残差分析
什么是残差分析如何利用残差分析来检验回归模型的适用性

什么是残差分析如何利用残差分析来检验回归模型的适用性残差分析是统计学中一种常用的方法,用于评估回归模型的适用性。
在回归分析中,我们希望通过建立数学模型来描述自变量与因变量之间的关系。
残差分析则是用来检验模型是否能准确地描述实际数据。
残差(residual)是指观测值与回归方程预测值之间的差异。
回归方程可以表示为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε,其中Y是因变量,X1、X2、...、Xn是自变量,β0、β1、β2、...、βn是回归系数,ε是误差。
残差计算公式为:残差 = 观测值 - 预测值。
当回归模型适用性良好时,残差应该随机分布在零附近,没有明显的模式或趋势。
接下来,我们将介绍如何利用残差分析来检验回归模型的适用性。
1. 绘制残差图(Residual Plot)残差图是一种展示残差分布的可视化方式。
在横轴上绘制观测值或预测值,纵轴上绘制残差。
如果残差图中的点随机分布在零附近,并且没有明显的模式,则说明回归模型适用性较好。
如果残差图中存在模式或趋势,那么回归模型可能存在问题,需要重新评估模型的可靠性。
2. 检查残差的正态性回归模型通常假设误差项(ε)满足正态分布。
我们可以通过绘制残差的直方图或概率图来检查残差是否服从正态分布。
如果残差近似服从正态分布,则说明回归模型的适用性较好。
3. 检查残差的独立性残差的独立性是指残差之间没有相关性。
我们可以通过绘制残差的自相关图(Autocorrelation Plot)来检验残差是否独立。
如果残差之间没有显示出明显的相关性,则说明回归模型的适用性较好。
4. 检查残差的等方差性等方差性是指残差的方差在自变量的不同取值范围内是恒定的。
我们可以绘制残差的散点图,以观察残差的方差是否与预测值相关。
如果散点图呈现出均匀分布且没有明显的锥形或漏斗形状,则说明回归模型的适用性较好。
总结来说,残差分析是用于检验回归模型适用性的重要方法。
残差分析(Residual Analysis)

残差分析(Residual Analysis)论文作者:金玟洙会计学中关于残差分析(Residual Analysis)的定义是将扣除有形资产的来衡量公司的剩余资产,最后的剩余资产来分析品牌资产的。
然而,在市场营销中这意味着产品被最终消费者所选择的概率结果。
或通过比较一个特定的品牌的选好度、属性、知名度、非属性和其他品牌后扣除的结果。
Srinivasan(1979), Rangaswamy et al(1993), Kamakara andRussell(1993), Park and Srinivasan(1994)都相继进行了这方面的相关研究。
下面我就用近期发表的Park and Srinivasan(1994)研究来解释一下。
残差分析的框架如下:客户对于某特定品牌有好感度应该表现为以下三个第一,对于该特定品牌的购买量第二,与购买品牌平均量相比,客户个人选择特定品牌概率更多第三,该特定品牌的单位贡献利润特定品牌的资产包含以下两种。
首先,顾客一个人预期的品牌资产乘以特定品牌的顾客抽样数其次,从对应的总销售的客户抽样数分为有关产品总销售额总之,在上述过程中,再加上特定品牌的销售乘以客户选择特定品牌比其他任何品牌更多获取的概率。
下边这些内容更了解说明:首先,对品牌的收益性的定义如下品牌的收益性由两部分组成。
一部分是基本的收益性,另一部分是由于品牌的收益性。
即使没有相关品牌也可以产生原有的利润,这是基本的收益性。
因为有了企业的品牌,所以会使产品的需求量增加。
我们认为品牌的出现使销售收入增长得益于品牌的收益性。
我们用以下形式表达品牌收益性= 基本收益性+品牌的收益性其次,单位贡献利润的定义如下,单位贡献利润加上扣除每单位可变成本的价值即得到了品牌的价值。
残差分析使用的是属于平均价格的溢价,并且要细分化价格溢价与得到的平均市场价格的贡献差益。
即,从品牌价格扣除属于平均产品的价格,你可以得到价格溢价。
从属于平均产品的价格扣除每单位的单位贡献利润,你可以得到从平均市场上获得的单位贡献利润。
回归模型的残差分析
回归模型的残差分析山东 胡大波判断回归模型的拟合效果是回归分析的重要内容,在回归分析中,通常用残差分析来判断回归模型的拟合效果。
下面具体分析残差分析的途径及具体例子。
一、 残差分析的两种方法1、差分析的基本方法是由回归方程作出残差图,通过观测残差图,以分析和发现观测数据中可能出现的错误以及所选用的回归模型是否恰当;在残差图中,残差点比较均匀地落在水平区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,说明模型的拟合精度越高,回归方程的预报精度越高。
2、可以进一步通过相关指数∑∑==---=n i ini i iy yy yR 1212^2)()(1来衡量回归模型的拟合效果,一般规律是2R 越大,残差平方和就越小,从而回归模型的拟合效果越好。
二、 典例分析:例1、某运动员训练次数与运动成绩之间的数据关系如下:试预测该运动员训练47次以及55次的成绩。
解答:(1)作出该运动员训练次数x 与成绩y 之间的散点图,如图1所示,由散点图可 知,它们之间具有线性相关关系。
(2)列表计算:由上表可求得875.40,25.39==y x ,12656812=∑=i ix,13731812=∑=i i y ,1318081=∑=ii i yx ,所以∑∑==---=81281)())((i ii i ix xy y x xβ.0415.18812281≈--=∑∑==i ii ii xxy x yx00302.0-≈-=x y βα,所以回归直线方程为.00302.00415.1^-=x y(3)计算相关系数将上述数据代入∑∑∑===---=8181222281)8)(8(8i i i i i ii y y x x yx yx r 得992704.0=r,查表可知707.005.0=r ,而05.0r r >,故y 与x 之间存在显着的相关关系。
(4)残差分析:作残差图如图2,由图可知,残差点比较均匀地分布在水平带状区域中,说明选用的模型比较合适。
高考复习资料:回归模型的残差分析

回归模型的残差分析山东胡大波判断回归模型的拟合效果是回归分析的重要内容,在回归分析中,通常用残差分析来判断回归模型的拟合效果。
下面具体分析残差分析的途径及具体例子。
一、残差分析的两种方法1、差分析的基本方法是由回归方程作出残差图,通过观测残差图,以分析和发现观测数据中可能出现的错误以及所选用的回归模型是否恰当;在残差图中,残差点比较均匀地落在水平区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,说明模型的拟合精度越高,回归方程的预报精度越高。
2、可以进一步通过相关指数∑∑==---=niiniiiyyyyR1212^2)()(1来衡量回归模型的拟合效果,一般规律是2R越大,残差平方和就越小,从而回归模型的拟合效果越好。
二、典例分析:例1、某运动员训练次数与运动成绩之间的数据关系如下:次数/x 30 33 35 37 39 44 46 50成绩/y 30 34 37 39 42 46 48 51试预测该运动员训练47次以及55次的成绩。
解答:(1)作出该运动员训练次数x与成绩y之间的散点图,如图1所示,由散点图可知,它们之间具有线性相关关系。
次数ix成绩iy2ix2iyixiy30 30 900 900 90033 34 1089 1156 112235 37 1225 1369 129537 39 1369 1521 144339 42 1521 1764 163844 46 1936 2116 202446 48 2116 2304 220850 51 2500 26012550由上表可求得875.40,25.39==y x ,12656812=∑=i ix,13731812=∑=i i y ,1318081=∑=ii i yx ,所以∑∑==---=81281)())((i ii i ix xy y x xβ.0415.18812281≈--=∑∑==i ii ii xxy x yx00302.0-≈-=x y βα,所以回归直线方程为.00302.00415.1^-=x y(3)计算相关系数将上述数据代入∑∑∑===---=8181222281)8)(8(8i i i i i ii y y x x yx yx r 得992704.0=r ,查表可知707.005.0=r ,而05.0r r >,故y 与x 之间存在显著的相关关系。
如何做残差分析
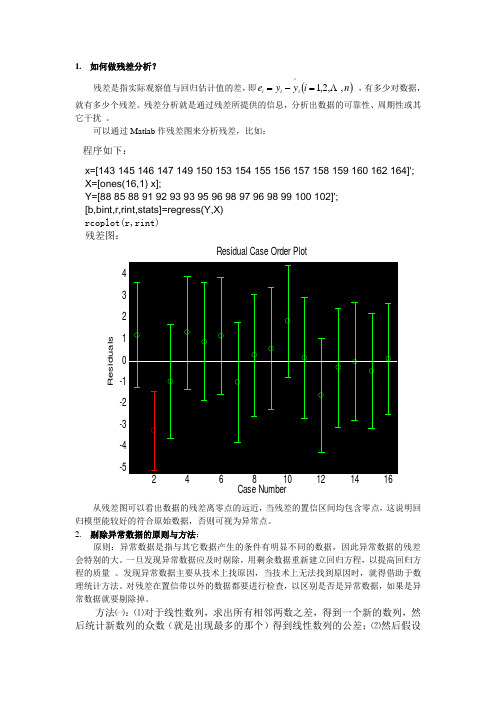
1. 如何做残差分析?残差是指实际观察值与回归估计值的差,即()n i y y e i i i ,,2,1^Λ=-= ,有多少对数据,就有多少个残差。
残差分析就是通过残差所提供的信息,分析出数据的可靠性、周期性或其它干扰 。
可以通过Matlab 作残差图来分析残差,比如: 程序如下:x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; X=[ones(16,1) x];Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';[b,bint,r,rint,stats]=regress(Y,X)rcoplot(r,rint)残差图:-5-4-3-2-11234Residual Case Order PlotR e s i d u a l s Case Number从残差图可以看出数据的残差离零点的远近,当残差的置信区间均包含零点,这说明回归模型能较好的符合原始数据,否则可视为异常点。
2. 剔除异常数据的原则与方法;原则:异常数据是指与其它数据产生的条件有明显不同的数据,因此异常数据的残差会特别的大。
一旦发现异常数据应及时剔除,用剩余数据重新建立回归方程,以提高回归方程的质量 。
发现异常数据主要从技术上找原因,当技术上无法找到原因时,就得借助于数理统计方法。
对残差在置信带以外的数据都要进行检查,以区别是否是异常数据,如果是异常数据就要剔除掉。
方法㈠:⑴对于线性数列,求出所有相邻两数之差,得到一个新的数列,然后统计新数列的众数(就是出现最多的那个)得到线性数列的公差;⑵然后假设第一个数是非异常数字;⑶假设数据不断加公差,看看绝大大多数是不是在原线性数列中,分情况:①若是,则第一个数以及第一个数加公差与原数列相同的元素均为非异常数据,其他则为异常数据;②若不是,则第一个数为异常数列,再假设第2个非异常数据,返回到第⑶步。
第5章 残差分析
异常值的原因是由自变量异常与因变量异常两个原因共同引起的。
异常值与强影响值
异常值原因
异常值消除方法
1.数据登记误差,存在抄写或录入 重新核实数据 的错误
第5章 残差分析
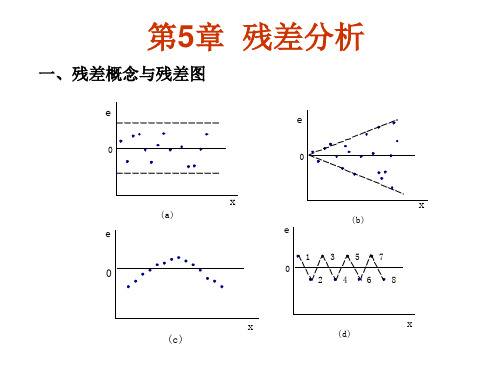
一、残差概念与残差图
e
e
0
0
(a)
e
0
x
e
x
(b)
1 3 57
0 2 46 8
x (c)
x
(d)
残差分析
一、残差概念与残差图
4
3
2
1
0
-1
-2
-3
-4
0
1
2
3
4
5
6
7
X
火灾损失数据残差图
残差分析
二、残差的性质
性质1 E (ei)=0
证明: E(ei ) E( yi ) E( yˆi )
chii=杆值 chii的平均值是
i 1
ch
1 n
n
chii
i 1
p n
异常值与强影响值
二、关于自变量x的异常值
虽然强影响点并不总是y的异常值点,不能单纯根据 杠杆值hii的大小判断强影响点是否异常,但是我们对强影 响点应该有足够的重视。为此引入库克距离,用来判断强 影响点是否为y的异常值点。库克距离的计算公式为:
i 1
残差分析
三、改进的残差
标准化残差
ZREi
ei
ˆ
学生化残差
SREi ˆ
线性回归方程的残差分析课件

利用线性回归分析方法预测某城市未来气温变化,并通过残差分析评估模型的可 靠性和精度。
详细描述
收集某城市近几年的气温数据,利用线性回归分析方法建立气温预测模型。通过 残差分析评估模型的可靠性和精度,如计算残差均值、残差标准差、残差图等。 根据分析结果提出气温预测的建议,如加强气象观测和数据收集等。
检验残差是否具有恒定 的方差,异方差性可能 导致模型预测不准确。
自相关检验
检验残差是否具有时间 上的自相关性,自相关 性可能导致模型预测不
稳定。
CHAPTER
残差分析基 础
残差的定义与计算
残差 计算方法
残差的正态性检验
目的
方法
残差的同方差性检验
目的
方法
CHAPTER
残差图分析
残差图绘制
残差图是一种用于分析回归模型预测 准确性的工具,通过将实际观测值与 预测值进行比较,可以直观地展示模 型的预测误差。
通过残差分析,可以发现模型中可能存在的多重共线性、异方差性等问题,并采取 相应措施进行解决,提高模型的稳定性和可靠性。
利用残差分析进行模型选择与评估
利用残差分析进行预测与决策
CHAPTER
案例研究
案例一:某公司销售收入的线性回归分析
总结词
通过分析某公司销售收入与广告投入、销售人员数量等因素之间的线性关系,评估线性回归方程的拟合效果和预 测能力。
线性回归方程的残差 分析课件
目录
• 线性回归方程概述 • 残差分析基础 • 残差图分析 • 残差分析在实践中的应用 • 案例研究
CHAPTER
线性回归方程概述
线性回归方程的定义
01
02
03
04
线性回归方程
多元回归的模型检验指标

多元回归的模型检验指标多元回归是一种经济学和统计学中常用的分析方法,用于研究多个自变量对一个因变量的影响程度。
在多元回归模型中,我们需要考虑多个自变量对因变量的联合作用,以及各自变量之间的相互关系。
在进行多元回归分析时,我们需要使用一些模型检验指标来评估模型的拟合程度和统计显著性。
本文将介绍几个常用的多元回归模型检验指标,并解释其含义和应用。
1. 残差分析残差分析是多元回归模型检验中最常用的方法之一。
残差是指模型预测值与实际观测值之间的差异,通过分析残差的分布情况可以评估模型的拟合程度。
常见的残差分析方法包括绘制残差散点图、残差直方图和残差-拟合值图等。
如果残差呈现随机分布、均值接近0且方差稳定的趋势,则说明模型拟合良好。
2. 线性关系检验线性关系检验用于检验自变量与因变量之间是否存在线性关系。
常用的方法包括绘制自变量与残差的散点图,观察其是否呈现线性趋势。
另外,还可以使用F检验来检验自变量的整体显著性,即自变量对因变量的联合作用是否显著。
3. 多重共线性检验多重共线性是指自变量之间存在高度相关性,可能会影响模型的稳定性和解释力。
常用的多重共线性检验指标包括方差膨胀因子(VIF)和条件数。
VIF越大,说明自变量之间的相关性越强,可能存在多重共线性问题。
条件数越大,说明矩阵X的条件数越大,可能存在多重共线性问题。
一般来说,VIF大于10或条件数大于30可以被认为存在多重共线性。
4. 拟合优度检验拟合优度检验用于评估模型的拟合程度。
常用的拟合优度检验指标包括决定系数(R²)、调整决定系数(adjusted R²)和残差平方和(RSS)。
R²越接近1,说明模型拟合效果越好;adjusted R²考虑了自变量个数对模型拟合的影响,可以更准确地评估模型的拟合程度;RSS越小,说明模型拟合效果越好。
5. 统计显著性检验统计显著性检验用于判断模型的统计显著性。
常用的统计显著性检验指标包括t检验和F检验。
第四节__残差分析

第四节残差分析、预报和控制一、残差分析前面咱们介绍了线性回归方程的成立和查验。
在实际问题中,由于观察人员的粗心或偶然因素的干扰。
常会使咱们所取得的数据不完全靠得住, 即出现异样数据。
有时即便通过相关系数或F查验证明回归方程靠得住,也不能排除数据存在上述问题。
残差分析的目的就在于解决这一问题。
所谓残差是指实际观察值与回归估量值的差,即(2-1-26)显然,有多少对数据,就有多少个残差。
残差分析就是通过残差所提供的信息,分析出数据的靠得住性、周期性或其它干扰。
第一介绍如何检查异样数据。
异样数据是指与其它数据产生的条件有明显不同的数据,因此异样数据的残差会特别的大。
一旦发觉异样数据应及时剔除,用剩余数据从头成立回归方程,以提高回归方程的质量。
发觉异样数据主要从技术上找原因,当技术上无法找到原因时,就得借助于数理统计方式。
由数理统计方式能够证明(2-1-27) 或记为(2-1-28)这说明残差的方差D(e)是x的函数,且二者呈曲线关系。
以回归方程及方程和作图。
见方开泰《实用回归分析》P45图考虑到较小,当n较大时(2-1-29) 现在图中的两条曲线可近似于两条平行直线。
从而有(2-1-30) 或近似地(2-1-31)这表明,当n较大时y i落在图2-1-3的长条形带子中的概率约为95%,只要明白,就可以够取得残差的置信区域。
一般是未知的,通常常利用残差标准差来估量。
可用下式求得(2-1-32) 由此可得残差置信带(2-1-33)对残差在置信带之外的数据都要进行检查,以区别是不是是异样数据,若是是异样数据就要剔除掉。
此刻咱们对例1做残差检查。
由式(2-1-32)残差置信带为,。
计算5个实验点的预报值与残差值(见表2-1-4),并作出残差检查图(见图2-1-4)表2-1-4 例1的残差值图2-1-4 例1的残差图由图2-1-4可见,例1中全数数据的残差都在置信带内,没有异样数据。
除此之外,残差图还能够为咱们提供许多有效信息。
3.2 残差分析知识分享

如果某组数据可能采取几种不同回归方程进行回归
分析,则可以通过比较R2的值来做出选择,即选取R2 较大的模型作为这组数据的模型。
总的来说:
相关指数R2是度量模型拟合效果的一种指标。
在线性模型中,它代表自变量刻画预报变量的能力。
例 关于x与y有如下数据:
x
2
4
5
6
8
y
30 40 60 50 70
有如下的两个线性模型:
y
i
yi)
是随机误差的效应,
例如,编号为6的女大学生,计算残差为:
6 1 ( 0 .8 4 9 1 6 5 8 5 .7 1 2 ) 6 .6 2 7
对每名女大学生计算这个差异,然后分别将所得的值平方后加起来,用数学符号
n
表示为: ( yi y i )2 称为残差平方和, 类似于方差的定义 i 1
在例1中,残差平方和约为128.361。
残差分析与残差图的定义:
在研究两个变量间的关系时,首先要根据散点图来粗略判断它们是否线 性相关,是否可以用回归模型来拟合数据。
然后,我们可以通过残差 e1,e2, ,en 来判断模型拟合的效果,判断原始
数据中是否存在可疑数据,这方面的分析工作称为残差分析。
表1-4列出了女大学生身高和体重的原始数据以及相应的残差数据。
假设随机误差对体重没有影响,也就是说,体重仅受身高的影响,那么散 点图中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落 在回归直线上。这些点散布在回归直线附近,所以一定是随机误差把这些点从 回归直线上“推”开了。
称
e
因此,数据点和它在回归直线上相应位置的差异( i =yi yi 为残差。
编号 身高/cm 体重/kg
回归模型的残差分析

回归模型的残差分析 The latest revision on November 22, 2020回归模型的残差分析山东 胡大波判断回归模型的拟合效果是回归分析的重要内容,在回归分析中,通常用残差分析来判断回归模型的拟合效果。
下面具体分析残差分析的途径及具体例子。
一、 残差分析的两种方法1、差分析的基本方法是由回归方程作出残差图,通过观测残差图,以分析和发现观测数据中可能出现的错误以及所选用的回归模型是否恰当;在残差图中,残差点比较均匀地落在水平区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,说明模型的拟合精度越高,回归方程的预报精度越高。
2、可以进一步通过相关指数∑∑==---=n i ini i iy yy yR 1212^2)()(1来衡量回归模型的拟合效果,一般规律是2R 越大,残差平方和就越小,从而回归模型的拟合效果越好。
二、 典例分析:解答:(1)作出该运动员训练次数x 与成绩y 之间的散点图,如图1所示,由散点图可知,它们之间具有线性相关关系。
由上表可求得875.40,25.39==y x ,12656812=∑=i ix ,13731812=∑=i i y ,1318081=∑=ii i yx ,所以∑∑==---=81281)())((i ii i ix xy y x xβ.0415.18812281≈--=∑∑==i ii ii xxy x yx00302.0-≈-=x y βα,所以回归直线方程为.00302.00415.1^-=x y (3)计算相关系数将上述数据代入∑∑∑===---=8181222281)8)(8(8i i i i i ii y y x x yx yx r 得992704.0=r ,查表可知707.005.0=r ,而05.0r r >,故y 与x 之间存在显着的相关关系。
(4)残差分析:作残差图如图2,由图可知,残差点比较均匀地分布在水平带状区域中,说明选用的模型比较合适。
第5章 残差分析

0
残差分析
二、残差的性质
性质2
var(ei
)
1
1 n
( xi
x)2 Lxx
2
(1 hii ) 2
其中
hii
1 n
(xi x)2 Lxx
称为杠杆值
残差分析
二、残差的性质
性质3. 残差满足约束条件:
n
ei 0
i 1 nxiei 0 Nhomakorabeae(i) -1165
23 -110 716 -429 841 139
74 76 -677 65 -223 -224 189 1179
SRE(i) -1.1658 0.1293 -0.7824 1.1963 -1.1498 0.9320 0.9448 0.7015 0.6008 -0.9199 0.2702 -1.4544 -1.7424 1.1528 1.1939
第5章 残差分析
一、残差概念与残差图
e
e
0
0
(a)
e
0
x
e
x
(b)
1 3 57
0 2 46 8
x (c)
x
(d)
残差分析
一、残差概念与残差图
4
3
2
1
0
-1
-2
-3
-4
0
1
2
3
4
5
6
7
X
火灾损失数据残差图
残差分析
二、残差的性质
性质1 E (ei)=0
证明: E(ei ) E( yi ) E( yˆi )
chii 0.375 0.043 0.054 0.432 0.068 0.280 0.036 0.070 0.060 0.100 0.021 0.040 0.052 0.029 0.339
计量经济学-残差图分析

X
···· · ·
数据拟合不充分时的残差图
5.随机误差项存在异方差性
如果Var(i)= (i2 不为常数(i=1,2, …,n),即对 应于每个xi,有一个 i2与之对应,则称随机误 差项具有异方差性。其标准残差图往往表现出
呈现渐增或渐减的形状,如下图所示。
ˆ *
ˆ *
+2
O
-2
························
ˆt*
ˆt*
+2 +2ຫໍສະໝຸດ O·t O
t
-2
-2
(a)
(b)
随机误差项存在自相关性时的残差图
(a)
+2
O -2
X
(b)
回归方程具有曲线形式的残差图
3.样本数据中存在一个或多个异常点
当样本数据中存在异常点时,一个最明显的 特征是,这些异常点明显地离开大多数数据点, 见下图。
ˆ *
· 异常点
+2
O -2
·· · ···· ········· ··········
X
异常点
·
样本数据中存在异常点时的残差图
如果样本回归模型对数据拟合是良好的话,
那,么 即iˆ的i 应估近计似ˆ服i 就从应N该(反0,映的2)这。些分布特性
从而有 ˆi / ~N(0,1),并称ˆi / 为标
准化残差。
考虑到 一般是未知的,用
ˆ RSS /(n 2) MSR
来代替,通常用s表示,从而有:
X
+2
O
-2
·
· · ·
···············
X
(a)
(b)
回归模型的残差分析

欢迎共阅回归模型的残差分析山东 胡大波判断回归模型的拟合效果是回归分析的重要内容,在回归分析中,通常用残差分析来判断回归模型的拟合效果。
下面具体分析残差分析的途径及具体例子。
一、 残差分析的两种方法1、差分析的基本方法是由回归方程作出残差图,通过观测残差图,以分析和发现观测数据中可能出现的错误以及所选用的回归模型是否恰当;在残差图由上表可求得875.40,25.39==y x ,12656812=∑=i ix ,13731812=∑=i i y ,1318081=∑=ii i yx ,所以∑∑==---=81281)())((i ii i ix xy y x xβ.0415.18812281≈--=∑∑==i ii ii xxy x yx00302.0-≈-=x y βα,所以回归直线方程为.00302.00415.1^-=x y (3)计算相关系数∑-88ii yx yx (3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性回归方程y =bx +a );(4)按一定规则估计回归方程中的参数(如最小二乘法);(5)得出结果后分析残差图是否有异常(个别数据对应残差过大,或残差呈现不随机的规律性等等),若存在异常,则检查数据是否有误,或模型是否合适等。
例2、某城区为研究城镇居民月家庭人均生活费支出和月人均收入的相关关费的预报值。
将x=1100代入回归方程得y=784.59元;将x=1200代入回归方程得y=850.58元。
故预测月人均收入分别为1100元和1200元的两家庭的月人均生活费分别为784.59元和850.58元。
回归模型的残差分析

欢迎共阅回归模型的残差分析山东 胡大波判断回归模型的拟合效果是回归分析的重要内容,在回归分析中,通常用残差分析来判断回归模型的拟合效果。
下面具体分析残差分析的途径及具体例子。
一、 残差分析的两种方法1、差分析的基本方法是由回归方程作出残差图,通过观测残差图,以分析和发现观测数据中可能出现的错误以及所选用的回归模型是否恰当;在残差图由上表可求得875.40,25.39==y x ,12656812=∑=i ix ,13731812=∑=i i y ,1318081=∑=ii i yx ,所以∑∑==---=81281)())((i ii i ix xy y x xβ.0415.18812281≈--=∑∑==i ii ii xxy x yx00302.0-≈-=x y βα,所以回归直线方程为.00302.00415.1^-=x y (3)计算相关系数∑-88ii yx yx (3)由经验确定回归方程的类型(如我们观察到数据呈线性关系,则选用线性回归方程y =bx +a );(4)按一定规则估计回归方程中的参数(如最小二乘法);(5)得出结果后分析残差图是否有异常(个别数据对应残差过大,或残差呈现不随机的规律性等等),若存在异常,则检查数据是否有误,或模型是否合适等。
例2、某城区为研究城镇居民月家庭人均生活费支出和月人均收入的相关关费的预报值。
将x=1100代入回归方程得y=784.59元;将x=1200代入回归方程得y=850.58元。
故预测月人均收入分别为1100元和1200元的两家庭的月人均生活费分别为784.59元和850.58元。
第十六讲 残差分析

变量变换
• 线性模型假设 E(y|x)的线性性, 和误差方差齐性: E(y|x)=a+b’x var(y|x)=常数 • 我们知道(y,x)联合正态分布时,该假设是正确的。 • 实际问题中,若x,y都是连续变量,通常对x或y或两者做 变换,使得变换之后(x,y)近似服从正态分布。 • 若某些自变量是因子(x1),其它自变量(x2)是连续型,那 么, 变换,使得(y,x2)|x1~正态。
变换的一般原则
• 总的原则是变换后每个变量都比较对称、均衡,换言之联合分布接近 正态。变换包括
– – – – Log变换 或 Box-Cox变换, 连续变量离散化, 有次序的因子变量的连续化, 无次序因子变量的合并
•
log 原则 如果一个非负变量的取值不在一个尺度或量级(magnitude)上,则取对数 后分析可能是有益的. 如果一个变量的取值在一个尺度或量级内,任何变换都可能无益. 不容易确定何种变换时,采用Box-Cox变换。
(b) 若x, z不独立 ⇒ var( y | x)一般依赖于x,除非 var( z | x)不依赖于x ⇒ var( y | x) = 常数 若( z , x) ~ 正态, 则
(3) δ = y-{α + β ' x} = a + b' x + c' z − {α + β ' x} = a − α + (b − β )' x + c' z
δ与x是否相关可通过 (1), (2)部分地检查,但一般无 法完全验证。
注:通常我们只有“工作模型”而不知道完全模型,只能通过 工作模型的残差探讨其拟合好坏。
残差分析
• 残差分析:拟合线性回归模型之后,通过 分析残差特征,检查拟合的好坏,即检查 数据是否满足模型假设
残差分析专题知识

公共卫生学院
一. 序言
回归分析旳目旳:
设法找出变量间旳依存(数量)关系, 用函数关系 式体现出来
二、基本概念
1、应变量(dependent variable) 2、自变量(independent variable)
3、一元线性回归 直线回归方程旳模型是:yi=a+bxi+ei
其中 (1)a是截距 (2)b是回归系数(regression coefficient)(回归直线旳
(2)回归模型残差旳独立性检验 用Durbin--Watson检验,其参数称为Dw或D。 D旳取值范围是0<D<4。其统计学意义为: D≈2,残差与自变量相互独立; D<2,残差与自变量正有关; D>2,残差与自变量负有关。
(3)残差旳方差齐性检验 以上都是对残差旳分析,称为残差分析。
残差分析还能够1)检出奇异点 2)评判预测效果。
y/
x)2 / n
n
l xy l xx
a ybx y bx
n
n
多元线性回归时,比较复杂,一般需要用计算机 处理。
五、线性回归旳检验
1、回归方程旳检验 方差分析法:
应变量旳总变异
_
( y y)2
可分解为 回归平方和(regression sum of squares):可用线
性回归解释旳部分
旳情况下,某一自变量每变化一种单位,应变量平均 变化旳单位数。 假就数如等,全于用部符0,参号b加b11,‘分,b析2b,旳2’…变,,量…b都,n 就是bn变原‘表成则达了化。原旳则变化量偏,回这归时系b0 bi’= bi*sxi/sy 因量为旳b相i’对没作有用量大纲小,。所以能够相互比较大小,反应自变 (3) ei是残差
残差分析课程设计案例

残差分析课程设计案例一、教学目标本节课的教学目标是使学生掌握残差分析的基本概念、方法和应用。
知识目标包括:理解残差的定义和性质,掌握残差分析的基本方法和步骤,了解残差分析在实际应用中的重要性。
技能目标包括:能够运用残差分析方法解决实际问题,能够正确地进行残差分析并解释分析结果。
情感态度价值观目标包括:培养学生对数据分析的兴趣和热情,培养学生勇于探索、严谨求实的科学态度。
二、教学内容本节课的教学内容主要包括残差分析的基本概念、方法和应用。
首先,介绍残差的概念和性质,让学生了解残差分析的基本对象。
其次,讲解残差分析的方法和步骤,包括残差的计算、残差图的绘制和残差分析的判断标准。
最后,通过实际案例介绍残差分析在实际应用中的重要性,如线性回归模型的评价和修正。
三、教学方法为了达到本节课的教学目标,将采用多种教学方法进行教学。
首先,采用讲授法,系统地讲解残差分析的基本概念、方法和应用。
其次,采用案例分析法,通过分析实际案例使学生更好地理解和掌握残差分析的方法和步骤。
此外,还采用讨论法,鼓励学生积极参与课堂讨论,培养学生的思考能力和团队协作精神。
四、教学资源为了支持本节课的教学内容和教学方法的实施,将准备以下教学资源。
教材:《统计学原理》,其中涉及残差分析的相关内容。
参考书:《线性回归分析与应用》,供学生课后进一步学习残差分析的详细知识。
多媒体资料:制作课件和残差图的演示,帮助学生更好地理解和掌握残差分析的方法和步骤。
实验设备:计算机和投影仪,用于展示多媒体资料和进行课堂讨论。
五、教学评估本节课的评估方式将包括平时表现、作业和考试三个部分。
平时表现主要评估学生在课堂上的参与程度、提问和回答问题的积极性等。
作业主要评估学生对课堂所学知识的掌握程度,包括残差分析的计算和案例分析等。
考试则是对学生全面掌握残差分析知识的评估,包括理论知识和实际应用能力的考察。
评估方式将力求客观、公正,全面反映学生的学习成果。
六、教学安排本节课的教学安排将分为五个课时,每个课时45分钟。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则回归直线yˆ bˆx aˆ 0.06x 0.32
(3)当x 6时, yˆ 0.06 6 0.32 0.68
由于所有的样本点不共线,而只是散布在某一直线的附近, 所以身高和体重的关系可以用线性回归模型来表示:
y bx a e
其中a和b为模型的未知参数,e称为随机 误差.
步骤1:计算线性回归方 例程1的线性回归方程为$y 0.849x 85.712(①散点图,②线性回归计算)
步骤2:计算残差,列表
编号 身高/cm
1
2
3
4
5
6
7
8
165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
体重估计/kg 54.373 54.373 47.581 58.618 62.863 54.373 45.883 58.618
ei yi bxi a,i 1, 2,...n,其估计值为ei yi yi yi b xi a,i 1, 2,...n
ei 称为相应于点(xi,yi)的残差。
4.如何发现数据中的错误?如何衡量随机模型的拟合
效果?
(1)计算线性回归方程$y=b$x a$.
残差
-6.373 2.627 2.419 -4.618 1.137 6.627 -2.883 0.382
步骤3:画残差图(横坐标可以是编号、体重、体重估计值,纵坐标是
残差)
残差
身8
高6
异
与4
常
体2
重
O -2
1234567
8 9 编号
残 -4
点
差 -6
图 -8
步骤4:残差分析
第一个样本点和第6个样本点的残差比较大,需要确认在采集过程中是否有人为错误。如果数据采集 错误,就予以纠正,然后再重新利用线性回归模型拟合数据;如果数据采集没有错误,则需寻找其他原
x 135 7 y 2.2 4.3 4.8 6.7
(1).画出散点图 (2).求x, y满足的线性回归方程. (3).预测x 6时y的值.
时间x 1 2 3 4 5 命中率y 0.4 0.4 0.5 0.6 0.6
(1).画出散点图 (2).求x, y满足的线性回归方程. (3).预测小李打篮球6小时的投篮命中率.
时间x 1 2 3 4 5 命中率y 0.4 0.4 0.5 0.6 0.6
(2).求x, y满足的线性回归方程. (3).预测小李打篮球6小时的投篮命中率.
函数模型与“回归模型”的关系
函数模型:因变量y完全由自变量x确定 回归模型: 预报变量y完全由解释变量x和随机误差e确定
问题二:在线性回归模型中,e是用bx+a预报真 实值y的随机误差,它是一个不可观测的量,那么 应如何研究随机误差呢?
e=y-(bx+a)
残差:一般的对于样本点(x1,y1),(x2,y2),...,(xn,yn ),它们的随机误差为
解(2):设所求的线性回归方程为yˆ bˆx aˆ
n
n
x 3, y 0.5 , xi yi 8.1, xi2 =55.
n
i 1
i 1
bˆ
xi yi
i1
n
xi2
nxy
2
nx
8.1 55
5 3 0.5 5 32
0.06
i1
aˆ y bˆx 0.5 0.063 0.32
回归分析的基本思想及其初步应用 第2课时
问题1:现实生活中两个变量间的关系有哪些
呢?
不相关
函数关系:确定性关系 1、两个变量的关系
线性相关$y b$x a$
相关关
系
非线性相关
相关关系:对于两个变量,当自变量取值一定时, 因变量的取值带有一定随机性的两个变量之间的关 系。
随堂练习
3.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系, 下表记录了小李某月1号到5号每天打篮球时间x(单位 : 小时)与当 天投篮命中率y之间的关系:
(2)计算eµi yi µyi yi b$xi a$ (i 1,2,...n)
①查找异常样本数据
(4)分析残差图
②拟合效果
模型合适:残差点分布在水平带状区域中 拟合高精度 : 带状区域的宽度窄
范例点击
(1).画出散点图 (2).求x, y满足的线性回归方程. (3).画残差图
作业
已知x, y的取值如下表所示
x
246 8
y
4.5 7.8 10.7 13.6
(1).画出散点图 (2).求x, y满足的线性回归方程. (3).预测x 5时y的值. (4).画出残差图.
作业
已知x, y的取值如下表所示
另外,残差点比较均匀地落在水平的带状区域中,说明选用的模型计较合适,这样的带状区域的宽 说明模型拟合精度越高,回归方程的预报精度越高。
随堂练习
为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系, 下表记录了小李某月1号到5号每天打篮球时间x(单位 : 小时)与当 天投篮命中率y之间的关系:
时间x 1 2 3 4 5 命中率y 0.4 0.4 0.5 0.6 0.6
