第二章(3,4)
3~4第二章 例题

中国石油大学(华东)储运工程系
现改烧焦炉煤煤的热值27210kjkg某居住小区共有居民860户每户居民按3口计算居民用气量指标2800mj人年计算从中低压调压站至小区庭院管入口管线小时计算用气量某楼居民40户30户装了燃气热水器双眼灶热负荷23450kjh热水器热负荷25590kjh煤气低热值17074kjm3计算该楼供气管道的小时计算用量已知某城市人口50万标况下燃气低热值36000kjnm托儿所用气定额取2000mj人
求其每天燃气的使用 量?
唐建峰
中国石油大学(华东)储运工程系
例2 固体液体燃料的折算
一居民用户原用煤作燃 料,每天用煤量为 3kg/d;现改烧焦炉煤 气, 计算条件如下:
煤的热值 27210kJ/kg 煤炉的效率20% 焦炉煤气热值17580kJ/kg 民用灶效率55%
求其每天燃气的使用 量?
Qy3 =
例1 华白指数计算
已知混合气体的体积 组分为:
甲烷23.4; 氢59.2; 一氧化碳8.6; 乙烷2.0; 氧1.2; 氮3.6; 二氧化碳2.0
求该混合气体的华白 指数
唐建峰
中国石油大学(华东)储运工程系
例1 华白指数计算
已知混合气体的体积 组分为:
甲烷23.4; 氢59.2; 一氧化碳8.6; 乙烷2.0; 氧1.2; 氮3.6; 二氧化碳2.0
居民
Nkq 50 × 10000 × 0.9 × 2500 × 1000 Q1 = = = 31250000 Nm 3 / a Hl 36000
(
)
唐建峰
中国石油大学(华东)储运工程系
公共建筑
Q2 = MNq 50 × 10000 × 150 × 2000 × 1000 = = 4166667 Nm 3 / a Hl 1000 × 36000
第二章 土的渗透性和渗流问题(3-4节)

式中,kx、kz—分别为x和z方向的渗透系数; h—测管水头。
7
将式(2-29)和(2-30)代入式(2- 28)可得出:
2h 2h kx 2 kz 2 0 x z
(2 - 31)
8
对于各向同性的均质土,kx=kz,则式(2 -31)可表达为:
h h 2 0 2 x z
(2 - 49)
31
对于二元渗流,当流网绘出后,即可方 便地求出流网中任意网格上的渗透力及 其作用方向(图2-24) 。作用于该网格 土体上的单宽总渗透力为:
J jV ( wi) (sl 1)
h w sl w hs l
注意:J作用于流网网格的形心上,方向 与流线平行。 32
ua hua w
(2 - 34)
注意:图中所示a、b两点位于同一根等 势线上,其测管水头虽然相同(位置水 头与压力水头之和,h=z+u/w)即 ha=hb, 但其孔隙水压力却不同,即ua≠ub。
20
3.水力坡降
h 流网中任意网格的平均水力坡降 i , l
l为该网格处流线的平均长度。
11
2.数值解法 有限差分法和有限单元法。 3.实验法 实验法是指采用一定比例的模型来摸拟 真实的渗流场,用实验手段测定渗流场 中的渗流要素。例如电比拟法、电网络 法和沙槽模型法等。
12
4.图解法 图解法是指采用绘制流网的方法求解拉 普拉斯方程的近似解。 该法具有简便、迅速的优点,并能用于 建筑物边界轮廓较复杂的情况。
式中M为流网中的流槽数,数值上等于流 线数减1。 通过坝底的总渗流量
Q qL
式中L为坝基长度。
第二章 习题及练习答案

第2章第二章习题及练习答案2.1 选择题A,B,C,C,A2.2 填空题1.在Python中,字典和集合都是用一对__大括号___作为定界符,字典的每个元素有两部分组成,即_键_和值,其中__键___不允许重复。
2.假设有列表a = ['name','age','sex']和b = ['Dong',38,'Male'],请使用一个语句将这两个列表的内容转换为字典,并且以列表a中的元素为键,以列表b中的元素为值,这个语句可以写为__c = dict(zip(a,b))__。
3.假设有一个列表a,现要求从列表a中每3个元素取1个,并且将取到的元素组成新的列表b,可以使用语句___b = a[::3]__。
4.使用列表推导式生成包含10个数字5的列表,语句可以写为__[5 for i in range(10)]_。
5. ___不可以________(可以、不可以)使用del命令来删除元组中的部分元素。
2.3 简答题1.为什么应尽量从列表的尾部进行元素的增加与删除操作?答:当列表增加或删除元素时,列表对象自动进行内存扩展或收缩,从而保证元素之间没有缝隙,但这涉及到列表元素的移动,效率较低,应尽量从列表尾部进行元素的增加与删除操作以提高处理速度。
2.简单解释Python的字符串驻留机制。
答:Python支持字符串驻留机制,即:对于短字符串,将其赋值给多个不同的对象时,内存中只有一个副本,多个对象共享该副本。
这一点不适用于长字符串,即长字符串不遵守驻留机制。
2.4 编程题1.编写程序,生成包含1000个0到100之间的随机整数,并统计每个元素的出现次数。
(提示:使用集合。
)答:import randomx = [random.randint(0,100) for i in range(1000)]d = set(x)for v in d:print(v, ':', x.count(v))2.假设有一段英文,其中有单独的字母“I”误写为“i”,请编写程序进行纠正。
有机化学(第二版)_ 课后答案

第二章 烷烃作业参考答案1、 共有九种:CH 3-CH 2-CH 2-CH 2-CH 2-CH 2-CH 3CH 3-CH-CH 2-CH 2-CH 2-CH 32CH 3-CH 2-CH-CH 2-CH 2-CH 33CH 3-CH-CH-CH 2-CH 3CH 3CH 3CH 3-CH-CH 2-CH-CH 33CH 3CH 3-C-CH 2-CH 2-CH 3CH 3CH 3CH 3-CH 2-C-CH 2-CH 3CH 3CH 3-CH 2-CH-CH 2-CH 2CH 2-CH 3CH 3-C3CH 3CH-CH 3CH 32、(1)3-甲基戊烷 (2)2,5-二甲基-3,4-二乙基己烷(3)2,2,3,4-四甲基戊烷 (4)2-甲基-5-乙基庚烷 (5)2-甲基-3-环丁基丁烷(6)顺-1-甲基-3-乙基环戊烷(7)反-1-甲基-4-乙基环己烷 (8)1-甲基-4-乙基-3-叔丁基环己烷 3、(1) (2)CH 3-CH-CH 2-CH 2-CH 33CH 3-C-CH 2CH 3CH 3CH 3(3) (4)CH 3-CH-CH-CH-CH-CH 3CH 33CH 2CH 32CH 33)34、(1) (2)CH 3CH 2-C CH 3CH-CH 3CH 3CH 3-C-CH-CH-CH 3CH 3CH 3CH 3 CH 3-CH-C-CH 2-CH 3CH 3CH 3CH3CH 3-C-CH 2-CH-CH 3CH 3CH 3CH 35、(1)错。
改为:2,2-二甲基丁烷(2)错。
改为:2,2,5-三甲基-4-乙基己烷 (3)正确 (4)错。
改为:2,2-二甲基丁烷6、(1)改为:H H 3CC 2H 5CH 3H HCH 3CH 2CHCH 2CH 3C H 33-甲基戊烷(2)CH(CH 3)2H 3CClCH 3H HCH 3-CH 2-C-CH(CH)2CH 3Cl2,3-二甲基2-氯丁烷7、C 1-C 2旋转:2H 52H 525优势构象 C 2-C 3旋转:333优势构象 8、(1) (2) (3)CH 2CH 2CH 3CH 2CH 3CH 3CH(CH 3)2OHCH 2CH 3H 3C9、(1)>(2)>(3)>(4)10、A:B:CH 3-CH 2-CH 2-CH 2-CH 3C:CH 3-CH-CH 2-CH 3CH 3CH 3-C-CH 3CH 3CH 311、 (4) > (3) > (1) >(2) 12、CH 3CH 2CH 3CH 3褪色:不褪色:CH 3CH 3CH 2CH 314(1) HICH 3-CH-CH 2CH 3IC H 3(2)C 2H 5C H 3H 2SO 4CH 3-CH 2-C C H 2CH 2C H 3C H 3OSO 3HCH 3-CH 2-CH 2C H 2CH 3C H 3OHH 2O第三章 烯烃 炔烃 二烯烃习题参考答案1、(1)2-甲基-4-乙基-3-己烯 (2)(Z )-3-甲基-2-戊烯 (3)4-甲基-2-丙基-1-戊烯 (4)(Z )-4-甲基-3-庚烯 (5)2,2-二甲基-5-乙基-3-庚炔 (6)(E )-3-甲基-2-溴-2-戊烯 (7)(2Z ,4Z )-3,5-二甲基-2,4-庚二烯 (8)3E-2,4-二甲基-1,3-己二烯2、(1) (2) (3) (4)(CH 3)2C=C CH 2CH 3CH 3C=CCl 3H H 3C CH 2=C-CH=CH 2CH 3 CH 2=CH-CH 2-CH=CH 2(5) (6)C=CH 3C CH 3HCH 2CH 2CH 3C=CH 3C C=C HHH CH 3H3、 (1)CH 3C=C CH 32CH 3C-CH CH 3Br 4CH 3CH 3(2)CH 3-C=CH-CH 3CH 322CH 3-C C H 3C H -C H 3OH +Br CH 3-C C H 3C H -C H 3Br Br(3)CH 3-C=CH-CH 33CH 3-C CH-CH 3CH 3Cl(4)CH 3-C=CH-CH 3CH 3HBr / 过氧化物CH 3-C CH-CH 3CH 3Br(5)CH 3-C=CH-CH 3CH 324CH 3-C CH 2-CH 3CH 3OSO 3HH 2OCH 3-C CH 2-CH 3CH 3OH(6)CH 3-C=CH-CH 3CH 34+CH 3-C=OCH 3+CH 3COOH(7)CH 3-C=CH-CH 33O 3C H 3CH 3CO CHCH 3H 2O / Zn CH 3-C=OCH 3+CH 3CHO4、(1)CH 3CH 2C=CHHBr(2mol)3CH 2C CH 3BrCH 3CH 2C OCH 3CH 3CH 2COOH+CO 2+H 2O3CH 2C=CH 2CN(2)H 3C+HBrH 3C(3)CH 3-C=CH-CH 3CH 32+HBr CH 3-C CH 2-CH 3CH 3CH 3-C CH-CH 3CH 3Cl ++CH 3-C CH 2-CH 3CH 3OH(4) CH 3-CH=CH 2CH 2-CH=CH 2C l22C H 2C l(5)CH 2=CH-CH=CH 3-CH=CH-CH 2Cl CO 2+H 2OC=O H H+O=C-C=O H H CHO5(1)CH 3-CH 2-CH 3CH 2=CH-CH 3CH=C-CH 3abc3)2+(2)CH 3-CH 2-aCH 2=CH-CH 2-CH 2CH 3b C=C-CH 2-CH 2CH 3cCH 2=CH-CH=CH-CH 3d 褪色不褪色aKMnO 4/HAg(NH 3)2无白cb,d顺丁烯二酸酐S 无d b CH HC CH HCCHCH C C O OO CH 36、(1)CH 3C CH 3CH 3+>CH 3-CH-CH 2-CH 3+>CH 3-CH-CH 2CH 3+(2)CH 2=CHCH 2+>CH 3CHCH 3+>CH 3CH 2CH 2+>CH 3+(3)CH 2+H 3CCH 2+CH 2+O 2N>>7、用浓H 2SO 4 8、(1) (2) (3)C=CH-CH 3H 3C H 3CCH 3CHCH 2CH=CH 2CH 2CH 3CH 39、 (3)、(4)具有—共轭体系;(2)具有缺电子的p —共轭体系; (3)具有多电子的p —共轭体系;(1)、(4)具有—共轭体系;10、(A)C H 3(B)CH 3-CH 2-CH-CH 3C H 3(C)CH 3CH 2CH=CH 2(C)CH 3CH 2CH=CH 2(A)CH 3HBr(B)CH 3-CH 2-CH-CH 311、(A)CH 3CH=CHCH(CH 3)2(B)CH 3CH 2CH=C(CH 3)2(C)CH 3CH 2CH 2CH(CH 3)212、CH 3CH-CH 2C=CHA:B:CH 3-C=CH 2-CH=CH 2C H 3CH 313、2Cl22CH 2Br BrCl (1)CH 2=CH —CH 3CH 2=CH —CH 2Cl 2Cl222CH 22BrCl (2)CH 2=CH —CH 3CH 2=CH —CH 2(3)CH 3C=CH +H 2OH 2S O 4, HgS O 4CH 3-C-CH 3O14、属于单环单萜(1(22属于倍半萜(3属于二萜4)属于倍半萜15、 CH 3C=CHH 3CCH 2CH 2C=CHCH 3CH 3第四章 芳香烃作业参考答案1、(1)邻硝基甲苯 (2)3-羟基苯磺酸 (3)3-甲基-4-氯苯甲酸 (4)1,4-二甲基萘 (5)4-甲基-3-苯基-1-戊烯 (6)6-氯-2-萘酚 2、(1) (2) (3) (4) (5)COOH NO2CH=CH2ClSO3HCH3ClNO2CH3CH(CH3)2CH2CH3(6)H3COClCOOH3、(1)C OOHCl2C OOHC l (2)CH3Cl HNO3H2SO4CH3ClCH3ClO2NNO2+(3)CH(CH3)2C(CH3)2Cl (4)OCH3+(CH3CO)2O无水3OCH3C-CH3OOCH3+C-CH3O(5)C(CH3)3CH2CH2CH3KMNO4H+C(CH3)3COOH(6)CH2CH=CH2CH2CH3KMNO4H+COOHCOOH(7)CH3CH2CH2CH2Cl+无水3CH-CH2CH3CH3(8)CH 2CH 3HNO 3H 2SO 4CH 2CH 3NO 2KMNO 4H +COOHNO 22FeCOOHNO 2Br4、 (1)OH>C H 3>>C l>N O 2(2)CH 3>CH 3CH 3>COOH>CH 3COOH>COOHCOOH5、 (1)a b c褪色:ba,cCH 3CH 3ab褪色:c不褪色:a(2)a b c褪色:b,caCH 2CH 3CH=CH2C=CHab c:C 无沉淀:b6、(1) (2) (3) (4) (5)323H(6)(7)(8)(9)3227、(1)无水3+CH3CH3KMNO4H+COOHHNO24COOHNO2(2)无水3+CH3CH3Cl(3)+(CH3CO)2O无水3C-C H3OBr2FeC-C H3OBr(4)3CH32CH2Cl23(5)3C H33Br2FeC H3BrO2(6)3CH333CH3CH3322 8、有芳香性的是:(2),(4),(5),(8)9、CH 3CH 2CH 310、C=CHCH 3AH 2CH 2CH 3CH 3B-H 2OCC O OO CD第五章旋光异构作业参考答案2、对:(6)(7)。
华南理工大学线性代数 课后习题答案

n
0 0 0
0
0 0 0
解:D (1) n 1 0
习题一部分讲解
第 一 章 7 题 : 求 A 2 和 A 2 n 1 , 其 中 1 1 A 1 1 1 1 2 解: A 1 1 4 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 4 0 0 0 1 4 0 0 0 4 0 0 0 4 0 0 1 1 1 1
T
a11 证: 设A a n1 c11 T 令AA C c n1
a1n ann c1n O cnn
n k 1
n k 1
n k 1
aik aik aik 2 =0 (i=1,2,...,n) cii aik aki 则 aik 0 (i 1, 2,..., n; k 1, 2,..., n) 0 0 所以,A O 0 0 第一章14 题: (E A)(E A A A ) E
(是方阵)
(2) (En uu )(En uu ) En ( (u u ) )uu En
T T T T
令
当u O, 矩阵uu T O, 则数( (u T u ) ) 0 当 u u 1 0,
T
uT u 1
第一章25题 : 设 A为 n阶矩阵, x是每个元素都是1的 n维列向量。 证明:(1) 列向量 Ax的 第 i个 元 素等于 A的 第 i行 元素之和 ; 1 a11 a1n 证: 记 A , x a n1 ann 1 a11 a12 a1n 1 n a1 j A第1行 元素之和 a21 a22 a2 n j 1 Ax 1 n A第 n行 元素之和 a a 1 nj a a n2 nn n1 j 1 所以,列向量 Ax的第 i个元素等于 A的第 i行 元素之和
蹴球竞赛规则

蹴球竞赛规则[日期:2010-04-01][字体:大中小]第一章比赛1 定义蹴球比赛是按照竞赛规则,双方运动员用脚底“蹴”球,使球通过脚底向前滚动,依据所“蹴”之球碰击对方或本方球的情况计算得分,以任一方先达到或超过规定分数而决定胜负的体育竞赛项目。
第二章比赛场地及器材2 比赛场地2.1 场地规格:长10米、宽10米的正方形平坦地面。
2.2 画线:线宽不得超过5厘米,边线及各线段均为场内和各区内的一部分。
2.3 停球区:在场地正中心,为一个半径20厘米的圆圈。
2.4 中心圆:在场地中央,为一个半径2.4米的圆圈。
2.5 发球区:在场地四角,每角一个,为半径0.5米的扇面,按逆时针方向编号为1、2、3、4区。
(图1)3 比赛用球3.1 比赛用球为硬塑实心球,直径10厘米±0.2厘米,重量1000克±10克。
3.2 比赛用球分两种鲜明颜色,分别标有1、2、3、4号。
1、3号球为同一颜色。
2、4号球为同一颜色。
第三章运动员和教练员4 运动员4.1 运动员须按比赛规程或赛会要求统一进入赛场。
4.2 除不可抗拒原因可以由本队教练员或领队代替挑号外,队员必须按时到达赛场进行挑号。
4.3 队员必须接受裁判员对其进行的装备检查,凡不符合规定者,应立即更换。
4.4 上场队员,须穿佩大会统一号衣或号码布。
号码按1、2、3、4排列,单、双号分别同色。
号码宽20厘米,高14厘米。
4.5 运动员必须穿平底运动鞋,并不得对鞋底进行特别加工。
4.6 每局交换发球顺序后,同时交换号码。
4.7 在临场比赛的任何时间,队员均不得擅自退到挡板外接受指导或饮水。
4.8 参赛队的所有人员必须遵守竞赛规则、规程,并对自己的行为负责,不得做出妨碍比赛、干扰对方、破坏比赛气氛的任何行为。
4.9 运动员有权提示裁判员及时更正计分错误。
5 教练员5.1 教练员应按赛会要求在指定地点进行观赛或指挥,未经裁判员允许,不得进入挡板或限制线内。
第二章 汉字 习题及参考答案

第二章汉字习题及参考答案第一节现代汉字概述(P76—P77)练习题一、填空。
1. 汉字是世界上历史最悠久的一种独立发展的文字。
2. 除中国外,现在使用汉字的国家还有日本、韩国、新加坡和马来西亚等。
3. 现代世界各国所用的文字可分为表意文字和表音文字两种性质不同的文字,汉字属于表意性质的文字,日文的假名属于表音性质的文字。
4. 大多数拼音文字是线性文字,汉字是平面性文字。
5. 先进的电脑与古老的汉字正在有机地结合起来。
这种结合使汉字不再仅仅是人与人之间交流信息的工具,而且成为人与机器沟通信息的纽带。
1.现代汉字有哪五个特点?这些特点对汉字的学习和使用有什么影响?现代汉字有五大特点:(1)汉字基本上是一种表意文字。
(2)汉字基本上是一种语素文字。
(3)汉字在形体上表现为方块形。
(4)汉字在语音上代表一个音节。
(5)汉字在书面上不实行分词连写。
总之,现代汉字是一种表意性质的语素文字。
这是它区别于纯粹表音的音素文字或音节文字的基本特点。
从这个基本观点出发,汉字教学应正确估价并充分利用汉字的表意作用,同时要加强汉字的字音教学,以弥补汉字表音功能薄弱的缺点。
2. “森”表示树多貌,“淼”表示大水貌,运用同样的造字法所造的汉字,你还能举出4—5个例字来吗?磊品晶焱犇众卉鑫3. 新造字的造字方法有哪几种跟传统的方法不同的?请举例说明。
新造字是指现代新造的汉字。
新造字除了大量使用形声法和少量使用会意法外,还有一些新的造字法,例如:(1)切音合形造字法,就是两个字合成一个字,意义也合,但是读音则利用切音方法,前字取声母,后字取韵母和声调。
例如方言字“甭”(béng),是“不”和“用”的切音;字义是“不用”,是“不”和“用”的合义。
(2)省形的切音合形造字法,语音和意义跟上面的方法相同,只是字形也各取一半。
例如科技用字“巯”(qiú),是“氢”和“硫”的切音,字义是:有机化合物中含“氢”和“硫”的基。
运筹学第二章课后题
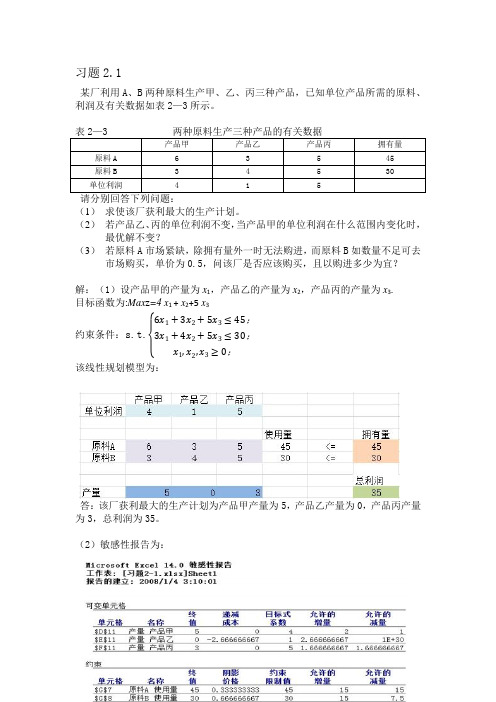
习题2.1某厂利用A 、B 两种原料生产甲、乙、丙三种产品,已知单位产品所需的原料、利润及有关数据如表2—3所示。
表2—3 两种原料生产三种产品的有关数据产品甲 产品乙 产品丙 拥有量 原料A 6 3 5 45 原料B 3 4 5 30 单位利润 4 1 5 请分别回答下列问题:(1) 求使该厂获利最大的生产计划。
(2) 若产品乙、丙的单位利润不变,当产品甲的单位利润在什么范围内变化时,最优解不变?(3) 若原料A 市场紧缺,除拥有量外一时无法购进,而原料B 如数量不足可去市场购买,单价为0.5,问该厂是否应该购买,且以购进多少为宜?解:(1)设产品甲的产量为x 1,产品乙的产量为x 2,产品丙的产量为x 3. 目标函数为:Max z =4 x 1 + x 2+5 x 3约束条件:s.t.{ 6x 1+3x 2+5x 3≤45;3x 1+4x 2+5x 3≤30;x 1,x 2,x 3≥0;该线性规划模型为:答:该厂获利最大的生产计划为产品甲产量为5,产品乙产量为0,产品丙产量为3,总利润为35。
(2)敏感性报告为:答:如数据显示,产品甲的单位利润变化范围为:[3,6]。
(3)敏感性报告为:由敏感性报告显示原料B允许的增量为15,其影子价格为0.667,又因为市场上原料B单价为0.5,此时,总利润为37.5。
答:该厂可购买15。
习题2.3已知某工厂计划生产三种产品,各产品需要在设备A、B、C上加工,有关数据如表2—5所示。
表2—5 生产三种产品的有关数据产品A产品B产品C每月设备有效台时设备A8210300设备B1058400设备C21310420单位利润(千元)32 2.9请分别回答下列问题:(1)如何充分发挥设备能力,才能使生产盈利最大?(2)为了增加产量,可借用其他工厂的设备B,若每月可借用60台时,租金为1.8万元,问借用设备B是否合算?(3)若另有两种新产品(产品4和产品5),其中生产每件新产品4需用设备A、B、C各12、5、10台时,单位赢利2.1千元;生产每件新产品5需用设备A、B、C各4、4、12台时,单位赢利1.87千元。
无机及分析化学课后习题答案

第二章 原子结构和元素周期律 习题解答1.简单说明四个量子数的物理意义和量子化条件。
2.定性画出s, p, d 所有等价轨道的角度分布图。
3.下列各组量子数哪些是不合理的?为什么?(1)2, 1, 0n l m ===; (2)2, 2, 1n l m ===-;(3) 3, 0, 0n l m ===; (4)3, 1, 1n l m ===+;(5)2, 0, 1n l m ===-;(6)2, 3, 2n l m ===+。
解 (2),(5),(6)组不合理。
因为量子数的取值时要求l < n ,m ≤ l 。
4.用合理的量子数表示(1)3d 能级;(2)2p z 原子轨道;(3)4s 1电子。
解 (1)3d 能级的量子数为:n = 3,l = 2。
(2)2p z 原子轨道的量子数为:n = 2,l = 1,m = 0。
(3)4s 1电子的量子数为:n = 4,l = 0,m = 0,m s =12+。
5.在下列各组量子数中,恰当填入尚缺的量子数。
(1) n =?,l =2,m =0,m s = +1/2; (2) n =2,l =?,m =-1,m s =-1/2; (3) n =4,l =2,m =0,m s = ?; (4) n =2,l =0,m =?,m s = +1/2。
解 (1)n ≥ 3正整数; (2)l = 1; (3)m s = +½(或-½); (4)m = 0。
6.下列轨道中哪些是等价轨道?x x x y z 2s, 3s, 3p , 4p , 2p , 2p , 2p 。
解 对氢原子: (n 相同)(x y z 2s, 2p , 2p , 2p );(x 3s, 3p 3s ,3p x )。
对多电子原子:(n 、l 相同)(x y z 2p , 2p , 2p )。
7.下列各元素原子的电子分布式各自违背了什么原理?请加以改正。
草房子第二章主要内容

草房子第二章主要内容第二章中,我们看到了主人公四姐妹的成长历程,以及她们在家庭和社会中所面临的困境和挑战。
在这一章节中,作者通过细腻的描写和真实的情感,展现了四姐妹在不同环境下的成长和变化,同时也反映了当时社会的一些现实问题。
首先,第二章中描述了四姐妹在农村的生活。
她们在艰苦的环境中长大,学会了勤劳和坚韧。
作者通过对她们生活细节的描写,展现了她们对家庭的责任和对生活的勇敢面对。
在这一部分,读者可以感受到四姐妹的纯真和坚强,以及她们对家庭的深厚情感。
其次,第二章还描述了四姐妹在城市的生活。
随着时代的变迁,她们离开了农村,来到了城市,开始了全新的生活。
在城市中,她们面对着各种陌生和挑战,但她们并没有被打倒,而是努力适应和奋斗。
通过对她们在城市生活的描写,读者可以看到她们面对新环境时的坚定和勇敢,以及她们对未来的憧憬和追求。
最后,第二章还反映了当时社会的一些现实问题。
在农村,四姐妹所面临的困境和苦难,反映了当时农村的贫困和落后;而在城市,她们所遇到的挑战和困难,则反映了当时城市的竞争和压力。
通过对四姐妹生活的描写,读者可以看到作者对当时社会现实的深刻观察和思考,以及对社会问题的关注和呼吁。
总的来说,第二章是草房子中非常重要的一部分,它展现了主人公四姐妹的成长历程和所面临的困境,同时也反映了当时社会的一些现实问题。
通过对四姐妹生活的细腻描写,读者可以更加深入地了解当时社会的风貌和人们的生活状态,同时也可以感受到作者对生活的热爱和对社会的关怀。
这一章节不仅让人感叹生活的不易,更让人对未来充满了希望和勇气。
信息论与编码习题参考答案(全)
111
(1)在W4=011中,接到第一个码字“0”后获得关于a4的信息量I(a4;0);
(2)在收到“0”的前提下,从第二个码字符号“1”中获取关于a4的信息量I(a4;1/0);
(3)在收到“01”的前提下,从第三个码字符号“1”中获取关于a4的信息量I(a4;1/01);
(4)从码字W4=011中获取关于a4的信息量I(a4;011)。
其中N=2FT,б2X是信号的方差(均值为零),б2N是噪声的方差(均值为零).
再证:单位时间的最大信息传输速率
信息单位/秒
(证明详见p293-p297)
5.12设加性高斯白噪声信道中,信道带宽3kHz,又设{(信号功率+噪声功率)/噪声功率}=10dB.试计算改信道的最大信息传输速率Ct.
解:
5.13在图片传输中,每帧约有2.25×106个像素,为了能很好的重现图像,需分16个量度电平,并假设量度电平等概率分布,试计算每分钟传输一帧图片所需信道的带宽(信噪功率比为30dB).
(2)求信源的极限熵H∞;
(3)求当p=0,p=1时的信息熵,并作出解释。
解:
3.10设某马尔柯夫信源的状态集合S:{S1S2S3},符号集X:{α1α2α3}。在某状态Si(i=1,2,3)下发发符号αk(k=1,2,3)的概率p(αk/Si) (i=1,2,3; k=1,2,3)标在相应的线段旁,如下图所示.
证明:
3.5试证明:对于有限齐次马氏链,如果存在一个正整数n0≥1,对于一切i,j=1,2,…,r,都有pij(n0)>0,则对每个j=1,2,…,r都存在状态极限概率:
(证明详见:p171~175)
3.6设某齐次马氏链的第一步转移概率矩阵为:
第二章直线的投影

例2-10 求点C 到任意倾斜直线AB的距离。
§2-7 直线的辅助投影
各投影都相交,投影的交点符合点 虽然投影也相交,但投影的交点不符 的投影规律,所以AB与CD相交。 合点的投影规律,故EF和GH不相交。
§2-5 两直线的相对位置
例2-3 试判断两直线AB 和CD 是否相交。 解: 各投影的交点不符合点的投影规律, 所以两直线不相交。
§2-5 两直线的相对位置
例2-4 已知平行两直线 AB、CD,试作一直线KL与AB、CD 都相交,且该直线 距H 面为10。 解:
点击后自动演播
§2-5 两直线的相对位置
三、两直线交错
若两直线既不平行也不相交,那必然是交错两直线,也称交 叉两直线,即异面直线。 下面这些都是交错直线。
交错直线同面投影的交点是两直线上一对重影点的投影,对 此重影需进行可见性判断。
§2-5 两直线的相对位置
例2-5 试判断交错两直线AB、CD之重影的可见性。 解: zⅣ>zⅢ,所以4可见,3不可见。
§2-2 直线上的点
一、直线上的点 从属性:直线上的点其投影必在直线的同面投影上。 定比性:直线线段上一点把线段分成两段,其长度之比, 等于这两段在同一投影面上的投影长度之比。
ac∶cb=a'c'∶c'b'= a"c"∶c"b"=AC∶CB
§2-2 直线上的点
例2-1 已知线段EF的两投影,试在其上取一点K,使EK∶KF =3∶4。 解:
求任意倾斜直线段的实长和倾角的基本方法是直角三角形 法。下图表示它的原理和作图过程。
§2-3 直线的倾角和直线段的实长
例2-2 已知直线CD 的正面投影c'd'和点C 的水平投影c,且知 直线CD 对H 面的倾角α=30°,求作线段CD 的H 面投影。 解:
导图系列(3-4):八年级数学(北师大版)各章知识点思维导图集合

第三章 图形的平移与旋转
第四章 因式分解 第五章 分式与分式方程
第六章 平行四边形
任它本身;负数的绝对值是它的相反数;0 的绝对值是 0。(反之,若 5 绝对值
性质 |a|=a,则 a≥0;若|a|=-a,则 a≤0。)
互为相反数的两个数的绝对值相等。
两个负数比较大小,绝对值大的反而小。
如果两个数只有符号不同,那么称其中一个数为另一个的相反数,也称这两个数互
性质 负数。
一般地,形如 的代数式叫做二次根式,a 叫做被开方数。
二次根 一般地,被开方数不含分母,也不含能开得尽方的因数或因式的二次根式叫最简二次根式。
11
式
·
( , ),
(,)
第三章 位置与坐标
序号 1
知识点 确定位置
第三章 位置与坐标
内容 在平面内,确定一个物体的位置一般需要 2 个数据。 在平面内,两条互相垂直且有公共原点的两条数轴构成平面直角坐标系。通常,两条 数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向。水平 的数轴叫做 x 轴或横轴,垂直的数轴叫做 y 轴或纵轴,x 轴和 y 轴统称为坐标轴,它们的 公共原点 O 称为直角坐标系的原点。建立了平面直角坐标系,平面内的点就可以用一组有 序实数对(a,b)来表示了。 在平面直角坐标系中,两条坐标轴将坐标平面分成了四部分,右上方的部分叫做第一 象限,其它三部分按逆时针方向依次叫做第二、三、四象限。坐标轴上的点不在任何一个 象限内。
性质 一个正数有两个平方根,它们互为相反数;0 的平方根是 0;负数没有平方根。
算数 定义 一般地,如果一个正数 x 的平方等于 a, ,那么这个正数 x 就叫做 a 的算数平方根。 9
平方根 性质 一个正数的算数平方根是正数;0 的算数平方根是 0;负数没有算数平方根。
第二章 烷烃习题解答

第二章 烷烃1.写出庚烷的同分异构体的构造式,用系统命名法命名(汉英对照)。
(共9种,略)2.写出下列化合物的汉英对照名称(1) 2-甲基戊烷(2-methylpentane) 或异己烷(isohexane) (2)3,3-二甲基-4-乙基己烷(4-ethyl-3,3-dimethylhexane) (3)2,3,6-三甲基-6-乙基辛烷(6-ethyl-2,3,6-trimethyloctane) (4)3,5,5,6-四甲基壬烷(3,5,5,6--tetramethylnonane)3. 下列烃类化合物按沸点降低的顺序排列:2-甲基庚烷 > 正庚烷 > 2-甲基己烷 > 3,3-二甲基戊烷 > 正戊烷4. 写出下列化合物一氯代时的全部产物的构造式 (1)正己烷hv++CH 3(CH 2)4CH 3Cl(CH 2)5CH 3CH 3CHCH 2CH 2CH 2CH 3ClCH 3CH 2CHCH 2CH 2CH 3Cl15.8%42.1%42.1%(2)异己烷hv+++ClCH 2CHCH 2CH 2CH 3CH 3CH 3CCH 2CH 2CH 3Cl CH 3CH 3CHCHCH 2CH 3Cl CH 3220%16.7%26.65%CH 3CHCH 2CH 2CH 3CH 3CH 3CHCH 2CHCH 3CH 3ClCH 3CHCH 2CH 2CH 2ClCH 326.6510%%(3)2,2-二甲基丁烷hv++40%45%CH 3CCH 2CH 3CH 3CH 315%ClCH 2CCH 2CH 3CH 3CH 3CH 3CCH 2CH 2ClCH 3CH 3CH 3C CH 3CH 3CHCH 3Cl5. 写出下列各取代基的构造式:C CH 3CH 3CH 3CH 2(1) Et-CH 3CH 2(2) i-Pr-CH 3CHCH 3(3) i-Bu-CH 3CHCH 2CH 3(4) s-Bu-CH 3CH 2CHCH 3(5)异戊基CH 3CHCH 2CH 2CH 3(6)新戊基(7) 三级戊基CH 3CCH 2CH 3CH 36. 写出乙烷氯代的自由基历程:Cl 2Cl2Cl++++CH 3CH 3HCl CH 3CH CH 3CH Cl ClCH 3CH 2ClCl链的引发链的增长与传递7.(1) 把下列三个透视式写成纽曼投影式,它们是否相同的构象? 答: 由于同一个碳原子上连有三个氢,它们是相同的构象。
高中数学新教材同步必修第一册 第2章 习题课 不等式恒成立、能成立问题

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
3.已知不等式x2+ax+4<0的解集为空集,则a的取值范围是
√A.{a|-4≤a≤4}
C.{a|a≤-4或a≥4}
B.{a|-4<a<4} D.{a|a<-4或a>4}
解析 由题意得,Δ=a2-16≤0,解得-4≤a≤4.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
4.已知不等式-x2+4x≥a2-3a在R上有解,则实数a的取值范围为
√A.{a|-1≤a≤4}
C.{a|a≥4或a≤-1}
B.{a|-1<a<4} D.{a|-4≤a≤1}
解析 由题意知,-(x-2)2+4≥a2-3a在R上有解, ∴a2-3a≤4,即(a-4)(a+1)≤0,∴-1≤a≤4.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
9.∀x∈{x|2≤x≤3},不等式mx2-mx-1<0恒成立,求m的取值范围.
解 由不等式mx2-mx-1<0,得m(x2-x)<1,
因为x∈{x|2≤x≤3},所以x2-x>;x2-1 x,
1234
4.定义运算ac
db=ad-bc,则不等式a1x
1 x+1<0
对任意
x∈R
恒成立,
则实数 a 的取值范围是_-__4_<_a_≤__0__.
解析 原不等式为ax(x+1)-1<0, 即ax2+ax-1<0,a=0时,不等式为-1<0,符合题意, 当 a≠0 时,有aΔ<=0,a2+4a<0 ⇒-4<a<0, 综上所述,a的取值范围是-4<a≤0.
《现代控制理论》刘豹著(第3版)课后习题答案(最完整版)

第一章习题答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解:系统的模拟结构图如下:)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CC L L R L L R x x x 。
现代控制理论基础第二章习题答案
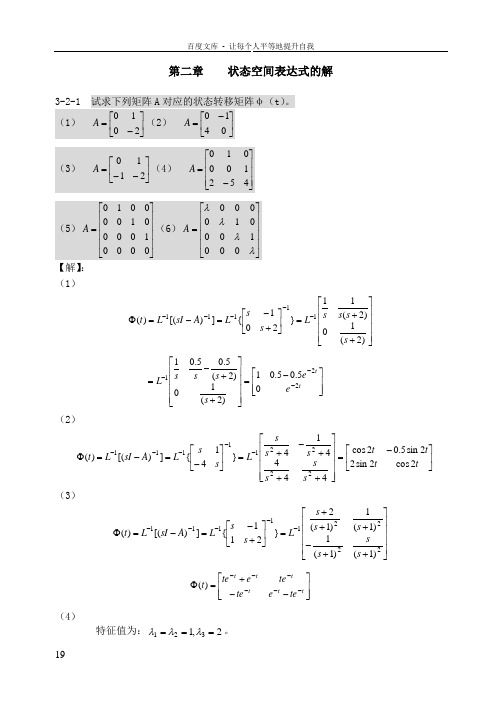
第二章 状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ(t )。
(1) ⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0410A (3) ⎥⎦⎤⎢⎣⎡--=2110A (4) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A (5)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000100001000010A (6)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ000100010000A 【解】:(1)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----)2(10)2(11}201{])[()(11111s s s s L s s L A sI L t ⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-=---t t e e s s s s L 22105.05.01)2(10)2(5.05.01(2)⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎦⎤⎢⎣⎡-=-=Φ-----t tt ts s s s s sL s s L A sI L t 2cos 2sin 22sin 5.02cos 444414}41{])[()(222211111(3)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-+++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----222211111)1()1(1)1(1)1(2}211{])[()(s s s s s s L s s L A sI L t ⎥⎥⎦⎤⎢⎢⎣⎡--+=Φ------t t tt tt te e te te e te t )((4)特征值为:2,1321===λλλ。
由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-200010011~1AP P A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=t t t t tA e e te e e2~0000 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡===Φ-1211321200000421211101)(21~t t t ttA At e te e eP Pe e t ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--++-----++-----++--=Φt t t tt t t t t t t t t t t tt t t t t t t t tt e te e e te e e te e e te e e te e e te e e te e e te e te e t 34838424225342222322)(222222222 (5)为结构四重根的约旦标准型。
最新人教版初中数学教材目录(全)

最新人教版初中数学教材目录(全)七年级上册(61)第1章有理数(19)第2章整式的加减(8)第3章一元一次方程(18)第4章图形认识初步(16)七年级下册(62)第5章相交线与平行线(14)第6章平面直角坐标系(7)第7章三角形(8)第8章二元一次方程组(12)第9章不等式与不等式组(12)第10章数据库的收集整理与描述(9)八年级上册(62)第11章全等三角形(11)第12章轴对称(13)第13章实数(8)第14章一次函数(17)第15章整式的乘除与因式分解(13)八年级下册(61)第16章分式(14)第17章反比例函数(8)第18章勾股定理(8)第19章四边形(16)第20章数据的分析(15)九年级上册(62)第21章二次根式(9)第22章一元二次方程(13)第23章旋转(8)第24章圆(17)第25章概率初步(15)九年级下册(48)第26章二次函数(12)第27章相似(13)第28章锐角三角函数(12)第29章投影与视图(11)七年级上册第一章有理数1.1 正数和负数阅读与思考用正负数表示加工允许误差1.2 有理数1.3 有理数的加减法实验与探究填幻方阅读与思考中国人最先使用负数1.4 有理数的乘除法观察与思考翻牌游戏中的数学道理1.5 有理数的乘方数学活动小结复习题1 第二章整式的加减2.1 整式阅读与思考数字1与字母X的对话2.2 整式的加减信息技术应用电子表格与数据计算数学活动小结复习题2 第三章一元一次方程3.1 从算式到方程阅读与思考“方程”史话3.2 解一元一次方程(一)——合并同类项与移项实验与探究无限循环小数化分数3.3 解一元一次方程(二)——去括号与去分母3.4 实际问题与一元一次方程数学活动小结复习题3 第四章图形认识初步4.1 多姿多彩的图形阅读与思考几何学的起源4.2 直线、射线、线段阅读与思考长度的测量4.3 角4.4 课题学习设计制作长方体形状的包装纸盒数学活动小结复习题4 部分中英文词汇索引七年级下册第五章相交线与平行线5.1 相交线5.2 平行线5.3 平行线的性质5.4 平移数学活动小结复习题5 第六章平面直角坐标系6.1 平面直角坐标系6.2 坐标方法的简单应用数学活动小结复习题6 第七章三角形7.1 与三角形有关的线段7.2 与三角形有关的角7.3 多边形及其内角和7.4 课题学习镶嵌数学活动小结复习题7 第八章二元一次方程组8.1 二元一次方程组8.2 消元8.3 再探实际问题与二元一次方程组数学活动小结复习题8 第九章不等式与不等式组9.1 不等式9.2 实际问题与一元一次不等式9.3 一元一次不等式组9.4 课题学习利用不等关系分析比赛(1)数学活动小结复习题9 第十章实数10.1 平方根10.2 立方根10.3 实数数学活动小结复习题10 部分中英文词汇索引八年级上册第十一章一次函数11.1 变量与函数信息技术应用用计算机画函数图象11.2 一次函数阅读与思考科学家如何测算地球的年龄11.3 用函数观点看方程(组)与不等式数学活动小结复习题11 第十二章数据的描述12.1 几种常见的统计图表12.2 用图表描述数据信息技术应用利用计算机画统计图阅读与思考作者可能是谁12.3 课题学习从数据谈节水数学活动小结复习题12 第十三章全等三角形13.1 全等三角形13.2 三角形全等的条件阅读与思考为什么要证明13.3 角的平分线的性质数学活动小结复习题13 第十四章轴对称14.1 轴对称14.2 轴对称变换信息技术应用探索轴对称的性质14.3 等腰三角形实验与探究三角形中边与角之间的不等关系数学活动小结复习题14 第十五章整式15.1 整式的加减15.2 整式的乘法15.3 乘法公式阅读与思考杨辉三角15.4 整式的除法15.5 因式分解观察与猜想x2+(p+q)x+pq型式子的因式分解数学活动小结复习题15 八年级下册第十六章分式16.1 分式16.1 分式的运算阅读与思考容器中的水能倒完吗16.1 分式方程数学活动小结复习题16 第十七章反比例函数17.1 反比例函数17.1 实际问题与反比例函数阅读与思考生活中的反比例关系数学活动小结复习题17 第十八章勾股定理18.1 勾股定理18.2 勾股定理的逆定理数学活动小结复习题18 第十九章四边形19.1 平行四边形19.1 特殊的平行四边形实验与探究巧拼正方形19.1 梯形观察与猜想平面直角坐标系中的特殊四边形数学活动小结复习题19 第二十章数据的分析20.1 数据的代表20.2 数据的波动信息技术应用用计算机求几种统计量阅读与思考数据波动的几种度量20.3 课题学习体质健康测试中的数据分析数学活动小结复习题20 九年级上册第二十一章二次根式21.1 二次根式21.2 二次根式乘除阅读与思考海伦──秦九韶公式数学活动小结复习题21 第二十二章一元二次方程22.1 一元二次方程22.2 降次──解一元二次方程阅读与思考黄金分割数22.3 实际问题与一元二次方程观察与猜想发现一元二次方程根与系数的关系数学活动小结复习题22 第二十三章旋转23.1 图形的旋转23.2 中心对称信息技术应用探索旋转的性质23.3 课题学习图案设计数学活动小结复习题23 第二十四章圆24.1 圆24.2 与圆有关的位置关系24.3 正多边形和圆阅读与思考圆周率π 24.4 弧长和扇形面积实验与研究设计跑道数学活动小结复习题24 第二十五章概率初步25.1 概率25.2 用列举法求概率阅读与思考概率与中奖25.3 利用频率估计概率阅读与思考布丰投针实验25.4 课题学习键盘上字母的排列规律数学活动小结复习题25 九年级下册第二十六章二次函数26.1 二次函数实验与探究推测植物的生长与温度的关系26.2 用函数观点看一元二次方程信息技术应用探索二次函数的性质26.3 实际问题与二次函数数学活动小结复习题26 第二十四章相似27.1 图形的相似27.2 相似三角形观察与猜想奇妙的分形图形27.3 位似信息技术应用探索位似的性质数学活动小结复习题27 第二十八章锐角三角函数28.1 锐角三角函数阅读与思考一张古老的三角函数28.2 解直角三角形数学活动小结复习题28 第二十九章投影与视图29.1 投影29.2 三视图阅读与思考视图的产生与应用29.3 课题学习制作立体模型数学活动小结复习题29 。
第二章_值机工作过程

第二章_值机工作过程第二章值机工作过程学习目标:通过本章的学习,了解值机岗位设置和各岗位基本要求,掌握始发站、经停站和到达站值机业务的工作流程,掌握中转服务的要求。
第一节值机业务一、旅客的航空旅行程序1、国内旅客的航空旅行程序购票办理乘机手续、托运行李安全检查候机登机乘机旅行下机、领取行李出机场2、国际旅客的航空旅行程序签证和护照航程设计和购票海关和卫检办理乘机手续、托运行李安检和边检候机、登机乘机旅行下机、领取行李海关通道移民局出机场国际值机工作与国内值机工作最大的不同就是涉及一个出境问题。
随之而来的工作就变得复杂起来。
客票查验是国际客票,旅客证件是国际证件,行李运输要符合国际运输规则。
从业务学习上讲,国内值机业务是国际值机业务的基础,国际值机业务是我们学习的重点和难点。
二、值机业务流程★值机区域控制和准备工作区域控制如整个值机区的供电问题、离港系统的运行准备工作至少在航班起飞前4小时开始,如了解航班动态情况并将有关信息及时传达到现场各相关岗位。
★旅客引导以前属于值机工作范围,通过导乘台等进行,白云机场现在已独立成单独的部门★值机过程★旅客服务★登机服务★中转服务★到达服务第二节值机岗位设置及各岗位基本要求一、地面服务岗位1、地面服务岗位:候机楼服务、值机服务、机场售票、隔离厅服务、外场调度等2、值机服务:值机控制、值机操作。
值机控制叫内值机,值机操作叫外值机。
以前配载是内值机,国际值机员常常也身兼配载平衡的工作,现在配载划分到签派了。
我们学习的重点是外值机。
二、外值机岗位设置:白云机场:值班主任柜台、值机柜台、随到随办柜台、头等舱柜台、逾重柜台等南航:普通值机柜台无行李交运柜台随到随办柜台头等舱、公务舱柜台特殊服务柜台等目前的柜台设置大致有两种,一种是指定航班设置,一个航班的旅客集中在一个柜台办理。
优势:方便值机员集中接收,提高了效率。
劣势:大型机场航班多,一方面浪费资源,人员结构臃肿,另一方面增加了旅客的不便(寻找值机柜台增加了旅客的时间成本)。
结构力学龙驭球第四版第二章课后习题答案
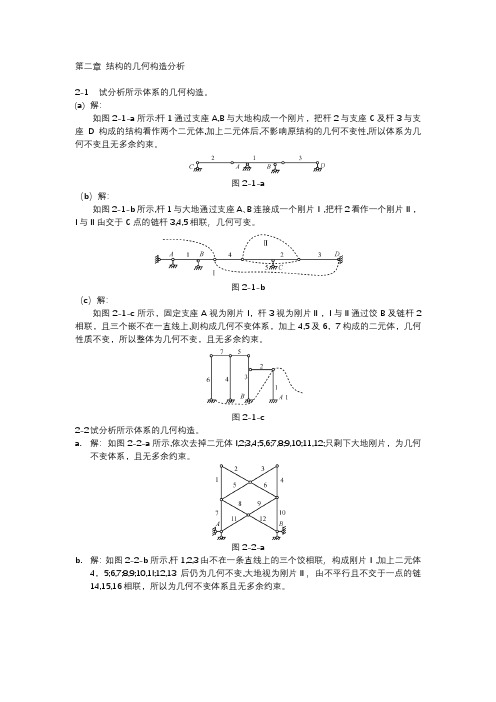
图 2-10-a b. 解:如图 2-10-b 所示刚片 I,ll,IⅢl,三刚片分别由饺(1,3),(2,3)及杆 1,2 交于无穷
图 2-8-a b. 解:如图 2-8-b 所示刚片Ⅰ﹐及大地Ⅲ,I,Ⅱ交于无穷远处饺(1,2),l,Ⅲ由支座链杆相
联交于(1,3),ll,Ⅲ交于(2,3); (1,3)及(2,3)的连线与杆 5,6 平行﹐故体系为瞬变。
图 2-8-b 2-9 试分析所示体系的几何构造。 a. 解:按一般思路分析,如图 2-9-a 所示刚片 I,ll,大地刚片Ⅲ,分别交于饺 A,(1,3),(2,3),
4,5;6,7;8,9;10,1l;12,13 后仍为几何不变,大地视为刚片Ⅱ﹐由不平行且不交于一点的链 14,15,16 相联,所以为几何不变体系且无多余约束。
图 2-2-b c. 解:去掉二元体 8,9,不予考虑。如图 2-2-c 所示刚片 I,ll,Ⅲ由三饺相联,但三个铰在一
条直线上,不满足规则要求,为瞬变体系。
图 2-1-c 2-2 试分析所示体系的几何构造。 a. 解:如图 2-2-a 所示,依次去掉二元体 l,2;3,4;5,6;7,8;9,10;11,12;只剩下大地刚片,为几何
不变体系,且无多余约束。
图 2-2-a b. 解:如图 2-2-b 所示,杆 1,2,3 由不在一条直线上的三个饺相联﹐构成刚片Ⅰ,加上二元体
w= 2j-b= 2×10-(16+4)= o b. 解:w = 3m-(3g +2h+b
=3×14-(3 ×2+2×18) =o
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f(x)
1 2
e
( x )2 2 2
x
其中μ,σ( σ > 0)为未知参数,则称
X 服从参数为μ,σ的正态分布,记为:
X ~ N ( , 2 )
正态分布密度函数图形
y
1 2
y
1 2
e
( x )2 2 2
F () lim F ( x ) 0;
x x
F () lim F ( x ) 1;
3、右连续性:对任意实数x,
F ( x 0) F ( x)
反之,具有上述三个性质的实函数,必是某
个随机变量的分布函数。故该三个性质是
分布函数的充分必要性质。
由定义知 X 落在区间( a ,b ] 里的概率可 用分布函数来计算:
k: xk x
1
pk
p1 x1
p2 x2
pk xk x
pn
xn x
离散型随机变量的分布函数F( x) 的图像是 呈阶梯状上升的右连续曲线, 在 X 的可能取值 xk 处发生间断, 间断点为第一类跳跃间断点, 在 间断点处有跳跃值 pk P( X xk )
F( x ) P( X x )
例4.长途汽车起点站于每时的10分、25分、55分发车
,设乘客不知发车时间,于每小时的任意时刻随机地到 达车站,求乘客候车时间超过10分钟的概率.
15 45
解:设A—乘客候车时间超过10分钟
X—乘客于某时X分钟到达,则XU(0,60)
P( A) P{10 X 15} P(25 X 45} P{55 X 60}
3.若 X ~ N ( , 2 ),则
F( x ) P{ X x } P { X
1 中损坏的只数为Y ~ B( 3 , ) 3
1 P(Y 1 ) C 3
1 3
1
1 1 3
31
4 9
例2 设随机变量 X 的分布函数为:
0, x 0 2 F( x ) x , 0 x 1 1, x1
(1) 求X取值在区间 (0.3,0.7)的概率;
p P{x 1000}
1 e 1000 2000
x 2000
dx e0.5 0.6065
从而 Y~b(4,0.6065)
所求概率为:
k k 4k C (0.6065) (1 0.6065) P{Y 3} 4 k 3 4
0.4865
3.正态分布
f ( x)
则称 X 服从区间[ a , b ] 上的均匀分布。 记作 X ~ U ( a,b )
x a b
例3 解:
若 X ~ U ( a,b ) ,求 F (x) 。
f ( x) a b
x<a
a xb
x
0 xa f ( t )dt b a 1
x
而且只要有不少于3个元件正常工作,该系统就能正常运行, 求该系统能正常运行1000小时以上的概率为多少?
解: 设Y为系统中寿命超过1000小时的元件数,
则Y~b(4,p), 其中
p P{X 1000}
x 1 2000 e ,x 0 X ~ f ( x) 2000 0 x0
FZ ( x ) P{ Z x } P{ X
P{ X x }
x}
x
1 2
e
( t )2 2 2
dt
令 u
t
或 t u dt du
x
1 2
e
u2 2
du ( x )
lim { F( a ) F( a x )} F( a ) F( a 0 ) x0
用分布函数表示概率
P( a X b ) F( b ) F( a )
P( X a ) F( a ) F( a 0 )
请 填 空
P( a X b ) P( a X b )
k: xk x
pk
§2.4 连续型随机变量的分布
定义 对任意实数 x , 若随机变量 X 的 分布函数可写成:
F( x ) f ( t )dt
x
x
其中 f ( x ) 0 ,则称 X 是连续型随机 变量,称f ( x )为X 的概率密度函数, 简称 为密度函数或概率密度。 记为:
(2) 求X的概率密度。
解: (1) P(0.3<X<0.7) =F(0.7)-F(0.3) = 0.72- 0.32 = 0.4
(2)
dF ( x ) f(x)= dx
2x, 0 x 1 0, 其它
0, x 0 2 F( x ) x , 0 x 1 1, x1
如零件的尺寸;纤维的强度和张力;农作物
的产量,小麦的穗长、株高;测量误差,射
击目标的水平或垂直偏差;信号噪声等等,
都服从或近似服从正态分布。
设X~ N ( , ) ,
2
X的分布函数是
( t )2 2 2
1 F ( x) 2
x
e
dt , x
正态分布由它的两个参数μ和σ唯 一确定, 当μ和σ不同时,是不同的正 态分布。
1
(2) P( X 1700
c = 1000
1500 X 2000 )
P( 1500 X 2000 )
P( X 1700 ,1500 X 2000 )
P( 1500 X 1700 )
P( 1500 X 2000 )
2000 1500
1700 1500
P( a X b ) P( X b ) P( X a )
F( b ) F( a )
a
b
x
P( X a ) 1 P( X a ) 1 F( a )
]
a
x
P( X a ) ?
a-Δx
P( X a )
x 0
a
lim
x
P{ a x X a }
下面我们介绍一种最重要的正态分布
标准正态分布
当 =0 , =1 时 , 称 X 服从标准正态分布
概率密度函数为: 分布函数为: ( x )
x
( x )
1 2 e
t2 2
1 2
e
x2 2
dt
记为: X ~ N ( 0 ,1 )
( x) 的数值可查标准正态分布表(附录)
(2) 计算 P( X 1700
1500 X 2000 );
(3) 已知一设备装有3个这样的电子管, 每个 电子管能否正常工作相互独立, 求在使用 的最初1500小时只有一个损坏的概率。
解: (1 ) 令
f(x )dx
1000
c dx 2 x
c c 1000 x 1000
X ~ f(x)
几何 意义 y
x
f ( t )dt
y = f(x)
x X
x
x
F( x ) P{ X x } f ( t )dt
概率密度 f(x) 的性质
1. f ( x ) 0
2.
f ( t )dt 1
常利用这两个性质检验一个函数能 否作为连续性随机变量的密度函数,或 求其中的未知参数。
3.在 f (x) 的连续点处有 f ( x ) F ( x ) 4. 对连续型随机变量 X 有: 1). P( X a ) F( a ) F( a 0 ) 0
2). P( a X b ) P( a X b )
P( a X b ) P( a X b )
f ( t )dt F( b ) F( a )
a b
3). P{ x X x dx } f ( x )dx
例1 已知某型号电子管的使用寿命 X 为连 续随机变量, 其密度函数为:
c f(x) , 2 x 0 x 1000 其他
(1) 求常数 c ;
15 10 45 1 60 1 1 5 20 5 1 dx dx dx 25 60 55 60 60 60 2
2.指数分布
1 x / ,x 0 e 若X ~ f ( x)= 0, x 0
f (x)
0为常数
0
x
则称X服从参数为 的指数分布。 其分布函数为 x
例:
X ~ N ( 0,1 )
பைடு நூலகம்
求P{ X 1 }
查表
P{ X 1 } ( 1) 0.8413
正态分布的几个结论: 1. ( x ) 1 ( x )
-x
0
x
2.(引理):
若 X ~ N ( , ),则 Z
2
X
: N ( 0,1 ) .
证: Z 的分布函数为:
1000 dx 2 x
1000 dx 2 x
4
51 6
1
24 51
(3) 设A 表示一个电子管的寿命小于1500小时
P(A) P{ 0 X 1500 }
1500 1000
1500
0
f ( x )dx
1000 1 dx 2 x 3
