北师大版九年级数学上2.5 一元二次方程的根与系数的关系同步练习(含答案)

合集下载

原创2023学年一元二次方程的根与系数的关系九年级数学

北师大版九年级数学上册第二章2.5一元二次方程的根与系数的关系假期同步测试一．选择题1.如果一元二次方程x 2-3x-1=0的两根为x 1、x 2，那么x 1+x 2=（） A ．-3 B ．3 C ．-1 D ．12.一元二次方程x 2+4x-3=0的两根为1x 、2x ，则1x •2x 的值是（） A ．4 B ．-4 C ．3 D ．-33．一元二次方程3x 2﹣4x ﹣5=0的两实数根的和与积分别是（） A ．，﹣ B ．， C ．﹣，﹣D ．﹣，4.一元二次方程x 2-3x-2=0的两根为x 1，x 2，则下列结论正确的是（） A ．x 1=-1，x 2=2 B ．x 1=1，x 2=-2 C ．x 1+x 2=3D ．x 1x 2=25. 设x 1，x 2是一元二次方程2x -2x-3=0的两根，则2211x x =（） A ．6 B ．8 C ．10 D ．12 6．关于x 的一元二次方程x 2+bx ﹣1=0的判别式为（） A ．1﹣b2B ．b 2﹣4C ．b 2+4D ．b 2+17. 已知x 1，x 2是一元二次方程x 2-4x+1=0的两个实数根，则x 1x 2-x 1-x 2的值等于（）A ．-3B ．0C ．3D ．58.若关于x 的方程x 2-2x+c=0有一根为-1，则方程的另一根为（）A．-1 B．-3 C．1 D．39.若关于x的一元二次方程x2-3x+p=0（p≠0）的两个不相等的实数根分别为a和b，且a2-ab+b2=18，则a b的值是（）b aA．3 B．-3 C．5 D．-510.判断一元二次方程式x2-8x-a=0中的a为下列哪一个数时，可使得此方程式的两根均为整数？（）A．12 B．16 C．20 D．24 11．（2019•贵港）若α，β是关于x的一元二次方程x2﹣2x+m＝0的两实根，且+＝﹣，则m等于（）A．﹣2 B．﹣3 C．2 D．3 12．（2019•广东）已知x1，x2是一元二次方程x2﹣2x＝0的两个实数根，下列结论错误的是（）A．x1≠x2B．x12﹣2x1＝0 C．x1+x2＝2 D．x1•x2＝2 13．已知关于的一元二次方程有两个不相等的实数根，若，则的值是A．2 B．–1 C．2或–1 D．不存在14．已知一元二次方程的两个根分别是x＝2和x＝－3，则这个一元二次方程是( )A．x2－6x＋8＝0 B．x2＋2x－3＝0C．x2－x－6＝0 D．x2＋x－6＝0二．填空题15.已知x1=3是关于x的一元二次方程x2-4x+c=0的一个根，则方程的另一个根x2是_______16.设m、n是一元二次方程x2+2x-7=0的两个根，则m2+3m+n= .17．若关于x的一元二次方程（m﹣2）x2﹣4x+3=0有实数解，则m的取值范围为．18.方程2x2-3x-1=0的两根为x1，x2，则x12+x22= ．19.关于x的方程2x2-ax+1=0一个根是1，则它的另一个根为 .20.已知一元二次方程x2+3x-4=0的两根为x1、x2，则x12+x1x2+x22= .21．已知关于x的一元二次方程x2﹣5x+1﹣m=0的一个根为2，则另一个根是22.设m，n分别为一元二次方程x2+2x-2018=0的两个实数根，则m2+3m+n= .23．（2019•娄底）已知方程x2+bx+3＝0的一根为+，则方程的另一根为．24．已知关于x的一元二次方程x2﹣4x+m﹣1=0的实数根x1，x2，满足3x1x2﹣x1﹣x2>2，则m的取值范围是__________．三．解答题25．若关于x的方程x2＋mx＋7＝0的一个根为3－2，求方程的另一个根及m的值．26．（2019•孝感）已知关于x的一元二次方程x2﹣2（a﹣1）x+a2﹣a ﹣2＝0有两个不相等的实数根x1，x2．（1）若a为正整数，求a的值；（2）若x1，x2满足x12+x22﹣x1x2＝16，求a的值．27．已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1、x2．（1）求m的取值范围；（2）若x12+x22=6x1x2，求m的值．28.已知直角三角形的两条直角边的长恰好是方程2x2-8x+7=0的两个根，求这个直角三角形的斜边长29.已知：关于x的方程x2+2mx+m2-1=0（1）不解方程，判别方程根的情况；（2）若方程有一个根为3，求m 的值．30．已知关于x的方程x2－(2k－1)x＋k2－2k＋3＝0有两个不相等的实数根．(1)求实数k的取值范围．(2)设方程的两个实数根分别为x1，x2，是否存在这样的实数k，使得|x1|－|x2|＝5成立？若存在，求出这样的k值；若不存在，请说明理由．答案提示1.A；2.D；3．A；4.C；5. C；6．C；7.A；8.D；9.D；10.C；11．B；12．D；13．A；14．D.15.1； 16. 5； 17．m≤且m≠2； 18.134； 19.12； 20.13； 21．3；22. 2016； 23．﹣； 24．3<m≤5．25．解：设方程的另一个根为t，根据题意，得(3－2)t＝7，∴t＝73－2＝3＋ 2.所以－m＝3－2＋3＋2＝6，即m＝－6.即方程的另一个根为3＋2，m的值为－6.26．解：（1）∵关于x的一元二次方程x2﹣2（a﹣1）x+a2﹣a﹣2＝0有两个不相等的实数根，∴△＝[﹣2（a﹣1）]2﹣4（a2﹣a﹣2）＞0，解得：a＜3，∵a为正整数，∴a＝1，2；（2）∵x1+x2＝2（a﹣1），x1x2＝a2﹣a﹣2，∵x12+x22﹣x1x2＝16，∴（x1+x2）2﹣3x1x2＝16，∴[2（a﹣1）]2﹣3（a2﹣a﹣2）＝16，解得：a1＝﹣1，a2＝6，∵a＜3，∴a＝﹣1．27．解: （1）∵方程有两个实数根，∴△≥0，即（﹣2）2﹣4（m﹣1）≥0，解得m≤2；（2）由根与系数的关系可得x1+x2=2，x1x2=m﹣1，∵x12+x22=6x1x2，∴（x1+x2）2﹣2x1x2=6x1x2，即（x1+x2）2=8x1x2，∴4=8（m﹣1），解得m=1.5．28.解: 设直角三角形的斜边为c，两直角边分别为a与b．∵直角三角形的两条直角边的长恰好是方程2x2-8x+7=0的两个根，∴a+b=4，ab=3.5；根据勾股定理可得：c2=a2+b2=（a+b）2-2ab=16-7=9，∴c=329.解：（1）∵a=1，b=2m，c= m2-1，∵△=b2-4ac=（2m）2-4×1×（m2-1）=4＞0，∴方程x2+2mx+m2-1=0有两个不相等的实数根；（2）∵x2+2mx+m2-1=0有一个根是3，∴32+2m×3+ m2-1=0，解得，m=-4或m=-2．30．解：(1)∵原方程有两个不相等的实数根，∴Δ＝[－(2k－1)]2－4(k2－2k＋3)＝4k－11＞0，解得k ＞114.(2)存在．∵x 1＋x 2＝2k －1，x 1x 2＝k 2－2k ＋3＝(k －1)2＋2＞0， ∴将|x 1|－|x 2|＝5两边平方，可得x 12－2x 1x 2＋x 22＝5，即(x 1＋x 2)2－4x 1x 2＝5， ∴(2k －1)2－4(k 2－2k ＋3)＝5，即4k －11＝5，解得k ＝4. ∵4>114，∴k ＝4.。

北师大版数学九年级上册《一元二次方程的根与系数的关系》同步练习题含答案

北师⼤版数学九年级上册《⼀元⼆次⽅程的根与系数的关系》同步练习题含答案第⼆章⼀元⼆次⽅程 2.5 ⼀元⼆次⽅程的根与系数的关系1．已知关于x的⼀元⼆次⽅程x2－x－3＝0的两个实数根分别为α，β，则(α＋3)(β＋3)等于( )A. 8B. 9C. 10D. 122. 设x1，x2是⽅程5x2－3x－2＝0的两个实数根，则1x1＋1x2的值为( )A. －4B. －3C. －2D. －323. 若关于x的⼀元⼆次⽅程x2－(a＋5)x＋8a＝0的两个实数根分别为2和b，则ab等于( )A. 4B. 3C. 2D. 14. 已知a，b是⽅程x2－x－3＝0的两个根，则代数式5a2＋b2－5a－b＋5的值为( )A. 20B. 22C. 23D. 255. 设m，n是⼀元⼆次⽅程x2＋2x－7＝0的两个根，则m2＋3m＋n等于( )A. 9B. 7C. 5D. 36. 已知⼀元⼆次⽅程-4x +3=0两根为x1、x2，则x1?x2=( )A. 4B. 3C. -4D. -37. 判断⼀元⼆次⽅程式x2-8x-a=0中的a为下列哪⼀个数时，可使得此⽅程式的两根均为整数？( )A. 12B. 16C. 20D. 248. 若关于x的⼀元⼆次⽅程x2-4x+5-a=0有实数根，则a的取值范围是( )A. a≥1B. a＞1C. a≤1D. a＜19. 已知x1，x2是⼀元⼆次⽅程x2-4x+1=0的两个实数根，则x1x2-x1-x2的值等于( )A. -3B. 0C. 3D. 510. 如果⼀元⼆次⽅程x2-3x-1=0的两根为x1、x2，那么x1+x2=( )A. -3B. 3C. -1D. 111. 若关于x的⽅程x2+3x+a=0有⼀个根为-1，则另⼀个根为12. 设x1，x2是⼀元⼆次⽅程-2x-3=0的两根，则 =13. 设α，β是⼀元⼆次⽅程x2＋2x－1＝0的两个根，则αβ的值是14. 若m，n是⼀元⼆次⽅程x2＝5x＋2的两个实数根，则m－mn＋n的值是15. 关于x的⽅程x2－ax＋2a＝0的两根的平⽅和是5，则a的值是16. 已知x1，x2是关于x的⽅程x2＋ax－2b＝0的两实数根，且x1＋x2＝－2，x1·x2＝1，则b a的值是17. 已知关于x的⽅程x2＋3x＋a＝0有⼀个根为－2，则另⼀个根为18. 已知m，n是关于x的⼀元⼆次⽅程x2－3x＋a＝0的两个根，若(m－1)(n －1)＝－6，则a＝19. 若关于x⼀元⼆次⽅程x2-x-m+2=0的两根x1，x2满⾜（x1-1）（x2-1）=-1，则m的值为20. 已知⽅程x2+mx+3=0的⼀个根是1，则它的另⼀个根是_______，m的值是_______21. 已知关于x的⼀元⼆次⽅程x2+2x+m=0有实数根，则m的取值范围是_______22. 在解⽅程x2＋px＋q＝0时，甲同学看错了p，解得⽅程的根为x1＝1，x2＝－3；⼄同学看错了q，解得⽅程的根为x1＝4，x2＝－2，则⽅程中的p＝______，q＝________．23. 已知直⾓三⾓形的两条直⾓边的长恰好是⽅程2x2-8x+7=0的两个根，则这个直⾓三⾓形的斜边长是_________24. 关于x 的⼀元⼆次⽅程（m-2）x 2+2x+1=0有实数根，求m 的取值范围.25. 设x 1，x 2是⼀元⼆次⽅程2x 2－x －3＝0的两根，求下列代数式的值．(1)x 12＋x 22；(2)x 2x 1＋x 1x 2；(3)x 12＋x 22－3x 1x 2.26. 若关于x 的⼀元⼆次⽅程x 2－4x ＋k －3＝0的两个实数根为x 1，x 2，且满⾜x 1＝3x 2，试求出⽅程的两个实数根及k 的值．27. 已知关于x 的⼀元⼆次⽅程x 2－6x ＋(2m ＋1)＝0有实数根．(1)求m 的取值范围；(2)如果⽅程的两个实数根为x 1，x 2，且2x 1x 2＋x 1＋x 2≥20，求m 的取值范围．。

北师大新版数学初三上册《一元二次方程的根与系数的关系》同步练习(有解析)

北师大新版数学初三上册《2一．选择题（共12小题）1．若一元二次方程x2+2x+m=0中的b2﹣4ac=0，则那个方程的两根为（）A．x1=1，x2=﹣1 B．x1=x2=1 C．x1=x2=﹣1 D．不确定2．已知关于x的方程kx2+（2k+1）x+（k﹣1）=0有实数根，则k的取值范畴为（）A．k≥﹣B．k＞﹣C．k≥﹣且k≠0 D．k＜﹣3．若关于x的方程kx2﹣6x+9=0有实数根，则k的取值范畴是（）A．k＜1 B．k≤1 C．k＜1且k≠0 D．k≤1且k≠04．关于x的一元二次方程（a﹣1）x2﹣2x+3=0有实数根，则整数a的最大值是（）A．2 B．1 C．0 D．﹣15．假如关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根，那么k的取值范畴是（）A．k＜B．k＜且k≠0 C．﹣≤k＜D．﹣≤k＜且k ≠06．关于x的一元二次方程x2﹣2x+k+2=0有实数根，则k的取值范畴在数轴上表示正确的是（）A．B．C．D．7．关于x的方程rx2+（r+2）x+r﹣1=0有根只有整数根的一切有理数r的值有（）个．A．1 B．2 C．3 D．不能确定8．若实数a、b满足a2﹣8a+5=0，b2﹣8b+5=0，则的值是（）A．﹣20 B．2 C．2或﹣20 D．9．下列一元二次方程中，只有方程（）的根为1与﹣2．A．x2﹣x﹣2=0 B．x2+x﹣2=0 C．x2﹣x+2=0 D．x2+x+2= 010．若函数y=kx﹣3的图象如图所示，则一元二次方程x2+x+k﹣1=0根的存在情形是（）A．有两个不相等的实数根B．有两个相等的实数根C．没有实数根D．无法确定11．设x1、x2是二次方程x2+x﹣3=0的两个根，那么x13﹣4x22+19的值等于（）A．﹣4 B．8 C．6 D．012．已知α，β满足α2+2α﹣1=0，β2+2β﹣1=0，则的值为（）A．2 B．﹣6 C．2或﹣6 D．﹣2或6二．填空题（共10小题）13．已知关于x的方程x2+（a﹣6）x+a=0的两根差不多上整数，则a 的值等于．14．关于x的一元二次方程（m﹣5）x2+2x+2=0有实根，则m的最大整数解是．15．若方程x2+2（1+a）x+3a2+4ab+4b2+2=0有实根，则=16．假如关于x的一元二次方程x2+bx+c=0没有实数根，则符合条件的一组b，c的实数值能够是b=，c=．17．若实数a、b、c满足，b+c﹣1=0，a﹣bc﹣1=0，则a的取值范畴是．18．假如关于x的方程（m﹣2）x2﹣2x+1=0有实数根，那么m的取值范畴是．19．若a＞b＞c＞0，一元二次方程（a﹣b）x2+（b﹣c）x+（c﹣a）=0的两个实根中，较大的一个实根等于．20．已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1、x2，则（x 1﹣1）2+（x2﹣1）2的最小值是．21．关于一切正整数n，关于x的一元二次方程x2﹣（n+3）x﹣3n2=0的两个根记为an、bn，则++…+=．22．若，若x1，x2是一元二次方程kx2+ax+b=0的两个实数根且满足，则k=．三．解答题（共6小题）23．已知：关于x的一元二次方程x2﹣2（2m﹣3）x+4m2﹣14m+8=0，（1）若m＞0，求证：方程有两个不相等的实数根；（2）若12＜m＜40的整数，且方程有两个整数根，求m的值．24．已知关于x的方程（x﹣1）（x﹣4）=k2，k是实数．（1）求证：方程有两个不相等的实数根：（2）当k的值取时，方程有整数解．（直截了当写出3个k的值）25．已知关于x的方程（k﹣1）x2+（2k﹣3）x+k+1=0有两个不相等的实数根．（1）求k的取值范畴；（2）假如k是符合条件的最大整数，且一元二次方程x2﹣4x+k=0与x 2+mx﹣1=0有一个相同的根，求现在m的值．26．已知关于x的方程x2﹣5x﹣m2﹣2m﹣7=0．（1）若此方程的一个根为﹣1，求m的值；（2）求证：不管m取何实数，此方程都有两个不相等的实数根．27．已知关于x一元二次方程x2﹣4x+c=0．（1）当c=1时，试解那个方程；（2）若方程的两个实数根为x1，x2，且x12﹣2x1x2+x22=0，求c的值．28．已知关于x的方程x2﹣（k+2）x+2k=0．①小明同学说：不管k取何实数，方程总有实数根，你认为他说的有道理吗？②若等腰三角形的一边a=1，另两边b、c恰好是那个方程的两个根，求△ABC的周长和面积．参考答案一．选择题1．C．2．A．3．B．4．C．5．D．6．C．7．B．8．C．9．B10．A．11．D．12．C．二．填空题13．0或16．14．m=4．15．﹣．16．b=2，c=3．答案不唯独．17．a≤．18．m≤3．19．1．20．8．21．﹣22．﹣2或1．三．解答题23．证明：（1）△=b2﹣4ac=[﹣2（2m﹣3）]2﹣4（4m2﹣14m+8）=8 m+4，∵m＞0，∴8m+4＞0．∴方程有两个不相等的实数根．（2）解：由求根公式得：∵方程有两个整数根，∴必须使为整数且m为整数．∴2m+1必是奇数，∴是奇数又∵12＜m＜40，∴25＜2m+1＜81．∴5＜＜9．∴m=24．24．（1）证明：原方程可变形为x2﹣5x+4﹣k2=0．∵△=（﹣5）2﹣4×1×（4﹣k2）=4k2+9＞0，∴不论k为任何实数，方程总有两个不相等的实数根；（2）解：原方程可化为x2﹣5x+4﹣k2=0．∵方程有整数解，∴x=为整数，∴k取0，2，﹣2时，方程有整数解．25．解：（1）△=（2k﹣3）2﹣4×（k﹣1）（k+1）=4k2﹣12k+9﹣4k2+4=﹣12k+13，∵方程（k﹣1）x2+（2k﹣3）x+k+1=0有两个不相等的实数根，∴﹣12k+13＞0，解得，k＜，又k﹣1≠0，∴k＜且k≠1时，方程有两个不相等的实数根；（2）∵k是符合条件的最大整数，x2﹣4x=0，x=0或4，当x=0时，x2+mx﹣1=0无意义；当x=4时，42+4m﹣1=0m=．26．（1）解：把x=﹣1代入x2﹣5x﹣m2﹣2m﹣7=0得1+5﹣m2﹣2m ﹣7=0，解得m1=m2=﹣1，即m的值为1；（2）证明：△=（﹣5）2﹣4（﹣m2﹣2m﹣7）=4（m+1）2+49，∵4（m+1）2≥0∴△＞0，∴方程都有两个不相等的实数根．27．解：（1）当c=1时，原方程为x2﹣4x+1=0，解得：x===2±，∴x1=2+，x2=2﹣．（2）∵x12﹣2x1x2+x22=0，∴（x1﹣x2）2=0，∴x1=x2，∴△=（﹣4）2﹣4c=16﹣4c=0，解得：c=4．∴c的值为4．28．解：（1）∵△=（k+2）2﹣4×1×2k=k2+4k+4﹣8k=k2﹣4k+4=（k ﹣2）2≥0，∴方程不管k取何值，总有实数根，∴小明同学的说法合理；（2）①当b=c时，则△=0，即（k﹣2）2=0，方程可化为x2﹣4x+4=0，∴x1=x2=2，而b=c=2，∴C△ABC=5，S△ABC=；②当b=a=1，∵x2﹣（k+2）x+2k=0．∴（x﹣2）（x﹣k）=0，∴x=2或x=k，∵另两边b、c恰好是那个方程的两个根，∴k=1，∴c=2，∵a+b=c，∴不满足三角形三边的关系，舍去；综上所述，△ABC的周长为5．。

2.5二次函数与一元二次方程课时练习(含答案解析)

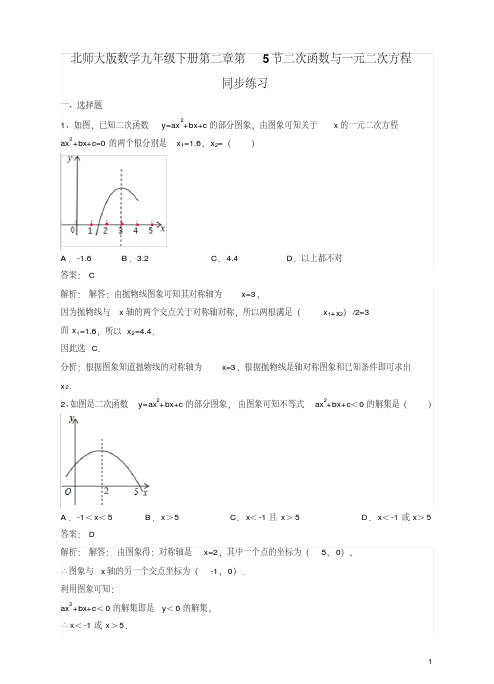
北师大版数学九年级下册第二章第5节二次函数与一元二次方程同步练习一、选择题1、如图，已知二次函数y=ax2+bx+c的部分图象，由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.6，x2=（）A．-1.6 B．3.2 C．4.4 D．以上都不对答案：C解析：解答：由抛物线图象可知其对称轴为x=3，因为抛物线与x轴的两个交点关于对称轴对称，所以两根满足（x1+x2）/2=3而x1=1.6，所以x2=4.4．因此选C．分析：根据图象知道抛物线的对称轴为x=3，根据抛物线是轴对称图象和已知条件即可求出x2．2、如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（）A．-1＜x＜5 B．x＞5 C．x＜-1且x＞5 D．x＜-1或x＞5 答案：D解析：解答：由图象得：对称轴是x=2，其中一个点的坐标为（5，0），∴图象与x轴的另一个交点坐标为（-1，0）．利用图象可知：ax2+bx+c＜0的解集即是y＜0的解集，∴x＜-1或x＞5．因此选：D．分析：利用二次函数的对称性，可得出图象与x轴的另一个交点坐标，结合图象可得出ax2+bx+c＜0的解集3、二次函数y= -x2+2x+k的部分图象如图所示，则关于x的一元二次方程-x2+2x+k=0的一个解x1=3，另一个解x2=（）A．1 B．-1 C．-2 D．0答案：B解析：解答：由抛物线图象可知其对称轴为x=1，因为抛物线与x轴的两个交点关于对称轴对称，其中一个点的坐标为（3，0），所以图象与x轴的另一个交点坐标为（-1，0）所以选B．分析：根据图象知道抛物线的对称轴为x=1，根据抛物线是轴对称图象和已知条件即可求出x2．4、如图，已知抛物线与x轴的一个交点A（1，0），对称轴是x= -1，则该抛物线与x轴的另一交点坐标是（）A．（-3，0）B．（-2，0）C．x= -3 D．x= -2答案：A解析：解答：由抛物线图象可知其对称轴为x= -1，因为抛物线与x轴的两个交点关于对称轴对称，其中一个点的坐标为（1，0），所以图象与x轴的另一个交点坐标为（-3，0）所以选A．分析：根据图象知道抛物线的对称轴为x= -1，根据抛物线是轴对称图象和已知条件即可求出另一个交点坐标为（-3，0）．5、抛物线y=ax2+bx+c（a≠０）与x轴的交点是（-2，0）和（4，0），这条抛物线的对称轴是（）A．直线x=1 B．直线x= -1 C．直线x=2 D．直线x= -2答案：A解析：解答：∵抛物线y=ax2+bx+c（a≠０）与x轴的交点是（-2，0）和（4，0），∴这条抛物线的对称轴是：x=（-2+4）/2，即x=1；所以选A．分析：根据对称轴的定义知x=(x1+x2)/26、若x1，x2（x1＜x2）是方程（x-a）（x-b）=1（a＜b）的两个根，则实数x1，x2，a，b的大小关系为（）A．x1＜x2＜a＜b B．x1＜a＜x2＜bC．x1＜a＜b＜x2D．a＜x1＜b＜x2答案：C解析：解答：用作图法比较简单，首先作出（x-a）（x-b）=0图象，随便画一个（开口向上的，与x轴有两个交点），再向下平移一个单位，就是（x-a）（x-b）=1，这时与x轴的交点就是x1，x2，画在同一坐标系下，很较易发现：答案是：x1＜a＜b＜x2．所以选C．分析：因为x1和x2为方程的两根，所以满足方程（x-a）（x-b）=1，再由已知条件x1＜x2、a ＜b结合图象，可得到x1，x2，a，b的大小关系．7、已知抛物线y=ax2-2x+1与x轴没有交点，那么该抛物线的顶点所在的象限是（）A．第四象限 B．第三象限 C．第二象限 D．第一象限答案：D解析：解答：∵抛物线y=ax2-2x+1与x轴没有交点，∴△=4-4a＜0，解得：a＞1，∴抛物线的开口向上，∴抛物线的顶点只能在第一象限或第二象限。

北师大版九年级数学上册 2.5 一元二次方程的根与系数的关系同步练习题(含答案,教师版)

北师大版九年级数学上册第二章2.5 一元二次方程的根与系数的关系同步练习题一、选择题1．已知x1，x2是一元二次方程x2＋2x－k－1＝0的两根，且x1x2＝－3，则k的值为(B) A．1 B．2 C．3 D．42．若一元二次方程x2－2x－1＝0的两根分别为x1，x2，则1x1＋1x2的值为(B)A．1 B．-2 C．3 D．-43．已知关于x的一元二次方程x2＋bx＋c＝0的两个实数根分别为x1，x2.若b＋2c＝0，则1x1＋1x2＋x1x2x1＋x2的值为（D）．A．52B．-32C．32D．-524．若一元二次方程x2－3x－2＝0的两根分别是m，n，则m3－3m2＋2n＝（A）A．6 B．5 C．3 D．45．对于任意实数a，b，定义：a◆b＝a2＋ab＋b2.若方程(x◆2)－5＝0的两根记为m，n，则m2＋n2＝（D）．A．3 B．4 C．5 D．66.已知关于x的方程ax2＋bx＋1＝0的两根为x1＝1，x2＝2，则方程a(x＋1)2＋b(x＋1)＋1＝0的两根之和为（A）．A．1 B．2 C．3 D．4二、填空题7．已知关于x的一元二次方程x2－2kx－8＝0的一个根是2，则此方程的另一个根是－4．8．已知关于x的方程x2＋mx－2n＝0的两根之和为－2，两根之积为1，则m＋n的值为32．9．写一个以5，－2为根的一元二次方程(化为一般形式)x2－3x－10＝0．10．已知m，n是一元二次方程x2－2x－3＝0的两根，则m＋n＋mn＝－1．11．若x1＋x2＝3，x21＋x22＝5，则以x1，x2为根的一元二次方程是x2－3x＋2＝0．12．已知实数m ，n 满足条件m 2－7m ＋2＝0，n 2－7n ＋2＝0，则n m ＋m n 的值是452或2．13．已知a ，b 是方程x 2＋2x －5＝0的两个实数根，则a 2b ＋ab 2的值为10．14．已知关于x 的方程kx 2－3x ＋1＝0有两个实数根，分别为x 1和x 2.当x 1＋x 2＋x 1x 2＝4时，k ＝1．15．若方程2x 2＋4x －3＝0的两根为x 1，x 2，则1x 21＋1x 22＝289．三、解答题16．已知x 1，x 2是一元二次方程x 2－3x －1＝0的两根，不解方程求下列各式的值： (1)x 21＋x 22；解：x 21＋x 22＝(x 1＋x 2)2－2x 1x 2 ＝32－2×(－1) ＝11.(2)1x 1＋1x 2. 解：1x 1＋1x 2＝x 1＋x 2x 1x 2＝3－1＝－3.17．已知关于x 的一元二次方程x 2－2(a －1)x ＋a 2－a －2＝0有两个不相等的实数根x 1，x 2.(1)若a 为正整数，求a 的值；(2)若x 1，x 2满足x 21＋x 22－x 1x 2＝16，求a 的值．解：(1)∵关于x 的一元二次方程x 2－2(a －1)x ＋a 2－a －2＝0有两个不相等的实数根， ∴Δ＝[－2(a －1)]2－4(a 2－a －2)＞0.解得a ＜3. ∵a 为正整数， ∴a ＝1或2.(2)∵x 21＋x 22－x 1x 2＝16， ∴(x 1＋x 2)2－3x 1x 2＝16.∵x 1＋x 2＝2(a －1)，x 1x 2＝a 2－a －2， ∴[2(a －1)]2－3(a 2－a －2)＝16. 解得a 1＝－1，a 2＝6. 又由(1)知a ＜3， ∴a ＝－1.18．已知x 1，x 2是一元二次方程4kx 2－4kx ＋k ＋1＝0的两个实数根，求使x 1x 2＋x 2x 1－2的值为整数的实数k 的整数值．解：根据题意，得Δ＝(－4k)2－4×4k(k＋1)≥0，且k≠0，解得k ＜0. ∵x 1＋x 2＝1，x 1x 2＝k ＋14k ，∴x 1x 2＋x 2x 1－2＝（x 1＋x 2）2－2x 1x 2x 1x 2－2 ＝（x 1＋x 2）2x 1x 2－4＝1k ＋14k－4 ＝－4k ＋1.∵k 为整数，且－4k ＋1为整数，∴k ＋1＝±1，±2，±4. 又∵k＜0，∴k ＝－5，－3，－2.19．已知关于x 的方程3x 2＋2x －m ＝0没有实数解，求实数m 的取值范围．解：∵3x 2＋2x －m ＝0没有实数解， ∴Δ＝4－4×3×(－m)＜0，解得m ＜－13.故实数m 的取值范围是m ＜－13.20．已知实数m ，n 满足3m 2＋6m －5＝0，3n 2＋6n －5＝0，求m n ＋n m 的值．解：若m≠n，∵实数m ，n 满足3m 2＋6m －5＝0，3n 2＋6n －5＝0， ∴m ，n 是方程3x 2＋6x －5＝0的两根． ∴m ＋n ＝－2，mn ＝－53.∴m n ＋n m ＝m 2＋n 2mn ＝（m ＋n ）2－2mn mn （－2）2－2×（－53）－53＝－225. 若m ＝n ，则m n ＋nm ＝1＋1＝2.综上可知，m n ＋n m 的值为－225或2.21．已知关于x 的一元二次方程x 2－2x ＋m －1＝0. (1)当m 取何值时，方程有两个不相等的实数根？ (2)若方程的两根都是正数，求m 的取值范围；(3)设x 1，x 2是这个方程的两个实数根，且1＋x 1x 2＝x 21＋x 22，求m 的值．解：(1)∵方程有两个不相等的实数根，∴Δ＝(－2)2－4(m －1)＝－4m ＋8＞0.∴m＜2. ∴当m ＜2时，方程有两个不相等的实数根．(2)设x 1，x 2是这个方程的两个实数根，则x 1＞0，x 2＞0，∴x 1x 2＝m －1＞0.∴m＞1. ∵方程的两根都是正数，∴Δ≥0.∴m ≤2.∴m 的取值范围是1＜m≤2. (3)由题意可得x 1＋x 2＝2，x 1x 2＝m －1. ∵1＋x 1x 2＝x 21＋x 22，∴1＋x 1x 2＝(x 1＋x 2)2－2x 1x 2，即1＋m －1＝22－2(m －1)．解得m ＝2.22．已知k 为非负实数，关于x 的方程x 2－(k ＋1)x ＋k ＝0和kx 2－(k ＋2)x ＋k ＝0. (1)求证：前一个方程必有两个非负实数根；(2)当k 取何值时，上述两个方程有一个相同的实数根？解：(1)证明：x 2－(k ＋1)x ＋k ＝0，Δ＝[－(k ＋1)]2－4k ＝k 2－2k ＋1＝(k －1)2≥0，∴方程x 2－(k ＋1)x ＋k ＝0的根为x ＝（k ＋1）±（k －1）22.∴x 1＝k ，x 2＝1. ∵k 为非负实数，∴方程x 2－(k ＋1)x ＋k ＝0必有两个非负实数根． (2)方程kx 2－(k ＋2)x ＋k ＝0中，∵k ≥0，当k≠0时，Δ＝(k ＋2)2－4k 2＝(k ＋2＋2k)(k ＋2－2k)＝(3k ＋2)(2－k)． ∵k ＞0，∴3k ＋2＞0.∴要使(3k ＋2)(2－k)≥0，需满足2－k≥0，即k≤2，且k≠0.当k ＝0时，x ＝0.∴k ≤2时，方程有实数根．当相同的根是k 时，把x ＝k 代入方程kx 2－(k ＋2)x ＋k ＝0，得k 3－(k ＋2)k ＋k ＝0，解得k ＝0或k ＝1＋52或k ＝1－52.∵k 为非负实数，∴k ＝0或1＋52.满足k≤2. 当相同的根是1时，把x ＝1代入方程kx 2－(k ＋2)x ＋k ＝0，得k －(k ＋2)＋k ＝0，解得k ＝2.满足k≤2.∴当k ＝2或0或1＋52时，上述两个方程有一个相同的实数根．。

北师大新版九年级数学同步试卷：一元二次方程的根与系数的关系

北师大新版九年级（上）中考题同步试卷：2.5 一元二次方程的根与系数的关系（01）一、选择题（共18小题）1．若关于x的方程x2+x﹣a+＝0有两个不相等的实数根，则实数a的取值范围是（）A．a≥2B．a≤2C．a＞2D．a＜22．若关于x的一元二次方程4x2﹣4x+c＝0有两个相等实数根，则c的值是（）A．﹣1B．1C．﹣4D．43．一元二次方程x2﹣2x﹣1＝0的根的情况为（）A．有两个相等的实数根B．有两个不相等的实数根C．只有一个实数根D．没有实数根4．若关于x的一元二次方程kx2﹣4x+3＝0有实数根，则k的非负整数值是（）A．1B．0，1C．1，2D．1，2，35．若关于x的一元二次方程（a﹣1）x2﹣2x+2＝0有实数根，则整数a的最大值为（）A．﹣1B．0C．1D．26．下列一元二次方程中，没有实数根的是（）A．4x2﹣5x+2＝0B．x2﹣6x+9＝0C．5x2﹣4x﹣1＝0D．3x2﹣4x+1＝0 7．方程（m﹣2）x2﹣x+＝0有两个实数根，则m的取值范围（）A．m＞B．m≤且m≠2C．m≥3D．m≤3且m≠2 8．关于x的一元二次方程（m﹣2）x2+（2m+1）x+m﹣2＝0有两个不相等的正实数根，则m的取值范围是（）A．m＞B．m＞且m≠2C．﹣＜m＜2D．＜m＜29．若关于x的一元二次方程x2+（2k﹣1）x+k2﹣1＝0有实数根，则k的取值范围是（）A．k≥B．k＞C．k＜D．k≤10．关于x的一元二次方程x2+x+m＝0有实数根，则m的取值范围是（）A．m≥B．m≤C．m≥D．m≤11．下列方程有两个相等的实数根的是（）A．x2+x+1＝0B．4x2+2x+1＝0C．x2+12x+36＝0D．x2+x﹣2＝012．下列一元二次方程中有两个不相等的实数根的方程是（）A．（x﹣1）2＝0B．x2+2x﹣19＝0C．x2+4＝0D．x2+x+l＝0 13．等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程x2﹣6x+n﹣1＝0的两根，则n的值为（）A．9B．10C．9或10D．8或1014．已知关于x的一元二次方程3x2+4x﹣5＝0，下列说法正确的是（）A．方程有两个相等的实数根B．方程有两个不相等的实数根C．没有实数根D．无法确定15．若一元二次方程x2﹣2x﹣m＝0无实数根，则一次函数y＝（m+1）x+m﹣1的图象不经过第（）象限．A．四B．三C．二D．一16．一元二次方程x2+x+＝0的根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．无实数根D．无法确定根的情况17．一元二次方程4x2+1＝4x的根的情况是（）A．没有实数根B．只有一个实数根C．有两个相等的实数根D．有两个不相等的实数根18．有两个一元二次方程M：ax2+bx+c＝0；N：cx2+bx+a＝0，其中a•c≠0，a≠c．下列四个结论中，错误的是（）A．如果方程M有两个相等的实数根，那么方程N也有两个相等的实数根B．如果方程M的两根符号相同，那么方程N的两根符号也相同C．如果5是方程M的一个根，那么是方程N的一个根D．如果方程M和方程N有一个相同的根，那么这个根必是x＝1二、填空题（共7小题）19．关于x的方程kx2﹣4x﹣＝0有实数根，则k的取值范围是．20．如果关于x的一元二次方程x2+4x﹣m＝0没有实数根，那么m的取值范围是．21．一元二次方程x2﹣5x+c＝0有两个不相等的实数根且两根之积为正数，若c是整数，则c＝．（只需填一个）．22．已知关于x的一元二次方程x2+x﹣1＝0有两个不相等的实数根，则k的取值范围是．23．关于x的一元二次方程（k﹣1）x2﹣2x+1＝0有两个不相等的实数根，则实数k的取值范围是．24．关于x的一元二次方程2x2﹣4x+m﹣1＝0有两个相等的实数根，则m的值为．25．若关于x的一元二次方程ax2+2x﹣1＝0无解，则a的取值范围是．三、解答题（共5小题）26．已知关于x的方程x2+2x+a﹣2＝0．（1）若该方程有两个不相等的实数根，求实数a的取值范围；（2）当该方程的一个根为1时，求a的值及方程的另一根．27．已知关于x的一元二次方程x2﹣（2m+3）x+m2+2＝0．（1）若方程有实数根，求实数m的取值范围；（2）若方程两实数根分别为x1、x2，且满足x12+x22＝31+|x1x2|，求实数m的值．28．关于x的一元二次方程x2+（2k+1）x+k2+1＝0有两个不等实根x1，x2．（1）求实数k的取值范围．（2）若方程两实根x1，x2满足|x1|+|x2|＝x1•x2，求k的值．29．已知：关于x的方程x2+2mx+m2﹣1＝0（1）不解方程，判别方程根的情况；（2）若方程有一个根为3，求m的值．30．已知关于x的一元二次方程（x﹣3）（x﹣2）＝|m|．（1）求证：对于任意实数m，方程总有两个不相等的实数根；（2）若方程的一个根是1，求m的值及方程的另一个根．北师大新版九年级（上）中考题同步试卷：2.5 一元二次方程的根与系数的关系（01）参考答案一、选择题（共18小题）1．C；2．B；3．B；4．A；5．B；6．A；7．B；8．D；9．D；10．D；11．C；12．B；13．B；14．B；15．D；16．B；17．C；18．D；二、填空题（共7小题）19．k≥﹣6；20．m＜﹣4；21．4；22．k≥1；23．k＜2且k≠1；24．3；25．a＜﹣1；三、解答题（共5小题）26．；27．；28．；29．；30．；北师大新版九年级（上）中考题同步试卷：2.5 一元二次方程的根与系数的关系（02）一、选择题（共14小题）1．方程x2﹣2x+3＝0的根的情况是（）A．有两个相等的实数根B．只有一个实数根C．没有实数根D．有两个不相等的实数根2．若关于x的一元二次方程x2﹣2x+kb+1＝0有两个不相等的实数根，则一次函数y＝kx+b 的大致图象可能是（）A．B．C．D．3．已知关于x的方程x2﹣2x+3k＝0有两个不相等的实数根，则k的取值范围是（）A．k＜B．k＞C．k＜且k≠0D．k＞且k≠0 4．若关于x的一元二次方程x2﹣4x+5﹣a＝0有实数根，则a的取值范围是（）A．a≥1B．a＞1C．a≤1D．a＜15．若关于x的方程x2+2x+a＝0不存在实数根，则a的取值范围是（）A．a＜1B．a＞1C．a≤1D．a≥16．关于x的一元二次方程（m﹣2）x2+2x+1＝0有实数根，则m的取值范围是（）A．m≤3B．m＜3C．m＜3且m≠2D．m≤3且m≠2 7．关于x的一元二次方程kx2+2x+1＝0有两个不相等的实数根，则k的取值范围是（）A．k＞﹣1B．k≥﹣1C．k≠0D．k＜1且k≠0 8．判断一元二次方程式x2﹣8x﹣a＝0中的a为下列哪一个数时，可使得此方程式的两根均为整数？（）A．12B．16C．20D．249．已知一元二次方程2x2﹣5x+3＝0，则该方程根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．两个根都是自然数D．无实数根10．若一元二次方程x2+2x+a＝0的有实数解，则a的取值范围是（）A．a＜1B．a≤4C．a≤1D．a≥111．下列一元二次方程有两个相等实数根的是（）A．x2﹣2x+1＝0B．2x2﹣x+1＝0C．4x2﹣2x﹣3＝0D．x2﹣6x＝0 12．若a满足不等式组，则关于x的方程（a﹣2）x2﹣（2a﹣1）x+a+＝0的根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．没有实数根D．以上三种情况都有可能13．下列一元二次方程中，有两个相等实数根的是（）A．x2﹣8＝0B．2x2﹣4x+3＝0C．9x2+6x+1＝0D．5x+2＝3x2 14．一元二次方程2x2+3x+1＝0的根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．没有实数根D．无法确定二、填空题（共11小题）15．若关于x的一元二次方程x2﹣3x+m＝0有两个相等的实数根，则m＝．16．若关于x的一元二次方程x2﹣x+m＝0有两个不相等的实数根，则m的值可能是（写出一个即可）．17．关于x的方程mx2+x﹣m+1＝0，有以下三个结论：①当m＝0时，方程只有一个实数解；②当m≠0时，方程有两个不等的实数解；③无论m取何值，方程都有一个负数解，其中正确的是（填序号）．18．若关于x的一元二次方程ax2+3x﹣1＝0有两个不相等的实数根，则a的取值范围是．19．关于x的方程x2+2x﹣m＝0有两个相等的实数根，则m＝．20．已知k＞0，且关于x的方程3kx2+12x+k+1＝0有两个相等的实数根，那么k的值等于．21．关于x的一元二次方程x2﹣x+m＝0没有实数根，则m的取值范围是．22．已知关于x的一元二次方程x2+2x+m＝0有实数根，则m的取值范围是．23．若一元二次方程（m﹣1）x2﹣4x﹣5＝0没有实数根，则m的取值范围是．24．关于x的一元二次方程ax2+bx+＝0有两个相等的实数根，写出一组满足条件的实数a，b的值：a＝，b＝．25．已知关于x的方程x2﹣2x+a＝0有两个实数根，则实数a的取值范围是．三、解答题（共5小题）26．已知关于x的一元二次方程x2﹣4x+m＝0．（1）若方程有实数根，求实数m的取值范围；（2）若方程两实数根为x1，x2，且满足5x1+2x2＝2，求实数m的值．27．已知关于x的方程x2+（2m﹣1）x+4＝0有两个相等的实数根，求m的值．28．已知关于x的一元二次方程（x﹣1）（x﹣4）＝p2，p为实数．（1）求证：方程有两个不相等的实数根；（2）p为何值时，方程有整数解．（直接写出三个，不需说明理由）29．已知关于x的方程mx2﹣（m+2）x+2＝0．（1）证明：不论m为何值时，方程总有实数根；（2）m为何整数时，方程有两个不相等的正整数根．30．已知关于x的一元二次方程mx2+mx+m﹣1＝0有两个相等的实数根．（1）求m的值；（2）解原方程．北师大新版九年级（上）中考题同步试卷：2.5 一元二次方程的根与系数的关系（02）参考答案一、选择题（共14小题）1．C；2．B；3．A；4．A；5．B；6．D；7．D；8．C；9．A；10．C；11．A；12．C；13．C；14．A；二、填空题（共11小题）15．；16．0；17．①③；18．a＞﹣且a≠0；19．﹣1；20．3；21．m＞；22．m ≤1；23．m＜；24．4；2；25．a≤1；三、解答题（共5小题）26．；27．；28．；29．；30．；北师大新版九年级（上）中考题同步试卷：2.5 一元二次方程的根与系数的关系（03）一、选择题（共13小题）1．若关于x的方程式x2﹣x+a＝0有实数根，则a的值可以是（）A．2B．1C．0.5D．0.252．下列关于x的一元二次方程有实数根的是（）A．x2+1＝0B．x2+x+1＝0C．x2﹣x+1＝0D．x2﹣x﹣1＝0 3．已知关于x的一元二次方程x2+2x﹣a＝0有两个相等的实数根，则a的值是（）A．4B．﹣4C．1D．﹣14．一元二次方程x2﹣4x+5＝0的根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．只有一个实数根D．没有实数根5．下列关于x的方程有实数根的是（）A．x2﹣x+1＝0B．x2+x+1＝0C．（x﹣1）（x+2）＝0D．（x﹣1）2+1＝06．关于x的一元二次方程x2﹣3x+m＝0有两个不相等的实数根，则实数m的取值范围为（）A．B．C．D．7．一元二次方程ax2+bx+c＝0（a≠0）有两个不相等的实数根，则b2﹣4ac满足的条件是（）A．b2﹣4ac＝0B．b2﹣4ac＞0C．b2﹣4ac＜0D．b2﹣4ac≥08．若+|n﹣2|＝0，且关于x的一元二次方程ax2+mx+n＝0有实数根，则a的取值范围是（）A．a≥8B．a＜8且a≠0C．a≤8D．a≤8且a≠0 9．下列方程没有实数根的是（）A．x2+4x＝10B．3x2+8x﹣3＝0C．x2﹣2x+3＝0D．（x﹣2）（x﹣3）＝1210．一元二次方程x2﹣2x+m＝0总有实数根，则m应满足的条件是（）A．m＞1B．m＝1C．m＜1D．m≤111．若关于x的一元二次方程（k﹣1）x2+2x﹣2＝0有不相等实数根，则k的取值范围是（）A．k＞B．k≥C．k＞且k≠1D．k≥且k≠1 12．下列方程中，没有实数根的是（）A．x2﹣4x+4＝0B．x2﹣2x+5＝0C．x2﹣2x＝0D．x2﹣2x﹣3＝0 13．关于x的一元二次方程x2+2（m﹣1）x+m2＝0的两个实数根分别为x1，x2，且x1+x2＞0，x1x2＞0，则m的取值范围是（）A．m≤B．m≤且m≠0C．m＜1D．m＜1且m≠0二、填空题（共12小题）14．如果关于x的方程x2﹣6x+m＝0有两个相等的实数根，那么m＝．15．关于x的一元二次方程x2﹣5x+k＝0有两个不相等的实数根，则k可取的最大整数为．16．若关于x的一元二次方程x2+x+m＝0有两个相等的实数根，则m＝．17．如果关于x的方程x2﹣2x+k＝0（k为常数）有两个不相等的实数根，那么k的取值范围是．18．一元二次方程2x2﹣3x+k＝0有两个不相等的实数根，则k的取值范围是．19．关于x的一元二次方程x2﹣3x+b＝0有两个不相等的实数根，则b的取值范围是．20．若一元二次方程x2﹣6x+m＝0有两个相等的实数根，则m的值为．21．已知关于x的方程x2+（1﹣m）x+＝0有两个不相等的实数根，则m的最大整数值是．22．关于x的反比例函数y＝的图象如图，A、P为该图象上的点，且关于原点成中心对称．△P AB中，PB∥y轴，AB∥x轴，PB与AB相交于点B．若△P AB的面积大于12，则关于x的方程（a﹣1）x2﹣x+＝0的根的情况是．23．关于x的一元二次方程x2﹣3x+k＝0有两个不相等的实数根，则k的取值范围是．24．关于x的一元二次方程x2+a＝0没有实数根，则实数a的取值范围是．25．已知关于x的一元二次方程x2﹣2x﹣k＝0有两个相等的实数根，则k值为．三、解答题（共5小题）26．已知关于x的方程（k﹣1）x2﹣（k﹣1）x+＝0有两个相等的实数根，求k的值．27．一元二次方程mx2﹣2mx+m﹣2＝0．（1）若方程有两实数根，求m的范围．（2）设方程两实根为x1，x2，且|x1﹣x2|＝1，求m．28．已知关于x的一元二次方程x2+2（m+1）x+m2﹣1＝0．（1）若方程有实数根，求实数m的取值范围；（2）若方程两实数根分别为x1，x2，且满足（x1﹣x2）2＝16﹣x1x2，求实数m的值．29．已知关于x的方程x2+ax+a﹣2＝0（1）若该方程的一个根为1，求a的值及该方程的另一根；（2）求证：不论a取何实数，该方程都有两个不相等的实数根．30．已知关于x的方程mx2﹣（m+2）x+2＝0（m≠0）．（1）求证：方程总有两个实数根；（2）若方程的两个实数根都是整数，求正整数m的值．北师大新版九年级（上）中考题同步试卷：2.5 一元二次方程的根与系数的关系（03）参考答案一、选择题（共13小题）1．D；2．D；3．D；4．D；5．C；6．B；7．B；8．D；9．C；10．D；11．C；12．B；13．B；二、填空题（共12小题）14．9；15．6；16．；17．k＜1；18．k＜；19．b＜；20．9；21．0；22．没有实数根；23．k＜；24．a＞0；25．﹣3；三、解答题（共5小题）26．；27．；28．；29．；30．；。

北师大版初三上册用公式法解一元二次方程同步练习(含解析)

北师大版初三上册2一、选择题1.用公式法解方程x2-2=-3x时，a ，b ，c的值依次是（）A.0，-2，-3B.1，3，-2C.1，-3，-2D.1，-2，-32.用公式法解方程（x+2）2=6（x+2）-4时，b2-4ac的值为（）A.52B.32C.2D.-123.方程-x2+3x=1用公式法求解，先确定a ，b ，c的值，正确的是（）A.a=-1，b=3，c=-1B.a=-1，b=3，c=1C.a=-1，b=-3，c=-1D.a=1，b=-3，c=-14.假如一元二次方程ax2+bx+c=0（a≠0）能用公式法求解，那么必须满足的条件是（）A.b2-4ac≥0B.b2-4ac≤0C.b2-4ac＞0D.b2-4ac＜05.方程x2-3x+2=0的最小一个根的倒数是（）A.1B.2C.D.46.方程（x-1）（x-2）=1的根是（）A.x1=1，x2=2B.x1=-1，x2=-2C.x1=0，x2=3 D.以上都不对7.已知a是一元二次方程x2﹣2x﹣1=0较大的实数根，则对a的值估量正确的是（）A.0＜a＜1 B.1＜a＜2 C.2＜a＜3 D.3＜a＜4二、填空题8.一元二次方程x2-3x-2=0的解是________9.写出方程x2+x-1=0的一个正根________10.当x=________时，代数式x2-8x+12的值是-4．11.利用解一元二次方程的方法，在实数范畴内分解因式x2﹣2x﹣1=__ ______．12.已知k＞0，且关于x的方程3kx2+12x+k+1=0有两个相等的实数根，那么k的值等于________．13.假如关于x的一元二次方程x2+2ax+a+2=0有两个相等的实数根，那么实数a的值为________14.关于x的方程3kx2+12x+2=0有实数根，则k的取值范畴是_______ _．三、解答题15.用公式法解方程：（1）；（2）（3）（4）16.已知关于x的方程x(x－k)＝2－k的一个根为2．（1）求k的值；（2）求方程2y(2k－y)＝1的解．17.已知直角三角形的两条直角边的长恰好是方程2x2-8x+7=0的两个根，求那个直角三角形的斜边长18.已知关于x的方程x2+（2m﹣1）x+4=0有两个相等的实数根，求m 的值．19.已知关于x的一元二次方程（x﹣1）（x﹣4）=p2 ，p为实数．（1）求证：方程有两个不相等的实数根；（2）p为何值时，方程有整数解．（直截了当写出三个，不需说明理由）20.定义新运算：关于任意实数m、n都有m☆n=m2n+n，等式右边是常用的加法、减法、乘法及乘方运算．例如：﹣3☆2=（﹣3）2×2+2=20．依照以上知识解决问题：若2☆a的值小于0，请判定方程：2x2﹣bx+a=0的根的情形．答案解析部分一、选择题1.【答案】B【考点】公式法解一元二次方程【解析】【解答】整理得：x2+3x-2=0，那个地点a=1，b=3，c=-2．故选B．【分析】方程整理为一样形式，找出a ， b ，c的值即可2.【答案】C【考点】公式法解一元二次方程【解析】【解答】∵（x+2）2=6（x+2）-4∴x2-2x-4=0∴a=1，b=-2，c=-4∴b2-4ac =4+16=20．故选C．【分析】此题考查了公式法解一元一次方程，解此题时第一把方程化简为一样形式，然后找a、b、c ，最后求出判别式的值3.【答案】A【考点】解一元二次方程-公式法【解析】【解答】将-x2+3x=1整理为一样形式得：-x2+3x-1=0，可得出a=-1，b=3，c=-1．故选A【分析】将一元二次方程整理为一样形式，找出二次项系数a ，一次项系数b及常数项c即可．4.【答案】A【考点】解一元二次方程-公式法【解析】【解答】若一元二次方程ax2+bx+c=0（a≠0）能用公式法求解，则b2-4ac≥0；故选A．【分析】若一元二次方程能用公式法求解，则根的判别式必大于或等于0，由此可判定出正确的选项．5.【答案】A【考点】一元二次方程的求根公式及应用【解析】【解答】解：x2-3x+2=0，（x-1）（x-2）=0，x-1=0或x-2=0，x1=1或x2=2，因此方程x2-3x+2=0的最小一个根的倒数是1，故答案为：A．【分析】观看方程右边为0，左边能够分解因式，因此利用因式分解法求出方程的解，再求出方程的解中较小一个根的倒数。

北师大版九年级数学上册 2 5一元二次方程根与系数的关系测试题(含答案)

一元二次方程根与系数的关系测试题一、选择题1.关于x的一元二次方程3x2+2x+1=0的根的情况，下列判断正确的是（）A．有两个相等的实数根 B．有两个不相等的实数根C．没有实数根 D．无法判断2.一元二次方程x2+px+q=0的两个根为p,q,则p+q等于（）A.0B.1C.0或-2D.0或-13.若关于x的一元二次方程（k-5）x2-2x+2=0有实数根，则整数k的最大值为（）A.4B.5C.6D.74.定义新运算a*b：对于任意实数a,b满足a*b=（a+b）（a-b）-1，其中等式右边是通常的加法、减法、乘法运算，例如3*2=（3+2）（3-2）-1=5-1=4．若x*k=2x（k为实数）是关于x的方程，则它的根的情况是（）A．有一个实数根 B．有两个不相等的实数根C．有两个相等的实数根 D．没有实数根5.设x1，x2是方程x2-2003x+2005=0的两个实根，实数a,b满足：ax12003+bx22003=2003，ax12004+bx22004=2004，则ax12005+bx22005的值为（）A．2005 B．2003 C．-2005 D．-20036.对于一元二次方程ax2+bx+c=0（a≠0），下列说法：①若a+b+c=0，则b2-4ac≥0；②若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根；③若c是方程ax2+bx+c=0的一个根，则一定有ac+b+1=0成立；ax2+bx+c=0的根，则b2−4ac＝(2ax0+b)2④若x0是一元二次方程其中正确的（）A．只有①② B．只有①②④ C．①②③④ D．只有①②③二．填空题8.已知：m、n是方程x2+2x-1=0的两根，则（m2+3m+3）（n2+3n+3）= ．9.如果关于x的一元二次方程ax2+bx+c=0有两个实数根，且其中一个根为另外一个根的2倍，则称这样的方程为“倍根方程”，以下关于倍根方程的说法，正确的有（填序号）①方程x2-x-2=0是倍根方程；②若（x-2）（mx+n）=0是倍根方程：则4m2+5mn+n2=0；③若p,q满足pq=2，则关于x的方程px2+3x+q=0是倍根方程；④若方程以ax2+bx+c=0是倍根方程，则必有2b2=9ac.三、解答题10.当m为何值时，一元二次方程2x2-（4m+1）x+2m2-1=0．（1）有两个不相等的实数根？（2）有两个相等的实数根？（3）没有实数根？11.已知关于x的一元二次方程（a+c）x2+2bx+（a-c）=0，其中a,b,c分别为△ABC三边的长．（1）如果x=-1是方程的根，试判断△ABC的形状，并说明理由；（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；（3）如果△ABC是等边三角形，试求这个一元二次方程的根．12.已知关于x的方程x2-（k+2）x+2k=0．（1）求证：k取任何实数值，方程总有实数根；（2）若等腰△ABC的一边长为4，另两边长m,n恰好是这个方程的两个根，求△AB C的周长．一元二次方程根与系数的关系测试题（解析）一、选择题1.关于x的一元二次方程3x2+2x+1=0的根的情况，下列判断正确的是（）B．有两个相等的实数根 B．有两个不相等的实数根C．没有实数根 D．无法判断【答案】C【分析】根据根的判别式即可求出答案．【解答】解：Δ=22-4×1×3=4-12=-8，故原方程无实数根，故选：C．2.一元二次方程x2+px+q=0的两个根为p,q,则p+q等于（）A.0B.1C.0或-2D.0或-1【答案】D【分析】利用根据根与系数的关系得，p+q=-p,pq=q,当q≠0时，p=1，当q=0时，p=0，然后计算p+q的值．【解答】解：根据根与系数的关系得，p+q=-p,pq=q,解得p=1，q=-2或p=q=0，所以p+q=-1或p+q=0．故选：D．3.若关于x的一元二次方程（k-5）x2-2x+2=0有实数根，则整数k的最大值为（）A.4B.5C.6D.7【答案】A【解答】解：∵关于x 的一元二次方程（k-5）x 2-2x+2=0有实数根，，解得：k≤211且k≠5． ∵k 为整数， ∴k 的最大值为4．故选：A ．【答案】Dx2是方程x2-2003x+2005=0的两个实根可得：x1+x2=2【分析】由根与系数关系，x1，003，x1×x2=2005；化简式子ax2005+bx22005的值为：（x1+x2）（ax12004+bx22004）-x1x2（ax12003+bx22003）；1=2003，x1×x2=2005，ax12003+bx22003=2003，ax12004+bx22004=2004代入即可得出将x1+x2结果．x2是方程x2-2003x+2005=0的两个实根可得：x1+x2=2003，x1×x2=2【解答】解：x1，005，故ax2005+bx22005=（x1+x2）（ax12004+bx22004）-x1x2（ax12003+bx22003），1=2003×2004-2005×2003，=-2003．故选：D．6.对于一元二次方程ax2+bx+c=0（a≠0），下列说法：①若a+b+c=0，则b2-4ac≥0；②若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根；③若c是方程ax2+bx+c=0的一个根，则一定有ac+b+1=0成立；ax2+bx+c=0的根，则b2−4ac＝(2ax0+b)2④若x0是一元二次方程其中正确的（）A．只有①② B．只有①②④ C．①②③④ D．只有①②③【答案】B【分析】按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论，可得答案．【解答】解：①若a+b+c=0，则x=1是方程ax2+bx+c=0的解，由一元二次方程的实数根与判别式的关系可知Δ=b2-4ac≥0，故①正确；②∵方程ax2+c=0有两个不相等的实根，∴Δ=0-4ac＞0，∴-4ac＞0，则方程ax2+bx+c=0的判别式Δ=b2-4ac＞0，二．填空题8.已知：m、n是方程x2+2x-1=0的两根，则（m2+3m+3）（n2+3n+3）= ．【解答】解：∵m、n是方程x2+2x-1=0的两根，∴m+n=-2，mn=-1，m2+2m-1=0，n2+2n-1=0，∴（m2+3m+3）（n2+3n+3）=（m2+2m-1+m+4）（n2+2n-1+n+4）=（m+4）（n+4）=mn+4（m+n）+16=-1+4×（-2）+16=7，故答案为：7．9.如果关于x的一元二次方程ax2+bx+c=0有两个实数根，且其中一个根为另外一个根的2倍，则称这样的方程为“倍根方程”，以下关于倍根方程的说法，正确的有（填序号）①方程x2-x-2=0是倍根方程；②若（x-2）（mx+n）=0是倍根方程：则4m2+5mn+n2=0；③若p,q满足pq=2，则关于x的方程px2+3x+q=0是倍根方程；④若方程以ax2+bx+c=0是倍根方程，则必有2b2=9ac.【解答】解：①解方程x2-x-2=0得，x1=2，x2=-1，得，x1≠2x2，∴方程x2-x-2=0不是倍根方程；故①不正确；②若（x-2）（mx+n）=0是倍根方程，x，1=2或x2=4，因此x2=1时，m+n=0，当x2=1当x时，4m+n=0，2=4∴4m2+5mn+n2=（m+n）（4m+n）=0，故②正确；∴2b2=9ac.故④正确，故答案为：②③④11.已知关于x的一元二次方程（a+c）x2+2bx+（a-c）=0，其中a,b,c分别为△ABC三边的长．（1）如果x=-1是方程的根，试判断△ABC的形状，并说明理由；（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；（3）如果△ABC是等边三角形，试求这个一元二次方程的根．【分析】（1）把x=-1代入方程得a+c-2b+a-c=0，整理得a=b,从而可判断三角形的形状；（2）根据判别式的意义得Δ=（2b）2-4（a+c）（a-c）=0，即b2+c2=a2，然后根据勾股定理可判断三角形的形状；（3）利用等边三角形的性质得a=b=c,方程化为x2+x=0，然后利用因式分解法解方程．【解答】解：（1）△ABC是等腰三角形；理由：把x=-1代入方程得a+c-2b+a-c=0，则a=b,所以△ABC为等腰三角形；（2）△ABC为直角三角形；理由：根据题意得Δ=（2b）2-4（a+c）（a-c）=0，即b2+c2=a2，所以△ABC为直角三角形；（3）∵△ABC为等边三角形，∴a=b=c,∴方程化为x2+x=0，解得x1=0，x2=-1．12.已知关于x的方程x2-（k+2）x+2k=0．（1）求证：k取任何实数值，方程总有实数根；（2）若等腰△ABC的一边长为4，另两边长m,n恰好是这个方程的两个根，求△AB C的周长．【分析】（1）计算其判别式，得出判别式不为负数即可；（2）当边长为4的边为腰时，则可知方程有一个根为4，代入可求得k的值，则可求得方程的另一根，可求得周长；当边长为4的边为底时，可知方程有两个相等的实数根，可求得k的值，再解方程即可．【解答】（1）证明：∵Δ=（k+2）2-8k=k2+4k+4-8k=（k-2）2≥0，∴无论k取何值，方程总有实数根；（2）解：当边长为4的边为腰时，则可知方程有一个实数根为4，∴16-4（k+2）+2k=0，解得k=4，∴方程为x2-6x+8=0，解得x=4或x=2，∴m、n的值分别为2、4，∴△ABC的周长为10；当边长为4的边为底时，则m=n,即方程有两个相等的实数根，∴Δ=0，即（k-2）2=0，解得k=2，∴方程为x2-4x+4=0，解得m=n=2，此时2+2=4，不符合三角形的三边关系，舍去；综上可知△ABC的周长为10．。

北师大版数学九年级上册：2.5 一元二次方程的根与系数的关系同步练习(含答案)

2.5 一元二次方程的根与系数的关系一、选择题1.设方程x2-3x+2=0的两根分别是x1,x2,则x1+x2的值为()A.3B.-32C.32D.-22.已知x1,x2是关于x的方程x2-ax-2=0的两根,下列结论一定正确的是 ()A.x1≠x2B.x1+x2>0C.x1·x2>0D.x1<0,x2<03.已知实数x1,x2满足x1+x2=7,x1x2=12,则以x1,x2为根的一元二次方程可以是()A.x2-7x+12=0B.x2+7x+12=0C.x2+7x-12=0D.x2-7x-12=04.关于x的一元二次方程x2-(k-1)x-k+2=0有两个实数根x1,x2,若(x1-x2+2)(x1-x2-2)+2x1x2=-3,则k的值为()A.0或2B.-2或2C.-2D.2二、填空题5.若关于x的一元二次方程x2-kx-2=0的一个根为1,则这个一元二次方程的另一个根为.6.若关于x的一元二次方程x2+2x-2m+1=0的两实数根之积为负,则实数m的取值范围是.7.若x1,x2是方程x2-4x-2020=0的两个实数根,则代数式x12-2x1+2x2的值等于.三、解答题8.不解方程,求下列方程的两根之和与两根之积:(1)x2-3x-11=0;(2)3x2-1=2x2-5x.9.已知方程3x2-x-1=0的两根分别为α,β,求下列各式的值:(1)α2+β2;(2)1α+1β.10.已知关于x的一元二次方程x2-(t-1)x+t-2=0.(1)求证:对于任意实数t,方程都有实数根;(2)当t为何值时,方程的两个根互为相反数?请说明理由.11. 已知一直角三角形的两条直角边长是关于x的一元二次方程x2+(2k-1)x+k2+3=0的两个不相等的实数根,如果此直角三角形的斜边长是5,求它的两条直角边长.详解详析1.A[解析] 由x2-3x+2=0可知,其二次项系数a=1,一次项系数b=-3,由根与系数的关系,得x1+x2=-ba =--31=3.故选A.2.A[解析] A项,∵Δ=(-a)2-4×1×(-2)=a2+8>0,∴x1≠x2,A项正确.B项,∵x1,x2是关于x的方程x2-ax-2=0的两根,∴x1+x2=a.∵a的正负不确定,∴B项不一定正确.C项,∵x1,x2是关于x的方程x2-ax-2=0的两根,∴x1·x2=-2<0,C项错误.D项,∵x1·x2=-2,∴x1,x2异号,D项错误.故选A.3.A4.D[解析] ∵关于x的一元二次方程x2-(k-1)x-k+2=0有两个实数根x1,x2, ∴x1+x2=k-1,x1x2=-k+2.∵(x1-x2+2)(x1-x2-2)+2x1x2=-3,即(x1+x2)2-2x1x2-4=-3,∴(k-1)2+2k-4-4=-3,解得k=±2.当k=2时,原方程为x2-x=0,∴Δ=(-1)2-4×1×0=1>0,∴该方程有两个不相等的实数根,∴k=2符合题意;当k=-2时,原方程为x2+3x+4=0,∴Δ=32-4×1×4=-7<0,∴该方程无解,∴k=-2不合题意,舍去.故k=2.故选D.5.-2[解析] ∵a=1,b=-k,c=-2,∴x1·x2=ca=-2.∵关于x 的一元二次方程x 2-kx-2=0的一个根为1, ∴另一个根为-2÷1=-2. 故答案为-2.6. m>12 [解析] 设x 1,x 2为关于x 的方程x 2+2x-2m+1=0的两个实数根.由题意,得{Δ>0,x 1x 2<0,即{4-4(1-2m )>0,-2m +1<0, 解得m>12. 故答案为m>12.7.2028 [解析] ∵x 1,x 2是方程x 2-4x-2020=0的两个实数根,∴x 1+x 2=4,x 12-4x 1-2020=0,即x 12-4x 1=2020,则原式=x 12-4x 1+2x 1+2x 2=x 12-4x 1+2(x 1+x 2)=2020+2×4=2020+8=2028. 故答案为2028. 8.解:(1)a=1,b=-3,c=-11, Δ=b 2-4ac=(-3)2-4×1×(-11)=53>0, ∴方程有两个实数根. 设方程的两个根为x 1,x 2,根据根与系数的关系得x 1+x 2=3,x 1x 2=-11. (2)原方程可变形为x 2+5x-1=0. a=1,b=5,c=-1,Δ=b 2-4ac=52-4×1×(-1)=29>0, ∴方程有两个实数根.设方程的两个根为x 1,x 2,根据根与系数的关系得x 1+x 2=-5,x 1x 2=-1. 9.解:由根与系数的关系,得α+β=13,αβ=-13. (1)α2+β2=(α+β)2-2αβ=132-2×-13=19+23=79.(2)1α+1β=α+βαβ=13-13=-1.10.解:(1)证明:∵在方程x 2-(t-1)x+t-2=0中,Δ=[-(t-1)]2-4×1×(t-2)=t 2-6t+9=(t-3)2≥0,∴对于任意实数t,方程都有实数根.(2)当t=1时,方程的两个根互为相反数.理由:设方程的两个根分别为m,n.∵方程的两个根互为相反数,∴m+n=t-1=0,解得t=1.∴当t=1时,方程的两个根互为相反数.11.[解析] 首先根据根的判别式求出k的取值范围,再根据根与系数的关系得到x1+x2=1-2k;x1x2=k2+3,再根据勾股定理得到x12+x22=52,接着利用完全平方公式变形得到(x1+x2)2-2x1x2=25,则(1-2k)2-2(k2+3)=25,求出k的值,进而求出两条直角边长.解:∵关于x的一元二次方程x2+(2k-1)x+k2+3=0有两个不相等的实数根,∴Δ>0,即(2k-1)2-4(k2+3)>0,.∴-4k-11>0,∴k<-114令方程的两根分别为x1,x2,则x1+x2=1-2k,x1x2=k2+3.∵此方程的两个根分别是一直角三角形的两条直角边长,且此直角三角形的斜边长为5, ∴x12+x22=52,∴(x1+x2)2-2x1x2=25,即(1-2k)2-2(k2+3)=25,∴k2-2k-15=0,解得k1=5,k2=-3.∵k<-11,∴k=-3.4把k=-3代入原方程,得x2-7x+12=0,解得x1=3,x2=4,∴直角三角形的两条直角边长分别为3和4.。

2.5一元二次方程的根与系数的关系-九年级上册初三数学(北师大版)

4.总结回顾环节，我发现部分学生对于一元二次方程根与系数关系的掌握程度仍有待提高。在今后的教学中，我会加强对于这一知识点的巩固练习，确保学生能够熟练掌握。
5.课堂氛围较为活跃，学生提问积极性较高，这说明他们在课堂上愿意思考、探究。作为老师，我要继续保持这种良好的课堂氛围，鼓励学生提问，培养他们的质疑精神。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解一元二次方程的根与系数关系的基本概念。一元二次方程的根与系数关系是指方程的三个系数a、b、c与其根x1、x2之间的数学关系。这个关系在解决实际问题中起着关键作用。
2.案例分析：接下来，我们来看一个具体的案例。这个案例将展示如何通过已知的根来求解方程的系数，以及如何利用系数关系来解决实际问题。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了一元二次方程的根与系数关系的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对这个知识点的理解。我希望大家能够掌握这些知识点，并在解决实际问题中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
五、教学反思
在今天的教学中，我重点关注了一元二次方程的根与系数关系这一章节。通过引入日常生活中的问题，我希望能够激发学生的兴趣，帮助他们理解数学与实际的联系。在授课过程中，我发现以下几点值得反思：
1.学生对于根的判别式Δ的理解存在困难。在讲解这一部分时，我应该更加形象地使用抛物线图像来帮助学生理解Δ值与方程根的关系。今后，我可以在课堂上增加更多直观的示例，以加深学生的理解。
2.教学难点
-理解根的判别式Δ的含义及其与方程根的关系。

秋北师大版九年级数学上册习题课件：2.5 一元二次方程的根与系数的关系(共22张PPT)

(2)(x＋1)2＝4x(x－1)．解：整理得：3x2－6x－1＝0， x1＋x2＝2, x1x2＝－13.
4. 若关于 x 的一元二次方程 x2－4x＋k－3＝0 的两个实数根为 x1，x2，且满足 x1＝3x2，试求出方程的两个实数根及 k 的值．
解：x1＝3，x2＝1，k＝6.
5. (2017·南充)已知关于 x 的一元二次方程 x2－(m －3)x－m＝0.
◎基础训练
1. (2017·烟台)若 x1，x2 是方程 x2－2mx＋m2－m－
1＝0 的两个根，且 x1＋x2＝1－x1x2，则 m 的值为( D )
A．－1 或 2
B．1 或－2
C．－2
D．1
【解析】由题意，x1＋x2＝2m，x1x2＝m2－m－1， ∵x1＋x2＝1－x1x2，∴2m＝1－(m2－m－1)，解得
7. 若两个不等实数 m、n 满足条件：m2－2m－k＝0， n2－2n－k＝0.
(1)求 k 的取值范围； (2)若 m2＋n2 的值是 6，求 k 的值．
解：(1)由已知得 m、n 分别是方程 x2－2x－k＝0 不
相等的实数根，Δ＝4＋4k>0，得：k>－1.
(2)由 m＋n＝2，mn＝－k， m2＋n2＝(m＋n)2－2mn，得 4＋2k＝6, 解得 k＝1.
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/9/122021/9/122021/9/122021/9/129/12/2021 14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年9月12日星期日2021/9/122021/9/122021/9/12 15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年9月2021/9/122021/9/122021/9/129/12/2021 16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021/9/122021/9/12September 12, 2021 17、儿童是中心，教育的措施便围绕他们而组织起来。2021/9/122021/9/122021/9/122021/9/12

数学北师大版初三上册一元二次方程的根与系数之间的关系同步练习(含解析)

数学北师大版初三上册2一、选择题1.若关于x的方程x2+3x+a=0有一个根为-1，则另一个根为（）A.-2B.2C.4D.-32.设a，b是方程x2+x﹣2021=0的两个实数根，则a2+2a+b的值为（）A.2021B.2021C.2021D.20213.下列一元二次方程中，两个实数根之和为1的是()A.x²+x+2=0 B.x²+x-2= 0 C.x²-x+2= 0 D.x²-x-2=04.假如一元二次方程x2-3x-1=0的两根为x1、x2 ，那么x1+x2=（）A.-3B.3C.-1D.15.在Rt△ABC中，斜边AB=5，而直角边BC，AC之长是一元二次方程x2-（2m-1）x+4（m-1）=0的两根，则m的值是（）A.4B.-1C.4或-1D.-4或16.已知m，n是关于x的一元二次方程x2﹣2tx+t2﹣2t+4=0的两实数根，则（m+2）（n+2）的最小值是（）A.7B.11C.12D.167.关于x的一元二次方程：x2﹣4x﹣m2=0有两个实数根x1、x2 ，则m2（）=（）A.B.C.4D.﹣48.关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正，关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正.给出三个结论：①这两个方程的根差不多上负根；②(m-1)2+(n-1)2≥2；③-1≤2 m-2n≤1.其中正确结论的个数是（）A.0个B.1个C.2个D.3个二、填空题9.已知关于x的一元二次方程x2+kx﹣6=0有一个根为﹣3，则方程的另一个根为________．10.已知实数m，n满足3m2+6m﹣5=0，3n2+6n﹣5=0，且m≠n，则________.11.若x1 ，x2是一元二次方程x2+3x﹣5=0的两个根，则x12x2+x1 x22的值是________．12.设m、n是一元二次方程x2+2x﹣7=0的两个根，则m2+3m+n=___ _____13.关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为负，则实数m的取值范畴是________．14.通过学习，爱好摸索的小明发觉，一元二次方程的根完全由它的系数确定，即一元二次方程ax2+bx+c=0（a≠0），当b2﹣4ac≥0时有两个实数根：x1= ，x2= ，因此：x1+x2= ，x1•x2= 、这确实是闻名的韦达定理．请你运用上述结论解决下列问题：关于x的一元二次方程x2+kx+k+1=0的两实数根分别为x1 ，x2 ，且x12+x22=1，则k的值为________．三、解答题15.已知关于x的一元二次方程x2＋x＋m2-2m＝0有一个实根为-1，求m的值及方程的另一个实根.16.已知关于x的方程（的两根之和为，两根之差为1，•其中a,b,c是△ABC的三边长．（1）求方程的根；（2）试判定△ABC的形状．17.关于x的一元二次方程有两个不等实根（1）求实数k的取值范畴．（2）若方程两实根满足，求k的值．18.已知关于x的一元二次方程（x-1）（x-4）=p2 ，p为实数．（1）求证：方程有两个不相等的实数根；（2）p为何值时，方程有整数解．（直截了当写出三个，不需说明理由）19.设x1 ，x2是一元二次方程2x2－x－3＝0的两根，求下列代数式的值．（1）x12＋x22；（2）；（3）x12＋x22－3x1x2.20.已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 ，x2 ．（1）求m的取值范畴；（2）当x12+x22=6x1x2时，求m的值．21.已知在关于x的分式方程①和一元二次方程（2﹣k）x2+3m x+（3﹣k）n=0②中，k、m、n均为实数，方程①的根为非负数．（1）求k的取值范畴；（2）当方程②有两个整数根x1、x2 ，k为整数，且k=m+2，n=1时，求方程②的整数根；（3）当方程②有两个实数根x1、x2 ，满足x1（x1﹣k）+x2（x2﹣k）=（x1﹣k）（x2﹣k），且k为负整数时，试判定|m|≤2是否成立？请说明理由．答案解析部分一、选择题1.【答案】A【考点】根与系数的关系【解析】解答: 设一元二次方程的另一根为，则依照一元二次方程根与系数的关系，得-1+ =-3，解得：=-2．故选A．分析: 依照一元二次方程根与系数的关系，利用两根和，两根积，即可求出a的值和另一根2.【答案】C【考点】一元二次方程的解，根与系数的关系【解析】【解答】解：∵a是方程x2+x﹣2021=0的根，∴a2+a﹣2021=0，∴a2=﹣a+2021，∴a2+2a+b=﹣a+2021+2a+b=2021+a+b，∵a，b是方程x2+x﹣2021=0的两个实数根，∴a+b=﹣1，∴a2+2a+b=2021﹣1=2021．故选C．【分析】先依照一元二次方程的解的定义得到a2=﹣a+2021，则a2+2a+b=2 021+a+b，然后依照根与系数的关系得到a+b=﹣1，再利用整体代入的方法运算．3.【答案】D【考点】一元二次方程根的判别式及应用，一元二次方程的根与系数的关系【解析】【解答】解：A．△=1－4×1×2=－7＜0，∴方程无实数根，故不符合题意；B．两根之和=－1，故不符合题意；C．△=1－4×1×2=－7＜0，∴方程无实数根，故不符合题意；D．两根之和=1，故符合题意．故答案为：D．【分析】依照根与系数的关系和根的判别式可求解。

九年级数学：一元二次方程根与系数的关系练习题(有答案)

、单项选择题: 一元二次方程根与系数的关系习题1.关于x 的方程ax 2 2x 1 0中,如果a 0,那么根的情况是( B ) (A) (C) 有两个相等的实数根没有实数根 (B)有两个不相等的实数根 (D)不能确定解: (2)2 4a 4a 0 原方程有两个不相等的实数根.2.设 (A) 解: X i 4 4a 4 4a 0 X 1,X 2是方程2x 215 (B) 12 方程两根为 X 23, x 1x 2 6x (C) 6 X i, X 2 3 0的两根,那么 (D) 3 2 X 1 3.以下方程中,有两个相等的实数根的是((A)2y 2+5=6y (B) x 2+5=2 5 x (C) 3 x 2 (此题为找出 0〞的方程即可)2 X 1 2 X 22 X 2的值是( (X i 32B ) —2 x+2=0 4.以方程X 2+2X —3=0的两个根的和与积为两根的 (A) y 2+5y —6=0 (B) y 2+5y + 6=0 解：设方程两根为X1, X2,那么: x 1 x 2 2, x 1x 23为根的一元二次方程为 5.如果X 1, X 2是两个不相等实数,且满足 (A) 2(B) -2 X 2)2 21 2x 1x 2 (D) 3x 2—2^x+1=0 二次方程是 (C) y 2-5y + 6=0 (D) 2 - y [( 2)( 3)]y ( 即：y (C) 5y解：X ：22x 1 1, x 2 2X 2 x n X 2可看作是方程x2x 二、填空题: 1、如果二次方程 4x k 2 解：方程X 2 4x k 2有两个相等的实数根2X 1 2x 12X2(D)的两根X 1X22)( 3) 02x 2 1,那么X i ? X 2等于0有两个相等的实数根,那么 k= 2.16 4k 22、如果关于x的方程2x2(4 k 1)x 2k20有两个不相等的实数根,那么k的取值范围是k 9.解：方程2x2 (4 k 1)x 2k2 1 0 8k有两个不相等的实数根[(4k 1)]2 8(2k21)3、x1,x2是方程2x27x 4 0的两根,那么x17 2 x2 = 一 , x〔x? = 2 , (x1 x2)= 2(x1 x2)2 4x1 x2274、假设关于x的方程(m2 2)x2 (m 2)x 1 0的两个根互为倒数,那么m = d3.解：设方程两根为x1, x2,那么: ,32[(m 2)]2 24(m2 2) 0 方程两根互为倒数 2[(m 2)]2 24(m2 2) 014x2 - ------- 1m 2m = 4时,方程mx 4 0有两个相等的实数根;解: 方程x2mx 4 0有两个相等的实数根解:m216m 4且m 0时,方程mx24x 1 0有两个不相等的实数根; 方程mx24x 1 0有两个不相等的实数根16 4m 0 且m 04且m 0时,原方程有两个不相等的实数根.6、关于x的方程10x2 (m 3)x m 7 0,假设有一个根为0,那么m=7,这时方程的另一个根是1；假设…,3 … 八、,、………8 ■两根之和为一工,那么m = 9,这时方程的两个本!!为X 1x 2 1.5—— 5解乂1)设方程 10x 2 (m 3)x m 7 0m 7 y---------- ②10由②,得:(5x 8)( x 1) 0m 7, x 1 1时,方程一根为0 x8或x 157、如果x 2 2(m 1)x m 2 5是一个完全平方式,那么方程x 2 2( m 1)x m 2 5 0W 两个相等实根m 2[2(m 1)]2 4(m 2 5) 08、方程2x(mx 4) x 2 6没有实数根,那么最小的整数 m = 2；解：将方程 2x( mx 4) x 2 648 m 88 0化简,得：(2m 1)x 2 8x 6 0原方程没有实数根64 24 (2m 1) 0另一根为 X i,那么:10m 7100 X i m 3 —— a 10 、一一 3原方程两根之和为 -5将m 7代入①,得:原方程可化为：5x 2 3x 8 09、方程2(x 1)(x 3m) x(m 4)两根的和与两根的积相等,那么m =2;(2)设原方程两根为a 、b,那么:0?X i10 5m =2 ；解：令 x 2 2( m 1)x m 2 5 0 4(m 2 2m 1) 4m 2 20 0x 2 2(m 1)x m 2 5是完全平方式8m 16 0x 1 1 11 m -6最小整数m 为2解：将方程 2(x 1)(x 3m) x(m 4)化简,得：2x 2 (7m 2)x 6m 0 设方程两根为x1,x 2,那么：7m 2x 1 x 2 ---, x 1x 2 3m方程两根的和与两根的积相等m 2当 m 2时,[(7m 2)]2 48m 0将m 8代入①,得：n 2将m 8, n2代入③,得: k 8 ( 2)16k 16解：原方程有实数根3 m -4 3 .当m -时,原万程有两个实数根.4解：方程两根为2、；3和2 73,(2 .3)- (2 、3) p , (2 .,3)(2 .3) q解之,得:10、设关于x 的方程x 2 6x k0的两根是m 和n ,且3m 2n20,那么k 值为16;①X 2-③,得:当 k16时, 36 4k 011、假设方程 x 2 (2m 1)x m 2 1 0有实数根,那么 m 的取值范围是 m12、一元二次方程 x 2px q 0两个根分别是273 和 2 13,那么 p= 4 ,q= 1;7m 2 23m解：m 、n 是方程的两根r m n 6①* mn k ②I 3m 2n 20 ③4m 3[(2m 1)]2 4(m 2 1) 01,24m 4m 14m4 0p 4'' q 1 p4, q 113、方程3x219x m 0的一个根是1,那么它的另一个根是16X — , m=16;3解：设方程的另一根为X i,那么:m 16mX1 3当a 16时, 19212a 0由①,得：X116方程另一根为16m 1&方16 , _ 口将X 一代入②,得:314、假设方程x2mx 1 0的两个实数根互为相反数,那么m的值是0;解：设方程两根为X1,X2,那么:x1 x2m 0时,m2 4 0 方程两根互为相反数0时,原方程两根互为相反数.X1x2m 015、m、n是关于x的方程x2(2m 1)X m2 1 0的两个实数根,那么代数式m n =1o解: m、n是方程的两根将①代入②,得:m n 2m 1 m(m 1)2mn m化简,得: 1代入①,得:2mn m (1)216、方程X23x 1 0 的两个根为a ,3,那么a +3=3, "3=1;17、如果关于x的方程x24x m 0与x2x 2m 0有一个根相同,那么m的值为0或3 ;解：方程有一个相同的根将x m代入x24x m 0,得:2 , 2 cx 4x m x x 2m 2m 4m m 0(4 1)x 2m m m(m 3) 0这个相同的根为:18、方程2x23x 0的两根之差为22 ,那么k= 2;解：设方程两根为x1, x2, 那么:2k254x i x2 21 22时,9 8k 0(x i x2)2254关于x的方程2x23x k 0两根19、解:20、解: x1 x2)24x1 x2254、,,1 ,差为2—时,k 22假设方程x2(a22)x 3 0的两根是1和一3,那么a= 2; 方程两根1和(3) (a2 2)D、假设关于x的方程设方程两根为义, x2, x2 2(m 1), x1x2方程两根互为倒数2x1 x2 4m 12(m那么:4m21)x 4m20有两个实数根,且这两个根互为倒数,②、关于x的一元二次方程(a2 1)x2F 1那么m的值为一；2[2(m 1)]2[2(m 1)]216m216m2(a 1)x 1 0两根互为倒数,那么a=J2.a 1 x 1 x 22——,x 1 x 2a 1方程两根互为倒数1 a2 1当 a.2时, (a 1)2 4(a 2 1) 0 当 a..2时,(a 1)24(a 2 1) 0a .. 2a 2 1 1解：设方程的另一根为 x v 那么:a . 2 1当 a 2 1时,2 4a 0方程另一根为x 1, a .2 1将x 1 1代入②,得:36 4k 4k 8k 8寸,36 4k 0 (2)关于x 的方程x 6x k 0的两根23、方程2x 2 mx 40两根的绝对值相等,那么 m=0ox 〔 x 2差为2时,k 8.解：设方程两根为x1, x 2,那么:a 、,221、如果关于x 的一元二次方程x 2 J2x a 0的一个根是1— &,那么另一个根是 x 1,a 的值为J2 1.解：设方程两根为x1, x 2,那么: 当 x 〔 x 2时,x 〔 x 2 0x 1 x 2x 1x 2 x 1 x 21 a2 1( 1 V2 x 1 <2①1(1 &)x 〔 a ②由①,得：x 1 22、如果关于x 的方程x 2 6x k0的两根差为2,那么k=8.解：设方程两根为x1, x 2,那么:x 1 x 2 6, x 1x 2 k x 1 x 2 2(x 〔 x 2)242(x 1 x 2) 4x 1 x 24x1 X2M£X1x2当x i x2 时,m2 32 0 m232 0当m 0时, m232 0 2x2mx 4 0两根绝对值相等时,m 0.x i x2qx r 0( p 0)的两根为0和一1,贝U q ： p=1:1.解: 设方程两根为x2, 那么:方程两根为0和x i X29p(1)25、方程3x2x 1 0 ,要使方程两根的平方和为13—,9那么常数项应改为2.解: 设方程两根为xi, x2, (¥2m3139并设方程的常数项为i 6m 13x i x2 1 3,x/22x i 2 x2 1392时,i 12m 0x2)22X1X2139常数项应改为2.26、方程x24x 2m 0的一个根a比另一个根3小4,那么a = 4 ;=0 ；m=0 .解：据题意,得：「 4 ①< 2m ②1 4③①+③,得：4将4代入①,得：0将4, 0代入②,得：m 0当m 0时, 16 8m 04, 0, m 02 1 13 1 27、关于x的万程x 3mx 2(m 1) 0的两根为x1,x2,且———一,那么m= 一.24、一元二次方程px2解：设方程2x 2 3x两根为x1,x 2,那么:9-0 m -时,方程有两个正根8m 0当m 0时,方程有一根为0.(2)、方程有一个正根,一个负根三、解答以下各题：1、3-也是方程x 2 mx 7 0的一个根,求另一个根及 m 的值. 解：设方程的另一根为刈,那么:(3 j2)x1 7②答：方程另一根为3 <2 ,由②,得：x 13 22m 6.解：方程两根为x 1, x 2,那么:X i X 2 3 x 1 x 2 4 3m 3 x 1 x 2 3m, x 1x 2 2(m 1) 一2(m 1)41 1 3 一— — 12m 6( m 1)x 1 x 2 4 m 1时, (3m)2 8(m 1) 0328、关于x 的方程2x 2 3x m _ _ 9 .................................. 0,当0 m 一时,万程有两个正数根；当8m 0时,方程有一个正根,个负根；当m 0时,方程有一个根为 0.x 1 x 2 (1)、方程有两个正数根方程有一个正根,一个负根9 8m 0x 1, x 2 m 0又方程有两个正数根 9 8m 09 m8m 0当m 0时,方程有一正一负两个根(3)、方程有一根为0x 1, x 23 2将x1 3 代入①,得：2、m取什么值时,方程2x2 (4m 1)x 2m2 1 0(1)有两个不相等的实数根,(2)有两个相等的实数根,(3)没有实数根；解：(4 m 1)2 8(2m2 1)16m28m 1 16m288m 9(1)有两个不相等的实数根8m 9 09 m -8, 9-当m -时,原方程有两个8不相等的实数根.(2)有两个相等的实数根3、求证：方程(m2 1)x2 2mx (m2 4)证实：(2m)2 4(m2 1)(m2 4)4m2 4(m4 5m2 4)4m416m2164(m4 4m2 4)2 24(m2 2)24、求证：不管k为何实数,关于x的式子(x解：令(x 1)(x 2) k2 0即:8m 9 09 m8, 9-当m -时,原方程有两个8相等的实数根.(3)没有实数根8m 9 09 m8当m 9时,原方程无实根.80没有实数根.m22 04(m2 2)2 0即：0方程(m2 1)x2 2mx (m2 4) 0没有实数根.21)(x 2) k都可以分解成两个一次因式的积.x2 33x 2 k209 4(2 k2)4k214k2024k 1 0方程(x 1)(x 2) k2 0有两个不相等的实数根不管k为何实数,关于x的式子 2 .... (x 1)(x 2) k都可以分解成两个一次因式的积.解：令2x2 (4k 1)x 2k2 1 0 8k 9 0a是实数,且方程x22ax 10有两个不相等的实根,试判别方程x2 2ax 1 1(a2x2 a2 1)2解：x2 2ax 1 1(a2x2 a2 2 0有无实根？1) 0 4a24 00 a214a44,20 a2204a4 20a2 24 0即：04a420a224 2 12 2 2万程x 2ax 1 -(ax a 1) 07、关于x的方程mx2nx 2 0两根相等,方程x24mx 3n 0的一个根是另一个根的3倍.求证: 方程x2 (k n)x (k m) 0 一定有实数根.2 2 2 2 」2x 4ax 2 a x a 1 (2 a2)x2 4ax a23 016a2 4(2 a2)(a2 3)16a2 4(2 a2)(a2 3)5、当k取什么实数时,二次三项式2x2 2 ,(4k 1)x 2k 1可因式分解当2x2 (4k 1)x 2k2 1 0 有两个实根时,原二次项式可因式分解2 2(4k 1)2 8( 2k2 1) 0 2x29 , 一,-时,二次三项式8(4 k 1)x 2k2 1可因式分解.方程x22ax 1 0有两个不等实根有两个不相等的实数根.m 2 n 4将m 2, n 4代入方程x 5 (k n)x (k m) 0得： x 2 (k 4)x (k 2) 0#： (k 4)2 4(k 2)k 2 8k 16 4k 8 k 2 4k 242(k 2)2202(k 2)2 0 (k 2)2 20 0方程 x 2 (k n)x (k m) 0 一定有实数根.25mx 3n 0的两根之比为 2 : 3,方程x 2nx 8m 0的两根相等(mnw0).求证：对的两根比为2:3设此方程两根为2a 和3a,那么:i52a 3a mI23 2a?3a -n2n m 2①mx 2 (n k 1)x k 1 0#： 2x 2 (4 k 1)x k 1 02(3 k)28( k 1) _ _2 一一9 6k k 8k 8 k 2 2k 152证实：方程2x 5mx 3n 0 将m 2, n 4代入方程证实：方程mx nx 2 0 两根相等m 0 2n 8m 0①方程 x 2 4mx 3n 0 一根是另一根的设方程一根为x 1 3x 1 x 1 ?3x 12n m将②代入①,得：4m 8m 0m(m 3 8) 0m 0 或 m 2 m 03倍x 1,另一根为3x 1,那么: 4m 3n2)8、方程2x 2方程x22nx 8m 0两根相等 2(k 1)2 4n232m 0 (k 1)2 08m8m 对于任意实数k,方程m(m3 8) 2mX (n k 1)x k 1 0m mn 0或m24恒有实数根.9、设X i, X2是方程2x24X0的两根,利用根与系数关系求以下各式的值:⑴、(X i 1)(X21) 1 ⑵、一X1X2X2X1(31 —X1 X2,八 2 .(4)、x1 x1x2 2x1解: X1, X2是一元二次方程x2(3) >— X1X1X22X24X 3 0的两根2X1 2 X2 X1X2X 1 X2 2, X1X2(x1 x2)2 2x1x2X1X2⑴、〔X11)(X2 1)2 3(2)2 2 ( 2)3X1 X2x1 x214 3~~3227 (3)21 143(4)、X1 X1X2 2X11 1⑵、X1 x2X1(X1 X2 2)2 2⑴ X i X2 (2) X i X2 解：X1, X2是一元二次方程4X27X 3 0的两根7 3X i X2 — X X i X24 42 2⑴ X i X22(x i x2) 2x i x2(7)2 2 34 425i6(2)X i X2..(X i X2)2(X i X2)2 4X i X2 (3)1r x i 匹(4) X i X2(3) ,X i X2X i X27.3.3i 一2(4 ) X i X2(xix2 )(X i X2)2 4X i X20的两个根,利用根与系数的关系,求以下各式的值: 第i4页共26页2~~3243x1?010、设方程4x27x 3 0的两根为X1, X2,不解方程,求以下各式的值ii、x1,x2是方程2x23x i解:Xi, X 2是一元二次方程 2 ( 9) 9 1612、解: 19 2x 23x 1 0的两根16X i X 2⑴(2 X i4x i x 24x i x 2实数s 、 19s 231 一,X iX 2一2 23)(2X 2 3) 6X 1 6(X 1 6X 2 9X 2)3 (2) Xi X 2X i X 2(Xi3X 1X 2X i X 2[(X iI)2X 22) X 2)2 2X 1X 2](1) 13t 分别满足方程 99s 1 0 99t t 2 0 1s 、1可看作是方程 t 19x 2 99x 1 0的两根 19s 2 99s1 0和且19st 4s t 4s s 一 t(SI)99 19 99t t 2cst 4s 10求代数式——t —— 的值.4?s4 19 99 19, s?1t 1995 1913、设: 3a 2 6a 11 3b 2 6b 11 0 且aw b,求a 4b 4的值.解: _ 2_3a 6a 11 0 3b 2 6b 11 0 2 2X 2(a b )2a 2b 2a、b 可看作是方程2_2_22[(a b) 2ab] 2a b3x 26x 11 0的两根[22 2 ( ?)]2 2 ( 4) 3 311 a b 2, ab31156 242 914 "Q - "-9"14、 a 2 1 a, b 2 1b ,且 awb,求(a — 1)(b —1)的值.2原方程可化为：x 2x 1 01 ( 1) 1 1, o1115、 m 2 m 4 0,-- n n解：m 2m 4 0x 2 x 4 0的两根1 1m, m —1, m ?一 —4nn n1 一代数式m —的值为 1.n3st 2s 3(2)———s-^. tst 1⑴、—p s1C 「3(s -) 2?s?- t t解：a 2 1 aa b 1, ab 1 b 2 1 b (a 1)(b 1) a 、b 可看作是方程 ab a b 1 x 2 1 x 的两根ab (a b) 116、 2s 2 4s 74t 2 0 , s, t 为实数,且stw1.求以下各式的值:27t 2 4t 2 03st 2s 3 ⑵ c 2s3s —— t2x 2 4x 7 0的两根3 ( 2) 2 ( |)0 , m, n 为实数,且m 1 ,求代数式m n的值m 、1可看作是方程 nst 1 ⑴一p;解：2s 2 4s 71 1 7s 2, s? 6 ( 7) 1t t 217、关于x的方程x2—(k+1)x+k+2=0的两根的平方和等于6,求k的值;解：设方程两根为x「x2,那么k 3x1 x2k 1, x1x2k 22乂22(x1 x2) 2x1 x2 6 (k 1)2 2(k 2) 62(k 1)2 4(k 2)当k 3寸, 0,不符合题意,应舍去当k 3时, 0,符合题意k的值为3.k2918、方程x2+3x+m=0中的m是什么数值时,方程的两个实数根满足:(1) 一个根比另一个根大2; (2) 一个根是另一个根的3倍；(3)两根差的平方是17解：设方程两根为％、x2,那么9 / 3、27一(一)一4 4 16x〔x2 3, x〔x2 m , 27当m 27时,160,符合题意9 4m⑴、当x〔x2 2时,1 5x1 2,x2 21,55m —(一)一2 2 4当m 5时, 0,符合题意4 m 一时,方程一根是另一根的笳. 16 (3)、当(X x2)2 17时,2(x1 x2) 4x1 x2 179 4m 17m 25时,方程一根比另一根4 2时, 0大2. 2时,方程两根差的平方是17.⑵、当x1 3x2时,9 3X i-, X 2 —4419、a,b,c 是三角形的三边长,且方程 (a 2+b?+c2)x 2+2(a+b+c)x+3=0有两个相等的实数根,求证：这个三角形是正三角形证实：方程有两个相等实根[2(a b c)]2 12(a 2 b 2 c 2) 02222(a b c)23(a 2 b 2c 2)0 -2-2-2---2a2b2c2ab2ac 2bc22_22_22_(a 2b 22ab) (a 2c 22ac) (b 2c 22bc) 0 22 2(a b)2(a c)2 (b c)2ab0, ac0, b c 0求这个直角三角形的面积. 解：设方程两根为x 、x 2,那么x 〔 x 2 2a 1, x 〔x 2 4(a 1) x 1、x 2是斜边长为5的直角三角形的两直角边2 2x 1 x 225(x 1 x 2)2 2x 1x 2 25 (2a 1)2 8(a 1) 25a 2 3a 4 0x 1、x 2是三角形的两边 x 1 x 2 2a 1 0 且 x 1x 2 4(a 1) 0a ]且a 12a 1只能取a 41 1 S^1x 2 2 4(4 1)(a 4)(a 1) 0解：设方程两根为x 1、x 2,那么4m 2 1 0 或 m 2 2m 3 021、关于x 的一元二次方程3x 2(4 m 2 1)x m(m 2) 0的两实根之和等于两个实根的倒数和,求m 的值.这个三角形是正三角形20、关于x 的方程x 2(2a 1)x 4(a 1) 0的两个根是斜边长为 5的直角三角形的两条直角边的长,X1 X24 m23 一,X〔X21m1 m2p m33, m4 1X1 X24m2134m213 m(4m2[(4m21)]2 12m(m 2) X iX iX2X2X1X24m213m(m 2)34m21m(m 2)1)(m 2) 3(4m 1)(4m2 1)(m22m 3) 0, 1-当m1 一时,2当m i0,不符合题意,应舍去0,符合题意当m1当m i 1时,答：m的值为0,符合题意0,不符合题意,应舍去22、是否存在实数k ,使关于X的方程9X2 (4k 7)X 6k2 0的两个实根X1,X2,满足上-,如果存X2 2 在,试求出所有满足条件的k的值,如果不存在,请说明理由.解：假设存在.据题意 ,得:4k 7X1 X2 9 , X1 X2 2k2 3X1 3X2 2上3或x1 3X2 2 X2 2 少X1 3 3 当一一时,X1 -X2 X2 2 2 当上3时,X1 3X2 X2 2 24k 7 2(4k 7) x1x294k 7 2(4k 7) 2 2------- ? - k3 ------ 9 3(4k 7)2 9k20(4k 7 3k)(4k 7 3k) 0X 1 3(4 k 7) 2(4k 7)453(4k 7)02(4k 7)45 45 [(4k 2 27)]2 4 9?( 6k2)(4k 7)2 225k2当k 1时, 0,符合题意241k256k 49 当k 7时, 0,符合题意5624 241 49 存在k值,当此方程无实根; 方程两根满足X1 X223、关于x的方程2x2(m 1)x 0的两根满足关系式X1 X2 1,求m的值及两个根.解: 设方程两根为X1、x2,那么1或m 11X i X2 m 1——,X1X22m 1""2"2(m 1)]2 8(m 1)X 1 X2 1 1时,4 0, 此时方程两根为: X10, X2 1X 111时,4 0, 此时方程两根为: X12, X2 31?m 3. 4答：m 1时, 方程两根为: X10, X2 1；(m 1)(m 3) 8(m 1) m 11时,方程两根为: X1 2, X2 3. (m 1)(m 3 8) 024、3是关于X的方程4X2 4mxm24m 0的两个实根,并且满足( 1)(1) 2,求m的值.解: 是方程的两根m, m2 4m416m2一, 2、16(m 4m)1) ( 1)2时,0,不符合题意,应舍去2时,0,符合题意4m4m的值为2.m 0,根据以下条件,分别求出m 的值：1⑶有一根为零；(4)有一本为1; (5)两根的平万和为 ——.64(4)、方程有一根为18 (2m 1) m 0 m 7当m 7时, 0m 7时,方程有一根为11(5)、万程两根的平万和为一642 21x 〔 x 26421(x 1 x 2) 2x 1x 2 一64即 3 1)6 m A644 64625、一元二次方程 8x 2 (2m 1)x(1)两根互为倒数；(2)两根互为相反数；解：设方程两根为x 1、x 2,那么2m 1 m x i x 2, x 〔 x 2882[(2m 1)]232 m(1)、两根互为倒数m 1 8m 8当m 8时,m 8寸,方程两根互为倒数(2)、两根互为相反数Q 0 81 m -2 1当m1时,21m 1时,万程两根互为相反数2(3)、方程有一根为0 m 0当m 0时, 0m 3m 0m(m 3) 0m 0或m 3当m 0 寸, 0当m 3时, 0,不符合题意,应舍去1 m 0时,万程两根的平万和为——6413 , ___ _ ______ _13时,两方程相同的根为：3a 1或 a 3_― 22[2(a 2)]4(a5)16a 36当a 1时,0,符合题意当a 3寸, 0,不符合题意,应舍去答：a 的值为1.28、方程x 2 bx c 0有两个不相等的正实根,两根之差等于解：设方程两根为x 1、x 2,那么x 〔 x 2 b, x#2 cx 2 3m 0时,方程有一根为026、方程x 2 mx 4 0和x 2 (m 2)x 16 0有一个相同的根,求 m 的值及这个相同的根.解：方程有一个相同的根2, 2 /x mx 4 x (m2)x 16(3m 13)(m 4) 0(m m 2)x 20这个相同的根为:10将x 工-代入x 21 mmx0,4时,两方程相同的根为(10 )2 10m1 m 1 m13 , ___ ______13时,两方程相同的根为：33；23m m 52当m 4时,两方程相同的根为：x27、关于x 的二次方程2(a 2)x a 2 5 0有实数根,且两根之积等于两根之和的2倍,求a 的值.解：设方程两根为x 1、x 2,那么2 Lx 〔 x 2 2(a 2), x 1x 2 a 52(x 1 x 2) x 〔x 224(a 2) a 2 52a 24a 3 0 (a 1)(a 3) 03,两根的平方和等于 29,求b 、c 的值.b22c 29②①-②得：c 10将c 10代入①,得: b 7b 3cb 3------ ?—— c2 2b24c 9 ①2 2x1 x229(x1 x2)2 2x1x229方程有两个不相等正实根x1 x2b 0, x1x2c 0b 7答：b 7, c 1029、一元二次方程(2k 3)x2 4kx 2k 5 0,且4k+1是腰长为7的等腰三角形的底边长,求：当取何整数时,方程有两个整数根.解：方程有两个实根即:(4k)2 4(2k 3)(2k 5) 04k 1是腰长为7的等腰三角形的底边长4k 1 144k134当k 1时,原方程可化为：x24x 3 0其解为1和3,满足条件当k 2时,原方程可化为：x28x 1 0其解不是整数,不满足条件,应舍去当k 3寸,原方程可化为：3x212x 1 0其解不是整数,不满足条件,应舍去答：当k 1时,原方程两根为整数.15 , 13—k -16 4整数k可能为1、2、330、x1,x2是关于x的方程x2px q 20的两根,x1 1, x2 1是关于x的方程x qx p 0的两根,求常数p、q的值.解：据题意,得:, x〔x2 px〔x2 q将p 1代入⑥,得：q 3答：p 1 , q 320的两个实数根；y b y 2是关于y 的万程y 5my 7 0的两个实数根,且x 1 y 1 2, x 2 解：据题意,得：2x 〔 x 2m )网 ny 〔 y 25m, y 〔 y 2 7x 1 y 1 2, X2 y 2 2 X y 〔 x 2 y 24m 7( 5m) 4m 25m 4 02 ,求m n 的值.(m 1)(m 4) 0 m 1或 m 4当m 1时,方程y 2m 4当m 4时,方程x 216 4n 0答：m 4, n 41 1 n?h2 21K.m 21n 22 24712x 1 1 x 2 1 q ③ p (2p 1) 2(X i 1)(x 2 1) p ④0,其中m n 分别是个等腰三角形的腰长和底边长Om 、n 分别是一个等腰三角形的腰长和底边在等腰三角形中,h . m 2将①代入③,得：p q 2⑤将①、②代入④,得：31、x 1, x 2是关于x 的方程x 1 2 * 4 m 2x n5my 7 0无实根2m x n 0有两个实根42m n 0,2m n 012这个方程有两个不相等实根. n.'m2 - n2 48②\ 4(2)、设方程两根为x「X2,并设三角形的高为h 将①代入②,得：n 12x1 x282x1 x2642(x1 x2) 4x1x2 64 m 2 A(舍负)该三角形的周长为2m n 4.13 12px q 0时,小张看错了p,解得方程的根为1与一3;小王看错了q,解得方程的根为4与-2.这个方程的根应该是什么将p 2, q 3代入原方程,得:x22x 3 0(x 3)( x 1) 0x1 3, x2 1答：这个方程的根是3和1.34、方程x2ax b 0的两根为x1,x2,且4x1 x? 0 ,又知根的判别式二25,求a, b的值. 解：据题意得x x1 x2 a ①4 4x1 x2 0 ②、x1x2b ③②-①,得：a _x1 —④3将④代入①,得：4a …x2—⑤4a29b 0 ⑥25a24b 25 ⑦⑥-⑦X 4,得：b 4将b 4代入⑥,得: a 3x1 x22m, x1x21 2-n4将n 12代入①,得:33、在解方程x2解：小张看错了pq 1 ( 3) 3小王看错了qP 4 ( 2)任息头数k,万程mx (n k 1)x k 1 0恒有实数根. 1 一,,一、一 s 、1可看作是方程 t1 o32、关于x 的万程x 2mx -n 4(1)求证：这个方程有两个不相等的实根；(2)假设方程两实根之差的绝对值是 8,等腰三角形的面积是 12,求这个三角形的周长.(1)、证实： 4m 2 n 24m 2 n 2 64(2m n)(2m n)m - n 16①4将④、⑤代入③,得: 答：a 3, b 435 x1,x 2 2次万程 x4 mx n 0 的两个实数根,2 x 1 2 x 2 (x 1 x 2)2 3 士 x 1 2-2 X2解: x1, x 2 是元二次方程 2m 4n5n 2mx n 0的两根, 将①代入②, 得:x i x 2 m, x 1x 2 5n 2 2n 2 x 1 2 x 2(x 1 x 2)2 (5n3)(n 1)2( x 2)22-2x 12?32x 1x 2 (x 1x 2)2 32n2-2x 2乂2〕2 〔泅〕2x 1x 2 2 1时,4n21 1021 10'3. 一 ...........3不符合题意,应舍去52(-m) 2n2 ? --------- 2 ------ 5n。

九年级数学上册《一元二次方程的根与系数的关系》测试题含答案

九年级数学上册《一元二次方程的根与系数的关系》测试题复习巩固1．下列方程中，两个实数根之和为2的一元二次方程是()A．x2＋2x－3＝0 B．x2－2x＋3＝0C．x2－2x－3＝0 D．x2＋2x＋3＝02．设一元二次方程x2－2x－4＝0的两个实根为x1和x2，则下列结论正确的是() A．x1＋x2＝2 B．x1＋x2＝－4C．x1x2＝－2 D．x1x2＝43．已知x1，x2是一元二次方程x2＋2ax＋b＝0的两根，且x1＋x2＝3，x1x2＝1，则a，b 的值分别是()A．a＝－3，b＝1 B．a＝3，b＝1C．3=2a-，b＝－1 D．3=2a-，b＝14．若一元二次方程x2＋kx－3＝0的一个根是x＝1，则该方程的另一个根是() A．3 B．－1C．－3 D．－25．已知方程x2－5x＋2＝0的两个根分别为x1，x2，则x1＋x2－x1x2的值为()A．－7 B．－3 C．7 D．36．(2013山东莱芜)已知m，n是方程x2＋22x＋1＝0的两根，则代数式223m n mn++的值为()A．9 B．±3 C．3 D．57．已知方程x2－4x－7＝0的根是x1和x2，则x1＋x2＝__________，x1x2＝__________.8．若方程x2－2x＋a＝0的一个根是3，则该方程的另一个根是__________，a＝__________.9．若x1，x2是一元二次方程x2－3x－2＝0的两个实数根，则x21＋3x1x2＋x22的值为__________．10．已知方程x2＋3x－1＝0的两实数根为α，β，不解方程求下列各式的值．(1)α2＋β2；(2)α3β＋αβ3；(3)βααβ+.能力提升11．关于x的一元二次方程x2－mx＋2m－1＝0的两个实数根分别是x1，x2，且x12＋x22＝7，则(x1－x2)2的值是()A．1 B．12 C．13 D．2512．若关于x 的一元二次方程x 2＋(m 2－9)x ＋m －1＝0的两个实数根互为相反数，则m 的值是__________．13．设a ，b 是方程x 2＋x －2 015＝0的两个不相等的实数根，则a 2＋2a ＋b 的值为__________．14．在解方程x 2＋px ＋q ＝0时，小张看错了p ，解得方程的根为1与－3；小王看错了q ，解得方程的根为4与－2.这个方程正确的根应该是什么？15．已知关于x 的方程x 2－2(k －1)x ＋k 2＝0有两个实数根x 1，x 2.(1)求k 的取值范围；(2)若|x 1＋x 2|＝x 1x 2－1，求k 的值．16．阅读材料：已知p 2－p －1＝0,1－q －q 2＝0，且pq ≠1，求1pq q +的值．解：由p 2－p －1＝0,1－q －q 2＝0，可知p ≠0，q ≠0.又因为pq ≠1，所以p ≠1q .所以1－q －q 2＝0可变形为2111=0q q ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭.所以p 与1q 是方程x 2－x －1＝0的两个不相等的实数根．故p ＋1q ＝1，即1pq q+＝1. 根据阅读材料所提供的方法，完成下面的解答．已知2m 2－5m －1＝0，2152=0n n +-，且m ≠n ，求11m n+的值．参考答案复习巩固1．C 选项B 中的方程无实数根．本题易误选为B.2．A3．D 由根与系数的关系知，x 1＋x 2＝－2a ，x 1x 2＝b .因此－2a ＝3，b ＝1，即32a =-，b ＝1.故选D. 4．C 设方程的另一个根为x 1，由x 1·1＝－3，得x 1＝－3.5．D 由根与系数的关系，得x 1＋x 2＝5，x 1x 2＝2.故x 1＋x 2－x 1x 2＝5－2＝3. 6．C 根据一元二次方程的根与系数的关系，得m ＋n ＝22-，mn ＝1.故222232213m n mn m n mn ++=(+)+=(-)+=.7．4 －78．－1 －3 设方程的另一个根是x 1，则113=23=x x a +⎧⎨⎩，，解得x 1＝－1，a ＝－3. 9．7 x 12＋3x 1x 2＋x 22＝(x 1＋x 2)2＋x 1x 2＝32＋(－2)＝7. 10．解：因为α，β是方程x 2＋3x －1＝0的两个实数根，所以α＋β＝－3，αβ＝－1.(1)α2＋β2＝(α＋β)2－2αβ＝(－3)2－2×(－1)＝11.(2)α3β＋αβ3＝αβ(α2＋β2)＝(－1)×11＝－11.(3)2211111βααβαβαβ++===--. 能力提升11．C 由根与系数的关系，得x 1＋x 2＝m ，x 1x 2＝2m －1，则(x 1－x 2)2＝2212x x +－2x 1x 2＝7－2(2m －1)＝9－4m ；又因为(x1－x2)2＝(x1＋x2)2－4x1x2＝m2－4(2m－1)，所以9－4m＝m2－8m＋4，解得m1＝5，m2＝－1.当m＝5时，Δ＜0，故m＝－1.此时(x1－x2)2＝9－4×(－1)＝13.12．－3由根与系数的关系，得－(m2－9)＝0，解得m＝±3.但当m＝3时，原方程无实根，故m＝－3.13．2 014因为a，b是方程x2＋x－2 015＝0的两个不相等的实数根，故由根与系数的关系可得a＋b＝－1①，由根的定义，得a2＋a－2 015＝0，即a2＋a＝2 015②.再由①＋②得a2＋2a＋b＝2 014.14．解：由题意，得1×(－3)＝q,4＋(－2)＝－p.从而可得p＝－2，q＝－3.因此原方程为x2－2x－3＝0，解得x1＝3，x2＝－1.故这个方程正确的根为3与－1.15．解：(1)依题意，得Δ≥0，即[－2(k－1)]2－4k2≥0，解得12 k≤.(2)依题意，得x1＋x2＝2(k－1)，x1x2＝k2.以下分两种情况讨论：①当x1＋x2≥0时，则有x1＋x2＝x1x2－1，即2(k－1)＝k2－1，解得k1＝k2＝1.因为12k≤，所以k1＝k2＝1不合题意，舍去．②x1＋x2＜0时，则有x1＋x2＝－(x1x2－1)，即2(k－1)＝－(k2－1)．解得k1＝1，k2＝－3.因为12k≤，所以k＝－3.综合①②可得k＝－3.16．解：由2m 2－5m －1＝0知m ≠0. 因为m ≠n ，所以11m n ≠. 所以21520m m +-=. 根据21520m m +-=与21520n n +-=的特征，可知1m 与1n 是方程x 2＋5x －2＝0的两个不相等的实数根．所以根据根与系数的关系，得115m n+=-.。