2009年湖南高考数学试题及答案(理数)

合集下载

2009年湖南高考数学文科卷及答案

2009年普通高等学校招生全国统一考试（湖南卷）含答案数学（文史类）一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.2log 的值为【 D 】A ． B.C. 12-D. 122. 抛物线2y =-8x 的焦点坐标是【 B 】A ．（2，0） B. （- 2，0） C. （4，0） D. （- 4，0） 3．设n s 是等差数列｛n a ｝的前n 项和，已知1a =3，5a =11，则7s 等于【 C 】 A ．13 B. 35 C. 49 D. 634．如图1 D ，E ，F 分别是∆ABC 的边AB ，BC ，CA 的中点，则【 A 】A ．AD + BE + CF=0 B ．BD CE DF -+ =0 C ．AD CE CF +- =0D ．BD BE FC --=0 图15．某地政府召集5家企业的负责人开会，其中甲企业有2人到会，其余4家企业各有1人到会，会上有3人发言，则这3人来自3家不同企业的可能情况的种数为【 B 】 A ．14 B. 16 C. 20 D. 486．平面六面体ABCD - 1A 1B 1C 1D 中，既与AB 共面也与1CC 共面的棱的条数为【 C 】 A ．3 B. 4 C.5 D. 67．若函数y=f(x)导函数在区间［a,b ］是增函数，则函数y=f(x)在区间［a,b ］上的图象可能是（A ）8. 设函数()y f x =在(,)-∞+∞内有定义，对于给定的正数K ，定义函数{(),(),()()f x f x k k k f x kf x ≤>=取函数()2xf x -=。

当K =12时，函数()k f x 的单调递增区间为【C 】 A (,0)-∞ B (0,)+∞ C (,1)-∞- D (1,)+∞二填空题：本大题共七小题，没小题5分，共35分，把答案填在答题卡中对应题号后的横线上。

2009年全国高考理科数学试题及答案-湖南卷

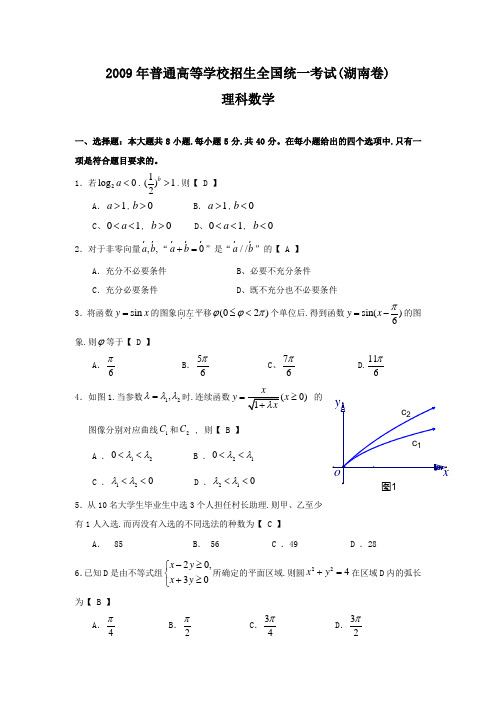
2009年普通高等学校招生全国统一考试(湖南卷)理科数学一、选择题：本大题共8小题.每小题5分.共40分。

在每小题给出的四个选项中.只有一项是符合题目要求的。

1．若2log 0a <.1()12b>.则【 D 】A ．1a >,0b >B ．1a >,0b <C 、01a <<, 0b >D 、01a <<, 0b <2．对于非零向量,,a b “0a b +=”是“//a b ”的【 A 】A ．充分不必要条件 B 、必要不充分条件C ．充分必要条件 D 、既不充分也不必要条件3．将函数sin y x =的图象向左．．平移(02)ϕϕπ≤<个单位后.得到函数sin()6y x π=-的图象.则ϕ等于【 D 】A ．6π B ．56π C 、76π D.116π4．如图1.当参数12,λλλ=时.连续函数0)y x =≥ 的图像分别对应曲线1C 和2C , 则【 B 】A ．120λλ<< B ．210λλ<<C ．120λλ<<D ．210λλ<<5．从10名大学生毕业生中选3个人担任村长助理.则甲、乙至少有1人入选.而丙没有入选的不同选法的种数为【 C 】A ． 85 B ． 56 C ．49 D ．286．已知D 是由不等式组20,30x y x y -≥⎧⎨+≥⎩所确定的平面区域.则圆224x y +=在区域D 内的弧长为【 B 】A ．4π B ．2π C ．34π D ．32π1 7．正方体1111ABCD A BC D-的棱上到异面直线AB.C1C的距离相等的点的个数为【 C 】A．2 B．3 C． 4 D．58．设函数()y f x=在(,)-∞+∞内有定义.对于给定的正数K.定义函数(),(),(),().Kf x f x Kf xK f x K≤⎧=⎨>⎩取函数()f x=2xx e---。

2009年湖南高考数学试题及答案(理数)

2009年湖南高考数学试题及答案数学（理科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若2log 0a <, 1()12b >, 则A ．1a >，0b >B ．1a >，0b <C ．01a <<，0b >D ．01a <<，0b < 【D 】2．对于非零向量a , b , “+=0a b ”是“a b ∥”的 A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【A 】3．将函数sin y x =的图象向左．．平移ϕ(02<π)ϕ≤个单位后，得到函数sin ()6y x π=-的图象，则ϕ等于 A ．6πB ．65πC ．67πD ．611π 【D 】4．如图1，当参数λ1λ=, 2λ时，连续函数y =(0)x ≥的图象分别对应曲线1C 和2C ，则 A ．120λλ<<B ．210λλ<<C ．120λλ<<D ．210λλ<<【B 】 5．从10名大学毕业生中选3人担任村长助理，则甲、乙至少有1人入选，而丙没有入选的不同选法的种数为 A ．85B ．56C ．49D ．28 【C 】 6．已知D 是由不等式组20,30x y x y -⎧⎨+⎩≥≥所确定的平面区域，则圆224x y +=在区域D 内的弧长为A ．4πB ．2πC ．43πD ．23π 【B 】7．正方体1111ABCD A B C D -的棱上到异面直线AB , 1CC 的距离相等的点的个数为 A ．2 B ．3 C ．4 D ．5 【C 】 8．设函数()y f x =在(,-+)∞∞内有定义．对于给定的正数K , 定义函数图1取函数()2e x f x x -=--．若对任意的(,)x ∈-+∞∞，恒有()()K f x f x =，则A ．K 的最大值为2B ．K 的最小值为2C ．K 的最大值为1D ．K 的最小值为1 【D 】二、填空题：本大题共7小题，每小题5分，共35分. 把答案填在答题卡．．．中对应题号后的横线上．9．某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为 12 ． 10．在333(1)(1)(1x +++++的展开式中，x 的系数为 7 （用数字作答）．11．若(0,)x π∈2，则2tan tan ()x x π+-212. 已知以双曲线C 的两个焦点及虚轴的两个端点为顶点的四边形，其中一个内角为60°，则双曲线C 的离心率为6/213．一个总体分为A , B 两层，其个体数之比为4:1, 用分层抽样方法从总体中抽取一个容量为10的样本．已知B 层中甲、乙都被抽到的概率为128, 则总体中的个体数为 40 ．14．在半径为13的球面上有A , B , C 三点，6A B =, 8B C =, 10C A =, 则（1）球心到平面ABC 的距离为 12 ；（2）过A , B 两点的大圆面与平面ABC 所成二面角（锐角）的正切值为 3 ． 15．将正ABC ∆分割成2n （2n ≥, n *∈N ）个全等的小正三角形（图2, 图3分别给出了2n =,3的情形），在每个三角形的顶点各放置一个数，使位于ABC∆的三边及平行于某边的任一直线上的数（当数的个数不少于3时）都分别依次成等差数列．若顶点A , B , C 处的三个数互不相同且和为1，记所有顶点上的数之和为()f n , 则有(2)2f =, (3)f = , … , ()f n = ． 1031(1)(2)6n n ++(),(),(),().K f x f x K f x K f x K ⎧=⎨>⎩≤B C AB AC 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．（本小题满分12分）在ABC ∆中，已知22|||3AB AC AB AC BC ⋅=⋅= , 求角A , B , C 的大小.解设BC a =，AC b =，AB c =．由2|||AB AC AB AC ⋅=⋅得2cos bc A =，所以cos A =．又(0,A ∈π)，因此6A π=．2|||3AB AC BC ⋅= 得2bc =．于是2sin sin C B A ⋅==所以5sin sin ()6C C π⋅-=，1sin (cos )2C C C ⋅+=，因此22sin cos C C C ⋅+=，sin 220C C -=，即sin (2)03C π-=．由6A π=知506C π<<，所以42333C πππ-<-<，从而203C π-=，或23C π-=π．即6C π=，或23C π=．故6A π=，23B π=，6C π=，或6A π=，6B π=，23C π=．17．（本小题满分12分）为拉动经济增长，某市决定新建一批重点工程，分为基础设施工程、民生工程和产业建设工程三类. 这三类工程所含项目的个数分别占总数的12, 13, 16. 现有3名工人独立地从中任选一个项目参与建设.(Ⅰ) 求他们选择的项目所属类别互不相同的概率；(Ⅱ) 记ξ为3人中选择的项目属于基础设施工程或产业建设工程的人数，求ξ的分布列及数学期望.解记第i 名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件i A ，i B ，i C ，1i =，2，3．由题意知1A ，2A ，3A 相互独立，1B ，2B ，3B 相互独立，1C ，2C ，3C 相互独立，i A ，j B ，k C （i ，j ，k =1，2，3，且i ，j ，k 互不相同）相互独立，且1()2i P A =，1()3i P B =，1()6i P C =．C ACA图2图3ACA 1B 1C 1DE （Ⅰ）他们选择的项目所属类别互不相同的概率P =1231233!()6()()()P A B C P A P B P C = ．（Ⅱ）解法1 设3名工人中选择的项目属于民生工程的人数为η，由已知，1(3,)3B η ，且3=-ξη，所以 33311(0)(3)C ()327P P ξh =====， 223122(1)(2)C ()()339P P ξh =====， 123124(2)(1)C ()()339P P ξh =====，03328(3)(0)C ()327P P ξh =====．故ξ的分布列是ξ的数学期望124801232279927E ξ=⨯+⨯+⨯+⨯=．解法2 记第i 名工人选择的项目属于基础设施工程或产业建设工程分别为事件i D ，1i =，2，3．由已知，1D ，2D ，3D 相互独立，且()()()()i i i i i P D P A C P A P C =+=+112263=+=,所以2(3,)3B ξ ，即3321()C ()()33k k kP k ξ-==，k =0，1，2，3．故ξ的分布列是ξ的数学期望2323E =⨯=ξ．18．（本小题满分12分）如图4，在正三棱柱111ABC A B C -中, 1A B A =, 点D 是11A B 的中点，点E 在11A C 上，且DE AE ⊥.(Ⅰ) 证明：平面ADE ⊥平面11ACC A ；(Ⅱ) 求直线AD 和平面1ABC 所成角的正弦值. 图4解（Ⅰ）如图所示，由正三棱柱111ABC A B C -的性质知 1AA ⊥平面111A B C ．又D E ⊂平面111A B C ，所以1DE AA ⊥．111162366=⨯⨯⨯=而DE AE ⊥，1AA AE A = ，所以DE ⊥平面11ACC A ．又D E ⊂平面AD E ，故平面ADE ⊥平面11ACC A ．（Ⅱ）解法1 如图所示，设F 是AB 的中点，连结D F ，1D C ，1C F ．由正三棱柱111ABC A B C -的性质及D 是11A B 的中点知，111A B C D ⊥，11A B DF ⊥．又1C D DF D = ，所以11A B ⊥平面1C DF ．而AB 11//A B ，所以AB ⊥平面1C DF ．又AB ⊂平面1ABC ，故平面1ABC ⊥平面1C DF ．过点D 作D H 垂直1C F 于点H ，则DH ⊥平面1ABC．连结AH ，则HAD ∠是直线AD 和平面1ABC 所成的角. 由已知1AB =，不妨设1AA =2AB =，DF =1D C =，1C F =，AD ==，11D F D C D H C F⋅===所以 sin DH HAD AD ∠==. 即直线AD 和平面1ABC .解法2 如图所示，设O 是A C 的中点，以O 为原点建立空间直角坐标系. 不妨设1AA =，则2AB =，相关各点的坐标分别是(0,1,0)A -， (,0,0)B ，1(0,1,C ，1(,,2D -. 易知 (,1,0)AB =，1(0,2,)AC =，1(,,AD =.设平面1ABC 的一个法向量为 (,,)x y z =n 10,20.AB y AC y ⎧⋅=+=⎪⎨⋅=+=⎪⎩n n 解得x y =-，z =-.故可取 (1,-n =. 所以，cos,||||A DA DA D ⋅===⋅ n n n 由此即知，直线AD 和平面1ABC 519．（本小题满分13分）某地建一座桥，两端的桥墩已建好，这两墩相距m 米. 余下工程只需建两端桥墩之间的桥HFE DC 1B 1A 1CBAyx面和桥墩. 经测算，一个桥墩的工程费用为256万元；距离为x 米的相邻两墩之间的桥面工程费用为(2)x+万元. 假设桥墩等距离分布，所有桥墩都视为点，且不考虑其它因素.记余下工程的费用为y 万元. (Ⅰ) 试写出y 关于x 的函数关系式；(Ⅱ) 当640m =米时，需新建多少个桥墩才能使y 最小？解（Ⅰ）设需新建n 个桥墩，则 (1)n x m +=，即 1m n x=-，所以()256(1)(2y f x n n x ==+++256(1)(2m m xx x=-++2562256mm x=++-．（Ⅱ）由（Ⅰ）知，1222561()2m f x mx x-=-+′322(512)2m x x=-．令()0f x =′，得 32512x =，所以 64x =．当064x <<时，()0f x <′，()f x 在区间(0,64 )内为减函数；当64640x <<时，()0f x >′，()f x 在区间(64,640 )内为增函数．所以()f x 在64x =处取得最小值．此时 64011964m n x=-=-=．故需新建9个桥墩才能使y 最小．20．（本小题满分13分）在平面直角坐标系xOy 中，点P 到点(3,0)F 的距离的4倍与它到直线2x =的距离的3倍之和记为d . 当点P 运动时，d 恒等于点P 的横坐标与18之和. (Ⅰ) 求点P 的轨迹C ；(Ⅱ) 设过点F 的直线l 与轨迹C 相交于M , N 两点，求线段M N 长度的最大值. 解（Ⅰ）设点P 的坐标为(,)x y ，则3|2|d x =+-．由题设，18d x =+，即3|2|18x x -=+． ……① 当2x >时得，……②化简得．当2x ≤时，由①得3x +，……③化简得 212y x =．162x -2213627y x +=y故点P 的轨迹C 是由椭圆1C ：2213627y x +=在直线2x =的右侧部分与抛物线2C ：212y x =在直线2x =的左侧部分（包括它与直线2x =的交点）所组成的曲线，参见图1．（Ⅱ）如图2所示，易知直线2x =与1C ，2C的交点都是(2,)A ，(2,B -，直线AF ，BF 的斜率分别为AF k=-，BF k = 当点P 在1C 上时，由②知1||62PF x=-． ……④当点P 在2C 上时，由③知||3PF x =+． ……⑤若直线l 的斜率k 存在，则直线l 的方程为 (3)y k x =-．（ⅰ）当AF k k ≤，或BF k k ≥，即k-≤，或k ≥时，直线l 与轨迹C 的两个交点11(,)M x y ，22(,)N x y 都在1C 上，此时由④知11||62M F x =-，21||62N F x =-，从而 1211||||||(6)(6)22M N M F N F x x =+=-+-12112()2x x =-+．由22(3)13627y k x y x =-⎧⎪⎨+=⎪⎩，得 2222(34)24361080k x k x k +-+-=．则1x ，2x 是这个方程的两根，所以21222434k x x k +=+，||MN 12112()2x x =-+22121234k k=-+．因为当k-≤k ≥时，224k ≥，所以222121001212||1212123311344424k M N kk=-=--=+++≤．当且仅当k =±（ⅱ）当AF BF k k k <<，即k -<<，直线l 与轨迹C 的两个交点图2yxAMEB2x =NOF2x =11(,)M x y ，22(,)N x y 分别在1C ，2C 上，不妨设点M 在1C 上，点N 在2C 上，则由④，⑤知，11||62M F x =-，2||3NF x =+．设直线AF 与椭圆1C 的另一交点为00(,)E x y ，则01x x <，22x <．1011||66||22M F x x EF =-<-=，2||332||NF x AF =+<+=，所以||||||||||||MN MF NF EF AF AE =+<+=．而点A ，E 都在1C 上，且AE k =-，由（ⅰ）知100||11AE =，所以 100||11M N <．若直线l 的斜率不存在，则123x x ==，此时121001||12(9211M N x x =-+<）=．综上所述，线段M N 长度的最大值为10011．21．（本小题满分13分）对于数列{}n u , 若存在常数0M >, 对任意的n *∈N , 恒有1121||||||n n n n u u u u u u +--+-++- M≤,则称数列{}n u 为B -数列.(Ⅰ) 首项为1, 公比为q (||1)q <的等比数列是否为B -数列？请说明理由； (Ⅱ) 设n S 是数列{}n x 的前n 项和. 给出下列两组论断：A 组：① 数列{}n x 是B -数列， ② 数列{}n x 不是B -数列； B组：③ 数列{}n S 是B -数列， ④ 数列{}n S 不是B -数列.请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题. 判断所给命题的真假，并证明你的结论；(Ⅲ) 若数列{}n a , {}n b 都是B -数列，证明：数列{}n n a b 也是B -数列. 解（Ⅰ）设满足题设的等比数列为{}n a ，则1n n a q -=．于是1221|||||||1|n n n n n a a qqq q -----=-=-，2n ≥．因此 211121|||||||1|(1||||||)n n n n n a a a a a a q q q q -+--+-++-=-++++ ．因为||1q <，所以 211||11||||||1||1||nn q q q q q q --++++=<-- ．即1121|1|||||||1||n n n n q a a a a a a q +---+-++-<- ．故首项为1，公比为(||1)q q <的等比数列是B -数列．（Ⅱ）命题1：若数列{}n x 是B -数列, 则数列{}n S 是B -数列．此命题为假命题．事实上，设1n x =，*n ∈N ，易知数列{}n x 是B -数列．但n S n =，1121||||||n n n n S S S S S S n+--+-++-= ．由n 的任意性知，数列{}n S 不是B -数列．命题2：若数列{}n S 是B -数列，则数列{}n x 是B -数列．此命题为真命题．事实上，因为数列{}n S 是B -数列，所以存在正数M ，对任意的*n ∈N ，有1121||||||n n n n S S S S S S M+--+-++- ≤，即 12||||||n n x x x M ++++ ≤．于是1121||||||n n n n x x x x x x +--+-++-1121||2||2||2||||n n n x x x x x +-+++++ ≤12||M x +≤，所以数列{}n x 是B -数列．（注：按题中要求组成其它命题解答时，仿上述解法）（Ⅲ）若数列{}n a ， {}n b 是B -数列, 则存在正数1M ，2M , 对任意的*n ∈N , 有11211||||||n n n n a a a a a a M +--+-++- ≤； 11212||||||n n n n b b b b b b M +--+-++- ≤．注意到 112211||||n n n n n a a a a a a a a ---=-+-++-+112211||||||||n n n n a a a a a a a ----+-++-+ ≤11||M a +≤.同理，21||||n b M b +≤.记111||K M a =+，221||K M b =+，则有111111||||n n n n n n n n n n n n a b a b a b a b a b a b ++++++-=-+-1112111||||||||||||n n n n n n n n n n b a a a b b K a a K b b +++++-+--+-≤≤.因此 11112211||||||n n n n n n n n a b a b a b a b a b a b ++---+-++-21121(||||||)n n n n K a a a a a a +--+-++- ≤+11121(||||||)n n n n K b b b b b b +--+-++- 2112K M K M +≤.故数列{}n n a b 是B -数列.。

2009年全国高考文科数学试题及答案-湖南卷

2009年普通高等学校招生全国统一考试（湖南卷）含答案数学（文史类）一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.2log 的值为【 D 】A ． B.C. 12-D. 122. 抛物线2y =-8x 的焦点坐标是【 B 】A ．（2，0） B. （- 2，0） C. （4，0） D. （- 4，0） 3．设n s 是等差数列｛n a ｝的前n 项和，已知1a =3，5a =11，则7s 等于【 C 】 A ．13 B. 35 C. 49 D. 634．如图1 D ，E ，F 分别是∆ABC 的边AB ，BC ，CA 的中点，则【 A 】A ．AD + BE + CF =0B ．BD CE DF -+=0C ．AD CE CF +-=0D ．BD BE FC --=0 图15．某地政府召集5家企业的负责人开会，其中甲企业有2人到会，其余4家企业各有1人到会，会上有3人发言，则这3人来自3家不同企业的可能情况的种数为【 B 】 A ．14 B. 16 C. 20 D. 486．平面六面体ABCD - 1A 1B 1C 1D 中，既与AB 共面也与1CC 共面的棱的条数为【 C 】 A ．3 B. 4 C.5 D. 67．若函数y=f(x)导函数在区间［a,b ］是增函数，则函数y=f(x)在区间［a,b ］上的图象可能是（A ）8. 设函数()y f x =在(,)-∞+∞内有定义，对于给定的正数K ，定义函数{(),(),()()f x f x kk k f x kf x ≤>=取函数()2xf x -=。

2009年湖南省高考数学试卷(理科)答案与解析

2009年湖南省高考数学试卷（理科）参考答案与试题解析一、选择题（共8小题，每小题5分，满分40分）1．（5分）（2009•湖南）若log2a＜0，＞1，则（）A．a＞1，b＞0 B．0＜a＜1，b＞0 C．a＞1，b＜0 D．0＜a＜1，b＜0【考点】对数函数的单调区间．【分析】根据指数函数与对数函数的图象和单调性直接解出a，b即可．【解答】解：依题意，根据指数函数与对数函数的图象和单调性知0＜a＜1，b＜0，故选D【点评】本题考查利用指对函数的图象或单调性解不等式，属基本题．2．（5分）（2009•湖南）对于非0向量，“”是“”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件【考点】向量的共线定理；充要条件．【专题】常规题型．【分析】利用向量垂直的充要条件，得到由前者推出后者；通过举反例得到后者推不出前者；利用充要条件的定义得到选项．【解答】解：∵⇒⇒反之，推不出，例如满足两个向量平行但得到所以是的充分不必要条件故选A【点评】本题考查向量共线的充要条件、考查说明一个命题不成立只要举一个反例即可、考查条件判断条件的方法．3．（5分）（2009•湖南）将函数y=sinx的图象向左平移φ（0≤φ＜2π）个单位后，得到函数y=sin（x﹣）的图象，则φ等于（）A．B．C．D．【考点】函数y=Asin（ωx+φ）的图象变换．【专题】计算题．【分析】先根据图象变换得到平移后的函数y=sin（x+φ），然后结合诱导公式可得到sin（x+π）=sin（x﹣），进而可确定答案．【解答】解：将函数y=sinx向左平移φ（0≤φ＜2π）个单位得到函数y=sin（x+φ）．根据诱导公式知当φ=π时有：y=sin（x+π）=sin（x﹣）．故选D．【点评】本题主要考查图象变换和诱导公式的应用．考查对基础知识的综合运用．4．（5分）（2009•湖南）如图，当参数λ分别取λ1，λ2时，函数y=（x≥0）的部份图象分别对应曲线C1和C2，则（）A．0＜λ1＜λ2B．0＜λ2＜λ1 C．λ1＜λ2＜0 D．λ2＜λ1＜0【考点】函数的图象．【专题】数形结合．【分析】根据图象先判定λ的正负，然后利用图象的高低列出不等式即可．【解答】解：∵曲线C1和C2在第一象限且成递增趋势取点（2x，f（2x）与（0，f（0），连接之后，取其中点（x，[f（2x）+f（0）]/2），根据图象（凸函数）可知，这个中点的纵坐标是小于f（x）（即点（x，f（x））的，由此，[f（2x）+f（0）]/2＜f（x），因为x＞=0，可解得λ＞0，∴λ1，λ2均大于0根据图象有＞∴1+λ1x＜1+λ2x∴λ1x＜λ2x∵x≥0∴0＜λ1＜λ2故选A．【点评】本题考查了根据图象列出不等式的知识，做题时注意分式不等式中分母的关系．5．（5分）（2009•湖南）从10名大学生毕业生中选3个人担任村长助理，则甲、乙至少有1人入选，而丙没有入选的不同选法的种数位（）A．85 B．56 C．49 D．28【考点】排列、组合的实际应用．【专题】计算题；分类讨论．【分析】由题意知丙没有入选，只要把丙去掉，把总的元素个数变为9个，甲、乙至少有1人入选，包括甲乙两人只选一个的选法和甲乙都选的选法两种情况，根据分类计数原理得到结果．【解答】解：∵丙没有入选，∴只要把丙去掉，把总的元素个数变为9个，∵甲、乙至少有1人入选，∴由条件可分为两类：一类是甲乙两人只选一个的选法有：C21•C72=42，另一类是甲乙都选的选法有C22•C71=7，根据分类计数原理知共有42+7=49，故选C．【点评】本题考查分类加法，在题目中有三个元素有限制条件，解题时先安排有限制条件的元素排列，在安排没有限制条件的元素，注意做到不重不漏．6．（5分）（2009•湖南）已知D是由不等式组，所确定的平面区域，则圆x2+y2=4在区域D内的弧长为（）A．B．C．D．【考点】二元一次不等式（组）与平面区域；弧长公式．【专题】图表型；数形结合；转化思想．【分析】先依据不等式组，结合二元一次不等式（组）与平面区域的关系画出其表示的平面区域，再利用圆的方程画出图形，最后利用弧长公式计算即可．【解答】解：如图阴影部分表示，确定的平面区域，所以劣弧的弧长即为所求．∵k OB=﹣，k OA=，∴tan∠BOA=||=1，∴∠BOA=．∴劣弧AB的长度为2×=．故选B．【点评】本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．7．（5分）（2009•湖南）正方体ABCD﹣A1B1C1D1的棱上到异面直线AB，CC1的距离相等的点的个数为（）A．2 B．3 C．4 D．5【考点】简单组合体的结构特征；点、线、面间的距离计算．【专题】计算题；压轴题；数学模型法．【分析】画出正方体，结合正方体中线面、线线垂直，先找定点、再找棱的中点，找出符合条件的所有的点．【解答】解：如图：正方体ABCD﹣A1B1C1D1，E、F分别是BC和A1D1的中点，连接AF 和FC1，根据正方体的性质知，BB1⊥AB，C1C⊥B1C1，故B1到异面直线AB，CC1的距离相等，同理可得，D到异面直线AB，CC1的距离相等，又有AB⊥BC，C1C⊥BC，故E到异面直线AB，CC1的距离相等，F 为A1D1的中点，易计算FA=FC1，故F到异面直线AB，CC1的距离相等，共有4个点．故选C．【点评】本题考查了正方体体的结构特征，考查了线面、线线垂直定理的应用，利用异面直线之间距离的定义进行判断，考查了观察能力和空间想象能力．8．（5分）（2009•湖南）设函数y=f（x）在（﹣∞，+∞）内有定义．对于给定的正数K，定义函数，取函数f（x）=2﹣x﹣e﹣x．若对任意的x∈（+∞，﹣∞），恒有f k（x）=f（x），则（）A．K的最大值为2 B．K的最小值为2 C．K的最大值为1 D．K的最小值为1 【考点】函数恒成立问题．【专题】计算题；压轴题；转化思想．【分析】根据新定义的函数建立f k（x）与f（x）之间的关系，通过二者相等得出实数k满足的条件，利用导数或者函数函数的单调性求解函数的最值，进而求出k的范围，进一步得出所要的结果．【解答】解：由题意可得出k≥f（x）最大值，由于f′（x）=﹣1+e﹣x，令f′（x）=0，e﹣x=1=e0解出﹣x=0，即x=0，当x＞0时，f′（x）＜0，f（x）单调递减，当x＜0时，f′（x）＞0，f（x）单调递增．故当x=0时，f（x）取到最大值f（0）=2﹣1=1．故当k≥1时，恒有f k（x）=f（x）．因此K的最小值是1．故选D．【点评】本题考查学生对新定义型问题的理解和掌握程度，理解好新定义的分段函数是解决本题的关键，将所求解的问题转化为求解函数的最值问题，利用了导数的工具作用，体现了恒成立问题的解题思想．二、填空题（共7小题，每小题5分，满分35分）9．（5分）（2009•湖南）某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为12．【考点】交、并、补集的混合运算．【专题】应用题；集合．【分析】设两者都喜欢的人数为x人，则只喜爱篮球的有（15﹣x）人，只喜爱乒乓球的有（10﹣x）人，由此可得（15﹣x）+（10﹣x）+x+8=30，解之即可两者都喜欢的人数，然后即可得出喜爱篮球运动但不喜爱乒乓球运动的人数．【解答】解：设两者都喜欢的人数为x人，则只喜爱篮球的有（15﹣x）人，只喜爱乒乓球的有（10﹣x）人，由此可得（15﹣x）+（10﹣x）+x+8=30，解得x=3，所以15﹣x=12，即所求人数为12人，故答案为：12．【点评】本题考查了集合的混合运算，属于应用题，关键是运用集合的知识求解实际问题．10．（5分）（2009•湖南）在（1+x）3+（1+）3+（1+）3的展开式中，x的系数为7（用数字作答）．【考点】二项式系数的性质．【分析】展开式中x的系数是二项式（1+x）3，，的展开式的x的系数和，再利用二项展开式的通项公式求出各二项展开式的x的系数．【解答】解：C31+C32+C33=23﹣1=7．故答案为7【点评】本题考查二项展开式的通项公式解决二项展开式的特定项问题．11．（5分）（2009•湖南）若x∈（0，）则2tanx+tan（﹣x）的最小值为2．【考点】基本不等式在最值问题中的应用．【专题】计算题．【分析】先利用诱导公式把tan（﹣x）转化成，然后根据x的范围判断出tanx＞0，利用基本不等式求得其最小值．【解答】解：2tanx+tan（﹣x）=2tanx+∵x∈（0，），∴tanx＞0，∴2tanx+≥2=2（当且仅当tanx=时，等号成立）故答案为：2．【点评】本题主要考查了基本不等式在最值问题中的应用．解题过程中注意等号成立的条件．12．（5分）（2009•湖南）已知以双曲线C的两个焦点及虚轴的两个端点为原点的四边形中，有一个内角为60°，则双曲线C的离心率为．【考点】双曲线的简单性质．【专题】计算题．【分析】根据题设条件，先设∠B2F1B1=60°，求出双曲线的离心率．再设∠F1B2F2=60°，求出双曲线的离心率．解题的同时要进行验根，避免出现不必要的错误．【解答】解：设双曲线C的焦点坐标是F1和F2，虚轴两个端点是B1和B2，则四边形F1B1F2B2为菱形．若∠B2F1B1=60°，则∠B2F1F2=30°．由勾股定理可知c=b．∴，故双曲线C的离心率为．若∠F1B2F2=60°，则∠F1B2B1=30°，由勾股定理可知b=c，不满足c＞b，所以不成立．综上所述，双曲线C的离心率为．答案：．【点评】解题时应该分∠B2F1B1=60°和∠F1B2F2=60°两种情况求出双曲线的离心率．解题时要注意a，b，c中c最大．13．（5分）（2009•湖南）一个总体分为A，B两层，其个体数之比为4：1，用分层抽样方法从总体中抽取一个容量为10的样本，已知B层中甲、乙都被抽到的概率为，则总体中的个体数是40．【考点】分层抽样方法；等可能事件的概率．【分析】设出B层中的个体数，根据条件中所给的B层中甲、乙都被抽到的概率值，写出甲和乙都被抽到的概率，使它等于，算出n的值，由已知A和B之间的比值，得到总体中的个体数．【解答】解：设B层中有n个个体，∵B层中甲、乙都被抽到的概率为，∴=，∴n2﹣n﹣56=0，∴n=﹣7（舍去），n=8，∵总体分为A，B两层，其个体数之比为4：1∴共有个体（4+1）×8=40故答案为：40．【点评】本题是分层抽样的相关知识．容易出错的是不理解分层抽样的含义或与其它混淆．抽样方法是数学中的一个小知识点，但一般不难，故也是一个重要的得分点，不容错过．14．（5分）（2009•湖南）在半径为13的球面上有A，B，C 三点，AB=6，BC=8，CA=10，则（1）球心到平面ABC的距离为12；（2）过A，B两点的大圆面与平面ABC所成二面角为（锐角）的正切值为3．【考点】球内接多面体．【专题】计算题；压轴题．【分析】（1）由题意说明△ABC是直角三角形，平面ABC是小圆，圆心在AC的中点，利用勾股定理直接求出球心到平面ABC的距离．（2）如图作出过A，B两点的大圆面与平面ABC所成二面角，直接求出它的正切值即可．【解答】解：（1）AB=6，BC=8，CA=10，△ABC是直角三角形，平面ABC是小圆，圆心在AC的中点D，AO=13，AD=5，球心到圆心的距离就是球心到平面ABC的距离，即：OD=12（2）过D作DE垂直AB于E，连接OE则∠OED就是过A，B两点的大圆面与平面ABC 所成二面角．易得DE=4所以tan∠OED==3故答案为：（1）12；（2）3．【点评】本题是基础题，考查球的截面问题，二面角的求法，考查空间想象能力，计算能力，能够正确作出图形是解好本题个前提，也是空间想象能力的具体体现．15．（5分）（2009•湖南）将正△ABC分割成n2（n≥2，n∈N）个全等的小正三角形（图1，图2分别给出了n=2，3的情形），在每个三角形的顶点各放置一个数，使位于△ABC的三边及平行于某边的任一直线上的数（当数的个数不少于3时）都分别依次成等差数列，若顶点A，B，C处的三个数互不相同且和为1，记所有顶点上的数之和为f（n），则有f（2）=2，f（3）=…，f（n）=．【考点】数列的应用．【专题】应用题；压轴题．【分析】根据等差中项法分别求解n=2，3，4时的值，由此归纳出f（n）的值即可．【解答】解：由题意可得，（各点放的数用该点的坐标表示）当n=2时，根据等差数列的性质可得，A+B=2D，A+C=2E，B+C=2F，且A+B+C=12（D+E+F）=2（A+B+C）=2，D+E+F=1∴f（2）=2=当n=3时，根据等差数列的性质可得，A+B=D+E，A+C=I+H，B+C=F+G，且A+B+C=1从而可得D+E+H+I+F+F=2（A+B+C）=2同样根据等差中项可得，M的数为∴f（3）=3+==同理可得，f（4）=5=f（n）=故答案为：，【点评】本题目主要考查了数列的通项公式的求解在实际问题中的应用，解题的关键是灵活利用等差中项，进行求解．考查了考试发现问题、解决问题的能力．三、解答题（共6小题，满分75分）16．（12分）（2009•湖南）在△ABC，已知2=32，求角A，B，C的大小．【考点】平面向量数量积的运算；余弦定理的应用．【分析】先用向量的数量积求出角A，再用三角形的内角和为180°得出角B，C的关系，用三角函数的诱导公式解之．【解答】解：设BC=a，AC=b，AB=c由2得2abcocA=bc所以cosA=又A∈（0，π）因此A=由=32得bc=；于是sinCsinB==所以sinCsin（）=，∴即sin（2C﹣）=0∵∴∴∴故A=或【点评】考查向量的数量积及三角函数的诱导公式．向量与三角结合是高考常见题型．17．（12分）（2009•湖南）为拉动经济增长，某市决定新建一批重点工程，分别为基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目的个数分别占总数的，，，现在3名工人独立地从中任选一个项目参与建设，选择哪个工程是随机的．（I）求他们选择的项目所属类别互不相同的概率；（II）记X为3人中选择的项目属于基础设施工程的人数，求X的分布列及数学期望．【考点】离散型随机变量及其分布列；相互独立事件的概率乘法公式．【专题】计算题．【分析】（I）由题意知3名工人独立地从中任选一个项目参与建设，根据三类工程的概率和相互独立事件同时发生的概率，写出他们选择的项目所属类别互不相同的概率．（II）由题意知X为3人中选择的项目属于基础设施工程的人数，X的取值为：0，1，2，3．结合变量对应的事件，写出事件的概率，写出分布列和期望．【解答】解：（I）3名工人独立地从中任选一个项目参与建设设一次选择基础设施工程、民生工程和产业建设工程依次为事件A、B、C．则，他们选择的项目所属类别互不相同的概率是：（II）由题意知X为3人中选择的项目属于基础设施工程的人数，X的取值为：0，1，2，3．P（X=0）=；；；．∴X的分布列为：X 0 1 2 3P∴．【点评】本题考查离散型随机变量的分布列和期望，考查相互独立事件同时发生的概率，是一个综合题，注意规范答题，这是一个送分的题目．18．（12分）（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=AA1，点D是A1B1的中点，点E在A1C1上，且DE⊥AE．（1）证明：平面ADE⊥平面ACC1A1；（2）求直线AD和平面ABC1所成角的正弦值．【考点】平面与平面垂直的判定；直线与平面所成的角．【专题】计算题；证明题．【分析】（1）先由正三棱柱ABC﹣A1B1C1的性质知AA1⊥平面A1B1C1，⇒DE⊥AA1．再由DE⊥AE⇒DE⊥平面ACC1A1．即可得出结论；（2）设O是AC的中点．先建立一个以O为原点建立空间直角坐标系，得到相关各点的坐标．再利用线面角的求法在空间直角坐标系内找到直线AD和平面ABC1所成角的正弦值即可．【解答】解：（1）证明：如图所示，由正三棱柱ABC﹣A1B1C1的性质知AA1⊥平面A1B1C1．又DE⊂平面A1B1C1，所以DE⊥AA1．而DE⊥AE．AA1∩AE=A，所以DE⊥平面ACC1A1．又DE⊂平面ADE，故平面ADE⊥平面ACC1A1．（2）如图所求，设O是AC的中点，以O为原点建立空间直角坐标系，不妨设AA1=，则AB=2，相关各点的坐标分别是A（0，﹣1，0），B（，0，0），C1（0，1，），D（，﹣，）．易知=（，1，0），=（0，2，），=（，，）．设=（x，y，z）是平面ABC1的一个法向量，则有解得x=﹣y，z=﹣y．故可取=（1，﹣，）．于是cos＜＞===由此即知，直线AD和平面ABC1所成角的正弦值为．【点评】本题考查平面和平面垂直的判定和性质．在证明面面垂直时，其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直19．（13分）（2009•湖南）某地建一座桥，两端的桥墩已建好，这两墩相距m米，余下的工程只需要建两端桥墩之间的桥面和桥墩．经预测一个桥墩的工程费用为256万元，距离为x 米的相邻两墩之间的桥面工程费用为万元．假设桥墩等距离分布，所有桥墩都视为点，且不考虑其他因素，记余下工程的费用为y万元．（Ⅰ）试写出y关于x的函数关系式；（Ⅱ）当m=640米时，需新建多少个桥墩才能使y最小？【考点】根据实际问题选择函数类型；利用导数求闭区间上函数的最值．【专题】应用题．【分析】（Ⅰ）设出相邻桥墩间距x米，需建桥墩个，根据题意余下工程的费用y为桥墩的总费用加上相邻两墩之间的桥面工程总费用即可得到y的解析式；（Ⅱ）把m=640米代入到y的解析式中并求出y′令其等于0，然后讨论函数的增减性判断函数的最小值时m的值代入中求出桥墩个数即可．【解答】解：（Ⅰ）相邻桥墩间距x米，需建桥墩个则（Ⅱ）当m=640米时，y=f（x）=640×（+）+1024f′（x）=640×（﹣+）=640×∵f′（26）=0且x＞26时，f′（x）＞0，f（x）单调递增，0＜x＜26时，f′（x）＜0，f（x）单调递减∴f（x）最小=f（x）极小=f（26）=8704∴需新建桥墩个．【点评】考查学生会根据实际问题选择函数关系的能力，会利用导数研究函数的增减性以及求函数最值的能力．20．（13分）（2009•湖南）在平面直角坐标系xOy中，点P到点F（3，0）的距离的4倍与它到直线x=2的距离的3倍之和记为d，当P点运动时，d恒等于点P的横坐标与18之和（Ⅰ）求点P的轨迹C；（Ⅱ）设过点F的直线I与轨迹C相交于M，N两点，求线段MN长度的最大值．【考点】圆与圆锥曲线的综合．【专题】综合题；压轴题；数形结合．【分析】（1）由题意，要求动点的轨迹方程，由于已经告诉了动点所满足的约束条件所以利用直接法求其轨迹即可：（2）由题意及解析式画出图形，利用直线与曲线的轨迹方程联立，通过图形讨论直线与轨迹的交点，利用两点间的距离公式求解即可．【解答】解（Ⅰ）设点P的坐标为（x，y），由题设则3︳x﹣2︳①由题意轨迹图（1）如下：（图1）当x＞2时，由①得，化简得．当x≤2时由①得化简得y2=12x故点P的轨迹C是椭圆在直线x=2的右侧部分与抛物线C2：y2=12x在直线x=2的左侧部分（包括它与直线x=2的交点）所组成的曲线，参见图1（Ⅱ）如图2所示，易知直线x=2与C1，C2的交点都是A（2，），B（2，），直线AF，BF的斜率分别为k AF=，k BF=．图2当点P在C1上时，由②知．④当点P在C2上时，由③知|PF|=3+x⑤若直线l的斜率k存在，则直线l的方程为y=k（x﹣3）（1）当k≤k AF，或k≥k BF，即k≤﹣2时，直线I与轨迹C的两个交点M（x1，y1），N（，）都在C1上，此时由④知|MF|=6﹣x 1|NF|=6﹣从而|MN|=|MF|+|NF|=（6﹣x 1）+（6﹣）=12﹣（x1+）由得（3+4k2）x2﹣24k2x+36k2﹣108=0则x1，x是这个方程的两根，所以x 1+=*|MN|=12﹣（x1+）=12﹣因为当，或时，k2≥24，．当且仅当时，等号成立．（2）当时，直线L与轨迹C的两个交点M（x1，y1），N（x2，y2）分别在C1，C2上，不妨设点M在C1上，点C2上，则④⑤知，设直线AF与椭圆C1的另一交点为E（x0，y0），则x0＜x1，x2＜2.所以|MN|=|MF|+|NF|＜|EF|+|AF|=|AE|．而点A，E都在C1上，且，有（1）知若直线ι的斜率不存在，则x1=x2=3，此时综上所述，线段MN长度的最大值为．【点评】（1）此问重点考查了直接法求动点的轨迹方程，还考查了对于含绝对值的式子化简时的讨论；（2）此问重点考查了利用图形抓住题目中的信息，分类讨论的思想，还考查了圆锥曲线中的焦半径公式（用点的一个坐标表示），还考查了两点间的距离公式．21．（13分）（2009•湖南）对于数列{u n}若存在常数M＞0，对任意的n∈N'，恒有|u n+1﹣u n|+|u n ﹣u n﹣1|+…+|u2﹣u1|≤M则称数列{u n}为B﹣数列（1）首项为1，公比为q（|q|＜1）的等比数列是否为B﹣数列？请说明理由；（2）设S n是数列{x n}的前n项和，给出下列两组论断；A组：①数列{x n}是B﹣数列②数列{x n}不是B﹣数列B组：③数列{S n}是B﹣数列④数列{S n}不是B﹣数列请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题．判断所给命题的真假，并证明你的结论；（3）若数列{a n}，{b n}都是B﹣数列，证明：数列{a n b n}也是B﹣数列．【考点】数列的应用．【专题】证明题；综合题；压轴题；新定义；开放型．【分析】（1）根据B﹣数列的定义，首项为1，公比为q（|q|＜1）的等比数列，验证|u n+1﹣u n|+|u n﹣u n﹣1|+…+|u2﹣u1|≤M即可；（2）首项写出两个命题，根据B﹣数列的定义加以证明，如果要说明一个命题不正确，则只需举一反例即可；（3）数列{a n}，{b n}都是B﹣数列，则有|a n+1﹣a n|+|a n﹣a n﹣1|+…+|a2﹣a1|≤M1，|b n+1﹣b n|+|b n ﹣a n﹣1|…++|b2﹣b1|≤M2，下面只需验证|a n+1b n+1﹣a n b n|+|a n b n﹣a n﹣1b n﹣1|+…+|a2b2﹣a1b1|≤M．【解答】解（1）设满足题设的等比数列为{a n}，则a n=q n﹣1，于是|a n﹣a n﹣1|=|q n﹣1﹣q n﹣2|=|q|n ﹣2|q﹣1|，n≥2因此|a n+1﹣a n|+|a n﹣a n﹣1|+…+|a2﹣a1|=|q﹣1|（1+|q|+|q|2++|q|n﹣1）．因为|q|＜1，所以1+|q|+|q|2+…+|q|n﹣1=，即|a n+1﹣a n|+|a n﹣a n1|+…+|a2﹣a1|＜故首项为1，公比为q（|q|＜1）的等比数列是B﹣数列．（2）命题1：若数列{x n}是B﹣数列，则数列{S n}是B﹣数列．此命题为假命题．事实上，设x n=1，n∈N•，易知数列{x n}是B﹣数列，但S n=n|S n﹣1﹣S n|+|S n﹣S n+1|+…+|S2﹣S1|=n由n的任意性知，数列{S n}是B﹣数列此命题为假命题．命题2：若数列{S n}是B﹣数列，则数列{x n}是B﹣数列此命题为真命题事实上，因为数列{S n}是B﹣数列，所以存在正数M，对任意的n∈N*，有|S n+1﹣S n|+|S n﹣S n﹣1|+…+|S2﹣S1|≤M即|x n+1|+|x n|+…+|x2|≤M．于是|x n+1﹣x n|+|x n﹣x n﹣1|+…+|x2﹣x1|≤|x n+1|+2|x n|+2|x n﹣1|+…+2|x2|+2|x1|≤2M+|x1|所以数列{x n}是B﹣数列．（3）若数列{a n}{b n}是B﹣数列，则存在正数M1．M2，对任意的n∈N•，有|a n+1﹣a n|+|a n﹣a n﹣1|+…+|a2﹣a1|≤M1，|b n+1﹣b n|+|b n﹣a n﹣1|…++|b2﹣b1|≤M2注意到|a n|=|a n﹣a n﹣1+a n﹣1+a n﹣2+…+a2﹣a1+a1|≤|a n﹣a n﹣1|+|a n﹣1﹣a n﹣2|+…+|a2﹣a1|+|a1|≤M1+|a1|同理：|b n|≤M2+|b1|记K2=M2+|b2|，则有K2=M2+|b2||a n+1b n+1﹣a n b n|=|a n+1b n+1﹣a n b n+1+a n b n+1﹣a n b n|≤|b n+1||a n+1﹣a n|+|a n||b n+1﹣b n|≤K1|a n+1﹣a n|+k1|b n+1﹣b n|因此K1（|b n+1﹣b n|+|b n﹣b n﹣1|+|a2﹣a1|）≤k2M1+k1M2+K1（|b n+1﹣b n|+|b n﹣b n﹣1|+|a2﹣a1|）≤k2M1+k1M2故数列{a n b n}是B﹣数列．【点评】考查学生理解数列概念，灵活运用数列表示法的能力，旨在考查学生的观察分析和归纳能力，特别是问题（2）（3）的设置，增加了题目的难度，综合性较强，属难题．。

2009年全国高考文科数学试题及答案-湖南卷

2009年普通高等学校招生全国统一考试（湖南卷）含答案数学（文史类）一、选择题：本大题共8小题.每小题5分.共40分。

在每小题给出的四个选项中.只有一项是符合题目要求的。

1.2log 的值为【 D 】A ．BC 、12-D 、122、抛物线2y =-8x 的焦点坐标是【 B 】A ．（2.0）B 、（- 2.0）C 、（4.0）D 、（- 4.0） 3．设n s 是等差数列｛n a ｝的前n 项和.已知1a =3.5a =11.则7s 等于【 C 】 A ．13 B 、35 C 、49 D 、634．如图1 D.E.F 分别是∆ABC 的边AB.BC.CA 的中点.则【 A 】A ．AD + BE + CF=0 B ．BD CE DF -+ =0 C ．AD CE CF +- =0D ．BD BE FC --=0 图15．某地政府召集5家企业的负责人开会.其中甲企业有2人到会.其余4家企业各有1人到会.会上有3人发言.则这3人来自3家不同企业的可能情况的种数为【 B 】 A ．14 B 、16 C 、20 D 、486．平面六面体ABCD - 1A 1B 1C 1D中.既与AB 共面也与1CC 共面的棱的条数为【 C 】 A ．3 B 、4 C.5 D 、67．若函数y=f(x)导函数在区间［a,b ］是增函数.则函数y=f(x)在区间［a,b ］上的图象可能是（A ）8、设函数()y f x =在(,)-∞+∞内有定义.对于给定的正数K.定义函数{(),(),()()f x f x kk k f x kf x ≤>=取函数()2xf x -=。

当K =12时.函数()k f x 的单调递增区间为【C 】 A (,0)-∞ B (0,)+∞ C (,1)-∞- D (1,)+∞二填空题：本大题共七小题.没小题5分.共35分.把答案填在答题卡中对应题号后的横线上。

9 、某班共30人.其中15人喜爱篮球运动.10人喜爱乒乓球运动.8人对这两项运都不喜爱.则喜爱篮球运动但不喜爱乒乓球运动的人数为 12 .10、若0x >.则2x x+11、在4(1的展开式中.x 的系数为 6 (用数字作答)。

2009年湖南高考数学试题及答案(理数)

4）基层为柔性防水层时，应加设一道无纺布做隔离层。
（2）做隔离层：
1）在细石混凝土防水层与基层之间设置隔离层，依据设计可采用于干铺无纺布、塑料薄膜或者低强度等级的砂浆，施工时避免钢筋破坏防水层，必要时可在防水层上做砂浆保护层。
2）采用低强度等级的砂浆的隔离层表面应压光，施工后的隔离层应表面平整光洁，厚薄一致，并具有一定的强度。在浇筑细石混凝土前，应做好隔离层成品保护工作，不能踩踏破坏，待隔离层干燥，并具有一定的强度后，细石混凝土防水层方可施工。
（二）操作工艺：
1）刚性防水层的基层宜为整体现浇钢筋混凝土板或找平层，应为结构找坡或找平层找坡，此时为了缓解基层变形对刚性防水层的影响，在基层与防水层之间设隔离层。
2）基层为装配式钢筋混凝土板时，板端缝应先嵌填密封材料处理。
交底人签字：
日期：
附页
3）刚性防水层的基层为保温屋面时，保温屋可兼做隔离层，但保温层必须干燥。
2）钢筋的品种、规格、位置及保护层厚度，必须符合设计要求和规程规定。检验方法：可检查钢筋隐蔽验收记录和观察检查。
3）防水层完工后严禁有渗漏现象。可蓄水30-100㎜高，持续24H观察。
（3）一般项目：
1）细石混凝土防水层的坡度，必须符合排水要求，不积水，可用坡度尺检查或浇水观察。
2）细石混凝土防水层的外观质量应厚度一致、表面平整、压实抹光、无裂缝、起壳、起砂等缺陷。
（二）主要机具：
序号
机具名称
型号
备注
序号
机具名称
型号
备注
1
混凝土搅拌机
J750
6
平板振动器
2
运输小车
7
滚筒
3
铁锹
8
塑料薄膜
4

2009年湖南省高考数学试卷(文科)

2009年湖南省高考数学试卷（文科）一、选择题（共8小题，每小题5分，满分40分）1．（5.00分）（2009•湖南）log2的值为（）A．﹣B．C．﹣ D．2．（5.00分）（2009•湖南）抛物线y2=4x的焦点坐标是（）A．（4，0） B．（2，0） C．（1，0） D．3．（5.00分）（2009•湖南）设S n是等差数列{a n}的前n项和，已知a2=3，a6=11，则S7等于（）A．13 B．35 C．49 D．634．（5.00分）（2009•湖南）如图，D，E，F分别是△ABC的边AB，BC，CA的中点，则（）A．++=B．﹣+=C．+﹣=D．﹣﹣= 5．（5.00分）（2009•湖南）某地政府召集5家企业的负责人开会，已知甲企业有2人到会，其余4家企业各有1人到会，会上有3人发言，则这3人来自3家不同企业的可能情况的种数为（）A．14 B．16 C．20 D．486．（5.00分）（2009•湖南）平行六面体ABCD﹣A1B1C1D1中，既与AB共面也与CC1共面的棱的条数为（）A．3 B．4 C．5 D．67．（5.00分）（2009•湖南）若函数y=f（x）的导函数在区间[a，b]上是增函数，则函数y=f（x）在区间[a，b]上的图象可能是（）A．B．C．D．8．（5.00分）（2009•湖南）设函数=f（x）在（﹣∞，+∞）内有定义，对于给定的正数K，定义函数f K（x）=取函数f（x）=2﹣|x|．当K=时，函数f K（x）的单调递增区间为（）A．（﹣∞，0）B．（0，+∞）C．（﹣∞，﹣1）D．（1，+∞）二、填空题（共7小题，每小题5分，满分35分）9．（5.00分）（2009•湖南）某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为．10．（5.00分）（2009•湖南）若x＞0，则x+的最小值为．11．（5.00分）（2009•湖南）在的展开式中，x的系数为．12．（5.00分）（2009•湖南）一个总体分为A，B两层，用分层抽样方法从总体中抽取一个容量为10的样本．已知B层中每个个体被抽到的概率都为，则总体中的个体数为．13．（5.00分）（2009•湖南）过双曲线C：﹣=1（a＞0，b＞0）的一个焦点作圆x2+y2=a2的两条切线，切点分别为A、B．若∠AOB=120°（O是坐标原点），则双曲线C的离心率为．14．（5.00分）（2009•湖南）在锐角△ABC中，BC=1，B=2A，则的值等于，AC的取值范围为．15．（5.00分）（2009•湖南）如图所示，把两块斜边长相等的直角三角板拼在一起，若=x+y，则x=，y=．三、解答题（共6小题，满分75分）16．（12.00分）（2009•湖南）已知向量=（sinθ，cosθ﹣2sinθ），=（1，2）．（1）若，求tanθ的值；（2）若，求θ的值．17．（12.00分）（2009•湖南）为拉动经济增长，某市决定新建一批重点工程，分别为基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目的个数分别占总数的，，，现在3名工人独立地从中任选一个项目参与建设，选择哪个工程是随机的．（I）求他们选择的项目所属类别互不相同的概率；（II）记X为3人中选择的项目属于基础设施工程的人数，求X的分布列及数学期望．18．（12.00分）（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=，点D是BC的中点，点E在AC上，且DE⊥A1E．（1）证明：平面A1DE⊥平面ACC1A1；（2）求直线AD和平面A1DE所成角的正弦值．19．（13.00分）（2009•湖南）已知函数f（x）=x3+bx2+cx的导函数的图象关于直线x=2对称．（1）求b的值；（2）若f（x）在x=t处取得极小值，记此极小值为g（t），求g（t）的定义域和值域．20．（13.00分）（2009•湖南）已知椭圆C的中心在原点，焦点在x轴上，以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形（记为Q）（1）求椭圆C的方程；（2）设点P是椭圆C的左准线与x轴的交点，过点P的直线l与椭圆C相交于M、N两点，当线段MN的中点落在正方形Q内（包括边界）时，求直线l的斜率的取值范围．21．（13.00分）（2009•湖南）对于数列{u n}若存在常数M＞0，对任意的n∈N+，﹣u n|+|u n﹣u n1|+…+|u2﹣u1|≤M则称数列u n为B﹣数列恒有|u n+1（1）首项为1，公比为的等比数列是否为B﹣数列？请说明理由；（2）设s n是数列{x n}的前n项和，给出下列两组判断：A组：①数列{x n}是B﹣数列．②数列{x n}不是B﹣数列．B组③数列{s n}是B﹣数列．④数列{s n}不是B﹣数列请以其中一组的一个论断条件，另一组中的一个论断为结论组成一个命题判断所给命题的真假，并证明你的结论；（3）若数列{a n}是B﹣数列，证明：数列{a n2}也是B﹣数列．2009年湖南省高考数学试卷（文科）参考答案一、选择题（共8小题，每小题5分，满分40分）1．；2．；3．；4．；5．；6．；7．；8．；二、填空题（共7小题，每小题5分，满分35分）9．12；10．．；11．6；12．120；13．2；14．2；（）；15．；；三、解答题（共6小题，满分75分）16．；17．；18．；19．；20．；21．；。

历年高考试题荟萃之排列组合+高考数学排列组合常见题型及解题策略+排列组合高考题及解析

排列与组合第一部六年高考荟萃2010年高考题一、选择题 1．（2010年高考山东卷理科8）某台小型晚会由6个节目组成，演出顺序有如下要求：节目甲必须排在第四位、节目乙不能排在第一位，节目丙必须排在最后一位，该台晚会节目演出顺序的编排方案共有（A ）36种（B ）42种 (C)48种（D ）54种【答案】B【解析】分两类：第一类：甲排在第一位，共有44A =24种排法；第二类：甲排在第二位，共有1333A A =18⋅种排法，所以共有编排方案241842+=种，故选B 。

【命题意图】本题考查排列组合的基础知识，考查分类与分步计数原理。

2．（ 2010年高考全国卷I 理科6）某校开设A 类选修课3门，B 类选择课4门，一位同学从中共选3门，若要求两类课程中各至少选一门，则不同的选法共有(A) 30种 (B)35种 (C)42种 (D)48种2.A【命题意图】本小题主要考查分类计数原理、组合知识,以及分类讨论的数学思想.【解析】:可分以下2种情况:(1)A 类选修课选1门,B 类选修课选2门,有1234C C 种不同的选法;(2)A 类选修课选2门,B类选修课选1门,有2134C C 种不同的选法.所以不同的选法共有1234C C +2134181230C C =+=种.3．(2010年高考天津卷理科10)如图，用四种不同颜色给图中的A 、B 、C 、D 、E 、F 六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色。

则不同的涂色方法共有（A ） 288种（B ）264种（C ） 240种（D ）168种【答案】B【解析】分三类：（1）B 、D 、E 、F 用四种颜色，则有441124A ⨯⨯=种方法；（2）B 、D 、E 、F 用三种颜色，则有3422A ⨯⨯+34212192A ⨯⨯⨯=种方法；（3）B 、D 、E 、F 用二种颜色，则有242248A ⨯⨯=，所以共有不同的涂色方法24+192+48=264种。

2009年湖北省高考数学试题(理数)

2009年湖北省高考数学试题（理数)数学试题（理科）一、填空题（56分） 1、函数1()2f x x =-的反函数为1()fx -= 。

2、若全集U R =，集合{|1}{|0}A x x x x =≥≤ ，则U C A = 。

3、设m 为常数，若点(0,5)F 是双曲线2219yxm-=的一个焦点，则m = 。

4、不等式13x x+<的解为。

5、在极坐标系中，直线(2cos sin )2ρθθ+=与直线cos 1ρθ=的夹角大小为。

6、在相距2千米的A 、B 两点处测量目标C ，若0075,60C AB C BA ∠=∠=，则A 、C 两点之间的距离是千米。

7、若圆锥的侧面积为2π，底面积为π，则该圆锥的体积为。

8、函数sin()cos()26y x x ππ=+-的最大值为。

9、马老师从课本上抄录一个随机变量ε的概率分布律如下表请小牛同学计算ε的数学期望，尽管“！”处无法完全看清，且两个“？”处字迹模糊，但能肯定这两个“？”处的数值相同。

据此，小牛给出了正确答案E ε= 。

10、行列式a b cd（,,,{1,1,2}a b c d ∈-）的所有可能值中，最大的是。

11、在正三角形ABC 中，D 是B C 上的点，3,1AB BD ==，则AB AD ⋅=。

12、随机抽取9个同学中，至少有2个同学在同一月出生的概率是（默认每月天数相同，结果精确到0.001）。

13、设()g x 是定义在R 上、以1为周期的函数，若()()f x x g x =+在[3,4]上的值域为[2,5]-，则()f x 在区间[10,10]-上的值域为。

14、已知点(0,0)O 、0(0,1)Q 和0(3,1)R ，记00Q R 的中点为1P ，取01Q P 和10P R 中的一条，记其端点为1Q 、1R ，使之满足11(||2)(||2)0O Q O R --<；记11Q R 的中点为2P ，取12Q P 和21P R 中?!?321P(ε=x )x的一条，记其端点为2Q 、2R ，使之满足22(||2)(||2)0O Q O R --<；依次下去，得到点12,,,,n P P P ，则0lim ||n n Q P →∞= 。

(精校版)湖南省数学(文)卷文档版(含答案)-2009年普通高等学校招生统一考试

2009年普通高等学校招生全国统一考试(湖南卷)文科数学一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．2log 2的值为【 D 】A ．2-B 2C ．12-D ． 122．抛物线28y x =-的焦点坐标是【 B 】A ．（2，0）B ．（- 2，0）C ．（4，0）D ．（- 4，0）3．设n S 是等差数列{}n a 的前n 项和，已知23a =，611a =，则7S 等于【 C 】A ．13B ．35C ．49D ． 634．如图1， D ，E ，F 分别是∆ABC 的边AB ，BC ，CA 的中点，则【 A 】A ．0AD BE CF ++=B ．0BD CF DF -+=C ．0AD CE CF +-=D．0BD BE FC --=图15．某地政府召集5家企业的负责人开会，其中甲企业有2人到会，其余4家企业各有1人到会，会上有3人发言，则这3人来自3家不同企业的可能情况的种数为【 B 】A ．14 B ．16 C ．20 D ．486．平面六面体1111ABCD A BC D -中，既与AB 共面也与1CC 共面的棱的条数为【 C 】A ．3 B ．4 C ．5 D ．67．若函数()y f x =的导函数．．．在区间[,]a b 上是增函数，则函数()y f x =在区间[,]a b 上的图象可能是【 A 】A ．B ．C ．D ．8．设函数()y f x =在(,)-∞+∞内有定义，对于给定的正数K ，定义函数(),(),(),().K f x f xK f x K f x K ≤⎧=⎨>⎩取函数()2xf x -=。

当K =12时，函数()K f x 的单调递增区间为【 C 】A ．(,0)-∞ B ．(0,)+∞ C ．(,1)-∞- D ．(1,)+∞ 二、填空题：本大题共7小题，每小题5分，共35分.把答案填在答题卡．．．中对应题号后的横线上。

【历年经典】2009年全国高考理科数学试题及答案-湖南卷

2009年普通高等学校招生全国统一考试(湖南卷)理科数学一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若2log 0a <，1()12b>，则【 D 】A ．1a >,0b >B ．1a >,0b <C 、01a <<, 0b >D 、01a <<, 0b <2．对于非零向量,,a b “0a b +=”是“//a b ”的【 A 】A ．充分不必要条件 B 、必要不充分条件C ．充分必要条件 D 、既不充分也不必要条件3．将函数sin y x =的图象向左．．平移(02)ϕϕπ≤<个单位后，得到函数sin()6y x π=-的图象，则ϕ等于【 D 】A ．6π B ．56π C 、76π D.116π4．如图1，当参数12,λλλ=时，连续函数0)y x =≥ 的图像分别对应曲线1C 和2C , 则【 B 】A ．120λλ<< B ．210λλ<<C ．120λλ<<D ．210λλ<<5．从10名大学生毕业生中选3个人担任村长助理，则甲、乙至少有1人入选，而丙没有入选的不同选法的种数为【 C 】A ． 85 B ． 56 C ．49 D ．286．已知D 是由不等式组20,30x y x y -≥⎧⎨+≥⎩所确定的平面区域，则圆224x y +=在区域D 内的弧长为【 B 】A ．4π B ．2π C ．34π D ．32π1 7．正方体1111ABCD A BC D-的棱上到异面直线AB，C1C的距离相等的点的个数为【 C 】A．2 B．3 C． 4 D．58．设函数()y f x=在(,)-∞+∞内有定义.对于给定的正数K，定义函数(),(),(),().Kf x f x Kf xK f x K≤⎧=⎨>⎩取函数()f x=2xx e---。

2009年湖南高考数学试题及答案(理数)

2009年普通高等学校招生全国统一考试（湖南卷）数学试题卷（文史类）本试卷满分150分，考试时间120分钟第Ⅰ卷考生注意：1．答题前，务必将自己的姓名、准考证号、填写清楚，并贴好条形码．请认真核准条形码上的准考证号、姓名和科目．2．每小题选出答案后，用2Ｂ铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．在试题卷上作答无效．3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．4．所有题目必须在答题卡上作答，在试题卷上答题无效． 5．考试结束后，将试题卷和答题卡一并交回．参考公式：如果事件A B ，互斥，那么 ()()()P A B P A P B +=+ 如果事件A B ，相互独立，那么 ()()()P A B P A P B =如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k 次的概率()(1)(01,2)k k n kn nP k C P P k n -=-= ，，，以R 为半径的球体积：34π3V R =一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个备选项中，只有一项是符合题目要求的。

1．圆心在y 轴上，半径为1，且过点（1，2）的圆的方程为（）A ．22(2)1x y +-= B ．22(2)1x y ++= C ．22(1)(3)1x y -+-=D ．22(3)1x y +-=【答案】A解法1（直接法）：设圆心坐标为(0,)b ，则由题意知2(1)(2)1o b -+-=，解得2b =，故圆的方程为22(2)1x y +-=。

解法2（数形结合法）：由作图根据点(1,2)到圆心的距离为1易知圆心为（0，2），故圆的方程为22(2)1x y +-=解法3（验证法）：将点（1，2）代入四个选择支，排除B ，D ，又由于圆心在y 轴上，排除C 。

2．命题“若一个数是负数，则它的平方是正数”的逆命题是（）A ．“若一个数是负数，则它的平方不是正数”B ．“若一个数的平方是正数，则它是负数”C ．“若一个数不是负数，则它的平方不是正数”D ．“若一个数的平方不是正数，则它不是负数” 【答案】B解析因为一个命题的逆命题是将原命题的条件与结论进行交换，因此逆命题为“若一个数的平方是正数，则它是负数”。

2009年高考试题——数学理(湖南卷)解析版

2009年普通高等等学校招生全国统一考试(湖南卷)数学（理工农医类）一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．若2log a ＜0，1()2b＞1，则 (D)A ．a ＞1,b ＞0B ．a ＞1,b ＜0 C. 0＜a ＜1, b ＞0 D. 0＜a ＜1, b ＜0 【答案】：D【解析】由2log 0a <得0,a <<由1()12b>得0b <，所以选D 项。

2．对于非0向时a,b,“a//b ”的确良（A ） A ．充分不必要条件 B. 必要不充分条件 C ．充分必要条件 D. 既不充分也不必要条件【答案】：A【解析】由0a b +=，可得a b =-，即得//a b ，但//a b ，不一定有a b =-，所以“0a b +=”是“//a b 的充分不必要条件。

3．将函数y=sinx 的图象向左平移ϕ(0 ≤ϕ＜2π)的单位后，得到函数y=sin ()6x π-的图象，则ϕ等于（D ） A ．6π B ．56π C. 76π D.116π【答案】：D【解析】解析由函数sin y x =向左平移ϕ的单位得到sin()y x ϕ=+的图象，由条件知函数sin()y x ϕ=+可化为函数s i n ()6y x π=-，易知比较各答案，只有11sin()6y x π=+s i n ()6x π=-，所以选D 项。

4．如图1，当参数2λλ=时，连续函数(0)1xy x xλ=≥+ 的图像分别对应曲线1C 和2C , 则 [ B]A 10λλ<<B 10λλ<<C 120λλ<<D 210λλ<<【答案】：B【解析】解析由条件中的函数是分式无理型函数，先由函数在(0,)+∞是连续的，可知参数120,0λλ>>，即排除C ，D 项，又取1x =，知对应函数值12y y ==，由图可知12,y y <所以12λλ>，即选B 项。

2009年高考数学(湖南)文

（Ⅲ）若数列是数列，证明：数列也是数列．
13．过双曲线C：的一个焦点作圆的两条切线，切点分别为A，B．若（O是坐标原点），则双曲线C的离心率为．
14．在锐角中，，则的值等于，的取值范围为．
15．如图2，两块斜边长相等的直角三角板拼在一起，若，则，．
三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．
9．某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为．
10．若，则的最小值为．
11．在的展开式中，的系数为（用数字作答）．
12．一个总体分为A，B两层，用分层抽样方法从总体中抽取一个容量为10的样本．已知B层中每个个体被抽到的概率都为，则总体中的个体数为．
21．（本小题满分13分）
对于数列，若存在常数，对任意的，恒有
，
则称数列为数列．
（I）首项为1，公比为的等比数列是否为数列？请说明理由；
（Ⅱ）设是数列的前项和．给出下列两组论断：
A组：①数列是数列，②数列不是数列；
B组：③数列是数列，④数列不是数列．
请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题．判断所给命题的真假，并证明你的结论；
6．平面六面体中，既与AB共面也与共面的棱的条数为（）
A．3B．4C．5D．6
7．若函数导函数在区间是增函数，则函数在区间上的图象可能是（）
8．设函数在内有定义，对于给定的正数K，定义函数
取函数．当K= 时，函数的单调递增区间为（）
A． B． C． D．
二、填空题：本大题共7小题，每小题5分，共35分．把答案填在答题卡中对应题号后的横线上．

湖南高考数学试题及答案

湖南高考数学试题及答案一、选择题1. 设函数 f(x) = e^(2x)，则 f'(x) =A. 2e^(2x)B. e^(2x)C. 2e^(2x)D. 02. 若函数 f(x) = x^2 - 4x + 3，则其图像关于 x = 2 对称的另一点是A. (1, 2)B. (3, 0)C. (2, 1)D. (4, -1)3. 设复数 z = a + bi，且 z^2 = -8 - 6i，则复数 a 和 b 的值分别为A. -4，3B. 2，-3C. -2，3D. 4，-3二、解答题1. 已知函数 f(x) 的定义域为实数集 R，f(x) = ax^2 + bx + c，且对任意的实数 x 都有 f(2x) = f(x)，求常数 a，b，c 的值。

解：由已知条件可得：f(2x) = a(2x)^2 + b(2x) + c = ax^2 + bx + c即 4ax^2 + 2bx + c = ax^2 + bx + c化简得 3ax^2 + (b - 2b)x = 0由于对任意的 x 都成立，因此方程两边的系数均为零：3a = 0，b - 2b = 0解得 a = 0，b = 0而 c 是任意实数，因此常数 a，b，c 的值可以为任意实数。

2. 设集合 A = {1, 2, 3}，则集合 A 与集合 B = {{1}, {3}, {1, 2, 3}}的交集、并集分别为多少？解：集合的交集是指同时存在于多个集合中的共有元素，而并集则是指包含了所有集合中的元素的集合。

集合 A 与集合 B 的交集为 {1, 3}，因为只有元素 1 和 3 同时存在于两个集合中。

集合 A 与集合 B 的并集为 {1, 2, 3}，因为包含了所有集合 A 和集合B 的元素。

三、解析题1. 已知函数 f(x) = 3x^2 - 2x - 1，求 f(x) 的极值点和最值。

解：首先求导数 f'(x) = 6x - 2，令其为零得到 x = 1/3。

2009年高考理科数学(湖南)卷

2008年普通高等学校招生全国统一考试（湖南卷）数学（理工农医类）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若2log 0a <, 1()12b >, 则A ．1a >，0b >B ．1a >，0b <C ．01a <<，0b >D ．01a <<，0b <2．对于非零向量a , b , “+=0a b ”是“a b ∥”的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件3．将函数sin y x =的图象向左．．平移ϕ(02<π)ϕ≤个单位后，得到函数sin ()6y x π=-的图象，则ϕ等于A ．6πB ．65πC ．67πD ．611π4．如图1，当参数λ1λ=, 2λ时，连续函数y (0)x ≥的图象分别对应曲线 1C 和2C ，则A ．120λλ<<B ．210λλ<<C ．120λλ<<D ．210λλ<< 5．从10名大学毕业生中选3人担任村长助理，则甲、乙至少有1人入选，而丙没有入选的不同选法的种数为 A ．85 B ．56C ．49D ．286．已知D 是由不等式组所确定的平面区域，则圆224x y +=在区域D 内的弧长为A ．4πB ．2π C ．43π D ．23π7．正方体1111ABCD ABC D -的棱上到异面直线AB , 1CC 的距离相等的点的个数为A ．2B ．3C ．4D ．58．设函数()y f x =在(,-+)∞∞内有定义．对于给定的正数K , 定义函数取函数()2e x f x x -=--．若对任意的(,)x ∈-+∞∞，恒有()()K f x f x =，则A ．K 的最大值为2B ．K 的最小值为2C ．K 的最大值为1D ．K 的最小值为1二、填空题：本大题共7小题，每小题5分，共35分. 把答案填在答题卡．．．中对应题号后的横线上．9．某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为．10．在333(1)(1(1x +++的展开式中，x 的系数为（用数字作答）． 11．若(0,)x π∈2，则2tan tan ()x x π+-2的最小值为．12、已知以双曲线C 的两个焦点及虚轴的两个端点为原点的四边形中，有一个内角为60 o，则双曲线C 的离心率为 .13．一个总体分为A , B 两层，其个体数之比为4:1, 用分层抽样方法从总体中抽取一个容量为10的样本．已知B 层中甲、乙都被抽到的概率为128, 则总体中的个体数为．14．在半径为13的球面上有A , B , C 三点，6AB =, 8BC =, 10CA =, 则（1）球心到平面ABC 的距离为；（2）过A , B 两点的大圆面与平面ABC 所成二面角（锐角）的正切值为． 15．将正ABC ∆分割成2n （2n ≥, n *∈N ）个全等的小正三角形（图2, 图3分别给出了2n =,3的情形），在每个三角形的顶点各放置一个数，使位于ABC ∆的三边及平行于某边的任一直线上的数（当数的个数不少于3时）都分别依次成等差数列．若顶点A , B , C 处的三个数互不相同且和为1，记所有顶点上的数之和为()f n , 则有(2)2f =, (3)f = , … , ()f n = ．B C AB AC(),(),(),().K f x f x K f x K f x K ⎧=⎨>⎩≤图2图3三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤． 16．（本小题满分12分）在ABC ∆中，已知 22|||3AB AC AB AC BC ⋅⋅= , 求角A , B , C 的大小.17．（本小题满分12分）为拉动经济增长，某市决定新建一批重点工程，分为基础设施工程、民生工程和产业建设工程三类. 这三类工程所含项目的个数分别占总数的12, 13, 16. 现有3名工人独立地从中任选一个项目参与建设.(Ⅰ) 求他们选择的项目所属类别互不相同的概率；(Ⅱ) 记ξ为3人中选择的项目属于基础设施工程或产业建设工程的人数，求ξ的分布列及数学期望.18．（本小题满分12分）如图4，在正三棱柱111ABC A B C -中, 1AB , 点D 是11A B 的中点，点E 在11AC 上，且DE AE ⊥.(Ⅰ) 证明：平面ADE ⊥平面11ACC A ；(Ⅱ) 求直线AD 和平面1ABC 所成角的正弦值.19．（本小题满分13分）某地建一座桥，两端的桥墩已建好，这两墩相距m 米. 余下工程只需建两端桥墩之间的桥面和桥墩. 经测算，一个桥墩的工程费用为256万元；距离为x 米的相邻两墩之间的桥面工程费用为(2)x 万元. 假设桥墩等距离分布，所有桥墩都视为点，且不考虑其它因素. 记余下工程的费用为y 万元. (Ⅰ) 试写出y 关于x 的函数关系式；(Ⅱ) 当640m =米时，需新建多少个桥墩才能使y 最小？20．（本小题满分13分）在平面直角坐标系xOy 中，点P 到点(3,0)F 的距离的4倍与它到直线2x =的距离的3倍之和记为d . 当点P 运动时，d 恒等于点P 的横坐标与18之和.(Ⅰ) 求点P 的轨迹C ；(Ⅱ) 设过点F 的直线l 与轨迹C 相交于M , N 两点，求线段MN 长度的最大值.21．（本小题满分13分）对于数列{}nu , 若存在常数0M >, 对任意的n *∈N , 恒有1121||||||n n n n u u u u u u +--+-++- M ≤,则称数列{}nu 为B -数列.(Ⅰ) 首项为1, 公比为q (||1)q <的等比数列是否为B -数列？请说明理由； (Ⅱ) 设n S 是数列{}nx 的前n 项和. 给出下列两组论断：A 组：① 数列{}n x 是B -数列， ② 数列{}n x 不是B -数列； B 组：③ 数列{}n S 是B -数列， ④ 数列{}n S 不是B -数列.请以其中一组中的一个论断为条件，另一组中的一个论断为结论组成一个命题. 判断所给命题的真假，并证明你的结论； (Ⅲ) 若数列{}n a , {}n b 都是B -数列，证明：数列{}n n a b 也是B -数列.1参考答案及解析一、选择题：本大题共8小题，每小题5分，共40分．1．解:由2log001a a<⇒<<,1()102b b>⇒<，易知D正确.2．解:0a b a b+=⇒=-，//a b∴；反之不成立，故选A.3．解:依题意得11sin()sin(2)sin()666y x x xππππ=-=-+=+，116πϕ∴=，易知D正确.4．解: 易知0λ>，故可排除C,D,再取特殊值1x=，结合图像可得210λλ<<，故选B.5．解: 除开丙，由间接法得3397843549C C-=-=，故选C.6．解:作图，由12111123,,tan111234123k kπθθ+==-⇒==∴=-⨯，故弧长为242l Rππθ==⨯=，选B.7．解:如图，用列举法知合要求的点的个数为：BC的点E、11A D的点F、1B、D，共4个，故选C.8．解: 由()K f x≥恒成立知min()K f x≥,故K有最小值，可排除A,C,又由直觉思维得在0x=时，()22011xf x x e-=--=--=，排除B,因此选D.二、填空题：本大题共7小题，每小题5分，共35分.9．解: 设所求人数为x，则只喜爱乒乓球运动的人数为10(15)5x x--=-，故15530812x x+-=-⇒=.注：最好作出韦恩图！或由1510(308)315312+--=⇒-=人.10．解:13,r rrT C b+⇒=故有：12330333327C C C C++=-=，得x的系数为7.11．解:(0,)2tan tan()2tan22x x x xππ∈⇒+-=+，当且仅当12tan tantan2x xx=⇒=时取等号.12、解: 设双曲线C的左右焦点为12,F F，虚轴的上下两个端点为12,B B，由于,c b>故11260F B F∠≠ ,则有122126030tan303bB F B B F Oc∠=⇒∠=⇒==, 2223c a⇒=,2223,2ce ea∴==⇒=13．解: 设B 层中的个体数为n ，则211828nn C =⇒=，则总体中的个体数为8540.⨯= 14．解: 由AB=6，BC=8，CA=10得ABC ∆是以B 为直角顶点的直角三角形，（1）设斜边AC 的中点为O ',则5r BO '==，故12d ===;（2）作O H AB '⊥,则4O H '=，故12tan 3.4d OHO O H '∠===' 15．解: 若依题意顶点A ,B ,C 处的三个数互不相同且和为1，按等差数列的性质进行计算则显然运算量较大,故常规思维不可取！可偏偏特取A ,B ,C 处的数均为13（极限法）来思考：则图2中有26a =个13，得1(2)623f =⨯=；故图3中有310a =个13，得 1(3)101033f =⨯=；易知4n =时有415a =个13，探讨数列26,a =310,a =415,a = 13(2)1,n n a a n n --=+-=+ （可参考2006湖南卷: 逆序数）由叠加法推知:6[456(11)](1)(2)2n a n n n =++++++++=个13,1(1)(2))6(.n f n n +∴+= 三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤． 16．（本小题满分12分）解设BC a =，AC b =，AB c =．由2|||AB AC AB AC ⋅⋅得 2cos bc A =，所以cos A =又(0,A ∈π)，因此6A π=．2|||3AB AC BC ⋅= 得 2bc =．于是 2sin sin C B A ⋅==所以 5sin sin ()6C C π⋅-=，1sin (cos )2C C C ⋅+=22sin cos C C C ⋅+sin 20C C =，即sin(2)03C π-=．由6A π=知506C π<<，所以42333C πππ-<-<，从而203C π-=，或23C π-=π．即6C π=，或23C π=．故6A π=，23B π=，6C π=，或6A π=，6B π=，23C π=．17．（本小题满分12分）解记第i 名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件i A ，i B ，i C ，1i =，2，3．由题意知1A ，2A ，3A 相互独立，1B ，2B ，3B 相互独立，1C ，2C ，3C 相互独立，i A ，j B ，k C （i ，j ，k =1，2，3，且i ，j ，k 互不相同）ACA 1B 1C 1DE 相互独立，且1()2i P A =，1()3i P B =，1()6i P C =．（Ⅰ）他们选择的项目所属类别互不相同的概率P =1231233!()6()()()P AB C P A P B P C = ．（Ⅱ）解法1 设3名工人中选择的项目属于民生工程的人数为η，由已知，1(3,)3B η ，且3=-ξη，所以 33311(0)(3)C ()327P P ξh =====， 223122(1)(2)C ()()339P P ξh =====，123124(2)(1)C ()()339P P ξh =====， 03328(3)(0)C ()327P P ξh =====．故ξ的分布列是ξ的数学期望124801232279927E ξ=⨯+⨯+⨯+⨯=．解法2 记第i 名工人选择的项目属于基础设施工程或产业建设工程分别为事件i D ， 1i =，2，3．由已知，1D ，2D ，3D 相互独立，且()()()()i i i i i P D P A C P A P C =+=+112263=+=,所以2(3,)3B ξ ，即3321()C ()()33kk k P k ξ-==，k =0，1，2，3．故ξ的分布列是ξ的数学期望2323E =⨯=ξ．18．（本小题满分12分）解（Ⅰ）如图所示，由正三棱柱111ABC ABC -的性质知 1AA ⊥平面111A B C ．又DE ⊂平面111A B C ，所以1DE AA ⊥．而DE AE ⊥，1AA AE A = ，所以DE ⊥平面11ACC A ．又DE ⊂平面A D E ，故平面ADE ⊥平面11ACC A ．（Ⅱ）解法1 如图所示，设F 是AB 的中点，连结DF ，1DC ，1C F ．由正三棱柱111ABC ABC -的性质及D 是11A B 的中点知，111AB C D ⊥，11AB DF ⊥．又1C D DF D = ，所以11AB ⊥平面1C DF ．111162366=⨯⨯⨯=而AB 11//A B ，所以AB ⊥平面1C DF ．又AB ⊂平面1ABC ，故平面1ABC ⊥平面1C DF ．过点D 作DH 垂直1C F 于点H ，则D H ⊥平面1ABC ．连结AH ，则H A D ∠是直线AD 和平面1ABC 所成的角.由已知1AB ，不妨设1AA =，则2AB =，DF =1DC =1C F =，AD ，11DF DC DH C F⋅==. 所以 sin DH HAD AD ∠==即直线AD 和平面1ABC .解法2 如图所示，设O 是AC 的中点，以O 为原点建立空间直角坐标系. 不妨设1AA =2AB =，相关各点的坐标分别是(0,1,0)A -， (0,0)B ，1(0)C ，1,,2D -. 易知 (0)AB = ，1(0,2,AC =，1(,2AD = .设平面1ABC 的一个法向量为 (,,)x y z =n 10,20.AB y AC y ⎧⋅=+=⎪⎨⋅=+=⎪⎩n n 解得x y =-，z =.故可取 (1,n =.所以，cos ,||||AD AD AD ⋅===⋅n n n 由此即知，直线AD 和平面1ABC 19．（本小题满分13分）解（Ⅰ）设需新建n 个桥墩，则 (1)n x m +=，即 1m n x=-，所以 ()256(1)(2y f x n n x ==+++256(1)(2m m x x x=-++2562256mm x=+-．（Ⅱ）由（Ⅰ）知，1222561()2m f x mx x -=-+′32(512)2m x x =-．令()0f x =′，得 32512x =，所以 64x =．HFE DC 1B 1A 1CBA图1yx2x =y 当064x <<时，()0f x <′，()f x 在区间(0,64 )内为减函数；当64640x <<时，()0f x >′，()f x 在区间(64,640 )内为增函数．所以()f x 在64x =处取得最小值．此时 64011964m n x =-=-=．故需新建9个桥墩才能使y 最小．20．（本小题满分13分）解（Ⅰ）设点P 的坐标为(,)x y ，则 3|2|d x =-．由题设，18d x =+，即3|2|18x x -=+． ……①当2x >时，由①得，……②化简得．当2x ≤3x =+，……③化简得 212y x =．故点P 的轨迹C 是由椭圆 1C ：221y x +=在直线2x =的右侧部分与抛物线2C ：212y x =在直线2x =的左侧部分（包括它与直线2x =的交点）所组成的曲线，参见图1．（Ⅱ）如图2所示，易知直线2x =与1C ，2C 的交点都是(2,A ，(2,B -，直线AF ，BF 的斜率分别为AF k =-BF k = 当点P 在1C 上时，由②知 1||6PF x =-． ……④当点P 在2C 上时，由③知 ||3PF x =+． ……⑤若直线l 的斜率k 存在，则直线l 的方程为 (3)y k x =-．（ⅰ）当AF k k ≤，或BF k k ≥，即k -≤，或k ≥时，直线l 与轨迹C 的两个交点11(,)M x y ，22(,)N x y 都在1C 上，此时由④知图2y xAMEB2x =NOF162x =-2213627y x +=2x 2x =11||62MF x =-，21||62NF x =-，从而 1211||||||(6)(6)22MN MF NF x x =+=-+-12112()2x x =-+．由22(3)13627y k x y x =-⎧⎪⎨+=⎪⎩，得 2222(34)24361080k x k x k +-+-=．则1x ，2x 是这个方程的两根，所以21222434k x x k +=+，||MN 12112()2x x =-+22121234k k=-+．因为当k -≤k ≥时，224k ≥，所以222121001212||1212123311344424k MN kk=-=--=+++≤．当且仅当k =±时，等号成立．（ⅱ）当AF BF k k k <<，即k -<<l 与轨迹C 的两个交点 11(,)M x y ，22(,)N x y 分别在1C ，2C 上，不妨设点M 在1C 上，点N 在2C 上，则由④，⑤知，11||62MF x =-，2||3NF x =+．设直线AF 与椭圆1C 的另一交点为00(,)E x y ，则01x x <，22x <．1011||66||22MF x x EF =-<-=，2||332||NF x AF =+<+=，所以||||||||||||MN MF NF EF AF AE =+<+=．而点A ，E 都在1C 上，且AE k =-由（ⅰ）知100||11AE =，所以 100||11MN <．若直线l 的斜率不存在，则123x x ==，此时121001||12(9211MN x x =-+<）=．综上所述，线段MN 长度的最大值为10011．21．（本小题满分13分）解（Ⅰ）设满足题设的等比数列为{}n a ，则1n n a q -=．于是1221|||||||1|n n n n n a a q q q q -----=-=-，2n ≥．因此 211121|||||||1|(1||||||)n n n n n a a a a a a q q q q -+--+-++-=-++++ ．因为||1q <，所以 211||11||||||1||1||nn q q q q q q --++++=<-- ．即1121|1|||||||1||n n n n q a a a a a a q +---+-++-<- ．故首项为1，公比为(||1)q q <的等比数列是B -数列．（Ⅱ）命题1：若数列{}n x 是B -数列, 则数列{}n S 是B -数列．此命题为假命题．事实上，设1n x =，*n ∈N ，易知数列{}n x 是B -数列．但n S n =，1121||||||n n n n S S S S S S n +--+-++-= ．由n 的任意性知，数列{}n S 不是B -数列．命题2：若数列{}n S 是B -数列，则数列{}n x 是B -数列．此命题为真命题．事实上，因为数列{}n S 是B -数列，所以存在正数M ，对任意的*n ∈N ，有1121||||||n n n n S S S S S S M +--+-++- ≤，即 12||||||n n x x x M ++++ ≤．于是1121||||||n n n n x x x x x x +--+-++-1121||2||2||2||||n n n x x x x x +-+++++ ≤12||M x +≤，所以数列{}n x 是B -数列．（注：按题中要求组成其它命题解答时，仿上述解法）（Ⅲ）若数列{}n a ，{}n b 是B -数列, 则存在正数1M ，2M , 对任意的*n ∈N , 有11211||||||n n n n a a a a a a M +--+-++- ≤； 11212||||||n n n n b b b b b b M +--+-++- ≤．注意到 112211||||n n n n n a a a a a a a a ---=-+-++-+112211||||||||nn n n a a a a a a a ----+-++-+ ≤11||M a +≤.同理，21||||n b M b +≤.记111||K M a =+，221||K M b =+，则有111111||||n n n n n n n n n n n n a b a b a b a b a b a b ++++++-=-+-1112111||||||||||||n n n n n n n n n n b a a a b b K a a K b b +++++-+--+-≤≤.因此 11112211||||||n n n n n n n n a b a b a b a b a b a b ++---+-++-21121(||||||)n n n n K a a a a a a +--+-++- ≤+11121(||||||)n n n n K b b b b b b +--+-++- 2112K M K M +≤.故数列{}n n a b 是B -数列.。