第11章恒定磁场

合集下载

真空中的磁场

I
讨论：
当直线电流为“无限长”时
β1
π
2
β2
π
2
β 1 β 2 dB a
B
=
μo
2π
I a
结束返回
2. 载流圆线圈轴线上的磁场
dB
=
μ
4π
o
Idl sina
r2
=
μo
4π
Idl r2
由对称性：
a = 90 0
I dl
r
IR
θ x
y dB θ P x
By= Bz=0
I dl r z
dB
B = dB x = dB
2 ( R 2 + l 2 )3 2
dI = n I dl
l = R ctgβ dl = R cscβ2 dβ
由上面得到：l = Rctgβ ，dl = R cscβ2 dβ
dB = μ on I d l R 2
2 ( R 2 +l 2 )3 2
μ
=
on 2
I (
( R2
R cscβ2 dβ ) R 2 + R 2ctg2β )3 2
洛伦兹力
荷兰物理学家
洛伦兹
H.A.Lorentz （1853-1928）
§11-6 带电粒子在磁场中所受作用及其运动
一、洛伦兹力
带电粒子在磁场中当 v、B 相互垂直时，
受力最大，且 Fm =q vB 在一般情况下：
F
B
F =q vB sinq
F 垂直于由v、B 所决定的平面
q
q
v
F = q v× B
q
v
d
N
sin ( v , r r2

第十一章电磁学恒定磁场 Ma 2016

0 qnS d lv er dB 4 r2
d B 0 qv er B d N 4 r 2 方向根据右手螺旋法则， B 垂直 v 、正， B 为 v r 的方向；q为负， B 与
q
+
r B
v
q－
q为 r组成的平面。 v r 相反。
μ0 I B (cos θ1 cos θ 2 ) 4πr0
0 π
2
I
无限长载流长直导线的磁场
θ1 θ2
μ0 I B 2πr0
注意用右手螺旋关系判断方向。半无限长载流长直导线的磁场
1
r0
P
θ1 θ2

2 π

μ0 I B 4πr0
I
r0
P
大学物理电磁学
2、载流圆线圈轴线上的磁场真空中，半径为R的载流导线，通有电流I，称圆电流。求其轴线上一点 P的磁感强度的方向和大小
1、5 点： dB 0
7

6 5
Idl
R
×
× 3
3、7点： dB
0 Idl 4 π R2
4
2、4、6、8 点：
dB
0 Idl
4π R
2
sin 45
0
大学物理电磁学
3. 毕—萨定律应用举例
dB 的方向均
沿x 轴负方向
(1) 载流长直导线的磁场
z
dz
解
2

dB
大学物理电磁学
磁现象与电现象有没有联系？
静电场？
静止的电荷运动的电荷
1820年奥斯特：发现电流的磁效应
N

磁场的介绍

解：在管上取一小段dl，
电流为dI=nIdl ，
该电流在P点的磁场为：
......d..l.... ........... ...
1
. r
2
lP
dB
oR
2 l2
2nIdl R2 3
2
r2 l2 R2
r
R
sin
l Rctg dl
则：dB onI sin d
R d sin 2
2
B
do2BnIco12so2n1Iscionsd2
对 LB dl 无贡献
安培环路定理揭示磁场是非保守场（涡旋场）
§11-5 安培环路定理的应用
一、无限长均匀载流圆柱体 I , R 内外磁场。
IR
o r P
L
dB'
L
o
dI•r dI•'
dB
P
对称性分析：
在 I 平面内，作以 o为中心、半径 r 的圆环 L， L上各点等价： B大小相等，方向沿切向。以 L为安培环路，逆时针绕向为正: +
L2
L2
管外空间B0
三、载流长直螺线管内部的磁场单位长度上的匝数 n，
I
B
线密绕 B外 0
对称性分析： B 只有平行于轴线的分量平行于轴的任一直线上各点 B 大小相等，
方向沿轴
B 0nI
长直螺线管内为均匀磁场
在长直螺线管的两端点处的磁场为中间的一半：
BS
1 2
0nI
I
B
0nI
1 2
基本概念：电流元 Idl
dl
I
dl
rB
一、毕奥 — 萨伐尔定律
dB

大学物理稳恒磁场

第十一章稳恒磁场磁场由运动电荷产生。

磁场与电场性质有对称性，学习中应注意比照。

§11－1 根本磁现象磁性，磁力，磁现象；磁极，磁极指向性，N极，S极，同极相斥，异极相吸。

磁极不可分与磁单极。

一、电流的磁效应1819年，丹麦科学家奥斯特发现电流的磁效应；1820年，法国科学家安培发现磁场对电流的作用。

二、物质磁性的电本质磁性来自于运动电荷，磁场是电流的场。

注：1932年，英国物理学家狄拉克预言存在“磁单极〞，至今科学家一直在努力寻找其存在的证据。

§11－2 磁场磁感强度一、磁场磁力通过磁场传递，磁场是又一个以场的形式存在的物质。

二、磁感强度磁感强度B 的定义：〔1〕规定小磁针在磁场中N 极的指向为该点磁感强度B 的方向。

假如正电荷沿此方向运动，其所受磁力为零。

〔2〕正运动电荷沿与磁感强度B 垂直的方向运动时，其所受最大磁力F max 与电荷电量q 和运动速度大小v 的乘积的比值，规定为磁场中某点磁感强度的大小。

即：qvF B max=磁感强度B 是描写磁场性质的根本物理量。

假如空间各点B 的大小和方向均相等，如此该磁场为均匀磁场．．．．；假如空间各点B 的大小和方向均不随时间改变，称该磁场为稳恒磁场．．．．。

磁感强度B 的单位：特斯拉〔T 〕。

§11－3 毕奥－萨伐尔定律一、毕－萨定律电流元: l Id电流在空间的磁场可看成是组成电流的所有电流元l Id 在空间产生元磁感强度的矢量和。

304r rl Id B d ⨯=πμ式中μ0：真空磁导率， μ0＝4π×10－7NA 2 dB 的大小： 20sin 4r Idl dB θπμ=d B 的方向： d B 总是垂直于Id l 与r 组成的平面，并服从右手定如此。

一段有限长电流的磁场： ⎰⎰⨯==l l rrl Id B d B 304πμ二、应用1。

一段载流直导线的磁场)cos (cos 42100θθπμ-=r IB说明：〔1〕导线“无限长〞：02r I B πμ=〔2〕半“无限长〞： 00004221r I r IB πμπμ==2。

大学物理下-吴百诗-ch11恒定电流的磁场ppt课件

②、载流导线在磁场中运动时，磁场力要作功—磁场具有能量…
三、磁感应强度
1、引入电场——电场强度
需要一个既具有大小又有方向的物理量来定量描述
磁场。
完整最新ppt
10
ch11
2、实验：运动电荷在磁场中的受力情况，确定空间一点的磁感应强度
①、类比：静电场中用试探电荷研究电场
测 F ，出 E ＝用 F /q 描述电 E 表场示强电度场。，
带电粒子在磁场中沿
其力他垂方直向于运v与动时所B ，组其成受
的平面
在磁场中的任一点，当带电粒子在磁场中垂直于 B方向运动时受力最大，且F max 大小是一确定值
qv
与 q,无v关
完整最新ppt
13
ch11
3、磁感应强度的定义
•磁场中任一点都存在一个特殊的方向和确定的比值
Fmax /qv •反映了磁场在该点的方向特征和强弱特征
两带电线上的电流为导体带电量线密度单位长度上的导线所受的安培力ch11两带电线单位长度上的电荷之间的库仑力导体带电量线密度在一般情况下磁场力远小于电场力ch11二磁场对平面载流线圈的作用如图所示均匀磁场中有一矩形刚性载流线圈mnop线圈中的电流为i磁感应强度b沿水平方向与线圈平面成求磁场对四条载流导线边的作用力根据方向相反不在一条直线上方向相反作用在同一直线上线圈在磁场中无平动线圈在磁场中有无转动
I Ild d B B d 完B 整最新ppt
16
ch11
2.电流元矢量 Idl
如图，I为回路导线中的电流， dl 为闭合回路导线中沿着电流
Idl
I
Idl
方向所取的一个长为dl的矢量线元，
大小：直线元的长度乘以I 方向：该点直线上电流的方向

大学物理(下)十一章十二章作业与解答

大学物理(下)十一章十二章作业与解答————————————————————————————————作者：————————————————————————————————日期：第十一章恒定磁场一. 选择题1．在一平面内，有两条垂直交叉但相互绝缘的导线，流经两条导线的电流大小相等，方向如图，在哪些区域中有可能存在磁感应强度为零的点？(A) 在Ⅰ、Ⅲ象限(B) 在Ⅰ、Ⅳ象限(C) 在Ⅱ、Ⅲ象限(D) 在Ⅱ、Ⅳ象限[ ]2. 载流导线在同一平面内，形状如图，在圆心O处产生的磁感应强度大小为(A)(B)(C)(D) [ ]注意见第11章课件最后的总结的那个图，半圆载流回路在圆心处的磁感强度是多少？3. 一圆形回路1及一正方形回路2，圆的直径与正方形边长相等，二者中通有大小相同电流，则它们在各自中心处产生的磁感应强度大小之比为(A) 0.90(B) 1.00(C) 1.11(D) 1.22 [ ]注意教材page304,及课件最后总结的那个图4. 在磁感应强度为的均匀磁场中做一半径为r的半球面S，S边线所在平面的法线方向单位矢量与的夹角为θ，则通过半球面S的磁通量（取半球面向外为正）为(A)(B)(C)(D)[ ]5. 如图，无限长载流直导线附近有一正方形闭合曲面S，当S向导线靠近时，穿过S的磁通量和S上各点的磁感应强度的大小B将(A) 增大，B增强(B) 不变，B不变(C) 增大，B不变(D) 不变，B增强[ ]6. 取一闭合积分回路L，使若干根载流导线穿过它所围成的面，若改变这些导线之间的相互间隔，但不越出积分回路，则(A) 回路L内的电流的代数和不变，L上各点的不变(B) 回路L内的电流的代数和不变，L上各点的改变(C) 回路L内的电流的代数和改变，L上各点的不变(D) 回路L内的电流的代数和改变，L上各点的改变[ ]7. 如图，两根导线ab和cd沿半径方向被接到一个截面处处相等的铁环上，恒定电流I 从a端流入而从d端流出，则磁感应强度沿闭合路径L的积分等于(A)(B)(C)(D)[ ]8. 一电荷为q的粒子在均匀磁场中运动，下列说法正确的是(A) 只要速度大小相同，粒子所受的洛仑兹力就相同(B) 在速度不变的前提下，若电荷q变为 -q，则粒子受力反向，数值不变(C) 粒子进入磁场后，其动能和动量都不变(D) 洛仑兹力与速度方向垂直，所以带电粒子运动的轨迹必定是圆[ ]9. 质量为m、电量为q的粒子，以速度v垂直射入均匀磁场中，则粒子运动轨道包围范围的磁通量与磁感应强度的大小之间的关系曲线为[ b ]注意见P317,(11.30)10. 如图，长直载流导线与一圆形电流共面，并与其一直径相重合(两者间绝缘),设长直电流不动，则圆形电流将(A) 向上运动(B) 绕旋转(C) 向左运动(D) 向右运动(E) 不动[ ]11. 磁场中有一载流圆线圈，其既不受力也不受力矩作用，这说明(A) 该磁场一定均匀，且线圈的磁矩方向一定与磁场方向平行(B) 该磁场一定不均匀，且线圈的磁矩方向一定与磁场方向平行(C) 该磁场一定均匀，且线圈的磁矩方向一定与磁场方向垂直(D) 该磁场一定不均匀，且线圈的磁矩方向一定与磁场方向垂直[ ]注意见P325 第二段表述，11.36式12. 用细导线均匀密绕成长为l、半径为a（l >>a）、总匝数为N的螺线管，管内充满相对磁导率为的均匀磁介质，线圈中载有电流I，则管中任一点(A) 磁感应强度大小为(B) 磁感应强度大小为(C) 磁场强度大小为(D) 磁场强度大小为[ ]二. 填空题13.如图，电流元在P点产生的磁感应强度的大小为___________________.14. 真空中有一载有电流I的细圆线圈，则通过包围该线圈的闭合曲面S的磁通量Φ=________________. 若通过S面上某面元的磁通为，而线圈中电流增加为2I时，通过该面元的磁通为，则_______________.0 ； 1︰215. 如图，两平行无限长载流直导线中电流均为I，两导线间距为a，则两导线连线中点P的磁感应强度大小，磁感应强度沿图中环路L的线积分_______________________.0 ；16. 恒定磁场中，磁感应强度对任意闭合曲面的积分等于零，其数学表示式是____________，这表明磁感应线的特征是_________________________. ；闭合曲线17. 一长直螺线管是由直径的导线密绕而成，通以的电流，其内部的磁感应强度大小B =_____________________.（忽略绝缘层厚度）18. 带电粒子垂直磁感应线射入匀强磁场，它做______________运动；带电粒子与磁感应线成300角射入匀强磁场，则它做__________________运动；若空间分布有方向一致的电场和磁场，带电粒子垂直于场方向入射，则它做__________________运动.圆周；螺旋线；变螺距的螺旋线19. 在霍尔效应实验中，通过导电体的电流和的方向垂直（如图）.如果上表面的电势较高，则导电体中的载流子带___________电荷；如果下表面的电势较高，则导电体中的载流子带___________电荷.正；负20. 如图，一载流导线弯成半径为R的四分之一圆弧，置于磁感应强度为的均匀磁场中，导线所受磁场力大小为______________，方向为_____________.； y轴正向注意：积分IRBdθ，θ的积分上下限？21. 如图，半径为R的半圆形线圈通有电流I，线圈处在与线圈平面平行指向右的均匀磁场中，该载流线圈磁矩大小为___________，方向____________；线圈所受磁力矩的大小为_________________，方向_____________.；垂直纸面向外；；向上22. 磁场中某点，有一半径为R、载有电流I的圆形实验线圈，其所受的最大磁力矩为M，则该点磁感应强度的大小为_________________.注意见教材324页三. 计算题23. 如图，两长直导线互相垂直放置，相距为d，其中一根导线与z轴重合，另一与x轴平行且在Oxy平面内，设导线中皆通有电流I，求y轴上与两导线等距的P点处的磁感应强度.解：长直载流导线在距其r处的磁感应强度为两长直载流导线在P点产生的磁感应强度方向一沿z轴方向，一沿x轴负方向且方向平行于Oxz平面与Oxy面成45o，如图示。

川师大学物理第十一章恒定电流的磁场习题解

第十一章恒定电流的磁场11–1 如图11-1所示，几种载流导线在平面内分布，电流均为I ，求它们在O 点处的磁感应强度B 。

（1）高为h 的等边三角形载流回路在三角形的中心O 处的磁感应强度大小为，方向。

（2）一根无限长的直导线中间弯成圆心角为120°，半径为R 的圆弧形，圆心O 点的磁感应强度大小为，方向。

…解：（1）如图11-2所示，中心O 点到每一边的距离为13OP h =，BC 边上的电流产生的磁场在O 处的磁感应强度的大小为012(cos cos )4πBC IB dμββ=-^00(cos30cos150)4π/34πI I h hμ︒︒=-=方向垂直于纸面向外。

另外两条边上的电流的磁场在O 处的磁感应强度的大小和方向都与BC B 相同。

因此O 处的磁感应强度是三边电流产生的同向磁场的叠加，即3BC B B ===方向垂直于纸面向外。

（2）图11-1（b ）中点O 的磁感强度是由ab ，bcd ，de 三段载流导线在O 点产生的磁感强度B 1，B 2和B 3的矢量叠加。

由载流直导线的磁感强度一般公式012(cos cos )4πIB dμββ=-可得载流直线段ab ，de 在圆心O 处产生的磁感强度B 1，B 3的大小分别为01(cos0cos30)4cos60)IB R μ︒=︒-︒π(0(12πI R μ=031(cos150cos180)4πcos60IB B R μ︒==︒-︒0(12πI R μ= 】IB 2图11–2图11–1…B（a ）AE（b ）方向垂直纸面向里。

半径为R ，圆心角α的载流圆弧在圆心处产生的磁感强度的大小为04πI B Rμα=圆弧bcd 占圆的13，所以它在圆心O 处产生的磁感强度B 2的大小为00022π34π4π6II I B R R Rμμαμ=== 方向垂直纸面向里。

因此整个导线在O 处产生的总磁感强度大小为000012333(1)(1)0.212π2π6I I II B B B B R R R Rμμμμ=++=-+-+=方向垂直纸面向里。

第十一章真空中的恒定磁场(1)讲述

（3）当带电粒子沿与上述
特定方向垂直的方向运动时所
即： Fmax qv 受到的磁力最大(记为Fm )，
并且Fm与q v的比值是与q、v
Fmax qv
无关的确定值。
大小与 q,无v关
第十一章真空中的恒定磁场
定
磁感应强度
B
:
反映空间某点的磁场大小和方向
义大小： B Fmax qv
方向：小磁针平衡时N 极的指向
第十一章真空中的恒定磁场
例1 长直电流的磁场.
dB 方向均垂
直指向里
q2
Idl q r
Il
od
q1
解
dB
0
4π
Idl sinq
r2
B
dB
0I
4π
dl sinq
r2
l d cotq, r d / sinq
*P dB
dl d dq / sin2 q
B 0I q2 sinq dq 4 π d q1
第十一章真空中的恒定磁场
第十一章真空中的恒定磁场
静电荷静电场
运动电荷电场磁场
稳恒电流稳恒磁场
学习方法：类比法
第十一章真空中的恒定磁场
§11-1 磁感应强度磁场的高斯定理
一、基本磁现象 (1) 天然磁铁吸引铁、钴、镍等物质。 (2) 条形磁铁两端磁性最强，称为磁极。
一只能够在水平面内自由转动的条形磁铁，平衡时总是顺
第十一章真空中的恒定磁场
规定：通过垂直于磁感应线方向的单位面积的磁感应线条数等于该点磁感应强度的大小。即
B dN
dN
dS
B
dN是穿过
dS
面的磁感应线条数。

大学物理第十一章习题解答..

第十一章：恒定电流的磁场习题解答1．题号：40941001分值：10分如下图所示，是一段通有电流I 的圆弧形导线，它的半径为R ，对圆心的张角为θ。

求该圆弧形电流所激发的在圆心O 处的磁感强度。

解答及评分标准：在圆弧形电流中取一电流元l Id （1分），则该电流元l Id 在圆心处的磁感强度为： θπμπμd R I RIdl dB 490sin 40020==（2分）其中θRd dl =则整段电流在圆心处的磁感强度为：θπμθπμθR I d R I dB B 44000===⎰⎰（2分）2．题号：40941002分值：10分一无限长的载流导线中部被弯成圆弧形，如图所示，圆弧形半径为cm R 3=，导线中的电流为A I 2=。

求圆弧形中心O 点的磁感应强度。

解答及评分标准：两根半无限长直电流在O 点的磁感应强度方向同为垂直图面向外，大小相等，以垂直图面向里为正向，叠加后得RI R I B πμπμ242001-=•-= （3分）圆弧形导线在O 点产生的磁感应强度方向垂直图面向里，大小为R I R I B 83432002μμ==（3分）二者叠加后得 T RI R I B B B 500121081.1283-⨯=-=+=πμμ （3分）方向垂直图面向里。

（1分）3．题号：40941003分值：10分难度系数等级：1一段导线先弯成图（a ）所示形状，然后将同样长的导线再弯成图（b ）所示形状。

在导线通以电流I 后，求两个图形中P 点的磁感应强度之比。

（a ）（b ）解答及评分标准：图中（a ）可分解为5段电流。

处于同一直线的两段电流对P 点的磁感应强度为零，其他三段在P 点的磁感应强度方向相同。

长为l 的两段在P 点的磁感应强度为 lI B πμ4201= （2分）长为2l 的一段在P 点的磁感应强度为 l I B πμ4202=（2分）所以lI B B B πμ22012=+= （2分）图（b ）中可分解为3段电流。

物理学教程-第十一章恒定磁场

Shanghai Institute of Technology
Chapter 11
恒定磁场
上海应用技术学院
理学院
谭默言
§11-1、§11-2 、 §11-3 教学基本要求
了解电流、电流密度的基本概念；
了解电源作用和电源电动势的定义；
掌握磁场及磁感强度的概念及特点。
·2 ·
§ 11-1 恒定电流
8 2
d 1、5 点： B 0
3、7点：dB +3
+
7
Idl
R
6
0 Idl
4π R
2
2、4、6、8 点：
+4
5
dB
0 Idl
4π R
sin 45 0 2
·13 ·
二
毕奥---萨伐尔定律应用举例
解 dB
例1 载流长直导线的磁场.
0 Idz sin
4π r
2
z
0 I B1 dl1 B2 dl2 d 2π
d
B1
B1 dl1 B2 dl2 0
B d l 0
l
I
B2 dl 2 dl
1
r1
r2
l
·31 ·
证明:
多电流情况
B B1 B2 B3 I 1 B d l ( B1 B2 B3 ) d l l l B1 d l B2 d l B3 d l
dB
P *
r

Idl
I
0 I dl er B dB 4 π r2

大学物理答案第11章

第十一章恒定磁场11－1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管，两个螺线管的长度相同，R ＝2r ，螺线管通过的电流相同为I ，螺线管中的磁感强度大小r R B B 、满足（）（A ） r R B B 2= （B ） r R B B = （C ） r R B B =2 （D ）r R B B 4=分析与解在两根通过电流相同的螺线管中，磁感强度大小与螺线管线圈单位长度的匝数成正比．根据题意，用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为（C ）.11－2 一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量为（）（A ）B r 2π2 （B ） B r 2π（C ）αB r cos π22（D ） αB r cos π2题 11-2 图分析与解作半径为r 的圆S ′与半球面构成一闭合曲面，根据磁场的高斯定理，磁感线是闭合曲线，闭合曲面的磁通量为零，即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量；S B ⋅=m Φ．因而正确答案为（D ）．11－3 下列说法正确的是（）（A ）闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过（B ）闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零（C ）磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D ）磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零分析与解由磁场中的安培环路定律，磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度不一定为零；闭合回路上各点磁感强度为零时，穿过回路的电流代数和必定为零.因而正确答案为（B ）．11－4 在图（ａ）和（ｂ）中各有一半径相同的圆形回路L1 、L2 ，圆周内有电流I1 、I2 ，其分布相同，且均在真空中，但在（ｂ）图中L2 回路外有电流I3 ，P 1 、P 2 为两圆形回路上的对应点，则（）（A ） ⎰⎰⋅=⋅21L L d d l B l B ，21P P B B =（B ） ⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B = （C ） ⎰⎰⋅=⋅21L L d d l B l B ，21P P B B ≠ （D ） ⎰⎰⋅≠⋅21L L d d l B l B ，21P P B B≠题 11-4 图分析与解由磁场中的安培环路定律，积分回路外的电流不会影响磁感强度沿回路的积分；但同样会改变回路上各点的磁场分布．因而正确答案为（C ）．11－5 半径为R 的圆柱形无限长载流直导体置于均匀无限大磁介质之中，若导体中流过的恒定电流为I ，磁介质的相对磁导率为μｒ（μｒ＜1），则磁介质内的磁化强度为（）（A ）()r I μr π2/1-- （B ） ()r I μr π2/1- （C ） r I μr π2/- （D ） r μI r π2/分析与解利用安培环路定理可先求出磁介质中的磁场强度，再由M ＝（μｒ－1）H 求得磁介质内的磁化强度，因而正确答案为（B ）．11－6 北京正负电子对撞机的储存环是周长为240 m 的近似圆形轨道，当环中电子流强度为8 mA 时，在整个环中有多少电子在运行？已知电子的速率接近光速. 分析一个电子绕存储环近似以光速运动时，对电流的贡献为c I e I /Δ=，因而由lNec I =，可解出环中的电子数.解通过分析结果可得环中的电子数10104⨯==ecIlN 11－7 已知铜的摩尔质量M ＝63.75 ｇ·mol －1，密度ρ ＝8.9 g · cm －3，在铜导线里，假设每一个铜原子贡献出一个自由电子，（1）为了技术上的安全，铜线内最大电流密度26.0A mm m j -=⋅ ，求此时铜线内电子的漂移速率v d ；（2）在室温下电子热运动的平均速率是电子漂移速率v d 的多少倍？分析一个铜原子的质量A N M m /=,其中N A 为阿伏伽德罗常数，由铜的密度ρ 可以推算出铜的原子数密度m ρn /=根据假设，每个铜原子贡献出一个自由电子，其电荷为e ，电流密度d m ne j v = ．从而可解得电子的漂移速率v d ．将电子气视为理想气体，根据气体动理论，电子热运动的平均速率em kTπ8=v 其中k 为玻耳兹曼常量，m e 为电子质量．从而可解得电子的平均速率与漂移速率的关系．解（1）铜导线单位体积的原子数为M ρN n A /=电流密度为j m 时铜线内电子的漂移速率14A s m 1046.4--⋅⨯===eN M j ne j m m d ρv （2）室温下（T ＝300 Ｋ）电子热运动的平均速率与电子漂移速率之比为81042.2π81⨯≈=edd m kTv v v 室温下电子热运动的平均速率远大于电子在恒定电场中的定向漂移速率．电子实际的运动是无规热运动和沿电场相反方向的漂移运动的叠加．考虑到电子的漂移速率很小，电信号的信息载体显然不会是定向漂移的电子．实验证明电信号是通过电磁波以光速传递的． 11－8 有两个同轴导体圆柱面，它们的长度均为20 m ，内圆柱面的半径为3.0 mm ，外圆柱面的半径为9.0 mm.若两圆柱面之间有10 μA 电流沿径向流过，求通过半径为6.0 mm 的圆柱面上的电流密度．题 11-8 图分析如图所示是同轴柱面的横截面，电流密度j 对中心轴对称分布．根据恒定电流的连续性，在两个同轴导体之间的任意一个半径为r 的同轴圆柱面上流过的电流I都相等，因此可得rlI j π2=解由分析可知，在半径r ＝6.0 mm 的圆柱面上的电流密度2m A μ3.13π2-⋅==rlIj 11－9 如图所示，已知地球北极地磁场磁感强度B 的大小为6.0×10－5T ．如设想此地磁场是由地球赤道上一圆电流所激发的，此电流有多大？流向如何？解设赤道电流为I ，则由教材第11－4节例2 知，圆电流轴线上北极点的磁感强度()RIRR IR B 24202/32220μμ=+=因此赤道上的等效圆电流为A 1073.12490⨯==μRBI 由于在地球地磁场的Ｎ极在地理南极，根据右手螺旋法则可判断赤道圆电流应该是由东向西流，与地球自转方向相反．题 11-9 图11－10 如图所示，有两根导线沿半径方向接触铁环的a 、b 两点，并与很远处的电源相接.求环心O 的磁感强度．题 11-10 图分析根据叠加原理，点O 的磁感强度可视作由ef 、be 、fa 三段直线以及acb 、a d b 两段圆弧电流共同激发．由于电源距环较远，0=ef B ．而be 、fa 两段直线的延长线通过点O ，由于0Idl r ⨯=，由毕奥－萨伐尔定律知0be fa ==B B ．流过圆弧的电流I 1 、I 2的方向如图所示，两圆弧在点O 激发的磁场分别为21101π4r l I μB =,22202π4r l I μB = 其中l 1 、l 2 分别是圆弧acb 、a d b 的弧长，由于导线电阻R 与弧长l 成正比，而圆弧acb 、a d b又构成并联电路，故有2211l I l I =将21B B 、叠加可得点O 的磁感强度B ．解由上述分析可知，点O 的合磁感强度0π4π42220211021=-=-=r l I μr l I μB B B 11－11 如图所示，几种载流导线在平面内分布，电流均为I ，它们在点O 的磁感强度各为多少？题 11-11 图分析应用磁场叠加原理求解．将不同形状的载流导线分解成长直部分和圆弧部分，它们各自在点O 处所激发的磁感强度较容易求得，则总的磁感强度∑=iB B 0.解（ａ）长直电流对点O 而言，有0d =⨯rl I ，因此它在点O 产生的磁场为零，则点O 处总的磁感强度为1/4 圆弧电流所激发，故有RIμB 800=B 0 的方向垂直纸面向外．（ｂ）将载流导线看作圆电流和长直电流，由叠加原理可得RIμR I μB π22000-=B 0 的方向垂直纸面向里．（c ）将载流导线看作1/2 圆电流和两段半无限长直电流，由叠加原理可得RIμR I μR I μR I μR I μB 4π24π4π4000000+=++=B 0 的方向垂直纸面向外．11－12 载流导线形状如图所示（图中直线部分导线延伸到无穷远），求点O 的磁感强度B ．题 11-12 图分析由教材11－4 节例题2的结果不难导出，圆弧载流导线在圆心激发的磁感强度RαI μB π40=，其中α为圆弧载流导线所张的圆心角，磁感强度的方向依照右手定则确定；半无限长载流导线在圆心点O 激发的磁感强度R IμB π40=，磁感强度的方向依照右手定则确定.点O 的磁感强度O B 可以视为由圆弧载流导线、半无限长载流导线等激发的磁场在空间点O 的叠加. 解根据磁场的叠加在图（ａ）中，k i k k i B RI μR I μR I μR I μR I μπ24π4π44000000--=---= 在图（ｂ）中，k i k i i B RI μR I μR I μR I μR I μπ41π14π44π4000000-⎪⎭⎫ ⎝⎛+-=---= 在图（c ）中，k j i B RIμR I μR I μπ4π4830000---= 11－13 如图(a)所示，载流长直导线的电流为I ，试求通过矩形面积的磁通量．题 11-13 图分析由于矩形平面上各点的磁感强度不同，故磁通量Φ≠BS ．为此，可在矩形平面上取一矩形面元d S ＝l d x ，如图（ｂ）所示，载流长直导线的磁场穿过该面元的磁通量为x l xId π2d d 0μ=⋅=ΦS B矩形平面的总磁通量ΦΦ⎰=d解由上述分析可得矩形平面的总磁通量⎰==Φ211200lnπ2d π2d dd d Ilx l xIμμ 11－14 已知10 mm 2裸铜线允许通过50 A 电流而不会使导线过热．电流在导线横截面上均匀分布．求导线内、外磁感强度的分布.题 11-14 图分析可将导线视作长直圆柱体，电流沿轴向均匀流过导体，故其磁场必然呈轴对称分布，即在与导线同轴的圆柱面上的各点，B 大小相等、方向与电流成右手螺旋关系．为此，可利用安培环路定理，求出导线表面的磁感强度．解围绕轴线取同心圆为环路L ，取其绕向与电流成右手螺旋关系，根据安培环路定理，有∑⎰=⋅=⋅I μB 0πr 2d l B在导线内r ＜R ， 2222ππRIr r R I I ==∑，因而 202πR IrμB =在导线外r ＞R ，I I =∑，因而rIμB 2π0=磁感强度分布曲线如图所示．11－15 有一同轴电缆，其尺寸如图（ａ）所示．两导体中的电流均为I ，但电流的流向相反，导体的磁性可不考虑．试计算以下各处的磁感强度：（1） r ＜R 1 ；（2） R 1 ＜r ＜R 2 ；（3） R 2 ＜r ＜R 3 ；（4） r ＞R 3 ．画出B －r 图线．题 11-15 图分析同轴电缆导体内的电流均匀分布，其磁场呈轴对称，取半径为r 的同心圆为积分路径，πr 2d ⋅=⋅⎰B l B ，利用安培环路定理∑⎰=⋅I μ0d l B ，可解得各区域的磁感强度．解由上述分析得r ＜R 122101ππ12πr R μr B =⋅ 21012πR Ir μB =R 1 ＜r ＜R 2I μr B 022π=⋅rI μB 2π02=R 2 ＜r ＜R 3()()⎥⎦⎤⎢⎣⎡---=⋅I R R R r I μr B 22232203ππ2π 2223223032πR R r R r I μB --= r ＞R 3()02π04=-=⋅I I μr B04=B磁感强度B （r ）的分布曲线如图（ｂ）．11－16 如图所示，N 匝线圈均匀密绕在截面为长方形的中空骨架上．求通入电流I 后，环内外磁场的分布．题 11-16 图分析根据右手螺旋法则，螺线管内磁感强度的方向与螺线管中心轴线构成同心圆，若取半径为r 的圆周为积分环路，由于磁感强度在每一环路上为常量，因而πr 2d ⋅=⋅⎰B l B依照安培环路定理∑⎰=⋅I μ0d l B ，可以解得螺线管内磁感强度的分布．解依照上述分析，有∑=⋅I μr B 02πr ＜R 102π1=⋅r B01=BR 2 ＞r ＞R 1NI μr B 022π=⋅rNI μB 2π02=r ＞R 202π3=⋅r B 03=B在螺线管内磁感强度B 沿圆周，与电流成右手螺旋．若112R R R <<- 和R 2 ，则环内的磁场可以近似视作均匀分布，设螺线环的平均半径()1221R R R +=，则环内的磁感强度近似为 RNIμB 2π0≈11－17 电流I 均匀地流过半径为R 的圆形长直导线，试计算单位长度导线内的磁场通过图中所示剖面的磁通量．题 11-17 图分析由题11－14 可得导线内部距轴线为r 处的磁感强度()202πR Irμr B =在剖面上磁感强度分布不均匀，因此，需从磁通量的定义()S B d ⎰=r Φ来求解．沿轴线方向在剖面上取面元ｄS ＝l ｄr ，考虑到面元上各点B 相同，故穿过面元的磁通量ｄΦ＝B ｄS ，通过积分，可得单位长度导线内的磁通量⎰=Sr B Φd解由分析可得单位长度导线内的磁通量4πd 2π0020Iμr R Ir μΦR==⎰11－18 已知地面上空某处地磁场的磁感强度40.410T B -=⨯，方向向北．若宇宙射线中有一速率715.010m s -=⨯v 的质子，垂直地通过该处．求：（1）洛伦兹力的方向；（2）洛伦兹力的大小，并与该质子受到的万有引力相比较．题 11-18 图解（1）依照B F ⋅=v q L 可知洛伦兹力L F 的方向为B ⊥v 的方向，如图所示．（2）因B ⊥v ，质子所受的洛伦兹力N 102.316-⨯==B F v q L在地球表面质子所受的万有引力N 1064.126p -⨯==g m G因而，有101095.1/⨯=G F L ，即质子所受的洛伦兹力远大于重力．11－19 霍尔效应可用来测量血流的速度，其原理如图所示．在动脉血管两侧分别安装电极并加以磁场．设血管直径为d ＝2.0 mm ，磁场为B ＝0.080 T ，毫伏表测出血管上下两端的电压为U H ＝0.10 mV ，血流的流速为多大？题 11-19 图分析血流稳定时，有H qE B q =v由上式可以解得血流的速度．解依照分析m/s 63.0===dBU B E HH v 11－20 带电粒子在过饱和液体中运动，会留下一串气泡显示出粒子运动的径迹．设在气泡室有一质子垂直于磁场飞过，留下一个半径为3.5 cm 的圆弧径迹，测得磁感强度为0.20 Ｔ，求此质子的动量和动能．解根据带电粒子回转半径与粒子运动速率的关系有m /s kg 1012.121⋅⨯===-ReB m p vkeV 35.222==mp E k11－21 从太阳射来的速度为0.80×108m/ｓ的电子进入地球赤道上空高层范艾伦辐射带中，该处磁场为4.0 ×10－7Ｔ，此电子回转轨道半径为多大？若电子沿地球磁场的磁感线旋进到地磁北极附近，地磁北极附近磁场为2.0 ×10－5Ｔ，其轨道半径又为多少？解由带电粒子在磁场中运动的回转半径高层范艾伦辐射带中的回转半径m 101.1311⨯==eB m R v地磁北极附近的回转半径m 2322==eB m R v11－22 如图（ａ）所示，一根长直导线载有电流I 1 ＝30 A ，矩形回路载有电流I 2 ＝20 A ．试计算作用在回路上的合力．已知d ＝1.0 cm ，b ＝8.0 cm ，l ＝0.12 m ．题 11-22图分析矩形上、下两段导线受安培力F 1 和F 2 的大小相等，方向相反，对不变形的矩形回路来说，两力的矢量和为零．而矩形的左右两段导线，由于载流导线所在处磁感强度不等，所受安培力F 3 和F 4 大小不同，且方向相反，因此线框所受的力为这两个力的合力．解由分析可知，线框所受总的安培力F 为左、右两边安培力F 3 和F 4 之矢量和，如图（ｂ）所示，它们的大小分别为d lI I μF π22103=()b d l I I μF +=π22104故合力的大小为()N 1028.1π2π2321021043-⨯=+-=-=b d lI I μd l I I μF F F 合力的方向朝左，指向直导线．11－23 一直流变电站将电压为500kV 的直流电，通过两条截面不计的平行输电线输向远方．已知两输电导线间单位长度的电容为3.0×10－11F ·m －1，若导线间的静电力与安培力正好抵消．求：（1）通过输电线的电流；（2）输送的功率．分析当平行输电线中的电流相反时，它们之间存在相互排斥的安培力，其大小可由安培定律确定．若两导线间距离为d ，一导线在另一导线位置激发的磁感强度dIμB π20=,导线单位长度所受安培力的大小BI F B =．将这两条导线看作带等量异号电荷的导体，因两导线间单位长度电容C 和电压U 已知，则单位长度导线所带电荷λ＝CU ，一导线在另一导线位置所激发的电场强度dελE 0π2=，两导线间单位长度所受的静电吸引力λE F E =．依照题意，导线间的静电力和安培力正好抵消，即0=+E B F F从中可解得输电线中的电流．解（1）由分析知单位长度导线所受的安培力和静电力分别为d I μBI F B π220==dεU C λE F E 022π2== 由0=+E BF F 可得dεU C d I μ02220π2π2=解得A 105.4300⨯==μεCUI （2）输出功率W 1025.29⨯==IU N11－24 在氢原子中，设电子以轨道角动量π2/h L =绕质子作圆周运动，其半径为m 1029.5110-⨯=a ．求质子所在处的磁感强度．h 为普朗克常量，其值为s J 1063.634⋅⨯-分析根据电子绕核运动的角动量π20h a m L ==v 可求得电子绕核运动的速率v ．如认为电子绕核作圆周运动，其等效圆电流v/π20a e T e i ==在圆心处，即质子所在处的磁感强度为02a i μB =解由分析可得，电子绕核运动的速率π2ma h=v其等效圆电流2020π4/π2ma he v a e i ==该圆电流在圆心处产生的磁感强度T 5.12π82202000===ma heμa i μB 11－25 如图[a]所示，一根长直同轴电缆，内、外导体之间充满磁介质，磁介质的相对磁导率为μr （μr ＜1），导体的磁化可以忽略不计．沿轴向有恒定电流I 通过电缆，内、外导体上电流的方向相反．求：（1）空间各区域内的磁感强度和磁化强度；*（2）磁介质表面的磁化电流．题 11-25 图分析电流分布呈轴对称，依照右手定则，磁感线是以电缆对称轴线为中心的一组同心圆．选取任一同心圆为积分路径，应有⎰⋅=⋅r H d π2l H ，利用安培环路定理⎰∑=⋅fI d l H求出环路内的传导电流，并由H μB =，()H μM r 1-=，可求出磁感强度和磁化强度．再由磁化电流的电流面密度与磁化强度的关系求出磁化电流．解（1）取与电缆轴同心的圆为积分路径，根据磁介质中的安培环路定理，有∑=fπ2I r H对r ＜R 1221f ππrR I I =∑ 得2112πR IrH =忽略导体的磁化（即导体相对磁导率μr =1），有01=M ，21012πR IrμB =对R 2 ＞r ＞R 1I I=∑f得rI H 2π2=填充的磁介质相对磁导率为μr ，有()r I μM r 2π12-=，rI μμB r 2π02= 对R 3 ＞r ＞R 2()()2223223ππR r R R I I I f -⋅--=∑ 得()()222322332πR R r r R I H --= 同样忽略导体的磁化，有03=M ，()()2223223032πR R r r R I μB --= 对r ＞R 30=-=∑I I If得04=H ，04=M ，04=B（2）由r M I s 2π⋅=，磁介质内、外表面磁化电流的大小为()()I μR R M I r si 12π112-=⋅= ()()I μR R M I r se 12π222-=⋅=对抗磁质（1r μ<），在磁介质内表面（r ＝R 1 ），磁化电流与内导体传导电流方向相反；在磁介质外表面（r ＝R 2 ），磁化电流与外导体传导电流方向相反．顺磁质的情况与抗磁质相反．H （r ）和B （r ）分布曲线分别如图（ｂ）和（c ）所示．。

大学普通物理学习题答案-第十一章-恒定电流与恒定磁场

第十一章恒定电流与恒定磁场一、选择题1.如图11-1所示，有两根载有相同电流的无限长直导线，分别通过x1=1m、x2=3m的点，且平行于y轴，则磁感应强度B等于零的地方是（）。

A.x=2m的直线上B.在x>2m的区域C.在x<1m的区域D.不在x、y平面上图11-11.【答案】A。

解析：根据对称性可得，两条载流导线在x=2m的直线上产生的磁感应强度大小相等；用右手螺旋定则可判断两磁感应强度的方向相反，相互抵消，合磁感应强度为零，故选A。

2.图11-2中6根无限长导线互相绝缘，通过电流均为I，区域Ⅰ、Ⅰ、Ⅰ、Ⅰ均为全等的正方形，哪一个区域指向纸内的磁通量最大（）。

A. Ⅰ区域B. Ⅰ区域C. Ⅰ区域D. Ⅰ区域2.【答案】B。

解析：通过Ⅰ区域的磁通量为0，通过Ⅰ区城的磁通量最大且指向纸内，通过Ⅰ区域的磁通量最大但指向纸外，通过IV区域的磁通量为0。

故选B。

3.如图11-3所示，在一圆形电流I所在的平面内，选取一个同心圆形闭合回路L，则由安培环路定理可知（）。

A.d 0LB l ⋅=⎰，且环路上任意一点B =0 B.d 0LB l ⋅=⎰，且环路上任意一点B ≠0 C.d 0LB l ⋅≠⎰，且环路上任意一点B ≠0 D.d 0LB l ⋅≠⎰，且环路上任意一点B =常量3.【答案】B 。

解析：根据安培环路定理，闭合回路内没有电流穿过，所以环路积分等于0.但是由于圆形电流的存在，环路上任意一点的磁感应强度都不等于0。

故选B 。

4.无限长直圆柱体，半径为R ，沿轴向均匀流有电流，设圆柱体内（r <R ）的磁感应强度为B i ，圆柱体外（r>R ）的磁感应强度为B e ，则有：（）。

A.B i 、B e 均与r 成正比B.B i 、B e 均与r 成反比C.B i 与r 成反比，B e 与r 成正比D.B i 与r 成正比，B e 与r 成反比4.【答案】B 。

解析：导体横截面上的电流密度2πR I J =，以圆柱体轴线为圆心，半径为r 的同心圆作为安培环路，当r <R ，20ππ2r J r B i ⋅=⋅μ，20π2R IrB i μ=；当r <R ，I r B e ⋅=⋅0π2μ，rIB e π20μ=；所以选D 。

大学物理电磁学第11章恒定磁场

四、毕-萨定律的应用
dB
0 4
Idl r r2
方法：
(1)将电流分解为无数个电流元
(2)由电流元求dB (据毕—萨定律)
(3)对dB积分求B = dB 矢量积分须化作分量积分去做
Bx dBx , By dBy , Bz dBz
例题1 直线电流在P点的磁场
2
解：
任取电流元 I dl
所有磁现象可归纳为：
运动电荷
运动电荷
载流导体
磁场
载流导体
磁体
磁体
磁场的宏观性质：对运动电荷(或电流)有力的作用，磁场有能量
二、磁感应强度
B 1、磁场的描述:磁感应强度
方向：磁针静止时，N极指向即B的正方向
S
N
2、B的大小：
以磁场对载流导线的作用为例
电流元所受到的磁场力
dF Idl sin
l
r
B
3）说明磁场为非保守场称为涡旋场
静电场是保守场、无旋场
二、简证(用特例说明安培环路定理的正确性)
(1)闭合路径L环绕电流
L在垂直于导线的平面内
B 0I 2 r
L
I d
o
B
r
dl
磁感线
(2)闭合路径L不包围电流
B dl1 dl2 L
P
·
I
d
o
dl2
dl1
L2
L1
磁感线
·
Q
三、运用安培环路定理求磁场安培环路定理适用于任何形状恒定电流的载流体
P·
Idl r
B
dB
0 4
Idl r r2
B
dB
0 4
Idl r r2

大学物理恒定磁场

11-1 恒定电流电流密度磁现象：我国是世界上最早发现和应用磁现象的国家之一，早在公元前300年久发现了磁铁矿石吸引铁的现象。

在11世纪，我国已制造出航海用的指南。

在1820年之前，人们对磁现象的研究仅局限于铁磁极间的相吸和排斥，而对磁与电两种现象的研究彼此独立，毫无关联。

1820年7月丹麦物理学家奥斯特发表了《电流对磁针作用的实验》，公布了他观察到的电流对磁针的作用，从此开创了磁电统一的新时代。

奥斯特的发现立即引起了法国数学家和物理学家安培的注意，他在短短的几个星期内对电流的磁效应作出了系列研究，发现不仅电流对磁针有作用，而且两个电流之间彼此也有作用，如图所示；位于磁铁附近的载流线圈也会受到力或力矩的作用而运动。

此外，他还发现若用铜线制成一个线圈，通电时其行为类似于一块磁铁。

这使他得出这样一个结论：天然磁性的产生也是由于磁体内部有电流流动。

每个磁性物质分子内部，都自然地包含一环形电流，称为分子电流，每个分子电流相当于一个极小的磁体，称为分子磁矩。

一般物体未被磁化时，单个分子磁矩取向杂乱无章，因而对外不显磁性；而在磁性物体内部，分子磁矩的取向至少未被完全抵消，因而导致磁铁之间有“磁力”相互作用。

1820年是人们对电磁现象的研究取得重大成果的一年。

人们发现，电荷的运动是一切磁现象的根源。

一方面，运动电荷在其周围空间激发磁场；另一方面，运动电荷在空间除受电场力作用之外，还受磁场力作用。

电磁现象是一个统一的整体，电学和磁学不再是两个分立的学科。

11-1 恒定电流电流密度如前所述，电荷的运动是一切磁现象的根源。

电荷的定向运动形成电流，称为传导电流；若电荷或宏观带电物体在空间作机械运动，形成的电流称为运流电流。

常见的电流是沿着一根导线流动的电流，其强弱用电流强度来描述，它等于单位时间通过某一截面的电量，方向与正电荷流动的方向相同，其数学表达式为dtdq I ，虽然我们规定了电流强度的方向，但电流强度I 是标量而不是矢量，因为电流的叠加服从代数加减法则，而不服从矢量叠加的平行四边形法则。

第十一章稳恒磁场

于π)的正弦成正比，即：结论
式的中单K位为有比关例。系数，其值与介质的种dB类和选用
14
在国际单位制中， μ0称为真空磁导率，
K
0
0
4
/ 4P
10r7 Tθ
mId lA
I
1
故有：
dB的方向用右手螺旋法则确定：
右手弯曲的四指由Idl的方
向沿小于180°的θ角转向 r的方向，则伸直拇指的指向就是dB 的方向。
5
一、磁感应强度
为了描述磁场中各点的磁场强弱和方向，引入磁感应强度。用B表示，
定义
B Fm q0v
单位：特斯拉（T）。
比值B是一个与运动电荷的性质无关、仅与该点磁场的性质有关的常量。
B为矢量，其方向用右手螺旋法则确定:
6
特斯拉
右手螺旋法则：
将右手拇指与其余四指垂直，先将四指的指向与 7 Fm方向相同，再使其向的v方向弯曲，这时拇指
大多数生物大分子是抗磁质，少数是顺磁质，极少呈铁磁质
43
三、超导体及其磁学特性
1、超导体超导现象：当物质的温度下降到某一定值时，该物质的电阻完全消失的现象称为超导现象。超导性：物质失去电阻的性质叫超导性。超导体：具有超导性的物质叫超导体。超导体失去电阻的温度称为临界温度Tc，可能成为超导体的物质是：①位于元素周期表中部的金属元素（除一价金属、铁磁质、和抗磁质）②许多化合物或合金。
磁感应线的特点:
I
I
通电螺线管的磁感应线
磁感应线是闭合的曲线，密集的地方磁场较
强，稀疏的地方磁场较弱。
9
1、磁通量
通过某曲面磁感应线的总数称为通过该曲面的磁通量。
用Φ表示。
通过面积元dS的磁通量为：

第十一章恒定电流的磁场作业磁介质磁介质中的安培环路定理小结

作业11.1、11.211.4、11.8、11.9、11.15、11.1787磁介质90顺磁质B B >（铝、氧、锰等）弱磁质B B >>铁磁质（铁、钴、镍等）强磁性物质B B <抗磁质（铜、铋、氢等）弱磁质抗磁质顺磁质SI SI B L宏观上构成沿介质表面的等效环形电流, 称为表面束缚电流或磁化电流。

B AI 0I cbad.l113五、磁场对载流导线和运动电荷的作用（1）磁场对载流导线的作用力—安培力微分形式积分形式B l I F ⨯=d d Bl I F l⨯=⎰d 其中，是载流导线上的电流元，是所在处的磁感应强度。

l Id l I d B（2）均匀磁场对平面载流线圈的作用合力=∑F 磁力矩B p M m ⨯=式中，是载流线圈的磁矩，，其中N 是线圈匝数，I 是线圈中的电流，S 是线圈的面积，且S 的方向与电流环绕方向满足右螺旋法则。

m p S NI p m=114（3）磁力的功⎰=m1m2m d ΦΦΦI A mm1m2)(ΦI ΦΦI ∆=-=磁力的功等于电流强度I 乘以通过回路磁通量的增量∆Φm 。

（4）磁场对运动电荷的作用Bq F⨯=v 洛仑兹力:116六、磁介质（1）磁介质的分类抗磁质1<r μ顺磁质1>r μ铁磁质1>>r μ（2）磁介质的磁化在外磁场中固有磁矩沿外磁场的取向或感应磁矩的产生使磁介质的表面（或内部）出现束缚电流。

第11 章恒定电流的磁场

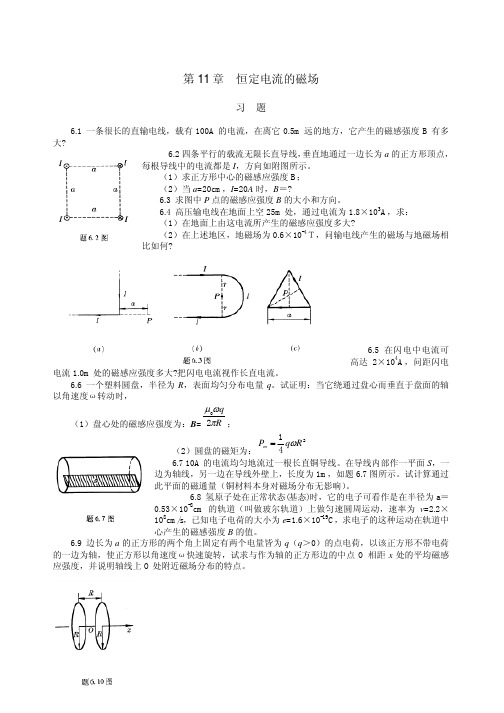
第11章恒定电流的磁场习题6.1 一条很长的直输电线，载有100A 的电流，在离它0.5m 远的地方，它产生的磁感强度B 有多大?6.2四条平行的载流无限长直导线，垂直地通过一边长为a 的正方形顶点，每根导线中的电流都是I ，方向如附图所示。

（1）求正方形中心的磁感应强度B ；（2）当a =20cm ，I =20A 时，B ＝?6.3 求图中P 点的磁感应强度B 的大小和方向。

6.4 高压输电线在地面上空25m 处，通过电流为1.8×103A ，求：（1）在地面上由这电流所产生的磁感应强度多大?（2）在上述地区，地磁场为0.6×10-4Ｔ，问输电线产生的磁场与地磁场相比如何?6.5 在闪电中电流可高达2×104A ，问距闪电电流1.0m 处的磁感应强度多大?把闪电电流视作长直电流。

6.6 一个塑料圆盘，半径为R ，表面均匀分布电量q 。

试证明：当它绕通过盘心而垂直于盘面的轴以角速度ω转动时，（1）盘心处的磁感应强度为：B =R qπωµ20；（2）圆盘的磁矩为：241R q P m ω=6.7 10A 的电流均匀地流过一根长直铜导线。

在导线内部作一平面S ，一边为轴线，另一边在导线外壁上，长度为1m ，如题6.7图所示。

试计算通过此平面的磁通量（铜材料本身对磁场分布无影响）。

6.8 氢原子处在正常状态(基态)时，它的电子可看作是在半径为a ＝0.53×10-8cm 的轨道（叫做玻尔轨道）上做匀速圆周运动，速率为v =2.2×108cm/s ，已知电子电荷的大小为e =1.6×10-19C ，求电子的这种运动在轨道中心产生的磁感强度B 的值。

6.9 边长为a 的正方形的两个角上固定有两个电量皆为q （q ＞0）的点电荷，以该正方形不带电荷的一边为轴，使正方形以角速度ω快速旋转，试求与作为轴的正方形边的中点O 相距x 处的平均磁感应强度，并说明轴线上O 处附近磁场分布的特点。

第十一章恒定磁场

S1 ( B R2 ) 0
S1 BR 2
(3i 2 j ) Si 3S
例3、两平行载流直导线
求 1.两线中点 B A
I1
2.过图中矩形的磁通量解：1.I1、I2在A点的磁场
BA
r2
A
I2
l
r3
0 I1 B1 B2 2 d 2
r1
2.0 10 T
第十一章恒定磁场静止的电荷产生静电场，静电场是一种物质。运动电荷周围既有电场又有磁场，磁场也是一种物质。恒定电流（运动电荷）的磁场在研究方法上与静电场有许多相似之处，因此要与静电场部分类比学习。
电流密度（矢量）
用来细致刻画电流在截面上分布的物理量。
垂直通过单位截面的电流强度，称为此处的电流密度。
0 I sin dy B 2 4 r 2 0 I sin d 1 4a
0 I B (cos 1 cos 2 ) 4a
I
2
dy

1 r0
r
y
O
dB
P
a
X
0 I B (cos 1 cos 2 ) 4a
无限长载流直导线
I 2
Ek dl Ek dl
L
单位正电荷绕闭合回路一周时，电源中非静电力所做的功。电动势描述电路中非静电力做功本领电势差描述电路中静电力做功本领注意：电动势是标量
基本的磁现象
天然磁石同极相斥异极相吸
S
N
S
N
电流的磁效应 1820年奥斯特
S
N
I
F
I
F
电子束
E dl

新编基础物理学答案_第11章

第11章恒定电流与真空中的恒定磁场11-1 电源中的非静电力与静电力有什么不同答：在电路中，电源中非静电力的作用是，迫使正电荷经过电源内部由低电位的电源负极移动到高电位的电源正极，使两极间维持一定的电位差。

而静电场的作用是在外电路中把正电荷由高电位的地方移动到低电位的地方，起到推动电流的作用；在电源内部正好相反，静电场起的是抵制电流的作用。

电源中存在的电场有两种：1、非静电起源的场；2、稳恒场。

把这两种电场与静电场比较，静电场由静止电荷所激发，它不随时间的变化而变化。

非静电场不由静止电荷产生，它的大小决定于单位正电荷所受的非静电力，k F E q=vv 。

当然电源种类不同，k F v的起因也不同。

11-2静电场与恒定电场有什么相同处和不同处为什么恒定电场中仍可应用电势概念答：稳恒电场与静电场有相同之处，即是它们都不随时间的变化而变化，基本规律相同，并且都是位场。

但稳恒电场由分布不随时间变化的电荷产生，电荷本身却在移动。

正因为建立稳恒电场的电荷分布不随时间变化，因此静电场的两条基本定理，即高斯定理和环路定理仍然适用，所以仍可引入电势的概念。

11-3一根铜导线表面涂以银层，当两端加上电压后，在铜线和银层中，电场强度是否相同电流密度是否相同电流强度是否相同为什么答：此题涉及知识点：电流强度d sI =⋅⎰r rj s ，电流密度概念，电场强度概念，欧姆定律的微分形式j E σ=rr 。

设铜线材料横截面均匀，银层的材料和厚度也均匀。

由于加在两者上的电压相同，两者的长度又相等，故铜线和银层的场强E r相同。

由于铜线和银层的电导率σ不同，根据j E σ=r r 知，它们中的电流密度j r 不相同。

电流强度d sI =⋅⎰r r j s ，铜线和银层的j r不同但相差不太大，而它们的横截面积一般相差较大，所以通过两者的电流强度，一般说来是不相同的。

11-4一束质子发生侧向偏转，造成这个偏转的原因可否是：（1）电场（2）磁场（3）若是电场或者是磁场在起作用，如何判断是哪一种场答：造成这个偏转的原因可以是电场或磁场。

第十一章恒定电流的磁场(一) 作业及参考答案 2014

一.选择题:1．（基础训练1）［D ］载流的圆形线圈(半径a1)与正方形线圈(边长a2 )通有相同电流I．若两个线圈的中心O1、O2处的磁感强度大小相同，则半径a1与边长a2之比a1∶a2为(A) 1∶1 (B) π2∶1(C) π2∶4 (D) π2∶8提示()82,,22135cos45cos244,2212212121ππμπμμ===-⨯⨯⨯==aaBBaIaIBaIBoooo得由2．(基础训练3)［B ］.有一无限长通电流的扁平铜片，宽度为a，厚度不计，电流I在铜片上均匀分布，在铜片外与铜片共面，离铜片右边缘为b处的P点(如图)的磁感强度B的大小为(A))(2baI+πμ．(B)bbaaI+πln2μ．(C)bbabI+πln2μ．(D))2(baI+πμ．提示：bbaaIrdraIrrdIdBdraIdIabb+======⎰⎰⎰+ln222dIBBB,BdB,2P,)(drrPπμπμπμπμ的大小为：，的方向也垂直纸面向内据方向垂直纸面向内；根处产生的它在，电流为导线相当于一根无限长的直的电流元处选取一个宽度为点为在距离3. .(基础训练4)［D ］如图，两根直导线ab和cd沿半径方向被接到一个截面处处相等的铁环上，稳恒电流I从a端流入而从d端流出，则磁感强度B沿图中闭合路径L的积分⎰⋅LlBd(A) I0μ．(B) I031μ．(C) 4/Iμ．(D) 3/2Iμ．提示⎰∑⎰=⋅∴=-==∴===⋅LLIl dBIIslIIslIslIIIl dB32322)(RRRIRI11122112122111Lμρρρμμ得为两条支路的电阻。

，，其中，而内4. 自测提高7［C ］如图，正方形的四个角上固定有四个电荷量均为q 的点电荷．此正方形以角速度ω 绕AC 轴旋转时，在中心O 点产生的磁感应强度大小为B 1；此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时，在O 点产生的磁感应强度的大小为B 2，则B 1与B 2间的关系为(A) B 1 = B 2． (B) B 1 = 2B 2．(C) B 1 =21B 2． (D) B 1 = B 2 /4．提示：设正方形边长为a ,)22(a b b OC AO ===式中，两种情况下正方形旋转时的角速度ω 相同，所以每个点电荷随着正方形旋转时形成的等效电流相同，为 πω2q I =当正方形绕AC 轴旋转时，一个点电荷在O 点产生的磁感应强度的大小为bIB 20μ=，实际上有两个点电荷同时绕AC 旋转产生电流，在O 点产生的总磁感应强度的大小为b IbIB B 001222μμ=⨯==同理，当正方形绕过O 点垂直于正方形平面的轴旋转时，在O 点产生的磁感应强度的大小为bIb IB B 0022244μμ=⨯== 故有122B B =5. 附录C 2［ B ］有一半径为R 的单匝圆线圈，通以电流I ，若将该导线弯成匝数为2=N 的平面圆线圈，导线长度不变，并通以同样的电流，则线圈中心的磁感应强度和磁矩分别是原来的：(A) 4倍和1/8 (B) 4倍和1/2 (C) 2倍和1/4 ． (D) 2倍和1/2提示：由半径为R 的单匝线圈弯成匝数为2=N 的线圈以后，每一个线圈的半径变为R r 21=，故磁感应强度变为原来的4倍，磁矩变为原来的1/2，总的变化为4倍和1/2二. 填空题6.（基础训练11）均匀磁场的磁感强度B与半径为r 的圆形平面的法线n的夹角为α ，今以圆周为边界，作一个半球面S ，S 与圆形平面组成封闭面如所示．则通过S 面的磁通量Φ = απcos 2B r -。

第11章 恒定磁场