初中数学平面直角坐标系提高题与常考题和培优题(含解析)

合集下载

第5章平面直角坐标系(中考经典常考题)-江苏省2023-2024学年上学期八年级数学单元培优

第5章平面直角坐标系（中考经典常考题）-江苏省2023-2024学年上学期八年级数学单元培优专题练习（苏科版）一．选择题（共10小题）1．（2023•盐城）在平面直角坐标系中，点A（1，2）在（）A．第一象限B．第二象限C．第三象限D．第四象限2．（2023•常州）在平面直角坐标系中，若点P的坐标为（2，1），则点P关于y轴对称的点的坐标为（）A．（﹣2，﹣1）B．（2，﹣1）C．（﹣2，1）D．（2，1）3．（2022•扬州）在平面直角坐标系中，点P（﹣3，a2+1）所在象限是（）A．第一象限B．第二象限C．第三象限D．第四象限4．（2022•常州）在平面直角坐标系xOy中，点A与点A1关于x轴对称，点A与点A2关于y轴对称．已知点A1（1，2），则点A2的坐标是（）A．（﹣2，1）B．（﹣2，﹣1）C．（﹣1，2）D．（﹣1，﹣2）5．（2020•淮安）在平面直角坐标系中，点（3，2）关于原点对称的点的坐标是（）A．（2，3）B．（﹣3，2）C．（﹣3，﹣2）D．（﹣2，﹣3）6．（2020•扬州）在平面直角坐标系中，点P（x2+2，﹣3）所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限7．（2020•南通）以原点为中心，将点P（4，5）按逆时针方向旋转90°，得到的点Q所在的象限为（）A．第一象限B．第二象限C．第三象限D．第四象限8．（2018•扬州）在平面直角坐标系的第二象限内有一点M，点M到x轴的距离为3，到y 轴的距离为4，则点M的坐标是（）A．（3，﹣4）B．（4，﹣3）C．（﹣4，3）D．（﹣3，4）9．（2017•南通）在平面直角坐标系中．点P（1，﹣2）关于x轴对称的点的坐标是（）A．（1，2）B．（﹣1，﹣2）C．（﹣1，2）D．（﹣2，1）10．（2017•南京）过三点A（2，2），B（6，2），C（4，5）的圆的圆心坐标为（）A．（4，）B．（4，3）C．（5，）D．（5，3）二．填空题（共10小题）11．（2023•宿迁）平面直角坐标系中，点A（2，3）关于x轴的对称的点的坐标是．12．（2023•连云港）画一条水平数轴，以原点O为圆心，过数轴上的每一刻度点画同心圆，过原点O按逆时针方向依次画出与正半轴的角度分别为30°、60°、90°、120°、…、330°的射线，这样就建立了“圆”坐标系．如图，在建立的“圆”坐标系内，我们可以将点A、B、C的坐标分别表示为A（6，60°）、B（5，180°）、C（4，330°），则点D 的坐标可以表示为．13．（2021•扬州）在平面直角坐标系中，若点P（1﹣m，5﹣2m）在第二象限，则整数m的值为．14．（2021•南京）如图，在平面直角坐标系中，△AOB的边AO，AB的中点C，D的横坐标分别是1，4，则点B的横坐标是．15．（2020•泰州）以水平数轴的原点O为圆心，过正半轴Ox上的每一刻度点画同心圆，将Ox逆时针依次旋转30°、60°、90°、…、330°得到11条射线，构成如图所示的“圆”坐标系，点A、B的坐标分别表示为（5，0°）、（4，300°），则点C的坐标表示为．16．（2018•常州）已知点P（﹣2，1），则点P关于x轴对称的点的坐标是．17．（2016•淮安）点A（3，﹣2）关于x轴对称的点的坐标是．18．（2018•宿迁）在平面直角坐标系中，将点（3，﹣2）先向右平移2个单位长度，再向上平移3个单位长度，则所得点的坐标是．19．（2018•南京）在平面直角坐标系中，点A的坐标是（﹣1，2），作点A关于y轴的对称点，得到点A'，再将点A'向下平移4个单位，得到点A″，则点A″的坐标是（，）．20．（2015•南京）在平面直角坐标系中，点A的坐标是（2，﹣3），作点A关于x轴的对称点，得到点A′，再作点A′关于y轴的对称点，得到点A″，则点A″的坐标是（，）．第5章平面直角坐标系（中考经典常考题）-江苏省2023-2024学年上学期八年级数学单元培优专题练习（苏科版）参考答案与试题解析一．选择题（共10小题）1．（2023•盐城）在平面直角坐标系中，点A（1，2）在（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】A【解答】解：∵点A（1，2）的横坐标和纵坐标均为正数，∴点A（1，2）在第一象限．故选：A．2．（2023•常州）在平面直角坐标系中，若点P的坐标为（2，1），则点P关于y轴对称的点的坐标为（）A．（﹣2，﹣1）B．（2，﹣1）C．（﹣2，1）D．（2，1）【答案】C【解答】解：点P的坐标是（2，1），则点P关于y轴对称的点的坐标是（﹣2，1），故选：C．3．（2022•扬州）在平面直角坐标系中，点P（﹣3，a2+1）所在象限是（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】B【解答】解：∵a2≥0，∴a2+1≥1，∴点P（﹣3，a2+1）所在的象限是第二象限．故选：B．4．（2022•常州）在平面直角坐标系xOy中，点A与点A1关于x轴对称，点A与点A2关于y轴对称．已知点A1（1，2），则点A2的坐标是（）A．（﹣2，1）B．（﹣2，﹣1）C．（﹣1，2）D．（﹣1，﹣2）【答案】D【解答】解：∵点A与点A1关于x轴对称，已知点A1（1，2），∴点A的坐标为（1，﹣2），∵点A与点A2关于y轴对称，∴点A2的坐标为（﹣1，﹣2），故选：D．5．（2020•淮安）在平面直角坐标系中，点（3，2）关于原点对称的点的坐标是（）A．（2，3）B．（﹣3，2）C．（﹣3，﹣2）D．（﹣2，﹣3）【答案】C【解答】解：点（3，2）关于原点对称的点的坐标是：（﹣3，﹣2）．故选：C．6．（2020•扬州）在平面直角坐标系中，点P（x2+2，﹣3）所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】D【解答】解：∵x2+2＞0，∴点P（x2+2，﹣3）所在的象限是第四象限．故选：D．7．（2020•南通）以原点为中心，将点P（4，5）按逆时针方向旋转90°，得到的点Q所在的象限为（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】B【解答】解：如图，∵点P（4，5）按逆时针方向旋转90°，得点Q所在的象限为第二象限．故选：B．8．（2018•扬州）在平面直角坐标系的第二象限内有一点M，点M到x轴的距离为3，到y 轴的距离为4，则点M的坐标是（）A．（3，﹣4）B．（4，﹣3）C．（﹣4，3）D．（﹣3，4）【答案】C【解答】解：由题意，得x＝﹣4，y＝3，即M点的坐标是（﹣4，3），故选：C．9．（2017•南通）在平面直角坐标系中．点P（1，﹣2）关于x轴对称的点的坐标是（）A．（1，2）B．（﹣1，﹣2）C．（﹣1，2）D．（﹣2，1）【答案】A【解答】解：点P（1，﹣2）关于x轴的对称点的坐标是（1，2），故选：A．10．（2017•南京）过三点A（2，2），B（6，2），C（4，5）的圆的圆心坐标为（）A．（4，）B．（4，3）C．（5，）D．（5，3）【答案】A【解答】解：如图，设△ABC的外心E（4，t），则CE＝5﹣t，EM＝t﹣2，∵EC＝AE，∴5﹣t＝，解得t＝，可得结论．故选：A．二．填空题（共10小题）11．（2023•宿迁）平面直角坐标系中，点A（2，3）关于x轴的对称的点的坐标是　（2，﹣3）　．【答案】见试题解答内容【解答】解：点A（2，3）关于x轴的对称点的坐标是（2，﹣3），故答案为：（2，﹣3）．12．（2023•连云港）画一条水平数轴，以原点O为圆心，过数轴上的每一刻度点画同心圆，过原点O按逆时针方向依次画出与正半轴的角度分别为30°、60°、90°、120°、…、330°的射线，这样就建立了“圆”坐标系．如图，在建立的“圆”坐标系内，我们可以将点A、B、C的坐标分别表示为A（6，60°）、B（5，180°）、C（4，330°），则点D 的坐标可以表示为　（3，150°）　．【答案】（3，150°）．【解答】解：∵点D与圆心的距离为3，射线OD与x轴正方向之间的夹角为150°，∴点D的坐标为（3，150°）．故答案为：（3，150°）．13．（2021•扬州）在平面直角坐标系中，若点P（1﹣m，5﹣2m）在第二象限，则整数m的值为　2　．【答案】见试题解答内容【解答】解：由题意得：，解得：，∴整数m的值为2，故答案为：2．14．（2021•南京）如图，在平面直角坐标系中，△AOB的边AO，AB的中点C，D的横坐标分别是1，4，则点B的横坐标是　6　．【答案】6．【解答】解：∵边AO，AB的中点为点C、D，∴CD是△OAB的中位线，CD∥OB，∵点C，D的横坐标分别是1，4，∴CD＝3，∴OB＝2CD＝6，∴点B的横坐标为6．故答案为：6．15．（2020•泰州）以水平数轴的原点O为圆心，过正半轴Ox上的每一刻度点画同心圆，将Ox逆时针依次旋转30°、60°、90°、…、330°得到11条射线，构成如图所示的“圆”坐标系，点A、B的坐标分别表示为（5，0°）、（4，300°），则点C的坐标表示为　（3，240°）　．【答案】见试题解答内容【解答】解：如图所示：点C的坐标表示为（3，240°）．故答案为：（3，240°）．16．（2018•常州）已知点P（﹣2，1），则点P关于x轴对称的点的坐标是　（﹣2，﹣1）　．【答案】见试题解答内容【解答】解：点P（﹣2，1），则点P关于x轴对称的点的坐标是（﹣2，﹣1），故答案为：（﹣2，﹣1）．17．（2016•淮安）点A（3，﹣2）关于x轴对称的点的坐标是　（3，2）　．【答案】见试题解答内容【解答】解：点A（3，﹣2）关于x轴对称的点的坐标是（3，2）．故答案为：（3，2）．18．（2018•宿迁）在平面直角坐标系中，将点（3，﹣2）先向右平移2个单位长度，再向上平移3个单位长度，则所得点的坐标是　（5，1）　．【答案】见试题解答内容【解答】解：∵将点（3，﹣2）先向右平移2个单位长度，∴得到（5，﹣2），∵再向上平移3个单位长度，∴所得点的坐标是：（5，1）．故答案为：（5，1）．19．（2018•南京）在平面直角坐标系中，点A的坐标是（﹣1，2），作点A关于y轴的对称点，得到点A'，再将点A'向下平移4个单位，得到点A″，则点A″的坐标是（　1　，　﹣2　）．【答案】见试题解答内容【解答】解：∵点A的坐标是（﹣1，2），作点A关于y轴的对称点，得到点A'，∴A′（1，2），∵将点A'向下平移4个单位，得到点A″，∴点A″的坐标是：（1，﹣2）．故答案为：1，﹣2．20．（2015•南京）在平面直角坐标系中，点A的坐标是（2，﹣3），作点A关于x轴的对称点，得到点A′，再作点A′关于y轴的对称点，得到点A″，则点A″的坐标是（　﹣2　，　3　）．【答案】见试题解答内容【解答】解：∵点A的坐标是（2，﹣3），作点A关于x轴的对称点，得到点A′，∴A′的坐标为：（2，3），∵点A′关于y轴的对称点，得到点A″，∴点A″的坐标是：（﹣2，3）．故答案为：﹣2；3．。

初一数学平面直角坐标系30道必做题(含答案和解析及考点)

初一数学平面直角坐标系30道必做题（含答案和解析及考点）1、如图是小刚画的一张脸，他对妹妹说“如果我用（1,3）表示左眼，用（3,3）表示右眼，那么嘴的位置可以表示成.答案：（2,1）.解析：略.考点：函数——平面直角坐标系——点的位置与坐标.2、如图所示，小颖从家到达莲花中学要穿过一个居民小区，若小区的道路均是正南或正东方向，小颖走下面哪条线路不能到达学校（）.A.（0,4）（0,0）（4,0）B.（0,4）（4,4）（4,0）C.（0,4）（1,4）（1,1）（4,1）（4,0）D.（0,4）（3,4）（4,2）（4,0）答案：D.解析：（3,4）（4,2）所走路线为斜线，不符合题意，不能正常到达学校．考点：函数——平面直角坐标系.3、如图，围棋盘放置在某个平面直角坐标系内，白棋②的坐标为（-7,-4），白棋④的坐标为（-6,-8），那么，黑棋的坐标应该分别是．答案：（-6,-6），（-4,-7）.解析：黑棋①的坐标是（-6,-6），黑棋③的坐标是（-4,-7）.考点：函数——平面直角坐标系——点的位置与坐标.4、如果点A（x,y）在第三象限，则点B（-x,y-1）在（）．A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案: D.解析:∵点A（x,y）在第三象限，∴{x＜0y＜0.∴-x＞0，y-1＜0.∴点B（-x,y-1）在第四象限．考点：函数——平面直角坐标系——点的位置与坐标.5、如图的坐标平面上有P、Q两点，其坐标分别为（5,a）、（b,7）．根据图中P、Q两点的位置，判断点（）落在第象限．答案：四.解析：由图象可知，b＜5，a＜7.∴6-b＞0，a-10＜0.∴点（6-b,a-10）落在第四象限．考点：函数——平面直角坐标系——点的位置与坐标.6、已知A（-2,0），B（a,0）且AB=5，则B点坐标为．答案：（3,0）或（-7,0）.解析：由题知︱a+2︱=5，∴a=3或-7.∴B点坐标为（3,0）或（-7,0）.考点：函数——平面直角坐标系——坐标与距离.7、若点A（-2,n）在x轴上，则点B（n-1,n+1）在（）．A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案：B.解析：略.考点：函数——平面直角坐标系——点的位置与坐标.8、点P（m+3,m+1）在直角坐标系的x轴上，则点P的坐标为（）．A.（1,-2）B.（2,0）C.（4,0）D.（0,-4）答案：B.解析：∵点P（m+3,m+1）在直角坐标系的轴上.∴m+1=0.∴m=-1.∴点P的坐标为（2,0）.考点：函数——平面直角坐标系——点的位置与坐标.9、已知点M（3a-8,a-1）．（1）若点M在第二象限，并且a为整数，则点M的坐标为．（2）若点N的坐标为（3,-6），并且直线MN∥x轴，则点M的坐标为．答案：（1）（-2,1）.（2）（-23,-6）.解析：（1）若点M在第二象限，3a＜0，a-1＞0.∴1＜a＜8，又a为整数.3∴a=2.∴M（-2,1）.（2）若点N的坐标为（3，-6），并且直线MN∥x轴.∴a-1=-6，即a=7.∴点M（-23,-6）.考点：函数——平面直角坐标系——点的位置与坐标.10、若点P（-1,a），Q（b,2），且PQ∥x轴，则a ，b .答案：a=2.b≠-1.解析：∵PQ∥x轴.∴PQ两点的纵坐标相同.∴a=2.又∵P、Q应为不重合的两点.∴b≠-1.考点：函数——平面直角坐标系——点的位置与坐标.11、点P（a,b）是平面直角坐标系内的点，请根据点的坐标判断点P的特征：（1）若a=b，则P点在.（2）若a+b=0，则P点在.答案：（1）一三象限坐标轴夹角平分线上.（2）二四象限坐标轴夹角平分线上.解析：（1）略.（2）略.考点：函数——平面直角坐标系——点的位置与坐标.12、若点M在第一、三象限的角平分线上，且点M到x轴的距离为2，则点M的坐标是（）．A.（2,2）B.（-2,-2）C.（2,2）或（-2,-2）D.（2,-2）或（-2,2）答案：C.解析：略.考点：函数——平面直角坐标系——坐标与距离.13、已知点（3-2k2,4k-3）在第一象限的角平分线上，则k= ．答案：1.解析：略.考点：函数——平面直角坐标系——点的位置与坐标.14、若点M（5-a，2a-6）在第四象限，且点M到x轴与y轴的距离相等，试求（a-2）2014-a-2015的值．答案：0.解析：由题意得，5-a+2a-6=0.解得a=1.所以，（a-2）2014-a-2015=（1-2）2014-1-2015=1-1=0.考点：函数——平面直角坐标系——坐标与距离.15、若点P位于y轴左方，距y轴3个单位长，位于x轴上方，距x轴四个单位长，则点P的坐标是．答案：（-3,4）.解析：略.考点：函数——平面直角坐标系——特殊点的坐标.16、在平面直角坐标系中，点P（-3,6）关于y轴的对称点的坐标为．答案：（3,6）.解析：根据关于谁对称，谁不变，可知，点P（-3,6）关于y轴的对称点的坐标为（3,6）. 考点：几何变换——图形的对称——关于x轴、y轴对称的点的坐标.17、在平面直角坐标系中，点P（-1,2）关于y轴的对称点为.答案：（1,2）.解析：由关于谁对称谁不变，可知点P（-1,2）关于y轴的对称点为（1,2）.考点：几何变换——图形的对称——关于x轴、y轴对称的点的坐标.18、在平面直角坐标系中，点P（-1,2）关于x轴的对称点在第象限．答案：三.解析：点P（-1,2）满足点在第二象限的条件．关于x轴的对称点的横坐标与P点的横坐标相同，是-2.纵坐标互为相反数，是-3.则P关于x 轴的对称点是（-2，-3），在第三象限．考点：几何变换——图形的对称——关于x轴、y轴对称的点的坐标.19、平面直角坐标系中，将线段OA向左平移2个单位，平移后，点O 、A的对应点分别为点O1 、A1，则点O1 、A1的坐标分别是（）．A.（0,0），（1,4）B.（0,0），（3,4）C.（-2,0），（1,4）D.（-2,0），（-1,4）答案：D.解析：∵线段OA向左平移2个单位，点O（0,0），A（1,4）.∴点O1，A1的坐标分别是（-2,0），（-1,4）.考点：几何变换——图形的平移——坐标与图形变化：平移.20、已知三角形的三个顶点坐标分别是（-2,1），（2,3），（-3,-1），把△ABC运动到一个确定位置，在下列各点坐标中，（）是平移得到的．A.（0,3），（0,1），（-1,-1）B.（-3,2），（3,2），（-4,0）C.（1,-2），（3,2），（-1,-3）D.（-1,3），（3,5），（-2,1）答案：D.解析：由（-2,1）→（-1,3），（2,3）→（3,5），（-3,-1）→（-2,1）可以看作点向右平移1个单位长度，向上平移2个单位长度，而图形的平移是相同的，所以D对，A、B、C错．考点：函数——平面直角坐标系——点的位置与坐标.几何变换——图形的平移——点的平移.21、线段CD是由线段AB平移得到的，点A（-1,4）的对应点为，则点B（-4,-1）的对应点D坐标为（）.A.（2,9）B.（5,3）C.（1,2）D.（-9,-4）答案：C.解析：略.考点：函数——平面直角坐标系——点的位置与坐标.22、已知点A（0,0），B（3,0），点C在y轴上，且△ABC的面积为6，则点C的坐标是．答案：（0,4）或（0，-4）.解析：由题意可知1AC·AB=6.2∴AC=4.∴点C的坐标是（0,4）或（0，-4）.考点：函数——平面直角坐标系——坐标与面积.23、如图所示，半圆AB平移到半圆CD的位置时所扫过的面积为（）．A.3B.3+πC.6D.6+π答案：C.解析：扫过面积即为矩形ABDC的面积.∴扫过面积=2×3=6.考点：函数——平面直角坐标系——坐标与面积.24、在正方形网格上有一个△ABC ，网格上最小正方形的边长为1．（1）把△ABC 平移，使点A 移动到点A’的位置，画出平移后的△A’B’C’，写出结论：__________．（2）△A’B’C’的面积为__________．（3）若点A 的坐标是（-5,2），点C’为坐标是（0,-2），在图中画出平面直角坐标系，点B’的坐标是__________．答案：（1）结论：A’B’∥AB （答案不唯一）．（2）△A’B’C’的面积是为5．（3）点B’的坐标是（-3,-3）.解析：（1）平移后的△A’B’C’如图所示，结论：A’B’∥AB （答案不唯一）．（2）观察图形可知，△A’B’C’内接在一个长为4，宽为3的长方形中.S △A’B’C’=4×3 −12×1×3−12×1×3−12×2×4=5. ∴△A’B’C’的面积是为5．（3）平面直角坐标系如图所示，点B’的坐标是（-3,-3）.考点：三角形——三角形基础——三角形面积及等积变换.几何变换——图形的平移——平移的性质——坐标与图形变化：平移——作图：平移变换.25、定义：f （a,b ）=（b,a ），g （m,n ）=（-m,-n ）.例如f （2,3）=（3,2），g （-1,-4）=（1,4）．则g[f （-5,6）] 等于．答案：（-6,5）.解析：根据所给定义，g[f （-5,6）]=g （6,-5）=（-6,5）. 考点：式——探究规律——定义新运算.函数——平面直角坐标系.26、在平面直角坐标系中，对于平面内任一点（m ,n ），规定以下两种变换①f （m ,n ）=（m ,-n ），如f （2,1）=（2,-1）；②g （m ,n ）=（-m ,-n ），如g （2,1）=（-2,-1）.按照以上变换有：f[g （3,4）]=f （-3,-4）=（-3,4），那么g[f （-3,2）] 等于（）． A.（3,2） B.（3,-2） C.（-3,2） D.（-3,-2）答案：A.解析：∵f （-3,2）=（-3,-2）.∴g[f （-3,2）]=g （-3,-2）=（3,2）. 考点：式——探究规律——定义新运算.27、观察下列有规律的点的坐标：A 1（1,1），A 2（2,-4），A 3（3,4），A 4（4,-2），A 5（5,7），A 6（6,−43），A 7（7,10），A 8（8,-1）依此规律，A 11的坐标为，A 12的坐标为． A.（12,16），（12,−23） B.（11,15），（11,−23）C.（11,16），（11,−23） D.（11,16），（12,−23）答案：D. 解析：略.考点：函数——平面直角坐标系——点的位置与坐标.28、如图，边长为1,2的长方形ABCD 以右下角的顶点为中心旋转90°，此时A 点的坐标为；依次旋转2011次，则顶点A 的坐标为． A.（3,3），（3027,0） B.（3,3），（3017,0） C.（3,2），（3027,0） D.（3,2），（3017,0）答案：D. 解析：略.考点：式——探究规律.方程与不等式.函数——平面直角坐标系.29、一个粒子在第一象限内及x 轴、y 轴上运动，在第1min 内它从原点运动到（1,0），而后接着按如图所示方式在与x 轴、y 轴平行的方向上来回运动，且每分钟移动1个单位长度，那么，在2011min 后，求这个粒子所处的位置坐标．A.（41,13）B.（41,14）C.（44,13）D.（44,14）答案：C.解析：弄清粒子的运动规律，并求出靠近2011min 后粒子所在的特殊点的坐标，最后确定所求点的坐标．对于这种运算数较大的题目，我们首先来寻找规律，先观察横坐标与纵坐标相同的点：（0,0），粒子运动了0min. （1,1），粒子运动了1×2=2（min ），向左运动．（2,2），粒子运动了2×3=6（min ），向下运动．（3,3），粒子运动了3×4=12（min），向左运动．（4,4），粒子运动了4×5=20（min），向下运动．……于是点（44,44）处粒子运动了44×45=1980（min）．这时粒子向下运动，从而在运动了2011后，粒子所在的位置是（44,44-31），即（44,13）.考点：函数——平面直角坐标系.30、在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位．其行走路线如图所示．①填写下列各点的坐标：A1（，），A3（，），A12（，）.②写出点A4n的坐标为（是正整数）.③指出蚂蚁从点A100到A101的运动方向为.A. ①（1,1），（1,0），（5,0）；②（2n，0）；③ 从下到上.B. ①（1,1），（1,0），（6,0）；②（2n，0）；③ 从上到下.C. ①（0,1），（1,0），（5,0）；②（2n，0）；③ 从上到下.D. ①（0,1），（1,0），（6,0）；②（2n，0）；③ 从下到上.答案：D.解析：略.考点：函数——平面直角坐标系——点的位置与坐标——坐标与距离.。

初中数学平面直角坐标系提高题与常考题和培优题(含解析)-

初中数学直角坐标系提高题与常考题和培优题(含解析)一．选择题（共12小题）1．已知点P（x+3，x﹣4）在x轴上，则x的值为（）A．3 B．﹣3 C．﹣4 D．42．如图，在平面直角坐标系中，点P的坐标为（）A．（3，﹣2）B．（﹣2，3）C．（﹣3，2）D．（2，﹣3）3．已知点P（0，m）在y轴的负半轴上，则点M（﹣m，﹣m+1）在（）A．第一象限B．第二象限C．第三象限D．第四象限4．已知点A（﹣1，0）和点B（1，2），将线段AB平移至A′B′，点A′于点A对应，若点A′的坐标为（1，﹣3），则点B′的坐标为（）A．（3，0） B．（3，﹣3）C．（3，﹣1）D．（﹣1，3）5．对于任意实数m，点P（m﹣2，9﹣3m）不可能在（）A．第一象限B．第二象限C．第三象限D．第四象限6．如图为A、B、C三点在坐标平面上的位置图．若A、B、C的x坐标的数字总和为a，y坐标的数字总和为b，则a﹣b之值为何？（）A．5 B．3 C．﹣3 D．﹣57．如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（﹣3，2），（b，m），（c，m），则点E的坐标是（）A．（2，﹣3）B．（2，3） C．（3，2） D．（3，﹣2）8．如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b 的值为（）A．2 B．3 C．4 D．59．如图，小手盖住的点的坐标可能是（）A．（6，﹣4）B．（5，2） C．（﹣3，﹣6）D．（﹣3，4）10．如图，将△PQR向右平移2个单位长度，再向下平移3个单位长度，则顶点P平移后的坐标是（）A．（﹣2，﹣4）B．（﹣2，4）C．（2，﹣3）D．（﹣1，﹣3）11．在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出下列定义：若b′=，则称点Q为点的限变点．例如：点（2，3）的限变点的坐标是（2，3），点（﹣2，5）的限变点的坐标是（﹣2，﹣5），如果一个点的限变点的坐标是（，﹣1），那么这个点的坐标是（）A．（﹣1，） B．（﹣，﹣1）C．（，﹣1） D．（，1）12．在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换：①f（a，b）=（﹣a，b）．如：f（1，3）=（﹣1，3）；②g（a，b）=（b，a）．如：g（1，3）=（3，1）；③h（a，b）=（﹣a，﹣b）．如，h（1，3）=（﹣1，﹣3）．按照以上变换有：f（g（h（2，﹣3）））=f（g（﹣2，3））=f（3，﹣2）=（﹣3，﹣2），那么f（g（h（﹣3，5）））等于（）A．（﹣5，﹣3）B．（5，3） C．（5，﹣3）D．（﹣5，3）二．填空题（共13小题）13．点P（3，﹣2）到y轴的距离为个单位．14．点P（x﹣2，x+3）在第一象限，则x的取值范围是．15．线段AB的长为5，点A在平面直角坐标系中的坐标为（3，﹣2），点B的坐标为（3，x），则点B的坐标为．16．在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换：①△（a，b）=（﹣a，b）；②○（a，b）=（﹣a，﹣b）；③Ω（a，b）=（a，﹣b），按照以上变换例如：△（○（1，2））=（1，﹣2），则○（Ω（3，4））等于．17．将点A（1，﹣3）沿x轴向左平移3个单位长度，再沿y轴向上平移5个单位长度后得到的点A′的坐标为．18．已知点P（2﹣a，2a﹣7）（其中a为整数）位于第三象限，则点P坐标为．19．如图是利用网格画出的太原市地铁1，2，3号线路部分规划示意图，若建立适当的平面直角坐标系，表示双塔西街点的坐标为（0，﹣1），表示桃园路的点的坐标为（﹣1，0），则表示太原火车站的点（正好在网格点上）的坐标是．20．定义：直线l1与l2相交于点O，对于平面内任意一点P1点P到直线l1与l2的距离分别为p、q则称有序实数对（p，q）是点P的“距离坐标”．根据上述定义，“距离坐标”是（3，2）的点的个数有个．21．在平面直角坐标系中，小明玩走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位，…，依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位；当n被3除，余数为1时，则向右走1个单位；当n被3除，余数为2时，则向右走2个单位，当走完第8步时，棋子所处位置的坐标是；当走完第2016步时，棋子所处位置的坐标是．22．如图，在平面直角坐标系中，每个最小方格的边长均为1个单位长，P1，P2，P3，…，均在格点上，其顺序按图中“→”方向排列，如：P1（0，0），P2（0，1），P3（1，1），P4（1，﹣1），P5（﹣1，﹣1），P6（﹣1，2）…根据这个规律，点P2016的坐标为．23．如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P60的坐标是．24．在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一条长为2016个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A﹣…．的规律紧绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是．25．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…按这样的运动规律，经过第2016次运动后，动点P的坐标是．三．解答题（共15小题）26．在如图所示的直角坐标系中描出下列各点：A（﹣2，0），B（2，5），C（﹣，﹣3）27．在如图中，确定点A、B、C、D、E、F、G的坐标．请说明点B和点F有什么关系？28．求图中四边形ABCD的面积．29．在平面直角坐标系中，点A（2m﹣7，m﹣5）在第四象限，且m为整数，试求的值．30．如图，一个小正方形网格的边长表示50米．A同学上学时从家中出发，先向东走250米，再向北走50米就到达学校．（1）以学校为坐标原点，向东为x轴正方向，向北为y轴正方向，在图中建立直角坐标系：（2）B同学家的坐标是；（3）在你所建的直角坐标系中，如果C同学家的坐标为（﹣150，100），请你在图中描出表示C同学家的点．31．如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负．如果从A到B记为：A→B（+1，+4），从B→A（﹣1，﹣4），其中第一个数表示左右方向，第二个数表示上下方向．（1）图中B→C （，），C→（+1，）；（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；（3）若图中另有两个格点M、N，且M→A（3﹣a，b﹣4），M→N（5﹣a，b﹣2），则N→A应记作什么？32．如图，已知A（﹣2，3）、B（4，3）、C（﹣1，﹣3）（1）求点C到x轴的距离；（2）求△ABC的面积；（3）点P在y轴上，当△ABP的面积为6时，请直接写出点P的坐标．33．已知：A（0，1），B（2，0），C（4，3）（1）求△ABC的面积；（2）设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．34．已知：如图，在平面直角坐标系xOy中，A（4，0），C（0，6），点B在第一象限内，点P从原点O出发，以每秒2个单位长度的速度沿着长方形OABC移动一周（即：沿着O→A→B→C→O的路线移动）．（1）写出B点的坐标（）；（2）当点P移动了4秒时，描出此时P点的位置，并求出点P的坐标；（3）在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．35．如图，某校七年级的同学从学校O点出发，要到某地P处进行探险活动，他们先向正西方向走8千米到A处，又往正南方向走4千米到B处，又折向正东方向走6千米到C处，再折向正北方向走8千米到D处，最后又往正东方向走2千米才到探险处P，以点O为原点，取O点的正东方向为x轴的正方向，取O点的正北方向为y轴的正方向，以2千米为一个长度单位建立直角坐标系．（1）在直角坐标系中画出探险路线图；（2）分别写出A、B、C、D、P点的坐标．36．已知：P（4x，x﹣3）在平面直角坐标系中．（1）若点P在第三象限的角平分线上，求x的值；（2）若点P在第四象限，且到两坐标轴的距离之和为9，求x的值．37．在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah．例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20．已知点A（1，2），B（﹣3，1），P（0，t）．（1）若A，B，P三点的“矩面积”为12，求点P的坐标；（2）直接写出A，B，P三点的“矩面积”的最小值．38．如图，在平面直角坐标系中，原点为O，点A（0，3），B（2，3），C（2，﹣3），D（0，﹣3）．点P，Q是长方形ABCD边上的两个动点，BC交x轴于点M．点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动，同时点Q 也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动．当点Q 运动到点M时，两动点均停止运动．设运动的时间为t秒，四边形OPMQ的面积为S．（1）当t=2时，求S的值；（2）若S＜5时，求t的取值范围．39．问题情境：在平面直角坐标系xOy中有不重合的两点A（x1，y1）和点B（x2，y2），小明在学习中发现，若x1=x2，则AB∥y轴，且线段AB的长度为|y1﹣y2|；若y1=y2，则AB∥x轴，且线段AB的长度为|x1﹣x2|；【应用】：（1）若点A（﹣1，1）、B（2，1），则AB∥x轴，AB的长度为．（2）若点C（1，0），且CD∥y轴，且CD=2，则点D的坐标为．【拓展】：我们规定：平面直角坐标系中任意不重合的两点M（x1，y1），N（x2，y2）之间的折线距离为d（M，N）=|x1﹣x2|+|y1﹣y2|；例如：图1中，点M（﹣1，1）与点N（1，﹣2）之间的折线距离为d（M，N）=|﹣1﹣1|+|1﹣（﹣2）|=2+3=5．解决下列问题：（1）如图1，已知E（2，0），若F（﹣1，﹣2），则d（E，F）；（2）如图2，已知E（2，0），H（1，t），若d（E，H）=3，则t=．（3）如图3，已知P（3，3），点Q在x轴上，且三角形OPQ的面积为3，则d （P，Q）=．40．小明在学习了平面直角坐标系后，突发奇想，画出了这样的图形（如图），他把图形与x轴正半轴的交点依次记作A1（1，0），A2（5，0），…A n，图形与y轴正半轴的交点依次记作B1（0，2），B2（0，6），…B n，图形与x轴负半轴的交点依次记作C1（﹣3，0），C2（﹣7，0），…C n，图形与y轴负半轴的交点依次记作D1（0，﹣4），D2（0，﹣8），…D n，发现其中包含了一定的数学规律．请根据你发现的规律完成下列题目：（1）请分别写出下列点的坐标：A3，B3，C3，D3；（2）请分别写出下列点的坐标：A n，B n，C n，D n；（3）请求出四边形A5B5C5D5的面积．初中数学直角坐标系提高题与常考题和培优题(含解析)参考答案与试题解析一．选择题（共12小题）1．（2017•河北一模）已知点P（x+3，x﹣4）在x轴上，则x的值为（）A．3 B．﹣3 C．﹣4 D．4【分析】直接利用x轴上点的纵坐标为0，进而得出答案．【解答】解：∵点P（x+3，x﹣4）在x轴上，∴x﹣4=0，解得：x=4，故选：D．【点评】此题主要考查了点的坐标，正确把握x轴上点的坐标性质是解题关键．2．（2016•柳州）如图，在平面直角坐标系中，点P的坐标为（）A．（3，﹣2）B．（﹣2，3）C．（﹣3，2）D．（2，﹣3）【分析】根据平面直角坐标系以及点的坐标的定义写出即可．【解答】解：点P的坐标为（3，﹣2）．故选A．【点评】本题考查了点的坐标，熟练掌握平面直角坐标系中点的表示是解题的关键．3．（2016•临夏州）已知点P（0，m）在y轴的负半轴上，则点M（﹣m，﹣m+1）在（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据y轴的负半轴上点的横坐标等于零，纵坐标小于零，可得m的值，根据不等式的性质，可得到答案．【解答】解：由点P（0，m）在y轴的负半轴上，得m＜0．由不等式的性质，得﹣m＞0，﹣m+1＞1，则点M（﹣m，﹣m+1）在第一象限，故选：A．【点评】本题考查了点的坐标，利用点的坐标得出不等式是解题关键．4．（2017•禹州市一模）已知点A（﹣1，0）和点B（1，2），将线段AB平移至A′B′，点A′于点A对应，若点A′的坐标为（1，﹣3），则点B′的坐标为（）A．（3，0） B．（3，﹣3）C．（3，﹣1）D．（﹣1，3）【分析】根据平移的性质，以及点A，B的坐标，可知点A的横坐标加上了4，纵坐标减小了1，所以平移方法是：先向右平移4个单位，再向下平移1个单位，根据点B的平移方法与A点相同，即可得到答案．【解答】解：∵A（﹣1，0）平移后对应点A′的坐标为（1，﹣3），∴A点的平移方法是：先向右平移2个单位，再向下平移3个单位，∴B点的平移方法与A点的平移方法是相同的，∴B（1，2）平移后B′的坐标是：（3，﹣1）．故选：C．【点评】本题考查了坐标与图形的变化﹣平移，解决问题的关键是运用平移中点的变化规律：横坐标右移加，左移减；纵坐标上移加，下移减．5．（2016•乌鲁木齐）对于任意实数m，点P（m﹣2，9﹣3m）不可能在（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】根据点所在象限中横纵坐标的符号即可列不等式组，若不等式组无解，则不能在这个象限．【解答】解：A、当点在第一象限时，解得2＜m＜3，故选项不符合题意；B、当点在第二象限时，解得m＜3，故选项不符合题意；C、当点在第三象限时，，不等式组无解，故选项符合题意；D、当点在第四象限时，解得m＞0，故选项不符合题意．故选C．【点评】本题考查了点的坐标，理解每个象限中点的坐标的符号是关键．6．（2016•台湾）如图为A、B、C三点在坐标平面上的位置图．若A、B、C的x 坐标的数字总和为a，y坐标的数字总和为b，则a﹣b之值为何？（）A．5 B．3 C．﹣3 D．﹣5【分析】先求出A、B、C三点的横坐标的和为﹣1+0+5=4，纵坐标的和为﹣4﹣1+4=﹣1，再把它们相减即可求得a﹣b之值．【解答】解：由图形可知：a=﹣1+0+5=4，b=﹣4﹣1+4=﹣1，a﹣b=4+1=5．故选：A．【点评】考查了点的坐标，解题的关键是求得a和b的值．7．（2016•滨州）如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（﹣3，2），（b，m），（c，m），则点E的坐标是（）A．（2，﹣3）B．（2，3） C．（3，2） D．（3，﹣2）【分析】由题目中A点坐标特征推导得出平面直角坐标系y轴的位置，再通过C、D点坐标特征结合正五边形的轴对称性质就可以得出E点坐标了．【解答】解：∵点A坐标为（0，a），∴点A在该平面直角坐标系的y轴上，∵点C、D的坐标为（b，m），（c，m），∴点C、D关于y轴对称，∵正五边形ABCDE是轴对称图形，∴该平面直角坐标系经过点A的y轴是正五边形ABCDE的一条对称轴，∴点B、E也关于y轴对称，∵点B的坐标为（﹣3，2），∴点E的坐标为（3，2）．故选：C．【点评】本题考查了平面直角坐标系的点坐标特征及正五边形的轴对称性质，解题的关键是通过顶点坐标确认正五边形的一条对称轴即为平面直角坐标系的y 轴．8．（2016•菏泽）如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（）A．2 B．3 C．4 D．5【分析】直接利用平移中点的变化规律求解即可．【解答】解：由B点平移前后的纵坐标分别为1、2，可得B点向上平移了1个单位，由A点平移前后的横坐标分别是为2、3，可得A点向右平移了1个单位，由此得线段AB的平移的过程是：向上平移1个单位，再向右平移1个单位，所以点A、B均按此规律平移，由此可得a=0+1=1，b=0+1=1，故a+b=2．故选：A．【点评】本题考查了坐标系中点、线段的平移规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．9．（2016•盐城校级一模）如图，小手盖住的点的坐标可能是（）A．（6，﹣4）B．（5，2） C．（﹣3，﹣6）D．（﹣3，4）【分析】先判断手所在的象限，再判断象限横纵坐标的正负即可．【解答】解：因为小手盖住的点在第四象限，第四象限内点的坐标横坐标为正，纵坐标为负，且横坐标的绝对值大于纵坐标的绝对值．故只有选项A符合题意，故选：A．【点评】解答此题的关键是熟记平面直角坐标系中各个象限内点的坐标符号，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．10．（2016•安顺）如图，将△PQR向右平移2个单位长度，再向下平移3个单位长度，则顶点P平移后的坐标是（）A．（﹣2，﹣4）B．（﹣2，4）C．（2，﹣3）D．（﹣1，﹣3）【分析】直接利用平移中点的变化规律求解即可．【解答】解：由题意可知此题规律是（x+2，y﹣3），照此规律计算可知顶点P（﹣4，﹣1）平移后的坐标是（﹣2，﹣4）．故选A．【点评】本题考查了图形的平移变换，平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．11．（2016•临澧县模拟）在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出下列定义：若b′=，则称点Q为点的限变点．例如：点（2，3）的限变点的坐标是（2，3），点（﹣2，5）的限变点的坐标是（﹣2，﹣5），如果一个点的限变点的坐标是（，﹣1），那么这个点的坐标是（）A．（﹣1，） B．（﹣，﹣1）C．（，﹣1） D．（，1）【分析】根据新定义的叙述可知：这个点和限变点的横坐标不变，当横坐标a≥1时，这个点和限变点的纵坐标不变；当横坐标a＜1时，纵坐标是互为相反数；据此可做出判断．【解答】解：∵＞1∴这个点的坐标为（，﹣1）故选C．【点评】本题考查了点的坐标和对新定义的阅读理解，准确找出这个点与限变点的横、纵坐标与a的关系即可．12．（2016•高新区一模）在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换：①f（a，b）=（﹣a，b）．如：f（1，3）=（﹣1，3）；②g（a，b）=（b，a）．如：g（1，3）=（3，1）；③h（a，b）=（﹣a，﹣b）．如，h（1，3）=（﹣1，﹣3）．按照以上变换有：f（g（h（2，﹣3）））=f（g（﹣2，3））=f（3，﹣2）=（﹣3，﹣2），那么f（g（h（﹣3，5）））等于（）A．（﹣5，﹣3）B．（5，3） C．（5，﹣3）D．（﹣5，3）【分析】根据f（a，b）=（﹣a，b）．g（a，b）=（b，a）．h（a，b）=（﹣a，﹣b），可得答案．【解答】解：f（g（h（﹣3，5）））=f（g（3，﹣5）=f（﹣5，3）=（5，3），故选：B．【点评】本题考查了点的坐标，利用f（a，b）=（﹣a，b）．g（a，b）=（b，a）．h （a，b）=（﹣a，﹣b）是解题关键．二．填空题（共13小题）13．（2017春•海宁市校级月考）点P（3，﹣2）到y轴的距离为3个单位．【分析】求得3的绝对值即为点P到y轴的距离．【解答】解：∵|3|=3，∴点P（3，﹣2）到y轴的距离为3个单位，故答案为：3．【点评】本题主要考查了点的坐标的几何意义：点到x轴的距离为点的纵坐标的绝对值，到y轴的距离为点的横坐标的绝对值．14．（2016•衡阳）点P（x﹣2，x+3）在第一象限，则x的取值范围是x＞2．【分析】直接利用第一象限点的坐标特征得出x的取值范围即可．【解答】解：∵点P（x﹣2，x+3）在第一象限，∴，解得：x＞2．故答案为：x＞2．【点评】此题主要考查了点的坐标，正确得出关于x的不等式组是解题关键．15．（2017•涿州市一模）线段AB的长为5，点A在平面直角坐标系中的坐标为（3，﹣2），点B的坐标为（3，x），则点B的坐标为（3，3）或（3，﹣7）．【分析】由线段AB的长度结合点A、B的坐标即可得出关于x的含绝对值符号的一元一次方程，解之即可得出x值，由此即可得出点B的坐标．【解答】解：∵线段AB的长为5，A（3，﹣2），B（3，x），∴|﹣2﹣x|=5，解得：x1=3，x2=﹣7，∴点B的坐标为（3，3）或（3，﹣7）．故答案为：（3，3）或（3，﹣7）．【点评】本题考查了坐标与图形性质、两点间的距离公式以及含绝对值符号的一元一次方程，根据两点间的距离公式找出关于x的含绝对值符号的一元一次方程是解题的关键．16．（2016•黔南州）在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换：①△（a，b）=（﹣a，b）；②○（a，b）=（﹣a，﹣b）；③Ω（a，b）=（a，﹣b），按照以上变换例如：△（○（1，2））=（1，﹣2），则○（Ω（3，4））等于（﹣3，4）．【分析】根据三种变换规律的特点解答即可．【解答】解：○（Ω（3，4））=○（3，﹣4）=（﹣3，4）．故答案为：（﹣3，4）．【点评】本题考查了点的坐标，读懂题目信息，理解三种变换的变换规律是解题的关键．17．（2016•广安）将点A（1，﹣3）沿x轴向左平移3个单位长度，再沿y轴向上平移5个单位长度后得到的点A′的坐标为（﹣2，2）．【分析】根据向左平移横坐标减，向上平移纵坐标加求解即可．【解答】解：∵点A（1，﹣3）沿x轴向左平移3个单位长度，再沿y轴向上平移5个单位长度后得到点A′，∴点A′的横坐标为1﹣3=﹣2，纵坐标为﹣3+5=2，∴A′的坐标为（﹣2，2）．故答案为（﹣2，2）．【点评】本题考查了坐标与图形变化﹣平移，平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．18．（2016•鞍山二模）已知点P（2﹣a，2a﹣7）（其中a为整数）位于第三象限，则点P坐标为（﹣1，﹣1）．【分析】根据第三象限点的坐标性质得出a的取值范围，进而得出a的值，即可得出答案．【解答】解：∵点P（2﹣a，2a﹣7）（其中a为整数）位于第三象限，∴，解得：2＜a＜3.5，故a=3，则点P坐标为：（﹣1，﹣1）．故答案为：（﹣1，﹣1）．【点评】此题主要考查了点的坐标，正确得出a的取值范围是解题关键．19．（2016•山西）如图是利用网格画出的太原市地铁1，2，3号线路部分规划示意图，若建立适当的平面直角坐标系，表示双塔西街点的坐标为（0，﹣1），表示桃园路的点的坐标为（﹣1，0），则表示太原火车站的点（正好在网格点上）的坐标是（3，0）．【分析】根据双塔西街点的坐标可知：1号线起点所在的直线为x轴，根据桃园路的点的坐标可知：2号线起点所在的直线为y轴，建立平面直角坐标系，确定太原火车站的点的坐标．【解答】解：由双塔西街点的坐标为（0，﹣1）与桃园路的点的坐标为（﹣1，0）得：平面直角坐标系，可知：太原火车站的点的坐标是（3，0）；故答案为：（3，0）【点评】本题考查了利用坐标确定位置，解题的关键就是确定坐标原点和x、y 轴的位置．20．（2016•厦门校级模拟）定义：直线l1与l2相交于点O，对于平面内任意一点P1点P到直线l1与l2的距离分别为p、q则称有序实数对（p，q）是点P的“距离坐标”．根据上述定义，“距离坐标”是（3，2）的点的个数有4个．【分析】首先根据“距离坐标”的含义，可得“距离坐标”是（3，2）到直线l1与l2的距离分别为3、2，然后根据到直线l1的距离是3的点在与直线l1平行且与l1的距离是3的两条平行线上，到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线上，一共有4个交点，所以“距离坐标”是（3，2）的点的个数有4个，据此解答即可．【解答】解：“距离坐标”是（3，2）到直线l1与l2的距离分别为3、2，因为到直线l1的距离是3的点在与直线l1平行且与l1的距离是3的两条平行线上，到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线上，一共有4个交点，所以“距离坐标”是（3，2）的点的个数有4个．故答案为：4．【点评】此题主要考查了点的“距离坐标”的含义以及应用，考查了分析推理能力，考查了分类讨论思想的应用，要熟练掌握，解答此题的关键是要明确：“距离坐标”是（3，2）到直线l1与l2的距离分别为3、2．21．（2016•汕头校级自主招生）在平面直角坐标系中，小明玩走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位，…，依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位；当n被3除，余数为1时，则向右走1个单位；当n被3除，余数为2时，则向右走2个单位，当走完第8步时，棋子所处位置的坐标是（9，2）；当走完第2016步时，棋子所处位置的坐标是（2016，672）．【分析】设走完第n步时，棋子所处的位置为点P n（n为自然数），根据走棋子的规律找出部分点P n的坐标，根据坐标的变化找出变化规律“P3n+1（3n+1，n），P3n+2（3n+3，n），P3n+3（3n+3，n+1）”，依此规律即可得出结论．【解答】解：设走完第n步时，棋子所处的位置为点P n（n为自然数），观察，发现规律：P1（1，0），P2（3，0），P3（3，1），P4（4，1），…，∴P3n+1（3n+1，n），P3n+2（3n+3，n），P3n+3（3n+3，n+1）．∵8=3×2+2，∴P8（9，2）．∵2016=3×671+3，∴P 2016（2016，672）．故答案为：（9，2）；（2016，672）．【点评】本题考查了规律型中的点的坐标变化，解题的关键是找出变化规律“P 3n +1（3n +1，n ），P 3n +2（3n +3，n ），P 3n +3（3n +3，n +1）”．本题属于中档题，难度不大，解决该题型题目时，根据点的变化找出变化规律是关键．22．（2016•岳阳）如图，在平面直角坐标系中，每个最小方格的边长均为1个单位长，P 1，P 2，P 3，…，均在格点上，其顺序按图中“→”方向排列，如：P 1（0，0），P 2（0，1），P 3（1，1），P 4（1，﹣1），P 5（﹣1，﹣1），P 6（﹣1，2）…根据这个规律，点P 2016的坐标为（504，﹣504）．【分析】根据各个点的位置关系，可得出下标为4的倍数的点在第四象限的角平分线上，被4除余1的点在第三象限的角平分线上，被4除余2的点在第二象限的角平分线上，被4除余3的点在第一象限的角平分线上，点P 2016的在第四象限的角平分线上，且横纵坐标的绝对值=2016÷4，再根据第四项象限内点的符号得出答案即可．【解答】解：由规律可得，2016÷4=504，∴点P 2016的在第四象限的角平分线上，∵点P 4（1，﹣1），点P 8（2，﹣2），点P 12（3，﹣3），∴点P 2016（504，﹣504），故答案为（504，﹣504）．【点评】本题考查了规律型：点的坐标，是一个阅读理解，猜想规律的题目，解答此题的关键是首先确定点所在的大致位置，所在正方形，然后就可以进一步推得点的坐标．23．（2016•三明）如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，﹣1），P5（2，﹣1），P6（2，0），…，则点P60的坐标是（20，0）．【分析】根据图形分别求出n=3、6、9时对应的点的坐标，可知点P3n（n，0），将n=20代入可得．【解答】解：∵P3（1，0），P6（2，0），P9（3，0），…，∴P3n（n，0）当n=20时，P60（20，0），故答案为：（20，0）．【点评】本题考查了点的坐标的变化规律，仔细观察图形，分别求出n=3、6、9时对应的点的对应的坐标是解题的关键．24．（2016•金华模拟）在平面直角坐标系中，A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），把一条长为2016个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A﹣…．的规律紧绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（0，﹣2）．【分析】根据点的坐标求出四边形ABCD的周长，然后求出另一端是绕第几圈后的第几个单位长度，从而确定答案．【解答】解：∵A（1，1），B（﹣1，1），C（﹣1，﹣2），D（1，﹣2），∴AB=1﹣（﹣1）=2，BC=1﹣（﹣2）=3，CD=1﹣（﹣1）=2，DA=1﹣（﹣2）=3，∴绕四边形ABCD一周的细线长度为2+3+2+3=10，2016÷10=201…6，∴细线另一端在绕四边形第202圈的第6个单位长度的位置，即CD中间的位置，点的坐标为（0，﹣2），故答案为：（0，﹣2）．【点评】本题利用点的坐标考查了数字变化规律，根据点的坐标求出四边形ABCD 一周的长度，从而确定2016个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键．25．（2016•乐亭县一模）如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…按这样的运动规律，经过第2016次运动后，动点P的坐标是（2016，0）．【分析】观察动点P运动图象可知，运动次数为偶数时，P点在x轴上，比较其横坐标与运动次数发现规律，根据规律即可解决问题．【解答】解：结合图象可知，当运动次数为偶数次时，P点运动到x轴上，且横坐标与运动次数相等，∵2016为偶数，∴运动2016次后，动点P的坐标是（2016，0）．故答案为：（2016，0）．【点评】本题考查了点的坐标以及数的变化，解题的关键是发现“当运动次数为偶数次时，P点运动到x轴上，且横坐标与运动次数相等”这已变化规律．本题属于基础题，难度不大，解题时可先看求什么？根据所求再去寻找规律能够简化很多．三．解答题（共15小题）26．（2016春•黄埔区期末）在如图所示的直角坐标系中描出下列各点：A（﹣2，0），B（2，5），C（﹣，﹣3）【分析】根据平面直角坐标系中点的表示方法找出各点的位置即可．【解答】解：如图所示．【点评】本题考查了点坐标，熟练掌握平面直角坐标系中的点的表示方法是解题的关键．27．（2016秋•商河县校级月考）在如图中，确定点A、B、C、D、E、F、G的坐标．请说明点B和点F有什么关系？【分析】从图形中找到各点对应的横纵坐标，从而进行求解．【解答】解：各点的坐标为：A（﹣4，4）、B（﹣3，0）、C（﹣2，﹣2）、D（1，﹣4）、E（1，﹣1）、F（3，0）、G（2，3），点B和点F关于y轴对称，且关于原点对称．【点评】本题考查了在平面直角坐标系中确定点的坐标，是一道简单的基础题．28．（2017春•滨海县月考）求图中四边形ABCD的面积．【分析】由图可得：四边形ABCD的面积=矩形EFGH的面积﹣△AEB的面积﹣△AHD的面积﹣△BFC的面积﹣△CGD的面积，即可解答．【解答】解：如图，S四边形ABCD=S矩形EFGH﹣S△AEB﹣S△AHD﹣S△BFC﹣S△CDG==25．【点评】本题考查了坐标与图形性质，解决本题的关键是结合图形四边形ABCD 的面积=矩形EFGH的面积﹣△AEB的面积﹣△AHD的面积﹣△BFC的面积﹣△CGD的面积．29．（2016春•垦利县期末）在平面直角坐标系中，点A（2m﹣7，m﹣5）在第四象限，且m为整数，试求的值．【分析】根据第四象限的点的横坐标是正数，纵坐标是负数列不等式组求出m 的取值范围，再根据m是整数解答即可．【解答】解：∵点A（2m﹣7，m﹣5）在第四象限，∴解得：．∵m为整数，∴m=4．∴．【点评】本题考查了点的坐标，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．。

中考数学总复习《平面直角坐标系中点的坐标规律探索》专项提升练习题(附答案)

中考数学总复习《平面直角坐标系中点的坐标规律探索》专项提升练习题（附答案)学校:___________班级：___________姓名：___________考号：___________一、单选题1．在平面直角坐标系xOy中，对于点P(x,y)，我们把P1(y−1,−x−1)叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4，这样依次得到各点，若A1的坐标为(1,2)，则A2024的友好点是（）A．(−3,2)B．(1,2)C．(−5,−2)D．(−3,4)2．如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标(1,2)，则经过第2024次变换后点A的对应点的坐标为（）A．(1,−2)B．(−1,−2)C．(−1,2)D．(1,2)3．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点(1,1)，第2次接着运动到点(2,0)，第3次接着运动到点(3,2)，第4次接着运动到点(4,0)…按这样的运动规律经过第2023次运动后，动点P的坐标是（）A．(2020,0)B．(2022,2)C．(2023,2)D．(2023,0)4．如图A1(1,0)，A2(1,1)，A3(−1,1)，A4(−1,−1)，A5(2,−1)…按此规律，点A2022的坐标为（）A．(505,505)B．(−506,506)C．(506,506)D．(−505,−505)5．小静同学观察台球比赛，从中受到启发，抽象成数学问题如下：如图，已知长方形OABC，小球P从(0,3)出发，沿如图所示的方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，第一次碰到长方形的边时的位置为P1(3,0)，当小球P第2024次碰到长方形的边时，若不考虑阻力，点P2024的坐标是（）A．(1,4)B．(7,4)C．(0,3)D．(3,0)6．在平面直角坐标系中直线l：y=x−1与x轴交于点A1如图所示依次作正方形A1B1C1O正方形A2B2C2C1… 正方形使得点A1A2A3… 在直线l上点C1C2C3… 在y轴正半轴上则点B2024的坐标为（）A．(22023,22024−1)B．(22024,22024)C．(22023,22023−1)D．(22023,22024+1)7．如图在平面直角坐标系中半径均为1个单位长度的半圆O1半圆O2半圆O3半圆O4… 组成一的坐标是()A．(2035,−1)B．(2035,0)C．(2036,0)D．(2036,−1)8．如图已知点A(2,1)B(−1,1)C(−1,−3)D(2,−3)点P从点A出发以每秒1个单位长度的速度沿A−B−C−D−A⋅⋅⋅的规律在四边形ABCD的边上循环运动则第2023秒时点P的坐标为（）A．(2,1)B．(−1,1)C．(−1,−3)D．(2,−3)二填空题9．在平面直角坐标系中已知点A(m,4)与点B(5,n)关于y轴对称则(m+n)2023的值为．10．点P在数轴上从0开始第1次向右移动1个单位紧接着第2次向左移动2个单位第3次向右移动3个单位第4次向左移动4个单位…… 依此规律移动当它移动160次时落在数轴上的点表示的数是．11．如图平面直角坐标系中一个点从原点O出发按向右→向上→向右→向下的顺序依次不断移动每次移动1个单位其移动路线如图所示第一次移到点A1第二次移到点A2第三次移到点A3…第n次移到点A n则点A2023的坐标是．12．如图所示长方形ABCD的两边BC、CD分别在x轴y轴上点C与原点重合点A的坐标为(2,3)将长方形ABCD沿x轴无滑动向右翻滚经过一次翻滚点A的对应点记为A1；经过第二次翻滚点A的对应点记为A2；……依次类推经过第2022次翻滚点A的对应点A2022的坐标为．13．如图,△ABC的顶点A,B分别在x轴,y轴上,∠ABC=90°,OA=OB=1,BC=2√2,将△ABC绕点O顺时针旋转,每次旋转90°,则第2023次旋转结束时,点C的坐标为．14．如图在平面直角坐标系xOy中已知点A的坐标是(0,1)以OA为边在右侧作等边三角形OAA1过点A1作x轴的垂线垂足为O1以O1A1为边在右侧作等边三角形O1A1A2再过点A2作x轴的垂线垂足为O2以O2A2为边在右侧作等边三角形O2A2A3……按此规律继续作下去则点A2024的纵坐标为．15．如图所有正方形的中心均在坐标原点且各边与坐标轴平行从内到外它们的边长依次为2 4 6 8 … 顶点依次为A1A2A3A4… 则顶点A2024的坐标是．16．如图所示抛物线y=x2在第一象限内经过的整数点（横坐标纵坐标都为整数的点）依次为A1A2 A3… A n将抛物线y=x2沿直线l：y=x向上平移得到一系列抛物线且满足条件：①抛物线的顶点M1M2M3… M n都在直线y=x上；②抛物线依次经过点A1A2A3… A n则顶点M2021的坐标为．三解答题17．已知点P(2m−6,m+2)．(1)若点P在x轴上求m的值及P点的坐标；(2)若点P横纵坐标互为相反数求点P在第几象限？(3)若点P和点Q都在过A(2,3)点且与y轴平行的直线上PQ=4求Q点的坐标．18．在平面直角坐标系xOy中对于点P(x,y)若点Q的坐标为(ax+y,x+ay)则称点Q是点P的“a级关联点”．级关联点”是点A′；(1)已知点A(−2,6)的“12(2)已知点M(m−1,2m)的“−3级关联点”N位于x轴上求点N的坐标；(3)在（2）的条件下若存在点H且HM=2直接写出H点坐标．19．如图在平面直角坐标系中设一点M自P0(1，0)处向上运动1个单位长度至P1(1，1)然后向左运动2个单位长度至P2处再向下运动3个单位长度至P3处再向右运动4个单位长度至P4处再向上运动5个单位长度至P5处… 如此继续运动下去设P n(x n，y n)n=1，2，3，……．(1)计算x1+x2+x3+x4．(2)计算x1+x2+⋅⋅⋅+x2023+x2024的值．20．如图动点P在平面直角坐标系中按图中箭头所示方向运动：第一次：原点(00)→P1(−1,2)；第二次：P1(−12)→P2(−2,0)；第三次：P2(−20)→P3(−3,4)；第四次：P3(−34)→P4(−4,0)；第五次：P4(−40)→P5(−5,2)；…归纳上述规律完成下列任务．(1)直接写出下列坐标：P7:P13:P14:；(2)第2023次运动后P2023的坐标为________；(3)点P199距x轴的距离为点P199距y轴的距离为．21．如图在平面直角坐标系中第一次将△OAB变换成△OA1B1第二次将△OA1B11变换成△OA2B2第三次将△OA2B2变换成△OA3B3.(1)观察每次变换前后的三角形的变化规律若将△OA3B3变换成△OA4B4则A4的坐标是B4的坐标是．(2)若按第（1）题找到的规律将△OAB进行n次变换得到△OA n B n比较每次变换中三角形顶点坐标有何变化找出规律推测A n的坐标是B n的坐标是．(3)若按第（1）题找到的规律将△OAB进行n次变换得到△OA n B n则△OA n B n的面积S为．22．在平面直角坐标系xOy中对于点P和正方形OABC给出如下定义：若点P关于y轴的对称点P′到正方形OABC的边所在直线的最大距离是最小距离的k倍则称点P是正方形OABC的“k倍距离点”．已知：点A（a0）B（a a）．(1)当a=4时①点C的坐标是；②在P1(−1,1),P2(−2,2),P3(2,2)三个点中是正方形OABC的“3倍距离点”；(2)当a=6时点P(−2,n)（其中n>0）是正方形OABC的“2倍距离点” 求n的取值范围；(3)点M(−2,2),N(−3,3)．当0<a<6时线段MN上存在正方形OABC的“2倍距离点” 直接写出a的取值范围．参考答案：1．解：∵A1的坐标为(1,2)∵A2(2−1,−1−1)即：A2(1,−2)∵A3(−2−1,−1−1)即：A3(−3,−2)∵A4(−2−1,3−1)即：A4(−3,2)∵A5(2−1,3−1)即：A6(1,2)．．．∵每四次一循环∵2024÷4=506则A2024的友好点是A2025(1,2)故选：B．2．解：点A第一次关于y轴对称后在第二象限点A第二次关于x轴对称后在第三象限点A第三次关于y轴对称后在第四象限点A第四次关于x轴对称后在第一象限即点A回到原始位置所以每四次对称为一个循环组依次循环∵2024÷4=506∵经过第2022次变换后所得的A点与第四次变换的位置相同回到原位坐标为(1,2)．故选：D．3．解：根据动点P在平面直角坐标系中按图中箭头所示方向运动第1次从原点运动到点(1,1)第2次接着运动到点(2,0)第3次接着运动到点(3,2)第4次运动到点(4,0)第5次接着运动到点(5,1)…以此类推可知横坐标为运动次数纵坐标依次为1 0 2 0 每4次为一个循环依次出现∵2023÷4=505⋅⋅⋅3∵经过第2023次运动后动点P的横坐标是2023 纵坐标为2∵经过第2023次运动后动点P的坐标是(2023,2)．故选：C．4．解：由题可知第一象限的点：A2,A6,A10……角标除以4余数为2；第二象限的点：A3,A7,A11……角标除以4余数为3；第三象限的点：A4,A8,A12……角标除以4余数为0；第四象限的点：A5,A9,A13……角标除以4余数为1；由上规律可知：2022÷4=505⋯2∵点A2022在第一象限．观察图形得：点A2的坐标为(1,1)点A6的坐标为(2,2)点A10的坐标为(3,3)……（n为角标）∵第一象限点的横纵坐标数字隐含规律：点的横纵坐标=n+24∵点A2022的坐标为(506,506)．故选：C．5．解：按照反弹时反射角等于入射角画出图形如下图：P(0,3)P1(3,0)P2(7,4)P3(8,3)P4(5,0)P5(1,4)P6(0,3)…通过以上变化规律可以发现每六次反射一个循环∵2024÷6=337 (2)∵P2024=P2∵点P2024的坐标是(7,4)．故选：B．6．解：直线l：y=x−1与x轴交于点A1∵当y=0时x=1∵A1(1,0)∵A1B1C1O为正方形∵B1(1,1)同理可得：A2(2,1)A3(4,3)A4(8,7)A5(16,15)…B2(2,3)B3(4,7)B4(8,15)B5(16,31)…∵B n(2n−1,2n−1)（n为正整数）∵点B2024的坐标为(22023,22024−1)故选：A．×2π×1=π7．解：半径为1个单位长度的半圆的周长为12个单位长度∵点P从原点O出发沿这条曲线向右运动速度为每秒π2π当点P从原点O出发沿这条曲线向右运动运动时间为1秒时点P的坐标为(1,1)∵点P1每秒走12当点P从原点O出发沿这条曲线向右运动运动时间为2秒时点P的坐标为(2,0)当点P从原点O出发沿这条曲线向右运动运动时间为3秒时点P的坐标为(3,−1)当点P从原点O出发沿这条曲线向右运动运动时间为4秒时点P的坐标为(4,0)当点P从原点O出发沿这条曲线向右运动运动时间为5秒时点P的坐标为(5,1)当点P从原点O出发沿这条曲线向右运动运动时间为6秒时点P的坐标为(6,0)…∵2035÷4=508 (3)∵P的坐标是(2035,−1)故选：A．8．解：由点A(2,1)B(−1,1)C(−1,−3)D(2,−3)可知ABCD是长方形∴AB=CD=3CB=AD=4∵点P从点A出发沿着A−B−C−D−A⋅⋅⋅回到点A所走路程是：3+3+4+4=14∵2023÷14=144⋯7∵第2023秒时P点在第三象限∴P(−1,−3)故选：C．9．解：∵点A(m,4)与点B(5,n)关于y轴对称∵m=−5n=4∵(m+n)2023=(−5+4)2023=−1．故答案为：−1．10．解：根据题意得：第一次落点可以用1表示第二次落点可以用−1表示第三次落点可以用2表示第四次落点可以用−2表示.......第160次落点可以用−80表示1−2+3−4+5−6+⋅⋅⋅+159−160=−80所以当它移动160次时落到数轴上的点表示的数为−80故答案为：−80．11．解：观察图象可知点A的纵坐标每4个点循环一次∵2023÷4=505⋅⋅⋅3∵点A2023的纵坐标与点A3的纵坐标相同∵A3(2,1)A7(4,1)A11(6,1)……∵A4n−1(2n,1)（n为正整数）∵当4n−1=2023时n=506∵2n=1012∵点A2023的坐标是（(1012,1)．故答案为：(1012,1)．12．解：如图所示：观察图形可得经过4次翻滚后点A对应点一循环2022÷4=505⋯2∵点A(2,3)长方形的周长为：2(2+3)=10∴经过505次翻滚后点A对应点A2022的坐标为(10×505+3+2,0)即(5055,0)．故答案为：(5055,0)．13．解:∵∠ABC=90°,OA=OB=1,∵∠ABO=45°,过点C作CD⊥y轴交y轴与点D,,∵∠CBD=45°,∵BC=2√2,∵DB=2,∵C(2,3),∵将△ABC 绕点O 顺时针旋转,每次旋转90°,∵第一次旋转得到C 的坐标为(3,−2),第二次旋转得到C 的坐标为(−2,−3),第三次旋转得到C 的坐标为(−3,2),第四次旋转得到C 的坐标为(2,3),第五次旋转得到C 的坐标为(3,−2),可以发现C 的坐标四次一循环,∵第2023次旋转结束时:2023÷4=505......3,∵第2023次旋转结束时点C 的坐标为:C(−3,2),故答案为:(−3,2)．14．解：∵点A 的坐标为(0,1) 三角形OAA 1是等边三角形∵OA 1=OA =1 ∠AA 1O =∠AOA 1=60°∵∠A 1OO 1=∠AOO 1−∠AOA 1=90°−60°=30°∵A 1O 1⊥x 轴∵在Rt △A 1OO 1中 ∠A 1OO 1=30° OA 1=1 则A 1O 1=12A 1O =12OO 1=√3A 1O 1=√32 ∵A 1(√32,12) 则点A 1的纵坐标为12同理 A 2O 2=12A 1O 1=(12)2=14A 3O 3=12A 2O 2=(12)3=18…∵A n O n =(12)n∵点A 2024的纵坐标为(12)2024故答案为：(12)2024．15．（506 -506）16．解：设M 1(a 1，a 1) M 2(a 2，a 2) M 3(a 3，a 3)∵抛物线y =x 2沿直线l ：y =x 向上平移∵以M 1(a 1，a 1)为顶点的抛物线为y =(x −a 1)2+a 1∵y=(x−a1)2+a1与y=x2的交点为A1∵(x−a1)2+a1=x2即2a1x=a12+a1解得x=12(a1+1)∵A1为整数点∵a1=1M1(1，1)；同理可求M2(3，3)；M3(5，5)；∵M n(2n−1，2n−1)∵M2021(2×2021−1，2×2021−1)即M2021(4041，4041)故答案为：(4041，4041)．17．（1）解：∵点P在x轴上∴m+2=0解得m=−2∴2m−6=2×(−2)−6=−10∴P点的坐标为(−10,0)；（2）解：根据题意得2m−6+m+2=0解得m=43∴2m−6=2×43−6=−103<0m+2=43+2=103>0∴点P在第二象限；（3）解：∵点P和点Q都在过A(2,3)点且与y轴平行的直线上∴点P和点Q的横坐标都为2∴2m−6=2解得：m=4∴m+2=6∴P(2,6)∵PQ=4∴Q点的纵坐标为10或2∴Q点的坐标为(2,10)或(2,2)．18．（1）解：由题意得：A′(12×(−2)+6,(−2)+12×6)即A′(5,1)；（2）解：由题意得：N(−3m+3+2m,−6m+m−1)∵N位于x轴上∵−6m+m−1=0解得：m=−15∵N(165,0)；（3）解：由（2）得：m=−15∵M(−65,−25)∵HM∥x轴且HM=2∵H(45,−25)或H(−165,−25)．19．（1）解：由题意可知P1(1，1)，P2(−1，1)，P3(−1，−2)，P4(3，−2)，P5(3，3)，P6(−3，3)，P7(−3，−4)，P8(5，−4)，……于是得到x1，x2，x3，x4的值为1 −1−13∵x1+x2+x3+x4=1−1−1+3=2（2）解：∵x5，x6，x7，x8的值分别为3 −3−35∵x5+x6+x7+x8=3−3−3+5=2；∵x1+x2+x3+x4=1−1−1+3=2x5+x6+x7+x8=3−3−3+5=2…x2021+x2022+x2023+x2024=2∵2024÷4=506∵x1+x2+⋯+x2023+x2024=2×506=1012．20．解：（1）由题知因为P1(−1,2)P2(−2,0)P3(−3,4)P4(−4,0)…所以点P2n的坐标为(−2n,0)点P4n−3的坐标为(3−4n,2)点P4n−1的坐标为(1−4n,4)(为正整数）．令4n−1=7解得n=2所以1−4n=−7．即点P7的坐标为(−7,4)．同理可得点P13的坐标为(−13,2)点P14的坐标为(−14,0)．故答案为：(−7,4)(−13,2)(−14,0)．（2）根据（1）的发现可知令4n−1=2023解得n=506所以点P2023的坐标为(−2023,4)．故答案为：(−2023,4)．（3）根据（1）的发现可知令4n−1=199解得n=50所以点P199的坐标为(−199,4)．则点P199到x轴的距离是4 到y轴的距离是199．故答案为：4 199．21．解：（1）∵A(1，3)，A1(2，3)，A2(4，3，)，A3(8，3)∵A4(16，3)；∵B(2，0)，B1(4，0)，B2(8，0)，B3(16，0)∵B4(32，0)．故答案为：(16，3)；(32，0)．（2）解：由（1）可知A1、A2、A3、⋯A n的横坐标每次扩大2倍,纵坐标为3 B1、B2、B3、⋯B n的横坐标每次扩大2倍纵坐标不变∵A n(2n，3)B n(2n+1，0)故答案为：(2n，3)(2n+1，0)；（3）∵A n(2n，3)B n(2n+1，0)∵OB n=2n+1，A n B n﹣1=3∵S=12OB n⋅A n B n﹣1=3×2n故答案为：3×2n．22．（1）解：①当a=4时如图1点A（40）B（44）．∵四边形OABC是正方形∴OC=OA=4点C的坐标是（04）故答案为：（04）；②∵点P1(−1,1)关于y轴的对称点坐标为（11）而点（11）到正方形OABC的边所在直线AB的最大距离是4−1=3到OA的最小距离为1∴点P1是正方形OABC的“3倍距离点”；同理可得点P2(−2,2)是正方形OABC的“1倍距离点”；同理可得点P3(2,2)是正方形OABC的“3倍距离点”；∴P1,P3是正方形OABC的“3倍距离点”故答案为：P1,P3；（2）当a=6时如图2点A（60）B（66）C（06）∵点P(−2,n)关于y轴的对称点坐标为（2n）n>0当0<n<2时P到BC的距离>2倍的P到OA的距离当2≤n≤4时P到BC的距离=2倍的P到OA的距离当4<n<6时P到BC的距离>2倍的P到OA的距离当n≥6时P到BC的距离=2倍的P到OA的距离∴nn−6=2∴n=12综上所述：点P(−2,n)（其中n>0）是正方形OABC的“2倍距离点”时n的取值范围是2≤n≤4或n=12；（3）解：∵点M(−2,2),N(−3,3)关于y轴的对称点坐标为M′(2,2),N′(3,3)设直线M′N′的解析式为y=kx+ b代入M′(2,2),N′(3,3)得{2k+b=23k+b=3解得：{k=1 b=0∴直线M′N′的解析式为y=x 设线段M′N′上一点P（m m）则2≤m≤3当P在正方形内时①a−mm=2∴a=3m∴6≤a≤9（舍去）；②ma−m=2∴a=32m∴3≤a≤92；当P在正方形外时mm−a=2∴a=12m∴1≤a≤32；此时不存在m−am=2的情况∴线段MN上存在正方形OABC的“2倍距离点”a的取值范围是1≤a≤32或3≤a≤92．。

中考数学知识点过关培优训练卷：平面直角坐标系(含解析答案)

中考数学知识点过关培优训练卷:平面直角坐标系一•选择题1在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，则目标的坐标可能是( )个单位，贝U E点的坐标为为( )7. 在平面直角坐标系中，对于点P (x, y),我们把点P (- y+1, x+1)叫做点P伴随点已2.3.4.5.B. (- 1 , —6)C. (—3, 10)D.(乙 3)如图，在平面直角坐标系中，点B的坐标点P (4, 3)到x轴的距离为(A. 4B. 3在平面直角坐标系中，点(- 2,A.第一象限B. 第二象限在平而直角坐标系中，点(0,C.C.2品),/ AOC= 45°,/ ACO= 30°,则3) 一定在(C.第三象限D. 7D.第四象限E在x轴上方, y轴的左侧，距离轴3个单位，距离y轴46.A. ( 3,- 4)B. (4,- 3)C. (- 4, 3)D. (- 3, 4)点P (a+3, b+1) 在平面直角坐标系的x轴上，并且点P到y轴的距离为2，则a+b的值A. - 1B.- 2C.- 1 或—6D.- 2 或-6A. ( 5,—4)知点A的伴随点为A，点A的伴随点为A,点A的伴随点为A,…，这样依次得到点A, AA,」…，A,…若点A i的坐标为（2, 4）,点他19的坐标为（）A. （- 3, 3）B. （- 2, - 2）C. （3,- 1）D. （2, 4）8. 小王和小丽下棋，小王执圆子，小丽执方子，如图是在直角坐标系中棋子摆出的图案，若再摆放一圆一方两枚棋子，使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则这两枚棋子的坐标分别是（）10•如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1, 1）,第2次接着运动到点（2 , 0）,第3次接着运动到点（3 , 2）,……,按这样的运动二.填空题11•如果点P （- 5 , y）在第三象限，请写出一个符合条件的点P的坐标________ .12. 已知P （2+x , 3x - 2）到x轴的距离是到y轴的距离的2倍，贝U x的值为 _________ .13. 在平面直角坐标系中，线段AB= 5 , AB// x轴，若A点坐标为（-1 , 3）,贝U B点坐标为_______ .14. 如图，等边三角形ABC的边长为1,顶点B与原点O重合，点C在x轴的正半轴上，过A.圆子（2, 3）,方子（1 , .3 ）C.圆，子（2, 3），方子（4, 0）9 .若点A（ m+2, 2m- 5 ）在y轴上，则点B.圆子（1, 3）,方子（2, 3）D.圆子（4 , 0）,方子（2 , 3）A的坐标是（）A. (0, - 9)B. (2.5 , 0)C. ( 2.5 , - 9)D. (- 9 , 0)点B 作BA 丄AC 于点A,过点作AB// OA 交OC 于点3;过点点A作AB// OA 交OC 于点&;•••,按着这个规律进行下去，点16.平面直角坐标系 xOy 中，已知线段AB 与 x 轴平行，且AB= 5, 则点B 的坐标是17•如图，把“ QQ 笑脸图标放在直角坐标系中，已知左眼 A 的坐标是（-2, 3）,右眼B的坐标为（0, 3）,则嘴唇C 点的坐标是 __________ .18.已知点A （2a +3, a - 4）在二、四象限的角平分线上，贝U a= _______ .19. 如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“T ”方向排列，如（1，0），（2，0），（2，1），（ 1，1），（1，2），（2，2）…根据这个规律，第2019个点的横坐标为 _______ .B i 作BA 丄AC 于点A,过A 的坐标是ABC 是边长为a 的等边三角形，点 B 始终落在y 轴上，点A若点A 的坐标为（3, 2）,20. 如图，在一单位为 1的方格纸上，△ AiA 人3，厶AAA ，^ A 5A 6A 7……，都是斜边在上、斜边长分别为2，4, 6,……的等腰直角三角形，若厶AAA 的顶点坐标分别为三•解答题21. 已知平面直角坐标系中有一点 M( 2m — 3， m +1).(1) 若点M 到y 轴的距离为2时，求点M 的坐标; (2) 点N (5,- 1)且M M x 轴时，求点 M 的坐标.6m +4= 0, b +2m — 8 = 0.(1 )当a = 1时，点P 到x 轴的距离为(2) 喏点P 在第一三象限的角平分线上，求点 P 的坐标;(3)当av b 时，贝U m 的取值范围是23.如图，在正方形网格中，若点 A 的坐标是(1，1)，点B 的坐标是(2，0).(1) 依题意，在图中建立平面直角坐标系;A l (2,22.在平面直角坐标系 xOy 中，有一点P (a ，b )，实数a ，b ，m 满足以下两个等式: a , 2a —Afe 018的坐标为(3) 若点D 的坐标为(3,- 1),在图中标出点 D 的位置；(4) 将点B 向左平移3个单位长度，再向上平移 1个单位长度，则所得的点 B '的坐标是 _______ ，△ ABC 的面积为 ________44—15B24.对于平面直角坐标系xOy 中的点P (a , b ),若点P'的坐标为(a +kb , 为常数，且0),则称点P'为点P 的“ k 属派生点”.例如：P (1, 4)的“ 2属派生点”为 2X 1+4),即 P'( 9, 6).(I)点P (- 2, 3)的“ 3属派生点” P'的坐标为 _____________ ; (H)若点P 的“ 5属派生点” P'的坐标为(3, - 9),求点P 的坐标；(川)若点P 在x 轴的正半轴上，点 P 的“k 属派生点”为P'点，且线段线段OP 长度的2倍，求k 的值.ka +b )(其中 kP'( 1+2X 4,PP 的长度为25.如图，四边形 ABC 曲平行四边形，OD= 3, CD= AB= 5，点A 坐标为(-2, 0)(1)请写出B 、C 、D 各点的坐标;26.已知：A (0, 1), B ( 2, 0), C (4, 3)(1)在坐标系中描出各点，画出△ ABC(2 )求厶ABO的面积；(3)设点P在坐标轴上，且△ ABP W^ ABC的面积相等，求点P的坐标.OA= 2cm OB= 2.5 cm OP= 4cm 点C 为OP的中点，回答下列问题:(1)图中距小明家距离相同的是哪些地方？(2)学校、商场、公园、停车场分别在小明家的什么方位？哪两个地方的方位是相同的?(3)若学校距离小明家400m那么商场和停车场分别距离小明家多少米?28.如图，四边形ABCD各个顶点的坐标分别为(- 2, 8),(- 11, 6) , (- 14, 0) (0, 0).(1 )确定这个四边形的面积，你是怎么做的？(2)如果把原来ABCD各个顶点纵坐标保持不变，横坐标增加2,所得的四边形面积又是多少?29.如图1在平面直角坐标系中，点 A B C D均在坐标轴上，AB// CD(1 )求证：/ ABO/CD© 90°;(2)如图2, BM平分/ ABC交x轴于点M DN平分/ CDC交y轴于点N,求/ BMOZ OND的值.P (3, 3),点A B分别在x轴正半轴和y轴负半轴上, 且PA= PB.30.如图1,在平面直角坐标系中,I- 4 ■■:J L I■亠H»・・亠1-=T:4f-rK«nO图1(1) 求证：PAL PB;(2) ____________________________________ 若点A(9, 0),则点B的坐标为____________________ ;(3) 当点B在y轴负半轴上运动时，求OA 0B的值;(4) 如图2，若点B在y轴正半轴上运动时，直接写出OA+OB的值.参考答案一•选择题1解：因为目标在第四象限，所以其坐标的符号是( 故选：A.2•解：连接 BC 过点B 作BDL CO 于 D,•••/ AOC= 45°, •••/ BO B 45°,•/点B 的坐标(0, 2 _), • OB= 2 _,•. BD^ 0亠•,；：：， ••• A , 0 B, C 四点共圆， :丄 CAO / CB B 180 ° ,•••/ AOC= 45°,/ ACO= 30° ,•••/ CAO= 105 ° ,• / CBO= 75°, • / CB B 30°,•- CD- 7,•••CO=「+ 7,故选：A.•••点P ( 4, 3)到x 轴的距离为|3| = 3, 故选：B.3•解：•••点 P ( 4, 3),+ ,-),观察各选项只有A 符合题意,4•解：T a2+3>3>0,2 c C• •—a —3 v 0,•••点(-2，- a2-3)—定在第三象限.故选：C.5. 解：•••点E在x轴上方，y轴的左侧，•••点E在第二象限，•• •距离x轴3个单位长度，距离y轴4个单位长度，•••点E的横坐标为-4，纵坐标为3,•••点E的坐标是(-4, 3).故选：C.6. 解：•••点P ( a+3, b+1)在平面直角坐标系的x轴上，并且点P到y轴的距离为2,••b+1 = 0, | a+3| = 2,•- a=- 1 或-5, b=- 1,•- a+b=- 2 或-6,故选：D.7. 解：观察发现：A (2, 4), A, (- 3 , 3),人(-2, - 2) , A ( 3 , - 1), % (2 , 4), A(-3 , 3)…•••依此类推，每4个点为一个循环组依次循环，2019-4= 504 余3 ,•••点A2019的坐标与A的坐标相同，为(-2, - 2),故选：B.&解：如图所示：9枚棋子组成的图案既是轴对称图形又是中心对称图形，•这两枚棋子的坐标分别是圆子( 2 , 3),方子(1 , .3 ),9.解：•••点A ( m+2 , 2m- 5)在y 轴上,• m+2= 0 ,解得：m=- 2 ,故2m- 5 =- 9,故点A的坐标为：（0,- 9）.故选：A.10•解：分析图象可以发现，点P的运动每4次位置循环一次•每循环一次向右移动四个单位.2019= 4X 504+3,当第504循环结束时，点P位置在（2016, 0）,在此基础之上运动三次到（2019, 2）, 故选：D.二.填空题（共10小题）11. 解：•••点P （- 5, y）在第三象限，.y v 0,.符合条件的点P的坐标，可以是（-5, - 3）等，故答案为：（-5,- 3）（答案不唯一）.12. 解：•••点P （2+x, 3x- 2）到x轴的距离是到y轴距离的2倍，.2|2+x| = |3x- 2| ,.2 （2+x）= 3x- 2 或2 （2+x ）=-（3x- 2）,9解得x= 6或x =-=59故答案为：，=或6.513. 解：T AB// x 轴，A点坐标为（-1, 3）,•••点B的纵坐标为3,当点B在点A的左边时，••• AB= 5,•••点B的横坐标为-1 - 5=- 5,此时点B （- 6, 3）,当点B在点A的右边时，T AB= 5,•••点B的横坐标为-1+5 = 4,此时点B （4, 3）,综上所述，点B的坐标为（-6 , 3 ）或（4, 3）.故答案为：（-6, 3）或（4, 3）.14. 解：•••△ ABC是等边三角形,••• AB= AC= BC= 1,Z ABC F Z A=Z ACB= 60 ° ,••• A (吉，逅)，C (1, 0), 2 2•/ BA丄AC•・AA i= A)C?• A i (：,=),4 4•/ A1B1// OA•••/ A1B1C=Z ABC= 60°,• △ A i B i C是等边三角形,• A是AC的中点,• A(,：~)8同理A3(-T,故答案为：则0D= ..AB= . a,C»： a.在^ OCD L OBCD> OC所以，当点O D C三点共线时，OC的长度最大, 最大值为'a^a= _2 2 2a.•/ 452= 2025 , 45 是奇数, •••第 2025 个点是（45, 0）, 第2019个点是(45, 6),故答案为：a .216•解：•••线段 AB 与 x 轴平行， •••点B 的纵坐标为2,点B 在点A 的左边时，3 - 5 =- 2, 点B 在点A 的右边时，3+5= 8,•••点B 的坐标为（-2, 2）或（8, 2） • 故答案为：（-2, 2）或（8, 2） •17.解：•••左眼 A 的坐标是（-2, 3），右眼B 的坐标为（0, 3）, •嘴唇C 的坐标是（-1,1）, 故答案是：（-1, 1）.18.解：•••点 A （2a +3, a -4）在二、四象限的角平分线上, •- 2a +3+a - 4= 0, 解得a =亍故答案为：〒19•解：根据图形，以最外边的矩形边长上的点为准，点的总个数等于 x 轴上右下角的点的横坐标的平方,例如：右下角的点的横坐标为 1，共有1个，1 = 12,右下角的点的横坐标为 2时，共有4个，4 = 22, 右下角的点的横坐标为 3时，共有9个，9 = 32, 右下角的点的横坐标为4时，共有16个，16= 42,右下角的点的横坐标为n 时，共有n 2个,所以，第2019个点的横坐标为45.故答案为：45.20. 解：•••各三角形都是等腰直角三角形，•••直角顶点的纵坐标的长度为斜边的一半，A (1, - 1), d (2 , 2), A6 (1 , - 3), A8 (2 , 4), A io (1, - 5), A12 (2 , 6),■I •…•••当脚码是2、6、10…时，横坐标为1,纵坐标为脚码的一半的相反「数•••点A2018在第四象限，横坐标是1,纵坐标是-2018-2 =- 1009 ,•A2018 的坐标为(1 , - 1009).故答案为(1, - 1009).三.解答题(共10小题)21. 解：(1)v点M(2m- 3 , n+1),点M到y轴的距离为1 ,•|2 m- 3| = 2 ,解得m= 2.5 或m= 0.5 ,当m= 2.5时，点M的坐标为(2 , 3.5 ),当n= 0.5时，点M的坐标为(-2 , 0);综上所述,点M的坐标为(2 , 3.5 )或(-2 , 0);(2)•••点M (2m- 3 , n+1),点N (5 , - 1 )且MN/ x 轴，•n+1=- 1,解得n=- 2 ,故点M的坐标为(-7 , - 1).22. 解：(1)当a= 1 时，贝U 2X 1 - 6n+4 = 0,解得n= 1.把n= 1代入b+2in- 8= 0中，得b = 6.所以P点坐标为(1 , 6),所以点P到x轴的距离为6.故答案为6.(2)当点P在第一、三象限的角平分线上时，根据点的横、纵坐标相等，可得a= b.由2a- 6n+4= 0 ,可得a= 3rn- 2；由b+2n- 8= 0,可得b=- 2n+8.贝U 3in—2 =- 2n+8 , 解得n= 2.把m= 2分别代入2a - 6n +4= 0, b +2m- 8 = 0中，解得a = b =4,所以P 点坐标为（4,4）. （3）由（2）中解答过程可知 a = 3m- 2, b =- 2m +8.若a < b ,即卩3m- 2v- 2m +8,解得 2. 故答案为m <2.（3）如图所示：D 点即为所求; (4) B (- 1 , 1); △ ABC 的面积■: = 3.故答案为：(-1,- 2); (- 1, 2); (- 1, 1) ; 3 .24. 解：(I)点 P (- 2, 3)的 “ 3 属派生点” P'的坐标为(-2+3X 3, - 2X 3+3),即(7,故答案为：（7，- 3）;(H)设 P (x , y ),依题意，得方程组:"沪-2解得*,尸1•••点 P (- 2, 1).（川）•••点 P （a , b ）在x 轴的正半轴上， • b = 0, a >0.•••点P 的坐标为（a , 0）,点P'的坐标为（a , ka ）, •线段PP'的长为点P'到x 轴距离为| ka | , •/ P 在x 轴正半轴，线段 0P 的长为a ,23.解:（1）如图所示.\+5y=35耳十y 二-9(2) C (- 1,- 2); C根据题意，有|PP* = 2|OP ,--1 ka|= 2a,••• a> 0,• -1 k| = 2.从而k=± 2.25. 解:(1)v OD= 3,••• D (0, 3),•••CD= AB= 5,点A坐标为(-2, 0),•C的坐标为(5, 3), B(3, 0);(2)平行四边形ABC［的面积=AB?OD- 5X 3= 15.26. 解:(1)如图所示:（2）过点C向x、y轴作垂线，垂足为D E.•四边形DOEC的面积=3X 4 = 12 , △ BCD的面积=■'= 3, △ ACE的面积=4 y c.= 4, △ AOB的面积=［乂v >■；:.：= 1.£U• △ ABC的面积=四边形DOEC勺面积-△ ACE的面积-△ BCD的面积-△ AOB的面积=12 - 3 - 4 - 1 = 4.当点p在x轴上时，△ ABP的面积=［『「：= 4,即：丄J r.---,解得：BP= 8 ,所点P的坐标为（10 , 0）或（-6 , 0）;当点P在y轴上时，△ ABP的面积=丄"厂；4,即丄；—门_ -,解得：AF= 4.所以点P的坐标为（0 , 5）或（0 , - 3）.所以点P的坐标为(0, 5)或(0,- 3)或(10, 0)或(-6, 0).27. 解:(1)v点C为OP的中点,二OC= OP= X 4= 2cm2 2•/ OA= 2cm• ••距小明家距离相同的是学校和公园；(2)学校北偏东45 °，商场北偏西30 °，公园南偏东60 °，停车场南偏东60 °;公园和停车场的方位相同；(3)图上1cm表示：400十2= 200m,商场距离小明家： 2.5 X 200= 500m停车场距离小明家： 4 X 200= 800m28•解：(1)过点B, A分别作BF, AE垂直于x轴，所以四边形的面积=X 3X 6+X (6+8) X 9+厶X 2 X 8= 80; 2(2 )根据平移的性质可知，平移后的图形形状和大小不变，所以所得的四边形面积是80.29. (1)证明：T AB// CD•••/ ABO Z DCO•••/ DCO/ CD= 90 ° ;•Z ABO Z CD= 90, ° ;(2)T BM平分Z ABO DN平分Z CDO•Z MB◎专Z ABO Z ND=号Z CDO•••/ MBO/ NDO 丄(/ ABO /CDQ = 45 2•••/ BMO/ ON B 135 °.30. (1)证明：如图1,过点P 作PE L x 轴于E ,作PF 丄y 轴于F ,••• P (3, 3),• PE= PF = 3,• Rt △ APE^ Rt △ BPF( HL ,• / APE=/ BPF • / APB=/ APE ■/ BPE=/ BPf +Z BPE=/ EPF= 90°,• PALPB(2) 解：由(1)证得，Rt △ APE^ Rt △ BPF• PF = PE•四边形OEPF!正方形，• OE= OF= 4,••• A (9, 0),• OA= 9,• AE= OA- OE= 9- 3=6,•/ Rt △ APE^ Rt △ BPF• AE= BF = 6 ,• OB= BF _ OF == 6 - 3= 3 ,•点B 的坐标为(0 , - 3),故答案为：(0 , - 3);(3) 解：I Rt △ APE^Rt △ BPF• AE= BF,••• AE= OA - OE= OA- 3 ,BF = OBOF= OB 3 ,• O AT 3 = OB^3 ,在 Rt △ APE 和 Rt △ BPF 中(PA=PB1P 匪PFOA OB= 6;(4)解：如图2,过点P作PE!x轴于E,作PF丄y轴-，于F, 同（1）可得，Rt △ AP降Rt △ BPF••• AE= BF,•/ AE= OA- OE= OA- 3,BF= OF- OB= 3- OB•- OA-3 = 3 - OB。

人教版七年级数学下册第七章平面直角坐标系培优专题测试训练(含答案)

人教版七年级数学下册第七章平面直角坐标系培优专题测试训练一、选择题1. 点(－2,1)在平面直角坐标系中所在的象限是( )A．第一象限 B．第二象限 C．第三象限 D．第四象限2. 已知点A的坐标为(2，1)，将点A向下平移4个单位长度，得到的点A'的坐标是 ( )A.(6，1)B.(-2，1)C.(2，5)D.(2，-3)3.图是某动物园的平面示意图，若以猴山为原点，向右的水平方向为x轴正方向，向上的竖直方向为y轴正方向建立平面直角坐标系，则熊猫馆所在的象限是 ( )A.第一象限B.第二象限C.第三象限D.第四象限4.在平面直角坐标系中，将点P(x，y)先向左平移4个单位长度，再向上平移3个单位长度后得到点P'(1，2)，则点P的坐标为( )A.(2，6)B.(-3，5)C.(-3，1)D.(5，-1)5.小明为画一个零件的轴截面，以该轴截面底边所在的直线为x轴，对称轴为y轴，建立如图所示的平面直角坐标系.若坐标轴的单位长度取1 mm，则图中转折点P的坐标表示正确的是( )A.(5，30)B.(8，10)C.(9，10)D.(10，10)6. 平面直角坐标系中，点P(－2，3)关于x轴对称的点的坐标为( )A. (－2，－3)B. (2，－3)C. (－3，2)D. (3，－2)7.如图，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，…，组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第21秒时，点P的坐标为( )A.(21，-1)B.(21，0)C.(21，1)D.(22，0)8.如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点O运动到点(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)……按这样的运动规律，经过第2021次运动后，动点P的坐标是( )A.(2021，1)B.(2021，0)C.(2021，2)D.(2022，0)二、填空题9. 点P(-6，-7)到x轴的距离为，到y轴的距离为 .10. 已知点P(3－m，m)在第二象限，则m的取值范围是________．11.如图，线段AB经过平移得到线段A'B'，其中点A，B的对应点分别为点A'，B'，这四个点都在格点上.若线段AB上有一点P(a，b)，则点P在A'B'上的对应点P'的坐标为 .12.五子棋是一种两人对弈的棋类游戏，起源于中国古代的传统黑白棋种，规则是在正方形棋盘中，由黑方先行，白方后行，轮流弈子，下在棋盘横线与竖线的交叉点上，直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图，这一部分棋盘是两个同学的对弈图.若白子A的坐标为(0，-2)，白子B的坐标为(-2，0)，为了不让白方马上获胜，此时黑方应该下在坐标为的位置.(写出一处即可)13.如图，在三角形ABC中，已知点A(0，4)，C(3，0)，且三角形ABC的面积为10，则点B的坐标为 .14. 将自然数按以下规律排列：第一列第二列第三列第四列第五列…第一行1451617第二行23615…第三行98714…第四行10111213…第五行………………表中数2在第二行、第一列，与有序数对(2，1)对应，数5与有序数对(1，3)对应，数14与有序数对(3，4)对应.根据这一规律，数2021对应的有序数对为 .15.如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位长度，依次得到点P1(0，1)，P2(1，1)，P3(1，0)，P4(1，-1)，P5(2，-1)，P6(2，0)，…，则点P60的坐标是 .16.在平面直角坐标系中，规定把一个三角形先沿着x轴翻折，再向右平移两个单位称为一次变换．如图，已知等边三角形ABC的顶点B、C的坐标分别是(－1，－1)，(－3，－1)，把△ABC经过连续九次这样的变换得到△A′B′C′，则点A的对应点A′的坐标是__________．三、解答题17. 在如图所示的平面直角坐标系中，描出下列各点:(0，4)，(-1，1)，(-4，1)，(-2，-1)，(-3，-4)，(0，-2)，(3，-4)，(2，-1)，(4，1)，(1，1)，(0，4).依次连接各点，观察得到的图形，你觉得它像什么?18.常用的确定物体位置的方法有两种.如图，在4×4的边长为1的小正方形组成的网格中，标有A ，B两点(点A，B之间的距离为m).请你用两种不同的方法表述点B相对于点A的位置.19. 如图所示，已知单位长度为1的方格中有一个三角形ABC.(1)请画出三角形ABC先向上平移3格，再向右平移2格所得的三角形A'B'C'(点A，B，C的对应点分别为点A'，B'，C');(2)请以点A为坐标原点，水平向右为x轴正方向，竖直向上为y轴正方向建立平面直角坐标系(在图中画出)，然后写出点B，B'的坐标.20. 如图，在平面直角坐标系中，A(3，4)，B(4，1)，求三角形AOB的面积.21.如图，在长方形OABC中，O为平面直角坐标系的原点，点A的坐标为(4，0)，点C的坐标为(0，6)，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O-A-B-C-O的路线移动(即沿着长方形的边移动一周).(1)点B的坐标为 ;(2)当点P移动了4秒时，求出点P的坐标，并在图中描出此时点P的位置;(3)在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间.22.如图，在平面直角坐标系中，已知A(2，3)，B(0，2)，C(3，0).将三角形ABC的一个顶点平移到坐标原点O处，写出平移方法和另两个对应顶点的坐标.23. 如图，若三角形A 1B 1C 1是由三角形ABC 平移后得到的，且三角形ABC 中任意一点P (x ，y )经过平移后的对应点为P 1(x-5，y+2).(1)求点A 1，B 1，C 1的坐标;(2)求三角形A 1B 1C 1的面积.24. 【阅读】在平面直角坐标系中，以任意两点P (x 1，y 1)、Q (x 2，y 2)为端点的线段中点坐标为1212,22x x y y ++⎛⎫ ⎪⎝⎭.【运用】(1)如图，矩形ONEF 的对角线交于点M ，ON 、OF 分别在x 轴和y 轴上，O 为坐标原点，点E 的坐标为(4,3)，求点M 的坐标；(2)在直角坐标系中，有A (－1,2)，B (3,1)，C (1,4)三点，另有一点D 与点A ，B ，C 构成平行四边形的顶点，求点D 的坐标．答案一、选择题1.B　2.D　3.B　4.D5.C　[解析] 如图，过点C作CD⊥y轴于点D，∴CD=50÷2-16=9，OA=OD-AD=40-30=10，∴P(9，10).故选C.6.A　【解析】本题考查了直角坐标平面内的点关于x轴的对称点，点如果关于x轴对称，则它的横坐标不变，纵坐标互为相反数，于是点(－2，3)关于x轴对称的点的坐标为(－2，－3)，故选A .7.C　[解析] 半径为1的半圆的弧长是×2π×1=π，由此可列下表：故选C.8.A　[解析]点P坐标的变化规律可以看作每运动四次一个循环，且横坐标与运动次数相同，纵坐标规律是：第1次纵坐标为1，第3次纵坐标为2，第2次和第4次纵坐标都是0.∵2021=505×4+1，∴经过第2021次运动后，动点P 的坐标是(2021，1).故选A .二、填空题9.7　6　10.m ＞3　【解析】∵点P 在第二象限，∴其横坐标是负数，纵坐标是正数，则根据题意得出不等式组，解得m ＞3. {3－m <0m >0)11.(a-2，b+3)　[解析]由图可知线段AB 向左平移了2个单位长度，向上平移了3个单位长度，所以P'(a-2，b+3).12.(2，0)或(-2，4)13.(-2，0)　[解析] S 三角形ABC =BC ·4=10，解得BC=5，∴OB=5-3=2，∴点B 的坐标为(-2，0).14.(45，5)　[解析] 观察表格发现：偶数列的第一行数是“列数”的平方数，奇数行的第一列数是“行数”的平方数.下面从奇数行着手：(1，1)表示1，即12;(3，1)表示9，即32;(5，1)表示25，即52;依此类推可知(45，1)表示452，即2025，于是(45，2)表示2024，(45，3)表示2023，…，(45，5)表示2021.故填(45，5).15.(20，0)　[解析] 因为P 3(1，0)，P 6(2，0)，P 9(3，0)，…，所以P 3n (n ，0).当n=20时，P 60(20，0).16.(16,1＋)　3解析：可以求得点A (－2，－1－)，则第一次变换后点A 的坐标为A 1(0,1＋)，第二次变换33后点A 的坐标为A 2(2，－1－)，可以看出每经过两次变换后点A 的y 坐标就还原，每经过一次3变换x 坐标增加2.因而第九次变换后得到点A 9的坐标为(16,1＋)．3三、解答题17.解:描点连线如图所示，它像五角星.18.解:方法一:用有序数对(a ，b )表示.比如:以点A为原点，水平向右为x轴正方向，竖直向上为y轴正方向建立平面直角坐标系，则点B相对于点A的位置是(3，3).方法二:用方向和距离表示.比如:点B位于点A的东北方向(或北偏东45°方向)，距离点A m处.19.解：(1)如图.(2)如图，以点A为坐标原点，水平向右为x轴正方向，竖直向上为y轴正方向建立平面直角坐标系，则B(1，2)，B'(3，5).20.[解析]三角形AOB的三边均不与坐标轴平行，不能直接利用三角形的面积公式求面积，需通过作辅助线，用“添补”法间接计算.解:如图，过点A作AE⊥y轴于点E，过点B作BF⊥x轴于点F，延长EA，FB交于点C，则四边形OECF为长方形.由点A，B的坐标可知AE=3，OE=4，OF=4，BF=1，CE=4，CF=4，所以AC=1，BC=3，所以S三角形AOB=S长方形OECF-S三角形OAE-S三角形ABC-S三角形BOF=4×4-×4×3-×3×1-×4×1=6.5.21.解:(1)(4，6)(2)因为点P的移动速度为每秒2个单位长度，所以当点P移动了4秒时，它移动了8个单位长度，此时点P的坐标为(4，4)，图略.(3)当点P到x轴的距离为5个单位长度时，有两种情况:①若点P在AB上，则点P移动了4+5=9(个)单位长度，此时点P移动了9÷2=4.5(秒);②若点P在OC上，则点P移动了4+6+4+1=15(个)单位长度，此时点P移动了15÷2=7.5(秒).综上所述，当点P到x轴的距离为5个单位长度时，点P移动了4.5秒或7.5秒.22.解：(1)若将点A平移到原点O处，则平移方法(不唯一)是向左平移2个单位长度，再向下平移3个单位长度.另两个顶点B，C的对应点的坐标分别是(-2，-1)，(1，-3).(2)若将点B平移到原点O处，则平移方法是向下平移2个单位长度.另两个顶点A，C的对应点的坐标分别是(2，1)，(3，-2).(3)若将点C平移到原点O处，则平移方法是向左平移3个单位长度.另两个顶点A，B的对应点的坐标分别是(-1，3)，(-3，2).23.解：(1)∵三角形ABC中任意一点P(x，y)经过平移后的对应点为P1(x-5，y+2)，∴三角形ABC 向左平移5个单位长度，再向上平移2个单位长度(平移方法不唯一)得到三角形A 1B 1C 1.∵A (4，3)，B (3，1)，C (1，2)，∴点A 1的坐标为(-1，5)，点B 1的坐标为(-2，3)，点C 1的坐标为(-4，4).(2)三角形A 1B 1C 1的面积=三角形ABC 的面积=3×2-×1×3-×1×2-×1×2=.24.解：(1)∵四边形ONEF 是矩形，∴点M 是OE 的中点．∵O (0,0)，E (4,3)，∴点M 的坐标为.(2，32)(2)设点D 的坐标为(x ，y )．若以AB 为对角线，AC ，BC 为邻边构成平行四边形，则AB ，CD 的中点重合∴Error!，解得，Error!.若以BC 为对角线，AB ，AC 为邻边构成平行四边形，则AD ，BC 的中点重合∴Error!，解得，Error!.若以AC 为对角线，AB ，BC 为邻边构成平行四边形，则BD ，AC 的中点重合∴Error!，解得，Error!.综上可知，点D 的坐标为(1，－1)或(5,3)或(－3,5)．。

第七章-平面直角坐标系培优提高卷(含答案)

\平面直角坐标系培优提高、选择题。

C . 4单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位…依此类推,1. 某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第K 棵树种植在P kk -1(X k ,Y k )处，其中 X 1=1 , Y 1=1，当 k>2 时，X k =X k - + 1-5([0 ：-5:：) ,Y k =Y k -5+ ［匚1［匚2:, : a :表示非负实数a 的整数部分，例如［2.55按此方案，第2013棵树种植点的坐标是（6： = 2, :0. 2： = 0,2. A . ( 3, 402) B . (3, 403) C .( 4, 403) D . (5, 403)如图，在平面直角坐标系中，已知点 A(-1, 1), B (- 1 , - 2)，将线段 AB 向下平移2个单位，再向右平移3个单位得到线段 A /B /,设点P （x,y ）为线段上任意一点，则x,y 满足的条件为（3. 4. C . 如图, x=3 , -4<y<—1-4 <x < —1 , y = 3A(-In I)(第 2 题)在平面直角坐标系中,B . x=2 , - 4<y<-1 D. -4<x<—1 , y = 2A*1XCD(1,1), B (- 1,1), 一条长为2014个单位长度且没有弹性的细线并按标是如图, A - B -C -D -A …的规律绕在四边形 (-1, 0)B . ( 1 , - 2)C (- 1,- 2),D ( 12).把（线的粗细忽略不计）的一端固定在点 A 处,ABCD 的边上，则细线另一端所在位置的点的坐A ,B 的坐标为（2, 0）,（ 0, 1），若将线段AB 平移至A 1B 1,D . (- 1 , - 1)则a+b 的值为（5. 在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个(第 3 )占）第n 步的走法是：当n 能被3整除时，则向上走1个单位；当n 被3除，余数为1时，则向 n 被3除，余数为2时，则向右走2个单位，当走完第100步时，棋子所处位置的坐标是(对于平面内任一点(m, n )，规定以下两种变换：①f (m, n ) = (m ,_n如 f (2, 1)=(2, —1 卜② g(m, n )=(—m ，— n )，如 g(2, 1)=(—2 -1).按照以上变换有:f fg (3, 4)]=f (—3,— 4)=(—3, 4 )，那么 g [f (—3, 2)]]等于(7•如图，矩形 OABC 的边0A 、0C 分别在x 轴、y 轴上，点B 的坐标为(3, 2) •点D 、E 分别，以点(0, 1)为位似中心，在 y 轴左方作^ ABC与^ A'B'C 的位似比为1 : 2•若设点C 的纵坐标是 m ,则其对应点C 的纵坐标是( 二、填空题。

七年级数学竞赛培优平面直角坐标系含解析

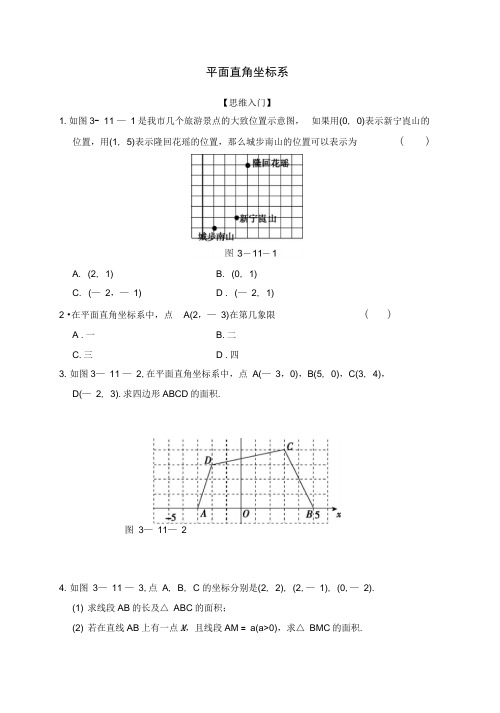
平面直角坐标系【思维入门】1.如图3- 11 —1是我市几个旅游景点的大致位置示意图，如果用(0, 0)表示新宁崀山的位置，用(1, 5)表示隆回花瑶的位置，那么城步南山的位置可以表示为()A. (2, 1)B. (0, 1)C. (—2，—1) D . (—2, 1)2 •在平面直角坐标系中，点A(2，—3)在第几象限()A .一B.二C.三 D .四3. 如图3—11 —2,在平面直角坐标系中，点A(—3，0)，B(5, 0)，C(3, 4)，D(—2, 3).求四边形ABCD的面积.图3—11—24. 如图3—11 —3,点A, B, C 的坐标分别是(2, 2), (2,—1), (0,—2).(1) 求线段AB的长及△ ABC的面积；(2) 若在直线AB上有一点M，且线段AM = a(a>0)，求△ BMC的面积.5. 在平面直角坐标系中有两点A( —2, 2), B(3, 2), C是坐标轴上的一点，若△ ABC是直角三角形，则满足条件的点有()A . 1个B . 2个C. 4个 D . 6个6 •在平面直角坐标系中，0为坐标原点，点A的坐标为(1，.3)，M为坐标轴上一点，且使得△MOA为等腰三角形，则满足条件的点M的个数为()A . 4B . 5 C. 6 D . 87.如图3—11 —4,在直角坐标系中，0是原点，已知A(4，3)，P是坐标轴上的一点，若以0, A，P三点组成的三角形为等腰三角形，则满足条件的点P共有____ 个，写出其中一个点P的坐标是_____ .8.如图3—11 —5,已知坐标平面内的三个点A(1, 3), B(3, 1), 0(0, 0),求厶ABO的面积.【思维升华】9•如图3- 11 —6，弹性小球从点P（0, 3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…，第n次碰到矩形的边时的点为P n，贝U点P3的坐标是____ ;点P2 014的坐标是_____ .10.如图3—11 —7,在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次不断地移动，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1,0），A4（2, 0）,…，那么点A4n+1（n是自然数）的坐标为 .图3—11—711.如图3—11 —8,在平面直角坐标系中，点A, B, C的坐标分别为（1, 0）, （0, 1）,（—1, 0）.一个电动玩具从坐标原点O出发，第一次跳跃到点P1，使得点P1与点O关于点A成中心对称；第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称；第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称；第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称；第五次跳跃到点P5，使得点P5与点P4关于点B成中心对称，….照此规律重复下去，则点P2 013的坐标为________________ .—----- 4---------- ——1 -- 1——>C °A耳图3- 11—812•在平面直角坐标系xOy中，对于点P(x, y)，我们把点P'—y+ 1, x+ 1)叫做点P的伴随点，已知点A1的伴随点为A2，点A2的伴随点为A3，点A的伴随点为A4,这样依次得到A1, A2, ______ A3,…，A n,…，若点A1的坐标为(3，1)，则点A3的坐标为，点A2014的坐标为____ ;若点A1的坐标为(a, b),对于任意的正整数n,点A n均在x轴上方，则a, b应满足的条件为 _____ .平面直角坐标系【思维入门】1.如图3- 11 —1是我市几个旅游景点的大致位置示意图，如果用(0, 0)表示新宁崀山的位置，用(1, 5)表示隆回花瑶的位置，那么城步南山的位置可以表示为A. (2, 1)B. (0, 1)C. (—2，—1) D . (—2, 1)2 •在平面直角坐标系中，点A(2，—3)在第几象限(D )A .一B.二C.三 D .四3.如图3—11 —2,在平面直角坐标系中，点A(—3，0)，B(5, 0)，C(3, 4)，D(—2, 3).求四边形ABCD的面积.-r - - T -- nt- - - -ir ■-! 1 1 V 1 1 1 I i i i fl&-i - = - -i- - - ii1 l< 1 4 1 Vi ii i ii i i1 1 i i i I1 1 i I 1 11 H 1 1 1 1I b 丨厂i i * 1i 1 h i IP * 1 \ «■1_ _ J_ - JL____________ Y J _ I I1 1 1 * p ■1[I 1 1 f1 ■」K H 1 \ H 1 * i B i \i i iJ 1 \ I _ n1'! 1 P / 1 1i 1 1 i f1 11 1 1 1 f1 1r I \ i ii h 1 i \ 1 11 N 1 «\ ■1r■ r7" -n J i r -i i ■i ■；11 !r 1 1= = i (- A r--1»i> i i \i »、i i i j r i：4-5 ：\A\:0 ：；；: #5 ；戈图3—11—2解：作DE丄x轴于E, CF丄x轴于F，如答图，1 1 1四边形ABCD 的面积=ADE + S四边形CDEF+BCF = ?X 1 X 3+(3 + 4) X (3 + 2) + 2 X 4 = 23.4•如图3- 11 —3,点A, B, C 的坐标分别是(2, 2), (2,—1), (0,—2).⑴求线段AB的长及△ ABC的面积；(2)若在直线AB上有一点M，且线段AM = a(a>0)，求△ BMC的面积.解：(1) •••点A, B的坐标分别是(2, 2), (2,—1),••• AB丄x轴，二AB= 2—(—1)= 3,1S A ABC = 2 X 3X 2 = 3.⑵当M点在BA的延长线上时，MB = a+ 3,1△ BMC 的面积=2X2X (a+ 3)= a+ 3;当M点在线段AB上时，0<a<3, MB = 3 —a,1△ BMC 的面积=2X 2X (3 —a) = 3 —a；当M点在AB的延长线上时，a>3, MB = a —3,1△ BMC 的面积=^X 2X (a—3)= a — 3.【思维拓展】5.在平面直角坐标系中有两点A( —2, 2), B(3, 2), C是坐标轴上的一点，若△ ABC是直角三角形，则满足条件的点有(D )A . 1个B . 2个C. 4个 D . 6个【解析】因为A, B的纵坐标相等，所以AB// x轴•因为C是坐标轴上的一点，所以过点A向x轴引垂线，过点B向x轴引垂线，分别可得一点，以AB为直径作圆，可与坐标轴交于4点，所以满足条件的点共有6个.6 •在平面直角坐标系中，0为坐标原点，点A的坐标为(1，3)，M为坐标轴上一点，且使得△MOA为等腰三角形，则满足条件的点M的个数为(C )A . 4B . 5 C. 6 D . 8【解析】如答图，满足条件的点M的个数为6,分别为(—2, 0)，(2, 0)，(0，2 3)，(0，2), (0, —2), 0,斗3.故选 C.r r 4 :'甌! 1* 1 3-----T -------------- -- 1 ----- i1 n ■* 1 t ! U…上II 1 J( 11 11 11 |L _ _ L1 1 H ■1 七\ \帆1 1; --- 「［-■「1/M L42 0 11II 1;1 2M2_________ J__________ ::;-1i 1Il i1；：：■；：：：* 1 p 1 ____ L - 1- ■------------------- ----------- ---------------- ----------第6题答图7•如图3—11 —4,在直角坐标系中，O是原点，已知A(4, 3), P是坐标轴上的一点，若以O, A, P三点组成的三角形为等腰三角形，则满足条件的点P共有一8—个，写出其中一个点P的坐标是(0, 6),答案不唯一.8.如图3- 11 —5,已知坐标平面内的三个点A(1, 3), B(3, 1), 0(0, 0),求厶ABO的面积.3= 4+ 3- 3= 4.-gxix解：如答图，S A ABO=第8题答图【思维升华】9•如图3- 11 — 6，弹性小球从点P(0, 3)出发，沿所示方向运动，每当小球碰到矩形OABC 的边时反弹，反弹时反射角等于入射角，当小球第 1次碰到矩形的边时的点为 P 1,第2次碰到矩形的边时的点为 P 2,…，第n 次碰到矩形的边时的点为 P n ，贝U 点 P 3的坐标是 —(8, 3)__;点P2 014的坐标是__(5，0)__,当点P 第3次碰到矩形的边时，点P 3的坐标为(8, 3);••• 2 014 £= 335……4 ,•••当点P 第2 014次碰到矩形的边时为第336个循环组的第4次反弹，点P 2 014的坐标为(5, 0).10. 如图3— 11 — 7,在平面直角坐标系中，一动点从原点O 出发，按向上、向右、向下、向右的方向依次不断地移动，每次移动一个单位，得到点 A 1(0, 1), A 2(1, 1), A 3(1, 0), A 4(2, 0),…，那么点A 4n +1(n 是自然数)的坐标为__(2n , 1)__.J h y A 2 A .沖 4 凡 ^10 /h1 j t 1 鼻 1 J (. 1 * 1 t 一 t A 0 〒 k 尸 k Aj J 44 A lx A ]2 【解图 3- 11— 7【解析】由图可知，n = 1时，4X 1+ 1 = 5•点A 5(2, 1),n = 2 时，4X 2+ 1 = 9,点 A 9(4, 1),n = 3 时，4X 3+ 1 = 13,点 A 13(6, 1),所以，点 A 4n + 1(2n , 1).11. 如图3— 11 — 8,在平面直角坐标系中，点A , B , C 的坐标分别为(1, 0), (0, 1),(— 1, 0). —个电动玩具从坐标原点 O 出发，第一次跳跃到点 P 1，使得点P 1与点O 关于点A 成中心对称；第二次跳跃到点P 2,使得点P 2与点P 1关于点B 成中心对称；第三次跳跃到点P 3,使得点P 3与点P 2关于点C 成中心对称；第四次跳跃到点 P 4,使得点P 4与点P 3关于点A 成中心对称；第五次跳跃到点 P 5，使得点P 5与点P 4关于点 B 成中心对称，….照此规律重复下去，则点P2 013的坐标为_(0,— 2)_ .7 +-4 ------------- b ——' -- 1——>C 0 A 兀图 3— 11— 8【解析】点 P 1（2, 0）, P 2（ — 2, 2）, P 3（0,— 2）, P 4（2, 2）, P 5（ — 2, 0）, P 6（0, 0）,P 7(2, 0),从而可得出6次一个循环,•••点P 2 013的坐标为（0,— 2）. 12. 在平面直角坐标系xOy 中，对于点P(x , y)，我们把点P '—y + 1, x + 1)叫做点P 的伴随点，已知点A 1的伴随点为A 2,点A 2的伴随点为A 3,点A 3的伴随点为A 4,这样依次得到A 1, A 2, A 3,…，A n ，…，若点A 1的坐标为(3, 1),则点A 3的坐标为 (— 3, 1)__,点A2 014的坐标为_(0, 4)_；若点A 1的坐标为(a , b)，对于任意的正整数n ,点A n 均在x 轴上方，则a , b 应满足的条件为1v a v 1且0v b v 2 .【解析】：A 1的坐标为(3, 1),•-A 2(0, 4), A 3( — 3, 1), A 4(0,— 2), A 5(3, 1),…， 2 013= 6 =335 3,以此类推，每4个点为一个循环组依次循环，2 014-4 = 503……2,•••点A 014的坐标与A2的坐标相同，为（0, 4）;•••点A i的坐标为（a，b）,• - A2（—b + 1，a+ 1），A3（—a，—b+ 2），A4（b—1，—a + 1），A5（a，b），…，以此类推，每4个点为一个循环组依次循环，•••对于任意的正整数n,点A n均在X轴上方，a+ 1>0，•丿…a+ 1>0，b+ 2>0，4>0，解得—1<a<1，0<b<2.。

平面直角坐标系培优训练题(精品)

平面直角坐标系培优训练题一、坐标在平面直角坐标系中的性质1.若a 为整数，且点(39,210)M a a --在第四象限内，则21a +的值为（） . 2、在平面坐标系中，若点(1,3)M 与点(,3)N x 之间的距离是5，则x 的值是＿＿＿ . 3.平面直角坐标系中的点1(2,)2P m m -关于x 轴的对称点在第四象限内，则m 的取值范围为＿＿＿＿＿＿ .4、已知点M(－2,b)在第三象限，那么点N(b, 2 )在5、若点P （a ，b ）在第四象限，则点M （b-a ，a-b ）在。

6、已知点P （a,b ）,且ab ＞0,a ＋b ＜0,则点P 在7、若点P （x ,y ）的坐标满足xy=0(x ≠y)，则点P 在（）A ．原点上B ．x 轴上C ．y 轴上D ．x 轴上或y 轴上8、点P （m ＋3, m ＋1）在x 轴上，则m = ，点P 坐标为。

9、已知点P(m ，2m －1)在y 轴上，则P 点的坐标是。

10、点P 的横坐标是-3，且到x 轴的距离为5，则P 点的坐标是（） 11、已知点P （x ，y ）在第四象限，且│x│=3，│y│=5，则点P 的坐标是（）12、点P （x,y ）位于x 轴下方，y 轴左侧，且x =2 ，y =4，点P 的坐标是（）二、平面直角坐标系中坐标的对称性13.（1）若(,8)P a 和(7,)Q b 关于y 轴对称，则2010()a b + =＿＿＿＿＿＿.14.已知(2+3,2)A a b -和(8,32)B a b +关于x 轴对称，那么a b +=＿＿＿＿＿＿ . 15、点A （1-a ，5），B （3，b ）关于原点对称，则a+b=_______．三、坐标的平移16.如图，围棋盘放置在某个平面直角坐标系内，白棋②的坐标为(7,4)--，白棋④的坐标为(6,8)--，那么，黑棋的坐标应该分别是＿＿＿＿＿＿ .17.如图，在直角坐标系中，已知点(3,0)A -，(0,4)B 且5AB =，对OAB ∆连续作旋转变换，依次得到三角形①，②,③，④，…，则三角形⑩的直角顶点的坐标为＿＿＿＿＿＿ .18.以平行四边形的顶点A 为原点、直线AD 为x 轴建立直角坐标系，已知B 、D 两点的坐标分别为（1,3），（4,0），把平行四边形向上平移2个单位，那么C 点平移后相应的点的坐标是（）.A.(3,3)B.(5,3)C.(3,5)D.(5,5)19、将点A （-4，2）向上平移3个单位长度得到的点B 的坐标是（） 20、线段CD 是由线段AB 平移得到的,点A （–1，4）的对应点为C （4，7），则点B （-4，–1）的对应点D 的坐标为（）四、利用坐标求面积 21.如图，在平面直角坐标系中，四边形各顶点的坐标分别为：(00),(70),(95),(27)A BCD ，，，，.（1）求此四边形的面积（2）在坐标轴上，你能否找到一点P ，使50PBC S ∆=？若能，求出点P 的坐标；若不能，请说明理由._ 17 _ 16图②图①22.如果四边形ABCD 顶点的坐标依次为 (12)(25)(73)(51)A B C D ，、，、，、，，那么四边形ABCD 的面积为＿＿＿＿＿＿ .23、如图，在平面直角坐标系中，点A ，B 的坐标分别为（－1，0），（3，0），现同时将点A ，B 分别向上平移2个单位，再向右平移1个单位，分别得到点A ，B 的对应点C ，D ，连接AC ，BD ，CD ．(1)、求点C ，D 的坐标及平行四边形ABDC 的面积ABDC S 四边形(2)、在y 轴上是否存在一点P ，连接PA ，PB ，使PAB S ∆＝2ABDC S 四边形，若存在这样一点，求出点P 的坐标，若不存在，试说明理由．五、动点问题24.（1）如图①，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2008次，点P 依次落在点1232008,,,...,P P P P 的位置，求点2008P 的横坐标.（2）如图②，在平面直角坐标系中，一颗棋子从P 点处开始依次关于点A 、B 、C 作循环对称跳动，即第一次跳到点P 关于点A 的对称点M 处，接着跳到点M 关于点B 的对称点N 处，第三次再跳到点N 关于点C 的对称点处,…，如此下去.① 在图中画出点M 、N ，并写出点M 、N 的坐标.② 求经过第2008次跳动之后，棋子落点与点P 的距离.25.在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位.其行走路线如图所示. （1）填写下列各点的坐标：1(_,_)A ；3(_,_)A ；12(_,_)A . （2）写出点4n A 的坐标（n 是正整数）.（3）指出蚂蚁从点100A 到点101A 的移动方向.26.如图，已知(20)(22)A B --，、，，线段AB 交y 轴于点C . （1）求点C 的坐标.（2）若(60)D ，，动点P 从点D 开始在x 轴上以每秒3个单位向左运动，同时，动点Q 从点C 开始在y 轴上以每秒1个单位向下运动.问经过多少秒，APC AOQ S S ∆∆= ?_ 12 _ 11 _ 8_7 _4_3_。

中考数学总复习《平面直角坐标系》专题训练(附带答案)

中考数学总复习《平面直角坐标系》专题训练(附带答案)学校:___________班级：___________姓名：___________考号：___________一、单选题1．若点A到x轴的距离为2，到y轴的距离为5，且点A在第四象限，则点A的坐标是（）A．(2,−5)B．(5,−2)C．(−2,5)D．(−5,2)2．若点P(m+5,m−3)在x轴上，则点P的坐标为（）A．(8,0)B．(0,−8)C．(4,0)D．(0,−4)3．在平面直角坐标系中，若直线AB经过点(3，−4)和(−3，4)，则直线AB() A．平行于x轴B．平行于y轴C．经过原点D．无法确定4．在平面直角坐标系中，将点P(−1,5)绕原点O顺时针旋转90°得到P′，则点P′的坐标为（）A．(1,5)B．(5,1)C．(−1,−5)D．(−5,−1) 5．点P坐标为(6−3a,a+2)，且点P到两坐标轴的距离相等，则点P的坐标是（）A．(3,3)B．(3,−3)C．(3,3)或(−6,6)D．(3,−3)或(6,−6)6．在平面直角坐标系中，点A(3,4)，B(−1,b)，当线段AB最短时，b的值为（）A．5B．4C．3D．07．如图，雷达探测器测得六个目标A，B，C，D，E，F，目标E，F的位置分别表示为E(3,330°),F(2,30°)按照此方法，目标A，B，C，D的位置表示不正确的是（）A．A(5,60°)B．B(3,120°)C．C(3,210°)D．D(5,270°) 8．如图A1(1,0)，A2(1,1)，A3(−1,1)，A4(−1,−1)，A5(2,−1)…按此规律，点A2022的坐标为（）A．(505,505)B．(−506,506)C．(506,506)D．(−505,−505)二、填空题9．电影票上“10排8号”记作(10,8)，那么(15,9)表示的意义是10．已知A(a，−4)与B(3，4)两点关于x轴对称，则a的值为11．已知点A(m+1,2)和点B(3,m−1)，若直线AB∥x轴，则A的坐标为．12．如图，在平面直角坐标系xOy中，Rt△OAB的斜边OB在x轴上∠ABO=30°，若点A的横坐标为1，则点B的坐标为．13．如图，△ABC为等腰直角三角形∠ABC=90°，点B、C在坐标轴上，已知点A坐标为(3,4)，则△ABC的面积为．14．在平面直角坐标系中，用大小、形状完全相同的长方形纸片摆放成如图所示的图案，已知点A的坐标为(−1,3)，则点B的坐标为．15．如图所示，在平面直角坐标系xOy中，点A的坐标是(2,0)，点B的坐标是(0,4)，点C 在x轴上运动（不与点A重合），点D在y轴上运动（不与点B重合），当点C的坐标为时，以点C，O，D为顶点的三角形与△AOB全等．16．如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到(1,1)，第2次接着运动到点(2,0)，第3次接着运动到点(3,2)，按这样的运动规律，经过第2023次运动后，动点P的坐标是．三、解答题17．为了更好的开展古树名木的系统保护工作，某公园对园内的4棵百年古树都利用坐标确定了位置，并且定期巡视．(1)请在如图所示的正方形网格中建立平面直角坐标系xOy，使得古树A，B的位置分别表示为A(2,1)，B(5,5)；(2)在（1）建立的平面直角坐标系xOy中．①表示古树C的位置的坐标为______，并在网格中标出古树E(4,−1)的位置；②现需要在沿y轴的道路某处P点向古树A，B修建两条步道，使得点P到古树A，B的距离和最小．请在网格中画出点P（保留作图痕迹，不写作图过程）；该距离和的最小值为______．18．已知平面直角坐标系中有一点M(m−1,2m+3)．(1)当点M到x轴的距离为1时，求点M的坐标；(2)当点M到两坐标轴的距离相等时，求点M的坐标．19．如图，已知△ABC的三个顶点的坐标分别为A(−6，0),B(−2，3),C(−1，0)．(1)将△ABC绕坐标原点O逆时针旋转90°．画出对应的△A′B′C′图形，直接写出点A的对应点A′的坐标；(2)在格点图内，若四边形A′B′C′D′为平行四边形，请直接写出第四个顶点D′的坐标．20．如图，在直角坐标系中A(0,1)，B(2,0)，C(4,3)．(1)在平面直角坐标系中描点，画出△ABC；并作出△ABC关于y轴对称的图形△A1B1C1；(2)求△ABC的面积；(3)设点P在y轴上，且△ABP与△ABC的面积相等，直接写出点P的坐标．21．如图，已知△ABC的顶点分别为A(−2,2)，B(−4,5)，C(−5,1)．(1)作出△ABC关于x轴对称的图形△A1B1C1(2)写出点C1的坐标(3)在x轴上找一点P，使得AP+CP最小（画出图形，找到点P的位置）．22．如图，在平面直角坐标系中，设一点M自P0(1，0)处向上运动1个单位长度至P1(1，1)，然后向左运动2个单位长度至P2处，再向下运动3个单位长度至P3处，再向右运动4个单位长度至P4处，再向上运动5个单位长度至P5处…如此继续运动下去，设P n(x n，y n)，n=1，2，3，……．(1)计算x1+x2+x3+x4．(2)计算x1+x2+⋅⋅⋅+x2023+x2024的值．参考答案1．解：设A(x,y)∵点A到x轴的距离为2，到y轴的距离为5∴x=±5,y=±2∵点A在第四象限∴x>0,y<0∴x=5,y=−2∴A(5,−2)故选：B．2．解：依题意得：m−3=0，即：m=3∴m+5=3+5=8∴点P的坐标为(8,0)故选A．3．解：点(3，−4)和(−3，4)的横纵坐标互为相反数故点(3，−4)和(−3，4)关于原点对称故直线AB经过原点．故选：C．4．解：如图，过P、P′分别向x轴作垂交于H、K根据旋转的定义可知OP=OP′，∠POP′=90°∴∠POH+∠P′OK=90°，∠P′OK+∠P′=90°∴∠POH=∠P′∴∠PHO=∠P′KO=90°∴△PHO≌△P′OK(AAS)．∴PH=OK=5，OH=P′K=1即P′(5,1)．故选B．5．解：由点(6−3a,a+2)到两坐标轴的距离相等，得6−3a=a+2，或6−3a+a+2=0解得a=1，或a=4则该点的坐标为(3,3)或(−6,6)故选：C．6．解：由题意知，点B(−1,b)在直线x=−1上运动∴当AB⊥直线x=−1时，线段AB最短此时b=4．故选：B．7．解：∴E(3,330°)，F(2,30°)∴A(5,60°)，B(3,120°)，C(4,210°)，D(5,270°)故选：C8．解：由题可知第一象限的点：A2,A6,A10，……角标除以4余数为2；第二象限的点：A3,A7,A11……角标除以4余数为3；第三象限的点：A4,A8,A12……角标除以4余数为0；第四象限的点：A5,A9,A13……角标除以4余数为1；由上规律可知：2022÷4=505⋯2∴点A2022在第一象限．观察图形，得：点A2的坐标为(1,1)，点A6的坐标为(2,2)，点A10的坐标为(3,3)，……∴第一象限点的横纵坐标数字隐含规律：点的横纵坐标=n+2（n为角标）4∴点A2022的坐标为(506,506)．故选：C．9．解：∴“10排8号”记为(10,8)∴(15,9)表示的意义是15排9号．故答案为：15排9号．10．解：∴A(a，−4)与B(3，4)两点关于x轴对称∴a=3故答案为：3．11．解：∴直线AB∥x轴∴m−1=2∴m=3∴m+1=4即点A坐标：A(4,2)故答案为：(4,2)．12．解：过点A作x轴的垂线，垂足为点C ∴Rt△OAB中∠ABO=30°∴∠AOB=60°∴AC⊥OB∴∠OAC=30°∴点A的横坐标为1∴OC=1∴OA=2OC=2∴∠ABO=30°∴OB=2OA=4∴点B的坐标为(4,0)故答案为：(4,0)．13．解：如图所示，过点A作AD⊥y轴于点D∴△ABC是等腰直角三角形∴AB =BC ，∠ABC=90°∴∠ABD =90°−∠OBC =∠OCB又∠ADB =∠BOC =90°∴△ADB ≌△BOC (AAS)∴AD =OB,DB =OC∴点A 坐标为(3,4)∴AD =OB =3∴S △ABC =S 梯形−S △ABD −S △OBC =12(1+3)×4−12×1×3−12×1×3=5 故答案为：5．14．解：设每个长方形纸片的宽为x ，长为y由题意可得：{2y −x −y =12x +y =3解得{x =23y =53∴点B 的到x 轴的距离为x +y =73，到y 轴的距离为2y −x =83 ∴点B 的坐标为(−83,73)．故答案为：(−83,73)．15．解：如图（1）所示当点C 在x 轴负半轴上，点D 在y 轴负半轴上时若△AOB ≌△COD ，则CO =AO =2∴点C 的坐标为(−2,0)；若△AOB ≌△DOC ，则OC =OB =4∴点C 的坐标为(−4,0)；如图（2）所示当点C在x轴负半轴上，点D在y轴正半轴上时若△AOB≌△DOC，则CO=BO=4∴点C的坐标为(−4,0)．若△AOB≌△COD，则CO=AO=2∴点C的坐标为(−2,0)；如图（3）所示当点C在x轴正半轴上，点D在y轴正半轴上时同理可得C的坐标为(4,0)；如图（4）所示当点C在x轴正半轴上，点D在y轴负半轴上时，同理可得点C的坐标为(4,0)；综上所述，点C的坐标为(−4,0)或(−2,0)或(4,0)故答案为：(−4,0)或(−2,0)或(4,0)．16．解：由图可得，动点P的横坐标和运动的次数相同，纵坐标以1，0，2，0为一个循环组依次循环∴经过第2023次运动后，动点P的横坐标为2023∴2023÷4=505 (3)∴经过第2023次运动后，动点P的纵坐标为2∴动点P的坐标是(2023,2)故答案为：(2023,2)．17．解：（1）如图所示（2）①点C(−2,2)，点E(4,−1)的位置如图所示；②过点A作关于y轴的对称点为A′，则A′(−2,1)，连接A′B与y轴交于点P，此时PA+PB最小等于A′B的长度；A′B=√[5−(−2)]2+(5−1)2=√72+42=√65∴点P到古树A，B的距离和的最小值为√65；故答案为：√6518．解：（1）∵|2m+3|=1∴2m+3=1或2m+3=−1解得：m=−1或m=−2∴点M的坐标是(−2,1)或(−3,−1)；（2）∵|m−1|=|2m+3|∴m−1=2m+3或m−1=−2m−3解得：m=−4或m=−23∴点M的坐标是：(−5,−5)或(−53,5 3 ).19．（1）解：△A′B′C′如图所示∴A′(0,−6)；（2）解：如图平行四边形A′B′C′D′即为所求：根据平行四边形性质可得D′(3,−5)故答案为：D′(3,−5)．20．（1）解：如图所示，△ABC即为所求；△A1B1C1即为所求．（2）S△ABC=3×4−12×1×2−12×2×4−12×2×3=4；（3）当点P在y轴上时，△ABP的面积=12AP×|x B|=4即12AP×2=4解得：AP=4．∴点P的坐标为(0,5)或(0,−3)．21．解：（1）如图1所示，△A1B1C1即为所求；（2）点C1的坐标为(−5,−1)；（3）如图2所示，点P即为所求．22．（1）解：由题意可知P1(1，1)，P2(−1，1)，P3(−1，−2)，P4(3，−2)，P5(3，3)，P6(−3，3)，P7(−3，−4)，P8(5，−4)，……于是得到x1，x2，x3，x4的值为1，-1，-1，3∴x1+x2+x3+x4=1−1−1+3=2（2）解：∴x5，x6，x7，x8的值分别为3，-3，-3，5∴x5+x6+x7+x8=3−3−3+5=2；∴x1+x2+x3+x4=1−1−1+3=2x5+x6+x7+x8=3−3−3+5=2…x2021+x2022+x2023+x2024=2∴2024÷4=506∴x1220232024。

《平面直角坐标系》精编测试题及答案(提高难)

《平面直角坐标系》精编测试题（提高）一、单选题1．已知点A(m,n)位于第二象限，并且n≤2m+5，m、n均为整数，则满足条件的点A个数有（）A．2个B．3个C．4个D．5个2．如图，象棋盘上，若“马”位于点(6，1)，则“将”位于（）A．(3，－2) B．(2，－2) C．(0，－1) D．(－3，0)3．若点P(3-a,2a+9)到两坐标轴的距离相等，则点P的坐标是（）A．(5，5) B．(2，2) C．(5，5)或(15，-15) D．(2，2)或(12，-12) 4．已知点A(－3，－1)，B(2，5)，将线段AB平移得到线段CD，若点A的对应点C在x 轴上，点B的对应点D在y轴上，则点C的坐标是()A．(3，0) B．(-1，0) C．(0，4) D．(－5，0)5.对平面坐标系上任意一点(a，b)，定义f1，f2两种变换：f1 (a，b)＝(﹣a，-b)，例如f1 (2，-1)＝(﹣2，1)；f2 (a，b)＝(a，-b)，例如f2 (1，5)＝(1，-5)；则f2 [f1 (2，﹣8)]的值是（）A．(2，8) B．(2，﹣8) C．(﹣2，8) D．(-2，-8)6．已知点A(-2n，n+1)，B(4，2n+1)，线段AB//y轴，则△AOB的面积为()A．4 B．6 C．8 D．107．已知点A（x，y）到x轴的距离为5，到y轴的距离为2，且x+y＞0，xy＜0，则点A的坐标为（）A．（﹣2，5）B．（2，5）C．（﹣2，-5）D．（2，-5）8．已知点A(a，b)在x轴上方，在y轴左侧，则点A到x轴、y的距离分别为() A．a，-b B．-a，b C．b，-a D．-b，a9．如图，在平面直角坐标系中，点,A C在x轴上，点C的坐标为(-1,0)，AC=3，将Rt△ABC先绕点C逆时针旋转90°，再向右平移5个单位长度，则变换后点A的对应点坐标是()A．(-1,8) B．(-1,-7) C．(4,4) D．(4,-3)10．如图，矩形ABCD的两边BC、CD分别在x轴、y轴上，点C与原点重合，点A(-1,2)，将矩形ABCD沿x轴向右翻滚，经过一次翻滚点A对应点记为A1，经过第二次翻滚点A对应点记为A2依此类推，经过3次翻滚后点A对应点A3的坐标为（）A ．(3,0)B ．(2,2)C ．(2,1)D ．(1,2)11．如图，线段AB 经过平移得到线段A ＇B ＇，其中点A 、B 的对应点分别为点A ＇、B ＇，这四个点都在格点上，若线段AB 上有一个点P （a,b ），则点P 在A ＇B ＇上的对应点P ＇的坐标为( )A ．(a+2,b-3)B ．(a-2,b+3)C ．(-a-2,b-3)D ．(a+2,b-3)12．如图，直角坐标平面xOy 内，动点P 按图中箭头所示方向依次运动，第1次从点（﹣1，0）运动到点（0，1），第2次运动到点（1，0），第3次运动到点（2，﹣2）…按这样的运动规律，动点P 第2023次运动到点的坐标是( )A ．(2021,0)B ．(2022,0)C ．(2023,0)D ．(2024,0) 二、填空题13．已知坐标平面内长方形ABCD 的三个顶点的坐标为A(2，12)，B(－7，12)，C(－7，－3)，则顶点D 的坐标为__________．14．如图，已知A(0，a)，B(b ，0)，第四象限的点C(c ，m)到x 轴的距离为3，若a ，b 满足2|2|(2)22a b b c c -+++=-+-，则点A 、B 、C 点坐标分别为________________． 15．在平面直角坐标系中，若A （4，0），B （0，3），C （m ，7），三角形ABC 的面积为14，则m 的值为_________．（第15题）（第16题）16．△ABC 中，A 、B 、C 三点坐标分别为()0,0、()4,1、()1,3，△ABC 中的面积为______． 17．在平面直角坐标系中，点P （x ，y ）经过某种变换后得到点P ′（﹣y ＋1，x ＋2），我们把点P ′（﹣y ＋1，x ＋2）叫做点P （x ，y ）的终结点．已知点P 1的终结点为P 2，点P 2的终结点为P 3，点P 3的终结点为P 4，这样依次得到P 1、P 2、P 3、P 4、…Pn … 若点P 1的坐标为（2，0），则点P2023的坐标为_________．三、解答题18．在平面直角坐标系中，P(1，4)，点A在坐标轴上，且S△PAO＝4，求点A的坐标．19．如图所示，在平面直角坐标系中，在△ABC中，OA＝2，OB＝4，点C的坐标为(0，3)．（1）求A，B两点坐标及S△ABC；（2）若点M在x轴上，且23ACM ABCS S，试求点M的坐标．（3）若点D是第一象限的点，且满足△CBD是以BC为直角边的等腰直角三角形，请直接写出满足条件的点D的坐标．20．如图，在平面直角坐标系中，△AA1C1是边长为1的等边三角形，点C1在y轴的正半轴上，以A A1=2为边长画等边△AA2C2；以AA2=4为边长画等边△AA2C3…按此规律继续画等边三角形，求点A2023和A n的坐标.21.如图，已知点O(0,0)，A(2,0)，，B(-1,2)．（1）求△OAB的面积；（2）点C是在坐标轴上异于点A的一点，且△OBC的面积等于△OAB的面积，求满足条件的点C的坐标；（3）若点D的坐标为（m，2），且m＜-1，连接AD交OB于点E，在x轴上有一点F，使△BDE的面积等于△BEF的面积，请直接写出点F的坐标__________（用含m的式子表示）．参考答案一、选择题CACDD AACDA BB二、填空题13. (2,-3)14. (0,-4)、(-2,0)、(2,-3)15. 416. 11/217. (-3,3)三、解答题18．解：（1）当点A在x轴上时，设A（x，0），|x|×4=4，解得x=±2 ∴A（-2，0）或（2，0）∵S△PAO=4，A（1，4）∴12|y|×1=4，解得x=±8 （2）当点A在y轴上时，设A（0，y）∵S△PAO=4，A（1，4）∴12∴A（-8，0）或（8，0）综上所述，A点坐标为（-2，0）或（2，0）或（-8，0）或（8，0）．19．解：（1）∵OA=2，OB=4，且A在原点左侧，B在原点右侧，∴A （-2，0），B （4，0） ∵C （0，3） ∴OC=3 ∴16392ABC S =⨯⨯= （2）设M 的坐标为（m ，0），则AM=()22m m --=+ ∵9ABC S = ∴2963ACM S =⨯= ∴12362m ⨯+⨯=，解得m=2或m=-6 ∴M 点的坐标是（2，0）或（-6，0）（3）如图，符合条件的D 点有两个，①△2BD E ≌△CBO ∴24D E OB ==，OE=OB+BE=7 ∴()274D ，②△1C D F ≌△BCO ∴CF=BO=4∴OF=4+3=7 ∴13D F OC == ∴()137D ，，综上所述，D 点坐标是（3，7）或（7，4）20. (22022-0.5，0)、(2n-1-0.5，0)21.解：（1）1122222OAB B S OA y =⋅⋅=⨯⨯=．（2）作如下图形，进行分类讨论：①当点C 在y 轴正半轴上时 111||22OBC B SOC x =⋅⋅=114,(0,4)OC C ∴=； ②当点C 在y 轴负半轴上时，221||22OBC B S OC x =⋅⋅= 224,(0,4)OC C ∴=- ③当点C 在x 轴负半轴上时，33122OBC B S OC y =⋅⋅= 332,(2,0)OC C ∴=- 因此符合条件的C 点坐标有3个，分别是(0,4),(0,4),(2,0)--．（3）BDE BEF S S = 1122D F BE h BE h ∴⋅⋅=⋅⋅ DF h h ∴=，即D 与F 点到OB 的距离相等12OBD D S OB h =⋅⋅12OBF F S OB h =⋅⋅OBD OBF S S ∴= ∴由BDE BEF S S =可推出OBD OBF S S =①F 位于x 轴负半轴上时，11(1)2122OBD B SBD y m m =⋅⋅=⨯--⨯=-- 11111122BOF B B S OF y OF y OF =⋅⋅=⋅⋅=11OF m ∴=-- 1(1,0)F m ∴+ ②F 位于x 轴正半轴上时，222112BOF B S OF y OF m =⋅⋅==-- 2(1,0)F m ∴-- 综上所述，点F 的坐标为1(1,0)F m +或2(1,0)F m --．。

九年级中考数学复习《平面直角坐标系》专项练习题-附带答案

九年级中考数学复习《平面直角坐标系》专项练习题-附带答案一、单选题1．在平面直角坐标系中，点P（3，﹣2）在第（）象限A．一B．二C．三D．四2．在平面直角坐标系中，已知线段PQ=4，且PQ⊥x轴，若点P的坐标为(5，−2)，则点Q的坐标为（）A．(5，2)B．(9，−2)C．(5，2)或(5，−6)D．(9，−2)或(1，−2)3．在平面直角坐标系中，点P（m﹣2，2m+n）在y轴正半轴上，且点P到原点O的距离为6，则m+3n的值为（）A．5 B．6 C．7 D．84．在平面直角坐标系中，点A，B，C，D，E，F的位置如图所示，如果点E的坐标是（﹣3，0），点F的坐标是（3，0），则在第三象限上的点是（）A．点A B．点B C．点C D．点D5．图，线段AB经过平移得到线段A1B1，若点A1(3，0)、B1(0，−4)，A(−1，2)，则点B的坐标为（）A．(−2，−3)B．(−4，−1)C．(−4，−2)D．(−2，−2)6．如图，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（0，1），将线段AB平移，使其一个端点到C（3，2），则平移后另一端点的坐标为（）A．（1，3）B．（5，1）C．（1，3）或（3，5）D．（1，3）或（5，1）7．如图，在平面直角坐标系xOy中，四边形ABCO是正方形，已知点A的坐标为(2，1)，则点C的坐标为（）A．(−1，2)B．(1，−2)C．(−1，√5)D．(−2，1)8．如图，把线段AB经过平移得到线段CD，其中A，B的对应点分别为C，D．已知A（﹣1，0），B（﹣2，3），C（2，1），则点D的坐标为（）A．．（1，4）B．．（1，3）C．．（2，4）D．．（2，3）二、填空题9．点A，点B同在平行于x轴的直线上，则点A与点B的坐标相等．10．已知点P（x﹣3，2x﹣4）在纵轴上，则x的值是.11．如果将点A（-3，-1）向右平移2个单位长度，再向下平移3个单位得到点B，那么点B的坐标是．12．将点A(3，－4)沿Ｘ轴负方向平移3个单位长度，得到A′点的坐标为，再将A′沿Ｙ轴正方向平移4个单位长度，得到A″点的坐标为13．北京中轴线南起永定门，北至钟鼓楼，全长7.8千米．如图是利用平面直角坐标系画出的中轴线及其沿线部分地点分布图，若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示天安门的点的坐标为(0，−1)，表示王府井的点的坐标为(1，−1)，则表示永定门的点的坐标为．三、解答题14．在雷达探测区域，可以建立平面直角坐标系表示位置.在某次行动中，当我两架飞机在A（－1，2）与B（3，2）位置时，可疑飞机在（－1，－3）位置，你能找到这个直角坐标系的横、纵坐标的位置吗？把它们表示出来并确定可疑飞机的位置，说说你的做法．15．多多和爸爸、妈妈周末到动物园游玩，回到家后，她利用平面直角坐标系画出了动物园的景区地图，如图所示．可是她忘记了在图中标出原点和x轴、y轴．只知道马场的坐标为（﹣3，﹣3），你能帮她建立平面直角坐标系并求出其他各景点的坐标？16．如图,已知A(-4，-1)，B(-5，-4)，C(-1，-3)，△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)（1）请在图中作出△A′B′C′；（2）写出点A′、B′、C′的坐标.17．如图是某校的平面示意图，已知图书馆、行政楼的坐标分别为(－3，2)，(2，3)．完成以下问题：（1）请根据题意在图上建立直角坐标系；（2）写出图上其他四个地点实验楼、校门口、综合楼、信息楼的坐标；（3）在图中用点P表示体育馆(－1，－3)的位置．18．在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位．其行走路线如图．（1）填写下列各点的坐标：A4（，），A8（，）；（2）点A4n﹣1的坐标（n是正整数）为（3）指出蚂蚁从点A2013到点A2014的移动方向．参考答案1．D2．C3．D4．C5．C6．D7．A8．A9．纵10．311．（-1，-4）12．(0,-4)；（0,0）13．(0，−7)14．解：能．如下图，先把AB四等分，然后过靠近A点的分点M作AB的垂线即为y轴，以AM为单位长度沿y轴向下2个单位即为O点，过点O作x轴垂直于y轴，然后描出敌机位置为点N．15．解：建立坐标系如图：∴南门（0，0），狮子（﹣4，5），飞禽（3，4）两栖动物（4，1）．16．（1）解：∵△ABC中任意一点P（x1，y1）平移后的对应点为P′（x1+6，y1+4）∴平移规律为：向右平移6个单位，向上平移4个单.如图所示：（2）解：A′（2，3），B′（1，0），C′（5，1）.17．（1）解:由图书馆、行政楼的坐标分别为(－3，2)，(2，3)可找到O(0,0)点，从而建立平面直角坐标系，如下图；（2）解: 根据（1）中的平面直角坐标系，可得其他四个地点的坐标．故实验楼(-4，0)；校门口(1，0)；综合楼(-5，-3)；信息楼(1，-2)；（3）解: 根据平面直角坐标系，P(－1，－3)的位置如下图18．【解答】解：（1）由图可知，A4，A8都在x轴上，∵小蚂蚁每次移动1个单位，∴OA4=2，OA8=4，∴A4（2，0），A8（4，0）；故答案为：2，0；4，0；（2）根据（1）OA4n=4n÷2=2n，∴点A4n﹣1的坐标（2n﹣1，0）；（3）∵2013÷4=503…1，∴从点A2013到点A2014的移动方向与从点A1到A2的方向一致，为→。