2013保险精算第七章解析

现金价值产生的原因
• 寿险是长期契约，在契约有效期内，投保人可能 由于经

保险人应不应该退还给投保人所缴纳的保费？ 若要退还，该退还多少？

保险业的发展史上，有两种极端的说法 保单是有法律效力的合约，中途 不退一分钱
退保应视为违约，理应受到惩罚

退还全部所缴保费
保费是为了对付被保险人的风 险才缴纳的，而现在被保险人 并没有出险
保单现金价值
• 不丧失价值条款 – 保险合同中一般设有专门条款（不丧失利益条款） 保障投保人的合法权益，当被保人退保时，保险公 司支付给保单持有人一定的金额。 • 不丧失保单利益(保单持有人的退保收益) – 被保人在退保后所得到的金额（因为缴纳了保费， 对保险公司的准备金有贡献，属于被保险人的资产、 保险人的责任，如若退保，责任不存在，应该退还 给被保险人） – 保险监管机构一般都规定最低的现金价值标准
• 评估假设（死亡率、预定利率费用率等）和评估方法（过去 法、未来法）比较保守，从而会产生较高的负债额。
• 不同国家规定有所不同，我国的精算规定也分别给出传统人 寿保险、新型寿险（分红保险、投资连结保险、万能保险） 法定责任准备金的评估假设和计算方法
– 如，中国保监会规定：会计年度末保单法定未到期责任准备金应当 采用“未来法”逐单计算，对确实不能采用“未来法”逐单计算的 条款，经中国保险监管委员会同意，可以采用“过去法”逐单计算。
保费差公式推导 (以完全连续n年定期两全保险为例)
t
V ( Ax:n ) Ax t:n t P ( Ax:n )ax t:n t Ax t:n t P ( Ax:n ) ax t:n t ax t:n t P ( Ax t:n t ) P ( Ax:n ) ax t:n t
责任准备金的分类
• 按覆盖责任分：
– 净责任准备金（受益责任准备金） – 费用责任准备金 – 修正责任准备金
• 按被保险人缴费、保险人赔付的方式分：
– 完全连续责任准备金（死亡即刻赔付，连续缴费） – 完全离散责任准备金（死亡年末赔付，生存期初缴费） – 半连续责任准备金（死亡即刻赔付，生存期初缴费）

ax t
1 Ax t

ax t 1 Ax t tVx 1 1 ax 1 Ax
半连续责任准备金的确定
• 以h次缴费n年定期两全保险为例
h t
x t:n t V ( Ax:n ) Ax t:nt h P( Ax:n )a i 1 i 1 1 1 x t:n t Ax t:nt Ax t:nt ( h Px:n h Px:n )a UDD i h 1 h 1 tVx:n tVx:n ,t h
净责任准备金的确定
• 将来亏损的期望即该时刻的净责任准备金
U V ( A ) E [ L ] E [ v ] PE[aU ] t x t
Ax t Pax t
• 用这种原理确定责任准备金的方法 称为将来法
将来法亏损方差
Var[ t L] Var[v PaU ]
U
[1 P ] Var[v ]
净责任准备金的确定原理（以完 全连续终身寿险为例）
• 将来亏损（prospective loss）
U L v paU t J 1 J 1 L v pa k
• 其中：
r.vU . 、J 是 ( x t ) 的 剩 余 寿 命 ， f (u ) u px t x t u u0 k, j Z f ( j ) j px k qx k j j qx k
• 其他险种场合可以同理推导。半连续责任准 备金都可以转换为完全离散责任准备金的函 数
1
– – – – – –
第七章
准备金
• 净责任准备金（受益责任准备金）
净责任准备金的定义 净责任准备金确定原理 用将来法确定常见险种的净责任准备金 完全连续型寿险的责任准备金递推公式 完全离散型寿险责任准备金的递推公式 半连续责任准备金的确定
法定责任准备金(偿付能力准备金)
• 是保险监管机构为确保保险公司财务状况而确定的准备金数 额的最小值，保险公司所提留的准备金必须高于这个值。
缴清保费公式推导
t
V ( Ax:n ) Ax t:n t P ( Ax:n )ax t:n t P ( Ax:n )ax t:n t 1 Ax t:n t Ax t:n t
P ( Ax:n ) 1 Ax t:n t P ( Ax t:n t )
差值
责任准备 金
未来 责任
未来 收入
0
t
w
责任 准备 金
差值
=
=
仍在保障范围内的
被保险人数
对每位仍在保 障范围内的被 保险人的未尽 责任现值
净责任准备金的主要计算方法
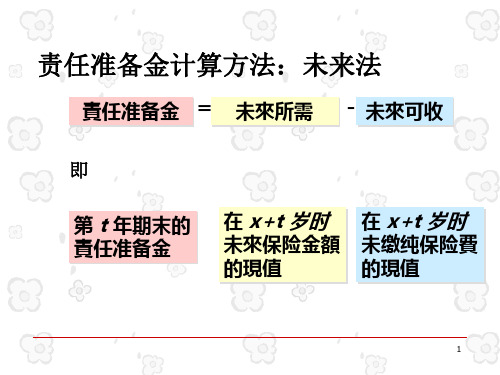
• 过去法： 过去已收纯保费的精算积累值－过去已给付的 保险金的精算积累值 • 未来法： 未来保险金给付的精算现值－未来应收纯保费 的精算现值
盈余准备金
• 侧重于体现盈余的真实性：在公平合理的基础 上提供一个收益水平的衡量 • 考虑准备金的盈余公式： 盈余=保费收入+投资收入-赔付支出-相关费用提存的准备金 • 计算的假设和方法不像法定责任准备金那么保 守，将费用在各保单年度进行分摊，使保险公 司的收益在未来的保单年度合理分配，此时计 算的准备金就是盈余准备金
责任准备金的其它确定方法
• 保费差公式（premium-difference formula） – 责任准备金等于剩余缴费期内保费差的精算现值。 • 缴清保险公式（paid-up insurance formula） – 责任准备金等于部分受益的精算现值。 • 过去法（retrospective method） – 责任准备金是已付保费积累值与保险成本积累值 （accumulated cost of insurance）之差。
净责任准备金的定义
• 定义： – 保险公司在任意时刻对每个仍在保障范围内的被保 险人的未尽责任现时值，就称为净责任准备金。 – 或者说是每个现存被保险人将来的受益现值，所以 也称为受益责任准备金。 • 实质 – 责任准备金是现存被保险人未来受益与未来 缴费现时值之差
责任准备金图解
未来 未来 责任 收入
其它公式
Ax t 1 ax t tVx Ax t Pax t 1 ( P)ax t 1 ax ax t 1 ( ) ax t 1 ax ax ax 1 Ax Ax 1 ( ) ax t ax
x t
ax 10
x t
tV ( Ax ) Ax t P ( Ax ) a
2
0
P ( Ax ) 2 2 Var ( t L) 1 A A x x 0.25
例题：
• 王某在40岁时投保了20年定期寿险，保 险金额为10000元。若保险费限期10年缴 清，预定利率为6%，以中国人寿保险业 经验生命表为依据，试计算： • （1）投保第5年末的责任准备金 • （2）投保第15年末的责任准备金 • （3）投保第20年末的责任准备金
2 U
[1 P ] [ Ax t A ]
2 2 2 x t
• 例题1：已知： 0.04, 0.06 • 利用将来法确定完全连续终身寿险在未来任意 时刻t的净责任准备金及将来损失的方差。
0.04, 0.06
Ax 0.4, 2 Ax 0.25, ax 10, P ( Ax ) 0.04 Ax t Ax 0.4, a