北师大版九年级数学上期中数学试题.docx

合集下载

北师大版九年级数学上册期中试卷及答案【完整】

北师大版九年级数学上册期中试卷及答案【完整】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．2020的相反数是（）A ．2020B ．2020-C ．12020D ．12020- 2．已知一个布袋里装有2个红球，3个白球和a 个黄球，这些球除颜色外其余都相同．若从该布袋里任意摸出1个球，是红球的概率为13，则a 等于（）A ．1B ．2C ．3D ．43．施工队要铺设1000米的管道，因在中考期间需停工2天，每天要比原计划多施工30米才能按时完成任务．设原计划每天施工x 米，所列方程正确的是（）A ．1000100030xx -+=2 B ．1000100030x x -+=2 C ．1000100030x x --=2 D ．1000100030x x--=2 4．为考察甲、乙、丙、丁四种小麦的长势，在同一时期分别从中随机抽取部分麦苗，获得苗高（单位：cm ）的平均数与方差为：x 甲=x 丙=13，x 乙=x 丁=15：s 甲2=s 丁2=3.6，s 乙2=s 丙2=6.3．则麦苗又高又整齐的是（）A ．甲B ．乙C ．丙D ．丁 5．在数轴上，点A ，B 在原点O 的两侧，分别表示数a ，2，将点A 向右平移1个单位长度，得到点C ．若CO=BO ，则a 的值为（）A ．-3B ．-2C ．-1D ．16．如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（）A．主视图改变，左视图改变B．俯视图不变，左视图不变C．俯视图改变，左视图改变D．主视图改变，左视图不变7．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（）A．30°B．25°C．20°D．15°8．如图，在平面直角坐标系中，已知点A（―3，6）、B（―9，一3），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（）A．（―1，2） B．（―9，18）C．（―9，18）或（9，―18） D．（―1，2）或（1，―2）9．如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时，则∠MPN的度数为（）A．140°B．100°C．50°D．40°10．下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）A ．B ．C ．D ．二、填空题（本大题共6小题，每小题3分，共18分）1．计算(31)(31)+-的结果等于___________．2．分解因式：x 3﹣16x ＝_____________．3．函数132y x x =--+中自变量x 的取值范围是__________． 4．如图，抛物线2y ax c =+与直线y mx n =+交于A(-1,P)，B(3,q)两点，则不等式2ax mx c n ++>的解集是__________．5．如图所示，一次函数y=ax+b 的图象与x 轴相交于点（2，0），与y 轴相交于点（0，4），结合图象可知，关于x 的方程ax+b=0的解是__________．6．如图，直线l x ⊥轴于点P ，且与反比例函数11k y x=（0x >）及22k y x =（0x >）的图象分别交于A 、B 两点，连接OA 、OB ，已知OAB ∆的面积为4，则12k k =﹣________．三、解答题（本大题共6小题，共72分）1．解方程23111x x x -=--2．已知关于x 的一元二次方程220x x k +-=有两个不相等的实数根．（1）求k 的取值范围；（2）若方程的两个不相等实数根是a ，b ，求111a ab -++的值．3．正方形ABCD 的边长为3，E 、F 分别是AB 、BC 边上的点,且∠EDF=45°.将△DAE 绕点D 逆时针旋转90°，得到△DCM.（1）求证：EF=FM（2）当AE=1时，求EF 的长．4．如图，在Rt △ABC 中，∠ACB ＝90°，过点C 的直线MN ∥AB ，D 为AB 边上一点，过点D 作DE ⊥BC ，交直线MN 于E ，垂足为F ，连接CD 、BE ．（1）求证：CE ＝AD ；（2）当D 在AB 中点时，四边形BECD 是什么特殊四边形？说明你的理由；（3）若D 为AB 中点，则当∠A 的大小满足什么条件时，四边形BECD 是正方形？请说明你的理由．5．随着科技的进步和网络资源的丰富，在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论.为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图.根据图中信息，解答下列问题：（1）求本次调查的学生总人数，并补全条形统计图；（2）求扇形统计图中“在线讨论”对应的扇形圆心角的度数；（3）该校共有学生2100人，请你估计该校对在线阅读最感兴趣的学生人数.6．某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．(1)降价前商场每月销售该商品的利润是多少元？(2)要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、A3、A4、D5、A6、D7、B8、D9、B10、B二、填空题（本大题共6小题，每小题3分，共18分）1、22、x （x +4）（x –4）.3、23x -<≤4、3x <-或1x >．5、x=26、8．三、解答题（本大题共6小题，共72分）1、2x =2、（1）k>-1；（2）13、(1)略；（2） 52.4、（1）略；（2）四边形BECD 是菱形，理由略；（3）当∠A ＝45°时，四边形BECD 是正方形，理由略5、（1）90人，补全条形统计图见解析；.（2）48︒；（3）560人.6、(1) 4800元；(2) 降价60元.。

北师大版2022～2023学年九年级数学第一学期期中质量检测题【含答案】

北师大版2022～2023学年九年级数学第一学期期中质量检测题（分值：150分）本试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间为120分钟.答卷前，请考生务必将自己的姓名、座号和准考证号填写在答题卡上，并同时将考点、姓名、准考证号和座号填写在试卷规定的位置.考试结束后，只交答题卡.第Ⅰ卷（选择题共60分）一、选择题（本题共15个小题，每题只有一个正确答案，每小题4分，共60分）1．菱形不具备的性质是（）A ．四条边都相等B ．对角线一定相等C ．是轴对称图形D ．是中心对称图形2．已知平行四边形ABCD ，下列条件中，不能判定这个平行四边形为矩形的是（）A ．∠A＝∠B B ．∠A＝∠C C ．AC ＝BD D ．AB⊥BC3．解一元二次方程x2﹣8x﹣5=0，用配方法可变形为（）A ．（x+4）2=11B ．（x﹣4）2=11C ．（x+4）2=21D ．（x﹣4）2=214．若x0是方程ax2+2x+c=0（a≠0）的一个根，设M=1﹣ac，N=（ax0+1）2，则M 与N 的大小关系正确的为（）A ．M ＞NB ．M=NC ．M ＜ND ．不确定5．一个盒子内装有大小、形状相同的四个球，其中红球1个、绿球1个、白球2个，小明摸出一个球不放回，再摸出一个球，则两次都摸到白球的概率是（）　A ．21B ．41C ．61D ．1216.在一个暗箱里放有a 个除颜色外其它完全相同的球，这a 个球中红球只有3个．每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在25%，那么可以推算出a 大约是（）A ．12B ．9C ．4D ．37.如图，在△ABC 中，DE ∥BC ，AD =6，BD =3，AE =4，则EC 的长为（）A.1 B .2 C.3 D. 4第7题图第8题图第9题图第10题图8.如图，下列条件不能判定△ADB ∽△ABC 的是（）A ．∠ABD ＝∠ACB B ．∠ADB ＝∠ABC B ．AB 2＝AD •AC D ．AD AB AB BC=9．如图，点D 、E 分别为△ABC 的边AB 、AC 上的中点，则△ADE 的面积与四边形BCED 的面积的比为（）A ．1：2B ．1：3C ．1：4D ．1：110.如图，在直角坐标系中，有两点A (6，3)、B (6，0)．以原点O 为位似中心，相似比为31，在第一象限内把线段AB 缩小后得到线段CD ，则点C 的坐标为（）A ．(2，1)B ．(2，0)C ．(3，3)D ．(3，1)11.已知点A （-2，y 1），B （-3，y 2）是反比例函y=x 6-图象上的两点，则有（）A ．y 1＞y 2B ．y 1＜y 2C ．y 1＝ y 2 D.不能确定12.函数xa y ＝（0≠a ）与a ax y －＝（0≠a ）在同一平面直角坐标系中的大致图象是（）13.某村耕地总面积为 50 公顷，且该村人均耕地面积 y （单位：公顷/人）与总人口x （单位：人）的函数图象如图所示，则下列说法正确的是（）A ．该村人均耕地面积随总人口的增多而增多B ．该村人均耕地面积 y 与总人口 x 成正比例C ．若该村人均耕地面积为 2 公顷，则总人口有 100 人A CBD ．当该村总人口为 50 人时，人均耕地面积为 1 公顷14. 如图，菱形ABCD 的边AD⊥y 轴，垂足为点E ，顶点A 在第二象限，顶点B 在y 轴的正半轴上，反比例函数()0,0y >≠=x k x k 的图象同时经过顶点C.D ，若点C 的横坐标为5，BE=3DE.则k 的值为( ) A.25B.3C.415D.515.如图，在正方形ABCD 中，点P 是AB 上一动点（不与A 、B 重合），对角线AC 、BD 相交于点O ，过点P 分别作AC 、BD 的垂线，分别交AC 、BD 于点E 、F ，交AD 、BC 于点M 、N.下列结论：①△APE≌△AME；②PM+PN=AC；③PE 2+PF 2=PO 2；④△POF∽△BNF；⑤当△PMN∽△AMP 时，点P 是AB 的中点.其中正确的结论有（）A ．5个B ．4个C ．3个D ．2个第Ⅱ卷（非选择题共90分）二、填空题（本题共7个小题，每题4分，共28分）16.若3x=5y ，则y x = ；已知0,2≠++===f d b f e d c b a 且，则fd be c a ++++= .17. 一天晚上，小伟帮助妈妈清洗两个只有颜色不同的有盖茶杯，突然停电了，小伟只好把杯盖和茶杯随机地搭配在一起，则颜色搭配正确的概率是 .18.把长度为20cm 的线段进行黄金分割，则较长线段的长是________cm ．（结果保留根号）19.如图所示，一个底面为等边三角形的三棱柱，底面边长为2，高为4，如图放置，则其左视图的面积是 .主视图俯视图左视图20.如下图，为了测量校园内一棵不可攀的树的高度，实验学校“玩转数学”社团做了如下的探索：根据《自然科学》中的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把镜子放在离树（AB ）9米的点E 处，然后沿着直线BE 后退到点D ，这是恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.7米，观察者目高CD=1.8米，则树（AB）的高度为____________米.第20题图第21题图21．如图，点A为函数y=（x＞0）图象上一点，连结OA，交函数y=（x＞0）的图象于点B，点C是x轴上一点，且AO=AC，则△ABC的面积为．22.如图，在RT△A BC中，∠C=90°，BC=8，AC=6，动点Q从B点开始在线段BA上以每秒2个单位长度的速度向点A移动，同时点P从A点开始在线段AC上以每秒1个单位长度的速度向点C移动．当一点停止运动，另一点也随之停止运动．设点Q，P移动的时间为t秒．当t= 秒时△APQ与△ABC相似.三.解答题23.（8分）同一时刻，物体的高与影子的长成比例，某一时刻，高1.6m的人影长1.2m，一电线杆影长为9m，则电线杆的高为多少米？24.（8分）在校园文化艺术节中，九年级一班有1名男生和2名女生获得美术奖，另有2名男生和2名女生获得音乐奖.（1）从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会，求刚好是男生的概率；（2）分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会，用列表或树状图求刚好是一男生一女生的概率.25.（8分）如图，在△ABC 中, 点D,E 分别是AB,AC 边上的两点，且AB=8,AC=6,AD=3,AE=4,DE=6,求BC 的长.26.（12分）如图，△ABC 为锐角三角形，AD 是BC 边上的高，正方形EFGH 的一边FG 在BC 上，顶点E 、H 分别在AB 、AC 上，已知BC=40cm ，AD=30cm ．（1）求证：△AEH∽△ABC；（2）求这个正方形的边长与面积.27.（12分）如图，已知反比例函数x k y =与一次函数b x y +=的图象在第一象限相交于点A （1，4+-k ）.（1）试确定这两个函数的表达式；（2）求出这两个函数的另一个交点B的坐标，并求出△AOB的面积.（3）直接写出当反比例函数值大于一次函数值时，x的取值范围.28（14分）已知：如图，在Rt△ACB中，∠C=90°，AC=3cm，BC=3cm，点P由B点出发沿BA方向向点A匀速运动，速度为2cm/s；点Q由A点出发沿AC方向向点C匀速运动，速度为cm/s；若设运动的时间为t（s）（0＜t＜3），解答下列问题：（1）如图①，连接PC，当t为何值时△APC∽△ACB，并说明理由；（2）如图②，当点P，Q运动时，是否存在某一时刻t，使得点P在线段QC的垂直平分线上，请说明理由；（3）如图③，当点P，Q运动时，线段BC上是否存在一点G，使得四边形PQGB为菱形？若存在，试求出BG长；若不存在请说明理由．数学试题答案一选择题1—5BB DB C 6～10 ABDBA 11～15 AADCB二填空题16. 35 217. 用A 和a 分别表示第一个有盖茶杯的杯盖和茶杯；12用B 和b 分别表示第二个有盖茶杯的杯盖和茶杯、经过搭配所能产生的结果如下：Aa 、Ab 、Ba 、Bb ．所以颜色搭配正确的概率是．1218. （105—10）注：无括号也不再扣分19. 4320. 621. 622. 13501130或三解答题23.解设电线杆高x 米，由题意得：x 1.6=91.2 ---------------------------------------------------5分 X=12 ---------------------------------------------------7分答：电线高为12米 --------------------------------------------------8分24.解：（1）从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会，刚好是男生的概率=433 =73；---------------------------------------------2分（2）画树状图为：---------------5分共有12种等可能的结果数，------------------------6分其中刚好是一男生一女生的结果数为6，----------------------------7分所以刚好是一男生一女生的概率==．----------------------8分25解：∵，-------------------------------1分， -----------------------------------2分∴AC AD =AB AE-------------------------------------3分∵∠A=∠A ，---------------------------------4分∴△ADE ∽△ACB.----------------------------------5分∴21==AC AD BC DE 即216=BC --------------------------------------7分∴BC=12---------------------------------------------8分26解：（1）证明：∵四边形EFGH 是正方形，∴EH ∥BC ，-----------------------1分∴∠AEH=∠B ，----------------------2分∠AHE=∠C ，-----------------------3分∴△AEH ∽△ABC ．-------------------4分（2）解：如图设AD 与EH 交于点M ．-----------------------5分∵∠EFD=∠FEM=∠FDM=90°，∴四边形EFDM 是矩形，∴EF=DM ，设正方形EFGH 的边长为x ，-------------------6分∵△AEH ∽△ABC ，∴=，-------------------------------------------8分∴=，-------------------------------------10分∴x=，-----------------------------------------11分∴正方形EFGH 的边长为cm ，面积为cm 2．------------------------12分27题（1）∵点A （1，4k -+）在反比例函数k y x =的图象上∴=4k k -+解得=2k ----------------------------------------------------1分∴A （1，2）∵点A （1，2）在一次函数y x b =+的图象上∴12b +=解得1b =-----------------------------------------2分反比例函数的解析式为2y x =，一次函数的解析式为1y x =+-------4分（2）解方程组12y x y x =+⎧⎪⎨=⎪⎩得21x y =-⎧⎨=-⎩或12x y =⎧⎨=⎩∵点B 在第三象限 ∴点B 坐标为2-1------------------6分∵1y x =+，当0y =时1x =-∴点C 坐标为1-0------------7分∴S △A O B =23-----------------------------10分（3）x<- 2或0<x<1----------------------------------12分注：写出一种情况给1分28题已知：如图，在Rt △ACB 中，∠C=90°，AC=3cm ，BC=3cm ，点P 由B 点出发沿BA 方向向点A 匀速运动，速度为2cm/s ；点Q 由A 点出发沿AC 方向向点C 匀速运动，速度为cm/s ；若设运动的时间为t （s ）（0＜t ＜3），解答下列问题：（1）如图①，连接PC，当t为何值时△APC∽△ACB，并说明理由；（2）如图②，当点P，Q运动时，是否存在某一时刻t，使得点P在线段QC的垂直平分线上，请说明理由；（3）如图③，当点P，Q运动时，线段BC上是否存在一点G，使得四边形PQGB为菱形？若存在，试求出BG长；若不存在请说明理由．【考点】相似形综合题．【分析】（1）先根据勾股定理求出AB，再用△APC∽△ACB，得出，即：，求出时间；（2）先用垂直平分线的性质得出QM=CM=CQ=（3﹣t），然后用平行线分线段成比例建立方程求出结论；（3）先由平行四边形的性质建立方程求出时间t，即求出PQ，PB，即可得到PQ≠PB判断出四边形PQGB不可能是菱形．解：（1）在Rt△ACB中，∠C=90°，AC=3cm，BC=3cm，∴AB=6，由运动知，BP=2t，AQ=t，∴AP=6﹣2t，∵△APC∽△ACB，∴，∴，∴t=；（2）存在，理由：如图②，由运动知，BP=2t，AQ=t，∴AP=6﹣2t，CQ=3﹣t，∵点P是CQ的垂直平分线上，∴QM=CM=CQ=（3﹣t），∴AM=AQ+QM=t﹣（3﹣t）=（t﹣1）过点P作PM⊥AC，∵∠ACB=90°，∴PM∥BC，∴，∴，∴t=或t=（舍），∴t=．（3）不存在，理由：由运动知，BP=2t，AQ=t，∴AP=6﹣2t，假设线段BC上是存在一点G，使得四边形PQGB为平行四边形，∴PQ∥BG，PQ=BG，∴△APQ∽△ABC，∴，∴，∴t=，PQ=，∴BP=2t=3，∴PQ≠BP，∴平行四边形PQGB不可能是菱形．即：线段BC上不存在一点G，使得四边形PQGB为菱形．【点评】此题是相似形综合题，主要考查了勾股定理，线段的垂直平分线的性质，相似三角形的判定和性质，平行四边形的性质，菱形的判定，解本题的关键是用方程的思想解决问题．。

北师大版数学九年级上册期中考试试卷(含答案)

北师大版数学九年级上册期中考试试卷(含答案)北师大版数学九年级上册期中考试试卷一、选择题（本大题共12小题）1.下列方程是一元二次方程的是（）A、ax2+bx+c=0B、x2-y+1=0C、x2=0D、(1/2)x+1=22.如图，由∠1=∠2，BC=DC，AC=EC，得△ABC≌△EDC的根据是（）A、SASB、ASAC、AASD、SSS3.关于x的方程(3m+1)x+2mx-1=0的一个根是1，则m的值是（）A、2/3B、-2/3C、-3/2D、3/24．如图，平行四边形ABCD的周长为16cm，AC、BD 相交于点O，OE⊥AC交AD于E，求△DCE的周长。

A、4cmB、6cmC、8cmD、10cm5.根据下列表格的对应值，判断ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的取值范围是（）x。

ax2+bx+c3.23.-0.063.24.-0.023.25.0.033.26.0.09A、3＜x＜3.23B、3.23＜x＜3.24C、3.24＜x＜3.25D、3.25＜x＜3.266.设M表示直角三角形，N表示等腰三角形，P表示等边三角形，Q表示等腰直角三角形，则下列四个图中，能表示它们之间关系的是（）7．下列图形：线段、正三角形、平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形，其中既是中心对称图形，又是轴对称图形的共有（）A、3个B、4个C、5个D、6个8.某型号的手机连续两次降价，每个售价由原来的1185元降到了580元，设平均每次降价的百分率为x，列出方程正确的是（）A、580(1+x)2=1185B、1185(1+x)2=580C、580(1-x)2=1185D、1185(1-x)2=5809．如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（）A、30°B、36°C、45°D、70°10.如图，已知AC平分∠PAQ，点B，B′分别在边AP，AQ上，如果添加一个条件，即可推出AB=AB′，那么该条件不可以是（）A、BB′⊥ACB、BC=B′CC、∠ACB=∠ACB′D、∠ABC=∠AB′C11.若等腰梯形两底的差等于一腰的长，则最小的内角是（）12.如图，小亮拿一张矩形纸，沿虚线对折一次得到图（2），再将对角两顶点重合折叠得到图（3）。

新北师大版九年级数学上册期中考试题(完美版)

新北师大版九年级数学上册期中考试题（完美版）班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．2-的相反数是（）A ．2-B ．2C ．12D ．12- 2．若二次根式51x -有意义，则x 的取值范围是（）A ．x ＞15B ．x ≥15C ．x ≤15D ．x ≤53．在实数|﹣3|，﹣2，0，π中，最小的数是（）A ．|﹣3|B ．﹣2C ．0D ．π 4．已知整式252x x -的值为6，则整式2x 2-5x+6的值为（） A ．9 B ．12 C ．18 D ．245．《九章算术》是我国古代数学名著，卷七“盈不足”中有题译文如下：今有人合伙买羊，每人出5钱，会差45钱；每人出7钱，会差3钱．问合伙人数、羊价各是多少？设合伙人数为x 人，所列方程正确的是（）A ．54573x x -=-B ．54573x x +=+C ．45357x x ++=D ．45357x x --= 6．已知二次函数242y x x =-+，关于该函数在﹣1≤x ≤3的取值范围内，下列说法正确的是（）A ．有最大值﹣1，有最小值﹣2B ．有最大值0，有最小值﹣1C ．有最大值7，有最小值﹣1D ．有最大值7，有最小值﹣27．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（）A ．30°B ．25°C ．20°D ．15° 8．如图，A ，B 是反比例函数y=4x在第一象限内的图象上的两点，且A ，B 两点的横坐标分别是2和4，则△OAB 的面积是（）A ．4B ．3C ．2D ．19．如图，函数 y 1＝﹣2x 与 y 2＝ax +3 的图象相交于点 A （m ，2），则关于 x 的不等式﹣2x ＞ax +3 的解集是（）A ．x ＞2B ．x ＜2C ．x ＞﹣1D ．x ＜﹣110．下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）A ．B ．C ．D ．二、填空题（本大题共6小题，每小题3分，共18分）181____________．2．分解因式：2242a a ++=___________．3．若22(3)16x m x +-+是关于x 的完全平方式，则m =__________．4．如图，直线1y x =+与抛物线245y x x =-+交于A ，B 两点，点P 是y 轴上的一个动点，当PAB ∆的周长最小时，PAB S ∆=__________．5．如图，C 为半圆内一点，O 为圆心，直径AB 长为2 cm ，∠BOC=60°，∠BCO=90°，将△BOC 绕圆心O 逆时针旋转至△B ′OC ′，点C ′在OA 上，则边BC 扫过区域（图中阴影部分）的面积为_________cm 2．6．PM2.5是指大气中直径小于或等于0.0000025m 的颗粒物，将0.0000025用科学计数法表示为___________.三、解答题（本大题共6小题，共72分）1．解分式方程：2311x x x x +=--2．关于x 的一元二次方程2223()0m x mx m +++=-有两个不相等的实数根．（1）求m 的取值范围；（2）当m 取满足条件的最大整数时，求方程的根．3．如图①,已知抛物线y=ax 2+bx+c 的图像经过点A （0，3)、B （1，0），其对称轴为直线l ：x=2，过点A 作AC ∥x 轴交抛物线于点C ，∠AOB 的平分线交线段AC 于点E ，点P 是抛物线上的一个动点，设其横坐标为m.（1）求抛物线的解析式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当m为何值时，四边形AOPE面积最大，并求出其最大值；（3）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由.4．某蔬菜生产基地的气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜．如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度y （℃）与时间x（h）之间的函数关系，其中线段AB、BC表示恒温系统开启阶段，双曲线的一部分CD表示恒温系统关闭阶段．请根据图中信息解答下列问题：（1）求这天的温度y与时间x（0≤x≤24）的函数关系式；（2）求恒温系统设定的恒定温度；（3）若大棚内的温度低于10℃时，蔬菜会受到伤害．问这天内，恒温系统最多可以关闭多少小时，才能使蔬菜避免受到伤害？485的选修情况，学校采取随机抽样的方法进行问卷调查（每个被调查的学生必须选择而且只能选择其中一门）．对调查结果进行了整理，绘制成如下两幅不完整的统计图，请结合图中所给信息解答下列问题：（1）本次调查的学生共有人，在扇形统计图中，m的值是；（2）将条形统计图补充完整；（3）在被调查的学生中，选修书法的有2名女同学，其余为男同学，现要从中随机抽取2名同学代表学校参加某社区组织的书法活动，请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率．6．某商场准备购进A，B两种书包，每个A种书包比B种书包的进价少20元，用700元购进A种书包的个数是用450元购进B种书包个数的2倍，A种书包每个标价是90元，B种书包每个标价是130元．请解答下列问题：（1）A，B两种书包每个进价各是多少元？（2）若该商场购进B种书包的个数比A种书包的2倍还多5个，且A种书包不少于18个，购进A，B两种书包的总费用不超过5450元，则该商场有哪几种进货方案？（3）该商场按（2）中获利最大的方案购进书包，在销售前，拿出5个书包赠送给某希望小学，剩余的书包全部售出，其中两种书包共有4个样品，每种样品都打五折，商场仍获利1370元．请直接写出赠送的书包和样品中，A种，B 种书包各有几个？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、B3、B4、C5、B6、D7、B8、B9、D10、B二、填空题（本大题共6小题，每小题3分，共18分）1、32、22(1)a +3、7或-14、125．5、4π6、2.5×10-6三、解答题（本大题共6小题，共72分）1、x=32、（1）6m <且2m ≠；（2）12x =-，243x =- 3、（1）y=x 2-4x+3.（2）当m=52时，四边形AOPE 面积最大，最大值为758.（3）P 点的坐标为：P 1P 2352，），P 3），P 4.4、（1）y关于x的函数解析式为210(05)20(510)200(1024)x xy xxx⎧⎪+≤<⎪=≤<⎨⎪⎪≤≤⎩；（2）恒温系统设定恒温为20°C；（3）恒温系统最多关闭10小时，蔬菜才能避免受到伤害．5、（1）50、30%．（2）补图见解析；（3）35.6、（1）A，B两种书包每个进价各是70元和90元；（2）共有3种方案，详见解析；（3）赠送的书包中，A种书包有1个，B种书包有个，样品中A种书包有2个，B种书包有2个.。

北师大版九年级数学上册期中考试卷及答案【完美版】

北师大版九年级数学上册期中考试卷及答案【完美版】班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．4的平方根是（） A ．±2B ．2C ．﹣2D ．162．实数a 、b 在数轴上的位置如图所示，且|a|＞|b|，则化简2a a b -+的结果为（）A ．2a+bB ．-2a+bC ．bD ．2a-b3．已知关于x 的分式方程21m x -+=1的解是负数，则m 的取值范围是（） A ．m ≤3B ．m ≤3且m ≠2C ．m ＜3D ．m ＜3且m ≠24．关于x 的一元二次方程2(1)20x k x k ---+=有两个实数根12,x x ，()1212122(2)2x x x x x x -+--+3=-，则k 的值（）A ．0或2B ．-2或2C ．-2D ．25．下列各组数中，能作为一个三角形三边边长的是（） A ．1，1，2B ．1，2，4C ．2，3，4D ．2，3，56．如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（）A ．主视图改变，左视图改变B ．俯视图不变，左视图不变C ．俯视图改变，左视图改变D ．主视图改变，左视图不变7．下列四个图形中，线段BE 是△ABC 的高的是（）A ．B ．C ．D ．8．如图，AB 是⊙O 的直径，BC 与⊙O 相切于点B ，AC 交⊙O 于点D ，若∠ACB=50°，则∠BOD 等于（）A ．40°B ．50°C ．60°D ．80°9．甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y （米）与甲出发的时间t （分）之间的关系如图所示，下列结论：①甲步行的速度为60米/分； ②乙走完全程用了32分钟；③乙用16分钟追上甲；④乙到达终点时，甲离终点还有300米。

北师大版九年级(上)期中数学试卷(含解析)

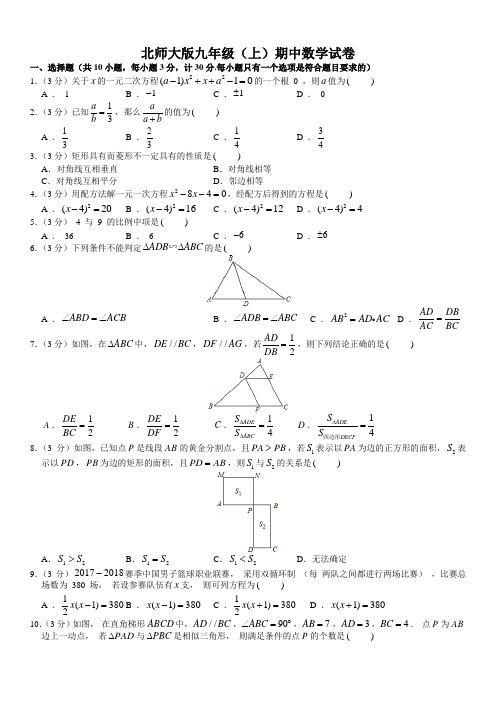
北师大版九年级（上）期中数学试卷一、选择题（共10小题，每小题3分，计30分.每小题只有一个选项是符合题目要求的） 1．（3分）关于x 的一元二次方程22(1)10a x x a -++-=的一个根 0 ，则a 值为( ) A ． 1 B ．1- C ．1± D ． 02．（3分）已知13a b =，那么aa b +的值为( ) A ．13 B ．23 C ．14D ．343．（3分）矩形具有而菱形不一定具有的性质是( )A ．对角线互相垂直B ．对角线相等C ．对角线互相平分D ．邻边相等 4．（3分）用配方法解一元一次方程2840x x --=，经配方后得到的方程是( ) A ．2(4)20x -= B ．2(4)16x -= C ．2(4)12x -=D ．2(4)4x -= 5．（3分） 4 与 9 的比例中项是( )A ． 36B ． 6C ．6-D ．6±6．（3分）下列条件不能判定ADB ABC ∆∆∽的是( )A ．ABD ACB ∠=∠B ．ADB ABC ∠=∠ C ．2AB AD AC = D ．AD DBAC BC= 7．（3分）如图，在ABC ∆中，//DE BC ，//DF AG ，若12AD DB =，则下列结论正确的是( )A ．12DE BC = B ．12DE DF = C ．14ADE ABC S S ∆∆= D ．14ADE DECF S S ∆=四边形 8．（3分）如图，已知点P 是线段AB 的黄金分割点，且PA PB >，若1S 表示以PA 为边的正方形的面积，2S 表示以PD ，PB 为边的矩形的面积，且PD AB =，则1S 与2S 的关系是( )A ．12S S >B ．12S S =C ．12S S <D ．无法确定9．（3分）20172018-赛季中国男子篮球职业联赛，采用双循环制（每两队之间都进行两场比赛），比赛总场数为 380 场，若设参赛队伍有x 支，则可列方程为( )A ．1(1)3802x x -= B ．(1)380x x -= C ．1(1)3802x x += D ．(1)380x x += 10．（3分）如图，在直角梯形ABCD 中，//AD BC ，90ABC ∠=︒，7AB =，3AD =，4BC =．点P 为AB 边上一动点，若PAD ∆与PBC ∆是相似三角形，则满足条件的点P 的个数是( )A ． 1 个B ． 2 个C ． 3 个D ． 4 个二、填空题（共4小题，每小题3分，计12分） 11．（3分）在 0 、 1 、 2 三个数字中，任取两个，组成两位数，则在组成的两位数中，是奇数的概率是． 12．（3分）如图，在正方形ABCD 外侧，作等边三角形ADE ，AC ，BE 相交于点F ，则BFC ∠为度．13．（3分）如图，已知ABC DEF ∆∆∽，且相似比为k ，则k 的值为．14．（3分）如图，在矩形ABCD 中，10AB =，5BC =，若点M 、N 分别是线段AC 、AB 上的两个动点，则BM MN +的最小值为．三、解答题（共11小题，计78分.解答应写出过程） 15．（9分）解方程：（1）24(1)36x +=；（2）2560y y --=；（3）22410m m --=． 16．（7分）如图，O 是菱形ABCD 对角线AC 与BD 的交点，5CD cm =，3OD cm =；过点C 作//CE DB ，过点B 作//BE AC ，CE 与BE 相交于点E ．（1）求OC 的长；（2）求四边形OBEC 的面积．17．（5分）如图，已知ABC ∆，在AB 边上找一点M ，在AC 边上找一点N ，使MB MN =，且AMN ABC ∆∆∽，请利用没有刻度的直尺和圆规，作出符合条件的线段MN （注：不写作法，保留作图痕迹，对图中涉及到的点用字母进行标注）．18．（5分）已知关于x 的一元二次方程220x x a -+=的两实数根1x ，2x 满足12120x x x x ++>，求a 的取值范围． 19．（6分）党的十八大提出，倡导富强、民主、文明、和谐，倡导自由、平等、公正、法治，倡导爱国、敬业、诚信、友善，积极培育和践行社会主义核心价值观，这 24 个字是社会主义核心价值观的基本内容．其中： “富强、民主、文明、和谐”是国家层面的价值目标； “自由、平等、公正、法治”是社会层面的价值取向；“爱国、敬业、诚信、友善”是公民个人层面的价值准则．小明同学将其中的“文明”、 “和谐”、 “自由“平等”的文字分别贴在 4 张硬纸板上，制成如图所示的卡片．将这 4 张卡片背面朝上洗匀后放在桌子上，从中随机抽取一张卡片，不放回，再随机抽取一张卡片．请你用列表法或画树状图法，帮助小明求出两次抽取卡片上的文字一次是国家层面价值目标、一次是社会层面价值取向的概率．（卡片名称可用字母表示）． 20．（6分）在图的方格纸中，OAB ∆的顶点坐标分别为(0,0)O 、(2,1)A --、(1,3)B --，△111O A B 与OAB ∆是以点P 为位似中心的位似图形（1）在图中标出位似中心P 的位置，并写出点P 及点B 的对应点1B 的坐标；（2）以原点O 为位似中心，画出OAB ∆的位似图形△22OA B ，使它与OAB ∆都在位似中心的同侧且它与OAB ∆的位似比为2:1，并写出点B 的对应点2B 的坐标；（3）OAB ∆内部一点M 的坐标为(,)a b ，写出M 在△22OA B 中的对应点2M 的坐标；（4）判断△22OA B 能否看作是由△111O A B 经过某种变换得到的图形．若能，请指出是怎样变换得到的（直接写答案）．21．（6分）如图，已知：AD DE AEAB BC AC==，求证：CAE BAD ∠=∠．22．（8分）在水果销售旺季，某水果店购进一优质水果，进价为 20 元/千克，售价不低于 20 元/千克，且不超过 32 元/千克，根据销售情况，发现该水果一天的销售量y （千克）与该天的售价x （元/千克）满销售量y （千克） ⋯34.8 32 29.6 28 ⋯ 售价x （元/千克） ⋯22.62425.226⋯（1） /（2）如果某天销售这种水果获利 150 元，那么该天水果的售价为多少元？ 23．（8分）李爱数同学发现操场中有一个不规则的封闭图形ABC 如图所示，为了知道它的面积，他在封闭图形内画出了一个半径为 1 米的圆，在不远处向圆内掷石子，结果记录如下：石子落在圆内（含圆上）的次数 14 43 93 150 石子落在阴影内的次数2391186300请根据以上信息，回答问题：（1）求石子落在圆内的频率；（2）估计封闭图形ABC 的面积．24．（8分）如图，在矩形ABCD 中，4AB =，3AD =，M 是边CD 上一点，将ADM ∆沿直线AM 对折，得到AMM ∆．（1）当AN 平分MAB ∠时，求DM 的长；（2）连接BN ，当1DM =时，求BN 的长．25．（10分）在四边形ABCD 中，对角线AC 、BD 相交于点O ，过点O 的两条直线分别交边AB 、CD 、AD 、BC 于点E 、F 、G 、H ．【感知】如图①，若四边形ABCD 是正方形，且AG BE CH DF ===，则AEOG S =四边形 ABCD S 正方形；【拓展】如图②，若四边形ABCD 是矩形，且14ABCD AEOG S S =矩形四边形，设AB a =，AD b =，BE m =，求AG 的长（用含a 、b 、m 的代数式表示）；【探究】如图③，若四边形ABCD 是平行四边形，且3AB =，5AD =，1BE =，试确定F 、G 、H 的位置，使直线EF 、GH 把四边形ABCD 的面积四等分．参考答案与试题解析一、选择题（共10小题，每小题3分，计30分.每小题只有一个选项是符合题目要求的）【解答】解：把0x =代入方程得：210a -=，解得：1a =±，22(1)10a x x a -++-=是关于x 的一元二次方程， 10a ∴-≠，即1a ≠，a ∴的值是1-．故选：B ．【解答】解：13a b =， ∴设a k =，3(0)b k k =≠，则134a k a b k k ==++．故选：C ．【解答】解：矩形具有的性质：对角线相等，对角线互相平分；菱形具有的性质：邻边相等，对角线互相平分，对角线互相垂直；∴矩形具有而菱形不一定具有的性质是：对角线相等．故选：B ．【解答】解：284x x -=，2816164x x ∴-+=+，即2(4)20x -=，故选：A ．【解答】解：设它们的比例中项是x ，则249x =⨯， 6x =±．故选：D ．【解答】解：A 、ABD ACB ∠=∠，A A ∠=∠，ABC ADB ∴∆∆∽，故此选项不合题意； B 、ADB ABC ∠=∠，A A ∠=∠，ABC ADB ∴∆∆∽，故此选项不合题意；C 、2AB AD AC =，∴AC ABAB AD=，A A ∠=∠，ABC ADB ∆∆∽，故此选项不合题意； D 、AD DBAC BC =不能判定ADB ABC ∆∆∽，故此选项符合题意．故选：D ．【解答】解：//DE BC ，//DF AG ， ADE ABC ∴∆∆∽，BDF BAC ∆∆∽． 12AD DB =， 11123DE BC ∴==+，22213BD BA ==+， 21()9ADE ABC S DE S BC ∆∆∴==，24()9BDF BAC S BD S BA ∆∆==， 19ADE ABC S S ∆∆∴=，49BDF ABC S S ∆∆=，49ABC DECF S S ∆∴=四边形，14ADE DECF S S ∆∴=四边形．故选：D ．【解答】解：P 是线段AB 的黄金分割点，且PA PB >，2PA PB AB ∴=，又1S 表示PA 为一边的正方形的面积，2S 表示长是AB ，宽是PB 的矩形的面积，21S PA ∴=，2S PB AB =， 12S S ∴=．故选：B ．【解答】解：设参赛队伍有x 支，则 (1)380x x -=．故选：B ．【解答】解：AB BC ⊥， 90B ∴∠=︒． //AD BC18090A B ∴∠=︒-∠=︒， 90PAD PBC ∴∠=∠=︒．设AP 的长为x ，则BP 长为7x -．若AB 边上存在P 点，使PAD ∆与PBC ∆相似，那么分两种情况： ①若APD BPC ∆∆∽，则::AP BP AD BC =，即:(7)3:4x x -=，解得：3x =②若APD BCP ∆∆∽，则::AP BC AD BP =，即:43:(7)x x =-，解得：4x =或 3 ．∴满足条件的点P 的个数是 2 个，故选：B ．二、填空题（共4小题，每小题3分，计12分）【解答】解：画树状图得：∴共有 6 种情况，是奇数的有 1 种情况，∴是奇数的概率是16．【解答】解：四边形ABCD 是正方形，AB AD ∴=，又ADE ∆是等边三角形，AE AD DE ∴==，60DAE ∠=︒， AB AE ∴=，ABE AEB ∴∠=∠，9060150BAE ∠=︒+︒=︒， (180150)215ABE ∴∠=︒-︒÷=︒，又45BAC ∠=︒，451560BFC ∴∠=︒+︒=︒．故答案为： 60 ．【解答】解：ABC DEF ∆∆∽，∴相似比等于：1()()()2AB AC BC a b c DE DF EF b a a c c b ++++==+++++++．12k ∴=．故答案为：12．【解答】解：过B 点作AC 的垂线，使AC 两边的线段相等，到E 点，过E 作EN AB ⊥于N 点，交AC 于M ，则BM MN +的最小值EN =， 10AB =，5BC =，2210555AC ∴=+=，AC ∴边上的高为10555⨯，所以45BE =，ABC ENB ∆∆∽，∴AB ACEN BE =， 8EN ∴=．故答案为：8．三、解答题（共11小题，计78分.解答应写出过程）【解答】解：（1）24(1)36x +=，2(1)9x ∴+=， 13x ∴+=±，则12x =，24x =-；（2）2560y y --=，(8)(7)0y y ∴-+=，则80y -=或70y +=，解得：18y =，27y =-；（3）2a =，4b =-，1c =-， ∴△1642(1)240=-⨯⨯-=>，则4262642m ±==．【解答】解：（1）ABCD 是菱形， AC BD ∴⊥，∴直角OCD ∆中，2222534()OC CD OD cm =-=-=；（2）//CE DB ，//BE AC ， ∴四边形OBEC 为平行四边形，又AC BD ⊥，即90COB ∠=︒， ∴平行四边形OBEC 为矩形， 0OB D =， ()24312OBEC S OB OC cm ∴=⋅=⨯=矩形．【解答】解：如图 2 所示，作B ∠的平分线BN ，交AC 于G ，作BN 的垂直平分线MG ，交AB 于M ，MN 即为所求．【解答】解：该一元二次方程有两个实数根，∴△2(2)41440a a =--⨯⨯=-，解得：1a ，由韦达定理可得12x x a =，122x x +=，12120x x x x ++>， 20a ∴+>，解得：2a >-， 21a ∴-<．【解答】解：画树状图为：共有 12 种等可能的结果数，其中两次抽取卡片上的文字一次是国家层面价值目标、一次是社会层面价值取向的结果数为 8 种，所以两次抽取卡片上的文字一次是国家层面价值目标、一次是社会层面价值取向的概率82123==．【解答】解：（1）点P 的位置如图所示，点(5,1)P --，点1(3,5)B -；（2）△22OA B 如图所示．点2B 的坐标(2,6)--；（3）OAB ∆内部一点M 的坐标为(,)a b ，写出M 在△22OA B 中的对应点2M 的坐标(2,2)a b ；（4）△22OA B 能看作是由△111O A B 经过平移变换得到的图形．△111O A B 向左平移 5 个单位，向下平移应该单位得到△22OA B ．【解答】证明：AD DE AEAB BC AC==， ABC ADE ∴∆∆∽， BAC DAE ∴∠=∠，BAD DAC DAC CAE ∴∠+∠=∠+∠， CAE BAD ∴∠=∠．【解答】解：（1）设y 与x 之间的函数关系式为y kx b =+，将(22.6,34.8)、(24,32)代入y kx b =+，22.634.82432k b k b +=⎧⎨+=⎩，解得：280k b =-⎧⎨=⎩， y ∴与x 之间的函数关系式为280y x =-+．当23.5x =时，28033y x =-+=．答：当天该水果的销售量为 33 千克．（2）根据题意得：(20)(280)150x x --+=，解得：135x =，225x =．2032x ， 25x ∴=．答：如果某天销售这种水果获利 150 元，那么该天水果的售价为 25 元．【解答】解：（1）观察表格得：随着投掷次数的增大，石子落在圆内的频率值稳定在13；（2）设封闭图形的面积为a ，根据题意得：13a π=，解得：3a π=，则封闭图形ABC 的面积为3π平方米．【解答】解：（1）由折叠性质得：ANM ADM ∆≅∆， MAN DAM ∴∠=∠，AN 平分MAB ∠，MAN NAB ∠=∠， DAM MAN NAB ∴∠=∠=∠，四边形ABCD 是矩形， 90DAB ∴∠=︒， 30DAM ∴∠=︒，3tan 3tan 30333DM AD DAM ∴=∠=⨯︒=⨯=；（2）如图，作NE AB ⊥于E ，延长EN 交CD 于F ．则NF CD ⊥．90MFN MNA AEN ∠=∠=∠=︒，90MNF ANE ∴∠+∠=︒，90ANE NAE ∠+∠=︒， FNM NAE ∴∠=∠， MNF NAE ∴∆∆∽， ∴MN MF FNAN NE AE ==，设MF x =，FN y =，则有1331x yy x ==-+，解得0.8x =，0.6y =，1.8AE ∴=，2.4NE =， 2.2BE AB AE =-=222226522245BN BE NE ∴=+=+=【解答】解：【感知】如图①，四边形ABCD 是正方形，45OAG OBE ∴∠=∠=︒，OA OB =，在AOG ∆与BOE ∆中，AG BE AOG BOE AO BO =⎧⎪∠=∠⎨⎪=⎩，AOG BOE ∴∆≅∆，14AOB ABCD AEOG S S S ∆∴==正方形四边形；故答案为：14；【拓展】如图②，过O 作ON AD ⊥于N ，OM AB ⊥于M ，14AOB ABCD S S ∆=矩形，14ABCD AEOG S S =矩形四边形，AOB AEOG S S ∆∴=四边形，AOB BOE AOE S S S ∆∆∆=+，AOG AOE AEOG S S S ∆∆=+四边形，BOE AOG S S ∆∆∴=，11112224BOE S BE OM m b mb ∆===，11112224AOG S AG ON AG a AG a ∆===，∴1144mb AG a =， mbAG a∴=；【探究】如图③，过O 作KL AB ⊥，PQ AD ⊥，则2KL OK =，2PQ OQ =，ABCD S AB KL AD PQ =⋅=⋅平行四边形， 3252OK OQ ∴⨯=⨯， ∴53OK OQ =， 14AOB ABCD S S ∆=平行四边形，14AEOG ABCD S S =四边形平行四边形，AOB AEOG S S ∆∴=四边形，BOE AOG S S ∆∆∴=，11122BOE S BE OK OK ∆==⨯⨯，12AOG S AG OQ ∆=，∴11122OK AG OQ ⨯⨯=，∴53OK AG OQ ==， ∴当53AG CH ==，1BE DF ==时，直线EF 、GH 把四边形ABCD 的面积四等分．。