椭圆知识点总结及经典习题.docx
椭圆知识点总结及练习
椭圆知识点总结及典型方法知识点一：椭圆的定义平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距.知识点二：椭圆的标准方程1．当焦点在x 轴上时，椭圆的标准方程：12222=+by a x )0(>>b a ，其中222b a c -=2．当焦点在y 轴上时，椭圆的标准方程：12222=+bx a y )0(>>b a ，其中222b a c -=；知识点三：椭圆的简单几何性质椭圆：12222=+by a x )0(>>b a 的简单几何性质（1）对称性：对于椭圆标准方程12222=+b y a x )0(>>b a ：说明：把x 换成x -、或把y 换成y -、或把x 、y 同时换成x -、y -、原方程都不变，（2）范围：椭圆上所有的点都位于直线a x ±=和b y ±=所围成的矩形内，所以椭圆上点的坐标满足a x≤，b y ≤。
（3）顶点：①椭圆的对称轴与椭圆的交点称为椭圆的顶点。
②椭圆12222=+by a x )0(>>b a 与坐标轴的四个交点即为椭圆的四个顶点，坐标分别为 )0,(1a A -，)0,(2a A ，),0(1b B -，),0(2b B③线段21A A ，21B B 分别叫做椭圆的长轴和短轴，a A A 221=,b B B 221=。
a 和b 分别叫做椭圆的长半轴长和短半轴长。
（4）离心率：①椭圆的焦距与长轴长度的比叫做椭圆的离心率，用e 表示，记ac a c e ==22。
知识点四：椭圆12222=+b y a x 与 12222=+bx a y )0(>>b a 的区别和联系知识点五: 椭圆的第二定义：平面内与一个定点（焦点）和一定直线（准线）的距离的比为常数e ，（0＜e ＜1）的点的轨迹为椭圆。
(完整版)椭圆知识点及经典例题汇总,推荐文档
（3）顶点：①椭圆的对称轴与椭圆的交点称为椭圆的顶点。
x2
②椭圆
y2
1 (a b 0) 与坐标轴的四个交点即为椭圆的四个顶点，坐标分别为
a2 b2
A1 (a,0) ， A2 (a,0) ， B1 (0,b) ， B2 (0,b)
③线段 A1 A2 ， B1B2 分别叫做椭圆的长轴和短轴， A1 A2 2a , B1B2 2b 。 a 和 b 分
( BF1 BF2 a) ； ( OF1 OF2 c) ； A1B A2 B a 2 b2 ；
（3） A1F1 A2 F2 a c ； A1F2 A2 F1 a c ； a c PF1 a c ；
知识点四：椭圆第二定义
一动点到定点的距离和它到一条定直线的距离的比是一个 (0,1) 内常数 e ，那么这个点的轨
若 ( PF1 PF2 F1F2 ) ，则动点 P 的轨迹无图形.
知识点二：椭圆的标准方程
1．当焦点在 x 轴上时，椭圆的标准方程： x 2 y 2 1 (a b 0) ，其中 c 2 a 2 b2 a2 b2
2．当焦点在 y 轴上时，椭圆的标准方程： y 2 x 2 1 (a b 0) ，其中 c 2 a 2 b2 ； a2 b2
3.椭圆的参数方程
x
y
a b
cos sin
(为参数)
注意：1．只有当椭圆的中心为坐标原点，对称轴为坐标轴建立直角坐标系时，才能得到椭圆
的标准ቤተ መጻሕፍቲ ባይዱ程；
2．在椭圆的两种标准方程中，都有 (a b 0) 和 c 2 a 2 b2 ；
3．椭圆的焦点总在长轴上.
当焦点在 x 轴上时，椭圆的焦点坐标为 (c,0) ， (c,0) ；
椭圆知识点归纳总结和经典例题
椭圆的基本知识1 •椭圆的定义：把平面内与两个定点 F 「F 2的距离之和等于常数(大于 F ,F 2)的点的轨迹叫做椭圆•这两个定点叫做椭圆的焦点，两焦点的距离叫做焦距 (设为2c ).2.椭圆的标准方程：焦点在坐标轴上的椭圆标准方程有两种情形，为了计算简便，可设方程为 虑焦点位置，求出方程 3.求轨迹方程的方法：定义法、待定系数法、相关点法、直接法例1如图，已知一个圆的圆心为坐 标原点,半径为2.从这个圆上任意一点P 向x 轴作垂线的解:段PP ,求线段PP 中点M 的轨迹•关点法)设点Mx , y ), 点Rx o , y o ), 贝 y x =x o , y = 匹 得 x o =x , y o = 2y.2x o 2+ y o 2= 4,得 x 2+ (2 y ) 2= 4,即- y 21.所以点M 的轨迹是一个椭圆42 2 2 24.范围.x < a , y < b ,••• | x| < a , | y| < b . 椭圆位于直线x =± a 和y =± b 围成的矩形里.5.椭圆的对称性 椭圆是关于y 轴、x 轴、原点都是对称的.坐标轴是椭圆的对称轴. 原点是椭圆的对称中心.椭圆的对称中心叫做椭圆的中心.6.顶点 只须令x = 0,得y =± b ,点Bi(0, — b )、R(0, b )是椭圆和y 轴的两个交点；令 y = 0,得x =± a ,点A ( —a ,0)、A(a ,0)是椭圆和x 轴的两个交点.椭圆有四个顶点：A ( — a , 0)、A(a , 0)、B(0, — b )、B(0, b ).椭圆和它的对称轴的四个交点叫椭圆的顶点. 线段AA 、BB 分别叫做椭圆的长轴和短轴 . 长轴的长等于2a .短轴的长等于2b . a 叫做椭圆的 长半轴长.b 叫做椭圆的短半轴长.y| BH | = |BF 2| = | BH| = | BF 2| = a .在 Rt △ OBF 2中，|OF |2= | BaF 2| 2 — | 0团 2, AZ b即 c 2 = a 2 — b 2.x7.椭圆的几何性质:mx2+ny2=1(m>0 n>0)不必考2 2a b2 2a b椭圆的几何性质可分为两类：一类是与坐标系有关的性质，如顶点、焦点、中心坐标；一类是与坐和召Hi¥厂1,J /1 .PjAJ4j对 关T r 轴・，、轴・燮标原点荊称荒于J 鞋*孑轴・坐肺腺点时称(K 点Ai ( —Un 0 ) a HI O) fihCOi —At tO-B — a J » A* a }(CXr-CI) a几点说明:(1)长轴：线段 AA ，长为2a ；短轴：线段B 1B 2，长为2b ；焦点在长轴上。
椭圆基本知识点与题型总结
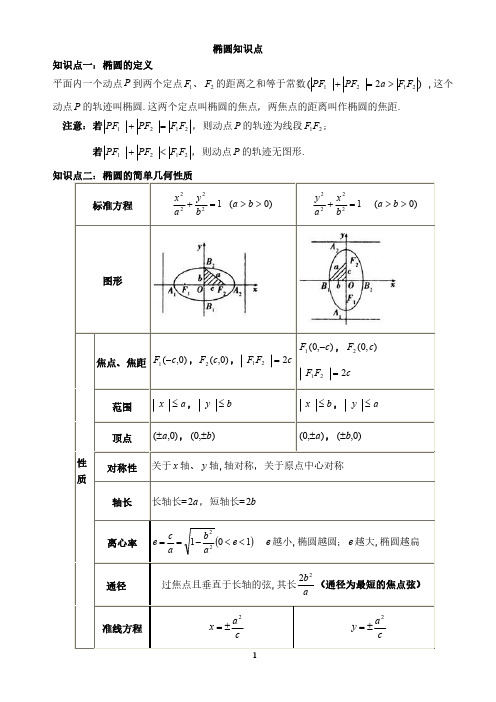
椭圆知识点知识点一：椭圆的定义平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距.注意：若2121F F PF PF =+，则动点P 的轨迹为线段21F F ；若2121F F PF PF <+，则动点P 的轨迹无图形.知识点二：椭圆的简单几何性质标准方程12222=+by a x )0(>>b a 12222=+bx a y )0(>>b a 图形性质焦点、焦距)0,(1c F -，)0,(2c F ，cF F 221=),0(1c F -，),0(2c F cF F 221=范围a x ≤，b y ≤b x ≤，ay ≤顶点)0,(a ±，),0(b ±),0(a ±，)0,(b ±对称性关于x 轴、y 轴,轴对称，关于原点中心对称轴长长轴长=a 2，短轴长=b2离心率()10122<<-==e ab ac e e 越小,椭圆越圆；e 越大,椭圆越扁通径过焦点且垂直于长轴的弦,其长ab 22（通径为最短的焦点弦）准线方程ca x 2±=ca y 2±=焦半径01ex a PF +=,02ex a PF -=01ey a PF +=，02ey a PF -=1.椭圆标准方程中的三个量c b a ,,的几何意义222c b a +=（见右图）2.椭圆的一般方程：22Ax By C +=()B A C B A 0ABC ≠≠同号，，，，且3.椭圆的参数方程：{cos sin x a y b ϕϕ==（其中ϕ为参数）4.椭圆焦点三角形问题（1）焦点三角形周长：ca 22+（2）在21F PF ∆中，有余弦定理：()θcos 2P P 22122212PF PF F F c -+=经常变形为：()()θcos 22-PF 221212212PF PF PF PF PF c -+=即：()()θcos 22-22212122PF PF PF PF a c -=（3）焦点三角形面积2tan cos 1sin sin 21S 2221P 21θθθθb b PF PF y c p F F =+=⋅=⋅=∆，其中21PF F ∠=θ5.最大角:p 是椭圆上一点，当p 是椭圆的短轴端点时，21PF F ∠为最大角。
椭圆知识点总结及经典习题
圆锥曲线与方程-－椭圆知识点一．椭圆及其标准方程1.椭圆的定义：平面内与两定点Ｆ1,Ｆ2距离的和等于常数()212F F a >的点的轨迹叫做椭圆，即点集M={P| |PF 1|+|PF 2|=2a,2a ＞|F 1F 2｜=2c};这里两个定点F 1，F 2叫椭圆的焦点，两焦点间的距离叫椭圆的焦距2c 。
(212F F a =时为线段21F F ,212F F a <无轨迹）。
2．标准方程: 222ca b =-①焦点在x 轴上：12222=+by a x （ａ＞ｂ＞0）; 焦点F(±ｃ，０）②焦点在y 轴上：12222=+bx a y （a ＞b ＞０）;焦点F(０, ±ｃ）注意：①在两种标准方程中,总有a>ｂ＞０，并且椭圆的焦点总在长轴上;②两种标准方程可用一般形式表示:221x y m n+= 或者 mx 2+ny 2=1 二．椭圆的简单几何性质： 1.范围(１)椭圆12222=+by a x （ａ＞ｂ>0） 横坐标-a ≤x ≤a ，纵坐标-b ≤ｘ≤b(2)椭圆12222=+bx a y (a>b ＞0） 横坐标-b ≤x ≤b,纵坐标-a ≤x ≤a２．对称性椭圆关于x 轴y 轴都是对称的，这里,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心叫做椭圆的中心 ３.顶点（1）椭圆的顶点：A 1(-a,0)，A 2(ａ，0),B １（０,-b)，B 2（0，b ）(2）线段A 1A ２，B １B ２ 分别叫做椭圆的长轴长等于2a,短轴长等于2b ，ａ和b 分别叫做椭圆的长半轴长和短半轴长。
4．离心率(1）我们把椭圆的焦距与长轴长的比22ca,即a c 称为椭圆的离心率，ﻫ记作e （10<<e )，22221()be a a==-ce 0=是圆；e 越接近于0 （ｅ越小)，椭圆就越接近于圆;e 越接近于１ （e 越大）,椭圆越扁;注意：离心率的大小只与椭圆本身的形状有关，与其所处的位置无关。
九年级下册《椭圆》知识点总结
九年级下册《椭圆》知识点总结
1.椭圆的定义
椭圆是平面上到两个固定点的距离之和等于常数的点的轨迹。
2.椭圆的性质
长轴和短轴：椭圆的两个轴分别为长轴和短轴，长轴的长度大于短轴的长度。
焦点和准线：椭圆的两个焦点是确定椭圆形状的关键点，准线是与焦点垂直且通过椭圆中心的直线。
离心率：椭圆的离心率表示椭圆形状的圆心偏离焦点的程度。
3.椭圆的方程
椭圆的标准方程：(x - h)^2 / a^2 + (y - k)^2 / b^2 = 1，其中 (h。
k) 是椭圆中心的坐标，a 和 b 分别是长轴和短轴的半径长度。
4.椭圆的图像特点
椭圆的图像是一个闭合的曲线，呈现出拉伸的圆形。
焦点在椭圆的长轴上，并且与准线对称。
椭圆的离心率小于1，且离心率越小，椭圆形状越接近圆形。
5.椭圆的应用
椭圆曲线加密：椭圆曲线加密算法是一种公钥加密算法，广泛应用于信息安全领域。
太阳能聚焦器：通过椭圆形状的反射面将太阳光聚焦在一个点上，实现能量的集中利用。
以上是九年级下册《椭圆》的知识点总结。
椭圆是数学中重要的几何图形，在应用中有广泛的用途和意义。
(完整)高中数学椭圆知识点与例题,推荐文档
2知识点一：椭圆的定义第一定义：平面内一个动点 P 到两个定点F i 、F 2的距离之和为定值焦点的距离叫作椭圆的焦距知识点二：椭圆的标准方程椭圆的焦点总在长轴上题型一、椭圆的定义 1、方程.x 22 y 2x 2 2 y 2 10化简的结果是2、若 ABC 的两个顶点 A 4,0 ,B 4,0 , ABC 的周长为18，则顶点C 的轨迹方程是2 2椭圆(PF i2aF 1F 2）,这个动点P 的轨迹叫椭圆•这两个定点叫椭圆的焦点，两注意：若（PRPF 2F i F 2 ），则动点 P 的轨迹为线段F i F 2 ；若(PF iF 1F 2），则动点P 的轨迹不存在.1 .当焦点在x2X~2a 2厂(a b 0),其中 c 2a 2b 22.当焦点在y 轴上时，椭圆的标准方程:2 ya2X d 21(a b 0),b 2其中a 2b 2.注意： 只有当椭圆的中心为坐标原点，对称轴为坐标轴建立直角坐标系时,才能得到椭圆的标准方程;在椭圆的两种标准方程中，都有（b 0)和c 2a 2b 2 ；当焦点在X 轴上时，椭圆的焦点坐标为(c,0) , ( c,0)； 当焦点在y 轴上时，椭圆的焦点坐标为 (0,c) , (0, c)3、椭圆—L 1上的点M到焦点F1的距离为2, N为MF_!的中点，贝y ON （O为坐25 9标原点）的值为（）A. 4B. 2C. 83 D.—X y24、椭圆———1两焦点为Fp F2, A 3,1 ,点P在椭圆上，贝U PR PA的最大值25 16为____ ，最小值为____题型二、椭圆的标准方程5、方程Ax2+By2=C表示椭圆的条件是(A) A, B同号且A M B ( B) A, B同号且C与异号(C) A, B, C同号且A M B ( D)不可能表示椭圆2 26、若方程—- 1 ,5 k k 3(1)表示圆，则实数k的取值是_____________ . __________(2) ______________________________________________________ 表示焦点在x轴上的椭圆，则实数k的取值范围是 _______________________________________ . __________(3) ______________________________________________________ 表示焦点在y型上的椭圆，则实数k的取值范围是 _______________________________________ . __________(4)表示椭圆，则实数k的取值范围是______________ . _________227、椭圆—y_1的焦距为2，贝U m =4m8、已知椭圆 2 mx3y2 6m0的一个焦点为(0, 2)求m的值9、已知椭圆的中心在原点，且经过点P 3,0 , a 3b，求椭圆的标准方程.2 210、求与椭圆4x 9y 36共焦点，且过点(3, 2)的椭圆方程。
(完整版)椭圆知识点总结
椭圆知识点知识要点小结：知识点一：椭圆的定义平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距. 注意：若)(2121F F PF PF =+，则动点P 的轨迹为线段21F F ； 若)(2121F F PF PF <+，则动点P 的轨迹无图形.知识点二：椭圆的标准方程1．当焦点在x 轴上时，椭圆的标准方程：12222=+by a x )0(>>b a ，其中222b a c -=2．当焦点在y 轴上时，椭圆的标准方程：12222=+bx a y )0(>>b a ，其中222b a c -=；注意：1．只有当椭圆的中心为坐标原点，对称轴为坐标轴建立直角坐标系时， 才能得到椭圆的标准方程； 2．在椭圆的两种标准方程中，都有)0(>>b a 和222b ac -=； 3．椭圆的焦点总在长轴上.当焦点在x 轴上时，椭圆的焦点坐标为)0,(c ，)0,(c -； 当焦点在y 轴上时，椭圆的焦点坐标为),0(c ，),0(c - 知识点三：椭圆的简单几何性质椭圆：12222=+by a x )0(>>b a 的简单几何性质（1）对称性：对于椭圆标准方程12222=+b y a x )0(>>b a ：说明：把x 换成x -、或把y 换成y -、或把x 、y 同时换成x -、y -、原方程都不变，所以椭圆12222=+by a x 是以x 轴、y 轴为对称轴的轴对称图形，并且是以原点为对称中心的中心对称图形，这个对称中心称为椭圆的中心。
（2）范围：椭圆上所有的点都位于直线a x ±=和b y ±=所围成的矩形内，所以椭圆上点的坐标满足a x ≤，b y ≤。
（3）顶点：①椭圆的对称轴与椭圆的交点称为椭圆的顶点。
椭圆知识点总结附例题
圆锥曲线与方程 椭 圆知识点一．椭圆及其标准方程1．椭圆的定义：平面内与两定点F 1，F 2距离的和等于常数()212F F a >的点的轨迹叫做椭圆，即点集M={P| |PF 1|+|PF 2|=2a ，2a ＞|F 1F 2|=2c}；这里两个定点F 1，F 2叫椭圆的焦点，两焦点间的距离叫椭圆的焦距2c 。
（212F F a =时为线段21F F ，212F F a <无轨迹）。
2．标准方程：222c a b =- ①焦点在x 轴上：12222=+by a x （a ＞b ＞0）； 焦点F （±c ，0）②焦点在y 轴上：12222=+bx a y （a ＞b ＞0）； 焦点F （0, ±c ）注意：①在两种标准方程中，总有a ＞b ＞0，并且椭圆的焦点总在长轴上；②两种标准方程可用一般形式表示：221x y m n+= 或者 mx 2+ny 2=1 二．椭圆的简单几何性质： 1.范围（1）椭圆12222=+by a x （a ＞b ＞0） 横坐标-a ≤x ≤a ,纵坐标-b ≤x ≤b（2）椭圆12222=+bx a y （a ＞b ＞0） 横坐标-b ≤x ≤b,纵坐标-a ≤x ≤a2.对称性椭圆关于x 轴y 轴都是对称的，这里，坐标轴是椭圆的对称轴，原点是椭圆的对称中心，椭圆的对称中心叫做椭圆的中心 3.顶点（1）椭圆的顶点：A 1（-a ，0），A 2（a ，0），B 1（0，-b ），B 2（0，b ）（2）线段A 1A 2，B 1B 2 分别叫做椭圆的长轴长等于2a ，短轴长等于2b ，a 和b 分别叫做椭圆的长半轴长和短半轴长。
4．离心率（1）我们把椭圆的焦距与长轴长的比22c a ，即ac称为椭圆的离心率， 记作e （10<<e ），22221()b e a a==-c e 0=是圆；e 越接近于0 （e 越小），椭圆就越接近于圆; e 越接近于1 （e 越大），椭圆越扁；注意：离心率的大小只与椭圆本身的形状有关，与其所处的位置无关。
椭圆 知识点+例题+练习
教学内容椭圆教学目标掌握椭圆的定义，几何图形、标准方程及其简单几何性质．重点椭圆的定义，几何图形、标准方程及其简单几何性质难点椭圆的定义，几何图形、标准方程及其简单几何性质教学准备教学过程椭圆知识梳理1．椭圆的定义(1)第一定义：平面内与两个定点F1，F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两个焦点的距离叫做焦距．(2)第二定义：平面内与一个定点F和一条定直线l的距离的比是常数e(0<e<1)的动点的轨迹是椭圆，定点F叫做椭圆的焦点，定直线l叫做焦点F相应的准线，根据椭圆的对称性，椭圆有两个焦点和两条准线．2．椭圆的标准方程和几何性质标准方程x2a2＋y2b2＝1(a>b>0)y2a2＋x2b2＝1(a>b>0)图形性质范围－a≤x≤a－b≤y≤b－b≤x≤b－a≤y≤a对称性对称轴：坐标轴；对称中心：原点顶点A1(－a,0)，A2(a,0)B1(0，－b)，B2(0，b)A1(0，－a)，A2(0，a)B1(－b,0)，B2(b,0)轴长轴A1A2的长为2a；短轴B1B2的长为2b教学效果分析教学过程考点二椭圆的几何性质【例2】已知F1、F2是椭圆的两个焦点，P为椭圆上一点，∠F1PF2＝60°.(1)求椭圆离心率的范围；(2)求证：△F1PF2的面积只与椭圆的短轴长有关．规律方法(1)椭圆上一点与两焦点构成的三角形，称为椭圆的焦点三角形，与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、|PF1|＋|PF2|＝2a，得到a，c的关系．(2)椭圆的离心率是椭圆最重要的几何性质，求椭圆的离心率(或离心率的取值范围)，常见有两种方法：①求出a，c，代入公式e＝ca；②只需要根据一个条件得到关于a，b，c的齐次式，结合b2＝a2－c2转化为a，c的齐次式，然后等式(不等式)两边分别除以a或a2转化为关于e的方程(不等式)，解方程(不等式)即可得e(e的取值范围)．【训练2】(1)(2013·四川卷改编)从椭圆x2a2＋y2b2＝1(a>b>0)上一点P向x轴作垂线，垂足恰为左焦点F1，A是椭圆与x轴正半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP(O是坐标原点)，则该椭圆的离心率是________．(2)(2012·安徽卷)如图，F1，F2分别是椭圆C：x2a2＋y2b2＝1(a>b>0)的左、右焦点，A教学效果分析教学过程设条件建立有关参变量的等量关系．(2)涉及到直线方程的设法时，务必考虑全面，不要忽略直线斜率为0或不存在等特殊情形．【训练3】(2014·山东省实验中学诊断)设F1，F2分别是椭圆：x2a2＋y2b2＝1(a＞b＞0)的左、右焦点，过F1倾斜角为45°的直线l与该椭圆相交于P，Q两点，且|PQ|＝43a.(1)求该椭圆的离心率；(2)设点M(0，－1)满足|MP|＝|MQ|，求该椭圆的方程．1．椭圆的定义揭示了椭圆的本质属性，正确理解掌握定义是关键，教学效果分析|BF |＝8，cos ∠ABF ＝45，则C 的离心率为________．6．(2014·无锡模拟)设椭圆x 2m 2＋y 2n 2＝1(m >0，n >0)的右焦点与抛物线y 2＝8x 的焦点相同，离心率为12，则此椭圆的方程为________． 7．已知F 1，F 2是椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的两个焦点，P 为椭圆C 上的一点，且PF 1→⊥PF 2→.若△PF 1F 2的面积为9，则b ＝________. 8．(2013·福建卷)椭圆Γ：x 2a 2＋y 2b 2＝1(a >b >0)的左，右焦点分别为F 1，F 2，焦距为2c .若直线y ＝3(x ＋c )与椭圆Γ的一个交点M 满足∠MF 1F 2＝2∠MF 2F 1，则该椭圆的离心率等于________．二、解答题9．已知椭圆的两焦点为F 1(－1,0)，F 2(1,0)，P 为椭圆上一点，且2|F 1F 2|＝|PF 1|＋|PF 2|. (1)求此椭圆的方程；(2)若点P 在第二象限，∠F 2F 1P ＝120°，求△PF 1F 2的面积．10．(2014·绍兴模拟)如图，椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1(－c,0)，F 2(c,0)．已知点M ⎝ ⎛⎭⎪⎫3，22在椭圆上，且点M 到两焦点距离之和为4. (1)求椭圆的方程；。
椭圆知识点总结加例题
椭圆知识点总结加例题一、椭圆的定义和性质1.1 椭圆的定义在平面上，椭圆的定义为：对于给定的两个不重合的实点F1和F2，以及一个实数2a （a>0），定义为到点F1和点F2的距离的和等于2a的点的轨迹，这个轨迹就是椭圆。
1.2 椭圆的几何性质（1）焦点性质：椭圆上到焦点的距离之和是一个常数2a。
（2）长短轴性质：椭圆有两个互相垂直的对称轴，其中较长的轴称为长轴，较短的轴称为短轴。
（3）离心率性质：椭圆的离心率e定义为焦距与长轴的比值，介于0和1之间。
（4）焦点到顶点的连线和短轴的交点为端点的线段称为短轴的焦径。
（5）焦点到顶点的连线和长轴的交点为端点的线段称为长轴的焦径。
1.3 椭圆的方程和标准方程椭圆的一般方程为：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, 其中a、b分别为椭圆长轴和短轴的半轴长。
通过坐标平移和旋转，可以得到椭圆的标准方程：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, 椭圆长轴在x轴上，且椭圆的中心为原点。
1.4 椭圆的参数方程和极坐标方程椭圆的参数方程：$\begin{cases}x=a\cos \theta\\ y=b\sin \theta\end{cases}$, $\theta \in [0, 2\pi)$。
椭圆的极坐标方程：$r(\theta)=\frac{ab}{\sqrt{b^2\cos^2\theta+a^2\sin^2\theta}}$。
二、椭圆的相关性质2.1 椭圆的离心率和焦距的关系设椭圆的长轴和短轴分别为2a和2b，焦点到几点段为2c，则椭圆的离心率e满足关系：$e=\frac{c}{a}$。
2.2 椭圆的面积和周长椭圆的面积：$S=\pi ab$。
椭圆的周长：$L=4aE(e)$，其中E(e)为第二类完全椭圆积分。
2.3 椭圆的切线和法线对于椭圆上任一点P(x，y)，其切线的斜率为$k=-\frac{b^2x}{a^2y}$，切线的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，且斜率为$k$的切线方程为$y-kx+ka^2=0$。
椭圆知识点总结附例题
圆锥曲线与方程 椭 圆知识点一．椭圆及其标准方程1．椭圆的定义：平面内与两定点F 1，F 2距离的和等于常数()212F F a >的点的轨迹叫做椭圆，即点集M={P| |PF 1|+|PF 2|=2a ，2a ＞|F 1F 2|=2c}；这里两个定点F 1，F 2叫椭圆的焦点，两焦点间的距离叫椭圆的焦距2c 。
（212F F a =时为线段21F F ，212F F a <无轨迹）。
2．标准方程：222c a b =-①焦点在x 轴上：12222=+by a x （a ＞b ＞0）； 焦点F （±c ，0）②焦点在y 轴上：12222=+bx a y （a ＞b ＞0）； 焦点F （0, ±c ）注意：①在两种标准方程中，总有a ＞b ＞0，并且椭圆的焦点总在长轴上；②两种标准方程可用一般形式表示：221x y m n+= 或者 mx 2+ny 2=1 二．椭圆的简单几何性质： 1.范围（1）椭圆12222=+by a x （a ＞b ＞0） 横坐标-a ≤x ≤a ,纵坐标-b ≤x ≤b（2）椭圆12222=+bx a y （a ＞b ＞0） 横坐标-b ≤x ≤b,纵坐标-a ≤x ≤a2.对称性椭圆关于x 轴y 轴都是对称的，这里，坐标轴是椭圆的对称轴，原点是椭圆的对称中心，椭圆的对称中心叫做椭圆的中心 3.顶点（1）椭圆的顶点：A 1（-a ，0），A 2（a ，0），B 1（0，-b ），B 2（0，b ）（2）线段A 1A 2，B 1B 2 分别叫做椭圆的长轴长等于2a ，短轴长等于2b ，a 和b 分别叫做椭圆的长半轴长和短半轴长。
4．离心率（1）我们把椭圆的焦距与长轴长的比22c a ，即ac称为椭圆的离心率， 记作e （10<<e ），22221()b e a a==-c e 0=是圆；e 越接近于0 （e 越小），椭圆就越接近于圆; e 越接近于1 （e 越大），椭圆越扁；注意：离心率的大小只与椭圆本身的形状有关，与其所处的位置无关。
(完整版)椭圆知识点总结,推荐文档
椭圆知识点知识点一：椭圆的定义平面内一个动点 P 到两个定点 F 1、 F 2 的距离之和等于常数( PF 1 + PF 2 = 2a > F 1 F 2 ) ,这个动点 P 的轨迹叫椭圆.这两个定点叫椭圆的焦点，两焦点的距离叫作椭圆的焦距. 注意：若 PF 1 + PF 2 = F 1 F 2 ，则动点 P 的轨迹为线段 F 1F 2 ；若 PF 1 + PF 2 < F 1F 2 ，则动点 P 的轨迹无图形.知识点二：椭圆的简单几何性质x 2 + y 2y 2 x 2椭圆： a 2 b 2 = 1 (a > b > 0) 与a 2 +b 2= 1 (a > b > 0) 的简单几何性质F 1F 2 = 2c F 1F 2 = 2c x ≤ a ， y ≤ bx ≤ b ， y ≤ aA 1 F 1 = A 2 F 2= a - c ； A 1 F 2 = A 2 F 1 = a + c ； a - c ≤ PF 1 ≤ a + c ；e = c(0 < e < 1)a离心率长轴长= 2a ，短轴长= 2b 长半轴长= a ，短半轴长= b （注意看清题目）轴长(0,±a ) ， (±b ,0)(±a ,0) ， (0,±b ) 顶点关于 x 轴、 y 轴和原点对称对称性 范围 焦距 F 1 (0,-c ) ， F 2 (0, c ) F 1 (-c ,0) ， F 2 (c ,0) 焦点性质图形(a > b > 0) 1 2 2+ = y x a 2 b2 1 (a > b > 0) x 2 + y 2 =a 2b 2标准方程注意：①与坐标系无关的椭圆本身固有的性质，如：长轴长、短轴长、焦距、离心率等；②与坐标系有关的性质，如：顶点坐标、焦点坐标等知识点三：椭圆相关计算1.椭圆标准方程中的三个量a, b, c 的几何意义a 2=b2+c 22. 通径:过焦点且垂直于长轴的弦,其长2b 2a焦点弦：椭圆过焦点的弦。
(完整word版)椭圆总结(全),推荐文档
椭圆一．知识清单1.椭圆的两种定义：①平面内与两定点F1，F2的距离的和等于定长2a 2a F1 F2的动点P 的轨迹，即点集M={P||PF|+|PF |=2a ， 2a＞ |F F |} ；（2a F1 F2时为线段 F1F2，2a F1F2无轨迹）。
此中两定1212点 F1， F2叫焦点，定点间的距离叫焦距。
②平面内一动点到一个定点和必定直线的距离的比是小于 1 的正常数的点的轨迹，即点集M={P|PF e， 0＜ e＜ 1 的常数。
（ e1为抛物线； e1为双曲线）d（利用第二定义 , 能够实现椭圆上的动点到焦点的距离与到相应准线的距离相互转变，定点为焦点，定直线为准线） .2 标准方程：（ 1）焦点在 x 轴上，中心在原点：x2y 21 （a＞b＞0）；a2 b 2焦点 F （－ c， 0）， F（ c，0）。
此中c a2b2（一个 Rt 三角形）12（ 2）焦点在 y 轴上，中心在原点：y 2x 21（a＞b＞0）；a2b2焦点 F1（ 0，－ c）， F2（ 0， c）。
此中c a 2 b 2注意：①在两种标准方程中，总有a＞ b＞ 0，c a 2b2而且椭圆的焦点总在长轴上；②两种标准方程可用一般形式表示：Ax2+By2=1 （A＞ 0，B＞ 0，A≠ B），当 A＜ B 时，椭圆的焦点在 x 轴上， A＞ B 时焦点在 y 轴上。
3 参数方程：焦点在 x 轴，x a cos（为参数）y b sin4 一般方程：Ax2By 21( A0,B 0)5. 性质：对于焦点在 x 轴上，中心在原点：x2y21（ a＞ b＞ 0）有以下性质：a2b2坐标系下的性质：①范围： |x|≤a， |y|≤b；② 对称性：对称轴方程为x=0， y=0，对称中心为O（0， 0）；③极点：A1（-a，0），A2（a，0），B1（0，-b），B2（0，b），长轴|A1A2|=2a，短轴|B1B2|=2b；（ a 半长轴长，b半短轴长）；④ 椭圆的准线方程：对于 x2y 21，左准线 l 1 : x a 2；右准线 l 2 : x a2a 2b 2c c对于 y 2x 21，下准线 l1 : y a 2；上准线 l 2 : y a 2a 2b 2c c焦点到准线的距离 pa 2 a 2 c 2b 2 cc（焦参数）cc椭圆的准线方程有两条，这两条准线在椭圆外面，与短轴平行，且对于短轴对称⑤ 焦半径公式： P （ x 0，y 0）为椭圆上任一点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆锥曲线与方程--椭圆知识点一•椭圆及其标准方程1椭圆的定义：平面内与两定点Fι, F2距离的和等于常数2a ■ F1F21J的点的轨迹叫做椭圆，即点集M={P∣∣PF ι∣+∣PF 2∣=2a，2a>∣F1F2∣=2c};这里两个定点F i, F2叫椭圆的焦点，两焦点间的距离叫椭圆的焦距2c。
(2a = F1F2时为线段F i F2, 2a C RF?无轨迹)。
2 2 22•标准方程：c= a- b2 2χ+y _ 1①焦点在X轴上：盲TT = 1( a> b> 0);焦点F(± C, 0)a b2 2y X②焦点在y轴上：—2 = 1(a>b>0)；焦点F (0, ±C)a b注意：①在两种标准方程中，总有a> b> 0,并且椭圆的焦点总在长轴上；2 2②两种标准方程可用一般形式表示：X y =1或者mχ2+ny2=1m n二•椭圆的简单几何性质：1. 范围2 2(1)椭圆X- y- =1 (a> b> 0)横坐标-a ≤x≤a ,纵坐标-b ≤X≤ba2b22 2(2)椭圆-y2x2 =1 (a>b>0) 横坐标-b ≤X≤b,纵坐标-a ≤x≤aa2b22. 对称性椭圆关于X轴y轴都是对称的，这里，坐标轴是椭圆的对称轴，原点是椭圆的对称中心，椭圆的对称中心叫做椭圆的中心3. 顶点(1)椭圆的顶点：A (-a , 0), A (a, 0), B (0, -b), B- (0, b)(2)线段AA, BB分别叫做椭圆的长轴长等于2a,短轴长等于2b, a和b分别叫做椭圆的长半轴长和短半轴长。
4 .离心率(1) 我们把椭圆的焦距与长轴长的比 2c ,即E 称为椭圆的离心率,2a ae = O 是圆；e 越接近于O (e 越小)，椭圆就越接近于圆 e 越接近于1( e 越大)，椭圆越扁；注意：离心率的大小只与椭圆本身的形状有关，与其所处的位置无关 小结一：基本元素 (1) 基本量：a 、b 、c 、e 、(共四个量)， 特征三角形 (2) 基本点：顶点、焦点、中心(共七个点) (3) 基本线：对称轴(共两条线) 5 •椭圆的的内外部2 2 x 2 y 2 亠—x o + yo W 1 (1) 点 P(X O , Y O )在椭圆-2 -每=1(a b - 0)的内部 J 2 U21a ba b2 2 x 2 y 2亠XO* y O 彳(2)点 P(x 0, y 0)在椭圆-2 =1(a b 0)的外部 2 TT 1.a ba b6. 几何性质(1) 点P 在椭圆上， 最大角∙ F 1PF 2max =∕F 1B 2F 2,(2) 最大距离，最小距离 7. 直线与椭圆的位置关系(1) 位置关系的判定：联立方程组求根的判别式； (2) 弦长公式： ________________________ (3) 中点弦问题：韦达定理法、点差法记作 e ( 0 < e < 1),例题讲解: 一.椭圆定义：1 •方程-2 2 y^ . X 2 2 y 2 =10化简的结果是 __________________________2•若. ABC 的两个顶点A -4,0 ,B 4,0 , ABC 的周长为18 ,则顶点C 的轨迹方程是 ____________2—=1上的一点P 到椭圆一个焦点的距离为9二•利用标准方程确定参数2 21. 若方程 厶 +丄=1 (1)表示圆，则实数k 的取值是5 _k k _3(2) _____________________________________________________ 表示焦点在X 轴上的椭圆，则实数 k 的取值范围是 ______________________________________ . ________ (3) _____________________________________________________ 表示焦点在y 型上的椭圆，则实数k 的取值范围是 _______________________________________ . ________ (4) _______________________________________ 表示椭圆，则实数k 的取值范围是 . 2. 椭圆4X 2 25y 2 =100的长轴长等于 _______________ ，短轴长等于 _____________ ,顶点坐标 是 _______________ , ____________ 焦点的坐标是 __________ , ________ 焦距是 _________ ，离心率等于—, ____2 23•椭圆 — -1的焦距为 2 ,贝U m= ______________ 。
4 m4. _____________________________________________ 椭圆5X 2 ky 2 =5的一个焦点是(0,2),那么k = ______________________________________________ 。
三•待定系数法求椭圆标准方程1. _____________________________________________________ 若椭圆经过点(-4,0) , (0,-3),则该椭圆的标准方程为 _____________________________________ 。
2. 焦点在坐标轴上，且a 2 =13 , c 2 =12的椭圆的标准方程为 _____________3. 焦点在X 轴上，a:b=2:1 , c =∙∕6椭圆的标准方程为 ________________4. 已知三点P (5, 2)、F 1 ( — 6, 0)、F 2 (6, 0),求以F 1、F 2为焦点且过点P 的椭圆的标x 23.已知椭圆一4 163,则P 到另一焦点距离为 _______准方程；变式：求与椭圆4χ2∙9y2 =36共焦点，且过点(3, -2)的椭圆方程。
四•焦点三角形2 21椭圆—-1的焦点为F I、F2, AB是椭圆过焦点F I的弦，则ABF2的周长是。
9 252•设F i, F2为椭圆16x2∙ 25y2 =400的焦点，P为椭圆上的任一点，贝:PF1F2的周长是多少？CPF I F2的面积的最大值是多少？2 23•设点P是椭圆—-y 1上的一点，F i, F2是焦点，若• F1PF2是直角，贝UCFI PF2的面积25 16为_________ 。
变式：已知椭圆9x2 16y2 =144 ,焦点为F1、F2，P是椭圆上一点•若.F1 PF^ 60，求APF I F2的面积.五•离心率的有关问题2 2 11. 椭圆H =1的离心率为-,则m =4 m 22. 从椭圆短轴的一个端点看长轴两端点的视角为1200,贝吐匕椭圆的离心率e为___________3. 椭圆的一焦点与短轴两顶点组成一个等边三角形，贝U椭圆的离心率为___________4. 设椭圆的两个焦点分别为R、、F2,过F2作椭圆长轴的垂线交椭圆于点卩，若厶FPF为等腰直角三角形，求椭圆的离心率。
5. 在厶ABC中，.A =300,∣AB∣=2,S.ABC j.3 .若以A B为焦点的椭圆经过点C ,则该椭圆的离心率e =__________ .六、最值问题：21、已知椭圆一∙ y2=1 , A(1 , 0) , P为椭圆上任意一点，求|PA|的最大值____________ 最小44值_________ 。
22. 椭圆L + y2=ι两焦点为F1、F2,点P在椭圆上，则∣PF1∣2 ∣PF2∣的最大值为______ ,七、弦长、中点弦问题1、已知椭圆4χ2■ y2=1及直y =X - m线.(1)当m为何值时，直线与椭圆有公共点？(2)若直线被椭圆截得的弦长为2卫，求直线的方程.522已知椭圆Xr宀1，(1)求过点(1,0 )且被椭圆截得的弦长为2. 2的弦所在直线的方程(2)求过点丐‘2且被P平分的弦所在直线的方程；同步测试1已知只(-8 , 0) , F2(8 , 0),动点P满足∣PF1∣+∣PF2∣=16 ,则点P的轨迹为() A圆B 椭圆C 线段D 直线2 22、椭圆X - y=1左右焦点为F1、F2, CD为过F1的弦，则也CDF的周长为16 92 22 23已知方程—y 1表示椭圆，则k的取值范围是()1+k 1 -kA -1<k<1B k>0C k ≥0D k>1 或k<-14、求满足以下条件的椭圆的标准方程(1)长轴长为10,短轴长为6 _______________(2) 长轴是短轴的2倍，且过点(2 , 1) ________________(3) 经过点(5 , 1) , (3 , 2) ______________45. 椭圆笃-Zτ=1(a b 0)的左右焦点分别是F i、F2,过点F i作X轴的垂线交椭圆于P点a b若∠ F1PF2=6O则椭圆的离心率为___________2 26已知椭圆的方程为—y 1，P点是椭圆上的点且.F i PF^ 60 ,求.PF1F2的面积_________________4 37.若椭圆的短轴为AB,它的一个焦点为F i,则满足△ ABF为等边三角形的椭圆的离心率为2 28. 椭圆- y 1上的点P到它的左焦点的距离是12,那么点P到它的右焦点的距离是 _100 36 —2 29. 已知椭圆χy+ L = 1(a>5)的两个焦点为F1、F2,且F1F2=8 ,弦AB过点F1,则△ ABF2a 25的周长_____________2 2 2 210、椭圆—+仝=1与椭圆—+ ^ = A- 0)有3 2 2 3(A)相等的焦距(B) 相同的离心率(C)相同的准线(D) 以上都不对2 2 2 211、椭圆—y1与n =I (0<k<9)的关系为25 9 9—k 25—扎(A)相等的焦距(B) 相同的的焦点(C)相同的准线(D) 有相等的长轴、短轴2 2 I12•点P为椭圆—-y 1上的动点,F L F2为椭圆的左、右焦点,则PF1 PF2的最小值为25 16__________ ,此时点P的坐标为 __________________ .感受咼考2 2X V1分别过椭圆孑+ b 2= 1(a>b>0)的左、右焦点F l 、F 2作两条互相垂直的直线11、∣2,它们 的交点在椭圆的内部，则椭圆的离心率的取值范围是 (A . (0,1)2 22•椭圆10θ+ 64=1的焦点为F l 、F 2,椭圆上的点P 满足∠ F 1PF 2= 60°则厶F 1PF 2的面 积是()3•已知椭圆E 的短轴长为6,焦点F 到长轴的一个端点的距离等于 9,则椭圆E 的离心 率等于()2 24已知点F , A 分别是椭圆a 2+ b 2= 1(a>b>0)的左焦点、右顶点，B(0, b)满足FB AB = 0,225. 已知椭圆X + N 2 = 1的左右焦点分别为F 1、F 2,过F 2且倾角为45°的直线I 交椭圆于A 、 8B 两点，以下结论中：①△ ABF 1的周长为8;②原点到I 的距离为1;③IABi = 正确结论的个数为()A . 3B . 2C . 1D . 06. 已知圆(x + 2)2+ V 2= 36的圆心为M ,设A 为圆上任一点，N(2,0),线段AN 的垂直平 分线交MA 于点P ,则动点P 的轨迹是( )A •圆B •椭圆C .双曲线D •抛物线2 27. 过椭圆C :》+ *= 1(a>b>0)的一个顶点作圆X 2+ b 2= b 2的两条切线，切点分别为 A , B ,若∠ AOB = 90o (O 为坐标原点)，则椭圆C 的离心率为 _________ .C.A. 64. 3 3B∙⅜3则椭圆的离心率等于() A H2B^C^≡1C. 2D.5+ 122 28若椭圆a 2+ b 2= 1(a>b>0)与曲线x 2+ y 2 = a 2- b 2无公共点，则椭圆的离心率 e 的取值范 围是 ________ •2 2X V10.已知椭圆C : a 2+ b 2= 1(a>b>0)的长轴长为4.(1)若以原点为圆心、椭圆短半轴为半径的圆与直线 y =x + 2相切，求椭圆C 的焦点坐标;111 •椭圆E 经过点A(2,3),对称轴为坐标轴，焦点 F 1, F 2在X 轴上，离心率e =勺(1) 求椭圆E 的方程；9 .已知△ ABC 顶点2 2X VA( — 4,0)和C(4,0),顶点B 在椭圆25+首= 1上，则sinA + Si nC Si nB。