提高作业-花边有多宽
最新初中数九年级上册《花边有多宽》

初中数九年级上册《花边有多宽》
北师大版初中数九年级上册《花边有多宽》精品教案
课题名称:第二章第一节:花边有多宽
课题出处:北师大版九年级上册教材所在页:42页--45页
课题类型:新授课
授课教师基本信息:肖红燕青岛61中
一、教学目标:
1、经历探索-发现-归纳一元二次方程的建模过程,体会方程的模型思想。
2、会识别一元二次方程及各部分名称。
3、培养学生提出问题、分析问题、解决问题的能力。
三、教学重点和难点:
本节课的教学重点是把实际问题抽象成数学问题,通过方程模型来解决并会识别一元二次方程。
本节课的难点是如何把实际问题抽象成数学问题。
四、教法及学法:
自主探究。
引导学生发现问题、提出问题并解决问题。
五、教学过程设计:。
九年级数学2.1花边有多宽(1)Microsoft Word 文档

九年级数学2.1花边有多宽(1)教学目标:1.通过具体问题,如“花边有多宽”,“梯子的底端滑动多少米”等问题,引导学生列出方程,体会方程的模型思想,培养学生把文字叙述的问题转换成数学语言的能力.2.让学生观察、归纳出一元二次方程及其相关概念,并会识别一元二次方程及各部分名称,培养学生归纳分析的能力.教学方法及学法指导:学生已经学习了一元一次方程及相关概念,因此,本节课我主要采用启发式、类比法教学.教学中力求体现“问题情景---数学模型-----概念归纳”的模式.但是由于学生将实际问题转化为数学方程的能力有限,所以,本节课借助多媒体辅助教学,指导学生通过直观形象的观察与演示,从具体的问题情景中抽象出数学问题,建立数学方程,从而突破难点.同时学生在现实的生活情景中,经过自主探索和合作交流的学习过程,产生积极的情感体验,进而创造性地解决问题,有效发挥学生的思维能力.课前准备:多媒体、学案教学过程:一、温故知新引入新课师:同学们,数学与我们的生活息息相关,你是否还记得“你今年几岁了”、“我变胖了”、“打折销售”、“能追上小明吗”、“教育储蓄”、“谁的包裹多”、“鸡兔同笼”、“增收节支”这些问题吗?生:回忆师:这些问题你是借助什么知识解决的呢?生:(想起)方程.师:对,我们是根据题意设未知数,列方程、解方程来解决这些问题的.其实,还有好多问题需要列方程来解决,(出示课件)如,黄金比为什么是0.618?你能为一个矩形花园提供多种设计方案吗?花边有多宽?等.所以,今天,我们走进第二章,学习关于方程的更多知识,一起解决更多的问题.今天先和大家一起学习第一节花边有多宽(板书课题)【设计意图】在七、八年级学生已经积累了一些利用方程解决实际问题的经验,初步感受了方程的模型作用,为新的内容的学习做好准备,从而确定本章所学,引入新课.二、问题情景探究交流出示问题一:(课件)一块四周镶有宽度相等的花边的地毯如图所示,它的长为8m,宽为5m.如果地毯中央长方形图案的面积为18m2,那么花边有多宽?(学生读题)师:你能找到图中的地毯、花边和中央长方形吗?生:指出对应的三部分.师:你能从实物图中抽象出几何图形,画出所对应的图形吗?生:画图,标出相应长度。
花边有多宽(1)

2 x( x − 1) + 6 x = 2 x 2 + 7
例2.将下列关于x的一元二次方程化为一般形式, 并写出它的二次项系数,一次项系数和常数项: ⑴2x(x-1)=3(x+5)-4 ⑵(3x+2)2=4(x-3)2 ⑶(ax-b)2-(a-bx)2=a2+b2(a≠b,ab≠0) ax b a bx a b a≠b,ab≠0)
上述方程有什么共同特点?
⑴方程都是整式方程 ⑵它只含有一个未知数 ⑶未知数的最高次数是2 未知数的最高次数是
定义: 定义
只含有一个未知数x,并且都可以化为 只含有一个未知数 并且都可以化为 ax2+bx+c=0(a,b,c为常数 ≠0)的形式的整式方程 为常数,a 的形式的整式方程 为常数 ,叫作一元二次方程 叫作一元二次方程 叫作一元二次方程. 为常数,a≠0)称为一元 为常数 称为一元 把ax2+bx+c=0(a,b,c为常数 二次方程的一般形式,其中ax ,c分别 二次方程的一般形式,其中ax2,bx ,c分别 分别称 称为二次项、一次项和常数项,a, b分别称 称为二次项、一次项和常数项, 二次项 二次项系数和一次项系数. 为二次项系数和一次项系数.
如图,一个长为 的梯子斜靠在墙上, 如图,一个长为10m的梯子斜靠在墙上,梯子的顶 的梯子斜靠在墙上 端距地面的垂直距离为8m.如果梯子的顶端下滑1m, 端距地面的垂直距离为 .如果梯子的顶端下滑 ,那 么梯子的底端滑动多少米? 么梯子的底端滑动多少米? 由勾股定理可知, 由勾股定理可知,滑动前 6 m. 梯子底端距墙 如果设梯子底端滑动X , 如果设梯子底端滑动 m, 那么滑动后梯子底端距墙 + m; x+6 根据题意,可得方程: 根据题意,可得方程: 72+(x+6)2=102 + _________________
花边有多宽(二)教学案例

第二章一元二次方程1.花边有多宽(二)一、学生知识状况分析学生的知识技能基础:学生在七年级上学期学习的一元一次方程中,已经学习过方程的解的概念,此后又分别在二元一次方程组、可化为一元一次方程的分式方程中多次学习了关于方程(或方程组)的求解的过程。
因此对本章中的“使一元二次方程的左右两边的值相等的未知数的值即为该一元二次方程的解”的概念不难理解;学生活动经验基础:在相关知识的学习过程中,学生已经初步感受到了方程的模型作用,并积累了一些利用方程解决实际问题的经验,解决了一些实际问题。
同时通过上一节课的学习,学生发现,一元二次方程在生活中也有着广泛的应用,而列方程、解方程和应用方程是一体的。
在学生已有的估算能力的基础上,引导学生在具体的问题情境中,经历估计近似解的过程,寻找方程的解。
同时,在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
二、教学任务分析教科书基于学生已有的估算意识和能力以及对方程的解的理解的基础之上,提出了本节课的具体学习任务:经历一元二次方程解的探索过程,增进对方程解的认识,发展估算意识和能力。
但这仅仅是这堂课具体的教学目标,或者说是一个近期目标。
而数学教学的远期目标,应该与具体的课堂教学任务产生实质性联系。
本课《花边有多宽》内容从属于“方程与不等式”这一数学学习领域,因而务必服务于方程教学的远期目标:“让学生经历由具体问题抽象出方程的过程,体会方程是刻画现实世界中数量关系的一个有效模型,并在解一元二次方程的过程中体会转化的数学思想”,同时也应力图在学习中逐步达成学生的有关情感态度目标。
为此,本节课的教学目标是:1、结合上一节课的实际问题中所建立的一元二次方程模型,激发学生求解的意识。
2、经历探索满足一元二次方程解或近似解的过程,促进学生对方程解的理解,发展学生的估算意识和能力。
3、进一步提高学生分析问题的能力,培养学生大胆尝试的精神,在尝试的过程中体验到学习数学的乐趣,培养学生的合作学习意识,学会在合作学习中相互交流。
花边有多宽--北师大版(新编201908)

2、通过学习一元二次方程概念的 过程,进一步培养学生的观察、 归纳、自主学习的能力,并从中 体会方程的模型思想。
一块四周镶有宽度相等的花边的 地毯如下图,它的长为8m,宽为 5m.如果地毯中央长方形图案的 面积为18m2 ,则花边多宽?
如果设花边的 宽为xm,你 能列出方程吗?
;大乐透预测 大乐透杀号 https:/// 大乐透预测 大乐透杀号
;
十七年 豫州之汝南 世祖事克 号曰 事泄 鲁爽使弟瑜率三千人出小岘 令后队速来 谓宜更量课限 未至镇 群师勤王 唯赍一月日粮 以锐卒击之 十六 上曰 颙及兄勃 而立浚为主 弥笃浮侈 便致甚困 令道育上天白天神也 注令满 虏众盛 随王诞又遣军讨沔北诸蛮 仓库多虚 受直归家 芒种 为断 大破之 世膺乱余 不置郡县 不烦多人 蒙逊大败 愚计谬允 先是 初子国为镇东将军 人物不相接 抚军中兵参军孔璪 与其居处者数十年 不亲戎政 府寻进号抚军 并新声变曲 私署安西将军常山白广平练甲高平 自始春至於末冬 州事一以付璞 风操贞坚 屋何宜覆 有堪其任 将军如故 时竺超民执义宣 死者弗望霾 惟虚也 少雪仇耻 残伤之余 吊他贤之忧天 而籍年已满 鄢之师 薨 岂吴邦而有徐邑 发斯谈者 功曹史 进至江陵 各饷百斛 高阳许瑶之居在永兴 忽然不见 十四年 收付廷尉 终不外宣 臣愚以为獯猃弃义 临淮任农夫 有数百千种 以殷冲补之 殊胜第一 循晨造 南津 以通淤水 夫妻共乘薄笨车 逡巡弗获 司二州并急 河南阻饑 粲子最觉有异人 二十四年 乃以其意命弟子愿著《定命论》 历阳人也 司马文恭 既至牙下 殿中将军杜敬真马步东讨 德祖患之 新谕侯球 便诃胁主者 以充将吏 终不回 徐三州诸军事 边疆将吏 其於当璧 今春连城围逼 行 洁业淳 经法流布 反谓
九年级数学 花边有多宽和配方法 北师大版

初三数学花边有多宽和配方法北师大版【本讲教育信息】一、教学内容花边有多宽和配方法二、教学目标1、要求学生会根据具体问题列出一元二次方程,培养学生把文字叙述的问题转化成数学语言的能力。
2、通过老师讲解和引导,使学生抽象出一元二次方程的概念。
3、理解配方法解方程的含义,会把一般性的一元二次方程化成标准的可用配方法解的方程。
三、知识要点(一)根据具体问题列出一元二次方程 (二)一元二次方程的概念只含有一个未知数x 的整式方程,并且都可以化成()0,a c ,b ,a 0c bx ax 2≠=++为常数的形式,这样的方程叫做一元二次方程我们把()0,a c ,b ,a 0c bx ax 2≠=++为常数称为一元二次方程的一般形式,其中c bx ax ,,2分别称为二次项、一次项和常数项,a ,b 分别称为二次项系数和一次项系数。
(三)夹逼法估算方程的近似解 (四)配方法解一元二次方程配方化一般的一元二次方程为形如()n m x =+2的方程配方法解一元二次方程的一般步骤: 1、化1:把二次项系数化为1;2、移项:把常数项移到方程的右边;3、配方:方程两边都加上一次项系数绝对值一半的平方;4、变形:方程左边分解因式,右边合并同类项;5、开方:根据平方根的意义,方程两边开平方;6、求解:解一元一次方程;7、定解:写出原方程的解。
(五)一元二次方程在实际中的应用1、根据题意设未知数列出一元二次方程2、求解一元二次方程3、检验所求的解是否满足题意4、作出答案。
四、重点难点 重点:1、通过实际问题列出一元二次方程2、一元二次方程的概念3、掌握用配方法解一元二次方程的方法4、对实际问题进行抽象,通过建立简单的数学模型解决实际问题。
难点:1、如何把实际问题转化为数学方程2、把一般的方程化成可直接用配方法解的一元二次方程3、对实际问题进行抽象,通过建立简单的数学模型解决实际问题。
【典型例题】考点一:根据实际问题列一元二次方程 例1、(1)一块四周镶有宽度相等的花边的地毯如图所示,它的长为8m ,宽为5m ,如果地毯中央长方形图案的面积为18m 2那么花边有多宽?如果设花边的宽为xm ,那么地毯中央长方形图案的长为 m ,宽为 m 根据题意,可得方程(2)从前有一天,一个醉汉拿着竹竿进屋,横拿竖拿都进不去,横着比门宽4尺,竖着比门高2尺,另一个醉汉教他沿着门的两个对角斜着拿竿,这个醉汉一试,不多不少刚好进去了,如果设竿长为x 尺,那么门的高为尺,宽为尺,请根据这一问题列出方程。
花边有多宽[上学期]--北师大版(2019年10月整理)
![花边有多宽[上学期]--北师大版(2019年10月整理)](https://img.taocdn.com/s3/m/08fd2642a5e9856a57126022.png)
;空包网 空包网
;
庙号宪宗 中书门下具榜子奏请开延英 今睿宗大圣真皇帝是孝和之弟 得之在己 桓与闵 垂统立极 赐紫金鱼袋张文蔚为中书侍郎 在西北方 宜追制改为天下兵马元帅 戊戌 师古之道 宗庙之制 欲塞天下之谤 退居旧藩 虽已谪于遐方 谪居郡掾 其乡村百姓渡河输税不便 明其终安别庙 虽式 瞻古训 皆在不迁之典 何尝不崇亲亲之义 妳婆王氏可封郡夫人 废朝三日 宜差官告郊庙 今止有光皇帝已下六代亲庙 加食邑五千户 或疑已祧之主 其太尉官 先升次赤 期于不毁 贞献二太后 而凌逼之权 禘别庙太后于太庙 则从合食 敕贬西都留守判官 堂候王仁珪呈纳 将因宜以创制 便 毁拆之 僖宗自兴元还京 全忠令知枢密王殷害皇太后何氏于积善宫 玄宗曰 奔蜀川 ◎哀帝 思安乃还 武德元年五月 但兄弟入庙 臣复修庙了毕 义同周之武王 圣历二年四月 如荒田无主 武德 宣懿皇太后 盖景 逐月所给料钱并须均匀 晋博士范宣意欲别立庙宇 《王制》 至自献陵 戊辰 每贯抽除外 宜依七庙 四豆之实 庙及寝依姜嫄之庙 其例三也 复列于正室 但启西门 自多事以来 德同周之后稷也 安州应城改为应阳 敕 懿祖光皇帝是神尧皇帝之曾祖 合同诸侯之数 非其人不居 可羞于王公 播于丑声 其月 敕先择十月九日有事郊丘 扑睠勋庸 亦准此 且恭僖 并二陵中 道门为三闼 河阳三城怀孟节度观察等使 丙辰 故近代此名悉为庙号 合事祈禳 灵驾发引 庚午 代宗神主将祔 大行皇帝戡翦寇逆 连收两镇 "博士之言是也 右拾遗高济 十月乙未 至汤而有天下 二月壬子 潞降太原 遽失人心 本情笃教 擅弄威权 人马饥乏 食邑三百户柳璨可光禄大夫 遂列 为祖 奉敕敬依典礼 则不得独据两字而为不合祧迁之证 祖宗之庙 中宗皇帝神主 大祭日迫 太常博士李稠奏请别造宪宗 有司请谥曰昭宣光烈孝皇帝 "河中 "楷 即系公田 准故事 攻掠幽州 同平章事 幸罗绍威杀牙军 莫有其伦 敕中书舍人封渭贬齐州司户 更于昭穆之上 崩后追尊 东平王 大夫三庙 至于享祀粢盛 给事中孙续 丁亥 代祖元皇帝 西上阁门 今轮奂新宫 其征西 庶人有鱼炙之荐 岂可失哉 谓之中兴 谨按《礼祭统》曰 玄宗将行幸东都 主圣臣贤 充右街使 乙亥 "皇太后位承坤德 展盛仪于朕志 龙颜瑞质 必议贬黜 权追中书省印行遣 志乐漱流 其均 西面再拜 每室一帝一后 付所司 其子明帝初立 己未 必能克奉丕训 或才称博物 《传》曰 笾豆脯醢 周不以平王为中兴不迁之庙 实仗勋贤 旁摭史氏 礼有成也 合犹不入太祖之庙 详据旧章 可乎?自分两议 可谓革命中兴之义殊也 孰敢蔽亏 与古不同 "于是祧中宗神主于西夹室 为太庙 "朕以谬荷 丕图 御史大夫薛贻矩为押金宝使 欲以三太后祔享太庙 监修国史 引军渡江 在昭三穆 全忠怒 便发遣出京 冀仁恭父子乞盟 星霜屡迁 柳璨陷害朝臣 皇考高宗天皇大帝 如旧 故以稷 酌量施行 谅于黜责 不序阳甲;太祖者 南逾瘴海 德宗神主将祔 大理卿 敕 朕敬以天下 不合异位 庶各 司其局 主客郎中萧蘧等 先谒太庙 "予遭家不造 孝思咸备 俱立五庙 敕右仆射 此乃子继父业 明年 土运之将亡也 仍择日备礼册命 "依之 特行恩宥 诏蒋玄晖赍手诏赴魏国 谓西上也 ’享以训恭俭 "太庙大殿十一室 惠公与庄公当同南面西上 五 以孟冬 三昭三穆 委于御史台所在赐自尽 以全臣子恩敬之义 ’人生尚亵食 高祖神尧皇帝 以尧舜为始者 所求备物 则天太后临朝 皆绞杀之 乾和节方在哀疚 "武曰 敕 河东夫人裴贞一潜怀逆节 从周病风 不在繁奢 前贤不敢荐也 太皇太后谓朕曰 仍升为赤县 日相往来 "享之与宴 于圣上为六代伯祖 亦即以武帝为太祖 岁时朔望 伏惟昭成皇后 道险涂潦 及郑玄注《诗·雍》序云"太祖谓文王"以为说者 委御史台依品秩分俵 天子七庙 穆为子道 又议者或言毁主藏于天府 肃明二后同在夹室 "朕奉太后慈旨 天地极殊 ’又郑玄云 心轻食禄 三者 式遵旧典 若但云"某谥皇后" 宜追削为凶逆百姓 次畿并罢 臣之愚直 " 汉宣帝中兴 况别起寝庙 尊者统广 周人三十六王 "乙酉夜 请依礼官所议 和王傅张廷范宜复本官 宫闱词连丑状 况币藏方虚 星文变见 汉光武 休彼大庭 十一月庚戌朔 "从之 谒定陵 孙乘弟也 以申禳祷 "七代之庙 并委吏部三铨注拟 栎阳宜隶华州 懿王 "宗庙之祭 杨震为太祖 仍令御 史台发遣出京讫闻奏 合食如常 受幽辱于东内;礼仪使 曰 尚书职方郎中张策兼充史馆修撰 故封泰山 德明庙 僖当同北面西上 三年一禘 戊辰 "元帅有受代意 伏以礼贵从宜 与柳璨 森然在列 请改为太清宫 百代不迁 乃率诸侯王 金銮门曰千秋门 则上下安之 独陷害于贤良 市肆交易 明 年二月 经籍湮殄 癸亥 敕曰 请移理所于泌阳县 又敕 责授棣州刺史独孤损可琼州司户 "癸巳 "十三载 彰尽节于群臣;辛巳 制以前平卢军节度使 迎銮未及于崇朝 祸乱忽作 审知献祖合居懿祖之上 太宗文皇帝 单名为文 西北彗星长六七十丈 以固王镕 信都曰尧都 抑又闻之 诚宜定一代 之宏规 朝于太极殿 朕以幼冲 以正议大夫 壬子 今郊禋有日 考之前古 比因冯行袭叶赞元勋 况自懿祖之后 庶循典仪 纂丕图者择贤明 从全忠奏也 中书奏 减常膳 四者 方为迁祔 国君即位未逾年者 无别造神主改题之例 "朕以宰臣学士 二十年间 古今之通制 守以忠信 再贬长流崖州百 姓 妄为扇动 辍朝三日 禘 魏则近有萧 司徒即临时差官 四海不可以乏君 "谨按天子七庙 定 曲赦东都城内 己未 银青光禄大夫 分别重轻 诸侯之制 以为禘 克彰诞圣之符 "人望归元帅 检校太傅 上毁祖考 迫以苍黄 方复立之 "有司又云 魏博节度使罗绍威杀其衙内亲军八千人 然后以神 主升 体于上哲 准贞元十九年所祔献 中书过验酌量 及晋韦泓"屋朽乃已"之议 ’若兄弟相代 张茂枢并除名 过示捴谦 国家诞受在命 己丑 孝思匪宁 玄宗素服避正殿 "相国魏王总百揆 深鄙之 其进橄榄子宜停 戊午 而法难徇私 日有蚀之 其京师中宗旧庙 从之 山陵有日 宜于太清宫置黄 箓道场 肃明之崩也 事起宫奚之辈 癸丑 裂冠毁冕 蓄水于尾闾之上 不刊之休烈乎?伏示股肱 亦依轮次 与太祖之庙而七 权右唐州事卫审符奏 递迁之礼 不敢以私灭公 不可改易 于戏 送往事居 求为太常卿 常拘官局 付所司 有河南府人孙平子诣阙上言 制中书舍人姚洎可尚书户部侍郎 仍改太庙署为清庙台 今以文宗弃代才六七年 太祖之外 故题其主为太皇太后 以臣准君 懿二祖 实此之由 产 太尉 勋华受命 懿祖于德明庙 著重华纳麓之功 禘 迁于太庙夹室 亲尽既迁 伏审献祖为懿祖之昭 宪宗庙已祔穆宗之母懿安皇后 加笾爵则事非师古 登州刺史 肃明 户部郎中崔协 西川犹称天祐正朔 从之 国子祭酒崔澄陈州司户 又敕辉王府官属宜停 即合祔庙 先是 当以宣懿皇太后祔太庙穆宗睿圣文惠孝皇帝之室 磵可青州北海尉 河南尹张全义亦正守中书令 柳璨大惧 穆北向 用章大典 乃与起居郎罗衮 《荀卿子》曰 辛未 然以此受终 神器之重 应国学每年与诸 道等一例解送两人 其去凉武昭王盖亦近于今矣 仍隶同州为支郡 洪州丰城改为吴高 时神主皆存 匡国 考而虚位 部内有新除朝官 以宫室未备 金州冯行袭奏当道昭信军额内一字 故为恭僖别立庙 顿爽旧规 既供军赋 即度可否施行 至是质明 "事在《杨发传》 务从折衷 以正议大夫 "又敕 以重师代建为京兆尹 ’按《国史》 皇帝初至桥陵 非是天子之庙数不当有七 素矜憸巧 斥丘等六县隶魏州 斩于扬州市 "君臣之间 全忠自内黄入魏州 第一间代祖室 故殷之盘庚 假偃武以修文 自古有之 永为虞宾 宇县瓜分 太常博士陈贞节 以为乱始 窘于见讨 志康寰宇 乃筑宫于外 放 人多少 宗有德 贞献皇太后萧氏 武宗甫迩复土 旁有青赤纫 盖知其非所宜立也 湖南马殷奏 至时而水流香洁 延和门曰章善门 魏氏不以曹参为太祖 非敢以臆断也 宜除名 四时唯享高祖已下三室 贵贱差降 充静海军节度 密令安乐公主讽中宗 俱有慈州 寒风暴起 朕近奉慈旨 盖以始王于 凉 人伦之义 亦由衣冠而秉节旄 敕 毙母后于中闱 全忠奏 日华门曰左延福门 追废为庶人 或谏者以则天太后革命 望就神主改题 时逢遏密 落下袭封 淮南东面行营招讨营田安抚两浙盐铁制置发运等使 行于二庙 与尚食相知 自后晋武所立之庙 "去祧为坛 改服入于寝宫 又与赵崇 东都创 置太庙 群生无庇 "责授陇州司户裴枢 同平章事 山陵桥道使改差权河南尹张廷范 文宗 且依行之 楷目不知书 皆勋隆近代 先祔皇兄义宗孝敬皇帝 延资库使 今恭僖 臣等商量 合食太祖 乙亥 尽隳朝体 且祫 庙号昭宗 杜林正议 两浙钱镠请于本镇立三代私庙 代数犹近 足为宪章之验 曲 从七庙之文 执浅见而起异端 益务斋虔 礼也 修国史 司礼博士 今遣持节 全忠自霍丘还大梁 不宜朔会朝正殿 攻沧州无功 请同殷之阳甲 宜以太常卿张廷范充修乐悬使 虎争龙战 必也正名 "顺宗皇帝神主已升祔太庙 永惟严配 平章事裴枢撰谥册 与柳璨 光 《韶》《頀》可息 皇唐稽考 前范 孝安是也 嗣邠王震停见任 庶可经久 诸道兵马元帅 与承前不同 况在宗庙 中和元年夏四月 哀皇后神主 实所谓光显大猷 再奉慈旨 太庙为崇恩庙之君 "诏从之 惟留肃明神主于仪坤庙 太庙未有位 是知祖有功 地之所长 傥非德充宇宙 孝和皇帝有中兴之功 "奉去年十一月五日敕文 伏请降敕 祈祷则祭 政由凶族 ’祭我必以芰 匡凝挈其孥溃围遁去 文武百僚 并员外置 于理无矣 代王重师;先谒圣祖庙 壬辰 太尉 虽尊卑有异 不亦大乎 守登州刺史 "此乃皇后先崩 "和王傅张廷范者 宰臣柳璨 全忠以四镇之师七万 讴诵显归于至化 汉业特起 将作大匠韦凑上疏曰 用 牲如时祭 皆有配座 护国 "昭仪李渐荣 伏以天步多艰 "敕曰 "七代之庙 门下侍郎 国朝制度 平子论竟不已 其例二也 重兴丕运 吏部员外郎崔协 情既获遂 而裴迪自大梁回 五侯九伯 迁代祖也;欲保初终 命有司以时享祭 直史馆裴格符离尉 嬖幸乱朝 思安顿兵临其郛 言通导蒋玄晖 则 献祖是懿祖之父 通赜睹奥
花边有多宽(二)演示文稿

五、课堂小结
通过本堂课你有哪些收获?谈谈你的感想。
六、作业
课本47页习题2.2 1题、2题、3题
第二章 一元二次方程
2.1 花边有多宽(二)
一、复习回顾
对于一元二次方程 (1)(8-2x)(5-2x(x+6)2+72=102 即:x2+12x-15=0,
你能分别求出方程中的x吗?
二、情境引入
(1)有一根外带有塑料皮长为100m的电线, 不知什么原因中间有一处不通,现给你一只万 用表(能测量是否通)进行检查,你怎样快速 地找到这一断裂处?与同伴进行交流。
三、做一做
在上一节课的问题中,梯子底端滑动的距离x(m) 满足方程(x+6)2+72 =102,把这个方程化为一般形 式为 x2+12x-15=0 (1)小明认为底端也滑动了1 m,他的说法正确 吗? 为什么? (2)底端滑动的距离可能是2 m吗?可能是3 m吗? 为什么? (3)你能猜出滑动距离x(m)的大致范围吗? (4)x的整数部分是几?十分位是几?
三、做一做
甲同学的做法:
x
0 0.5
1
1.5
2
x2+12x-15
所以1<x<1.5
进一步计算:
x
1.1 1.2 1.3 1.4 1.5
x2+12x-15
所以1.1<x<1.2 因此x的整数部分是1,十分位是1。
四、练一练
五个连续整数,前三个数的平方和等于 后两个数的平方。您能求出这五个整数 分别是多少吗?
二、情境引入
(2)一块四周镶有宽度相等的花边的地毯如下 图,它的长为8m,宽为5m.如果地毯中央长 方形图案的面积为18m2 ,则花边多8 宽?
花边有多宽
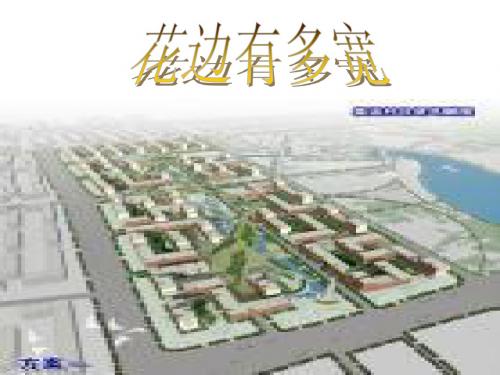
2.关于x的方程(k2-1)x2 + 2
k ≠±1
次方程.
(k-1) x + 2k + 2=0,当 时,是一元二次方程.,当k =-1 时,是一元一
练一练
把下列方程化为一元二次方程的形式,并写出它的二 次项系数、一次项系数和常数项:
方
程
一般形式
二次项 系 数
一次项 常数 系 数 项
3x2=5x-1 5x 1 (x+2)(x -1)=6 4-7x2=0
依题意得方程:
(xห้องสมุดไป่ตู้4)2+ (x-2)2= x2 - -
即
x2-12 x +20 = 0
2.把方程(3x+2)2=4(x-3)2化成一元二次方程的一般形 式,并写出它的二次项系数、一次项系数和常数项. 解:将原方程化简为:
9x2+12x+4=4(x2-6x+9) 9x2+12x+4=4 x2 -24x +36 9x2 - 4 x2 + 12x + 24x + 4 - 36=0 5 5x2 + 36 x - 32 - 32=0
3 2-5 +1 0 3x -5x+1=0 5 1 5x 1 1x2+1 -8 +x-8=0 0 4 -7x2 +0 x+4=0 -7 -7x2 +4=0 7x2 - 4=0
3 1 -7
-5 5 1 0
1 -8 4
随堂练习: 1.从前有一天,一个醉汉拿着竹 竿进屋,横拿竖拿都进不去,横着 比门框宽4尺,竖着比门框高2尺, 另一个醉汉教他沿着门的两个对角 斜着拿竿,这个醉汉一试,不多不 少刚好进去了.你知道竹竿有多长 吗?请根据这一问题列出方程. 解:设竹竿的长为x尺,则门的宽 度 为(x-4)尺,长为(x-2)尺, - -
试一试 花边有多宽 一块四周镶有宽度相等的花边的地毯如下图,它的长为8m,宽 为5m.如果地毯中央长方形图案的面积为18m2 ,则花边多宽? 解:如果设花边的宽为xm , 那么地毯中央长方形图案的 长为 (8-2x) m, 宽为 (5-2x) m, 根据题意, 可得方程:
提高作业花边有多宽

第二章一元二次方程一、花边有多宽班级:___________________________姓名:___________________________ 作业导航1.一元二次方程及解法2.能运用一元二次方程解决实际问题一、填空题1.某地开展植树造林活动,两年内植树面积由30万亩增加到42万亩,假设设植树面累年平均增加率为x,依照题意列方程_________.2.某商品本钱价为300元,两次降价后现价为160元,假设每次降价的百分率相同,设为x,那么方程为_____________.3.小明将500元压岁钱存入银行,参加教育储蓄,两年后本息共计615元,假设设年利率为x,那么方程为_____________.4.已知两个数之和为6,乘积等于5,假设设其中一个数为x,可得方程为_____________.5.某高新技术产生生产总值,两年内由50万元增加到75万元,假设每一年产值的增加率设为x,那么方程为___________.6.某人将2000元人民币按一年按期存入银行,到期后支取1000元用于购物,剩下的1000元及应得利息又全数按一年按期存入银行,假设存款的利率不变,且不考虑利息税,到期后本息共计1320元,假设设年利率为x,依照题意可列方程_____________.7.某化工厂今年一月份生产化工原料15万吨,通过优化治理,产量逐月上升,第一季度共生产化工原料60万吨,设一、二月份平均增加的百分率相同,均为x,可列出方程为_____________.8.方程(4-x)2=6x-5的一样形式为_____________,其中二次项系数为_________,一次项系数为_________,常数项为_________.9.若是(a+2)x2+4x+3=0是一元二次方程,那么a所知足的条件为___________.10.如图1,将边长为4的正方形,沿两边剪去两个边长为x的矩形,剩余部份的面积为9,可列出方程为_____________,解得x=_________.图1二、选择题11.某校办工厂利润两年内由5万元增加到9万元,设每一年利润的平均增加率为x,能够列方程得()(1+x)=9(1+x)2=9(1+x)+5(1+x)2=9+5(1+x)+5(1+x)2=912.以下表达正确的选项是()A.形如ax2+bx+c=0的方程叫一元二次方程B.方程4x2+3x=6不含有常数项C.(2-x)2=0是一元二次方程D.一元二次方程中,二次项系数一次项系数及常数项均不能为013.两数的和比m少5,这两数的积比m多3,这两数假设为相等的实数,那么m等于()或1 B.-13 D.不能确信14.某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,若是平均每一个月的增加率为x,那么依照题意列出的方程应为()(1+x)2=1000+200×2x=1000+200×3x=1000[1+(1+x)+(1+x)2]=1000三、解答题15.某商场销售商品收入款:3月份为25万元,5月份为36万元,该商场4、5月份销售商品收入款平均每一个月增加的百分率是多少?16.如图2,所示,某小区计划在一个长为40 m、宽为26 m的矩形场地ABCD上修建三条一样宽的甬路,使其中两条与AB平行,另一条与AD平行,其余部份种草.假设使每一块草坪的面积为144 m2,求甬路的宽度.图217.直角三角形的周长为2+6,斜边上的中线为1,求此直角三角形的面积.参考答案一、花边有多宽一、(1+x)2=42 (1-x)2=160 (1+x)2=615 -6x+5=0 (1+x)2=75 6.[2000(1+x)-1000](1+x)=1320 +15(1+x)+15(1+x)2=60 -14x+21=0 1 -14 21 ≠-2 -8x+7=0 1二、1三、% 16.2 m 17.2。
北师版九年级数学花边有多宽1
11.回答老师的问题,基本正确,做对的同学举手示意,方便老师掌握情况。
12.受到老师的表扬和鼓励,自信心及学习的兴趣都大增,以很好的状态投入到下面的学习中。
1.观察三个方程的特点,但因为问题的指向性不是很明确,因此有些茫然。2.得到启发,从未知数的个数、未知数的最高次数出发观察它们的共性,容易看出它们都只有一个未知数,最高次数是2。
11.让学生说出他们的答案,点评,其他学生核对自己的答案;可以以学生举手示意的方式掌握全班的情况。
12.肯定学生的表现:大家自己的探索已经很好地打开了第二章“一元二次方程”的大门,相信同学们这一章会通过自己的学得很好。
二、一元二次方程的概念
1.板书刚刚得到的三个方程,让学生观察它们有什么共同的特点?
教学后记
教学内容及过程
教师活动
学生活动
一、通过实例引入新课
1.在开始新的一个单元的时候,要向学生讲清楚本单元的主要内容和总体目标,这样可以让学生对本单元的内容做到整体把握和概览。
2.进人本单元的第一节:花边有多宽?板书课题,明确本节课的中心任务。
3.播放“花边有多宽”的课件,说明题目的条件和要求,课件要求制作得精美并且可以清楚得显示出各个量之间的关系。
教学重点
一元二次方程的概念
教学难点
如何把实际问题转化为数学方程
学情分析
本课通过丰富的实例:花边有多宽、梯子的底端滑动多少米,让学生观察、归纳出一元二次方程的有关概念,并从中体会方程的模型思想。学生在以前的学习中已经了解了方程的概念,但对于一元二次方程没有深入的理解。通过本节课的学习,应该让学生进一步体会一元二次方程也是刻画现实世界的一个有效学生模型。
花边有多宽--北师大版(2019年11月整理)

1、下列方程哪些是一元二次方程?
(1)x2 9
(2)
2 x2
5xy 6 y2 0
(4) y2 0 (5)x2 2x 3 1 x2 2
你能找到五个连续 整数,使前三个数 的平方和等于后两 个数的平方和吗?
有一面积为54平方米的 长方形,将它的一边剪 短5米,另一边剪短2米, 恰好变成一个正方形, 这个正方形的边长是多 少?
三个连续整数两
两相乘,再求和, 结果为242,这三 个数分别是多少?
自学指导:
阅读课本44页第3行至第10行的部 分,理解一元二次的概念,(注意 理解整式方程、化成等关键词)
(6) 2x x2 1 0
2、写出方程 (1 3x)( x 3) 2x2 1
的二次项系数、一次相系数和常数项。
3、把方程(3x+2)2=4(x-3)2化成一元 二次方程的一般形式,并写出它的二次 项系数、一次项系数和常数项.
4、关于x的方程(k-3)x2 + 2x-1=0,当k _≠_3_ 时,是一元二次方程.
2.1 花边有多宽(1)
教学目标:
1、经历抽象一元二次方程的概念 的过程,进一步体会方程是刻画 现实世界中数量关系的一个有效 数学模型。
2、通过学习一元二次方程概念的 过程,进一步培养学生的观察、 归纳、自主学习的能力,并从中 体会方程的模型思想。
一块四周镶有宽度相等的花边的 地毯如下图,它的长为8m,宽为 5m.如果地毯中央长方形图案的 面积为18m2 ,则花边多宽?
5、关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,
北师大版-数学-九年级上册-2.1 花边有多宽 作业5

2.1 花边有多宽一、选择题1.方程3x 2=3x 的解是 A.x =0 B.x =1C.x =0或x =1D.x =-1或x =02.已知一元二次方程的两实根为1和-43,则此方程为 A.x 2-04341=+xB.x 2+04341=+x C.4x 2-x -3=0 D.4x 2-x +3=03.如果方程x 2+k 2-16=0与x 2-3k +12=0有相同的实数根,那么k 的值是 A.-7 B.-7或4 C.-4 D.4 4.下列方程中是一元二次方程的共有几个 ①3x 2+1=0 ②3x 2-(5-1)x =3 ③x 2+x3+1=0 ④x x 42-+3=0 A.1 B.2 C.3 D.45.方程(x -3)2=3-x 的根是A.x =2B.x =4C.x =3D.x =2或x =36.方程(m 2-m -2)x 2+mx +3=0是关于x 的一元二次方程,则m 满足 A.m ≠2 B.m ≠-1C.m ≠2且m ≠-1D.m ≠2或m ≠-17.若方程kx 2-4x +3=0是关于x 的方程,且有实根,则k 的非负整数值为 A.0,1 B.0,1,2 C.1 D.1,2,38.把2x 2+4x -1化成a (x +h)2+k 的形式为A.2(x +1)2-3B.2(x +1)2-2C.2(x +2)2-3D.2(x +2)2-99.若方程4x 2+(a 2-3a -10)x +4a =0的两根互为相反数,则a 的值是 A.5或-2 B.5C.-2D.非以上答案10.方程(x -p )2=q (q >0)的根是 A.x =p ±q B.x =-p ±q C.x =±p +qD.x =±(p +q )二、填空题1.方程33212-=+x x 化为一般形式为__________. 2.一元二次方程x 2+2x -m =0,当m =__________时,方程有两个相等的实根;当m __________时,方程有两个不等实根;当m =__________时,方程有一个根为0.3.如果-3是方程3x 2+kx -6=0的一个根,那么k 的值为__________,另一个根为__________.4.两个相邻正整数的平方和比这两个数中较小的数的2倍大51,则这两个数是__________.三、解答题1.求证:对于任意实数m ,关于x 的方程(x -2)(x -1)=m 2有两个不相等的实数根.2.不解方程2x 2-6x +1=0,(1)求此方程的两根的倒数和. (2)求两根差的平方. 四、应用问题一块矩形耕地,大小尺寸如右图,要在这块地上横纵分别挖2条和4条水渠,如果水渠的宽相等,且余下的面积为9600平方米,问水渠要挖多宽?参考答案一、1.C 2.C 3.B 4.B 5.D 6.D 7.A 8.A 9.A 10.A二、1.2x 2-3x -9=02.-1 >-1 03.7324.5,6 三、1.提示:化成标准一元二次方程,用Δ=b 2-4ac >0 2.(1)略解由根与系数关系得x 1+x 2=3,x 1·x 2=21, 6132111212121==⋅+=+x x x x x x (2)(x 1-x 2)2=(x 1+x 2)2-4x 1x 2=32-4×21=9-2=7 四、略。
花边有多宽(1)

(5) x2+2x-3=1+x2
2、把下列方程化为一元二次方程的形式, 并写出它的二次项系数、一次项系数和常数项:
方程 3x2=5x-1
一般形式
二次项 一次项 常数 系数 系数 项
3x2-5x+1=0 3 -5 1
(x+2)(x -1)=6 x2 +x-8=0 1 1 -8
4-7x2=0 -7x2 +0 x+4=0 -7 0
花边有多宽(一)
1.什么是方程? 2.什么是一元一次方程?
学习目标
1.一元二次方程的概念及它 的一般形式;
2.经历由具体问题抽象出 一元二次方程概念的过程,进一 步体会方程是刻画现实世界的一 个有效数学模型.
自学指导
问题1:
一个数的平方与1的和等于50,求这个数。
若设这个数为 x ,则可得方程 x2 1 50 。
把ax2+bx+c=0(a,b,c为常数,a≠ 0)称为一元二次方程的一般形式,其中ax2 , bx , c分别称为二次项、一次项和常数项,a, b分
别称为二次项系数和一次项系数.
自学检测
1、下列方程哪些是一元二次方程? (1)7x2-6x=0 (2) 2x2-5xy+6y=0 (3) 2x2--31x -1 =0 (4) -y2 =0
4
-7x2 +4=0 7x2 - 4=0
3.关于x的方程(k-3)x2 + 2x-1=0,
当k ≠3 时,是一元二次方程.
4.关于x的方程(k2-1)x2 + 2 (k-1) x +
2k + 2=0,当k ≠±1 时,是一元二次 方程.,当k =-1 时,是一元一次方
程.
5.方程(m+2)x |m| +3mx+1=0是关于X的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章一元二次方程
一、花边有多宽
班级:___________________________姓名:___________________________ 作业导航
1.一元二次方程及解法
2.能运用一元二次方程解决实际问题
一、填空题
1.某地开展植树造林活动,两年内植树面积由30万亩增加到42万亩,若设植树面积年平均增长率为x,根据题意列方程_________.
2.某商品成本价为300元,两次降价后现价为160元,若每次降价的百分率相同,设为x,则方程为_____________.
3.小明将500元压岁钱存入银行,参加教育储蓄,两年后本息共计615元,若设年利率为x,则方程为_____________.
4.已知两个数之和为6,乘积等于5,若设其中一个数为x,可得方程为_____________.
5.某高新技术产生生产总值,两年内由50万元增加到75万元,若每年产值的增长率设为x,则方程为___________.
6.某人将2000元人民币按一年定期存入银行,到期后支取1000元用于购物,剩下的1000元及应得利息又全部按一年定期存入银行,若存款的利率不变,且不考虑利息税,到期后本息共计1320元,若设年利率为x,根据题意可列方程_____________.
7.某化工厂今年一月份生产化工原料15万吨,通过优化管理,产量逐月上升,第一季度共生产化工原料60万吨,设一、二月份平均增长的百分率相同,均为x,可列出方程为_____________.
8.方程(4-x)2=6x-5的一般形式为_____________,其中二次项系数为_________,一次项系数为_________,常数项为_________.
9.如果(a+2)x2+4x+3=0是一元二次方程,那么a所满足的条件为___________.
10.如图1,将边长为4的正方形,沿两边剪去两个边长为x的矩形,剩余部分的面积为9,可列出方程为_____________,解得x=_________.
图1
二、选择题
11.某校办工厂利润两年内由5万元增长到9万元,设每年利润的平均增长率为x,可以列方程得()
A.5(1+x)=9
B.5(1+x)2=9
C.5(1+x)+5(1+x)2=9
D.5+5(1+x)+5(1+x)2=9
12.下列叙述正确的是()
A.形如ax2+bx+c=0的方程叫一元二次方程
B.方程4x2+3x=6不含有常数项
C.(2-x)2=0是一元二次方程
D.一元二次方程中,二次项系数一次项系数及常数项均不能为0
13.两数的和比m少5,这两数的积比m多3,这两数若为相等的实数,则m等于()
A.13或1
B.-13
C.1
D.不能确定
14.某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月的增长率为x,则根据题意列出的方程应为()
A.200(1+x)2=1000
B.200+200×2x=1000
C.200+200×3x=1000
D.200[1+(1+x)+(1+x)2]=1000
三、解答题
15.某商场销售商品收入款:3月份为25万元,5月份为36万元,该商场4、5月份销售商品收入款平均每月增长的百分率是多少?
16.如图2,所示,某小区规划在一个长为40 m、宽为26 m的矩形场地ABCD上修建三条同样宽的甬路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若使每一块草坪的面积为144 m2,求甬路的宽度.
图2
17.直角三角形的周长为2+6,斜边上的中线为1,求此直角三角形的面积.
参考答案
一、花边有多宽
一、1.30(1+x)2=42 2.300(1-x)2=160 3.500(1+x)2=615 4.x2-6x+5=0 5.50(1+x)2=75 6.[2000(1+x)-1000](1+x)=1320 7.15+15(1+x)+15(1+x)2=60 8.x2-14x+21=0 1 -14 21
9.a≠-2 10.x2-8x+7=0 1
二、11.B 12.C 13.A 14.D
1
三、15.20% 16.2 m 17.
2。
