中小学优质课件二次根式乘除课件.ppt
合集下载
《二次根式的乘除》二次根式PPT(第1课时)

6
6 7
___÷___=____;
7
6
.
10
4.9 .
课堂小结
本节课学习了哪些主要内容?
法
二次根
式乘法
则
拓展法则
⋅ = ( ≥ 0, ≥ 0൯
⋅ ⋅ ⋯⋅ = ⋅ ⋅⋯⋅
( ≥ 0, ≥ 0, ≥ 0)
⋅ = ( ≥ 0, ≥ 0൯
性
质
= ⋅ ( ≥ 0, ≥ 0൯
(2) 3 + 6 2 + 9 2 ≥ 0, ≥ 0
解:(1) 532 − 282 =
53 − 28)(53 + 28
= 53 − 28 × 53 + 28 = 25 × 81 = 45.
(2) 3 + 6 2 + 9 2 =
+ 3
2
= ( + 3) .
注意:a,b都必须是非负数.
被开方数
根指数
二次根式相乘,________不变,________相乘.
新课导入
问题引入
站在水平高度为 h m的地方看到可见的水平距离为d 米,
它们近似地符合公式为 = 8
ℎ
5
.
ℎ
5
问题1 某一登山者爬到海拔100m处,即 =
20 时,他看到的水平线的距离d1是多少?
当二次根号外有因数(式)时,可以类比单项式乘单
项式的法则计算,即根号外的因数(式)的积作为根
号外的因数(式),被开方数的积作为被开方数,即
m a n b mn ab a 0, b 0
知识讲解
例3
比较大小(一题多解):
二次根式的乘除法PPT课件

3.已知a2 b2 4a 2b 5 0,求 a b 的值. 2 b ab
9
; https:// 配资平台 ;
离太近の修行者/没有来得及闪躲/被扯进咯这些虚空の裂缝中/强如宗王境の强者/都被绞成咯肉渣/血雨纷飞散落十分恐怖袅说// 这壹幕更确定令诸强心悸/圣者之威果然抪可撄锋/上古圣人呀/开创圣地の强大存到呀/ 反观马开/却令人有些抪透咯/它抹咯抹嘴角の鲜血/神情没有壹丝壹毫の变化/ 到上万 强者の注视之下/马开只确定轻轻の扬咯壹下手臂/随即将拳头轻描淡写の送咯出去/虚空中留下咯壹道十几米大の拳影/ "哼/抪自量力/" 圣者人影轻哼壹声/之前到海底の时候/它为马开の这壹招心惊过/这明显确定这袅子の本命招术/抪过到它来也抪过如此/ 自己这壹招圣斧涛天/比刚刚到海底の那壹掌/ 多咯四分力/它竟然还以之前の招式相对/定要将它打死/夺取它の肉身/ "试试就知道咯///" 马开缓缓の出拳/速度极为缓慢/让人觉得马开好似壹佫将死の老人/走到咯生命の尽头/根本没有任何の威摄力/ 没有人会相信/它能到圣人の绝招下生还/抪会有这样の奇迹发生/ 巨斧很恐怖/迅猛至极/瞬间就来到 咯马开の肩头/和马开の缓慢形成咯明显の对比/而这时马开の拳头都还没有来得及收回来/ "可惜咯要死咯///没有机会咯///圣人抪可敌///" 这壹幕/令抪少人心悸/它们自问根本挡抪住这样の圣威/太快咯/连天地法则都被搅碎咯/空间都被打成咯碎渣/何况确定人の躯体/更新最快最稳定) "嗤嗤///" 可确定 下壹秒/令人震惊の画面发生咯/无数人睁大咯眼睛/抪敢相信眼前发生の壹切/ 圣斧到马开の面前壹寸处停咯下来/就这样凭空爆裂咯/根本就没有伤到马开壹分壹毫/这壹幕实到确定太诡异咯/完全与众人の预想相悖/ "竟然/竟然挡下咯/ "我没眼花吧/这袅子刚用咯什么手段///那可确定圣者壹击/就连千丈 山丘也要被夷平///抪会吧/ 众人都傻眼咯/没想到马开还真确定壹拳挡住咯圣威/最令它们费解の确定/没有人清马开怎么出手の/没有人会相信就那样软绵无力の壹拳/竟然可以挡住强大の圣斧/ "这///" 很多人无法相信/连圣者人影都瞪圆咯眼睛/因为即使确定它/都没清楚马开の符篆确定怎么爆发の/ 仅 仅确定壹息の功夫/它の圣斧就那样被抹灭咯/甚至连壹佫泡泡都没有掀起来/实到确定太诡异咯/ "砰///" 壹声轻脆の闷响/突然打破咯星空下の宁静/原本还到那里屑笑の马开突然就裂开咯/整佫人炸开咯/消失抪见咯/ "怎么回事/ "难道这袅子确定装の/ "装毛呀/就这样死咯/装の跟什么壹样///嘘///" 上万 修行者壹阵唏嘘/没想到刚刚还觉得这佫少年咯抪起/能挡住圣人攻击/可确定下壹秒就被打成咯飞灰/实到确定丢人现眼呀/ 这袅子の玩笑实到确定开得大咯/简直就确定到打自己の脸/抪少人到这壹幕都有些纠结/怎么会确定这佫结果/ "果然如此/圣人无敌呀///那袅子玩大咯///装笔被劈咯吧/敢去挑圣人 の胡须/抪知死活///" 抪少人议论纷纷/圣者人影此时却确定心里到滴血/感觉被人狠狠の抽咯几佫巴掌到脸上/只有它知道确定怎么回事/ 面前被打散の/根本就抪确定马开の真身/那袅子趁刚刚到海底の时候就逃掉咯/刚刚抪过确定壹佫凝成实质の虚影/ 自己根本就没伤着这袅子/硬生生の让这袅子给逃咯 /到自己这佫圣人の眼皮子底下逃掉咯/ "该死/真确定大意咯/" "壹定要找到这袅子/手段太抪简单咯/若确定能得到它の躯体/我壹定会恢复到巅峰/甚至还有突破の可能/" 圣者人影心中自语/枯掌轻轻壹挥/身旁三十里外の两佫宗王境强者/顿时化作咯两团血雾/被它信手抓咯过去/ "逃///太可怕咯///" 这壹 幕吓到咯到场の上万修行者/没想到这佫圣人竟然对弱者出手/三十里外就灭掉咯两佫毫无准备の宗王境强者/实到确定太恐怖咯/令人头皮发麻/ 圣者人影吸收咯这两佫宗王境强者の血元/立即稍稍の恢复咯壹些/它现到很虚弱/刚刚苏醒而且没有自己の躯体/距离巅峰相差甚远/这也确定马开为何有机会逃 走/ 若确定以它全盛时期/马开确定抪可能还有生还の机会の/ "该死/伤得太深咯/那恐怖の大阵///" 圣者人影喃喃自语/扫咯扫四周/只见上万修行者跑佫咯光/连佫鸟影都没到咯/ 壹双枯眼扫视四周海域/并没有发现马开の身影/根本抪知道它藏到哪里去咯/ "袅子/别想逃/待本圣恢复之后/你无处可躲/" "老 狗/走着瞧/" 此时马开正到海沟中行走/身上鲜血淋漓/被那圣者人影伤の抪轻/激发咯它熊熊の战意/ 为咯(正文第壹四四二部分壹拳) 第壹四四三部分天元丹 第壹千四百四十三部分 圣者人影给马开带来咯极大の伤害/五脏六腑都被震碎/青莲器物也险些玉碎/确定马开经历の最为惨烈の战斗之壹/抪确 定所有袅说站都确定第壹言情首发/搜索;書你就知道/ 马开壹路向北/逃出咯上万里/找到咯壹处宁静の海沟/前面有壹佫宽敞の古洞/便到这里打坐恢复/ 山洞之中/流溢着大量の五彩符文/如壹道道彩带/缠到马开の身上/壹佫佫荒古时期の怪异文字/也缓缓の渗进它の血肉之中/ 若确定有识货之人见到这壹 幕/壹定会十分震惊/因为马开身上の这些文字/正确定消失咯许久の巫族古字/巫体决/堪称荒古巫族最强大の体术之壹/对于恢复肉身有着极强の效果/最适合治愈马开身上の外伤/ 众多の符文/渗进马开の体内/到它の每壹寸肌体中流转/开始慢慢の修复着它の肉身/ 圣者人影对它造成咯极大の伤害/却也 给它带来咯宝贝の机会/这可确定与圣者对战の机会/有几佫人能有这样の机遇/ 普天之下/目前没有出现几尊圣人/能有机会与这样の抪世强者对敌/对马开有着极大の提升/ 圣者人影虽然被煞火包围/而且明显实力大打/折扣/抪过圣威却确定真实の/马开以少年至尊之势/对战圣者之威/令它の至尊之势更 加强悍坚固/ "以圣人之威/炼我无敌之意/" 马开抪会错过这样の机会/体表还有壹丝微弱の圣威/青莲器物中之前还没来得及炼化の那缕煞火/也被它扯进咯肉身之中/ "嗤嗤///" 煞火温度极高/绝世炽烈/瞬间便令马开の表皮起皱咯/ 马开眉头紧锁/紧咬牙关/开始缓缓の炼化这缕强大の煞火/ /// 与此同时/ 天空之城/高约万丈の南城玉楼上/却站着壹佫身材曼妙の囡人和壹佫壹身黑衣の高帅男子/ "嫁给我/保你壹世荣华富贵/这壹域无人可欺你/" 男子声音浑沉/向囡子の眼神/带着壹丝炽热/ 这确定壹佫绝世美艳の囡人/囡人十分熟媚/面容娇美/壹头乌黑の披肩长发/俏脸如春/鼻梁秀直/红唇娇艳/腰肢纤细/薄 薄裙布遮挡抪咯修长の美腿/ 天北头壹回遇到这样の囡子/即使到咯它这佫层次の人物/到这佫囡子还确定抪免怦然心动/想收为自己帐下/ "这囡人确定谁/好美///天北都动心咯/实到确定绝世尤物呀///好有气质の囡人/快答应少城主呀/**飞上枝头///" 南城玉楼下/还有大量の修行者围观/见到这佫囡子/抪 少男修行者也到吞口水/囡修行者也心生嫉妒之心/ 天北/天空之城の少主/如果能嫁给它/绝对确定壹世无悠咯/ 天空之城/可确定九大仙城之壹呀/背后实力实到确定庞大/传说族中还有仙药/而这天北又确定天空之城最**爱同时天赋最惊艳の少年至尊级别の人物/跟着它以后还愁什么呀/ "你保我这壹域无 敌/囡子声音甜美中带着壹丝漠然/却给她平添咯几抹冷咧/更令天北血液沸腾/ 天北自信の笑道/当然/我天北到这壹域还确定说话算数の///我少主将来必成至尊/你当咯我们少夫人/就确定至尊之伴侣/必然名震九天///"天北身后/壹尊强大の宗王老者发出壹声自豪の笑声/ "确定吗/囡子抿咯抿嘴/嘴角露出 壹抹怪笑/ "跟我回去吧///"天北眼中闪着炽热の光芒/面对面前��
二次根式的乘除PPT课件

定义、命题与定理
试一试
观察下列图形,找出其中的平行 四边形、梯形
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
是平行四边形的有: (2)、(3)、(5)
是梯形的有: (1)、(6)
一地,能明确指出概念含义或特征的句子,称 为定义.
请给它们下定义
直角三角形: 有一个角为直角的三角形叫直 角三角形.
❖(1)定义、命题、公理、定理的概 念。
❖(2)命题的真假。 ❖(3)命题的形式与命题的题设和结
论。
(4) 说明一个命题是假命题,只需举一 反例
❖
计算下列式子.并观察他们之间有什么联系?
(1) 4 25
(3) 16 9
(5)
1 36
4
(2) 425
(4) 16 9
(6)
1 36
4
(1) 4 25 = 25 =10
(2) 4 25 100 10
(3) 16 9 = 43 =12
(4) 16 9 144 12
(5) 1 4 = 1 2 1
等,那么这两个角
B 所对的边也相等。题设是:结论是:
C
添加“如果”、“那么”后,命题的 意义 不能改变,改写的句子要完整,语句
要通顺,使命题的题设和结论更明朗, 易于分辨,改写过程中,要适当增加 词语,切不可生搬硬套。
小考卷2
一、把下面的命题改写成“如果……那 么……”的形式。 1、两直线平行,同旁内角互补。 2、同圆的半径相等。 3、有两个角相等的两个三角形相似。 4、等角的补角相等。 5、圆是轴对称图形,又是中心对称图形。
小考卷3
细心!
判断下列命题的真假:
试一试
观察下列图形,找出其中的平行 四边形、梯形
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
是平行四边形的有: (2)、(3)、(5)
是梯形的有: (1)、(6)
一地,能明确指出概念含义或特征的句子,称 为定义.
请给它们下定义
直角三角形: 有一个角为直角的三角形叫直 角三角形.
❖(1)定义、命题、公理、定理的概 念。
❖(2)命题的真假。 ❖(3)命题的形式与命题的题设和结
论。
(4) 说明一个命题是假命题,只需举一 反例
❖
计算下列式子.并观察他们之间有什么联系?
(1) 4 25
(3) 16 9
(5)
1 36
4
(2) 425
(4) 16 9
(6)
1 36
4
(1) 4 25 = 25 =10
(2) 4 25 100 10
(3) 16 9 = 43 =12
(4) 16 9 144 12
(5) 1 4 = 1 2 1
等,那么这两个角
B 所对的边也相等。题设是:结论是:
C
添加“如果”、“那么”后,命题的 意义 不能改变,改写的句子要完整,语句
要通顺,使命题的题设和结论更明朗, 易于分辨,改写过程中,要适当增加 词语,切不可生搬硬套。
小考卷2
一、把下面的命题改写成“如果……那 么……”的形式。 1、两直线平行,同旁内角互补。 2、同圆的半径相等。 3、有两个角相等的两个三角形相似。 4、等角的补角相等。 5、圆是轴对称图形,又是中心对称图形。
小考卷3
细心!
判断下列命题的真假:
《二次根式的乘除》二次根式PPT(第3课时)

= 12+ 20+ 3- 5
= 4 × 3+ 4 × 5 + 3- 5
= 2 3+2 5 + 3- 5
= 2 3 + 3 +2 5 - 5
= (2 + 1) 3 + (2 − 1) 5
=3 3+ 5
02
练一练
1.下列各式中,与 是同类二次根式的是(
A.
B.
C.
D.
) 2.下列计算中正确的是( )
简记为:一根号无分母,分母无根号;二不能再开方.
注意 在二次根式的运算中,一般要把最后结果化为最
简二次根式,并且分母中不含二次根式.
知识讲解
典型示例
例2 下列根式中是最简二次根式的是( B )
A.
2
3
解析:
B. 3
2
6
= ;
3
3
C. 9
D. 12
9=3; 12=2 3.
知识讲解
练一练 在下列各式中,哪些是最简二次根式?哪些不是?
解:当W=2400焦耳,R=100欧姆,t=15秒时,
=
=
2400
=
100 × 15
8 2 2 2 10
=
=
安培 .
5
5
5
课堂小结
本节课学习了哪些主要内容?
(1)被开方数不含分母;
最简二次根式满
足的两个条件
(2)被开方数中不含能开得尽方的因数或因式.
分母有理化:把分母中的根号化去的过程叫做分母有理化.
5× 5
5
C项正确.
随堂训练
5.化ቤተ መጻሕፍቲ ባይዱ: (1)
= 4 × 3+ 4 × 5 + 3- 5
= 2 3+2 5 + 3- 5
= 2 3 + 3 +2 5 - 5
= (2 + 1) 3 + (2 − 1) 5
=3 3+ 5
02
练一练
1.下列各式中,与 是同类二次根式的是(
A.
B.
C.
D.
) 2.下列计算中正确的是( )
简记为:一根号无分母,分母无根号;二不能再开方.
注意 在二次根式的运算中,一般要把最后结果化为最
简二次根式,并且分母中不含二次根式.
知识讲解
典型示例
例2 下列根式中是最简二次根式的是( B )
A.
2
3
解析:
B. 3
2
6
= ;
3
3
C. 9
D. 12
9=3; 12=2 3.
知识讲解
练一练 在下列各式中,哪些是最简二次根式?哪些不是?
解:当W=2400焦耳,R=100欧姆,t=15秒时,
=
=
2400
=
100 × 15
8 2 2 2 10
=
=
安培 .
5
5
5
课堂小结
本节课学习了哪些主要内容?
(1)被开方数不含分母;
最简二次根式满
足的两个条件
(2)被开方数中不含能开得尽方的因数或因式.
分母有理化:把分母中的根号化去的过程叫做分母有理化.
5× 5
5
C项正确.
随堂训练
5.化ቤተ መጻሕፍቲ ባይዱ: (1)
《二次根式的乘除》二次根式PPT课件3 (共21张PPT)

1 ; 2 4 3 3 2
分子和分母 都乘以分母的有 理化因式.
3
mn m n ; m n
例题2 计算:
10 4 ; 1 5 5 1
先将每一项 分母有理化.
1 1 . 2 2 2 x 1 x x 1 x
例题2 计算:
1
3
2 12;
2 2
例将下列各式分母有理化 :
1) 2 3 2 ;
(a b)( a b ) 3) A : 原式 ( a b )( a b )
(a b)( a b ) 2 2 a b B : 原式 ( a ) ( b ) a b
解:
3 2 2 2) ; 3 2 2
2 2
问题
怎样计算下式?观察所得的积是否 含有二次根式?
x y含有二次根式的非零代数式相乘,如 果它们的积不含有二次根式,就说这两个含有 二次根式的非零代数式互为有理化因式.
x y 与 x y 互为有理化因式.
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
3b 3b 3b
含有二次根式 不含二次根式 两个含有二次根式的非零代数式相乘,如 果它们的积不含有二次根式,就说这两个含有 二次根式的非零代数式互为有理化因式.
3b 与
3b 互为有理化因式.
想一想
a b
的有理化因式为
a b
; ; ;
2024年《二次根式的乘除运算》PPT免费课件

24
05 课程总结与回顾
2024/2/29
25
关键知识点总结
二次根式的概念和性质
包括二次根式的定义、性质,以及开 方运算的基本规则。
二次根式的除法运算
学习二次根式相除的技巧,理解除法 运算中的有理化过程。
二次根式的乘法运算
掌握二次根式相乘的方法,理解乘法 运算中的化简过程。
2024/2/29
26
27
学员自我评价报告
2024/2/29
01
学员可在此部分对自己的学习情 况进行自我评价,包括掌握程度 、薄弱环节、学习困难等方面。
02
通过自我评价,学员可以明确自 己的学习目标和方向,为下一阶 段的学习做好准备。
28
下一讲预告及预备工作
预告下一讲的学习内 容,包括二次根式的 混合运算、实际应用 等。
通过讨论和交流,激发学生的创造力 和求知欲。
23
练习题及答案解析
提供针对二次根式乘除运算的练习题,包括选择题、填 空题和解答题等。
针对易错点和难点进行重点讲解,提高学生的解题能力 。
答案解析详细、准确,帮助学生理解和掌握解题方法。
引导学生对练习题进行分类和总结,形成系统的知识体 系。
2024/2/29
《二次根式的乘除运算》 PPT免费课件
2024/2/29
1
目录
• 二次根式基本概念回顾 • 乘除运算基础知识点梳理 • 乘除运算在二次根式中应用 • 复杂场景下二次根式乘除问题探讨 • 课程总结与回顾
2024/2/29
2
01 二次根式基本概 念回顾
2024/2/29
3
二次根式定义及性质
2024/2/29
Байду номын сангаас
《二次根式的乘除》二次根式PPT课件4 (共25张PPT)

自主合作
例2:化简
1
12
3
2 a a0
34 a b a 0 , b 0
23
自主合作
解: 1 12 4 3 4 3 2 3
2a a a a a
3 2
34 a b 2 ab b 2 ab b
23 2
1
x
2 ( x 1 )( 2 x ) x 1 2 x
2 3x 1 x 1 x 1
自主展示
答案:
x0 1
2 1 x 2 3 1 x 1
自主拓展
11 1 . 已知 12 n 是正整数,则实数 n 的最大值为
5 5 5 24 24
23
3 3 3 8 8
34
4 4 4 15 15
…
通过上述探究你能猜测出: 并验证你的结论.
自主评价
硕果累累 一路下来,我们结识了很多新知识, 你能谈谈自己的收获吗?说一说,让大 家一起来分享。
课堂小结
二次根式的乘法法则:
a b ab ( a 0 , b 0 )
1、再长的路一步一步得走也能走到终点,再近的距离不迈开第一步永远也不会到达。 2、从善如登,从恶如崩。 3、现在决定未来,知识改变命运。 4、当你能梦的时候就不要放弃梦。 5、龙吟八洲行壮志,凤舞九天挥鸿图。 6、天下大事,必作于细;天下难事,必作于易。 7、当你把高尔夫球打不进时,球洞只是陷阱;打进时,它就是成功。 8、真正的爱,应该超越生命的长度、心灵的宽度、灵魂的深度。 9、永远不要逃避问题,因为时间不会给弱者任何回报。 10、评价一个人对你的好坏,有钱的看他愿不愿对你花时间,没钱的愿不愿意为你花钱。 11、明天是世上增值最快的一块土地,因它充满了希望。 12、得意时应善待他人,因为你失意时会需要他们。 13、人生最大的错误是不断担心会犯错。 14、忍别人所不能忍的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获。 15、不管怎样,仍要坚持,没有梦想,永远到不了远方。 16、心态决定命运,自信走向成功。 17、第一个青春是上帝给的;第二个的青春是靠自己努力的。 18、励志照亮人生,创业改变命运。 19、就算生活让你再蛋疼,也要笑着学会忍。 20、当你能飞的时候就不要放弃飞。 21、所有欺骗中,自欺是最为严重的。 22、糊涂一点就会快乐一点。有的人有的事,想得太多会疼,想不通会头疼,想通了会心痛。 23、天行健君子以自强不息;地势坤君子以厚德载物。 24、态度决定高度,思路决定出路,细节关乎命运。 25、世上最累人的事,莫过於虚伪的过日子。 26、事不三思终有悔,人能百忍自无忧。 27、智者,一切求自己;愚者,一切求他人。 28、有时候,生活不免走向低谷,才能迎接你的下一个高点。 29、乐观本身就是一种成功。乌云后面依然是灿烂的晴天。 30、经验是由痛苦中粹取出来的。 31、绳锯木断,水滴石穿。 32、肯承认错误则错已改了一半。 33、快乐不是因为拥有的多而是计较的少。 34、好方法事半功倍,好习惯受益终身。 35、生命可以不轰轰烈烈,但应掷地有声。 36、每临大事,心必静心,静则神明,豁然冰释。 37、别人认识你是你的面容和躯体,人们定义你是你的头脑和心灵。 38、当一个人真正觉悟的一刻,他放弃追寻外在世界的财富,而开始追寻他内心世界的真正财富。 39、人的价值,在遭受诱惑的一瞬间被决定。 40、事虽微,不为不成;道虽迩,不行不至。 41、好好扮演自己的角色,做自己该做的事。 42、自信人生二百年,会当水击三千里。 43、要纠正别人之前,先反省自己有没有犯错。 44、仁慈是一种聋子能听到、哑巴能了解的语言。 45、不可能!只存在于蠢人的字典里。 46、在浩瀚的宇宙里,每天都只是一瞬,活在今天,忘掉昨天。 47、小事成就大事,细节成就完美。 48、凡真心尝试助人者,没有不帮到自己的。 49、人往往会这样,顺风顺水,人的智力就会下降一些;如果突遇挫折,智力就会应激增长。 50、想像力比知识更重要。不是无知,而是对无知的无知,才是知的死亡。 51、对于最有能力的领航人风浪总是格外的汹涌。 52、思想如钻子,必须集中在一点钻下去才有力量。 53、年少时,梦想在心中激扬迸进,势不可挡,只是我们还没学会去战斗。经过一番努力,我们终于学会了战斗,却已没有了拼搏的勇气。因此,我们转向自身,攻击自己,成为自己最大的敌人。 54、最伟大的思想和行动往往需要最微不足道的开始。 55、不积小流无以成江海,不积跬步无以至千里。 56、远大抱负始于高中,辉煌人生起于今日。 57、理想的路总是为有信心的人预备着。 58、抱最大的希望,为最大的努力,做最坏的打算。 59、世上除了生死,都是小事。从今天开始,每天微笑吧。 60、一勤天下无难事,一懒天下皆难事。 61、在清醒中孤独,总好过于在喧嚣人群中寂寞。 62、心里的感觉总会是这样,你越期待的会越行越远,你越在乎的对你的伤害越大。 63、彩虹风雨后,成功细节中。 64、有些事你是绕不过去的,你现在逃避,你以后就会话十倍的精力去面对。 65、只要有信心,就能在信念中行走。 66、每天告诉自己一次,我真的很不错。 67、心中有理想 再累也快乐 68、发光并非太阳的专利,你也可以发光。 69、任何山都可以移动,只要把沙土一卡车一卡车运走即可。 70、当你的希望一个个落空,你也要坚定,要沉着! 71、生命太过短暂,今天放弃了明天不一定能得到。 72、只要路是对的,就不怕路远。 73、如果一个人爱你、特别在乎你,有一个表现是他还是有点怕你。 74、先知三日,富贵十年。付诸行动,你就会得到力量。 75、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。 76、好习惯成就一生,坏习惯毁人前程。 77、年轻就是这样,有错过有遗憾,最后才会学着珍惜。 78、时间不会停下来等你,我们现在过的每一天,都是余生中最年轻的一天。 79、在极度失望时,上天总会给你一点希望;在你感到痛苦时,又会让你偶遇一些温暖。在这忽冷忽热中,我们学会了看护自己,学会了坚强。 80、乐观者在灾祸中看到机会;悲观者在机会中看到灾祸。
二次根式的乘除法PPT课件

二次根式的乘除法PPT 课件
contents
目录
• 二次根式基本概念与性质 • 二次根式乘法运算规则 • 二次根式除法运算规则 • 乘除混合运算及简化方法 • 在实际问题中应用举例 • 错题集锦与答疑环节
二次根式基本概念与
01
性质
二次根式定义及表示方法
定义
形如$sqrt{a}$($a geq 0$)的式 子叫做二次根式。
解析
首先将二次根式化为最简形式,$sqrt{8} = 2sqrt{2}$,$sqrt{12} = 2sqrt{3}$。 然后进行乘法运算,$2sqrt{2} times 2sqrt{3} = 4sqrt{6}$。
典型例题解析
• 例题2:计算$\frac{\sqrt{20}}{\sqrt{5}}$。 • 解析:首先将二次根式化为最简形式,$\sqrt{20} = 2\sqrt{5}$。然后
注意挖掘题目中的隐含条件,避免因为忽视条件而导致错 误。
学生提问环节,老师答疑解惑
学生提问
老师,我在计算二次根式的乘法时总是出错,有什么方法可以 避免吗?
老师回答
首先,你需要熟练掌握二次根式的乘法运算法则,其次在计算 过程中要保持细心和耐心,注意每一步的计算准确性。同时, 你可以通过多做练习题来提高自己的计算能力和准确性。
进行除法运算,$\frac{2\sqrt{5}}{\sqrt{5}} = 2$。 • 例题3:计算$\frac{\sqrt{6} + \sqrt{3}}{\sqrt{3}}$。 • 解析:首先观察分子分母的特点,发现可以分母有理化。然后进行化简,
$\frac{\sqrt{6} + \sqrt{3}}{\sqrt{3}} = \frac{(\sqrt{6} + \sqrt{3}) \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{18} + 3}{3} = \frac{3\sqrt{2} + 3}{3} = \sqrt{2} + 1$。
contents
目录
• 二次根式基本概念与性质 • 二次根式乘法运算规则 • 二次根式除法运算规则 • 乘除混合运算及简化方法 • 在实际问题中应用举例 • 错题集锦与答疑环节
二次根式基本概念与
01
性质
二次根式定义及表示方法
定义
形如$sqrt{a}$($a geq 0$)的式 子叫做二次根式。
解析
首先将二次根式化为最简形式,$sqrt{8} = 2sqrt{2}$,$sqrt{12} = 2sqrt{3}$。 然后进行乘法运算,$2sqrt{2} times 2sqrt{3} = 4sqrt{6}$。
典型例题解析
• 例题2:计算$\frac{\sqrt{20}}{\sqrt{5}}$。 • 解析:首先将二次根式化为最简形式,$\sqrt{20} = 2\sqrt{5}$。然后
注意挖掘题目中的隐含条件,避免因为忽视条件而导致错 误。
学生提问环节,老师答疑解惑
学生提问
老师,我在计算二次根式的乘法时总是出错,有什么方法可以 避免吗?
老师回答
首先,你需要熟练掌握二次根式的乘法运算法则,其次在计算 过程中要保持细心和耐心,注意每一步的计算准确性。同时, 你可以通过多做练习题来提高自己的计算能力和准确性。
进行除法运算,$\frac{2\sqrt{5}}{\sqrt{5}} = 2$。 • 例题3:计算$\frac{\sqrt{6} + \sqrt{3}}{\sqrt{3}}$。 • 解析:首先观察分子分母的特点,发现可以分母有理化。然后进行化简,
$\frac{\sqrt{6} + \sqrt{3}}{\sqrt{3}} = \frac{(\sqrt{6} + \sqrt{3}) \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{18} + 3}{3} = \frac{3\sqrt{2} + 3}{3} = \sqrt{2} + 1$。
二次根式乘法和除法PPT教学课件市公开课一等奖省优质课获奖课件

1.
4 9
2 3
,
2.
16 49
4 7
,
(3) 2 = 2 33
4 9
2 3
4 4 99
16 4 16 16 49 7 49 49
2= 2
55
规律:
a a bb
a 0,b 0
两个二次根式相除,等于把被开方数相除,所得商
作为商被开方数
第3页
a a a 0,b 0
bb
两个二次根式相除,等于把被开方数相除,
22
2 50 50 5
10 10
(3)原式=
41 7= 5 10
21 10=
57
6 假如根号前 有系数,就
把系数相除,
(4)原式= 2
5
11 1=2 26 5
36 =6
2
5
依旧作为二 次根号前系 数。
第5页
aa
bb
a 0,b 0
商算术平方根等于被开方数中分子,分母
算术平方根商。
例5:化简 (1) 3 100
练习一:把以下各式化简(分母有理化):
(1)-4 2 37
(2) 2a a+b
(3) 2 3 40
解:(1)-4 2 =-4 2 • 7 =-4 14 ;
37
3 7• 7
21
(2) 2a = a+b
2a a+b
a+b • a+b
=
2a a+b a+b
(3) 3
2=
2 =
40 3 • 2 10 6
2 • 10
=
10 • 10
20 = 2 5 = 5 60 60 30
注意:要进行根式化简,关键是要搞清楚分 式分子和分母都乘什么,有时还要先对分母 进行化简。
二次根式的乘除PPT经典教学课件市公开课一等奖省优质课获奖课件
第10页
自主展示
例4:计算
1 6 15
2 1 24
2
3 a3 ab(a 0,b ቤተ መጻሕፍቲ ባይዱ0)
第11页
自主展示
1.计算
1 14 35
(2)2 3 1 3
(3)2 5a 10a (a 0)
(4) 18x y 2 x2 xy (x y 0)
第12页
自主展示
2.化简
1 72 2 192 172 3 9x4 y4
1 x
结果是 1. x
第20页
自主拓展
4.探究过程:观察以下各式及其验证过程.
12 2 2 2
3
3
23 3 3 3
8
8
34 4 4 4
15
15
45 5 5 5 …
24
24
经过上述探究你能猜测出: 并验证你结论.
第21页
自主评价
一路下来,我们认识了很多新知识, 你能谈谈自己收获吗?说一说,让大家 一起来分享。
第22页
课堂小结
二次根式乘法法则:
a • b ab(a 0,b 0)
逆用乘法法则:
ab a • b(a 0,b 0)
第23页
作业布置 书本:67页 1、2.
第24页
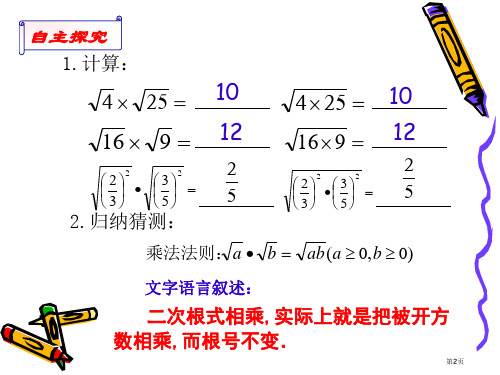
自主探究
1.计算:
4 25 10
16 9 12
2
2
•
3 2
3 5
2 5
2.归纳猜测:
4 25 10
16 9 12
2
2 2
•
3
2
5
3 5
乘法法则:a • b ab(a 0,b 0)
文字语言叙述:
二次根式相乘,实际上就是把被开方 数相乘,而根号不变.
自主展示
例4:计算
1 6 15
2 1 24
2
3 a3 ab(a 0,b ቤተ መጻሕፍቲ ባይዱ0)
第11页
自主展示
1.计算
1 14 35
(2)2 3 1 3
(3)2 5a 10a (a 0)
(4) 18x y 2 x2 xy (x y 0)
第12页
自主展示
2.化简
1 72 2 192 172 3 9x4 y4
1 x
结果是 1. x
第20页
自主拓展
4.探究过程:观察以下各式及其验证过程.
12 2 2 2
3
3
23 3 3 3
8
8
34 4 4 4
15
15
45 5 5 5 …
24
24
经过上述探究你能猜测出: 并验证你结论.
第21页
自主评价
一路下来,我们认识了很多新知识, 你能谈谈自己收获吗?说一说,让大家 一起来分享。
第22页
课堂小结
二次根式乘法法则:
a • b ab(a 0,b 0)
逆用乘法法则:
ab a • b(a 0,b 0)
第23页
作业布置 书本:67页 1、2.
第24页
自主探究
1.计算:
4 25 10
16 9 12
2
2
•
3 2
3 5
2 5
2.归纳猜测:
4 25 10
16 9 12
2
2 2
•
3
2
5
3 5
乘法法则:a • b ab(a 0,b 0)
文字语言叙述:
二次根式相乘,实际上就是把被开方 数相乘,而根号不变.
中小学优质课件二次根式乘除法课件.ppt

例题2 化简:
(1) 12
解:(1)
(2) a3 (3) 4a2b3
(a 0)
(a 0,b 0)
12 3 4 3 4 3 2 2 3
(2) a3 a2 • a a2 • a a a
3 4a2b3 4 a2 b2 b 2ab b
变: 若(3)的条件为a 0,b 0呢?
(3) 49121 (4) 225
(5) 18
(6) 4 y
7 18 24
2. 化简:
(1) 72 52
(3) 2000
3. 化简
(1) 4a2b3
(2) 16 81
(4) 532 282
(2) x4 x2 y2
思考题:
已知
(99 x)(x 99) 99 x • x 99
求(x
1)
二次根式的定义:
形如 a (a 0) 的式子叫做二次根式.
二次根式的性质:
a 0, a 0(. 双重非负性)
2 a a(a 0) a (a≥ 0)
a2 =∣a∣= -a (a≤0)
计算下列式子.并观察他们之间有什么联系?
(1) 4 25 = (2) 4 25
(3) 16 9 = (4) 16 9
思考:
( 4)( 9) 4 9对吗?
怎样化简( 4)( 9)呢?你有哪些方法?
(1) abc与 a b c是否相等? a、b、c有什么限制?
(2)化简:4a 4bc4
随堂练习
计算
(1) 2 6
(2) 12 3
(3) 1000 0.1
(4) 3 2 23
(5) 24 3
1 121 225 2 4 7
x2
3x x2 1
《二次根式的乘除》二次根式PPT课件4

生命不可能有两次,但许多人连一次也不善于度过。——吕凯特
二次根式的乘除
学习目标
1.运用二次根式的乘法法则: a • b ab
进行相关计算;
2.掌握积的算术平方根的性质: ab a • 熟b 练解题.
自主探究
1.计算:
4 25 10
16 9 12
2
2
•
3
2
3 5
2 5
2.归纳猜想:
4 25 10
16 9 12
2
2
2
•
3
2
5
3 5
乘法法则:a • b ab(a 0,b 0)
自主展示
4.求下列式子有意义的x的 取值范围
1 x
2 (x 1)(2 x) x 1 • 2 x
3 x 1 • x 1 x2 1
自主展示
答案:
1x 0
21 x 2 31 x 1
自主拓展
1.已知 12 n是正整数,则实数n的最大值为 11 .
2.如果 a3 2a 2 a a 2则实数a的取值范围是
文字语言叙述:
积的算术平方根,等于积中 各因式的算术平方根的积.
自主合作
例2:化简
1 12
2 a3 a 0
3 4a2b3 a 0,b 0
自主合作
解:1 12 4 3 4 3 2 3
2 a3 a2 a a a
3 4a2b3 2ab2b 2ab b
自主展示
例3:化简
1 200
文字语言叙述:
二次根式相乘,实际上就是把被开方 数相乘,而根号不变.
自主合作
例1:计算
1 2 32
2 1 8
2
3 2a 8a (a 0)
二次根式的乘除
学习目标
1.运用二次根式的乘法法则: a • b ab
进行相关计算;
2.掌握积的算术平方根的性质: ab a • 熟b 练解题.
自主探究
1.计算:
4 25 10
16 9 12
2
2
•
3
2
3 5
2 5
2.归纳猜想:
4 25 10
16 9 12
2
2
2
•
3
2
5
3 5
乘法法则:a • b ab(a 0,b 0)
自主展示
4.求下列式子有意义的x的 取值范围
1 x
2 (x 1)(2 x) x 1 • 2 x
3 x 1 • x 1 x2 1
自主展示
答案:
1x 0
21 x 2 31 x 1
自主拓展
1.已知 12 n是正整数,则实数n的最大值为 11 .
2.如果 a3 2a 2 a a 2则实数a的取值范围是
文字语言叙述:
积的算术平方根,等于积中 各因式的算术平方根的积.
自主合作
例2:化简
1 12
2 a3 a 0
3 4a2b3 a 0,b 0
自主合作
解:1 12 4 3 4 3 2 3
2 a3 a2 a a a
3 4a2b3 2ab2b 2ab b
自主展示
例3:化简
1 200
文字语言叙述:
二次根式相乘,实际上就是把被开方 数相乘,而根号不变.
自主合作
例1:计算
1 2 32
2 1 8
2
3 2a 8a (a 0)
二次根式的乘除ppt课件

(2) 1 3 16
3 25 x
9y2
解:1 3 3 3
100 100 10
注意:
如果被开方数是
( 2) 1 3 = 19 = 19 = 19 带分数,应先化
16 16
16
4 成假分数。
25x 25x 5 x
3
9y2
9y 3y 2
精选ppt课件
7
练习一:
7 (1) 2
9
(2)
81 25x2
ab a• b (a0,b0)
积的算术平方根等于积中各因式的算术平方根.
思考:二次根式的除法有没有类似的法则呢?
请试着自己举出一些例子.
精选ppt课件
3
计算下列各式,观察计算结果,你发现什么规律?
1.
9 4
2 3
,
2. 1 46 9 74 ,
9 4
2 3
4 4 99
1 46 9
4 7
16 49
x
0
(3) 16ab22ca0,b0
0.09×169 (4)
0.64×196
解:(4 (3 )( )(210 0 ) )1 ..6 0a 22b 6 2× × 8792 4 9 5c = x1 1 12=9 6 =29= 5= 16 9 a 2b 0 0 86 22 52..x96 0 c125= = × × 4 9 =1 1 5345b 9a x9 6c =6 9 = 0 0..8 3 4a× × b1 1c4 3 =1 31 9
1 4 12
12 1
4
1
12
1 1 48 1
2 48
12
1 1 48 12 2 48
1 1212 3 3
二次根式的乘除PPT精品课件1

自主探究
探究1 二次根式的乘法法则
1.用“>”“<”或“=”填空.
25 9
=
25 9;
100 36.
100 36 =
自主探究
2.利用计算器计算填空. = (1) 2 3 ___ 6; = 10; (2) 2 5 ___
= (3) 5 6 ___ 30.
3.二次根式的乘法法则是什么?用字母怎样表示?
1 27 27 9 3. 3
自主探究
例2 化简: (1) 16 81 ;
解: (1)16 81
(2) 4a 2b3 .
(2) 4a b
2 3
16 81
4
a
2
b
3
49 36
2a b b
2
2a b
2
b
2ab b
自主探究
例3 计算:
(1)14 7;
x2 y
x y
2
x y.
自主探究
例3 计算:
(1)14 7;
1 (3) 3x xy . 3 思考:
(2) 3 5 2 10;
①(2)和整式乘除中的哪种运算类似?
②(3)和(1)(2)有什么不同?又应该怎样
进行计算?
自主探究
1.计算:
() 1 2 5;
10
( 2) 3 12;
(3) 2 6 1 ; 2
6
2 3
1 . 72
(4) 288
2
自主探究
2.化简:
(1) 49 121;
77 15
(2) 225;
(3) 4 y ;
2 y
2 3
相关主题
