空间向量与几何高考题汇总
高考数学空间向量与立体几何选择题

高考数学空间向量与立体几何选择题1. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)2. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)3. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)4. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)5. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)6. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)7. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)8. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)9. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)10. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)11. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)12. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)13. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)14. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)D. \(-1\)15. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)16. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)17. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?B. \(-3\)C. \(1\)D. \(-1\)18. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)19. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)20. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)21. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)22. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)23. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)24. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)25. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)C. \(-\vec{a}\)D. \(-\vec{b}\)26. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)27. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)28. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)29. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)30. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)31. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)32. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)33. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)34. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)35. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)36. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)C. \(2\)D. \(-2\)37. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)38. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)39. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)40. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)41. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)42. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)43. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)44. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)C. \(1\)D. \(-1\)45. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)46. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)47. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?A. \(3\)B. \(-3\)D. \(-1\)48. 题目:已知向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=-2\),且向量\(\vec{c}\)与\(\vec{a}\)和\(\vec{b}\)的夹角分别为30°和60°,则\(\vec{c}\cdot\vec{a}\)的值是多少?A. \(1\)B. \(-1\)C. \(2\)D. \(-2\)49. 题目:若向量\(\vec{a}\)和\(\vec{b}\)满足\(\vec{a}\cdot\vec{b}=0\),则下列哪个向量不可能与\(\vec{a}\)和\(\vec{b}\)共线?A. \(\vec{a}\)B. \(\vec{b}\)C. \(-\vec{a}\)D. \(-\vec{b}\)50. 题目:若两个向量\(\vec{a}\)和\(\vec{b}\)的夹角为120°,则\(\vec{a}\cdot\vec{b}\)的值是多少?B. \(-3\)C. \(1\)D. \(-1\)。
空间向量与立体几何高考真题
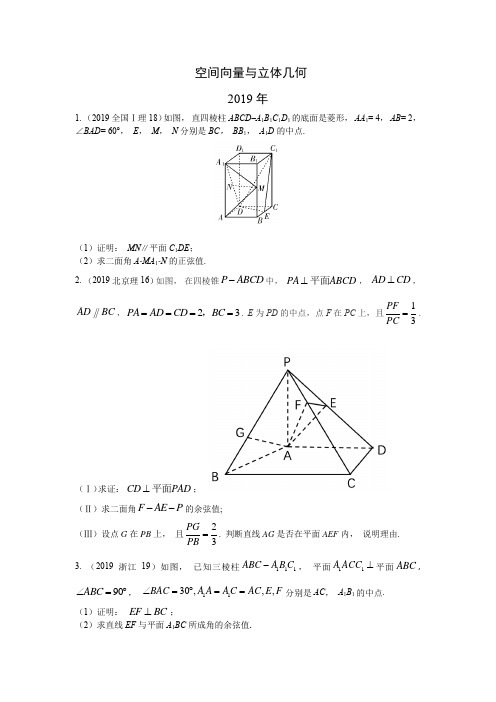
空间向量与立体几何2019年 1. (2019全国Ⅰ理18)如图,直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形, AA 1= 4, AB = 2,∠BAD = 60°, E , M , N 分别是BC , BB 1, A 1D 的中点.(1)证明: MN ∥平面C 1DE ; (2)求二面角A -MA 1-N 的正弦值.2. (2019北京理16)如图, 在四棱锥中, , , , . E 为PD 的中点, 点F 在PC 上, 且.(Ⅰ)求证: ;(Ⅱ)求二面角的余弦值;(Ⅲ)设点G 在PB 上, 且. 判断直线AG 是否在平面AEF 内, 说明理由. 3. (2019浙江19)如图, 已知三棱柱, 平面平面,, 分别是AC , A 1B 1的中点. (1)证明: ;(2)求直线EF 与平面A 1BC 所成角的余弦值.P ABCD -PA ABCD ⊥平面AD CD ⊥ADBC 2PA AD CD BC ====,13PF PC =CD PAD ⊥平面F AE P --23PG PB =111ABC A B C -11A ACC ⊥ABC 90ABC ∠=︒1130,,,BAC A A AC AC E F ∠=︒==EF BC ⊥4. (2019江苏16)如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB= BC.求证:(1)A1B1∥平面DEC1;(2)BE⊥C1E.5. (2019全国Ⅲ理19)图1是由矩形ADEB、R t△ABC和菱形BFGC组成的一个平面图形,其中AB= 1,BE= BF= 2,∠FBC= 60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B-CG-A的大小.6. (2019全国Ⅱ理17)如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明: BE ⊥平面EB 1C 1;(2)若AE = A 1E , 求二面角B –EC –C 1的正弦值.7. (2019北京理16)如图, 在四棱锥中, , ,, . E 为PD 的中点, 点F 在PC 上, 且.(Ⅰ)求证: ;(Ⅱ)求二面角的余弦值;(Ⅲ)设点G 在PB 上, 且. 判断直线AG 是否在平面AEF 内, 说明理由. 8. (2019浙江19)如图, 已知三棱柱, 平面平面,, 分别是AC , A 1B 1的中点. (1)证明: ;(2)求直线EF 与平面A 1BC 所成角的余弦值.P ABCD -PA ABCD ⊥平面AD CD ⊥ADBC 2PA AD CD BC ====,13PF PC =CD PAD ⊥平面F AE P --23PG PB =111ABC A B C -11A ACC ⊥ABC 90ABC ∠=︒1130,,,BAC A A AC AC E F ∠=︒==EF BC ⊥9. (2019全国Ⅲ理19)图1是由矩形ADEB、R t△ABC和菱形BFGC组成的一个平面图形,其中AB= 1,BE= BF= 2,∠FBC= 60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B-CG-A的大小.10. (2019全国Ⅱ理17)如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE= A1E,求二面角B–EC–C1的正弦值.11. (全国Ⅰ理18)如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1= 4,AB= 2,∠BAD= 60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明: MN ∥平面C 1DE ; (2)求二面角A -MA 1-N 的正弦值.12. (2019北京理16)如图, 在四棱锥中, , , , . E 为PD 的中点, 点F 在PC 上, 且.(Ⅰ)求证: ; (Ⅱ)求二面角的余弦值;(Ⅲ)设点G 在PB 上, 且. 判断直线AG 是否在平面AEF 内, 说明理由. 13. (2019天津理17)如图, 平面, , .(Ⅰ)求证: 平面;(Ⅱ)求直线与平面所成角的正弦值;(Ⅲ)若二面角的余弦值为, 求线段的长. P ABCD -PA ABCD ⊥平面AD CD ⊥ADBC 2PA AD CD BC ====,13PF PC =CD PAD ⊥平面F AE P --23PG PB =AE ⊥ABCD ,CF AE AD BC ∥∥,1,2AD AB AB AD AE BC ⊥====BF ∥ADE CE BDE E BD F --13CF。
历届数学高考中的试题空间向量与立体几何
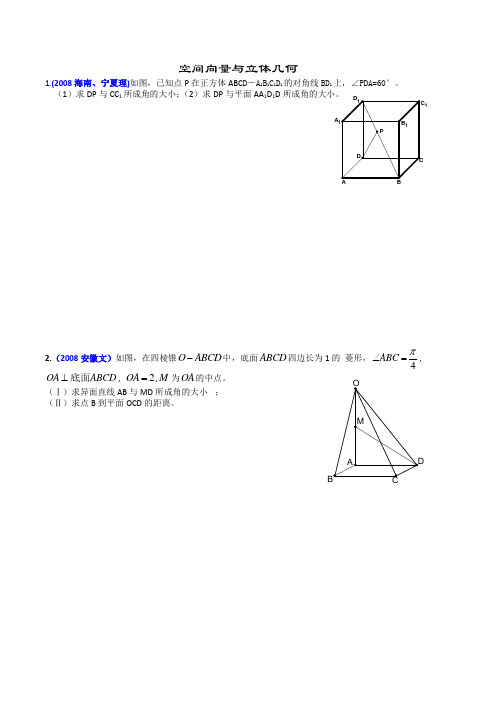
空间向量与立体几何1.(2008海南、宁夏理)如图,已知点P 在正方体ABC D -A 1B 1C 1D 1的对角线BD 1上,∠PDA=60°。
(1)求DP 与CC 1所成角的大小;(2)求DP 与平面AA 1D 1D2.(2008安徽文)如图,在四棱锥O ABCD -中,底面ABCD 四边长为1的 菱形,4ABC π∠=,OA ABCD ⊥底面, 2OA =,M 为OA 的中点。
(Ⅰ)求异面直线AB 与MD 所成角的大小; (Ⅱ)求点B 到平面OCD 的距离。
1A3.(2005湖南文、理)如图1,已知ABCD 是上、下底边长分别为2和6,高为3的等腰梯形,将它沿对称轴OO 1折成直二面角,如图2。
(Ⅰ)证明:AC ⊥BO 1; (Ⅱ)求二面角O -AC -O 1的大小。
4.(2007安徽文、理)如图,在六面体1111D C B A ABCD -中,四边形ABCD 是边长为2的正方形,四边形1111D C B A 是边长为1的正方形,⊥1DD 平面1111D C B A ,⊥1DD 平面ABCD ,DD 1=2。
(Ⅰ)求证:11C A 与AC 共面,11D B 与BD 共面. (Ⅱ)求证:平面;1111BDD B ACC A 平面⊥ (Ⅲ)求二面角C BB A --1的大小.A BC D O O 1 A B O C O 1 D5.(2007海南、宁夏理)如图,在三棱锥S ABC -中,侧面SAB 与侧面SAC 均为等边三角形,90BAC ∠=°,O 为BC 中点. (Ⅰ)证明:SO ⊥平面ABC ; (Ⅱ)求二面角A SC B --的余弦值.6.(2007四川理)如图,PCBM 是直角梯形,∠PCB =90°,PM ∥BC ,PM =1,BC =2,又AC =1,∠ACB =120°,AB ⊥PC ,直线AM 与直线PC 所成的角为60°. (Ⅰ)求证:平面PAC ⊥平面ABC ; (Ⅱ)求二面角B AC M --的大小; (Ⅲ)求三棱锥MAC P -的体积.OS B AC7.(2006全国Ⅰ卷文、理)如图,1l 、2l 是互相垂直的异面直线,MN 是它们的公垂线段.点A 、B 在1l 上,C 在2l 上,AM MB MN ==。
(完整word版)高三数学空间向量专题复习附答案

一、利用向量处理平行与垂直问题例1、 在直三棱柱111C B A ABC -中,090=∠ACB , 030=∠BAC ,M A A BC ,6,11==是1CC 得中点。
求证:AM B A ⊥1练习:棱长为a 的正方体ABCD —A 1B 1C 1D 1中,在棱DD 1上是否存在点P 使B 1D ⊥面P AC ?例2 如图,已知矩形ABCD 和矩形ADEF 所在平面互相垂直,点N M ,分别在对角线AE BD ,上,且AE AN BD BM 31,31==,求证://MN 平面CDE练习1、在正方体1111D C B A ABCD -中,E,F 分别是BB 1,,CD 中点,求证:D 1F ⊥平面ADE2、如图,在底面是菱形的四棱锥P —ABCD 中, ︒=∠60ABC ,,2,a PD PB a AC PA ====点E 在PD 上,且PE :ED = 2: 1.在棱PC 上是否存在一点F, 使BF ∥平面AEC?证明你的结论.二、利用空间向量求空间的角的问题例1 在正方体1111D C B A ABCD -中,E 1,F 1分别在A 1B 1,,C 1D 1上,且E 1B 1=41A 1B 1,D 1F 1=41D 1C 1,求BE 1与DF 1所成的角的大小。
例2 在正方体1111D C B A ABCD -中, F 分别是BC 的中点,点E 在D 1C 1上,且=11E D 41D 1C 1,试求直线E 1F 与平面D 1AC例3 在正方体1111D C B A ABCD -中,求二面角1C BD A --的大小。
zx1CFD CBA例4 已知E,F分别是正方体1111DCBAABCD-的棱BC和CD的中点,求:(1)A1D与EF所成角的大小;(2)A1F与平面B1EB所成角的大小;(3)二面角BBDC--11的大小。
三、利用空间向量求空间的距离的问题例1 直三棱柱AB C-A1B1C1的侧棱AA1,底面ΔAB C求点B1到平面A1B C的距离。
高考数学压轴专题(易错题)备战高考《空间向量与立体几何》全集汇编及解析

新高考数学《空间向量与立体几何》练习题一、选择题1.已知三棱锥P ABC -中,PA PB PC ==,APB BPC CPA ∠>>∠,PO ⊥平面ABC 于O ,设二面角P AB O --,P BC O --,P CA O --分别为,,αβγ,则( ) A .αβγ>>B .γβα>>C .βαγ>>D .不确定【答案】A【解析】【分析】 D 为AB 中点,连接,DP DO ,故PD AB ⊥,计算sin cos 2POAPB a α=∠,sin cos 2PO CPB a β=∠,sin cos 2PO CPA a γ=∠,得到大小关系. 【详解】如图所示:设PA PB PC a ===,D 为AB 中点,连接,DP DO ,故PD AB ⊥, PO ⊥平面ABC ,故PDO ∠为二面角P AB O --的平面角.cos 2APB PD a ∠=,sin cos 2PO PO APB PD a α==∠, 同理可得: sin cos 2PO CPB a β=∠,sin cos 2PO CPA a γ=∠, APB BPC CPA ∠>∠>∠,故sin sin sin αβγ>>,故αβγ>>. 故选:A .【点睛】本题考查了二面角,意在考查学生的计算能力和空间想象能力. 2.已知某几何体的三视图如图所示,则该几何体的体积为A.273B.276C.274D.272【答案】D【解析】【分析】先还原几何体,再根据锥体体积公式求结果.【详解】几何体为一个三棱锥,高为33333,,所以体积为1127=33333=322V⨯⨯⨯,选D.【点睛】(1)解决本类题目的关键是准确理解几何体的定义,真正把握几何体的结构特征,可以根据条件构建几何模型,在几何模型中进行判断;(2)解决本类题目的技巧:三棱柱、四棱柱、三棱锥、四棱锥是常用的几何模型,有些问题可以利用它们举特例解决或者学会利用反例对概念类的命题进行辨析.3.鲁班锁(也称孔明锁、难人木、六子联方)起源于古代中国建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.如图1,这是一种常见的鲁班锁玩具,图2是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )A .8(6623)+B .6(8823)+C .8(632)+D .6(8832)+【答案】A【解析】【分析】该鲁班锁玩具可以看成是一个正方体截去了8个正三棱锥所余下来的几何体,然后按照表面积公式计算即可.【详解】 由题图可知,该鲁班锁玩具可以看成是一个棱长为222+的正方体截去了8个正三棱锥所余下来的几何体,且被截去的正三棱锥的底面边长为22,则该几何体的表面积为2116(222)42282322S ⎡=⨯+-⨯+⨯⨯⎢⎣8(623)=+. 故选:A.【点睛】本题考查数学文化与简单几何体的表面积,考查空间想象能力和运算求解能力.4.如图,棱长为1的正方体1111ABCD A B C D -,O 是底面1111D C B A 的中心,则O 到平面11ABC D 的距离是( )A .12B .24C .22D .32【答案】B【解析】【分析】如图建立空间直角坐标系,可证明1A D ⊥平面11ABC D ,故平面11ABC D 的一个法向量为:1DA u u u u r ,利用点到平面距离的向量公式即得解.【详解】如图建立空间直角坐标系,则:1111(,,1),(0,0,1),(1,0,0),(1,1,0),(0,1,1)22O D A B C 111(,,0)22OD ∴=--u u u u r 由于AB ⊥平面111,ADD A AD ⊂平面11ADD A1AB A D ∴⊥,又11AD A D ⊥,1AB AD I1A D ∴⊥平面11ABC D 故平面11ABC D 的一个法向量为:1(1,0,1)DA =u u u u rO ∴到平面11ABC D 的距离为: 1111||224||2OD DA d DA ⋅===u u u u r u u u u r u u u u r 故选:B【点睛】本题考查了点到平面距离的向量表示,考查了学生空间想象,概念理解,数学运算的能力,属于中档题.5.已知ABC V 的三个顶点在以O 为球心的球面上,且22cos A =,1BC =,3AC =,三棱锥O ABC -的体积为146,则球O 的表面积为( ) A .36πB .16πC .12πD .163π 【答案】B【解析】【分析】 根据余弦定理和勾股定理的逆定理即可判断三角形ABC 是直角三角形,根据棱锥的体积求出O 到平面ABC 的距离,利用勾股定理计算球的半径OA ,得出球的面积.【详解】由余弦定理得22229122cos 26AB AC BC AB A AB AC AB +-+-===g ,解得22AB =, 222AB BC AC ∴+=,即AB BC ⊥.AC ∴为平面ABC 所在球截面的直径.作OD ⊥平面ABC ,则D 为AC 的中点,11114221332O ABC ABC V S OD OD -∆==⨯⨯⨯⨯=Q g , 7OD ∴=. 222OA OD AD ∴=+=.2416O S OA ππ∴=⋅=球.故选:B .【点睛】本题考查了球与棱锥的关系,意在考查学生对这些知识的理解掌握水平,判断ABC ∆的形状是关键.6.如图,网格纸上小正方形的边长为1,粗实(虚)线画出的是某多面体的三视图,则该多面体的体积为( )A .64B .643C .16D .163【答案】D【解析】根据三视图知几何体是:三棱锥D ABC -为棱长为4的正方体一部分,直观图如图所示:B 是棱的中点,由正方体的性质得,CD ⊥平面,ABC ABC ∆的面积12442S =⨯⨯=,所以该多面体的体积1164433V =⨯⨯=,故选D.7.三棱柱111ABC A B C -中,底面边长和侧棱长都相等,1160BAA CAA ︒∠=∠=,则异面直线1AB 与1BC 所成角的余弦值为( )A.3 B.6C.4 D【答案】B【解析】【分析】设1AA c =u u u v v ,AB a =u u u v v ,AC b =u u u v v ,根据向量线性运算法则可表示出1AB u u u v 和1BC u u u u v;分别求解出11AB BC ⋅u u u v u u u u v 和1AB u u u v ,1BC u u u u v ,根据向量夹角的求解方法求得11cos ,AB BC <>u u u v u u u u v ,即可得所求角的余弦值.【详解】设棱长为1,1AA c =u u u v v ,AB a =u u u v v ,AC b =u u u v v由题意得:12a b ⋅=v v ,12b c ⋅=v v ,12a c ⋅=v v 1AB a c =+u u u v v v Q ,11BC BC BB b a c =+=-+u u u u v u u u v u u u v v v v()()22111111122AB BC a c b a c a b a a c b c a c c ∴⋅=+⋅-+=⋅-+⋅+⋅-⋅+=-++=u u u v u u u u v v v v v v v v v v v v v v v v 又1AB ===u u u v1BC ===u u u u v111111cos ,6AB BC AB BC AB BC ⋅∴<>===⋅u u u v u u u u v u u u v u u u u v u u u v u u u u v 即异面直线1AB 与1BC 本题正确选项:B【点睛】 本题考查异面直线所成角的求解,关键是能够通过向量的线性运算、数量积运算将问题转化为向量夹角的求解问题.8.已知四棱锥S ABCD -的底面是正方形,侧棱长均相等,E 是线段AB 上的点(不含端点).设SE 与BC 所成的角为α,SE 与平面ABC D 所成的角为β,二面角S-AB-C 的平面角为γ,则( )A .αβγ≤≤B .βαγ≤≤C .a βγ≤≤D .γβα≤≤【答案】C【解析】【分析】 根据题意,分别求出SE 与BC 所成的角α、SE 与平面ABC D 所成的角β、二面角S-AB-C 的平面角γ的正切值,由正四棱锥的线段大小关系即可比较大小.【详解】四棱锥S ABCD -的底面是正方形,侧棱长均相等,所以四棱锥为正四棱锥,(1)过E 作//EF BC ,交CD 于F ,过底面中心O 作ON EF ⊥交EF 于N ,连接SN ,取AB 中点M ,连接OM ,如下图(1)所示:则tan SN SN NE OMα==;(2)连接,OE 如下图(2)所示,则tan SO OEβ=;(3)连接OM ,则tan SO OMγ= ,如下图(3)所示:因为,,SN SO OE OM ≥≥所以tan tan tan αγβ≥≥,而,,αβγ均为锐角,所以,αγβ≥≥故选:C.【点睛】本题考查了异面直线夹角、直线与平面夹角、平面与平面夹角的求法,属于中档题.9.如图,平面四边形ABCD 中,1AB AD CD ===,2BD =,BD CD ⊥,将其沿对角线BD 折成四面体A BCD '-,使平面A BD '⊥平面BCD ,若四面体A BCD '-的顶点在同一个球面上,则该球的表面积为( )A .3πB 3C .4πD 3 【答案】A【解析】【分析】 设BC 的中点是E ,连接DE ,由四面体A′BCD 的特征可知,DE 即为球体的半径.【详解】设BC 的中点是E ,连接DE ,A′E ,因为AB =AD =1,BD 2由勾股定理得:BA ⊥AD又因为BD ⊥CD ,即三角形BCD 为直角三角形所以DE 为球体的半径32DE = 23432S ππ== 故选A【点睛】 求解球体的表面积、体积的问题,其实质是求球体的半径,解题的关键是构造关于球体半径R 的方程式,构造常用的方法是构造直角三角形,再利用勾股定理建立关于半径R 的方程.10.设A ,B ,C ,D 是同一个球面上四点,ABC ∆是斜边长为6的等腰直角三角形,若三棱锥D ABC -体积的最大值为27,则该球的表面积为( )A .36πB .64πC .100πD .144π 【答案】C【解析】【分析】由题意画出图形,求出三棱锥D ABC -的外接球的半径,代入表面积公式求解.【详解】解:如图,ABC ∆是斜边BC 长为6的等腰直角三角形,则当D 位于直径的端点时,三棱锥D ABC -体积取最大值为27,由AB AC =,AB AC ⊥,6BC =,可得斜边BC 上的高3AE =,32AB AC ==, 由1132322732DE ⨯⨯⨯⨯=,解得9DE =, 则21AE EF DE==. ∴球O 的直径为10DE EF +=,则球O 的半径为11052⨯=. ∴该球的表面积为245100S ππ=⨯=.故选C .【点睛】本题考查多面体外接球表面积的求法,考查数形结合的解题思想方法,是中档题.11.设,为两条不同的直线,,为两个不同的平面,下列命题中,正确的是( )A .若,与所成的角相等,则B .若,,则 C .若,,则 D .若,,则 【答案】C【解析】试题分析:若,与所成的角相等,则或,相交或,异面;A 错. 若,,则或,B 错. 若,,则正确. D .若,,则 ,相交或,异面,D 错考点:直线与平面,平面与平面的位置关系12.四棱锥P ABCD -所有棱长都相等,M 、N 分别为PA 、CD 的中点,下列说法错误的是( )A .MN 与PD 是异面直线B .//MN 平面PBCC .//MN ACD .MN PB ⊥【答案】C【解析】【分析】 画出图形,利用异面直线以及直线与平面平行的判定定理,判断选项A 、B 、C 的正误,由线线垂直可判断选项D .【详解】由题意可知四棱锥P ABCD -所有棱长都相等,M 、N 分别为PA 、CD 的中点,MN 与PD 是异面直线,A 选项正确;取PB 的中点为H ,连接MH 、HC ,四边形ABCD 为平行四边形,//AB CD ∴且AB CD =,M Q 、H 分别为PA 、PB 的中点,则//MH AB 且12MH AB =, N Q 为CD 的中点,//CN MH ∴且CN MH =,则四边形CHMN 为平行四边形, //MN CH ∴,且MN ⊄平面PBC ,CH ⊂平面PBC ,//MN ∴平面PBC ,B 选项正确;若//MN AC ,由于//CH MN ,则//CH AC ,事实上AC CH C ⋂=,C 选项错误; PC BC =Q ,H 为PB 的中点,CH PB ∴⊥,//MN CH Q ,MN PB ∴⊥,D 选项正确.故选:C .【点睛】本题考查命题的真假的判断与应用,涉及直线与平面的平行与垂直的位置关系的判断,是中档题.13.已知底面是等腰直角三角形的三棱锥P -ABC 的三视图如图所示,俯视图中的两个小三角形全等,则( )A .PA ,PB ,PC 两两垂直B .三棱锥P -ABC 的体积为83 C .||||||6PA PB PC ===D .三棱锥P -ABC 的侧面积为35【答案】C 【解析】 【分析】 根据三视图,可得三棱锥P -ABC 的直观图,然后再计算可得.【详解】 解:根据三视图,可得三棱锥P -ABC 的直观图如图所示,其中D 为AB 的中点,PD ⊥底面ABC .所以三棱锥P -ABC 的体积为114222323⨯⨯⨯⨯=, 2AC BC PD ∴===,2222AB AC BC ∴=+=,||||||2DA DB DC ∴===()22||||||226,PA PB PC ∴===+=222PA PB AB +≠Q ,PA ∴、PB 不可能垂直,即,PA ,PB PC 不可能两两垂直, 1222222PBA S ∆=⨯=Q ()22161252PBC PAC S S ∆∆==-=Q∴三棱锥P -ABC 的侧面积为2522故正确的为C.故选:C.【点睛】 本题考查三视图还原直观图,以及三棱锥的表面积、体积的计算问题,属于中档题.14.某四面体的三视图如图所示,正视图,俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为( )A .22B .23C .4D .26【答案】B【解析】 解:如图所示,该几何体是棱长为2的正方体中的三棱锥P ABC - , 其中面积最大的面为:1232232PAC S V =⨯⨯= . 本题选择B 选项.点睛:三视图的长度特征:“长对正、宽相等,高平齐”,即正视图和侧视图一样高、正视图和俯视图一样长,侧视图和俯视图一样宽.若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法.15.已知四面体P ABC -的外接球的球心O 在AB 上,且PO ⊥平面ABC ,23AC AB =,若四面体P ABC -的体积为32,求球的表面积( )A .8πB .12πC .83πD .123π【答案】B【解析】【分析】 依据题意作出图形,设四面体P ABC -的外接球的半径为R ,由题可得:AB 为球的直径,即可求得:2AB R =,3AC R =, BC R =,利用四面体P ABC -的体积为32列方程即可求得3R =,再利用球的面积公式计算得解。
(完整word版)高三数学空间向量专题复习附答案

一、利用向量处理平行与垂直问题例1、 在直三棱柱111C B A ABC -中,090=∠ACB , 030=∠BAC ,M A A BC ,6,11==是1CC 得中点。
求证:AM B A ⊥1练习:棱长为a 的正方体ABCD —A 1B 1C 1D 1中,在棱DD 1上是否存在点P 使B 1D ⊥面P AC ?例2 如图,已知矩形ABCD 和矩形ADEF 所在平面互相垂直,点N M ,分别在对角线AE BD ,上,且AE AN BD BM 31,31==,求证://MN 平面CDE练习1、在正方体1111D C B A ABCD -中,E,F 分别是BB 1,,CD 中点,求证:D 1F ⊥平面ADE2、如图,在底面是菱形的四棱锥P —ABCD 中, ︒=∠60ABC ,,2,a PD PB a AC PA ====点E 在PD 上,且PE :ED = 2: 1.在棱PC 上是否存在一点F, 使BF ∥平面AEC?证明你的结论.二、利用空间向量求空间的角的问题例1 在正方体1111D C B A ABCD -中,E 1,F 1分别在A 1B 1,,C 1D 1上,且E 1B 1=41A 1B 1,D 1F 1=41D 1C 1,求BE 1与DF 1所成的角的大小。
例2 在正方体1111D C B A ABCD -中, F 分别是BC 的中点,点E 在D 1C 1上,且=11E D 41D 1C 1,试求直线E 1F 与平面D 1AC例3 在正方体1111D C B A ABCD -中,求二面角1C BD A --的大小。
zx1CFD CBA例4 已知E,F分别是正方体1111DCBAABCD-的棱BC和CD的中点,求:(1)A1D与EF所成角的大小;(2)A1F与平面B1EB所成角的大小;(3)二面角BBDC--11的大小。
三、利用空间向量求空间的距离的问题例1 直三棱柱AB C-A1B1C1的侧棱AA1,底面ΔAB C求点B1到平面A1B C的距离。
2024年高考数学复习大题全题型专练:空间向量与立体几何(解析版)

专题9立体几何中的探索性问题1.(2022·全国·高考真题)如图,直三棱柱111ABC A B C 的体积为4,1A BC 的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1A C 的中点,1AA AB ,平面1A BC 平面11ABB A ,求二面角A BD C 的正弦值.【答案】(2)2【解析】【分析】(1)由等体积法运算即可得解;(2)由面面垂直的性质及判定可得BC 平面11ABB A ,建立空间直角坐标系,利用空间向量法即可得解.(1)在直三棱柱111ABC A B C 中,设点A 到平面1A BC 的距离为h ,则1111111111433333A A BC A A ABC A ABC AB BC C C B V S h h V S A A ,解得h所以点A 到平面1A BC ;(2)取1A B 的中点E ,连接AE ,如图,因为1AA AB ,所以1AE A B ,又平面1A BC 平面11ABB A ,平面1A BC ∩平面111ABB A A B ,且AE 平面11ABB A ,所以AE ⊥平面1A BC ,在直三棱柱111ABC A B C 中,1BB 平面ABC ,由BC 平面1A BC ,BC 平面ABC 可得AE BC ,1BB BC ,又1,AE BB 平面11ABB A 且相交,所以BC 平面11ABB A ,所以1,,BC BA BB 两两垂直,以B 为原点,建立空间直角坐标系,如图,由(1)得AE 12AA AB,1A B 2BC ,则 10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以1A C 的中点 1,1,1D ,则 1,1,1BD , 0,2,0,2,0,0BA BC ,设平面ABD 的一个法向量 ,,m x y z ,则020m BD x y z m BA y ,可取 1,0,1m ,设平面BDC 的一个法向量 ,,n a b c ,则020m BD a b c m BC a,可取 0,1,1n r ,则1cos ,2m n m n m n ,所以二面角A BD C2.(2022·浙江·高考真题)如图,已知ABCD 和CDEF 都是直角梯形,//AB DC ,//DC EF ,5AB ,3DC ,1EF ,60BAD CDE ,二面角F DC B 的平面角为60 .设M ,N 分别为,AE BC的中点.(1)证明:FN AD ;(2)求直线BM 与平面ADE 所成角的正弦值.【答案】(1)证明见解析;【解析】【分析】(1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点G 、H ,由平面知识易得FC BC ,再根据二面角的定义可知,60BCF ,由此可知,FN BC ,FN CD ,从而可证得FN 平面ABCD ,即得FN AD ;(2)由(1)可知FN 平面ABCD ,过点N 做AB 平行线NK ,所以可以以点N 为原点,NK ,NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N xyz ,求出平面ADE 的一个法向量,以及BM ,即可利用线面角的向量公式解出.(1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点交于点G 、H .∵四边形ABCD 和EFCD 都是直角梯形,//,//,5,3,1AB DC CD EF AB DC EF ,60BAD CDE ,由平面几何知识易知,2,90DG AH EFC DCF DCB ABC ,则四边形EFCG 和四边形DCBH 是矩形,∴在Rt EGD 和Rt DHA,EG DH ∵,DC CF DC CB ,且CF CB C ,∴DC 平面,BCF BCF 是二面角F DC B 的平面角,则60BCF ,∴BCF △是正三角形,由DC 平面ABCD ,得平面ABCD 平面BCF ,∵N 是BC 的中点, FN BC ,又DC 平面BCF ,FN 平面BCF ,可得FN CD ,而BC CD C ,∴FN 平面ABCD ,而AD 平面ABCD FN AD .(2)因为FN 平面ABCD ,过点N 做AB 平行线NK ,所以以点N 为原点,NK ,NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N xyz ,设(3,(1,0,3)A B D E,则32M,33,,(2,(2BM AD DE设平面ADE 的法向量为(,,)n x y z 由00n AD n DE,得20230x x z,取n ,设直线BM 与平面ADE 所成角为 ,3.(2022·青海·海东市第一中学模拟预测(理))如图,在三棱柱111ABC A B C 中,11222A C AA AB AC BC ,160BAA.(1)证明:平面ABC 平面11AA B B .(2)设P 是棱1CC 的中点,求AC 与平面11PA B 所成角的正弦值.【答案】(1)证明见解析(2)4【解析】【分析】(1)设2AB,由余弦定理求出1A B 1A B AB ,1A B BC ,进而证明出线面垂直,面面垂直;(2)建立空间直角坐标系,利用空间向量求解线面角的正弦值.(1)设2AB .在四边形11AA B B 中,∵12AA AB ,160BAA ,连接1A B ,∴由余弦定理得2221112cos6012A B AA AB AA AB,即1A B ∵22211A B AB AA ,∴1A B AB .又∵22211A B BC A C ,∴1A B BC ,AB BC B ,∴1A B 平面ABC ,∵1A B 平面11AA B B ,∴平面ABC 平面11AA B B .(2)取AB 中点D ,连接CD ,∵AC BC ,∴CD AB ,由(1)易知CD 平面11AA B B,且CD 如图,以B 为原点,分别以射线BA ,1BA 为x ,y 轴的正半轴,建立空间直角坐标系B -xyz,则(2,0,0)A,1A,C,1(B,1(C,P .11(2,0,0)A B,1(0,A P ,设平面11PA B 的法向量为(,,)n x y z ,则11100n A B n A P,得200x,令1y ,则取(0,1,1)n,(AC u u u r,||cos ,4||||AC n AC n AC n ,AC 与平面11PA B4.(2022·内蒙古·赤峰红旗中学松山分校模拟预测(理))如图,在四棱锥P —ABCD 中,底面ABCD 为正方形,PD 底面ABCD ,M 为线段PC 的中点,PD AD ,N 为线段BC 上的动点.(1)证明:平面MND 平面PBC(2)当点N 在线段BC 的何位置时,平面MND 与平面PAB 所成锐二面角的大小为30°?指出点N 的位置,并说明理由.【答案】(1)证明见解析(2)点N 在线段BC 的中点【解析】【分析】(1)由PD 底面ABCD ,可得PD BC ,而CD BC ,可证得BC 平面PCD ,从而得BC DM ,而DM PC ,所以DM 平面PBC ,再由面面垂直的判定定理可得结论,(2)设1PD AD ,以D 为原点,以,,DA DC DP 所在的直线分别为,,x y z 轴建立空间直角坐标系,然后利用空间向量求解即可(1)证明:因为PD 底面ABCD ,BC 底面ABCD ,所以PD BC ,因为CD BC ,CD PD D ∩,所以BC 平面PCD ,因为DM 平面PCD ,所以BC DM ,因为四边形ABCD 为正方形,PD AD ,所以PD CD ,因为在PDC △中,PD CD ,M 为线段PC 的中点,所以DM PC ,因为PC BC C ,所以DM 平面PBC ,因为DM 平面DMN ,所以平面MND 平面PBC ,(2)当点N 在线段BC 的中点时,平面MND 与平面PAB 所成锐二面角的大小为30°,理由如下:因为PD 底面ABCD ,, DA DC 平面ABCD ,所以,PD DA PD DC ,因为DA DC ,所以,,DA DC DP 两两垂直,所以以D 为原点,以,,DA DC DP 所在的直线分别为,,x y z 轴建立空间直角坐标系,如图所示,设1PD AD ,则11(0,0,0),(1,0,0),(1,1,0),(0,0,1),(0,1,0),0,,22D A B P C M,设(,1,0)(01)N ,则11(1,0,1),(0,1,0),(,1,0),0,,22AP AB DN DM,设(,,)m x y z 为平面PAB 的法向量,则00m AP x z m AB y,令1x ,则=(1,0,1)m u r ,设(,,)n a b c 为平面MND 的法向量,则011022n DN a b n DM b c,令1a ,则(1,,)n ,因为平面MND 与平面PAB 所成锐二面角的大小为30°,所以cos ,2m n m n m n ,化简得24410 ,得12 ,所以当点N 在线段BC 的中点时,平面MND 与平面PAB 所成锐二面角的大小为30°5.(2022·四川·成都七中模拟预测(理))如图1,在边上为4的菱形ABCD 中,60DAB ,点M ,N 分别是边BC ,CD 的中点,1AC BD O ,AC MN G .沿MN 将CMN △翻折到PMN 的位置,连接PA ,PB ,PD ,得到如图2所示的五棱锥P ABMND .(1)在翻折过程中是否总有平面PBD 平面PAG ?证明你的结论;(2)当四棱锥P MNDB 体积最大时,求直线PB 和平面MNDB 所成角的正弦值;(3)在(2)的条件下,在线段PA 上是否存在一点Q ,使得二面角Q MN P 点Q 的位置;若不存在,请说明理由.【答案】(1)在翻折过程中总有平面PBD 平面PAG ,证明见解析(3)Q 存在且Q 为线段PA 的中点【解析】【分析】(1)证明出BD 平面PAG ,进而证明面面垂直;(2)找到当PG 平面MNDB 时,四棱锥P MNDB 体积最大,直线PB 和平面MNDB 所成角的为PBG ,求出PG ,BG PB ,从而求出PBG 的正弦值;(3)建立空间直角坐标系,利用空间向量和二面角的大小,列出方程,确定点Q 的位置(1)在翻折过程中总有平面PBD 平面PAG ,证明如下:∵点M ,N 分别是边CD ,CB 的中点,又60DAB ,∴BD MN ∥,且PMN 是等边三角形,∵G 是MN 的中点,∴MN PG ,∵菱形ABCD 的对角线互相垂直,∴BD AC ,∴MN AC ,∵AC PG G ,AC 平面PAG ,PG 平面PAG ,∴MN 平面PAG ,∴BD 平面PAG ,∵BD 平面PBD ,∴平面PBD 平面PAG .(2)由题意知,四边形MNDB 为等腰梯形,且4DB ,2MN ,1O G所以等腰梯形MNDB 的面积 242S 要使得四棱锥P MNDB 体积最大,只要点P 到平面MNDB 的距离最大即可,∴当PG 平面MNDB 时,点P 到平面MNDB此时四棱锥P MNDB 体积的最大值为133V ,直线PB 和平面MNDB 所成角的为PBG ,连接BG ,在直角三角形PBG 中,PG BG ,由勾股定理得:PB .30sin10PG PBG PB.(3)假设符合题意的点Q 存在.以G 为坐标原点,GA ,GM ,GP 所在直线分别为x 轴、y 轴、z 轴,建立如图所示空间直角坐标系,则 A , 0,1,0M , 0,1,0N , P ,由(2)知,AG PG ,又AG MN ,且MN PG G ,MN 平面PMN ,PG 平面PMN ,AG 平面PMN ,故平面PMN 的一个法向量为�1=1,0,0,设AQ AP (01 ≤≤),∵AP ,AQ ,故1 ,∴ 0,2,0NM,1,1,QM ,平面QMN 的一个法向量为 2222,,n x y z ,则20n NM ,20n QM ,即222220,10,y x y z 令21z ,所以 220,31y x211,0,1,0,313131n,则平面QMN 的一个法向量 ,0,31n ,设二面角Q MN P 的平面角为 ,则11cos 10n n n n ,解得:12 ,故符合题意的点Q 存在且Q 为线段PA 的中点.6.(2022·全国·南京外国语学校模拟预测)如图,在三棱台111ABC A B C 中,AB AC ,4AB AC ,1112A A A B ,侧棱1AA 平面ABC ,点D 是棱1CC 的中点.(1)证明:平面1BB C 平面1AB C ;(2)求二面角C BD A的正弦值.【答案】(1)证明见解析(2)15【解析】【分析】(1)先根据线面垂直的性质与判定证明1AC BB ,再根据勾股定理证明11AB BB ,进而根据线面垂直得到1BB 平面1AB C ,从而根据面面垂直的判定证明即可(2)A 为坐标原点,AB ,AC ,1AA 的所在的直线分别为x ,y ,z 轴建立空间直角坐标系,再分别求解平面,ABD CBD 的一个法向量,进而得到面面角的正弦即可(1)证明:因为1A A 平面ABC ,AC 平面ABC ,所以1AA AC ,又AB AC ,1AA AB A ∩,1AA ,AB Ì平面11ABB A ,所以AC 平面11ABB A .又1BB 平面11ABB A ,所以1AC BB .又因为1AB1BB ,所以22211AB AB BB ,所以11AB BB .又1AB AC A ∩,1AB ,AC 平面1AB C ,所以1BB 平面1AB C ,因为1BB 平面1BB C ,所以平面1BB C 平面1AB C .(2)以A 为坐标原点,AB ,AC ,1AA 的所在的直线分别为x ,y ,z 轴建立空间直角坐标系,如图所示.因为4AB AC ,111112A A A B A C ,所以 0,0,0A , 4,0,0B , 0,4,0C , 10,2,2C , 0,3,1D .设平面ABD 的一个法向量为 1111,,x n y z ,设平面CBD 的一个法向量为 2222,,n x y z ,且 4,0,0AB , 0,3,1AD ,4,4,0CB , 0,1,1CD ,因为110,0,AB n AD n 所以1110,30,x y z 令11y ,则10x ,13z ,所以 10,1,3n .又因为220,0.CB n CD n所以22220,0,x y y z 令21x ,则21y ,21z ,所以 21,1,1 n .所以12121230cos ,15n n n n n n .设二面角C BD A 的大小为,则sin 所以二面角C BD A 的正弦值为19515.7.(2022·青海·模拟预测(理))如图,在四棱锥A -BCDE 中,底面BCDE 为矩形,M 为CD 中点,连接BM ,CE 交于点F ,G 为△ABE 的重心.(1)证明://GF 平面ABC(2)已知平面ABC ⊥BCDE ,平面ACD ⊥平面BCDE ,BC =3,CD =6,当平面GCE 与平面ADE 所成锐二面角为60°时,求G 到平面ADE 的距离.【答案】(1)证明见解析【解析】(1)延长EG 交AB 于N ,连接NC ,因为G 为△ABE 的重心,所以点N 为AB 的中点,且2EG GN ,因为//CM BE ,故CMF EBF ∽,所以2EF BE CF CM,故EF EG CF GN ,故//GF NC ,而NC 平面ABC ,GF 平面ABC,故//GF 平面ABC ;(2)由题意知,平面ABC ⊥平面BCDE ,平面ABC ∩平面BCDE=BC ,DC BC ,DC 平面BCDE ,故DC 平面ABC,AC 平面ABC,则DC AC ,同理BC AC ,又,,BC DC C BC DC ∩平面BCDE,所以AC 平面BCDE ,以C 为原点,以CB,CD,CA 所在直线分别为x,y,z轴,建立空间直角坐标系,设点G 到平面BCDE 的距离为(0)t t ,则(0,0,3),(3,0,0),(3,6,0),(2,2,),(0,6,0)A t B E G t D ,故(2,2,),(3,6,0),(0,6,3),(3,0,0)CG t CE AD t DE ,设平面GCE 的法向量为111(,,)m x y z ,则00m CG m CE,即11111220360x y tz x y ,取11y ,则112,,2,z x t 即2(2,1,m t,设平面ADE 的法向量为222(,,)n x y z ,则00n AD n DE,即22263030y tz x ,取22z ,则2y t ,则(0,,2)n t ,所以4||||1cos 602||||t m n t m n,解得212,t t ,又(2,4,DG ,故点G 到平面ADE的距离为||||DG n d n 8.(2022·北京市第九中学模拟预测)如图,在四棱锥P ABCD 中,底面ABCD 是边长为2的正方形,△PAB 为正三角形,且侧面PAB ⊥底面ABCD ,M 为PD的中点.(1)求证:PB //平面ACM ;(2)求直线BM 与平面PAD 所成角的正弦值;(3)求二面角C PA D 的余弦值.【答案】(1)证明见解析;(2)32;(3)7.【解析】【分析】(1)连接BD AC N ∩,连MN ,证明//PB MN ,再利用线面平行的判定推理作答.(2)(3)取AB 中点O ,连PO ,证明PO 平面ABCD ,以点O 为原点建立空间直角坐标系,借助空间向量求线面角的正弦,二面角的余弦作答.(1)连接BD AC N ∩,连MN ,如图,正方形ABCD 中,N 为BD 的中点,而M 为PD 的中点,则//PB MN ,而MN 平面ACM ,PB 平面ACM ,所以//PB 平面ACM .(2)取AB 中点O ,连PO ,如图,正PAB △中,PO AB,因侧面PAB 底面ABCD ,侧面PAB 底面ABCD AB ,PO 侧面PAB ,则PO 平面ABCD ,在平面ABCD 内过O 作Oy AB ,则射线,,OB Oy OP 两两垂直,以点O 为原点,射线,,OB Oy OP 分别为x ,y ,z 轴非负半轴建立空间直角坐标系,则1(1,0,0),(1,0,0),(1,2,0),(),(1,2,0)2B A D P M C,3(0,2,0),()2AD AP BM ,设平面PAD 的法向量111(,,)m x y z,则111200m AD y m AP x,令11z,得(m ,设直线BM 与平面PAD 所成角为,则||sin |cos ,|222||||m BM m BM m BM ,所以直线BM 与平面PAD所成角的正弦值是2.(3)由(2)知,(2,2,0)AC u u u r ,设平面CPA 的法向量222(,,)n x y z,则22222200n AC x y n AP x ,令21z,得(n ,于是得cos ,7||||m n m n m n ,显然二面角C PA D 大小为锐角,所以二面角C PA D 的余弦值为277.9.(2022·内蒙古·海拉尔第二中学模拟预测(理))已知四棱锥S ABCD 中,四边形ABCD 为菱形,SAB SBA ,.SD AB (1)求证:ABD △是等边三角形;(2)22SA SD AD ,求SC 与平面SAD 所成角的正弦值.【答案】(1)证明见解析(2)4214【解析】【分析】(1)取AB 的中点O ,连接SO 、OD ,证明出AB 平面SDO ,可得出AB DO ,可得出AD BD ,再利用菱形的性质可证得结论成立;(2)证明出SO DO ,以点O 为坐标原点,OA 、OD 、OS 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量法可求得SC 与平面SAD 所成角的正弦值.(1)证明:取AB 的中点O ,连接SO 、OD ,因为SAB SBA ,O 为AB 的中点,则SO AB ,因为SD AB ,SO SD S ∩,AB 平面SDO ,OD ∵平面SDO ,则 OD AB ,故AD BD ,因为四边形ABCD 为菱形,则AB AD ,所以,AD AB BD ,因此,ABD △为等边三角形.(2)解:由已知2SA SB ,2AB ,则222SA SB AB ,SA SB ,O ∵为AB 的中点,所以,112SO AB ,因为ABD △是边长为2的等边三角形,则2sin33DO ,因为2SD ,则222SO DO SD ,SO DO ,因为AB 平面SDO ,以点O 为坐标原点,OA 、OD 、OS 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则 1,0,0A、 D、C 、 0,0,1S ,设平面SAD 的法向量为 ,,n x y z,AD , 1,0,1AS ,则00n AD x n AS x z,取xn,1SC,42cos ,14SC n SC n SC n .因此,SC 与平面SAD 所成角的正弦值为4214.10.(2022·广东茂名·二模)如图,四棱锥P ﹣ABCD 的底面是等腰梯形,AD ∥BC ,BC =2AD ,60ABC ,E 是棱PB 的中点,F 是棱PC 上的点,且A 、D 、E 、F四点共面.(1)求证:F 为PC 的中点;(2)若△PAD 为等边三角形,二面角P AD B 的大小为120 ,求直线BD 与平面ADFE 所成角的正弦值.【答案】(1)证明见解析(2)4【解析】【分析】(1)先由线面平行的判定定理证明AD ∥平面PBC ,再根据线面平行的性质定理即可证明EF ∥AD ,即可证明结论;(2)建立空间直角坐标系,求得相关各点坐标,求得平面ADFE 的法向量,根据向量的夹角公式即可求得答案.(1)证明:四棱锥P ﹣ABCD 中,AD ∥BC ,BC ⊂平面PBC ,∴AD ∥平面PBC .由题意A 、D 、E 、F 四点共面,平面ADFE ∩平面PBC =EF ,∴AD ∥EF ,而AD ∥BC ,∴EF ∥BC ,∵E 是棱PB 的中点,∴F 为PC 中点.(2)如图,以BC 为x 轴,连接BC 中点O 和AD 中点G ,以OG 为y 轴,过点O 作垂直于平面ABCD 的直线作为z 轴,建立如图所示空间直角坐标系,因为AB =CD ,BC =2AD ,60ABC设AD =a ,则BC =2a ,AB CD a ,所以,(,,0),((,,0),(,0,0)22222a a OG A a B a D a C a ,3(,0),(,0,0)2BD a AD a ,因为△PAD 为等边三角形,所以PG ⊥AD ,由题意知OG AD ,所以∠PGO 为二面角P AD B 的平面角,又二面角P AD B 的大小为120 ,所以120PGO ,因为PG ⊥AD ,GO ⊥AD ,,,PG GO G PG GO ∩平面PGO ,所以AD ⊥平面PGO ,过P 作PH 垂直于y 轴于点H ,因为PH ⊂平面PGO ,所以AD ⊥PH ,又PH ⊥GH ,,GH AD 平面ABCD ,GH AD G ∩,所以PH 垂直于平面ABCD ,且60PGH ,3,,4PG a PH a a GH a ,244OH OG GH a a a ,∴3,4P a,因为E ,F 分别为PB ,PC 的中点,所以33(,),(,),(0,,)282838a a E a a F a a AE a a ,设平面ADFE 的法向量为(,,)n x y z ,则00n AE n AD,所以30880ay az ax,取z =1,n ,设BD 与平面ADFE 所成角为θ,则32sin |cos ,|4a BD n ,即直线BD 与平面ADFE11.(2022·安徽省舒城中学三模(理))在四棱锥P ABCD 中,PAB △为正三角形,四边形ABCD 为等腰梯形,M 为棱AP 的中点,且2224AB AD BC CD,DM 퐴 =14퐴.(1)求证:平面ODM 平面ABCD ;(2)求直线AP 与平面PBC 所成角的正弦值.【答案】(1)证明见解析;(2)13.【解析】【分析】(1)E 为AB 中点,连接,,OM PE DE ,易得BCDE 为平行四边形,即知△ADE 为等腰三角形,进而有 OD AB ,由等边三角形性质有PE AB ,根据中位线、平行线的推论知OM AB ,再根据线面垂直的判定、面面垂直的判定证结论.(2)构建空间直角坐标系,求出直线AP 方向向量和平面PBC 的法向量,应用空间向量夹角的坐标表示求线面角的正弦值.(1)若E 为AB 中点,连接,,OM PE DE ,由//CD BE 且2CD BE ,故BCDE 为平行四边形,所以2BC DE ,又2AD 且퐴=14퐴 ,即O 为AE 中点,等腰△ADE 中OD AE ,即 OD AB ,又PAB 为正三角形,故PE AB ,因为,O M 分别为AE ,AP 中点,故//OM PE ,则OM AB ,由OM OD O ∩,,OM OD 面OMD ,故AB 面OMD ,而AB Ì面ABCD ,则平面ODM 平面ABCD ;(2)过O 作Oz 面ABCD ,由(1)可构建以O 为原点,,,OB OD Oz为,,x y z轴的空间直角坐标系,所以(1,0,0),(3,0,0),A B C,而OM OD DM,则3)2M ,所以P,故((1,0,3)AP BP CP ,若(,,)m x y z 是面PBC的一个法向量,则23030m BP x z m CP x z,令1z,则m,所以|cos ,|||||||m AP m AP m AP ,故直线AP 与平面PBC 所成角的正弦值31313.12.(2022·广东·大埔县虎山中学模拟预测)如图,在四棱台1111ABCD A B C D 中,2AB ,111A B ,四边形ABCD 为平行四边形,点E 为棱BC 的中点.(1)求证:1//D E 平面11ABB A ;(2)若四边形ABCD 为正方形,1AA 平面ABCD ,12A A AB ,求二面角1A DE C 的余弦值.【答案】(1)证明见解析;(2)23.【解析】【分析】(1)连1A B ,利用给定条件证明四边形11A D EB 为平行四边形,再利用线面平行的判定推理作答.(2)以点A 为原点建立空间直角坐标系,借助空间向量求解作答.(1)在四棱台1111ABCD A B C D 中,四边形ABCD 为平行四边形,且112AB A B ,点E 为棱BC 的中点,连1A B ,如图,则有1112A D AD BE ,11////A D AD BE ,即四边形11A D EB 为平行四边形,则11//D E A B ,又1D E 平面11ABB A ,1A B 平面11ABB A ,所以1//D E 平面11ABB A .(2)以A 为坐标原点,AB 为x 轴,AD 为y 轴,1AA 为z 轴,建立如图所示的空间直角坐标系,则 10,0,2A , 0,2,0D , 2,1,0E , 10,2,2DA , 2,1,0ED ,设平面1A DE 的一个法向量为 ,,n x y z ,则122020DA n y z ED n x y,令1x ,得 1,2,2n ,平面DEC 的一个法向量为 0,0,1m ,则22cos ,133||||m n m n m n ,显然二面角1A DE C 的平面角为钝角,所以二面角1A DE C 的余弦值为23.13.(2022·全国·模拟预测(理))如图,在四棱锥A BCDE 中,AC 平面BCDE ,AD DE ,BCE 为等边三角形,60ECD.(1)求证:DE 平面ACD ,且//BE 平面ACD .(2)已知3AC ,2BC ,求平面ADE 与平面ABE 所成锐二面角的余弦值.【答案】(1)证明见解析(2)1020【解析】【分析】(1)由线面垂直性质可得AC DE ,结合AD DE 可证得DE 平面ACD ;根据//BE CD ,由线面平行的判定可证得结论;(2)以D 为坐标原点可建立空间直角坐标系,利用二面角的向量求法可求得结果.(1)AC ∵平面BCDE ,DE 平面BCDE ,AC DE ,又AD DE ,AC AD A ∩,,AC AD 平面ACD ,DE 平面ACD ;BCE QV 为等边三角形,60BEC ,又60ECD ,//BE CD ,CD ∵平面ACD ,BE 平面ACD ,//BE 平面ACD .(2)DE ∵平面ACD ,CD 平面ACD ,DE CD ;以D 为坐标原点,,DC DE 为,x y 轴正方向,作z 轴//AC ,可建立如图所示空间直角坐标系,则 0,0,0D , 1,0,3A, B, E ,1,0,3DA, DE,3AB , 2,0,0BE ,设平面ADE 的法向量 111,,n x y z ,则111300DA n x z DE n,令11z ,则13x ,10y , 3,0,1n ;设平面ABE 的法向量 222,,m x y z ,则22223020AB m x z BE m x,令21z ,则20x,2ym;cos ,20m n m n m n , 平面ADE 与平面ABE 1020.14.(2022·浙江绍兴·模拟预测)如图,三棱台111ABC A B C 中,90ABC,111A A A B A C 2AB BC.(1)证明:111A C A B ;(2)求直线11A C 与平面1A CB 所成的角.【答案】(1)证明见解析(2)π6【解析】【分析】(1)由题,取AC 中点D ,连接1A D BD 、,11AC A C ∥,先由线线垂直证AC 面1A BD ,即可由线面垂直证1AC A B ,即可证111A C A B ;(2)分别以1DB DC DA 、、为x y 、、z 轴建立如图空间直角坐标系,即可由向量法求所求线面角.(1)由题,取AC 中点D ,连接1A D BD 、,由11A A A C ,AB BC ,则1AC A D AC BD 、,又1A D BD 、面1A BD ,故AC 面1A BD ,因为1A B 面1A BD ,故1AC A B ,又11AC A C ∥,则111A C A B ,得证;(2)由题,90ABC ,则AD BD CD ,又11A A A B ,11A D A D ,故11AA D BA D ,故1190A DB A DA .分别以1DB DC DA 、、为x y 、、z 轴建立如图空间直角坐标系,易得2,0,0B , 0,2,0C , 10,0,1,0,2,0A A , 10,2,1A C , 12,0,1A B ,0,22,0AC ,设平面1A CB 法向量 ,,n x y z ,则112020n A B x z n A C y z ,令1x ,则1,1,2n ,故221cos ,2222n AC ,故直线AC 与平面1A CB 所成的角为π6.即直线11A C 与平面1A CB 所成的角为π6.15.(2022·辽宁实验中学模拟预测)如图所示正四棱锥,2,7P ABCD AB PA(1)求证:PA BD(2)若沿侧棱将此四棱锥剪开,四个侧面向外旋转,PAD 旋转至1,P AD PCD 旋转至2P CD 如图所示,其中二面角1P AD B与二面角2P CD B 相同,当12DP DP 时,求平面1P AD 与2P CD 所成的锐二面角的余弦值【答案】(1)证明见解析(2)34【解析】【分析】(1)连接,BD AC ,交于点O ,连接PO ,PO 面ABCD ,得PO BD ,从而证得BD 平面PAC ,得线线垂直;(2)以D 为原点,DA 为x 轴,DC 为y 轴,过点D 且垂直于平面ABCD 的直线为z 轴建立空间直角坐标系,设是二面角1P AD B 大小为 ,表示出12,P P 的坐标,由向量垂直求出 ,得12,P P 的坐标,再求出平面1P AD 与平面2P CD 的一个法向量,则法向量夹角得二面角.(1)证明:连接,BD AC ,交于点O ,连接PO ,PO 面ABCD ,BD 平面ABCD ,PO BD ,又BD AC ∵,PO AC O ∩,,PO AC 平面PAC ,所以BD 平面PAC ,又PA ∵平面PAC ,BD PA .(2)以D 为原点,DA 为x 轴,DC 为y 轴,过点D 且垂直于平面ABCD 的直线为z 轴建立空间直角坐标系,设点E 为DA中点,则1PE ,设F 是BC 中点,则EF AD ,又1P E AD ,所以1PEF 是二面角1P AD B 的平面角,即1P EF ,1)P ,同理2)P 21248sin 0DP DP u u u r u u u r 解得:3cos 2,1sin 2 ,12(1,(P P��1=(1,−6,23),�퐴=(2,0,0)设1(,,)n x y z 为平面1P AD 的法向量,则10n DA ,20x ,0x ,�1⋅��1=0,60x y ,取1y,则z ∴�1=(0,1,3)��2=(−6,1,23),(0,2,0)DC ,设�2=(�,�,�)为平面2P CD 的法向量,则20n DC ,20s ,0s ,�2⋅��2=0,60m ,取1m,则t ∴�2=(1,0,3),푐��<�1,�2>==34,平面1P AD 与平面2PCD 所成的锐二面角的余弦值为34.16.(2022·福建·三明一中模拟预测)如图,四边形ABCD 为菱形,2,60AB ABC ,将ACD △沿AC 折起,得到三棱锥D ABC ,点M ,N分别为ABD △和ABC 的重心.(1)证明:CD ∥平面BMN ;(2)当三棱锥D ABC 的体积最大时,求二面角N BM D 的余弦值.【答案】(1)证明见解析(2)【解析】【分析】(1)延长BM 交AD 于点P ,延长BN 交AC 于O 点,连接PO ,证明PO CD ∥即可.(2)证明,,OC OD OB 两两垂直,以O 为坐标原点,,,OB OC OD 分别为x ,y ,z 轴建立空间直角坐标系Oxyz ,求出两个平面的法向量,利用二面角的向量公式求解即可.(1)延长BM 交AD 于点P ,延长BN 交AC 于O 点,连接PO .因为点M ,N 分别为ABD △和ABC 的重心,所以点P,O 分别为AD 和AC 的中点,所以PO CD ∥,又CD 平面BMN ,PO 平面BMN ,所以//CD 平面BMN .(2)当三棱锥D ABC 的体积最大时,点D 到底面ABC 的距离最大,即平面DAC 平面ABC ,连接DO ,因为ADC 和ABC 均为正三角形,于是,DO AC BO AC ,又平面DAC 平面ABC AC ,所以DO 平面ABC ,所以,,OC OD OB 两两垂直,以O 为坐标原点,,,OB OC OD 分别为x ,y ,z 轴建立空间直角坐标系Oxyz ,则1(0,0,0),(0,1,0),0,2O A B D P,所以11,(0,22BP BD OB OP,又二面角N BM D 即二面角O BP D ,设平面BPD 的一个法向量为(,,)n x y z ,则0,0n BP n BD可得1020y,取1z,则(1,n ,同理设平面OBP 的一个法向量为(,,)m a b c ,则00m OB m OP ,即013022b,取b,则m ,所以cos ,5||||m n m n m n ,由图可知二面角N BM D 为钝角,所以二面角N BM D的余弦值为17.(2022·浙江湖州·模拟预测)已知四棱锥P ABCD 中,底面ABCD 为等腰梯形,//AB CD ,24AB CD,AD BC ,PAB △是斜边为AP的等腰直角三角形.(1)若PC PBC 平面ABCD ;(2)若PC PD 与平面ABCD 所成的角的正弦值.【答案】(1)证明见解析;【解析】【分析】(1)根据给定条件,证明PB BC ,再利用线面垂直、面面垂直的判定推理作答.(2)作出二面角C AB P 的平面角并求出其大小,再建立空间直角坐标系,借助空间向量求解作答.(1)因PC,BC 4PB ,则有222PB BC PC ,即有PB BC ,又PB AB ,且AB BC B ,,AB BC 平面ABCD ,于是得PB 平面ABCD ,而PB 平面PBC ,所以平面PBC 平面ABCD .(2)在平面ABCD 内,过B 作直线垂直于AB ,交直线CD 于E ,有1CE ,1BE,如图,则EBP 为二面角C AB P 的平面角,AB 平面EBP ,AB PE ,于是得CE PE ,Rt PEC中,1PC CE,则PE PBE △中,PE 1BE ,4PB ,由余弦定理得2221cos 22PB BE PE PBE PB BE ,则有2π3PBE ,显然平面ABP 平面EBP ,在平面EBP 内过B 作Bz BP ,则Bz 平面ABP ,以B 为原点,分别以射线,BA BP Bz ,为x ,y ,z 轴非负半轴建立空间直角坐标系,则11(4,0,0),(1,),(3,(0,),(0,4,0)222,0,0),2A C D P B ,(4,0,0)BA ,1(1,,)22BC ,设平面ABCD 的法向量(,,)n x y z,则10240n BC x y n BA x ,令1z,得n 而93(3,,)22PD ,设PD 与平面ABCD 所成的角为,||sin |cos ,||5|||n PD n PD n PD 所以PD 与平面ABCD 所成的角的正弦值为105.18.(2022·四川·成都七中模拟预测(理))如图1,在等边ABC 中,点D ,E 分别为边AB ,AC 上的动点且满足//DE BC ,记DE BC.将△ADE 沿DE 翻折到△MDE 的位置并使得平面MDE ⊥平面DECB ,连接MB ,MC 得到图2,点N 为MC 的中点.(1)当EN ∥平面MBD 时,求λ的值;(2)试探究:随着λ值的变化,二面角B -MD -E 的大小是否改变?如果改变,请说明理由;如果不改变,请求出二面角B MD E 的正弦值大小.【答案】(1)12(2)【解析】【分析】(1)首先取MB 的中点为P ,连接DP ,PN ,再结合线面平行的性质即可得到12(2)利用空间向量法求解即可.(1)取MB 的中点为P ,连接DP ,PN ,因为MN CN ,MP BP ,所以NP ∥BC ,又DE ∥BC ,所以NP ∥DE ,即N ,E ,D ,P 四点共面,又EN ∥平面BMD ,EN ⊂平面NEDP ,平面NEDP ∩平面MBD =DP ,所以EN ∥PD ,即NEDP 为平行四边形,所以NP =DE ,则DE =12BC ,即λ=12.(2)取DE 的中点O ,连接MO ,则MO ⊥DE ,因为平面MDE ⊥平面DECB ,平面MDE ∩平面DECB =DE ,且MO ⊥DE ,所以MO ⊥平面DECB ,如图建立空间直角坐标系,不妨设2BC,则 M , ,0,0D, 1,0B ,所以 ,0,MD,11,0DB ,设平面BMD 的法向量为 ,,m x y z,则0(1))0MD m x z DB m x y,即,x x ,令x1,1m .又平面EMD 的法向量 0,1,0n ,所以cos ,m n m n m n即随着 值的变化,二面角B MD E 的大小不变.且sin ,5m n .所以二面角B MD E.19.(2022·全国·模拟预测(理))如图,在四棱锥P ABCD 中,1AB BC ,2DC ,PD PC ,90DPC ,90DCB CBA ,平面PDC 平面ABCD .(1)证明:PD 平面PBC ;(2)求二面角A PC B 的余弦值.【答案】(1)证明见解析;(2)63.【解析】【分析】(1)由面面、线面垂直的性质可得BC PD ⊥,且BC CD ,根据线面垂直的判定即可证结论;(2)构建空间直角坐标系,求面APC 、面BPC 的法向量,应用空间向量夹角的坐标表示求二面角的余弦值.(1)由题设,BC CD ,又面PDC 面ABCD ,面PDC ∩面ABCD CD ,BC 面ABCD ,所以BC 面PDC ,而PD 面PDC ,则BC PD ⊥,由90DPC 得:PC PD ,又BC PC C ,则PD 平面PBC .(2)若O 是CD 的中点,连接,OP OA ,由PD PC ,1AB BC ,2DC ,90DCB CBA ,所以,OP CD OA CD ,面PDC 面ABCD ,面PDC ∩面ABCD CD ,OA 面ABCD ,所以OA 面PDC ,OP 面PDC ,则OA OP .综上,可构建如下空间直角坐标系,90DPC ,所以(1,0,0),(1,1,0),(0,1,0),(0,0,1)A B C P ,则(1,0,1),(0,1,1),(1,1,1)AP CP BP ,若(,,)m x y z 是面APC 的法向量,则00AP m x z CP m y z ,令1z ,则(1,1,1)m ,若(,,)n a b c 是面BPC 的法向量,则00BP m a b c CP m b c,令1c ,则(0,1,1)n ,所以|cos ,|||||||m n m n m n A PC B.20.(2022·上海市光明中学模拟预测)如图所示,设有底面半径为3的圆锥.已知圆锥的侧面积为15 ,D 为PA 中点,3AOC.(1)求圆锥的体积;(2)求异面直线CD 与AB 所成角.【答案】(1)12 (2)2【解析】【分析】(1)由圆锥侧面积公式可求得母线长,进而得到圆锥的高,利用圆锥体积公式可求得结果;(2)解法一:取OA 边上中点E ,由线面垂直的判定可证得AB 平面CDE ,由线面垂直性质得AB CD ,由此可得结果;解法二:取圆弧AB 中点E ,连结OE ,以O 为坐标原点可建立空间直角坐标系,由向量运算可得0AB CD ,知AB CD ,由此可得结果.(1)设圆锥母线长为l ,315S rl l ∵侧,5l ,即5PA PB ,圆锥的高4h OP ,2 1119412333V S h OA OP 底.(2)解法一:取OA 边上中点E ,连结DE ,CE ,AC ,DE ∵是AOP 的中位线,//DE OP ;OP ∵垂直于底面,DE 垂直于底面,DE AB ∴;CA CO ∵,E 为OA 中点,CE OA ,即AB CE ^;CE DE E ∵,,CE DE 平面CDE ,AB 平面CDE ,又CD 平面CDE ,AB CD ,即异面直线AB 与CD 所成角为2.解法二:取圆弧AB 中点E ,连结OE ,则OE AB ;以O 为坐标原点,,,OE OB OP 的正方向为,,x y z轴,可建立如图所示空间直角坐标系,则 0,3,0A , 0,3,0B,3,02C ,30,,22D , 0,6,0AB,2CD,0AB CD ,即AB CD , 异面直线AB 与CD 所成角为2.。
高中数学高考总复习立体几何空间向量空间直角坐标系习题及详解

高中数学高考总复习立体几何空间向量空间直角坐标系习题及详解一、选择题1.已知四边形ABCD 满足:AB →·BC →>0,BC →·CD →>0,CD →·DA →>0,DA →·AB →>0,则该四边形为( )A .平行四边形B .梯形C .平面四边形D .空间四边形[答案] D[解析] ∵AB →·BC →>0,∴∠ABC >π2,同理∠BCD >π2,∠CDA >π2,∠DAB >π2,由内角和定理知,四边形ABCD 一定不是平面四边形,故选D.2.如图,点P 是单位正方体ABCD -A 1B 1C 1D 1中异于A 的一个顶点,则AP →·AB →的值为( )A .0B .1C .0或1D .任意实数 [答案] C[解析] AP →可为下列7个向量:AB →,AC →,AD →,AA 1→,AB 1→,AC 1→,AD 1→,其中一个与AB →重合,AP →·AB →=|AB →|2=1;AD →,AD 1→,AA 1→与AB →垂直,这时AP →·AB →=0;AC →,AB 1→与AB →的夹角为45°,这时AP →·AB →=2×1×cos π4=1,最后AC 1→·AB →=3×1×cos ∠BAC 1=3×13=1,故选C.3.如图,在平行六面体ABCD -A 1B 1C 1D 1中,M 为AC 与BD 的交点,N 为BB 1的靠近B 的三等分点,若A 1B 1→=a ,A 1D 1→=b ,A 1A →=c ,则MN →等于( )A .-12a +12b +13cB.12a +12b -13cC.12a -12b -13c D .-12a -12b +23c[答案] C[解析] MN →=MB →+BN →=12D 1B 1→+13BB 1→=12(A 1B 1→-A 1D 1→)-13A 1A →=12a -12b -13c . 4.已知A (2,-5,1),B (2,-2,4),C (1,-4,1),则AC →与AB →的夹角为( ) A .30° B .45° C .60°D .90°[答案] C[解析] AB →=(0,3,3),AC →=(-1,1,0).设〈AB →,AC →〉=θ,则cos θ=AB →·AC →|AB →|·|AC →|=332·2=12,∴θ=60°. 5.已知a =(2,-1,3),b =(-1,4,-2),c =(7,5,λ),若a ,b ,c 三向量共面,则实数λ等于( )A.627 B.637 C.647D.657[答案] D[解析] ∵a ,b ,c 三向量共面, ∴存在实数m ,n 使c =m a +n b , 即(7,5,λ)=(2m -n ,-m +4n,3m -2n ), ∴⎩⎪⎨⎪⎧2m -n =7-m +4n =5λ=3m -2n,∴λ=657.6.(2010·山东青岛)在空间四边形ABCD 中,AB →·CD →+AC →·DB →+AD →·BC →的值为( )A .0 B.32C .1D .无法确定[答案] A[解析] AB →·CD →+AC →·DB →+AD →·BC →=AB →·(BD →-BC →)+(BC →-BA →)·DB →+(BD →-BA →)·BC →=AB →·BD →-AB →·BC →+BC →·DB →-BA →·DB →+BD →·BC →-BA →·BC →=0,故选A.7.△ABC 的顶点分别为A (1,-1,2),B (5,-6,2),C (1,3,-1),则AC 边上的高BD等于( )A .5 B.41 C .4D .2 5[答案] A[解析] 设AD →=λAC →,D (x ,y ,z ),则(x -1,y +1,z -2)=λ(0,4,-3), ∴x =1,y =4λ-1,z =2-3λ. ∴BD →=(-4,4λ+5,-3λ), 又AC →=(0,4,-3),AC →⊥BD →, ∴4(4λ+5)-3(-3λ)=0, ∴λ=-45,∴BD →=⎝⎛⎭⎫-4,95,125, ∴|BD →|=(-4)2+⎝⎛⎭⎫952+⎝⎛⎭⎫1252=5. 8.已知正方体ABCD -A 1B 1C 1D 1的棱长为1,AM →=12MC →,点N 为B 1B 的中点,则线段MN 的长度为( )A.216B.66C.156D.153[答案] A[解析] MN →=AN →-AM →=AN →-13AC →=AB →+BN →-13()AB →+AD →+AA 1→ =23AB →+16AA 1→-13AD →. ∴MN =|MN →|=49|AB →|2+136|AA 1→|2+19|AD →|2=216. 9.设空间四点O 、A 、B 、P 满足OP →=OA →+tAB →,其中0<t <1,则有( ) A .点P 在线段AB 上 B .点P 在线段AB 的延长线上 C .点P 在线段BA 的延长线上 D .点P 不一定在直线AB 上 [答案] A[解析] ∵OP →=OA →+tAB →,∴AP →=tAB →,∵0<t <1,∴点P 在线段AB 上.10.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 、N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值等于( )A.32B.1010C.35D.25[答案] D[解析] AM →=AA 1→+A 1M →=AA 1→+12AB →,CN →=CB →+BN →=-AD →+12AA 1→,AM →·CN →=-AA 1→·AD →-12AB →·AD →+12|AA 1→|2+14AA 1→·AB →=12,|AM →|2=|AA 1→|2+14|AB →|2+AA 1→·AB →=54,|CN →|2=|AD →|2+14|AA 1|2-12AD →·AA 1→=54,∴cos 〈AM →,CN →〉=AM →·CN →|AM →|·|CN →|=25,故选D.二、填空题11.已知a =(1,2x -1,-x ),b =(x +2,3,-3),若a ∥b ,则x =________. [答案] 1[解析] ∵a ∥b ,∴1x +2=2x -13=-x -3,由1x +2=2x -13得,2x 2+3x -5=0,∴x =1或-52, 由2x -13=-x-3得x =1,∴x =1. 12.设向量a =(-1,3,2),b =(4,-6,2),c =(-3,12,t ),若c =m a +n b ,则m +n =________. [答案]112[解析] m a +n b =(-m +4n,3m -6n,2m +2n ), ∴(-m +4n,3m -6n,2m +2n )=(-3,12,t ). ∴⎩⎪⎨⎪⎧-m +4n =-33m -6n =122m +2n =t,解得⎩⎪⎨⎪⎧m =5,n =12,t =11.∴m +n =112.13.若|a |=17,b =(1,2,-2),c =(2,3,6),且a ⊥b ,a ⊥c ,则a =________. [答案] (-185,2,15)或(185,-2,-15)[解析] 设a =(x ,y ,z ), ∵a ⊥b ,∴x +2y -2z =0.① ∵a ⊥c ,∴2x +3y +6z =0.② ∵|a |=17.∴x 2+y 2+z 2=17.③ ∴联立①②得x =-18z ,y =10z . 代入③得425z 2=17,∴z =±15.∴a =(-185,2,15)或(185,-2,-15).14.直三棱柱ABC -A 1B 1C 1中,∠ACB =90°,∠BAC =30°,BC =1,AA 1=6,M 是CC 1的中点,则异面直线AB 1与A 1M 所成角为________.[答案] π2[解析] 由条件知AC 、BC 、CC 1两两垂直,以C 为原点,CB ,CA ,CC 1分别为x 轴,y 轴,z 轴建立空间直角坐标系,则B (1,0,0),A (0,3,0),B 1(1,0,6),M (0,0,62),A 1(0,3,6),∴AB 1→=(1,-3,6),A 1M →=(0,-3,-62),cos 〈AB 1→,A 1M →〉=AB 1→·A 1M →|AB 1→|·|A 1M →|=0,∴〈AB 1→,A 1M →〉=π2,即直线AB 1与A 1M 所成角为π2.三、解答题15.已知向量b 与向量a =(2,-1,2)共线,且满足a ·b =18,(k a +b )⊥(k a -b ),求向量b 及k 的值.[解析] ∵b ≠0,a ,b 共线,∴存在实数λ,使a =λb ,∵a =(2,-1,2),∴|a |=3, ∴a ·b =λa 2=λ|a |2=9λ=18, ∴λ=2.∴b =(4,-2,4).∵(k a +b )⊥(k a -b ),∴(k a +b )·(k a -b )=0. ∴(k a +2a )·(k a -2a )=0. ∴(k 2-4)|a |2=0.∴k =±2.16.(2010·上海松江区模拟)设在直三棱柱ABC -A 1B 1C 1中,AB =AC =AA 1=2,∠BAC =90°,E ,F 依次为C 1C ,BC 的中点.(1)求异面直线A 1B 、EF 所成角θ的大小(用反三角函数值表示); (2)求点B 1到平面AEF 的距离.[解析] 以A 为原点建立如图所示空间直角坐标系,则各点坐标为A 1(0,0,2),B (2,0,0),B 1(2,0,2),E (0,2,1),F (1,1,0),(1)A 1B →=(2,0,-2),EF →=(1,-1,-1), cos θ=A 1B →·EF →|A 1B →|·|EF →|=422×3=63,∴θ=arccos63. (2)设平面AEF 的一个法向量为n =(a ,b ,c ), ∵AE →=(0,2,1),AF →=(1,1,0), 由⎩⎪⎨⎪⎧n ·AE →=0n ·AF →=0得,⎩⎪⎨⎪⎧2b +c =0a +b =0,令a =1可得n =(1,-1,2),∵AB 1→=(2,0,2),∴d =|AB 1→·n ||n |=66= 6.∴点B 1到平面AEF 的距离为 6.17.如图,平面ABEF ⊥平面ABCD ,四边形ABEF 与ABCD 都是直角梯形,∠BAD =∠F AB =90°,BC 綊12AD ,BE 綊12F A ,G 、H 分别为F A 、FD 的中点.(1)证明:四边形BCHG 是平行四边形; (2)C 、D 、F 、E 四点是否共面?为什么? (3)设AB =BE ,证明:平面ADE ⊥平面CDE .[解析] 由题设知,F A 、AB 、AD 两两互相垂直.如图,以A 为坐标原点,射线AB 为x 轴正半轴,建立如图所示的直角坐标系A -xyz .(1)设AB =a ,BC =b ,BE =c ,则由题设得A (0,0,0),B (a,0,0),C (a ,b,0),D (0,2b,0),E (a,0,c ),G (0,0,c ),H (0,b ,c ),F (0,0,2c ).所以,GH →=(0,b,0),BC →=(0,b,0), 于是GH →=BC →.又点G 不在直线BC 上, 所以四边形BCHG 是平行四边形. (2)C 、D 、F 、E 四点共面.理由如下: 由题设知,F (0,0,2c ),所以EF →=(-a,0,c ),CH →=(-a,0,c ),EF →=CH →, 又C ∉EF ,H ∈FD ,故C 、D 、F 、E 四点共面.(3)由AB =BE ,得c =a ,所以CH →=(-a,0,a ),AE →=(a,0,a ) 又AD →=(0,2b,0),因此CH →·AE →=0,CH →·AD →=0 即CH ⊥AE ,CH ⊥AD ,又AD ∩AE =A ,所以CH ⊥平面ADE .故由CH ⊂平面CDFE ,得平面ADE ⊥平面CDE .[点评] 如果所给问题中存在两两垂直的直线交于一点,容易将各点的坐标表示出来时,可用向量法求解.如果其所讨论关系不涉及求角,求距离或所求角、距离比较容易找(作)出时,可不用向量法求解,本题解答如下:(1)由题设知,FG =GA ,FH =HD ,所以GH 綊12AD .又BC 綊12AD ,故GH 綊BC ,所以四边形BCHG 是平行四边形.(2)C 、D 、F 、E 四点共面.理由如下: 由BE 綊12AF ,G 是F A 的中点知,BE 綊GF ,所以EF ∥BG ,由(1)知BG ∥CH ,所以EF ∥CH ,故EC 、FH 共面. 又点D 直线FH 上,所以C 、D 、F 、E 四点共面.(3)连结EG ,由AB =BE ,BE 綊AG ,及∠BAG =90°知ABEG 是正方形, 故BG ⊥EA .由题设知,F A 、AD 、AB 两两垂直,故AD ⊥平面F ABE , 因此EA 是ED 在平面F ABE 内的射影,∴BG ⊥ED . 又EC ∩EA =E ,所以BG ⊥平面ADE .由(1)知,CH ∥BG ,所以CH ⊥平面ADE .由(2)知F ∈平面CDE ,故CH ⊂平面CDE ,得平面ADE ⊥平面CDE .。
2023-2024学年高考数学空间向量与立体几何专项练习题(附答案)

A .B .223.若直线的方向向量为,平面l bA .()(1,0,0,2,0,0b n ==-()(0,2,1,1,0,1b n ==--A .B .5136.如图,在平行六面体ABCDA.1122a b c -++C.1122a b c --+7.如图,在四面体OABC中,1-16.已知四棱锥P ABCDPC棱上运动,当平面1.C【分析】根据已知结合向量的坐标运算可得出,且.然后根据向量的数量积a b a +=- 14a = 运算求解,即可得出答案.【详解】由已知可得,且.()1,2,3a b a+=---=-14a =又,()7a b c +⋅= 所以,即有,7a c -⋅= cos ,14cos ,7a c a c a c -⋅=-=所以,.1cos ,2a c =-又,所以.0,180a c ≤≤ ,120a c =︒ 故选:C.2.C【分析】利用中点坐标公式求出中点的坐标,根据空间两点间的距离公式即可得出中线BC 长.【详解】由图可知:,,,(0,0,1)A (2,0,0)B (0,2,0)C 由中点坐标公式可得的中点坐标为,BC (1,1,0)根据空间两点间距离公式得边上的中线的长为.BC 22211(1)3++-=故选:C 3.D【分析】若直线与平面平行,则直线的方向向量与平面的法向量垂直,利用向量数量积检验.【详解】直线的方向向量为,平面的法向量为,l bαn 若可能,则,即.//l αb n ⊥r r 0b n ⋅=r r A 选项,;()1220b n =⨯-⋅=-≠B 选项,;11305160b n =⨯⨯⋅+⨯+=≠C 选项,;()()01201110b n =⨯-+⨯+⨯-⋅=-≠D 选项,;()1013310b n =⨯+-⨯=⋅+⨯因为,,3AB =4BC =2PA =所以()()(0,0,2,3,0,0,0,0,1P B Q 设平面的法向量为BQD (m x =()(),,3,0,1m BQ x y z ⎧设,2AB AD AS ===则()()()0,0,0,0,0,2,2,2,0,A S C P 设,()0,,2M t t -(1,1,2OM t =--所以1120OM AP t t ⊥=-+-+-=点到平面与平面的距离和为为定值,D 选项正确.M ABCD SAB 22t t -+=,,()2,0,0B ()()2,0,2,0,2,0SB BC =-=设平面的法向量为,SBC (),,n x y z =则,故可设,22020n SB x z n BC y ⎧⋅=-=⎪⎨⋅==⎪⎩()1,0,1n = 要使平面,又平面,//OM SBC OM ⊄SBC 则,()()1,1,21,0,11210OM n t t t t ⋅=---⋅=-+-=-=解得,所以存在点,使平面,B 选项正确.1t =M //OM SBC 若直线与直线所成角为,又,OM AB 30︒()2,0,0AB =则,()()222213cos3022661122OM ABOM ABt t t t ⋅-︒====⋅-++-+-⨯ 整理得,无解,所以C 选项错误.23970,8143730t t -+=∆=-⨯⨯=-<故选:ABD.10.BCD【分析】根据向量的多边形法则可知A 正确;根据向量的三角不等式等号成立条件可知,B 错误;根据共线向量的定义可知,C 错误;根据空间向量基本定理的推论可知,D 错误.【详解】对A ,四点恰好围成一封闭图形,根据向量的多边形法则可知,正确;对B ,根据向量的三角不等式等号成立条件可知,同向时,应有,即必要,a b a b a b+=+ 性不成立,错误;对C ,根据共线向量的定义可知,所在直线可能重合,错误;,a b对D ,根据空间向量基本定理的推论可知,需满足x +y +z =1,才有P 、A 、B 、C 四点共面,错误.故选:BCD .11.AB【分析】以,,作为空间的一组基底,利用空间向量判断A ,C ,利用空间向量法ABAD AA 可得面,再用向量法表示,即可判断B ,利用割补法判断D ;1AC ⊥PMN AH【详解】依题意以,,作为空间的一组基底,ABAD AA 则,,11AC AB AD AA =++ ()1122MN BD AD AB ==-因为棱长均为2,,11π3A AD A AB ∠=∠=所以,,224AB AD == 11π22cos 23AA AD AA AB ⋅=⋅=⨯⨯= 所以()()1112D A A C MN AD A A B AA B++⋅⋅=- ,()2211102AB AD AB AD AB AD AA AD AA AB ⋅-+-⋅+==⋅+⋅故,即,故A 正确;1AC MN ⊥1AC MN ⊥同理可证,,面,面,PN AC ⊥MN PN N ⋂=MN ⊂PMN PN ⊂PMN 所以面,即面,即为正三棱锥的高,1AC ⊥PMN AH ⊥PMN AH A PMN -所以()()1133AH AN NH AN NP NM AN AP AN AM AN=+=++=+-+- ,()13AP AM AN =++又,,分别是,,的中点,,P M N 1AA AB AD π3PAM PAN MAN ∠=∠=∠=所以,则三棱锥是正四面体,1PA AM AN PM MN PN ======P AMN -所以()11111133222AH AP AM AN AA AB AD ⎛⎫=++=⨯++ ⎪⎝⎭ ,()111166AA AB AD AC =++=所以,故B 正确;116AH AC =因为()211AC AB AD AA =++ ()()()222111222AB ADAA AB AD AB AA AD AA =+++⋅+⋅+⋅ ,2426==()21111111=AC AA AB AD AA AA AB AA AD AA AA ⋅=++⋅⋅+⋅+ ,11222222=822=⨯⨯+⨯⨯+⨯设直线和直线所成的角为,1AC 1BB θ则,故C 错误;1111111186cos cos ,cos ,3262AC AA AC BB AC AA AC AA θ⋅=====⨯ ,11111111111111A B D C ABCD A B C D A B D A C B D A B ABC D ADCV V V V V V ------=----其中,1111111111116ABCD A B C D A B D A C B D C B ABC D ADC V V V V V -----====所以,故D 错误.1111113A B D C ABCD A B C D V V --=故选:AB.关键点睛:本题解决的关键点是利用空间向量的基底法表示出所需向量,利用空间向量的数量积运算即可得解.12.AC【分析】对于A ,根据即可算出的值;对于B ,根据计算;对于C ,根据||2a = m a b ⊥ m 计算即可;对于D ,根据求出,从而可计算出.a b λ= 1a b ⋅=- m a b + 【详解】对于A ,因为,所以,解得,故A 正确;||2a = 2221(1)2m +-+=2m =±对于B ,因为,所以,所以,故B 错误;a b ⊥ 2120m m -+-+=1m =对于C ,假设,则,a b λ= (1,1,)(2,1,2)m m λ-=--所以,该方程组无解,故C 正确;()12112m m λλλ=-⎧⎪-=-⎨⎪=⎩对于D ,因为,所以,解得,1a b ⋅=- 2121m m -+-+=-0m =所以,,所以,故D 错误.(1,1,0)a =- (2,1,2)b =-- (1,2,2)+=-- a b 故选:AC.13.15【分析】根据线面垂直,可得直线的方向向量和平面的法向量共线,由此列式计算,即得答案.【详解】∵,∴,∴,解得,l α⊥u n ∥ 3123a b ==6,9a b ==∴,15a b +=故1514.2【分析】根据垂直得到,得到方程,求出.()0a a b λ⋅-= 2λ=【详解】,()()()2,1,31,2,12,12,3a b λλλλλ-=---=--- 因为,所以,()a a b λ⊥- ()0a a b λ⋅-= 即,()()2,12,3241293702,1,134λλλλλλλ----=-++-+-=+⋅-=解得.2λ=故215.17【分析】利用向量的加法,转化为,直接求模长即可.CD CA AB BD =++ 【详解】因为.CD CA AB BD =++ 所以()22CD CA AB BD =++ 222222CA CA AB AB AB BD BD CA BD=+⋅++⋅++⋅ 222132022042342⎛⎫=+⨯++⨯++⨯⨯⨯- ⎪⎝⎭17=所以.17CD = 故答案为.1716.33【分析】首先建立空间直角坐标系,分别求平面和平面的法向量,利用法向量垂MBD PCD 直求点的位置,并利用向量法求异面直线所成角的余弦值,即可求解正弦值.M 【详解】如图,以点为原点,以向量为轴的正方向,建立空间直角坐标A ,,AB AD AP ,,x y z 系,设,2AD AP ==,,,,()2,0,0B ()0,2,0D ()002P ,,()2,2,0C 设,()()()0,2,22,2,22,22,22DM DP PM DP PC λλλλλ=+=+=-+-=-- ,,,()2,2,0BD =-u u u r ()2,0,0DC =u u u r ()0,2,2DP =- 设平面的法向量为,MBD ()111,,m x y z =r ,()()11111222220220DM m x y z DM m x y λλλ⎧⋅=+-+-=⎪⎨⋅=-+=⎪⎩33故。
高考数学必做题--立体几何与空间向量 (后附参考答案与详解)

立体几何与空间向量-高考必做题123平行的截面,则截得的三;截得的平面图形中,面积最大的值是.4的中点,为线段上的动点,过点,,则下列命题正确的是.5与四棱锥的表面的交线,并写出作图的步骤.7是正方体棱上一点(不包括棱的端点),.,则的取值范围是.8的最大值为满足9的中点,沿将矩形折起使得分别为中点.10C.3个D.4个分别为棱,上的点. 已知下列判断:上的正投影是面积为定值的三角形;平行的直线;所成的二面角(锐角)的大小与点的位置有关,与点的位置无关.11,,,与平面所12的位置,使得平面,并证明你的13,坐标平面上的一组正投影图像如.14如图是圆的直径,垂直圆所在的平面,是圆上的点.求证:平面平面.(1)15 16 17 18椭圆的一部分 D.抛物线的一部分19 D.,所成角都相等的直线条数为所成角都相等的直线的条数为,则下面结论正确的是(20分别是棱的中点,是侧面长度的取值范围是().21D.D.③④分别是棱,的中点,过直线,,给出以下四个命题:22为正方形,,则三棱锥2324 2526 272829 30A. B.C. D.立体几何与空间向量-高考必做题123为边长为的等边三角形,面积为截得的平面图形中,正六边形如图所示分别为各边中点,边长为,面积为.故答案为;.立体几何与空间向量立体几何初步空间几何体4如图,在棱长为的正方体的中点,点在线段上.点到直线的距离的最小值为.∵,底面,∴四边形是矩形.∴,又平面,平面∴平面.∴直线上任一点到平面的距离是两条异面直线∵平面平面.5当时,为中点,此时可得截面为等腰梯形;当点向移动时,满足即可得截面为四边形,①正确;对于②,当时,如图所示,延长至,使,连接交于,连接可证,由可得故可得,∴截面对于③,由②知当此时的截面形状仍然为上图所示的五边形对于④,当时,与可证,且,可知截面故答案为:①②④.立体几何与空间向量立体几何初步空间几何体点、直线、平面间的位置关系6与四棱锥的表面的交线,并写出作图的步骤.为平面与四棱锥的表面的交线.分别是线段,上的,的菱形,,,,,,所以,设平面的法向量为,则由可得令因为,所以直线与平面的成角的正弦值为法1:延长,分别交,延长线于,,连接,,则四边形为平面法2:记平面与直线的交点为,设由.所以即为点.所以连接,,则四边形为平面平面向量平面向量的基本概念向量的加法与减法平面向量的数量积数量积立体几何与空间向量立体几何初步点、直线、平面间的位置关系空间中的平行空间向量空间直角坐标系空间向量的应用789的最大值为满足,所以,所以.,接下来研究这个二次函数的性质可函数函数的概念与表示最值单调性对称性二次函数立体几何与空间向量立体几何初步空间几何体点、直线、平面间的位置关系空间中的垂直10,,则中位线且又且,所以且所以四边形是平行四边形,所以,又平面,法二:如图,延长因为且,所以为中点,所以中位线,又平面,面,所以法一:如图,因为,所以又.所以∴,∴,又∵,,∴平面,面,∴又,所以平面,又为中点,所以所以平面,,所以中,,,∴二面角的余弦值为法二:如图,∵,∴∴,∴∴,∴,,又∵,,∴平面,面,∴,又,所以平面,面,∴则,,,而是平面的一个法向量,设平面的法向量为则令,则,面的一个法向量为所以所以,二面角的余弦值为立体几何与空间向量立体几何初步点、直线、平面间的位置关系空间中的平行空间中的垂直空间向量空间直角坐标系空间向量及其运算空间向量的应用11中,,分别为棱D.4个平面,而两个平面面与面上的正投影是面积为定值的三角形,此是一个正确的结点在面上的投影到此棱的距离是定平行的直线,此两平面相交,一个面内平行于两个平面的交线一定平行于另一个平面,此结论正确;所成的二面角(锐角)的大小与点的位置有关,与点的位置无关,此结论不对,与两者都有关系,可代入几个特殊点进行验证,如与重重合时的情况就不一样,故此命题不正点、直线、平面间的位置关系空间中的平行空间中的垂直12的位置,使得平面,并证明你的,∵与平面所成角为,即,∴,由,知,,则,,,∴,,设平面的法向量为,则,即,令,则,∵平面,∴为平面的法向量,∴又∵二面角为锐角,∴二面角的余弦值为.点是线段上一个动点,设,则,∵平面,∴,即,解得:,此时,点坐标为,.平面向量平面向量的基本定理及坐标表示平面向量的坐标运算用坐标表示平面向量共线的条件立体几何与空间向量立体几何初步点、直线、平面间的位置关系空间中的平行空间中的垂直空间向量空间向量及其运算空间向量的应用答案解析该几何体还原如图所示,易得体积为.立体几何与空间向量立体几何初步空间几何体体积和表面积的计算三视图14是圆的直径,垂直圆所在的平面,是圆上的点.求证:平面平面.,,,求:二面角的余弦值.(1)答案见解析.(2)答案见解析.(1)由是圆的直径,得.由平面,平面,得.在中,∵,,∴立体几何初步空间中的垂直空间向量空间向量的应用1516三角函数与解三角形解三角形立体几何与空间向量立体几何初步空间几何体点、直线、平面间的位置关系17动点从到,再到,到再回到,,则经过的最短路径为:一个半圆和一个即.立体几何与空间向量立体几何初步空间几何体18如图,三棱锥的顶点、、等边三角形,点,分别为线段体积的最大值为19椭圆的一部分 D.抛物线的一部分的交线的距离分别为和.,D.,所成角都相等的直线条数为所成角都相等的直线的条数为,则下面结论正确的是(2021D.连结,可以证明平面,所以点位于线段上,把三角形拿到平面上,则有,所以当点位于时,最大,当位于中点时,最小,此时所以,即所以线段长度的取值范围是22D.③④在正方体中,平面,∴平面平面,①正确;②连接,∵平面,四边形的对角线是固定的,要使面积最小,只需的长度最小即可,此时为棱中点,,长度最小,对应四边形②正确;③∵,∴四边形是菱形,当时,长度由大变小,当时,长度由小变大,∴函数不是单调函数,③错误;④连接,,,四棱锥分割成两个小三棱锥,以为底,分别以、为顶点,∵面积是个常数,、到平面的距离是个常数,2324函数图象的交点函数的零点三角函数与解三角形三角函数任意角与弧度制三角函数的定义立体几何与空间向量立体几何初步空间几何体解析几何曲线与方程25)成。
高考数学空间向量与立体几何解答题专题复习题

高考数学空间向量与立体几何解答题专题复习题1.已知空间三点(023)(216)(115)A B C −−,,,,,,,,.(1)求以AB AC ,为边的平行四边形的面积.(2)若=a a 分别与AB AC ,垂直,求向量a 的坐标.2.三棱柱ABC −A 1B 1C 1的所有棱长都相等,∠A 1AB =∠A 1AC =60∘,点M 为△ABC 的重心,AM 的延长线交BC 于点N ,连接A 1M .设AB ⃗⃗⃗⃗⃗ =a ,AC ⃗⃗⃗⃗⃗ =b ⃗ ,A 1A ⃗⃗⃗⃗⃗⃗⃗ =c .(1)用a ,b ⃗ ,c 表示A 1M ⃗⃗⃗⃗⃗⃗⃗⃗ ; (2)证明:A 1M ⊥AB .第2题图 第3题图3.在正方体1111D C B A ABCD −中,如图E 、F 分别是1BB ,CD 的中点.(1)求证:⊥F D 1平面ADE ;(2)1,EF CB 的夹角. 4.在几何体ABCD P −中,底面ABCD 为矩形,侧棱⊥PA 底面ABCD ,3=AB ,1=BC ,2=PA ,E 为PD 的中点.(1)求直线AC 与PB 所成角的余弦值.(2)在侧面PAB 内找一点N ,使⊥NE 平面PAC ,并求出N 点到AB 和AP 的距离.第4题图 第5题图5.在底面为矩形的四棱锥P ABCD −中,平面PAD ⊥平面ABCD .A B C DP(1)证明:AB PD ⊥.(2)若,90PA PD AB APD ==∠=︒,设Q 为PB 中点,求直线AQ 与平面PBC 所成角的余弦值.6.如图,在三棱柱111ABC A B C −中,1CC ⊥平面,,2ABC AC BC AC BC ⊥==,13CC =,点,D E 分别在棱1AA 和棱1CC 上,且12,AD CE M ==为棱11A B 的中点.(1)求证:11C M B D ⊥.(2)求二面角1B B E D −−的正弦值.(3)求直线AB 与平面1DB E 所成角的正弦值.第6题图 第7题图 第8题图7.在四棱锥P ABCD −中,PD ⊥底面ABCD ,底面ABCD 是矩形,M 是线段PC 的中点.已知2PD CD ==,1AD =.(1)求证://PA 平面BDM(2)求二面角M BD C −−的余弦值.(3)直线BD 上是否存在点N ,使得MN 与PA 垂直?若存在,求MN 的长;若不存在,请说明理由.8.在四棱锥P ﹣ABCD 中,P A ⊥平面ABCD ,AB ⊥AD ,BC ∥AD ,点M 是棱PD 上一点,且AB =BC =2,AD =P A =4.(1)若PM :MD =1:2,求证:PB ∥平面ACM .(2)求二面角A ﹣CD ﹣P 的正弦值.(3)若直线AM 与平面PCD ,求MD 的长.。
高考必刷大题 空间向量与立体几何

故 2λ=-2,2λ+2μ-μt=0, 3μt= 3,
解得
t=23,从而D→F=0,43,2
3
3.
123456
所以直线AE与DF所成角的余弦值为
|cos〈A→E,D→F〉|=|AA→→EE|·|DD→→FF|=
2 7×2
7=37. 3
123456
4.(2023·成都模拟)如图所示,直角梯形ABDE和三角形ABC所在平面互相 垂直,DB⊥AB,ED∥AB,AB=2DE=2BD=2,AC=BC,异面直线DE 与AC所成角为45°,点F,G分别为CE,BC的中点,点H是线段EG上靠近 点G的三等分点.
则有nn··B—C→CC→=1 =x+-x+3y=30z,=0,
可取 n=( 3,-1,1),又—BA→1 =(1,0, 3),
—→
所以点
A1 到平面
BCC1B1 的距离为| BA|n1|·n|=2
3=2 5
515,
所以所求距离为2 515.
123456
3.(2024·丹东模拟)如图,平行六面体ABCD-A1B1C1D1的所有棱长都相等, 平面CDD1C1⊥平面ABCD,AD⊥DC,二面角D1-AD-C的大小为120°, E为棱C1D1的中点.
(1)求证:A,B,F,H四点共面;
123456
如图,取AB的中点O,连接OC,OE, 因为AC=BC,故∠BAC为锐角, 又ED∥AB, 故∠BAC即为异面直线DE与AC所成角, 则∠BAC=45°, 则∠ACB=90°,即AC⊥CB, 因为直角梯形ABDE和三角形ABC所在平面互相垂直,DB⊥AB, 平面ABDE∩平面ABC=AB,DB⊂平面ABDE,
123456
设平面PBD的法向量为n=(x,y,z), 则nn··PP→→DB==22xy--22zz==00,, 取 x=1,得 n=(1,1,1), ∵A→M=n,∴AM⊥平面 PBD.
空间向量与立体几何高考题汇编

1.(2009北京卷)(本小题共14分)如图,四棱锥P ABCD 的底面是正方形,PD ABCD 底面,点E 在棱PB 上. (Ⅰ)求证:平面AEC PDB 平面;(Ⅱ)当2PDAB 且E 为PB 的中点时,求AE 与平面PDB 所成的角的大小.解:如图,以D 为原点建立空间直角坐标系D xyz ,设,,AB a PD h 则,0,0,,,0,0,,0,0,0,0,0,0,A a B a a C a D P h ,(Ⅰ)∵,,0,0,0,,,,0ACa a DPh DBa a ,∴0,0AC DPAC DB,∴AC ⊥DP ,AC ⊥DB ,∴AC ⊥平面PDB ,∴平面AECPDB 平面.(Ⅱ)当2PD AB 且E 为PB 的中点时,1120,0,2,,,222P a E a a a ,设AC ∩BD=O ,连接OE ,由(Ⅰ)知AC ⊥平面PDB 于O ,∴∠AEO 为AE 与平面PDB 所的角,∵1122,,,0,0,2222EAa a a EOa ,∴2cos 2EA EO AEOEAEO,∴45AOE ,即AE 与平面PDB 所成的角的大小为45.2.(2009山东卷)(本小题满分12分)如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB//CD ,AB=4, BC=CD=2,AA 1=2, E 、E 1、F 分别是棱AD 、AA 1、AB 的中点。
(1)证明:直线EE 1//平面FCC 1;(2)求二面角B-FC 1-C 的余弦值。
EABCFE 1A 1B 1C 1D 1D解法二:(1)因为AB=4, BC=CD=2, F 是棱AB 的中点, 所以BF=BC=CF,△BCF 为正三角形, 因为ABCD 为等腰梯形,所以∠BAC=∠ABC=60°,取AF 的中点M, 连接DM,则DM ⊥AB,所以DM ⊥CD,以DM 为x 轴,DC 为y 轴,DD 1为z 轴建立空间直角坐标系,,则D (0,0,0),A (3,-1,0),F (3,1,0),C (0,2,0),C 1(0,2,2),E (32,12,0),E 1(3,-1,1),所以131(,,1)22EE ,(3,1,0)CF,1(0,0,2)CC 1(3,1,2)FC 设平面CC 1F 的法向量为(,,)n x y z 则100n CF n CC 所以30x y z 取(1,3,0)n ,则1311310022n EE ,所以1n EE ,所以直线EE 1//平面FCC 1.(2)(0,2,0)FB,设平面BFC 1的法向量为1111(,,)n x y z ,则11100n FB n FC 所以11110320y x y z ,取1(2,0,3)n ,则12130032n n ,2||1(3)2n ,221||20(3)7n ,所以11127cos ,7||||27n n n n n n ,由图可知二面角B-FC 1-C 为锐角,所以二面角B-FC 1-C的余弦值为77.3.(2009全国卷Ⅱ)(本小题满分12分)如图,直三棱柱111ABCA B C 中,,AB AC D 、E 分别为1AA 、1B C 的中点,DE平面1BCC (I )证明:AB AC(II )设二面角A BD C 为60°,求1B C 与平面BCD 所成的角的大小。
【新高考数学】23个立体几何与空间向量专题

是圆的直径,ADB 60o ,BDC 45o ,PD 垂直于底面 ABCD ,PD 2 2R ,E, F
分别是 PB,CD 上的点,且 PE DF ,过点 E 作 BC 的平行线交 PC 于G . EB FC
⑴求 BD 与平面 ABP 所成角 的正弦值 sin ;
P
⑵当 PE 1 时,求 EFG 的面积 S . EB 2
是 CD 的中点, PA 底面 ABCD , PA 3 . ⑴证明:平面 PBE 平面 PAB ; ⑵求二面角 A BE P 的 大小.
F P
E
G
H
D
C
E
A
图 21
B
A
D
B
C 图 22
例 22 、如图 22,平面 ABEF 平面 ABCD ,四边形 ABEF 与四边形 ABCD 都是直角梯形,
D
PE
A
C
C
A
O
F
B 图1
D O
B
图2 E
C
例 2 、如图 2,四面体 ABCD 中, O, E 分别是 BD, BC 的中点, CA CB CD BD 2 ,
AB AD 2 ⑴ 求异面直线 AB 与 CD 所成角的余弦值 cos ;
⑵ 求点 E 到平面 ACD 的距离 d .
例 3 、如图 3 所示,四棱锥 P ABCD 的底面 ABCD 是半径为 R 的圆的内接四边形,其中 BD
例 19 、 如 图 19 , 直 三 棱 柱 ABC A1B1C1 中 , D、E 分 别 是 AB、BB1 的 中 点 .
AA1 AC CB
2 2
AB ,求二面角 D
A1C
E 的正弦值 sin
.
高考数学压轴专题(易错题)备战高考《空间向量与立体几何》全集汇编及答案解析

【高中数学】数学高考《空间向量与立体几何》复习资料一、选择题1.如图,平面四边形ABCD 中,1AB AD CD ===,2BD =,BD CD ⊥,将其沿对角线BD 折成四面体A BCD '-,使平面A BD '⊥平面BCD ,若四面体A BCD '-的顶点在同一个球面上,则该球的表面积为( )A .3πB 3C .4πD 3 【答案】A【解析】【分析】 设BC 的中点是E ,连接DE ,由四面体A′BCD 的特征可知,DE 即为球体的半径.【详解】设BC 的中点是E ,连接DE ,A′E ,因为AB =AD =1,BD 2由勾股定理得:BA ⊥AD又因为BD ⊥CD ,即三角形BCD 为直角三角形所以DE 为球体的半径3DE = 2343S ππ== 故选A【点睛】 求解球体的表面积、体积的问题,其实质是求球体的半径,解题的关键是构造关于球体半径R 的方程式,构造常用的方法是构造直角三角形,再利用勾股定理建立关于半径R 的方程.2.若四面体的三视图如图所示,则该四面体的四个面中,直角三角形的面积和为( )A .2B .25+C .425+D .4【答案】B【解析】【分析】 根据四面体的三视图可知:一侧面垂直于底面,且底面是以该侧面与底面的交线为直角边的直角三角形,然后根据面面垂直的性质定理,得到与底面的另一直角边为交线的侧面为直角三角形求解.【详解】由四面体的三视图可知:平面PAB ⊥平面ABC ,BC AB ⊥,所以BC ⊥平面PAB ,所以BC PB ⊥,所以,ABC PBC V V 是直角三角形,如图所示:所以直角三角形的面积和为:11112252252222ABC PBC S S AB BC PB BC +=⨯⨯+⨯⨯=⨯⨯+=+V V 故选:B【点睛】本题主要考查三视图的应用以及线面垂直,面面垂直的关系,还考查了运算求解的能力,属于中档题.3.如图,网格纸是由边长为1的小正方形构成,若粗实线画出的是某几何体的三视图,则该几何体的表面积为( )A .920π+B .926π+C .520π+D .526π+【答案】C【解析】【分析】 根据三视图还原为几何体,结合组合体的结构特征求解表面积.【详解】由三视图可知,该几何体可看作是半个圆柱和一个长方体的组合体,其中半圆柱的底面半圆半径为1,高为4,长方体的底面四边形相邻边长分别为1,2,高为4,所以该几何体的表面积2112141222S ππ=⨯+⨯⨯⨯+⨯⨯14224520π+⨯⨯+⨯=+,故选C. 【点睛】本题主要考查三视图的识别,利用三视图还原成几何体是求解关键,侧重考查直观想象和数学运算的核心素养.4.已知正方体1111A B C D ABCD -的棱1AA 的中点为E ,AC 与BD 交于点O ,平面α过点E 且与直线1OC 垂直,若1AB =,则平面α截该正方体所得截面图形的面积为( ) A .64 B .62C .32 D .34【答案】A【解析】【分析】根据正方体的垂直关系可得BD ⊥平面11ACC A ,进而1BD OC ⊥,可考虑平面BDE 是否为所求的平面,只需证明1OE OC ⊥即可确定平面α.【详解】如图所示,正方体1111ABCD A B C D -中,E 为棱1AA 的中点,1AB =,则2113122OC =+=,2113424OE =+=,2119244EC =+=, ∴22211OC OE EC +=,1OE OC ∴⊥;又BD ⊥平面11ACC A ,1BD OC ∴⊥,且OE BD O =I ,1OC ∴⊥平面BDE ,且1136222BDE S BD OE ∆==⨯⨯=g , 即α截该正方体所得截面图形的面积为6. 故选:A .【点睛】本题考查线面垂直的判定,考查三角形面积的计算,熟悉正方体中线面垂直关系是解题的关键,属于中档题.5.如图,在正方体1111ABCD A B C D -,点P 在线段1BC 上运动,则下列判断正确的是( )①平面1PB D ⊥平面1ACD②1//A P 平面1ACD③异面直线1A P 与1AD 所成角的取值范围是0,3π⎛⎤ ⎥⎝⎦④三棱锥1D APC -的体积不变A .①②B .①②④C .③④D .①④【答案】B【解析】【分析】由面面垂直的判定定理判断①,由面面平行的性质定理判断②,求出P 在特殊位置处时异面直线所成的角,判断③,由换底求体积法判断④.【详解】正方体中易证直线AC ⊥平面11BDD B ,从而有1AC B D ⊥,同理有11B D AD ^,证得1B D ⊥平面1ACD ,由面面垂直判定定理得平面1PB D ⊥平面1ACD ,①正确;正方体中11//A B CD ,11//BC AD ,从而可得线面平行,然后可得面面平行,即平面11A BC //平面1ACD ,而1A P ⊂平面11A BC ,从而得1//A P 平面1ACD ,②正确; 当P 是1BC 中点时,1A P 在平面11A B CD 内,正方体中仿照上面可证1AD ⊥平面11A B CD ,从而11AD A P ⊥,1A P 与1AD 所成角为90︒.③错;∵11D APC P AD C V V --=,由1//BC 平面1ACD ,知P 在线段1BC 上移动时,P 到平面1ACD 距离相等,因此1P AD C V -不变,④正确.故选:B .【点睛】本题考查面面垂直的判定定理、面面平行的性质定理、异面直线所成的角、棱锥的体积等知识,考查学生的空间想象能力,属于中档题.6.如图,正方形网格纸中的实线图形是一个多面体的三视图,则该多面体各表面所在平面互相垂直的有( )A .2对B .3对C .4对D .5对【答案】C【解析】【分析】 画出该几何体的直观图P ABCD -,易证平面PAD ⊥平面ABCD ,平面PCD ⊥平面PAD ,平面PAB ⊥平面PAD ,平面PAB ⊥平面PCD ,从而可选出答案.【详解】该几何体是一个四棱锥,直观图如下图所示,易知平面PAD ⊥平面ABCD ,作PO⊥AD于O,则有PO⊥平面ABCD,PO⊥CD,又AD⊥CD,所以,CD⊥平面PAD,所以平面PCD⊥平面PAD,同理可证:平面PAB⊥平面PAD,由三视图可知:PO=AO=OD,所以,AP⊥PD,又AP⊥CD,所以,AP⊥平面PCD,所以,平面PAB⊥平面PCD,所以该多面体各表面所在平面互相垂直的有4对.【点睛】本题考查了空间几何体的三视图,考查了四棱锥的结构特征,考查了面面垂直的证明,属于中档题.7.已知一个几何体的三视图如图所示(正方形边长为1),则该几何体的体积为()A.34B.78C.1516D.2324【答案】B【解析】【分析】【详解】由三视图可知:该几何体为正方体挖去了一个四棱锥A BCDE-,该几何体的体积为1111711132228⎛⎫-⨯⨯+⨯⨯= ⎪⎝⎭ 故选B 点睛:思考三视图还原空间几何体首先应深刻理解三视图之间的关系,遵循“长对正,高平齐,宽相等”的基本原则,其内涵为正视图的高是几何体的高,长是几何体的长;俯视图的长是几何体的长,宽是几何体的宽;侧视图的高是几何体的高,宽是几何体的宽.8.已知,m l 是两条不同的直线,,αβ是两个不同的平面,则下列可以推出αβ⊥的是( )A .,,m l m l βα⊥⊂⊥B .,,m l l m αβα⊥⋂=⊂C .//,,m l m l αβ⊥⊥D .,//,//l m l m αβ⊥【答案】D【解析】【分析】A ,有可能出现α,β平行这种情况.B ,会出现平面α,β相交但不垂直的情况.C ,根据面面平行的性质定理判断.D ,根据面面垂直的判定定理判断.【详解】对于A ,m l ⊥,m β⊂,若l β⊥,则//αβ,故A 错误;对于B ,会出现平面α,β相交但不垂直的情况,故B 错误;对于C ,因为//m l ,m α⊥,则l α⊥,又因为l βαβ⊥⇒∥,故C 错误; 对于D ,l α⊥,m l m α⇒⊥∥,又由m βαβ⇒⊥∥,故D 正确.故选:D【点睛】本题考查空间中的平行、垂直关系的判定,还考查学生的空间想象能力和逻辑推理能力,属于中档题.9.在四面体ABCD 中,AB ,BC ,BD 两两垂直,4AB BC BD ===,E 、F 分别为棱BC 、AD 的中点,则直线EF 与平面ACD 所成角的余弦值( )A.13B.33C.223D.63【答案】C【解析】【分析】因为AB,BC,BD两两垂直,以BA为X轴,以BD为Y轴,以BC为Z轴建立空间直角坐标系,求出向量EFu u u r与平面ACD的法向量nr,再根据cos,||||EF nEF nEF n⋅〈〉=u u u r ru u u r ru u u r r,即可得出答案.【详解】因为在四面体ABCD中,AB,BC,BD两两垂直,以BA为X轴,以BD为Y轴,以BC为Z轴建立空间直角坐标系,又因为4AB BC BD===;()4,0,0,(0,0,0),(0,4,0),(0,0,4)A B D C,又因为E、F分别为棱BC、AD的中点所以(0,0,2),(2,2,0)E F故()2,2,2EF=-u u u r,(4,4,0)AD=-u u u r,(4,0,4)AC=-u u u r.设平面ACD的法向量为(,,)n x y z=r,则n ADn AC⎧⋅=⎨⋅=⎩u u u vvu u u vv令1,x=则1y z==;所以(1,1,1)n=r1cos,3||||332EF nEF nEF n⋅〈〉===⨯u u u r ru u u r ru u u r r设直线EF与平面ACD所成角为θ,则sinθ=cos,EF n〈〉u u u r r所以222cos1sinθθ=-=故选:C【点睛】本题主要考查线面角,通过向量法即可求出,属于中档题目.10.我国南北朝时期数学家祖暅,提出了著名的祖暅原理:“缘幂势既同,则积不容异也”.“幂”是截面积,“势”是几何体的高,意思是两等高几何体,若在每一等高处的截面积都相等,则两几何体体积相等.已知某不规则几何体与右侧三视图所对应的几何体满足“幂势既同”,其中俯视图中的圆弧为14圆周,则该不规则几何体的体积为( )A .12π+B .136π+C .12π+D .1233π+ 【答案】B【解析】【分析】根据三视图知该几何体是三棱锥与14圆锥体的所得组合体,结合图中数据计算该组合体的体积即可.【详解】解:根据三视图知,该几何体是三棱锥与14圆锥体的组合体, 如图所示;则该组合体的体积为21111111212323436V ππ=⨯⨯⨯⨯+⨯⨯⨯=+; 所以对应不规则几何体的体积为136π+. 故选B .【点睛】本题考查了简单组合体的体积计算问题,也考查了三视图转化为几何体直观图的应用问题,是基础题.11.已知正三棱柱111ABC A B C -的所有棱长都相等,D 是11A B 的中点,则AD 与平面11BCC B 所成角的正弦值为( )A .5B .25C .1010D .15 【答案】D【解析】【分析】先找出直线AD 与平面11BCC B 所成角,然后在1B EF V 中,求出1sin EB F ∠,即可得到本题答案.【详解】如图,取AB 中点E ,作EF BC ⊥于F ,连接11,B E B F ,则1EB F ∠即为AD 与平面11BCC B 所成角.不妨设棱长为4,则1,2BF BE ==,13,25EF B E ∴=1315sin 25EB F ∴∠==. 故选:D【点睛】 本题主要考查直线与平面所成角的求法,找出线面所成角是解决此类题目的关键.12.四棱锥P ABCD -所有棱长都相等,M 、N 分别为PA 、CD 的中点,下列说法错误的是( )A .MN 与PD 是异面直线B .//MN 平面PBC C .//MN ACD .MN PB ⊥【答案】C【解析】【分析】画出图形,利用异面直线以及直线与平面平行的判定定理,判断选项A 、B 、C 的正误,由线线垂直可判断选项D .【详解】由题意可知四棱锥P ABCD -所有棱长都相等, M 、N 分别为PA 、CD 的中点,MN 与PD 是异面直线,A 选项正确;取PB 的中点为H ,连接MH 、HC ,四边形ABCD 为平行四边形,//AB CD ∴且AB CD =,M Q 、H 分别为PA 、PB 的中点,则//MH AB 且12MH AB =, N Q 为CD 的中点,//CN MH ∴且CN MH =,则四边形CHMN 为平行四边形, //MN CH ∴,且MN ⊄平面PBC ,CH ⊂平面PBC ,//MN ∴平面PBC ,B 选项正确;若//MN AC ,由于//CH MN ,则//CH AC ,事实上AC CH C ⋂=,C 选项错误; PC BC =Q ,H 为PB 的中点,CH PB ∴⊥,//MN CH Q ,MN PB ∴⊥,D 选项正确.故选:C .【点睛】本题考查命题的真假的判断与应用,涉及直线与平面的平行与垂直的位置关系的判断,是中档题.13.设三棱锥V ﹣ABC 的底面是A 为直角顶点的等腰直角三角形,VA ⊥底面ABC ,M 是线段BC 上的点(端点除外),记VM 与AB 所成角为α,VM 与底面ABC 所成角为β,二面角A ﹣VC ﹣B 为γ,则( )A .2παββγ+<,>B .2παββγ+<,<C .2παββγ+>,>D .2παββγ+>,< 【答案】C【解析】【分析】由最小角定理得αβ>,由已知条件得AB ⊥平面VAC ,过A 作AN VC ⊥,连结BN ,得BNA γ=∠,推导出BVA γ>∠,由VA ⊥平面ABC ,得VMA β=∠,推导出MVA γ>∠,从而2πβγ+>,即可得解.【详解】 由三棱锥V ABC -的底面是A 为直角顶点的等腰直角三角形,VA ⊥平面ABC ,M 是线段BC 上的点(端点除外),记VM 与AB 所成角为α,VM 与底面ABC 所成角为β,二面角A VC B --为γ, 由最小角定理得αβ>,排除A 和B ;由已知条件得AB ⊥平面VAC ,过A 作AN VC ⊥,连结BN ,得BNA γ=∠, ∴tan tan AB BNA AN γ=∠=, 而tan AB BVA AV∠=,AN AV <,∴tan tan BNA BVA ∠>∠, ∴BVA γ>∠,∵VA ⊥平面ABC ,∴VMA β=∠,∴2MVA πβ+∠=, ∵tan AM MVA AV∠=,AB AM >,∴tan tan BVA MVA ∠>∠, ∴MVA γ>∠,∴2πβγ+>.故选:C .【点睛】本题查了线线角、线面角、二面角的关系与求解,考查了空间思维能力,属于中档题.14.已知底面是等腰直角三角形的三棱锥P -ABC 的三视图如图所示,俯视图中的两个小三角形全等,则( )A .PA ,PB ,PC 两两垂直B .三棱锥P -ABC 的体积为83 C .||||||6PA PB PC ===D .三棱锥P -ABC 的侧面积为35【答案】C 【解析】 【分析】 根据三视图,可得三棱锥P -ABC 的直观图,然后再计算可得.【详解】 解:根据三视图,可得三棱锥P -ABC 的直观图如图所示,其中D 为AB 的中点,PD ⊥底面ABC .所以三棱锥P -ABC 的体积为114222323⨯⨯⨯⨯=, 2AC BC PD ∴===,2222AB AC BC ∴=+=,||||||2DA DB DC ∴===()22||||||226,PA PB PC ∴===+=222PA PB AB +≠Q ,PA ∴、PB 不可能垂直,即,PA ,PB PC 不可能两两垂直, 1222222PBA S ∆=⨯=Q ()22161252PBC PAC S S ∆∆==-=Q∴三棱锥P -ABC 的侧面积为2522故正确的为C.故选:C.【点睛】 本题考查三视图还原直观图,以及三棱锥的表面积、体积的计算问题,属于中档题.15.已知四面体P ABC -的外接球的球心O 在AB 上,且PO ⊥平面ABC ,23AC AB =,若四面体P ABC -的体积为32,求球的表面积( )A .8πB .12πC .83πD .123π【答案】B【解析】【分析】 依据题意作出图形,设四面体P ABC -的外接球的半径为R ,由题可得:AB 为球的直径,即可求得:2AB R =,3AC R =, BC R =,利用四面体P ABC -的体积为32列方程即可求得3R =,再利用球的面积公式计算得解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1(2010辽宁理19))已知三棱锥P -ABC 中,PA ⊥面ABC ,AB ⊥AC ,PA=AC=12AB ,N 为AB 上一点,AB=4AN,M,S 分别为PB,BC 的中点.证明:CM ⊥SN ; 审题要津:本题空间坐标系易建立,可用坐标法. 证明:设PA=1,以A 为原点,射线AB ,AC ,AP 分别为x ,y ,z 轴正向建立空间直角坐标系如图,则P (0,0,1),C (0,1,0),B (2,0,0),M (1,0,12),N (12,0,0),S (1,12,0) 111(1,1,),(,,0)222CM SN =-=-- ,因为110022CM SN ∙=-++= , 所以CM ⊥SN .【点评】对坐标系易建立的空间线线垂直判定(证明)问题,常用向量法,即通过证明所证直线的方向向量的数量积为0证明两直线垂直.例2(2010天津理19) 在长方体1111ABCD A BC D -中,E 、F 分别是棱BC ,1CC 上的点,CF =AB =2CE , 1::AB AD AA =1:2:4.证明AF ⊥平面1A ED审题要津:本题空间坐标系易建立,可用坐标法.解析:如图所示,建立空间直角坐标系,点A 为坐标原点,设1AB =,依题意得(0,2D ,(1,2,1)F ,1(0,0,4)A ,31,,02E ⎛⎫⎪⎝⎭已知(1,2,1)AF = ,131,,42EA ⎛⎫=-- ⎪⎝⎭ ,11,,02ED ⎛⎫=- ⎪⎝⎭ 于是AF ·1EA =0,AF ·ED =0.因此,1AF EA ⊥,AF ED ⊥,又1EA ED E ⋂= 所以AF ⊥平面1A ED【点评】对坐标系易建立的空间线面垂直问题,通常用向量法,先求出平面的法向量和直线的方向向量,证明平面法向量与直线的方向向量平行或者直接用向量法证明直线与平面内两条相交直线垂直,再用线面垂直判定定理即可.例 3 (2010年山东文)在如图所示的几何体中,四边形ABCD 是正方形,MA ⊥平面ABCD ,//PD MA ,E 、G 、F 分别为MB 、PB 、PC 的中点,且2AD PD MA ==.求证:平面EFG ⊥平面PDC .审题要津:本题空间坐标系易建立,可用坐标法.解析:以A 为原点,向量DA ,AB ,AM分别为x 轴、y 轴、z 轴的正方向,如图建立坐标系,设AM=1,则AD=AB=PD=2,则B(0,2,0),C (-2,2,0),D(-2,0,0),P(-2,0,2), M(0,0,1),则E(0,1,12),G(-1,1,1),F(-2,1,1), ∴EG=(-1,0,12),GF=(-1,0,0),设平面EFG 的法向量m =(x ,y ,z ),则 EG ∙ m =12x z -+=0且GF ∙ m =x -=0,取y =1,则x =z =0,∴m =(0,1,0),易证面PDC 的法向量为DA=(2,0,0), ∵DA ∙ m =200100⨯+⨯+⨯=0,∴m ⊥DA, ∴平面EFG ⊥平面PDC【点评】对于易建立空间坐标系的面面垂直问题,常向量法,即先建立坐标系,求出两个平面的法向量,通过证明这两个平面的法向量垂直,即得面面垂直. 考点2.利用空间向量处理空间平行关系空间线线、线面、面面平行关系问题是高考考查的另一个重点内容,考查的形式灵活多样,常与探索性问题、垂直问题、空间角问题结合,可以是小题,也可以是解答题的一个小题,题目的难度一般不大,是高考中的得分点之一.例4(2010 湖南理18)在正方体1111ABCD A BC D -,E 是棱1DD 的中点。
在棱11C D 上是否存在一点F ,使1B F ∥平面1A BE ?证明你的结论。
审题要津:本题坐标系易建立,可用向量法求解.解析:以A 为坐标原点,如图建立坐标系,设正方形的棱长为2,则B(2,0,0),E(0,2,1),1A (0,0,2),1B (2,0,2),∴BE =(-2,2,1),1BA=(-2,0,2), 设面1BEA 的法向量为m =(x ,y ,z ),则BE ∙m =22x y z -++=0且1BA ∙ m =22x z +=0,取x =1,则z =-1,y =32,∴m =(1,32,-1), 假设在棱11C D 上存在一点F ,使1B F ∥平面1A BE ,设F(0x ,2,2)(0≤0x ≤2),则BF =(02x -,2,2), 则BF ∙ m =031(2)2(1)22x ⨯-+⨯+-⨯=0,解得0x =1, ∴当F 为11C D 中点时,1B F ∥平面1A BE .【点评】对于易建立坐标系的线面平行问题的向量解法,有两种思路:(1)用共面向量定理,证明直线的方向向量能用平面内两条相交直线的方向向量表示出来,即这三个向量共线,根据共面向量概念和直线在平面外,可得线面平行;(2)求出平面法向量,然后证明法向量与直线的方向向量垂直即可.对于探索性问题,通常先假设成立,设出相关点的坐标,利用相关知识,列出关于坐标的方程,若方程有解,则存在,否则不存在.注意,(1)设点的坐标时,利用点在某线段上,设出点分线段所成的比,用比表示坐标可以减少未知量,简化计算;(2)注意点的坐标的范围.例5在三棱柱111ABC A B C -中,侧棱垂直于底面,在底面ABC 中ABC ∠=090,D 是BC 上一点,且1A B ∥面1AC D ,1D 为11B C 的中点,求证:面11A BD∥面1AC D .审题要津:本题的坐标系容易建立,可用向量法.解析:以B 点为原点,如图建立坐标系,设AB=a ,BC=2b ,1BB =c ,则A (a ,0,0),1C (0,2b ,c ),1B (0,0, c ),1A (a ,0,c ), ∴1D (0,b ,c ),设D(0,0y ,0)(0≤0y ≤2b ),∴AD=(-a ,0y ,0),1AC =(-a ,2b ,c ),1BA =(a ,0,c ),1BD=(0,b ,c ), 设面1A C D的法向量为m =(1x ,1y ,1z ),则AD ∙m =101ax y y -+=0且1AC ∙ m =1112ax by cz -++=0,取1y =a ,则1x =0y ,1z =02ay abc-, 则m =(0y ,a ,02ay abc-), 又∵1A B ∥面1AC D , ∴1BA ∙ m =002ay ab ay c c -+⨯=0,解得0y =b , ∴m =(b ,a ,abc-), 设面11A BD 的法向量为n =(2x ,2y ,2z ),则1BA ∙ n =22ax cz +=0且1BD ∙n =22by cz +=0,取2z =1,则2x =c a -,2y =c b -,则n =(c a -,cb-,1), ∴n =cab-m , ∴m ∥n , ∴面11A BD ∥面1AC D . 【点评】对面面平行问题的向量方解法有两种思路,(1)利用向量证明一个面内两条相交直线分别与另一个平面平行,根据面面判定定理即得;(2)求出两个平面的法向量,证明这两个法向量平行,则这两个面就平行.考点3利用空间向量处理异面直线夹角、线面角、二面角等空间角问题异面直线夹角、线面角、二面角等空间角问题是高考考查的热点和重点,常与探索性问题、平行问题、垂直等问题结合,重点考查综合利用空间向量、空间平行与垂直的有关定理、空间角的相关概念解决空间角问题的能力,是立体几何中的难点,难度为中档难度.例6(2010天津理19) 在长方体1111ABCD A BC D -中,E 、F 分别是棱BC ,1CC 上的点,2CF AB CE ==,1::1:2:4AB AD AA =(1)求异面直线EF 与1A D 所成角的余弦值;(2)求二面角1A ED F --的正弦值。
审题要津:本题坐标系易建立,可以向量法.解析:如图所示,建立空间直角坐标系,点A 为坐标原点,设1AB =,依题意得(0,2,0)D ,(1,2,1)F ,1(0,0,4)A ,31,,02E ⎛⎫⎪⎝⎭(1)证明:易得10,,12EF ⎛⎫= ⎪⎝⎭,1(0,2,4)A D =- ,于是1113c o s ,5E F A D E F A D E F A D ==-, 所以异面直线EF 与1A D 所成角的余弦值为35(2)解:设平面EFD 的法向量n =(,,)x y z ,则EF ∙ n =12y z +=0且ED ∙ n =12x y -+=0,不妨令x =1,可得n =(1,2,-1),设平面1A ED 的法向量m =(m ,n ,p )则ED ∙m =12m n -+=0且1DA ∙ m =24n p -+=0, 取p =1,则n =2,m =1,则m =(1,2,1) 于是2cos ,==|3∙n m n m n ||m |,从而sin ,nm ,所以二面角1A -ED-F的正弦值为3【点评】(1)对异面直线夹角问题,先求出两条异面直线的方向向量分别为m 、n ,在求出m 、n 的夹角,设两异面直线的夹角θ,利用cos θ=|cos |m,n 求出异面直线的夹角,注意:(1)异面直线夹角与向量夹角的关系;(2)对二面角l αβ--的大小问题,先求出平面α、β的法向量m 、n ,再求出m 、n 的夹角,在α内取一点A ,在β内取一点B ,设二面角l αβ--大小为θ,若AB ∙ n 与AB ∙ m 同号,则θ=m,n ,若AB ∙ n 与AB∙ m 异号,则θ=π-m,n ,注意二面角大小与法向量夹角的关系.例7( 2010全国卷I 理7)正方体ABCD-1111A B C D 中,B 1B 与平面AC 1D 所成角的余弦值为23D 审题要津:本题是正方体中的线面关系问题,可用空间向量法求解.解析:如图建立坐标系,设正方体棱长为1,1BB 与面1ACD 的夹角为θ,则D(0,0,0),C(0,1,0),B(1,1,0),A(1,0,0),1D (0,0,1),1B (1,1,1), ∴AC =(-1,1,0),1AD =(-1,0,1),1BB =(0,0,1),设面1ACD 的法向量n =(x ,y ,z ),则0=AC ∙ n =x y -+且0=1AD ∙ n =x z -+,取x =1,则y =1,z =1, ∴n =(1,1,1),∴sin θ=11||||BB BB ∙∙n |n |cos θD.【点评】对于线面夹角问题,若容易建立坐标系,则常用坐标法,建立坐标系,求出线面夹角问题中三位直线的方向向量m 和平面法向量n ,设线面角为θ,则直线方向向量m 在平面法向量n 方向上的投影的长度|∙|m n |n |与直线方向向量m 的模之|m |比||∙|m n |m |n |就是线面夹角的正弦值,即sin θ=||∙|m n |m |n |.历届高考中的空间向量与立体几何试题选讲1.(2008海南、宁夏理)如图,已知点P 在正方体ABC D -A 1B 1C 1D 1的对角线BD 1上,∠PDA=60°。
