【人教A版】高中数学必修2教学同步讲练第二章《平面与平面平行的判定》练习题(含答案)
【人教A版】高中数学必修2教学同步讲练第二章《平面与平面垂直的性质》练习题(含答案)

第二章点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质2.3.3 直线与平面垂直的性质2.3.4 平面与平面垂直的性质A级基础巩固一、选择题1.在空间中,下列命题正确的是()A.垂直于同一条直线的两直线平行B.平行于同一条直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行2.关于直线m,n与平面α,β,有下列四个命题:①若m∥α,n∥β,且α∥β,则m∥n;②若m⊥α,n⊥β,且α⊥β,则m⊥n;③若m⊥α,n∥β,且α∥β,则m⊥n;④若m∥α,n⊥β且α⊥β,则m∥n.其中真命题的序号是()A.①②B.③④C.①④D.②③3.若平面α⊥平面β,平面β⊥平面γ,则()A.a∥γB.α⊥γC.α与γ相交但不垂直 D.以上都有可能4.在圆柱的一个底面上任取一点(该点不在底面圆周上),过该点作另一个底面的垂线,则这条垂线与圆柱的母线所在直线的位置关系是()A.相交B.平行C.异面D.相交或平行5.在正方体ABCD-A1B1C1D1中,若E为A1C1的中点,则直线CE垂直于()A.AC B.BDC.A1D D.A1A二、填空题6.已知AF⊥平面ABCD,DE⊥平面ABCD,如图所示,且AF =DE,AD=6,则EF=________.7.设a,b是两条不同的直线,α,β是两个不同的平面,有下列四个说法:①若a⊥b,a⊥α,b⊄α,则b∥α;②若a∥α,a⊥β,则α⊥β;③若a⊥β,α⊥β,则a∥α或a⊂α;④若a⊥b,a⊥α,b⊥β,则α⊥β.其中正确的个数为________.8.已知直二面角α-l-β,点A∈α,AC⊥l,点C为垂足,B∈β,BD⊥l,点D为垂足.若AB=2,AC=BD=1,则CD的长为________.三、解答题9.如图所示,ABCD为正方形,SA⊥平面ABCD,过点A且垂直于SC的平面分别交SB,SC,SD于点E,F,G.求证:AE⊥SB.10.(2015·广东卷)如图所示,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC.(1)证明:BC∥平面PDA;(2)证明:BC⊥PD.B级能力提升1.如图所示,在正方形SG1G2G3中,E、F分别是G1G2、G2G3的中点,现在沿SE、SF、EF把这个正方形折成一个四面体,使G1、G2、G3重合,重合后的点记为G.给出下列关系:①SG⊥平面EFG;②SE⊥平面EFG;③GF⊥SE;④EF⊥平面SEG.其中成立的有()A.①与②B.①与③C.②与③D.③与④2.在三棱锥P-ABC中,平面PAC⊥平面ABC,∠PCA=90°,△ABC是边长为4的正三角形,PC=4,M是AB边上的一动点,则PM的最小值为________.3.如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M,N 分别是AB,PC的中点.(1)求证:MN⊥CD;(2)若∠PDA=45°,求证:MN⊥平面PCD.参考答案第二章点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质2.3.3 直线与平面垂直的性质2.3.4 平面与平面垂直的性质A级基础巩固一、选择题1.在空间中,下列命题正确的是()A.垂直于同一条直线的两直线平行B.平行于同一条直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行解析:A项中垂直于同一条直线的两直线可能平行、异面或相交;B项中平行于同一条直线的两个平面可能平行或相交;C项中垂直于同一平面的两个平面可能平行或相交;D项正确.答案:D2.关于直线m,n与平面α,β,有下列四个命题:①若m∥α,n∥β,且α∥β,则m∥n;②若m⊥α,n⊥β,且α⊥β,则m⊥n;③若m⊥α,n∥β,且α∥β,则m⊥n;④若m∥α,n⊥β且α⊥β,则m∥n.其中真命题的序号是()A.①②B.③④C.①④D.②③解析:①m,n可能异面、相交或平行,④m,n可能平行、异面或相交,所以①④错误.答案:D3.若平面α⊥平面β,平面β⊥平面γ,则()A.a∥γB.α⊥γC.α与γ相交但不垂直 D.以上都有可能解析:两个平面都垂直于同一个平面,则这两个平面可能平行,也可能相交,故A,B,C都有可能.答案:D4.在圆柱的一个底面上任取一点(该点不在底面圆周上),过该点作另一个底面的垂线,则这条垂线与圆柱的母线所在直线的位置关系是()A.相交B.平行C.异面D.相交或平行解析:由线面垂直的性质可得.答案:B5.在正方体ABCD-A1B1C1D1中,若E为A1C1的中点,则直线CE垂直于()A.AC B.BDC.A1D D.A1A解析:如图所示,连接AC,BD,因为BD⊥AC,A1C1∥AC,所以BD⊥A1C1,因为BD⊥A1A,所以BD⊥平面ACC1A1,因为CE ⊂平面ACC1A1,所以BD⊥CE.答案:B二、填空题6.已知AF⊥平面ABCD,DE⊥平面ABCD,如图所示,且AF =DE,AD=6,则EF=________.解析:因为AF⊥平面ABCD,DE⊥平面ABCD,所以AF∥DE,又AF=DE,所以四边形AFED是平行四边形,所以EF=AD=6.答案:67.设a,b是两条不同的直线,α,β是两个不同的平面,有下列四个说法:①若a⊥b,a⊥α,b⊄α,则b∥α;②若a∥α,a⊥β,则α⊥β;③若a⊥β,α⊥β,则a∥α或a⊂α;④若a⊥b,a⊥α,b⊥β,则α⊥β.其中正确的个数为________.解析:①若a⊥b,a⊥α,可得出b∥α或b⊂α,又b⊄α,可得出b∥α,①正确;②若a∥α,a⊥β,由线面平行的性质定理可以得出在α内存在一条线c⊥β,故可得出α⊥β,②正确;③由a⊥β,α⊥β,可得出a∥α或a⊂α,③正确;④由a⊥b,a⊥α,可得出b∥α或b⊂α,又b⊥β,可得出α⊥β,④正确.答案:48.已知直二面角α-l-β,点A∈α,AC⊥l,点C为垂足,B∈β,BD⊥l,点D为垂足.若AB=2,AC=BD=1,则CD的长为________.解析:如图,连接BC.因为二面角α-l-β为直二面角,AC⊂α,且AC⊥l,α∩β=l,所以AC⊥β.又BC⊂β,所以AC⊥BC,所以BC2=AB2-AC2=3.又BD⊥CD,所以CD=BC2-BD2= 2.答案:2三、解答题9.如图所示,ABCD为正方形,SA⊥平面ABCD,过点A且垂直于SC的平面分别交SB,SC,SD于点E,F,G.求证:AE⊥SB.证明:因为SA⊥平面ABCD,所以SA⊥BC.因为四边形ABCD是正方形,所以AB⊥BC.因为SA∩AB=A,所以BC⊥平面SAB.因为AE⊂平面SAB,所以BC⊥AE.因为SC⊥平面AGFE,所以SC⊥AE.又因为BC∩SC=C,所以AE⊥平面SBC.而SB⊂平面SBC,所以AE⊥SB.10.(2015·广东卷)如图所示,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC.(1)证明:BC∥平面PDA;(2)证明:BC⊥PD.证明:(1)因为在长方形ABCD中,BC∥AD,BC⊄平面PDA,AD⊂平面PDA,所以BC∥平面PDA.(2)取CD的中点H,连接PH.因为PD=PC,所以PH⊥CD.又平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,PH ⊂平面PDC.所以PH⊥平面ABCD.又BC⊂平面ABCD,所以PH⊥BC.因为在长方形ABCD中,BC⊥CD,PH∩CD=H,所以BC⊥平面PDC.又PD⊂平面PDC,所以BC⊥PD.B级能力提升1.如图所示,在正方形SG1G2G3中,E、F分别是G1G2、G2G3的中点,现在沿SE、SF、EF把这个正方形折成一个四面体,使G1、G2、G3重合,重合后的点记为G.给出下列关系:①SG⊥平面EFG;②SE⊥平面EFG;③GF⊥SE;④EF⊥平面SEG.其中成立的有()A.①与②B.①与③C.②与③D.③与④解析:由SG⊥GE,SG⊥GF,得SG⊥平面EFG,排除C、D;若SE⊥平面EFG,则SG∥SE,这与SG∩SE=S矛盾,排除A.答案:B2.在三棱锥P-ABC中,平面PAC⊥平面ABC,∠PCA=90°,△ABC是边长为4的正三角形,PC=4,M是AB边上的一动点,则PM的最小值为________.解析:如图,连接CM,则由题意知PC⊥平面ABC,可得PC⊥CM,所以PM=PC2+CM2,要求PM的最小值只需求出CM的最小值即可,在△ABC中,当CM⊥AB时CM有最小值,此时有CM=4×32=23,所以PM的最小值为27.答案:273.如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M,N 分别是AB,PC的中点.(1)求证:MN⊥CD;(2)若∠PDA=45°,求证:MN⊥平面PCD.证明:(1)如图所示,取PD的中点E,连接AE,NE.11因为N 为PC 的中点,E 为PD 的中点,所以NE ∥CD 且NE =12CD . 而AM ∥CD ,且AM =12AB =12CD , 所以NE ∥AM 且NE =AM ,所以四边形AMNE 为平行四边形,所以MN ∥AE .又PA ⊥平面ABCD ,所以PA ⊥CD .又因为四边形ABCD 为矩形,所以AD ⊥CD .而AD ∩PA =A ,所以CD ⊥平面PAD ,所以CD ⊥AE .又AE ∥MN ,所以MN ⊥CD .(2)由(1)可知CD ⊥AE ,MN ∥AE .又∠PDA =45°,所以△PAD 为等腰直角三角形.又E 为PD 的中点,所以AE ⊥PD ,所以AE ⊥平面PCD .又AE ∥MN ,所以MN ⊥平面PCD .。
最新人教版高中数学必修2第二章《平面与平面平行的判定》课后训练
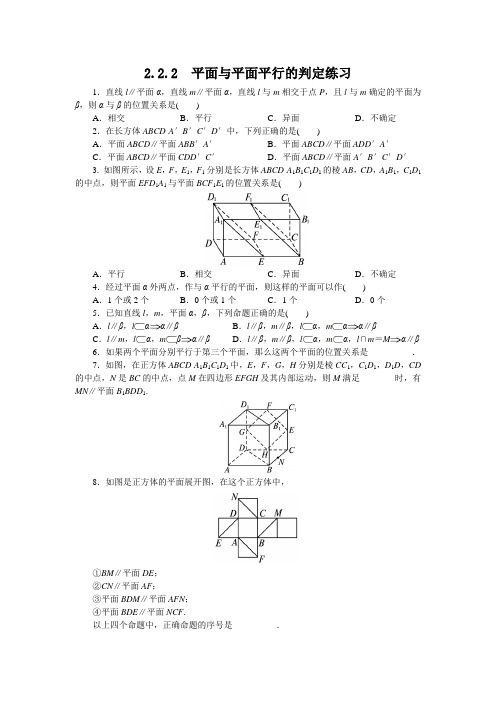
2.2.2 平面与平面平行的判定练习1.直线l∥平面α,直线m∥平面α,直线l与m相交于点P,且l与m确定的平面为β,则α与β的位置关系是()A.相交B.平行C.异面D.不确定2.在长方体ABCD-A′B′C′D′中,下列正确的是()A.平面ABCD∥平面ABB′A′B.平面ABCD∥平面ADD′A′C.平面ABCD∥平面CDD′C′D.平面ABCD∥平面A′B′C′D′3. 如图所示,设E,F,E1,F1分别是长方体ABCD-A1B1C1D1的棱AB,CD,A1B1,C1D1的中点,则平面EFD1A1与平面BCF1E1的位置关系是()A.平行B.相交C.异面D.不确定4.经过平面α外两点,作与α平行的平面,则这样的平面可以作()A.1个或2个B.0个或1个C.1个D.0个5.已知直线l,m,平面α,β,下列命题正确的是()A.l∥β,lαα∥βB.l∥β,m∥β,lα,mαα∥βC.l∥m,lα,mβα∥βD.l∥β,m∥β,lα,mα,l∩m=Mα∥β6.如果两个平面分别平行于第三个平面,那么这两个平面的位置关系是__________.7.如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱CC1,C1D1,D1D,CD 的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足________时,有MN∥平面B1BDD1.8.如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是__________.9. 如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC和SC的中点.求证:平面EFG∥平面BDD1B1.10. 如图,E,F,G,H分别是正方体ABCD-A1B1C1D1的棱BC,CC1,C1D1,AA1的中点,求证:(1)GE∥平面BB1D1D;(2)平面BDF∥平面B1D1H.参考答案1. 答案:B2. 答案:D3. 答案:A4. 答案:B5. 答案:D6. 答案:平行7. 答案:M ∈线段FH8. 答案:①②③④9. 答案:证明: 如图所示,连接SB ,SD .∵F ,G 分别是DC ,SC 的中点,∴FG ∥SD .又∵SD 平面BDD 1B 1,FG 平面BDD 1B 1, ∴直线FG ∥平面BDD 1B 1.同理可证EG ∥平面BDD 1B 1.又∵直线EG 平面EFG ,直线FG 平面EFG , 直线EG ∩直线FG =G ,∴平面EFG ∥平面BDD 1B 1.10. 答案:证明: (1)取B 1D 1的中点O ,连接GO ,OB ,易证OG ∥12B 1C 1,且OG =12B 1C 1,BE ∥12B 1C 1,且BE =12B 1C 1. ∴OG ∥BE 且OG =BE ,∴四边形BEGO 为平行四边形,∴OB ∥GE .∵OB 平面BDD 1B 1,GE 平面BDD 1B 1, ∴GE ∥平面BB 1D 1D .(2)由正方体的性质,易知B 1D 1∥BD ,且易证BF ∥D 1H . ∵B 1D 1平面BDF ,BD平面BDF ,∴B 1D 1∥平面BDF .∵HD1平面BDF,BF平面BDF,∴HD1∥平面BDF.又∵B1D1∩HD1=D1,∴平面BDF∥平面B1D1H.。
【人教A版】高中数学必修2教学同步讲练第二章《平面与平面平行的性质》练习题(含答案)

第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.2.4 平面与平面平行的性质A级基础巩固一、选择题1.已知平面α∥平面β,过平面α内的一条直线a的平面γ,与平面β相交,交线为直线b,则a、b的位置关系是() A.平行B.相交C.异面D.不确定2.已知l是过正方体ABCD-A1B1C1D1的顶点A,B1,D1的平面与下底面ABCD所在平面的交线,下列结论中错误的是() A.D1B1∥l B.BD∥平面AD1B1C.l∥平面A1B1C1D1D.l⊥B1C13.五棱柱的底面为α和β,且A∈α,B∈α,C∈β,D∈β,且AD∥BC,则AB与CD的位置关系为()A.平行B.相交C.异面D.无法判断4.P是△ABC所在平面外一点,平面α∥平面ABC,α交线段PA,PB,PC于A′,B′,C′,若PA′∶AA′=2∶3,则S△A′B′C′∶S△ABC=()A.2∶25 B.4∶25C.2∶5 D.4∶55.下列说法正确的个数是()①两平面平行,夹在两平面间的平行线段相等;②两平面平行,夹在两平面间的相等的线段平行;③如果一条直线和两个平行平面中的一个平行,那么它和另一个平面也平行;④平行直线被三个平行平面截得的线段对应成比例.A.1 B.2C.3 D.4二、填空题6.如图所示,在三棱柱ABC-A′B′C′中,截面A′B′C与平面ABC 交于直线a,则直线a与直线A′B′的位置关系为________.7.如图所示,平面四边形ABCD所在的平面与平面α平行,且四边形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边形,则四边形ABCD的形状一定是________.8.正方体ABCD-A1B1C1D1的棱长为3,点E在A1B1上,且B1E =1,平面α∥平面BC1E,若平面α∩平面AA1B1B=A1F,则AF的长为________.三、解答题9.如图所示,已知E,F分别是正方体ABCD-A1B1C1D1棱AA1,CC1上的点,且AE=C1F.求证:四边形EBFD1是平行四边形.10.如图所示,平面α∥平面β∥平面γ,两条直线l,m分别与平面α,β,γ相交于点A,B,C和点D,E,F.已知AC=15 cm,DE=5 cm,AB∶BC=1∶3,求AB,BC,EF的长.B级能力提升1.已知a,b表示直线,α,β,γ表示平面,下列推理正确的是()A.α∩β=a,b⊂α⇒a∥bB.α∩β=a,a∥b⇒b∥a,且b∥βC.a∥β,b∥β,a⊂α,b⊂α⇒α∥βD.α∥β,α∩γ=a,β∩γ=b⇒a∥b2.如图,棱长为2的正方体ABCD-A1B1C1D1中,M是棱AA1的中点,过C,M,D1作正方体的截面,则截面的面积是________.3.如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?参考答案第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.2.4 平面与平面平行的性质A级基础巩固一、选择题1.已知平面α∥平面β,过平面α内的一条直线a的平面γ,与平面β相交,交线为直线b,则a、b的位置关系是() A.平行B.相交C.异面D.不确定解析:两平行平面α,β被第三个平面γ所截,则交线a、b平行.答案:A2.已知l是过正方体ABCD-A1B1C1D1的顶点A,B1,D1的平面与下底面ABCD所在平面的交线,下列结论中错误的是() A.D1B1∥l B.BD∥平面AD1B1C.l∥平面A1B1C1D1D.l⊥B1C1解析:因为正方体的上底面与下底面平行,由面面平行的性质定理可得选项A正确,再由线面平行的判定定理可得选项B、C正确.选项D错误,因为D1B1∥l,所以l与B1C1所成角是45°.答案:D3.五棱柱的底面为α和β,且A∈α,B∈α,C∈β,D∈β,且AD∥BC,则AB与CD的位置关系为()A.平行B.相交C .异面D .无法判断解析:因为AD ∥BC 所以ABCD 共面,由面面平行的性质定理知AB ∥CD .答案:A4.P 是△ABC 所在平面外一点,平面α∥平面ABC ,α交线段PA ,PB ,PC 于A ′,B ′,C ′,若PA ′∶AA ′=2∶3,则S △A ′B ′C ′∶S △ABC =( )A .2∶25B .4∶25C .2∶5D .4∶5解析:易知平面ABC ∥平面A ′B ′C ′,所以AC ∥A ′C ′,BC ∥B ′C ′,AB ∥A ′B ′.所以△A ′B ′C ′∽△ABC .又因为PA ′∶AA ′=2∶3,所以PA ′PA =A ′C ′AC =25.所以S △A ′B ′C ′S △ABC =425. 答案:B5.下列说法正确的个数是( )①两平面平行,夹在两平面间的平行线段相等;②两平面平行,夹在两平面间的相等的线段平行;③如果一条直线和两个平行平面中的一个平行,那么它和另一个平面也平行;④平行直线被三个平行平面截得的线段对应成比例.A .1B .2C .3D .4解析:①正确;②错误,这两条相等的线段可能相交或异面;③错误,直线可能在另一个平面内;④正确.答案:B二、填空题6.如图所示,在三棱柱ABC -A ′B ′C ′中,截面A ′B ′C 与平面ABC 交于直线a ,则直线a 与直线A ′B ′的位置关系为________.解析:在三棱柱ABC-A′B′C′中,A′B′∥AB,AB⊂平面ABC,A′B′⊄平面ABC,所以A′B′∥平面ABC.又A′B′⊂平面A′B′C,平面A′B′C∩平面ABC=a,所以A′B′∥a.故填平行.答案:平行7.如图所示,平面四边形ABCD所在的平面与平面α平行,且四边形ABCD在平面α内的平行投影A1B1C1D1是一个平行四边形,则四边形ABCD的形状一定是________.解析:因为平面AC∥α,平面AA1B1B∩α=A1B1,平面AA1B1B ∩平面ABCD=AB,所以AB∥A1B1,同理可证CD∥C1D1,又A1B1∥C1D1,所以AB∥CD,同理可证AD∥BC,所以四边形ABCD是平行四边形.答案:平行四边形8.正方体ABCD-A1B1C1D1的棱长为3,点E在A1B1上,且B1E =1,平面α∥平面BC1E,若平面α∩平面AA1B1B=A1F,则AF的长为________.解析:由题意知,因平面α∥平面BC1E,所以A1F綊BE,所以Rt△A1AF≌Rt△BB1E,所以B1E=FA=1.答案:1三、解答题9.如图所示,已知E,F分别是正方体ABCD-A1B1C1D1棱AA1,CC1上的点,且AE=C1F.求证:四边形EBFD1是平行四边形.证明:如图,在平面A1ADD1中,作EG∥AD交D1D于点G,连接GC,易证EG綊AD綊BC,所以四边形GEBC为平行四边形,所以EB綊GC.又AE=C1F,所以D1G綊FC,所以四边形D1GCF为平行四边形,所以D1F綊GC,所以EB綊D1F,所以四边形EBFD1是平行四边形.10.如图所示,平面α∥平面β∥平面γ,两条直线l,m分别与平面α,β,γ相交于点A,B,C和点D,E,F.已知AC=15 cm,DE=5 cm,AB∶BC=1∶3,求AB,BC,EF的长.解:如图所示,连接AF,交β于点G,连接BG,GE,AD,CF.因为平面α∥平面β∥平面γ,所以BG ∥CF ,GE ∥AD .所以AB BC =AG GF =DE EF =13. 所以AB AB +BC =14. 所以AB =154cm , EF =3DF =15 cm ,BC =AC -AB =454cm. B 级 能力提升1.已知a ,b 表示直线,α,β,γ表示平面,下列推理正确的是( )A .α∩β=a ,b ⊂α⇒a ∥bB .α∩β=a ,a ∥b ⇒b ∥a ,且b ∥βC .a ∥β,b ∥β,a ⊂α,b ⊂α⇒α∥βD .α∥β,α∩γ=a ,β∩γ=b ⇒a ∥b解析:A 项中,α∩β=a ,b ⊂α,则a ,b 可能平行也可能相交;B 项中,α∩β=a ,a ∥b ,则可能b ∥α,且b ∥β,也可能b 在平面α或β内;C 项中,a ∥β,b ∥β,a ⊂α,b ⊂α,根据面面平行的判定定理,若再加上条件a ∩b =A ,才能得出α∥β;D 项为面面平行的性质定理的符号语言,正确.答案:D2.如图,棱长为2的正方体ABCD -A 1B 1C 1D 1中,M 是棱AA 1的中点,过C ,M ,D 1作正方体的截面,则截面的面积是________.解析:在正方体ABCD-A1B1C1D1中,因为平面MCD1∩平面DCC1D1=CD1,所以平面MCD1∩平面ABB1A1=MN,且MN∥CD1,所以N为AB的中点(如图),所以该截面为等腰梯形MNCD1;因为正方体的棱长为2,易知,MN=2,CD1=22,MD 1=5,所以等腰梯形MNCD 1的高MH = (5)2-⎝ ⎛⎭⎪⎫222=32 2. 所以截面面积为12(2+22)×322=92. 答案:923.如图,在正方体ABCD -A 1B 1C 1D 1中,O 为底面ABCD 的中心,P 是DD 1的中点,设Q 是CC 1上的点,问:当点Q 在什么位置时,平面D 1BQ 与平面PAO 平行?解:如图,设平面D 1BQ ∩平面ADD 1A 1=D 1M ,点M 在AA 1上,由于平面D 1BQ ∩平面BCC 1B 1=BQ ,平面ADD 1A 1∥平面BCC 1B 1,由面面平行的性质定理可得BQ ∥D 1M .假设平面D1BQ∥平面PAO,由平面D1BQ∩平面ADD1A1=D1M,平面PAO∩平面ADD1A1=AP,可得AP∥D1M,所以BQ∥D1M∥AP.因为P为DD1的中点,所以M为AA1的中点,所以Q为CC1的中点,故当Q为CC1的中点时,平面D1BQ∥平面PAO.。
人教A版高中数学必修二2.2.1直线与平面平行的判定平面与平面平行的判定同步练习(I)卷

人教A版高中数学必修二 2.2.1直线与平面平行的判定平面与平面平行的判定同步练习(I)卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分)若两个平面与第三个平面相交,有两条交线且两条交线互相平行,则这两个平面()A . 有公共点B . 没有公共点C . 平行D . 平行或相交2. (2分)(2018·中山模拟) 如图,在正方形中,分别是的中点,沿把正方形折成一个四面体,使三点重合,重合后的点记为,点在内的射影为 .则下列说法正确的是()A . 是的垂心B . 是的内心C . 是的外心D . 是的重心3. (2分) (2018高二上·拉萨月考) 设表示不同的直线,表示不同的平面,给出下列四个命题:①若,且,则;②若,,,则;③若,,则;④如果,,,则 .则错误的命题个数为()A . 4B . 3C . 2D . 14. (2分)已知直线m∥平面α,直线n在α内,则m与n的关系为()A . 平行B . 相交C . 相交或异面D . 平行或异面5. (2分) (2017高一下·瓦房店期末) 已知为直线,为平面,,,则与之间的关系是()A . 平行B . 垂直C . 异面D . 平行或异面6. (2分)已知a,b表示直线,α,β,γ表示平面,则下列推理正确的是()A . α∩β=a,b⊂α⇒a∥bB . α∩β=a,a∥b⇒b∥α且b∥βC . a∥β,b∥β,a⊂α,b⊂α⇒α∥βD . α∥β,α∩γ=a,β∩γ=b⇒a∥b7. (2分) (2020高二上·遂宁期末) 设是两条不同的直线,是两个不同的平面,下列四个命题为假命题的是()A . 若,则;B . 若面,面,,则面C . 若,则 .D . 若,,则8. (2分)设m,n是两条不同的直线,是两个不同的平面,则下列命题正确的是()A . 若m⊥n,m⊥α,n∥β,则α∥βB . 若m∥α,n∥β,α∥β则m∥nC . 若m∥n,m∥α,n∥β则α∥βD . 若m⊥α,n∥β,α∥β,则m⊥n二、填空题 (共3题;共4分)9. (2分)在下面给出的条件中,若条件足够能推出a∥α,则在横线上填“OK”;若条件不能保证推出a∥α,则请在横线上补足条件:(1)条件:a∥b,b∥c,c⊂α,________ ,结论:a∥α,(2)条件:α∩β=b,a∥b,a⊂β,________ ,结论:a∥α.10. (1分) (2018高一下·包头期末) 给出下列命题:①如果,是两条直线,且,那么平行于经过的任何平面;②如果直线和平面满足,那么直线与平面内的任何直线平行;③如果直线,和平面满足,,那么;④如果直线,和平面满足,,,那么;⑤如果平面,,满足,,那么 .其中正确命题的序号是________.11. (1分)如图,在直角梯形ABCD中,BC⊥DC ,AE⊥DC , M , N分别是AD , BE的中点,将三角形ADE沿AE折起,则下列说法正确的是________(填序号).①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D 折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.三、解答题 (共3题;共30分)12. (5分)如图空间四边形ABCD,E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD,AC⊥BD,试判断四边形EFGH的形状,并证明.13. (10分) (2016高二上·西湖期中) 如图,在棱长为ɑ 的正方体ABCD﹣A1B1C1D1中,E、F、G分别是CB.CD.CC1的中点.(1)求直线 A1C与平面ABCD所成角的正弦的值;(2)求证:平面A B1D1∥平面EFG.14. (15分) (2016高二下·韶关期末) 如图,在长方体ABCD﹣A1B1C1D1中,AA1=AD=1,E为CD中点.(1)求证:C1D∥平面AB1E;(2)求证:BC1⊥B1E;(3)若AB= ,求二面角E﹣AB1﹣B的正切值.参考答案一、单选题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共3题;共4分)9-1、10-1、11-1、三、解答题 (共3题;共30分)12-1、13-1、13-2、14-1、14-2、第11 页共11 页。
【人教A版】高中数学必修2教学同步讲练第二章《直线与平面平行的性质》练习题(含答案)

第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.2.3 直线与平面平行的性质A级基础巩固一、选择题1.已知直线l∥平面α,P∈α,那么过点P且平行于l的直线()A.只有一条,不在平面α内B.只有一条,在平面α内C.有两条,不一定都在平面α内D.有无数条,不一定都在平面α内2.如果l∥平面α,则l平行于α内()A.全部直线B.唯一确定的直线C.任一直线D.过l的平面与α的交线3.若两个平面与第三个平面相交有两条交线且两条交线互相平行,则这两个平面()A.有公共点B.没有公共点C.平行D.平行或相交4.如图所示,长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG与AB的位置关系是()A.平行B.相交C.异面D.平行和异面5.如图所示,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则()A.MN∥PDB.MN∥PAC.MN∥ADD.以上均有可能二、填空题6.如图所示,在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,EH∥FG.则EH与BD的位置关系是______.7.如图所示,正方体ABCD-A1B1C1D1中,AB=2,点E为AD 的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.8.如图,ABCDA1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的关系是________.三、解答题9.如图,AB,CD为异面直线,且AB∥α,CD∥α,AC,BD 分别交α于M,N两点,求证AM∶MC=BN∶ND.10.如图所示,四面体A-BCD被一平面所截,截面EFGH是一个矩形.(1)求证:CD∥平面EFGH;(2)求异面直线AB、CD所成的角.B级能力提升1.下列命题中,正确的命题是()A.若直线a上有无数个点不在平面α内,则a∥αB.若a∥α,则直线a与平面α内任意一条直线都平行C.若a⊂α,则a与α有无数个公共点D.若a⊄α,则a与α没有公共点2.对于平面M与平面N,有下列条件:①M、N都垂直于平面Q;②M、N都平行于平面Q;③M内不共线的三点到N的距离相等;④l,m为两条平行直线,且l∥M,m∥N;⑤l,m是异面直线,且l∥M,m∥M;l∥N,m∥N,则可判定平面M与平面N平行的条件是________(填正确结论的序号).3.如图所示,已知P是▱ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PBC∩平面PAD=l.(1)求证:l∥BC.(2)问:MN与平面PAD是否平行?试证明你的结论.参考答案第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.2.3 直线与平面平行的性质A级基础巩固一、选择题1.已知直线l∥平面α,P∈α,那么过点P且平行于l的直线()A.只有一条,不在平面α内B.只有一条,在平面α内C.有两条,不一定都在平面α内D.有无数条,不一定都在平面α内解析:如图所示,因为l∥平面α,P∈α,所以直线l与点P确定一个平面β,α∩β=m,所以P∈m,所以l∥m且m是唯一的.答案:B2.如果l∥平面α,则l平行于α内()A.全部直线B.唯一确定的直线C.任一直线D.过l的平面与α的交线解析:利用线面平行的性质定理知,选D.答案:D3.若两个平面与第三个平面相交有两条交线且两条交线互相平行,则这两个平面()A.有公共点B.没有公共点C.平行D.平行或相交答案:D4.如图所示,长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于G、H,则HG与AB的位置关系是()A.平行B.相交C.异面D.平行和异面解析:因为E,F分别是AA1,BB1的中点,所以EF∥AB.又AB⊄平面EFGH,EF⊂平面EFGH,所以AB∥平面EFGH.又AB⊂平面ABCD,平面ABCD∩平面EFGH=GH,所以AB∥GH.答案:A5.如图所示,四棱锥P-ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则()A.MN∥PDB.MN∥PAC.MN∥ADD.以上均有可能解析:因为MN∥平面PAD,MN⊂平面PAC,平面PAD∩平面PAC=PA,所以MN∥PA.答案:B二、填空题6.如图所示,在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,EH∥FG.则EH与BD的位置关系是______.解析:因为EH∥FG,FG⊂平面BCD,EH⊄平面BCD,所以EH∥平面BCD.因为EH⊂平面ABD,平面ABD∩平面BCD=BD,所以EH∥BD.答案:平行7.如图所示,正方体ABCD-A1B1C1D1中,AB=2,点E为AD 的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.解析:由于在正方体ABCD-A1B1C1D1中,AB=2,所以AC=2 2.又E为AD的中点,EF∥平面AB1C,EF⊂平面ADC,平面ADC∩平面AB1C=AC,所以EF∥AC,所以F为DC的中点,所以EF=12AC= 2.答案:28.如图,ABCDA1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的关系是________.解析:因为AC∥面A1B1C1D1,根据线面平行的性质知l∥AC.答案:平行三、解答题9.如图,AB,CD为异面直线,且AB∥α,CD∥α,AC,BD 分别交α于M,N两点,求证AM∶MC=BN∶ND.证明:连接AD 交α于点P ,连接MP ,NP ,因为CD ∥α,面ACD ∩α=MP ,所以CD ∥MP ,所以AM MC =AP PD. 同理可得NP ∥AB ,AP PD =BN ND, 所以AM MC =BN ND. 10.如图所示,四面体A -BCD 被一平面所截,截面EFGH 是一个矩形.(1)求证:CD ∥平面EFGH ;(2)求异面直线AB 、CD 所成的角.(1)证明:因为截面EFGH 是矩形,所以EF ∥GH .又GH ⊂平面BCD ,EF ⊄平面BCD .所以EF⊂平面ACD,平面ACD∩平面BCD=CD,所以EF∥CD.又EF⊂平面EFGH,CD⊄平面EFGH,所以CD∥平面EFGH.(2)解:由(1)知CD∥EF,同理AB∥FG,由异面直线所成角的定义知,∠EFG即为所求.故AB、CD所成的角为90°.B级能力提升1.下列命题中,正确的命题是()A.若直线a上有无数个点不在平面α内,则a∥αB.若a∥α,则直线a与平面α内任意一条直线都平行C.若a⊂α,则a与α有无数个公共点D.若a⊄α,则a与α没有公共点解析:对于A,直线a与平面α有可能相交,所以A错;对于B,平面α内的直线和直线a可能平行,也可能异面,所以B错;对于D,因为直线a与平面α可能相交,此时有一个公共点,所以D错.答案:C2.对于平面M与平面N,有下列条件:①M、N都垂直于平面Q;②M、N都平行于平面Q;③M内不共线的三点到N的距离相等;④l,m为两条平行直线,且l∥M,m∥N;⑤l,m是异面直线,且l∥M,m∥M;l∥N,m∥N,则可判定平面M与平面N平行的条件是________(填正确结论的序号).解析:由面面平行的判定定理及性质定理知,只有②⑤能判定M∥N.答案:②⑤3.如图所示,已知P是▱ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PBC∩平面PAD=l.(1)求证:l∥BC.(2)问:MN与平面PAD是否平行?试证明你的结论.证明:(1)因为BC∥AD,BC⊄平面PAD,AD⊂平面PAD,所以BC∥平面PAD.又BC⊂平面PBC,平面PBC∩平面PAD=l,所以l∥BC.(2)平行.如图所示,取PD的中点E,连接AE,NE.因为N是PC的中点,所以EN綊12CD.因为M为▱ABCD边AB的中点,所以AM綊12CD.所以EN綊AM,所以四边形AMNE为平行四边形,所以MN∥AE.又MN⊄平面PAD,AE⊂平面PAD,所以MN∥平面PAD.。
【人教A版】高中数学必修2教学同步讲练第二章《平面与平面垂直的判定》练习题(含答案)

第二章点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质2.3.2 平面与平面垂直的判定A级基础巩固一、选择题1.一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角()A.相等B.互补C.不确定D.相等或互补2.对于直线m,n和平面α,β,能得出α⊥β的一个条件是() A.m⊥n,m∥α,n∥βB.m⊥n,α∩β=m,n⊂αC.m∥n,n⊥β,m⊂αD.m∥n,m⊥α,n⊥β3.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,则二面角B-PA-C的大小为()A.90°B.60°C.45°D.30°4.如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD =45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成几何体A-BCD,则在几何体A-BCD中,下列结论正确的是()A.平面ABD⊥平面ABC B.平面ADC⊥平面BDCC.平面ABC⊥平面BDC D.平面ADC⊥平面ABC5.已知m,n为不重合的直线,α,β,γ为不重合的平面,则下列命题中正确的是()A.m⊥α,n⊂β,m⊥n⇒α⊥βB.α⊥γ,β⊥γ⇒α∥βC.α∥β,m⊥α,n∥β⇒m⊥nD.α⊥β,α∩β=m,n⊥m⇒n⊥β二、填空题6.如图所示,检查工作的相邻两个面是否垂直时,只要用曲尺的一边紧靠在工件的一个面上,另一边在工件的另一个面上转动,观察尺边是否和这个面密合就可以了,其原理是________.7.过正方形ABCD的顶点A作线段AP⊥平面ABCD,且AP =AB,则平面ABP与平面CDP所成的二面角的度数是________.8.如图所示,在三棱锥S-ABC中,△SBC,△ABC都是等边三角形,且BC=1,SA=32,则二面角S-BC-A的大小为________.三、解答题9.在正方体ABCD-A1B1C1D1中,求证:面A1CD1⊥面C1BD.10.如图所示,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC的中点.(1)证明SO⊥平面ABC;(2)求二面角A-SC-B的余弦值.B级能力提升1.在空间四边形ABCD中,若AD⊥BC,AD⊥BD,那么有() A.平面ABC⊥平面ADCB.平面ABC⊥平面ADBC.平面ABC⊥平面DBCD.平面ADC⊥平面DBC2.矩形ABCD的两边AB=3,AD=4,PA⊥平面ABCD,且PA=435,则二面角A-BD-P的度数为________.3.(2015·课标全国Ⅰ卷节选)如图所示,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.证明:平面AEC⊥平面AFC.参考答案第二章点、直线、平面之间的位置关系2.3 直线、平面垂直的判定及其性质2.3.2 平面与平面垂直的判定A级基础巩固一、选择题1.一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角()A.相等B.互补C.不确定D.相等或互补答案:C2.对于直线m,n和平面α,β,能得出α⊥β的一个条件是() A.m⊥n,m∥α,n∥βB.m⊥n,α∩β=m,n⊂αC.m∥n,n⊥β,m⊂αD.m∥n,m⊥α,n⊥β解析:因为m∥n,n⊥β,所以m⊥β.又m⊂α,所以α⊥β.答案:C3.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,则二面角B-PA-C的大小为()A.90°B.60°C.45°D.30°解析:因为PA⊥平面ABC,BA⊂平面ABC,CA⊂平面ABC,所以BA⊥PA,CA⊥PA,因此,∠BAC为二面角BPAC的平面角,又∠BAC=90°.答案:A4.如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD =45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成几何体A-BCD,则在几何体A-BCD中,下列结论正确的是()A.平面ABD⊥平面ABC B.平面ADC⊥平面BDCC.平面ABC⊥平面BDC D.平面ADC⊥平面ABC解析:由已知得BA⊥AD,CD⊥BD,又平面ABD⊥平面BCD,所以CD⊥平面ABD,从而CD⊥AB,故AB⊥平面ADC.又AB⊂平面ABC,所以平面ABC⊥平面ADC.答案:D5.已知m,n为不重合的直线,α,β,γ为不重合的平面,则下列命题中正确的是()A.m⊥α,n⊂β,m⊥n⇒α⊥βB.α⊥γ,β⊥γ⇒α∥βC.α∥β,m⊥α,n∥β⇒m⊥nD.α⊥β,α∩β=m,n⊥m⇒n⊥β解析:α∥β,m⊥α⇒m⊥β,n∥β⇒m⊥n.答案:C二、填空题6.如图所示,检查工作的相邻两个面是否垂直时,只要用曲尺的一边紧靠在工件的一个面上,另一边在工件的另一个面上转动,观察尺边是否和这个面密合就可以了,其原理是________.解析:如图,因为OA⊥OB,OA⊥OC,OB⊂β,OC⊂β且OB∩OC =O,根据线面垂直的判定定理,可得OA⊥β.又OA⊂α,根据面面垂直的判定定理,可得α⊥β.答案:面面垂直的判定定理7.过正方形ABCD的顶点A作线段AP⊥平面ABCD,且AP =AB,则平面ABP与平面CDP所成的二面角的度数是________.解析:可将图形补成以AB、AP为棱的正方体,不难求出二面角的大小为45°.答案:45°8.如图所示,在三棱锥S-ABC中,△SBC,△ABC都是等边三角形,且BC=1,SA=32,则二面角S-BC-A的大小为________.解析:如图所示,取BC的中点O,连接SO,AO.因为AB=AC,O是BC的中点,所以AO⊥BC,同理可证SO⊥BC,所以∠SOA是二面角S-BC-A的平面角.在△AOB中,∠AOB=90°,∠ABO=60°,AB=1,所以AO=1·sin 60°=32.同理可求SO=3 2.又SA=32,所以△SOA是等边三角形,所以∠SOA=60°,所以二面角S-BC-A的大小为60°.答案:60°三、解答题9.在正方体ABCD-A1B1C1D1中,求证:面A1CD1⊥面C1BD.证明:因为ABCD-A1B1C1D1为正方体,所以AC⊥BD,因为AA1⊥平面ABCD,所以AA1⊥BD.又因为AA1∩AC=A,所以BD⊥平面ACA1,又因为A1C⊂平面ACA1,所以BD⊥A1C,同理BC1⊥A1C,因为BD∩BC1=B,所以A1C⊥平面C1BD,因为A1C⊂平面A1CD1,所以面A1CD1⊥面C1BD.10.如图所示,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC的中点.(1)证明SO⊥平面ABC;(2)求二面角A-SC-B的余弦值.(1)证明:如图所示,由题设AB=AC=SB=SC=SA.连接OA,△ABC为等腰直角三角形,所以OA=OB=OC=22SA,且AO⊥BC.又△SBC为等腰三角形,故SO⊥BC,且SO=22SA.从而OA 2+SO 2=SA 2,所以△SOA 为直角三边形,SO ⊥AO .又AO ∩BC =O ,所以SO ⊥平面ABC .(2)解:取SC 的中点M ,连接AM ,OM .由(1)知SO =OC ,SA =AC ,得OM ⊥SC ,AM ⊥SC . 所以∠OMA 为二面角A -SC -B 的平面角.由AO ⊥BC ,AO ⊥SO ,SO ∩BC =O ,得AO ⊥平面SBC .所以AO ⊥OM .又AM =32SA ,AO =22SA ,故sin ∠AMO =AO AM =23=63.所以二面角A -SC -B 的余弦值为33.B 级 能力提升1.在空间四边形ABCD 中,若AD ⊥BC ,AD ⊥BD ,那么有()A .平面ABC ⊥平面ADCB .平面ABC ⊥平面ADBC .平面ABC ⊥平面DBCD .平面ADC ⊥平面DBC解析:因为AD ⊥BC ,AD ⊥BD ,BC ∩BD =B ,所以AD ⊥平面DBC .又因为AD ⊂平面ADC ,所以平面ADC ⊥平面DBC .答案:D2.矩形ABCD 的两边AB =3,AD =4,PA ⊥平面ABCD ,且PA =435,则二面角A -BD -P 的度数为________. 解析:过点A 作AE ⊥BD ,连接PE ,则∠AEP 为所求角.因为由AB =3,AD =4知BD =5,又AB ·AD =BD ·AE ,所以AE =125.所以tan ∠AEP =435125=33.所以∠AEP =30°. 答案:30°3.(2015·课标全国Ⅰ卷节选)如图所示,四边形ABCD 为菱形,∠ABC =120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE =2DF ,AE ⊥EC .证明:平面AEC ⊥平面AFC .证明:连接BD,设BD∩AC=G,连接EG,FG,EF.在菱形ABCD中,不妨设GB=1.由∠ABC=120°,可得AG=GC= 3.由BE⊥平面ABCD,AB=BC,可知AE=EC.又AE⊥EC,所以EG=3,且EG⊥AC.在Rt△EBG中,可得BE=2,故DF=22.在Rt△FDG中,可得FG=62.,可得EF 在直角梯形BDFE中,由BD=2,BE=2,DF=22=322.从而EG2+FG2=EF2,所以EG⊥FG.又AC∩FG=G,可得EG⊥平面AFC.因为EG⊂平面AEC,所以平面AEC⊥平面AFC.。
贵州省人教A版高中数学必修二2.2.2平面与平面平行的判定同步训练

贵州省人教A版高中数学必修二2.2.2平面与平面平行的判定同步训练姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)已知l∥α,m∥α,l∩m=P且l与m确定的平面为β,则α与β的位置关系是()A . 相交B . 平行C . 相交或平行D . 不确定2. (2分) (2017高二上·汕头月考) 已知两直线、,两平面、,且 .则下面四个命题中正确的有()个.①若,则有;②若,则有;③若,则有;④若,则有 .A . 0B . 1C . 2D . 34. (2分)下列命题正确的是()A . 若两条直线与同一个平面所成的角相等,则这两条直线平行B . 若一条直线垂直于一个平面内的两条直线,则这条直线垂直于这个平面C . 若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D . 若两个平面都垂直于第三个平面,则这两个平面平行5. (2分)已知直线a和两个平面,给出下列两个命题:命题p:若a∥,a⊥,则⊥;命题q:若a∥,a∥,则∥。
那么下列判断正确的是()A . p为假B . 为假C . p∧q为真D . p∨q为真6. (2分)已知是两两不重合的三个平面,下列命题中错误的是()A . 若,则B . 若,则C . 若,则D . 若,则7. (2分)下列叙述中,正确的是()A . 四边形是平面图形B . 有三个公共点的两个平面重合。
C . 两两相交的三条直线必在同一个平面内D . 三角形必是平面图形。
8. (2分)下列说法正确的是()A . 空间三个点确定一个平面B . 两个平面一定将空间分成四部分C . 梯形一定是平面图形D . 两个平面有不在同一条直线上的三个交点9. (2分) (2018高二上·浙江期中) 在下列条件中,可判定平面与平面平行的是()A . ,都平行于直线B . 内存不共线的三点到的距离相等C . ,是内的两条直线,且,D . ,是两条异面直线,且,,,10. (2分) (2018高二上·万州月考) 在空间中,两不同直线a、b,两不同平面、,下列命题为真命题的是()A . 若,则B . 若,则C . 若,则D . 若,则二、填空题 (共4题;共4分)11. (1分)若夹在两个平面间的三条平行线段相等,那么这两个平面的位置关系为________.12. (1分)已知平面α和β ,在平面α内任取一条直线a ,在β内总存在直线b∥a ,则α与β的位置关系是________(填“平行”或“相交”).13. (1分)正四面体的各条棱比为a,点P在棱AB上移动,点Q在棱CD上移动,则点P和点Q的最短距离是________.14. (1分)如右图所示,在正方体ABCD-A1B1C1D1中,E、F、G、H分别为棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足________时,有MN∥平面B1BDD1.三、解答题 (共4题;共25分)15. (5分) (2018高二上·万州月考) 如图,在三棱锥P—ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC、(Ⅰ)证明:AB⊥PC;(Ⅱ)证明:平面PAB//平面FGH16. (10分)在正方体ABCD-A1B1C1D1中,M、N、P分别是AD1、BD和B1C的中点,求证:(1)MN∥平面CC1D1D.(2)平面MNP∥平面CC1D1D.17. (5分) (2018高二上·万州月考) 如图,在四棱锥P﹣ABCD中,底面ABCD是边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4 .(I)求证:PD∥面ACE;(Ⅱ)求三棱锥E﹣ABC的体积。
高中数学 第二章 2.2.2 平面与平面平行的判定练习 新人教A版必修2

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学习资料专题2.2.2 平面与平面平行的判定【选题明细表】1.经过平面外两点与这个平面平行的平面( C )(A)只有一个 (B)至少有一个(C)可能没有 (D)有无数个解析:当这两点的连线与平面相交时,则没有平面与这个平面平行;当这两点的连线与平面平行时,有且只有一个平面与这个平面平行,所以选C.2.设直线l,m,平面α,β,下列条件能得出α∥β的有( D )①l⊂α,m⊂α,且l∥β,m∥β②l⊂α,m⊂β,且l∥m ③l∥α,m∥β,且l∥m(A)1个(B)2个(C)3个(D)0个解析:由两平面平行的判定定理可知,得出α∥β的个数为零.3.已知两个不重合的平面α,β,给定以下条件:①α内不共线的三点到β的距离相等;②l,m是α内的两条直线,且l∥β,m∥β;③l,m是两条异面直线,且l∥α,l∥β,m∥α,m∥β.其中可以判定α∥β的是( D )(A)① (B)② (C)①③ (D)③解析:①中,若三点在平面β的两侧,则α与β相交,故不正确.②中,α与β也可能相交.③中,若把两异面直线l,m平移到一个平面内,即为两相交直线,由判定定理知正确.4.(2018·武汉月考)a,b,c为三条不重合的直线,α,β,γ为三个不重合的平面,现给出六个命题:①⇒a∥b;②⇒a∥b;③⇒α∥β;④⇒α∥β;⑤⇒a∥α;⑥⇒a∥α.其中正确的命题是( C )(A)②③ (B)①④⑤(C)①④ (D)①③④解析:由空间平行线的传递性,知①正确;②错误,a,b还可能相交或异面;③错误,α与β可能相交;由面面平行的传递性,知④正确;⑤⑥错误,a可能在α内.故选C.5.如图所示,已知四棱锥P ABCD底面ABCD为平行四边形,E,F分别为AB,PD的中点.求证:AF ∥平面PCE.证明:如图所示.取CD中点M,连接MF,MA,则在△PCD中,MF∥PC,又MF⊄平面PCE,PC⊂平面PCE,所以MF∥平面PCE.又因为ABCD为平行四边形,E,M分别为AB,CD中点,所以AE CM.所以四边形EAMC为平行四边形,所以MA∥CE,又MA⊄平面PCE,CE⊂平面PCE.所以MA∥平面PCE.又MA∩MF=M,所以平面MAF∥平面PCE.又因为AF⊂平面MAF,所以AF∥平面PCE.6.平面α内有不共线的三点到平面β的距离相等且不为零,则α与β的位置关系为( C )(A)平行 (B)相交(C)平行或相交(D)可能重合解析:若三点分布于平面β的同侧,则α与β平行,若三点分布于平面β的两侧,则α与β相交.故选C.7.(2018·江西九江一模)在正方体ABCD A 1B1C1D1中,AB=4,M,N分别为棱A1D1,A1B1的中点,过点B的平面α∥平面AMN,则平面α截该正方体所得截面的面积为.解析:如图所示,截面为等腰梯形BDPQ,故截面的面积为×(2+4)×3=18.答案:188.如图所示的是正方体的平面展开图.有下列四个命题:①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.其中,正确命题的序号是.解析:展开图可以折成如图(1)所示的正方体.在正方体中,连接AN,如图(2)所示,因为AB∥MN,且AB=MN,所以四边形ABMN是平行四边形.所以BM∥AN.因为AN⊂平面DE,BM⊄平面DE,所以BM∥平面DE.同理可证CN∥平面AF,所以①②正确;如图(3)所示,可以证明BM∥平面AFN,BD∥平面AFN,进而得到平面BDM∥平面AFN,同理可证平面BDE∥平面NCF,所以③④正确.答案:①②③④9.在正方体ABCD A 1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC,SC的中点.求证:(1)直线EG∥平面BDD1B1;(2)平面EFG∥平面BDD1B1.证明:(1)如图,连接SB,因为E,G分别是BC,SC的中点,所以EG∥SB.又因为SB⊂平面BDD1B1,EG⊄平面BDD1B1.所以直线EG∥平面BDD1B1.(2)连接SD,因为F,G分别是DC,SC的中点,所以FG∥SD.又因为SD⊂平面BDD1B1,FG⊄平面BDD1B1,所以FG∥平面BDD1B1.又EG∥平面BDD1B1,且EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,所以平面EFG∥平面BDD1B1.10.如图所示,在正方体ABCD A 1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?解:当Q为CC1的中点时,平面D1BQ∥平面PAO.因为Q为CC1的中点,P为D1D的中点,所以PQ∥DC.又DC∥AB,所以PQ∥AB且PQ=AB,所以四边形ABQP为平行四边形,所以QB∥PA.又PA⊂平面PAO,QB⊄平面PAO,所以BQ∥平面PAO.连接BD,则O∈BD,又O为DB的中点,P为D1D的中点,所以PO∥D1B.PO⊂平面PAO,D1B⊄平面PAO,所以D1B∥平面PAO.又D1B∩BQ=B,所以平面D1BQ∥平面PAO.。
【优质文档】人教A版必修2第二章2.2.2《平面与平面平行的判定》精选题高频考点(含答案)-2

/ / 的一个充分条件是
B .存在一条直线 a , a / / , a / / .
C.存在一条直线 a , a a, a / / .
D .存在两条平行直线 a, b , a , b ,a / / , b / / a .
2.在正方体 ABCD -A1B1C1D1 中, E,F ,G 分别是 A1 B1, B1C1,BB1 的中点,给出下列 四个推断:
A .平行
B.相交
C .平行或相交
D .平行或在平面内
()
试卷第 4 页,总 12 页
二、填空题
21.如图, ABCD 是空间四边形, E、 F、 G、H 分别是其四边上的点且共面,
面 EFGH , AC = m, BD= n,当 EFGH 是菱形时, AE ______. EB
AC ∥平
22.已知,如图, A 、 B、 C、 D 四点不共面,且 AB ∥ α, CD ∥ α, AC∩α= E, AD∩α = F,BD∩α= H, BC∩α= G,则四边形 EFHG 的形状是 ______.
23.下列四个命题中,正确的命题为 ________(填序号 ).
① α∥ β, β⊥ γ,则 α⊥ γ
② α∥ β, β∥ γ,则 α∥ γ
③ α⊥ β, γ⊥ β,则 α⊥ γ
④ α⊥ β, γ⊥ β,则 α∥ γ
24.已知 m,n 是两条不重合的直线 , , 是三个两两不重合的平面 .给出下列四个命题 :
B .若 ?? ⊥??, ?? ⊥??, ??∥??,则 ??∥??
C.若 ?? ? ??, ??∥??, m, n 共面于 ??,则 ?? ∥??
D .若, ?? ⊥??,??⊥??, ??,??不平行,则 m, n 为异面直线
(同步练习)人教A版高中数学必修二2.2.2平面与平面平行的判定 同

人教A版高中数学必修二2.2.2平面与平面平行的判定同步训练B卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2017高二下·河北期末) 设,是不同的直线,,,是不同的平面,有以下四个命题其中正确的命题是()A . ①④B . ①③C . ②③D . ②④2. (2分)已知直线a和两个平面,给出下列两个命题:命题p:若a∥,a⊥,则⊥;命题q:若a∥, a∥,则∥。
那么下列判断正确的是()A . p为假B . 为假C . p∧q为真D . p∨q为真3. (2分) (2018高二上·万州月考) 在空间中,两不同直线a、b,两不同平面、,下列命题为真命题的是()A . 若,则B . 若,则C . 若,则D . 若,则4. (2分) (2019高二上·佛山月考) 已知平面α与平面β、γ都相交,则这三个平面可能的交线有()A . 1条或2条B . 2条或3条C . 1条或3条D . 1条或2条或3条5. (2分)设m,n是两条不同的直线,是三个不同的平面,则下列为假命题的是()A . 若,则B . 若,则C . 若,则D . 若,则6. (2分)能够判定两个平面α,β平行的条件是()A . 平面α,β都和第三个平面相交,且交线平行B . 夹在两个平面间的线段相等C . 平面α内的无数条直线与平面β无公共点D . 平面α内的所有的点到平面β的距离都相等7. (2分) (2018高二上·万州月考) 若、、是互不相同的空间直线,、是不重合的平面,则下列命题正确的是()A . 若∥ ,则B . 若∥ ,∥ ,则、、共面C . 若,则∥D . 若、、共点,则、、共面8. (2分) (2020高一下·隆化期中) 不重合的两个平面可以把空间分成()部分A . 2B . 3或4C . 4D . 2或3或410. (2分) (2017高二上·汕头月考) 已知两直线、,两平面、,且 .则下面四个命题中正确的有()个.①若,则有;②若,则有;③若,则有;④若,则有 .A . 0B . 1C . 2D . 3二、填空题 (共4题;共4分)11. (1分) (2019高二上·河北月考) 已知正四棱锥底面边长为,体积为32,则此四棱锥的侧棱长为________.12. (1分)若夹在两个平面间的三条平行线段相等,那么这两个平面的位置关系为________.13. (1分)已知平面α和β ,在平面α内任取一条直线a ,在β内总存在直线b∥a ,则α与β的位置关系是________(填“平行”或“相交”).14. (1分)如右图所示,在正方体ABCD-A1B1C1D1中,E、F、G、H分别为棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足________时,有MN∥平面B1BDD1.三、解答题 (共4题;共30分)15. (5分) (2019高一上·咸阳月考) 已知正方体,求证:平面平面 .16. (10分) (2020高二上·安徽月考) 如图所示,在四棱锥中,四边形是正方形,点分别是线段的中点.(1)求证: ;(2)线段上是否存在一点 ,使得面面 ,若存在,请找出点并证明;若不存在,请说明理由.17. (10分) (2020高二上·柯桥期末) 如图,四棱锥中,,底面为矩形,平面平面,O、E分别是棱、的中点.(1)求证:平面;(2)求二面角的大小.18. (5分) (2018高二上·万州月考) 如图,在三棱锥P—ABC中,E、F、G、H分别是AB、AC、PC、BC的中点,且PA=PB,AC=BC、(Ⅰ)证明:AB⊥PC;(Ⅱ)证明:平面PAB//平面FGH参考答案一、单选题 (共10题;共20分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:10-1、考点:解析:二、填空题 (共4题;共4分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:三、解答题 (共4题;共30分)答案:15-1、考点:解析:答案:16-1、答案:16-2、考点:解析:答案:17-1、答案:17-2、考点:解析:答案:18-1、考点:解析:。
【人教A版】高中数学必修2教学同步讲练第二章《平面与平面之间的位置关系》练习题(含答案)

第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.3 空间中直线与平面之间的位置关系2.1.4 平面与平面之间的位置关系A级基础巩固一、选择题1.与同一平面平行的两条直线()A.平行B.相交C.异面D.平行、相交或异面2.过平面外一条直线作平面的平行平面()A.必定可以并且只可以作一个B.至少可以作一个C.至多可以作一个D.一定不能作3.若直线a不平行于平面α,则下列结论成立的是()A.α内的所有直线均与a异面B.α内不存在与a平行的直线C.α内的直线均与a相交D.直线a与平面α有公共点4.与两个相交平面的交线平行的直线和这两个平面的位置关系是()A.都平行B.都相交C.在两平面内D.至少和其中一个平行5.平面α与平面β平行且a⊂α,下列三种说法:①a与β内的所有直线都平行;②a与β平行;③a与β内的无数条直线平行,其中正确的个数是()A.0 B.1C.2 D.3二、填空题6.在长方体ABCD-A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有________个.7.若a与b异面,则过a与b平行的平面有________个.8.若平面α与平面β平行,a⊂α,b⊂β,则a与b的位置关系是________.三、解答题9.如图所示,在正方体ABCD-A1B1C1D1中,指出B1C,D1B所在直线与正方体各面所在平面的位置关系.10.如图所示,ABCDA1B1C1D1是正方体,画出图中阴影部分的平面与平面ABCD的交线,并给出证明.B级能力提升1.已知a,b,c为三条不重合的直线,α,β为两个不重合的平面.①a∥c,b∥c⇒a∥b;②a∥β,b∥β⇒a∥b;③a∥c,c∥α⇒a∥α;④a∥β,a∥α⇒α∥β;⑤a⊄α,b⊂α,a∥b⇒a∥α.其中正确的命题是()A.①⑤B.①②C.②④D.③⑤2.给出下列命题:①如果平面α与平面β相交,那么它们只有有限个公共点;②两个平面的交线可能是一条线段;③经过空间任意三点的平面有且只有一个;④如果两个平面有三个不共线的公共点,那么这两个平面就重合为一个平面.其中正确命题的序号为________.3.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别为B1C1,A1D1的中点.求证:平面ABB1A1与平面CDFE相交.参考答案第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.1.3 空间中直线与平面之间的位置关系2.1.4 平面与平面之间的位置关系A级基础巩固一、选择题1.与同一平面平行的两条直线()A.平行B.相交C.异面D.平行、相交或异面解析:与同一平面平行的两条直线的位置关系有三种情况:平行、相交或异面.答案:D2.过平面外一条直线作平面的平行平面()A.必定可以并且只可以作一个B.至少可以作一个C.至多可以作一个D.一定不能作解析:因为直线在平面外包含两种情况:直线与平面相交和直线与平面平行.当直线与平面相交时,不能作出符合题意的平面;当直线与平面平行时,可作出唯一的一个符合题意的平面.答案:C3.若直线a不平行于平面α,则下列结论成立的是()A.α内的所有直线均与a异面B.α内不存在与a平行的直线C.α内的直线均与a相交D.直线a与平面α有公共点解析:若直线a不平行平面α,则a∩α=A或a⊂α,故D项正确.答案:D4.与两个相交平面的交线平行的直线和这两个平面的位置关系是()A.都平行B.都相交C.在两平面内D.至少和其中一个平行解析:若该直线不属于任何一个平面,则其与两平面平行;若该直线属于其中一个平面,则其必和另一个平面平行.答案:D5.平面α与平面β平行且a⊂α,下列三种说法:①a与β内的所有直线都平行;②a与β平行;③a与β内的无数条直线平行,其中正确的个数是()A.0 B.1C.2 D.3解析:因为α∥β,a⊂α,所以a与β无公共点,所以a∥β,故②正确,所以a与β内的所有直线都没有公共点,所以a与β内的直线平行或异面,故①不正确,③正确.答案:C二、填空题6.在长方体ABCD-A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有________个.解析:如图所示,结合图形可知AA1∥平面BB1C1C,AA1∥平面DD1C1C,AA1∥平面BB1D1D.答案:37.若a与b异面,则过a与b平行的平面有________个.解析:当a与b异面时,如图,过a上任意一点M作b′∥b,则a与b′确定了唯一的平面α,且b∥α,故过a与b平行的平面有1个.答案:18.若平面α与平面β平行,a⊂α,b⊂β,则a与b的位置关系是________.解析:由两平面平行的定义可知,a与b没有公共点,所以a与b平行或异面.答案:平行或异面三、解答题9.如图所示,在正方体ABCD-A1B1C1D1中,指出B1C,D1B所在直线与正方体各面所在平面的位置关系.解:B1C所在直线与正方体各面所在平面的位置关系是:B1C是平面BB1C1C内,B1C∥平面AA1D1D,B1C与平面ABB1A1,平面CDD1C1,平面ABCD,平面A1B1C1D1都相交.D1B所在直线与正方体各面所在平面都相交.10.如图所示,ABCDA1B1C1D1是正方体,画出图中阴影部分的平面与平面ABCD的交线,并给出证明.证明:如图,过点E作EN⊥CD于点N,连接NB并延长,交EF的延长线于点M,连接AM,因为直线EN∥BF,所以B,N,E,F四点共面,因此EF与BN相交,交点为M.因为M∈EF,且M∈NB,而EF⊂平面AEF,NB⊂平面ABCD,所以M是平面ABCD与平面AEF的公共点.又因为点A是平面AEF和平面ABCD的公共点,所以AM为这两平面的交线.B级能力提升1.已知a,b,c为三条不重合的直线,α,β为两个不重合的平面.①a∥c,b∥c⇒a∥b;②a∥β,b∥β⇒a∥b;③a∥c,c∥α⇒a∥α;④a∥β,a∥α⇒α∥β;⑤a⊄α,b⊂α,a∥b⇒a∥α.其中正确的命题是()A.①⑤B.①②C.②④D.③⑤解析:由公理4知①正确,由直线与平面平行的位置关系知⑤正确,从而选 A.其中②是错误的,因为平行于同一平面的两条直线可能平行、可能相交,也可能异面,③是错误的.因为当a∥c,c∥α时,可能a∥α,也可能a⊂α,对于④,α,β可能平行,也可能相交.答案:A2.给出下列命题:①如果平面α与平面β相交,那么它们只有有限个公共点;②两个平面的交线可能是一条线段;③经过空间任意三点的平面有且只有一个;④如果两个平面有三个不共线的公共点,那么这两个平面就重合为一个平面.其中正确命题的序号为________.解析:两个平面相交,则两个平面就是一条公共的交线,故①②错误;若空间中的任意三点在一条直线上,则经过这三点就有无数个平面,故③错误;④是正确的.答案:④3.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别为B1C1,A1D1的中点.求证:平面ABB1A1与平面CDFE相交.证明:在正方体ABCD-A1B1C1D1中,E为B1C1的中点,所以EC与B1B不平行,则延长CE与BB1必须相交于一点H,所以H∈EC,H∈B1B.又知B1B⊂平面ABB1A1,CE⊂平面CDFE,所以H∈平面ABB1A1,H∈平面CDFE,故平面ABB1A1与平面CDFE相交.。
高一数学人教A版必修2同步课时作业2.2.2平面与平面平行的判定(有答案)

高一数学人教A 版必修2同步课时作业2.2.2平面与平面平行的判定一、选择题1.如图,在长方体1111ABCD A B C D -中,若,,,E F G H 分别是棱 111111,,,A B BB CC C D 的中点,则必有( )A .1BD GH ∥B .BD EF ∥C .平面EFGH ∥平面ABCD D .平面EFGH ∥平面11A BCD2.平面//α平面β的一个条件是( ) A.存在一条直线,//,//a a a αβ B.存在一条直线,,//a a a αβ⊂C.存在两条平行直线,,,,//,//a b a b a b αββα⊂⊂D.存在两条异面直线 ,,,,//,//a b a b a b αββα⊂⊂ 3.两个平面平行的条件是( )A.一个平面内一条直线平行于另一个平面B.一个平面内两条直线平行于另一个平面C.一个平面内的无数条直线平行于另一个平面D.一个平面内的任意一条直线平行于另一个平面4.在下列条件中,可判定平面α与平面β平行的是( ) A.αβ、 都垂直于平面rB.α内存在不共线的三点到β的距离相等C.,l m 是α内两条直线,且//,//l m ββD.,l m 是两条异面直线,且//,//,//,//l m l m ααββ5.如图所示,在正方体1111ABCD A B C D -中,点,,,,E F G P Q 分别为棱111111AB C D D A D D C C ,,,,的中点,则下列叙述中正确的是( )A.直线//BQ 平面EFGB.直线1//A B 平面EFGC.平面//APC 平面EFGD.平面1//A BQ 平面EFG6.已知直线,a b 与平面,,αβγ,下列条件中能推出//αβ的是( ) A .a α⊥且a β⊥B .αγ⊥且βγ⊥C .a α⊂,b β⊂,//a bD .a α⊂,b α⊂,//a β,//b β7.已知两个不重合的平面,αβ,给定以下条件: ①α内任意不共线的三点到β的距离都相等; ②,l m 是α内的两条直线,且//,//l m ββ;③,l m 是两条异面直线,且//,//,//,//l l m m αβαβ; 其中可以判定//αβ的是( ) A.① B.② C.①③D.③8.下列命题正确的是 ( )①一个平面内有两条直线都与另外一个平面平行,则这两个平面平行; ②一个平面内有无数条直线都与另外一个平面平行,则这两个平面平行; ③一个平面内任何直线都与另外一个平面平行,则这两个平面平行; ④一个平面内有两条相交直线都与另外一个平面平行,则这两个平面平行. A .①③ B .②④ C .②③④ D .③④二、填空题9.若夹在两个平面间的三条平行线段相等,则这两个平面的位置关系是__________.10.经过直线外一点有__________个平面与已知直线平行;经过直线外一点有__________条直线与已知直线平行.11.如果两个平面分别平行于第三个平面,那么这两个平面的位置关系是__________. 三、解答题12.如图所示,在三棱柱111ABC A B C -,中,点,D E 分别是BC 与11B C 的中点.求证:平面1//A EB 平面ADC .参考答案1.答案:D解析:对于A,由图形知1BD 与GH 是异面直线,∴A 错误; 对于B ,由题意知BD 与EF 也是异面直线,∴B 错误; 对于C ,平面EFGH 与平面ABCD 是相交的,∴C 错误; 对于D,平面//EFGH 平面11A BCD ,理由是:由,,,E F G H 分别是棱111111,,,A B BB CC C D 的中点, 得出111//,//EF A B EH A D ,所以//EF 平面11A BCD ,//EF 平面11A BCD , 又EF EH E =,所以平面//EFGH 平面11A BCD . 故选:D. 2.答案:D解析:对于选项A,当,αβ两平面相交,直线a 平行于交线时,满足要求,故A 不对;对于选项B,当两平面,αβ相交,a 在平面α内且a 平行于交线时,满足要求,故B 不对;对于选项C ,同样在α与β相交,,a b 分别在,αβ内且与交线都平行时满足要求,故C 不对;对于选项D,因为,a b 异面,故在β内一定有一条直线a '与a 平行且与b 相交,同样,在α内也一定有一条直线b '与b 平行且与a 相交,由面面平行判定的推论可知其正确.3.答案:D解析:由两平面平行的定义及判定定理知A 、B 、C 不正确.故选D. 4.答案:D解析:A 中:教室的墙角的两个平面都垂直底面,但是不平行,错误B 中:如果三个点在平面的两侧,满足不共线的三点到β的距离相等,这两个平面相交,B 错误C 中:如果这两条直线平行,那么平面α与β可能相交,所以C 错误 故选D 5.答案:D解析:如图,由于平面过点E ,F ,G ,结合该平面与正方体的上下两个面相交,因此该平面与下底面也有一条交线,此交线即为下底面内过点E 且与直线GF 平行的直线,因此另一个交点为BC 的中点I ,同理可得该平面与两个侧面的交线GH ,IQ ,由此可得截面为如图所示的正六边形EIQFGH .直线BQ平面EFG Q =,故A 错误;1//A B HE ,1A B ⊄平面EFG ,HE ⊂平面EFG ,1//A B 平面EFG ,故B 正确;在平面11AA D D 上,直线GH 与AP 必相交,故平面APC 与平面EFG相交,故C 错误;平面1A BQ 与平面EFG 相交,故D 错误.6.答案:A解析:选项A,根据垂直于同一直线的两个平面平行,可知正确; 选项B, αγ⊥,βγ⊥可能推出,αβ相交,所以B 不正确; 选项C, a α⊂,b β⊂,//a b ,α与β可能相交,故不正确;选项D, a α⊂,b α⊂, //a β, //b β,如果//a b 推出,αβ 相交,所以D 不正确; 故选:A 7.答案:D解析:对于命题①,α内不共线的三点到β的距离相等,那么两个平面可以相交,故错误;对于命题②,由面面平行的判定可知,若l ,m 平行,则不一定能够推理得到//αβ,故②错误;对于命题③,由l ,m 是两条异面直线,通过平移可以在同一个平面内,则该平面与α,β都平行,由平行于同一平面的两个平面平行这一性质可知,//αβ,故③正确.所以满足条件的是③. 8.答案:D解析:如果两个平面没有任何一个公共点,那么我们就说这两个平面平行,也即是两个平面没有任何公共直线.对于①:一个平面内有两条直线都与另外一个平面平行,如果这两条直线不相交,而是平行,那么这两个平面相交也能够找得到这样的直线存在.对于②:一个平面内有无数条直线都与另外一个平面平行,同①.对于③:一个平面内任何直线都与另外一个平面平行,则这两个平面平行.这是两个平面平行的定义.对于④:一个平面内有两条相交直线都与另外一个平面平行,则这两个平面平行.这是两个平面平行的判定定理.所以只有③④正确,故选D .点睛: 如果两个平面没有任何一个公共点,那么我们就说这两个平面平行,也即是两个平面没有任何公共直线.两个平面平行,其中一个平面内的任一直线与另一个平面必平行.平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面分别平行,则这两个平面平行.9.答案:相交或平行解析:若夹在两个平面间的三条平行线段相等,则这两个平面平行或相交. 10.答案:无数; 一解析:经过直线外一点有无数个平面与已知直线平行经过直线外一点有一条直线与已知直线平行. 11.答案:平行解析:如果两个平面分别平行于第三个平面,那么这两个平面平行. 12.答案:由棱柱的性质,知1111//,,,B C BC BV BC D E =分别为BC ,11B C 的中点,所以,则四边形1C DBE 为平行四边形,因此1//EB C D ,又1C D ⊂平面1,ADC EB ⊄平面1ADC , 所以//EB 平面1ADC . 如图,连接DE ,则因为,所以则四边形1EDAA 为平行四边形, 所以1//A E AD .又1A E ⊄平面1ADC ,AD ⊂平面1ADC , 所以1//A E 平面1ADC . 又1A E EB E ⋂=所以平面1//A EB 平面1ADC .。
人教A版高中数学必修第二册8.5.3 平面与平面平行(第2课时)平面与平面平行的性质 练习(原卷版)

8.5.3 平面与平面平行第2课时 平面与平面平行的性质一、选择题1.,,a b αβαβ//////,则a 与b 位置关系是 ( )A .平行B .异面C .相交D .平行或异面或相交2.两个平行平面与另两个平行平面相交所得四条直线的位置关系是( )A .两两相互平行B .两两相交于一点C .两两相交但不一定交于同一点D .两两相互平行或交于同一点3.如图,在多面体ABC DEFG -中,平面//ABC 平面,//DEFG EF DG ,且,2AB DE DG EF ==,则 ( )A .//BF 平面ACGDB .//CF 平面ABEDC .//BC FGD .平面//ABED 平面CGF4.如图所示,已知正方体1111ABCD A B C D -的棱长为3,点E 在11A B 上,且11B E =,记图中阴影平面为平面α,且平面α平面1BC E .若平面α平面111AA B B A F =,则AF 的长为( )A .1B .1.5C .2D .35.(多选题)已知直线a ,两个不重合的平面,αβ.若α//β,a α⊂,则下列四个结论中正确的是( )A.a 与β内的所有直线平行;B.a 与β内的无数条直线平行;C.a 与β内任何一条直线都不垂直;D.a 与β没有公共点.A .①②B .②④C .②③D .③④6.(多选题)已知平面//α平面β,P 是α,β外一点,过点P 的直线m 与α,β分别交于A ,C 两点,过点P 的直线n 与α,β分别交于B ,D 两点,且6PA =,8PD =,9AC =,则BD 的长为( )A .16B .24C .14D .245二、填空题7.如图,过正方体1111ABCD A B C D -的顶点1B 、1D 与棱AB 的中点P 的平面与底面ABCD 所在平面的交线记为l ,则l 与11B D 的位置关系为_________.8.如图所示,P 是ABC 所在平面外一点,平面α∥平面ABC ,α分别交线段PA PB PC ,,于A B C ''',,,若:2:3PA AA ''=,则A B C ABC S S '''∆∆=________.9.如图,平面α平面β∥平面γ,两条异面直线,l m 分别与平面,,αβγ相交于点,,A B C 和点,,D E F ,已知2AB =cm,3BC cm =,4DE cm =,则EF =_______.10. 已知直线a //平面α,平面α//平面β,则直线a 与平面β的位置关系为________ 或 。
2021年高中数学 2.2.2平面与平面平行的判定练习 新人教A版必修2

2021年高中数学 2.2.2平面与平面平行的判定练习新人教A版必修2一、选择题1.在长方体ABCD-A′B′C′D′中,下列正确的是( )A.平面ABCD∥平面ABB′A′B.平面ABCD∥平面ADD′A′C.平面ABCD∥平面CDD′C′D.平面ABCD∥平面A′B′C′D′[答案] D2.两个平面平行的条件是( )A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内的无数条直线平行于另一个平面D.一个平面内的任意一条直线平行于另一个平面[答案] D[解析] 任意一条直线平行于另一个平面,即平面内所有的直线都平行于另一个平面.3.如果一个角的两边与另一个角的两边分别平行,下列结论一定成立的是( ) A.这两个角相等B.这两个角互补C.这两个角所在的两个平面平行D.这两个角所在的两个平面平行或重合[答案] D[解析] 这两个角相等或互补;这两个角所在的两个平面平行或重合.4.如图所示,设E,F,E1,F1分别是长方体ABCD-A1B1C1D1的棱AB,CD,A1B1,C1D1的中点,则平面EFD1A1与平面BCF1E1的位置关系是( )A.平行B.相交C.异面D.不确定[答案] A[解析] ∵E1和F1分别是A1B1和D1C1的中点,∴A1D1∥E1F1,又A1D1⊄平面BCF1E1,E1F1⊂平面BCF1E1,∴A1D1∥平面BCF1E1.又E1和E分别是A1B1和AB的中点,∴A1E1綊BE,∴四边形A1EBE1是平行四边形,∴A1E∥BE1,又A1E⊄平面BCF1E1,BE1⊂平面BCF1E1,∴A1E∥平面BCF1E1,又A1E⊂平面EFD1A1,A1D1⊂平面EFD1A1,A1E∩A1D1=A1,∴平面EFD1A1∥平面BCF1E1.5.已知直线l,m,平面α,β,下列命题正确的是( )A.l∥β,l⊂α⇒α∥βB.l∥β,m∥β,l⊂α,m⊂α⇒α∥βC.l∥m,l⊂α,m⊂β⇒α∥βD.l∥β,m∥β,l⊂α,m⊂α,l∩m=M⇒α∥β[答案] D[解析] 如右图所示,在长方体ABCD-A1B1C1D1中,直线AB∥CD,则直线AB∥平面DC1,直线AB⊂平面AC,但是平面AC与平面DC1不平行,所以选项A错误;取BB1的中点E,CC1的中点F,则可证EF∥平面AC,B1C1∥平面AC.又EF⊂平面BC1,B1C1⊂平面BC1,但是平面AC与平面BC1不平行,所以选项B错误;直线AD∥B1C1,AD⊂平面AC,B1C1⊂平面BC1,但平面AC与平面BC1不平行,所以选项C错误;很明显选项D是两个平面平行的判定定理,所以选项D正确.6.若平面α∥平面β,直线a∥α,点B∈β,则在平面β内过点B的所有直线中( ) A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一一条与a平行的直线[答案] A[解析] 当直线a⊂β,B∈a上时满足条件,此时过B不存在与a平行的直线,故选A.二、填空题7.如果两个平面分别平行于第三个平面,那么这两个平面的位置关系是________.[答案] 平行8.已知平面α和β,在平面α内任取一条直线a,在β内总存在直线b∥a,则α与β的位置关系是________(填“平行”或“相交”).[答案] 平行[解析] 假若α∩β=l,则在平面α内,与l相交的直线a,设a∩l=A,对于β内的任意直线b,若b过点A,则a与b相交,若b不过点A,则a与b异面,即β内不存在直线b∥a.故α∥β.三、解答题9. (xx·福建厦门六中月考)如图所示,四棱锥P-ABCD的底面ABCD为矩形,E,F,H 分别为AB,CD,PD的中点.求证:平面AFH∥平面PCE.[证明] 因为F为CD的中点,H为PD的中点,所以FH∥PC,所以FH∥平面PCE.又AE∥CF且AE=CF,所以四边形AECF为平行四边形,所以AF∥CE,所以AF∥平面PCE.由FH⊂平面AFH,AF⊂平面AFH,FH∩AF=F,所以平面AFH∥平面PCE.10.如图,F,H分别是正方体ABCD-A1B1C1D1的棱CC1,AA1的中点,求证:平面BDF∥平面B1D1H.[证明] 取DD1中点E,连AE、EF.∵E、F为DD1、CC1的中点,∴EF綊CD.∴EF綊AB,∴四边形EFBA为平行四边形.∴AE∥BF.又∵E、H分别为D1D、A1A的中点,∴D1E綊HA,∴四边形HAED1为平行四边形.∴HD1∥AE,∴HD1∥BF,由正方体的性质易知B1D1∥BD,且已证BF∥D1H.∵B1D1⊄平面BDF,BD⊂平面BDF,∴B1D1∥平面BDF.∵HD1⊄平面BDF,BF⊂平面BDF,∴HD1∥平面BDF.又∵B1D1∩HD1=D1,∴平面BDF∥平面B1D1H.能力提升一、选择题1.下列说法正确的是( )A.平面α内有一条直线与平面β平行,则平面α与平面β平行B.平面α内有两条直线与平面β平行,则平面α与平面β平行C.平面α内有无数条直线与平面β平行,则平面α与平面β平行D.平面α内所有直线都与平面β平行,则平面α与平面β平行[答案] D[解析] 两个平面平行⇔两个平面没有公共点⇔平面α内的所有直线与平面β没有公共点⇔平面α内的所有直线都与β平行.2.经过平面α外两点,作与α平行的平面,可以作( )A.1个B.2个C.0个或1个D.无数个[答案] C[解析] 当两个点在平面α同侧且连线平行于平面α时,可作一个平面与α平行;当两个点在平面α异侧或同侧且连线与平面α不平行时,不能作出平面与α平行.3.下列结论中:(1)过不在平面内的一点,有且只有一个平面与这个平面平行;(2)过不在平面内的一条直线,有且只有一个平面与这个平面平行;(3)过不在直线上的一点,有且只有一条直线与这条直线平行;(4)过不在直线上的一点,有且仅有一个平面与这条直线平行.正确的序号为( )A.(1)(2) B.(3)(4)C.(1)(3) D.(2)(4)[答案] C4.过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有( )A .4条B .6条C .8条D .12条[答案] D[解析] 如右图所示,以E 为例,易证EH ,EM ∥平面DBB 1D 1.与E 处于同等地位的点还有F 、G 、H 、M 、N 、P 、Q ,故有符合题意的直线8×22=8条.以E 为例,易证QE ∥平面DBB 1D 1,与E 处于同等地位的点还有H 、M 、G 、F 、N 、P ,故有符合题意的直线4条.∴共有8+4=12(条).二、填空题5.如图是四棱锥的平面展开图,其中四边形ABCD 为正方形,E ,F ,G ,H 分别为PA ,PD ,PC ,PB 的中点,在此几何体中,给出下面四个结论:①平面EFGH ∥平面ABCD ; ②平面PAD ∥BC ; ③平面PCD ∥AB ; ④平面PAD ∥平面PAB .其中正确的有________.(填序号) [答案] ①②③[解析] 把平面展开图还原为四棱锥如图所示,则EH ∥AB ,所以EH ∥平面ABCD .同理可证EF ∥平面ABCD ,所以平面EFGH ∥平面ABCD ;平面PAD ,平面PBC ,平面PAB ,平面PDC 均是四棱锥的四个侧面,则它们两两相交.∵AB ∥CD ,∴平面PCD ∥AB .同理平面PAD ∥BC .6.如下图所示,在正方体ABCD -A 1B 1C 1D 1中,E 、F 、G 、H 分别为棱CC 1、C 1D 1、D 1D 、CD 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 满足________时,有MN ∥平面B 1BDD 1.[答案] 点M在FH上[解析] ∵FH∥BB1,HN∥BD,FH∩HN=H,∴平面FHN∥平面B1BDD1,又平面FHN∩平面EFGH=FH,∴当M∈FH时,MN⊂平面FHN,∴MN∥平面B1BDD1.三、解答题7.如下图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E,F,G分别是BC,DC 和SC的中点.求证:平面EFG∥平面BDD1B1.[分析]证明平面与平面平行转化为证明线面平行,即转化为证明直线FG∥平面BDD1B1,EG∥平面BDD1B1.[证明] 如下图所示,连接SB,SD.∵F,G分别是DC,SC的中点,∴FG∥SD.又∵SD⊂平面BDD1B1,FG⊄平面BDD1B1,∴直线FG∥平面BDD1B1.同理可证EG∥平面BDD1B1.又∵直线EG⊂平面EFG,直线FG⊂平面EFG,直线EG∩直线FG=G,∴平面EFG∥平面BDD1B1.8.已知点S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB边AB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.[分析1] 观察图形容易看出SG∥平面DEF.要证明此结论成立,只须证明SG与平面DEF内的一条直线平行.考虑到题设条件中众多的中点,可应用三角形中位线性质.观察图形可以看出:连接CG与DE相交于H,连接FH,FH就是适合题意的直线.怎样证明SG∥FH?只需证明H是CG的中点.[证法1] 连接CG交DE于点H,∵DE是△ABC的中位线,∴DE∥AB.在△ACG中,D是AC的中点,且DH∥AG,∴H是CG的中点.∴FH是△SCG的中位线,∴FH∥SG.又SG⊄平面DEF,FH⊂平面DEF,∴SG∥平面DEF.[分析2]由题设条件中,D、E、F都是棱的中点,不难得出DE∥AB,DF∥SA,从而平面DEF∥平面SAB,又SG⊂平面SAB,从而得出SG∥平面DEF.[证法2] ∵EF为△SBC的中位线,∴EF∥SB.∵EF⊄平面SAB,SB⊂平面SAB,∴EF∥平面SAB.同理:DF∥平面SAB,EF∩DF=F,∴平面SAB∥平面DEF,又∵SG⊂平面SAB,∴SG∥平面DEF.[点评] 要证面面平行,应先证线线或线面平行,已知面面平行也可以得出线面平行,它们之间可以相互转化.34126 854E 蕎40823 9F77 齷23048 5A08 娈30276 7644 癄`31893 7C95 粕20731 50FB 僻34572 870C 蜌f22963 59B3 妳G29383 72C7 狇31447 7AD7 竗。
人教A版必修2第二章2.2.2《平面与平面平行的判定》精选题高频考点(含答案)-1

人教A 版必修2第二章2.2.2《平面与平面平行的判断》精选题高频考点(含答案)-1学校:___________姓名:___________班级:___________考号:___________一、单选题1.对于直线m ,n 和平面α,β,则α//β的一个充分条件是( ) A ..m α⊂,n β⊂,m //β,n //αB .m //n ,m //α,n //βC .m //n ,m α⊥,n β⊥D .m n ⊥,m α⊥,n β⊥ 2.平面α与平面β平行的条件可以是( )A .平面α内有无穷多条直线都与β平行B .平面α内的任何直线都与β平行C .直线//,//m m αβ,且直线m 不在α内,也不在β内D .直线m α⊂,直线l β⊂,且//,//m l βα3.如图所示,在棱长为1的正方体1111ABCD A B C D -中,点E F ,分别是棱1BC CC ,的中点,P 是侧面11BCC B 内一点,若1A P P 平面AEF ,则线段1A P 长度的取值范围是( )A .12⎡⎢⎣⎦,B .42⎡⎢⎣⎦,C .2⎣D . 4.在立体几何中,用一个平面去截一个几何体得到的平面图形叫截面,如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点E 、F 分别是棱B 1B 、B 1C 中点,点G 是棱CC 1的中点,则过线段AG 且平行于平面A 1EF 的截面图形为( )A .矩形B .三角形C .正方形D .等腰梯形 5.如图,多面体ABCD ﹣A 1B 1C 1D 1为正方体,则下面结论正确的是( )A .A 1B ∥B 1CB .平面CB 1D 1⊥平面A 1B 1C 1D 1C .平面CB 1D 1∥平面A 1BDD .异面直线AD 与CB 1所成的角为30°6.已知α,β是不同的平面,m ,n 是不同的直线,则下列命题不正确的是( ) A .若m ⊥α,m ∥n ,n ⊂β,则α⊥βB .若m ∥n ,α∩β=m ,则n ∥α,n ∥βC .若m ∥n ,m ⊥α,则n ⊥αD .若m ⊥α,m ⊥β,则α∥β7.在正方体1111ABCD A B C D -中,E 、F 分别是棱AB 、1AA 的中点,M 、N 分别是线段1D E 与1C F 上的点,则与平面ABCD 平行的直线MN 有( )A .0条B .1条C .2条D .无数条 8.对于平面α和两条直线,m n , 下列命题中真命题是( )A .若m α⊥,m n ⊥,则//n αB .若//m α,//n α,则//m nC .若,m n 与α所成的角相等,则//m nD .若m α,//m n ,且n 在平面α外,则//n α9.已知两条不重合的直线,m n 和两个不重合的平面,,αβ有下列命题:①若,m n m α⊥⊥,则//n α; ②若,,//,m n m n αβ⊥⊥则//;αβ③若,m n 是两条异面直线,,,//,//,m n m n αββα⊂⊂则//;αβ④若,,,,m n n m αβαββ⊥⋂=⊂⊥则n α⊥.其中正确命题的个数是A .1B .2C .3D .410.平面α∥β平面的一个充分条件是( )A .存在一条直线a ,a ∥α,a ∥βB .存在一条直线a ,a ⊂α,a ∥βC .存在两条平行直线a ,b ,a ⊂α,b ⊂β,a ∥β,b ∥αD .存在两条异面直线a ,b ,a ⊂α,b ⊂β,a ∥β,b ∥α11.如图,长方体1111ABCD A B C D -中,4AB BC ==,122BB =点E ,F ,M 分别为11A B ,11A D ,11B C 的中点,过点M 的平面α与平面AEF 平行,且与长方体的面相交,则交线围成的几何图形的面积为( )A .65B .66C .12D .2412.给出下列四个说法,其中正确说法的序号为( )①平行于同一直线的两平面平行;②平行于同一平面的两平面平行;③垂直于同一直线的两平面平行;④垂直于同一平面的两平面平行A .①②B .②③C .①②③D .②③④13.已知平面α,β,γ和直线l ,则“αβ∥”的充分不必要条件是( ) A .α内有无数条直线与β平行B .l α⊥且l β⊥C .γα⊥且γβ⊥D .α内的任何直线都与β平行14.设m ,n 是两条不同的直线,α,β是两个不同的平面,且m α⊂,n ⊂α,则“αβ∥”是“m βP 且n βP ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件15.下列命题正确的是( )A .若两个平面都垂直于第三个平面则这两个平面平行B .若两条直线和同一个平面所成的角相等,则这两条直线平行C .若两个平面不平行,则两个平面内存在互相平行的直线D .若一条直线不平行于一个平面,则这个平面内不存在与该直线平行的直线 16.设l 为直线,α,β是两个不同的平面,下列命题中正确的是( )A .若l ∥α,l ∥β,则α∥βB .若l ⊥α,l ⊥β,则α∥βC .若l ⊥α,l ∥β,则α∥βD .若α⊥β,l ∥α,则l ⊥β 17.设,a b 是两条直线,,,αβγ是三个平面,下列推导错误的是( )A .,,a b b a a βββ⊂⊄⇒P PB .a b a b αα⊥⇒⊥∥,C .,,a b a b αβαγβγ==⇒I I ∥∥D .,,,a b a b ααββαβ⊂⊂⇒P P P 18.α,β是两个不重合的平面,在下列条件中,可判断平面α,β平行的是( ) A .m ,n 是平面α内两条直线,且//m β,//n βB .α内不共线的三点到β的距离相等C .α,β都垂直于平面γD .m ,n 是两条异面直线,m α⊂,n β⊂,且//m β,//n α19.已知m ,n 是两条不同的直线,α,β是两个不同的平面,给出下列命题: ①若αβ∥,m α⊂,n β⊂,则m n P ;②若m αP ,m n P ,则n αP ;③若m ,n是异面直线,则存在α,β,使m α⊂,n β⊂,且αβ∥;④若α,β不垂直,则不存在m α⊂,使m β⊥.其中正确的命题有( ).A .1个B .2个C .3个D .4个 20.如图所示,在三棱台111ABC A B C -中,点D 在11A B 上,且1AA BD ∥,点M 是111A B C △内(含边界)的一个动点,且有平面BDM P 平面1A C ,则动点M 的轨迹是( )A .平面B .直线C .线段,但只含1个端点D .圆二、填空题 21.已知两条不同直线l ,m 和两个不同的平面α,β,有如下命题:①若l ⊂α,m ⊂α,l ∥β,m ∥β,则α∥β;②若l ⊂α,l ∥β,α∩β=m ,则l ∥m ;③若α⊥β,l ⊥β,则l ∥α.其中正确的命题是________.22.在如图直四棱柱1111ABCD A B C D -中,底面ABCD 为菱形,124AA AB ==,60BAD ∠=︒,点M 为棱1AA 的中点,若N 为菱形1111D C B A 内一点(不包含边界),满足MN ∥平面1BDC ,设直线MN 与直线1CC 所成角为α,则tan α的最小值为______.23.已知a ,b 为直线,,αβ为平面.在下列四个命题中,正确的命题是______(填序号).①若a α⊥,b α⊥,则a b ∥;②若a P α,b P α,则a b ∥;③若a α⊥,a β⊥,则αβ∥;④若a b ∥,b βP ,则a β∥.24.在正方形1111ABCD A B C D -中,M 、N 、Q 分别是棱11D C 、11A D 、BC 的中点,点P 在1BD 上且123BP BD =.则以下四个说法:________(填序号). ①//MN 平面APC ;②1//C Q 平面APC ;③A 、P 、M 三点共线;④平面//MNQ 平面APC .25.给出下列结论:①一条直线垂直于一个平面,则这条直线就和这个平面内的任何直线垂直; ②过平面外一点有只有一个平面和这个平面垂直;③过直线外一点有且只有一个平面和这条直线平行;④如果两个平面平行,那么其中一个平面内的任一直线平行于另一个平面. 其中正确的是__________.(写出所有正确结论的序号)26.如图所示,在正方体1111ABCD A B C D -中,E F G H ,,,分别是棱111CC C D ,1D D CD ,的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 满足______时,有MN ∥平面11B BDD .27.如图是一几何体的平面展开图,其中四边形ABCD 为正方形, E F G H ,,,分别为PA PD PC PB ,,,的中点,在此几何体中,给出下面五个结论:①平面EFGH P 平面ABCD ;②PA P 平面BDG ;③EF P 平面PBC ;④FH P 平面BDG ;⑤EF P 平面BDG .其中正确结论的序号是________.28.如图所示,在三棱柱111ABC A B C -中,E F G H ,,,分别是1111AB AC A B A C ,,,的中点,则与平面BCHG 平行的平面为________.29.a b c ,,为三条不重合的直线,αβγ,,为三个不重合的平面,现给出下面六个命题:①若a c b c ∥,∥,则a b ∥;②若a b γγ∥,∥,则a b ∥;③若c c αβ∥,∥,则αβ∥;④若αγβγ∥,∥,则αβ∥;⑤若c a c α∥,∥,则a P α;⑥若a γαγ∥,∥,则a P α.其中真命题是_________(填序号).30.如图,在棱长均相等的正四棱锥P ABCD -最终,O 为底面正方形的重心,,M N 分别为侧棱,PA PB 的中点,有下列结论:①//PC 平面OMN ;②平面//PCD 平面OMN ;③OM PA ⊥;④直线PD 与直线MN 所成角的大小为90o .其中正确结论的序号是______.(写出所有正确结论的序号)31.如图,棱长为2的正方体1111ABCD A B C D -中,M 是棱AA 1的中点,过C ,M ,D 1作正方体的截面,则截面的面积是________.32.设αβγ,,为彼此不重合的三个平面,l 为直线,给出下列结论:①若αβαγ⊥‖, ,则 βγ⊥ ②若αγβγ⊥⊥,,且αβ⋂= l 则l γ⊥ ③若直线l 与平面α内的无数条直线垂直,则 l α⊥④若α内存在不共线的三点到β的距离相等,则αβ‖ 上面结论中,正确的序号为_______.33.(A 类题)已知α,β是两个不同的平面,a ,b 是两条不同的直线,给出条件:①αβφ⋂=;②a α⊥,a β⊥;③a P α,b P α,b β⊂,上述条件中能推出平面αP 平面β的是__________(填写序号)34.设α、β是两个不重合的平面,a ,b 是两条不同的直线,给出下列条件: ①α、β都平行于直线a 、b ;②a 、b 是α内两条直线,且a ∥β,b ∥β;③若a 、b 相交,且都在α、β外,a ∥α,a ∥β,b ∥α,b ∥β.其中可判定α∥β的条件的序号为________.35.已知点S 是正三角形ABC 所在平面外一点,点D ,E ,F 分别是SA ,SB ,SC 的中点,则平面DEF 与平面ABC 的位置关系是________.36.如图,E ,F ,G 分别是四面体ABCD 的棱BC ,CD ,DA 的中点,则此四面体中与过点E ,F ,G 的截面平行的棱是__________ .37.如图,在正方体1111ABCD A B C D -中,E ,F 分别是棱BC ,C 1D 1的中点,则EF 与平面BDD 1B 1的位置关系是___________ .38.已知直线a //平面α,平面α//平面β,则直线a 与平面β的位置关系为_______________.39.设,,l m n 是三条不同的直线,,,αβγ是三个不同的平面,现给出四个命题: ①若l n P 且m n P ,则l m P ;②若l αP 且m αP ,则l m P ;③若n αP 且n βP ,则αβP ;④若αγP 且βγP ,则αβP .其中正确命题的序号是________________.(把正确命题的序号都填上)40.a 、b 、c 为三条不重合的直线,α、β、γ为三个不重合平面,现给出六个命题. ①a c b c ⎫⎬⎭P P ⇒a ∥b ;②a b γγ⎫⎬⎭P P ⇒a ∥b ;③c c αβ⎫⎬⎭P P ⇒α∥β; ④αγβγ⎫⎬⎭P P ⇒α∥β;⑤c a c α⎫⎬⎭P P ⇒a ∥α;⑥a γαγ⎫⎬⎭P P ⇒a ∥α. 其中正确的命题是________.(填序号)三、解答题41.判断下列命题的真假.(1)如果两个平面不相交,那么它们就没有公共点;(2)如果一个平面内有两条直线平行于另一个平面,那么这两个平面平行;(3)如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行;(4)分别在两个平行平面内的两条直线平行.42.如图所示,四棱锥P -ABCD 的底面ABCD 为矩形,E 、F 、H 分别为AB 、CD 、PD 的中点.求证:平面AFH ∥平面PCE .43.已知底面是平行四边形的四棱锥P ABCD -中,点E 在PD 上,且:2:1PE ED =,在棱PC 上是否存在一点F ,使BF ∥平面AEC ?证明你的结论.44.在如图所示的几何体中,D 是AC 的中点,EF DB ∥,G H ,分别是EC 和FB 的中点.求证:GH P 平面ABC .45.如图,已知点P 是平行四边形ABCD 所在平面外一点,M 、N 分别是AB 、PC 的中点.(1)求证:MN ∥平面PAD ;(2)在PB 上确定一个点Q ,使平面MNQ ∥平面PAD .46.如图,长方体1111ABCD A B C D -中,11AA AB ==,2AD =,E 为BC 的中点,M ,N 分别为棱1DD ,11A D 的中点.(1)求证:平面//CMN 平面1A DE ;(2)求直线CN 和平面11AAC C 所成角的正弦值.47.如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,//CD AB ,AD AB ⊥,AD =11122CD PD AB PA ====,点E 、F 分别为AB 、AP 的中点.﹙1﹚求证:平面//PBC 平面EFD ;﹙2﹚求三棱锥P EFD -的体积.48.如图,a b ,是异面直线,,//,,//a a b b αββα⊂⊂,求证://αβ.49.如图,正方体1111ABCD A B C D -中,M ,N ,E ,F 分别是棱A 1B 1,A 1D 1,B 1C 1,C1D1的中点,求证:平面AMN∥平面EFDB.50.如图,四边形ABCD是平行四边形,点E,F,G分别为线段BC,PB,AD的中点.(1)证明:EF∥平面P AC;(2)证明:平面PCG∥平面AEF;(3)在线段BD上找一点H,使得FH∥平面PCG,并说明理由.参考答案1.C2.B3.B4.D5.C6.B7.D8.D9.C10.D11.A12.B13.B14.A15.C16.B17.D18.D19.B20.C21.②2223.①③24.②③25.①④26.M∈FH27.①②③④28.平面1A EF29.①④30.①②③【答案】9 232.①②33.①②34.③35.平行【答案】BD,AC【答案】平行38.直线a平行于平面β或直线a在平面β内39.①④40.①④41.(1)真命题;(2)假命题;(3)真命题;(4)假命题. 42.详见解析.43.见解析44.见解析45.(1)见解析;(2)见解析.46.(1)证明见解析;(2.47.(1)证明见解析;﹙2﹚12.48.证明见解析49.见解析50.(1)见解析(2)见解析(3)见解析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质
2.2.1 直线与平面平行的判定
2.2.2 平面与平面平行的判定
A级基础巩固
一、选择题
1.下列图形中能正确表示语句“平面α∩β=l,a⊂α,b⊂β,a∥β”的是()
2.能保证直线与平面平行的条件是()
A.直线与平面内的一条直线平行
B.直线与平面内的所有直线平行
C.直线与平面内的无数条直线平行
D.直线与平面内的所有直线不相交
3.在正方体ABCD-A1B1C1D1中,M是棱CD上的动点,则直线MC1与平面AA1B1B的位置关系是()
A.相交B.平行C.异面D.相交或平行
4.已知m,n是两条直线,α,β是两个平面.有以下命题:①m,n相交且都在平面α,β外,m∥α,m∥β,n∥α,n∥β,
则α∥β;②若m ∥α,m ∥β,则α∥β;③若m ∥α,n ∥β,m ∥n ,则α∥β.其中正确命题的个数是( )
A .0
B .1
C .2
D .3
5.平面α与△ABC 的两边AB ,AC 分别交于D ,E ,且AD DB =AE EC
,如图所示,则BC 与平面α的关系是( )
A .平行
B .相交
C .异面
D .BC ⊂α
二、填空题
6.在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE ∶EB =CF ∶FB =1∶3,则对角线AC 与平面DEF 的位置关系是________.
7.若空间四边形ABCD 的两条对角线AC ,BD 的长分别是8,12,过AB 的中点E 且平行于BD ,AC 的截面四边形的周长为________.
8.下图是正方体的平面展开图,在这个正方体中:
①BM ∥平面DE ;
②CN ∥平面AF ;
③平面BDM ∥平面AFN ;
④平面BDE ∥平面NCF .
以上四个命题中,正确命题的序号是________.
三、解答题
9.如图所示的三棱柱ABC-A1B1C1中,M,N分别为BC,B1C的中点,求证:MN∥面ACC1A1.
10.如图所示,在已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC.
B级能力提升
1.如图所示,在下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP 的图形的序号是()
①②
③④
A.①③B.①④
C.②③D.②④
2.已知a和b是异面直线,且a⊂平面α,b⊂平面β,a∥β,b∥α,则平面α与β的位置关系是________.
3.在长方体ABCD-A1B1C1D1中,E,F,E1,F1分别是AB,CD,A1B1,C1D1的中点.求证:平面EFD1A1∥平面BCF1E1.
参考答案
第二章点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质
2.2.1 直线与平面平行的判定
2.2.2 平面与平面平行的判定
A级基础巩固
一、选择题
1.下列图形中能正确表示语句“平面α∩β=l,a⊂α,b⊂β,a∥β”的是()
解析:A中不能正确表达b⊂β;B中不能正确表达a∥β;C中也不能正确表达a∥β;D正确.
答案:D
2.能保证直线与平面平行的条件是()
A.直线与平面内的一条直线平行
B.直线与平面内的所有直线平行
C.直线与平面内的无数条直线平行
D.直线与平面内的所有直线不相交
解析:A不正确,因为直线可能在平面内;B不正确;C不正确,直线也可能在平面内;D正确,因为直线与平面内所有直线不相交,依据直线和平面平行的定义可得直线与平面平行.
答案:D
3.在正方体ABCD -A 1B 1C 1D 1中,M 是棱CD 上的动点,则直线MC 1与平面AA 1B 1B 的位置关系是( )
A .相交
B .平行
C .异面
D .相交或平行
解析:MC 1⊂平面DD 1C 1C ,而平面AA 1B 1B ∥平面DD 1C 1C ,故MC 1∥平面AA 1B 1B .
答案:B
4.已知m ,n 是两条直线,α,β是两个平面.有以下命题:①m ,n 相交且都在平面α,β外,m ∥α,m ∥β,n ∥α,n ∥β,则α∥β;②若m ∥α,m ∥β,则α∥β;③若m ∥α,n ∥β,m ∥n ,则α∥β.其中正确命题的个数是( )
A .0
B .1
C .2
D .3
解析:把符号语言转换为文字语言或图形语言.可知①是面面平行的判定定理;②③中平面α,β还有可能相交,所以选B.
答案:B
5.平面α与△ABC 的两边AB ,AC 分别交于D ,E ,且AD DB =AE EC
,如图所示,则BC 与平面α的关系是( )
A .平行
B .相交
C .异面
D .BC ⊂α
解析:因为AD DB =AE EC
,所以ED ∥BC ,又DE ⊂α,BC ⊄α, 所以BC ∥α.
答案:A
二、填空题
6.在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE ∶EB =CF ∶FB =1∶3,则对角线AC 与平面DEF 的位置关系是________.
解析:因为AE ∶EB =CF ∶FB =1∶3,所以EF ∥AC .又因为AC ⊄平面DEF ,EF ⊂平面DEF ,所以AC ∥平面DEF .
答案:平行
7.若空间四边形ABCD 的两条对角线AC ,BD 的长分别是8,12,过AB 的中点E 且平行于BD ,AC 的截面四边形的周长为________.
解析:设所求截面四边形为EFGH ,且F ,G ,H 分别是BC ,CD ,DA 的中点,所以EF =GH =4,FG =HE =6.所以截面四边形EFGH 的周长为2×(4+6)=20.
答案:20
8.下图是正方体的平面展开图,在这个正方体中:
①BM∥平面DE;
②CN∥平面AF;
③平面BDM∥平面AFN;
④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.
解析:以ABCD为下底面还原正方体,如图,则易判定四个命题都是正确的.
答案:①②③④
三、解答题
9.如图所示的三棱柱ABC-A1B1C1中,M,N分别为BC,B1C的中点,求证:MN∥面ACC1A1.
证明:因为M,N分别为BC,B1C的中点,
所以MN∥BB1,又BB1∥AA1,
所以MN∥AA1,
又MN⊄面ACC1A1,AA1⊂面ACC1A1,所以MN∥面ACC1A1.
10.如图所示,在已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC.
证明:因为PM∶MA=BN∶ND=PQ∶QD,
所以MQ∥AD,NQ∥BP.
因为BP⊂平面PBC,NQ⊄平面PBC,
所以NQ∥平面PBC.
又因为底面ABCD为平行四边形,
所以BC∥AD,所以MQ∥BC.
因为BC⊂平面PBC,MQ⊄平面PBC,
所以MQ∥平面PBC.
又因为MQ∩NQ=Q,
所以根据平面与平面平行的判定定理,得平面MNQ∥平面PBC.
B级能力提升
1.如图所示,在下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP 的图形的序号是()
①②
③④
A.①③B.①④
C.②③D.②④
答案:B
2.已知a和b是异面直线,且a⊂平面α,b⊂平面β,a∥β,b∥α,则平面α与β的位置关系是________.
解析:在b上任取一点O,则直线a与点O确定一个平面γ,设γ⊂β=l,则l⊂β,
因为a∥β,所以a与l无公共点,
所以a∥l,所以l∥α.
又b∥α,根据面面平行的判定定理可得α∥β.
答案:平行
3.在长方体ABCD-A1B1C1D1中,E,F,E1,F1分别是AB,CD,A1B1,C1D1的中点.求证:平面EFD1A1∥平面BCF1E1.。
