小学奥数知识名师点拨 例题精讲 解题思路 平移、旋转、割补.教师版
四下第1讲 平移、旋转和轴对称(解题思路)

第1讲平移、旋转和轴对称考点1:平移的两要素例1.如图所示:图形(1)向平移了格.图形(2)向平移了格.图形(3)向平移了格.【思路分析】找出各个图形平移后的对应关键点,即可得到平移的方向和距离,由此得解.【规范解答】解:如图所示:图形(1)向上平移了2格.图形(2)向左平移了4格.图形(3)向右平移了6格.故答案为:上,2,左,4,右,6.【名师点评】此题考查了利用平移进行图形变化的方法的灵活应用.练习1.(1)长方形向上平移了格.(2)六边形向平移了格.(3)五角星向平移了格.【思路分析】根据题意,结合图形,由平移的概念找出图形平移的方向,和平移的格数,即可求解.【规范解答】解:观察图形可知:(1)长方形向上平移了6格.(2)六边形向左平移了5格.(3)五角星向下平移了6格.故答案为:上,6,左,5,下,6.【名师点评】本题考查平移的基本概念及平移规律,关键是要观察比较平移前后物体的位置.2.填一填.(1)①向上平移了格.(2)②向平移了格.(3)③向平移了格.【思路分析】先找清楚方向,看原图到现在的图是向哪个方向平移的,然后在原图中选择一个点,找出这个点在后来图中的位置,然后数出这两个点之间的小格数即可.【规范解答】解:(1)①向上平移了2格.(2)②向左平移了4格.(3)③向右平移了6格.故答案为:上、2;左、4;右、6.【名师点评】解决本题关键是要数清楚平移的格子数.考点2:作平移后的图形例2.画出网格中图形向上平移1格,再向右平移3格后的图形.【思路分析】根据平移图形的特征,把平行图形的各个顶点分别向上平移1格,再向右平移3格,然后顺次连接各点即可.【规范解答】解:【名师点评】作平移后的图形关键是把对应点的位置画正确.练习1.(1)房子向右平移5格.(2)小船向下平移4格,再向左5格.【思路分析】(1)根据平移的特征,把小房子的各顶点分别向右平移5格,再依次连结即可得到向右平移5格后的图形.(2)同理即可画出小船向下平移4格,再向左平移5格后的图形.【规范解答】解:(1)房子向右平移5格(下图):(2)小船向下平移4格,再向左5格(下图):【名师点评】平移作图要注意:①方向;②距离.整个平移作图,就是把整个图案的每一个特征点按一定方向和一定的距离平行移动.考点3:运用平移的知识解决问题例3.一块平行四边形地底是18m,高是12m,地中间有两条1米宽的小路(如图),在这块地里种菜,种菜的面积是多少?【思路分析】将小路两旁部分向中间平移,直至小路消失,那么种菜的面积就是底为(181)--米,高为(121)米的平行四边形的面积,根据平行四边形的面积=底⨯高计算即可得出种菜的面积.【规范解答】解:(181)(121)-⨯-=⨯1711=(平方米)187答:种菜的面积是187平方米.【名师点评】此题主要考查平行四边形面积的计算.关键是求出图形切拼后平行四边形的底和高.练习1.如图,求图中阴影部分的面积.(单位:厘米)【思路分析】如图所示:阴影部分①和空白部分②的面积相等,将①平移到②的位置,则阴影部分就变成了一个长方形,利用长方形的面积公式S ab=即可求解.【规范解答】解:据思路分析可知,阴影部分的面积为:(12)2+⨯=⨯32=(平方厘米)6答:阴影部分的面积是6平方厘米.【名师点评】规范解答此题的关键是:利用平移的方法,将不规则图形转化成规则图形,再根据规则图形的面积公式即可求解.2.一块草地形状如图的阴影部分,阴影部分的面积是多少平方米?【思路分析】把草地上左边的半圆放在右边就变成了一个长为10米,宽为6米的长方形,这个长方形的面积就是草地的面积.【规范解答】解:把左边的半圆平移到右边的半圆上后草地就变成了一个长方形,它的面积是:10660⨯=(平方米);答:阴影部分的面积是60平方米.【名师点评】求组合图形的面积时经常用平移、旋转、填补、切割等方法把复杂的图形变成较简单的图形来算.考点4:旋转的三要素例4.根据图,回答问题.①号三角形是绕A点按顺时针方向旋转了度.②号梯形是绕B点按时针方向旋转了度.③号三角形是绕C点按时针方向旋转了度.④号平行四边形是绕D点按时针方向旋转了度.【思路分析】根据图形旋转的特征,一个图形绕某点顺时针(或逆时针)旋转一定的度数,某点的位置不动,其余各点(边)均绕某点按相同的方向旋转相同的度数.【规范解答】解:①号三角形绕A点按顺时针方向旋转了90度.②号梯形绕B点按逆时针方向旋转了90度.③号三角形绕C点按逆时针方向旋转了90度.④号平行四边形绕D点按顺时针方向旋转了90度.故答案为:顺,90,逆,90,逆,90,顺,90.【名师点评】本题是考查图形的旋转,关键是弄清旋转的方向与角度.练习1.①图形D绕点O按方向旋转︒到图形A所在的位置.②图形A绕点O按方向旋转︒到图形C所在的位置.③图形C绕点O按方向旋转︒到图形B所在的位置.【思路分析】旋转的要素是旋转方向,旋转中心,旋转角,据此即可解决问题.【规范解答】解:①图形D绕点O按逆时针方向旋转90︒到图形A所在的位置.②图形A绕点O按逆时针方向旋转180︒到图形C所在的位置.③图形C绕点O按顺时针方向旋转90︒到图形B所在的位置.故答案为:逆时针,90;逆时针,180;顺时针,90.【名师点评】本题主要考查了旋转的要素,是需要熟记的内容.3.如图:(1)指针从“1”绕点O顺时针旋转60︒后指向.(2)指针从“1”绕点O逆时针旋转90︒后指向.(3)指针从“12”绕点O顺时针旋转︒后指向“3”.(4)指针从“12”绕点O逆时针旋转︒后指向“8”.(5)指针从7:15到7:40绕点O顺时针旋转度.【思路分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆心角是3601230︒÷=︒,即每两个相邻数字间的夹角是30︒,即指针从一个数字走到下一个数字时,绕中心轴旋转了30︒,由此规范解答即可.【规范解答】解:(1)指针从“1”绕点O顺时针旋转60︒后指向3.(2)指针从“1”绕点O逆时针旋转90︒后指向9.(3)指针从“12”绕点O顺时针旋转90︒后指向“3”.(4)指针从“12”绕点O逆时针旋转120︒后指向“8”.(5)指针从7:15到7:40绕点O顺时针旋转150度.故答案为:3,9,90,120,150.【名师点评】关键弄清在钟面上指针绕中心从一个数字旋转到相邻的另一个数字旋转了多少度.考点5:作旋转一定角度后的图形例5.我会操作.(1)画出三角形绕点“A”顺时针旋转90度后的图形,并标为图1.(2)画出三角形绕点“B”逆时针旋转180度后的图形,并标为图2.【思路分析】(1)根据旋转的特征,三角形ABO绕点“A”顺时针旋转90︒,点“A”的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形1.(2)同理,三角形ABO绕点“B”逆时针旋转180︒,点“B”的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形2.【规范解答】解:(1)画出三角形绕点“A”顺时针旋转90度后的图形,并标为图1(图中红色部分).(2)画出三角形绕点“B”逆时针旋转180度后的图形,并标为图2(图中绿色部分).【名师点评】经过旋转,图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.(旋转前后两个图形的对应线段相等、对应角相等.练习1.画出小旗绕点O逆时针旋转90︒后得到的图形.【思路分析】根据旋转的意义,找出图中三角旗3个关键处,再画出绕O点按逆时针方向旋转90度后的形状即可.【规范解答】解:作图如下:【名师点评】本题考查了图形的旋转变化,学生主要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错.考点6:轴对称图形的辨识例6.下面图形不是轴对称图形的是()A.B.C.【思路分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可.【规范解答】解:根据轴对称图形的意义可知:选项A、B都是轴对称图形,而C不是轴对称图形;故选:C.【名师点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.练习1.下面9个交通标志图案中,有()个图形是轴对称图形.A.4B.5C.6D.7【思路分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可.【规范解答】解:根据轴对称图形的意义可知:是轴对称图形;故选:A.【名师点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.2.成轴对称的两个数字是()A.B.C.【思路分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;依次进行判断即可.【规范解答】解:根据轴对称图形的意义可知:选项A、B都不是轴对称图形,只有C是轴对称图形;故选:C.【名师点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.考点7:画轴对称图形的对称轴例7.按要求画出下面轴对称图形的对称轴.【思路分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此画图规范解答即可.【规范解答】解:【名师点评】本题考查了轴对称图形的对称轴的确定,根据轴对称图形的对称轴两边的部分关于对称轴折叠能够完全重合作图即可,比较简单.练习1.画出下列图形的所有对称轴.【思路分析】(1)有三条对称轴,即过每个圆圆心与另外两个圆交点的直线.(2)有两条对称轴,即过个两个箭头顶点的直线,及箭头两个顶点间线段的垂直平分线.(3)等腰有一条对称轴,底边高所在的直线.【规范解答】解:【名师点评】此题是考查确定轴对称图形对称轴的条数及位置.关键是轴对称图形的意义及各图形的特征.考点8:作轴对称图形的另一半例8.动手画一画:以虚线为对称轴,画出下列图形的轴对称图形.【思路分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出原图的关键对称点,依次连结即可.【规范解答】解:【名师点评】求作一个几何图形关于某条直线对称的图形,可以转化为求作这个图形上的特征点关于这条直线对称的点,然后依次连结各对称点即可.练习1.先画出下面这个轴对称图形的另一半,再画出这个轴对称图形向右平移8格后的图形.【思路分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的下边画出图形的关键对称点,顺次连结.然后根据平移的特征,把图形的各点分别向右平移8格,再依次连结即可.【规范解答】解:先画出下面这个轴对称图形的另一半,再画出这个轴对称图形向右平移8格后的图形,作图如下:【名师点评】本题是考查作轴对称图形、作平移的图形.关键是确定对称点(对应点)的位置.2.下面的图形都是由相同的小正方形组成的,请分别在各图形上画一个同样大小的小正方形,使它们成为轴对称图形.【思路分析】因为如果一个图形沿着一条直线对折,直线两边的图形能够完全重合,这样的图形叫做轴对称图形,据此规范解答.【规范解答】解:作图如下【名师点评】此题是考查了轴对称图形的意义.考点9:镜面对称问题例9.如图是小明在平面镜中看到时钟形成的像,它的实际时间是()A.21:05B.12:02C.12:05D.15:02【思路分析】根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称.【规范解答】解:如图实际时间是12:05.故选:C.【名师点评】此题主要明白镜面对称的特点是:上下前后方向一致,左右方向相反,镜中与实际景物大小不变.练习1.如图的钟面是从镜子里看到的,实际钟面上的时刻是.【思路分析】镜面对称的特点是:上下前后方向一致,左右方向相反;图中镜子里看到的时间是6:40,由镜面对称左右方向相反特点,镜中时针在6与7之间,实际是在5与6之间,是5时,镜中分针指刻度8,实际中是指刻度4,即20分;据此规范解答.【规范解答】解:因为镜中时针在6与7之间,实际是在5与6之间,是5时,镜中分针指着刻度8,实际中是指刻度4,即20分,所以实际钟面上的时刻是5:20.故答案为:5:20.【名师点评】此题主要明白镜面对称的特点是:上下前后方向一致,左右方向相反.2.一位司机从反光镜中看到后面汽车的车牌是,这个车牌号实际是浙F.8765A.【思路分析】根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称.【规范解答】解:如图,这个车牌实际是:浙F.8765A.故答案为:浙F.8765A.【名师点评】此题主要明白镜面对称的特点是:上下前后方向一致,左右方向相反,镜中与实际景物大小不变.3.从镜子里看的样子是()A.B.C.【思路分析】镜面对称的特点是:上下前后方向一致,左右方向相反,在镜中的样子,上下前后的样子不变,只有左右方向相反,所以.【规范解答】解:从镜子里看的样子是;故选:C.【名师点评】此题考查了镜面对称的特点:上下前后方向一致,左右方向相反.注意左右方向是相反的.考点10:运用平移、对称和旋转综合作图例10.按要求在方格纸上画一画.①把三角形先向右平移10格,再向上平移4格.②把长方形绕点A顺时针旋转90︒.③把最右边的图形补全,使它成为轴对称图形.【思路分析】①根据平移的特征,把三角形的各顶点分别向右平移10格,依次连结即可得到向右平移10格后的图形;用同样的方法即可把平移后的图形再向上平移4格.②根据旋转的特征,长方形绕点A顺时针旋转90︒,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形.③根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的左边画出右半图的关键对称点,依次连结即可.【规范解答】解:①把三角形先向右平移10格(图中灰色部分),再向上平移4格(图中红色部分).②把长方形绕点A顺时针旋转90︒(图中绿色部分).③把最右边的图形补全,使它成为轴对称图形(图中蓝色部分).【名师点评】作平移后的图形、作旋转一定度数后的图形、作轴对称图形的关键是确定对应点(对称点)的位置.练习1.如图(1)将图形A先绕点O顺时针旋转90 ,再向左平移6格,得到图形C.(2)将图形B向右平移5格后得到图形D.(3)以直线l为对称轴作图形D的轴对称图形E.【思路分析】(1)以点O为旋转中心,把图形A的另外几个顶点,分别绕点O顺时针旋转90后,再依次连接起来,得到的图形再把各个顶点分别向左平移6格,依次连接起来即可得出图形C;(2)把图形B的各个顶点分别向左平移5格,再依次连接起来,即可得出图形D.(3)据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,画出图形D的轴对称图形E即可规范解答问题.【规范解答】解:根据题干思路分析可得:【名师点评】此题考查利用轴对称、旋转、平移进行图形变换的方法.。
12平移与旋转--知识讲解及其练习 含答案

平移与旋转--知识讲解【学习目标】1.理解平移、旋转的基本概念,掌握平移、旋转的基本特征,并能利用平移与旋转的性质进行证明有关问题;2.知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质,能用平移变换有关知识说明一些简单问题及进行图形设计;理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质;3.能够按要求作出简单平面图形旋转后的图形,并能利用旋转进行简单的图案设计.【要点梳理】要点一、平移1. 定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移.要点诠释:(1)图形的平移的两要素:平移的方向与平移的距离.(2)图形的平移不改变图形的形状与大小,只改变图形的位置.2. 性质:图形的平移实质上是将图形上所有点沿同一方向移动相同的距离,平移不改变线段、角的大小,具体来说:(1)平移后,对应线段平行(或共线)且相等;(2)平移后,对应角相等;(3)平移后,对应点所连线段平行(或共线)且相等;(4)平移后,新图形与原图形的形状与大小不变.要点诠释:(1)“连接各组对应点的线段”的线段的长度实际上就是平移的距离.(2)要注意“连接各组对应点的线段”与“对应线段”的区别,前者是通过连接平移前后的对应点得到的,而后者是原来的图形与平移后的图形上本身存在的.3. 作图:平移作图是平移基本性质的应用,在具体作图时,应抓住作图的“四步曲”——定、找、移、连.(1)定:确定平移的方向和距离;(2)找:找出表示图形的关键点;(3)移:过关键点作平行且相等的线段,得到关键点的对应点;(4)连:按原图形顺次连接对应点.要点二、旋转的概念把一个图形绕着某一点O转动一个角度的图形变换叫做旋转.点O叫做旋转中心,转动的角叫做旋转角(如∠AOA′),如果图形上的点A经过旋转变为点A′,那么,这两个点叫做这个旋转的对应点.要点诠释:旋转的三个要素:旋转中心、旋转方向和旋转角度.要点三、旋转的性质(1)对应点到旋转中心的距离相等(OA=OA′);(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前、后的图形的形状与大小不变.要点诠释:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转.要点四、旋转的作图在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键点沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.要点诠释:作图的步骤:(1)连接图形中的每一个关键点与旋转中心;(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角);(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;(4)连接所得到的各对应点.【典型例题】类型一、平移1.如图所示,平移△ABC,使点A移动到点A′,画出平移后的△A′B′C′.【思路点拨】平移一个图形,首先要确定它移动的方向和距离,连接AA′后这个问题便获得解决.根据平移后的图形与原来的图形的对应线段平行(或在一条直线上)且相等,容易画出所求的线段.【答案与解析】解:如图所示,(1)连接AA′,过点B作AA′的平行线l,在l上截取BB′=AA′,则点B′就是点B的对应点.(2)用同样的方法做出点C的对应点C′,连接A′B′、B′C′、C′A′,就得到平移后的三角形A′B′C′.【总结升华】平移一个图形,首先要确定它移动的方向和距离.连接AA′,这个问题就解决了,然后分别把B、C按AA′的方向平移AA′的长度,便可得到其对应点B′、C′,这就是确定了关键点平移后的位置,依次连接A′B′,B′C′,C′A′便得到平移后的三角形A′B′C′.2.(•东台市模拟)如图,将△ABC平移到△A′B′C′的位置(点B′在AC边上),若∠B=55°,∠C=100°,则∠AB′A′的度数为______.【答案】25°【解析】∵∠B=55°,∠C=100°,∴∠A=180°﹣∠B﹣∠C=180°﹣55°﹣100°=25°,∵△ABC平移得到△A′B′C′,∴AB∥A′B′,∴∠AB′A′=∠A=25°.【总结升华】图形在平移的过程有“一变两不变”、“一变”是位置的变化,“两不变”是形状和大小不变.本例中由△ABC经过平移得到△A′B′C′.则有AB=A′B′,BC=B′C′,AC=A′C′,∠A=∠A′,∠C=∠C,∠B=∠B′.举一反三:【变式】(•临淄区一模)如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为.【答案】20;解:∵△ABC沿BC方向平移2cm得到△DEF,∴CF=AD=2cm,AC=DF,∵△ABC的周长为16cm,∴AB+BC+A C=16cm,∴四边形ABFD的周长=AB+BC+CF+DF+AD=AB+BC+AC+CF+AD=16cm+2cm+2cm=20cm.故答案为:20cm.类型二、旋转的概念及性质3.如图,把四边形AOBC绕点O旋转得到四边形DOEF.在这个旋转过程中:(1)旋转中心是谁?(2)旋转方向如何?(3)经过旋转,点A、B的对应点分别是谁?(4)图中哪个角是旋转角?(5)四边形AOBC与四边形DOEF的形状、大小有何关系?(6)AO与DO的长度有什么关系? BO与EO呢?(7)∠AOD与∠BOE的大小有什么关系?【答案与解析】(1)旋转中心是点O;(2)旋转方向是顺时针方向;(3)点A的对应点是点D,点B的对应点是点E;(4)∠AOD和∠BOE;(5)四边形AOBC与四边形DOEF的图形全等,即形状一致,大小相等;(6)AO=DO,BO=EO;(7)∠AOD=∠BOE.【总结升华】通过具体实例认识旋转,了解旋转的概念和性质.举一反三【变式】如图所示:O为正三角形ABC的中心.你能用旋转的方法将△ABC分成面积相等的三部分吗?如果能,设计出分割方案,并画出示意图.【答案】下面给出几种解法:解法一:连接OA、OB、OC即可.如图甲所示;解法二:在AB边上任取一点D,将D分别绕点O旋转120°和240°得到D1、D2,连接OD、OD1、 OD2即得,如图乙所示.解法三:在解法二中,用相同的曲线连结OD、OD1、OD2即得如图丙所示4.如图,将图(1)中的正方形图案绕中心旋转180°后,得到的图案是( )【答案】C.【解析】抓住图形特征,观察图中的每个小的图形绕中心点旋转180°后能否与自身重合.【总结升华】在解题的过程中,可看出如果选取的基本图形不同,可得到不同的形成过程,甚至所选取的基本图形相同,也有不同的形成过程,因此分析图案的形成过程旨在了解图形的变化规律,而不必强求分析的一致性.类型三、旋转的作图5. 如图,已知△ABC与△DEF关于某一点对称,作出对称中心.【答案与解析】【总结升华】确定关于某点成中心对称的两个图形的对称中心的方法:⑴利用中心对称的性质:对称点所连线段被对称中心所平分,所以连接任意一对对称点,取这条线段的中点,则该点即为对称中心;⑵利用中心对称的性质:对称点所连线段都经过对称中心,所以连接任意两对对称点,则这两条线段的交点即为对称中心.6.(•南宁)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).(1)画出△ABC 关于y 轴对称的△A 1B 1C 1;(2)将△ABC 绕着点B 顺时针旋转90°后得到△A 2BC 2,请在图中画出△A 2BC 2,并求出线段BC 旋转过程中所扫过的面积(结果保留π).【思路点拨】(1)根据题意画出△ABC 关于y 轴对称的△A 1B 1C 1即可;(2)根据题意画出△ABC 绕着点B 顺时针旋转90°后得到△A 2BC 2,线段BC 旋转过程中扫过的面积为扇形BCC 2的面积,求出即可. 【答案与解析】解:(1)如图所示,画出△ABC 关于y 轴对称的△A 1B 1C 1;(2)如图所示,画出△ABC 绕着点B 顺时针旋转90°后得到△A 2BC 2,由勾股定理得,BC=222+3=13,线段BC 旋转过程中所扫过得面积S=π21134⨯()=.【总结升华】此题考查了作图﹣旋转变换,对称轴变换,以及扇形面积,作出正确的图形是解本题的关键. 举一反三【变式】如图,画出ABC ∆绕点O 逆时针旋转100︒所得到的图形.【答案】(∠AOA′=∠BOB′=∠COC′=100°)平移与旋转--巩固练习【巩固练习】一、选择题1.如图所示的图形中的小三角形可以由△ABC平移得到的有 ( )A.3个 B.4个 C.5个 D.6个2.(•株洲)如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是()A.50°B.60°C.70°D.80°3.下面生活中的物体的运动情况可以看成平移的是().(1)摆动的钟摆;(2)在笔直的公路上行驶的汽车;(3)随风摆动的旗帜;(4)摇动的大绳;(5)汽车玻璃上雨刷的运动;(6)从楼顶自由落下的球(球不旋转).A.(1)(3) B.(4)(5) C.(3)(5) D.(2)(6)4.如图,4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( ).A.点A B.点B C.点C D.点D5.如图①,在宽为20m、长为30m的矩形地面上修建两条同样宽度的道路,余下部分作为耕地.根据图中数据,可得耕地的面积为 ( )A.600m2 B.551m2 C.550m2 D.500m26.如图,在正方形ABCD中,E为DC边上的点,连结BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连结EF,若∠BEC=60°,则∠EFD的度数为( )A.10°B.15°C.20°D.25°二、填空题7.(春•博野县期末)图形在平移时,下列特征中不发生改变的有(把你认为正确的序号都填上),①图形的形状;②图形的位置;③线段的长度;④角的大小;⑤垂直关系;⑥平行关系.8.如图所示,△ABC经过平移得到△A′B′C′,图中△_________与△_________大小形状不变,线段AB与A′B′的位置关系是________,线段CC′与BB′的位置关系是________.9.(•吉林)如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为cm.10.(春•新化县期末)钟表的分针匀速旋转一周需要60min,经过20min,分针旋转了_______度.11.如图,在等腰直角△ABC中,B=90°,将△ABC绕顶点A逆时针方向旋转60°后得到△AB′C′,则等于__________度.12.如图,△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则△ABB′是______三角形.三.解答题13.如图,将四边形ABCD平移到四边形EFGH的位置,根据平移后对应点所连的线段平行且相等,写出图中平行的线段和相等的线段.14.(吉安校级期中)等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.(1)求出点B的坐标;(2)当A1与B1的纵坐标相同时,求出a的值;(3)在(2)的条件下直接写出点B1的坐标.15.如图所示,在长为50m,宽为22m的长方形地面上修筑宽度都为2 m的道路,余下的部分种植花草,求种植花草部分的面积.【答案与解析】一、选择题1.【答案】C ;【解析】图中小三角形△BDE ,△CEF ,△DGH ,△EHI ,△FIJ 都可以由△ABC 平移得到.2.【答案】B ;【解析】解:∵在三角形ABC 中,∠ACB=90°,∠B=50°,∴∠A=180°﹣∠ACB ﹣∠B=40°.由旋转的性质可知:BC=B′C,∴∠B=∠BB′C=50°.又∵∠BB′C=∠A+∠ACB′=40°+∠ACB′,∴∠ACB′=10°,∴∠COA′=∠AOB′=∠OB′C +∠ACB′=∠B+∠ACB′=60°.故选B .3.【答案】D ;【解析】(1)摆动的钟摆,方向发生改变,不属于平移;(2)在笔直的公路上行驶的汽车沿直线运动,属于平移;(3)随风摆动的旗帜,形状发生改变,不属于平移;(4)摇动的大绳,方向发生改变,不属于平移;(5)汽车玻璃上雨刷的运动,方向发生改变,不属于平移;(6)从楼顶自由落下的球沿直线运动,属于平移.∴可以看成平移的是(2)(6).故选D.4.【答案】B ;【解析】连接对应点111,,PP MM NN ,做三条线段的垂直平分线,交点即是旋转中心.5.【答案】B ;6.【答案】B ;【解析】因为△BCE 旋转90°得到△DCF ,所以EC=CF,∠CFD=∠CEB=60°,即∠EFC=45°,所以∠EFD=60°-45°=15°.二、填空题7.【答案】①③④⑤⑥;【解析】解:由图形平移的性质,知图形在平移时,其特征不发生改变的有①③④⑤⑥.8.【答案】ABC , A ′B ′C ′,平行,平行;【解析】平移的性质.9.【答案】42;【解析】解:∵将△ABC 绕点B 顺时针旋转60°,得到△BDE,∴△ABC≌△BDE,∠CBD=60°,∴BD=BC=12cm,∴△BCD为等边三角形,∴CD=BC=CD=12cm,在Rt△ACB中,AB==13,△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=5+13+12+12=42(cm),故答案为:42.10.【答案】120°;【解析】2036012060⨯︒=︒.11.【答案】105°;【解析】∠BAC′=∠BAB′+∠B′AC′=60°+45°=105°.12.【答案】等边三角形;【解析】因为△ABC旋转60°得到△''ABC,则AB= AB′,∠BAB′=60°,所以是等边三角形.三、解答题13.【解析】解:平行的线段:AE∥BG∥DH,相等的线段:AE=BF=OG=DH.14.【解析】解:(1)如图1所示过点B作BC⊥OA,垂足为C.∵△OAB为等边三角形,∴∠BOC=60°,OB=BA.∵OB=AB,BC⊥OA,∴OC=CA=1.在Rt△OBC中,,∴BC=.∴点B的坐标为(1,).(2)如图2所示:∵点B1与点A1的纵坐标相同,∴A1B1∥OA.①如图2所示:当a=300°时,点A1与点B1纵坐标相同.如图3所示:当a=120°时,点A1与点B1纵坐标相同.∴当a=120°或a=300°时,点A1与点B1纵坐标相同.(3)如图2所示:由旋转的性质可知A1B1=AB=2,点B的坐标为(1,2),∴点B1的坐标为(﹣1,).如图3所示:由旋转的性质可知:点B1的坐标为(1,﹣).∴点B1的坐标为(﹣1,)或(1,﹣).15.【解析】解:如图所示②把几条2米宽的小路分别平移到大长方形的上边缘和左边缘,则种植花草部分汇集成一个长方形,显然,这个长方形的长是50-2=48(m),宽是22-2=20(m),于是种植花草部分的面积为48×20=960(m2).。
小学奥数 几何类 几何图形周长和面积的基本计算 平移、旋转、割补.题库版

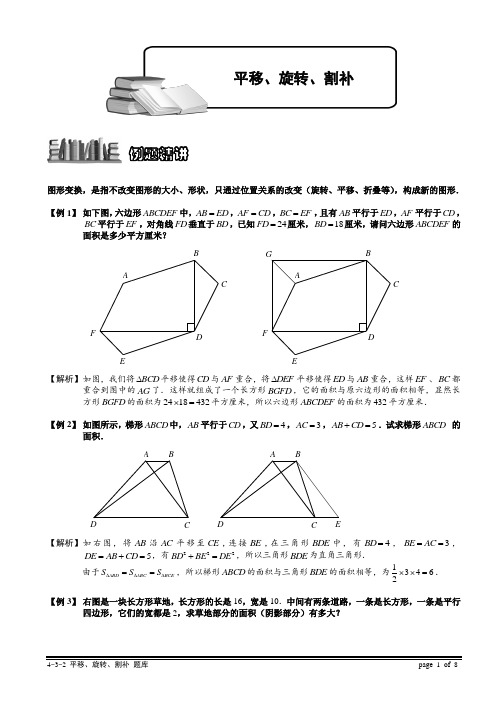
图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形. 【例 1】 右图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积(阴影部分)有多大?【考点】平移、旋转、割补 【难度】2星 【题型】解答 【解析】 如图所示,将道路平移后的()()162102112-⨯-=。
【答案】112【例 2】 如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个.请算出阴影部分的面积.1cm【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 如图,将阴影部分分割成一个正六边形和12个小三角形,再把正六边形分割成6个正三角形,由于正十二边形的每个内角为()180********︒⨯-÷=︒,所以阴影小三角形的顶角等于15060230︒-︒⨯=︒,每个顶角的两边和与其相邻的正三角形的底边所成的角都是306090︒+︒=︒,所以通过如右上图所示的平移可以组成6个边长为1厘米的正方形,所以所求阴影部分面积为2166⨯=平方厘米.【答案】6【例 3】 如图所示,梯形ABCD 中,AB 平行于CD ,又4BD =,3AC =,5AB CD +=.试求梯形ABCD 的面积.D CBAEDCBA【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 如右图,将AB 沿AC 平移至CE ,连接BE ,在三角形BDE 中,有4BD =,3BE AC ==,5DE AB CD =+=,有222BD BE DE +=,所以三角形BDE 为直角三角形.由于ABD ABC BCE S S S ∆∆∆==,所以梯形ABCD 的面积与三角形BDE 的面积相等,为13462⨯⨯=.例题精讲4-2-5.平移、旋转、割补【例 4】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FD BAGFE DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【答案】432【例 5】 如图2,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若PBC 、PEF 的面积为3与4,则正六边形ABCDEF 的面积是.E【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】2007年,迎春杯、中年级、初赛、7题【解析】 这是一道几何问题,考察同学们对常见图形性质的认识.正六边形的六条边都相等,每个角都是,每一组对边都互相平行,正六边形可以看作是由六个正三角形拼成的(如图(1)).其中正六边形的面积是正三角形面积的6倍.每相邻两个正三角形拼成的是一个平行四边形.如图(2),连结BF ,三角形ABF 的面积是平行四边形ABFO 面积的一半.六边形ABCDEF 的面积是平行四边形ABFO 的3倍,故六边形ABCDEF 的面积是三角形ABF 的面积的6倍. 如图(3),连结BF ,CE ,三角形BCP 的面积与三角形EFP 的面积和是平行四边形BFEC 面积的一半.而六边形ABCDEF 的面积是平行四边形BFEC 的1.5倍,故六边形ABCDEF 的面积是三角形BCP 的面积与三角形EFP 的面积和的3倍.图(1)OAB CDEF图(2)OB ACDEF图(3)E所以,由PBC △、PEF △的面积分别为3与4, 可知正六边形ABCDEF 的面积是(34)321+⨯=.【例 6】 正六边形A1A2A3A4A5A6的面积是2009平方厘米,B1,B2,B3,B4,B5,B6分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.A 3【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】2009年、迎春杯、六年级、初赛、14题【解析】 如图,设62B A 与13B A 的交点为O ,则图中空白部分由6个与23A OA △一样大小的三角形组成,只要求出了23A OA △的面积,就可以求出空白部分面积,进而求出阴影部分面积.4A 3A 654连接63A A 、61B B 、63B A设116A B B △的面积为“1”,则126B A B △面积为“1”,126A AB △面积为“2”,那么636A A B △面积为126A A B △的2倍,为“4”,梯形1236A A A A 的面积为224212⨯+⨯=,263A B A △的面积为“6”,123BAA △的面积为2 根据蝴蝶定理,1263261316B A B A A B B O A O S S ===△△∶∶,故21233612167A OAB A A S S ==+△△, 所以231236A A A A 121277A OA S S =△梯形∶∶∶1∶,即23A OA △的面积为梯形1236A A A A 面积的17,故为六边形123456A A A A A A 面积的114,那么空白部分的面积为正六边形面积的136147⨯=,所以阴影部分面积为32009111487⎛⎫⨯-= ⎪⎝⎭(平方厘米).【答案】1148【例 7】 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm 和4cm ,乙三角形两条直角边分别为3cm 和6cm ,求图中阴影部分的面积.【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 如右图,我们将三角形甲与乙进行平移,就会发现平行四边形面积等于平移后两个长方形面积之和.所以阴影部分面积为:2346236242211cm ⨯+⨯-⨯÷+⨯÷=()()【答案】11【例 8】在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 阴影总值是一个梯形.我们用三种方法解答.⑴ 割补法从顶点作底边上的高,得到两个相同的直角三角形.将这两个直角三角形拼成一个长方形(见下图).显然,阴影部分正好是长方形的13,所以原题阴影部分占整个图形面积的13.⑵ 拼补法将两个这样的三角形拼成一个平行四边形(下页左上图).显然,图中阴影面积占平行四边形面积的13.根据商不变性质,将阴影面积和平行四边形面积同时除以2,商不变.所以原题阴影部分占整个图形面积的13.⑶ 等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,所以阴影部分占整个图形面积的3193=. 注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立. 【答案】13【例 9】 如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点P 为中心转动一个正方形.当5AB =厘米,13BC =厘米,12CA =厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).P【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 右图由左图旋转而得,则右图中的8个空白小三角形都是完全相同的,右图中重叠部分的面积等于正方形面积减去4个小三角形的面积,从右图中可以看出正方形的边长为5131230++=厘米,所以重叠部分的面积为:2304(5122)780-⨯⨯÷=(平方厘米).【答案】780【例 10】 如图,在直角三角形中有一个正方形,已知10BD =厘米,7DC =厘米,求阴影部分的面积.【考点】平移、旋转、割补 【难度】4星 【题型】解答【解析】 绕D 点逆时针旋转CED ∆,使E 与F 重合,则C 点落在AB 边上的'C 点处,且'C D CD =.则阴影部分面积转化为直角三角形'BC D 的面积,所以阴影部分的面积为107235⨯÷=平方厘米.【答案】35【例 11】 四边形ABCD 中,AB =30,AD =48,BC =14,CD =40.又已知∠ABD +∠BDC =900,求四边形ABCD 的面积.DBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如下图,以BD 的垂直平分线为对称轴L ,做△ABD 关于L 的对称图形△A 'BD .连接A 'C .A 1IABCD因为∠ABD +∠BDC =9000而∠ABD =∠A 'DB =900,所以有∠A 'DB +∠BDC =900. 那么A 'CD 为直角三角形,由勾股定理知2A C '=22AB CD +=2500,所以50A C '=.而在△A 'BC 中,有A 'B =AD =48,有482+142=2500,即A 'B 2+BC 2=A 'C 2,即△A 'BC 为直角三角形. 有A CD A BCSS''+130402=⨯⨯114489362+⨯⨯=. 而|ABCDS 四边形A CD A BC S S ''=+936=.评注:Ⅰ.本题以∠ABC +∠BDC =900突破口,通过对称变换构造出与原图形相关的角三角形Ⅱ.对于这道题我们还可以将△BCD 作L 的对称图形.如下:C 1lABCD【答案】936【例 12】 如图,在三角形ABD 中,当AB 和CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.DCAB?30°40°【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 因为AB =CD ,于是可以将三角形ABC 的边BA 边与CD 对齐,如下图. 在下图中有∠BCA =110°,所以∠ACD =70°于是∠AC C '=∠ACD +∠DC C '=∠ACD +∠ABC =70°+40°=110°;A 1D C 1CB 1BA即∠AC C '=110°=∠CC D ';又因为C A ''只是CA 移动的变化,所以C A ''=CA ;则A B CA ''是一等腰梯形.于是,∠ADC '=180°-110°=70°;又∠CDC '=30°,所以∠ADC =70°-30°=40°.【答案】40°【例 13】 如图所示的四边形的面积等于多少?DB13131212【考点】平移、旋转、割补 【难度】4星 【题型】解答【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【答案】144【例 14】 如图,三角形ABC 是等腰直角三角形,P 是三角形外的一点,其中90BPC ∠=︒,10cm AP =,求四边形ABPC 的面积.P DCBAP'PDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 因为BAC ∠和BPC ∠都是直角,和为180︒,所以ABP ∠和ACP ∠的和也为180︒,可以旋转三角形APC ,使AC 和AB 重合,则四边形的面积转化为等腰直角三角形'AP P ,面积为1010250⨯÷=平方厘米.【答案】50【例 15】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】2008年、武汉明心奥数【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【答案】10【例 16】 如图,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,将腰CD 以D 为中心逆时针旋转90︒至ED ,连接AE 、CE ,则ADE ∆的面积是 .ED CBAH FEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】2008年、武汉明心奥数【解析】 如图所示,将ADE ∆以D 为中心顺时针旋转90︒,到FDC ∆的位置.延长FD 与BC 交于H .由于ABCD 是直角梯形,AD 与FD 垂直,则四边形ADHB 是长方形,则BH AD =.由于ADE ∆与FDC ∆面积相等,而FDC ∆的底边2FD AD ==,高321CH BC BH =-=-=,所以FDC ∆的面积为2121⨯÷=,那么ADE ∆的面积也为1.【答案】1【例 17】 如图,正方形ABCD 和DEFG 有一个公共点D ,试比较三角形ADG 和三角形CDE 的面积.GFEDC BAA'GFEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 因为ADC ∠和GDE ∠是直角,所以ADG ∠和CDE ∠是互补角,将三角形ADG 顺时针旋转90︒到达'A DE ∆的位置,则'A 、D 、C 在同一条直线上,且'A D AD CD ==,即D 是'A C 的中点,所以三角形CDE 和三角形'A DE 面积相等,则三角形CDE 和三角形ADG 面积相等.【答案】相等【例 18】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE的面积.F【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】2008年、资优杯【解析】 如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==,所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ).又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ).那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ),所以12.52OBE BDE S S ∆∆==(2cm ).【答案】2.5【例 19】 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++= 2cm .EDCBADEC 'A 'CBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】2008年、迎春杯、高年级、复赛、10题【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系: ''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=.【答案】50【例 20】 如图所示的四边形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==厘米,连接对角线BD ,30ABD ∠=︒.求四边形ABCD 的面积.DCB A DECBA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】第八届、华杯总决赛【解析】 由45A ∠=°,30ABD ∠=︒,可得1804530105ADB ∠=︒-︒-︒=︒,1053075DBC ∠=︒-︒=︒.将DBC ∆剪下来,翻转,再贴在BD 边上,即将B 点粘在D 点上,D 点粘在B 点上,如右上图所示.则C 点在E 点的位置.由于10575180ADB EDB ∠+∠=︒+︒=︒,所以A 、D 、E 三点在同一条直线上.由于45A E C ∠=∠=∠=°,所以90ABE ∠=︒,即ABE ∆是等腰直角三角形,它的面积就等于四边形ABCD 的面积,所以四边形ABCD 的面积为1515112.52⨯=平方厘米.【答案】112.5【例 21】 如图,在ABD ∆中,AB CD =,求“?”的度数.40°30°?DCBAD【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如图,由于AB CD =,可以将ABC ∆移动到DCE ∆,由于180(3040)110AC B ∠=︒-︒+︒=︒,18011070ACD ∠=︒-︒=︒,所以7040110ACE ∠=︒+︒=︒,又110CED ∠=︒,而AC DE =,所以四边形ACED 是等腰梯形,有180********ADE CED ∠=︒-∠=︒-︒=︒,703040ADC ∠=︒-︒=︒.点评:通过构造全等三角形来转化.【答案】40°【例 22】 下图三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,点D 在BC边上,:2:3BD DC =.当三角形ABC 的面积是250cm 时,三角形ADE 的面积是多少?EDCB AGP R Q F EDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 以点A 为中心,由三个三角形ABC 可拼成右图:连结QE 、RF 、GD ,则DEQFRG 是一个正六边形.连结RD 、DQ 、RQ ,显然RDQ 是一个等边三角形,并且它的面积是正六边形面积的一半,所以是三角形ADE 的面积的3倍.由于23150cm PBC ABC S S ∆∆=⨯=,根据“鸟头定理”,22336cm 3223DQC PBC S S ∆∆=⨯⨯=++, 所以2342cm RDQ PBC DQC S S S ∆∆∆=-⨯=,则2342314cm ADE RDQS S ∆∆=÷=÷=.【答案】14【例 23】 如图,正方形PQRS 有三个顶点分别在ABC ∆的三条边上,BQ QC =.求正方形PQRS 的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如下图,我们设ABC ∆的面积为1,有161279341()122132111311143a e c db =---+=-⨯-⨯-⨯=,所以682143a e ==,751143bcd a ++=-=, 所以6875a b c d =++.如下图左,将三角形c 和三角形d 分别以P 、R 为中心按箭头方向旋转90︒,形成由两个直角三角形连在一起的一个四边形,如下图右,b 、c 、d 被虚线分成两个直角三角形,它们的面积之和为:276292230cm b c d ++=⨯÷+⨯÷=,所以2683027.2(cm )75a =⨯=.【答案】27.2【例 24】 如下图,△ABC 是边长为1的等边三角形,△BCD 是等腰三角形BD =CD ,顶角∠BDC =1200,∠MDN =600,求△AMN 的周长.120°60°M BD CNA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 如下图, 延长AC 至P ,使CP =MB ,连接DP .120°60°M BD C NA则有∠MBD =600+1163ADEDQRDEQSRT SS S ==正六边形01801202-=∠PCD ;CP =BM ;BD =CD ,所以有△MBD ≌△PCD .于是∠MDC =∠PDC ;又因为∠MDB +∠NDC =600,所以∠PDC +∠NDC =∠NDP =600; MD =PD ,在△MDN 、△PND 中,∠NDM =∠NDP ,ND =ND ,MD =PD ,于是△MND ≌△PND .有MN =PN .因为NP =NP =NC +CP ,而AM =AB -MB =AB -CP , 所以AM +AN +MN =(AB -CP )+AN +(NC +CP )=AB +AN +NC =2.即△AMN 的周长为2.【答案】2【例 25】若干个大小相同的正五边形如右图排成环状,下图中所示的只是3个五边形.那么要完成这一圈共需个正五边形.【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】2009年、迎春杯、六年级、初赛、5题【解析】 如图,设O 为圆心,A 、B 、C 、D 为五边形的顶点,连接OA 、OB 、OC .DC BAO从图中可以看出,OAB △和OBC △是完全相同的,所以OBA OBC ∠=∠,又五边形内角和为540°,所以正五边形的每个内角都为5405108÷=°°,即108ABD CBD ∠=∠=°, 那么3601082144ABC ∠=︒-︒⨯=︒,则144272OBA ∠=÷=°°, 又OAB OBA ∠=∠,所以18072236AOB ∠=︒-︒⨯=︒ 所以要用3603610+=°°个正五边形才能围成一圈.【答案】10【例 26】 如图,ABCD 是矩形,BC =6cm , AB=10cm ,AC 和BD 是对角线,图中的阴影部分以C 为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)【考点】平移、旋转、割补 【难度】3星 【题型】解答 【关键词】2006年,第十一届、华杯赛、决赛、第11题【解析】 ①设三角形BCO 以CD 为轴旋转一周所得到的立体的体积是s ,S 等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆锥的体积。
小学数学知识归纳认识平移旋转和翻折的变换

小学数学知识归纳认识平移旋转和翻折的变换一、平移变换平移是指将一个图形在平面上沿着某个方向进行移动,新的图形与原来的图形相等,只是位置改变了。
平移变换可用向量来表示。
例如,我们有一个三角形ABC,要将它向右平移3个单位长度,我们可以使用向量加法的方式来进行表示。
假设向右为正方向,则平移向量为3i(i表示单位向量,指向x轴正方向),则新的三角形A'B'C'可表示为A'B'C'=ABC+3i。
平移变换有以下几个特点:1. 平移后的图形与原图形形状相同。
2. 平移后图形的顶点与原图形的对应顶点连线平行且长度相等。
3. 平移后的图形与原图形之间的距离保持不变。
4. 平移变换是可逆的,即可以通过相反方向移动同样的距离回到原来的位置。
二、旋转变换旋转是指将一个图形绕某一点进行旋转,旋转变换也是以向量为基础的。
例如,我们有一个矩形ABCD,要将它绕点O逆时针旋转90°,我们可以使用向量旋转公式进行计算。
设原矩形的四个顶点坐标分别为A(x1, y1), B(x2, y2), C(x3, y3), D(x4, y4),绕点O逆时针旋转90°后的新坐标分别为A'(x1', y1'), B'(x2', y2'), C'(x3', y3'), D'(x4', y4'),则有以下关系式:x1' = y1-y1' + x1y1' = x1'-x1 + y1x2' = y2-y1' + x1y2' = x2'-x1 + y1x3' = y3-y1' + x1y3' = x3'-x1 + y1x4' = y4-y1' + x1y4' = x4'-x1 + y1旋转变换有以下几个特点:1. 旋转后的图形与原图形形状相同。
小学奥数教程之 图形的平移、旋转、割补计算题

图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形. 【例 1】 右图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积(阴影部分)有多大?【考点】平移、旋转、割补 【难度】2星 【题型】解答 【解析】 如图所示,将道路平移后的()()162102112-⨯-=。
【答案】112【例 2】 如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个.请算出阴影部分的面积.1cm【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 如图,将阴影部分分割成一个正六边形和12个小三角形,再把正六边形分割成6个正三角形,由于正十二边形的每个内角为()180********︒⨯-÷=︒,所以阴影小三角形的顶角等于15060230︒-︒⨯=︒,每个顶角的两边和与其相邻的正三角形的底边所成的角都是306090︒+︒=︒,所以通过如右上图所示的平移可以组成6个边长为1厘米的正方形,所以所求阴影部分面积为2166⨯=平方厘米.【答案】6【例 3】 如图所示,梯形ABCD 中,AB 平行于CD ,又4BD =,3AC =,5AB CD +=.试求梯形ABCD 的面积.D CBAEDBA【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如右图,将AB 沿AC 平移至CE ,连接BE ,在三角形BDE 中,有4BD =,3BE AC ==,5DE AB CD =+=,有222BD BE DE +=,所以三角形BDE 为直角三角形.由于ABD ABC BCE S S S ∆∆∆==,所以梯形ABCD 的面积与三角形BDE 的面积相等,为13462⨯⨯=.【答案】6【例 4】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形例题精讲4-2-5.平移、旋转、割补ABCDEF 的面积是多少平方厘米?FD BAGFE DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【答案】432【例 5】 如图2,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若PBC 、PEF 的面积为3与4,则正六边形ABCDEF 的面积是.E【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、中年级、初赛、7题 【解析】 这是一道几何问题,考察同学们对常见图形性质的认识.正六边形的六条边都相等,每个角都是,每一组对边都互相平行,正六边形可以看作是由六个正三角形拼成的(如图(1)).其中正六边形的面积是正三角形面积的6倍.每相邻两个正三角形拼成的是一个平行四边形.如图(2),连结BF ,三角形ABF 的面积是平行四边形ABFO 面积的一半.六边形ABCDEF 的面积是平行四边形ABFO 的3倍,故六边形ABCDEF 的面积是三角形ABF 的面积的6倍. 如图(3),连结BF ,CE ,三角形BCP 的面积与三角形EFP 的面积和是平行四边形BFEC 面积的一半.而六边形ABCDEF 的面积是平行四边形BFEC 的1.5倍,故六边形ABCDEF 的面积是三角形BCP 的面积与三角形EFP 的面积和的3倍.图(1)OAB CDEF图(2)OB ACDEF图(3)E所以,由PBC △、PEF △的面积分别为3与4, 可知正六边形ABCDEF 的面积是(34)321+⨯=.【答案】21【例 6】 正六边形A1A2A3A4A5A6的面积是2009平方厘米,B1,B2,B3,B4,B5,B6分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.4A 3【考点】平移、旋转、割补 【难度】5星 【题型】解答【关键词】迎春杯、六年级、初赛、14题 【解析】 如图,设62B A 与13B A 的交点为O ,则图中空白部分由6个与23A OA △一样大小的三角形组成,只要求出了23A OA △的面积,就可以求出空白部分面积,进而求出阴影部分面积.4A 3A 654连接63A A 、61B B 、63B A设116A B B △的面积为“1”,则126B A B △面积为“1”,126A A B △面积为“2”,那么636A A B △面积为126A A B △的2倍,为“4”,梯形1236A A A A 的面积为224212⨯+⨯=,263A B A △的面积为“6”,123B A A △的面积为2根据蝴蝶定理,1263261316B A B A A B B O A O S S ===△△∶∶,故21233612167A OAB A A S S ==+△△, 所以231236A A A A 121277A OA S S =△梯形∶∶∶1∶,即23A OA △的面积为梯形1236A A A A 面积的17,故为六边形123456A A A A A A 面积的114,那么空白部分的面积为正六边形面积的136147⨯=,所以阴影部分面积为32009111487⎛⎫⨯-= ⎪⎝⎭(平方厘米).【答案】1148【例 7】 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm 和4cm ,乙三角形两条直角边分别为3cm 和6cm ,求图中阴影部分的面积.【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 如右图,我们将三角形甲与乙进行平移,就会发现平行四边形面积等于平移后两个长方形面积之和.所以阴影部分面积为:2346236242211cm ⨯+⨯-⨯÷+⨯÷=()()【答案】11【例 8】在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 阴影总值是一个梯形.我们用三种方法解答.⑴ 割补法从顶点作底边上的高,得到两个相同的直角三角形.将这两个直角三角形拼成一个长方形(见下图).显然,阴影部分正好是长方形的13,所以原题阴影部分占整个图形面积的13.⑵ 拼补法将两个这样的三角形拼成一个平行四边形(下页左上图).显然,图中阴影面积占平行四边形面积的13.根据商不变性质,将阴影面积和平行四边形面积同时除以2,商不变.所以原题阴影部分占整个图形面积的13.⑶ 等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,所以阴影部分占整个图形面积的3193=. 注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立. 【答案】13【例 9】 如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点P 为中心转动一个正方形.当5AB =厘米,13BC =厘米,12CA =厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).P【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 右图由左图旋转而得,则右图中的8个空白小三角形都是完全相同的,右图中重叠部分的面积等于正方形面积减去4个小三角形的面积,从右图中可以看出正方形的边长为5131230++=厘米,所以重叠部分的面积为:2304(5122)780-⨯⨯÷=(平方厘米).【答案】780【例 10】 如图,在直角三角形中有一个正方形,已知10BD =厘米,7DC =厘米,求阴影部分的面积.【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 绕D 点逆时针旋转CED ∆,使E 与F 重合,则C 点落在AB 边上的'C 点处,且'C D CD =.则阴影部分面积转化为直角三角形'BC D 的面积,所以阴影部分的面积为107235⨯÷=平方厘米.【答案】35【例 11】 四边形ABCD 中,AB =30,AD =48,BC =14,CD =40.又已知∠ABD +∠BDC =900,求四边形ABCD 的面积.DBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,以BD 的垂直平分线为对称轴L ,做△ABD 关于L 的对称图形△A 'BD .连接A 'C .A 1IABCD因为∠ABD +∠BDC =9000而∠ABD =∠A 'DB =900,所以有∠A 'DB +∠BDC =900.那么A 'CD 为直角三角形,由勾股定理知2A C '=22AB CD +=2500,所以50A C '=.而在△A 'BC 中,有A 'B =AD =48,有482+142=2500,即A 'B 2+BC 2=A 'C 2,即△A 'BC 为直角三角形.有A CD A BCSS''+130402=⨯⨯114489362+⨯⨯=. 而|ABCD S 四边形A CD A BC S S ''=+936=.评注:Ⅰ.本题以∠ABC +∠BDC =900突破口,通过对称变换构造出与原图形相关的角三角形Ⅱ.对于这道题我们还可以将△BCD 作L 的对称图形.如下:C 1lABCD【答案】936【例 12】 如图,在三角形ABD 中,当AB 和CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.DCAB?30°40°【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为AB =CD ,于是可以将三角形ABC 的边BA 边与CD 对齐,如下图. 在下图中有∠BCA =110°,所以∠ACD =70°于是∠AC C '=∠ACD +∠DC C '=∠ACD +∠ABC =70°+40°=110°;A 1D C 1C B 1BA即∠AC C '=110°=∠CC D ';又因为C A ''只是CA 移动的变化,所以C A ''=CA ;则ABC A ''是一等腰梯形.于是,∠ADC '=180°-110°=70°;又∠CDC '=30°,所以∠ADC =70°-30°=40°.【答案】40°【例 13】 如图所示的四边形的面积等于多少?DB13131212【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【答案】144【例 14】 如图,三角形ABC 是等腰直角三角形,P 是三角形外的一点,其中90BPC ∠=︒,10cm AP =,求四边形ABPC 的面积.P DCBAP'PDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为BAC ∠和BPC ∠都是直角,和为180︒,所以ABP ∠和ACP ∠的和也为180︒,可以旋转三角形APC ,使AC 和AB 重合,则四边形的面积转化为等腰直角三角形'AP P ,面积为1010250⨯÷=平方厘米.【答案】50【例 15】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数 【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【答案】10【例 16】 如图,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,将腰CD 以D 为中心逆时针旋转90︒至ED ,连接AE 、CE ,则ADE ∆的面积是 .ED CBAH FEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数 【解析】 如图所示,将ADE ∆以D 为中心顺时针旋转90︒,到FDC ∆的位置.延长FD 与BC 交于H .由于ABCD 是直角梯形,AD 与FD 垂直,则四边形ADHB 是长方形,则BH AD =.由于ADE ∆与FDC ∆面积相等,而FDC ∆的底边2FD AD ==,高321CH BC BH =-=-=,所以FDC ∆的面积为2121⨯÷=,那么ADE ∆的面积也为1.【答案】1【例 17】 如图,正方形ABCD 和DEFG 有一个公共点D ,试比较三角形ADG 和三角形CDE 的面积.GFEDCBAA'GFEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为ADC ∠和GDE ∠是直角,所以ADG ∠和CDE ∠是互补角,将三角形ADG 顺时针旋转90︒到达'A DE ∆的位置,则'A 、D 、C 在同一条直线上,且'A D AD CD ==,即D 是'A C 的中点,所以三角形CDE 和三角形'A D E 面积相等,则三角形CDE 和三角形ADG 面积相等.【答案】相等【例 18】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE的面积.F【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】资优杯 【解析】 如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==,所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ).又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ).那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ),所以12.52OBE BDE S S ∆∆==(2cm ).【答案】2.5【例 19】 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++=2cm .EDCBADEC 'A 'CBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、高年级、复赛、10题 【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系: ''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=.【答案】50【例 20】 如图所示的四边形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==厘米,连接对角线BD ,30ABD ∠=︒.求四边形ABCD 的面积.DCB A DECBA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】第八届、华杯总决赛 【解析】 由45A ∠=°,30ABD ∠=︒,可得1804530105ADB ∠=︒-︒-︒=︒,1053075DBC ∠=︒-︒=︒.将DBC ∆剪下来,翻转,再贴在BD 边上,即将B 点粘在D 点上,D 点粘在B 点上,如右上图所示.则C 点在E 点的位置.由于10575180ADB EDB ∠+∠=︒+︒=︒,所以A 、D 、E 三点在同一条直线上.由于45A E C ∠=∠=∠=°,所以90ABE ∠=︒,即ABE ∆是等腰直角三角形,它的面积就等于四边形ABCD 的面积,所以四边形ABCD 的面积为1515112.52⨯=平方厘米.【答案】112.5【例 21】 如图,在ABD ∆中,AB CD =,求“?”的度数.40°30°?DCBAD【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如图,由于AB CD =,可以将ABC ∆移动到D C E ∆,由于180(3040)110A C B ∠=︒-︒+︒=︒,18011070ACD ∠=︒-︒=︒,所以7040110ACE ∠=︒+︒=︒,又110CED ∠=︒,而AC DE =,所以四边形ACED 是等腰梯形,有180********ADE CED ∠=︒-∠=︒-︒=︒,703040ADC ∠=︒-︒=︒. 点评:通过构造全等三角形来转化.【答案】40°【例 22】 下图三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,点D 在BC边上,:2:3BD DC =.当三角形ABC 的面积是250cm 时,三角形ADE 的面积是多少?ECBAGP R Q F EDCA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 以点A 为中心,由三个三角形ABC 可拼成右图:连结QE 、RF 、GD ,则DEQFRG 是一个正六边形.连结RD 、DQ 、RQ ,显然RDQ 是一个等边三角形,并且它的面积是正六边形面积的一半,所以是三角形ADE 的面积的3倍.由于23150cm PBC ABC S S ∆∆=⨯=,根据“鸟头定理”,22336cm 3223DQC PBC S S ∆∆=⨯⨯=++,所以2342cm RDQ PBC DQC S S S ∆∆∆=-⨯=,则2342314cm ADE RDQ S S ∆∆=÷=÷=. 【答案】14【例 23】 如图,正方形PQRS 有三个顶点分别在ABC ∆的三条边上,BQ QC =.求正方形PQRS 的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如下图,我们设ABC ∆的面积为1,有161279341()122132111311143a e c db =---+=-⨯-⨯-⨯=,所以682143a e ==,751143bcd a ++=-=, 所以6875a b c d =++.如下图左,将三角形c 和三角形d 分别以P 、R 为中心按箭头方向旋转90︒,形成由两个直角三角形连在一起的一个四边形,如下图右,b 、c 、d 被虚线分成两个直角三角形,它们的面积之和为:276292230cm b c d ++=⨯÷+⨯÷=,所以2683027.2(cm )75a =⨯=.【答案】27.2【例 24】 如下图,△ABC 是边长为1的等边三角形,△BCD 是等腰三角形BD =CD ,顶角∠BDC =1200,∠MDN =600,求△AMN 的周长.120°60°M BD CNA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 如下图, 延长AC 至P ,使CP =MB ,连接DP .120°60°M BD C NA则有∠MBD =600+1163ADEDQRDEQSRT SS S ==正六边形01801202-=∠PCD ;CP =BM ;BD =CD ,所以有△MBD ≌△PCD .于是∠MDC =∠PDC ;又因为∠MDB +∠NDC =600,所以∠PDC +∠NDC =∠NDP =600; MD =PD ,在△MDN 、△PND 中,∠NDM =∠NDP ,ND =ND ,MD =PD ,于是△MND ≌△PND .有MN =PN .因为NP =NP =NC +CP ,而AM =AB -MB =AB -CP , 所以AM +AN +MN =(AB -CP )+AN +(NC +CP )=AB +AN +NC =2.即△AMN 的周长为2.【答案】2【例 25】 若干个大小相同的正五边形如右图排成环状,下图中所示的只是3个五边形.那么要完成这一圈共需个正五边形.【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、六年级、初赛、5题 【解析】 如图,设O 为圆心,A 、B 、C 、D 为五边形的顶点,连接OA 、OB 、OC .DC B A O从图中可以看出,OAB △和OBC △是完全相同的,所以OBA OBC ∠=∠,又五边形内角和为540°,所以正五边形的每个内角都为5405108÷=°°,即108ABD CBD ∠=∠=°,那么3601082144ABC ∠=︒-︒⨯=︒,则144272OBA ∠=÷=°°,又OAB OBA ∠=∠,所以18072236AOB ∠=︒-︒⨯=︒所以要用3603610+=°°个正五边形才能围成一圈.【答案】10【例 26】 如图,ABCD 是矩形,BC =6cm , AB=10cm ,AC 和BD 是对角线,图中的阴影部分以C 为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)【考点】平移、旋转、割补 【难度】3星 【题型】解答【关键词】华杯赛、决赛、第11题【解析】 ①设三角形BCO 以CD 为轴旋转一周所得到的立体的体积是s ,S 等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆锥的体积。
六年级下册奥数试题——平移、旋转、割补(含答案)人教版
【例 11】 (武汉明心奥数挑战赛)如图所示,ABC 中,ABC 90 , AB 3 , BC 5 ,以 AC 为一边 向 ABC 外作正方形 ACDE ,中心为 O ,求 OBC 的面积.
E
E
D O
D O
A
A
3
3
B
5
C
B
5
C
F
【解析】如图,将 OAB 沿着 O 点顺时针旋转 90 ,到达 OCF 的位置. 由于 ABC 90 , AOC 90 ,所以 OAB OCB 180 .而 OCF OAB , 所以 OCF OCB 180 ,那么 B 、 C 、 F 三点在一条直线上. 由于 OB OF , BOF AOC 90 ,所以 BOF 是等腰直角三角形,且斜边 BF 为 5 3 8 ,所
那么 EAF EAB BAF EAB DAE 90 ,而 AEB 也是 90 ,所以四边形 AFBE 是直角梯 形,且 AF AE 3 ,
所以梯形 AFBE 的面积为:
3 5 3 1 12 ( cm2 ).
2
又因为 ABE 是直角三角形,根据勾股定理, AB2 AE2 BE2 32 52 34 ,所以
平移、旋转、割补
例题精讲
图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形.
【例 1】 如下图,六边形 ABCDEF 中,AB ED ,AF CD ,BC EF ,且有 AB 平行于 ED ,AF 平行于 CD , BC 平行于 EF ,对角线 FD 垂直于 BD ,已知 FD 24厘米,BD 18 厘米,请问六边形 ABCDEF 的 面积是多少平方厘米?
.
F
E
E
A
D
最新小升初奥数巧求面积---割补法知识讲解

解析
从顶点作底边上的高,得到两个相同的直角三角 形。将这两个直角三角形拼成一个长方形见右图。 显然,阴影部分正好是长方形的三分之一,所以 原题阴影部分占整个图形面积的三分之一。 还可以拼成一个平行四边形或将其分成9个三 角形。
例5. 如下图所示,在一个等腰直角三角形中,削去一个三角形后, 剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。 求这个梯形的面积。
小升初奥数巧求面积---割 补法
知识梳理
相加法
相减法
割补法
平移法 旋转法
巧求 面积
放大法 等量代换法
直接求法 重叠法 引辅助线法
典型例题精讲
例1. 下图中四个圆的半径都是5厘米,求阴影部分的面积。
解析
同学们请看图,我们将图形进行割补。 把阴影部分割补成四个半圆形和一个正方形, 求出阴影部分面积就可以了。 2S圆=5× 5× 3.14× 2=157(平方厘米)
9厘米 5厘米
例6.ABC是三个圆的圆心,圆的半径都是10分米,求阴 影部分的面积。
D
B
F
A
C
E
解析
我们用割补法,将阴影部分割补 成一个半圆形,求出阴影部分面 积就可以了。 S半圆=10× 10× 3.14÷ 2=157平方 分米
D
B
F
A
C
E
例7.如图所示,空白部分占正方形面积的 几分之几?
解析
9厘米 5厘米
解析
因为不知道梯形的高,所以不能直接求出梯形的面 积。可以从等腰直角三角形与正方形之间的联系上考 虑。将四个同样的等腰直角三角形拼成一个正方形, 图中阴影部分是边长9厘米与边长5厘米的两个正方 形面积之差,也是所求梯形面积的4倍。所以所求梯 形面积是(9× 9-5× 5)÷4=14(平方厘米)。
小学思维数学讲义:组合图形之平移、旋转、割补-带详解

图形之平移、旋转、割补图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形. 【例 1】 右图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积(阴影部分)有多大?【考点】平移、旋转、割补 【难度】2星 【题型】解答 【解析】 如图所示,将道路平移后的()()162102112-⨯-=。
【答案】112【例 2】 如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个.请算出阴影部分的面积.1cm【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如图,将阴影部分分割成一个正六边形和12个小三角形,再把正六边形分割成6个正三角形,由于正十二边形的每个内角为()180********︒⨯-÷=︒,所以阴影小三角形的顶角等于15060230︒-︒⨯=︒,每个顶角的两边和与其相邻的正三角形的底边所成的角都是306090︒+︒=︒,所以通过如右上图所示的平移可以组成6个边长为1厘米的正方形,所以所求阴影部分面积为2166⨯=平方厘米.【答案】6【例 3】 如图所示,梯形ABCD 中,AB 平行于CD ,又4BD =,3AC =,5AB CD +=.试求梯形ABCD 的面积.D CBAEDCBA【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如右图,将AB 沿AC 平移至CE ,连接BE ,在三角形BDE 中,有4BD =,3BE AC ==,5DE AB CD =+=,有222BD BE DE +=,所以三角形BDE 为直角三角形.由于ABD ABC BCE S S S ∆∆∆==,所以梯形ABCD 的面积与三角形BDE 的面积相等,为13462⨯⨯=.【答案】6【例 4】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?例题精讲FED BAGFE DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【答案】432【例 5】 如图2,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若PBC 、PEF 的面积为3与4,则正六边形ABCDEF 的面积是 .E【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、中年级、初赛、7题 【解析】 这是一道几何问题,考察同学们对常见图形性质的认识.正六边形的六条边都相等,每个角都是,每一组对边都互相平行,正六边形可以看作是由六个正三角形拼成的(如图(1)).其中正六边形的面积是正三角形面积的6倍.每相邻两个正三角形拼成的是一个平行四边形.如图(2),连结BF ,三角形ABF 的面积是平行四边形ABFO 面积的一半.六边形ABCDEF 的面积是平行四边形ABFO 的3倍,故六边形ABCDEF 的面积是三角形ABF 的面积的6倍. 如图(3),连结BF ,CE ,三角形BCP 的面积与三角形EFP 的面积和是平行四边形BFEC 面积的一半.而六边形ABCDEF 的面积是平行四边形BFEC 的1.5倍,故六边形ABCDEF 的面积是三角形BCP 的面积与三角形EFP 的面积和的3倍.图(1)OAB CDEF图(2)OB ACDEF图(3)E所以,由PBC △、PEF △的面积分别为3与4, 可知正六边形ABCDEF 的面积是(34)321+⨯=.【答案】21【例 6】 正六边形A1A2A3A4A5A6的面积是2009平方厘米,B1,B2,B3,B4,B5,B6分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.A 3【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、六年级、初赛、14题【解析】 如图,设62B A 与13B A 的交点为O ,则图中空白部分由6个与23A OA △一样大小的三角形组成,只要求出了23A OA △的面积,就可以求出空白部分面积,进而求出阴影部分面积.4A 3A 654连接63A A 、61B B 、63B A设116A B B △的面积为“1”,则126B A B △面积为“1”,126A A B △面积为“2”,那么636A A B △面积为126A A B △的2倍,为“4”,梯形1236A A A A 的面积为224212⨯+⨯=,263A B A △的面积为“6”,123B A A △的面积为2根据蝴蝶定理,1263261316B A B A A B B O A O S S ===△△∶∶,故21233612167A OAB A A S S ==+△△, 所以231236A A A A 121277A OA S S =△梯形∶∶∶1∶,即23A OA △的面积为梯形1236A A A A 面积的17,故为六边形123456A A A A A A 面积的114,那么空白部分的面积为正六边形面积的136147⨯=,所以阴影部分面积为32009111487⎛⎫⨯-= ⎪⎝⎭(平方厘米).【答案】1148【例 7】 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm 和4cm ,乙三角形两条直角边分别为3cm 和6cm ,求图中阴影部分的面积.【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 如右图,我们将三角形甲与乙进行平移,就会发现平行四边形面积等于平移后两个长方形面积之和.所以阴影部分面积为:2346236242211cm ⨯+⨯-⨯÷+⨯÷=()()【答案】11【例 8】 在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 阴影总值是一个梯形.我们用三种方法解答.⑴ 割补法从顶点作底边上的高,得到两个相同的直角三角形.将这两个直角三角形拼成一个长方形(见下图).显然,阴影部分正好是长方形的13,所以原题阴影部分占整个图形面积的13.⑵拼补法将两个这样的三角形拼成一个平行四边形(下页左上图).显然,图中阴影面积占平行四边形面积的1 3 .根据商不变性质,将阴影面积和平行四边形面积同时除以2,商不变.所以原题阴影部分占整个图形面积的1 3.⑶等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,所以阴影部分占整个图形面积的3193=.注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立.【答案】1 3【例9】如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点P为中心转动一个正方形.当5AB=厘米,13BC=厘米,12CA=厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).P【考点】平移、旋转、割补【难度】3星【题型】解答【解析】右图由左图旋转而得,则右图中的8个空白小三角形都是完全相同的,右图中重叠部分的面积等于正方形面积减去4个小三角形的面积,从右图中可以看出正方形的边长为5131230++=厘米,所以重叠部分的面积为:2304(5122)780-⨯⨯÷=(平方厘米).【答案】780【例10】如图,在直角三角形中有一个正方形,已知10BD=厘米,7DC=厘米,求阴影部分的面积.【考点】平移、旋转、割补【难度】4星【题型】解答【解析】绕D点逆时针旋转CED∆,使E与F重合,则C点落在AB边上的'C点处,且'C D CD=.则阴影部分面积转化为直角三角形'BC D的面积,所以阴影部分的面积为107235⨯÷=平方厘米.【答案】35【例11】四边形ABCD中,AB=30,AD=48,BC=14,CD=40.又已知∠ABD+∠BDC=900,求四边形ABCD的面积.DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,以BD 的垂直平分线为对称轴L ,做△ABD 关于L 的对称图形△A 'BD .连接A 'C .A 1IABCD因为∠ABD +∠BDC =9000而∠ABD =∠A 'DB =900,所以有∠A 'DB +∠BDC =900.那么A 'CD 为直角三角形,由勾股定理知2A C '=22AB CD +=2500,所以50A C '=.而在△A 'BC 中,有A 'B =AD =48,有482+142=2500,即A 'B 2+BC 2=A 'C 2,即△A 'BC 为直角三角形. 有A CD A BCSS''+130402=⨯⨯114489362+⨯⨯=. 而|ABCDS 四边形A CD A BC S S ''=+936=.评注:Ⅰ.本题以∠ABC +∠BDC =900突破口,通过对称变换构造出与原图形相关的角三角形Ⅱ.对于这道题我们还可以将△BCD 作L 的对称图形.如下:C 1lABCD【答案】936【例 12】 如图,在三角形ABD 中,当AB 和CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.DCAB?30°40°【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为AB =CD ,于是可以将三角形ABC 的边BA 边与CD 对齐,如下图. 在下图中有∠BCA =110°,所以∠ACD =70°于是∠AC C '=∠ACD +∠DC C '=∠ACD +∠ABC =70°+40°=110°;A 1D C 1C B 1BA即∠AC C '=110°=∠CC D ';又因为C A ''只是CA 移动的变化,所以C A ''=CA ;则ABC A ''是一等腰梯形.于是,∠ADC '=180°-110°=70°;又∠CDC '=30°,所以∠ADC =70°-30°=40°.【答案】40°【例 13】 如图所示的四边形的面积等于多少?DB13131212【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【答案】144【例 14】 如图,三角形ABC 是等腰直角三角形,P 是三角形外的一点,其中90BPC ∠=︒,10cm AP =,求四边形ABPC 的面积.P DCBAP'PDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为BAC ∠和BPC ∠都是直角,和为180︒,所以ABP ∠和ACP ∠的和也为180︒,可以旋转三角形APC ,使AC 和AB 重合,则四边形的面积转化为等腰直角三角形'AP P ,面积为1010250⨯÷=平方厘米.【答案】50【例 15】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数 【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【答案】10【例 16】 如图,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,将腰CD 以D 为中心逆时针旋转90︒至ED ,连接AE 、CE ,则ADE ∆的面积是 .ED CBAH FEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数 【解析】 如图所示,将ADE ∆以D 为中心顺时针旋转90︒,到FDC ∆的位置.延长FD 与BC 交于H .由于ABCD 是直角梯形,AD 与FD 垂直,则四边形ADHB 是长方形,则BH AD =.由于ADE ∆与FDC ∆面积相等,而FDC ∆的底边2FD AD ==,高321CH BC BH =-=-=,所以FDC ∆的面积为2121⨯÷=,那么ADE ∆的面积也为1.【答案】1【例 17】 如图,正方形ABCD 和DEFG 有一个公共点D ,试比较三角形ADG 和三角形CDE 的面积.GFEDCBAA'GFEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为ADC ∠和GDE ∠是直角,所以ADG ∠和CDE ∠是互补角,将三角形ADG 顺时针旋转90︒到达'A DE ∆的位置,则'A 、D 、C 在同一条直线上,且'A D AD CD ==,即D 是'A C 的中点,所以三角形CDE 和三角形'A DE 面积相等,则三角形CDE 和三角形ADG 面积相等.【答案】相等【例 18】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.F【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】资优杯 【解析】 如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==,所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ).又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ).那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ),所以12.52OBE BDE S S ∆∆==(2cm ).【答案】2.5【例 19】 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++= 2cm .EDCBADEC 'A 'CBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、高年级、复赛、10题 【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系: ''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=.【答案】50【例 20】 如图所示的四边形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==厘米,连接对角线BD ,30ABD ∠=︒.求四边形ABCD 的面积.DCB A DECBA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】第八届、华杯总决赛 【解析】 由45A ∠=°,30ABD ∠=︒,可得1804530105ADB ∠=︒-︒-︒=︒,1053075DBC ∠=︒-︒=︒.将DBC ∆剪下来,翻转,再贴在BD 边上,即将B 点粘在D 点上,D 点粘在B 点上,如右上图所示.则C 点在E 点的位置.由于10575180ADB EDB ∠+∠=︒+︒=︒,所以A 、D 、E 三点在同一条直线上.由于45A E C ∠=∠=∠=°,所以90ABE ∠=︒,即ABE ∆是等腰直角三角形,它的面积就等于四边形ABCD 的面积,所以四边形ABCD 的面积为1515112.52⨯=平方厘米.【答案】112.5【例 21】 如图,在ABD ∆中,AB CD =,求“?”的度数.40°30°?DCBAD【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图,由于AB CD =,可以将ABC ∆移动到DCE ∆,由于180(3040)110AC B ∠=︒-︒+︒=︒,18011070ACD ∠=︒-︒=︒,所以7040110ACE ∠=︒+︒=︒,又110CED ∠=︒,而AC DE =,所以四边形ACED 是等腰梯形,有180********ADE CED ∠=︒-∠=︒-︒=︒,703040ADC ∠=︒-︒=︒. 点评:通过构造全等三角形来转化.【答案】40°【例 22】 下图三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,点D 在BC边上,:2:3BD DC =.当三角形ABC 的面积是250cm 时,三角形ADE 的面积是多少?ECBAGP R Q F EDCA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 以点A 为中心,由三个三角形ABC 可拼成右图:连结QE 、RF 、GD ,则DEQFRG 是一个正六边形.连结RD 、DQ 、RQ ,显然RDQ 是一个等边三角形,并且它的面积是正六边形面积的一半,所以是三角形ADE 的面积的3倍.由于23150cm PBC ABC S S ∆∆=⨯=,根据“鸟头定理”,22336cm 3223DQC PBC S S ∆∆=⨯⨯=++,所以2342cm RDQ PBC DQC S S S ∆∆∆=-⨯=,则2342314cm ADE RDQ S S ∆∆=÷=÷=. 【答案】14【例 23】 如图,正方形PQRS 有三个顶点分别在ABC ∆的三条边上,BQ QC =.求正方形PQRS 的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如下图,我们设ABC ∆的面积为1,有161279341()122132111311143a e c db =---+=-⨯-⨯-⨯=,所以682143a e ==,751143bcd a ++=-=, 所以6875a b c d =++.如下图左,将三角形c 和三角形d 分别以P 、R 为中心按箭头方向旋转90︒,形成由两个直角三角形连在一起的一个四边形,如下图右,b 、c 、d 被虚线分成两个直角三角形,它们的面积之和为:276292230cm b c d ++=⨯÷+⨯÷=,所以2683027.2(cm )75a =⨯=.P SR dcb6cm 2cmd QPS R CBA2cm 9cm6cm7cmc b c d【答案】27.2【例 24】 如下图,△ABC 是边长为1的等边三角形,△BCD 是等腰三角形BD =CD ,顶角∠BDC =1200,∠MDN =600,求△AMN 的周长.120°60°M BD CNA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 如下图, 延长AC 至P ,使CP =MB ,连接DP .120°60°M BD PC NA则有∠MBD =600+1163ADEDQRDEQSRT SS S ==正六边形01801202-=∠PCD ;CP =BM ;BD =CD ,所以有△MBD ≌△PCD .于是∠MDC =∠PDC ;又因为∠MDB +∠NDC =600,所以∠PDC +∠NDC =∠NDP =600; MD =PD ,在△MDN 、△PND 中,∠NDM =∠NDP ,ND =ND ,MD =PD ,于是△MND ≌△PND .有MN =PN .因为NP =NP =NC +CP ,而AM =AB -MB =AB -CP , 所以AM +AN +MN =(AB -CP )+AN +(NC +CP )=AB +AN +NC =2.即△AMN 的周长为2.【答案】2【例 25】 若干个大小相同的正五边形如右图排成环状,下图中所示的只是3个五边形.那么要完成这一圈共需个正五边形.【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、六年级、初赛、5题 【解析】 如图,设O 为圆心,A 、B 、C 、D 为五边形的顶点,连接OA 、OB 、OC .11 DC B A O从图中可以看出,OAB △和OBC △是完全相同的,所以OBA OBC ∠=∠,又五边形内角和为540°,所以正五边形的每个内角都为5405108÷=°°,即108ABD CBD ∠=∠=°,那么3601082144ABC ∠=︒-︒⨯=︒,则144272OBA ∠=÷=°°,又OAB OBA ∠=∠,所以18072236AOB ∠=︒-︒⨯=︒所以要用3603610+=°°个正五边形才能围成一圈.【答案】10【例 26】 如图,ABCD 是矩形,BC =6cm , AB=10cm ,AC 和BD 是对角线,图中的阴影部分以C 为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)【考点】平移、旋转、割补 【难度】3星 【题型】解答【关键词】华杯赛、决赛、第11题【解析】 ①设三角形BCO 以CD 为轴旋转一周所得到的立体的体积是s ,S 等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆锥的体积。
小学奥数:平移、旋转、割补.专项练习及答案解析

图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形.【例 1】 右图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积(阴影部分)有多大?【考点】平移、旋转、割补 【难度】2星 【题型】解答 【解析】 如图所示,将道路平移后的()()162102112-⨯-=。
【答案】112【例 2】 如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个.请算出阴影部分的面积.1cm1cm 1cm【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如图,将阴影部分分割成一个正六边形和12个小三角形,再把正六边形分割成6个正三角形,由于正十二边形的每个内角为()180********︒⨯-÷=︒,所以阴影小三角形的顶角等于15060230︒-︒⨯=︒,每个顶角的两边和与其相邻的正三角形的底边所成的角都是306090︒+︒=︒,所以通过如右上图所示的平移可以组成6个边长为1厘米的正方形,所以所求阴影部分面积为2166⨯=平方厘米.【答案】6【例 3】 如图所示,梯形ABCD 中,AB 平行于CD ,又4BD =,3AC =,5AB CD +=.试求梯形ABCD 的面积.D CBAEDCBA【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如右图,将AB 沿AC 平移至CE ,连接BE ,在三角形BDE 中,有4BD =,3BE AC ==,5DE AB CD =+=,有222BD BE DE +=,所以三角形BDE 为直角例题精讲4-2-5.平移、旋转、割补三角形.由于ABD ABC BCE S S S ∆∆∆==,所以梯形ABCD 的面积与三角形BDE 的面积相等,为13462⨯⨯=. 【答案】6【例 4】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FED CBAGFE DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【答案】432【例 5】 如图2,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若PBC 、PEF 的面积为3与4,则正六边形ABCDEF 的面积是 .E【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、中年级、初赛、7题 【解析】 这是一道几何问题,考察同学们对常见图形性质的认识.正六边形的六条边都相等,每个角都是,每一组对边都互相平行,正六边形可以看作是由六个正三角形拼成的(如图(1)).其中正六边形的面积是正三角形面积的6倍.每相邻两个正三角形拼成的是一个平行四边形.如图(2),连结BF ,三角形ABF 的面积是平行四边形ABFO 面积的一半.六边形ABCDEF 的面积是平行四边形ABFO 的3倍,故六边形ABCDEF 的面积是三角形ABF 的面积的6倍. 如图(3),连结BF ,CE ,三角形BCP 的面积与三角形EFP 的面积和是平行四边形BFEC 面积的一半.而六边形ABCDEF 的面积是平行四边形BFEC 的1.5倍,故六边形ABCDEF 的面积是三角形BCP 的面积与三角形EFP 的面积和的3倍.图(1)OAB CDEF图(2)OB ACDEF图(3)E所以,由PBC △、PEF △的面积分别为3与4,可知正六边形ABCDEF 的面积是(34)321+⨯=.【答案】21【例 6】 正六边形A1A2A3A4A5A6的面积是2009平方厘米,B1,B2,B3,B4,B5,B6分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.A 3【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、六年级、初赛、14题 【解析】 如图,设62B A 与13B A 的交点为O ,则图中空白部分由6个与23A OA △一样大小的三角形组成,只要求出了23A OA △的面积,就可以求出空白部分面积,进而求出阴影部分面积.43A 654连接63A A 、61B B 、63B A设116A B B △的面积为“1”,则126B A B △面积为“1”,126A A B △面积为“2”,那么636A A B △面积为126A A B △的2倍,为“4”,梯形1236A A A A 的面积为224212⨯+⨯=,263A B A △的面积为“6”,123B A A △的面积为2根据蝴蝶定理,1263261316B A B A A B B O A O S S ===△△∶∶,故21233612167A OAB A A S S ==+△△, 所以231236A A A A 121277A OA S S =△梯形∶∶∶1∶,即23A OA △的面积为梯形1236A A A A 面积的17,故为六边形123456A A A A A A 面积的114,那么空白部分的面积为正六边形面积的136147⨯=,所以阴影部分面积为32009111487⎛⎫⨯-= ⎪⎝⎭(平方厘米).【答案】1148【例 7】 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm 和4cm ,乙三角形两条直角边分别为3cm 和6cm ,求图中阴影部分的面积.【考点】平移、旋转、割补【难度】3星【题型】解答【解析】如右图,我们将三角形甲与乙进行平移,就会发现平行四边形面积等于平移后两个长方形面积之和.所以阴影部分面积为:2346236242211cm⨯+⨯-⨯÷+⨯÷=()()【答案】11【例 8】在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【考点】平移、旋转、割补【难度】3星【题型】解答【解析】阴影总值是一个梯形.我们用三种方法解答.⑴割补法从顶点作底边上的高,得到两个相同的直角三角形.将这两个直角三角形拼成一个长方形(见下图).显然,阴影部分正好是长方形的13,所以原题阴影部分占整个图形面积的13.⑵拼补法将两个这样的三角形拼成一个平行四边形(下页左上图).显然,图中阴影面积占平行四边形面积的13.根据商不变性质,将阴影面积和平行四边形面积同时除以2,商不变.所以原题阴影部分占整个图形面积的13.⑶等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,所以阴影部分占整个图形面积的31 93 =.注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立.【答案】1 3【例 9】如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点P为中心转动一个正方形.当5AB=厘米,13BC=厘米,12CA=厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).P【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 右图由左图旋转而得,则右图中的8个空白小三角形都是完全相同的,右图中重叠部分的面积等于正方形面积减去4个小三角形的面积,从右图中可以看出正方形的边长为5131230++=厘米,所以重叠部分的面积为:2304(5122)780-⨯⨯÷=(平方厘米).【答案】780【例 10】 如图,在直角三角形中有一个正方形,已知10BD =厘米,7DC =厘米,求阴影部分的面积.【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 绕D 点逆时针旋转CED ∆,使E 与F 重合,则C 点落在AB 边上的'C 点处,且'C D CD =.则阴影部分面积转化为直角三角形'BC D 的面积,所以阴影部分的面积为107235⨯÷=平方厘米.【答案】35【例 11】 四边形ABCD 中,AB =30,AD =48,BC =14,CD =40.又已知∠ABD +∠BDC =900,求四边形ABCD 的面积.DBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,以BD 的垂直平分线为对称轴L ,做△ABD 关于L 的对称图形△A 'BD .连接A 'C .A 1IABCD因为∠ABD +∠BDC =9000而∠ABD =∠A 'DB =900,所以有∠A 'DB +∠BDC =900.那么A 'CD 为直角三角形,由勾股定理知2A C '=22AB CD +=2500,所以50A C '=.而在△A 'BC 中,有A 'B =AD =48,有482+142=2500,即A 'B 2+BC 2=A 'C 2,即△A 'BC 为直角三角形.有A CD A BC S S ''+V V 130402=⨯⨯114489362+⨯⨯=. 而|ABCDS 四边形A CD A BC S S ''=+V V 936=.评注:Ⅰ.本题以∠ABC +∠BDC =900突破口,通过对称变换构造出与原图形相关的角三角形Ⅱ.对于这道题我们还可以将△BCD 作L 的对称图形.如下:C 1lABCD【答案】936【例 12】 如图,在三角形ABD 中,当AB 和CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.DCAB?30°40°【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为AB =CD ,于是可以将三角形ABC 的边BA 边与CD 对齐,如下图. 在下图中有∠BCA =110°,所以∠ACD =70°于是∠AC C '=∠ACD +∠DC C '=∠ACD +∠ABC =70°+40°=110°;A 1D C 1C B 1BA即∠AC C '=110°=∠CC D ';又因为C A ''只是CA 移动的变化,所以C A ''=CA ;则ABC A ''是一等腰梯形.于是,∠ADC '=180°-110°=70°;又∠CDC '=30°,所以∠ADC =70°-30°=40°. 【答案】40°【例 13】 如图所示的四边形的面积等于多少?DB13131212【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【答案】144【例 14】 如图,三角形ABC 是等腰直角三角形,P 是三角形外的一点,其中90BPC ∠=︒,10cm AP =,求四边形ABPC 的面积.P DCBAP'PDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为BAC ∠和BPC ∠都是直角,和为180︒,所以ABP ∠和ACP ∠的和也为180︒,可以旋转三角形APC ,使AC 和AB 重合,则四边形的面积转化为等腰直角三角形'AP P ,面积为1010250⨯÷=平方厘米.【答案】50【例 15】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数 【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【答案】10【例 16】 如图,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,将腰CD 以D 为中心逆时针旋转90︒至ED ,连接AE 、CE ,则ADE ∆的面积是 .ED CBAH FEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数 【解析】 如图所示,将ADE ∆以D 为中心顺时针旋转90︒,到FDC ∆的位置.延长FD 与BC交于H .由于ABCD 是直角梯形,AD 与FD 垂直,则四边形ADHB 是长方形,则BH AD =. 由于ADE ∆与FDC ∆面积相等,而FDC ∆的底边2FD AD ==,高321CH BC BH =-=-=,所以FDC ∆的面积为2121⨯÷=,那么ADE ∆的面积也为1. 【答案】1【例 17】 如图,正方形ABCD 和DEFG 有一个公共点D ,试比较三角形ADG 和三角形CDE 的面积.GFEDCBAA'GFEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为ADC ∠和GDE ∠是直角,所以ADG ∠和CDE ∠是互补角,将三角形ADG 顺时针旋转90︒到达'A DE ∆的位置,则'A 、D 、C 在同一条直线上,且'A D AD CD ==,即D 是'A C 的中点,所以三角形CDE 和三角形'A DE 面积相等,则三角形CDE 和三角形ADG 面积相等.【答案】相等【例 18】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.F【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】资优杯 【解析】 如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置. 那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==, 所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ).又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ).那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ),所以12.52OBE BDE S S ∆∆==(2cm ).【答案】2.5【例 19】 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++=2cm .EDCBADEC 'A 'CBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、高年级、复赛、10题 【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90o ,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系:''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=W .【答案】50【例 20】 如图所示的四边形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==厘米,连接对角线BD ,30ABD ∠=︒.求四边形ABCD 的面积.DCB A DECBA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】第八届、华杯总决赛 【解析】 由45A ∠=°,30ABD ∠=︒,可得1804530105ADB ∠=︒-︒-︒=︒,1053075DBC ∠=︒-︒=︒.将DBC ∆剪下来,翻转,再贴在BD 边上,即将B 点粘在D 点上,D 点粘在B 点上,如右上图所示.则C 点在E 点的位置.由于10575180ADB EDB ∠+∠=︒+︒=︒,所以A 、D 、E 三点在同一条直线上.由于45A E C ∠=∠=∠=°,所以90ABE ∠=︒,即ABE ∆是等腰直角三角形,它的面积就等于四边形ABCD 的面积,所以四边形ABCD 的面积为1515112.52⨯=平方厘米.【答案】112.5【例 21】 如图,在ABD ∆中,AB CD =,求“?”的度数.40°30°?DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图,由于AB CD =,可以将ABC ∆移动到DCE ∆,由于180(3040)110ACB ∠=︒-︒+︒=︒,18011070ACD ∠=︒-︒=︒,所以7040110ACE ∠=︒+︒=︒,又110CED ∠=︒,而AC DE =,所以四边形ACED 是等腰梯形,有180********ADE CED ∠=︒-∠=︒-︒=︒,703040ADC ∠=︒-︒=︒. 点评:通过构造全等三角形来转化.【答案】40°【例 22】 下图三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,点D 在BC 边上,:2:3BD DC =.当三角形ABC 的面积是250cm 时,三角形ADE 的面积是多少?EDCBAGP R Q F ECBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 以点A 为中心,由三个三角形ABC 可拼成右图:连结QE 、RF 、GD ,则DEQFRG是一个正六边形.连结RD 、DQ 、RQ ,显然RDQ 是一个等边三角形,并且它的面积是正六边形面积的一半,所以是三角形ADE 的面积的3倍. 由于23150cm PBC ABC S S ∆∆=⨯=,根据“鸟头定理”,22336cm 3223DQC PBC S S ∆∆=⨯⨯=++,所以2342cm RDQ PBC DQC S S S ∆∆∆=-⨯=,则2342314cm ADE RDQ S S ∆∆=÷=÷=.【答案】14【例 23】 如图,正方形PQRS 有三个顶点分别在ABC ∆的三条边上,BQ QC =.求正方形PQRS 的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,我们设ABC ∆的面积为1,有161279341()122132111311143a e c db =---+=-⨯-⨯-⨯=,所以682143a e ==,751143b c d a ++=-=, 所以6875a b c d =++.如下图左,将三角形c 和三角形d 分别以P 、R 为中心按箭头方向旋转90︒,形成由两个直角三角形连在一起的一个四边形,如下图右,b 、c 、d 被虚线分成两个直角三角形,它们的面积之和为:276292230cm b c d ++=⨯÷+⨯÷=,所以2683027.2(cm )75a =⨯=.【答案】27.2【例 24】 如下图,△ABC 是边长为1的等边三角形,△BCD 是等腰三角形BD =CD ,顶角∠BDC =1200,∠MDN =600,求△AMN 的周长.120°60°M BD CNA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 如下图, 延长AC 至P ,使CP =MB ,连接DP .120°60°M BD PC NA则有∠MBD =600+1163ADEDQRDEQSRT S S S ==V V 正六边形001801202-=∠PCD ;CP =BM ;BD =CD , 所以有△MBD ≌△PCD .于是∠MDC =∠PDC ;又因为∠MDB +∠NDC =600,所以∠PDC +∠NDC =∠NDP =600; MD =PD ,在△MDN 、△PND 中,∠NDM =∠NDP ,ND =ND ,MD =PD ,于是△MND ≌△PND .有MN =PN .因为NP =NP =NC +CP ,而AM =AB -MB =AB -CP ,所以AM+AN+MN=(AB-CP)+AN+(NC+CP)=AB+AN+NC=2.即△AMN的周长为2.【答案】2【例 25】若干个大小相同的正五边形如右图排成环状,下图中所示的只是3个五边形.那么要完成这一圈共需个正五边形.【考点】平移、旋转、割补【难度】4星【题型】解答【关键词】迎春杯、六年级、初赛、5题【解析】如图,设O为圆心,A、B、C、D为五边形的顶点,连接OA、OB、OC.DCBAO从图中可以看出,OAB△和OBC△是完全相同的,所以OBA OBC∠=∠,又五边形内角和为540°,所以正五边形的每个内角都为5405108÷=°°,即108ABD CBD∠=∠=°,那么3601082144ABC∠=︒-︒⨯=︒,则144272OBA∠=÷=°°,又OAB OBA∠=∠,所以18072236AOB∠=︒-︒⨯=︒所以要用3603610+=°°个正五边形才能围成一圈.【答案】10【例 26】如图,ABCD是矩形,BC=6cm, AB=10cm,AC和BD是对角线,图中的阴影部分以C 为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)【考点】平移、旋转、割补【难度】3星【题型】解答【关键词】华杯赛、决赛、第11题【解析】①设三角形BCO以CD为轴旋转一周所得到的立体的体积是s,S等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆锥的体积。
五年级上册第10讲 平移、旋转、割补

【典型例题】
例3:按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角 形.已知甲三角形两条直角边分别为2cm和4cm ,乙三角形两条直角边分别为 3cm和6cm ,求图中阴影部分的面积.
S阴= S甲 + S乙-S长
1 2 S甲 : 4×2÷2=4cm2
S乙 : 6×3÷2=9cm2
S长 : (3-2)×(6-4)=2cm2 S阴 : 4+9-2=11cm2
第10讲 平移、旋转、割补
五年级奥数班
【知识点拨】
图形变换,是指不改变图形的大小、形状,只通过位置 关系的改变(旋转、平移、折叠等),构成新的图形。
平移
【典型例题】
例1:右图是一块长方形草地,长方形的长是16 ,宽是10.中间有两条道路, 一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积 (阴影部分)有多大?
10×7÷2=35cm2 答:阴影部分的面积是35平方厘米。
11
【典型例题】
例6:如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点 为中 心转动一个正方形.当AB=5厘米,BC=13厘米,CA=12 厘米时(如下右图), 求右图中的两个正方形相重叠部分的面积。
A B
5
12
C
13 5
S重叠= S正 - 4S△
2米
10米
(16-2)×(10-2)=112 答:草地部分的面积是112。
16米
13
【课堂精练】
2.如图所示,求阴影部分的面积(单位:厘米)。
6cm
a1
a2 c1
c2
4cm
a + b +c = a + b +c
1 1 1 2 2
小学数学 平移、旋转、割补.教师版

4-2-5.平移、旋转、割补例题精讲图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形.【例1】右图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积(阴影部分)有多大?【考点】平移、旋转、割补【难度】2星【题型】解答【解析】如图所示,将道路平移后的()()162102112-⨯-=。
【答案】112【例2】如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个.请算出阴影部分的面积.【考点】平移、旋转、割补【难度】3星【题型】解答【解析】如图,将阴影部分分割成一个正六边形和12个小三角形,再把正六边形分割成6个正三角形,由于正十二边形的每个内角为()180********︒⨯-÷=︒,所以阴影小三角形的顶角等于15060230︒-︒⨯=︒,每个顶角的两边和与其相邻的正三角形的底边所成的角都是306090︒+︒=︒,所以通过如右上图所示的平移可以组成6个边长为1厘米的正方形,所以所求阴影部分面积为2166⨯=平方厘米.【答案】6【例3】如图所示,梯形ABCD 中,AB 平行于CD ,又4BD =,3AC =,5AB CD +=.试求梯形ABCD 的面积.【考点】平移、旋转、割补【难度】3星【题型】解答【解析】如右图,将AB 沿AC 平移至CE ,连接BE ,在三角形BDE 中,有4BD =,3BE AC ==,5DE AB CD =+=,有222BD BE DE +=,所以三角形BDE 为直角三角形.由于ABD ABC BCE S S S ∆∆∆==,所以梯形ABCD 的面积与三角形BDE 的面积相等,为13462⨯⨯=.【答案】6【例4】如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?【考点】平移、旋转、割补【难度】5星【题型】解答【解析】如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【答案】432【例5】如图2,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若PBC 、PEF 的面积为3与4,则正六边形ABCDEF 的面积是.【考点】平移、旋转、割补【难度】4星【题型】解答【关键词】迎春杯、中年级、初赛、7题【解析】【解析】这是一道几何问题,考察同学们对常见图形性质的认识.正六边形的六条边都相等,每个角都是,每一组对边都互相平行,正六边形可以看作是由六个正三角形拼成的(如图(1)).其中正六边形的面积是正三角形面积的6倍.每相邻两个正三角形拼成的是一个平行四边形.如图(2),连结BF ,三角形ABF 的面积是平行四边形ABFO 面积的一半.六边形ABCDEF 的面积是平行四边形ABFO 的3倍,故六边形ABCDEF 的面积是三角形ABF 的面积的6倍.如图(3),连结BF ,CE ,三角形BCP 的面积与三角形EFP 的面积和是平行四边形BFEC 面积的一半.而六边形ABCDEF 的面积是平行四边形BFEC 的1.5倍,故六边形ABCDEF 的面积是三角形BCP 的面积与三角形EFP 的面积和的3倍.所以,由PBC △、PEF △的面积分别为3与4,可知正六边形ABCDEF 的面积是(34)321+⨯=.【答案】21【例6】正六边形A1A2A3A4A5A6的面积是2009平方厘米,B1,B2,B3,B4,B5,B6分别是正六边形各边的中点;那么图中阴影六边形的面积是平方厘米.【考点】平移、旋转、割补【难度】5星【题型】解答【关键词】迎春杯、六年级、初赛、14题【解析】【解析】如图,设62B A 与13B A 的交点为O ,则图中空白部分由6个与23A OA △一样大小的三角形组成,只要求出了23A OA △的面积,就可以求出空白部分面积,进而求出阴影部分面积.连接63A A 、61B B 、63B A 设116A B B △的面积为“1”,则126B A B △面积为“1”,126A A B △面积为“2”,那么636A A B △面积为126A A B △的2倍,为“4”,梯形1236A A A A 的面积为224212⨯+⨯=,263A B A △的面积为“6”,123B A A △的面积为2根据蝴蝶定理,1263261316B A B A A B B O A O S S ===△△∶∶,故21233612167A OAB A A S S ==+△△,所以231236A A A A 121277A OA S S =△梯形∶∶∶1∶,即23A OA △的面积为梯形1236A A A A 面积的17,故为六边形123456A A A A A A 面积的114,那么空白部分的面积为正六边形面积的136147⨯=,所以阴影部分面积为32009111487⎛⎫⨯-= ⎪⎝⎭(平方厘米).【答案】1148【例7】按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm 和4cm ,乙三角形两条直角边分别为3cm 和6cm ,求图中阴影部分的面积.【考点】平移、旋转、割补【难度】3星【题型】解答【解析】如右图,我们将三角形甲与乙进行平移,就会发现平行四边形面积等于平移后两个长方形面积之和.所以阴影部分面积为:2346236242211cm ⨯+⨯-⨯÷+⨯÷=()()【答案】11【例8】在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【考点】平移、旋转、割补【难度】3星【题型】解答【解析】阴影总值是一个梯形.我们用三种方法解答.⑴割补法从顶点作底边上的高,得到两个相同的直角三角形.将这两个直角三角形拼成一个长方形(见下图).显然,阴影部分正好是长方形的13,所以原题阴影部分占整个图形面积的13.⑵拼补法将两个这样的三角形拼成一个平行四边形(下页左上图).显然,图中阴影面积占平行四边形面积的13.根据商不变性质,将阴影面积和平行四边形面积同时除以2,商不变.所以原题阴影部分占整个图形面积的13.⑶等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,所以阴影部分占整个图形面积的3193=.注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立.【答案】13【例9】如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点P 为中心转动一个正方形.当5AB =厘米,13BC =厘米,12CA =厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).P【考点】平移、旋转、割补【难度】3星【题型】解答【解析】右图由左图旋转而得,则右图中的8个空白小三角形都是完全相同的,右图中重叠部分的面积等于正方形面积减去4个小三角形的面积,从右图中可以看出正方形的边长为5131230++=厘米,所以重叠部分的面积为:2304(5122)780-⨯⨯÷=(平方厘米).【答案】780【例10】如图,在直角三角形中有一个正方形,已知10BD =厘米,7DC =厘米,求阴影部分的面积.【考点】平移、旋转、割补【难度】4星【题型】解答【解析】绕D 点逆时针旋转CED ∆,使E 与F 重合,则C 点落在AB 边上的'C 点处,且'C D CD =.则阴影部分面积转化为直角三角形'BC D 的面积,所以阴影部分的面积为107235⨯÷=平方厘米.【答案】35【例11】四边形ABCD 中,AB =30,AD =48,BC =14,CD =40.又已知∠ABD +∠BDC =900,求四边形ABCD 的面积.【考点】平移、旋转、割补【难度】5星【题型】解答【解析】如下图,以BD 的垂直平分线为对称轴L ,做△ABD 关于L 的对称图形△A 'BD .连接A 'C .因为∠ABD +∠BDC =9000而∠ABD =∠A 'DB =900,所以有∠A 'DB +∠BDC =900.那么A 'CD 为直角三角形,由勾股定理知2A C '=22AB CD +=2500,所以50A C '=.而在△A 'BC 中,有A 'B =AD =48,有482+142=2500,即A 'B 2+BC 2=A 'C 2,即△A 'BC 为直角三角形.有A CD A BC S S ''+ 130402=⨯⨯114489362+⨯⨯=.而|ABCD S 四边形A CD A BC S S ''=+ 936=.评注:Ⅰ.本题以∠ABC +∠BDC =900突破口,通过对称变换构造出与原图形相关的角三角形Ⅱ.对于这道题我们还可以将△BCD 作L 的对称图形.如下:【答案】936【例12】如图,在三角形ABD 中,当AB 和CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.【考点】平移、旋转、割补【难度】5星【题型】解答【解析】因为AB =CD ,于是可以将三角形ABC 的边BA 边与CD 对齐,如下图.在下图中有∠BCA =110°,所以∠ACD =70°于是∠AC C '=∠ACD +∠DC C '=∠ACD +∠ABC =70°+40°=110°;即∠AC C '=110°=∠CC D ';又因为C A ''只是CA 移动的变化,所以C A ''=CA ;则ABC A ''是一等腰梯形.于是,∠ADC '=180°-110°=70°;又∠CDC '=30°,所以∠ADC =70°-30°=40°.【答案】40°【例13】如图所示的四边形的面积等于多少?【考点】平移、旋转、割补【难度】4星【题型】解答【解析】题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【答案】144【例14】如图,三角形ABC 是等腰直角三角形,P 是三角形外的一点,其中90BPC ∠=︒,10cm AP =,求四边形ABPC 的面积.P D C B A P'PD CB A【考点】平移、旋转、割补【难度】5星【题型】解答【解析】因为BAC ∠和BPC ∠都是直角,和为180︒,所以ABP ∠和ACP ∠的和也为180︒,可以旋转三角形APC ,使AC 和AB 重合,则四边形的面积转化为等腰直角三角形'AP P ,面积为1010250⨯÷=平方厘米.【答案】50【例15】如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【考点】平移、旋转、割补【难度】5星【题型】解答【关键词】武汉明心奥数【解析】如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠,所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【答案】10【例16】如图,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,将腰CD 以D 为中心逆时针旋转90︒至ED ,连接AE 、CE ,则ADE ∆的面积是.ED C B A H FE DCB A 【考点】平移、旋转、割补【难度】5星【题型】解答【关键词】武汉明心奥数【解析】如图所示,将ADE ∆以D 为中心顺时针旋转90︒,到FDC ∆的位置.延长FD 与BC 交于H .由于ABCD 是直角梯形,AD 与FD 垂直,则四边形ADHB 是长方形,则BH AD =.由于ADE ∆与FDC ∆面积相等,而FDC ∆的底边2FD AD ==,高321CH BC BH =-=-=,所以FDC ∆的面积为2121⨯÷=,那么ADE ∆的面积也为1.【答案】1【例17】如图,正方形ABCD 和DEFG 有一个公共点D ,试比较三角形ADG 和三角形CDE 的面积.GFDC B AA'G F D C B A 【考点】平移、旋转、割补【难度】5星【题型】解答【解析】因为ADC ∠和GDE ∠是直角,所以ADG ∠和CDE ∠是互补角,将三角形ADG 顺时针旋转90︒到达'A DE∆的位置,则'A 、D 、C 在同一条直线上,且'A D AD CD ==,即D 是'A C 的中点,所以三角形CDE 和三角形'A DE 面积相等,则三角形CDE 和三角形ADG 面积相等.【答案】相等【例18】如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.【考点】平移、旋转、割补【难度】5星【题型】解答【关键词】资优杯【解析】如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==,所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ).又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ).那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ),所以1 2.52OBE BDE S S ∆∆==(2cm ).【答案】2.5【例19】如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++=2cm.【考点】平移、旋转、割补【难度】5星【题型】解答【关键词】迎春杯、高年级、复赛、10题【解析】将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90 ,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系:''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯= .【答案】50【例20】如图所示的四边形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==厘米,连接对角线BD ,30ABD ∠=︒.求四边形ABCD 的面积.【考点】平移、旋转、割补【难度】4星【题型】解答【关键词】第八届、华杯总决赛【解析】由45A ∠=°,30ABD ∠=︒,可得1804530105ADB ∠=︒-︒-︒=︒,1053075DBC ∠=︒-︒=︒.将DBC ∆剪下来,翻转,再贴在BD 边上,即将B 点粘在D 点上,D 点粘在B 点上,如右上图所示.则C 点在E 点的位置.由于10575180ADB EDB ∠+∠=︒+︒=︒,所以A 、D 、E 三点在同一条直线上.由于45A E C ∠=∠=∠=°,所以90ABE ∠=︒,即ABE ∆是等腰直角三角形,它的面积就等于四边形ABCD 的面积,所以四边形ABCD 的面积为1515112.52⨯=平方厘米.【答案】112.5【例21】如图,在ABD ∆中,AB CD =,求“?”的度数.40°30°?DC B A【考点】平移、旋转、割补【难度】5星【题型】解答【解析】如图,由于AB CD =,可以将ABC ∆移动到DCE ∆,由于180(3040)110ACB ∠=︒-︒+︒=︒,18011070ACD ∠=︒-︒=︒,所以7040110ACE ∠=︒+︒=︒,又110CED ∠=︒,而AC DE =,所以四边形ACED 是等腰梯形,有180********ADE CED ∠=︒-∠=︒-︒=︒,703040ADC ∠=︒-︒=︒.点评:通过构造全等三角形来转化.【答案】40°【例22】下图三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,点D 在BC 边上,:2:3BD DC =.当三角形ABC 的面积是250cm 时,三角形ADE 的面积是多少?E C B A GPR Q FE C B A【考点】平移、旋转、割补【难度】5星【题型】解答【解析】以点A 为中心,由三个三角形ABC 可拼成右图:连结QE 、RF 、GD ,则DEQFRG 是一个正六边形.连结RD 、DQ 、RQ ,显然RDQ 是一个等边三角形,并且它的面积是正六边形面积的一半,所以是三角形ADE 的面积的3倍.由于23150cm PBC ABC S S ∆∆=⨯=,根据“鸟头定理”,22336cm 3223DQC PBC S S ∆∆=⨯⨯=++,所以2342cm RDQ PBC DQC S S S ∆∆∆=-⨯=,则2342314cm ADE RDQ S S ∆∆=÷=÷=.【答案】14【例23】如图,正方形PQRS 有三个顶点分别在ABC ∆的三条边上,BQ QC =.求正方形PQRS 的面积.【考点】平移、旋转、割补【难度】5星【题型】解答【解析】如下图,我们设ABC ∆的面积为1,有161279341()122132111311143a e c d b =---+=-⨯--⨯=,所以682143a e ==,751143bcd a ++=-=,所以6875a b c d =++.如下图左,将三角形c 和三角形d 分别以P 、R 为中心按箭头方向旋转90︒,形成由两个直角三角形连在一起的一个四边形,如下图右,b 、c 、d 被虚线分成两个直角三角形,它们的面积之和为:276292230cm b c d ++=⨯÷+⨯÷=,所以2683027.2(cm )75a =⨯=.【答案】27.2【例24】如下图,△ABC 是边长为1的等边三角形,△BCD 是等腰三角形BD =CD ,顶角∠BDC =1200,∠MDN =600,求△AMN 的周长.【考点】平移、旋转、割补【难度】4星【题型】解答【解析】如下图,延长AC 至P ,使CP =MB ,连接DP .则有∠MBD =600+1163ADE DQR DEQSRT S S S == 正六边形001801202-=∠PCD ;CP =BM ;BD =CD ,所以有△MBD ≌△PCD .于是∠MDC =∠PDC ;又因为∠MDB +∠NDC =600,所以∠PDC +∠NDC =∠NDP =600;MD =PD ,在△MDN 、△PND 中,∠NDM =∠NDP ,ND =ND ,MD =PD ,于是△MND ≌△PND .有MN =PN .因为NP =NP =NC +CP ,而AM =AB -MB =AB -CP ,所以AM +AN +MN =(AB -CP )+AN +(NC +CP )=AB +AN +NC =2.即△AMN 的周长为2.【答案】2【例25】若干个大小相同的正五边形如右图排成环状,下图中所示的只是3个五边形.那么要完成这一圈共需个正五边形.【考点】平移、旋转、割补【难度】4星【题型】解答【关键词】迎春杯、六年级、初赛、5题【解析】【解析】如图,设O 为圆心,A 、B 、C 、D 为五边形的顶点,连接OA 、OB 、OC .DC B A O从图中可以看出,OAB △和OBC △是完全相同的,所以OBA OBC ∠=∠,又五边形内角和为540°,所以正五边形的每个内角都为5405108÷=°°,即108ABD CBD ∠=∠=°,那么3601082144ABC ∠=︒-︒⨯=︒,则144272OBA ∠=÷=°°,又OAB OBA ∠=∠,所以18072236AOB ∠=︒-︒⨯=︒所以要用3603610+=°°个正五边形才能围成一圈.【答案】10【例26】如图,ABCD 是矩形,BC =6cm ,AB=10cm ,AC 和BD 是对角线,图中的阴影部分以C 为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)【考点】平移、旋转、割补【难度】3星【题型】解答【关键词】华杯赛、决赛、第11题【解析】①设三角形BCO 以CD 为轴旋转一周所得到的立体的体积是s ,S 等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆锥的体积。
五年级奥数平移、旋转、割补教师版

五年级奥数平移、旋转、割补教师版【例 1】 右图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积(阴影部分)有多大?【考点】平移、旋转、割补 【难度】2星 【题型】解答 【解析】 如图所示,将道路平移后的()()162102112-⨯-=。
【答案】112【例 2】 如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个.请算出阴影部分的面积.1cm1cm【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如图,将阴影部分分割成一个正六边形和12个小三角形,再把正六边形分割成6个正三角形,由于正十二边形的每个内角为()180********︒⨯-÷=︒,所以阴影小三角形的顶角等于15060230︒-︒⨯=︒,每个顶角的两边和与其相邻的正三角形的底边所成的角都是306090︒+︒=︒,所以通过如右上图所示的平移可以组成6个边长为1厘米的正方形,所以所求阴影部分面积为2166⨯=平方厘米.【答案】6【例 3】 如图所示,梯形ABCD 中,AB 平行于CD ,又4BD =,3AC =,5AB CD +=.试求梯形ABCD 的面积.D CBAEDCBA【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如右图,将AB 沿AC 平移至CE ,连接BE ,在三角形BDE 中,有4BD =,3BE AC ==,5DE AB CD =+=,有222BD BE DE +=,所以三角形BDE 为直角三角形.由于ABD ABC BCE S S S ∆∆∆==,所以梯形ABCD 的面积与三角形BDE 的面积相等,为例题精讲4-2-5.平移、旋转、割补13462⨯⨯=. 【答案】6【例 4】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FD CBAGFE DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【答案】432【例 5】 如图2,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若PBC 、PEF 的面积为3与4,则正六边形ABCDEF 的面积是 .E【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、中年级、初赛、7题 【解析】 这是一道几何问题,考察同学们对常见图形性质的认识.正六边形的六条边都相等,每个角都是,每一组对边都互相平行,正六边形可以看作是由六个正三角形拼成的(如图(1)).其中正六边形的面积是正三角形面积的6倍.每相邻两个正三角形拼成的是一个平行四边形.如图(2),连结BF ,三角形ABF 的面积是平行四边形ABFO 面积的一半.六边形ABCDEF 的面积是平行四边形ABFO 的3倍,故六边形ABCDEF 的面积是三角形ABF 的面积的6倍. 如图(3),连结BF ,CE ,三角形BCP 的面积与三角形EFP 的面积和是平行四边形BFEC 面积的一半.而六边形ABCDEF 的面积是平行四边形BFEC 的1.5倍,故六边形ABCDEF 的面积是三角形BCP 的面积与三角形EFP 的面积和的3倍.图(1)OAB CDEF图(2)OB ACDEF图(3)E所以,由PBC △、PEF △的面积分别为3与4, 可知正六边形ABCDEF 的面积是(34)321+⨯=.【答案】21【例 6】 正六边形A1A2A3A4A5A6的面积是2009平方厘米,B1,B2,B3,B4,B5,B6分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.4A 3【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、六年级、初赛、14题 【解析】 如图,设62B A 与13B A 的交点为O ,则图中空白部分由6个与23A OA △一样大小的三角形组成,只要求出了23A OA △的面积,就可以求出空白部分面积,进而求出阴影部分面积.43A 654连接63A A 、61B B 、63B A设116A B B △的面积为“1”,则126B A B △面积为“1”,126A A B △面积为“2”,那么636A A B △面积为126A A B △的2倍,为“4”,梯形1236A A A A 的面积为224212⨯+⨯=,263A B A △的面积为“6”,123B A A △的面积为2根据蝴蝶定理,1263261316B A B A A B B O A O S S ===△△∶∶,故21233612167A OAB A A S S ==+△△, 所以231236A A A A 121277A OA S S =△梯形∶∶∶1∶,即23A OA △的面积为梯形1236A A A A 面积的17,故为六边形123456A A A A A A 面积的114,那么空白部分的面积为正六边形面积的136147⨯=,所以阴影部分面积为32009111487⎛⎫⨯-= ⎪⎝⎭(平方厘米). 【答案】1148【例 7】 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm 和4cm ,乙三角形两条直角边分别为3cm 和6cm ,求图中阴影部分的面积.【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如右图,我们将三角形甲与乙进行平移,就会发现平行四边形面积等于平移后两个长方形面积之和.所以阴影部分面积为:2346236242211cm ⨯+⨯-⨯÷+⨯÷=()()【答案】11【例 8】 在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 阴影总值是一个梯形.我们用三种方法解答.⑴ 割补法从顶点作底边上的高,得到两个相同的直角三角形.将这两个直角三角形拼成一个长方形(见下图).显然,阴影部分正好是长方形的13,所以原题阴影部分占整个图形面积的13.⑵ 拼补法将两个这样的三角形拼成一个平行四边形(下页左上图).显然,图中阴影面积占平行四边形面积的13.根据商不变性质,将阴影面积和平行四边形面积同时除以2,商不变.所以原题阴影部分占整个图形面积的13.⑶ 等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,所以阴影部分占整个图形面积的3193=.注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立. 【答案】13【例 9】 如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点P 为中心转动一个正方形.当5AB =厘米,13BC =厘米,12CA =厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).P【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 右图由左图旋转而得,则右图中的8个空白小三角形都是完全相同的,右图中重叠部分的面积等于正方形面积减去4个小三角形的面积,从右图中可以看出正方形的边长为5131230++=厘米,所以重叠部分的面积为:2304(5122)780-⨯⨯÷=(平方厘米).【答案】780【例 10】 如图,在直角三角形中有一个正方形,已知10BD =厘米,7DC =厘米,求阴影部分的面积.【考点】平移、旋转、割补 【难度】4星 【题型】解答【解析】 绕D 点逆时针旋转CED ∆,使E 与F 重合,则C 点落在AB 边上的'C 点处,且'C D CD =.则阴影部分面积转化为直角三角形'BC D 的面积,所以阴影部分的面积为107235⨯÷=平方厘米.【答案】35【例 11】 四边形ABCD 中,AB =30,AD =48,BC =14,CD =40.又已知∠ABD +∠BDC =900,求四边形ABCD 的面积.DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,以BD 的垂直平分线为对称轴L ,做△ABD 关于L 的对称图形△A 'BD .连接A 'C .A 1IABCD因为∠ABD +∠BDC =9000而∠ABD =∠A 'DB =900,所以有∠A 'DB +∠BDC =900. 那么A 'CD 为直角三角形,由勾股定理知2A C '=22AB CD +=2500,所以50A C '=.而在△A 'BC 中,有A 'B =AD =48,有482+142=2500,即A 'B 2+BC 2=A 'C 2,即△A 'BC 为直角三角形.有A CD A BCSS''+130402=⨯⨯114489362+⨯⨯=. 而|ABCDS 四边形A CD A BC S S ''=+936=.评注:Ⅰ.本题以∠ABC +∠BDC =900突破口,通过对称变换构造出与原图形相关的角三角形Ⅱ.对于这道题我们还可以将△BCD 作L 的对称图形.如下:C 1lABCD【答案】936【例 12】 如图,在三角形ABD 中,当AB 和CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.DCAB?30°40°【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为AB =CD ,于是可以将三角形ABC 的边BA 边与CD 对齐,如下图. 在下图中有∠BCA =110°,所以∠ACD =70°于是∠AC C '=∠ACD +∠DC C '=∠ACD +∠ABC =70°+40°=110°;A 1D C 1C B 1BA即∠AC C '=110°=∠CC D ';又因为C A ''只是CA 移动的变化,所以C A ''=CA ;则ABC A ''是一等腰梯形.于是,∠ADC '=180°-110°=70°;又∠CDC '=30°,所以∠ADC =70°-30°=40°.【答案】40°【例 13】 如图所示的四边形的面积等于多少?DB13131212【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【答案】144【例 14】 如图,三角形ABC 是等腰直角三角形,P 是三角形外的一点,其中90BPC ∠=︒,10cm AP =,求四边形ABPC 的面积.P DCBAP'PDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为BAC ∠和BPC ∠都是直角,和为180︒,所以ABP ∠和ACP ∠的和也为180︒,可以旋转三角形APC ,使AC 和AB 重合,则四边形的面积转化为等腰直角三角形'AP P ,面积为1010250⨯÷=平方厘米.【答案】50【例 15】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数 【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【答案】10【例 16】 如图,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,将腰CD 以D 为中心逆时针旋转90︒至ED ,连接AE 、CE ,则ADE ∆的面积是 .ED CBAH FEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数 【解析】 如图所示,将ADE ∆以D 为中心顺时针旋转90︒,到FDC ∆的位置.延长FD 与BC 交于H .由于ABCD 是直角梯形,AD 与FD 垂直,则四边形ADHB 是长方形,则BH AD =. 由于ADE ∆与FDC ∆面积相等,而FDC ∆的底边2FD AD ==,高321CH BC BH =-=-=,所以FDC ∆的面积为2121⨯÷=,那么ADE ∆的面积也为1.【答案】1【例 17】 如图,正方形ABCD 和DEFG 有一个公共点D ,试比较三角形ADG 和三角形CDE的面积.GFEDCBAA'GFEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为ADC ∠和GDE ∠是直角,所以ADG ∠和CDE ∠是互补角,将三角形ADG 顺时针旋转90︒到达'A DE ∆的位置,则'A 、D 、C 在同一条直线上,且'A D AD CD ==,即D 是'A C 的中点,所以三角形CDE 和三角形'A DE 面积相等,则三角形CDE 和三角形ADG 面积相等.【答案】相等【例 18】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.F【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】资优杯 【解析】 如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==, 所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ).又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ).那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ),所以12.52OBE BDE S S ∆∆==(2cm ).【答案】2.5【例 19】 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++=2cm .EDCBADEC 'A 'CBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、高年级、复赛、10题 【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系:''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=.【答案】50【例 20】 如图所示的四边形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==厘米,连接对角线BD ,30ABD ∠=︒.求四边形ABCD 的面积.DCB A DECBA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】第八届、华杯总决赛 【解析】 由45A ∠=°,30ABD ∠=︒,可得1804530105ADB ∠=︒-︒-︒=︒,1053075DBC ∠=︒-︒=︒.将DBC ∆剪下来,翻转,再贴在BD 边上,即将B 点粘在D 点上,D 点粘在B 点上,如右上图所示.则C 点在E 点的位置.由于10575180ADB EDB ∠+∠=︒+︒=︒,所以A 、D 、E 三点在同一条直线上.由于45A E C ∠=∠=∠=°,所以90ABE ∠=︒,即ABE ∆是等腰直角三角形,它的面积就等于四边形ABCD 的面积,所以四边形ABCD 的面积为1515112.52⨯=平方厘米.【答案】112.5【例 21】 如图,在ABD ∆中,AB CD =,求“?”的度数.40°30°?DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图,由于AB CD =,可以将ABC ∆移动到DCE ∆,由于180(3040)110ACB ∠=︒-︒+︒=︒,18011070ACD ∠=︒-︒=︒,所以7040110ACE ∠=︒+︒=︒,又110CED ∠=︒,而AC DE =,所以四边形ACED 是等腰梯形,有180********ADE CED ∠=︒-∠=︒-︒=︒,703040ADC ∠=︒-︒=︒. 点评:通过构造全等三角形来转化.【答案】40°【例 22】 下图三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,点D 在BC 边上,:2:3BD DC =.当三角形ABC 的面积是250cm 时,三角形ADE 的面积是多少?ECBAGP R Q F EDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 以点A 为中心,由三个三角形ABC 可拼成右图:连结QE 、RF 、GD ,则DEQFRG是一个正六边形.连结RD 、DQ 、RQ ,显然RDQ 是一个等边三角形,并且它的面积是正六边形面积的一半,所以是三角形ADE 的面积的3倍.由于23150cm PBC ABC S S ∆∆=⨯=,根据“鸟头定理”,22336cm 3223DQC PBC S S ∆∆=⨯⨯=++,所以2342cm RDQ PBC DQC S S S ∆∆∆=-⨯=,则2342314cm ADE RDQ S S ∆∆=÷=÷=. 【答案】14【例 23】 如图,正方形PQRS 有三个顶点分别在ABC ∆的三条边上,BQ QC =.求正方形PQRS 的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,我们设ABC∆的面积为1,有161279341()122132111311143a e c d b =---+=-⨯-⨯-⨯=, 所以682143a e ==,751143bcd a ++=-=, 所以6875a b c d =++.如下图左,将三角形c 和三角形d 分别以P 、R 为中心按箭头方向旋转90︒,形成由两个直角三角形连在一起的一个四边形,如下图右,b 、c 、d 被虚线分成两个直角三角形,它们的面积之和为:276292230cm b c d ++=⨯÷+⨯÷=,所以2683027.2(cm )75a =⨯=.【答案】27.2【例 24】 如下图,△ABC 是边长为1的等边三角形,△BCD 是等腰三角形BD =CD ,顶角∠BDC =1200,∠MDN =600,求△AMN 的周长.120°60°M BD CNA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 如下图, 延长AC 至P ,使CP =MB ,连接DP .120°60°M BD PC NA则有∠MBD =600+1163ADEDQRDEQSRT SS S ==正六边形001801202-=∠PCD ;CP =BM ;BD =CD ,所以有△MBD ≌△PCD .于是∠MDC =∠PDC ;又因为∠MDB +∠NDC =600,所以∠PDC +∠NDC =∠NDP =600; MD =PD ,在△MDN 、△PND 中,∠NDM =∠NDP ,ND =ND ,MD =PD ,于是△MND ≌△PND .有MN =PN .因为NP =NP =NC +CP ,而AM =AB -MB =AB -CP , 所以AM +AN +MN =(AB -CP )+AN +(NC +CP )=AB +AN +NC =2.即△AMN 的周长为2.【答案】2【例 25】 若干个大小相同的正五边形如右图排成环状,下图中所示的只是3个五边形.那么要完成这一圈共需个正五边形.【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、六年级、初赛、5题 【解析】 如图,设O 为圆心,A 、B 、C 、D 为五边形的顶点,连接OA 、OB 、OC .DC BAO从图中可以看出,OAB △和OBC △是完全相同的,所以OBA OBC ∠=∠,又五边形内角和为540°,所以正五边形的每个内角都为5405108÷=°°,即108ABD CBD ∠=∠=°,那么3601082144ABC ∠=︒-︒⨯=︒,则144272OBA ∠=÷=°°, 又OAB OBA ∠=∠,所以18072236AOB ∠=︒-︒⨯=︒ 所以要用3603610+=°°个正五边形才能围成一圈.【答案】10【例 26】 如图,ABCD 是矩形,BC =6cm , AB=10cm ,AC 和BD 是对角线,图中的阴影部分以C为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)【考点】平移、旋转、割补 【难度】3星 【题型】解答 【关键词】华杯赛、决赛、第11题 【解析】 ①设三角形BCO 以CD 为轴旋转一周所得到的立体的体积是s ,S 等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆锥的体积。
(小学奥数)平移、旋转、割补

圖形變換,是指不改變圖形的大小、形狀,只通過位置關係的改變(旋轉、平移、折疊等),構成新的圖形.【例 1】右圖是一塊長方形草地,長方形的長是16,寬是10.中間有兩條道路,一條是長方形,一條是平行四邊形,它們的寬都是2,求草地部分的面積(陰影部分)有多大?【考點】平移、旋轉、割補 【難度】2星 【題型】解答 【解析】 如圖所示,將道路平移後的()()162102112-⨯-=。
【答案】112【例 2】如圖所示,一個正十二邊形的邊長是1釐米,空白部分是等邊三角形,一共有12個.請算出陰影部分的面積.1cm1cm 1cm【考點】平移、旋轉、割補 【難度】3星 【題型】解答【解析】 如圖,將陰影部分分割成一個正六邊形和12個小三角形,再把正六邊形分割成6個正三角形,由於正十二邊形的每個內角為()180********︒⨯-÷=︒,所以陰影小三角形的頂角等於15060230︒-︒⨯=︒,每個頂角的兩邊和與其相鄰的正三角形的底邊所成的角都是306090︒+︒=︒,所以通過如右上圖所示的平移可以組成6個邊長為1釐米的正方形,所以所求陰影部分面積為2166⨯=平方釐米.【答案】6例題精講4-2-5.平移、旋轉、割補【例 3】如圖所示,梯形ABCD 中,AB 平行於CD ,又4BD =,3AC =,5AB CD +=.試求梯形ABCD 的面積.DCBAEDCBA【考點】平移、旋轉、割補 【難度】3星 【題型】解答【解析】 如右圖,將AB 沿AC 平移至CE ,連接BE ,在三角形BDE 中,有4BD =,3BE AC ==,5DE AB CD =+=,有222BD BE DE +=,所以三角形BDE 為直角三角形.由於ABD ABC BCE S S S ∆∆∆==,所以梯形ABCD 的面積與三角形BDE 的面積相等,為13462⨯⨯=. 【答案】6【例 4】如下圖,六邊形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行於ED ,AF 平行於CD ,BC 平行於EF ,對角線FD 垂直於BD ,已知24FD =釐米,18BD =釐米,請問六邊形ABCDEF 的面積是多少平方釐米?FED CBAGFEDCBA【考點】平移、旋轉、割補 【難度】5星 【題型】解答 【解析】 如圖,我們將BCD ∆平移使得CD 與AF 重合,將DEF ∆平移使得ED 與AB 重合,這樣EF 、BC 都重合到圖中的AG 了.這樣就組成了一個長方形BGFD ,它的面積與原六邊形的面積相等,顯然長方形BGFD 的面積為2418432⨯=平方釐米,所以六邊形ABCDEF 的面積為432平方釐米.【答案】432【例 5】如圖2,六邊形ABCDEF 為正六邊形,P 為對角線CF 上一點,若PBC 、PEF 的面積為3與4,則正六邊形ABCDEF 的面積是 .E【考點】平移、旋轉、割補 【難度】4星 【題型】解答 【關鍵字】迎春杯、中年級、初賽、7題【解析】 這是一道幾何問題,考察同學們對常見圖形性質的認識.正六邊形的六條邊都相等,每個角都是,每一組對邊都互相平行,正六邊形可以看作是由六個正三角形拼成的(如圖(1)).其中正六邊形的面積是正三角形面積的6倍.每相鄰兩個正三角形拼成的是一個平行四邊形.如圖(2),連結BF ,三角形ABF 的面積是平行四邊形ABFO 面積的一半.六邊形ABCDEF 的面積是平行四邊形ABFO 的3倍,故六邊形ABCDEF 的面積是三角形ABF 的面積的6倍. 如圖(3),連結BF ,CE ,三角形BCP 的面積與三角形EFP 的面積和是平行四邊形BFEC 面積的一半.而六邊形ABCDEF 的面積是平行四邊形BFEC 的1.5倍,故六邊形ABCDEF 的面積是三角形BCP 的面積與三角形EFP 的面積和的3倍.图(1)OAB CDEF 图(2)OB ACDEF图(3)E所以,由PBC △、PEF △的面積分別為3與4, 可知正六邊形ABCDEF 的面積是(34)321+⨯=.【答案】21【例 6】正六邊形A1A2A3A4A5A6的面積是2009平方釐米,B1,B2,B3,B4,B5,B6分別是正六邊形各邊的中點;那麼圖中陰影六邊形的面積是 平方釐米.A 3【考點】平移、旋轉、割補 【難度】5星 【題型】解答【關鍵字】迎春杯、六年級、初賽、14題 【解析】 如圖,設62B A 與13B A 的交點為O ,則圖中空白部分由6個與23A OA △一樣大小的三角形組成,只要求出了23A OA △的面積,就可以求出空白部分面積,進而求出陰影部分面積.4A 3A 654連接63A A 、61B B 、63B A設116A B B △的面積為“1”,則126B A B △面積為“1”,126A A B △面積為“2”,那麼636A A B △面積為126A A B △的2倍,為“4”,梯形1236A A A A 的面積為224212⨯+⨯=,263A B A △的面積為“6”,123B A A △的面積為2 根據蝴蝶定理,1263261316B A B A A BB O A O S S ===△△∶∶,故21233612167A OAB A A S S ==+△△, 所以231236A A A A121277A OA S S =△梯形∶∶∶1∶,即23A OA △的面積為梯形1236A A A A 面積的17,故為六邊形123456A A A A A A 面積的114,那麼空白部分的面積為正六邊形面積的136147⨯=,所以陰影部分面積為32009111487⎛⎫⨯-= ⎪⎝⎭(平方釐米). 【答案】1148【例 7】按照圖中的樣子,在一平行四邊形紙片上割去了甲、乙兩個直角三角形.已知甲三角形兩條直角邊分別為2cm 和4cm ,乙三角形兩條直角邊分別為3cm 和6cm ,求圖中陰影部分的面積.【考點】平移、旋轉、割補 【難度】3星 【題型】解答 【解析】 如右圖,我們將三角形甲與乙進行平移,就會發現平行四邊形面積等於平移後兩個長方形面積之和.所以陰影部分面積為:2346236242211cm ⨯+⨯-⨯÷+⨯÷=()()【答案】11【例 8】在一個等腰三角形中,兩條與底邊平行的線段將三角形的兩條邊等分成三段(見右圖),求圖中陰影部分的面積占整個圖形面積的幾分之幾.【考點】平移、旋轉、割補 【難度】3星 【題型】解答【解析】 陰影總值是一個梯形.我們用三種方法解答.⑴ 割補法從頂點作底邊上的高,得到兩個相同的直角三角形.將這兩個直角三角形拼成一個長方形(見下圖).顯然,陰影部分正好是長方形的13,所以原題陰影部分占整個圖形面積的13.⑵ 拼補法將兩個這樣的三角形拼成一個平行四邊形(下頁左上圖).顯然,圖中陰影面積占平行四邊形面積的13.根據商不變性質,將陰影面積和平行四邊形面積同時除以2,商不變.所以原題陰影部分占整個圖形面積的13.⑶ 等分法將原圖等分成9個小三角形(見右上圖),陰影部分占3個小三角形,所以陰影部分占整個圖形面積的3193=.注意,後兩種方法對任意三角形都適用.也就是說,將例題中的等腰三角形換成任意三角形,其他條件不變,結論仍然成立. 【答案】13【例 9】如下左圖,有兩個大小相同的完全重疊在一起的正方形,現在以點P 為中心轉動一個正方形.當5AB =釐米,13BC =釐米,12CA =釐米時(如下右圖),求右圖中的兩個正方形相重疊部分的面積(注意,圖的尺寸不一定準確).P【考點】平移、旋轉、割補 【難度】3星 【題型】解答【解析】 右圖由左圖旋轉而得,則右圖中的8個空白小三角形都是完全相同的,右圖中重疊部分的面積等於正方形面積減去4個小三角形的面積,從右圖中可以看出正方形的邊長為5131230++=釐米,所以重疊部分的面積為:2304(5122)780-⨯⨯÷=(平方釐米).【答案】780【例 10】 如圖,在直角三角形中有一個正方形,已知10BD =釐米,7DC =釐米,求陰影部分的面積.【考點】平移、旋轉、割補 【難度】4星 【題型】解答 【解析】 繞D 點逆時針旋轉CED ∆,使E 與F 重合,則C 點落在AB 邊上的'C 點處,且'C D CD =.則陰影部分面積轉化為直角三角形'BC D 的面積,所以陰影部分的面積為107235⨯÷=平方釐米.【答案】35【例 11】 四邊形ABCD 中,AB =30,AD =48,BC =14,CD =40.又已知∠ABD +∠BDC =900,求四邊形ABCD 的面積.DBA【考點】平移、旋轉、割補 【難度】5星 【題型】解答【解析】 如下圖,以BD 的垂直平分線為對稱軸L ,做△ABD 關於L 的對稱圖形△A 'BD .連接A 'C .A 1IABCD因為∠ABD +∠BDC =9000而∠ABD =∠A 'DB =900,所以有∠A 'DB +∠BDC =900.那麼A 'CD 為直角三角形,由畢氏定理知2A C '=22AB CD +=2500,所以50A C '=.而在△A 'BC 中,有A 'B =AD =48,有482+142=2500,即A 'B 2+BC 2=A 'C 2,即△A 'BC 為直角三角形.有A CD A BCSS''+130402=⨯⨯114489362+⨯⨯=. 而|ABCD S 四边形A CDA BCSS''=+936=.評注:Ⅰ.本題以∠ABC +∠BDC =900突破口,通過對稱變換構造出與原圖形相關的角三角形Ⅱ.對於這道題我們還可以將△BCD 作L 的對稱圖形.如下:C 1lABCD【答案】936【例 12】 如圖,在三角形ABD 中,當AB 和CD 的長度相等時,請求出“?”所示的角是多少度,給出過程.DCAB?30°40°【考點】平移、旋轉、割補 【難度】5星 【題型】解答【解析】 因為AB =CD ,於是可以將三角形ABC 的邊BA 邊與CD 對齊,如下圖. 在下圖中有∠BCA =110°,所以∠ACD =70°於是∠AC C '=∠ACD +∠DC C '=∠ACD +∠ABC =70°+40°=110°;A 1D C 1CB 1BA即∠AC C '=110°=∠CC D ';又因為C A ''只是CA 移動的變化,所以C A ''=CA ;則ABC A ''是一等腰梯形.於是,∠ADC '=180°-110°=70°;又∠CDC '=30°,所以∠ADC =70°-30°=40°.【答案】40°【例 13】 如圖所示的四邊形的面積等於多少?DB13131212【考點】平移、旋轉、割補 【難度】4星 【題型】解答 【解析】 題目中要求的四邊形既不是正方形也不是長方形,難以運用公式直接求面積.我們可以利用旋轉的方法對圖形實施變換: 把三角形OAB 繞頂點O 逆時針旋轉,使長為13的兩條邊重合,此時三角形OAB 將旋轉到三角形OCD 的位置.這樣,通過旋轉後所得到的新圖形是一個邊長為12的正方形,且這個正方形的面積就是原來四邊形的面積. 因此,原來四邊形的面積為1212144⨯=.(也可以用畢氏定理) 【答案】144【例 14】 如圖,三角形ABC 是等腰直角三角形,P 是三角形外的一點,其中90BPC ∠=︒,10cm AP =,求四邊形ABPC 的面積.PDCBAP'PDCBA【考點】平移、旋轉、割補 【難度】5星 【題型】解答 【解析】 因為BAC ∠和BPC ∠都是直角,和為180︒,所以ABP ∠和ACP ∠的和也為180︒,可以旋轉三角形APC ,使AC 和AB 重合,則四邊形的面積轉化為等腰直角三角形'AP P ,面積為1010250⨯÷=平方釐米.【答案】50【例 15】 如圖所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 為一邊向ABC ∆外作正方形ACDE ,中心為O ,求OBC ∆的面積.【考點】平移、旋轉、割補 【難度】5星 【題型】解答 【關鍵字】武漢明心奧數 【解析】 如圖,將OAB ∆沿著O 點順時針旋轉90︒,到達OCF ∆的位置.由於90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那麼B 、C 、F 三點在一條直線上.由於OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜邊BF 為538+=,所以它的面積為218164⨯=.根據面積比例模型,OBC ∆的面積為516108⨯=. 【答案】10【例 16】 如圖,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,將腰CD 以D 為中心逆時針旋轉90︒至ED ,連接AE 、CE ,則ADE ∆的面積是 .ED CB AH FEDCBA【考點】平移、旋轉、割補 【難度】5星 【題型】解答 【關鍵字】武漢明心奧數 【解析】 如圖所示,將ADE ∆以D 為中心順時針旋轉90︒,到FDC ∆的位置.延長FD 與BC交於H .由於ABCD 是直角梯形,AD 與FD 垂直,則四邊形ADHB 是長方形,則BH AD =. 由於ADE ∆與FDC ∆面積相等,而FDC ∆的底邊2FD AD ==,高321CH BC BH =-=-=,所以FDC ∆的面積為2121⨯÷=,那麼ADE ∆的面積也為1.【答案】1【例 17】 如圖,正方形ABCD 和DEFG 有一個公共點D ,試比較三角形ADG 和三角形CDE 的面積.GFEDCBAA'GFEDCBA【考點】平移、旋轉、割補 【難度】5星 【題型】解答 【解析】 因為ADC ∠和GDE ∠是直角,所以ADG ∠和CDE ∠是互補角,將三角形ADG 順時針旋轉90︒到達'A DE ∆的位置,則'A 、D 、C 在同一條直線上,且'A D AD CD ==,即D 是'A C 的中點,所以三角形CDE 和三角形'A DE 面積相等,則三角形CDE 和三角形ADG 面積相等.【答案】相等【例 18】 如圖,以正方形的邊AB 為斜邊在正方形內作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交於O .已知AE 、BE 的長分別為3cm 、5cm ,求三角形OBE 的面積.F【考點】平移、旋轉、割補 【難度】5星 【題型】解答 【關鍵字】資優杯 【解析】 如圖,連接DE ,以A 點為中心,將ADE ∆順時針旋轉90︒到ABF ∆的位置.那麼90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四邊形AFBE 是直角梯形,且3AF AE ==, 所以梯形AFBE 的面積為:()1353122+⨯⨯=(2cm ). 又因為ABE ∆是直角三角形,根據畢氏定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ). 那麼()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ), 所以1 2.52OBE BDE S S ∆∆==(2cm ).【答案】2.5【例 19】 如圖,已知4cmAB AE ==,BC DC=,90BAE BCD ∠=∠=︒,10cmAC =,則S ABC ACE CDE S S ∆∆∆++=2cm .ED CB A D EC 'A 'CBA【考點】平移、旋轉、割補 【難度】5星 【題型】解答【關鍵字】迎春杯、高年級、復賽、10題【解析】 將三角形ABC 繞A 點和C 點分別順時針和逆時針旋轉90,構成三角形'AEC 和'A DC ,再連接''A C ,顯然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 關於正方形的中心O 中心對稱,在中心對稱圖形''ACA C 中有如下等量關係:''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=. 所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=. 【答案】50【例 20】 如圖所示的四邊形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==釐米,連接對角線BD ,30ABD ∠=︒.求四邊形ABCD 的面積.D CB A DEC B A【考點】平移、旋轉、割補 【難度】4星 【題型】解答【關鍵字】第八屆、華杯總決賽【解析】 由45A ∠=°,30ABD ∠=︒,可得1804530105ADB ∠=︒-︒-︒=︒,1053075DBC ∠=︒-︒=︒.將DBC ∆剪下來,翻轉,再貼在BD 邊上,即將B 點粘在D 點上,D 點粘在B 點上,如右上圖所示.則C 點在E 點的位置.由於10575180ADB EDB ∠+∠=︒+︒=︒,所以A 、D 、E 三點在同一條直線上.由於45A E C ∠=∠=∠=°,所以90ABE ∠=︒,即ABE ∆是等腰直角三角形,它的面積就等於四邊形ABCD 的面積,所以四邊形ABCD 的面積為1515112.52⨯=平方釐米. 【答案】112.5【例 21】 如圖,在ABD ∆中,AB CD =,求“?”的度數.40°30°?D C B AD【考點】平移、旋轉、割補 【難度】5星 【題型】解答【解析】 如圖,由於AB CD =,可以將ABC ∆移動到DCE ∆,由於180(3040)110ACB ∠=︒-︒+︒=︒,18011070ACD ∠=︒-︒=︒,所以7040110ACE ∠=︒+︒=︒,又110CED ∠=︒,而AC DE =,所以四邊形ACED 是等腰梯形,有180********ADE CED ∠=︒-∠=︒-︒=︒,703040ADC ∠=︒-︒=︒.點評:通過構造全等三角形來轉化.【答案】40°【例 22】 下圖三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,點D 在BC 邊上,:2:3BD DC =.當三角形ABC 的面積是250cm 時,三角形ADE 的面積是多少?ED C B A G PR QFE C B A【考點】平移、旋轉、割補 【難度】5星 【題型】解答【解析】 以點A 為中心,由三個三角形ABC 可拼成右圖:連結QE 、RF 、GD ,則DEQFRG是一個正六邊形.連結RD 、DQ 、RQ ,顯然RDQ 是一個等邊三角形,並且它的面積是正六邊形面積的一半,所以是三角形ADE 的面積的3倍.由於23150cm PBC ABC S S ∆∆=⨯=,根據“鳥頭定理”,22336cm 3223DQC PBC S S ∆∆=⨯⨯=++, 所以2342cm RDQ PBC DQC S S S ∆∆∆=-⨯=,則2342314cm ADE RDQ S S ∆∆=÷=÷=.【答案】14【例 23】 如圖,正方形PQRS 有三個頂點分別在ABC ∆的三條邊上,BQ QC =.求正方形PQRS 的面積.【考點】平移、旋轉、割補 【難度】5星 【題型】解答 【解析】 如下圖,我們設ABC ∆的面積為1,有161279341()122132111311143a e c db =---+=-⨯-⨯-⨯=, 所以682143a e ==,751143bcd a ++=-=, 所以6875a b c d =++.如下圖左,將三角形c 和三角形d 分別以P 、R 為中心按箭頭方向旋轉90︒,形成由兩個直角三角形連在一起的一個四邊形,如下圖右,b 、c 、d 被虛線分成兩個直角三角形,它們的面積之和為:276292230cm b c d ++=⨯÷+⨯÷=,所以2683027.2(cm )75a =⨯=.【答案】27.2【例 24】 如下圖,△ABC 是邊長為1的等邊三角形,△BCD 是等腰三角形BD =CD ,頂角∠BDC =1200,∠MDN =600,求△AMN 的周長.120°60°MBD C NA【考點】平移、旋轉、割補 【難度】4星 【題型】解答【解析】 如下圖, 延長AC 至P ,使CP =MB ,連接DP .120°60°MBD P C NA則有∠MBD =600+1163ADE DQR DEQSRT S S S ==正六边形001801202-=∠PCD ;CP =BM ;BD =CD ,所以有△MBD ≌△PCD .於是∠MDC =∠PDC ;又因為∠MDB +∠NDC =600,所以∠PDC +∠NDC =∠NDP =600; MD =PD ,在△MDN 、△PND 中,∠NDM =∠NDP ,ND =ND ,MD =PD ,於是△MND ≌△PND .有MN =PN .因為NP =NP =NC +CP ,而AM =AB -MB =AB -CP ,所以AM +AN +MN =(AB -CP )+AN +(NC +CP )=AB +AN +NC =2.即△AMN 的周長為2.【答案】2【例 25】 若干個大小相同的正五邊形如右圖排成環狀,下圖中所示的只是3個五邊形.那麼要完成這一圈共需 個正五邊形.【考點】平移、旋轉、割補 【難度】4星 【題型】解答【關鍵字】迎春杯、六年級、初賽、5題【解析】 如圖,設O 為圓心,A 、B 、C 、D 為五邊形的頂點,連接OA 、OB 、OC .DC B A O從圖中可以看出,OAB △和OBC △是完全相同的,所以OBA OBC ∠=∠,又五邊形內角和為540°,所以正五邊形的每個內角都為5405108÷=°°,即108ABD CBD ∠=∠=°,那麼3601082144ABC ∠=︒-︒⨯=︒,則144272OBA ∠=÷=°°,又OAB OBA ∠=∠,所以18072236AOB ∠=︒-︒⨯=︒所以要用3603610+=°°個正五邊形才能圍成一圈.【答案】10【例 26】 如圖,ABCD 是矩形,BC =6cm , AB=10cm ,AC 和BD 是對角線,圖中的陰影部分以C 為軸旋轉一周,則陰影部分掃過的立體的體積是多少立方釐米?(π取3.14)【考點】平移、旋轉、割補 【難度】3星 【題型】解答【關鍵字】華杯賽、決賽、第11題【解析】 ①設三角形BCO 以CD 為軸旋轉一周所得到的立體的體積是s ,S 等於高為10釐米,底面半徑是6釐米的圓錐的體積減去2個高為5釐米,底面半徑是3釐米的圓錐的體積。
【精编】奥数精编训练-平移、旋转、割补

图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形.【例1】右图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积(阴影部分)有多大?【例2】如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个.请算出阴影部分的面积.1cm1cm【例3】如图所示,梯形ABCD中,AB平行于CD,又4BD=,3AC=,5AB CD+=.试求梯形ABCD的面积.D CBAEDCBA【例4】如下图,六边形ABCDEF中,AB ED=,AF CD=,BC EF=,且有AB平行于ED,AF平行于CD,BC平行于EF,对角线FD垂直于BD,已知24FD=厘米,18BD=厘米,请问六边形ABCDEF的面积是多少平方厘米?例题精讲4-2-5.平移、旋转、割补FE DC BAGFE DC BA【例5】如图2,六边形ABCDEF为正六边形,P为对角线CF上一点,若PBC、PEF的面积为3与4,则正六边形ABCDEF的面积是.E【例6】正六边形A1A2A3A4A5A6的面积是2009平方厘米,B1,B2,B3,B4,B5,B6分别是正六边形各边的中点;那么图中阴影六边形的面积是平方厘米.A3【例7】按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm和4cm,乙三角形两条直角边分别为3cm和6cm,求图中阴影部分的面积.【例 8】 在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【例 9】 如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点P 为中心转动一个正方形.当5AB =厘米,13BC =厘米,12CA =厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).P【例 10】 如图,在直角三角形中有一个正方形,已知10BD =厘米,7DC =厘米,求阴影部分的面积.【例 11】 四边形ABCD 中,AB =30,AD =48,BC =14,CD =40.又已知∠ABD +∠BDC =900,求四边形ABCD 的面积.DBA【例 12】 如图,在三角形ABD 中,当AB 和CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.DCAB?30°40°【例 13】 如图所示的四边形的面积等于多少?DB13131212【例 14】 如图,三角形ABC 是等腰直角三角形,P 是三角形外的一点,其中90BPC ∠=︒,10cm AP =,求四边形ABPC 的面积.PDCBAP'PDCBA【例 15】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【例 16】 如图,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,将腰CD 以D 为中心逆时针旋转90︒至ED ,连接AE 、CE ,则ADE ∆的面积是 .ED CBAH FEDCBA【例 17】 如图,正方形ABCD 和DEFG 有一个公共点D ,试比较三角形ADG 和三角形CDE 的面积.GEDCBAA'GFEDC BA【例 18】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.F【例 19】 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++=2cm .EDCBADEC 'A 'CBA【例 20】 如图所示的四边形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==厘米,连接对角线BD ,30ABD ∠=︒.求四边形ABCD 的面积.DCB A DECBA【例 21】 如图,在ABD ∆中,AB CD =,求“?”的度数.40°30°?DCBA【例 22】 下图三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,点D 在BC 边上,:2:3BD DC =.当三角形ABC 的面积是250cm 时,三角形ADE 的面积是多少?EDCBAGP R Q F EDCBA【例 23】 如图,正方形PQRS 有三个顶点分别在ABC ∆的三条边上,BQ QC =.求正方形PQRS的面积.【例 24】 如下图,△ABC 是边长为1的等边三角形,△BCD 是等腰三角形BD =CD ,顶角∠BDC =1200,∠MDN =600,求△AMN 的周长.120°60°M BD CNA【例 25】 若干个大小相同的正五边形如右图排成环状,下图中所示的只是3个五边形.那么要完成这一圈共需个正五边形.【例26】如图,ABCD是矩形,BC=6cm, AB=10cm,AC和BD是对角线,图中的阴影部分以C为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)【例27】一个半径为1厘米的圆盘沿着一个半径为4厘米的圆盘外侧做无滑动的滚动,当小圆盘的中心围绕大圆盘中心转动90度后(如图2),小圆盘运动过程中扫出的面积是()平方厘米。
(精品)小学奥数4-2-5 平移、旋转、割补.专项练习及答案解析

图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形.【例 1】 右图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积(阴影部分)有多大?【考点】平移、旋转、割补 【难度】2星 【题型】解答 【解析】 如图所示,将道路平移后的()()162102112-⨯-=。
【答案】112【例 2】 如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个.请算出阴影部分的面积.1cm【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如图,将阴影部分分割成一个正六边形和12个小三角形,再把正六边形分割成6个正三角形,由于正十二边形的每个内角为()180********︒⨯-÷=︒,所以阴影小三角形的顶角等于15060230︒-︒⨯=︒,每个顶角的两边和与其相邻的正三角形的底边所成的角都是306090︒+︒=︒,所以通过如右上图所示的平移可以组成6个边长为1厘米的正方形,所以所求阴影部分面积为2166⨯=平方厘米.【答案】6【例 3】 如图所示,梯形ABCD 中,AB 平行于CD ,又4BD =,3AC =,5AB CD +=.试求梯形ABCD 的面积.D CBAEDCBA【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如右图,将AB 沿AC 平移至CE ,连接BE ,在三角形BDE 中,有4BD =,3BE AC ==,5DE AB CD =+=,有222BD BE DE +=,所以三角形BDE 为直角例题精讲4-2-5.平移、旋转、割补三角形.由于A B D A B C B C S S S ∆∆∆==,所以梯形ABCD 的面积与三角形BDE 的面积相等,为13462⨯⨯=. 【答案】6【例 4】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FD BAGFE DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【答案】432【例 5】 如图2,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若PBC 、PEF 的面积为3与4,则正六边形ABCDEF 的面积是 .E【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、中年级、初赛、7题 【解析】 这是一道几何问题,考察同学们对常见图形性质的认识.正六边形的六条边都相等,每个角都是,每一组对边都互相平行,正六边形可以看作是由六个正三角形拼成的(如图(1)).其中正六边形的面积是正三角形面积的6倍.每相邻两个正三角形拼成的是一个平行四边形.如图(2),连结BF ,三角形ABF 的面积是平行四边形ABFO 面积的一半.六边形ABCDEF 的面积是平行四边形ABFO 的3倍,故六边形ABCDEF 的面积是三角形ABF 的面积的6倍. 如图(3),连结BF ,CE ,三角形BCP 的面积与三角形EFP 的面积和是平行四边形BFEC 面积的一半.而六边形ABCDEF 的面积是平行四边形BFEC 的1.5倍,故六边形ABCDEF 的面积是三角形BCP 的面积与三角形EFP 的面积和的3倍.图(1)OAB CDEF图(2)OB ACDEF图(3)E所以,由PBC △、PEF △的面积分别为3与4,可知正六边形ABCDEF 的面积是(34)321+⨯=.【答案】21【例 6】 正六边形A1A2A3A4A5A6的面积是2009平方厘米,B1,B2,B3,B4,B5,B6分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.A 3【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、六年级、初赛、14题 【解析】 如图,设62B A 与13B A 的交点为O ,则图中空白部分由6个与23A OA △一样大小的三角形组成,只要求出了23A OA △的面积,就可以求出空白部分面积,进而求出阴影部分面积.4A 3A 654连接63A A 、61B B 、63B A设116A B B △的面积为“1”,则126B A B △面积为“1”,126A A B △面积为“2”,那么636A AB △面积为126A A B △的2倍,为“4”,梯形1236A A A A 的面积为224212⨯+⨯=,263A B A △的面积为“6”,123B A A △的面积为2根据蝴蝶定理,1263261316B A B A A B B O A O S S ===△△∶∶,故21233612167A OAB A A S S ==+△△, 所以231236A A A A 121277A OA S S =△梯形∶∶∶1∶,即23A OA △的面积为梯形1236A A A A 面积的17,故为六边形123456A A A A A A 面积的114,那么空白部分的面积为正六边形面积的136147⨯=,所以阴影部分面积为32009111487⎛⎫⨯-= ⎪⎝⎭(平方厘米).【答案】1148【例 7】 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm 和4cm ,乙三角形两条直角边分别为3cm 和6cm ,求图中阴影部分的面积.【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 如右图,我们将三角形甲与乙进行平移,就会发现平行四边形面积等于平移后两个长方形面积之和.所以阴影部分面积为:2346236242211cm ⨯+⨯-⨯÷+⨯÷=()()【答案】11【例 8】 在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 阴影总值是一个梯形.我们用三种方法解答.⑴ 割补法从顶点作底边上的高,得到两个相同的直角三角形.将这两个直角三角形拼成一个长方形(见下图).显然,阴影部分正好是长方形的13,所以原题阴影部分占整个图形面积的13.⑵ 拼补法将两个这样的三角形拼成一个平行四边形(下页左上图).显然,图中阴影面积占平行四边形面积的13.根据商不变性质,将阴影面积和平行四边形面积同时除以2,商不变.所以原题阴影部分占整个图形面积的13.⑶ 等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,所以阴影部分占整个图形面积的3193=.注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立.【答案】13【例 9】 如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点P 为中心转动一个正方形.当5AB =厘米,13BC =厘米,12CA =厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).P【考点】平移、旋转、割补 【难度】3星 【题型】解答 【解析】 右图由左图旋转而得,则右图中的8个空白小三角形都是完全相同的,右图中重叠部分的面积等于正方形面积减去4个小三角形的面积,从右图中可以看出正方形的边长为5131230++=厘米,所以重叠部分的面积为:2304(5122)780-⨯⨯÷=(平方厘米).【答案】780【例 10】 如图,在直角三角形中有一个正方形,已知10BD =厘米,7DC =厘米,求阴影部分的面积.【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 绕D 点逆时针旋转CED ∆,使E 与F 重合,则C 点落在AB 边上的'C 点处,且'C D CD =.则阴影部分面积转化为直角三角形'BC D 的面积,所以阴影部分的面积为107235⨯÷=平方厘米.【答案】35【例 11】 四边形ABCD 中,AB =30,AD =48,BC =14,CD =40.又已知∠ABD +∠BDC =900,求四边形ABCD 的面积.DBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,以BD 的垂直平分线为对称轴L ,做△ABD 关于L 的对称图形△A 'BD .连接A 'C .A 1IABCD因为∠ABD +∠BDC =9000而∠ABD =∠A 'DB =900,所以有∠A 'DB +∠BDC =900.那么A 'CD 为直角三角形,由勾股定理知2A C '=22AB CD +=2500,所以50A C '=.而在△A 'BC 中,有A 'B =AD =48,有482+142=2500,即A 'B 2+BC 2=A 'C 2,即△A 'BC 为直角三角形.有A CD A BCSS''+130402=⨯⨯114489362+⨯⨯=. 而|ABCD S 四边形A CD A BC S S ''=+936=.评注:Ⅰ.本题以∠ABC +∠BDC =900突破口,通过对称变换构造出与原图形相关的角三角形Ⅱ.对于这道题我们还可以将△BCD 作L 的对称图形.如下:C 1lABCD【答案】936【例 12】 如图,在三角形ABD 中,当AB 和CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.DCAB?30°40°【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为AB =CD ,于是可以将三角形ABC 的边BA 边与CD 对齐,如下图. 在下图中有∠BCA =110°,所以∠ACD =70°于是∠AC C '=∠ACD +∠DC C '=∠ACD +∠ABC =70°+40°=110°;A 1D C 1C B 1BA即∠AC C '=110°=∠CC D ';又因为C A ''只是CA 移动的变化,所以C A ''=CA ;则ABC A''是一等腰梯形.于是,∠ADC '=180°-110°=70°;又∠CDC '=30°,所以∠ADC =70°-30°=40°. 【答案】40°【例 13】 如图所示的四边形的面积等于多少?DB13131212【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【答案】144【例 14】 如图,三角形ABC 是等腰直角三角形,P 是三角形外的一点,其中90BPC ∠=︒,10cm AP =,求四边形ABPC 的面积.P DCBAP'PDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为BAC ∠和BPC ∠都是直角,和为180︒,所以ABP ∠和ACP ∠的和也为180︒,可以旋转三角形APC ,使AC 和AB 重合,则四边形的面积转化为等腰直角三角形'AP P ,面积为1010250⨯÷=平方厘米.【答案】50【例 15】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数 【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【答案】10【例 16】 如图,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,将腰CD 以D 为中心逆时针旋转90︒至ED ,连接AE 、CE ,则ADE ∆的面积是 .ED CBAH FEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数【解析】 如图所示,将ADE ∆以D 为中心顺时针旋转90︒,到F D C ∆的位置.延长FD 与BC交于H .由于ABCD 是直角梯形,AD 与FD 垂直,则四边形ADHB 是长方形,则BH AD =.由于ADE ∆与FDC ∆面积相等,而FDC ∆的底边2FD AD ==,高321CH B C B H =-=-=,所以FDC ∆的面积为2121⨯÷=,那么ADE ∆的面积也为1. 【答案】1【例 17】 如图,正方形ABCD 和DEFG 有一个公共点D ,试比较三角形ADG 和三角形CDE 的面积.GFEDCBAA'GFEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 因为ADC ∠和GDE ∠是直角,所以ADG ∠和CDE ∠是互补角,将三角形ADG 顺时针旋转90︒到达'A DE ∆的位置,则'A 、D 、C 在同一条直线上,且'A D A D C D ==,即D 是'A C 的中点,所以三角形CDE 和三角形'A D E 面积相等,则三角形CDE 和三角形ADG 面积相等.【答案】相等【例 18】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.F【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】资优杯 【解析】 如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置. 那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==, 所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ).又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ).那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ),所以12.52OBE BDE S S ∆∆==(2cm ).【答案】2.5【例 19】 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++=2cm .EDCBADEC 'A 'CBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、高年级、复赛、10题 【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系:''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=.【答案】50【例 20】 如图所示的四边形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==厘米,连接对角线BD ,30ABD ∠=︒.求四边形ABCD 的面积.DCB A DECBA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】第八届、华杯总决赛【解析】 由45A ∠=°,30ABD ∠=︒,可得180453A D B ∠=︒-︒-︒=︒,1053075DBC ∠=︒-︒=︒.将DBC ∆剪下来,翻转,再贴在BD 边上,即将B 点粘在D 点上,D 点粘在B 点上,如右上图所示.则C 点在E 点的位置.由于10575180ADB EDB ∠+∠=︒+︒=︒,所以A 、D 、E 三点在同一条直线上.由于45A E C ∠=∠=∠=°,所以90ABE ∠=︒,即ABE ∆是等腰直角三角形,它的面积就等于四边形ABCD 的面积,所以四边形ABCD 的面积为1515112.52⨯=平方厘米.【答案】112.5【例 21】 如图,在ABD ∆中,AB CD =,求“?”的度数.40°30°?DCBAD【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如图,由于AB CD =,可以将ABC ∆移动到D C E ∆,由于180(3040)110ACB ∠=︒-︒+︒=︒,18011070ACD ∠=︒-︒=︒,所以7040A C E ∠=︒+︒=︒,又110CED ∠=,而AC DE =,所以四边形ACED 是等腰梯形,有180********ADE CED ∠=︒-∠=︒-︒=︒,703040ADC ∠=︒-︒=︒. 点评:通过构造全等三角形来转化.【答案】40°【例 22】 下图三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,点D 在BC 边上,:2:3BD DC =.当三角形ABC 的面积是250cm 时,三角形ADE 的面积是多少?EDCBAGP R Q F EDCA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 以点A 为中心,由三个三角形ABC 可拼成右图:连结QE 、RF 、GD ,则DEQFRG是一个正六边形.连结RD 、DQ 、RQ ,显然RDQ 是一个等边三角形,并且它的面积是正六边形面积的一半,所以是三角形ADE 的面积的3倍. 由于23150cm PBC ABC S S ∆∆=⨯=,根据“鸟头定理”,22336cm 3223DQC PBC S S ∆∆=⨯⨯=++,所以2342cm RDQ PBC DQC S S S ∆∆∆=-⨯=,则2342314cm ADE RDQ S S ∆∆=÷=÷=.【答案】14【例 23】 如图,正方形PQRS 有三个顶点分别在ABC ∆的三条边上,BQ QC =.求正方形PQRS 的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,我们设ABC ∆的面积为1,有161279341()122132111311143a e c db =---+=-⨯-⨯-⨯=,所以682143a e ==,751143b c d a ++=-=, 所以6875a b c d =++.如下图左,将三角形c 和三角形d 分别以P 、R 为中心按箭头方向旋转90︒,形成由两个直角三角形连在一起的一个四边形,如下图右,b 、c 、d 被虚线分成两个直角三角形,它们的面积之和为:276292230cm b c d ++=⨯÷+⨯÷=,所以2683027.2(cm )75a =⨯=.【答案】27.2【例 24】 如下图,△ABC 是边长为1的等边三角形,△BCD 是等腰三角形BD =CD ,顶角∠BDC =1200,∠MDN =600,求△AMN 的周长.120°60°M BD CNA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 如下图, 延长AC 至P ,使CP =MB ,连接DP .120°60°M BD PC NA则有∠MBD =600+1163ADEDQRDEQSRT SS S ==正六边形001801202-=∠PCD ;CP =BM ;BD =CD ,所以有△MBD ≌△PCD .于是∠MDC =∠PDC ;又因为∠MDB +∠NDC =600,所以∠PDC +∠NDC =∠NDP =600; MD =PD ,在△MDN 、△PND 中,∠NDM =∠NDP ,ND =ND ,MD =PD ,于是△MND ≌△PND .有MN =PN .因为NP =NP =NC +CP ,而AM =AB -MB =AB -CP ,所以AM +AN +MN =(AB -CP )+AN +(NC +CP )=AB +AN +NC =2.即△AMN 的周长为2. 【答案】2【例 25】 若干个大小相同的正五边形如右图排成环状,下图中所示的只是3个五边形.那么要完成这一圈共需个正五边形.【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、六年级、初赛、5题 【解析】 如图,设O 为圆心,A 、B 、C 、D 为五边形的顶点,连接OA 、OB 、OC .DC BAO从图中可以看出,OAB △和OBC △是完全相同的,所以OBA OBC ∠=∠,又五边形内角和为540°,所以正五边形的每个内角都为5405108÷=°°,即108ABD CBD ∠=∠=°, 那么3601082144ABC ∠=︒-︒⨯=︒,则144272OBA ∠=÷=°°, 又OAB OBA ∠=∠,所以18072236AOB ∠=︒-︒⨯=︒ 所以要用3603610+=°°个正五边形才能围成一圈. 【答案】10【例 26】 如图,ABCD 是矩形,BC =6cm , AB=10cm ,AC 和BD 是对角线,图中的阴影部分以C为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)【考点】平移、旋转、割补 【难度】3星 【题型】解答 【关键词】华杯赛、决赛、第11题【解析】 ①设三角形BCO 以CD 为轴旋转一周所得到的立体的体积是s ,S 等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆锥的体积。
小学奥数4-2-5 平移、旋转、割补.专项练习及答案解析

图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形.【例 1】 右图是一块长方形草地,长方形的长是16,宽是10.中间有两条道路,一条是长方形,一条是平行四边形,它们的宽都是2,求草地部分的面积(阴影部分)有多大?【考点】平移、旋转、割补 【难度】2星 【题型】解答 【解析】 如图所示,将道路平移后的()()162102112-⨯-=。
【答案】112【例 2】 如图所示,一个正十二边形的边长是1厘米,空白部分是等边三角形,一共有12个.请算出阴影部分的面积.1cm【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 如图,将阴影部分分割成一个正六边形和12个小三角形,再把正六边形分割成6个正三角形,由于正十二边形的每个内角为()180********︒⨯-÷=︒,所以阴影小三角形的顶角等于15060230︒-︒⨯=︒,每个顶角的两边和与其相邻的正三角形的底边所成的角都是306090︒+︒=︒,所以通过如右上图所示的平移可以组成6个边长为1厘米的正方形,所以所求阴影部分面积为2166⨯=平方厘米.【答案】6例题精讲4-2-5.平移、旋转、割补【例 3】 如图所示,梯形ABCD 中,AB 平行于CD ,又4BD =,3AC =,5AB CD +=.试求梯形ABCD 的面积.D CBAEDCBA【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 如右图,将AB 沿AC 平移至CE ,连接BE ,在三角形BDE 中,有4BD =,3BE AC ==,5DE AB CD =+=,有222BD BE DE +=,所以三角形BDE 为直角三角形.由于A B D A B C B C ES S S ∆∆∆==,所以梯形ABCD 的面积与三角形BDE 的面积相等,为13462⨯⨯=. 【答案】6【例 4】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FD CBAGF EDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【答案】432【例 5】 如图2,六边形ABCDEF 为正六边形,P 为对角线CF 上一点,若PBC 、PEF的面积为3与4,则正六边形ABCDEF 的面积是 .E【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、中年级、初赛、7题【解析】 这是一道几何问题,考察同学们对常见图形性质的认识.正六边形的六条边都相等,每个角都是,每一组对边都互相平行,正六边形可以看作是由六个正三角形拼成的(如图(1)).其中正六边形的面积是正三角形面积的6倍.每相邻两个正三角形拼成的是一个平行四边形.如图(2),连结BF ,三角形ABF 的面积是平行四边形ABFO 面积的一半.六边形ABCDEF 的面积是平行四边形ABFO 的3倍,故六边形ABCDEF 的面积是三角形ABF 的面积的6倍. 如图(3),连结BF ,CE ,三角形BCP 的面积与三角形EFP 的面积和是平行四边形BFEC 面积的一半.而六边形ABCDEF 的面积是平行四边形BFEC 的1.5倍,故六边形ABCDEF 的面积是三角形BCP 的面积与三角形EFP 的面积和的3倍.图(1)OAB CDEF图(2)OB ACDEF图(3)E所以,由PBC △、PEF △的面积分别为3与4, 可知正六边形ABCDEF 的面积是(34)321+⨯=.【答案】21【例 6】 正六边形A1A2A3A4A5A6的面积是2009平方厘米,B1,B2,B3,B4,B5,B6分别是正六边形各边的中点;那么图中阴影六边形的面积是 平方厘米.A 3【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、六年级、初赛、14题【解析】 如图,设62B A 与13B A 的交点为O ,则图中空白部分由6个与23A OA △一样大小的三角形组成,只要求出了23A OA △的面积,就可以求出空白部分面积,进而求出阴影部分面积.43A 654连接63A A 、61B B 、63B A设116A B B △的面积为“1”,则126B A B △面积为“1”,126A A B △面积为“2”,那么636A AB △面积为126A A B △的2倍,为“4”,梯形1236A A A A 的面积为224212⨯+⨯=,263A B A △的面积为“6”,123B A A △的面积为2根据蝴蝶定理,1263261316B A B A A B B O A O S S ===△△∶∶,故21233612167A OAB A A S S ==+△△, 所以231236A A A A 121277A OA S S =△梯形∶∶∶1∶,即23A OA △的面积为梯形1236A A A A 面积的17,故为六边形123456A A A A A A 面积的114,那么空白部分的面积为正六边形面积的136147⨯=,所以阴影部分面积为32009111487⎛⎫⨯-= ⎪⎝⎭(平方厘米).【答案】1148【例 7】 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为2cm 和4cm ,乙三角形两条直角边分别为3cm 和6cm ,求图中阴影部分的面积.【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 如右图,我们将三角形甲与乙进行平移,就会发现平行四边形面积等于平移后两个长方形面积之和.所以阴影部分面积为:2346236242211cm ⨯+⨯-⨯÷+⨯÷=()()【答案】11【例8】在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【考点】平移、旋转、割补【难度】3星【题型】解答【解析】阴影总值是一个梯形.我们用三种方法解答.⑴割补法从顶点作底边上的高,得到两个相同的直角三角形.将这两个直角三角形拼成一个长方形(见下图).显然,阴影部分正好是长方形的13,所以原题阴影部分占整个图形面积的13.⑵拼补法将两个这样的三角形拼成一个平行四边形(下页左上图).显然,图中阴影面积占平行四边形面积的13.根据商不变性质,将阴影面积和平行四边形面积同时除以2,商不变.所以原题阴影部分占整个图形面积的13.⑶等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,所以阴影部分占整个图形面积的31 93 =.注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立.【答案】1 3【例9】如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点P为中心转动一个正方形.当5AB=厘米,13BC=厘米,12CA=厘米时(如下右图),求右图中的两个正方形相重叠部分的面积(注意,图的尺寸不一定准确).P【考点】平移、旋转、割补 【难度】3星 【题型】解答【解析】 右图由左图旋转而得,则右图中的8个空白小三角形都是完全相同的,右图中重叠部分的面积等于正方形面积减去4个小三角形的面积,从右图中可以看出正方形的边长为5131230++=厘米,所以重叠部分的面积为:2304(5122)780-⨯⨯÷=(平方厘米).【答案】780【例 10】 如图,在直角三角形中有一个正方形,已知10BD =厘米,7DC =厘米,求阴影部分的面积.【考点】平移、旋转、割补 【难度】4星 【题型】解答【解析】 绕D 点逆时针旋转CED ∆,使E 与F 重合,则C 点落在AB 边上的'C 点处,且'C D CD =.则阴影部分面积转化为直角三角形'BC D 的面积,所以阴影部分的面积为107235⨯÷=平方厘米.【答案】35【例 11】 四边形ABCD 中,AB =30,AD =48,BC =14,CD =40.又已知∠ABD +∠BDC =900,求四边形ABCD 的面积.DBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如下图,以BD 的垂直平分线为对称轴L ,做△ABD 关于L 的对称图形△A 'BD .连接A 'C .A 1IABCD因为∠ABD +∠BDC =9000而∠ABD =∠A 'DB =900,所以有∠A 'DB +∠BDC =900.那么A 'CD 为直角三角形,由勾股定理知2A C '=22AB CD +=2500,所以50A C '=.而在△A 'BC 中,有A 'B =AD =48,有482+142=2500,即A 'B 2+BC 2=A 'C 2,即△A 'BC 为直角三角形.有A CD A BCSS''+130402=⨯⨯114489362+⨯⨯=. 而|ABCD S 四边形A CDA BCSS''=+936=.评注:Ⅰ.本题以∠ABC +∠BDC =900突破口,通过对称变换构造出与原图形相关的角三角形Ⅱ.对于这道题我们还可以将△BCD 作L 的对称图形.如下:C 1lABCD【答案】936【例 12】 如图,在三角形ABD 中,当AB 和CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.DCAB?30°40°【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 因为AB =CD ,于是可以将三角形ABC 的边BA 边与CD 对齐,如下图. 在下图中有∠BCA =110°,所以∠ACD =70°于是∠AC C '=∠ACD +∠DC C '=∠ACD +∠ABC =70°+40°=110°;A 1D C 1C B 1BA即∠AC C '=110°=∠CC D ';又因为C A ''只是CA 移动的变化,所以C A ''=CA ;则ABC A ''是一等腰梯形.于是,∠ADC '=180°-110°=70°;又∠CDC '=30°,所以∠ADC =70°-30°=40°.【答案】40°【例 13】 如图所示的四边形的面积等于多少?DB13131212【考点】平移、旋转、割补 【难度】4星 【题型】解答【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【答案】144【例 14】 如图,三角形ABC 是等腰直角三角形,P 是三角形外的一点,其中90BPC ∠=︒,10cm AP =,求四边形ABPC 的面积.PDCBAP'PDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 因为BAC ∠和BPC ∠都是直角,和为180︒,所以ABP ∠和ACP ∠的和也为180︒,可以旋转三角形APC ,使AC 和AB 重合,则四边形的面积转化为等腰直角三角形'AP P ,面积为1010250⨯÷=平方厘米.【答案】50【例 15】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【答案】10【例 16】 如图,直角梯形ABCD 中,AD BC ∥,AB BC ⊥,2AD =,3BC =,将腰CD以D 为中心逆时针旋转90︒至ED ,连接AE 、CE ,则AD E ∆的面积是 .ED CBAH FEDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】武汉明心奥数【解析】 如图所示,将AD E ∆以D 为中心顺时针旋转90︒,到FDC ∆的位置.延长FD 与BC 交于H .由于ABCD 是直角梯形,AD 与FD 垂直,则四边形ADHB 是长方形,则BH AD =. 由于A D E ∆与FDC ∆面积相等,而FDC ∆的底边2F D A D ==,高321C H B CB H =-=-=,所以FDC ∆的面积为2121⨯÷=,那么AD E ∆的面积也为1.【答案】1【例 17】 如图,正方形ABCD 和DEFG 有一个公共点D ,试比较三角形ADG 和三角形CDE 的面积.GFEDCBAA'GFEDC BA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 因为ADC ∠和GDE ∠是直角,所以ADG ∠和CDE ∠是互补角,将三角形ADG 顺时针旋转90︒到达'A DE ∆的位置,则'A 、D 、C 在同一条直线上,且'A D AD CD ==,即D 是'A C 的中点,所以三角形CDE 和三角形'A D E 面积相等,则三角形CDE 和三角形ADG 面积相等.【答案】相等【例 18】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.F【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】资优杯【解析】 如图,连接DE ,以A 点为中心,将AD E ∆顺时针旋转90︒到ABF ∆的位置. 那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==,所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ). 又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ). 那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ),所以12.52OBE BDE S S ∆∆==(2cm ).【答案】2.5【例 19】 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++= 2cm .EDCBADEC 'A 'CBA【考点】平移、旋转、割补 【难度】5星 【题型】解答 【关键词】迎春杯、高年级、复赛、10题【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系: ''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S∆∆∆∆∆∆++=++==⨯⨯=. 【答案】50【例 20】 如图所示的四边形ABCD 中,45A C ∠=∠=°,105ABC ∠=°,15AB CD ==厘米,连接对角线BD ,30ABD ∠=︒.求四边形ABCD 的面积.DCB A DCBA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】第八届、华杯总决赛【解析】 由45A ∠=°,30ABD ∠=︒,可得1804530A D B ∠=︒-︒-︒=︒,1053075DBC ∠=︒-︒=︒.将DBC ∆剪下来,翻转,再贴在BD 边上,即将B 点粘在D 点上,D 点粘在B 点上,如右上图所示.则C 点在E 点的位置.由于10575180ADB EDB ∠+∠=︒+︒=︒,所以A 、D 、E 三点在同一条直线上.由于45A E C ∠=∠=∠=°,所以90ABE ∠=︒,即ABE ∆是等腰直角三角形,它的面积就等于四边形ABCD 的面积,所以四边形ABCD 的面积为1515112.52⨯=平方厘米. 【答案】112.5【例 21】 如图,在ABD ∆中,AB CD =,求“?”的度数.40°30°?DCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 如图,由于AB CD =,可以将ABC ∆移动到D C E ∆,由于180(3040)110ACB ∠=︒-︒+︒=︒,18011070ACD ∠=︒-︒=︒,所以7040110ACE ∠=︒+︒=︒,又110CED ∠=︒,而AC DE =,所以四边形ACED 是等腰梯形,有180********ADE CED ∠=︒-∠=︒-︒=︒,703040ADC ∠=︒-︒=︒.点评:通过构造全等三角形来转化.【答案】40°【例 22】 下图三角形ABC 是等腰三角形,AB AC =,120BAC ∠=︒.三角形ADE 是正三角形,点D 在BC 边上,:2:3BD DC =.当三角形ABC 的面积是250cm 时,三角形ADE 的面积是多少?EDCBAGR Q F EDCBA【考点】平移、旋转、割补 【难度】5星 【题型】解答【解析】 以点A 为中心,由三个三角形ABC 可拼成右图:连结QE 、RF 、GD ,则DEQFRG 是一个正六边形.连结RD 、DQ 、RQ ,显然RDQ 是一个等边三角形,并且它的面积是正六边形面积的一半,所以是三角形ADE 的面积的3倍. 由于23150cm PBC ABC S S ∆∆=⨯=,根据“鸟头定理”,22336cm 3223DQC PBC S S ∆∆=⨯⨯=++, 所以2342cm RDQ PBC DQC S S S ∆∆∆=-⨯=,则2342314cm ADE RDQ S S ∆∆=÷=÷=. 【答案】14【例 23】 如图,正方形PQRS 有三个顶点分别在ABC ∆的三条边上,BQ QC =.求正方形PQRS 的面积.【考点】平移、旋转、割补 【难度】5星 【题型】解答 【解析】 如下图,我们设ABC∆的面积为1,有161279341()122132111311143a e c db =---+=-⨯-⨯-⨯=, 所以682143a e ==,751143b c d a ++=-=, 所以6875a b c d =++.如下图左,将三角形c 和三角形d 分别以P 、R 为中心按箭头方向旋转90︒,形成由两个直角三角形连在一起的一个四边形,如下图右,b 、c 、d 被虚线分成两个直角三角形,它们的面积之和为:276292230cm b c d ++=⨯÷+⨯÷=,所以2683027.2(cm )75a =⨯=.【答案】27.2【例 24】 如下图,△ABC 是边长为1的等边三角形,△BCD 是等腰三角形BD =CD ,顶角∠BDC =1200,∠MDN =600,求△AMN 的周长.120°60°M BD CNA【考点】平移、旋转、割补 【难度】4星 【题型】解答 【解析】 如下图, 延长AC 至P ,使CP =MB ,连接DP .120°60°M BD PC NA则有∠MBD =600+1163ADEDQRDEQSRT SS S ==正六边形001801202-=∠PCD ;CP =BM ;BD =CD ,所以有△MBD ≌△PCD .于是∠MDC =∠PDC ;又因为∠MDB +∠NDC =600,所以∠PDC +∠NDC =∠NDP =600;MD =PD ,在△MDN 、△PND 中,∠NDM =∠NDP ,ND =ND ,MD =PD ,于是△MND ≌△PND .有MN =PN .因为NP =NP =NC +CP ,而AM =AB -MB =AB -CP , 所以AM +AN +MN =(AB -CP )+AN +(NC +CP )=AB +AN +NC =2.即△AMN 的周长为2. 【答案】2【例 25】 若干个大小相同的正五边形如右图排成环状,下图中所示的只是3个五边形.那么要完成这一圈共需 个正五边形.【考点】平移、旋转、割补 【难度】4星 【题型】解答 【关键词】迎春杯、六年级、初赛、5题【解析】 如图,设O 为圆心,A 、B 、C 、D 为五边形的顶点,连接OA 、OB 、OC .DC BAO从图中可以看出,OAB △和OBC △是完全相同的,所以OBA OBC ∠=∠,又五边形内角和为540°,所以正五边形的每个内角都为5405108÷=°°,即108ABD CBD ∠=∠=°, 那么3601082144ABC ∠=︒-︒⨯=︒,则144272OBA ∠=÷=°°, 又OAB OBA ∠=∠,所以18072236AOB ∠=︒-︒⨯=︒ 所以要用3603610+=°°个正五边形才能围成一圈. 【答案】10【例 26】 如图,ABCD 是矩形,BC =6cm , AB=10cm ,AC 和BD 是对角线,图中的阴影部分以C 为轴旋转一周,则阴影部分扫过的立体的体积是多少立方厘米?(π取3.14)【考点】平移、旋转、割补 【难度】3星 【题型】解答 【关键词】华杯赛、决赛、第11题【解析】 ①设三角形BCO 以CD 为轴旋转一周所得到的立体的体积是s ,S 等于高为10厘米,底面半径是6厘米的圆锥的体积减去2个高为5厘米,底面半径是3厘米的圆锥的体积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A1 B6
B1
A2
B2
A6
A3
B5
B3
A5
B4
A4
4-2-5.平移、旋转、割补 题库
page 2 of 11
【考点】平移、旋转、割补 【难度】5 星 【题型】解答 【关键词】迎春杯、六年级、初赛、14 题 【解析】如图,设 B6 A2 与 B1 A3 的交点为 O ,则图中空白部分由 6 个与 △A2OA3 一样大小的三角形组成,只要
【例 9】 如下左图,有两个大小相同的完全重叠在一起的正方形,现在以点 P 为中心转动一个正方形.当 AB 5 厘米, BC 13 厘米, CA 12 厘米时(如下右图),求右图中的两个正方形相重叠部分的面积 (注意,图的尺寸不一定准确).
P
【考点】平移、旋转、割补 【难度】3 星 【题型】解答 【解析】右图由左图旋转而得,则右图中的 8 个空白小三角形都是完全相同的,右图中重叠部分的面积等于
3
3
⑵ 拼补法
将两个这样的三角形拼成一个平行四边形(下页左上图).显然,图中阴影面积占平行四边形面积的 1 . 3
根据商不变性质,将阴影面积和平行四边形面积同时除以 2 ,商不变.所以原题阴影部分占整个图形 面积的 1 .
3
⑶ 等分法 将原图等分成 9 个小三角形(见右上图),阴影部分占 3 个小三角形,所以阴影部分占整个图形面积的 31. 93 注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条 件不变,结论仍然成立. 【答案】 1 3
腰梯形.于是,∠ ADC =180° 110°=70°;又∠ CDC =30°,所以∠ ADC =70° 30°=40°.
【答案】 40 °
【例 13】 如图所示的四边形的面积等于多少?
【考点】平移、旋转、割补 【难度】4 星 【题型】解答 【解析】题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.
∠ACD=70°于是∠ AC C =∠ ACD +∠ DC C =∠ ACD +∠ ABC =70°+40°=110°;
A
B
D
C
A1
B1
C1
即∠ AC C =110°=∠ CCD ;又因为 CA 只是 CA 移动的变化,所以 CA = CA ;则 ABCA 是一等
4-2-5.平移、旋转、割补 题库
page 5 of 11
重合到图中的 AG 了.这样就组成了一个长方形 BGFD ,它的面积与原六边形的面积相等,显然长 方形 BGFD 的面积为 24 18 432 平方厘米,所以六边形 ABCDEF 的面积为 432 平方厘米. 【答案】 432
【例 5】 如图 2,六边形 ABCDEF 为正六边形, P 为对角线 CF 上一点,若 PBC 、 PEF 的面积为 3 与 4 , 则正六边形 ABCDEF 的面积是 .
A
I
A1
B
D
C
因为∠ABD+∠BDC=9000 而∠ABD=∠ A DB=900,所以有∠ A DB+∠BDC=900.
那么 A CD 为直角三角形,由勾股定理知 AC 2 AB2 CD2 =2500,所以 AC 50 . 而在△ A BC 中,有 A B=AD=48,有 482+142=2500,即 A B2+BC2= A C2,即△ A BC 为直角三角形.
【考点】平移、旋转、割补 【难度】2 星 【题型】解答
【解析】如图所示,将道路平移后的 16 2 10 2 112 。
【答案】112
【例 2】 如图所示,一个正十二边形的边长是 1 厘米,空白部分是等边三角形,一共有 12 个.请算出阴影 部分的面积.
1cm
1cm
1cm
【考点】平移、旋转、割补 【难度】3 星 【题型】解答 【解析】如图,将阴影部分分割成一个正六边形和 12 个小三角形,再把正六边形分割成 6 个正三角形,由于
有
SA ACD
SA ABC
30 40
1 2
14 48
1 2
936 .
而| S四边形ABCD SA ACD SA ABC 936 .
评注:Ⅰ.本题以∠ABC+∠BDC=900 突破口,通过对称变换构造出与原图形相关的角三角形
Ⅱ.对于这道题我们还可以将△BCD 作 L 的对称图形.如下:
A l
B
D
我们可以利用旋转的方法对图形实施变换:
把三角形 OAB 绕顶点 O 逆时针旋转,使长为 13 的两条边重合,此时三角形 OAB 将旋转到三角形 OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12 的正方形,且这个正方形的面积就 是原来四边形的面积. 因此,原来四边形的面积为12 12 144 .(也可以用勾股定理) 【答案】144
正 十 二 边 形 的 每 个 内 角 为 180 12 2 12 150 , 所 以 阴 影 小 三 角 形 的 顶 角 等 于
150 60 2 30 ,每个顶角的两边和与其相邻的正三角形的底边所成的角都是 30 60 90 ,所
以通过如右上图所示的平移可以组成 6 个边长为 1 厘米的正方形,所以所求阴影部分面积为12 6 6 平方厘米. 【答案】 6
△B1 A2 A3 的面积为 2
根据蝴蝶定理, B1O
A O S ∶S 3
△B1 A2 B6
△ A3 A2 B6
1∶6 ,故 S△A2OA3
1
6
6
S△B1
A2
A3
12 7
,
所以
S ∶S △A2OA3
梯形A1A 2 A3 A 6
12∶12∶1∶7 7
,
即
△
A2OA3
的
面
积
为
梯
形
A1 A2 A3 A6 面积的
正方形面积减去 4 个小三角形的面积,从右图中可以看出正方形的边长为 5 13 12 30 厘米,所以 重叠部分的面积为: 302 4 (5 12 2) 780 (平方厘米). 【答案】 780
【例 10】 如图,在直角三角形中有一个正方形,已知 BD 10 厘米, DC 7 厘米,求阴影部分的面积.
【例 3】 如图所示,梯形 ABCD 中, AB 平行于 CD ,又 BD 4 , AC 3 , AB CD 5 .试求梯形 ABCD 的面积.
A
B
A
B
D
C
D
C
E
【考点】平移、旋转、割补 【难度】3 星 【题型】解答
【 解 析 】 如 右 图 , 将 AB 沿 AC 平 移 至 CE ,连 接 BE ,在 三 角 形 BDE 中 , 有 BD 4 , BE AC 3 ,
4-2-5.平移、旋转、割补
例题精讲
图形变换,是指不改变图形的大小、形状,只通过位置关系的改变(旋转、平移、折叠等),构成新的图形. 【例 1】 右图是一块长方形草地,长方形的长是 16,宽是 10.中间有两条道路,一条是长方形,一条是平
行四边形,它们的宽都是 2,求草地部分的面积(阴影部分)有多大?
C
C1
【答案】 936
【例 12】 如图,在三角形 ABD 中,当 AB 和 CD 的长度相等时,请求出“?”所示的角是多少度,给出过程.
A
30°
40°
B
C
? D
【考点】平移、旋转、割补 【难度】5 星 【题型】解答 【解析】因为 AB=CD,于是可以将三角形 ABC 的边 BA 边与 CD 对齐,如下图. 在下图中有∠BCA=110°,所以
4-2-5.平移、旋转、割补 题库
page 4 of 11
【例 11】 四边形 ABCD 中,AB=30,AD=48,BC=14,CD=40.又已知∠ABD+∠BDC=900,求四边形 ABCD 的面积.
A
B
D
C
【考点】平移、旋转、割补 【难度】5 星 【题型】解答
【解析】如下图,以 BD 的垂直平分线为对称轴 L,做△ABD 关于 L 的对称图形△ A BD.连接 A C.
C
D
O
B
E
C B
D
O E
C BP
D E
A
F
图 图 1图
A
F
图 图 2图
所以,由 △PBC 、 △PEF 的面积分别为 3 与 4,
可知正六边形 ABCDEF 的面积是 (3 4) 3 21 .
【答案】 21
A
F
图 图 3图
【例 6】 正六边形 A1A2A3A4A5A6 的面积是 2009 平方厘米,B1,B2,B3,B4,B5,B6 分别是正六边形各边的中点; 那么图中阴影六边形的面积是 平方厘米.
1 7
,故为六边形
A1 A2 A3 A4
A5 A6
面积的
1 14
,那么空白部分的面积为正六边形面积的
1 14
6
3 7
,所以阴影部分面积为
2009
1
3 7Βιβλιοθήκη 1148(平方厘米).
【答案】1148
【例 7】 按照图中的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角 边分别为 2cm 和 4cm ,乙三角形两条直角边分别为 3cm 和 6cm ,求图中阴影部分的面积.
【考点】平移、旋转、割补 【难度】4 星 【题型】解答 【解析】绕 D 点逆时针旋转 CED ,使 E 与 F 重合,则 C 点落在 AB 边上的 C ' 点处,且 C ' D CD .则阴影
部分面积转化为直角三角形 BC ' D 的面积,所以阴影部分的面积为10 7 2 35 平方厘米. 【答案】 35
4-2-5.平移、旋转、割补 题库
