微积分 第四章 第五节 曲线的凸性、拐点与渐近线
合集下载
3.7凸性、拐点及
例1 判断曲线 y x 3 的凹凸性.
解 y 3 x 2 , y 6 x ,
当x 0时， y 0,
曲线 在( ,0]为凸的；
当x 0时， y 0,
曲线 在[0,)为凹的；
注意到, 点(0,0)是曲线由凸变凹的分界 点.
连续曲线上凹凸的分界点称为曲线的拐点.
o
x
o
x
二、曲线凹凸的判定
y
y f ( x)
A
B
y
y f ( x)
B
A
o
a
b
x
o
a
b
x
tan
f ( x ) 递增
y 0
tan
f ( x ) 递减
y 0
定理1 如果 f ( x ) 在 [a , b] 上连续, 在 (a , b ) 内具有
二阶导数 , 若在 ( a , b ) 内 (1) f ( x ) 0, 则 f ( x ) 在 [a , b] 上的图形是凹的; ( 2) f ( x ) 0, 则 f ( x ) 在 [a , b] 上的图形是凸的 .
2 3 5 3
1 4 解 当x 0时, y x , y x , 3 9 x 0是不可导点, y, y均不存在.
但在( ,0)内, y 0, 曲线在( ,0]上是凹的 ; 在(0,)内, y 0, 曲线在[0,)上是凸的.
点(0,0)是曲线 y 3 x的拐点.
8
6
4
2
-15
-10
-5
5
10
15
-2
-4
-6
-8
三、曲线的渐近线
定义（曲线的渐近线）：
微积分课件曲线的凹凸性与拐点
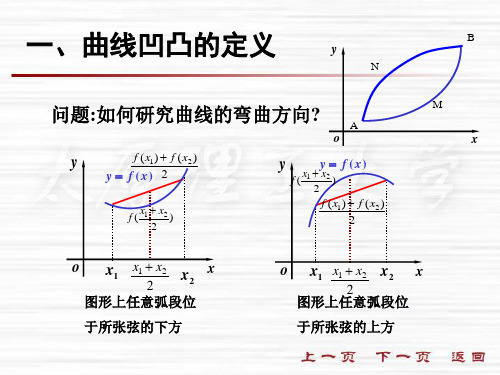
二、曲线凹凸的判定
y
y f ( x)
A
B
y
y f ( x)
B
A
o
a
b
x
o
a
f ( x ) 递增
y 0
f ( x ) 递减
b x y 0
定理1 如果 f ( x ) 在 [a , b] 上连续, 在 (a , b) 内具有
二阶导数 , 若在 (a , b ) 内 (1) f ( x ) 0, 则 f ( x ) 在 [a , b] 上的图形是凹的; ( 2) f ( x ) 0, 则 f ( x ) 在 [a , b] 上的图形是凸的 .
(3) x0两近旁 f ( x)变号,点( x0 , f ( x0 ))即为拐点 ;
x0两近旁 f ( x)不变号 ,点( x0 , f ( x0 ))不是拐点 .
4 3 求曲线 y 3 x 4 x 1 的拐点及 例2 凹、凸的区间 .
解
2 y 12 x 12 x , y 36 x( x ). 3 2 令y 0, 得 x1 0, x2 . 3
如果对(a , b)内任意两点 x1 , x2 , 恒有 x1 x2 f ( x1 ) f ( x2 ) f( ) , 2 2 那末称 f ( x )在(a , b)内的图形是凸的;
y
y f ( x)
A
B
y
y f ( x)
B
A
o
a
b
x
o
a
b
x
曲线上任意一点切线都在曲线弧的下方。 凹弧： 凸弧： 曲线上任意一点切线都在曲线弧的上方。
即证：
f ( 2 ) f (1 ) 0
高数课件-曲线的凹凸性与拐点
4.5 曲线的凹凸性与拐点
4.5.1 曲线的凹凸性 4.5.2 拐点
17-<#>
2021-10-3
前面讨论了函数的单调性和极值．从几何上讲，单调性 反映的是曲线的升降，极值反映的曲线的“峰值”或“谷底”．
单从单调性和极值来研究曲线是不够的．
比如当函数 f x 在某区间单调增加时，其方式是多样的
(见图4-4-6)．具体表现在曲线弯曲的方向不同，有凸有凹．曲 线的这种性态称为凹凸性．
设 f ( x)在(a, b)内二阶可导，且 f ( x0 ) 0 ， 其中 x0 (a, b)，则( x0 , f ( x0 ))是否一定为 曲线 f ( x)的拐点？举例说明.
f
(x0 )
f (1)(x1
x0 )
f (xቤተ መጻሕፍቲ ባይዱ )
1 2
(
x2
x1) f (1) ，
f
(x2 )
f
(x0 )
f
(2 )(x2
x0 )
f
(x0 )
1 2 (x2
x1)
f
(2 ) ．
17-1
续证
2021-10-3
两式相加，从而有
f
(x1)
f
( x2 )
2f
(x0)
x2
2
x1 [
故 0，f 0是曲线 y f x的拐点.选（C）.
17-1
例
f x x x n 假定 ( )在 = 0處具有直到 階的連續導數，且
f ( x0 ) f ( x0 ) f (n1)( x0 ) 0,但 f (n)( x0 ) 0
n 這裏 為奇數>3，
则( x0 , f ( x0 ))是拐点
4.5.1 曲线的凹凸性 4.5.2 拐点
17-<#>
2021-10-3
前面讨论了函数的单调性和极值．从几何上讲，单调性 反映的是曲线的升降，极值反映的曲线的“峰值”或“谷底”．
单从单调性和极值来研究曲线是不够的．
比如当函数 f x 在某区间单调增加时，其方式是多样的
(见图4-4-6)．具体表现在曲线弯曲的方向不同，有凸有凹．曲 线的这种性态称为凹凸性．
设 f ( x)在(a, b)内二阶可导，且 f ( x0 ) 0 ， 其中 x0 (a, b)，则( x0 , f ( x0 ))是否一定为 曲线 f ( x)的拐点？举例说明.
f
(x0 )
f (1)(x1
x0 )
f (xቤተ መጻሕፍቲ ባይዱ )
1 2
(
x2
x1) f (1) ，
f
(x2 )
f
(x0 )
f
(2 )(x2
x0 )
f
(x0 )
1 2 (x2
x1)
f
(2 ) ．
17-1
续证
2021-10-3
两式相加，从而有
f
(x1)
f
( x2 )
2f
(x0)
x2
2
x1 [
故 0，f 0是曲线 y f x的拐点.选（C）.
17-1
例
f x x x n 假定 ( )在 = 0處具有直到 階的連續導數，且
f ( x0 ) f ( x0 ) f (n1)( x0 ) 0,但 f (n)( x0 ) 0
n 這裏 為奇數>3，
则( x0 , f ( x0 ))是拐点
3-5 凹凸性 拐点.渐近线
0
0
f ( x ) 递增
y 0
f ( x ) 递减
y 0
机动
目录
上页
下页
返回
结束
例1. 判断曲线
解: 函数的定义域为
的凹凸性.
1 y , x 1 y 2 x
所以在函数的定义域 由定理1知 曲线
1 内，y 2 0 x
是凸的.
机动
目录
上页
下页
2 x 2 3x b lim [ f ( x) x] lim 2 x x x 2 x 3
y x 2 为曲线的斜渐近线 . 无水平渐近线 .
机动 目录 上页 下页 返回 结束
y 0是曲线的水平渐近线
1 x lim +ln(1+e ) = x 0 x
x 0是曲线的垂直渐近线
机动
目录
上页
下页
返回
结束
1 例3 求曲线y=f(x)= +ln(1+e x )的渐近线 x f ( x) 1 ln(1+e x ) lim 2 + 考虑斜渐近线. lim x x x x x
第五节
第三章
曲线的凹凸性,拐点与渐近线
一、曲线的凹凸性 二、曲线的拐点 三、渐近线
机动
目录
上页
下页
返回
结束
1、曲线凹凸性的概念
定义 . 设函数 在区间 I 上连续 ,
(1) 若恒有
图形是凹的; (2) 若恒有
B
则称
则称
A 图形是凸的 .
yy
oo
x1 x x1 x x1x1 2 2x2x2 x x 2 2
微积分课件3-5曲线的凹凸性与拐点
例3 求曲线 y sin x cos x ([0,2]内) 的拐点.
解 y cos x sin x , y sin x cos x ,
y cos x sin x .
令 y 0, f (3)
4
得
x1
3 4
,
x2
7 4
.
2 0, f (7) 2 0,
2
x2
,
x2
),
f (x2)
f ( x1 x2 ) 2
f (2 )( x2
x1 x2 ) 2
f (2 )
x2 2
x1
两式相加为：
[
f
(x1)
f
(
x1
2
x2
)]
[
f
( x2 )
f
(
x1
2
x2
)]
[
f
(2
)
f
(1 )]
x2
2
x1
(1) f ( x) 0,则 f ( x) 在 [a,b] 上的图形是凹的;
(2) f ( x) 0,则 f ( x) 在 [a,b] 上的图形是凸的.
证明：1） 任取两点 x1, x2( x1 x2 )
分析： 要证 f ( x1 x2 ) f ( x1 ) f ( x2 )
注1:拐点处的切线必在拐点 处穿过曲线. 注2、拐点是用坐标（x0 , f ( x0 ))来表示的， 不同于极值点的表示.
2 拐点的必要条件
定理 2 如果 f ( x)在( x0 , x0 )内存在二阶导
数,则点x0 , f ( x0 )是拐点的必要条件是 f "( x0 ) 0.
曲线的凹凸性、拐点与渐近线
x1 x2 f ( x 1 ) f ( x2 ) f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凸的(凸弧)。 x x y y f( )
如果恒有
1
2
f ( x1 ) f ( x2 ) f ( x1 ) 2 x x2 f( 1 ) 2 x1 x2 2
f ( x2 )
2013-9-12 9
§2.4.2 曲线的凹凸性、拐点与渐近线
注 如果 f ( x) (1)lim 不存在； x x f ( x) (2)lim a , 但 lim[ f ( x ) ax ]不存在， x x x 则可以判断y f ( x )不存在斜渐近线。
2013-9-12
§2.4.2 曲线的凹凸性、拐点与渐近线
1.函数的凹凸性与拐点 定义1：设 f ( x )在区间 I 上连续，如果对于 I 上任意两点 x1 , x2， x1 x2 f ( x 1 ) f ( x2 ) 恒有 f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凹的(凹弧)；
2013-9-12
13
§2.4.2 曲线的凹凸性、拐点与渐近线
x2 例8 求曲线 f ( x ) 的渐近线。 x 1
2013-9-12
14x x 来自则直线 y C 是曲线 y f ( x )的水平渐近线。
(2)垂直渐近线 若曲线 y f ( x )在点 x0处间断，且 lim f ( x ) 或 lim f ( x ) ,
x x0 x x0
则直线 x x0是曲线 y f ( x )的垂直渐近线。 f ( x) (3)斜渐近线 若 lim a , lim[ f ( x ) ax ] b, x x x 则直线y ax b是曲线 y f ( x )的斜渐近线。
如果恒有
1
2
f ( x1 ) f ( x2 ) f ( x1 ) 2 x x2 f( 1 ) 2 x1 x2 2
f ( x2 )
2013-9-12 9
§2.4.2 曲线的凹凸性、拐点与渐近线
注 如果 f ( x) (1)lim 不存在； x x f ( x) (2)lim a , 但 lim[ f ( x ) ax ]不存在， x x x 则可以判断y f ( x )不存在斜渐近线。
2013-9-12
§2.4.2 曲线的凹凸性、拐点与渐近线
1.函数的凹凸性与拐点 定义1：设 f ( x )在区间 I 上连续，如果对于 I 上任意两点 x1 , x2， x1 x2 f ( x 1 ) f ( x2 ) 恒有 f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凹的(凹弧)；
2013-9-12
13
§2.4.2 曲线的凹凸性、拐点与渐近线
x2 例8 求曲线 f ( x ) 的渐近线。 x 1
2013-9-12
14x x 来自则直线 y C 是曲线 y f ( x )的水平渐近线。
(2)垂直渐近线 若曲线 y f ( x )在点 x0处间断，且 lim f ( x ) 或 lim f ( x ) ,
x x0 x x0
则直线 x x0是曲线 y f ( x )的垂直渐近线。 f ( x) (3)斜渐近线 若 lim a , lim[ f ( x ) ax ] b, x x x 则直线y ax b是曲线 y f ( x )的斜渐近线。
微积分4.4曲线的凹凸性、拐点与渐近线
点和阶导数不存在的点; (3) 用(2)中求出的点将函数定义域分成若干个部分区间,
在各个部分区间内讨论二阶导数的符号, 确定曲线是否存在 拐点, 若在拐点, 求出拐点.
例2 判断曲线 y(x1)3 x5 的凸性, 并求其拐点. 解 定 义 域 为 (- ,)
15
而 y 8x5 3 5x2 3, y 10 4 x 1
x -
x
其 中 a 和 b 为 常 数 ,且 a 0 ,则称直线 y = ax + b为曲线
y =ƒ(x) 的斜渐近线. (如图)
y
αM˘•
•
Q
y=ƒ(x)
•
L:y=ax+b
o »α
x
22
分析: 如果曲线 y =ƒ(x)有斜渐近线 y = ax + b, 则由定义知,
必有
lim[f(x)ax]b 或lim [f(x)ax]b
f (x0) 0 或 f ( x0 )不存在.
但是, 若f (x0) 0或 f ( x0 )不存在时, 曲线 y f (x)
上的点 (x0, f (x0))不一定是拐点, 还必须用下面的定理判断.
13
定理4.4.3 (拐点存在的充分条件) 设函数 y = ƒ(x)在 x0 的某邻域内二阶可导 (f(x0)可 以 不 存 在 ),且f(x0)0 或 f(x0)不 存 在 ,
从而, 当 f ( x ) 存在时, 则可用二阶导数的符号来判别
曲线的凹凸性.
6
定理4.4.1 设函数 y = ƒ(x)在 I 内有二阶导数, 则
(1 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凹 的 ；
(2 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凸 的 .
在各个部分区间内讨论二阶导数的符号, 确定曲线是否存在 拐点, 若在拐点, 求出拐点.
例2 判断曲线 y(x1)3 x5 的凸性, 并求其拐点. 解 定 义 域 为 (- ,)
15
而 y 8x5 3 5x2 3, y 10 4 x 1
x -
x
其 中 a 和 b 为 常 数 ,且 a 0 ,则称直线 y = ax + b为曲线
y =ƒ(x) 的斜渐近线. (如图)
y
αM˘•
•
Q
y=ƒ(x)
•
L:y=ax+b
o »α
x
22
分析: 如果曲线 y =ƒ(x)有斜渐近线 y = ax + b, 则由定义知,
必有
lim[f(x)ax]b 或lim [f(x)ax]b
f (x0) 0 或 f ( x0 )不存在.
但是, 若f (x0) 0或 f ( x0 )不存在时, 曲线 y f (x)
上的点 (x0, f (x0))不一定是拐点, 还必须用下面的定理判断.
13
定理4.4.3 (拐点存在的充分条件) 设函数 y = ƒ(x)在 x0 的某邻域内二阶可导 (f(x0)可 以 不 存 在 ),且f(x0)0 或 f(x0)不 存 在 ,
从而, 当 f ( x ) 存在时, 则可用二阶导数的符号来判别
曲线的凹凸性.
6
定理4.4.1 设函数 y = ƒ(x)在 I 内有二阶导数, 则
(1 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凹 的 ；
(2 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凸 的 .
高等数学--4.5曲线凸性、拐点与渐近线
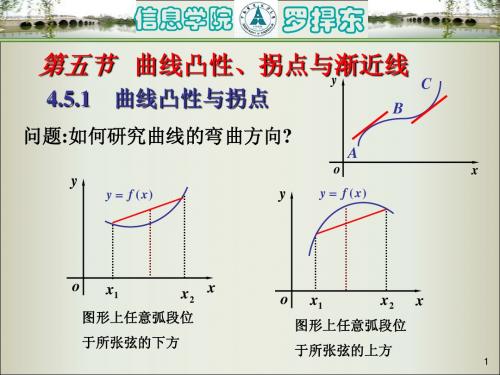
点 ( 0 , 0 ) 是曲线
y
3
x的拐点 .
9
信息学院
考研题欣赏
罗捍东
（2004年3，4）设 f ( x ) x ( x 1) ，则 (A)x=0是f(x)的极值点，但(0,0)不是曲线y=f(x)的拐点。 (B)x=0不是f(x)的极值点，但(0,0)是曲线y=f(x)的拐点。 (C)x=0是f(x)的极值点，且(0,0)是曲线y=f(x)的拐点。
规范的定义：如果函数y=f(x)在(a，b )内任意 两点x1，x2都满足： f ( 则称该曲线为上凸。 足： f ( x
x2 2
x1 x 2 2
)
f ( x1 ) f ( x 2 ) 2
如果函数y=f(x)在(a，b )内任意两点x1，x2都满
1
)
f ( x1 ) f ( x 2 ) 2
( 2 ,0 )
0
不存在
( 0 , )
0
拐点
( 3, 26 9 )
0
间 断 点
23
极值点
3
信息学院
补充点 : ( 1
A ( 1 , 2 ),
罗捍东
(1 3 , 0 );
C ( 2 ,1 ).
B
3 , 0 ),
B ( 1 , 6 ), y
6
作图
1
3
证： f ( x ) 二阶可导 , f ( x ) 存在且连续 ,
又 ( x 0 , f ( x 0 ) ) 是拐点 ,
则 f ( x ) [ f ( x ) ] 在 x 0 两边变号 ,
f ( x ) 在 x 0 取得极值 ,
第五节曲线的凹凸性拐点与渐近线
例3 讨论曲线 f (x) x4 2x3 1 拐点.
解 f ( x)的定义域为(,)
f ( x) 4x3 6x2
f ( x) 12x( x 1)
令 f ( x) 0 得 x 0, x 1
x
f ( x) f (x)
( ,0) 0 (0,1)
0
拐点(0,1)
1 (1, )
0
拐点(1,0)
x0
x0
故有垂直渐近线 x 0.
练习 求曲线
y
(1
1 1
x)e x
的渐近线.
解
(3)
lim
f (x)
lim(1
1
1
)e
1 x
e0
x x
x
x
1 1
lim [ f ( x) ex ] lim[(1 x)e x ex]
x
x
1 1
1 1
1 1
lim[e x x(e x e)] e l i m x(e x e)
例4 讨论曲线 f ( x) ( x 1)3 x5 的凹凸性与拐点 解 f ( x)的定义域为(,)
f
( x)
8
5
x3
5
2
x3
33
令
f
(
x)
0
得
x
1 4
f ( x) 10 4x 1 9 3x
另 f (0) 不存在
x ( ,0) 0
1 (0, )
4
1 4
( 1 , ) 4
f (x)ຫໍສະໝຸດ 不存在 利用凹凸性证明不等式
例2
试证明0
x
时,有
sinx 2
x
.
微积分4-5
x2 x0
由此得
f (x0 )
x2 x0 x2 x1
f (x1)
x0 x1 x2 x1
f (x2 )
而由x0=λx1+(1－λ)x2可得
x2 x0 ,
x2 x1
1 x0 x1
x2 x1
将其代入上式,即得
f (x0) f [x1 (1 )x2] f (x1) (1 ) f (x2)
该曲线的凸区间为(－∞,0)和(0,1), 凹区间为(1,+∞); 拐点为(1,4.6).
判定连续曲线y=f(x)的凸性与拐点的一般步骤是: (1)求出使f''(x) 0 与 f''(x) 不存在的点,并以这些
点为分界点,将函数f(x)的定义域划分为若干个 子空间; (2)按照定理4.10确定曲线y=f(x)在各子区间上的 凸性; (3)讨论拐点:若 f''(x) 在分界点x0的左、右两侧异 号,则点(x0,f(x0))为曲线y=f(x)的拐点;若同号, 则(x0,f(x0))不是拐点.
y''
2 3
x1
3
2 3
x4
3
2 3
(x
1) x 4
3
令y'' 0 ,得x1=1;
在点x2=0,二阶导数y'' 不存在. 以x1=1,x2=0为分界点,将函数定义域
(－∞,+∞)分为三个子区间, 讨论函数在各子
区间上的凹凸性,
区间
(－∞,0)
y''
－
y
0
(0,1)
1
不存在
－
0
不是拐点
拐点
《高等数学》曲线的凹凸性与拐点
曲线的凹凸性与拐点上一节我们利用导数研究了函数的单调性和极值。
函数的单调性反映在图形上，就是曲线的上升和下降，但曲线在上升或下降的过程中还有一个弯曲方向的问题。
例如，图143--中有两条曲线弧，虽然它们都是上升的，但图形却有显著不同，ACB 是向上凸的曲线弧，而ADB 是向上凹的曲线弧，它们的凹凸性不同，接下来我们就来研究曲线的凹凸性及其拐点。
一、曲线凹凸性的定义从几何上看，在有的曲线弧上，如果任取两点，则联结着两点间的弦总位于这两点间的弧段的上方（图)(243a --），而有的曲线弧，则正好相反（图)(243b --）。
曲线的这种性 图143-- 质就是曲线的凹凸性 。
因此曲线的凹凸性可以用联结曲线弧上任意两点的弦的中点与曲线弧上相应点（即具有相同横坐标的点）的位置关系来描述，下面给出曲线凹凸性的定义。
)(a )(b图243--定义1 设)(x f 在区间I 连续，若对于I 上任意两点1x 和2x ，恒有2)()()2(2121x f x f x x f +<+ 则称)(x f 在I 上的图形是（向上）凹的（或凹弧）；若恒有2)()()2(2121x f x f x x f +>+ 则称)(x f 在I 上的图形是（向上）凸的（或凸弧）。
一般情况下，在函数的整个定义域内，其曲线的凹凸性并不一致。
通常把连续曲线上凹弧与凸弧的分界点称为曲线的拐点。
二、曲线凹凸性的判定曲线的凹凸性有明显的几何特征。
当x 逐渐增加时，对于凹曲线，其上每一点的切线斜率是逐渐增加的（如图)(343a --），即导函数)(x f '是单调增加函数；而对于凸曲线，其上每一点的切线斜率是逐渐减少的（如图)(343b --），即导函数)(x f '是单调减少函数。
与此几何特征相对应，有下述判断曲线凹凸性的定理。
)(a )(b图343--定理1 设函数)(x f 在I 内具有一阶和二阶导数，若在I 内 （1）0)(>''x f ，则曲线)(x f 在I 上的图形是凹的； （2）0)(<''x f ，则曲线)(x f 在I 上的图形是凸的。
微积分 第四章 第五节 曲线的凸性、拐点与渐近线
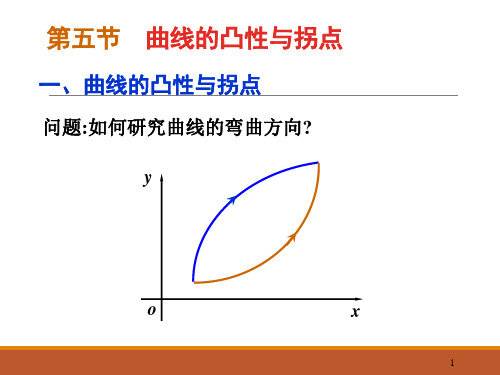
2 3
(23 ,)
f ( x)
0
0
f (x)
下凸
拐点
(0,1)
拐点
上凸 (2 3 ,1127)
下凸
8
拐点的求法：
1.找出二阶导数为零的点或不可导点； 2.若它两侧的二阶导数值异号,则为 拐点；若同号则不是拐点.
注意：拐点要写出纵坐标.
例3 求曲线 y 3 x 的拐点.
解
当x 0时,
y
1
x
2
3,
当x 0时， y 0,
曲线 在 [0,) 为下凸的；
点(0,0)是曲线的拐点.
y
y x3
Ox
7
例2 求曲线 y 3x4 4 x3 1的凹凸区间及拐点.
解 D : (,)
y 12x3 12x2, y 36 x( x 2).
3
令y 0,
得
x1
0,
x2
2. 3
x
(,0)
0
(0, 2 3)
y
2
x
5 3
,
3
9
x 0 是不可导点, y, y 均不存在.
但在(,0)内, y 0, 在(0,)内, y 0,
点(0,0)是曲线 y 3 x的拐点.
9
例4 求 曲 线 y x2 3 的 拐 点.
解
y
2
x
1 3
，y
4
x
4 3
，
3
9
x 0是不可导点, y, y均不存在.
当 x 0 和当 x 0 时,均有 y 0 ,
故 (0, 0) 不是拐点.
所以曲线无拐点.
y
y 3 x2
o
微积分课件3-5曲线的凹凸性与拐点
注1:拐点处的切线必在拐点 处穿过曲线. 注2、拐点是用坐标（x0 , f ( x0 ))来表示的， 不同于Biblioteka 值点的表示.2 拐点的必要条件
定理 2 如果 f ( x)在( x0 , x0 )内存在二阶导
数,则点x0 , f ( x0 )是拐点的必要条件是 f "( x0 ) 0.
凸弧：曲线上任意一点切线都在曲线弧的上方。
二、曲线凹凸的判定
y
y f (x) B
y y f (x)
B
A A
oa
bx
f ( x) 递增 y 0
oa
bx
f ( x) 递减 y 0
定理1 如果 f ( x) 在 [a,b] 上连续,在 (a,b) 内具有
二阶导数 ,若在 (a,b)内
2
2
即证
[
f ( x1 )
f
(
x1
2
x2
)] [
f
( x2 )
f
( x1
2
x2 )]
0
1
(
x1 ,
x1
2
x2
),
f ( x1 )
f ( x1 2
x2 )
f (1 )( x1
x1 x2 ) 2
f (1 )
x1 x2 2
2
(
x1
2
x2
,
x2
),
f (x2)
f ( x1 x2 ) 2
f (2 )( x2
x1 x2 ) 2
f (2 )
x2 2
x1
两式相加为：
[
f
(x1)
定理 2 如果 f ( x)在( x0 , x0 )内存在二阶导
数,则点x0 , f ( x0 )是拐点的必要条件是 f "( x0 ) 0.
凸弧：曲线上任意一点切线都在曲线弧的上方。
二、曲线凹凸的判定
y
y f (x) B
y y f (x)
B
A A
oa
bx
f ( x) 递增 y 0
oa
bx
f ( x) 递减 y 0
定理1 如果 f ( x) 在 [a,b] 上连续,在 (a,b) 内具有
二阶导数 ,若在 (a,b)内
2
2
即证
[
f ( x1 )
f
(
x1
2
x2
)] [
f
( x2 )
f
( x1
2
x2 )]
0
1
(
x1 ,
x1
2
x2
),
f ( x1 )
f ( x1 2
x2 )
f (1 )( x1
x1 x2 ) 2
f (1 )
x1 x2 2
2
(
x1
2
x2
,
x2
),
f (x2)
f ( x1 x2 ) 2
f (2 )( x2
x1 x2 ) 2
f (2 )
x2 2
x1
两式相加为：
[
f
(x1)
简明微积分曲线凹凸与拐点
凹的. (2) 若在(a,b)内 f(x)0，则曲线弧y=f(x)在[a,b]上为
凸的.
例1 判定曲线弧y=xarctan x的凹凸性. 解 所给曲线在 (,)内为连续曲线弧.由于
yHale Waihona Puke rctxa1nxx2, y 1 1 x2 (1 (1 x 2)x 2) x 2 2 x(1 2 x2)2 0 ,
(3)y3 1 3x2 3,y3 9 2x5 3.y3 在 x0处不 . 存在
1
当 x0时 ， y3 0 ， 曲线 y3x3 弧 为凹 . 的
1
当 x0时y3 ， 0 ， 曲线 y3x3 弧 为凸 . 的
1
从而知点(0,0)为曲线弧 y3 x 3 的拐点.
例5 讨论曲线 y(x1)3 x2的凹凸性，并求其拐点.
解 所给函数 在(,)内为连续函数.
52
y[x (1)3x2][x3x3]
2
5x3
2
1
x 3,
33
1 4
4
y1x0 32x31x0 3(x1).
99 9
5
当x0时， y为连续. 函数
当x0时 ,y不存. 在 令 y0，可 x得 1.
(2) 若对于任意的x0(a,b)，曲线弧y=f(x)过点(x0,f(x0)) 的切线总位于曲线弧y=f(x)的上方，则称曲线弧 y=f(x)在[a,b]上为凸的.
如果y=f(x)在(a,b)内二阶可导，则可以利用二阶 导数的符号来判定曲线的凹凸性. 定理(曲线凹凸的判定法) 设函数y=f(x)在[a,b]上连续， 在(a,b)内二阶可导. (1) 若在(a,b)内 f(x)0，则曲线弧y=f(x)在[a,b]上为
(2)y2 5 3x2 3,y2 1 9x 01 3,y2 在 x0处不 . 存在
凸的.
例1 判定曲线弧y=xarctan x的凹凸性. 解 所给曲线在 (,)内为连续曲线弧.由于
yHale Waihona Puke rctxa1nxx2, y 1 1 x2 (1 (1 x 2)x 2) x 2 2 x(1 2 x2)2 0 ,
(3)y3 1 3x2 3,y3 9 2x5 3.y3 在 x0处不 . 存在
1
当 x0时 ， y3 0 ， 曲线 y3x3 弧 为凹 . 的
1
当 x0时y3 ， 0 ， 曲线 y3x3 弧 为凸 . 的
1
从而知点(0,0)为曲线弧 y3 x 3 的拐点.
例5 讨论曲线 y(x1)3 x2的凹凸性，并求其拐点.
解 所给函数 在(,)内为连续函数.
52
y[x (1)3x2][x3x3]
2
5x3
2
1
x 3,
33
1 4
4
y1x0 32x31x0 3(x1).
99 9
5
当x0时， y为连续. 函数
当x0时 ,y不存. 在 令 y0，可 x得 1.
(2) 若对于任意的x0(a,b)，曲线弧y=f(x)过点(x0,f(x0)) 的切线总位于曲线弧y=f(x)的上方，则称曲线弧 y=f(x)在[a,b]上为凸的.
如果y=f(x)在(a,b)内二阶可导，则可以利用二阶 导数的符号来判定曲线的凹凸性. 定理(曲线凹凸的判定法) 设函数y=f(x)在[a,b]上连续， 在(a,b)内二阶可导. (1) 若在(a,b)内 f(x)0，则曲线弧y=f(x)在[a,b]上为
(2)y2 5 3x2 3,y2 1 9x 01 3,y2 在 x0处不 . 存在
高等数学(经济类)3.12函数的凸性,拐点与渐近线
3
所以有垂直渐近线 x 3 及 x 1
又因
a lim x
f (x) x
lim
x
x2
x2 2x
3
b
lim [
x
f
(
x)
x]
lim
x
2x2 x2 2x
3x 3
y x 2为曲线的斜渐近线 .
y x2 1
机动 目录 上页 下页 返回 结束
y
拐点要写成坐标形式 a, f a
a 定o义3-6
设函数
f x
x
定理3-20(凹凸判定法)
设函数 (1) 在 I 内 (2) 在 I 内
在区间I 上有二阶导数 则 在 I 内图形是下凸的 ; 则 在 I 内图形是上凸的 .
机动 目录 上页 下页 返回 结束
例 判断曲线
的凸性.
y
解: y 4x3,
x
x 1
lim 2(x 2)(x 3) 2x(x 1) 4,
x
x 1
y 2x 4 是曲线的一条斜渐近线 .
机动 目录 上页 下页 返回 结束
例 求曲线
的渐近线 .
解 y
x3
, lim y ,
(x 3)(x 1) x3
(或x 1)
上任一点处的切线都在曲线的上方,则称该曲线为向上凸的,
称区间 a,b 为曲线的上凸区间; 如果曲线 y f x
上任一点处的切线都在曲线的下方,则称该曲线为向下凸的,
称区间 a,b 为曲线的下凸区间.
机动 目录 上页 下页 返回 结束
定义3-7 连续曲线上向上凸与向下凸弧线的分界点称 为拐点 .
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当x 0时， y 0,
曲线 在 [0,) 为下凸的；
点(0,0)是曲线的拐点.
y
y x3
Ox
7
例2 求曲线 y 3x4 4 x3 1的凹凸区间及拐点.
解 D : (,)
y 12x3 12x2, y 36 x( x 2).
3
令y 0,
得
x1
0,
x2
2. 3
x
(,0)
0
(0, 2 3)
， ex(1) y e x (1 )e y
取 ，即得 ． 1
ex ey
x y
e 2
2
2
11
故 (0, 0) 不是拐点.
所以曲线无拐点.
y
y 3 x2
o
x
10
利用函数曲线弧的凹凸性可以证 明一些不等式
*例 4
试证明 ex
ey
x y
e 2
，其中 x
y．
2
证 令 y ex ，显然 y ex 0 ，所以 y 在 ex (,) 上是凹的，
据定义有，对于任意 x y 及 (0,1) ，有
第五节 曲线的凸性与拐点
一、曲线的凸性与拐点
问题:如何研究曲线的弯曲方向? y
o
x
1
曲线的上、下凸性就是曲线弯曲的方向.
设 f ( x) 是定义在区间 I 上的函数， P1 , P2 是曲线 C：
y f ( x) ( x I ) 上的任意两点, 线段 P1P2 称为曲线 C 的
弦，C 上介于 P1 , P2 之间的曲线段 P1P2 称为 C 的弧.
y f (x)
o x1 x1 x2 x2
2
xo
x1 x1 x2 x2
2
下凸：f ( x1 x2 ) f ( x1 ) f ( x2 )
2
2
上凸：f ( x1 x2 ) f ( x1 ) f ( x2 )
2
2
x
4
曲线凸性的判定
观察与思考： 曲线的凹向与函数的导数的单调性有什么关系？ 当曲线是下凸时， f (x)单调增加. 当曲线是上凸时， f (x)单调减少.
2 3
(23 ,)
Байду номын сангаас
f ( x)
0
0
f (x)
下凸
拐点
(0,1)
拐点
上凸 (2 3 ,1127)
下凸
8
拐点的求法：
1.找出二阶导数为零的点或不可导点； 2.若它两侧的二阶导数值异号,则为 拐点；若同号则不是拐点.
注意：拐点要写出纵坐标.
例3 求曲线 y 3 x 的拐点.
解
当x 0时,
y
1
x
2
3,
y
C : y f (x)
P2
P1
o
x 2
定义 如果曲线C : y f ( x) ( x I ) 上任意两点P1, P2
的弦 P1P2 总在弧 P1, P2 之下，则称曲线 C 是上凸的；
如果曲线C : y f ( x) ( x I ) 上任意两点P1, P2
的弦 P1P2 总在弧 P1, P2 之上，则称曲线 C 是下凸的.
曲线下凸与上凸的分界点称为曲线的拐点.
拐点
下凸
上凸
5
y
y f (x) B
y f (x)
y
B
A
oa
bx
f ( x) 递增 y 0
A oa
f ( x) 递减
bx y 0
定理 设函数 f ( x) 在[a, b] 上连续，在(a, b) 内
二阶可导.
(1) 如果 f ( x) 0 , x (a, b) ,
y
C : y f (x) P2
y
C : y f (x)
P2
P1
o
x
上凸—凸
P1
o
x
下凸—凹
3
实际上，只要考虑[ x1 , x2 ] 的中点就可以了.
y
y f (x) y
f ( x1 ) f ( x2 )
2
f ( x1 x2 ) 2
f ( x1 x2 ) 2
f ( x1 ) f ( x2 ) 2
y
2
x
5 3
,
3
9
x 0 是不可导点, y, y 均不存在.
但在(,0)内, y 0, 在(0,)内, y 0,
点(0,0)是曲线 y 3 x的拐点.
9
例4 求 曲 线 y x2 3 的 拐 点.
解
y
2
x
1 3
，y
4
x
4 3
，
3
9
x 0是不可导点, y, y均不存在.
当 x 0 和当 x 0 时,均有 y 0 ,
则曲线 y f ( x) 在[a, b] 上是下凸的；
(2) 如果 f ( x) 0 , x (a, b) ,
则曲线 y f ( x) 在[a, b] 上是上凸的. 证略.
6
例1 判断曲线 y x3 的凹凸性.
解 y 3x2, y 6x, 当x 0时，y 0,
曲线 在 (,0] 为上凸的；
曲线 在 [0,) 为下凸的；
点(0,0)是曲线的拐点.
y
y x3
Ox
7
例2 求曲线 y 3x4 4 x3 1的凹凸区间及拐点.
解 D : (,)
y 12x3 12x2, y 36 x( x 2).
3
令y 0,
得
x1
0,
x2
2. 3
x
(,0)
0
(0, 2 3)
， ex(1) y e x (1 )e y
取 ，即得 ． 1
ex ey
x y
e 2
2
2
11
故 (0, 0) 不是拐点.
所以曲线无拐点.
y
y 3 x2
o
x
10
利用函数曲线弧的凹凸性可以证 明一些不等式
*例 4
试证明 ex
ey
x y
e 2
，其中 x
y．
2
证 令 y ex ，显然 y ex 0 ，所以 y 在 ex (,) 上是凹的，
据定义有，对于任意 x y 及 (0,1) ，有
第五节 曲线的凸性与拐点
一、曲线的凸性与拐点
问题:如何研究曲线的弯曲方向? y
o
x
1
曲线的上、下凸性就是曲线弯曲的方向.
设 f ( x) 是定义在区间 I 上的函数， P1 , P2 是曲线 C：
y f ( x) ( x I ) 上的任意两点, 线段 P1P2 称为曲线 C 的
弦，C 上介于 P1 , P2 之间的曲线段 P1P2 称为 C 的弧.
y f (x)
o x1 x1 x2 x2
2
xo
x1 x1 x2 x2
2
下凸：f ( x1 x2 ) f ( x1 ) f ( x2 )
2
2
上凸：f ( x1 x2 ) f ( x1 ) f ( x2 )
2
2
x
4
曲线凸性的判定
观察与思考： 曲线的凹向与函数的导数的单调性有什么关系？ 当曲线是下凸时， f (x)单调增加. 当曲线是上凸时， f (x)单调减少.
2 3
(23 ,)
Байду номын сангаас
f ( x)
0
0
f (x)
下凸
拐点
(0,1)
拐点
上凸 (2 3 ,1127)
下凸
8
拐点的求法：
1.找出二阶导数为零的点或不可导点； 2.若它两侧的二阶导数值异号,则为 拐点；若同号则不是拐点.
注意：拐点要写出纵坐标.
例3 求曲线 y 3 x 的拐点.
解
当x 0时,
y
1
x
2
3,
y
C : y f (x)
P2
P1
o
x 2
定义 如果曲线C : y f ( x) ( x I ) 上任意两点P1, P2
的弦 P1P2 总在弧 P1, P2 之下，则称曲线 C 是上凸的；
如果曲线C : y f ( x) ( x I ) 上任意两点P1, P2
的弦 P1P2 总在弧 P1, P2 之上，则称曲线 C 是下凸的.
曲线下凸与上凸的分界点称为曲线的拐点.
拐点
下凸
上凸
5
y
y f (x) B
y f (x)
y
B
A
oa
bx
f ( x) 递增 y 0
A oa
f ( x) 递减
bx y 0
定理 设函数 f ( x) 在[a, b] 上连续，在(a, b) 内
二阶可导.
(1) 如果 f ( x) 0 , x (a, b) ,
y
C : y f (x) P2
y
C : y f (x)
P2
P1
o
x
上凸—凸
P1
o
x
下凸—凹
3
实际上，只要考虑[ x1 , x2 ] 的中点就可以了.
y
y f (x) y
f ( x1 ) f ( x2 )
2
f ( x1 x2 ) 2
f ( x1 x2 ) 2
f ( x1 ) f ( x2 ) 2
y
2
x
5 3
,
3
9
x 0 是不可导点, y, y 均不存在.
但在(,0)内, y 0, 在(0,)内, y 0,
点(0,0)是曲线 y 3 x的拐点.
9
例4 求 曲 线 y x2 3 的 拐 点.
解
y
2
x
1 3
，y
4
x
4 3
，
3
9
x 0是不可导点, y, y均不存在.
当 x 0 和当 x 0 时,均有 y 0 ,
则曲线 y f ( x) 在[a, b] 上是下凸的；
(2) 如果 f ( x) 0 , x (a, b) ,
则曲线 y f ( x) 在[a, b] 上是上凸的. 证略.
6
例1 判断曲线 y x3 的凹凸性.
解 y 3x2, y 6x, 当x 0时，y 0,
曲线 在 (,0] 为上凸的；