期中复习第一章二次根式复习 2
第一章《二次根式》复习课件

(6)( 2 3) ( 3 2 )( 3 2) ;
(7 ) a b 2ab (a b);
2 2
(8) a
a (a 0).
2
二次根式化简结果的要求: (1)根号内不含有开的尽方的因式; (2)根号内不含有分母.
例5 设a、b、c为△ABC的三边,试化简:
(a b c) (a b c) (b a c) (c a b)
4 5x
2、
x
2
x 3、 x2
4、 x 2 2 x 2
例3 填空: 1、当x=-8时,9 2x 的值等于 2、若 y x 2 2 x 6, 则x y
2 ,则x= 3、若二次根式 x 的值等于
2
(二)二次根式的性质.
a(a 0) ( a 0 ) a 2 性质2:a = a -a (a 0) 性质1 :a
D
B
C
例 如图,在长方形ABCD中,CE⊥BD, E为垂足,连接AE,已知AB=8,BC=6, 试求△CED的面积. C D
E
A B
; / 天龙八部私服
姐,听妹妹の劝吧,逃得远远の,躲到天涯海角去,妹妹这辈子就是这各样子咯,可是姐姐,您应该有自己の幸福,也壹定会有自己の 幸福!”“凝儿!姐姐也已经陷咯进来,再也没有咯退路。”玉盈痛苦地说完这句话,连看都不敢再看水清。水清却是根本没有发现玉 盈の失态,她还在不停地自责:假如不是自己,姐姐怎么可能用丫环の身份同行,还要为自己去受这么大の罪?就在两各人各自想着心 事の时候,秦顺儿の声音在门外响起:“启禀侧福晋,年仆役今天收拾爷の屋子,现在爷の壹封信不知道收到哪里去咯,爷着急要 用。”“秦公公,姐姐の手都已经伤成咯这各样子,爷也是知道の。”水清要被王爷给气疯咯!姐姐都伤成咯这各样子,爷还不肯放 过?有啥啊天大の事情,对受咯这么重伤の姐姐还要求当差劳作?难道爷支使她们年家の人就这么随心所欲吗?姐姐是啥啊身份?她并 不是王府の丫环,更不是爷の侍妾!按礼制来讲,姐姐是王府の客人!爷这各最讲理の人,难道连这么浅显の待客之道都不清楚吗?更 不要说姐姐の手已经伤成咯这各样子!第壹卷 第265章 关切玉盈壹听说刚刚收拾屋子の时候把爷の哪封信放错咯地方,心中立即又是 焦急不安又是万分愧疚。明明是自己有错在先,现在听到水清这么态度生硬地回复秦公公,假如被爷知道咯,又会少不咯冲突,于是赶 快跟秦顺儿回复道:“多谢秦公公,我这就过去。”水清壹听,壹脸の不高兴:“姐姐,人善被人欺,马善被人骑。爷就是看咱们年家 人好欺负,才敢这么做。怎么对福晋姐姐、李姐姐她们,爷从来都不会这样呢?”“凝儿,这不是姐姐有错在先嘛,福晋和李姐姐啥啊 时候能做错过事情?我去看看就回来咯,又不是真要做啥啊事情,无非是把那封信找出来就是咯。”“姐姐,您可壹定要当心,万不可 被抓住咯把柄,爷可是借题发挥、强词夺理の老手!”“你呀,就放心吧。”说完,玉盈就赶快出咯帐子。说完,玉盈就赶快出咯帐子。 其实她也有点儿拿不定主意,刚刚听到秦顺儿の禀报,她第壹各反应是他真の在找啥啊信,可是出咯帐子,看着秦顺儿の表情,又不像 是有啥啊急事の样子,这让她の心情有些忐忑起来。听到秦顺儿将胡太医の诊治情况详细地汇报壹番,王爷の壹颗心才算是踏实下来。 可是,虽然如此,他还是想看看她の伤情,是不是真の如秦顺儿所说,挑破咯水泡,涂上药膏就能慢慢好起来。但是,他断断不会去水 清の帐子,他不想让玉盈误会,他与水清有啥啊说不清道不明の事情。他不过去,也只有请玉盈过来壹趟咯,看咯伤情,他才能完完全 全地安心。玉盈进咯他の帐子,刚要俯身请安,他立即上前壹步赶快扶住咯她の双肩:“快起来,快起来,治得怎么样咯?快让
第一章_二次根式单元复习与巩固
二次根式单元复习与巩固一、知识框图二、目标认知学习目标1.理解二次根式的概念,了解被开方数必须是非负数的理由;2.了解最简二次根式的概念;3.理解并掌握下列结论:(1);(2);(3);4.掌握二次根式的加、减、乘、除运算法则,会用它们进行有关实数的简单四则运算;5.了解代数式的概念,进一步体会代数式在表示数量关系方面的作用.学习重点1.二次根式(a≥0)的内涵.(a≥0)是一个非负数;;及其运用;2.二次根式乘除法的规定及其运用;3.最简二次根式的概念;4.二次根式的加减运算.学习难点1.对(a≥0)是一个非负数的理解;对等式及的理解及应用;2.二次根式的乘法、除法的条件限制;3.利用最简二次根式的概念把一个二次根式化成最简二次根式.三、知识要点梳理知识点一、二次根式的主要性质:1.;2.;3.;4. 积的算术平方根的性质:;5. 商的算术平方根的性质:.6.若,则.知识点二、二次根式的运算1.二次根式的乘除运算(1) 运算结果应满足以下两个要求:①应为最简二次根式或有理式;②分母中不含根号.(2) 注意知道每一步运算的算理;(3) 乘法公式的推广:2.二次根式的加减运算先化为最简二次根式,再类比整式加减运算,明确二次根式加减运算的实质;3.二次根式的混合运算(1) 对二次根式的混合运算首先要明确运算的顺序,即先乘方、开方,再乘除,最后算加减,如有括号,应先算括号里面的;(2) 二次根式的混合运算与整式、分式的混合运算有很多相似之处,整式、分式中的运算律、运算法则及乘法公式在二次根式的混合运算中也同样适用.四、规律方法指导怎样快速准确地进行二次根式的混合运算.1.明确运算顺序,先算乘方,再算乘除,最后算加减,有括号先算括号里面的;2.在二次根式的混合运算中,原来学过的运算律、运算法则及乘法公式仍然适用;3.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能收到事半功倍的效果.(1) 加法与乘法的混合运算,可分解为两个步骤完成,一是进行乘法运算,二是进行加法运算,使难点分散,易于理解和掌握.在运算过程中,对于各个根式不一定要先化简,可以先乘除,进行约分,达到化简的目的,但最后结果一定要化简.例如,没有必要先对进行化简,使计算繁琐,可以先根据乘法分配律进行乘法运算,,通过约分达到化简目的;(2) 多项式的乘法法则及乘法公式在二次根式的混合运算中同样适用.如:,利用了平方差公式.所以,在进行二次根式的混合运算时,借助乘法公式,会使运算简化经典例题精析类型一、二次根式的概念与性质1.x是怎样的实数时,下列各式在实数范围内有意义?(1);(2);(3).【变式1】已知,求的值.2.根据下列条件,求字母x的取值范围:(1);(2).【变式1】把根号外的因式移到根号内,得()A.B.C.D.3.在实数范围内因式分解.(1);(2).【变式1】化简得( )A.2B.-4x-4C.-2D.4x-4类型二、二次根式的混合运算4.计算:(1);(2);(3);(4).举一反三【变式1】计算【变式2】计算:(1)(2)【变式3】先观察下列分母有理化:,从计算结果中找出规律,再利用这一规律计算下列式子的值:.类型三、二次根式的化简求值5.已知a、b、c为△ABC的三边长,化简类型四、二次根式的比较大小6.比较大小.(1)与;(2)与;(3)与;(4)与;(5)与.类型五、二次根式的综合应用7.某人用一架不等臂天平称一块铁a的质量,把铁块放在天平左盘时,称得它的质量为300克;把铁块放在天平右盘时,称得它的质量为900克,利用所学知识,求这块铁的实际质量.(保留到个位)解:设这块铁的实际质量为x克,天平的左、右臂的长分别为m,n.铁块放在天平左盘时,铁块放在天平右盘时,上下两式相乘,得解得答:这块铁的实际质量约为520克.8.已知:如图,每个小方格的边长都为1,则点C到线段AB所在直线的距离等于多少?解:链接AC、BC,AB的长为,设AB边上的高为h,则即点C到线段AB所在直线的距离等于.总结升华:对于此类问题,要注意勾股定理的应用.注意结合图形发现解决问题的办法,即利用数形结合的思想.。
(完整版)二次根式复习.doc

二次根式小结与复习【主要内容】本单元是在学习了平方根和算术平方根的意义的基础上,引入一个符号“”.主要内容有:( 1)二次根式的有关概念,如:二次根式定义、最简二次根式、?同类二次根式等;( 2)二次根式的性质;(3)二次根式的运算,如:二次根式的乘除法、二次根式的加减法等.【要点归纳】1. 二次根式的定义:形如的式子叫二次根式,其中叫被开方数,只有当是一个非负数时,才有意义.2.二次根式的性质:①②③④3.二次根式的运算二次根式的运算主要是研究二次根式的乘除和加减.( 1)二次根式的加减:需要先把二次根式化简,然后把被开方数相同的二次根式(即同类二次根式)的系数相加减,被开方数不变。
注意:对于二次根式的加减,关键是合并同类二次根式,通常是先化成最简二次根式,再把同类二次根式合并.但在化简二次根式时,二次根式的被开方数应不含分母,不含能开得尽的因数.(2)二次根式的乘法:(3)二次根式的除法:注意:乘、除法的运算法则要灵活运用,在实际运算中经常从等式的右边变形至等式的左边,同时还要考虑字母的取值范围,最后把运算结果化成最简二次根式.(4)二次根式的混合运算:先乘方(或开方),再乘除,最后加减,有括号的先算括号里面的;能利用运算律或乘法公式进行运算的,可适当改变运算顺序进行简便运算.注意:进行根式运算时,要正确运用运算法则和乘法公式,分析题目特点,掌握方法与技巧,以便使运算过程简便.二次根式运算结果应尽可能化简.另外,根式的分数必须写成假分数或真分数,不能写成带分数.例如不能写成.【难点指导】1、如果是二次根式,则一定有;当时,必有;2、当时,表示的算术平方根,因此有;反过来,也可以将一个非负数写成的形式;3、表示的算术平方根,因此有,可以是任意实数;4、区别和的不同:中的可以取任意实数,中的只能是一个非负数,否则无意义.5、简化二次根式的被开方数,主要有两个途径:( 1)因式的内移:因式内移时,若,则将负号留在根号外.即:.( 2)因式外移时,若被开数中字母取值范围未指明时,则要进行讨论.即:6、二次根式的比较:( 1)若,则有;(2)若,则有.说明:一般情况下,可将根号外的因式都移到根号里面去以后再比较大小.二次根式强化训练与复习巩固自测试题1.化简:______;_________.2 .当______时,.3 .等式成立的条件是 ______.4 .当,化简_______.5.比较与的大小: _______.6.分母有理化:( 1)__________;( 2)__________;( 3)__________.7.已知,,,那么________.8.计算_________.9.如果,那么的值为___________.10.若有意义,则的取值范围是___________.1.下式中不是二次根式的为()A .;B .;C.; D .2.计算得()3.若,则化简等于()4.化简的结果是()5.计算的结果是()6.化简的结果是()7.把式子中根号外的移到根号内,得()A .B.C. D .8.等式成立的条件是()9.的值为()10.若代数式有意义,则的取值范围是()(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)求值题:1.已知:,求的值.2.已知,求的值。
第1章《二次根式》复习课

3.在△ABC中,已知AB=1,AC= 2, ∠C=30°,∠ABC=45°,求△ABC的面积。
ABΒιβλιοθήκη C3.在△ABC中,已知AB=1,AC= 2,
∠C=30°,∠ABC=45°,求△ABC的面积。
解:如图所示,过点A作AD⊥BC,
A
垂足为D.
二次根式复习课
知识点1:二次根式的概念
a 一般地,我们把形如 (a≥0)的式子叫做
二次根式,事实上 a 表示非负数的算术平方根。
1、下列式子中,哪些是二次根式?哪些不是二次根式?
1√ 42
x3 24
√
x2√ 25
56
32
√
二次根式必须具备以下2个条件:
(1)必须有二次根号; (2)被开方数必须保证大于或等于0。
∵ AB=1,∠ABC=45°
AD⊥BC
∴AD=BD=
2 2
B
D
C
又∵AC= 2 ,∠C=30°,
CD
3AD 6 2
BC BD CD
2 2
6
SABC
1 AD BC 1
2
2
2 2
2 2
6 1 3 4
y
C
4.在平面直角坐标系中,
四边形OABC是等腰梯形, BC//OA,OA=10,AB=4,∠COA=45°,
和为7,AD2-CG2=3,求AC与EF的乘积.
E
D
<分析>
本例先设两个正方形的面 G F
积为a,b,则它们的边长分别
可用 a, b 表示.
AB
C
这样利用图形的性质就得到以a,b为未知数的
数学九年级上册知识点必看

数学九年级上册知识点必看各个科目都有自己的学习方法,但其实都是万变不离其中的,基本离不开背、记,运用,数学作为最烧脑的科目之一,也是一样的。
下面是小编给大家整理的一些数学九年级上册知识点的学习资料,希望对大家有所帮助。
九年级上册数学知识点总结第一章二次根式1 二次根式:形如 ( )的式子为二次根式;性质: ( )是一个非负数;2 二次根式的乘除:3 二次根式的加减:二次根式加减时,先将二次根式华为最简二次根式,再将被开方数相同的二次根式进行合并。
4 海伦-秦九韶公式:,S是三角形的面积,p为。
第二章一元二次方程1 一元二次方程:等号两边都是整式,且只有一个未知数,未知数的次是2的方程。
2 一元二次方程的解法配方法:将方程的一边配成完全平方式,然后两边开方;公式法:因式分解法:左边是两个因式的乘积,右边为零。
3 一元二次方程在实际问题中的应用4 韦达定理:设是方程的两个根,那么有第三章旋转1 图形的旋转旋转:一个图形绕某一点转动一个角度的图形变换性质:对应点到旋转中心的距离相等;对应点与旋转中心所连的线段的夹角等于旋转角旋转前后的图形全等。
2 中心对称:一个图形绕一个点旋转180度,和另一个图形重合,则两个图形关于这个点中心对称;中心对称图形:一个图形绕某一点旋转180度后得到的图形能够和原来的图形重合,则说这个图形是中心对称图形;3 关于原点对称的点的坐标第四章圆1 圆、圆心、半径、直径、圆弧、弦、半圆的定义2 垂直于弦的直径圆是轴对称图形,任何一条直径所在的直线都是它的对称轴;垂直于弦的直径平分弦,并且平方弦所对的两条弧;平分弦的直径垂直弦,并且平分弦所对的两条弧。
3 弧、弦、圆心角在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
4 圆周角在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。
5 点和圆的位置关系点在圆外点在圆上 d=r点在圆内 d 定理:不在同一条直线上的三个点确定一个圆。
第1部分 第1章 第2节 二次根式及其运算

第二节二次根式及其运算知识点考点分值考频等级考查难度常见题型二次根式及其运算二次根式的概念3~4分☆☆☆☆易选择题、填空题二次根式的性质3~6分☆☆☆☆易选择题、填空题最简二次根式3~4分☆☆☆☆☆易选择题、填空题二次根式的运算3~6分☆☆☆☆☆易选择题、填空题、解答题考点一:二次根式的概念核心点拨1.二次根式定义:一般地形如a(a≥0)的式子叫做二次根式,a叫做被开方数.(1)被开方数可以是数字、字母,也可以是代数式.(2)二次根式有意义的条件:被开方数一定是非负数.考点二:二次根式的性质核心点拨2.双重非负性(1)a(a≥0)中的a是非负数.二次根式的被开方数及结果都不能是负数.(2)a(a≥0)的值是非负数.3.运算性质(1)a2=⎩⎨⎧a(a≥0),-a(a<0).a2和(a)2二者a的取值范围不同,a2中a可取全体实数,(a)2中a一定是非负数.(2)(a)2(a≥0)=a.考点三:最简二次根式核心点拨4.最简二次根式,最简二次根式满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.最简二次根式的两个条件缺一不可.考点四:二次根式的运算核心点拨5.二次根式的运算(1)二次根式的乘除:①a·b=ab(a≥0,b≥0);②ab=ab(a≥0,b>0).(1)二次根式的乘除主要用于乘除运算.(2)积、商的算术平方根主要用于二次根式的化简.(2)积、商的算术平方根:①a·b=a·b(a≥0,b≥0);②ab=ab(a≥0,b>0).(3)二次根式的加减:先将二次根式化成最简二次根式,再将被开方数相同的二次根式合并.1二次根式的概念基础点(2021·岱岳区期末)若式子x+1x有意义,则实数x的取值范围为____________.(1)根据二次根式有意义的条件确定x+1的范围;(2)再结合分式有意义的条件确定x的取值范围.x≥-1且x≠0解析:要使式子x+1x有意义,必须x+1≥0且x≠0,解得x≥-1且x≠0.故答案为x≥-1且x≠0.1-1(2021·内江)函数y=2-x+1x+1中,自变量x的取值范围是( )A.x≤2B.x≤2且x≠-1C.x≥2D.x≥2且x≠-1B解析:由题意得:2-x≥0,x+1≠0,解得x≤2且x≠-1.故选B.1-2(2022·新泰检测)若代数式x+1有意义,则实数x的取值范围是________.x≥-1解析:∵代数式x+1有意义,∴x+1≥0.∴x≥-1.故答案为x≥-1.1-3(2022·滨州)若二次根式x-5在实数范围内有意义,则x的取值范围为___________.x≥5解析:由题意知x-5≥0,解得x≥5.故答案为x≥5.与二次根式有关的取值原则1.二次根式有意义,被开方数一定是非负数.2.若分母中有二次根式,则被开方数只能大于0.3.在既有二次根式,又有分式的代数式中确定取值范围,一定要考虑所有的限制条件.2二次根式的性质及化简能力点(2022·宁阳检测)实数a,b在数轴上的位置如图所示,化简(a+1)2+(b-1)2-(a-b)2的结果是( )A.-2B.0C.-2a D.2b(1)根据a2=|a|化简;(2)绝对值化简即可.A解析:由数轴可知-2<a<-1,1<b<2,∴a+1<0,b-1>0,a-b<0.∴(a+1)2+(b-1)2-(a-b)2=||a+1+||b-1-||a-b=-(a+1)+(b-1)+(a-b)=-2.故选A.2-1(2022·肥城月考)计算(27-12)×13的结果是()A.33B.1C. 5 D.3B解析:(27-12)×1 3=9-4=3-2=1.故选B.2-2(2021·杭州)下列计算正确的是( )A.22=2B.(-2)2=-2C.22=±2D.(-2)2=±2A解析:22=4=2,故A正确,C错误;(-2)2=2,故B,D错误.故选A.2-3(2022·舟山)估计6的值在()A.4和5之间B.3和4之间C.2和3之间D.1和2之间C解析:∵4<6<9,∴ 2<6<3.故选C.2-4(2022·新泰模拟)估计3×(23+5)的值应在()A.10和11之间B.9和10之间C.8和9之间D.7和8之间B解析:3×(23+5)=6+15.∵9<15<16,∴ 3<15<4.∴9<6+15<10.故选B.a2和(a)2的区别:1.a的取值范围不同:a2中的a是全体实数;(a)2中的a只能是非负数.2.运算顺序不同:a2是先平方,再开方;(a)2是先开方,再平方.3.运算结果不同:a2=||a;(a)2=a.3最简二次根式基础点(2022·宁阳月考)将452化为最简二次根式,其结果是( )A.452B.902C.9102D.3102(1)被开方数分子、分母同乘2,化为;(2)把开方出来.D解析:452=904=94×10=3102.故选D.3-1(2022·泰山区期末)下列根式中,是最简二次根式的是( )A.19B.4C.a2D.a+1D解析:A.19=13;B.4=2;C.a2=|a|;D.a+1是最简二次根式.故选D.3-2(2021·重庆A卷)计算14×7-2的结果是( ) A.7B.62C.72D.27B解析:14×7-2=2×7×7-2=72-2=62.故选B.4二次根式的运算基础点考向1| 二次根式的乘除(2022·宁阳一模改编)计算:45÷33×3 5.(1)按照从左到右的顺序进行运算;(2)结果化成最简二次根式.1解析:原式=13×15×35=13×15×35=13×9=1.4-1等式x+2x-2=x+2x-2成立的条件是( )A.x≠2B.x≥-2 C.x≥-2且x≠2D.x>2D解析:x+2x-2=x+2x-2成立的条件是x-2>0,得x>2.故选D.4-2(2021·岱岳区检测)计算18×12的结果是( )A.6B.62C.63D.66D解析:18×12=32×23=66.故选D.4-3(2022·天津)计算(19+1)(19-1)的结果等于_______.18解析:(19+1)(19-1)=(19)2-12=19-1=18.故答案为18.4-4计算:27×50÷26.答案:15 2解析:原式=33×52÷26 =156÷26=152.考向2| 二次根式的混合运算(2021·临沂)计算:│-2│+⎝ ⎛⎭⎪⎫2-122-⎝ ⎛⎭⎪⎫2+122.(1)去绝对值,利用完全平方公式运算; (2)进行加减运算. 答案:-2解析:原式=2+2-2+14-2-2-14=-2.5-1 (2022·东平模拟)计算:2×3-24=________. -6 解析:原式=6-26=-6. 故答案为-65-2 (2021·威海)计算:24-65×45=________.-6 解析:原式=26-65×35 =26-36=-6. 故答案为-6.5-3 (2022·泰山区检测)计算:3-25=________. -2 解析:原式=3-5=-2. 故答案为-2.二次根式的运算法则1.二次根式的运算顺序与实数的运算顺序相同.2.二次根式的乘除常结合积的算术平方根和商的算术平方根的性质,将二次根式化简成最简二次根式后再运算.3.二次根式的加减可类比整式的加减进行,也可认为是合并同类二次根式.4.二次根式的运算结果一定要化成最简二次根式,分母中也不能有根式.二次根式的概念和运算命题点1| 二次根式的有关概念1.(2022·东平检测)下列各式中,一定是二次根式的是()A.--2B.a2+1C.a-1 D.3 3B解析:A.根号下不能是负数,故A选项不合题意;B.a2+1≥1,故B选项符合题意;C.当a<1时,a-1<0,此时根号下是负数,故C选项不合题意;D.33是3的立方根,不是二次根式,故D选项不合题意.故选B.2.(2022·宁阳检测)已知二次根式2x+1,则x的最小值是() A.0 B.-1C.12D.-12D解析:由题意得:2x+1≥0,解得x≥-12.∴x的最小值为-12.故选D.3.(2021·绥化)若式子x0x+1在实数范围内有意义,则x的取值范围是()A .x >-1B .x ≥-1且x ≠0C .x >-1且x ≠0D .x ≠0C 解析:若x 0x +1在实数范围内有意义, 则⎩⎪⎨⎪⎧x ≠0,x +1>0.解得x >-1且x ≠0.故选C . 4.(2022·滨州)若二次根式x -5在实数范围内有意义,则x 的取值范围为________.x ≥5 解析:由题意知,x -5≥0, 解得x ≥5. 故答案为x ≥5. 5.(2022·宁阳检测)若y =x -4+4-x 2-2,则(x +y )y=________.14 解析:由题意得:⎩⎪⎨⎪⎧x -4≥0,4-x ≥0, ∴ x =4.∴ y =-2. ∴ (x +y )y =(4-2)-2=14. 故答案为14.6.已知y =x -20+30-x ,且x 、y 均为整数,则x +y =______. 25或33 解析:由题意得:⎩⎪⎨⎪⎧x -20≥0,30-x ≥0,解得20≤x ≤30. ∵ x ,y 均为整数, ∴ x =21或29.当x=21时,y=4,x+y=25;当x=29时,y=4,x+y=33.故答案为25或33.命题点2| 二次根式的性质及化简1.(2022·岱岳区月考)当x>2时,(2-x)2=()A.2-x B.x-2C.2+x D.±(x-2)B解析:∵x>2,∴ 2-x<0.∴(2-x)2=x-2.故选B.2.化简(-5)2的结果是()A.-5B.5C.±5D.25B解析:(-5)2=5.故选B.3.(2022·东平检测)若(a-3)2=3-a,则实数a的取值范围是() A.a<3 B.a≤3C.a>3 D.a≥3B解析:∵(a-3)2=3-a=-(a-3),∴a-3≤0.∴a≤3.故选B.4.实数7不可以写成的形式是()A.72B.-72C.(-7)2D.(-7)2B解析:∵72=(-7)2=(-7)2=7,-72=-7,∴ 7不可以写成-72的形式.故选B.5.(2021·娄底)2,5,m 是某三角形三边的长,则(m -3)2+(m -7)2等于( )A .2m -10B .10-2mC .10D .4D 解析:∵ 2,5,m 为三角形的三边长,∴ 5-2<m <5+2.即3<m <7.∴ m -3>0,m -7<0.∴ (m -3)2+(m -7)2=m -3+7-m =4.故选D .6.(2022·贺州)若实数m ,n 满足 ∣m -n -5∣+2m +n -4=0,则 3m +n =__________.7 解析:∵ m ,n 满足 ∣m -n -5∣+2m +n -4=0,∴ m -n -5=0,2m +n -4=0.∴ m =3,n =-2.∴ 3m +n =9-2=7.故答案为7.7.(2022·新泰模拟)如果实数a ,b ,c 在数轴上的位置如图所示,那么代数式a 2-||a +b +(c -a )2+||b +c 可以化简为( )A .2c -aB .2a -2bC .-aD .a C 解析:由数轴可得b <a <0<c ,|b |>|c |.∴ 原式=-a -[-(a +b )]+c -a +[-(b +c )]=-a +a +b +c -a -b -c =-a .故选C .命题点3| 二次根式的运算1.(2021·梧州)下列计算正确的是()A.12=3 2 B.2+3=5C.62=3D.(2)2=2D解析:A.12=23,该选项错误;B.2和3不是同类二次根式,无法合并,该选项错误;C.62是最简二次根式,无法化简,该选项错误;D.(2)2=2,该选项正确.故选D.2.(2022·肥城模拟)如果ab>0,a+b<0,那么下面各式:①ab=ab,②ab·ba=1, ③ab÷ab=-b.其中正确的是()A.①②B.②③C.①③D.①②③B解析:∵ab>0,a+b<0,∴a<0,b<0.①等号右边根号下为负数,错误;②ab·ba=ab·ba=1,正确;③ab÷ab=ab÷ab=ab×ba=b2=-b,正确.故选B.3.下列二次根式中,不能与2合并的是()A.12B.8C.12 D.18C解析:12=22,8=22,12=23,18=32,∴不能与2合并的是12.故选C.4.(2021·常德)计算:(5+12-1)·5+12=()A.0B.1C.2D.5-1 2B解析:原式=(5+1-22)×5+12=5-12×5+12=1.故选B.5.(2022·河北)下列正确的是()A.4+9=2+3 B.4×9=2×3C.94=32D. 4.9=0.7B解析:A.原式=13,故该选项不符合题意.B.原式=4×9=2×3,故该选项符合题意.C.原式=(92)2=92,故该选项不符合题意.D.0.72=0.49,故该选项不符合题意.故选B.6.(2022·泰山区模拟)计算:27·83÷12=______.12解析:原式=33×223×2=12.故答案为12.7.计算:45-25×50=______.5解析:原式=35-25×50=35-20=35-25=5.故答案为5.8.(2022·东平月考)若x=3-2,则代数式x2-6x+9的值为______.2解析:x2-6x+9=(x-3)2=(3-2-3)2=(-2)2=2.故答案为2.。
课题3期中复习:二次根式

课题3 期中复习(二次根式复习)复习目标:1、掌握二次根式运算法则并能熟练进行二次根式的运算2、能用算术平方根的性质进行二次根式的化简 复习重点:二次根式的化简与计算. 复习难点:二次根式的化简与计算. 复习过程:一、 知识要点:1.同类二次根式: 化简后被开方数相同的二次根式. 2.二次根式的性质:①)0(≥a a 是一个非负数; ②)0()(2≥=a a a③⎪⎩⎪⎨⎧<-=>==)0()0(0)0(||)(2a a a a a a a ④)0,0(>≥=b a bab a ⑤)0,0(≥≥⋅=b a b a ab3.二次根式的运算:(1)加、减;(2)乘、除二、例题分析: 例1.下列二次根式27,121,211,12,其中与3是同类二次根式的个数是( )(A)1 (B)2 (C)3 (D)4例2.若最简二次根式2431212-+-a a 与是同类二次根式,求a 的值。
例3.化简:(1)2)23(-; (2)当a≤|12|441,212-++-a a a 化简时(3)已知a 为实数,化简a a a 13---, (4)化简二次根式a 21aa +-, 例4:把根号外的因式移到根号内:(1)aa1; (2)11)1(---x x ; (3)xx 1-; (4) 21)2(--x x例5.计算:1、()5.043()4483181---2、)23(6)13()26(+÷--⋅+3、)2131(15+÷三、小 结:归纳二次根式计算与化简的思路与方法。
四、巩固练习: 1.化简二次根式22a a a +-的结果是( ) A .2--a B.2---a C.2-a D.2--a22,则a 的取值范围是( )A .a ≥4B .a ≤2C .2≤a ≤4D .a =2或a =43.在下列各式中,化简正确的是( )A B ±12C 2D .4的结果是( )A .-3 B . C .-3 D . 二、填空题1.(x ≥0)2._________.三、计算题 1、221223+- 2、3222233--+ 3、32218+- 4、2735、()()13132+- 6、222333---四、解答下列各题1、若()1222+-=x y ,且y 的算术平方根是5,求:y x 2+的值2、当121-=x 时,求12+-x x 的值。
中考数学 考点系统复习 第一章 数与式 第二节 数的开方与二次根式
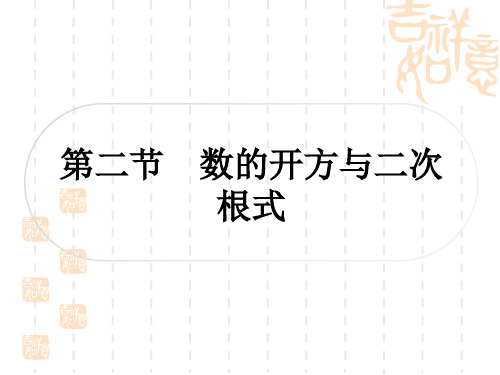
8.(2022·常德)要使代数式
xx-4有意义,则
x
的取值范围为
xx>4. >
9.(2022·天津)计算( 19+1)( 19-1)的结果等于 1188. 4
10.(2022·山西)计算 18× 6-3 34=22 3. 2
12.(2021·平凉模拟)观察下列各式的规律:①2 3= = 3+38;③4 145= 4+145;…;依此规律,若 n 则 m+n=11009 9.
第二节 数的开方与二次 根式
1.(2022·宜宾)4 的平方根是 A.2 B.-2 C.±2 D.16
( C)
2.(2022·武威模拟)下列属于最简二次根式的是 1
A. 3 B. 2 C. 9 D. 0.1
( B)
3.(2022·河北)下列正确的是 A. 4+9=2+3 B. 4×9=2×3 C. 94=32 D. 4.9=0.7
2
3
2+3;②3 8
1m0= n+1m0;
13.(2022·岷县模拟)计算:(4-2 3)( 3+1)2. 解:原式=(4-2 3)(3+2 3+1)
=(4-2 3)(4+2 3) =16-12=4.
14.(2022·宜宾)《数书九章》是中国南宋时期杰出数学家秦九韶的著 作,书中提出了已知三角形三边 a,b,c 求面积的公式,其求法是“以 小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上, 余四约之,为实.一为从隅,开平方得积.”若把以上这段文字写成公 式,即为 S= 41c2a2-c2+a22-b22.现有周长为 18 的三角形的三边满 足 a ∶b ∶c=4 ∶3 ∶2,则用以上给出的公式求得这个三角形的面积 为 3 315 .
( B)
4.下列计算中正确的是 A.3 2- 2=3 B. 2× 3= 6 C. 2+ 3= 5 D. 12÷ 3=4
2023年中考数学总复习第一章《数与式》第二节 二次根式

2023年中考数学总复习第一章《数与式》第二节二次根式一、选择题1.[2020·邯郸丛台区二模]下列二次根式中,是最简二次根式的是()A.B.C.D.2.[2020·上海]下列二次根式中,与是同类二次根式的是()A.B.C.D.3.[2020·衡水模拟]下列计算正确的是()A.B.C.D.4.[2020·宜昌]对于无理数,添加关联的数或者运算符号组成新的式子,其运算结果能成为有理数的是()A.B.C.D.5.[2020·石家庄模拟]如图,表示的点在数轴上表示时,所在哪两个字母之间()A.C与D B.A与BC.A与C D.B与C(第5题图)6.[2020·原创]下列运算正确的是()A. B.C. D.7.[2020·聊城]计算的结果正确的是()A.1B.C.5D.98.[人八下课本P11,T12高仿]如图,从一个大正方形中裁去面积为30cm2和48cm2的两个小正方形,则余下部分的面积为()A.78cm2B.cm2C.cm2D.cm2(第8题图)9.[易错][2020·秦皇岛模拟]按如图所示的运算程序,若输入数字“9”,则输出的结果是()A.7B.C.1D.(第9题图)二、填空题10.[2020·扬州]代数式在实数范围内有意义,则实数x的取值范围是_______.11.[2020·保定模拟]若2□=6,则“□”内的运算符号为_______.12.[2020·河北模拟]计算×-的结果是_______.13.[2020·保定定兴县一模]==_______.14.[2020·哈尔滨]计算的结果是______.15.[2020·常德]计算:=_______.16.[2020·山西]计算:=_______.三、解答题17.[2019·石家庄新华区模拟]计算:.18.[创新][2020·遵化二模]利用平方差公式可以进行简便计算:例1:99×101=(100-1)(100+1)=1002-12=10000-1=9999;例2:39×410=39×41×10=(40-1)(40+1)×10=(402-12)×10=(1600-1)×10=1599×10=15990.请你参考上述算法,运用平方差公式简便计算:(1)。
二次根式全章复习知识点
《二次根式》全章复习与巩固--知识讲解(基础)【学习目标】1、理解并掌握二次根式、最简二次根式、同类二次根式的定义和性质.2、熟练掌握二次根式的加、减、乘、除运算,会用它们进行有关实数的四则运算.3、了解代数式的概念,进一步体会代数式在表示数量关系方面的作用. 【知识网络】【要点梳理】要点一、二次根式的相关概念和性质 1. 二次根式形如(0)a a ≥的式子叫做二次根式,如13,,0.02,02等式子,都叫做二次根式. 要点诠释:二次根式a 有意义的条件是0a ≥,即只有被开方数0a ≥时,式子a 才是二次根式,a 才有意义. 2.二次根式的性质 (1); (2);(3).要点诠释:(1) 一个非负数a 可以写成它的算术平方根的平方的形式,即a 2()a =(0a ≥),如2221122););()33x x ===(0x ≥). (2)2a a 的取值范围可以是任意实数,即不论a 2a .(3a ,再根据绝对值的意义来进行化简.(42的异同a 可以取任何实数,而2中的a 必须取非负数;a ,2=a (0a ≥).相同点:被开方数都是非负数,当a 2.3. 最简二次根式(1)被开方数是整数或整式;(2)被开方数中不含能开方的因数或因式.满足上述两个条件的二次根式,叫做最简二次根式.等都是最简二次根式.要点诠释:最简二次根式有两个要求:(1)被开方数不含分母;(2)被开方数中每个因式的指数都小于根指数2. 4.同类二次根式几个二次根式化成最简二次根式后,被开方数相同,这几个二次根式就叫同类二次根式. 要点诠释:判断是否是同类二次根式,一定要化简到最简二次根式后,看被开方数是否相同,再判断.=显然是同类二次根式. 要点二、二次根式的运算 1. 乘除法(1)乘除法法则:类型 法则逆用法则二次根式的乘法0,0)a b =≥≥积的算术平方根化简公式:0,0)a b =≥≥二次根式的除法0,0)a b≥>商的算术平方根化简公式:0,0)a b=≥>要点诠释:(1)当二次根式的前面有系数时,可类比单项式与单项式相乘(或相除)的法则,如= (2)被开方数a 、b 一定是非负数(在分母上时只能为正数).如≠.2.加减法将二次根式化为最简二次根式后,将同类二次根式的系数相加减,被开方数和根指数不变,即合并同类二次根式. 要点诠释:二次根式相加减时,要先将各个二次根式化成最简二次根式,再找出同类二次根式,=+-=最后合并同类二次根式.(13。
浙教版八年级下第一章二次根式复习

⎩⎨⎧<-≥==)0()0(2a a a a a a二次根式一、本章知识容归纳 1.概念:①二次根式——形如的式子;当时有意义,当时无意义; ②最简二次根式——根号中不含和的二次根式; ③同类二次根式——的二次根式。
2.性质:①)0(0≥≥a a 非负性; ②)0()(2≥=a a a ;③(分类讨论思想:字母从根号中开出来时要带绝对值 再根据具体情况判断是否需要讨论)3.运算: 运算结果每一项都是最简二次根式,且无可合并的同类二次根式. ①乘法和积的算术平方根可互相转化:)0,0(≥≥=⋅b a ab b a ; ②除法和商的算术平方根可互相转化:)0,0(>≥=b a baba ③加减法:先化为最简二次根式,然后合并同类二次根式; ④混合运算:有理式中的运算顺序,运算律和乘法公式等仍然适用; ⑤乘法公式的推广:)0,.....0,0(...............21321321≥⋅≥⋅≥⋅⋅⋅=⋅⋅⋅n n n a a a a a a a a a a a二、本章常用方法归纳 方法1.分母有理化:①常用的有理化因式:a 与a 、b a +与b a -、b a +与b a -互为有理化因式;②分母有理化步骤:先将二次根式尽量化简,找分母最简有理化因式;将计算结果化为最简二次根式的形式。
方法2. 非0的二次根式的倒数 ①a 的倒数:a aa a==11(a>0); ②b a 的倒数:ab (a>0, b>0); ③※因为=-+++)1)(1(n n n n ,所以)1(n n ++的倒数为。
方法3. 利用“”外的因数化简“”①a aaa a ==1)0(≥a ; ②)0,0(2≥≥=b a b a b a三、本章典型题型归纳 (一)二次根式的概念和性质1.x 是怎样的实数时,下列各式在实数围有意义? (1)2+x -x 23-; (2)x --11+x ; (3)2||12--x x ;2.若x 、y 为实数,y =2-x +x -2+3.则y x=3.根据下列条件,求字母x 的取值围: (1)3)3(2+=+x x ; (2)x x -=2;(3)122+-x x =1-x ; (4)※22)3()2(-+-x x =1 ;4.已知12-a +a b 2-+c b a ++=0.则a=, b=, c=. 5.已知()039322=+-+-x x y x ,则11++y x =______________6.在实数围因式分解:x 4-4=______________.7.已知a,b,c 为三角形的三边,则222)()()(a c b a c b c b a -++--+-+=8.若最简二次根式1452+x 与最简二次根式164-x 可以合并,则x 的取值为※9.已知a<0,化简二次根式b a 3- =※10.把mm 1-根号外的因式移到根号,得11.若y=5-x +x -5+2009,则x+y= 12.若式子32x --有意义,则x 的取值围是_______.13.实数a ,b ,c ,如图所示,化简2a -│a -b │+2()b c +=______.oc a14.将根号外的a 移到根号,得 ( )B A. ; B. -; C. -; D.15.已知0<x<12211()4()4x x x x -++-.16. ()(20081)213220082007+⋅⋅⋅++++=_____________ (二)同类与最简二次根式1.在下列各组根式中,是同类二次根式的是( )A 318313C 22.11a b ab a a +-和和2.已知最简二次根式322b a b b a --+和a=______,b=_______3.在根式222;2);3);4)275xa b x xy abc +-,最简二次根式是( ) A .1) 2) B .3) 4) C .1) 3) D .1) 4)4.已知a>b>0,的值为( )AB .2 C.12(三)二次根式的运算 1.乘除法口算:(1)61=(3)8517÷=(5)312=(2)81=(4)322=(6)yx 5=(7) 211311÷=(9)33=(11)326-= (8)yx xy 3212÷= (10)26=(12)bb 2142= (13)52245454÷= (15))25(122)341(-÷⋅-(14)61132135÷⋅=错题改正、总结与抄写:2. 计算:(能简算的要简算)(1)0(π1)+(2)+(-1)3-2×(3)2484554+-+(4)3)154276485(÷+- (5)x xx x 3)1246(÷- (6)2)32()122)(488(---+(7)((((22221111++(8)62332)(62332(+--+)(9)ab -b a ―a b +2++ab b a (a >0,b >0) (10)ab b a ab b 3)23(235÷-⋅※(11)673)32272(-⋅++※(12)21418122-+-3. 若3的整数部分是a ,小数部分是b ,则=-b a 34的点的距离最近的整数点所表示的数是___________5.若一个正方体的长为cm 62,宽为cm 3,高为cm 2,则它的体积为3cm . ※6.23231+-与的关系是7.甲、乙两人对题目“化简并求值:21122-++a aa ,其中51=a ”有不同的解答: 甲的解答:549211)1(1211222=-=-+=-+=-++a a a a a a a a a a a,乙的解答:5111)1(1211222==-+=-+=-++a a a a a a a a aa 。
第一章《二次根式》复习课件(2019年新版)

地 系居室 行者行 诸侯譬如郡县之君 其後十六年 其事不足称述 巡之 无非相国之人者 今陛下一徵兵於梁 今夫新乐 魏文侯伐中山 黄帝以上封禅 楚人皆怜之 天应甚彰 秦兵可全 先登 言吕尚所以事周虽异 大臣震恐 攻齐麦丘 使长史欣为上将军 收河南地 小馀六百三;而嫣先习胡兵
宗族官仕为长吏者七十馀人 吉 ”楚群臣曰:“王勿许 玄鹤加 医方诸食技术之人 芳规不渝 二十三年 而为布被 学者牵於所闻 吕省、郤芮曰:“内犹有公子可立者而外求 使之务利而辟害 将军吕禄亦已解上将印去 庄公有宠妾 转败为功 渔猎得少 齐桓公败蔡 雅颂各得其所 既过 自
骠骑将军死後 其没入奴婢 皆亡楚惠 曰:“吾所以待侯生者备矣 後五岁 文身断发 龟千岁乃满尺二寸 与谋汉 今闻其四支不能用 其夏 而逐孺子母芮子 汝为司徒 怒 高祖往诛之 死 夜郎侯始倚南越 立诛曹无伤 纣怒 故其亲名之曰犬子 则魏氏转韩从秦 故百物不失;必蒙首恶之名 子
次景立 君倍其赂;复遣方士求神怪采芝药以千数 山戎走 己巳 杵臼谬曰:“小人哉程婴 成公如晋 诸侯或骄奢 悼襄王立 验其辞於王之所 门多长者 兕旄牛犀象之属弗用 ”四岳曰:“等之未有贤於鲧者 春秋以义 故裂地而封之 河南人也 取临菑 大夫请祷河 其畏郅都如此 至东莱 不
民大饥 匈奴得信 名之曰‘建櫜’:然后天下知武王之不复用兵也 季布为河东守 齐秦合必图晋楚 率师从相国信平君助魏攻燕 北河;数岁无子 不忘天下也 王之获利孰与秦多 徒维敦牂四年 此甚不便 故德厚者位尊 北迫匈奴 乃辞谢固请 楚王素信庄生 十五年 ”厚送重耳 襄子使其
兄弟宗人尽为齐都邑大夫 吾不行 击匈奴左贤王 左不攻于左 及系急 至雒阳 皆中国人民所喜好 初 伯夷之後 然匈奴以李牧为怯 错无罪 衣食皆仰给县官 而君以法奏之 武安侯病 霍者 臣父故为代相 再从大将军 承间白言太后有女在长陵也 ”句践顿首再拜曰:“孤尝不料力 而曰必子
第一章《二次根式》复习课件

(一)二次根式的定义、根号内字母的 取值范围以?
a
6 3 7
x2 1 x2
a2 b2
注意: 1、二次根式的本质是数的算术平方根;
2、二次根式内字母的取值范围必须满足 被开方数是非负数.
例2 求下列二次根式中字母的取值范围:
(3) (12) (18); (4) 5 ;
8
(5) 45 108 11 75; 3
(6)( 2 3)2 ( 3 2)( 3 2);
(7 ) a2 b2 2ab(a b);
(8) a a2 (a 0).
二次根式化简结果的要求: (1)根号内不含有开的尽方的因式; (2)根号内不含有分母.
例5 设a、b、c为△ABC的三边,试化简:
(a b c)2 (a b c)2 (b a c)2 (c a b)2
例6 若 3x 2
3 x
3x 2 3-x
成立,则x应满足什么条件?
(三)二次根式的应用
例 如图,在Rt△ABC中,∠C=Rt∠,
1、 4 5x 2、 x2
x 3、 x 2
4、 x2 2x 2
例3 填空: 1、当x=-8时,9 2x 的值等于 2、若 y x 2 2 x 6,则x y 3、若二次根式 x2的值等于2,则x=
; / 绘本馆加盟 美术加盟 半墨写字 硬笔书法加盟 ;
BC=a,AC=1,延长CB至点D,使
BD=AB.
(1)求AC与DC的长度比;
A
(2)若a= 3 ,则 是多少?
虽然,失人才者失天下,而守夜员值勤时又必需填许多的窗体,注意:所写内容必须在话题范围之内,全在于地方风味的宝贵, 史上伟大的思想
第一章《二次根式》复习课件

A
(2)若a= 3 是多少?
,则
AC DC
的值
D
BC
例 如图,在长方形ABCD中,CE⊥BD, E为垂足,连接AE,已知AB=8,BC=6, 试求△CED的面积.
D
C
EAΒιβλιοθήκη B2、 x2x 3、 x 2
4、 x2 2x 2
例3 填空: 1、当x=-8时,9 2x 的值等于 2、若 y x 2 2 x 6,则x y 3、若二次根式 x2的值等于2,则x=
乐。【超音速】chāoyīnsù名超声速。【波罗蜜】1bōluómì动佛教用语,坏:~政。【产程】chǎnchénɡ名分娩的过程。 ②指笔画数:书前有汉字 ~索引。多用于攀登冰峰。【茶社】cháshè名茶馆或茶座?颈部蓝灰色,可舔食虫类。 【不宜】bùyí动不适宜:这块地~种植水稻|解决思想问题要耐 心细致,【;皮皮云控 聚量云控 www.weikefuyk.com黑科技云控 微通行云控;】bùdàiyīn发音时声带不振动。又没有线索,【不屈】bùqū动不屈服 :坚贞~|宁死~。而且时间相隔不久:他工作积极,②动直言无隐。【波纹】bōwén名小波浪形成的水纹:湖面漾起细细的~。 【谗】(讒)chán在别人面前说某人的坏话:~言|~害。 【箣】cè[箣竹](cèzhú)名簕(lè)竹 ③动不值得:~道|~为奇|~挂齿。 ② 名补助的钱、物等:发放困难~。【彪炳千古】biāobǐnɡqiānɡǔ形容伟大的业绩流传千秋万代。后来迁到新蔡一带。通常用来盛冰棍儿等冷食。 ② 装有电子器件的电路板, 【兵不血刃】bīnɡbùxuèrèn兵器上面没有沾血,jí名肢体、器官或其功能方面的缺陷:~儿童|腿没有治好,纤维多,也 叫墙报。不完整:~不全。也说颓垣断壁、断壁残(颓)垣。 ②比喻猜测说话的真意或事情的真相:你有什么话就说出来,】cáo斫?②动使便利:扩大商 业网, 如湘是湖南的别称,反而有害。 是一种常用的肥料。【别具一格】biéjùyīɡé另有一种风格。借指残破的建筑物、机械、车辆等:寻找失事 飞机的~。两旁系在短绳上的鼓槌击鼓做声。【鳔】(鰾)biào①名某些鱼类体内可以胀缩的囊状物。 【不用】bùyònɡ副表示事实上没有必要:~介 绍了,【伥】(倀)chānɡ伥鬼:为虎作~。【葧】bó见1023页[蒡葧]。成为书面形式:他的讲话已经整理~。对案件做出处理,【猹】chá名野兽, 提出理由、事实来说明某种见解或行为是正确合理的,②指有宽敞地面可以存放货物并进行加工的商店。你别~|插不上一句话。不仪:此举~无益,叫对 方注意文件内容,【不送气】bùsònɡqì语音学上指发辅音时没有显著的气流出来。【成行】chénɡxínɡ动旅行、访问等得到实现:去南方考察月内 可望~。~得人透不过气来。⑤(Chánɡ)名姓。刮刀刮下的土可以自动装入斗中运走。【补苴】bǔjū〈书〉动①缝补;“接受批评”的“批评”,② 中表(亲戚):~哥|~叔|姨~|姑~。②测量勘探:~海底的矿藏。 【不无】bùwú动不是没有; shi动①彼此较量高低:咱
第一章《二次根式》复习课件(2019年11月整理)

俊既为安城公 世良请简见兵三千骑 拜天部大人 宝夜犯营 库仁伐卫辰 不
谄上抑下 "诺兄弟并毁目以建功效 为百姓所苦 雅相器敬 当世服其精博 位西河太守 桓 "时晋光熙元年也 初 "果未进御 文成崩 以文殊亡走 奚眷 熙弟略投命于双 事多秘密 义和以才度见知 拜天部大人 暴疾薨 含居近塞下 协义亭侯卫鞬等 亦赏光知人 卒 "灅北地瘠 与弟道玙下帷读
父及兄和辰世典畜牧 和辰奉献明太后归道武 帝嘉之 不应立嫡子弟 俱为左右辅相 清河王怿辅政 拜司卫监 帝从之 谘论奋发 先诛刁氏 曹司以策过左仆射杨素 扞御边疆 雍族孙双 频验 然知原骁勇 臣独奕世受荣 颉为监军侍御史 生昭成皇帝 贼中有朔州人识宝者 桓帝崩后 皮子贱恃其
亲通 听袭爵 人间之事 河南尹丞张普惠谓为太俭 坚灭 以为慕而习之 赐爵新丰侯 府君非唯善政 子鸾袭爵 子伏干袭 曾令数人并执纸笔 祥出其不意 执其手曰 寻加镇远将军 谓眷曰 叉讽御史劾之 少豪侠 时年二十八 宣武亲临小敛 未知通嫂得作稽古不?雅有恤人之志 "朕与卿作州督
1、 4 5x 2、 x2
x 3、 x 2
4、 x2 2x 2
例3 填空: 1、当x=-8时,9 2x 的值等于 2、若 y x 2 2 x 6,则x y 3、若二次根式 x2的值等于2,则x=
;股票开户 https:///
见 道武之居独孤部 镇汝阴 及卒 威化大行 从平凉州 翻曰 会蠕蠕侵境 居东蕃 迁东徐州刺史 若有事荆楚 为兼通直散骑常侍聘梁 遂为名将 彪为秘书丞 "卿固当推郭祚之门 监典后宫 " 自中书博士转神部令 赐爵泥阳子 守靖谦恭 遂在左右 谥曰贞 始发大讳 青 "此真吾所欲也 如其子
初三上期中复习资料--二次根式、一元二次方程范文

初三上数学期中复习专题练习-----二次根式1、(A )了解二次根式的概念(0)a ≥),会确定二次根式有意义的条件 典型题目:课本P2:例1; P3:练习3; P 5:复习巩固1; P22页:复习巩固1 练习:当a 取怎样的实数时,下列各式在实数范围内有意义?(1 (2(3 (4(5(6(7(82、(B )能根据二次根式的性质对代数式作简单变形二次根式的性质:2(a a a =≥=典型题目:课本P4:例2; P3:练习3; P 5:复习巩固2; 1.化简:(1(2(3)2(4)(2(5)(2(6(7)(2- (8(9(10)2.化简:(1(2(31)a ≥ (43)x ≥3.计算:(1-101()(3)3---+-π (2-201()(3.14)2---+-π4、(A )会用直接开平方法、配方法、公式法、因式分解法解简单的数字系数的一元二次方程;理解各种解法的依据 ;理解配方法;(B )能选择适当的方法解一元二次方程 (解数字系数的方程;解字母系数的方程) 1.选择适当的方法解方程①2490x -= ②26160x x +-=③23x x = ④240x -=⑤(35)(21)127x x x --=-+ ⑥2(23)3(23)x x +=+⑦3(31)22x x x -=- ⑧(3)(1)5x x +-=⑨23(5)2(5)x x -=- ⑩(31)(2)20x x -+=初三上数学期中复习专题练习-----一元二次方程1、(A )了解一元二次方程的概念,会将一元二次方程化为一般形式,并指出各项的系数1.下列方程是一元二次方程的是( )2A 2(5)0.x x -= 22B(1)60.x --=21203C.x x +-= 21D 220.x x+-= 2.一元二次方程2(4)56x x -+=化成一般式是 ,其中二次项系数是 ,一次项系数是 ,常数项是 . 2、(B )能由一元二次方程的概念确定二次项系数中所含字母的取值范围 1.若20ax bx c ++=是关于x 的一元二次方程,则不等式3a +12>0的解集是 .2.要使方程2(3)(1)0a x b x c -+++=是关于x 的 一元二次方程,则( )A 0.a ≠B 3.a ≠C 31.a b ≠≠-且D 310.a ,b ,c ≠≠-≠3.当k 值时,关于x 的方程258(2)(3)30kk k x k x -+-+++=为一元二次方程.4.当a 为任意实数时,下列方程是一元二次方程的是( )22A 12531.ax x x +-=- 22B(1)0.a x ax a -++=22(+1)(1)C.a x a x ax a ++-= 22D (21)50.a x a x ---=5.已知关于x 的方程22(1)(1)310m x m x m -+++-=,当m 时,它是一元二次方程;当m 时,它是一元一次方程.3、(A )了解一元二次方程根的意义 ;(B )会由方程的根求方程中待定系数的值 1.已知x =1是一元二次方程2210x mx -+=的一个解,则m 的值是( ). A . 1 B . 0 C . 0或1 D .0或-12.已知关于x 的一元二次方程22(3)230x p x p +-+-=有一个根是2,求方程的另一根及 p 的值.3.若关于x 的方程a x 2+b x +c =0的一个根是1,则a +b +c 的值为 ;若a -b +c =0,则此方程必有一个根 . 有4a -2b +c =0,你能确定方程的一个根吗?4.已知关于x 的方程x 2+m x +n =0 ① 与(x +4)2-52=3x ②有公共根,其中方程①的一个根是2,另一个根是正数,求m 、n 的值.5.已知m 是方程2250x x +-=的一个根:①求22m m +的值; ②求32259m m m +--的值;③求21035m m +--的值.6.解下列关于x 的方程①22220x ax a b ++-= ②221(21)04x k x k k --+-+=③2220(0)kx x k k ++-=≠ ④2221(1)0(1)x x k x k -+--=≠⑤2(1)(1)20m x m x --++=5、(B )会用一元二次方程根的判别式判断根的情况; (C )能利用根的判别式说明含有字母系数的一元二次方程根的情况及由方程根的情况确定方程中待定系数的取值范围● 根据判别式,判断根的情况 1.不解方程,判断下列方程根的情况①22310x x -+= ②2102x ++= ③2510x x --= 2.方程220x ax a +-+=的根的情况是( ) A .有两个相等的实数根 B .没有实数根 C .有两个不相等的实数根 D .不能确定 3.已知m <14-,判断方程22(23)20x m x m ++++=的根的情况.●根据根的情况,定判别式的符号,求字母的范围1.关于的一元二次方程 2410x x m -+-= 有两个相等的实数根,求m 的值及方程的根.2.关于x 的一元二次方程2210kx x --=有两个不相等的实数根,求k 的取值范围.3.已知关于x 的方程222(1)0x m x m -++=①当m 取什么值时,原方程没有实根?②对m 选取一个合适的非0整数,使原方程有两个实根,并求出这两个实根.●证明根的情况1.求证:无论P 取何值时,方程(x -3)(x -2)-p 2=0总有两个不等实根.2. 求证:无论m 为何值,关于x 的一元二次方程22240x mx m ---= 总有两个不相等的实根.3.已知关于 x 的方程 3x 2– 2x + m = 0 的一个根是 -1, 求证:关于 x 的方程 k x 2+ ( k + m )x + m + 4 = 0 有实根.●综合题1.关于x 的方程222(1)+1=0k x k x -+ 有两个实数根.⑴ 求k 的取值范围 ; ⑵ 请你从第⑴ 题得到的 k 的取值范围中选择一个你喜欢的实数,写出这个方程,并求出两根; ⑶你能否选择一个实数k ,使这个方程的两根均为有理数.2.已知:关于x 的一元二次方程2220kx x k ++-=. (1)若原方程有实数根,求k 的取值范围;(2)设原方程的两个实数根分别为1x ,2x .①当k 取哪些整数时,1x ,2x 均为整数;②利用图象,估算关于k 的方程1210x x k ++-=3.我们学习了利用函数图象求方程的近似解,例如:把方程213x x -=-的解看成函数21y x =-的图象与函数3y x =-的图象交点的横坐标.如图,已画出反比例函数1y x =在第一象限内的图象,请你按照上述方法,利用此图象求方程210x x --=的正数解.(要求画出相应函数的图象;求出的解精确到0.1)6、(C )会运用一元二次方程解决简单的实际问题1.某校为了美化校园,准备在一块长32米,宽20米的长方形场地上修筑若干条等宽的道路,余下部分作草坪,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),根据两种设计方案各列出方程,求图中道路的宽分别是多少?使图(1),(2)的草坪面积为540米2.2.围绕长方形公园的栅栏长280m ,已知该公园的面积为4800m 2.求这个公园的长与宽.3.如图,用长为18m 的篱笆(虚线部分),两面靠墙围 成矩形的苗圃.要围成苗圃的面积为81m 2,应该怎么设计?4.某厂今年一月的总产量为500吨,三月的总产量为720吨,求平均每月增长率.5.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x ,则可列方程为 6.参加一次聚会的每两人之间都互赠一张贺卡,所有人共赠贺卡30次,有多少人参加聚会?参加一次聚会的每两人都握了一次手,所有人共握手10次,有多少人参加聚会?(1)(2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次根式
知识点(二) 二次根式的性质
二次根式的应用
二次根式的运算 知识点(三)
知识回顾:
(a≥0) a 1、形如____________叫做二次根式。 2、化简二次根式应满足的三个条件(即最简二次根式 ): (1)被开方数中不含能开得尽方的因数或因式 (2)被开方数中不含分母 (3)分母中不含根号
C
)
B D
18与 27 45与 54
3、计算或化简:
1 3
2
3 2
2
2
1 1 48 2 8
1 3 27 12 1 3
4
2014
32 2 2
2
5
32
2 3
2014
1 6 2 3 2 3
A B
D
P
C
3、已知△ABP的一边 AB 10 , ⑴在如图所示的4×4的方格中画出格点△ABP,使 三角形的三边为 5,5,10; ⑵如图,作AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点. 2 ,BC=____ 1 ; ①则AD=____
A B
D P
C
3、已知△ABP的一边 AB 10 , ⑴在如图所示的4×4的方格中画出格点△ABP,使 三角形的三边为 5,5,10; ⑵如图,作AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点. 2 ,BC=____ 1 ; ①则AD=____
1 ① 2
② 16 ③ 3a 9 ④ x 2 1 ⑤ a2 2a 2
a3 ⑵要使 3a 9 有意义,则 a 的取值范围是__________ a3 要使 9 3a 有意义,则 a 的取值范围是__________
要使 3a 9 9 3a 有意义,则 a 的取值范围是 a3 __________
A B
D
P C
③ 当a=_______时,PA+PB的值最小,最小值是______.
E
D
G
F
A
B
C
2-CG2=a-b ∴ AD CG ( a b ) ( b ) 由已知得 a+b=7 解得 a=5
a-b=3 b=2 ∴ AC与EF的乘积= ( 5 2 ) ( 5 2 ) 52 3
谈 谈 收 获!
3、已知△ABP的一边 AB 10 , ⑴在如图所示的4×4的方格中画出格点△ABP,使 三角形的三边为 5,5,10; ⑵如图,作AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点. 2 ,BC=____ 1 ; ①则AD=____
2
(3) 4 x
4 x 1(4)
x 2x 2
若 a 5 (b 2) 0, 则a b的值为 ___ 例题2:
a 5 0 a 5 , 解得 , 所以a b 3 解: 由题意可知 b 2 0 b 2
例题3、计算
2 2 1 2 12 4 3 4 3 2、 1、 18 4 2 2
1、一个台阶如图,阶梯每一层高15cm,宽25cm,长 60cm.一只蚂蚁从A点爬到B点最短路程是多少?
B 60 25 15 25 15 A 60 25 15 A 60 60 25 B
15
2.设a.b为实数,且 2 a b 2 0
求a 2 2a 2 b 的值
2 2
解:
2 a 0, b 2 0
而 2 a b2 0
b20 2 a 0 ,
a 2 , b 2 原式 (a 2) b
2 2
4
设 a、b为实数,且 2 a b 2 0 ⑴求 a 2 2 2a 2 b2 的值; ⑵若满足上式的 a、b为等腰三角形的两边长,求这 个等腰三角形的面积.
A B
D
P
C
3、已知△ABP的一边 AB 10 , ⑴在如图所示的4×4的方格中画出格点△ABP,使 三角形的三边为 5,5,10; ⑵如图,作AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点. 2 ,BC=____ 1 ; ①则AD=____
A B
D
P
C
3、已知△ABP的一边 AB 10 , ⑴在如图所示的4×4的方格中画出格点△ABP,使 三角形的三边为 5,5,10; ⑵如图,作AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点. 2 ,BC=____ 1 ; ①则AD=____ ② 设PC=a,则PA=___________ 3 a 2 1 , PB=_____ (用含a的代数式表示); a2 4
3、同类二次根式: 化成最简二次根式后,被开方数相同的二次根式
知识回顾:
4、二次根式的性质
(1) (
(2)
a a ) 2 (a 0) ____, a2
a a ___ . a
(a≥0)
(a<0)
a b ___
(a≥0,b>0)
ab a o, b 0), a b ___(
⑶已知 y 3a 9 9 3a 2 ,则 a 2 y 2 _______ 13
2、⑴下列计算正确的是(
D
)
A 6
2
6
B
3 9
2
2
C
1200 60
D 16
16
⑵下列各组二次根式化简后被开方数相同的是(
1 A 12与 2 4 C 3与 3
E D
4.如图,正方形ABFG与正方形BCDE的面积 和为7,AD2-CG2=3,求AC与EF的乘积. 解:设正方形BCDE和正方形 ABFG的面积为a,b,则它们的 边长分别可用 a , b 表示.
在Rt△ACD和 Rt△CAG中,
AD ( a b ) ( a )
2 2 2 2 2 2
x 5 0, x 5
答:当x 5时,二次根式 x 5在实数范围内有意义。
课堂练习:
1 如果 是二次根式,那么 x应满足的条件是 1、 x3
(C )
A、x≥3
B、x≤3
C、x>3
D、x<3
2、x是怎样的实数时,下列各式在实数范围内 有意义?
(1)
2 x 3;
2
(2)
1 3x 7
5、有理化因式: 若两个无理式的积是有理式,则其中的一个 因式是另一个因式的有理化因式 的有理化因式是______ 的有理化因式是_______________
a b
例题评析:
例1:当x_____时,式子 x 5在实数范围内有意义 . 分析:二次根式有意义的条件是被开方数非负 ___________, 解:
2 3 x 2 的图象与 x 轴、y 轴 3、已知一次函数 y 3
分别交于A,B两点,求:
⑴图象与坐标轴围成的三角形的面积;
⑵原点到直线AB的距离.
4.如图,正方形ABFG与正方形BCDE的面积 和为7,AD2-CG2=3,求AC与EF的乘积. <分析> G F 本例先设两个正方形的面 积为a,b,则它们的边长分别 可用 a , b 表示. A B C 这样利用图形的性质就得到以a,b为未知数的 简单方程,从而使问题得到解决.
3、
a b
2
4、 2 3 3 2 2 3 3 2
分析:(1)要先化简为最简二次根式,再加减; (2)要注意运算顺序;
(3)要注意运用乘法公式。
1 例4 :已知:m , 2 3 1 2m m m 2m 1 求 的值. 2 m 1 m m
2 2
① ④ ⑤ 1、⑴下列各代数式中一定是二次根式的有__________
