八年级数学等腰梯形的轴对称性2
八年级数学下册22.5(1)等腰梯形的性质

A 15
D
∴BE=AD=15 ,DE=AB=20 20
20
∵AB=DC
∴DE=DC ∵四边形ABCD是等腰梯形
B
15 E
C
∴∠C=∠B=60°(等腰梯形同一底边上的两内角相等)
∴△DEC是等边三角形. ∴EC=DE=20
∴BC=BE+EC=15+20=35
练一练:
如图,在等腰梯形ABCD中,AD∥BC,AB=DC,对角线
AC⊥BD于点O,AD=4,BC=8,求BD。求S梯形ABCD
解:过点D作DE∥AC交BC的延长线于点E
∴∠1=∠AOD=90°
A4 D
∵AD∥BC
∴四边形ACED是平行四边形
(平行四边形的定义)
∴DE=AC CE=AD=4
(平行四边形的对边相等)
1 O
∵在等腰梯形ABCD中,
AC=BD(等腰梯形的两条B对角线相等) 8
用一个等腰三角形纸片过两腰在三角
形内部用尺裁出一个梯形,并判断这个梯形 是否为等腰梯形.
E
A \ B
D /
C
A
D
等腰梯形
B
C
探索
折一折你手中的等腰梯形纸片
A B
(1) 两腰相等
AB=CD D (2)是轴对称图形
对称轴:两底中点的连 线所在的直线
C (3)同底上两内角相等 ∠A= ∠D, ∠B= ∠C 如何说明?
AB=DC,若AC=3cm,则BD= 3 cm
x+x
B
C
第1,3题图
A
D
3.已知等腰梯形的一个内角等于70°, B
第2题图 C
则其他三个内角的度数是 110°,110 °,70 ° 。
八年级数学等腰三角形的轴对称性2

课本34页 练习 3
习题:6 B E C
●本节课你还有哪些疑问?
D F
C
练习: 书 33 2
一个四边形的四个内角度数之比为 1:1:2:2时,这个四边形是梯形吗?
1.代号①, ②, ③, ④的4张三角形纸片都有一个 角为50°,如果它们另有一个角的度数分别为 50°,70°,80°,90°,那么其中只有_①__③___ 的纸片能沿直线剪一刀得到等腰梯形.
2.如图,等腰梯形ABCD中,AD∥BC,AD=5, AB=6,BC=8,且AB∥DE, △DEC的周长是 _1_5___.
怎样说明你的猜想的正确性呢?
E
A
D
B
C
在同一底上的2个角相等的梯形是等腰梯形.
符号语言:
∵梯形ABCD中,AD∥BC,∠B=∠C;
∴四边形ABCD是等腰梯形.
娇艳和自在……前面高耸怪异、奇光闪烁的三烟神塔就是表演巨校博士级的创意表演场,整个三烟神塔由七座菊花形的碳黑色大型建筑和一座高达八百多层的,葱绿色 的六球云朵形的主厦构成。在雪白色的天空和暗红色的云朵映衬下显得格外醒目。远远看去。千烟神塔的底部,二十根超大的美丽钢门柱威猛挺拔……水蓝色的墙裙上 ,纯红色的美丽钢雕塑闪着病态的奇光。千烟神塔的墙体,全部用深红色的美丽钢和深红色的美丽钢镶嵌。而神秘中带着妖艳的窗体则采用了大胆的鲜红色鬼光玻璃。 千烟神塔顶部是一个巨大的,淡青色的水晶体。那是用几乎透明的天明铜和星光玉,经过特殊工艺镶嵌而成。整个千烟神塔给人一种又美玉般的静幽又壮观而疯狂,等 到夜幕降临,这里又会出现另一番迷离异样的光彩……一条飘舞代表但又威猛欢快的大道通向千烟神塔主楼……放眼望去,整个路面上摇晃着紫葡萄色的迷彩银和土黄 色的水晶……大道两旁跳动着满天乱舞的金灿灿,乱茫茫,圆滚滚的彩丝……彩丝后面隐约生长排列着五彩斑斓、华丽精髓的如同毒虫般的低矮植物和沉甸甸,轻飘飘 ,飘悠悠的怪异瓜果……两列高高的瓦刀模样的闪着灵光的花柱在怪物丛中突兀而立,只见从闪着灵光的花柱顶部垂下缕缕簇簇弧光般的光影,看上去仿佛天青色的瀑 布伴随着深黄色的钻石飘飘而下……大道左侧不远处是一片浅绿色的湖光,湖光旁边红、蓝、褐三色相交的林带内不时出现闪动的异影和怪异的叫声……大道右侧远处 是一片水白色的珊瑚丛,那里似乎还跳跃着一片鹅黄色的土桃树林和一片深灰色的妖藤树林……见有客到,大道两旁水蓝色的悬影钢基座上,正在喧闹的银兔神和奇鹿 魔立刻变成了一个个凝固的雕像……这时,静静的泉水也突然喷出一簇簇、一串串直冲云霄的五光十色的钻石般的水柱和水泡般的水花……突然,满天遍地飞出数不清 的彗星,顷刻间绚丽多姿的彗星就同时绽放,整个大地和天空立刻变成了怪异的海洋……空气中瞬间游动出神奇的幽光之香……飞进主楼巍巍的淡青色莲花形大门,空 阔安静、古朴出色的大厅立刻让人眼前一亮,但扑面而来的空气也让人感到一种沧桑威猛的味道……大厅的地面是用明亮怪异的亮雾色云光石和湖金色迷彩银铺成,四 周高大的透明钢墙壁雕绘着辉宏而刺激的巨幅壁画……大厅前方,隐隐可见一座光彩亮丽、正被仙雾光环笼罩的圣坛,但见仙雾朦胧萦绕,光环耀眼梦幻,所以很难看 清圣坛上的身影和圣人……通向圣坛的豪华地毯两旁摆放着两排精美的硕大花盆,花盆中生长着整齐繁茂、鲜花盛开、香气四溢的巨大乔本花卉……每个花盆前面都摆 放着一只精巧怪
八年级数学等腰梯形的轴对称性2

轴对称再认识(二)

镜像对称变换
定义
镜像对称变换是指将图形关于某一直线进行对称,与原图形重合 的变换。
举例
直线、抛物线、双曲线等具有镜像对称性。例如,将一条直线画在 纸上,然后折叠纸片,直线两侧的部分会重合。
应用
镜像对称变换在物理学、工程学等领域有广泛应用。例如,在电路 设计中,常常需要利用镜像对称性来简化电路。
绘画和雕塑
在绘画和雕塑作品中,轴对称经常被用来创造平 衡和和谐的感觉,如达芬奇的《蒙娜丽莎》。
音乐
音乐作品中的旋律和节奏有时也会呈现出轴对称 的特点,使音乐具有更丰富的表现力和美感。
文学作品
在文学作品中,作者有时会采用对称的句式或结 构来增强作品的艺术效果。
05
轴对称的数学问题解析
轴对称与几何证明
轴对称再认识(二)
目录 CONTENT
• 轴对称的定义与性质 • 轴对称的图形分类 • 轴对称的变换方法 • 轴对称在生活中的应用 • 轴对称的数学问题解析
01
轴对称的定义与性质
轴对称的定义
轴对称是指一个平面图形沿着一条直 线折叠后,直线两旁的部分能够互相 重合,那么这个图形叫做轴对称图形 ,这条直线叫做对称轴。
轴对称与代数方程
对称方程
在代数方程中,有些方程关于某直线或点对称,如二次方程的根 与系数的关系等。
解法
利用代数方程的对称性,可以简化方程的求解过程,如利用根与 系数的关系求解二次方程等。
应用
代数方程的对称性在数学、物理、工程等领域有广泛的应用,如 物理学中的波传播、电路分析等。
感谢您的观看
THANKS
1 2 3
函数图像的对称性
一些函数图像具有轴对称性,如正弦函数、余弦 函数等。这些函数的图像关于某些直线对称。
八年级数学下册课后补习班辅导等腰梯形的轴对称性讲学案苏科版

八年级数学下册课后补习班辅导等腰梯形的轴对称性讲学案苏科版【本讲教育信息】一、教学内容:等腰梯形的轴对称性[目标]探索等腰梯形的轴对称性及其相关性质。
二、重、难点:等腰梯形及其性质和四边形是等腰梯形的条件。
三、知识要点:1、梯形平面中,有一组对边平行且不相等的四边形是梯形。
梯形中,平行的一组对边称为底,不平行的一组对边称为腰。
如:在梯形EBCD中,ED∥BC,EB、CD叫梯形的腰,ED、BC叫梯形的两底,∠EBC、∠DCB、∠BED、∠CDE叫梯形的底角。
☆ 边与角满足什么条件的四边形为梯形。
① 只有一组对边平行的四边形为梯形② 只有一组邻角互补的四边形为梯形2、等腰梯形(a)定义:两腰相等的梯形叫做等腰梯形。
(b)等腰梯形是轴对称图形,过两底的中点的直线是它的对称轴。
(c)等腰梯形的性质:① 等腰梯形的对角线相等;② 等腰梯形在同一底上的两个角相等。
③ 在同一底上的两个角相等的梯形是等腰梯形。
(判定定理)【典型例题】例1、如图,有九个点在平面上形成33的方阵,以这些点为顶点的等腰梯形有()(A)0个(B)2个(C)4个(D)8个分析:只能以最长的对角线作为等腰梯形的底边。
一共有2条这样长的对角线,而每条对角线可组成2个等腰梯形。
所以共有4个。
答:C例2、如图,在梯形ABCD中,AD∥BC,E、F分别是AD、BC的中点,且EF⊥BC,则梯形ABCD_________(填“是”或“不是”)等腰梯形。
分析:分别作AG⊥BC于G,DH⊥BC于H;由已知易证△ABG≌△DCH,∴ AB=DC,∴梯形ABCD是等腰梯形。
答:是例3、(1)等腰梯形上底的长与腰长相等,而一条对角线与一腰垂直,则梯形上底角的度数是____________。
(2)已知等腰梯形的一个底角等于60 ,它的两底分别为13cm和37cm,它的周长为___________。
(3)如图在等腰梯形ABCD中,AD∥BC,AB =AD,BD = BC,求∠C的度数。
八年级数学基础巩固与拓展提优:第一章 第10课时 等腰梯形的轴对称性(2)

第10课时等腰梯形的轴对称性(2)(附答案)【基础巩固】1.在梯形ABCD中,AB∥DC,∠A=130°,∠C=50°,则∠B=_______,∠D=_______,该梯形是_______.2.一个四边形的四个内角的度数之比是2:2:1:1,则此四边形的形状为_______.3.如图,在梯形ABCD中,AD∥BC,E、F分别是AD、BC的中点,且EF⊥BC,则梯形ABCD_______(填“是”或“不是”)等腰梯形.4.如图,在梯形ABCD中,AD∥BC,试添加一个适当的条件使梯形ABCD是等腰梯形,你添加的条件可以是_______.(写出所有可能的条件)5.如图,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,以下四个结论:①∠ABC=∠DCB,②OA=OD,③∠BCD=∠BDC,④S△AOB=S△DOC,其中正确的是 ( ) A.①② B.①④C.②③④D.①②④6.在梯形中,若有两个角相等,那么它一定为 ( )A.等腰梯形B.直角梯形 C.一般梯形 D.直角梯形或等腰梯形7.如图,AB=AC,过点A的直线DE∥CB,CD⊥AC,BE⊥AB.梯形BCDE是等腰梯形吗?为什么?8.如图,在梯形ABCD中,AD∥BC,AC=BD.求证:梯形ABCD是等腰梯形.9.如图,在△ABC中,AB=AC,BD、CE分别是角平分线,连接DE.(1)△ADE是等腰三角形吗?为什么?(2)四边形BCDE是等腰梯形吗?为什么?(3)根据你的理解,说一说等腰梯形和等腰三角形的相互关系.10.如图,在梯形ABCD中,BC∥AD,延长CB到E,使BE=AD,若同时有∠E=∠ACE,则梯形ABCD是等腰梯形吗?为什么?11.如图,在梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD交CD的延长线于点E,且∠C=2∠E.(1)求证:梯形ABCD是等腰梯形;(2)若∠BDC=30°,AD=5,求CD的长.【拓展提优】12.如图,有9个点在平面上形成3×3的方阵,以这些点为顶点的等腰梯形有 ( ) A.0个 B.2个 C.4个 D.8个13.如图,在梯形ABCD中,已知AB与CD不平行,∠ABD=∠ACD,请你添加一个条件:_______,使得加上这个条件后能够推出AD∥BC且AB=CD.14.你能数出下列图形中有多少个等腰梯形吗?(图中三角形均为等边三角形)15.如图,在梯形ABCD中,AD∥BC,点M是BC的中点,且MA=MD.求证:四边形ABCD是等腰梯形.16.如图,△ABP和△CDP全等且均为等边三角形,且AP⊥PD.(1)求∠PCB的度数;(2)求证:四边形ABCD是等腰梯形.17.如图,在梯形ABCD中,AD∥BC,AB=DC.试在它所在的平面内找一点P,使得△PAB、△PBC、△PCD、△PDA均为等腰三角形,这样的点你能找几点?在图中画出来.18.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14 cm,AD=18 cm,BC=21 cm,点P从点A出发,沿边AD向点D以1 cm/s的速度移动,点Q从点C出发沿边CB向点B以2 cm/s 的速度移动,若有一点运动到端点时,另一点也随之停止.如果P、Q同时出发,能否有四边形PQCD成等腰梯形?如果存在,求经过几秒后;如果不存在,请说明理由.参考答案【基础巩固】1.130°50°等腰梯形2.等腰梯形3.是4.AB=CD或∠A=∠D或∠B=∠C 5.D 6.D 7.是等腰梯形,理由略8.略9.(1)是等腰三角形,理由略(2)是等腰梯形,理由略(3)略10.是等腰梯形11.(1)略(2)CD=10【拓展提优】12.C 13.∠DAC=∠ADB.∠BAD=∠CDA,∠DBC=∠ACB,∠ABC=∠DCB,OB=CC,OA=OD(任选其一) 14.18 15.略16.(1)15° (2)略17.5个18.能,经过8s。
八年级数学等腰梯形的性质
思
考
1、用一块面积为800 cm 2 的等腰
梯形彩纸做风筝 ,为牢固起见,
用竹条作梯形的对角线,对角
线恰好互相垂直,那么至少需 要竹条 80 cm
A
D
解: ∵四边形ABCD是等腰梯形
∴设AC=BD=x
B
C
又∵AC⊥BD
∴ 1 x 2 = 800
2
解得:x=40
∴至少需要竹条 80 cm
“横断面”的概念
3
S2
5
4
D、S1 = S2
7
练习二
3、如图:若a=4 , b=6 , c=7 ,d=3 , 以它们为边作梯形,其中a∥b , 你认为这样的梯形能作出吗?
若能请作出图形,若不能,
Aa D
c
d
请说明 解: 这样的梯形不能作出
B
Hb C
过A点作AH∥CD 交BC于H点,得到 AHCD
∴AH=CD=d=3 , AD=HC= a = 4
A、m>h B、m<h C、m=h D、不能确定 B 解:
D
h
EC H
2 1 2 1 2 1
∟
过D作DH∥AC交BC 延长线于H点 ∴ BD=DH
∵AC⊥BD
又过D作DE ⊥ BH于E点
∴BD ⊥ DH
∴ DE= BH
又∵ AD ∥ BH , DH ∥ AC ∴四边形ACHD是平行四边形
= (BC+CH)
“横断面”的概念
梯形的性质应用1
横断面
梯形的性思质应用考
2、河流的一个横断面,如图,根据下表中的测量数据计算断面面积
离河一岸的距离(m) 0 2 3 5 9 11
水 深(m)
八年级数学上册第2章知识归纳:轴对称和轴对称图形(青岛版)

知识归纳:轴对称和轴对称图形
轴对称
1、一个图形沿着某一条直线折叠,如果直线两侧的图形能够重合,就说这一个图形是轴对称图形。
这条直线叫做图形的对称轴。
2、轴对称图形一定有对称轴,而且至少有1条对称轴,常见的例如:等腰三角形、等腰梯形、线段、角;有两条对称轴的常见图形有长方形;有三条对称轴的常见图形有等边三角形;正方形有4条对称轴;五角星和正五边形有5条对称轴;圆有无数条对称轴。
轴对称图形的画法
1、轴对称图形的性质:
(1)对称轴两边的图形一定完全相同
(2)对应点也关于对称轴对称
(3)对应点的连线垂直于对称轴
(4)对应点到对称轴的距离相等
2、轴对称图形的画法:
(1)根据题意确定已知图形以及对称轴位置
(2)找出已知图形的关键点
(3)一次过每个点作垂直于对称轴的虚线
(4)在对称轴另一侧确定各对应点位置
(5)标明各点对应名称,顺次连接各对应点得到轴对称图形。
确定轴对称图形的对称轴
沿某条直线对折之后,两边的图形能够完全重叠,这条直线就是
图形的对称轴。
轴对称和成轴对称。
苏教版八年级数学全册知识点总结
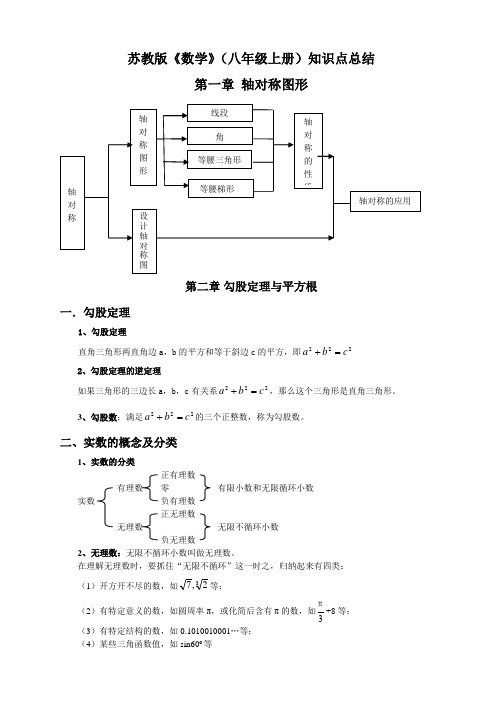
苏教版《数学》(八年级上册)知识点总结第一章 轴对称图形第二章 勾股定理与平方根一.勾股定理1、勾股定理直角三角形两直角边a ,b 的平方和等于斜边c 的平方,即222c b a =+ 2、勾股定理的逆定理如果三角形的三边长a ,b ,c 有关系222c b a =+,那么这个三角形是直角三角形。
3、勾股数:满足222c b a =+的三个正整数,称为勾股数。
二、实数的概念及分类1、实数的分类 正有理数有理数 零 有限小数和无限循环小数 实数 负有理数 正无理数无理数 无限不循环小数 负无理数2、无理数:无限不循环小数叫做无理数。
在理解无理数时,要抓住“无限不循环”这一时之,归纳起来有四类: (1)开方开不尽的数,如32,7等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如3π+8等; (3)有特定结构的数,如0.1010010001…等; (4)某些三角函数值,如sin60o 等轴对称轴对称的性质轴对称图形线段 角 等腰三角形 轴对称的应用等腰梯形设计轴对称图案三、平方根、算数平方根和立方根1、算术平方根:一般地,如果一个正数x 的平方等于a ,即x 2=a ,那么这个正数x 就叫做a 的算术平方根。
特别地,0的算术平方根是0。
表示方法:记作“a ”,读作根号a 。
性质:正数和零的算术平方根都只有一个,零的算术平方根是零。
2、平方根:一般地,如果一个数x 的平方等于a ,即x 2=a ,那么这个数x 就叫做a 的平方根(或二次方根)。
表示方法:正数a 的平方根记做“a ±”,读作“正、负根号a ”。
性质:一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根。
开平方:求一个数a 的平方根的运算,叫做开平方。
0≥a注意a 的双重非负性:a ≥03、立方根一般地,如果一个数x 的立方等于a ,即x 3=a 那么这个数x 就叫做a 的立方根(或三次方根)。
表示方法:记作3a性质:一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
数学等腰梯形

数学等腰梯形知识点总结归纳等腰梯形(isosceles trapezium)是一组对边平行(不相等),另一组对边不平行但相等的四边形。
等腰梯形是一个平面图形,是一种特殊的梯形。
一、等腰梯形的性质1. 等腰梯形的两条腰相等。
2. 等腰梯形在同一底上的两个角相等。
3. 等腰梯形的两条对角线相等。
4. 等腰梯形是轴对称图形,对称轴是上下底中点的连线所在直线(过两底中点的直线)。
二、等腰梯形的判定1. 两腰相等的梯形是等腰梯形;2. 同一底上的两个角相等的梯形是等腰梯形;3. 对角线相等的梯形是等腰梯形。
三、等腰梯形的其他相关性质1. 等腰梯形中,高、中线、角平分线重合(即“三线合一”)。
2. 等腰梯形对角线互相垂直。
3. 等腰梯形中位线长是上底加下底和的一半。
四、等腰梯形的面积公式设等腰梯形的上底长为a,下底长为b,高为h,则等腰梯形的面积公式为:面积= (a + b) × h / 2。
五、等腰梯形与三角形的联系等腰梯形可以划分成三个等腰直角三角形。
等腰梯形的上底与下底的垂直平分线即为等腰三角形的高,上下底之间的距离即为等腰三角形的高,等腰三角形的底即为等腰梯形的腰。
等腰梯形的两腰即为两个等腰直角三角形的腰。
六、等腰梯形与平行四边形的联系若等腰梯形上底为0,即为平行四边形。
七、等腰梯形与矩形的联系若等腰梯形两腰垂直于底,则为矩形。
八、等腰梯形与正方形的联系若等腰梯形两腰垂直于底且上底为0,即为正方形。
九、实例解析1. 已知等腰梯形两腰长分别为5cm和5cm,上底长为3cm,下底长为7cm,求等腰梯形的面积。
解:根据等腰梯形的面积公式,面积= (a + b) × h / 2,其中a为上底长,b为下底长,h为高。
因为等腰梯形的两腰相等,所以梯形的高即为腰与上下底垂直平分线的长度。
这里可以使用勾股定理求解高,设高为h,则有h² = 5² - (2)² = 21,所以h = √21cm。
等腰梯形的性质

19.3 等腰梯形的性质(人教版数学八年级下册第十九章第三节)【教学设想】本节课主要是对等腰梯形的性质进行探索,通过对梯形、等腰梯形图形及相关性质的分析,培养学生猜测、动手实验及几何证明的能力,给学生创造自主学习、自主探索、合作交流的机会,并借此培养和锻炼学生的观察能力、思维能力、表达能力、解决问题的能力。
【教学目标分析】1.知识技能:了解和掌握梯形、等腰梯形、直角梯形的有关概念,探寻等腰梯形的对称性,掌握并证明等腰梯形的两个重要性质。
2.数学思考:①通过观察、猜想、实验、推理等数学活动,发现和找寻等腰梯形的对称性及性质,培养和发展学生的推理能力、动手操作能力、几何论证能力。
②培养学生化归的思想、添加辅助线的能力和证明能力。
3.解决问题:通过对等腰梯形性质的探索过程,体验利用手持式图形计算设备充当数学认知工具的乐趣,感受平面几何图形的美,丰富学生从事数学活动的经验与体验,感受数学思考过程的条理性及解决问题策略的多样性,发展学生的实践能力及创新意识。
4.情感态度:在操作活动及观察、分析过程中发展学生的自主探索、勇于质疑和独立思考的习惯及相互合作的意识和品质,并从中体会到发现的快乐。
【重、难点分析】教学重点:梯形的有关概念及等腰梯形的性质。
教学难点:添加辅助线,把梯形问题转化为平行四边形或三角形问题等。
【学习者特征分析】学生的知识技能基础:学生对梯形的概念已经有所了解和掌握,并且已经学习了轴对称知识,为接下来的学习奠定了知识和技能基础。
学生活动经验基础:在相关知识的学习过程中,学生已经经历了利用《数学画板》探索验证数学结论的活动,解决了一些简单的现实问题,获得了一些数学活动经验的基础;同时在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
【教学媒体】多媒体投影、数码学习机、《数学画板》软件。
【教学过程】(一)结合实际, 创设情境,引入新知:教师活动:1、观察一组图片,在图中有你熟悉的图形吗?多媒体课件引入。
等腰梯形及其性质

两腰相等的梯形叫做等腰梯形(isosceles trapezium)。
(来自《沪教版八年级(下)数学》22.4 梯形)等腰梯形是一种特殊的梯形。
2辅助线编辑1、平移一腰。
2、过上底两点向下底两点做垂线。
3、延长两腰交于一点。
4、平移一条对角线。
3性质编辑1、等腰梯形同一底上的两个内角相等。
2、两腰相等,两底平行,对角线相等。
3、由托勒密定理可得等腰梯形ABCD,有AB×CD+BC×AD=AC×BD。
4、中位线长是上下底边长度和的一半。
5、两条对角线相等,是轴对称图形,只有一条对称轴,上底和下底的中垂线就是它的对称轴。
6、对角线分成的四个三角形有3对全等形,一对相似形。
7、等腰梯形的面积公式:S=(上底+下底)×高×1/2。
8、特殊面积计算:当对角线垂直时:S=(BD×AC)/2。
9、等腰梯形对角线的平方等于腰的平方与上、下底积的乘积和。
BD2=AC2=AB2+AD·BC=CD2+AD·BC1、一组对边相等且不平行,另一组对边平行的四边形是等腰梯形。
2、同一底上的两个角相等的梯形是等腰梯形。
3、对角线相等的梯形是等腰梯形。
4、两腰相等的梯形是等腰梯形以下判定不作为定理使用:5、对角线相等且能形成两个等腰三角形的四边形是等腰梯形。
6、对角互补的梯形是等腰梯形。
5面积公式编辑梯形的面积=(上底+下底)×高/2;用“a”、“b”、“h”分别表示梯形的上底、下底、高,“S”表示梯形的面积则S=(a+b)h/2。
特殊情况:1.若对角线互相垂直,则面积为1/2两对角线的乘积。
2.在已知中位线情况下,中位线乘高。
(中位线等于(a+b)/2)面积推导:设有两个完全一样的等腰梯形,将这两个梯形拼成一个平行四边形,则平行四边形底=等腰梯形上底和下底之和,平行四边形高=等腰梯形的高,故设上底为a,下底为b,高为h,平行四边形面积=(a+b)h,所以等腰梯形面积=(a+b)h/2。
等腰梯形的性质定理和判定定理及其证明

等腰梯形的性质定理和判定定理及其证明32.4等腰梯形的性质定理和判定定理及其证明教学目标:知识目标:理解和掌握等腰梯形的性质定理的内容及简单的应用;能力目标:通过动手操作,探索等腰梯形的性质及其证明方法,初步培养学生探索问题和研究问题的能力;情感目标:营造一个相互协作的课堂气氛,引领学生自主探究、集体讨论,激发学生的学习热情;教学重点与难点: 1、等腰梯形性质的探究及证明; 2、等腰梯形性质定理的简单应用。
教学过程: 1、复习旧知,引入新课填空(1)的四边形是平行四边形;(2)的四边形是平行四边形;(3)的四边形是平行四边形;(4)的四边形是平行四边形;(5)的四边形是平行四边形;(6)一组对边平行,一组对边相等的四边形是平行四边形;用举反例的方法举出有一组对边平行,一组对边相等但并不是平行四边形的图形即等腰梯形,从而由这个错误的判定引出梯形、等腰梯形、直角梯形的定义;我们这节课就来研究等腰梯形的性质。
2、自主探索、提出猜想把学生分成以四个人一组的若干小组,提供给每个小组一个等腰梯形的模型,让同学们用各种数学工具通过各种数学方法,如翻折、旋转等来探索等腰梯形有哪些性质?同学们可能会得出下面一些结论:(1)两腰相等;(2)两个底角相等;(3)等腰梯形是轴对称图形,不是中心对称图形;(4)两条对角线相等;………… 3、交流反馈、共同论证结论(1)由等腰梯形的定义可以得到而不用证明;结论(2)的证明探索:(学生讨论交流,提出各自的证明思路)(如果学生没有思路,教师可以引导证明两个角相等的两种思路:)一是把两个角转化到同一个三角形中,用“等边对等角”证明;二是把两个角转化到两个全等三角形中,用“全等三角形的对应角相等”证明;完善结论后得到:等腰梯形的性质定理等腰梯形的同一条底边上的两个内角相等。
结论(3):观察翻折、旋转的动画演示后,由轴对称图形和中心对称图形的定义可以直接得到:等腰梯形是轴对称图形,经过两底中点的直线是它的对称轴。
北京课改初中数学八下《16.8等腰梯形与直角梯形》word教案(2)

DB⊥ AD.那么∠ DBC=______ , ∠ C=_______ .
A
C B
三、课堂小结: 通过本讲的学习应掌握: 1、梯形、直角梯形、等腰梯形的概念. 2、 等腰梯形的性质: (1) 等腰梯形同一底上的两个角相等. (2) 等腰梯形的两条对角线相等.
四、课后作业:
第 2 课时
等腰梯形的判定
(2)化归的思想;
3. 总结梯形中常用的辅助线,掌握化归的思想 .
梯形中添加辅助线常常可以将梯形化归为三角形、平行四边形、矩形、直角梯形等
. 同时,
还可以集中梯形中分散的已知条件, 如右图中将梯形的两腰、 两底角、 两边之差集中到了一
个三角形中 .
另外还要注意: ( 1)从图形变换及化归角度理解梯形中
一、问题,引导探索
1、复习:等腰梯形的定义是什么?学生回答。教师点评。我们知道,定义既可以作为性
质定理,又可以作为判定定理使用。
议一议:除了运用定义外,还有判定等腰梯形的其他方法吗? 鼓励学生大胆猜想,小心求证。
二、构造几何模型,探究证法 :
已知:梯形 ABCD, AD∥ BC,∠ B=∠ C,
求证:梯形 ABCD是等腰梯形。
关系:
想一想: “既是ቤተ መጻሕፍቲ ባይዱ角梯形,又是等腰梯形” 学生思考后回答。
,这样的梯形存在吗?
下面我们研究等腰梯形的性质。 议一议: 在等腰三角形中,有“等角对等边” 性质? 引导学生思考、讨论、交流。并写出已知、求证。
,那么,在等腰梯形中,是不是也有类似的
A
D
已知:如图,在梯形 ABCD中, AD∥ BC, AB= CD,
例 1 如图, 延长等腰梯形 ABCD的两腰 BA 与 CD交于点 E,说出图中的等腰三角形,
初中数学等腰梯形的性质知识点详解

初中数学等腰梯形的性质知识点详解初中数学等腰梯形的性质知识点详解对于数学的学习中,下面是对等腰梯形的性质知识点的内容讲解,学习。
等腰梯形的性质①两底平行,两腰相等②等腰梯形在同一底上的两个角相等③等腰梯形的两条对角线相等④等腰梯形是轴对称图形,只有一条对称轴,一底的垂直平分线是它的对称轴通过上面对数学中等腰梯形的性质知识点的内容讲解学习,相信同学们已经能很好的掌握了吧,希望同学们会从中学习的更好。
初中数学相关的角与性质知识点详解对于数学的学习中,下面是对相关的角与性质知识点的内容讲解,学习。
相关的角与性质相关的角:1、对顶角:一个角的两边分别是另一个角的两边的反向延长线,这两个角叫做对顶角。
2、互为补角:假如两个角的和是一个平角,这两个角做互为补角。
3、互为余角:假如两个角的和是一个直角,这两个角叫做互为余角。
4、邻补角:有公共顶点,一条公共边,另两条边互为反向延长线的两个角做互为邻补角。
注意:互余、互补是指两个角的数量关系,与两个角的位置无关,而互为邻补角那么要求两个角有特殊的位置关系。
角的性质1、对顶角相等。
2、同角或等角的余角相等。
3、同角或等角的补角相等。
通过上面对数学中相关的角与性质知识点的内容讲解学习,相信同学们已经能很好的掌握了吧,希望同学们会从中学习的更好。
初中数学菱形的定义与性质知识点详解下面是教师对数学中菱形的定义与性质相关知识讲解,希望给同学们的复习学习提供很好的帮助。
菱形的定义与性质1、定义:邻边相等的平行四边形是菱形。
2、性质:〔1〕菱形的四边形都相等。
〔2〕菱形的对角线互相垂直,并且每一条对角线平分一组对角,〔3〕菱形的面积等于对角线乘积的一半。
〔4〕菱形既是中心对称图形,又是轴对称图形,有2条对称轴。
相信上面对数学中菱形的定义与性质知识的讲解学习,同学们已经能很好的掌握了吧,希望同学们在考试中获得优异成绩。
初中数学梯形定义知识点详解下面是教师对数学中梯形定义相关知识讲解,希望给同学们的复习学习提供很好的帮助。
八年级数学三线合一教案

(2)b=8,c=17,则S△ABC=_______。
3、求下列图中表示边的未知数x、y、z的值.
x
y
z
576
625
144
169
144
81
3、
三、互学互助:
1、学生互相批改自测题;
2、各小组汇报典型错误;
3、师生共同探讨解决疑难问题
四、导学导练
1、如图,在△ABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB与D,
五、课堂小结:
六、教、学反思:
④课题:1.6等腰梯形的轴对称性(1)
课型:新授时间:11、9、9
执笔:杨丙才审核:八年级数学备课组
[学习目标] 1.知道等腰梯形的基本概念、等腰梯形的轴对称性
2.掌握等腰梯形的性质,并能运用性质解决问题
3.进一步培养学生有条理的思考和表达能力,渗透转化、类比的数学思想
(2)经过折叠后所得的△ABC,在所得的三角形中∠1=∠2。那么请同学们度量边AC,BC的长度,你们有什么发现?
(3)在一张薄纸上画线段AB,并在AB同侧利用量角器画两个相等的锐角∠BAM和∠ABM.设AM与BN相交于点C.量一量AC与BC的长度,AC和BC相等吗?你和同学所得的结论相同吗?
二、自学自测:
四:导学导练
1.如图,在等边三角形ABC的边AB、AC上分别截取AD=AE,△ADE是等边三角形吗?试说明理由.
2.如图,P、Q是△ABC的BC边上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.
3、如图,点A是BC上一点,⊿ABD、⊿ACE都是等边三角形。
试说明:
(1)BE=CD;(2)求∠DOM的度数;(3)AM=AN;(4)MN∥BC。
22.5(1)-等腰梯形的性质
资源信息表22.5(1)等腰梯形的性质民办文绮中学林红教学目标1.经历由平行四边形的性质类比探索等腰梯形性质的过程,掌握等腰梯形的性质定理、并能应用进行计算和证明;2.会添加适当的辅助线,将等腰梯形问题转化成三角形、平行四边形等熟知的几何图形来解决问题;3.提高探索等腰梯形性质的活动,提高类比、归纳能力,感受类比、分类讨论和转化等数学思想和方法在解决问题中的作用.教学重点及难点掌握等腰梯形的性质定理、并能应用进行计算和证明;会添加适当的辅助线,将等腰梯形问题转化成三角形、平行四边形等熟知的几何图形来解决问题.教学用具准备直尺、多媒体课件.教学流程设计温故知新新课讲授课堂练习小结教学过程设计一、创设问题情境,鼓励学生讨论1.什么是平行四边形?有哪些性质?2.什么是等腰梯形?3.观察图形,猜想等腰梯形会有哪些性质?(板书课题:等腰梯形的性质)二、新课讲授1、问题类比,提出猜想将学生分组,讨论第三个问题,很快得出猜想(命题):命题:等腰梯形两底平行,两腰相等.(定义往往可以做为性质定理直接运用)命题:等腰梯形在同一底上的两个角相等.命题:等腰梯形的对角线相等.(学生对命题的叙述不一定准确,教师引导学生得出叙述准确的命题,并提出应对命题的正确性加以证明.)2.分析探索、寻求证明:已知:如图,在梯形ABCD中,AD∥BC,AB=DC求证:∠B=∠C启发与思考:问题一:证明两角相等通常采用什么办法?(可能的答案:1.证明所在的两三角形全等.2.证明是等腰三角形.3.证角平分线,等等.)依据学生的回答,让学生观察图形,发现可能采用的证法与所给的已知条件相距甚远.因此,引出新的问题:问题二:对于研究新问题(未知的、复杂的问题),通常采用什么数学思想解决?( “转化”的思想,也就是将未知的转化为已知的,将复杂的图形转化为熟悉的基本图形进行研究.)问题三:怎样转化?(添加辅助线.)问题四:怎样添加辅助线,可以将问题转化为大家熟悉的图形,并利用已知图形的性质及已知条件进行证明和研究?这个问题是教学中的难点和关键,为突破这个教学难点,教学中必须注意引导学生联系问题一中所提到的方案,即添加辅助线后能将梯形问题转化为问题一中所涉及的已知(熟悉的)图形,或者是转化后能将分散的、没有联系的条件聚拢到一起,建立直接联系.并利用已知图形的性质及已知条件进行证明.教学中将学生分组讨论,并证明.可能的添法:(一) 过梯形的顶点作腰的平行线,将梯形转化为一个平行四边形和一个三角形.如图所示:B E C(二) 过上底的端点作下底的垂线,将梯形转化成为一个矩形和两个直角三角形.如图所示:教学中一定要注意添加辅助线是关键,要注意学生的思维过程,引导学生克服思维障碍.引出辅助线后,证明比较简单,可由两位学生到黑板板演,检查书写规范.问题五:上述证明中的辅助线是如何将问题转化的?(教师引导学生总结.)第一种添加辅助线的方法:1)可理解为将梯形转化为平行四边形和等腰三角形来研究.2)可理解为将梯形的一腰平移,使这个腰与另一个腰产生直接联系(构成等腰三角形).第二种添加辅助线的方法:可理解为构造两个全等三角形,从而使问题得证.(让学生想一想,还可以用什么样的方法作辅助线来解决梯形问题,多找几名学生回答,然后教师总结,可借助多媒体演示见图).(1)“作高”:使两腰在两个直角三角形中.(2)“移对角线”:使两条对角线在同一个三角形中.(3)“延腰”:构造具有公共角的两个等腰三角形.(4)“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形.综上所述:解决梯形问题的基本思想和方法就是通过添加适当的辅助线,把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决.练习:证明,等腰梯形的两条对角线相等.4.对称性:等腰梯形是轴对称图形.对称轴是上底(下底)的垂直平分线.5. 例题选讲:如图:等腰梯形ABCD 中,AD//BC,腰BA 和CD 的延长线交于点E.求证:△EAD 是等腰三角形方法探讨:交流:方法一:等角对等边;方法二:大边减小边. 练习1.如图:等腰梯形ABCD 中,AD//BC,BA =CD,E 是AD 延长线上一点,CE=CD.求证:∠B=∠E. 再考虑:四边形ABCE 是平行四边形吗?为什么?练习2.如图:等腰梯形ABCD 中,AD//BC,AD =AB,BD ⊥CD, 求:∠C 的度数.三. 本课小结: A D B EE C BA D A1)有关概念:等腰梯形的性质:边、角、对角线、对称性2)方法:梯形问题一般通过添加平行线,或作高,将梯形问题转化为平行四边形、矩形、直角三角形的问题来解决的.四.布置作业:练习册第48页习题22.5(1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5878棋牌老版
[单选]具有强筋壮骨,和胃健脾用于治疗和预防小儿佝偻病、软骨病的是()A.龙牡壮骨颗粒B.琥珀抱龙丸C.牛黄抱龙丸D.肥儿丸E.一捻金 [单选]胃壁固有肌层声像图上显示层次为()。A.6层B.5层C.4层D.3层E.2层 [判断题]为了预防、减少和避免学生伤害事故的发生,除应对学生加强安全意识和提高自我保护能力以及培养健康的心理素质外,还应对其强化纪律观念,尽量减少因自违纪行为而导致的伤害事故的发生。A.正确B.错误 [单选]下列属于终末质量评价的是()。A.病区管理合格率B.消毒隔离管理合格率C.年度护理差错发生率D.一人一针一管执行率E.护理技术操作合格率 [单选,A2型题,A1/A2型题]关于造影剂的使用,哪项是错误的()A.胆影葡胺--胆道造影B.医用硫酸钡--消化道造影C.碘化油--心血管造影D.空气--脑室造影E.泛影葡胺--尿路造影 [单选]属于"早期发现"的探测器是(),它对燃烧或热解产生的固体或液体微粒予以响应,可以探测物质初期燃烧所产生的气溶胶或烟粒子浓度,因此广泛采用。A.感温火灾探测器B.感烟火灾探测器C.感光火灾探测器D.复合式火灾探测器 [单选]下列哪项不属妇科杂病范畴()A.癥瘕B.不孕症C.阴痒D.妇人脏躁E.转胞 [单选,A2型题,A1/A2型题]下列哪项不是慢性淋巴细胞白血病的特点().A.多见于老年人B.常并发自身免疫性溶血性贫血C.白细胞计数增高D.骨髓中见到大量幼稚淋巴细胞E.骨髓中见到大量成熟淋巴细胞 [单选]安装A形井架应采用水平安装,整体吊升的方法,主要方法有()。A.撑杆法和扒杆法B.扒杆法和人字架法C.旋转扒杆法D.撑杆法和人字架法 [单选,案例分析题]某电网企业110kV变电站,两路电源进线,两路负荷出线(电缆线路),进线、出线对端均为系统内变电站,四台主变压器(电压比为110/10.5kV);110kV为单母线分段接线,每段母线接一路进线,一路出线,两台主变;主变高压侧套管CT电流比为3000/1A,其余110kVCT电流 [单选]对于螺内酯试验,说法错误的是()A.螺内酯是醛固酮的竞争性拮抗剂B.螺内酯可以抑制醛固酮的分泌C.不可以判断是原发性还是继续性D.服药后,血钾升高E.服药后,尿钾降低 [单选,A2型题,A1/A2型题]甲状旁腺功能减退症患者对维生素D制剂的使用,下列说法正确的是()。A.用钙剂时常规加用维生素D制剂B.应尽可能快速大量应用维生素D制剂,以尽快控制症状C.较重患者须加用维生素D制剂,应从小剂量开始D.以上都不对E.钙剂加量时亦应增加维生素D制剂的用量 [判断题]元认知调节策略与监控策略无关。()A.正确B.错误 [判断题]材料的伸长率、断面收缩率数值越小,表明其塑性越好。()A.正确B.错误 [名词解释]俄狄浦斯情结(05年十月已考) [单选]建构招标采购合同体系的方法包括()。A.责任分配矩阵B.带状结构分解C.网状结构分解D.义务分配矩阵 [单选,A1型题]儿童意外伤害的预防措施包括()A.伤害监测B.伤害干预C.伤害干预措施研究D.伤害的急救和康复E.以上都有 [填空题]在集邮门市前台业务管理子系统,提供两种预订方式,即()和暂发收据。 [多选]水灰比可以影响到水泥商品混凝土的()A、坍落度B、耐久性C、工艺性D、强度 [单选]头针进针时,应达到的解剖组织层是()。A.皮内B.皮下C.肌肉D.帽状腱膜E.骨膜 [单选]泵的轴承箱的的温度要求不大于()。A.65℃B.70℃C.80℃ [填空题]在政治上,齐国采取了“因其俗,()其礼”,鲁国采取了“革其俗,革其礼”的政策。 [单选]月经周期中,子宫内膜增生期主要是下列哪项激素的作用?()A.绒毛膜促性腺激素B.雌激素C.孕激素D.雄激素E.促性腺激素 [单选]飞机在地面连接上地面电源车时,GPCU(地面电源控制组件)由谁供电()A.地面电源车和直流电瓶汇流条;B.只由直流电瓶汇流条供电;C.只由地面电源车供电。 [单选]高血压病脑出血时,最常见的出血部位是()A.小脑齿状核B.小脑皮质C.脑桥D.基底节E.延脑 [单选]下列不符合化妆品定义的产品是()。A.含抑制螨虫剂的洗头水B.香皂C.含抑汗剂的爽身粉D.防蛀漱口水E.脱毛霜 [单选]目前测定中药中重金属及有害元素(铅、镉、汞、铜、砷)最常用的方法是A.紫外-可见分光光度法B.红外分光光度法C.原子吸收分光光度法D.薄层色谱扫描法E.高效液相色谱法 [单选]矫治g之间B.强度在60~350g之间C.强度小于60gD.强度在500~1000g之间E.强度大于1000g,但小于1500g [单选]下列有关行政机关公务员处分的说法哪一项是正确的?()A.处分决定自送达之日起生效B.处分决定机关负责人的回避,由机关集体讨论决定C.除案情复杂或有特殊情形外,给予行政机关公务员处分,应自批准立案之日起6个月作出决定D.如被撤销处分的行政机关公务员的工资福利受到损 [单选]与固定增长股票的价值呈反方向变化的是()。A.股利的增长率B.上一期刚支付的股利C.投资的必要报酬率D.下一期预计支付的股利 [多选]关于近曲小管的描述正确的是()。A.细胞呈锥体形或立方形,界限清楚B.腔面有刷状缘?C.细胞基部有纵纹D.胞质嗜酸性E.细胞核圆形,位于细胞中央 [单选]()既标识了一个网络,又标识了该网络上的一台特定主机。A.主机名B.MAC地址C.IP地址D.物理地址 [单选]关于水灰比对混凝土拌合物特性的影响,说法不正确的是()。A.水灰比越大,粘聚性越差B.水灰比越小,保水性越好C.水灰比过大会产生离析现象D.水灰比越大,坍落度越小 [判断题]出口电池产品的制造商在电池产品出口前,应向国家质检总局申请备案。()A.正确B.错误 [填空题]一般来讲,浅基础的地基破坏模式有三种:()、()和()。 [单选]骨软化症的特点不包括()A.患者多于青春期发病,与维生素D缺乏有关B.主要表现为骨痛、肌无力,还可出现骨骼变形C.X线检查有助于本病的诊断D.以骨基质矿化障碍为特点的一种疾病E.血清碱性磷酸酶可轻、中度升高 [单选]根据所有观测点在堤防上的平面位置和累计沉降量可绘制成()。A.堤防沉降量平面分布图B.堤防横断面图C.堤防平面图D.堤防纵断面图 [单选,A4型题,A3/A4型题]女,49岁,上腹胀满5年,2个月来食欲不振,全身无力,体检无明显异常发现,X线钡餐未见异常。胃镜活检:炎性细胞浸润及肠上皮化生,未见腺体萎缩。浅表性胃炎胃镜改变正确的是()A.皱襞平坦B.皱襞变细C.粘膜苍白D.可透见粘膜下血管网E.粘膜红白相间, [单选,A2型题]热性惊厥发作中最首要的处理是()A.给氧、保持气道通畅B.降低颅内压C.降低体温D.控制感染E.控制惊厥发作 [单选,A2型题,A1/A2型题]以下自杀的相关因素不正确的是()A.重大的负性应激事件可能成为自杀的直接原因或诱因B.独身、离婚、丧偶者自杀率高于婚姻状况稳定者C.从事专门职业的医生、律师、作家、音乐家等的自杀率低于普通人群D.西方国家的自杀率大多是男多于女,而我国则相差不大
