2017-2018学年河南省豫南九校高二上学期期末联考数学(理)试题 扫描版
河南省豫南九校2018-2019学年高二上学期第三次联考数学(理)试题(含解析)
河南省豫南九校2018-2019学年高二上学期第三次联考数学（理）试题一、选择题（本大题共12小题，共60.0分）1.命题“若，则”的逆命题是A. 若，则B. 若，则C. 若，则D. 若，则【答案】A【解析】解：命题的逆命题需将条件和结论交换，因此逆命题为：若，则．故选：A．根据命题的逆命题需将条件和结论交换即可求出．本题考查了四种命题的之间的关系，属于基础题．2.椭圆的长轴长是A. 2B.C. 4D.【答案】D【解析】解：椭圆的标准方程为，即有，则椭圆的长轴长为，故选：D．将椭圆方程化为标准方程，可得椭圆的a，进而得到椭圆的长轴长2a的值．本题考查椭圆的方程和性质，主要考查椭圆的长轴长，注意化椭圆为标准方程，属于基础题．3.若x，y满足，则的最大值为A. 0B. 3C. 4D. 5【答案】C【解析】解：作出不等式组对应的平面区域如图：阴影部分．设得，平移直线，由图象可知当直线经过点A时，直线的截距最大，此时z最大．由，解得，即，代入目标函数得．即目标函数的最大值为4．故选：C．作出不等式组对应的平面区域，目标函数的几何意义是直线的纵截距，利用数形结合即可求z的取值范围．本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．4.数列的通项公式为，当取到最小时，A. 5B. 6C. 7D. 8【答案】C【解析】解：令，解得．当取到最小时，．故选：C．令，解出即可得出．本题考查了数列的通项公式与求和公式、数列的单调性，考查了推理能力与计算能力，属于中档题．5.过抛物线的焦点F作与对称轴垂直的直线交抛物线于A，B两点，则以AB为直径的圆的标准方程为A. B. C.D.【答案】B【解析】解：由抛物线的性质知AB为通径，焦点坐标为，直径，即，所以圆的标准方程为，故选：B．由抛物线的性质知AB为通径，焦点坐标为，直径，求得即可．本题考查了抛物线的性质，属于基础题．6.当时不等式恒成立，则实数a的取值范围是A. B. C. D.【答案】A第2页，共11页【解析】解：当时，表达式，当且仅当时取等号．当时，不等式恒成立，则实数a的取值范围是．故选：A．化简不等式的左侧，利用基本不等式求出表达式的最小值，然后求出a的范围．本题考查函数恒成立，基本不等式的应用，考查分析问题解决问题的能力．7.成等差数列的三个正数的和等于12，并且这三个数分别加上1，4，11后成为等比数列中的，，，则数列的通项公式为A. B. C. D.【答案】A【解析】解：设成等差数列的三个正数分别为，a，，可得，解得，即成等差数列的三个正数分别为，4，，这三个数分别加上1，4，11后成为等比数列中的，，，可得，解方程可得舍去，则，，，即有，则，故选：A．设成等差数列的三个正数分别为，a，，由条件可得，再由等比数列中项的性质，可得d的方程，解得，求得等比数列的公比为2，首项为2，即可得到数列的通项公式．本题考查等差数列的通项公式和等比数列的中项的性质和通项公式，考查运算能力，属于基础题．8.的内角A、B、C的对边分别是a、b、c，若，，，则A. B. 2 C. D. 1【答案】B【解析】解：，，，由正弦定理得：，，由余弦定理得：，即，解得：或经检验不合题意，舍去，则．故选：B．利用正弦定理列出关系式，将，a，b的值代入，利用二倍角的正弦函数公式化简，整理求出的值，再由a，b及的值，利用余弦定理即可求出c的值．此题考查了正弦、余弦定理，二倍角的正弦函数公式，熟练掌握定理是解本题的关键．9.等差数列中，m，n，s，，则是的A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件【答案】B【解析】解：在等差数列中，若，则，，，成立，即充分性成立，当为常数列时，则，但不成立，即必要性不成立，则是的充分不必要条件，故选：B．根据等差数列的通项公式以及充分条件和必要条件的定义进行判断即可．本题主要考查充分条件和必要条件的判断，结合等差数列的通项公式和性质是解决本题的关键．10.在中，若，则圆C：与直线l：的位置关系是A. 相切B. 相交C. 相离D. 不确定【答案】A【解析】解：，，即．圆心到直线l的距离，又圆的半径，直线l与圆相切．故选：A．根据正弦定理化简得出a，b，c的关系，根据距离公式求出圆心到直线l的距离，与半径比较得出结论．本题考查了直线与圆的位置关系判断，属于基础题．11.在中，内角A，B，C所对应的边分别为a，b，c，若，且，则的值为A. B. C. 2 D. 4【答案】C第4页，共11页【解析】解：中，由，利用正弦定理得，，故B．由余弦定理得，即，又，所以，求得，故选：C．先由条件利用正弦定理求得角B，再由余弦定理列出关于a，c的关系式，然后进行合理的变形，求得的值．本题考查正弦定理、余弦定理得应用解题先由正弦定理求得角B，再由余弦定理列出关于a，c的关系式，然后进行合理的变形，求得的值，属于中档题．12.已知抛物线C的顶点在坐标原点，焦点，P为抛物线上的任一点，过点P作圆E：的切线，切点分别为M，N，则四边形PMEN的面积最小值为A. B. C. D.【答案】D，抛物线的准线方程为抛物线方程为：，设，过点P作圆E：的切线，切点分别为M，N，PE取得最小值时，四边形PMEN的面积取得最小值，，的最小值为：．，．四边形故选：D．求出圆的圆心与半径，设，F为抛物线的焦点，求出抛物线方程，然后转化求解PE的最小值，即可求解四边形面积的最小值．本题考查了抛物线的性质，圆的切线的性质，数形结合思想的应用，属于中档题．二、填空题（本大题共4小题，共20.0分）13.抛物线的焦点坐标是______．【答案】【解析】解：抛物线的标准方程为：，所以抛物线的焦点坐标为：．故答案为：．利用抛物线方程直接求解抛物线的焦点坐标即可．本题考查抛物线的简单性质的应用，是基础题．14.内角A，B，C的对边分别为a，b，c，若，则______．【答案】【解析】解：中，，由正弦定理得，即，，，．故答案为：．由题意，利用正弦定理、两角和的正弦公式即可求得角C的值．本题考查了正弦定理与三角形的内角和定理的应用问题，是基础题．15.“斐波那契数列”由十三世纪意大利数学家列昂纳多斐波那契发现，因为斐波那契以兔子繁殖为例子而引入，故又称该数列为“兔子数列”斐波那契数列满足：，，，记其前n项和为，设为常数，则______用t表示．【答案】t【解析】解：斐波那契数列满足：，，，设则：，，，，．故答案为：t直接利用题中的信息，进一步求出关系式，再求出结果．本题考查的知识要点：信息题在数列中的应用．16.已知等比数列的前n项和，则函数的最小值为______．【答案】16第6页，共11页【解析】解：因为，而题中，易知，故 ； 所以，即，等号成立条件为， 所以最小值为16． 故答案为：16先根据 是等比数列的前n 项和求出a 的值，再利用基本不等式求函数的最值． 本题考查等比数列前n 项和的性质以及基本不等式在求函数最值中的应用，属于中档题．三、解答题（本大题共6小题，共70.0分）17. 求抛物线 上的点到直线 的距离的最小值．【答案】解：如图，设与直线 平行且与抛物线 相切的直线为 ， 切线方程与抛物线方程联立得， 去y 整理得 ， 则 ，解得， 所以切线方程为，抛物线 上的点到直线 距离的最小值是这两条平行线间的距离：．【解析】画出图形，设出切线方程，联立方程组利用韦达定理求出b ，然后通过平行线之间的距离求解即可．本题考查直线与抛物线的位置关系的应用，平行线之间的距离的求法，考查计算能力．18. 已知等差数列 的公差为d ，且关于x 的不等式 的解集为 ．求数列 的通项公式； 若，求数列 前n 项和 ．【答案】解： 由x 的不等式 的解集为 ， 可得 ，3为 的两根，得解得， 故数列 的通项公式为 ，即．由知，所以，所以．【解析】由题意可得，3为的两根，运用韦达定理解方程可得数列的首项和公差，即可得到所求通项公式；求得，再由数列的裂项相消求和，计算可得所求和．本题考查等差数列的通项公式的运用，考查数列的裂项相消求和，化简整理的运算能力，属于中档题．19.已知的内角A，B，C满足．求角A；若的外接圆半径为1，求的面积S的最大值．【答案】解：设内角A、B、C所对的边分别为a、b、c，根据，可得，，分，分又，；分由正弦定理得，，分由余弦定理得，分的面积为，当且仅当时取等号，面积S的最大值为分【解析】根据题意，利用正弦、余弦定理，即可求出角A的值；由正弦、余弦定理，利用三角形面积公式与基本不等式，即可求得面积的最大值．本题考查了正弦、余弦定理的应用问题，也考查了三角形面积公式与基本不等式的应用问题，是中档题．第8页，共11页20.解不等式；已知a，b，，求证：．【答案】解：（1）由不等式＞，得（x-2）（x2+3x+2）＞0，即（x-2）（x+1）（x+2）＞0，解得-2＜x＜-1，或x＞2，故不等式的解集为：；（2）因为a，b，c＞0，所以===≥2+2=2+2=4，当且仅当a=b+c时等号成立．故．【解析】（1）由分式不等式的解法、高次不等式的解法得：（x-2）（x2+3x+2）＞0，即（x-2）（x+1）（x+2）＞0，解得-2＜x＜-1，或x ＞2，故不等式的解集为：；（2）由重要不等式的应用得：== =≥2+2=2+2=4，当且仅当a=b+c时等号成立．命题得证．本题考查了分式不等式的解法、高次不等式的解法及重要不等式的应用，属中档题．21.已知命题p：，．若p为真命题，求实数m的取值范围；若有命题q：，，当为真命题且为假命题时，求实数m的取值范围．【答案】解：，，时不成立．且，解得．为真命题时，．对于命题q：，，，又时，，．为真命题且为假命题时，真q假或p假q真，当p假q真，有，解得；当p真q假，有，解得；为真命题且为假命题时，或．【解析】根据二次函数的性质求出p为真时m的范围即可；，，时不成立可得且，解得m范围对于命题q：，，根据时，利用函数的单调性即可得出由为真命题且为假命题时，可得p真q假或p假q 真．本题考查了函数与不等式的性质、不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．22.已知，，点C是动点，且直线AC和直线BC的斜率之积为．求动点C的轨迹方程；设直线l与中轨迹相切于点P，与直线相交于点Q，且，求证：．【答案】解：设，则依题意得，又，，所以有，整理得，动点C的轨迹方程为．证明：证法1：设直线l：，与，联立得，即，依题意，即，设直线l与动点C的轨迹交于点，，，得，，而，得，又，又，则知，即．证法2：设，则曲线C在点P处切线PQ：，令，得，又，知，即．第10页，共11页【解析】设，依题意得，由，，得，由此能求出动点C的轨迹方程．法1：设直线l：，与联立，得，利用根的判别式、韦达定理、圆的性质，结合已知条件能证明．法2：设，则曲线C在点P处切线PQ：，令，得，由，则由，能证明．本题考查点的轨迹方程的求法，考查角为直角的证明，考查椭圆、直线方程的斜率、根的判别式、韦达定理等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．。
河南省豫南九校2017届高三第四次联考(数学理)(含答案)word版
D1C 1B 1A 1DC BA豫南九校2016——2017学年高三第四次联考数学试题（理科）命题教师：泌阳一高数学组考试时间：150分钟 试卷满分150分本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，其中第II 卷第（22）-（23）题为选考题，其他题为必考题。
考生作答时，将答案答在答题卡上，在本试卷上答题无效。
考试结束后，将本试卷和答题卡一并交回。
注意事项： 一、选择题1．已知集合A ，B 都是非空集合，则“()x A B ∈ ”是“x A ∈且x B ∈”的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ． 既不是充分条件，也不是必要条件2．定义一种运算如下：11122122x y x y x y x y ⎡⎤=-⎢⎥⎣⎦，复数1i z i i ⎤-=⎥⎥⎦（i 是虚数单位）的共轭复数是（ ）A11)i +B11)i -C11)i + D11)i - 3．根据表格中的数据，可以判定方程20xe x --=的一个根所在的区间为(,1)()k k k N +∈，则k 的值为（ ）A ．-1B ．0C ．1D ．24．若)(x f 是偶函数，且当0)1(,1)(,),0[<--=+∞∈x f x x f x 则时的解集是（ ）A ．（－1，0）B ．（－∞，0）∪（1，2）C ．（1，2）D ．（0，2）5．在正方体ABCD －A 1B 1C 1D 1中，直线A 1B 与平面BC 1D 1所成角的正切值为（ ）ABC ．1D6．已知函数321()22f x x x m =-+的图象上A 点处的切线与直线30x y -+=的夹角为45°，则A 点的横坐标为（ ）.A ．0B ．1C ．0或16D ．1或167．设数列{}n a 是以2为首项，1为公差的等差数列，{}n b 是以1为首项，2为公比的等比数列，则1210b b b a a a +++=… （ ）A ．1033B ．1034C ．2057D ．20588. 一个算法的程序框图如图所示，若该程序输出的结果是45，则判断框中应填入的条件是（ ） A ．6i > B ． 6i < C ．5i > D ． 5i <9．图中共顶点的椭圆①、②与双曲线③、④的离心率分别为 1234e e e e ﹑﹑﹑，其大小关系为（ ）A. 1234e e e e <<<B. 2134e e e e <<<C. 1243e e e e <<<D. 2143e e e e <<< 10．设2()3sin()43f x x π=+，若12,()()()x f x f x f x ∀∈≤≤R ，则12||x x -的最小值为 A. 8 B. 4 C. 2 D. 111. 设O 为坐标原点，点M 坐标为)2,3(，若点(,)N x y 满足不等式组：53,4200≤≤⎪⎪⎩⎪⎪⎨⎧≤+≤+≥≥s x y s y x y x 当 时，则∙的最大值的变化范围是（ ） A ．[7，8] B ．[7，9] C ．[6，8] D ．[7，15]12. 若A, B 是平面内的两个定点, 点P 为该平面内动点, 且满足向量AB 与AP夹角为锐角θ, |PB||AB|+PA AB=0∙, 则点P 的轨迹是（ ）A ．直线 （除去与直线AB 的交点） B ．圆 （除去与直线AB 的交点）C ．椭圆 （除去与直线AB 的交点）D ．抛物线（除去与直线AB 的交点）二、填空题13．26(1)(1)ax x -+的展开式中，3x 项的系数为16-，则实数a 的值为14．若,a b 是正常数，a b ≠，,(0,)x y ∈+∞，则222()a b a b x y x y++≥+，当且仅当a b x y =时上式取等号. 利用以上结论，可以得到函数29()12f x x x =+-（1(0,)2x ∈）的最小值为 ．15．已知P 为圆22(1)1x y +-=上任意一点，直线OP 的倾斜角为θ弧度，O 为坐标原点，记d OP =，以(,)d θ为坐标的点的轨迹为C ，则曲线C 与x 轴围成的封闭图形的面积为 16. 下列正确结论的序号是 ①命题.01,:01,22<++∃>++∀x x x x x x 的否定是②命题“若0,0,0===b a ab 或则”的否命题是“00,0≠≠≠b a ab 且则若”③已知线性回归方程是,23ˆx y+=则当自变量的值为2时，因变量的精确值为7; ④若]1,0[,∈b a ，则不等式4122<+b a 成立的概率是4π.三、解答题17．（本小题满分12分）已知2(2sin ,)OA a x a =，(1cos 1)OB x x =-+ ，O 为坐标原点，0a ≠，设()f x OA OB b =⋅+，b a >．（1）若0a >，写出函数()y f x =的单调递增区间；（2）若函数()y f x =的定义域为[,]2ππ，值域为[2,5]，求实数a 与b 的值．18．（本小题满分12分）一个多面体的直观图和三视图如图所示（1）求证:BD PA ⊥；（2）是否在线段PD 上存在一Q 点,使二面角D AC Q --的平面角为30，设DQλ=，若存在，求λ；若不存在，说明理由19．（本小题满分12分）．某科技公司遇到一个技术难题，紧急成立甲、乙两个攻关小组，按要求各自单独进行为期一个月的技术攻关，同时决定对攻关期满就攻克技术难题的小组给予奖励．已知此技术难题在攻关期满时被甲小组攻克的概率为23，被乙小组攻克的概率为34． （1）设ξ为攻关期满时获奖的攻关小组数，求ξ的分布列及E ξ；（2）设η为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方，记“函数7()2xf x η=-在定义域内单调递减”为事件C ，求事件C 的概率．20.（本小题满分12分）设)0(1),(),,(22222211>>=+b a bx a y y x B y x A 是椭圆上的两点，已知11(,)x y m b a = ，22(,)x y n b a = ，若0m n ∙= 且椭圆的离心率,23=e 短轴长为2，O 为坐标原点.（1）求椭圆的方程；（2）若直线AB 过椭圆的焦点F （0，c ），（c 为半焦距），求直线AB 的斜率k 的值；（3）试问：△AOB 的面积是否为定值？如果是，请给予证明；如果不是，请说明理由。
【全国校级联考】河南省豫南九校2017-2018学年下学期高二第二次联考数学(理)试题(原卷版)
豫南九校2017-2018学年下期第二次联考高二数学（理）试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 复数（为虚数单位）在复平面内对应的点位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限2. 抛物线的焦点坐标是（）A. B. C. D.3. 下列说法正确的是（）A. 命题“若，则”的否命题是“若，则”B. 若，则“”是“”的必要不充分条件C. 函数的最小值为D. 命题“，”的否定是“，”4. 已知函数，则函数的图象在处的切线方程为（）A. B. C. D.5. 已知函数在上单调递增，则实数的取值范围是（）A. B. C. D.6. 甲、乙、丙、丁四位同学被问到是否去过市时，甲说：我没去过，乙说：丙去过，丙说：丁去过，丁说：我没去过.在以上的回答中只有一人回答正确，且只有一人去过市.根据以上条件，可以判断去过市的人是（）A. 甲B. 乙C. 丙D. 丁7. 用数学归纳法证明不等式“”时的过程中，由到，不等式的左边增加的项为（）A. B.C. D.8. 已知为等差数列，，.若为等比数列，，则类似的结论是（）A. B.C. D.9. 将标号分别为，，，，的个小球放入个不同的盒子中，每个盒子至少放一球，则不同的方法种数为（）A. B. C. D.10. 已知数列是公比为的等比数列，满足.设等差数列的前项和为，若，则（）A. B. C. D.11. 已知椭圆与抛物线的交点为，连线经过抛物线的焦点，且线段的长度等于椭圆的短轴长，则椭圆的离心率为（）A. B. C. D.12. 已知函数是函数的导函数，（其中为自然对数的底数），对任意实数，都有，则不等式的解集为（）A. B. C. D.第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 设复数满足，则__________．14. 计算__________．15. 已知，是双曲线的两个焦点，为双曲线上一点，且，若的面积为，则__________．16. 若为的各位数字之和，如，，则.记，，，……，，，则__________．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知的展开式中各项的二项式系数之和为.（1）求的值；（2）求的展开式中项的系数；（3）求展开式中的常数项.18. 已知的三个内角，，的对边分别为，，，且.（1）求角的大小；（2）若，，求.19. 设命题实数满足，命题实数满足.（1）若，为真命题，求的取值范围；（2）若是的充分不必要条件，求实数的取值范围.20. 如图，在多面体中，四边形，，均为正方形，点是的中点，点在上，且与平面所成角的正弦值为.......（1）证明：平面；（2）求二面角的大小.21. 已知椭圆的一个焦点为，且过点.（1）求椭圆的方程；（2）已知直线与椭圆交于，两点，求（为坐标原点）的面积取最大值时直线的方程.22. 已知函数.（1）求函数的极值；（2）若函数（其中为自然对数的底数），且对任意的总有成立，求实数的取值范围.。
河南省豫南九校2017-2018学年高二上学期期末联考地理试题
河南省豫南九校高二17-18学年上学期期末联考地理一、选择題（本大题共30小題，每小题2分，共50分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
）读下面108°E的地形剖面图，据图完成下列问题。
1、下列判断正确的是A、①为云贵高原B、③为黄河谷地C、⑤汾河谷地D、⑥为内蒙古高原2、符合⑥地地形特征的是A、有喀斯特地貌分布B、海拔较高，起伏不大C、千沟万壑的景观D、远看成山，近看成川3、关于④地形区形成原因的说法，正确的是A、主要是流水侵蚀形成B、主要是冰川侵蚀形成C、主要是受挤压向上拱起形成D、主要是断层受挤压，一侧上升形成民居的特点受自然条件和生产方式的影响，读图完成下列问题。
4、图中建筑物设计最有利于防大风的建筑是A、甲B、乙C、丙D、丁5、图乙所在的地区是我国水土流失严重的地区，下列水土流失治理措施中，属于黄土高原保持水土根本措施的是A、平整土地B、修筑梯田C、造林种草D、深耕改土读下图完成下列问题。
6、粮食输出前两位的省份发展商品农业的有利条件是①人口稀少，本地消费量较小②水源充足，土壤肥沃③地形平坦，光热充足④交通便利，机械化水平高A、①②③④B、①②③C、①②④D、②③④7、江浙地区号称“鱼米之乡”，浙江却成为第二粮食调入大省，最主要的原因是A、山区较多，土地贫瘠，单产低B、自然灾害频发，影响粮食生产C、经济发展迅速，粮食播种面积下降D、制造乙醇汽油，消耗大量粮食下图为“某旅友时期自行车骑行途经地点的手机截屏图”，完成下列问题。
8、图中各区域有明确边界的是A、亚热带地区B、台湾省C、江南丘陵区D、湿润地区9、记录旅友骑行途经地点位置的地理信息技术是A、遥感B、数字地球C、地理信息系统D、全球定位系统下图是某城市部分地区经过数字化处理的功能分区图层和地价图层（单位：十万元）。
读图完成下列问题。
10、功能分区图层中最适合布局电子装配工业的是A、①B、②C、③D、④有中亚明珠之称的伊赛克湖位于天山山脉北麓，中国古称图斯池、热海、清池，终年不结冰，以“热湖”著称，气候温和干燥，年降水量约200－300毫米，部分地区可达800－1000毫米，湖泊东西两岸降水量相差悬殊，西岸年降水量仅115毫米，东岸年降水量则达569毫米。
河南省豫南九校2018-2019学年高二上学期第三次联考数学(理)试题
河南省豫南九校2018-2019学年高二上学期第三次联考数学（理）试题本试题卷共6页，23题（含选考题）。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项：1、答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后，请将本试题卷和答题卡一并上交。
一、选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.命题“若2018a >，则2017a >”的逆命题是（ ） A ．若2017a >，则2018a > B ．若2017a ≤，则2018a > C ．若2017a >，则2018a ≤ D ．若2017a ≤，则2018a ≤2.椭圆2228x y +=的长轴长是（ ） A ．2B．C ．4D．3.若x ，y 满足2030x y x y x -≤⎧⎪+≤⎨⎪≥⎩，则2x y +的最大值为（ ）A ．0B ．3C ．4D ．54.数列{}n a 的通项公式为323n a n =-，当n S 取到最小时，n =（ ） A ．5B ．6 C. 7D ．85.过抛物线24y x =的焦点F 作与对称轴垂直的直线交抛物线24y x =于A ，B 两点，则以AB 为直径的圆的标准方程为（ ）A ．22(1)4x y ++=B ．22(1)4x y -+= C. 22(1)4x y ++= D ．22(1)4x y +-=6.当1x >时不等式11x a x +≥-恒成立，则实数a 的取值范围是（ ） A ．(,3]-∞ B ．[3,)+∞C.(,2]-∞ D ．[2,)+∞7.成等差数列的三个正数的和等于12，并且这三个数分别加上1，4，11后成为等比数列{}n b 中的2b ，3b ，4b ，则数列{}n b 的通项公式为（ ） A ．2n n b = B ．3n n b =C. 12n n b -= D ．13n n b -=8.ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，若2B A =，1a =，b =c =（ ）A ．1或2B ．2D ．19.等差数列{}n a 中，*,,,m n s t N ∈，则m n s t +=+是m n s t a a a a +=+的（ ） A ．充要条件B ．充分不必要条件 C. 必要不充分条件D ．既不充分也不必要条件10.在ABC ∆中，若sin sin sin 0a A b B c C +-=，则圆22:1C x y +=与直线:0l ax by c ++=的位置关系是（ ）A ．相切B ．相交C.相离 D ．不确定11.设ABC ∆的内角A ，B ，C 所对边的长分别为a ，b ，c ，若sin cos 0b A B =，且2b ac =，则a cb+的值为（ ）A B C. 2D ．412.已知抛物线C 的顶点在坐标原点，焦点(2,0)F ，P 为抛物线上的任一点，过点P 作圆22:12340E x y x +-+=的切线，切点分别为M ，N ，则四边形PMEN 的面积最小值为（ ）A B ．D ．二、填空题（本大题共4小题，每小题5分，共20分）13.抛物线24y ax =（a R ∈且0a ≠）的焦点坐标为 ．14.ABC ∆内角A ，B ，C 的对边分别为a ，b ，c ，若2cos 2c B a b =+，则C ∠= ． 15.“斐波那契数列”由十三世纪意大利数学家列昂纳多•斐波那契发现，因为斐波那契以兔子繁殖为例子而引入，故又称该数列为“兔子数列”，斐波那契数列{}n a 满足：11a =，21a =，*12(3,)n n n a a a n n N --=+≥∈，记其前n 项和为n S ，设2018a t =（t 为常数），则2016201520142013S S S S +--= ．（用t 表示） 16.已知等比数列{}n a 的前n 项和1133n n S t -=⋅-，则函数(2)(10)(0)x x y x x t++=>+的最小值为 ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17.（本小题满分10分）求抛物线2y x =-上的点到直线4380x y +-=的距离的最小值. 18.（本小题满分12分）已知等差数列{}n a 的公差为d ，且关于x 的不等式2130a x dx --<的解集为(1,3)-. （1）求数列{}n a 的通项公式； （2）若1(3)n n b n a =+，求数列{}n b 前n 项和n S .19.（本题满分12分）已知ABC ∆的内角A ，B ，C 满足sin sin sin sin A B C C -+sin sin sin sin BA B C=+-.（1）求角A ；（2）若ABC ∆的外接圆半径为1，求ABC ∆的面积S 的最大值. 20.（本小题满分12分） （1）解不等式22032x x x ->++； （2）已知,,a b c R +∈，求证：11()()4a b c ab c+++≥+. 21.（本小题满分12分）已知命题:p x R ∀∈，240mx x m ++≤.（1）若p 为真命题，求实数m 的取值范围；（2）若有命题:[2,8]q x ∃∈，2log 10m x +≥，当p q ∨为真命题且p q ∧为假命题时，求实数m 的取值范围. 22.（本小题满分12分）已知(2,0)A -，(2,0)B ，点C 是动点，且直线AC 和直线BC 的斜率之积为34-. （1）求动点C 的轨迹方程；（2）设直线l 与（1）中轨迹相切于点P ，与直线4x =相交于点Q ，且(1,0)F ，求证：90PFQ ∠=︒.高二数学（理）参考答案一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1-5: ADCCB 6-10: AABBA 11、12：CD1. 【解析】命题的逆命题需将条件和结论交换，因此逆命题为：若2017a >，则2018a >.2. 【解析】椭圆方程变形为22148x y +=，28a =，∴a =2a =. 3. 【解析】作出如图可行域，则当2z x y =+经过点P 时，取最大值，而(1,2)P ，∴所求最大值为4，故选C .4. 【解析】∵数列{}n a 的通项公式323n a n =-，∴数列{}n a 为公差为3的递增的等差数列，令3230n a n =-≥可得233n ≥，∴数列{}n a 的前7项为负数，从第8项开始为正数∴S 取最小值时，n 为7，故选C .5. 【解析】由抛物线的性质知AB 为通径，焦点坐标为(1,0)，直径2||24R AB p ===，即2R =，所以圆的标准方程为22(1)4x y -+=，故选B .6. 【解析】∵1x >∴111111x x x x +=-++≥--13=，当且仅当111x x -=-即2x =时等号成立，所以最小值为3∴3a ≤，实数a 的取值范围是(,3]-∞ 7. 【解析】设成等差数列的三个正数为a d -，a ，a d +，即有312a =，计算得出4a =，根据题意可得41d -+，44+，411d ++成等比数列，即为5d -，8，15d +成等比数列，即有(5)(15)64d d -+=，计算得出1d =（11-舍去），即有4，8，16成等比数列，可得公比为2，则数列{}n b 的通项公式为2222422n n n n b b --==⨯=.8. 【解析】∵2B A =，1a =，b =sin sin a bA B=得：1sin sin sin 22sin cos A B A A A ===，∴cos 2A =， 由余弦定理得：2222cos a b c bc A =+-，即2133c c =+-， 解得：2c =或1c =（经检验不合题意，舍去），则2c =，故选B .9. 【解析】由等差数列的性质知：*,,,m n s t N ∈，m n s t +=+时m n s t a a a a +=+成立.反之：等差数列{}n a 为常数列，m n s t a a a a +=+对任意*,,,m n s t N ∈成立，故选B .10. 【解析】因为sin sin sin 0a A b B c C +-=，所以2220a b c +-=，圆心(0,0)C 到直线:0l ax by c ++=的距离1d r ===，故圆22:1C x y +=与直线:0l ax by c ++=相切，故选A .11. 【解析】由sin cos 0b A B =可得sin sin cos 0B A A B =，从而tan B =3B π=，从2b ac =可联想到余弦定理：2222cos b a c ac B =+-22a c ac =+-，所以有222()0a c ac ac a c +-=⇒-=，从而a c =.再由2b ac =可得a b c ==，所以a cb+的值为2.12. 【解析】由题意可知抛物线的方程为28y x =，圆E 的圆心为(6,0)E ，半径为r =设(,)P x y ，则||PM ====.所以当2x =时，切线长||PM PMEN 的面积取得最小值，最小值为min ||PM r ⨯==D . 二、填空题（本大题共4小题，每小题5分，共20分）13. 1(0,)16a14. 120︒ 15. t 16.16 13. 【解析】由题意可得214x y a =，所以焦点在y 轴上，且124p a =∴18p a=则焦点坐标为1(0,)16a. 14. 【解析】方法一：∵2cos 2c B a b =+，∴222222a c b c a b ac +-⨯=+，即222a b c ab +-=-， ∴2221cos 22a b c C ab +-==-，∴120C =︒. 方法二：∵2cos 2c B a b =+，∴2sin cos C B 2(sin cos cos sin )sin C B C B B =++ ∴1cos 2C =-，∴120C =︒. 15. 【解析】2016201520142013S S S S +--2015201620152014a a a a =+++201720162018a a a t =+==.16. 【解析】因为111(1)111n n n a q a a S q q q q-==----，而题中11133333n n n t S t -=⋅-=⋅-，易知133t -=-，故1t =；所以(2)(10)x x y x t ++=+(2)(10)1x x x ++=+91101x x =++++，即1016y ≥=，等号成立条件为9121x x x +=⇒=+，所以最小值为16. 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） 17. 【解析】法一：如图，设与直线4380x y +-=平行且与抛物线2y x =-相切的直线为430x y b ++=，切线方程与抛物线方程联立得2430y x x y b ⎧=-⎨++=⎩去y 整理得2340x x b --=，则16120b ∆=+=，解得43b =-，所以切线方程为44303x y +-=，抛物线2y x =-上的点到直线4380x y +-=距离的最小值是这两条平行线间的距离4|8|4353d -==.法二：设2(,)P x x -，则点P 到直线4380x y +-=的距离2d =21220|3()|533x =-+ 2324()533x =-+，在抛物线2y x =-中，x R ∈，所以当23x =时，d 取得最小值43，即抛物线2y x =-上的点到直线4380x y +-=距离的最小值是4318. 【解析】（1）由题意，得112,33,d a a ⎧=⎪⎪⎨⎪-=-⎪⎩解得12,1.d a =⎧⎨=⎩故数列{}n a 的通项公式为12(1)n a n =+-，即21n a n =-. （2）由（1）知21n a n =-，所以2122n b n n ==+1(1)111()2(1)21n n n n n n +-⋅=⋅-++所以n S =111111[(1)()()]22231n n -+-+⋅⋅⋅+-+， 11(1)212(1)nn n =-=++ 19. 【解析】（1）设内角A ，B ，C 所对的边分别为a ，b ，c .根据sin sin sin sin A B C C -+sin sin sin sin BA B C =+-，可得a b c bc a b c-+=+-222a b c bc ⇒=+-，所以2221cos 222b c a bc A bc bc +-===，又因为0A π<<，所以3A π=. （2）2sin a R A =2sin a R A ⇒=2sin 3π== 所以223b c bc =+-2bc bc bc ≥-=，所以1sin 2S bc A=132≤⨯=（b c =时取等号）.故三角形面积最大值为420. 【解析】 （1）由不等式22032x x x ->++，得2(2)(32)0x x x -++>，即(2)(1)(2)0x x x -++>， 解得21x -<<-，或2x >（2）因为,,0a b c >，所以11()()a b c ab c ++++11[()]()a b c a b c=++++ 11a b cb c a +=++++ 2a b cb c a+=+++224≥+=当且仅当a b c =+时等号成立. 21. 【解析】（1）∵x R ∀∈，240mx x m ++≤， ∴0m <且21160m ∆=-≤，解得01144m m m <⎧⎪⎨≤-≥⎪⎩或，∴p 为真命题时，14m ≤-. （2）[2,8]x ∃∈，2log 10[2,8]m x x +≥⇒∃∈，21log m x≥-. 又[2,8]x ∈时，211[1,]log 3x -∈--， ∴1m ≥-.∵p q ∨为真命题且p q ∧为假命题时，∴p 真q 假或p 假q 真，当p 假q 真，有114m m ≥-⎧⎪⎨>-⎪⎩，解得14m >-； 当p 真q 假，有114m m <-⎧⎪⎨≤-⎪⎩，解得1m <-；∴当p q ∨为真命题且p q ∧为假命题时，1m <-或14m >-. 22. 【解析】（1）设(,)C x y ，则依题意得34AC BC k k ⋅=-，又(2,0)A -，(2,0)B ，所以有 3(0)224y y y x x ⋅=-≠+-， 整理得221(0)43x y y +=≠，即为所求轨迹方程. （2）设直线:l y kx m =+，与223412x y +=联立得2234()12x kx m ++=，即222(34)84120k x kmx m +++-=，依题意222(8)4(34)(412)0km k m ∆=-+-=，即2234k m +=，∴122834km x x k -+=+，得122434kmx x k -==+， ∴2243(,)3434km m P k k -++，而2234k m +=，得43(,)k P m m-，又(4,4)Q k m +， 又(1,0)F ，则FP FQ ⋅=43(1,)(3,4)k k m m m--⋅+0=，知FP FQ ⊥， 即90PFQ ∠=︒.。
理数答案
豫南九校2017—2018学年上期第二次联考高二数学（理）答案一、选择题：本大题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有 一项是符合题目要求的。
1．答案：B 2．答案：C 当41<<k 且23≠k 时表示椭圆 3．答案：D ,R x ∈∃使得02<x4．答案：D 11713,918271377122===⇒==+a S a a a a5．答案：B 3122112c c c c c c n n n ⋅=⇒⋅=+-因为0>n c 所以92=c6．答案：B 由),2(62512≥-=-=⇒-=-n n S S a n n S n n n n 当1=n 时也满足再由73<<k a 得 7623<-<n 解得k= 5和6 7．答案：C 命题p 为假 命题q 为真8．答案：C 2,4==b a 时C 不成立9．答案：C 由正弦定理结合已知可得22sin =A 再由大边对大角的4π=A10．答案：B由正弦定理结合已知可得A A A C A cos sin 42sin 2sin 2sin 3===43cos =A 8114321c o s 22c o s c o s 22=-⎪⎭⎫⎝⎛⨯=-==A A C11．答案：B A 选项公比为-1不成立，C 选项公差为0不成立，D 选项q 为0不成立12．答案：B 因为P 在线段A F 2的中垂线上，所以PA PF =2所以2111124F F AF PF PA PF PF >==+=+所以P 点的轨迹是以21,F F 为焦点的椭圆，且53,22=∴==b a c 故选B二、填空题：本题共4小题，每小题5分，共20分。
13．答案：14由)(10071*∈<<N n n 得)(141*∈≤≤N n n14由︒=∠+∠180ANC ANB 得ANC ANB ∠=∠cos cos462321693225922=⨯-+-=⨯-+m mm m m 46=∴BC 15．答案：1>q 由0>n S 知01>a 由()01111>-=--+q q a a a n n n 得1>q16．答案：[]3,1- 画出不等式表示的平面区域知y x +在点()3,3处取最大值6，在点()32,-m m 处取最小值33-m 由 6336≤-≤-m 得31≤≤-m 三、解答题：本大题共6个小题，共70分。
【全国校级联考】河南省商丘市九校2017-2018学年高二上学期期末联考数学(理)试题(解析版)
2017---2018学年上期期末联考高二数学试题（理科）注意：1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，时间120分钟。
2、全部答案在答题卡上完成,答在本试题上无效。
3、每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。
第I卷(共60分)一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若命题“”为假，且“”为假，则（）A. “”为假B. 假C. 真D. 不能判断的真假【答案】B【解析】试题分析：因为“”为假，所以“”为真，又“”为假，所以为假，故选B．考点：1、复合命题的真假；2、命题的否定．2. 已知是等差数列，且……，则（）A. 3B. 6C. 9D. 36【答案】B【解析】因为,选B3. 在中，，则的面积为（）A. B. C. 或 D. 或【答案】B....... ........考点：余弦定理及三角形面积的求法．4. 在如图所示的正方体A1B1C1D1-ABCD中，E是C1D1的中点，则异面直线DE与AC夹角的余弦值为( )．A. －B. －C.D.【答案】D【解析】试题分析：取中点,连接则即为异面直线夹角，设边长为1由余弦定理的考点：异面直线所成角点评：先将异面直线平移为相交直线找到所求角，再在三角形中求三边余弦定理求角5. 已知，则f（x）在点P（－1,2）处的切线与坐标轴围成的三角形面积等于（）A. 4B. 5C.D.【答案】C【解析】f（x）在点P（－1,2）处的切线方程为与坐标轴围成的三角形面积等于 ,选C6. 过抛物线y2=8x的焦点作直线交抛物线于A，B两点，若线段AB的中点的横坐标为4，则∣AB∣等于（）A. 12B. 8C. 6D. 4【答案】A【解析】∣AB∣,选A.7. 已知等差数列满足,,则前n项和取最大值时，n的值为A. 20B. 21C. 22D. 23【答案】B【解析】试题分析：由得，由,所以数列前21项都是正数，以后各项都是负数，故取最大值时，n的值为21考点：本小题主要考查等差数列的性质.点评：等差数列是一类比较特殊也比较重要的数列，要充分利用等差数列的性质解决问题，可以简化运算.8. 是的导函数，的图象如右图所示，则的图象只可能是（）A. B. C. D.【答案】D【解析】试题分析：首先观察函数的图象，与x轴的交点即为的极值点，然后根据函数与其导数的关系进行判断．由图可以看出函数的图象是一个二次函数的图象，在a与b之间，导函数的值是先增大后减小故在a与b之间，原函数图象切线的斜率是先增大后减小，故选D．考点：函数的单调性与导数的关系9. 已知是抛物线的准线与双曲线的两条渐近线所围成的三角形平面区域内（含边界）的任意一点，则的最大值为（）A. 3B. 4C. 5D. 6【答案】C【解析】约束条件为可行域如图,所以直线过点A(2,-1)时取最大值5,选C.10. 如图：的二面角的棱上有两点，直线分别在这个二面角的两个半平面内，且都垂直于.已知则的长为( )A. B. 6 C. D. 8【答案】A【解析】选A11. 若上是减函数，则的取值范围是（）A. B. C. D.【答案】C【解析】由题意得上恒成立,即,选C12. 已知椭圆的左焦点为F,椭圆C与过原点的直线相交于A、B两点,连接AF、BF. 若|AB|=10,|BF|=8，cos∠ABF=,则C的离心率为( )A. B. C. D.【答案】B【解析】试题分析：由余弦定理得，所以有勾股定理得，设是右焦点，根据椭圆的对称性知四边形是矩形.所以，，，故选B.考点：1、椭圆的定义和几何性质；2、余弦定理及勾股定理.第Ⅱ卷(共90分)二、填空题（本大题共4小题，每小题5分，共20分。
(全优试卷)河南省豫南九校高二上学期期末联考理科数学试题Word版含答案
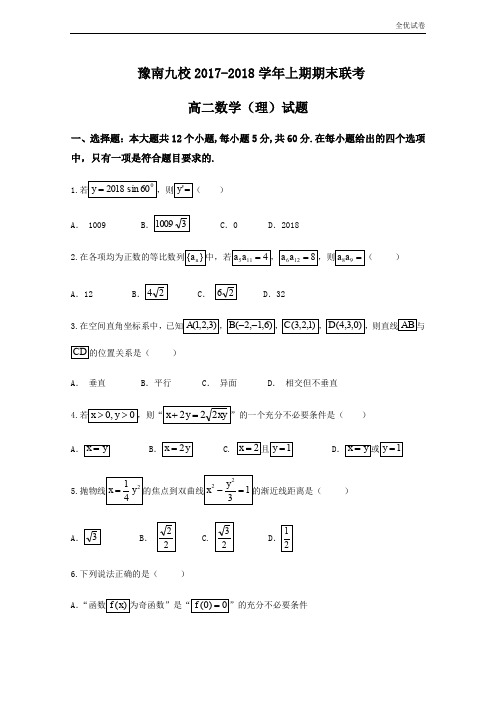
豫南九校2017-2018学年上期期末联考高二数学（理）试题一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.）A． 1009 B．0 D．20182.）A．12 B．．323.在空间直角坐标系中，）A．垂直 B．平行 C．异面 D．相交但不垂直4.）A5.）A．6.下列说法正确的是（）A．BC.D7.）A8.）A ．2B ． 4 C. 5 D．69.）A ．10.（ ）A ． 7B ．4 C. 0 D ．-411.）A12.范围为（）A．二、填空题（每题5分，满分20分，将答案填在答题纸上）13.14.的取值范围是．15.16.的最小值为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. （1（2.18.（1（219..（1（2.（1（2.21.（1（2.22.离等于3.（1（2.试卷答案一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1—5CBBCC 6—10DBDAA 11—12CD1．C2．B3．B【解析】由题意得4．C是5．C【解析】（可由抛物线的焦点F（1,0）直接求距离）6．D故选项A错误；因为是在三角形中，所以是故选项B错误；则p,q至少有一个为假命题，故选项C错误；故选D．7．B以8．D【解析】作出可行域如图，C6．9．AA．10．A11．C=C ．12．D二、填空题（本大题共4小题，每小题5分，共20分）1314 15 1613．14，，即，ABE 中，又i nn b =+，则44n mm n．(当且仅当“=”)三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）17．（1R（2,4<545x-=x=118．解：（1（219．解：（1OD OA∴==DO O=AC∴⊥面AEC，EO∴面AEC（2,∠，EFO改成角的余弦值为（亦可以建系完成）20．解：（1（221．（1）设椭圆E所以椭圆E（2）由（1）知F1(-2,0)，F2(2,0)，所以直线AF1直线AF2由椭圆E设P(x,y)其斜率为负，不合题意，舍去．22．解：（1（2）解法1因为(=-·FA FB xFA FB=．，所以0解法2FA FB=．。
河南省豫南九校2017-2018学年高二上学期期末联考化学试题+扫描版
豫南九校2017—2018学年上期期末联考高二化学答案一、选择题（每个小题只有一个选项符合题意，选对得3分，共42分。
）1—5BCCBA 6—10ADDBB 11—14BBDD二、（本大题为必答题，包含4个小题，共38分）15．【答案】（6分）（1）淀粉溶液（1分）（2）碱（1分）（3）滴入最后一滴标准液，溶液由蓝色变成无色且半分钟内不恢复蓝色（2分）（4）B（2分）16．【答案】（8分）（1）Cu2++2H 2O Cu（OH）2+2H+（2分）（2）因为Cu2++2e-−−→Cu，使Cu2+水解平衡向左移动，c（H+）减小，pH上升（2分）（3）电解过程中溶液的pH逐渐降低（2分）（4）CuCl 2电解Cu+ Cl2↑，Cl2+H2O HCl+ HClO，使溶液酸性增强，pH降低（2分）17．【答案】（10分）（1）CO（g）+1/2O2（g）=CO2（g）△H=-283 kJ·mol-l（2分）（2）大于（1分）AC（2分）（3）①10-3.45（或3.5×10-4）[当c(F-)=c(HF)时，K a=c(H+)，查图中的交点处即为c(F-)=c(HF)，故所对应的pH即为K a的负对数] （2分）②当pH=4.0时，溶液中的c(F-)=1.6×10-3mol/L，溶液中c(Ca2+)=2.0×l0-4 mol/L，c( Ca2+)×c2(F-)= 5.l×10-10> K sp( CaF2)，有沉淀产生（3分）18．【答案】（14分）（1）增大（2分）（2）200（2分）（3）①＜（2分）；②0.1（2分）；③2（2分）（4）A（2分）；D（2分）三、（本大题为选做题，请在下列两个考试模块中任选一个模块作答，请先把要选择答题的模块涂黑，20分）选作（一）【物质结构与性质部分】19．【答案】（1）A（2）C（3）D20．【答案】（11分）（1）ds（1分）（1分）K、Cr（1分）（2）1s22s22p63s23p5 （1分）Ar（1分）HClO4 （1分）正四面体（1分）（3）氟的原子半径小于氯原子，氢氟键的键能大于氢氯键，分子稳定（2分）；氟化氢分子间可以形成氢键，沸点反常的高（2分）选作（二）【有机化学基础部分】19．【答案】（1）A（2）C（3）A20．【答案】（11分）（1）（2分）（2）法拉第（1分）6（2分）79（2分）（3）（2分）加成反应（1分）（4）C12H10 （1分）。
2017-2018学年河南省豫南九校高二上学期期末联考物理试题扫描版含答案
豫南九校2017—2018学年上期期末联考高二物理答案一、选择题（共50分，其中1～6题为单选题，每小题5分，每小题给出的四个选项中，只有一个选项是正确的；7～10题为多选题，每小题5分，在每小题给出的四个选项中，有多个选项是正确的，全部选对的得5分，选对但不全的得3分，有选错的得0分．)1．【答案】C【解析】法拉第认为电荷的周围存在着由它产生的电场，并采用了电场线来简洁地描述它，故C 正确；安培通过实验测定了磁场对电流的作用力，故B 错误；奥斯特发现了电流的磁效应，是安培提出了分子电流假说，故A 错误；库仑通过扭秤实验建立了库仑定律，密立根比较精确地测定了元电荷e 的数值，故D 错误。
2．【答案】A【解析】试题分析：粒子受到的电场力指向轨迹弯曲的一侧，所以该粒子受到的电场力指向带负电的A 电荷，所以该粒子带的是正电，所以A 正确，B 错误；因为，根据等量异种点电荷电场线及等势面分布特点可知，所以大于，大于，试探电荷在M 处的电势能大于在N 处的电势能，所以CD 错误。
考点：电场线；电势能．3．【答案】B【解析】根据左手定则知，导体棒开始所受的安培力方向水平向右，根据F=BIL 知，安培力在第一个T/2内做匀加速直线运动，在第二个T/2内，安培力方向水平向左，大小不变，做匀减速直线运动，根据运动的对称性知，一个周期末速度为零，金属棒的速度方向未变．知金属棒一直向右移动，先向右做匀加速直线运动，再向右做匀减速运动，速度随时间周期性变化．安培力在一个周期内先做正功，后做负功，故AC 正确，B 错误．因为电流周期性变化，则安培力也周期性变化．故D 正确．此题选择不正确的选项，故选B ．4．【答案】C【解析】A 项：根据2m vq v B r=可知，q B r v m =，粒子获得的最大动能为：2222211222k q B R q B R E m v m m m ⎛⎫=== ⎪⎝⎭，所以要想粒子获得的最大动能增大，可增加D 形盒的半径，故A 错误；。
2017-2018学年河南省豫南九校高二上学期期末联考数学(理)试题扫描版含答案
豫南九校2017—2018学年上期期末联考高二数学（理）答案一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1—5CBBCC6—10DBDAA11—12CD1．C【解析】根据求导法则易知0y '=．2．B【解析】由等比数列的性质有，．3．B【解析】由题意得,(3,3,3),(1,1,1)AB CD =--=-,所以3AB CD =-，所以AB CD ∥．4．C【解析】，，当且仅当时取等号．故“”是“”的充分不必要条件．5．C【解析】双曲线2213yx-=的焦点(20)，到渐近线距离为2134x y⇒=的焦点(10)，到渐近线距离为32．（可由抛物线的焦点F （1,0）直接求距离）6．D【解析】函数()f x 的定义域为R 才成立，故选项A 错误；因为是在三角形中，所以“A B <”是“sin sin A B <”成立的充要条件，故选项B 错误；若命题p q ∧为假命题，则p ,q 至少有一个为假命题，故选项C 错误；故选D ． 7．B【解析】令1n =，得111233S a =+，11a =，当2n ≥时，111233n n S a --=+，所以111133n n n n n S S a a a ---=-=，所以112n n a a -=-，所以数列{}n a 是以1为首项，12-为公比的等比数列，所以11()2n n a -=-．。
河南省中原名校(即豫南九校)2017-2018学年高二上学期第二次联考数学(理)试题含答案
豫南九校2017-2018学年上期第二次联考高二数学（理)试题 第Ⅰ卷（共60分）一、选择题:本大题共12个小题,每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1。
已知集合{}2|23A x y x x ==--，{}|30B x x =+>，则AB =（ ）A ．[1,2)-B ．[]3,1--C ．(3,2]-D ．(2,1]-2.“14k <<"是“方程22141x y k k +=--表示椭圆”的什么条件（）A ．充分不必要条件B ．充要条件C ．必要不充分条件D ．既不充分也不必要条件3。
命题“x R ∀∈，使得20x ≥”的否定形式是（）A ．x R ∀∈，使得20x < B ．x R ∀∈，使得20x≤ C ．x R ∃∈，使得20x≥D ．x R ∃∈，使得20x <4.设nS 是等差数列{}na 的前n 项和，若21218a a +=,则13S =（）A ．91B ．126C ．234D ．1175。
数列{}nc 满足112ln ln ln nn n c c c -+=+，若13c =，327c =，则2c 等于（）A ．9-B ．9C ．9±D ．以上都不对6。
已知数列{}n a 的前n 项和25n S n n =-，若它的第k 项满足37k a <<，则k =(）A ．4和5B ．5和6C ．6和7D ．7和87。
已知命题p ：0x R ∃∈，使得06sin x =；命题q :在ABC ∆中，若A B >，则sin sin A B >，下列判断正确的是( ）A ．q 为假B ．p q ∨为假C ．p q ∧为假D ．p 为真8。
若1a b >>，则下列结论不一定成立的是（ )A ．11a b <B >C ．b aa b >D ．loglog ba ab >9。
河南省豫南九校2018-2019学年高二上学期第三次联考数学(理)试题(精品解析)
{
由图象可知当直线������ =‒ 2������ + ������经过点 A 时，直线������ =‒ 2������ + ������的截距最大， 此时 z 最大． 由{������ + ������ = 3，解得{������ = ������ = 1
故选：A． 化简不等式的左侧，利用基本不等式求出表达式的最小值，然后求出 a 的范围． 本题考查函数恒成立，基本不等式的应用，考查分析问题解决问题的能力． 成等差数列的三个正数的和等于 12，并且这三个数分别加上 1，4，11 后成为等 比数列{������������}中的������2，������3，������4，则数列{������������}的通项公式为( )
6.
������ + ������ ‒ 1 ≥ ������ 当������ > 1时不等式 恒成立，则实数 a 的取值范围是( )
1
A. ( ‒ ∞,3]
【答案】A
B. [3, + ∞)
C. ( ‒ ∞,2]
D. [2, + ∞)
第 2 页，共 11 页
【解析】解：当������ > 1时，表达式 当且仅当������ = 2时取等号． 当������ >
23 3
=7+3
2
．
本题考查了数列的通项公式与求和公式、数列的单调性，考查了推理能力与计算能力， 属于中档题．
2 2 过抛物线������ = 4������的焦点 F 作与对称轴垂直的直线交抛物线������ = 4������于 A，B 两点， 则以 AB 为直径的圆的标准方程为( ) 2 2 2 2 2 2 2 2 A. (������ + 1) + ������ = 4 B. (������ ‒ 1) + ������ = 4 C. ������ + (������ + 1) = 4 D. ������ + (������ ‒ 1) = 4
河南省豫南九校2018-2019学年高二上学期第三次联考数学(理)试题(含解析)
代入目标函数������ = 2������ + ������得������ = 1 × 2 + 2 = 4． 即目标函数������ = 2������ + ������的最大值为 4． 故选：C． 作出不等式组对应的平面区域，目标函数的几何意义是直线的纵截距，利用数形结合 即可求 z 的取值范围． 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想 是解决此类问题的基本方法． 数列{������������}的通项公式为������������ = 3������ ‒ 23，当������������取到最小时，������ = ( )
6.
������ + ������ ‒ 1 ≥ ������ 当������ > 1时不等式 恒成立，则实数 a 的取值范围是( )
1
A. ( ‒)
C. ( ‒ ∞,2]
D. [2, + ∞)
第 2 页，共 11 页
【解析】解：当������ > 1时，表达式 当且仅当������ = 2时取等号． 当������ >
则������ = 2．
故选：B． 利用正弦定理列出关系式，将������ = 2������，a，b 的值代入，利用二倍角的正弦函数公式化 简，整理求出������������������������的值，再由 a，b 及������������������������的值，利用余弦定理即可求出 c 的值． 此题考查了正弦、余弦定理，二倍角的正弦函数公式，熟练掌握定理是解本题的关 键．
3 2， ������ ������ 1 3 3 3
2
������ ‒ 1
= 2������，
8.
数学---河南省豫南九校2017-2018学年高二上学期第一次联考(10月)(文)
河南省豫南九校2017-2018学年 高二上学期第一次联考（10月）（文）（考试时间：120分钟 试卷满分：150分）一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.已知角α的终边过点P （3a ，4a ），且a<0，那么cosα等于（ ） A.-54 B.54 C.-53 D.532.已知向量a =（sinα，cosα），b =（cosβ，sinβ），且a ∥b ，若α，β∈[0,2π]，则α＋β=（ ） A.0 B.2π C.π43D.π 3.已知数列{a n }是等比数列，数列{b n }是等差数列，若a 1·a 5·a 9=-8，b 2+b 5+b 8=6π，则cosaa bb 73641⋅-+的值是（ ）A.21 B.23 C.-21 D.-23 4.若向量a =（1，x ），b =（2x+3，-x ）互相垂直，其中x ∈R ，则b a -等于（ ） A.-2或0 B.2 C.2或-2 D.2或105.已知α∈（-4π，0）且sin2α=-2524，则sinα+cosα=（ ）A.51B.-51C.-57D.57 6.△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若bc<cosA ，则△ABC 为（ ）A.钝角三角形B.直角三角形C.锐角三角形D.等边三角形 7.已知数列{a n }是等差数列，若aa1112+1<0，且它的前n 项和S n 有最大值，则使得S n >0的n的最大值为（ ）A.11B.12C.21D.22 8.不解三角形，确定下列判断中正确的是（ ）A.b=9，c=10，B=60°，无解B.a=7，b=14，A=30°，有两解C.a=6，b=9，A=45°，有两解D.a=30，b=25，A=150°，有一解9.已知02≠=b a ，且关于x 的方程x 2+ax+a ·b =0有实根，则a 与b 的夹角取值范围是（ ） A.⎥⎦⎤⎢⎣⎡6,0π B.⎥⎦⎤⎢⎣⎡ππ,3 C.⎥⎦⎤⎢⎣⎡32,3ππ D.⎥⎦⎤⎢⎣⎡x ,6π 10.函数f （x ）=Asin （ϕω+x ）（A>0，ω>0,0<ϕ<π）的图象如图所示，则下列有关 f （x ）性质的描述正确的是（ ） A.ϕ=32πB.x=ππk +127，k ∈Z 为其所有对称轴C.⎥⎦⎤⎢⎣⎡++2127,212ππππk k ，k ∈Z 为其减区间 D.f （x ）向左移12π可变为偶函数 11.设等比数列{a n }的前项和S n =2n -1（n ∈N *）,则a 12+a 22+…+a n 2=（ ） A.31（4n -1） B.4n -1 C.(2n -1)2 D.31(2n -1)2 12.给出下列语句：①若α、β均为第一象限角，且α>β，且sinα>sinβ； ②若函数y=2cos ⎝⎛⎪⎭⎫-3πax 的最小正周期是4π，则a=21；③函数y=21sin -x 的周期是π； ④函数y=sinx+sin x 的值域是[]2,0。
河南省豫南九校20172018学年高二数学上学期第一次联考(10月)试题文(含解析)
豫南九校2017—2018学年上学期第一次联考高二数学（文科）试题一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知角α的终边过点P（3a，4a），且a<0，那么cosα等于（）A. -B.C. -D.【答案】C【解析】由题意得，选C.2. 已知向量=（sinα，cosα），=（cosβ，sinβ），且∥，若α，β[0,]，则α＋β=（）A. 0B.C.D.【答案】B【解析】由向量平行可得，即，选B.3. 已知数列{a n}是等比数列，数列{b n}是等差数列，若a1·a5·a9=-8，b2+b5+b8=6，则的值是（）A. B. C. - D. -【答案】C【解析】由题意得a1·a5·a9=，b2+b5+b8=，所以=，选C.4. 若向量=（1，x），=（2x+3，-x）互相垂直，其中x R，则等于（）A. -2或0B. 2C. 2或-2D. 2或10【答案】D【解析】同两向量垂直可得或x=-1,当x=3时=，当x=-1时，=，选D.5. 已知α（-，0）且sin2α=-，则sinα+cosα=（）A. B. - C. - D.【答案】A【解析】,又α（-，0），所以，且，，所以，选A.6. △ABC中，角A，B，C所对的边分别为a，b，c，若<cosA，则△ABC为（）A. 钝角三角形B. 直角三角形C. 锐角三角形D. 等边三角形【答案】A【解析】由正弦定理可得，即，所以是钝角，选A.7. 已知数列{a n}是等差数列，若，且它的前n项和S n有最大值，则使得S n>0的n的最大值为（）A. 11B. 12C. 21D. 22【答案】C【解析】由题意得，由前n项和S n有最大值可知等差数列{a n}为递减，d<0.所以，所以，所以n=21,选C.8. 不解三角形，确定下列判断中正确的是（）A. b=9，c=10，B=60°，无解B. a=7，b=14，A=30°，有两解C. a=6，b=9，A=45°，有两解D. a=30，b=25，A=150°，有一解【答案】D【解析】A选项，两解，错。
河南省中原名校(即豫南九校)2017_2018学年高二数学上学期第二次联考试题理(含解析)
豫南九校2017-2018学年上期第二次联考高二数学（理）试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，，则（）A. B. C. D.【答案】B【解析】集合，∴故选：点睛：1.用描述法表示集合，首先要弄清集合中代表元素的含义，再看元素的限制条件，明确集合类型，是数集、点集还是其他的集合．2．求集合的交、并、补时，一般先化简集合，再由交、并、补的定义求解．3．在进行集合的运算时要尽可能地借助Venn图和数轴使抽象问题直观化．一般地，集合元素离散时用Venn图表示；集合元素连续时用数轴表示，用数轴表示时要注意端点值的取舍2. “”是“方程表示椭圆”的什么条件（）A. 充分不必要条件B. 充要条件C. 必要不充分条件D. 既不充分也不必要条件【答案】C【解析】若方程表示椭圆，则，解得：∴“”是“方程表示椭圆”的必要不充分条件故选：C点睛：本题考查所给方程表示椭圆的充要条件，同时考查了椭圆的标准方程，是一道易错题，即当分母相等时，一般表示的是圆，而圆并不是椭圆的特殊形式，要把这种情况去掉.3. 命题“，使得”的否定形式是（）A. ，使得B. ，使得C. ，使得D. ，使得【答案】D【解析】命题“，使得”的否定形式是，使得故选：D4. 设是等差数列的前项和，若，则（）A. 91B. 126C. 234D. 117【答案】D【解析】是等差数列的前项和，,选D.5. 数列满足，若，，则等于（）A. B. C. D. 以上都不对【答案】B【解析】由数列满足，可知：，且∴数列为等比数列∴，又，，∴故选:B6. 已知数列的前项和，若它的第项满足，则（）A. 4和5B. 5和6C. 6和7D. 7和8【答案】B【解析】当n=1时，，即当时，令，解得：，∴故选：B7. 已知命题：，使得；命题：在中，若，则，下列判断正确的是（）A. 为假B. 为假C. 为假D. 为真【答案】C【解析】∵，∴命题p为假命题；∵，∴，由正弦定理易得：，命题q为真命题；∴为假命题故选：C8. 若，则下列结论不一定成立的是（）A. B. C. D.【答案】C【解析】∵，∴＜，＞，故A，B成立当a=4，b=2时，，故C错误；..................故选：C．9. 设的内角，，所对的边长分别为，，，若，，，则（）A. B. C. D. 或【答案】C【解析】，则为锐角，根据正弦定理，，则，则，选C.10. 在中，内角，，所对的边分别是，，，已知，，则（）A. B. C. D.【答案】B【解析】，，，，，，选B. 11. 下列结论正确的是（）A. 若为等比数列，是的前项和，则，，是等比数列B. 若为等比数列，是的前项和，则，，是等差数列C. 若为等比数列，“”是“”的充要条件D. 满足（，为常数的数列为等比数列【答案】B【解析】对于A，当公比为时，,,,∴，，不是等比数列；对于B，若为等差数列，是的前项和，则，，是等差数列；对于C，若为常数列，，显然1+102+3，对于D，当q=0时，显然数列不为等比数列故选：B12. 已知圆：，定点，是圆上的一动点，线段的垂直平分线交半径于点，则点的轨迹的方程是（）A. B. C. D.【答案】B【解析】连结，则 =PA，∵+ =PA+==6＞，由椭圆的定义可得点的轨迹为以点、为焦点，长轴为6的椭圆∴2a=6，即a=3，又∵焦点为（2，0），即c=2，∴b2=a2﹣c2=9﹣4=5，故点P的轨迹C的方程为：故选：B点睛：求与圆有关的轨迹问题时，根据题设条件的不同常采用以下方法：①直接法：直接根据题目提供的条件列出方程．②定义法：根据圆、直线等定义列方程．③几何法：利用圆的几何性质列方程．④代入法：找到要求点与已知点的关系，代入已知点满足的关系式等．第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 100以内的正整数有__________个能被7整除的数．【答案】14【解析】它们分别为，共计14个.14. 在中，，，是的中点，，则等于__________．【答案】【解析】延长至N，使，连接，则四边形为平行四边形，，在中，，在中，，，.15. 等比数列的前项和，若，为递增数列，则公比的取值范围__________．【答案】【解析】时，有，恒成立，若，，即成立，若只要，若，需要恒成立，当时，恒成立，当时，也恒成立，当时，若为偶数时，也不可能恒成立，所以的取值范围为16. 设，实数，满足若，则实数的取值范围是__________．【答案】【解析】根据题意得可行域所围成的三角形必在两平行线和之间，由图可知，实数的取值范围是，填.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知：，：（），若是的充分不必要条件，求实数的取值范围．【答案】．【解析】试题分析：首先落实集合A与B，解一元二次不等式求出集合A，由于解一元二次不等式得出集合B，根据p找出非p,由于若是的充分不必要条件，说明非p对应的集合是q对应的集合的真子集，借助集合的包含关系列出不等式，解出a的范围；试题解析：由得，由得．又因为是的充分不必要条件,所以解得．【点睛】有关充要条件问题有两种解释，第一是从逻辑关系的角度去解决，若，但推不出，则是的充分不必要条件；第二从命题所对应的集合的包含关系的角度去解决，是的充分不必要条件说明对应的集合是所对应的集合的真子集.18. 要制作一个体积为，高为的有盖长方体容器，已知该容器的底面造价是每平方米10元，侧面造价是每平方米5元，盖的总造价为100元，求该容器长为多少时，容器的总造价最低为多少元？【答案】长为3，容器的总造价最低为250元．【解析】试题分析：此题首先需要由实际问题向数学问题转化，设池底长和宽分别为，，该容器的造价为y，建立函数关系式，然后利用基本不等式求出最值即可求出所求．试题解析：设该长方体容器长为，则宽为，又设该容器的造价为元，则，因为（当且仅当即时取“=”），所以．答：该容器长为3米时，容器的总造价最低为250元．点睛：在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误19. 已知数列为等差数列，且，．（1）求数列的通项公式；（2）若（），是的前项和，求证：．【答案】（1）．（2）见解析.【解析】试题分析：（1）由等差数列的基本公式求得数列的通项公式；（2）由（1）得到的通项公式，利用裂项相消法求和，易证所给不等式.试题解析：（1）因为数列为等差数列,设公差为,,所以，∴，，∴．（2），，∴．20. 已知的边，三角形内角、满足．（1）求角的值；（2）点在以，为焦点的椭圆上，求椭圆离心率的取值范围．【答案】(1) ;(2)．试题解析：(1)在中,由得，因为A,B为的内角,所以即，所以．(2)又因为点A在以B,C为焦点的椭圆上 ,所以椭圆的焦距而椭圆长轴，在中，，∴，所以椭圆离心率的值范围：．21. 数列的前项和为，已知，（）．（1）求数列的通项公式；（2）求数列的前项和．【答案】（1）（2）．【解析】试题分析：(1)由与的关系得到数列的通项公式；(2)利用错位相减法得到数列的前项和．试题解析：（1），，当，=2不满足上式，（2）由（1）知∴．点睛：用错位相减法求和应注意的问题(1)要善于识别题目类型，特别是等比数列公比为负数的情形；(2)在写出“S n”与“qS n”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S n－qS n”的表达式；(3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于1和不等于1两种情况求解.22. 已知椭圆：经过，且椭圆的离心率为．（1）求椭圆的方程；（2）设斜率存在的直线与椭圆交于，两点，为坐标原点，，且与圆心为的定圆相切，求圆的方程．【答案】（1）．（2）．【解析】试题分析：(1)利用待定系数法得到椭圆的方程；(2)联立方程，可得：，利用根与系数的关系代数化，得到，结合直线与圆相切即可得到圆的方程．试题解析：（1）因为C经过点（0，），所以，又因为椭圆C的离心率为所以，所以椭圆C的方程为：．（2）设的方程为由得，，，∴，成立，因为l与圆心为O的定圆W相切所以O到l的距离即定圆W的方程为．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
豫南九校2017—2018学年上期期末联考高二数学（理）答案一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1—5CBBCC 6—10DBDAA 11—12CD1．C【解析】根据求导法则易知错误！未找到引用源。
．2．B【解析】由等比数列的性质有，．3．B【解析】由题意得,错误！未找到引用源。
,所以错误！未找到引用源。
，所以错误！未找到引用源。
．4．C【解析】，，当且仅当时取等号．故“”是“”的充分不必要条件．5．C【解析】双曲线错误！未找到引用源。
的焦点错误！未找到引用源。
到渐近线距离为错误！未找到引用源。
的焦点错误！未找到引用源。
到渐近线距离为错误！未找到引用源。
．（可由抛物线的焦点F（1,0）直接求距离）6．D【解析】函数错误！未找到引用源。
的定义域为错误！未找到引用源。
才成立，故选项A错误；因为是在三角形中，所以“错误！未找到引用源。
”是“错误！未找到引用源。
”成立的充要条件，故选项B错误；若命题错误！未找到引用源。
为假命题，则p,q至少有一个为假命题，故选项C错误；故选D．7．B【解析】令错误！未找到引用源。
，得错误！未找到引用源。
，错误！未找到引用源。
，当错误！未找到引用源。
时，错误！未找到引用源。
，所以错误！未找到引用源。
，所以错误！未找到引用源。
，所以数列错误！未找到引用源。
是以1为首项，错误！未找到引用源。
为公比的等比数列，所以错误！未找到引用源。
．8．D【解析】作出可行域如图，当直线过点C 时，错误！未找到引用源。
最大，由得，所以错误！未找到引用源。
的最大值为6． 9．A【解析】sin()2sin cos 2sin cos cos sin A C B C A C A C ++=+ 所以2sin cos sin cos 2sin sin 2B C A C B A b a =⇒=⇒=，选A ．10．A【解析】，又由题意知，．11．C【解析】补成四棱柱错误！未找到引用源。
,则所求角为错误！未找到引用源。
错误！未找到引用源。
错误！未找到引用源。
, 因此错误！未找到引用源。
，故选C ． 12．D【解析】依题意，错误！未找到引用源。
解得错误！未找到引用源。
，因为直线 错误！未找到引用源。
，故错误！未找到引用源。
;设错误！未找到引用源。
的中点为错误！未找到引用源。
，则 错误！未找到引用源。
错误！未找到引用源。
,错误！未找到引用源。
即错误！未找到引用源。
，化简可得 错误！未找到引用源。
，所以点错误！未找到引用源。
的轨迹是以错误！未找到引用源。
为圆心，错误！未找到引用源。
为半径的圆，所以 错误！未找到引用源。
的取值范围为错误！未找到引用源。
，所以错误！未找到引用源。
的取值范围为错误！未找到引用源。
．二、填空题（本大题共4小题，每小题5分，共20分）13．错误！未找到引用源。
14．错误！未找到引用源。
15． 错误！未找到引用源。
16．错误！未找到引用源。
13．【解析】由题意错误！未找到引用源。
是奇函数错误！未找到引用源。
．14．【解析】，，即，即，解得，又，错误！未找到引用源。
．15．【解析】取BC中点E，DC中点F，由题意错误！未找到引用源。
，△ABE中，错误！未找到引用源。
，错误！未找到引用源。
，又错误！未找到引用源。
，错误！未找到引用源。
．16．【解析】圆心为错误！未找到引用源。
，则代入直线得：错误！未找到引用源。
，即错误！未找到引用源。
，观察所求式子形式；不妨令错误！未找到引用源。
，则错误！未找到引用源。
错误！未找到引用源。
．(当且仅当错误！未找到引用源。
，亦即错误！未找到引用源。
取“=”；此时错误！未找到引用源。
．)三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）17．（1）解：设错误！未找到引用源。
．则关于x的不等式错误！未找到引用源。
的解集不是空集错误！未找到引用源。
在R上能成立错误！未找到引用源。
，即错误！未找到引用源。
解得a≥．（或由错误！未找到引用源。
的解集非空得错误！未找到引用源。
亦可得） (5)a≤-或26分（2）解：错误！未找到引用源。
，当且仅当错误！未找到引用源。
，解得x=1或错误！未找到引用源。
而错误！未找到引用源。
即错误！未找到引用源。
时，上式等号成立，故当错误！未找到引用源。
时，错误！未找到引用源。
． (10)分18．解：（1）因为错误！未找到引用源。
，错误！未找到引用源。
，即错误！未找到引用源。
，得错误！未找到引用源。
，错误！未找到引用源。
，所以错误！未找到引用源。
．…………………5分（2）错误！未找到引用源。
，…………………6分错误！未找到引用源。
，…………8分错误！未找到引用源。
………………10分错误！未找到引用源。
错误！未找到引用源。
．…………………12分19．解：（1）错误！未找到引用源。
为错误！未找到引用源。
的中点，错误！未找到引用源。
错误！未找到引用源。
设错误！未找到引用源。
为错误！未找到引用源。
的中点，连接错误！未找到引用源。
，则错误！未找到引用源。
，错误！未找到引用源。
错误！未找到引用源。
错误！未找到引用源。
，错误！未找到引用源。
从而错误！未找到引用源。
，错误！未找到引用源。
错误！未找到引用源。
面错误！未找到引用源。
，错误！未找到引用源。
，错误！未找到引用源。
面错误！未找到引用源。
错误！未找到引用源。
面错误！未找到引用源。
，错误！未找到引用源。
面错误！未找到引用源。
面错误！未找到引用源。
………………6分（2）设错误！未找到引用源。
为错误！未找到引用源。
的中点,连接错误！未找到引用源。
,则错误！未找到引用源。
平行且等于错误！未找到引用源。
错误！未找到引用源。
∥错误！未找到引用源。
错误！未找到引用源。
∥错误！未找到引用源。
不难得出错误！未找到引用源。
面错误！未找到引用源。
（错误！未找到引用源。
错误！未找到引用源。
）错误！未找到引用源。
面错误！未找到引用源。
面错误！未找到引用源。
错误！未找到引用源。
在面错误！未找到引用源。
射影为错误！未找到引用源。
，错误！未找到引用源。
的大小为错误！未找到引用源。
与面错误！未找到引用源。
所成角的大小．设错误！未找到引用源。
，则错误！未找到引用源。
，错误！未找到引用源。
,错误！未找到引用源。
即错误！未找到引用源。
与错误！未找到引用源。
改成角的余弦值为错误！未找到引用源。
．（亦可以建系完成）…………12分20．解：（1）因为错误！未找到引用源。
由正弦定理，得错误！未找到引用源。
，………………2分所以错误！未找到引用源。
，又错误！未找到引用源。
所以错误！未找到引用源。
…………………………………………4分所以错误！未找到引用源。
，所以错误！未找到引用源。
，即错误！未找到引用源。
为直角。
……………………6分（2）设错误！未找到引用源。
，则错误！未找到引用源。
在△错误！未找到引用源。
中，因为错误！未找到引用源。
，错误！未找到引用源。
所以错误！未找到引用源。
，所以错误！未找到引用源。
…………8分在错误！未找到引用源。
中，错误！未找到引用源。
，即错误！未找到引用源。
，所以错误！未找到引用源。
，……………………………10分所以错误！未找到引用源。
，即错误！未找到引用源。
，整理得错误！未找到引用源。
所以错误！未找到引用源。
．……………………………12分21．（1）设椭圆E的方程为错误！未找到引用源。
．由错误！未找到引用源。
，得错误！未找到引用源。
…………………2分所以错误！未找到引用源。
，将错误！未找到引用源。
代入，有错误！未找到引用源。
，解得错误！未找到引用源。
……………3分所以椭圆E的方程为错误！未找到引用源。
．…………………4分（2）由（1）知F1(-2,0)，F2(2,0)，所以直线AF1的方程为错误！未找到引用源。
即错误！未找到引用源。
…………………5分直线AF2的方程为错误！未找到引用源。
．由椭圆E的图形知，错误！未找到引用源。
的角平分线所在直线的斜率为正数．…………6分设P(x,y)为错误！未找到引用源。
的角平分线所在直线上任一点，则有错误！未找到引用源。
……………………………………8分若错误！未找到引用源。
，得错误！未找到引用源。
其斜率为负，不合题意，舍去．于是错误！未找到引用源。
,即错误！未找到引用源。
．所以错误！未找到引用源。
的角平分线所在直线的方程为错误！未找到引用源。
…………12分22．解：（1）抛物线的准线方程为错误！未找到引用源。
，所以点错误！未找到引用源。
错误！未找到引用源。
到焦点的距离为错误！未找到引用源。
．……………………………1分解得错误！未找到引用源。
．所以抛物线错误！未找到引用源。
的方程为错误！未找到引用源。
． (2)分（2）解法1：设直线错误！未找到引用源。
的方程为错误！未找到引用源。
．........................3分将错误！未找到引用源。
代入错误！未找到引用源。
并整理得错误！未找到引用源。
， (4)分由错误！未找到引用源。
，解得错误！未找到引用源。
．……………………………………5分设错误！未找到引用源。
，错误！未找到引用源。
，错误！未找到引用源。
，则错误！未找到引用源。
，错误！未找到引用源。
，……………………………6分因为错误！未找到引用源。
…7分因为错误！未找到引用源。
，所以错误！未找到引用源。
．即错误！未找到引用源。
，又错误！未找到引用源。
，解得错误！未找到引用源。
．……………………………8分所以直线错误！未找到引用源。
的方程为错误！未找到引用源。
．设错误！未找到引用源。
的中点为错误！未找到引用源。
,则错误！未找到引用源。
，错误！未找到引用源。
，………………………9分所以直线错误！未找到引用源。
的中垂线方程为错误！未找到引用源。
．因为错误！未找到引用源。
的中垂线方程为错误！未找到引用源。
，所以△错误！未找到引用源。
的外接圆圆心坐标为错误！未找到引用源。
．…………………………………10分因为圆心错误！未找到引用源。
到直线错误！未找到引用源。
的距离为错误！未找到引用源。
，且错误！未找到引用源。
，所以圆的半径错误！未找到引用源。
．………………11分所以△错误！未找到引用源。
的外接圆的方程为错误！未找到引用源。
．………………………12分解法2：依题意可设直线错误！未找到引用源。
．………………………3分将直线错误！未找到引用源。
与抛物线错误！未找到引用源。
联立整理得错误！未找到引用源。
．…………4分由错误！未找到引用源。
，解得错误！未找到引用源。
．……………………5分设错误！未找到引用源。
则错误！未找到引用源。
．……………………………………6分所以错误！未找到引用源。
，因为错误！未找到引用源。
，…………………7分因为错误！未找到引用源。