简案(18)二次函数中角度关系与坐标专题专题

合集下载

二次函数角度问题解法

二次函数角度问题解法一、介绍在数学中，二次函数是一种常见的函数形式，具有形如 y = ax^2 + bx + c 的特点。

二次函数角度问题解法是指在给定二次函数的情况下，通过求解函数的相关角度问题，来对函数进行分析和理解的方法。

二、相关角度问题二次函数角度问题包括函数的顶点、对称轴、开口方向、最值等问题。

通过对这些角度进行求解和分析，可以帮助我们更好地理解和应用二次函数。

2.1 顶点二次函数的顶点坐标可以通过求解函数的导数来确定。

对于一般形式的二次函数 y = ax^2 + bx + c，其导函数为y’ = 2ax + b。

令导数等于零，即 2ax + b = 0，解得 x = -b/2a。

将 x 值代入原函数，即可求得对应的 y 值。

这样就可以确定二次函数的顶点坐标。

2.2 对称轴二次函数的对称轴是指与函数图像关于直线 x = p 对称的直线。

对于一般形式的二次函数 y = ax^2 + bx + c，其对称轴的方程式为 x = -b/2a，该方程式由顶点的横坐标给出。

这表明，二次函数图像关于直线 x = -b/2a 对称。

2.3 开口方向二次函数的开口方向可以通过二次项系数 a 的正负来确定。

如果 a > 0，则二次函数的图像开口向上；如果 a < 0，则二次函数的图像开口向下。

这个特点对于理解二次函数的凹凸性以及判断最值都非常重要。

2.4 最值二次函数的最值可以通过函数的开口方向和顶点的纵坐标来确定。

当二次函数开口向上时，函数不取最小值，即不存在最小值；当二次函数开口向下时，函数的最小值即为顶点的纵坐标。

类似地，最大值也可以通过函数开口方向和顶点坐标的判断来确定。

三、解决方法在解决二次函数角度问题时，我们可以按照以下步骤进行：1.根据函数形式确定二次函数的各项系数 a、b、c。

2.求解顶点坐标：通过导数求解，令导数等于零，求得顶点的横坐标 x，再代入原函数求得顶点的纵坐标 y。

二次函数角度类问题(带答案)

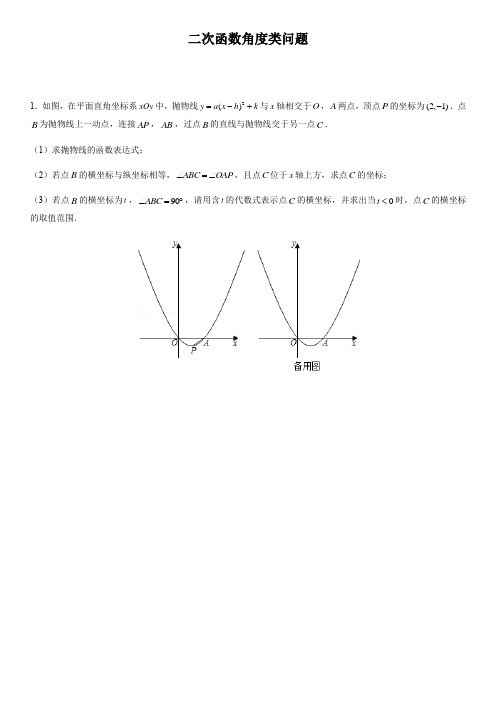
二次函数角度类问题1．如图，在平面直角坐标系xOy中，抛物线2=-+与x轴相交于O，A两点，顶点P的坐标为(2,1)y a x h k()-．点B为抛物线上一动点，连接AP，AB，过点B的直线与抛物线交于另一点C．（1）求抛物线的函数表达式；（2）若点B的横坐标与纵坐标相等，ABC OAP∠=∠，且点C位于x轴上方，求点C的坐标；（3）若点B的横坐标为t，90t<时，点C的横坐标ABC∠=︒，请用含t的代数式表示点C的横坐标，并求出当0的取值范围．2．如图，抛物线22(3)(69)y mx m x m =++-+与x 轴交于点A 、B ，与y 轴交于点C ，已知(3,0)B ．（1）求m 的值和直线BC 对应的函数表达式；（2）P 为抛物线上一点，若PBC ABC S S ∆∆=，请直接写出点P 的坐标；（3）Q 为抛物线上一点，若45ACQ ∠=︒，求点Q 的坐标．3．如图，抛物线(1)()a>与x轴交于A、B两点，交y轴于点C．y x x a=+-（其中1)（1）直接写出OCA∠的度数和线段AB的长（用a表示）；（2）若点D为ABC∆4，求此抛物线的解析式；∆的外心，且BCD∆与ACO（3）在（2）的前提下，试探究抛物线(1)()=+-上是否存在一点P，使得CAP DBAy x x a∠=∠？若存在，求出点P 的坐标；若不存在，请说明理由．4．如图，抛物线2=++经过点(2,0)y ax bx cA-，(4,0)B，与y轴正半轴交于点C，且2OC OA=，抛物线的顶点为D，对称轴交x轴于点E．直线y mx n=+经过B，C两点．（1）求抛物线及直线BC的函数表达式；（2）点F是抛物线对称轴上一点，当FA FC+的最小值；+的值最小时，求出点F的坐标及FA FC（3）连接AC，若点P是抛物线上对称轴右侧一点，点Q是直线BC上一点，试探究是否存在以点E为直角顶点的∆，且满足tan tanRt PEQEQP OCA∠=∠．若存在，求出点P的坐标；若不存在，请说明理由．5．如图，已知抛物线24(0)y ax bx a=++≠与x轴交于点(1,0)A和B，与y轴交于点C，对称轴为直线52x=．（1）求抛物线的解析式；（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由；（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且2DQE ODQ∠=∠．在y轴上是否存在点F，得BEF∆为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．6．如图，在平面直角坐标系中，直线132y x=-+与x轴交于点A，与y轴交于点B，抛物线213y x bx c=++经过坐标原点和点A，顶点为点M．（1）求抛物线的关系式及点M的坐标；（2）点E是直线AB下方的抛物线上一动点，连接EB，EA，当EAB∆的面积等于252时，求E点的坐标；（3）将直线AB向下平移，得到过点M的直线y mx n=+，且与x轴负半轴交于点C，取点(2,0)D，连接DM，求证：45ADM ACM∠-∠=︒．7．如图，在平面直角坐标系中，已知抛物线24(0)=++≠经过点(2,0)y ax bx aA-和点(4,0)B．（1）求这条抛物线所对应的函数表达式；（2）点P为该抛物线上一点（不与点C重合），直线CP将ABC∆的面积分成2:1两部分，求点P的坐标；（3）点M从点C出发，以每秒1个单位的速度沿y轴移动，运动时间为t秒，当OCA OCB OMA∠=∠-∠时，求t的值．8．如图，抛物线22=++经过(1,0)y ax bxB两点，与y轴交于点C，连接BC．A-，(4,0)（1）求该抛物线的函数表达式；（2）如图2，直线:3=+经过点A，点P为直线l上的一个动点，且位于x轴的上方，点Q为抛物线上的一个l y kx动点，当//PQ y轴时，作QM PQ⊥，交抛物线于点M（点M在点Q的右侧），以PQ，QM为邻边构造矩形PQMN，求该矩形周长的最小值；（3）如图3，设抛物线的顶点为D，在（2）的条件下，当矩形PQMN的周长取最小值时，抛物线上是否存在点F，使得CBF DQM∠=∠？若存在，请求出点F的坐标；若不存在，请说明理由．9．已知二次函数．（1）若，，求方程的根的判别式的值；（2）如图所示，该二次函数的图象与轴交于点，、，，且，与轴的负半轴交于点，点在线段上，连接、，满足，． ①求证：；②连接，过点作于点，点在轴的负半轴上，连接，且，求的值．2(0)y ax bx c a =++>12a =2bc ==-20ax bx c ++=x 1(A x 0)2(B x 0)120x x <<y C D OC AC BD ACO ABD ∠=∠1b c x a-+=AOC DOB ∆≅∆BC D DE BC ⊥E 12(0,)F x x -y AF ACO CAF CBD ∠=∠+∠1cx10．如图，抛物线交轴于点，，是抛物线的顶点，是抛物线上的动点，点的横坐标为，交直线于点，交于点，交轴于点．（1）求抛物线的表达式；（2）设的面积为，的面积为，当时，求点的坐标；（3）连接，点在抛物线的对称轴上（位于第一象限内），且，在点从点运动到点的过程中，点也随之运动，直接写出点的纵坐标的取值范围．23y ax bx =+-x (1,0)A -(3,0)B D P P (03)m m //AE PD 1:22l y x =+E AP DE F y Q PDF ∆1S AEF ∆2S 12S S =P BQ M 45BMQ ∠=︒P B C M Mt11．抛物线过点，点，顶点为．（1）求抛物线的表达式及点的坐标；（2）如图1，点在抛物线上，连接并延长交轴于点，连接，若是以为底的等腰三角形，求点的坐标；（3）如图2，在（2）的条件下，点是线段上（与点，不重合）的动点，连接，作，边交轴于点，设点的横坐标为，求的取值范围．23y ax bx =++(1,0)A -(3,0)B C C P CP x D AC DAC ∆AC P E AC A C PE PEF CAB ∠=∠EF x F F mm12．如图，已知：抛物线与直线交于点，，与轴另一交点为．（1）求抛物线的解析式；（2）在抛物线上找一点，使的内心在轴上，求点的坐标；（3）是抛物线上一动点，过点作轴的垂线，垂足为，连接．在（2）的条件下，是否存在点，使？若存在，请求出点的坐标；若不存在，请说明理由．2y x bx c =++l (1,0)A -(2,3)C -x B P ACP ∆x P M M x N BM M MBN APC ∠=∠M13．如图，在平面直角坐标系中，抛物线与轴交于点和点，与轴交于点．（1）求抛物线的函数表达式．（2）若点为第三象限内抛物线上一动点，作轴于点，交于点，过点作的垂线与抛物线的对称轴和轴分别交于点、，设点的横坐标为．①求的最大值；②连接、，若，求的值．2y x bx c =++x A (1,0)B y (0,3)C -P PD x ⊥D AC E E AC y F G Pm PE DF DG 45FDG ∠=︒m14．如图1，抛物线与轴负半轴交于点，与轴正半轴交于点，与轴的负半轴交于点，．（1）求抛物线的解析式；（2）点、在第四象限内抛物线上，点在点下方，连接，，，设点的横坐标为，点的横坐标为，求与的函数关系式；（3）如图2，在（2）条件下，连接交于点，过点作于，连接，，是否存在点，使，若存在，求出点的坐标；若不存在，请说明理由．214y x bx c =++x A x B y C 10OC OB ==P Q P Q CP CQ 180OCP OCQ ∠+∠=︒Q m P n m n AP CO D Q QE AB ⊥E BQ DE P 2AED EQB ∠=∠P15．如图1，在平面直角坐标系中，抛物线交轴于和两点，交轴于点，点是线段上一动点，连接，将线段绕点顺时针旋转得到线段，过点作直线轴于，交抛物线于点，过点作于．（1）求抛物线解析式．（2）如图2，当点恰好在抛物线上时（与点重合），①求线段的长；②连接，求的值；③试探究在直线上，是否存在点，使？若存在，请直接写出点的坐标；若不存在，请说明理由．23y ax bx =++x (1,0)A -(5,0)B y C D OB CD CD D 90︒DE E l x ⊥H M C CF l ⊥F F M EH DF tan FDE ∠lG 45EDG ∠=︒G16．已知：在平面直角坐标系中，抛物线交轴于、两点．（1）如图1，求抛物线的解析式；（2）如图2，过点作射线轴，点是射线上一点，射线交抛物线于点，交轴于点，将线段绕点逆时针旋转得到线段，射线交轴于点，设点的横坐标为，长为，求与的函数关系式（不要求写出自变量的取值范围）；（3）如图3，在（2）的条件下，延长交抛物线于点，交轴于点，过点作轴于点，交于点，延长与过点且垂直于的直线交于点，连接、，若，求的值．xOy 2y x bx c =++x (1,0)A -(3,0)B (0,2)D //DR x E DR AE P y H AE E 90︒EF FB y C P t CH d d t t FE Q x G Q QM x ⊥M DR N QM F QF K AK GK 2180GKF AKG ∠+∠=︒d17．如图，在平面直角坐标系中，抛物线与轴交于点、，与轴交于点，直线经过、两点．（1）求抛物线的解析式；（2）若点为线段上的一个动点，过点作轴，交抛物线于点，过作轴，交直线于点，以、为边作矩形，矩形的周长能为10吗？如果能，请求出点的横坐标；如果不能，请说明理由；（3）点是抛物线上的一个动点，当时，请直接写出点的坐标．232y ax x c =-+x A B y C 122y x =+A C D AC D //DE y E E EF y ⊥AC F DE EF DEFG DEFG E P PCA BCO ∠=∠P18．如图所示：二次函数的图象与轴交于，两点，与轴交于点，连接，．（1）求直线的函数表达式；（2）如图1，若点为抛物线上线段右侧的一动点，连接，．求面积的最大值及相应点的坐标；（3）如图2，该抛物线上是否存在点，使得？若存在，请求出所有点的坐标；若不存在，请说明理由．26y x x =--x A B y C AC BC BC M BC CM BM BMC ∆M P ACO BCP ∠=∠P19．如图1，在平面直角坐标系中，一次函数的图象与轴交于点，与轴交于点，抛物线的图象经过、两点，且与轴的负半轴交于点．（1）求二次函数的表达式；（2）若点在直线下方的抛物线上，如图1，连接、，设四边形的面积为，求的最大值；（3）若点在抛物线上，如图2，过点作于点，试问是否存在点，使得中的某个角恰好等于？若存在，请求点的横坐标；若不存在，请说明理由．122y x =-x B y C 212y x bx c =++B C x A D BC DC DB OCDB S S D D DM BC ⊥M D CDM ∆ABC ∠D20．如图抛物线与轴交于、两点在的右侧），且与直线交于，两点，已知点的坐标为．（1）求抛物线的函数表达式；（2）点是线段上一点，且满足； ①若点为直线上方抛物线上一动点，设点的横坐标为，当为何值时，的面积最大； ②过点向轴作垂线，交轴于点，在抛物线上是否存在一点，使得．若存在，直接写出点的坐标，若不存在，请说明理由．2y x bx c =-++x A B (B A 2y x =+A C B (6,0)E AC 16CE AE =P AC P t t PEA ∆E x x F N NAC FEB ∠=∠N21．如图①，在平面直角坐标系中，已知抛物线与轴交于，两点，与轴交于点．（1）求该抛物线的解析式；（2）如图②，若点是抛物线上一动点，设点的横坐标为，连接，，当的面积等于面积的2倍时，求的值；（3）抛物线上是否存在点，使？若存在，请求出点的坐标；若不存在，请说明理由．23(0)y ax bx a =++≠x (1,0)A -(3,0)B y C D D (03)m m <<CD BD BCD ∆AOC ∆m P CBP ACO ABC ∠+∠=∠P22．已知：抛物线经过点和点，与轴交于另一点．（1）求抛物线的解析式；（2）点为第四象限内抛物线上的点，连接，，．设点的横坐标为．①如图1，当时，求的值；②如图2，连接，过点作轴的垂线，垂足为点．过点作的垂线，与射线交于点，与轴交于点．当时，求的值．2y x bx c =++(1,0)A -(0,3)C -x B P CP AP AC P (03)m m <<CP AC ⊥tan PAB ∠AC P x D C AP PD E x F EAD ACO ∠=∠m23．如图，抛物线与轴交于点，，与轴交于点，直线为．（1）求抛物线的解析式．（2）过点作直线与抛物线在第一象限的交点为．当时，确定直线与的位置关系．（3）在第二象限抛物线上求一点，使．2y ax c =+x A B y CBC 2y x =-A AD D 3ABD ABC S S ∆∆=AD BC P 15PCA ∠=︒24．已知抛物线与轴交于点，点，与轴交于点，顶点为点，如图1所示．（1）求抛物线的解析式；（2）若点在抛物线上，点在轴上，是否存在以点、、、为顶点的四边形是平行四边形，若存在，请直接写出点的坐标；若不存在，请说明理由；（3）如图2所示，抛物线的对称轴与轴交于点，连接，将绕着点顺时针旋转得到△，在旋转过程中，连接，当首次出现时．求直线的函数表达式．23y ax bx =++x (1,0)A -(3,0)B y CD P Q x A C P Q P x N CN OCN ∆N O C N ''OO 'O ON OCN '∠=∠C O ''25．综合与探究：如图，抛物线与轴交于点，（点在点的左侧），与轴交于点，直线经过，两点．（1）求，两点的坐标及直线的函数表达式．（2）点是直线上方抛物线上一点，其横坐标为，过点作直线轴于点，交直线于点．当时，求点的坐标．（3）在（2）的条件下，在轴上是否存在点，使得？若存在，请直接写出点的坐标；若不存在，请说明理由．2168y x x =-++x A B A B y C l B C A B l D l m D DE x ⊥E l F 2DF EF =D y P 2PAB DAB ∠=∠P26．如图，已知抛物线的对称轴为直线且与轴相交于点，与轴相交于点，直线经过点．（1）求该抛物线与直线的表达式；（2）设动点在该抛物线上，当时，求的值．212y x bx c =++52x =-x (6,0)A -y C :2l y x b =+C l (,)P m n 45PAC ∠=︒m27．综合与探究：如图1，已知抛物线与轴交于点，（点在点的左侧），与轴交于点，顶点为，．（1）求抛物线的函数表达式；（2）判断的形状并说明理由；（3）如图2，是下方的抛物线上的一个动点，且点的横坐标为，求面积与的函数关系式及的最大值；（4）在抛物线上是否存在一点，使得，若存在，请直接写出点的坐标；若不存在，请说明理由．2y x bx c =++x A B A B y C D 3OA OC ==ACD ∆N AC N n CAN ∆S n S N NAB ABC ∠=∠N（1）求抛物线的解析式；（2）为轴上一动点，过点作轴，交直线于点，交抛物线于点，连接． ①点在线段上运动，若直角三角形，求点的坐标；②点在轴的正半轴上运动，若．请直接写出的值．(,0)E m x E ED x ⊥AB D P BP E OA BPD ∆E E x 45PBD CBO ∠+∠=︒m（1）求抛物线的解析式．（2）是抛物线对称轴上的一点连接，，求的最小值．（3）若为轴正半轴上一动点，过点作直线轴，交直线于点，交抛物线于点，连接，，当时，请求出的值．M BM CM BM CM +(,0)E m x E ED x ⊥AB D P BP BC 45PBD CBO ∠+∠=︒m30．抛物线交轴于，两点在的左边），交轴于，直线经过，两点．（1）求抛物线的解析式；（2）如图1，为直线上方的抛物线上一点，轴交于点，过点作于点．设，求的最大值及此时点坐标；（3）如图2，点在轴负半轴上，点绕点顺时针旋转，恰好落在第四象限的抛物线上点处，且，求点坐标．213y x bx c =-++x A B (A B y C 4y x =-+B C P BC //PD y BC D D DE AC ⊥E 1021m PD DE =+m P N y A N M 180ANM ACM ∠+∠=︒N答案与解析1．【答案】（1）y 2211(2)144y x x x =--=-（2）(6,3)或5(1,)4-（3）当0t <时，点C 的横坐标的取值范围是12C x 【详解】（1）抛物线2()y a x h k =-+，顶点P 的坐标为(2,1)-，2h ∴=，1k =-，即抛物线2()y a x h k =-+为2(2)1y a x =--，抛物线2()y a x h k =-+经过O ，即2(2)1y a x =--的图象过(0,0)，20(02)1a ∴=--，解得14a =， ∴抛物线的函数表达为2211(2)144y x x x =--=-；（2）在214y x x =-中，令y x =得214x x x =-，解得0x =或8x =，(0,0)B ∴或(8,8)B ，①当(0,0)B 时，过B 作//BC AP 交抛物线于C ，此时ABC OAP ∠=∠，如图：在214y x x =-中，令0y =，得2104x x -=，解得0x =或4x =，(4,0)A ∴，设直线AP 解析式为y kx b =+，将(4,0)A 、(2,1)P -代入得：0412k b k b =+⎧⎨-=+⎩，解得122k b ⎧=⎪⎨⎪=-⎩， ∴直线AP 解析式为122y x =-， //BC AP ，∴设直线BC 解析式为12y x b '=+，将(0,0)B 代入得0b '=， ∴直线BC 解析式为12y x =，由21214y x y x x ⎧=⎪⎪⎨⎪=-⎪⎩得00x y =⎧⎨=⎩（此时为点O ，舍去）或63x y =⎧⎨=⎩， (6,3)C ∴；②当(8,8)B 时，过P 作PQ x ⊥轴于Q ，过B 作BH x ⊥轴于H ，作H 关于AB 的对称点M ，作直线BM 交抛物线于C ，连接AM ，如图：(2,1)P -，(4,0)A ，1PQ ∴=，2AQ =，Rt APQ ∆中，1tan 2PQ OAP AQ ∠==， (8,8)B ，(4,0)A ，4AH ∴=，8BH =，Rt ABH ∆中，1tan 2AH ABH BH ∠==，OAP ABH ∴∠=∠， H 关于AB 的对称点M ，ABH ABM ∴∠=∠，ABM OAP ∴∠=∠，即C 是满足条件的点，设(,)M x y ， H 关于AB 的对称点M ，4AM AH ∴==，8BM BH ==，∴222222(4)(0)4(8)(8)8x y x y ⎧-+-=⎨-+-=⎩，两式相减变形可得82x y =-，代入即可解得80x y =⎧⎨=⎩（此时为H ，舍去）或85165x y ⎧=⎪⎪⎨⎪=⎪⎩， 8(5M ∴，16)5，设直线BM 解析式为y cx d =+，将8(5M ，16)5，(8,8)B 代入得； 8816855c d c d =+⎧⎪⎨=+⎪⎩，解得342c d ⎧=⎪⎨⎪=⎩， ∴直线BM 解析式为324y x =+，解232414y x y x x ⎧=+⎪⎪⎨⎪=-⎪⎩得154x y =-⎧⎪⎨=⎪⎩或88x y =⎧⎨=⎩（此时为B ，舍去）， 5(1,)4C ∴-，综上所述，C 坐标为(6,3)或5(1,)4-；（3）设BC 交y 轴于M ，过B 作BH x ⊥轴于H ，过M 作MN BH ⊥于N ，如图：点B 的横坐标为t ，21(,)4B t t t ∴-，又(4,0)A ， |4|AH t ∴=-，21||4BH t t =-，||OH t MN ==， 90ABC ∠=︒，90MBN ABH BAH ∴∠=︒-∠=∠，且90N AHB ∠=∠=︒，ABH BMN ∴∆∆∽， ∴AH BH BN MN=，即21|||4|4||t t t BN t --= 22|4|41||4t t BN t t -∴==-， 2144NH t t ∴=-+， 21(0,4)4M t t ∴-+，设直线BM 解析式为2144y ex t t =+-+，将21(,)4B t t t -代入得2211444t t et t t -=+-+， 4e t∴=-，∴直线BC 解析式为24144y x t t t =-+-+，由22144144y x x y x t t t ⎧=-⎪⎪⎨⎪=-+-+⎪⎩得22141444x x x t t t -=-+-+，解得1(x t B =的横坐标），22416164t t x t t t-+=-=--+， ∴点C 的横坐标为164t t--+；当0t <时，164C x t t=--+224=++212=+，∴=时，C x 最小值是12，此时4t =-，∴当0t <时，点C 的横坐标的取值范围是12C x ．2．【答案】（1）1m =-，3y x =-（2）(2,1)，(1,0)，，（3）7(2Q ∴，5)4-．：（1）将(3,0)B 代入22(3)(69)y mx m x m =++-+，化简得，20m m +=，则0m =（舍)或1m =-，1m ∴=-，243y x x ∴=-+-．(0,3)C ∴-，设直线BC 的函数表达式为y kx b =+，将(3,0)B ，(0,3)C -代入表达式，可得，033k b b =+⎧⎨-=⎩，解得，13k b =⎧⎨=-⎩，∴直线BC 的函数表达式为3y x =-．（2）如图，过点A 作1//AP BC ，设直线1AP 交y 轴于点G ，将直线BC 向下平移GC 个单位，得到直线23P P ．由（1）得直线BC 的表达式为3y x =-，(1,0)A ，∴直线AG 的表达式为1y x =-，联立2143y x y x x =-⎧⎨=-+-⎩，解得10x y =⎧⎨=⎩，或21x y =⎧⎨=⎩， 1(2,1)P ∴或(1,0)，由直线AG 的表达式可得(0,1)G -，2GC ∴=，2CH =，∴直线23P P 的表达式为：5y x =-，联立2543y x y x x =-⎧⎨=-+-⎩，解得，x y ⎧=⎪⎪⎨⎪=⎪⎩，或，x y ⎧=⎪⎪⎨⎪=⎪⎩，2P ∴，3P；综上可得，符合题意的点P 的坐标为：(2,1)，(1,0)，，；（3）如图，取点Q 使45ACQ ∠=︒，作直线CQ ，过点A 作AD CQ ⊥于点D ，过点D 作DF x ⊥轴于点F ，过点C 作CE DF ⊥于点E ，则ACD ∆是等腰直角三角形，AD CD ∴=，()CDE DAF AAS ∴∆≅∆，AF DE ∴=，CE DF =．设DE AF a ==，则1CE DF a ==+，由3OC =，则3DF a =-，13a a ∴+=-，解得1a =．(2,2)D ∴-，又(0,3)C -，∴直线CD 对应的表达式为132y x =-，设1(,3)2Q n n -，代人243y x x =-+-， ∴213432n n n -=-+-，整理得2702n n -=．又0n ≠，则72n =． 7(2Q ∴，5)4-． 3．【答案】（1）45OCA ∴∠=︒，1AB a ∴=+（2）2(1)(2)2y x x x x =+-=--（3）存在，(1,2)-或1(2-，5)4-【详解】（1）定义抛物线(1)()y x x a =+-，令0y =，可得1x =-或a ， (1,0)B ∴-，(,0)A a ，令0x =，得到y a =-，(0,)C a ∴-，OA OC a ∴==，1OB =，1AB a ∴=+．90AOC ∠=︒，45OCA ∴∠=︒．（2）AOC ∆是等腰直角三角形，45OAC ∴∠=︒，点D 是ABC ∆的外心，290BDC CAB ∴∠=∠=︒，DB DC =， BDC ∴∆也是等腰直角三角形，DBC OAC ∴∆∆∽，∴BC AC =，∴=，解得2a =或2(2--不是分式方程的根舍弃）， ∴抛物线的解析式为2(1)(2)2y x x x x =+-=--．（3）作点C 关于抛物线的对称轴12x =的对称点C '，连接AC '．(0,2)C -，(1,2)C '-，//PC AB ∴， BC ，AC '关于直线12x =对称， CB AC ∴='，∴四边形ABCP 是等腰梯形，CBA C AB ∴∠=∠'，45DBC OAC ∠=∠=︒，ABD CAC ∴∠=∠'，∴当点P 与点C '重合时满足条件，(1,2)P ∴-．作点P 关于直线AC 的对称点(0,1)E -，则EAC PAC ABD ∠=∠=∠，作直线AE 交抛物线于P '，点P '满足条件， (2,0)A ，(0,1)E -，∴直线AE 的解析式为112y x =-，由21122y x y x x ⎧=-⎪⎨⎪=--⎩，解得20x y =⎧⎨=⎩（即点)A 或1254x y ⎧=-⎪⎪⎨⎪=-⎪⎩， 1(2P ∴'-，5)4-，综上所述，满足条件的点P 的坐标为(1,2)-或1(2-，5)4-．4．【答案】（1）4y x =-+（2）3）存在，或【详解】（1）由点A 的坐标知，2OA =， 24OC OA ==，故点C 的坐标为(0,4)，将点A 、B 、C 的坐标代入抛物线表达式得：42016404a b c a b c c -+=⎧⎪++=⎨⎪=⎩，解得1214a b c ⎧=-⎪⎪=⎨⎪=⎪⎩，故抛物线的表达式为2142y x x =-++；将点B 、C 的坐标代入一次函数表达式得：044m n n =+⎧⎨=⎩，解得14m n =-⎧⎨=⎩，故直线BC 的表达式为4y x =-+；（2）点A 、B 关于抛物线的对称轴对称，设抛物线的对称轴交BC 于点F ，则点F 为所求点，此时，当FA FC +的值最小，理由：由函数的对称性知，AF BF =，则AF FC BF FC BC +=+=为最小，当1x =时，43y x =-+=，故点(1,3)F ，由点B 、C 的坐标知，4OB OC ==，则BC ==即点F 的坐标为(1,3)、FA FC +的最小值为（3）存在，理由：设点P 的坐标为21(,4)2m m m -++、点Q 的坐标为(,4)t t -+， ①当点Q 在点P 的左侧时，如图2，过点P 、Q 分别作x 轴的垂线，垂足分别为N 、M ，由题意得：90PEQ ∠=︒，90PEN QEM ∴∠+∠=︒，90EQM QEM ∠+∠=︒，PEN EQM ∴∠=∠，90QME ENP ∴∠=∠=︒，QME ENP ∴∆∆∽， ∴21tan tan 42PN EN PE OA EPQ OCA ME QM QE OC ===∠=∠===，则2142PN m m =-++，1ME t =-，1EN m =-，4QM t =-+， ∴214112142m m m t t -++-==--+，解得m =，当m =2142m m -++=故点P的坐标为． ②当点Q 在点P 的右侧时，分别过点P 、Q 作抛物线对称轴的垂线，垂足分别为N 、M ，则1MQ t =-，4ME t =-，2142NE m m =-++、1PN m =-，同理可得：QME ENP ∆∆∽， ∴tan 2MQ ME EQ PQE EN PN PE===∠=，即21421142t t m m m --==--++，解得m =（舍去负值），故m =故点P的坐标为，故点P的坐标为或． 5．【答案】（1）254y x x =-+（2）见解析（3）存在，(0,1)或(0,1)-或25(0,)8 【详解】（1）由题意得：40522a b b a ++=⎧⎪-⎨=⎪⎩，解得15a b =⎧⎨=-⎩，故抛物线的表达式为254y x x =-+①；（2）对于254y x x =-+，令2540y x x =-+=，解得1x =或4，令0x =，则4y =，故点B 的坐标为(4,0)，点(0,4)C ，设直线BC 的表达式为y kx t =+，则440t k t =⎧⎨+=⎩，解得14k t =-⎧⎨=⎩，故直线BC 的表达式为4y x =-+，设点P 的坐标为(,4)x x -+，则点Q 的坐标为2(,54)x x x -+，则22(4)(54)4PQ x x x x x =-+--+=-+，10-<，故PQ 有最大值，当2x =时，PQ 的最大值为4CO =，此时点Q 的坐标为(2,2)-；PQ CO =，//PQ OC ，故四边形OCPQ 为平行四边形；（3）D 是OC 的中点，则点(0,2)D ，由点D 、Q 的坐标，同理可得，直线DQ 的表达式为22y x =-+，过点Q 作QH x ⊥轴于点H ，则//QH CO ，故AQH ODA ∠=∠，而2DQE ODQ ∠=∠．HQA HQE ∴∠=∠，则直线AQ 和直线QE 关于直线QH 对称，故设直线QE 的表达式为2y x r =+，将点Q 的坐标代入上式并解得6r =-，故直线QE 的表达式为26y x =-②，联立①②并解得54x y =⎧⎨=⎩（不合题意的值已舍去），故点E 的坐标为(5,4)，设点F 的坐标为(0,)m ，由点B 、E 的坐标得：222(54)(40)17BE =-+-=，同理可得，当BE BF =时，即21617m +=，解得1m =±；当BE EF =时，即225(4)17m +-=，方程无解；当BF EF =时，即221625(4)m m +=+-，解得258m =；故点F 的坐标为(0,1)或(0,1)-或25(0,)8． 6．【答案】（1）21233y x x =-=-，(3,3)-（2）5(1,)3-或7(2，35)12-（3）见解析【详解】（1）对于132y x =-+，令1302y x =-+=，解得6x =，令0x =，则3y =，故点A 、B 的坐标分别为(6,0)、(0,3)，抛物线213y x bx c =++经过坐标原点，故0c =，将点A 的坐标代入抛物线表达式得：103663b =⨯+，解得2b =-，故抛物线的表达式为2123y x x =-；则抛物线的对称轴为3x =，当3x =时，21233y x x =-=-，则点M 的坐标为(3,3)-；（2）如图1，过点E 作//EH y 轴交AB 于点H ，设点E 的坐标为21(,2)3x x x -，则点1(,3)2H x x -+，则EAB ∆的面积21111256(32)22232EHB EHA S S EH OA x x x ∆∆=+=⨯⨯=⨯⨯-+-+=，解得1x =或72，故点E 的坐标为5(1,)3-或7(2，35)12-；（3）直线AB 向下平移后过点(3,3)M -，故直线CM 的表达式为113(3)3222y x x =---=--，令13022y x =--=，解得3x =-，故点(3,0)C -；过点D 作DH CM ⊥于点H ，直线CM 的表达式为1322y x =--，故1tan 2MCD ∠=，则sin MCD ∠=则sin (23)DH CD MCD =∠=+=由点D 、M 的坐标得，DM则sin DH HMD MD ∠=== 故4545HMD DMC ADM ACM ∠=︒=∠=∠-∠=︒，45ADM ACM ∴∠-∠=︒．7．【答案】（1）2142y x x =-++（2）(6,8)-（3）2t =或10 【详解】（1）设抛物线的表达式为12()()y a x x x x =--，则2(2)(4)28y a x x ax ax a =+-=--，即84a -=，解得12a =-，故抛物线的表达式为2142y x x =-++①；（2）由点A 、B 的坐标知，2OB OA =，故CO 将ABC ∆的面积分成2:1两部分，此时，点P 不在抛物线上；如图1，当123BH AB ==时，CH 将ABC ∆的面积分成2:1两部分，即点H 的坐标为(2,0)，则CH 和抛物线的交点即为点P ，由点C、H的坐标得，直线CH的表达式为24y x=-+②，联立①②并解得68xy=⎧⎨=-⎩（不合题意的值已舍去），故点P的坐标为(6,8)-；（3）在OB上取点(2,0)E，则ACO OCE∠=∠，OCA OCB OMA∠=∠-∠，故AMO ECB∠=∠，过点E作EF BC⊥于点F，在Rt BOC∆中，由OB OC=知，45OBC∠=︒，则2)EF BF==-，由点B、C的坐标知，BC=则CF BC BF=-=则1tan tan3EFECB AMOCF∠===∠，则21tan 3AO AMO OM OM ∠===，则6OM =，故642CM OM OC =±=±=或10，则2t =或10．8．【答案】（1）213222y x x =-++（2）314（3）存在，(1,0)-或，【详解】（1）设抛物线的表达式为12()()y a x x x x =--，即22(1)(4)(34)34y a x x a x x ax ax a =+-=--=--，即42a -=，解得12a =-，故抛物线的表达式为213222y x x =-++；（2）将点A 的坐标代入直线l 的表达式得：03k =-+，解得3k =，故直线l 的表达式为33y x =+，设点Q 的坐标为213(,2)22x x x -++，则点P 的坐标为(,33)x x +，由题意得，点Q 、M 关于抛物线对称轴对称，而抛物线的对称轴为直线32x =，故点M 的横坐标为3x -，则332QM x x x =--=-，设矩形周长为C ，则22132()2[3233(2)]822C PQ QM x x x x x x =+=-++--++=-+， 10>，故C 有最小值，当12x =时，矩形周长最小值为314；（3）当12x =时，213212228y x x =-++=，即点Q 的坐标为1(2，21)8，由抛物线的表达式知，点D 的坐标为3(2，25)8， 5(328)9过点D作DK QM⊥于点K，则25211882D QDK y y=-=-=，同理可得，1QK=，则1 tan2DKDQMQK∠==，CBF DQM∠=∠，故1 tan tan2CBF DQM∠=∠=，在BOC∆中，21 tan42COCBOOB∠===，故BF和BO重合，故点F和点A重合，即点F的坐标为(1,0)-，当点F在直线BC的上方时，5AC=BC=5AB=，222AB AC BC∴=+，90ACB∴∠=︒，则点A关于BC的对称点(1,4)A'，∴直线BF的解析式为41633y x=-+，由24163313222y x y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩，解得40x y =⎧⎨=⎩或53289x y ⎧=⎪⎪⎨⎪=⎪⎩， 5(3F ∴，28)9，综上所述，满足条件的点F 的坐标为(1,0)-或， 9．【答案】（1）△（2）见解析【详解】（1）当，时，△；（2）①设，则，，则，即，，，，，；②，，，，故，，则，则，则， 5(328)92214(2)4(2)82b ac =-=--⨯⨯-=12a =2b c ==-2214(2)4(2)82b ac =-=--⨯⨯-=20ax bx c ++=12b x x a +=-12c x x a =12b x x c a +=-=2x c OC =-=121c x x a a=÷=-2OB x CO ==ACO ABD ∠=∠90COA BOD ∠=∠=︒()AOC DOB ASA ∴∆≅∆OCA CAF CFA ∠=∠+∠ACO CAF CBD ∠=∠+∠CBD AFO ∴∠=∠OB OC =45OCB ∠=︒1CD OC OD OC OA c a=-=-=--1)DE c CE a==+=1)BE BC CE CE c a =-=-=-+11)tan 1c c DE a CBD BE c a ++∠===-。

二次函数与角度综合问题(教师版)

二次函数与几何综合专题--角问题【模型解读】二次函数与角综合问题，常见的主要有三种类型： 1. 特殊角问题：（1）利用特殊角的三角函数值找到线段之间的数量关系（2）遇到特殊角可以构造特殊三角形，如遇到45°构造等腰直角三角形，遇到30°、60°构造等边三角形，遇到90°构造直角三角形2.角的数量关系问题（1）等角问题：借助特殊图形的性质、全等和相似的性质来解决；构造圆，利用圆周角的性质来解决（2）二倍角问题：利用角平分线的性质、等腰三角形的性质、对称、辅助圆等知识来解答（3）角的和差问题3.角的最值问题：利用辅助圆等知识来解答【引例】如图，在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，3OA OC ==，顶点为D ，对称轴交x 轴于点E ．（1）求抛物线的解析式、对称轴及顶点D 的坐标．（2）在抛物线上是否存在点P ，使PAO OCE ∠=∠，若存在，求出点P 的坐标；若不存在，说明理由．（3）该抛物线上是否存在点P，使得PCA CAD∠=∠？若存在，求出所有点P的坐标；若不存在，请说明理由．∠的平分线与y轴的交点M的坐标．（4）直线AC与抛物线的对称轴交于点F，请求出CDF∠=∠，若存在，求出点P的坐标；若不存在，请说明理（5）在抛物线上是否存在点P，使得POC PCO由．（6）过点B 的直线交直线AC 于点M ，当直线AC 与BM 的夹角等于ACB ∠的2倍时，求点M 的坐标．（7）在y 轴上是否存在点N ，使得BCO BNO BAC ∠+∠=∠，若存在，求出点N 的坐标；若不存在，请说明理由．（8）在对称轴左侧的抛物线上有一点M ，在对称轴右侧的抛物线上有一点N ，满足90MDN ∠=︒．求证：MN 恒过定点，并求出定点坐标．【答案】（1）223y x x =+-，对称轴为：直线x ＝－1，顶点坐标为：D （－1，－4）；（2）存在，P 的坐标为（43，139）或（23，119-）；（3）存在，点P 的坐标为（－4，5）或（52-，74-）；（4）点M 的坐标为（0－3）；（5）存在，P 1，－32）或（1-，－32）；（6）点M 的坐标为（52-，12-）或（12，72-）；（7）在y 轴上存在点N ，点N 的坐标为（0，±2）；（8）见解析，（－1，－3）．【详解】答案：（1）解：∵3OA OC ==， ∴A （－3，0），C （0，－3），∴()20333b c c ⎧=--+⎪⎨-=⎪⎩，解得：23b c =⎧⎨=-⎩，∴抛物线的解析式为：223y x x =+-，对称轴为：直线x ＝－1，顶点坐标为：D （－1，－4）．（2）解：假设存在，如图，当点P 在x 轴上方时，过点P 作PH ⊥x 轴于点H ，设点P 的坐标为（a ，223a a +-），则90PHA COE ∠=∠=︒，∵点A （－3，0），点C （0，－3），点E （－1，0），点P （a ，223a a +-）， ∴AH ＝a －（－3）＝a ＋3，PH ＝223a a +-，OC ＝3，EO ＝1，∵PAO OCE ∠=∠，90PHA COE ∠=∠=︒， ∴PHA EOC △∽△， ∴PH AHEO OC=， ∴223313a a a +-+=，解得：143a =，23a =-（不符合题意，舍去），此时2164132323939a a +-=+⨯-=， ∴点P 的坐标为（43，139），当点P 在x 轴下方时，如图，过点P '作P F '⊥x 轴于点F ，设点P '的坐标为（b ，223b b +-），则90P FA COE '∠=∠=︒，∵点A （－3，0），点C （0，－3），点E （－1，0），点P '（b ，223b b +-）， ∴AF ＝b －（－3）＝b ＋3，P F '＝223b b --+，OC ＝3，EO ＝1， ∵P AO OCE '∠=∠，90P FA COE '∠=∠=︒， ∴P FA EOC '△∽△， ∴P F AFEO OC'=， ∴223313b b b --++=，解得：123b =，23b =-（不符合题意，舍去），此时242112323939b b +-=+⨯-=-， ∴点P '的坐标为（23，119-），综上所述，在抛物线上存在点P ，使PAO OCE ∠=∠，此时点P 的坐标为（43，139）或（23，119-）．（3）解：假设存在，如图，当点P 在直线AC 的右上方时，设直线AD 为y kx b =+，将A （－3，0），D （－1，－4）代入，得304k b k b -+=⎧⎨-+=-⎩，解得：26k b =-⎧⎨=-⎩，∴直线AD 为26y x =--， ∵PCA CAD ∠=∠， ∴//PC AD ，∴设直线PC 为12y x b =-+，将C （0，－3）代入，得13b =-， ∴直线PC 为23y x =--，将23y x =--与223y x x =+-联立方程，得22323x x x +-=--，解得：14x =-，20x =（不符合题意，舍去）当4x =-时，235y x =--=， ∴点P 的坐标为（－4，5）；如图，当点P '在直线AC 的左下方时，延长CP '交x 轴于点G ，延长AD 交y 轴于点H ，∵直线AD 为26y x =--， ∴当x ＝0时，y ＝－6， ∴OH ＝6，∵P CA CAD '∠=∠，45OCA OAC ∠=∠=︒， ∴P CA OCA CAD OAC '∠+∠=∠+∠，即：P CO OAD '∠=∠， ∴在△GOC 与△HOA 中，OCG OAH OC OA COG AOH ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△GOC ≌△HOA （ASA ）， ∴OG ＝OH ＝6，∴点G 的坐标为（－6，0），设直线CG 为22y k x b =+，将G （－6，0），C （0，－3）代入，得603k b b -+=⎧⎨=-⎩，解得：123kb⎧=-⎪⎨⎪=-⎩，∴直线CG为132y x=--，将132y x=--与223y x x=+-联立方程，得21 2332x x x+-=--，解得：15 2x=-，20x=（不符合题意，舍去）当52x=-时，17324y x=--=-，∴点P的坐标为（52-，74-），综上所述，抛物线上存在点P，使得PCA CAD∠=∠，此时点P的坐标为（－4，5）或（52-，74-）．（4）解：如图，过点D作DH⊥y轴于点H，∵点D为（－1，－4），点C为（0，－3），∴DE＝OH＝4，OC＝3，DH＝1，∴CH＝OH－OC＝1，∴在Rt△CDH中，CD∵DM平分CDF∠，∴∠CDM＝∠FDM，∵DF//y轴，∴∠CMD＝∠FDM，∴∠CMD＝∠CDM，∴CM＝CD∴OM＝OC－CM＝3又∵点M在y轴的负半轴上，∴点M 的坐标为（03）．（5）解：假设存在，∵POC PCO ∠=∠， ∴PC ＝PO ，∴点P 在OC 的垂直平分线上， ∵O （0，0），C （0，－3），∴OC 的垂直平分线为直线y ＝－32，将y ＝－32代入223y x x =+-，得23232x x +-=-，解得：11x ，21x =，∴在抛物线上存在点P ，使得POC PCO ∠=∠，此时点P 1，－32）或（1，－32）．（6）解：若点M 在点C 的左上方时，满足2AMB ACB ∠=∠，如图，过点M 作MH ⊥AB 于点H ，过点C 作CG ⊥MH ，交HM 的延长线于点G ，∵2AMB ACB MBC ACB ∠=∠+∠=∠， ∴ACB MBC ∠=∠， ∴MB MC =，设直线AC 为y kx b =+，将A （－3，0），C （0，－3）代入，得303k b b -+=⎧⎨=-⎩，解得：13k b =-⎧⎨=-⎩，∴直线AC 为3y x =--， ∵点M 在直线AC 上，∴设点M 的坐标为（x ，－x －3），又∵点B （1，0），点C （0，－3），∴MH ＝x ＋3，BH ＝1－x ，MG ＝－x －3－（－3）＝－x ，CG ＝－x ， ∴在Rt △MHB 中，22222(3)(1)MB MH BH x x =+=++-，在Rt △MGC 中，222222()()2MC MG CG x x x =+=-+-=， ∵MB MC =， ∴22MB MC =， ∴222(3)(1)2x x x ++-=，解得：52x =-，将52x =-代入3y x =--，得12y =-，∴此时点M 的坐标为（52-，12-），若点M '在点C 的右下方时，满足2PM B ACB '∠=∠，如图，过点M '作M N AB '⊥于点N ，∵2PM B ACB '∠=∠，2AMB ACB ∠=∠，∴AMB PMB '∠=∠， ∴MBMB '=，设点M '的坐标为（m ，－m －3），又∵点B （1，0），点M （52-，12-），∴MH ＝52-＋3＝12，BH ＝1－（52-）＝72，M 'N ＝－m －3，BN ＝1－m ，∴在Rt △MHB 中，222221725()()222MB MH BH =+=+=，在Rt M NB '△中，22222(3)(1)M B M N BN m m ''=+=--+-，∵MBMB '=， ∴22M B MB '=， ∴2225(3)(1)2m m --+-=，解得：112m =，252m =-（不符合题意，舍去），将12x m ==代入3y x =--，得72y =-，∴此时点M '的坐标为（12，72-），综上所述，当直线AC 与BM 的夹角等于ACB ∠的2倍时，点M 的坐标为（52-，12-）或（12，72-）．（7）解：假设在y 轴的正半轴上存在点N ，使得BCO BNO BAC ∠+∠=∠，如图，过点N 作NM ⊥BN ，交CB 的延长线于点M ，过点M 作MH ⊥y 轴于点H ，则∠MHN ＝∠MNB ＝∠BON ＝90°，∵点A （－3，0），点C （0，－3）， ∴OA ＝OC ＝3，又∵∠AOC ＝90°， ∴∠BAC ＝∠OCA ＝45°， ∴45BCO BNO BAC ∠+∠=∠=︒， ∴45MBN BCO BNO ∠=∠+∠=︒， ∵∠MNB ＝90°，∴∠NMB ＝∠MBN ＝45°， ∴NB ＝MN ，∵∠MHN ＝∠MNB ＝90°，∴∠HMN ＋∠HNM ＝∠ONB ＋∠HNM ＝90°， ∴∠HMN ＝∠ONB ， ∴在△HMN 与△ONB 中，MHN NOB HMN ONB MN BN ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△HMN ≌△ONB （AAS ）， ∴HM ＝ON ，HN ＝OB ， ∵点B 坐标为（1，0）， ∴HN ＝OB ＝1，设HM ＝ON ＝a ，则OH ＝ON ＋HN ＝a ＋1， ∴点M 的坐标为（a ，a ＋1），设直线BC 为y kx b =+，将B （1，0），C （0，－3）代入，得3k b b +=⎧⎨=-⎩，解得：33k b =⎧⎨=-⎩，∴直线BC 为33y x =-，将点M （a ，a ＋1）代入得：133a a +=-，解得：2a =，∴点N 的坐标为（0，2），当点N 在y 轴的负半轴时，如图所示，根根轴对称的性质可得此时点N 的坐标为（0，－2），综上所述，在y 轴上存在点N ，使得BCO BNO BAC ∠+∠=∠，此时点N 的坐标为（0，±2）．（8）解：如图，过点D 作直线l ⊥y 轴，过点M 、N 分别作直线l 的垂线，垂足分别为点H 、G ，设点M 的坐标为（m ，223m m +-），点N 的坐标为（n ，223n n +-）， ∵顶点D 的坐标为（－1，－4），且M 、N 分别位于点D 的左右两侧， ∴2223(4)21MH m m m m =+---=++，1HD m =--，2223(4)21NG n n n n =+---=++，(1)1DG n n =--=+，根据题意可得90MHD DGN MDN ∠=∠=∠=︒， ∴90MDH HMD MDH GDN ∠+∠=∠+∠=︒， ∴HMD GDN ∠=∠， ∴HMD GDN △∽△， ∴MH HDDG NG=， ∴22211121m m mn n n ++--=+++，即22(1)(1)1(1)m m n n +-+=++， ∴(1)(1)1m n -++=，整理得：20mn m n +++=，设直线MN 为y kx b =+，将M （m ，223m m +-），N （n ，223n n +-）代入，得222323km b m m kn b n n ⎧+=+-⎨+=+-⎩，解得：23k m n b mn =++⎧⎨=--⎩，∴直线MN 为(2)3y m n x mn =++--， ∵20mn m n +++=， ∴2m n mn ++=-，∴直线MN 为3(1)3y mnx mn mn x =---=-+-， ∴当10x +=即=1x -时，=3y -，∴无论m ，n 取何值，直线MN 总会经过定点（－1，－3）， ∴直线MN 恒过定点，该定点坐标为（－1，－3）．【模型实例】1．如图，在平面直角坐标系xOy 中，抛物线()2y a x h k =-+与x 轴相交于O ，A 两点，顶点P 的坐标为()2,1-．点B 为抛物线上一动点，连接,AP AB ，过点B 的直线与抛物线交于另一点C ．（1）求抛物线的函数表达式；（2）若点B 的横坐标与纵坐标相等，ABC OAP ∠=∠，且点C 位于x 轴上方，求点C 的坐标；（3）若点B 的横坐标为t ，90ABC ∠=︒，请用含t 的代数式表示点C 的横坐标，并求出当0t <时，点C 的横坐标的取值范围．【答案】（1）214y x x =-或21(2)14y x =--；（2）点C 的坐标为(6,3)或51,4⎛⎫- ⎪⎝⎭；（3）164t t --+；12C x ≥【分析】（1）设抛物线的解析式为()221y a x =--，把点O (0，0)代入即可求解；（2）求得B (0，0)或B (8，8)，分两种情况讨论，①当点B 的坐标为(0，0)时，过点B 作BC ∥AP 交抛物线于点C ，利用待定系数法求得直线BC 的解析式为12y x =，解方程组即可求解；②点B 的坐标为(8，8)时，作出如图的辅助线，利用三角形函数以及轴对称的性质求得M (85，165)，同①可求解；（3）作出如图的辅助线，点B 的坐标为(t ，214t t -)，得到AH =4t -，BH =214t t -，OH =t =MN ，由AH =4t -，BH =214t t -，OH =t =MN ，△ABH ~△BMN 得到M (0，2144t t -+)，求得BC 的解析式为：24144y x t t t =-+-+，解方程组求得点C 的横坐标为164t t--+，即可求解．【详解】（1）∵抛物线的顶点坐标为P (2，-1)，∴设抛物线的解析式为()221y a x =--， ∵抛物线经过原点O ，即经过点O (0，0)， ∴()20021a =--，解得：14a =， ∴抛物线的解析式为()22112144y x x x =--=-；（2）在()21214y x =--中，令y x =，得：()21214x x =--，解得0x =或8x =， ∴B (0，0)或B (8，8)，①当点B 的坐标为(0，0)时，过点B 作BC ∥AP 交抛物线于点C ，此时∠ABC =∠OAP ，如图：在()21214y x =--中，令0y =，得：()212104x --=，解得：0x =或4x =， ∴A (4，0)，设直线AP 的解析式为1y kx b =+，将A (4，0)，P (2，-1)代入得110412k b k b =+⎧⎨-=+⎩，解得：1122k b ⎧=⎪⎨⎪=-⎩， ∴直线AP 的解析式为122y x =-，∵BC ∥AP ，∴设直线BC 的解析式为212y x b =+，将B (0，0)代入得20b =， ∴直线BC 的解析式为12y x =，由()2121214y x y x ⎧=⎪⎪⎨⎪=--⎪⎩，得：00x y =⎧⎨=⎩(此点为点O ，舍去)或63x y =⎧⎨=⎩， ∴点C 的坐标为(6，3)；②点B 的坐标为(8，8)时，过点P 作PQ ⊥x 轴于点Q ，过点B 作BH ⊥x 轴于点H ，作H 关于AB 的对称点M ，作直线BM 交抛物线于C ，连接AM ，如图：∵A (4，0)，P(2，-1)， ∴PQ =1，AQ =2，在Rt △APQ 中，1tan 2PQ OAP AQ ∠==， ∵A (4，0)，B (8，8)， ∴AH =4，BH =8，在Rt △ABH 中，1tan 2AH ABH BH ∠==， ∴∠OAP =∠ABH ，∵H 关于AB 的对称点为M ， ∴∠ABM =∠ABH ，∴∠ABC =∠OAP ，即C 为满足条件的点，设M (x ，y )，∵H 关于AB 的对称点为M ，∴AM =AH =4，BM =BH =8，∴()()()()222222404888x y x y ⎧-+-=⎪⎨-+-=⎪⎩ 两式相减得：82x y =-，代入即可解得： 80x y =⎧⎨=⎩(此点为点H ，舍去)或85165x y ⎧=⎪⎪⎨⎪=⎪⎩， ∴M (85，165)，同理求得BM 的解析式为：324y x =+，解()23241214y x y x ⎧=+⎪⎪⎨⎪=--⎪⎩得：88x y =⎧⎨=⎩(此点为点B ，舍去)或154x y =-⎧⎪⎨=⎪⎩，∴点C 的坐标为(-1，54)；综上，点C 的坐标为(6，3)或(-1，54)；（3）设BC 交y 轴于点M ，过点B 作BH ⊥x 轴于点H ，过点M 作MN ⊥BH 于点N ，如图：∵点B 的横坐标为t ，∴点B 的坐标为(t ，214t t -)，又A (4，0)，∴AH =4t -，BH =214t t -，OH =t =MN ， ∵∠ABC =90°，∴∠MBN =90°-∠ABH =∠BAH ，且∠N =∠AHB =90°， ∴△ABH ~△BMN ，∴AH BH BN MN=，即2144t t t BN t--=， ∴BN =224414t tt t -=-，∴HN =2144t t -+，∴M (0，2144t t -+)，同理求得BC 的解析式为：24144y x t t t =-+-+，由22144144y x x y x t t t ⎧=-⎪⎪⎨⎪=-+-+⎪⎩，得22141444x x x t t t -=-+-+，解得x t =(点B 的横坐标)，或2416164t t x t t t-+=-=--+，∴点C 的横坐标为164t t --+，当0t <时，164C x t t=--+224=++212=+，=C x 的最小值是12，此时4t =-；∴当0t <时，点C 的横坐标的取值范围是12C x ≥．【点睛】本题考查二次函数综合知识，涉及解析式、锐角三角函数、对称变换、两条直线平行、两条直线互相垂直、解含参数的方程等，综合性很强，难度较大，解题的关键是熟练掌握、应用各种综合知识，用含字母的式子表示线段长度及函数解析式．2.如图，在平面直角坐标系xOy 中，抛物线E ：y ＝﹣（x ﹣m ）2+2m 2（m ＜0）的顶点P 在抛物线F ：y ＝ax 2上，直线x ＝t 与抛物线E ，F 分别交于点A ，B ．（1）求a 的值；（2）将A ，B 的纵坐标分别记为y A ，y B ，设s ＝y A ﹣y B ，若s 的最大值为4，则m 的值是多少？（3）Q 是x 轴的正半轴上一点，且PQ 的中点M 恰好在抛物线F 上．试探究：此时无论m 为何负值，在y 轴的负半轴上是否存在定点G ，使∠PQG 总为直角？若存在，请求出点G 的坐标；若不存在，请说明理由．【分析】（1）由抛物线的顶点式可直接得出顶点P的坐标，再代入抛物线F即可得出结论；（2）根据题意可分别表达A，B的纵坐标，再根据二次函数的性质可得出m的值；（3）过点Q作x轴的垂线KN，分别过点P，G作x轴的平行线，与KN分别交于K，N，则△PKQ∽△QNG，设出点M的坐标，可表达点Q和点G的坐标，进而可得出结论．【解答】解：（1）由题意可知，抛物线E：y＝﹣（x﹣m）2+2m2（m＜0）的顶点P的坐标为（m，2m2），∵点P在抛物线F：y＝ax2上，∴am2＝2m2，∴a＝2．（2）∵直线x＝t与抛物线E，F分别交于点A，B，∴y A＝﹣（t﹣m）2+2m2＝﹣t2+2mt+m2，y B＝2t2，∴s＝y A﹣y B＝﹣t2+2mt+m2﹣2t2＝﹣3t2+2mt+m2＝﹣3（t﹣m）2+m2，∵﹣3＜0，∴当t＝m时，s的最大值为m2，∵s的最大值为4，∴m2＝4，解得m＝±，∵m＜0，∴m＝﹣．（3）存在，理由如下：设点M的坐标为n，则M（n，2n2），∴Q（2n﹣m，4n2﹣2m2），∵点Q在x轴正半轴上，∴2n﹣m＞0且4n2﹣2m2＝0，∴n＝﹣m，∴M（﹣m，m2），Q（﹣m﹣m，0）．如图，过点Q作x轴的垂线KN，分别过点P，G作x轴的平行线，与KN分别交于K，N，∴∠K＝∠N＝90°，∠QPK+∠PQK＝90°，∵∠PQG＝90°，∴∠PQK+∠GQN＝90°，∴∠QPK＝∠GQN，∴△PKQ∽△QNG，∴PK：QN＝KQ：GN，即PK•GN＝KQ•QN．∵PK＝﹣m﹣m﹣m＝﹣m﹣2m，KQ＝2m2，GN＝﹣m﹣m，∴（﹣m﹣2m）（﹣m﹣m）＝2m2•QN解得QN＝．∴G（0，﹣）．3.如图，在平面直角坐标系中，抛物线y＝ax2+bx+2经过A（，0），B（3，）两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P在抛物线上，过P作PD⊥x轴，交直线BC于点D，若以P、D、O、C为顶点的四边形是平行四边形，求点P的横坐标；（3）抛物线上是否存在点Q，使∠QCB＝45°？若存在，请直接写出点Q的坐标；若不存在，请说明理由．【分析】（1）根据待定系数法，将点A，点B代入抛物线解析式，解关于b，c的二元一次方程组，即可求得抛物线的解析式；（2）设出点P的坐标，确定出PD∥CO，由PD＝CO，列出方程求解即可；（3）过点D作DF⊥CP交CP的延长线于点F，过点F作y轴的平行线EF，过点D作DE⊥EF于点E，过点C作CG⊥EF于点G，证明△DEF≌△FGC（AAS），由全等三角形的性质得出DE＝FG，EF＝CG，求出F点的坐标，由待定系数法求出直线CF的解析式，联立直线CF和抛物线解析式即可得出点P的坐标．【解答】解：（1）将点A（﹣，0），B（3，）代入到y＝ax2+bx+2中得：，解得：，∴抛物线的解析式为y＝﹣x2+x+2；（2）设点P（m，﹣m2+m+2），∵y＝﹣x2+x+2，∴C（0，2），设直线BC的解析式为y＝kx+c，∴，解得，∴直线BC的解析式为y＝x+2，∴D（m，m+2），∴PD＝|﹣m2+m+2﹣m﹣2|＝|m2﹣3m|，∵PD⊥x轴，OC⊥x轴，∴PD∥CO，∴当PD＝CO时，以P、D、O、C为顶点的四边形是平行四边形，∴|m2﹣3m|＝2，解得m＝1或2或或，∴点P的横坐标为1或2或或；（3）①当Q在BC下方时，如图，过B作BH⊥CQ于H，过H作MN⊥y轴，交y轴于M，过B作BN⊥MH于N，∴∠BHC＝∠CMH＝∠HNB＝90°，∵∠QCB＝45°，∴△BHC是等腰直角三角形，∴CH＝HB，∴∠CHM+∠BHN＝∠HBN+∠BHN＝90°，∴∠CHM＝∠HBN，∴△CHM≌△HBN（AAS），∴CM＝HN，MH＝BN，∵H（m，n），∵C（0，2），B（3，），∴，解得，∴H（，），设直线CH的解析式为y＝px+q，∴，解得，∴直线CH的解析式为y＝﹣x+2，联立直线CF与抛物线解析式得，解得或，∴Q（，）；②当Q在BC上方时，如图，过B作BH⊥CQ于H，过H作MN⊥y轴，交y轴于M，过B作BN⊥MH于N，同理得Q（，）．综上，存在，点Q的坐标为（，）或（，）．4.如图1，在平面直角坐标系中．抛物线y＝ax2+bx+2与x轴交于A（﹣4，0）和B（1，0），与y轴交于点C，连接AC，BC．（1）求该抛物线的解析式；（2）如图2，点M为直线AC上方的抛物线上任意一点，过点M作y轴的平行线，交AC于点N，过点M作x轴的平行线，交直线AC于点Q，求△MNQ周长的最大值；（3）点P为抛物线上的一动点，且∠ACP＝45°﹣∠BAC，请直接写出满足条件的点P的坐标．【分析】（1）用待定系数法可得抛物线的解析式为y＝﹣x2﹣x+2；（2）设直线AC解析式为y＝kx+2，用待定系数法得直线AC解析式为y＝x+2，设M（x，﹣x2﹣x+2），则N（x，x+2），即得MN＝﹣x2﹣2x，可证△QMN∽△AOC，有＝＝，故MQ＝2MN，NQ＝MN，可得△MNQ周长MN+MQ+NQ＝MN+2MN+MN＝﹣（x﹣2）2+6+2，即得当x＝2时，△MNQ周长最大值为6+2；（3）在x轴负半轴上取D，使OC＝OD，连接CD交抛物线于P，此时∠ACP＝45°﹣∠BAC，P是满足条件的点，由C（0，2），D（2，0），得直线CD解析式为y＝x+2，即可解得P（﹣5，﹣3），作D关于直线AC的对称点E，连接CE并延长交抛物线于P'，由对称性知∠ACP'＝∠ACP，P'是满足条件的点，设E （m，n），可得，可解得E（﹣，），从而可得直线CE解析式为：y＝x+2，即可解得P'（﹣，）．【解答】解：（1）把A（﹣4，0）和B（1，0）代入y＝ax2+bx+2得：，解得，∴抛物线的解析式为y＝﹣x2﹣x+2；（2）由y＝﹣x2﹣x+2可得C（0，2），设直线AC解析式为y＝kx+2，把A（﹣4，0）代入得：﹣4k+2＝0，解得k＝，∴直线AC解析式为y＝x+2，设M（x，﹣x2﹣x+2），则N（x，x+2），∴MN＝﹣x2﹣x+2﹣（x+2）＝﹣x2﹣2x，∵MQ∥x轴，MN∥y轴，∴∠MQN＝∠CAO，∠NMQ＝∠AOC＝90°，∴△QMN∽△AOC，∴＝＝，即＝＝，∴MQ＝2MN，NQ＝MN，∴△MNQ周长MN+MQ+NQ＝MN+2MN+MN＝（3+）MN＝（3+）×（﹣x2﹣2x）＝﹣（x+2）2+6+2，∵﹣＜0，∴当x＝﹣2时，△MNQ周长最大值为6+2；（3）在x轴负半轴上取D，使OC＝OD，连接CD交抛物线于P，如图：∴D（﹣2，0），∠CDO＝45°，此时∠ACP＝45°﹣∠BAC，P是满足条件的点，∵C（0，2），D（2，0），∴直线CD解析式为y＝x+2，由得或，∴P（﹣5，﹣3），作D关于直线AC的对称点E，连接CE并延长交抛物线于P'，由对称性知∠ACP'＝∠ACP，P'是满足条件的点，设E（m，n），根据AE＝AD，CE＝CD可得：，解得或，∴E（﹣，），由E（﹣，），C（0，2）可得直线CE解析式为：y＝x+2，解得或，∴P'（﹣，），综上所述，P的坐标为（﹣5，﹣3）或（﹣，）．5.抛物线y＝x2﹣4x+c与直线I：y＝kx交于点G（1，m）和点H，﹣1≤m＜0，直线x＝m﹣1交直线l于点A，交抛物线于点B．（1）求c和k的值（用含m的代数式表示）；（2）过点A作x轴的平行线交抛物线于M，N两点（M在N的左侧），交y轴于点C．求的取值范围；（3）在（2）的条件下，过点B作x轴的平行线，与抛物线另一个交点为D，若点E是线段BD的中点，探究∠MEN与∠ABC的数量关系，并说明理由．【分析】（1）把点G（1，m）分别代入y＝x2﹣4x+c与y＝kx，即可求得答案；（2）由题意可得A（m﹣1，m2﹣m），B（m﹣1，m2﹣5m+8），M（m+1，m2﹣m），求得＝＝﹣2m+4，再根据一次函数的性质即可求得的取值范围；（3）先求出D（﹣m+5，m2﹣5m+8），E（2，m2﹣5m+8），F（2，m2﹣m），利用三角函数定义可得：tan ∠ABC＝＝，tan∠MEF＝＝，tan∠NEF＝＝，得出∠MEF＝∠NEF＝∠ABC，进而可得∠MEN＝2∠ABC．【解答】解：（1）∵抛物线y＝x2﹣4x+c与直线I：y＝kx交于点G（1，m），∴m＝12﹣4×1+c，m＝k×1，∴c＝m+3，k＝m；（2）∵直线x＝m﹣1交直线l于点A，∴y＝m（m﹣1）＝m2﹣m，∴A（m﹣1，m2﹣m），∵直线x＝m﹣1交抛物线于点B，∴y＝x2﹣4x+m+3＝（m﹣1）2﹣4（m﹣1）+m+3＝m2﹣5m+8，∴B（m﹣1，m2﹣5m+8），∴AB＝﹣4m+8，∵过点A作x轴的平行线交抛物线于M，N两点（M在N的左侧），交y轴于点C，∴C（0，m2﹣m），点M的纵坐标与点A的纵坐标相等，∴m2﹣m＝x2﹣4x+m+3，解得：x1＝m+1，x2＝﹣m+3，∴M（m+1，m2﹣m），N（﹣m+3，m2﹣m），∴AM＝m+1﹣（m﹣1）＝2，∴＝＝﹣2m+4，∵﹣2＜0，且﹣1≤m＜0，∴的值随着m的增大而减小，当m＝﹣1时，＝﹣2×（﹣1）+4＝6，当m＝0时，＝﹣2×0+4＝4，∴4≤≤6；（3）∠MEN＝2∠ABC．理由如下：∵BD∥x轴，∴点D的纵坐标与点B的纵坐标相等，∴m2﹣5m+8＝x2﹣4x+m+3，解得：x1＝m﹣1，x2＝﹣m+5，∴D（﹣m+5，m2﹣5m+8），∵点E是线段BD的中点，∴E（2，m2﹣5m+8），如图，设直线x＝2交直线MN于点F，则F（2，m2﹣m），∴MF＝NF＝﹣m+1，EF＝m2﹣5m+8﹣（m2﹣m）＝﹣4m+8，∵AC＝0﹣（m﹣1）＝﹣m+1，AB＝﹣4m+8，∴tan∠ABC＝＝，∵tan∠MEF＝＝，tan∠NEF＝＝，∴∠MEF＝∠NEF＝∠ABC，∴∠MEN＝2∠ABC．6.抛物线y＝ax2﹣2ax﹣3a与x轴交于A、B两点（点A在点B的左边），与y轴的正半轴交于C点，△ABC的面积为6．（1）直接写出点A、B的坐标为A（﹣1，0），B（3，0）；抛物线的解析式为y＝﹣x2+2x+3．（2）如图1，连结AC，若在第一象限抛物线上存在点D，使点D到直线AC的距离为，求点D的坐标；（3）如图2，平行于AC的直线交抛物线于M、N两点，在抛物线上存在点P，当PQ⊥y轴时，PQ恰好平分∠MPN，求P点坐标．【分析】（1）令y＝0，可求出x的值，进而可得出A，B的坐标；令x＝0，可求出y的值，可得出点C的坐标，得出线段OC的长，利用三角形的面积公式可得出a的值；（2）过点O作OQ⊥AC于点Q，根据三角形面积的等积法可求出OQ的长，进可得出点D的位置，利用全等三角形的性质求出直线QA′的解析式，联立可求出点D的坐标；（3）过点M作ME⊥DE于E，过点N作NF⊥DE于F，根据∠MPE＝∠NPE，∠MEP＝∠NFP＝90°，可得△MPE∽△NPF，设出M、N、P三点的坐标（只设横坐标，纵坐标用横坐标表示），分别用横坐标之差、纵坐标之差表示出两个相似三角形的直角边，列出比例等式；设出MN的解析式，与抛物线方程联立，得出两根之和的关系式，结合前面的比例等式解出P点的横坐标，进而算出纵坐标．【解答】解：（1）令y＝0，即ax2﹣2ax﹣3a＝0，解得x＝﹣1或x＝3，∴A（﹣1，0），B（3，0）；令x＝0，则y＝﹣3a，∴C（0，﹣3a），即OC＝﹣3a，∴S＝×4×（﹣3a）＝6，解得a＝﹣1，∴函数解析式为：y＝﹣x2+2x+3．故答案为：A（﹣1，0），B（3，0）；y＝﹣x2+2x+3．（2）由（1）知，A（﹣1，0），B（3，0），C（0，3），∴OA＝1，OC＝3，AB＝，过点O作OG⊥AC于点G，∴S△OAC＝•OA•OB＝•AC•OG∴×1×3＝×•OG，∴OG＝，设点D到直线AC的距离h＝＝2OG，延长GO到点G′，使得OG′＝OG，过点G′作AC的平行线与x轴交于点A′，与抛物线在第一象限内交于点D，∴∠GAO＝∠G′A′O，∵∠GOA＝∠G′OA′，∴△GAO≌△G′A′O（AAS），∴OA＝OA′＝1，∴A′（1，0），∵A（﹣1，0），C（0，3），∴直线AC的解析式为：y＝3x+3，∴直线A′G′的解析式为：y＝3x﹣3，令3x﹣3＝﹣x2+2x+3，解得x＝2或x＝﹣3，∵点D在第一象限，∴D（2，3）．（3）如图，过点M作ME⊥DE于E，过点N作NF⊥DE于F，设M（x1，﹣x12+2x1+3），N（x2，﹣x22+2x2+3），P（x0，﹣x02+2x0+3），则：ME＝﹣x12+2x1+3﹣（﹣x02+2x0+3）＝﹣x12+2x1+x02﹣2x0＝﹣（x1﹣x0）（x1+x0）+2（x1﹣x0）＝（x0+x1﹣2）（x0﹣x1），PE＝x0﹣x1，FN＝﹣x02+2x0+3﹣（﹣x22+2x2+3）＝﹣（x0+x2﹣2）（x0﹣x2），PF＝x0﹣x2，∵PQ恰好平分∠MPN，即∠MPE＝∠NPE，∠MEP＝∠NFP＝90°，∴△MPE∽△NPF，∴＝，∴＝，∴x0＝，∵A（﹣1，0），C（0，﹣3），∵MN∥AC，∴设直线MN的解析式为y＝3x+b，令3x+b＝﹣x2+2x+3，由消去y整理得：x2+x﹣3+b＝0，由韦达定理可知：x1+x2＝﹣1，∴x＝，∴x−2x−3＝，∴P（，）．7.如图，抛物线y＝mx2+3mx﹣2m+1的图象经过点C，交x轴于点A（x1，0），B（x2，0）（点A在点B左侧），且x2﹣x1＝5，连接BC，D是AC上方的抛物线一点．（1）求抛物线的解析式；（2）连接BC，CD，S△DCE：S△BCE是否存在最大值？若存在，请求出其最大值及此时点D的坐标；若不存在，请说明理由；（3）第二象限内抛物线上是否存在一点D，DF垂直AC于点F，使得△DCF中有一个锐角等于∠BAC的两倍？若存在，求点D的横坐标，若不存在，请说明理由．【分析】（1）利用抛物线与x轴的交点的横坐标与一元二次方程根的联系，用一元二次方程根与系数的关系定理列出关于m的方程，解方程即可得出结论；（2）过点D作DH⊥x轴于点H，交AC于点M，过点B作BN⊥x轴于点B，交直线AC于点N，利用待定系数法求得直线AC的解析式，设D（a，a+2），则M（a，a+2），求得线段DM，BN的长，利用同高的三角形的面积关系列出S△DCE：S△BCE关于a的等式，利用配方法和二次函数的性质解答即可；（3）利用分类讨论的思想方法分两种情况讨论解答：①当∠DCF＝2∠BAC时，②当∠FDC＝2∠BAC时：取AB的中点P，连接OP，过点D作DR⊥y轴于点R，延长交AC于点G，利用勾股定理的逆定理判定△ABC为直角三角形，∠ACB＝90°，设D（a，a+2），则DR＝﹣a，OR＝a+2，利用直角三角形的边角关系定理列出关于a的方程，解方程即可得出结论．【解答】解：（1）∵抛物线y＝mx2+3mx﹣2m+1的图象交x轴于点A（x1，0），B（x2，0），∴x1，x2是方程mx2+3mx﹣2m+1＝0的两根，∴x1+x2＝﹣3，x1•x2＝．∵x2﹣x1＝5，∴＝25．即：﹣4x1•x2＝25，∴9﹣4×＝25．解得：m＝﹣．∴抛物线的解析式为y＝﹣﹣x+2．（2）S△DCE：S△BCE存在最大值，此时点D的坐标为（﹣2，3），理由：令y＝0，则﹣﹣x+2＝0，解得：x＝﹣4或1，∴A（﹣4，0），B（1，0），令x＝0，则y＝2，∴C（0，2）．设直线AC的解析式为y＝kx+b，∴，解得：，∴直线AC的解析式为y＝x+2．过点D作DH⊥x轴于点H，交AC于点M，过点B作BN⊥x轴于点B，交直线AC于点N，如图，则DM∥BN，∴△EDM∽△EBN，∴．设D（a，a+2），则M（a，a+2），∴DM＝（a+2）﹣（a+2）＝﹣﹣2a．当x＝1时，y＝×1+2＝，∴N（1，）．∴BN＝．∵等高的三角形的面积比等于底的比，∴S△DCE：S△B∁E＝．∴S△DCE：S△B∁E＝＝﹣﹣a＝﹣（a+2）2+，∵＜0，∴当a＝﹣2时，S△DCE：S△BCE有最大值为，此时点D（﹣2，3）；（3）第二象限内抛物线上存在一点D，DF垂直AC于点F，使得△DCF中有一个锐角等于∠BAC的两倍，点D的横坐标为﹣2或﹣，理由：∵A（﹣4，0），B（1，0），C（0，2），∴OA＝4，OB＝1，OC＝2，∴AC＝＝2，BC＝＝，AB＝OA+OB＝5．∵AC2+BC2＝25＝AB2，∴△ABC为直角三角形，∠ACB＝90°．取AB的中点P，连接OP，则P（﹣，0），∴OP＝．∴P A＝PB＝PC＝，∴∠BAC＝∠PCA．∵∠CPB＝∠BAC+∠PCA，∴∠CPB＝2∠BAC．过点D作DR⊥y轴于点R，延长交AC于点G，如图，①当∠DCF＝2∠BAC时，设D（m，m+2），则DR＝﹣m，OR＝m+2，∴CR＝OR﹣OC＝m．∵DR⊥y轴，OA⊥y轴，∴DR∥AB，∴∠G＝∠BAC．∵∠DCF＝∠G+∠CDG，∠DCF＝2∠BAC，∴∠CDG＝∠G＝∠BAC．∵tan∠BAC＝，∴tan∠CDR＝．∴，∴解得：m＝﹣2或0（舍去），∴m＝﹣2．∴点D的横坐标为﹣2；②当∠FDC＝2∠BAC时，∵∠CPB＝2∠BAC，∴∠FDC＝∠CPB．∵tan∠CPB＝，∴tan∠FDC＝，∵tan∠FDC＝，∴，设FC＝4n，则DF＝3n，∴CD＝＝5n．∵tan∠G＝tan∠BAC＝，∴tan∠G＝，∴FG＝6n．∴CG＝FG﹣FC＝2n．∵tan∠G＝，∴RC＝n，∴DR＝＝n，∴，解得：a＝或0（舍去），∴a＝﹣，即点D的横坐标为﹣，综上，第二象限内抛物线上存在一点D，DF垂直AC于点F，使得△DCF中有一个锐角等于∠BAC的两倍，点D的横坐标为﹣2或﹣．【课后练习】1.如图1，抛物线y＝ax2+bx+3经过A（1，0）、B（3，0）两点，与y轴交于点C，（1）求抛物线的函数解析式；（2）如图2，M是x轴下方的抛物线上一点，连接MO、MB、MC，若△MOC的面积是△MBC面积的3倍，求点M的坐标；（3）如图3，连接AC、BC，在抛物线上是否存在一点N（不与点A重合），使得∠BCN＝∠ACB？若存在，求点N的横坐标；若不存在，请说明理由．【分析】（1）由于抛物线y＝ax2+bx+3过A（1，0）、B（3，0）两点，那么可以得到方程ax2+bx+3＝0的两根为x＝1或x＝3，然后利用根与系数即可确定a、b的值．（2）利用待定系数法求出直线BC的解析式，设点M（m，m2﹣4m+3），过点M作MN∥y轴，交BC于点N，则N（m，﹣m+3），根据△MOC的面积是△MBC面积的3倍，即可得到点M的坐标；（3）过点B作BE⊥AB交CN与E，证明△ABC≌△EBC（ASA），根据全等三角形的性质得BE＝AB＝2，求得E的坐标，由点E、C的坐标可得直线CN的解析式，联立y＝x2﹣4x+3即可求得N点的坐标．【解答】解：（1）∵抛物线y＝ax2+bx+3过A（1，0）、B（3，0）两点，∴方程ax2+bx+3＝0的两根为x＝1或x＝3，∴1+3＝﹣，1×3＝，∴a＝1，b＝﹣4，∴二次函数解析式是y＝x2﹣4x+3；（2）∵二次函数解析式是y＝x2﹣4x+3，∴C（0，3）．设直线BC的解析式为y＝kx+t（k≠0），则，解得：．∴直线BC的解析式为y＝﹣x+3．设点M（m，m2﹣4m+3），过点M作MN∥y轴，交BC于点N，∴N（m，﹣m+3），∴MN＝﹣m+3﹣m2+4m﹣3＝﹣m2+3m，∵A（1，0）、B（3，0），C（0，3）．∴S△MOC＝OC•m＝m，S△MBC＝MN•OB＝﹣m2+m，∵△MOC的面积是△MBC面积的3倍，∴m＝3（﹣m2+m），∴m＝0（舍去）或，∴点M的坐标为（，﹣）；（3）抛物线上存在一点N，使得∠BCN＝∠ACB．过点B作BE⊥AB交CN与E，∵B（3，0），C（0，3）．∴OB＝OC＝3，∴∠OBC＝45°，∴∠OBC＝∠EBC＝45°，∵BC＝BC，∠BCN＝∠ACB．∴△ABC≌△EBC（ASA），∴BE＝AB＝2，∴E（3，2），设直线CN的解析式为y＝mx+n，∴，解得，∴直线CN的解析式为y＝﹣x+3，联立y＝x2﹣4x+3得，或（舍去），∴抛物线上存在一点N，使得∠BCN＝∠ACB．点N的横坐标为．2.如图，抛物线与x轴交于点A和点C（﹣1，0），与y轴交于点B（0，3），连接AB，BC，对称轴PD交AB与点E．（1）求抛物线的解析式；（2）如图2，试探究：线段BC上是否存在点M，使∠EMO＝∠ABC，若存在，求出点M的坐标；若不存在，请说明理由；（3）如图3，点Q是抛物线的对称轴PD上一点，若以点Q、A、B为顶点的三角形是锐角三角形，请直接写出点Q纵坐标n的取值范围．【分析】（1）用待定系数法即可求解；（2）先求出A（4，0），可得抛物线的对称轴为x＝＝，证明∠ACB＝∠ABC，△MCO∽△EBM，可得MC•BM＝BE•CO，求出MC，即可求解；（3）当∠BAQ为直角时，求出直线BQ的表达式为y＝x+3，得到n＝5；当∠BQA为直角时，利用解直角三角形的方法求出n＝；当∠BAQ为直角时，同理可得，n＝﹣，进而求解．【解答】解：（1）由题意得：，解得，故抛物线的表达式为y＝﹣x2+x+3；（2）对于y＝﹣x2+x+3，令y＝﹣x2+x+3＝0，解得x＝4或﹣1，故点A的坐标为（4，0），∵点A（4，0），B（0，3），C（﹣1，0），∴抛物线的对称轴为x＝＝，直线AB的表达式为y＝﹣x+3，AB＝＝5＝AC．∴∠ACB＝∠ABC，点E（，），∵∠CME＝∠CMO+∠OME＝∠ABC+∠MEB，∠ABC＝∠OME，∴∠CMO＝∠BEM．∴△MCO∽△EBM，∴，∴MC•BM＝BE•CO，∵B（0，3），E（，），∴BE＝＝，∴MC•BM＝，∵MC+BM＝BC＝＝．∴MC＝或MC＝．∴＝或＝，如图，过M作MK⊥x轴于K，则MK∥y轴，∴△CMK∽△CBO，∴＝或，即＝或，∴MK＝或，∵B（0，3），C（﹣1，0），∴直线BC的解析式为y＝3x+3，∴M的﹣横坐标为﹣或﹣，∴点M的坐标为（﹣，）或（﹣，）；（3）设点Q的坐标为（，n），当∠ABQ为直角时，如图，设BQ交x轴于点H，∵∠ABQ＝90°，∴∠BAO+∠BHA＝90°，∵∠BAO+∠ABO＝90°，∴∠ABO＝∠BHA，∵tan∠ABO＝，∴tan∠BHO＝，故设直线BQ的表达式为y＝x+t，∵该直线过点B（0，3），∴t＝3，∴直线BQ的表达式为y＝x+3，当x＝时，y＝x+3＝5，即n＝5；②当∠BQA为直角时，过点Q作直线MN交y轴于点N，交过点A与y轴的平行线于点M，∵∠BQN+∠MQA＝90°，∠MQA+∠MAQ＝90°，∴∠BQN＝∠MAQ，∴tan∠BQN＝tan∠MAQ，即，则，解得n＝；③当∠BAQ为直角时，同理可得，n＝﹣；综上，以点Q、A、B为顶点的三角形是锐角三角形，则△ABQ不为直角三角形，故点Q纵坐标n的取值范围为﹣＜n＜或＜n＜5．3.如图1，抛物线y＝ax2﹣x+c与x轴交于A（﹣2，0）、B（4，0）两点，与y轴交于点C，直线l与抛物线交于A、D两点，其中D点的横坐标为2．（1）求抛物线的解析式以及直线AD的解析式；（2）点P是抛物线上位于直线AD下方的动点，过点P作x轴，y轴的平行线，交AD于点E、F，当PE+PF取最大值时，求点P的坐标；（3）如图2，连接AC，点Q在抛物线上，且满足∠QAB＝2∠ACO，求点的坐标．【分析】（1）将A（﹣2，0），B（4，0）代入y＝ax2﹣x+c，求出抛物线的解析式，求出D点坐标后，利用待定系数法求直线AD的解析式；（2）由题意可得PF＝PE，设P（x，x2﹣x﹣4），F（x，﹣x﹣2），则PF＝﹣x2+2，当PF最大时，PF+PE就最大，由此求解即可；（3）在BO上截取ON＝OA，连接CN，过点A作AH⊥CN，证明△OCN≌△OCA（SAS），则可推导出∠QAB＝∠NCA，再由S△ANC＝AN×OC＝AH×CN，求出tan∠NCA＝，分两种情况讨论：当点Q在AB的下方时，设AQ与y轴交于点I，tan∠NCA＝tan∠QAB＝，可求点I（0，﹣），求出直线AQ解析式为y＝﹣x﹣，联立方程组得：，可求点Q坐标为（，﹣），当点Q在AB的上方时，同理可求直线AQ解析式为：y＝x+，联立方程组得：，可求点Q坐标为（，）．【解答】解：（1）将A（﹣2，0），B（4，0）代入y＝ax2﹣x+c，得，解得，∴抛物线解析式为y＝x2﹣x﹣4，当x＝2时，y＝﹣4，∴D（2，﹣4），设直线AD的解析式为y＝kx+b，将A（﹣2，0）D（2，﹣4）代入，得，解得，∴直线AD的解析式为y＝﹣x﹣2；（2）根据题意作图，如图1，在y＝﹣x﹣2上，当x＝0时，y＝﹣2，∴AD与y轴的交点M的坐标为（0，﹣2），∴OA＝OM，∠AOM＝90°，∴∠OAB＝45°，∵PE∥x轴，PF∥y轴，∴∠PEF＝∠OAB＝45°，∠EPF＝90°，∴PF＝PE，设P（x，x2﹣x﹣4），F（x，﹣x﹣2），∴PF＝﹣x2+2，∵P在AD的下方，∴﹣2＜x＜2，当x＝0时，PF有最大值为2，此时PF+PE最大，∴P（0，﹣4）；（3）在BO上截取ON＝OA，连接CN，过点A作AH⊥CN，如图2，∵点A（﹣2，0），点C（0，﹣4），∴OA＝2，OC＝4，∴AC＝2，∵ON＝OA，∠CON＝∠COA＝90°，OC＝OC，∴△OCN≌△OCA（SAS），∴∠ACO＝∠NCO，CN＝AC＝2，∴∠NCA＝2∠ACO，∵∠QAB＝2∠ACO，∴∠QAB＝∠NCA，∵S△ANC＝AN×OC＝AH×CN，∴AH＝，∴CH＝，∴tan∠NCA＝，如图3，当点Q在AB的下方时，设AQ与y轴交于点I，∵∠QAB＝∠NCA，∴tan∠NCA＝tan∠QAB＝，∴OI＝，∴点I（0，﹣），又∵点A（﹣2，0），∴直线AQ解析式为：y＝﹣x﹣，联立方程组得：，解得：或（不合题意舍去），∴点Q坐标为（，﹣），当点Q在AB的上方时，同理可求直线AQ解析式为：y＝x+，联立方程组得：，解得：（不合题意舍去）或，∴点Q坐标为（，），综上所述：点Q的坐标为（，﹣）或（，）．。

中考二次函数与角度有关的问题知识解读

二次函数与角度有关的问题知识解读【专题说明】二次函数背景下与角有关的存在性问题，是各地中考和模拟考试压轴题的热点问题，这种类型的题目综合性较强，更重要的是涉及方程与函数思想、数形结合思想、分类讨论等重要的思想方法，对学生分析、解决问题的能力具有较高的要求。

为此，下面将与角度有关的常见压轴题题型及解法做统一整理【知识点梳理】类型一：将等角问题转化成等腰三角形或平行线问题。

如例1：抛物线y=-x+3x+4,与坐标轴交于点A、B、C，CP⊥y轴交抛物线与点P，点M为A、C间抛物线上一点（包括端点），求满足∠MPO=∠POA的点M的坐标。

分析：显然符合条件的点M有两个，OP上方一个，OP下方一个、当M在OP 上方时，由∠MPO=∠POA可知PM//OA,则M与C点重合。

当M在OP下方时，∠MPO=∠POA，这两角组成的三角形是等腰三角形。

设PM与x轴交于点D，坐标为D(n,0)，由两点间距离公式可表示出OD、PD长，根据OD=PD列方程即可求出D点坐标，再求出PD直线表达式与抛物线表达式联立，进而求出M点坐标。

类型二：将等角问题转化成等角所在三角形相似或等角对应的三角函数（通常是正切值）相等问题。

这类问题有两种情况：一种是所求角的一边与坐标轴平行（重合）；例2如图，抛物线y=x221+bx+c 与x 轴交于A 、B 两点，与y 轴交于点C ，其对称轴交抛物线于点D ，交x 轴于点E ，已知OB=OC=6.（1）求抛物线的解析式及点D 的坐标；（2）连接BD ，F 为抛物线上一动点，当∠FAB=∠EDB 时，求点F 的坐标；解析：通过已知条件易得抛物线表达式为6221y 2+−=x x 及各定点坐标，第二问中的F 有两种情况：x 轴上方一个，x 轴下方一个。

在Rt ⊿BDE 中，可知tan ∠EDB=21，则tan ∠FAB=21，过F 作x 轴垂线，构造∠FAB 所在直角三角形，接着通过设F 点坐标，表示FH 和AH 长，根据tan ∠FAB=21=AH FH 列方程，或利用相似三角形对应边成比例列式，从而求出点F 坐标，由于表示FH 时加了绝对值，已经考虑到了上下两种情况，这样两个F 就都求出来了。

二次函数中角度问题

二次函数中角度问题二次函数是高中数学中非常重要的一章内容，其中涉及到许多重要的概念和知识点，其中一个比较重要的问题就是二次函数中角度问题。

本文将从以下几个方面进行详细的阐述。

一、什么是角度问题在二次函数中，我们经常会遇到关于角度的问题。

例如，我们可以将二次函数表示为 $y = a\sin^2(x) + b\cos^2(x)$ 的形式，其中$a$ 和 $b$ 是常数。

这个式子中的 $x$ 就代表了一个角度。

此外，在解决一些实际问题时，我们也经常需要用到角度概念。

例如，在物理学中，我们需要计算物体在斜面上滑动时的倾斜角度；在工程学中，我们需要计算建筑物或桥梁的倾斜角度等等。

因此，在二次函数中涉及到角度问题时，我们需要对角度有一个清晰准确的认识。

二、如何理解角度在数学中，我们通常使用弧度来表示角度。

弧度是一个长度单位，它表示弧长与半径之比。

例如，在一个半径为 $r$ 的圆上走过弧长为$l$ 的弧所对应的弧度就是 $\theta = l/r$。

在初学者中，我们通常使用度数来表示角度。

一个圆的周长是 $2\pi r$，因此一个完整的圆的角度是 $360$ 度。

因此，我们可以将一个任意角度 $\theta$ 转换为弧度制：$$\theta_{\text{弧度}} = \frac{\theta_{\text{度}}}{180^\circ}\pi$$例如，$45^\circ$ 对应的弧度是 $\pi/4$。

三、如何解决二次函数中的角度问题在二次函数中，我们经常需要用到三角函数和反三角函数。

例如，在上面提到的二次函数 $y = a\sin^2(x) + b\cos^2(x)$ 中，我们需要用到正弦和余弦函数。

在解决这些问题时，我们需要掌握以下几个重要的知识点：1. 三角函数的定义域和值域正弦和余弦函数都是周期为 $2\pi$ 的周期函数。

它们的定义域是实数集合 $\mathbb{R}$，值域是区间 $[-1, 1]$。

二次函数与角度问题解题技巧

二次函数与角度问题解题技巧一、引言二次函数是中学数学中重要的概念之一，在解题中经常会涉及到与角度相关的问题。

本文将从几个角度探讨二次函数与角度问题的解题技巧，帮助读者更好地理解和应用这些知识。

二、二次函数的基本特征在深入讨论二次函数与角度问题之前，我们首先需要理解二次函数的基本特征。

二次函数的标准形式为：f(x)=ax2+bx+c，其中a、b和c分别是常数，a≠0。

2.1 零点二次函数的零点是函数图像与x轴交点的横坐标。

要求二次函数的零点，可以通过解方程f(x)=0来得到。

常用的求根公式是一元二次方程的解法之一，即$ x = $。

2.2 顶点二次函数的顶点是函数图像的最高或最低点。

顶点的横坐标是通过x=−b计算得2a到的，纵坐标是将横坐标代入函数中得到的。

2.3 对称轴二次函数的对称轴是通过顶点且垂直于x轴的直线。

对称轴的方程可以通过x=−b得到。

2a2.4 开口方向二次函数的开口方向可以根据系数a的正负来确定。

当a>0时，二次函数开口向上；当a<0时，开口向下。

三、角度问题的解题技巧在解决与角度相关的二次函数问题时，我们需要掌握一些解题技巧。

本节将从几个角度探讨这些技巧。

3.1 求解函数图像与坐标轴交点当需要求解二次函数的图像与x轴或y轴交点时，我们可以将函数设置为0，得到方程f(x)=0或f(y)=0。

通过解这些方程，我们可以得到函数图像与坐标轴交点的坐标。

3.2 求解函数图像的对称性二次函数的图像关于其顶点对称。

通过计算顶点的坐标，我们可以确定函数图像的对称轴、开口方向以及顶点的位置。

3.3 求解函数的最大值或最小值当需要求解二次函数的最大值或最小值时，我们可以利用顶点的纵坐标。

根据开口方向，最大值或最小值就是函数图像的顶点。

3.4 求解角度问题在一些角度问题中，我们需要根据给定的条件，建立二次函数的方程，并通过解方程求解。

一般情况下，可以利用三角函数的性质将角度转化为弧度，然后建立二次函数方程，最后通过求解方程得到结果。

二次函数中角度的存在性问题

二次函数中角度的存在性问题类型一：等角构造法（作垂直，找相似）例1：如图，抛物线y＝x2-4x＋3与x轴交于点A，B两点，与y轴交C，连接AC.抛物线上是否存在点M，使∠OBM ＝∠OCA.若存求出点M的坐标；若不存在，请说明理由.分析：1.假设∠OBM=∠OCA，过M作ME垂直x轴，构造∆MEB~∆AOC，利用对应边成比例，可求出M点坐标。

2.利用对称性，求出点M的对称点H,可得∠HBO=∠OBM，延长BH交抛物线于点M’，则点M’就为所求的。

类型二：2倍角构造法（作垂直平分线，构造等腰三角形，则外角就为已知角的两倍）例2.如图，直线y＝-3x＋3与x轴交于点A，与y轴交于点B，抛物线y＝-x2＋bx＋c经过点A，B．抛物线上是否存在点M，使直线AM与y轴所夹锐角是∠ABO的2倍？若存在，请求出点M的坐标；若不存在，请说明理由.分析：1.作AB的垂直平分线CD,交y轴于点D,则构造等腰三角形BDA，所以∠ODA=2∠OBA，延长AD交抛物线于点M，则联立解析式可求点M坐标。

2.利用对称性可求点M的对称点H（或者求D点的对称点），则延长AH交抛物线于M’。

类型三：半角构造法（作角平分线或向外延长作等腰三角形）例3：如图，抛物线交x 轴于A ，C 两交y 轴于点B ，连接AB .抛物线上是否存在点M ，使∠ACM ＝？若存在，请求出点M 的坐标；若不存在，请说明理由.分析：方法1：作∠OAB 的J 角平分线AE ，求出E 点坐标及AE 解析式。

过点C 作CM ∥AE ，则∠MCA=∠OAE=∠OAB ，则点M 就为所求作的。

然后利用对称性，可求点M ’.4x 31x 31y 2+--=BAO ∠2121方法2：延长OA 至D ，使AD 等于AB ，构造等腰三角形BAD,则∠ADB=∠OAB ，过C 点作CM ∥BD,则点M 就为所求作的。

然后一样利用对称性求出点M ’。

21。

二次函数角度问题

二次函数角度问题1. 什么是二次函数二次函数是一种形式为f(x) = ax^2 + bx + c的函数，其中a、b和c是实数，并且a不等于0。

二次函数的图像通常是一个开口朝上或朝下的抛物线。

2. 什么是二次函数的角度二次函数的角度是指抛物线与其自身的对称轴之间的夹角。

对称轴是一个垂直于x轴的线，通过抛物线的顶点。

角度的大小决定了抛物线的形状和方向。

3. 如何确定二次函数的角度要确定二次函数的角度，我们可以使用二次函数的标准形式f(x) = a(x-h)^2 + k，其中(h, k)是抛物线的顶点坐标。

对称轴的方程为x = h，因此角度可以通过计算抛物线开口朝上或朝下的倾斜程度来确定。

4. 如何计算二次函数的角度计算二次函数的角度，可以使用函数的一阶导数。

一阶导数表示函数的斜率，也就是抛物线在某一点处的斜率。

当斜率为正时，抛物线开口朝上；当斜率为负时，抛物线开口朝下。

我们可以对二次函数f(x) = ax^2 + bx + c求导，得到f'(x) = 2ax + b。

通过求解f'(x) = 0，可以找到抛物线与对称轴的交点。

这个交点的x坐标可以代入原函数，得到对称轴的方程x = h。

如果a大于0，则抛物线开口朝上，角度为锐角。

如果a小于0，则抛物线开口朝下，角度为钝角。

角度的大小与a的绝对值成正比。

5. 如何解释二次函数角度对抛物线的影响二次函数的角度决定了抛物线的形状和开口的方向。

角度较小时，抛物线较为陡峭；角度较大时，抛物线较为平缓。

当角度比较小的时候，抛物线的增长或减少速度较快，曲线较为陡峭。

这意味着函数的值在x轴附近迅速变化，对应于一个较为敏感的函数。

当角度比较大的时候，抛物线的增长或减少速度较慢，曲线较为平缓。

这意味着函数的值在x轴附近变化得较为缓慢，对应于一个较为平滑的函数。

因此，角度对二次函数的图像具有重要影响，它决定了函数的形状、敏感性和平滑度。

总结起来，二次函数是一种具有角度的函数，角度决定了抛物线的形状和开口的方向。

二次函数与角的有关问题专项辅导资料

二次函数与角的有关问题专项辅导资料要理解二次函数与角的有关问题，首先需要了解二次函数的基本性质和角度的概念。

在此基础上，我们将讨论二次函数与角度的关系，以及如何利用角度解决二次函数的问题。

一、二次函数的基本性质二次函数是形如f(x) = ax^2+bx+c的函数，其中a、b和c是常数，并且a≠0。

二次函数的图像是一个抛物线，其开口方向由a的正负决定。

如果a>0，则抛物线开口向上，如果a<0，则抛物线开口向下。

二次函数的顶点坐标为(-b/2a, f(-b/2a))，其对称轴为直线x=-b/2a。

二、角的概念角度是平面上两条射线所夹的空间部分。

角度通常用度（°）来表示，一个完整的角度为360°。

我们可以通过不同的单位来表示角度，如弧度和百分度。

其中，360°等于2π弧度。

三、二次函数与角的关系1.抛物线的开口方向与角度的对应关系二次函数的开口方向与角度的对应关系如下：-当抛物线开口向上时，与x轴正半轴的夹角是锐角。

-当抛物线开口向下时，与x轴正半轴的夹角是钝角。

2.抛物线的顶点与角度的对应关系二次函数的顶点与角度的对应关系如下：-抛物线的顶点左侧的区域对应于一个小于180°的角度区间。

-抛物线的顶点右侧的区域对应于一个大于180°的角度区间。

3.求解二次函数与角度的交点可以利用角度的概念来求解二次函数与角度的交点。

假设二次函数的表达式为f(x)，要求解f(x)=k（k为常数）的交点，可以通过以下步骤：- 将f(x) = k转化为ax^2+bx+c = k的形式。

- 将该方程转化为标准形式ax^2+bx+(c-k)=0，并解出方程。

-得到方程的根之后，可以将根代入f(x)中求得交点的坐标。

四、利用角度解决二次函数的问题1.求解二次函数的极值问题二次函数的极值问题可以通过角度的方法来解决。

假设二次函数的表达式为f(x)，要求解f(x)的最小（或最大）值，可以通过以下步骤：- 将二次函数转化为标准形式ax^2+bx+c。

数学专题7——二次函数的角度问题

二次函数中的角度问题知识要点：一模中二次函数的角度问题的主体是角度相等问题角度相等问题有以下解决策略策略一：作垂线，构造两个包含目标角的直角三角形，则这两个直角三角形相似，结合三角比等工具解决问题策略二：将角度进行转化，构造等腰三角形策略三：构造相似三角形，利用对应边成比例求解策略四：求出其中一个已知角的三角比，利用此三角比得到直线斜率，结合直线方程求解【练习1】在平面直角坐标系中，已知抛物线2(0)y ax bx c a =++>与x 轴交于(1,0)A -、B 两点（点A 在点B 的左侧），与y 轴交于点C ，抛物线的顶点为点D ，对称轴为直线1x =，交x 轴于点E ，1tan 2BDE ∠=．（1）求抛物线的表达式；（2）若点P 是对称轴上一点，且DCP BDE ∠=∠，求点P 的坐标．【练习2】如图，在平面直角坐标系xOy 中，直线AB 与抛物线2y ax bx =+交于点(6,0)A 和点(1,5)B -．（1）求这条抛物线的表达式和直线AB 的表达式；（2）如果点C 在直线AB 上，且BOC ∠的正切值是32，求点C 的坐标．【练习3】如图，抛物线212y x bx c =-++经过点(2,0)A -，点(0,4)B ．（1）求这条抛物线的表达式；（2）P 是抛物线对称轴上的点，联结AB 、PB ，如果PBO BAO ∠=∠，求点P 的坐标；（3）将抛物线沿y 轴向下平移m 个单位，所得新抛物线与y 轴交于点D ，过点D 作//DE x 轴交新抛物线于点E ，射线EO 交新抛物线于点F ，如果2EO OF =，求m 的值．【练习4】如图，在平面直角坐标系xOy 中，二次函数26(y ax bx a =++、b 都是常数，且0)a <的图象与x 轴交于点(2,0)A -、(6,0)B ，顶点为点C ．（1）求这个二次函数的解析式及点C 的坐标；（2）过点B 的直线132y x =-+交抛物线的对称轴于点D ，联结BC ，求CBD ∠的余切值；（3）点P 为抛物线上一个动点，当PBA CBD ∠=∠时，求点P 的坐标．【练习5】已知：在平面直角坐标系xOy 中，抛物线2y ax bx =+经过点(5,0)A 、(3,4)B -，抛物线的对称轴与x 轴相交于点D ．（1）求抛物线的表达式；（2）联结OB 、BD ．求BDO ∠的余切值；（3）如果点P 在线段BO 的延长线上，且PAO BAO ∠=∠，求点P 的坐标．二次函数中的角度问题参考解析【练习1】在平面直角坐标系中，已知抛物线2(0)y ax bx c a =++>与x 轴交于(1,0)A -、B 两点（点A 在点B 的左侧），与y 轴交于点C ，抛物线的顶点为点D ，对称轴为直线1x =，交x 轴于点E ，1tan 2BDE ∠=．（1）求抛物线的表达式；（2）若点P 是对称轴上一点，且DCP BDE ∠=∠，求点P 的坐标．【解析】解：（1）依照题意，画出图形，如图1所示．点A 的坐标为(1,0)-，抛物线的对称轴为直线1x =，∴点E 的坐标为(1,0)，2BE AE ∴==． 1tan 2BE BDE DE ∠==， 24DE BE ∴==，∴点D 的坐标为(1,4)-．∴抛物线的表达式可设为2(1)4y a x =--．将(1,0)-代入2(1)4y a x =-+，得：440a -=，解得：1a =，∴抛物线的表达式为2(1)4y x =--，即223y x x =--．（2）取点(5,0)F ，连接DF ，过点C 作CM ⊥直线DE ，垂足为点M ，过点B 作BN ⊥直线DF ，垂足为点N ，如图2所示．点D 的坐标为(1,4)-，4EF DE ∴==，DEF ∴∆为等腰直角三角形，45EDF EFD ∴∠=∠=︒，DF =BN DF ⊥，BNF ∴∆为等腰直角三角形，NB NF ∴===，DN DF NF ∴=-=1tan 3BN BDN DN ∴∠==．当0x =时，2233y x x =--=-，∴点C 的坐标为(0,3)-．点D 的坐标为(1,4)-，CM DE ⊥，1CM DM ∴==，CDM ∴∆为等腰直角三角形， 45DCM CDM ∴∠=∠=︒．①当点P 在点D 下方时，45CDM DCP CPM ∠=∠+∠=︒，45BDE BDN ∠+∠=︒，CPM BDN ∴∠=∠，1tan 3CM CPM MP ∴∠==，即113MP =， 3MP ∴=，6EP EM MP ∴=+=，∴点P 的坐标为(1,6)-；②当点P 在点D 上方时，45PCD PCM ∠+∠=︒，45BDE BDN ∠+∠=︒，PCM BDN ∴∠=∠，1tan 3MP PCM CM ∴∠==， 13MP ∴=，103EP EM MP ∴=+=， ∴点P 的坐标为10(1,)3-．综上所述，点P 的坐标为(1,6)-或10(1,)3-．【练习2】如图，在平面直角坐标系xOy 中，直线AB 与抛物线2y ax bx =+交于点(6,0)A 和点(1,5)B -．（1）求这条抛物线的表达式和直线AB 的表达式；（2）如果点C 在直线AB 上，且BOC ∠的正切值是32，求点C 的坐标．【解析】解：（1）把点(6,0)A 和点(1,5)B -代入抛物线2y ax bx =+得： 36605a b a b +=⎧⎨+=-⎩，解得：16a b =⎧⎨=-⎩， ∴这条抛物线的表达式：26y x x =-，设直线AB 的解析式为：y kx b =+，把点(6,0)A 和点(1,5)B -代入得：605k b k b +=⎧⎨+=-⎩，解得：16k b =⎧⎨=-⎩，则直线AB 的解析式为：6y x =-；（2）当0x =时，6y =，当0y =时，6x =，6OA OH ∴==，90AOH ∠=︒， 45OAH ∴∠=︒，过B 作BG x ⊥轴于G ，则ABG ∆是等腰直角三角形，AB ∴=过O 作OE AB ⊥于E ， 1122AOH S AH OE OA OH ∆==，66OE =⨯，OE =，BE AB AE ∴=-=Rt BOE ∆中，3tan 2OE OBE BE ∠===， BOC ∠的正切值是32， BOC OBE ∴∠=∠，作OB 的垂直平分线交AB 于C ，交OB 于F ，过C 作CD x ⊥轴于D ，连接OC ，设(,6)C m m -，则)AC m =-，OC BC =，22(6))]m m m ∴+-=-，174m =， 17(4C ∴，7)4-．【练习3】如图，抛物线212y x bx c =-++经过点(2,0)A -，点(0,4)B ．（1）求这条抛物线的表达式；（2）P 是抛物线对称轴上的点，联结AB 、PB ，如果PBO BAO ∠=∠，求点P 的坐标；（3）将抛物线沿y 轴向下平移m 个单位，所得新抛物线与y 轴交于点D ，过点D 作//DE x 轴交新抛物线于点E ，射线EO 交新抛物线于点F ，如果2EO OF =，求m 的值．【解析】解：（1）抛物线经过点(2,0)A -，点(0,4)B ∴2204b c c --+=⎧⎨=⎩，解得14b c =⎧⎨=⎩∴抛物线解析式为2142y x x =-++，（2）221194(1)222y x x x =-++=--+，∴对称轴为直线1x =，如图1，过点P 作PG y ⊥轴，垂足为G ，PBO BAO ∠=∠，tan tan PBO BAO ∴∠=∠，∴PG BO BG AO = ∴121BG =，12BG ∴= 72OG ∴=， 7(1,)2P ∴，（3）如图2设新抛物线的表达式为2142y x x m =-++-则(0,4)D m -，(2,4)E m -，2DE = 过点F 作FH y ⊥轴，垂足为H ，//DE FH ，2EO OF =∴21DE EO DO FH OF OH ===， 1FH ∴=，①点D 在y 轴的正半轴上，则5(1,)2F m --，52OH m ∴=-∴42512DO m OH m -==-， 3m ∴=，②点D 在y 轴的负半轴上，则9(1,)2F m -，92OH m ∴=-，∴42912DO m OH m -==-， 5m ∴=∴综上所述m 的值为3或5．【练习4】如图，在平面直角坐标系xOy 中，二次函数26(y ax bx a =++、b 都是常数，且0)a <的图象与x 轴交于点(2,0)A -、(6,0)B ，顶点为点C ．（1）求这个二次函数的解析式及点C 的坐标；（2）过点B 的直线132y x =-+交抛物线的对称轴于点D ，联结BC ，求CBD ∠的余切值；（3）点P 为抛物线上一个动点，当PBA CBD ∠=∠时，求点P 的坐标．【解析】解：（1）将(2,0)A -，(6,0)B 代入26y ax bx =++，得：426036660a b a b -+=⎧⎨++=⎩，解得：122a b ⎧=-⎪⎨⎪=⎩，∴二次函数的解析式为21262y x x =-++．221126(2)822y x x x =-++=--+，∴点C 的坐标为(2,8)．（2）当2x =时，1322y x =-+=，∴点D 的坐标为(2,2)．过点D作DE BC ⊥，垂足为点E ，设抛物线对称轴与x 轴的交点为点F ，如图1所示．抛物线的顶点坐标为(2,8)，∴点F 的坐标为(2,0)．点B 的坐标为(6,0)，8CF ∴=，6CD =，2DF =，4BF =，BCBD = sin BF DE BCF BC CD ∴∠==6DE =，DE ∴=BE ∴=，4cot 3BE CBD DE ∴∠===．（3）设直线PB 与y 轴交于点M ，如图2所示． PBA CBD ∠=∠，4cot 3OB PBA OM ∴∠==，即643OM =， 92OM ∴=， ∴点M 的坐标为9(0,)2或9(0,)2-．设直线BP 的解析式为(0)y mx n m =+≠，将(6,0)B ，9(0,)2M 代入y mx n =+，得：6092m n n +=⎧⎪⎨=⎪⎩，解得：3492m n ⎧=-⎪⎪⎨⎪=⎪⎩， ∴直线BP 的解析式为3942y x =-+．同理，当点M 的坐标为9(0,)2-时，直线BP 的解析式为3942y x =-．联立直线BP 与抛物线的解析式成方程组，得：239421262y x y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩或239421262y x y x x ⎧=-⎪⎪⎨⎪=-++⎪⎩，解得：1112398x y ⎧=-⎪⎪⎨⎪=⎪⎩，2260x y =⎧⎨=⎩或1172578x y ⎧=-⎪⎪⎨⎪=-⎪⎩，2260x y =⎧⎨=⎩，∴点P 的坐标为1(2-，39)8或7(2-，57)8-．【练习5】已知：在平面直角坐标系xOy 中，抛物线2y ax bx =+经过点(5,0)A 、(3,4)B -，抛物线的对称轴与x 轴相交于点D ．（1）求抛物线的表达式；（2）联结OB 、BD ．求BDO ∠的余切值；（3）如果点P 在线段BO 的延长线上，且PAO BAO ∠=∠，求点P 的坐标．【解析】解：（1）将(5,0)A ，(3,4)B -代入2y ax bx =+，得：2550934a b a b +=⎧⎨-=⎩，解得：1656a b ⎧=⎪⎪⎨⎪=-⎪⎩， ∴所求抛物线的表达式为21566y x x =-．（2）抛物线的表达式为21566y x x =-， ∴抛物线的对称轴为直线52x =， ∴点D 的坐标为5(2，0)．过点B 作BC x ⊥轴，垂足为点C ，如图1所示．点B 的坐标为(3,4)-，点D 的坐标为5(2，0)， 4BC ∴=，3OC =，511322CD =+=，11cot 8CD BDO CB ∴∠==．（3）设点P 的坐标为(,)m n ，过点P 作PQ x ⊥轴，垂足为点Q ，如图2所示．则PQ n =-，OQ m =，5AQ m =-．在Rt ABC ∆中，90ACB ∠=︒， 8cot 24AC BAC BC ∴∠∠===． PAO BAO ∠=∠，5cot 2AQ m PAO PQ n -∴∠===-，即25m n -=①． BC x ⊥轴，PQ x ⊥轴， 90BCO PQA ∴∠=∠=︒， //BC PQ ∴， ∴BC OC PQ OQ=， ∴43n m=-，即43m n =-②．由①、②得：2543m n m n -=⎧⎨=-⎩，解得：15112011m n ⎧=⎪⎪⎨⎪=-⎪⎩， ∴点P 的坐标为15(11，20)11-．。

二次函数与角度问题解题技巧

二次函数与角度问题解题技巧二次函数与角度问题解题技巧是高中数学教学中的一个重要内容，本文将为大家详细介绍有关二次函数与角度问题解题的相关内容。

一、二次函数的基本性质二次函数y=ax²+bx+c是一个常见的函数形式，其中a、b、c都是常数，a不能为0。

通过对二次函数的研究，我们可以得到以下几个基本性质。

1.对称轴：二次函数的图像关于直线x=-b/2a对称。

2.开口方向：当a>0时，二次函数开口朝上；当a<0时，二次函数开口朝下。

3.零点：二次函数的零点为x=(-b±√(b²-4ac))/2a。

4.最值：当a>0时，二次函数的最小值为c-b²/4a；当a<0时，二次函数的最大值为c-b²/4a。

二、角度的基本概念在解题时涉及到角度问题，我们需要先了解一些角度的基本概念。

1.度数：度数是衡量角度大小的单位，一个完整的圆是360°。

角度小于360°的称为锐角或者钝角，大于360°的称为扩角。

2.弧度：弧度是衡量角度大小的另一种单位，一个完整的圆对应的弧度是2π。

一般情况下，我们可以通过角度制转换成弧度制，即1°=π/180。

3.三角函数：三角函数包括正弦函数、余弦函数和正切函数。

它们是角度的函数，可以用来计算三角形中各个边和角度之间的关系。

三、我们可以通过二次函数与角度问题解题来加深对这两个知识点的理解。

下面分别介绍两种不同的解题方法。

1.将角度问题转换成二次函数问题有时我们会遇到一些角度问题，如正弦函数、余弦函数和正切函数等，可以通过转换成二次函数的形式来解决。

如题：已知正弦函数的最小正周期为6，函数图像通过点(0,-1)，求这个正弦函数的解析式。

解：因为正弦函数的最小正周期为6，所以这个函数的表达式应该是y=Asin(2π/6x)+B。

又因为这个函数图像通过点(0,-1)，所以B=-1。

初三讲义。二次函数当中的角度问题

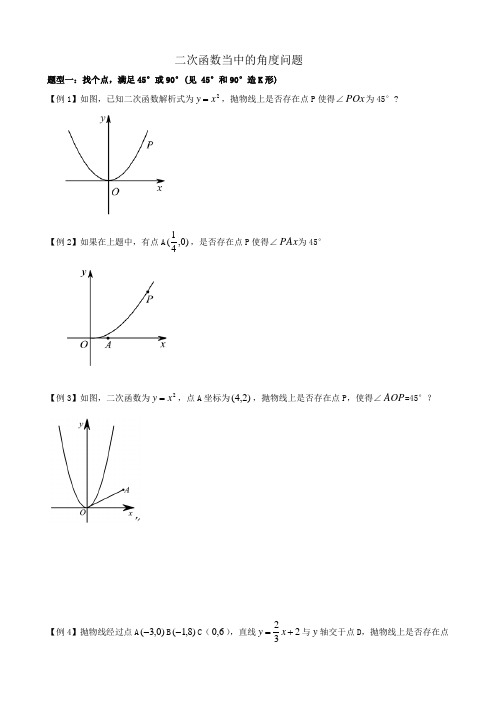
二次函数当中的角度问题题型一：找个点，满足45°或90°(见 45°和90°造K 形)【例1】如图，已知二次函数解析式为2x y =，抛物线上是否存在点P 使得∠POx 为45°?【例2】如果在上题中，有点A )0,41(，是否存在点P 使得∠PAx 为45°【例3】如图，二次函数为2x y =，点A 坐标为)2,4(，抛物线上是否存在点P ，使得∠AOP =45°？【例4】抛物线经过点A )0,3(-B )8,1(-C （6,0），直线232+=x y 与y 轴交于点D ，抛物线上是否存在点P 使得∠PAD =45°？【例5】已知二次函数为322--=x x y ，与x 轴交于A 、B 两点。

在抛物线上是否存在点P 使得∠PAC 为锐角？若存在，请求出x 的取值范围。

【实战演练】1.如图，抛物线432++-=x x y 与x 轴交于A 、B 两点，与y 轴交于点C ，点D(3，4)在抛物线上，连接BD ，点P 为抛物线上一点，且∠DBP =45°，求点P 的坐标．2.抛物线a bx ax y 42-+=经过点A （1,0）和C （0,4），与x 轴交于另一点B 。

（1）求抛物线解析式（2）已知点D （m,1-m ）在抛物线第二象限上，求点D 关于直线BC 对称点坐标。

（3）在（2）的条件下，连接BD ，在抛物线上是否存在点P 使得∠DBP=45°，求点P 坐标。

题型二找个点满足角度相等【例1】抛物线322++-=x x y 与并轴分别交于A 、B 两点，与y 轴的正半轴交于C 点，抛物线的顶点为D ，连接BC 、BD ，抛物线上是否存在一点P ，使得∠PCB=∠CBD ，若存在，求P 点的坐标，不存在，说明理由。

【例2】抛物线解析式为322--=x x y ，交x 轴于A 、B 两点，图形上是否存在点P 使得∠PCO ＞∠ACO 若存在，请求出x 的取值范围。

二次函数与角度问题

二次函数专题一：角度一、有关角相等1、已知抛物线2y ax bx c =++的图象与x 轴交于A 、B 两点（点A 在点B 的左边），与y 轴交于点(0C ，3)，过点C 作x 轴的平行线与抛物线交于点D ，抛物线的顶点为M ，直线5y x =+经过D 、M 两点.（1）求此抛物线的解析式；（2）连接AM 、AC 、BC ，试比较MAB ∠和ACB ∠的大小，并说明你的理由.思路点拨：对于第（1）问，需要注意的是CD 和x 轴平行（过点C 作x 轴的平行线与抛物线交于点D ）对于第（2）问，比较角的大小a 、如果是特殊角，也就是我们能分别计算出这两个角的大小，那么他们之间的大小关系就清楚了b 、如果这两个角可以转化成某个三角形的一个外角和一个不相邻的内角，那么大小关系就确定了c 、如果稍难一点，这两个角转化成某个三角形的两个内角，根据大边对大角来判断角的大小d 、除了上述情况外，那只有可能两个角相等，那么证明角相等的方法我们学过什么呢，全等三角形、相似三角形和简单三角函数，从这个题来看，很明显没有全等三角形，剩下的就是相似三角形和简单三角函数了，其实简单三角函数证明角相等和相似三角形证明角相等的本质是一样的，都是对应边的比相等e 、可能还有人会问，这么想我不习惯，太复杂了，那么我再说一个最简单的方法，如何快速的找出题目的结论问题，在本题中，需要用到的点只有M 、C 、A 、B 这四个点，而这四个点的坐标是很容易求出来的，那么请你把这四个点规范的在直角坐标系内标出来，再用量角器去量这两个角大大小，你就能得出结论了，得出结论以后你再看d 这一条解：（1）∵CD∥x 轴且点C （0，3），∴设点D 的坐标为(x ，3) ． ∵直线y= x+5经过D 点， ∴3= x+5．∴x=－2．即点D(－2，3) ．根据抛物线的对称性，设顶点的坐标为M （－1，y ），又∵直线y= x+5经过M 点，∴y =－1+5，y =4．即M （－1，4）．∴设抛物线的解析式为2(1)4y a x =++． ∵点C （0，3）在抛物线上，∴a=－1．即抛物线的解析式为223y x x =--+．…………3分（2）作BP⊥AC 于点P ，MN⊥AB 于点N ．由（1）中抛物线223y x x =--+可得点A （－3，0），B （1，0）， ∴AB=4，AO=CO=3，AC=32．∴∠PAB＝45°．∵∠ABP=45°，∴PA=PB=22． ∴PC=AC－PA=2．在Rt△BPC 中，tan∠BCP=PBPC =2．在Rt△ANM 中，∵M（-1，4），∴MN=4．∴AN=2．tan∠NAM=MNAN =2．∴∠BCP＝∠NAM．即∠ACB＝∠MAB．后记：对于几何题来说，因为组成平面图形的最基本的元素就是线段和角（圆分开再说），所以几何的证明无非就是线段之间的关系，角之间的关系，在二次函数综合题里，我主张首先要想到的是利用角之间的关系来解题，其次才是利用线段之间的关系来解题，除非你很快就能看出利用线段之间的关系来解题很简单，因为在直角坐标系里要求两点之间的距离是很麻烦的，尤其是不知道某个点的确切坐标时，那么这个题给了我们一个如果判断角之间关系的基本思路2、（2012朝阳一模第24题8分）24. 在平面直角坐标系xOy 中，抛物线23y ax bx =++经过点N （2,－5），过点N 作x 轴的平行线交此抛物线左侧于点M ，MN =6. （1）求此抛物线的解析式；（2）点P （x ,y ）为此抛物线上一动点，连接MP 交此抛物线的对称轴于点D ，当△DMN 为直角三角形时，求点P 的坐标；（3）设此抛物线与y 轴交于点C ，在此抛物线上是否存在点Q 若不存在，说明理由.24. 解：（1）∵32++=bx ax y 过点M 、N （2，－5），MN 由题意，得M （4-，5-）.∴⎩⎨⎧-=+--=++.53416,5324b a b a解得 ⎩⎨⎧-=-=.2,1b a∴此抛物线的解析式为322+--=x x y . …………………………………2分（2）设抛物线的对称轴1-=x 交MN 于点G ，若△DMN 为直角三角形，则32121===MN GD GD . ∴D 1（1-，2-），2D （1-，8-）. ………………………………………4分直线MD 1为1-=x y ，直线2MD 为9--=x y . 将P （x ，322+--x x ）分别代入直线MD 1，2MD 的解析式，得1322-=+--x x x ①，9322--=+--x x x ②.解①得 11=x ，42-=x （舍），∴1P （1,0）. …………………………………5分解②得 33=x ，44-=x （舍），∴2P （3,－12）. ……………………………6分（3）设存在点Q （x ，322+--x x ），使得∠QMN =∠CNM .① 若点Q 在MN 上方，过点Q 作QH ⊥MN ，交MN 于点H ，则4tan =∠=CNM MHQH. 即）（445322+=++--x x x .解得21-=x ，42-=x （舍）.∴1Q （2-，3）. ……………………………7分 ② 若点Q 在MN 下方，同理可得2Q （6，45-）. …………………8分3、（2012西城一模25题8分）25．平面直角坐标系xOy 中，抛物线244y ax ax a c =-++与x 轴交于点A 、点B ，与y 轴的正半轴交于点C ，点 A 的坐标为(1, 0)，OB =OC ，抛物线的顶点为D ．(1) 求此抛物线的解析式；(2) 若此抛物线的对称轴上的点P 满足∠APB =∠ACB ，求点P 的坐标；(3) Q 为线段BD 上一点，点A 关于∠AQB 的平分线的对称点为A '，若2=-QB QA ，求点Q 的坐标和此时△QAA '的面积．25．解：（1）∵ 2244(2)y ax ax a c a x c =-++=-+，∴ 抛物线的对称轴为直线2x =．∵ 抛物线244y ax ax a c =-++与x 轴交于点A 、点B ，点A 的坐标为(1,0)，∴ 点B 的坐标为(3,0)，OB ＝3．…………… 1分可得该抛物线的解析式为(1)(3)y a x x =--． ∵ OB =OC ，抛物线与y 轴的正半轴交于点C ， ∴ OC =3，点C 的坐标为(0,3)．将点C 的坐标代入该解析式，解得a =1．……2分∴ 此抛物线的解析式为243y x x =-+．（如图9（2）作△ABC 的外接圆☉E ，设抛物线的对称轴与x 轴的交点为点F ，设☉E 与抛物线的对称轴位于x 轴上方的部分的交点为点1P ，点1P 关于x 轴的对称点为点2P ，点1P 、点2P 均为所求点.（如图10）可知圆心E 必在AB 边的垂直平分线即抛物线的对称轴直线2x =上．∵ 1APB ∠、ACB ∠都是弧AB 所对的圆周角， ∴ ACB B AP ∠=∠1，且射线FE 上的其它点P 都不满足ACB APB ∠=∠．由（1）可知 ∠OBC=45°，AB=2，OF=2．可得圆心E 也在BC 边的垂直平分线即直线y x =上．∴ 点E 的坐标为(2,2)E ．………………………………………………… 4分∴ 由勾股定理得 EA∴ 1EP EA ==∴ 点1P 的坐标为1(2,2P+．…………………………………………… 5分由对称性得点2P 的坐标为2(2,2P -． ……………………………… 6分∴符合题意的点P 的坐标为1(2,2P +、2(2,2P --. （3）∵ 点B 、D 的坐标分别为(3,0)B 、(2,1)D -，可得直线BD 的解析式为3y x =-，直线BD 与x 轴所夹的锐角为45°． ∵ 点A 关于∠AQB 的平分线的对称点为A '，（如图11）若设AA '与∠AQB 的平分线的交点为M ，则有 QA QA '=，AM A M '=，AA QM '⊥，Q ，B ，A '三点在一条直线上．∵ QA QB -=∴ .2''=-=-=QB QA QB QA BA作A N '⊥x 轴于点N ．∵ 点Q 在线段BD 上， Q ，B ，A '三点在一条直线上， ∴ sin451A N BA ''=⋅︒=，cos451BN BA '=⋅︒=． ∴ 点A '的坐标为(4,1)A '． ∵ 点Q 在线段BD 上，∴ 设点Q 的坐标为(,3)Q x x -，其中23x <<． ∵ QA QA '=，∴ 由勾股定理得 2222(1)(3)(4)(31)x x x x -+-=-+--．解得114x =．经检验，114x =在23x <<的范围内．∴ 点Q 的坐标为111(,)44Q -． …………………………………………… 7分此时1115()2(1)2244QAA A AB QAB A Q S S S AB y y '''∆∆∆=+=⋅⋅+=⨯⨯+=．… 8分二、特殊角（一）、450角1、如图，在平面直角坐标系xoy 中，点P 为抛物线2x y =上一动点，点A 的坐标为（4,2），若点P 使∠AOP ＝450，请求出点P 的坐标。

题型九二次函数综合题类型四二次函数与角度有关的问题(专题训练)(解析版)

题型九二次函数综合题类型四二次函数与角度有关的问题（专题训练）1.已知抛物线23y ax bx =+-与x 轴相交于(1,0)A -，(3,0)B 两点，与y 轴交于点C ，点(,0)N n 是x 轴上的动点．（1）求抛物线的解析式；（2）如图1，若3n <，过点N 作x 轴的垂线交抛物线于点P ，交直线BC 于点G ．过点P 作PD BC ^于点D ，当n 为何值时，PDG BNG V V ≌；（3）如图2，将直线BC 绕点B 顺时针旋转，使它恰好经过线段OC 的中点，然后将它向上平移32个单位长度，得到直线1OB ．①1tan BOB Ð=______；②当点N 关于直线1OB 的对称点1N 落在抛物线上时，求点N 的坐标．【答案】（1）223y x x =--；（2）n =；（3）①12；②或．【分析】（1）根据点,A B 的坐标，利用待定系数法即可得；（2）先根据抛物线的解析式可得点,C P 的坐标，再利用待定系数法可得直线BC 的解析式，从而可得点G 的坐标，然后分别求出,PG BG 的长，最后根据全等三角形的性质可得PG BG =，由此建立方程求解即可得；（3）①先利用待定系数法求出直线BD 的解析式，再根据平移的性质可得直线1OB 的解析式，从而可得点E 的坐标，然后根据正切三角函数的定义即可得；②先求出直线1NN 的解析式，再与直线1OB 的解析式联立求出它们的交点坐标，从而可得点1N 的坐标，然后代入抛物线的解析式求解即可得．【详解】解：（1）将点(1,0)A -，(3,0)B 代入23y ax bx =+-得：309330a b a b --=ìí+-=î，解得12a b =ìí=-î，则抛物线的解析式为223y x x =--；（2）由题意得：点P 的坐标为2(,23)P n n n --，对于二次函数223y x x =--，当0x =时，3y =-，即(0,3)C -，设直线BC 的解析式为y kx c =+，将点(3,0)B ，(0,3)C -代入得：303k c c +=ìí=-î，解得13k c =ìí=-î，则直线BC 的解析式为3y x =-，(,3)G n n \-，223(23)3PG n n n n n \=----=-+，(3BG n ==-PDG BNG @V QV ，PG BG \=，即23(3n n n -+=-，解得n =3n =（与3n <不符，舍去），故当n =PDG BNG @V V ；（3）①如图，设线段OC 的中点为点D ，过点B 作x 轴的垂线，交直线1OB 于点E ，则点D 的坐标为3(0,2D -，点E 的横坐标为3，设直线BD 的解析式为00y k x c =+，将点(3,0)B ，3(0,2D -代入得：0003032k c c +=ìïí=-ïî，解得001232k c ì=ïïíï=-ïî，则直线BD 的解析式为1322y x =-，由平移的性质得：直线1OB 的解析式为12y x =，当3x =时，32y =，即3(3,)2E ，33,2OB BE \==，11tan 2BE BOB OB Ð==\，故答案为：12；②由题意得：11NN OB ^，则设直线1NN 的解析式为12y x c =-+，将点(,0)N n 代入得：120n c -+=，解得12c n =，则直线1NN 的解析式为22y x n =-+，联立2212y x n y x =-+ìïí=ïî，解得4525x n y n ì=ïïíï=ïî，即直线1NN 与直线1OB 的交点坐标为42(,)55n n ，设点1N 的坐标为1(,)N s t ，则4250225s n n t n +ì=ïïí+ï=ïî，解得3545s n t n ì=ïïíï=ïî，即134(,)55N n n ，将点134(,)55N n n 代入223y x x =--得：2334()55235n n n -´-=，整理得：2507509n n --=，解得n =或n =则点N的坐标为或．【点睛】本题考查了二次函数与一次函数的综合、全等三角形的性质、正切三角函数等知识点，熟练掌握待定系数法和二次函数的性质是解题关键．2.二次函数2()40y ax bx a =++¹的图象经过点(4,0)A -，(1,0)B ，与y 轴交于点C ，点P 为第二象限内抛物线上一点，连接BP 、AC ，交于点Q ，过点P 作PD x ^轴于点D ．（1）求二次函数的表达式；（2）连接BC ，当2DPB BCO Ð=Ð时，求直线BP的表达式；（3）请判断：PQ QB是否有最大值，如有请求出有最大值时点P 的坐标，如没有请说明理由．【答案】（1）234y x x =--+；（2）151588y x =-+；（3）PQ QB 有最大值为45，P 点坐标为()2,6-【分析】（1）将(4,0)A -，(1,0)B 代入2()40y ax bx a =++¹中，列出关于a 、b 的二元一次方程组，求出a 、b 的值即可；（2）设BP 与y 轴交于点E ，根据//PD y 轴可知，DPB OEB Ð=Ð，当2DPB BCO Ð=Ð，即2OEB BCO Ð=Ð，由此推断OEB V 为等腰三角形，设OE a =，则4CE a =-，所以4BE a =-，由勾股定理得222BE OE OB =+，解出点E 的坐标，用待定系数法确定出BP 的函数解析式即可；（3）设PD 与AC 交于点N ，过B 作y 轴的平行线与AC 相交于点M ．由A 、C 两点坐标可得AC 所在直线表达式，求得 M 点坐标，则5BM =，由//BM PN ，可得PNQ BMQ △∽△，5PQ PN PN QB BM ==，设20000(,34)(40)P a a a a --+-<<，则00(,4)N a a +22200000034(4)4(2)4555a a a a a a PQ QB --+-+---++===，根据二次函数性质求解即可．【详解】解：（1）由题意可得：2(4)(4)40+40a b a b ì×-+×-+=í+=î解得：13a b =-ìí=-î，∴二次函数的表达式为234y x x =--+；（2）设BP 与y 轴交于点E ，∵//PD y 轴，DPB OEB Ð=Ð∴，2DPB BCO Ð=Ð∵，2OEB BCO Ð=Ð∴，ECB EBC \Ð=Ð，BE CE \=，设OE a =，则4CE a =-，4BE a =-∴，在Rt BOE V 中，由勾股定理得222BE OE OB =+，222(4)1a a -=+∴解得158a =，150,8E æöç÷èø∴，设BE 所在直线表达式为(0)y kx e k =+¹150,81+0.k e k e ì×+=ï\íï×=î解得15,815.8k e ì=-ïïíï=ïî∴直线BP 的表达式为151588y x =-+．（3）设PD 与AC 交于点N ．过B 作y 轴的平行线与AC 相交于点M．由A 、C 两点坐标分别为(4,0)-，(0,4)可得AC 所在直线表达式为4y x =+∴M 点坐标为(1,5)，5BM =由//BM PN ，可得PNQ BMQ △∽△，5PQ PN PN QB BM ==∴设20000(,34)(40)P a a a a --+-<<，则00(,4)N a a +22200000034(4)4(2)4555a a a a a a PQ QB --+-+---++===∴，∴当02a =-时，PQ QB有最大值0.8，此时P 点坐标为()2,6-．【点睛】本题主要考查二次函数以及一次函数解析式的确定，函数图像的性质，相似三角形，勾股定理等知识点，熟练运用待定系数法求函数解析式是解题关键，本题综合性强，涉及知识面广，难度较大，属于中考压轴题．3.如图，抛物线()223(69)y mx m x m =++-+与x 轴交于点A 、B ，与y 轴交于点C ，已知(3,0)B ．（1）求m 的值和直线BC 对应的函数表达式；（2）P 为抛物线上一点，若PBC ABC S S =△△，请直接写出点P 的坐标；（3）Q 为抛物线上一点，若45ACQ Ð=°，求点Q 的坐标．【答案】（1）1m =-，3y x =-；（2）()2,1P ，P ，P ；（3）75,24æö-ç÷èøQ 【分析】（1）求出A ，B 的坐标，用待定系数法计算即可；（2）做点A 关于BC 的平行线1AP ，联立直线1AP 与抛物线的表达式可求出1P 的坐标，设出直线1AP 与y 轴的交点为G ，将直线BC 向下平移，平移的距离为GC 的长度，可得到直线23P P ，联立方程组即可求出P ；（3）取点Q ，连接CQ ，过点A 作AD CQ ^于点D ，过点D 作DF x ^轴于点F ，过点C 作CE DF ^于点E ，得直线CD 对应的表达式为132y x =-，即可求出结果；【详解】（1）将()3,0B 代入()()22369=++-+y mx m x m ，化简得20m m +=，则0m =（舍）或1m =-，∴1m =-，得：243y x x =-+-，则()0,3C -．设直线BC 对应的函数表达式为y kx b =+，将()3,0B 、()0,3C -代入可得033k b b =+ìí-=î，解得1k =，则直线BC 对应的函数表达式为3y x =-．（2）如图，过点A 作1AP ∥BC ，设直线1AP 与y 轴的交点为G ，将直线BC 向下平移 GC 个单位，得到直线23P P ，由（1）得直线BC 的解析式为3y x =-，()1,0A ，∴直线AG 的表达式为1y x =-，联立2143y x y x x =-ìí=-+-î，解得：10x y =ìí=î（舍），或21x y =ìí=î，∴()12,1P ，由直线AG 的表达式可得()1,0G -，∴2GC =，2CH =，∴直线23P P 的表达式为5y x =-，联立2543y x y x x =-ìí=-+-î，解得：11x y ìïïíï=ï，22xy ìïïíï=ïî，∴3P ，2P ，∴()2,1P ，P ，P ．（3）如图，取点Q ，连接CQ ，过点A 作AD CQ ^于点D ，过点D 作DF x ^轴于点F ，过点C 作CE DF ^于点E ，∵45ACQ Ð=°，∴AD=CD ，又∵90ADC Ð=°，∴90ADF CDE Ð+Ð=°，∵90CDE DCE Ð+Ð=°，∴DCE ADF Ð=Ð，又∵90E AFD Ð=Ð=°，∴CDE DAF D D ≌，则AF DE =，CE DF =．设==DE AF a ，∵1OA =，OF CE =，∴1CE DF a ==+．由3OC =，则3=-DF a ，即13+=-a a ，解之得，1a =．所以()2,2D -，又()0,3C -，可得直线CD 对应的表达式为132y x =-，设1,32Q m m æö-ç÷èø，代入243y x x =-+-，得213432-=-+-m m m ，2142=-+m m m ，2702-=m m ，又0m ¹，则72m =．所以75,24æö-ç÷èøQ ．【点睛】本题主要考查了二次函数综合题，结合一元二次方程求解是解题的关键．4.如图，抛物线(1)()y x x a =+-（其中1a >）与x 轴交于A 、B 两点，交y 轴于点C ．（1）直接写出OCA Ð的度数和线段AB 的长（用a 表示）；（2）若点D 为ABC V 的外心，且BCD △与ACO △:4，求此抛物线的解析式；（3）在（2）的前提下，试探究抛物线(1)()y x x a =+-上是否存在一点P ，使得CAP DBA Ð=Ð若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）∠OCA=45°，AB= a +1；（2）2y x x 2=--；（3）存在，P 1（12-，54-），P 2（1，-2）．【分析】（1）根据二次函数解析式可得A （a ，0），C （0，-a ），B （-1，0），即可得出OA=OB=a ，OB=1，即可证明△OCA 是等腰直角三角形，可得∠OCA=45°，根据线段的和差关系可表示AB 的长；（2）如图，作△ABC 的外接圆⊙D ，根据等腰直角三角形的性质可得，利用两点间距离公式可用a 表示出BC 的长，根据圆周角定理可得∠D=2∠OAC=90°，可得△DBC 是等腰直角三角形，即可证明△DBC ∽△OCA ，根据相似三角形周长之比等于相似比列方程求出a 值即可得答案；（3）如图，过点D 作DH ⊥AB 于H ，过点C 作AC 的垂线，交x 轴于F ，过点O 作OG ⊥AC 于G ，连接AP 交CF 于E ，可得△OCF 是等腰直角三角形，利用待定系数法可得直线CF 的解析式，根据外心的定义及等腰直角三角形的性质可求出点D 坐标，即可得出BH 、DH 的长，根据CAP DBA Ð=Ð，∠BHD=∠ACE=90°可证明△BHD ∽△ACE ，根据相似三角形的性质可求出CE 的长，根据两点间距离公式可得点E 坐标，利用待定系数法可得直线AE 解析式，联立直线AE 与抛物线的解析式求出点P 坐标即可得答案．【详解】（1）∵抛物线(1)()y x x a =+-（其中1a >）与x 轴交于A 、B 两点，交y 轴于点C ．∴当x=0时，y=-a ，当y=0时，(1)()0x x a +-=，解得：11x =-，2x a =，∴A （a ，0），C （0，-a ），B （-1，0），∴OB=1，OA=OC=a ，∴△OCA 是等腰直角三角形，∴∠OCA=45°，AB=OA+OB=a+1．（2）如图，作△ABC 的外接圆⊙D ，∵点D 为ABC V 的外心，∴DB=DC ，∵△OCA 是等腰直角三角形，OA=a ，∴∠OAC=45°，，∵∠BDC 和∠BAC 是 BC所对的圆心角和圆周角，∴∠BDC=2∠BAC=90°，∴∠DBC=45°，∴∠DBC=∠OAC ，∴△DBC ∽△OCA ，∵BCD △与ACO △:4，∴BC AC ==，解得：2a =±，经检验：2a =±是原方程的根，∵1a >,∴a=2，∴抛物线解析式为：(1)(2)y x x =+-=22x x --．（3）如图，过点D 作DH ⊥AB 于H ，过点C 作AC 的垂线，交x 轴于F ，过点O 作OG ⊥AC 于G ，连接AP 交CF 于E ，∵a=2，∴C （0，-2），A （2，0），AC=，∵∠OCA=45°，∴∠OCF=45°，∴△OCF 是等腰直角三角形，∴F （-2，0），设直线CF 的解析式为y=kx+b ，∴202k b b -+=ìí=-î，解得：12k b =-ìí=-î，∴直线CF 的解析式为2y x =--，∵△OCA 是等腰直角三角形，OG ⊥AC ，∴OG 所在直线为AC 的垂直平分线，点G 为AC 中点，∵点D 为ABC V 的外心，∴点D 在直线OG 上，∵A （2，0），C （0，-2），∴G （1，-1），设直线OG 的解析式y=mx ，∴m=-1，∴直线OG 的解析式y=-x ，∵点D 为△ABC 的外心，∴点D 在AB 的垂直平分线上，∴点D 的横坐标为122-+=12，把x=12代入y=-x 得y=-12，∴D （12，-12），∴DH=12，BH=1+12=32，∵CAP DBA Ð=Ð，∠BHD=∠ACE=90°，∴△BHD ∽△ACE ，∴DH BHCE AC=，即12CE =解得：CE =，∵点E 在直线CF 上，∴设点E 坐标为（n ，-n-2），∴，解得：23n =±，∴1E （23-，43-），2E （23，83-），设直线AE 1的解析式为y=k 1x+b 1，∴1111243320k b k b ì-+=-ïíï+=î，解得：11121k b ì=ïíï=-î，∴直线AE 1的解析式为112y x =-，同理：直线AE 2的解析式为24y x =-，联立直线AE 1解析式与抛物线解析式得21122y x y x x ì=-ïíï=--î，解得：111254x y ì=-ïïíï=-ïî，1220x y =ìí=î（与点A 重合，舍去），∴P 1（12-，54-），联立直线AE 2解析式与抛物线解析式得2242y x y x x =-ìí=--î，解得：1112x y =ìí=-î，2220x y =ìí=î（与点A 重合，舍去），∴P 2（1，-2）．综上所述：存在点P ，使得CAP DBA Ð=Ð，点P 坐标为P 1（12-，54-），P 2（1，-2）．【点睛】本题考查二次函数的综合，考查了二次函数的性质、待定系数法求一次函数解析式、圆周角定理、等腰三角形的性质、相似三角形的判定与性质，熟练掌握相关性质及定理是解题关键5.已知二次函数图象过点A （﹣2，0），B （4，0），C （0，4）．（1）求二次函数的解析式．（2）如图，当点P 为AC 的中点时，在线段PB 上是否存在点M ，使得∠BMC ＝90°？若存在，求出点M 的坐标；若不存在，请说明理由．（3）点K 在抛物线上，点D 为AB 的中点，直线KD 与直线BC 的夹角为锐角θ，且tan θ=53，求点K 的坐标．【分析】（1）设二次函数的解析式为y ＝a （x+2）（x ﹣4），将点C 坐标代入可求解；（2）利用中点坐标公式可求P （﹣1，2），点Q （2，2），由勾股定理可求BC 的长，由待定系数法可求PB 解析式，设点M （c ，―25c +85），由两点距离公式可得（c ﹣2）2+（―25c +85―2）2＝8，可求c ＝4或―2429，即可求解；（3）过点D 作DE ⊥BC 于点E ，设直线DK 与BC 交于点N ，先求出DE ＝BE=角三角函数可求NE =DEtanθDK 与射线EC 交于点N （m ，4﹣m ）和DK 与射线EB 交于N （m ，4﹣m ）两种情况讨论，求出直线DK 解析式，联立方程组可求点K 坐标．【解析】（1）∵二次函数图象过点B （4，0），点A （﹣2，0），∴设二次函数的解析式为y ＝a （x+2）（x ﹣4），∵二次函数图象过点C （0，4），∴4＝a （0+2）（0﹣4），∴a =―12，∴二次函数的解析式为y =―12（x+2）（x ﹣4）=―12x 2+x+4；（2）存在，理由如下：如图1，取BC 中点Q ，连接MQ ，∵点A （﹣2，0），B （4，0），C （0，4），点P 是AC 中点，点Q 是BC 中点，∴P （﹣1，2），点Q （2，2），BC =设直线BP 解析式为：y ＝kx+b ，由题意可得：2=―k +b 0=4k +b ，解得：k =―25b =85∴直线BP 的解析式为：y =―25x +85，∵∠BMC ＝90°∴点M 在以BC 为直径的圆上，∴设点M （c ，―25c +85），∵点Q 是Rt △BCM 的中点，∴MQ =12BC ＝∴MQ 2＝8，∴（c ﹣2）2+（―25c +85―2）2＝8，∴c ＝4或―2429，当c ＝4时，点B ，点M 重合，即c ＝4，不合题意舍去，∴c =―2429，则点M 坐标（―2429，5629），故线段PB 上存在点M （―2429，5629），使得∠BMC ＝90°；（3）如图2，过点D 作DE ⊥BC 于点E ，设直线DK 与BC 交于点N ，∵点A （﹣2，0），B （4，0），C （0，4），点D 是AB 中点，∴点D （1，0），OB ＝OC ＝4，AB ＝6，BD ＝3，∴∠OBC ＝45°，∵DE ⊥BC ，∴∠EDB ＝∠EBD ＝45°，∴DE ＝BE∵点B （4，0），C （0，4），∴直线BC 解析式为：y ＝﹣x+4，设点E （n ，﹣n+4），∴﹣n+4=32，∴n =52，∴点E （52，32），在Rt △DNE 中，NE =DEtanθ253=①若DK 与射线EC 交于点N （m ，4﹣m ），∵NE ＝BN ﹣BE ，4﹣m ）―∴m =85，∴点N （85，125），∴直线DK 解析式为：y ＝4x ﹣4，联立方程组可得：y =4x ―4y =―12x 2+x +4，解得：x 1=2y 1=4或x 2=―8y 2=―36，∴点K 坐标为（2，4）或（﹣8，﹣36）；②若DK 与射线EB 交于N （m ，4﹣m ），∵NE ＝BE ﹣BN ，―4﹣m ），∴m =175，∴点N （175，35），∴直线DK 解析式为：y =14x ―14，联立方程组可得：y =14x ―14y =―12x 2+x +4，解得：x 3=y 3=x 4=y 4=∴点K ，综上所述：点K 的坐标为（2，4）或（﹣8，﹣3616）．6.如图，在平面直角坐标系xOy 中，直线y ＝kx+3分别交x 轴、y 轴于A ，B 两点，经过A ，B 两点的抛物线y ＝﹣x 2+bx+c 与x 轴的正半轴相交于点C （1，0）．（1）求抛物线的解析式；（2）若P 为线段AB 上一点，∠APO ＝∠ACB ，求AP 的长；（3）在（2）的条件下，设M 是y 轴上一点，试问：抛物线上是否存在点N ，使得以A ，P ，M ，N 为顶点的四边形为平行四边形？若存在，求出点N 的坐标；若不存在，请说明理由．【分析】（1）利用待定系数法解决问题即可．（2）求出AB，OA，AC，利用相似三角形的性质求解即可．（3）分两种情形：①PA为平行四边形的边时，点M的横坐标可以为±2，求出点M的坐标即可解决问题．②当AP为平行四边形的对角线时，点M″的横坐标为﹣4，求出点M″的坐标即可解决问题．【解析】（1）由题意抛物线经过B（0，3），C（1，0），∴c=3―1+b+c=0，解得b=―2 c=3，∴抛物线的解析式为y＝﹣x2﹣2x+3（2）对于抛物线y＝﹣x2﹣2x+3，令y＝0，解得x＝﹣3或1，∴A（﹣3，0），∵B（0，3），C（1，0），∴OA＝OB＝3OC＝1，AB＝∵∠APO＝∠ACB，∠PAO＝∠CAB，∴△PAO∽△CAB，∴APAC =AOAB，∴AP4∴AP＝（3）由（2）可知，P（﹣1，2），AP＝①当AP为平行四边形的边时，点N的横坐标为2或﹣2，∴N（﹣2，3），N′（2，﹣5），②当AP为平行四边形的对角线时，点N″的横坐标为﹣4，∴N″（﹣4，﹣5），综上所述，满足条件的点N的坐标为（﹣2，3）或（2，﹣5）或（﹣4，﹣5）．。

简案(18)二次函数中角度关系与坐标专题专题

年级九科目数学班型一对一学生姓名第次课课题名称二次函数与角度问题授课老师授课时间2018年3月22日15:00——17:00教学目标掌握二次函数中与角度有关问题常见的思路和方法；教学重点在抛物线上找点，满足特殊角的方法与解题思路教学难点在抛物线上找点，满足特殊角的方法与解题思路教学过程：一、知识点睛：解决“二次函数中存在性问题”的基本步骤：①画图分析．研究确定图形，先画图解决其中一种情形．②分类讨论.先验证①的结果是否合理，再找其他分类，类比第一种情形求解．③验证取舍.结合点的运动范围，画图或推理，对结果取舍．二、典型例题1.如图，抛物线y=-x2+bx+c经过A、B、C三点，且3OA=OB=OC(1)求此二次函数解析式.(2)D为抛物线y=-x2+bx+c上一点，连接DC、AC，使DCB ACO∠=∠，求D点的坐标.(3)E为抛物线y=-x2+bx+c上一点，且直线CE与直线AC相交所成锐角为450，求E点坐标.(4)F 为抛物线y=-x 2+bx+c 上一点，连接AF 、AC 使FAB ACO ∠=∠，求F 点坐标.(5)G 为抛物线y=-x 2+bx+c 上一点，连接AG 、AC 、BC 使GAC ABC ∠=∠，求G 点坐标.2.如图，二次函数y=-21x 2+bx+c 经过点C （0,3）且对称轴x=21， (1)求此二次函数解析式.(2)M 为抛物线y=-21x 2+bx+c 上一点，直线BM 交y 轴一点K ，连接AK ，当∠AKB=450时，求M 点坐标.(3)N 为抛物线y=-21x 2+bx+c 上一点，直线BN 交y 轴一点G ，连接AG ，当∠AGB=1350时，求N 点坐标.三、练习：1.如图所示，已知直线l:y kx m =+与x 轴、y 轴分别交于A 、C 两点，抛物线C ：2y x bx c =-++经过A 、C 两点，点B 是抛物线与x 轴的另一个交点，当12x =-时，y 取最大值254.（1）求抛物线和直线的解析式；（2）设点E 是x 轴上一点，若∠DCE=90°，求点E 的坐标；（3）若点F 是AC 上的动点，当∠AFB=90°，求点F 的坐标；（4）设直线l 1：y=21x+t 与抛物线C 相交于M 、N 两点，是否存在t ，使得∠MCN=90°，若存在，求t 的值，ACO Bxy若不存在，说明理由；（5）设点G 在x 轴上，且∠GCB=∠GBC,求点G 的坐标；（6）在抛物线上是否存在一点H ，使得∠HAC=∠HCA ，若存在，求点H 的坐标，若不存在，说明理由；（7）在抛物线上是否存在一点P ，使得∠PCA=∠BAC ，若存在，求点P 的坐标，若不存在，说明理由；（8）设直线y=-ax+3与直线AC 的交点为P （不与C 重合），与y 轴的交点为H ，若∠HPC=∠OCA ，求点P 的坐标及a 的值.四、课堂达标检测：1.如图，抛物线432++-=x x y 与x 轴交于A 、B 两点，与y 轴交于点C ，点D(3，4)在抛物线上，连接BD ，点P 为抛物线上一点，且∠DBP =45°，求点P 的坐标．2.抛物线322++-=x x y 与并轴分别交于A 、B 两点，与y 轴的正半轴交于C 点，抛物线的顶点为D ，连接BC 、BD ，抛物线上是否存在一点P ，使得∠PCB=∠CBD ，若存在，求P 点的坐标，不存在，说明理由，3.若抛物线24y x x =+-的顶点为B ，与轴正半轴交于A 点，在抛物线对称轴右侧一点P ，使tan 13PBA ∠=，求P 点的坐标；4．抛物线342+-=x x y ，交x 轴于M 、N 点（M 点N 点左边），交y 轴于D 点，点E 为第一象限抛物线上的点，若∠EMN =2∠ODM，求E 点坐标．5．如图，抛物线342+-=x x y 交x 轴于A(l ，O)、B 两点，交，，轴于C(0，3)；抛物线上是否存在点P ，使∠PCB+ ∠ACB= 45°?若存在，求出P点坐标；若不存在，请说明理由；五、课堂小结与收获：角度存在性的处理思路1.和角度相关的存在性问题通常要放在直角三角形中处理，通过三角函数将角的特征转化为边的比例特征来列方程求解．一般过定点构造直角三角形．2.当两个角相等时，常转化为两个直角三角形相似的问题来处理六、作业布置（另附）：课后反思检查人：日期：家庭作业（要求：字迹清楚、过程规范）学生姓名1．抛物线y=ax 2+bx-4a 经过A （1，0）、C （0，4）两点，与x 轴交于另一点B ．（1）求抛物线的解析式；（2）已知点D （m ，1-m ）在第二象限的抛物线上，求点D 关于直线BC 的对称点的坐标；（3）在（2）的条件下，连接BD ，点P 为抛物线上一点，且∠DBP=45°，求出点P 的坐标．【探索1】如图，在平面直角坐标系XOY 中，点P 为抛物线2y x =上一动点，是否存在点P ，使POX ∠为45°，若存在，请求出点P 的坐标；不存在，说明理由。

二次函数专题三：角度问题-含答案

二次函数与几何图形综合题角度问题1.如图，在平面直角坐标系xOy 中，二次函数y ＝ax 2＋bx －3(a ，b 是常数)的图象与x 轴交于点A(－3，0)和点B (1，0)，与y 轴交于点C.动直线y ＝t (t 为常数)与抛物线交于不同的两点P 、Q.(1)求a 和b 的值及t 的取值范围； (2)若∠PCQ ＝90°，求t 的值．1. 解：(1)将点A 、点B 的坐标代入y ＝ax 2＋bx －3中可得：⎩⎨⎧=+=03-03-3-9b a b a ，解得⎩⎨⎧==21b a ；∴抛物线的解析式为y ＝x 2＋2x －3 动直线y ＝t ，联立两个解析可得：x 2＋2x －3＝t ，即x 2＋2x －(3＋t )＝0.∵动直线y ＝t (t 为常数)与抛物线交于不同的两点，∴b 2－4ac ＝4＋4(3＋t )＞0，解得t ＞－4；(3)∵y ＝x 2＋2x －3＝(x ＋1)2－4， ∴抛物线的对称轴为直线x ＝－1. 当x ＝0时，y ＝－3，∴C(0，－3)．设点Q 的坐标为(m ，t )，则P (－2－m ，t)．如解图，设PQ 与y 轴交于点D ，则CD ＝t ＋3，DQ ＝m ，DP ＝m ＋2.∵∠PCQ ＝∠PCD ＋∠QCD ＝90°，∠DPC ＋∠PCD ＝90°， ∴∠QCD ＝∠DPC ，又∠PDC ＝∠QDC ＝90°，∴△QCD ∽△CPD ，∴DQ DC ＝DC PD，即3+t m ＝23++m t ，整理得：t 2＋6t ＋9＝m 2＋2m ， ∵Q (m ，t )在抛物线上，∴t ＝m 2＋2m －3，∴m 2＋2m ＝t ＋3，∴t 2＋6t ＋9＝t ＋3，化简得：t 2＋5t ＋6＝0，解得t ＝－2或t ＝－3，当t ＝－3时，动直线y ＝t 经过点C ，故不合题意，舍去．∴t ＝－2.2. 如图①，若二次函数y ＝36x 2＋bx ＋c 的图象与x 轴交于A(－2，0)、B(3，0)两点，点A 关于正比例函数y ＝3x 的图象的对称点为C. (1)求b 、c 的值；(2)证明：点C 在所求的二次函数的图象上；(3)如图②，过点B 作DB ⊥x 轴交正比例函数y ＝3x 的图象于点D ，连接AC ，交正比例函数y ＝3x 的图象于点E ，连接AD 、CD ，如果动点P 从点A 沿线段AD 方向以每秒2个单位的速度向点D 运动，同时动点Q 从点D 沿线段DC 方向以每秒1个单位的速度向点C 运动，当其中一个点到达终点时，另一个点随之停止运动，连接PQ 、QE 、PE ，设运动时间为t 秒，是否存在某一时刻，使PE 平分∠APQ ，同时QE 平分∠PQC ，若存在，求出t 的值；若不存在，请说明理由．3. (1)解：∵点A (－2，0)，B (3，0)在抛物线y ＝36x 2＋bx ＋c 上， ∴将A ，B 两点代入抛物线解析式得：⎩⎨⎧36×4－2b ＋c ＝036×9＋3b ＋c ＝0，解得：b ＝－36，c ＝－3；(2)证明：设点F 在直线y ＝3x 上，且F (2，23)．如解图①所示，过点F 作FH ⊥x 轴于点H ，则FH ＝23，OH ＝2， ∴tan ∠FOB ＝FHOH＝3，∴∠FOB ＝60°，∴∠AOE ＝∠F O B ＝60°，连接OC ，过点C 作CK ⊥x 轴于点K ，∵点A 、C 关于直线y ＝3x 对称， ∴OC ＝OA ＝2，∠COE ＝∠AOE ＝60°∴∠COK ＝180°－∠AOE －∠COE ＝60°，在Rt △COK 中，CK ＝OC ·sin60°＝2×32＝3，OK ＝OC ·cos60°＝2×12＝1，∴C(1，－3)，又由(1)得抛物线解析式为：y ＝36x 2－36x －3，当x ＝1时，y ＝－ 3.∴点C 在所求二次函数的图象上．(3)解：假设存在．如解图①所示，在Rt △ACK 中，由勾股定理得：AC ＝AK 2＋CK 2＝32＋（3）2＝2 3. 如解图②所示，∵OB ＝3， ∴BD ＝33，AB ＝OA ＋OB ＝5.在Rt △ABD 中，由勾股定理得：AD ＝AB 2＋BD 2＝52＋（33）2＝213.∵A 、C 关于直线y ＝3x 对称，∴C D ＝AD ＝213，∠DAC ＝∠DCA ，AE ＝CE ＝12AC ＝ 3.连接PQ 、PE 、QE ，则∠APE ＝∠QPE ，∠PQE ＝∠CQE .在四边形APQC 中，∠DAC ＋∠APQ ＋∠PQC ＋∠DCA ＝360°(四边形内角和等于360°)，即2∠DAC ＋2∠APE ＋2∠CQE ＝360°，∴∠DAC ＋∠A P E ＋∠CQE ＝180°. 又∵∠DAC ＋∠APE ＋∠AEP ＝180°(三角形内角和定理)，∴∠AEP ＝∠CQE . 在△APE 与△CEQ 中，∵∠DAC ＝∠DCA ，∠AEP ＝∠C Q E ，∴△APE ∽△CEQ ，∴CQ AE ＝CE AP，即213－t 3＝32t ，整理得：2t 2－413t ＋3＝0，解得：t ＝213－462或213＋462(t ＜13，舍去)∴存在某一时刻，使PE 平分∠APQ ，同时，QE 平分∠PQC ，此时t ＝213－462.3.如图，在平面直角坐标系中，直线y ＝12x ＋2与x 轴交于点A ，与y 轴交于点C ，抛物线y ＝－12x 2＋bx ＋c 经过A 、C 两点，与x 轴的另一交点为点B .(1)求抛物线的函数表达式；(2)点D 为直线AC 上方抛物线上一动点．①连接BC 、CD ，设直线BD 交线段AC 于点E ，△CDE 的面积为S 1，△BCE 的面积为S 2，求S 1S 2的最大值； ②过点D 作DF ⊥AC ，垂足为点F ，连接CD ，是否存在点D ，使得△CDF 中的某个角恰好等于∠BAC 的2倍？若存在，求点D 的横坐标；若不存在，请说明理由．备用图3 解：(1)据题意得，A (－4，0)，C(0，2)，∵y ＝－12x 2＋bx ＋c 过A 、C 两点，∴⎪⎩⎪⎨⎧=+⨯=cc b 24-1621-0，∴⎪⎩⎪⎨⎧==223-c b ， ∴y ＝－12x 2－32x ＋2；(2)①如解图①，令y ＝0，∴－12x 2－32x ＋2＝0，解得x 1＝－4，x 2＝1，∴B (1，0)，过D 作DM ⊥x 轴交AC 于M ，过B 作BN ⊥x 轴交AC 延长线于N ，∴DM ∥BN ， ∴△DME ∽△BNE ，∴DE BE ＝DMBN，∴设点C 到BD 的距离为h ，则S 1S 2＝h BE h DE ·21·21＝DE BE ＝DM BN，令D (a ，－12a 2－32a ＋2)，∴M (a ，12a ＋2)，∵B (1，0)，∴N(1，52)，∴DM ＝(－12a 2－32a ＋2)－(12a ＋2)＝－12a 2－2a ，BN ＝52，∴S 1S 2＝DM BN ＝252-21-2aa ＝－15(a ＋2)2＋45，∴当a ＝－2时，S 1S 2取最大值为45； ②存在．D 的横坐标为－2或－2911；如解图②，∵A(－4，0)，B (1，0)，C (0，2)， ∴AC ＝25，BC ＝5，AB ＝5， ∴AC 2＋BC 2＝AB 2，∴△A B C 是以∠ACB 为直角的直角三角形，取AB 的中点P ，∴P (－32，0)，∴P A ＝PC ＝PB ＝52，∴∠CPO ＝2∠BAC ，∴tan ∠CPO ＝tan(2∠BAC )＝43；(ⅰ)当∠DCF ＝2∠BAC 时，如解图③，过D 作x 轴的平行线交y 轴于点R ，交AC 的延长线于点G ，则∠DGF ＝∠BAC ，∵∠DCF ＝∠G ＋∠CDG ， ∴∠CDG ＝∠G ＝∠BAC ，∴tan ∠CDG ＝tan ∠BAC ＝12，即RC DR ＝12，令D (n ，－12n 2－32n ＋2)，∴DR ＝－n ，RC ＝－12n 2－32n ，∴nnn -23-21-2＝12， ∴n 1＝0(舍去)，n 2＝－2，∴x D ＝－2. (ⅱ)当∠CDF ＝2∠BAC 时，∴tan ∠FDC ＝43，令FC ＝4k ，∴DF ＝3k ，DC ＝5k ，tan ∠DGC ＝3k FG ＝12，∴FG ＝6k ，∴CG ＝2k ，DG ＝35k ，∴RC ＝255k ，RG ＝455k ， DR ＝35k －455k ＝1155k ，∴DRRC ＝kk5525511＝n n n 23-21--2，∴n 1＝0(舍去)，n 2＝－2911，∴x D ＝－2911，综上所述，D 的横坐标为－2或－2911.4.在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A B ，两点（点A 在点B 的左侧），与y 轴交于点C ，点B 的坐标为(30)，，将直线y kx =沿y 轴向上平移3个单位长度后恰好经过B C ，两点．（1）求直线BC 及抛物线的解析式；（2）设抛物线的顶点为D ，点P 在抛物线的对称轴上，且APD ACB ∠=∠，求点P 的坐标；（3）连结CD ，求OCA ∠与OCD ∠两角和的度数． 24．解：（1）y kx =沿y 轴向上平移3个单位长度后经过y 轴上的点C ，(03)C ∴，．设直线BC 的解析式为3y kx =+．(30)B ，在直线BC 上，330k ∴+=．解得1k =-∴直线BC 的解析式为3y x =-+．抛物线2y x bx c =++过点B C ，，9303b c c ++=⎧∴⎨=⎩，．解得43b c =-⎧⎨=⎩，． ∴抛物线的解析式为243y x x =-+．（2）由243y x x =-+．可得(21)(10)D A -，，，．3OB ∴=，3OC =，1OA =，2AB =．可得OBC △是等腰直角三角形．45OBC ∴∠=，如图1，设抛物线对称轴与x 轴交于点F ，12AF ∴=过点A 作AE BC ⊥于点E ．90AEB ∴∠=．可得BE AE ==CE =在AEC △与AFP △中，90AEC AFP ∠=∠=，∠AEC AFP ∴△∽△．xAE CEAF PF∴=，1PF =．解得2PF =．点P 在抛物线的对称轴上，∴点P 的坐标为(22)，或(22)-，．（3）解法一：如图2，作点(10)A ，关于y 轴的对称点A '，则(10)A '-，．连结A C A D ''，，可得A C AC '==OCA OCA '∠=∠．由勾股定理可得220CD =，210A D '=．又210A C '=，222A D A C CD ''∴+=．A DC '∴△是等腰直角三角形，90CA D '∠=，45DCA '∴∠=．45OCA OCD '∴∠+∠=． 45OCA OCD ∴∠+∠=．即OCA ∠与OCD ∠两角和的度数为45．解法二：如图3，连结BD．同解法一可得CD =AC = 在Rt DBF △中，90DFB ∠=，1BF DF ==，DB ∴==在CBD △和COA △中，1DB AO ==3BC OC ==CD CA == DB BC CDAO OC CA∴==．CBD COA ∴△∽△．BCD OCA ∴∠=∠． 45OCB ∠=，45OCA OCD ∴∠+∠=．即OCA ∠与OCD ∠两角和的度数为45．x图35.已知抛物线y=x2﹣2x+c与x轴交于A．B两点，与y轴交于C点，抛物线的顶点为D点，点A的坐标为（﹣1，0）．（1）求D点的坐标；（2）如图1，连接AC，BD并延长交于点E，求∠E的度数；（3）如图2，已知点P（﹣4，0），点Q在x轴下方的抛物线上，直线PQ交线段AC于点M，当∠PMA=∠E时，求点Q的坐标．，又∵∴即：∴解得：xmm∴﹣）或（﹣，﹣）6.如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点．（1）求这条抛物线的解析式；（2）E为抛物线上一动点，是否存在点E使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；（3）若将直线BC平移，使其经过点A，且与抛物线相交于点D，连接BD，试求出∠BDA的度数．解：（1）∵该抛物线过点C（0，2），∴可设该抛物线的解析式为y=ax2+bx+2．将A（﹣1，0），B（4，0）代入，得，解得，∴抛物线的解析式为：y=﹣x2+x+2．（2）存在．由图象可知，以A、B为直角顶点的△ABE不存在，所以△ABE只可能是以点E为直角顶点的三角形．在Rt△BOC中，OC=2，OB=4，∴BC==．在Rt△BOC中，设BC边上的高为h，则×h=×2×4，∴h=．∵△BEA∽△COB，设E点坐标为（x，y），∴=，∴y=±2将y=2代入抛物线y=﹣x2+x+2，得x1=0，x2=3．当y=﹣2时，不合题意舍去．∴E点坐标为（0，2），（3，2）．（3）如图2，连结AC，作DE⊥x轴于点E，作BF⊥AD于点F，∴∠BED=∠BFD=∠AFB=90°．设BC的解析式为y=kx+b，由图象，得，∴，y BC=﹣x+2．由BC∥AD，设AD的解析式为y=﹣x+n，由图象，得0=﹣×（﹣1）+n,∴n=﹣，y AD=﹣x﹣．∴﹣x2+x+2=﹣x﹣，解得：x1=﹣1，x2=5∴D（﹣1，0）与A重合，舍去，D（5，﹣3）．∵DE⊥x轴，∴DE=3，OE=5．由勾股定理，得BD=．∵A（﹣1，0），B（4，0），C（0，2），∴OA=1，OB=4，OC=2．∴AB=5在Rt△AOC中，Rt△BOC中，由勾股定理，得AC=，BC=2，∴AC2=5，BC2=20，AB2=25，∴AC2+BC2=AB2∴△ACB是直角三角形，∴∠ACB=90°．∵BC∥AD，∴∠CAF+∠ACB=180°，∴∠CAF=90°．∴∠CAF=∠ACB=∠AFB=90°，∴四边形ACBF是矩形，∴AC=BF=，在Rt△BFD中，由勾股定理，得DF=，∴DF=BF，∴∠ADB=45°．7.如图，抛物线24y ax bx a =+-经过()10A -，、()04C ，两点，与x 轴交于另一点B ． ⑴求抛物线的解析式；⑵已知点()1D m m +，在第一象限的抛物线上，求点D 关于直线BC 对称的点的坐标； ⑶在⑵的条件下，连接BD ，点P 为抛物线上一点，且45DBP ∠=︒，求点P 的坐标．解：⑴∵抛物线24y ax bx a =+-经过()10A -，， ()04C ，两点，∴4044a b a a --=⎧⎨-=⎩,解得13a b =-⎧⎨=⎩∴抛物线的解析式为234y x x =-++．⑵∵点()1D m m +，在抛物线上，∴2134m m m +=-++，即2230m m --=，∴1m =-或3m =．∵点D 在第一象限，∴点D 的坐标为()34，．由⑴知OC OB =，∴45CBA ∠=︒．设点D 关于直线BC 的对称点为点E ．∵()04C ，，∴CD AB ∥，且3CD =，∴45ECB DCB ∠=∠=︒， ∴E 点在y 轴上，且3CE CD ==．∴1OE =，∴(01E ，即点D 关于直线BC 对称的点的坐标为()01，． ⑶方法一：作PF AB ⊥于F ，DE BC ⊥于E ．由⑴有：4OB OC ==，∴45OBC ∠=︒， ∵45DBP ∠=︒，CBD PBA ∠=∠．∵()04C ，，()34D ，，∴CD O B ∥且3CD =．∴45DCE CBO∠=∠=︒，∴DE CE =∵4OB OC ==，∴BC =∴2BE BC CE =-=，∴3tan tan 5DE PBF CBD BE ∠=∠==．设3PF t =，则5BF t =，∴54OF t =-，∴()543P t t -+，． ∵P 点在抛物线上，∴()()23543544t t t =--++-++，∴0t =（舍去）或2225t =， ∴266525P ⎛⎫- ⎪⎝⎭，．方法二：过点D 作BD 的垂线交直线PB 于点Q ，过点D 作轴于H ．过Q 点作QG DH ⊥于G ．∵45PBD ∠=︒,∴QD DB =．∴90QDG BDH ∠+∠=︒，又90DQG QDG ∠+∠=︒，∴DQG BDH ∠=∠． ∴QDG DBH △≌△，∴4QG DH ==，1DG BH ==．由⑵知()34D ，，∴()13Q -，．∵()40B ，，∴直线BP 的解析式为31255y x =-+．解方程组23431255y x x y x ⎧=-++⎪⎨=-+⎪⎩得1140x y =⎧⎨=⎩，22256625x y ⎧=-⎪⎪⎨⎪=⎪⎩，点P 的坐标为266525⎛⎫- ⎪⎝⎭，．8.如图，抛物线2y x bx c =-++与直线122y x =+交于,C D 两点，其中点C 在y 轴上，点D 的坐标为732⎛⎫ ⎪⎝⎭，．点P 是y 轴右侧的抛物线上一动点，过点P 作PE x ⊥轴于点E ，交CD 于点F .⑴ 求抛物线的解析式；⑵ 若点P 的横坐标为m ，当m 为何值时，以O ，C ，P ，F 为顶点的四边形是平行四边形？请说明理由．⑶ 若存在点P ，使45PCF ∠=︒，请直接写出相应的点P 的坐标．⑴ ∵直线122y x =+经过点C ，∴()02C ，． ∵抛物线2y x bx c =-++经过点(02)C ，，732D ⎛⎫ ⎪⎝⎭，，∴227332cb c =⎧⎪⎨=-++⎪⎩∴722b c ⎧=⎪⎨⎪=⎩． ∴抛物线的解析式为2722y x x =-++ ⑵ ∵点P 的横坐标为m 且在抛物线上，∴2722P m m m ⎛⎫-++ ⎪⎝⎭，，122F m m ⎛⎫+ ⎪⎝⎭，∵PF CO ∥，∴当PF CO =时，以O ，C ，P ，F 为顶点的四边形是平行四边形． ①当3m ＜时，227122322PF m m m m m ⎛⎫=-++-+=-+ ⎪⎝⎭，∴232m m -+=，解得：11m =，22m =．即当1m =或2时，四边形OCPF 是平行四边形．②当3m ≥时，221722322PF m m m m m ⎛⎫⎛⎫=+--++=- ⎪ ⎪⎝⎭⎝⎭232m m -=，解得：1m =2m =（舍去）即当1m =时，四边形OCFP 是平行四边形． ⑶ 如图，当点P 在CD 上方且45PCF ∠=︒时，作PM CD ⊥，CN PF ⊥，则PMF CNF △∽△，∴212PM CN mMF FN m ===，∴2PM CM CF ==∴5522PF CN m ===== 又∵23PF m m =-+，∴2532m m m -+=解得：112m =，20m =（舍去），∴1722P ⎛⎫ ⎪⎝⎭，．同理可以求得：另外一点为2313618P ⎛⎫⎪⎝⎭，．。

第二章二次函数之二次函数中的角度问题专题训 2024—2025学年北师大版数学九年级下册

第二章二次函数之二次函数中的角度问题专题训北师大版2024—2025学年九年级下册一、二次函数中的45度角（一）构造等腰直角三角形求直线与曲线的交点问题1.如图，抛物线y＝﹣x2+3x+4经过A（﹣1，0）、C（0，4）两点，与x轴交于另一点B，连接AC，BC．过点C作x轴的平行线交抛物线于另一点D，连接BD，点P为抛物线上一点，且∠DBP＝45°，求点P的坐标；2.如图，抛物线y＝﹣x2+x+3，与x轴交于A（﹣2，0）、B（6，0）两点，与y轴交于点C．直线l与抛物线交于A、D两点，与y轴交于点E，点D的坐标为（4，3）．点Q是y 轴上的点，且∠ADQ＝45°，求点Q的坐标．3.如图，抛物线y＝﹣x2+3x+4与x轴交于A、B两点，与y轴交于C点，点D在抛物线上且横坐标为3．（1）求tan∠DBC的值；（2）点P为抛物线上一点，且∠DBP＝45°，求点P的坐标．（二）定弦定角4.如图，已知抛物线y＝﹣+x+4交x轴于A（﹣3，0），B（4，0）两点，交y轴于点C，点P是抛物线上一点，连接AC、BC．在抛物线的对称轴上是否存在点Q，使得∠AQC＝45°？若存在，求出点Q的坐标；若不存在，请说明理由．二、函数中的其他特殊角度问题（一）构造一线三垂直1.如图，抛物线y＝﹣x2+x+2与x轴交于点A和点B．点D的坐标D(1,2)连接BD，P为抛物线上一点，且∠DBP＝135°，求点P的坐标2.如图，抛物线y＝（x﹣）（x﹣3）与x轴交于A，B两点，与y轴交于点C，点D 是抛物线的对称轴l与x轴的交点，点P是抛物线上一点，且∠DCP＝30°，则符合题意的点P的坐标为．3.如图，已知抛物线y＝﹣x2﹣2x+3；与直线AB相交于A（﹣3，0），B（0，3）两点．设C是抛物线对称轴上的一动点，求使∠CBA＝90°的点C的坐标；（二）、函数中已知一个角的正切求点的坐标1.如图，已知抛物线y＝（x﹣1）2与y轴交于点B（0，），点C为抛物线的顶点．点A在抛物线上，且AC⊥BC，求点A的坐标．2．如图，已知点A（﹣8，0），点B（﹣5，﹣4），直线y＝2x+m过点B交y轴于点C，交x轴于点D，抛物线；经过点A、C、D，连接AB、AC．E为直线AC上方的抛物线上一点，且tan∠ECA＝，求点E的坐标；3.如图，在平面直角坐标系xOy中，直线AB与抛物线y＝x2﹣6x交于点A（6，0）和点B（1，﹣5）．直线AB的表达式y＝x﹣6；如果点C在直线AB上，且∠BOC的正切值是，求点C的坐标．三、二次函数中的角度问题（一）等腰三角形直线与抛物线交点1．如图，在平面直角坐标系中，抛物线y＝x2+2x﹣3与坐标轴的交点分别为点A（﹣3，0），B（1，0），C（0，﹣3）．D（﹣1，﹣4），连接BC，作直线CD，已知直线CD上有一动点P，满足∠PBC＝∠BCO，求点P的坐标；（也可以用角平分线分线段成比例）2.如图，抛物线经过点A（﹣2，0），点B（0，4）．P是抛物线对称轴上的点，联结AB、PB，如果∠PBO＝∠BAO，求点P的坐标；3.如图1，已知y＝的图象与x轴交于A，B两点，点P是抛物线上在第四象限的点，且tan∠BAP＝．（1）求点P的坐标；（2）抛物线的对称轴交x轴于点Q，若抛物线上存在点C，使得∠CPQ＝∠PQB，求点C的坐标；4.如图，在平面直角坐标系中，直线y＝﹣x+3交坐标轴于B，C两点，抛物线y＝﹣x2+2x+3．经过B，C两点，且交x轴于另一点A（﹣1，0）．点D为第一象限内抛物线上一动点，过点D作DQ∥CO，交BC于点P，交x轴于点Q．设点P的横坐标为m，在点D移动的过程中，存在∠DCP＝∠ACO，求出此时m的值；（利用角的正切值相等）5.如图，抛物线y＝﹣x2﹣2x+c的经过D（﹣2，3），与x轴交于A、B两点（点A在点B的左侧）、与y轴交于点C．（1）在抛物线的对称轴上有一点P，使得∠OAP＝∠BCO，求点P的坐标；（2）点M在抛物线上，点N在抛物线对称轴上．当∠ACM＝90°时，求点M的坐标；6．如图，在平面直角坐标系中，抛物线y＝x2+x﹣4．的图象与x轴交于点A（2，0）、B （﹣4，0），与y轴交于点D．在抛物线上有一点M，过点M、A的直线MA交y轴于点C，连接BC，若∠MBO＝∠BCO，请直接写出点M的坐标．（二）二次函数的倍角关系1.如图，抛物线y＝x2+2x﹣3交x轴于A、B两点，其中点A坐标为（1，0），与y轴交于点C（0，﹣3）．连接AC，点P在抛物线上，且满足∠P AB＝2∠ACO．求点P的坐标；2.如图1，抛物线y＝﹣x2+6x﹣5．交x轴于A、B两点，交y轴于点C．直线y＝x﹣5经过点B、C，连接AC，当∠AMB＝2∠ACB时，求点M的坐标（外角加对称）．3.如图，在平面直角坐标系中，直线y＝﹣x+2与x轴交于点A，与y轴交于点B，抛物线y＝﹣x2+x+2经过A，B两点且与x轴的负半轴交于点C．点D为直线AB上方抛物线上的一个动点，当∠ABD＝2∠BAC时，求点D的坐标；4.如图，抛物线；交x轴于A（﹣1，0）、B（3，0）两点，交y轴于点C，连接BC．点P是抛物线上一点，设P点的横坐标为m．请直接写出使∠PBA＝∠ABC 的点P的坐标（三）二次函数中角的和差关系1.如图1，已知抛物线y＝﹣x2﹣2x+3过点A（1，0），B（﹣3，0）．顶点C（﹣1，4），的设点D是x轴上一点，当tan（∠CAO+∠CDO）＝4时，求点D的坐标（母子模型相似）；．2.如图，在平面直角坐标系中，已知抛物线y＝x2+x﹣2与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，直线l经过A，C两点，连接BC．取点G（0，﹣1），连接AG，在第一象限内的抛物线上，是否存在点P，使∠BAP＝∠BCO﹣∠BAG？若存在，求出点P的坐标；若不存在，请说明理由．3.如图，经过点A（0，﹣4）的抛物线y＝x2﹣x﹣4．与x轴相交于B（﹣2，0），C两点，O为坐标原点．设点M在y轴上，∠OMB+∠OAB＝∠ACB，求AM的长．4.如图，抛物线y＝﹣x2+x+5．与x轴交于A、B（A左B右），与y轴交于C，直线y＝﹣x+5经过点B、C．点P为第二象限抛物线上一点，设点P横坐标为m，点P到直线BC的距离为d，求d与m的函数解析式；若∠PCB+∠POB＝180°，求d的值（四点共圆）．5.如图，抛物线y＝ax2﹣ax﹣6a与x轴交于A、B两点（A在B点左边），与y轴负半轴交于C点，OC＝2OA．E是x轴上方，抛物线上一点，若∠AEB+∠BAE＝45°，求E点纵坐标；练习：如图1，抛物线y＝x2+（m﹣3）x﹣4与y轴交于C点，与直线y＝mx交于A，B两点（点B，A分别在第一、三象限）．（1）求的值；（2）若AC⊥AB，求m的值；（3）如图2，连接AC，点P是y轴上的一定点，当m的值发生变化时，∠BPO＝∠ACO 恒成立，求定点P的坐标．。

二次函数角度存在性问题解题策略(非定弦定角类)

二次函数任意角解题策略（非定弦定角类）针对已知角的动点，求角一边与抛物线或直线的交点例1、如图，抛物线y＝x2+2x﹣3与x轴交于A（1，0），、B（﹣3，0）两点，与y轴交于点C（0，﹣3），点D是y轴左侧的抛物线上一动点，连接AC，当∠DAB＝∠ACO时，求点D的坐标．分析：D的坐标，坐标即“横平竖直”，横纵坐标比即为直角三角形，两直角边的关系。

由于∠DAB＝∠ACO ，tan∠DAB＝tan∠ACO，则很容易得到点D坐标的绝对值之比。

然后通过二次函数解析式表示D的坐标，利用比值求解。

解：过点D作x轴的垂线，交x轴于点H，如图2所示．设点D的坐标为（m，m2+2m﹣3）．∵∠DAB＝∠ACO，∴tan∠DAB＝tan∠ACO，即＝，∴总结：一般来说，角度问题都可通过正切处理解决，有定角，则该角的正切值定，可得坐标的横纵比。

此题简单在所求角的一边是确定的，刚好在X轴上，易于构造直角三角形解决问题。

倘若，角的一边不在坐标轴上，那问题又该如何处理，上述做法是否仍然可行？且看下例。

例2、如图，抛物线y＝﹣x2+x+2．与直线y＝x+2交于C、D两点，其中点C在y轴上，点D的坐标为（3，）．点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点N．若存在点P，使∠PCN＝45°，请写出相应的点P的坐标．分析：首先根据题意可大概画出图形，应有两种可能，一种是点P在CD 上方，一种是在CD下方。

点N 对解题并无影响，∠PCN即为∠PCD。

点C（0,2），若能再在PC上得一个点的坐标求出直线CP解析式，联立二次函数求交点，问题便迎刃而解。

由于45°是特殊角，可构造等腰直角三角形，在利用一线三直角模型，得全等三角形，进一步得到点的坐标。

如何构造一线三直角模型呢，关键是直角顶点的选取，首先探究当点P在CD上方的情况。

法一：如图1-1所示,易证△CEG≌△EDF（AAS），想办法求出点E的坐标，结合点C即可求直线CP.法二：如图1-2所示。

简案(18)二次函数中角度关系与坐标专题专题

二次函数角度问题解法

二次函数角度类问题(带答案)

二次函数与角度综合问题(教师版)

中考二次函数与角度有关的问题知识解读

二次函数中角度问题

二次函数与角度问题解题技巧

二次函数中角度的存在性问题

二次函数角度问题

二次函数与角的有关问题专项辅导资料

数学专题7——二次函数的角度问题

二次函数与角度问题解题技巧

初三讲义。二次函数当中的角度问题

二次函数与角度问题

题型九 二次函数综合题 类型四 二次函数与角度有关的问题(专题训练)(解析版)

简案(18)二次函数中角度关系与坐标专题专题

二次函数专题三：角度问题-含答案

第二章二次函数之二次函数中的角度问题专题训 2024—2025学年北师大版数学九年级下册

二次函数角度存在性问题解题策略(非定弦定角类)

题型九二次函数综合题类型四二次函数与角度有关的问题(专题训练)(解析版)