微积分 - 四川大学
(NEW)四川大学《690高等数学(微积分、级数)》历年考研真题汇编

6 (12分)一质量为m的物体,最初静止于x0处,在力F=-k/x2 的作用下沿直线运动,试求物体在任意位置x处的速度.
7 (13分)质量为m的摩托车,在恒定的牵引力F的作用下工作, 它所受的阻力与其速率的平方成正比,它能达到的最大速率是vm.试计 算从静止加速到vm/2所需的时间以及所走过的路程.
3 求下列不定积分(共50分): (1) (2)
(3)
(4) (5) (6) (7) (8) (9) (10)
4 用级数展开计算下列积分的近似值(计算前三项)(共20 分):
(1) (2)
5 (5分)甲乙两船同时从一码头出发,甲船以30km/h的速度向北 行驶,乙船以40km/h的速度向东行驶,求两船间距离增加的速度为多 少?
2012年四川大学690高等数学(微 积分、级数)考研真题
2013年四川大学690高等数学(微 积分、级数)考研真题
2014年四川大学690高等数学(微 积分、级数)考研真题
2015年四川大学690高等数学(微 积分、级数)考研真题
2016年四川大学690高等数学(川大学690高等数学(微 积分、级数)考研真题
1 请写出下列初等函数的级数展开式(共20分): (1)ax (2)sin(x/2) (3) (4)ln(1+x) (5)1/(1+x)
2 求下列平面图形的面积(共30分): (1)曲线y=x3与y轴和直线y=1所围成的图形; (2)曲线y=x2与y=2-x2所围成的图形.
目 录
2012年四川大学690高等数学(微积分、级数)考研真题 2013年四川大学690高等数学(微积分、级数)考研真题 2014年四川大学690高等数学(微积分、级数)考研真题 2015年四川大学690高等数学(微积分、级数)考研真题 2016年四川大学690高等数学(微积分、级数)考研真题 2017年四川大学690高等数学(微积分、级数)考研真题
2014-15(2)四川大学微积分期末试卷 解答

因为 d = 9 5 3 ,从而最短距离为 9 − 5 3 ,最长距离为 9 + 5 3 .
x x
2. 设函数 ϕ ( x ) 连续, 且满足 ϕ ( x ) = e + tϕ ( t )dt − x
x 0
∫
∫
0
ϕ ( t )dt , 求 ϕ ( x ) .
解: 等式两边对 x 求导得 再求导得微分方程 微分方程的特征方程为
2 2 2 2 2
Lx = 2 x − 2 xλ + µ = 0 (1) L = 2 y − 2 yλ + µ = 0 (2) y Lz = 2 z + λ + µ = 0 (3) z x2 + y 2 (4) = 1 (5) x + y + z =
(1)-(2)得: ( x − y )(1 − λ ) = 0 即 = λ 1或 = x y 若 λ = 1 ,带回(1)得 µ = 0 ,由(3)可得 z = − 故 y = x ,由(4) ,可得 z = 2 x ,代入(5)式
′ f= lim y (0, 0)
∆y → 0
f (0, 0 + ∆y ) − f (0, 0) 0 = lim = 0 ∆ → y 0 ∆y ∆y
假设 f ( x, y ) 在 (0, 0) 处的可微,则 = dz
f x′(0, 0)∆x + f y′(0, 0) = ∆y 0
考虑 lim
ρ →0
0 0
2
2
2
= ∫ (− y 2 + xy 3 ) dx = ∫ (−4 + 8 x)dx = (−4 x + 4 x 2 ) = 8 .
四川大学《常微分方程》课程考评方式与标准

四川大学《常微分方程》课程考评方式与标准常微分方程(Ordinary Differential Equations), 是本科数学专业的核心基础课程,授课对象为数学学院本科二年级学生。
它是学习泛函、偏微、微分几何等课程的基础,是数学在工程技术中发挥作用的拳头之一。
在工程力学、流体力学、天体力学、电路振荡分析、工业自动控制以及化学、生物、经济等领域都有广泛的应用。
通过本课程学习,不仅为后续课程打下基础,而且以穿插其中的在历史上成功利用微分方程解释实际现象的著名范例来培养学生用数学理论解决实际问题的意识和初步能力。
因此本课程的教学目的是,一方面让课程内容紧贴工程实际,使学生从生活中去体悟教学的内容,另一方面让课程内容面向学科前沿、面向科研热点、面向新时代,培养学生动手能力和初步的科研能力。
基于上述思想,我们采用“大班授课、小班研讨”的教学方式,即由主讲教师设计课程改革方案并承担大班教学工作,研究生助教负责组织小班研讨及其他辅助工作。
小班研讨围绕课程内容,就常微分方程与动力系统的学科发展中相关的问题展开讨论。
同时将过去单一的“作业-考试”模式改为作业(Assignment)、报告(Presentation)、咨询(Inquiry)、讨论(Discussion)、专题论述(Essay)、考试(Test)的全方位开放式APIDET教学模式。
增强师生互动,把学生从应考能手培养成具有创新意识和动手能力的科研好手。
与这一教学模式相适应,我们对课程考试进行了改革,注意加强教学过程考核,全面检查教学内容的阶段完成情况。
尝试多种形式的考试评分办法,学生期末成绩由作业、课堂报告、课堂讨论、专题论述、半期考试和期末考试成绩来综合评定,避免由一次考试来决定学生期末总成绩。
半期考试和期末考试实行教考分离,即把教学和考试分开,任课老师不参与本课程的考试出题、监考和评卷。
具体方法与标准如下:1.平时作业:占期末总成绩的10%。
督促学生应按时完成平时作业,及时批改作业。
川大理工科数学I,II,III之微积分和线性代数教学大纲

课程号:20113740课程名称:大学数学(I) 微积分开课学期:秋季春季(学年课)学分:秋季4 春季5先修课程:初等数学基本目的:介绍微积分的基本知识,为非数学类各专业后继课程提供基本的数学工具,初步培养学生应用数学知识分析、解决实际问题的意识与能力内容提要:一、函数与极限(约22学时)函数,函数与数列极限的定义与性质,无穷小与无穷大,无穷小比较,极限四则运算,极限存在准则与两个重要极限,函数的连续性与间断点,初等函数连续性,闭区间上连续函数性质。
二、一元函数微分学(约26学时)导数的定义与性质,基本求导方法与导数公式,微分,高阶导数,微分中值定理,泰勒公式,洛必达法则,导数的应用三、一元函数积分学(约30学时)不定积分与定积分的概念与性质,牛顿-莱布尼茨公式,换元积分法与分部积分法,定积分的应用与近似计算。
四、空间解析几何与矢量代数(约16学时)矢量及矢量的运算,坐标系及矢量的坐标,平面与直线,曲面与曲线,二次曲面的标准型五、多元函数微分学(约20学时)多元函数的概念,偏导数与全微分,复合函数,隐函数的微分法,微分法在几何上的应用,多元函数的极值,矢量分析六、重积分(约12学时)二重积分的概念与性质,二重积分的计算及应用,三重积分七、曲线积分和曲面积分(约14学时)第一、二型曲线积分,格林公式及曲线积分与路程径无关的条件,第一、二型曲面积分,高斯公式与散度,斯托克斯公式与旋度。
八、无穷级数(约17学时)常数项级数,幂级数,傳里叶级数九、广义积分与含参变量的积分(约3学时)广义积分,含参变量的积分十、常微分方程(约14学时)微分方程的基本概念,一阶微分方程的初等解法,可降阶的高阶微分方程,高阶线性方程教学方式:秋季每周授课5学时,共85学时左右;春季每周授课6学时,共102学时,其中每周习题课1学时教材与参考书:1)杨志和等,微积分(上、下册),高等教育出版社2)同济大学应用数学系,高等数学,高等教育出版社3)马知恩等,工科分析基础,高等教育出版社4)杨志和等,微积分学习指导,自编讲义(待出版)学生成绩评定方法:平时(作业、出勤率)10%,期中考试20%,期末考试70%课程名称:大学数学(II)微积分开课学期:秋季、春季(学年课)学分:每期各4 学分先修课程:初等数学基本目的:介绍微积分的基本知识,为非数学类各专业后继课程提供基本的数学工具,初步培养学生应用数学知识分析、解决实际问题的意识与能力内容提要:一、函数与极限(约16学时)函数,数列与函数的极限,无穷小与无穷大,极限运算法则,极限存在准则,函数的连续性与间断点,初等函数连续性,闭区间上连续函数性质。
四川大学锦城学院

四川大学锦城学院教学大纲授课时间:专业名称:课程名称:主讲教师:授课班级:系(教研室)主任:年月日四川大学锦城学院课程教学大纲一、课程基本信息课程名称:《大学数学(3)微积分-1》(Calculus(3)-1)《大学数学(3)微积分-2》(Calculus(3)-2)课程编码: 00017030,00018040总学时:48+64=112学时学分:3+4=7学分适应专业:行政管理、市场营销、人力资源、旅游管理、会计学、审计学、ACCA、财务管理、金融学、国际经贸、保险、投资学、国际商务、建筑学、城市规划、信息管理与信息系统、电子商务课程性质:专业基础课教材:《经济数学——微积分》吴传生编高等教育出版社教学辅助资料:《大学数学微积分同步练习册》齐薇、钱小瑞主编重庆大学出版社推荐读物:《高等数学》高等教育出版社《微积分》魏有德编四川大学出版社出版二、课程目标及要求:(一)本课程目标“微积分”是大学数学中最重要的一门基础课,它的理论和方法在理、工、医、农、经济、管理、金融等各个学科中都得到了广泛的应用,是学习各专业课程必不可少的数学工具。
通过学习,使学生获得微积分、微分方程、空间解析几何、级数等的基本知识,掌握基本概念、基本理论;培养一定的逻辑思维能力、空间想象能力和计算能力,为学习后继课程和伴随科学发展进一步扩大数学知识打下较好的基础。
(二)本课程要求1.微分法和积分法是“微积分”最基本最重要的两个运算,在全书各章中都要用到,因此,必须熟练理解基本概念、掌握其计算方法和技巧。
2.在学习相关的数学理论时,要注意数学概念、公式、定理的经济背景及经济应用,如复利模型、微观经济学中的边际分析理论、弹性、最大利润原理等。
三、本课程与相关课程的关系:初等数学的函数相关知识;简单的极限求法。
后续课程为《线性代数》、《概率统计》。
四、课程内容及学时分配:1第一学期教学进度安排如下:第一学期:(48学时)第一章:函数(4学时)[教学目的和要求] 通过学习,掌握集合、实数集、函数的概念;掌握分段函数、基本初等函数及其图像;了解初等函数的概念;掌握函数的奇偶性、单调性、周期性、有界性;掌握反函数和复合函数;会建立一些实际问题的函数关系;了解常见的需求函数、供给函数、成本利润函数等。
四川大学高数微积分I(上)考前复习用2018年期末真题试卷(含答案)

x
1
x4
2
x2
d 1
x
而
1 0
x4
2x 2x2
dx 1
1 2d x 2,
0
1
x4
2x 2x2
dx 1
1
2 x3
d
x
1,
故原无穷限广义积分也收敛.
三、解答题(每小题 10 分,共 20 分)
1.设两曲线为 l1 : y x2 ,l2 : x y 2 .
n1
n n1 n
(1)n1 1 xn
n1
n
f
(2017) (0)
a2017
2017!
2 2017
2017!
2 2016!
注 前一问 6 分,后一问 2 分.
6.判断无穷限广义积分
0
x4
2x 2x2
d 1
x
的敛散性.
解 1
2x
f ( x2 y) (2xy x2 dy ) e x y (1 dy ) 1
dx
dx
解之得 dy dx
f
( x2 f (
y x
)
2
2xy e x y) x2 e
x
y
y
1
.
y) 2xy e x y f ( x2 y) x2 e x y
(2) 由(1)知, x0 为极值点,所以 f ( x0 ) 0. 将函数 f ( x) 在点 x x0 处展开,得
f (x)
f ( x0 )
f ( x0 )( x x0 )
浅析微积分在经济学中的应用

浅析微积分在经济学中的应用黄尹艺(四川大学锦城学院,会计2班,130410236)[摘 要]经济学中的很多经济现象、经济理论都能够用数学知识去解释。
本文本着“数学为体,经济为用”的原则,对于微积分在经济学领域中的连续复利、边际分析、弹性分析、最优化问题作一些初步分析。
[关键词] 微积分;导数;极限;边际分析;弹性分析随着数学理论的不断完善和经济的飞速发展,数学与经济学的联系越来越紧密。
数学是经济学理论研究的理想工具,借助数学模型研究经济学,具有清晰、深入、严密三大优势。
微积分学作为数学的一个基础分支学科,在经济学中有着极为广泛的应用。
经济量化分析已成为经济学研究的主要手段。
现主要从微积分与经济的相关联系出发,简要讨论微积分在经济学中的应用及其存在的经济学意义。
一、 微积分的基本思想微积分学是数学的一个基础分支学科,源于代数和几何。
内容主要包括函数、极限、导数、微分学、积分学及其应用。
微积分有两个基本想法:其一是微分学,包括求导数的运算,是一套关于变化率的理论。
它使得函数,速度,加速度和曲线的斜率等均可在一个通用的符号化基础上进行讨论;其二是积分学,包括积分的运算,为计算被一个函数图像所包的面积提供一套通用的方法,引入诸如体积的相关概念。
微积分局部求近似、极限求精确的基本思想方法贯穿于整个微积分学体系中。
二、 微分在经济学中的应用在经济学领域中,微积分被运用十分基础和广泛,是学好经济学、剖析现实经济现象的基本工具。
1、 极限在经济学中的应用极限概念是微积分中最基本的概念,在极限的概念基础上面,很多微积分的概念理论得到发展,很多经济学的知识也得到有效的解决。
比如利用极限解决连续复利问题。
例 设银行存款现值P 和将来值B ,年利率为r ,则t 年后的本利和即将来值为t r)(1B +=若一年分n 次计算复利,则每期利率为三,一年后的本利和即将来值为 n nr P B )1(+= 而t 年后的本利和即将来值为 tn nrp B )1(+= 当∞→n 时,则t 年后的本利和即将来值为 t tn n pe nr p B =+=∞→)1(lim 从而现值p 和将来值B 之间的关系为t pe =B或者 t Be p -=现值P 为1,利息r 为100%,1t =,则得 e B =例子中的极限应用体现了在经济学中当一个数值含有极限的意义即趋向无穷大或0时,利用微积分中的极限的思想去解题可以步骤简化,思路清晰的解决很多经济学的这些问题。
四川大学微积分下册 习题册级数部分 答案

= 1 2 .所以R = 2,原级
∞ n1 n=1 (−1) n 收
∞ 1 n=1 n 发散.当t
= −2即x = −1时,级数为
解
=( 2.
∞ n−1 . n=1 nx n−1 = ∞ (xn ) s(x) = ∞ n=1 nx n=1 ∞ x 1 n n=1 x ) =( 1−x ) = (1−x)2
第一节 级数的概念与性质
一、 (1) 对级数 ∞ 则( ). n=1 un , 若limn→∞ un = 0 , ∞ A. 必收敛; B. 必发散; C.不能判断 n=1 un 的收敛性; D. Sn = u1 + u2 + · · · + un = 0
(2) 若级数
∞ 则级数 n=1 un 收敛于S, ∞ n=1 (un
2.
∞ n 2n−1 . n=1 ( 3n−1 )
解 由根值判别法limn→∞ 原级数收敛。
3. 4.
∞ n=1 n+1 n .
√ n
un =limn→∞ ( 3nn −1 )
2n−1 n
=1 9 <1
解 级数通项的极限为1, 不为零.原级数收敛。 解 当a = 1时级数的通项趋于无穷,极限不存在。级数发散。当a = 1时,由比 1 1 lnn+3 a+ n n 1 0 1 n+1 值判别法limn→∞ uu = lim ) =ae = a ( .当a < 1时,原级数发散, n →∞ 1 lnn +2 n a+ a+ 1
1.
解 级数的通项极限不存在, 级数发散.
3. √ ∞ n=1 ( n √
解 Sn = 四、 判别下列级数的敛散性.
四川大学锦城学院

四川大学锦城学院教学大纲授课时间:________________________________ 专业名称:_______________________________ 课程名称:_______________________________ 主讲教师:_______________________________ 授课班级:________________________________系(教研室)主任:____________________四川大学锦城学院课程教学大纲一、课程基本信息课程名称:《大学数学(3)微积分-1》(Calculus(3)-1 )《大学数学(3)微积分-2》(Calculus(3)-2 )课程编码:00017030,00018040总学时:48+64=112学时学分:3+4=7学分适应专业:行政管理、市场营销、人力资源、旅游管理、会计学、审计学、ACCA 财务管理、金融学、国际经贸、保险、投资学、国际商务、建筑学、城市规划、信息管理与信息系统、电子商务课程性质:专业基础课教材:《经济数学一一微积分》吴传生编高等教育出版社教学辅助资料:《大学数学微积分同步练习册》齐薇、钱小瑞主编重庆大学出版社推荐读物:《高等数学》高等教育出版社《微积分》魏有德编四川大学出版社出版二、课程目标及要求:(一)本课程目标“微积分”是大学数学中最重要的一门基础课,它的理论和方法在理、工、医、农、经济、管理、金融等各个学科中都得到了广泛的应用,是学习各专业课程必不可少的数学工具。
通过学习,使学生获得微积分、微分方程、空间解析几何、级数等的基本知识,掌握基本概念、基本理论;培养一定的逻辑思维能力、空间想象能力和计算能力,为学习后继课程和伴随科学发展进一步扩大数学知识打下较好的基础。
(二)本课程要求1 •微分法和积分法是“微积分”最基本最重要的两个运算,在全书各章中都要用到,因此,必须熟练理解基本概念、掌握其计算方法和技巧。
高等数学微积分课件6.1.1 点集

D 的边界是圆周
上一页 | 首页 | 下一页
四川大学数学学院 2005
既不开,也不闭的集合
半开半闭区间
A {x | a x b} (a, b]
a
(a, b] 的边界点是 a 和 b
上一页 | 首页 | 下一页
四川大学数学学院 2005
b
既不开,也不闭的集合
内开外闭的圆环
D {( x, y ) | a x y b }
例子
A {( x, y ) | 0 x y a }
2 2 2
有界开区域:有界、开、连通
上一页 | 首页 | 下一页
四川大学数学学院 2005
B {( x, y ) | a x y b }
2 2 2 2
有界闭区域:有界、闭、连通
上一页 | 首页 | 下一页
四川大学数学学院 2005
邻域(neighborhood) 回忆: R 中的邻域:
U ( x0 , ) {x | x x0 }
{x | x0 x x0 } ( x0 , x0 )
x
x0 x 0 上一页 | 首页 | x 下一页 0
四川大学数学学院 2005
上一页 | 首页 | 下一页
四川大学数学学院 2005
内点(interior point) 点 M 0 是点集 V 的一个内点,如果存在
使
0
U (M 0 , ) V
M0
V 的内点属于V
V
上一页 | 首页 | 下一页
四川大学数学学院 2005
外点(exterior point) 点 M 0 是点集 V 的一个外点,如果存在
微积分-四川大学数学学院

习题课教学大纲(微积分II)(征求意见稿)课程名称:大学数学-微积分II英文名称:Calculus课程性质:必修课程代码:20113830(上册)20112530(下册)面向专业:大学数学II各专业习题课指导丛书名称:高等数学(第五版)出版单位:高等教育出版社出版日期:2002年7月主编:同济大学应用数学系习题课讲义名称:大学数学习题课系列教材--微积分编写单位:四川大学数学学院编写日期:2006年8月主编:四川大学数学学院高等数学教研室第一章函数与极限1.函数与极限2学时(1)基本内容函数的概念,函数的表示,函数的几种特性,复合函数,分段函数,极限的概念及性质,极限存在准则,重要极限,无穷小量与无穷大量,极限的计算,函数的连续与间断,闭区间上连续函数的性质。
(2)基本要求处理作业批改中发现的问题。
通过具体例子讲解极限的计算问题,连续性讨论问题,复合函数定义域及分段函数的复合问题。
第二章导数与微分2学时(1)基本内容:导数及高阶导数的定义;复合函数隐函数参数方程决定的函数和分段函数的求导;微分。
(2)基本要求:处理作业批改中发现的问题;举列说明复合函数隐函数参数方程决定的函数和分段函数的一阶二阶求导;会求微分。
第三章微分中值定理与导数的应用2学时1.中值定理及洛必达法则(1) 基本内容:中值定理的应用;洛必达法则求极限.(2)基本要求:处理作业批改中发现的问题;通过具体例子讲解中值定理的题型和解题步骤;求各种不定形的极限并注意化简和变形技巧.2.不等式的证明和函数曲线(1)基本内容:函数单调性凹凸性的判定;函数的最值;泰勒定理.(2)基本要求:处理作业批改中发现的问题;举例说明函数导数二阶导数曲线关系;举例讲解利用曲线特征证明函数不等式;举例说明函数最值的应用;泰勒中值定理的应用方法.第四章不定积分2学时一、基本内容:复习原函数和不定积分的概念,不定积分的基本性质及基本积分公式,总结换元积分法和分部积分法,有理函数、三角函数的有理式和简单无理函数的积分的计算方法。
四川大学微积分 第一章 函数

集合的交:A B={x|x A 且x B}
集合的差:A-B={x|x A 且x B}
微积分
函数-集合
区 在一条直线上指定了一点作为原点O,再指 间 定了正向,此外又规定了单位长度,这条直 线就称为数轴。
数轴上的点与实数之间可以建立一一对应的 关系。有时为了形象化起见,把数x称为点x, 就是指数轴上与数x对应的那个点。
O -1 0 1
x
微积分
函数-集合
闭区间:[a,b]={x|a≤x≤b}
O
有 限 区 间
a
O
b
x
开区间:(a,b)={x|a<x<b} x 左闭右开区间:[a,b)={x|a≤x<b}
a
b
O a
b
x
左开右闭区间:(a,b]={x|a<x≤b}
O
a
b
x
微积分
函数-集合
[a, + ∞)={x|a≤x}
R={x|x为实数}
微积分
函数-集合
子集 如果集合A的元素都是集合B的元素,即若 xA 则 必 xB , 就 说 A 是 B 的 子 集 , 记 作 AB(读作A包含于B)或BA(读作B包含A)
如果A B且或AB,则称A与B相等。
1. AA即集合A是其自己的子集。 2. 传递性 AB、B C 则A C。 3. A,即空集是任何集合A的子集。
定义域R
o
x
在自变量的不同变化范围中, 对应法则用不同的 式子来表示的函数,称为分段函数.
例如 , 2 x 1, f ( x) 2 x 1, x0 x0
y x2 1
y 2x 1
微积分
高等数学教材 四川大学

高等数学教材四川大学高等数学是大学数学中的一门重要课程,对于理工科学生来说尤为重要。
四川大学作为中国一流的综合性大学,其高等数学教材在教育界享有很高的声誉。
本文将从教材概述、教材特色、教材优势等方面对四川大学高等数学教材进行介绍。
一、教材概述四川大学高等数学教材是根据教学大纲编写的,内容涵盖了高等数学的各个分支,包括微积分、线性代数、概率论等。
教材内容丰富,选取了大量的实际问题和例题,旨在培养学生的数学建模和解题能力。
二、教材特色1. 理论与实践相结合四川大学高等数学教材注重理论与实践相结合,理论内容严谨、全面,但并不仅仅停留在理论层面,更注重将理论应用到实际问题中。
教材在每个章节都穿插了一些例题,帮助学生将理论应用到实践中,提高学生解决实际问题的能力。
2. 突出问题求解的方法与思路教材在讲解问题求解的过程中,注重培养学生的问题解决思维和方法。
教材中详细介绍了各种问题解决的方法和技巧,引导学生灵活运用这些方法解决实际问题。
3. 强调数学与实际的联系四川大学高等数学教材注重数学与实际的联系,将抽象的数学内容与实际问题相结合,让学生更好地理解数学的内涵和意义。
教材中的例题和习题都是以实际问题为背景,激发学生对数学的兴趣和学习的动力。
三、教材优势1. 知识点体系完整四川大学高等数学教材的知识点体系完整,内容覆盖面广。
学生通过学习教材可以系统地掌握高等数学的各个方面。
2. 章节设置合理教材的章节设置合理,从基础知识到高级知识层层递进,循序渐进。
每个章节都设有总结和习题,方便学生巩固和运用所学知识。
3. 难易程度适中教材难易程度适中,对于初学者而言较容易理解,同时对于进阶学习和拓展也有相应的内容设置,使学生能够逐步提升自己的数学水平。
总之,四川大学高等数学教材准确满足了大学生学习高等数学的需求,具有一定的教材特色和优势。
通过学习该教材,学生能够全面提高自己的数学素养和解决实际问题的能力。
四川大学高等数学教材以其丰富的内容和全面的知识点体系,为学生打下坚实的数学基础。
四川大学电气信息学院电气工程及其自动化专业课表
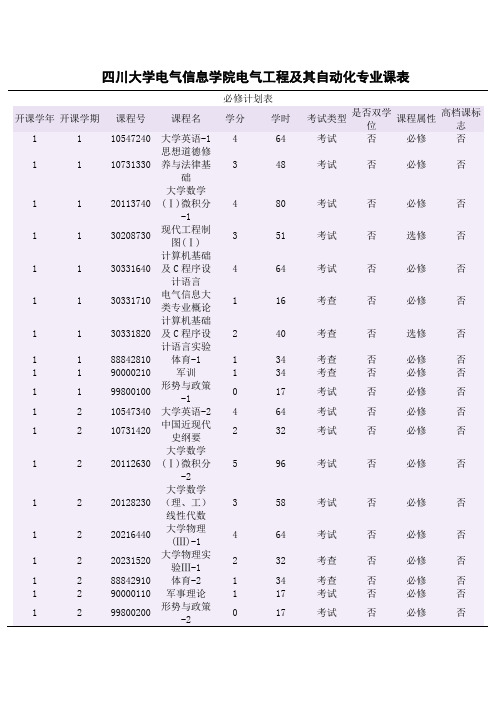
四川大学电气信息学院电气工程及其自动化专业课表必修计划表开课学年开课学期课程号课程名学分学时考试类型是否双学位课程属性高档课标志1 1 10547240 大学英语-1 4 64 考试否必修否1 1 10731330 思想道德修养与法律基础3 48 考试否必修否1 1 20113740大学数学(Ⅰ)微积分-14 80 考试否必修否1 1 30208730 现代工程制图(Ⅰ)3 51 考试否选修否1 1 30331640 计算机基础及C程序设计语言4 64 考试否必修否1 1 30331710 电气信息大类专业概论1 16 考查否必修否1 1 30331820 计算机基础及C程序设计语言实验2 40 考查否选修否1 1 88842810 体育-1 1 34 考查否必修否1 1 90000210 军训 1 34 考查否必修否1 1 99800100 形势与政策-10 17 考试否必修否1 2 10547340 大学英语-2 4 64 考试否必修否1 2 10731420 中国近现代史纲要2 32 考试否必修否1 2 20112630大学数学(Ⅰ)微积分-25 96 考试否必修否1 2 20128230大学数学(理、工)线性代数3 58 考试否必修否1 2 20216440 大学物理(Ⅲ)-14 64 考试否必修否1 2 20231520 大学物理实验Ⅲ-12 32 考查否必修否1 2 88842910 体育-2 1 34 考查否必修否1 2 90000110 军事理论 1 17 考试否必修否1 2 99800200 形势与政策-20 17 考试否必修否2 1 10510340 大学英语-34 64 考试否必修否2 1 10731530 马克思主义基本原理概论3 48 考试否必修否2 1 20100320工程数学复函数与积分变换2 32 考试否选修否2 1 20113620工程数学数值计算方法2 32 考试否选修否2 1 20128430大学数学(理、工)概率统计3 58 考试否必修否2 1 20216530 大学物理(Ⅲ)-23 48 考试否选修否2 1 20231610 大学物理实验Ⅲ-21 16 考查否选修否2 1 30203120 工程训练(Ⅰ)2 64 考查否必修否2 1 30330820 MATLAB编程与工程应用2 32 考试否选修否2 1 30332250 电路原理 5 80 考试否必修否2 1 30332510 电路实验 1 20 考查否必修否2 1 30334730 电工电子测量技术及实验3 48 考试否选修否2 1 88801610 体育-3 1 34 考查否必修否2 1 99800300 形势与政策-30 17 考试否必修否2 2 10510440 大学英语-4 4 64 考试否必修否2 2 10731660毛泽东思想、邓小平理论和“三个代表”重要思想概论6 96 考试否必修否2 2 30307240 模拟电子技术基础4 64 考试否必修否2 2 30309940 信号与系统(Ⅰ)4 64 考试否必修否2 2 30313430 电磁场3 48 考试否选修否2 2 30313710 模拟电子技术基础实验1 24 考查否必修否2 2 30313810 数字电子技术基础实验1 21 考查否必修否2 2 30332620计与实践2 40 考查否必修否2 2 30334440 数字电子技术基础4 64 考试否必修否2 2 88801710 体育-4 1 34 考查否必修否2 2 99800400 形势与政策-40 17 考试否必修否2 2 99905220中华文化(文学篇)3 48 考试否必修否2 2 99905320中华文化(历史篇)3 48 考试否必修否2 2 99905420中华文化(哲学篇)3 48 考试否必修否3 1 30301030 单片机原理及应用3 48 考试否选修否3 1 30301420 电机电器CAD技术2 32 考试否选修否3 1 30307820 数据库技术 2 32 考试否选修否3 1 30308830 通信工程 3 48 考试否选修否3 1 30314310 数据库技术实验1 16 考试否选修否3 1 30316830 自动控制原理(II)3 48 考试否必修否3 1 30332450 微机原理与接口技术5 80 考试否必修否3 1 30332860 电机学 6 96 考试否必修否3 1 99800500 形势与政策-50 17 考试否必修否3 2 30302420 电力拖动 2 32 考试否选修否3 2 30306230 计算机网络与通信3 51 考试否必修否3 2 30306620 可编程控制器原理及应用2 32 考试否选修否3 2 30314530 DSP原理及应用3 48 考试否选修否3 2 30315430 计算机控制系统3 48 考试否选修否3 2 30317020 电力电子CAD2 32 考试否选修否3 2 30317120 自动测试系统2 32 考试否选修否3 2 30320030 电子商务技术3 48 考试否选修否3 2 30320920 的电力电子技术2 32 考试否选修否3 2 30330520 PCB计算机辅助设计2 32 考试否选修否3 2 30332710 计算机网络实践1 20 考查否必修否3 2 30332930 电力电子技术3 48 考试否必修否3 2 30333010 生产实习(Ⅰ)1 16 考查否必修否3 2 30334540 电力系统分析理论4 64 考试否必修否3 2 30334630 发电厂电气部分3 48 考试否必修否3 2 99800600 形势与政策-60 17 考试否必修否4 1 30303120 电力谐波分析2 32 考试否选修否4 1 30303520 电能质量与控制技术2 32 考试否选修否4 1 30303710 电气工程新理论和新技术1 16 考试否选修否4 1 30305020 高压直流输电2 32 考试否选修否4 1 30312430 毕业实习(I)3 51 考查否必修否4 1 30314820 电力系统自动装置2 32 考试否选修否4 1 30314920 电力技术经济2 32 考试否选修否4 1 30315020 电力市场营销2 32 考试否选修否4 1 30315230 调度自动化及信息管理系统3 48 考试否选修否4 1 30315320 电力系统远动原理2 32 考试否选修否4 1 30315540 电力系统继电保护原理4 64 考试否选修否4 1 30315620 电力市场理论2 32 考试否选修否4 1 30315730 高电压技术 3 48 考试否选修否4 1 30315820 发电厂变电站综合自动化2 32 考试否选修否4 1 30315930 电力市场运营系统3 48 考试否选修否4 1 30316020 配电网自动化及管理信息系统2 32 考试否选修否4 1 30316730 高频开关电源技术3 48 考试否选修否4 1 30316820 建筑电气及楼宇自动化2 32 考试否选修否4 1 30316940 电气传动自动控制系统4 64 考试否选修否4 1 30320025 微机保护 3 48 考试否选修否4 1 30330220 智能电器及其应用2 32 考试否选修否4 1 30330420 电气设备故障诊断与信息技术2 32 考试否选修否4 1 30330720 电器控制技术2 32 考试否选修否4 1 30331020 电力系统分析的计算机算法2 32 考试否选修否4 1 30332020 电力营销管理信息系统2 32 考查否选修否4 1 30333110 课程设计(Ⅰ)1 16 考查否必修否4 1 30335020 电力系统电压稳定及无功电压优化控制2 32 考试否选修否4 1 30335220 电能质量控制技术与设备2 32 考试否选修否4 1 30337920 供用电技术 2 32 考查否选修否4 1 99800700 形势与政策-70 17 考试否必修否4 2 30312780 毕业设计(I)16 256 考查必修4 2 99800800 形势与政策-82 17 考试否必修否。
高等数学微积分习题册上册答案

三、根据函数极限的定义证明下列极限.
(1)
lim
x→∞
1 x2
= 0;
证明:对任意ε>0,解不等式
|
1 x2
− 0 |=
1 x2
<ε
→|
x |>
1 ε
四川大学数学学院高等数学教研室编
3
学院
姓名
学号
日期
取X
= 1 ,当| x |> ε
X,
|
1 x2
−
0
|<
ε
,所以
lim
x→∞
1 x2
= 0。
1.3 函数的极限
证明:对任意ε>0, 解不等式 | x2 − 4 + 4 |=| x + 2 |< ε x+ 2
取δ = ε ,当 0 <| x + 2 |< δ , | x2 − 4 + 4 |< ε ,所以 lim x2 − 4 = −4 。
x+2
x→−2 x + 2
二、证明 lim(4x −1) = 11,并求正数δ ,使得当| x − 3 |< δ 时,就有| (4x −1) −11|< 0.001. x→3
学院
姓名
学号
一、根据数列极限的定义证明下列极限:
日期
1.2 数列的极限
(1)
lim
n→∞
(−1) n2
n
= 0;
证明:对任意ε,解不等式
|
(−1)n n2
−
0 |=
1 n2
<
ε
→
n
>
1 ε
四川大学期末考试试题(闭卷)2018-2019春微积分

四川大学期末考试试题(闭卷)(2018——2019 学年第 2 学期) A 卷课程号:201138040 课序号:01~50 课程名称:微积分(I)-2 任课教师:成绩:第 1 页,共 2 页第 2 页,共 2 页⎨2018-2019 春微积分(I )-2 A 卷参考答案一.填空题(每小题 4 分,共 5 分)1.曲面 z = 2x 3 - y 2 在点(1,1,1)处的切平面方程是 ( 6x - 2 y - z- 3 = 0 ).解: dz = 6x 2dx - 2 ydy , 6x - 2 y - z - 3 = 02. 设= lnarctan y, 则 x=( 3 ).x = 2, y =1 5解 :∂z = 1 2x - 1 - y =x + y , ∂z =3∂x 2 x 2+y2y 2x21 +x2x 2 + y 2∂x x = 2, y =1 53 设 f ( x , y ) =+ ⎰⎰ x 2+ y 2≤1f (x , y )dxdy ,则⎰⎰x 2+ y2≤1f ( x ,y )dxdy =2π ().3(π-1)解:f ( x , y )dxdy = k = k )dxdy = 2π k π ⎰⎰⎰⎰ 3 +x 2 + y 2 ≤1x 2 + y 2 ≤14. f (x ) 是周期为2π的周期函数, f (x ) = ⎧cos x - 2, -π≤ x < 0, ⎩sin x + 2, 0 < x < π设 s (x ) 是其傅里叶级数的和函数, 则 s (π) = ( -1).2解: s (π) = 1 [ lim f ( x ) + lim f ( x )] = - 12 x →-π+x →π-2 5. 二阶微分方程 y y ''+ y '2= 1 的通解是(y 2 = x 2 + c x + c ).∂z ∂xy 2 = 2 ( x + c )dx = x 2 + ⎰ yy '=x + c ,12二.计算题(每小题 7 分,共 28 分)6.设e z + x - 2xy + z - 1 = 0 确定的函数 z = z ( x , y ) ,∂z ∂ 2z求(1) ∂y, (2)∂y ∂x. ( 0,0) 解:(1)方程两边同时对 y 求偏导:(1) (e z+ 1)∂z- 2x = 0,∂y…………………………………………..(2 分)∂z=2x, .............................. (1 分)∂y e z + 1(2) 方程 两边再同时对 x 求偏导:∂z ∂z ∂ 2z (2) e z⋅ + (e z + 1) - 2 = 0 …………………………..(2 分)∂x ∂y ∂x ∂y把 x =0,y =0 代入原方程可得 z = 0 ,( 0,0) = 2xe z + 1 = 0 , …(1 分)∂ 2 z=2=再代入方程(2), 得 ∂x ∂y e z +11 ................ (1 分)7. 空间闭曲面∑ 由 x 2 + y 2 = 1, z = 0和z = 4 + y 围成, 求它的表面积.解: S = π+⎰x 2 + y 2 =1(4 + y )ds +⎰⎰x 2 + y 2 ≤11dxdy…………………………..(4 分)= π+ 8π+2π=(9 + 2)π ……………………………..…………..(3 分)8. 计算曲线积分 I = ⎰L(e x sin y - 2 y )dx + (e x cos y - 3)dy ,其中 L 为由点 A:(2,0)到点 B;(1,2)再到原点 O (0,0)的折线段.解: ∂P =∂y ∂Q = ∂x ∂ (e x sin y - 2 y ) = e x cos y - 2 ,∂y∂(e x cos y - 3) = e x cos y ,∂x ∴ ∂P ≠ ∂y∂Q ∂x , 曲线积分与路径有关 .................... (1 分)∂z ∂y ( 0,D⎰⎰ =⎰⎰ ( ∂Q - ∂P )dxdy = 2⎰⎰ dxdy = 4,………………………… (3 分)ABOA ∂x ∂y D⎰OA= 20 ⋅ dx + (e x- 3) ⋅ 0 ⋅ dx = 0 , ............................ (1 分) 0因此∴ I =⎰AMOA- ⎰OA= 4- 0 = 4. ………………………… (1 分)⎰⎨⎩xy9. 设可导函数φ(x ) 满足φ(x ) c os x + 2 xφ(t )sin t d t = x +1, 求φ(x ) .解:设 y =φ(x ) , 两边对 x 求导,得y 'cos x + ysin x = 1其通解为 y = c cos x +sin x .………………………… (2 分)………………………… (4 分)因为 x = 0时, y = 1, 得c = 1. 所以 y = cos x + sin x .…………(1 分)三. 解答题(每小题 9 分,共 27 分)⎧ x k y10. 设二元函数 f ( x , y ) = ⎪ 4 x 2 + y 2, ( x , y ) ≠ (0, 0) . ⎪ 0,( x , y ) = (0, 0)(1) 当k 为何值时 f ( x , y ) 在点(0,0)处连续;(2) 当k 为何值时 f ( x , y ) 在点(0,0)处可微. 解:(1)令 x = ρcos θ, y = ρsin θ,lim f ( x , y ) = lim ρk -1 cos θsin θx →0 y →0ρ→0 1+ 3cos 2 θ 因为∀θ, cos θsin θ 有界,1+ 3cos 2 θ所以当k > 1时 f ( x , y ) 在点(0,0)处连续 ............. (3 分)(2)根据偏导数定义f (0, 0) = lim h →0f (0, 0) = lim k →0f (h , 0) - f (0, 0) = 0 hf (0, k ) - f (0,0)= 0 k…………………………… (2 分)讨论极限ρ→0 ρ= lim ρk -2 cos θsinθρ→0 1+3cos2 θ所以当k > 2 时f ( x, y) 在点(0,0)处可微............ (2 分)1+1+∞n =0⎩ 1 21 211. 设 f (x )=1x1+x 2∞+ arctan x , (1)把 f (x ) 展开成 x 的幂级数; (2)求 f (2019) (0) .n n解:= ∑(-1)x ,n =0x ∈(-1,1)…………………… (1 分)∴ x = 1+ x 2x ∑ n =0 (-1)nx 2n = ∑ n =0 (-1)nx 2n+1, x ∈(-1,1)…………………… (2 分)1 1 1 ∞ n 2narctan x = ⎰0 2 dx = ⎰0 ( ∑(-1) xn =0)dx= ∑(-1)nx 2n +1 , x ∈[-1,1]…………………… (3 分)n =02n +1f (x ) = x+ arctan x = ∞2n + 2 (-1)n x 2n +11+ x 2f (2019) (0) = 2019!a2019∑ 2n+1= -2019! 2020= -2020 ⋅ 2018!2019…………………… (1 分)…………………… (2 分)⎧ y ' - 3 y ' + 2 y = - xe x12 求初值问题⎨y (0) =y '(0) = 1的特解.解:对应特征方程为r 2 - 3r + 2 = 0 ,其特征根为r = 1, r = 212所以齐次方程的通解为 y = C e x+ C e 2 x ................................. (3 分)因为λ= 1 是单根, 设非齐次方程特解为 y * = x (ax +b )e x……… (2 分)代入原方程,化简得a =1, b = 1 . 所以 y * = ( 122x 2 + x )e x , .... (2 分)从而原方程的通解为 y = C e x+ C e 2 x+ ( 1 x 2 + x )e x…………………… (1 分)∞ ∞由y(0) =y '(0) = 1 , 得c1=-1, c2= 2所以初值问题的特解为y = ( 12x 2 +x + 2)e x -e 2 x ........................... (1 分)四. 证明题(7 分)13.证明级数∑n=1(-1)n-11条件收敛于ln 2 .n∞n n ⎰ 1 2∞ n -1 1 ∞ 1证明: ∑(-1)n =1 =∑ 是调和级数, 发散; n =1 …………………… (1 分)又由莱布尼茨判别法,交错级数∑(-1) n =1 n -1 1 收敛, n…………………… (1 分)则∑(-1)n =1 n -1 1 条件收敛. n …………………… (1 分)考虑幂级数 s (x ) = ∑(-1)n =1n -1 1x n n ,收敛半径为 1, ....................................... (1 分)在绝对收敛区间为(-1,1)内,s '(x ) = ∑(-1)n =1 n -11 (x nn ) ' = ∑(-1) n =1 n -1x n -1 = 1 , 1+ x …………………… (3 分) s (x ) =x 1 dx =ln(1 + x ) 0 1+ x因为 x=1 时, 级数收敛,则 s (1) = lim ln(1+ x ) = ln 2. x →1-…………………… (1 分)五.应用题(每小题 9 分,共 18 分)14. 求曲面 x 2 + y 2 - 4x - 4 y + 7 = 0 和平面 x + z = 8 交线上的点到 y 轴的最长距离和最短距离.解:点( x , y , z ) 到 y 轴的距离为. …………………… (2 分)令F = x 2 + z 2 + λ( x 2 + y 2 - 4x - 4 y - 7) + λ( x + z - 8) , (2 分) ⎧F = 2x + λ(2x - 4) + λ = 0⎪ x 1 2 ⎪F y = λ1 (2 y - 4) = 0 F = 2z + λ = 0 …………………… (2 分)⎨ z 2 ⎪F = x 2 + y 2 - 4x - 4 y - z - 7 = 0 ∞ ∞ ∞ ∞ ∞⎪ λ1 ⎪F = x + z - 8 = 0⎩ λ2解得(x , y , z ) = (1, 2, 7)或(3, 2, 5) ....................................................................(1分) 将这两个点分别代入目标函数,可得最大值5 和最小值 .……… (2 分) 34 2∑121 2 2 15. 设空间曲面∑: z 2 = x 2 + y 2 (1 ≤ z ≤ 2部分) ,方向指向外侧,计算曲面积分 I = ⎰⎰ cos( y + z )dydz + y 2dzdx + ( x + z 2 )dxdy .解:作辅助面∑1: z = 1, ( x , y ) ∈ D : x 2 + y 2 ≤ 1 ,方向指向下侧;辅助面∑2: z = 2, ( x , y ) ∈ D : x 2 + y 2 ≤ 4 ,方向指向上侧 (2 分) ∑+∑1+∑2 围成空间闭区域Ω ,方向指向外侧, 根据高斯公式, 有⎰⎰∑+∑ +∑ = ⎰⎰⎰Ω (2 y + 2z )dxdydz = 2⎰⎰⎰Ωzdxdydz = ⎰ ⎰⎰ ⎰2 2 15 2 zdz dxdy = 2π 1 D z 1 z ⋅ z dz = π, 2…………………… (4 分) ⎰⎰∑⎰⎰∑ = -⎰⎰x 2 + y 2 ≤ 1 ( x + 1)dxdy = -π,= ⎰⎰x 2 + y 2 ≤ 4 ( x + 4)dxdy =16π,…………………… (1 分) …………………… (1 分) ∴ I = ⎰⎰1 1 2∑+∑1 +∑2-⎰⎰∑-⎰⎰∑2=15π+π- 16π=-15π.2 2.……… (1 分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题课指导丛书名称:微积分
出版单位: 中国人民大学出版社 出版日期:2002年7月
主编:赵树嫄
一、课程学时学分:
课程总学时:120 课程总学分:6
习题课总学时:20 习题课总学分:0
二:习题课的地位、作用与目的:
微积分习题课是微积分课程的重要组成部分,是学生学习这门课程的一个必要环节。通过对微积分学习各类习题的讲解,能使学生加深对该课程内容的理解,获得对求解微分积分等数学习题所必要的技能技巧;也能使学生在学习过程中,获得应用微积分知识解决实际问题的能力,为学生进一步学习概率统计、经济类等课程以及为将来可能从事的科研工作打下良好的基础。
读书以过目成诵为能,最是不济事。——郑板桥
第九章 微分方程 2学时
(1)基本内容 常微分方程的阶、解、通解、特解等基本概念,线性微分方程解的性质与通解的结构,一阶(高阶)微分方程可积类型和二阶常系数线性齐次(非齐次)微分方程的解法,微分方程的简单应用。
(2) 基本要求 处理作业批改中发现的问题,复习本讲微分方程的基本概念、解的结构和例题,举例说明如何对实际问题分析等量关系并建立微分方程,举例讲解求微分方程的通解或特解的解题思路和技巧,特别是二阶常系数线性齐次(非齐次)微分方程的解法。
读书以过目成诵为能,最是不济事。——郑板桥
习题课教学大纲(微积分Ⅲ)
(征求意见稿)
课程名称:大学数学-微积分Ⅲ
英文名称:Calculus
课程性质:必修 课程代码:
第五章 不定积分 2学时
一、基本内容:复习原函数和不定积分的概念,不定积分的基本性质及基本积分公式,总结换元积分法和分部积分法,有理函数、三角函数的有理式和简单无理函数的积分的计算方法。
二、基本要求:处理作业批改中发现的问题,举例说明原函数与不定积分之间的关系,
讲解,演练换元积分法与分部积分法,补充求有理函数、三角函数的有理式和简单无理函数的积分的例题讲解。
处理作业批改中发现的问题。通过具体例子讲解极限的计算问题,连续性讨论问题,复合函数定义域及分段函数的复合问题。
第三章 导数与微分 2学时
(1)基本内容:导数及高阶导数的定义;复合函数 隐函数 参数方程决定的函数和分段函数的求导;微分。
(2)基本要求:处理作业批改中发现的问题;举列说明复合函数 隐函数 参数方程决定的函数和分段函数的一阶二阶求导;会求微分。
第八章 多元函数微分法极其应用 4学时
基本内容 1.空间直角坐标系简介;空间中两点距离及二次曲面方程
2.复习多元函数的概念,二元函数的极限与连续以及有界闭区域上连续函数的性质,偏导数和全微分的概念,全微分存在的必要条件和充分条件;复合函数一阶、二阶偏导数的求法,计算隐函数的偏导数,多元函数极值和条件极值的概念,二元函数极值的充分条件,计算二元函数的无条件极值和条件极值地方法和简单函数的最大值和最小值的应用题解法。
3. 二重积分的定义及性质,二重积分的计算-直角坐标与极坐标方法
基本要求
1、讲评本章批改作业中的典型问题
2、讲解多元函数的一、二阶偏导数与全微分的例题,重点举多元复合函数及隐函数求导例子, 使学生能熟练掌握它们的计算方法。本章的基本应用拉格朗日条件极值求最大值应用问题。
3、举例讲解二重积分化成二次积分直角坐标及极坐标方法。
第六章 定积分及应用 2学时
一、 基本内容:式,定积分的换元积分法和分部积分法。无穷限广义积分和无界函数的广义积分,函数。
二、基本要求
(1)复习定积分的概念和定积分的基本性质, 理解变上限函数并掌握其求导方法,举例说明掌握牛顿-莱布尼茨公式的应用,定积分的换元积分法与分部积分法,广义积分的概念和计算广义积分,了解函数,通过课堂练习消化上述内容。
(2)基本要求:处理作业批改中发现的问题;举例说明利用定积分计算一些几何量 (平面图的面积、旋转体的体积及侧面积)
第七章 无穷级数 2学时
(1)基本内容: 常数项级数的概念和性质和审敛法。幂级数以及函数展开成幂级数。函数幂级数展开式的应用。傅里叶级数和一般周期的傅里叶级数。
(2)基本要求: 处理作业批改中发现的问题。讲解常数项级数的常用审敛法应用实例,以及如何求幂级数的收敛半径。对于函数展开成幂级数的性质和应用,可以选择用方法复习讲解。对于傅里叶级数则重点讲解和函数的表示以及傅里叶系数的求法。
第四章 微分中值定理与导数的应用 2学时
1.中值定理及洛必达法则
(1) 基本内容:中值定理的应用;洛必达法则求极限.
(2)基本要求:处理作业批改中发现的问题;通过具体例子讲解中值定理的题型和解题步骤;求各种不定形的极限并注意化简和变形技巧.
2.边际与弹性
基本要求:处理作业批改中发现的问题;举例说明弹性在经济中的需求、收益中应用.
三、习题课课程基本要求:
第一、二章 函数与极限
1.函数与极限 2学时
(1)基本内容
函数的概念,函数的表示,函数的几种特性,复合函数,分段函数,极限的概念及性质,极限存在准则,重要极限,无穷小量与无穷大量,极限的计算,函数的连续与间断,闭区间上连续函数的性质。
(2)基本要求
