沪科版九年级数学上册第22章 相似形测试题
沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,小颖身高为160cm,在阳光下影长AB=240cm,当她走到距离墙角(点D)150cm处时,她的部分影子投射到墙上,则投射在墙上的影子DE的长度为()A.50B.60C.70D.802、下列图形相似的是()(1)放大镜下的图片与原来的图片;(2)幻灯的底片与投影在屏幕上的图象;(3)天空中两朵白云的照片;(4)卫星上拍摄的长城照片与相机拍摄的长城照片.A.4组B.3组C.2组D.1组3、如图,,,,则的长为().A. B. C.4 D.64、下列所给条件中,不能使△ABC与△A’B’C’相似的是( )A.AB=AC, A'B'=A'C',∠A=∠A'B.∠A=40°,∠B=80°,∠A'=40°,∠C'=60°C. , ∠B=∠B'D. ,∠A=∠A'5、如图,在△ABC中,DE∥BC,= ,四边形DECB的面积是10,则△ABC 的面积为()A.4B.8C.18D.96、已知a,b,c,d是成比例线段,其中a=3cm,b=2cm,c=6cm,则d的长度为()A.4cmB.5cmC.6cmD.9cm7、如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD=1,BD=2,则的值为()A. B. C. D.8、如图,D是AB的中点,E是AC的中点,则△ADE与四边形BCED的面积比是()A.1B.C.D.9、下列命题为真命题的是()A.有两边及一角对应相等的两个三角形全等B.方程 x 2+2x+3=0有两个不相等的实数根C.面积之比为1∶2的两个相似三角形的周长之比是1∶4D.顺次连接任意四边形各边中点得到的四边形是平行四边形10、如图,直线l1∥l2∥l3,直线AC和直线DF在l1, l2, l3上的交点分别为:A,B,C,D,E,F.已知AB=6,BC=4,DF=9,则DE=()A.5.4B.5C.4D.3.611、如图,,两条直线与三条平行线分别交于点和.已知,则的值为()A. B. C. D.12、勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以勾股图为背景的邮票。
沪科版九年级数学上册《第二十二章相似形》单元测试卷-带参考答案

沪科版九年级数学上册《第二十二章相似形》单元测试卷-带参考答案一、单选题1.已知三个数1,2,4,若添一个数使得四个数成比例,这个数可以是( )A .8B .8-C .3D .3-2.已知35x y =,则x x y+的值为( ) A .25 B .38C .32 D .233.已知2a =3b (a≠0,b≠0),那么下列变形中错误的是( )A .23b a = B .32a b = C .32a b= D .b :a =2:34.若x 是3和6的比例中项,则x 的值为( )A .32B .32-C .23±D .32±5.如图,在△ABC 中,DE△BC ,AD =5,AB =12,AE =3,则EC 的长是( )A .365B .215C .20D .156.已知点P 是线段MN 的黄金分割点,MP >NP ,且MP=51)cm ,则NP 等于( )A .2cmB .(35cmC .5﹣1)cmD .5+1)cm7.如图,直线 123l //l //l ,一等腰 Rt ABC 的三个顶点 A 、 B 、 C 分别在直线 1l 、 2l 和 3l上, ACB 90∠=︒ , AC 交 2l 于点 D. 若 1l 与 2l 的距离为 1 , 1l 与 3l 的距离为 4 ,则ABBD的值是( )A 2B 34C 42D 528.如图,AD△BE△CF ,直线l 1、l 2这与三条平行线分别交于点A ,B ,C 和点D ,E ,F .已知AB=1,BC=3,DE=2,则EF 的长为( )A .4B .5C .6D .89.如图,△ABC 中,AD 是中线,BC =8,△B =△DAC ,则线段AC 的长为( )A .4B .42C .6D .4 310.下列各组数中,能成比例的是( )A .3,4,5,6B .-1,-2, 2,4C .-3,1,3,0D .-1,2,-3,4二、填空题11.如图,已知AB CD EF ,若632AC CE DF ===,,,则BD 的长为 .12.如图,△ABC 是边长为a 的等边三角形,将三角板的30°角的顶点与A 重合,三角板30°角的两边与BC 交于D 、E 两点,则DE 长度的取值范围是 .13.如图,在等腰直角△ABC 中,AB=4,点D 在边AC 上一点且AD=1,点E 是AB 边上一点,连接DE ,以线段DE 为直角边作等腰直角△DEF( D 、E 、F 三点依次呈逆时针方向),当点F 恰好落在BC 边上时,则AE 的长是 .三、解答题14.已知:如图,在△ABC 中,△ACB =90°,CD △AB ,垂足为D ,AD =3,BD =6,求CD 的长.15.如图,在矩形ABCD 中,E 是BC 的中点,DF△AE ,垂足为F .(1)求证:△ABE△△DFA . (2)若AB=6,BC=4,求DF 的长.16.在△ABC 中,点D 、E 分别边AB 、AC 上的点,若AD =2,DB =7,AE =3,EC =3,求DE :BC的值.17.如图,四边形ABCD 和四边形EFGH 相似,求△α、△β 的大小和EH 的长度.四、综合题18.在矩形 ABCD 中,点 O 是对角线 AC 、 BD 的交点,直角 EPF ∠ 的顶点 P 与 O 重合, OE 、 OF 分别与 AB 、 BC 边相交于 E 、 F ,连接 EF , BC k AB =⋅ ( k 为常数).(1)发现问题:如图1,若 1k = ,猜想:OEOF= ; (2)类比探究:如图2, 1k ≠ 探究线段 OE , OF 之间的数量关系,并说明理由;(3)拓展运用:如图3,在(2)的条件下,若 FO FC = , 2k =和 6OD =,求 EF 的长.19.如图,点C 、D 在线段AB 上,△PCD 是等边三角形,且CD 2=AD •BC .(1)求证:△APD △△PBC ; (2)求△APB 的度数.20.定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.(1)如图1,在四边形 ABCD 中 80ABC ∠=︒ , 140ADC ∠=︒ 对角线 BD 平分ABC ∠ .求证: BD 是四边形 ABCD 的“相似对角线”;(2)如图2,已知 FH 是四边形 EFGH 的“相似对角线” 30EFH HFG ∠=∠=︒ .连接EG ,若 EFG ∆ 的面积为 3,求 FH 的长.21.(教材呈现)下图是华师版九年级上册数学教材第78页的部分内容.例2 如图:在ABC 中,D 、E 分别是边BC 、AB 的中点, AD 、CE 相交于点G .求证:13GE GD CE AD ==. 证明:连接ED .(1)请根据教材提示,结合图①,写出完整的证明过程.(2)(结论应用)如图②,在ABC 中,D 、F 分别是边BC 、AB 的中点,AD 、CF 相交于点G ,GE AC 交BC 于点E ,GH AB 交BC 于点H ,则EGH 与ABC 的面积的比值为 .答案解析部分1.【答案】A【解析】【解答】解:设添加的数是x根据题意得 124x =:: 即24=1x ⨯⨯ 解得:=8x 故答案为:A .【分析】如果两个数的比值与另两个数的比值相等 就说这四个数成比例 据此解答即可.2.【答案】B【解析】【解答】解:∵35x y =∴设x=3k y=5k∴33358x k x y k k ==++故答案为:B .【分析】根据35x y = 设x=3k y=5k 再将x 、y 的值代入x x y+计算即可。
沪科版九年级数学上册试题 第22章《相似形》单元测试卷(含答案详解)

第22章《相似形》单元测试卷一、单选题(本大题共10小题,每小题3分,共30分)1.两千多年前,古希腊数学家欧多克索斯发现了黄金分割,即:如图,点P 是线段AB 上一点(AP >BP ),若满足,则称点P 是AB 的黄金分割点.黄金分割在日常生活中处处可见,例如:主持人在舞台上主持节目时,站在黄金分割点上,观众看上去感觉最好.若舞台长20米,主持人从舞台一侧进入,设他至少走x 米时恰好站在舞台的黄金分割点上,则x 满足的方程是( )A .(20﹣x )2=20xB .x 2=20(20﹣x )C .x (20﹣x )=202D .以上都不对2.如图,点D ,E ,F 分别在的边上,,,,点M 是的中点,连接并延长交于点N ,则的值是( )A .B .C .D .3.将含有的三角板按如图所示放置,点在直线上,其中,分别过点,作直线的平行线,,点到直线,的距离分别为,,则的值为( )BP APAP AB=ABC V 13AD BD =DE BC ∥EF AB ∥EF BM AC ENAC32029161730︒ABC A DE 15BAD ∠=︒B C DE FG HIB DE HI 1h 2h 12h hA .1 BCD4.如图,点D 是△ABC 中AB 边上靠近A 点的四等分点,即4AD =AB ,连接CD ,F 是AC 上一点,连接BF 与CD 交于点E ,点E 恰好是CD 的中点,若S △ABC =8,则四边形ADEF 的面积是( )A .4B .C .2D .5.如图,在边长为的小正方形组成的网格中,建立平面直角坐标系,的三个顶点均在格点(网格线的交点)上.以原点为位似中心,画使它与的相似比为,则点的对应点的坐标是( )A .B .C .或D .或6.如图,已知、,与相交于点,作于点,点是的中点,于点,交于点,若,,则值为( )11-1181171ABC V O 111A B C △ABC V 2B 1B ()42,()42--,()42,()42--,()42,()42,-AB BC ⊥DC BC ⊥AC BD O OM BC ⊥M E BD EF BC ⊥G AC F 4AB =6CD =OM EF -A.B .C .D .7.如图,在平面直角坐标系中,为原点,为平面内一动点,,连接,点是线段上的一点,且满足.当线段取最大值时,点的坐标是( )A .B .C .D .8.如图,四边形是矩形,平分,,、的延长线交于点,连接,连接交于点.下列结论错误的是()A .图中共有三个等腰直角三角形B .C .D .9.如图,在平面直角坐标系中,点,点B 是线段上任意一点,在射线上取一点C ,使,在射线上取一点D ,使.所在直线的关系式为,点F 、G分别为线段的中点,则的最小值是()751253525O OA OB ==C 32BC =AC M AC :1:2CM MA =OM M36,55⎛⎫ ⎪⎝⎭612,55⎛⎫ ⎪⎝⎭ABCD CE BCD ∠AE CE ⊥EA CB F DE BD CE G DGC EBC∠=∠AB AD CG CE⋅=⋅∽CDG CEBV V ()E OE OA OB BC =BC BD BE =OA 12y x =OC DE 、FGABC .D .4.810.如图所示,正方形由四个全等的直角三角形和一个小正方形组成,且内接于正方形,连接,.已知正方形与正方形面积之比为,若,则( )A BCD .二、填空题(本大题共8小题,每小题4分,共32分)11.已知,且,则 .12.在中,M ,N 分别是BC ,AC 边上一点,连接AM ,BN 交于点P ,若,,则 .13.正方形中,E ,F 分别是,上的点,连结交对角线于点G ,若恰好平分,,则的值为 .ABCD FGHI DE BE CE>ABCD FGHI 59DE CH ∥BECE=32::3:5:7a b c =10a b c -+=a b c ++=ABC V :2:3BM CM =:1:4AN CN =:AP MP =ABCD AD DC EF BD BE AEF ∠413DG GB =DE AE14.宽与长的比等于黄金比的矩形称为黄金矩形.古希腊很多矩形建筑中宽与长的比都等于黄金比,如图,矩形ABCD 为黄金矩形,AB <AD ,以AB 为边在矩形ABCD 内部作正方形ABEF ,若AD =1,则DF = .15.如图,矩形的两条对角线相交于点O ,,垂足为E ,F 是的中点,连接交于点P,那么.16.如图,中,,,,若正方形的顶点在上,顶点、都在上,射线交边于点,则长为 .17.如图:等腰直角三角形中,E 为边上一点,.将沿着翻折得到线段,连接,若.ABCD AC BD ,OE AB ⊥OC EF OB OPPB=ABC V 90ACB ∠=︒2BC =4AC =DEFC D AB F G AC AF BC H CH ABC BC 3BE CE =AB AE AD CD AB =CD =18.如图,在矩形中,,,点在直线上,从点出发向右运动,速度为每秒,点在直线上,从点出发向右运动,速度为每秒,相交于点,则的最小值为 .三、解答题19.(8分)如图,,于点D ,M 是的中点,交于点P ,.若,求的长.ABCD 5cm AB =6cm BC =E AD A 0.5cm F BC B 2cm BE AF 、G BG CG +cm AB AC =AD BC ⊥AD CM AB DN CP ∥6cm AB =PN20.(8分)如图,四边形ABCD 中,AB=AC=AD ,AC 平分∠BAD ,点P 是AC 延长线上一点,且PD ⊥AD .(1)证明:∠BDC=∠PDC ;(2)若AC 与BD 相交于点E ,AB=1,CE :CP=2:3,求AE 的长.21.(10分)如图,在斜坡的顶部有一铁塔AB ,B 是CD 的中点,CD 是水平的,在阳光的照射下,塔影DE 留在坡面上.若铁塔底座宽CD=12m ,塔影长 m ,小明和小华的身高都是1.6m ,同一时刻小明站在点E 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m 和1m ,求塔高AB.18DE22.(10分)如图1,在,,,D 为上一点,连接,分别过点A 、B 作于点N ,于点M .(1)求证:;(2)若点D 满足,求的长;(3)如图2,若点E 为中点,连接,求证:.图1 图2Rt ABC △90ACB ∠=︒1AC BC ==AB CD AN CD ⊥BM CD ⊥ACN CBM V V ≌21BDAD =∶∶DM AB EM 45EMN ∠=︒23.(10分)如图,在正方形中,点是对角线上一点,的延长线交于点,交的延长线于点,连接.(1)求证:;(2)求证:;(3)若的长.ABCD G BD CG AB E DA F AG CG AG =2AB BE DF =⋅GE =GC =EF24.(12分)如图,在平面直角坐标系中,点A 在轴的正半轴上,点在轴的负半轴上,点在轴的正半轴上,且,线段、的长是一元二次方程的两个根,且.(1)求点A 、点的坐标;(2)求点的坐标;(3)若直线过点A 交线段于点,且,求点坐标;(4)在平面内是否存在一点,使得以为直角顶点的与相似,若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.x B x C y 90ACB ∠=︒OB OA 213360x x -+=OB OA <B C l BC D :1:2ABD ADC S S =△△D P P APC △ABC V P答案一、单选题1.A【分析】点P 是AB 的黄金分割点,且PB <PA ,PB =x ,则PA =20−x ,则,即可求解.解:由题意知,点P 是AB 的黄金分割点,且PB <PA ,PB =x ,则PA =20−x ,∴,∴(20−x )2=20x ,故选:A .2.A【分析】过点F 作交AC 于点G,可证.同理,可得,,;由,得,于是;设,则,,,从而得.解:过点F 作交AC 于点G,∴∴.BP AP AP AB=BP AP AP AB =FG BN ∥EN GN =13AE AD EC DB ==3EC AE =13AE BF EC FC ==FG BN ∥13BF NG FC GC ==3GC NG =EN NG a ==3=GC a 5EC a =203AC a =320EN AC =FG BN ∥1EN EM GN FM==EN GN =∵,∴.∴.∵,∴.∵,∴.∴.设,则,∴∴.∴.∴.∴.故选:A3.B【分析】设交于点,由,得三角形BCM 为等腰直角三角形,再由含30度角直角三角形三边长比及等腰直角三角形的边长比,设BC 为x ,可得MA 为,再由平行线分线段成比例求解.解:设交于点,∵,,DE BC ∥13AE AD EC DB ==3EC AE =EF AB ∥13AE BF EC FC ==FG BN ∥13BF NG FC GC ==3GC NG =EN NG a ==3=GC a 5EC EN NG GC a=++=35EC AE a ==53AE a =520+533AC AE EC a a a =+==320203EN a AC a ==CE FG M 45DAC BAD CAB ∠=∠+∠=︒MA x =-CE FG M 30CAB ∠=︒15BAD ∠=︒∴,∵,∴,三角形为等腰直角三角形,在Rt △ABC 中,设长为,则,∵,∴,∴,∵,∴,故选:B .4.D【分析】过D 点作DG∥EF ,连接AE ,,GF =FC ,再计算△ADE 和△AEF 的面积即可.解:过D 点作DG ∥EF ,连接AE ,∵点E 恰好是CD 的中点,4AD =AB ,∴,GF =FC ,设AG =k ,则AF =4k ,GF =3k ,FC =3k ,∴,∵,S △ABC =8,∴,∴,∵,∴,∴=.45DAC BAD CAB ∠=∠+∠=︒//FG DE 45CMB DAC ∠=∠=︒BCM BC x CM BC x ==30CAB ∠=︒CA ==MA x =-////HI FG DE 121h MA h CM ===14AG AD AF AB ==14AG AD AF AB ==43AF FC =14ACD ABC S AD S AB ∆∆==124ACD ABC S S ∆∆==112ADE AEC ACD S S S ∆∆∆===43AEFCEF S AF S CF ∆∆==4477AEF AEC S S ∆∆==417ADE AEF ADEF S S S ∆∆=+=+四边形117故选:D .5.C【分析】直接利用位似图形的性质画出三角形顶点的对应点,再顺次连接即可画出图形,根据点的位置写出坐标即可.解:如图所示,当和在原点同侧时,∵与的相似比为2,,∴,即;如图所示,当和在原点两侧时,∵与的相似比为2,,∴,即;综上所述,或,故选C.1B ABC V 111A B C △111A B C △ABC V ()2,1B ()122,12B ⨯⨯()142B ,ABC V 111A B C △111A B C △ABC V ()2,1B ()122,12B -⨯-⨯()142B --,()142B --,()142B ,6.A【分析】证明,,,,求出,求出,,得出即可得出答案.解:、,,∴,,,∴,,∴,,∴,,∴,点是的中点,,,,∴,,∴,∴,故选:.7.DCOM CAB △∽△BOM BDC V V ∽OM CM AB BC =OM BM DC BC =125OM =132EG CD ==122FG AB ==1EF EG FG =-=AB BC ⊥ DC BC ⊥OM BC ⊥OM AB CD ∥∥COM CAB ∴V V ∽BOM BDC V V ∽OM CM AB BC =OM BM DC BC =4OM CM BC =6OM BM BC=125OM =EF BC ⊥ EG AB CD ∥∥ E BD BE DE ∴=BG CG ∴=CF AF ∴=132EG CD ==122FG AB ==1EF EG FG =-=75OM EF -=A【分析】由题意可得点在以点为圆心,为半径的上,在轴的负半轴上取点,连接,分别过、作,,垂足为、,先证,得,从而当取得最大值时,取得最大值,结合图形可知当,,三点共线,且点在线段上时,取得最大值,然后分别证,,利用相似三角形的性质即可求解.解:∵点为平面内一动点,,∴点在以点为圆心,为半径的上,在轴的负半轴上取点,连接,分别过、作,,垂足为、,∵∴∴,∵,∴,∵,∴,∴,∴当取得最大值时,取得最大值,结合图形可知当,,三点共线,且点在线段上时,取得最大值,C B 32OB x 0D ⎛⎫ ⎪ ⎪⎝⎭BD C M CF OA ⊥ME OA ⊥F E OAM DAC V V ∽23OM OA CD AD ==CD OM D B C B DC CD BDO CDF V V ∽AEM AFC V V ∽C 32BC =C B 32OB x 0D ⎛⎫ ⎪ ⎪⎝⎭BD C M CF OA ⊥ME OA ⊥F E OA OB ==AD OD OA =+=23OA AD =:1:2CM MA =23OA CM AD AC==OAM DAC ∠∠=OAM DAC V V ∽23OM OA CD AD ==CD OM D B C B DC CD∵∴,∴,∵,∴,∵轴轴,,∴,∵,∴,∴,解得同理可得,,∴,解得∴∴当线段取最大值时,点的坐标是,故选D .8.A【分析】根据矩形的性质以及角平分线的性质得,是等腰直角三角形,,是等腰直角三角形,由证明,可得,,则,是等腰直角三角形,由,可得,由三角形外角的性质可得,证明,列比例式并结合等量代换可得.OAOB ==OD =BD =152==9CD BC BD =+=23OM CD =6OM =y x ⊥CF OA ⊥90DOB DFC ∠∠==︒BDO CDF ∠∠=BDO CDF V V ∽OB BD CF CD =1529=CF =AEM AFC V V ∽23ME AM CF AC ==23=ME =OE ===OM M 45DCE BCE ∠=∠=︒CEF △45F DCE ∠=∠=︒ABF △SAS (SAS)≌EBF EDC V V FEB CED ∠=∠BE ED =90FEB CEB CEB CED ∠+∠=∠+∠=︒BED V EBF EDC △≌△FEB CED ∠=∠DGC EBC ∠=∠∽CDG CEB V V AB AD CG CE ⋅=⋅解:如图:四边形是矩形,,,,平分,,,,是等腰直角三角形,,,是等腰直角三角形,,,,,,,,是等腰直角三角形,是等腰直角三角形,故A 错误;,,,,故B 正确;,,故D正确;ABCD AB CD ∴=90ABC BCD ADC ∠=∠=∠=︒90ABF ∴∠=︒CE BCD ∠45DCE BCE ∴∠=∠=︒AE CE ⊥ 90FEC ∴∠=︒CEF ∴V EF CE ∴=45F ∠=︒ABF ∴V BF AB CD ∴==45F DCE ∠=∠=︒ (SAS)≌EBF EDC ∴V △FEB CED ∴∠=∠BE ED =90FEB CEB CEB CED ∴∠+∠=∠+∠=︒BE ED = BED ∴V DCH V 45EBD ∴∠=︒45DGC GCB CBG CBG ∠=∠+∠=︒+∠ 45EBC EBD CBG CBG ∠=∠+∠=︒+∠DGC EBC ∴∠=∠DCG ECB ∠=∠ ∽CDG CEB ∴V V,,,,,故C 正确.故选:A .9.A【分析】如图所示,连接,设射线交射线于H ,过点H 作于M ,连接,先根据三线合一定理得到,,进而证明四边形是矩形,得到,,故当点B 与点M 重合时,最小,即最小,最小值为,设,则,求出,利用相似三角形的性质求出(舍去),则的最小值为.解:如图所示,连接,设射线交射线于H ,过点H 作于M ,连接,∵,,点F 、G 分别为线段的中点,∴,,∵,∴,即,∴四边形是矩形,∴,,∴当最小时,最小,∴当点B 与点M 重合时,最小,即最小,最小值为,∵点H 在直线上,∴可设,∴,∵,CD CG CE CB∴=CD AB = BC AD =AB CG CE AD∴=AB AD CG CE ∴⋅=⋅BF BG ,ED OA HM OE ⊥BH BF OC BG DE ⊥,⊥OBF CBF DBG EBG ==∠∠,∠∠BFHG FG BH =90OHE ∠=︒BH FG HM ()2H m m ,2OM m HM m ==,OE =OMH HME △∽△m =0m =FG BF BG ,ED OA HM OE ⊥BH OB BC =BD BE =OC DE 、BF OC BG DE ⊥,⊥OBF CBF DBG EBG ==∠∠,∠∠180OBF CBF DBG EBG +++=︒∠∠∠∠90CBF DBG +=︒∠∠90FBG ∠=︒BFHG FG BH =90OHE ∠=︒BH FG BH FG HM 12y x =()2H m m ,2OM m HM m ==,()E∴∵,∴,又∵,∴,∴,∴∴(舍去),经检验,∴,故选A .10.A【分析】设,,则,根据正方形与正方形面积之比为,得到,求出,作交于点M ,作交于点P ,证明出,设,则然后利用相似三角形的性质得到,然后解方程求解即可.解:由题意可得,∴设,,则,∵,∴,OE =90MEH HOE MHO MOH +=︒=+∠∠∠∠MHO MEH =∠OMH HME =∠∠OMH HME △∽△OM HM HM ME=2m m =m =0m =m =FG CI DH a ==CH b =IH a b =+ABCD FGHI 59()22259a b a b +=+2BI CH a ==BM GH ⊥GH NE BM ⊥BM BPE ENC ∽V V CN m =IN BP a m ==+a m a a m +=BIC CHD ≌V V CI DH a ==CH b =IH a b =+90H ∠=︒22222CD CH DH a b =+=+∵正方形与正方形面积之比为,∴,即,∴整理得,∴,解得或(舍去),∴,∴,如图所示,作交于点M ,作交于点P ,由题意可得,,∵,∴四边形,是矩形,∴,,∴,∴设,则,∵,∴,∵,∴,∴,又∵,∴,ABCD FGHI 592259CD IH =()22259a b a b +=+222520a ab b -+=25220a a b b ⎛⎫-+= ⎪⎝⎭12a b =2a b=2b a =2BI CH a ==BM GH ⊥GH NE BM ⊥BM AGD DHC ≌V V ED CH ∥BINP ENHD 2PN BI a ==EN DH a ==PE PN EN a =-=CN m =IN BP a m ==+BE CE ⊥90BEP CEN ∠+∠=︒BP PN ⊥90BEP PBE ∠+∠=︒CEN PBE ∠=∠90BPE ENC ∠=∠=︒BPE ENC ∽V V∴,即,∴整理得,∴,∴解得,∴故选:A .二、填空题11.30【分析】设,,,根据得到,求得,从而得出,,,代入进行计算即可.解:,设,,,,,解得:,,,,,故答案为:30.12.【分析】过点M 作,交于点Q ,根据平行线分线段成比例可得,设,求出,即可求解.解:过点M 作,交于点Q ,BP PE BE EN CN CE ==a m a a m+=220a am m -+=210a a m m ⎛⎫-+= ⎪⎝⎭a m =BE CE =3a k =5b k =7c k =10a b c -+=35710k k k -+=2k =6a =10b =14c =::3:5:7a b c = ∴3a k =5b k =7c k =10a b c -+= 35710k k k ∴-+=2k =6a ∴=10b =14c =6101430a b c ∴++=++=5:8MQ BN ∥AC 23BM NQ CM CQ ==2,3NQ k CQ k ==54k AN =MQ BN ∥AC∵,∴,设,∴,∵,∴,则,∵,∴,故答案为:.13.或4【分析】延长交于R ,作于T ,不妨设,,,可证得是等腰三角形,可推出,进而表示出,然后解,从而求出x 的值,进而可得结果.解:如图,延长交于R ,作于T ,,不妨设,,则,设,MQ BN ∥23BM NQ CM CQ ==2,3NQ k CQ k ==5CN NQ CQ k =+=:1:4AN CN =154AN k =54k AN =MQ PN ∥55428kAP AN MP NQ k ===5:812EF BC GT DE ⊥4DG =13GB =4DE x =REB V 413EG DE DG RG BR BG ===EG DEG △EF BC GT DE ⊥ 413DG GB =∴4DG =13GB =17BD =4DE x =四边形是正方形,,,,,,恰好平分,,,,,在中,,由勾股定理得,解得,,当,当,综上所述,或4,故答案为:或4.14【分析】先根据黄金矩形求出AB ,再利用正方形的性质求出AF ,然后进行计算即可解答.解:∵矩形ABCD 为黄金矩形,AB <AD ,ABCD ∴BC AD ∥AD ==∴EBC AEB ∠=∠4AE AD DE x =-=413EG DE DG RG BR BG ===∴13BR x = BE AEF ∠∴AEB FEB ∠=∠∴EBC FEB ∠=∠∴13ER BR x ==∴4521717EG ER x ==Rt EGT V GT DT DG ===4ET DE DT x =-=-((22252417x x ⎛⎫+-= ⎪⎝⎭1x =2x =∴4DE x ==DE =AE ==∴4DE AE=DE =AE ==∴12DE AE =12DE AE =12∴∴∵四边形ABEF 是正方形,∴∴DF=AD -AF=15.【分析】根据矩形性质得到,利用三角形的三线合一得,过O 作交于点Q ,则有,,计算即可.解:∵是矩形,∴,∵F 是的中点,∴,又∵,∴,过O 作交于点Q ,∴,,∴,故答案为:.16.AB AD =AB AD ==1=13OA OB OC ==AE EB =OQ AB P EF OQF AEF V V ∽OQP BEP V V ∽ABCD OA OB OC ==OC 1122OF OC OA ==OA OB =OE AB⊥AE EB =OQ AB P EF OQF AEF V V ∽OQP BEP V V ∽13OP OQ OQ OF PB BE AE AF ====1343【分析】证明,,由相似三角形的性质得出 , ,设, 可得,, 从而可得出答案.解:∵四边形为正方形, ,∴,,∴,, ∴, , 设, ∴,, ∴, ∴, ∴.故答案为 .17.2【分析】如图,作,使,连接,,交于,过作于,可得,,可得,求解,,可得,由对折可得:,,,证明,可得,再证明,可得,有,,求解,可得,从而可得答案.解:∵等腰直角三角形,∴,如图,作,使,连接,,交于,过作于,△∽△ADG ABC AEF AHC V V ∽DG AG BC AC=EF AF CH AC =DG EF x ==24x AG =4x AG x CH +=DGFE 90ACB ∠=︒DG EF BC ∥∥DG EF =△∽△ADG ABC AEF AHC V V ∽DG AG BC AC=EF AF CH AC =DG EF x ==24xAG =4x AG x CH +=2AG x =24x x x CH +=43CH =43AH AE ⊥AH AE =DE EH CH DE K A AF BC ⊥F BAE CAH ∠=∠BC ==12AF CF BC ===()SAS BAE CAH ≌△△454590BCH ∠=︒+︒=︒BE CH ==CE EF ==AH AE ===52EH ==AB AD ==BAE DAE ∠=∠DE BE =45ADE ABE ∠=∠=︒()SAS AEC AHD V V ≌90ECH EDH ∠=∠=︒()Rt Rt HL HEC EHD V V ≌HED CHE ∠=∠CH DE ==EK HK =CK DK =EK HK ==CK DK ===HKE CKD V V ∽ABC AB =AB AC ==BC =AH AE ⊥AH AE =DE EH CH DE K A AF BC ⊥F∵等腰直角三角形,∴,,∴,∴,∴,,∴,∵,∴,,∴∴,由对折可得:,,,∵,∴,∴,∵,,∴,∴,∴,∴,∵,,∴,ABC 90BAC EAH ∠=︒=∠AB AC ==45B ACB ∠=∠=︒BAE CAH ∠=∠BC ==12AF CF BC ===()SAS BAE CAH ≌△△BE CH =45B ACH ∠=∠=︒454590BCH ∠=︒+︒=︒3BE CE =BE CH ==CE EF ==AH AE ===52EH =AB AD ==BAE DAE ∠=∠DE BE ==45ADE ABE ∠=∠=︒90BAC EAH ∠=∠=︒90BAE EAC DAE DAH ∠+∠=︒=∠+∠EAC DAH ∠=∠AE AH =AB AC AD ==()SAS AEC AHD V V ≌45ACE AHD ∠=∠=︒CE HD ==454590EDH ∠=︒+︒=︒90ECH EDH ∠=∠=︒EH EH =CE DH =()Rt Rt HL HEC EHD V V ≌∴,,∴,,由勾股定理可得:,∴,∴,∴,∴,,∴,∴,∴,故答案为:218.10【分析】过点作直线,分别交、于点,过点作直线,分别交、于点,易知四边形、、为矩形,证明,由相似三角形的性质可得;设两点运动时间为,则,,易得,;作点关于直线的对称点,由轴对称的性质可得,故当三点共线时,的值最小,即取最小值,此时,在中,由勾股定理求得的值,即可获得答案.解:如下图,过点作直线,分别交、于点,过点作直线,分别交、于点,HED CHE ∠=∠CH DE ==EK HK =CK DK =222EK CE CK =+222EK EK ⎫=-+⎪⎪⎭EK HK ==CK DK ===45DK CK EK HK ===HKE DKC ∠=∠HKE CKD V V ∽45CD CK HE HK ==4452552CD EH ==⨯=G MN BC ⊥AD BC M N 、G PQ CD ∥AB DC P Q 、ABNM PBNG GNCQ GAE GFB V V ∽AE GM BF GN =E F 、t 0.5AE t =2BF t =1cm GM =4cm GN =C PQ K CG KG =B G K 、、BG KG +BG CG +Rt BCK △BK G MN BC ⊥AD BC M N 、G PQ CD ∥AB DC P Q 、易知四边形、、为矩形,,∵四边形为矩形,∴,∴,,∴,∴,设两点运动时间为,则,,则有,即,∵,∴,,∵四边形为矩形,∴,作点关于直线的对称点,如图,则,,由轴对称的性质可得,当三点共线时,的值最小,即取最小值,此时,在中,,∴的最小值为.故答案为:10.三、解答题19.ABNM PBNG GNCQ 5cm MN AB ==ABCD AD BC ∥AB DC∥GAE GFB ∠=∠GEA GBF ∠=∠GAE GFB VV ∽AEGM BF GN=E F 、t 0.5AE t =2BF t =0.5124GM t GN t ==4GN GM =5cm MN =1cm GM =4cm GN =GNCQ 4cm QC GN ==C PQ K 4cm QK QC ==8cm KC QK QC =+=CG KG =B G K 、、BG KG +BG CG +Rt BCK △10cm BK ===BG CG +10cm解:∵,,∴,又∵,∴,∴,∵点M 是线段的中点,,∴,∴,∴,∵,∴.20.解:(1)证明:∵AB=AD ,AC 平分∠BAD ,∴AC ⊥BD ,∴∠ACD+∠BDC=90°,∵AC=AD ,∴∠ACD=∠ADC ,∴∠ADC+∠BDC=90°,∵PD ⊥AD ,∴∠ADC+∠PDC=90°,∴∠BDC=∠PDC ;(2)解:过点C 作CM ⊥PD 于点M ,AB AC =AD BC ⊥BD DC =DN CM ∥1BN BD PN DC==BN NP =AD DN CM ∥1AP AM PN MD==AP PN =13PN AB =6cm AB =()1162cm 33PN AB ==⨯=∵∠BDC=∠PDC ,∴CE=CM ,∵∠CMP=∠ADP=90°,∠P=∠P ,∴△CPM ∽△APD ,∴=,设CM=CE=x ,∵CE :CP=2:3,∴PC=x ,∵AB=AD=AC=1,∴=,解得:x=,故AE=1-=.21.解:如图,过点D 作,交AE 于点F ,过点F 作,垂足为点G.由题意得,,∴,∵,,∴,∴,答:塔高AB 为24m.CM AD PC PA32x 13x 23x 12+131323DF CD ⊥FG AB ⊥1.62DF DE =18 1.6214.4(m)DF =⨯÷=16m 2GF BD CD === 1.61AG GF =1.669.6(m)AG =⨯=14.49.624(m)AB =+=22.解:(1)证明:∵,,∴,,又∵,∴,∴∵,∴;(2)解:∵,,∴,∴,设,则,由(1)知,,∵,∴,∴,∴,∴,∴;(3)解:延长,相交于点H,AN CD ⊥BM CD ⊥90ANC ∠=︒90BMC ∠=︒90ACB ∠=︒90ACN BCM BCN CBM ∠+∠=∠+∠=︒ACN CBM∠=∠AC BC =()ACN CBM ASA V V ≌AND BMD ∠=∠ADN BDM ∠=∠AND BMD V V ∽12AN DN AD BM DM DB ===AN x =2BM x =AN CM x ==2BM CN x ==222AN CN AC +=()22221x x +=x =CM =CN =MN 2233DM MN ===ME AN∵E 为的中点,∴∵,,∴,∴,,∴,∴,又∵,∴,又∴,∴,∴.23.解:(1)证明:∵是正方形的对角线,∴,,在和中,,∴,∴;(2)证明:∵四边形是正方形,∴,,,AB AE BE=90ANM ∠=︒90BMN ∠=︒AN BM ∥HAE MBE ∠=∠AHE BME ∠=∠()AAS AHE BME V V ≌AH BM =BM CN =CN AH =CM AN=MN HN =45HMN ∠=︒45EMB ∠=︒BD ABCD 45C D B A D B ∠=∠=︒DC DA =CDG V ADG △DC DA CDG ADG DG DG =⎧⎪∠=∠⎨⎪=⎩()SAS CDG ADG ≌△△CG AG =ABCD 90CBE FDC ∠=∠=︒CB CD AB ==CB DF ∥∴,∴,∴,即,∴;(3)解:∵∴,∵四边形是正方形,∴,,,∴,∴,,∴,∴,设,则,∴,∵,∴,,∴,∴,∴,∴的长为24.(1)解:∵,∴.∴.∵点A 在轴的正半轴上,点在轴的负半轴上,BCE DFC ∠=∠BCE DFC ∽△△CB FD BE DC =AB FD BE AB=2AB BE DF =⋅GE =GC =CE CG GE =+=ABCD CD AB ∥CD AB =CB AD ∥BE CD ∥EBG CDG ∠=∠BEG DCG ∠=∠BEG DCG ∽△△BE GE DC GC ==BE =6CD x =(66AE AB BE CD BE x x =-=-==AF CB ∥FAE CBE ∠=∠AFE BCE ∠=∠AFE BCE △∽△EF AE EC BE==EF =EF 213360x x -+=(4)(9)0x x --=124,9x x ==x B x∴A 点坐标为,B 点坐标为,(2)∵A 点坐标为,B 点坐标为,∴,设点C 的坐标为,则,∵,,∴,∴,∴,∴,∴,解得,经检验,是方程的解且符合题意,∴点C 的坐标是;(3)过点D 作轴于点E ,轴于点F ,如图,则,∴,,∵,∴.∴;,∵,,∴;,()9,0()4,0-()9,0()4,0-9,4OA OB ==()0,t ()0t >OC t =90ACB ∠=︒90AOC COB ∠=∠=︒90OCB ACO OCB OBC ∠+∠=∠+∠=︒ACO OBC ∠=∠ACO CBO V V ∽OC AO OB OC=94tt =6t =6t =()0,6DE x ⊥DF y ⊥DE OC ∥DF OB∥BED BOC V V ∽CDF CBO V V ∽:1:2ABD ADC S S =△△:1:2BD DC =13DE BD OC BC ==23DF CD BO BC ==4OB =6OC =2DE =243DF =解得.∴.(4)解:存在,求解过程如下:设,由题意可得:,,当时,,即,,解得,或,即点坐标为或,当时,,即,,解得或,即点坐标为或,综上可知,满足条件的P 点为:或或或83DF =8,23D ⎛⎫- ⎪⎝⎭(,)P x y 13AB OB OA =+=BC ===AC ===AP =CP =APC ACB △∽△AP AC PC AC AB CB ==29AC AP AB===6AC CB CP AB ⨯===00x y =⎧⎨=⎩721310813x y ⎧=⎪⎪⎨⎪=⎪⎩P (0,0)72108,1313⎛⎫⎪⎝⎭APC BCA △∽△AP AC PC BC AB AC ==6AC BC AP AB ⨯===29AC CP AB===96x y =⎧⎨=⎩45133013x y ⎧=⎪⎪⎨⎪=-⎪⎩P ()9,64530,1313⎛⎫- ⎪⎝⎭(0,0)72108,1313⎛⎫ ⎪⎝⎭()9,64530,1313⎛⎫- ⎪⎝⎭。
沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、图中的两个三角形是位似图形,它们的位似中心是()A.点PB.点OC.点MD.点N2、如图,已知△ACD∽△ADB,AC=4,AD=2,则AB的长为()A.1B.2C.3D.43、以下变换可以改变图形的大小的是()A.位似变换B.旋转变换C.轴对称变换D.平移变换4、如图,直线l1∥l2∥l3,直线AC分别交l1, l2, l3于点A,B,C;直线DF分别交l1, l2, l3于点D,E,F.AC与DF相交于点H,且AH=2,HB=1,BC=5,则的值为()A. B.2 C. D.5、如图,△ABC∽△ADE ,则下列比例式正确的是()A. B. C. D.6、已知2x=5y(y≠0),则下列比例式成立的是( )A. B. C. D.7、如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端、树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距6m,与树相距15m,则树的高度为( )A.4mB.5mC.7mD.9m8、在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是()A. B. C. D.9、如图,在中,点D为AB边上一点,E、F分别为AC、BC边上的点,,连接AF交DE于点G,则下列结论中一定正确的是()A. B. C. D.10、下列各组中的四条线段成比例的是()A.a=1,b=3,c=2,d=4B.a=4,b=6,c=5,d=10C.a=2,b=4,c=3,d=6 D.a=2,b=3,c=4,d=511、某一时刻,身髙1.6m的小明在阳光下的影长是0.4m,同一时刻同一地点测得某旗杆的影长是5m,则该旗杆的高度是()A.1.25mB.10mC.20mD.8m12、已知P,Q是线段AB的两个黄金分割点,且AB=10,则PQ长为()A.5( -1)B.5( +1)C.10( -2)D.5(3- )13、书画经装裱后更便于收藏.如图,画心ABCD为长90cm、宽30cm的矩形,装裱后整幅画为矩形A′B′C′D′,两矩形的对应边互相平行,且AB与A′B'的距离、CD与C′D′的距离都等于4cm.当AD与A′D′的距离、BC与B'C′距离都等于acm,且矩形ABCD∽矩形A′B′C′D'时,整幅书画最美观此时,a的值为()A.4B.6C.12D.2414、如图,D、E分别是△ABC的边AB、AC的中点,H、G是边BC上的点,且=12,则图中阴影部分的面积为()HG= BC,S△ABCA.6B.4C.3D.215、如图,在菱形ABCD中,点E为边AD的中点,且∠ABC=60°,AB=6,BE交AC于点F,则AF=()A.1B.2C.2.5D.3二、填空题(共10题,共计30分)16、已知AM是△ABC中BC边上的中线,P是△ABC的重心,过P作EF(EF∥BC),分别交AB、AC于E、F,则=________.17、已知点P把线段分割成AP和PB两段(AP>PB),如果AP是AB和PB的比例中项,那么AP:AB的值等于________ .18、已知线段a=2cm,b=8 cm,若线段c是a,b的比例中项,那么c=________cm19、将一个矩形沿着一条对称轴翻折,如果所得到的矩形与这个矩形相似,那么我们就将这样的矩形定义为“白银矩形”.事实上,“白银矩形”在日常生活中随处可见.如,我们常见的A纸就是一个“白银矩形”.请根据上述信息4纸的较长边与较短边的比值.这个比值是________求A420、如图,内接于,于点,若,,的半径,则的值为________.21、如图,点,分别在的边,的延长线上,.若,的面积为3,则的面积为________.22、如图,在直角坐标系中,点,,以O为位似中心,按2:1的相似比把缩小为,则点E的对应点的坐标为________ .23、一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C 的坐标为(﹣3,0),∠B=30°,则点B的坐标为________ .24、如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE 沿CE折叠,使点B落在矩形内点F处,下列结论正确的是________(写出所有正确结论的序号)①当E为线段AB中点时,AF∥CE;②当E为线段AB中点时,AF=;③当A、F、C三点共线时,AE=;④当A、F、C三点共线时,△CEF≌△AEF.25、小颖测得2m高的标杆在太阳下的影长为1.2m,同时又测得一棵树的影长为2.4m,请你帮助小颖计算出这棵树的高度为________m.三、解答题(共5题,共计25分)26、已知xyz≠0且,求k的值.27、如图,小明在地面上放置一个平面镜来测量铁塔的高度,镜子与铁塔的距离米,镜子与小明的距离米时,小明刚好从镜子中看到铁塔顶端.已知小华的眼睛距地面的高度CD=1.6米,求铁塔的高度.(根据光的反射原理,)28、如图,在△ABC中,AB=8,AC=6,D是AC上的一点,且AD=2,试在AB上确定一点E,使得△ADE与原三角形相似,并求出AE的长.29、如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,求球拍击球的高度h.30、如图,△ABC中,DE∥BC,EF∥AB求证:△ADE∽△EFC.参考答案一、单选题(共15题,共计45分)1、A2、A3、A4、D5、D6、C7、C8、C9、C10、C11、C12、C14、A15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、29、30、。
沪科版九年级上册数学第22章 相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,在正方形中,点是边的中点,连接,交边于点,已知,则的长为()A. B. C.1 D.22、下列四组线段中,是成比例线段的是()A.5cm,6cm,7cm,8cmB.3cm,6cm,2cm,5cmC.2cm,4cm,6cm,8cmD.12cm,8cm,15cm,10cm3、下列命题中不成立的是()A.矩形的对角线相等B.三边对应相等的两个三角形全等C.两个相似三角形面积的比等于其相似比的平方D.一组对边平行,另一组对边相等的四边形一定是平行四边形4、如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2, AC=3, BC=6,则⊙O的半径是()A.3B.4C.4D.25、下列各选项的两个图形(实线部分),不属于位似图形的是()A. B. C. D.6、在一比例尺为1:100 000的地图上,一块绿地面积为3cm2,则这块绿地实际面积为()A.300000cm 2B.300m 2C.900000m 2D.3×10 6m 27、在相同时刻的物高与影长成比例,如果高为1.5m的测杆的影长为2.5m,那么影长为30m的旗杆是()A.20mB.16mC.18mD.15m8、如图,△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC和△ACB相似的条件是()A.①②④B.①③④C.②③④D.①②③9、如图,在正方形中,为中点,.联结.那么下列结果错误的是()A. 与相似B. 与相似C. 与相似 D. 与相似10、两个相似三角形的面积比为1∶4,那么这两个三角形的周长比为()A.1∶2;B.1∶4;C.1∶8;D.1∶16.11、如图,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )A.4B.2C.4D.值不确定12、如图,在△ABC中,∠BAC=90°,F是BA延长线上一点,FD⊥BC于D,交AC于点E,则图中相似三角形共有几对()A.6对B.5对C.4对D.3对13、生活中到处可见黄金分割的美.如图,点C将线段AB分成AC、CB两部分,且AC>BC,如果,那么称点C为线段AB的黄金分割点.若C是线段AB的黄金分割点,AB=2,则分割后较短线段长为()A. B. C. D.14、下列说法中,错误的是()A.两个全等三角形一定是相似形B.两个等腰三角形一定相似C.两个等边三角形一定相似D.两个等腰直角三角形一定相似15、如图,点D、E分别在AB、AC上,且若,,;则AB的长为(A.16B.8C.10D.5二、填空题(共10题,共计30分)16、甲、乙两盏路灯底部间的距离是30米,一天晚上,当小华走到距路灯乙底部5米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.5米,那么路灯甲的高为________米.17、如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x 轴上(C与A不重合)当点C的坐标为________时,使得△BOC∽△AOB.18、在△ABC中,AB=9,AC=12,BC=18,D是AC边上一点,DC= AC,在AB边上取一点E,连接DE,若两个三角形相似,则DE的长为________.19、如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则的值为________.20、如图,已知点A在反比例函数y=(x<0)上,作Rt ABC,点D是斜边AC的中点,连接DB并延长交y轴于点E,若BCE的面积为7,则k的值为________.21、在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,则高楼的高度是________米.22、如图,中,平分,,,,,则________.23、如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点F为DM中点,点E为DC上的动点.当∠DFE=45°时,则DE=________ .24、如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB 的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点P的坐标是________ .25、如图,O为坐标原点,点C的坐标为(1,0),∠ACB=90°,∠B=30°,当点A在反比例函数y= 的图象上运动时,点B在函数________(填函数解析式)的图象上运动.三、解答题(共5题,共计25分)26、已知xyz≠0且,求k的值.27、如图,▱ABCD的对角线AC、BD相交于点O,点E、F、G、H分别是线段OA、OB、OC、OD的中点,那么▱ABCD与四边形EFGH是否是位似图形?为什么?28、如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且.(1)∠1与∠2相等吗?为什么?(2)判断△ABE与△ACD是否相似?并说明理由.29、如图,等腰的顶角,请用尺规作图法,在边上求作一点,使得∽.(保留作图痕迹,不写作法)30、如图,已知,求证:△ABD∽△ACE参考答案一、单选题(共15题,共计45分)1、C2、D3、D4、D5、C6、D7、C8、D9、C10、A11、A12、A13、B14、B15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题,共计25分)26、28、30、。
沪科版九年级上册数学第22章 相似形 含答案
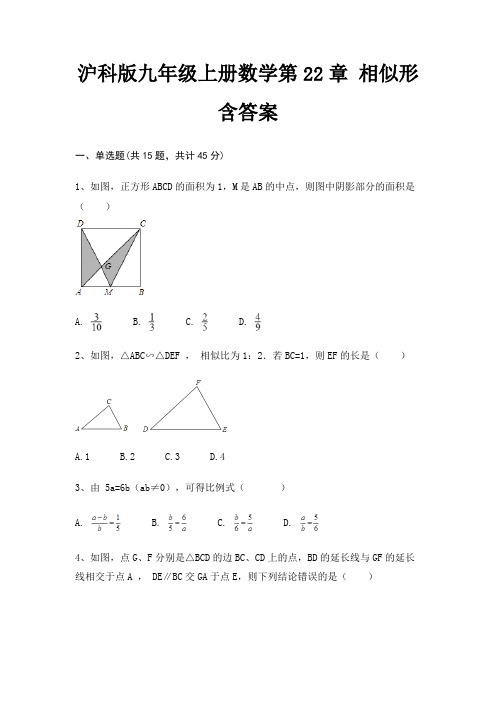
沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,正方形ABCD的面积为1,M是AB的中点,则图中阴影部分的面积是()A. B. C. D.2、如图,△ABC∽△DEF ,相似比为1:2.若BC=1,则EF的长是()A.1B.2C.3D.43、由 5a=6b(ab≠0),可得比例式()A. B. C. D.4、如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A , DE∥BC交GA于点E,则下列结论错误的是()A. B. C. D.5、如图,□ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC 等于()A.3:2B.3:1C.1:1D.1:26、已知=,那么下列等式中,不一定正确的是()A.2a=5bB. =C.a+b=7D. =7、如图,△ABC内接于⊙O,AD⊥BC于点D,AD=2cm,AB=4cm,AC=3cm,则⊙O 的直径是( )A.2cmB.4cmC.6cmD.8cm8、如图,在中,于点,若,则的值为()A. B. C. D.9、如图,直线l1∥l2∥l3,直线AC分别交l1, l2, l3于点A , B ,C;直线DF分别交l1, l2, l3于点D , E , F . AC与DF相交于点H ,且AH=2,HB=1,BC=5,则的值为().A. B.2 C. D.10、已知x:y=3:2,则下列各式中不正确的是()A. B. C. D.11、下列各组图形中一定相似的有()A.两个矩形B.两个等腰梯形C.两个等腰三角形D.两个等边三角形12、如图,△ABC中,D是边AC上的一点,且∠DBC=∠A,BC=, AC=3,则CD的长是 ( )A.1B.C.2D.13、雨后初晴,一学生在运动场上玩耍,从他前面2米远一块小积水处,他看到旗杆顶端的倒影,如果旗杆底端到积水处的距离为40米,该生的眼部高度是1.5米,那么旗杆的高度是()A.30米B.40米C.25米D.35米14、已知,那么的值为()A. B. C. D.15、如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB,若AB=3BD。
沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,AD是的一条角平分线,点E在AD上.若,,则与的面积比为()A.1:5B.5:1C.3:20D.20:32、如图,Rt△ABC中,AB⊥AC,AB=3,AC=4,P是BC边上一点,作PE⊥AB于E,PD⊥AC于D,设BP=x,则PD+PE=()A. B. C. D.3、下列两个图形一定相似的是)A.任意两个矩形B.任意两个等腰三角形C.任意两个正方形D.任意两个菱形4、如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是()A. B. C. D.5、如图,△ABC 与△A′B′C′是位似图形,点O 是位似中心,若OA=2AA′,S △ABC =8,则S △A′B′C′=( )A.18B.12C.32D.166、如图,Rt△ABC 中,∠BAC=90°,AD⊥BC 于点D ,若BD :CD=3:2,则= ( )A. B. C. D.7、如图,中,,则下列等式中不成立的是( )A.B.C.D.8、已知△ABC∽△DEF,且相似比为2:3,则△ABC 与△DEF 的对应高之比为( )A.2:3B.3:2C.4:9D.9:4 9、如图所示,不能判定△ABC∽△DAC 的条件是( )A.∠B=∠DACB.∠BAC=∠ADCC.AD 2=BD•BCD.AC 2=DC•BC10、如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=,则△ABC的边长是()A.3B.4C.5D.611、已知:,下列式子中错误的是()A. B. C. D.12、如图△ABC∽△ACD,则下列式子中不成立的是()A. =B. =C.AC 2=AD•ABD. =13、按100分制60分及格来算,满分是150分的及格分是()A.60分B.72分C.90分D.105分14、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有()A.1个B.2个C.3个D.4个15、如图所示,E为□ABCD的边AD上的一点,且AE∶ED=3∶2,CE交BD于F,则BF∶FD ()A.3∶5B.5∶3C.2∶5D.5∶2二、填空题(共10题,共计30分)16、如图是的中线,是上一点,且,的延长线交于点,若,则________.17、在同一时刻,太阳光下身高1.6m的小强的影长是1.2m,学校旗杆的影长是15m,则旗杆高为________ m18、如图,已知顶点,以原点为位似中心,把缩小到原来的,则与点对应的点的坐标是________.19、如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为________时,△ADP和△ABC相似.20、如图,在方格纸中,以每个小方格的边长为单位1,△ABC和△EPD的顶点均在格点上,请你提供一个符合条件的点P,使△ABC与以E,P,D为顶点的三角形相似,则点P所在的格点坐标可以是________21、如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②;③△PMN为等边三角形;④当∠ABC=45°时,BN=PC.其中正确的是________ .22、如图,内接于,于点D,,若的半径,则的长为________.23、如图,某风景区在建设规划过程中,需要测量两岸码头A、B之间的距离.设计人员在O点设桩,取OA、OB的三等分点C、D,测得CD=25m,则AB=________ .24、如图,A的坐标是(0,2),点C是x轴上的一个动点,点B与点O在直线AC两侧,∠BAC=∠OAC,BC⊥AC,点B的坐标为(x,y),y与x的函数关系式为________.25、如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD,AB=2,OD=3,则BC的长为________.三、解答题(共5题,共计25分)26、已知a、b、c满足,且,分别求出a、b、c 的值.27、如图:已知等边三角形ABC,D为AC边上的一动点,CD=nDA,连线段BD,M为线段BD上一点,∠AMD=60°,AM交BC于E.(1)若n=1,则= .= ;(2)若n=2,求证:BM=6DM;(3)当n= 时,M为BD中点.(直接写结果,不要求证明)28、已知:如图,Rt△ABC中,∠ACB=90°,P是边AB上一点,AD⊥CP,BE⊥CP,垂足分别为D、E,已知AB=3, BC=3, BE=5.求DE的长.29、如图,小明在地面上放置一个平面镜来测量铁塔的高度,镜子与铁塔的距离米,镜子与小明的距离米时,小明刚好从镜子中看到铁塔顶端.已知小华的眼睛距地面的高度CD=1.6米,求铁塔的高度.(根据光的反射原理,)30、如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E。
沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、在平面直角坐标系中,,,若把线段扩大倍得线段,若,则的坐标可以是()A. B. C. D.2、若a、b、c、d是成比例线段,其中a=5cm,b=2.5cm,c=10cm,则线段d的长为()A.2cmB.4cmC.5cmD.6cm3、如图,菱形ABCD中,点M,N在AC上,ME⊥AD, NF⊥AB. 若NF = NM = 2,ME = 3,则AN =()A.3B.4C.5D.64、如图,将△ABC的三边分别扩大一倍得到△A1B1C1(顶点均在格点上),若它们是以P点为位似中心的位似图形,则P点的坐标是()A.(-3,-3)B.(-4,-4)C.(-4,-3)D.(-3,-4)5、如图,Rt△ABC中,∠ACB=90°,CD为斜边上的高,AC=2,AD=1,则BC的长是()A.4B.3C.D.6、如图,在平面直角坐标系中有一个四边形ABCD,现将四边形ABCD各顶点的横坐标和纵坐标都乘2,得到四边形A1B1C1D1,则四边形A1B1C1D1的面积与四边形ABCD的面积之比为()A.2:1B.3:1C.4:1D.5:17、如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB CF;③CF=FD;④△ABE∽△AEF.其中正确的有()A.1个B.2个C.3个D.4个8、如图,在平面直角坐标系中,动点A、B分别在x轴上和函数y=x的图象上,AB=4,CB⊥AB,BC=2,则OC的最大值为()A.2 +2B.2 +4C.2D.2 +29、一个油桶高0.8m,桶内有油,一根长lm的木棒从桶盖小口插入桶内,一端到达桶底,另一端恰好在小口处,抽出木棒量得浸油部分长0.8m,则油桶内的油的高度是()A.0.8mB.0.64mC.1mD.0.7m10、如图,□ABCD中,EF∥AB,DE∶EA = 2∶3,EF = 4,则CD的长为()A. B.8 C.10 D.1611、将一副三角板如图叠放,交点为O则△AOB与△COD面积之比是().A. B. C. D.12、若一个图形的面积为2,那么将它与成中心对称的图形放大为原来的两倍后的图形面积为()A.8B.6C.4D.213、有以下命题:.①如果线段d是线段a、b、c的第四比例项,则有②如果点C是线段AB的中点,那么AC是AB、BC的比例中项③如果点C是线段AB的黄金分割点,且AC>BC,那么AC是AB、BC的比例中项④如果点C是线段AB的黄金分割点,且AC>BC,且AB=2,则AC= -1其中正确的有( )A.1个B.2个C.3个D.4个14、如图,一次函数的图象与x轴,y轴交于A,B两点,与反比例函数的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接.有下列四个结论:①与的面积相等;②;③;④.其中正确的结论是()A.1个B.2个C.3个D.4个15、如图,在△ABC中,DE∥BC ,则下列比例式中,不成立的是().A. B. C. D.二、填空题(共10题,共计30分)16、如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长为________17、如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是________.18、高6m的旗杆在水平地面上的影子长4m,同一时刻附近有一建筑物的影子长20米,则该建筑物的高为________19、在如图所示方格纸中,已知△DEF是由△ABC经相似变换所得的像,那么△DEF的每条边都扩大到原来的________ 倍.20、如图所示,△ABC中,DE∥BC,AE:EB=2:3,若△AED的面积是4m2,则四边形DEBC的面积为________21、如图,在平行四边形ABCD中,AB=3,AD=4 ,AF交BC于E,交DC的延长线于F,且CF=1,则CE的长为________.22、如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x <3),矩形EFGH的面积为y,那么y关于x的函数解析式是________.23、如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么的值等于________.24、如图,四边形ABCD与四边形EFGH的对应边平行,AD是△PHE的中位线,若四边形ABCD的面积4,则四边形EFGH面积是________.25、如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于点E, cos B=,则=________.三、解答题(共5题,共计25分)26、如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.27、如图,在△ABC中,EF∥BC且EF= BC=2cm,△AEF的周长为10cm,求梯形BCFE的周长.=2,四边形A′28、如图,四边形ABCD和四边形A′B′C′D′位似,位似比k1B′C′D′和四边形A″B″C″D″位似,位似比k=1.四边形A″B″C″D″和2四边形ABCD是位似图形吗?位似比是多少?29、如图△ABC中,D、E是AB、AC上点,AB=7.8,AD=3,AC=6,AE=3.9,试判断△ADE与△ABC是否会相似.30、如图,△ABC中,点D在AB上,∠ACD=∠ABC,若AD=2,AB=6,求AC的长.参考答案一、单选题(共15题,共计45分)1、C2、C3、B4、C5、D6、C7、C8、A9、B10、C11、B12、A13、C14、D15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、28、30、。
沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,在△ABC中,点D是AB边上的一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )A.4B.3C.2D.12、如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE 的是()A. =B. =C.∠B=∠DD.∠C=∠AED3、手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是()A. B. C. D.4、矩形的两边长分别为a、b,下列数据能构成黄金矩形的是()A.a=4,b= +2B.a=4,b= ﹣2C.a=2,b=+1 D.a=2,b= ﹣15、已知点把线段分成两条线段、,且,下列说法错误的是()A.如果,那么线段被点黄金分割B.如果,那么线段被点黄金分割 C.如果线段被点黄金分割,那么与的比叫做黄金比 D. 是黄金比的近似值6、在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,则旗杆高为()A.16mB.18mC.20mD.22m7、如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有()A.1条B.2条C.3条D.4条8、如图,△ABC中,AB=AC=10,点D在BC上,连接AD,若CD=AB,AD=BD,则BC的长为()A.-5+5B.5+5C.10+5D.15-59、下列四条线段成比例的是()A. B. C.D.10、若=(a≠0,b≠0),则=()A. B. C. D.11、如图,已知AB、CD、EF互相平行,且AB=1,CD=4,那么EF的长是()A. B. C. D.12、如图,已知P是△ABC边AB上的一点,连接CP.以下条件中不能判定△ACP∽△ABC的是()A.∠ACP=∠BB.∠APC=∠ACBC.AC 2=AP•ABD. =13、如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①=;②若点D是AB的中点,则AF=AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若=,则S△ABC =9S△BDF,其中正确的结论序号是()A.①②B.③④C.①②③D.①②③④14、如图,△ABC中,DE∥BC,若AD:DB=2:3,则下列结论中正确的()A. =B. =C. =D. =15、△ADE∽△ABC,且相似比为1:3,若△ADE的面积为5,则△ABC的面积为()A.10B.15C.30D.45二、填空题(共10题,共计30分)16、如图,平面直角坐标系中有正方形和正方形,若点和点的坐标分别为,,则两个正方形的位似中心的坐标是________.17、《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门位于的中点,南门位于的中点,出东门15步的处有一树木,求出南门多少步恰好看到位于处的树木(即点在直线上)?请你计算的长为________步.18、如图,在中,D,E为边的三等分点,,H为与的交点.若,则________.19、在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF 与DC交于点F,若AB=9,DF=2FC,则BC=________.(结果保留根号)20、如图,正方形的边在的边上,顶点D、G分别在、上,,如果,,那么正方形的边长等于________.21、如果线段a、b满足,那么的值等于________.22、已知图中的每个小正方格都是边长为1的小正方形,若△ABC与是位似图形,且顶点都在小正方形顶点上,则它们的位似中心的坐标是________.23、在ΔABC 中,AC=4,BC=2. 点 D 在射线 AB 上,在构成的图形中,ΔACD 为等腰三角形,且存在两个互为相似的三角形,则 CD 的长是________.24、如图,已知点A、B分别在反比例函数y=(x>0),y=﹣(x>0)的图象上,且OA⊥OB,则的值为________.25、勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则APn的长度是________.三、解答题(共5题,共计25分)26、解方程.534%-2x=0.5627、如图为三个并列的边长相同的正方形,试说明:∠1+∠2+∠3=90°.28、如果一个矩形ABCD(AB<BC)中,≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE(如图),请问矩形ABFE是否是黄金矩形?请说明你的结论的正确性.29、如图,已知:AB∥FG,AC∥EH,BG=CH,求证:EF∥BC.30、将三角形各边向外平移1个单位并适当延长,得到如图(1)所示的图形,变化前后的两个三角形相似吗?如果把三角形改为正方形、长方形呢?(如图(2)(3))参考答案一、单选题(共15题,共计45分)1、B2、B3、D4、D5、C6、C7、C8、B9、C11、D12、D13、C14、B15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题,共计25分)26、28、30、。
沪科版九年级上册数学第22章 相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶()A.0.5mB.0.55mC.0.6mD.2.2m2、下列说法正确的是()A.分别在△ABC的边AB,AC的反向延长线上取点D,E,使DE∥BC,则△ADE是△ABC放大后的图形B.两位似图形的面积之比等于位似比C.位似多边形中对应对角线之比等于位似比D.位似图形的周长之比等于位似比的平方3、如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于()A.2B.3C.D.4、如图,在正△ABC中,D,E分别在AC,AB上,且,AE=BE,则有()A.△AED∽△ABCB.△ADB∽△BEDC.△BCD∽△ABCD.△AED∽△CBD5、如图,P是Rt△ABC的斜边BC上异于B,C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有()A.1条B.2条C.3条D.4条6、如图,在大小为4×4的正方形网格中,是相似三角形的是()A.①和②B.②和③C.①和③D.②和①7、如图,点G是的重心,过点G作,分别交、于点D、E,则与的关系为()A. B. C. D.8、如图,DE是△ABC的中位线,已知△ABC的面积为8 ,则△ADE的面积为( ) .A.2B.4C.6D.89、下列结论中,错误的有:()①所有的菱形都相似;②放大镜下的图形与原图形不一定相似;③等边三角形都相似;④有一个角为110度的两个等腰三角形相似;⑤所有的矩形不一定相似.A.1个B.2个C.3个D.4个10、如图,给出下列条件:①;②;③;④其中单独能够判定的个数为()A.1B.2C.3D.411、如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②= ;③DP2=PH•PB;④tan∠DBE=2﹣.其中正确的是()A.①②③④B.①②④C.②③④D.①③④12、如图,△ABC中,点D在AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F,连接CD,交EF于点G,则下列说法错误的是()A. B. C. D.13、如图,正方形ABCD的面积为12,M是AB的中点,连接AC、DM,则图中阴影部分的面积是()A.6B.4.8C.4D.314、如图,的面积为12,点D、E分别是边AB、AC的中点,则的面积为()A.6B.5C.4D.315、如图,中,,,.将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是()A. B. C.D.二、填空题(共10题,共计30分)16、如图,在平面直角坐标系中,点O为坐标原点,A(﹣8,0),B(﹣8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转后得到四边形OA′B′C′,此时线段OA′,B′C′分别与直线BC相交于点P,Q.当四边形OA′B′C′的顶点B′落在y轴的正半轴上,的值为________.17、如图,O是四边形ABCD对角线的交点,已知∠BAD+∠BCA=180°,AB=5,AC=4,AD=3,=,则BC=________.18、如果两个相似多边形对应边的比是2:3,那么这两个相似多边形周长的比是________19、如图,,如果,,,那么________.20、有一个三角形的三边长为2,4,5,若另一个和它相似的三角形的最短边为4,则第二个三角形的周长为________。
沪科版九年级上册数学第22章 相似形 含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD 于点E、F,连接BD、DP,,BD与CF相交于点给出下列结论:①BE=2AE;②△DFP∽△BPA:③:④DP2=PH.PC其中正确的是()A.①②③④B.①③④C.②③D.①②④2、如图,△ABC是一张锐角三角形的纸片,AD是边BC上的高,已知BC=20cm,AD=15cm,从这张纸片上剪一下一个矩形,使矩形的一边在BC上,另两个顶点分别在AB、AC上。
则下列结论不正确的是()A.当△AHG的面积等于矩形面积时,HE的长为5cmB.当HE的长为6cm 时,剪下的矩形的边HG是HE的2倍C.当矩形的边HG是HE的2倍时,矩形面积最大D.当矩形的面积最大时,HG的长是10cm3、如图,DE∥BC,则下列不成立的是()A. B. C. D.4、如图,∠1=∠2,则下列各式中,不能说明△ABC∽△ADE的是( )A.∠D=∠BB.∠E=∠CC.D.5、如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为()A.5B.6C.7D.86、在△ABC中,点D、E分别在AB、AC上,如果AD=2,BD=3,那么由下列条件能够判定DE∥BC的是()A. =B. =C. =D. =7、如图,平面直角坐标系中,,反比例函数的图象分别与线段交于点,连接.若点关于的对称点恰好在上,则()A. B. C. D.8、如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE :S△COB等于()A.1:2B.1:3C.1:4D.2:39、△ABC∽△A′B′C′,且∠A=68°,则∠A′=().A.22°B.44°C.68°D.80°10、如果两个相似多边形的相似比为1:5,则它们的面积比为()A.1:25B.1:5C.1:2.5D.1:11、若△ABC∽△A′B′C′,AB=2,BC=3,A′B′=1,则B′C′等于( )A.1.5B.3C.2D.112、如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是()A.BO:BC=1:2B.CD:AB=2:1C.CO:BC=1:2 D.AD:DO=3:113、若,则的值是()A. B. C. D.14、下列关于相似的说法:①所有的等腰直角三角形一定相似;②所有的菱形一定相似;③所有的全等三角形一定相似;④所有的有一个角为60°的等腰梯形一定相似.其中说法正确的有( )A.1个B.4个C.3个D.2个15、在□ABCD中,是上一点,交于点,若,,则的长为()A.4B.5C.6D.7二、填空题(共10题,共计30分)16、如图,在矩形ABCD中,AB=4,AD=3,以点C为圆心作⊙C与直线BD相切,点P是⊙C上一个动点,连接AP交BD于点T,则的最大值是________.17、已知等腰直角△ABC,∠C=90°,AC=2,D为边AC上一动点,连结BD,在射线BD上取一点E使BE•BD=AB2.若点D由A运动到C,则点E运动的路径长为________.18、如图所示是一块含30°角的直角三角板,直角顶点位于坐标原点,斜边轴,顶点在函数的图像上,顶点在的图像上,,则________19、如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为________.20、如图,和都是等边三角形,且点A、C、E在同一直线上,与、分别交于点F、M,与交于点N.下列结论正确的是________(写出所有正确结论的序号).①;②;③;④21、如图:平行四边形ABCD中,E为AB中点,,连E、F交AC于G,则AG:GC=________;22、已知点是线段的黄金分割点,,且,则等于________ .23、在Rt△ABC纸片上剪出9个如图所示的正方形,点E,F落在AB边上,每个正方形的边长为1,则Rt△ABC的面积为________。
沪科版九年级数学上册试题 第22章 相似形 单元检测卷(含答案)

第22章《相似形》单元检测卷一、单选题(本大题共10小题,每小题3分,共30分)1.若、、、是成比例线段,其中,,,则线段的长为( )A .2B .3C .6D .272.如图,有三个矩形,其中是相似矩形的是( )A .甲与乙B .甲与丙C .乙与丙D .以上都不对3.若△ABC 的三边长分别为1△DEF的三边长分别2,,则与( )A .一定相似B .一定不相似C .不一定相似D .无法判定是否相似4.如图,在中,、分别是边、上的点,下列命题中,假命题是( )A .若,则与相似B .若,则与相似C .若,则与相似 D .若,则与相似5.在平行四边形ABCD 中,E 是上一点,,连接相交于F ,则的值为( )a b c d 15a =5b =9c =d ABC V DEFV ABC V D E AC AB AD DEAC BC=ADE V ABC V AD AEDC EB=ADE V ABC V AD AEAB AC=ADE V ABC V ADE B ∠=∠ADE V ABC V AD 23AE DE =BE AC 、BCF AEF S S △△A.B .C .D .6.在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是( )A .B .C .或D .或7.将三角形纸片按如图所示的方式折叠,使点落在边上,记为点,折痕为.已知,,若,那么的长度是( )A .B .4C .D .28.如图,点D 、E 、F 分别在的边上,且,,下列4个式子中,不正确的是( )A .B .C .D .9.如图,已知在矩形中,,,作对角线,按以下步骤作图:①以点为圆心、适当长为半径作弧,分别交边,于点,;②分别以点,为圆心、大于的长为半径作弧,两弧交于点;③作射线交于点,交于点,交的延长线于点.则( )329425457()6,2A ()6,2B -O 12ABO V A A '()12,4()3,1--()3,1()3,1--()12,4-()12,4ABC V B AC B 'EF 6AB AC ==8BC =FB C ABC '∽△△BF 247127ABC V AB AC BC 、、DE BC ∥EF AB ∥AD AEAB AC =BD BF AD FC=AE BFEC FC =AD BF AB BC=ABCD 3AB =5BC =AC B BA BC E F E F 12EF H BH AC G AD I CD J :JID JBC S S =V VA. B .C .D .10.如图,在平行四边形ABCD 中,,,,点E 为边上一动点,连接并延长至点F ,使得,以,为邻边构造,连接交于点O .当的长最小时,的长为( )A B.1 C .2 D .二、填空题(本大题共8小题,每小题4分,共32分)11.如果两个相似三角形的周长比是,那么它们的面积比是 .12.已知是线段上的黄金分割点若,若,则 .13.已知:如下图,,,,,则 .14.如图,,请你补充一个条件: ,使.15.如图,已知,,,,要使,只要.9254253525=60B ∠︒9AB =6AD =AB ED 14DF DE =EC EF EFGC Y EG DC EG AE 1+2M AB .AM BM <2cm AB =BM =cm BC DE ∥3AD =4AE =9AB =CE =12∠=∠ABC ADE △△∽90ACB ADC ∠=∠= 3BC =4AC =ABC ACD V V ∽CD =16.如图,E 为的中点,,,,则的长为 .17.如图,在正方形中,为中点,、分别是、边上的点,若,,则的长为 .18.如图,在中,E 、F 分别是的中点,,动点P 在射线上,交于D ,的平分线交于Q ,当时,则的值为 .三、解答题(本大题共6小题,共58分)19.(8分)如图,已知AB ∥DC ,点E 、F 在线段BD 上,AB =2DC ,BE =2DF .(1)求证:△ABE ∽△CDF .(2)若BD =8,DF =2,求EF的长.AB ADE B ∠=∠12AB =9AC =CD ABCD E AB G F AD BC 5AG BF +=90GEF ∠=︒GF ABC V ,AB AC 6,5BC CE ==EF BP CE CBP ∠CE 18EP BP +=CQ20.(8分)如图为平行四边形的边延长线上一点,分别交、于、.(1)求证:;(2)若,,求.21.(10分)每年的秋冬季节,青竹湖湘一外国语学校的银杏大道是学校最为靓丽的一条风景线,数学彭老师有一天为了测量一棵高不可攀的银杏树高度,他利用了反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离银杏树m 的点处,然后观测者沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得m ,观测者目高m ,则树高约是多少米?F ABCD AD BF CD ACG E GE BEEB EF=32EF =8GE =BE ()8AB E BE D A 2DE =1.75CD =AB22.(10分)观察与发现:如图:小明将一个边长为的正方形纸片折叠,使得点D 落在边上的点E 处(不与A ,B 重合),折痕交于点F ,交于点H ,点C 落在Q 处,与交于点G ,(1)小明认为,你同意吗?请说明理由.(2)实践与探究:在上图中,当时,请你计算的周长.23.(10分)感知:(1)数学课上,老师给出了一个模型:6cm ABCD AB FH AD BC EQ BC AEF BGE V V ∽2cm AE BGE △如图1,,由,,可得;又因为,可得,进而得到______.我们把这个模型称为“一线三等角”模型.应用:(2)实战组受此模型的启发,将三等角变为非直角,如图2,在中,,,点P 是BC 边上的一个动点(不与B 、C 重合),点D 是AC 边上的一个动点,且.①求证:;②当点P 为BC 中点时,求CD 的长;拓展:(3)在(2)的条件下如图2,当为等腰三角形时,请直接写出BP 的长.90BAD ACB AED ∠=∠=∠=︒12180BAD ∠+∠+∠=︒2180D AED ∠+∠+∠=︒1D ∠=∠90ACB AED =∠=︒ABC DAE △△∽BCAC=ABC V 10AB AC ==12BC =APD B ∠=∠ABP PCD △△∽APD △24.(12分)感知:如图①,在四边形 ABCD 中,AB CD ,∠B=90°,点 P 在 BC 边上,当∠APD=90°时,△ABP 与△PCD 是否相似? (填“是”或“否”).探究:如图②,在四边形 ABCD 中,点 P 在 BC 边上,当∠B=∠C=∠APD 时,求证:△ABP ∽△PCD .拓展:如图③,在△ABC 中,点 P 是边 BC 的中点,点 D 、E 分别在边 AB 、AC 上.若∠B=∠C=∠DPE=45°,BC=,CE=9,则 DE 的长为.∥答案一、单选题1.B【分析】如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.根据定义,将a ,b 及c 的值代入即可求得d .解:已知a ,b ,c ,d 是成比例线段,根据比例线段的定义得:,代入,,,解得:.故选:B .2.B【分析】根据矩形相似的条件,判断对应边的比是否相等即可.解:矩形甲长与宽比为,矩形乙长与宽比为,矩形丙长与宽比为,∴所以甲和丙的长与宽的比相等,故这两个矩形相似,故选:B .3.A【分析】求出三组对应边的比,观察是否相等即可作出判断.解:.故选:A .ad cb =ad cb =15a =5b =9c =95315d ⨯==322.551.53=1.5312=12ABC DEF ∴∽△△4.A【分析】三角形相似的判定方法:两边成比例且夹角相等的两个三角形相似;三边成比例的两个三角形相似;两角对应相等的两个三角形相似;根据三角形相似的判定方法容易得出结论.解:若,不满足三角形相似的判定方法,不一定相似,A 是假命题;若,则DE ∥BC ,△ADE~ △ACB B 正确;若又∠A=∠A,△ADE~△ACB, C 正确;若∠ADE=∠B,又∠A=∠A,△ADE~△ABC, D 正确;所以选A.5.C【分析】根据题目已知条件求证,再找到相似三角形的相似比即可表示出其面积比.解:∵四边形是平行四边形,∴,,∴,,∴,又∵,∴,∴,∴,故选:C .6.C【分析】根据位似变换的性质计算,得到答案.解:以原点为位似中心,相似比为 把缩小, ,AD DEAC BC=∴AD AEDC EB=∴∴AD AEAB AC= ∴∴ ∴∴AEF CBF ∽△△ABCD AD BC ∥=AD BC EAF BCF ∠=∠AEF CBF ∠=∠AEF CBF ∽△△23AE DE =25AE BC =2252452AEF CBF S AE S BC ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭△△254BCFAEFS S=△△O 1,2ABO V ()6,2A则点的对应点的坐标为 或 即或,故选:C.7.B【分析】设,根据折叠的性质用x 表示出和,最后根据两三角形相似对应边成比例即可求解.解:设,则由折叠的性质可知:,,当时,有,即:,解得:;故选:B .8.B【分析】证明,可判断选项A ;由平行线分线段成比例,可判断选项B 和C ;证明,推导出四边形是平行四边形,可判断选项D .解:∵,∴,∴,故A 正确,不符合题意;∵,∴,∵,∴,,故B 错误,符合题意;∵,∴,故C 正确,不符合题意;∵,∴,A A '1(6,2⨯12)2⨯116,2,22⎛⎫-⨯-⨯ ⎪⎝⎭()3,1()3,1--BF x =B F 'FC BF x =B F x '=8FC x =-FB C ABC '∽△△B F FC BA AC='866xx -=4x =ADE ABC △△∽ADE ABC △△∽BDEF DE BC ∥ADE ABC △△∽AD AE AB AC=DE BC ∥BD CE AD EA=EF AB ∥CF FB EACE =BD CF AD FB=EF AB ∥AE BF EC FC=DE BC ∥ADE ABC △△∽∴,∵,,∴四边形是平行四边形,∴,∴,故D 正确,不符合题意.故选:B .9.B【分析】利用相似三角形的性质解决问题即可.解:∵四边形是矩形,∴,,,由作图可知,平分,∴,∴,∴,∴,∵,∴,∴故选∶ B .10.B【分析】利用证明,根据已知条件求出与的线段比例关系,从而得出的长最小时,的长最小,即可求出.根据和推出四边形的形状,进而证明,即可求出的长度.解:过点A 作交于M ,AD DE AB BC=DE BC ∥EF AB ∥BDEF DE BF =AD BF AB BC=ABCD AD BC ∥5AD BC ==90ABC BAD ∠∠==︒BJ ABC ∠45ABJ CBJ ∠∠==︒45ABI AIB ∠∠==︒3AB AI ==2DI AD AI =-=AD BC ∥JDI JCB ∽V V 2425JID JBC S DI S BC ⎛⎫== ⎪⎝⎭V V EFGC Y DOE COG V :V EG OE OE EG OE AB ⊥ABCD Y AM DC ⊥AEMO AE OM =AE AM DC ⊥DC∵,∴.∵为平行四边形,∴,,∴,,∴.∴, ∴,∴的长最小时,的长最小,∴,∵在中,,,∴,∵,∴.∵,,∴,∵在平行四边形ABCD 中,,∴四边形为平行四边形.∵,,∴,∴.故选:B .14DF DE =45DE EF =EFGC EF CG =EF CG ∥EDO OCG ∠=∠DEO OGC ∠=∠DOE COG V :V 45DO OE DE CO OG CG ===49OE EG =OE EG OE AB ⊥ABCD Y 60B ADC ∠=∠=︒AM DC ⊥180180609030DAM ADC AMD ∠=︒-∠-∠=︒-︒-︒=︒6AD =132DM AD ==OE CD ⊥AM DC ⊥AM OE ∥AB CD P AEMO 9AB =45DO CO =4DO =1AE OM DO DM ==-=二、填空题11.【分析】根据相似三角形的性质求解即可.解:∵两个相似三角形的周长比是,∴这两个三角形的相似比为∴这两个三角形的面积比是;故答案为:.12.【分析】根据黄金分割点的定义,知是较长线段;则,代入数据即可得出的长.解:∵点M 为线段的黄金分割点,且,,∴,故答案为:.13.8【分析】根据平行线分线段成比例求出,减去可得结果.解:∵,∴,即,∴,∴,故答案为:8.14.(答案不唯一)【分析】再添加一组角可以利用有两组角对应相等的两个三角形相似来进行判定.解:添加条件,理由如下:∵,∴,即,又∵,∴,4:522222:4:5=4:5)1BM BM AB =AM AB AM BM <2cm AB =)21cm bM AB ===-)1AC AE BC DE ∥AD AE AB AC =349AC=12AC =1248CE AC AE =-=-=B D ∠=∠B D ∠=∠12∠=∠12CAD CAD ∠+∠=∠+∠BAC DAE ∠=∠B D ∠=∠ABC ADE △△∽故答案为:(答案不唯一).15.【分析】根据对应边成比例的两个三角形互为相似三角形可以求解.解:∠ACB=,AC=4,BC=3,,要使,有,,,故答案为:16.1【分析】先求解,再证明,可得,再建立方程求解,从而可得答案.解:∵,E 为的中点,∴,∵,,∴,∴,而,∴,解得:,∴,故答案为:117.5【分析】首先证明,从而推出对应边成比例:,因为,可得,再根据进行化简可得,进而得到答案.B D ∠=∠125o 905∴=ABC ACD V V ∽AB BC AC CD=534CD =12CD=51256AE BE ==ADE ABC △△∽AE AD AC AB =12AB =AB 6AE BE ==ADE B ∠=∠A A ∠=∠ADE ABC △△∽AE AD AC AB =9AC =6912AD =8AD =981CD AC AD =-=-=∽AEG BFE △△AE AGFB BE =AE BE =2AE AG BF =⋅2222222GF GE EF AG AE BE BF =+=+++22()GF AG BF =+解:四边形是正方形,,,,,,,.,,又,,的长为5.故答案为:5.18.【分析】延长,交的延长线于点M ,由三角形的中位线定理可得,继而可证明,由等角对等边可得,再证明,利用相似三角形的性质求解即可.解:延长,交的延长线于点M ,∵的平分线交于Q ,ABCD 90A B ∴∠=∠=︒90AGE AEG ∴∠+∠=︒90BFE FEB ∠+∠=︒90GEF ∠=︒ 90GEA FEB ∴∠+∠=︒AGE FEB ∴∠=∠AEG EFB ∠=∠AEG BFE ∴△∽△∴AE AG FB BE =AE BE = 2AE AG BF ∴=⋅2222222222222222222()25GF GE EF AG AE BE BF AG BF AE BE AG BF AE AG BF AG BF AG BF ∴=+=+++=+++=++=++=+=g GF ∴54BQ EF EF BC ∥PBM M ∠=∠PB PM =EQM CQB V V ∽BQ EF CBP ∠CE∴,∵E 、F 分别是的中点,∴,∴,∴,∴,∴,∵,∴∆EQM ∽∆CQB ,∴,∵,∴,故答案为:.三、解答题19.解:(1)证明:∵AB ∥DC ,∴∠B =∠D ,∵AB =2DC ,BE =2DF ,∴AB :DC =BE :DF =2,∴△ABE ∽△CDF ;(2)解:∵BE =2DF ,DF =2,∴ ,∵BD =8,∴EF =BD ﹣DF ﹣BE =2.20.解:(1)证明:平行四边形PBM CBM ∠=∠,AB AC EF BC ∥M CBM ∠=∠PBM M ∠=∠PB PM =18EM PE PM PE PB =+=+=EQM CQB ∠=∠EM EQ CB CQ=6,5BC CE ==54CQ =544BE =ABCD∴,∴,∴(2):由(1)中证明得:∵,代入后得∴21.解:根据题意,易得,,则,则,即,解得:AB=7m ,答:树高AB 约是7m .22.(1)解:同意.理由如下:根据折叠的性质可得.∵,∴.∵,∴;(2)解:设,则,∴,∴,即,.∵,DC AB ∥BC AD∥GE CE EB AE =CE BE AE EF =GE BE EB EF=GE BE EB EF=32EF =8GE =832BE EB =16BE =90CDE ABE ∠=∠=︒CED AEB ∠=∠ABE CDE ∆∆∽BE AB DE CD=82 1.75AB =90FEQ D EF DF ∠=∠=︒=,9090AEF BEG AEF AFE ∠+∠=︒∠+∠=︒,AFE BEG ∠=∠90A B ∠=∠=︒AEF BGE V V ∽AF x =6DF EF x ==-()22226x x +=-83x =83AF =103EF =AEF BGE V V ∽∴,即,∴,∴的周长为.23.解:感知:(1)∵△ABC ∽△DAE ,∴,∴,故答案为:;应用:(2)①∵∠APC=∠B+∠BAP ,∠APC=∠APD+∠CPD ,∠APD=∠B ,∴∠BAP=∠CPD ,∵AB=AC ,∴∠B=∠C ,∴△ABP ∽△PCD ;②BC=12,点P 为BC 中点,∴BP=PC=6,·∵△ABP ∽△PCD ,∴,即,解得:CD=3.6;拓展:(3)当PA=PD 时,△ABP ≌△PCD ,∴PC=AB=10,∴BP=BC -PC=12-10=2;当AP=AD 时,∠ADP=∠APD ,∵∠APD=∠B=∠C ,∴∠ADP=∠C ,不合题意,∴AP ≠AD ;AFAE EFBE BG GE ==8102334BG GE==35BG GE ==,BGE △()34512cm ++=BCACAE DE =BCAEAC DE =AEDE AB BP PC CD =1066CD =当DA=DP 时,∠DAP=∠APD=∠B ,∵∠C=∠C ,∴△BCA ∽△ACP ,∴,即,解得:,∴,综上所述,当为等腰三角形时, BP 的长为2或.24.解:感知:∵∠APD=90°,∴∠APB+∠DPC=90°,∵∠B=90°,∴∠APB+∠BAP=90°,∴∠BAP=∠CPD ,∵AB ∥CD ,∠B=90°,∴∠C=180°-∠B=90°=∠B ,∴△ABP ∽△DCP ,故答案为:是;探究:∵∠APC=∠BAP+∠B ,∠APC=∠APD+∠CPD ,∴∠BAP+∠B=∠APD+∠CPD .∵∠B=∠APD ,∴∠BAP=∠CPD .∵∠B=∠C ,∴△ABP ∽△PCD ,拓展:同探究的方法得出,△BDP ∽△CPE ,∴,∵点P 是边BC 的中点,BC AC AC CP =121010CP=253CP =25111233BP BC CP =-=-=APD △113BD BP CP CE=∴BP=CP=∵CE=9,∴BD=8,∵∠B=∠C=45°,∴∠A=180°﹣∠B ﹣∠C=90°,即AC ⊥AB 且AC=AB ,∴,∴AD=AB﹣BD=4,AE=AC ﹣CE=3,在Rt △ADE 中,.故答案是:5.=12AB AC BC ===5=。
沪科版九年级上册数学第22章 相似形含答案

沪科版九年级上册数学第22章相似形含答案一、单选题(共15题,共计45分)1、如图,在平面直角坐标系中,Rt△ABC的顶点A,C的坐标分别是(0,3),(3、0)。
∠ACB=90°,AC=2BC,若函数y= (k>0,x>0)的图象经过点B,则k 的值为()A. B.9 C. D.2、如图所示,一般书本的纸张是原纸张多次对开得到矩形ABCD沿EF对开后,再把矩形EFCD沿MN对开,以此类推,若各种开本的矩形都相似,那么等于()A.0.618B.C.D.23、给出4个判断:①所有的等腰三角形都相似,②所有的等边三角形都相似,③所有的直角三角形都相似,④所有的等腰直角三角形都相似.其中判断正确的个数有()A.1个B.2个C.3个D.4个4、如图,在□ABCD中,E是BC的中点,且∠AEC=∠DCE,下列结论不正确的是( )A.BF= DFB.S△FAD =2S△FBEC.四边形AECD是等腰梯形D.∠AEB=∠ADC5、如图,AB为⊙O的直径,BC,CD是⊙O的切线,切点分别为点B,D,点E 为线段OB上的一个动点,连接OD,CE,DE,已知AB=2 ,BC=2,当CE+DE的值最小时,则的值为()A. B. C. D.6、利用复印机的缩放功能,将原图中边长为5cm的一个等边三角形放大成边长为20cm的等边三角形,则放大前后的两个三角形的面积比为()A.1:2B.1:4C.1:8D.1:167、如图,在△ABC中,∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC =6,则CE长为()A. B. C. D.8、如图,把其中的一个小正方形看作基本图形,这个图形中不含的变换是()A.相似(相似比不为1)B.平移C.对称D.旋转9、如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O 为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是()A.(-1,2)B.(-9,18)C.(-9,18)或(9,-18)D.(-1,2)或(1,-2)10、下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则在网格图中的三角形与△ABC相似的是()A. B. C.D.11、如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG AE,垂足为G,BG=,则△CEF的周长为()A.8B.9.5C.10D.11.512、平面直角坐标系中,已知点O(0,0)、A(0,2)、B(1,0),点P是反比例函数y=-图象上的一个动点,过点P作PQ⊥x轴,垂足为点Q.若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有()A.1个B.2个C.3个D.4个13、如图,点是正方形的边延长线一点,连接交于,作,交的延长线于,连接,当时,作于,连接,则的长为()A. B. C. D.14、如图,四边形ABCD是矩形,点E、F是矩形ABCD外两点,AE⊥CF于H,AD=3,DC=4,DE= ,∠EDF=90°,则DF的长是()A. B. C. D.15、已知⊙O的半径为2,A为圆内一定点,AO=1.P为圆上一动点,以AP为边作等腰△APG,AP=PG,∠APG=120°,OG的最大值为()A.1+B.1+2C.2+D.2 ﹣1二、填空题(共10题,共计30分)16、如图,小伟在打网球时,击球点距离球网的水平距离是10米,已知网高是0.9米,要使球恰好能打过网,且落在离网5米的位置,则拍击球的高度h为________米.17、已知线段AB=2,点C为线段AB的黄金分割点(AC>BC),则AC=________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第22章相似形一、选择题(每小题4分,共40分)1.已知2x=3y(y≠0),则下面结论成立的是()A. xy=32 B.x3=2y C.xy=23 D.x2=y32.如图22-Z-1,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E与B,D,F.若AC=4,CE=6,BD=3,则DF的长是()A.4 B.4.5 C.5 D.5.5图22-Z-13.若△ABC∽△DEF,相似比为3∶2,则对应高的比为()A.3∶2 B.3∶5 C.9∶4 D.4∶94.如图22-Z-2,在△ABC中,点D,E分别在边AB,AC上,DE∥BC.若BD=2AD,则()A. ADAB=12 B.AEEC=12 C.ADEC=12 D.DEBC=12图22-Z-25.如图22-Z-3,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC 与△DEF的面积之比为()A.1∶2 B.1∶4 C.1∶5 D.1∶6图22-Z-36.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,下列条件不能判定它们相似的是()A.∠A=∠B′B.AC=BC,A′C′=B′C′C.AB=3BC,A′B′=3B′C′D.△ABC中有两边长为3,4,△A′B′C′中有两边长为6,87.如图22-Z-4,某校数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE 高1.5 m,测得AB=2 m,BC=14 m,则旗杆CD的高度是()A.9 m B.10.5 m C.12 m D.16 m图22-Z-48.如图22-Z-5,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC 的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是()A. EABE=EGEF B.EGGH=AGGD C.ABAE=BCCF D.FHEH=CFAD图22-Z-59.如图22-Z-6,边长为12的正方形ABCD中有一个小正方形EFGH,其中点E,F,G分别在AB,BC,FD上.若BF=3,则小正方形的边长为()A.12B. 154C. 5 D.6图22-Z-610.如图22-Z-7,已知矩形ABCD的顶点A,D分别落在x轴、y轴上,OD=2OA=6,AD∶AB=3∶1,则点C的坐标是()A.(2,7)B.(3,7)C.(3,8)D.(4,8)图22-Z -7二、填空题(每小题5分,共20分)11.若4x =3y ,则y x +y=________. 12.如图22-Z -8,AE ,BD 相交于点C ,BA ⊥AE 于点A ,ED ⊥BD 于点D .若AC =4,AB =3,CD =2,则CE =________.图22-Z -813.如图22-Z -9,小明同学用自制的直角三角形纸板DEF 测量树的高度AB ,他调整自己的位置,设法使斜边DF 保持水平,并且边DE 与点B 在同一直线上.已知纸板的两条直角边DE =40 cm ,EF =20 cm ,测得边DF 离地面的高度AC =1.5 m ,CD =8 m ,则树高AB =________m.图22-Z -9三、解答题(共40分)14.如图22-Z -10,在矩形ABCD 中,F 是DC 上一点,BF ⊥AC ,垂足为E ,AD AB =12,△CEF 的面积为S 1,△AEB 的面积为S 2,则S 1S 2的值等于________. 图22-Z -1015.(8分)如图22-Z -11,已知菱形AMNP 内接于△ABC ,点M ,N ,P 分别在边AB ,BC ,AC 上,如果AB =21 cm ,CA =15 cm ,求菱形AMNP 的周长.图22-Z -1116.(10分)如图22-Z -12,在由边长为1的小正方形组成的网格中建立平面直角坐标系,已知△ABC 三个顶点分别为A (-1,2),B (2,1),C (4,5).(1)画出△ABC 关于x 轴对称的△A 1B 1C 1;(2)以原点O 为位似中心,在x 轴的上方画出扩大后的△A 2B 2C 2,使△A 2B 2C 2与△ABC 位似,且相似比为2.图22-Z -1217.(10分)如图22-Z -13,正方形ABCD 的顶点A 在等腰直角三角形DEF 的斜边EF 上,EF 与BC 交于点G ,连接CF .(1)求证:△DAE ≌△DCF ;(2)求证:△ABG ∽△CFG .图22-Z -1318.(12分)如图22-Z -14,在△ABC 中,AB =AC ,P ,D 分别是BC ,AC 边上的点,且∠APD =∠B .(1)求证:AC ·CD =CP ·BP ;(2)若AB =10,BC =12,当PD ∥AB 时,求BP 的长.图22-Z -141.A2.B [解析] ∵a ∥b ∥c ,∴AC CE =BD DF ,即46=3DF,解得DF =4.5.故选B . 3.A [解析] 因为△ABC ∽△DEF ,根据相似三角形的性质“相似三角形对应高之比等于相似比”可知选A .4.B [解析] ∵点D ,E 分别在边AB ,AC 上,DE ∥BC ,∴AD BD =AE EC.∵BD =2AD ,∴AD BD =AE EC =12.故选B . 5.B6. D7.C [解析] 依题意得BE ∥CD ,∴△AEB ∽△ADC ,∴AB AC =BE CD ,即22+14=1.5CD,解得CD =12(m ).故选C .8.C9.B [解析] 先得出△BEF ∽△CFD ,再由勾股定理求出DF 的长,最后由相似三角形的对应边成比例得出边长EF.10.A [解析] 如图,作CE ⊥y 轴,垂足为E.∵OD =2OA =6,∴OA =3.易得Rt △CED ∽Rt △DOA ,∴CE DO =DE AO =CD AD. 又∵CD =AB ,∴CE 6=DE 3=13, ∴CE =2,DE =1,∴OE =7,∴C 点的坐标为(2,7).11. 37[解析] 设x =4k ,y =3k , ∴y x +y =3k 4k +3k =37. 12.2.5 [解析] ∵BA ⊥AE ,AC =4,AB =3,∴BC =32+42=5.∵BA ⊥AE ,ED ⊥BD ,∴∠A =∠D =90°.又∵∠ACB =∠DCE ,∴△ABC ∽△DEC ,∴AC BC =DC CE ,即45=2CE,∴CE =2.5.故答案为2.5.13.5.5 [解析] 利用Rt △DEF 和Rt △BCD 相似,求得BC 的长后加上AC 的长,即为树高AB.14. 116 [解析] ∵AD AB =12,∴设AD =BC =a ,则AB =CD =2a ,∴AC =5a.∵BF ⊥AC ,∴△CBE ∽△CAB ,△AEB ∽△ABC ,∴BC 2=CE·AC ,AB 2=AE·AC ,∴a 2=CE·5a ,(2a)2=AE·5a ,∴CE =5a 5,AE =4 5a 5, ∴CE AE =14. ∵△CEF ∽△AEB ,∴S 1S 2=(CE AE )2=116. 故答案为116. 15.解:∵四边形AMNP 是菱形,∴PN ∥AB ,∴△CPN ∽△CAB ,∴CP ∶CA =PN ∶AB.∵PN =PA ,∴CP ∶CA =PA ∶AB ,即CP ∶15=PA ∶21,从而CP ∶PA =15∶21=5∶7,∴(CP +PA)∶PA =(5+7)∶7,∴AC ∶PA =12∶7,即15∶PA =12∶7,解得PA =354, ∴菱形AMNP 的周长是354×4=35(cm ). 16.解:(1)如图所示,△A 1B 1C 1就是所求三角形.(2)如图所示,△A 2B 2C 2就是所求三角形.17.证明:(1)∵△DEF 是等腰直角三角形,四边形ABCD 是正方形,∴DE =DF ,DC =DA ,∠B =∠EDF =∠ADC =90°,∠EFD =∠DEF =45°. ∵∠CDF +∠ADF =∠ADE +∠ADF =90°,∴∠CDF =∠ADE.在△DAE 与△DCF 中,∵⎩⎨⎧DA =DC ,∠ADE =∠CDF ,DE =DF ,∴△DAE ≌△DCF.(2)由(1)中△DAE ≌△DCF ,得∠DFC =∠DEA =45°.又∵∠EFD =45°,∴∠CFG =∠DFC +∠EFD =90°,∴∠CFG =∠B.又∵∠CGF =∠AGB ,∴△ABG ∽△CFG .18.解:(1)证明:∵∠APC =∠APD +∠DPC =∠PAB +∠B ,且∠APD =∠B , ∴∠DPC =∠PAB.又∵AB =AC ,∴∠ABP =∠PCD ,∴△ABP ∽△PCD ,∴AB CP =BP CD. 又∵AB =AC , ∴AC CP =BP CD , 即AC·CD =CP·BP.(2)∵PD ∥AB ,∴∠DPC =∠B.由(1)中知∠DPC =∠PAB ,∴∠PAB =∠B. 又∵∠B =∠C , ∴∠PAB =∠C.又∵∠PBA =∠ABC , ∴△PBA ∽△ABC , ∴BP AB =AB BC, ∴BP =AB 2BC =10212=253.。
