正方体的截面图形
正方体截面地总结(最全,适用于公务员图形推理)
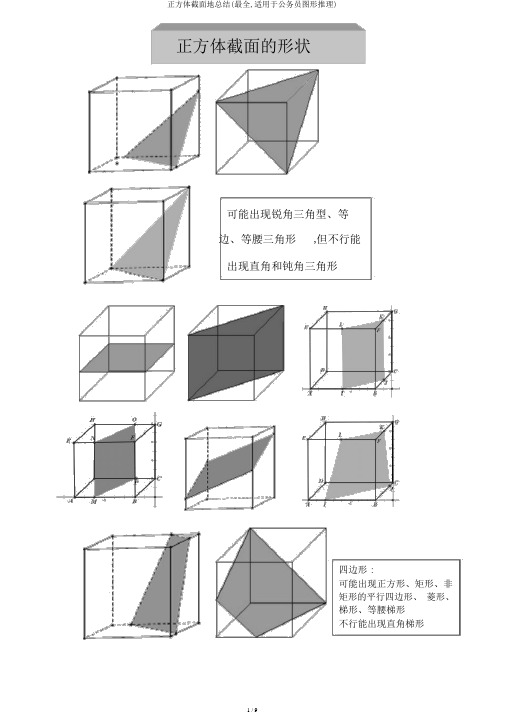
正方体截面的形状可能出现锐角三角型、等边、等腰三角形,但不行能出现直角和钝角三角形四边形 :可能出现正方形、矩形、非矩形的平行四边形、菱形、梯形、等腰梯形不行能出现直角梯形结论以下:1、可能出现的:锐角三角型、等边、等腰三角形,正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形2、不行能出现:钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形正方体的截面形状一:问题背景在家做饭时,切菜特别是切豆腐时,发现截面有好多形状。
若用不一样的截面去截一个正方体,获得的截面会有哪几种不一样的形状?二:研究方法先进行猜想,再利用土豆和萝卜经过切割实验研究。
三:猜想及其余可能的证明:1.正方形:由于该立体几何图形是正方体,所以用从随意地点与该正方体上下底面平行的平面进行截取能够获得,或许和侧面平前进行截取,由以下图示证明:====》》》由图示可知,水平方向截取正方体,获得的截面为正方形。
====》》》由图示可知,竖直方向截取正方体,获得的截面为正方形。
2.矩形:由于正方形也属于矩形,所以对正方形的证明同合用于矩形。
其次,当长宽不等的矩形截面的图示以下:由上图所示可知,按不一样角度截取正方体能够获得矩形。
比如,正方体的六个对角面都是矩形。
3.平行四边形:当平面与正方体的各面都不平行时,所得截面为平行四边形,图示以下:==》由上图所示可知,当截面不与正方体的各面平行时,所得截面可能为平行四边形。
4.三角形:依据必定角度过正方体的三条棱进行截取能够获得三角形的截面,图示以下:==》》》由上图可知,正方体能够截得三角形截面。
但必定是锐角三角形,包含等腰和等边三角形特其余,当截面恰好经过三个面的对角线时,所得的三角形截面为正三角形,图示以下:==》获得:正三棱锥5.猜想以外的截面形状:(1)菱形:以以下图所示,当A,B 为所在棱的中点时,该截面为菱形:(2)梯形:以下图,当按必定角度使截面在正方体的上下底面上所存在的线段长短有异时,所得截面可能是梯形:==》》》(3)五边形:以下图,能够截得五边形截面:=》经过实践及资料查问可知,没法获得正五边形。
正方体截面总结(最全适用于公事员图形推理)

正方体截面的形状可能出现锐角三角型、等边、等腰三角形,但不可能出现直角和钝角三角形四边形:可能出现正方形、矩形、非矩形的平行四边形、结论如下:1、可能显现的:锐角三角型、等边、等腰三角形,正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能显现:钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形正方体的截面形状一:问题背景在家做饭时,切菜尤其是切豆腐时,觉察截面有很多形状。
假设用不同的截面去截一个正方体,取得的截面会有哪几种不同的形状?二:研究方式先进行猜想,再利用马铃薯和萝卜通过切割实验研究。
三:猜想及其他可能的证明:1.正方形:因为该立体几何图形是正方体,因此用从任意位置与该正方体上下底面平行的平面进行截取能够取得,或和侧面平行进行截取,由以下图示证明:====》》》由图示可知,水平方向截取正方体,取得的截面为正方形。
====》》》由图示可知,竖直方向截取正方体,取得的截面为正方形。
2.矩形:因为正方形也属于矩形,因此对正方形的证明同适用于矩形。
第二,当长宽不等的矩形截面的图示如下:由上图所示可知,按不同角度截取正方体能够取得矩形。
例如,正方体的六个对角面都是矩形。
3.平行四边形:当平面与正方体的各面都不平行时,所得截面为平行四边形,图示如下:==》由上图所示可知,当截面不与正方体的各面平行时,所得截面可能为平行四边形。
4.三角形:依照必然角度过正方体的三条棱进行截取能够取得三角形的截面,图示如下:==》》》由上图可知,正方体能够截得三角形截面。
但必然是锐角三角形,包括等腰和等边三角形专门的,当截面恰好通过三个面的对角线时,所得的三角形截面为正三角形,图示如下:==》取得:正三棱锥5.猜想之外的截面形状:(1)菱形:如以下图所示,当A,B为所在棱的中点时,该截面为菱形:(2)梯形:如下图,当按必然角度使截面在正方体的上下底面上所存在的线段长短有异时,所得截面可能是梯形:==》》》(3)五边形:如下图,能够截得五边形截面:=》通过实践及资料查询可知,无法取得正五边形。
正方体截面的三视图

正方体截面的三视图1、打开一个“新绘图”,建立直角坐标系。
2、用[画圆]工具画单位圆。
作出单位圆与y轴正半轴的交点C、负半轴交点D。
3、[标记]向量AB,依向量AB平移点B到B’;[标记]向量AC,依向量AC平移点C到C’;[标记]向量AD,依向量AD平移点D到D’。
4、[标记]原点A为“旋转中心”,把点D绕A旋转-45度,得到D’,用[文本编辑]工具把D’的标签改为D”。
5、用[画点]工具在屏幕上任意画三点E、F、G,用[画线段]工具连结AE、AF、AG。
6、用[选择]工具先后选择点E、点A,并选择[编辑]菜单中的[操作类按钮]、[移动],选择“慢速地”后产生“→移动E->A按钮”。
用[文本编辑]工具把“→移动E->A按钮”改为“主视”。
7、用[选择]工具先后选择点E、B’、F、A,并选择[编辑]菜单中的[操作类按钮]、[移动],选择“慢速地”后产生“移动”。
用[文本编辑]工具把“移动”改为“左视”。
8、用[选择]工具先后选择点E、D’、G、A,并选择[编辑]菜单中的[操作类按钮]、[移动],选择“慢速地”后产生“→移动”。
用[文本编辑]工具把“→移动”改为“俯视”。
9、用[选择]工具先后选择点E、D”、F、B、G、C,并选择[编辑]菜单中的[操作类按钮]、[移动],选择“中速”后产生“→移动”。
用[文本编辑]工具把“→移动”改为“还原”。
10、用[画点]工具在平面上任画一点H。
11、依向量AE平移点H,得到H’,立即把H’的标签改为I;依向量AF两次平移点H,得到H”,立即把H”的标签改为J;依向量AG两次平移点H,得到H”,立即把H”的标签改为K.12、以HI、HJ、HK为从一点出发的三条棱,完成平行六面体。
用[文本编辑]工具改写一些点的标签。
13、用[画线段]工具连结IK、LJ’,作出它们的中点,用[文本编辑]工具把标签分别改为M、N。
14、用[选择]工具先后选择K、M、L、N,并选择[作图]菜单中的[多边形内部],给多边形填充。
细说正方体的截面图形

细说正方体的截面图形在实际生活中时常出现实物几何体的切面所形成的截面图形形状,在中学数学中也学习了几何体的截面图形,截面是一个平面去截一个几何体得到的平面图形或一个平面与几何体表面交线围成的封闭图形,。
截面图形更好的将平面几何与立体几何联系起来,探究具体几何体的截面图形有助于更深入的认识几何体,发展正确的空间观念。
对于一个几何体不同的切截方式所得到的截面图形可能出现不同的情况。
现具体以正方体为例来探究正方体的截面图形形状。
一个平面截正方体与各面的交线都是线段,因此正方体的截面图形都是平面图形。
正方体有六个面,用一个平面去截正方体至少要经过正方体的三个面而最多要经过六个面,所有出现的截面图形边数至少是三条而最多是六条,则只可能出现三角形、四边形、五边形、六边形。
一、截面图形是三角形用一平面去截正方体经过正方体三个面时得到的截面图形是三角形1.截面图形是锐角三角形如下图,一个平面截正方体任意三个面得到截面△EFG ,BE=a,BF=b,BG=c.可得EF=22b a +,EG=22c a +,FG=22c b +.(1)如图①,当a ≠b ≠c 时,则EG ≠FG ≠EF,即截面△EFG 是一般三角形。
(2)如图②,当a=b ≠c 时,则EG=FG ≠EF 即截面△EFG 是等腰三角形。
同理可得a=c ≠b 或b=c ≠a 时截面△EFG 是等腰三角形。
(3)如图③,当a=b=c 时EF=FG=EG 即截面△EFG 是等边三角形2.截面图形不能是直角三角形如图①,2EF =22b a +,2FG =22c b +,2EG =22c a +,则222EG FG EF +<,222EG EF FG +<,222EG FG EF +<,所以截面三角形不可能是直角三角形。
3.截面图形不可能是钝角三角形如图①,cos ∠FEG=EG EF FG EG EF ⋅-+2222=22222222222ca b a c b c a b a +⋅+--+++ =22222c a b a a +⋅+>0,则0<∠FEG< 90.同理可得0<∠EFG< 90.0<∠EGF< 90. 所有截面图形不可能是钝角三角形。
正方体的截面形状

①截面可以是三角形:等边三角形、等腰三角形、一般三角形;
②截面三角形是锐角三角形;截面三角形不能是直角三角形、钝角三角形;
③截面可以是四边形:平行四边形、矩形、菱形、正方形、梯形、等腰梯形;截面为四边形时,这个四边形中至少有一组对边平行;
④截面不能是直角梯形;
⑤截面可以是五边形;截面五边形必有两组分别平行的边,同时有两个角相等;截面五边形不可能是正五边形;
⑥截面可以是六边形;截面六边形必有分别平行的边,同时有两个角相等;
⑦截面六边形可以是等角(均为120°)的六边形,特别地可以是正六边形.
对应截面图形如下图中各图形所示.。
正方体的几种截面

正方体的几种截面正方体是一种具有六个相等的正方形面的立体图形。
它的截面有多种形式,每一种截面都展现了正方体在不同方向上的特性和特点。
本文将以几种常见的正方体截面为标题,详细介绍它们的特点和应用。
一、正方形截面正方形截面是正方体最基本的截面形式。
它的特点是四条边相等且内角均为90度。
正方形截面在建筑、工程和设计领域中广泛应用。
例如,在建筑结构设计中,正方形截面的柱子能够提供较好的稳定性和承重能力,因此常用于大型建筑物的支撑结构。
二、长方形截面长方形截面是正方体的另一种常见截面形式。
它的特点是两对相等的边,且每一对边长度可以不相等。
长方形截面在工程和建筑领域中有着广泛的应用。
例如,在桥梁设计中,长方形截面的梁能够提供较好的强度和刚度,从而能够承受大量的荷载。
三、三角形截面正方体的三角形截面是指由正方体的三个顶点和与它们相连的三条边所围成的图形。
三角形截面具有较高的稳定性和刚度,因此常用于建筑中的支撑结构或桥梁中的支撑柱。
此外,三角形截面还常用于设计飞机或汽车的支撑杆,以提高结构的强度和稳定性。
四、菱形截面菱形截面是指由正方体的四个角点和与它们相连的四条边所围成的图形。
菱形截面具有较好的强度和稳定性,因此常用于建筑物的支撑结构或桥梁中的支撑柱。
此外,在船舶设计中,菱形截面的船体能够提供较好的抗风浪能力,因此被广泛应用于各类船舶的设计和制造。
五、圆形截面正方体的圆形截面是指由正方体的四个角点围成的圆形。
圆形截面具有较好的强度和稳定性,因此常用于建筑物的支撑结构或桥梁中的支撑柱。
此外,在机械工程领域中,圆形截面的轴能够提供较好的扭转刚度,因此被广泛应用于各类机械设备的设计和制造。
六、椭圆形截面椭圆形截面是指由正方体的四个角点围成的椭圆形。
椭圆形截面具有较好的强度和刚度,因此常用于建筑物的支撑结构或桥梁中的支撑柱。
此外,在电子工程中,椭圆形截面的导线能够提供较好的电流传输能力,因此被广泛应用于各类电子设备的设计和制造。
正方体截面总结(最全-适用于公务员图形推理)

正方体截面的形状.可能出现锐角三角型、等边、等腰三角形,但不可能出现直角和钝角三角形结论如下:1、可能出现的:锐角三角型、等边、等腰三角形,正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现:钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形正方体的截面形状一:问题背景在家做饭时,切菜尤其是切豆腐时,发现截面有很多形状。
若用不同的截面去截一个正方体,得到的截面会有哪几种不同的形状?二:研究方法先进行猜想,再利用土豆和萝卜通过切割实验研究。
三:猜想及其他可能的证明:1.正方形:因为该立体几何图形是正方体,所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到,或者和侧面平行进行截取,由下列图示证明:====》》》由图示可知,水平方向截取正方体,得到的截面为正方形。
====》》》由图示可知,竖直方向截取正方体,得到的截面为正方形。
2.矩形:因为正方形也属于矩形,所以对正方形的证明同适用于矩形。
其次,当长宽不等的矩形截面的图示如下:由上图所示可知,按不同角度截取正方体可以得到矩形。
例如,正方体的六个对角面都是矩形。
3.平行四边形:当平面与正方体的各面都不平行时,所得截面为平行四边形,图示如下:==》由上图所示可知,当截面不与正方体的各面平行时,所得截面可能为平行四边形。
4.三角形:根据一定角度过正方体的三条棱进行截取可以得到三角形的截面,图示如下:==》》》由上图可知,正方体可以截得三角形截面。
但一定是锐角三角形,包括等腰和等边三角形特别的,当截面刚好经过三个面的对角线时,所得的三角形截面为正三角形,图示如下:==》得到:正三棱锥5.猜想之外的截面形状:(1)菱形:如下图所示,当A,B为所在棱的中点时,该截面为菱形:(2)梯形:如图所示,当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时,所得截面可能是梯形:==》》》(3)五边形:如图所示,可以截得五边形截面:=》通过实践及资料查询可知,无法得到正五边形。
截面为六边形的正方体

截面为六边形的正方体在这片神奇的数学世界里,有一种形状叫六边形,真是个妙不可言的存在。
六边形啊,听起来就像是个大大的巧克力饼干,边边角角都有趣味。
咱们要说的正方体,嘿,简直是个完美的家伙,六个面,统统都是正方形,像极了咱们日常生活中的纸盒子。
可当这两者相遇,奇妙的事情就发生了。
你能想象吗,一个正方体的切面,竟然能变成六边形!真的是让人忍不住想要去探个究竟。
想象一下,一个正方体静静地坐在那儿,咱们用刀子一刀切下去,刀锋划过,咔嚓一声,正方体的面就变成了六边形。
哇,这可真是个“魔法时刻”!这六边形的边边角角,恰好是那样的均匀,仿佛是大师精心雕琢的艺术品。
每一条边都是一样长,仿佛在跟你悄悄地说:“嘿,看看我多完美!”这种对称的美,简直能让人拍手叫好,直呼过瘾。
好吧,咱们得深入聊聊这六边形的魅力。
六边形可不是普通的形状,它在自然界中到处可见。
蜂巢里的小房子,就是这个六边形的。
蜜蜂们可真是聪明,它们用六边形来储存蜂蜜,既节省空间又稳固。
听说,科学家们还认为,六边形的结构是最有效的。
这让我想到了咱们的生活,越是简单的东西,反而越能让人省心,是吧?再说回这正方体切割出的六边形,想想它的用途,多得数不胜数。
比如说,在建筑设计中,六边形可以带来奇特的视觉效果。
你见过那种像是蜂巢一样的建筑吗?大气又好看,绝对能让你过目不忘。
六边形的地砖铺成的花纹,走在上面,仿佛在走入了一片迷宫,恍若置身于梦境,真是太酷了!六边形还有个让人惊讶的特性,那就是它的角度,都是120度。
你有没有想过,为什么不选其他的角度?120度可不是随便的数字,这让六边形在平面上能完美地拼接,不留缝隙,真是个聪明的家伙。
生活中,很多时候,我们也得学会这种智慧,选择那些能让我们更有效率的方案,毕竟,时间就是金钱啊!这时候,咱们再回头看看正方体。
它在我们的日常生活中,无处不在。
无论是盒饭、快递,还是那一排整齐的书籍,都是正方体的身影。
你想想,正方体的面那么平整,容易叠放,又节省空间,简直是居家必备的好帮手。
正方体的截面(数字故事)

让我们来看一看同学们的探究 学生探究1
让我们来看一看同学们的探究 学生探究2
让我们来看一看同学们的探究 学生探究3
开动脑筋,使用身边材料, 动手操作,验证猜想,这才是 我们知识探索与获取的最佳方 法。
正方体是由六个完全相同的正 方形围成的立体图形,生活中我们 经常见到它。
用一个平面去截正方体, 截面会是什么形状呢?
我们来试试看 是三角形!
我们来试试看! 是梯形!
我们来试试看 是正方形!
我们来试试看! 是长方形!
ቤተ መጻሕፍቲ ባይዱ
我们来试试看! 是五边形!
我们来试试看 是六边形!
正方体的截面通过动手探究 发现有如下几种:三角形、四 边形、五边形和六边形。
正方体截面总结(最全,适用于公务员图形推理)

正方体截面的形状IIII II II 1 1 II II II II四边形:可能出现正方形、矩形、非矩形的平行四边形、菱形、梯形、等腰梯形不可能出现直角梯形y' J7 /\ /J-X z/F -\/<、H I ■亠*T〕结论如下:1可能出现的:锐角三角型、等边、等腰三角形,正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现:钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边正方体的截面形状:问题背景在家做饭时,切菜尤其是切豆腐时,发现截面有很多形状。
若用不同的截面去截一个正方体,得到的截面会有哪几种不同的形状?二:研究方法先进行猜想,再利用土豆和萝卜通过切割实验研究。
三:猜想及其他可能的证明:1.正方形:因为该立体几何图形是正方体,所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到,或者和侧面平行进行截取,由下列图示证明:==》》》由图示可知,水平方向截取正方体,得到的截面为正方形。
由图示可知,竖直方向截取正方体,得到的截面为正方形。
2矩形:因为正方形也属于矩形,所以对正方形的证明同适用于矩形。
其次,当长宽不等的矩形截面的图示如下:==》》》由上图所示可知,按不同角度截取正方体可以得到矩形。
例如,正方体的六个对角面都是矩形。
3. 平行四边形:当平面与正方体的各面都不平行时,所得截面为平行四边形,图示如下:由上图所示可知,当截面不与正方体的各面平行时,所得截面可能为平行四边形。
4. 三角形:根据一定角度过正方体的三条棱进行截取可以得到三角形的截面,图示如下==》》》由上图可知,正方体可以截得三角形截面。
但一定是锐角三角形,包括等腰和等边三角形特别的,当截面刚好经过三个面的对角线时,所得的三角形截面为正三角形,图示如下:ClCl 111A,IK==》得到:正三棱锥5. 猜想之外的截面形状:(1)菱形:如下图所示,当A,B为所在棱的中点时,该截面为菱形:(2)梯形:如图所示,当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时,所得截面可能是梯形:(3)五边形:如图所示,可以截得五边形截面:通过实践及资料查询可知,无法得到正五边形。
正方体截面总结(最全,适用于公务员图形推理)

M / * B结论如下:1可能出现的:锐角三角型、等边、等腰三角形,正方形、矩形、边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现:钝角三角形、直角三角形、直角梯形、正五边形、非矩形的平行四七边形或更多边正方体的截面形状一:问题背景在家做饭时,切菜尤其是切豆腐时,发现截面有很多形状。
若用不同的截面去截一个正方体,得到的截面会有哪几种不同的形状?二:研究方法先进行猜想,再利用土豆和萝卜通过切割实验研究。
三:猜想及其他可能的证明:1•正方形:因为该立体几何图形是正方体,所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到,或者和侧面平行进行截取,由下列图示证明:由图示可知,水平方向截取正方体,得到的截面为正方形。
由图示可知,竖直方向截取正方体,得到的截面为正方形。
2矩形:因为正方形也属于矩形,所以对正方形的证明同适用于矩形。
其次,当长宽不等的矩形截面的图示如下: 由上图所示可知,按不同角度截取正方体可以得到矩形。
例如,正方体的六个对角面都是矩形。
3. 平行四边形:当平面与正方体的各面都不平行时,所得截面为平行四边形,图示如下:==》》》 ==》》》由上图所示可知,当截面不与正方体的各面平行时,所得截面可能为平行四边形。
4. 三角形:根据一定角度过正方体的三条棱进行截取可以得到三角形的截面,图示如下==》由上图可知,正方体可以截得三角形截面。
但一定是锐角三角形,包括等腰和等边三角形特别的,当截面刚好经过三个面的对角线时,所得的三角形截面为正三角形,图示如下:==》得到: 正三棱锥5. 猜想之外的截面形状:(1)菱形:如下图所示,当A,B 为所在棱的中点时,该截面为菱形:(2)梯形:如图所示,当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时,所得截面可能是梯形:(3 )五边形:(4 )六边形:如图所示,可以截得六边形截面:==》》》如图所示,可以截得五边形截面:通过实践及资料查询可知,无法得到正五边形。
正方体的截面

正方体的截面引言截面是指一个物体被一个平面所切割后的形状。
正方体是一个具有六个相等的正方形面的立方体。
在本文中,我们将讨论正方体的截面形状和性质。
正方体的基本概念正方体是一种特殊的立方体,具有六个相等的正方形面。
它的每个面都与其他三个面相邻,形成直角相交。
正方体的边长被定义为所有正方形面的边长。
正方体的截面形状正方体的截面形状取决于截割平面的方向和位置。
根据截面与正方体边长的相对位置,可以将截面分为以下几种情况:1. 水平截面当截割平面与正方体的底面平行时,截面为一个正方形。
正方形的边长等于正方体的边长。
2. 垂直截面当截割平面与正方体的一个侧面平行时,截面为一个长方形。
长方形的边长等于正方体的边长,而宽度则取决于截割平面与正方体的相对位置。
3. 平面截面当截割平面与正方体的一个角相交时,截面为一个不规则多边形。
多边形的形状取决于截割平面的位置和角度。
4. 对角线截面当截割平面通过正方体的两个相对角点时,截面为一个菱形。
菱形的对角线为正方体的对角线。
5. 中心截面当截割平面通过正方体的中心点时,截面为一个正六边形。
正六边形的边长等于正方体的边长。
正方体截面的性质正方体的截面具有一些特殊的性质,这些性质可以用来解决一些几何问题。
以下是一些常见的性质:1. 截面面积正方体的截面面积取决于截割平面的形状和位置。
对于水平和垂直截面,其面积等于正方体的底面积。
对于其他类型的截面,其面积可以通过几何计算方法进行求解。
2. 截面形状对称性正方体的截面形状具有一定的对称性。
例如,水平和垂直截面是关于正方体的中心点对称的。
对称性可以帮助我们简化计算和分析截面的性质。
3. 截面相对位置正方体的截面相对位置可以用来确定截面之间的关系。
例如,两个水平截面之间的距离等于正方体的高度。
总结正方体的截面形状和性质是几何学中的重要概念。
通过研究截面,我们可以更好地理解正方体的结构和特性。
了解正方体截面的形状和性质对于解决几何问题和应用数学都具有重要的意义。
