深圳市罗湖区-学年八-上-期末测试卷(含答案)

合集下载

深圳罗湖区罗湖中学八年级上册生物期末试卷及答案-百度文库

深圳罗湖区罗湖中学八年级上册生物期末试卷及答案-百度文库一、选择题1．海蜇是湛江常见的海洋生物，也是吴川的三宝之一，它属于（）A．原生动物B．腔肠动物C．软体动物D．节肢动物2．蚯蚓比蛔虫在进化上的高等之处主要在于A．身体有分节B．营自由生活C．有口有肛门D．生殖器官发达3．下列哪种动物在捕捉食物时，使用触手？（）A．水蛭B．乌贼C．扇贝D．海蜇4．观察鸟的形态结构示意图，下列说法与鸟适于飞行生活没有关系的是( )A．有发达的胸肌B．骨骼轻、薄，有的愈合在一起C．有坚硬的角质喙D．身体呈流线型，体表被覆羽毛5．如图是家鸽体内部分结构分布示意图，以下描述正确的是（）A．家鸽呼吸时只在c处进行气体交换B．b和c都能进行气体交换C．a是气管b是肺c是气囊D．气体进入体内的途径是a→b→c6．下列珍稀动物中，属于两栖动物的是（）A．扬子鳄B．大鲵C．中华鲟D．白鳍豚7．“四处野鸭和菱藕，秋收满畈稻谷香…”一曲优美的《洪湖水浪打浪》描述出江汉平原鱼米之乡的富庶和美丽．下列相关叙述中，不正确的是（）A．野鸭的形态结构既适于游泳，也适于飞行B．野鸭一年一度的迁徙行为受遗传物质控制C．莲藕和水稻都不分昼夜地进行着呼吸作用D．菱和莲藕与水稻一样，都只能进行有性生殖8．十二生肖是华夏先民图腾崇拜和早期天文学的结晶，让每个人都具有与生俱来的属相，代表着这个民族所有人的精神风貌。

下列哪项是亥猪、巳蛇和酉鸡的共同特征：（）A．胎生哺乳B．体温恒定C．身体被毛D．用肺呼吸9．如图是人体运动的有关结构模式图，说法错误的是（）A．图1中的1从4中脱落出来叫脱臼B．图1与灵活性有关的是5和3内的滑液C．图2伸肘时9收缩，7舒张D．图2中9的两端肌腱都连在同一根肱骨上10．如图是长骨的结构示意图，下列关于长骨结构的叙述错误的是（）A．①内的骨髓终生具有造血功能B．③内红骨髓变成黄骨髓后便永远失去造血功能C．骨折后对骨的愈合起作用的是④内的成骨细胞D．②致密坚硬，抗压力强11．下图是人的屈肘动作示意图，下列相关叙述正确的是（）A．该运动过程中，2起支点的作用B．1是肱三头肌，由肌腱和肌腹两部分组成C．关节囊及里面和外面的韧带使3具有牢固性D．该动作是由骨骼、骨连结和骨骼肌三者协调配合完成的12．运动时消化系统、呼吸系统和循环系统共同配合为骨骼肌提供了（）A．维生素B．无机盐C．能量D．水13．鲤鱼和鹰的运动方式分别是（）A．爬行、飞行B．爬行、行走C．游泳、行走D．游泳、飞行14．下列对动物行为的叙述，正确的是A．学习行为是动物后天学习所得，与遗传因素无关B．先天性行为和学习行为是两种截然不同、互不相关的行为类型C．具有社会行为的动物群体中，往往是年长者为“首领”D．动物的行为多种多样，有利于它们的存活和繁殖后代15．下面描述的生物现象中，属于社会行为的是（）A．成群的蚂蚁结成“圆球”过河B．黑猩猩从洞穴中钓取白蚁作为食物C．养鸡厂内成群的母鸡在“咯咯”地叫D．乌贼受到威胁时会释放墨汁16．动物具有“学习行为”，主要与动物的什么有关（）A．大脑皮层B．小脑皮层C．激素水平D．运动器官17．“母鸡孵卵”这种动物的行为具有的特点是（）①由体内的遗传物质所决定的②生来就有的③由动物所在的生活环境所决定的④由生活经验获得的A．①②B．③④C．①③D．②④18．关于“小鼠走迷宫”的探究实验，下列说法正确的是A．这是探究小鼠的先天性行为B．小鼠“尝试与错误”的次数远少于蚯蚓C．不同小鼠熟悉迷宫的能力都一样D．小鼠一旦学会走迷宫，就不会忘记19．动物的行为多种多样，既有先天性行为，又有学习行为，这些行为有利于动物的生存和繁殖，下列有关动物行为的叙述、错误的是（）A．先天性行为由遗传物质决定B．先天性行为是学习行为的基础C．学习行为一旦形成，就不会改变D．学习行为在个体生活经历中获得20．观察图中几种动物的行为，下列说法错误的是（）A．从动物行为的功能来看，图中①属于取食行为，④属于防御行为B．从动物行为获得途径来看，图中②属于学习行为，③属于先天性行为，二者都与遗传物质有关C．学习行为是在生活过程中，通过积累生活经验和“学习”逐渐建立起来的D．动物的复杂行为只受神经系统的调控21．下列关于动物在自然界中的作用叙述正确的是( )A．蜜蜂采集花粉时不利于植物传粉B．动物通过呼吸作用将体内部分有机物分解成无机物，不利于生态系统的物质循环C．昆虫吃掉蔬菜人为捕杀某种动物以及随意引进某种动物都不会影响生态平衡D．松鼠将收获的松子储存在地面下,可以帮助植物传播种子22．关于动物在生物圈中的作用叙述中，哪项是错误的（）A．动物能帮助植物传播花粉和种子B．动物能影响和改变环境C．动物是食物链的结构成分D．动物能光能合成有机物，能够净化空气23．如图是五种不同的微生物结构图，下列叙述正确的是（）A．它们都有细胞膜、细胞质和遗传信息B．B、C、D属于真核生物C．E的生活方式是寄生或腐生D．D可以用来发酵生产酸奶24．下列叙述不正确的是A．乳酸菌可进行分裂生殖，酵母菌也能进行孢子生殖B．菌落是多种细菌或真菌繁殖后形成的集合体C．流感病毒是一种球状的病原体，它没有细胞结构D．乳酸菌和酵母菌相比，乳酸菌的细胞结构中没有成形的细胞核25．酸奶的营养价值比牛奶高，是因为酸奶在发酵过程中营养成分转变成更易于被人体消化和吸收的营养物质，并产生多种维生素。

2023-2024学年广东省深圳市罗湖区八年级(上)期末数学试卷及答案解析

2023-2024学年广东省深圳市罗湖区八年级（上）期末数学试卷一、选择题（共10小题，每题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．（3分）下列四个数中，是无理数的是（）A．3.14B．C．D．02．（3分）下列各组数据中，能作为直角三角形的三边长的是（）A．2，3，4B．3，4，5C．5，6，7D．7，8，9 3．（3分）根据下列描述，能够确定一个点的位置的是（）A．学校图书馆前面B．凤凰电影院3排6座C．和谐号第2号车厢D．北偏东40°方向4．（3分）甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数都是9.2环，方差分别为，，，，则射击成绩最稳定的是（）A．甲B．乙C．丙D．丁5．（3分）已知一次函数y＝x﹣1，则该函数的图象是（）A．B．C．D．6．（3分）如图，小颖绘制一个潜望镜原理示意图，两个平面镜的镜面AB与CD平行，入射光线a与出射光线b平行．若入射光线a与镜面AB的夹角∠1＝45°，则∠4的度数为（）A．30°B．45°C．60°D．90°7．（3分）如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，则∠ECD等于（）A．40°B．45°C．50°D．55°8．（3分）下列命题是真命题的是（）A．同旁内角互补B．相等的角是对顶角C．4的算术平方根是±2D．三角形的一个外角大于任何一个和它不相邻的内角9．（3分）《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，木长多少尺？若设绳子长x尺，木长y尺，所列方程组正确的是（）A．B．C．D．10．（3分）如图，在平面直角坐标系中，点A在y轴上，点B在x轴上，以AB为边作正方形ABCD，点C的坐标（﹣7，3）在一次函数y＝kx+6上，一次函数与x轴交于点E，与y轴交于点F，将正方形ABCD沿x轴向右平移a个单位长度后，点D刚好落在直线EF上，则a的值为（）A．B．C．D．二、填空题（本题共5小题，每小题3分，共15分）11．（3分）计算：＝．12．（3分）比较大小：．（填“＞”、“＝”或“＜”）13．（3分）如图，阴影部分是两个正方形，其他三个图形是一个正方形和两个直角三角形，则阴影部分的面积之和为．14．（3分）如图，直线y＝2x+6与直线l：y＝kx+b交于点P（﹣1，m），则方程组的解为．15．（3分）如图，在△ABC中，∠ACB＝90°，AC＝BC，点D是△ABC外的一个点，连接AD，BD，且AD＝2，∠ADB＝135°，四边形ACBD的面积是，则BD的长为．三、解答题（共7小题，共55分，其中16题6分，17题8分，18题6分，19题8分，20题8分，21题9分，22题10分）16．（6分）计算：（1）；（2）（1﹣）2+3．17．（8分）解方程组：（1）；（2）．18．（6分）杭州亚运会开幕式惊艳了世界，这背后离不开志愿者们的默默奉献，这些志愿者很多都来自高校．在志愿者招募之时，A，B两所大学就积极组织了志愿者选拔活动，对报名的志愿者进行现场测试，现从这两所大学参加测试的志愿者中分别随机抽取了20名志愿者的综合测试成绩进行整理和分析，下面给出部分信息．综合以上信息，解答下列问题：A，B两所大学被抽取的志愿者测试成绩的平均分、中位数、众数如下表：学校平均分中位数众数A校a b95B校93.595c（1）填空：a＝，b＝，c＝；（2）B校志愿者的成绩的扇形统计图中的圆心角α＝°，请补全A校志愿者的成绩的条形统计图；（3）如果你是组委会成员，你倾向招哪所大学的志愿者？请说明理由．19．（8分）为进一步落实“德、智、体、美、劳”五育并举工作，有效开展“阳光体育”活动，某中学计划从体育用品商场购买乒乓球拍和乒乓球用于学生社团活动．若购买2副球拍和3盒乒乓球则共需75元；若购买3副球拍和2盒乒乓球则共需100元．（1）求每副乒乓球拍和每盒乒乓球的价格．（2）学校计划采购乒乓球拍20副和乒乓球30盒．元旦期间，商场搞促销活动：甲商场全部商品打9折出售，乙商场买2副乒乓球拍送一盒乒乓球，请问在哪个商场采购合算？请说明理由．20．（8分）如图，已知直线与x轴，y轴分别交于点A和点B，M为线段OB上一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处．（1）求A，B两点的坐标．（2）求直线AM的函数表达式．21．（9分）我们学习了平移、旋转、轴对称等图形变换，这些图形变换不仅可以应用到精美的图案设计上，还可以解决生活实际问题．【图案设计】如图1，在平面直角坐标系中，A（3，4），B（1，2），C（5，1）．（1）作出△ABC关于y轴的对称图形△DEF，并标注出点D，E，F；【拓展应用】（2）如图1，点P是x轴上一动点，并且满足PA+PB的值最小，请在图中找出点P的位置（保留作图痕迹），并直接写出PA+PB的最小值为．【实际应用】（3）如图2，某地有一块三角形空地ABC，已知∠ABC＝45°，G是△ABC内一点，连接GB后测得GB＝20米，现当地政府欲在三角形空地ABC中修一个三角形花坛GMN，点M，N分别是AB，BC边上的任意一点（不与各边顶点重合），请问△GMN的周长最少约多少米？（保留整数）（≈1.41，≈1.73）22．（10分）【综合探究】在数学综合与实践活动课上，兴趣小组的同学用两个完全相同的长方形纸片展开探究活动，这两张长方形纸片的长为8cm，宽为4cm．（1）【实践探究】小红将两个完全相同的长方形纸片ABCD和EFGQ摆成图1的形状，点A与点E重合，边AD与边EF重合，边AB，QE在同一直线上．请判断：△ACG的形状为．（2）【解决问题】如图2，在（1）的条件下，小明将长方形EFGQ绕点A顺时针转动m°（转动角度小于45°），即∠DAF＝m°，边EF与边CD交于点M，连接BM，BN平分∠MBC，交CD于点N，∠AMB+∠AMC＝180°，求∠CBN的度数．（3）【拓展研究】从图2开始，小亮将长方形EFGQ绕点A顺时针转动一周，若边EF 所在的直线恰好经过线段BQ的中点O时，连接BF，FQ，请直接写出△BFQ的面积．2023-2024学年广东省深圳市罗湖区八年级（上）期末数学试卷参考答案与试题解析一、选择题（共10小题，每题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．【分析】根据有理数和无理数的定义，对题目中的四个选项逐一进行判断即可得出答案．【解答】解：对于选项A，3.14是有理数，不合题意；对于选项B，是有理数，不合题意；对于选项C，是无理数，符合题意；对于选项D，0是有理数，不合题意．故选：C．【点评】此题主要考查了实数的意义，熟练掌握有理数和无理数的定义是解决问题的关键．2．【分析】根据勾股定理的逆定理对题目中的四个选项逐一进行判断即可得出答案．【解答】解：对于选项A，∵22+32＝13，42＝16，∴22+32≠42，∴选项A中的数据作为三角形三边长，不是直角三角形，故该选项不符合题意；对于选项B，∵32+42＝25，52＝25，∴32+42＝52，∴选项B中的数据作为三角形三边长，是直角三角形，故该选项符合题意；对于选项C，∵52+62＝61，72＝49，∴52+62≠72，∴选项C中的数据作为三角形三边长，不是直角三角形，故该选项不符合题意；对于选项D，∵72+82＝113，92＝81，∴72+82≠92，∴选项D中的数据作为三角形三边长，不是直角三角形，故该选项不符合题意．故选：B．【点评】此题主要考查了勾股定理的逆定理，熟练掌握勾股定理的逆定理是解决问题的关键．3．【分析】根据确定一个点的位置必须有两个数据来判断．【解答】解：A选项中，学校图书馆前面，不能确定具体的一个点，故不符合题意；B选项中，凤凰电影院3排6座，能确定具体的一个点，故符合题意；C选项中，和谐号第2号车厢，不能确定具体的一个点，故不符合题意；D选项中，北偏东40°方向，不能确定具体的一个点，故不符合题意，故选：B．【点评】本题考查了坐标确定位置的问题，关键知道确定一个点的位置必须有两个数据来判断．4．【分析】根据方差的意义“方差越小越稳定”，比较方差大小，选择方差最小的即可．【解答】解：∵，，，，∴，∴甲的方差最小，∴射击成绩最稳定的是甲，故选：A．【点评】本题主要考查了方差的意义，熟记方差的意义“方差越小越稳定”是解题的关键．5．【分析】先由y＝x﹣1得该一次函数是过点（1，0）和点（0，﹣1）的一条直线，由此对题目中给出的四个选项逐一进行判断即可得出答案．【解答】解：对于y＝x﹣1，当x＝0时，y＝﹣1，当y＝0时，x＝1，∴一次函数y＝x﹣1是过点（1，0）和点（0，﹣1）的一条直线，对于选项A，符合题意；对于选项B，函数的图象经过点（﹣1，0）和点（0，1），故该选项不符合题意；对于选项C，函数的图象经过点（1，0）和点（0，1），故该选项不符合题意；对于选项D，函数的图象经过点（﹣1，0）和点（0，﹣1），故该选项不符合题意；故选：A．【点评】此题主要考查了一次函数的图象，熟练掌握一次函数的图象是解决问题的关键．6．【分析】在图中标注∠5，∠6，由AB∥CD，直线a∥直线b，利用“两直线平行，内错角相等”，可得出∠2＝∠3，∠5＝∠6，再结合∠1+∠2+∠5＝180°，∠3+∠4+∠6＝180°，即可求出∠4的度数．【解答】解：在图中标注∠5，∠6，如图所示．∵AB∥CD，直线a∥直线b，∴∠2＝∠3，∠5＝∠6．又∵∠1+∠2+∠5＝180°，∠3+∠4+∠6＝180°，∴∠4＝∠1＝45°．故选：B．【点评】本题考查了平行线的性质，牢记“两直线平行，同位角相等”是解题的关键．7．【分析】根据三角形外角性质求出∠ACD，根据角平分线定义求出即可．【解答】解：∵∠A＝60°，∠B＝40°，∴∠ACD＝∠A+∠B＝100°，∵CE平分∠ACD，∴∠ECD＝∠ACD＝50°，故选：C．【点评】本题考查了角平分线定义和三角形外角性质，能熟记三角形外角性质的内容是解此题的关键．8．【分析】利用平行线的性质、对顶角的定义、算术平方根的定义及三角形的外角的性质分别判断后即可确定正确的选项．【解答】解：A、两直线平行，同旁内角互补，故原命题错误，是假命题，不符合题意；B、相等的角不一定是对顶角，故错误，是假命题，不符合题意；C、4的算术平方根是2，故原命题错误，是假命题，符合题意；D、三角形的一个外角大于任何一个和它不相邻的内角，正确，是真命题，符合题意．故选：D．【点评】本题考查了命题与定理的知识，解题的关键是了解有关的定义及定理，难度不大．9．【分析】根据“用绳子去量长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺”，即可得出关于x，y的二元一次方程组，此题得解．【解答】解：∵用绳子去量长木，绳子还剩余4.5尺，∴x﹣y＝4.5；∵将绳子对折再量长木，长木还剩余1尺，∴．∴所列方程组为．故选：B．【点评】本题考查了由实际问题抽象出二元一次方程组，找准等量关系，正确列出二元一次方程组是解题的关键．10．【分析】由点C的坐标，利用一次函数图象上点的坐标特征，可求出k值，进而可得出直线EF的函数解析式，过点C作CM⊥x轴于点M，过点D作DN⊥y轴于点N，则△OAB≌△MBC及△OAB≌△NDA，利用全等三角形的性质，可求出点D的坐标，利用一次函数图象上点的坐标特征，可求出点D平移后的横坐标，结合平移前点D的横坐标，即可求出结论．【解答】解：∵点C的坐标（﹣7，3）在一次函数y＝kx+6上，∴3＝﹣7k+6，解得：k＝，∴直线EF的函数解析式为y＝x+6.过点C作CM⊥x轴于点M，过点D作DN⊥y轴于点N，如图所示．∵四边形ABCD是正方形，∴AB＝BC＝CD＝DA，∠ABC＝∠BAD＝90°．∵∠ABO+∠OAB＝90°，∠ABO+∠MBC＝180°﹣90°＝90°，∴∠OAB＝∠MBC．在△OAB和△MBC中，，∴△OAB≌△MBC（AAS），∴OB＝MC＝3，OA＝MB＝7﹣3＝4，∴点A的坐标为（0，4），点B的坐标为（﹣3，0）．同理，可证出△OAB≌△NDA（AAS），∴AN＝BO＝3，DN＝AO＝4，∴ON＝OA+AN＝4+3＝7，∴点D的坐标为（﹣4，7）．当y＝7时，x+6＝7，解得：x＝，∴a＝﹣（﹣4）＝．故选：D．【点评】本题考查了全等三角形的判定与性质、正方形的性质以及一次函数图象上点的坐标特征，利用全等三角形的性质，求出点D的坐标是解题的关键．二、填空题（本题共5小题，每小题3分，共15分）11．【分析】根据立方根的定义即可求解．【解答】解：＝﹣2．故答案为：﹣2．【点评】本题考查了立方根，如果一个数的立方等于a，那么这个数叫做a的立方根或三次方根．12．【分析】首先比较出与的平方的大小关系，然后根据：两个正实数，平方大的，这个数也大，判断出与的大小关系即可．【解答】解：＝50，＝27，∵50＞27，∴＞．故答案为：＞．【点评】此题主要考查了实数大小比较的方法，解答此题的关键是要明确：正实数＞0＞负实数，两个正实数，平方大的，这个数也大．13．【分析】由勾股定理求出CD2＝64，AB2＝AF2+BF2＝CD2＝64，再由正方形的性质即可得出结论．【解答】解：如图．∵四边形ABCD是正方形，∴AB＝CD，在Rt△CDE中，由勾股定理得：CD2＝CE2﹣DE2＝102﹣62＝64，在Rt△ABF中，由勾股定理得：AB2＝AF2+BF2＝CD2＝64，∴阴影部分的面积之和＝AF2+BF2＝AB2＝64，故答案为：64．【点评】本题考查的是勾股定理以及正方形的性质等知识，熟练掌握勾股定理和正方形的性质是解题的关键．14．【分析】将点P（﹣1，m）代入y＝2x+6，求出m的值，即可得点P的坐标，根据两函数图象交点的横纵坐标的值为两函数解析式组成的方程组的解可得答案．【解答】解：将点P（﹣1，m）代入y＝2x+6，得m＝﹣2+6＝4，∴点P坐标为（﹣1，4），∴方程组的解为．故答案为：．【点评】本题考查一次函数与二元一次方程（组），熟知两函数图象交点的横纵坐标的值为两函数解析式组成的方程组的解是解题的关键．15．【分析】过点B作BE⊥AD，交AD的延长线于点E，证出ED＝BD，设ED＝EB＝x，得出DB＝x，AE＝2+x，由四边形ACBD的面积求出x＝1，则可得出答案．【解答】解：过点B作BE⊥AD，交AD的延长线于点E，∵∠ADB＝135°，∴∠EDB＝45°，∴∠EDB＝∠EBD，∴ED＝BD，设ED＝EB＝x，∴DB＝＝x，AE＝2+x，∴AB2＝BE2+AE2＝x2+（2+x）2＝2x2+4x+4，过点C作CF⊥AB于点F，∵∠ACB＝90°，AC＝BC，∴CF＝AB，∴，∵四边形ACBD的面积是，∴，∴（x﹣1）（x+5）＝0，解得x1＝1，x2＝﹣5（舍去），∴DE＝1，∴BD＝．故答案为：．【点评】本题考查了勾股定理，等腰直角三角形的性质，解一元二次方程，熟练掌握以上知识是解题的关键．三、解答题（共7小题，共55分，其中16题6分，17题8分，18题6分，19题8分，20题8分，21题9分，22题10分）16．【分析】（1）先根据二次根式的性质进行计算，再根据二次根式的加法法则进行计算，再根据二次根式的除法法则进行计算即可；（2）先根据二次根式的性质和完全平方公式进行计算，再二次根式的加减法法则进行计算即可．【解答】解：（1）＝＝＝5；（2）（1﹣）2+3＝1﹣2+3+＝4﹣．【点评】本题考查了二次根式的混合运算，能正确根据二次根式的运算法则进行计算是解此题的关键，注意运算顺序．17．【分析】（1）方程组利用代入消元法求出解即可；（2）方程组利用加减消元法求出解即可．【解答】解：（1），将①代入②得：x+2x＝12，解得：x＝4，将x＝4代入①得y＝8，则原方程组的解是；（2），①+②得5x＝10，解得：x＝2，将x＝2代入①得：y＝3，则原方程组的解是．【点评】此题考查了解二元一次方程组，此题的关键是把二元一次方程组转化成一元一次方程，题目比较典型，难度适中．18．【分析】（1）先求出A校90分的人数，再根据平均数公式求a即可，根据中位数和众数的定义即求出b、c的值；（2）用360°乘80分所占的百分比即可求出圆心角α，根据A校90分的人数补全条形统计图即可；（3）依据表格中平均数、中位数、众数比较做出判断即可．【解答】解：（1）A校90分的人数为20﹣1﹣1﹣9﹣4＝5（人），∴a＝＝93.5，将A校被抽取的20名志愿者分数按从小到大的顺序排列后，第10，11个数据分别为95，95，所以中位数b＝＝95，由扇形统计图可知B校志愿者的成绩100分的百分比最大，所以众数c＝100，故答案为：93.5，95，100；（2）B校志愿者的成绩的扇形统计图中的圆心角α＝360°×（1﹣20%﹣15%﹣20%﹣40%）＝18°，补全A校志愿者的成绩的条形统计图：故答案为：18；（3）倾向招B所大学的志愿者，理由如下：∵两所大学的平均分和中位数都相等，但B所大学众数大于A所大学的众数，∴倾向招B所大学的志愿者．【点评】本题考查条形统计图、扇形统计图、统计表的意义和表示数据的特征，理解平均数、中位数、众数的意义是正确解答的前提，从统计图表中获取有用信息是解题的关键．19．【分析】（1）设出每副乒乓球拍和每盒乒乓球的价格，再列二元一次方程组，解出即可；（2）分别求出在甲商场和乙商场购买的价格，再比较即可得出在哪个商场采购合算．【解答】解：（1）设每副乒乓球拍的价格为x元，每盒乒乓球的价格为y元，根据题意，得，解得，答：每副乒乓球拍的价格为30元，每盒乒乓球的价格为5元；（2）在甲商场采购合算．理由如下：在甲商场采购：（20×30+30×5）×0.9＝675（元），在乙商场采购：20×30+（30﹣）×5＝700（元），∵675＜700，∴在甲商场采购合算．【点评】本题考查二元一次方程组的应用，理解题意，弄清题目中的等量关系并列出方程组是解题的关键．20．【分析】（1）令x＝0可得点B的坐标，令y＝0可得点A的坐标；（2）先根据勾股定理求AB的长，由折叠可得BM＝B'M＝4，设OM＝x，则BM＝B'M＝8﹣x，由勾股定理列式得：x2+42＝（8﹣x）2，解方程可得x的值，利用待定系数法求AM的解析式；【解答】解：（1）当x＝0时，y＝﹣x+8＝8，∴B（0，8），当y＝0时，x＝6，∴A（6，0）；（2）∵A（6，0），B（0，8），∴AB＝＝10，∴AB′＝AB＝10，∴B′（﹣4，0），设OM＝x，则B′M＝BM＝BO﹣MO＝8﹣x，B′O＝AB′﹣AO＝10﹣6＝4∴x2+42＝（8﹣x）2x＝3∴M（0，3）设AM：y＝kx+b，则，解得，∴直线AM的解析式为y＝﹣x+3．【点评】本题为一次函数的综合应用，涉及折叠的性质、待定系数法、勾股定理等知识．在（1）中利用函数与坐标轴的交点列方程是解题的关键，在（2）中求得M点的坐标是解题的关键．21．【分析】（1）分别作点A，B，C关于y轴的对称点D，E，F，连接DE、EF、DF，则△DEF就是所求的图形；（2）作点B关于x轴的对称点G，连接AG交x轴于点P，连接BP，则PB＝PG，所以PA+PB＝PA+PG＝AG，此时PA+PB的值最小，即可由A（3，4），G（1，﹣2），求得AG＝＝2，于是得到问题的答案；（3）分别作点G关于直线AB、BC的对称点L、H，连接LH分别交AB、BC于点M，N，连接GL、GH、GM、GN、BL、BH，则GM+GN+MN＝LM+HN+MN＝LH，此时△GMN的周长最小，可求得∠LBH＝∠GBL+∠GBH＝2（∠ABG+∠CBG）＝90°，再根据勾股定理求得LH＝＝20≈28（米），则△GMN的周长最少约28米．【解答】解：（1）如图1，分别作点A，B，C关于y轴的对称点D，E，F，连接DE、EF、DF，△DEF就是所求的图形.（2）如图1，作点B关于x轴的对称点G，连接AG交x轴于点P，连接BP，点P就是所求的图形．理由：∵PB＝PG，∴PA+PB＝PA+PG＝AG，∴此时PA+PB的值最小，∵A（3，4），B（1，2），∴G（1，﹣2），∴AG＝＝2，∴PA+PB的最小值为2，故答案为：2．（3）如图2，分别作点G关于直线AB、BC的对称点L、H，连接LH分别交AB、BC 于点M，N，连接GL、GH、GM、GN、BL、BH，∵AB垂直平分GL，BC垂直平分GH，∴GM＝LM，GN＝HN，∴GM+GN+MN＝LM+HN+MN＝LH，∴此时△GMN的周长最小，∵LB＝GB＝20米，BA⊥GL，HB＝GB＝20米，BC⊥GH，∴∠ABL＝∠ABG，∠CBH＝∠CBG，∴∠GBL＝2∠ABG，∠GBH＝2∠CBG，∴∠LBH＝∠GBL+∠GBH＝2（∠ABG+∠CBG）＝2∠ABC＝2×45°＝90°，∴LH＝＝＝20≈20×1.41≈28（米），答：△GMN的周长最少约28米．【点评】此题重点考查图形与坐标、轴对称的性质、勾股定理、两点之间线段最短等知识，此题综合性强，难度较大，正确地作出所需要的辅助线是解题的关键．22．【分析】（1）可推出AG＝AC，∠CAG＝90°，从而得出结果；（2）作MX⊥AB于X，可推出BM＝AB，进而得出MX＝BM，从而∠ABM＝30°，进一步得出结果；（3）当线段FE与BQ交于点O时，作BV⊥AF于V，可证得△EOQ≌△VOB，从而BV＝EQ＝2，OV＝OE，进而得出∠BEF＝30°，从而得出AV＝BV＝4，进而得出OF＝8﹣2，进一步得出结果；当EF的延长线交BQ于点O时，同样得方法得出结果．【解答】解：（1）∵长方形纸片ABCD和EFGQ是两个完全相同的长方形，∴AC＝AG，∠BAC＝∠GAF，∴∠BAC+∠CAD＝∠GAF+∠CAD，∴∠GAC＝∠BAD＝90°，∴△ACG是等腰直角三角形，故答案为：等腰直角三角形；（2）如图1，∵四边形ABCD是长方形，∴AB∥CD，∠ABC＝∠D＝∠DAB＝90°，∴∠BAM+∠AMC＝180°，∵∠AMB+∠AMC＝180°，∴∠BAM＝∠AMB，∴BM＝AB＝4，作MX⊥AB于X，∴∠AXM＝90°，∴四边形ADMX是矩形，∴MX＝AD＝2，∴MX＝BM，∴∠ABM＝30°，∴∠CBM＝60°，∵BN平分∠MBC，∴∠CBN＝；（3）如图2，当线段FE与BQ交于点O时，作BV⊥AF于V，∵O是BQ的中点，∴OB＝OQ，∵∠QEF＝∠BVE＝90°，∠EOQ＝∠BOV，∴△EOQ≌△VOB（AAS），∴BV＝EQ＝4，OV＝OE，∴BV＝EB，∴∠BEF＝30°，∴AV＝BV＝4，∴OA＝2，∴OF＝8﹣2，＝S△BOF+S△FOQ＝OF•（AQ+BV）＝＝32﹣8，∴S△BFQ如图3，当EF的延长线交BQ于点O时，由上知：OE＝OV＝2，∴OF＝EF+OE＝8+2，＝S△BOF+S△FOQ＝OF•（AQ+BV）＝＝32+8，∴S△BFQ综上所述：△BFQ的面积是32+8或32﹣8．【点评】本题考查了矩形的性质，等腰三角形的判定，直角三角形的性质，全等三角形的判定和性质等知识，解决问题的关键是作辅助线，构造全等三角形。

深圳罗湖区罗湖中学八年级上册生物期末试卷及答案-百度文库

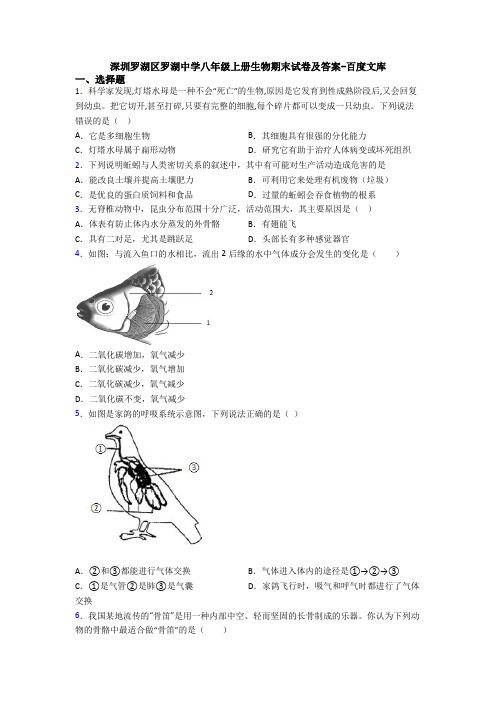
深圳罗湖区罗湖中学八年级上册生物期末试卷及答案-百度文库一、选择题1．科学家发现,灯塔水母是一种不会“死亡”的生物,原因是它发育到性成熟阶段后,又会回复到幼虫。

把它切开,甚至打碎,只要有完整的细胞,每个碎片都可以变成一只幼虫。

下列说法错误的是（）A．它是多细胞生物B．其细胞具有很强的分化能力C．灯塔水母属于扁形动物D．研究它有助于治疗人体病变或坏死组织2．下列说明蚯蚓与人类密切关系的叙述中，其中有可能对生产活动造成危害的是A．能改良土壤并提高土壤肥力B．可利用它来处理有机废物（垃圾）C．是优良的蛋白质饲料和食品D．过量的蚯蚓会吞食植物的根系3．无脊椎动物中，昆虫分布范围十分广泛，活动范围大，其主要原因是（）A．体表有防止体内水分蒸发的外骨骼B．有翅能飞C．具有二对足，尤其是跳跃足D．头部长有多种感觉器官4．如图：与流入鱼口的水相比，流出2后缘的水中气体成分会发生的变化是（）A．二氧化碳增加，氧气减少B．二氧化碳减少，氧气增加C．二氧化碳减少，氧气减少D．二氧化碳不变，氧气减少5．如图是家鸽的呼吸系统示意图，下列说法正确的是（）A．②和③都能进行气体交换B．气体进入体内的途径是①→②→③C．①是气管②是肺③是气囊D．家鸽飞行时，吸气和呼气时都进行了气体交换6．我国某地流传的“骨笛”是用一种内部中空、轻而坚固的长骨制成的乐器。

你认为下列动物的骨骼中最适合做“骨笛”的是（）A．草鱼B．东北虎C．鹤D．蛇7．爬行动物是真正适应陆地环境的脊椎动物，主要原因是（）A．用肺呼吸B．卵表面有坚韧的卵壳C．体表覆盖角质的鳞片或甲D．生殖和发育摆脱了对水环境的依赖8．家兔与食草生活相适应的特征是（）A．体表被毛B．发达的神经系统C．有发达的门齿和臼齿D．有发达的犬齿9．下列关于骨骼肌、骨和关节的说法不正确．．．的是（）A．人体的骨骼肌有600多块B．骨与骨的连结叫关节C．人体有206块骨D．骨松质中，终生具有红骨髓10．下图是人屈肘时上臂的两组肌肉协调活动示意图，此时，肱二头肌和肱三头肌所处的状态分别是：A．均收缩B．均舒张C．收缩和舒张D．舒张和收缩11．关节炎是一种常见疾病，患者关节腔内有大量积液并伴有肿胀疼痛，其病变部位应是（）A．关节面B．关节软骨C．关节囊D．关节腔12．教育部、国家体育总局和共青团中央提出“阳光体育”——“每天锻炼一小时，健康生活一辈子”，关于体育锻炼作用的叙述，下面哪一项最全面A．能使关节囊和韧带增厚B．能加强骨的营养C．能使肌肉发达D．以上三项都是13．蜗牛、羚羊和大象的运动方式分别是：A．爬行、攀援、行走B．爬行、跳跃、行走C．行走、跳跃、奔跑D．行走、爬行、奔跑14．动物社会行为的特征不包括（）A．群体内部成员之间分工合作B．群体内部成员各自独立生活C．有的群体中还形成等级D．群体内部成员之间进行信息交流15．下列几种动物中，不具有社会行为的是（）A．东北虎B．蚂蚁C．白蚁D．狒狒16．在走“T”形迷宫实验中，蚯蚓大约要经过200次“尝试和错误”后，才能学会直接爬向潮湿的暗室；鸟类大约经过几次就可以学会绕过障碍取食。

2022-2023深圳罗湖区八年级(上)期末语文答案

2022-2023学年广东省深圳市罗湖区八年级（上）期末语文试卷参考答案与试题解析一、积累运用（30分）.1．【分析】本题考查学生对古诗文名句的识记能力。

解答此类题目，我们需要在平时的学习中，做好积累，根据提示语句写出相应的句子，尤其要注意不能出现错别字。

理解性识记，注意结合语境填充。

【解答】（1）似曾相识燕归来（2）老骥伏枥（重点字：骥）（3）绿杨阴里白沙堤（4）折戟沉沙铁未销东风不与周郎便（5）贫贱不能移（6）报君黄金台上意提携玉龙为君死白头搔更短浑欲不胜簪2．【分析】本题考查根据拼音写汉字。

需要学生在平时读课文时，养成仔细观察的习惯，注意读音、字形，并注意在具体语境中体会读音及书写。

【解答】答案：（1）浩瀚（2）濒临（3）巧妙绝伦（4）长途跋涉3．【分析】本题考查学生正确使用词语的能力。

解答此题，我们平时要积累大量的词语，还要结合句意表述，从词性、词义轻重、感情色彩、习惯用法等多方面考虑。

【解答】ABD.正确；C.有误，精疲力尽：形容非常疲乏，一点力气也没有了。

词义和“精神抖擞”矛盾。

故选：C。

4．【分析】本题考查病句辨析及修改能力。

常见的病句类型有成分残缺、搭配不当、语序混乱、结构混乱、语意不明、语言赘余等。

先通读所有句子，凭语感判断正误，如果不能判断的，可以压缩句子，看搭配是否得当，找出病因。

【解答】ACD.正确；B.有误，本句病因应是重复累赘，“当务之急”已包含“目前”之意，正确修改应是删去“目前”。

故选：B。

5．【分析】（1）本题考查拟写新闻标题。

解答此题，先从新闻中找出关键语句“我校‘品读经典放飞青春’经典诵读比赛在学校多功能厅举行”，由题干可知“我校”为“阳光中学”，将以上信息进行概括，即可得出答案：阳光中学举行经典诵读比赛。

解答时，要注意字数要求。

（2）本题考查提取句子主干。

该句主语中心语是“比赛”，“根据参赛作品的内容”是状语。

谓语中心语是“分为”，“篇章”是宾语中心语。

句子主干是：比赛分为篇章。

2023-2024学年广东省深圳市罗湖区八年级上学期期末考英语试卷含答案

2023—2024学年第一学期学业质量检测八年级英语2024.1本试卷考试时间90分钟，满分100分；第一部分选择题（50分）Ⅰ.完形填空（10分）阅读下面短文，从短文后所给的A、B、C、D四个选项中选出能填入相应空白处的最佳选项，并在答题卡上将相应的字母编号涂黑。

（共10小题，每小题1分）Did you get a gift from your parents,classmates or teachers when you were leaving primary school?Was there 1special about it?A2was going to leave college.Her father said,“Dear,I want to give you an old3.I bought it a long time ago,you know.Before I give it to you,take it to a car dealer(经销商)in the city and see how much they offer for it.”The girl did as the father ing back,she said,“They offered$1,000because it4very old.”“OK.Take it to the second-hand car dealer,”the father said.The girl5again and said,“They offered$100because it is a very old car and it needs a lot of work.”The father asked his daughter to6the car to a car club.This time the girl get something different.“Some people in the club offered me$100,000because it is a rare(少见的)car,it’s super7to find,but it is still in good condition.”The father8,“Dear,remember this.You are not worth anything if you are not in the right place.If they don’t like you,do not be9.That means you are in the10place.Don’t stay in a place where no ones sees your value.”1.A.everything B.nothing C.something D.anything2.A.daughter B.son C.sister D.aunt3.A.coat B.car C.watch D.pen4.A.smells B.feels C.looks D.sounds5.A.came back B.came on C.looked back D.gave back6.A.give B.break C.show D.challenge7.A.easy B.boring C.strange D.difficult8.A.cried B.smiled C.asked D.checked9.A.happy B.confident C.angry D.correctfortable B.popular C.local D.wrongⅡ.阅读理解（40分）第一节阅读下列短文，从下面每小题所给的A、B、C、D四个选项中，选出最佳选项，并在答题卡上将相应的字母编号涂黑。

2021-2022学年广东省深圳市罗湖区八年级(上)期末数学试卷(附详解)

2021-2022学年广东省深圳市罗湖区八年级（上）期末数学试卷一、选择题（本大题共10小题，共30.0分）1.下列四个实数中，为无理数的是()D. √4A. 0B. πC. 342.若一直角三角形的两边长分别是6，8，则第三边长为()A. 10B. 2√7C. 10或2√7D. 143.在平面直角坐标系中，点A的坐标是(−2,1)，点B与点A关于y轴对称，则点B的坐标是()A. (1,−2)B. (2,−1)C. (2,1)D. (−1,−2)4.甲、乙、丙、丁四人各进行了10次射击测试，他们的平均成绩相同．方差分别是S甲2=0.6，S乙2=1.1，S丙2=1.2，S丁2=0.9.则射击成绩最稳定的是()A. 甲B. 乙C. 丙D. 丁5.下列运算正确的是()A. √2+√3=√5B. 2√3−√3=2C. 2√2×3√2=6√2D. √6÷√2=√36.如图，AB//DF，AC⊥CE于点C，BC与DF交于点E，若∠A=20°，则∠CED等于()A. 20°B. 50°C. 70°D. 110°7.下列命题是假命题的是()A. 无理数都是无限小数B. −1的立方根是它本身C. 三角形内角和都是180°D. 内错角相等8.如图，一次函数y=kx+b的图象经过点(0,4)，则下列结论正确的是()A. 图象经过一、二、三象限B. 关于x 方程kx +b =0的解是x =4C. b <0D. y 随x 的增大而减小9. 《九章算术》是中国古代第一部数学专著，它的出现标志着中国古代数学形成了完整的体系，在其方程章中有一道题：今有甲乙二人，不知其钱包里有多少钱，若乙把其钱的一半给甲则甲的钱数为50；若甲把其钱的23给乙，则乙的钱数也能为50，问甲、乙各有多少钱？若设甲持钱为x ，乙持钱为y ，则可列方程组( )A. {x +23y =50y +12x =50B. {x +12y =50y +23x =50 C. {x −12y =50y −23x =50 D. {x −23y =50y −12x =50 10. 现有一楼房发生火灾，消防队员决定用消防车上的云梯救人．如图(1)已知云梯最多只能伸长到15m ，消防车高3m.救人时云梯伸长至最长，在完成从12m 高处救人后，还要从15m 高处救人．这时消防车要从原处再向着火的楼房靠近的距离AC 为( )A. 3米B. 5米C. 7米D. 9米二、填空题（本大题共5小题，共15.0分）11. 16的算术平方根是______．12. 某学校决定招聘数学教师一名，一位应聘者测试的成绩如下表：测试项目笔试面试测试成绩(分) 80 90将笔试成绩，面试成绩按6：4的比例计入总成绩，则该应聘者的总成绩是______分．13. △ABC 中，∠A 比∠B 大10°，∠C =50°，则∠A =______．14. 已知一次函数y =kx +4(k ≠0)的图象与两坐标轴围成的三角形面积为4，则k =______．15. 如图，Rt △ABC 中，∠ACB =90°，AC =3，BC =4，将边AC 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B′处，两条折痕与斜边AB 分别交于点E 、F ，以下四个结论：①∠ECF =45°；②△CEF 是等腰直角三角形；③S △CDF =3625；④B′F =45，其中正确结论的序号有______．三、解答题（本大题共7小题，共55.0分）16. 计算：(1)2√18−√32+√2；(2)(√12−√24)÷√6−2√12．17. 解方程：{x +y =8x −3y =4．18.如图所示，在平面直角坐系中，△ABC的顶点坐标分别是A(a,−4)，B(−1,2)，C(4,4)．(1)已知点A(a,−4)关于x轴的对称点P的坐标为(−5,b)，求a，b的值；(2)画出△ABC，且△ABC的面积为______；(3)画出△ABC关于y轴成对称的图形△A2B2C2，并写出各个顶点的坐标．19.在第二十二届深圳读书月来临之际，为了解某学校八年级学生每天平均课外阅读时间的情况，随机抽查了该学校八年级部分同学，对其每天平均课外阅读时间进行统计，并绘制了如图所示的不完整的统计图，请根据相关信息，回答下列问题：(1)该校抽查八年级学生的人数为______，图中的a值为______；(2)请将条形统计图补充完整；(3)求被抽查的学生每天平均课外阅读时间的众数、中位数和平均数．(4)根据统计的样本数据，估计该校八年级400名学生中，每天平均课外阅读时间为2小时的学生有多少人？20.请解答下列各题：(1)阅读并回答：科学实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等．如图1，一束平行光线AB与DE射向一个水平镜面后被反射．此时∠1=∠2，∠3=∠4．①由条件可知：∠1=∠3，依据是______，∠2=∠4，依据是______．②反射光线BC与EF平行，依据是______．(2)解决问题：如图2，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b镜反射，若b射出的光线n平行于m，且∠1=42°，则∠2=______；∠3=______．21.为丰富同学们的课余活动，某校成立了篮球课外兴趣小组，计划购买一批篮球，需购买A，B两种不同型号的蓝球共300个，已知购买3个A型蓝球和2个B型蓝球共需340元，购买2个A型蓝球和1个B型篮球共需要210元．(1)求购买一个A型蓝球、一个B型篮球各需多少元？(2)若该校计划投入资金W元用于购买这两种篮球，设购进的A型蓝球为t个，求W关于t的函数关系式；(3)学校在体育用品专卖店购买A、B两种型号篮球共300个，经协商，专卖店给出如下优惠：A种球每个降价8元，B种球打9折．计算下来，学校共付费16740元．学校购买A、B两种篮球各多少个？22.如图1，直线AB的解析式为y=kx+6，D点坐标为(8,0)，O点关于直线AB的对称点C点在直线AD上．(1)求直线AB的解析式；(2)如图2，在x轴上是否存在点F，使△ABC与△ABF的面积相等，若存在求出F点坐，若不存在，请说明理由；(3)如图3，过点G(5,2)的直线l：y=mx+b，当它与直线AB夹角等于45°时，求出相应m的值．答案和解析1.【答案】B【解析】解：A.0是整数，属于有理数，故本选项不合题意；B.π是无理数，故本选项符合题意；C.3是分数，属于有理数，故本选项不合题意；4D.√4=2，是整数，属于有理数，故本选项不合题意；故选：B．无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．本题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．2.【答案】C【解析】【分析】本题考查了利用勾股定理解直角三角形的能力，当已知条件中没有明确哪是斜边时，要注意讨论，一些学生往往忽略这一点，造成丢解．本题已知直角三角形的两边长，但未明确这两条边是直角边还是斜边，因此两条边中的较长边8既可以是直角边，也可以是斜边，所以求第三边的长必须分类讨论，即8是斜边或直角边的两种情况，然后利用勾股定理求解．【解答】解：设第三边为x，①当8是直角边时，则x=√62+82=10，②当8是斜边时，x=√82−62=2√7．∴第三边长为10或2√7．故选：C．【解析】解：∵点A 与点B 关于y 轴对称，点A 的坐标是(−2,1)，∴点B 的坐标是：(2,1)．故选：C ．直接利用关于y 轴的对称点的坐标特点：横坐标互为相反数，纵坐标不变，进而得出答案．此题主要考查了关于y 轴对称点的性质，正确记忆横纵坐标的关系是解题关键．4.【答案】A【解析】解：∵S 甲2=0.6，S 乙2=1.1，S 丙2=1.2，S 丁2=0.9，∴S 甲2<S 丁2<S 乙2<S 丙2，∴射击成绩最稳定的是甲，故选：A ．根据方差的意义求解即可．本题主要考查方差，方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越差；反之，则它与其平均值的离散程度越小，稳定性越好．5.【答案】D【解析】解：A ．√2与√3不能合并，所以A 选项不符合题意；B .2√3−√3=√3，所以B 选项不符合题意；C .2√2×3√2=6×2=12，所以C 选项不符合题意；D .√6÷√2=√6÷2=√3，所以D 选项符合题意．故选：D ．根据二次根式的加减法对A 、B 进行判断；根据二次根式的乘法法则对C 进行判断；根据二次根式的除法法则对D 进行判断．本题考查了二次根式的混合运算：熟练掌握二次根式的性质、二次根式的乘法法则和除法法则是解决问题的关键．【解析】解：∵AC⊥CE，∴∠C=90°，∵∠A=20°，∴∠ABC=70°，∵AB//DF，∴∠CED=∠ABC=70°．故选：C．由AC⊥CE与∠A=20°，即可求得∠ABC的度数，又由AB//DF，根据两直线平行，同位角相等，即可求得∠CED的度数．此题考查了平行线的性质与垂直的定义．应用两直线平行，同位角相等是解题关键．7.【答案】D【解析】解：A、无理数都是无限小数，正确，是真命题，A选项不符合题意；B、−1的立方根是它本身，正确，是真命题，B选项不符合题意；C、三角形的内角和都是180°，正确，是真命题，C选项不符合题意；D、两直线平行，内错角相等，故原命题错误，是假命题，D选项符合题意．故选：D．利用无理数的定义、立方根的定义、三角形的内角和及平行线的性质分别判断后即可确定正确的选项．考查了命题与定理的知识，解题的关键是了解无理数的定义、立方根的定义、三角形的内角和及平行线的性质，难度不大．8.【答案】A【解析】解：由一次函数y=kx+b的图象可知图象经过一、二、三象限，∴k>0，b>0，y随x的增大而增大，∵一次函数y=kx+b的图象经过点(0,4)，∴关于x方程kx+b=0的解是x=−4，k故A正确，B、C、D错误，根据一次函数的性质，一次函数与一元一次方程的关系对各小题分析判断即可得解．本题主要考查了一次函数的性质，一次函数与一元一次方程，利用数形结合是求解的关键．9.【答案】B【解析】解：设甲持钱为x ，乙持钱为y ，则可列方程组：{x +12y =50y +23x =50．故选：B ．直接利用“乙把其钱的一半给甲则甲的钱数为50；甲把其钱的23给乙，则乙的钱数也能为50”分别得出等式组成方程组即可得出答案．此题主要考查了由实际问题抽象出二元一次方程组，正确得出等式是解题关键． 10.【答案】A【解析】解：在Rt △ABO 中，∵∠AOB =90°，AB =15m ，OB =12−3=9(m)， ∴AO =√AB 2−OB 2=√152−92=12(m)，在Rt △COD 中，∵∠COD =90°，CD =15m ，OD =15−3=12(m)，∴OC =√CD 2−OD 2=√152−122=9(m)，∴AC =OA −OC =3(m)，答：消防车要从原处再向着火的楼房靠近的距离AC 为3m ，故选：A ．在Rt △ABO 中，根据勾股定理得到AO =√AB 2−OB 2=√152−92=12(m)，在Rt △COD 中，根据勾股定理得到OC =√CD 2−OD 2=√152−122=9(m)，于是得到结论．本题考查了勾股定理的应用，熟练掌握勾股定理是解题的关键．11.【答案】4【解析】此题主要考查了算术平方根的定义．一个正数的算术平方根就是其正的平方根．根据算术平方根的定义即可求出结果．【解答】解：∵42=16，∴√16=4．故答案为：4．12.【答案】84【解析】解：由题意知，80×66+4+90×46+4=84(分)，故答案为：84．按6：4的比例计算总成绩即可．本题主要考查加权平均分的计算，根据题意按比例求出加权平均分是解题的关键．13.【答案】70°【解析】解：∵∠A比∠B大10°，∴∠B=∠A−10°，∵∠A+∠B+∠C=180°，∠C=50°，∴∠A+∠A−10°+50°=180°，解得：∠A=70°．故答案为：70°．由题意可得∠B=∠A−10°，结合三角形的内角和即可求解．本题主要考查三角形的内角和定理，解答的是熟记三角形的内角和为180°．14.【答案】±2【解析】解：一次函数y=kx+4与x轴的交点为(−4k,0)，与y轴的交点为(0,4)，∴函数图象与坐标轴围成三角形面积为S=12×|−4k|×4=|−8k|=4，∴k=±2，故答案为±2．分别求出函数与x轴、y轴的交点坐标，再由三角形面积可得S=12×|−4k|×4=|−8k|=4，从而求出k的值．本题考查一次函数图象上点的坐标特点；能够求出一次函数图象与坐标轴的交点，并结合直角三角形的面积公式求解是关键．15.【答案】①②④【解析】解：由折叠可知，AE=ED，BF=B′F，AC=CD，∠ACE=∠ECD，∠BCF=∠B′CF，∴∠ECF=12∠ACB，∵∠ACB=90°，∴∠ECF=45°，故①正确；∵CE⊥AD，∴∠CEF=90°，∵∠ECF=45°，∴△CEF是等腰直角三角形；故②正确；∵AC=3，BC=4，∴BC=5，∴S△ABC=12×AC×BC=12×AB×CE，∴CE=125，∵AC=3，∴AE=95，∵ED=AE，∴ED=95，∵CE=EF=125，∴DF=35，∴S△CDF=12×DF×CE=12×35×125=1825，故③不正确；∵AE =DE =95，CE =EF =125， ∴BF =5−95−125=45， ∵BF =B′F ，∴B′F =45；故④正确；故答案为：①②④．①由折叠可知∠ECF =12∠ACB =45°；②由折叠可知∠CEF =90°，又由∠ECF =45°，则△CEF 是等腰直角三角形；③由面积S △ABC =12×AC ×BC =12×AB ×CE ，求出CE =125，AE =ED =95，则DF =35，所以S △CDF =12×DF ×CE =1825；④AE =DE =95，CE =EF =125，B′F =AB −AE −CE =45．本题考查图形的折叠，熟练掌握直角三角形的性质，折叠的性质是解题的关键．16.【答案】解：(1)原式=6√2−4√2+√2=3√2；(2)原式=(2√3−2√6)÷√6−2×√22=2√3÷√6−2√6÷√6−√2=√2−2−√2=−2．【解析】(1)直接化简二次根式，进而合并得出答案；(2)直接化简二次根式，再利用二次根式的除法运算法则化简得出答案．此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．17.【答案】解：{x +y =8①x −3y =4②， ①−②得4y =4，解得y =1，把y =1代入①得x =7．故方程组的解为{x =7y =1．【解析】利用加减消元法解方程组即可求解．此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．18.【答案】14.5【解析】解：(1)∵点A(a,−4)关于x轴的对称点P的坐标为(−5,b)，∴a=−5，b=4；(2)△ABC的面积=12×8×9−12×2×5−2×3−12×3×7=14.5；故答案为：14.5；(3)如图所示：A2(4,−5)，B2(1,2)，C2(−4,4)．(1)根据关于x轴对称的两点横坐标相等、纵坐标互为相反数得出答案；(2)根据三角形面积公式解答即可；(3)根据点A、B、C坐标可作出△ABC，再分别作出三个顶点关于y轴的对称点，然后首尾顺次连接即可得．本题主要考查作图−轴对称变换，解题的关键是掌握轴对称变换的定义与性质、割补法求三角形的面积等知识点．19.【答案】10018【解析】解：(1)该校抽查八年级学生的人数为：30÷30%=100，a%=18÷100×100%=18%，故答案为：100，18；(2)100−12−30−18=40(人)，补图如下：平均数是：(12×0.5+30×1+40×1.5+18×2)÷100=1.32(小时)，众数是1.5小时，中位数是1.5小时，即每周平均课外阅读时间的样本数据的平均数是1.32小时、众数是1.5小时、中位数是1.5小时；(3)400×18%=72(人)，答：该校八年级每周平均课外阅读时间为2ℎ的学生有72人．(1)根据阅读时间为1小时的人数和所占的百分比可以求得该校抽查八年级学生的人数，然后即可计算出a的值；(2)用总人数100−12−30−18可得阅读时间为1.5小时的人数，完成统计图；(3)根据统计图中的数据，可以计算出平均数，再根据统计图中的数据可以得到众数和中位数；(4)根据统计图中的数据，可以计算出该校八年级每周平均课外阅读时间为2ℎ的学生人数．本题考查条形统计图和扇形统计图、用样本估计总体、加权平均数、中位数、众数，解答本题的关键是明确题意，利用数形结合的思想解答．20.【答案】两直线平行，同位角相等等量代换同位角相等，两直线平行84°90°【解析】解：(1)①由条件可知：∠1=∠3，依据是：两直线平行，同位角相等；∠2=∠4，依据是：等量代换；②反射光线BC与EF平行，依据是：同位角相等，两直线平行；故答案为：①两直线平行，同位角相等；等量代换．②同位角相等，两直线平行．(2)如图，∵∠1=42°，∴∠4=∠1=42°，∴∠6=180°−42°−42°=96°，∵m//n ，∴∠2+∠6=180°，∴∠2=84°，∴∠5=∠7=180°−∠22=48°，∴∠3=180°−48°−42°=90°．故答案为：84°，90°．(1)根据平行线的判定与性质逐一求解可得；(2)根据入射角等于反射角得出∠1=∠4，∠5=∠7，求出∠6，根据平行线性质即可求出∠2，求出∠5，根据三角形内角和求出∠3即可．本题考查了平行线的性质和判定，熟练掌握平行线的判定与性质是解题的关键．21.【答案】解：(1)设购买一个A 型蓝球a 元、一个B 型篮球b 元，由题意可得：{3a +2b =3402a +b =210，解得{a =80b =50，答：购买一个A 型蓝球80元、一个B 型篮球50元；(2)设购进的A 型蓝球为t 个，则购进B 型篮球(300−t)个，由题意可得：W =80t +50(300−t)=30t +15000，即W 关于t 的函数关系式是W =30t +15000；(3)设购进的A 型蓝球为x 个，则购进B 型篮球(300−x)个，由题意可得：(80−8)x +50×0.9×(300−x)=16740，解得x =120，∴300−x=180，答：学校购买A、B两种篮球分别为120个、180个．【解析】(1)根据购买3个A型蓝球和2个B型蓝球共需340元，购买2个A型蓝球和1个B型篮球共需要210元，可以列出二元一次方程组，然后求解即可；(2)根据题意和(1)中的结果，可以写出W关于t的函数关系式；(3)根据题意和(1)中的结果，可以列出相应的方程，然后求解即可．本题考查一次函数的应用、二元一次方程组的应用，解答本题的关键是明确题意，找出等量关系，列出相应的方程，写出相应的函数关系式．22.【答案】解：(1)∵y=kx+6，∴A(0,6)，∴OA=6，∵D(8,0)，∴OD=8，x+6，∴直线AD的解析式为y=−34在Rt△ABD中，AD=√AO2+OD2=√36+64=10，∵O点、点C关于直线AB对称，∴设OB=BC=a，OA=AC=6，∴CD=4，∴BD=8−a，在Rt△BCD中，a2+42=(8−a)2，∴a=3，∴B(3,0)，∴0=3k+6，∴k=−2，∴直线AB的解析式为y=−2x+6；(2)∵AC=AO，AB=AB，OB=BC，∴△ABO≌△ABC(SSS)，∴S△ABO=S△ABC，×6×3=9，∴S△ABC=12设点F坐标为(x,0)，∴S△ABF=12×6×|x−3|=9，∴x=0或6，∴点F(0,0)或(6,0)；(3)如图3，设直线l与AB的交点为E和F，过点G作HN⊥x轴，过点E作EH⊥HN于H，过点F作FN⊥HN于N，设点E(a,−2a+6)，∵点G(5,2)，∴EH=5−a，HG=−2a+6−2=−2a+4，∵直线l与直线AB夹角等于45°，∴∠GEF=∠GFE=45°，∴EG=GF，∠EGF=90°，∴∠EGH+∠FGN=90°=∠EGH+∠GEH，∴∠FGN=∠GEH，又∵∠H=∠N=90°，EG=FG，∴△EGH≌△FGN(AAS)，∴EH=GN=5−a，FN=HG=−2a+4，∴点F的坐标为(1+2a,a−3)，∵点F在直线AB上，∴a−3=−2(1+2a)+6，∴a=75，∴点E(75,165)，点F(195,−25)，∴直线EG的解析式为：y=−13x+113，直线FG的解析式为：y=2x−8，∴m=−1或2．3【解析】(1)先求点A，点B的坐标，代入解析式可求解；(2)设点F坐标为(x,0)，由三角形的面积公式可求解；(3)如图3，设直线l与AB的交点为E和F，过点G作HN⊥x轴，过点E作EH⊥HN于H，过点F作FN⊥HN于N，由全等三角形的性质求出点E，点F坐标，即可求解．本题是一次函数综合题，考查了待定系数法，全等三角形的判定和性质，轴对称的性质，勾股定理等知识，利用数形结合思想解决问题是解题的关键．。

广东省深圳市罗湖区2021-2022学年八年级上学期期末数学试题(解析版)

八年级（上）期末学业质量与学科素养评价数学2022.01一、选择题1. 下列四个实数中，为无理数的是（） A. 0 B.πC.34D.【答案】B 【解析】【分析】根据无理数的定义：“无限不循环的小数是无理数”，逐项分析判断即可【详解】A. 0是有理数，故该选项不符合题意； B. π是无理数，故该选项符合题意； C. 34是有理数，故该选项不符合题意； D.2=是有理数，故该选项不符合题意；故选B【点睛】本题考查了无理数，解答本题的关键掌握无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．2. 若一直角三角形的两边长分别是6，8，则第三边长为（）A. 10B.C. 10或D. 14【答案】C 【解析】【详解】有两种情况，当810=当8所以，第三边的长为10或故选C ．【点睛】本题考查了勾股定理.运用分类讨论是解题的关键．3. 在平面直角坐标系中，点A 的坐标是()2,1−，点B 与点A 关于y 轴对称，则点B 的坐标是（） A. ()1,2− B. ()2,1−C. ()2,1D. ()1,2−−【答案】C【解析】【分析】根据关于y 轴对称的点坐标的特征：纵坐标不变，横坐标互为相反数，即可求解．【详解】解：点A 的坐标是()2,1−，点B 与点A 关于y 轴对称，∴B 的坐标为()2,1，故选：C ．【点睛】本题主要是考查了关于y 轴对称的点坐标的特征，熟练掌握关于坐标轴对称的点的特征，是解决该类问题的关键．4. 甲、乙、丙、丁四人各进行了10次射击测试，他们的平均成绩相同，方差分别是21.2S =甲，21.1S =乙，20.6S =丙，20.9S =丁，则射击成绩最稳定的是( ) A. 甲 B. 乙 C. 丙 D. 丁【答案】C 【解析】【分析】根据方差是用来衡量一组数据波动大小的量，故由甲乙丙丁的方差可直接作出判断．【详解】∵2S 1.2=甲，2S 1.1=乙，2S 0.6=丙，2S 0.9=丁， ∴2S 丙＜2S 丁＜2S 乙＜2S 甲， ∴射击成绩最稳定的是丙，故选C.【点睛】本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定． 5. 下列运算正确的是（）B. 2−=C. 【答案】D 【解析】【分析】根据二次根式的性质对A 进行判断；根据二次根式的加减法对B 进行判断；根据二次根式的乘法法则对C 进行判断；根据二次根式的除法法则对D 进行判断．【详解】解：A A 选项不符合题意；B ．−B 选项不符合题意；C ．12=，所以C 选项不符合题意； DD 选项符合题意．故选：D ．【点睛】本题考查了二次根式的混合运算，熟练掌握二次根式的性质、二次根式的乘法和除法法则是解决问题的关键．6. 如图，AB DF ∥，AC CE ⊥于点C ，BC 与DF 交于点E ，若20A ∠=°，则CED ∠等于（）A. 20°B. 50°C. 70°D. 110°【答案】C 【解析】【分析】由AC CE ⊥与20A ∠=°，即可求得ABC ∠的度数，又由AB DF ∥，根据两直线平行，同位角相等，即可求得CED ∠的度数．【详解】解：∵AC CE ⊥， ∴90C ∠=°， ∵20A ∠=°， ∴70ABC ∠=°， ∵AB DF ∥，∴70CED ABC ∠=∠=°．故选：C ．【点睛】题目主要考查了平行线的性质与垂直的性质、三角形内角和定理，熟练掌握平行线的性质是解题关键．7. 下列命题是假命题的是（） A. 无理数都是无限小数 B. 1−的立方根是它本身 C. 三角形内角和都是180° D. 内错角相等【答案】D 【解析】【分析】根据无理数的定义、立方根、三角形内角和定理、平行线的性质，分别进行判断，即可得到答案．【详解】解：A 、无理数都是无限小数；原命题是真命题，故不符合题意； B 、1−的立方根是它本身；原命题是真命题，故不符合题意； C 、三角形内角和都是180°；原命题是真命题，故不符合题意； D 、两直线平行，内错角相等；原命题是假命题，故符合题意；故选：D【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．8. 如图，一次函数y kx b =+的图象经过点()0,4，则下列结论正确的是（）A. 图像经过一、二、三象限B. 关于x 方程0kx b +=的解是4x =C. 0b <D. y 随x 的增大而减小【答案】A 【解析】【分析】根据函数图象可知图象经过一、二、三象限，即可判断A 选项，从图象上无法得知与x 轴的交点坐标，无法求得方程0kx b +=的解，即可判断B 选项，根据图象与y 轴的交点，可知4b =，进而可知0b >，即可判断C 选项，根据图象经过一、二、三象限，0k >，即可知y 随x 的增大而增大，进而判断D 选项【详解】A. 图像经过一、二、三象限,故该选项正确，符合题意； B. 关于x 方程0kx b +=的解不一定是4x =，不正确，不符合题意C. 根据图象与y 轴的交点，可知4b =，则0b >，故该选项不正确，不符合题意；D. 图象经过一、二、三象限，0k >，y 随x 的增大而增大，故该选项不正确，不符合题意；故选A【点睛】本题考查了一次函数图象的性质，与坐标轴交点问题，增减性，熟练掌握一次函数图象的性质是解题的关键．9. 《九章算术》是中国古代第一部数学专著，它的出现标志着中国古代数学形成了完整的体系，在其方程章中有一道题：今有甲乙二人，不知其钱包里有多少钱，若乙把其钱的一半给甲，则甲的钱数为50；若甲把其钱的23给乙，则乙的钱数也能为50，问甲、乙各有多少钱？若设甲持钱为x，乙持钱为y，则可列方程组()．A.25031502x yy x+=+=B.15022503x yy x+=+=C.15022503x yy x−=−=D.25031502x yy x−=−=【答案】B 【解析】【分析】由乙把其钱的一半给甲，则甲的钱数为50；若甲把其钱的23给乙，则乙的钱数也能为50，列出方程组求解即可．【详解】解：由题意得：15022503x yy x+=+=，故选B．【点睛】本题考查了二元一次方程组的应用，解答本题的关键是理解题意列出方程组．10. 现有一楼房发生火灾，消防队员决定用消防车上的云梯救人，如图（1）已知云梯最多只能伸长到15m，消防车高3m．救人时云梯伸长至最长，在完成从12m高处救人后，还要从15m高处救人，这时消防车要从原处再向着火的楼房靠近的距离AC为（）A. 3米B. 5米C. 7米D. 9米【答案】A 【解析】【分析】根据题意结合图形可得：3OE =m ，1239OB =−=m ，15312OD =−=m ，15AB CD ==m ，在两个直角三角形ABO ∆和COD ∆中，分别运用勾股定理求出AO ，CO ，即可得出移动的距离．【详解】解：如图所示：3OE =m ，1239OB =−=m ，15312OD =−=m ，15AB CD ==m ，在Rt ABO ∆中，12AO =m ，Rt COD ∆中，9CO m ，3AC AO CO =−=m ，故选：A ．在【点睛】题目主要考查勾股定理的应用，理解题意，找出相应的线段运用勾股定理是解题关键．二、填空题11. 16的算术平方根是___________．【答案】4 【解析】【详解】解：∵2(4)16±= ∴16的平方根为4和-4 ∴16的算术平方根为412. 某学校决定招聘数学教师一名，一位应聘者测试的成绩如表：测试项目笔试面试测试成绩（分） 8090将笔试成绩，面试成绩按6:4的比例计入总成绩，则该应聘者的总成绩是______分．【答案】84 【解析】【分析】根据求加权平均数的方法求解即可【详解】解：6480904836841010×+×=+= 故答案为：84【点睛】本题考查了求加权平均数，掌握加权平均数计算公式是解题的关键．加权平均数计算公式为：1122()1k k xx f x f x f n++…+，其中12k f f f …，，，代表各数据的权. 13. ABC 中，A ∠比B Ð大10°，50C ∠=°，则A ∠=______．【答案】70° 【解析】【分析】根据三角形内角和定理可得130A B ∠+∠=°，由题意A ∠比B ∠大10°，可得10A B ∠−∠=°，组成方程组求解即可．【详解】解：∵50C ∠=°， ∴130A B ∠+∠=°，∵A ∠比B ∠大10°， ∴10A B ∠−∠=°，∴13010A B A B ∠+∠=°∠−∠=°，解得：7060A B ∠=°∠=°，故答案为：70°．【点睛】题目主要考查三角形内角和定理及二元一次方程组的应用，理解题意，列出代数式组成方程组是解题关键．14. 已知一次函数()40y kx k =+≠的图象与两坐标轴围成的三角形面积为4，则k =______．【答案】2或-2##-2或2 【解析】【分析】由函数解析式确定与x 轴的交点坐标为4(0)k−，，与y 轴的交点坐标为（0，4），然后根据函数图象与坐标轴的面积为4列出方程求解即可．【详解】解：∵在4(0)y kx k =+≠中，当0x =时，4y =；当0y =时，4x k=−， ∴4y kx =+的图象与x 轴的交点坐标为4(0)k−，，与y 轴的交点坐标为（0，4），由题意可得：14442k⋅−⋅=，解得：2k =±．故答案为：2或-2．【点睛】题目主要考查一次函数解析式的确定及其与坐标轴围成面积的计算方法，理解题意，得出方程是解题关键．15. 如图，Rt ABC 中，90ACB ∠=°，3AC =，4BC =，将边AC 沿CE 翻折，使点A 落在AB 上点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B ′处，两条折痕与斜边AB 分别交于点E 、F ，以下四个结论：①45ECF ∠=°；②CEF △是等腰直角三角形；③3625CDF S =△；④45B F ′=．其中正确结论的序号有______．的【答案】①②④ 【解析】【分析】根据折叠的性质，3CD AC ==，4B C BC ′==，B F BF ′=，∠=∠ACE DCE ，BCF B CF ′∠=∠，CE AB ⊥，然后结合等腰三角形的性质，直角三角形的性质，以及勾股定理，分别对每个选项进行判断，即可得到答案．【详解】解：由折叠的性质可知，3CD AC ==，4B C BC ′==，B F BF ′=，∠=∠ACE DCE ，BCF B CF ′∠=∠，CE AB ⊥，∴DCE B CF ACE BCF ′∠+∠=∠+∠， ∵90ACB ∠=°，∴45ECF DCE B CF ′∠=∠+∠=°；故①正确； ∵90CEF ∠=°，∴45CFE ECF ∠=∠=°，∴CEF △是等腰直角三角形；故②正确；由勾股定理，则5AB ，∵1122ABCS AC BC AB CE ∆== ， ∴1134522CE ××=××， ∴125CE =，∴125EF =，由勾股定理，则95DE =， ∴1293555DF EF DE =−=−=，∴1131218225525CDFS DF CE==××=△，故③错误；∵91245555 BF AB AE EF=−−=−−=，∴45B F BF′==；故④正确；∴正确的选项有①②④；故答案为：①②④；【点睛】本题考查了折叠的性质，勾股定理，等腰三角形的判定和性质，三角形的面积公式等知识，解题的关键是掌握折叠的性质，正确得到边相等、角相等．三、解答题16. 计算：（1）+（2）−【答案】（1）（2）2−【解析】【分析】（1）由二次根式的性质进行化简，然后合并同类二次根式，即可得到答案；（2）先二次根式的除法，再计算减法运算，即可得到答案．【详解】解：（1）+原式=2×==（2）−原式22−−2=2−．【点睛】本题考查了二次根式的性质，二次根式的加减乘除混合运算，解题的关键是掌握运算法则，正确的进行化简．17. 解方程：834x y x y += −=【答案】方程组的解是71= =x y ．【解析】【分析】根据加减消元法求解方程组即可；【详解】解：834x y x y += −=①② ①－②，得44y =，解得1y =，将1y =代入①得，解得7x =，所以方程组的解是71= =x y ．【点睛】本题主要考查了二元一次方程组的求解，熟练掌握运用加减消元法是解题关键．18. 如图所示，在平面直角坐标系中，ABC 顶点坐标分别是(),4A a −，()1,2B −和()4,4C −．（1）已知点(),4A a −关于x 轴的对称点P 的坐标为()5,b −，求a ，b 的值；（2）画出ABC ，且ABC 的面积为；（3）画出与ABC 关于y 轴成对称的图形111A B C △，并写出各个顶点的坐标．的【答案】（1）5a =−，4b =；（2）作图见详解；13；（3）作图见详解；()15,4A −，()11,2B ，()14,4C ．【解析】【分析】（1）利用关于x 轴的对称点的坐标特点（横坐标不变，纵坐标互为相反数）直接写出答案即可；（2）先确定A 、B 、C 点的位置，然后顺次连接，最后运用割补法计算三角形面积即可；（3）先确定A 、B 、C 三点关于y 轴对称的对称点位置，然后顺次连接即可；最后直接写出三个点的坐标即可．【详解】解：（1）∵点(),4A a −关于x 轴的对称点P 的坐标为()5,b −，∴5a =−，4b =；（2）如图：ABC 即为所求，1118418326413222ABC S ∆=×−××−××−××=，故答案为：13；（3）如图：A 、B 、C 点关于y 轴的对称点为：()15,4A −，()11,2B ，()14,4C ，顺次连接，∴111A B C 即为所求()15,4A −，()11,2B ，()14,4C ．【点睛】此题主要考查了轴对称变换的作图题，确定组成图形关键点的对称点是解答本题的关键． 19. 在第二十二届深圳读书月来临之际，为了解某学校八年级学生每天平均课外阅读时间的情况，随机抽查了该学校八年级部分同学，对其每天平均课外阅读时间进行统计，并绘制了如图所示的不完整的统计图．请根据相关信息，解答下列问题：（1）该校抽查八年级学生的人数为，图中的a值为；（2）请将条形统计图补充完整；（3）求被抽查的学生每天平均课外阅读时间的众数、中位数和平均数；（4）根据统计的样本数据，估计该校八年级400名学生中，每天平均课外阅读时间为2小时的学生有多少人？【答案】（1）100,18；（2）见解析；（3）1.5,1.5,1.32（4）72人【解析】【分析】（1）根据每天平均课外阅读时间为1小时的占30%，共30人，即可求得总人数；（2）根据总数减去其他三项即可求得每天平均课外阅读时间为1.5小时的人数进而补充条形统计图；（3）根据条形统计图可知阅读时间为1.5小时的人数最多，故学生每天平均课外阅读时间的众数为1.5，根据第50和51个都落在阅读时间为1.5小时的范围内，即可求得中位数为1.5，根据求平均数的方法，求得100个学生阅读时间的平均数（4）根据扇形统计图可知，每天平均课外阅读时间为2小时的比例为18%，400乘以18%即可求得．÷=（人）；【详解】（1）总人数为：3030%10018100%18%100×=故答案为：100,18−−−=（人）（2）每天平均课外阅读时间为1.5小时的人数为：10012301840补充条形统计图如下：（3）根据条形统计图可知抽查的学生每天平均课外阅读时间的众数为1.5中位数为1.5，平均数为()10.512130 1.540182 1.32100××+×+×+×=；（4）40018%72×=（人）∴估计该校八年级400名学生中，每天平均课外阅读时间为2小时的学生有72人【点睛】本题考查了条形统计图与扇形统计图信息关联，求众数、中位数和平均数，样本估算总体，从统计图中获取信息是解题的关键．20. 请解答下列各题：（1）阅读并回答：科学实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等．如图1，一束平行光线AB 与DE 射向一个水平镜面后被反射，此时12∠=∠，34∠=∠．①由条件可知：13∠=∠，依据是，24∠∠=，依据是．②反射光线BC 与EF 平行，依据是．（2）解决问题：如图2，一束光线m 射到平面镜a 上，被a 反射到平面镜b 上，又被b 镜反射，若b 射出的光线n 平行于m ，且142∠=°，则2∠=；3∠= ．【答案】（1）①两直线平行，同位角相等；等量代换．②同位角相等，两直线平行．（2）84°；90°；【解析】【分析】（1）根据平行线的判定与性质逐一求解可得；（2）根据入射角等于反射角得出∠1=∠4，∠5=∠7，求出∠6，根据平行线性质即可求出∠2，求出∠5，根据三角形内角和求出∠3即可．【详解】解：（1）①由条件可知：∠1=∠3，依据是：两直线平行，同位角相等；∠2=∠4，依据是：等量代换；②反射光线BC 与EF 平行，依据是：同位角相等，两直线平行；故答案为：①两直线平行，同位角相等；等量代换．②同位角相等，两直线平行．（2）如图，∵∠1=42°，∴∠4=∠1=42°，∴∠6=180°-42°-42°=96°，∵m ∥n ，∴∠2+∠6=180°，∴∠2=84°，∴∠5=∠7=1802482°−∠=°， ∴∠3=180°-48°-42°=90°．故答案为：84°；90°；【点睛】本题考查了平行线的性质和判定，三角形的内角和定理的应用，熟练掌握平行线的判定与性质是解题的关键．21. 为丰富同学们的课余活动，某校成立了篮球课外兴趣小组，计划购买一批篮球，需购买A 、B 两种不同型号的篮球共300个．已知购买3个A 型篮球和2个B 型篮球共需340元，购买2个A 型篮球和1个B 型篮球共需要210元．（1）求购买一个A 型篮球、一个B 型篮球各需多少元？（2）若该校计划投入资金W 元用于购买这两种篮球，设购进的A 型篮球为t 个，求W 关于t 的函数关系式；（3）学校在体育用品专卖店购买A 、B 两种型号篮球共300个，经协商，专卖店给出如下优惠：A 种球每个降价8元，B 种球打9折，计算下来，学校共付费16740元，学校购买A 、B 两种篮球各多少个？【答案】（1）一个A 型篮球为80元，一个B 型篮球为50元；（2）函数解析式为：()30150000300W t t =+≤≤；（3）A 型篮球120个，则B 型篮球为180个．【解析】【分析】（1）设一个A 型篮球为x 元，一个B 型篮球为y 元，根据题意列出方程组求解即可得；（2）A 型篮球t 个，则B 型篮球为()300t −个，根据单价、数量、总价的关系即可得；（3）根据A 型篮球与B 型篮球的优惠政策求出单价，然后代入（2）解析式中求解即可得．【详解】解：（1）设一个A 型篮球为x 元，一个B 型篮球为y 元，根据题意可得：323402210x y x y += +=，解得：8050x y = =， ∴一个A 型篮球为80元，一个B 型篮球为50元；（2）A 型篮球t 个，则B 型篮球为()300t −个，根据题意可得：()()805030030150000300W t t t t =+−=+≤≤，∴函数解析式为：()30150000300W t t =+≤≤；（3）根据题意可得：A 型篮球单价为()808−元，B 型篮球单价为500.9×元，则()()16740808500.9300t t =−+××−，解得：120t =，300180t −=，∴A 型篮球120个，则B 型篮球为180个．【点睛】题目主要考查二元一次方程组及一次函数的应用，理解题意，列出相应方程是解题关键．22. 如图1，直线AB 的解析式为6y kx =+，D 点坐标为()8,0，O 点关于直线AB 的对称点C 点在直线AD 上．（1）求直线AB 解析式；（2）如图2，在x 轴上是否存在点F ，使ABC 与ABF 的面积相等，若存在求出F 点坐标，若不存在，请说明理由；（3）如图3，过点()5,2G 的直线:l y mx b =+．当它与直线AB 夹角等于45°时，求出相应m 的值．【答案】（1）直线AB 的解析式为26y x =−+；（2）()6,0F ；（3）13m =−或3m =．【解析】【分析】（1）在Rt AOD ∆中，利用勾股定理确定10AD =，由对称设OB BC a ==，6OAAC ==，4CD =，再利用勾股定理即可确定点B 的坐标，然后代入解析式即可；（2）由（1）得，BC =OB =3，根据O 点关于直线AB 的对称点C 点在直线AD 上，可得AOB ABC ∆≅∆，即两个三角形的面积相同，使ABF ∆的面积与ABC ∆的面积相同，只需要找到ABF ∆的面积与AOB ∆的面积相同的点即可，设点(),0F x ，两个三角形的高均为线段OA 长度，只需要底相同即可，根据底相同列出方程求解即可得；（3）设若直线GE 、GF 与直线AB 夹角等于45°，由图可得GEF ∆为等腰直角三角形，作EM GM ⊥于M ，FN GN ⊥于N ，可得90EMG GNF ∠=∠=°，GE GF =，利用全等三角形的判定及性质可得EM GN =，GM FN =，直线l 过()5,2G ，直线l 的解析式为：+25y mx m −，设E 坐标为(),26t t −+，则()5,26M t −+，由各线段间的数量关系可得F 点坐标为()12,3t t +−，将其代入直线AB 的解析式，即可得出t 的值，然后点E 、F 坐标，代入解析式求解即可．【详解】解：（1）6y kx =+ ， ()0,6A ∴，即6OA =，又()8,0D ，8OD ∴=，的设直线AD 的解析式为6y nx =+，将点()8,0D 代入得，直线AD 的解析式为364y x =−+.在Rt AOD ∆中，10AD =，点O 、点C 关于直线AB 对称，∴设OB BC a ==，6OAAC ==，4CD =， 8BD a ∴=−，在Rt BCD ∆中，()22248a a +=−，3a ∴=， ()3,0B ∴，将点B 代入6y kx =+ ∴直线AB 的解析式为26y x =−+；（2）由（1）得，BC =OB =3，如图所示：∵O 点关于直线AB 的对称点C 点在直线AD 上，∴AOB ABC ∆≅∆， ∴AOB ABC S S ∆∆=，使ABF ABC S S ∆∆=，则设点(),0F x ，两个三角形的高均为线段OA 长度，使底相同即：33x OB x −=−=，解得：6x =或0x =（舍去），∴()6,0F ；（3）如图，设若直线GE 、GF 与直线AB 夹角等于45°，即GEF ∆为等腰直角三角形，作EM GM ⊥于M ，FN GN ⊥于N ，∴90EMG GNF ∠=∠=°，GE GF =，∵90EGN ∠=°，∴90EGM FGN ∠+∠=°， ∵90EGM MEG ∠+∠=°，∴MEG FGN ∠=∠，在MEG ∆与NGF ∆中， EMG GNF MEG FGN GE GF ∠=∠ ∠=∠ =， ∴GEM FGN ∆∆≌，EM GN ∴=，GM FN =，直线l 过()5,2G ，即25m b =+，解得：25b m =−， ∴直线l 的解析式为：+25y mx m −，设E 坐标为(),26t t −+，则()5,26M t −+，5EM GN t ==−，26224GM FN t t ==−+−=−+，由线段间的关系可得：F ∴点坐标为()12,3t t +−，F 点在直线AB 上，()2126t t ∴=−++，解得：75t =， 716,55E ∴ ，198,55F −，当直线l 过E 点时，7162555m m +−=，解得：13m =−；当直线l 过F 点时，1982555m m +−=−，解得：3m =；所以13m =−或3m =．【点睛】本题主要考查了一次函数综合应用，涉及勾股定理、全等三角形的判定和性质等知识点，作出相应图象，根据图象之间的关系进行求解是本题解题的关键．的。

广东省深圳市罗湖区2022-2023学年八年级上学期期末英语试题(含解析)

广东省深圳市罗湖区2022-2023学年八年级上学期期末英语试题学校:___________姓名：___________班级：___________考号：___________9．A．yesterday B．today C．tomorrow D．next week 10．A．worse B．better C．longer D．shorter二、阅读单选①A 64-year-old Chinese carpenter’s（木工的）traditional skills have become very popular as he creates woodwork with nothing more than a single piece of wood, without glues, screws（螺丝）or nails（钉子）.②Wang Dewen, known as “Grandpa Amu” on YouTube, has been honored with “the modern day Lu Ban”, thanks to his wonderful carpentry knowledge.③Grandpa Amu’s most popular video, which shows him making a wooden bridge, has spread widely on YouTube, getting more than 40 million views.④“If you do something, you have to love it, and you have to be interested in it; however being interested doesn’t mean there’s only happiness and no pain.” Grandpa Amu shared when talking about his excellent carpentry skills.⑤Grandpa Amu follows an ancient Chinese mortise（卯眼）and tenon（榫）technique, which means no nails or glues are used in the whole process of building the bridge.⑥The master carpenter has also made several wooden toys for his grandson using the same technique. His young grandson’s favorites include a walking Peppa Pig and a bubble blowing machine. Attracting over 1.17 million fans on YouTube, Grandpa Amu’s videos so far have gained more than 300 million views.11．Why did the old carpenter become famous?A．He creates woodwork only with wood.B．He makes wooden toys like Peppa Pig.C．He is good at making funny videos.D．He teaches us how to make woodwork. 12．How many views did Wang Dewen’s most popular video get?A．1, 170, 000.B．40, 000, 000.C．300, 000, 000.D．340, 000, 000. 13．What can we learn from Wang’s words in Paragraph 4?A．We can do everything well if we are interested in it.B．If we are interested in something, we must do it well.C．With only interest and love, we can do something well easily.D．To do something well, we need both interest and hard work.14．According to the passage, which of the following is TRUE?三、阅读还原6选5don’t do that again.35．You looked so worried and nervous. Just ________. The exam may not be as difficult as you think.A．sleep on it—to think about something for a while before making a decisionB．take it easy—relaxC．go bananas—become crazyD．cry wolf—to ask for help when you don’t need itE．let the cat out of the bag—to tell a secret carelessly or by mistakeF．be over the moon—be very happy七、用所给单词的正确形式填空九、用所给单词的正确形式填空十、单句选词填空十二、单句选词填空十三、用所给单词的正确形式填空十五、用所给单词的正确形式填空十六、语法填空十七、材料作文To learn about how students use cell phones, we did a survey in our grade last week.___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ ___________________________________________________________________________ _________________________________________________参考答案：1．D 2．A 3．B 4．C 5．D 6．A 7．B 8．A 9．C 10．B【导语】本文主要讲述了一个人自己设计并建造房子，虽然开始房子很漂亮，但是随着时间的推移，房子开始出现一些问题，然而这个人总是拖延到明天去处理这些问题，最终导致房子变得越来越糟糕。

2022-2023学年深圳市罗湖区八年级(上)期末语文试卷与答案

2022-2023学年深圳市罗湖区八年级（上）期末语文试卷一、积累运用（30分）.1．（10分）默写古诗文。

（1）无可奈何花落去，。

（晏殊《浣溪沙》）（2），志在千里。

（曹操《龟虽寿》）（3）浅草才能没马蹄。

最爱湖东行不足，。

（白居易《钱塘湖春行》）（4），自将磨洗认前朝。

，铜雀春深锁二乔。

（杜牧《赤壁》）（5）富贵不能淫，。

（孟子《富贵不能淫》）（6）诗人常在诗词中表达家国情怀。

如李贺在《雁门太守行》中用“，”表达忠君报国之情；杜甫在《春望》用，”表达忧国思家的情怀。

2．（4分）根据拼音写出相应的词语。

（1）hào hàn 的大海可以做证：为了这一梦想成真，古老的中华民族，已经等了近百年。

（2）但他不放心，怕茶房不妥帖，颇chóu chú了一会。

（3）桥的设计完全合乎科学原理，施工技术更是qiǎo miào jué lún 。

（4）近处小路上骑驴而行的则是cháng tú bá shè的行旅。

3．（3分）下列句子中加点的词语使用不恰当的一项是（）A．大学刚毕业时，他心中燃烧着一股强烈而炽热．．的浪漫主义激情。

B．李云龙和战友吹嘘．．自己的独立团有八个营，上万人的兵力。

C．同学们上完体育课，依然个个精神抖擞、筋疲力尽．．．．的样子。

D．中华民族精神是中华民族赖以生存和发展的物神支撑，是中华民族自强不息，团结奋进、不折不挠．．．．的不竭动力。

4．（3分）下列对病句的修改不正确．．．的一项是（）A．一个人能否成为真正的读者，关键在于青少年时期要养成良好的阅读习惯。

（把“否”删去）B．防止疫情向学校扩散，守护师生安康，维护校园稳定，这是教育系统目前的当务之急。

（把“扩散”改为“传播”）C．新公布的香港国安法得到大家拥护的原因，是因为其尊重香港实际，符合国际惯例。

（应删去“使”的原因”）D．通过展示具体的5G信号使用范例，使人们能更清楚地了解5G可以为日常生活带来改变。

2020-2021学年深圳市罗湖区八年级上学期期末数学试卷(含解析)

2020-2021学年深圳市罗湖区八年级上学期期末数学试卷一、选择题（本大题共10小题，共30.0分）1.将式子a√−1(a<0)中根号外的因式移到根号里面，其中正确的是()aA. √−aB. −√−aC. √aD. −√a2.下列计算正确的是()A. √2+√3=√5B. 4√3−3√3=1C. 2√1=√2 D. 3÷√2=2√623.研究表明，当每公顷钾肥和磷肥的施用量一定时，氮肥施用量与土豆的产量有如表所示的关系：氮肥施用量/千克03467101135202259336404471土豆产量/吨15.1821.3625.7232.2934.0539.4543.1543.4640.8330.75下列说法错误的是()A. 氮肥施用量是自变量，土豆产量是因变量B. 当氮肥的施用量是101千克/公顷时，土豆的产量是32.29吨/公顷C. 如果不施氮肥，土豆的产量是15.18吨/公顷D. 氮肥施用量404千克/公顷比氮肥施用量336千克/公顷时的土豆的产量更高4. 在平面直角坐标系中，点A(2,3)与点B关于y轴对称，则点B的坐标为()A. (−2,3)B. (−2,−3)C. (2,−3)D. (−3,−2)5. 在△ABC中，AB=3，BC=3√3，AC=6，则△ABC的面积是()D. 18√3A. 9B. 9√3C. 9√326. 如图，将一副三角板如图放置．若AE//BC，则∠AFD=()A. 90°B. 85°C. 75°D. 65°7. 春节期间，某医药超市某品牌口罩从初一到初六这六天的销售量(单位：只)分别为285，280，330，310，300，310，这六天该超市这种品牌口罩销售量的中位数和众数分别是()A. 300，310B. 305，310C. 310，310D. 295，3108. 如图，点P为反比例函数y=2x上的一动点，作PD⊥x轴于点D，△POD的面积为k，则函数y=kx−1的图象为()A.B.C.D.9. 如图，已知△ABC，△DCE，△FEG，△HGI是4个全等的等腰三角形，底边BC，CE，EG，GI在同一直线上，且AB=2，BC=1.连接AI，交FG于点Q，则QI=()A. 1B. √616C. √666D. 4310. 如图，在△ABC中，AB=AC=10，BC=12，点D是BC上一点，DE//AC，DF//AB，则△BED与△DFC的周长的和为()A. 34B. 32C. 22D. 20二、填空题（本大题共5小题，共15.0分）11. 一个立方体的体积变为原来的6倍，则它的棱长变为原来的______倍．12. 在平面直角坐标系中，已知A(1,0)、B( −1,0)，△ABC 为等边三角形，则点C 的坐标是____________________;13. 如图所示，∠CAB 的外角等于120°，∠B 等于40°，则∠C 的度数是______ ．14. 如果一个正数的平方根分别是2a +1和5−a ，则这个正数为______．15. 在如图所示的4×4正方形网格中．∠1+∠2+∠3+∠4+∠5+∠6+∠7= 度．三、解答题（本大题共7小题，共55.0分）16. 计算：(−1)2012−(12)−1×√8317. (1)计算：√83+|√2−3|−√25+√2；(2)已知(1−x)3=−8，求x 的值．(3)已知实数x ，y 满足：{4x −3y =112x −y =13，求x −y 的值．18. 某学校为了了解本校学生体能健康状况，从本校学生中选取了总人数的10%做为一个样本，进行调查统计，根据收集的数据绘制了下面两幅不完整的统计图表．根据要求回答下列问题：成绩频数百分比不及格9%及格良好优秀56a合计b100%(1)直接写出a，b的值；(2)已知身体状况“及格”人数比“良好”人数少34人，且这两部分学生分别占总数百分比的和是63%，求样本中身体状况“及格”和“良好”的学生各有多少人？(3)补全条形统计图；(4)求本校共有多少名学生？其中全校学生中体能状况“优秀”的学生有多少人？19. 已知：点A、C分别是∠B的两条边上的点，点D、E分别是直线BA、BC上的点，直线AE、CD相交于点P．(1)点D、E分别在线段BA、BC上，若∠B=60°(如图1)，且AD=BE，BD=CE，求∠APD的度数；(2)如图2，点D、E分别在线段AB、BC的延长线上，若∠B=90°，AD=BC，∠APD=45°，求证：BD=CE．20. 某工厂现有15m3木料，准备制作各种尺寸的圆桌和方桌，如果用部分木料制作桌面，其余木料制作桌腿．(1)已知一张圆桌由一个桌面和一条桌腿组成，如果1m3木料可制作40个桌面，或制作20条桌腿．要使制作出的桌面、桌腿恰好配套，直接写出制作桌面的木料为多少m3？(2)已知一张方桌由一个桌面和四条桌腿组成．根据所给条件，解答下列问题．①如果1m3木料可制作50个桌面，或制作300条桌腿，应怎样计划用料才能使做好的桌面和桌腿恰好配套？②如果3m3木料可制作20个桌面，或制作320条桌腿，应怎样计划用料才能制作尽可能多的桌子？21. 在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点(点D不与点B、C重合)，以AD为直角边在AD右侧作等腰三角形ADE，使∠DAE=90°，连接CE．探究：如图①，当点D在线段BC上时，证明BC=CE+CD．应用：在探究的条件下，若AB=√2，CD=1，则△DCE的周长为______．拓展：(1)如图②，当点D在线段CB的延长线上时，BC、CD、CE之间的数量关系为______．(2)如图③，当点D在线段BC的延长线上时，BC、CD、CE之间的数量关系为______．22. 在平面直角坐标系中，边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点，现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N(如图)．(1)旋转过程中，当MN和AC平行时，求正方形OABC旋转的角度；(2)试证明旋转过程中，△MNO的边MN上的高为定值；(3)折△MBN的周长为p，在旋转过程中，p值是否发生变化？若发生变化，说明理由；若不发生变化，请给予证明，并求出p的值．参考答案及解析1.答案：B解析：解：a√−1a(a<0)=−√a2×(−1 a )=−√−a．故选：B．利用二次根式的性质直接化简得出即可．此题主要考查了二次根式的化简，正确确定二次根式的符号是解题关键．2.答案：C解析：解：A、√2与√3不能合并，所以A选项错误；B、原式=√3，所以B选项错误；C、原式=2×√22=√2，所以C选项正确；D、原式=3√2=3√22，所以D选项错误．故选：C．根据二次根式的加减法对A、B进行判断；根据二次根式的性质对C进行判断；二次根式的除法法则对D进行判断．本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．3.答案：D解析：解：A、氮肥施用量是自变量，土豆产量是因变量，原说法正确，故选项不符合题意；B、当氮肥的施用量是101千克/公顷时，土豆的产量是32.29吨/公顷，原说法正确，故选项不符合题意；C、如果不施氮肥，土豆的产量是15.18吨/公顷，原说法正确，故选项不符合题意；D、氮肥施用量404千克/公顷比氮肥施用量336千克/公顷时的土豆的产量更低，原说法错误，故选项符合题意．故选：D．根据图表数据可得，土豆产量随氮肥施用量的变化而变化，并且氮肥施用量在小于或等于336千克/公顷时，土豆的产量是逐渐增加的，而氮肥施用量在大于或等于404千克/公顷时，土豆的产量是逐渐减少的，据此解对各选项分析判断即可．本题主要考查了函数的定义和结合实际土豆产量和施用氮肥量确定函数关系．函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．4.答案：A解析：解：点A(2,3)关于y轴对称点的坐标为B(−2,3)故选A。