静水力学
水力学知识点总结

水力学知识点总结1. 水的基本性质水是自然界中非常重要的物质,它具有一系列独特的物理、化学性质。
如水的密度、粘度、表面张力等重要性质对水力学研究有着重要的影响。
2. 水动力学水动力学是研究流体的运动规律及其与物体之间的相互作用的科学。
水动力学是水力学的基础,分为静水力学和流体力学。
静水力学研究静止的流体,而流体力学则研究流体的运动。
3. 流体静力学流体静力学是研究静止流体中的压力、浮力和力的平衡问题。
在水力学中,流体静力学主要用于水库、坝体等结构的压力分析。
4. 流体动力学流体动力学是研究流体运动及其产生的压力、阻力以及对物体的作用力。
在水力学中,流体动力学主要应用于河流、渠道等流体动力学性质的研究。
5. 流态力学流体力学是研究流体运动状态与性质的学问。
在水力学中,流态力学主要应用于分析水流的速度、流量、流向、涡流情况等。
6. 水流的稳定性水流的稳定性是水力学中的重要概念,它指的是水体流动时所产生的稳定的流态特性,包括流态的平稳性、安定性和可操作性等。
7. 水力工程水利工程是利用水资源进行灌溉、供水、发电等利用的工程。
水利工程设计要考虑水力学的各种知识,如水流的稳定性、水利工程的结构和设备等方面。
8. 水道工程水道工程是为了改善河流、渠道等水道的通航、排涝等目的的工程项目。
在水道工程设计中,水力学知识对水流速度、水位变化、水力坡等方面有着重要影响。
9. 水电站在水力学中,水电站是一个重要的应用领域。
水力功率的计算、水轮机的设计、水库的水位控制等都需要水力学知识。
10. 河流水文学河流水文学是研究河流的水文特性、水位变化规律、涨落情况等方面的科学。
水文学是水力学中应用最广泛的一个分支,水利工程、水资源评价等方面都需要水文学的知识。
11. 液压机械液压机械是以流体静力学和流体动力学的理论为基础,利用液体作为传动介质的机械装置。
水力学的理论基础对液压机械的设计、制造和使用都有着重要的影响。
12. 水资源评价水力学的知识还被应用于水资源评价领域,通过水文学、水文模型等方法来评价水资源的分布、利用、保护等问题。
第二章 水静力学

第二章 水静力学水静力学(Hydrostatics )是研究液体处于静止状态时的力学规律及其在实际工程中的应用。
“静止”是一个相对的概念。
这里所谓“静止状态”是指液体质点之间不存在相对运动,而处于相对静止或相对平衡状态的液体,作用在每个液体质点上的全部外力之和等于零。
绪论中曾指出,液体质点之间没有相对运动时,液体的粘滞性便不起作用,故静止液体质点间无切应力;又由于液体几乎不能承受拉应力,所以,静止液体质点间以及质点与固壁间的相互作用是通过压应力(称静水压强)形式呈现出来。
水静力学的主要任务是根据力的平衡条件导出静止液体中的压强分布规律,并根据其分布规律,进而确定各种情况下的静水总压力。
因此,水静力学是解决工程中水力荷载问题的基础,同时也是学习水动力学的基础。
§2-1 静水压强及其特性1.静水压强的定义 在静止的液体中,围绕某点取一微小作用面,设其面积为ΔA ,作用在该面积上的压力为ΔP ,则当ΔA 无限缩小到一点时,平均压强A P ∆∆/便趋近于某一极限值,此极限值便定义为该点的静水压强(Hydrostatic Pressure),通常用符号p 表示,即dA dP A P p A =∆∆=→∆0lim (2-1) 静水压强的单位为2/m N (Pa(帕)),量纲为[][]21--=T ML p 。
2.静水压强的特性静水压强具有两个重要的特性:(1)静水压强方向与作用面的内法线方向重合。
在静止的液体中取出一团液体,用任意平面将其切割成两部分,则切割面上的作用力就是液体之间的相互作用力。
现取下半部分为隔离体,如图2-1所示。
假如切割面上某一点M 处的静水压强p 的方向不是内法线方向而是任意方向,则p 可以分解为切应力τ和法向应力p n 。
从绪论中知道,静止的液体不能承受剪切力也不可能承受拉力,否则将平衡破坏,与静止液体的前提不符。
所以,静水压强唯一可能的方向就是和作用面的内法线方向一致。
(2)静水压强的大小与其作用面的方位无关,亦即任何一点处各方向上的静水压强大小相等。
第二章水静力学

n
= p • D Ax
p =
n n
•
1 2
Dy
•
Dz
代入第一式
F F F px pncos(n, x) x =0 则:
1 2
Dy
Dz
px
1 2
Dy
Dz
pn
1 6
Dx Dy
Dz
fx
=
0
整理后,有
px
pn
1 Dx
3
fx
=
0
当四面体无限缩小到A点时,Dx
p x
=
p n
同理,我们可以推出:
0 因此:
△h
G
z1
2p 2
z2
0
h
G
p
0
(a)
(b)
圆柱上表面的静水压力 F1 = p1DA
圆柱下表面的静水压力 F2 = p2DA
小水柱体的重力
G = gDADh
力的平衡方程 p2DA p1DA gDADh = 0
p 0 ▽
h1 h2
△h
p
11
G
z1
2p 2
z2
0
(a)
p 0 ▽
h
G
p
0 (b)
单位重量的液体在某点所具有的位置势能(单位位
能):
z1
=
mgz1 mg
z 的能量意义是单位重量液体所具有的位置势能,
称为单位位能。
pa
p1 g
h12
1
z1
pa
p2 g
z2
0
0
Z Fpy
D Fpn Fpx
z
A y CBOFpzYX
相应面上的总压力为
第二部分 水静力学

§2—2 液体平衡的微 分方程及其积分
1.液体平衡的微分方程
设正交六面体中心 点处的静水压强为p,是 坐标的连续函数,即 p=p(x,y,z),用泰勒级数 展开得M和N点的压强为
pM
p 1 p dx 2 x
pN
p
1 p dx 2 x
ABCD面上的力(p 1 p dx)dydz 2 x
dp=ρ(Xdz+Ydy+Zdz)
积分:p= —ρ(a x +g z)+ C
由边界条件x = z = 0 ,p = p0 C = P0对任一点B(x ,y )
p p0 (ax gz)
p0
(a g
x
z)
p0
a g
x z
p0 (z z ) p0 h
pc p0 h2 p0 h1 (h2 h1) pA h
p p0 h
水静力学基本方程常用表达式 说明:
(1) 静水压强随深度按线性规律增加。
(2) 液体内任一点的静水压强由两部分组成, 一部分是自由液面上的表面压强po; 另一部分是单位面积上的垂直液柱重量γh 。
§2-3重力作用下静水压强的分布规律
思考: 点A质量为M的液体: 静止时有重力Mg,方向?与Z轴方向??在X、Y轴方向的投影为? 则:单位质量力为Mg / M = g ,方向??
任一点的单位质量力均为g,方向??
1 .水静力学基本方程
dp=ρ(Xdz+Ydy+Zdz)
液体平衡微分方程综合式
X 0, Y 0, Z g
思考: 平面上各点的静水压力方向?? 曲面上各点的静水压力方向??
《水力学》第一章 水静力学
理论证明静水压力具有各项同性
四面体体积:V 1 xyz
6
总质量力在三个坐标
方向的投影为:
Fpx
1 6
xyzf x
Fpy
1 6
xyzf y
按照平衡条件,所有
Fpz
1 6
xyzf z
作用于微小四面体上
的外力在各坐标轴上
投影的代数和应分别 为零。
即在绕中心轴作等角速旋转的液体中有:只有r值相同的 那些点,即位于同心圆柱面上的各点 z p 才保持不变。
g
29
例1-1 有一圆柱形容器,内径为R,原
盛水深度为H,将容器以等角速度
绕中心轴oz旋转,试求运动稳定后容器 中心及边壁处的水深。
30
解 : 在 容 器 边 壁 处 r = R , Zs=Zw ,
1-3 等压面
等压面:静水压强值相等的点连接成的面(可
能是平面也可能是曲面)。
等压面性质:
1.在平衡液体中等压面即是等势面。 2.等压面与质量力正交。
15
1-3 等压面
等压面性质: dp ( U dx U dy U dz) dU
x
y
dz
1.在平衡液体中等压面即是等势面。
17
等压面性质2:等压面与质量力正交。
力 F 沿 ds 移动所做的功可写作矢量F与ds的数性积:
W F ds ( fxdx f ydy fzdz)dm W dUdm
因等压面上 dU=0 ,所以W=F*ds=0。也即质量力必 须与等压面正交。
注意: (1) 静止液体质量力仅为重力时,等压面必定 是水平面;
以 p' 表示绝对压强,p表示相对压强,pa 则表示当地
2第二章 水静力学

A
p0 h z z0
式中,h=z0-z 表示该点在自由面以下的液柱高度。 上式即计算静水压强的基本公式。它表明,静止液体内任 意点的静水压强由两部分组成:一部分是自由面上的气体 压强p0(当自由面与大气相通时, p0=pa ,为当地大气压 强),另一部分是γh ,相当于单位面积上高度为 h 的水柱 重量。
∆P dP = ∆A→0 ∆A dA lim
静水压力的单位为N或kN; 静水压强的单位为Pa或kPa 。
• 二、静水压强的特性
静水压强有两个重要的特性: 1.静水压强的方向与受压面垂直并指向受压面(垂直指向性)
在平衡液体中静水压强的方向与作用面垂直并指向作用面, 即静水压力只能是垂直的压力。
2.静水压强各向同性(各向等值性):任一点静水压强的大 小和受压面方向无关,或者说作用于同一点上个方向的静水压 强大小相等。
dp = ρ(−adx − gdz) 积分得 p = ρ(−ax − gz) + C
当x=z=0时,p=p0,故C=p0,从而 a p = ρ(−ax − gz) + C 或 p = p0 + γ (− x − z)
g
令p0=98kPa,x=-1.5m,z=-1.0m,代入上式,得A点压强为
p A = 98 + 9.8[− 0.98 (−1.5) − (−1.0)] = 109.27kPa 9.8
例题分析
一洒水车,以0.98m/s2的等加速度向前行驶,设以水面中心点为 原点,建立xOz坐标系,试求自由表面与水平面的夹角θ;又自 由表面压强p0=98kPa,车壁某点A的坐标为x=-1.5m,z=-1.0m, 求A点的压强。
例题分析
水力学课件 第一章 水静力学

§1.1 静水压强及其特征
联立上面各式代入后得:
1 2
pxyz
1 2
pnyz
1 6
xyzf x
0
1 2
p y xz
1 2
pnxz
1 6
xyzf y
0
1 2
pz xy
1 2
pnxy
1 6
xyzf z
0
联立上面各式代入后得:
1 2
pxyz
1 2
pnyz
1 6
xyzf x
0
1 2
p y xz
1 2
pnxz
§1.4 等压面
一、等压面(Isobaric Surface):在平衡的液体中, 由压强相等的各点所组成的面叫做等压面。 等压面的重要特性是: 1.在静止的或相对平衡的液体中,等压面同时也是
等势面(Isopotential Surface)。 dp dU
2.在相对平衡的液体中,等压面与质量力正交。
条件:只适用于静止、同种、连续液体
三、气体压强计算
p p0
§ 1.5几种质量力同时作用下的液体平衡
z
gm h z
zs
o
x
以z轴为对称轴的旋转抛物面方程:
R
o
r
x
m
F
y 1 2rBiblioteka gz C 2§ 1.5几种质量力同时作用下的液体平衡 平衡微分方程: dp ( fxdx f ydy fzdz) 质量力:离心惯性力和重力 F m 2r, mg 单位质量力: fx 2 x, f y 2 y, fz g 自由面上压强不变为大气压: dp 0
§ 1.5几种质量力同时作用下的液体平衡
2、圆筒中液体内任一点静水压强分布规律:
工程力学中的静水力学与流体压力分析

工程力学中的静水力学与流体压力分析工程力学是研究物体受力和运动规律的学科,并且在工程领域中有着广泛的应用。
其中,静水力学和流体压力分析是工程力学的重要分支,对于许多工程项目的设计和实施起着至关重要的作用。
一、静水力学的基本概念和原理静水力学是研究液体静止状态下的力学行为的学科,主要涉及液体压力、浮力和液压机械等内容。
在工程力学中,静水力学的应用非常广泛,例如在水坝、水塔、水管等工程结构的设计和施工过程中,都需要进行静水力学的分析。
静水力学的基本概念和原理主要包括以下几点:1. 压力:压力是指单位面积上受到的力的大小,常用的单位是帕斯卡(Pa)。
在静水力学中,液体的压力是由于液体自身的重力和所受到的外力所引起的。
2. 浮力:浮力是指物体在液体中受到的向上的力,其大小等于被物体排开的液体的重量。
根据阿基米德原理,当一个物体浸入液体中时,被物体排开的液体体积所受到的力等于物体受到的浮力。
3. 压力传递:液体的压力在静水力学中可以沿任意方向传递,即帕斯卡定律。
根据帕斯卡定律,液体内的压力作用在液体上的任意一点,其大小和方向都相同。
二、流体压力分析的方法和应用流体压力分析是研究流体静力学和动力学的学科,主要涉及流体静力学方面的内容。
在工程力学中,流体压力分析广泛应用于液压系统、风洞实验、涡轮机械等领域。
流体压力分析的方法可以通过以下几种途径实现:1. 简化模型分析:根据问题的复杂度和要求,可以对流体系统进行简化处理,采用理论分析或者经验公式得到近似解。
2. 数值模拟方法:利用计算机数值模拟方法,通过建立流体力学方程组,采用数值求解方法,得到流体系统的详细分布情况。
3. 实验测量方法:通过实验仪器对流体系统进行测量,得到不同位置的压力分布和压力变化情况。
流体压力分析在工程中的应用非常广泛,例如在液压系统中,通过对液体压力的分析,可以实现机械设备的运动控制;在风洞实验中,通过对气流压力的分析,可以模拟飞行器在不同速度和角度下的气动性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
Z
p0 在液面上,z=z0,p=p0,则 c z0 g
故有
p p0 g ( z0 z)
p p0 gh
x y
(2)静水压强的基本公式 液面上的气体压强p0
压强由两部分组成: 举例
单位面积上高度为h的水柱重ρgh
p0=pa
已知:p0=98kN/m2,h=1m, 求:该点的静水压强 解:
用pk来表示
pk pa p
举例
例1:如图已知,p0=98kN/m2,h=1m, 求:该点的绝对压强及相对压强
p 解: p0 gh 98 1 9.81 107.8kN / m p p pa 107.8 98 9.8kN / m2
2
p0=pa
Y 的力矩为 各分力dFp对OX轴的力矩为 A 则有: I c IX=Ic+Yc2A Y Y dFP Y sinαdAα dAρgsinsinαdA 2dA (2) ρgY ρgYsinD Yc αY 2 Y (2) Y ρgYc A dFP Y A A A
FP hD hc
O
Y
答:该闸门上所受静水总压力的大小为246kN,方向向右, 在水面下8.03m处。
p fx x
(1)
整理化简得:
p fx x
p fy y
(2)
Euler平衡微分方程式
静水压强沿某一方向的变化率与 该方向的单位体积质量力相等。
p fz z
将(2)中各式分别乘以dx,dy和dz,然后相加得:
p p p dx dy dz ρ f x dx f y dy f z dz x y z
P1=ρgh=1000kg/m3×9.81m/s2×4.83m=47.3kN/m2 P2=ρgH=1000kg/m3×9.81m/s2×7m=68.6 kN/m2
p1 p2 ab 290kN 2 a 2b b2 e . 1 1.17m 3 b1 b2
返回
P
H
h
P1
P2
60°
a
e
A
(1) FP YD ρgsinαYc A YD 整理可得静水总压力的压力中心位置: 为平面对OX轴的惯性矩 I X Y 2 dA
Ic表示平面对于通过其形心C并与OX轴平行的轴线的惯性矩。 Yc A YD I X I c Yc A Yc A YD Y 2 dA (1)=(2)
作为零点计量的压强,用p′表示 用p表示。
相对压强 ——以当地大气压作为零点计量的压强,
若将当地大气压强用pa表示,则有
p p pa
举例
例1:如图已知,p0=98kN/m2,h=1m, 求:该点的绝对压强及相对压强
p 解: p0 gh 98 1 9.81 107.8kN / m p p pa 107.8 98 9.8kN / m2
h
例2:如图已知, p0=50kN/m2,h=1m, 求:该点的绝对压强及相对压强 解:p p0 gh 50 1 9.8 1 59.8kN / m2
p p pa 59.8 98 38.2kN / m2
h
p0
相对压强为什么是负值? 什么位置处相对压强为零?
(3) (4)
dp ( f x dx f y dy f z dz)
静水压强的分布规律是由单位质量力所决定的
3 重力作用下静水压强的分布规律
(1) 基本公式
只受重力作用:fx=0,fy=0,fz=-g
z
p0
h A Z0
dp ( f x dx f y dy f z dz) gdz
1.按一定比例,用线段长度代表该点静水压强的大小 举例
2.用箭头表示静水压强的方向,并与作用面垂直
画出下列AB或ABC面上的静水压强分布图
P ρgh
A A B
ρghB
B
C
A
ρgh1
B
ρgh2
返回
图解法——作用于矩形平面上的静水总压力的计算
静水压强分布图的绘制规则:
1.按一定比例,用线段长度代表该点静水压强的大小 其中b为矩形受压面的宽度; 举例 2.用箭头表示静水压强的方向,并与作用面垂直 Ω为静水压强分布图形的面 积;
2
p0=pa
h
例2:如图已知, p0=50kN/m2,h=1m, 求:该点的绝对压强及相对压强 解:p p0 gh 50 1 9.8 1 59.8kN / m2
p p pa 59.8 98 38.2kN / m2
h
p0
相对压强为什么是负值? 什么位置处相对压强为零?
静的 水三 总要 压素 力
大小:
FP b
方向:垂直并指向受压面 作用点:通过压强分布体的重心
举例
例:某底孔引水洞进口处设矩形平
面闸门,高度a=2.5m,宽度 b=2.0m。闸门前水深H=7.0m,闸 门倾斜角为60°,求作用于闸门上 的静水总压力。 解: h=H-asin60°=7.0m-2.5m×0.867=4.83m
p FP A
p lim
FP A 0 A
单位:N/m2、kN/m2 、Pa 、kPa
1 静水压强的特性
F
n
F
× 1.静水压强垂直指向受压面 证明
M
Fτ
2.作用于同一点上各方向的静水压强的大小相等
p1 p2 B
2 液体平衡微分方程式
表征液体处于平衡状态时作用于液体上各种力之间的关系式
作用于六面体上的力有表面力和质量力 (1)表面力:周围液体作用于六个面 z 上的压力 形心点A ( x, y, z )的压强为p (2)质量力:
返回
3 压强的计示及测量
(2) 压强的计示及测量 绝对压强 ——以设想没有大气存在的绝对真空状态 压强的计示
作为零点计量的压强,用p′表示
相对压强 ——以当地大气压作为零点计量的压强,
用p表示。
若将当地大气压强用pa表示,则有
p p pa
举例
——指绝对压强小于大气压强的数值, 真空度(或真空压强)
A
其中
YdA Y A
c A
为平面对OX轴的面积矩
A为受压面的面积。
(1) FP ρgsinαY其中pcρghc A A 为受压面形心点的压强; c 所以静水总压力的大小为
FP P A c
解析法——作用于任意形状平面上的静水总压力
(2) 静水总压力的方向 Fp垂直指向受压面 (3) 静水总压力的作用点 总压力Fp对OX轴的力矩为
ρfxdxdydz ρfydxdydz ρfzdxdydz
p p dx dx ( p p )dydz x x 2 2
dx
A dy
dz
p (p
p p dx dx )dydz x x2 2
依平衡条件: Fx 0
y
x
则
p dx p dx (p )dydz ( p )dydz f x dxdydz 0 x 2 x 2
2
举例
例:一垂直放置的圆形平板闸门,已
知闸门半径R=1m,形心在水下的淹 没深度hc=8m,试用解析法计算作用 于闸门上的静水总压力。 解: F p A gh R2 246kN P c c
R 4
Ic YD Yc hc 4 8.03m Yc A hc A
p p0 gh 98kN / m2 1000kg / m3 9.8m / s 2 1m 1000 107.8kN / m2
h A p
pa
在容器壁面上同水深处的一点所受到的压强有多大? 该点所受到的有效作用力有多大?
返回
3 重力作用下静水压强的分布规律
(2) 压强的计示及测量 绝对压强 ——以设想没有大气存在的绝对真空状态 压强的计示
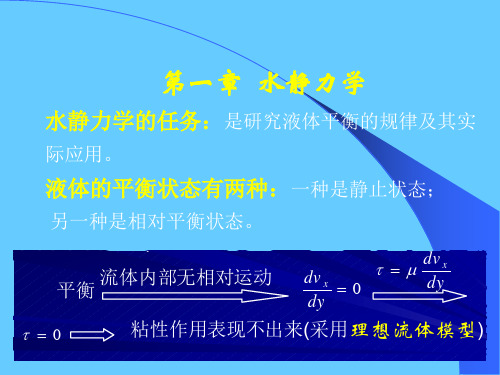
水静力学的任务是研究液体平衡的规律及其实际应用。
液体平衡
主要内容
静止状态
相对平衡状态
1 静水压强及其特性 工程应用主要是确定水对水工建筑物表面的作用力。 2 3 4
液体平衡微分方程 重力作用下静水压强的分布规律 作用于平面上的静水总压力
1 什么是静水压强
FP FP
平衡液体内部相邻两部分之间相互作用的力或 液体对固体壁面的作用力为静水压力,用FP表示。 面平均静水压强 静水压强
静水总压力大小
P Ωb
按梯形形心公式得
解析法——作用于任意形状平面上的静水总压力
(1) 静水总压力的大小
hc
dFP O (b) α h
dFP ρghdA ρgYsinαdA
FP dFP ρgYsinαdA
A A
C dA Y M(X,Y) C YC
X
ρgsinα YdA
pk pa p 98 59.8 38.2kN / m2
返回
4 作用于平面上的静水总压力
静 水 总 压 力
图解法—适用于矩形平面
解析法—适用于任意形状平面
图解法——作用于矩形平面上的静水总压力的计算 表示静水压强沿受压面分布情况的几何图
形,称为静水压强分布图。
静水压强分布图的绘制规则:
