静水压强分布图及其绘制(精)
合集下载
液体作用在平面上的总压力
则有
P dP sinyc A
hc A pc A
2、总压力作用点(压心)
设总压力P的作用点为D点 合力矩定理:
P yD y dP sin y2dA
A
受压面A对ox轴的惯性矩 A y 2dA Io Ic yc2 A
则有
yD
sin Io
P
Io yc A
yc
Ic yc A
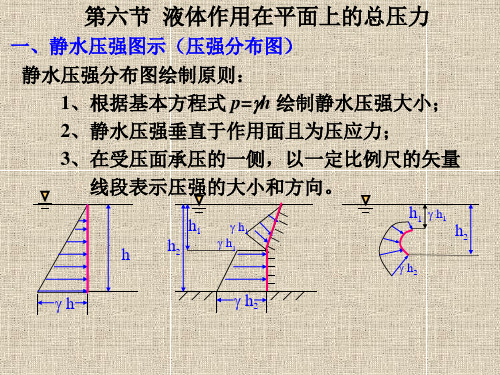
第六节 液体作用在平面上的总压力
一、静水压强图示(压强分布图) 静水压强分布图绘制原则:
1、根据基本方程式 p=h 绘制静水压强大小;
2、静水压强垂直于作用面且为压应力; 3、在受压面承压的一侧,以一定比例尺的矢量
线段表示压强的大小和方向。
h1பைடு நூலகம்
h1
h
h2
h1
h1 h1 h2
h2
h
h2
❖受压面为平面的情况下,压强分布图的外包线为 直线;当受压面为曲面时,曲面的长度与水深不成 直线函数关系,故压强分布图外包线亦为曲线。
(一)为何要重视老年人用药?
2 老年人用药机会多 上海市药品不良反应监测中心正在进行的一项“上海
市 中老年人群药物流行病学研究”显示,上海市54%的
中 老年人(50岁以上)患有各种慢性疾病,每个月有58 %的中老年人会看病,每年有91%的中老年人会服用 药物,每个月会有78%的中老年人会服用药物。
二、 药物商品选择的原则即合理用药的基本要素
安全性 (首要条件)
有效性
要素
经济性
适当性
第一节 药物商品的选择和使用
给药的适当性
治疗目标 疗程
药物 剂型
病人 途径
剂量 时间
第一节 药物商品的选择和使用
P dP sinyc A
hc A pc A
2、总压力作用点(压心)
设总压力P的作用点为D点 合力矩定理:
P yD y dP sin y2dA
A
受压面A对ox轴的惯性矩 A y 2dA Io Ic yc2 A
则有
yD
sin Io
P
Io yc A
yc
Ic yc A
第六节 液体作用在平面上的总压力
一、静水压强图示(压强分布图) 静水压强分布图绘制原则:
1、根据基本方程式 p=h 绘制静水压强大小;
2、静水压强垂直于作用面且为压应力; 3、在受压面承压的一侧,以一定比例尺的矢量
线段表示压强的大小和方向。
h1பைடு நூலகம்
h1
h
h2
h1
h1 h1 h2
h2
h
h2
❖受压面为平面的情况下,压强分布图的外包线为 直线;当受压面为曲面时,曲面的长度与水深不成 直线函数关系,故压强分布图外包线亦为曲线。
(一)为何要重视老年人用药?
2 老年人用药机会多 上海市药品不良反应监测中心正在进行的一项“上海
市 中老年人群药物流行病学研究”显示,上海市54%的
中 老年人(50岁以上)患有各种慢性疾病,每个月有58 %的中老年人会看病,每年有91%的中老年人会服用 药物,每个月会有78%的中老年人会服用药物。
二、 药物商品选择的原则即合理用药的基本要素
安全性 (首要条件)
有效性
要素
经济性
适当性
第一节 药物商品的选择和使用
给药的适当性
治疗目标 疗程
药物 剂型
病人 途径
剂量 时间
第一节 药物商品的选择和使用
静水总压力

Байду номын сангаас
C
D
C
C
5
2
总压力作用点
hc P F
h dP
α E
O
O O
D
C
dA
对Ob轴取矩得
2 A A
L
2
PLD Lp dA g L sin dA g sin L d A
A
令 I L A
2 b A
L’
6
表示平面EF对Ob轴的面积惯性矩。
由平行移轴定律得 化简
I b I c Lc A
方向: 垂直指向受压面
2
P 作用点:过 压强分布图 形心,且位于 对称轴上.
A
B
P C
3
(2)
O
解
析 法:
hc
P
F
h dP
α E
O
C D L
dA
P g sin Lc A g hc A pc A
4
大小: P=pcA, pc—形心处压强
方向: 垂直指向受压平面 作用点:
I y =y + y A
2
Ic LD Lc Lc A
(1-50)
可见,LD > LC 即,总压力的作用点在形心之下 (平面水平放置时重合)
上式控制总压力作用点深度位置。
7
bD 的确定:将静水压力对OL轴取矩,则
Pb D bp d A bL sin d A sin Lb d A
1-9
一
作用于平面上的静水总压力
压力图法(图解法), 解析法
两种方法:
静水压强分布图的绘制
•用一定比例的线段长度代表静水压强的大小; •用与作用面垂直的箭头表示静水压强方向。
静水力学

h
p0
相对压强为什么是负值? 什么位置处相对压强为零?
pk pa p 98 59.8 38.2kN / m2
返回
4 作用于平面上的静水总压力
静 水 总 压 力
图解法—适用于矩形平面
解析法—适用于任意形状平面
图解法——作用于矩形平面上的静水总压力的计算 表示静水压强沿受压面分布情况的几何图
为平面对OX轴的面积矩
A为受压面的面积。
其中p ρgh A (1) FP ρgsinαYc A c为受压面形心点的压强; c
所以静水总压力的大小为
FP Pc A
解析法——作用于任意形状平面上的静水总压力
(2) 静水总压力的方向 Fp垂直指向受压面 (3) 静水总压力的作用点 总压力Fp对OX轴的力矩为
液体平衡微分方程 重力作用下静水压强的分布规律 作用于平面上的静水总压力
1 什么是静水压强
FP Байду номын сангаасP
平衡液体内部相邻两部分之间相互作用的力或 液体对固体壁面的作用力为静水压力,用FP表示。 面平均静水压强 静水压强
p FP A
p lim
FP A0 A
单位:N/m2、kN/m2 、Pa 、kPa
ρfxdxdydz ρfydxdydz ρfzdxdydz
p p dx dx ( p p )dydz x x 2 2
dx
A dy
dz
p (p
p p dx dx )dydz x x2 2
依平衡条件: Fx 0
y
x
则
p dx p dx (p )dydz ( p )dydz f x dxdydz 0 x 2 x 2
p0=pa
p0
相对压强为什么是负值? 什么位置处相对压强为零?
pk pa p 98 59.8 38.2kN / m2
返回
4 作用于平面上的静水总压力
静 水 总 压 力
图解法—适用于矩形平面
解析法—适用于任意形状平面
图解法——作用于矩形平面上的静水总压力的计算 表示静水压强沿受压面分布情况的几何图
为平面对OX轴的面积矩
A为受压面的面积。
其中p ρgh A (1) FP ρgsinαYc A c为受压面形心点的压强; c
所以静水总压力的大小为
FP Pc A
解析法——作用于任意形状平面上的静水总压力
(2) 静水总压力的方向 Fp垂直指向受压面 (3) 静水总压力的作用点 总压力Fp对OX轴的力矩为
液体平衡微分方程 重力作用下静水压强的分布规律 作用于平面上的静水总压力
1 什么是静水压强
FP Байду номын сангаасP
平衡液体内部相邻两部分之间相互作用的力或 液体对固体壁面的作用力为静水压力,用FP表示。 面平均静水压强 静水压强
p FP A
p lim
FP A0 A
单位:N/m2、kN/m2 、Pa 、kPa
ρfxdxdydz ρfydxdydz ρfzdxdydz
p p dx dx ( p p )dydz x x 2 2
dx
A dy
dz
p (p
p p dx dx )dydz x x2 2
依平衡条件: Fx 0
y
x
则
p dx p dx (p )dydz ( p )dydz f x dxdydz 0 x 2 x 2
p0=pa
水力学1(4

ρg
18
说明静水压强对该液体质点作的功为 dm g 的这种做功本领称为液体的压强势能。
p1 。液体压强 ρg
所以, 1 ρg 就是单位重量液体在1点相对于大气压的压强 p 势能,即单位压能。 由于位能和压能均为势能,所以又将液体的单位位能z与单位
压能 p1 ρg 之和称为单位重量液体的势能,简称单位势能。 能量意义:在质量力仅为重力作用的同种相互连通的平衡液体中, 任意点相对同一位置和压强基准的单位势能都相等。 它反映了重力作用下平衡液体中能量的守恒与转换的规律, 位能和压能二者等值相互转换,总和不变。
11
2 液柱单位
根据的关系可知,任何一种压强(包括绝对压强、相对压
强和真空压强)的大小,都可以等效地用某种已知容重液体的
液柱高度来表示。
工程中,常用的液柱高度为水柱高度和汞柱高度,其单位
为mH2O、mmH2O和mmHg。 1mH2O产生的压强为9.8kPa和1000kgf/m2;
1mmH2O产生的压强为9.8Pa和1kgf/m2;
(2)用箭头在线段的一端标出静水压强的方向,并垂直指向受
压面; (3)在线段的另一端画出压强分布的外包络线。
1
2
第四节 液柱式测压计
液柱式测压计是以水静力学基本方程原理为基础,将被测压 强转换成液柱的高差进行测量的测压计。其简单、直观、精度较 高,但测量范围较小,故常用在实验室或实际生产中测量低压、
p f(x.y.z)
9
讨论: (1)设液面的 z 轴坐标用zs表示,则将 p=p0 代入上(A)式可 得液面方程为
ω2 2 ω2r 2 zs x y2 2g 2g 上式表明,液面为一旋转抛物面。因为液体中任一点的水深,则
18
说明静水压强对该液体质点作的功为 dm g 的这种做功本领称为液体的压强势能。
p1 。液体压强 ρg
所以, 1 ρg 就是单位重量液体在1点相对于大气压的压强 p 势能,即单位压能。 由于位能和压能均为势能,所以又将液体的单位位能z与单位
压能 p1 ρg 之和称为单位重量液体的势能,简称单位势能。 能量意义:在质量力仅为重力作用的同种相互连通的平衡液体中, 任意点相对同一位置和压强基准的单位势能都相等。 它反映了重力作用下平衡液体中能量的守恒与转换的规律, 位能和压能二者等值相互转换,总和不变。
11
2 液柱单位
根据的关系可知,任何一种压强(包括绝对压强、相对压
强和真空压强)的大小,都可以等效地用某种已知容重液体的
液柱高度来表示。
工程中,常用的液柱高度为水柱高度和汞柱高度,其单位
为mH2O、mmH2O和mmHg。 1mH2O产生的压强为9.8kPa和1000kgf/m2;
1mmH2O产生的压强为9.8Pa和1kgf/m2;
(2)用箭头在线段的一端标出静水压强的方向,并垂直指向受
压面; (3)在线段的另一端画出压强分布的外包络线。
1
2
第四节 液柱式测压计
液柱式测压计是以水静力学基本方程原理为基础,将被测压 强转换成液柱的高差进行测量的测压计。其简单、直观、精度较 高,但测量范围较小,故常用在实验室或实际生产中测量低压、
p f(x.y.z)
9
讨论: (1)设液面的 z 轴坐标用zs表示,则将 p=p0 代入上(A)式可 得液面方程为
ω2 2 ω2r 2 zs x y2 2g 2g 上式表明,液面为一旋转抛物面。因为液体中任一点的水深,则
静水压强分布图实例ppt课件

p p pa 107.8 98 9.8kN / m2
p0=pa h
例2:如图已知, p0=50kN/m2,h=1m, 求:该点的绝对压强及相对压强
p0
pa
h
解:p p0 gh 50 1 9.81 59.8kN / m2
p p pa 59.8 98 38.2kN / m2
由液面上的压强p0;另一部分是该点到自由液面的单位面积上的液柱重
量gh 。 (3)在静止液体中,位于同一深度(h=常数)的各点的静压
强相等,即任一水平面都是等压面。
20
z
Z
y
p0 h
A
Z0
x
21
[例题]已知:p0=98kN/m2, h=1m,
求:该点的静水压强
p0=pa
h
p
pa
解: p p0 gh
§2-3 压强的计算基准和量度单位
一、压强的表示
1. 计算基准
绝对压强:以完全真空时的绝对零压强(p=0)为基准来计 量的压强称为绝对压强;
相对压强:
以当地大气压强为基准来计量的压强称为相对压强。
绝对压强与相对压强之间的关系可在下面导出。当 自由液面上的压强是当地大气压强pa时,则液体中任一点的
压强可写成 p pa gh
为了正确区别和理解绝对压强、计示压强和真空之间 的关系,可用图来说明。
25
计示压强
绝对压强
真空 绝对压强
图 绝对压强、计示压强和真空之间的关系
26
流体静压强的量度单位主要有三种:应力单位,大气压的 倍数和液注高度。为了便于换算,现将常遇到的几种压强单位 及其换算系数列于表中。
表 压强的单位及其换算表
p0=pa h
例2:如图已知, p0=50kN/m2,h=1m, 求:该点的绝对压强及相对压强
p0
pa
h
解:p p0 gh 50 1 9.81 59.8kN / m2
p p pa 59.8 98 38.2kN / m2
由液面上的压强p0;另一部分是该点到自由液面的单位面积上的液柱重
量gh 。 (3)在静止液体中,位于同一深度(h=常数)的各点的静压
强相等,即任一水平面都是等压面。
20
z
Z
y
p0 h
A
Z0
x
21
[例题]已知:p0=98kN/m2, h=1m,
求:该点的静水压强
p0=pa
h
p
pa
解: p p0 gh
§2-3 压强的计算基准和量度单位
一、压强的表示
1. 计算基准
绝对压强:以完全真空时的绝对零压强(p=0)为基准来计 量的压强称为绝对压强;
相对压强:
以当地大气压强为基准来计量的压强称为相对压强。
绝对压强与相对压强之间的关系可在下面导出。当 自由液面上的压强是当地大气压强pa时,则液体中任一点的
压强可写成 p pa gh
为了正确区别和理解绝对压强、计示压强和真空之间 的关系,可用图来说明。
25
计示压强
绝对压强
真空 绝对压强
图 绝对压强、计示压强和真空之间的关系
26
流体静压强的量度单位主要有三种:应力单位,大气压的 倍数和液注高度。为了便于换算,现将常遇到的几种压强单位 及其换算系数列于表中。
表 压强的单位及其换算表
静水压强与静水总压力PPT课件

作用点:过FPx和FPz的交点,作与水平方 向成α角的线延长交曲面于D点
第14页/共28页
前进
y
oM
N
x
z
h dFp E dFp dFpz
F
K
L
dFpx
K
(dA)x
L
❖曲面上静水总压力的水平分力等于(dA) z
曲面在铅垂投影面上的静水总压力。
Fpx ghc Ax Pc Ax
❖曲面上静水总压力的垂直压力等于 压力体内的水体重。 FPz gV
静水总压力与水平方向的夹角:
arctan
FPz FPx
29.68
静水总压力的作用点:ZD R sin 2 sin 29.68 1m
答:略。
返回
第26页/共28页
结束
第27页/共28页
谢谢您的观看!
第28页/共28页
F三角
分布图叠加,直接求总压力
h1
e F矩形
h2
FP
b
(h2
h1) ( gh1
2
gh2 )
b
117.6kN
方向向右
依力矩定理:
Fp
e
F三角
[h2
h1
3
h2
]
F矩形
h2 2
可解得:e=1.56m
答:略
返回
第24页/共28页
一垂直放置的圆形平板闸门如
O
图所示,已知闸门半径R=1m,形心 在水下的淹没深度hc=8m,试用解析
注意:
1.平衡液体的自由表面是等压面。 2.不同流体的交界面是等压面。 3.讨论等压面必须保证是同一种连续介质
连通容器
连通容器
第6页/共28页
第14页/共28页
前进
y
oM
N
x
z
h dFp E dFp dFpz
F
K
L
dFpx
K
(dA)x
L
❖曲面上静水总压力的水平分力等于(dA) z
曲面在铅垂投影面上的静水总压力。
Fpx ghc Ax Pc Ax
❖曲面上静水总压力的垂直压力等于 压力体内的水体重。 FPz gV
静水总压力与水平方向的夹角:
arctan
FPz FPx
29.68
静水总压力的作用点:ZD R sin 2 sin 29.68 1m
答:略。
返回
第26页/共28页
结束
第27页/共28页
谢谢您的观看!
第28页/共28页
F三角
分布图叠加,直接求总压力
h1
e F矩形
h2
FP
b
(h2
h1) ( gh1
2
gh2 )
b
117.6kN
方向向右
依力矩定理:
Fp
e
F三角
[h2
h1
3
h2
]
F矩形
h2 2
可解得:e=1.56m
答:略
返回
第24页/共28页
一垂直放置的圆形平板闸门如
O
图所示,已知闸门半径R=1m,形心 在水下的淹没深度hc=8m,试用解析
注意:
1.平衡液体的自由表面是等压面。 2.不同流体的交界面是等压面。 3.讨论等压面必须保证是同一种连续介质
连通容器
连通容器
第6页/共28页
静水压强分布图实例

1 FX p X dA X p n dAn cos( n, X ) Xdxdydz 0 6
因为
1 dAn cos( n, X ) dAx dydz 2
代入上式得:
3 当四面体无限地缩小到0点时,上述方程中最后一项近于 零,取极限得, 即 p p
X n
p X pn
②质量力:(只有重力、静止)如图所示
1 其质量为 dxdydz ,单位质量力在各方向上的分别为 6
X、Y、Z,则质量力在各方向上的分量为
1 1 1 Xdxdydz , Ydxdydz , Zdxdydz 6 6 6
FX 0, FY 0, FZ 0
•以X方向为例:
学习重点
1、静水压强的两个特性及有关基本概念。 2、重力作用下静水压强基本公式和物理意 义。 3、静水压强的表示和计算。 4、静水压强分布图和平面上的流体总压力 的计算。 5、压力体的构成和绘制以及曲面上静水总 压力的计算。 6、处于相对平衡状态的液体中压强的计算。
§2-1
若在静止液体中任取两点l和2,点1和点2压强各为p1和p2, 位置坐标各为z1和z2,则可把式
p z c g
改写成另一表达式,即: z1
p1
p1 p2 z2 g g
1
z1
p2
2
z2
0 0 静压强基本方程的几何意义和物理意义
为了进一步理解静水压强基本方程式,现在来讨 论该方程的物理意义和几何意义 1.物理意义 式中:
pA g
A
Z
x y
如图所示,在一密闭容器中盛有密度为ρ 的液体,若自由液面上的 压强为p0、位置坐标为z0,则在液体中位置坐标为z的任意一点A的压强 p可由该式得到,即
水力学_静水压力ppt课件

sinJ x
si yC
说明各项意义,一般情况下D在C下方。
实际工程中的受压面多是轴对称面,总压力P的作用点 必位于对称轴上,这就完全确定了D的位置。
15
§2-8 作用在曲面上的静水总压力
一、原则 Px dpx
PZ dpZ
P Px2 Pz2
二、静水总压力的水平分力
p1d p2d (z1 z2 )d 0
整理
z1
p1
z2
p2
即 z+ p = c
(2-2-2)
4
或
p1d p2d hd 0
整理
p2 p1 h
(2-2-1)
当p柱=p体0 +上h底面与液面齐平时,若液面压强为p0,则(2-2-3)
式(2-2-2)和(2-2-3)为重力作用下水静力学基本方程的两 种表现形式,
❖
P =P -pa
abs
如图:若 p0 为相对压强,
P P rh P P rh P
B
0
Babs
0
a
7
若P0 为绝对压强,
p Babs
p 0
h
若开口(不封闭) p h B
p p h p
B
0
a
p p h
Babs
a
以后无特殊说明,指相对压强。
3、真空及真空度:当液体中某一点
的绝对压强小于当地大气压强时,
12
右图示: P1 h1lb
e1
2
P2
1
2
(h2
h1 )b
e2 3
P
P1
P2
1 2
(h1
h2
)b
Px P1e1 P2e2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 -
版权所有,仿冒及翻印必究
水力分析与计算
水力分析与计算
静水压强分布图及其绘制
1.静水压强分布图
根据静水压强的基本公式h p γ=知道,压强p 的大小与水深h 成线性函数关系,因此可以将作用面上的压强沿水深的分布绘制成几何图形,即静水压强分布图。
2.静水压强分布图的绘制方法如下:
(1)用静水压强的基本公式计算出静水压强的数值,
用一定的比例尺箭杆长度代表该点静水压强的大小。
(2)用箭头表示静水压强的方向(垂直作用面)。
(3)连接箭杆的尾部构成的几何图形,就构成受压面
上的静水压强分布图。
对于平面壁,压强p 沿水深h 方
向呈直线分布,只要确定两个点的压强值,就可以确定
该直线。
如右图所示,一矩形平板闸门AB ,一侧挡水,水深
为h ,水面为大气压p a ,闸门顶、底两点的压强值分别为0=A p ,h p B γ=。
由B 点作垂直AB 面的箭杆,以线段B B '表示B p 的大小,连接B A '构成的直角三角形B AB '即为AB 面上的静水压强分布图。
下图中绘出了几种有代表性受压面的相对压强分布图。
静水压强分布图可以叠加,对于建筑物上下游都受水压力的情况,如下图 (b )叠加之后静水压强分布图为矩形,这样做可简化静水总压力的计算。
