第二章水静力学(1)
武汉大学水力学教材答案第二章

武汉⼤学⽔⼒学教材答案第⼆章第⼆章⽔静⼒学1、相对压强必为正值。
( )2、图⽰为⼀盛⽔容器。
当不计瓶重时, 作⽤于地⾯上的⼒等于⽔作⽤于瓶底的总压⼒。
( )3、静⽔总压⼒的压⼒中⼼就是受⼒⾯⾯积的形⼼。
( )4、⼆向曲⾯上的静⽔总压⼒的作⽤点就是静⽔总压⼒的⽔平分⼒与铅直分⼒的交点。
( )5、⼀个任意形状的倾斜平⾯与⽔⾯的夹⾓为α。
则该平⾯上的静⽔总压⼒P=ρgy D A sinα。
(y D为压⼒中⼼D的) ()b,长度L及倾⾓α均相等,则⼆板上的静⽔总压⼒作( )( )8、静⽔压强仅是由质量⼒引起的。
( )9、在⼀盛⽔容器的侧壁上开有两个⼩孔A、B,并安装⼀U 形⽔银压差计,如图所⽰。
由于A、B两点静⽔压强不h 的差值。
( )10、物体在⽔中受到的浮⼒等于作⽤于物体表⾯的静⽔总压⼒。
( )11、选择下列正确的等压⾯: ( )(3) C ? C (4) D ? D( )(1) 淹没⾯积的中⼼;(2) 压⼒体的中⼼;(3) 总压⼒的作⽤点;(4) 受压⾯的形⼼。
13、平衡液体中的等压⾯必为( )(1) ⽔平⾯;(2) 斜平⾯;(3) 旋转抛物⾯;(4) 与质量⼒相正交的⾯。
14、图⽰四个容器内的⽔深均为H,则容器底⾯静⽔压强最⼤的是( )(1) a ; (2) b ; (3) c ; (4) d 。
15、欧拉液体平衡微分⽅程( ) (1) 只适⽤于静⽌液体;(2) 只适⽤于相对平衡液体;(3) 不适⽤于理想液体;(4) 理想液体和实际液体均适⽤。
16、容器中盛有两种不同重度的静⽌液体,如图所⽰,作⽤在容器A B 壁⾯上的静⽔压强分布图应为( ) (1) a (2) d17、液体某点的绝对压强为58 kP a,则该点的相对压强为( )(1) 159.3 kP a;(2) 43.3 kP a;(3) -58 kP a(4) -43.3 kP a。
18、图⽰的容器a 中盛有重度为ρ1的液体,容器b中盛有密度为ρ1和ρ2的两种液体,则两个容器中曲⾯AB 上压⼒体及压⼒应为( )(1) 压⼒体相同,且压⼒相等;(2) 压⼒体相同,但压⼒不相等;(3) 压⼒体不同,压⼒不相等;1 m 时〔虚线位置〕,闸门上的静⽔总压⼒。
水力学 水静力学 水静力学

压力中心位置:
0.6
Ph D dP h
1 h 2 [0.5 2 (0.6 h) cot 600 ]dh 0.37m P 0
1 hD dP h P0
h
受压面为梯形,是对称图形,所以其压力中心位于对称轴上。
§2.5 平面上静水总压力计算 2.5.1 图解法(矩形平面)
PyD ydP gyy sin dA
A
g sin y 2 dA g sin I x
A
yD
g sin I x
P
g sin I x I x g sin yc A yc A
2 (惯性矩平行移轴定理 ) I x I C Ayc
yD
2 I xC Ayc I yc C yc A yc A
dx 1 p pM p x , y, z p dx 2 2 x dx 1 p pN p x , y, z p dx 2 2 x
质量力在x轴的分量为:
fx dx dy dz
X方向的平衡方程:
1 p 1 p dx dydz p dx dydz f x dxdydz 0 p 2 x 2 x
2.3
重力场中流体静压强的分布规律
液体中任一点的压强为:
dp ( f x dx f y dy f z dz )
质量力只有重力:fx= fy =0, fz =-g,可得:
dp gdz
p c z c 积分可得: p gz g g p C 也可变形为 z g
微小面元dA上水压力
dP pdA ghdA
作用在平面上的总水压力 是平行分布力的合力
第二章 水静力学

第二章 水静力学水静力学(Hydrostatics )是研究液体处于静止状态时的力学规律及其在实际工程中的应用。
“静止”是一个相对的概念。
这里所谓“静止状态”是指液体质点之间不存在相对运动,而处于相对静止或相对平衡状态的液体,作用在每个液体质点上的全部外力之和等于零。
绪论中曾指出,液体质点之间没有相对运动时,液体的粘滞性便不起作用,故静止液体质点间无切应力;又由于液体几乎不能承受拉应力,所以,静止液体质点间以及质点与固壁间的相互作用是通过压应力(称静水压强)形式呈现出来。
水静力学的主要任务是根据力的平衡条件导出静止液体中的压强分布规律,并根据其分布规律,进而确定各种情况下的静水总压力。
因此,水静力学是解决工程中水力荷载问题的基础,同时也是学习水动力学的基础。
§2-1 静水压强及其特性1.静水压强的定义 在静止的液体中,围绕某点取一微小作用面,设其面积为ΔA ,作用在该面积上的压力为ΔP ,则当ΔA 无限缩小到一点时,平均压强A P ∆∆/便趋近于某一极限值,此极限值便定义为该点的静水压强(Hydrostatic Pressure),通常用符号p 表示,即dA dP A P p A =∆∆=→∆0lim (2-1) 静水压强的单位为2/m N (Pa(帕)),量纲为[][]21--=T ML p 。
2.静水压强的特性静水压强具有两个重要的特性:(1)静水压强方向与作用面的内法线方向重合。
在静止的液体中取出一团液体,用任意平面将其切割成两部分,则切割面上的作用力就是液体之间的相互作用力。
现取下半部分为隔离体,如图2-1所示。
假如切割面上某一点M 处的静水压强p 的方向不是内法线方向而是任意方向,则p 可以分解为切应力τ和法向应力p n 。
从绪论中知道,静止的液体不能承受剪切力也不可能承受拉力,否则将平衡破坏,与静止液体的前提不符。
所以,静水压强唯一可能的方向就是和作用面的内法线方向一致。
(2)静水压强的大小与其作用面的方位无关,亦即任何一点处各方向上的静水压强大小相等。
第二章水静力学

n
= p • D Ax
p =
n n
•
1 2
Dy
•
Dz
代入第一式
F F F px pncos(n, x) x =0 则:
1 2
Dy
Dz
px
1 2
Dy
Dz
pn
1 6
Dx Dy
Dz
fx
=
0
整理后,有
px
pn
1 Dx
3
fx
=
0
当四面体无限缩小到A点时,Dx
p x
=
p n
同理,我们可以推出:
0 因此:
△h
G
z1
2p 2
z2
0
h
G
p
0
(a)
(b)
圆柱上表面的静水压力 F1 = p1DA
圆柱下表面的静水压力 F2 = p2DA
小水柱体的重力
G = gDADh
力的平衡方程 p2DA p1DA gDADh = 0
p 0 ▽
h1 h2
△h
p
11
G
z1
2p 2
z2
0
(a)
p 0 ▽
h
G
p
0 (b)
单位重量的液体在某点所具有的位置势能(单位位
能):
z1
=
mgz1 mg
z 的能量意义是单位重量液体所具有的位置势能,
称为单位位能。
pa
p1 g
h12
1
z1
pa
p2 g
z2
0
0
Z Fpy
D Fpn Fpx
z
A y CBOFpzYX
相应面上的总压力为
水力学第二章(1)

静水压强各向同性证明
D py dx z
O
px pn dy pz C
dz A
B y
x
dx,dy,dz为四面体 为四面体ABCD dx,dy,dz为四面体ABCD 的棱长;dA为斜平面BCD的 为斜平面BCD 的棱长;dA为斜平面BCD的 面积; 面积; cos(n,x),cos(n,y),cos(n,z)为 为 斜平面BCD外法线n BCD外法线 斜平面BCD外法线n的方向 余弦; 余弦; px,py,pz ,pn分别表示 与坐标轴一致的平面和斜 面上的平均压强
第二章 水静力学
主要内容: 主要内容: §2-1 静水压强及其特性 §2-2 液体平衡微分方程及其积分 §2-3 重力作用下静水压强的分布规律
水静力学的任务: 水静力学的任务 是研究液体平衡的基本规 律及其实际应用。 律及其实际应用。 液体的平衡 状态有两种 静止状态 相对平衡状态
• 液体处于平衡状态时,液体质点之间没有相 液体处于平衡状态时, 对运动,液体内部不存在切应力; 对运动,液体内部不存在切应力; • 液体质点间的相互作用是通过压强的形式表 现出来的。 现出来的。
同理, 轴方向可推出类似结果, 同理,对y、z轴方向可推出类似结果,从而可得 液体平衡微分方程
1 ∂p = 0 ρ ∂x 1 ∂p Y− =0 ρ ∂y 1 ∂p Z− = 0 ρ ∂z X−
上式的物理意义为:液体处于平衡状态时, 上式的物理意义为:液体处于平衡状态时,单位 质量液体所受的表面力与质量力彼此相等。 质量液体所受的表面力与质量力彼此相等。 注意: 注意:该方程对于不可压缩液体和可压缩液体均 适用。 适用。
p = lim ∆P ∆A → 0 ∆ A
国际单位制中,静水压强p的单位为Pa(N/m )。 国际单位制中,静水压强p的单位为Pa(N/m²)。 Pa
第二章 流体静力学

d
例题3
考虑左侧水的作用
a a
a
a
b
b
b
b
c
c
c
c
ab段曲面(实 压力体)
bc段曲面(虚 压力体)
阴影部分相 互抵消
abc曲面(虚压 力体)
例题3
考虑右侧水的作用
a
b
c
bc段曲面 (实压力体)
例题3
合成
a a
a
a
b
b
b
b
c
c
c
c
左侧水的作 用
右侧水的作 用
abc曲面(虚压 力体)
例4
圆柱形压力水罐,半径R=0.5m,长l=2m,压 力表读值p=23.72kN/M2,试求(1)端部平 面盖板所受水压力;(2)上、下半圆筒所 受水压力。
分析思路
流体作用在曲面各微元面积上的压力 不是平行的,不能直接相加,而是采取 力学中“先分解,后合成”的方法确定总压 力。
§2.5 作用在曲面上的静水总压力
压力大小
dP ghd
一、静水总压力的水平分力
水平分力
dPx dP cos ghd cos ghd x
hd 为压力体体积
z
z
压力体
z
h d z
定义: 压力体相当于从曲面向上引至液 面(自由液面)的无数微小柱体的 体积总和,它是纯数学概念,与这 个体积内是否充满液体无关。
画法: (1)自由液面 (2)曲面 (3)根据静压强作用的方向找特殊点 (4)分段 (5)沿曲面的边界引垂直液面的铅垂面
空气 A 水
故A点的真空值为
p v p a p A (h2 h1 ) 1000 9.8 (2 1) 9800 Pa
《水力学》第二章答案

第二章:水静力学 一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h 高的水头具有大小为ρgh 的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中,z 表示某点在基准面以上的高度,称为位置水头,g p ρ表示在该点接一根测压管,液体沿测压管上升的高度,称为测压管高度或压强水头,g p z ρ+称为测压管水头,即为某点的压强水头高出基准面的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A 是等压面,C-C,B-B 都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了Ap∆,水面以下同一高度的各点压强都增加Ap∆。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
水静力学
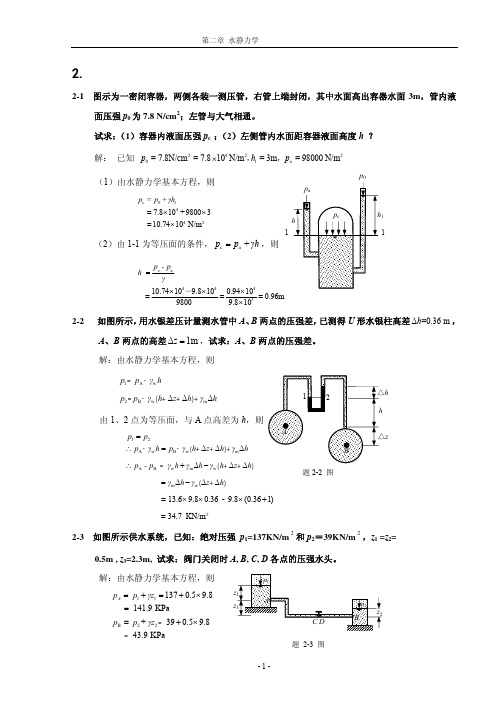
2-5 如图所示容器,上层为空气,中层为容重 8170N/m 3 的石油,下层为容重
12250N/ m 3 的甘油,试求:当测压管中的甘油表面高程为 9.14m 时压力表 G 的读数。
解:由已知条件,则
γ2 = 8.17 KN/m3 ,γ3 = 12.25 KN/m3 h1 = 9.14 - 7.62 = 1.52 m h2 = 7.62 - 3.66 = 3.96 m 由水静力学基本方程,取甘油与石油交界面
= 6.284 rad/s
ω
R2
R1
题 2-9 图
2-10 如图所示为一复式水银测压计,用来测水箱中的表面压强 p0。试求:根据图 中读数(单位
为 m)计算水箱中液面处的绝对压强 p0。
解:从右向左写液体静水压强平衡方程,则
pa + γh (2.3- 1.2)- γw (2.5 −1.2)+ γh (2.5- 1.4) = p0 + γw (3.0 −1.4) p0 = pa + γh (2.3- 1.2)+ γh (2.5- 1.4)
1
2
△h
h
由 1、2 点为等压面,与 A 点高差为 h,则
p1 = p2
A
∴ pA - γw h = pB- γw (h+ ∆z+ ∆h)+ γm∆h
△z B
∴ pA - pB = γw h + γm∆h − γw (h+ ∆z+ ∆h) = γm∆h − γw (∆z+ ∆h)
题 2-2 图
= 13.6× 9.8× 0.36 - 9.8× (0.36 +1)
解: 图中虚线表示假想的自由液面,其方程为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章水静力学1、相对压强必为正值。
( )2、图示为一盛水容器。
当不计瓶重时, 作用于地面上的力等于水作用于瓶底的总压力。
( )3、静水总压力的压力中心就是受力面面积的形心。
( )4、二向曲面上的静水总压力的作用点就是静水总压力的水平分力与铅直分力的交点。
( )5、一个任意形状的倾斜平面与水面的夹角为α。
则该平面上的静水总压力P=ρgy D A sinα。
(y D为压力中心D的) ()b,长度L及倾角α均相等,则二板上的静水总压力作( )( )8、静水压强仅是由质量力引起的。
( )9、在一盛水容器的侧壁上开有两个小孔A、B,并安装一U 形水银压差计,如图所示。
由于A、B两点静水压强不∆h 的差值。
( )10、物体在水中受到的浮力等于作用于物体表面的静水总压力。
( )11、选择下列正确的等压面: ( )(3) C − C (4) D − D( )(1) 淹没面积的中心;(2) 压力体的中心;(3) 总压力的作用点;(4) 受压面的形心。
13、平衡液体中的等压面必为( )(1) 水平面;(2) 斜平面;(3) 旋转抛物面;(4) 与质量力相正交的面。
14、图示四个容器内的水深均为H,则容器底面静水压强最大的是( )(1) a ; (2) b ; (3) c ; (4) d 。
15、欧拉液体平衡微分方程( ) (1) 只适用于静止液体;(2) 只适用于相对平衡液体;(3) 不适用于理想液体;(4) 理想液体和实际液体均适用。
16、容器中盛有两种不同重度的静止液体,如图所示,作用在容器A B 壁面上的静水压强分布图应为( ) (1) a (2) d17、液体某点的绝对压强为58 kP a,则该点的相对压强为( )(1) 159.3 kP a;(2) 43.3 kP a;(3) -58 kP a(4) -43.3 kP a。
18、图示的容器a 中盛有重度为ρ1的液体,容器b中盛有密度为ρ1和ρ2的两种液体,则两个容器中曲面AB 上压力体及压力应为( )(1) 压力体相同,且压力相等;(2) 压力体相同,但压力不相等;(3) 压力体不同,压力不相等;1 m 时〔虚线位置〕,闸门上的静水总压力。
( )(3) 不变;(4) 无法确定。
3 m 水柱高,当地大气压为一个工程大气压,其相应的绝对压强值等于( )(1) 3 m 水柱高;(2) 7 m 水柱高;(3) -3 m 水柱高;(4) 以上答案都不对。
21、液体中,测管水头(z + p/ρg) 的能量意义是______________________。
22、液体中,位置高度z 的能量意义是_______________;压强高度p/ρg 的能量意义是_______________。
23、真空压强的最小值是__________________;真空压强的最大值是___________________。
24、比重为0.81 的物体放入比重为0.9 的液体中,则出露部分体积与总体积之比为__________________。
25、容器A、B分别以加速度a和等角速度 运动,如图所示。
分别绘出液面下深度h处的等压面形状,并标明该等压面上任一质点的质量力F的方向。
2627、绘出图示圆柱体上水平压强分布图和压力体图。
并标出水压力铅直分力的方向。
28、三个圆球各充满液体后的测压管液面如图示,试绘出各球面的压力体图,并标出力的方向。
30、压力水箱上角装有一圆柱体压力表读数为19.60 kPa,箱中盛满水。
试绘出作用于圆柱面ABC上的水平压强分布图和压力体。
31、有一圆柱形容器,顶部设一通气管,如图所示。
已知圆柱半径 R =0.5 m ,通气管中的水面与容器顶盖齐平。
容器以等角速度ω=2π s -1绕铅垂中心轴旋转,求容器顶盖的总压力P 。
(N 937.9 1P =)32、一封闭容器如图所示。
容器中水面的绝对压强 p 0=91.5Pa 。
中间插入一两端开口的玻璃管。
当空气恰好充 满全管而不流动时, 求管伸入水中的深度 h 。
(=h 0.663 m )33、在物体上装置一个直径很小的盛水 U 形管,以测定物体作直线运动的加速度(如图)。
若 L =0.3m ,h =0.15 m ,求物体的加速度 a 。
(a =4.9 m/s 2)α=120︒,如图所示可绕 A 轴转动,如图所受。
已知 L = 2 m 。
不计门重及摩擦力,求闸门开 始自动倾倒时的水深 h 。
(h=3.759 m )35、一曲面的形状为 3/4 个圆柱面,半径 R =0.8 m ,宽度(垂直于纸面)为1 m 。
圆心位于液面以下h =2.58 m ,如图所受。
容器中盛有密度为 ρ1=816 kg/m 3的液体,其深度 h 1=0.98 m ,其下为密度ρ2=1000 kg/m 3的液体。
(1) 绘制曲面的水平分力的压强分布图和垂直分力的压力体图。
(2) 求作用于曲面的静水总压力的大小和方向。
(kN 15.68P x ==; kN 33.58P z =;=P 37.06 kN ;=θ64.97︒)加速度 a 垂直向上运动,如图所示。
试导出液体中任一点压强 p 的表达式。
(h gag p z a g p a )1()(++++-=ρρ)37、一容器左侧盛油,右侧盛水,上、下各接一水银压差计。
各液面标高如图所示。
已知油的密度ρ=816 kg/m 3。
求容器顶部压差计液面高差h 。
(h =0.2018 m )(不计重量)在密度分别为ρ1和ρ2的两种液体作用下处于平衡状态。
试导出D 与ρ1, ρ2,h 1,h 2之间的关系式。
( gg )gh gh (3D 211122ρ+ρρ-ρ=)39、一矩形水箱,箱中盛有液体,水箱沿倾斜角为θ的斜面以加速度a 向下滑动(如图)。
试确定箱内液体表面的 形状。
(液面方程为0=g)z -sin a (x )cos (a θ+θ ;液面对水平面的倾斜角θθ=βasin -g cos a x z =tan )40、图示为一空心弯管,下端插入水中,其水平段长度R =30 cm 。
当弯管绕铅直z 轴作等角速度旋转时,管内水 面上升至下游水面以上h =20 cm 。
求角速度ω。
(=ω 6.6 rad/s )41、在石油库斜壁的圆孔上装有一直径D =1.2 m 的半球形盖(如图)。
半球形盖中心O 点在液面下的深度H =4 m 。
斜壁与液面的夹角α=30︒,石油的密度ρ=900 kg/m 3。
求螺栓a 、b 上的总拉力。
(42.70kN )42、杯式水银真空计如图所示。
已知杯的直径D =60 mm ,管的直径d =6 mm 。
杯顶接大气时,测压管液面读数 为零。
杯顶封闭时,若测得测压管读数h =300 mm ,求杯中气体的真空压强。
(=0p 40.384 kPa )43、用U 形水银测压计测量A 点的静水压强,其读数为h ( mm ),如图所示。
令A 点压强不变,若将U 形管下将高 度H ( mm )。
则水银测压计读数放大为h +∆h( mm )。
试证明: ∆h=H/13.1。
44、蜡块A 沉浸在充满油和水的容器中,如图所示。
已知蜡块密度ρn =960 kg/m 3,油的密度ρ0=900 kg/m 3。
试确定蜡块沉没在水中和油中的体积占百分之几。
(V 6.0V 2=;V 4.0V 1=)45、在盛满液体的容器壁上装有一个均质圆柱体,如图所示。
由于圆柱体浸在液体中,必受到一个向上的浮力作用。
若摩擦力很小,在浮力产生的力矩的作用下,此圆柱体可绕O 轴不停转动,这种说法对不对?为什么?H 和 底面积 A 均相等时,问:(1) 容器底部所受的静水压强是否相等? (2) 底面所受的静水压力是否相等?(3) 桌面上受的压力是否相等?为什么?47、一圆锥形开口容器,下接一弯管。
当容器空着时,弯管上读数如图所示。
问圆锥内充满水后,弯管上读数为多少? (h=4.08m ,l=1.065m )48、图示一倒U 形差压计,左边管内为水,右边管内为相对密度(即比重)9.0s 1=的油。
倒U 形管顶部为相对密度8.0s 2=的油。
已知左管内A 点的压强2A m /KN 98p =,试求右边管内B 点的压强。
(p B =97.4Kpa )49、一容器如图所示,当A 处真空表读数为22cm 汞柱高,求E 、F 两管中的液柱高21h ,h 值。
并求容器左侧U 形管中的h 值。
(h 1=126cm , h 2=600.8cm , h=80.9cm )50、两液箱具有不同的液面高程,液体重度均为'γ,用两个测压计连接如图,试证:212211'h h h h +γ+γ=γ51、密闭容器盛水如图,已知m 3h =,,m 2h ,m 5.2h A B ==求容器内点A ,点B 及液面上的相对压强及绝对压强,并求图中所示y 值。
(p A =-19600pa , p B =24500pa , p 0=-29400pa ;绝对压强: p A =78400pa , p B =122500pa , p 0=63600pa ;y=3m )52、如图所示为一铅直安装的煤气管。
为求管中静止煤气的密度,在高度差m 20H =的两个断面安装U 形管测压计,内装水。
已知管外空气的密度3a m /kg 28.1=ρ,测压计读数为mm 115h ,mm 100h 21==。
与水相比,U 形管中气柱的影响可以忽略。
求管内煤气的密度。
(0.53Kg/m 3)53、试按图示复式水银测压计的读数计算出锅炉中水面上蒸汽的绝对压强p 。
已,m 3.2h ,m 2.1h ,m 5.2h ,m 4.1h ,m 3H 4321=====水银的相对密度6.13s =。
(362.8Kpa )54、如图所示为双液式微压计,A ,B 两杯的直径均为mm 50d 1=,用U 形管连接,U 形管直径mm 5d 2=,A 杯内盛有酒精,密度31m /kg 870=ρ,B 杯内盛有煤油32m /kg 830=ρ。
当两杯上的压强差0p =∆时,酒精与煤油的分界面在0-0线上。
试求当两种液体的分界面上升到0‘-0’位置、mm 280h =时p ∆等于多少?(156.6Pa )55、一水箱装置如图,箱底高出地面m 3h 2=,箱中水深m 2h 1=,其表面压强以绝对压强计为0.7个工程大气压,要求:(1)以地面为基准面,求出A 、B 两点的单位位能与单位压能,并在图上标明;(2)以水箱中水面为基准面,求出A 、B 两点的单位位能与单位压能,并在图上标明。
(Z A1=5m , Z B1=3m ,p A1/γ=-3m , p B1/γ=-1m ;Z A2=2m , Z B2=0m ,p A1/γ=-3m , p B1/γ=-1m )56、图示为一沉没于海中的潜艇的横断面图,气压计测出潜艇内的绝对压强cm 84p s =(水银柱),已知海水的相对密度03.1s =,试求潜艇的沉没深度y 。
