05 弯曲应力
材料力学第五章弯曲应力

式中 : M 横截面上的弯矩
Iz
横截面对中性轴的惯性矩
y
求应力的点到中性轴的距离
I z A y2dA
m 惯性矩是面积与距离平方的乘积,恒为正值,单位为 4
My
IZ
讨论
应用公式时,一般将 M,y 以绝对值代入。根据梁变 形的情况直接判断 的正,负号。 以中性轴为界,梁 变形后凸出边的应力为拉应力( 为正号)。凹入边 的应力为压应力,( 为负号)。
max M (x) WZ
RA
P
A
C
5m 10m
RB B
a
12.5
z
166
例题1 :图示简支梁由 56 a 工字钢制成 ,其横截面见图 p = 150kN。求 (1) 梁上的最大正应力 max
(2) 同一截面上翼缘与腹板交界处 a 点的应力
解:
C 截面为危险截面。最大弯矩
+
M max 375KN.m
查型钢表,56 a 工字钢
I z 65586 cm6
W z 2342cm2
(1) 梁的最大正应力 +
σ max
M max WZ
160MPa
(2) a点的正应力
a点到中性轴的距离为
ya
560 2
21
所以 a 点的正应力为
σ a M max ya 145MPa IZ
12.5
My
IZ
最大正应力发生在横截面上离中性轴最远的点处 当 中性轴为对称轴时 ,ymax 表示最大应力点到中性轴 的距离,横截面上的最大正应力为
max M ymax Iz
WZ
IZ ymax
材料力学第5章弯曲应力

M
M
中性轴
z
m
n
y
o
o
dA
z
mn
y
dx
Mzy
Iz
max
Mz Wz
M
MZ:横截面上的弯矩
y:到中性轴的距离
IZ:截面对中性轴的惯性矩
M
中性轴
§5-2 惯性矩的计算
一、静矩 P319
y
Sz ydA
A
z dA
zc
c y
S y zdA
yc
A
o
z
分别为平面图形对z 轴和 y 轴的静矩。
ySc Az ydA
F M
F
a
B
F
Fa
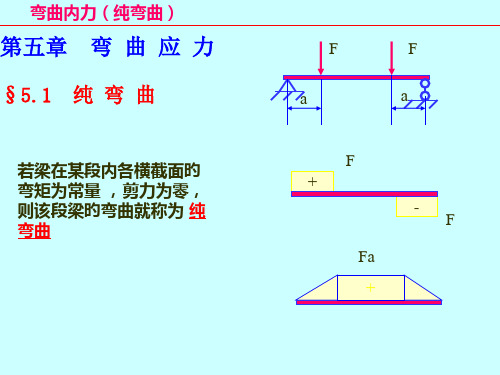
5.3 梁弯曲时的正应力
若梁在某段内各横截
面上的弯矩为常量, F
F
a
a
剪力为零, 则该段梁 A 的弯曲就称为纯弯曲。
B
Fs
在 AC 和 DB 段 内 横 截 面上既有弯矩又有剪 M 力, 这种情况称为横 力弯曲或剪切弯曲。
F F
Fa
平面假设
变形前原为平面的梁的横截面变形后仍保持为 平面, 并绕垂直于纵对称面的某一轴旋转, 且仍 然垂直于变形后的梁轴线。这就是弯曲变形的 平面假设。
C y'
a
x'
xc
b
注意!C点必须为截面形心。
六、组合截面的惯性矩
Iy Iyi
Iz Izi
例2:求对倒T字型形心 轴yC和zC的惯性矩。
解:1. 取参考轴yOz 2. 求形心
2cm y(yc)
1 c1
6 cm
yc
Ai yi A
y
c 1
工程力学5第五章弯曲应力 ppt课件

M
dM Iz
S
* z
dF ddx
dM dx = FS
FS
S
* z
Izd
S
* z
b( h 2
h1 2
)[ h1 2
1 2
(h 2
h1 2
)]
d
(
h1 2
y)[ y
1 2
(
h1 2
y)]
1 h2 [b(
h12
)
d ( h12
y2 )]
2 44
2PPT课件
z
280
PPT课件
60
y
4.13MPa 4.34MPa
38
例3:一矩形截面外伸梁,如图所示。现自梁
中1.2.3.4点处分别取四个单元体,试画出单
元体上的应力,并写出应力的表达式。
q
1
A
l /4
2
4 h /4
3
B
l
l /4
h
z τmax
bτ
PPT课件
39
解:(1)求支座反力:
q
3 FA 4 ql
腹板
δ d
yz
FS——横截面上剪力。
y
翼缘
矩形截面的两个假定同样适用。
PPT课件
24
δ
h h1
y
δ
FN1
b
dF z
dx
dF FN 2 FN1
FN2
式中:FN1
dA M
A*
Iz
A*
第五章 弯曲应力

第五章弯曲应力§5-1 梁弯曲正应力§5-2 惯性矩计算§5-3 梁弯曲剪应力*§5-4 梁弯曲时的强度计算§5-5 塑性弯曲的概念*§5-6 提高梁抗弯能力的措施§5-1 梁弯曲正应力一、梁弯曲时横截面上的应力分布一般情况下,梁受外力而弯曲时,其横截面上同时有弯矩和剪力两个内力。
弯矩由分布于横截面上的法向内力元σdA所组成,剪力由切向内力元τdA组成,故横截面上同时存在正应力和剪应力。
MσdAτdA Q当梁较长时,正应力是决定梁是否破坏的主要因素,剪应力则是次要因素。
二、弯曲分类P P a aAC DB ACD +−BC D+P PPa 梁AC 、BD 段的横截面上既有剪力又有弯矩,称为剪切弯曲(横力弯曲)。
CD 段梁的横截面上只有弯矩而无剪力,称为纯弯曲。
此处仅研究纯弯曲时梁横截面上正应力与弯矩的关系。
三、纯弯曲实验1.准备A BC DE F G H 在梁侧面画上AB 、CD 、EF 、GH 四条直线,且AB ∥CD 、EF ∥GH。
在梁两端对梁施加纯弯矩M 。
A B C D E F G H M MA BC DE F G H 2.现象•变形后横向线AB 、CD 发生了相对转动,仍为直线,但二者不再平行;仍与弧线垂直。
•纵向线EF 、GH 由直线变成曲线,且EF 变短,GH 变长;•曲线EF 、GH 间的距离几乎没有变化;•横截面上部分沿厚度方向变宽,下部分变窄。
3.假定•梁的任意一个横截面,如果在变形之前是平面,在变形后仍为平面,只是绕截面的某一轴线转过了一个角度,且与变形后的轴线垂直。
——平截面假定。
•梁上部分纤维受压而下部分纤维受拉,中间一层纤维既不受拉也不受压,这一层叫中性层或中性面。
•中性层与横截面的交线叫中性轴。
梁弯曲变形时横截面绕中性轴转动。
中性层纵向对称面中性轴•梁的纵向纤维之间无挤压力作用,故梁的纵向纤维只受拉伸或压缩作用——单向受力假设。
弯曲应力-材料力学

弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
另外,根据不同的弯曲形式和受力情 况,还可以采用其他计算公式来求解 弯曲应力,如均布载荷下的简支梁、 集中载荷下的悬臂梁等。
弯曲应力的计算方法
根据材料力学的基本原理,弯曲应力 的计算公式为:σ=M/Wz,其中σ为 弯曲应力,M为弯曲力矩,Wz为截面 对中性轴的抗弯截面系数。
弯曲应力可能导致材料发生弯曲变形,影响结构的稳定性和精度。
弯曲应力对材料刚度的影响
弯曲应力对材料的刚度有影响,材料的刚度随着弯曲应力的增大而 减小。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
弯曲应力
材料的韧性和强度都会影响其弯曲应力的大小和分布。韧性好的材料能够更好地分散和 吸收弯曲应力,而高强度的材料则能够承受更大的弯曲应力而不发生断裂。
材料韧性、强度与弯曲应力的关系
韧性
是指材料在受到外力作用时吸收能量的能力。韧性好的材料能够吸收更多的能量,从而 减少因弯曲应力而产生的脆性断裂。
强度
剪切应力的分布
剪切应力在材料截面的边缘最大,向中性轴方向 逐渐减小。
3
剪切应力和弯曲应力的关系
剪切应力和弯曲应力共同作用,影响梁的承载能 力和稳定性,在设计时需要考虑两者的相互作用。
弯曲应力与剪切应力的关系
1 2
剪切应力在弯曲应力中的作用
在弯曲过程中,剪切应力会在材料截面的边缘产 生,它与弯曲应力相互作用,影响梁的承载能力 和稳定性。
材料力学第五章-弯曲应力知识分享

材料力学第五章-弯曲应力注:由于本书没有标准答案,这些都是我和同学一起做的答案,其中可能会存在一些错误,仅供参考。
习 题6-1厚度mm h 5.1=的钢带,卷成直径 D=3m 的圆环,若钢带的弹性模量E=210GPa ,试求钢带横截面上的最大正应力。
解: 根据弯曲正应力公式的推导: Dy E yE 2..==ρσ MPa D h E 1053105.110210.39max =⨯⨯⨯==-σ 6—2直径为d 的钢丝,弹性模量为E ,现将它弯曲成直径为D 的圆弧。
试求钢丝中的最大应力与d /D 的关系。
并分析钢丝绳为何要用许多高强度的细钢丝组成。
解: ρσyE .= Dd E ED d .22max ==σ max σ与Dd成正比,钢丝绳易存放,而引起的最大引力很小.6—3 截面形状及尺寸完全相同的一根钢梁和一根木梁,如果所受的外力也相同,则内力是否相同?横截面上正应力的变化规律是否相同?对应点处的正应力与纵向线应变是否相同? 解: 面上的内力相同,正应力变化规律相同。
处的正应力相同,线应变不同6—4 图示截面各梁在外载作用下发生平面弯曲,试画出横截面上正应力沿高度的分布图.6—5 一矩形截面梁如图所示,已知F=1.5kN 。
试求(1) I —I 截面上A 、B 、C 、D 各点处的正应力; (2) 梁上的最大正应力,并指明其位置。
解:(1)m N F M .3002.0*10*5.12.0*3===MPa M I y M z A 11110*30*1812*10*15*.1233===--σ A B σσ-= 0=C σMPa M D 1.7410*30*1812*10*)5.15(*1233==--σ MPa W Fl z 5.16610*30*186*10*300*10*5.19233max ===--σ 位置在:固定端截面上下边缘处。
6—6 图示矩形截面简支梁,受均布载荷作用。
已知载荷集度q=20kN /m ,跨长l =3,截面高度=h 24cm ,宽度=b 8cm 。
材料力学第五章 弯曲应力

F F d F 0 N 2 N 1 S
将FN2、FN1和dFS′的表达式带入上式,可得
* M M d M * S S b d x 0 z z
I z I z
简化后可得
dM S z* dx I z b
dM F S ,代入上式得 由公式(4-2), dx
* 式中 S z
A1
y1dA ,是横截面距中性轴为 y 的横线 pq 以下的面积对中性轴的静矩。同理,
可以求得左侧面 rn 上的内力系的合力 FN 1 为
M * FN 1 S z Iz
在顶面rp上,与顶面相切的内力系的合力是
d F b d x S
根据水平方向的静平衡方程
F 0 ,可得
综上所述,对于各横截面剪力相同的梁和剪力不相同的
细长梁(l>5h),在纯弯曲情况下推导的弯曲正应力公式 (5-2)仍然适用。
例5-1
图5-10(a)所示悬臂梁,受集中力F与集中力
偶Me作用,其中F=5kN,Me=7.5kN· m,试求梁上B点左邻 面1-1上的最大弯曲正应力、该截面K点处正应力及全梁的 最大弯曲正应力。
第五章 弯曲应力
5.1 弯曲正应力 5.2 弯曲切应力简介 5.3 弯曲强度条件及其应用 5.4 提高梁弯曲强度的主要措施
5.1 弯曲正应力
上一章研究表明,一般情况下,梁横截面上同时存在
剪力FS和弯矩M。由于只有切向微内力τ dA才可能构成剪力, 也只有法向微内力σdA才可能构成弯矩,如图5-1(a)所示。 因此,在梁的横截面上将同时存在正应力σ和切应力τ(见图 5-1(b))。梁弯曲时横截面上的正应力与切应力分别称为 弯曲正应力与弯曲切应力。
第五章弯曲应力

弯曲应力/横力弯曲时的正应力
§5.3横力弯曲时的正应力
材料力学
弯曲应力/横力弯曲时的正应力
现实中常见的弯曲问题多为横力弯曲
横力弯曲的特点:
梁的横截面上不但有正应力还有切应力,
横截面不再保持为平面。
注意:
纯弯曲时的正应力计算公式 仍然适用于横力弯曲。
材料力学
弯曲应力/横力弯曲时的正应力
第五章 弯曲应力
材料力学
§5.1 纯弯曲
材料力学
弯曲应力/纯弯曲 横力 F 弯曲 a F (+) (-)
FS 图
纯弯曲
F
一. 纯弯曲和横力弯曲: 横力
弯曲
纯弯曲:梁弯曲变形时, 横截面上只有弯矩而无剪
a L
力(
M 0 , Fs 0
)。
横力弯曲:梁弯曲变形
Fa
-F
时,横截面上既有弯矩又 有剪力(
M 图
材料力学
弯曲应力/提高弯曲强度的措施
3.减小支座跨度或增加支座
F A L 0.125FL (+)
M 图
F BA 0.2L 0.6L 0.2L 0.025FL (+) 0.02FL
M 图
F BA 0.5L
9 512
B
0.5L
9 512
FL
FL
(+) 0.02FL
1 32 FL
(+)
M 图
h
材料力学
弯曲应力/纯弯曲时的正应力
圆形截面:
实心:
d z
Iz
空心:
64
d
4
D d z
IZ
D (1 )
第五章弯曲应力解析

•梁的长度比横截面度量尺寸大得多(长梁),平截面假 定仅适应于长梁,若梁长度与横截面度量尺寸的比值 小于5,由弹性力学知,平截面假定就不适用. •平截面假定一般不适用于曲梁.
§5-2 纯弯曲时的正应力
同圆轴扭转的应力公式推导过程一样,从变形几何关系、 物理关系和静力学关系三方面考虑.
M σdA
FS τdA
当梁较长时,正应力是决定梁是否破坏的主要因素, 切应力则是次要因素.
➢二、弯曲分类
梁AC、BD段的横截面上既有剪 A 力又有弯矩,称为剪切弯曲.
aP
C P
Pa
D
B
CD段梁的横截面上只有弯矩 而无剪力,称为纯弯曲.
+
A
C
D −B
此处仅研究纯弯曲时梁横截面 上正应力与弯矩的关系.
FN=0
M
FN
AdA
A
E
ydA
E
A
ydA
0
zM
Ox
y
σdA
y
因 E 0 故 ydA 0
A
由中值定理知
A ydA yC .A S z
—横截面图形对z 轴的静矩.
故 yC .A 0 yC 0 —横截面图形形心坐标.
即横截面形心在z轴上,故中性轴必通过横截面形心.
My=0
M
M y
第五章 弯曲应力
§5-1 纯弯曲 §5-2 纯弯曲时的正应力 §5-3 惯性矩计算 §5-4 剪切弯曲时的正应力 §5-5 弯曲切应力 §5-6 提高梁抗弯能力的措施
§5-1 纯弯曲
➢一、梁弯曲时横截面上的应力分布
一般情况下,梁受外力而弯曲时,其横截面上同时 有弯矩和剪力两个内力.弯矩由分布于横截面上的 法向内力元σdA所组成,剪力由切向内力元τdA组 成,故横截面上同时存在正应力和切应力.
材料力学05 弯曲应力

–x
qL
2
max
1.5
F max S A
1.5 5400 0.12 0.18
0.375MPa 0.9MPa []
M
qL2
应力之比
+
8 Mmax
max M max 2 A L 16.7
max
Wz
3
F
m S
ax
h
x
§5-5 提高弯曲强度的措施
弯曲正应力是控制梁强度的主要因素,故弯曲正应力强度 条件是设计梁的主要依据。
7
(3)结论:
mn
变形前原为平面的梁的横截
aa
面变形后仍保持为平面,且
仍垂直于变形后的梁的轴
线。——平面假设
bb mn
(4)推论: ①横截面变形后仍为平面,只是
M
mn
M
绕中性轴发生转动,距中性轴等
aa
高处,变形相等。
bb mn
②对于纯弯曲,认为各纵向纤维 之间无挤压,仅承受拉应力或压 应力。即纵向纤维间无正应力, 只有横截面上有正应力。
max
M max ymax Iz
[ ]
工作正应力最大值
许用正应力
引入记号:
Wz
Iz ymax
称为抗弯截面系数
则弯曲正应力强度条件可改写为:
max
M max Wz
[
]
3.弯曲正应力强度条件的应用(以等截面梁为例)
① 校核强度: max [ ]
② 设计截面尺寸:
Wz
1
第五章 弯曲应力
§5–1 引言 §5–2 纯弯曲时的正应力 §5–3 横力弯曲时的正应力 §5–4 弯曲切应力 §5–5 提高弯曲强度的措施
第五章弯曲应力

变形前 变形后
ab= dx= o1o2 = ρdθ a'b' = (ρ + y)dθ
弯曲应力/ 弯曲应力/纯弯曲时的正应力
所以纵向纤维ab的应变为 所以纵向纤维 的应变为: 的应变为
∆ ab ( ρ + y)dθ − ρdθ yd θ y = = ε= = ρdθ dx ab ρ
轴向变形规律: 轴向变形规律: 轴向变形程度的大小与到中性层的距离成正 离中性轴越远,变形越大。 比,离中性轴越远,变形越大。
一.纯弯曲正应力的分布规律 1.纯弯曲变形几何关系 1.纯弯曲变形几何关系
m
o1
o
ρ
a´ a´ b´ ´
n
o2
dx
变形后 y b
a m
n
y——任意纵向纤维至中性层的距离 任意纵向纤维至中性层的距离 任意纵向纤维至 的曲率半径, 曲率中心, ρ——中性层o1o2的曲率半径, o——曲率中心, 中性层 曲率中心 纵向纤维ab: 纵向纤维
材料力学
弯曲应力/ 弯曲应力/纯弯曲
现象二: 现象二:
M M
M
纵向纤维间距离不变 说明横截面上没有切应力。 说明横截面上没有切应力。
材料力学
弯曲应力/ 弯曲应力/纯弯曲
现象三: 现象三:
M M
M
横截面变形后仍保持为平面, 横截面变形后仍保持为平面,且仍然垂直于 变形后的轴线,此即弯曲的平面假设。 变形后的轴线,此即弯曲的平面假设。
-F
时,横截面上既有弯矩又 有剪力( 有剪力( M ≠ 0, Fs ≠ 0 )。
(+) M-图 图
材料力学
弯曲应力/ 弯曲应力/纯弯曲
二. 纯弯曲实验观察 对 比 弯 曲 前 后 梁 的 变 化
第五章 弯曲应力

三类条件
物理关系
静力关系
1.变形几何关系
m a
n
a
m a o b m
n a o dx
b m
dx
b n
b n
假设oo层为中性层 变形前:aa = bb = oo = dx
m M a
o b m
n a M M
d M
dx
o b n
m o
b′
n o
b′
m
n
变形后:假设中性层oo层变形后的曲率半径为,则
max
M [ ] Wz max
(2) 设计截面尺寸
(3) 计算许用载荷
M Wz [ ]
M max Wz [ ]
例2. T形截面铸铁梁,已知[σt]=30MPa,[σc]=60MPa, 试 80 校核梁的强度。
9kN
A 1m
4kN
B D 1m
20
CLeabharlann 1m120讨论: 1.横截面是绕中性轴转动。 (中性层不伸长也不缩短,中性轴是中性层与横截
面的交线 。) 上部受压
当M > 0时 下部受拉 上部受拉 下部受压
当M < 0时
讨论: 2.纵向纤维的伸长或者缩短与它到中性层的
距离成正比。
m
n′
n a
y
a
y
b m
b
中性层 n′
中性轴 横截面
n
定量分析
与圆轴扭转问题相似,弯曲问题的理论分析也 必须包含三类条件。 变形几何关系
结论: 1.横截面上只存在正应力。
(纵向线与横向线保持直角。)
2.正应力分布不是均匀的。
(纵向线中既有伸长也有缩短的。)
材料力学第5章弯曲应力

欢迎来到材料力学第5章弯曲应力的世界!在本章中,我们将深入探讨什么是 弯曲应力,并研究其在不同形状截面中的计算方法和应用。
弯曲应力的定义和概念
什么是弯曲应力?
弯曲应力是物体受到外力作用时,在横截面上产生的力分布状态。
应变张量与应力张量
了解应变张量和应力张量的关系是理解弯曲应力的基础。
应力-应变曲线与弯曲应力
探索材料的应力-应变曲线与弯曲应力之间的关系。
弯曲应力在工程中的应用
建筑结构
了解弯曲应力在建筑结构中的应 用,如桥梁和楼梯等。
机械设计
探索弯曲应力在机械设计中的重 要性,如机械零件和工具。
航空航天工程
了解弯曲应力在航空航天工程中 的关键应用,如飞机和火箭。
梯形截面
探索梯形截面的弯曲应力计算方法。
弯曲应力的影响因素
1 外力
外力的大小和方向将直接影响到物体的弯曲应力。
2 截面形状
不同形状的截面将对弯曲应力的分布产生影响。
3 材料的力学性质
材料的弯曲应力极限和应力-应变关系是必须考虑的因素。
材料的弯曲应力极限
如何确定材料的弯曲应力极限
了解如何通过实验和模拟来确定材料的弯曲应力极限。
材料力学中的弯曲应力方程
一般弯曲应力方程
通过一般弯曲应力方程,我们可以计算出材料在弯曲时 的应力。
悬臂梁的弯曲应力
悬臂梁的弯曲应力方程与一般情况下的方程有所不同, 的弯曲应力计算方法
1
圆形截面
2
了解计算圆形截面的弯曲应力的公式和步骤。
3
矩形截面
学习如何计算矩形截面的弯曲应力。
弯曲应力CL专业知识
大正应力。
A
C 5kN
φ60
B
φ40
3kN E
400
1000
200
M
+
FRA=41/14(kN) FRB=71/14(kN)
-
X
M图
弯曲内力(横力弯曲时旳正应力)
解:1.C截面
max2.BMW右cc侧
1.17 106
603
32
55.3MPa
max
MB WB
0.9 106
603(1 ( 40)4 )
(+) (b)
C
z
形心
(-)
解:
Fb/2 作梁旳弯矩图(图c),最大副弯矩在
20
20
截面B上,最大正弯矩在截面C上,其值
y
分别为:
MB
Fb 2
,
MC Fb 4
弯曲内力(横力弯曲时旳正应力)
由横截面旳尺寸可见,中性轴到上下边沿旳距离分别为:
y2 86mm, y1 134mm
经分析可知,不论是对截面C还是对截面B而言,该梁旳强度
46.2MPa 60MPa
弯曲内力(横力弯曲时旳正应力)
M(kN.m) 2.5 B
C
4 y1
y1
x y2
80
2 0
120
20
y2
y1=52mm
C截面 B截面
Cl
MC y2 IZ
2.5103(120 20 52)103 763(102 )4
28.8MPa
30MPa
弯曲内力(横力弯曲时旳正应力) M(kN.m) 2.5
弯曲内力(纯弯曲)
第五章 弯 曲 应 力
§5.1 纯 弯 曲
05弯曲应力

例题5-1
q=60kN/m
A
1m
FAy
C
l = 3m
120
1.C 截面上K点正应力 2.C 截面上最大正应力
B
x
180
K
30 3.全梁上最大正应力 z 4.已知E=200GPa,
FBy
C 截面的曲率半径ρ y
FS 90kN
M ql 2 / 8 67.5kN m
x 90kN
n
I y
I yi
i 1
n
I z
I zi
i 1
(2)平行移轴公式
以形心为原点,建立与原坐标轴平行 y
x
dyAC
的坐标轴如图
xaxC
yb
yC
y
a
C
xC x
b
I x I xC b2 A SxCAyC 0
I x
y 2dA
A
(
A
yC
b)
2
dA
(
A
yC2
5.832 105
61.7 106 Pa 61.7MPa (压应力)
42
q = 60kN/m
A
1m
FAY
C
l = 3m
FS 90kN
B
x
FBY
x 90kN
180
120
2. C 截面最大正应力
30 C 截面弯矩
K
z
M C 60kN m
y
C 截面惯性矩
IZ 5.832 105 m 4
bh3 12
) /(h0
T05弯曲应力

材料力学习题 第五章 弯曲应力 P166,5-3已知:如图。
AB 段直径D =0.06m ,BE 段外径D =0.06m ,内径d =0.045m 求:σmax 。
解:1. 内力:危险截面C 、B2. 应力:截面C MP a38.63m 10121.232m,.kN 344.1353==⨯===-W M D W M CC σπ截面B MP a09.62m 10450.1)1(32m,.kN 9.03543==⨯=-==-W M D W M BB σαπP168,5-11已知:内力及截面如图。
材料4[σt ]= [σc ]。
求:合理的b 。
解:1. 根据强度条件:最佳的截面设计可以使122121t 4,][][][],[y y y y y I My I Mt t c zc t z ======即σσσσσσ2. 根据截面高可得:32080,4002121===+y y y y ,3. 按照z 轴为形心轴的要求:)(5100506010203016032030021mm b b S S ==⨯+⨯⨯+-⨯⨯=+)(P168,5-12已知:受力及截面如图。
材料 [σt ] =40MPa ,[σc ] =160MPa 。
I z =1.018×10-4m 4,h 1=0.0964m ,h 2=0.1536m 。
求:[F ]。
解:1. 内力:危险截面A 、C ,M A =0.8F ,M B =0.6F2. 应力:截面A 2221116.1328.0][],[80.528.0][],[F kN h I F h I M F kN h I F h I M c z c z A c t z t z A t ==≤≤===≤≤=σσσσσσ截面C 4113226.2816.0][],[18.446.0][],[F kN h I F h I M F kN h I F h I M c z c z C c t z t z C t ==≤≤===≤≤=σσσσσσ3. 结论:34321},,,m in{][F F F F F F ==P168,5-13已知:内力及截面如图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
EIz
ρ
=M
惯性矩
曲率半径 ρ
1
y
dx
1
曲率
ρ
M y σ= Iz 3、静力关系
M
M
中性轴
M ——横截面上的弯矩 横截面上的弯矩 y ——到中性轴的距离 到中性轴的距离
截面对中性轴的惯性矩 Iz ——截面对中性轴的惯性矩
σ
M
m
n
z
y
o
dA
σ
m
dx
n
z
y
M
M y σ= Iz
向下为正的原因) (y 向下为正的原因)
Mmax ymax 横力弯曲最大正应力 σmax = Iz
抗弯截面系数
Iz W= ymax
类比: 类比:扭转
Mmax σmax = W
Tmax τmax = W t
三种典型截面对中性轴的惯性矩 1.矩形截面 1.矩形截面 2.实心圆截面 2.实心圆截面
Wt — 抗扭截面系数 3.截面为外径 、内径d 3.截面为外径D、内径 截面为外径 的空心圆: (α=d/D) 的空心圆:
q = 2 kN m
100
200 200
4m
100
2 qL 8
2 qL M Pa σmax = max = 82 = 6 M bh W 6 横放 2 qL M Pa σmax = max = 82 =12 M hb W 6
竖放
§5-3 横力弯曲时的正应力
弯曲正应力的强度条件 弯曲正应力的强度条件 M max y max σ max = ≤ [σ ] Iz 1.弯矩最大的截面上 1.弯矩最大的截面上 2.离中性轴最远处 2.离中性轴最远处 3.非常规截面或变截面梁要综合考虑 3.非常规截面或变截面梁要综合考虑 M 与 I z 4.脆性材料抗拉和抗压性能不同, 4.脆性材料抗拉和抗压性能不同,二方面都要考虑 脆性材料抗拉和抗压性能不同
[σ ] = 60MPa. 试校核轮轴的强度。 试校核轮轴的强度。
变截面梁
分析( 分析(1) σ max =
M
max
Wz
≤ [σ ]
(2)考察弯矩 M 最大的截面 (3)考察抗弯截面系数 Wz 最小的截面
( 解: 1)计算简图 C A B (2)绘弯矩图 截面, (3)B 截面,C 截面需校核 (4)强度校核 B 截面: 截面:
9kN
4kN
A
1m
B C
1m 1m
D
分析: 非对称截面, 分析: 非对称截面,要确定中性轴位置 中性轴是通过截面形心的直线 作弯矩图,寻找需要校核的截面(可能的危险截面) 作弯矩图,寻找需要校核的截面(可能的危险截面) 要同时满足 σ t ,max ≤ [σ t ] , σ c ,max ≤ [σ c ]
最大应力并不总发生在最大弯矩处 (5)结论:满足强度要求 结论:
§5-3 横力弯曲时的正应力
P146例题5.3 P146例题5.3 例题
[ T 型截面铸铁梁,截面尺寸如图示。σ t ] = 30MPa, [σ c ] = 160MPa, 型截面铸铁梁,截面尺寸如图示。
试校核梁的强度。 试校核梁的强度。 非常规截面梁
y2 ——叠梁2上点对Z2轴(中性轴)的距离
M y 横截面上正应力的画法: σ = Iz
σmin
M
σmin
M
σmax
σmax
公式适用范围: ①线弹性范围—正应力小于比例极限σp; ②精确适用于纯弯曲梁; ③对于横力弯曲的细长梁(跨度与截面高度比L/h>5), 上述公式的误差不大,但公式中的M应为所研究截面 上的弯矩,即为截面位置的函数。
I z1 ——叠梁1截面对Z1轴(中性轴)的惯性矩
I z 2 ——叠梁2截面对Z2轴(中性轴)的惯性矩
由ε= 即
y
ρ
得
σ1 =
σ1 =
E1 y1
ρ
σ2 =
E2 y2
ρ
E1 y1M E1 I z1 + E2 I z 2
σ2 =
E2 y2 M E1 I z1 + E2 I z 2
y1 ——叠梁1上点到Z1轴(中性轴)的距离
Байду номын сангаасx x
=−61.7×106 Pa =−61.7M (压应力) Pa 压应力)
§5-3 横力弯曲时的正应力
q=60kN/m
180 120
2. C 截面最大正应力
30
A
1m
FAy
B C
l = 3m
C 截面弯矩
MC = 60kN⋅ m
x
K
z y
FBy
C 截面惯性矩
FS 90kN
Iz = 5.832×10−5 m4
B C
l = 3m
x
K
3. 全梁最大正应力 30 最大弯矩 z Mmax = 67.5kN⋅ m 截面惯性矩
Iz = 5.832×10−5 m4
FBy
y
FS 90kN
(+)
(−)
x 90kN
Mmax ymax σmax = Iz 180 67.5×103 × ×10−3 2 = 5.832×10−5 =104.17×106 Pa =104.17M Pa
σB =
Fa 62.5 × 267 × 32 = 3 WzB π d1 π × 0.163 32 = 41.5 ×106 Pa = 41.5MPa< [σ ] MB =
Fb Fa C 截面: 截面:
σC =
MC WzC =
Fb 62.5 ×160 × 32 = = 46.4 ×106 Pa = 46.4MPa< [σ ] 3 π d2 π × 0.133 32
σ t , max ≤ [σ t ]
σ c , max ≤ [σ c ]
§5-3 横力弯曲时的正应力
例题1 q=60kN/m
180 120
A
1m
FAy
B C
l = 3m
x
K
FBy
FS 90kN
y 解:1. 求支反力 FAy = 90kN FBy = 90kN
MC = 90×1−60×1×0.5 = 60kN⋅ m
1 MB = − FL 2
bh3 Iz = 12
12
§5-3 横力弯曲时的正应力
横力弯曲:既有弯矩又有剪力。 横力弯曲:既有弯矩又有剪力。
由于切应力的影响,横截面不能再保持为平面。 由于切应力的影响,横截面不能再保持为平面。
§5-3 横力弯曲时的正应力 M y 纯弯曲,F 为零,由 纯弯曲 S为零 由 纯弯曲正应力分布 σ = dM/dx=FS=0, Iz
M
ql 2 / 8 = 67.5kN⋅ m
(+)
x
EIz 200×109 ×5.832×10−5 = ρC = 60×103 MC =194.4m
§5-3 横力弯曲时的正应力
例题2
图示为火车轮轴的简图。 图示为火车轮轴的简图。已知 d1 =160mm, d2 =130mm, a = 0.267m, b = 0.16m, F = 62.5kN, 材料的许用应力为
第五章 弯曲应力
第五章
§5-1 纯弯曲
弯曲应力
§5-2 纯弯曲时的正应力 §5-3 横力弯曲时的正应力 §5-4 弯曲切应力 §5-5 *关于弯曲理论的基本假设 §5-6 提高弯曲强度的措施
回顾与比较 拉伸、 拉伸、压缩
§5-1 纯弯曲
内力 应力
F σ= A
扭转
Tρ τ= Ip
M
弯曲
FAy
FS
σ =? τ =?
将梁的轴线取为 x 轴,
O
z
向下为正) 横截面的对称轴取为 y 轴,(向下为正 向下为正 中性轴取为 z 轴。 y z z
O O
x
y
x
y
§5-2 纯弯曲时的正应力
1、变形几何关系 、 2、物理关系 、 3、静力关系 、
综合考虑
F
m
n
F
(ρ + y)dθ − ρdθ y ε= = ρdθ ρ
m
n
中性轴
1、变形几何关系 y σ = Eε = E
M
M
ρ
m
n
z
y
o
dA
σ
E 2、物理关系 σ FN =∫A dA = ∫ ydA = 0 ρ A
o
静矩
m
dx
n
z
Miy =∫ zσdA =
A
A
E
∫ zydA= 0 ρ
A
惯性积
y
ρ dθ
Miz =∫ yσdA =
M = 曲率 ρ EIz
抗弯刚度
E
ρ∫
A
y dA =
Fa
横力弯曲:既有弯矩又有 剪力。如AC段和DB段 纯弯曲:只有弯矩,没有 剪力。如CD段
F
F
横向线
m n
F 纵向线
实验现象: 实验现象:
1、变形前互相平行的纵向 直线、变形后变成弧线,且 凹边纤维缩短、凸边纤维伸 长。 2、变形前垂直于纵向线的 横向线,变形后仍为直线, 且仍与弯曲了的纵向线正交, 但两条横向线间相对转动了 一个角度。
m
n
平面假设: 平面假设:
变形前原本为平面的横截面变形后仍保持为平面。 变形前原本为平面的横截面变形后仍保持为平面。且 仍垂直于变形后的轴线, 仍垂直于变形后的轴线,只是横截面绕某一轴旋转了 一个角度。 一个角度。
中性层:梁内一层纤维既不伸长也不缩短, 中性层:梁内一层纤维既不伸长也不缩短,因而纤维不 受拉应力和压应力,此层纤维称为中性层。(阴影) 受拉应力和压应力,此层纤维称为中性层。(阴影) 。(阴影 中性轴:中性层与横截面的交线称为中性轴。 中性轴:中性层与横截面的交线称为中性轴。 中性轴与纵向对称面垂直。 中性轴与纵向对称面垂直。
