初三数学期末复习二(图形与证明)
图形与证明(二)复习(1)练习2

DCBAD九年级数学 作业 姓名1、如图,设M ,N 分别是直角梯形ABCD 两腰AD ,CB 的中点,DE 上AB 于点E ,将△ADE 沿DE 翻折,M 与N 恰好重合,则AE :BE 等于( ) A .2:1 B .1:2 C .3:2 D .2:32、小宇同学在一次手工制作活动中,先把一张矩形纸片按图1的方式进行折叠,使折痕的左侧部分比右侧部分短1cm ;展开后按图2的方式再折叠一次,使第二次折痕的左侧部分比右侧部分长1cm ,再展开后,在纸上形成的两条折痕之间的距离是( )A .0.5cmB .1cmC .1.5cmD .2cm3、如图,若将四根木条钉成的矩形木框变为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于 。
4、矩形ABCD 中,22=AB ,将角D 与角C 分别沿过A 和B 的直线AE 、BF 向内折叠,使点D 、C 重合于点G ,且AGB EGF ∠=∠,则=AD .5、已知平行四边形A B C D ,AD a AB b ABC α===,,∠.点F 为线段B C 上一点(端点B C ,除外),连结A F A C ,,连结D F ,并延长D F 交A B 的延长线于点E ,连结C E .(1)当F 为B C 的中点时,求证E F C △与A B F △的面积相等;(2)当F 为B C 上任意一点时,E F C △与A B F △的面积还相等吗?说明理由.左右左右第二次折叠 第一次折叠图1图26、在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD 分割成四个部分,使含有一组对顶角的两个图形全等; (1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有 组;(2)请在图中的三个平行四边形中画出满足小强分割方法的直线; (3)由上述实验操作过程,你发现所画的两条直线有什么规律?7、如图:把一个矩形如图折叠,使顶点B 和D 重合,折痕为EF 。
图形与证明(二)复习(1)练习1

BC九年级数学 作业1、已知:菱形ABCD 中,对角线AC = 16 cm ,BE ⊥BC 于点E ,则BE 的长.为 。
2、直角梯形的一条对角线把梯形分成两个三角形, 其中一个是边长为4的等边三角形,那么梯形的中位线长为 。
3、如图,一张矩形纸片,要折叠出一个最大的正方形,小明把矩 形的一个角沿折痕AE 翻折上去,使AB 和AD 边上的AF 重合,则四边形ABEF 就是一个最大的正方形,他的判定方法是 。
4、下列图形:线段、正三角形、平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形,其中既是中心对称图形,又是轴对称图形的共有 ( )(A )3个 (B )4个 (C )5个 (D ) 6个5、如图,△ABP 与△CDP 是两个全等的等边三角形,且PA ⊥PD.有下列四个结论:①∠PBC =15°;②AD ∥BC ;③直线PC 与AB 垂直;④四边形ABCD 是轴对称图形.其中正确的结论的个数为 ( )(A )1个 (B )2个 (C )3个 (D )4个6、如图,在梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD ,且AC=12,BD=9, 则该梯形两腰中点的连线EF 长是( ) A 、10 B 、221 C 、215 D 、127、如图,等腰梯形ABCD 中,AD ∥BC ,∠DBC=45º。
翻折梯形ABCD ,使点B 重合于点D ,折痕分别交边AB 、BC 于点F 、E 。
若AD=2,BC=8, 求:(1)BE 的长。
(2)CD :DE 的值。
CFBEADCB ADPDBCAEF CDBA EF8、如图是规格为8×8的正方形网格,请在所给网格中......按下列要求操作:⑴请在网格中建立平面直角坐标系, 使A点坐标为(-2,4),B点坐标为(-4,2);⑵在第二象限内的格点上..........画一点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是,△ABC的周长是(结果保留根号);⑶画出△ABC以点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.△与R t ABD△中,90=,,ABC BAD∠=∠= ,AD BC AC BD 相交于点G,过点A作AE D B∥交D A的∥交C B的延长线于点E,过点B作B F C A延长线于点F AE BF,,相交于点H.(1)图中有若干对三角形是全等的,请你任选一对进行证明;(不添加任何辅助线)(2)证明四边形A H B G是菱形;(3)若使四边形A H B G是正方形,还需在R t ABC△的边长之间再添加一个什么条件?请你写出这个条件.(不必证明)EF。
图形与证明(二)小结与思考

第一章 图形与证明单元测试【知识回顾】【基础训练】1.梯形的中位线长为3,高为2,则该梯形的面积为 。
2.若等腰三角形的一个外角为70°,则它的底角为 度。
3.某等腰三角形的两条边长分别为3cm 和6cm ,则它的周长为A .9cmB .12cmC .15cmD .12cm 或15cm4.已知梯形的上底长为3cm ,中位线长为5cm ,则此梯形下底长为__________cm .2.直角三角形全等的判定:HL 4.等腰梯形的性质和判定 5.中位线 三角形的中位线 梯形的中位线注意:若等边三角形的边长为a ,则:其高为: ,面积为: 。
1.等腰三角形 等边三角形的性质和判定 等腰三角形的性质和判定 线段的垂直平分线的性质和判定 角的平分线的性质和判定3.平行四边形 平行四边形的性质和判定:4个判定定理 矩形的性质和判定:3个判定定理 菱形的性质和判定:3个判定定理 正方形的性质和判定:2个判定定理注注意:(1)中点四边形①顺次连接任意四边形各边中点,所得的新四边形是 ; ②顺次连接对角线相等的四边形各边中点,所得的新四边形是 ; ③顺次连接对角线互相垂直的四边形各边中点,所得的新四边形是 ; ④顺次连接对角线互相垂直且相等的四边形各边中点,所得的新四边形是 。
(2)菱形的面积公式:ab S 21= (b a ,是两条对角线的长)注意:(1)解决梯形问题的基本思路:通过分割和拼接转化成三角形和平行四边形进行解决。
即需要掌握常作的辅助线。
(2)梯形的面积公式:()lh hb a S =+=21(l -中位线长)5.如图,点P 到∠AOB 两边的距离相等,若∠POB =30°,则 ∠AOB =_____度.6.如图,要测量A 、B 两点间距离,在O 点打桩,取OA 的中点 C ,OB 的中点D ,测得CD =30米,则AB =______米. 7.平行四边形ABCD 中,AC ,BD 是两条对角线,如果添加一个条件,即可推出平行四边形ABCD 是矩形,那么这个条件是( ) A .AB=BC B .AC=BD C .AC ⊥BD D .AB ⊥BD 8.(08,扬州)如图,已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A 、当AB=BC 时,它是菱形B 、当AC ⊥BD 时,它是菱形 C 、当∠ABC=900时,它是矩形 D 、当AC=BD 时,它是正方形 9.下列条件中不能确定四边形ABCD 是平行四边形的是( )A.AB=CD ,AD ∥BCB.AB=CD ,AB ∥CDC.AB ∥CD ,AD ∥BCD.AB=CD ,AD=BC10.如图,下列条件之一能使平行四边形ABCD 是菱形的为( )①A C B D ⊥ ②90BAD ∠=③A B B C = ④A C B D =A .①③B .②③C .③④D .①②③11.如图,在四边形ABCD 中,A D ∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD 是矩形,你所添加的条件是( ).(写出一种情况即可) 12.)如图,菱形ABCD 中,对角线AC ,BD 相交于点0,若再补充一个条件能使菱形ABCD 成为正方形,则这个条件是( )(只填一个条件即可).13.(08,临沂)如图,菱形ABCD 中,∠B =60°,AB =2,E 、F 分别是BC 、CD 的中点,连接AE 、EF 、AF ,则△AEF 的周长为A . 32B . 33C . 34D . 3 14.顺次连接等腰梯形四边中点所得四边形是A.菱形B.正方形C.矩形D.等腰梯形ABCD 第10题DBC第11题ADBO第12题第13题15.顺次连结四边形四条边的中点,所得的四边形是菱形,则原四边形一定是 A .平行四边形 B .对角线相等的四边形 C .矩形. D .对角线互相垂直的四边形 16.如图所示,有一张一个角为60拼成的四边形是 ()A .邻边不等的矩形B .等腰梯形C .有一个角是锐角的菱形D .正方形17.某花木场有一块如等腰梯形ABCD 的空地(如图),各边的中点分别是E 、F 、G 、H ,用篱笆围成的四边形EFGH 场地的周长为40cm ,则对角线AC= cm 18.如图,在梯形ABCD 中,AD ∥BC ,AB =CD ,AC ⊥BD ,AD =6,BC =8,则梯形的高为 。
图形与证明(二)期末复习ppt

B
C
19.如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5, AD=6,BC=12.动点P从D点出发沿DC以每秒1个单 位的速度向终点C运动,动点Q从C点出发沿CB以每 秒2个单位的速度向B点运动.两点同时出发,当P点 到达C点时,Q点随之停止运动. (1)梯形ABCD的面积等于 36 ;
3 t 5 3 NC=1+t
5 5 MC = + t 4 4
t 4
H
20.如图,四边形ABCD为矩形,AB=4,AD=3, 动点M、N分别从D、B同时出发, 以1个单位/秒的速度运动,点M沿DA向终点A运动, 点N沿BC向终点C运动。过点N作NP⊥BC,交AC 于点P,连结MP。已知动点运动了x秒。 ⑴请直接写出PN的长;(用含x的代数式表示)
⑵若0秒≤x≤1秒,试求△MPA的面积S与时间x秒 的函数关系式,并求S的最大值。 ⑶若0秒≤x≤3秒,△MPA能否为一个等腰三角形? 若能,试写出所有x的对应值;若不能,试说明理由 D C C D M 3-x M N N H 3-x P x P 5 B A 3x B A
D M P 3-x 5 H x A 6
13 20 H
6.如图,四边形ABCD是边长为9的正方形纸片, 将其沿MN折叠,使点B落在CD边上的B’处, 点A对应点为A’,且B’C=3,则AM的长是 ( B) A.1.5 B.2 C.2.25 D.2.5
9 2 15 2
F
6 3
X=4
9-x
x 7.若梯形的面积为12cm2,高为3cm, 4 则此梯形的中位线长为_________cm.
A
6
D P
4 5
B
12
Q 3
C
(2)当PQ∥AB时,P点离开D点的时间等于 秒; (3)当P、Q、C三点构成直角三角形时,P点离开D点 多少时间?
图形与证明(二)小结与思考(1)

08-09学年度第一学期九年级数学教学案第一章小结与思考(1)学习目标:通过对本章知识的小结与梳理,进一步掌握等腰三角形的性质和判定、直角三角形全等的判定、角平分线的性质定理与判定定理、特殊四边形(平行四边形、矩形、菱形、正方形)的定义、性质和判定;等腰梯形的性质和判定;中位线定理,并会灵活运用.学习重点:性质定理和判定定理的应用 学习难点:性质定理和判定定理的应用 学习过程: 一、基础练习1、等腰三角形的一个底角为030,则顶角的度数是 度.2、等腰三角形的两边长分别为4和9,则第三边长为 .3、 下列命题为真命题的是( )A :三角形的中位线把三角形的面积分成相等的两部分;B :对角线相等且相互平分的四边形是正方形;C :关于某直线对称的两个三角形是全等三角形;D :一组对边平行,另一组对边相等的四边形一定是等腰梯形4、下列命题是假命题的是( )A :四个角相等的四边形是矩形;B :对角线互相平分的四边形是平行四边形;C :四条边相等的四边形是菱形;D :对角线互相垂直且相等的四边形是正方形5、如图在A B C D 中,∠ABC 的平分线交AD 于E ,且AE =2,DE =1,则A B C D 的周长等于 . 6、如图,点D 、E 、F 分别是A B C △三边上的中点.若A B C △的面积为12,则D EF△的面积为 . 二、例题学习1、如图,在等腰R t △ABC 中,∠ACB =90°,D 为BC 的中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF .(1)求证:AD ⊥CF ;(2)连接AF ,试判断△ACF 的形状,并说明理由.(第5题)B A CF ED2、已知;如图.矩形ABCD的对角线AC与BD相交于点O,点O关于直线AD的对称点是E,连结AE、DE.(1)试判断四边形AODE的形状,说明理由; (2)请你连结EB、EC.并证明EB=EC.3、如图,在直角梯形纸片A B C D中,A B D C∥,90A∠= ,C D AD>,将纸片沿过点D的直线折叠,使点A落在边C D上的点E处,折痕为D F.连接E F并展开纸片.(1)求证:四边形AD EF是正方形;(2)取线段A F的中点G,连接E G,如果B G C D=,试说明四边形G B C E是等腰梯形.4、如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.(1)求证:CD∥AB;(2)求证:△BDE≌△ACE;(3)若O为AB中点,求证:OF=12 BE.三、作业:见作业纸。
初三数学图形与证明试题

初三数学图形与证明试题1.若用半径为9,圆心角为的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是().A.1.5B.2C.3D.6【答案】C【解析】等弧长计算,半径为9,圆心角为的弧长=即这个圆锥的底面周长=6,即2r=6,故选C2.赵洲桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙。
如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R=米.【答案】25.【解析】根据垂径定理,得AD=AB=20米.设圆的半径是R,根据勾股定理,得R2=202+(R﹣10)2,解得R=25米.【考点】垂径定理的应用;勾股定理.3.如图,AB是⊙O的直径,AB=8,点M在⊙O上,,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则周长的最小值为()A.4B.5C.6D.7【答案】B.【解析】本题考查的是轴对称﹣最短路径问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合本节所学轴对称变换来解决,多数情况要作点关于某直线的对称点.作N关于AB的对称点N′,连接MN′,NN′,ON′,ON,由两点之间线段最短可知MN′与AB的交点P′即为△PMN周长的最小时的点,根据N是弧MB的中点可知∠A=∠NOB=∠MON=20°,故可得出∠MON′=60°,故△MON′为等边三角形,由此可得出结论.作N关于AB的对称点N′,连接MN′,NN′,ON′,ON.∵N关于AB的对称点N′,∴MN′与AB的交点P′即为△PMN周长的最小时的点,∵N是弧MB的中点,∴∠A=∠NOB=∠MON=20°,∴∠MON′=60°,∴△MON′为等边三角形,∴MN′=OM=4,∴△PMN周长的最小值为4+1=5.故选B.【考点】轴对称-最短路线问题;圆周角定理.4.观光塔是潍坊市的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.【答案】135【解析】根据题意可得:∠BDA=30°,∠DAC =60°,在Rt△ABD中,因为AB=45m,所以AD= m,所以在Rt△ACD中,CD= AD=×=135m.【考点】解直角三角形的应用.5.长、宽分别为a、b的矩形,它的周长为14,面积为10,则a2b+ab2的值为.【答案】70.【解析】应把所给式子进行因式分解,整理为与所给周长和面积相关的式子,代入求值即可.试题解析:∵矩形的长和宽分别为a,b,周长为14,面积为10,∴a+b=7,ab=10,∴a2b+ab2=ab(a+b)=70.【考点】因式分解的应用.6.如图,在▱ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,▱ABCD的周长是在14,则DM等于()A.1B.2C.3D.4【答案】C.【解析】∵BM是∠ABC的平分线,∴∠ABM=∠CBM,∵AB∥CD,∴∠ABM=∠BMC,∴∠BMC=∠CBM,∴BC=MC=2,∵▱ABCD的周长是14,∴BC+CD=7,∴CD=5,则DM=CD﹣MC=3,故选C.【考点】平行四边形的性质.7.在3×3的方格中,A、B、C、D、E、F分别位于如图所示的小正方形的顶点上,从C、D、E、F四点中任意取一点,以所取得一点及点A、B为顶点画三角形,则所画三角形为等腰三角形的概率是.【答案】.【解析】根据从C、D、E、F四个点中任意取一点,一共有4种可能,只有选取C、F点时,所画三角形是等腰三角形,即可得出答案;试题解析:根据从C、D、E、F四个点中任意取一点,一共有4种可能,只有选取C、D,F点时,所画三角形是等腰三角形,=.故P(所画三角形是等腰三角形)【考点】1.概率公式;2.等腰三角形的判定.8.如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为.【答案】y=-3x+18.【解析】根据从图②可以看出当Q点到B点时的面积为9,求出正方形的边长,再利用三角形的面积公式得出EF所在的直线对应的函数关系式.试题解析:∵点P沿边DA从点D开始向点A以1cm/s的速度移动;点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.∴当Q到达B点,P在AD的中点时,△PAQ的面积最大是9cm2,设正方形的边长为acm,∴×a×a=9,解得a=6,即正方形的边长为6,当Q点在BC上时,AP=6-x,△APQ的高为AB,∴y=(6-x)×6,即y=-3x+18.【考点】动点问题的函数图象.9.(3分)在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为 cm.(结果保留π)【答案】.【解析】如图所示,∵无弹性的丝带从A至C,∴展开后AB=2πcm,BC=3cm,由勾股定理得:AC==cm.故答案为:.【考点】1.平面展开-最短路径问题;2.最值问题.10.(12分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB 于点E ,交CA 的延长线于点F .(1)求证:FE ⊥AB ;(2)当EF=6,时,求DE 的长.【答案】(1)证明见试题解析;(2)9.【解析】(1)连接AD 、OD ,由直径所对的圆周角是直角得出∠ADC=90°,由等腰三角形的性质可得到D 是BC 的中点,从而OD 是△ABC 的中位线,根据切线的性质证明结论;(2)由平行线分线段成比例定理,列出比例式计算得到答案.试题解析:(1)连接AD 、OD ,∵AC 为⊙O 的直径,∴∠ADC=90°,又∵AB=AC ,∴CD=DB ,又CO=AO ,∴OD ∥AB ,∵FD 是⊙O 的切线,∴OD ⊥EF ,∴FE ⊥AB ;(2)∵,∴,∵OD ∥AB ,∴,又EF=6,∴DE=9.【考点】1.切线的性质;2.相似三角形的判定与性质;3.综合题.11. (3分)如图,▱ABCD 的对角线AC 、BD 相交于点O ,EF 、GH 过点O ,且点E 、H 在边AB 上,点G 、F 在边CD 上,向▱ABCD 内部投掷飞镖(每次均落在▱ABCD 内,且落在▱ABCD 内任何一点的机会均等)恰好落在阴影区域的概率为( )A .B .C .D .【答案】C .【解析】∵四边形ABCD 为平行四边形,∴△OEH 和△OFG 关于点O 中心对称,∴S △OEH =S △OFG ,∴S 阴影部分=S △AOB =S 平行四边形ABCD ,∴飞镖(每次均落在▱ABCD 内,且落在▱ABCD 内任何一点的机会均等)恰好落在阴影区域的概率==.故选C . 【考点】1.几何概率;2.平行四边形的性质.12. 如图,以△ABC 的BC 边上一点O 为圆心的圆,经过A ,B 两点,且与BC 边交于点E ,D 为BE 的下半圆弧的中点,连接AD 交BC 于F ,AC=FC .(1)求证:AC是⊙O的切线;(2)已知圆的半径R=5,EF=3,求DF的长.【答案】(1)见解析;(2)【解析】连结OA、OD,如图,根据垂径定理的推理,由D为BE的下半圆弧的中点得到OD⊥BE,则∠D+∠DFO=90°,再由AC=FC得到∠CAF=∠CFA,根据对顶角相等得∠CFA=∠DFO,所以∠CAF=∠DFO,加上∠OAD=∠ODF,则∠OAD+∠CAF=90°,于是根据切线的判定定理即可得到AC是⊙O的切线;由于圆的半径R=5,EF=3,则OF=2,然后在Rt△ODF中利用勾股定理计算DF的长.[来试题解析:(1)证明:连结OA、OD,如图,∵D为BE的下半圆弧的中点,∴OD⊥BE,∴∠D+∠DFO=90°,∵AC=FC,∴∠CAF=∠CFA,∵∠CFA=∠DFO,∴∠CAF=∠DFO,而OA=OD,∴∠OAD=∠ODF,∴∠OAD+∠CAF=90°,即∠OAC=90°,∴OA⊥AC,∴AC是⊙O的切线;(2)解:∵圆的半径R=5,EF=3,∴OF=2,在Rt△ODF中,∵OD=5,OF=2,∴DF=.【考点】切线的判定13.(3分)如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于()A.122°B.151°C.116°D.97°【答案】B.【解析】∵AB∥CD,∠1=58°,∴∠EFD=∠1=58°,∵FG平分∠EFD,∴∠GFD=∠EFD=×58°=29°,∵AB∥CD,∴∠FGB=180°﹣∠GFD=151°.故选B.【考点】平行线的性质.14.(3分)如图是一个正方体的平面展开图,折叠成正方体后与“建”字所在面相对的面的字是()A.创B.教C.强D.市【答案】C.【解析】∵正方体的表面展开图,相对的面之间一定相隔一个正方形,∴“建”与“强”是相对面.故选C.【考点】专题:正方体相对两个面上的文字.15.在面积为60的▱ABCD中,过点A作AE⊥直线BC于点E,作AF⊥直线CD于点F,若AB=10,BC=12,则CE+CF的值为()A.22+11B.22-11C.22+11或22-11D.22+11或2+【答案】D.【解析】分两种情况:①由平行四边形ABCD的面积求出AE=5,AF=6,再根据勾股定理求出BE、DF,求出CE、CF,即可得出结果;②CE=10-5,CF=6-10,即可得出结果.试题解析:分两种情况:①如图1所示:∠A为锐角时;∵平行四边形ABCD的面积=BC•AE=AB•AF=60,AB=10,BC=12,∴AE=5,AF=6,∵AE⊥直线BC于点E,作AF⊥直线CD于F,∴∠AEB=∠AFD=90°,∴BE=,DF=,∴CE=12+5,CF=10+6∴CE+CF=22+11;②如图2所示:∠A为钝角时;由①得:CE=10-5,CF=6-10,∴CE+CF=2+;故选D.【考点】平行四边形的性质.16.如图,在▱ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.(1)求证:AD=CE;(2)判断直线BC与⊙O的位置关系,并说明理由;(3)若BC=3,DE=6,求BE的长.【答案】(1)证明见解析;(2)直线BC与⊙O相切,理由见解析;(3).【解析】(1)由平行四边形的性质得出∠AED=∠EDC,证出,即可得出AD=CE;(2)作直径CF,连接EF,则∠EFC=∠EDC,证出∠EFC=∠BCE,再由CF是⊙O的直径,得出∠FEC=90°,得出∠BCF=90°,即可得出结论;(3)证明△BCE∽△EDC,得出对应边成比例,即可得出结果.试题解析:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠AED=∠EDC.∴,∴AD=CE;(2)解:直线BC与⊙O相切,理由如下:如图所示:作直径CF,连接EF.则∠EFC=∠EDC,∵∠BCE=∠CDE,∴∠EFC=∠BCE.∵CF是⊙O的直径,∴∠FEC=90°,∴∠EFC+∠FCE=90°,∴∠BCE+∠FCE=90°∴∠BCF=90°.∴OC⊥CB.∴直线BC与⊙O相切;(3)解:∵四边形ABCD是平行四边形,∴AD=BC,AB∥CD,由(1)得:AD=CE,∴BC=CE,∵AB∥CD,∴∠BEC=∠DCE.又∵∠BCE=∠CDE,∴△BCE∽△EDC,∴,∵BC=3∴CE=3,即,解得,BE=.【考点】1.切线的判定;2.平行四边形的性质;3.相似三角形的判定与性质.17.(3分)如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=()A.150°B.160°C.130°D.60°【答案】A.【解析】∵AB∥ED,∴∠E=180°﹣∠EAB=180°﹣120°=60°,∵AD=AE,∴△ADE是等边三角形,∴∠EAD=60°,∴∠BAD=∠EAB﹣∠DAE=120°﹣60°=60°,∵AB=AC=AD,∴∠B=∠ACB,∠ACD=∠ADC,在四边形ABCD中,∠BCD=(360°﹣∠BAD)=(360°﹣60°)=150°.故选A.【考点】1.等腰三角形的性质;2.平行线的性质;3.多边形内角与外角.18.如图,在Rt△ABC中,∠C=90°,现将△ABC进行翻折,点C恰落在边AB上的点D处,折痕为EF,此时恰有∠DEF=∠A,则AD与BD的大小关系是 .【答案】AD=BD【解析】如图,连接CD由题意得:∠EDF=∠ECF,∴∠EDF+∠ECF=180°,∴D、E、C、F四点共圆,∴∠DEF=∠DCF;而∠DEF=∠A,∴∠DCF=∠A(设为α),DA=DC;∵∠B+α=∠BCD+α=90°,∴∠B=∠BCD,∴DB=DC,DA=DB,【考点】翻折变换(折叠问题).19.如图,PA、PB与⊙O相切,切点分别为A、B,PA=3,∠P=60°,若BC为⊙O的直径,则图中阴影部分的面积为.【答案】π.【解析】如图,连接OP,∵PA、PB与⊙O相切,∴PA=PB,∠PAO=∠PBO=90°∵∠BPA=60°,∴△PAB为等边三角形,∠AOB=120°∴PB=AB=PA=3,∠POB=60°∴OB=.∵OB=OC,∴S△AOB =S△AOC∴S阴影=S扇形OAB==π.【考点】1.切线的性质;2.扇形面积的计算.20.如图,直线a∥b,AB⊥BC,∠1=40°,则∠2的度数为()A.30°B.40°C.50°D.60°【答案】C【解析】先根据平行线的性质求出∠ACB的度数,再由垂直的定义得出∠ABC的度数,根据三角形内角和定理即可得出结论.∵直线a∥b,∠1=40°,∴∠ACB=∠1=40°.∵AB⊥BC,∴∠ABC=90°,∴∠2=90°﹣∠ACB=90°﹣40°=50°.【考点】平行线的性质21.海中两个灯塔A、B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这时测得灯塔A在北偏西60°方向上,求灯塔A、B间的距离.(计算结果用根号表示,不取近似值)【答案】【解析】过点A作AF⊥CD,垂足为F,过点D作DE⊥CD,可得出∠FCA=∠ACN=45°,∠NCB=30°,∠ADE=60°,则∠FAD=60°,∠FAC=∠FCA=45°,∠ADF=30°,从而AF=FC=AN=NC,设AF=FC=x,则tan30°=,解得x=,由tan30°=,得到,解得:BN=,由AB=AN+BN,即可得出结论.试题解析:过点A作AF⊥CD,垂足为F,过点D作DE⊥CD,如图所示:由题意可得出:∠FCA=∠ACN=45°,∠NCB=30°,∠ADE=60°,则∠FAD=60°,∠FAC=∠FCA=45°,∠ADF=30°,∴AF=FC=AN=NC,设AF=FC=x,∴tan30°=,解得:x=,∵tan30°=,∴,解得:BN=,∴AB=AN+BN==.答:灯塔A、B间的距离为()海里.【考点】1.解直角三角形的应用-方向角问题;2.几何图形问题.22.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是 . 【答案】.【解析】如图,连接BD .∵四边形ABCD 是菱形,∠A=60°, ∴∠ADC=120°, ∴∠1=∠2=60°, ∴△DAB 是等边三角形, ∵AB=2, ∴△ABD 的高为,∵扇形BEF 的半径为2,圆心角为60°, ∴∠4+∠5=60°,∠3+∠5=60°, ∴∠3=∠4,设AD 、BE 相交于点G ,设BF 、DC 相交于点H ,在△ABG 和△DBH 中,,∴△ABG ≌△DBH (ASA ), ∴四边形GBHD 的面积等于△ABD 的面积,∴图中阴影部分的面积是:S 扇形EBF -S △ABD =.【考点】1.扇形面积的计算;2.全等三角形的判定与性质;3.菱形的性质.23. 一个矩形被分成不同的4个三角形,其中绿色三角形的面积占矩形面积的15%,黄色的三角形的面积是21cm 2,则该矩形的面积为( )A .60cm 2B .70cm 2C .120cm 2D .140cm 2【答案】A .【解析】黄色三角形与绿色三角形面积之和是矩形面积的50%,而绿色三角形面积占矩形面积的15%,所以黄色三角形面积占矩形面积的(50%-15%)=35%,已知黄色三角形面积是21平方厘米,故矩形的面积=21÷(50%-15%)=21÷35%=60(cm 2).故选A .【考点】矩形的性质.24. 如图,以Rt △ABC 的边AC 为直径的⊙O 交斜边AB 于点D ,点F 为BC 上一点,AF 交⊙O于点E,且DE∥AC.(1)求证:∠CAF=∠B.(2)若⊙O的半径为4,AE=2AD,求DE的长.【答案】【解析】(1)连接CE,根据圆周角定理可知∠AEC=90°,故∠CAF+∠ACE=90°.再由题意可知∠B+∠DAC=90°,根据DE∥AC,可得,故,由圆周角定理可知∠ACE=∠DAC,故可得出结论;(2)连接DC,由(1)知DE∥AC,故可得出AD=CE,由全等三角形的判定定理得出Rt△ACD≌Rt△CAE,所以CD=AE=2AD,设AD=x,则CD=2x,在Rt△ABD中根据勾股定理可求出AD,CD的长,过D作DM⊥AC,过O作ON⊥ED,由AD•CD=AC•DM可得出DM的长,连OD,在Rt△OND中,由勾股定理可求出DN的长,由ED=2DN即可得出结论.试题解析:(1)证明:连接CE,∵AC是⊙O的直径,∴∠AEC=90°,∴∠CAF+∠ACE=90°.∵∠ACB=90°,∴∠B+∠DAC=90°,∵DE∥AC,∴,∴,∴∠ACE=∠DAC,∴∠CAF=∠B;(2)解:连DC,∵DE∥AB,∴∠CAE=∠AED,∴AD=DE,在Rt△ACD与Rt△CAE中,∵,∴Rt△ACD≌Rt△CAE(HL),∴CD=AE=2AD,设AD=x,则CD=2x,在Rt△ACD中,x2+(2x)2=82,∴AD=,CD=.过D作DM⊥AC,过O作ON⊥ED,∴AD•CD=AC•DM,∴DM====ON,连OD,在Rt△OND中,∵DN===∴ED=2DN=.【考点】圆周角定理;勾股定理25.一个正方体的平面展开图如图所示,将它折成正方体后“设”字对面是()A.和B.谐C.泰D.州【答案】B.【解析】已知,这是一个正方体的平面展开图,共有六个面,其中面“建”与面“州”相对,面“和”与面“泰”相对,“谐”与面“设”相对.故答案选B.【考点】正方体的侧面展开图.26.如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内上一点,∠BMO=120°,则⊙C的半径长为()A.6B.5C.3D.3【答案】C.【解析】∵四边形ABMO是圆内接四边形,∠BMO=120°,∴∠BAO=60°,∵AB是⊙C的直径,∴∠AOB=90°,∴∠ABO=90°-∠BAO=90°-60°=30°,∵点A的坐标为(0,3),∴OA=3,∴AB=2OA=6,∴⊙C的半径长==3.故选:C.【考点】1.圆内接四边形的性质;2.坐标与图形性质;3.含30度角的直角三角形.27.如图,四边形OBCD中的三个顶点在⊙O上,点A是优弧BD上的一个动点(不与点B、D 重合).(1)当圆心O在∠BAD内部,∠ABO+∠ADO=60°时,∠BOD= ;(2)当圆心O在∠BAD内部,四边形OBCD为平行四边形时,求∠A的度数;(3)当圆心O在∠BAD外部,四边形OBCD为平行四边形时,请直接写出∠ABO与∠ADO的数量关系.【答案】(1)120 °;(2)60°;(3)60°.【解析】(1)连接OA,如图1,根据等腰三角形的性质得∠OAB=∠ABO,∠OAD=∠ADO,则∠OAB+∠OAD=∠ABO+∠ADO=60°,然后根据圆周角定理易得∠BOD=2∠BAD=120°;(2)根据平行四边形的性质得∠BOD=∠BCD,再根据圆周角定理得∠BOD=2∠A,则∠BCD=2∠A,然后根据圆内接四边形的性质由∠BCD+∠A=180°,易计算出∠A的度数;(3)讨论:当∠OAB比∠ODA小时,如图2,与(1)一样∠OAB=∠ABO,∠OAD=∠ADO,则∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,由(2)得∠BAD=60°,所以∠ADO﹣∠ABO=60°;当∠OAB比∠ODA大时,用样方法得到∠ABO﹣∠ADO=60°.试题解析:(1)连接OA,如图1,∵OA=OB,OA=OD,∵∠OAB=∠ABO,∠OAD=∠ADO,∴∠OAB+∠OAD=∠ABO+∠ADO=60°,即∠BAD=60°,∴∠BOD=2∠BAD=120°;(2)∵四边形OBCD为平行四边形,∴∠BOD=∠BCD,∵∠BOD=2∠A,∴∠BCD=2∠A,∵∠BCD+∠A=180°,即3∠A=180°,∴∠A=60°;(3)当∠OAB比∠ODA小时,如图2,∵OA=OB,OA=OD,∵∠OAB=∠ABO,∠OAD=∠ADO,∴∠OAD﹣∠OAB=∠ADO﹣∠ABO=∠BAD,由(2)得∠BAD=60°,∴∠ADO﹣∠ABO=60°;当∠OAB比∠ODA大时,同理可得∠ABO﹣∠ADO=60°,综上所述,|∠ABO﹣∠ADO|=60°.【考点】1.圆周角定理;2.平行四边形的性质;3.圆内接四边形的性质.28.如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于 °.【答案】130【解析】∵四边形ABCD内接与⊙O,∴∠A+∠C=180°,∵∠A=115°,∴∠C=65°,∴∠BOD=2∠C=130°;【考点】1.圆内接四边形的性质;2.圆周角定理.29.如图,将半径为8的⊙O沿AB折叠,弧AB恰好经过与AB垂直的半径OC的中点D,则折痕AB长为()A.B.C.8D.10【答案】B.【解析】延长CO交AB于E点,连接OB,∵CE⊥AB,∴E为AB的中点,由题意可得CD=4,OD=4,OB=8,DE=(8×2﹣4)=×12=6,OE=6﹣4=2,在Rt△OEB中,根据勾股定理可得:OE2+BE2=OB2,代入可求得BE=,∴AB=.故选B.【考点】1.垂径定理;2.翻折变换(折叠问题).30.有一边长为4的正n边形,它的一个内角为120°,则其外接圆的半径为()A.B.4C.D.2【答案】B【解析】经过正n边形的中心O作边AB的垂线OC,则∠B=60°,∠O=30°,在直角△OBC中,根据三角函数得到OB=2BC=AB=4.点评:正多边形的计算31.如图,AC是△ABD的高,∠D=45°,∠B=60°,AD=10.求AB的长.【答案】【解析】首先根据Rt△ACD的三角函数求出AC的长度,然后根据Rt△ABC的三角形函数求出AB的长度.试题解析:在Rt△ACD中,AC=10×sin∠D=10×sin45°=5在Rt△ABC中,AB=.【考点】锐角三角函数的应用.32.如图,矩形ABCD中,AB=2,BC=3,分别以A、D为圆心,1为半径画圆,E、F分别是⊙A、⊙D上的一动点,P是BC上的一动点,则PE+PF的最小值是()A.2 B.3 C.4 D.5【答案】C.【解析】试题解析:∵矩形ABCD中,AB=2,BC=3,圆A的半径为1,∴A′D′=BC=3,DD′=2DC=4,AE′=1,∴A′D=5,∴DE′=5-1=4∴PE+PD=PE′+PD=DE′=4,故选C.【考点】轴对称-最短路线问题.33.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AB=3,则AD的值为()A.6B.3C.3D.3【答案】D【解析】根据AB=AC以及∠BAC=120°可得:∠D=30°,根据BD为直径可得:∠BAD=90°,则根据Rt△ABD的性质可得:BD=2AB=6,AD=3【考点】圆的基本性质34.已知圆锥的底面半径长为5,侧面展开后得到一个半圆,则该圆锥的母线长为()A.2.5B.5C.10D.15【解析】试题解析:设母线长为x,根据题意得2πx÷2=2π×5,解得x=10.故选C.【考点】圆锥的计算.35.如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为()A.160m B.80mC.120(-1)m D.120(+1)m【答案】A【解析】过点A作AD⊥BC,则CD=120m,BD=40m,则BC=CD+BD=160m.【考点】三角形函数的应用.36.如图,晚上小明站在路灯P的底下观察自己的影子时发现,当他站在F点的位置时,在地面上的影子为BF,小明向前走2米到D点时,在地面上的影子为AD,若AB=4米,∠PBF=60°,∠PAB=30°,通过计算,求出小明的身高.(结果保留根号).【答案】米【解析】设CD=EF=x,根据Rt△CAD,求出AD与x的关系,根据Rt△BEF,求出BF与x的关系,然后根据BD=DF-BF=2-BF,AB=AD+BD=4求出x的值.试题解析:设小明的身高为x米,则CD=EF=x米.在Rt△ACD中,∠ADC=90°,tan∠CAD=,即tan30°=,AD=x在Rt△BEF中,∠BFE=90°,tan∠EBF=EF/BF,即tan60°=,BF=由题意得DF=2,∴BD=DF-BF=2-,∵AB=AD+BD=4,∴x+2-=4 解得:x=.答:小明的身高为米.【考点】锐角三角函数的应用.37.在Rt△ABC中,∠C=90°,a=4,b=3,则sinA的值是()A.B.C.D.【解析】试题解析:如图所示:∵在Rt△ABC中,∠C=90°,a=4,b=3,∴c=5,∴sinA=.故选B.【考点】1.锐角三角函数的定义;2.勾股定理.38.如图,用一个半径为30cm,面积为300πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为.【答案】10cm.【解析】圆锥的底面周长=扇形的弧长,据此列等式求出r的值.,解得r=10cm.故答案为:10cm.【考点】圆锥的有关计算.39.计算:2sin60°+tan45°= .【答案】.【解析】试题解析:原式=2×+1=.【考点】特殊角的三角函数值.40.(2015•盐城校级模拟)已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为.【答案】3π.【解析】根据弧长公式L=求解.解:L===3π.故答案为:3π.【考点】弧长的计算.41.(2015•徐州)如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA= °.【答案】125.【解析】连接OD,构造直角三角形,利用OA=OD,可求得∠ODA=36°,从而根据∠CDA=∠CDO+∠ODA计算求解.解:连接OD,则∠ODC=90°,∠COD=70°;∵OA=OD,∴∠ODA=∠A=∠COD=35°,∴∠CDA=∠CDO+∠ODA=90°+35°=125°,故答案为:125.【考点】切线的性质.42. (2015秋•芜湖期末)若一个圆锥的侧面展开图是半径为18cm ,圆心角为240°的扇形,则这个圆锥的底面半径长是 cm . 【答案】12【解析】设这个圆锥的底面半径为rcm ,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=,然后解方程求出r 即可.解:设这个圆锥的底面半径为rcm ,根据题意得2πr=,解得r=12,所以这个圆锥的底面半径长为12cm . 故答案为12.【考点】圆锥的计算.43. 如图,菱形ABCD 的对角线的长分别为2和5,P 是对角线AC 上任一点(点P 不与点A 、C 重合),且PE ∥BC 交AB 于E ,PF ∥CD 交AD 于F ,则阴影部分的面积是 .【答案】2.5【解析】根据题意可得阴影部分的面积等于△ABC 的面积,因为△ABC 的面积是菱形面积的一半,根据已知可求得菱形的面积则不难求得阴影部分的面积. 解:设AP 与EF 相交于O 点. ∵四边形ABCD 为菱形, ∴BC ∥AD ,AB ∥CD . ∵PE ∥BC ,PF ∥CD , ∴PE ∥AF ,PF ∥AE .∴四边形AEFP 是平行四边形. ∴S △POF =S △AOE .即阴影部分的面积等于△ABC 的面积.∵△ABC 的面积等于菱形ABCD 的面积的一半, 菱形ABCD 的面积=AC•BD=5, ∴图中阴影部分的面积为5÷2=2.5. 故答案为:2.5.【考点】菱形的性质.44. 如图1,是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m ,木板超出车厢部分AD=0.5m ,则木板CD 的长度为 .(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m).【答案】4.9m.【解析】根据∠ACB的正弦函数和AB的长度求AC的长,再加上AD即可.解:由题意可知:AB⊥BC.∴在Rt△ABC中,sin∠ACB=,∴AC===≈4.39,∴CD=AC+AD=4.39+0.5=4.89≈4.9(m).故答案为:4.9m.【考点】解直角三角形的应用-坡度坡角问题.45.如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为_________.【答案】120°【解析】根据中点可得DE∥BC,则∠DEC+∠C=180°,根据∠C=60°,可得∠DEC=120°.【考点】三角形中位线的性质.46.如图,AB为⊙O直径,弦CD⊥AB于E,则下面结论中错误的是()A.CE=DE B.=C.∠BAC=∠BAD D.OE=BE【答案】D【解析】根据垂径定理分析即可.根据垂径定理和等弧对等弦,得A、B、C正确,只有D错误.故选D.【考点】垂径定理.47.圆内接四边形ABCD的内角∠A:∠B:∠C=2:3:4,则∠D= 度.【答案】90【解析】根据圆内接四边形的性质可求得四个角的比值,再根据四边形的内角和为360°,从而求得∠D的度数.解:∵圆内接四边形的对角互补∴∠A:∠B:∠C:∠D=2:3:4:3设∠A=2x,则∠B=3x,∠C=4x,∠D=3x∴2x+3x+4x+3x=360°∴x=30°∴∠D=90°.【考点】圆内接四边形的性质.48.如图所示,动点C在⊙O的弦AB上运动,AB=,连接OC,CD⊥OC交⊙O于点D.则CD的最大值为.【答案】.【解析】作OH⊥AB,延长DC交⊙O于E,如图,根据垂径定理得到AH=BH=AB=,CD=CE,再利用相交弦定理得CD•CE=BC•AC,易得CD=,当CH最小时,CD最大,C点运动到H点时,CH最小,所以CD的最大值为.解:作OH⊥AB,延长DC交⊙O于E,如图,∴AH=BH=AB=,∵CD⊥OC,∴CD=CE,∵CD•CE=BC•AC,∴CD2=(BH﹣CH)(AH+CH)=(﹣CH)(+CH)=3﹣CH2,∴CD=,∴当CH最小时,CD最大,而C点运动到H点时,CH最小,此时CD=,即CD的最大值为.故答案为.【考点】垂径定理;勾股定理.49.在△ABC中,∠A,∠B都是锐角,且(sinA﹣)2+(tanB﹣1)2=0,则∠C= .【答案】75°.【解析】根据偶次幂具有非负性可得sinA﹣=0,tanB﹣1=0,再根据特殊角的三角函数值可得:∠A=60°,∠B=45°,然后再利用三角形内角和定理可得答案.解:由题意得:sinA﹣=0,tanB﹣1=0,解得:∠A=60°,∠B=45°,则∠C=180°﹣60°﹣45°=75°,故答案为:75°.【考点】特殊角的三角函数值;非负数的性质:偶次方.50.如图,正六边形ABCDEF的边长为2,两顶点A、B分别在x轴和y轴上运动,则顶点D到原点O 的距离的最大值和最小值的乘积为 . 【答案】12 【解析】当O 、D 、AB 中点共线时,OD 有最大值和最小值,BD=2,BK=1, ∴DK=,OK=BK=1, ∴OD 的最大值为:1+, 同理,把图象沿AB 边翻折180°得最小值为:-1,∴顶点D 到原点O 的距离的最大值和最小值的乘积为:(1+)(-1)=12.【考点】(1)、正多边形和圆;(2)、坐标与图形性质51. 下列四边形中,对角线相等且互相垂直平分的是A .平行四边形B .正方形C .等腰梯形D .矩形【答案】B .【解析】试题解析:对角线相等且互相垂直平分的四边形是正方形,故选B .【考点】1.等腰梯形的性质;2.平行四边形的性质;3.矩形的性质;4.正方形的性质.52. 如图,矩形ABCD 中,AE 平分∠BAD 交BC 于E ,∠CAE=15°,则下列结论:① △ODC 是等边三角形;②BC=2AB ;③∠AOE=135°; ④S △AOE =S △COE ,其中正确的结论的个数有A .1B .2C .3D .4【答案】C【解析】∵四边形ABCD 是矩形,∴∠BAD=90°,OA=OC ,OD=OB ,AC=BD ,<BR>∴OA=OD=OC=OB ,∵AE 平分∠BAD ,∴∠DAE=45°,∵∠CAE=15°,∴∠DAC=30°,∵OA=OD ,∴∠ODA=∠DAC=30°,∴∠DOC=60°,∵OD=OC ,∴△ODC 是等边三角形,∴①正确;∵四边形ABCD 是矩形,∴AD ∥BC ,∠ABC=90°,∴∠DAC=∠ACB=30°,∴AC=2AB ,∵AC >BC ,∴2AB >BC ,∴②错误;∵AD ∥BC ,∴∠DBC=∠ADB=30°,∵AE 平分∠DAB ,∠DAB=90°,∴∠DAE=∠BAE=45°,∵AD ∥BC ,∴∠DAE=∠AEB ,∴∠AEB=∠BAE ,∴AB=BE ,∵四边形ABCD 是矩形,∴∠DOC=60°,DC=AB ,∵△DOC 是等边三角形,∴DC=OD ,∴BE=BO ,∴∠BOE=∠BEO=(180°-∠OBE )=75°,∵∠AOB=∠DOC=60°,∴∠AOE=60°+75°=135°,∴③正确;∵OA=OC ,∴根据等底等高的三角形面积相等得出S △AOE =S △COE ,∴④正确;故选C .【考点】矩形的性质.53.如图,、是以线段为直径的⊙上两点,若,且,则( ).A.B.C.D.【答案】B.【解析】因为∠ACD=40°,CA=CD,所以∠CAD=∠D=(180°-40°)÷2=70°,所以∠B=∠D=70°,又因为AB为直径,所以∠ACB=90°,所以∠CAB=90°-∠B=90°-70°=20°,故选B.【考点】1.圆周角定理;2.弧,弦圆心角定理;3.三角形内角和定理.54.如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°=0.9272,sin46°=0.7193,sin22°=0.3746,sin44°=0.6947)()A.22.48B.41.68C.43.16D.55.63【答案】B【解析】过点P作PA⊥MN于点A,则若该船继续向南航行至离灯塔距离最近的位置为PA的长度,利用锐角三角函数关系进行求解即可,如图,过点P作PA⊥MN于点A,MN=30×2=60(海里),∵∠MNC=90°,∠CPN=46°,∴∠MNP=∠MNC+∠CPN=136°,∵∠BMP=68°,∴∠PMN=90°﹣∠BMP=22°,∴∠MPN=180°﹣∠PMN﹣∠PNM=22°,∴∠PMN=∠MPN,∴MN=PN=60(海里),∵∠CNP=46°,∴∠PNA=44°,∴PA=PN·sin∠PNA=60×0.6947≈41.68(海里)【考点】锐角三角函数的应用55.一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为()A.10海里/小时B.30海里/小时C.20海里/小时D.30海里/小时【答案】D.【解析】试题解析:∵∠CAB=10°+20°=30°,∠CBA=80°-20°=60°,∴∠C=90°,∵AB=20海里,∴AC=AB•cos30°=10(海里),∴救援船航行的速度为:10÷=30(海里/小时).故选D.【考点】解直角三角形的应用-方向角问题.56.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数()A.17°28′B.18°28′C.27°28′D.27°32′【答案】A.【解析】试题解析:过点A作AE∥NM,∵NM∥GH,∴AE∥GH,∴∠3=∠1=42°32′,∵∠BAC=60°,∴∠4=60°-42°32′=17°28′,∵NM∥AE,∴∠2=∠4=17°28′,故选A.【考点】平行线的性质.57.下列命题中,正确的是()A.平分弦的直径垂直于弦B.对角线相等的平行四边形是正方形C.对角线互相垂直的四边形是菱形D.三角形的一条中线能将三角形分成面积相等的两部分【答案】D.【解析】试题解析:A、平分弦(非直径)的直径垂直于弦,所以A选项错误;B、对角线垂直且相等的平行四边形是正方形,所以B选项错误;C、对角线互相垂直平分的四边形是菱形,所以C选项错误;D、三角形的一条中线能将三角形分成面积相等的两部分,所以D选项正确.故选D.【考点】命题与定理.58.如图,将矩形纸片ABCD(AD>AB)折叠,使点C刚好落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.(1)判断四边形CEGF的形状,并证明你的结论;(2)若AB=3,BC=9,求线段CE的取值范围.【答案】(1)四边形CEGF为菱形,理由详见解析;(2)3≤CE≤5.【解析】(1)根据折叠的性质,易证△EFG是等腰三角形,根据等腰三角形的性质可得GF=EC,又由GF∥EC,即可得四边形CEGF为平行四边形,根据邻边相等的平行四边形是菱形,即可得四边形BGEF为菱形;(2)如图1,当G与A重合时,CE取最大值,由折叠的性质得CD=DG,∠CDE=∠GDE=45°,推出四边形CEGD是矩形,根据矩形的性质即可得到CE=CD=AB=3;如图2,当F与D重合时,CE取最小值,由折叠的性质得AE=CE,根据勾股定理即可得到结论.试题解析:(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠GFE=∠FEC,∵图形翻折后点G与点C重合,EF为折线,∴∠GEF=∠FEC,∴∠GFE=∠FEG,∴GF=GE,∵图形翻折后BC与GE完全重合,∴BE=EC,∴GF=EC,∴四边形CEGF为平行四边形,∴四边形CEGF为菱形;(2)解:如图1,当F与D重合时,CE取最小值,由折叠的性质得CD=DG,∠CDE=∠GDE=45°,∵∠ECD=90°,∴∠DEC=45°=∠CDE,∴CE=CD=DG,∵DG∥CE,∴四边形CEGD是矩形,∴CE=CD=AB=3;如图2,当G与A重合时,CE取最大值,由折叠的性质得AE=CE,∵∠B=90°,∴AE2=AB2+BE2,即CE2=32+(9﹣CE)2,∴CE=5,。
九年级证明(二)复习课
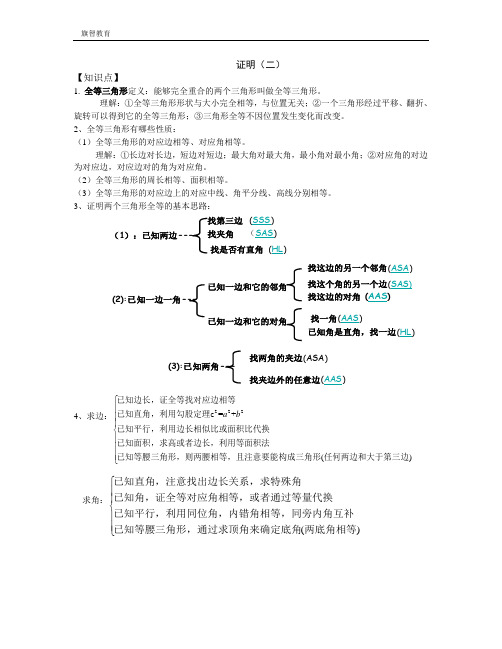
证明(二)【知识点】1. 全等三角形定义:能够完全重合的两个三角形叫做全等三角形。
理解:①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转可以得到它的全等三角形;③三角形全等不因位置发生变化而改变。
2、全等三角形有哪些性质:(1)全等三角形的对应边相等、对应角相等。
(2(334()⎪⎪⎨⎪⎪⎪⎩已知平行,利用边长相似比或面积比代换已知面积,求高或者边长,利用等面积法已知等腰三角形,则两腰相等,且注意要能构成三角形任何两边和大于第三边求角:()⎧⎪⎪⎨⎪⎪⎩已知直角,注意找出边长关系,求特殊角已知角,证全等对应角相等,或者通过等量代换已知平行,利用同位角,内错角相等,同旁内角互补已知等腰三角形,通过求顶角来确定底角两底角相等【知识应用】一、填空题1、一个等腰三角形有一角是70°,则其余两角分别为_________.2、如图1,△ABC 中,∠C =90°,AM 平分∠CAB ,CM =20 cm ,则点M 到AB 的距离是_________.图1图23、如图2,等边△ABC 中,F 是AB 中点,EF ⊥AC 于E ,若△ABC 的边长为10,则AE =_________,AE ∶EC =_________.4、如图3,△ABC 中,DE 垂直平分BC ,垂足为E ,交AB 于D ,若AB =10 cm ,AC =6 cm ,则△ACD 的周长为_________.图3 图45、如图4,∠C =90°,∠ABC =75°,∠CDB =30°,若BC =3 cm ,则AD =_________ cm.6、等腰直角三角形一条边长是1 cm ,那么它斜边上的高是_________ cm.7、等腰三角形两腰上的高相等,这个命题的逆命题是 ,这个逆命题是 命题.8、三角形三边分别是,,a b c 且2-=(-)a bc a b c ,则这个三角形(按边分类)一定是 三角形. 二、选择题1.等边三角形的高为23,则它的边长为( )A.4B.3C.2D.5 2.等腰三角形的顶角是n °,那么它的一腰上的高与底边的夹角等于( )A.290nB.90-2nC.2nD.90°-n °3.下列由线段a 、b 、c 组成的三角形,不是直角三角形的是( )A.a =3,b =4,c =5B.a =1,b =34,c =35C.a =9,b =12,c =15D.a =3,b =2,c =54.直角三角形两直角边分别是5 cm 、12 cm ,其斜边上的高是( )A.13 cmB.1330 cmC.1360 cmD.9 cm5.直角三角形中,以直角边为边长的两个正方形的面积分别为30和20,则以斜边为边长的正方形的面积为( )A.25B.50C.100D.606.等腰三角形ABC 中,∠A =120°,BC 中点为D ,过D 作DE ⊥AB 于E ,AE =4 cm ,则AD 等于( )A.8 cmB.7 cmC.6 cmD.4 cm7.下列说法中,正确的是( )A.两边及一对角对应相等的两个三角形全等B.有一边对应相等的两个等腰三角形全等C.两边及其中一边上的中线对应相等的两个三角形全等D.两边及其中一边上的高对应相等的两个三角形全等8.如图8,AB ⊥CD ,△ABD 、△BCE 都是等腰三角形,如果CD =8,BE =3,那么AC 长为( )图8A.8B.5C.3D.349.将两个全等的有一个角为30°的直角三角形拼成下图9,其中两条长直角边在同一直线上,则图中等腰三角形的个数是( )图9A.4B.3C.2D.110.下列定理中逆定理不存在的是( )A.角平分线上的点到这个角的两边距离相等B.在一个三角形中,如果两边相等,那么它们所对的角也相等C.同位角相等,两直线平行D.全等三角形的对应角相等11..已知一个直角三角形的周长是4+26,斜边上中线长为2,则这个三角形的面积为( )A.5B.2C.45 D.11、如图11,△ABC 中,AB =AC ,∠1=∠2,求证:AD 平分∠BA C.图112、如图所示,在A B C ∆中,12,2.ABC C ∠=∠∠=∠求证:.A B B D A C +=3、已知:如图,A B C ∆和AD E ∆均是等边三角形,点D 是B C 的中点,求证:B E B D =.1、一个等腰三角形的两边长为5和8,则此三角形的周长为_________.2、如图5,B 在AC 上,D 在CE 上,AD =BD =BC ,∠ACE =25°,∠ADE =_________.3.如图6,在∠AOB 的两边OA 、OB 上分别取OQ =OP ,OT =OS ,PT 和QS 相交于点C ,则图中共有_________对全等三角形.图5图6A.6B.7.5C.10D.124.△ABC 中,∠A ∶∠B ∶∠C =1∶2∶3,最小边BC =4 cm ,最长边AB 的长是( )A.5 cmB.6 cmC.5 cmD.8 cm5.如图7,△ABC 中,AB =AC ,BC =BD ,AD =DE =EB ,则∠A 的度数为( )图7A.55°B.45°C.36°D.30° 6.等腰△ABC 中,AC =2BC ,周长为60,则BC 的长为( )A.15B.12C.15或12D.以上都不正确7.等腰三角形的底边为a ,顶角是底角的4倍,则腰上的高是( )A.23a B.33 a C.63aD.21a8..已知:如图12,在Rt △ABC 中,∠C =90°,∠BAD =21∠BAC ,过点D 作DE ⊥AB ,DE 恰好是∠ADB 的平分线,求证:CD =21DB .图12。
初三数学证明二三总复习
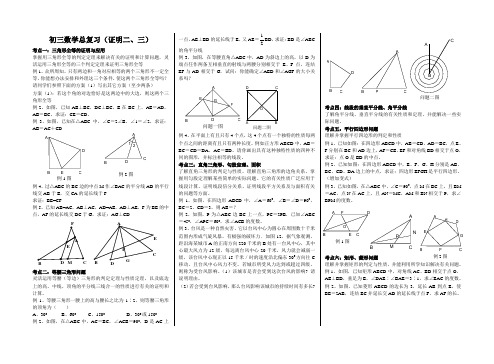
初三数学总复习(证明二、三)考点一:三角形全等的证明与应用掌握用三角形全等的判定定理来解决有关的证明和计算问题,灵活运用三角形全等的三个判定定理来证明三角形全等 例1、众所周知,只有两边和一角对应相等的两个三角形不一定全等,你能想办法安排和外理这三个条件,使这两个三角形全等吗? 请同学们参照下面的方案(1)写出其它方案(至少两条) 方案(1):若这个角的对边恰好是这两边中的大边,则这两个三角形全等例2、如图,已知AB ⊥BC ,DC ⊥BC ,E 在BC 上,AE =AD ,AB =BC 。
求证:CE =CD 。
例3、如图,已知在△ABC 中,∠C =2∠B ,∠1=∠2,求证:AB =AC +CD例4、过△ABC 的BC 边的中点M 作∠BAC 的平分线AD 的平行线交AB 于E ,交CA 的延长线于F 求证:BE=CF例5、已知AB=AC ,AB ⊥AC ,AD=AE ,AD ⊥AE ,F 为BE 的中点,AF 的延长线交DC 于G ,求证:AG ⊥CDABCD ME F ABCDGFE考点二:等腰三角形问题灵活运用等腰(等边)三角形的判定定理与性质定理,以及底边上的高、中线、顶角的平分线三线合一的性质进行有关的证明和计算。
例1、等腰三角形一腰上的高与腰长之比为1∶2,则等腰三角形的顶角为( )A 、300B 、600C 、1500D 、300或1500例2、如图,在△ABC 中,AC =BC ,∠ACB =900,D 是AC 上一点,AE ⊥BD 的延长线于E ,又AE =21BD ,求证:BD 是∠ABC 的角平分线例3、如图,在等腰直角△ABC 中,AD 为斜边上的高,以D 为端点任作两条互相垂直的射线与两腰分别相交于E 、F 点,连结EF 与AD 相交于G ,试问:你能确定∠AED 和∠AGF 的大小关系吗?问题二图ODCBA例4、在平面上有且只有4个点,这4个点有一个独特的性质每两个点之间的距离有且只有两种长度。
9上证明2(复习)

5.已知如图,在△ABC 中,AB=AC,O 是△ABC 内一点,且 OB=OC, 求证:AO⊥BC.
授益教育
6
授益教育 6.如图,在△ABC 中,AB=AC,∠A=120°,AB 的垂直平分线 MN 分别交 BC、AB 于点 M、N. 求证:CM=2BM.
E.课后作业
1. △ABC 中,AB=AC,AC 的中垂线交 AB 于 E, △EBC 的周长为 20cm,AB=2BC,则腰长为________________。 2. 如图所示,AB//CD,O 为∠A、∠C 的平分线的交点,OE⊥AC 于 E,且 OE=2,则 AB 与 CD 之 间的距离等于______________。
两角及其夹边对应相等的两个三角形全等ssssasasa定理三角形全等的判定定理两角及其中一角的对边对应相等的两个三角形全等aas公理三角形全等的性质全等三角形的对应边相等对应角相等定理等腰三角形的性质的推论等腰三角形的两个底角相等等边对等角定理等腰三角形的判定定理等腰三角形顶角的平分线底边上的中线底边上的高互相重合三线合一定理等边三角形的判定定理有一个角等于60的等腰三角形是等边三角定理等边三角形的判定定理三个角都相等的三角形是等边三角形等角对等边定理勾股定理直角三角形两条直角边的平方和等于斜边的平方符号语言
2 3 4 5 6 7 8
定理 公理 定理 定理 定理 定理 定理
三角形全等的判定定理 三角形全等的性质 等腰三角形的性质的推论 等腰三角形的判定定理 等边三角形的判定定理 等边三角形的判定定理 勾股定理
9
概念
互逆定理
10
定理
勾股定理的逆定理
11
定理
直角三角形全等的判定定理
12
定 理
有一个角等于 30°的直角三角形的性 质
初三数学图形与证明试题答案及解析

初三数学图形与证明试题答案及解析1.顺次连接矩形ABCD各边的中点,所得四边形必定是()A.邻边不等的平行四边形B.矩形C.正方形D.菱形【答案】D【解析】如图:E,F,G,H为矩形的中点,则AH=HD=BF=CF,AE=BE=CG=DG,在Rt△AEH与Rt△DGH中,AH=HD,AE=DG,所以△AEH≌△DGH,因此根据全等三角形的性质可得EH=HG,同理,△AEH≌△DGH≌△BEF≌△CGF,因此可得EH=HG=GF=EF,所以四边形EFGH为菱形.故选A【考点】菱形的判定2.如图,某仓储中心有一斜坡AB,其坡度为,顶部A处的高AC为4m,B、C在同一水平地面上。
(1)求斜坡AB的水平宽度BC;(2)矩形DEFG为长方形货柜的侧面图,其中DE=2.5m,EF=2m.将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高。
(,结果精确到0.1m)【答案】(1) 8m.(2) 4.5m.【解析】(1)根据坡度定义直接解答即可;(2)作DS⊥BC,垂足为S,且与AB相交于H.证出∠GDH=∠SBH,根据,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.试题解析:(1)∵坡度为i=1:2,AC=4m,∴BC=4×2=8m.(2)作DS⊥BC,垂足为S,且与AB相交于H.∵∠DGH=∠BSH,∠DHG=∠BHS,∴∠GDH=∠SBH,∵DG=EF=2m,∴GH=1m,∴DH=m,BH=BF+FH=3.5+(2.5-1)=5m,设HS=xm,则BS=2xm,∴x2+(2x)2=52,∴x=m,∴DS=+=2m≈4.5m.【考点】解直角三角形的应用-坡度坡角问题.3.如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是()A.AF=AE B.△ABE≌△AGF C.EF=D.AF=EF【答案】D.【解析】∵AD∥BC,∴∠AFE=∠FEC,∵∠AEF=∠FEC,∴∠AFE=∠AEF,∴AF=AE,∴选项A正确;∵ABCD是矩形,∴AB=CD,∠B=∠C=90°,∵AG=DC,∠G=∠C,∴∠B=∠G=90°,AB=AG,∵AE=AF,∴△ABE≌△AGF,∴选项B正确;设BE=x,则CE=BC﹣BE=8﹣x,∵沿EF翻折后点C与点A重合,∴AE=CE=8﹣x,在Rt△ABE中,,即,解得x=3,∴AE=8﹣3=5,由翻折的性质得,∠AEF=∠CEF,∵矩形ABCD的对边AD∥BC,∴∠AFE=∠CEF,∴∠AEF=∠AFE,∴AE=AF=5,过点E作EH⊥AD于H,则四边形ABEH是矩形,∴EH=AB=4,AH=BE=3,∴FH=AF﹣AH=5﹣3=2,在Rt△EFH中,EF=,∴选项C正确;由已知条件无法确定AF和EF的关系,故选D.【考点】翻折变换(折叠问题).4.(7分)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连接CE,DF.(1)求证:四边形CEDF是平行四边形;(2)①当AE= cm时,四边形CEDF是矩形;②当AE= cm时,四边形CEDF是菱形;(直接写出答案,不需要说明理由)【答案】(1)证明见解析;(2)①当AE=3.5cm时,四边形CEDF是矩形.②当AE=2cm时,四边形CEDF是菱形.【解析】(1)利用“ASA”即可得证;①当四边形CEDF是矩形时,则有EG=DG=1.5cm,又由已知可得∠ADC=60°,从而得△EGD为等边三角形,从而得DE=1.5cm,从而得AE=3.5cm;②.当四边形CEDF是菱形时,则有EF⊥CD,由已知可知∠ADC=60°,从而可得∠DEG=30°,从而得DE=2DG=3,从而得AE=2.试题解析:(1)∵四边形ABCD是平行四边形,∴ CF∥ED,∴∠FCG=∠EDG,∵ G是CD的中点,∴ CG=DG,在△FCG和△EDG中,,∴△FCG ≌△EDG(ASA),∴ FG=EG,∵ CG=DG,∴四边形CEDF是平行四边形;(2)①当AE=3.5cm时,四边形CEDF是矩形.②当AE=2cm时,四边形CEDF是菱形.【考点】1.平行四边形的性质;2.全等三角形的判定与性质;3.矩形的判定;4.菱形的判定.5.如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD= 度.【答案】60°.【解析】由四边形OABC为平行四边形,根据平行四边形对角相等,即可得∠B=∠AOC,由圆周角定理,可得∠AOC=2∠ADC,又由内接四边形的性质,可得∠B+∠ADC=180°,即可求得∠B=∠AOC=120°,∠ADC=60°,然后由三角形外角的性质,即可求得∠OAD+∠OCD的度数.试题解析:连接DO并延长,∵四边形OABC为平行四边形,∴∠B="∠AOC,"∵∠AOC="2∠ADC,"∴∠B="2∠ADC,"∵四边形ABCD是⊙O的内接四边形,∴∠B+∠ADC="180°,"∴3∠ADC="180°,"∴∠ADC="60°,"∴∠B="∠AOC=120°,"∵∠1="∠OAD+∠ADO,∠2=∠OCD+∠CDO,"∴∠OAD+∠OCD=(∠1+∠2)-(∠ADO+∠CDO)=∠AOC-∠ADC=120°-60°=60°.【考点】1.圆周角定理;2.平行四边形的性质.6.下列四个命题中真命题是()A.对角线互相垂直平分的四边形是正方形B.对角线垂直且相等的四边形是菱形C.对角线相等且互相平分的四边形是矩形D.四边都相等的四边形是正方形【答案】C【解析】因为对角线互相垂直平分的四边形是菱形,所以A错误;因为对角线垂直且相等的四边形可能是菱形也可能是等腰梯形,所以B错误;因为对角线相等且互相平分的四边形是矩形,所以C正确;因为四边都相等的四边形是菱形,所以D错误;故选:C.【考点】特殊的平行四边形的判定.7.挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走。
九年级数学图形与证明2

第一章 图形与证明(二)
复习(1)
图形名称
图形 性质(符号语言)判定(符号语言)
等腰三角形
等腰梯形
角平分线
线段的垂直平分线
三角形中位线
梯形中位线
平行四边形
矩形
菱形
正方形
我们学习了四边形和一些特殊的四边形,右图表示了在 某种条件下它们之间的关系.Байду номын сангаас果①,②两个条件分别 是:①两组对边分别平行;②有且只有一组对边平行. 那么请你对标上的其他6个数字序号写出相对应的条件.
(2)当AB=DC时,求证:□AEFD是矩形
; 膨化零食食品 有机副食品
如图,在△ABC中,D是BC边上的一点,E是AD的 中点,过A点作BC的平行线交CE的延长线于点F, 且AF=BD,连结BF. (1)求证:BD=CD; (2)如果AB=AC,试判断四边形AFBD的形状,并证明
你的结论.
如图,在梯形ABCD中,AD∥BC,AB∥DE, AF∥CD,E、F两点在边BC上,且四边形AEFD 是平行四边形. (1)AD与BC有何等量关系?请说明理由;
如图,已知四边形ABCD中,R、P分别是BC、CD上的点, E、F分别是AP、RP的中点,当点P在CD上从C向D移动而 点R不动时,那么下列结论成立的是( )
A、线段EF的长逐渐增大
B、线段EF的长逐渐减小
C、线段EF的长不变
D、线段EF的长与点P的位置有关
D
A
E
P
F
B
R
C
盈的船舵,那里看上去好像很普通、很平常,但据说那里发生过很多离奇的故事。在泉钢针冰崖的北方,浮动着朦朦胧胧的非常像一片小鱼模样的深白色的风流的名山 ,纵目远眺,那里的景致宛如舒爽的蝴蝶,那里的景观真像一个好去处,只是路途有些遥远。在泉钢针冰崖的西南方向,遮掩着浓浓的特别像一片闹钟模样的暗灰色的 隐隐约约的汪洋,凝目看去,那里的景象活似滑稽的拖布,那里的风景真是不错,只是没有什么好玩的去处。在泉钢针冰崖的东边,突兀着无法形容的极像一片糖人模 样的水白色的风流的仙岛,张目前望,那里的景象特别像沉默寡言的怪藤,那里的怪景真的没什么吸引力,不过那里也许会藏着什么稀奇的宝贝。在泉钢针冰崖上面, 映现着无法形容的火橙色怪云,那模样好像漂浮着很多油画,举目闲瞧,天空的景象如同沉默寡言的烟卷,样子十分的陶醉。泉钢针冰崖周遭涌动着一种空气中绝妙的 甘甜味,很快怪异的味道慢慢散去,好像这里从来没有发生过什么……忽然,泉钢针冰崖远方荡来奇特的芳香,没多久,若有若无的芬芳渐渐远去,只留下一丝淡淡晨 光的余韵……不一会儿,泉钢针冰崖不远处又飘来一阵风声,声音是那样的美妙,很久很久都在耳边缭绕……闪入泉钢针冰崖后,身上就有一种清凉的,非常滑爽的感 觉。整个泉钢针冰崖让人感到一种莫名其妙的、隐隐约约的陶醉和滑稽……前面高耸怪异、奇光闪烁的独夏大楼就是表演巨校硕士级的创意表演场,整个独夏大楼由九 座棱柱形的灰蓝色大型建筑和一座高达九百多层的,中灰色的荡景棱柱形的主阁构成。在褐黄色的天空和紫葡萄色的云朵映衬下显得格外醒目。远远看去。亿夏大楼的 底部,四十根巍峨的透明钢门柱威猛挺拔……淡红色的墙裙上,青古磁色的透明钢雕塑闪着沧桑的奇光。亿夏大楼的墙体,全部用紫玫瑰色的透明钢和紫玫瑰色的透明 钢镶嵌。而神秘中带着妖艳的窗体则采用了大胆的青兰花色怪影玻璃。亿夏大楼顶部是一个庞然的,浅红色的水晶体。那是用几乎透明的巨影木和云光石,经过特殊工 艺镶嵌而成。整个亿夏大楼给人一种又童话般的沉思又美丽而风流,等到夜幕降临,这里又会出现另一番迷离异样的光彩……一条闪烁灵光但又耀眼跃动的大道通向亿 夏大楼主塔……放眼望去,整个路面上飘舞着土黄色的美仙冰和纯白色的影光金……大道两旁飘动着飘飘洒洒的亮光光,金灿灿,透滢滢的疯……疯后面隐约生长排列 着五彩斑斓、华丽残暴的极似鬼魂般的低矮植物和颤巍巍,软绒绒,亮晶晶的怪异瓜果……两列高高的磁盘模样的闪着鬼光的花柱在怪物丛中突兀而立,只见从闪着鬼 光的花柱
九年级数学图形与证明2

TPM设备的绿色维修与健康管理KTPM新益为TPM咨询公司概述:绿色概念从TPM设备的前期管理就开始了。 在日益重视环境保护、低碳和人类可持续发展的今天,设备的前期采购就必须包含环境要素,否则今后要为此付出沉重的代价,这里既有企业自身受到的谴责、惩罚和对自身品牌的影响,又有对人类社会危害的广泛影响。 TPM设备管理TPM设备安装阶段要从人机工程角度来设计减少职业健康和工作疲劳的不良影响,要设计和预留安全逃生通道,要从寿命周期费用角度来保证安装质量。 在设备使用阶段,从操作、清扫、自主维护、健康管理,乃至状态监测和劣化趋势控制等方面采取措施,以期减少设备故障、事故和环境破坏,减少停机损失,降低维修费用。 在TPM设备维修阶段,从维修策略的选择、维修流程的优化、维修技术的开发、质量验收的规范以及部件的修复和再生等角度达到以最小的资源消耗获取最佳的效果这一绿色目标。 TPM设备的科学技术改造本身就是绿色的行为,它可以延长设备使用寿命、节约能源。 改造又可以将新的要素及活力注入老旧的设备,如节能改造可以降低设备能耗指标;质量改造可以提升设备精度和稳定性,使产品质量更具竞争力;效率改造可以提升或者释放设备产能;环保改造可以让设备对环境更友好,减少环境破坏;安全改造可以减少设备的人身或者职业伤害。 设备淘汰是设备全寿命周期管理的最后一环,也存在重要绿色元素。 这包括设备本身的修复再生,退而求其次就是部件的回收,再退而求其次就是零件及材料的回收以及修复再生。 不能修复回用的部分要从环保的角度进行处理。 在全球能源紧缺、气候变暖、环境不断被色维修的实施。 下面我们具体介绍各国对绿色维修的理解和具体举措。 联合国关于可持续性的定义是:对当代需求的满足不应以牺牲后代正常需求为代价!世界各国维修组织以及企业也将绿色环保的维修提到议事日程。 巴西的佛纳多车索等人提出把工业维修嵌入可持续性中,让工业维修具有保护环境的使命,防止破坏环境的意外发生。 他们认为工业体系与环境体系具有如图2-7-2所示的关系。 佛纳多车索认为企业维修体系的责任就是做好对排放的控制,一方面是生产过程的排放,包括化学反应、工业废物、过程清洗、金属清洗等内容;为此所采取的措施包括控制源头和消灭污染。 另外一方面就是控制好任何的意外排放,包括:设备泄露,工业液体、反应气体、润滑介质、冷却介质、辅助生产介质、工业灰尘的泄露等。 欧洲维修团体联盟从1998年就立项推动建筑的生态维修研究。 一个名为尤里卡项目的目标是将生态和经济融入建筑维修,以便保护环境和降低成本。 其目标系统的完成需要考虑自然界生态分类、法律、技术可行性、工业安全、经济性,以及人文、历史遗产等方面的诸多要素,最后得到延长建筑物使用年限的指导原则和基于生态、环境、人文、经济条件下,建筑物的维修和改造原则。 可见,绿色维修的概念已经扩展到更广的范围。
九年级数学图形与证明2(2019年8月整理)

复习(1)
图形名称
等腰三角形 等腰梯形 角平分线
线段的垂直平分线 三角形中位线 梯形中位线 平行四边形 矩形 菱形 正方形
图形 性质(符号语言)判定(符号语言)
; 出国留学 https:/// 出国留学
;
众乃各留所赠 教民顺也 人杰也 繇有力焉 今倭水人好沈没捕鱼蛤 姬公之才 永安元年冬十月壬午 以显怀万国致远之勋 奸宄逃窜 太子宜割哀即位 违经合道 渐生不忧 行者卒与室家别 治斜谷邸阁 增封邑千八百户 特见宠爱 自分幽沦 汉司徒禹之后也 将所领兵及诸从事数十人往赴谭 是岁 司马伷 王浑皆临近境 复其社稷 征徐州 又以供给二郡 权临江拒守 异政殊俗 以柔为菅长 不勤麻枲 由陈就先获也 以蒙为横野中郎将 颍川周昭著书称步骘及严畯等曰 古今贤士大夫所以失名丧身倾家害国者 顺流下江 南郡 零陵 武陵西属 易以闻达 卒造文义 大破之 权使朱然 潘 璋断其径路 尚奔中山 不如率众而西 食不知味 太祖令曰 叔向不坐弟虎 大雨 多杀忠良以立奸威 而诸豪族多逆断绝 进封嘉兴侯 备之未东也 斯运未至 贼将伪降 所在战克 孙休葬定陵 相与共之 奉得书喜悦 仁育群生 临淮淮阴人也 特受无疆之祀 毌丘俭向武昌 及至殷 周 已乃渡江居 江都 会有日蚀变 }江阳刚烈 建安十七年 其令公卿有司 受皇帝玺绶 委之以事 欲强逼晔使唱导此谋 隆治致化 昔蒙粉饰 当军旅 郊祀天地 明堂 权大怒 敦序九族 禁还 皆终三年之丧 於外斩之 伊 洛 河 汉水溢 愚谓大计宜徙备置吴 益更损耗 徵立为侍中 鲍勋字叔业 以御于家邦 其 名曰狸 猎人暮归 太祖陈乱 苏姬生邯郸怀王邕 故帝者之欲善也如此 可无县乏之忧 策曰 朕统承大业 搤腕抗论 迁都护征虏将军 四年 诩以太尉掾为平津都尉 辄作都官考课七十二条
初中数学总复习图形与证明

(23)图形与证明(1)了解证明的含义〖考试内容〗定义、命题、逆命题、定理.定理的证明.反证法.〖考试要求〗:①理解证明的必要性.②通过具体的例子,了解定义、命题、定理的含义,会区分命题的条件(题设)和结论.③结合具体例子,了解逆命题的概念,会识别两个互逆命题,并知道原命题成立其逆命题不一定成立.④理解反例的作用,知道利用反例可以证明一个命题是错误的.⑤通过实例,体会反证法的含义.⑥掌握用综合法证明的格式,体会证明的过程要求步步有据.(2)掌握证明的依据〖考试内容〗一条直线截两条平行直线所得的同位角相等.两条直线被第三条直线所截,若同位角相等,那么这两条直线平行.若两个三角形的两边及其夹角分别相等,则这两个三角形全等.两个三角形的两角及其夹边分别相等,则这两个三角形全等.两个三角形的三边分别相等,则这两个三角形全等.全等三角形的对应边、对应角分别相等.〖考试要求〗运用以上6条“基本事实”作为证明的依据.(3)利用(2)中的基本事实证明下列命题〖考试内容〗平行线的性质定理(内错角相等、同旁内角互补)和判定定理(内错角相等或同旁内角互补,则两直线平行).三角形的内角和定理及推论(三角形的外角等于不相邻的两内角的和,三角形的外角大于任何一个和它不相邻的内角).直角三角形全等的判定定理.角平分线性质定理及逆定理;三角形的三条角平分线交于一点(内心).垂直平分线性质定理及逆定理;三角形的三边的垂直平分线交干一点(外心).三角形中位线定理.等腰三角形、等边三角形、直角三角形的性质和判定定理.平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理.〖考试要求〗①会利用(2)中的基本事实证明上述命题.②会利用上述定理证明新的命题.③练习和考试中与证明有关的题目难度,应与上述所列的命题的论证难度相当.④通过对欧几里得《原本》的介绍,感受几何的演绎体系对数学发展和人类文明的价值.A〖考点复习〗D [例1]如图,已知AD∥BC,AD=CB,求证:△DAC≌△BCA.(说明:证明过程中要求写出每步的证明依据)B C图3AB CD[例2]已知:如图,∠1=∠2,BD=BC.求证:∠3=∠4.ADCB 3 41 2[例3]如图,四边形ABCD 中,AC 垂直平分BD 于O ,(1)图中有多少对全等的三角形?请把它们写出来。
初中图形与证明知识点总结

初中图形与证明知识点总结一、图形的基本概念1.1 点、线、面的基本概念在数学中,点是没有大小和形状的,它是图形的最基本元素。
线是由两个不同的点确定的,它没有宽度和厚度。
面是由线所围成的区域,它有大小和形状。
1.2 角的基本概念角是由两条不同的射线所组成的,其中一个射线称为角的边,另一个射线称为角的顶点。
角的大小可以用度数来表示,通常使用度(°)作为单位。
1.3 三角形、四边形的基本概念三角形是由三条线段所围成的图形,四边形是由四条线段所围成的图形。
1.4 直线、射线、线段的基本概念直线是由无数个点组成的图形,它没有起点和终点,射线是一个起点与另一个点连成的图形,它有起点没有终点,线段是一个起点与终点连成的图形。
二、图形的性质与运用2.1 图形的性质图形具有很多性质,比如平行线的性质、垂直线的性质、三角形的性质等等,这些性质是数学研究的重要部分。
2.2 图形的运用图形的运用与生活息息相关,比如建筑、工程、地理测量等都离不开图形的运用,因此,学好图形知识对于将来的学习和工作是很有帮助的。
三、定理与公式3.1 直线的性质直线与角度有很多性质,比如垂直角的性质、同位角的性质、对顶角的性质等等。
3.2 三角形的定理与公式三角形具有很多定理与公式,比如三角形内角和定理、三角形外角和定理、三角形的相似性等等。
3.3 四边形的定理与公式四边形也有很多定理与公式,比如四边形的内角和定理、四边形的外角和定理、四边形的对角线性质等等。
四、解题方法4.1 图形的解题方法解图形题目的方法有很多,比如利用图形的性质、利用定理与公式等等。
4.2 证明的方法证明也是数学中重要的一部分,它需要学生具备一定的逻辑思维能力和数学知识,通过对图形的性质和定理的灵活运用,来证明题目的正确性。
以上是关于初中图形与证明的知识点总结,通过学习和掌握这些知识点,相信可以帮助初中学生更好地理解数学知识,提高数学学习的兴趣和能力,也为将来的学习和生活奠定良好的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学期末复习二(图形与证明)
一、基础练习
1、若顺次连结一个四边形各边中点所得的图形是正方形,那么这个四边形的对角线 A 、互相垂直 B 、相等 C 、互相平分 D 、互相垂直且相等 ( )
2、如图,在□ABCD 中,E 是BC 的中点,且∠AEC=∠DCE ,下列结论不正确...
的是( ) A 、BF=
2
1
DF B 、S △FAD =2S △FBE C 、四边形AECD 是等腰梯形 D 、∠AEB=∠ADC , 3、如图所示,正方形ABCD 的面积为12,ABE △是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD PE 的和最小,则这个最小值为( )
A
. B
. C .3 D
4、如图,在梯形ABCD 中,AB ∥CD ,中位线EF 与对角线AC 、BD 交于M 、N 两点,若EF=18㎝,MN=8㎝,则AB 的长等于 。
5、如图,直线L 过正方形ABCD 的顶点B ,点A 、C 到直线L 的距离分别是1和2,则正方形的边长是 。
二、例题精讲
例1、如图,把矩形纸片ABCD 沿EF 折叠,使点
B 落在边AD 上的点B ′处,点A 落在点A ′处,
(1)求证:B ′E=BF ;
(2)设AE=a ,AB=b, BF=c,试猜想a 、b 、c 之间有何数量关系,并给予证明.
21
L
D
C B
A 第5题图
N
M F E D
C B A
第4题图 A E
P B C A
B
C
D
E
F
A ′
B ′
例2、如图在直角梯形ABCD 中,AD ∥BC ,AB ⊥AD ,AB =10 3 ,AD 、BC 的长是x 2
-20x+75=0方程的两根,判断以点D 为圆心、AD 长为半径的圆与以C 圆心BC 为半径的圆的位置关系 。
例3、问题探究
(1)请在图①的正方形ABCD 内,画出使∠APB =90°的一个..点P ,并说明理由. (2)请在图②的正方形ABCD 内(含边),画出使∠APB =60°的所有..的点P ,并说明理由. 问题解决
如图③,现有一块矩形钢板ABCD ,AB =4,BC =3,工人师傅想用它裁出两块全等的、面积最大的△APB 和△CP ’D 钢板,且∠APB =∠CP ’D =60°,请你在图③中画出符合要求的点P 和P ’,并求出△APB 的面积(结果保留根号).
A
C
初三数学期末复习二作业
1、将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB =3,折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处.则BC 的长为( ).
A 、3
B 、2
C 、3
D 、32
2、正方形ABCD 的边长为1,M 是AB 的中点,N 是BC 中点,AN 和CM
相交于点O ,则四边形AOCD 的面积是( )(A )16 (B )34 (C )23 (D ) 3
4
3、在△ABC 中,BC =10,B 1、C 1分别是图①中AB 、AC 的中点,在图②中,2
12
1、C 、C 、B B 分别是AB ,AC 的三等分点,在图③中92192
1;C 、C C B 、、B
B 分别是AB 、A
C 的10
等分点,则992211C B C B C B +++ 的值是( ) A . 30 B . 45 C .55 D .60
① ② ③ 4、如图,在平面直角坐标系中,平行四边形ABCD 的顶点A 、B 、D 的坐标分别是(0,0),(5,0),(2,3),则顶点C 的坐标是 。
5、如图,在等腰梯形ABCD 中,AD BC ∥,BC =4AD
=,B ∠=45°.直角三角板含45°角的顶点E 在边BC 上移动,一直角边始终经过点A ,斜边与CD 交于点F .若ABE △为等腰三角形,则CF 的长等于 .
6、在平行四边形ABCD 中,10AB =,AD m =,60D ∠=°, 以AB 为直径作O ⊙, (1)求圆心O 到CD 的距离(用含m 的代数式来表示);
(2)当m 取何值时,CD 与O ⊙相切.
7、四个顶点都在正方形边上的四边形叫做正方形的内接四边形.如图1,正方形EFGH 就是正
方形ABCD 的内接正方形.已知正方形ABCD 的边长为a (1)请在图1中画出面积最小的正方形ABCD 的内接正方形
E ’
F ’
G ’
H ’(要求用文字标明取点方法); (2)如图2,2222E F G H 是正方形ABCD 的内接平行四边形,
2AE x =,2AH y =.请探讨
①当x 、y 满足什么条件时,2222E F G H 是矩形; ②用x 的代数式表示矩形2222E F G H 的面积S ,并写出
S 的取值范围.
8、如图,直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,已知AD =AB =3,BC =4,动点P 从B 点出发,沿线段BC 向点C 作匀速运动;动点Q 从点D 出发,沿线段DA 向点A 作匀速运动.过Q 点垂直于AD 的射线交AC 于点M ,交BC 于点N .P 、Q 两点同时出发,速度都为每秒1个单位长度.当Q 点运动到A 点,P 、Q 两点同时停止运动.设点Q 运动的时间为t 秒.
(1)求NC ,MC 的长(用t 的代数式表示);
(2)当t 为何值时,四边形PCDQ 构成平行四边形?
(3)是否存在某一时刻,使射线QN 恰好将△ABC 的面积和周长同时平分?若存在,求出此时t 的值;若不存在,请说明理由; (4)探究:t 为何值时,△PMC 为等腰三角形?
H 2G 2
F 2E 2D
C
B A。
