南昌大学第九届高数竞赛(数学专业类11级)试题及答案

南昌大学高数试题及答案

南昌大学 2006～2007学年第一学期期末考试试卷一、填空题 (每空 3 分，共 15 分) : 1.函数1()lg(5)3f x x x =++--的定义域为_______________.2. 设函数 ,0,()ln(),0,x e x f x a x x -⎧<=⎨+≥⎩ 则a 为_____值时,()f x 在x =0处连续.(a >0) 3. 若函数()f x 在x =0可导, 且f (0)=0,则0()limx f x x→=__________. 4.设()f x =在[1, 4]上使Lagrange(拉格朗日)中值定理成立的ξ=_____.5. 设220()sin ,xF x t dt =⎰则()dF x =_______________. 二、单项选择题 (每题 3 分，共15分):1. 0x =是函数1()sin f x x x=的( ).(A) 跳跃间断点. (B) 可去间断点. (C) 无穷间断点. (D) 振荡间断点. 2. 设曲线21x y e-=与直线1x =-相交于点P,曲线过点P 处的切线方程为( ).(A) 210.x y ++= (B) 230.x y +-= (C) 230.x y -+= (D) 220.x y --=3. 若函数()f x 在区间(,)a b 内可导,1x 和2x 是区间(,)a b 内任意两点, 且12x x <, 则至少存在一点ξ使( ). (A) ()()'()(),f b f a f b a ξ-=- 其中.a b ξ<< (B) 11()()'()(),f b f x f b x ξ-=- 其中1.x b ξ<< (C) 2121()()'()(),f x f x f x x ξ-=- 其中12.x x ξ<< (D) 22()()'()(),f x f a f x a ξ-=- 其中2.a x ξ<<4. 设函数()f x 在(,)-∞+∞上连续,则()d f x dx ⎡⎤⎣⎦⎰等于( ).(A) ().f x (B) ().f x dx (C) ().f x C + (D) '().f x dx5. 设43()()'()d d I f x dx f x dx f x dx dx dx=++⎰⎰⎰存在, 则I =( ).(A) 0. (B) ().f x(C) 2().f x (D) 2().f x C +三、计算下列极限 (共2小题, 每小题7分, 共14分) :1. 0lim.1cos x x→-2. tan 2(sin ).lim x x x π→四. 解下列各题 (共3小题, 每小题7分, 共21分):1.设ln y =求''(0).y2. 设函数()y y x =由方程23ln()sin x y x y x +=+确定,求'(0).y3. 设2022(),(),t x f u du y f t ⎧=⎪⎨⎡⎤⎪=⎣⎦⎩⎰ 其中()f u 具有二阶导数, 且()0,f u ≠ 求22.d y dx五.求下列不定积分 (共2小题,每小题7分,共14分): 1、81.(1)dx x x +⎰2. 2sin .x xdx ⎰六.已知1(2),'(2)0,2f f ==及20()1,f x dx =⎰求120''(2).x f x dx ⎰(7分)七.已知函数222,(1)x y x =-试求其单增、单减区间, 并求该函数的极值和拐点. (9分)八.设()f x 在[,)a +∞上连续,''()f x 在(,)a +∞内存在且大于零,记()()()().f x f a F x x a x a-=>- 证明:()F x 在(,)a +∞内单调增加. (5分)南昌大学 2006～2007学年第一学期期末考试试卷及答案一、填空题 (每空 3 分，共 15 分) : 1.函数1()lg(5)3f x x x =++--的定义域为（ 2335;x x ≤<<<与）2. 设函数 ,0,()ln(),0,x e x f x a x x -⎧<=⎨+≥⎩ 则a 为（ e ）值时,()f x 在x =0处连续.(a >0) 3. 若函数()f x 在x =0可导, 且f (0)=0,则0()limx f x x→=（ '(0)f ） 4.设()f x =在[1, 4]上使Lagrange(拉格朗日)中值定理成立的ξ=（ 9/4 ）一、 5. 设220()sin ,xF x t dt =⎰则()dF x =（22sin(4)x dx ）二、单项选择题 (每题 3 分，共15分):1. 0x =是函数1()sin f x x x=的( B ).(A) 跳跃间断点. (B) 可去间断点. (C) 无穷间断点. (D) 振荡间断点. 2. 设曲线21x y e-=与直线1x =-相交于点P,曲线过点P 处的切线方程为( C ).(A) 210.x y ++= (B) 230.x y +-= (C) 230.x y -+= (D) 220.x y --=3. 若函数()f x 在区间(,)a b 内可导,1x 和2x 是区间(,)a b 内任意两点, 且12x x <, 则至少存在一点ξ使( C ). (A) ()()'()(),f b f a f b a ξ-=- 其中.a b ξ<< (B) 11()()'()(),f b f x f b x ξ-=- 其中1.x b ξ<< (C) 2121()()'()(),f x f x f x x ξ-=- 其中12.x x ξ<< (D) 22()()'()(),f x f a f x a ξ-=- 其中2.a x ξ<<4. 设函数()f x 在(,)-∞+∞上连续,则()d f x dx ⎡⎤⎣⎦⎰等于( B ). (A) ().f x (B) ().f x dx (C) ().f x C + (D) '().f x dx5. 设43()()'()d d I f x dx f x dx f x dx dx dx=++⎰⎰⎰存在, 则I =( D ).(A) 0. (B) ().f x(C) 2().f x (D) 2().f x C +三、计算下列极限 (共2小题, 每小题7分, 共14分) :1. 0lim.1cos x x→- 解：0x →时，211cos 2xx -，()2224111cos 22x x x -= ∴0lim1cos xx →=-022x x →=2. tan 2(sin ).lim x x x π→解：(1) 令()tan sin xy x = ln tan lnsin y x x =(2)2ln lim x y π→=2tan lnsin lim x x x π→= 2lnsin cot lim x xx π→==221cos sin 0csc lim x xx x π→=- (3) tan 2(sin )lim x x x π→=2lim x y π→ln 021lim y x e e π→===四. 解下列各题 (共3小题, 每小题7分, 共21分):1. 设ln y=求''(0).y 解：21[ln(1)ln(1).2y x x ==--+22112112'. 3212111x x y x x x x -⎡⎤⎛⎫∴=-=-+ ⎪⎢⎥--++⎣⎦⎝⎭分222222222112(1)411''.2(1)(1)2(1)(1) x x x y x x x x ⎡⎤+--=-+=--⎢⎥-+-+⎣⎦ 13''(0)1.722y =--=-于是分2. 设函数()y y x =由方程23ln()sin x y x y x +=+确定,求'(0).y解：方程两边对x 求导,得()23212'3'cos . 4x y x y x y x x y+=+++分0,1,'(0) 1. 7x y y ===当时由原方程得代入上式得分3. 设2022(),(),t x f u du y f t ⎧=⎪⎨⎡⎤⎪=⎣⎦⎩⎰ 其中()f u 具有二阶导数, 且()0,f u ≠ 求22.d y dx 解: 222 4()'(),().dy dx tf t f t f t dt dt==22222222224()'()4'(). ()4'()8''(). ()dydy tf t f t dt tf t dx dx f t dtdy d dy dx d d y f t t f t dx dt dx dx dx f t dt∴===⎛⎫⎪⎛⎫⎝⎭ ⎪+⎝⎭∴=== 五.求下列不定积分 (共2小题,每小题7分,共14分): 1、81.(1)dx x x +⎰解: 原式 =()78888888811111dx =dx 88(1)11x dx x x x x x x ⎛⎫=- ⎪++⎝⎭+⎰⎰⎰ 81ln ||ln |1|.8x x C =-++2. 2sin .x xdx ⎰解: 原式1cos211cos2224x xdx xdx x xdx -==-⎰⎰⎰ 211sin 2cos 2.448x x x x C =--+六.已知1(2),'(2)0,2f f ==及20()1,f x dx =⎰求120''(2).x f x dx ⎰(7分)解: 设2,t x = 则2122001''()''()24t x f x dx f t dt =⎰⎰222200011'()2'()2()88t f t tf t dt tdf t ⎡⎤⎡⎤=-=-⎣⎦⎣⎦⎰⎰ 220011()()(11)0.44t f t f t dt ⎡⎤=--=--=⎣⎦⎰ 七.已知函数222,(1)x y x =-试求其单增、单减区间, 并求该函数的极值和拐点. (9分)解: 34484',''.(1)(1)xx y y x x +==-- 1'0,0;''0,.y x y x ====-令得令得故(0,1)为单增区间,(,0)(1,);-∞+∞和为单减区间函数在0x =处取得极小值,极小值为0;点(1/2,2/9)-为拐点.八.设()f x 在[,)a +∞上连续,''()f x 在(,)a +∞内存在且大于零,记()()()().f x f a F x x a x a-=>- 证明:()F x 在(,)a +∞内单调增加. (5分)证明: 1()()'()'().f x f a F x f x x a x a -⎡⎤=-⎢⎥--⎣⎦由拉格朗日中值定理知存在(,),a x ξ∈使()()'().f x f a f x aξ-=- []1'()'()'().F x f x f x aξ∴=--由''()0f x >可知'()f x 在(,)a +∞内单调增加,因此对任意x 和(),a x ξξ<<有'()'(),f x f ξ>从而'()0,F x >故()F x 在(,)a +∞内单调增加.南昌大学 2009～2010学年第一学期期末考试试卷一、填空题(每空 3 分，共 15 分)1. 设函数()arcsin ln 13xy x =+-，则它的定义域为。

2017-2018学年度第九届高等数学竞赛(答案)

中山大学新华学院第九届高等数学竞赛姓名学号班级成绩一、填空题（每题3分，共18分） 1.函数()11y ln x =++()()1,00,-⋃+∞。

2. 2111.dx x+∞=⎰。

3.曲线236x x y +=的拐点横坐标为=x 2-;4. 11(1x x -+=⎰2π. 5.a =6.设A =“某人投注的号码中一等奖”，则P （A ）=861331615.64310C C -=⨯二、计算题（每题7分，共49分） 1. 设)1ln(2x x y ++=，求dy ． )1ln(2++=x x d dy )1(1122++++=x x d x x ............3分dx x xx x ⎪⎪⎭⎫⎝⎛++++=111122 ----------5分.112dx x +=------------7分2、已知函数32()f x x ax bx =++在1x =处有极小值2-，(1) 求a 与b 的值； (2) 求()f x 的极大值点与极大值。

解：（1）由(1)2f =-且为极小值知，12320a b a b ++=-⎧⎨++=⎩，解得0;3a b =⎧⎨=-⎩------------------ 2分（2）322()3,()333(1)3(1)(1),f x x x f x x x x x '=-=-=-=+-由上表可得，极大值(1)2f -=。

------------------ 7分 3.设函数()f x 在0x =处有二阶导数,且 0()lim0,x f x x→=(0)4,f ''= 求(0),(0),f f '10()lim 1.xx f x x →⎛⎫+ ⎪⎝⎭解：4、设211()x x f x e-⎧⎪+=⎨⎪⎩00x x >≤，求31(2)d f x x -⎰. 解：令2=-t x，则d d =x t ，当1=x 时，1=-t ; 当3=x 时，1=t ------------------ 3分3101111(2)d ()d ()d ()d ---==+⎰⎰⎰⎰f x x ft t f t t f t t 0211d 1+x x -=⎰1-0e d x x +⎰114eπ=-+ ------------------ 7分5. 计算40⎰t =，则2,2x t dx tdt == ------------------ 2分4202t te dt =⎰⎰ ------------------- 4分222220002()2422(1)t t t te e dt e e e =-=-=+⎰ -----------------7分2000011()1()()lim ln 1lim lim 0000()1()(0)1limlim (0)222002()(0)lim ()lim 000,()(0)()(0)lim lim 0,()lim 1.x x x x f x f x f x xx x xx xx x x x f x f x f f xxx x f x f f x x xf x f f x f x xf x e eex eeee →→→→⎛⎫+•⎪⎝⎭→→→==→'''-''→→===⨯=-'===⎛⎫+= ⎪⎝⎭====6.解：)1ln(y xe e xzy x y x +++=∂∂++, ------------------ 2分yx xe y z y x +++=∂∂+11, ------------------ 4分于是 =)0,1(dz dy e edx )2(2++. ------------------ 7分7. 计算二次积分 23120y xx I dx e dy =⎰⎰．解：被积函数是22y e ，对于y 而言，它的原函数不能用初等函数表示，需改变积分次序才能进行．区域D ： 3,01,y x y y ⎧≤≤⎨≤≤⎩ 如图所示．--------- 2分2312y xxI dx e dy=⎰⎰2312y yye dy dx=⎰⎰=2122201(1)2y e y dy -⎰，令22y u =，由上式得----- 4分 1112220111222(12)212()|23uuu u u I e u du e du ue du e ue e e =-=-=---=-⎰⎰⎰------------------ 7分三、（10分）0()()()()2.().设有任意阶导数，且满足试求xf x x t f t dt f x x f x -=-⎰12()()()2()+()()()2()=()2()()()xxxxx x f t dt tf t dt f x xx f t dt x f x xf x f x f t dt f x x f x f x f x c e c e -=-'⋅-'-''==+⎰⎰⎰⎰000解：由题意：等式两端对变量求导：-=即：等式两端再次对变量求导: 上式微分方程对应通解为：12 0,(0)0,(0)21,()xx x x f f c c f x e e --'=====-令可得，从而=-1,故.四、应用题（每题9分，共18分）3x y =oxy x=-111 1y o1. 解：如图（略），曲线与x 轴的交点为)0,1(-和)0,1(，..........2分(1) ⎰112)1(--=dx x S 34=............5分(2) 12V dy π=⎰()12101122y dy y y πππ⎛⎫=-=-= ⎪⎝⎭⎰ .......9分 2. 解：设L 为获得的总利润,L R C =-= 1p 1q +2p 2q -C=1p ()1120.1p -+2p ()220.01p --(())123540q q ++=2211220.1160.01 2.4595p p p p -+-+- (2)分解方程组1112220.2160,0.02 2.40,p p L p p L p p =-+=⎧⎪⎨=-+=⎪⎩解得1p =80, 2p =120,唯一驻点是(80,120)．又 ..........6分A =L 11=－0.2<0,B =L 12=0,C =L 22=－0.02<0,因此 Δ=AC －B 2=0.004>0．故L 在驻点(80,120)处有极大值. .........8分于是可以断定,当两个市场售价分别为80和120个单位时,利润最大,最大利润为L (80,120)=189． ...............9分五、综合拓展题（5分）兄妹二人沿某街分别在离家3公里与2公里处同向散步回家，家中的狗一直在二人之间来回奔跑。

第九届全国大学生数学竞赛非数类参考答案(白兔兔)

学校
由 α 的任意性得
"
fx p0, 0q “ 0 fy p0, 0q “ 0
, 从而 p0, 0q 是 f px, yq 的驻点.
˘ d2 gα pt q d` fx cos α ` fy sin α “ 2 dt dt ` ˘ ˘ ` “ fxx cos α ` fxy sin α cos α ` fyx cos α ` fyy sin α sin α 省市 “ fxx cos2 α ` 2 fxy sin α cos α ` fyy sin2 α “ ‰ “ sin α cos α fxx cot2 α ` 2 fxy ` fyy tan2 α
所以 f p0, 0q 是 f px, yq 极小值. 三、 (本题满分 14 分) 设曲线 Γ 为曲线 x ě 0, y ě 0, z ě 0 ∫ 上从点 Ap1, 0, 0q 到点 Bp0, 0, 1q 的一段. 求曲线积分 I “ y dx ` z dy ` x dz
Γ
x2 ` y2 ` z2 “ 1 ,
Γ1 Σ
第 4 页, 共 6 页
曲线 Γ 在 xOy 面上投影的方程为
` ˘2 x´ 1 y2 2 ` 1 ˘2 ` ` 1 ˘2 “ 1 座位号
2 ? 2
又该投影（半个椭圆）的面积得知 1 π 这样就有 I “ ´ ? 2 2 2
Σ
π dx dy “ ? . 同理, 4 2
Σ
π dy dz “ ? 4 2
密封线答题时不要超过此线姓名
一、 (本题满分 42 分, 共 6 小题, 每小题 7 分) ∫ x 1. 已知可导函数 f pxq cos x ` 2 f pt q sin t dt “ x ` 1 满足则 f pxq “

全国大学生数学竞赛第九届(非数学)决赛试卷

xi2 − xi xi+1 ， n ≥ 2 .
=i 1=i 1
(1) 证明：对任一非零 x ∈ Rn ， H (x) > 0 ； (2) 求 H (x) 满足条件 xn = 1的最小值.
得分评阅人
六 (本题满分 12 分)
{ } 设函数 f (x, y) 在区= 域 D (x, y) x2 + y2 ≤ a2 上具
第九届全国大学生数学竞赛决赛试卷
得分
(非数学类, 2018 年 3 月)
评阅人
添加作者个人微信，备注知乎数学竞赛，可进入300多人的数学竞赛微信群
二 (本题满分 11 分)
设函数 f (x) 在区间 (0,1) 内连续，且存在两两互异的点 x1, x2 , x3, x4 ∈ (0,1) ，使得
题号满分
−x 1 1 1
cz = dab ， d w = abc ，则行列式 1 − y 1
1 = ＿＿＿＿＿＿＿.
1 1 −z 1
1 1 1 −w
省市____________学校____________准考证号____________姓名____________考场号______座位号______ 密封线密封线密封线
有一阶连续偏导数，且满足 f (x, y) x2 + y2 = a2 = a2 ，以及
∫∫ max
( x, y )∈D

∂f ∂x
2
+

∂f ∂y
2

= a2 ，其中
a
>
0
.
证明：
D
f (x, y)dxdy
≤ 4πa4 . 3
全国大学生数学竞赛决赛（非数学类,2018）-4

第九届全国大学生数学竞赛决赛试题参考答案及评分标准

第九届全国大学生数学竞赛决赛试题参考答案及评分标准(非数学类, 2018 年 3 月)一、填空题(满分 30 分，每小题 6 分)：(1) 极限lim tan x - sin x =1.x →0 x ln(1+ s in 2 x )2(2) 设一平面过原点和点(6, -3, 2) ，且与平面4x - y + 2z = 8 垂直，则此平面方程为 2x + 2 y - 3z = 0 .(3) 设函数 f (x , y ) 具有一阶连续偏导数，满足d f (x , y ) = ye y d x + x (1+ y )e y d y ，及 f (0, 0) = 0 ，则 f (x , y ) =xye y .d u (t ) 1 2e t - e +1 (4) 满足 d t = u (t ) + ⎰0 u (t )d t 及u (0) = 1的可微函数u (t ) =3 - e.(5) 设a , b , c , d 是互不相同的正实数，x , y , z , w 是实数，满足a x = bcd ，b y = cda ， c z = dab ， d w = abc ，则行列式= 0.二、(本题满分 11 分) 设函数 f (x ) 在区间(0,1) 内连续，且存在两两互异的点 x 1, x 2 , x 3, x 4 ∈(0,1) ，使得α =f (x 1) - f (x 2 ) < x 1 - x 2 f (x 3 ) - f (x 4 ) =β ，x 3 - x 4证明：对任意λ ∈(α , β ) ，存在互异的点 x , x ∈(0,1) ，使得λ = f (x 5 ) - f (x 6 ) . 5 6 x - x56【证】不妨设 x 1 < x 2 , x 3 < x 4 ，考虑辅助函数F (t ) =f ((1- t )x 2 + tx 4 ) - f ((1- t )x 1 + tx 3 )，……… 4 分(1- t )(x 2 - x 1) + t (x 4 - x 3 )则 F (t ) 在闭区间[0, 1] 上连续，且 F (0) = α < λ < β = F (1) . 根据连续函数介值定理，存在t 0 ∈(0,1) ，使得 F (t 0 ) = λ .………………… 3 分-x 11 1 1 - y11 1 1 -z11 11 -wn n !1⎣ ⎦- ∑π令 x 5 = (1- t 0 )x 1 + t 0 x 3 ， x 6 = (1- t 0 )x 2 + t 0 x 4 ，则 x 5, x 6 ∈(0,1) ， x 5 < x 6 ，且λ = F (t ) = f (x 5 ) - f (x 6 ).………………… 4 分x - x5 6三、(本题满分 11 分)设函数 f (x ) 在区间[0,1] 上连续且⎰1f (x )d x ≠ 0 ，证明：在区间[0,1] 上存在三个不同的点x 1，x 2，x 3 ，使得π1f (x )d x =⎡ 1x 1f (t ) d t + f (x ) arctan⎤8 ⎰⎢1 + x 2 ⎰01x 1 ⎥ x 3⎣ 1 = ⎡ 1x 2 f (t ) d t + f (x ) a rctan x ⎦ ⎤ (1 - x ). ⎢1 + x 2 ⎰0 2 2 ⎥ 3 ⎣ 2 ⎦【证】令 F (x ) = 4 arctan x ⎰0 ，则F (0) = 0, F (1) = 1且函数F (x )在闭⎰f (t )d t区间[0,1] 上可导. 根据介值定理，存在点x 3 ∈(0,1) ，使F (x 3 ) = 1. 2………………… 5 分再分别在区间[0, x 3 ] 与[x 3，1]上利用拉格朗日中值定理，存在x 1 ∈(0,x 3) ，使得F (x 3) - F (0) = F '(x 1)(x 3 - 0) ，即π1⎡ 1 x 1⎤8 ⎰0 f (x )d x = ⎢1 + x 2 ⎰0 f (x ) d x + f (x 1) arctan x 1 ⎥ x 3 ； ……… 3 分⎣ 1 ⎦且存在x 2 ∈(x 3 ,1) ，使F (1) - F (x 3) = F '(x 2 )(1 - x 3) ，即π1f (x )d x =⎡ 1x 2f (x ) d x + f (x) arctan x ⎤(1 - x ) .8 ⎰⎢1 + x 2 ⎰022⎥ 3⎣2⎦………………… 3 分四、(本题满分 12 分) 求极限： lim ⎡n +1 (n +1)! - n n !⎤ .n →∞【解】注意到n +1(n +1)! - n⎡ n +1 (n +1)! n !=n ⎢ ⎤ 1⎥ ，而 ………… 3 分 ⎢ nn ! ⎦⎥ nlim1 nk lnln x d x1lim= en →∞ n k =1n = e ⎰0= ，…………… 3 分nn !xf (t )d t1n n en n ! nn ! ∑∑ 【证】 (1) 二次型 H (x ) = ∑ x -⎝ ⎭n -1 ⎭n n +1- 1 ⋅1 ∑n +1lnk=(n +1)n[(n +1)!] (n !)n +1 = (n +1)n (n +1)= e(n +1)!n n +1k =1 n +1， …… 3 分利用等价无穷小替换e x -1 x (x → 0) ，得lim ⎡ n +1 (n +1)! ⎤ n - 1 n +1 k 1n →∞ nn ! 1⎥ = - lim n +1∑ln n +1 = -⎰0 ln x d x = 1 ， ⎢⎣因此，所求极限为⎦⎥ n →∞⎤k =1⎡ n +1 (n +1)! ⎤ 1lim - = limlim n ⎢ -1⎥ = . …… 3 分n →∞⎦ n →∞ n n →∞ ⎢⎣n n ! ⎦⎥ enn -1五、(本题满分 12 分) 设 x = (x , x , , x )T ∈ R n ，定义 H (x ) =x 2 -xx，n ≥ 2 .1 2 ni =1ii i +1i =1(1)证明：对任一非零 x ∈ R n ， H (x ) > 0 ；(2)求 H (x ) 满足条件 x n = 1的最小值.nn -1 2ii i 1的矩阵为i =1⎛i =11 ⎫2 ⎪ ⎪ - 1 1 - 1 ⎪ 2 2 ⎪ 1 ⎪A = -2 ⎪ ， ……………3 分⎪ 1 ⎪ 1 - ⎪2 ⎪ - 11⎪⎪ ⎝ 2 ⎭因为 A 实对称，其任意k 阶顺序主子式∆k > 0 ，所以 A 正定，故结论成立. ………………… 3 分 (2) 对 A 作分块如下 A = ⎛ A n -1 α ⎫ ，其中α = (0, , 0, - 1)T ∈ R n -1 ，取可逆矩⎛ I - A -1 α ⎫α T 1 ⎪ ⎛ A n -1 2 0 ⎫ ⎛ A n -1 0 ⎫ 阵 P = n -1 n -1 ⎪ ，则 P T AP = ⎪ = ⎪ ，其中⎝ 01 ⎭ ⎝ 0 1- α T A -1α ⎝ 0 a ⎭ n +1(n +1)!nn !⎡n +1 (n +1)! ⎣⎢ 1 -n -1 ⎛ f ⎫ ∂x ∂y a = 1- α T A -1α .………………… 3 分记 x = P (x ,1)T ，其中 x = (x , x , , x )T ∈ R n -1 ，因为12n -1H (x ) = x T Ax = (x T ，1)P T (P T )-1 ⎛ An -10 ⎫ P -1P ⎛ x 0 ⎫ = x TA x + a ，0 0a ⎪ 1 ⎪ 0 n -1 0⎝⎭ ⎝ ⎭且 A 正定，所以 H (x ) = x T A x + a ≥ a ，当 x = P (x ,1)T = P (0,1)T 时， H (x ) = a .n -10 n -1 0因此， H (x ) 满足条件 x n = 1的最小值为a .………………… 3 分六、(本题满分 12 分) 设函数 f (x , y ) 在区域 D = {(x , y ) x 2 + y 2 ≤ a 2}上具有一阶连续偏导数，且满足 f (x , y )⎡ ∂ 2 = a 2，以及 max ⎢⎛ ∂f ⎫2⎤ +⎥ = a 2 ，其x 2 + y 2 =a 2中a > 0 . 证明： ⎰⎰ f (x , y )d x d y ≤ 4π a 4 .( x , y )∈D⎪ ⎢⎣⎝ ⎭ ⎪ ⎝ ⎭ ⎥⎦D3 【解】在格林公式P (x , y )d x + Q (x , y )d y = ⎛ ∂Q - ∂P ⎫d x d y ⎰ ⎰⎰ ∂x ∂y ⎪C D ⎝⎭中，依次取 P = yf (x , y ) ， Q = 0 和取 P = 0 ， Q = xf (x , y ) ，分别可得⎰⎰ f (x , y )d x d y = - ⎰ yf (x , y )d x - ⎰⎰ y ∂fd x d y ， D C D ∂y⎰⎰ f (x , y )d x d y = ⎰ xf (x , y )d y - ⎰⎰ x ∂fd x d y .两式相加，得D C D ∂x= a 2 -+- 1⎛ ∂f +∂f ⎫= + ⎰⎰ f (x , y )d x d y2⎰ y d x x d y 2 ⎰⎰ x∂x y ∂y ⎪d x d y I 1 I 2DCD ⎝ ⎭ ………………… 4 分a224对 I 1 再次利用格林公式，得 I 1 =2⎰ - y d x + x d y = a ⎰⎰ d x d y = π a ， …… 2 分CD对 I 2 的被积函数利用柯西不等式，得I 2 ≤ 1⎰⎰ x∂f+ yd x d y ≤1 ⎰⎰d x d y∂f ∂y2 D ∂x2 Dn n =1≤ax d y = 1π a 4 ，………………… 4 分2 D3因此，有⎰⎰f (x , y )d x d y ≤ π a 4 + 1 π a 4= 4 π a 4 . …………… 2 分D七、(本题满分 12 分) 设0 < a 3 3ln 1< 1 ,n = 1, 2, ，且lim a n= q (有限或+ ∞ ).nn →∞ln n∞∞(1)证明：当q > 1 时级数∑ a n 收敛，当q < 1 时级数∑ a n 发散；n =1n =1(2)讨论q = 1 时级数∑ a n 的收敛性并阐述理由.n =1证: (1)若 q > 1 ，则∃ p ∈ R ,s.t. q > p > 1 .根据极限性质， ∃N ∈ Z + ，s.t.ln 1a n1 ∞1∞∀n > N ，有ln n> p ，即a n <n p，而 p > 1时∑n p 收敛,所以∑ a n 收敛.n =1n =1若q < 1 ，则 ………………… 3 分∃ p ∈ R ，s.t. q < p < 1. 根据极限性质，∃N ∈ Z + ,s.t. ∀n > N ，ln 1a n1∞1∞有 ln n < p ，即a n > n p ，而 p < 1时∑ n p 发散,所以∑ a n 发散. n =1 n =1………………… 3 分(2) 当q = 1 时，级数∑ an可能收敛，也可能发散.n =11∞例如： a n = 满足条件，但级数∑ a n 发散； ………………… 3 分n =11 ∞又如： a n =n ln 2 n满足条件，但级数∑ a n 收敛. ………………… 3 分∞∞。

2018年第九届决赛

一.填空题（每小题6分，共30分）
4. 满足 du(t) u(t) 1 u(t)dt及u(0) 1,则可微函数u(t) ________ .
dt
0
方程 du(t ) u(t ) 1 u(t )dt两边对t求导得微分方程
dt
0
u(t ) u(t ) u(t ) C1et C2
u(0) 1 u(t ) C1et 1 C1 u(0) C1
x3 ).
证明 : 令
F ( x) arctan x
x
f (t)dt
1
f ( x)dx
0
80
则F (0)
1
f ( x)dx,
F (1)
1 f ( x)dx,且F ( x)在[0,1]上可导
80
80
F (0) F (1) 0
证明 : 根据介值定理存在x3 (0,1),使F ( x3 ) 0
b y cda,cz dab,d w abc,则行列式 1 y 1 1 ___0_____ . 1 1 z 1 1 1 1 w
二（11分）设函数 f ( x)在(0,1)内连续且存在两两互异的点
x1 , x2 , x3 , x4 (0,1),使得
f ( x1 ) f ( x2 ) x1 x2
1
e
0
e
1
0 ln xdx 1
五.(12分）设 x ( x1, x2 , n 2.
n
n1
, xn )T Rn , H ( x) xi2 xi xi1,
i 1
i 1
(1)证明：对于任意的非零x Rn , H ( x) 0;
(2)求H ( x)满足条件xn 1的最小值.
1
1 2

高等数学统考卷11-12届附答案

高等数学统考卷 1112届附答案一、选择题（每题1分，共5分）1. 下列函数中，哪个函数是奇函数？A. y = x^3B. y = x^2C. y = x^4D. y = |x|A. 积分的上下限互换，积分值不变B. 被积函数乘以常数，积分值也乘以该常数C. 积分区间可加性D. 积分中值定理3. 下列极限中，哪个是正确的？A. lim(x→0) (sin x) / x = 0B. lim(x→0) (1 cos x) / x^2 = 1C. lim(x→∞) (1 / x) = 0D. lim(x→∞) (x^2 1) / x = 1A. ∫∫(x^2 + y^2) dxdyB. ∫∫xy dxdyC. ∫∫x dxdyD. ∫∫y dxdy5. 下列级数中，哪个是收敛的？A. 1 + 1/2 + 1/3 + 1/4 + …B. 1 1/2 + 1/3 1/4 + …C. 1 + 2/3 + 4/9 + 8/27 + …D. 1 + 1/2 + 1/4 + 1/8 + …二、判断题（每题1分，共5分）1. 高斯公式可以用来计算曲面积分。

（）2. 泰勒公式可以用来近似计算函数值。

（）3. 无穷小量相乘仍为无穷小量。

（）4. 拉格朗日中值定理是罗尔定理的推广。

（）5. 偏导数连续必可微。

（）三、填空题（每题1分，共5分）1. 函数f(x) = e^x 在x = 0处的导数值为______。

2. 曲线y = x^3 在点(1, 1)处的切线方程为______。

3. 若f(x, y) = x^2 + y^2，则f_x(1, 2) =______。

4. 设A为矩阵，若|A| = 0，则A为______矩阵。

5. 空间曲线r(t) = (cos t, sin t, t) 在t = π/2处的切线方向向量为______。

四、简答题（每题2分，共10分）1. 简述罗尔定理的内容。

2. 解释复合函数求导法则。

3. 举例说明什么是隐函数。

历年全国大学生数学竞赛初赛真题全(数学类)十一届试卷高清无水印(2009-2019)

（数学类）试卷第一题：(15分)求经过三平行直线1:L x y z ==，2:11L x y z -==+，3:11L x y z =+=-的圆柱面的方程.第二题：(20分)设n nC ⨯是n n ⨯复矩阵全体在通常的运算下所构成的复数域C 上的线性空间，12100010*******n n n a a a F a --⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪- ⎪⎝⎭. (1)假设111212122212n n n n nn aa a a a a A a a a ⎛⎫ ⎪ ⎪⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭，若AF FA =，证明： 121112111n n n n A a F a F a F a E ---=++++ ；(2)求n nC⨯的子空间{}()|n n C F X C FX XF ⨯=∈=的维数.第三题：(15分)假设V 是复数域C 上n 维线性空间（0n >），,f g 是V 上的线性变换. 如果fg gf f -=，证明：f 的特征值都是0，且,f g 有公共特征向量.第四题：(10分)设{}()n f x 是定义在,a b ⎡⎤⎢⎥⎣⎦上的无穷次可微的函数序列且逐点收敛，并在,a b ⎡⎤⎢⎥⎣⎦上满足()nf x M '≤.（1）证明{}()n f x 在,a b ⎡⎤⎢⎥⎣⎦上一致收敛；（2）设()lim ()n n f x f x →∞=，问()f x 是否一定在,a b ⎡⎤⎢⎥⎣⎦上处处可导, 为什么？第五题：(10分)设320sin d sin n nt a t t t π=⎰，证明11nn a ∞=∑发散.第六题：(15分)(,)f x y 是{}22(,)|1x y x y +≤上二次连续可微函数，满足222222f f x y x y ∂∂+=∂∂，计算积分221d d x y I x y +≤⎛⎫=⎰⎰第七题：(15分)假设函数()f x 在[0,1]上连续，在()0,1内二阶可导，过点(0,(0))A f ，与点(1,(1))B f 的直线与曲线()y f x =相交于点(,())C c f c ，其中01c <<. 证明：在 ()0,1内至少存在一点ξ，使()0f ξ''=.（数学类）试卷一、（本题共10分）设(0,1)ε∈，0x a =，1sin 0,1,2).n n x a x n ε+=+= （证明lim n n x ξ→+∞=存在，且ξ为方程sin x x a ε-=的唯一根.二、（本题共15分）设01030002010000B ⎛⎫⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭. 证明2X B =无解，这里X 为三阶未知复方阵.三、（本题共10分）设2D ⊂ 是凸区域，函数(,)f x y 是凸函数. 证明或否定：(,)f x y 在D 上连续.注：函数(,)f x y 为凸函数的定义是(0,1)α∀∈以及1122(,),(,)x y x y D ∈，成立12121122((1),(1))(,)(1)(,)f x x y y f x y f x y αααααα+-+-≤+-.四、（本题共10分）设()f x 在0,1⎡⎤⎢⎥⎣⎦上黎曼(Riemann)可积，在1x =可导，(1)0,f =(1)f a '=. 证明：120lim ()d .n n n x f x x a →+∞=-⎰五、（本题共15分）已知二次曲面∑（非退化）过以下九点：(1,0,0),(1,1,2),(1,1,2),(3,0,0),(3,1,2),(3,2,4),(0,1,4),(3,1,2),(5,8).A B C D E F G H I ------问∑是哪一类曲面？六、（本题共20分）设A 为n n ⨯实矩阵（未必对称），对任一n 维实向量T 1(,,),0n A ααααα=≥ （这里T α表示α的转置），且存在n 维实向量β使得T 0A ββ=. 同时对任意n 维实向量x 和y ，当T 0xAy ≠时有TT 0xAy yAx +≠. 证明：对任意n 维实向量v ，都有T0.vA β=七、(本题共10分) 设f 在区间0,1⎡⎤⎢⎥⎣⎦上黎曼(Riemann)可积，0 1.f ≤≤ 求证：对任何0ε>，存在只取值为0和1的分段（段数有限）常值函数()g x ，使得,0,1αβ⎡⎤⎡⎤∀⊆⎢⎥⎢⎥⎣⎦⎣⎦，()()().f x g x dxβαε-<⎰八、(10分) 已知:(0,)(0,)ϕ+∞→+∞是一个严格单调下降的连续函数，满足0lim (),t t ϕ+→=+∞且10()d ()d ,t t t t a ϕϕ+∞+∞-==<+∞⎰⎰其中1ϕ-表示ϕ的反函数. 求证：32212001()d ()d .2t t t t a ϕϕ+∞+∞-⎡⎤⎡⎤+≥⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰（数学类）试卷一、（本题15分）已知四点(1,2,7),(4,3,3),(5,1,0).-试求过这四点的球面方程。

第九届全国大学生数学竞赛参考答案(非数学类)

2017年数学竞四川赛区（非数学类）试题评分标准及参考答案一 1. 已知可导函数满足, 则()f x解：在方程两边求导得'()c o s +()s i n f x x f x x =,'()+()tan sec f x f x x x =.从而tan tan ()sec xdx xdx f x e xe dx c -⎛⎫⎰⎰=+ ⎪⎝⎭⎰l nc o sl n c o s211==cos cos cos x x e e dx c x dx c x x --⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎰⎰ ()=c o s t a n =s i n co s xx c x cx ++ 由于(0)1f =，故()sin cos f x x x =+。

2．求()n n n +∞→22sin lim π解由于 ()=+n n 22sin π()ππn n n -+22sin=2sin 1⎛⎫→。

3. 设(,)w f u v =具有二阶连续偏导数，且==+u x cy v x cy -，，其中c 为非零常数。

则21xx yy w w c-=_________。

解: 12+x w f f =，1112222xx w f f f =++，21()y w c f f =-，()()()22111122122111222=2yy w cf f c cf cf cf cf c f f f y∂=-=--+-+∂。

所以1221=4xx yy w w f c-。

4. 设()f x 有二阶导数连续，且(0)'(0)0,"(0)6f f f ===，则24(s i n )l i m x f xx →=______解：21()(0)'(0)"()2f x f f x f x ξ=++，所以241(sin )"()sin 2f x f x ξ=。

这样244400(sin )"()sin lim=lim 32x x f x f xx x ξ→→=。

大学生高等数学竞赛试题汇总及答案

前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

）2009-2010年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(16/15，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，⎰-=12d 1u uu （*）令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f ,则=)(x f ____________.解:令⎰=2d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。

因此3103)(2-=x x f 。

3．曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解:因平面022=-+z y x 的法向量为)1,2,2(-，而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面2222-+=y x z 平行平面 022=-+z y x 的切平面方程是0122=--+z y x 。

高等数学竞赛模拟试题【精品】

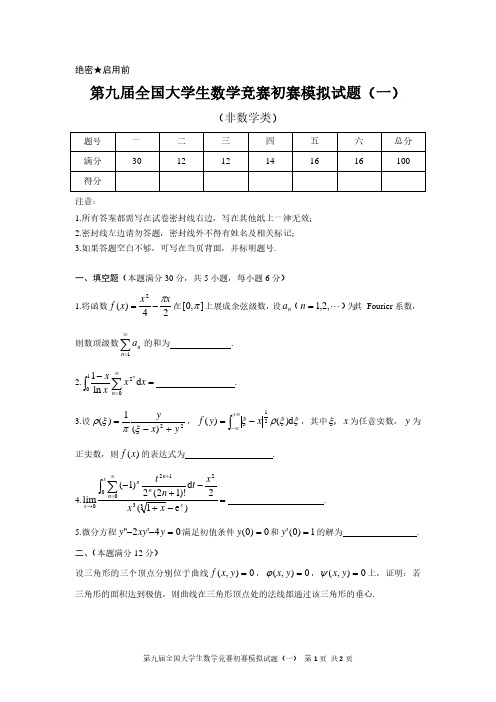
1 1 a + b f (b) = f (a) + (b − a ) f ' (a ) + f ' (b) + 4 f ' − (b − a ) 5 f (5) (ξ ). 6 2 2880
四、（本题满分 14 分）求经过三条平行直线 L1 : x = y = z ， L2 : x − 1 = y = z + 1 ， L3 : x = y + 1 = z − 1 的圆柱面的方程.
（2）求
∑
k =1
1
∏ ( k + m)
m =0
2017
.
第九届全国大学生数学竞赛初赛模拟试题（二）第 1 页共 2 页
三、（本题满分 14 分）计算三重积分
∫∫∫ xyzdxdydz ，其中 Ω 位于第一象限，由下列曲面所围成：x
Ω
2
+ y 2 = mz ，
x 2 + y 2 = nz ， xy = a 2 ， xy = b 2 ， y = αx ， y = βx ，其中 0 < a < b ， 0 < α < β ，
.
(−1) n 2.使级数 ∑ ln 1 + n p n=2
( p > 0) 条件收敛的 p 的取值范围为
.
3.设 f (u , v) 具有一阶连续偏导数，且满足 f (tu , tv ) = t 2 f (u , v) ， f (1,2) = 0, f u (1,2) = 3 ，
n →∞
. .
2.设 f ( x) =
∫
1
0
ln x − t dt ，则 max f ( x) =

数学竞赛11试题及答案

数学竞赛11试题及答案数学竞赛试题及答案试题一：计算下列表达式的值：\[ 2^3 + 3^2 - 4 \]试题二：解方程：\[ x^2 - 5x + 6 = 0 \]试题三：如果一个直角三角形的两条直角边分别为3和4，求斜边的长度。

试题四：一个圆的半径为7，求这个圆的面积。

试题五：一个数列的前三项为2, 3, 5，如果这个数列是等差数列，求第四项。

试题六：证明：对于任意正整数\( n \)，\( 1^3 + 2^3 + ... + n^3 = (1 + 2 + ... + n)^2 \)。

试题七：如果一个函数\( f(x) = ax^2 + bx + c \)在点\( x = 2 \)处取得极值，求\( b \)的值。

试题八：在平面直角坐标系中，点A(1,2)和点B(4,6)，求直线AB的斜率。

试题九：一个长方体的长、宽、高分别为2, 3, 4，求这个长方体的体积。

试题十：如果一个函数\( g(t) = t^3 - 6t^2 + 11t - 6 \)在区间\( [1, 3] \)上单调递增，求\( t \)的取值范围。

试题十一：求圆心在原点，半径为5的圆的方程。

答案：试题一：\( 2^3 + 3^2 - 4 = 8 + 9 - 4 = 13 \)试题二：\( (x - 2)(x - 3) = 0 \)，所以\( x = 2 \)或\( x = 3 \)试题三：根据勾股定理，斜边长度为\( \sqrt{3^2 + 4^2} = 5 \)试题四：圆的面积为\( \pi r^2 = 49\pi \)试题五：等差数列的公差为\( 3 - 2 = 1 \)，所以第四项为\( 5 + 1 = 6 \)试题六：根据等差数列求和公式，左边为\( \frac{n(n+1)}{2} \)的平方，右边也是\( \frac{n(n+1)}{2} \)的平方，两者相等。

试题七：\( f(x) \)的导数\( f'(x) = 2ax + b \)，在\( x = 2 \)处导数为0，所以\( 4a + b = 0 \)，如果\( a \neq 0 \)，则\( b = -4a \)。

全国大学生数学竞赛赛试题(1-9届)

全国大学生数学竞赛赛试题(19届)一、试题概述全国大学生数学竞赛是由中国数学会主办的一项面向全国高校本科生的数学竞赛。

自2009年首届竞赛举办以来，已成功举办九届。

竞赛旨在激发大学生对数学的兴趣，提高他们的数学素养和综合能力，同时选拔优秀数学人才。

每届竞赛均设有预赛和决赛两个阶段，预赛为全国范围内的统一考试，决赛则在全国范围内选拔出的优秀选手中进行。

二、竞赛内容全国大学生数学竞赛的试题内容主要包括高等数学、线性代数、概率论与数理统计等基础数学知识。

试题难度适中，既考查参赛选手的基础知识掌握程度，又注重考查他们的综合应用能力和创新思维能力。

三、竞赛特点1. 公平公正：竞赛试题由全国数学教育专家命题，确保试题质量，保证竞赛的公平公正。

2. 注重基础：竞赛试题主要考查参赛选手对基础数学知识的掌握程度，有利于引导大学生重视基础数学学习。

3. 综合应用：试题设计注重考查参赛选手的综合应用能力，培养他们的创新思维和实践能力。

4. 激发兴趣：竞赛通过丰富多样的试题形式，激发大学生对数学的兴趣，培养他们的数学素养。

四、竞赛组织全国大学生数学竞赛由各省、市、自治区数学会负责组织本地区的预赛，中国数学会负责全国范围内的决赛。

竞赛组织工作包括试题命制、竞赛宣传、选手选拔、竞赛监督等环节，确保竞赛的顺利进行。

五、竞赛影响全国大学生数学竞赛自举办以来，受到了广大高校和数学爱好者的广泛关注和热情参与。

竞赛不仅为优秀数学人才提供了展示才华的舞台，也为全国高校数学教育提供了有益的借鉴和启示。

通过竞赛，大学生们不仅提高了自己的数学水平，还结识了许多志同道合的朋友，拓宽了视野，激发了学习热情。

六、竞赛历程自2009年首届全国大学生数学竞赛举办以来，竞赛规模逐年扩大，影响力不断提升。

参赛选手涵盖了全国各大高校的本科生，包括综合性大学、理工科院校、师范院校等。

随着竞赛的普及，越来越多的学生开始关注并参与其中，竞赛逐渐成为衡量高校数学教育水平和学生数学素养的重要标志。

大学生高等数学竞赛试题汇总与答案

=。。。
上式可以得到一个微分方程，求解即可。
四、（15分）设
n
a0,Sa,证明：
nnk
k1
（1）当1时，级数
a
n
S
nn
1
收敛；
（2）当1且()
sn时，级数
n
a
n
S
nn
1
发散。
解：
（1）
a>0,
n
s单调递增
n
当
n1
a收敛时，
n
aa
nn
ss
n1
，而
a
n
s
1
收敛，所以
a
n
s
n
收敛；
当
n1
a发散时，lim
n
解：
（1）椭球上一点P(x,y,z)到直线的距离
由轮换对称性，
（2）abc
当1时，
4
22
Iabc(ab)
max
15
当1时，
4
22
Iabc(bc)
min
15
六、(15分)设函数(x)具有连续的导数，在围绕原点的任意光滑的
简单闭曲线C上，曲线积分
c
2xydx(x)dy
42
xy
的值为常数。
（1）设L为正向闭曲线
1kk...
12
使得
k
i
1a1
n
2
s
kn
i
成立，所以
k
N
1
a
n
s
n
N
1
2
当n时，N，所以
a
n
s
nn
1
发散
五、（15分）设l是过原点、方向为(,,)，（其中

历届全国大学生高等数学竞赛真题及答案非数学类.docx

前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

）2009年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分，共20分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=10210d 1)ln (1ln d )d ln 1d 1ln (u u u u u u u u u u v v u uv u u u u u ⎰-=12d 1u uu （*）令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 151651322153=⎥⎦⎤⎢⎣⎡+-=t t t 2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解:令⎰=20d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。

因此3103)(2-=x x f 。

3．曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解:因平面022=-+z y x 的法向量为)1,2,2(-，而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。

历届全国大学生高等数学竞赛真题及答案非数学类.docx

前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

）2009年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分，共20分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解:令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=10210d 1)ln (1ln d )d ln 1d 1ln (u u u u u u u u u u v v u uv u u u u u ⎰-=12d 1u uu （*）令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 151651322153=⎥⎦⎤⎢⎣⎡+-=t t t 2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解:令⎰=20d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。

因此3103)(2-=x x f 。

3．曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解:因平面022=-+z y x 的法向量为)1,2,2(-，而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。

历届全国大学生数学竞赛真题与答案非数学类

高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

）2009 年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5 分，共 20 分）(xy) ln(1 y)1．计算xdxdy ____________ ，其中区域 D 由直线 x y 1与两D1 x y坐标轴所围成三角形区域.1解 : 令 xy u, x v ，则 xv, y u v ，11( x y) ln(1y ) Dx dxdy1 xyu ln u u ln v dudvD1 u1u ln uu uu(udvln vdv)du0 1 01 u 0 1u 2 ln u u(u ln u u) 01 u 1 u du1u 2du（ * ）1 u令 t 1 u ，则u 1 t 2du2tdt ， u 21 2t 2t 4 ， u(1 u) t 2 (1 t)(1 t) ，(*)0 ( 12t2t 4)d t2112 t31 t 512t 4)dt 2 t2 (1 2t352．设 f ( x) 是连续函数，且满足f (x)3x 22f (x)dx16152 , 则 f (x)____________.令 A 23x2A 2 ，解:f (x)dx ，则 f ( x)A 2A 2)d x 82(A 2)4 2A ,( 3x 2解得 A4 。

因此 f (x) 3x 2 10 。

3 3 ．曲面 z x 2y 2 2 平行平面 2x 2 y z0 的切平面方程是 __________. 32解: 因平面2x2 yz 0 的法向量为 (2,2,1) ，而曲面 z x 2 y 22 在2 ( x 0 , y 0 ) 处的法向量为 ( z x (x 0 , y 0 ), z y ( x 0 , y 0 ), 1)，故( z x ( x 0 , y 0 ), z y ( x 0 , y 0 ), 1) 与 ( 2,2, 1) 平行，因此，由 z x x ， z y 2y 知2 z x ( x 0 , y 0 ) x 0 ,2 z y (x 0 , y 0 )2y 0 ，即 x 02, y 0 1 ，又 z( x 0 , y 0 ) z( 2,1) 5 ，于是曲面 2x 2yz 0 在( x 0 , y 0 , z( x 0 , y 0 )) 处的切平面方程是 2( x 2) 2( y 1) ( z5)0 ，即曲面zx 2 y 2 2 平行平面22x 2 y z 0 的切平面方程是 2x 2y z 1 0 。