14.3.1提公因式法同步练习含答案
八年级数学人教版上册同步练习提公因式法(解析版)

14.3.1提公因式法一、单选题1.在3257x x x k +++中,若有一个因式为(2)x +,则k 的值为( )A .2B .2-C .6D .6- 【答案】A【分析】根据因式分解的意义可设()()322572x x x k x x mx n +++=+++,再利用整式乘法计算()()22x x mx n +++后得()()32222x m x n m x n +++++,即可根据因式分解与整式乘法的关系求解.【详解】设()()322572x x x k x x mx n +++=+++, ∵()()22x x mx n +++ 322222x mx nx x mx n =+++++()()32222x m x n m x n =+++++3257x x x k =+++,∴25m ,27n m +=, 2k n =,解得3m =,1n =,2k =.故选:A .【点评】本题考查了因式分解的意义,掌握因式分解与整式乘法的关系是解题的关键.2.下列各式由左边到右边是因式分解且分解结果正确的是( )A .()3a 43a 12-=-B .()()24x 94x 34x 3-=+-C .()22x 4x 4x 2-+=-D .()3224a 6a 2a 2a 2a 3a ++=+ 【答案】C【分析】根据因式分解的意义求解即可.【详解】A 、()34312a a -=-是整式的乘法,故A 不符合题意;B 、()()2492323x x x -=+-,原式分解不正确,故B 不符合题意;C 、()22442x x x -+=-,分解正确,故C 符合题意;D 、()3224622231a a a a a a ++=++,原式分解不正确,故D 不符合题意;故选:C .【点评】本题考查了因式分解的意义,利用因式分解是把一个多项式转化成几个整式积的形式.3.下列从左到右是因式分解的是( ).A .(a +b )(a -b )=a 2-b 2B .(a +b )2 =a 2+2ab +b 2C .(x +2)(x -5)=x 2-3x +10D .x 2+2x -15=(x -3)(x +5) 【答案】D【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【详解】A 、是整式的乘法,故A 错误;B 、是整式的乘法,故B 错误;C 、是整式的乘法,故C 错误;D 、符合因式分解,故D 正确;故选:D .【点评】本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式,注意因式分解与整式乘法的区别.4.下列等式中,从左到右的变形正确的是( )A .()22242x x x ++=+B .()()2444x x x -=+-C .()222244x y x xy y +=++D .()()2x 2x 3x 6+-=-【答案】C【分析】分别对各选项进行变形,然后对照进行判断即可得到答案.【详解】A 、()22241+3x x x ++=+,原选项变形错误,故不符合题意;B 、()()2422x x x -=+-,原选项变形错误,故不符合题意;C 、()222244x y x xy y +=++,原选项变形正确,故符合题意;D 、2(2)(3)6x x x x +=---,原选项变形错误,故不符合题意;故选:C .【点评】此题主要考查了整式的乘法和因式分解,熟练掌握运算法则是解答此题的关键.5.对于①2(2)(1)2x x x x +-=+-,②4(14)x xy x y -=-,从左到右的变形,表述正确的是( ) A .都是因式分解B .都是乘法运算C .①是因式分解,②是乘法运算D .①是乘法运算,②是因式分解【答案】D 【分析】根据因式分解的定义(把一个多项式化成几个整式积的形式,叫因式分解,也叫分解因式判断即可.将多项式×多项式变得多项式,是乘法运算.【详解】①2(2)(1)2x x x x +-=+-,从左到右的变形是整式的乘法;②4(14)x xy x y -=-,从左到右的变形是因式分解;所以①是乘法运算,②因式分解.故选:D .【点评】此题考查了因式分解与乘法运算的定义的认识,解题的关键是掌握因式分解及乘法运算的定义. 6.下列各式由左边到右边的变形中,是分解因式的为( )A .2105525x x x x x -=⋅-B .()a x y ax ay +=+C .()22442x x x -+=-D .()()2163443x x x x x -+=-++ 【答案】C【分析】将多项式写成整式的积的形式,叫做将多项式分解因式,根据定义解答.【详解】A 、2105525x x x x x -=⋅-,不是分解因式;B 、()a x y ax ay +=+,不是分解因式;C 、()22442x x x -+=-,是分解因式;D 、()()2163443x x x x x -+=-++,不是分解因式; 故选:C .【点评】此题考查多项式的分解因式,熟记定义及分解因式后式子的特点是解题的关键.7.下列各式从左到右的变形中,属于分解因式的是( )A .a (m+n )=am+anB .10x 2﹣5x =5x (2x ﹣1)C .x 2﹣16+6x =(x+4)(x ﹣4)+6xD .a 2﹣b 2﹣c 2=(a ﹣b )(a+b )﹣c 2【答案】B【分析】根据分解因式的定义逐个判断即可.【详解】A .等式由左到右的变形属于整式乘法,不属于分解因式,故本选项不符合题意;B .等式由左到右的变形属于分解因式,故本选项符合题意;C .等式由左到右的变形不属于分解因式,故本选项不符合题意;D .等式由左到右的变形不属于分解因式,故本选项不符合题意;故选:B .【点评】此题考查了因式分解的定义.掌握其定义是解答此题的关键.8.(﹣2)2019+(﹣2)2020等于( )A .﹣22019B .﹣22020C .22019D .﹣2【答案】C【分析】直接提取公因式(−2)2019,进而计算得出答案.【详解】(−2)2019+(−2)2020=(−2)2019×(1−2)=22019.故选:C .【点评】此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.二、填空题目9.多项式39x -,29x -与269x x -+的公因式为______.【答案】3x -【分析】根据公因式定义,对各选项整理然后即可选出有公因式的项.【详解】因为3x ﹣9=3(x ﹣3),x 2﹣9=(x +3)(x ﹣3),x 2﹣6x +9=(x ﹣3)2,所以多项式3x ﹣9,x 2﹣9与x 2﹣6x +9的公因式为(x ﹣3).故答案:3x -.【点评】此题考查的是公因式的定义,找公因式的要点是:(1)公因式的系数是多项式各项系数的最大公约数;(2)字母取各项都含有的相同字母;(3)相同字母的指数取次数最低的.在提公因式时千万别忘了“﹣1”.10.已知22()()24x my x ny x xy y -+=+-,则22m n mn -的值为______.【答案】8.-【分析】由22()()24x my x ny x xy y -+=+-可得()222224,x n m xy mny x xy y +--=+-可得:2,4,n m mn -=-=-即2,4,m n mn -=-=再把22m n mn -分解因式,再整体代入求值即可.【详解】 22()()24x my x ny x xy y -+=+-,222224,x nxy mxy mny x xy y ∴+--=+-()222224,x n m xy mny x xy y ∴+--=+-2,4,n m mn ∴-=-=-2,4,m n mn ∴-=-=∴ ()22m n m n mn mn =--()428.=⨯-=-故答案为:8.-【点评】本题考查的是整式的乘法,多项式的恒等,因式分解的应用,掌握以上知识是解题的关键. 11.多项式22y y m ++因式分解后有一个因式是(1)y -,则m =_______.【答案】3-【分析】由于x 的多项式y 2+2y+m 分解因式后有一个因式是(y-1),所以当y=1时多项式的值为0,由此得到关于m 的方程,解方程即可求出m 的值.【详解】∵多项式y 2+2y+m 因式分解后有一个因式为(y-1),∵当y=1时多项式的值为0,即1+2+m=0,解得m=-3.故答案为:-3.【点评】本题考查了因式分解的意义,有公因式时,要先考虑提取公因式;注意运用整体代入法求解. 12.已知x 2-3x -1=0,则2x 3-3x 2-11x +1=________.【答案】4【分析】根据x 2-3x -1=0可得x 2-3x =1,再将所求代数式适当变形后分两次整体代入即可求得值.【详解】∵x 2-3x -1=0,∴x 2-3x =1,∴3223111x x x --+=223132611x x x x -+-+=()22233111x x x x x -+-+将x 2-3x =1代入原式=221113x x x +-+=23)13(x x -+将x 2-3x =1代入原式=314+=,故答案为:4.【点评】本题考查代数式求值,因式分解法的应用.解决此题的关键是掌握“降次”思想和整体思想.三、解答题13.仔细阅读下面例题:例题:已知二次三项式25x x m ++有一个因式是x +2,求另一个因式以及m 的值.解:设另一个因式px +n ,得25x x m ++=(x +2)(px +n ),对比等式左右两边x 的二次项系数,可知p =1,于是25x x m ++=(x +2)(x +n ).则25x x m ++=2x +(n +2)x +2n ,∴n +2=5,m =2n ,解得n =3,m =6,∴另一个因式为x +3,m 的值为6依照以上方法解答下面问题:(1)若二次三项式2x ﹣7x +12可分解为(x ﹣3)(x +a ),则a = ;(2)若二次三项式22x +bx ﹣6可分解为(2x +3)(x ﹣2),则b = ;(3)已知代数式23x +2x +kx ﹣3有一个因式是2x ﹣1,求另一个因式以及k 的值.【答案】(1)-4;(2)-1;(3)另一个因式为2x +x +3,k 的值为5.【分析】(1)仿照题干中给出的方法计算即可;(2)仿照题干中给出的方法计算即可;(3)设出另一个因式为(2ax bx c ++),对比两边三次项系数可得a =1,再参照题干给出的方法计算即可.【详解】(1)∵2(3)()33x x a x x ax a -+=-+-=2(3)3x a x a +--=2712x x -+.∴a ﹣3=﹣7,﹣3a =12,解得:a =﹣4.(2)∵2(23)(2)2346x x x x x +-=+--=226x x --.=226x bx +-.∴b =﹣1.(3)设另一个因式为(2ax bx c ++),得32223(21)()x x kx x ax bx c ++-=-++.对比左右两边三次项系数可得:a =1.于是32223(21)()x x kx x x bx c ++-=-++.则3232232232222(21)(2)x x kx x x bx bx cx c x b x c b x c ++-=-+-+-=+-+--.∴﹣c =﹣3,2b ﹣1=1,2c ﹣b =k .解得:c =3,b =1,k =5.故另一个因式为23x x ++,k 的值为5.【点评】本题以阅读材料给出的方法为背景考查了因式分解、整式乘法、合并同类项等知识,熟练掌握以上知识是解题关键.14.解答下列各题:(1)计算:()()()22x 12x 52x 5+-+-(2)分解因式:()225m 2x y 5mn --. 【答案】(1)426x +;(2)()()5m 2x y+n 2x y n ---【分析】(1)利用完全平方公式和平方差公式分别计算前后两部分,然后进行加减运算即可;(2)先提取公因式5m ,再利用平方差公式计算.【详解】(1)原式2241=4425x x x +++-=426x +(2)原式()22=5m 2x y n -⎡⎤-⎣⎦()()=5m 2x y+n 2x y n ---【点评】本题考查整式的混合运算和因式分解,解题的关键是熟练掌握完全平方公式和平方差公式的法则. 15.将下列各式因式分解:(1)324x xy -;(2)(x ﹣y )2x +6xy (y ﹣x )+9(x ﹣y )2y .【答案】(1)x (x+2y )(x-2y );(2)(x ﹣y )2(3)x y -.【分析】(1)先提取公因式x ,后变形成为22(2)x y -,用平方差公式分解即可;(2)先将6xy (y ﹣x )变形为-6xy (x﹣y),后提取公因式,再用完全平方公式分解即可.【详解】(1)324x xy -=22(4)x x y -=22[(2)]x x y -=x (x+2y )(x-2y );(2)(x ﹣y )2x +6xy (y ﹣x )+9(x ﹣y )2y=(x ﹣y )2x -6xy (x ﹣y )+9(x ﹣y )2y=(x ﹣y )(2x -6xy +92y )=(x ﹣y )2(3)x y -.【点评】本题考查了提取公因式法,平方差公式法,完全平方公式法分解因式,熟练掌握先提后套用公式分解因式是解题的关键.16.我们常利用数形结合思想探索整式乘法的一些法则和公式.类似地,我们可以借助一个棱长为a 的大正方体进行以下探索:(1)在大正方体一角截去一个棱长为()<b b a 的小正方体,如图1所示,则得到的几何体的体积为________;(2)将图1中的几何体分割成三个长方体①、②、③,如图2所示,∵BC a =,AB a b =-,CF b =,∴长方体①的体积为()ab a b -.类似地,长方体②的体积为________,长方体③的体积为________;(结果不需要化简)(3)将表示长方体①、②、③的体积相加,并将得到的多项式分解因式的结果为________;(4)用不同的方法表示图1中几何体的体积,可以得到的等式为________.(5)已知4a b -=,2ab =,求33a b -的值.【答案】(1)33a b -;(2)()2b a b -,()2a a b -;(3)()+ab a b -()2b a b -()2+a a b -()()22a b a ab b =-++;(4)()()3322a b a b a ab b -=-++;(5)88.【分析】(1)由大的正方体的体积为3,a 截去的小正方体的体积为3,b 从而可得答案;(2)由,,ED OD b DM a b ===-,,GH HJ a HN a b ===-利用长方体的体积公式直接可得答案; (3)提取公因式-a b ,即可得到答案;(4)由(1)(3)的结论结合等体积的方法可得答案;(5)利用()2222,a b a b ab +=-+先求解22,a b + 再利用()()3322a b a b a ab b -=-++,再整体代入求值即可得到答案.【详解】(1)由大的正方体的体积为3,a 截去的小正方体的体积为3,b所以截去后得到的几何体的体积为:33,a b -故答案为:33.a b -(2),,ED OD b DM a b ===-由长方体的体积公式可得:长方体②的体积为()2b a b -,,,GH HJ a HN a b ===-所以长方体③的体积为()2,aa b - 故答案为:()2b a b -,()2.a a b -(3)由题意得:()+ab a b -()2b a b -()2+a a b -()()22.a b a ab b =-++故答案为:()+ab a b -()2b a b -()2+a a b -()()22.a b a ab b =-++(4)由(1)(3)的结论,可以得到的等式为:()()3322.a b a b a ab b -=-++故答案为:()()3322.a b a b a ab b -=-++(5) 4a b -=,2ab =,()222216420,a b a b ab ∴+=-+=+=()()3322a b a b a ab b -=-++,()33420288.a b ∴-=⨯+=【点评】本题考查的是完全平方公式的变形,提公因式分解因式,代数恒等式的几何意义,掌握利用不同的方法表示同一个几何体的体积得到代数恒等式,以及应用得到的恒等式解决问题是解题的关键. 17.已知7,12a b ab -==-(1)求22ab a b -的值(2)求22a b +的值【答案】(1)84;(2)25.【分析】(1)先提取公因式ab -将所求式子因式分解为()ab a b --,再将已知式子的值代入即可得; (2)利用完全平方公式进行变形求值即可得.【详解】(1)7,12a b ab -==-,()22ab a b ab a b ∴-=--,()127=--⨯,84=;(2)7,12a b ab -==-,()249a b ∴-=,22249a b ab ∴+-=,()2221249a b ∴+-⨯-=,2225a b ∴+=.【点评】本题考查了利用因式分解和完全平方公式进行变形求值,熟练掌握因式分解的方法和完全平方公式是解题关键.18.设333201720182019x y z ==,322222x mx nx x mx n =+++++,且=.求111x y z++的值. 【答案】1.【分析】由322222x mx nx x mx n =+++++,可得000x y z >>>,,,令333201720182019x y z k ===,由=变形得=可得2111111x y z x y z ⎛⎫++=++ ⎪⎝⎭因式分解11111110x y z x y z ⎛⎫⎛⎫++++-= ⎪⎪⎝⎭⎝⎭,由000x y z >>>,,,1110x y z ++>,可得1111x y z ++=. 【详解】∵322222x mx nx x mx n =+++++,∴000x y z >>>,,,或,,x y z 一正,两负,333201720182019x y z ==说明x ,y ,z 同号,∴000x y z >>>,,,令333201720182019x y z k ===,=++,=+,=+,111x y z ⎛⎫=++ ⎪⎝⎭,111x y z=++, ∴2111111x y z x y z ⎛⎫++=++ ⎪⎝⎭, ∴11111110x y z x y z ⎛⎫⎛⎫++++-= ⎪⎪⎝⎭⎝⎭, ∵000x y z >>>,,,1110x y z++>, ∴1111x y z++=. 【点评】本题考查立方根条件求值问题,掌握立方根的性质,巧秒恒等变形使实际问题简化,利用等式两边平方,因式分解求出代数式的值是解题关键.19.已知5x y +=,4xy =,求下列各式的值.(1)x y -;(2)33x y xy +.【答案】(1)3±;(2)68【分析】(1)根据完全平方公式的变形公式(x ﹣y )2=(x+y)2﹣4xy 进行求解即可;(2)利用完全平方公式求解x 2+y 2,再将所求代数式因式分解,进而代入数值即可求解.【详解】(1)∵5x y +=,4xy =,∴(x ﹣y )2=(x+y)2﹣4xy=52﹣4×4=9,∴x ﹣y=±3;(2)∵(x+y )2= x 2+y 2+2xy ,∴x 2+y 2=52﹣2×4=17,∴33x y xy +=xy(x 2+y 2)=4×17=68.【点评】本题考查代数式求值、完全平方公式、平方根、因式分解、有理数的混合运算,熟记完全平方公式,灵活运用公式是解答的关键.20.仔细阅读下面的例题:例题:已知二次三项式25x x m ++有一个因式是2x +,求另一个因式及m 的值.解:设另一个因式为x n +,得25(2)()x x m x x n ++=++,则225(2)2x x m x n x n ++=+++,25n ∴+=,2m n =,解得3n =,6m =,∴另一个因式为3x +,m 的值为6.依照以上方法解答下列问题:(1)若二次三项式254x x -+可分解为(1)()x x a -+,则a =________;(2)若二次三项式226x bx +-可分解为(23)(2)x x +-,则b =________;(3)已知二次三项式229x x k +-有一个因式是21x -,求另一个因式以及k 的值.【答案】(1)4-;(2)1-;(3)另一个因式为5x +,k 的值为5.【分析】(1)将(1)()x x a -+展开,根据所给出的二次三项式即可求出a 的值;(2)(2x +3)(x ﹣2)展开,可得出一次项的系数,继而即可求出b 的值;(3)设另一个因式为(x +n ),得2x 2+9x ﹣k =(2x ﹣1)(x +n ),可知2n ﹣1=9,﹣k =﹣n ,继而求出n 和k 的值及另一个因式.【详解】(1)∵(1)()x x a -+=x 2+(a ﹣1)x ﹣a =254x x -+,∴a ﹣1=﹣5,解得:a =﹣4;故答案是:﹣4(2)∵(2x +3)(x ﹣2)=2x 2﹣x ﹣6=2x 2+bx ﹣6,∴b =﹣1.故答案是:﹣1.(3)设另一个因式为(x+n),得2x2+9x﹣k=(2x﹣1)(x+n),则2x2+9x﹣k=2x2+(2n﹣1)x﹣n,∴2n﹣1=9,﹣k=﹣n,解得n=5,k=5,∴另一个因式为x+5,k的值为5.【点评】本题考查因式分解的意义,解题关键是对题中所给解题思路的理解,同时要掌握因式分解与整式乘法是相反方向的变形,即互逆运算,二者是一个式子的不同表现形式.祝福语祝你考试成功!。
【人教版八年级数学上册同步练习试题及答案】《14.3.1提公因式法》同步练习及答案

§14.3.1提公因式法一.精心选一选1.下列各式从左到右的变形中,是因式分解的是()。
A.(x+3)(x-3)=x²-9B.x²+1=x(x+1x )C.3x²-3x+1=3x(x-1)+1D.a²-2ab+b²=(a-b)²2多项式- 6a²b+18a²b³x+24ab2y的公因式是( )A.mx+my和x+yB.3a(x+y)和2y+2xC.3a-3b和6(b-a)D.-2a-2b和 a²-ab4.下列各多项式因式分解错误的是()A.( a-b) ³-(b-a)=(a-b)2(a-b-1)B.x(a-b-c)-y(b+c-a)=(a-b-c)(x+y)C.P(m-n)3-Pq(n-m)3=P(m-n)3(1+q)D.(a-2b)(7a+b)-2(2b-a)2=(a-2b)(5a+5b)5.将多项式(3a-4b)(7a-8b)-(11a-12b)(8b-7a)分解因式正确的结果是()A.8(7a-8b)(a-b)B.2(7a-8b) ²C.8(7a-8b)(b-a)D.-2(7a-8b) ²6已知多项式3x²-mx+n分解因是的结果为(3x+2)(x-1)则,m,n的值分别为()A.m=1 n=-2 B.m-1 n=-2Cm=2 n=-2 D.m=-2 n=-27.多项式(m+1)(m-1)+(m-1)提取公因式(m-1)后,另一个因式为()A.m+1B.2mC.2D.m+28.a是有理数,则整式a²(a²-2)-2a²+4的值()A.不是负数B.恒为正数C.恒为负数D.不等于0二.细心填一填9.分解因式3x(x-2)-(2-x)=10.利用因式分解计算:3.68×15.7-31.4+15.7×0.32=11.分解因式:(x+y)²-x-y=12.已知a+b=9 ab=7 则a²b+ab²=13.观察下列各式:①abx-adx ②2x²y+6xy²③8m³-4m²+1④(p+q)x²y-5x²(p+q)+6(p+q)²⑤(x+y)(x-y)-4b(y+x)-4ab其中可以用提取公因式法分解的因式( )。
14.3.1提公因式法

注意:首项为负,应提出负号。
例题精讲
例4 分解因式:
(1) x( x y) y( x y)
2
(2)5a b( x y) 10a b ( y x)
3 2 4 3
3
把括号看作整体
相同(相反)的括号看作一个整体。
归纳总结
提公因式法:
如果多项式的各项有公因式,可以把这 个公因式提出来,将多项式写成公因式 与另一个因式的乘积的形式。这种分解 因式的方法叫做提公因式法。
.
3.(盐城·中考)因式分解 2a 2 4a ______.
2 【解析】用提公因式法因式分解: a 4 a 2 a (a 2)
2
答案:2a(a-2)
4.写出下列多项式各项的公因式.
(1)ma+mb m
(2)4kx-8ky 4k
(3)5y3+20y2 5y2 ab
(4)a2b-2ab2+ab
提公因式法的一般步骤 :
1、确定提取的公因式; 2、提取公因式。
诊断
小明解的有误吗?
把12x2y+18xy2分解因式 解:原式 =3xy(4x + 6y)
错误
公因式没有提尽, 还可以提出公因式2
正确解:原式=6xy(2x+3y)
注意:公因式要提尽。
小亮解的有误吗?
把3x2 - 6xy+x分解因式
m
4k
5y2
ab 2x
(5) 4x2-8ax+2x
(6) 3(a+b)2-6(a+b)3
3(a+b)2
【例题】
【例1】把8a3b2 + 12ab3c 分解因式. 分析:找公因式 1.系数的最大公约数 2.找相同字母 ab 4
2021最新人教版八年级数学上册第十四章 14.3.1提公因式法 同步练习题( 教师版)

人教版八年级数学上册第十四章14.3.1 提公因式法同步练习题一、选择题1.多项式a2-4a分解因式,结果正确的是(A)A.a(a-4) B.(a+2)(a-2)C.a(a+2)(a-2) D.(a-2)2-42.把2(a-3)+a(3-a)提取公因式a-3后,另一个因式为(A)A.2-a B.a+2 C.a-2 D.-2-a3.下列各式从左边到右边的变形,是因式分解的是(B)A.ab+ac+d=a(b+c)+dB.a2-1=(a+1)(a-1)C.(a+b)2=a2+2ab+b2D.a2b=ab·a4.(2x+a)(2x-a)是下列哪个多项式因式分解的结果(B)A.4x2+a2B.4x2-a2C.-4x2+a2D.-4x2-a25.把多项式x2+ax+b分解因式,得(x+1)(x-3),则a,b的值分别是(B)A.a=2,b=3B.a=-2,b=-3C.a=-2,b=3D.a=2,b=-36.多项式8a3b2+12ab3c的公因式是(C)A.abcB.ab2C.4ab2D.4ab2c7.下列各组式子中没有公因式的是(B)A.4a2bc与8abc2B.a3b2+1与a2b3-1C.b(a-2b)2与a(2b-a)2D.x+1与x2-18.下列多项式中,能用提公因式法因式分解的是(B)A.x2-yB.x2-2xC.x2+y2D.x2-xy+y29.在下列各式中,从左到右的变形正确的是(D)A.y-x=+(x-y)B.(y-x)2=-(x-y)2C.(y-x)3=(x-y)3D.(y-x)4=(x-y)410.-m(m+x)(x-n)与mn(m-x)(n-x)的公因式是(B)A.-mB.m(n-x)C.m(m-x)D.(m+x)(x-n)11.把多项式m2(a-2)+m(2-a)因式分解,结果正确的是(C)A.(a-2)(m2-m)B.m(a-2)(m+1)C.m(a-2)(m-1)D.m(2-a)(m-1)12.把-a(x-y)-b(y-x)+c(x-y)分解因式,正确的结果是(B)A.(x-y)(-a-b+c)B.(y-x)(a-b-c)C.-(x-y)(a-b+c)D.-(y-x)(a+b-c)13.多项式x2m-x m提取公因式x m后,另一个因式是(B)A.x2-1B.x m-1C.x mD.x2m-114.若9a2(x-y)2-3a(y-x)3=M·(3a+x-y),则M等于(C)A.y-xB.x-yC.3a(x-y)2D.-3a(x-y)二、填空题15.因式分解:(1)ab-7a=a(b-7);(2)ax-ay=a(x-y).16.分解因式:-12x3-6x2+9x=-3x(4x2+2x-3).17.因式分解:(1)x(x+2)-x-2=(x+2)(x-1);(2)(a-b)2-(b-a)=(a-b)(a-b+1).18.若a+b=4,ab=1,则a2b+ab2=4.19.分解因式:6a2b-12ab2+3ab3=3ab(2a-4b+b2).20.已知a+b=3,ab=2,则a2b+ab2=6.三、解答题21.用提公因式法因式分解:(1)3x3+6x4;解:原式=3x3(1+2x).(2)4a3b2-10ab3c;解:原式=2ab2(2a2-5bc).(3)-3ma3+6ma2-12ma;解:原式=-3ma(a2-2a+4).(4)6p(p+q)-4q(p+q).解:原式=2(p+q)(3p-2q).22.将下列各式分解因式:(1)x4+x3+x;解:原式=x(x3+x2+1).(2)6x(a-b)+4y(b-a);解:原式=6x(a-b)-4y(a-b)=2(a -b)(3x -2y).(3)(a 2-ab)+c(a -b);解:原式=a(a -b)+c(a -b)=(a +c)(a -b).(4)4q(1-p)3+2(p -1)2.解:原式=4q(1-p)3+2(1-p)2=2(1-p)2(2q -2pq +1).23.16.9×18+15.1×18能被4整除吗?解:因为16.9×18+15.1×18=18×(16.9+15.1)=18×32=4.所以16.9×18+15.1×18能被4整除.24.认真阅读下列分解因式的过程,再回答所提出的问题: 1+x +x(1+x)+x(1+x)2=(1+x)[1+x +x(1+x)]=(1+x)2(1+x)=(1+x)3.(1)上述分解因式的方法是提公因式法;(2)分解因式:1+x +x(1+x)+x(1+x)2+x(1+x)3;(3)猜想:1+x+x(1+x)+x(1+x)2+…+x(1+x)n分解因式的结果是(1+x)n+1. 解:原式=(1+x)[(1+x)+x(1+x)+x(1+x)2]=(1+x)2[(1+x)+x(1+x)]=(1+x)3(1+x)=(1+x)4.。
新人教版《14.3.1提公因式法》同步练习及答案

§14.3.1提公因式法一.精心选一选1.下列各式从左到右的变形中,是因式分解的是()。
A.(x+3)(x-3)=x²-9B.x²+1=x(x+1x )C.3x²-3x+1=3x(x-1)+1D.a²-2ab+b²=(a-b)²2多项式- 6a²b+18a²b³x+24ab2y的公因式是( )A.mx+my和x+yB.3a(x+y)和2y+2xC.3a-3b和6(b-a)D.-2a-2b和 a²-ab4.下列各多项式因式分解错误的是()A.( a-b) ³-(b-a)=(a-b)2(a-b-1)B.x(a-b-c)-y(b+c-a)=(a-b-c)(x+y)C.P(m-n)3-Pq(n-m)3=P(m-n)3(1+q)D.(a-2b)(7a+b)-2(2b-a)2=(a-2b)(5a+5b)5.将多项式(3a-4b)(7a-8b)-(11a-12b)(8b-7a)分解因式正确的结果是()A.8(7a-8b)(a-b)B.2(7a-8b) ²C.8(7a-8b)(b-a)D.-2(7a-8b) ²6已知多项式3x²-mx+n分解因是的结果为(3x+2)(x-1)则,m,n的值分别为()A.m=1 n=-2 B.m-1 n=-2Cm=2 n=-2 D.m=-2 n=-27.多项式(m+1)(m-1)+(m-1)提取公因式(m-1)后,另一个因式为()A.m+1B.2mC.2D.m+28.a是有理数,则整式a²(a²-2)-2a²+4的值()A.不是负数B.恒为正数C.恒为负数D.不等于0二.细心填一填9.分解因式3x(x-2)-(2-x)=10.利用因式分解计算:3.68×15.7-31.4+15.7×0.32=11.分解因式:(x+y)²-x-y=12.已知a+b=9 ab=7 则a²b+ab²=13.观察下列各式:①abx-adx ②2x²y+6xy²③8m³-4m²+1④(p+q)x²y-5x²(p+q)+6(p+q)²⑤(x+y)(x-y)-4b(y+x)-4ab其中可以用提取公因式法分解的因式( )。
部编版人教初中数学八年级上册《14.3.1提公因式法 同步训练习题(含答案)》最新精品优秀

前言:该同步训练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点,精心编辑而成。
以高质量的同步训练习题助力考生查漏补缺,在原有基础上更进一步。
(最新精品同步训练习题)14.3因式分解14.3.1 提公因式法[学生用书P89]1.下列等式从左到右的变形,属于因式分解的是( )A.a(x-y)=ax-ayB.x2+2x+1=x(x+2)+1C.(x+1)(x+3)=x2+4x+3D.x3-x=x(x+1)(x-1)【解析】 A,B,C三项右边不是整式的积的形式,不是因式分解,故错误;D.符合因式分解的形式,且分解正确,故选D.2.下列用提公因式法分解因式正确的是( )A.5x3+4x2-x=x(5x2+4x)B.4x2y-8xy2+16xy=2xy(2x-4y+8)C.p(a-b)3-pq(b-a)3=p(a-b)3(1-q)D.-12a2b-3ab2c+a3b3c=-12ab(a+6b c-2a2b2c)3.[2016·滨州]把多项式x2+ax+b分解因式,得到(x+1)(x-3),则a,b的值分别是( )A.a=2,b=3 B.a=-2,b=-3C.a=-2,b=3 D.a=2,b=-34.分解因式:(1)[2016·海南]ax-ay=____;(2)[2016·无锡]ab-a2=___;(3)[2016·广州]2a2+ab=____;(4)[2016·南京]2a(b+c)-3(b+c)=__ __.5.因式分解:(1)-x3z+x4y;(2)36aby-12abx+6ab;(3)3x(a-b)+2y(b-a);(4)12a2b-18ab2-24a3b3.6.计算:(1)39×37-13×91;(2)29×20.17+72×20.17+13×20.17-20.17×14.7.已知a+b=2,ab=1,则a2b+ab2=___.8.[2015·大连]若a=49,b=109,则ab-9a的值为__ __.9.已知(2x-21)(3x-7)-(3x-7)(x-13)可因式分解为(3x+a)(x+b),其中a,b均为整数,则a+3b=__ _.。
14.3.1 提公因式法
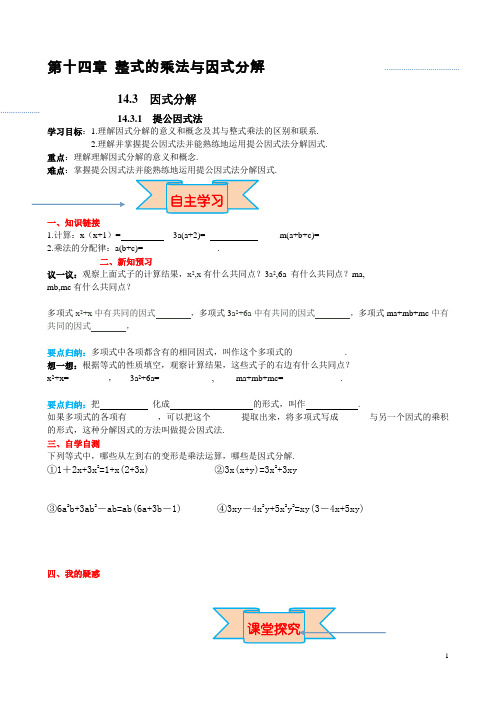
第十四章整式的乘法与因式分解14.3 因式分解14.3.1 提公因式法学习目标:1.理解因式分解的意义和概念及其与整式乘法的区别和联系.2.理解并掌握提公因式法并能熟练地运用提公因式法分解因式.重点:理解理解因式分解的意义和概念.难点:掌握提公因式法并能熟练地运用提公因式法分解因式.一、知识链接1.计算:x(x+1)= 3a(a+2)= m(a+b+c)=2.乘法的分配律:a(b+c)=_________________.二、新知预习议一议:观察上面式子的计算结果,x2,x有什么共同点?3a2,6a 有什么共同点?ma,mb,mc有什么共同点?多项式x2+x中有共同的因式,多项式3a2+6a中有共同的因式,多项式ma+mb+mc中有共同的因式,要点归纳:多项式中各项都含有的相同因式,叫作这个多项式的____________.想一想:根据等式的性质填空,观察计算结果,这些式子的右边有什么共同点?x2+x=_________,3a2+6a=____________, ma+mb+mc=_____________.要点归纳:把化成的形式,叫作.如果多项式的各项有_______,可以把这个_______提取出来,将多项式写成_______与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.三、自学自测下列等式中,哪些从左到右的变形是乘法运算,哪些是因式分解.①1+2x+3x2=1+x(2+3x) ②3x(x+y)=3x2+3xy③6a2b+3ab2-ab=ab(6a+3b-1) ④3xy-4x2y+5x2y2=xy(3-4x+5xy)四、我的疑惑___________________________________________________________________________________________ ___________________________________________________________一、要点探究探究点1:因式分解例1:下列从左到右的变形中是因式分解的有()①x2-y2-1=(x+y)(x-y)-1;②x3+x=x(x2+1);③(x-y)2=x2-2xy+y2;④x2-9y2=(x+3y)(x-3y).A.1个B.2个C.3个D.4个方法总结:因式分解与整式乘法是相反方向的变形,即互逆运算,二者是一个式子的不同表现形式.因式分解的右边是两个或几个因式积的形式,整式乘法的右边是多项式的形式.辩一辩:在下列等式中,从左到右的变形是因式分解的有___________,不是的,请说明为什么?①am+bm+c=m(a+b)+c ____________________________________;②24x2y=3x ·8xy ____________________________________;③x2-1=(x+1)(x-1) ____________________________________;④(2x+1)2=4x2+4x+1 ____________________________________;⑤x2+x=x2(1+1x) ____________________________________;⑥2x+4y+6z=2(x+2y+3z) ____________________________________.探究点2:公因式问题1:如何确定一个多项式的公因式?找一找:3x 2- 6 xy的公因式.(1)多项式3x 2- 6 xy有____项,分别为__________、_________,它们的系数分别是______、_______,最大公约数是____________,它们含有的共同字母是___________,该字母的指数分别为____、_____. (2)该多项式的公因式为______________.方法归纳:正确找出多项式的公因式的步骤:1.定系数:公因式的系数是多项式各项系数的_______________.2.定字母:字母取多项式各项中都含有的________的字母.3.定指数:相同字母的指数取各项中______的一个,即字母最_____次数.填一填:下列各多项式的公因式是什么?将其填在横线上.(1) 3x+6y ___________; (2)ab-2ac ___________;(3) a2 - a3 ___________ ; (4)4 (m+n) 2 +2(m+n) ___________;(5)9m2n-6mn ___________; (6)-6x2y-8 xy 2 ___________;探究点3:用提公因式法分解因式例2:把下列各式分解因式(1)8a3b2+12ab3c;(2)2a(b+c)-3(b+c);(3)(a+b)(a-b)-a-b.方法总结:提公因式法步骤(分两步)第一步:找出公因式;第二步:提取公因式,即将多项式化为两个因式的乘积.辩一辩:下列同学分解因式的结果正确吗?不正确的话,请说明理由,并改正.(1)分解因式12x2y+18xy2=3xy(4x + 6y). ____________(填“正确”或“错误”)理由:_______________________________正解:________________________________(2)分解因式3x2 - 6xy+x =x(3x-6y).____________(填“正确”或“错误”)理由:_______________________________正解:________________________________(3)- x 2+xy-xz= - x(x+y-z)____________(填“正确”或“错误”)理由:_______________________________正解:________________________________易错归纳:(1)提取公因式后,多项式中各项还含有公因式.(2)提取公因式后,漏掉另一个因式中商是1的项;(3)找底数互为相反数的幂的公因式时符号出错;例3:计算:(1)39×37-13×91;(2)29×20.16+72×20.16+13×20.16-20.16×14.方法总结:在计算求值时,若式子各项都含有公因式,用提取公因式的方法可使运算简便.例4: 已知a +b =7,ab =4,求a 2b +ab 2的值.方法总结:含a ±b ,ab 的求值题,通常要将所求代数式进行因式分解,将其变形为能用a ±b 和ab 表示的式子,然后将a ±b ,ab 的值整体带入即可.1.下列各式变形中,是因式分解的是( )A.a 2-2ab +b 2-1=(a -b )2-1 B.)11(22222xx x x +=+ C .(x +2)(x -2)=x 2-4 D.x 4-1=(x 2+1)(x +1)(x -1)2.多项式6ab 2c -3a 2bc +12a 2b 2中各项的公因式是( )A .abcB .3a 2b 2C .3a 2b 2cD .3ab3.把a 2-4a 多项式分解因式,结果正确的是( )A .a (a-4)B .(a+2)(a-2)C .a (a+2)(a-2)D .(a-2)2-44.当a ,b 互为相反数时,代数式a 2+ab-2的值为( )A .2B .0C .-2D .-15.分解因式(1)a 2b –2ab 2+ab ; (2)2(a-b )-4(b-a);(3)a 2b (a -b )+3ab (a -b ); (4)y 2(2x +1)+y (2x +1)2.A.5mn B.5m2n2 C.5m2n D.5mn22.把多项式(x+2)(x-2)+(x-2)提取公因式(x-2)后,余下的部分是()A.x+1 B.2x C.x+2 D.x+33.下列多项式的分解因式,正确的是()A.12xyz-9x2y2=3xyz(4-3xyz)B.3a2y-3ay+6y=3y(a2-a+2)C.-x2+xy-xz=-x(x2+y-z)D.a2b+5ab-b=b(a2+5a)4.把下列各式分解因式:(1)8 m2n+2mn=_____________;(2)12xyz-9x2y2=_____________;(3)p(a2 + b2 )- q(a2 + b2 )=_____________;(4) -x3y3-x2y2-xy=_______________;(5)(x-y)2+y(y-x)=_____________.5.若9a2(x-y)2-3a(y-x)3=M·(3a+x-y),则M等于_____________.6.简便计算:(1) 1.992+1.99×0.01 ; (2)20132+2013-20142; (3)(-2)101+(-2)100.7.(1)已知: 2x+y=4,xy=3,求代数式2x2y+xy2的值.(2)化简求值:(2x+1)2-(2x+1)(2x-1),其中x=12. .拓展提升8.△ABC的三边长分别为a、b、c,且a+2ab=c+2bc,请判断△ABC是等边三角形、等腰三角形还是直角三角形?并说明理由.。
人教初中数学八年级上册 14.3.1 提公因式法同步练习

14.3.1提公因式法【知识巩固】1、 分解因式:7a 2b 2-14ab 3c=2、 若xy=6,x-y=5,则x 2y-xy 2=3、 在下列四个式子中:①6a 2b=2a 2 .3b ;②x 2-4-3x=(x+2)(x-2)-3x ;③ab 2-2ab=a b(b-2);④-a 2+4=(2-a)(2+a)。
从左到右的变形,是因式分解的有 ( )A 、4个B 、3个C 、2个D 、1个4、多项式 x 3-25x, x 2-25, x 3y+3x 2y-10xy 的公因式应当是 ( )A 、x-5B 、x+5C 、没有公因式D 、以上都不对5、用提公因式法分解因式:3a(x-y) -9b(y-x) 的公因式应当是 ( )A 、3a-9bB 、3a+9bC 、x-yD 、3( x-y)6、把多项式-8a 2b 3c+16a 2b 2c 2-24a 3bc 3分解因式,应提公因式是 ( )A 、2ab 2c 3B 、-4abcC 、-8a 2bcD 、24a 3b 3c 37、把多项式()()a p a p -+-112分解因式的结果是( )A 、()()p p a +-21B 、()()p p a --21C 、()()11--p a p8、因式分解:(1)cx-cy-cz(2) x 6y-2x 4z(3) (m-n)(p+q)-(m-n)(p-q)(4) x(x-y)2- y(x-y)(5)()y x y x m +--2【拓展探究】9、两个连续偶数的平方差能够被4整除吗?请说明理由。
10、阅读下列因式分解的过程,再回答所提出的问题:1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x)=(1+x)3(1)上述分解因式的方法是 ,共应用了 次.(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2012,则需应用上述方法 次,结果是 .(3)分解因式:1+x+x(x+1)+x(x+1)2+…+ x(x+1)n (n 为正整数).【答案】1、7ab 2(a-2bc);2、30;3、C ;4、B ;5、D ;6、C ;7、C ;8、(1)原式=c(x-y-z);(2)原式=x 4(x 2y-2z);(3)原式=(m-n)(p+q-p+q)=2q(m-n);(4)原式=(x-y)(x 2-xy-y);(5)原式=(x-y)(mx-my-1);9、解:设较小的偶数为2n,则另一个偶数为2n+2,则两个连续偶数的平方差为:(2n+2)2-(2n)2=(2n+2+2n)(2n+2-2n)=2(4n+2)=4(2n+1)∴两个连续偶数的平方差能够被4整除;10、(1)提公因式法,3;(2)2013,(1+x)2013;(3)(1+x)n+1。
人教版 八年级数学上册 第14.3.1用提公因式法因式分解专题 (含答案)

人教版 八年级数学上册 第14.3.1用提公因式法因式分解练习题(含答案)1. 把下列各式因式分解(1)-+--+++a x abx acx ax m m m m 2213(2)a a b a b a ab b a ()()()-+---32222解:-+--=--+++++a x abx acx ax ax ax bx c x m m m m m 221323()(2)有时将因式经过符号变换或将字母重新排列后可化为公因式,如:当n 为自然数时,()()()()a b b a a b b a n n n n -=--=----222121;,是在因式分解过程中常用的因式变换。
解:a a b a b a ab b a ()()()-+---32222 )243)((]2)(2))[(()(2)(2)(222223b b ab a b a a b b a a b a b a a b a ab b a a b a a ++--=+-+--=-+-+-=2. 利用提公因式法简化计算过程例:计算1368987521136898745613689872681368987123⨯+⨯+⨯+⨯ 解:原式)521456268123(1368987+++⨯==⨯=987136813689873. 在多项式恒等变形中的应用例:不解方程组23532x y x y +=-=-⎧⎨⎩,求代数式()()()22332x y x y x x y +-++的值。
解:()()()()()()()223322233253x y x y x x y x y x y x x y x y +-++=+-+=+- 把2x y +和53x y -分别为3和-2带入上式,求得代数式的值是-6。
4. 在代数证明题中的应用例:证明:对于任意自然数n ,323222n n n n ++-+-一定是10的倍数。
分析:首先利用因式分解把代数式恒等变形,接着只需证明每一项都是10的倍数即可。
人教版八年级数学上14.3《提公因式法》测试(含答案及解析)

提公因式法测试时间:60分钟总分:100一、选择题(本大题共10小题,共30.0分)1.多项式①2①2−①,①(①−1)2−4(①−1)+4,①(①+1)2−4①(①+1)+4,①−42−1+4①;分解因式后,结果含有相同因式的是()A. ①①B. ①①C. ①①D. ①①2.多项式12①①3①+8①3①的各项公因式是()A. 4①2B. 4abcC. 2①①2D. 4ab3.①4−①4和①2+①2的公因式是()A. ①2−①2B. ①−①C. +①D. ①2+①24.计算(−2)100+(−2)99的结果是()A. 2B. −2C. −299D. 2995.将下列多项式因式分解,结果中不含有因式①+1的是()A. ①2−1B. ①2+①C. ①2+①−2D. (①+2)2−2(①+2)+16.把(①−①)3−(①−①)2分解因式的结果为()A. (①−①)2(①−①+1)B. (①−①)2(①−①−1)C. (①−①)2(①+①)D. (①−①)2(①−①−1)7.下列多项式中,能用提取公因式法分解因式的是()A. ①2−①B. ①2+2①C. 2+①2D. ①2−①①+①2第1页/共14页8.将3(①−①)−9①(①−①)因式分解,应提的公因式是()A. 3①−9①B. 3①+9①C. ①−①D. 3(①−①)9.把多项式(①+1)(①−1)+(①−1)提取公因式(①−1)后,余下的部分是()A. ①+1B. 2mC. 2D. ①+210.把①①+3+①①+1分解因式得()A. ①①+1(①2+1)B. ①①(①3+①)C.①(①①+2+①) D. ①①+1(①2+①)二、填空题(本大题共10小题,共30.0分)11.已知①+①=10,①①=16,则①2①+①①2的值为______ .12.若+①=10,①①=1,则①3①+①①3=______ .13.若①+①=3,①①=6,则①①2+①2①的值为______ .14.计算21×3.14+79×3.14的结果为______ .15.已知①+①=3,①①=2,则①2①+①①2=______ .16.分解因式:①2+①=______ .17.分解因式:①2+2①=______.18.因式分解①(①−3)2+①(3−①)2=______ .19.若①−①=3,①①=−2,则2①2①−2①①2+1的值为______ .20.计算9999×9999+9999=_______ .三、计算题(本大题共4小题,共24.0分)21.分解因式:(1)3①−12①2(2)①2−4①①+4①2(3)①2(①−2)−①(2−①)(4)(2+4①2)2−16①2①2.22.分解因式:(1)15①2−5①(2)(①2+1)2−4①2(3)①2−2①①+①2−1(4)4①3①2−12①2①2+8①①2.23.计算:(1)(−①①)2⋅3①2①÷9①4①2;(2)①(①−1)+2①(①+1)−3①(2①−5).第3页/共14页24.计算与化简:(1)3(①−①)2−(2①+①)(−①+2①)(2)已知2①−①=8,①①=3,求2①2①+8①2①2−①①2的值.四、解答题(本大题共2小题,共16.0分)25.分解因式:2①(①−①)2−8①2(①−①)26.简便计算:1.992+1.99×0.01.第5页/共14页答案和解析【答案】1. A2. D3. D4. D5. C6. B7. B8. D9. D10. A11. 16012. 813. 1814. 31415. 616. ①(①+1)17. ①(①+2)18. (①−3)2(①+①)19. −1120. 9999000021. 解:(1)原式=3①(1−4①);(2)原式=(①−2①)2;(3)原式=①2(①−2)+①(①−2)=①(①−2)(①+1);(4)原式=(①2+4①2+4①①)(①2+4①2−4①①)=(①+2①)2(①−2①)2.22. 解:(1)原式=5(3①−1);(2)原式=(①2+1+2①)(①2+1−2①)=(①+1)2(①−1)2;(3)原式=(①−①)2−1=(①−①+1)(①−①−1);(4)原式=4①①2(①2−3①+2)=4①①2(①−1)(①−2).23. 解:(1)原式=①2①2⋅3①2①⋅429①=2①332.(2)原式=①2−①+2①2+2①−6①2+15①=−3①2+16①.24. 解:(1)原式=3(①2−2①①+①2)−(4①2−①2)=3①2−6①①+3①2−4①2+①2=−①2−6①+4①2;(2)当2①−①=8、①①=3时,原式=①①(2①+8①①−)=3×(8+8×3)=96.25. 解:2①(①−①)2−8①2(①−①)=2①(①−①)[(①−①)+4①]=2①(①−①)(5①−①).26. 解:1.992+1.99×0.01=1.99×(1.99+0.01)=3.98.【解析】1. 解:①2①2−①=①(2①−1);①(①−1)2−4(①−1)+4=(①−3)2;①(①+1)2−4①(①+1)+4无法分解因式;①−4①2−1+4①=−(4①2−4①+1)=−(2−1)2.所以分解因式后,结果中含有相同因式的是①和①.第7页/共14页故选:A.根据提公因式法和完全平方公式把各选项的多项式分解因式,然后再找出结果中含有相同因式的即可.本题主要考查了提公因式分解因式和利用完全平方公式分解因式,熟练掌握公式结构是求解的关键.2. 解:12①①3①+8①3①=4①①(3①2①+2①2),4ab是公因式,故选:D.根据公因式定义,对各选项整理然后即可选出有公因式的项.此题考查的是公因式的定义,找公因式的要点是:(1)公因式的系数是多项式各项系数的最大公约数;(2)字母取各项都含有的相同字母;(3)相同字母的指数取次数最低的.在提公因式时千万别忘了“−1”.3. 解:∵①4−①4=(①2+①2)(①2−①2)=(①2+①2)(①−①)(①+①).∴①4−①4和①2+①2的公因式是①2+①2,故选D.将原式分解因式,进而得出其公因式即可.此题主要考查了公因式,正确分解因式是解题关键.4. 解:原式=(−2)99[(−2)+1]=−(−2)99=299,故选:D.根据提公因式法,可得负数的奇数次幂,根据负数的奇数次幂是负数,可得答案.本题考查了因式分解,提公因式法是解题关键,注意负数的奇数次幂是负数,负数的偶数次幂是正数.5. 【分析】先把各个多项式分解因式,即可得出结果.本题考查了因式分解的意义与方法;熟练掌握因式分解的方法是解决问题的关键.【解答】解:①.∵①2−1=(①+1)(①−1),B.①2+①=①(①+1),C.2+①−2=(①+2)(①−1),D.(①+2)2−2(①+2)+1=(①+2−1)2=(①+1)2,∴结果中不含有因式①+1的是选项C.故选C.6. 解:原式=(①−①)3−(①−①)2=(①−①)2(①−①−1),故选B原式变形后,提取公因式即可得到结果.此题考查了因式分解−提公因式法,熟练掌握提取公因式的方法是解本题的关键.7. 解:A、不符合要求,没有公因式可提,故本选项错误;B、2+2①可以提取公因式x,正确;C、不符合要求,没有公因式可提,故本选项错误;D、不符合要求,没有公因式可提,故本选项错误;故选B.根据找公因式的要点提公因式分解因式.要明确找公因式的要点:(1)公因式的系数是多项式各项系数的最第9页/共14页大公约数;(2)字母取各项都含有的相同字母;(3)相同字母的指数取次数最低的.8. 【分析】此题考查了因式分解−提取公因式法,熟练掌握分解因式的方法是解本题的关键.原式变形后,找出公因式即可.【解答】解:将3①(①−①)−9①(①−①)=3①(①−①)+9①(−①)因式分解,应提的公因式是3(①−①).故选D.9. 解:(①+1)(①−1)+(①−1),=(①−1)(①+1+1),=(①−1)(①+2).故选D.先提取公因式(①−1)后,得出余下的部分.先提取公因式,进行因式分解,要注意①−1提取公因式后还剩1.10. 解:①①+3+①①+1=①①+1(①2+1).故选:A.直接找出公因式,进而提取公因式得出答案.此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.11. 解:∵①+①=10,①①=16,∴①2①+①①2=①①(①+①)=10×16=160.故答案为:160.首先提取公因式xy,进而将已知代入求出即可.此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.12. 解:当①+①=10,①①=1时,①3①+①①3=①①(①2+①2)=①①[(①+①)2−2①①]=1×(102−2×1)=8,故答案为:8.将①+①、xy代入①3①+①①3=①①[(①+①)2−2①①]中计算即可得.本题主要考查代数式的求值,熟练掌握提公因式和完全平方公式是解题的关键.13. 解:∵①+①=3,①①=6,∴①①2+2①=①①(①+①)=3×6=18.故答案为:18.直接利用提取公因式法分解因式,进而将已知代入求出答案.此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.14. 解:原式=3.14×(21+79)=100×3.14=314.第11页/共14页故答案为314.先提公因式3.14,再计算即可.本题考查了因式分解−提公因式法,因式分解的方法还有公式法,掌握平方差公式和完全平方公式是解题的关键.15. 解:∵①+①=3,①①=2,∴①2①+①①2=①①(①+①)=6.故答案为:6.首先将原式提取公因式ab,进而分解因式求出即可.此题主要考查了提取公因式法分解因式,正确找出公因式再分解因式是解题关键.16. 解:①2+①=①(①+1).故答案为:①(①+1).直接提取公因式分解因式得出即可.此题主要考查了提取公因式法分解因式,正确得出公因式是解题关键.17. 解:原式=①(①+2)故答案为:①(①+2)根据提取公因式法即可求出答案.本题考查因式分解,解题的关键是熟练运用提取公因式法,本题属于基础题型.18. 解:原式=①(−3)2+①(①−3)2=(①−3)2(①+①).故答案为:(①−3)2(①+①).直接提取公因式(①−3)2即可.此题主要考查了提公因式法分解因式,关键是正确找出公因式.19. 解:∵2①2①−2①①2+1=2①①(①−①)+1将①−①=3,①①=−2代入得:原式=2①①(①−①)+1=2×(−2)×3+1=−11.故答案为:−11.直接提取公因式2mn,进而将已知代入求出即可.此题主要考查了提取公因式法的应用以及代数式求值,正确找出公因式是解题关键.20. 解:9999×9999+9999=9999(9999+1)=99990000.故答案为:99990000.提取公因式9999后即可确定正确的答案.本题考查了因式分解的知识,解题的关键是能够确定公因式,难度不大.21. (1)原式提取公因式即可得到结果;(2)原式利用完全平方公式分解即可;(3)原式变形后,提取公因式即可得到结果;(4)原式利用完全平方公式及平方差公式分解即可.此题考查了因式分解−运用公式法,熟练掌握平方差公式是解本题的关键.22. (1)原式提取公因式即可;(2)原式利用平方差公式化简,再利用完全平方公式分解即可;(3)原式前三项利用完全平方公式分解,再利用平方差公式分解即第13页/共14页可;(4)原式提取公因式,再利用十字相乘法分解即可.此题考查了因式分解−运用公式法,以及提公因式法,熟练掌握因式分解的方法是解本题的关键.23. (1)先计算乘方、除法转化为乘法,再约分即可得;(2)先计算乘法,再合并同类项即可得.本题主要考查整式和分式的运算,解题的关键是熟练掌握分式的乘除运算和整式的混合运算顺序和运算法则.24. (1)先计算乘方和乘法,再去括号、合并同类项即可得;(2)将已知等式的值代入原式=①①(2①+8①①−①),计算可得.本题主要考查整式的运算与因式分解,解题的关键是掌握完全平方公式和平方差公式及提公因式法因式分解的能力.25. 直接找出公因式,进而提取公因式得出答案.此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.26. 直接提取公因式1.99,进而计算得出答案.此题主要考查了提取公因式,正确找出公因式是解题关键.。
人教版八年级上册 因式分解专项练习14.3.1提公因式法(含答案)

人教版八年级上册因式分解专项练习-提公因式法(含答案)1.请把下列各式分解因式(1)x(x-y)-y(y-x) (2)-12x3+12x2y-3xy2(3)(x+y)2+mx+my (4)a(x-a)(x+y)2-b(x-a)2(x+y)(5)15×(a-b)2-3y(b-a)(6)(a-3)2-(2a-6)(7)(m+n)(p-q)-(m+n)(q+p)2.因式分解:(1)3x2﹣6xy+x;(2)﹣4m3+16m2﹣28m;(3)18(a﹣b)2﹣12(b﹣a)3.3.因式分解:-2m3+8m2-12m;4.用提公因式法分解多项式:3223048x y x yz -+5.分解因式:(1)−4ab −8b 2+10b (2)2(n −m)2−m(m −n)(3)15y(a −b)2−3y(b −a) (4)6(m −n)3−12(n −m)2(5)x 2+3x +1=0,求2x 2010+6x 2009+2x 2008的值 6.分解因式:3210()5()ab a b b b a ---7.把下列各式分解因式:(1)4x 3-6x 2; (2)2a 2b+5ab+b ; (3)6p(p+q)-4q(p+q);(4) (x -1)2-x+1; (5)-3a 2b +6ab 2-3ab.8.把下列各式分解因式:(1)236x y xy - (2)2332525x y x y -(4)3241626m m m -+- (4)22(3)3a a --+(5)23()2()m x y y x --- (6)2318()12()b a b a b ---(7)1532223520x y x y x y +- (8)6x(x+y)-4y(x+y)(8)()()()a x a b a x c x a -+--- (10)()()()()m n p q m n p q ++-+-9.把下列各式分解因式:(1)a(b -c)+c -b ; (2)15b(2a -b)2+25(b -2a)2.10.()()x x y y y x ---11.把下列各式分解因式:(1)2x 2-xy ; (2)-4m 4n +16m 3n -28m 2n.12.分解因式① -49a 2bc -14ab 2c+7ab ①(2a+b)(2a -3b)-8a(2a+b)13.分解因式:a(x +y -z)-b(z -x -y)-c(x -z +y).14.因式分解:(y ﹣x )(a ﹣b ﹣c )+(x ﹣y )(b ﹣a ﹣c )15.因式分解:12a 2b(x -y)-4ab(y -x).16.因式分解: 53242357a b c a b c a bc +-17.因式分解:26()2()()x y x y x y +-+-18.计算:(1)a (a+b )﹣b (a ﹣b ); (2)(x ﹣2y )(2y+x )+(2y+x )2﹣2x (x+2y )19.因式分解(1)-3x 2+6xy -3y 2 (2)a 2(x -y)+16(y -x)20.用提取公因式法将下列各式分解因式:(1)6xyz-3xz2;(2)x4y-x3z;(3)x(m-x)(m-y)-m(x-m)(y-m).参考答案1.(1)(x-y)(x+y);(2)-3x(2x-y)2;(3)(x+y)(x+y+m);(4)(x-a)(x+y)(ax+ay-bx+ab);(5)3(a-b)(5ax-5bx+y);(6)(a-3)(a-5);(7)-2q(m+n)【解析】试题分析:(1)运用提取公因式法因式分解即可;(2)运用提取公因式法因式分解即可,注意先提取负号;(3)先分组,提公因式,再利用整体法运用提取公因式法因式分解即可;(4)运用提取公因式法因式分解即可,注意整体思想的应用;(5)根据a-b与b-a互为相反数,利用整体法提取公因式法因式分解即可;(6)运用提取公因式法因式分解即可;(7)运用提取公因式法因式分解即可,注意符号变化.试题解析:(1)x(x-y)-y(y-x)=(x-y)(x+y)(2)-12x3+12x2y-3xy2=-3x(4x2-4xy+y2)=-3x(2x-y)2(3)(x+y)2+mx+my=(x+y)2+m(x+y)=(x+y)(x+y+m)(4)a(x-a)(x+y)2-b(x-a)2(x+y)=(x-a)(x+y)[a(x+y)-b(x-a)]=(x-a)(x+y)(ax+ay-bx+ab)(5)15x(a-b)2-3y(b-a)=15x(a-b)2+3y(a-b)=3(a-b)(5ax-5bx+y);(6)(a-3)2-(2a-6)=(a-3)2-2(a-3)=(a-3)(a-5);(7)(m+n)(p-q)-(m+n)(q+p)=(m+n)(p-q-q-p)=-2q(m+n)2.(1)x(3x﹣6y+1);(2)﹣4m(m2﹣4m+7);(3)6(a﹣b)2(3+2a﹣2b).【解析】【分析】(1)利用提取公因式法分解因式得出即可;(2)利用提取公因式法分解因式得出即可;(3)利用提取公因式法分解因式得出即可. 【详解】(1)解:3x 2﹣6xy+x=x (3x ﹣6y+1)(2)解:﹣4m 3+16m 2﹣28m=﹣4m (m 2﹣4m+7)(3)解:18(a ﹣b )2﹣12(b ﹣a )3=6(a ﹣b )2(3+2a ﹣2b ) 【点睛】考查因式分解,熟练掌握提取公因式法是解题的关键. 3.-2m(m 2-4m+6) 【解析】 【分析】直接运用提公因式法.即提出公因式-2m 即可. 【详解】解:-2m 3+8m 2-12m=-2m (m 2-4m+6) 【点睛】本题考核知识点:因式分解. 解题关键点:找出公因式. 4.()2658x y xy z --【解析】试题分析:根据提公因式法--因式分解,确定公因式后提取公因式即可. 试题解析:()32223048658x y x yz x y xy z -+=--.5.(1)-2b (2a+4b -5);(2)(n -m )(2n -m );(3)3y (a -b )[5a -5b+1];(4)6(n -m )2(m -n -2);(5)0 【解析】【分析】(1)直接提取公因式﹣2b 分解即可;(2)首先把m −n 变为−(m −n),再提取公因式n -m 分解即可; (3)首先把b −a 变为−(a -b ),再提取公因式a -b 分解即可;(4)首先把6(m −n)3变为−6(n −m)3,再提取公因式6(n −m)2分解即可;(5)首先把2x 2010+6x 2009+2x 2008变为2x 2008(x 2+3x +1) ,再把x 2+3x +1=0代入即可; 【详解】(1)−4ab −8b 2+10b = -2b (2a+4b -5);(2)2(n −m)2−m (m −n )=2(n −m )2+m (n −m )=(n -m )(2n -m );(3)15y(a −b)2−3y (b −a )=15y (a −b )2+3y (a −b )=3y (a −b )[5a −5b )+1] (4)6(m −n)3−12(n −m)2=6(m −n)3−12(m −n)2=6(m −n)2(m −n −2) (5)2x 2010+6x 2009+2x 2008=2x 2008(x 2+3x +1)=0 【点睛】本题主要考查了提取公因式法分解因式,正确找出公因式是解题关键. 6.225()(221)b a b a ab --- 【解析】分析:提取公因式法进行因式分解即可. 详解:原式()()32105,ab a b b a b =---()()2521.b a b a a b ⎡⎤=---⎣⎦ ()()225221.b a b a ab =---点睛:本题主要考查因式分解,常见的因式分解的方法有:提取公因式法,公式法,十字相乘法.注意:分解一定要彻底.7.(1)2x 2(2x -3);(2)b(2a 2+5a+1);(3)2(p+q)(3p -2q);(4)(x -1)(x -2);(5)-3ab(a -2b +1). 【解析】 【分析】(1)直接利用提取公因式法,提取公因式2x 2,进而分解因式得出答案; (2)直接利用提取公因式法,提取公因式b ,进而分解因式得出答案; (3)直接利用提取公因式法,提取公因式2(p +q ),进而分解因式得出答案; (4)直接利用提取公因式法,提取公因式(x ﹣1),进而分解因式得出答案. (5)直接利用提取公因式法,提取公因式﹣3ab ,进而分解因式得出答案. 【详解】(1)原式=222223x x x ⋅-⋅=22(23)x x -; (2)原式= b •2a 2+ b •5a + b •1=b (2a 2+5a +1); (3)原式=2(p +q )•3p -2(p +q )•2q =2(p +q )(3p -2q ); (4)原式=(x -1)2-(x -1)=(x -1)(x -1-1)= (x -1)(x -2);(5)原式=-3ab •a +(-3ab )•(-2b )+(-3ab )•1=-3ab (a -2b +1). 【点睛】本题考查了提取公因式法分解因式,正确找出公因式是解题的关键.8.(1)3xy(x -2); (2)225(5)x y y x -; (3)22(2813m m m --+); (4)3)(27)a a --(; (5)()(322)x y m x y --+; (6)26()(52a b b a --);(7) 225314)x y xy y +-(;(8)2(x+y)(3x -2y); (9)()()x a a b c ---; (10)2()q m n +.试题分析:都利用提公因式法分解因式即可.试题解析:(1)原式=3xy(x -2);(2)原式=()2255x y y x -;(3)原式=22(2813m m m --+);(4)()3)27a a =--原式(; (5)原式=()()322x y m x y --+;(6)原式=()26(52a b b a --);(7)原式= 225314)x y xy y +-(;(8)原式=2(x+y)(3x -2y);(9)原式=()()x a a b c ---;(10)原式=()2q m n +.9.(1)(b -c)(a -1)(2) 5(2a -b)2(3b +5)【解析】试题分析:(1)先确定公因式是(b -c ),将公因式(b -c )提到括号外,可得(b -c )(a -1) , (2)先确定公因式是5(2a -b )2,将公因式5(2a -b )2提到括号外,可得5(2a -b )2(3b +5).试题解析:(1)原式=a (b -c )-(b -c )=(b -c )(a -1),(2)原式=15b (2a -b )2+25(2a -b )2=5(2a -b )2(3b +5).10.()()x y x y -+试题分析:后一项变号后,提取公因式(x-y)即可.试题解析:解:原式=x(x-y)+y(x-y)=(x-y)(x+y).11.(1) x(2x-y)(2)-4m2n(m2-4m+7)【解析】试题分析:(1)先确定公因式,将公因式提到括号外,括号里为原多项式中每一项除以公因式所得结果, (2)先确定公因式,将公因式提到括号外,括号里为原多项式中每一项除以公因式所得结果.试题解析:(1)原式=x(2x-y),(2)原式=-4m2n(m2-4m+7).12.①-7ab(7ac+2bc-1);①-3(2a+b)2【解析】试题分析:本题考查了因式分解.①直接用提公因式-7ab即可;①把(2a+b)作为一个整体提取.①原式=-7ab(7ac+2bc-1)①原式=(2a+b)(2a-3b-8a)=(2a+b)(-6a-3b)=-3(2a+b) 213.(x+y-z)(a+b-c)【解析】试题分析:先确定公因式(x+y-z),提公因式可得: (x+y-z) (a+b-c),试题解析:原式=a(x+y-z)+b(x+y-z)-c(x+y-z)=(x+y-z) (a+b-c).14.2(y﹣x)(a﹣b)【解析】试题分析:先提取公因式(y-x)后,再提取公因式2即可.试题解析:原式=(y ﹣x )(a ﹣b ﹣c )﹣(y ﹣x )(b ﹣a ﹣c )=(y ﹣x )(a ﹣b ﹣c ﹣b+a+c )=2(y ﹣x )(a ﹣b ).15.4ab(x -y)(3a+1)【解析】【分析】直接提取公因式4ab (x -y ),即可求得答案.【详解】原式=12a 2b(x -y)+4ab(x -y)=4ab(x -y)(3a+1)【点睛】此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.16.a 3bc (a 2b 2c+5ab -7)【解析】【分析】根据题意提取公因式即可.【详解】解:原式=322(57)a bc a b c ab +-【点睛】本题主要考查提取公因式,根据每个字母的最低次数提取即可.17.4(x +y )(x +2y ).【解析】首先提公因式2(x+y),再整理括号里面的3(x+y)﹣(x﹣y),再提公因式2即可.【详解】原式=2(x+y)[3(x+y)﹣(x﹣y)]=2(x+y)(2x+4y)=4(x+y)(x+2y).【点睛】本题考查了提公因式法分解因式,关键是公因式提取要彻底.18.(1)a2+b2;(2)0.【解析】【分析】(1)(2)按照先去括号,后合并同类项的步骤化简即可;【详解】解:(1)原式=a2+ab﹣ab+b2=a2+b2(2)法一:原式=x2﹣4y2+x2+4xy+4y2﹣2x2﹣4xy=(x2+x2﹣2x2)+(﹣4y2+4y2)+(4xy﹣4xy)=0法二:原式=(x+2y)(x﹣2y+2y+x﹣2x)=(x+2y)×0=0本题考查平方差公式、完全平方公式、提公因式等知识,解题的关键是灵活运用所学知识解决问题,记住平方差公式、完全平方公式.19.(1)−3(x−y)2(2)(x−y)(a−4)(a+4)【解析】试题分析:(1)先提取公因式-3,再对余下的多项式利用完全平方公式继续分解;(2)先提取公因式(x-y),再对余下的多项式利用完全平方公式继续分解.试题解析:(1)原式= −3(x2−2xy+y2)= −3(x−y)2(2)原式=a2(x−y)−16(x−y)=(x−y)(a2−16)=(x−y)(a−4)(a+4)【点睛】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.20.(1) 3xz(2y-z);(2) x3(xy-z);(3)-(m-x)2(m-y).【解析】【分析】分别提取公因式3xz,x3,(m-x)(m-y)即可得答案,注意符号.【详解】解:(1)6xyz-3xz2=3xz(2y-z).(2)x4y-x3z=x3(xy-z).(3)x(m-x)(m-y)-m(x-m)(y-m)=x(m-x)(m-y)-m(m-x)(m-y)=(m-x)(m-y)(x-m)=-(m-x)2(m-y).【点睛】本题考查的知识点是提公因式,解题的关键是熟练的掌握提公因式.。
2022年人教版八年级上册《提公因式法》同步练习(附答案)

14.3 因式分解14.3.1 提公因式法1.以下各式从左到右的变形中,是因式分解的是〔〕。
A.(x+3)(x-3)=x²²+1=x(x+1x )²²-2ab+b²=(a-b)²2多项式- 6a²b+18a²b³x+24ab2y的公因式是〔 )A.mx+my和x+yB.3a(x+y)和2y+2xC.3a-3b和6〔b-a)D.-2a-2b和 a²-ab4.以下各多项式因式分解错误的选项是〔〕A.( a-b) ³-(b-a)=〔a-b)2(a-b-1)B.x(a-b-c)-y(b+c-a)=(a-b-c)(x+y)C.P(m-n)3-Pq(n-m)3=P(m-n)3(1+q)D.(a-2b)(7a+b)-2(2b-a)2=(a-2b)(5a+5b)5.将多项式〔3a-4b)(7a-8b)-(11a-12b)(8b-7a)分解因式正确的结果是〔〕A.8(7a-8b)(a-b)B.2(7a-8b) ²C.8(7a-8b)(b-a)D.-2(7a-8b) ²6多项式3x²-mx+n分解因是的结果为(3x+2)(x-1)那么,m,n的值分别为〔〕A.m=1 n=-2 B.m-1 n=-2Cm=2 n=-2 D.m=-2 n=-27.多项式〔m+1〕(m-1)+〔m-1〕提取公因式〔m-1〕后,另一个因式为〔〕A.m+1B.2mC.2D.m+28.a是有理数,那么整式a²〔a²-2〕-2a²+4的值〔〕9.分解因式3x(x-2)-(2-x)=××0.32=11.分解因式:〔x+y)²-x-y=12.a+b=9 ab=7 那么a²b+ab²=13.观察以下各式:①abx-adx ②2x²y+6xy²③8m³-4m²+1④(p+q)x²y-5x²(p+q)+6(p+q)²⑤(x+y)(x-y)-4b(y+x)-4ab其中可以用提取公因式法分解的因式( 〕。
人教版八年级数学14.3.1提公因式法(包含答案)

14.3.1提公因式法知识要点:1.定义:把一个多项式化成几个整式的乘积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式.2.提公因式法的定义:一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.3.提公因式法分解因式的一般步骤:①确定公因式:先确定系数,再确定字母和字母的指数;②提公因式并确定另一个因式;③把多项式写成这两个因式的积的形式.一、单选题1.下列多项式中,能进行因式分解的是( )A .x²+xB .x²-yC .x²+y²D .x²-xy+y² 【答案】A2.把2-a a 分解因式,正确的是( )A .(1)a a -B .(1)a a +C .()21a a -D .(1)a a - 【答案】A3.下式等式从左到右的变形,属于因式分解的是( )A .()()22a b a b a b +-=-;B .()21+4+41a a a a +=+; C .()()311x x x x x -=-+; D .2111x x x x x ⎛⎫++=++ ⎪⎝⎭. 【答案】C4.在下列各式中,从左到右的变形是因式分解的是( )A .2(3)(3)9x x x -+=-B .2524(3)(8)x x x x +-=-+C .223(2)3x x x x +-=+-D .211()x x x x-=- 【答案】B 5.已知,多项式212x mx --可因式分解为()()34x x +-,则m 的值为( ) A .-1B .1C .-7D .7 【答案】B6.三角形的三边a 、b 、c 满足a (b ﹣c )+2(b ﹣c )=0,则这个三角形的形状是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰直角三角形 【答案】A7.多项式x 2m ﹣x m 提取公因式x m 后,另一个因式是( )A .x 2﹣1B .x m ﹣1C .x mD .x 2m ﹣1 【答案】B8.把x n+3+x n+1分解因式得( )A .()n 12x x 1++B .()n 3x x x +C .()n 2n x x x ++D .()n 12x x x ++ 【答案】A9.若多项式mx +n 可分解为m (x -y ),则n 表示的整式为( )A .mB .myC .-yD .-my【答案】D10.8和24的最大公因数是( )A .4B .8C .16D .24【答案】B11.已知xy =﹣3,x +y =2,则代数式x 2y +xy 2的值是( )A .﹣6B .6C .﹣5D .﹣1【答案】A12.-28a 2b +21ab 2-7ab 等于( )A .7ab(4a -3b +1)B .7ab(-4a -3b -1)C .-7ab(4a -3b +1)D .-7ab(4a -3b)【答案】C二、填空题13.因式分解:2m m +=_______.【答案】(1)m m +14.已知23x y y +=-=,,则22x y xy +=____.【答案】3015.因式分解:2232x x -=________.【答案】()2116x x -16.分解因式b 2(x ﹣3)+b (x ﹣3)=_____.【答案】b (x ﹣3)(b+1)17.因式分解:(a +1)(a ﹣1)﹣2a +2=_____.【答案】(a ﹣1)2.18.因式分解:()()2a b b a ---=_______;【答案】(a -b )(a -b+1)19.若a ,b 互为相反数,则22a b ab +=________.【答案】0三、解答题20.(1)分解因式:a (a ﹣b )﹣b (a ﹣b );(2)已知x+2y =4,求3x 2+12xy+12y 2的值.【答案】(1)(a ﹣b )2;(2)48.21.分解因式:6(a −b)2+3(a −b);【答案】3(a −b)(2a −2b +1)22.已知x +y =1,xy =-12,求x (x +y )(x -y )-x (x +y )2的值(可以利用分解因式求).【答案】24.23.已知x+y=a,试求(x+y)3(2x+2y)3(3x+3y)3的值.【答案】216a9.24.阅读下列因式分解的过程,再回答所提出的问题:1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x)=(1+x)3(1)上述分解因式的方法是,共应用了次.(2)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2019,则需应用上述方法次,结果是.(3)分解因式:1+x+x(x+1)+x(x+1)2+…+x(x+1)n(n为正整数)结果是.【答案】(1)提公因式法;2;(2)2019;(x+1)2020;(3)(x+1)n+1.。
新人教版八年级上《14.3.1提公因式法》课文练习含答案

14.3 因式分解14.3.1提公因式法课前预习要点感知多项式的各项中都含有公共的因式叫做这个多项式的________.如果一个多项式的各项含有公因式,把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做________.预习练习1-1多项式8a3b2+12a3bc-4a2b中,各项的公因式是( )A.a2b B.4a2b C.-4a2b2D.-a2b1-2(南宁中考)因式分解:ax+ay=________.当堂训练知识点1因式分解的定义1.下列式子是因式分解的是( )A.(x+1)(x-1)=x2-1B.2a+4=2(a+1)C.a2+2a=a(a+2)D.x2+3x+2=x(x+3)+2知识点2用提公因式法分解因式2.用提公因式法分解因式:(1)3x3+6x4;(2)4a3b2-10ab3c;(3)-3ma3+6ma2-12ma;(4)6p(p+q)-4q(p+q).课后作业3.(河北中考)下列等式从左到右的变形,属于因式分解的是( )A.a(x-y)=ax-ayB.x2+2x+1=x(x+2)+1C.(x+1)(x+3)=x2+4x+3D.x3-x=x(x+1)(x-1)4.(威海中考)若m-n=-1,则(m-n)2-2m+2n的值是( )A.3 B.2 C.1 D.-15.(来宾中考)分解因式:x3-2x2y=________.6.将下列各式分解因式:(1)x(x-y)+y(y-x);(2)(a2-ab)+c(a-b);(3)4q(1-p)3+2(p-1)2.挑战自我7.△ABC的三边长分别为a,b,c,且a+2ab=c+2bc,请判断△ABC是等边三角形、等腰三角形还是直角三角形?说明理由.参考答案要点感知 公因式 提公因式法预习练习1-1 B 1-2 a(x +y)当堂训练1.C2.(1)原式=3x 3(1+2x). (2)原式=2ab 2(2a 2-5bc). (3)原式=-3ma(a 2-2a +4). (4)原式=2(p +q)(3p -2q).课后作业3.D 4.A 5.x 2(x -2y) 6.(1)原式=x(x -y)-y(x -y)=(x -y)(x -y)=(x -y)2.(2)原式=a(a -b)+c(a -b)=(a +c)(a -b). (3)原式=4q(1-p)3+2(1-p)2=2(1-p)2(2q -2pq +1).挑战自我7.△ABC 是等腰三角形.理由:∵a +2ab =c +2bc ,∴(a -c)+2b(a -c)=0.∴(a -c)(1+2b)=0.故a =c 或1+2b =0.显然b ≠-12,故a =c.∴此三角形为等腰三角形.。
人教版八年级数学上册《14.3.1 提公因式法》基础测试(含答案解析)

人教版八年级数学上册《14.3.1 提公因式法》基础测试1. 下列各式从左到右的变形是因式分解的是( ) A.()222312x x x ++=++ B.()()22x y x y x y +-=-C.()222x xy y x y xy-+=-+D.()222x y x y -=-2. 下列各式从左到右的变形中,属于因式分解的是( ) A.()a x y ax ay-=-B.()22121x x x x ++=++C.()()21343x x x x ++=++D.()()311x x x x x -=+-3. 多项式284nnx x -的公因式是( )A.4nx B.21n x - C.41n x - D.12n x -4. 多项式1124n n a a -+-的公因式是M ,则M 等于( )A.12n x- B.2na - C.12n a-- D.12n a+-5. 分解因式22422x y xy xy -+-的结果是( ) A.()221xy x y --+B.()22xy x y -+C.()221xy xy y -+-D.()221xy x y -+-6.把多项式()()232x y y x ---分解因式正确的是( )A. ()()322x y x y ---B. ()()322x y x y --+C. ()()322x y x y -+-D. ()()322y x x y -+-7. 已知m 为有理数,则整式()22211m m m --+的值( )A.不是负数B.恒为负数C.恒为正数D.不等于08.把多项式321640x x y -+提出个公因式28x -后,另一个因式是 .9. 因式分解:(1)()()()23223;a b a b a --+-(2)()()()2232;x y x y x y -+--(3)()()()()()()23332312357.a b x b a x a b x -+-----•+10. 若3,25,ab a b =--=则222a b ab -的值是( )A.-15B.15C.2D.-811. 设681×2019-681×2018=a ,2015×2016-2013×2018=b ,=c ,则a ,b ,c 的大小关系是( ) A.b<c<a B.a<c<b C.b<a<c D.c<b<a 12. 化简:()()()299111...1a a a a a a a ++++++++= .13.先化简,再求值:()()22,a ab a b +-+其中3, 5.a b ==14. 如图,长和宽分别为,a b 的长方形的周长为10,面积为6,求22a b ab +的值.参考答案1. 答案:D解析:A选项,()222312x x x++=++不是因式分解,错误:B选项,()()22x y x y x y+-=-不是因式分解,错误C选项,()222x xy y x y xy-+=-+不是因式分解,错误;D选项,()222x y x y-=-是因式分解,正确故选D.2. 答案:D解析:A、C选项中的变形是整式乘法,不是因式分解B选项中变形结果是()2x x+与1的和,不是因式分解;D选项中()()()32111,x x x x x x x-=-=+-是因式分解故选D.3. 答案:A解析:()284=421n n n nx x x x--∴,公因式是4n x.4. 答案:A解析:()111224=212,n n na a a a-+---故选A.5. 答案:A解析:()22422=221.x y xy xy xy x y-+---+故选A.6. 答案:B解析:()()()()()()2232=32322.x y y x x y x y x y x y------=--+故选B.7. 答案:A解析:原式=()()()2222211=10m m m m----≥,即不是负数.8. 答案:25x y-解析:()()3221640825.x x y x x y-+÷-=-9. 答案:【解】()()()()()()()()()()()123223=23232322232.a b a b aa b a b aa ab ba a b--+-----=---=--()()()()()()()22232=23252.x y x y x y x y x y x y y x y -+---+-+=-()()()()()()()()()()()()()()()()()()()()()32333231235723323312357=2333157235325.a b x b a x a b x a b x a b x a b x a b x x x a b x b a x -+-----•+=-++----•+-++--+⎡⎤⎣⎦=---=-+10. 答案:A 解析:()223,25,223515.ab a b a b ab ab a b =--=∴-=-=-⨯=-11. 答案:A 解析:()68120196812018=68120192018=681a =⨯-⨯⨯-,2015b =⨯()()()201512015220153+--⨯+22=20152015201532015220156+--⨯+⨯+()=20151326=6⨯-++,c =======b c a ∴<<,故选A.12. 答案:()1001a +解析:原式=()()()()()29821111...11a a a a a a a a a ⎡⎤+++++++++=+⎣⎦()()()()2973111...1=1a a a a a a a a ⎡⎤+++++++++⎣⎦()()()()296100111...1=...=1.a a a a a a a a ⎡⎤+++++++++⎣⎦ 13. 答案:【解】原式=()()()()222.a b a a b a b a b a b +--=+-=-当3,5a b ==时,原式=2235=16.--14. 答案:【解】∵长和宽分别为,a b 的长方形的周长为10,面积为6,a b ∴+=5,ab =6,()225630.a b ab ab a b ∴+=+=⨯=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§14.3.1提公因式法
一.精心选一选
1.下列各式从左到右的变形中,是因式分解的是()。
A.(x+3)(x-3)=x²-9
B.x²+1=x(x+1
x )
C.3x²-3x+1=3x(x-1)+1
D.a²-2ab+b²=(a-b)²
2多项式- 6a²b+18a²b³x+24ab2y的公因式是( )
A.mx+my和x+y
B.3a(x+y)和2y+2x
C.3a-3b和6(b-a)
D.-2a-2b和 a²-ab
4.下列各多项式因式分解错误的是()
A.( a-b) ³-(b-a)=(a-b)2(a-b-1)
B.x(a-b-c)-y(b+c-a)=(a-b-c)(x+y)
C.P(m-n)3-Pq(n-m)3=P(m-n)3(1+q)
D.(a-2b)(7a+b)-2(2b-a)2=(a-2b)(5a+5b)
5.将多项式(3a-4b)(7a-8b)-(11a-12b)(8b-7a)分解因式正确的结果是()
A.8(7a-8b)(a-b)
B.2(7a-8b) ²
C.8(7a-8b)(b-a)
D.-2(7a-8b) ²
6已知多项式3x²-mx+n分解因是的结果为(3x+2)(x-1)则,m,n的值分别为()A.m=1 n=-2 B.m-1 n=-2
Cm=2 n=-2 D.m=-2 n=-2
7.多项式(m+1)(m-1)+(m-1)提取公因式(m-1)后,另一个因式为()
A.m+1
B.2m
C.2
D.m+2
8.a是有理数,则整式a²(a²-2)-2a²+4的值()
A.不是负数
B.恒为正数
C.恒为负数
D.不等于0
二.细心填一填
9.分解因式3x(x-2)-(2-x)=
10.利用因式分解计算:3.68×15.7-31.4+15.7×0.32=
11.分解因式:(x+y)²-x-y=
12.已知a+b=9 ab=7 则a²b+ab²=
13.观察下列各式:①abx-adx ②2x²y+6xy²③8m³-4m²+1
④(p+q)x²y-5x²(p+q)+6(p+q)²⑤(x+y)(x-y)-4b(y+x)-4ab
其中可以用提取公因式法分解的因式( )。
(填序号)
14.若x m=5 x n=6 叫x m- x m+2n=
15.不解方程组 2x+y=6 则7y(x-3y)2-2(3y-x)3=
x-3y=1
16.计算 20142-2014×2013+1=
17.分解因式-7m(m-n)3+21mn(n-m)2=
18.若(2x)n-81=(4x2+9)(2x+3)(2x-3)则n=
三、解答题:
19.分解因式
① -49a2bc-14ab2c+7ab
②(2a+b)(2a-3b)-8a(2a+b)
20.试说明817-279-913必能被45整除
21.已知△ABC的三边长a,b,c满足a²-bc-ab+ac=0求证△ABC为等腰三角形
22. 先化简.在求值:
30x²(y+4)-15x(y+4),其中x=2,y=-2
23.已知:m²=n+2 n²=m+2 (m≠n)求m³-2mn+n3的值。
14.3.1答案
一.1. D 2. B 3. D 4 . D
5. B
6. A
7. D
8. A
二.9. (x-2)(3x+1) 10. 31.4 11. (x+y)(x+y-1)
12. 63 13. ①②④ 14.-175 15. 3 16.2015
17. -7m(m-n)2(m-4n) 18. 4
三.19. ①原式=-7ab(7ac+2bc-1)
②原式=(2a+b)(2a-3b-8a)
=(2a+b)(-6a-3b)
=-3(2a+b) 2
20.解:817-279-913
=(34)7-(33)9-(32)13
=328-327-326
=326(32-3-1)
=326×5=324×45
∴817-279-913能被45整除。
21. 证明:∵ a2-bc-ab+ac=0
∴ (a-b)(a+c)=0
∵ a,b为△ABC三边
∴ a+c>0,则a-b=0,即a=b
∴△ABC为等腰三角形
22. 解:原式=15x(y+4)(2x-1)
当x=2, y=-2时
原式=15×2×(-2+4)(2×2-1)=180
23. 解:∵ m2=n+2 n2=m+2
∴ m3=mn+2m n3=mn+2n
∴ m3+n3=2mn+2(m+n)
∴ m3-2mn+n3=2(m+n)
而m2-n2=(n+2)-(m+2)=n-m
∵ m≠n ∴ m-n≠0
∴ m+n=-1
∴ m3-2mn+n3=-1×2=-2。
