二重积分计算1
合集下载
高等数学A10-2二重积分的计算(1)
前赤壁赋
10-2 二重积分的计算
（宋）苏轼
寄蜉蝣于天地,
渺沧海之一粟.
哀吾生之须臾，
羡长江之无穷.
10-2 二重积分的计算
第二节 二重积分的计算
一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 三、小结与思考
10-2 二重积分的计算
一、利用直角坐标系计算二重积分
(1) 在直角坐标系下用平行于 y
坐标轴的直线网来划分区域 D，
则面积元素为
d dxdy
o
D
x
故二重积分可写为
f ( x, y)d f ( x, y)dxdy
D
D
10-2 二重积分的计算
(2) 如果积分区域 D如图所示，那么可用不等式表示为
a x b, 1( x) y 2( x). ［X－型］
其中ri 为 ri与 ri ri 的平均值.由此当 ri , i 充分小 时，极坐标系下的面积元素 d rdrd.
10-2 二重积分的计算
其次, 直角坐标系与极坐标系有如下变换关系
x r cos
y
r
sin
最后, 两坐标系下积分区域 D 形状不变，因此有
f ( x, y)d f (r cos , r sin )rdrd .
D
o
10-2 二重积分的计算
D
D
以下我们讨论极坐标下的二重积分的计算．
r 1( ) r 2( )
DD
r 1( )
r 2( ) D
r 2( )
D
o
Ao
Ao
A
r 1( ) 0
10-2 二重积分的计算
（宋）苏轼
寄蜉蝣于天地,
渺沧海之一粟.
哀吾生之须臾，
羡长江之无穷.
10-2 二重积分的计算
第二节 二重积分的计算
一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 三、小结与思考
10-2 二重积分的计算
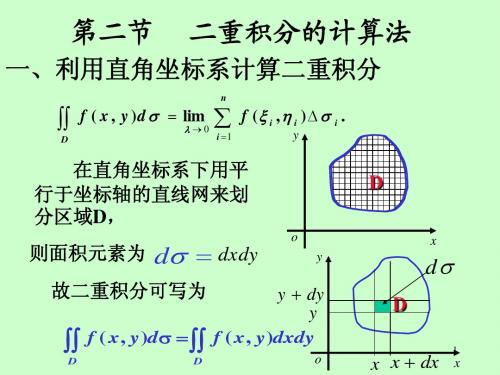
一、利用直角坐标系计算二重积分
(1) 在直角坐标系下用平行于 y
坐标轴的直线网来划分区域 D，
则面积元素为
d dxdy
o
D
x
故二重积分可写为
f ( x, y)d f ( x, y)dxdy
D
D
10-2 二重积分的计算
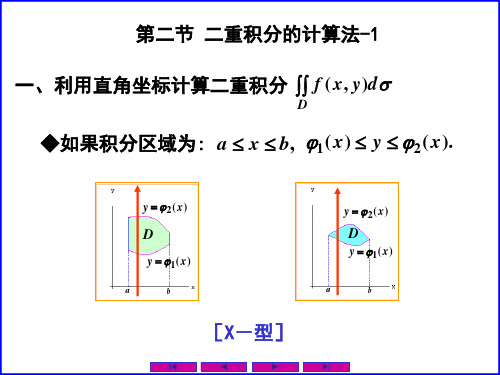
(2) 如果积分区域 D如图所示，那么可用不等式表示为
a x b, 1( x) y 2( x). ［X－型］
其中ri 为 ri与 ri ri 的平均值.由此当 ri , i 充分小 时，极坐标系下的面积元素 d rdrd.
10-2 二重积分的计算
其次, 直角坐标系与极坐标系有如下变换关系
x r cos
y
r
sin
最后, 两坐标系下积分区域 D 形状不变，因此有
f ( x, y)d f (r cos , r sin )rdrd .
D
o
10-2 二重积分的计算
D
D
以下我们讨论极坐标下的二重积分的计算．
r 1( ) r 2( )
DD
r 1( )
r 2( ) D
r 2( )
D
o
Ao
Ao
A
r 1( ) 0
0902二重积分的计算法-1
D
b ϕ2( x) f ( x , y )dy ; = dx a ϕ1 ( x )
∫
∫∫ f ( x , y )dσ ∫
D
d ϕ2 ( y) f ( x , y )dx . = dy c ϕ1 ( y )
∫
［混合型］ 混合型］ （在积分过程中要正确选择积分次序） 在积分过程中要正确选择积分次序） 积分次序
y
A(x)
a
x
y = ϕ2 ( x)
b
x
D
y = ϕ1( x)
b ϕ ( x) ∴ ∫∫ f ( x , y )dσ =∫a dx ∫ϕ 2( x ) f ( x , y )dy . ……二次积分公式 ? 1 二次积分公式
D
◆如果积分区域为：c ≤ y ≤ d , ϕ1 ( y ) ≤ x ≤ ϕ 2 ( y ). 如果积分区域为：
π
练习1 练习 改变下列积分的积分次 序
∫
1 2 x− x2 2 2− x dx f ( x , y )dy + dx f ( x , y )dy . 0 0 1 0
∫
∫
∫
解 积分区域如图： 积分区域如图：
y = 2− x
原式 = ∫0 dy ∫
1
2− y
2
y = 2x − x2
1− 1− y
f ( x , y )dx.
1
o
1
x
2.设f ( x , y )在D上连续 , 其中 D是由直线 y = x , y = a及x = b (b > a )所围成的闭区域 , 证明 :
(1)∫
b x dx a a
∫ f ( x , y )dy = ∫
b b dy y a
b ϕ2( x) f ( x , y )dy ; = dx a ϕ1 ( x )
∫
∫∫ f ( x , y )dσ ∫
D
d ϕ2 ( y) f ( x , y )dx . = dy c ϕ1 ( y )
∫
［混合型］ 混合型］ （在积分过程中要正确选择积分次序） 在积分过程中要正确选择积分次序） 积分次序
y
A(x)
a
x
y = ϕ2 ( x)
b
x
D
y = ϕ1( x)
b ϕ ( x) ∴ ∫∫ f ( x , y )dσ =∫a dx ∫ϕ 2( x ) f ( x , y )dy . ……二次积分公式 ? 1 二次积分公式
D
◆如果积分区域为：c ≤ y ≤ d , ϕ1 ( y ) ≤ x ≤ ϕ 2 ( y ). 如果积分区域为：
π
练习1 练习 改变下列积分的积分次 序
∫
1 2 x− x2 2 2− x dx f ( x , y )dy + dx f ( x , y )dy . 0 0 1 0
∫
∫
∫
解 积分区域如图： 积分区域如图：
y = 2− x
原式 = ∫0 dy ∫
1
2− y
2
y = 2x − x2
1− 1− y
f ( x , y )dx.
1
o
1
x
2.设f ( x , y )在D上连续 , 其中 D是由直线 y = x , y = a及x = b (b > a )所围成的闭区域 , 证明 :
(1)∫
b x dx a a
∫ f ( x , y )dy = ∫
b b dy y a
第九章第2节二重积分的计算(1)
y + dy y ∫∫ f ( x, y)dσ =∫∫ f ( x, y)dxdy
D D
dσ
D
x
o
x x + dx
1
x
直角坐标系下的计算公式
a 如果积分区域为： 如果积分区域为： ≤ x ≤ b, ϕ 1 ( x ) ≤ y ≤ ϕ 2 ( x ).
y = ϕ2 ( x )
y = ϕ2 ( x )
ϕ1 ( x )
f ( x , y )dy
4
如果积分区域为： 如果积分区域为：
c ≤ y ≤ d , ϕ 1 ( y ) ≤ x ≤ ϕ 2 ( y ).
d
d
x = ϕ1 ( y )
D
x = ϕ2 ( y)
x = ϕ1 ( y )
D
c
c
x = ϕ2 ( y)
∫∫ f ( x , y )dσ = ∫
π
例4. 求 ∫∫ x e
D
2 − y2
dxdy ，其中 D 是以(0,0), (1,1),
(0,1)为顶点的三角形.
解 Q∫ e
− y2
dy 无法用初等函数表示
∴ 积分时必须考虑次序
∫∫ x e
D
2 − y2
dxdy = ∫ dy ∫ x e
0 0
1
y
2 − y2
dx
=∫ e
0
1
− y2
y ⋅ dy = − 3
2 2 2
2
2
2
利用对称性, 考虑第一卦限部分, 其曲顶柱体的顶为
R
o x
R2 −x2
x2 + y2 = R2
z = R2 − x2 0 ≤ y ≤ R2 − x2 (x, y) ∈D: 0 ≤ x ≤ R
9-2二重积分的计算(1)13801
应用计算“已知平行截面面积的立体求体积” 的方法(简称平行截面法), 可求此体积. 步骤： 1º 求平行于坐标面的截面面积 A(x)
x0 [a, b],
作平行于 yOz 面的平面 x = x0 . 这个平面截曲顶 柱体所得到的截面是一
个以区间[ 1(x0), 2(x0) ]
为底，曲线 z = f (x0 , y)
为曲边的曲边梯形.
其面积：
2 ( x0 )
A( x0 )
1 ( x 0 )
f ( x0 , y ) d y
即x [a , b], 有
A( x )
b a
2 ( x )
1 ( x )
f ( x , y ) d y —— 已知平行截面面积
2 V A( x ) d x
2 ( x )
1 ( x )
2( y)
f ( x , y )dy f ( x , y )dx .
x 1 ( y)
dy
d
1( y)
D y y 1 ( x) c x o a bx
3 对于X 型区域D， 用直线 x x由下
至上穿D，穿入点所对应的纵坐标为 (出 ) y y 2 ( x) 内层积分的下限. (上 ) D y 1 ( x ) f ( x , y ) d D O a x b x 2 ( x) b
y 2 ( x) y 1 ( x )
x0
x
x0 b x
特点：用直线 x x0 (a x0 b)穿区域D，
该直线与D的边界至多有两个交点 .
定理
设 f ( x , y )在有界闭区域D上连续,
则
f ( x, y ) d f ( x, y ) d x d y
x0 [a, b],
作平行于 yOz 面的平面 x = x0 . 这个平面截曲顶 柱体所得到的截面是一
个以区间[ 1(x0), 2(x0) ]
为底，曲线 z = f (x0 , y)
为曲边的曲边梯形.
其面积：
2 ( x0 )
A( x0 )
1 ( x 0 )
f ( x0 , y ) d y
即x [a , b], 有
A( x )
b a
2 ( x )
1 ( x )
f ( x , y ) d y —— 已知平行截面面积
2 V A( x ) d x
2 ( x )
1 ( x )
2( y)
f ( x , y )dy f ( x , y )dx .
x 1 ( y)
dy
d
1( y)
D y y 1 ( x) c x o a bx
3 对于X 型区域D， 用直线 x x由下
至上穿D，穿入点所对应的纵坐标为 (出 ) y y 2 ( x) 内层积分的下限. (上 ) D y 1 ( x ) f ( x , y ) d D O a x b x 2 ( x) b
y 2 ( x) y 1 ( x )
x0
x
x0 b x
特点：用直线 x x0 (a x0 b)穿区域D，
该直线与D的边界至多有两个交点 .
定理
设 f ( x , y )在有界闭区域D上连续,
则
f ( x, y ) d f ( x, y ) d x d y
高数讲义第二节二重积分的计算(一)
解：先画出积分区域 D ， 并确定 D 的类型
方法一：将 D 看做 Y 型区域
y x2
y x y2
(4 , 2)
2
y
x y2
0 1
x
(1 , 1)
1 y 2 , y2 x y2
x y d x d y
2 1
d
y
y2 y2
xy d x
D
x y d x d y
2 1
d
y
y2 y2
xy d x
D
1 2
x
2
1 0
y
(
d xd
x2
y
x4
)
1 2
dx
1 x2
0
1 2
(1 ( x3
3
x2)dx x5) 1
5
0
1 15
例 2 求 ( x2 y)dxdy，其中D是由抛物线
D
y x2和 x y2所围平面闭区域.
解：画积分区域 两曲线的交点
x y2
y x2
x
(0,0) y2
, (1,1),
· y M 2 y 2( x )
y
· M 2 y 2( x )
D
D
· M 1 y 1( x )
0a x b x
· M 1 y 1( x )
0 a x bx
类型 I （X 型）：D 由直线 x = a , x = b 与曲线
y 1( x ) 和 y 2( x ) 所围成，即
D { ( x, y ) | a x b, 1( x) y 2( x) }
dx
y
A(x)
0
a
z f ( x, y)
y 1( x )
方法一：将 D 看做 Y 型区域
y x2
y x y2
(4 , 2)
2
y
x y2
0 1
x
(1 , 1)
1 y 2 , y2 x y2
x y d x d y
2 1
d
y
y2 y2
xy d x
D
x y d x d y
2 1
d
y
y2 y2
xy d x
D
1 2
x
2
1 0
y
(
d xd
x2
y
x4
)
1 2
dx
1 x2
0
1 2
(1 ( x3
3
x2)dx x5) 1
5
0
1 15
例 2 求 ( x2 y)dxdy，其中D是由抛物线
D
y x2和 x y2所围平面闭区域.
解：画积分区域 两曲线的交点
x y2
y x2
x
(0,0) y2
, (1,1),
· y M 2 y 2( x )
y
· M 2 y 2( x )
D
D
· M 1 y 1( x )
0a x b x
· M 1 y 1( x )
0 a x bx
类型 I （X 型）：D 由直线 x = a , x = b 与曲线
y 1( x ) 和 y 2( x ) 所围成，即
D { ( x, y ) | a x b, 1( x) y 2( x) }
dx
y
A(x)
0
a
z f ( x, y)
y 1( x )
二重积分的计算1
z
y
D
z = f (x, y)
O
a x0 b x
目录 上页 下页 返回 结束
设曲顶柱的底为
y = ϕ2 (x)
z z = f (x, y)
ϕ1(x) ≤ y ≤ ϕ2 (x) D = (x, y) a ≤ x ≤b
任取 截面积为 故曲顶柱体体积为 平面 截柱体的
y
D
O
a x0 b x y = ϕ1(x)
D
x
∫c d y∫ψ ( y)
1
d
ψ 2 ( y)
c f (x, y) dx O =ψ ( y) x x 1
当被积函数 f (x, y) 在D上变号 变号时,结论仍成立。 变号
目录 上页 下页 返回 结束
说明: 说明 (1) 若积分区域既是 X - 型区域又是Y - 型区域 , 则有
∫∫D
b a d
V = ∫∫ f (x, y) dσ = ∫ A(x)记 d x
ϕ2 (x) f (x,y) dy ]d x = d x = [ f (x,y)dy a ϕ1( x) a ϕ1(x)
b
∫ ∫
D b ϕ2 ( x)
a
作
∫
b
∫
目录
上页
下页
返回
结束
同样, 曲顶柱的底为
D = { (x, y) ψ1( y) ≤ x ≤ψ2 ( y), c ≤ y ≤ d }
−4
y
−2
y2 = x
x
y
=[
12y − 1 y2 − 1 y3 2 3
D
注: 计 ∫∫ 算
2 ] −[ ] = 52 3 −4 −2 f (x, y) dσ 时 若 f (x, y) 可 展 D , 扩 到 1
y
D
z = f (x, y)
O
a x0 b x
目录 上页 下页 返回 结束
设曲顶柱的底为
y = ϕ2 (x)
z z = f (x, y)
ϕ1(x) ≤ y ≤ ϕ2 (x) D = (x, y) a ≤ x ≤b
任取 截面积为 故曲顶柱体体积为 平面 截柱体的
y
D
O
a x0 b x y = ϕ1(x)
D
x
∫c d y∫ψ ( y)
1
d
ψ 2 ( y)
c f (x, y) dx O =ψ ( y) x x 1
当被积函数 f (x, y) 在D上变号 变号时,结论仍成立。 变号
目录 上页 下页 返回 结束
说明: 说明 (1) 若积分区域既是 X - 型区域又是Y - 型区域 , 则有
∫∫D
b a d
V = ∫∫ f (x, y) dσ = ∫ A(x)记 d x
ϕ2 (x) f (x,y) dy ]d x = d x = [ f (x,y)dy a ϕ1( x) a ϕ1(x)
b
∫ ∫
D b ϕ2 ( x)
a
作
∫
b
∫
目录
上页
下页
返回
结束
同样, 曲顶柱的底为
D = { (x, y) ψ1( y) ≤ x ≤ψ2 ( y), c ≤ y ≤ d }
−4
y
−2
y2 = x
x
y
=[
12y − 1 y2 − 1 y3 2 3
D
注: 计 ∫∫ 算
2 ] −[ ] = 52 3 −4 −2 f (x, y) dσ 时 若 f (x, y) 可 展 D , 扩 到 1
二重积分运算
二重积分运算
二重积分运算是微积分中的一个重要概念，它是对二元函数在一个有限区域内的积分运算。
在实际应用中，二重积分运算被广泛应用于物理、工程、经济学等领域，是解决实际问题的重要工具。
二重积分运算的定义是：设f(x,y)在闭区域D上连续，则在D上的二重积分为：
∬Df(x,y)dxdy
其中，D表示二元函数f(x,y)的定义域，dxdy表示对x和y的积分运算。
二重积分运算的结果是一个数值，表示在D上f(x,y)的积分值。
二重积分运算的计算方法有两种：直接计算和变量代换法。
直接计算法是将二元函数f(x,y)在D上分割成若干个小区域，然后对每个小区域进行积分运算，最后将所有小区域的积分值相加得到二重积分的结果。
变量代换法是将二元函数f(x,y)在D上的积分转化为在另一个区域上的积分，然后再进行计算。
二重积分运算在实际应用中有着广泛的应用。
例如，在物理学中，二重积分运算可以用来计算物体的质心、重心、转动惯量等物理量；在工程学中，二重积分运算可以用来计算材料的强度、应力、变形等参数；在经济学中，二重积分运算可以用来计算市场需求、供给、价格等经济指标。
二重积分运算是微积分中的一个重要概念，它在实际应用中有着广泛的应用。
掌握二重积分运算的计算方法和应用技巧，对于解决实际问题具有重要的意义。
高等数学二重积分的计算(1)
0
0
1
0
积分次序.
解：积分区域如图
y 3
x 3 y
f (x, y)d
d
[
2(y)
f
(x, y)dx]dy
D
c 1(y)
d
dy
2 ( y)
f
(x, y)dx
c 1(y)
先对x后对y
的二次积
分
应用公式时注意：
1) 首先应判定区域D是否为X-型或Y型区域。
画出积分区域 D 的图形. 2) 若 D 既是 x－型 区域又是 y－型 区域 则有：
块为好；
②根据被积函数f(x,y)特点，选择积分次序，以积分 简便或能够进行积分为原则，
如被积函数是：e
1 x
,
sin
x
,
cos
x
,
1
y
, ex2 , e x等应选择先积y，后积x.
x x ln x
（3）确定二次积分的上、下限，把二重积分化 为二次积分计算即可。 定限方法归纳如下
①先定限后积②域内划条线③先交为下限④后交为上限
解: 设两个直圆柱方程为
z
x2 y2 R2, x2 z2 R2
利用对称性, 考虑第一卦限部分,
R
其曲顶柱体的顶为 z R2 x2
OR
(x,
y)
D
:
0 0
y x
R
R2
x2
则所求体积为
x x2 z2 R2
y
R
8
R2 x2 d x
R2 x2
dy
0
0
8 R (R2 x2 ) d x 16 R3
0
3
例 2 试将 f (x, y)d 化为两种不同次序的累次
10.2二重积分的计算(1)
xydx]dy
2
1
[
y
x2 ] y dy 21
2
1
[
y3 2
y ]dy 2
y4 [
8
y2 4
]
12
1
1 8
.
例 2 计算 y 1 x2 y2d , 其中 D 是由直线 D
y x、x 1和 y 1 所围成的闭区域.
解 如图, D 既是 X 型, 又是Y 型.若视为X
型, 则
11
原积分 [ y 1 x2 y2dy]dx 1 x
第二节 二重积分的计算法（1）
一、利用直角坐标系计算二重积分 二、交换二次积分次序 三、对称性、奇偶性的应用
一、利用直角坐标系(right angle coordinate system)计算二重积分
如果积分区域为：a x b, 1( x) y 2( x).
［X－型］
y 2(x)
D
y 1( x)
y2 x 及直线 y x 2所围成的闭区域.
解 如图,
D 既是 X 型, 也是Y 型. 但易见选择前者计算
较麻烦, 需将积分区域划分为两部分来计算, 故选
择后者.
2 y2
xyd
[ 1 y2
xydx]dy
D
2 [ x2 1 2
y]
y y2
2
dy
1 2
2
[ y( y 2)2 y5 ]dy
)(e
y
1 0
)
(e
1)2 .
例 6 求两个底圆半径都等于 R 的直交圆柱面所围
成的立体的体积.
解 设两个圆柱面的方程分别为 x2 y2 R2 及
d
dy
2 ( y) f ( x, y)dx.
二重积分计算1
y2x y 2xx2
原 式 0 1d1 2 y y 1 y2f(x ,y)d.x
例 3改 变 积 分 0 2adx2 2a a x xx2f(x,y)dy(a0)
的 次 序 .
解：
2a
y 2ax
a
y 2axx2 xaa2y2
a 2a
= 原式
D
a 1(x)
f(x ,y)ddd y 2(y)f(x ,y)d［.x Y－型］ c 1(y)
D
在积分中要正确选择积分次序与正确给出积分
限，且定积分中的各种技巧在这里仍然适用。
练习一：将二重积分化成二次积分 If(x,y)dxdy
D: 由四条直线 : x=3，x=5, y
sin ydxd y1dyysin ydx o
Dy
y 0 y2
x
1
0(siynysiny)dy
1si1n
二次积分中的第一次积分要易于计算， 且最终形成只是关于第二个变量的函数。
(练习)将二重积分化成二次积分 If(x,y)dxdy
一、 先对x积分
D
y
b
o
D
ax
b
a
I dya f(x,y)dx
2 先对 y 积分（从下到上）
y
1
xydxdy
dx
x
xydy
D
x
x
xdx ydy
x
1 1(x3 x5)dx 1
20
24
D
3 先对 x 积分（从左到右）
0
1x
xydxdy d y
D
二重积分中值定理数一
二重积分中值定理数一二重积分中值定理是数学中的一条重要定理，它可以帮助我们更好地理解二重积分的基本概念和性质，同时也是计算复杂积分的重要工具之一。
其中的一条数学公式——“二重积分中值定理数一”在二重积分中起到了非常核心的作用，下面我们将围绕这一公式来讲解它的相关内容。
1. 数学公式“二重积分中值定理数一”是什么？在二元连续有界函数$f(x,y)$定义的矩形区域 $D$ 上，存在一点$(\xi,\eta)$，使得$$\frac{1}{S(D)} \iint\limits_{D}f(x,y)dxdy = f(\xi,\eta)$$其中，$S(D)$表示矩形区域$D$的面积。
2. 公式的含义和作用二重积分中值定理数一是一条非常重要的中值定理，它表明在矩形区域（积分区域）上，必定存在一个点$(\xi,\eta)$，使得函数$f(x,y)$在该点处的值等于其在整个矩形区域上的平均值，也就是二重积分的结果。
换言之，这条公式为我们提供了一种计算“平均值”的方法，将一个复杂的积分问题转化为在一个点上求解函数值的问题，从而使得我们的计算更加简单、明了。
3. 具体实例假设我们要计算函数$f(x,y)=xy$在矩形区域$D=[0,2]\times[0,1]$上的平均值，按照二重积分的定义，我们需要计算$I=\frac{1}{S(D)}\iint_Df(x,y)dxdy$。
然而，根据定理，我们知道$I=f(\xi,\eta)$其中点$(\xi,\eta)$是在矩形区域$D$上存在的一点。
那么我们该如何确定$(\xi,\eta)$的值呢？我们可以通过找到该函数在$D$上的极值点来得到答案。
首先，我们计算一下$f(x,y)$在合适的某个区域$D_1$内的最大值和最小值，假设$f(x,y)$在$D_1=[0,1]\times[0,1]$内取得最大值$M$，最小值$m$。
那么我们有$S(D_1)\leq S(D)$，则$\frac{1}{S(D)}\iint_Df(x,y)dxdy\leq\frac{1}{S(D_1)}\iint_{D_ 1}f(x,y)dxdy\leq M$。
10.2二重积分计算(1)
y
y = 4 − x2
D = D + D2 (如图所示 如图所示) 如图所示 1
显然, 在D 上, f (−x, y) = − f (x, y) 显然 1
D 1
o D2 1 x
x =1
在D2上, f (x,−y) = − f (x, y)
∴ I = ∫∫ x ln(y + 1+ y2 )dxdy
D 1
z
D
o
(曲边梯形的面积 曲边梯形的面积) 曲边梯形的面积
a x0 b x y = ϕ1(x)
V = ∫∫ f (x, y) dσ = ∫ A(x)d x D
b
为第二次积分的 被积函数的因子
b
=∫ [ ∫
a
b
ϕ2 ( x)
a
ϕ1( x)
f (x,y) dy ]d x ∆∫ dx∫
a
ϕ2 ( x)
ϕ1 ( x)
D3
∫∫(xy + cos xsin y)d xd y = 0 + 2∫∫cos xsin yd xd y
D2 D 1
例.计算 计算 所围成. y = 4 − x2, y = −3x, x =1 所围成 解: 令 f (x, y) = x ln(y + 1+ y )
2
其中D 其中 由
4
y = −3x
= ∫∫ f (x, y)dxdy
D
性质: 性质
(有和定积分完全对应的性质 条) 有和定积分完全对应的性质:7条 有和定积分完全对应的性质
D
1. ∫∫ k f (x, y)dσ = k ∫∫ f (x, y) dσ ( k 为常数) 为常数 D
假 定 下 列 性 质 中 出 现 的 二 重 积 分 存 在
1二重积分的计算
解 根据对称性有 D = 4D1
在极坐标系下
D1
x2 + y2 = a2 ⇒ r = a,
( x2 + y2 )2 = 2a2 ( x2 − y2 ) ⇒ r = a 2cos 2θ ,
由⎨⎧r ⎩
=
a r
2cos2θ =a
,
得交点A = (a, π), 6
所求面积σ = ∫∫ dxdy = 4∫∫ dxdy
D
f ( x, y) 为曲顶柱体的体积． z
z = f (x, y)
应用计算“平行截
面面积为已知的立
体求体积”的方法,
y
A(x0 )
y = ϕ2(x)
x
b
x0 a
得
f (x, y)dσ =
b
ϕ2 (x)
f
(x,
y = ϕ1(x)
y)dydx.
∫∫ ∫ ∫ D
a ϕ1 ( x )
=
b
dx
ϕ2 (x) f (x, y)dy.
∫∫ 1. 计算 I
=
D
sin y dσ y
，其中区域 D 为曲线 y =
x 及直线
y=x 所围成。
∫∫ 2． 计算 I = ln(1+ x2 + y2 )dσ ，其中区域 D 为曲线 x2 + y2 = 1及 D 坐标轴围成的第一象限的部分。
作业
P153. 1(1,4),3,6(1,2,4,5,6) ,8,9,10,15
D
c
ϕ1( y)
1
∫∫ ∫ ∫ D
f ( x, y)dσ =
d⎡ c ⎢⎣
φ2 ( y ) φ1 ( y )
f
转动惯量二重积分公式(一)
转动惯量二重积分公式(一)
转动惯量二重积分公式
1. 转动惯量的定义
转动惯量是刚体在某一轴周围旋转时，对于该轴通过的力矩所起
的抵抗作用。
它的公式可以表示为：
I=∬r2dm
其中，I表示转动惯量，r表示质点到轴的距离，dm表示质量元。
2. 转动惯量二重积分公式
转动惯量可以通过二重积分来计算。
对于一个边界已知、密度分
布连续的平面区域D上的刚体，转动惯量I可以表示为：
I=∬r2
ρ(x,y) dA
D
其中，r表示质点到轴的距离，ρ(x,y)表示点(x,y)处的密度，dA表示面积元素。
3. 转动惯量二重积分公式的举例
考虑一个均匀密度的矩形薄板，边长分别为a和b。
假设薄板
的中心与原点重合，按照x轴方向为横轴，y轴方向为纵轴建立平面
直角坐标系。
根据转动惯量二重积分公式，可以将转动惯量表示为：
I=∬r2
D
ρ(x,y) dA
对于该矩形薄板，其转动惯量可以表示为：
I=∬(x2+y2)
D
ρ dA
由于矩形薄板的密度是均匀的，则ρ为常数，可以将其提出积分号外：
I=ρ∬(x2+y2)
D
dA
将矩形薄板的边界确定为x∈[−a
2,a
2
]，y∈[−b
2
,b
2
]，建立二重积
分的限定范围。
计算二重积分的结果即可得到转动惯量的值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
原式
1
2 y
dy 0
1 1 y2
f ( x, y)dx.
例 3
改变积分
2a
dx
0
2ax
2axx2 f ( x, y)dy (a 0)
的次序.
解：
2a
y 2ax
a
y 2ax x2 x a a2 y2
a
2a
= 原式
a
a a2 y2
dy
0
y2
f ( x, y)dx
D
D: y1(x) y y2(x) axb
y
y2(x)
D
y1(x)
0
［a X－型x ］b x
I=
y ( x) f ( x, y)dy y ( x )
二重积分计算的两种积分顺序
D: x1(y) x x2(y) cyd
y
d y
x1 (y)
c
x2(y)
D
0
. ［Y－型］ x
I =
d
dy
x ( y) f ( x , y)dx
z=f (x,y)
0
c
y
a
b
D
x
d
y
二重积分的计算1 (D是矩形区域)
z
I f ( x, y)dxdy
D
D是矩形区域 [a,b ; c,d]
b
Q( y ) = a f ( x , y)dx
Id
c Q( y)dy
0
a
z f (x, y) y y
c
b
V a A( x)dx
z=f (x,y)
c
x2(y)
D
0
［Y－型］ x
I=
x ( y) f ( x, y)dx x ( y)
I f ( x, y)dxdy
D
二重积分计算的两种积分顺序
D: x1(y) x x2(y) cyd
y
d y
x1 (y)
c
x2(y)
D
0
. ［Y－型］ x
I=
x ( y) f ( x, y)dx x ( y)
Y型区域的特点：穿过区域且平行于x轴的直线
与区域边界相交不多于两个交点. 积分次序：先X后Y。 若区域如图，则须进行分割.
在分割后的三个区域上分别 使用积分公式
D3 D1
D2
.
D
D1
D2
D3
如果积分区域即是X-型又是Y-型的 ，则重积分既可以 转化为先对x后对y的 ，也可以转化为先y后x的二次积分（ 累次积分）
cyd
ψ( y)
Q( y ) = f ( x, y)dx φ( y) d
I = c Q( y)dy
0
c
d
ψ( y)
dy f ( x, y)dx
c
φ( y)
z=f (x,y)
y
x=(y)
d
y
D
.
.
x
x=(y)
二重积分计算的两种积分顺序
D: x1(y) x x2(y) cyd
y
d y
x1 (y)
D
c
1( y)
二重积分的计算2（D是曲线梯形区域）
z
I f ( x, y)dxdy
D
D: (y) x (y)
cyd
0
c
z=f (x,y)
y
x=(y)
d
y
D
x=(y) x
二重积分的计算2（D是曲线梯形z区域）
I f ( x, y)dxdy
D
D: (y) x (y)
cyd
z f (x, y)
第二节 重积分的计算
• 直角坐标系下计算二重积分 • 举例 • 小结
定积分中已知截面面积为 A(x)的立体---元素法/微元法
b
V a A( x)dx .
dV=A(x)dx
A(x)
a
V x
b
x
二重积分的计算1 (D是矩形区域)z
I f ( x, y)dxdy
D
D是矩形区域 [a,b ; c,d]
z=f (x,y)
y
d
y
二次积分 .
.
b
.
x
同理，也可以先对 y 积分
D
b
d
I a dxc f ( x, y)dy
二次积分
积分区域的类型：
如果积分区域为：a x b,
［X－型］
y 2(x)
D
y 1( x)
a
b
1( x) y 2( x).
y 2(x)
D
y 1( x)
a
b
其中函数1( x) 、2( x) 在区间 [a,b]上连续.
y y
.
z=f (x,y)
ψ( y)
Q( y ) = f ( x, y)dx φ( y)
I
=
d
c
Q( y)dy0c NhomakorabeaQ( y)
y
x=(y)
d
y
.
D
.
x=(y)
x
问题：Q( y)是什么图形？ 也是曲边梯形 !
二重积分的计算2（D是曲线梯形区域）
z
I f ( x, y)dxdy
D
D: (y) x (y)
c
x ( y)
I f ( x, y)dxdy
D
D: y1(x) y y2(x) axb
y
y2(x)
D
y1(x)
0
a
x bx
［X－型］
I =
b
dx
y ( x)
f ( x, y)dy
a
y ( x )
X型区域的特点： 穿过区域且平行于y轴的直线
与区域边界相交不多于两个交点. 积分次序：先Y后X。
例 1
改变积分
1
dx
1 x
f ( x, y)dy 的次序.
00
解： 积分区域如图
原式
1 1 y
dy f ( x, y)dx.
00
y 1 x
例2 改变积分
1
dx
2 x x2
f ( x, y)dy
2
dx
2x f ( x, y)dy的次序.
0
0
1
0
解： 积分区域如图
y2 x y 2x x2
y
y2(x)
D
y1(x)
0
a
x bx
［X－型］
I=
y ( x) f ( x, y)dy y ( x )
二重积分计算的两种积分顺序
D: x1(y) x x2(y) cyd
y
d y
x1 (y)
c
x2(y)
D
0
［Y－型］ x
.
I =
d
dy
x ( y) f ( x , y)dx
c
x ( y)
I f ( x, y)dxdy
y
d
y
Q( y)
.
b
D
x
问. 题：Q( y)是什么图形？ 是曲边梯形。
二重积分的计算1 (D是矩形区域)
z
I f ( x, y)dxdy
D
D是矩形区域 [a,b ; c,d]
b
Q( y ) = a f ( x , y)dx
Id
c Q( y)dy
c
d
b
0
c dya f ( x , y)dx a
I f ( x, y)dxdy
D
二重积分计算的两种积分顺序
D: x1(y) x x2(y) cyd
y
d y
x1 (y)
c
x2(y)
D
0
. ［Y－型］ x
I =
d
dy
x ( y) f ( x , y)dx
c
x ( y)
I f ( x, y)dxdy
D
D: y1(x) y y2(x) axb
f ( x, y)d
b
dx
2 ( x) f ( x, y)dy.
D
a
1( x)
如果积分区域为：c y d , 1( y) x 2( y). ［Y－型］
d
x 1( y) D x 2( y)
c
d
x 1( y)
c
D
x 2( y)
f ( x, y)d
d
dy
2 ( y) f ( x, y)dx.