六下统计问题的考点分析+模拟试题(含答案)
人教版六年级下册小学数学小升初复习统计与概率专项复习卷(附参考答案)

统计与概率专项复习卷班级:姓名:一、冷静思考,正确填写。
1.2024年6月以来,我国大部分地区在暖高压带控制下,高温天气增多,为了解某地区7月上旬气温变化情况,宜采用( )统计图;2024年7月15日国家统计局发布我国上半年国家经济运行情况报告,要体现第一、第二、第三产业产值情况,宜采用( )统计图;要体现货物进出口占比情况,宜采用( )统计图。
2.如图是实验小学六年级同学最喜欢的体育活动人数占比情况。
(1)从图中我们可以得出最喜欢跳绳的人数占总人数的( )%。
(2)如果最喜欢打篮球的有40人,那么最喜欢踢足球的有( )人。
(3)如果最喜欢跳绳的比最喜欢踢毽子的多6人,那么最喜欢跳绳的有( )人。
3.将1、3、5、7四张数字卡片反扣在桌面上(卡片背面完全相同),从中任意抽出两张,这两张数字卡片的和( )是偶数。
(填“一定”“可能”或“不可能”)4.盒子里有大小完全相同的红球6个,黄球3个,蓝球3个,任意摸出1个球,摸出( )球的可能性最大。
要使摸出三种球的可能性相同,可以( )。
5.李冰期末考试语文、英语、科学的平均成绩是76分,数学成绩公布后,他的平均成绩提高了3分,李冰的数学成绩是( )分。
6.盒子里放着三张卡片,分别写着7、8、9三个数字。
从盒子里任意摸出一张卡片,如果是质数,算笑笑赢;如果是合数,算淘气赢,那么( )赢的可能性大。
若想两人赢的可能性相等,可以在盒子里再放入一张写着数字( )的卡片。
(任意写出一种答案)7.根据统计图,填一填。
(1)6月收入( )万元,支出( )万元。
(2)( )月的收入和支出相差最少,相差( )万元。
(3)8月与( )月收入相同。
(4)11月的收入比10月增长( )%。
(5)根据折线统计图,请你提出一个数学问题。
8.下图是株洲市某年1~12月各月气温和降水量统计图。
估一估,填一填。
(1)这一年株洲市年降水量大约是( )毫米。
(结果保留整数)(2)这一年株洲市月平均气温大约是( )摄氏度(结果保留整数),株洲市气温的总体变化趋势是。
青岛版小学(六三制)数学六年级下册《统计与概率》知识点及典型题目训练试题(含答案)

回顾整理——统计与概率一、知识点解读 1.统计知识点:统计表分为单式统计表和复式统计表。
单式统计表是只对某一项目的数量进行统计的表格,复式统计表是统计项目在两个或两个以上的统计表格,复式统计表也叫复合统计表。
统计图分为条形统计图,折线统计图和扇形统计图。
条形统计图是用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来。
从图中,能清晰的看出数量的多少,便于相互比较。
折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来,以折线的上升或下降来表示统计数量增减变化。
从图中,不但可以表示出数量的多少,而且还能够清楚地表示出数量增减变化的情况。
扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数。
从图中,能清楚地看出各部分与总数的百分比,部分与部分之间的关系。
《统计与概率》知识框架统 计与 统计量1.平均数: 总数量除以平均分成的份数。
2.中位数:一组数据按照从大到小的顺序排列,中间的数就是这组数据的中位数。
当数据的个数为偶数时, 中间两个数的平均数是这组数据的中位数。
3.众数:一组数据中出现次数最多的数称为这组数据的众 数, 一组数据可能没有众数, 也可能有一个或两个。
统计表4.统计表:分为单式统计表和复式统计表统计图5.统计图 (1)认识条形统计图、折线统计图、扇形统计图, 能够掌握各种统计图的特征, 会选用相应的统计图描述数据(2)绘制三种统计图的方法 (3) 读懂三种统计图,能利用统计图中的信息解决问题可能性6.可能性 (1) 用一定、 可能、 不可能描述事件发生的概率 (2) 用分数表示事件发生的可能性的多 少 (3) 游戏的公平性: 参与游戏各方获胜的可能性相等就公平, 如果不相等就不公平统计量:平均数。
平均数是指在一组数据中所有数据之和再除以数据的个数。
平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标。
通用版数学六年级下册总复习专题:统计3 含答案

統計一.填空題我能行。
1.學校統計全校各年級人數及總人數,應選用( )統計圖;氣象局統計一晝夜氣溫情況,應選用( )統計圖。
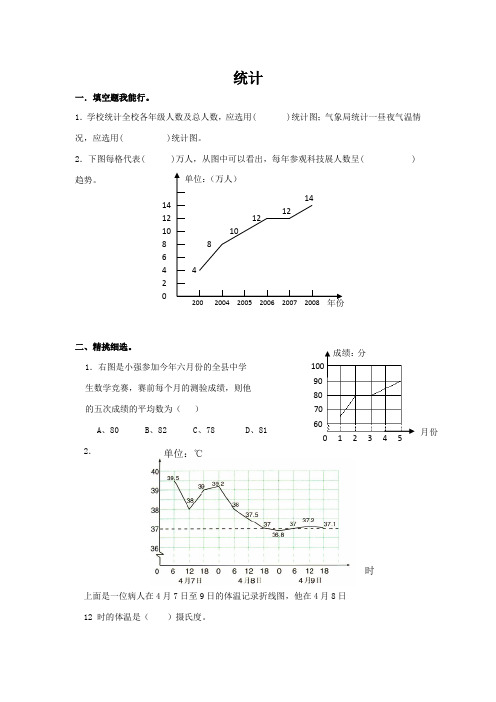
2.下圖每格代表( )萬人,從圖中可以看出,每年參觀科技展人數呈( )趨勢。
二、精挑細選。
1.右圖是小強參加今年六月份的全縣中學 生數學競賽,賽前每個月的測驗成績,則他 的五次成績的平均數為( )A 、80B 、82C 、78D 、81 2.上面是一位病人在4月7日至9日的體溫記錄折線圖,他在4月8日 12 時的體溫是( )攝氏度。
年份單位:(萬人)2 4 6 8 10 12 142002004 2005 2006 2007 2008 48 10 12 1214單位:攝氏度時70 6080 90 100 1 0 2 3 4 5月份成績:分單位:℃A 、38B 、37.5C 、37D 、39.2 三.統計樂園。
1.幸福社區2005 ~2009年每百戶居民電腦平均擁有量如下圖。
⑴ 幸福社區2005~2009年每百戶居民電腦平均擁有量一共增加了( )臺。
⑵( )年到( ) 年這一年電腦平均擁有量增長的幅度最小。
( )年到( ) 年這一年電腦平均擁有量增長的幅度最大。
⑶ 根據圖中的資訊預測,2010年幸福社區每百人電腦平均擁有量大約( )臺。
2.中國人的驕傲。
第24--29屆奧運會中國獲金牌數量統計圖40302010030屆數量/臺2005年 2006年 2007年 2008年 2009年年份屆(1)根據統計表中的數據,完成統計圖。
(2)( )屆取得的奧運金牌數最多,最多的那一屆比最少的那一屆多( )枚。
(3)中國獲得奧運金牌數的整體是( )趨勢。
(4)請你預測第30屆奧運會中國代表團能獲得多少枚金牌?在圖上畫出來。
並說出你的理由。
(5)你還能提出什麼數學問題?3.下麵是某地2009年月平均溫度變化情況統計圖,看圖回答下列問題。
(1)上面的統計圖是( )統計圖。
(2)哪個月的平均氣溫最高?哪個月的平均氣溫最低?(3)哪兩個月之間的平均氣溫上升得最快?哪兩個月之間的平均氣溫下降得最快?4.小曼身高一年級時115釐米,二年級時120釐米,三年級時130釐米,四年級時135釐米,五年級時140釐米。
【小升初专项复习】小学数学毕业考专项复习卷(5)统计与概率 全国通用(含答案、详解)

六下数学毕业考专项复习卷(5)统计与概率姓名:___________ 班级:___________ 学号:___________一、填空题1.要描述六年级学生参加各课外小组人数占全年级总人数的百分比情况,应选用(________)统计图;要记录某地区12个月的气温变化情况,应选用(________)统计图;要直观表示我国几大河流——长江、黄河、黑龙江、珠江的长度,应选用(________)统计图。
2.箱子里有10个球,要使箱子里摸出蓝色球的可能性是710,箱子里应该有________个蓝色球.3.20以内所有质数相加的和是(_____),它们的平均数是(_____)。
4.盒子里有同样大小的红球、黄球、篮球各7个,要想摸出的球一定有2个同色的,至少要摸_____个球.5.在一个盒子里装着只有颜色不同的若干黑、白、红三种颜色的珠子,其中红色珠子的颗数是白色的,黑色珠子的颗数是红色珠子的50%.如果从盒子中任意摸出一颗珠子,摸出黑色珠子的可能性是________.6.根据统计图,解决问题。
(1)(_____)先到达终点。
(2)开赛初(_____)领先,开赛(_____)min两人相遇,然后(_____)领先,小强最多领先小刚(_____)m。
(3)小刚的平均速度约是(_____),小强的平均速度约是(_____)。
(得数保留整数)7.在一个不透明的口袋里放入12个除颜色外其余完全相同的球,要使摸到红球的可能性为56,应放入(_____)个红球。
8.笑笑从家去相距5千米远的图书馆借书,经过情况如下图。
回来时的速度是____千米/时。
9.“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘凯随机调查了城区若干名学生和家长对小学生带手机现象的看法,统计整理并制作了如下的统计图:(1)这次调查的家长人数为________,并补全图①________;(2)图①中表示家长“赞成”的圆心角的度数为________;(3)预测一下,若有2500名家长接受调查,估计有________名家长持反对态度.二、解答题10.五个裁判员给一名体操运动员评分,去掉一个最高分和一个最低分,平均得分为9.58分;去掉一个最高分,平均得分为9.46分;去掉一个最低分,平均得分为9.66分.这名体操运动员的最高分和最低分相差多少分?11.育才小学六(2)班第一学期期末考试成绩情况统计图(1)这是一幅统计图,它的特点是.(2)如果这个班共有60人参加考试,获得不及格有人.(3)如果在这次考试中共有2人不及格,这个班共获得优秀的有人.(4)获得及格等级的人数比获得不及格等级的人数多%.12.下面是王芳家8月份支出及储蓄情况的统计图。
2020新人教小学六年级数学下册统计专项考点练习(含答案)

新人教小学六年级数学下册统计专项考点练习
1. 某校六年级有370人,六年级里面一定有()个人的生日是同一天.
A .2
B .4
C .5
2. ()能表示一组男生的跳绳成绩。
A .条形统计图
B .折线统计图
C .扇形统计图
3. 刘翔在2008年北京奥运会上()能拿冠军。
A .不可能
B .可能
C .一定
4. 把红、黄、蓝、白四种颜色的球各8个放到一个袋子里,至少要取()个球,才可以保证取到三个颜色相同的球.
A .9
B .8
C .5
D .13
5. 可以清楚地表示部分和整体关系的统计图是()
A .条形统计图
B .扇形统计图
C .单式折线统计图
D .复式折线统计图
6. 下面各组数中互为倒数的是().
A .。
六年级数学下册《统计与可能性》专项练习题及答案(人教版)

六年级数学下册《统计与可能性》专项练习题及答案(人教版)统计与可能性(一)【学习内容】统计图表(课本109、110页)【学习目标】1、进一步掌握复式条形统计图和复式折线统计图,加深对复式条形统计图和复式折线统计图特点的理解。
2、能正确根据需要选择统计图有效地表示数据并根据统计结果做出简单的判断和预测。
【学习过程】一、知识梳理1.简单的统计图有()统计图、()统计图和()统计图。
2.这三种统计图表各自的特点是什么?3.为了表示某地区一年内月平均气温变化的情况,可以把月平均气温制成()统计图,为了解全班同学血型情况,可以制作()统计图,为了统计全校喜欢各项体育活动的人数,可以制作()统计图。
二、课堂练习六年级同学爱吃的食物的人数统计图1.看图回答问题。
(1)统计图纵轴表示________.(2)从整体上看两个班中学生喜欢吃__________的人数最多。
(3)二班中喜欢吃蔬菜的人数占全班人数的______%;(4)一班中喜欢吃肉禽类的人数是喜欢吃蔬菜的_________倍。
(5)两个班中喜欢吃蔬菜的同学人数是爱吃虾类人数_____%。
(6)你有什么建议?2.下面两个统计图,反映的是甲、乙两位同学在复习阶段数学自测成绩和在家学习时间分配情况。
请看图回答以下问题:(1)从折线统计图看出()的成绩提高得快。
(2)从条形统计图看出()的反思时间少一些,少()%。
(3)你喜欢谁的学习方式,为什么?(4)你喜欢谁的学习方式,就求出他最后三次自测的平均成绩。
3、六(2)班同学的血型情况如右图。
(1)从图中你能看出哪些信息?(2)该班有50人,各种血型各有多少人?三、当堂检测1、根据右图回答下列问题。
(1)上午9时的温度是()。
(2)这一天的最低温度大约是(),是()时达到的。
(3)这一天的温差是(),从最低温到最高温经过了()小时。
(4)图中的A点表示(),B点表示()。
(5)从统计图中你还能得到什么信息?(至少写两条)2、我国领土面积960万平方千米,下图是我国地形分布情况。
六年级数学下册《统计与概率综合》练习题及答案解析

六年级数学下册《统计与概率综合》练习题及答案解析学校:___________姓名:___________班级:_____________一、填空题1.孙亮家去年的总收入为50000元,各项收入来源情况如图。
其中占总收入比重最大的是( )收入,是( )元。
其中卖核桃的收入占总收入的( )%。
2.把一个正方体的3个面涂成蓝色,2个面涂成黄色,1个面涂成黑色,任意抛一次,( )色面朝上的可能性最大,( )色面朝上的可能性最小。
3.小军家2016年各季度电费情况如下图:小军家2016年各季度电费情况统计图(1)每格代表( )元。
(2)小军家第( )季度电费最多,是( )元。
(3)小军家电费第一季度比第二季度多( )元。
(4)小军家全年电费( )元。
4.体育老师对某班女生进行仰卧起坐测试。
以1分钟能做30个为达标,超过的个数用正数表示,不足的个数用负数表示。
老师记录的其中7个女生的成绩是:﹢4、﹣2、﹣9、﹢15、﹢12、﹢8、0。
这7个女生仰卧起坐的达标率是( )%,她们平均每人做了( )个仰卧起坐。
二、选择题5.要反映小林一学期数学成绩变化情况,选用()统计图比较合适。
A.复式条形B.单式折线C.复式折线6.小明想从下面的盒子中摸出一颗黑球,从()盒中摸是最好的选择。
A.B.C.D.7.今天是星期一,7天后()是星期一。
A.可能B.不可能C.一定8.小华身高145cm,他在平均水深是120cm的小河游泳,()危险。
A.没有B.可能有C.一定有9.下列几种统计情况,用复式折线统计图反映比较合适的是()。
A.陈晓本学期数学单元测式成绩的波动情况B.苏宁电器1月份销售各种品牌冰箱的百分比C.晋江市和惠安县近5年财政收入变化情况D.实验小学合唱团和舞蹈队的男、女生人数情况三、解答题10.暑假快到了,学校号召六年级的同学们参与劳动实践活动,同学们依据自己的情况选择了相关的劳动项目,主要有以下四种:A.清除小广告;B.捡拾垃圾;C.指导垃圾分类;D.去敬老院打扫卫生。
六年级下册数学试题-《统计与概率》易错题专项复习(含解析)人教版

【专题复习】2019-2020学年人教新版小升初《统计与概率》易错题专项复习(提高版)【学生版】一.选择题(共12小题)1.小冬爸爸5月份的工资总收入约是8000元,按照如图进行支配,那么用于教育费用约是()A.4000元B.1200元C.2000元D.900元2.明天()下雨.A.一定B.可能C.不可能3.口袋里有1个红球、1个黄球、1个白球.从口袋里任意摸出1个球,摸到球的颜色一共有()种不同的可能.A.1种B.2种C.3种4.抛一枚硬币,朝上的可能性()A.正面大B.反面大C.正反两面差不多5.把3个白球和5个红球放在盒子里,任意摸出一个,()是蓝色的.A.可能B.一定C.不可能6.某班有50人,其中三好学生10人,优秀学生干部5人,在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是()A.72°,36°B.100°,50°C.120°,60°D.80°,40°7.如图,甲摸到白球得1分,乙摸到黑球得1分,在()箱中摸最公平.A.B.C.D.8.从写有1~6的6张卡片中任抽一张,抽到是2的可能性是()A.B.C.D.9.刘翔在2016年巴西里约热卢奥运会上()能拿冠军.A.不可能B.可能C.一定10.太阳()是东升西落.A.一定B.不一定C.不会11.笑笑和淘气玩“剪刀、石头、布”游戏,下面说法中正确的是()A.笑笑一定胜B.淘气一定胜C.淘气可能胜12.明天()会下雨.A.可能B.一定C.不可能二.填空题(共9小题)13.用0,3,5,8可以组成个没有重复数字的两位数,其中最大的两位数是,最小的两位数是.14.箱子里放着3个苹果,5个橘子,2个桃子,7个梨,小明随便拿出一个水果,有种可能,拿到的可能性最小,要想让这种水果的可能性最大,至少还要加个.15.鱼不可能会在天上飞..16.有三把锁和三把钥匙,现在用三把钥匙去打开三把锁,最多要试次.17.在一块并排10垄的田地中,选择2垄种植A、B两种作物,每种作物种植一垄.为有利于作物生长,要求A、B两种作物的间隔不小于6垄,则不同的选垄种植方法有种.18.有一楼梯共12级,如规定每次只能跨上一级或两级,要登上第12级,共有不同的走法.19.一桶水,需2人一起抬.3人把一桶水从离家600米远的地方抬回家,平均每人要抬米.20.用0、1、2、3四个数字,可以组成个不同的三位数.21.下面是数学学习小组6名同学的测验成绩:李刚95分,王聪92分,王冬88分,范华93分,张兰94分,周兵96分.(1)这六位同学的平均分数多少?(2)如果把他们的平均成绩记住0,那么这6名同学的成绩分别记作多少?三.判断题(共5小题)22.在制作扇形统计图时,总的数量越多,所画的圆就越大..(判断对错)23.冬天一定会下雪..(判断对错)24.小明所在班级同学的平均身高比小强所在班级的平均身高高些,所以小明比小强要高些..(判断对错)25.三(1)班同学的平均体重是35千克,三(1)班不可能有体重低于32千克的同学..(判断对错)26.在一次彩票有奖销售活动中,中奖的可能性是.李叔叔买了100张彩票,一定能有20张中奖.(判断对错)四.应用题(共5小题)27.下图是小华骑自行车到6千米远的森林公园去游玩的情况.(1)小华从出发到返回,一共经过了多长时间?(2)返回前,小华在路上用的时间比在公园里玩的时间多多少分钟?(3)返回时,小华骑自行车每分钟行走多少米?28.某次考试,的学生取得优秀成绩,这些学生的平均分比优秀的分数线高4分,而没达到优秀的学生的平均分比优秀的分数线低11分,所有学生的平均分是87分.那么,优秀的分数线是多少分?29.某电视节目评选优秀选手,专家组与观众代表的评分如下表.(1)专家组的平均分是多少?(2)观众代表的平均分是多少?(3)总平均分是多少?30.2017年某店“双十一”销售额比2016年“双十一”销售额增加了多少亿元?31.某小学参加兴趣小组情况如图:已知参加体育的有136人,参加“其它”兴趣小组的共有多少人?五.解答题(共15小题)32.工人叔叔要修一条长85米的公路,已经修了5天,还剩13.5米,平均每天修了多少米?33.昨天和今天共售出996张票,每天放映3场,平均每场售出多少张票?34.袋子里放了6个球:〇〇〇〇〇●任意摸一个再放回.小胖连续摸了5次,都是白球,他第六次摸到的球是黑球.(填“一定”、“不可能”或“可能”)35.小英4次语文测验的平均成绩是89分,第5次测验得了94分.问她5次测验的平均成绩是多少?36.有一种奖券的中奖率是1%,所以买100张奖券就一定能中奖..37.一个小组在一班工作时间内,前3小时每小时生产零件170个,后5小时每小时生产零件186个,平均每小时生产零件多少个?38.李大爷带900元买了22袋同一种化肥,还剩20元.平均每袋化肥多少元?39.按要求涂一涂.(1)图1摸出的一定是黑球;(2)图2摸出的不可能是黑球;(3)图3摸出黑球的可能性最大40.星期天,小华乘公交车从家到图书馆看书,后来打的回家,如图表示的是这段时间里小华离家距离的变化情况.请你仔细观察,回答问题.(1)小华在图书馆呆了分钟.(2)回来打的时平均速度是每小时千米.(3)乘公交车所用的时间比回来多用%.41.求下面图形的面积或体积.(1)求如图1中的阴影面积(单位:m)(2)求玩具陀螺的体积.(单位:cm)42.下面是5位同学的体重:小李38千克,小王42千克,小张36千克,小林43千克,小许41千克.先计算他们的平均体重,再用正数和负数来表示他们的体重与平均体重相差的部分.单位:千克43.刘小强4次数学测验的平均成绩是90分,第5次数学测验得95分,小强这5次测验的平均成绩是多少?44.聪聪家2015年11月支出情况统计如图.聪聪家2015年11月的总支出是3600元.请你回答问题:(1)这个月哪项支出最多?支出了多少元?(2)购买衣物的支出比文化教育支出少百分之几?少支出了多少元?45.实验小学去年四个季度用水情况统计如下表:这个小学去年平均每个月用水多少吨?46.如图是某班数学期末考试的统计图,可惜已经破损了.已知:这个班数学期末考试的及格率为95%.成绩优秀的人数占全班的35%.成绩“良好”的人数比“优秀”的人数多.请你算一算:(1)该班一共有人参加了这次考试;(2)其中成绩达到优秀的一共有人;(3)成绩良好的有人.【教师版】一.选择题(共12小题)1.小冬爸爸5月份的工资总收入约是8000元,按照如图进行支配,那么用于教育费用约是()A.4000元B.1200元C.2000元D.900元【解答】解:如图,教育可以用占15%8000×15%=1200(元).故选:B.2.明天()下雨.A.一定B.可能C.不可能【解答】解:因为明天下不下雨,属于可能性中的不确定事件,在一定条件下可能发生,也可能不发生的事件;故选:B.3.口袋里有1个红球、1个黄球、1个白球.从口袋里任意摸出1个球,摸到球的颜色一共有()种不同的可能.A.1种B.2种C.3种【解答】解:口袋里有1个红球、1个黄球、1个白球.从口袋里任意摸出1个球,摸到球的颜色一共有红、黄、白3种不同的可能.故选:C.4.抛一枚硬币,朝上的可能性()A.正面大B.反面大C.正反两面差不多【解答】解:1÷2=,正面朝上和反面朝上的可能性都是,即可能性相等;故选:C.5.把3个白球和5个红球放在盒子里,任意摸出一个,()是蓝色的.A.可能B.一定C.不可能【解答】解:把3个白球和5个红球放在盒子里,任意摸出一个,不可能是蓝色的;故选:C.6.某班有50人,其中三好学生10人,优秀学生干部5人,在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是()A.72°,36°B.100°,50°C.120°,60°D.80°,40°【解答】解:(1)表示三好学生的圆心角:360°×(10÷50)=360°×20%=72°;(2)表示优秀学生干部人数的圆心角:360°×(5÷50)=360°×10%=36°;答:在扇形统计图上表示三好学生和优秀学生干部人数的圆心角分别是72°和36°.故选:A.7.如图,甲摸到白球得1分,乙摸到黑球得1分,在()箱中摸最公平.A.B.C.D.【解答】解:从图中看出:B箱中黑球个数和白球个数相等,即可能性一样大;最公平;故选:B.8.从写有1~6的6张卡片中任抽一张,抽到是2的可能性是()A.B.C.D.【解答】解:抽到一张牌,即占;故选:D.9.刘翔在2016年巴西里约热卢奥运会上()能拿冠军.A.不可能B.可能C.一定【解答】解:刘翔在2016年伦敦奥运会上可能能拿冠军,属于可能性中的不确定事件,在一定条件下可能发生,也可能不发生的事件;故选:B.10.太阳()是东升西落.A.一定B.不一定C.不会【解答】解:由分析可知:太阳东升西落,是客观规律,属于确定事件中的必然事件;故选:A.11.笑笑和淘气玩“剪刀、石头、布”游戏,下面说法中正确的是()A.笑笑一定胜B.淘气一定胜C.淘气可能胜【解答】解:笑笑和淘气玩“剪刀、石头、布”的游戏是公平的,他们赢的可能性为:1÷3=;因此都有赢的机会,但不能确定,所以选项A、B错误,他们只有赢的可能性;故选:C.12.明天()会下雨.A.可能B.一定C.不可能【解答】解:明天可能会下雨,属于不确定事件中的可能事件;故选:A.二.填空题(共9小题)13.用0,3,5,8可以组成9 个没有重复数字的两位数,其中最大的两位数是85 ,最小的两位数是30 .【解答】解:0、3、5、8四个数字可以组成的两位数有:30,35,38;50,53,58;80,83,85,共有9个不同的两位数;其中最大的是85,最小的两位数是30,故答案为:9,85,3014.箱子里放着3个苹果,5个橘子,2个桃子,7个梨,小明随便拿出一个水果,有 4 种可能,拿到桃子的可能性最小,要想让这种水果的可能性最大,至少还要加 6 个.【解答】解:(1)因为箱子里放着3个苹果,5个橘子,2个桃子,7个梨,小明随便拿出一个水果可能摸到苹果,也可能摸到橘子,还可能摸到桃子或者是梨,因此有4种可能;(2)因为有3个苹果,5个橘子,2个桃子,7个梨,7>5>3>2,所以从箱子里任意摸出一个水果,摸到桃子的可能性最小;要想让这种水果的可能性最大,至少还要加7+1﹣2=6个,故答案为:4,桃子,6.15.鱼不可能会在天上飞.正确.【解答】解:由分析可知:鱼不可能会在天上飞,属于确定事件中的不可能事件;故答案为:正确.16.有三把锁和三把钥匙,现在用三把钥匙去打开三把锁,最多要试 6 次.【解答】解:3+2+1=6(次).答:最多要试6次.故答案为:6.17.在一块并排10垄的田地中,选择2垄种植A、B两种作物,每种作物种植一垄.为有利于作物生长,要求A、B两种作物的间隔不小于6垄,则不同的选垄种植方法有12 种.【解答】解:(3+2+1)×2=6×2=12(种);答:则不同的选垄种植方法有12种.故答案为:12.18.有一楼梯共12级,如规定每次只能跨上一级或两级,要登上第12级,共有233 不同的走法.【解答】解:1级:1种;2级:2种;(走1级或走2级)3级:3种;(全走1级,走1+2或2+1)4级:5种;(全走1级,2+1+1,1+2+1,1+1+2,2+2)5级:8种;(全走1级,2+1+1+1,1+2+1+1,1+1+2+1,1+1+1+2,2+2+1,2+1+2,1+2+2)…【兔子数列】1、2、3、5、8、13、21、34、55、89、144、233.答:共有233种不同的走法.19.一桶水,需2人一起抬.3人把一桶水从离家600米远的地方抬回家,平均每人要抬400 米.【解答】解:600×2÷3=1200÷3=400(米)答:平均每人要抬400米.故答案为:400.20.用0、1、2、3四个数字,可以组成18 个不同的三位数.【解答】解:组成的三位数有:120、102、210、201、310、130、301、103、230、203、320、302、123、132、213、231、321、312;一共有18个.故答案为:18.21.下面是数学学习小组6名同学的测验成绩:李刚95分,王聪92分,王冬88分,范华93分,张兰94分,周兵96分.(1)这六位同学的平均分数多少?(2)如果把他们的平均成绩记住0,那么这6名同学的成绩分别记作多少?【解答】解:(1)六位同学的平均数为:(95+92+88+93+94+96)÷6=558÷6=93(分).答:这六位同学的平均分数93分.(2)若平均成绩记作0,则李刚的分数为:95﹣93=2(分),王聪的分数为:92﹣93=﹣1(分),王冬的分数为:88﹣93=﹣5(分),范华的分数为:93﹣93=0(分),张兰的分数为:94﹣93=1(分),周兵的分数为:96﹣93=3(分).答:李刚的分数为2分,王聪的分数为﹣1分,王冬的分数为﹣5分,范华的分数为0分,张兰的分数为1分,周兵的分数为3分.三.判断题(共5小题)22.在制作扇形统计图时,总的数量越多,所画的圆就越大.×.(判断对错)【解答】解:根据扇形统计图的特点可知:在制作扇形统计图时,总的数量不论多少,都用所画的圆表示单位“1”,所以原题说法错误;故答案为:×.23.冬天一定会下雪.错误.(判断对错)【解答】解:冬天一定会下雪,说法错误;故答案为:错误.24.小明所在班级同学的平均身高比小强所在班级的平均身高高些,所以小明比小强要高些.错误.(判断对错)【解答】解:因为平均数反映的是一组数据的特征,不是其中每一个数据的特征,平均数反映的是一组数据的特征,不是其中每一个数据的特征.所以小明所在班级同学的平均身高比小强所在班级的平均身高高些,并不是说小明比小强要高些,所以判断错误.故答案为:错误.25.三(1)班同学的平均体重是35千克,三(1)班不可能有体重低于32千克的同学.错误.(判断对错)【解答】解:因为,我们班同学的平均体重是35千克,并不是每个同学的体重都是35千克,有的同学的体重比35千克高的多,也有的同学的体重比35千克低的多,也可能有低于32千克的同学;所以,三(1)班同学的平均体重是35千克,三(1)班不可能有体重低于32千克的同学说法错误的;故答案为:错误.26.在一次彩票有奖销售活动中,中奖的可能性是.李叔叔买了100张彩票,一定能有20张中奖×.(判断对错)【解答】解:100×=20(张),可能有20张中奖;说一定中奖是错误的;故答案为:×.四.应用题(共5小题)27.下图是小华骑自行车到6千米远的森林公园去游玩的情况.(1)小华从出发到返回,一共经过了多长时间?(2)返回前,小华在路上用的时间比在公园里玩的时间多多少分钟?(3)返回时,小华骑自行车每分钟行走多少米?【解答】解:(1)3=3=(小时)答:一共经过了2小时.(2)1﹣=1﹣=(小时)答:返回前,小华在路上用的时间比在公园里玩的时间多20分钟.(3)小时=小时=40分钟,6千米=6000米6000÷40=150(米)答:返回时,小华骑自行车每分钟行走150米.28.某次考试,的学生取得优秀成绩,这些学生的平均分比优秀的分数线高4分,而没达到优秀的学生的平均分比优秀的分数线低11分,所有学生的平均分是87分.那么,优秀的分数线是多少分?【解答】解:等号两边除以x得y=87+5y=92答:优秀的分数线是92分.29.某电视节目评选优秀选手,专家组与观众代表的评分如下表.(1)专家组的平均分是多少?(2)观众代表的平均分是多少?(3)总平均分是多少?【解答】解:(1)(8+8.5+8+9.5+10+9+8.5+8.5)÷8 =70÷8=8.75(分)答:这8个专家打的平均分是8.75分.(2)(8.5+8.5+9.5+8.5+8.5+9.5+9.5+9.5)÷8=72÷8=9(分)答:这8个观众代表打的平均分是9分.(3)(8.75+9)÷2=17.75÷2=8.875(分)答:总平均分是8.875分.30.2017年某店“双十一”销售额比2016年“双十一”销售额增加了多少亿元?【解答】解:350×=220(亿元)答:2017年某店“双十一”销售额比2016年“双十一”销售额增加了220亿元.31.某小学参加兴趣小组情况如图:已知参加体育的有136人,参加“其它”兴趣小组的共有多少人?【解答】解:136÷34%=400(人)400×(1﹣34%﹣18%﹣26%)=400×22%=88(人)答:参加“其它”兴趣小组的共有88人.五.解答题(共15小题)32.工人叔叔要修一条长85米的公路,已经修了5天,还剩13.5米,平均每天修了多少米?【解答】解:(85﹣13.5)÷5=71.5÷5=14.3(米).答:平均每天修了14.3米.33.昨天和今天共售出996张票,每天放映3场,平均每场售出多少张票?【解答】解:996÷2÷3,=996÷6,=166(张),答:平均每场售出166张票.34.袋子里放了6个球:〇〇〇〇〇●任意摸一个再放回.小胖连续摸了5次,都是白球,他第六次摸到的球可能是黑球.(填“一定”、“不可能”或“可能”)【解答】解:因为袋子里放了6个球,有黑球,也有白球,小胖第六次摸到的球可能黑球,属于不确定事件中的可能性事件;故答案为:可能.35.小英4次语文测验的平均成绩是89分,第5次测验得了94分.问她5次测验的平均成绩是多少?【解答】解:解法一:(89×4+94)÷5=90(分);解法二:89+(94﹣89)÷5,=89+5÷5,=90(分);答:5次测验的平均成绩是90分.36.有一种奖券的中奖率是1%,所以买100张奖券就一定能中奖.×.【解答】解:一种有奖征卷的中奖率是1%,买100张这样的奖券,有可能中奖一次,但属于不确定事件中的可能性事件;所以本题中说买100张,一定会中奖,说法错误.故答案为:×.37.一个小组在一班工作时间内,前3小时每小时生产零件170个,后5小时每小时生产零件186个,平均每小时生产零件多少个?【解答】解:(170×3+186×5)÷(3+5),=(510+930)÷8,=1440÷8,=180(个);答:平均每小时生产零件180个.38.李大爷带900元买了22袋同一种化肥,还剩20元.平均每袋化肥多少元?【解答】解:(900﹣20)÷22=880÷22=40(元)答:平均每袋化肥40元.39.按要求涂一涂.(1)图1摸出的一定是黑球;(2)图2摸出的不可能是黑球;(3)图3摸出黑球的可能性最大【解答】解:40.星期天,小华乘公交车从家到图书馆看书,后来打的回家,如图表示的是这段时间里小华离家距离的变化情况.请你仔细观察,回答问题.(1)小华在图书馆呆了70 分钟.(2)回来打的时平均速度是每小时12 千米.(3)乘公交车所用的时间比回来多用50 %.【解答】解:(1)小华在图书馆呆了:100﹣30=70(分钟);(2)返回时用的时间:120﹣100=20(分钟)=(小时),返回时的车速:4÷=12(千米);(3)(30﹣20)÷20=10÷20=50%答:乘公交车所用的时间比回来多用50%.故答案为:70,12,50.41.求下面图形的面积或体积.(1)求如图1中的阴影面积(单位:m)(2)求玩具陀螺的体积.(单位:cm)【解答】解:(1)6×(6÷2)﹣3.14×(6÷2)2÷2 =18﹣14.13=3.87(m2)答:阴影面积是3.87m2.(2)3.14×(3÷2)2×4+3.14×(3÷2)2×3×=3.14×1.52×4+3.14×1.52×(3×)=3.14×2.25×4+3.14×2.25×1=7.056×4+7.056=7.056×5=35.325(cm3)答:玩具陀螺的体积是35.325cm3.42.下面是5位同学的体重:小李38千克,小王42千克,小张36千克,小林43千克,小许41千克.先计算他们的平均体重,再用正数和负数来表示他们的体重与平均体重相差的部分.单位:千克【解答】解:(1)(38+42+36+43+41)÷5=200÷5=40(千克)答:他们的平均体重是340千克.(2)将平均体重记为0千克,超过记为正数,不足记为负数,这六个人的体重可以记作:38﹣40=﹣242﹣40=+236﹣40=﹣443﹣40=+341﹣40=+143.刘小强4次数学测验的平均成绩是90分,第5次数学测验得95分,小强这5次测验的平均成绩是多少?【解答】解:(90×4+95)÷5=455÷5=91(分)答:小强这5次测验的平均成绩是91分.44.聪聪家2015年11月支出情况统计如图.聪聪家2015年11月的总支出是3600元.请你回答问题:(1)这个月哪项支出最多?支出了多少元?(2)购买衣物的支出比文化教育支出少百分之几?少支出了多少元?【解答】解:(1)3600×35%=1260(元)答:这个月伙食支出最多,支出了1260元(2)(25%﹣20%)÷25%=0.05÷0.25=0.2=20%答:购买衣物的支出比文化教育支出少20%.3600×25%=3600×0.25=900(元)3600×20%=3600×0.2=720(元)900﹣720=180(元)答:少支出了180元.45.实验小学去年四个季度用水情况统计如下表:这个小学去年平均每个月用水多少吨?【解答】解:(167+215+362+156)÷12=900÷12=75(吨);答:这个小学去年平均每个月用水75吨.46.如图是某班数学期末考试的统计图,可惜已经破损了.已知:这个班数学期末考试的及格率为95%.成绩优秀的人数占全班的35%.成绩“良好”的人数比“优秀”的人数多.请你算一算:(1)该班一共有40 人参加了这次考试;(2)其中成绩达到优秀的一共有14 人;(3)成绩良好的有18 人.【解答】解:(1)2÷(1﹣95%)=2÷0.05=40(人);答:该班一共有40人参加了这次考试.(2)40×35%=14(人);答:其中成绩达到优秀的一共有14人.(3)14×(1+)=14×=18(人);答:成绩良好的有18人;故答案为:40,14,18.。
2024年数学统计图表解读基础练习题六年级下册(含答案)

2024年数学统计图表解读基础练习题六年级下册(含答案)试题部分一、选择题:A. 扇形图B. 折线图C. 条形图D. 散点图A. 平均数B. 中位数C. 众数D. 方差3. 某班级学生体重数据的众数是40千克,那么这组数据的平均数可能是多少?()A. 35千克B. 40千克C. 45千克D. 50千克A. 扇形图B. 折线图C. 条形图D. 饼图A. 平均数B. 中位数C. 众数D. 极差A. 扇形图B. 折线图C. 条形图D. 散点图A. 折线图B. 条形图C. 扇形图D. 饼图A. 平均数B. 中位数C. 众数D. 方差A. 扇形图B. 折线图C. 条形图D. 散点图A. 扇形图B. 折线图C. 条形图D. 饼图二、判断题:1. 平均数、中位数和众数都是描述数据集中趋势的统计量。
()2. 扇形图可以表示部分在总体中所占比例。
()3. 折线图适合表示一段时间内数据的变化趋势。
()4. 方差越大,说明数据的波动越小。
()5. 条形图可以清晰地表示各部分在总体中所占比例。
()6. 散点图适合表示两个变量之间的关系。
()7. 众数不受极端值影响。
()8. 饼图可以表示各班级学生人数的分布情况。
()9. 中位数不受极端值影响。
()10. 平均数、中位数和众数在描述数据时,可能得到相同的结果。
()三、计算题:1. 某班级10名学生的体重(单位:kg)如下:45, 48, 50, 52, 45, 48, 50, 52, 45, 48。
求这组数据的平均数。
2. 某班级5名学生的身高(单位:cm)如下:160, 165, 162, 158, 163。
求这组数据的中位数。
3. 某商品一周内每天的销售量(单位:件)如下:30, 35, 40, 35, 40, 45, 50。
求这组数据的众数。
4. 某班级6名学生的成绩(单位:分)如下:85, 90, 88, 92, 87, 89。
求这组数据的方差。
5. 某班级7名学生的年龄如下:12, 12, 13, 12, 13, 12, 14。
六年级下册数学单元测试-5.统计 青岛版(六三)(含答案)

六年级下册数学单元测试-5.统计一、单选题1.爸爸把家庭每月各种支出情况绘制成扇形统计图,是为了()。
A. 能直观地看出每项支出的多少B. 能看出每项支出的变化趋势C. 能直观地看出每项支出与月总支出的关系D. 形象、美观2.六年级一班有40名学生,选举班长的得票数为:小何20票,小赵10票,小邓6票,小李4票。
下面三幅图中,( )图准确地表示了这一结果。
A. B. C.3.下图表示的是六(1)班和六(2)班男、女生人数的情况。
如果每个班都有48人,那么六(1)班的男生人数比六(2)班的多( )人。
A. 16B. 10C. 84.要表示某城市晚报的广告栏出的四类广告信息的条数的多少,最好选()A. 条形统计图B. 折线统计图C. 扇形统计图5.为了表示某学生在小学六年中各次期末考试的数学成绩的变化情况,应选用()A. 扇形统计图B. 折线统计图C. 条形统计图二、判断题6.表示一个星期的气温变化情况,选用扇形统计图比较合适。
7.扇形统计图能形象、直观地展示各部分数量与总数量间的关系,但不能明确各部分具体的数量。
8.在制作扇形统计图时,总的数量越多,所画的圆就越大.9.既要表示各个项目数量的多少,又要表示数量变化的趋势,就制一幅折线统计图.三、填空题10.下面是某校六年级男生喜爱球类运动的情况统计图.根据图中信息填空.(1)喜欢________的人数最少(2)喜欢乒乓球的人有35人,六年级男生有________人.(3)喜欢排球的人有________人.(4)喜欢篮球的大约占________%,喜欢足球的大约占________%.(5)学校准备举办一次球类运动的比赛,报名参加________比赛的人数可能最多.11.反映某地本周气温变化情况用________统计图表示最好。
12.医生把病人的血压变化情况制成统计图,最佳选择是________;学校选用________来反映各年级人数的多少。
13.右图是六(1)班学生最喜欢的运动项目统计图。
必考点解析人教版(五四制)六年级数学下册第十章数据的收集、整理与描述定向练习试卷(含答案解析)

六年级数学下册第十章数据的收集、整理与描述定向练习考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、在一个样本中,50个数据分别落在5个小组内,第1、2、3、5小组数据的个数分别是2、8、15、5,则第4小组的频率是()A.0.3 B.0.4 C.0.5 D.0.62、某学校对七年级随机抽取若干名学生进行“创建文明城市"知识答题,成绩分为1分,2分,3分,4分共4个等级,将调查结果绘制成如下图所示的条形统计图和扇形统计图,根据图中信息,这些学生中得1分或2分的共有()人.A.10 B.11 C.12 D.133、下列调查中,适合采取抽样调查的是()A.对某小区的卫生死角的调查B.对某市初中学生视力状况的调查C.对某校九(1)班学生的心理健康状况的调查D.对“神舟十二号”载人飞船发射前零部件质量情况的调查4、七年级10个班开展“学雷锋做好人好事”活动,为了清楚表明三月份各班做好人好事的件数是多少,最好选用()A.折线统计图B.条形统计图C.扇形统计图D.以上都不对5、为了完成下列任务,你认为最适合采用普查的是()A.了解某品牌电视的使用寿命B.了解一批西瓜是否甜C.了解某批次烟花爆竹的燃放效果D.了解某隔离小区居民新冠核酸检查结果6、下列调查中,适合采用抽样调查的是().A.了解全市中学生每周使用手机的时间B.对乘坐飞机的乘客进行安全检查C.调查我校初一某班的视力情况D.检查“北斗”卫星重要零部件的质量7、为了了解2017年我县九年级6023名学生学业水平考试的数学成绩,从中随机抽取了200名学生的数学成绩,下列说法正确的是( )A.2017年我县九年级学生是总体B.每一名九年级学生是个体C.200名九年级学生是总体的一个样本D.样本容量是2008、七年级10个班开展“学雷锋做好人好事”活动,为了清楚表明三月份各班做好人好事的件数是多少,最好选用()A.折线统计图B.条形统计图C.扇形统计图D.以上都不对9、下列事件中,调查方式选择合理的是()A.为了解某批次汽车的抗撞击能力,选择全面调查B.为了解某市中学生每天阅读时间的情况,选择全面调查C.为了解某班学生的视力情况,选择全面调查D.为选出某校短跑最快的学生参加全市比赛,选择抽样调查10、某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对本校100名学生家长进行调查.这次调查的样本是()A.100名学生B.100名学生家长C.被抽取的100名学生家长D.被抽取的100名学生家长的意见第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、去年某市有9万名初中毕业生参加升学考试,为了了解这9万名考生的数学成绩,从中取2000名考生数学成绩进行统计分析.在这个抽样中,总体是________,个体是________,样本是________,样本容量是________.2、绘制频数分布直方图的一般步骤:(1)计算最大值与最小值的差______;(2)决定______与______;(3)列 ______;(4)以______表示数据,纵轴表示频数,画频数分布直方图.3、九年级体育测试某班跳绳成绩的频数分布表如下:跳绳次数x在160≤x<180范围的学生占全班学生的_____(用百分数表示).4、某学校在开展“节约每一滴水”的活动中,从九年级的200名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理成下表:请你估计这200名同学的家庭一个月节约用水的总量大约是__________.5、一个盒子中有5个红球和若干个白球,它们除颜色外都相同,从中随机摸出一个球,记下它的颜色后再放回盒子中.不断重复这个过程,共摸了100次球,发现有25次摸到红球,请估计盒子中白球大约有_____个.三、解答题(5小题,每小题10分,共计50分)1、为了了解我校学生对英语单词掌握的情况,现对全校学生进行英语百词测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,现将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请根据图中所给的信息解答下列问题:(1)本次随机抽取的人数是人,并将以上两幅统计图补充完整;(2)若“一般”和“优秀”均被视为达标成绩,则我校被抽取的学生中有人达标;(3)若我校学生有1800人,请你估计此次测试中,全校达标的学生有多少人?2、4月23日是“世界读书日”,我校校团委发起了“让阅读成为习惯”的读书活动,鼓励学生利用周末积极阅读课外书籍.为了解学生周末两天的读书时间,校团委随机调查了部分学生的读书时间x (单位:分钟),把读书时间分为四组:A(30≤x<60),B.(60≤x<90),C.(90≤x<120),D (120≤x<150).部分数据信息如下:a.B组和C组的所有数据:85 90 60 70 110 75 65 78 100 90 80 95 90b.根据调查结果绘制了如下尚不完整的统计图:请根据以上信息,回答下列问题:(1)被调查的学生共有多少人,并补全频数分布直方图;(2)在扇形统计图中,C组所对应的扇形圆心角是_____;(3)请结合统计图给全校学生发出一条合理化的倡议.3、某中学六年级共有学生200人,参加课外活动小组情况如图所示(每人只参加一项).(1)参加科技小组的学生有多少人?(2)参加美术小组的比参加体育小组的学生多多少人?4、2021年是航天大年,中国航天事业快速发展.2021年10月16日0时23分,神州十三号按照预定时间在酒泉卫星发射中心精准点火发射.12月9日15时40分,“天宫课堂”第一课开讲啦!神舟十三号乘组航天员翟志刚、王亚平、叶光富3名航天员在轨介绍展示中国空间站工作生活场景,演示微重力环境下细胞学实验、物体运动、液体表面张力等现象,并与地面课堂进行实时交流.课堂中展示了四个实验:A.浮力消失实验、B.水膜张力实验、C.水球光学实验、D.泡腾片实验.某校七年级数学兴趣小组成员随机抽取了本年级的部分同学,调查他们在这四个实验中最感兴趣的一个,并绘制了以下两幅不完整的统计图.学生最感兴趣实验条形统计图学生最感兴趣实验扇形统计图请你根据图中提供的信息解答下列问题:(1)本次被调查的学生一共有人,扇形统计图中“D”所在扇形的圆心角的度数为 ;(2)补全条形统计图;(3)若该校七年级共有800名学生,估计全年级对水膜张力实验最感兴趣的学生有多少人?5、带头盔对保护骑电动车人的安全尤为重要.志愿者在金华市区随机抽取部分骑电动车的人,对此进行佩戴头盔情况调查(调查内容为:“很少戴头盔”、“有时戴头盔”、“常常戴头盔”、“总是戴头盔”).将调查数据整理后,绘制成部分统计图如下所示.请根据图中信息,解答下列问题:(1)该调查的样本容量为______;(2)请你补全条形统计图,并求出“总是戴头盔”所占的圆心角的度数;(3)据金华市区骑电动车人数约55万人,请你估计金华市区“很少带头盔”的有多少人?-参考答案-一、单选题1、B【解析】【分析】根据总数计算出第4小组的频数,用第4小组的频数除以数据总数就是第4小组的频率.【详解】解:第4小组的频数:50-2-8-15-5=20,第4小组的频率为:20÷50=0.4.∴第4小组的频率为0.4.故选:B.【点睛】本题考查了频率的计算方法,理解频率的计算公式是解题的关键.2、B【解析】【分析】先求出抽取的总人数,再求出得3分的人数,即可求出得1分或2分的人数.【详解】解:抽取的总人数为12÷30%=40(人),得3分的人数为40×42.5%=17(人),得1分或2分的人数为40-17-12=11(人).故选:B.【点睛】本题主要考查了条形统计图与扇形统计图,解题的关键是能从条形统计图与扇形统计图得出准信息.3、B【解析】【分析】结合题意,根据抽样调查和全面调查的性质分析,即可得到答案.【详解】对某小区的卫生死角的调查,适合全面调查,故选项A不符合题意,对某市初中学生视力状况的调查,适合抽样调查,故选项B符合题意;对某校九(1)班学生的心理健康状况的调查,适合全面调查,故选项C不符合题意,对“神舟十二号”载人飞船发射前零部件质量情况的调查,适合全面调查,故选项D不符合题意故选:B.【点睛】本题考查了统计调查的知识;解题的关键是熟练掌握抽样调查的性质,从而完成求解.4、B【解析】【分析】根据三种统计图的特点,判断即可.【详解】解:七年级10个班开展“学雷锋做好人好事”活动,为了清楚表明三月份各班做好人好事的件数是多少,最好选用:条形统计图,故选:B.【点睛】本题考查了统计图的选择,熟练掌握三种统计图的特点是解题的关键.5、D【解析】【分析】普查和抽样调查的选择,需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,普查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.【详解】解:A、了解某品牌电视的使用寿命,调查带有破坏性,应用抽样调查方式,故此选项不合题意;B、了解一批西瓜是否甜,调查带有破坏性,应用抽样调查方式,故此选项不合题意;C、了解某批次烟花爆竹的燃放效果,调查带有破坏性,适合选择抽样调查,故此选项不符合题意;D、了解某隔离小区居民新冠核酸检查结果,对结果的要求高,结果必须准确,应用全面调查方式,故此选项符合题意.故选:D.【点睛】本题考查了抽样调查和全面调查,由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.6、A【解析】【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.【详解】解:A、了解全市中学生每周使用手机的时间,适合采用抽样调查,符合题意;B、对乘坐飞机的乘客进行安全检查,适合采用全面调查,不符合题意;C、调查我校初一某班的视力情况,适合采用全面调查,不符合题意;D、检查“北斗”卫星重要零部件的质量,适合采用全面调查,不符合题意,故选:A.【点睛】本题考查了抽样调查和全面调查的区别,解题的关键是掌握选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.7、D【解析】【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.根据总体、个体、样本、样本容量的定义,做出判断.【详解】解: 2017年我县九年级学生的数学成绩是总体,故A不符合题意;每一名九年级学生的数学成绩是个体,故B不符合题意;200名九年级学生的数学成绩是总体的一个样本,故C不符合题意;样本容量是200,故D符合题意;故选D【点睛】考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.8、B【解析】【分析】根据三种统计图的特点,判断即可.【详解】解:七年级10个班开展“学雷锋做好人好事”活动,为了清楚表明三月份各班做好人好事的件数是多少,最好选用:条形统计图,故选:B.【点睛】本题考查了统计图的选择,熟练掌握三种统计图的特点是解题的关键.9、C【解析】【分析】全面调查是指对总体中每个个体都进行的调查,一般适用于总体中个体数量不太多的情况;抽样调查是指不必要或不可能对总体进行全面调查时,就从总体中抽取一部分个体进行调查,然后根据调查数据来推断总体的情况;根据全面调查与抽样调查的含义即可确定正确答案.【详解】了解汽车的抗撞击能力具有破坏性,用抽样调查,∴A选项不合题意,某市中学生人数较多,适合抽样调查,∴B选项不合题意,一个班的学生人数较少,适合选择全面调查,∴C选项符合题意,选出短跑最快的学生,每个学生都有可能,应选择全面调查,∴D选项不符合题意,故选:C.【点睛】本题考查了全面调查与抽样调查,掌握两者的含义是本题的关键.10、D【解析】【分析】总体是指考察的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量这四个概念时,首先找出考察的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.【详解】解:某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对本校100名学生家长进行调查.这次调查的样本是被抽取的100名学生家长的意见.故选:D.【点睛】此题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考察对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.二、填空题1、 9万名考生的数学成绩每名考生的数学成绩被抽出的2000名考生的数学成绩 2000【解析】【分析】根据抽样中总体、个体、样本以及样本容量的概念解答即可.【详解】根据题意,在这个抽样中,总体是9万名考生的数学成绩,个体是每名考生的数学成绩,样本是被抽出的2000名考生的数学成绩,样本容量是2000.故答案为:9万名考生的数学成绩;每名考生的数学成绩;被抽出的2000名考生的数学成绩;2000.【点睛】本题主要考查了对抽样中总体、个体、样本以及样本容量的理解,属于基础题,掌握总体、个体、样本以及样本容量的概念是解题关键.2、极差组距组数频数分布表横轴【解析】略3、26%【解析】【分析】用此范围的频数除以总数,再乘以100%即可得到答案.【详解】解:跳绳次数x在160≤x<180范围的学生占全班学生的百分比为13100%=26% 2326136⨯++++,故答案为:26%.【点睛】此题考查利用频数求百分比,掌握百分比的计算公式是解题的关键.4、240t【解析】【分析】计算出选出的10名同学家庭一个月平均节水的吨数,把这个平均数作为200名同学的每个家庭一个月节约用水量,即可计算出总的节约用水量.【详解】选出的10名同学家庭一个月平均节水:20.5314 1.5121.210⨯+⨯+⨯+⨯=(t)则这200名同学的家庭一个月节约用水的总量大约是:200×1.2=240(t)故答案为:240t【点睛】本题考查了用样本估计总体,这里是用样本的平均数作为总体的平均数,掌握此点是关键.5、15【解析】【分析】由共摸了100次球,发现有25次摸到红球知摸到红球的概率为0.25,设盒子中白球有x 个,可得50.255x=+,解之即可. 【详解】解:设盒子中白球大约有x 个, 根据题意,得:50.255x=+, 解得15x =,经检验15x =是分式方程的解,所以估计盒子中白球大约有15个,故答案为:15.【点睛】本题考查用样本估计总体,从一个总体得到一个包含大量数据的样本,我们很难从一个个数字中直接看出样本所包含的信息,解题的关键是用频率分布直方图来表示相应样本的频率分布,从而去估计总体的分布情况.三、解答题1、(1)120,统计图补充见详解;(2)96;(3)1440人.【解析】【分析】(1)用不合格人数24除以占比20%即可求出抽取人数未120人,用1减去优秀占比和不合格占比即可求出一般占比,用120乘以优秀占比50%即可求出优秀人数,再补充两幅统计图即可;(2)用120乘以优秀与一般占比之和,即可求出抽取学生中达标人数;(3)用1800乘以优秀与一般占比之和,即可估算出全校达标学生数.【详解】解:(1)24÷20%=120(人),1-50%-20%=30%,120×50%=60(人),故答案为:120,统计图补充如图:;(2)120×(50%+30%)=96(人),故答案为:96;(3)1800×(50%+30%)=1440(人),答:此次测试中,全校达标的人数约为1440人.【点睛】本题考查了扇形统计图与条形统计图,用样本估计总体等知识,根据两幅统计图提供的公共信息得到样本容量是解题关键.2、 (1)20,作图见解析(2)108°(3)书是人类进步的阶梯,同学们周末两天只有少部分人读书时间在两小时以上,需增加读书的时间.(答案不唯一)【解析】【分析】(1)由扇形统计图中A所占扇形比例为20%和频数分布直方图中A组频数为4,即可得总人数为4÷20%=20人,再由题干可求得B组人数为7人,D组人数为3人,补全频数分布直方图即可.(2)由(1)知频数分布直方图中C组频数为6,故C组所对应扇形圆心角为6 36010820︒⨯=︒(3)与统计图的数据相关即可,答案不唯一(1)总人数为4÷20%=20人B组人数为13-6=7人D组人数为20-4-6-7=3人补全频数分布直方图如图所示(2)636010820︒⨯=︒故C组所对应的扇形圆心角是108°.(3)书是人类进步的阶梯、同学们周末两天只有少部分人读书时间在两小时以上,需增加读书的时间.(答案不唯一)【点睛】本题考查了数据的调查及整理.频数分布直方图是用小长方形的面积来反映数据落在各个小组内的频数的大小的统计图.扇形统计图,特点:扇形统计图能清楚地表示出各部分在总体中所占的百分比,缺点:在两个扇形统计图中,若一个统计图中的某一个量所占的百分比比另一个统计图中的某一个量所占的百分比多,容易造成第一个统计量大于第二个统计量的错觉.注意:扇形统计图中,用圆代表总体,扇形的大小代表各部分数量占总体数量的百分数,但是没有给出具体数值,因此不能通过两个扇形统计图来比较两个统计量的多少.3、 (1)参加科技小组的学生有70人;(2)参加美术小组的比参加体育小组的学生多10人.【解析】【分析】(1)根据“科技小组”所占的百分比,根据频率=频数÷总数即可求出科技小组的人数;(2)求出参加美术小组的比参加体育小组的学生多的所占的百分比即可.(1)解:参加科技小组的学生有200×35%=70(人),答:参加科技小组的学生有70人;(2)解:参加体育小组所占的百分比为1-35%-25%-20%=20%,参加美术小组的比参加体育小组的学生多的人数为200×(25%-20%)=10(人),答:参加美术小组的比参加体育小组的学生多10人.【点睛】本题考查扇形统计图,理解扇形统计图表示数据的特征是解决问题的前提,掌握频率=频数÷总数是正确解答的关键.4、 (1)50,108(2)补全图形见解析(3)144人【解析】【分析】(1)由喜欢C有12人,占比24%,可得总人数,再求解喜欢D人数,可得D所在扇形的圆心角;(2)由喜欢D有15人,再补充条形统计图即可;(3)由喜欢B所占的百分比乘以总人数可得全年级对水膜张力实验最感兴趣的学生人数.(1)解:由喜欢C有12人,占比24%,所以本次被调查的学生一共有1250 24%人.所以喜欢D有501491215人,所以扇形统计图中“D”所在扇形的圆心角的度数为15360108. 50故答案为:50,108.(2)解:由喜欢D15人,补全图形如下:(3)解:该校七年级共有800名学生,估计全年级对水膜张力实验最感兴趣的学生有:980014450人. 【点睛】本题考查的是从条形图与扇形图中获取信息,画条形统计图,求解扇形图中某部分的圆心角,利用样本估计总体,掌握以上统计基础知识是解题的关键.5、 (1)200(2)147.6︒(3)3.85万人.【解析】【分析】(1)利用“常常戴头盔”的人数除以所占的百分比,即可求解;(2)先求出“有时戴头盔”的人数,再利用360°乘以“总是戴头盔”所占的百分比,即可求解;(3)用55万乘以“很少带头盔”所占的百分比,即可求解.(1)解:该调查的样本容量为6432%200÷= ;(2)解:“有时戴头盔”的人数为()20014648240-++=,补全图形如下图所示:“总是戴头盔”所占的圆心角的度数为82360147.6 200⨯=︒;(3)1455 3.85200⨯=(万)答:很少带头盔约有3.85万人.【点睛】本题主要考查了条形统计图和扇形统计图,能准确从统计图获取信息是解题的关键.。
青岛版小学(六三制)数学六年级下册《统计与概率》知识点及典型题目训练试题(含答案)

回顾整理——统计与概率一、知识点解读 1.统计知识点:统计表分为单式统计表和复式统计表。
单式统计表是只对某一项目的数量进行统计的表格,复式统计表是统计项目在两个或两个以上的统计表格,复式统计表也叫复合统计表。
统计图分为条形统计图,折线统计图和扇形统计图。
条形统计图是用一个单位长度表示一定的数量,根据数量的多少画成长短不同的直条,然后把这些直条按一定的顺序排列起来。
从图中,能清晰的看出数量的多少,便于相互比较。
折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来,以折线的上升或下降来表示统计数量增减变化。
从图中,不但可以表示出数量的多少,而且还能够清楚地表示出数量增减变化的情况。
扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数。
从图中,能清楚地看出各部分与总数的百分比,部分与部分之间的关系。
《统计与概率》知识框架统 计与 统计量1.平均数: 总数量除以平均分成的份数。
2.中位数:一组数据按照从大到小的顺序排列,中间的数就是这组数据的中位数。
当数据的个数为偶数时, 中间两个数的平均数是这组数据的中位数。
3.众数:一组数据中出现次数最多的数称为这组数据的众 数, 一组数据可能没有众数, 也可能有一个或两个。
统计表4.统计表:分为单式统计表和复式统计表统计图5.统计图 (1)认识条形统计图、折线统计图、扇形统计图, 能够掌握各种统计图的特征, 会选用相应的统计图描述数据(2)绘制三种统计图的方法 (3) 读懂三种统计图,能利用统计图中的信息解决问题可能性6.可能性 (1) 用一定、 可能、 不可能描述事件发生的概率 (2) 用分数表示事件发生的可能性的多 少 (3) 游戏的公平性: 参与游戏各方获胜的可能性相等就公平, 如果不相等就不公平统计量:平均数。
平均数是指在一组数据中所有数据之和再除以数据的个数。
平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标。
小学统计试题及答案

小学统计试题及答案一、选择题(每题2分,共20分)1. 统计中,用来表示一组数据的集中趋势的量数是()。
A. 平均数B. 中位数C. 众数D. 方差答案:A2. 以下哪个选项不是统计图的类型?()A. 条形图B. 折线图C. 饼图D. 表格答案:D3. 一组数据中出现次数最多的数值称为()。
A. 平均数B. 中位数C. 众数D. 方差答案:C4. 统计中,用来表示一组数据的离散程度的量数是()。
A. 平均数B. 中位数C. 众数D. 方差5. 下列哪个选项是统计数据收集的方法?()A. 观察法B. 实验法C. 调查法D. 以上都是答案:D6. 统计中,用来表示一组数据的中间位置的量数是()。
A. 平均数B. 中位数C. 众数D. 方差答案:B7. 以下哪个选项是统计图的类型?()A. 条形图B. 折线图C. 饼图D. 所有选项答案:D8. 一组数据中所有数值的总和除以数据的个数,得到的是()。
A. 平均数B. 中位数C. 众数D. 方差答案:A9. 统计中,用来表示一组数据的分布情况的量数是()。
B. 中位数C. 众数D. 标准差答案:D10. 以下哪个选项不是统计数据整理的方法?()A. 排序B. 计算平均数C. 制作统计表D. 制作条形图答案:D二、填空题(每题2分,共20分)1. 统计图中,用来表示数据大小的图形是______。
答案:条形图2. 一组数据中,位于中间位置的数值是______。
答案:中位数3. 统计中,用来表示一组数据的波动大小的量数是______。
答案:标准差4. 统计图的类型包括______、折线图、饼图等。
答案:条形图5. 统计数据收集的方法包括观察法、______、调查法等。
答案:实验法6. 一组数据中,所有数值的总和除以数据的个数,得到的是______。
答案:平均数7. 统计中,用来表示一组数据的集中趋势的量数是______。
答案:平均数8. 一组数据中,出现次数最多的数值是______。
六年级数学统计和概率试题答案及解析

六年级数学统计和概率试题答案及解析1.常用的统计图有统计图,统计图,统计图三种.【答案】条形,折线,扇形.【解析】根据统计图的分类即可解答.解:根据统计图的分类,常用的统计图有条形统计图、折线统计图和扇形统计图三种.故答案为:条形,折线,扇形.【点评】此题主要考查统计图的分类,理解和掌握它们的特点和作用,能够根据它们的特点和作用,解决有关的问题.2.()不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况.A.条形统计图 B.折线统计图 C.扇形统计图【答案】B【解析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.解:根据折线统计图的特点可知:折线不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况;故选:B.【点评】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.3.学校组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行活动。
下面两幅统计图反映了学生报名参加夏令营的情况,请你根据图中的信息回答下列问题。
①该校报名参加本次活动的一共有()人。
算式:_______________。
②该校报名参加乙组的有()人。
请在条形统计图上画出来。
【答案】①50,25÷ 50%, ② 10 画图略【解析】思路分析:这是一道涉及百分数、扇形图、条形图的应用题,先根据丙组的人数和占比计算总人数,再根据总人数和乙组的占比,计算乙组的人数,根据条形图示例画出乙组的条形分布图。
名师详解:从条形分布图可以看出,丙组有25人报名参加。
从扇形分布图可以发现,丙组人数是总人数的50%。
所以,总是人数=丙组人数÷丙组人数占总人数的百分数=25÷50%=50人。
从扇形分布图可以发现,乙组人数是总人数的10%。
所以,乙组人数=总人数×乙组人数占总人数的百分数=50×20%=10人。
2024年数学六年级下册统计基础练习题(含答案)

2024年数学六年级下册统计基础练习题(含答案)试题部分一、选择题(请在下列选项中选择一个正确答案)A. 条形统计图B. 折线统计图C. 扇形统计图D. 散点图2. 在一组数据中,出现次数最多的数被称为这组数据的:A. 中位数B. 众数C. 平均数D. 极差A. 平均数B. 中位数C. 众数D. 极差A. 众数B. 中位数C. 平均数D. 极差5. 一组数据的极差是:A. 最大值与最小值的和B. 最大值与最小值的差C. 最大值与平均数的差D. 最小值与平均数的差A. 条形统计图B. 折线统计图C. 扇形统计图D. 散点图7. 某班级有男生30人,女生20人,则男生与女生的人数比为:A. 3:2B. 2:3C. 1:2D. 2:1A. 条形统计图B. 折线统计图C. 扇形统计图D. 散点图A. 平均数B. 中位数C. 众数D. 方差10. 在一组数据中,将数据按大小顺序排列,位于中间位置的数是:A. 平均数B. 中位数C. 众数D. 极差二、判断题(请在每个题目前写上“对”或“错”)1. 平均数是表示一组数据集中趋势的统计量。
()2. 中位数是一组数据中最大的数。
()3. 众数可以用来描述一组数据的离散程度。
()4. 扇形统计图可以清楚地表示出各部分数量与总数之间的关系。
()5. 方差越小,数据的离散程度越大。
()三、计算题:20道1. 某班级学生的体重数据如下:45kg, 50kg, 48kg, 52kg, 49kg, 51kg。
求这组数据的平均体重。
2. 一组数据的中位数是50,已知数据中包括两个数:45和55,其他数未知。
若这组数据共有9个数,求第三个数。
3. 一组数据的众数是8,已知数据中包括8, 10, 12, 8, 15, 8, 20,求这组数据的平均数。
4. 某班级有40名学生,其中男生身高平均为160cm,女生身高平均为150cm。
若男生和女生人数之比为3:2,求全班学生的平均身高。
2024年数学数据的收集与分析基础练习题六年级下册(含答案)

2024年数学数据的收集与分析基础练习题六年级下册(含答案)试题部分一、选择题:A. 条形统计图B. 折线统计图C. 扇形统计图D. 频率分布直方图A. 平均数B. 中位数C. 众数D. 极差3. 某班级学生体重数据如下:40kg、45kg、50kg、55kg、60kg,这组数据的平均数是()kg。
A. 45B. 50C. 55D. 60A. 方差B. 标准差C. 极差D. 中位数A. 平均数大于中位数B. 中位数大于众数C. 众数大于平均数D. 平均数等于中位数6. 某商店一周内销售记录如下:周一100元,周二120元,周三150元,周四130元,周五140元,周六160元,周日170元。
这组数据的众数是()元。
A. 100B. 120C. 150D. 160A. 条形统计图B. 折线统计图C. 扇形统计图D. 频率分布直方图A. 平均数B. 中位数C. 众数D. 方差9. 某城市一周内每天的最高气温分别为:28℃、30℃、29℃、31℃、32℃、33℃、34℃。
这组数据的中位数是()℃。
A. 30B. 31C. 32D. 33A. 平均数是表示数据集中趋势的量B. 中位数是表示数据集中趋势的量C. 众数是表示数据集中趋势的量D. 极差是表示数据集中趋势的量二、判断题:1. 平均数、中位数和众数都可以用来描述一组数据的集中趋势。
()2. 方差越大,数据的波动越小。
()3. 折线统计图可以清楚地表示出各部分在总体中所占的百分比。
()4. 条形统计图可以很容易地看出数量的多少。
()5. 扇形统计图能清楚地表示出各部分在总体中所占的百分比。
()6. 中位数受极端值的影响较大。
()7. 众数是一组数据中出现次数最多的数。
()8. 平均数、中位数和众数的大小关系总是相同的。
()9. 极差是一组数据中的最大值与最小值之差。
()10. 方差和标准差都是用来描述数据波动大小的统计量。
()三、计算题:1. 某班级10名学生的数学成绩如下:85, 92, 78, 88, 91, 80, 77, 90, 84, 。
通用版数学六年级下册总复习专题:统计3 含答案(附答案)
统计一.填空题我能行。
1.学校统计全校各年级人数及总人数,应选用( )统计图;气象局统计一昼夜气温情况,应选用( )统计图。
2.下图每格代表( )万人,从图中可以看出,每年参观科技展人数呈( )趋势。
二、精挑细选。
1.右图是小强参加今年六月份的全县中学 生数学竞赛,赛前每个月的测验成绩,则他 的五次成绩的平均数为( )A 、80B 、82C 、78D 、81 2.上面是一位病人在4月7日至9日的体温记录折线图,他在4月8日 12 时的体温是( )摄氏度。
年份单位:(万人)2 4 6 8 10 12 1448 10 12 1214单位:摄氏度时70 6080 90 100 1 0 2 3 4 5月份成绩:分单位:℃A 、38B 、37.5C 、37D 、39.2 三.统计乐园。
1.幸福小区2005 ~2009年每百户居民电脑平均拥有量如下图。
⑴ 幸福小区2005~2009年每百户居民电脑平均拥有量一共增加了( )台。
⑵( )年到( ) 年这一年电脑平均拥有量增长的幅度最小。
( )年到( ) 年这一年电脑平均拥有量增长的幅度最大。
⑶ 根据图中的信息预测,2010年幸福小区每百人电脑平均拥有量大约( )台。
2.中国人的骄傲。
第24--29届奥运会中国获金牌数量统计图40302010030届数量/台2005年 2006年 2007年 2008年 2009年年份届(1)根据统计表中的数据,完成统计图。
(2)( )届取得的奥运金牌数最多,最多的那一届比最少的那一届多( )枚。
(3)中国获得奥运金牌数的整体是( )趋势。
(4)请你预测第30届奥运会中国代表团能获得多少枚金牌?在图上画出来。
并说出你的理由。
(5)你还能提出什么数学问题?3.下面是某地2009年月平均温度变化情况统计图,看图回答下列问题。
(1)上面的统计图是( )统计图。
(2)哪个月的平均气温最高?哪个月的平均气温最低?(3)哪两个月之间的平均气温上升得最快?哪两个月之间的平均气温下降得最快?4.小曼身高一年级时115厘米,二年级时120厘米,三年级时130厘米,四年级时135厘米,五年级时140厘米。
西师大版六年级数学下册《统计综合应用》随堂练习及答案.doc

(西师大版)六年级数学下册统计综合应用班级______姓名______ 1.根据下面实验小学今年上半年各年级学生人数.完成下面统计表。
一年级258人二年级234人三年级280人四年级207人五年级305人六年级268人2(1(2)上半年平均每月生产机床多少台?3.根据下面某水泥厂第一季度产量统计表,解答下面的问题。
(1(2)3月份产量比1月份增产百分之几?(3)1月份产量是2月份的百分之几?4.根据下面前进汽车厂去年1~6月汽车产量,解答问题。
(1)平均每个月制造汽车多少辆?(2)6月份制造的汽车比1月份增长百分之几?(3)第一季度制造的汽车比第二季度少多少辆?5.下图中表示3个工人单独完成某项工作所用天数,请根据图中数据完成计算。
(1)甲、乙合做这项工作,多少天可以完成?(2)乙、丙合做多少天可以完成这项工作的 75%?(3(41.2.(1)(23.(1)(2(34.(1)(2(3答:第一季度制造的汽车比第二季度167辆.5.(1)1÷1160()15207+=(天)答:甲、乙合做这项工作,607天可以完成.(2)75%÷1125()20253+=(天)答:乙、丙合做253天可以完成这项工作的 75%.(3)1÷111300()15202547++=(天)答:甲、乙、丙三人合做这项工作,30047天可以完成.(4)11(13)201525-⨯÷=(天)答:甲先单独做3天,再由丙做,还需20天.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六下统计问题的考点分析+模拟试题(含答案)主要内容统计(补充说明: 2014年新版人教版教材,去掉了中位数和众数的内容,但是在各类选拔中仍会出现该内容,因此,对于这两类知识,大家可选择使用。
)学习目标1、使学生结合实例认识扇形统计图,能联系对百分数意义的理解,对扇形统计图提供的信息进行简单的分析,提出或解决简单的实际问题,初步体会扇形统计图描述数据的特点。
2、使学生通过具体的实例,初步理解众数的含义,会求一组简单数据的众数,并能根据具体的问题,选择适当的统计量表示一组数据的特征,体会不同统计量的特点。
3、使学生结合具体实例初步理解中位数的意义,会求一组简单数据的中位数。
能根据具体问题选择合适的统计量表示一组数据的整体特征。
三、考点分析1、扇形统计图可以清楚地表示出各部分数量同总数量之间的关系。
2、在一组数据中,出现的最多的数,叫做这组数据的众数。
3、一组数据的中位数,是指这组数据按大小顺序依次排列,处于最中间的那个数;如果正中间有两个数,中位数就是这两个数的平均数。
4、如果一组数据的众数出现的次数很多,这时的众数具有代表性;如果一组数据里有极端数据,这时的中位数具有代表性。
典型例题例1、(理解扇形统计图表示数据的方式,对扇形统计图进行简单的分析)看统计图回答问题。
小明家5月份支出情况统计图:(1)图中的这个圆表示什么什么?被分成了几部分?每一部分都是什么形状?(2)从图上看,哪项支出最多?哪项支出最少?(3)你还能获得哪些信息?分析与解:扇形统计图用一个圆表示总数量,用不同的扇形表示各部分量占总数量的百分比。
根据统计图,我们可以对数据进行简单的分析。
解答:(1)图中的这个圆看作单位“1”,表示小明家5月份支出情况。
被分成了6个扇形,分别表示服装、食品、赡养老人、水电气、文化、其他这6项的支出情况。
(2)从图上扇形的大小可以直观地看出,食品支出最多,其他支出最少。
当然也可以根据各项支出占总支出的百分数来比较。
(3)可以看出各项支出占总支出的百分数,如食品支出占总支出的36﹪,文化支出占总支出的20﹪┈┈┈点评:扇形统计图通过各个扇形的大小,反映各个部分的多少。
图的直观形象,容易引发比较、估计和判断。
当然所有量的扇形合起来是一个圆,总数量的分率是100﹪。
例2、(根据扇形统计图进行有关的计算)如果小明家5月份总支出是1600元,根据例1的统计图,填写下表。
分析与解:图中的这个圆表示总支出,看作单位“1”,可以根据每项支出占总支出的百分数,求出每项支出多少元。
解答:食品:1600 × 36﹪ = 576(元)服装:1600 × 10﹪ = 160(元)赡养老人:1600 × 16﹪ = 256(元)水电气:1600 × 10﹪ = 160(元)例3、(辨析)要表示各部分与总数的关系,就选用条形统计图。
分析与解:条形统计图用长短不同的直条表示出不同的数量,可以很容易地看出各种数量的多少。
但要反映各部分与总数的关系,应选用扇形统计图。
正确解答:要表示各部分与总数的关系,就选用扇形统计图。
例4、(理解众数的意义,并求一组数据的众数)江阳电子配件厂第一车间有12名工人,5月份每人的日均生产零件个数是:42、51、46、44、48、50、51、56、44、48、48、43。
找出这组日产量的众数。
分析与解:一组数据的众数是这组数据中出现次数最多的数。
在求众数的时候,只要数一数每个数出现的次数,出现次数最多的就是众数。
解答:48出现的次数最多,因此48是这组数据的众数。
点评:求众数的方法就是在一组数据中寻找出现次数最多的数例5、(根据统计表来求众数)某商店销售各种领口尺寸衬衫的情况如下表。
分析与解:应多进哪种衬衫,这种衬衫的尺寸就应该是众数。
从统计表上看,销售的每一件衬衫作为一个数据,每种尺寸的衬衫售出的件数,可以看作相应数据的个数。
如领口38厘米的衬衫售出13件,表示38这个数出现了13次。
解答:领口40厘米的衬衫售出34件,表示40这个数在一组数据中出现了34次,40是这组数据的众数。
所以应多进领口尺寸40厘米的衬衫。
例6、(比较平均数和众数在表示一组数据特征时哪个更合适)下面是某超市工作人员的月工资。
(单位:元)3000、2000、900、800、750、650、600、600、600、600、500请分别求出这组数据的平均数和众数,再比较哪个数据更能代表这组数据的特征。
分析与解:平均数反映一组数据的平均值,而众数是一组数据中出现次数最多的数。
它们都能表示一组数据的特征,但由于一组数据中数据的不同,它们在反映一组数据特征的时候代表性不同。
解答:求平均数:(3000 + 2000 + 900 + 800 + 750 + 650 + 600 + 600 + 600 + 600 + 500 )÷ 11 = 1000求众数:600出现了4次,所以600是这组数据的众数。
平均数是1000,但是大多数人的工资没有那么高,主要是前两个人的工资比其他人高得多,所以平均数不能反映这组数据的真实情况。
而众数600更能代表这组数据的特征。
例7、(辨析)一组数据的众数只有一个。
分析与解:一组数据的众数可以是一个,也可以是两个或两个以上。
如在1.71、1.75、1.73、1.75、1.72、1.71、1.75、1.71这组数据中,1.71和1.75都出现了3次,所以1.71和1.75都是这组数据的众数。
而在1、2、3、5、7这组数据中,每个数都出现了一次,这组数据没有众数。
解答:一组数据的众数可能是一个,也可能不止一个,也可能没有众数。
例8、(理解中位数的意义,会求一组数据的中位数)下面是9位同学的体重。
(单位:千克)35、42、30、29、52、44、39、36、33这组数据的中位数是多少?分析与解:求一组数据的中位数,首先将这组数据按从小到大(或从大到小)的顺序排列,如果这组数据的个数是奇数,找出中间的数就是中位数。
解答:将9位同学体重的数据按从小到大排列如下:29、30、33、35、36、39、42、44、52正中间的一个数是36,所以36是这组数据的中位数。
例9、(一组数据的个数是偶数时,中位数就是中间两个数的平均数)下面是8位同学的身高。
(单位:厘米)142、138、145、130、150、145、139、143这组数据的中位数是多少?分析与解:本组有8个数据,先将这组数据按大小顺序排列,然后取中间两个数的平均数就是中位数。
解答:将8位同学身高的数据按从小到大排列如下:130、138、139、142、143、145、145、150正中间的有两个数,是142、143。
(142 + 143)÷ 2 = 142.5这组数据的中位数是142.5。
例10、(辨析)中位数就是一组数据正中间的数。
分析与解:要求一组数据的中位数,先要把这组数据按从小到大(或从大到小)排列,然后再找中位数。
将一组数据从小到大(或从大到小)排列,如果数据有奇数个,正中间的数就是中位数;如果数据有偶数个,正中间两个的平均数是中位数。
例11、(综合题)李玲同学前几次的数学成绩分别是:96分、98分、95分、93分。
但最近一次的数学成绩是45分,原因是考试时她患感冒,正在发烧。
请你用一个合理的统计量来评价李玲的数学学习水平。
分析与解:李玲的数学成绩这组数据的中位数是95,平均数是85.4,很明显中位数更能代表李玲的数学学习水平,因为她考了一个45分,对平均数的影响很大,使平均数比中位数低了很多。
解答:用中位数能代表李玲的数学学习水平。
例12、(综合题)某公司的33名职工的月工资收入统计如下。
(1)求该公司职工月工资的平均数、中位数和众数。
(2)你认为用哪个数据更能代表这个公司员工的工资水平?结合此问题谈谈你的看法。
分析与解:先求出这组数据的平均数、中位数和众数,然后再进行分析。
解答:(1)平均数是2091,中位数是1500,众数是1500。
(2)在这个问题中,中位数或众数均能反映该公司员工的工资水平。
因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司员工的工资水平。
统计问题的模拟试题(含答案)1、下面是百花山公园占地分布情况统计图(1)()占地面积最大,()占地面积最小。
(2)山丘占百花山公园的()﹪。
(3)百花山公园占地1200公顷,请填写下表。
2、下面是小青家10月份支出及储蓄情况统计图。
(1)小青家10月份的伙食费共花了800元,小青家的支出及储蓄总共多少元?(2)请根据扇形统计图,把下表填写完整。
3、填空。
(1)在40、16、46、20、40、50、40这组数据中,众数是(),中位数是(),平均数是()。
(2)在52、60、48、55、71、60、60、58这组数据中,众数是(),中位数是(),平均数是()。
4、某鞋店上周销售各种尺码男式皮鞋的情况如下表。
讨论:假如你是这家鞋店的经理你最关心什么(哪种尺码销售最多)?假如让你去进货,你有什么想法?5、这是六(3)班同学的左眼视力情况统计:5.0 4.9 5.3 5.2 4.7 5.2 4.8 5.1 5.3 5.24.85.0 4.5 5.1 4.9 5.1 4.7 5.0 4.8 5.15.0 4.8 4.9 5.1 4.9 5.1 4.6 5.1 4.7 5.15.0 5.1 5.1 4.9 5.0 5.1 5.2 5.1 4.6 5.0(1)根据上面的数据完成下面的统计表(26、下面是从昆山人才市场获得的甲乙两家公司的员工招聘信息,胡老师有一位亲戚今年正好大学毕业,他应该去哪家公司应聘呢?甲公司:乙公司7这组数据的中位数是多少?8、出示:下面是第一小组9位同学家庭的住房面积。
(单位:平方米)86 84 50 92 87 80 93 43 88这组数据的平均数和中位数各是多少?9、出示:一次时装模特大奖赛上,一个模特刚刚表演完,主持人说:下面请评委亮分,“6分,8.5分,8.4分,8.9分,8.8分,8.3分,8.5分,8.7分,8.4分,8.5分。
去掉一个最高分,再去掉一个最低分。
该选手的最后得分是---------(1)如果不去掉一个最高分和一个最低分,这位选手平均分是()(2)如果去掉一个最高分和一个最低分,这位选手平均分是()(3)在10个原始得分中,中位数是()(4)两种算分的方式哪一种算出的得分更能代表这位选手的水平?统计问题的模拟试题参考答案1、下面是百花山公园占地分布情况统计图(1)(湖面)占地面积最大,(路面)占地面积最小。
(2)山丘占百花山公园的( 21 )﹪。
2、下面是小青家10月份支出及储蓄情况统计图。
