必修1第一章复习[上学期]新人教版
新人教版高中物理版必修一知识点总结

必修一知识点归纳第一章、运动学基本概念1.机械运动:物体在空间中所处位置发生变化,这样的运动叫做机械运动。
2.运动的特性:普遍性,永恒性,多样性3.参考系:(1)定义:为了研究一个物体运动而假定不动的另一个物体叫参考系。
(2)原则:参考系的选取是自由的。
但必须以能使问题简化方便解决为原则。
(2)比较两个物体的运动必须选用同一参考系。
(3)参照物不一定静止,但被认为是静止的。
4.质点(1)在研究物体运动的过程中,如果物体的大小和形状在所研究问题中可以忽略是,把物体简化为一个点,认为物体的质量都集中在这个点上,这个点称为质点。
(2).质点条件:1)物体中各点的运动情况完全相同(物体做平动)2)物体的大小(线度)<<它通过的距离(3)质点具有相对性,而不具有绝对性。
(4).理想化模型:根据所研究问题的性质和需要,抓住问题中的主要因素,忽略其次要因素,建立一种理想化的模型,使复杂的问题得到简化。
(为便于研究而建立的一种高度抽象的理想客体)5.时间与时刻(1).钟表指示的一个读数对应着某一个瞬间,就是时刻,时刻在时间轴上对应某一点。
两个时刻之间的间隔称为时间,时间在时间轴上对应一段。
△t=t2—t1(2).时间和时刻的单位都是秒,符号为s,常见单位还有min,h。
(3).通常以问题中的初始时刻为零点。
6.路程和位移(1).路程表示物体运动轨迹的长度,但不能完全确定物体位置的变化,是标量。
(2).从物体运动的起点指向运动的重点的有向线段称为位移,是矢量。
(3).物理学中,只有大小的物理量称为标量;既有大小又有方向的物理量称为矢量。
(4).只有在质点做单向直线运动是,位移的大小等于路程。
两者运算法则不同。
7.打点记时器:通过在纸带上打出一系列的点来记录物体运动时间信息的仪器。
(电火花打点记时器——火花打点,电磁打点记时器——电磁打点);一般打出两个相邻的点的时间间隔是0.02s。
8.速度:物体通过的与所用的时间之比叫做速度。
最新人教版高一数学必修1第一章《复习》教案

最新人教版高一数学必修1第一章《复习》教案本章的研究内容主要包括集合和函数的基本知识,以及抽象函数和复合函数的相关问题。
通过整合这些知识,可以帮助学生系统化、网络化地理解数学概念,培养他们的理性思维能力和抽象思维能力。
在研究过程中,我们将注重培养学生的分析、探究、思考能力,帮助他们综合运用基本知识解决问题。
同时,我们也会激发学生对数学的兴趣,培养他们的合作、交流和创新意识。
本章的教学重点包括集合与函数的基本知识,含字母问题的研究,以及抽象函数的理解。
教学难点则在于分类讨论的标准和抽象函数的理解。
为了更好地进行教学,我们准备了多媒体课件和投影仪,并计划用两个课时来完成本章的教学任务。
在教学过程中,我们首先对第一章的知识点进行了回顾,包括集合的含义、表示法、元素与集合的关系,集合间的基本关系以及函数的概念和表示方法等等。
我们还介绍了函数的单调性、奇偶性以及应用问题的解法。
在解决函数应用题的过程中,我们需要遵循“设、列、解、答”的步骤,即先分析题意设出变量,然后列出关系式建立函数模型,接着运用函数的性质解出要求的量,最后回到原实际问题作答。
这些步骤可以用框图来表示。
通过本章的研究,我们希望学生能够掌握集合和函数的基本知识,理解抽象函数和复合函数的相关问题,并能够综合运用这些知识解决实际问题。
同时,我们也希望能够培养学生的分析、探究、思考能力,激发他们对数学的兴趣和创新意识。
当涉及到多个变量时,需要寻找与所求量(y)之间的关系式。
确定一个自变量(x),并通过题目中的条件用x表示其他变量,最终得到函数模型y=f(x)。
在证明集合相等时,需要同时满足A包含于B和B包含于A。
判断两个函数是否相同,需要考虑它们的定义域和对应法则。
函数表达式可以通过定义法、换元法和待定系数法求得。
函数的定义域可以通过列出使函数有意义的自变量的不等式来求解。
常见的依据包括分母不为0、偶次根式中被开方数不小于0以及实际问题的实际意义。
新人教版高一生物必修一知识点复习总结

高一生物必修一知识点整理第一章走近细胞第一节从生物圈到细胞一、相关概念、细胞:是生物体结构和功能的基本单位。
除了病毒以外,所有生物都是由细胞构成的。
细胞是地球上最基本的生命系统生命系统的结构层次:细胞→组织→器官→系统(植物没有系统)→个体→种群→群落→生态系统→生物圈二、病毒的相关知识:1、病毒(Virus)是一类没有细胞结构的生物体。
主要特征:①、个体微小,一般在10~30nm之间,大多数必须用电子显微镜才能看见;②、仅具有一种类型的核酸,DNA或RNA,没有含两种核酸的病毒;③、专营细胞内寄生生活;④、结构简单,一般由核酸(DNA或RNA)和蛋白质外壳所构成。
2、根据寄生的宿主不同,病毒可分为动物病毒、植物病毒和细菌病毒(即噬菌体)三大类。
根据病毒所含核酸种类的不同分为DNA病毒和RNA病毒。
3、常见的病毒有:人类流感病毒(引起流行性感冒)、SARS病毒、人类免疫缺陷病毒(HIV)[引起艾滋病(AIDS)]、禽流感病毒、乙肝病毒、人类天花病毒、狂犬病毒、烟草花叶病毒等。
第二节细胞的多样性和统一性一、细胞种类:根据细胞内有无以核膜为界限的细胞核,把细胞分为原核细胞和真核细胞二、原核细胞和真核细胞的比较:1、原核细胞:细胞较小,无核膜、无核仁,没有成形的细胞核;遗传物质(一个环状DNA分子)集中的区域称为拟核;没有染色体,DNA 不与蛋白质结合,;细胞器只有核糖体;有细胞壁,成分与真核细胞不同。
2、真核细胞:细胞较大,有核膜、有核仁、有真正的细胞核;有一定数目的染色体(DNA与蛋白质结合而成);一般有多种细胞器。
3、原核生物:由原核细胞构成的生物。
如:蓝藻、细菌(如硝化细菌、乳酸菌、大肠杆菌、肺炎双球菌)、放线菌、支原体等都属于原核生物。
4、真核生物:由真核细胞构成的生物。
如动物(草履虫、变形虫)、植物、真菌(酵母菌、霉菌、粘菌)等。
三、细胞学说的建立:1、1665 英国人虎克(Robert Hooke)用自己设计与制造的显微镜(放大倍数为40-140倍)观察了软木的薄片,第一次描述了植物细胞的构造,并首次用拉丁文cella(小室)这个词来对细胞命名。
高一数学必修一人教版知识点:第一章

高一数学必修一人教版知识点:第一章(实用版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的教育资料,如幼儿教案、音乐教案、语文教案、知识梳理、英语教案、物理教案、化学教案、政治教案、历史教案、其他范文等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, this store provides various types of educational materials for everyone, such as preschool lesson plans, music lesson plans, Chinese lesson plans, knowledge review, English lesson plans, physics lesson plans, chemistry lesson plans, political lesson plans, history lesson plans, and other sample texts. If you want to learn about different data formats and writing methods, please stay tuned!高一数学必修一人教版知识点:第一章A列举法:把集合中的元素一一列举出来,然后用一个大括号括上。
最新人教版高一数学上册必修1第一章知识点总结

A
B
A∩B
U A CUA
A∪B 2、会借助数轴或者Venn图来求集合
如:设A={x|x>-2},B={x|x<3},求A∩B。此题利用数轴很简单。 设A={4,5,6,8},B={3,5,7,8},求A∪B。 此题利用Venn图简洁明了
3、(拓展)集合中元素的个数公式,此公式会在选择、填空中直接被应用
3、集合的三要素中的互异性是个考点,经常跟函数、不等式联系 起来作为选择题或者填空题考查。
如: 已知A={1,2a,a+b},B={4,2a-3,3},且A=B,求a,b的值。
§1.1.2集合间的基本关系
教学目的: (1)了解集合之间的包含、相等关系的含义; (2)理解子集、真子集的概念; (3)能利用Venn图表达集合间的关系; (4)了解与空集的含义。 教学重点:子集与空集的概念;用Venn图表达集合间的关系。 教学难点:弄清元素与子集 、属于与包含之间的区别;
高中数学必修1 第一章知识点总结
第一章、集合与函数概念 §1.1 .1 集合
教学目标: (1)通过实例,了解集合的含义,体会元素与集合的“属于”关系; (2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同 的具体问题,感受集合语言的意义和作用; 教学重点:集合的基本概念与表示方法; 教学难点:运用集合的两种常用表示方法——列举法与描述法,正确表示一 些简单的集合; 主要知识点: 1、 把研究的对象统称为元素,把一些元素组成的总体叫做集合。集合三要 素:确定性、互异性、无序性。 2、 只要构成两个集合的元素是一样的,就称这两个集合相等。 3、 常见集合:正整数集合:或,整数集合:,有理数集合:,实数集合:. 4、集合的表示方法:列举法、描述法.
高一上化学人教版必修第一册期末知识点复习总结

第一章物质及其变化一、物质的分类1.根据物质的组成对物质进行分类(1)由同一种元素形成的几种性质不同的单质,叫作这种元素的同素异形体如金刚石、石墨和C60;O2和O3(2)根据物质的组成对物质进行分类——树状分类法(3)从不同的角度对物质进行分类——交叉分类法碳酸钠为钠盐,也为碳酸盐2.根据物质的性质对物质进行分类酸性氧化物碱性氧化物定义能与碱反应生成盐和水的氧化物能与酸反应生成盐和水的氧化物实例CO2、SO3等CaO、Fe2O3等属类大多数非金属氧化物大多数金属氧化物例1 .以下为中学化学中常见的几种物质:①Fe ②熔融NaCl ③NaHSO4 ④CO2 ⑤H2SO4 ⑥酒精⑦KHCO3溶液⑧BaSO4⑨NaOH请回答下面问题。
属于电解质的是(填序号);属于酸的是;属于盐的是。
二、分散系及其分类1.分散系(1)基本概念(2)分类根据分散质粒子的直径大小分类:2.胶体(1)分类胶体分散剂实例液溶胶液体Fe(OH)3胶体气溶胶气体云、雾固溶胶固体有色玻璃(2)Fe(OH)3胶体的制备在小烧杯中,加入40 mL蒸馏水,加热至沸腾,向沸水中逐滴加入5~6滴FeCl3饱和溶液,继续煮沸至液体呈红褐色,停止加热,即可得到Fe(OH)3胶体。
化学方程式:FeCl 3+3H 2O=====△Fe(OH)3(胶体)+3HCl 。
(3)丁达尔效应①实验探究实验操作实验现象原因分析观察到一条光亮的“通路”胶粒的直径为1~100 nm ,能使光波发生散射无明显现象溶液中粒子的直径小于1__nm ,光的散射极其微弱②应用:该效应常用来区分胶体和溶液。
三、物质的转化1.实现物质转化的基本依据:在化学变化过程中,元素不会发生改变。
2.常见单质及其化合物的转化关系 (1)实例探究Ca ――→①CaO ――→②Ca (OH )2――→③CaCO 3 C ――→④CO 2――→⑤H 2CO 3――→⑥CaCO 3写出上述转化的化学方程式并注明反应类型:序号 化学方程式 反应类型 ① 2Ca +O 2===2CaO 化合反应 ② CaO +H 2O===Ca(OH)2化合反应 ③ Ca(OH)2+CO 2===CaCO 3↓+H 2O复分解反应 ④ C +O 2=====点燃CO 2 化合反应 ⑤ CO 2+H 2O===H 2CO 3化合反应 ⑥H 2CO 3+Ca(OH)2===CaCO 3↓+2H 2O复分解反应(2)探究归纳:单质到盐的转化关系3.确定制取物质的方法 (1)确定依据(2)实例——碱的制备(3)工业生产方法的选择①最适当方法的选择②实例——工业上制取NaOHa.不采用Na2O与H2O反应的原因:Na2O作为原料,来源少、成本高;b.主要采用方法:电解饱和食盐水;c.过去曾采用方法:盐(如Na2CO3)与碱[如Ca(OH)2]反应。
人教版教学课件-新人教[原创]必修1第一章总复习
![人教版教学课件-新人教[原创]必修1第一章总复习](https://img.taocdn.com/s3/m/439b3edeb14e852458fb5756.png)
真核细胞 较大(10 μm~100 μm) 没有由核膜包围的典型的细胞核, 有成形的、真正的细 只是把遗传物质储存、复制的场 胞核,有核膜、核仁 所称拟核 以DNA分子存在 以染色体形式存在
只有核糖体
举例
有线粒体等多种细胞 器 细胞壁不含纤维素,主要成分是 细胞壁的主要成分是 糖类与蛋白质形成的化合物(肽 纤维素和果胶 聚糖) 动物 植物 细菌 蓝藻(颤藻 念珠藻 发菜) 衣藻 绿藻 红藻 硅藻 放线菌 衣原体 支原体 真菌(酵母菌 霉菌 蘑
1.科学发现是很多科学家的共同参与, 共同努力的结果 2.科学发现的过程离不开技术的支持 3.科学发现需要理性思维和实验的结 合 4.科学学说的建立是一个不断开 拓.继承.修正和发展的过程
• 1.下列关于人体生命活动与细胞关系的叙述,错误的是 A.细胞的分裂和分化是人体发育的基础 • B.只有通过精子和卵细胞,子代方能获得亲本的遗传物 质 • C.人体是由细胞构成的,所以细胞的生长必然导致人体 的生长 • D.人体是由细胞构成的,所以细胞的分裂必然导致人体 的生长 • 2.如果把细胞搅碎,细胞将死亡;病毒不具有细胞结构, 如果把病毒搅碎,病毒将失去活性,这说明( ) • A.细胞和病毒失活是因为破坏了它们的化学成分 • B.细胞和病毒被搅碎都失活,可见两者的特点是一致的 • C.像病毒这样不具细胞结构的生物的存在,说明生命现 象不依赖于细胞结构 • D.生物体的生命活动必须建立在一定的结构基础之上
• • • • •
• 2.细胞的统一性
• 4.成人身体约有1014个细胞。这些细胞大约有20(种 不同的类型,根据分化程度的不同,又可分为600多 种,但是都有基本相同的结构,这说明( ) • A.体细胞既有多样性,又有统一性 • B.细胞的结构和功能基本相同 • C.200多种不同的类型就是200多种不同的组织 • D.人体细胞的基本结构与草履虫相同 • 5.(05年北京)在以下描述中可以将病毒与其他微生物 相区别的是 • A.能够使人或动物患病 B.没有细胞核,仅有核酸 • C.具有寄生性 D.由核酸和蛋白质装配进行增殖
人教版高一数学必修一-第一章-知识点与习题讲解

必修1第一章集合与函数基础知识点整理第1讲 §1。
1。
1 集合的含义与表示¤知识要点:1。
把一些元素组成的总体叫作集合(set ),其元素具有三个特征,即确定性、互异性、无序性.2. 集合的表示方法有两种:列举法,即把集合的元素一一列举出来,并用花括号“{ }”括起来,基本形式为123{,,,,}n a a a a ⋅⋅⋅,适用于有限集或元素间存在规律的无限集. 描述法,即用集合所含元素的共同特征来表示,基本形式为{|()x A P x ∈},既要关注代表元素x ,也要把握其属性()P x ,适用于无限集.3。
通常用大写拉丁字母,,,A B C ⋅⋅⋅表示集合. 要记住一些常见数集的表示,如自然数集N ,正整数集*N 或N +,整数集Z ,有理数集Q ,实数集R 。
4. 元素与集合之间的关系是属于(belong to )与不属于(not belong to ),分别用符号∈、∉表示,例如3N ∈,2N -∉.¤例题精讲:【例1】试分别用列举法和描述法表示下列集合:(1)由方程2(23)0x x x --=的所有实数根组成的集合; (2)大于2且小于7的整数。
解:(1)用描述法表示为:2{|(23)0}x R x x x ∈--=; 用列举法表示为{0,1,3}-.(2)用描述法表示为:{|27}x Z x ∈<<; 用列举法表示为{3,4,5,6}.【例2】用适当的符号填空:已知{|32,}A x x k k Z ==+∈,{|61,}B x x m m Z ==-∈,则有: 17 A ; -5 A ; 17 B 。
解:由3217k +=,解得5k Z =∈,所以17A ∈;由325k +=-,解得73k Z =∉,所以5A -∉;由6117m -=,解得3m Z =∈,所以17B ∈。
【例3】试选择适当的方法表示下列集合:(教材P 6 练习题2, P 13 A 组题4) (1)一次函数3y x =+与26y x =-+的图象的交点组成的集合; (2)二次函数24y x =-的函数值组成的集合; (3)反比例函数2y x =的自变量的值组成的集合。
人教版(新教材)高中数学第一册(必修1)精品课件:第一章集合与常用逻辑用语章末复习课

【例1】 (1)设集合A={1,2,4},集合B={x|x=a+b,a∈A,b∈A},则集合B中元
素的个数是( )
A.4
B.5
C.6
D.7
(2)已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是( )
A.1
B.3
ቤተ መጻሕፍቲ ባይዱ
C.5
D.9
解析 (1)∵a∈A,b∈A,x=a+b,所以x=2,3,4,5,6,8,∴B中有6个元素, 故选C. (2)当x=0,y=0时,x-y=0;当x=0,y=1时,x-y=-1;当x=0,y=2时,x-y =-2;当x=1,y=0时,x-y=1;当x=1,y=1时,x-y=0;当x=1,y=2时,x -y=-1;当x=2,y=0时,x-y=2;当x=2,y=1时,x-y=1;当x=2,y=2时, x-y=0.根据集合中元素的互异性知,B中元素有0,-1,-2,1,2,共5个. 答案 (1)C (2)C
【训练4】 (1)若p:x2+x-6=0是q:ax+1=0的必要不充分条件,则实数a的值为 ________. (2) 若 - a<x< - 1 成 立 的 一 个 充 分 不 必 要 条 件 是 - 2<x< - 1 , 则 a 的 取 值 范 围 是 ________.
解析 (1)p:x2+x-6=0,即x=2或x=-3. q:ax+1=0,当 a=0 时,方程无解;当 a≠0 时,x=-1a. 由题意知p q,q p,故a=0舍去;
当 a≠0 时,应有-1a=2 或-1a=-3,解得 a=-12或 a=13. 综上可知,a=-12或 a=13. (2)根据充分条件、必要条件与集合间的包含关系,应有{x|-2<x<-1} {x|-a<x< -1},故有a>2. 答案 (1)-12或13 (2)a>2
人教版高中数学必修一第一章知识点

第一章集合与函数概念〖1.1 〗集合【1.1.1 】集合的含义与表示(1)集合的概念集合中的元素具有确定性、互异性和无序性.( 2)常用数集及其记法N表示自然数集,N或N表示正整数集,Z表示整数集,Q表示有理数集,R表示实数集.( 3)集合与元素间的关系对象 a 与集合 M 的关系是a M ,或者 a M ,两者必居其一.(4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合 . ③描述法: { x | x具有的性质 } ,其中x为集合的代表元素 .④图示法:用数轴或韦恩图来表示集合.( 5)集合的分类①含有有限个元素的集合叫做有限集. ②含有无限个元素的集合叫做无限集. ③不含有任何元素的集合叫做空集 ().【 1.1.2 】集合间的基本关系( 6)子集、真子集、集合相等名称记号意义性质示意图A B(或子集B A)A B真子集(或B A)A中的任一元素都属于 BA B,且B中至少有一元素不属于 A(1)A A(2)A A(B)BA(3)若A B 且 B C,则A C(4)若A B 且 B A,则 A B或(1) A (A为非空子集)BA(2)若A B 且 B C,则 A CA 中的任一元素都属集合A B于B,B中的任一元素相等都属于 A (1)A BA(B) (2)B A( 7)已知集合A有n(n1) 个元素,则它有2n个子集,它有 2n1个真子集,它有 2n 1个非空子集,它有 2n2非空真子集.( 8)交集、并集、补集名称交集并集补集【 1.1.3】集合的基本运算记号意义性质示意图{ x | x A, 且(1)A A AA B(2)AA B(3)A B Ax B}A B B{ x | x A, 或(1)A A AA(2)A ABA B(3)A B Ax B}A B B1A(e A)2A (e U A)UUe A{ x | x U , 且x A}痧( A B)( U A)(?U B)UU痧(A B)(U A)(? B)U U【补充知识】含绝对值的不等式与一元二次不等式的解法( 1)含绝对值的不等式的解法不等式解集| x | a( a 0){ x | a x a}| x | a(a 0)x | xa 或 x a}把 ax b 看成一个整体,化成| x | a,| ax b |c,| ax b |c(c0)| x | a(a 0) 型不等式来求解(2)一元二次不等式的解法判别式b24ac000二次函数y ax2bx c(a0)的图象O一元二次方程2b b4ac2x1,22a x1 x2bax bx c0( a0)无实根2a(其中x1x2 )的根ax2bx c0(a0){ x | x x1或x x2}{ x | x b }R的解集2aax2bx c 0( a 0){ x | x1x x2}的解集〖1.2 〗函数及其表示【1.2.1 】函数的概念( 1)函数的概念①设 A、 B 是两个非空的数集,如果按照某种对应法则 f ,对于集合 A 中任何一个数x ,在集合 B中都有唯一确定的数 f ( x) 和它对应,那么这样的对应(包括集合 A ,B 以及 A 到 B 的对应法则 f )叫做集合 A到 B 的一个函数,记作 f : A B .②函数的三要素: 定义域、值域和对应法则.③只有定义域相同,且对应法则也相同的两个函数才是同一函数.( 2)区间的概念及表示法①设 a, b 是两个实数,且a b ,满足 a x b 的实数x的集合叫做闭区间,记做[a,b] ;满足a xb 的实数x的集合叫做开区间,记做(a,b) ;满足a x b ,或 a x b 的实数x的集合叫做半开半闭区间,分别记做[ a,b) , (a,b] ;满足 x a, x a, x b, x b 的实数 x 的集合分别记做.[a, ),( a,),(, b],(, b)注意:对于集合 { x | a x b} 与区间 (a, b) ,前者 a 可以大于或等于b,而后者必须a b .(3)求函数的定义域时,一般遵循以下原则:① f ( x) 是整式时,定义域是全体实数.② f ( x) 是分式函数时,定义域是使分母不为零的一切实数.③ f ( x) 是偶次根式时,定义域是使被开方式为非负值时的实数的集合.④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1.⑤y tan x 中,x k(k Z ) .2⑥零(负)指数幂的底数不能为零.⑦若 f ( x) 是由有限个基本初等函数的四则运算而合成的函数时,则其定义域一般是各基本初等函数的定义域的交集.⑧对于求复合函数定义域问题,一般步骤是:若已知 f (x) 的定义域为 [ a, b] ,其复合函数 f [ g( x)]的定义域应由不等式 a g ( x) b 解出.⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论.⑩由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义.(4)求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,只是提问的角度不同.求函数值域与最值的常用方法:①观察法:对于比较简单的函数,我们可以通过观察直接得到值域或最值.②配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的值域或最值.③判别式法:若函数y f ( x) 可以化成一个系数含有y 的关于 x 的二次方程a( y) x2b( y) x c( y)0 ,则在 a( y)0 时,由于 x, y 为实数,故必须有b2 ( y) 4a( y)c( y)0 ,从而确定函数的值域或最值.④不等式法:利用基本不等式确定函数的值域或最值.⑤换元法:通过变量代换达到化繁为简、化难为易的目的,三角代换可将代数函数的最值问题转化为三角函数的最值问题.⑥反函数法:利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值.⑦数形结合法:利用函数图象或几何方法确定函数的值域或最值.⑧函数的单调性法.【 1.2.2 】函数的表示法(5)函数的表示方法表示函数的方法,常用的有解析法、列表法、图象法三种.解析法:就是用数学表达式表示两个变量之间的对应关系.列表法:就是列出表格来表示两个变量之间的对应关系.图象法:就是用图象表示两个变量之间的对应关系.( 6)映射的概念①设 A、 B 是两个集合,如果按照某种对应法则 f ,对于集合 A 中任何一个元素,在集合 B 中都有唯一的元素和它对应,那么这样的对应(包括集合 A , B 以及 A 到 B 的对应法则 f )叫做集合 A 到B 的映射,记作 f : A B .②给定一个集合 A 到集合 B 的映射,且 a A, b B .如果元素 a 和元素b对应,那么我们把元素b 叫做元素a的象,元素a叫做元素 b 的原象.----〖 1.3 〗函数的基本性质【 1.3.1 】单调性与最大(小)值( 1)函数的单调性①定义及判定方法函数的图象定义性 质如果对于属于定义域I 内某个区间上的任意两个自变量y y=f(X)的值 x 1 、x 2 , 当 x 1 < x 2 时,都f(x 2 )...有 f(x 1)<f(x 2 ) , 那 么 就说.........f(x 1 )f(x) 在这个区间上是 增函数 ....o1x 2xx函数的单调性如果对于属于定义域I 内某yy=f(X)个区间上的任意两个自变量f(x 1)的值 x 1、 x 2 ,当 x 1 < x 2 时,都...判定方法( 1)利用定义( 2)利用已知函数的单调性( 3)利用函数图象(在某个区间图象上升为增)( 4)利用复合函数( 1)利用定义( 2)利用已知函数的单调性 ( 3)利用函数图象(在有 f(x 1)>f(x 2 ) , 那 么 就说f(x ).........2f(x) 在这个区间上是 减函数 .ox 1x 2...x某个区间图象下降为减)( 4)利用复合函数②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数.③ 对 于 复 合 函 数 yf [ g( x)], 令u g( x), 若y f (u)为 增 ,u g( x)为 增 , 则y f [ g (x)] 为增;若 yf (u) 为减, ug( x) 为减,则 yf [g (x)] 为增;若 y f (u) 为增, ug( x)为 减, 则yf [ g( x)]为 减; 若 yf (u)为 减,ug( x) 为 增, 则 yy f [ g (x)] 为减.( 2)打“√”函数f ( x) x a (a 0) 的图象与性质xf (x) 分别在 ( ,a ] 、 [ a ,) 上为增函数,分别在ox[a, 0) 、 (0, a ] 上为减函数.( 3)最大(小)值定义①一般地,设函数y f (x) 的定义域为 I ,如果存在实数M 满足:(1)对于任意的 xI ,都有 f ( x)M ;(2)存在 x 0 I ,使得 f (x 0 ) M .那么,我们称M 是函数 f ( x)的最大值,记作f ( x) M②一般地,设函数y f ( x) 的定义域为 I ,如果存在实数m 满足:(1)对于任意的x I ,都有f (x)m ;(2)存在 x0I ,使得 f ( x0 )m .那么,我们称 m 是函数 f (x) 的最小值,记作f max (x)m.【1.3.2 】奇偶性(4)函数的奇偶性①定义及判定方法函数的定义图象判定方法性质如果对于函数f(x)定义域内( 1)利用定义(要先任意一个 x,都有f(-x)=-判断定义域是否关于.......f(x),那么函数 f(x)叫做奇函原点对称)......数.( 2)利用图象(图象.关于原点对称)函数的奇偶性如果对于函数f(x)定义域内( 1)利用定义(要先任意一个 x,都有f(-x)=f(x) ,判断定义域是否关于..........那么函数 f(x)叫做偶函数.原点对称)...( 2)利用图象(图象关于 y 轴对称)②若函数 f ( x) 为奇函数,且在x 0处有定义,则 f (0)0.③奇函数在 y 轴两侧相对称的区间增减性相同,偶函数在y 轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.〖补充知识〗函数的图象( 1)作图利用描点法作图:①确定函数的定义域;②化解函数解析式;③讨论函数的性质(奇偶性、单调性);④画出函数的图象.利用基本函数图象的变换作图:要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象.①平移变换y f ( x)h 0,左移h个单位h0,右移 | h|个单位y f ( x)k 0,上移k个单位k0,下移 | k|个单位②伸缩变换y f (x h) y f (x) ky f ( x)01,伸y f ( x) 1,缩0A1,缩y f ( x) A 1,伸y Af ( x)③对称变换y f ( x)y f ( x)y f ( x)y f ( x) (2)识图x轴f (x)y f (x)y轴f (x)y y原点f ( x)y f ( x)直线y xy f1( x) y去掉y轴左边图象y f (| x |)保留y轴右边图象,并作其关于y轴对称图象保留x轴上方图象y| f ( x) |将x轴下方图象翻折上去对于给定函数的图象,要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性,注意图象与函数解析式中参数的关系.(3)用图函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,获得问题结果的重要工具.要重视数形结合解题的思想方法.7。
高一化学必修一第一章重难点:离子反应[新人教版]
![高一化学必修一第一章重难点:离子反应[新人教版]](https://img.taocdn.com/s3/m/41be620119e8b8f67d1cb926.png)
高一化学必修一第一章重难点:离子反应[新人教版]高一化学必修一第一章重难点:离子反应[新人教版]亲爱的同学,新学期就要开始了。
怀着梦想,背上行囊,走进英才,又一阶段的学习之旅启程了。
生命的辉煌,在这时奠基;青春作伴,正当立志奋发时!一起来看看高一化学必修一第一章重难点相关内容。
高一化学必修一第一章重难点:离子反应[新人教版]一、离子反应的概念离子反应是指有离子参加的反应。
也就是说,反应物中有离子或生成物中有离子的反应,均为离子反应。
由于中学阶段涉及的问题多数是指水溶液中的变化,所以水溶液中电解质间的相互反应便成了离子反应的常见问题。
但须注意的是,凡是离子化合物,就含有离子,有时固体状态的物质之间(如实验室判氨)或固体与气体之间(如碱石灰与氯化氢)发生的反应,也可以是离子反应,只是通常不书写类似这样过程的离子反应方程式。
在水溶液中发生离子反应的条件即复分解反应的三个条件(有难电离、难溶及易挥发物质生成)和氧化还原反应(比如置换反应等)。
二、离子共存问题凡是能发生反应的离子之间或在水溶液中水解相互促进的离子之间不能大量共存(注意不是完全不能共存,而是不能大量共存)。
一般规律是:A、①B、③ ④C、② ⑤D、① ④[解题分析] 本题全面考查离子共存知识,在题给的六组离子中,第①组ClO-与H+、I-不能大量共存,第②组中NH4+与OH-、HCO3-与OH-不能大量共存,第③④组中各离子可以共存,第⑤组H+与AlO2-、HSO3-不能大量共存,第⑥组中Ca2+与CO32-甚至SO42-不能大量共存。
因此,正确选项应为B。
例2:在pH=1的溶液中,可大量共存的离子组是A、Fe3+、I-、S2-、Cl-B、Al3+、Mg2+、SO42-、Cl-C、K+、Na+、AlO2-、NO3-D、K+、Na+、SO42-、S2O32- [解题分析] 本题先明确了溶液的环境为PH=1的酸性条件下,因此不仅要判断各离子组中离子能否共存,还要判断它们能否与H+大量共存。
第1章 走近细胞 知识点总结-高一上学期生物人教版必修1

第一章走进细胞第1节细胞是生命活动的基本单位1.细胞*是生物体结构和功能的基本单位(除病毒)。
2.细胞学说主要建立者:施莱登和施旺。
3.细胞学说内容*:①细胞是一个有机体,一切动植物都由细胞发育而来,并由细胞和细胞产物构成。
②细胞是一个相对独立的单位,既有它自己的生命,又对与其他细胞共同组成的整体的生命起作用。
③新细胞是由老细胞分裂产生的。
4.细胞学说建立过程:①维萨里:揭示了器官水平的结构。
②比夏:指出器官由组织构成。
③罗伯特·胡克*:第一位发现并命名细胞(死细胞)的人。
④列文虎克*:第一位观察活细胞的人。
⑤马尔比基:观察到了动植物的微细结构。
⑥耐格里:观察到新细胞的产生是细胞分裂的结果。
⑦魏尔肖:对施莱登的观点进行修正,总结“细胞通过分裂产生新细胞”。
5.细胞学说意义:①细胞学说*揭示了动植物的统一性,从而阐明了生物界的统一性。
(没有揭示多样性和差异性,仅局限于动物和植物)②使生物学研究进入细胞水平,并为后来进入分子水平打下基础。
③细胞学说中细胞分裂产生新细胞的结论,为生物进化论埋下伏笔。
6.归纳法分为完全归纳法和不完全归纳法。
不完全归纳法得出的结论很可能是可信的,可以用来预测和判断。
7.生物的生命活动离不开细胞的原因*?①单细胞生物依赖单个细胞完成各种生命活动。
②多细胞生物依赖各种分化的细胞密切合作共同完成生命活动。
③病毒只有寄生在活细胞体内才能显现出生命特征。
8.常见的单细胞生物:草履虫、变形虫、眼虫、衣藻、细菌等。
9.病毒相关知识*:①病毒是非细胞结构的生物。
②主要由核酸和蛋白质组成。
③病毒营寄生生活,只有寄生在活细胞体内才能显现出生命特征。
培养病毒不能用普通的全营养培养基,需要用宿主活细胞培养基培养。
④病毒按照核酸种类的不同分为:DNA病毒:如乙肝病毒、天花病毒、噬菌体等。
RNA病毒:如流感病毒、新冠病毒、HIV、SARS病毒等。
病毒按照宿主细胞的不同分为:动物病毒、植物病毒、噬菌体(细菌病毒)。
最新人教版高一数学必修1第一章《复习》教案

第一章单元复习从容说课通过对本章集合知识与函数知识结构的整合,使学生所学的知识系统化、网络化.本课从知识结构的整体出发,通过对集合知识与函数知识的综合运用,培养学生的理性思维能力,优化学生的数学认知结构.通过解决抽象函数、复合函数的有关问题,培养学生的抽象思维能力;利用分析、讨论的课堂教学手段,培养学生的合作、交流意识;结合函数知识解决实际问题,激发学生学习数学的兴趣,培养他们分析问题、解决问题的能力.三维目标一、知识与技能掌握集合、函数的有关概念,能综合运用集合与函数的基本知识解决问题.对复合函数与抽象函数有新的认识.二、过程与方程培养学生分析、探究、思考的能力,进一步培养学生综合运用基本知识解决问题的能力.三、情感态度与价值观激发学生学习数学的兴趣,培养他们合作、交流、创新意识以及分类讨论、抽象理解能力.教学重点集合与函数的基本知识,含字母问题的研究,抽象函数的理解.教学难点分类讨论的标准、抽象函数的理解.教具准备多媒体课件、投影仪.课时安排2课时教学过程一、知识回顾(一)第一章知识点1.集合:①集合的含义;②表示法;③元素与集合的关系.2.集合间的基本关系:①子集;②真子集;③集合相等.3.集合的运算:①并集;②交集;③补集.4.函数:①函数的概念;②三要素:定义域,值域,对应法则;③映射概念.5.函数的表示:①表示法:解析法,列表法,图象法;②求函数的解析式;③求函数的定义域;④求一些简单函数的值域和最值.6.函数的单调性:①函数单调性定义;②单调函数的概念;③单调区间;④判断或证明函数单调性的方法;⑤单调性的应用;⑥利用函数的单调性求最值.7.函数的奇偶性:①奇偶性的概念;②奇偶性的定义域特征;③判断函数奇偶性的步骤;④奇偶性图象特征.8.函数的应用问题:①解函数应用题的基本方法步骤;②与几何图形有关的应用题的解法;③与物理现象有关的应用题的解法;④与社会生活有关的实际问题的解法.9.(1)解函数应用题的主要步骤是:①“设”即分析题意设出变量;②“列”即列出关系式,建设函数模型;③“解”即运用函数的性质解出要求的量;④“答”即回到原实际问题作答.(2)解实际问题的步骤用框图可表示为(3)当实际问题中的变量较多时,首先寻找所求量(y )与这些变量间的关系式,然后根据实际要求确定一个自变量(x ),而其他变量通过题中条件再用x 表示出来,用代入法即可得到函数模型y =f (x ).(二)方法总结1.证明集合相等的方法:A =B ⇔①A ⊂B ;②A ⊃B (两点必须同时具备).2.相同函数的判定方法:①定义域相同;②对应法则相同(两点必须同时具备).3.函数表达式的求法:①定义法;②换元法;③待定系数法.4.函数的定义域的求法:列出使函数有意义的自变量的不等关系式,求解即得函数的定义域.常涉及到的依据为:①分母不为0;②偶次根式中被开方数不小于0;③实际问题要考虑实际意义等.5.函数值域的求法:①配方法(二次或四次);②判别式法;③反表示法;④换元法;⑤不等式法;⑥函数的单调性法.6.函数单调性的判定法:①设x 1、x 2是所研究区间内的任两个自变量,且x 1<x 2;②判定f (x 1)与f (x 2)的大小;③作差比较或作商比较.(注:做有关选择、填空题时,可采用复合函数单调性判定法,做解答题时必须用单调性定义和基本函数的单调性)7.函数奇偶性的判断:首先看函数的定义域是否关于原点对称,再看f (-x )与f (x )的关系.(1)图象的作法与平移:①据函数表达式,列表、描点、连光滑曲线;②利用熟知函数的图象的平移、翻转、伸缩变换;③利用函数图象的对称性描绘函数图象.(2)函数的应用举例(实际问题的解法). a.解决应用问题的一般程序是:①审题:弄清题意,分清条件和结论,理顺数量关系;②建模:将文字语言转化成数学语言,利用相应的数学知识模型. ③求模:求解数学模型,得到数学结论.④还原:将用数学方法得到的结论,还原为实际问题的意义.b.建模类型:①可化为一、二次函数的应用题的解法;②可化为分段函数的应用题解法. 8.常用函数的研究、总结与推广:(1)以二次函数为背景的函数问题(包括通过换元可转化为二次函数的问题).(2)研究函数y =b ax d cx ++(ac ≠b d)的图象性质. (3)研究函数y =x +x1的图象性质并推广.9.抽象函数(即不给出f (x )解析式,只知道f (x )具备的条件)的研究. (1)若f (a +x )=f (a -x ),则f (x )关于直线x =a 对称. (2)若对任意的x 、y ∈R ,都有f (x +y )=f (x )+f (y ),可利用赋值法研究抽象函数的性质.二、讲解新课 典型例题 【例1】 集合A ={x |x 2-mx -8≥0},B ={x |x 2-2mx -n <0},问能否找到两个实数m 、n ,使A ∩B ={x |4≤x <5}?若存在,求出m 、n 的值;若不存在,请说明理由.解:假设存在实数m 、n 满足条件.由题意可知,4是方程x 2-mx -8=0的一根,由韦达定理知方程的另一根为-2. ∴m =4+(-2)=2.∴B ={x |x 2-4x -n <0},A ={x |x ≥4或x ≤2}. 由题意可知,5是方程x 2-4x -n =0的一根,方程x 2-4x -n =0的另一根为x 0,则⎩⎨⎧-=⋅=+,5,4500n x x ∴⎩⎨⎧=-=.5,10n x综上,存在实数m =2,n =5满足题意.方法引导:本题通过集合与一元二次方程结合,给出一类开放性的问题,要求学生自己找出是否存在实数m 、n 能够满足题意.解题的关键就是能发现一元二次不等式解的特点.【例2】 设A ={x |-2≤x ≤a }≠∅,B ={y |y =2x +3,x ∈A },C ={z |z =x 2,x ∈A },且C ⊆B ,求实数a 的取值范围.解:∵A ={x |-2≤x ≤a },∴B ={y |y =2x +3,x ∈A }={y |-1≤y ≤2a +3}. 又C ={z |z =x 2,x ∈A },且C ⊆B ,①当-2≤a ≤0时,C ={z |z =x 2,x ∈A }={z |a 2≤z ≤4},∴⎩⎨⎧≥+-≥,432,12a a 得a ≥21,无解.②当0<a ≤2时,C ={z |0≤z ≤4},∴⎩⎨⎧+≤-≥,324,10a 得a ≥21.∴21≤a ≤2.③当a >2时,C ={z |0≤z ≤a 2}, ∴⎩⎨⎧+≤-≥,32,102a a 得-1≤a ≤3.∴2<a ≤3.综上21≤a ≤3. 方法引导:本题是集合与二次函数相结合的问题,通过对a 进行分类讨论,利用数轴分析集合间的包含关系来解决.【例3】 已知函数f (x )=xax x ++22,x ∈[1,+∞).(1)当a =21时,求函数f (x )的最小值;(2)若对任意x ∈[1,+∞),f (x )>0恒成立,试求实数a 的取值范围.(1)解:当a =21时,f (x )=x +x21+2.设1≤x 1<x 2,则f (x 2)-f (x 1)=(x 2-x 1)(1-2121x x ). ∵2x 1x 2>2,0<2121x x <21, ∴1-2121x x >0.又x 2-x 1>0, ∴f (x 2)-f (x 1)>0,即f (x 1)<f (x 2).∴f (x )在区间[1,+∞)上为增函数,则f (x )在区间[1,+∞)上的最小值为f (1)=27. (2)解法一:在区间[1,+∞]上,f (x )=xax x ++22>0恒成立⇔x 2+2x +a >0恒成立.设y =x 2+2x +a ,x ∈[1,+∞),y =x 2+2x +a =(x +1)2+a -1在区间[1,+∞)上递增, ∴当x =1时,y min =3+a .于是当且仅当y min =3+a >0时,函数f (x )>0恒成立,故a >-3.解法二:f (x )=x +xa+2,x ∈[1,+∞),当a ≥0时,函数f (x )的值恒为正;当a <0时,y =x +2与y =xa在[1,+∞)上都是增函数.所以f (x )=x +xa+2在[1,+∞)上是增函数.故当x =1时,y min =3+a ,于是当且仅当y min =3+a >0时,函数f (x )>0恒成立,故a >-3.方法引导:本题体现了函数思想在解题中的运用,第(1)题用函数单调性求函数的最小值,第(2)题用函数的单调性解决恒成立的问题.在第(2)题的解法一中,还可以这样解:要使x 2+2x +a >0恒成立,只要a >-x 2-2x =-(x +1)2+1恒成立,在[1,+∞)上,由函数单调性得-(x +1)2+1≤-3,所以只要a >-3.【例4】 已知f (x )=-x 2+ax -4a +21,x ∈[0,1],求f (x )的最大值g (a ),且求g (a )的最小值.解:∵f (x )=-x 2+ax -4a +21=-(x -2a )2+42a -4a +21,对称轴x =2a,∵x ∈[0,1],①当2a≤0,即a ≤0时,f (x )max =f (0)=-4a +21.②当0<2a<1,即0<a <2时,f (x )max =f (2a )=42a -4a +21.③当2a≥1,即a ≥2时,f (x )max =f (1)=43a-21.∴g (a )=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥-<<+-≤+-.2,2143,20,2144,0,2142a a a a aa a ①当a ≤0时,-4a +21≥21. ②当0<a <2时,42a -4a +21=41(a -21)2+167≥167.③当a ≥2时,43a-21≥1.∴g (a )min =167.方法引导:本题是含参数的二次函数最值问题,通过对称轴x =2a的移动,对a 进行分类讨论,得到的最大值g (a )是关于a 的一个分段函数的形式,注意分段函数的最小值,是每一段最小值的最小值.【例5】 对于任意非零实数x 、y ,已知函数y =f (x )(x ≠0)满足f (xy )=f (x )+f (y ). (1)求f (1),f (-1);(2)判断y =f (x )的奇偶性;(3)若y =f (x )在(0,+∞)上是增函数,且满足f (x )+f (x -21)≤0,求x 的取值范围.解:(1)∵对于任意非零实数x 、y ,有f (xy )=f (x )+f (y ), 取x =y =1,得f (1)=f (1)+f (1), ∴f (1)=0.取x =y =-1,得f (1)=f (-1)+f (-1),∴f (-1)=0.(2)对任意x ≠0,取y =-1,则f (-x )=f (x )+f (-1)=f (x )+0,即f (-x )=f (x ),∴f (x )是偶函数.(3)∵f (x )+f (x -21)≤0,∴f [x (x -21)]≤0.由f (x )是偶函数,得f (|x 2-21x |)≤f (1).又y =f (x )(x ≠0)在(0,+∞)上是增函数,∴0<|x 2-21x |≤1. ∴-1≤x 2-21x <0或0<x 2-21x ≤1. 解得0<x <21或4171-≤x <0或21<x ≤4171+.方法引导:本题求抽象函数的单调性与奇偶性,一般常用赋值法,给x 、y 取一些特殊的值,从而得到一些特殊的函数值,再结合函数的单调性与奇偶性的性质解题.【例6】 已知f (x )∈[83,21],求y =f (x )+)(21x f -的值域.解:∵f (x )∈[83,21],∴2f (x )∈[43,1].∴1-2f (x )∈[0,41].∴)(21x f -∈[0,21].令t =)(21x f -,t ∈[0,21],则f (x )=21(1-t 2).∴y =21(1-t 2)+t =-21(t -1)2+1.由于t ∈[0,21],所以21≤y ≤87.故函数y 的值域为[21,87].方法引导:本题利用换元法求函数的值域,设出新元以后必须给出新元的范围,对于)(21x f -的范围的研究通常由里向外,最后再根据二次函数的性质求值域.【例7】 如下图,灌溉渠的横断面是等腰梯形,底宽及两边坡总长度为a ,边坡的倾斜角为60°.(1)求横断面积y 与底宽x 的函数关系式;(2)已知底宽x ∈[4a ,2a ],求横断面面积y 的最大值和最小值. 解:(1)分别过A 、B 作AE 、BF 垂直于CD ,交CD 于点E 、F , ∵∠ADC =∠BCD =60°,且AB =x ,∴AD =BC =2xa -.∴D E=CF =2x a -·cos60°=4xa -,AE =2xa -·sin60°=4)(3x a -.∴y =21(AB +CD )·AE =21(x +x +2xa -)·4)(3x a -=163(a +3x )(a -x )(0<x<a ).(2)∵y =-1633(x -3a )2+123a 2,x ∈[4a ,2a],∴当x =3a时,y max =123a 2;当x =2a时,y min =6435 a 2.故横断面面积y 的最大值为123a 2,最小值为6435a 2.方法引导:本题是函数在几何图形方面的应用,运用几何图形的性质求出与面积有关的量(用x 表示),根据面积公式列出关系式,这个过程就是建立数学模型,得到的函数是二次函数,但定义域不是R ,而是实际的底宽[4a ,2a].【例8】 某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系用图甲所示的一条折线表示;西红柿的种植成本与上市时间的关系用图乙的抛物线表示:(1)写出如图甲表示的市场售价与时间的函数关系式P =f (t );写出如图乙表示的种植成本与时间的函数关系式Q =g (t ).(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价和种植成本的单位:元/102 kg ,时间单位:天)解:(1)由图甲可得市场售价与时间的函数关系为f (t )=⎩⎨⎧≤<-≤≤-.300200,3002,2000,300t t t t由图乙可得种植成本与时间的函数关系为g (t )=2001(t -150)2+100,0≤t ≤300. (2)设t 时刻的纯收益为h (t ),则由题意得h (t )=f (t )-g (t ),即h (t )=⎪⎪⎩⎪⎪⎨⎧≤<-+-≤≤++-.300200,2125272001,2000,217521200122t t t t t t当0≤t ≤200时,配方整理得h (t )=-2001(t -50)2+100,所以,当t =50时,h (t )取得区间[0,200]上的最大值100;当200<t ≤300时,配方整理得h (t )=-2001·(t -350)2+100,所以,当t =300时,h (t )取得区间(200,300)上的最大值87.5.综上,由100>87.5可知,h (t )在区间[0,300]上可以取得最大值100,此时t =50,即从2月1日开始的第50天时,上市的西红柿纯收益最大.方法引导:本题是现实生活中的实际问题,题中两图本来是通过实验分析得到相关数据抽象出来的数学模型,这里让我们通过识图找到相应的函数关系式,然后建立纯收益关于时间的分段函数,利用二次函数和分段函数的知识解决问题.【例9】 已知f (x )是定义在[-1,1]上的奇函数,且f (1)=1,若a 、b ∈[-1,1],a +b ≠0,有ba b f a f ++)()(>0.(1)判断函数f (x )在[-1,1]上是增函数还是减函数,并证明你的结论;(2)若满足f (x +21)<f (11-x ),求x 的取值范围;(3)若f (x )≤m 2-2am +1,对所有x ∈[-1,1],a ∈[-1,1]恒成立,求实数m 的取值范围.解:(1)任取-1≤x 1<x 2≤1,则x 1-x 2<0.∵ba b f a f ++)()(>0,∴2121)()(x x x f x f --+>0.∴f (x 1)+f (-x 2)<0.又∵f (x )是定义在[-1,1]上的奇函数,∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2). ∴函数f (x )在[-1,1]上是增函数.(2)∵函数f (x )在[-1,1]上是增函数,由f (x +21)<f (11-x ), 得⎪⎪⎪⎩⎪⎪⎪⎨⎧-<+≤--≥+,1121,111,121x x x x ⎪⎪⎩⎪⎪⎨⎧<<-<<≥-≥.2311,12,23x x x x x 或或 ∴-23≤x <-1. (3)∵f (x )≤m 2-2am +1,且对所有x ∈[-1,1],a ∈[-1,1]恒成立, ∴m 2-2am +1≥f (x )max =f (1),得m 2-2am ≥0,当a ∈[-1,1]时恒成立. 令f (a )=m 2-2am ,a ∈[-1,1],∴⎪⎩⎪⎨⎧≥+=-≥+-=,02)1(,02)1(22m m f m m f得⎩⎨⎧-≤≥≤≥.20,02m m m m 或或∴m ≥2或m ≤-2或m =0.方法引导:本题是函数的一个综合题,注意对于函数单调性的证明应该用定义法,利用函数的单调性求出自变量之间的关系以及利用最值解决恒成立问题,这是对函数性质的一个综合把握.三、课堂练习 (2课时的练习)课本P 51复习参考题A 组1,2,3,4,5,6,7,8,9. 答案:1.(1)A ={-3,3};(2)B ={1,2};(3)C ={1,2}. 2.(1)集合的点组成线段AB 的垂直平分线;(2)集合的点组成以O 为圆心,3 cm 为半径的圆. 3.三角形的外心.4.a 的值为0,-1,1.5.A ∩B ={(0,0)},A ∩C =∅,(A ∩B )∪(B ∩C )={(0,0),(53,-59}. 6.(1){x |x ≤-2或x ≥2}. (2){x |x ≥2}.(3){x |x ≥4且x ≠5}.7.(1)f (a )+1=a +12; (2)f (a +1)=-aa+2.8.证明:(1)f (-x )=22)(1)(1x x ---+=2211x x -+=f (x );(2)f (x 1)=22)1(1)1(1xx -+=1122-+x x =-2211x x -+=-f (x ). 9.(1)图象略.(2)最大高度为1.08 m. 四、课堂小结1.集合语言是现代数学的基本语言,使用集合语言可以简洁、准确地表达数学的内容.2.运用集合与对应的语言进一步描述了函数概念.与初中的函数概念相比较,突出了函数概念的本质:两个数集间的一种确定的对应关系;明确了函数的三要素.3.函数是描述变量之间依赖关系的重要数学模型.函数的表示方法主要有解析法、图象法、列表法三种.4.研究函数的基本性质不仅是解决实际问题的需要,也是数学本身的自然要求.例如:事物的变化趋势、对称性、用料最省、利润最大、效率最高等,就要研究函数的基本性质,如单调性、最大(小)值和奇偶性等.五、布置作业 (2课时的作业)课本P52复习参考题A组10,11,12,13,14;B组2,3,4,5,6,7,8.板书设计第一章单元复习方法归类要点例题及分析过程课堂小结与布置作业。
人教版高中数学必修一第一章知识点
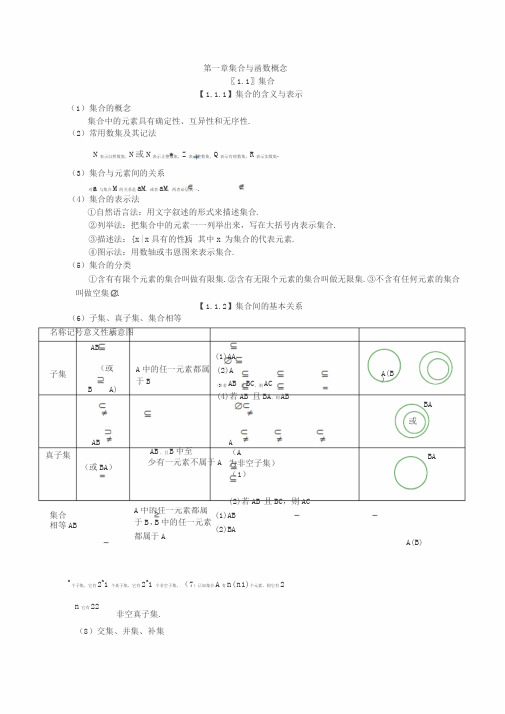
第一章集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示(1)集合的概念集合中的元素具有确定性、互异性和无序性.(2)常用数集及其记法N表示自然数集,N或N表示正整数集,Z表示整数集,Q表示有理数集,R表示实数集.(3)集合与元素间的关系对象a与集合M的关系是aM,或者aM,两者必居其一.(4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{x|x具有的性质},其中x为集合的代表元素.④图示法:用数轴或韦恩图来表示集合.(5)集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集().【1.1.2】集合间的基本关系(6)子集、真子集、集合相等名称记号意义性质示意图AB(1)AA子集B (或A)A中的任一元素都属于B(2)A(3)若AB且BC,则AC(4)若AB且BA,则ABA(B)BA或真子集AB(或BA)AB,且B中至少有一元素不属于AA(A为非空子集)(1)(2)若AB且BC,则ACBA集合相等AB A中的任一元素都属于B,B中的任一元素都属于A(1)AB(2)BAA(B)n个子集,它有2n1个真子集,它有2n1个非空子集,(7)已知集合A有n(n1)个元素,则它有2n它有22非空真子集. (8)交集、并集、补集1【1.1.3】集合的基本运算名称记号意义性质示意图AB 交集{x|x A,且(1)AAA(2)AAB(3)ABAxB}ABBAB 并集{x|x A,或(1)AAA(2)AAAB(3)ABAxB}ABB1A(e U A)2()AeAUU补集e U A{x|xU,且xA} 痧U(A B)(U A)(?U B)痧U(AB)(U A)(?U B)【补充知识】含绝对值的不等式与一元二次不等式的解法(1)含绝对值的不等式的解法不等式解集|x|a(a0){x|axa}|x|a(a0)x|xa或xa}把axb看成一个整体,化成|x|a,|axb|c,|axb|c(c0)|x|a(a0)型不等式来求解(2)一元二次不等式的解法判别式24bac000二次函数2(0)yaxbxcaO的图象一元二次方程20(0)axbxcax1,22bb4ac2abxx122a无实根(其中x1x2)的根20(0) axbxca的解集b{x|xx或xx2}{x|x}12aR 220(0)axbxca的解集{x|xxx}12〖1.2〗函数及其表示【1.2.1】函数的概念(1)函数的概念①设A、B是两个非空的数集,如果按照某种对应法则f,对于集合A中任何一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么这样的对应(包括集合A,B以及A到B的对应法则f)叫做集合A到B的一个函数,记作f:AB.②函数的三要素:定义域、值域和对应法则.③只有定义域相同,且对应法则也相同的两个函数才是同一函数.(2)区间的概念及表示法①设a,b是两个实数,且ab,满足a xb的实数x的集合叫做闭区间,记做[a,b];满足axb的实数x的集合叫做开区间,记做(a,b);满足a xb,或axb的实数x的集合叫做半开半闭区间,分别记做[a,b),(a,b];满足x a,xa,xb,xb的实数x的集合分别记做[a,),(a,),(,b],(,b).注意:对于集合{x|axb}与区间(a,b),前者a可以大于或等于b,而后者必须ab.(3)求函数的定义域时,一般遵循以下原则:①f(x)是整式时,定义域是全体实数.②f(x)是分式函数时,定义域是使分母不为零的一切实数.③f(x)是偶次根式时,定义域是使被开方式为非负值时的实数的集合.④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1.⑤ytanx中,()xkkZ.2⑥零(负)指数幂的底数不能为零.⑦若f(x)是由有限个基本初等函数的四则运算而合成的函数时,则其定义域一般是各基本初等函数的定义域的交集.⑧对于求复合函数定义域问题,一般步骤是:若已知f(x)的定义域为[a,b],其复合函数f[g(x)]的定义域应由不等式ag(x)b解出.⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论.⑩由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义.(4)求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,只是提问的角度不同.求函数值域与最值的常用方法:①观察法:对于比较简单的函数,我们可以通过观察直接得到值域或最值.②配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的值域或最值.③判别式法:若函数yf(x)可以化成一个系数含有y的关于x的二次方程2a(y)xb(y)xc(y)0,则在a(y)0时,由于x,y为实数,故必须有byaycy,从而确定函数的值域或最值.2()4()()0④不等式法:利用基本不等式确定函数的值域或最值.⑤换元法:通过变量代换达到化繁为简、化难为易的目的,三角代换可将代数函数的最值问题转化为三角函数的最值问题.⑥反函数法:利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值.⑦数形结合法:利用函数图象或几何方法确定函数的值域或最值.⑧函数的单调性法.【1.2.2】函数的表示法(5)函数的表示方法表示函数的方法,常用的有解析法、列表法、图象法三种.解析法:就是用数学表达式表示两个变量之间的对应关系.列表法:就是列出表格来表示两个变量之间的对应关系.图象法:就是用图象表示两个变量之间的对应关系.(6)映射的概念①设A、B是两个集合,如果按照某种对应法则f,对于集合A中任何一个元素,在集合B中都有唯一的元素和它对应,那么这样的对应(包括集合A,B以及A到B的对应法则f)叫做集合A到B的映射,记作f:AB.②给定一个集合A到集合B的映射,且aA,bB.如果元素a和元素b对应,那么我们把元素b叫做元素a的象,元素a叫做元素b的原象.〖1.3〗函数的基本性质 【1.3.1】单调性与最大(小)值(1)函数的单调性①定义及判定方法 函数的定义图象判定方法性质 如果对于属于定义域I 内某(1)利用定义个区间上的任意两个自变量 的值x2,当x . 1、x 1.<.x .2.时,都y y=f(X) f(x)2(2)利用已知函数的 单调性有f .(x ...).<.f(.x ...).,那么就说 12 f(x)在这个区间上是增函数. ...f(x)1(3)利用函数图象(在 某个区间图o x 1x 2x 象上升为增)函数的(4)利用复合函数 单调性(1)利用定义如果对于属于定义域I 内某yy=f(X)(2)利用已知函数的个区间上的任意两个自变量 11、x .<.x .的值x2,当x .2.时,都 有f .(x ..12.).,那么就说f(x) 1f(x) 2单调性 (3)利用函数图象(在 某个区间图f(x)在这个区间上是减函数. ...o xx 12x象下降为减)(4)利用复合函数②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为 增函数,减函数减去一个增函数为减函数.③对于复合函数yf[g(x)],令ug(x),若yf(u)为增,ug(x)为增,则yf[g(x)]为增;若yf(u)为减,ug(x)为减,则y f[g(x)]为增;若yf(u)为 增,ug(x)为减,则y f[g(x)]为减;若yf(u)为减,ug(x)为增,则yyf[g(x)]为减.a(2)打“√”函数()(0)fxxax的图象与性质 f(x)分别在(,a ]、[a ,)上为增函数,分别在ox[a,0)、(0,a]上为减函数.(3)最大(小)值定义①一般地,设函数yf(x)的定义域为I,如果存在实数M满足:(1)对于任意的xI,都有f(x)M;(2)存在x I,使得f(x0)M.那么,我们称M是函数f(x)的最大值,记作0f max(x)M.5②一般地,设函数yf(x)的定义域为I,如果存在实数m满足:(1)对于任意的xI,都有f(x)m;(2)存在x0I,使得f(x0)m.那么,我们称m是函数f(x)的最小值,记作f max(x)m.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法函数的定义图象判定方法性质如果对于函数f(x)定义域内(1)利用定义(要先任意一个x,都有.f(.-.x..)=.-.判断定义域是否关于f(x)....,那么函数f(x)叫做奇.函.原点对称)数..(2)利用图象(图象关于原点对称)函数的奇偶性如果对于函数f(x)定义域内(1)利用定义(要先任意一个x,都有f(-.x..)=.f.(x.)..,..判断定义域是否关于那么函数f(x)叫做偶.函.数..原点对称)(2)利用图象(图象关于y轴对称)②若函数f(x)为奇函数,且在x0处有定义,则f(0)0.③奇函数在y轴两侧相对称的区间增减性相同,偶函数在y轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.〖补充知识〗函数的图象(1)作图利用描点法作图:①确定函数的定义域;②化解函数解析式;③讨论函数的性质(奇偶性、单调性);④画出函数的图象.利用基本函数图象的变换作图:要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象.①平移变换yfxyfxh()h0,h()左移个单位右移|个单位h0,h|yfxyfxk()kk()0,上移个单位下移|个单位k0,k|变换②伸缩01,伸yf(x)yf(x)1,缩6yfxyAfx()0A1,缩()A1,伸③对称变换x轴yf(x)y轴yf(x)yf(x)yf(x)原点直线1yxyf(x)yf(x)yf(x)yf(x)去掉轴左边图象yyf(x)yf(|x|)保留y轴右边图象,并作其关于y轴对称图象保留轴上方图象yfxyfx()x|()|将轴下方图象翻折上去x(2)识图对于给定函数的图象,要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性,注意图象与函数解析式中参数的关系.(3)用图函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,获得问题结果的重要工具.要重视数形结合解题的思想方法.7。
期末考试第一单元复习卷【新教材】2020-2021学年人教版(2019)高一上学期生物必修一

高一生物期末复习(第一章)班级姓名一、选择题1.细胞是生命活动的基本单位。
下列选项中不能够支持这一说法的是()A.草履虫是单细胞生物,能进行运动和分裂B.人体发育离不开细胞的分裂和分化C.离体的叶绿体在一定的条件下能释放氧气D.用手抓握物体需要一系列神经细胞和肌肉细胞的协调配合2.下列有关原核细胞的叙述,错误的是()A.没有核膜包被的细胞核,有染色质B.蓝细菌细胞内含有叶绿素和藻蓝素C.蓝细菌有细胞壁,但其化学成分与植物细胞细胞壁不同D.原核细胞与真核细胞具有统一性3.新冠病毒是一种RNA病毒,由它引起的新冠肺炎严重威胁全世界人民的生命安全。
下列关于该病毒的叙述,正确的是()A.新冠病毒没有细胞结构,在分类上属于原核生物B.新冠病毒属于最基本的生命系统C.新冠病毒唯一的细胞器是核糖体D.新冠病毒只能在活细胞中增殖4.细胞学说的创立是生物学发展史上的一个里程碑,被恩格斯列为19世纪自然科学三大发现之一。
下列关于细胞学说内容及意义的描述,错误的是()A.细胞学说认为细胞是一个有机体B.细胞学说认为新细胞是由老细胞分裂产生的C.细胞学说揭示了动物和植物的统一性D.细胞学说阐明了生物界与非生物界的统一性5.正在肆虐全球的新冠病毒肺炎(COVID-19)是由新型冠状病毒(2019-nCoV)引起的。
该病原体是一种RNA病毒。
下列有关该病毒的叙述,错误的是()A.该病毒的遗传物质的元素组成有5种B.该病毒属于原核生物C.该病毒的蛋白质组成单位是氨基酸D.该病毒进入人体后,可在肺部细胞中增殖6.下列关于细胞与生命活动关系的叙述,错误的是()A.引起新型冠状病毒肺炎的病原体无细胞结构,所以其生命活动与细胞无关B.绿藻、酵母菌、草履虫等单细胞生物,只靠一个细胞就可以完成摄食、运动、分裂等多种生命活动C.缩手反射和膝跳反射的完成均需要多种细胞的密切合作D.一切生物的生命活动都在细胞内或细胞参与下完成7.T2噬菌体是一种DNA病毒,有关该病毒的叙述,正确的是()A.T2噬菌体含DNA和RNA B.T2噬菌体不具有细胞核C.T2噬菌体属于自养型生物D.T2噬菌体能独立合成自身蛋白8.一位动物学家正在研究一种驯鹿的千里踏雪大迁徙行为;一位果树专家正在研究某种果树的丰产措施。
【高中生物】必修一总复习课件 高一上学期生物人教版必修1

(2)结合水:细胞中与其他物质相结合的水,约占细胞内全部水分 的4.5% 功能:细胞结构的重要组成成分。
无机盐
1.存在形式:细胞中大多数无机盐以离子的形式存在。 2.含量:占细胞鲜重的1%—1.5% 3.功能 ① 构成复杂化合物的重要组成部分 ② 维持生物体正常的生命活动 ③ 维持生物体内的平衡
1864年 德 萨克斯 绿叶在暗处放置几小时 ——目的是消耗掉叶片中的营养
1941年 美 鲁宾和卡门 同位素标记实验
——光合作用产生的氧气全部来自水
美 卡尔文 14C标记的14CO2
——光合产物中有机物的碳来自CO2
2、光合作用的概念: 指绿色植物通过叶绿体,利用光能,把二氧化碳和水转化
成储存着能量的有机物,并且释放出氧气的过程。
存在于细胞质中。
DNA
甲基绿
绿色
RNA
吡罗红
红色
盐酸:能够改变细胞膜的通透性,加速染色剂进入细胞,同时使
染色质中的DNA与蛋白质分离,有利于DNA与染色剂结合
第四章:细胞的物质输入和输出
第1节 物质跨膜运输实例 第2节 生物膜的流动镶嵌模型 第3节 物质跨膜运输的方式
第1节 物质跨膜运输实例
你吃比较咸的食物时,例如你吃腌制的咸菜,连续嗑带盐的瓜子 等,你的口腔和唇的黏膜有什么感觉?为什么?
光
CO2+H2O 叶绿体 (CH2O)+O2
① 光反应阶段 有光才能进行 场所:类囊体薄膜上
光能 吸收
2H2O
O2+4[H]
ADP+Pi+能量 酶 ATP
② 暗反应阶段 有光、无光都能进行
第一章知识点总结 高一上学期生物人教版(2019)必修1

生物学必修一第1章知识点总结1.1 细胞是生命活动的基本单位一、细胞学说1. 建立者:和2. 内容:(1)细胞是一个有机体,一切都由细胞发育而来,并由和所构成。
(2)细胞是一个的单位,既有它自己的生命,又能与其他细胞共同组成整体的生命。
(3)新细胞是由老细胞产生。
3.建立过程(连线)a维萨里①用显微镜观察植物的木栓组织,发现并命名细胞b比夏②建立了细胞学说c罗伯特•胡克③通过尸体解剖研究,揭示了人体在器官水平的结构d列文虎克④提出细胞通过分裂产生新细胞,指出所有的细胞都来源于先前存在的细胞e施莱登和施旺⑤通过对器官的解剖观察,指出器官由组织构成f魏尔肖⑥用自制显微镜观察到了细菌、红细胞、精子等活细胞4、科学方法—(包括完全归纳法和不完全归纳法,施莱登和施旺运用的是)5. 意义(细胞学说被恩格斯列为19世纪自然科学三大发现之一)(1)细胞学说揭示了动物和植物的,从而阐明了生物界的;(2)细胞学说使人们认识到植物和动物有着共同的结构基础,打破了之间的壁垒,使解剖学、生理学、胚胎学等学科获得了共同的基础;(2)使生物学的研究进入水平;(3)为后来的确立埋下了伏笔二、细胞是基本的生命系统1、生命活动与细胞的关系(1)单细胞生物依靠独立完成各项生命活动;(2)多细胞生物依赖密切合作,共同完成生命活动(3)病毒细胞结构,必须在细胞中【结论】是生命活动的基本单位;生命活动离不开。
2、生命系统的结构层次细胞→_________→__________→系统→_________→_________→群落→_____________→生物圈【注意】(1)植物没有这一层次;(2)对单细胞生物而言,一个细胞就是一个,因此没有等层次。
(3)生态系统包括生物群落和;(4)最基本/最小的生命系统是;(5)最大的生命系统是。
(5)分子、原子或病毒等都生命系统1.2 细胞的多样性和统一性一、细胞的多样性和统一性(1)细胞的多样性体现在不同细胞的和不同(2)细胞的统一性体现在细胞都有相似的,如细胞膜、细胞质和细胞核二、真核细胞和原核细胞真核细胞与原核细胞的本质区别是:【注】1、如何判断某种菌是细菌:①带“杆”、“球”、“弧”、“螺旋”的都是细菌;②蓝细菌(旧称蓝藻)也属于细菌,如色球蓝细菌、颤蓝细菌、念珠蓝细菌、发菜等;1、细菌中的多数种类是营腐生或生活的生物;2、蓝细菌细胞内含有和,是能进行光合作用的生物(蓝细菌细胞内叶绿体)。
(新教材)部编人教版高中数学必修一第一章课后练习和习题汇总(附答案)

(新教材)部编人教版高中数学必修一第一章课后练习和习题汇总(附答案)目录第一章集合与常用逻辑用语.1.1 集合的概念1.2 集合间的基本关系1.3集合的基本运算1.4 充分条件与必要条件1.5全称量词与存在量小结复习参考题1第一章集合与常用逻辑用语1.1集合的概念练习1.判断下列元素的全体是否组成集合,并说明理由:(1)与定点A,B等距离的点;【答案解析】:是集合,因为这些点有确定性.(2)高中学生中的游泳能手.【答案解析】:不是,因为是否能手没有客观性,不好确定.2.用符号“∈”或“∉”填空:0___ N; -3___ N; 0.5__Z; √2__z; ⅓__Q; π__R.【答案解析】:根据自然数,整数,有理数,实数的定义即可判断.0是自然数,则0∈N ;-3不是自然数,则-3∉N ; 0.5,√2 不是整数,则0.5∉Z,√2∉Z;⅓是有理数,则⅓∈Q ;π 是无理数,则π∈R故答案为:(1)∈;(2)∉ ;(3)∉ ;(4)∉ ;(5)∈ ;(6)∈3.用适当的方法表示下列集合:(1)由方程x²-9=0的所有实数根组成的集合;【答案解析】:{-3, 3}.(2)一次函数y=x+3与y=-2x+6图象的交点组成的集合;【答案解析】: {(1, 4)}.(3)不等式4x- 5<3的解集.【答案解析】:{x | x<2}.习题1.1一、复习巩固1.用符号“∈”或“∉”填空:(1)设A为所有亚洲国家组成的集合,则中国____ A,美国____A,印度____A,英国____ A;【答案解析】:设A为所有亚洲国家组成的集合,则:中国∈A,美国∉A,印度∈A,英国∉A.(2)若A={x|x²=x},则-1____A;【答案解析】:A={x|x²=x}={0, 1},则-1∉A.(3)若B={x|x²+x-6=0},则3____B;【答案解析】:若B={x|x²+x-6=0}={x|(x+3)(x-2)=0}={-3,2},则3∉B; (4)若C={x∈N|1≤x≤10},则8____C, 9.1____C.【答案解析】:若C={x∈N|1≤x≤10}={1, 2, 3,4,5, 6,7, 8,9,10},则8∈C, 9.1∉C.2.用列举法表示下列集合:(1)大于1且小于6的整数;【答案解析】:大于1且小于6的整数有4个:2,3,4,5,所以集合为{2,3,4,5}.(2) A={x|(x-1)(x +2)=0};【答案解析】:(x- 1)(x+2)=0的解为x=1或x=-2,所以集合为{1, -2}.(3) B={x∈Z|-3<2x-1<3}.【答案解析】:由-3<2x-1<3,得-1<x<2.又因为x∈Z,所以x=0.或x=1,所以集合为{0,1}.二、综合运用3.把下列集合用另一种方法表示出来:(1) {2,4,6,8, 10};。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从那以后,表姐再回家,我们拒绝喝七分钱一杯的果子露,坚持要去知味观吃一毛钱一碗的阳春面和四毛五一客的小笼包子。在那个年代,知味观就是美味的代名词,知味观的的小笼包子和阳春面 在我们眼中就是盛宴大餐。
我的表姐因为母亲早亡,父亲远走他乡下落不明,一直由我父母收养。她要年长我们许多,其时已经工作,在杭州郊区的一个茶场做工,每月有三十六块钱的工资。表姐一周回家一次,每次回来都 会带我们兄弟姐妹几个去延安路上的一家冷饮店喝七分钱一杯的果子露。果子露虽然清凉甘甜,但它对一群饿得咕咕叫的肚子来说于事无补。大家开始向表姐诉苦,恳求她带我们去吃面条,吃包子。显 然,面条和包子的开销要高出果子露许多。表姐面露难色,但看到我们眼巴巴的馋样,听到我们肚子里的咕咕叫声,她心软了。bodog赢了钱冻结账户
终于,表姐带我们去了仁和路上一家名叫“知味观”的餐馆。她给我们四个孩子每人点了一碗阳春面,犹豫了一下,她又咬咬牙买了两客小笼包子。
面条端上来时我们每一个人都两眼发亮:淡淡的酱红色清汤里,卧着黄白色细软如丝的面条,上面撒着碧绿的葱花,猪油花像一朵朵涟漪飘在汤的表面,香气扑鼻。小笼包子更是诱人,皮儿薄得近 乎透明,馅儿是猪肉加蟹黄拌的,鲜得没法形容,咬一口,香浓的汁水漫过舌尖,让你含在口里不忍吞咽。
