平行线分线段成比例经典例题与变式练习
初中数学相似三角形知识库平行线分线段成比例经典例题与变式练习(精选题目)

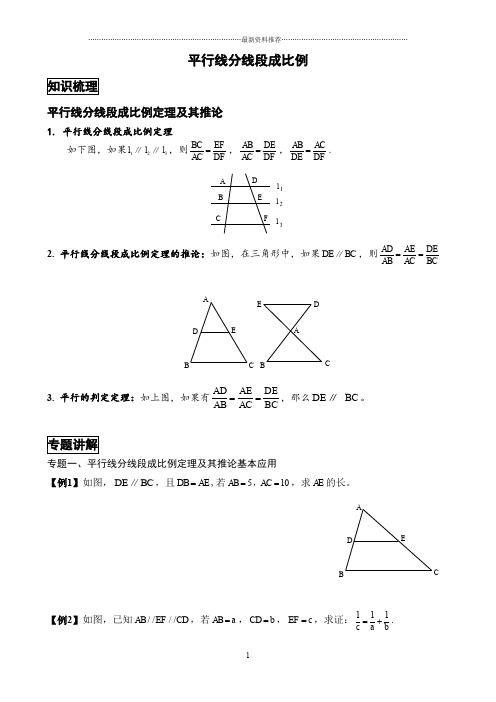
平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2007年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52 B.1 C.32D.2(1)MEDC BA(2)F ED CA【例5】 (2001年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O . (1)当1A 2AE C =时,求AOAD的值;E AO(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2003年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例经典例题与变式练习(精选题目)精编版
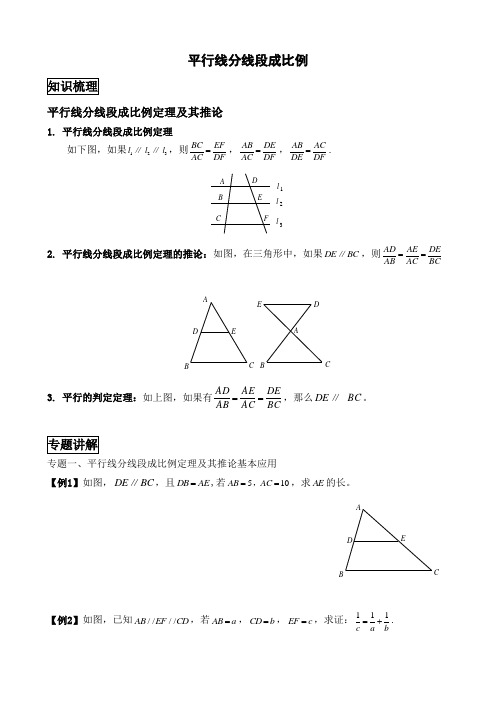
平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52B.1C.32D.2(1)MEDC BA(2)F ED CBA【例5】 (2011年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD的值;(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D E D CBAO不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
(完整版)平行线分线段成比例经典例题与变式练习(含标准答案..

1 / 14平行线分线段成比例知识梳理1. 1. 平行线分线段成比例定理平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2.平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCD E EDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥BC 。
专题讲解专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111cab=+.FEDCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111ABCDEF+=.FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论F EDCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作 EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题【例4】 (2007年北师大附中期末试卷)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EFAFFC FD + 的值为( )A.52 B.1 C.32D.2(1)MEDCBA(2)F ED CBA【例5】 (2001年河北省中考试卷)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD 的值; E AO(2)当11A 34AE C=、时,求AO AD 的值; (3)试猜想1A 1AE C n =+时AO AD 的值,并证明你的猜想.【例6】 (2003年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =;(2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段比例经典例题与变式练习(精选题目)31601
平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52 C.32(1)MEDC BA(2)F ED CBA【例5】 (2011年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD 的值;(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; E D CB AO(2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例经典例题与变式练习(题目)(教育相关)
A
E
D
M
N
P
B
C
【例10】 在 ABC 中,底边 BC 上的两点 E 、 F 把 BC 三等分, BM 是 AC 上的中 线, AE 、 AF 分别交 BM 于 G 、 H 两点,求证: BG :GH : HM 5:3: 2
A
M GH
BE
【例11】 如图, M 、 N 为 ABC 边 BC 上的两点,且满足 BM MN NC ,一条 平行于 AC 的直线分别交 AB 、 AM 和 AN 的延长线于点 D 、 E 和 F . 求证: EF 3DE .
AB AC BC
A D
E E
D A
B
CB
C
3. 平行的判定定理:如上图,如果有 AD AE DE ,那么 DE ∥ BC 。 AB AC BC
专题讲解
专题一、平行线分线段成比例定理及其推论基本应用 【例1】如图, DE ∥BC ,且 DB AE ,若 AB 5,AC 10 ,求 AE 的长。
(1)如图(1),在 ABC 中, M 是 AC 的中点, E 是 AB 上一点,且 AE 1 AB ,
4
连接 EM 并延长,交 BC 的延长线于 D ,则 BC _______.
CD
(2)如图(2),已知 ABC 中, AE : EB 1: 3, BD: DC 2:1, AD 与 CE 相交于 F ,则 EF AF
A
F E
B
D
C
【例7】(宁德市中考题)如图, ABC 中, D 为 BC 边的中点,延长 AD 至 E , 延长 AB 交 CE 的延长线于 P 。若 AD 2DE ,求证: AP 3AB 。
A
B P
平行线分线段成比例经典例题与变式练习(精选题目)备课讲稿

平行线分线段成比例经典例题与变式练习(精选题目)平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( ) A.52 B.1 C.32D.2 (1)MEDC BA(2)F ED CBA【例5】 (2011年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD的值;(2)当11A 34AE C =、时,求AOAD 的值; (3)试猜想1A 1AE C n =+时AOAD 的值,并证明你的猜想.E D CAO【例6】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
(完整word)初中数学相似三角形知识库平行线分线段成比例经典例题与变式练习(精选题目)
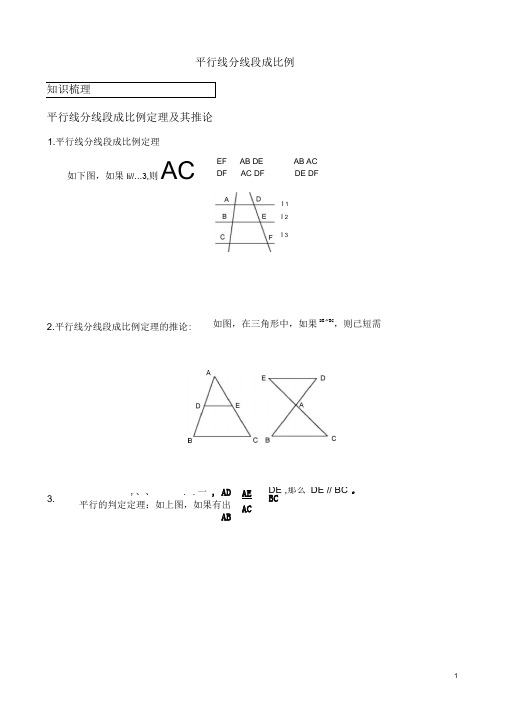
平行线分线段成比例知识梳理平行线分线段成比例定理及其推论1.平行线分线段成比例定理如下图,如果li//…3,则AC EF AB DE AB AC DF AC DF DE DFl 1l 2l 32.平行线分线段成比例定理的推论: 如图,在三角形中,如果DE"BC,则已短需3.,、、. .一, AD平行的判定定理:如上图,如果有出ABAEACDE ,那么DE // BC 。
BC专题一、平行线分线段成比例定理及其推论基本应用【例1】如图,DE // BC ,且DB AE ,若AB 5, AC 10 ,求AE 的长。
【例2】如图,已知AB//EF//CD ,若AB a , CD b , EF c ,求证:111, cab【巩固】如图,AB BD , CD BD ,垂足分别为B 、D, AC 和 BD 相交于点E, EF BD,垂足为F .证明:AB CD EF .【巩固】如图,找出S ABD 、S BED 、SBCD之间的关系,并证明你的结论【例3】如图,在梯形ABCD 中,AB // CD , AB 12 , CD 9,过对角线交点。
作专题二、定理及推论与中点有关的问题【例4】(2007年北师大附中期末试题)11 如图1 ,在ABC中,M是AC的中点,E是AB上一点,且AE - AB ,4 ' 连接EM并延长,交BC的延长线于D ,则CD(2)如图(2),已知ABC 中,AE:EB 1:3 , BD :DC 2:1 , AD与CE相交于F,贝汁豆FCAFFD的值为()A. 5B.1C.2【例5】(2001年河北省中考试题)如图,在AC边上的任意一点,BE交AD于点O .(1)当AE工时,求AO 的值;ABC中,D为BC边的中点,E为EF // CD 交AD , BC 于 E , F ,求EF 的长。
【巩固】(上海市数学竞赛题)如图,在梯形ABCD中,AD // BC , AD a , BC b, E , F分别是AD , BC的中点,AF交BE于P , CE交DF于Q ,求PQ的长。
平行线分线段成比例练习题

平行线分线段成比例练习题平行线分线段成比例练习题在几何学中,平行线是一种非常重要的概念。
当两条直线在同一平面上且永远不相交时,我们称它们为平行线。
平行线具有许多有趣的性质和特点,其中之一是平行线分线段成比例。
在这篇文章中,我们将通过一些练习题来加深对平行线分线段成比例的理解和应用。
练习题1:已知AB和CD是两条平行线,E是AB上的一点,F是CD上的一点。
如果AE 与CF的比例为2:3,求BE与DF的比例。
解答:根据平行线分线段成比例的性质,我们可以得出以下等式:AE/CF = BE/DF由已知条件AE/CF = 2/3,代入得:2/3 = BE/DF通过交叉相乘得:2DF = 3BE因此,BE与DF的比例为3:2。
练习题2:在平行线AB和CD上,分别取两个点E和F。
如果AE与CF的比例为4:5,且BE与DF的比例为3:2,求AE与DE的比例。
解答:首先,根据平行线分线段成比例的性质,我们可以得到以下等式:AE/CF = BE/DF代入已知条件得:AE/5 = 3/2通过交叉相乘得:2AE = 15因此,AE = 15/2 = 7.5接下来,我们需要求出DE的长度。
根据平行线分线段成比例的性质,我们可以得到以下等式:AE/DE = BE/DF代入已知条件得:7.5/DE = 3/2通过交叉相乘得:2DE = 22.5因此,DE = 22.5/2 = 11.25最后,我们可以求得AE与DE的比例:AE/DE = 7.5/11.25 = 2/3练习题3:在平行线AB和CD上,分别取两个点E和F。
如果AE与CF的比例为3:4,且BE与DF的比例为5:6,求AE与DE的比例。
解答:根据平行线分线段成比例的性质,我们可以得到以下等式:AE/CF = BE/DF代入已知条件得:AE/4 = 5/6通过交叉相乘得:6AE = 20因此,AE = 20/6 = 10/3接下来,我们需要求出DE的长度。
根据平行线分线段成比例的性质,我们可以得到以下等式:AE/DE = BE/DF代入已知条件得:(10/3)/DE = 5/6通过交叉相乘得:6DE = 50/3因此,DE = (50/3)/6 = 25/9最后,我们可以求得AE与DE的比例:AE/DE = (10/3)/(25/9) = 30/25 = 6/5通过以上练习题的解答,我们可以看到平行线分线段成比例的应用。
平行线分线段比例经典例题与变式练习31601

平行线分线段比例经典例题与变式练习31601(总14页)本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111cab=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( ) A.52 B.1 C.32D.2 (1)MEDC BA(2)F ED CBA【例5】 (2011年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD 的值;(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.E D CB AO(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例经典例题与变式练习(精选题目)

平行线分线段成比例平行线分线段成比例定理及其推论 1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB AC DE DF=. 2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DE AB AC BC== 3. 平行的判定定理:如上图,如果有BCDE AC AE AB AD ==,那么DE ∥BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE的长。
【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+. 【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=.【巩固】如图,找出ABD S∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论. 【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
【巩固】(上海市数学竞赛题)如图,在梯形ABCD中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
专题二、定理及推论与中点有关的问题【例4】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BC CD =_______.(2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AF FC FD + 的值为( ) A.52 B.1 C.32 D.2【例5】 (2011年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为AC 边上的任意一点,BE 交AD 于点O . (1)当1A 2AE C =时,求AO AD的值; (2)当11A 34AE C =、时,求AO AD的值; (3)试猜想1A 1AE C n =+时AO AD 的值,并证明你的猜想. ED CB AO【例6】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AE FC ED =⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
专题22.2平行线分线段成比例【十大题型】-2024-2025学年九年级数学上册举[含答案]
![专题22.2平行线分线段成比例【十大题型】-2024-2025学年九年级数学上册举[含答案]](https://img.taocdn.com/s3/m/33cdaba1c9d376eeaeaad1f34693daef5ff71305.png)
专题22.2平行线分线段成比例【十大题型】【沪科版】【题型1辨别相似图形】【题型2相似多边形的性质运用】【题型3“A”模型中的平行线分线段成比例】【题型4“8”模型中的平行线分线段成比例】【题型5“X”模型中的平行线分线段成比例】【题型6“#”模型中的平行线分线段成比例】【题型7多种模型的综合平行线分线段成比例】【题型8平行线分线段成比例与重心、中位线的综合运用】【题型9作平行线构造平行线分线段成比例】【题型10 作垂线构造平行线分线段成比例】知识点1:相似多边形定义1:形状相同的图形叫做相似图形.定义2:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做相似比.性质:相似多边形的对应角相等,对应边成比例.【题型1辨别相似图形】【例1】(23-24九年级·山东聊城·开学考试)1.下面各组图形中,不是相似形的是( )A.B.C.D.【变式1-1】(23-24九年级·安徽六安·期末)2.下列多边形一定相似的是( )A .两个等腰三角形B .两个平行四边形C .两个正五边形D .两个六边形【变式1-2】(23-24九年级·山西阳泉·期末)3.学校艺术节上,同学们绘制了非常美丽的画并且在其周围裱上等宽的边框做成艺术墙.下面是王亮从艺术墙上选取的四幅形状不同的作品,在同一幅作品中,内、外边框的图形不一定相似的是( )A .B .C .D .【变式1-3】(23-24九年级·全国·期末)4.下列说法中:①所有的等腰三角形都相似;②所有的正三角形都相似;③所有的正方形都相似;④所有的矩形都相似.其中说法正确的序号是 .【题型2 相似多边形的性质运用】【例2】(23-24九年级·河北邢台·期中)5.已知矩形ABCD 中,4,3AB BC ==,下面四个矩形中与矩形ABCD 相似的是( )A .B .C .D .【变式2-1】(23-24九年级·广东深圳·期末)6.如图,在矩形ABCD 中,4AB =,6BC =,点E ,F 分别在AD ,BC 上,且EF AB ∥,矩形ABCD 与矩形BFEA 相似,则矩形BFEA 的面积为( )A .16B .403C .323D .163【变式2-2】(23-24九年级·海南海口·期末)7.如图是两个形状相同的举重图案,则x 的值是.【变式2-3】(23-24九年级·山西太原·期末)8.如图,四边形ABCD 是一张矩形纸片.折叠该矩形纸片,使AB 边落在AD 边上,点B 的对应点为点F ,折痕为AE ,展平后连接EF ;继续折叠该纸片,使FD 落在FE 上,点D 的对应点为点H ,折痕为FG ,展平后连接H G .若矩形HECG ∽矩形ABCD ,1AD =,则CD 的长为( ).A .0.5B 1CD 知识点2:平行线分线段成比例两条直线被一组平行线所截,所得的对应线段成比例.如图:如果123l l l ∥∥,则AB DEBC EF =,AB DE AC DF =,BC EF AC DF=.推论:平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.【题型3 “A ”模型中的平行线分线段成比例】【例3】(23-24九年级·内蒙古包头·期末)9.如图,某位同学用带有刻度的直尺在数轴上作图,若PQ MN ∥,点Q ,点M 在直尺上,且分别与直尺上的刻度1和3对齐,在数轴上点N 表示的数是10,则点P 表示的数是( )A .52B .3C .103D .5【变式3-1】(23-24九年级·黑龙江哈尔滨·阶段练习)10.如图,在ABC V 中,DE BC ∥,DF AC ∥,则下列比例式中正确的是( )A .BD DFAD AC=B .BF AEFC EC=C .BF DFFC AC=D .BF CEFC AE=【变式3-2】(2024·黑龙江哈尔滨·模拟预测)11.如图,在ABC V 中,D 、E 分别为AB AC 、边的中点,连接DE ,点F 为BC 边上一点,2BF FC =,连接AF 交DE 于点N ,则下列结论中错误的是( )A .12AN AF =B .23DN DE =C .12AD AC =D .12NE FC =【变式3-3】(23-24九年级·河南平顶山·期末)12.如图,矩形ABCD 的四个顶点分别在直线1l ,3l ,4l ,2l 上,若直线123l l l ∥∥且相邻两直线间距离相等.若6AB =,4BC =,则2l ,3l 之间的距离为( ).A.5B.65C.125D.245【题型4“8”模型中的平行线分线段成比例】【例4】(23-24九年级·湖南岳阳·期末)13.如图,DE BC∥,则下列比例式错误的是()A.AD DEBD BC=B.AE ADEC BD=C.AB ACBD EC=D.AD AEAB AC=【变式4-1】(2024春·上海静安·九年级校考期中)14.已知ax bc=,求作x,那么下列作图正确的是()A.B.C.D.【变式4-2】(2024春·陕西西安·九年级高新一中校考阶段练习)15.如图,在平行四边形ABCD 中,ABC Ð的平分线BF 分别与AC 、AD 交于点E 、F ,3AB =,2FD =,则EFFB的值为( )A .25B .38C .37D .35【变式4-3】(2024春·全国·九年级专题练习)16.如图, 12l l ∥,:2:5AF BF =,:4:1BC CD =,则:AE EC 的值为( )A .5:2B .1:4C .2:1D .3:2【题型5 “X ”模型中的平行线分线段成比例】【例5】(23-24九年级·陕西渭南·期末)17.如图,123l l l ∥∥,两条直线与这三条平行线分别交于点、、A B C 和D E F 、、,已知32AB BC =,若10DF =,则DE 的长为( )A .2B .3C .5D .6【变式5-1】(23-24九年级·山西晋中·期中)18.如图,直线123l l l ∥∥,直线AC 和DF 被直线1l 、2l 、3l 所截,2AB =,5BC =,6EF =,则DE 的长为( )A .7B .125C .152D .245【变式5-2】(23-24九年级·湖南岳阳·期末)19.如图,123l l l ∥∥,直线a ,b 相交于点G ,与这三条平行线分别相交于点A 、B 、C 和点D 、E 、F ,下列比例式中错误的是( )A .AB DEBG EG =B .AG DGGC GF =C .BE BGFC BC=D .AD AGBE BG=【变式5-3】(2024春·吉林长春·九年级统考期末)20.如图 ,AB ∥CD ∥EF ,AF 与BE 相交于点G ,且AG =4,GD =2,DF =8,那么BCCE的值等于.【题型6 “#”模型中的平行线分线段成比例】【例6】(23-24九年级·江苏南京·期末)21.如图,123l l l ∥∥,则下列比例式成立的是( )A .AB DEAC EF=B .AB DEAC DF=C .AB BEAC CF=D .AB ADAC CF=【变式6-1】(23-24九年级·安徽六安·阶段练习)22.如图,AB CD EF ∥∥,20BF =.(1)若3AC =,5CE =,求DF 的长;(2)若:2:3AC CE =,求DF 的长.【变式6-2】(23-24九年级·贵州铜仁·期末)23.如图是某景区大门部分建筑,已知AD BE CF ∥∥,16m AC =,当:4:3DF DE =时,则AB 的长是( )A .10mB .11mC .12mD .13m【变式6-3】(23-24九年级·海南海口·期末)24.如图,123l l l ∥∥,若23AB BC =,6DF =,则DE 等于( )A .2.4B .3C .3.6D .4【题型7 多种模型的综合平行线分线段成比例】【例7】(23-24九年级·山东淄博·期末)25.如图,AB ,CD 相交于点E ,且AC ∥EF ∥DB ,点C ,F ,B 在同一条直线上,已知AC =p ,EF =r ,DB =q ,则p ,q ,r 之间满足的数量关系式是( )A .111r q p+=B .112p q r+=C .111p q r+=D .112q r p+=【变式7-1】(2024·黑龙江哈尔滨·一模)26.如图,在V ABC 中,点D 在AB 边上,点E 在BC 边上,过点D 作DG //BC ,交AC 于点G ,过点E 作EH //AB ,交AC 于点H ,DG 的延长线与EH 的延长线交于点F ,则下列式子一定正确的是( )A .AD DGDB BC=B .GF HCEC GH=C .FH GHAD AG=D .HE ECAB BE=【变式7-2】(23-24九年级·浙江温州·期末)27.如图,在ABCD Y 中,E ,F ,G 依次是对角线BD 上的四等分点,连结CG 并延长交AD 于点M ,连结MF 并延长交BC 于点H .若,1MF MC MG ==,MH 的长为( )A .4B .6C .7D .8【变式7-3】(23-24九年级·浙江宁波·期中)28.如图, 点P 是平行四边形ABCD 内部一点, 过P 分别作AB 和BC 的平行线交平行四边 形ABCD 的四边于E F G H ,,,. 连结AC 分别交EG FH ,于M 和N . 若四边形~FBGP 四边形EPHD ,且四边形FBCH 的面积是四边形`AFP E 的3倍. 下列选项正确的是( )A .EP PH =B .AN EP =C .2AN MN =D .2AM CM=【题型8 平行线分线段成比例与重心、中位线的综合运用】【例8】(23-24九年级·山东枣庄·期中)29.如图,在菱形ABCD 中,点E 、F 分别是边BC 、CD 的中点,连接AE 、AF 、EF .若菱形ABCD 的面积为16,则△AEF 的面积为( )A .3B .4C .5D .6【变式8-1】(23-24九年级·上海·期中)30.△ABC 中,AB=AC=10,重心G 到底边BC 的距离为2,那么AG= .【变式8-2】(23-24九年级·安徽宿州·期末)31.如图,60AOB Ð=°,C 、D 是边OA 上的两点,且8,2OD CD ==,点P 是OB 上的一动点,连接PD ,点Q 是PD 的中点,连接CQ ,则CQ 的最小值为( )A .1BCD .2【变式8-3】(2024·福建泉州·模拟预测)32.设AX ,BY ,CZ 是ABC V 的三条中线,求证:AX ,BY ,CZ 三线共点.【题型9 作平行线构造平行线分线段成比例】【例9】(23-24九年级·广东河源·期末)33.AD 是ABC V 的中线,E 是AD 上一点,14AE AD =,BE 的延长线交AC 于F ,则AF FC的值为( )A .14B .15C .16D .17【变式9-1】(23-24九年级·重庆·期中)34.如图,正方形ABCD 的边长为4,E 为CD 边中点,G 为BC 边上一点,连接AE ,DG ,相交于点F .若45DF FG =,则FE 的长度是( )A B C .12D .47【变式9-2】(23-24九年级·浙江湖州·期末)35.如图△ACB ,∠ACB=90°,点O 是AB 的中点,CD 平分∠BCO 交AB 于点D ,作AE ⊥CD分别交CO 、BC 于点G ,E . 记△AGO 的面积为S 1,△AEB 的面积为S 2,当12S S =25时,则OG BC 的值是( )A .25B .13C .411D .38【变式9-3】(23-24九年级·广西·期中)36.如图,在△ABC 中,M 是AC 的中点,P ,Q 为BC 边上的点,且BP=PQ=CQ ,BM 与AP ,AQ 分别交于D ,E 点,则BD ∶DE ∶EM 等于A .3∶2∶1B .4∶2∶1C .5∶3∶2D .5∶2∶1【题型10 作垂线构造平行线分线段成比例】【例10】(2024·浙江绍兴·一模)37.有一种有趣的读数法:如图,在图纸上确定纵轴与横轴,从交点O 处开始依次在两轴上画出单位相同的标度,再作两轴交角的角平分线OP ,OP 上的标度与纵轴上的标度在同一水平线上,拿一根直尺,使得它的两端分别架在横轴和纵轴上,且OA =a ,OB =b ,读出直尺与OP 的交点C 的标度就可以求出OC 的长度.当a =4,b =6时,读得点C 处的标度为()A .125B C .245D 【变式10-1】(23-24九年级·浙江·周测)38.如图,在ABC 中,90A Ð=°,6AB =,10BC =,ABC Ð的平分线交AC 于点D ,与BC 的垂线CE 相交于点E ,则:BD DE 为( )A .3:2B .5:3C .4:3D .2:1【变式10-2】(23-24九年级·山东聊城·期末)39.如图,正方形ABCD 边长为3,G ,F 是对角线BD 的三等分点,点E 在边AB 上,EG AD ∥,连接FC .(1)求EF 的长.(2)试判断EF 与FC 之间的位置关系,并说明理由.【变式10-3】(23-24九年级·广东佛山·期中)40.如图,在四边形ACBD 中,对角线AB CD ,相交于点O ,9010ACB BD CD Ð=°==,,16BC =,若2DAB ABC Ð=Ð,则AD AB 的值为 .1.B【分析】根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,依据定义即可解决.【详解】解:A、两幅国旗相似,故不符合题意;B、顶角不相等的两个等腰三角形不相似,故符合题意;C、两个五角星相似,故不符合题意;D、所有的圆都相似,故不符合题意,故选:B.【点睛】本题考查的是相似图形的识别,我们把形状相同的图形称为相似形.关键要联系实际,根据相似图形的定义得出.2.C【分析】本题主要考查了相似图形的判定,掌握相似形的定义(如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形相似)是解题的关键.根据相似三角形的定义逐项判断即可.【详解】解:A、两个等边三角形相似,但是两个等腰三角形并不一定相似,三个角度没有确定,故A不正确;B、两个平行四边形对应角度及对应边都不一定成比例,所以不一定相似,故B不正确;C、两个正五边形角度相等,放大缩小后可以完全重合,两图形相似,故C正确;D、两个正六边形相似,但是两个六边形并不一定相似,故D不正确.故选C.3.A【分析】根据图形相似的概念进行解答即可.【详解】解:两个矩形不一定相似,但两个正方形、两个等边三角形及两个圆一定相似,故选:A.【点睛】本题考查了两个图形的相似,掌握相似多边形的概念(即边数相同的两个多边形,如果对应角相等,对应边成比例)是解题的关键.4.②③【分析】根据正方形、矩形、等边三角形、等腰三角形的性质进行判断即可.【详解】①所有的等腰三角形都相似,错误;②所有的正三角形都相似,正确;③所有的正方形都相似,正确;④所有的矩形都相似,错误.故答案为②③.【点睛】本题考查了相似图形的知识,熟练掌握各特殊图形的性质是解题的关键,难度一般.5.A【分析】验证对应边是否成比例即可判断.【详解】解:A:432 1.5=,符合题意;B:4332¹,不符合题意;C:432 1.2¹,不符合题意;D:432.52¹,不符合题意;故选:A【点睛】本题考查了相似多边形的判定.熟记定理内容即可.6.C【分析】本题主要考查相似图形的性质,相似图形的对应边成比例,面积比等于相似比的平方.证明224469ABEFBCDAS ABS BCæöæö===ç÷ç÷èøèø矩形矩形,从而可得答案.【详解】解:∵矩形ABFE∽矩形BCDA,4AB=,6BC=,∴224469ABEFBCDAS ABS BCæöæö===ç÷ç÷èøèø矩形矩形,4624ABCDS=´=矩形,∴323ABEFS=矩形,故选:C.7.22.5【分析】本题考查了相似多边形的性质,如果两个多边形相似,那么它们对应边的比相等,对应角相等,对应周长的比都等于相似比;它们对应面积的比等于相似比的平方.根据相似多边形的性质:对应线段的比等于相似比列式求解即可.【详解】解:由题意得,30:20:15x=∴22.5x =.故答案为:22.5.8.C【分析】本题考查的是矩形的性质、翻折的性质及相似多边形性质,熟练应用矩形和相似多边形性质是解题关键,设CD x =,则()1,1EC x CG x x =-=--,根据两矩形相似求出即可.【详解】解:在矩形ABCD 中,设CD x =,则AB CD x ==,1AD BC ==,由翻折得,90AB AF x AFE B BAF ==Ð=Ð=Ð=°,\四边形ABEF 是正方形,同理,四边形DFHG 是正方形,,1BE AB x DF DG x \====-,()1,121CE x CG x x x \=-=--=-,Q 矩形HECG ∽矩形ABCD ,EC CG BC CD \=,即1211x x x--=,解得:x ,经检验,xCD \=故选:C .9.C【分析】利用平行线分线段成比例定理求解.【详解】解:∵PQ MN ∥,∴13OP OQ ON OM ==,∵10ON =,∴103OP =.故选:C .【点睛】本题考查作图﹣复杂作图,数轴,平行线的性质等知识,解题的关键是掌握平行线分线段成比例定理.10.D【分析】根据平行线分线段成比例判断各项即可.【详解】解:A .由DF AC ∥,得BD DF BA AC =,故A 选项错误;B .由DF AC ∥,得BF BD FC DA =,又由DE BC ∥,得BD CE DA EA =,则BF CE FC EA =,故B 选项错误,D 选项正确;C .由DF AC ∥,得BF DF BC AC =,故C 选项错误;故选:D .【点睛】本题考查了平行线分线段成比例,两条直线被一组平行线所截,所得的对应线段成比例,平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.11.C【分析】根据平行线分线段成比例定理,可推出AN NF =,根据中位线定理分析求解.【详解】解:∵D 、E 分别为AB AC 、边的中点,∴DE BC ∥.∴1AD AN DB NF ==∴12AN AF =,11,22NE CF DN BF == .∴12NE FC =.∵2BF FC =,∴2DN NE =.∴23DN DE =.所以,A,B,D 正确,C 错误;故选:C【点睛】本题考查平行线分线段成比例定理,中位线定理;由平行线的位置关系得到线段间数量关系是解题的关键.12.C【分析】本题主要考查了平行线分线段成比例,矩形的性质,勾股定理以及平行线的定义等知识,熟练掌握平行线分线段成比例以及平行线之间等距离是解答本题的关键.过A 点作3AN l ^于点N ,交2l 于点M ,根据平行线分线段成比例以及平行线之间等距离可得1AE AM EB NM ==,进而可得132AE EB AB ===,再利用勾股定理可得5ED ==,结合三角形的面积即可求解.【详解】过A 点作3AN l ^于点N ,交2l 于点M ,如图,∵在矩形ABCD 中,4BC =,∴4AD BC ==,90BAD Ð=°,∵直线123l l l ∥∥且相邻两直线间距离相等,3AN l ^,∴AM NM =,∴1AE AM EB NM==,∵6AB =,∴132AE EB AB ===,∴在Rt EAD V 中,5ED ==,∵11S 22EAD AE AD AM ED =´´=´´V ,∴125AE AD AM ED ´==,∴125MN AM ==,故选:C .13.A 【分析】根据平行线分线段成比例定理写出相应的比例式,即可得出答案.【详解】解:∵DE //BC ,∴,,AD AE AB AC AD AE BD EC BD EC AB AC===;∴A错误;故选:A.【点睛】此题考查了平行线分线段成比例定理,用到的知识点是平行线分线段成比例定理,关键是找准对应关系,避免错选其他答案.14.C【分析】根据平行线分线段成比例结合题意,依次对各选项进行判断即可.【详解】∵ax bc=,∴a cb x=或a bc x=.A.作出的为a a xb b c+=+,故不符合题意;B.该情况无法作图,故不符合题意;C.作出的为a cb x=,故符合题意;D.作出的为a cx b=,故不符合题意;故选C.【点睛】本题考查平行线分线段成比例定理,第四比例线段的作法.熟练掌握定理是解题的关键.15.B【分析】根据平行四边形的性质证得AD∥BC,AD=BC,再根据角平分线的定义和平行线的性质以及等角对等边证得AF=AB=3,BC=5,再根据平行线分线段成比例和比例性质求解即可.【详解】解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠AFB=∠CBF,∵BF平分∠ABC,∴∠ABF=∠CBF,∴∠ABF=∠AFB,∴AF=AB=3,又FD=2,∴BC=AD=AF+FD=5,∵AD∥BC,∴35=EF AF BE BC =,∴38EF FB =,故选:B .【点睛】本题考查平行四边形的性质、平行线的性质、角平分线的定义、等腰三角形的判定、平行线分线段成比例定理、比例性质等知识,熟练掌握相关知识的联系与运用是解答的关键.16.C【分析】本题考查相似三角形的判定和性质,根据12l l ∥可证GAF DBF V V ∽,GAE DCE ∽△△,利用相似三角形对应边成比例即可求解.【详解】解:Q 12l l ∥,\GAF DBF Ð=Ð,AGF BDF Ð=Ð,\GAF DBF V V ∽,\25AF GA BF DB ==,Q :4:1BC CD =,\15CD DB =,\21255GA DC =¸=,Q 12l l ∥,\GAE DCE Ð=Ð,AGE CDE Ð=Ð,\GAE DCE ∽△△,\2GA AE DC CE==,\:2:1AE EC =,故选C .17.D 【分析】本题主要考查平行线分线段成比例,根据题意可得AB DE BC EF=,设DE x =,则10EF x =-,由此即可求解,掌握平行线的分线段成比例,比例的性质,解方程的方法是解题的关键.【详解】解:根据题意可得,32AB DE BC EF ==,设DE x =,则10EF x =-,∴3210x x =-,解得,x =6,∴DE 的长为6,故选:D .18.B【分析】本题考查了平行线分线段成比例定理,根据平行线分线段成比例得出比例式代入即可.【详解】解:Q 123l l l ∥∥,\AB DE BC EF=,256DE \=,125DE \=.故选B .19.C【分析】平行线分线段成比例定理的内容是:一组平行线截两条直线,所截的线段对应成比例,根据以上内容判断即可.【详解】解:A 、∵123l l l ∥∥,∴AB DE BG EG=,结果正确,故本选项不符合题意;B 、∵123l l l ∥∥,∴AG DG GC GF=,结果正确,故本选项不符合题意;C 、∵123l l l ∥∥,∴BE BG FC GC=,结果错误,故本选项符合题意;D 、∵123l l l ∥∥,∴AD AG BE BG=,结果正确,故本选项不符合题意;故选:C .【点睛】本题考查了平行线分线段成比例定理,解题的关键是:一组平行线截两条直线,所截的线段对应成比例.20.34##0.75【分析】根据平行线分线段成比例定理列出比例式,把已知数据代入计算即可.【详解】解:////AB CD EF Q ,,BC AD AG GD CE DF DF+\==4,2,8,AG GD DF ===Q 423,84BC AD AG GD CE DF DF ++\====故答案为:3.4【点睛】本题主要考查了平行线分线段成比例定理,灵活运用定理,找准对应关系是解此题的关键.21.B【分析】根据平行线分线段比例定理,得到对应的线段成比例,判断出正确的选项.【详解】解:∵123l l l ∥∥,∴AB DE AC DF=,故选:B .【点睛】本题考查平行线分线段比例定理,解题的关键是掌握这个定理,根据平行的条件得到对应的线段成比例.22.(1)12.5DF =(2)12DF =【分析】本题主要考查了平行线分线段成比例,关键是灵活运用平行线分线段成比例定理.(1)由平行分线段成比例得出AC BD CE DF=,再代入数值计算;(2)由平行线分线段成比例的性质得出23BD DF =,再代入计算.【详解】(1)AB CD EF ∥∥Q ,\=AC BD CE DF,3AC =Q ,5CE =,20BF =,3205DF DF-\=,解得12.5DF =;(2)AB CD EF ∥∥Q ,:2:3AC CE =,23AC BD CE DF \==.20BF =Q ,2023DF DF -\=,解得12DF =.23.C 【分析】本题主要考查了平行线分线段成比例定理,根据平行线分线段成比例定理得到43DF AC AB DE ==,再由16m AC =可得结果.【详解】解:∵AD BE CF ∥∥,∴43DF AC AB DE ==,∵16m AC =,∴12m AB =,故选C .24.C【分析】本题考查了平行线分线段成比例定理,根据平行线分线段成比例定理,得到,DE EF 的关系,再根据6DF =可得到答案,正确运用定理找准对应关系是解题的关键.【详解】解:∵123l l l ∥∥,23AB BC =,∴32AB DE BC EF ==,∴35DE DF =,∵6DF =,∴3186 3.655DE =´==,故选:C .25.C 【分析】根据平行线分线段成比例,可证得EF BF AC BC =,EF CF BD BC=,两式相加即可得出结论.【详解】解://AC EF Q ,\EF BF AC BC=,//EF DB Q ,\EF CF BD BC =,\1EF EF BF CF BF CF BC AC BD BC BC BC BC ++=+===,即1r r p q +=,\111p q r+=.故选:C .【点睛】本题主要考查了平行线分线段成比例定理的运用,通过平行线分线段成比例定理得出线段的比是解题的关键.26.C【分析】根据平行线分线段成比例的性质进行逐一判断即可.【详解】解:∵DG //BC ,∴AD DG AB BC=,故A 选项错误;∵DG //BC ,∴GF GH EC HC=,故B 选项错误;∵EH //AB ,∴FH GH AD AG=,故C 选项正确;∵EH //AB ,∴HE EC AB BC=,故D 选项错误.故选:C .【点睛】此题主要考查线段的比,解题的关键是熟知平行线分线段成比例的性质.27.D【分析】根据AD ∥BC ,得到MD MG DG BC CG BG==,根据四等分点和MG 得到CG ,可得MC =MF =4,再证明1DF MF BF FH==可得HF ,可得MH .【详解】解:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴MD MG DG BC CG BG==,∵E ,F ,G 依次是对角线BD 上的四等分点,MG =1,∴113DG CG BG ==,∴CG =3,∴MF =MC =MG +CG =4,∵AD ∥BC ,∴1DF MF BF FH==,∴HF =4,∴MH =MF +HF =8,故选D .【点睛】本题考查了平行线分线段成比例,平行四边形的性质,解题的关键是根据平行线得到相应的比例式.28.D【分析】设EP x PH y BF kx BG ky ====,,,,利用平行线分线段成比例定理求得GM x FN y EM kx NH ky ====,,,,再利用已知条件求得2k =,据此即可求解.【详解】解:∵点P 是平行四边形ABCD 内部一点, 过P 分别作AB 和BC 的平行线交平行四边形ABCD 的四边于E F G H ,,,.四边形~FBGP 四边形EPHD ,∴四边形PFBG DEPH ,都是平行四边形,且相似,设EP x PH y BF kx BG ky ====,,,,∵FN BC ∥,∴FN AF GM GC BC AB AB BC==,,即(1)(1)(1)(1)FN x GM y k y k x k x k y ==++++,,∴GM x FN y EM kx NH ky ====,,,,∴CGM NFA CNH MAE ≌,≌,△△△△∴PGCH AFPE S S =四边形四边形,∵四边形FBCH 的面积是四边形`AFP E 的3倍.∴(1)3k y y+=,∴2k =,∴EP PH =、AN EP =、2AN MN =都不成立,2AM CM =成立,故选:D .【点睛】本题考查了平行四边形的判定和性质,平行线分线段成比例定理,熟练掌握平行四边形的性质是解题的关键.29.D【分析】连接AC 、BD ,交于点O ,AC 交EF 于点G ,根据菱形性质可得菱形面积公式,然后根据三角形中位线定理得EF 与BD 关系,最后根据三角形面积公式代入计算可得答案.【详解】解:连接AC 、BD ,交于点O ,AC 交EF 于点G ,∵四边形ABCD 是菱形,∴AO =OC ,菱形ABCD 的面积为:12AC •BD ,∵点E 、F 分别是边BC 、CD 的中点,∴EF ∥BD ,EF =12BD ,∴AC ⊥EF ,CF CG DF OG =,∴OG =CG ,∴AG =3CG ,设AC =a ,BD =b ,∴12ab =16,即ab =32,S △AEF =12EF •AG =12×12b ×34a =316ab =6.故选:D .【点睛】此题考查的是菱形的性质、平行线分线段成比例定理、三角形中位线定理,能够利用三角形面积公式得到答案是解决此题关键.30.4【分析】过点D 作//DE BF 交AC 于点E ,首先利用重心的概念和平行线分线段成比例得出2AG AF GD EF==,然后代入计算即可.【详解】如图,过点D 作//DE BF 交AC 于点E ,∵G 是△ABC 重心,∴AD ,BF 都是△ABC 的中线,,AF CF BD DC \==.//DE BF Q ,12CE EF CF \==, 2AF EF \= .//DE BF Q ,2AG AF GD EF\==. 2GD =Q ,4AG \=,故答案为:4.【点睛】本题主要考查平行线分线段成比例,掌握重心的概念和平行线分线段成比例的性质是解题的关键.31.B【分析】取OD 的中点M ,连接MQ ,过点C 作CQ MQ ¢^于点Q ¢,得MQ 是DOP △的中位线,连接DQ ¢并延长交OB 于点P ¢,可得Q 点的运动轨迹是射线MQ ,所以得CQ 的最小值为CQ ¢的长,然后利用含30度角的直角三角形性质即可解决问题.本题考查了三角形的中位线定理,含30度角的直角三角形的性质,轨迹,解决本题的关键是得到Q 点的运动轨迹是射线MQ .【详解】解:如图,取OD 的中点M ,连接MQ ,过点C 作CQ MQ ¢^于点Q ¢,Q 点Q 是PD 的中点,MQ \是DOP △的中位线,MQ 始终与OB 平行,连接DQ ¢并延长交OB 于点P ¢,∴1DM DQ OM Q P ¢=¢=¢DQ Q P ¢¢¢\=,Q \点的运动轨迹是射线MQ ,CQ \的最小值为CQ ¢的长,60CMQ AOB ¢Ð=Ð=°Q ,8OD =,M 是OD 的中点,142MD OD \==,2CD =Q ,2MC MD CD \=-=,112MQ MC ¢\==,CQ \=¢=¢CQ \故选:B32.见解析【分析】令,AX CZ 相交于点E ,延长AX ,使XE XD =,连接BD ,CD ,证明四边形BDCE 是平行四边形,则BE CD ∥,BD CE ∥,再证明ZE 为ABD △中位线,则点E 为AD 中点,最后证明EY 为ABD △中位线,得出EY CD ∥,即可根据过直线外一点有且只有一条直线与已知直线平行,进行求证.【详解】解:令,AX CZ 相交于点E ,延长AX ,使XE XD =,连接BD ,CD .∵AX 是ABC V 的中线,∴BX CX =,∵XE XD =,∴四边形BDCE 是平行四边形,∴BE CD ∥,BD CE ∥,∵CZ 是ABC V 的中线,∴点Z 为AB 中点,BD CE∥∴12AE AZ AD AB ==,∴ZE 为ABD △中位线,即点E 为AD 中点,∵BY 是ABC V 的中线,∴点Y 为AC 中点,BE CD∥∴12AE AY AD AC ==,∴EY 为ABD △中位线,∴EY CD ∥,∵EY CD ∥,BE CD ∥,∴点B 、E 、Y 在同一条直线上,∴AX ,BY ,CZ 三线共点.【点睛】本题主要考查了三角形重心的证明,解题的关键是掌握平行四边形的判定和性质,平行线分线段成比例定理,三角形中位线的判定和性质,以及在平面内过直线外一点有且只有一条直线与已知直线平行.33.C【分析】本题考查平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.作DH BF ∥交AC 于H ,根据三角形中位线定理得到FH HC =,根据平行线分线段成比例定理得到,计算得到答案.【详解】解:作DH BF ∥交AC 于H ,∵AD 是ABC V 的中线,∴BD DC =,∴FH HC =,∵DH BF ∥,且14AE AD =∴13AF AE HF ED ==, ∴16AF FC =::,故选:C34.A【分析】本题考查了平行线分线段成比例,正方形的性质,掌握平行线分线段成比例是解题的关键.作FH BC ∥交CD 于H ,则45DH DF HC FG ==,根据E 为CD 边中点,得19HE ED =,再根据FH AD ∥,得19FE HE AE DE ==,根据勾股定理得AE =FE .【详解】解:如图,作FH BC ∥交CD 于H ,则45DH DF HC FG ==,E Q 为CD 边中点,\19HE ED =,FH AD Q ∥,\19FE HE AE DE ==,AE ==QFE \故选:A .35.D【分析】连接BG ,过点O 作OT ∥AE 交BC 于点T ,首先证明41AG EG =,再利用平行线分线段成比例求解即可.【详解】解:如图所示,连接BG ,过点O 作OT ∥AE 交BC 于点T ,∵点O 是AB 的中点,∴AO =OB ,∴AOG OBG S S =n n ,∵25AOG ABE S S =n n ,∴41ABG BEG S S =n n ,∴41AG EG =,∵OT ∥AE ,AO =BO ,∴ET =TB ,∴OT =12AE ,∴25GE OT =,∵AE ⊥CD ,CD 平分∠BCO ,∴∠DCG =∠DCE ,∴∠CGE +∠DCG =90°,∠CEG +∠DCB =90°,∴∠CGE =∠CEG ,∴CG =CE ,∵∠CGE =∠COT ,∠CEG =∠CTD ,∴∠COT =∠CTD ,∴CO =CT ,∴OG =ET ,∵GE ∥OT ,∴25CE GE CT OT ==,∴23CE ET =,∴38OG BC =,故选:D .【点睛】题目主要考查平行线分线段成比例,三角形的面积,三角形中位线定理等,理解题意,学会添加辅助线,构造平行线是解题关键.36.C【分析】过A 作AF ∥BC 交BM 延长线于F ,设BC=3a ,则BP=PQ=QC=a ;根据平行线间的线段对应成比例的性质分别求出BD 、BE 、BM 的长度,再来求BD ,DE ,EM 三条线段的长度,即可求得答案.【详解】过A 作AF ∥BC 交BM 延长线于F ,设3BC a =,则BP PQ QC a ===;∵AM CM =,AF ∥BC ,∴1AF AM BC CM==,∴3AF BC a ==,∵AF ∥BP ,∴133BD BP a DF AF a ===,∴34DF BF BD ==,∵AF ∥BQ ,∴2233BE BQ a EF AF a ===,∴23EF BE =,即25BF BE =,∵AF ∥BC ,∴313BM BC a MF AF a===,∴BM MF =,即2BF BM =,∴235420BF BF BF DE BE BD =-=-=,22510BF BF BF EM BM BE =-=-=,∴3::::53242010BF BF BF BD DE EM ==::.故选:C .【点睛】本题考查了平行线分线段成比例定理以及比例的性质,正确作出辅助线是关键.37.A【分析】通过分别向横轴和纵轴作辅助线得到等腰三角形,建立线段之间的对应关系,同时利用平行线分线段成比例的推理,建立比例关系式即可求解.【详解】解:如图所示,过C 点分别向OA 、OB 作垂线,垂足分别为点D 、点E ,因为∠AOB =90°,OP 平分∠AOB ,∴∠BOC =∠AOC =45°,∴∠BOC =∠OCE =∠AOC =∠OCD =45°,∴OE =CE =CD =OD ,设OE =CE =CD =OD =x ,∴BE =6-x ,∵CE ∥OA ,∴BE CE OB OA =,∴664x x -=,∴125x =,∵OP 上的标度与纵轴上的标度在同一水平线上,∴点C 处的标度等于CD 的长,即为125,故选:A .【点睛】本题综合考查了等腰三角形的判定、角平分线的定义和平行线分线段成比例定理的推论等内容,解决本题的关键是正确理解题意与图形,能在图形中得到对应等量关系,能正确作出辅助线构造相似三角形等,本题蕴含了数形结合等思想方法.38.A【分析】过点D 作DF BC ^于点F ,由勾股定理得8AC =,再由角平分线的性质得DA DF =,进而由面积法求出3DF =,则5CD AC DA =-=,然后由勾股定理得4CF =,则6BF =,最后由平行线分线段成比例定理即可得出结论.【详解】解:过点D 作DF BC ^于点F ,∵90A Ð=°,6AB =,10BC =,∴DA BA ^,8AC ===,∵BD 平分ABC Ð,DF BC ^,∴DA DF =,∵ABC ABD BCD S S S =+△△△,∴111222AB AC AB DA BC DF ×=×+×,∴68610DF DF ´=+,。
平行线分线段成比例经典例题与变式练习(精选题目)精编版

平行线分线段成比例平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111cab=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA专题二、定理及推论与中点有关的问题 【例3】 (2012年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52 B.1 C.32D.2(1)MEDCBA(2)FED CBA【例4】 (2011年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD的值;(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想. 【例5】 (2013年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例经典例题与变式练习(精选题目) (2)

平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2007年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52B.1C.32D.2(1)MEDC BA(2)F ED CBA【例5】 (2001年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O . (1)当1A 2AE C =时,求AOAD的值;E D CAO(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2003年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例八大题型

【变式】如图,已知点 F 在 AB 上,且 AF:BF=1:2,点 D 是 BC 延长线上一点,BC:CD =2:1,连接 FD 与 AC 交于点 M,则 FN:ND= .
解:过点 F 作 FE∥BD,交 AC 于点 E,
∴=,
∵AF:BF=1:2,
∴ = 1,
3
∴ = 1,
3
即 FE= 13BC, ∵BC:CD=2:1,
C l3
【小结】若将所截出的小线段位置靠上的(如 AB )称为上,位置靠下的称为下,两条线段
上上 上上 下下
合成的线段称为全,则可以形象的表示为 下 下 , 全 全 , 全 全 .
【题型1 “井”字型】
【例 1】如图,直线 l1∥l2∥l3,直线 AC 和 DF 被 l1,l2,l3 所截,如果 AB=2,BC=3,EF =2,那么 DE 的长是( )
A.2
B
.4
3
C.1
D.34
【分析】根据平行线分线段成比例定理得出比例式,代入求出即可. 【解答】解:∵直线 l1∥l2∥l3, ∴=,
∵AB=2,BC=3,EF=2,
∴2 = ,
32
∴DE=
4,
3
故选:B.
【变式】如图,a∥b∥c,两条直线与这三条平行线分别交于点 A,B,C 和 D,E,F.已知 AB=3,BC=2,DE=6,则 DF 等于( )
∵ = = 1,
2
∴BG=2DG, ∵BE=4DG, ∴ = 1,
4
故 D 错误,符合题意; 故选:D.
【变式】已知,在△ABC 中,点 D 为 AB 上一点,过点 D 作 DE∥BC,DH∥AC 分别交 AC、 BC 于点 E、H,点 F 是 BC 延长线上一点,连接 FD 交 AC 于点 G,则下列结论中错误的 是( )
平行线分线段成比例经典例题与变式练习(精选题目)

平行线分线段成比例知识梳理平行线分线段成比例定理及其推论1.平行线分线段成比例定理如下图,如果h // I2 // I3,则BCACABDEACDF2.平行线分线段成比例定理的推论:3.平行的判定定理:AB DEAC12DF,EFDF如图,在三角形中,如果ADDE // BC,贝U --ABAEACDEBC 如上图,如果有ADABAEACDEBC,那么DE // BC专题讲解专题一、平行线分线段成比例定理及其推论基本应用【例1】如图,DE // BC,且DB AE,若AB 5, AC 10,求AE的长。
【例2】如图,已知AB//EF//CD,若AB a , CD b , EF c ,求证:111. cab 【巩固】如图,AB BD,CD BD,垂足分别为B、D,AC和【巩固】如图,找出S ABD、S BED、S BCD之间的关系,并证明你的结论BD相交于点E,EF BD,垂足为F .证明:1 1AB CD1EFA连接EM 并延长,交BC 的延长线于D , 则CC (2)如图(2),已知 ABC 中,AE:EB 1:3,BD :DC 2:1,AD 与CE 相交于F ,则EF FCAF FD的值为()A.|B.1C.【例5】(2001年河北省中考试题)如图,在 AC 边上的任意一点,BE 交AD 于点O .【例3】如图,在梯形ABCD 中,AB // CD , AB 12 , CD 9,过对角线交点0作EF // CD 交 AD , BC 于 E , F ,求 EF 的长。
【巩固】(上海市数学竞赛题)如图,在梯形 ABCD 中,AD // BC ,AD a ,BC b ,E ,F 分别 是AD ,BC 的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
专题二、定理及推论与中点有关的问题 【例4】(2007年北师大附中期末试题)1(1)如图(1),在 ABC 中,M 是AC 的中点,E 是AB 上一点,且AE - AB ,43 2D.2A(1)当AE-时,求AO的值;AC2AD(2)当AE 1 1 口」、—求A0的值;AC 3 4AD(3)试猜想AE 1AC n 1时A0的值,并证明你的猜想AD【例6】(2003年湖北恩施中考题)如图,AD是ABC的中线,点E在AD上,F 是BE延长线与AC的交点.(1)如果E是AD的中点,求证:圧 -;FC 2(2)由(1)知,当E是AD中点时,圧-成立,若E是AD上任意一点(E与A、DFC 2 ED不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.【巩固】(天津市竞赛题)如图,已知ABC中,AD是BC边上的中线,E是AD 上的一点,且BE AC,延长BE交AC于F。
平行线分线段成比例经典例题与变式练习(精选题目)(1)

平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2007年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52B.1C.32D.2(1)MEDC BA(2)F ED CBA【例5】 (2001年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O . (1)当1A 2AE C =时,求AOAD的值;E D CAO(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2003年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
(完整word)初中数学相似三角形知识库平行线分线段成比例经典例题与变式练习(精选题目)

平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
专题一、平行线分线段成比例定理及其推论基本应用【例1】 如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
EDCBA【例2】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【巩固】如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=. FEDCBA【巩固】如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例3】 如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作EF CD ∥交AD BC ,于E F ,,求EF 的长。
OFED CBA【巩固】(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
QPFED CBA专题二、定理及推论与中点有关的问题 【例4】 (2007年北师大附中期末试题)(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =, 连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( )A.52 B.1 C.32D.2(1)MEDC BA(2)F ED CA【例5】 (2001年河北省中考试题)如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O . (1)当1A 2AE C =时,求AOAD的值;E AO(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.【例6】 (2003年湖北恩施中考题)如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.F E DCBA【巩固】(天津市竞赛题)如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线分线段成比例
平行线分线段成比例定理及其推论
1. 平行线分线段成比例定理
如下图,如果1l ∥2l ∥3l ,则
BC EF AC DF =,AB DE AC DF =,AB AC
DE DF
=
.
2. 平行线分线段成比例定理的推论:如图,在三角形中, 如果DE BC ∥,则AD AE DE
AB AC BC
==
3. 平行的判定定理:如上图,如果有
BC
DE
AC AE AB AD =
=,那么DE ∥ BC 。
1、如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
2、 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,
求证:111
c a b
=+.
3、如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和
BD 相交于点E ,EF BD ⊥,垂足为F .证明:
111
AB CD EF
+=
.
4、如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.
l 3
l 2l 1F
E D C
B A A
B
C
D
E
E D
C B A
E
D
C
B
A
F
E D
C
B
A
F
E
D
C
B
A
E
C
A
5、如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对
角线交点O 作 EF CD ∥交AD BC ,于E F ,,求EF 的长。
6、(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,
AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
7、(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且1
4
AE AB =,
连接EM 并延长,交BC 的延长线于D ,则
BC
CD
=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,
:2:1BD DC =,AD 与CE 相交于F ,则EF AF
FC FD
+ 的值为( ) A.52 B.1 C.3
2
D.2
8、如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD
于点O . (1)当1A 2AE C =时,求
AO
AD 的值; (2)当
11A 34AE C =、时,求
AO
AD
的值; (3)试猜想
1A 1AE C n =
+时AO
AD
的值,并证明你的猜想.
9、如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.
(1)如果E 是AD 的中点,求证:
1
2
AF FC =; (2)由(1)知,当E 是AD 中点时,
12AF AE
FC ED
=⋅
成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.
10、如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
求证:AF EF =。
E
D C
B A
O
O
F
E
D
C
B
A
Q
P
F
E
D C
B
A
(1)
M
E
D
C B
A
(2)
F
E
D C
B A F E D
C
B
A
F
E
D
C
B A
11、如图,ABC ∆中,D 为BC 边的中点,延长AD 至E , 延长AB 交CE 的延长线于P 。
若2AD DE =,求证:3AP AB =。
12、如图, ABC ∆中,BC a =,若11D E ,分别是AB AC ,的中点,则1112
D E a =;
若22D E 、分别是11D B E C 、的中点,则2213
224a D E a a ⎛⎫=+= ⎪⎝⎭; 若33D E 、分别是22D B E C 、的中点,则3313724
8
D E a a a ⎛⎫=+= ⎪⎝⎭;
…………
若n n D E 、分别是-1-1n n D B E C 、的中点,则n n D E =_________.
13、如图,在四边形ABCD 中,AC 与BD 相交于点O ,直线l 平行于BD ,且 与AB 、DC 、BC 、AD 及AC 的延长线分别相交于点M 、N 、R 、S 和P . 求证:PM PN PR PS ⋅=⋅
14、已知,如图,四边形ABCD ,两组对边延长后交于E 、F ,对角线BD EF ∥,
AC 的延长线交EF 于G .求证:EG GF =.
15、已知:P 为ABC ∆的中位线MN 上任意一点,BP 、CP 的延长
线分别交对边AC 、AB 于D 、E ,求证:1AD AE
DC EB
+=
16、在ABC ∆中,底边BC 上的两点E 、F 把BC 三等分,BM 是AC 上的中 线,AE 、AF 分别交BM 于G 、H 两点,求证:::5:3:2BG GH HM =
17、如图,M 、N 为ABC ∆边BC 上的两点,且满足BM MN NC ==,一条 平行于AC 的直线分别交AB 、AM 和AN 的延长线于点D 、E 和F . 求证:3EF DE =.
E n D n E 3D 3
E 2D 2E 1
D 1C
B
A
P
E
D
C
B
A
l
S
R P
N
M
O D
C B
A
G
F
E
C
D
B
A
P
N
M
E
D C
B
A M
H G F E
C
B
A
F N
M
E D C
B
A
18、已知:如图,在梯形ABCD 中,//AB CD ,M 是AB 的中点,分别连 接AC 、BD 、MD 、MC ,且AC 与MD 交于点E ,DB 与MC 交于F . (1)求证://EF CD
(2)若AB a =,CD b =,求EF 的长.
19如图,在梯形ABCD 中,AD BC ∥,
396AD BC AB ===,,,4CD =,若EF BC ∥,且梯形AEFD 与梯形EBCF 的周长相
等,求EF 的长。
20、 如图,ABCD 的对角线相交于点O ,在AB 的延 长线上任取一点E ,连接OE 交BC 于点F ,若AB a AD c BE b ===,,,求BF 的值。
21、 已知等腰直角ABC ∆中,E 、D 分别为直角边BC 、AC 上的点,且 CE CD =,过E 、D 分别作AE 的垂线,交斜边AB 于L ,K .
求证:BL LK =.
【习题1】 如已知DE AB ∥,2OA OC OE =⋅,求证:AD BC ∥.
【习题2】 在ABC ∆中,BD CE =,DE 的延长线交BC 的延长线于P ,
求证:AD BP AE CP ⋅=⋅.
P
E D
C
B A
F
E
M D
C
B
A
F E
D
C
B
A O
F
E
D
C
B
A
L K
E D
C
B
A
D
O
E C
B
A
【习题3】 如图,在ABC ∆的边AB 上取一点D ,在AC 取一点E ,使AD AE =, 直线DE 和BC 的延长线相交于P ,求证:
BP BD
CP CE
=
P
E D
C
B
A。
