因动点产生的平行四边形

合集下载

中考数学动点问题归纳总结5.因动点产生的平行四边形问题

5.因动点产生的平行四边形问题1.如图，抛物线214y x bx c =++与x 轴交于()5,0A 、()1,0B -两点，过点A 作直线AC x ⊥轴，交直线2y x =于点C ．（1）求该抛物线的解析式；（2）求点A 关于直线2yx =的对称点A '的坐标，判定点A '是否在该抛物线上，并说明理由；（3）点P 是抛物线上一动点，过点P 作y 轴的平行线，交线段CA '于点M ，是否存在这样的点P ，使四边形PACM 是平行四边形？若存在，求出点P 的坐标；若不存在，请说明理由．解析：（1）∵抛物线214y x bx c =++与x 轴交于()5,0A 、()1,0B -两点 ∴25504104b c b c ⎧++=⎪⎪⎨⎪-+=⎪⎩解得154b c =-⎧⎪⎨=-⎪⎩ ∴抛物线的解析式为21544yx x =-- （2）过点A '作A E x '⊥轴于E ，AA '与OC 交于点D∵点C 在直线2y x =上，()5,10C ∴∵点A 和A '关于直线2yx =对称，OC AA '∴⊥，A D AD '= 5,10,OA AC ==OC ∴===1122OAC S OA AC OC AD ∆=⋅=⋅，AD AA '∴=∴=在Rt A EA '∆和Rt OAC ∆中90A AE A AC ''∠+∠=︒，90ACD A AC '∠+∠=︒A AE ACD '∴∠=∠又90A EA OAC '∠=∠=︒，A EA OAC '∆∆∽A E AE AA OA AC OC''∴==，即510A E AE '==4,8,3A E AE OE AE OA '∴===-=∴点A '的坐标为()3,4-当3x =-时，()21533444y =⨯-+-=∴点A '在该抛物线上（3）存在理由：设直线CA '的解析式为y kx b =+则51034k b k b +=⎧⎨-+=⎩解得34254k b ⎧=⎪⎪⎨⎪=⎪⎩ ∴直线CA '的解析式为32544y x =+ 设215,44P x x x ⎛⎫-- ⎪⎝⎭，则325,44M x x ⎛⎫+ ⎪⎝⎭ PM AC ∥∴要使四边形PACM 是平行四边形，只需PMAC = 又点M 在点P 的上方，232515104444x x x ⎛⎫∴+---= ⎪⎝⎭ 解得122,5x x ==（不合题意，舍去）当2x =时，94y =-∴当点P 运动到92,4⎛⎫- ⎪⎝⎭时，四边形PACM 是平行四边形 2.如图，抛物线()20y ax bx c a =++≠与y 轴交于点()0,4C ，与x 轴交于点A 和点B ，其中点A 的坐标为()2,0-，抛物线的对称轴1x =与抛物线交于点D ，与直线BC 交于点E ．（1）求抛物线的解析式；（2）在直线BC 上方的抛物线上是否存在点F ，使四边形ABFC 的面积为17，若存在，求出点F 的坐标；若不存在，请说明理由；（3）平行于DE 的动直线l 与直线BC 相交于点P ，与抛物线相交于点Q ，若以D 、E 、P 、Q 为顶点的四边形是平行四边形，求点P 的坐标．解析：（1）由抛物线经过点()0,4C可得4c = ① ∵对称轴1,22b x b a a =-=∴=- ② 又抛物线过点()2,0A -，042a b c ∴=-+③ 由①②③解得：1,1,42a b c =-== ∴抛物线的解析式为2142yx x =-++ （2）假设存在满足条件的点F ，连接BC 、CF 、OF ，作FHx ⊥轴于H ，FG y ⊥轴于G设点F 的坐标为21,42t t t ⎛⎫-++ ⎪⎝⎭，其中04t << 则2142FH t t =-++，FG t =221114428222OBF S OB FH t t t t ∆⎛⎫∴=⋅=⨯⨯-++=-++ ⎪⎝⎭ 114222OCF S OC FG t t ∆=⋅=⨯⨯= 224282412AOC OBF OFC ABFC S S S S t t t t t ∆∆∆∴=++=-+++=-++四边形令241217t t -++=，即2450t t -+=则()244540∆=--⨯=-<，方程无解故不存在满足条件的点F（3）设直线BC 的解析式为()0y kx bk =+≠，又过点()4,0B ，()0,4C044k b b =+⎧∴⎨=⎩解得14k b =-⎧⎨=⎩ ∴直线BC 的解析式为4yx =-+ 由()2211941222y x x x =-++=--+，得91,2D ⎛⎫ ⎪⎝⎭又点E 在直线BC 上，则点()1,3E于是93322DE =-= 由于DE PQ ∥，若以D 、E 、P 、Q 为顶点的四边形是平行四边形，只需DE PQ =设点(),4P m m -+，则21,42Q m m m ⎛⎫-++ ⎪⎝⎭①当04m <<时，()221144222PQ m m m m m =-++--+=-+ 由213222m m -+=，解得1m =或3m = 当1m =时，线段PQ 与DE 重合，1m =舍去3m ∴=，此时()13,1P②当0m <或4m >时，221144222PQ m m m m m ⎛⎫=-+--++=- ⎪⎝⎭由213222m m -=，解得2m =±此时，((232,2P P +--+综上所述，满足条件的点P 有三个，分别是()13,1P ，((232,2P P +--+. 3.如图，抛物线222y x x m=-与x 轴负半轴交于点A ，顶点为B ，且对称轴与x 轴交于点C ．（1）求点B 的坐标（用含m 的代数式表示）；（2）D 为BO 中点，直线AD 交y 轴于E ，若点E 的坐标为()0,2，求抛物线的解析式；（3）在（2）的条件下，点M 在直线BO 上，且使得AMC ∆的周长最小，P 在抛物线上，Q 在直线BC 上，若以A 、M 、P 、Q 为顶点的四边形是平行四边形，求点P 的坐标．解析：（1）222211222y x x x m m m m ⎛⎫=-=-- ⎪⎝⎭ ∴抛物线的顶点B 的坐标为11,22m m ⎛⎫- ⎪⎝⎭ （2）令2220x x m-=，解得10x =，2x m = ∵抛物线222y x x m=-与x 轴负半轴交于点A (),0A m ∴且0m <.过点D 作DF x ⊥轴于F由D 为BO 中点，DF BC ∥，可得12CF FO CO == 12DF BC ∴= 由抛物线的对称性得3,4AF AC OC AO =∴=DF EO ∥，ADF AEO ∴∆∆∽，DF AF EO AO∴= 由()0,2E ，11,22B m m ⎛⎫- ⎪⎝⎭，得12,4OE DF m ==- 13424m -∴=，6m ∴=- ∴抛物线的解析式为2123yx x =-- （3）依题意，得()6,0A -，()3,3B -，()3,0C -可得直线OB 的解析式为y x =-，直线BC 为3x =-作点C 关于直线BO 的对称点()10,3C ，连接1AC 交BO 于M ，则M 即为所求由()6,0A -，()10,3C ，可得直线1AC 的解析式为132y x =+ 由132y x y x⎧=+⎪⎨⎪=-⎩解得22x y =-⎧⎨=⎩ ∴点M 的坐标为()2,2-由点P 在抛物线2123yx x =--上，设21,23P t t t ⎛⎫-- ⎪⎝⎭①当AM 为平行四边形的一边时如图，过M 作MG x ⊥轴于G ，过P 作PHBC ⊥于H 则2,3G M H B x x x x ==-==-可证AMG PQH ∆∆≌，得4PH AG ==()34t ∴--=，1t ∴=171,3P ⎛⎫∴- ⎪⎝⎭如图，同理可4PH AG ==34,7t t ∴--=∴=-277,3P ⎛⎫∴-- ⎪⎝⎭ ②当AM 为平行四边形的对角线时如右图，过M 作MHBC ⊥于H ，过P 作PG x ⊥轴于G 则3,H B G P x x x x t ==-==可证APG MQH ∆∆≌，得1AG MH ==()61,5t t ∴--=∴=-35:5,3P ⎛⎫∴- ⎪⎝⎭ 综上，点P 的坐标为171,3P ⎛⎫∴- ⎪⎝⎭，277,3P ⎛⎫-- ⎪⎝⎭，355,3P ⎛⎫- ⎪⎝⎭4.已知正方形OABC 的边OC 、OA 分别在x 、y 轴的正半轴上，点B 坐标为()4,4，点(),0P t 是x 轴上一动点，过点O 作OH AP ⊥于点H ，直线OH 交直线BC 于点D ，连接AD ．（1）如图1，当点P 在线段OC 上时，求证：OP CD =；（2）在点P 运动过程中，AOP ∆与以A 、B 、D 为顶点的三角形相似时，求t 的值；（3）如图2，抛物线212463y x x =-++上是否存在点Q ，使得以P 、D 、Q 、C 为顶点的四边形为平行四边形？若存在，求出t 的值；若不存在，请说明理由．解析：（1）证明：正方形OABC ，OA OC ∴=，90AOP OCD ∠=∠=︒90OAP APO ∴∠+∠=︒OH AP ⊥，90COD APO ∴∠+∠=︒OAP COD ∴∠+∠，AOP OCD ∴∆∆≌OP CD ∴=（2）解：当点P 在线段OC 上时若AOP ABD ∆∆∽，AO AB =，AOP ABD ∴∆∆≌ ,2,2OP CD OP BD CD t ∴=∴===∴=当点P 在OC 延长线上时，如图1ADB ODC APO ∠>∠=∠∴若AOP DBA ∆∆∽，则AO OP DB AB= 可证AOP OCD ∆∆≌，OP CD ∴=，4DB PC t ∴==-444t t ∴=-，解得2t =-（舍去）或2t =+ 当点P 在CO 延长线上时，如图290COD ODC ∠+∠=︒，90HOP APO ∠+∠=︒又COD HOP ∠=∠，ODC APO ∴∠=∠ODC ADB ∠>∠，APO ADB ∴∠>∠∴若AOP DBA ∆∆∽，则AO OP DB AB= 可证AOP OCD ∆∆≌，OP CD ∴=,4DB PC t ∴==-444t t -∴=-，解得2t =+（舍去）或2t =-∴当AOP ∆与以A 、B 、D 为顶点的三角形相似时，2t=或2+或2- （3）①若CD 为平行四边形的对角线则,DQ PC DQ PC =∥（i ）当点P 在线段OC 上时，如图3,,4OP t DC OP t DQ PC t =∴====-()8,Q t t ∴-，代入212463y x x =-++，得 ()()21288463t t t --+-+=，解得2t =或4t =（舍去）（ii ）当点P 在CO 延长线上时，如图OP t =-，DC OP t ∴==-，4DQ PC t ==-()8,Q t t ∴-，代入212463y x x =-++，得 ()()21288463t t t --+-+=，解得2t =（舍去）或4t =（舍去） ②若CD 为平行四边形的边则,PQ DC PQ DC =∥（i ）当点P 在OC 延长线上时，如图5,OP t PQ DC OP t =∴===(),Q t t ∴-，代入212463y x x =-++，得 212463t t t -++=-，解得2t =-（舍去）或12t = （ii ）当点P 在CO 延长线上时，如图6、图7OP t =-，PQ DC OP t ∴===-(),Q t t ∴或(),Q t t -把(),Q t t 代入212463y x x =-++，得 212463t t t -++=，解得6t =-或4t =（舍去）把(),Q t t -代入212463y x x =-++，得 212463t t t -++=-，解得2t =-或12t =（舍去）综上所述，抛物上存在点Q ，使得以P 、D 、Q 、C 为顶点的四边形为平行四边形， t 的值为：12t =，212t =，36t =-，42t =-5.如图，在平面直角坐标系中，O 是坐标原点，矩形OABC 的顶点)A ，()0,1C ，将AOC ∆沿AC 翻折得APC ∆．（1）求点P 的坐标；（2）若抛物线243yx bx c =-++经过P 、A 两点，试判断点C 是否在该抛物线上，并说明理由；（3）设（2）中的抛物线与矩形OABC 的边BC 交于点D ，与x 轴交于另一点E ，点M 在x 轴上运动，N 在y 轴上运动，若以点E 、M 、D 、N 为顶点的四边形是平行四边形，试求点M 、N 的坐标．解析：（1）在Rt OAC ∆中，OA =1OC =，30,OAC ∴∠=︒过P 作PQ OA ⊥于Q ，如图1⑦在Rt PAQ ∆中，60,PAQ AP ∠=︒=2OQ AQ ∴==，32PQ =，322P ⎛⎫∴ ⎪⎝⎭（2）将P 、A 两点坐标代入抛物线的解析式中，得：312240c c ⎧-++=⎪⎨⎪-++=⎩解得1b c ⎧=⎪⎨=⎪⎩∴抛物线的解析式为2413yx =-++ 当0x =时，1y =，∴点()0,1C 在该抛物线上（3）①若DE 是平行四边形的对角线，如图2点C 在y 轴上，CD x ∥轴，∴过点D 作DM CE ∥交x 轴于M ，则四边形EMDC 为平行四边形把1y =代入抛物线解析式，得点D的坐标为4⎛⎫ ⎪⎝⎭把0y =代入抛物线解析式，得点E的坐标为4⎛⎫- ⎪⎝⎭2M ⎛⎫∴ ⎪⎝⎭，N 点即为C 点，坐标是()0,1②若DE 是平行四边形的边，如图3、图4过点A 作AN DE ∥交y 轴于N ，四边形DANE 是平行四边形2DE AN ∴====3ON OA =，30EAN ∴∠=︒ ,30AN DE DEA EAN ∴∠=∠=︒∥)(),0,1M N ∴- 同理过点C 作CM DE ∥交x 轴于M ，四边形CMED 是平行四边形()(),0,1M N ∴6.如图，已知抛物线211:4C y x bx c =-++与x 轴交于点A 、B （A 在B 的左侧），与y 轴交于点C ，抛物线2C 与抛物线1C 关于y 轴对称，点A 、B 的对称点分别是E 、D ，连接CD 、CB ，设AD m =．（1）当2m =时，求b 的值；（2）若点P 是抛物线1C 上的一个动点（P 不与点A 、B 重合），试判断点P 关于原点的对称点Q 是否在抛物线2C 上，请说明理由；（3）将CDB ∆沿直线BC 折叠，点D 的对应点为G ．是否存在实数m ，使得四边形CDBG 为平行四边形，且点G 恰好落在抛物线2C 上，若存在，求出m 的值；若不存在，请说明理由．解析：（1）∵抛物线211:4C y x bx c =-++的对称轴为直线2x b = 抛物线2C 与抛物线1C 关于y 轴对称∴抛物线2C 的对称轴为直线2x b =-12,222,2m b b b =∴--=∴=- （2）∵抛物线211:4C y x bx c =-++，抛物线2C 与抛物线1C 关于y 轴对称 ∴抛物线221:4C y x bx c =--+ 设(),P x y 是抛物线1C 上任意一点(0)y ≠则点P 关于原点的对称点()11,Qx y --，且21114y x bx c =-++ 将点Q 的横坐标代入抛物线2C 的解析式得2111114Q y x bx c y y =-++=≠- ∴点Q 不在抛物线2C 上（3）存在B 、D 关于y 轴对称，点C 在y 轴上，CD CB ∴=由折叠知CG CD =∵四边形CDBG 是平行四边形，CD BG ∴=CB CG BG ∴==，CGB ∴∆是等边三角形CDB ∴∆是等边三角形假设点G 恰好落在抛物线2C 上由抛物线和等边三角形的对称性可知B 点一定在抛物线2C 的对称轴上BD BE AD m ∴===1,2OD OB m ∴==31,0,,022A m B m ⎛⎫⎛⎫∴- ⎪ ⎪⎝⎭⎝⎭CDB ∆为等边三角形，2c CO m ∴=== 对于抛物线211:4C y x bx c =-++，根据根与系数的关系，有31422m m c -⋅=-314222m m m ∴-⋅=-⨯0,3m m ≠∴=∴存在实数3m =，使得四边形CDBG 为平行四边形，且点G 恰好落在抛物线2C 上 7.已知抛物线212y x c =+经过点()3,5A -，顶点为Q ，点P 是y 轴上位于点Q 上方的一个动点，连接AP 并延长，交抛物线于点B ，分别过点A 、B 作x 轴的垂线，垂足为C 、D ，连接AQ 、BQ ．（1）求抛物线的解析式；（1）当A 、Q 、B 三点构成直角三角形时，求点P 的坐标；（2）当AC 、AP 、BD 、BP 四条线段构成平行四边形时，求点P 的坐标．解析：（1）∵抛物线212y x c =+经过点()3,5A - ()21532c ∴=⨯-+，12c ∴= ∴抛物线的解析式为21122y x =+（2）21122y x =+，10,2Q ⎛⎫∴ ⎪⎝⎭①若90AQB ∠=︒过点Q 作EF x ∥轴，分别交AC 、BD 于E 、F 则195,322AE AC EC EQ =-=-== 易证AEQ QFB ∆∆∽，AE EQ QF FB ∴= 32AE FQ QE FB ∴== 设13,22B m m ⎛⎫+ ⎪⎝⎭，代入抛物线解析式，得49m = 425,318B ⎛⎫∴ ⎪⎝⎭可得直线AB 的解析式为5562y x =-+ 50,2P ⎛⎫∴ ⎪⎝⎭ ②若90QAB ∠=︒过点Q 作QE x ∥轴，交AC 于E()13,5,0,,22A Q AQ ⎛⎫-∴= ⎪⎝⎭易证AEQ QAP ∆∆∽，PQ AQ AQ AE ∴=，2132AQ PQ AE ∴== ()0,7P ∴③若90ABQ ∠=︒过点A 、Q 分别作x 轴的平行线，交BD 于E 、F 设211,22B n n ⎛⎫+ ⎪⎝⎭，则3,AE n QF n =+= 22119152222BE n n =--=-，2211112222BF n n =+-= 可证ABE BQF ∆∆∽，AE BE BF QF∴= 229132212n n n n -+∴=，即()()23340n n n +-+= 30n ∴+=，得3n =-（舍去）或2340n n -+=，方程无实数解∴当ABQ ∆为直角三角形时，点P 的坐标为50,2⎛⎫ ⎪⎝⎭或()0,7 （3）①若AC BD =，AP BP =，此时点A 与点B 关于y 轴对称()5,0,5OP AC P ∴==∴②若ACAP =，设()0,P y ，则()29525y +-= 解得1y=或9y = 当1y =时，则()0,1P此时直线AP 解析式为413yx =-+ 与抛物线的交点B 为19()35，59BP BD ∴=== 此时AC 、AP 、BD 、BP 四条线段能构成平行四边形()0,1P ∴符合题意当9y =时，则()0,9P此时直线AP 解析式为493y x =+ 与抛物线的交点B 为17149()39，过P 作PE BD ⊥于E ，则1731739PE ⨯==， 149684179999BE ⨯=-== 51785149999BP ⨯∴==<，即BP BD < 此时AC 、AP 、BD 、BP 四条线段不能构成平行四边形()0,9P ∴不符合题意 ③若AC BP =，则点P 必在点A 上方，AP BD ≠此时AC 、AP 、BD 、BP 四条线段不能构成平行四边形∴满足条件的点P 的坐标为()0,5或()0,1 8.如图，抛物线2y x bx c =-++与直线122y x =+交于C 、D 两点，其中点C 在y 轴上，点D 的坐标为7(3)2，．点P 是y 轴右侧的抛物线上一动点，过点P 作PE x ⊥轴于点E ，交CD 于点F ．（1）求抛物线的解析式；（2）若点P 的横坐标为m ，当m 为何值时，以O 、C 、P 、F 为顶点的四边形是平行四边形？请说明理由．（3）若存在点P ，使45PCF ∠=︒，请直接写出相应的点P 的坐标．解析：（1）在直线解析式122y x =+中，令0x =，得2y =， (02)C ∴，．∵点(02)C ，、7D(3)2，在抛物线2y x bx c =-++上， 27932c b c =⎧⎪∴⎨-++=⎪⎩，解得722b c ⎧=⎪⎨⎪=⎩， ∴抛物线的解析式为：2722yx x =-++．（2）PF OC ∥，且以O 、C 、P 、F 为顶点的四边形是平行四边形，2PF OC ∴==， ∴将直线122y x =+沿y 轴向上、下平移2个单位之后得到的直线，与抛物线y 轴右侧的交点，即为所求之交点．由答图1可以直观地看出，这样的交点有3个．将直线122y x =+沿y 轴向上平移2个单位，得到直线142y x =+，联立2142722y x y x x ⎧=+⎪⎪⎨⎪=-++⎪⎩，解得121,2x x ==，121,2m m ∴==；将直线122y x =+沿y 轴向下平移2个单位，得到直线12y x =，联立212722y x y x x ⎧=⎪⎪⎨⎪=-++⎪⎩，解得3433,22x x +-==（在y 轴左侧，不合题意，舍去），32m +∴=． ∴当m 为值为12，或2时，以O 、C 、P 、F 为顶点的四边形是平行四边形．（3）存在．理由：设点P 的横坐标为m ，则271,2,,222P m m m F m m ⎛⎫⎛⎫-+++ ⎪ ⎪⎝⎭⎝⎭．由答图2所示，过点C 作CM PE ⊥于点M ，则,2CM m EM ==，12F FM y EM m ∴=-=， tan 2CFM ∴∠=．在Rt CFM ∆中，由勾股定理得：2CF m =．过点P 作PN CD ⊥于点N ，则tan tan 2PN FN PEN FN CFMFN =⋅∠=⋅∠∠=45PCF ∠=︒，PN CN ∴=，而2PN FN =，,22FN CF m PN FN ∴====，在Rt PFN ∆中，由勾股定理得：52PF m ==． 227122322P F PF y y m m m m m ⎛⎫⎛⎫=-=-++-+=-+ ⎪ ⎪⎝⎭⎝⎭， 2532m m m ∴-+=，整理得：2102m m -=，解得0m =（舍去）或12m =， 17()22P ∴，；同理求得，另一点为2313()618P ，． ∴符合条件的点P 的坐标为17()22，或2313()618，．9.如图，抛物线22y x x c =-+的顶点A 在直线:5l y x =-上．（1）求抛物线顶点A 的坐标；（2）设抛物线与y 轴交于点B ，与x 轴交于点C 、D （C 点在D 点的左侧），试判断ABD ∆的形状；（3）在直线l 上是否存在一点P ，使以点P 、A 、B 、D 为顶点的四边形是平行四边形，若存在，求点P 的坐标；若不存在，请说明理由．解析：（1）∵顶点A 的横坐标为212x-=-=，且顶点A 在5y x =-上 ∴当1x =时，154y =-=-()1,4A ∴-（2）ABD ∆是直角三角形将(14)A -，代入22y x x c =-+，得124c -+=-，3c ∴=-223y x x ∴=--，(03)B ∴-，当0y =时，2230x x --=，121,3x x ∴=-=(10)C ∴-，，(30)D ，22218BD OB OD =+=，()2224312AB =-+=，()22231420AD =-+= 222BD AB AD +=，90ABD ∴∠=︒即ABD ∆是直角三角形（3）存在．由题意知：直线5yx =-交y 轴于点(05)E -，，交x 轴于点(50)F ，5OE OF ∴==，又3OB OD ==OEF ∴∆与OBD ∆都是等腰直角三角形BD l ∴∥，即PA BD ∥则构成平行四边形只能是PADB 或PABD ，如图,过点P 作y 轴的垂线，过点A 作x 轴的垂线并交于点G设11(5)P x x -，，则1(15)G x -，则11PG x =-，11541AG x x =--=-PA BD ==由勾股定理得：()()22111118x x -+-=，12x ∴=-或24x =(27)P ∴--，或(41)P -，∴存在点(27)P --，或(41)P -，使以点P 、A 、B 、D 为顶点的四边形是平行四边形10.抛物线2y axbx c =++与x 轴交于(20)A -，、(40)B ，两点，与y 轴负半轴交于点C ，且12ABC S ∆=．（1）求此抛物线的解析式；（2）如图1，P 为直线BC 上一点，若以O 、P 、B 为顶点的三角形与ABC ∆相似，求点P 的坐标；（3）如图2，过点A 作AM AC ⊥交抛物线于点M ，交y 轴于点D ，直线x m =与抛物线交于点Q ，与直线AM 交于点R ．问是否存在这样的m ，使C 、D 、Q 、R 四点构成平行四边形？若存在，求出m 的值，若不存在；说明理由．解析：（1）(20)A -，、(40)B ，2,46OA OB AB ∴===，1161222ABC S AB OC CO ∆=⋅=⨯⋅=，4OC ∴= ∵点C 在y 轴负半轴上，(04)C ∴-，42016404a b c a b c c -+=⎧⎪∴++=⎨⎪=-⎩解得1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴抛物线的解析式为2142y x x =-- （2）易知ABC ∆为锐角三角形∴若以O 、P 、B 为顶点的三角形与ABC ∆相似，点P 只能在线段BC 上过P 作PE OB ⊥于E ，设PE t = 当OP AC ∥时，OBP ABC ∆∆∽ 则EP OB OC AB =，446t ∴=，83t ∴= 4OB OC ==，45OBC ∴∠=︒BE PE t ∴==， 84433OE OB BE ∴=-=-= 148()33P ∴-，当BPO BAC ∠=∠时，PBO ABC ∆∆∽过A 作AH BC ⊥于H，则2AH AB ==EP OB AH BC ∴=，=，3t ∴=431OE ∴=-=2(13)P ∴-，（3）,AD AC ODA OAC ⊥∴∆∆∽OD OA OA OC∴=，224OD ∴= 1OD ∴=，5CD ∴=，(01)D ，，设直线AM 的解析式为y kx b =+则201k b b -+=⎧⎨=⎩解得121k b ⎧=⎪⎨⎪=⎩ ∴直线AM 的解析式为112y x =+ 设21(4)2Q m m m --，，则1(1)2R m m +，QR CD ∥，∴当QR CD =时，C 、D 、Q 、R 四点构成平行四边形 2114(1)522m m m ∴---+=解得32m ±= 或2111(4)522m m m +---= 解得0m =（舍去）或3m =∴当32m ±=或3m =时，C 、D 、Q 、R 四点构成平行四边形。

【初中数学】因动点产生的平行四边形问题

例 2014年河南省中考第23题如图1，抛物线y ＝－x 2＋bx ＋c 与x 轴交于A (－1, 0)、B (5, 0)两点，直线334y x =-+与y 轴交于点C ，与x 轴交于点D ，点P 是x 轴上方的抛物线上的一个动点，过点P 作PF ⊥x 轴于点F ，交直线CD 于点E ．设点P 的横坐标为m ．（1）求抛物线的解析式；（2）若PE ＝5EF ，求m 的值；（3）若点E ′是点E 关于直线PC 的对称点，是否存在点P ，使点E ′落在y 轴上？若存在，请直接写出相应的点P的坐标；若不存在，请说明理由．图1动感体验请打开几何画板文件名“14河南23”，拖动点P 运动，可以体验到，PE 与EF 的比值，有两个时刻等于5．当点E ′落在y 轴上时，四边形PE ′CE 是菱形．思路点拨1．用含有m 的式子表示PE 、EF 的长，注意EF 存在两种情况．2．第（3）题我们这样来思考：假如点E ′落在了点C 上方的某个位置，那么∠EC E ′其实是确定的，作角平分线就得到了点P 的位置．点P 确定了，就可以确定点E 、E ′的准确位置．此时比较容易观察到菱形PE ′CE ．根据EC ＝EP 解方程的时候，转化为m 的四次方程，把这个四次方程用开平方法转化为两个二次方程．解得到m 的四个根．这四个根的几何意义是当点E ′在C 上方时，角平分线所在直线与抛物线有两个交点；当点E ′在C 下方时，角平分线所在直线与抛物线也有两个交点．注意舍去x 轴下方的解．满分解答（1）因为抛物线y ＝－x 2＋bx ＋c 与x 轴交于A (－1, 0)、B (5, 0)两点，所以y ＝－(x ＋1)(x －5)＝－x 2＋4x ＋5．（2）点P 的横坐标为m ，那么P (m ,－m 2＋4m ＋5)，E (m ,334m -+)，F (m , 0)．所以22319(45)(3)244PE m m m m m =-++--+=-++．若PE ＝5EF ，存在两种情况：如图2，当E 在F 上方时，334EF m =-+．解方程219325(3)44m m m -++=-+，得m ＝2，或132m =（点P 在x 轴下方，舍去）．如图3，当E 在F 下方时，334EF m =-．解方程219325(3)44m m m -++=-，得m =m =（点P 在x 轴下方，舍去）．图2 图3（3）点P 的坐标为111(,)24-，或(4,5)，或(33)．考点伸展第（3）题的思路是这样的：如图4，当点E ′落在y 轴上时，四边形PE ′CE 是菱形．这是因为：根据对称性，CE ＝CE ′，∠PCE ＝∠PCE ′．又因为PE //CE ′，所以∠PCE ＝∠CPE ′．所以∠PCE ′＝∠CPE ′．所以CE ′＝PE ′．所以四边形PE ′CE 是平行四边形．所以四边形PE ′CE 是菱形．由E (m ,334m -+)、C (0, 3)，得2222325()416EC m m m =+-=．而21924PE m m =-++，由EP ＝EC ，可得两个方程：解方程2195244m m m -++=，得12m =-，或m ＝4（如图4所示）．解方程2195244m m m -++=-，得3m =或3m =+P 在x 轴下方，舍去）（如图5所示）．图4 图5例 2014年连云港市中考第26题已知二次函数y＝x2＋bx＋c，其图像抛物线交x轴于A(1, 0)、B(3, 0)两点，交y轴于点C．直线l过点C，且交抛物线于另一点E（点E不与A、B重合）．（1）求此二次函数关系式；（2）若直线l1经过抛物线的顶点D，交x轴于点F，且l1//l，则以C、D、E、F为顶点的四边形能否为平行四边形？若能，求出点E的坐标；若不能，请说明理由；（3）若过点A作AG⊥x轴，交直线l于点G，联结OG、BE，试证明OG//BE．动感体验请打开几何画板文件名“14连云港26”，拖动点E在抛物线上运动，可以体验到，以C、D、E、F为顶点的四边形有四次机会成为平行四边形．思路点拨1．四个点C、D、E、F中，C、D是确定的，以CD为分类标准，分两种情况讨论平行四边形．CD为对角线时，CF//ED；CD为边时，CD//EF．2．在坐标平面内，如果有平行线，那么构造直角边与坐标轴平行的直角三角形，通过三角比进行运算比较简便．满分解答（1）因为抛物线y＝x2＋bx＋c交x轴于A(1, 0)、B(3, 0)两点，所以y＝(x－1)(x－3)＝x2－4x＋3．（2）由y＝x2－4x＋3＝(x－2)2－1，得顶点D的坐标为(2,－1)．如图1，如果CF//ED，过点E作x轴的垂线，过点D作x轴的平行线，两条直线交于点H，那么△EDH≌△CFO．所以EH＝CO＝3，DH＝FO．设FO的长为m，那么点E的坐标可以表示为(2＋m, 2)．将E(2＋m, 3)代入y＝(x－2)2－1，得m2－1＝2．解得m所以点E的坐标为(2（如图1），或(2（如图2）．图1 图2如图3，如果CD//EF，那么△EFN≌△CDM．因此EN＝CM＝4，FN＝DM＝2．设OF＝m，那么点E的坐标可以表示为(m－2, 4)．所以(m－4)2－1＝4．解得m＝4．所以点E 的坐标为(2, 4)（如图3），或(2,4)（如图4）．图3 图4（3）如图5，设点E 的坐标为(x , x 2－4x ＋3)．过点G 、E 分别向y 轴作垂线，垂足分别为G ′、E ′，那么''''CG CE GG EE =．所以233(43)1G y x x x ---+=．解得y G ＝x －1．过点E 作EK ⊥x 轴于K ．因为24313EK x x x BK x -+==--，1GA x OA =-，所以EK GABK OA =．因此tan ∠EBK ＝tan ∠GOA ．所以∠EBK ＝∠GOA ，OG //BE ．图5考点伸展第（3）题也可以这样思考：如图5，设过点C (0, 3)的直线l 的解析式为y ＝kx ＋3．联立抛物线的解析式y ＝x 2－4x ＋3，可以将点E 的坐标表示为(k ＋4, k 2＋4k ＋3)．点G 是直线x ＝1和直线y ＝kx ＋3的交点，所以G (1,k ＋3)．于是243343EK k k k BK k ++==++-，3GA k OA =+，所以EK GABK OA =．例 2014年日照市中考第24题已知抛物线2y bx =++A (2, 0)，顶点为点P ，与x 轴的另一交点为点B ．（1）求b 的值，求出点P 、B 的坐标；（2）如图1，在直线y =上是否存在点D ，使四边形OPBD 为平行四边形？若存在，求出点D 的坐标；若不存在，请说明理由；（3）在x 轴下方的抛物线上是否存在点M ，使△AMP ≌△AMB ？如果存在,试举例验证你的猜想；如果不存在，试说明理由．图1动感体验请打开几何画板文件名“14日照24”，拖动点D 运动，可以体验到，四边形OPBD 可以成为平行四边形．拖动点M 运动，可以体验到，当△AMP ≌△AMB 时，点M 落在∠BAP 的平分线上．思路点拨1．有平行四边形，必然可以构造出两个全等的直角三角形，直角边与坐标轴平行．2．△AMP 与△AMB 有公共边AM ，如果△AMP ≌△AMB ，那么直线AM 就是对称轴．满分解答（1）将A (2, 0)代入2y x bx =++得20b +=．解得b =-．所以2y -+2812)x x -+2)(6)x x =--24)x --因此(4,P -，(6,0)B ．（2）如图2，过点P 作PE ⊥x 轴，垂足为E ．由于tan ∠OBP ＝PE BE =，所以BP 与直线y =平行．因此当BD//PO时，四边形OPBD为平行四边形．因此OD＝PB．过点D作DF⊥x轴，垂足为F．因为BP＝OD，所以DF＝PE＝OF＝BE＝2．所以点D的坐标为(2,．图2 图3 图4（3）如图4，由A(2, 0)、(4,P-、(6,0)B，得AB＝4，AP4．所以AB＝AP．因此∠BAP的平分线与抛物线的交点M，就满足△AMP≌△AMB．考点伸展第（3）题也可以用方程来解：设点D的坐标为()x．由OD＝PB，得OD2＝PB2．所以x2＋3x2＝16．解得x＝±2．当x＝2时，如图2所示。

因动点产生的平行四边形--课件

（1）若点E、F同时运动， A
D
当t为何值时，四边形
F
AECF是平行四边形；
E
O
B
C
新课探究
例2、如图,平行四边形ABCD的对角线AC、BD 相交于点O,BD=12cm,AC=8cm,E在线段BO上从点B以1cm/s的速度运动,点F在线段OD上从点O 以2cm/s的速度运动.设运动时间为t秒.
（2）在（1）的条件下，
巩固练习
如图，在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm, BC=30cm,动点P从A开始沿AD边向D以1cm/s的速度运动动点Q从点C开始沿CB边向B以3cm/s的速度运动.P、Q 分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为t秒．
(2)当t为何值时，四边形ABQP为矩形？
AOB 90
AB2 AO2 BO2 42 62 52 AB 2 13
∴当 AB= 2 13 时, 四边形AECF是菱形
A
D
F
EO
B
C
巩固练习
如图，在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm, BC=30cm,动点P从A开始沿AD边向D以1cm/s的速度运动动点Q从点C开始沿CB边向B以3cm/s的速度运动.P、Q 分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为t秒． (1)当t为何值时，四边形PQCD为平行四边形？
当t等于多少时,以 P、Q和四边形OABC中的其中两个顶点为顶点所形成的四边形
y CB
Q
为平行四边形?能否构成菱形
或者矩形？
OP
Ax
D

初三数学专题动点问题

因动点产生的平行四边形问题1、如图，已知抛物线y＝－x2＋bx＋c经过A(0, 1)、B(4, 3)两点．（1）求抛物线的解析式；（2）求tan∠ABO的值；（3）过点B作BC⊥x轴，垂足为C，在对称轴的左侧且平行于y轴的直线交线段AB 于点N，交抛物线于点M，若四边形MNCB为平行四边形，求点M的坐标．2、如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B(1, 0)、C(3, 0)、D(3, 4)．以A为顶点的抛物线y＝ax2＋bx＋c过点C．动点P从点A出发，沿线段AB向点B运动，同时动点Q从点C出发，沿线段CD向点D运动．点P、Q的运动速度均为每秒1个单位，运动时间为t秒．过点P作PE⊥AB交AC于点E．（1）直接写出点A的坐标，并求出抛物线的解析式；（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？（3）在动点P、Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C、Q、E、H为顶点的四边形为菱形？请直接写出t的值．3、已知平面直角坐标系xOy （如图），一次函数334y x =+的图象与y 轴交于点A ，点M 在正比例函数32y x =的图象上，且MO ＝MA ．二次函数 y ＝x 2＋bx ＋c 的图象经过点A 、M ．（1）求线段AM 的长；（2）求这个二次函数的解析式；（3）如果点B 在y 轴上，且位于点A 下方，点C 在上述二次函数的图象上，点D 在一次函数334y x =+的图象上，且四边形ABCD 是菱形，求点C 的坐标．4、将抛物线c 1：233y x =-+沿x 轴翻折，得到抛物线c 2，如图所示．（1）请直接写出抛物线c 2的表达式；（2）现将抛物线c 1向左平移m 个单位长度，平移后得到新抛物线的顶点为M ，与x 轴的交点从左到右依次为A 、B ；将抛物线c 2向右也平移m 个单位长度，平移后得到新抛物线的顶点为N ，与x 轴的交点从左到右依次为D 、E ．①当B 、D 是线段AE 的三等分点时，求m 的值；②在平移过程中，是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理由．5、如图1，抛物线23y ax ax b =-+经过A （－1，0），C （3，2）两点，与y 轴交于点D ，与x 轴交于另一点B 。

函数图象中的存在性问题----因动点产生的平行四边形

函数图象中的存在性问题——因动点产生的平行四边形例26 如图，在平面直角坐标系中，以坐标原点O 为圆心，2为半径画圆，P 是⊙O 上一动点且在第一象限内，过点P 作⊙O 的切线，与x 、y 轴分别交于点A 、B 。

求证：（1）、△OBP 与△OPA 相似；（2）、当点P 为AB 中点时，求出P 点坐标；（3）、在⊙O 上是否存在一点Q ，使得以Q 、O 、A 、P 为顶点的四边形是平行四边形。

若存在，试求出Q 点坐标；若不存在，请说明理由。

Py xB A O 2121-1-1例24．如图，抛物线223y x x =-++与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C ，顶点为D .（1）直接写出A 、B 、C 三点的坐标和抛物线的对称轴；（2）连接BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点，过点P 作PF DE ∥交抛物线于点F ，设点P 的横坐标为m ；①用含m 的代数式表示线段PF 的长，并求出当m 为何值时，四边形PEDF 为平行四边形？ ②设BCF △的面积为S ，求S 与m 的函数关系式.例27：:在平面直角坐标系中，已知抛物线经过A )0,4(-，B )4,0(-，C )0,2(三点．（1）求抛物线的解析式；（2）若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值．（3）若点P 是抛物线上的动点，点Q 是直线x y -=上的动点，判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标．例252009-2010北京大兴区九年级（上）期末数学试卷【023】如图，在梯形ABCD 中，24AD BC AD BC ==∥，，，点M 是AD 的中点，MBC △是等边三角形．（1）求证：梯形ABCD 是等腰梯形；（2）动点P 、Q 分别在线段BC 和MC 上运动，且60MPQ =︒∠保持不变．设PC x MQ y ==，，求y 与x 的函数关系式；（3）在（2）中：①当动点P 、Q 运动到何处时，以点P 、M 和点A 、B 、C 、D 中的两个点为顶点的四边形是平行四边形？并指出符合条件的平行四边形的个数；②当y 取最小值时，判断PQC △的形状，并说明理由．【033】已知抛物线22y x x a =-+（0a <）与y 轴相交于点A ，顶点为M .直线12y x a =-分别与x 轴，y 轴相交于B C ，两点，并且与直线AM 相交于点N .(1)填空：试用含a 的代数式分别表示点M 与N 的坐标，则()()M N ，，，；(2)如图，将NAC △沿y 轴翻折，若点N 的对应点N ′恰好落在抛物线上，AN ′与x 轴交于点D ，连结CD ，求a 的值和四边形ADCN 的面积；(3)在抛物线22y x x a =-+（0a <）上是否存在一点P ，使得以P A C N ，，，为顶点的四边形是平行四边形？若存在，求出P 点的坐标；若不存在，试说明理由.23（2012奉贤二模）．已知：直角坐标平面内有点A (-1，2)，过原点O 的直线l ⊥OA ，且与过点A 、O 的抛物线相交于第一象限的B 点，若OB =2OA 。

5.因动点产生的平行四边形问题[6页][001]

4因动点产生的平行四边形问题

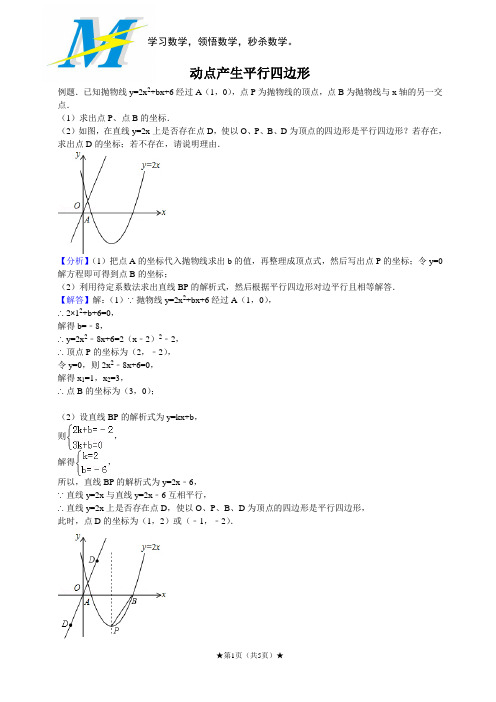
动点产生平行四边形例题．已知抛物线y=2x2+bx+6经过A（1，0），点P为抛物线的顶点，点B为抛物线与x轴的另一交点．（1）求出点P、点B的坐标．（2）如图，在直线y=2x上是否存在点D，使以O、P、B、D为顶点的四边形是平行四边形？若存在，求出点D的坐标；若不存在，请说明理由．【分析】（1）把点A的坐标代入抛物线求出b的值，再整理成顶点式，然后写出点P的坐标；令y=0解方程即可得到点B的坐标；（2）利用待定系数法求出直线BP的解析式，然后根据平行四边形对边平行且相等解答．【解答】解：（1）∵抛物线y=2x2+bx+6经过A（1，0），∴2×12+b+6=0，解得b=﹣8，∴y=2x2﹣8x+6=2（x﹣2）2﹣2，∴顶点P的坐标为（2，﹣2），令y=0，则2x2﹣8x+6=0，解得x1=1，x2=3，∴点B的坐标为（3，0）；（2）设直线BP的解析式为y=kx+b，则，解得，所以，直线BP的解析式为y=2x﹣6，∵直线y=2x与直线y=2x﹣6互相平行，∴直线y=2x上是否存在点D，使以O、P、B、D为顶点的四边形是平行四边形，此时，点D的坐标为（1，2）或（﹣1，﹣2）．练习：1．已知等腰梯形ABOC在直角坐标系中如图所示，AB∥OC，OB=2，OA=．（1）求点C的坐标；（2）求经过点B，O，C的抛物线解析式；（3）若点P为（2）中所求抛物线上一动点，点Q为y轴上一动点，请探索是否存在点P和点Q，使得以B，C，P，Q为顶点的四边形是平行四边形？若存在，请求出所有对应的P，Q的坐标；若不存在，请说明理由．2．（2011•梅州）如图，已知抛物线y=x2﹣4x+3与x 轴交于两点A、B，其顶点为C．（1）对于任意实数m，点M（m，﹣2）是否在该抛物线上？请说明理由；（2）求证：△ABC是等腰直角三角形；（3）已知点D在x轴上，那么在抛物线上是否存在点P，使得以B、C、D、P为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．3．（2012•宜宾）如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．（1）求抛物线顶点A的坐标；（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状；（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．4．（2015秋•台安县期中）如图，抛物线y=﹣x2+bx+c经过点A，B，C，已知点A（﹣1，0），点C （0，3）．（1）求抛物线的表达式；（2）P为线段BC上一点，过点P作y轴的平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；（3）设E是抛物线上的一点，在x轴上是否存在点F，使得A，C，E，F为顶点的四边形是平行四边形？若存在，求点E，F的坐标；若不存在，请说明理由．5．（2015秋•诸暨市校级月考）如图是二次函数y=（x+m）2+k的图象，其顶点坐标为M（1，﹣4）．（1）求出图象与x轴的交点A，B的坐标；（2）在二次函数的图象上是否存在点P，在对称轴存在点Q，使以A，B，P，Q四点构成的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．6．（2015•三亚校级模拟）如图，抛物线y=与x轴交于A，B两点，与y轴交于点C，且OA=2，OC=3．（1）求抛物线的解析式；（2）作Rt△OBC的高OD，延长OD与抛物线在第一象限内交于点E，求点E的坐标；（3）在x轴上方的抛物线上，是否存在一点P，使得四边形OBEP是平行四边形？若存在，求出点P 的坐标；若不存在，请说明理由．7．已知，二次函数y=（x+2）2的图象与x轴交于点A，与y轴交于点B．（1）求点A、点B的坐标；（2）求S△AOB；（3）求对称轴方程；（4）在对称轴上是否存在一点P，使以P，A，O，B为顶点的四边形为平行四边形？若存在，求P 点坐标；若不存在，请说明理由．1.P(-1,-3分之根号3)q（0,3分之4倍根号3）；p（-3，根号三）q（0,2倍根号三）；p（3,5倍根号三）q（0,4倍根号三）2.P的坐标是（2﹣，1）或（2+，1）．3.P（﹣2，﹣7）或P（4，﹣1）使以点A、B、D、P为顶点的四边形是平行四边形4.点E的坐标为：，E4（2，3）F的坐标是：，F4（﹣3，0）．5.求的P点坐标为：（1，﹣4）、（﹣3，12），（5，12）．6.存在一点P（﹣1，2）使得四边形OBEP是平行四边形7.点P的坐标为（﹣2，4）或（﹣2，﹣4）时，以P，A，O，B为顶点的四边形为平行四边形．。

--中考压轴题--1.4因动点产生的平行四边形问题含答案

１.4 因动点产生的平行四边形问题例1 成都市中考第28题如图1,在平面直角坐标系中,抛物线y=ａx２-2aｘ－３a（a＜0）与x轴交于A、Ｂ两点(点A在点Ｂ的左侧)，通过点A的直线l:y＝kx+b与ｙ轴负半轴交于点C，与抛物线的另一种交点为D，且CD=4AC.(1）直接写出点Ａ的坐标，并求直线l的函数体现式（其中ｋ、b用含a的式子表达)；（2）点Ｅ是直线l上方的抛物线上的动点,若△ACE的面积的最大值为,求a的值;(3）设Ｐ是抛物线的对称轴上的一点，点Q在抛物线上，以点A、Ｄ、Ｐ、Ｑ为顶点的四边形能否成为矩形？若能，求出点P的坐标;若不能，请阐明理由.图１备用图例2 陕西省中考第24题如图1,已知抛物线C:y＝－ｘ2＋bx＋ｃ通过A(－3,0)和Ｂ(0, 3）两点.将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为Ｎ.(1)求抛物线C的体现式；(２)求点Ｍ的坐标;(3）将抛物线C平移到抛物线Ｃ′,抛物线C′的顶点记为Ｍ′，它的对称轴与x轴的交点记为N′.如果以点M、N、M′、Ｎ′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C 如何平移?为什么?图1例3 上海市松江区中考模拟第24题如图１，已知抛物线y=-x2+bx＋c通过Ａ(0, 1)、B(4, 3）两点.（1）求抛物线的解析式;(2）求tan∠ABO的值；（3）过点B作BC⊥x轴,垂足为C，在对称轴的左侧且平行于y轴的直线交线段AB于点N，交抛物线于点M,若四边形MNCB为平行四边形,求点M的坐标．图1例4 福州市中考第２１题如图1，在Rt△ＡBC中，∠C=90°，AＣ＝６,BC=8,动点P从点A开始沿边AC向点C 以每秒１个单位长度的速度运动,动点Ｑ从点C开始沿边CB向点Ｂ以每秒2个单位长度的速度运动,过点P作PD/／BC,交AB于点D,联结ＰQ．点Ｐ、Ｑ分别从点A、C同步出发，当其中一点达到端点时，另一点也随之停止运动，设运动的时间为ｔ秒(t≥0)．(1）直接用含t的代数式分别表达:QＢ=＿___＿_＿,ＰＤ=__＿＿___；（2）与否存在t的值，使四边形PDBQ为菱形？若存在,求出t的值；若不存在，阐明理由,并探究如何变化点Q的速度（匀速运动）,使四边形PDBQ在某一时刻为菱形,求点Ｑ的速度；(3）如图2,在整个运动过程中,求出线段ＰQ的中点M所通过的途径长.图1 图2例５烟台市中考第2６题如图1，在平面直角坐标系中，已知矩形AＢCD的三个顶点B(1,　０)、C(3,　０)、D(3，4).以A为顶点的抛物线y＝ax２＋ｂx+c过点C．动点P从点Ａ出发，沿线段AＢ向点B运动，同步动点Q从点C出发，沿线段CＤ向点Ｄ运动.点P、Ｑ的运动速度均为每秒１个单位,运动时间为t秒.过点P作ＰＥ⊥AB交AC于点E.(１）直接写出点Ａ的坐标,并求出抛物线的解析式；（２）过点E作EＦ⊥AD于F,交抛物线于点G，当ｔ为什么值时,△ＡCG的面积最大？最大值为多少？（３）在动点Ｐ、Q运动的过程中，当ｔ为什么值时，在矩形ABCD内(涉及边界)存在点H，使以C、Q、E、H为顶点的四边形为菱形?请直接写出t的值.图１例6 上海市中考第２４题已知平面直角坐标系ｘOy (如图1)，一次函数的图象与y 轴交于点Ａ，点Ｍ334y x =+在正比例函数的图象上，且M Ｏ=M Ａ．二次函数32y x =y =x ２+ｂx +c 的图象通过点A 、M ．（1)求线段AM 的长;(2）求这个二次函数的解析式;（3)如果点Ｂ在y 轴上,且位于点Ａ下方，点Ｃ在上述二次函数的图象上，点D 在一次函数的图象上，且四边形ABCD 是菱形,求点Ｃ334y x =+的坐标．图1例7 江西省中考第24题将抛物线c 1:ｘ轴翻折，得到抛物线ｃ２,如图1所示.2y =（1）请直接写出抛物线c ２的体现式；（2)现将抛物线c 1向左平移m 个单位长度,平移后得到新抛物线的顶点为Ｍ，与ｘ轴的交点从左到右依次为A 、B ;将抛物线c 2向右也平移m 个单位长度,平移后得到新抛物线的顶点为Ｎ，与x 轴的交点从左到右依次为D 、E ．①当B 、D 是线段AE 的三等分点时，求m 的值；②在平移过程中,与否存在以点A 、Ｎ、E 、Ｍ为顶点的四边形是矩形的情形？若存在,祈求出此时ｍ的值;若不存在,请阐明理由．图11.4 因动点产生的平行四边形问题答案例1 成都市中考第28题如图1，在平面直角坐标系中，抛物线ｙ=ａｘ２-2ax－3ａ(a＜0)与x轴交于A、Ｂ两点（点Ａ在点B的左侧),通过点A的直线ｌ:y=kx＋ｂ与y轴负半轴交于点C，与抛物线的另一种交点为D，且CD＝４AＣ.（１）直接写出点Ａ的坐标，并求直线ｌ的函数体现式(其中k、b用含a的式子表达）；（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为，求ａ的值；(3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点Ａ、D、P、Q为顶点的四边形能否成为矩形？若能,求出点P的坐标;若不能，请阐明理由．图１备用图动感体验请打开几何画板文献名“1５成都28”，拖动点E 在直线AD 上方的抛物线上运动,可以体验到，当ＥC ⊥AC 时，△A ＣE 的面积最大．点击屏幕左下角的按钮“第(3）题”,拖动点H 在y 轴正半轴运动，观测点Q 和Ｑ′，可以看到点Q 和点Q ′都可以落在抛物线上．思路点拨１.过点E 作x 轴的垂线交AD 于Ｆ,那么△AEF 与△CEF 是共底的两个三角形．2．以AD 为分类原则讨论矩形,当AD 为边时,A Ｄ与QP 平行且相等，对角线AP ＝ＱＤ;当AD 为对角线时,ＡD 与ＰQ 互相平分且相等．满分解答(1)由y ＝ax 2-2ａx -３a ＝a (x +1)(x －３)，得A (-1, 0)．由CD =４AC ，得x D ＝4．因此D (4, 5ａ).由A (-１,　0)、Ｄ（４，　5a ）,得直线l 的函数体现式为y ＝ax ＋a ．(２)如图1，过点E 作x 轴的垂线交A Ｄ于F .设E (ｘ, ax ２-2ａx -3ａ）,F (x , ax +ａ),那么EF =ｙE -ｙF =ax 2－3ａx －4a .由S △AC Ｅ=Ｓ△ＡEF －Ｓ△ＣEF =11()()22E A E C EF x x EF x x ---===，1()2C A EF x x -21(34)2ax ax a --21325(228a x a --得△ＡCE 的面积的最大值为．解方程,得.258a -25584a -=25a =-（3）已知A (-１, 0)、Ｄ(4, 5a)，x P ＝1,以AD 为分类原则，分两种状况讨论:①如图2，如果AD 为矩形的边,那么ＡＤ／/ＱＰ，A Ｄ＝ＱP ，对角线AP =QD ．由x D －x A ＝x Ｐ-ｘQ ，得x Q ＝-4．当x ＝-4时,ｙ=a （x +１)(x －３)=2１a ．因此Q (-4, 21a ).由y D －y Ａ＝y P -y Ｑ,得y P =26a .因此P (1, ２6a ）.由AP ２=Q Ｄ2，得22+(26ａ）2＝８2＋（１6ａ）2．整顿,得7a 2＝1.因此Ｐ．a =(1，②如图3，如果AD 为矩形的对角线，那么AD 与PQ 互相平分且相等．由ｘD +x A =x P +ｘQ ,得x Ｑ=2.因此Q (2,－3ａ）．由ｙD +y A =y P ＋y Q ，得y P =８a .因此Ｐ(1，　8a )．由A Ｄ2=PQ ２，得52＋(５a )2=１2+(11a )2．整顿，得4a ２=1．因此.此时P .12a =-(14)-，图1 图2 图3考点伸展第(3）题也可以这样解.设P (1，n ).①如图２，当AD 时矩形的边时,∠QPD =90°,因此，即.AM DN MD NP =5553a n a -=-解得．因此P ．因此Q ．235a n a +=235(1,)a a +3(4,)a -将Q 代入y ＝a (x ＋1)(ｘ-3)，得.因此3(4,a -321a a=a =②如图３,当AD 为矩形的对角线时,先求得Q (2，-3a ）．由∠AQD =90°，得，即．解得.AG QK GQ KD=32335a a a -=--12a =-例２陕西省中考第24题如图１,已知抛物线Ｃ:ｙ=－x 2＋b ｘ＋c 通过Ａ（－3,０)和B （０，　3)两点．将这条抛物线的顶点记为M ，它的对称轴与x 轴的交点记为N .(1)求抛物线C 的体现式;（2)求点M 的坐标;（3)将抛物线Ｃ平移到抛物线C ′，抛物线C ′的顶点记为M ′,它的对称轴与x 轴的交点记为N ′.如果以点Ｍ、N 、Ｍ′、Ｎ′为顶点的四边形是面积为1６的平行四边形，那么应将抛物线C 如何平移？为什么？图1动感体验请打开几何画板文献名“１4陕西２4”,拖动右侧的点Ｍ′上下运动,可以体验到,以点M 、Ｎ、M ′、Ｎ′为顶点的平行四边形有四种状况.思路点拨１.抛物线在平移的过程中,M′N′与MN 保持平行,当M′N′=MN ＝4时，以点M 、N 、M ′、N ′为顶点的四边形就是平行四边形.２.平行四边形的面积为16,底边MN ＝4，那么高NN′＝4．３.M′N′=4分两种状况：点M′在点Ｎ′的上方和下方.　４．N Ｎ′＝4分两种状况:点N′在点N 的右侧和左侧.满分解答(1)将Ａ(-3，0)、B (0, 3）分别代入y =-ｘ2+b ｘ＋ｃ，得解得b ＝-2，ｃ＝3．930,3.b c c --+=⎧⎨=⎩因此抛物线C 的体现式为ｙ＝-x ２-２x +3．(２）由y ＝－x 2-２ｘ+３＝－(x+1)２+４,得顶点Ｍ的坐标为(－1,４）．（3)抛物线在平移过程中，M′N′与MN 保持平行,当M′N′＝MN=4时,以点M 、N 、Ｍ′、N ′为顶点的四边形就是平行四边形．由于平行四边形的面积为１6,因此M Ｎ边相应的高NN′=4．那么以点M 、N 、M ′、N ′为顶点的平行四边形有4种状况：抛物线C 直接向右平移4个单位得到平行四边形ＭN Ｎ′M ′（如图2）;抛物线C 直接向左平移４个单位得到平行四边形MNN ′M ′（如图2）;抛物线C 先向右平移4个单位，再向下平移８个单位得到平行四边形MNM ′Ｎ′（如图3）；抛物线C 先向左平移４个单位,再向下平移8个单位得到平行四边形M ＮM ′N ′（如图3).图2 图3考点伸展本题的抛物线C 向右平移m 个单位，两条抛物线的交点为Ｄ，那么△MM ′D 的面积Ｓ有关m 有如何的函数关系?如图4,△MM ′D 是等腰三角形，由M (－1,４）、M ′（-１+m ,　４),可得点D 的横坐标为.22m -将代入y =－（x ＋1）２＋4，得．因此DH ＝．22m x -=244m y =-+244m -因此S ＝.2311(4)2248m m m m -=-图4例3 上海市松江区中考模拟第24题如图1,已知抛物线ｙ=-x２＋bx＋c通过A(0，　１)、Ｂ（４, ３)两点．（１）求抛物线的解析式;(2)求taｎ∠ＡBO的值；(3）过点Ｂ作BC⊥x轴,垂足为C,在对称轴的左侧且平行于y轴的直线交线段AB于点N,交抛物线于点M，若四边形MNＣB为平行四边形,求点Ｍ的坐标．图1动感体验请打开几何画板文献名“１3松江24”,拖动点N在直线ＡＢ上运动，可以体验到,以M、Ｎ、Ｃ、B为顶点的平行四边形有4个,符合MN在抛物线的对称轴的左侧的平行四边形MNCＢ只有一种．请打开超级画板文献名“13松江２4”，拖动点N在直线ＡB上运动，可以体验到,MN有4次机会等于３，这阐明以M、Ｎ、Ｃ、B为顶点的平行四边形有４个，而符合MN在抛物线的对称轴的左侧的平行四边形ＭNCＢ只有一种．思路点拨１．第(2)题求∠ABO的正切值,要构造涉及锐角∠ABO的角直角三角形．2．第(3）题解方程ＭN＝ｙM－ｙN＝BC,并且检查x的值与否在对称轴左侧．满分解答（1）将Ａ(０, 1)、Ｂ(４,　3)分别代入y ＝－x 2＋ｂx ＋c ,得解得，ｃ=1．1,164 3.c b c =⎧⎨-++=⎩92b =因此抛物线的解析式是.2912y x x =-++(2)在R ｔ△B ＯC 中,OC ＝4，BC =3，因此OB =5．如图2，过点Ａ作AH ⊥O Ｂ,垂足为H .在R ｔ△AOH 中，OA ＝1，,4sin sin 5AOH OBC ∠=∠=因此．图24sin 5AH OA AOH =⋅∠=因此，. 35OH =225BH OB OH =-=在Rt △ABH 中，．4222tan 5511AH ABO BH ∠==÷=(3）直线AB 的解析式为.112y x =+设点Ｍ的坐标为，点N 的坐标为，29(,1)2x x x -++1(,1)2x x +那么．2291(1)(1)422MN x x x x x =-++-+=-+当四边形MN ＣB 是平行四边形时,MN ＝ＢC =3.解方程-ｘ2＋4x =3，得x ＝1或x ＝3.由于x =３在对称轴的右侧（如图4），因此符合题意的点Ｍ的坐标为（如图3）．9(1,2图3 图4考点伸展第（3）题如果改为:点Ｍ是抛物线上的一种点，直线M Ｎ平行于y 轴交直线A Ｂ于Ｎ,如果Ｍ、N 、B 、C 为顶点的四边形是平行四边形,求点M 的坐标.那么求点M 的坐标要考虑两种状况:MN ＝y Ｍ－y Ｎ或MN ＝y N －ｙM ．由y Ｎ-y M =4x －x 2,解方程x 2－4x ＝3，得(如图5）.2x =±因此符合题意的点Ｍ有4个：,,，.9(1,211(3,)2(2(2+图５例４福州市中考第2１题如图１，在Rt △A ＢＣ中,∠C ＝90°,ＡC ＝6,ＢC =8,动点P 从点Ａ开始沿边AC 向点C 以每秒1个单位长度的速度运动，动点Q 从点Ｃ开始沿边C Ｂ向点B 以每秒２个单位长度的速度运动，过点P 作ＰD //BC ,交AB 于点Ｄ,联结PQ .点P 、Q 分别从点A 、C 同步出发,当其中一点达到端点时,另一点也随之停止运动,设运动的时间为t 秒(t ≥0).（1)直接用含t 的代数式分别表达：Q Ｂ=__＿＿___,P Ｄ＝__＿____;（2）与否存在t 的值，使四边形PDBQ 为菱形?若存在,求出ｔ的值;若不存在，阐明理由，并探究如何变化点Q 的速度（匀速运动),使四边形PD ＢＱ在某一时刻为菱形，求点Q 的速度;(３）如图２,在整个运动过程中，求出线段PQ 的中点M 所通过的途径长．图1 图2动感体验请打开几何画板文献名“１２福州２１”，拖动左图中的点P 运动，可以体验到，PQ 的中点M 的运动途径是一条线段.拖动右图中的点Q 运动，可以体验到,当ＰＱ//AB 时,四边形PDB Ｑ为菱形．请打开超级画板文献名“1２福州2１”，拖动点Ｑ向上运动，可以体验到，PQ 的中点M 的运动途径是一条线段．点击动画按钮的左部，Q 的速度变成1．07，可以体验到,当PQ //ＡB 时，四边形PDBQ 为菱形．点击动画按钮的中部，Ｑ的速度变成1.思路点拨1．菱形ＰDB Ｑ必须符合两个条件,点P 在∠ＡB Ｃ的平分线上,ＰQ /／A Ｂ.先求出点P 运动的时间t ,再根据PQ ／/AB ，相应线段成比例求ＣQ 的长，从而求出点Q 的速度．2．探究点M 的途径,可以先取两个极端值画线段,再验证这条线段是不是点Ｍ的途径.满分解答（1)ＱB ＝8-2t ,PD ＝．43t （2）如图3，作∠ABC 的平分线交C Ａ于Ｐ,过点P 作PQ //AB 交BC 于Ｑ,那么四边形PDBQ 是菱形.过点P 作ＰE ⊥AB ，垂足为Ｅ,那么BE ＝ＢC =8．在Rt △ABC 中,AC ＝6，B Ｃ＝8,因此AB ＝１０. 在R ｔ△APE 中,,因此． 23cos 5AE A AP t ===103t =图3当ＰQ //ＡB 时，，即.解得.CQ CP CB CA =106386CQ -=329CQ =因此点Q 的运动速度为．3210169315÷=（３)以C 为原点建立直角坐标系．如图4,当t =０时，ＰQ 的中点就是AC 的中点E (3,0）.如图5,当t ＝4时，PQ 的中点就是ＰB 的中点F (1,4).直线E Ｆ的解析式是y =-２x +6．如图6，PQ 的中点M 的坐标可以表达为（，t ）.经验证,点M (，ｔ）在直线EF 62t -62t -上.因此PQ 的中点M的运动途径长就是线段E Ｆ的长，E Ｆ=图4 图5 图６考点伸展第（3)题求点M 的运动途径尚有一种通用的措施是设二次函数：当t ＝2时，PQ 的中点为（2,2).设点M 的运动途径的解析式为ｙ=ax 2+bx ＋ｃ,代入E (３，0)、Ｆ(1，4）和（2,２),得解得ａ=０，b =-2，c =６.930,4,42 2.a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩因此点M 的运动途径的解析式为y ＝－２x ＋6.例５烟台市中考第26题如图1，在平面直角坐标系中，已知矩形ABＣD的三个顶点B(1，0)、C(３, ０)、Ｄ(3, 4).以A为顶点的抛物线y＝ax2+bｘ+c过点C.动点P从点A出发,沿线段AＢ向点B运动，同步动点Ｑ从点C出发，沿线段CD向点D运动．点P、Ｑ的运动速度均为每秒1个单位,运动时间为t秒．过点P作PE⊥AB交AC于点E．(1）直接写出点A的坐标,并求出抛物线的解析式；(2)过点E作EF⊥AD于F,交抛物线于点G，当t为什么值时,△AＣＧ的面积最大?最大值为多少？(3）在动点P、Q运动的过程中,当t为什么值时,在矩形AＢCD内(涉及边界)存在点Ｈ，使以C、Q、E、H为顶点的四边形为菱形?请直接写出t的值．图1动感体验请打开几何画板文献名“1２烟台２６”,拖动点P在AＢ上运动，可以体验到，当P在AB 的中点时,△ACG的面积最大.观测右图，我们构造了和△ＣEQ中心对称的△FＱE和△ECH′，可以体验到,线段EQ的垂直平分线可以通过点C和F,线段CE的垂直平分线可以通过点Q和Ｈ′，因此以C、Q、E、H为顶点的菱形有2个.请打开超级画板文献名“12烟台26”,拖动点Ｐ在AＢ上运动,可以体验到，当P在AB的中点时,即t=2,△ACＧ的面积获得最大值1．观测CＱ,EQ,EC的值,发现以C、Q、E、Ｈ为顶点的菱形有2个．点击动画按钮的左部和中部,可得菱形的两种精确位置。

因动点产生的平行四边形问题

因动点产生的平行四边形问题例1（上海市中考第24题）已知平面直角坐标系xOy（如图1），一次函数334y x=+的图像与y轴交于点A，点M在正比例函数32y x=的图像上，且MO＝MA．二次函数y＝x2＋bx＋c的图像经过点A、M．（1）求线段AM的长；（2）求这个二次函数的解析式；（3）如果点B在y轴上，且位于点A下方，点C在上述二次函数的图像上，点D在一次函数334y x=+的图像上，且四边形ABCD是菱形，求点C的坐标．图1满分解答（1）当x＝0时，3334y x=+=，所以点A的坐标为(0，3)，OA＝3．如图2，因为MO＝MA，所以点M在OA的垂直平分线上，点M的纵坐标为32．将32y=代入32y x=，得x＝1．所以点M的坐标为3(1,)2．因此AM=．（2）因为抛物线y＝x2＋bx＋c经过A(0，3)、M3(1,)2，所以3,31.2cb c=⎧⎪⎨++=⎪⎩解得52b=-，3c=．所以二次函数的解析式为253 2y x x=-+．（3）如图3，设四边形ABCD为菱形，过点A作AE⊥CD，垂足为E．在Rt△ADE中，设AE＝4m，DE＝3m，那么AD＝5m．因此点C的坐标可以表示为(4m，3－2m)．将点C(4m，3－2m)代入253 2y x x=-+，得23216103m m m-=-+．解得12m=或者m＝0（舍去）．因此点C的坐标为（2，2）．图2 图3考点伸展如果第（3）题中，把“四边形ABCD是菱形”改为“以A、B、C、D为顶点的四边形是菱形”，那么还存在另一种情况：如图4，点C的坐标为727 (,) 416．图4例2（江西省中考第24题）将抛物线c1：2y=x轴翻折，得到抛物线c2，如图1所示．（1）请直接写出抛物线c2的表达式；（2）现将抛物线c1向左平移m个单位长度，平移后得到新抛物线的顶点为M，与x 轴的交点从左到右依次为A、B；将抛物线c2向右也平移m个单位长度，平移后得到新抛物线的顶点为N，与x轴的交点从左到右依次为D、E．①当B、D是线段AE的三等分点时，求m的值；②在平移过程中，是否存在以点A、N、E、M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由．图1满分解答（1）抛物线c2的表达式为2y=（2）抛物线c1：2y=+x轴的两个交点为(－1，0)、(1，0)，顶点为．抛物线c2：2y=x轴的两个交点也为(－1，0)、(1，0)，顶点为(0,．抛物线c1向左平移m个单位长度后，顶点M的坐标为(m-，与x轴的两个交点为(1,0)A m--、(1,0)B m-，AB＝2．抛物线c2向右平移m个单位长度后，顶点N的坐标为(,m，与x轴的两个交点为(1,0)D m-+、(1,0)E m+．所以AE＝(1＋m)－(－1－m)＝2(1＋m)．①B、D是线段AE的三等分点，存在两种情况：情形一，如图2，B在D的左侧，此时123AB AE==，AE＝6．所以2(1＋m)＝6．解得m＝2．情形二，如图3，B在D的右侧，此时223AB AE==，AE＝3．所以2(1＋m)＝3．解得12m=．图 2 图 3 图4②如果以点A、N、E、M为顶点的四边形是矩形，那么AE＝MN＝2OM．而OM2＝m2＋3，所以4(1＋m)2＝4(m2＋3)．解得m＝1（如图4）．考点伸展第（2）题②，探求矩形ANEM，也可以用几何说理的方法：在等腰三角形ABM中，因为AB＝2，AB所以△ABM是等边三角形．同理△DEN是等边三角形．当四边形ANEM是矩形时，B、D两点重合．因为起始位置时BD＝2，所以平移的距离m＝1．例3（2010年河南省中考第23题）如图1，在平面直角坐标系中，已知抛物线经过A(－4,0)、B(0,－4)、C(2,0)三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△MAB的面积为S，求S关于m的函数关系式，并求出S的最大值；（3）若点P是抛物线上的动点，点Q是直线y＝－x上的动点，判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．图1 图2满分解答(1) 因为抛物线与x 轴交于A(－4,0)、C(2,0)两点，设y ＝a(x ＋4)(x －2)．代入点B(0,－4)，求得12a =．所以抛物线的解析式为211(4)(2)422y x x x x =+-=+-． (2)如图2，直线AB 的解析式为y ＝－x －4．过点M 作x 轴的垂线交AB 于D ，那么2211(4)(4)222MD m m m m m =---+-=--．所以2142MDA MDB S S S MD OA m m ∆∆=+=⋅=--2(2)4m =-++．因此当2m =-时，S 取得最大值，最大值为4．(3) 如果以点P 、Q 、B 、O 为顶点的四边形是平行四边形，那么PQ//OB ，PQ ＝OB ＝4．设点Q 的坐标为(,)x x -，点P 的坐标为21(,4)2x x x +-．①当点P 在点Q 上方时，21(4)()42x x x +---=．解得2x =-±此时点Q 的坐标为(22-+-（如图3），或(22--+（如图4）． ②当点Q 在点P 上方时，21()(4)42x x x --+-=．解得4x =-或0x =（与点O 重合，舍去）．此时点Q 的坐标为(－4,4) （如图5）．图3 图4 图5考点伸展在本题情境下，以点P、Q、B、O为顶点的四边形能成为直角梯形吗？如图6，Q(2,－2)；如图7，Q(－2,2)；如图8，Q(4,－4)．图6 图7 图8例4（山西省中考第26题）在直角梯形OABC中，CB//OA，∠COA＝90°，CB＝3，OA＝6，BA＝分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系．（1）求点B的坐标；（2）已知D、E分别为线段OC、OB上的点，OD＝5，OE＝2EB，直线DE交x轴于点F．求直线DE的解析式；（3）点M是（2）中直线DE上的一个动点，在x轴上方的平面内是否存在另一点N，使以O、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．图1 图2满分解答(1)如图2，作BH⊥x轴，垂足为H，那么四边形BCOH为矩形，OH＝CB＝3．在Rt△ABH中，AH＝3，BA＝，所以BH＝6．因此点B的坐标为(3,6)．(2) 因为OE＝2EB，所以223E Bx x==，243E By y==，E(2,4)．设直线DE 的解析式为y ＝kx ＋b ，代入D(0,5)，E(2,4)，得5,2 4.b k b =⎧⎨+=⎩ 解得12k =-，5b =．所以直线DE 的解析式为152y x =-+．(3) 由152y x =-+，知直线DE 与x 轴交于点F(10,0)，OF ＝10，DF ＝①如图3，当DO 为菱形的对角线时，MN 与DO 互相垂直平分，点M 是DF 的中点．此时点M 的坐标为(5,52)，点N 的坐标为(－5,52)． ②如图4，当DO 、DN 为菱形的邻边时，点N 与点O 关于点E 对称，此时点N 的坐标为(4,8)．③如图5，当DO 、DM 为菱形的邻边时，NO ＝5，延长MN 交x 轴于P ．由△NPO ∽△DOF ，得NP PO NODO OF DF==，即510NP PO ==．解得NP =，PO =N 的坐标为(-．图3 图4考点伸展如果第（3）题没有限定点N 在x 轴上方的平面内，那么菱形还有如图6的情形．图5 图6例 5（福州市中考第21题）如图1，等边△ABC 的边长为4，E 是边BC 上的动点，EH ⊥AC 于H ，过E 作EF ∥AC ，交线段AB 于点F ，在线段AC 上取点P ，使PE ＝EB ．设EC ＝x （0＜x≤2）．（1）请直接写出图中与线段EF 相等的两条线段（不再另外添加辅助线）；（2）Q 是线段AC 上的动点，当四边形EFPQ 是平行四边形时，求平行四边形EFPQ 的面积（用含x 的代数式表示）；（3）当（2）中的平行四边形EFPQ 面积最大值时，以E 为圆心，r 为半径作圆，根据⊙E 与此时平行四边形EFPQ 四条边交点的总个数，求相应的r 的取值范围．图1满分解答（1）BE 、PE 、BF 三条线段中任选两条．（2）如图2，在Rt △CEH 中，∠C ＝60°，EC ＝x ，所以x EH 23=．因为PQ ＝FE ＝BE ＝4－x ，所以x x x x EH PQ S EFPQ 3223)4(232+-=-=⋅=平行四边形．（3）因为x x S EFPQ 32232+-=平行四边形322232+--=）（x ，所以当x ＝2时，平行四边形EFPQ 的面积最大．此时E 、F 、P 分别为△ABC 的三边BC 、AB 、AC 的中点，且C 、Q 重合，四边形EFPQ 是边长为2的菱形（如图3）．图2 图3过点E 点作ED ⊥FP 于D ，则ED ＝EH ＝3．如图4，当⊙E 与平行四边形EFPQ 的四条边交点的总个数是2个时，0＜r ＜3；如图5，当⊙E 与平行四边形EFPQ 的四条边交点的总个数是4个时，r ＝3；如图6，当⊙E 与平行四边形EFPQ 的四条边交点的总个数是6个时，3＜r ＜2；如图7，当⊙E 与平行四边形EFPQ 的四条边交点的总个数是3个时，r ＝2时；如图8，当⊙E 与平行四边形EFPQ 的四条边交点的总个数是0个时，r ＞2时．图4 图5 图6图7 图8考点伸展本题中E 是边BC 上的动点，设EC ＝x ，如果没有限定0＜x≤2，那么平行四边形EFPQ 的面积是如何随x 的变化而变化的？事实上，当x ＞2时，点P 就不存在了，平行四边形EFPQ 也就不存在了．因此平行四边形EFPQ 的面积随x 的增大而增大．例6（年江西省中考第24题）如图1，抛物线322++-=x x y 与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C ，顶点为D ．（1）直接写出A 、B 、C 三点的坐标和抛物线的对称轴；（2）连结BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点，过点P 作PF//DE 交抛物线于点F ，设点P 的横坐标为m ．①用含m 的代数式表示线段PF 的长，并求出当m 为何值时，四边形PEDF 为平行四边形？②设△BCF 的面积为S ，求S 与m 的函数关系．图1满分解答（1）A （－1，0），B （3，0），C （0，3）．抛物线的对称轴是x ＝1．（2）①直线BC 的解析式为y ＝－x ＋3．把x ＝1代入y ＝－x ＋3，得y ＝2．所以点E 的坐标为（1，2）．把x ＝1代入322++-=x x y ，得y ＝4．所以点D 的坐标为（1，4）．因此DE=2．因为PF//DE ，点P 的横坐标为m ，设点P 的坐标为)3,(+-m m ，点F 的坐标为)32,0(2++-m m ，因此m m m m m FP 3)3()32(22+-=+--++-=．当四边形PEDF 是平行四边形时，DE=FP ．于是得到232=+-m m ．解得21=m ，12=m （与点E 重合，舍去）．因此，当m=2时，四边形PEDF 是平行四边形时．②设直线PF 与x 轴交于点M ，那么OM+BM=OB=3．因此BM FP OM FP S S S S CPF BPF BCF ⋅+⋅=+==∆∆∆2121 m m m m 29233)3(2122+-=⨯+-=． m 的变化范围是0≤m≤3．图2 图3考点伸展在本题条件下，四边形PEDF 可能是等腰梯形吗？如果可能，求m 的值；如果不可能，请说明理由．如图4，如果四边形PEDF 是等腰梯形，那么DG=EH ，因此E P F D y y y y -=-．于是2)3()32(42-+-=++--m m m ．解得01=m （与点CE 重合，舍去），12=m （与点E 重合，舍去）．因此四边形PEDF 不可能成为等腰梯形．图4例 7（太原市中考第29题）如图，在平面直角坐标系xOy 中，直线与交于点A ，分别交x 轴于点B 和点C ，点D 是直线AC 上的一个动点．（1）求点A 、B 、C 的坐标．（2）当△CBD 为等腰三角形时，求点的坐标．（3）在直线AB 上是否存在点E ，使得以点E 、D 、O 、A 为顶点的四边形是平行四边形？如果存在，直接写出BECD的值；如果不存在，请说明理由．图1满分解答（1）在1y x =+中，当0y =时，1x =-，所以点的坐标为(1,0)-．在334y x =-+中，当0y =时，4x =，所以点的坐标为（4，0）．解方程组1,33,4y x y x =+⎧⎪⎨=-+⎪⎩ 得87x =，157y =．所以点的坐标为815,77⎛⎫ ⎪⎝⎭．（2）因为点D 在直线334y x =-+上，设点D 的坐标为3(,3)4x x +．当△CBD 为等腰三角形时，有以下三种情况：1y x =+334y x =-+D B C A①如图2，当DB ＝DC 时，设底边BC 上的高为DM ．在Rt △CDM 中，1522CM BC ==，所以31548DM CM ==．这时点D 的坐标为315,28⎛⎫ ⎪⎝⎭． ②如图3，当CD ＝CB ＝5时，点D 恰好落在y 轴上，此时点D 的坐标为（0，3）．根据对称性，点D 关于点C 对称的点D ′的坐标为（8，－3）．③如图4，当BC ＝BD 时，设BC 、DC 边上的高分别为DM 、BN ．在Rt △BCN 中，BC ＝5，所以CN ＝4，因此DC ＝8．在Rt △DCM 中，DC ＝8，所以32455DM DC ==，43255DM DC ==．这时点D 的坐标为1224,55⎛⎫- ⎪⎝⎭．综上所述，当△CBD 为等腰三角形时，点D 的坐标为315,28⎛⎫⎪⎝⎭、（0，3）、（8，－3）或1224,55⎛⎫- ⎪⎝⎭．图2 图3 图4（3）如图5，以点E 、D 、O 、A 为顶点的四边形是平行四边形有以下三种情形： ①当四边形AEOD为平行四边形时，BE CD =． ②当四边形ADEO为平行四边形时，10BE CD =． ③当四边形AODE为平行四边形时，20BE CD =．考点伸展如图5，第（3）题这样解：在△ABC 中，已知BC ＝5，BC 边上的高为157，解得AB，AC ＝257．由'15BE BO BA BC ==，得'BE =BE =图5由45CD CO CA CB ==，得207CD =，所以30'7CD =．结合图5，可以计算出20BE CD =，10或20．。

二次函数(2-1)-由动点生的平行四边行问题

抛物线与直线形（2）——由动点生成的平行四边形问题一、基本图形剖析１．若只有一个动点例：如图，点A（１，３），B（-１，０），C（４，１），点D为平面直角坐标系上一点，若以ＡＢＣＤ为顶点的四边形是平行四边形，求点D的坐标分析1：若AB为边，则过C点作AB的平行线，于是就有两种情况①AC为对角线②BC为对角线分析2：若AC为边，则过B点作AE的平行线，于是就有两种情况①BC为对角线（同分析1 的②）②AB为对角线分析3：若BC为边，则过A点作BC的平行线，于是就有两种情况①AC为对角线（同分析1 的①）①AB为对角线（同分析2 的②）分析4：小结２．若有两个动点例：如图，点A（１，３），B（t，０），C（４，１），点D为平面直角坐标系上一点，若以ＡＢＣＤ为顶点的四边形是平行四边形，求点D的坐标分析1：若AB为边，则过C点作AB的平行线，于是就有两种情况①AC为对角线②BC为对角线分析2：若AC为边，则过B点作AE的平行线，于是就有两种情况①BC为对角线（同分析1 的②）②AB为对角线分析3：若BC为边，则过A点作BC的平行线，于是就有两种情况①AC为对角线（同分析1 的①）①AB为对角线（同分析2 的②）二、二次函数与平行四边形经典例题【例1】如图，抛物线322--=x x y 与x 轴交B A ,两点（A 点在B 点左侧），直线l 与抛物线交于C A ,两点，其中C 点的横坐标为2．（1）求B A ,两点的坐标及直线AC 的函数表达式；（2）P 是线段AC 上的一个动点，过P 点作y 轴的平行线交抛物线于E 点，求线段PE 长度的最大值；（3）点G 抛物线上的动点，在x 轴上是否存在点F ，使G F C A ,,,这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F 点坐标；如果不存在，请说明理由．思路点拨对于（3），AF 可能为平行四边形的边或对角线，故四个点能组成四边形的情况由多种，需全面讨论。

因动点产生的平行四边形问题ppt课件

M1
x
M2
分类讨论数形结合
2
M3
如图，在平面直角坐标系中，已知抛物线过点A(-1,0) ，B(0,-5), C（3，4），（2）求经过A,B,C三点的抛物线函数解析式，若点P是抛物线上的动点，点Q是直线y=-x上的动点，若以B、O、P、Q 为顶点的四边形为平行四边形，求相应的点Q的坐标；
归纳：已知两个定点，再找两个点组成平行四边形。 1、如果两定点连接的线段为一边，则两动点连接的线段
与已知边平行且相等。 2、如果两定点连接线段没有确定为一边的情况下要进行
分类讨论，这条线段可以为边或对角线。
3
(3)、在（2）中所求的所有平行四边形中，探究：是否存在以OB为边的菱形？若存在，请予以证明；若不存在，那能否把直线y=-x绕着原点作适当旋转,使以OB为边、P、Q为顶点的四边形是菱形？一共有几个菱形？请直接写出点P在第一象限时，点Q的坐标和对应的直线的解析式。
1
例:如图，在平面直角坐标系中，已知抛物线过点A(-1,0), B(0,-5),C（3，4）.
（1）点M是坐标平面内的一点，若
以A、B、C、M为顶点的四边形为平
行四边形，写出点M的坐标；
y
M1(2， 9)或M2（4，-1）或M3（-4， -9）
方法归纳：已知三个点确定，找第四个点组成平行四边形时候，通常采用的方法有图形变换中的平移法、中点构造法、三角形全等等方法。
两种重要数学思想：分类讨论数形结合
6
4
能力提升
如图：在平面直角坐标系中，以坐标原点O为圆心，2 为半径画圆，P是圆O上一动点且在第一象限内，过点P作圆O的切线，与x轴、y轴分别交于点A、B.在圆O上求一点Q，使得以Q、O、A、P为顶点的四边形为平行四边形。

《动点中的平行四边形生成问题》微课程设计方案

《动点中的平行四边形生成问题》微课程设计方案
环节3：分析方程的获得过程
环节6：变二反三
问题变式2是将点的运动从平行线中移动到三角形的边上，由此提高学生对于“先定平行，再定方程”的理解和应用；同时学生可以自行先解决问题再继续观看视频：
问题的变式2：已知矩形ABCD中，AD=8，AB=4，AF=5，且四边形AFCE是菱形，动点
P，Q分别从A，C两点出发，沿△AFB和△CDE各边匀速运动一周，即点P自
A→F→B→A停止，点Q自C→D→E→C停止，已知点P的速度为每秒5个单位,点Q的速度为每秒4个单位,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t 的值将原来的线性运动方式变成平面图形上的运动，再次增加问题的难度，既让学生体会分类讨论思想，又让学生能够在分类讨论的过程中体会速度在问题中的作用，发展学生的分类讨论思想与方程思想，化归转化思想。

环节7：总结提升。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

因动点产生的平行四边形
问题：
（1）以平面上的点A,点B，点C为顶点，求构成平行四边形的第四个点。

（2）平面直角坐标系中已知平行四边形的三个点，求第四个点的坐标，要分类讨论。

例1: 在平面直角坐标系中，点A(1,0),B（4，0）,点C在y轴的正半轴上，且OB=2OC (1)求直线BC的解析式；
(2）在直角坐标平面内确定点M，使得以点M,A,B,C为顶点的四边形是平行四边形，请写出点M的坐标。

例2: 如图，在平面直角坐标系中，点O是坐标原点，正
比例函数y=kx的图象与双曲线交于点A，且点A
的横坐标为．
(1)求k的值．
(2)将直线y=kx向上平移4个单位得到直线BC，直线BC
分别交x轴、y轴于点B、C，如点D在直线BC上，在平
面直角坐标系中求一点P，使以O、B、D、P为顶点的四边
形是菱形．
例3: 如图，Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片，点O与原点重合，点A在x轴上，点C在y轴上，OC=，∠CAO=30度．将Rt△OAC
折叠，使OC边落在AC边上，点O与点D重合，折痕为CE．
(1)求折痕CE所在直线的解析式；
(2)求点D的坐标；
(3)设点M为直线CE上的一点，过点M作AC的平行线，交y
轴于点N，是否存在这样的点M，使得以M、N、D、C为顶点
的四边形是平行四边形？若存在，请求出符合条件的点M的
坐标；若不存在，请说明理由．
例4如图，在平面直角坐标系中，抛物线经过A(-1，0)，B(3，0)，C(0，-1)三点．
(1)求该抛物线的表达式；
(2)点Q在y轴上，点P在抛物线上，要使以点Q、P、A、B为顶点的四边形是平行四边形，求所有满足条件的点P的坐标．
例5: 在平面直角坐标系中，已知抛物线经过A(-4，0)，B(0，-4)，C(2，0)三点．
(1)求抛物线的解析式；
(2)若点P是抛物线上的动点，点Q是直线y=-x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
例6:已知：如图①，在Rt△ABC 中，∠C=90°，AC= 4cm，BC=3cm，点P由B 出发沿BA 方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t(s)(0<t<2)，解答下列问题：
(1)当t为何值时，QP∥BC ？
(2)设AQP 的面积为y(cm2) ，求y与t之间的函数关系式；
(3)是否存在某一时刻t，使线段PQ恰好把Rt△ACB 的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；
(4)如图②，连接PC，并把PQC沿QC翻折，得到四边形PQP'C ，那么是否存在某一时刻t ，使四边形PQP'C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．
旁触类通
1.如图，点A(m，m+1)，B(m+3，m-1)都在反比例函数的图象上．
(1)求m，k的值；
(2)如果M为x轴上一点，N为y轴上一点，以点A，B，M，N为
顶点的四边形是平行四边形，试求直线MN的函数表达式．
2.如图，对称轴为x=的抛物线经过点A(6，0)和B(0，4)．
(1)求抛物线解析式；
(2)设点E(，)是抛物线上一动点，且位于第四象限，四边形OEAF
是以OA为对角线的平行四边形，当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形？
（3）是否存在点E，使平行四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．
3、如图，在平面直角坐标系xOy中，半径为的⊙C与x轴交
于A(-1，0)、B(3，0)两点，且点C在x轴的上方．
(1)求圆心C的坐标；
(2)已知一个二次函数的图象经过点A、B、C，求这二次函数的解
析式；
(3)设点P在y轴上，点M在(2)的二次函数图象上，如果以点P、M、A、B为顶点的四边形是平行四边形，请你直接写出点M的坐标．
4、如图1，在Rt△ABC中，∠C=90°，AC=6，BC=8，动点P从点A开始沿边AC向点C以1个单位长度的速度运动，动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动，过点P作PD∥BC，交AB于点D，连接PQ分别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒(t≥0)．
(1)直接用含t的代数式分别表示：QB= _________ ，PD= _________ ．
(2)是否存在t的值，使四边形PDBQ为菱形？若存在，求出t的值；若不存在，说明理由．并探究如何改变Q的速度(匀速运动)，使四边形PDBQ在某一时刻为菱形，求点Q的速度；(3)如图2，在整个运动过程中，求出线段PQ中点M所经过的路径
长．
5、如图，抛物线经过A(-1，0)，B(5，0)，C(0，−)三点．
(1)求抛物线的解析式；
(2)在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；
(3)点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
6、如图，抛物线y=-x2+bx+c与直线y=x+2交于C、D两点，其中点C在y轴上，点D的坐
标为(3，)．点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F．
(1)求抛物线的解析式；
(2)若点P的横坐标为m，当m为何值时，以O、C、P、F为顶点的四边形是平行四边形？请说明理由．
(3)若存在点P，使∠PCF=45°，请直接写出相应的点P的坐标．。