复习单元过关平行性测试卷(理科)(立体几何
必修2立体几何单元测试题及答案

立体几何单元测验题一、选择题:把每小题的正确答案填在第二页的答题卡中,每小题4分,共60分 1.一个圆锥的底面圆半径为3,高为4,则这个圆锥的侧面积为A .152πB .10πC .15πD .20π 2.C B A ,,表示不同的点,l a ,表示不同的直线,βα,表示不同的平面,下列推理错误的是A .ααα⊂⇒∈∈∈∈lB l B A l A ,,, B .,,,AB l l AB l αβαβαβ=⊥⊂⊥⇒⊥C .,l A l A αα⊄∈⇒∉D .βαβα与不共线,,且⇒∈∈C B A C B A C B A ,,,,,,重合3.直线c b a ,,相交于一点,经过这3条直线的平面有A .0个B .1个C .3个D .0个或1个 4.下列说法正确的是A .平面α和平面β只有一个公共点B .两两相交的三条直线共面C .不共面的四点中,任何三点不共线D .有三个公共点的两平面必重合5. 直线b a 与是一对异面直线,a B A 是直线,上的两点,b D C 是直线,上的两点,N M ,分别是BD AC 和的中点,则a MN 和的位置关系为A .异面直线B .平行直线C .相交直线D .平行直线或异面直线6.已知正方形ABCD ,沿对角线ABC AC ∆将折起,设AD 与平面ABC 所成的角为α,当α最大时,二面角D AC B --等于( )A .090 B .060 C .045 D .030 7.已知异面直线b a ,分别在平面βα,内,且βα c =,直线c A .同时与b a ,相交 B .至少与b a ,中的一条相交 C .至多与b a ,中的一条相交 D .只能与b a ,中的一条相交 8.一个平面多边形的斜二侧图形的面积是S ,则这个多边形的面积是A B .2S C . D .4SMD'DCBA1A 9.直线l 在平面α外,则A .α//lB .α与l 相交C .α与l 至少有一个公共点D .α与l 至多有一个公共点10.如图,BD AB BD M AC M AB BD AC AB ,,平面,平面,⊥⊥⊂===1与平面M 成030角,则D C 、间的距离为( ) A .1 B .2 C .2 D .311.如果在两个平面内分别有一条直线,这两条直线互相平行,那么这两个平面的位置关系一定是A .平行B .相交C .平行或相交D .垂直相交 12.已知平面α及α外一条直线l ,下列命题中 (1)若l 垂直于α内的两条平行线,则α⊥l ;(2)若l 垂直于α内的所有直线,则α⊥l ;(3)若l 垂直于α内的两条相交直线,则α⊥l ;(4)若l 垂直于α内的任意一条直线,则α⊥l ;正确的有A .0 个B .1 个C .2个D .3个 13.与空间四点等距离的平面有A .7个B .2个C .9个D .7个或无穷多个 14.如果球的内接正方体的表面积为24,那么球的体积等于 A. B.C .D .315.直三棱柱111111ABC A B C AC AB AA AC A B-==中,,异面直线与 060所成的角为,则CAB ∠等于A . 090 B . 060 C .045 D .030姓名 班级 座位号二、解答题:(本大题共三个小题,共40分,要求写出求解过程) 16.(12分)在空间四边形ABCD 中,F E 、分别为BC AB 、中点。
2014高三理科数学单元过关(10)—立体几何

2014高三理科数学单元过关(10)考查单元:立体几何一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.三视图如图的几何体是 ( )A .三棱锥B .四棱锥C .四棱台D .三棱台 2.关于直线a 、b ,以及平面M 、N ,给出下列命题: ①若a ∥M ,b ∥M ,则a ∥b ;②若a ∥M ,b ⊥M ,则a ⊥b ; ③若a ∥b ,b ∥M ,则a ∥M ;④若a ⊥M ,a ∥N ,则M ⊥N . 其中正确命题的个数为 ( )A .0B .1C .2D .3 3.如果底面直径和高相等的圆柱的侧面积是S ,那么圆柱的体积等于 ( ) A.S 2S B.S 2S π C.S 4S D.S4Sπ4.如图,在正方体ABCD -A 1B 1C 1D 1中,若E 是AD 的中点,则直线A 1B 与直线C 1E 的位置关系是 ( ) A .平行 B .相交 C .共面 D .垂直5.已知两条不同直线l 1和l 2及平面α,则直线l 1∥l 2的一个充分条件是 ( ) A .l 1∥α且l 2∥α B .l 1⊥α且l 2⊥α C .l 1∥α且l 2⊄α D .l 1∥α且l 2⊂α 6.给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行; ②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; ③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,为真命题的是 ( ) A .①和② B .②和③ C .③和④ D .②和④7.一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的 两个全等的等腰直角三角形,则该几何体的外接球的表面积为 ( ) A .12π B .43π C .3π D .123π8.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,线段B 1D 1上 有两个动点E 、F ,且EF =12,则下列结论中错误..的是 ( ) A .AC ⊥BE B .EF ∥平面ABCDC .三棱锥A -BEF 的体积为定值D .△AEF 的面积与△BEF 的面积相等二、填空题(将答案填写在题中的横线上)9.如图是一个几何体的三视图.若它的体积是33,则a =________.10.在△ABC 中,∠ACB =90°,AB =8,∠ABC =60°,PC ⊥平面ABC ,PC =4,M 是AB 上一个动点,则PM 的最小值为________.11.如果三棱锥的三个侧面两两垂直,它们的面积分别为6 cm 2、4 cm 2、3 cm 2,那么它的外接球体积是________.12.如右图所示,点P 在正方形ABCD 所在平面外,PD ⊥平面ABCD ,PD =AD,则PA 与BD 所成角的度数为________.13.设P 是60°的二面角α-l -β内一点,PA ⊥α,PB ⊥β,A 、B 分别为垂足,PA =2, PB =4,则AB 的长是________. 14.如图所示,四棱锥P -ABCD的底面是一直角梯形,AB ∥CD ,CD =2AB , E 为PC 的中点,则BE 与平面PAD的位置 关系为________.三、解答题(解答应写出文字说明、证明过程或演算步骤)。
高三理科数学《立体几何》测试题带答案

高三理科数学《立体几何》测试题(带答案)1、如图,在C ∆AB 中,C 45∠AB =,点O 在AB 上,且2C 3OB =O =AB ,PO ⊥平面C AB ,D //A PO ,1D 2A =AO =PO . ()1求证://PB 平面C D O ;()2求二面角CD O --A 的余弦值.(1)证明:因为ABC PO 平面⊥,D//A PO,DA AB PO AB ⊥⊥所以4,21π=∠==AOD PO AO DA 所以又……………………2分 ,//4,,21PB OD OBP OP OB PO AO ,即所以即又π=∠==……………….4分 COD PB COD OD COD PB 平面所以平面平面又//,,⊂⊄。
……………….6分(2)解:过A 作,,,AN N CD MN M M DO AM 连接于作,过垂足为⊥⊥ 则的平面角。
即为二面角A CD O ANM --∠……………….8分,中,得,在直角中,得,在等腰直角设a MN COD a AM AOD a AD 3322=∆=∆=510cos 630=∠=∆ANM a AN AMN ,所以中,得在直角……………….12分2、如图,在棱长为2的正方体1111CD C D AB -A B 中,E 、F 分别为11D A 和1CC 的中点.()1求证:F//E 平面1CD A ;()2求异面直线F E 与AB 所成的角的余弦值;()3在棱1BB 上是否存在一点P ,使得二面角C P -A -B 的大小为30?若存在,求出BP 的长;若不存在,请说明理由.解:如图分别以DA 、DC 、DD 1所在的直线为x 轴、y 轴、z 轴建立空间直角坐标系D-xyz ,由已知得D (0,0,0)、A (2,0,0)、B (2,2,0)、C (0,2,0)、B 1(2,2,2)、D 1(0,0,2)、E (1,0,2 )、F (0,2,1).(1)取AD 1中点G ,则G (1,0,1),CG -→=(1,-2,1),又EF -→=(-1,2,-1),由EF -→=-→-CG ,∴EF -→与CG -→共线.从而EF∥CG,∵CG ⊂平面ACD 1,EF ⊄平面ACD 1,∴EF ∥平面ACD 1. ………………………………………………………………4分 (2) ∵AB =(0,2,0), cos<EF ,AB>=||||2EF AB EF AB ⋅==⋅, ∴异面直线EF 与AB 所成角的余弦值为36.…………………………………………………8分 (3)假设满足条件的点P 存在,可设点P (2,2,t )(0<t ≤2),平面ACP 的一个法向量为n =(x ,y ,z ),则0,0.n AC n AP ⎧⋅=⎪⎨⋅=⎪⎩ ∵AP =(0,2,t ), AC =(-2,2,0),∴220,20,x y y tz -+=⎧⎨+=⎩取2(1,1,)n t =-.易知平面ABC 的一个法向量1(0,0,2)BB =, 依题意知,<1BB ,n >=30°或<1BB ,n >=150°,∴|cos<1BB ,n4||-=,即22434(2)4t t =+,解得3t =∵(0,2]3∴在棱BB 1上存在一点P ,当BPP -AC -B 的大小为30°……………13分3、如图所示,在四棱锥CD P -AB 中,底面CD AB 为矩形,PA ⊥平面CD AB ,点E 在线段C P 上,C P ⊥平面D B E . ()1求证:D B ⊥平面C PA ;()2若1PA =,D 2A =,求二面角C B -P -A 的余弦值.(1) 证明:∵PA ABCD ⊥平面,BD ABCD ⊂平面 ∴PA BD ⊥.同理由PC BDE ⊥平面,可证得PC BD ⊥. 又PAPC P =,∴BD PAC ⊥平面.(2)解:如图,分别以射线AB ,AD ,AP 为x 轴,y 轴,z 轴的正半轴建立空间直角坐标系A xyz -.由(1)知BD PAC ⊥平面,又AC P A C ⊂平面, ∴BD AC ⊥.故矩形ABCD 为正方形,∴2AB BC CD AD ====. ∴00020022()()00(20001)()()A B C D P ,,,,,,,,,,,,,,. ∴ ()()()2,0,1,0,2,0,2,2,0PB BC BD ===-.设平面PBC 的一个法向量为(,,)n x y z =,则0n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩,即2000200x y z x y z +⋅-=⎧⎨⋅++⋅=⎩,∴20z xy =⎧⎨=⎩,取1x =,得(1,0,2)n =.∵BD PAC ⊥平面,∴(2,2,0)BD =-为平面PAC 的一个法向量.所以10cos ,10n BD n BD n BD⋅<>==-. 设二面角B PC A --的平面角为α,由图知02πα<<,则10cos cos ,D 10n α=B=∴二面角C B -P -A4、如图,平面CD AB ⊥平面D F A E ,其中CD AB 为矩形,D F A E 为梯形,F//D A E ,F F A ⊥E ,F D 2D 2A =A =E =.()1求异面直线F E 与C B 所成角的大小;()2若二面角F D A -B -的平面角的余弦值为13,求AB 的长.解:(1) 延长AD ,FE 交于Q .因为ABCD 是矩形,所以BC ∥AD ,所以∠AQF 是异面直线EF 与B C 所成的角.在梯形ADEF 中,因为DE ∥AF ,AF ⊥FE ,AF =2,DE =1得∠AQF =30°.………………………5分(2) 方法一:设AB =x .取AF 的中点G .由题意得 DG ⊥AF .因为平面ABCD ⊥平面ADEF ,A B ⊥AD ,所以AB ⊥平面ADEF ,所以AB ⊥DG .所以DG ⊥平面ABF . 过G 作GH ⊥BF ,垂足为H ,连结DH ,则DH ⊥BF , 所以∠DHG 为二面角A -BF-D 的平面角. 在直角△AGD 中,AD =2,AG =1,得DG 在直角△BAF中,由AB BF =sin ∠AFB =GH FG ,得GHx,所以GH.在直角△DGH 中,DGGH ,得DH =因为cos ∠DHG =GH DH =13,得x AB 15分方法二:设AB =x .以F 为原点,AF ,FQ 所在的直线分别为x 轴,y 轴建立空间直角坐标系Fxyz .则 F (0,0,0),A (-2,0,0),E (3,0,0),D (-10),B (-2,0,x ),所以DF =(10),BF =(2,0,-x ). 因为EF ⊥平面ABF所以平面ABF 的法向量可取1n =(0,1,0).设2n =(x 1,y 1,z 1)为平面BFD的法向量,则111120,0,x z x x -=⎧⎪⎨=⎪⎩所以,可取2n =1.因为cos<1n ,2n >=1212||||n n n n ⋅⋅=13,得xAB .5、如图,已知AB ⊥平面CD A ,D E ⊥平面CD A ,C ∆AB 为等边三角形, D D 2A =E =AB ,F 为CD 的中点. ()1求证:F//A 平面C B E ;()2求证:平面C B E ⊥平面CD E ;()3求直线F B 和平面C B E 所成角的正弦值.(1)证明:取CE 的中点G,连FG 、BG .可证得四边形GFAB 为平行四边形,则AF//BG即可证得AF//平面BCE. …………………………..(4分)(2)依题意证得BG ⊥平面CDE ,即可证得平面BCE ⊥平面CDE …….(8分) (3)解:设AD=DE=2AB=2,建立如图所示的坐标系A —xyz, 则A(0,0,0),C(2,0,0),B(0,0,1),D(1,3,0),E(1,3,2),F ()0,23,23 设平面BCE 的法向量为),,,(z y x =由0,0=⋅=⋅可取)2,3,1(-=,)1,23,23(-= 设BF 和平面BCE 所成的角为θ,则: sin θ42=……………………………(12分)6、如图,三棱柱111C C AB -A B 的底面是边长为4的正三角形,1AA ⊥平面C AB ,1AA =M 为11A B 的中点.()1求证:C M ⊥AB ;()2在棱1CC 上是否存在点P ,使得C M ⊥平面ABP ?若存在,确定点P 的位置;若不存在,请说明理由.()3若点P 为1CC 的中点,求二面角C B -AP -的余弦值.(1)解:取AB 中点O ,连结OM ,C O . M 为11A B 的中点 ∴1//MO A A1AA ⊥平面C AB ∴MO ⊥平面C AB∴MO ⊥AB …………2分7、如图,已知111C C AB -A B 是正三棱柱,它的底面边长和侧棱长都是2,D 为侧棱1CC 的中点,E 为11A B 的中点.()1求证:D AB ⊥E ;()2求直线11A B 到平面D AB 的距离;()3求二面角D C A -B -的正切值.(1)证明:连结C 1E,则C 1E ⊥A 1B 1, 又∵A 1B 1⊥C 1C ∴A 1B 1⊥平面EDC 1 ∴A 1B 1⊥DE, 而A 1B 1//AB ∴AB ⊥DE.(2) 取AB 中点为F,连结EF,DF,则EF ⊥AB ∴AB ⊥DF过E 作直线EH ⊥DF 于H 点,则EH ⊥平面DAB ∴EH 就是直线A 1B 1到平面DAB 的距离在矩形C 1EFC 中,∵AA 1=AB=2,∴EF=2,C 1E=3,DF=2, ∴在△DEF 中,EH=3,故直线A 1B 1到平面DAB 的距离为 3(3)过A 作AM ⊥BC 于M 点,则AM ⊥平面CDB 过M 作MN ⊥BD 于N 点,连结AN,则AN ⊥BD ∴∠ANM 即为所求二面角的平面角 在Rt △DCB 中,BC=2,DC=1,M 为BC 中点∴MN=55在Rt △AMN 中,tan ∠ANM=AMMN =158、如图,在直三棱柱111C C A B -AB 中,C AB ⊥A ,C 2AB =A =,14AA =,点D 是C B 的中点.()1求异面直线1A B 与1C D 所成角的余弦值;()2求平面1DC A 与平面1ABA 所成二面角的正弦值.(1)以},,{1→→→AA AC AB 为单位正交基底建立空间直角坐标系xyz A -, 则)0,0,0(A ,)0,0,2(B ,)0,2,0(C ,)4,0,0(1A ,)0,1,1(D ,)4,2,0(1C .)4,0,2(1-=∴→B A ,)4,1,1(1--=→D C10103182018,cos 111111==⋅>=<∴→→→→DC B A DC B AD C B A ∴异面直线B A 1与D C 1所成角的余弦值为10103. 6分(2))0,2,0(=→AC 是平面1ABA 的的一个法向量 设平面1ADC 的法向量为),,(z y x m =→,)0,1,1(=→AD ,)4,2,0(1=→AC ,由→→⊥AD m ,→→⊥1AC m 得 ⎩⎨⎧=+=+0420z y y x取1=z ,得2-=y ,2=x ,所以平面1ADC 的法向量为)1,2,2(-=→m . 设平面1ADC 与1ABA 所成二面角为θ .32324,cos cos =⨯-=⋅>=<=∴→→→→→mAC m AC m AC θ, 得35sin =θ. 所以平面1ADC 与1ABA 所成二面角的正弦值为35. 12分。
2023年高考备考三年 立体几何(解答题)(理科专用)(含答案)

又,1 ⊂ 平面11且相交,所以 ⊥ 平面11,
所以,,1两两垂直,以 B 为原点,建立空间直角坐标系,如图,
高考材料
高考材料
由〔1〕得 = 2,所以1 = = 2,1 = 2 2,所以 = 2,
角函数的根本关系计算可得;
(1)
证明:连接并延长交于点,连接、,
因为是三棱锥−的高,所以 ⊥ 平面,, ⊂ 平面,
所以 ⊥ 、 ⊥ ,
又 = ,所以 △ ≅ △ ,即 = ,所以∠ = ∠,
又因为, ⊂ 平面, ∩ = ,所以 ⊥ 平面,
因为 ⊂ 平面,所以平面 ⊥ 平面.
(2)
连接,由〔1〕知, ⊥ 平面,因为 ⊂ 平面,
1
所以 ⊥ ,所以 △ = 2 ⋅ ,
当 ⊥ 时,最小,即 △ 的面积最小.
则(0,2,0),1(0,2,2),(0,0,0),(2,0,0),所以1的中点(1,1,1),
则 = (1,1,1), = (0,2,0), = (2,0,0),
设平面的一个法向量 = (,,),则{
⋅ = + + = 0
,
⋅ = 2 = 0
以为坐标原点建立如下图的空间直角坐标系−,
则(1,0,0),(0, 3,0),(0,0,1),所以 = (−1,0,1), = (−1, 3,0),
设平面的一个法向量为 = (,,),
{
⋅ = − + = 0
则 ⋅ = − + 3 = 0 ,取 = 3,则 = (3, 3,3),
高考材料
高考材料
〔1〕证明: BF DE ;
〔2〕当 B1 D 为何值时,面 BB1C1C 与面 DFE 所成的二面角的正弦值最小
高三数学理科单元质检卷立体几何含答案
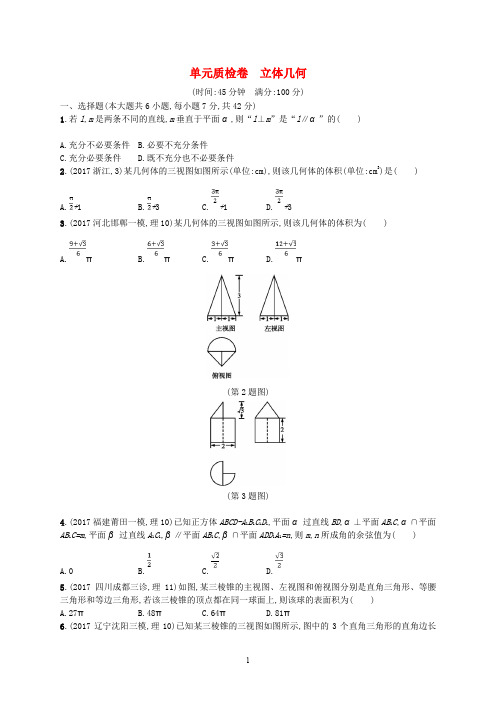
单元质检卷立体几何(时间:45分钟满分:100分)一、选择题(本大题共6小题,每小题7分,共42分)1.若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件2.(2017浙江,3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.+1B.+3C.+1D.+33.(2017河北邯郸一模,理10)某几何体的三视图如图所示,则该几何体的体积为()A.πB.πC.πD.π(第2题图)(第3题图)4.(2017福建莆田一模,理10)已知正方体ABCD-A1B1C1D1,平面α过直线BD,α⊥平面AB1C,α∩平面AB1C=m,平面β过直线A1C1,β∥平面AB1C,β∩平面ADD1A1=n,则m,n所成角的余弦值为()A.0B.C.D.5.(2017四川成都三诊,理11)如图,某三棱锥的主视图、左视图和俯视图分别是直角三角形、等腰三角形和等边三角形,若该三棱锥的顶点都在同一球面上,则该球的表面积为()A.27πB.48πC.64πD.81π6.(2017辽宁沈阳三模,理10)已知某三棱锥的三视图如图所示,图中的3个直角三角形的直角边长度已经标出,则在该三棱锥中,最短的棱和最长的棱所在直线所成角的余弦值为()A.B.C.D.(第5题图)(第6题图)二、填空题(本大题共2小题,每小题7分,共14分)7.(2017安徽安庆二模,理14)正四面体ABCD中,E,F分别为边AB,BD的中点,则异面直线AF,CE所成角的余弦值为.8.(2017山西太原二模,理15)已知三棱锥A-BCD中,AB=AC=BC=2,BD=CD=,点E是BC的中点,点A在平面BCD上的射影恰好为DE的中点,则该三棱锥外接球的表面积为.三、解答题(本大题共3小题,共44分)9.(14分)(2017河南郑州一中质检一,理18)如图,在三棱锥S-ABC中,平面SAB⊥平面ABC,△SAB是等边三角形,已知AC=2AB=4,BC=2.(1)求证:平面SAB⊥平面SAC;(2)求二面角B-SC-A的余弦值.10.(15分)(2017辽宁沈阳三模,理19)如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.(1)过B1作出三棱柱的截面,使截面垂直于AB,并证明;(2)求AC1与平面BCC1B1所成角的正弦值.11.(15分)(2017河南焦作二模,理19)在三棱柱ABC-A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AA1,A1B1上,且AE=,A1F=,CE⊥EF.(1)求证:平面ABB1A1⊥平面ABC;(2)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.参考答案单元质检卷立体几何1.B解析由“m⊥α且l⊥m”推出“l⊂α或l∥α”,但由“m⊥α且l∥α”可推出“l⊥m”,所以“l⊥m”是“l∥α”的必要不充分条件,故选B.2.A解析V=×3××π×12+×2×1+1,故选A.3.A解析由三视图可得,直观图为圆锥的与圆柱的组成的组合体,由图中数据可得几何体的体积为·π·12·π·12·2=π,故选A.4.D解析如图所示,∵BD1⊥平面AB1C,平面α过直线BD,α⊥平面AB1C,∴平面α即为平面DBB1D1.设AC∩BD=O,∴α∩平面AB1C=OB1=m.∵平面A1C1D过直线A1C1,与平面AB1C平行,而平面β过直线A1C1,β∥平面AB1C,∴平面A1C1D即为平面β.β∩平面ADD1A1=A1D=n,又A1D∥B1C,∴m,n所成角为∠OB1C,由△AB1C为正三角形,则cos∠OB1C=cos.故选D.5.C解析由三视图可知直观图如图所示.∵△ABC是边长为6的等边三角形,∴外接球的球心D在底面ABC的投影为△ABC的中心O.过点D作DE⊥VA于点E,则E为VA的中点,连接OA,DA,则DE=OA=×3=2,AE=VA=2,DA为外接球的半径r,∴r==4,∴外接球的表面积S=4πr2=64π.故选C.6.A解析由三视图还原原几何体如图.几何体是三棱锥A-BCD,满足平面ACD⊥平面BCD,且AD⊥CD,BC⊥CD.最短棱为CD,最长棱为AB.在平面BCD内,过点B作BE∥CD,且BE=CD,连接DE,∴四边形BEDC为正方形,可得AE=2,在Rt△AEB中,求得AB==3,∴cos∠ABE=.即最短的棱和最长的棱所在直线所成角的余弦值为.故选A.7.解析如图,连接CF,取BF的中点M,连接CM,EM,则ME∥AF,故∠CEM即为所求的异面直线所成角.不妨设这个正四面体的棱长为2,则AF=CE=CF=,EM=,CM=,∴cos∠CEM=.故答案为.8.π解析由题意,△BCD为等腰直角三角形,E是其外接圆的圆心,点A在平面BCD上的射影恰好为DE的中点F,则BF=,∴AF=,设球心到平面BCD的距离为h,则1+h2=,∴h=,r=, ∴该三棱锥外接球的表面积为4π×π.9.(1)证明在△BCA中,∵AB=2,CA=4,BC=2,∴AB2+AC2=BC2,故AB⊥AC.又平面SAB⊥平面ABC,平面SAB∩平面ABC=AB,∴AC⊥平面SAB.又AC⊂平面SAC,所以平面SAB⊥平面SAC.(2)解如图建立空间直角坐标系,A(0,0,0),B(2,0,0),S(1,0,),C(0,4,0),=(1,-4,),=(-2,4,0),=(0,4,0),设平面SBC的法向量n=(x,y,z),由则n=.设平面SCA的法向量m=(a,b,c),由∴m=(-,0,1),∴cos<n,m>=-,∴二面角B-SC-A的余弦值为.10.解 (1)设AB中点为O,连接OC,OB1,B1C,则截面OB1C为所求.证明:OC,OB1分别为△ABC,△ABB1的中线,所以AB⊥OC,AB⊥OB1,又OC,OB1为平面OB1C内的两条相交直线,所以AB⊥平面OB1C,(2)以O为原点,方向为x轴正方向建立如图所示的空间直角坐标系,易求得B(1,0,0),A(-1,0,0),C(0,,0),B1(0,0,),C1(-1,),=(1,-,0),=(1,0,-),=(0,),设平面BCC1B1的一个法向量为n=(x,y,z),由解得平面BCC1B1的一个法向量为n=(,1,1),|cos<,n>|=,所以AC1与平面BCC1B1所成角的正弦值为.11.(1)证明取AB的中点D,连接CD,DF,DE.∵AC=BC,D是AB的中点,∴CD⊥AB.∵侧面ABB1A1是边长为2的正方形,AE=,A1F=,∴A1E=,EF=,DE=,DF=,∴EF2+DE2=DF2,∴DE⊥EF,又CE⊥EF,CE∩DE=E,CE⊂平面CDE,DE⊂平面CDE,∴EF⊥平面CDE,又CD⊂平面CDE,∴CD⊥EF,又CD⊥AB,AB⊂平面ABB1A1,EF⊂平面ABB1A1,AB,EF为相交直线,∴CD⊥平面ABB1A1,又CD⊂平面ABC,∴平面ABB1A1⊥平面ABC.(2)解∵平面ABB1A1⊥平面ABC,∴三棱柱ABC-A1B1C1是直三棱柱,∴CC1⊥平面ABC.∵CA⊥CB,AB=2,∴AC=BC=.以C为原点,分别以CA,CB,CC1为x轴,y轴,z轴建立空间直角坐标系,如图所示.则A(,0,0),C(0,0,0),C1(0,0,2),E,F.∴=(-,0,2),.设平面CEF的法向量为n=(x,y,z),则∴令z=4,得n=(-,-9,4).∴·n=10,|n|=6,||=.∴cos<n,>=.∴直线AC1与平面CEF所成角的正弦值为.。
高二年数学(理科)《立体几何》单元测试卷

高二年数学(理科)《立体几何》单元测试卷一、选择题(共10小题,每小题5分,共50分,每个小题只有一个正确选项)1、现有四个图形①三角形 ②四边形 ③梯形 ④菱形.,可能不是平面图形的是( ) A.① B .② C.③ D .④2.直线和平面平行的性质定理的数学符号表示是( ) A .a ∥a b a ⇒=⋂⊂αββα,,∥b B . α⊄a ,a ∥b ,α⊂b ⇒a ∥α C .a ∥α,⇒⊂βa a ∥b D .a ∥α⇒=⋂b αβ,a ∥b3、如图,二面角βα--l 的大小为30°,α∈P ,点P 到β的距离为h ,则点P 到棱l 的距离为( )A.h B .3h C.21h D .2h 4、设a 、b 、c 表示直线,α、β、γ表示平面.给出四个命题( ) ① c ⊥a,a ∥b ⇒c ⊥b ②γ⊥α,α∥β⇒γ⊥β ③ a ⊥α,α∥β⇒a ⊥β ④a α⊥,a//b b α⇒⊥则正确命题的个数是( )A.4 B .3 C.2 D .15、教室内有根棍子,无论怎样放置,地面上总有这样的直线与棍子所在直线( ) A 、平行 B 、垂直 C 、相交但不垂直 D 、异面6、如图,是一个无盖正方体盒子的表面展开图,A 、B 、C 为其上的三个点,则在正方体盒子中,∠ABC 等于 ( ) ( ) A .45° B .60° C .90° D .120° 7、下列命题中正确的是( )A .若平面M 外的两条直线在平面M 内的射影为一条直线及此直线外的一个点,则这两条直线互为异面直线;B .若平面M 外的两条直线在平面M 内的射影为两条平行直线,则这两条直线相交;C .若平面M 外的两条直线在平面M内的射影为两条平行直线,则这两条直线平行;D .若平面M 外的两条直线在平面M 内的射影为两条互相垂直的直线,则这两条直线垂直。
8、如图,PA ⊥矩形ABCD ,下列结论中不正确的是( ) A . PD ⊥BD B .PD ⊥CDC .PB ⊥BCD .PA ⊥BDOADC B P9、如图,在长方体1111ABCD A BC D -中,AB=BC=2,1AA =1,则1AC 与平面1111A B C D 所成角的正弦值为( )A.3 B .23 C.4D .1310、如图,在四棱锥P-ABCD 中,已知底面ABCD 是边长为a 的正方形,PA ⊥平面ABCD ,且PA=2a,那么点A 到平面PBD 的距离是( ) A.a B .a 32 C.a 23 D .a 23二、填空题(共4小题,每小题5分,共20分)11.若点P 是△ABC 所在平面外一点,且PA=PB=PC,则点P 在平面ABC 内的射影O 是△ABC 的 心. 12.如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =3,AA 1=4,则异面直线AB 1与 A 1D 所成的角的余弦值为 .13.已知过球面上A 、B 、C 三点的截面和球心的距离等于球的半径的一半,且AB=BC=CA=2,则球面面积是_____________________.14、如图,在ABC ∆中,90ACB ︒∠=,AB=8,60ABC ︒∠=, PC ⊥平面ABC, PC=4,M 是AB 上的一个动点,则PM 的最小值为____________________第12题图 第14题图CDB C 1D 1A 1B 1A ODABCP C DBC 1D 1A 1B 1AC ABP三、解答题(本题共5小题,共70分。
2012届高考数学(理)一轮复习单元测试卷:立体几何

立体几何单元能力测试一、选择题(本大题共12小题,每小题5分,共60分.每小题中只有一项符合题目要求)1.如右图所示,是一个正方体的表面展开图,A 、B 、C 均为棱的中点,D 是顶点,则在正方体中,异面直线AB 和CD 的夹角的余弦值为( )A.25B.35C.105D.55 答案 C 解析把展开图复原为正方体后示意图如右图所示,∠EGF 为AB 和CD 所成的角,F 为正方体一棱的中点.∴EF =GF =52,EG = 2. ∴cos ∠EGF =105.2.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )A.8π3B.82π3 C .82π D.32π3答案 B解析 S 圆=πr 2=1⇒r =1,而截面圆圆心与球心的距离d =1,∴球的半径为R =r 2+d 2=2,∴V =43πR 3=82π3,故选B.3.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )A.13cm 3B.23cm C.43cm 3 D.83cm 3 答案 C解析 由三视图可知该几何体为三棱锥,如图所示,其中AC =AD ,平面ACD ⊥平面BCD ,E 为CD 的中点,则AE ⊥平面BCD ,且BE =AE =2,DC =2,∴V =13×12×BE ×DC ×AE =13×12×2×2×2=43cm 3,故选C.4.已知m 、n 是两条不同的直线,α、β是两个不同的平面,给出下列命题: ①若α⊥β,m ∥α,则m ⊥β;②若m ⊥α,n ⊥β,且m ⊥n ,则α⊥β;③若m ⊥β,m ∥α,则α⊥β;④若m ∥α,n ∥β,且m ∥n ,则α∥β.其中真命题的序号是( ) A .①④ B .②③ C .②④ D .①③ 答案 B解析 若α⊥β,m ∥α,则m 与β可能相交、平行或m 在平面β内,故①错;m∥α,n∥β,m∥n,则α与β可能平行,可能相交,故④错.故选B.5.(2010·湖北卷)用a,b,c表示三条不同的直线,γ表示平面,给出下列命题:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a⊥c;③若a∥γ,b∥γ,则a∥b;④若a⊥γ,b⊥γ,则a∥b.其中真命题的序号是()A.①②B.②③C.①④D.③④答案 C解析对于①,由公理“平行于同一直线的两条直线平行”可知,①正确;对于②,如在长方体ABCD-A1B1C1D1中,AB⊥AD,CD⊥AD,此时AB平行于CD,因此②不正确.对于③,如当平面α∥γ时,平面α内的任意两条直线a,b都平行于平面γ,显然此时直线a,b可能相交,因此③不正确.对于④,由“垂直于同一平面的两条直线平行”可知其正确性.综上所述,其中真命题的序号是①④,选C.6.如右图所示,正四棱锥P-ABCD的底面积为3,体积为22,E为侧棱PC的中点,则PA与BE所成的角为()A.π6 B.π4C.π3 D.π2答案 C解析连结AC、BD交于点O,连结OE,易得OE∥PA.∴所求角为∠BEO .由所给条件易得OB =62,OE =12PA =22,BE =2, ∴cos ∠OEB =12,∴∠OEB =60°,选C. 7.如图,在长方体ABCD —A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为( )A.63B.255C.155D.105 答案 D解析 连结A 1C 1,交B 1D 1于O ,依题意得,A 1C 1⊥B 1D 1,BB 1⊥A 1C 1,又B 1D 1∩BB 1=B 1,∴A 1C 1⊥平面BB 1D 1D .连结BO ,则∠C 1BO 为所求角,又OC 1=2,BC 1=5,∴sin C 1BO =C 1O BC 1=25=105,选D.8.圆台上、下底面面积分别是π、4π,侧面积是6π,这个圆台的体积是( ) A.233π B .23π C.736π D.733π 答案 D解析 上底半径r =1,下底半径R =2.∵S 侧=6π,设母线长为l ,则π(1+2)·l =6π,∴l =2,∴高h =l 2-R -r 2=3,∴V =13π·3(1+1×2+2×2)=733π.故选D.9.如图,四棱锥P -ABCD 的底面为正方形,PD ⊥底面ABCD ,PD =AD =1,设点C 到平面PAB 的距离为d 1,点B 到平面PAC 的距离为d 2,则有( )A .1<d 1<d 2B .d 1<d 2<1C .d 1<1<d 2D .d 2<d 1<1 答案 D解析 ∵CD ∥平面PAB .∴C 到平面PAB 的距离等于D 到平面PAB 的距离. 过D 作DE ⊥PA ,则DE ⊥平面PAB ,d 1=DE =22. B 与D 到平面PAC 的距离相等.设AC ∩BD =O ,则平面PDO ⊥平面PAC ,∴d 2等于D 到PO 的距离,可计算d 2=33,∴d 2<d 1<1.10.半径为4的球面上有A ,B ,C ,D 四点,且满足AB →·AC →=0,AD →·AC →=0,AB →·AD →=0,则△ABC ,△ACD ,△ADB 面积之和S △ABC +S △ACD +S △ADB 的最大值为( )A .8B .16C .32D .64 答案 C解析 设AB =a ,AC =b ,AD =c , 则S △ABC +S △ACD +S △ADB =12(ab +ac +bc )≤12(a 2+b 22+a 2+c 22+b 2+c 22)=12(a 2+b 2+c 2)=12×4R 2=12×4×42=32, 当且仅当a =b =c 时取“=”.11.二面角的棱上有A 、B 两点,直线AC 、BD 分别在这个二面角的两个半平面内,且都垂直于AB .已知AB =4,AC =6,BD =8,CD =217,则该二面角的大小为( )A .150°B .45°C .60°D .120° 答案 C解析 由条件,知CA →·AB →=0,AB →·BD →=0,CD →=CA →+AB →+BD →.∴|CD →|2=|CA →|2+|AB →|2+|BD →|2+2CA →·AB →+2AB →·BD →+2CA →·BD →=62+42+82+2×6×8cos 〈CA →,BD →〉=(217)2,∴cos 〈CA →,BD →〉=-12,〈CA →,BD →〉=120°,∴二面角的大小为60°,故选C.12.已知正方体ABCD -A 1B 1C 1D 1棱长为1,点P 在线段BD 1上,当∠APC 最大时,三棱锥P -ABC 的体积为( )A.124B.118C.19D.112答案 B解析 以B 为坐标原点,BA 为x 轴,BC 为y 轴,BB 1为z 轴建立空间直角坐标系,设BP →=λBD 1→,可得P (λ,λ,λ),再由cos ∠APC =AP →·CP →|AP →||CP →|可求得当λ=13时,∠APC 最大,故V P -ABC =13×12×1×1×13=118.二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)13.如图所示是一个几何体的三视图,根据图中标出的尺寸(单位:cm),可得该几何体的表面积为________cm 2.答案 36 解析由三视图可知,此几何体是一个以AA ′=2,AD =4,AB =2为棱的长方体被平面A ′C ′B 截去一个角后得到的,在△A ′C ′B 中,因为A ′C ′=BC ′=25,BA ′=22,所以S △A ′C ′B =12×22×252-22=6,故几何体表面积为2×4×2+2×2+12×4×2×2+12×2×2+6=36.14.如图,在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是菱形,∠BAD =60°,AA 1=AB =1,则截面ACC 1A 1的面积为________;异面直线AD 与D 1C 所成角的余弦值为________.答案3 24解析 截面ACC 1A 1为矩形. AA 1=1,AC =3,其面积S =3;BD =1,BD 1=2,在△BCD 1中,BC =1,CD 1=2,cos ∠BC D 1=24.则异面直线AD 与D 1C 所成角的余弦值为24. 15.如图是一几何体的平面展开图,其中ABCD 为正方形,E 、F 、分别为PA 、PD 的中点,在此几何体中,给出下面四个结论:①直线BE 与直线CF 异面; ②直线BF 与直线AF 异面 ③直线EF ∥平面PBC ; ④平面BCE ⊥平面PAD . 其中正确的有______个.答案 2解析 将几何体展开拼成几何体(如图),因为E 、F 分别为PA 、PD 的中点,所以EF ∥AD ∥BC ,即直线BE 与CF 共面,①错;因为B ∉平面PAD ,E ∈平面PAD ,E ∉AF ,所以BE 与AF 是异面直线,②正确;因为EF ∥AD ∥BC ,EF ⊄平面PBC ,BC ⊂平面PBC ,所以EF ∥平面PBC ,③正确;平面PAD 与平面BCE 不一定垂直,④错.16.直三棱柱ABC -A 1B 1C 1的各顶点都在同一球面上.若AB =AC =AA 1=2,∠BAC =120°,则此球的表面积等于________.答案 20π解析 设球心为O ,球半径为R ,△ABC 的外心是M ,则O 在底面ABC 上的射影是点M ,在△ABC 中,AB =AC =2,∠BAC =120°,∠ABC =12(180°-120°)=30°,AM =AC 2sin30°=2.因此,R 2=22+(AA 12)2=5,此球的表面积等于4πR 2=20π.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)在下面三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连结BC ′,证明:BC ′∥平面EFG .解析 (1)如图. (2)所求多面体的体积V =V 长方体-V 正三棱锥=4×4×6-13×⎝ ⎛⎭⎪⎫12×2×2×2=2843(cm 3).(3)证明:如图,在长方体ABCD -A ′B ′C ′D ′中,连结AD ′,则AD ′∥BC ′. 因为E 、G 分别为AA ′、A ′D ′的中点, 所以AD ′∥EG ,从而EG ∥BC ′.又BC ′⊄平面EFG ,所以BC ′∥平面EFG .第 10 页 共 14 页 金太阳新课标资源网18.(本小题满分12分)(2010·新课标全国,文)如图,已知四棱锥P -ABCD 的底面为等腰梯形,AB ∥CD ,AC ⊥BD ,垂足为H ,PH 是四棱锥的高.(1)证明:平面PAC ⊥平面PBD ;(2)若AB =6,∠APB =∠ADB =60°,求四棱锥P -ABCD 的体积.解析 (1)因为PH 是四棱锥P -ABCD 的高,所以AC ⊥PH .又AC ⊥BD ,PH ,BD 都在平面PBD 内,且PH ∩BD =H , 所以AC ⊥平面PBD , 故平面PAC ⊥平面PBD .(2)因为ABCD 为等腰梯形,AB ∥CD ,AC ⊥BD ,AB =6, 所以HA =HB = 3. 因为∠APB =∠ADB =60°, 所以PA =PB =6,HD =HC =1. 可得PH =3,等腰梯形ABCD 的面积为S =12AC ×BD =2+ 3. 所以四棱锥的体积为V =13×(2+3)×3=3+233.19.(本小题满分12分)如图,在四棱锥P -ABCD 中,底面是矩形且AD =2,AB =PA =2,PA ⊥底面ABCD ,E 是AD 的中点,F 在PC 上.(1)求F 在何处时,EF ⊥平面PBC ;(2)在(1)的条件下,EF 是否是PC 与AD 的公垂线段?若是,求出公垂线段的长度;若不是,说明理由.金太阳新课标资源网解析 (1)取CB 中点G ,连结EG 、FG∵EG ⊥BC ,EF ⊥面PBC∴BC ⊥面EFG ,∴BC ⊥FG∵BC ⊥PB ,∴FG ∥PB∵G 为中点,∴F 为PC 中点.(2)由(1)可知EF ⊥PC 且EF ⊥BC ,即EF ⊥AD ,∴EF 是PC 与AD 的公垂线段,其长为EF =1.20.(本小题满分12分)(2010·湖南卷,文)如图所示,在长方体ABCD -A 1B 1C 1D 1中,AB =AD =1,AA 1=2,M 是棱CC 1的中点.(1)求异面直线A 1M 和C 1D 1所成的角的正切值;(2)证明:平面ABM ⊥平面A 1B 1M .解析 (1)如图,因为C 1D 1∥B 1A 1,所以∠MA 1B 1为异面直线A 1M 与C 1D 1所成的角.因为A 1B 1⊥平面BCC 1B 1,所以∠A 1B 1M =90°.而A 1B 1=1,B 1M =B 1C 21+MC 21=2,故tan ∠MA 1B 1=B 1M A 1B 1= 2. 即异面直线A 1M 和C 1D 1所成的角的正切值为 2.(2)由A 1B 1⊥平面BCC 1B 1,BM ⊂平面BCC 1B 1,得A 1B 1⊥BM .① 由(1)知,B 1M =2,又BM =BC 2+CM 2=2,B 1B =2,所以B 1M 2+BM 2金太阳新课标资源网=B 1B 2,从而BM ⊥B 1M .②又A 1B 1∩B 1M =B 1,再由①②得BM ⊥平面A 1B 1M ,而BM ⊂平面ABM ,因此平面ABM ⊥平面A 1B 1M .21.(本小题满分12分)在几何体ABCDE 中,∠BAC =π2,DC ⊥平面ABC ,EB ⊥平面ABC ,AB =AC =BE =2,CD =1.(1)设平面ABE 与平面ACD 的交线为直线l ,求证:l ∥平面BCDE ;(2)设F 是BC 的中点,求证:平面AFD ⊥平面AFE ;(3)求几何体ABCDE 的体积.解析 (1)∵CD ⊥平面ABC ,BE ⊥平面ABC ,∴CD ∥BE .∵CD ⊄平面ABE ,BE ⊂平面ABE ,∴CD ∥平面ABE .又l =平面ACD ∩平面ABE ,∴CD ∥l .又l ⊄平面BCDE ,CD ⊂平面BCDE ,∴l ∥平面BCDE .(2)在△DFE 中,FD =3,FE =6,DE =3.∴FD ⊥FE .∵CD ⊥平面ABC ,∴CD ⊥AF ,又BC ⊥AF ,CD ∩BC =C ,∴AF ⊥平面BCDE ,∴AF ⊥FD ,∵EF ∩AF =F ,∴FD ⊥平面AFE .又FD ⊂平面AFD ,∴平面AFD ⊥平面AFE .(3)∵DC ⊥平面ABC ,BE ⊥平面ABC ,∴DC ∥BE∵AB =AC =2,且∠BAC =π2金太阳新课标资源网∴BC =2 2∴S BEDC =12(DC +BE )×BC =3 2由(2)知AF ⊥平面BCED∴V E -BCDE =13S BEDC ·AF =13×32×2=2.22.(本小题满分12分)如图,在长方体ABCD -A 1B 1C 1D 1中,AD =AA 1=1,AB >1,点E 在棱AB 上移动,小蚂蚁从点A 沿长方体的表面爬到点C 1,所爬的最短路程为2 2.(1)求证:D 1E ⊥A 1D ;(2)求AB 的长度;解析 (1)连结AD 1,由长方体的性质可知: AE ⊥平面AD 1,∴AD 1是ED 1在平面AD 1内的射影. 又∵AD =AA 1=1,∴AD 1⊥A 1D ,∴D 1E ⊥A 1D (三垂线定理).(2)设AB =x ,∵四边形ADD 1A 1是正方形, ∴小蚂蚁从点A 沿长方体的表面爬到点C 1, 可能有四种途径,如图甲、乙的最短路程为 |AC 1|=x 2+4,金太阳新课标资源网如图丙、丁的最短路程为|AC 1|=x +1 2+1=x 2+2x +2,∵x >1,∴x 2+2x +2>x 2+2+2=x 2+4, ∴x 2+4=22,∴x =2.。
高考数学复习专题过关检测—立体几何(含解析)

高考数学复习专题过关检测—立体几何一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2021·山东济宁二模)“直线m垂直于平面α内的无数条直线”是“m⊥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.(2021·重庆八中月考)已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则异面直线CD与PB所成角的余弦值为()A.√55B.2√55C.√510D.√95103.(2021·江西上饶三模)在正方体ABCD-A1B1C1D1中,G是线段BC1上一点,且A1G⊥B1D,则()A.BG=12BC1B.BC1=3GC1C.BG=3GC1D.G为线段BC1上任意一点4.(2021·辽宁葫芦岛一模)某保鲜封闭装置由储物区与充氮区(内层是储物区,用来放置新鲜易变质物品,充氮区是储物区外的全部空间,用来向储物区输送氮气从而实现保鲜功能)构成.如图,该装置外层上部分是半径为2的半球,下面大圆刚好与高度为3的圆锥的底面圆重合,内层是一个高度为4的倒置小圆锥,小圆锥底面平行于外层圆锥的底面,且小圆锥顶点与外层圆锥顶点重合,为了保存更多物品,充氮区的体积最小为()A.4πB.16π3C.28π3D.4π35.(2021·天津三模)在圆柱O1O2内有一个球O,球O分别与圆柱O1O2的上、下底面及母线均有且只有一个公共点.若O1O2=2,则圆柱O1O2的表面积为() A.4π B.5πC.6πD.7π6.(2021·广东深圳模拟)已知球O与棱长为2的正方体ABCD-A1B1C1D1的各个面都相切,M为棱DD1的中点,则平面AMC截球O所得截面的面积为()A.π3B.2π3C.πD.4π37.(2021·福建师大附中模拟)过正方形ABCD的顶点A作PA⊥平面ABCD,若AB=AP,则平面ABP与平面CDP的夹角的余弦值为()A.13B.√22C.√32D.√338.(2021·山东滨州二模)在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,P是底面ABCD内(包括边界)的一个动点,若MP∥平面A1BC1,则异面直线MP与A1C1所成角的取值范围是()A.(0,π3] B.[π6,π3]C.[π3,π2] D.[π3,π)二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.(2021·广东广州三模)对于空间中的两条不同直线a,b和两个不同平面α,β,下列说法正确的是()A.若a⊥α,b⊥α,则a∥bB.若a⊥b,b⊥β,则a∥βC.若a⊥α,b⊥β,α⊥β,则a⊥bD.若a∥α,α⊥β,则a⊥β10.(2021·湖北荆门月考)如图,在正方体ABCD-A1B1C1D1中,点P在线段BC1上运动,下列结论正确的是()A.三棱锥A-D1PC的体积不变B.直线AP与平面ACD1所成角的大小不变C.直线AP与直线A1D所成角的大小不变D.二面角P-AD1-C的大小不变11.(2021·福建龙岩三模)在意大利,有一座满是“斗笠”的灰白小镇阿尔贝罗贝洛,这些圆锥形屋顶的奇特小屋名叫Trullo,于1996年被收入世界文化遗产名录.现测量一个Trullo的屋顶,得到圆锥SO(其中S为顶点,O为底面圆心),母线SA的长为6 m,C是母线SA上靠近点S的三等分点.从点A到点C绕屋顶侧面一周安装灯光带,灯光带的最小长度为2√13 m.下面说法正确的是()A.圆锥SO 的侧面积为12π m 2B.过点S 的平面截此圆锥所得截面面积最大值为18 m 2C.圆锥SO 的外接球的表面积为72π m 2D.棱长为√3 m 的正四面体在圆锥SO 内可以任意转动12.(2021·新高考Ⅰ,12)在正三棱柱ABC-A 1B 1C 1中,AB=AA 1=1,点P 满足BP ⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ +μBB 1⃗⃗⃗⃗⃗⃗⃗ ,其中λ∈[0,1],μ∈[0,1],则( )A.当λ=1时,△AB 1P 的周长为定值B.当μ=1时,三棱锥P-A 1BC 的体积为定值C.当λ=12时,有且仅有一个点P ,使得A 1P ⊥BP D.当μ=12时,有且仅有一个点P ,使得A 1B ⊥平面AB 1P三、填空题:本题共4小题,每小题5分,共20分.13.(2021·辽宁大连期中)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为 .14.(2021·河北石家庄期末)如图,已知二面角A-EF-D 的大小为45°,四边形ABFE 与四边形CDEF 都是边长为1的正方形,则B ,D 两点间的距离是 .15.(2021·浙江绍兴二模)如图,在棱长为4的正方体ABCD-A 1B 1C 1D 1中,M 是棱A 1A 上的动点,N 是棱BC 的中点.当平面D 1MN 与平面ABCD 的夹角最小时,A 1M= .16.(2021·广东汕头二模)在菱形ABCD 中,AB=2,∠DAB=60°,E 为AB 的中点,将△ADE 沿DE 翻折成△A 1DE ,当三棱锥A 1-DEC 的体积最大时,三棱锥A 1-DEC 的外接球的表面积为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)(2021·广东韶关期中)如图,在直三棱柱ABC-A 1B 1C 1中,侧面ABB 1A 1,BCC 1B 1,ACC 1A 1的面积依次为16,12,20,E ,F 分别为A 1C 1,BC 的中点.求证:(1)平面ABE⊥平面BB1C1C;(2)C1F∥平面ABE.18.(12分)(2021·河北张家口一模)如图,四边形ABCD是正方形,PA⊥平面ABCD,PA∥EB,且PA=PB=3.(1)求证:CE∥平面PAD;PA,求直线PD与平面PCE所成角的正弦值.(2)若BE=1319.(12分)(2021·北京石景山区模拟)如图,四棱锥P-ABCD的底面为矩形,PD⊥底面ABCD,M为BC的中点,PB⊥AM.(1)求证:平面PAM⊥平面PBD;(2)若PD=DC=1,求四棱锥P-ABCD的体积.20.(12分)(2021·山东淄博三模)如图①,在平面图形ABCD中,△ABD是边长为4的等边三角形,DB是∠ADC的平分线,且BD⊥BC,M为AD的中点,沿BM将△ABM折起,得到四棱锥A1-BCDM,如图②.图①图②(1)设平面A1BC与平面A1DM的交线为l,在四棱锥A1-BCDM的棱A1C上求一点N,使直线BN∥l;(2)若二面角A1-BM-D的大小为60°,求平面A1BD与平面A1CD的夹角的余弦值.21.(12分)(2021·湖南长沙模拟)如图,C是以AB为直径的圆上异于点A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F分别是PC,PB的中点,设平面AEF与平面ABC的交线为直线l.(1)求证:直线l⊥平面PAC.(2)直线l上是否存在点Q,使直线PQ分别与平面AEF,直线EF所成的角互余?若存在,求出AQ的值;若不存在,请说明理由.22.(12分)(2021·重庆蜀都中学月考)如图①,在菱形ABCD 中,∠ABC=120°,动点E ,F 分别在边AD ,AB 上(不含端点),且存在实数λ,使EF ⃗⃗⃗⃗⃗ =λBD ⃗⃗⃗⃗⃗⃗ ,沿EF 将△AEF 向上折起得到△PEF ,使得平面PEF ⊥平面BCDEF ,如图②所示.图①图②(1)若BF ⊥PD ,设三棱锥P-BCD 和四棱锥P-BDEF 的体积分别为V 1,V 2,求V1V 2.(2)当点E 的位置变化时,二面角E-PF-B 是否为定值?若是,求出该二面角的余弦值;若不是,说明理由.答案及解析1.B解析由直线m垂直于平面α内的无数条直线不能推出m⊥α,但是由m⊥α一定能推出直线m垂直于平面α内的无数条直线,所以“直线m垂直于平面α内的无数条直线”是“m⊥α”的必要不充分条件.故选B.2.C解析连接AE,BE(图略),设AB=1,则PA=2,AE=√12+12-2×1×1×cos120°=√3,PE=√4+3=√7,BE=√3+1=2,PB=√4+1=√5.易知CD∥BE,所以∠PBE是直线CD与PB所成的角(或其补角).又cos∠PBE=2×2×√5=√510,所以直线CD与PB所成角的余弦值为√510.故选C.3.D解析如图,∵AD⊥平面ABB1A1,∴AD⊥A1B.又AB1⊥A1B,AB1∩AD=A,∴A1B⊥平面AB1D,∴A1B⊥B1D.同理BC1⊥B1D.又A1B∩BC1=B,∴B1D⊥平面A1BC1.又A1G⊂平面A1BC1,∴A1G⊥B1D.故G为线段BC1上任意一点.故选D.4.B解析由题意可知内层小圆锥底面半径最大为√22-12=√3,所以充氮区的体积最小为12×43π×23+13π×22×3-13π×(√3)2×4=16π3.故选B.5.C解析依题意,圆柱O1O2的底面半径r=1,高h=2,所以圆柱O1O2的表面积S=2πr·h+2πr2=4π+2π=6π.故选C.6.A解析设球心O到截面的距离为d,截面圆的半径为r,由V O-ACM=V M-AOC,得1 3·S△ACM·d=√23S△AOC.因为S△ACM=12×2√2×√3=√6,S△AOC=12×2√2×1=√2,所以d=√63.又d2+r2=1,所以r=√33,所以平面AMC截球O所得截面的面积为πr2=π3.故选A.7.B 解析 设AP=AB=1,以A 为原点,AB ,AD ,AP 所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系如图所示,则P (0,0,1),D (0,1,0),C (1,1,0),所以PC ⃗⃗⃗⃗⃗ =(1,1,-1),PD ⃗⃗⃗⃗⃗ =(0,1,-1). 设平面CDP 的法向量m =(x ,y ,z ),则{m ·PC⃗⃗⃗⃗⃗ =x +y -z =0,m ·PD ⃗⃗⃗⃗⃗ =y -z =0,取y=1,则x=0,z=1,所以m =(0,1,1)为平面CDP 的一个法向量.易知n =(0,1,0)为平面ABP 的一个法向量.设平面ABP 与平面CDP 的夹角为θ,则cos θ=|m ·n ||m ||n |=√2×1=√22.故选B .8.C 解析 如图,以D 为原点,DA ,DC ,DD 1所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系,设AB=2,则B (2,2,0),A 1(2,0,2),C 1(0,2,2),M (0,0,1),取AD 的中点E ,DC 的中点F ,连接ME ,EF ,MF ,则E (1,0,0),F (0,1,0).因为ME ⃗⃗⃗⃗⃗⃗ =(1,0,-1),C 1B ⃗⃗⃗⃗⃗⃗⃗ =(2,0,-2)=2ME ⃗⃗⃗⃗⃗⃗ ,所以C 1B ∥ME.同理EF ∥A 1C 1.又ME ⊄平面A 1BC 1,C 1B ⊂平面A 1BC 1,所以ME ∥平面A 1BC 1.同理MF ∥平面A 1BC 1.又MF ∩ME=M ,所以平面MEF ∥平面A 1BC 1.因为P 是底面ABCD 内(包括边界)的一个动点,MP ∥平面A 1BC 1,所以点P 在线段EF 上.因为EF ∥A 1C 1,所以异面直线MP 与A 1C 1所成的角即是直线MP 与EF 所成的角.当MP ⊥EF 时,异面直线MP 与A 1C 1所成的角最大为π2,当点P 与点E 或点F 重合时,异面直线MP 与A 1C 1所成的角最小为π3.故所求角的取值范围为[π3,π2].9.AC 解析 对于A,由线面垂直的性质定理知A 正确;对于B,若a ⊥b ,b ⊥β,则a ∥β或a ⊂β,所以B 错误;对于C,由a ⊥α,α⊥β,可知a ∥β或a ⊂β,又b ⊥β,所以a ⊥b ,所以C 正确;对于D,若a ∥α,α⊥β,则a ∥β或a ⊂β或a 与β相交,所以D 错误.故选AC .10.ACD 解析 对于A,因为BC 1∥平面AD 1C ,所以BC 1上任意一点到平面AD 1C 的距离都相等,所以三棱锥A-D 1PC 的体积不变,故A 正确;对于B,因为BC 1∥平面AD 1C ,所以点P 到平面ACD 1的距离不变,但AP 的长度随着点P 的移动而变化,所以直线AP 与平面ACD 1所成角的大小会改变,故B 错误;对于C,因为直线A 1D ⊥平面ABC 1D 1,AP ⊂平面ABC 1D 1,所以A 1D ⊥AP ,所以直线AP 与直线A 1D 所成角的大小不变;故C 正确;对于D,二面角P-AD 1-C 也就是二面角B-AD 1-C ,其大小不变,故D 正确.故选ACD .11.AD 解析 如图,设圆锥底面半径为r m,将圆锥侧面展开得到扇形ASA',在△A'SC 中,A'S=6 m,SC=2 m,A'C=2√13 m,则cos ∠A'SC=36+4-522×6×2=-12,所以∠A'SC=2π3,所以2πr=2π3×6=4π,r=2,所以圆锥的侧面积为π×2×6=12π(m 2),故A 正确.在△ASB 中,cos ∠ASB=SA 2+SB 2-AB 22SA ·SB=79,sin ∠ASB=√1-4981=4√29,易知过点S 的平面截此圆锥所得截面面积最大为S △SAB =12SA·SB·sin ∠ASB=12×6×6×4√29=8√2(m 2),故B 错误.设圆锥SO 的外接球的半径为R m,则R 2=(SO-R )2+r 2,又SO=√SA 2-r 2=√36-4=4√2,所以R 2=(4√2-R )2+4,解得R=9√24,所以圆锥SO 的外接球的表面积为4πR 2=81π2(m 2),故C 错误.设圆锥SO 的内切球的半径为t m,则4√2-t=13,解得t=√2,设棱长为√3 m 的正四面体的外接球的半径为r 1 m,将该正四面体放在棱长为√62的正方体中,可知该正四面体的外接球也是该正方体的外接球,易知r 1=12√3×(√62)2=3√24,因为r 1<t ,所以棱长为√3 m 的正四面体在圆锥SO 内可以任意转动,故D 正确.故选AD . 12.BD 解析图①A 项中,当λ=1时,BP ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +u BB 1⃗⃗⃗⃗⃗⃗⃗ ⇒BP ⃗⃗⃗⃗⃗ −BC ⃗⃗⃗⃗⃗ =CP ⃗⃗⃗⃗⃗ =u BB 1⃗⃗⃗⃗⃗⃗⃗ ,则CP ⃗⃗⃗⃗⃗ 与BB 1⃗⃗⃗⃗⃗⃗⃗ 共线,故点P 在线段CC 1(包括端点)上,如图①所示.在△AB 1P 中,|AB 1|=√2,|AP|=√1+u 2,|B 1P|=√1+(1-u )2, 故△AB 1P 的周长L=|AB 1|+|AP|+|B 1P|不为定值,故A 错误;图②B 项中,当u=1时,BP ⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ +BB 1⃗⃗⃗⃗⃗⃗⃗ ⇒BP ⃗⃗⃗⃗⃗ −BB 1⃗⃗⃗⃗⃗⃗⃗ =B 1P ⃗⃗⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ ,则B 1P ⃗⃗⃗⃗⃗⃗⃗ 与BC⃗⃗⃗⃗⃗ 共线,故点P 在线段B 1C 1(包括端点)上,如图②所示.由图②可知B 1C 1∥平面A 1BC ,即B 1C 1上的每一点到平面A 1BC 的距离都相等,因此三棱锥P-A 1BC 的体积为定值,故B 正确;图③C 项中,当λ=12时,分别取线段BC ,B 1C 1的中点D ,D 1,连接DD 1,可知点P 在线段DD 1(包括端点)上,如图③所示.取AC 的中点O ,建立如图所示的空间直角坐标系Oxyz ,则B √32,0,0,C 0,12,0,A 10,-12,1,P (√34,14,u),从而A 1P ⃗⃗⃗⃗⃗⃗⃗ =(√34,34,u -1),BP ⃗⃗⃗⃗⃗ =(-√34,14,u), 由A 1P ⃗⃗⃗⃗⃗⃗⃗ ·BP⃗⃗⃗⃗⃗ =u (u-1)=0,得u=0或u=1. 当点P 与点D 或D 1重合时,满足A 1P ⊥BP ,故C 错误;D 项中,当u=12时,分别取线段BB 1,CC 1的中点M ,N ,连接MN ,可知点P 在线段MN (包括端点)上,如图④所示.图④建系同选项C,则A 0,-12,0,A 10,-12,1,B √32,0,0,P √32−√32λ,λ2,12,从而A 1B ⃗⃗⃗⃗⃗⃗⃗ =√32,12,-1,AP ⃗⃗⃗⃗⃗ =√32−√32λ,λ2+12,12,四边形ABB 1A 1为正方形,显然A 1B ⊥AB 1. 要使A 1B ⊥平面AB 1P ,只需A 1B ⊥AP ,即A 1B ⃗⃗⃗⃗⃗⃗⃗ ·AP⃗⃗⃗⃗⃗ =12−λ2=0,解得λ=1. 当且仅当点P 与点N 重合时,A 1B ⊥平面AB 1P ,故D 正确. 综上所述,选BD .13.39π 解析 ∵体积V=13π×62·h=30π,∴高h=52,∴母线长l=√ℎ2+r 2=√(52)2+62=132,∴S 侧=πrl=π×6×132=39π. 14.√3-√2 解析 ∵BD ⃗⃗⃗⃗⃗⃗ =BF ⃗⃗⃗⃗⃗ +FE ⃗⃗⃗⃗⃗ +ED ⃗⃗⃗⃗⃗ ,∴|BD ⃗⃗⃗⃗⃗⃗ |2=|BF ⃗⃗⃗⃗⃗ |2+|FE ⃗⃗⃗⃗⃗ |2+|ED ⃗⃗⃗⃗⃗ |2+2BF ⃗⃗⃗⃗⃗ ·FE ⃗⃗⃗⃗⃗ +2FE ⃗⃗⃗⃗⃗ ·ED ⃗⃗⃗⃗⃗ +2BF ⃗⃗⃗⃗⃗ ·ED ⃗⃗⃗⃗⃗ .由题意可知|BF ⃗⃗⃗⃗⃗ |=|FE ⃗⃗⃗⃗⃗ |=|ED ⃗⃗⃗⃗⃗ |=1,BF ⃗⃗⃗⃗⃗ ·FE ⃗⃗⃗⃗⃗ =0,FE ⃗⃗⃗⃗⃗ ·ED ⃗⃗⃗⃗⃗ =0,BF ⃗⃗⃗⃗⃗ ·ED ⃗⃗⃗⃗⃗ =1×1×cos 135°=-√22,∴|BD⃗⃗⃗⃗⃗⃗ |=√3-√2.故B ,D 两点间的距离是√3-√2. 15.85 解析 如图,建立空间直角坐标系,则N (2,4,0),D 1(0,0,4),设M (4,0,a )(0≤a ≤4),所以MN ⃗⃗⃗⃗⃗⃗⃗ =(-2,4,-a ),D 1N ⃗⃗⃗⃗⃗⃗⃗⃗ =(2,4,-4).设平面D 1MN 的法向量为n =(x ,y ,z ),则{n·MN⃗⃗⃗⃗⃗⃗⃗ =0,n·D1N⃗⃗⃗⃗⃗⃗⃗⃗ =0,即{-2x+4y-az=0,2x+4y-4z=0,解得{x=(4-a)z4,y=(a+4)z8,令z=8,则x=8-2a,y=a+4,所以n=(8-2a,a+4,8)为平面D1MN的一个法向量.易知m=(0,0,1)为平面ABCD的一个法向量.设平面D1MN与平面ABCD的夹角为θ,则cos θ=|m·n||m||n|=√(8-2a)+(a+4)+64=√5a2-24a+144,当a=125时,cos θ取最大值,则θ取最小值,所以A1M=4-125=85.16.8π解析如图,由余弦定理,得DE=√AD2+AE2-2AD·AEcos60°=√3,CE=√BE2+BC2-2BE·BCcos(180°-60°)=√7,所以AE2+DE2=AD2,DC2+DE2=CE2,即AE⊥DE,DC⊥DE.分别取CE,A1C的中点F,M,连接FM,则F为Rt△DEC的外心,因为△DEC的面积为定值,所以当平面A1DE⊥平面DEC时,点A1到平面DEC的距离最大,此时三棱锥A1-DEC的体积最大,又A1E⊥DE,所以A1E⊥平面DEC.由F,M分别为CE,A1C的中点,得FM∥A1E,所以FM⊥平面DEC,易知M是三棱锥A1-DEC的外接球的球心.因为A1C2=A1E2+CE2=1+7=8,所以所求外接球的表面积S=4π(A1C2)2=8π.17.证明(1)在直三棱柱ABC-A1B1C1中,BB1⊥平面ABC,AB⊂平面ABC,∴BB1⊥AB.∵侧面ABB1A1,BCC1B1,ACC1A1的面积依次为16,12,20,∴AB∶BC∶AC=4∶3∶5,∴AB2+BC2=AC2,即AB⊥BC.又BB1∩BC=B,∴AB⊥平面BB1C1C,又AB⊂平面ABE,∴平面ABE⊥平面BB1C1C.(2)如图,取AB的中点G,连接EG,GF.∵G,F分别为AB,BC的中点,∴GF∥AC,GF=12AC.∵E为A1C1的中点,∴EC1=12A1C1=12AC.又A 1C 1∥AC ,∴EC 1∥GF ,EC 1=GF ,∴四边形EGFC 1为平行四边形,∴C 1F ∥EG.又C 1F ⊄平面ABE ,EG ⊂平面ABE ,∴C 1F ∥平面ABE. 18.(1)证明 因为四边形ABCD 是正方形,所以BC ∥AD.又AD ⊂平面PAD ,BC ⊄平面PAD ,所以BC ∥平面PAD. 同理EB ∥平面PAD.又BC ∩EB=B ,所以平面EBC ∥平面PAD. 又CE ⊂平面EBC ,所以CE ∥平面PAD.(2)解 以A 为原点,AD ,AB ,AP 所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系如图所示.因为PA=AB=3,所以BE=13PA=1,所以P (0,0,3),D (3,0,0),C (3,3,0),E (0,3,1), 所以PD ⃗⃗⃗⃗⃗ =(3,0,-3),PC ⃗⃗⃗⃗⃗ =(3,3,-3),PE⃗⃗⃗⃗⃗ =(0,3,-2). 设平面PCE 的法向量为m =(x ,y ,z ),则{m ·PC ⃗⃗⃗⃗⃗ =3x +3y -3z =0,m ·PE ⃗⃗⃗⃗⃗ =3y -2z =0,得{x =z3,y =2z 3,令z=3,则x=1,y=2,所以m =(1,2,3)为平面PCE 的一个法向量. 设直线PD 与平面PCE 所成的角为θ, 则sin θ=|cos <PD ⃗⃗⃗⃗⃗ ,m >|=|PD⃗⃗⃗⃗⃗⃗⃗ ·m ||PD ⃗⃗⃗⃗⃗⃗⃗||m |=3√2×√14=√77,所以直线PD 与平面PCE 所成角的正弦值为√77. 19.(1)证明 因为PD ⊥底面ABCD ,AM ⊂平面ABCD ,所以PD ⊥AM.又PB ⊥AM ,PB ∩PD=P ,所以AM ⊥平面PBD. 又AM ⊂平面PAM ,所以平面PAM ⊥平面PBD. (2)解 由(1)可知AM ⊥平面PBD ,所以AM ⊥BD ,所以△DAB ∽△ABM.设BM=x ,则AD=2x ,由BMAB =ABAD ,即x1=12x ,得2x 2=1,解得x=√22,所以AD=√2.因为PD ⊥底面ABCD ,所以四棱锥P-ABCD 的体积为13×1×√2×1=√23.20.解 (1)如图,延长CB ,DM 相交于点E ,连接A 1E.因为点A 1,E 既在平面A 1BC 内,又在平面A 1DM 内,所以直线A 1E 即为平面A 1BC 与平面A 1DM 的交线l.因为DB 是∠ADC 的平分线,且BD ⊥BC ,所以B 为EC 的中点. 取A 1C 的中点N ,连接BN ,则BN ∥A 1E ,即BN ∥l. 故当N 为棱A 1C 的中点时,BN ∥l.(2)由题意可知BM ⊥A 1M ,BM ⊥MD ,则∠A 1MD 为二面角A 1-BM-D 的平面角,所以∠AMD=60°.又A 1M=MD ,所以△A 1MD 为等边三角形. 取MD 的中点O ,连接A 1O ,则A 1O ⊥MD.由BM ⊥A 1M ,BM ⊥MD ,A 1M ∩MD=M ,可知BM ⊥平面A 1MD ,所以BM ⊥A 1O. 又BM ∩MD=M ,所以A 1O ⊥平面BCDM. 如图,建立空间直角坐标系.则D (-1,0,0),A 1(0,0,√3),C (-5,4√3,0),B (1,2√3,0),所以DA 1⃗⃗⃗⃗⃗⃗⃗⃗ =(1,0,√3),DC ⃗⃗⃗⃗⃗ =(-4,4√3,0),DB⃗⃗⃗⃗⃗⃗ =(2,2√3,0). 设平面A 1CD 的法向量m =(x ,y ,z ),则{m ·DA 1⃗⃗⃗⃗⃗⃗⃗⃗ =0,m ·DC ⃗⃗⃗⃗⃗ =0,即{x +√3z =0,-4x +4√3y =0, 令z=-√3,则x=3,y=√3,所以m =(3,√3,-√3)为平面A 1CD 的一个法向量. 设平面A 1BD 的法向量为n =(a ,b ,c ),则{n ·DA 1⃗⃗⃗⃗⃗⃗⃗⃗ =0,n ·DB ⃗⃗⃗⃗⃗⃗ =0,即{x +√3c =0,2a +2√3b =0, 令c=-√3,则a=3,b=-√3,所以n =(3,-√3,-√3)为平面A 1BD 的一个法向量. 设平面A 1BD 与平面A 1CD 的夹角为θ, 则cos θ=|cos <m ,n >| =√3×√3)√3)√3)|√3+(√3)+(-√3)×√3+(-√3)+(-√3)=35,所以平面A 1BD 与平面A 1CD 的夹角的余弦值为35.21.(1)证明 ∵E ,F 分别是PC ,PB 的中点,∴BC ∥EF.又EF ⊂平面AEF ,BC ⊄平面AEF ,∴BC ∥平面AEF. 又BC ⊂平面ABC ,平面AEF ∩平面ABC=l ,∴BC ∥l.∵BC ⊥AC ,平面PAC ∩平面ABC=AC ,平面PAC ⊥平面ABC ,BC ⊂平面ABC ,∴BC ⊥平面PAC.∴l ⊥平面PAC.(2)解 如图,建立空间直角坐标系,则A (2,0,0),B (0,4,0),P (1,0,√3),E 12,0,√32,F 12,2,√32.所以AE ⃗⃗⃗⃗⃗ =(-32,0,√32),EF⃗⃗⃗⃗⃗ =(0,2,0). 由题意可设Q (2,y ,0),平面AEF 的法向量为m =(x ,y ,z ), 则{AE⃗⃗⃗⃗⃗ ·m =-32x +√32z =0,EF ⃗⃗⃗⃗⃗ ·m =2y =0,取z=√3,则x=1,y=0,所以m =(1,0,√3)为平面AEF 的一个法向量. 又PQ ⃗⃗⃗⃗⃗ =(1,y ,-√3),所以|cos <PQ ⃗⃗⃗⃗⃗ ,EF⃗⃗⃗⃗⃗ >|=2√4+y =√4+y ,|cos <PQ ⃗⃗⃗⃗⃗ ,m >|=2√4+y =√4+y ,依题意,|cos <PQ ⃗⃗⃗⃗⃗ ,EF ⃗⃗⃗⃗⃗ >|=|cos <PQ ⃗⃗⃗⃗⃗ ,m >|,解得y=±1.故直线l 上存在点Q ,使直线PQ 分别与平面AEF ,直线EF 所成的角互余,此时AQ=1.22.解 (1)取EF 的中点G ,连接PG.因为EF⃗⃗⃗⃗⃗ =λBD ⃗⃗⃗⃗⃗⃗ ,所以EF ∥BD ,所以PE=PF , 所以PG ⊥EF.又平面PEF ⊥平面BCDEF ,平面PEF ∩平面BCDEF=EF ,PG ⊂平面PEF ,所以PG ⊥平面BCDEF.连接GC ,由题意可知GC ⊥EF.以G 为坐标原点,GF ,GC ,GP 所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系如图所示.设菱形的边长为2,则F (λ,0,0),B (1,√3(1-λ),0),P (0,0,√3λ),D (-1,√3(1-λ),0),所以FB ⃗⃗⃗⃗⃗ =(1-λ,√3(1-λ),0),DP ⃗⃗⃗⃗⃗ =(1,-√3(1-λ),√3λ).因为BF ⊥PD ,所以FB ⃗⃗⃗⃗⃗ ·DP ⃗⃗⃗⃗⃗ =1-λ-3(1-λ)2=0,解得λ=23或λ=1(舍去).设△BCD 的面积为S ,则S △AEF =49S ,所以S 四边形BDEF =59S.所以V 1V 2=S △BCD S 四边形BDEF=S 59S =95.(2)二面角E-PF-B 是定值.证明如下:由(1)知n 1=(0,1,0)为平面PEF 的一个法向量. 设平面PFB 的法向量为n 2=(x ,y ,z ),因为FB ⃗⃗⃗⃗⃗ =(1-λ,√3(1-λ),0),FP⃗⃗⃗⃗⃗ =(-λ,0,√3λ), 所以{n 2·FB ⃗⃗⃗⃗⃗ =0,n 2·FP⃗⃗⃗⃗⃗ =0,即{(1-λ)x +√3(1-λ)y =0,-λx +√3λz =0,取y=1,则x=-√3,z=-1,所以n 2=(-√3,1,-1)为平面PFB 的一个法向量. 设二面角E-PF-B 的平面角为θ,所以|cos θ|=|cos <n 1,n 2>|=1×√5=√55.由图可知θ为钝角,所以二面角E-PF-B 为定值,其余弦值来为-√55.。
北师大版(理科数学) 立体几何初步 单元测试(含答案)

一、选择题1.给出下列说法中正确的是()A.棱柱被平面分成的两部分可以都是棱柱B.底面是矩形的平行六面体是长方体C.棱柱的底面一定是平行四边形D.棱锥的底面一定是三角形考点多面体的结构特征题点多面体的结构特征答案 A解析平行于棱柱底面的平面可以把棱柱分成两个棱柱,故A正确;三棱柱的底面是三角形,故C错误;底面是矩形的平行六面体的侧面不一定是矩形,故它也不一定是长方体,故B错误;四棱锥的底面是四边形,故D错误.故选A.2.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积为()A.6 B.3 2C.6 2 D.12答案 D解析由斜二测画法规则可知,△OAB为直角三角形,且两直角边长分别为4和6,故面积为12.3.下列说法正确的是()A.经过空间内的三个点有且只有一个平面B.如果直线l上有一个点不在平面α内,那么直线上所有点都不在平面α内C.四棱锥的四个侧面可能都是直角三角形D.用一个平面截棱锥,得到的几何体一定是一个棱锥和一个棱台考点线、面关系的综合问题题点线、面关系的其他综合问题答案 C解析在A中,经过空间内的不共线的三个点有且只有一个平面,故A错误;在B中,如果直线l上有一个点不在平面α内,那么直线与平面相交或平行,则直线上最多有一个点在平面α内,故B错误;在C中,如图的四棱锥,底面是矩形,一条侧棱垂直底面,那么它的四个侧面都是直角三角形,故C正确;在D中,用一个平行于底面的平面去截棱锥,得到两个几何体,一个是棱锥,一个是棱台,故D错误.故选C.4.设α-l-β是二面角,直线a在平面α内,直线b在平面β内,且a,b与l均不垂直,则()A.a与b可能垂直也可能平行B.a与b可能垂直,但不可能平行C.a与b不可能垂直,但可能平行D.a与b不可能垂直,也不可能平行考点空间中直线与直线的位置关系题点空间中直线与直线的位置关系的判定答案 A解析∵α-l-β是二面角,直线a在平面α内,直线b在平面β内,且a,b与l均不垂直,∴当a∥l,且b∥l时,由平行公理得a∥b,即a,b可能平行,故B与D不正确;当a,b 垂直时,若二面角是直二面角,则a⊥l与已知矛盾,若二面角不是直二面角,则a,b可以垂直,且满足条件,故C不正确;∴a与b有可能垂直,也有可能平行,故选A.5.在空间中,a,b是不重合的直线,α,β是不重合的平面,则下列条件中可推出a∥b的是()A.aα,bβ,α∥βB.a∥α,bαC.a⊥α,b⊥αD.a⊥α,bα考点直线与平面垂直的性质题点应用线面垂直的性质定理判定线线平行答案 C解析对于A,若aα,bβ,α∥β,则a与b没有公共点,即a与b平行或异面;对于B,若a∥α,bα,则a与b没有公共点,即a与b平行或异面;对于C,若a⊥α,b⊥α,由线面垂直的性质定理,可得a∥b;对于D,若a⊥α,bα,则由线面垂直的定义可得a⊥b,故选C.6.《算数书》竹简于上世纪八十年代在湖北省张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“禾盖”的术:置如其周,令相乘也,又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈136L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V ≈7264L 2h 相当于将圆锥体积公式中的圆周率π近似取为( ) A.15750B.258C.237D.227考点 柱体、锥体、台体的体积 题点 锥体的体积 答案 D解析 设圆锥的底面半径为r ,则圆锥的底面周长L =2πr ,∴r =L 2π,∴V =13πr 2h =L 2h 12π.令L 2h12π=7264L 2h ,得π=227,故选D. 7.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( ) A.26B.36C.23D.22答案 A解析 由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点,因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,如图所示,S △ABC =34×AB 2=34, 高OD =12-⎝⎛⎭⎫332=63, ∴V S -ABC =2V O -ABC =2×13×34×63=26.8.在长方体ABCD -A 1B 1C 1D 1中,若AB =AD =23,CC 1=2,则二面角C 1-BD -C 的大小为( )A .30°B .45°C .60°D .90° 考点 二面角 题点 知题作角 答案 A解析 如图,连接AC 交BD 于点O ,连接OC 1.因为AB=AD=23,所以AC⊥BD,又易知BD⊥平面ACC1A1,所以BD⊥OC1,所以∠COC1为二面角C1-BD-C的一个平面角.因为在△COC1中,OC=6,CC1=2,所以tan∠COC1=3 3,所以二面角C1-BD-C的大小为30°.二、填空题9.圆台的母线长为2a,母线与轴的夹角为30°,一个底面圆的半径是另一个底面圆的半径的2倍,则两底面圆的半径分别为________.考点题点答案a,2a解析如图,画出圆台轴截面,由题设,得∠OP A=30°,AB=2a,设O1A=r,P A=x,则OB=2r,x+2a=4r,且x=2r,∴a=r,即两底面圆的半径分别为a,2a.10.一个正四面体木块如图所示,点P是棱VA的中点,过点P将木块锯开,使截面平行于棱VB和AC,若木块的棱长为a,则截面面积为________.考点直线与平面平行的性质题点与性质有关的计算问题答案 a 24解析 在平面VAC 内作直线PD ∥AC ,交VC 于D ,在平面VBA 内作直线PF ∥VB ,交AB 于F ,过点D 作直线DE ∥VB ,交BC 于E ,连接EF .∴PF ∥DE ,∴P ,D ,E ,F 四点共面,且面PDEF 与VB 和AC 都平行, 则四边形PDEF 为边长为12a 的正方形,故其面积为a 24.11.如图,若边长为4和3与边长为4和2的两个矩形所在平面互相垂直,则cos α∶cos β=________.考点 平面与平面垂直的性质 题点 有关面面垂直性质的计算 答案5∶2解析 由题意,两个矩形的对角线长分别为5,25, 所以cos α=525+4=529,cos β=2529,所以cos α∶cos β=5∶2. 三、解答题12.如图所示,在正三棱柱ABC -A 1B 1C 1中,AB =3,AA 1=4,M 为AA 1的中点,P 是BC 上的一点,且由P 沿棱柱侧面经过棱CC 1到M 的最短路线为29.设这条最短路线与CC 1的交点为N ,求:(1)该三棱柱的侧面展开图的对角线的长; (2)PC 和NC 的长.考点 多面体表面上绕线最短距离问题 题点 棱柱体表面上绕线最短距离问题解 (1)该三棱柱的侧面展开图是宽为4,长为9的矩形, 所以对角线的长为42+92=97.(2)将该三棱柱的侧面沿棱BB 1展开,如图所示.设PC 的长为x , 则MP 2=MA 2+(AC +x )2.因为MP =29,MA =2,AC =3,所以x =2(负值舍去),即PC 的长为2. 又因为NC ∥AM ,所以PC P A =NC AM ,即25=NC 2,所以NC =45.13.如图所示,在几何体ABCDFE 中,△ABC ,△DFE 都是等边三角形,且所在平面平行,四边形BCED 是边长为2的正方形,且所在平面垂直于平面ABC .(1)求几何体ABCDFE 的体积; (2)证明:平面ADE ∥平面BCF . 考点 题点(1)解 取BC 的中点为O ,ED 的中点为G ,连接AO ,OF ,FG ,AG .∵AO⊥BC,AO平面ABC,平面BCED⊥平面ABC,平面BCED∩平面ABC=BC,∴AO⊥平面BCED.同理FG⊥平面BCED.∵AO=FG=3,∴V ABCDFE=13×4×3×2=833.(2)证明由(1)知AO∥FG,AO=FG,∴四边形AOFG为平行四边形,∴AG∥OF.又∵DE∥BC,DE∩AG=G,DE平面ADE,AG平面ADE,FO∩BC=O,FO平面BCF,BC平面BCF,∴平面ADE∥平面BCF.四、探究与拓展14.如图所示,在长方体ABCD-A1B1C1D1中,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中成立的是()①EF与BB1垂直;②EF⊥平面BCC1B1;③EF与C1D所成的角为45°;④EF∥平面A1B1C1D1.A.②③B.①④C.③D.①②④考点线面平行、垂直的综合应用题点平行与垂直的判定答案 B解析显然①④正确,②③错误.15.在△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将△BAO沿AO折起,使B点与图中B′点重合.(1)求证:AO⊥平面B′OC;(2)当三棱锥B′-AOC的体积取最大时,求二面角A-B′C-O的余弦值;(3)在(2)的条件下,试问在线段B′A上是否存在一点P,使CP与平面B′OA所成的角的正弦值为53?证明你的结论,并求AP的长.考点空间角问题题点空间角的综合问题(1)证明∵AB=AC且O是BC的中点,∴AO⊥BC,即AO⊥OB′,AO⊥OC,又∵OB′∩OC=O,OB′平面B′OC,OC平面B′OC,∴AO⊥平面B′OC.(2)解在平面B′OC内,作B′D⊥OC于点D,则由(1)可知B′D⊥OA,又OC∩OA=O,∴B′D⊥平面OAC,即B′D是三棱锥B′-AOC的高,又B′D≤B′O,∴当D与O重合时,三棱锥B′-AOC的体积最大,过O作OH⊥B′C于点H,连接AH,如图.由(1)知AO⊥平面B′OC,又B′C平面B′OC,∴B′C⊥AO,∵AO∩OH=O,∴B′C⊥平面AOH,∴B′C⊥AH,∴∠AHO即为二面角A-B′C-O的平面角.在Rt△AOH中,AO=2,OH=22,∴AH=322,∴cos ∠AHO =OH AH =13,故二面角A -B ′C -O 的余弦值为13.(3)解 如图,连接OP ,在(2)的条件下,易证OC ⊥平面B ′OA ,∴CP 与平面B ′OA 所成的角为∠CPO , ∴sin ∠CPO =OC CP =53,∴CP =35. 又在△ACB ′中,sin ∠AB ′C =310=CP 2, ∴CP ⊥AB ′, ∴B ′P =22-CP 2=55,∴AP =455.。
2019福建高三总复习单元过关测试卷(理科)(立体几何—泉州市)(附答案)$799167

2016高三毕业班总复习单元过关形成性测试卷(理科)立体几何泉州市数学组一、选择题:本大题共6小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知某几何体的正视图和侧视图(如图所示),则该几何体的俯视图不可能是(2)已知某几何体的三视图(单位:cm )如图所示,则该几 何体的体积是(A )384cm (B ) 392cm(C ) 3100cm (D )3108cm(3)对于不重合的两条直线m l ,和不重合的两个平面βα,,下列命题正确的是(A )若ββ//,//,//m l m l 则 (B )若βαβα//,,l l m 则⊂=(C )若βαβα//,l l 则,⊥⊥ (D )若βααβ⊥⊥⊥⊥则,,,l m m l(4)在如图所示的空间直角坐标系O xyz -中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为(A )①和② (B )③和① (C )③和④ (D )④和②(5)已知一个直三棱柱,其底面是正三角形,一个体积为43π的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是(A ) (B ) (C ) (D )(6)空间中的一条线段PQ ,在其俯视图和侧视图中,该线段的投影的长度分别恒为1和2,则线段PQ 长的取值范围是(A )(0,1]PQ ∈ (B )[1,2]PQ ∈ (C )[2,3]PQ ∈ (D )PQ ∈二、填空题:本大题共4小题,每小题6分。
(7)正三棱柱111C B A ABC -的底面边长为2,侧棱长为,D 为BC 中点,则三棱锥11DC B A -的体积为_____________.(8)一个空间几何体的三视图如图所示,则该几何体的表面积为 .(9)已知点P 在正方体1111ABCD A B C D -的对角线1BD 上,60PDA ∠= ,则DP 与1CC 所成角的大小为___________.(10)已知三棱锥O A B C -底面ABC 的顶点在半径为4的球O 表面上,且6AB =,BC =,AC =O ABC -的体积为___________.三、解答题:解答应写出文字说明,证明过程或演算步骤。
数学基地校高三毕业班总复习 立体几何 平行性试卷(理)

2017高三毕业班总复习立体几何平行性试卷(理)一、选择题(共12小题,每小题5分,共60分)(1) 对两条不相交的空间直线a 与b ,必存在平面α,使得( )(A),a b αα⊂⊂ (B ),a bαα⊂(C) ,a b αα⊥⊥(D),a b αα⊂⊥(2) 如图,正三棱柱111ABC A B C -的主视图是边长为4的 正方形,则此正三棱柱的左视图的面积为( )(A )16 (B ) 23(C)43(D )83(3)设a ,b 是两条不同的直线,α,β是两个不同的平面,则下列命题错误的是( )(A )若,a bαα⊥,则a b ⊥(B)若,,a ba b αβ⊥⊂,则αβ⊥(C)若,,a b αβαβ⊥⊥,则a b (D )若,,aa αβ则αβ(4)在梯形ABCD 中,2ABC π∠=,//AD BC ,222BC AD AB ===。
将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )(A )23π(B )43π (C)53π (D )2π(5) 如图,在四面体ABCD 中,已知AB AC ⊥,BD AC ⊥,那么D 在面ABC 内的射影H 必在( ) A .直线AB 上 B .直线BC 上 C .直线AC 上 D .ABC ∆内部(6)某个长方体被一个平面所截,得到几何体的三视图 如图所示,则这个几何体的体积为( )(A )4 (B ) 22(C)203(D )8(7) 已知一个球与一个正三棱柱的三个侧面和两个底面相切,若这个球的体积是323π,则这个三棱柱的体积是( )(A )48 (B ) 246(C ) 243 (D )483(8) 某品牌香水瓶的三视图如图 (单位:cm),则该几何体的表面积为( ) (A)2952cm π⎛⎫- ⎪⎝⎭ (B ) 2942cmπ⎛⎫- ⎪⎝⎭(C )2942cm π⎛⎫+ ⎪⎝⎭ (D )2952cm π⎛⎫+ ⎪⎝⎭(9) 在四面体S ABC -中,,2,2AB BC AB BC SA SC ⊥====,二面角S AC B -- 的余弦值是33-,则该四面体外接球的表面积是( )(A) 86π(B )24π (C) 6π(D)6π(10)已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为()(11)如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题:①点M到AB的距离为2;2②三棱锥C DNE-的体积是16;π。
立体几何 平行垂直 练习题

空间立体几何练习题数学(理工农医类)考试范围:高中内容(人教版)考试时间:120分钟;命题人:题号一二三总分得分注意事项:1. 答题前填写好自己的姓名、班级、考号等信息2. 请将答案正确填写在答题卡上分卷I分卷I 选择题评卷人得分一、单选题(下面每题都四个选项但每题只有一个正确选项,并将正确选项填写在答题卡相应位置上,否则答案无效!)1、设、是不同的直线,、是不同的平面,则下列命题:①若,则;②若,则;③若,则;④若,则.其中正确命题的个数是()A.0B.1C.2D.32、设、是不同的直线,、是不同的平面,则下列命题:①若,则;②若,则;③若,则;④若,则.其中正确命题的个数是()A.0B.1C.2D.33、设,是两条不同的直线,是一个平面,则下列命题正确的是()A.若,,则B.若,,则C.,,则D.若,,则4、对于空间的两条直线,和一个平面,下列命题中的真命题是()A.若,,则B.若,,则C.若,,则D.若,,则5、设是三个互不重合的平面,是两条不重合的直线,则下列命题中正确的是()A.若,则B.若,,,则C.若,,则D.若,,,则6、设是两条不同直线,是两个不同的平面,下列命题正确的是()A.且则B.且,则C.则D.则7、在空间中,若、表示不同的平面,、、表示不同直线,则以下命题中正确的有()①若∥,∥,∥,则∥②若⊥,⊥,⊥,则⊥③若⊥,⊥,∥,则∥④若∥,,,则∥A.①④B.②③C.②④D.②③④8、设是两条不同的直线,是两个不同的平面,有下列四个命题:①若;②若;③若;④若其中正确命题的序号是()A.①③B.①②C.③④D.②③9、对于平面、、和直线、、、,下列命题中真命题是()A.若,则;B.若则;C .若,则;D.若,则.10、已知为异面直线,平面,平面.直线满足,则()A.,且B.,且C.与相交,且交线垂直于D.与相交,且交线平行于分卷II分卷II 非选择题评卷人得分二、填空题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)11、设是两条不同的直线,是两个不同的平面,则下列正确命题的序号是.①.若,,则;②.若,,则;③.若,,则;④.若,则.12、已知是两个互相垂直的平面,是一对异面直线,下列五个结论:(1),(2)(3)(4)(5)。
全国二卷立体几何真题及模拟题(理科)

立体几何(理科)立体几何解题中常用的判定定理及性质定理1.直线与平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.(线线平行⇒线面平行)若a⊂/α,b⊂α,a∥b,则a∥α.2.直线与平面平行的性质定理:如果一条直线和一个平面平行,过这条直线的任一平面与此平面的交线与该直线平行.(线面平行⇒线线平行)若a∥α,a⊂β,α⋂β=b,则a∥b.3.直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线垂直,则该直线与此平面垂直.若m⊂α,n⊂α,m⋂n=O,l⊥m,l⊥n,则l⊥α.4.直线与平面垂直的性质定理:垂直于同一个平面的两条直线平行.若a⊥α,b⊥α,则a∥b.5.平面与平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(线面平行⇒面面平行)若a⊂α,b⊂α,a⋂b=A,a∥β,b∥β,则α∥β.6.平面与平面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.若α∥β,α∩γ=a,β∩γ=b,则a∥b.7.两个平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.若l⊥α,l⊂β,则α⊥β.8.两个平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.若α⊥β,α∩β=l,a⊂α,a⊥l,则a⊥β.空间角的计算(1)两条异面直线所成角的求法设直线a,b的方向向量为a,b,其夹角为θ,则cos φ=|cos θ|=|a·b||a||b|(其中φ为异面直线a,b所成的角).(2)直线和平面所成角的求法如图所示,设直线l的方向向量为e,平面α的法向量为n,直线l与平面α所成的角为φ,两向量e与n的夹角为θ,则有sin φ=|cos θ|=|e·n| |e||n|.(3)二面角的求法①利用向量求二面角的大小,可以不作出平面角,如图所示,〈m,n〉即为所求二面角的平面角.②对于易于建立空间直角坐标系的几何体,求二面角的大小时,可以利用这两个平面的法向量的夹角来求.如图所示,二面角α-l-β,平面α的法向量为n1,平面β的法向量为n2,〈n1,n2〉=θ,则二面有α-l-β的大小为θ或π—θ.空间距离的计算直线到平面的距离,两平行平面的距离均可转化为点到平面的距离.点P 到平面α的距离,d =PM n n⋅ (其中n 为α的法向量,M 为α内任一点).空间角的范围(1)异面直线所成的角(θ):0<θ≤π2; (2)直线与平面所成的角(θ):0≤θ≤π2; (3)二面角(θ):0≤θ≤π.历年高考真题及解析(2013课标全国Ⅱ,理18)如图,直三棱柱111ABC A B C -中,,D E 分别是1,AB BB 的中点,12===AA AC CB AB . (1)证明:1BC ∥平面1A CD ;(2)求二面角1--DA C E 的正弦值.解:(1)连结AC 1交A 1C 于点F ,则F 为AC 1中点. 又D 是AB 中点,连结DF ,则BC 1∥DF . 因为DF ⊂平面A 1CD ,BC 1 ⊄平面A 1CD , 所以BC 1∥平面A 1CD .(2)由AC =CB =2AB 得,AC ⊥BC . 以C 为坐标原点,CA 的方向为x 轴正方向,建立如图所示的空间直角坐标系C -xyz .设CA =2,则D (1,1,0),E (0,2,1),A 1(2,0,2),CD =(1,1,0),CE =(0,2,1),1CA =(2,0,2).设n =(x 1,y 1,z 1)是平面A 1CD 的法向量, 则10,0,CD CA ⎧⋅=⎪⎨⋅=⎪⎩n n 即11110,220.x y x z +=⎧⎨+=⎩可取n =(1,-1,-1).同理,设m 是平面A 1CE 的法向量, 则10,0,CE CA ⎧⋅=⎪⎨⋅=⎪⎩m m 可取m =(2,1,-2). 从而cos 〈n ,m〉=||||3=·n m n m , 故sin 〈n ,m〉=3即二面角D -A 1C -E的正弦值为(2014课标全国Ⅱ,理18)如图,四棱锥P-ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D-AE-C 为60°,AP=1,,求三棱锥E-ACD 的体积. 解:(Ⅰ)设AC 的中点为G, 连接EG .在三角形PBD 中,中位线EG//PB ,且EG 在平面AEC 上,所以PB //平面AEC .(Ⅱ)设CD=m , 分别以,AB, AD,AP 为X,Y,Z轴建立坐标系,则xy。
【精品】2023年高考数学单元复习过关提升卷 立体几何(解析版)

专题09 立体几何学校:___________姓名:___________班级:___________考号:___________题型:15单选+4填空+3解答,满分150分一、单选题1.(北师大版必修2过关斩将第一章立体几何初步�5-�7综合拔高练)如图,在下列四个正方体中,,A B 为正方体的两个顶点,,,M N Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( )A .B .C .D .【答案】A【分析】利用线面平行的判定,结合正方体的性质判断直线AB 与平面MNQ 是否平行.【详解】A :由正方体的性质知:AB 平行于Q 与底面中心的连线,而该线段与面MNQ 交于Q 点,故AB 与面MNQ 不平行;B ://AB MQ 且AB ⊄平面,MNQ MQ ⊂平面MNQ ,则//AB 平面MNQ ;C ://AB MQ 且AB ⊄平面,MNQ MQ ⊂平面MNQ ,则//AB 平面MNQ ;D ://AB NQ 且AB ⊄平面,MNQ NQ ⊂平面MNQ ,则//AB 平面MNQ .故选:A .2.(北师大版必修2过关斩将第一章立体几何初步�1简单几何体1.2简单多面体)下面图形中,为棱锥的是( )A.①③B.①③④C.①②④D.①②【答案】C【分析】利用棱锥的定义对所给4个图形逐一分析判断作答.【详解】一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥,显然①②④满足棱锥定义,③不满足棱锥定义,所以①②④是棱锥,③不是棱锥.故选:C3.(北师大版(2019)必修第二册金榜题名第六章立体几何初步�1基本立体图形1.3简单旋转体——球、圆柱、圆锥和圆台)如图是由哪个平面图形旋转得到的()A.B.C.D.【答案】D【分析】根据圆柱、圆锥与圆台的定义,判断选项中的图形旋转一周后所得到的几何体的形状,进而可得结果. 【详解】A 中图形旋转得到两个圆锥与一个圆柱,不合题意;B 中图形旋转得到两个相同底面的圆锥,不合题意;C 中图形旋转得到相同底面的圆柱与圆锥,不合题意;D 中图形旋转得到一个圆台与一个圆锥,合题意.故选:D.4.(吉林省延边朝鲜族自治州延边第二中学2020-2021学年高一下学期期中数学试题)在空间中,下列命题正确的是( )A .三点确定一个平面B .若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行C .两两相交且不共点的三条直线确定一个平面D .如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行【答案】C【分析】根据平面、线面平行、线线平行、异面直线等知识确定正确选项.【详解】A ,不在同一条直线上的三个点确定一个平面,A 错误.B ,//l α,l 与α内的直线可以平行、异面,B 错误.C 选项,两两相交且不共点的三条直线确定一个平面,C 正确.D 选项,如果两条平行直线中的一条与一个平面平行,那么另一条可能在这个平面内,D 错误. 故选:C5.(北京市房山区2022届高三上学期入学测试数学试题)已知三条不同的直线,,l m n 和两个不同的平面,αβ ,下列四个命题中正确的是( )A .若//m α,//n α,则//m nB .若//l m ,m α⊂,则//l αC .若//l α,l β//,则//αβD .若//l α,l β⊥,则αβ⊥【答案】D【分析】由线线、线面的位置关系,结合平面的基本性质判断线线、线面、面面的位置关系.【详解】A :若//m α,//n α,则,m n 可能平行、相交、异面,错误;B :若//l m ,m α⊂,则//l α或l α⊂,错误;C :若//l α,l β//,则,αβ可能平行、相交或垂直,错误;D :若//l α,若过l 的平面交面α于直线k 则//l k ,由l β⊥知k β⊥,又k α⊂,由面面垂直的判定知αβ⊥,正确;故选:D6.(北师大版(2019)必修第二册金榜题名进阶篇四十九柱、锥、台的体积)长方体同一顶点上的三条棱长分别为2,2,3,则长方体的体积与表面积分别为( )A .12,32B .12,24C .22,12D .12,11 【答案】A【分析】根据长方体的体积公式和表面积公式可得正确的选项.【详解】长方体的体积为22312⨯⨯=,表面积为()222+23+2332⨯⨯⨯=,故选:A.7.(北师大版(2019)必修第二册金榜题名进阶篇四十九柱、锥、台的体积)设四棱锥的底面是对角线长分别为2和4的菱形,四棱锥的高为3,则该四棱锥的体积为( )A .12B .24C .4D .30【答案】C【分析】求出菱形的面积后可求四棱锥的体积.【详解】 所求的体积为11324432⨯⨯⨯⨯=, 故选:C.8.(北师大版(2019)必修第二册金榜题名进阶篇四十八柱、锥、台的侧面展开与面积)若圆锥的底面直径为6,高是4,则它的侧面积为( )A .12πB .24πC .15πD .30π【答案】C【分析】利用条件及圆锥的侧面积公式即求.【详解】作圆锥的轴截面如图,则高AD =4,底面半径CD =3,圆锥的母线AC =5,所以圆锥的侧面积为35=15ππ⨯⨯.故选:C.9.(吉林省延边第二中学2020-2021学年高一下学期第二次考试月考数学试题)若一个圆锥的侧面展开图是半径为R 的半圆,则该圆锥的高为( )A .3RB .2RC .32RD .22R 【答案】C【分析】设圆锥的底面半径为r ,则可得2r R ππ=,求出底面半径,再利用勾股定理可求出圆锥的高【详解】设圆锥的底面半径为r ,则由题意得2r R ππ=,所以2R r =, 所以圆锥的高为22322R R R ⎛⎫-= ⎪⎝⎭, 故选:C10.(北师大版(2019)必修第二册金榜题名进阶篇四十八柱、锥、台的侧面展开与面积)正六棱柱的底面边长为2,最长的一条对角线长为25,则它的表面积为( )A .4)B .2)C .1)D .8)【答案】B【分析】 根据正六棱柱的结构特征,求岀棱柱的高,再计算它的表面积.【详解】正六棱柱的底面边长为2,最长的一条对角线长为12BB =,它的表面积为)16=2622sin 6222412223S S S π=+⨯⨯⨯⨯⨯+⨯⨯==表面积底面积矩形.故选:B.11.(广东省深圳市罗湖区2022届高三上学期第一次质量检测数学试题)若将面积为2的等腰直角三角形,以其一条直角边所在的直线为旋转轴旋转而成一个圆锥,则该圆锥的体积为( )A .B .8πCD .83π 【答案】D【分析】根据三角形的面积求出它的边长,进而得到圆锥的高和底面圆半径,结合圆锥体积公式计算即可.【详解】由等腰直角三角形的面积为2,得其直角边长为2, 所以经过旋转得到圆锥的高为2,底面圆半径为2,所以圆锥的体积为:2182233V ππ=⨯⨯=. 故选:D12.(重庆市合川实验中学2020-2021学年高二上学期第一次月考数学试题)棱长为2的正方体的外接球的体积是( )A .B .C .D .【答案】B【分析】由正方体的性质求其外接球的直径,再利用球体体积公式求外接球体积.【详解】由题设,正方体的外接球的直径2R =∴外接球的体积343V R π==.13.(北师大版(2019)必修第二册金榜题名第六章立体几何初步�3空间点、直线、平面之间的位置关系3.2刻画空间点、线、面位置关系的公理(基本事实4、定理))在正四棱柱1111ABCD A B C D -中,1AB BC ==,13AA =,则异面直线1BC 与11D B 所成角的余弦值为( )A .24B .144C .77D .77【答案】A【分析】 作出两异面直线所成的角,然后由余弦定理求解.【详解】在正四棱柱中11//BD B D ,则异面直线1BC 与11D B 所成角为1DBC ∠或其补角,在1DBC 中,2BD =,22111(3)2BC DC =+=,12cos 222DBC ∠=⨯⨯ 所以异面直线1BC 与11D B 2 故选:A .14.(【百强校】2015-2016学年河北省冀州市中学高一下开学考试数学试卷(带解析))设PH ⊥平面 ABC ,且,,PA PB PC 相等,则 H 是ABC 的A .内心B .外心C .垂心D .重心【答案】B【详解】 PH ⊥平面ABC ,且,,PA PB PC 相等,则HA HB HC ==,故H 是ABC 的外心.【点睛】三角形中有三种主要线段:高、角平分线和中线,它们各自的交点就分别称为三角形的垂心、内心与重心.1、内心:三条角平分线的交点,也是三角形内切圆的圆心.性质:到三边距离相等.2、重心:三条中线的交点.性质:三条中线的三等分点.3、垂心:三条高所在直线的交点.性质:此点分每条高线的两部分乘积.4、外心:三条中垂线的交点,也是三角形外接圆的圆心.性质:到三个顶点等远.15.(江苏省无锡市2020-2021学年高二下学期期末数学试题)《九章算术·商功》:“斜解立方,得两塹堵,斜解塹堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以基,其形露矣.”文中“阳马”是底面为长方形且有一条侧棱与底面垂直的四棱锥.在阳马P ABCD -中,侧棱PA ⊥底面ABCD ,且1PA =,2AB AD ==,则点A 到平面PBD 的距离为( )A .23B .63C .62D .33 【答案】B 【分析】利用等体积法有P ABD A PBD V V --=,即可求A 到平面PBD 的距离.【详解】设A 到平面PBD 的距离为h ,则三棱锥PABD 的体积为:1133ABD PBD S PA S h ⨯⨯=⨯⨯△△,即有11112212233232h ⨯⨯⨯⨯=⨯⨯, ∴6h =. 故选:B .二、填空题16.(上海市嘉定区第一中学、金山中学2021-2022学年高二上学期9月月考数学试题)若直线a ⋂平面A α=,直线b ⊂平面α,则直线a 与直线b 的位置关系为___________①相交;②平行;③异面(将所有可能的代号写在横线上).【答案】①③【分析】分别在A b ∉和A b ∈两种情况下得到两直线位置关系即可.如图所示:若A b ∉,则直线b 与直线a 异面;若A b ∈,则直线b 与直线a 相交.故答案为:①③.17.(上海市复旦大学附属中学2022届高三上学期9月月考数学试题)一个圆柱的侧面展开图是一个面积为4π2的正方形,则这个圆柱的体积为___________;【答案】22π【分析】由题意可得圆柱的高和底面周长相等,均为2π,然后求出底面半径,从而可求出圆柱的体积【详解】设圆柱的底面半径为r ,因为圆柱的侧面展开图是一个面积为4π2的正方形,所以圆柱的高和底面周长相等,均为2π,所以22ππ=r ,得1r =,所以这个圆柱的体积为2222r πππ⋅=,故答案为:22π18.(北师大版必修2过关斩将第一章立体几何初步�7简单几何体的再认识7.3球)已知正方体的棱长为2,则与正方体的各棱都相切的球的表面积是_______.【答案】8π【分析】由球与正方体的各棱相切可得球的半径,从而可求其表面积.【详解】 过正方体的对角面作截面如图,故球的半径2r =∴其表面积242)8S ππ=⨯=.故答案为:8π.三、双空题19.(人教A 版(2019)必修第二册第八章立体几何单元测试)下列几何体中旋转体__________个,台体(棱台和圆台)__________个.【答案】3 2【分析】根据几何体的结构特征判断可得出结论.【详解】由图可知,(6)(7)(8)为旋转体,(5)(7)为台体.故答案为:3;2.【点睛】本题考查旋转体与台体的判断,属于基础题.四、解答题20.(【全国百强校】北京东城北京二中2017-2018学年高二上学期期中考试数学(理)试题)如图,四棱锥P ABCD -的底面ABCD 为菱形,PB PD =,E ,F 分别为AB 和PD 的中点.(1)求证:EF ∥平面PBC .(2)求证:BD ⊥平面PAC .【答案】(1) 证明见解析.(2)证明见解析.【详解】分析:(1)证明线面平行,只需在面内找一条直线与已知线平行即可,取PC 中点为G ,证明四边形BEFG是平行四边形即可;(2)证明线面垂直则需在面内找两条相交直线与已知线垂直即可,BD AC ⊥,BD PO ⊥即可得证.详解:(1)证明:取PC 中点为G ,∵在PCD 中,F 是PD 中点,G 是PC 中点,∴FG CD ,且12FG CD =, 又∵底面ABCD 是菱形,∴AB CD ,∵E 是AB 中点,∴BE CD ,且12BE CD =, ∴BE FG ,且BE FG =,∴四边形BEFG 是平行四边形,∴EF BG ,又EF ⊄平面PBC ,BG ⊄平面PBC ,∴EF 平面PBC .(2)证明:设AC BD O ⋂=,则O 是BD 中点,∵底面ABCD 是菱形,∴BD AC ⊥,又∵PB PD =,O 是BD 中点,∴BD PO ⊥,又AC PO O ⋂=,∴BD ⊥平面PAC .点睛:本题考查了空间直线平面的平行,垂直,关键是熟练掌握定理,定义,把空间问题转化为平面问题求解,属于中档题.21.(吉林省长春外国语学校2020-2021学年高二下学期期末考试数学(文科)试题)如图,在三棱柱111ABC A B C -中,1AA ⊥平面ABC ,1AB BC AC AA ===,D 是BC 的中点.(1)求证:1//A B 平面1AC D ;(2)求证:平面1AC D ⊥平面11BCC B .【答案】(1)证明见解析;(2)证明见解析;【分析】(1)连接1A C 交1AC 于O ,连接OD ,证明1//OD A B 利用线面平行判定定理证明;(2)证明AD ⊥平面11BCC B ,再利用面面垂直判定定理证明【详解】解:(1)如图,连接1A C 交1AC 于O ,连接OD ,∴O 是1A C 的中点,又D 是BC 的中点,∴OD 是1A BC 的中位线,∴1//OD A B∵1A B ⊂/平面1AC D ,OD ⊂平面1AC D ∴1//A B 平面1AC D(2)∵AB BC AC ==,D 是BC 的中点,∴AD BC ⊥,∵三棱柱111ABC A B C -中,1AA ⊥平面ABC ,∴1BB ⊥平面ABC∵AD ⊂平面ABC ,∴1BB AD ⊥,又1BB 、BC 是平面11BCC B 内的两条相交直线∴AD ⊥平面11BCC B ,∵AD ⊂平面1AC D ,∴平面1AC D ⊥平面11BCC B .22.(广东省江门市2020-2021学年高一下学期期末数学试题)如图,AB 是圆O 的直径,PA 垂直圆O 所在的平面,C 是圆O 上的点.(1)求证:BC ⊥平面PAC ;(2)设Q 为PA 的中点,G 为AOC △的重心,求证:面//OQG 平面PBC .【答案】(1)证明见解析;(2)证明见解析.【分析】(1)根据圆直径的性质,得BC AC ⊥,由PA ⊥平面ABC 得BC PA ⊥,利用线面垂直的判定定理,可证BC ⊥平面PAC ;(2)延长OG ,交AC 于M ,连结GM 、QM ,证出QM 是PAC △的中位线,得//QM PC .利用线面平行的判定定理证出//QM 平面PBC ,同理可得//QO 平面PBC ,根据面面平行的判定定理,可得平面//OQG 平面PBC .【详解】解:(1)∵AB 是圆O 的直径,∴BC AC ⊥,又∵PA ⊥平面ABC ,BC ⊂平面ABC ,∴BC PA ⊥. ∵PA AC A =,∴BC ⊥平面PAC ;(2)延长OG ,交AC 于M ,连结GM 、QM ,∵G 为AOC △的重心,∴OM 是AOC △的中线, ∵Q 为PA 的中点,M 为AC 的中点,∴//QM PC , ∵QM ⊄平面PBC ,PC ⊂平面PBC ,∴//QM 平面PBC , 同理可得//QO 平面PBC ,∵QM 、QO 是平面OQG 内的相交直线, ∴平面//OQG 平面PBC .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016高三毕业班总复习单元过关平行性测试卷(理科)立体几何 泉州市数学组一、选择题:本大题共6小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)在一个几何的三视图中,正视图和俯视图如右图所示,则相应的侧视图不可能是(A ) (B )(C ) (D )(2)如图是一个组合几何体的三视图,则该几何体的体积等于 (A )24128π+ (B )3672π+ (C )24128π+(D )36128π+ (3)如图,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为(A )23 (B )43(C )83(D )8(4)已知二面角l αβ--的大小为45,m α ,n α⊥,则下列四种位置关系中,一定不成立的是(A )m n ⊥ (B )m β⊥(C )m 与平面β所成的角等于45 (D )n 与平面β所成的角等于45(5)如图,直三棱柱111A B C A B C -中,16AA =,4AB AC ==,AB AC ⊥,点,E F 分别是线段11,AB CC 的动点,11,AE EB CF FC λμ== .则当14B EFB V -=三棱锥时,必有 (A )13λ=(B )13μ= (C )3λ= (D )3μ=(6),则该条棱的长度为(B)3 二、填空题:本大题共4小题,每小题6分。
(7)一个四面体的顶点在空间直角坐标系O xyz -的坐标分别是(0,1,1),(1,2,1),(1,1,2),(0,3,3),画出该四面体的正视图时,以平面yOz 为投影面,则得到的正视图的面积是_______.(8)已知三棱锥S ABC -的各个顶点都在一个半径为2的球面上,球心O 在AB 上,则三棱锥S ABC -的体积最大值为____________.(9)一个几何体的正视图为一个四边形,则这个几何体可能是下列几何体中的___________.(填入所有可能的几何体的编号)①三棱锥; ②四棱锥; ③圆锥; ④三棱柱; ⑤圆柱. (10)已知一个圆柱的两个底面都在同一个球面上,且圆柱的表面积是此球的表面积的34,则圆柱的体积与此球的体积的比值是___________.三、解答题:解答应写出文字说明,证明过程或演算步骤。
(11)(本小题满分10分)如图,在等腰梯形ABCD 中,AB CD ,3AB =, 1CD =,2AD BC ==,E 为AB 上的点且1AE =,将AED ∆沿DE 折起到1A ED 的位置,使得平面1A ED ⊥平面BCDE .(Ⅰ)求证:1A E BE ⊥;(Ⅱ)求二面角1B AC D --的余弦值.(12)(本小题满分15分)直三棱柱111ABC A B C -中,D 是AC 的中点,1A D 与1AC 交于点E ,F 在线段1AC 上,且12AF FC =,11AA =,2AB =,1AC =,60BAC ∠=.(Ⅰ)求证:1B F 平面1A BD ;(Ⅱ)求直线BC 与平面1A BD 所成的角的正弦值.(13)(本小题满分15分)如图,在三棱柱111ABC A B C -中,1AA ⊥平面ABC ,122AA AC AB ===,11BC AC ⊥.(Ⅰ)求证:AB ⊥平面1AC ;(Ⅱ)试探究线段1AA 上的点D 的位置,使得平面1ABC 与平面11B C D 所成的二面角.2016高三毕业班总复习单元过关平行性测试卷(理科)立体几何(参考答案) 泉州市数学组一.选择题.(1)选B . (2)选D. (3)选B. (4)选B. (5)选C. (6) 选A . 二、填空题.(7)填2. (8)填83. (9)填①②④⑤. (10). 三、解答题.(11)解:(Ⅰ)由题意,可知在等腰梯形ABCD 中,DE AB ⊥, 所以1A E DE ⊥,又平面1A ED ⊥平面BCDE ,平面1A ED 平面BCDE DE =, 1A E ⊂平面1A ED ,所以1A E ⊥平面BCDE , 又因为BE ⊂平面BCDE ,故1A E BE ⊥. ………………5分(Ⅱ)由(Ⅰ),可知1,,EA EB ED 两两垂直,故以E 为原点,分别以1,,EA EB ED所在直线为x 轴、y 轴、z 轴建立空间直角坐标系O xyz -.则1(1,0,0),(0,2,0),(0,1A B C D ,11(1,2,0),(0,1(1(0,1,0)AB BC AD CD =-=-=-=-,设平面1A BC 的一个法向量1111(,,)x y z =n ,则有1110,0,A B BC ⎧⋅=⎪⎨⋅=⎪⎩n n即20,0,x y y -+=⎧⎪⎨-=⎪⎩整理,得2,,x y z y =⎧⎪⎨=⎪⎩令z =1)=n ;设平面1ACD 的一个法向量2222(,,)x y z =n ,则有 2120,0,A D CD ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0,x y ⎧-+=⎪⎨-=⎪⎩整理,得,0,x y ⎧=⎪⎨=⎪⎩ 令1z =,得2=n ;设二面角1B AC D --的大小为θ,(,)2πθπ∈,所以121278⋅=⋅n n n n ,故7cos 8θ=-. …………10分(12)解1:(Ⅰ)连结1AB ,交1A B 于点G ,连结EG .则有1AG GB =. 由题意,可知11AD AC ,∴1111,ADE C A E DAE AC E ∠=∠∠=∠, ∴11ADE C A E ∆∆ ,11112AE AD EC C A ==, 又12AF FC =,∴1AE EF FC ==, ∴1B FEG , ………………6分又∵1B F ⊄平面1A BD ,EG ⊂平面1A BD , ∴1B F平面1A BD . ……………7分(Ⅱ)∵ 1CC ⊥平面ABC ,BC ⊂平面ABC ,∴1BC CC ⊥.在ABC ∆中,2AB =,1AC =,60BAC ∠=,∴2222cos 3BC AB AC AB AC BAC =+-∠=, 则222AB BC AC =+,∴090BCA ∠=,BC AC ⊥,又∵1CC ⊥平面ABC ,,AB AC ⊂平面ABC , ∴11,CC CA CC CB ⊥⊥,如图,以C 以原点,分别以1,,CA CC CB 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系O xyz -. …………10分则有B ,1(1,1,0)A ,1(,0,0)2D ,111((,1,0)22DB DA =-= ,CB = …………11分设平面1A BD 的一个法向量(,,)x y z =n ,直线BC 与平面1A BD 所成的角为θ.由100DB DA ⎧⋅=⎪⎨⋅=⎪⎩n n,得102102x x y ⎧-+=⎪⎪⎨⎪+=⎪⎩,整理得12z x y x ⎧=⎪⎪⎨⎪=-⎪⎩,令x =1A BD的一个法向量=n ,所以1sin 4CBCBθ⋅===⋅n n .故直线BC 与平面1A BD 所成的角的正弦值为14. …………15分解2:(Ⅰ)取11AC 的中点H ,连结1,,FH B H DH .则有1DH BB , ∴四边形1DHB B 为平形四边形, ∴1B HBD ,又1B H ⊄平面1A BD ,BD ⊂平面1A BD , ∴1B H平面1A BD . …………4分由题意,可知11AD AC ,∴1111,ADE C A E DAE AC E ∠=∠∠=∠, ∴ADE ∆∽11C A E ∆,11112AE AD EC C A ==, 又12AF FC =,∴1AE EF FC ==.又11A H HC =,∴1FH EA ,又FH ⊄平面1A BD ,1EA ⊂平面1A BD , ∴FH 平面1A BD , …………5分 又∵1,FH B H ⊂平面1B FH ,1FH B H H =, ∴平面1B FH平面1A BD .又1B F ⊂平面1B FH , ∴1B F平面1A BD . ………………7分(Ⅱ)同解法1.解3:(Ⅰ)∵ 1CC ⊥平面ABC ,BC ⊂平面ABC ,∴1BC CC ⊥.在ABC ∆中,2AB =,1AC =,60BAC ∠=,∴2222cos 3BC AB AC AB AC BAC =+-∠=, 则222AB BC AC =+,∴090BCA ∠=,BC AC ⊥,又∵1CC ⊥平面ABC ,,AB AC ⊂平面ABC , ∴11,CC CA CC CB ⊥⊥,如图,以C 以原点,分别以1,,CA CC CB 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系O xyz -. …………2分则有(1,0,0)A,B ,1(1,1,0)A,1(0,1B ,1(0,1,0)C ,1(,0,0)2D .∴111((,1,0)22DB DA =-= .设(,,0)F x y ,则(1,,0)AF x y =-,1(,1,0)FC x y =-- .∵12AF FC =,∴12,2(1),x x y y -=-⎧⎨=-⎩解得1,32,3x y ⎧=⎪⎪⎨⎪=⎪⎩即12(,,0)33F,111(,33FB =- .若令1FB = 1mDB nDA + ,可解得11,3m n ==, ∴存在11,3m n ==,使得1FB = 1mDB nDA + ,∴向量1FB 与1,DB DA 共面.又∵1B F ⊄平面1A BD ,∴1B F 平面1A BD . …………8分(Ⅱ)同解法1.(13)(Ⅰ)证明:∵1AA ⊥平面ABC ,,AB AC ⊂平面ABC ,∴1A A AB ⊥,1A A AC ⊥.…1分又∵1A A AC =,11//A A C C ,且11=A A C C , ∴侧面11A ACC 是正方形,11A C AC ⊥.………2分∵11BC AC ⊥,11,BC AC ⊂平面1ABC , ∴1AC ⊥平面1ABC .又∵AB ⊂平面1ABC ,∴1AC AB ⊥, 又∵1A A AB ⊥,11,⊂AC AA 平面1AC , ∴AB ⊥平面1AC . …………7分(Ⅱ)解:由(Ⅰ)可知,AB ⊥AC ,从而1,,AB AC AA 两两垂直,故以A 为原点,分别以1,,AB AC AA 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系O xyz -.∵122AA AC AB ===,∴1(0,0,2)A ,1(1,0,2)B,(0,2,0)C ,1(0,2,2)C , ∴1(0,2,2)CA =- ,11(1,2,0)BC =- . 设(0,0,)(02)D t t ≤≤,平面11B C D 的一个法向量为(,,)x y z =n ,则1(1,0,2)B D t =-- 且1110,0,B C B D ⎧⋅=⎪⎨⋅=⎪⎩n n, 即20,(2)0x y x t z -+=⎧⎨-+-=⎩,整理得1212y x z x t ⎧=⎪⎪⎨⎪=⎪-⎩,令2x =,则2(2,1,)2t =-n . 由(Ⅰ)可知,1AC ⊥平面1ABC , ∴1(0,2,2)CA =- 是平面1ABC 的一个法向量.设平面1ABC 与平面11B C D 所成的二面角的大小为θ,第 11 页 共 11 页则11cos 2CA CA θ⋅===⋅n n , 整理,得2320t t -+=,解得1t =或2t =,………14分 ∴当D 为线段1AA 的中点或与1A 重合时,平面1ABC 与平面11B C D 所……………15分。
