坡度问题专项练习题
湘教版九年级数学上册坡度问题同步练习题

4.4 解直角三角形的应用第2课时 坡度、坡比问题 1. 如图,已知一商场自动扶梯的长l 为13米,高度h 为5米,自动扶梯与地面所成的夹角为θ,则tan θ的值等于( )A .512B . 125C .513D .12132.(2014深圳中考)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12,的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )A .6002505-B .6003250-C .3503503+D .50033. (2014•上海中考)已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为_____米.☆4. 如图,某公园入口处原有三级台阶,每级台阶高为20cm ,深为30cm ,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A ,斜坡的起始点为C ,现设计斜坡的坡度i=1:5,则AC 的长度是_________.5.(2014•莱芜中考)如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)☆6. (2014•常德中考)如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为160米,400米,1000米,钢缆AB,BC分别与水平线AA2,BB2所成的夹角为30°,45°,求钢缆AB和BC的总长度.(结果精确到1米)☆7. (2014•山西中考)如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB、BC表示连接缆车站的钢缆,已知A、B、C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1:2,钢缆BC的坡度i2=1:1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)8. (2014•广安中考)为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB长602米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).(1)若修建的斜坡BE的坡比为3:1,求休闲平台DE的长是多少米?(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G,H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?考点综合专题:一元二次方程与其他知识的综合◆类型一一元二次方程与三角形、四边形的综合1.(雅安中考)已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是()A.5 B.7 C.5或7 D.102.(广安中考)一个等腰三角形的两条边长分别是方程x2-7x+10=0的根,则该等腰三角形的周长是()A.12 B.9C.13 D.12或93.(罗田县期中)菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x +12=0的一个根,则菱形ABCD的周长为()A.16 B.12 C.16或12 D.244.(烟台中考)等腰三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2-6x+n-1=0的两根,则n的值为()A.9 B.10C.9或10 D.8或105.(齐齐哈尔中考)△ABC的两边长分别为2和3,第三边的长是方程x2-8x +15=0的根,则△ABC的周长是.6.(西宁中考)若矩形的长和宽是方程2x2-16x+m=0(0<m≤32)的两根,则矩形的周长为.【方法8】7.已知一直角三角形的两条直角边是关于x的一元二次方程x2+(2k-1)x +k2+3=0的两个不相等的实数根,如果此直角三角形的斜边是5,求它的两条直角边分别是多少.【易错4】◆类型二一元二次方程与函数的综合8.(泸州中考)若关于x 的一元二次方程x 2-2x +kb +1=0有两个不相等的实数根,则一次函数y =kx +b 的大致图象可能是( )9.(安顺中考)若一元二次方程x 2-2x -m =0无实数根,则一次函数y =(m +1)x +m -1的图象不经过( )A .第四象限B .第三象限C .第二象限D .第一象限10.(葫芦岛中考)已知k 、b 是一元二次方程(2x +1)(3x -1)=0的两个根,且k >b ,则函数y =kx +b 的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限11.(广元中考)从3,0,-1,-2,-3这五个数中抽取一个数,作为函数y =(5-m 2)x 和关于x 的一元二次方程(m +1)x 2+mx +1=0中m 的值.若恰好使函数的图象经过第一、三象限,且使方程有实数根,则满足条件的m 的值是 .12.(甘孜州中考)若函数y =-kx +2k +2与y =k x(k ≠0)的图象有两个不同的交点,则k 的取值范围是 . .◆类型三 一元二次方程与二次根式的综合13.(达州中考)方程(m -2)x 2-3-mx +14=0有两个实数根,则m 的取值范围为( )A .m >52B .m ≤52且m ≠2 C .m ≥3 D .m ≤3且m ≠214.(包头中考)已知关于x 的一元二次方程x 2+k -1x -1=0有两个不相等的实数根,则k 的取值范围是 .考点综合专题:一元二次方程与其他知识的综合1.B 2.A 3.A 4.B 5.86.16 解析:设矩形的长和宽分别为x 、y ,根据题意得x +y =8,所以矩形的周长为2(x +y)=16.7.解:∵一元二次方程x 2+(2k -1)x +k 2+3=0有两个不相等的实数根,∴Δ>0,∴(2k -1)2-4(k 2+3)>0,即-4k -11>0,∴k<-114,令其两根分别为x 1,x 2,则有x 1+x 2=1-2k ,x 1·x 2=k 2+3,∵此方程的两个根分别是一直角三角形的两条直角边,且此直角三角形的斜边长为5,∴x 21+x 22=52,∴(x 1+x 2)2-2x 1·x 2=25,∴(1-2k)2-2(k 2+3)=25,∴k 2-2k -15=0,∴k 1=5,k 2=-3,∵k<-114,∴k =-3, ∴把k =-3代入原方程得到x 2-7x +12=0,解得x 1=3,x 2=4,∴直角三角形的两直角边分别为3和4.8.B9.D 解析:∵一元二次方程x 2-2x -m =0无实数根,∴Δ<0,∴Δ=4-4×1×(-m)=4+4m <0,∴m <-1,∴m +1<1-1,即m +1<0,m -1<-1-1,即m -1<-2,∴一次函数y =(m +1)x +m -1的图象不经过第一象限.故选D.10.B 11.-2 12.k>-12且k≠013.B 14.k≥1。
解直角三角形的应用-坡度坡角问题-初中数学习题集含答案

解直角三角形的应用-坡度坡角问题(北京习题集)(教师版)一.选择题(共2小题)1.(2019秋•石景山区期末)如图,某斜坡的长为,坡顶离水平地面的距离为,则这个斜坡的坡度为 A .B . CD . 2.(2016秋•丰台区期末)如果某个斜坡的坡度是,那么这个斜坡的坡角为 A .B .C .D .二.填空题(共3小题)3.(2019•朝阳区模拟)2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,一位同学乘滑雪板沿斜坡笔直滑下了200米,若斜坡与水平面的夹角为,则他下降的高度为 米.(用含的式子表示)4.(2018秋•通州区期中)一运动员乘雪橇沿坡比的斜坡笔直滑下,若下滑的垂直高度为1000米.则这名运动员滑到坡底的路程是 米.5.(2017秋•石景山区期末)“平改坡”是指在建筑结构许可条件下,将多层住宅的平屋顶改建成坡屋顶,并对外立面进行整修粉饰,达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为.如图是某小区对楼顶进行“平改坡”改造的示意图.根据图中的数据,如果要使坡面的坡度达到,那么立柱的长为 米.三.解答题(共4小题)6.(2017秋•昌平区校级期中)深圳市民中心广场上有旗杆如图1所示,某学校数学兴趣小组测量了该旗杆的高100m 50m ()30︒60︒12()30︒45︒60︒90︒ααBC 1:1.2AC度.如图2,某一时刻,旗杆的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长为16米,落在斜坡上的影长为8米,;同一时刻,太阳光线与水平面的夹角为,1米的标杆竖立在斜坡上的影长为2米,求旗杆的高度.7.(2017春•西城区校级期中)上海迪士尼乐园,是中国内地首座迪士尼主题乐园,于2016年6月16日正式开园.小明和妈妈在游玩迪士尼乐园的过程中,发现了一些娱乐设施中蕴含着数学问题,请你利用所学的知识帮助小明解答这些问题:(1)游乐园里的跷跷板(如图是深受大人和孩子青睐的娱乐设施之一,如图2是跷跷板示意图,横板绕其中点上下转动,立柱与地面垂直.若,那么点被跷起的最大高度为 .若将横板换成横板,且,仍为的中点,设点的最大高度为,则 (填“”、“ ”或“” (2)游乐园中的滑梯(如图是另一个备受小朋友喜爱的游戏.小朋友需从左侧攀爬上楼梯,再水平走至滑梯口,然后从右侧滑梯滑下,完成整个游戏过程.如图4为滑梯简图,已知左侧楼梯的倾斜角,右侧滑梯的倾斜角,整个过程中,小朋友运动的距离为,其中水平通道,那么楼梯 ,滑梯 .8.(2015秋•北京期末)北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如AB BC CD AB BC ⊥45︒EF FG 1)AB O OC 1OC m =B h m AB A B ''2A B AB ''=O A B ''B 'h 'h 'h ><=)3)45A ∠=︒30C ∠=︒5+1BD m =AB =m DC =m图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由降为,已知原斜坡坡面长为200米,点,,在同一水平地面上,求改善后的斜坡坡角向前推进的距离.(结果保留整9.(2016•朝阳区校级模拟)如图,是某公园“六一”前新增设的一架滑梯,该滑梯高度,滑梯着地点与梯架之间的距离.(1)求滑梯的长.(2)若规定滑梯倾斜面不超过45度属于安全范围,通过计算说明这架滑梯的倾斜角是否符合要求?45︒30︒AB D B C BD 1.41≈ 1.73≈ 2.45)≈2AC cm =B 4BC cm =AB ()ABC ∠解直角三角形的应用-坡度坡角问题(北京习题集)(教师版)参考答案与试题解析一.选择题(共2小题)1.(2019秋•石景山区期末)如图,某斜坡的长为,坡顶离水平地面的距离为,则这个斜坡的坡度为 A .B . CD . 【分析】首先根据,求出,再求正切即可.【解答】解:,, , ,, 故选:.【点评】此题主要考查了解直角三角形的应用,关键是掌握特殊角的三角函数值.2.(2016秋•丰台区期末)如果某个斜坡的坡度是,那么这个斜坡的坡角为 A .B .C .D .【分析】根据坡角的正切坡度,列式可得结果.【解答】解:设这个斜坡的坡角为,由题意得:, ; 故选:.【点评】本题考查了解直角三角形的应用坡度坡角问题,明确坡度实际就是一锐角的正切值;在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.100m 50m ()30︒60︒12100AB m =50BC m =30α=︒100AB m =Q 50BC m =501sin 1002α∴==30α∴=︒tan 30∴︒=∴C ()30︒45︒60︒90︒=αtan α==30α∴=︒A -二.填空题(共3小题)3.(2019•朝阳区模拟)2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,一位同学乘滑雪板沿斜坡笔直滑下了200米,若斜坡与水平面的夹角为,则他下降的高度为 米.(用含的式子表示)【分析】如图,设下滑的距离为米,下降的高度为线段.解直角三角形求出即可;【解答】解:如图,设下滑的距离为米,下降的高度为线段.在中,(米,故答案为.【点评】本题考查解直角三角形的应用,解题的关键是理解题意,属于中考常考题型.4.(2018秋•通州区期中)一运动员乘雪橇沿坡比的斜坡笔直滑下,若下滑的垂直高度为1000米.则这名运动员滑到坡底的路程是 2000 米.【分析】由坡比可得垂直高度与对应的水平宽度的比值,因而可求出垂直高度为1000米对应的水平宽度,再用勾股定理求出斜坡长即可.【解答】解:由坡比的定义得,坡面的铅直高度1000米与水平宽度之比为,所以水平宽度为(米,答:这名运动员滑到坡底的路程是2000米.故答案为:2000米.【点评】此题考查了解直角三角形坡度坡角问题,正确理解坡比的定义是解题的关键,注意坡比与坡角的区别.坡α200sin αg α200AB =AC AC 200AB =AC Rt ABC ∆sin 200sin AC AB αα==g g )200sin αg 2000=)-度是坡面的铅直高度和水平宽度的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用表示,常写成的形式.把坡面与水平面的夹角叫做坡角,坡度与坡角之间的关系为:.5.(2017秋•石景山区期末)“平改坡”是指在建筑结构许可条件下,将多层住宅的平屋顶改建成坡屋顶,并对外立面进行整修粉饰,达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为.如图是某小区对楼顶进行“平改坡”改造的示意图.根据图中的数据,如果要使坡面的坡度达到,那么立柱的长为 2.5 米.【分析】由坡度的概念得出,根据可得的长度. 【解答】解:根据题意知, ,, 解得:,故答案为:2.5.【点评】本题主要考查解直角三角形的应用坡度坡角问题,解题的关键是熟练掌握坡度的定义.三.解答题(共4小题)6.(2017秋•昌平区校级期中)深圳市民中心广场上有旗杆如图1所示,某学校数学兴趣小组测量了该旗杆的高度.如图2,某一时刻,旗杆的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长为16米,落在斜坡上的影长为8米,;同一时刻,太阳光线与水平面的夹角为,1米的标杆竖立在斜坡上的影长为2米,求旗杆的高度.【分析】由同一时间内,太阳光线照射的影长,都是成比例的,所以可过点作,交于点,则,则可求出的长;由太阳光线与水平面的夹角为,可过点作,可解得h l i 1:i m =αi α:tan i h l α==BC 1:1.2AC 11.2AC AB =3AB =AC 11.2AC AB =3AB =Q ∴13 1.2AC = 2.5AC =-AB BC CD AB BC ⊥45︒EF FG C PC BC ⊥AD P PCD EFG ∆∆∽PC 45︒P PQ AB ⊥米,从而解出答案.【解答】解:过点作,交于点,过点作,垂足为,,,, (米,四边形为矩形,(米,(米,在中,,(米,(米.答:旗杆的高度为 20 米.【点评】此题考查了解直角三角形的应用,用到的知识点是平行投影的性质、相似三角形的判定与性质以及解直角三角形,关键是根据题意画出辅助线,得出相似三角形.7.(2017春•西城区校级期中)上海迪士尼乐园,是中国内地首座迪士尼主题乐园,于2016年6月16日正式开园.小明和妈妈在游玩迪士尼乐园的过程中,发现了一些娱乐设施中蕴含着数学问题,请你利用所学的知识帮助小明解答这些问题:(1)游乐园里的跷跷板(如图是深受大人和孩子青睐的娱乐设施之一,如图2是跷跷板示意图,横板绕其中点上下转动,立柱与地面垂直.若,那么点被跷起的最大高度为 2 .若将横板换成横板,且,仍为的中点,设点的最大高度为,则 (填“”、“ ”或“”(2)游乐园中的滑梯(如图是另一个备受小朋友喜爱的游戏.小朋友需从左侧攀爬上楼梯,再水平走至滑梯口,16AQ PQ BC ===C PC BC ⊥AD P P PQ AB ⊥Q PCD EFG ∆∆Q ∽∴PC CD EF FG =∴812PC =4PC ∴=)Q PQBC 16PQ BC ∴==)4BQ PC ==)Q Rt APQ ∆45APQ ∠=︒16AQ PQ ∴==)16420AB AQ BQ ∴=+=+=)1)AB O OC 1OC m =B h m AB A B ''2A B AB ''=O A B ''B 'h 'h 'h ><=)3)然后从右侧滑梯滑下,完成整个游戏过程.如图4为滑梯简图,已知左侧楼梯的倾斜角,右侧滑梯的倾斜角,整个过程中,小朋友运动的距离为,其中水平通道,那么楼梯 ,滑梯 .【分析】(1)利用三角形的中位线定理即可解决问题.(2)如图4中,作于,于.则四边形是矩形,设,构建方程求出即可解决问题.【解答】解:(1)如图2中,作于.,,,,若将横板换成横板,且,仍为的中点,设点的最大高度为,同法可得, ,故答案为2,.(2)如图4中,作于,于.则四边形是矩形,,设,在中,,,,在中,,,45A ∠=︒30C ∠=︒5+1BD m =AB =m DC =m BE AC ⊥E DF AC ⊥F BEFD BE DF xm ==x BH AC ⊥H OA OB =Q OC BH ⊥AC CH ∴=22BH OC m ∴==AB A B ''2A B AB ''=O A B ''B 'h '2h m '=h h ∴='=BE AC ⊥E DF AC ⊥F BEFD BE DF ∴=BE DF xm ==Rt ABE ∆45A ∠=︒Q AE BE xm ∴==AB ∴=Rt DCF ∆30C ∠=︒Q 22CD DF xm ∴==,,,,故答案为4.【点评】本题考查解直角三角形的应用,三角形的中位线定理,梯形等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.8.(2015秋•北京期末)北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由降为,已知原斜坡坡面长为200米,点,,在同一水平地面上,求改善后的斜坡坡角向前推进的距离.(结果保留整【分析】根据题意和正切的概念分别求出、的长,计算即可.【解答】解:,,米,,5AB BD CD ++=+Q ∴125x ++=+2x ∴=AB ∴=24CD x m ==45︒30︒AB D B C BD 1.41≈ 1.73≈ 2.45)≈CB CD 90C ∠=︒Q 45ABC ∠=︒141AC BC ∴==≈tan AC D CD∠=米, 米,答:改善后的斜坡坡角向前推进的距离为104米.【点评】本题考查的是解直角三角形的应用坡度坡角问题,熟记锐角三角函数的定义是解题的关键.9.(2016•朝阳区校级模拟)如图,是某公园“六一”前新增设的一架滑梯,该滑梯高度,滑梯着地点与梯架之间的距离.(1)求滑梯的长.(2)若规定滑梯倾斜面不超过45度属于安全范围,通过计算说明这架滑梯的倾斜角是否符合要求?【分析】(1)直接利用勾股定理得出的长,进而得出答案;(2)直接利用特殊角的三角函数值,再结合,得出答案. 【解答】解:(1)由题意可得:在直角三角形中,,答:滑梯的长为;(2)因为:,, 所以,故符合要求.【点评】此题主要考查了解直角三角形的应用以及坡角问题,正确把握坡角的定义是解题关键.245tan 30AC CD ∴==≈︒104BD CD CB ∴=-=BD -2AC cm =B 4BC cm =AB ()ABC ∠AB 1tan 2AC B BC ==ABC )AB cm ==AB 1tan 2AC B BC ==tan 451︒=045B ︒<<︒。
【湘教版】九年级数学上册:4.4.2 与坡度、方位角有关的应用问题 同步练习(含答案)

第2课时 与坡度.方位角有关的应用问题要点感知1 山坡的坡面与地平面的夹角叫作坡角,如图所示,角α为斜面的坡角.如图所示,通常把坡面的铅直高度h 和水平宽度l 的比叫作坡度,通常用字母i 表示,即i =l h (坡度通常写成1∶m 的形式).坡度i 与坡角α的关系是i =lh =tanα.坡度越大,山坡越陡.预习练习1-1 如图,修建抽水站时,沿着坡度为i =1∶6的斜坡铺设管道,下列等式成立的是( )A.sinα=61B.cosα=61C.tanα=61D.以上都不对要点感知2 从正北方向或正南方向到目标方向所形成的小于90°的角叫作方位角.如图中点A 的方向角为北偏东60°.预习练习2-1 如图,C .D 是两个村庄,分别位于一个湖的南.北两端A 和B 的正东方向上,且D 位于C 的北偏东30°方向上,且CD =6 km ,则AB =_____km .知识点1 与坡度.坡角有关的应用问题1.某堤的横断面如图.堤高BC是5米,迎水斜坡AB的长是13米,那么斜坡AB的坡度是( )A.1∶3B.1∶2.6C.1∶2.4D.1∶22.拦水坝横断面如图所示,迎水坡AB的坡比是1∶3,坝高BC=10 m,则坡面AB的长度是( )A.15 mB.203mC.103mD.20 m知识点2 与方位角有关的应用问题3.如图,某海监船和一渔船同时从点A出发,海监船沿正北方向MN 航行,渔船往北偏东60°方向以40海里/小时的速度航行,渔船半小时后到达B处,此时渔船恰好在海监船的正东方向,则此时渔船与海监船的距离为( )A.20海里B.103海里C.202海里D.30海里4.(昭通中考)小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,2≈1.41,3≈1.73)5.钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.(1)请在图中作出该船在点B处的位置;(2)求钓鱼岛C到B处的距离.(结果保留根号)6.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到达事故船C 处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)7.某商场为方便顾客使用购物车,准备将滚动电梯的坡面坡度由1∶1.8改为1∶2.4(如图).如果改动后电梯的坡面长为13米,求改动后电梯水平宽度增加部分BC的长.挑战自我8.如图,在东西方向的海岸线MN上有A.B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.(参考数据:sin32°≈0.53,cos32°≈0.85,sin55°≈0.82,cos55°≈0.57) (1)求船P到海岸线MN的距离(精确到0.1海里);(2)若船A.船B分别以20海里/小时.15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.参考答案预习练习1-1 C要点感知2 331.C2.D3.B4.过P作PC⊥AB于C.在Rt△APC中,AP=200 m,∠ACP=90°,∠PAC=60°,∴PC=200×sin60°=200×3/2=1003.∵在Rt△PBC中,sin37°=PC/PB,∴PB=PC/sin37°=100×1.73/0.6≈288(m).答:小亮与妈妈相距约288米.5.AB=30×0.5=15(海里),由题意知CB⊥AB,在Rt△ABC中,∠BAC=30°,tan∠BAC=BC/AB,所以BC=ABtan∠BAC=ABtan30°=15×33=53(海里).答:钓鱼岛C到B处的距离为53海里.6.过点C作CD⊥AB交AB延长线于D.在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,∴CD=1/2AC=40海里.在Rt△CBD中,∵∠CDB=90°,∠CBD=90°-37°=53°,∴BC=CD/sin∠CBD≈400.8=50(海里),∴海警船到达事故船C处所需的时间大约为:50÷40=54(小时).答:海警船到达事故船C处所需时间约为54小时.7.在Rt△ADC中,∵AD∶DC=1∶2.4,AC=13,由AD2+DC2=AC2,得AD2+(2.4AD)2=132.∴AD=±5(负值不合题意,舍去).∴DC=12.在Rt△ABD中,∵AD∶BD=1∶1.8,∴BD=5×1.8=9.∴BC=DC-BD=12-9=3.答:改动后电梯水平宽度增加部分BC的长为3米.8.(1)过点P作PD⊥AB于点D.由题意,得∠PAB=90°-58°=32°,∠PBD=90°-35°=55°,AP=30,在Rt△ADP中,sin∠PAD=PD/AP,得PD=AP·sin∠PAD,即PD=30·sin32°≈15.9.答:船P到海岸线MN的距离约为15.9海里.(2)在Rt△BDP中,sin∠PBD=PD/BP,∴BP=PD/sin∠PBD=15.9/sin55°≈19.4,A船需要时间为30/20=1.5(小时),B船需要时间为19.4/15≈1.3(小时),∵1.5>1.3,∴B船先到达P处.答:B船先到达P处.。
解直角三角形的应用-坡度坡角问题精选题

解直角三角形的应用-坡度坡角问题精选题一.选择题(共15小题)1.如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为()(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)A.30.6B.32.1C.37.9D.39.42.如图,河坝横断面迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是()A.9m B.6m C.m D.m3.如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为()A.5cosαB.C.5sinαD.4.如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为()A.24m B.22m C.20m D.18m5.如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为米,则斜坡AB的长度为()A.米B.米C.米D.24米6.如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=4m,则坡面AB的长度是()A.m B.4m C.2m D.4m7.如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为()A.4cosα米B.4sinα米C.4tanα米D.米8.如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)()A.7.5米B.8米C.9米D.10米9.如图,一个长方体木箱沿斜面滑至如图位置时,AB=2m,木箱高BE=1m,斜面坡角为α,则木箱端点E距地面AC的高度表示为()m.A.+2sinαB.2cosα+sinαC.cosα+2sinαD.tanα+2sinα10.一辆汽车沿坡角为α的斜坡前进500米,则它上升的最大高度为()A.500sinαB.C.500cosαD.11.如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为()A.9米B.28米C.米D.(14+2)米12.如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AH与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为()(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)A.35.5米B.37.6米C.38.6米D.40.3米13.斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是()A.500•sinα米B.米C.500•cosα米D.米14.如图,河坝横断面迎水坡AB的坡比为1:.坝高BC为4m,则AB的长度为()A.4m B.8m C.8m D.16m15.如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是()米.A.7B.11C.13D.20二.填空题(共18小题)16.如图,我市在建高铁的某段路基横断面为梯形ABCD,DC∥AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为米(结果保留根号).17.如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB长26m,斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移m时,才能确保山体不滑坡.(取tan50°≈1.2)18.如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角α=20°,两树间的坡面距离AB=5m,则这两棵树的水平距离约为m(结果精确到0.1m,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364).19.已知一个斜坡的坡度i=1:,那么该斜坡的坡角的度数是度.20.如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是cm.21.如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是m.22.如图,某河堤迎水坡AB的坡比i=1:,堤高BC=5m,则坡面AB的长是m.23.如图,AB是一垂直于水平面的建筑物,BC是建筑物底端的一个平台,斜坡CD的坡度(或坡比)为i=1:0.75,坡长为10米,DE为地平面(A,B,C,D,E均在同一平面内),则平台距地面的高度为.24.某人沿着坡度i=1:的山坡向上走了300m,则他上升的高度为m.25.如图,某小型水库栏水坝的横断面是四边形ABCD,DC∥AB,测得迎水坡的坡角α=30°,已知背水坡的坡比为1.2:1,坝顶部宽为2m,坝高为6m,则坝底AB的长为.26.如图,斜坡AB长为100米,坡角∠ABC=30°,现因“改小坡度”工程的需要,将斜坡AB改造成坡度i=1:5的斜坡BD(A、D、C三点在地面的同一条垂线上),那么由点A到点D下降了米.(结果保留根号)27.如图,传送带把物体从地面送到离地面5米高的地方,如果传送带与地面所成的斜坡的坡度i=1:2.4,那么物体所经过的路程AB为米.28.如图,河坝的横断面AB的坡比是1:2,坝高BC=3米,则坡面AB的长度是米.29.如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=12米,BC=20米,CD的坡度为i=1:2;且此时测得1米杆在地面上的影长为2米,则电线杆的高度为米.30.如图,当小明沿坡度i=1:的坡面由A到B行走了6米时,他实际上升的高度BC =米.31.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为米.(结果保留根号)32.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度i=1:2.5,那么该斜坡的水平距离AC的长为m.33.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE=m,斜面坡角为30°,则木箱端点E距地面AC的高度EF为m.三.解答题(共8小题)34.如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.(1)求新传送带AC的长度;(2)如果需要在货物着地点C的左侧留出5m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.35.如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3m,背水坡AD的坡度i(即tan∠DAB)为1:0.5,坝底AB=14m.(1)求坝高;(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin37°≈,cos37°≈,tan37°≈)36.沿江大堤经过改造后的某处横断面为如图所示的梯形ABCD,高DH=12米,斜坡CD 的坡度i=1:1.此处大堤的正上方有高压电线穿过,PD表示高压线上的点与堤面AD的最近距离(P、D、H在同一直线上),在点C处测得∠DCP=26°.(1)求斜坡CD的坡角α;(2)电力部门要求此处高压线离堤面AD的安全距离不低于18米,请问此次改造是否符合电力部门的安全要求?(参考数据:sin26°≈0.44,tan26°≈0.49,sin71°≈0.95,tan71°≈2.90)37.小华同学将笔记本电脑水平放置在桌子上,当显示屏的边缘线OB与底板的边缘线OA 所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上,OA=OB=24cm,BC⊥AC,∠OAC=30°.(1)求OC的长;(2)如图④,垫入散热架后,要使显示屏的边缘线OB'与水平线的夹角仍保持120°,求点B′到AC的距离.(结果保留根号)38.某厂家新开发的一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A离地面距离1m.(1)该车大灯照亮地面的宽度BC约是多少(不考虑其它因素)?(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,从60km/h到摩托车停止的刹车距离是m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:,,,)39.如图,一座堤坝的横截面是梯形,根据图中给出的数据,求坝高和坝底宽(精确到0.1m)参考数据:≈1.414,≈1.73240.如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高1米的影子CE,而当光线与地面的夹角是45°时,办公楼顶A在地面上的影子F与墙角C有35米的距离(B,F,C在一条直线上).(1)求办公楼AB的高度;(2)若要在A,E之间挂一些彩旗,请求出A,E之间的距离.41.如图,拦水坝的横断面为梯形ABCD,AD=3m,坝高AE=DF=6m,坡角α=45°,β=30°,求BC的长.解直角三角形的应用-坡度坡角问题精选题41道参考答案与试题解析一.选择题(共15小题)1.如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为()(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)A.30.6B.32.1C.37.9D.39.4【解答】解:延长AB交DC于H,作EG⊥AB于G,如图所示:则GH=DE=15米,EG=DH,∵梯坎坡度i=1:,∴BH:CH=1:,设BH=x米,则CH=x米,在Rt△BCH中,BC=12米,由勾股定理得:x2+(x)2=122,解得:x=6,∴BH=6米,CH=6米,∴BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=(6+20)(米),∵∠α=45°,∴∠EAG=90°﹣45°=45°,∴△AEG是等腰直角三角形,∴AG=EG=(6+20)(米),∴AB=AG+BG=6+20+9≈39.4(米);故选:D.2.如图,河坝横断面迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是()A.9m B.6m C.m D.m【解答】解:在Rt△ABC中,BC=3米,tan A=1:;∴AC=BC÷tan A=3米,∴AB==6米.故选:B.3.如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为()A.5cosαB.C.5sinαD.【解答】解:如图,过点B作BC⊥AF于点C.∵BC=5米,∠CBA=∠α.∴AB==.故选:B.4.如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为()A.24m B.22m C.20m D.18m【解答】解:过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.由题意得:.(2分)∴DF=DE×1.6÷2=14.4(m).(1分)∴GF=BD=CD=6m.(1分)又∵.(2分)∴AG=1.6×6=9.6(m).(1分)∴AB=14.4+9.6=24(m).(1分)答:铁塔的高度为24m.故选:A.5.如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为米,则斜坡AB的长度为()A.米B.米C.米D.24米【解答】解:过B作BE⊥AD于E,过C作CF⊥AD于F,如图所示:则四边形BEFC是矩形,∴BE=CF,∵背水坡CD的坡比i=1:1,CD=米,∴CF=DF=CD=6(米),∴BE=CF=6米,又∵斜坡AB的坡比i=1:2=,∴AE=2BE=12(米),∴AB===6(米),故选:C.6.如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=4m,则坡面AB的长度是()A.m B.4m C.2m D.4m【解答】解:∵迎水坡AB的坡比是1:,∴BC:AC=1:,BC=4m,∴AC=4m,则AB==4(m).故选:D.7.如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为()A.4cosα米B.4sinα米C.4tanα米D.米【解答】解:过点A作AD⊥BC于点D,∵AB=AC=2米,AD⊥BC,∴BD=DC,∴cosα==,∴DC=2cosα(米),∴BC=2DC=2×2cosα=4cosα(米).故选:A.8.如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)()A.7.5米B.8米C.9米D.10米【解答】解:在Rt△ABC中,∠ACB=90°,BC=6米,∵sin∠BAC==sin37°≈0.6=,∴AB≈BC=×6=10(米),故选:D.9.如图,一个长方体木箱沿斜面滑至如图位置时,AB=2m,木箱高BE=1m,斜面坡角为α,则木箱端点E距地面AC的高度表示为()m.A.+2sinαB.2cosα+sinαC.cosα+2sinαD.tanα+2sinα【解答】解:过E作EN⊥AC于N,交AB于M,过B作BG⊥AC于G,BH⊥EN于H,如图所示:则四边形BHNG是矩形,∴HN=BG,在Rt△ABG中,∠BAG=α,sin∠BAG=,∴BG=AB•sin∠BAG=2sinα(m),∴HN=2sinα(m),∵∠EBM=∠ANM=90°,∠BME=∠AMN,∴∠BEM=∠MAN=α,在Rt△EHB中,∠BEM=α,BE=1m,∵oos∠BEM=,∴EH=BE•cos∠BEM=1×cosα=cosα(m),∴EN=EH+HN=(cosα+2sinα)m,即木箱端点E距地面AC的高度为(cosα+2sinα)m,故选:C.10.一辆汽车沿坡角为α的斜坡前进500米,则它上升的最大高度为()A.500sinαB.C.500cosαD.【解答】解:如图,∠A=α,AE=500.则EF=500sinα.故选:A.11.如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为()A.9米B.28米C.米D.(14+2)米【解答】解:延长AD交BC的延长线于F点,作DE⊥CF于E点.DE=8sin30°=4;CE=8cos30°=4;∵测得1米杆的影长为2米.∴EF=2DE=8∴BF=BC+CE+EF=20+4+8=28+4∴电线杆AB的长度是(28+4)=14+2米.故选:D.12.如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AH与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为()(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)A.35.5米B.37.6米C.38.6米D.40.3米【解答】解:如图,作EG′⊥AB于点G′,BP⊥DE于点P,则∠DBP=∠BFG′=30°,∵BD=30,∴DP=BD=15,BP=BD cos∠DBP=30×=15,∵DE=19,∴PE=BG′=DE﹣DP=4,∵∠AEG′=∠H=53°,∴∠EAG′=37°∴AG′==,则AB=AG′+BG′=+4≈38.6,故选:C.13.斜坡的倾斜角为α,一辆汽车沿这个斜坡前进了500米,则它上升的高度是()A.500•sinα米B.米C.500•cosα米D.米【解答】解:如图,∠A=α,AE=500.则EF=500sinα.故选:A.14.如图,河坝横断面迎水坡AB的坡比为1:.坝高BC为4m,则AB的长度为()A.4m B.8m C.8m D.16m【解答】解:∵迎水坡AB的坡比为1:,∴=,∵BC=4m,∴AC=4m,由勾股定理得:AB===8(m),故选:B.15.如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是()米.A.7B.11C.13D.20【解答】解:过D作DG⊥BC于G,EH⊥BC于H,∴GH=DE=2(米,∵DG=EH=15米,背水坡CD的坡度i=1:0.6,背水坡EF的坡度i=3:4,∴CG=9(米),HF=20(米),∴CF=GH+HF﹣CG=13(米),故选:C.二.填空题(共18小题)16.如图,我市在建高铁的某段路基横断面为梯形ABCD,DC∥AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为6米(结果保留根号).【解答】解:过点D作DE⊥AB于E,过点C作CF⊥AB于F.∵CD∥AB,DE⊥AB,CF⊥AB,∴DE=CF,在Rt△CFB中,CF=BC•sin45°=3(米),∴DE=CF=3(米),在Rt△ADE中,∵∠A=30°,∠AED=90°,∴AD=2DE=6(米),故答案为:6.17.如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE⊥AD,斜坡AB长26m,斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移10m时,才能确保山体不滑坡.(取tan50°≈1.2)【解答】解:在BC上取点F,使∠FAE=50°,过点F作FH⊥AD于H,∵BF∥EH,BE⊥AD,FH⊥AD,∴四边形BEHF为矩形,∴BF=EH,BE=FH,∵斜坡AB的坡比为12:5,∴=,设BE=12xm,则AE=5xm,由勾股定理得,AE2+BE2=AB2,即(5x)2+(12x)2=262,解得,x=2,∴AE=10m,BE=24m,∴FH=BE=24m,在Rt△F AH中,tan∠F AH=,∴AH=≈20(m),∴BF=EH=AH﹣AE=10(m),∴坡顶B沿BC至少向右移10m时,才能确保山体不滑坡,故答案为:10.18.如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角α=20°,两树间的坡面距离AB=5m,则这两棵树的水平距离约为 4.7m(结果精确到0.1m,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364).【解答】解:过点A作水平面的平行线AH,作BH⊥AH于H,由题意得,∠BAH=α=20°,在Rt△BAH中,cos∠BAH=,∴AH=AB•cos∠BAH≈5×0.940≈4.7(m),故答案为:4.7.19.已知一个斜坡的坡度i=1:,那么该斜坡的坡角的度数是30度.【解答】解:∵tanα=1:=,∴坡角=30°.20.如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是210cm.【解答】解:过点B作BD⊥AC于D,根据题意得:AD=2×30=60(cm),BD=18×3=54(cm),∵斜坡BC的坡度i=1:5,∴BD:CD=1:5,∴CD=5BD=5×54=270(cm),∴AC=CD﹣AD=270﹣60=210(cm).∴AC的长度是210cm.故答案为:210.21.如图,在坡度为1:2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,则斜坡上相邻两树间的坡面距离是3m.【解答】解:∵坡度为1:2,=,且株距为6米,∴株距:坡面距离=2:,∴坡面距离=株距×=3(米).另解:∵CB:AB=1:2,设CB=x,AB=2x,∴AC==x,∴=,∵AB=6m,∴AC=×6=3m.故答案为:3.22.如图,某河堤迎水坡AB的坡比i=1:,堤高BC=5m,则坡面AB的长是10m.【解答】解:∵坡比i=tan∠CAB===,∠ACB=90°,∴∠BAC=30°,∴AB=2BC,又∵BC=5m,∴AB=2BC=10m,故答案为:10.23.如图,AB是一垂直于水平面的建筑物,BC是建筑物底端的一个平台,斜坡CD的坡度(或坡比)为i=1:0.75,坡长为10米,DE为地平面(A,B,C,D,E均在同一平面内),则平台距地面的高度为8米.【解答】解:如图,延长AB交ED的延长线于F,过C作CG⊥EF于G,则BF=CG,在Rt△CDG中,i==1:0.75=,CD=10米,设CG=4x米,则DG=3x米,由勾股定理得:(4x)2+(3x)2=102,解得:x=2,∴CG=8(米),GD=6(米),∴BF=CG=8米,即平台距地面的高度为8米,故答案为:8米.24.某人沿着坡度i=1:的山坡向上走了300m,则他上升的高度为150m.【解答】解:如图所示.∵BC:AB=1:.∴∠A=30°.∵AC=300m,∴BC=300×sin30°=150(m).故答案为:150.25.如图,某小型水库栏水坝的横断面是四边形ABCD,DC∥AB,测得迎水坡的坡角α=30°,已知背水坡的坡比为1.2:1,坝顶部宽为2m,坝高为6m,则坝底AB的长为(7+6)m.【解答】解:如图所示:过点C作CE⊥AB,DF⊥AB,垂足分别为:E,F,∵坝顶部宽为2m,坝高为6m,∴DC=EF=2m,EC=DF=6m,∵α=30°,∴BE==6(m),∵背水坡的坡比为1.2:1,∴==,解得:AF=5(m),则AB=AF+EF+BE=5+2+6=(7+6)m,故答案为:(7+6)m.26.如图,斜坡AB长为100米,坡角∠ABC=30°,现因“改小坡度”工程的需要,将斜坡AB改造成坡度i=1:5的斜坡BD(A、D、C三点在地面的同一条垂线上),那么由点A到点D下降了(50﹣10)米.(结果保留根号)【解答】解:在Rt△ABC中,∠ABC=30°,∴AC=AB=50,BC=AB•cos∠ABC=50,∵斜坡BD的坡度i=1:5,∴DC:BC=1:5,∴DC=10,则AD=50﹣10,故答案为:(50﹣10).27.如图,传送带把物体从地面送到离地面5米高的地方,如果传送带与地面所成的斜坡的坡度i=1:2.4,那么物体所经过的路程AB为13米.【解答】解:∵传送带与地面所成的斜坡的坡度i=1:2.4,∴=,即=,解得,AC=12,由勾股定理得,AB===13,故答案为:13.28.如图,河坝的横断面AB的坡比是1:2,坝高BC=3米,则坡面AB的长度是3米.【解答】解:∵河坝的横断面AB的坡比是1:2,∴=,∵BC=3米,∴AC=6米,由勾股定理得:AB===3(米),故答案为:3.29.如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=12米,BC=20米,CD的坡度为i=1:2;且此时测得1米杆在地面上的影长为2米,则电线杆的高度为(14+4)米.【解答】解:过点D作DF⊥AB于F,DE⊥BC交BC的延长线于E,则四边形FBED为矩形,∴BF=DE,DF=BE,在Rt△DCE中,CD的坡度为i=1:2,设DE=x米,则CE=2x米,由勾股定理得:x2+(2x)2=122,解得:x1=4,x2=﹣4(舍去),∴BF=DE=4米,CE=8米,∴DF=BE=BC+CE=(20+8)米,由题意得:AF=DF=(10+4)米,∴AB=AF+BF=(14+4)米,故答案为:(14+4).30.如图,当小明沿坡度i=1:的坡面由A到B行走了6米时,他实际上升的高度BC =3米.【解答】解:∵i=1:,∴tan A==,∴∠A=30°,∴BC=AB=3(米),故答案为:3.31.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为10米.(结果保留根号)【解答】解:∵∠BDC=60°,∠A=30°,∴∠ABD=60°﹣30°=30°,∴∠ABD=∠A,∴BD=AD=20(米),在Rt△BDC中,sin∠BDC=,则BC=BD•sin∠BDC=10(米),故答案为:10.32.如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度i=1:2.5,那么该斜坡的水平距离AC的长为75m.【解答】解:∵斜坡的坡度i=1:2.5,∴BC:AC=1:2.5,∴AC=75(m),故答案为:75.33.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE=m,斜面坡角为30°,则木箱端点E距地面AC的高度EF为3m.【解答】解:连接AE,在Rt△ABE中,AB=3m,BE=m,则AE==2m,又∵tan∠EAB==,∴∠EAB=30°,在Rt△AEF中,∠EAF=∠EAB+∠BAC=60°,∴EF=AE×sin∠EAF=2×=3m.答:木箱端点E距地面AC的高度为3m.故答案为:3.三.解答题(共8小题)34.如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.(1)求新传送带AC的长度;(2)如果需要在货物着地点C的左侧留出5m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.【解答】解:(1)在Rt△ABD中,∠ABD=45°,∴AD=AB=4(m),在Rt△ACD中,∠ACD=30°,∴AC=2AD=8(m),答:新传送带AC的长度为8m;(2)在Rt△ACD中,∠ACD=30°,∴CD=AC•cos∠ACD=4(m),在Rt△ABD中,∠ABD=45°,∴BD=AD=4(m),∴BC=CD﹣BD=(4﹣4)m,∴PC=BP﹣BC=4﹣(4﹣4)=4(m),∵4<5,∴货物MNQP需要挪走.35.如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3m,背水坡AD的坡度i(即tan∠DAB)为1:0.5,坝底AB=14m.(1)求坝高;(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin37°≈,cos37°≈,tan37°≈)【解答】解:(1)作DM⊥AB于M,CN⊥AN于N.由题意:tan∠DAB==2,设AM=x,则DM=2x,∵四边形DMNC是矩形,∴DM=CN=2x,在Rt△NBC中,tan37°===,∴BN=x,∵x+3+x=14,∴x=3,∴DM=6,答:坝高为6m.(2)作FH⊥AB于H.设DF=y,则AE=2y,EH=3+2y﹣y=3+y,BH=14+2y﹣(3+y)=11+y,由△EFH∽△FBH,可得=,即=,解得y=﹣7+2或﹣7﹣2(舍弃),∴DF=2﹣7,答:DF的长为(2﹣7)m.36.沿江大堤经过改造后的某处横断面为如图所示的梯形ABCD,高DH=12米,斜坡CD 的坡度i=1:1.此处大堤的正上方有高压电线穿过,PD表示高压线上的点与堤面AD的最近距离(P、D、H在同一直线上),在点C处测得∠DCP=26°.(1)求斜坡CD的坡角α;(2)电力部门要求此处高压线离堤面AD的安全距离不低于18米,请问此次改造是否符合电力部门的安全要求?(参考数据:sin26°≈0.44,tan26°≈0.49,sin71°≈0.95,tan71°≈2.90)【解答】解:(1)∵斜坡CD的坡度i=1:1,∴tanα=DH:CH=1:1=1,∴α=45°.答:斜坡CD的坡角α为45°;(2)由(1)可知:CH=DH=12米,α=45°.∴∠PCH=∠PCD+α=26°+45°=71°,在Rt△PCH中,∵tan∠PCH==≈2.90,∴PD=22.8(米).22.8>18,答:此次改造符合电力部门的安全要求.37.小华同学将笔记本电脑水平放置在桌子上,当显示屏的边缘线OB与底板的边缘线OA 所在水平线的夹角为120°时,感觉最舒适(如图①).侧面示意图为图②;使用时为了散热,他在底板下面垫入散热架,如图③,点B、O、C在同一直线上,OA=OB=24cm,BC⊥AC,∠OAC=30°.(1)求OC的长;(2)如图④,垫入散热架后,要使显示屏的边缘线OB'与水平线的夹角仍保持120°,求点B′到AC的距离.(结果保留根号)【解答】解:(1)如图③,在Rt△AOC中,OA=24,∠OAC=30°.∴OC=OA=×24=12(cm);(2)如图④,过点B′作B′D⊥AC,垂足为D,过点O作OE⊥B′D,垂足为E,由题意得,OA=OB′=24(cm),当显示屏的边缘线OB'与水平线的夹角仍保持120°,可得,∠AOB′=150°∴∠B′OE=60°,∵∠ACO=∠B′EO=90°,∴在Rt△B′OE中,B′E=OB′×sin60°=12(cm),又∵OC=DE=12(cm),∴B′D=B′E+DE=12+12(cm),即:点B′到AC的距离为(12+12)cm.38.某厂家新开发的一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A离地面距离1m.(1)该车大灯照亮地面的宽度BC约是多少(不考虑其它因素)?(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,从60km/h到摩托车停止的刹车距离是m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:,,,)【解答】解:(1)过A作AD⊥MN于点D,在Rt△ACD中,tan∠ACD==,CD=5.6(m),在Rt△ABD中,tan∠ABD==,BD=7(m),∴BC=7﹣5.6=1.4(m).答:该车大灯照亮地面的宽度BC是1.4m;(2)该车大灯的设计不能满足最小安全距离的要求.理由如下:∵以60 km/h的速度驾驶,∴速度还可以化为:m/s,最小安全距离为:×0.2+=8(m),大灯能照到的最远距离是BD=7m,∴该车大灯的设计不能满足最小安全距离的要求.39.如图,一座堤坝的横截面是梯形,根据图中给出的数据,求坝高和坝底宽(精确到0.1m)参考数据:≈1.414,≈1.732【解答】解:在Rt△CDE中,∵sin∠C=,cos∠C=∴DE=sin30°×DC=×14=7(m),CE=cos30°×DC=×14=7≈12.124≈12.12,∵四边形AFED是矩形,∴EF=AD=6m,AF=DE=7m在Rt△ABF中,∵∠B=45°∴DE=AF=7m,∴BC=BF+EF+EC≈7+6+12.12=25.12≈25.1(m)答:该坝的坝高和坝底宽分别为7m和25.1m.40.如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高1米的影子CE,而当光线与地面的夹角是45°时,办公楼顶A在地面上的影子F与墙角C有35米的距离(B,F,C在一条直线上).(1)求办公楼AB的高度;(2)若要在A,E之间挂一些彩旗,请求出A,E之间的距离.【解答】解析(1)如图,过点E作EH⊥AB于点H.设AB=x米,则BF=AB=x米,∵FC=35米,∴BC=HE=(35+x)米,∵EC=1米,∴BH=EC=1米,∴AH=(x﹣1)米.在Rt△AHE中,tan22°=,即≈,解得x≈25.答:办公楼AB的高度约为25米.(2)由(1)得AH=x﹣1=24米,在Rt△AHE中,sin22°==,∴AE=≈24×=64(米).答:A,E之间的距离约为64米.41.如图,拦水坝的横断面为梯形ABCD,AD=3m,坝高AE=DF=6m,坡角α=45°,β=30°,求BC的长.【解答】解:过A点作AE⊥BC于点E,过D作DF⊥BC于点F,则四边形AEFD是矩形,有AE=DF=6,AD=EF=3,∵坡角α=45°,β=30°,∴BE=AE=6,CF=DF=6,∴BC=BE+EF+CF=6+3+6=9+6,∴BC=(9+6)m,答:BC的长(9+6)m.。
坡度坡角练习题
1坡度坡角练习题1、如图(1):水库大坝的横断面为梯形,坝顶宽6m ,坝高24m ,斜坡AD 的坡角为45°,斜坡BC 的坡度为i=1︰2,则坝底AB 的长为( ) A 、42m B 、(30-203) C 、78m D 、30m2、 如图(2):河堤横断面为梯形,上底为4m ,堤高为6m ,斜坡AD 的坡度为1︰3,斜坡CB 的坡度为45°,则河堤横断面的面积为( ) A 、48m 2 B 、96 m 2 C 、84 m 2 D 、192 m3、某一拦水坝的横断面是一个等腰梯形,它的上底长为6米,下底长为10米,高为23米,那么拦水坝的坡度和坡角分别为( 0 A 、33,60° B 、3 ,30° C 、3 ,60° D 、33,30° 4、如图(4):自动扶梯AB 的长度为20米,倾斜角A 为α,高度BC 为 米(结果用含α的三角函数表示)。
5、铁路的路基横断面是一个等腰梯形,如图(5),斜坡AB 的坡度为1︰3,坡面AB 的水平宽度为33m ,基面AD 的宽为2m ,则路基的高AE= m ,∠C ,路基底部BC= m 。
6 、如图:铁路的路基的横截面是等腰梯形,斜坡AB 的坡度为1∶3,BE 为33米,基面AD 宽2米,求路基的高AE ,基底的宽BC 及坡角B 的度数.(答案可带根号)7、 如图:水坝的横断面是梯形,迎水坡BC 的坡角∠B=30°,背水坡AD 的坡度为8、如图所示的燕服槽一个等腰梯形,外口AD 宽10cm ,燕尾槽深10cm ,AB 的坡度i=1:1,求里口宽BC 及燕尾槽的截面积.BCDA(1)(2) BCDAFE (5)CDA BE C(4) B A29、如图,斜坡AC 的坡度(坡比)为1:3 ,AC=10米.坡顶有一旗杆BC ,旗杆顶端B 点与A 点有一条彩带AB 相连,AB=14米.试求旗杆BC 的高度.10.如图,水坝的横断面是梯形,背水坡AB 的坡角∠BAD= 60,坡长AB=m 320,为加强水坝强度, 将坝底从A 处向后水平延伸到F 处,使新的背水坡 的坡角∠F= 45,求AF 的长度(结果精确到1米,参考数据: 414.12≈,732.13≈).11.施工队准备在一段斜坡上铺上台阶方便通行.现测得斜坡上铅垂的两棵树间水平距离AB =4米,斜面距离BC =4.25米,斜坡总长DE =85米. (1)求坡角∠D 的度数(结果精确到1°);(2)若这段斜坡用厚度为17c m 的长方体台阶来铺,需要铺几级台阶?12、如图,某堤坝的横截面是梯形ABCD ,背水坡AD 的坡度i (即tanα)为1:1.2,坝高为5米,现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD 加宽1米,形成新的背水坡EF ,其坡度为1:1.4,已知堤坝总长度为4000米.(1)求完成该工程需要多少土方?(2)该工程由甲、乙两个工程队同时合作完成.按原计划需要20天.准备开工前接到上级通知,汛期可能提前,要求两个工程队提高工作效率,甲队工作效率提高30%,乙队工作效率提高40%,结果提前5天完成.问这两个工程队原计划每天各完成多少土方?13、一座建于若干年前的水库大坝的横断面如图所示,其中背水面的整个坡面是长为90米、宽为5米的矩形.现需将其整修并进行美化,方案如下:①将背水坡AB 的坡度由1:0.75改为1:3;②用一组与背水坡面长边垂直的平行线将背水坡面分成9块相同的矩形区域,依次相间地种草与栽花.(1)求整修后背水坡面的面积;(2)如果栽花的成本是每平方米25元,种草的成本是每平方米20元,那么种植花草至少需要多少元?(10题图)17cm(第11题)ABCDEF。
中考数学复习《解直角三角形的应用-坡度坡角问题》专项练习题-附带有答案

中考数学复习《解直角三角形的应用-坡度坡角问题》专项练习题-附带有答案一、单选题1.如果一斜坡的坡比是1:2.4,那么该斜坡坡角的余弦值是()A.125B.512C.513D.12132.某村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离为()A.5cosαB.5cosαC.5sinαD.5sinα3.如图所示,河堤横断面迎水坡AB的坡比是1:2,堤高BC=4m,则坡面AB的长度是()mA.8 B.16 C.4√5D.4√34.某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距50海里.客轮以60海里/小时的速度沿北偏西60°方向航行23小时到达B处,那么tan∠BAP=()A.45B.65C.√55D.2√555.如图,斜面AC的坡度为1:2,AC=3 √5米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高度为()A.5米B.6米C.8米D.(3+ √5)米6.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了__米.(sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)()A.415 B.280 C.335 D.2507.如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,电梯坡面BC的坡度i=1:√3,则电梯坡面BC的坡角α为()A.15°B.30°C.45°D.60°8.如图是某厂家新开发的一款摩托车,它的大灯射出的光线AB,AC与地面MN的夹角分别为8°和10°,该大灯照亮地面的宽度BC的长为3.5米,则该大灯距地面的高度为()(参考数据:sin8°≈425tan8°≈17sin10°≈950tan10°≈528)A.3.5米B.2.5米C.4.5米D.5.5米二、填空题9.某人沿着坡度i=1:√3的山坡起点向上走了50米,则他离地面高米.(坡度:坡面铅直高度与水平宽度的比)10.如图,一辆小车沿着坡度为i=1:√3的斜坡向上行驶了90米,则此时该小车离水平面的垂直高度为米.11.如图,某单位门前原有四级台阶,每级台阶高为18cm,宽为30cm,为方便残疾人土,拟在门前台阶右侧改成斜坡,设台阶的起点为A点,斜坡的起点为C点,准备设计斜坡BC的坡度i=1:5,则AC的长度是cm.12.如图,山脚下有一棵树AB,小强从点B沿山坡向上走50m到达点D,用高为1.5m的测角仪CD测得树顶为10°,已知山坡的坡脚为15°,则树AB的高= (精确到0.1m)(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27).13.江边有一处高10米,背水坡角为45°的防洪大堤,大堤的横截面为梯形ABCD,其中CD∥AB,∠DAB= 45°(如图).某防洪指挥部发现该大堤急需加固,经调查论证,防洪指挥部专家组制定的加固方案是沿背水坡面AD用土石进行加固,使上底加宽3米,加固后背水坡EF的坡比为1:√3.则加固后坝底增加的宽度AF=米.三、解答题14.为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形DE= 10m,其坡度为i1=1:√3,将步梯DE改造为斜坡AF,其坡度为i2=1:4,求斜坡AF的长度.(结果精确到0.01m,参考数据:√3≈1.732√17≈4.122)15.如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地BC//AD,BE⊥AD斜坡AB长26m,斜坡AB 的坡比为12:5为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.(1)求BE的高度.(2)如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移多少m时,才能确保山体不滑坡.(取tan50°≈1.2)16.我国南水北调中线工程的起点是丹江口水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位,如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡底端水平方向增加的宽度AC.(结果精确到0.1米,参考数据:sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.5,√3≈1.73)17.为践行“绿水青山就是金山银山”的重要思想,我省森林保护区开展了寻找古树活动.如图,发现古树AB是直立于水平面,为测量古树AB的高度,小明从古树底端B出发,沿水平方向行走了26米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E 点处测得古树顶端A点的仰角∠AEF为15°(点A、B、C、D在同一平面内),斜坡CD的坡度(或坡比)i=1︰2.4.(1)求斜坡CD的高;(2)求古树AB的高?(已知sin15°≈0.26,cos15°≈0.97,tan15≈0.27°)18.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC//AD,BE⊥AD,斜坡AB长√106m,坡度i=9:5.为了减缓坡面,防止山体滑坡,保障安全,学校决定对该斜坡进行改造,为52地质人员勘测,当坡角不超过45∘时,可确保山体不滑坡.(1)求改造前坡顶到地面的距离BE.(2)如果改造时保持坡脚A不动,坡顶B沿BC削进到F处,问BF至少是多少米?答案1.D2.B3.C4.A5.A6.B7.B8.B9.2510.4511.27012.23.2m13.10√3−714.解:∵DE=10m,其坡度为i1=1:√3∴在Rt△DCE中∴解得DC=5∵四边形ABCD为矩形∴AB=CD=5∵斜坡AF的坡度为i2=1:4∴ABBF =14∴BF=4AB=20在Rt△ABF中AF=√AB2+BF2=5√17≈20.61(m)∴斜坡AF的长度为20.61米.15.(1)解:作∠DAG=50°,AG交BC于G,过点G作GH⊥AD于H则BEHG为矩形∴GH=BE BG=EH设BE=12xm∵斜坡AB的坡比为12:5∴AE=5xm由勾股定理得:(5x)2+(12x)2=262解得:x=2(负值舍去)∴BE=24m,AE=12m ∴GH=BE=24m;(2)解:在Rt△GAH中则24AH≈1.2解得:AH=20∴EH=AH−AE=10(m)∴BG=EH=10m 答:坡顶B沿BC至少向右移10m时,才能确保山体不滑坡.16.解:在Rt△BAE中,∠BAE=68°,BE=162米,∴AE= BEtan∠BAE ≈1622.5=64.8(米).在Rt△DEC中,∠DCE=60°,DE=176.6米,∴CE= DEtan∠DCE =√3≈102.08(米)∴AC=CE-AE≈102.08-64.8=37.28≈37.3(米),即工程完工后背水坡底端水平方向增加的宽度约为37.3米. 17.(1)解:如图,作EM⊥BC交BC的延长线于M∵斜坡CD的坡度(或坡比)i=1:2.4,DC=BC=26米,设DM=x米,则CM=2.4x米在Rt△DCM中,∵DM2+CM2=DC2,∴x2+(2.4x)2=262,解得x=10,即斜坡CD的高度为10米.(2)解:作EN⊥AB于N由⑴知CM=24米,EM=10+0.8=10.8米,BM=BC+CM=26+24=50米∵EN⊥AB,EM⊥BC,AB⊥BC∴四边形ENBM是矩形.∴EN=BM=50米,BN=EM=10.8米.在Rt△AEN中∵∠AEF=15°∴AN=EN﹒tan15°≈50×0.27≈13.5∴AB=AN+BN=13.5+10.8=24.3米.18.(1)解:∵坡度i=9:5∴BEAE =95,设BE=9x AE=5x根据勾股定理BE2+AE2=AB2则81x2+25x2=(52√106)2,解得x=52∴BE=52×9=452m;(2)解:如图,连接AF,过点F作FH⊥AD于点H由(1)得AE=52×5=252m设BF=xm∵FHAH=tan∠FAH=tan45°=1∴452x+252=1,解得x=10∴BF至少是10米。
专题28.6解直角三角形的应用:坡度坡角大题专项提升训练(重难点培优)-2022-2023学年九年级

2021-2022学年九年级数学下册尖子生培优题典【人教版】专题28.6解直角三角形的应用:坡度坡角大题专项提升训练(重难点培优)一.解答题(共24小题)1.(2022秋•长春期中)如图是某地铁站自动扶梯的示意图,自动扶梯AB的倾斜角(∠BAC)为30.5°,自动扶梯AB的长为17米.(1)求乘客从扶梯底端升到顶端上升的高度BC.(结果精确到0.1米)(2)如果一层楼的高度为2.8米,问这个扶梯升高的高度BC相当于几层楼高?(结果保留整数)【参考数据:sin30.5°=0.51,cos30.5°=0.86,tan30.5°=0.59】2.(2022春•江北区校级月考)图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角∠EAD为22°,长为3米的真空管AB与水平线AD的夹角为37°,安装热水器的铁架竖直管CE的长度为0.5米.(1)真空管上端B到水平线AD的距离.(2)求安装热水器的铁架水平横管BC的长度.(结果精确到0.1米)参考数据:sin37°≈,cos37°≈,tan37°≈,sin22°≈,cos22°≈,tan22°≈0.4.3.(2022秋•惠山区校级月考)某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米.(1)直接写出∠BAD=;(2)求旗杆的高度.(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)4.(2021秋•七里河区校级期末)某小区为了安全起见,决定将小区内的滑滑板的倾斜角由45°调为30°,如图,已知原滑滑板AB的长为4米,点D,B,C在同一水平地面上,求调整后滑滑板底部移动的距离.(结果精确到0.1米,参考数据:≈1.414,≈1.732,≈2.449)5.(2022秋•乳山市校级月考)如图,水库大坝的横断面是梯形ABCD,迎水坡BC的坡角为30,背水坡AD的坡度为1:1.2,坝顶宽DC为2.5米,坝高CF为4.5米.求:(1)坝底AB的长;(2)坡BC的长;(3)迎水坡BC的坡度.6.(2022秋•宁阳县校级月考)如图,某校教学楼后面紧邻着一个山坡,坡上面是一块平地.BC∥AD,BE ⊥AD,斜坡AB长26m,斜坡AB的坡比为12:5.为了减缓坡面,防止山体滑坡,学校决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,则坡顶B沿BC至少向右移多少m时,才能确保山体不滑坡.(取tan50°≈1.2)7.(2020秋•鲤城区校级期中)我市有一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.(参考数据:,)8.(2022•綦江区校级模拟)某小区拟建设地下停车库入口,将原步行楼梯入口AC改造为斜坡AD.已知入口高AB=3m,坡面AC的坡度i=1:1,新坡面坡角∠ADB=30°.(1)求斜坡底部增加的长度CD为多少米?(保留根号)(2)入口处水平线AE=5m,地下停车库坡道入口上方点E处有悬挂广告牌EF,EF⊥BD,EF=0.5m.若一辆高度为2米的货车沿斜坡AD驶入车库,行进中是否会碰到广告牌的下端F?请说明理由.(参考数据: 1.4, 1.7)9.(2022•徐州)如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面CQ,坡角∠QCN=30°.在阳光下,小明观察到AB在地面上的影长为120cm,在坡面上的影长为180cm.同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.10.(2022•南京模拟)如图是一座人行天桥的引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角的楼梯AD、BE和一段水平平台DE构成.已知天桥高度BC=4.5米,引桥水平跨度AC=8米.(参考数据:取sin37°=0.60,cos37°=0.80,tan37°=0.75)(1)求水平平台DE的长度;(2)若与地面垂直的平台立柱MN的高度为3米,求两段楼梯AD与BE的长度之比.11.(2022•菏泽)菏泽某超市计划更换安全性更高的手扶电梯,如图,把电梯坡面的坡角由原来的37°减至30°,已知原电梯坡面AB的长为8米,更换后的电梯坡面为AD,点B延伸至点D,求BD的长.(结果精确到0.1米.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)12.(2022•郯城县二模)如图所示,某人通过定滑轮拉动静止在水平面上的箱子,开始时与物体相连的绳和水平面间的夹角为37°,拉动一段距离后,绳与水平面间的夹角为53°,绳子的自由端竖直向下移动了3米,求箱子移动的距离.(绳子伸缩不计)(参考数据:sin37°=,sin53°=,tan37°=)13.(2022•南京模拟)小华在网上看到一个如图(1)的躺椅,他决定自己动手用木条制作一个简易的躺椅,如图(2)是简易躺椅的侧面,其中∠B=44°,∠ACB=17°,∠DEC=∠DCE=48°,AE=AC,若木条AB=5dm,请你计算木条AC,DE,DC的长.(相关数据:sin44°=0.69,cos44°=0.72,tan44°=0.97,sin17°=0.29,cos17°=0.96,tan17°=0.31,sin48°=0.74,cos48°=0.67,tan48°=1.11,结果保留一位小数)14.(2022•湖北模拟)周末爬山、郊游是现代市民常见的健康休闲生活方式.小明和小亮两家相约周末一起去天柱山游玩.如图,他们从天柱山西坡的B点出发,沿坡角为30°的山坡走了300m到达山腰E点处休息;然后又沿着坡角为45°的山坡走了150m到达山顶A处.求天柱山的高度.(结果精确到个位,参考数据:≈1.4,≈1.7)15.(2022春•重庆月考)图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角∠EAD为22°,长为3米的真空管AB的坡度为1:,安装热水器的铁架竖直管CE的长度为0.5米.(1)真空管上端B到水平线AD的距离.(2)求安装热水器的铁架水平横管BC的长度(结果精确到0.1米).(参考数据:sin22°≈,cos22°≈,tan22°≈0.4)16.(2022•莱西市一模)周末爬山、郊游是现代市民常见的健康休闲生活方式.小丁和小亮两家相约周末一起去“天然氧吧”大青山游玩.如图,他们从大青山西坡的B点出发,沿坡角为37°的山坡走了300米到达山腰E点处休息;然后又沿着坡角为45°的山坡走了150米到达山顶A处.求大青山的海拔高度.(结果精确到个位,参考数据:≈1.4,≈1.7,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)17.(2022•邯郸模拟)如图,某登山队沿山坡AB﹣BC上山后,再沿山坡CD下山.已知山坡AB的坡度为i=1:2.4,山坡BC的坡度为i=1:0.75,山坡CD的坡角∠D=30°,且山顶C点到水平面AD的距离为1000m,B点到水平面AD的距离为200m.(1)求山坡AB﹣BC的长:(2)已知登山队上山的速度保持不变,且下山速度是上山速度的2倍,若下山比上山少用26分钟,求下山的速度.18.(2022•南召县四模)2022年5月25日,郑州市城市隧道综合管理养护中心结合隧道情况,从人民至上、生命至上的角度出发,考虑增加多种安全措施,排除安全隐患.其中对京广路隧道,根据各段隧道空间情况,在不影响交通的情况下,加装了大小、形状不一的19条人行逃生爬梯.如图1,起初工程师计划修建一段坡度为4:3(即AF:BF=4:3),总长为7.5米的爬梯AB.从安全角度考虑,工程师对爬梯的设计进行了修改,如图2,修建了AC、DE两段爬梯,并在中间修建了1米的水平平台DC,其中∠ACD =135°,∠E=40°,爬梯AC长2米,点E、B、F三点共线.求修改后爬梯的底部E与修改前爬梯的底部B之间的距离.(结果精确到0.1米.参考数据:≈1.41,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)19.(2022•新野县三模)北京冬残奥会期间,为方便中外参赛运动员的生活起居、参赛出行,组委会在无障碍设施方面做了精心的安排,让运动员在细节里感受“中国温度”.如图1是一场馆内的无障碍坡道,其示意图如图2所示,台阶的垂直高度AB的长为1.4m,缓坡BD的坡角∠DBC=6°,缓坡FD的坡角∠EDF=8°,平台AF的长为2m,求BC的长.(结果精确到0.1m)(参考数据:sin6°≈0.10,cos6°≈0.99,tan6°≈0.11,sin8°≈0.14,cos8°≈0.99,tan8°≈0.14)20.(2022•鄂尔多斯)旗杆及升旗台的剖面如图所示,MN、CD为水平线,旗杆AB⊥CD于点B.某一时刻,旗杆AB的一部分影子BD落在CD上,另一部分影子DE落在坡面DN上,已知BD=1.2m,DE=1.4m.同一时刻,测得竖直立在坡面DN上的1m高的标杆影长为0.25m(标杆影子在坡面DN上),此时光线AE与水平线的夹角为80.5°,求旗杆AB的高度.(参考数据:sin80.5°≈0.98,cos80.5°≈0.17,tan80.5°≈6)21.(2022春•沙坪坝区校级期末)如图,已知教学楼前面的玻璃幕墙GH垂直于地面,为测量GH的高度,身高1.6米的小凯从教学楼底E点沿直线步行4米到达长度为10米的斜坡DC的底端D点处,在D处用仪器测得∠HDE=30°,然后再沿着斜坡DC上行到达C点(已知CM⊥DM且CM:DM=3:4),到达C点后继续沿平行于地面的平台直线行走了6米到达B点,此时他刚好踩着太阳光照射下楼顶G点的影子,这时小凯同学的影长BN=1.8米,用线段AB表示小凯同学身高,A,B,C,D,E,H,G,M,N在同一个平面内.且B,C,N和M,D,E在各自的同一水平线上,其中GE⊥EM,AB⊥BC,EM∥BC,GB∥AN.(1)求线段HE和EM的长度.(2)求玻璃幕墙GH的高度.(≈1.732,结果保留一位小数)22.(2022春•开州区期末)某商场拟将地下一楼改建为地下停车库,将原步行楼梯入口AC改造为车库斜坡入口AD.已知入口高AB=4m,且AB⊥BD,点C处测得∠ACB=45°,新坡面坡角∠ADB=30°.(1)求斜坡底部增加的长度CD为多少米?(保留根号)(2)入口处水平线AE=6m,地下停车库坡道入口上方点E处有悬挂广告牌EF,EF⊥BD,EF=1.3m.根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入,请求出限制高度为多少米?(结果精确到0.1,参考数据:≈1.4,≈1.7)23.(2022•景德镇模拟)如图1是一个长方体形家用冰箱,长宽高分别为0.5米、0.5米、1.7米,在搬运上楼的过程中,由于楼梯狭窄,完全靠一名搬运师傅背上楼.(1)如图2,为便于搬运师傅起身,冰箱通常与地面成60°角,求此时点D与地面的高度;(2)如图3,在搬运过程中,冰箱与水平面成80°夹角,最低点A与地面高度为0.3米,门的高度为2米,假如最高点C与门高相同时,刚好可以搬进去.若他保持冰箱与平面夹角不变,他要下蹲几厘米(结果保留整数)才刚好进门?(sin80°≈0.98,cos80°≈0.16,tan80°≈5.67)24.(2022•沙坪坝区校级模拟)如图是某景区登山路线示意图,其中AD是缆车游览路线,折线A﹣B﹣C ﹣D是登山步道,步道AB与水平面AE的夹角α为30°,步道CD与水平面的夹角β为45°,BC是半山观景平台,BC∥AE.现测得AB=300m,CD=450m,缆车路线AD=1000m.其中点A,B,C,D,E在同一平面内,DE⊥AE.(1)求点B到水平面AE的距离;(2)求半山观景平台BC的长度.(结果保留整数)(参考数据:≈1.414,≈1.732.)。
重庆数学中考专题之坡度

.选择题(共40小题)1. ( 2018?重庆)如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂 直,在教学楼底部 E 点处测得旗杆顶端的仰角/ AED = 58°,升旗台底部到教学楼底部 的距离DE = 7米,升旗台坡面 CD 的坡度i = 1 : 0.75,坡长CD = 2米, 面CD 的水平距离BC = 1米,则旗杆AB 的高度约为( )(参考数据:cos58°~ 0.53, tan58°~ 1.6)20米到达点C ,再经过一段坡度(或坡比)为 i = 1 : 0.75、坡长为10米的斜坡CD 到达点D ,然后再沿水平方向向右行走40米到达点E (A , B , C , D , E3. ( 2018?大渡口区二模)如图,为测量学校旗杆 AB 的高度,小明从旗杆正前方3米处的点C 出发,沿坡度为丄-1 ';的斜坡CD 前进…;米到达点D ,在点D 处放置测角仪,测得旗杆顶部 A 的仰角为37°,量得测角仪 DE 的高为1.5米,A 、B 、C , D 、E 在同一 平面内,且旗杆和测角仪都与地面垂直.则旗杆AB 的高度约为()(参考数据:sin37° 〜0.60, cos37°~= 0.80, tan37°~ 0.75, 「金 1.73.)中考专题之坡度若旗杆底部到坡 sin58°~ 0.85,A . 12.6 米B . 13.1 米C . 14.7 米 16.3 米2. ( 2018?重庆)如图, AB 是一垂直于水平面的建筑物,某同学从建筑物底端B 出发,先沿水平方向向右行走均在同一平面内).在E 处测得建筑物顶端 A 的仰角为24°,则建筑物AB 的高度约为(参sin24 °~ 0.41, cos24°~ 0.91, tan24=0.45)(A . 21.7 米B . 22.4 米C . 27.4 米D . 28.8 米考数据:5. ( 2018春?沙坪坝区校级期中)小明利用所学教学知识测量某薑筑物如下的方法:小明从与某建筑物底端 B 在同一水平线上的 A 点出发.先沿斜坡 AD 行走 260米至坡顶D 处,再从D 处沿水平方向继续前行若干米后至点 E 处,在E 点测得该建 筑物顶端c 的仰角为72 °,建筑物底端 B 的俯角为63°.其中点A 、B 、C 、D 、E 在同 平面内,斜坡AD 的坡度i = l : 2.4,根据小明的测量数据,计算得出建筑物 BC 的高度为( )米(计算结果精确到0.1米)6. ( 2018?九龙坡区模拟)如图,某学校教学楼正前方 AB 有一斜坡CD = 20米,其坡度i=B . 7.5 米C . 7.7 米D . 8.5 米4. ( 2018?重庆模拟)如图,小明为了测量大楼 AB 的高度,他从点 C 出发,沿着斜坡面 CD走52米到点D 处,测得大楼顶部点 A 的仰角为37°,大楼底部点 B 的俯角为45°,已知斜坡CD 的坡度为i = 1: 2.4.大楼AB 的高度约为( (参考数据:sin37°~ 0.60, cos37°~ 0.80, tan37°~ 0.75)B . 35 米C . 36 米D . 40 米BC 的高度,采用了〜0.89, tan63°~ 1.96A . 157.1B . 157.4C . 257. lD . 257.4A . 6.8 米 A . 32 米~ 3.08, sin631:二,在斜坡的顶部D看教学楼楼顶B的仰角为26。
2021年九上数学同步练习2-解直角三角形的应用﹣坡度坡角问题-单选题专训及答案

2021年九上数学同步练习2-解直角三角形的应用﹣坡度坡角问题-单选题专训及答案解直角三角形的应用﹣坡度坡角问题单选题专训1、(2020路南.九上期末) 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1:,则AB的长为()A . 12米B . 4 米C . 5 米D . 6 米2、(2016乐至.九上期末) 河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比是1:(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是()A . 5 米B . 10米C . 15米D . 10 米3、(2016怀柔.九上期末) 如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )A . 4 米B . 6 米C . 12 米D . 24米4、(2019黄浦.九上期末) 已知某条传送带和地面所成斜坡的坡度为1:2,如果它把一物体从地面送到离地面9米高的地方,那么该物体所经过的路程是( )A . 18米B . 4.5米C . 9 米D . 9 米.5、(2020苏州.九上期末) 如图是一斜坡的横截面,某人沿斜坡从M出发,走了13米到达 N处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是()A . 1∶5B . 12∶13C . 5∶13D . 5∶126、(2017天长.九上期末) 如图,某水库堤坝横断面迎水坡AB的斜面坡度是1:,堤坝高BC=50m,则迎水坡面AB的长度是()A . 100mB . 120mC . 50 mD . 100 m7、(2020石鼓.九上期末) 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比为1:,则AB的长为A . 12米B . 4 米C . 5 米D . 6 米8、(2020醴陵.九上期末) 如图,有一斜坡,坡顶B离地面的高度BC为30m,斜坡AB的坡度为1:2,则此斜坡AB为( )A . mB . 60mC . 30mD . 15m9、(2019龙华.九上期末) 下列命题中,是真命题的是()A . 对角线相等的平行四边形是正方形:B . 相似三角形的周长之比等于相似比的平方;C . 若方程kx2-2x-1=0有两个不相等的实数根,则k>-1;D . 若一个斜坡的坡度为1:,则该斜坡的坡角为30°.10、(2016潮州.九上期末) 如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A . sinA的值越大,梯子越陡B . cosA的值越大,梯子越陡C . tanA的值越小,梯子越陡D . 陡缓程度与∠A的函数值无关11、(2018定安.九上期末) 如图,修建抽水站时,沿着坡度为i=1:的斜坡铺设水管.若测得水管A处铅垂高度为8 m,则所铺设水管AC的长度为()A . 8mB . 12mC . 14mD . 16m12、(2019重庆.九上期末) 如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为()(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).A . 5.1米B . 6.3米C . 7.1米D . 9.2米13、(2016简阳.九上期末) 如图①,某超市从一楼到二楼有一自动扶梯,图②是侧面示意图.已知自动扶梯AB的坡度为1∶2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )A . 10.8米B . 8.9米C . 8.0米D . 5.8米14、(2017温江.九上期末) 一个公共房门前的台阶高出地面2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是()A . 斜坡AB的坡度是18°B . 斜坡AB的坡度是tan18°C . AC=2tan18°米D . AB= 米15、(2018拱墅.九上期中) 如图,河坝横断面迎水坡的坡比是(坡比是坡面的铅直高度与水平宽度之比),坝高,则坡面的长度是().A .B .C .D .16、(2019江阴.九上期中) 某人沿着坡度为1:2.4的斜坡向上前进了130m,那么他的高度上升了( )A . 50mB . 100mC . 120mD . 130m17、(2019晋江.九上期中) 如图是某商场一楼与二楼之间的手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,电梯坡面BC的坡度i=1:,则电梯坡面BC的坡角α为()A . 15°B . 30°C . 45°D . 60°18、(2019淮阳.九上期中) 河堤的横断面如图所示,堤高BC=5米,迎水坡AB的坡比1:,则AB的长是()A . 5B . 5C . 10D . 1019、(2018淅川.九上期中) 在坡度为1:1.5的山坡上植树,要求相邻两树间的水平距离为6m,则斜坡上相邻两树间的坡面距离为()A . 4mB . mC . 3mD . m20、(2018重庆.九上期中) 如图,在 A 处观察 C 测得仰角∠CAD=31°,且A、B的水平距离 AE=800米,斜坡 AB 的坡度i =1: 2 ,索道 BC 的坡度i = 2 : 3 ,CD⊥AD 于 D,BF⊥CD于F,则索道BC 的长大约是( )(参考数据:tan31°≈0. cos31°≈0.9,≈3.6)A . 1400B . 1440C . 1500D . 154021、(2018重庆.九上期中) 图中的阴影部分是某水库大坝横截面,小明站在大坝上的A处看到一棵大树CD的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面的夹角为60°,在A处测得树顶D的俯角为15°,如图所示,已知斜坡AB的坡度i= :1,若大树CD的高为8 米,则大坝的高为()米(结果精确到1米,参考数据≈1.414 ≈1.732)A . 18B . 19C . 20D . 2122、(2017沙坪坝.九上期中) 如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)()A . 10.8米B . 8.9米C . 8.0米D . 5.8米23、(2020常州.九上期末) 河堤横断面如图所示,斜坡AB的坡度=1: ,AB= 6m,则BC的长是()A . mB . 3mC . mD . 6m24、(2019济南.九上期末) 如图,一辆小车沿倾斜角为的斜坡向上行驶13米,已知,则小车上升的高度是()A . 5米B . 6米C . 6.5米D . 12米25、(2020来宾.九上期末) 堤坝的横断面如图,堤高BC是5米,迎水斜坡AB的长为13米,那么斜坡AB的坡度是()A . 1:3B . 1:2.6C . 1:2D . 1:2.426、(2020覃塘.九上期末) 已知一堤坝的坡度,堤坝的高度为米,则堤坝的斜坡长为()A . 米B . 米C . 米D . 米27、(2020平.九上期末) 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300,同一时刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为()A . 米B . 12米C . 米D . 10米28、(2020遂宁.九上期末) 如图,河堤横断面迎水坡AB的坡比是,堤高BC=10m,则坡面AB的长度是()A . 15mB .C . 20mD .29、(2021淮北.九上期末) 如图,大坝横截面的迎水坡AB的坡比为1:2,即BC:AC=1:2,若坡面AB的水平宽度AC为12米,则斜坡AB的长为()A . 4 米B . 6 米C . 6 米D . 24米30、(2020香坊.九上期末) 如图,滑雪场有一坡角α为20°的滑雪道,滑雪道AC 的长为200米,则滑雪道的坡顶到坡底垂直高度AB的长为()A . 200tan20°米B . 米C . 200sin20°米D . 200cos20°米解直角三角形的应用﹣坡度坡角问题单选题答案1.答案:A2.答案:A3.答案:B4.答案:D5.答案:D6.答案:A7.答案:A8.答案:A9.答案:D10.答案:A11.答案:D12.答案:A13.答案:D14.答案:B15.答案:B16.答案:A17.答案:B18.答案:D19.答案:B20.答案:B21.答案:B22.答案:D23.答案:B24.答案:A25.答案:D26.答案:C27.答案:A28.答案:29.答案:30.答案:。
坡度问题专项练习题

word 格式-可编辑-感谢下载支持A Bα5米CBA i =1︰4AB CD E45°60° 坡度问题一、填空题:1、若一段斜坡的水平宽度为12米,坡度i=1:3,则这斜坡的铅锤高度是________。
2、若一段斜坡的坡度是i=1:2,某人走在这斜坡上走了10米,则这个人的高度上升了________。
3、有一段山坡,坡面长为200米,山披坡高为100米,则此山坡的坡度为i=_______。
4、若一段斜坡的水平宽度为6米,坡度i=1:3,则这斜坡的坡面长为_________米5、已知一个坡的坡比i =1︰3,则此坡的坡角是 度.6、一斜坡的坡角为30度,那么这个斜坡的坡度 i = .7、如图,斜坡路面AB 的坡比i =1︰4,坡高BC =3米,则路面AB 长等于 米8、如果一条斜坡的坡度为1∶0.75,高为4米,那么这条斜坡的长度为 米.9、一斜面的坡度i =1︰0.75,一物体由斜面底部沿斜面向前推了10米, 那么这个物体升高了 米.10、有一山坡,高50米,山坡长130米,则此山坡的坡度为 (写成比的形式). 11.小明沿着坡度为1:2的山坡向上走了1000m ,则他升高了 米。
12、一斜面的坡角为30°,一物体沿斜面向上推了10米,那么这个物体升高了 米。
13、如图所示,铁路的路基横断面是等腰梯形,斜坡AB 的坡度为1:3,斜坡AB 的水平宽度BE =33m ,则斜坡AB =_____________m .14. 如图,先锋村准备在坡角为030=α山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB 为__________米.二、解答题: 1、(2010浙江嘉兴)设计建造一条道路,路基的横断面为梯形ABCD ,如图(单位:米).设路基高为h ,两侧的坡角分别为α和β,已知h=2, α=45°,1tan 2β=,CD=10. (1)求路基底部AB 的宽;(2)修筑这样的路基1000米,需要多少土石方?2、(2010江苏泰州)庞亮和李强相约周六去登山,庞亮从北坡山脚C 处出发,以24米/分钟的速度攀登,同时,李强从南坡山脚B 处出发.如图,已知小山北坡的坡度31∶=i ,山坡长为240米,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A ?(将山路AB 、AC 看成线段,结果保留根号)3、(2010江苏淮安)某公园有一滑梯,横截面如图薪示,AB 表示楼梯,BC 表示平台,CD 表示滑道.若点E ,F 均在线段AD 上,四边形BCEF 是矩形,且cos ∠BAF=53,AB=4.5米,BC=1米,CD=6米.求: (1) 梯角∠D 的度数; (2)滑梯地面宽度AD 的长.4、(2010江苏扬州)如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD .小明在山坡的坡脚A 处测得宣传牌底部D 的仰角为60°,沿山坡向上走到B 处测得宣传牌顶部C 的仰角为45°.已知山坡AB 的坡度i =1:3,AB =10米,AE =15米,求这块宣传牌CD 的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:2≈1.414,3≈1.732)αβA B C D α A D Eword 格式-可编辑-感谢下载支持5、(2010 四川泸州)如图5,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD )急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF 的坡比(1)求加固后坝底增加的宽度AF ;(2)求完成这项工程需要土石多少立方米?(结果保留根号)6.水坝的横截面是梯形ABCD (如图1),上底米,坝高3==DN AM 米,斜坡AB 的坡比3:11=i ,斜坡DC 的坡比1:12=i .(1)求坝底BC 的长(结果保留根号);(6分)(2)为了增强水坝的防洪能力,在原来的水坝上增加高度(如图2),使得水坝的上底2=EF 米,求水坝增加的高度(精确到1.0米,参考数据73.13≈).(6分)7、(2010新疆乌鲁木齐)某过街天桥的截面图为梯形,如图所示,其中天桥斜面CD 的坡度为i =CD 的长为10m ,天桥另一斜面AB 的坡角45=∠ABC (1)写出过街天桥斜面AB 的坡度; (2)求DE 的长;(3)若决定对该过街天桥进行改建,使AB 斜面的坡度变缓,将其45°坡角改为30°,方便过路群众,改建后斜面为AF ,试计算此改建需占路面的宽度FB 的长(结果精确到0.01)8、(2010云南昭通)云南2009年秋季以来遭遇百年一遇的全省特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形ABCD (如图7所示),AD∥BC,EF 为水面,点E 在DC 上,测得背水坡AB 的长为18米,倾角∠B=30°,迎水坡CD 上线段DE 的长为8米,∠ADC=120°. (1)请你帮技术员算出水的深度(精确到0.01米,参考数据732..13≈);(2)就水的深度而言,平均每天水位下降必须控制在多少米以内,才能保证现有水量至少能使用20天?(精确到0.01米)AB CDM N(图1)ABCDMNEF(图2)4=ADword 格式-可编辑-感谢下载支持10 2.5BA9、(2010贵州遵义)如图,水坝的横断面是梯形,背水坡AB 的坡角∠BAD=60°,坡长AB=203m,为加强水坝强度,将坝底从A 处向后水平延伸到F 处,使新的背水坡的坡角∠F=45 ,求AF 的长度(结果精确到1米,参考数据:2≈1.414, 3 ≈1.732)10、(2010四川广安)如图.是一座人行天桥的示意图,天桥的高是l0米,坡面的倾斜角为45°,为了方便行人安全过天桥,市政部门决定降低坡度.使新坡面的倾斜角为30°若新坡脚前需留2 .5米的人行道,问离原坡脚10米的建筑物是否需要拆除?请说明理由 (参考数据:2≈1.414, 3 ≈1.732)11. 如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB 长为4米. (1)求新传送带AC 的长度;(2)如果需要在货物着地点C 的左侧留出2米的通道,试判断距离B 点4米的货物MNQP 是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:2≈1.41,3≈1.73,5≈2.24,6≈2.45)12.(2010年山东省济南市)我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC ∥AD ,斜坡AB =40米,坡角∠BAD =600,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过450时,可确保山体不滑坡,改造时保持坡脚A 不动,从坡顶B 沿BC 削进到E 处,问BE 至少是多少米(结果保留根号)13、如图,某堤坝的横截面是梯形ABCD ,背水坡AD 的坡度i=1︰1.2,坝高为5米。
初中三年级上学期数学《坡度问题》作业

坡度问题作业1.如图斜坡长130 m ,坡顶离水平地面的距离为50 m ,那么这个斜坡与水平地面夹角的正切值等于( )A.513B.1213C.512D.13122.如图一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )A .斜坡AB 的坡度是10° B .斜坡AB 的坡度是tan10°C .AC =1.2tan10°米D .AB = 1.2cos10°米 3.如图河坝横断面迎水坡AB 的坡比为1∶3(坡比是坡面的铅直高度BC 与水平宽度AC 之比),坝高BC =3 m ,则坡面AB 的长度是( )A .9 mB .6 mC .6 3 mD .3 3 m4.如图,斜面AC 的坡度(CD 与AD 的比)为1∶2,AC =3 5米,坡顶有旗杆BC ,旗杆顶端B 点与A 点有一条彩带相连.若AB =10米,则旗杆BC 的高度为( )A .5米B .6米C .8米D .(3+5)米5.如图一水库大坝的横断面为梯形ABCD ,坝顶BC 宽6米,坝高20米,斜坡AB 的坡度i =1∶2.5,斜坡CD 的坡角为30°,则坝底AD =________米.6.如图,某公园入口处原有三级台阶,每级台阶高为18 cm,深为30 cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1∶5,则AC的长度是________cm.7.某景区为方便游客参观,在每个景点均设置两条通道,即楼梯和无障碍通道.如图K-44-8,已知在某景点P处,供游客上下的楼梯倾斜角为30°(即∠PBA=30°),长度为4 m(即PB=4 m),无障碍通道P A的倾斜角为15°(即∠P AB=15°),求无障碍通道的长度.(结果精确到0.1 m,sin15°≈0.26)8.2017·海南为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1∶1(即DB∶EB=1∶1),如图K-44-9所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)。
专题1.5 解直角三角函数应用-坡度坡角应用(专项训练)(原卷版)

专题1.5 解直角三角函数应用-坡度坡角应用(专项训练)1.(2021秋•济阳区期末)如图,一山坡的坡度i=1:,小明从A处爬到B处所走的直线距离AB=100米,则他在垂直方向上升的高度CB为 米.2.(2021秋•南召县月考)如图所示,某商场要在一楼和二楼之间搭建扶梯BC,已知一楼与二楼之间的地面高度差为3.5米,扶梯BC的坡度,则扶梯BC的长度为米.3.(2022•瑶海区三模)图1、图2分别是一滑雪运动员在滑雪过程中某一时刻的实物图与示意图,已知运动员的小腿ED与斜坡AB垂直,大腿EF与斜坡AB平行,且G、E、D 三点共线,若雪仗EM长为1m,EF=0.4m,∠EMD=30°,∠GFE=62°,求此刻运动员头部G到斜坡AB的高度h(精确到0.1m,参考数据:sin62°≈0.88、cos62°≈0.47、tan62°≈1.88)4.(2022•太平区一模)某商场从安全和便利的角度出发,提升顾客的购物体验,准备将自动扶梯由原来的阶梯式改造成斜坡式.如图,已知商场的层高AD为6m,坡角∠ABD为30°,改造后的斜坡式自动扶梯的坡角∠ACB为16°,请你计算改造后的斜坡式自动扶梯AC相比改造前AB增加的长度.(结果精确到0.1m,参考数据:sin16°≈0.28,cos16°≈0.96,tan16°≈0.29)5.(2022春•北碚区校级月考)如图,为了测量陶行知纪念馆AB的高度,小李在点C处放置了高度为1.5米的测角仪CD,测得纪念馆顶端A点的仰角∠ADE=51°,然后他沿着坡度i=1:2.4的斜坡CF走了6.5米到达点F,再沿水平方向走4米就到达了纪念馆底端点B.(结果精确到0.1,参考数据:sin51°≈0.78,cos51°≈0.63,tan51°≈1.23)(1)求点D到纪念馆AB的水平距离;(2)求纪念馆AB的高度约为多少米?6.(2022•黄岩区一模)如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4 m.(1)求新传送带AC的长度;(2)如果需要在货物着地点C的左侧留出5m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.7.(2022•铁岭模拟)某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB ⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).(1)求这个车库的高度AB;(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)8.(2022•瑶海区二模)2021年底中国高铁运营里程数已达4万公里,中国高铁发展速度之快、质量之高令全世界惊叹,是当之无愧的“国家名片”.如图所示某条高铁路基的横断面是四边形ABCD,AD∥BC,路基顶BC宽10米,斜坡AB长为15米,斜坡AB的坡角α是32°,斜坡CD的坡度i=1:2.5,求路基底AD的长.(结果精确到1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)9.(2022春•渝中区校级月考)图1是安装在倾斜屋顶上的热水器,图2是安装热水器的侧面示意图.已知屋面AE的倾斜角∠EAD为22°,长为3米的真空管AB与水平线AD的夹角为37°,安装热水器的铁架竖直管CE的长度为0.5米.(1)真空管上端B到水平线AD的距离.(2)求安装热水器的铁架水平横管BC的长度(结果精确到0.1米).(参考数据:sin37°≈,cos37°≈,tan37°≈,sin22°≈,cos22°≈,tan22°≈0.4)10.(2022•营口)在一次数学课外实践活动中,某小组要测量一幢大楼MN的高度,如图,在山坡的坡脚A处测得大楼顶部M的仰角是58°,沿着山坡向上走75米到达B处,在B处测得大楼顶部M的仰角是22°,已知斜坡AB的坡度i=3:4(坡度是指坡面的铅直高度与水平宽度的比),求大楼MN的高度.(图中的点A,B,M,N,C均在同一平面内,N,A,C在同一水平线上,参考数据:tan22°≈0.4,tan58°≈1.6)11.(2022•鄂州)亚洲第一、中国唯一的航空货运枢纽——鄂州花湖机场,于2022年3月19日完成首次全货运试飞,很多市民共同见证了这一历史时刻.如图,市民甲在C处看见飞机A的仰角为45°,同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°.若斜坡CF的坡比=1:3,铅垂高度DG=30米(点E、G、C、B在同一水平线上).求:(1)两位市民甲、乙之间的距离CD;(2)此时飞机的高度AB.(结果保留根号)12.(2021•内江)在一次课外活动中,某数学兴趣小组测量一棵树CD的高度.如图所示,测得斜坡BE的坡度i=1:4,坡底AE的长为8米,在B处测得树CD顶部D的仰角为30°,在E处测得树CD顶部D的仰角为60°,求树高CD.(结果保留根号)13.(2021•郴州)如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯AC的高度,测得斜坡AB=105米,坡度i=1:2,在B处测得电梯顶端C的仰角α=45°,求观光电梯AC的高度.(参考数据:≈1.41,≈1.73,≈2.24.结果精确到0.1米)。
(872)解直角三角形应用--坡度专项练习40题111 18+21页

解直角三角形应用--坡度专项练习40题1.若某斜面的坡度为1:,则该坡面的坡角为度.2.如图,斜坡AB的坡度是1:4,如果从点B测得离地面的铅垂线高度BC是6米,那么斜坡AB′的长度是米.3.某居民楼紧挨一座山坡AB,经过地质人员勘测,当坡度不超过45°时,可以确保山体不滑坡,如图所示,已知AE∥BD,斜坡AB的坡角∠ABD=60°,为防止滑坡,现对山坡进行改造,改造后,斜坡BC与地面BD成45°角,AC=10米.则斜坡BC=米.4.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=10米,背水坡CD的坡度i=1:,则背水坡的坡长CD为米.5.某人沿着坡度为1:3的山坡向上走了200m,则他升高了米.6.如图,小明沿着一个斜坡从坡底A向坡顶B行走的过程中发现,他毎向前走60m,他的高度就升高36m,则这个斜坡的坡度等于.7.如图,小车从4米高的A处沿斜坡滑到B处,若斜坡坡度为i=1:2,则斜坡AB的水平宽度BC为米.8.公园内有一小山坡AB,经测量,坡度∠ABC=30°,斜坡AB长为30千米,为方便游客行走,决定开挖小山坡,使斜坡比是1:3(即为CD与BC的长度之比),A,D两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.9.如图,一水库大坝的横断面为梯形ABCD,坝顶宽6米,坝高10米,斜坡AB的坡度i1=1:3,斜坡CD的坡度i2=1:1.(1)求斜坡AB的长(结果保留根号);(2)求坝底AD的长度;(3)求斜坡CD的坡角α.10.如图,长为10米的梯子AB斜靠在墙上,梯子的顶端A到地面的距离AC为8米,当梯子的顶端A下滑1米到A'时,底端B向外滑动到点B',求BB'的长(精确到0.01米).(参考数据:≈7.1414)11.如图,斜坡AB的坡度是i=1:2,坡角B处有一棵树BC,某一时刻测得树BC在斜坡AB 上的影子BD的长度是10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为多少米?(结果保留根号).12.为了游客的安全,某景点将原坡角为30°的斜坡AB改为坡度为1:3的斜坡AC,已知AB=100米,BC在同一水平线上,求改造后斜坡的坡脚向前移动距离BC的长.13.计划在楼层间修建一个坡角为35°的楼梯,若楼层间高度为2.7m,为了节省成本,现要将楼梯坡角增加11°,则楼梯的斜面长度约减少m.(用科学计算器计算,结果精确到0.01m).14.如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(1)求AB段山坡的高度EF;(2)求山峰的高度CF(结果保留根式).15.如图,一段河堤的斜坡BC=15米,为了加固河堤,斜坡的坡度由原来的1:2变成1:3,加固后斜坡AD的长是多少?(结果可化为最简根式)16.如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,求大厅两层之间的距离BC的长.(结果精确到0.1米)(参考数据:sin31°=0.515,cos31°=0.857,tan31°=0.60)17.如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积.18.如图,小明从点A处出发,沿着坡角为α的斜坡向上走了0.65千米到达点B,sinα=,然后又沿着坡度为i=1:4的斜坡向上走了1千米达到点C.问小明从A点到点C上升的高度CD是多少千米(结果保留根号)?19.如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.(1)求斜坡AB的水平宽度BC;(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(结果保留根号)20.如图,防洪大堤的横断面是梯形ABCD,其中AD∥BC,坡角α=60°,汛期来临前对其进行了加固,改造后的坡长为AE,背水面坡角β=45°.若原坡长AB=16m,求改造后的坡长AE(结果保留根号).21.如图,公园内有一棵景观树,AB的影子请好落在地图BC和地图CD上,经测量CD=4m,BC=10m,已知该坡面CD与地面成30°角,且此时测得2m的竹竿的影子是1m,求这棵景观树的高度.22.如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.(1)求斜坡AB的水平宽度BC;(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(≈2.236,结果精确到0.1m)23.如图,CE为水平线,斜坡AC的坡度(坡比)为1:,AC=10米,坡顶有一直立旗杆BA,现在想用一根彩带从旗杆顶端B点连接到坡底C点,如果已知旗杆AB长为3米,试求彩带BC 至少准备多长?24.如图,是某货运站传送货物的平面示意图.传送带AB长为4米,在离B点5米远的地方有一堆货物DEFG等待运输.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.但要保证货物着地点C的左侧留出2米的通道,试判断货物DEFG是否需要挪走.(结果精确到0.1米:参考数据:≈1.41,≈1.73,≈2.24,≈2.45)25.如图,斜坡AC的坡比为1:,AC=10米,坡顶有一旗杆BC,旗杆顶端B点与点A有一条彩带相连,AB=14米,试求旗杆BC的高度.26.如图,已知斜坡AB长为60米,坡角(即∠BAC)为45°,BC⊥AC.现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE,若修建的斜坡BE的坡比为:1,求休闲平台DE的长是多少米?(结果保留根号).27.如图,一侧面为矩形的建筑物ABCD,AP为建筑物上一灯杆(垂直于地面),夜晚灯杆顶端灯亮时,EH段是建筑物在斜坡EF上的影子.已知BC=8米,AP=12米,CE=6米,斜坡EF 的坡角∠FEG=30°,EH=4米,且B,C,E,G在同一水平线上,题中涉及的各点均在同一平面内,求建筑物的高度AB(结果保留根号).28.如图,有一段斜坡BC长为10米,坡角∠CBD=11°,为方便残疾人的轮椅车通行,现准备把坡角降为5°.(1)求坡高CD;(2)求斜坡新起点A到原起点B的距离(精确到0.1米).参考数据:sin11°≈0.19,cos11°≈0.98,tan5°≈0.09.29.如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米.(1)求广告牌与铁塔AB之间的水平距离;(2)求铁塔AB的高.(图中AB,CD均与水平面垂直,结果保留根号)30.小明从点A出发,沿着坡角为α的斜坡向上走了650米到达点B,且sinα=.然后又沿着坡度i=1:3的斜坡向上走了500米达到点C.(1)小明从A点到点B上升的高度是多少米?(2)小明从A点到点C上升的高度CD是多少米?(结果保留根号)31.如图,某水上乐园有一个滑梯AB,高度AC为6米,倾斜角为60°,暑期将至,为改善滑梯AB的安全性能,把倾斜角由60°减至30°(1)求调整后的滑梯AD的长度;(2)调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)(参考数据:≈1.41,,≈2.45)32.如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).33.某商场为了方便顾客使用购物车,将滚动电梯由坡角30°的坡面改为坡度为1:2.4的坡面.如图,BD表示水平面,AD表示电梯的铅直高度,如果改动后电梯的坡面AC长为13米,求改动后电梯水平宽度增加部分BC的长(结果保留根号).34.如图是某滑板俱乐部训练时的斜坡截面的示意图,该截面垂直于水平面,出于安全因素考虑,俱乐部决定将训练的斜坡AB改造成AD,这时斜坡的坡角由45°降为30°,已知原斜坡面AB的长为6米,点D,B,C在同一水平直线上,AE∥DC,改善后斜坡坡面AD的长为多少米?35.某建筑大楼后面紧邻着一个土坡,坡上面是一块平地,如图,BC∥AD,斜坡AB长20米,坡角∠BAD=60°,为防止山体滑坡,保障安全,决定对该土坡进行改造.经相关部门勘测,当坡角不超过45°时,可确保山体不滑坡.(1)求改造前坡顶到地面的距离BE的长;(2)为确保安全,在改造工程中保持坡脚A不动,坡顶B沿BC削进到点F处,问:BF至少为多少米?(结果保留根号)36.如图.斜坡AF的坡度(铅直高度与水平宽度的比)为1:2.4,斜坡A F上一棵与水平面垂直的大树BD在阳光的照射下,在斜坡上的影长BC=6.5米,此时光线与水平线恰好成30°角,求大树BD的高.(结果精确到0.1米,参考数据:≈1.414,≈1.732)37.如图,某拦河坝横截面的原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°.为了提高拦河大坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°.(1)请你计算这个拦河大坝的高度;(2)请你计算改造后拦河大坝坡面EF的长.(结果保留根号)(参考数据:sin72°≈,cos72°≈,tan72°≈)38.某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯AB长为10m,坡角∠ABD为30°;改造后的斜坡式自动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度,(结果精确到0.lm.温馨提示:sin15°≈0.26,cosl5°≈0.97,tan15°≈0.27)39.如图,为了将货物装入大型的集装箱卡车,需要利用传送带AB将货物从地面传送到高1.8米(即BD=1.8米)的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.(1)求传送带AB的长度;(2)因实际需要,现在操作平台和传送带进行改造,如图中虚线所示,操作平台加高0.2米(即BF=0.2米),传送带与地面所成斜坡的坡度i=1:2.求改造后传送带EF的长度.(精确到0.1米)(参考数值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41,≈2.24)40.重庆大坪时代天街已成为人们周末休闲娱乐的重要场所,时代天街从一楼到二楼有一自动扶梯(如图1),图2是侧面示意图.已知自动扶梯AC的坡度为i=1:2.4,AC=13m,BE是二楼楼顶,EF∥MN,B是EF上处在自动扶梯顶端C正上方的一点,且BC⊥EF,在自动扶梯底端A处测得B点仰角为42°.(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)(1)求二楼的层高BC约为多少米;(2)为了吸引顾客,开发商想在P处放置一个高10m的《疯狂动物城》的装饰雕像,并要求雕像最高点与二楼顶层要留出2m距离好放置灯具,请问这个雕像能放得下吗?如果不能,请说明理由.解直角三角形应用--坡度40题参考答案:1.【分析】坡度等于坡角的正切值.根据特殊角的三角函数值解答.【解答】解:∵某斜面的坡度为1:,∴tanα==,∴α=30°.故答案为:30.2.【分析】先利用坡度的定义,求出水平宽度AC的长,再利用勾股定理得出斜坡AB的长度.【解答】解:∵斜坡AB的坡度i=1:4,∴=,∵从点B测得离地面的铅垂线高度BC是6米,∴=,解得:AC=24,则斜坡AB的长为:==6(米).故答案为6.3.【分析】根据题意可以运用锐角三角函数表示出BC的长,从而可以解答本题.【解答】解:作AM⊥BD于点M,作CN⊥BD于点N,如右图所示,∵∠ABD=60°,∠CBD=45°,∴BN=,BM=,BC=,∵CN=AM,AC=BN﹣BM,AC=10米,∴BC=≈33.4米,即斜坡BC的长是33.4米.故答案为:33.44.【分析】由题意可得四边形AEFD是矩形,由AB的坡角α=45°,得出AE的长,利用背水坡CD的坡度i=1:得出∠C的度数,即可求解.【解答】解:∵迎水坡AB的坡角α=45°,坡长AB=10米,∴AE=10×sin45°=10(米),∵背水坡CD的坡度i=1:,∴tan∠C===,∴∠C=30°,则DC=2DF=2AE=20(米),故答案为:20.5.【分析】根据题意作出图形,然后根据坡度为1:3,设BC=x,AC=3x,根据AB=200m,利用勾股定理求解.【解答】解:∵坡度为1:3,∴设BC=x,AC=3x,∴AB=,即x=200,解得:x=20.故答案为:20.6.【分析】先根据勾股定理求出水平宽度,再根据坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式即可求解.【解答】解:∵小明沿着一个斜坡从坡底A向坡顶B行走的过程中发现,他毎向前走60m,他的高度就升高36m,=48(m),∴这个斜坡的坡度等于36:48=1:.故答案为:1:.7.【分析】根据坡度定义直接解答即可.【解答】解:∵坡度为i=1:2,AC=4m,∴BC=4×2=8m.故答案为:8.8.【分析】在直角△ABC中,利用三角函数即可求得BC、AC的长,然后在直角△BCD中,利用坡比的定义求得CD的长,根据AD=AC﹣CD即可求解.【解答】解:Rt△ABC中,∠ABC=30°,sin∠ABC=,∴AC=AB=×30=15,BC=ABcos∠ABC=30×=,∵斜坡BD的坡比是1:3,∴CD=BC=5,∴AD=AC﹣CD=15﹣5答:开挖后小山坡下降了(15﹣5)千米.9.【分析】(1)根据坡度的概念求出AE的长,根据勾股定理求出AB的长;(2)分别得出DF,EF的长,进而得出答案;(3)根据坡度是坡角的正切值计算即可.【解答】解:(1)过点B,作BE⊥AD于点E,∵坝高10米,斜坡AB的坡度i1=1:3,∴=,∴=,解得:AE=30m,则AB==10(m),答:斜坡AB的长为10m;(2)过点C作CF⊥AD于点F,∵斜坡CD的坡度i2=1:1,坝高10米,∴BC=EF=6m,CF=FD=10m,∴AD=AE+EF+FD=30+6+10=46(m),答:坝底AD的长度为46m;(3)∵斜坡CD的坡度i2=1:1,∴斜坡CD的坡角α为:tanα=1,则α=45°10.【分析】在Rt△ABC中,根据AC,AB的长可以求得BC的长,在Rt△A'B'C中,根据A'C 和A'B'的长可以求得B'C的长,即可求得BB'的长,即可解题.【解答】解:∵Rt△ABC中,AC=8m,AB=10m,∴BC==6m,∵Rt△A'B'C中,A'C=8m﹣1m=7m,A'B'=10m,∴B'C=m,∴BB′=B'C﹣BC=(﹣6)m≈1.14m.答:BB′的长约为1.14m.11.【分析】根据题意首先利用勾股定理得出DF,DE的长,再利用锐角三角函数关系得出EC 的长,进而得出答案.【解答】解:过点D作DF⊥BG,垂足为F,∵斜坡AB的坡度i=1:2,∴设DF=x,BF=2x,则DB=10m,∴x2+(2x)2=102,解得:x=2,故DE=4,BE=DF=2,∵测得太阳光线与水平线的夹角为60°,∴tan60°===,解得:EC=4,故BC=EC+BE=(2+4)(m).12.【分析】作AD⊥BC于D,解直角三角形即可得到结论.【解答】解:作AD⊥BC于D,在Rt△ABD中,∠ABD=30°,∴AD=AB•sin∠ABD=100•sin30°=50m,BD=AB•cos∠ABD=100cos30°=50m,∵AC的坡度为1:3,∴AD:CD=1:3,∴BC=CD﹣BD=(150﹣50)m,∴改造后斜坡的坡脚向前移动距离BC的长是(150﹣50)m.13.【分析】根据三角函数的定义分别求出坡角为35°,楼层间高度为2.7m时楼梯的斜面长度和将楼梯坡角增加11°后楼梯的斜面长度,即可求出楼梯的斜面长度约减少多少.【解答】解:、∵坡角为35°,楼层间高度为2.7m,∴楼梯的斜面长度==≈4.703(m),∵将楼梯坡角增加11°后,楼梯的斜面长度=≈3.755(m),∴楼梯的斜面长度约减少4.703﹣3.755≈0.95(m),故答案为:0.9514.【分析】(1)作BH⊥AF于H,如图,在Rt△ABH中根据正弦的定义可计算出BH的长,从而得到EF的长;(2)先在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.【解答】解:(1)作BH⊥AF于H,如图,在Rt△ABH中,∵sin∠BAH=,∴BH=800•sin30°=400,∴EF=BH=400米.答:AB段山坡的高度EF为400米;(2)在Rt△CBE中,∵sin∠CBE=,∴CE=200•sin45°=100,∴CF=CE+EF=(100+400)(米).答:山峰的高度CF为(100+400)米.15.【分析】过C作CE⊥AB,过D作DF⊥AB,垂足分别为E、F.设CE=x,根据坡度的定义得出BE=2x,AF=3x.在Rt△CEB中,利用勾股定理得出x2+(2x)2=152,解方程求出x=3,然后在Rt△ADF中,由勾股定理求出AD==x,将x的值代入计算即可.【解答】解:过C作CE⊥AB,过D作DF⊥AB,垂足分别为E、F.设CE=x,则BE=2x,DF=CE=x,AF=3x,∵在Rt△CEB中,∠BEC=90°,BC=12,∴x2+(2x)2=122,得:x=3.∵在Rt△ADF中,∠AFD=90°,∴AD===x=×3=15.答:加固后斜坡AD是15米.16.【分析】根据题意和锐角三角函数可以求得BC的长,从而可以解答本题.【解答】解:过B作地平面的垂线段BC,垂足为C,在Rt△ABC中,∵∠ACB=90°,∴BC=AB•sin∠BAC=12×0.515≈6.2(米),答:大厅两层之间的距离BC的长约为6.2米.17.【分析】根据坡比定义求得AE=50、DF=40,从而得出梯形的下底AD的长,由梯形面积公式求解可得.【解答】解:根据题意知BC=EF=5,BE=CF=20,∵=,=,∴AE=2.5BE=50,DF=2CF=40,则AD=AE+EF+DF=50+5+40=95,=×(BC+AD)×BE=×(5+95)×20=1000(平方米),∴S梯形ABCD答:大坝的截面面积为1000平方米.18.【分析】直接构造直角三角形,进而分别得出DF,CF的长进而得出答案.【解答】解:如图所示:过点B作BE⊥AD交于点E,过点B作BF⊥CD于点F,∵sinα=,∴设BE=5x,AB=13x,故AE=12x,∵AB=0.65千米,∴BE=0.25千米,则DF=0.25千米,∵沿着坡度为i=1:4的斜坡向上走了1千米达到点C,∴设CF=a,则BF=4a,故a2+(4a)2=12,解得:a=,故DC=CF+DF=(0.25+)千米,答:小明从A点到点C上升的高度CD为(0.25+)千米.19.【分析】(1)根据坡度定义直接解答即可;(2)作DS⊥BC,垂足为S,且与AB相交于H.证出∠GDH=∠SBH,根据=,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.【解答】解:(1)∵坡度为i=1:2,AC=4m,∴BC=4×2=8m.(2)作DS⊥BC,垂足为S,且与AB相交于H.∵∠DGH=∠BSH,∠DHG=∠BHS,∴∠GDH=∠SBH,∴=,∵DG=EF=2m,∴GH=1m,∴DH==m,BH=BF+FH=3.5+(2.5﹣1)=5m,设HS=xm,则BS=2xm,∴x2+(2x)2=52,∴x=m∴DS=+=2m.20.【分析】过A作AH⊥BC于H,在Rt△ABH中求出AH的长度,然后在Rt△AEH中求出AE 的长度.【解答】解:过A作AH⊥BC于H.在Rt△ABH中,∵α=60°,AB=16m,∴AH=AB•sinα=16×=8,在Rt△AEH中,∵β=45°,∴AE===8.答:改造后的坡长AE为8m.21.【分析】作DE⊥AB于点E,DF⊥BC于点F,在Rt△CDF中,利用含30°角的直角三角形的性质可得DF长,也就是BE的长,还可以求得CF的长,也就求得了BF的长,也就是ED的长;易得AE与影长DE构成的三角形和竹杆与影长构成的三角形相似,利用相似三角形的对应边成比例可得AB的长.【解答】解:作DE⊥AB于点E,DF⊥BC于点F.在Rt△CDF中,∵CD=4m,∠DCF=30°,∴DF=CD=2m,CF=DF=2m,∴BE=DF=2m,∴ED=BF=BC+CF=(10+2)m.∵同一时刻的光线是平行的,水平线是平行的,∴光线与水平线的夹角相等,又∵标竿与影长构成的角为直角,AE与ED构成的角为直角,∴AE与影长DE构成的三角形和竹竿与影长构成的三角形相似,∴=,解得AE=(20+4)m,∴AB=AE+BE=(22+4)m.答:AB的长为(22+4)m.22.【分析】(1)根据坡度定义直接解答即可;(2)作DS⊥BC,垂足为S,且与AB相交于H.证出∠GDH=∠SBH,根据=,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.【解答】解:(1)∵坡度为i=1:2,AC=4m,∴BC=4×2=8m.(2)作DS⊥BC,垂足为S,且与AB相交于H.∵∠DGH=∠BSH,∠DHG=∠BHS,∴∠GDH=∠SBH,∴=,∵DG=EF=2m,∴GH=1m,∴DH==m,BH=BF+FH=3.5+(2.5﹣1)=5m,设HS=xm,则BS=2xm,∴x2+(2x)2=52,∴x=m,∴DS=+=2m≈4.5m.23.【分析】延长BA交CE于D点,则BD⊥CE,在Rt△ACD中,得到tan∠ACD===,求出∠ACD=30°,再根据∠ACD的正弦、余弦值,求出AD、CD的长,从而得到BD的长,然后利用勾股定理求出BC的长.【解答】解:延长BA交CE于D点,则BD⊥CE,在Rt△ACD中,tan∠ACD===,故∠ACD=30°,由cos∠ACD=知,CD=AD•cos∠ACD=10×cos30°=5,由sin∠ACD=知AD=AC•sin∠ACD=10×=5,∴BD=BA+AD=3+5=8,在Rt△BCD中,BC====,∴<<∴BC≈12米.24.【分析】过A作AD⊥BC于D,在Rt△ABD中,根据特殊角的三角函数值求出AD,再根据在直角三角形中,30°所对的直角边等于斜边的一半求出AC,根据勾股定理求出CD,从而求出CB,最后根据DC=DB﹣CB求出DC,然后与2米进行比较,即可得出答案.【解答】解:如图,作AD⊥BC于点D;在Rt△ABD中,AD=BD=ABsin45°=4×=2,在Rt△ACD中,∵∠ACD=30°,∴AC=2AD=4;在Rt△ACD中,CD===2;∴CB=CD﹣BD=2﹣2≈2.1.∵DC=DB﹣CB≈5﹣2.1=2.9>2;∴货物DEFG不需要挪走.25.【分析】如果延长BC交AD于E点,则CE⊥AD,要求BC的高度,就要知道BE和CE的高度,就要先求出AE的长度.直角三角形ACE中有坡比,由AC的长,那么就可求出AE的长,然后求出BE、CE的高度,BC=BE﹣CE,即可得出结果.【解答】解:延长BC交AD于E点,则CE⊥AD.在Rt△AEC中,AC=10,由坡比为1:可知:∠CAE=30°,∴CE=AC•sin30°=10×=5,AE=AC•cos30°=5.在Rt△ABE中,BE===11.∵BE=BC+CE,∴BC=BE﹣CE=11﹣5=6(米).答:旗杆的高度为6米.26.【分析】由三角函数的定义,即可求得DF与BF的长,又由坡度的定义,即可求得EF的长,继而求得休闲平台DE的长.【解答】解:作DP⊥AC,垂足为点P,延长DE交BC于点F,∵FM∥CG,∴∠BDF=∠BAC=45°,∵斜坡AB长60米,D是AB的中点,∴BD=30米,∴DF=BD•cos∠BDF=30×=30(米),BF=DF=30米,∵斜坡BE的坡比为:1,∴=,解得:EF=10(米),∴DE=DF﹣EF=30﹣10(米).答:休闲平台DE的长是(30﹣10)米;27.【分析】作HM⊥BG于点M,延长DH交BG于点N,首先在直角三角形EMH中求得HM、EM的长,然后求得MN的长,最后利用三角形相似求得DC的长即可求得建筑物的高.【解答】解:作HM⊥BG于点M,延长DH交BG于点N,∵∠FEN=30°,EH=4∴HM=2,EM=2,∵△PAD∽△HMN,∴,即,解得:MN=,∴CN=CE+EM+MN=6+2+=+2,∵△PAD∽△DCN,∴即,解得:DC=11+3(米).答:建筑物的高为11+3米.28.【分析】(1)在Rt△CBD中,根据CD=BC•sin11°直接计算即可;(2)在Rt△CBD中,根据BD=10×cos11°≈0.98×10≈9.8米,进一步求出AD的长,AD﹣BD 即为AB的长.【解答】解:(1)在Rt△CBD中,CD=BC•sin11°≈10×0.19=1.9米,(2)在Rt△CBD中,BD=10×cos11°≈0.98×10≈9.8米,在Rt△ACD中,=tan5°,∴AD=≈≈21.1(米),∴AB=AD﹣BD=21.1﹣9.8=11.3(米).29.【分析】(1)过点C作CE⊥AB于E,过点B作BF⊥CD于F,过点B作BF⊥CD于F,在Rt △BFD中,分别求出DF、BF的长度,在Rt△ACE中,求出AE、CE的长度;(2)然后根据矩形BFCE的性质得到:CF=BE=CD﹣DF=1,然后通过解Rt△ACE求得AE=CE,结合图形来求得AB的长度.【解答】解:(1)过点C作CE⊥AB于E,过点B作BF⊥CD于F,过点B作BF⊥CD于F,在Rt△BFD中,∵∠DBF=30°,sin∠DBF==,cos∠DBF==,∵BD=6,∴DF=3,BF=3,∵AB∥CD,CE⊥AB,BF⊥CD,∴四边形BFCE为矩形,∴BF=CE=3(米),即广告牌与铁塔AB之间的水平距离的3米;(2)由(1)知,四边形BFCE为矩形,BF=CE=3.则CF=BE=CD﹣DF=1,在Rt△ACE中,∠ACE=45°,∴AE=CE=3,∴AB=3+1.即:铁塔AB的高为(3+1)米.30.【分析】(1)根据题意画出图形,进而利用锐角三角函数关系分别求出BF;(2)利用坡度的定义求得CE的长,即可得出点C相对于起点A升高的高度.【解答】解:(1)如图所示:过点B作BF⊥AD于点F,过点C作CD⊥AD于点D,由题意得:AB=650米,BC=1千米,∴sinα===,∴BF=650×=250米,∴小明从A点到点B上升的高度是250米;(2)∵斜坡BC的坡度为:1:3,∴CE:BE=1:3,设CE=x,则BE=3x,由勾股定理得:x2+(3x)2=5002解得:x=50,∴CD=CE+DE=BF+CE=250+50,答:点C相对于起点A升高了米.31.【分析】本题中两个直角三角形有公共的边,那么可利用这条公共直角边进行求解.(1)求AD长的时候,可在直角三角形ADC内,根据30°的角所对的直角边是斜边的一半求解.(2)在直角三角形ABC中求得AB的长后用AD﹣AB即可求得增加的长度.【解答】解:(1)Rt△ABD中,∵∠ADB=30°,AC=6米,∴AD=2AC=12(m)∴AD的长度为12米;(2)∵Rt△ABC中,AB=AC÷sin60°=4(m),∴AD﹣AB=12﹣4≈5.1(m).∴改善后的滑梯会加长5.1m.32.【分析】过点C作CE⊥AB于E,过点B作BF⊥CD于F,在Rt△BFD中,分别求出DF、BF 的长度,在Rt△ACE中,求出AE、CE的长度,继而可求得AB的长度.【解答】解:过点C作CE⊥AB于E,过点B作BF⊥CD于F,在Rt△BFD中,∵∠DBF=30°,sin∠DBF==,cos∠DBF==,∵BD=6,∴DF=3,BF=3,∵AB∥CD,CE⊥AB,BF⊥CD,∴四边形BFCE为矩形,∴BF=CE=3,CF=BE=CD﹣DF=1,在Rt△ACE中,∠ACE=45°,∴AE=CE=3,∴AB=3+1.答:铁塔AB的高为(3+1)m.33.【分析】在Rt△ADC中,已知了坡面AC的坡比以及坡面AC的值,通过勾股定理可求AD,DC的值,在Rt△ABD中,根据坡角为30°,求出坡面AC的坡比可求BD的值,再根据BC=DC ﹣BD即可求解.【解答】解:在Rt△ADC中,∵AD:DC=1:2.4,AC=13,由AD2+DC2=AC2,得AD2+(2.4AD)2=132.∴AD=±5(负值不合题意,舍去).∴DC=12.在Rt△ABD中,∵∠ABD=30°,∴AD:BD=:3,∴BD==5.∴BC=DC﹣BD=12﹣5.答:改动后电梯水平宽度增加部分BC的长为(12﹣5)米.34.【分析】过点A作AM⊥CD于M,由勾股定理就可以求出AM的值,在Rt△ADM中,由直角三角形的性质就可以求出AD的值.【解答】解:过点A作AM⊥CD于M,∴∠AMD=90°.∵∠ABM=45°,∴∠BAM=∠ABM=45°,∴AM=BM.在Rt△ABM中由勾股定理,得AM=3.∵∠D=30°,∴AD=2AM,∴AD=6.答:现在坡面AD的长为6米.35.【分析】(1)根据∠BAD=60°,AB=20米,利用三角函数求出BE的长度;(2)作FG⊥AD,G为垂足,连结FA,则FG=BE利用tan45°求出AG的长10m,利用cos60°求出AE长,让AG减AE即可.【解答】解:(1)作BE⊥AD,E为垂足,则BE=AB•sin60°=20sin60°=10(m);(2)作FG⊥AD,G为垂足,连结FA,则FG=BE.∵AG==10(m),AE=AB•cos60°=20cos60°=10(m),∴BF=AG﹣AE=10﹣10(m),即BF至少是(10﹣10)m.36.【分析】作CM⊥DB于点M,已知BC的坡度即可得到BM和CM的比值,则在直角△MBC 中,利用勾股定理即可求得BM和MC的长度,然后在直角△DCM中利用三角函数求得DM的长,则BD=BM+DM,据此即可求解.【解答】解:作CM⊥DB于点M,∵斜坡AF的坡度是1::2.4,∠A=∠BCM,∴,∴在直角△MBC中,设BM=5x,则CM=12x.由勾股定理可得:BM2+CM2=BC2,∴(5x)2+(12x)2=6.52,解得:x=,∴BM=5x=,CM=12x=6,在直角△MDC中,∠DCM=∠EDG=30°,∴DM=CM•tan∠DCM=6tan30°=6×=2,∴BD=DM+BM=+2≈2.5+2×1.732≈6.0(米).答:大树的高约为6.0米.37.【分析】(1)过点A作AM⊥CF于点M,过点E作EN垂直CF于点N,设拦河大坝的高度为xm,在Rt△ABM和Rt△EFN中分别求出BM和FN的长度,然后根据已知AE=10m,BF=4m,EN﹣AE=BF+BM,列方程求出x的值;(2)根据(1)求得EF的长度,即可求得坡面EF的长.【解答】解:(1)过点A作AM⊥CF于点M,过点E作EN垂直CF于点N,设拦河大坝的高度为xm,在Rt△ABM和Rt△EFN中,∵∠ABM=72°,∠EFN=45°,∴BM===,FN=x,∵AE=10m,BF=4m,FN﹣AE=BF+BM,∴x﹣10=4+,解得:x=24,即拦河大坝的高度为24m;(2)∵∠EFN=45°,∴EF=EN=24(m).答:改造后拦河大坝坡面EF的长为24m.38.【分析】先在Rt△ABD中,用三角函数求出AD,最后在Rt△ACD中用三角函数即可得出结论.【解答】解:在Rt△ABD中,∠ABD=30°,AB=10m,∴AD=ABsin∠ABD=10×sin30°=5,在Rt△ACD中,∠ACD=15°,sin∠ACD=,∴AC==≈≈19.2m,即:改造后的斜坡式自动扶梯AC的长度约为19.2米.39.【分析】(1)在直角△ABD中,利用正弦函数的定义可得AB=,将数值代入计算即可求解;(2)先求出DF=BD+BF=2米,再根据坡度的定义得出=,那么DE=2DF=4米,然后在直角△EFD中利用勾股定理即可求出EF.【解答】解:(1)在直角△ABD中,∵∠ADB=90°,∠BAD=37°,BD=1.8米,∴AB=≈=3(米).答:传送带AB的长度约为3米;(2)∵DF=BD+BF=1.8+0.2=2米,斜坡EF的坡度i=1:2,∴=,∴DE=2DF=4米,∴EF===2≈4.5(米).答:改造后传送带EF的长度约为4.5米.40.【分析】(1)延长CB交MN于点H,根据坡度的定义求出HC,AH的长,然后在直角△ACH 中利用三角函数即可求得BC的长;(2)利用(1)所求得出大厅层高进而得出答案.【解答】解:(1)如图所示:延长BC交MN于H∵BC⊥EF,EF∥MN,∴BH⊥MN,∵i=1:2.4=5:12=CH:AH,∴设CH=5k,则AH=12k在Rt△ACH中,由勾股定理AC==13k,∵AC=13m,∴k=1,∴CH=5m,AH=12m,设BC=x,在Rt△ACH中,tan∠BAH=,∴tan42°=,x≈5.8m,答:二楼层高约为5.8m;(2)由题得,大厅层高为BH=BC+CH=5.8+5=10.8(m),而10+2=12m>10.8m,∴雕像放不下.。
九年级数学下册《三角函数的应用》综合练习2(坡度、坡角)(含答案)

三角函数的应用(坡度、坡角)◆随堂检测1、某斜坡的坡度为i=1:3,则该斜坡的坡角为______度.2、以下对坡度的描述正确的是().A.坡度是指斜坡与水平线夹角的度数;B.坡度是指斜坡的铅直高度与水平宽度的比;C.坡度是指斜坡的水平宽度与铅直高度的比;D.坡度是指倾斜角的度数3、某人沿坡度为i=1:33的山路行了20m,则该人升高了().A.203m B.20340.103.33m C m D3m4、斜坡长为100m,它的垂直高度为60m,则坡度i等于().A.35B.45C.1:43D.1:0.755、在坡度为1:1.5的山坡上植树,要求相邻两树间的水平距离为6m,•则斜坡上相邻两树间的坡面距离为().A.4m B.213m C.3m D.413m◆典例分析水库拦水坝的横断面为梯形ABCD,背水坡CD的坡比i=1:3,•已知背水坡的坡长CD=24m,求背水坡的坡角α及拦水坝的高度.解:过D作DE⊥BC于E.∵该斜边的坡度为1:3,则tanα=3,∴α=30°,在Rt△DCE中,DE⊥BC,DC=24m.∴∠DCE=30°,∴DE=12(m).故背水坡的坡角为30°,拦水坝的高度为12m.点评:本题的关键是弄清坡度、坡角的概念,坡度和坡角的关系:坡度就是坡角的正切值,通过做高构造直角三角形,再利用三角函数值求出坡角即可.◆课下作业●拓展提高1、如图,沿倾斜角为30°的山坡植树,•要求相邻两棵树间的水平距离AC为2m,那么相邻两棵树的斜坡距离AB约为_______m(精确到0.1m).(•可能用到的数据2≈1.41,3≈1.73)1题图2题图2、如图,防洪大堤的横断面是梯形,坝高AC=6米,背水坡AB的坡度i=1:2,则斜坡AB的长为_______米.3、如图,在高2米,坡角为30°的楼梯表面铺地砖,•地毯的长度至少需________米(精确到0.1米).3题图4题图4、如图,梯形护坡石坝的斜坡AB的坡度i=1:3,坡高BC为2米,则斜坡AB 的长是()A.25米B.210米C.45米D.6米5、为了灌溉农田,某乡利用一土堤修筑一条渠道,在堤中间挖出深为1.2m,下底宽为2m,坡度为1:0.6的渠道(其横断面为等腰梯形),并把挖出的土堆在两旁,使土堤的高度比原来增加了0.6m,如图所示,求:(1)渠面宽EF;(2)修400m 长的渠道需挖的土方数.6、一勘测人员从A 点出发,沿坡角为30°的坡面以5km/h 的速度行到点D ,•用了10min ,然后沿坡角为45°的坡面以2.5km/h 的速度到达山顶C ,用了12min ,•求山高及A ,B 两点间的距离(精确到0.1km ).7、某村计划开挖一条长为1600m 的水渠,渠道的横断面为等腰梯形,渠道深0.8m ,下底宽1.2m ,坡度为1:1.实际开挖渠道时,每天比原计划多挖土方20m 3,结果比原计划提前4天完工,求原计划每天挖土多少立方米.(精确到0.1m 3)●体验中考1、(衢州)为测量如图所示上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道倾斜角α的正切值是( ) A .14B .4C .17D .172、(益阳市)如图,先锋村准备在坡角为 的山坡上栽树,要求相邻两树之间的520α20m水平距离为5米,那么这两树在坡面上的距离AB 为( ) A. αcos 5 B. αcos 5 C. αsin 5 D. αsin 53、(台州市)如图,有一段斜坡BC 长为10米,坡角12CBD ︒∠=,为方便残疾人的轮椅车通行,现准备把坡角降为5°. (1)求坡高CD ;(2)求斜坡新起点A 与原起点B 的距离(精确到0.1米).4、(山西省)有一水库大坝的横截面是梯形ABCD ,AD BC EF ∥,为水库的水面,点E 在DC 上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB 的长为12米,迎水坡上DE 的长为2米,135120BAD ADC ∠=∠=°,°,求水深.(精确到0.1米,2 1.41 1.73==,3)α5米A BDCB A5°12°ABCD EF 水深参考答案1.30°点拨:坡度是斜边铅直高度与水平宽度的比,坡角的正切值等于坡度.2.B 点拨:理解概念很关键.3.C 点拨:∴∠α=60°,∴h=20×sin60°.4.C 点拨:由题意可知,该坡的水平宽度为80,∴tanα=6080=34.5.B 点拨:坡度是指铅直高度与水平宽度的比拓展提高:1、2.32、3、5.54、B5、(1)过B作BM⊥AD.∵i=1:0.6,BM=1.2m,∴AM=0.72m.再过A作AN⊥EF,同理得EN=0.36m.∴EF=2+2×0.72+2×0.36=4.16m.(2)根据题意V土=12(AD+BC)×BM×400=12(2+3.44)×1.2×400=1 305.6m3.故渠面宽EF为4.16m,修400m长的渠道需挖1 305.6m3的土.6、过D作DE⊥AB于E,DF⊥BC于F,由题意可知,AD≈0.83km,在Rt△ADE中,AD=0.83km,∠DAE=30°,∴,DE=0.415km.在Rt△DCF中,DC=0.5km,∠CDF=45°,∴2≈0.35km , ∴3, BC=CF+BF=CF+DE=0.35+0.415≈0.8km ,故山高为0.8km ,A ,B 两点之间的距离为1.1km . 7、如图.过A 作AM ⊥CD ,垂足为M . ∵坡度为1:1,渠道深为0.8m . ∴DM=0.8m ,即CD=1.2+2×0.8=2.8m . 挖渠道共挖出的土方数为12(AB+CD )·AM×1600=2 560m 3. 设原计划每天挖xm 3的土,则实际每天挖(x+20)m 3, 根据题意得2560256020x x =++4. 解得x≈103.5m 3,x≈-123.5m 3(不符合题意,舍去). 经检验x=103.5m 3是原方程的根.故原计划每天挖土约103.5m 3. 体验中考: 1、A 2、B3、解:(1)在BCD Rt ∆中,︒=12sin BC CD 1.221.010=⨯≈(米). (2)在BCD Rt ∆中,︒=12cos BC BD8.998.010=⨯≈(米); 在ACD Rt ∆中,︒=5tan CD AD 2.123.330.09≈≈(米), 23.339.813.5313.5AB AD BD =-≈-=≈(米). 答:坡高2.1米,斜坡新起点与原起点的距离为13.5米4、解:分别过A D 、作AM BC ⊥于M DG BC ⊥,于G .过E 作EH DG ⊥于H ,则四边形AMGD 为矩形.,135120AD BC BAD ADC ∠=∠=Q ∥°,°. ∴456030B DCG GDC ∠=∠=∠=°,°,°.在Rt ABM △中,sin 12AM ABB ===·∴DG =在Rt DHE △中,cos 2DH DEEDH =∠==·∴ 1.41 1.73HG DG DH =-=⨯-6≈6.7. 答:水深约为6.7米.。
备考2024年中考数学二轮复习-解直角三角形的应用﹣坡度坡角问题-综合题专训及答案

备考2024年中考数学二轮复习-解直角三角形的应用﹣坡度坡角问题-综合题专训及答案解直角三角形的应用﹣坡度坡角问题综合题专训1、(2020开封.中考模拟) 如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).(1)求灯杆CD的高度;(2)求AB的长度(结果精确到0.1米).(参考数据: =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)2、(2012盘锦.中考真卷) 某校门前正对一条公路,车流量较大,为便于学生安全通过,特建一座人行天桥.如图,是这座天桥的引桥部分示意图,上桥通道由两段互相平行的楼梯AB、CD和一段平行于地面的平台CB构成.已知∠A=37°,天桥高度DH为5.1米,引桥水平跨度AH为8.3米.(1)求水平平台BC的长度;(2)若两段楼梯AB:CD=10:7,求楼梯AB的水平宽度AE的长.(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ )3、(2017.中考模拟) 如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:坡度1:201:161:12最大高度(米) 1.50 1.000.75(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;(2)求斜坡底部点A与台阶底部点D的水平距离AD.4、(2018奉贤.中考模拟) 如图,为了将货物装入大型的集装箱卡车,需要利用传送带AB将货物从地面传送到高1.8米(即BD=1.8米)的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.(1)求传送带AB的长度;(2)因实际需要,现在操作平台和传送带进行改造,如图中虚线所示,操作平台加高0.2米(即BF=0.2米),传送带与地面所成斜坡的坡度i=1:2.求改造后传送带EF的长度.(精确到0.1米)(参考数值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.41, ≈2.24)5、(2018苏州.中考模拟) 如图①,某超市从一楼到二楼的电梯的长为16. 50 m,坡角为32°.(1)求一楼与二楼之间的高度 (精确到0. 01 m) ;(2)电梯每级的水平级宽均是0.25m,如图②,小明跨上电梯时,该电梯以每秒上升2级的高度运行,10s后他上升了多少米?(精确到0. 01 m,参考数据: )6、(2018滨州.中考模拟) 已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:(1)坡顶A到地面PQ的距离;(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)7、(2016济宁.中考真卷) 某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.(1)求新坡面的坡角a;(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆桥?请说明理由.8、(2017新化.中考模拟) 某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.(1)求新坡面的坡角a;(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.9、(2017广东.中考模拟) 某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面AC的坡度为1:.(1)求新坡面AC的坡角∠CAB;(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆桥?请说明理由.10、(2019贵阳.中考模拟) 如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:的斜坡CD前进2 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.(1)求点D的铅垂高度(结果保留根号);(2)求旗杆AB的高度(结果保留根号).11、(2019桂林.中考模拟) 如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:(沿斜坡从B到D时,其升高的高度与水平前进的距离之比),另一段斜坡AD的长400米,在斜坡BD的坡顶D处测得山顶A的仰角为45°(1)求斜坡BD的坡顶D到地面BC的高度是多少米?(2)求BC.(结果保留根号)12、(2018遵义.中考模拟) 为纪念遵义会议80周年献礼,遵义市政府对城市建设进行了整改,如图,已知斜坡AB长60 米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).(1)若修建的斜坡BE的坡比为∶1,求休闲平台DE的长是多少米?(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H 在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?13、(2019合肥.中考模拟) 如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=10米,AE=15米.(i=1:是指坡面的铅直高度BH与水平宽度AH的比)(测角器的高度忽略不计,结果精确到0.1米.参考数据: 1.414, 1.732)(1)求点B距水平面AE的高度BH;(2)求广告牌CD的高度.14、(2019枣庄.中考模拟) 日照间距系数反映了房屋日照情况.如图①,当前后房屋都朝向正南时,日照间距系数=L:(H﹣H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面高度.如图②,山坡EF朝北,EF长为15m,坡度为i=1:0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到E点的距离为4m.(1)求山坡EF的水平宽度FH;(2)欲在AB楼正北侧山脚的平地FN上建一楼房CD,已知该楼底层窗台P处至地面C处的高度为0.9m,要使该楼的日照间距系数不低于1.25,底部C距F处至少多远?15、(2020拱墅.中考模拟) 如图,甲、乙两座建筑物的水平距离BC为78m.从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C 处的俯角为58°,求甲、乙建筑物的高度AB和DC.(结果取整数,参考数据:tan48°≈1.1,tan58°≈1.60)解直角三角形的应用﹣坡度坡角问题综合题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:11.答案:12.答案:13.答案:14.答案:15.答案:。
备考2024年中考数学二轮复习-解直角三角形的应用﹣坡度坡角问题

备考2024年中考数学二轮复习-解直角三角形的应用﹣坡度坡角问题解直角三角形的应用﹣坡度坡角问题专训单选题:1、(2017温州.中考真卷) 如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα= ,则小车上升的高度是()A . 5米B . 6米C . 6.5米D . 12米2、(2011宁波.中考真卷) 如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为α,那么滑梯长l为()A .B .C .D . h•sinα3、(2017东莞.中考模拟) 河堤横断面如图所示,坝高BC=6米,迎水坡AB的坡长比为1:,则AB的长为()A . 5 米B . 4 米C . 12米D . 6 米4、(2017江北.中考模拟) 如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是()米.A . 7B . 11C . 13D . 205、(2019盘龙.中考模拟) 如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)()A . 21.7米B . 22.4米C . 27.4米D . 28.8米6、(2019惠民.中考模拟) 一座人行天桥如图所示,坡面BC的铅直高度与水平宽度的比为1:2,为了方便市民推车过天桥,有关部门决定在保持天桥高度的前提下,降低坡度,使新坡面AC的坡度为1:3,AB=6m,则天桥高度CD为()A . 6mB . 6 mC . 7mD . 8m7、(2020长清.中考模拟) 如图,某建筑物上挂着“巴山渝水,魅力重庆”的宣传条幅,王同学利用测倾器在斜坡的底部处测得条幅底部的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡的坡度米,米(点在同平面内,,测倾器的高度忽略不计),则条幅的长度约为()(参考数据:)A . 12.5米B . 12.8米C . 13.1米D . 13.4米8、(2020宁德.中考模拟) 如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为()A .B .C .D .9、(2021玉林.中考模拟) 河堤横断面如图所示,堤高米,迎水坡的坡比为,则AB的长为()A . 米B . 米C . 18米D . 21米10、(2021北.中考模拟) 如图,河坝横断面迎水坡AB的坡比为1:,坝高BC=4m,则AB的长度为()A . 2 mB . 4 mC . 4 mD . 6m填空题:11、(2018长宁.中考模拟) 若某斜面的坡度为1:,则该坡面的坡角为________度.12、(2017奉贤.中考模拟) 如图,如果在坡度i=1:2.4 的斜坡上两棵树间的水平距离AC为3米,那么两树间的坡面距离AB是________米.13、(2020长宁.中考模拟) 如图,传送带把物体从地面送到离地面5米高的地方,如果传送带与地面所成的斜坡的坡度i=1:2.4,那么物体所经过的路程AB为________米.14、(2019上海.中考模拟) 一座拦河大坝的横截面是梯形ABCD,AD∥BC,∠B = 90°,AD =6米,坡面CD的坡度,且BC = CD,那么拦河大坝的高是________米.15、(2020湖州.中考模拟) 如图,是将一正方体货物沿坡面AB装进汽车货厢的平面示意图,已知长方体货厢的高度BC为2.6米,斜坡AB的坡比为1:2.4,现把图中的货物继续向前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,则货物的高度BD不能超过________米.16、(2020亳州.中考模拟) 如图,某水库大坝的橫断面是梯形ABCD,坝高为15米,迎水坡CD的坡度为1:2.4,那么该水库迎水坡CD的长度为________米.17、(2021长沙.中考模拟) 钓鱼岛是中国固有领土,2021年4月26日,国家自然资源部发布了钓鱼岛地形地貌调查报告,钓鱼岛中央山脊呈东西走向,北坡稍缓,南坡陡峭,已知主峰高华峰北坡坡度,海平面上BC的水平距离约为615米,则主峰高华峰的高度约为米.(精确到1米)18、如图,一条光线照在坡度为1:的斜坡上,被坡面上的平面镜反射成与地面平行的直线,求这条光线与坡面的夹角α解答题:19、(2017浙江.中考模拟) 如图所示,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为(即tan∠PAB= ),且O,A,B在同一条直线上,求电视塔OC的高度以及此人所在的位置点P的垂直高度.(侧倾器的高度忽略不计,结果保留根号)20、(2017普陀.中考模拟) 一段斜坡路面的截面图如图所示,BC⊥AC,其中坡面AB的坡比i1=1:2,现计划削坡放缓,新坡面的坡角为原坡面坡脚的一半,求新坡面AD的坡比i2(结果保留根号)21、(2017平顶山.中考模拟) 如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).22、(2017唐河.中考模拟) 如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).23、(2017娄底.中考模拟) 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?24、(2019贵阳.中考模拟) 如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1:的斜坡CD前进2 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.(1)求点D的铅垂高度(结果保留根号);(2)求旗杆AB的高度(结果保留根号).25、(2020海门.中考模拟) 某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).(1)求这个车库的高度AB;(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)解直角三角形的应用﹣坡度坡角问题答案1.答案:A2.答案:A3.答案:C4.答案:C5.答案:A6.答案:A7.答案:B8.答案:9.答案:10.答案:11.答案:12.答案:13.答案:14.答案:15.答案:16.答案:17.答案:18.答案:19.答案:20.答案:21.答案:22.答案:23.答案:24.答案:25.答案:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学校 班级 姓名 学号
装 定 线
A B α 5米
C
B
A i =1︰4
坡度问题
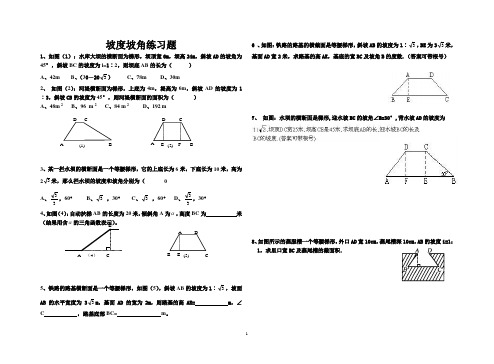
一、填空题:
1、若一段斜坡的水平宽度为12米,坡度i=1:3,则这斜坡的铅锤高度是________。
2、若一段斜坡的坡度是i=1:2,某人走在这斜坡上走了10米,则这个人的高度上升了________。
3、有一段山坡,坡面长为200米,山披坡高为100米,则此山坡的坡度为i=_______。
4、若一段斜坡的水平宽度为6米,坡度i=1:3,则这斜坡的坡面长为_________米
5、已知一个坡的坡比i =1︰3,则此坡的坡角是 度.
6、一斜坡的坡角为30度,那么这个斜坡的坡度 i = .
7、如图,斜坡路面AB 的坡比i =1︰4,坡高BC =3米,则路面AB 长等于 米
8、如果一条斜坡的坡度为1∶0.75,高为4米,那么这条斜坡的长度为 米.
9、一斜面的坡度i =1︰0.75,一物体由斜面底部沿斜面向前推了10米,
那么这个物体升高了 米.
10、有一山坡,高50米,山坡长130米,则此山坡的坡度为 (写成比的形式). 11.小明沿着坡度为1:2的山坡向上走了1000m ,则他升高了 米。
12、一斜面的坡角为30°,一物体沿斜面向上推了10米,那么这个物体升高了 米。
13、如图所示,铁路的路基横断面是等腰梯形,斜坡AB 的坡度为1:3,斜坡AB 的水平宽
度BE =33m ,则斜坡AB =_____________m .
14. 如图,先锋村准备在坡角为0
30=α山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB 为__________米.
二、解答题: 1、(2010浙江嘉兴)设计建造一条道路,路基的横断面为梯形ABCD ,如图(单位:米).设
路基高为h ,两侧的坡角分别为α和β,已知h=2, α=45°,1
tan 2
β=,CD=10.
(1)求路基底部AB 的宽;
(2)修筑这样的路基1000米,需要多少土石方? 2、(2010江苏泰州)庞亮和李强相约周六去登山,庞亮从北坡山脚C 处出发,以24米/分钟
的速度攀登,同时,李强从南坡山脚B 处出发.如图,已知小山北坡的坡度31
∶=i ,山坡长为240米,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A ?(将山路AB 、AC 看成线段,结果保留根号)
3、(2010江苏淮安)某公园有一滑梯,横截面如图薪示,AB 表示楼梯,BC 表示平台,CD 表
示滑道.若点E ,F 均在线段AD 上,四边形BCEF 是矩形,且cos ∠5
AB=4.5米,BC=1米,CD=6米.求: (1) 梯角∠D 的度数; (2)滑梯地面宽度AD 的长.
αβA
B C D
α A D E
B
A
4、(2010江苏扬州)如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD .小明在山坡的坡脚A 处测得宣传牌底部D 的仰角为60°,沿山坡向上走到B 处测得宣传牌顶部C 的仰角为45°.已知山坡AB 的坡度i =1:3,AB =10米,AE =15米,求这块宣传牌CD 的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:2≈1.414,3≈1.732)
5、(2010 四川泸州)如图5,某防洪指挥部发现长江边一处长500米,高10米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD )急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF 的坡比(1)求加固后坝底增加的宽度AF ;
(2)求完成这项工程需要土石多少立方米?(结果保留根号)
6.水坝的横截面是梯形ABCD (如图1),上底米,坝高3==DN AM 米,
斜坡AB 的坡比3:11=i ,斜坡DC 的坡比1:12=i .
(1)求坝底BC 的长(结果保留根号);(6分)
(2)为了增强水坝的防洪能力,在原来的水坝上增加高度(如图2),使得水坝的上底
2=EF 米,求水坝增加的高度(精确到1.0米,参考数据73.13≈)
.(6分)
7、(2010新疆乌鲁木齐)某过街天桥的截面图为梯形,如图所示,其中天桥斜面CD 的坡度为i =CD 的长为10m ,天桥另一斜面AB 的坡角
45=∠ABC (1)写出过街天桥斜面AB 的坡度; (2)求DE 的长;
(3)若决定对该过街天桥进行改建,使AB 斜面的坡度变缓,将其45°坡角改为30°,方便过路群众,改建后斜面为AF ,试计算此改建需占路面的宽度FB 的长(结果精确到0.01)
A
B C D
M N
(图1)
A
B C D
M N E
F
(图2) 4
=AD
学校 班级 姓名 学号
装 定 线 120°F E
D C
B A 10 2.5B
A
8、(2010云南昭通)云南2009年秋季以来遭遇百年一遇的全省特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形ABCD (如图7所示),AD∥BC,EF 为水面,点E 在DC 上,测得背水坡AB 的长为18米,倾角∠B=30°,迎水坡CD 上线段DE 的长为8米,∠ADC=120°. (1)请你帮技术员算出水的深度(精确到0.01米,参考数据732..13≈);
(2)就水的深度而言,平均每天水位下降必须控制在多少米以内,才能保证现有水量至少能使用20天?(精确到0.01米)
9、(2010贵州遵义)如图,水坝的横断面是梯形,背水坡AB 的坡角∠BAD=60°,坡长AB=203m,为加强水坝强度,将坝底从A 处向后水平延伸到F 处,使新的背水坡的坡角∠F=45 ,求AF 的长度(结果精确到1米,参考数据:2≈1.414,
3 ≈1.732)
10、(2010四川广安)如图.是一座人行天桥的示意图,天桥的高是l0米,坡面的倾斜角为
45°,为了方便行人安全过天桥,市政部门决定降低坡度.使新坡面的倾斜角为30°若新坡脚前需留2 .5米的人行道,问离原坡脚10米的建筑物是否需要拆除?请说明理由 (参考数据:2≈1.414, 3 ≈1.732)
11. 如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB 长为4米. (1)求新传送带AC 的长度;
(2)如果需要在货物着地点C 的左侧留出2米的通道,试判断距离B 点4米的货物MNQP 是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:2≈1.41,3≈1.73,5≈2.24,6≈2.45)
α
3
2
12.(2010年山东省济南市)我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,
如图所示,BC ∥AD
,斜坡AB =40米,坡角∠BAD =600
,为防夏季因瀑雨引发山体滑坡,保障安
全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过450
时,可确保山体不滑坡,改造时保持坡脚A 不动,从坡顶B
沿BC 削进到E 处,问BE 至少是多少米(结果保留根号)
13、如图,某堤坝的横截面是梯形ABCD ,背水坡AD 的坡度i=1︰1.2,坝高为5米。
现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD 加宽1米,形成新的背水坡EF ,其坡度为1︰1.4。
已知堤坝总长度为4000米。
(1)求完成该工程需要多少土方?(4分)
(2)该工程由甲、乙两个工程队同时合作完成,按原计划需要20天。
准备开工前接到上级通知,汛期可能提前,要求两个工程队提高工作效率。
甲队工作效率提高30%,乙队工作效率提高40%,结果提前5天完成。
问这两个工程队原计划每天各完成多少土方?(5分)
14、利用土埂修筑一条渠道,在埂中间挖去深为0.6米的一块(图6-35阴影部分是挖去部分),已知渠道内坡度为1∶0.5,渠道底面宽BC 为0.5米,求:①横断面(等腰梯形)ABCD 的面积;②修一条长为100米的渠道要挖去的土方数.
15、如图,在气象站台A 的正西方向的B 处有一台风中心,该台风中心以每小时20km 的速度沿北偏东o
60的BD 方向移动,在距离台风中心130km 内的地方都要受到其影响。
⑴台风中心在移动过程中,与气象台A 的最短距离是多少?。
