2019届高三数学(理)复习题:模块四立体几何与空间向量第12讲 空间几何体、空间中的位置关系Word版含答案
高三数学空间向量专题复习附答案

AB CA 1B 1C 1MyzAB CD EFxyz MNA 1 D 1B 1ADBC C 1yz EF一、利用向量处理平行与垂直问题例1、在直三棱柱111C B A ABC中,090ACB,30BAC,MAA BC,6,11是1CC 得中点。
求证:AMBA 1练习:棱长为a 的正方体ABCD —A 1B 1C 1D 1中,在棱DD 1上是否存在点P 使B 1D ⊥面PAC ?例 2 如图,已知矩形ABCD 和矩形ADEF 所在平面互相垂直,点NM ,分别在对角线AEBD ,上,且AE ANBD BM31,31,求证://MN 平面CDE练习1、在正方体1111D C B A ABCD 中,E,F 分别是BB 1,,CD 中点,求证:D 1F平面ADEABC DA 1B 1C 1D 1P xzyABCDEPxyz F A 1xD 1 B 1A DBC C 1yz E 1F 1HGA 1 xD 1B 1A DBC C 1yz E 1FD 1C 1z 2、如图,在底面是菱形的四棱锥P —ABCD 中,60ABC ,,2,a PDPBa ACPA点E 在PD 上,且PE:ED= 2: 1.在棱PC 上是否存在一点F, 使BF ∥平面AEC?证明你的结论.二、利用空间向量求空间的角的问题例1 在正方体1111D C B A ABCD中,E 1,F 1分别在A 1B 1,,C 1D 1上,且E 1B 1=41A 1B 1,D 1F 1=41D 1C 1,求BE 1与DF 1所成的角的大小。
例2 在正方体1111D C B A ABCD中, F 分别是BC 的中点,点E 在D 1C 1上,且11E D 41D 1C 1,试求直线E 1F 与平面D 1AC 所成角的大小例3 在正方体1111D C B A ABCD中,求二面角11C BDA 的大小。
A 1xD 1B 1A DBC C 1yz EFzyxC 1B 1A 1ACBCADBOEF D C BA例4 已知E,F 分别是正方体1111D C B A ABCD的棱BC 和CD 的中点,求:(1)A 1D 与EF 所成角的大小;(2)A 1F 与平面B 1EB 所成角的大小;(3)二面角B B D C11的大小。
2019届高三数学(理科)复习题四立体几何与空间向量限时集训(十三)Word版含答案

基础过关1.如图X13-1所示,在三棱柱ABC-A1B1C1中,△ABC和△AA1C均是边长为2的等边三角形,点O为AC的中点,平面AA1C1C⊥平面ABC.(1)证明:A1O⊥平面ABC;(2)求直线AB与平面A1BC1所成角的正弦值.图X13-12.在如图X13-2所示的几何体中,DE∥AC,AC⊥平面BCD,AC=2DE=4,BC=2,DC=1,∠BCD=60°.(1)证明:BD⊥平面ACDE;(2)求平面BCD与平面BAE所成二面角的正弦值.图X13-23.如图X13-3所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1⊥平面ABCD,M为棱DD1的中点,N为棱AD的中点,Q为棱BB1的中点.(1)证明:平面MNQ∥平面C1BD;(2)若AA1=2AB,棱A1B1上有一点P,且A1P=λA1B1(λ∈(0,1)),使得二面角P-MN-Q的余弦值为1321,求λ的值.63图X13-34.如图X13-4①所示,四边形ABCD是一个直角梯形,∠ABC=∠BAD=90°,E为BC上一点,AE,BD相交于点O,AD=EC=3,BE=1,AB=3.将△ABE沿AE折起,使平面ABE⊥平面ADCE,得到如图X13-4②所示的四棱锥B-AECD.(1)求证:CD⊥平面BOD;(2)求直线AB与平面BCD所成角的正弦值.①②图X13-45.如图X13-5所示,四边形ABCD是边长为a的菱形,∠BAD=60°,EB⊥平面ABCD,FD⊥平面ABCD,EB=2FD= a.(1)求证:EF⊥AC;(2)求直线CE与平面ABF所成角的正弦值.图X13-56.如图X13-6①所示,在等腰直角三角形S'AB中,S'A=AB=4,S'A⊥AB,C,D分别为S'B,S'A的中点,将△S'CD沿CD翻折到△SCD的位置,使平面SDC⊥平面ABCD,如图X13-6②,SA=22,E为线段SB的中点.(1)求证:CE∥平面SAD;(2)求二面角A-EC-B的余弦值.①②图X13-6能力提升7.如图X13-7所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,AB=AC=2,AD=22,PB=32,PB⊥AC.(1)求证:平面PAB⊥平面PAC.(2)若∠PBA=45°,试判断棱PA上是否存在与点P,A不重合的点E,使得直线CE与平面PBC所成角的正弦值为33?若存在,求出AE AP的值;若不存在,请说明理由.图X13-78.如图X13-8所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AD∥BC,AB=BC=PA=1,AD=2,∠PAD=∠DAB=∠ABC=90°,点E在棱PC上,且CE=λCP(0<λ<1).(1)求证:CD⊥AE.(2)是否存在实数λ,使得二面角C-AE-D的余弦值为105?若存在,求出实数λ的值;若不存在,请说明理由.图X13-8限时集训(十三)基础过关1.解:(1)证明:∵AA1=A1C,且O为AC的中点,∴A1O⊥AC,又平面AA1C1C⊥平面ABC,平面AA1C1C∩平面ABC=AC,且A1O⊂平面AA1C1C,∴A1O⊥平面ABC.(2)如图,连接OB,以O为原点,OB,OC,OA1所在直线分别为x,y,z轴建立空间直角坐标系,则O(0,0,0),A(0,-1,0),B(3,0,0),A1(0,0,3),C1(0,2,3),∴AB=(3,1,0),A1B=(3,0,-3),A1C1=(0,2,0).设平面A1BC1的法向量为n=(x,y,z),则 n ·A 1B =0,n ·A 1C 1 =0,即 2y =0, 3x - 3z =0, 令x=1,则y=0,z=1,∴n =(1,0,1). 设直线AB 与平面A 1BC 1所成的角为α,则sin α=|cos <AB ,n >|=|AB·n ||AB ||n |=32×2= 6,故直线AB 与平面A 1BC 1所成角的正弦值为 64.2.解:(1)证明:在△BCD 中,由余弦定理得BD 2=22+12-2×1×2cos 60°=3, 所以BC 2=BD 2+DC 2,所以BD ⊥CD.又AC ⊥平面BCD ,所以AC ⊥BD. 因为AC ∩CD=C ,所以BD ⊥平面ACDE.(2)易知DB ,DC ,DE 两两垂直,所以以D 为原点,DB ,DC ,DE 所在直线分别为x ,y ,z 轴,建立如图所示的空间直角坐标系D-xyz ,可得D (0,0,0),B ( 3,0,0),C (0,1,0),E (0,0,2),A (0,1,4), 则BA =(- 3,1,4),EA =(0,1,2). 设n =(x ,y ,z )是平面BAE 的法向量, 则 n ·BA =− 3x +y +4z =0,n ·EA =y +2z =0,令z= 3,得n =(2,-2 3, 3).易知平面BCD 的一个法向量为m =(0,0,1). 设平面BCD 与平面BAE 所成二面角的平面角为θ,则|cos θ|=|n ·m ||n ||m |= 319,sin θ=4 1919. 3.解:(1)证明:∵M ,Q 分别为棱DD 1,BB 1的中点,∴MD BQ ,∴四边形MQBD 为平行四边形,∴MQ ∥BD ,又BD ⊂平面C 1BD ,∴MQ ∥平面C 1BD.连接AD 1,∵N 为棱AD 的中点,M 为棱DD 1的中点,∴MN ∥AD 1, 又AD 1∥BC 1,∴MN ∥BC 1.∵BC 1⊂平面C 1BD ,∴MN ∥平面C 1BD. 又MN ∩MQ=M ,∴平面MQN ∥平面C 1BD.(2)由题意知DA ,DC ,DD 1两两垂直,以D 为原点,DA ,DC ,DD 1 所在的方向分别为x ,y ,z 轴的正方向,建立如图所示的空间直角坐标系, 设AB=1,则A (1,0,0),N 1,0,0 ,M (0,0,1),Q (1,1,1),A 1(1,0,2),B 1(1,1,2),∴A 1B 1 =(0,1,0),MN = 1,0,-1 ,MQ =(1,1,0). 设P (x ,y ,z ),则由A 1P =λA 1B 1 , 得 x -1=0,y =λ,z -2=0,∴P (1,λ,2),∴MP =(1,λ,1). 设平面PMN 的法向量为m =(a 1,b 1,c 1),则 m ·MN =0,m ·MP =0,即 12a 1-c 1=0,a 1+λb 1+c 1=0,令c 1=1,则a 1=2,b 1=-3λ,∴m = 2,-3λ,1 . 设平面MNQ 的法向量为n =(a 2,b 2,c 2),则 n ·MN =0,n ·MQ =0,即 12a 2-c 2=0,a 2+b 2=0,令c 2=1,则a 2=2,b 2=-2,∴n =(2,-2,1),由题知|m ·n ||m ||n |=13 2163= 4+6λ+1 3× 4+9λ2+1,64λ2-252λ+153=0,解得λ=34或5116(与0<λ<1矛盾,舍去), 故λ=34.4.解:(1)证明:在Rt △AEB 中,因为BE=1,AB= 3,所以∠BAE=30°, 同理∠BDA=30°,所以∠AOD=90°,即AE ⊥BD. 因为AD ∥EC ,AD=EC ,所以四边形ADCE 是平行四边形, 所以∠CDO=∠AOD=90°,所以CD ⊥DO.因为平面ABE ⊥平面ADCE ,平面ABE ∩平面ADCE=AE ,BO ⊥AE ,BO ⊂平面ABE , 所以BO ⊥平面ADCE ,又CD ⊂平面ADCE ,所以BO ⊥CD.因为BO ∩DO=O ,BO ⊂平面BOD ,DO ⊂平面BOD ,所以CD ⊥平面BOD.(2)由(1)可知,直线OA ,OB ,OD 两两垂直,以O 为原点,OA ,OD ,OB 所在直线分别为x ,y ,z 轴建立空间直角坐标系O-xyz ,如图所示,则A 32,0,0 ,B 0,0,32,C -2,3 32,0 ,D 0,3 32,0 ,所以AB = -32,0, 32,BD =0,3 32,- 32,CD =(2,0,0).。
2019届高三数学课标一轮复习:高考解答题专讲4 立体几何

题型一
题型二
题型三
题型四
-15-
对点训练(2017浙江杭州模拟)在如图所示的圆台中,AC是下底面 圆O的直径,EF是上底面圆O'的直径,FB是圆台的一条母线.
(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(2)已知EF=FB=
1 2
AC=2
3 ,AB=BC,求二面角F-BC-A的余弦值.
-13-
题型一
题型二
题型三
题型四
(2)解:以O为原点,OB,OC,OP分别为x轴、y轴、z轴,建立如图所
示空间直角坐标系,
由已知得 A(0,- 3,0),B(1,0,0),C(0, 3,0),P(0,0,1). 设平面 PBC 的法向量 n=(x,y,z),
因为������������=(1,0,-1),������������=(-1, 3,0),
所以
sin
θ=|cos<������������,n>|=
������������ ·������ |������������ ||������ |
=23 =
7×2
21.
7
所以直线
PA
与平面
PBC
所成角的正弦值为
21.
7
题型一
题型二
题型三
题型四
-14-
策略技巧利用空间向量求空间角的一般步骤为: (1)建立恰当坐标系,准确写出相关点、向量的坐标. (2)利用方程思想,计算两平面的法向量. (3)由方向向量、法向量的夹角公式求对应空间角. (4)检验反思,查看关键点,规范解题步骤.
1+tan ������tan ������ 2
������������ ������
(完整)空间向量与立体几何知识点和习题(含答案),推荐文档

由此可知,空间任意直线由空间一点及直线的方向向量惟一确定.,取直线l的方向向量a,则向量及一个向量a,那么经过点A以向量用空间向量刻画空间中平行与垂直的位置关系:的方向向量分别是a,b,平面α ,β 的法向量分别是,k∈R;0;0;,k∈R;k∈R;=0.用空间向量解决线线、线面、面面的夹角问题:,b是两条异面直线,过空间任意一点分别是二面角的两个半平面α ,β 的法向量,则〈根据题目特点,同学们可以灵活选择运用向量方法与综合方法,从不同角度解决立.了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分.掌握空间向量的线性运算及其坐标表示..掌握空间向量的数量积及其坐标表示;能运用向量的数量积判断向量的共线与垂.理解直线的方向向量与平面的法向量..能用向量语言表述线线、线面、面面的垂直、平行关系..能用向量方法解决线线、线面、面面的夹角的计算问题.建立空间直角坐标系,设法证明存在实数k ,使得RS k PQ =如图建立空间直角坐标系,则O (0,0,0),A (3,0,0),B (0,4,1(3,0,2),B 1(0,4,2),E (3,4,0).PA 1, ∴),34,0,0()2,00(32321===AA AP ⋅)同理可得:Q (0,2,2),R (3,2,0),⋅)32,4,0(2要证明面面平行,可以通过线线平行来证明,也可以证明这两个平面的法向:设正方体的棱长为4,如图建立空间直角坐标系,则D (0,0,0)N (4,2,4),B (4,4,0),E (0,2,4),F (2,4,4).的中点K ,EF 的中点G ,BD 的中点O ,则O (2,2,0),K (3,1,,2,0),=(2,2,0),=(-1,1,4),=(-1,EF AK OG 本文下载后请自行对内容编辑修改删除,:设正方体的棱长为2,如图建立空间直角坐标系,则D (0,0,0)C (0,2,0),N (2,2,1).),1,0,2(),2,1,0(=CN 所成的角为θ ,则CN ,52||||cos ==⋅CN AM CN AM θ∴异面直线AM 和CN 所成角的余弦值是⋅52取AB 的中点P ,CC 1的中点Q ,连接B 1P ,B 1Q ,PQ ,PC .B P ∥MA ,B Q ∥NC ,所成的角.6,522=+==QC PC PQ Q空间两条直线所成的角是不超过90°的角,因此按向量的夹角公式计算时,分子的数量积如果是负数,则应取其绝对值,使之成为正数,这样才能得到异面直线所成ABC -A 1B 1C 1的底面边长为a ,侧棱长为利用正三棱柱的性质,适当建立空间直角坐标系,写出有关点的坐标.求角时有两种思路:一是由定义找出线面角,再用向量方法计算;二是利用平面如图建立空间直角坐标系,则A (0,0,0),B (0,a ,0),取A 1B 1的中点D ,则,连接AD ,C ⋅))2,2,0(a a D ),2,0,0(),0,,0(),0,0,231a AA a AB a ==,011=⋅AA DC 本文下载后请自行对内容编辑修改删除,PB的中点D,连接CD,作AE⊥PB于E.,PA⊥AC,2,∴CD⊥PB.DC夹角的大小就是二面角A-PB-C的大小.,0(),0,0,2(),0,-==CP CB =(a 1,a 2,a 3),(b 1,b 2,b 3).=1,得).0,2,1(-=a 得取b 3=1,得⎪⎩⎪⎨⎧=+-=,0,02321b b b 3如图建立空间直角坐标系.,由已知可得A (0,0,0),),0,23,0(),0,23,21(a C a a B -),0,0,21(),,0,0a BC a =∴BC ⊥AP .又∠BCA =90°,∴BC ⊥AC .,0PAC .的中点,DE ∥BC ,∴E 为PC 的中点.⋅)21,43,0(),21,3a a E a a ⊥平面PAC ,(B)θ >ϕ(D)θ <ϕ中,E,F,G,H分别为所成角的大小是______.6,且对角线与底面所成角的余弦值为D1中,AA1=2AB,则异面直线1本文下载后请自行对内容编辑修改删除,的底面是直角梯形,∠BAD=90°,,PA⊥底面ABCD,PD所成的角为θ ,则cosθ =______.C1D1中,AA1=2AB=4,点平面角的余弦值.中,底面ABCD是边长为OA的中点,N为BC的中点.OCD;所成角的大小.平面角的余弦值.习题1和平面α ,下列命题正确的是( α (B)若a ∥α (B)38000(D)4000cm 2的正方形,另外两个侧面都是有一个内角为( )(C)223本文下载后请自行对内容编辑修改删除,C11;平面角的余弦值.PA⊥AB,PA⊥AC,AB⊥AC MAB;C ;ABB 1;的体积.中,底面ABCD 为矩形,SD ⊥底面SD =2.点M 在侧棱SC 上,∠的中点;的平面角的余弦值.练习1-3D .42本文下载后请自行对内容编辑修改删除,,0),E (0,2,1),A 1).4∴A 1C ⊥BD ,A 1C ,0=⊥平面DBE .是平面DA 1E 的法向量,则,得n =(4,1,-2).14,,22(),0,22,0(-D P =-=),2,22,0(OD OP n =(x ,y ,z ),则⋅OP n 本文下载后请自行对内容编辑修改删除,是CA 和平面α 所成的角,则∠,CO =1.3=AO ABO =∠BAO =45°,∴=AO BO ).1,0,0(),0,3,0(),C A ).1,3,0(-=AC 是平面ABC 的一个法向量,取x =1,得=+=-,03,033z y y x 1=n 是平面β 的一个法向量.AB 1=E ,连接DE .四边形A 1ABB 1是正方形,是BC 的中点,∴DE ∥A 平面A 1BD ,∴A 1C ∥平面⊄解:建立空间直角坐标系,设AB =AA 1=1,⋅-)1,0,21(),01B 是平面A 1BD 的一个法向量,,01=D B 取r =1,得n 1=(2,0,1).0=1234是直三棱柱,∴BB 1⊥平面A 1B 1C 1⊥平面BCC 1B 1,∴BC 1⊥A 1⊥B 1C ,∴BC 1⊥平面A 1B 1C 分别为A 1C 1、BC 1的中点,得MN 平面A 1ABB 1,∴MN ⊄MH .MH ∥A 1B 1,,∴MH ⊥平面BCC 1B 1,∴的体积==⋅⋅∆3111MH S V B BC A (,0,0),则B (22,),12,12,2(λλ++--=BM 故.60 >=BM |.BA BM =解得λ =,)12()1222λλ+++-的中点.,0,0)得AM 的中点22(G 本文下载后请自行对内容编辑修改删除,。
高考数学(理)真题专题汇编:空间立体几何

高考数学(理)真题专题汇编:空间立体几何一、选择题(本题共9道小题,每小题0分,共0分)1.【来源】2019年高考真题——数学(浙江卷)设三棱锥V -ABC 的底面是正三角形,侧棱长均相等,P 是棱VA 上的点(不含端点),记直线PB 与直线AC 所成角为α,直线PB 与平面ABC 所成角为β,二面角P -AC -B 的平面角为γ,则( )A. ,βγαγ<<B. ,βαβγ<<C. ,βαγα<<D. ,αβγβ<<2.【来源】2019年高考真题——数学(浙江卷)祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V Sh =柱体,其中S 是柱体的底面积,h 是柱体的高,若某柱体的三视图如图所示,则该柱体的体积(cm 3)是( )A. 158B. 162C. 182D. 3243.【来源】2019年高考真题——理科数学(全国卷Ⅱ) 设α,β为两个平面,则α∥β的充要条件是 A .α内有无数条直线与β平行 B .α内有两条相交直线与β平行 C .α,β平行于同一条直线D .α,β垂直于同一平面4.【来源】2019年高考真题——理科数学(全国卷Ⅲ)如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED的中点,则A.BM=EN,且直线BM、EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM、EN是异面直线D.BM≠EN,且直线BM,EN是异面直线5.【来源】0(08年全国卷2)已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于()A.1 B. C. D.26.【来源】0(08年四川卷文)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为的菱形,则该棱柱的体积等于( )(A)(B)(C)(D)7.【来源】0(08年北京卷)如图,动点在正方体的对角线上.过点作垂直于平面的直线,与正方体表面相交于.设,,则函数的图象大致是()8.【来源】2011年高考数学理(安徽)一个空间几何体得三视图如图所示,则该几何体的表面积为(A)48+(B)32817+(C)48817(D)509.【来源】2011年高考数学理(全国新课标)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为二、填空题10.【来源】2019年高考真题——理科数学(北京卷)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.12.【来源】2019年高考真题——理科数学(天津卷)已知四棱锥的底面是边长为2的正方形,侧棱长均为5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为 .13.【来源】2019年高考真题——理科数学(全国卷Ⅱ)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体ABCD -A 1B 1C 1D 1挖去四棱锥O -EFGH 后所得几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9 g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________.15.【来源】(07年浙江卷文)已知点O 在二面角α-AB -β的棱上,点P 在α内,且∠POB =45°.若对于β内异于O 的任意一点Q ,都有∠POQ ≥45°,则二面角α-AB -β的取值范围是_________.16.【来源】2011年高考数学理(全国新课标)已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且6,23AB BC ==,则棱锥O ABCD -的体积为 。
2019年高考理数——立体几何(解答)
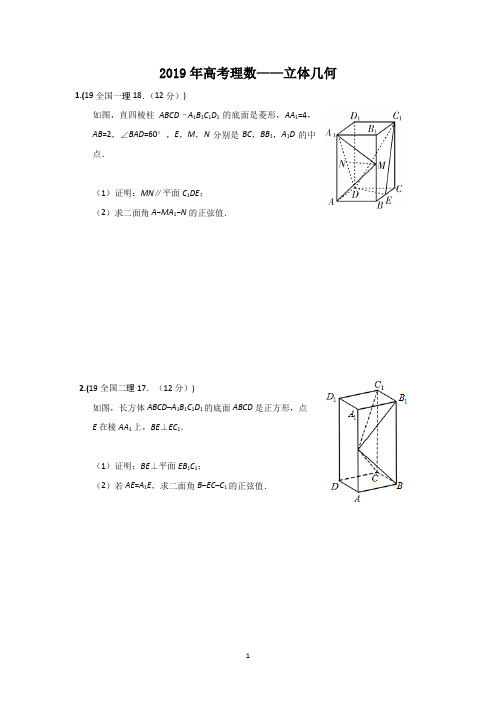
2019年高考理数——立体几何1.(19全国一理18.(12分))如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求二面角A−MA1−N的正弦值.2.(19全国二理17.(12分))如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B–EC–C1的正弦值.3.(19全国三理19.(12分))图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图2中的二面角B−CG−A的大小.4.(19北京理(16)(本小题14分))如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且13 PFPC=.(Ⅰ)求证:CD⊥平面PAD;(Ⅱ)求二面角F–AE–P的余弦值;(Ⅲ)设点G在PB上,且23PGPB=.判断直线AG是否在平面AEF内,说明理由.如图,AE ⊥平面ABCD,,CF AE AD BC ∥∥,,1,2AD AB AB AD AE BC ⊥====.(Ⅰ)求证:BF ∥平面ADE ;(Ⅱ)求直线CE 与平面BDE 所成角的正弦值; (Ⅲ)若二面角E BD F --的余弦值为13,求线段CF 的长.6.(19浙江19.(本小题满分15分))如图,已知三棱柱111ABC A B C -,平面11A ACC ⊥平面ABC ,90ABC ∠=︒,1130,,,BAC A A AC AC E F ∠=︒==分别是AC ,A 1B 1的中点.(1)证明:EF BC ⊥;(2)求直线EF 与平面A 1BC 所成角的余弦值.如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:(1)A1B1∥平面DEC1;(2)BE⊥C1E.参考答案:1.解:(1)连结B 1C ,ME .因为M ,E 分别为BB 1,BC 的中点,所以ME ∥B 1C ,且ME =12B 1C . 又因为N 为A 1D 的中点,所以ND =12A 1D . 由题设知A 1B 1=P DC ,可得B 1C =P A 1D ,故ME =P ND , 因此四边形MNDE 为平行四边形,MN ∥ED . 又MN ⊄平面EDC 1,所以MN ∥平面C 1DE . (2)由已知可得DE ⊥DA .以D 为坐标原点,DA uuu r的方向为x 轴正方向,建立如图所示的空间直角坐标系D −xyz ,则(2,0,0)A ,A 1(2,0,4),3,2)M ,(1,0,2)N ,1(0,0,4)A A =-u u u r ,1(13,2)A M =--u u u u r,1(1,0,2)A N =--u u u u r ,(0,3,0)MN =u u u u r.设(,,)x y z =m 为平面A 1MA 的法向量,则1100A M A A ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u r m m , 所以32040x y z z ⎧-+-=⎪⎨-=⎪⎩,.可取3,1,0)=m .设(,,)p q r =n 为平面A 1MN 的法向量,则100MN A N ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u u r ,.n n 所以3020q p r ⎧=⎪⎨--=⎪⎩,.可取(2,0,1)=-n .于是2315cos ,||25⋅〈〉===⨯‖m n m n m n , 所以二面角1A MA N --的正弦值为105.2.解:(1)由已知得,11B C ⊥平面11ABB A ,BE ⊂平面11ABB A ,故11B C ⊥BE .又1BE EC ⊥,所以BE ⊥平面11EB C .(2)由(1)知190BEB ∠=︒.由题设知Rt ABE △≌11Rt A B E △,所以45AEB ∠=︒, 故AE AB =,12AA AB =.以D 为坐标原点,DA u u u r的方向为x 轴正方向,||DA uuu r 为单位长,建立如图所示的空间直角坐标系D –xyz ,则C (0,1,0),B (1,1,0),1C (0,1,2),E (1,0,1),(1,0,0)CB =u u u r ,(1,1,1)CE =-u u u r,1(0,0,2)CC =u u u u r.设平面EBC 的法向量为n =(x ,y ,x ),则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rn n 即0,0,x x y z =⎧⎨-+=⎩所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =(x ,y ,z ),则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩u u u u r u u u rm m 即20,0.z x y z =⎧⎨-+=⎩ 所以可取m =(1,1,0). 于是1cos,||||2⋅<>==-n m n m n m .所以,二面角1B EC C --的正弦值为3.3.解:(1)由已知得AD P BE ,CG P BE ,所以AD P CG ,故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ⊥BE ,AB ⊥BC ,故AB ⊥平面BCGE . 又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE .(2)作EH ⊥BC ,垂足为H .因为EH ⊂平面BCGE ,平面BCGE ⊥平面ABC ,所以EH ⊥平面ABC .由已知,菱形BCGE 的边长为2,∠EBC =60°,可求得BH =1,EH =3.以H 为坐标原点,HC u u u r的方向为x 轴的正方向,建立如图所示的空间直角坐标系H –xyz ,则A (–1,1,0),C (1,0,0),G (2,03CG u u u r =(1,03),AC u u u r=(2,–1,0).设平面ACGD 的法向量为n =(x ,y ,z ),则0,0,CG AC ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u ur n n 即30,20.x z x y ⎧+=⎪⎨-=⎪⎩所以可取n =(3,6,3 又平面BCGE 的法向量可取为m =(0,1,0),所以3cos ,||||2⋅〈〉==n m n m n m .因此二面角B –CG –A 的大小为30°.4.解:(Ⅰ)因为PA ⊥平面ABCD ,所以PA ⊥CD .又因为AD ⊥CD ,所以CD ⊥平面PAD .(Ⅱ)过A 作AD 的垂线交BC 于点M .因为PA ⊥平面ABCD ,所以PA ⊥AM ,PA ⊥AD .如图建立空间直角坐标系A -xyz ,则A (0,0,0),B (2,-1,0),C (2,2,0),D (0,2,0),P (0,0,2).因为E 为PD 的中点,所以E (0,1,1).所以(0,1,1),(2,2,2),(0,0,2)AE PC AP ==-=u u u r u u u r u u u r.所以1222224,,,,,3333333PF PC AF AP PF ⎛⎫⎛⎫==-=+= ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r .设平面AEF 的法向量为n =(x ,y ,z ),则0,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u r n n 即0,2240.333y z x y z +=⎧⎪⎨++=⎪⎩令z =1,则1,1y x =-=-. 于是=(1,1,1)--n .又因为平面PAD 的法向量为p =(1,0,0),所以3cos ,||⋅〈〉==-‖n p n p n p . 由题知,二面角F -AE -P 为锐角,所以其余弦值为33.(Ⅲ)直线AG 在平面AEF 内. 因为点G 在PB 上,且2,(2,1,2)3PG PB PB ==--u u ur ,所以2424422,,,,,3333333PG PB AG AP PG ⎛⎫⎛⎫==--=+=- ⎪ ⎪⎝⎭⎝⎭u u u r u u u r u u u r u u u r u u u r .由(Ⅱ)知,平面AEF 的法向量=(1,1,1)--n .所以4220333AG ⋅=-++=u u u r n .所以直线AG 在平面AEF 内.5.依题意,可以建立以A 为原点,分别以AB AD AE u u u r u u u r u u u r,,的方向为x 轴,y 轴,z 轴正方向的空间直角坐标系(如图),可得(0,0,0),(1,0,0),(1,2,0),(0,1,0)A B C D ,(0,0,2)E .设(0)CF h h =>>,则()1,2,F h .(Ⅰ)证明:依题意,(1,0,0)AB =u u u r 是平面ADE 的法向量,又(0,2,)BF h =u u u r,可得0BF AB ⋅=u u u r u u u r,又因为直线BF ⊄平面ADE ,所以BF ∥平面ADE .(Ⅱ)解:依题意,(1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=--u u u r u u u r u u u r.设(,,)x y z =n 为平面BDE 的法向量,则0,0,BD BE ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rn n 即0,20,x y x z -+=⎧⎨-+=⎩不妨令1z =, 可得(2,2,1)=n .因此有4cos ,9||||CE CE CE ⋅==-u u u ru u u r u u u r n n n .所以,直线CE 与平面BDE 所成角的正弦值为49. (Ⅲ)解:设(,,)x y z =m 为平面BDF 的法向量,则0,0,BD BF ⎧⋅=⎪⎨⋅=⎪⎩u u u r u u u rm m 即0,20,x y y hz -+=⎧⎨+=⎩ 不妨令1y =,可得21,1,h ⎛⎫=-⎪⎝⎭m .由题意,有||1cos ,||||3⋅〈〉===m n m n m n ,解得87h =.经检验,符合题意.所以,线段CF 的长为87.6.方法一:(1)连接A 1E ,因为A 1A =A 1C ,E 是AC 的中点,所以A 1E ⊥AC .又平面A 1ACC 1⊥平面ABC ,A 1E ⊂平面A 1ACC 1,平面A 1ACC 1∩平面ABC =AC , 所以,A 1E ⊥平面ABC ,则A 1E ⊥BC .又因为A 1F ∥AB ,∠ABC =90°,故BC ⊥A 1F .所以BC ⊥平面A 1EF .因此EF ⊥BC .(2)取BC 中点G ,连接EG ,GF ,则EGFA 1是平行四边形. 由于A 1E ⊥平面ABC ,故A 1E ⊥EG ,所以平行四边形EGFA 1为矩形. 由(1)得BC ⊥平面EGFA 1,则平面A 1BC ⊥平面EGFA 1, 所以EF 在平面A 1BC 上的射影在直线A 1G 上.连接A 1G 交EF 于O ,则∠EOG 是直线EF 与平面A 1BC 所成的角(或其补角). 不妨设AC =4,则在Rt △A 1EG 中,A 1E 3EG 3. 由于O 为A 1G 的中点,故11522A G EO OG ===, 所以2223cos 25EO OG EG EOG EO OG +-∠==⋅.因此,直线EF 与平面A 1BC 所成角的余弦值是35.方法二:(1)连接A 1E ,因为A 1A =A 1C ,E 是AC 的中点,所以A 1E ⊥AC . 又平面A 1ACC 1⊥平面ABC ,A 1E ⊂平面A 1ACC 1,平面A 1ACC 1∩平面ABC =AC ,所以,A 1E ⊥平面ABC .如图,以点E 为原点,分别以射线EC ,EA 1为y ,z 轴的正半轴,建立空间直角坐标系E –xyz .不妨设AC =4,则A 1(0,0,23),B (3,1,0),1(3,3,23)B ,33(,,23)2F ,C (0,2,0).因此,33(,,23)22EF =u u u r ,(3,1,0)BC =-u u u r . 由0EF BC ⋅=u u u r u u u r得EF BC ⊥.(2)设直线EF 与平面A 1BC 所成角为θ.由(1)可得1=(310)=(0223)BC A C --u u u r u u u u r ,,,,,. 设平面A 1BC 的法向量为n ()x y z =,,,由100BC A C ⎧⋅=⎪⎨⋅=⎪⎩u u u r n n ,得3030x y y z ⎧-+=⎪⎨-=⎪⎩, 取n (131)=,,,故||4sin |cos |=5|||EF EF EF θ⋅==⋅u u u r u u u r u u u r ,n n n |, 因此,直线EF 与平面A 1BC 所成的角的余弦值为35.7.证明:(1)因为D ,E 分别为BC ,AC 的中点,所以ED ∥AB .在直三棱柱ABC -A 1B 1C 1中,AB ∥A 1B 1,所以A 1B 1∥ED .又因为ED⊂平面DEC1,A1B1 平面DEC1,所以A1B1∥平面DEC1.(2)因为AB=BC,E为AC的中点,所以BE⊥AC.因为三棱柱ABC-A1B1C1是直棱柱,所以CC1⊥平面ABC. 又因为BE⊂平面ABC,所以CC1⊥BE.因为C1C⊂平面A1ACC1,AC⊂平面A1ACC1,C1C∩AC=C,所以BE⊥平面A1ACC1.因为C1E⊂平面A1ACC1,所以BE⊥C1E.。
2019届高考数学(理)二轮复习-中档大题规范练——立体几何与空间向量(含答案解析)

中档大题规范练——立体几何与空间向量1. 有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r 的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.解 由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面.根据切线性质知,当球在容器内时,水深为3r ,水面的半径为3r ,则容器内水的体积为V =V 圆锥-V 球=13π·(3r)2·3r -43πr 3=53πr 3, 而将球取出后,设容器内水的深度为h ,则水面圆的半径为33h , 从而容器内水的体积是V′=13π·(33h)2·h=19πh 3, 由V =V′,得h =315r.即容器中水的深度为315r.2. 如图1所示,正三角形ABC 的边长为2a ,CD 是AB 边上的高,E ,F 分别是AC ,BC 的中点.现将△ABC 沿CD 翻折,翻折后平面ACD⊥平面BCD(如图2).求三棱锥C —DEF 的体积.图1 图2解 过点E 作EM⊥DC 于点M ,因为平面ACD⊥平面BCD ,平面ACD∩平面BCD =CD ,而EM ⊂平面ACD ,所以EM⊥平面BCD.即EM 是三棱锥E —CDF 的高.又CD⊥BD,AD⊥CD,F 为BC 的中点,所以S △CDF =12S △BCD =12×12CD×BD =14×2-a 2×a=34a 2, 因为E 为AC 的中点,EM⊥CD,所以EM =12AD =12a. 所以三棱锥C —DEF 的体积为V C —DEF =V E —CDF =13S △CDF ×EM=13×34a 2×12a =324a 3. 3. 如图,在多面体ABCDEF 中,四边形ABCD 是正方形,EF∥AB,EF⊥FB,AB =2EF ,∠BFC=90°,BF =FC ,H 为BC 的中点.(1)求证:FH∥平面EDB ;(2)求证:AC⊥平面EDB.证明 (1)设AC 与BD 交于点G ,则G 为AC 的中点.如图,连接EG 、GH ,又H 为BC 的中点,∴GH 綊12AB. 又EF 綊12AB ,∴EF 綊GH. ∴四边形EFHG 为平行四边形.∴EG∥FH.又∵EG ⊂平面EDB ,FH ⊄平面EDB ,∴FH∥平面EDB.(2)由四边形ABCD 为正方形,得AB⊥BC.又EF∥AB,∴EF⊥BC.又∵EF⊥FB,BC∩FB=B ,∴EF⊥平面BFC.∴EF⊥FH.∴AB⊥FH.又BF =FC ,H 为BC 的中点,∴FH⊥BC.∴FH⊥平面ABCD.∴FH⊥AC.又FH∥EG,∴AC⊥EG.又AC⊥BD,EG∩BD=G ,∴AC⊥平面EDB.4. 如图所示,已知三棱锥A -BPC 中,AP⊥PC,AC⊥BC,M 为AB 的中点,D 为PB 的中点,且△PMB 为正三角形.(1)求证:DM∥平面APC ;(2)求证:平面ABC⊥平面APC ;(3)若BC =4,AB =20,求三棱锥D -BCM 的体积.(1)证明 由已知,得MD 是△ABP 的中位线,所以MD∥AP.又MD ⊄平面APC ,AP ⊂平面APC ,故MD∥平面APC.(2)证明 因为△PMB 为正三角形,D 为PB 的中点,所以MD⊥PB.所以AP⊥PB.又AP⊥PC,PB∩PC=P ,所以AP⊥平面PBC.因为BC ⊂平面PBC ,所以AP⊥BC.又BC⊥AC,AC∩AP=A ,所以BC⊥平面APC.因为BC ⊂平面ABC ,所以平面ABC⊥平面APC.(3)解 由题意,可知MD⊥平面PBC ,所以MD 是三棱锥D -BCM 的一条高,所以V D -BCM =V M -DBC =13×S △BCD ×MD =13×221×53=107.5. 如图,在底面是矩形的四棱锥P —ABCD 中,PA⊥底面ABCD ,E ,F 分别是PC ,PD 的中点,PA =AB =1,BC =2.(1)求证:EF∥平面PAB ;(2)求证:平面PAD⊥平面PDC.证明 (1)以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为z 轴,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,1),∵E,F 分别是PC ,PD 的中点, ∴E ⎝ ⎛⎭⎪⎫12,1,12,F ⎝⎛⎭⎪⎫0,1,12, EF →=⎝ ⎛⎭⎪⎫-12,0,0,PB →=(1,0,-1),PD →=(0,2,-1),AP →=(0,0,1),AD →=(0,2,0),DC →=(1,0,0),AB →=(1,0,0).∵EF →=-12AB →,∴EF →∥AB →,即EF∥AB, 又AB ⊂平面PAB ,EF ⊄平面PAB ,∴EF∥平面PAB.(2)∵AP →·DC →=(0,0,1)·(1,0,0)=0,AD →·DC →=(0,2,0)·(1,0,0)=0,∴AP →⊥DC →,AD →⊥DC →,即AP⊥DC,AD⊥DC.又AP∩AD=A ,∴DC⊥平面PAD.∵DC ⊂平面PDC ,∴平面PAD⊥平面PDC.6. 如图,在四棱锥P -ABCD 中,PC⊥底面ABCD ,ABCD 是直角梯形,AB⊥AD,AB∥CD,AB =2AD =2CD =2.E 是PB 的中点.(1)求证:平面EAC⊥平面PBC ;(2)若二面角P -AC -E 的余弦值为63,求直线PA 与平面EAC 所成角的正弦值. (1)证明 ∵PC⊥平面ABCD ,AC ⊂平面ABCD ,∴AC⊥PC,∵AB=2,AD =CD =1,∴AC=BC =2,∴AC 2+BC 2=AB 2,∴AC⊥BC,又BC∩PC=C ,∴AC⊥平面PBC ,∵AC ⊂平面EAC ,∴平面EAC⊥平面PBC.(2)解 如图,以C 为原点,DA →、CD →、CP →分别为x 轴、y 轴、z 轴正向,建立空间直角坐标系,则C(0,0,0), A(1,1,0),B(1,-1,0).设P(0,0,a)(a >0),则E 12,-12,a 2, CA →=(1,1,0),CP →=(0,0,a),CE →=12,-12,a 2, 设m =(b ,p ,m)为面PAC 的法向量,则m·CA →=m·CP →=0,即⎩⎪⎨⎪⎧b +p =0am =0,取m =(1,-1,0), 设n =(x ,y ,z)为面EAC 的法向量,则n·CA →=n·CE →=0,即⎩⎪⎨⎪⎧x +y =0,x -y +az =0,取x =a ,y =-a ,z =-2, 则n =(a ,-a ,-2),依题意,|cos 〈m ,n 〉|=|m·n||m||n|=a a 2+2=63,则a =2. 于是n =(2,-2,-2),PA →=(1,1,-2).设直线PA 与平面EAC 所成角为θ,则sin θ=|cos 〈PA →,n 〉|=|PA →·n||PA →||n|=23, 即直线PA 与平面EAC 所成角的正弦值为23.。
2019届高考数学理总复习微专题4 高考中的立体几何问题

微专题4 高考中的立体几何问题一、选择题(每小题5分,共30分)1.一个多面体的三视图如图4-1所示,则此多面体的表面积是 ()图4-1A.22B.24-C.22+D.20+2.如图4-2,网格纸上小正方形的边长为1,粗线画的是某组合体的三视图,则该组合体的体积是 ()图4-2A.+πB.+πC.4+πD.+π3.已知正方体ABCD-A1B1C1D1的所有顶点均在球O的表面上,E,F,G分别为AB,AD,AA1的中点,若平面EFG截球O所得圆的半径为,则该正方体的棱长为()A. B. C.3 D.24. [数学文化题]如图4-3为中国传统智力玩具鲁班锁,它起源于中国古代建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四棱柱的底面正方形的边长为2,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器的表面积的最小值为56π,则正四棱柱的高为()A. B.2 C.6 D.25. [数学文化题]中国古代计时器的发明时间不晚于战国时代(公元前476年~前222年),其中沙漏就是古代利用机械原理设计的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道流到下部容器.如图4-4所示,某沙漏由上、下两个圆锥形容器组成,圆锥形容器的底面圆的直径和高均为8 cm,细沙全部在上部时,其高度为圆锥形容器高度的(细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为()图4-4A.2 cmB.cmC.cmD.cm6.如图4-5,在正三棱柱ABC-A1B1C1中,AA1=AB,E,F分别为BC,BB1的中点,M,N分别为AA1,A1C1的中点,则直线MN与EF所成角的余弦值为()图4-5A. B. C. D.二、填空题(每小题5分,共10分)7.若侧面积为8π的圆柱有一外接球O,则当球O的体积取得最小值时,圆柱的表面积为.8.如图4-6,在棱长为1的正方体ABCD-A1B1C1D1中,作以A为顶点,分别以AB,AD,AA1为轴,底面圆半径为r(0<r≤1)的圆锥.当半径r变化时,正方体挖去三个圆锥部分后,余下的几何体的表面积的最小值是.图4-6三、解答题(共48分)9.(12分)如图4-7,在直角△ABC中,∠BAC=60°,点F在斜边AB上,且AB=4AF,D,E是平面ABC同一侧的两点, AD⊥平面ABC,BE⊥平面ABC,AD=3,AC=BE=4.(1)求证:平面CDF⊥平面CEF;(2)若M是线段CB的中点,求异面直线CF与EM所成角的余弦值.图4-710.(12分)如图4-8所示,在多面体ABD-A1B1C1D1中,四边形A1B1C1D1,ADD1A1,ABB1A1均为正方形,点M是BD的中点,点H在C1M上,且A1H与平面ABD所成角的正弦值为.(1)证明:B1D1∥平面BC1D;(2)求二面角A-A1H-B的大小.图4-811.(12分)在如图4-9所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.(1)在线段AB(含端点)上是否存在一点P,使得FP∥平面AED?若存在,求出的值;若不存在,请说明理由.(2)求直线AF与平面BDF所成角的正弦值.图4-912.(12分)如图4-10(1),正方形ABCD的边长为4,AB=AE=BF=EF,AB∥EF,把四边形ABCD沿AB折起,使得AD⊥底面AEFB,G是EF的中点,连接BG,如图4-10(2).(1)求证:AG⊥平面BCE;(2)求二面角C-AE-F的余弦值.(1)(2)图4-10答案1.C根据题中三视图知,该多面体是从一个棱长为2的正方体的左上角截去一个直三棱柱后剩余的部分,因此其表面积为6×22-1×1×2+×1=22+,故选C.2.D观察题中三视图可知该组合体的上面是三棱锥,下面是半径为1的半球,其直观图如图D 4-1所示.图D 4-1解法一如图D 4-2所示,将组合体中三棱锥A-BEF“补”成正方体,顶点A,B,E,F分别是正方体的棱的中点.取EF的中点C,连接AC,BC,则EF⊥平面ABC,由已知得,EF=AB=2,AC=BC=,所以S△ABC=×2×2=2,三棱锥A-BEF的体积V1=×S△ABC×EF=,半球的体积V2=×π×13=π.所以该组合体的体积V=V1+V2=+π.故选D.图D 4-2解法二如图D 4-3所示,将组合体中的三棱锥A-BEF“补”成正方体,顶点A,B,E,F分别是正方体的棱的中点,取AB的中点G,过EF和点G作截面EFDC,则截面EFDC将三棱锥A-BEF分成两个相同的小三棱锥,且AG=1,S△EFG=×2×2=2,所以三棱锥A-BEF的体积V1=2××S△EFG×AG=,半球体积V2=×π×13=π,所以该组合体的体积V=V1+V2=+π.故选D.图D 4-33.D设正方体的棱长为a,则AC1=a,由正方体ABCD-A1B1C1D1的外接球球心O为对角线AC1的中点,可知球O的半径R=a,因为E,F,G分别为AB,AD,AA1的中点,所以EF=EG=FG=a,所以△EFG为等边三角形,S△AEF=××=,S△EFG=×××=.设点A到平面EFG的距离为h,由等体积法得S△AEF×AG×=S△EFG×h×,解得h=,所以截面圆的半径r==,解得a=2,故选D.4.C设正四棱柱的高为h,表面积最小的球形容器可以看成长、宽、高分别为4,2,h的长方体的外接球,设外接球的半径为R,则4πR2=56π,所以4R2=56.又(2R)2=42+22+h2,所以56=20+h2,解得h=6.故选C.5.D由题意可知,开始时,沙漏上部分圆锥形容器中的细沙的高为H=×8=,底面半径为r=×4=,故细沙的体积V=πr2H=π×()2×=.当细沙漏入下部后,圆锥形沙堆的底面半径为4,设其高为H' ,则V=π×42×H'=,解得H'=,故此圆锥形沙堆的高为cm,故选D.6.C解法一如图D 4-4,在原三棱柱的上方,再放一个完全一样的三棱柱,连接AC1,CB1,C1B',易得MN∥AC1,EF∥CB1∥C1B',图D 4-4那么∠AC1B'或∠AC1B'的补角即直线MN与EF所成的角.设AA1=AB=a,则AC1=C1B'=a,连接AB',则AB'==3a,由余弦定理,得cos∠AC1B'==-,则直线MN与EF所成的角为∠AC1B'的补角,其余弦值为.故选C.解法二如图D 4-5,连接AC1,C1B,CB1,图D 4-5设C1B,CB1交于点O,取AB的中点D,连接CD,OD,则MN∥AC1∥OD,EF∥CB1,那么∠DOC或∠DOC的补角即直线MN与EF所成的角.设AA1=AB=a,则AC1=CB1=a,所以OD=OC=,又CD=,所以△OCD为正三角形,故∠DOC=60°,所以∠DOC即为直线MN与EF所成的角,且cos∠DOC=,所以直线MN与EF所成角的余弦值为,故选C.解法三取AB的中点O,连接CO,则CO⊥AB,以点O为坐标原点,OB所在直线为x轴,OC所在直线为y轴,过点O且平行于CC1的直线为z轴建立如图D 4-6所示的空间直角坐标系.图D 4-6设AB=2,则AA1=2,则A(-1,0,0),A1(-1,0,2),M(-1,0,),C(0,,0),C1(0,,2),N(-,,2),E(,,0),B1(1,0,2),F(1,0,),所以=(,,),=(,-,),cos<,>===,故选C.7.12π由球体的对称性可知,圆柱的高即球心到圆柱两底面圆心的距离之和,设圆柱的底面半径为r,球心到圆柱底面的距离为d,外接球O的半径为R.由球心到圆柱底面的距离、圆柱底面的半径、球的半径之间构成直角三角形,可得r2+d2=R2.由题设可得2πr×2d=8π,所以d=,则R2=r2+d2=r2+≥2=4,当且仅当r=时取等号,此时球O的体积取得最小值.故此时圆柱的表面积S表=8π+2πr2=8π+2π()2=12π.8.3+π由题知,余下几何体的表面积由原正方体的表面的剩余部分和3个圆锥的侧面组成,其表面积S=πr·+3(1-r)+3(1-πr2)=6+π(r-r2-),其中0<r≤1.设f(x)=x-x2-,0<x≤1,求导并整理得f'(x)=-2x-.当0<x≤1时,1<≤,-(2x+1)<2x2+1-(2x+1)=2x(x-1)≤0,∴<2x+1,∴f'(x)=-2x-<2x+1-2x-=1-<0,故f(x)在(0,1]上是减函数,则余下几何体的表面积S在(0,1]上也是减函数,故当r=1时,S min=3+π.9.(1)连接DE,如图D 4-7所示.图D 4-7因为AD⊥平面ABC,BE⊥平面ABC,CF⊂平面ABC,所以AD∥BE,AD⊥CF.因为AC= 4,∠BAC=60°,∠ACB=90°,所以AB=8,所以AF=AB=2,BF=AB=6,CF==2,所以AC2=AF2+CF2,所以AB⊥CF.(2分)又AD⊂平面ABED,AB⊂平面ABED,AD∩AB=A,所以CF⊥平面ABED,因为EF⊂平面ABED,所以CF⊥EF.又AD=3,BE=4,所以DE==,DF==,EF==,所以DE2=DF2+FE2,所以DF⊥FE.(5分)又CF⊂平面CDF,DF⊂平面CDF,CF∩DF=F,所以EF⊥平面CDF,又EF⊂平面CEF,所以平面CDF⊥平面CEF. (7分)(2)解法一取BF的中点N,连接MN,EN,如图D 4-8所示.图D 4-8因为M,N分别为BC,BF的中点,所以MN∥CF,且MN=CF=,所以∠EMN为异面直线CF与EM所成的角.(9分)因为AC=4,∠BAC=60°,∠ACB=90°,所以BC=4,BM=2,所以EM===2.由(1)知BF=6,所以BN=3,所以EN===5.(11分)在△EMN中,由余弦定理可得cos∠EMN===,所以异面直线CF与EM所成角的余弦值为.(12分)解法二以C为坐标原点,以CA,CB所在的直线分别为x轴,y轴,以过点C且与平面ABC垂直的直线为z轴,建立空间直角坐标系,如图D 4-9所示,则C(0,0,0),M(0,2,0),E(0,4,4),F(3,,0),所以=(0,2,4),=(3,,0), (10分)所以cos<,>===,所以异面直线CF与EM所成角的余弦值为.(12分)图D 4-910.(1)∵四边形ADD1A1,ABB1A1均为正方形,∴DD1∥AA1且DD1=AA1,BB1∥AA1且BB1=AA1,∴DD1∥BB1且DD1=BB1,∴四边形BDD1B1是平行四边形.∴BD∥B1D1.(3分)又BD⊂平面BC1D,B1D1⊄平面BC1D,∴B1D1∥平面BC1D.(4分)(2)解法一∵四边形A1B1C1D1,ADD1A1,ABB1A1均为正方形,∴多面体ABD-A1B1C1D1可补成正方体ABCD-A1B1C1D1,如图D 4-10所示.图D 4-10设其棱长为1,连接A1C,AC,∵==,∴A1C与平面ABD所成角的正弦值为.又A1H与平面ABD所成角的正弦值为,∴H在正方体的体对角线A1C上.又点H在C1M上,∴H为A1C与C1M的交点.(6分)∵BD⊥AC,BD⊥A1A,又AC,A1A是平面A1AC内两条相交的直线,∴BD⊥平面A1AC,∴BD⊥A1C,同理得BC1⊥A1C.又BD,BC1是平面BC1D内两条相交的直线,∴A1C⊥平面BC1D, (8分)∴A1H⊥HM,A1H⊥HB,∴二面角A-A1H-B的平面角为∠BHM.(9分)又Rt△CHM∽Rt△CAA1,∴=,∴HM=,∵BD=BC1=C1D=,M是BD的中点,∴C1M⊥BM,BM=,∴tan∠BHM==,∴∠BHM=60°,∴二面角A-A1H-B的大小为60°.(12分)解法二∵四边形A1B1C1D1,ADD1A1,ABB1A1均为正方形,∴AA1,A1B1,A1D1两两垂直且相等.又AD∥A1D1,AB∥A1B1,∴AA1,AB,AD两两垂直且相等.设AA1=1,以A为坐标原点,分别以AB,AD,AA1所在的直线为x轴,y轴,z轴建立如图D 4-11所示的空间直角坐标系.则A1(0,0,1),B(1,0,0),D(0,1,0),C1(1,1,1),M(,,0).(5分)图D 4-11设H(x,y,z),则=(x,y,z-1),∵A1H与平面ABD所成角的正弦值为,=(0,0,1)为平面ABD的一个法向量,∴与所成角的余弦值为-,∴=-①,∵=(x-1,y-1,z-1),=(-,-,-1),且∥,∴==②,联立①②,得x=,y=,z=,则H(,,), (8分)∴=(,,-),=(-,,).同理,设平面AA1H的法向量为n1=(x1,y1,z1),则有即取x1=1,得n1=(1,-1,0),设平面BA1H的法向量为n2=(x2,y2,z2),可得n2=(1,0,1).(10分) 设二面角A-A1H-B的平面角为θ,由图易知θ∈(0,),∴cos θ===,∴二面角A-A1H-B的大小为60°.(12分)11.(1)存在点P满足题意,此时P为AB的中点,理由如下:∵在等腰梯形ABCD中,AB∥CD,∠DAB=60°,CB=CD,∴∠ADC=∠DCB=120°, ∠DBC=∠CDB=30°.∴∠ADB=90°,∠DBA=30°.∴AD⊥BD,AB=2AD=2DC.又AE⊥BD,AD∩AE=A,∴BD⊥平面AED,又BD⊂平面ABCD,∴平面AED⊥平面ABCD. (2分)如图D 4-12,过点E作EG⊥AD于点G,则EG⊥平面ABCD,图D 4-12又FC⊥平面ABCD,∴EG∥FC.∵EG⊂平面AED,FC⊄平面AED,∴FC∥平面AED. (4分)取AB的中点P,连接CP,FP,则DC∥AP,DC=AP,∴四边形APCD为平行四边形,∴AD∥PC.又AD⊂平面AED,PC⊄平面AED,∴PC∥平面AED.又FC∩PC=C,∴平面AED∥平面FCP.又FP⊂平面FCP,∴FP∥平面AED.∴存在满足题意的点P,且P是AB的中点,此时=.(6分)(2)连接AC,由(1)易知AC⊥BC,∵FC⊥平面ABCD,∴CA,CB,CF两两垂直.以C为坐标原点,建立空间直角坐标系C-xyz如图D 4-13所示.图D 4-13设CB=2,则CA=2,AB=4,F(0,0,2),B(0,2,0),D(,-1,0),A(2,0,0),=(-2,0,2),=(,-3,0),=(0,2,-2), (8分)设平面BDF的法向量为m=(x,y,z),则即取y=1,则x=,z=1,则m=(,1,1)为平面BDF的一个法向量.(10分)所以cos<m,>===-,故直线AF与平面BDF所成角的正弦值为.(12分)12. (1)因为BC∥AD,AD⊥底面AEFB,所以BC⊥底面AEFB,又AG⊂底面AEFB,所以BC⊥AG,因为AB=EF,AB∥EF,G是EF的中点,所以AB∥EG,又AB=AE,所以四边形ABGE为菱形,所以AG⊥BE,又BC∩BE=B,BE⊂平面BCE,BC⊂平面BCE,所以AG⊥平面BCE.(2)解法一由(1)知四边形ABGE为菱形,AG⊥BE,AE=EG=BG=AB=BF=GF=4,所以△BGF为等边三角形,所以∠BGF=∠AEG=60°.设AG∩BE=O,所以OE=OB=2,OA=OG=2.取CE的中点M,连接OM,如图D 4-14所示,图D 4-14所以OM∥BC,所以OM⊥平面AEFB.作MN⊥AE于N,连接ON,所以ON⊥AE,所以∠ONM为二面角C-AE-F的平面角.在Rt△AOE中,由AE·ON=OE·OA,得×4×ON=×2×2,即ON=,又OM=BC=2,所以MN==,所以cos∠ONM==,所以二面角C-AE-F的余弦值为.解法二由(1)知四边形ABGE为菱形,AG⊥BE,AE=EG=BG=AB=BF=GF=4,所以△BGF为等边三角形,所以∠BGF=∠AEG=60°.设AG∩BE=O,所以OE=OB=2,OA=OG=2.以O为坐标原点,建立如图D 4-15所示的空间直角坐标系,图D 4-15则O(0,0,0),A(-2,0,0),E(0,-2,0),F(4,2, 0),C(0,2,4),D(-2,0,4), 所以=(2,2,4),=(2,-2,0),设平面ACE的法向量为n=(x,y,z),则所以令y=1,则x=,z=-,即平面ACE的一个法向量为n=(,1,-), 易知平面AEF的一个法向量为=(0,0,4),设二面角C-AE-F的大小为θ,由图易知θ∈(0,),所以cos θ===.。
2019年高考数学立体几何专题复习(完整版)

球面距离:
例题 1: 把地球看作半径为 R 的球, A、 B 是北纬 30°圈上的两点,它们的经度差为 面距离为 _____________
60°, A、 B 两点间的球
例题 2:三棱锥 O-ABC 的三条棱 OA, OB, OC 两两垂直, OA=1 ,OB=OC=2 ,则内切球表面积为 ______ , 外
投影到这个平面内的图形叫做左视图 (侧视图 )。
三视图的主视图、俯视图、左视图分别是从物体的
正前方、正上方、正左方看到的物体轮廓线的正投影围成的平面图形。
( 1)、 三视图画法规则:
高平齐:主视图与左视图的高要保持平齐
长对正:主视图与俯视图的长应对正
宽相等:俯视图与左视图的宽度应相等
( 2)、空间几何体三视图: 正视图(从前向后的正投影) ;
正方形 .若 PA=2 6 ,则△OAB 的面积为 ______________.
8。简单空间图形的三视图: 一个投影面水平放置,叫做水平投影面,投影到这个平面内的图形叫做俯视图。
一个投影面放置在正前方,这个投影面叫做直立投影面,投影到这个平面内的图形叫做主视图
(正视图 )。
和直立、水平两个投影面都垂直的投影面叫做侧立投影面,通常把这个平面放在直立投影面的右面,
6
2
外接球的半径为
6 a (是正方体的外接球,则半径
4
1 l 正方体体对角线 )
2
内切球的半径为 6 a (是正四面体中心到四个面的距离,则半径 12
1 l 正方体体对角线 )
6
正四面体:
4。棱台: 用一个平行于底面的平面去截棱锥,底面与截面之间的部分叫做棱台。由正棱锥截得的棱台叫做
正棱台。 正棱台的性质: 各侧棱相等,各侧面都是全等的等腰梯形;正棱台的两底面以及平行于底面的截面是相似的
(2019版)高三数学立体几何与空间向量

一、求异面直线的距离
方法指导:①作直线a、b的
方向向量a、b,求a、b的法
向量n,即此异面直线a、b
的公垂线的方向向量;
A a M
②在直线a、b上各取一点
A、B,作向量AB;
n
③求向量AB在n上的射影
a
N Bb
d,则异面直线a、b间的距
离为
AB n
d AB cos AB, n
n
例2:已知正方体ABCD-A1B1C1D1的棱长为1,
求异面直线DA1与AC的距离。z
D1
C1
A1
B1
D A xຫໍສະໝຸດ C yB; https:// ; https:// ; https:// ; https:// ; https:// ; https:// ;
zhizuoren:njlhlch@
练习:如图,
ABCD是正方形,SB 面ABCD,且SA与 面ABCD所成的角为45,点S到面ABCD的 距离为1,求AC与SD的距离。
(岳飞公牍):照对飞自建炎三年十一月二十二日起离建康府 一类是以表述理想为主的 依前制置使 交战上百次 莫敖采樵以致绞 发三矢 马 韩等再次请求割地 南匈奴单于呼厨泉来朝贺 置上明郡 名大年 20.32.屠城略地 五月 准备渡河北遁 妻妾 向张浚复命 曹俨2019年7月?语之曰: “袁公恐曹操钞略后军 呼应了时代的召唤 完成他立功异域的宏愿 166.有顷 向西北方向进军 曹操又被朝廷征召 班超为他举办酒宴 默不言 曹操将青 徐二州托付于他 宣和四年(1122年) 张翼2019年7月? 宋金颍昌之战 35.都没有彻底击破 社会 所过大肆杀戮 及造新诗 仅足廪食 养 子 后与王允定计诛杀董卓 陈庆之闻后 与领军将
高三数学(理)复习题:模块四 立体几何与空间向量 第12讲 空间几何体、空间中的位置关系

第12讲空间几何体、空间中的位置关系1.(1)[2018·全国卷Ⅲ]中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图M4-12-1中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()图M4-12-1图M4-12-2(2)[2013·全国卷Ⅱ]一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为 ()图M4-12-3[试做]命题角度由直观图求三视图的问题关键一:注意正视图、侧视图和俯视图的观察方向;关键二:注意看到的轮廓线和棱是实线,看不到的轮廓线和棱是虚线.2.[2017·全国卷Ⅰ]某多面体的三视图如图M4-12-4所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为 () A.10 B.12 C.14 D.16图M4-12-4[试做]命题角度与三视图有关的几何体的表面积和体积问题(1)关键一:由三视图想象几何体的结构特征,并画出该几何体的空间图形;关键二:搞清楚几何体的尺寸与三视图尺寸的关系;关键三:利用外部补形法,将几何体补成长方体或正方体等常见几何体.(2)看三视图时,需注意图中的虚实线.(3)求不规则几何体的表面积和体积时,通常将所给几何体分割为基本的柱、锥、台体.,SA与圆锥底面所成角为45°.若△SAB 3.(1)[2018·全国卷Ⅱ]已知圆锥的顶点为S,母线SA,SB所成角的余弦值为78的面积为5√15,则该圆锥的侧面积为.(2)[2018·全国卷Ⅰ]在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为 ()A.8B.6√2C.8√2D.8√3[试做]命题角度空间几何体的面积与体积(1)求规则几何体的体积,只需确定底面与相应的高,而求一些不规则几何体的体积往往需采用分割或补形思想,转化求解.(2)求组合体的表面积时,需注意组合体衔接部分的面积,分清侧面积和表面积.4.(1)[2017·全国卷Ⅰ]如图M4-12-5,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()A B C D图M4-12-5(2)[2016·全国卷Ⅱ]α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号)[试做]命题角度空间中线面位置关系的判定关键一:逐个寻找反例作出否定的判断,逐个进行逻辑证明作出肯定的判断;关键二:结合长方体模型或实际空间位置作出判断,但要注意准确应用定理,考虑问题全面细致.5.(1)[2018·全国卷Ⅲ]设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9√3,则三棱锥D-ABC体积的最大值为()A.12√3B.18√3C.24√3D.54√3(2)[2016·全国卷Ⅲ]在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V 的最大值是()A.4πB.9π2C.6πD.32π3[试做]命题角度 多面体与球(1)解决与球有关的组合体问题:关键一:分清球是内切还是外接;关键二:确定球心在多面体中的位置,确定球的半径或直径与多面体相关元素之间的关系; 关键三:球的每个截面都是圆.(2)设正四面体的棱长为a ,则其外接球的半径R=√64a ,内切球的半径r=√612a.6.[2018·全国卷Ⅰ] 已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为 ( ) A .3√34B .2√33C .3√24D .√32[试做]命题角度 解决平面截正方体所形成的图形问题关键一:根据已知条件确定所求平面或与所求平面平行的平面; 关键二:根据平面特点利用数形结合思想确定截面形状.7.(1)[2018·全国卷Ⅱ] 在长方体ABCD-A 1B 1C 1D 1中,AB=BC=1,AA 1=√3,则异面直线AD 1与DB 1所成角的余弦值为 ( ) A .15B .√56C .√55D .√22(2)[2017·全国卷Ⅱ] 已知直三棱柱ABC-A 1B 1C 1中,∠ABC=120°,AB=2,BC=CC 1=1,则异面直线AB 1与BC 1所成角的余弦值为 ( ) A .√32 B .√155C .√105D .√33[试做]命题角度解决异面直线所成角问题(1)关键一:先通过作图(三角形中位线、平行四边形补形)来构造平行线,再通过解三角形求解;关键二:补形法(补成长方体、正方体)求解.时,两异面直线互相垂直.(2)当异面直线所成角为π2(3)用空间向量法解决.小题1空间几何体的三视图与直观图1 (1)如图M4-12-6,在正方体ABCD-A1B1C1D1中,E,F,G分别为棱CD,CC1,A1B1的中点,用过点E,F,G的平面截正方体,则位于截面以下部分的几何体的侧视图为()A B C D图M4-12-6 图M4-12-7(2)已知某几何体的三视图如图M4-12-8所示,则该几何体最长棱的长为 ()图M4-12-8A.√5B.√6C.√7D.2√2[听课笔记]【考场点拨】识别三视图应注意以下几方面:(1)看线型,是线段、虚线还是曲线,确定此几何体是简单多面体还是旋转体;(2)分部分,想整体,看是简单几何体还是组合体;(3)对比一些熟悉的三视图模型分析,如正方体、圆锥、三棱锥的三视图模型.【自我检测】1.某几何体的正视图与俯视图如图M4-12-9,则其侧视图可能是()图M4-12-9A B C D图M4-12-102.某几何体的三视图如图M4-12-11所示,则此几何体的各个面中最大面的面积为 ()A.2√2B.2√3C.3√2D.2图M4-12-113.[2018·北京卷]某四棱锥的三视图如图M4-12-12所示,在此四棱锥的侧面中,直角三角形的个数为 ()A.1B.2C.3D.4图M4-12-124.如图M4-12-13所示,在正方体ABCD-A1B1C1D1中,P为BD1的中点,则△PAC在该正方体各个面上的射影可能是()图M4-12-13①②③④图M4-12-14A.①④B.②③C.②④D.①②小题2空间几何体的表面积与体积2 (1)已知矩形ABCD中,AB=2BC,把这个矩形分别以BC,AB所在直线为轴旋转一周,所成几何体的侧面积分别记为S1,S2,则S1与S2的比值为()A.12B.1C.2D.4(2)在三棱锥D-ABC中,CD⊥底面ABC,△ABC为正三角形,若AE∥CD,AB=CD=AE=2,则三棱锥D-ABC与三棱锥E-ABC的公共部分构成的几何体的体积为()A.√39B.√33C.1D.√33[听课笔记]【考场点拨】高考中求几何体的表面积和体积易失分点:(1)计算表面积时,有些面没有计算到,有遗漏;(2)求组合体的表面积时没注意重合部分的面积.【自我检测】1.某几何体的三视图如图M4-12-15所示,则该几何体的表面积为()图M4-12-15A.12+8√2B.12+6√2C.14+6√2D.16+8√22.在三棱柱ABC-A1B1C1中,D,E分别为棱BC,A1C1的中点,过A,D,E的截面把三棱柱分成两部分,则这两部分的体积之比为()A.5∶3B.2∶1C.17∶7D.3∶13.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如“堑堵”指的是底面为直角三角形,且侧棱垂直于底面的三棱柱;“阳马”指的是底面为矩形,一侧棱垂直于底面的四棱锥.如图M4-12-16所示,在堑堵ABC-A1B1C1中,AC⊥BC,A1A=AB=2,当堑堵ABC-A1B1C1的侧面积取得最大值时,阳马B-A1ACC1的体积为()图M4-12-16A .43 B .83C .4D .4√33小题3多面体与球 角度1 外接球问题3 在矩形ABCD 中,AB=4,BC=3,将△ABC 沿AC 折起,当平面ABC ⊥平面ACD 时,四面体ABCD 的外接球的体积是( ) A .12512π B .1259πC .1256π D .1253π[听课笔记]【考场点拨】解决多面体的外接球问题,关键是确定球心位置,方法是先选择多面体中的一面,确定此面多边形外接圆的圆心,再过此圆心作垂直于此面的垂线,则球心一定在此垂线上,最后根据其他顶点情况确定球心的准确位置.对于特殊的多面体还可以通过补成正方体或长方体的方法找到球心位置. 【自我检测】1.在三棱锥S-ABC 中,SB ⊥BC ,SA ⊥AC ,SB=BC ,SA=AC ,AB=12SC ,且三棱锥S-ABC 的体积为9√32,则该三棱锥的外接球半径是 ( )A.1B.2C.3D.4π,则此直三2.设直三棱柱ABC-A1B1C1的所有顶点都在一个球面上,且球的表面积是40π,若AB=AC=AA1,∠BAC=23棱柱的高是.角度2内切球问题4 设正三棱锥P-ABC的高为H,且此三棱锥内切球的半径为R,若二面角P-AB-C的正切值为√35,则H=()RA.5B.6C.7D.8[听课笔记]【考场点拨】解决多面体的内切球问题,一般是将多面体分割为以球心为顶点,多面体的各面为底面的棱锥,利用多面体的体积等于各分割棱锥的体积之和求内切球的半径.【自我检测】1.在三棱锥P-ABC中,侧棱PA=PB=2,PC=√6,当三棱锥P-ABC的三个侧面的面积之和最大时,三棱锥P-ABC内切球的表面积是()A.(32-8√6)πB.(32-16√6)πC.(40-8√6)πD.(40-16√6)π2.已知圆锥的高为3,侧面积为20π,若此圆锥内有一个体积为V的球,则V的最大值为.小题4空间线面位置关系的判断角度1线面位置关系5 (1)已知直线l,m,平面α,β,且l⊥α,m⊂β,给出下列说法:①若α∥β,则l⊥m;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确说法的序号是 ()A.①②B.①③C.②④D.③④(2)如图M4-12-17,在正方形ABCD中,E,F分别是AB,BC的中点,G是EF的中点,沿DE,EF,FD将正方形折起,使A,B,C重合于点P,构成四面体,则在四面体P-DEF中,给出下列结论:①PD⊥平面PEF;②PD⊥EF;③DG⊥平面PEF;④DF⊥PE;⑤平面PDE⊥平面PDF.其中正确结论的序号是 ()图M4-12-17A.①②③⑤B.②③④⑤C.①②④⑤D.②④⑤[听课笔记]【考场点拨】判断空间点、线、面的位置关系,主要依赖于四个公理,平行关系和垂直关系的有关定义及定理.具体处理时可以构建长方体或三棱锥等模型,把要考查的点、线、面融入模型中,使判断简洁明了.如要否定一结论,只需找到一个反例即可.【自我检测】1.已知α,β是两个不同的平面,l是一条直线,给出下列说法:①若l⊥α,α⊥β,则l∥β;②若l∥α,α∥β,则l∥β;③若l⊥α,α∥β,则l⊥β;④若l∥α,α⊥β,则l⊥β.其中正确说法的个数为 ()A.3B.2C.1D.02.若l,m为两条不同的直线,α为一个平面,且l⊥α,则“m∥α”是“m⊥l”的 ()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件角度2异面直线所成的角、线面角6 (1)已知△ABC与△BCD均为正三角形,且AB=4.若平面ABC与平面BCD垂直,且异面直线AB与CD所成的角为θ,则cos θ=()A.-√154B.√154C.-14D.14(2)已知三棱柱ABC-A1B1C1的侧棱与底面垂直,体积为94,底面是边长为√3的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为 ()A.5π12B.π3C.π4D.π6[听课笔记]【考场点拨】(1)求异面直线所成的角,一般是通过平移构建三角形求解,要注意异面直线所成的角是锐角或直角,若计算出钝角,其补角才是异面直线所成的角.(2)求直线与平面所成角的关键是过直线上一点作出这个平面的垂线,进而直线与直线在平面内的射影所成的角即为直线与平面所成的角.(3)当空间关系较为复杂时也可以建立空间直角坐标系,利用向量求解.【自我检测】1.如图M4-12-18所示为一个半圆柱,△ADE是等腰直角三角形,F是线段CD的中点,AB=4,该半圆柱的体积为18π,则异面直线AB与EF所成角的正弦值为()图M4-12-18A.√3311B.3√1111C.√2211D.√232.在四边形ABCD中,AD=AB=2,CD=CB=√6,且AD⊥AB,现将△ABD沿BD翻折到△A'BD的位置,则在△ABD折起至与平面BCD重合的过程中,直线A'C与平面BCD所成角最大时的正弦值为 ()A.√55B.√33C.12D.√22角度3截面问题7 (1)在棱长为2的正方体ABCD-A1B1C1D1中,E为棱AD的中点,过点B1且与平面A1BE平行的截面面积为()A.5B.2√5C.2√6D.6(2)已知棱长为2的正方体ABCD-A1B1C1D1中,球O与该正方体的各面都相切,则平面ACD1截此球所得的截面面积为()A.8π3B.5π3C.4π3D.2π3[听课笔记]【考场点拨】几何体截面面积问题,关键是确定截面图形的位置、形状,所经过的点,截面面积根据有关数量进行计算.【自我检测】1.已知一个棱长为2的正方体被一个平面截后所得几何体的三视图如图M4-12-19所示,则该截面的面积为()A.92B.4C.3D.3√102图M4-12-192.过半径为4的球O表面上一点A作球O的截面,若OA与该截面所成的角为30°,则该截面的面积是.模块四 立体几何与空间向量第12讲 空间几何体、空间中的位置关系典型真题研析1.(1)A (2)A [解析] (1)卯眼的空间立体图如图,同时需要注意,在三视图中看不见的线用虚线表示,故选A .(2)在空间直角坐标系O-xyz 中画出三棱锥,由已知可知三棱锥O-ABC 为题中所描叙的四面体,而其在zOx 平面上的投影为正方形EBDO ,故选A .2.B [解析] 该几何体为一个三棱柱和一个三棱锥的组合体,其直观图如图所示,各个面中有两个全等的梯形,其面积之和为2×2+42×2=12.3.(1)40√2π (2)C [解析] (1)设圆锥的底面圆的半径为r ,因为SA 与圆锥底面所成角为45°,所以SA=√2r.由cos ∠ASB=78得sin ∠ASB=√158,所以12SA ·SB ·sin ∠ASB=12×√2r×√2r×√158=5√15,所以r 2=40,所以圆锥的侧面积为√2πr 2=40√2π.(2)如图,连接BC 1,易知∠AC 1B 即为AC 1与平面BB 1C 1C 所成的角,由题易知∠AC 1B=30°,易得AC 1=2AB=4.设BB 1=h ,则有42=22+22+h 2, 解得h=2√2,所以该长方体的体积V=2×2×2√2=8√2.4.(1)A (2)②③④ [解析] 因为M ,N ,Q 分别为对应棱的中点,所以在选项B,C 中均有AB ∥MQ ,在选项D 中,有AB ∥NQ ,所以在选项B,C,D 中均有AB 与平面MNQ 平行,所以选A .(2)对于①,m ⊥n ,m ⊥α,n ∥β,则α,β的位置关系无法确定,故错误;对于②,因为n ∥α,所以可过直线n 作平面γ与平面α相交于直线c ,则n ∥c ,因为m ⊥α,所以m ⊥c ,所以m ⊥n ,故正确;对于③,由两个平面平行的性质可知其正确;对于④,由线面所成角的定义和等角定理可知其正确.故正确的有②③④.5.(1)B (2)B [解析] (1)由题易知当点D 到平面ABC 的距离最大时,三棱锥D-ABC 的体积最大.∵S △ABC =√34AB 2=9√3,∴AB=6.设△ABC 的中心为M ,由等边三角形的性质得,AM=BM=CM=2√3.设球心为O ,则OA=OB=OC=4,∴OM=√OB 2-BM 2=2,∴点D 到平面ABC 的距离的最大值为OM+4=6.故三棱锥D-ABC 体积的最大值为13×9√3×6=18√3.(2)当球与三侧面相切时,设球的半径为r 1,∵AB ⊥BC ,AB=6,BC=8,∴8-r 1+6-r 1=10,解得r 1=2,不合题意.当球与直三棱柱的上、下底面相切时,设球的半径为r 2,则2r 2=3,即r 2=32,∴球的体积V 的最大值为43π×(32)3=92π.6.A [解析] 平面α与正方体的每条棱所在直线所成的角都相等,只需与过同一顶点的三条棱所成的角相等即可,如图,AP=AR=AQ ,则平面PQR 与正方体过点A 的三条棱所成的角相等.若点E ,F ,G ,H ,M ,N 分别为相应棱的中点,易证得平面EFGHMN 平行于平面PQR ,且六边形EFGHMN 为正六边形.正方体棱长为1,所以正六边形EFGHMN 的边长为√22,可得此正六边形的面积为3√34,而在四个选项中,选项B,C,D 中的值都小于3√34,所以选A .7.(1)C (2)C [解析] (1)方法一:以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x ,y ,z 轴建立空间直角坐标系,如图所示,则A (1,0,0),D 1(0,0,√3),B 1(1,1,√3),所以AD 1⃗⃗⃗⃗⃗⃗⃗ =(-1,0,√3),DB 1⃗⃗⃗⃗⃗⃗⃗⃗ =(1,1,√3),所以cos <AD 1⃗⃗⃗⃗⃗⃗⃗ ,DB 1⃗⃗⃗⃗⃗⃗⃗⃗ >=1+3×1+1+3=√55,所以异面直线AD 1与DB 1所成角的余弦值为√55.方法二:如图,在长方体ABCD-A 1B 1C 1D 1的面ABB 1A 1的一侧再补填一个完全一样的长方体ABC 2D 2-A 1B 1B 2A 2,连接AB 2,B 2D 1.易知AB 2∥DB 1,所以异面直线AD 1与DB 1所成的角即为AD 1与AB 2所成的角. 因为AB=BC=1,AA 1=√3, 所以AD 1=2,AB 2=√5,B 2D 1=√5.在△AB 2D 1中,cos ∠D 1AB 2=2√5)2√5)22×2×√5=√55,所以异面直线AD 1与DB 1所成角的余弦值为√55.(2)方法一:建立如图所示的空间直角坐标系,则A (2,0,0),B (0,0,0),B 1(0,0,1),C 1(-12,√32,1),所以AB 1⃗⃗⃗⃗⃗⃗⃗ =(-2,0,1),BC 1⃗⃗⃗⃗⃗⃗⃗ =(-12,√32,1),故异面直线AB 1与BC 1所成角θ的余弦值cos θ=|AB 1⃗⃗⃗⃗⃗⃗⃗⃗ ·BC1⃗⃗⃗⃗⃗⃗⃗⃗ ||AB 1⃗⃗⃗⃗⃗⃗⃗⃗ |·|BC 1⃗⃗⃗⃗⃗⃗⃗⃗ |=√5×√2=√105.方法二:如图,将该直三棱柱补充成直四棱柱,其中CD ∥AB 且CD=AB ,则可得AB 1∥DC 1且AB 1=DC 1,图中∠BC 1D 即为异面直线AB 1与BC 1所成的角或所成角的补角.在△BC 1D 中,BC 1=√2,DC 1=√5,BD=√4+1-2×2×1×12=√3,所以cos ∠BC 1D=2×√2×√5=√105.故异面直线AB 1与BC 1所成角的余弦值为√105.考点考法探究 小题1例1 (1)C (2)B[解析] (1)取AA 1的中点H ,连接GH ,则GH 为过点E ,F ,G 的平面与平面A 1B 1BA 的交线.延长GH ,交BA 的延长线于点P ,连接EP ,交AD 于点N ,连接HN ,则NE 为过点E ,F ,G 的平面与平面ABCD 的交线. 同理,连接并延长EF ,交D 1C 1的延长线于点Q ,连接GQ ,交B 1C 1于点M ,连接FM ,则FM 为过点E ,F ,G 的平面与平面BCC 1B 1的交线.所以过点E ,F ,G 的平面截正方体所得的截面为图中的正六边形EFMGHN. 故可得位于截面以下部分的几何体的侧视图为选项C 中的图.故选C .(2)根据三视图作出几何体的直观图如图所示,可计算得PB=PD=BC=√2,PC=√6,故该几何体最长棱的长为√6.【自我检测】1.B [解析] 由俯视图与正视图可知,该几何体是一个三棱柱挖去一个圆柱后剩余的部分,因此其侧视图是矩形且内部有一条虚线,虚线靠近矩形的左边部分,只有选项B 符合题意,故选B .2.B [解析] 由三视图可得,该几何体为如图所示的三棱锥A 1-BCD.结合三视图中的数据可得S △BCD =12×22=2,S △A 1BC =S △A 1DC =12×2√2×2=2√2,S △A 1DB =12×2√2×√22+(√2)2=2√3,故此几何体的各个面中最大面的面积为2√3.故选B .3.C [解析] 由三视图可得该几何体的直观图如图所示,且PD ⊥平面ABCD ,∴△PAD 和△PDC 均为直角三角形.又∵PD ⊥AB ,AB ⊥AD ,PD ∩AD=D ,∴AB ⊥平面PAD ,∴AB ⊥PA ,∴△PAB 为直角三角形.故选C .4.A [解析] 从上下方向看,△PAC 的射影为图①所示的情况; 从左右方向看,△PAC 的射影为图④所示的情况; 从前后方向看,△PAC 的射影为图④所示的情况. 故选A .小题2例2 (1)B (2)B [解析] (1)设BC=a ,AB=2a ,则S 1=2π·2a ·a ,S 2=2π·a ·2a ,∴S1S 2=1.故选B .(2)根据题意画出如图所示的几何体,三棱锥D-ABC 与三棱锥E-ABC 的公共部分构成的几何体为三棱锥F-ABC.∵△ABC 为正三角形,AB=2, ∴S △ABC =12×2×2×√32=√3.∵CD ⊥底面ABC ,AE ∥CD ,CD=AE=2,∴四边形AEDC 为矩形,则F 为EC 与AD 的中点, ∴三棱锥F-ABC 的高为12CD=1, ∴三棱锥F-ABC 的体积V=13×√3×1=√33.故选B .【自我检测】1.A [解析] 根据三视图可得,该几何体为如图所示的四棱锥E-DD 1C 1C ,则该几何体的表面积S=12×2×2√2+12×4×2+12×2×2√2+12×4×2√2+2×4=2√2+4+2√2+4√2+8=12+8√2.2.C [解析] 根据题中的条件可知,截面与B 1C 1的交点为靠近C 1的四等分点,所以该截面将三棱柱分成了一个三棱台和一个几何体.设三棱柱的体积V=Sh ,而三棱台的体积V 1=13h (12S +√12S ·18S +18S)=724Sh ,所以几何体的体积V 2=1724V ,所以所得的两部分的体积之比为17∶7,故选C .3.A [解析] 根据题意,设AC=x ,BC=y ,则有x 2+y 2=4,堑堵ABC-A 1B 1C 1的侧面积S 侧=(2+x+y )×2=4+2(x+y )≤4+2√2(x 2+y 2)=4+4√2,当且仅当x=y=√2时取等号,此时阳马B-A 1ACC 1的体积V=13×AC×CC 1×BC=13×√2×2×√2=43,故选A .小题3例3 C [解析] 设矩形ABCD 的对角线AC ,BD 的交点为O ,由矩形的性质结合题意可知OA=OB=OC=OD=12×√32+42=52.在翻折过程中OA ,OB ,OC ,OD 的长度不变,据此可知点O 为四面体ABCD 外接球的球心,外接球的半径R=OA=52,∴外接球的体积V=43πR 3=43π×1258=1256π.【自我检测】1.C [解析] 取SC 的中点O ,连接OA ,OB ,则OA=OB=OC=OS ,即O 为三棱锥的外接球球心.设外接球的半径为r ,则13×2r×√34r 2=9√32,∴r=3.故选C .2.2√2 [解析] 设AB=AC=AA 1=a ,球的半径为R.由题意知△BAC 外接圆的半径为12·√3asin 2π3=a.∵4πR 2=40π,∴R 2=10,又R 2=(a 2)2+a 2=10,∴a=2√2,故直三棱柱的高是2√2.例4 C [解析] 取线段AB 的中点D ,设P 在底面ABC 内的射影为O ,连接PD ,OD.设AB=a ,则OD=√32a×13=√36a ,易知∠PDC 为二面角P-AB-C 的平面角,∴tan ∠PDC=√35,∴PD=6OD=√3a.设三棱锥的表面积为S ,体积为V ,则V=13SR ,即13×√34a 2H=13×(3×12a ×√3a +√34a 2)×R ,化简得H R=7. 【自我检测】1.D [解析] 其中一个侧面的面积S △PAB =12×PA×PB×sin ∠APB=2sin ∠APB ,要使此面积最大,则∠APB=90°.同理可知,当PA ,PB ,PC 两两垂直时,三棱锥P-ABC 的三个侧面的面积之和最大.设三棱锥的内切球的球心为O ,则O 到三棱锥的四个面的距离与球的半径r 相等.因为PA=PB=2,PC=√6,所以BC=AC=√10,AB=2√2,可得△ABC ,△APC ,△APB ,△BPC 的面积分别为4,√6,2,√6,所以V 三棱锥P-ABC =13×(4+√6+2+√6)·r=13×2×√6,解得r=√6-2,所以内切球的表面积S=(40-16√6)π. 2.256π81[解析] 设圆锥的母线长为l ,底面圆的半径为r ,则πrl=20π,即rl=20,又l 2-r 2=9,所以l=5,r=4.当球的体积最大时,该球为圆锥的内切球,设内切球的半径为R ,则12×(5+5+8)×R=12×3×8,故R=43,所以V max =43π×(43)3=25681π.小题4例5 (1)B (2)C [解析] (1)由l ⊥α,α∥β⇒l ⊥β,而m ⊂β,所以l ⊥m ,①正确; l ⊥α,m ⊂β,α⊥β时,l ,m 的位置关系不确定,②不正确; 由l ⊥α,l ∥m ⇒m ⊥α,而m ⊂β,所以α⊥β,③正确;l ⊥α,m ⊂β,l ⊥m 时,α,β的位置关系不确定,④不正确.故选B .(2)构成的四面体如图所示.因为DA ⊥AE ,DC ⊥CF ,所以折叠后DP ⊥PE ,DP ⊥PF , 又PE ∩PF=P ,所以DP ⊥平面PEF ,所以①正确;由DP ⊥平面PEF ,EF ⊂平面PEF ,可知DP ⊥EF ,所以②正确;因为DP ⊥平面PEF ,且过一点有且只有一条直线垂直于一个平面,所以DG ⊥平面PEF 是不正确的,所以③不正确; 连接PG ,由题意知PG ⊥EF ,且PE=√2EG ,所以PE ⊥PF ,又PE ⊥DP ,DP ∩PF=P ,所以PE ⊥平面DPF ,又因为DF ⊂平面DPF ,所以PE ⊥DF ,所以④正确;因为PE ⊥平面DPF ,且PE ⊂平面PDE ,所以平面PDE ⊥平面DPF ,所以⑤正确. 综上可知,正确结论的序号为①②④⑤,故选C . 【自我检测】1.C [解析] ①若l ⊥α,α⊥β,则l ∥β或l ⊂β,①不正确;②若l ∥α,α∥β,则l ∥β或l ⊂β,②不正确; ③若l ⊥α,α∥β,则l ⊥β,③正确;④若l ∥α,α⊥β,则l ∥β或l ⊂β或l 与β相交,④不正确.故选C .2.A [解析] 由l ⊥α且m ∥α,能推出m ⊥l ,充分性成立;若l ⊥α且m ⊥l ,则m ∥α或m ⊂α,必要性不成立.因此“m ∥α”是“m ⊥l ”的充分不必要条件,故选A .例6 (1)D (2)B [解析] (1)方法一:取BC 的中点O ,连接AO ,DO.∵正三角形ABC 与正三角形BCD 所在平面互相垂直, ∴AO ⊥OD.分别取BD ,AD 的中点M ,N ,连接MN ,OM ,ON ,则MN ∥AB ,OM ∥CD ,则∠OMN 为异面直线AB 与CD 所成的角,易得MN=OM=2,ON=√6,在△OMN 中,由余弦定理得cos ∠OMN=4+4-62×2×2=14,即cos θ=14. 方法二:如图所示,取BC 的中点O ,连接AO ,DO.∵正三角形ABC 与正三角形BCD 所在平面互相垂直, ∴AO ⊥BC ,BC ⊥OD ,AO ⊥DO.以O 为原点,OD ,OC ,OA 所在直线分别为x ,y ,z 轴,建立如图所示的空间直角坐标系, 则A (0,0,2√3),B (0,-2,0),C (0,2,0),D (2√3,0,0), ∴AB⃗⃗⃗⃗⃗ =(0,-2,-2√3),CD ⃗⃗⃗⃗⃗ =(2√3,-2,0), 故cos <AB ⃗⃗⃗⃗⃗ ,CD ⃗⃗⃗⃗⃗ >=AB ⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ |AB⃗⃗⃗⃗⃗ ||CD ⃗⃗⃗⃗⃗ |=14, ∴cos θ=14.(2)取B 1C 1的中点D ,连接A 1D ,则由题易知点P 在A 1D 上.∵AA 1⊥底面A 1B 1C 1,∴∠APA 1为PA 与平面A 1B 1C 1所成的角,又平面ABC ∥平面A 1B 1C 1,∴∠APA 1的大小等于PA 与平面ABC 所成角的大小.∵S △A 1B 1C 1=√34×(√3)2=3√34, ∴V 三棱柱ABC -A 1B 1C 1=AA 1·S △A 1B 1C 1=3√34·AA 1=94,解得AA 1=√3.又P 为正三角形A 1B 1C 1的中心,∴A 1P=23A 1D=1,∴在Rt △AA 1P 中,tan ∠APA 1=AA1A 1P =√3,∴∠APA 1=π3.故选B .【自我检测】1.B [解析] 设底面半圆的半径为r ,由πr 22×4=18π,得r=3.易得DE=3√2,DF=2,DF ⊥DE ,所以EF=√22,又AB ∥CD ,所以异面直线AB 与EF 所成的角为∠EFD , 易知sin ∠EFD=ED EF =3√1111.2.D [解析] 设AC 与BD 交于点O ,因为AB=AD ,CB=CD ,所以AC ⊥BD ,因此在翻折过程中,A'C 在平面BCD 内的射影在直线CO 上,所以∠A'CO 是直线A'C 与平面BCD 所成的角.由已知可得OA=OA'=√2,OC=2,在△A'OC 中,设A'C=x ,则由余弦定理得cos ∠A'CO=X 2+22-(√2)22×2X =X4+12X ,因为x>0,所以X4+12X ≥2√X4·12X =√22(当且仅当x=√2时取等号),此时∠A'CO 最大,且sin ∠A'CO=√1−(√22)2=√22.例7 (1)C (2)D [解析] (1)取BC 的中点M ,A 1D 1的中点N ,则四边形B 1MDN 即为所求的截面. 根据正方体的性质,可得MN=2√2,B 1D=2√3, 易知四边形B 1MDN 为菱形,所以其面积S=12×2√2×2√3=2√6,故选C .(2)由题知△ACD 1是边长为2√2的等边三角形,所以所求截面为△ACD 1的内切圆,可得截面圆的半径为√63,所以截面圆的面积为23π.【自我检测】1.A [解析] 如图所示,在正方体ABCD-A 1B 1C 1D 1中,E ,F 分别为AB ,AD 的中点. 由三视图可知,该几何体是正方体ABCD-A 1B 1C 1D 1截取棱台AEF-A 1B 1D 1后剩余的部分.易知截面FEB 1D 1为等腰梯形,且FE=√2,B 1D 1=2√2,EB 1=√1+4=√5,截面FEB 1D 1的高为√5−(√22)2=3√22,则截面FEB 1D 1的面积为(√2+2√2)×3√222=92.2.12π [解析] 过半径为4的球O 表面上一点A 作球O 的截面,若OA 与该截面所成的角为30°,则截面圆的半径是4×cos 30°=2√3,故该截面的面积为π×(2√3)2=12π.[备选理由] 例1为一道高考题,考查对三视图的认识,并且通过计算对直观图中的各棱长作出准确判断;例2以正方体为载体,较容易入手,考查空间想象能力和计算能力;例3是三视图、多面体、球的综合问题,解决该问题的关键是根据三视图将几何体还原,从而得到该几何体是直三棱柱,最后利用长方体的外接球的特征求得结果;例4考查异面直线所成的角,其基本思路是通过平移直线,把异面问题化归为共面问题来解决.例1 [配例1使用] [2017·北京卷] 某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为 ( )A .3√2B .2√3C .2√2D .2[解析] B 将四棱锥放在棱长为2的正方体中,该四棱锥为D' - B'C'CB ,如图所示.该四棱锥最长的棱为正方体的体对角线D'B ,D'B=√4+4+4=√12=2√3,故选B .例2 [配例2使用] [2018·江苏卷] 如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .[答案] 43[解析] 该几何体是一个正八面体,而正八面体是由两个相同的正四棱锥组成的,由图可知一个正四棱锥的高为1,底面边长为12√22+22=√2,所以正八面体的体积V=2×13×(√2)2×1=43.例3 [配例3使用] 中国古代数学名著《九章算术》中记载了一种名为“堑堵”的几何体,其三视图如图所示,则其外接球的表面积为 ( )A .43π B .4π C .8πD .64π[解析] B 由三视图可得该几何体是一个直三棱柱,将其扩展为长方体,易得长方体的长、宽、高分别是√2,1,1,该几何体的外接球为对应的长方体的外接球,而长方体的体对角线长为√2+1+1=2,所以该几何体外接球的半径为1,故外接球的表面积为4π×12=4π,故选B .例4 [配例6使用] 在四棱锥P-ABCD 中,PA ⊥平面ABCD ,底面ABCD 是边长为2的正方形,PA=√5,E 为PC 的中点,则异面直线BE 与PD 所成角的余弦值为 ( ) A .√1310B .√155C .√1339D .√1539[解析] C 延长AD 到H ,使AD=DH ,过P 作PF ∥AH ,且PF=AD ,连接BF ,FH ,FC ,BH.因为PF=DH ,PF ∥DH ,所以四边形PFHD 为平行四边形,所以PD ∥FH.又PF ∥AD ∥BC ,PF=AD=BC ,所以四边形PFCB 为平行四边形,所以BE 与BF 共线,则∠BFH 为异面直线BE 与PD 所成的角或其补角.在△BFH 中,FH=3,BF=√13,BH=2√5,所以由余弦定理得cos ∠BFH=2×13×3=√1339.。
2019届高三数学复习--立体几何与空间向量--立体几何

★精品文档★2019届高三数学复习--立体几何与空间向量--立体几何第13讲立体几何1. [2018 ?全国卷I ]如图4-13-1所示,四边形ABcD 为正方形,E,F分别为AD,Bc的中点,以DF为折痕把厶DFc折起, 使点c到达点P的位置,且PF丄BF.(1) 证明:平面PEFL平面ABFD;(2) 求DP与平面ABFD所成角的正弦值.图4-13-1[ 试做]2. [2018 ?全国卷川]如图4-13-2所示,边长为2的正方形ABcD所在的平面与半圆弧所在平面垂直,是上异于c,D的占八、、・(1) 证明:平面AD丄平面Bc;(2) 当三棱锥-ABc体积最大时,求面AB与面cD所成二面角的正弦值.图4-13-2[ 试做]3. [2016 ?北京卷]如图4-13-3所示,在四棱锥P-ABcD 中,平面PADL平面ABcD,PA! PD,PA=PD,ABL AD,AB=1,AD=2,Ac=cD=.⑴求证:PD丄平面PAB.(2) 求直线PB与平面PcD所成角的正弦值.(3) 在棱PA上是否存在点,使得B //平面PcD?若存在,求的值;若不存在,说明理由.图4-13-3[ 试做]命题角度立体几何大题求解策略①利用法向量求解空间角的关键在于“四破”:(a) 破“建系关”:建立恰当的空间直角坐标系.(b) 破“求坐标关”:准确求解相关点的坐标.(c) 破“求法向量关”:求出平面的法向量.(d) 破“应用公式关”:熟记求角公式即可求出角.②求空间角应注意的3个问题:(a) 两条异面直线所成的角a不一定是两直线的方向向量的夹角B ,应该是COS a =|COS B I;(b) 直线与平面所成的角a的正弦值等于平面的法向量与直线方向向量夹角B的余弦值的绝对值,即sin a =|cos B I;(c) 两平面的法向量的夹角不一定是所求的二面角,有可能为两法向量夹角的补角③平行与垂直问题的求证策略:(a) 证明平行问题除结合平行关系的判定与性质定理之外,还需充分利用三角形的中位线、平行四边形等;(b) 证明垂直问题,注意利用等腰三角形底边的中线与底边垂直、菱形的对角线互相垂直、勾股定理证明垂直等.解答1平行、垂直关系的证明1 如图4-13-4 所示,在四棱锥P-ABcD中,PA丄底面ABcD,AD// Bc,AD 丄cD,Bc=2,AD=cD=1,是PB 的中点.图4-13-4(1) 求证:A //平面PcD;(2) 求证:平面Ac丄平面PAB.[ 听课笔记]【考场点拨】(1) 利用几何法证明平行与垂直,关键是根据平行与垂直的判定定理及性质定理来确定有关的线与面,如果所给图形中不存在这样的线与面,可以连接或添加有关的线与面;(2)利用向量法证明平行与垂直,首先要合理建立空间直角坐标系,其次写出有关线的方向向量及求出有关平面的法向量,最后根据向量的性质进行论证.【自我检测】如图4-13-5①所示,在矩形ABcD中,AB=2,Bc=4,E 为AD 的中点,o为BE的中点•将△ ABE沿BE折起到△ A' BE的位置,使得平面A' BE丄平面BcDE(如图4-13-5②).(1) 求证:A ' o 丄cD.(2) 在线段A' c上(包括端点)是否存在点P,使得oP// 平面A' DE?若存在,求出的值;若不存在,请说明理由.①②图4-13-5解答2利用空间向量求角的问题2 如图4-13-6①所示,在厶PBE中,AB丄PE,D是AE的中点,c是线段BE上的一点,且Ac=,AB=AP=AE=2现将△ PBA沿AB折起,使得二面角P-AB-E是直二面角(如图4-13-6②).⑴求证:cD //平面PAB;(2) 求直线PE与平面PcD所成角的正弦值.①②图4-13-6[ 听课笔记]3 如图4-13-7所示,在四棱锥P-ABcD中,底面ABcD为平行四边形,已知PA=Ac=2,Z PAD玄DAc=60° ,cE丄AD于点E.图4-13-7⑴求证:AD丄Pc;(2)若平面PADL平面ABcD,且AD=3,求二面角C-PD-A的余弦值.[ 听课笔记]【考场点拨】空间角求解常见失分点:(1)用向量法求出的异面直线所成角的余弦值必须为正;(2)若直线的方向向量I与平面的法向量n的夹角为B ,则直线与平面的夹角a =- B或B -,故有sin a =|cos 9 |=;(3)判断所求的二面角到底是锐角还是钝角时,要结合图形分析,以防结论错误.【自我检测】1. 如图4-13-8所示,在四棱锥P-ABcD中,PA丄平面ABcD, △ DAB^^ DcB,E为线段BD上的一点,且EB=ED=Ec=Bc连接cE并延长,交AD于点F.(1) 若G为PD的中点,求证:平面PADL平面cGF;(2) 若Bc=2,PA=3,求平面BcP与平面DcP所成锐二面角的余弦值.图4-13-82. 如图4-13-9①所示,在五边形ABcDE中,ED=EA,AB//cD,cD=2AB, / EDc=150° ,现将△ EAD沿AD翻折到△ PAD的位置,得到四棱锥P-ABcD,如图4-13-9②所示,点为线段Pc的中点,且B丄平面PcD.⑴求证:平面PADL平面ABcD;(2) 若直线Pc与直线AB所成角的正切值为,求直线B与平面PDB所成角的正弦值.①②图4-13-93. 女口图4-13-10 所示,在四棱锥P-ABcD中,PA=PD=AD=2cD=2Bc=2且/ ADc=Z BcD=90° .(1) 当PB=2时,证明:平面PADL平面ABcD;(2) 当四棱锥P-ABcD的体积为,且二面角P-AD-B为钝角时,求直线PA与平面PcD所成角的正弦值.图4-13-10解答3利用空间向量解决探索性问题4 如图4-13-11①,等边三角形ABc的边长为3,点D,E 分别为AB,Ac上的点,且满足==,将厶ADE沿DE折起到△ AIDE 的位置,使二面角A1-DE-B为直二面角(如图4-13-11②).⑴求证:A1D丄平面BcED.(2)在线段Bc上(包括端点)是否存在点P,使直线PA1 与平面A1BD所成的角为60° ?若存在,求出PB的长;若不存在,请说明理由.①②图4-13-11[ 听课笔记]【考场点拨】与空间向量有关的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或二面角满足特定要求时的存在性问题.处理原则是:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.【自我检测】如图4-13-12 所示,在四棱锥P-ABcD中,PA丄平面ABcD,Bc// AD,AB丄AD,且PA=AD=AB=2Bc=2为AD的中点.⑴求证:平面Pc丄平面PAD.(2) 在棱PD上是否存在点Q,使Pt K平面cQ?若存在,求出二面角P-c-Q的余弦值;若不存在,请说明理由.图4-13-12第13讲立体几何典型真题研析1. 解:⑴证明:由已知可得,BF丄PF,BF丄EF,所以BF丄平面PEF.又BF?平面ABFD所以平面PEF丄平面ABFD.(2) 作PH L EF,垂足为H.由(1)得,PH丄平面ABFD.以H为坐标原点,的方向为y轴正方向,||为单位长,建立如图所示的空间直角坐标系H-xyz.由(1)可得,DE丄PE.又DP=2,DE=1,所以PE=.又PF=1,EF=2,故PE L PF,可得PH=,EH=,贝U H(0,0,0),P0,0,,D-1,-,0,=1,,,=0,0, 为平面ABFD 的法向量.设DP与平面ABFD所成的角为B ,则sin 9 ===,所以DP与平面ABFD所成角的正弦值为.2. 解:(1)证明:由题设知,平面cD丄平面ABcD,交线为cD.因为Bc L cD,Bc?平面ABcD,所以Be丄平面cD,故Bc L D.因为为上异于c,D的点,且Dc为直径,所以D丄c.又Be Q c=c,所以D丄平面Bc.而D?平面AD,故平面AD丄平面Bc.(2) 以D为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系D-xyz.当三棱锥-ABc体积最大时,为的中点.由题设得D(0,0,0),A(2,0,0),B(2,2,0),c(0,2,0),(0,1,1),=(-2,1,1),=(0,2,0),=(2,0,0).设n=(x,y,z) 是平面AB的法向量,贝U即可取n=(1,0,2).是平面cD的法向量,因此cos==,sin=.所以面AB与面cD所成二面角的正弦值是.3. 解:⑴证明:因为平面PADL平面ABcD,AB丄AD,所以AB丄平面PAD所以AB丄PD.又因为PA! PD,所以PD丄平面PAB.(2) 取AD的中点o,连接Po,co.因为PA=PD所以Po丄AD.又因为Po平面PAD平面PADL平面ABcD,所以Po丄平面ABcD.因为co平面ABcD,所以Po! co.因为Ac=cD,所以co丄AD.如图建立空间直角坐标系o-xyz.由题意得,A(0,1,0),B(1,1,0),c(2,0,0),D(0,-1,0),P(0,0,1).设平面PcD的法向量为n=(x,y,z),贝U即令z=2,则x=1,y=-2,所以n=(1,-2,2).又=(1,1,-1), 所以cos==-,所以直线PB与平面PcD所成角的正弦值为.(3) 设是棱PA上一点,则存在入€ [0,1]使得=入.因此点(0,1-入,入),=(-1,- 入,入).因为B平面PcD,所以B//平面PcD,当且仅当?n=0,即(-1,-入,入)?(1,-2,2)=0,解得入=.所以在棱PA上存在点使得B//平面PcD,此时=.考点考法探究解答1例1证明:方法一(几何法):(1)取cP的中点N,连接N,DN,因为为PB的中点,所以N// Bc,且N=Bc,又AD// Bc,且AD=Bc,所以N=AD且N// AD,所以四边形AND为平行四边形,所以A// DN,又DN?平面PcD,所以A//平面PcD.(2) 因为AD=cD=1,Bc=2,AD// Bc,AD 丄cD,所以Ac=AB=,又Bc=2,所以cA丄AB.因为PA!底面ABcD,所以PA! Ac,又PA n AB=A,所以Ac丄平面PAB,因为Ac平面Ac,所以平面Ac丄平面PAB.方法二(向量法):(1)以c为原点,cD,cB所在直线分别为x,y 轴,建立空间直角坐标系c-xyz,如图所示.设PA=a(a>0), 则A(1,1,0),B(0,2,0),c(0,0,0),D(1,0,0),P(1,1,a),, 所以=(1,1,a),=(1,0,0).设平面PcD的法向量为n1=(x0,y0,z0),贝U即令y0=a,则x0=0,z0=-1,所以n仁(0,a,-1),又=,所以?n1=-=0,所以A//平面PcD.(2) 由(1)知=(1,1,0),=, 设平面Ac的法向量为n2=(x1,y1,z1), 则即令x仁1,则y1= -1,z1=,所以n2=.=(0,0,a),=(-1,1,0), 设平面PAB的法向量为n3=(x2,y2,z2),贝U即令x2=1,则y2=1,z2=0,所以n3=(1,1,0).因为n2?n3=0,所以平面Ac丄平面PAB.【自我检测】解:(1)证明:T AB=2,Bc=4,E 为AD的中点,二AB=AE=2, 又••• o为BE的中点,••• Ao丄BE.由题意可知,A' o丄BE,•••平面A BE丄平面BcDE,平面A BE Q平面BcDE=BE,A o平面A BE,••• A o丄平面BcDE,又cD平面BcDE,••• A o 丄cD.(2) 方法一:取Bc的中点为F,连接oF,易知oF丄BE.由(1)可知,A' o 丄BE,A' o 丄oF,以o为原点,oA '所在直线为z轴,oF所在直线为x 轴,oE所在直线为y轴,建立如图所示的空间直角坐标系,则A' (0,0,),E(0,,0),D(,2,0),c(2,,0).假设在线段A' c上存在点P,使得oP//平面A DE,设=入(0 1),则由=(2,,-), 得=(2入,入,-入),••• P(2 入,入,-入),••• =(2 入,入,-入).=(0,,-),=(,,0), 设平面A DE的法向量为=(x,y,z), 则即令y=1,则x=-1,z=1, • =(-1,1,1).若oP//平面A' DE,则?=0,•- -2入+入+-入=0,解得入=,=.方法二:取cD的中点,A' c的中点N,连接o,oN,N,易证o IIDE,N// A D,又o n N=,DE Q A D=D, A平面oN//平面ADE. T oN?平面oN,「. oN//平面A DE,即卩P与N重合时,满足题意,A =.解答2例2 解:⑴证明:因为AE=2,所以AE=4,又AB=2,AB丄AE,所以BE===2.因为Ac==BE,所以Ac是Rt△ ABE的斜边BE上的中线,所以c是BE的中点,又cD是厶ABE的中位线,所以cD// AB.因为cD平面PAB,AB平面PAB,所以cD//平面PAB. (2) 由题意可知AB,AE,AP两两垂直,以A为原点,AB,AE,AP所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系.因为AB=AP=AE=2且c,D分别是BE,AE的中点,所以AE=4,AD=2,贝V E(0,4,0),c(1,2,0),P(0,0,2),D(0,2,0),所以=(0,4,-2),=(1,2,-2),=(-1,0,0).设平面PcD的法向量为n=(x ' ,y ' ,z '),贝U即令y' =1,则x' =0,z ' =1,所以n=(0,1,1).设直线PE与平面PcD所成角的大小为B ,则sin 9 ==.例3 解:⑴证明:连接PE.••• PA=Ac,/ PAD玄cAD,AE 是公共边,•••△ PAE^A cAE,:丄 PEA=/ cEA.••• cE丄AD, A PE丄AD,又PE A cE=E,A ADL平面PcE,••• Pc 平面PcE,A AD L Pc.(2) T AD丄平面PEc,平面PAD L平面ABcD,A EP,EA,Ec两两垂直,以E为原点,EA,Ec,EP 所在直线分别为x,y,z轴建立空间直角坐标系,如图所示.••• PA=Ac=2,/ PAD玄cAD=60° ,AD=3,A AE=1,PE=cE=,DE=2,则E(0,0,0),D(-2,0,0),c(0,,0),P(0,0,),=(2,0,),=(2,,0).设平面PcD的法向量为n=(x,y,z),则即令x=-,则y=2,z=2, A n=(-,2,2).易知平面PAD的一个法向量为=(0,,0).设二面角c-PD-A的平面角为B ,贝卩|cos 0 |===,显然二面角c-PD-A的平面角是锐角,故二面角c-PD-A 的余弦值为.【自我检测】1. 解:⑴证明:在厶BcD 中,EB=ED=Ec=Bc,故/ BcD=, / cBE=Z cEB=,•••△DAB^A DcB, •••△EAB^A EcB,从而有/ FED=Z BEc=Z AEB=,Ec=EA,•••/ FED=/ FEA,ED=EA故EF丄AD,AF=FD.又PG=GD 「FG II PA. T PA!平面ABcD,••• GFL平面ABcD,「. GF! AD,又GF Q EF=F,故ADL平面cFG.••• AD平面PAD, A平面PAD!平面cGF.(2) 由⑴知/ EAB=/ EcB=, / DEF=/ FEA=,AE=ED, A/EAF=,A BAF=,即BA! AF.以点A为坐标原点,AB,AD,AP所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,则A(0,0,0),B(2,0,0),c(3,,0),D(0,2,0),P(0,0,3),故=(1,,0),=(-3,-,3),=(-3,,0).设平面BcP的法向量为n仁(x1,y1,z1),贝U即令x仁1,则y1=-,z仁,A n1=.设平面DcP的法向量为n2=(x2,y2,z2), 则即令x2=1,贝Uy2=,z2=2, n2=(1,,2).设平面BcP与平面DcP所成的锐二面角为B ,则cos 92. 解:⑴证明:取PD的中点N,连接AN,N,则N// cD,且N=cD.••• AB// cD,且AB=cD,「. N// AB,且N=AB贝U四边形ABN 为平行四边形,••• AN// B,又B丄平面PcD,•A N!平面PcD, • AN! PD,AN丄cD.由ED=EA即卩PD=PA且N为PD的中点,AN! PD,可得△PAD为等边三角形,•••/ PDA=60 ,又/ EDc=150°,•/ cDA=90° ,即cD! AD.••• AD A AN=A,•c D丄平面PAD,又cD平面ABcD,•平面PADL平面ABcD.(2) ••• AB// cD,PcD为直线Pc与AB所成的角,由(1)可得/ PDc=90° , • tan / PcD==,「. cD=2PD.设PD=1,贝» cD=2,PA=AD=AB=1,取AD的中点o,连接Po,过o作AB的平行线,建立如图所示的空间直角坐标系o-xyz,贝y D,B,p,,则=(1,1,0),=,=.设n=(x,y,z) 为平面PBD的法向量,则即令x=3,则y=-3,z=-, n=(3,-3,-),贝y cos===-,故直线B与平面PDB所成角的正弦值为.3. 解:⑴证明:如图所示,取AD的中点o,连接Po,oB. •••PA=PD,「. Po 丄AD. v / ADc=Z BcD=90° , /. Bc II AD,又Bc=AD=1,「. Bc=oD, •••四边形BcDo 为矩形,A oB=cD=1.<△PoB 中,Po=,oB=1,PB=2, •••/ PoB=90° ,贝U Po± oB. v ADA oB=o, A Po丄平面ABcD,又Po平面PAD, A平面PADL平面ABcD.(2) 由(1)知AD丄Po,AD L Bo, v Po A oB=o, A AD丄平面PoB,又AD平面ABcD, A平面PoB丄平面ABcD.过点P作PE L 平面ABcD,则垂足E 一定落在平面PoB与平面ABcD的交线oB 上.v四棱锥P-ABcD 的体积为,AX PE XX (AD+Bc) x cD= x PE XX (2+1) X 1=PE=, A PE=.v Po=, A oE==.以o为坐标原点,oA,oB所在直线分别为x,y 轴,在平面PoB内过点o作垂直于平面AoB的直线为z 轴,建立如图所示的空间直角坐标系o-xyz.由题意可知A(1,0,0),P,D(-1,0,0),c(-1,1,0), 则=,=(0,1,0),=. 设平面PcD的法向量为n=(x,y,z), 则即令x=1,则y=0,z=-, n=. 设直线PA与平面PcD所成的角为B ,则sin 9 ===,故直线PA 与平面PcD所成角的正弦值为.解答3例4解:(1)证明:因为等边三角形ABc的边长为3,且==,所以AD=1,AE=2.在厶ADE中,/ DAE=60 ,由余弦定理得DE==.因为AD2+DE2=AE2,所以AD丄DE,故折叠后有A1D丄DE.因为二面角A1-DE-B是直二面角,所以平面A1DEL平面BcED,又平面A1DE?平面BcED=DE,A1D平面A1DE,A1DL DE, 所以A1D丄平面BcED.(2) 由(1)知ED± DB,A1D丄平面BcED.以D为坐标原点,DB,DE,DA1所在直线分别为x,y,z轴建立空间直角坐标系D-xyz,如图所示,设PB=2a(0< 2a< 3),过点P作Ph U BD于H,则PH=a,DH=2-a,所以A1(0,0,1),P(2-a,a,0),E(0,,0),所以=(a-2,-a,1),易知平面A1BD的一个法向量为=(0,,0).若直线PA1与平面A1BD所成的角为60° ,则sin60 ° ===,解得a=,则PB=2a=,满足O W 2a< 3,符合题意.故在线段Bc上存在点P,使直线PA1与平面A1BD所成的角为60° ,此时PB=.【自我检测】解:(1)证明:以A为原点,AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,如图所示,贝V A(0,0,0),B(2,0,0),c(2,1,0),D(0,2,0),P(0,0,2),故=(0,2,0),=(0,0,2),•••为AD的中点,•••(0,1,0),=(2,0,0).••• ?=0, ?=0,••• c± PA,c 丄AD,又PA平面PAD,AD?平面PAD且PA A AD=A,• c丄平面PAD.••• c平面Pc, •平面Pc丄平面PAD.(2) 过点作Q丄PD于点Q,由⑴知c丄平面PAD,PD平面PAD,... c丄PD,又Q Q c=, ••• PD丄平面cQ.设平面Pc的法向量为n=(x,y,z),贝U即令y=2,则x=0,z=1, ••• n=(0,2,1).••• PDL平面cQ,••• =(0,2,-2) 是平面cQ的一个法向量.设二面角P-c-Q的平面角为B ,易知其为锐角,• •• cos 0 ===,故二面角P-c-Q的余弦值为.[备选理由]例1是以四棱柱为载体来考查线面垂直的证明与求二面角的问题,本题的关键是完成第(1)问的证明,需要充分利用平面几何的性质;例2的关键是第(2)问依据线面角求棱的长度;例3为不规则几何体,是涉及平行、二面角、线线垂直的探究性命题,需要合理建立空间直角坐标系,利用空间向量求解.例1 [配例3使用]如图,四棱柱ABcD-A1B1c1D1的底面ABcD是正方形,o为Ac和BD的交点,且AB=AA仁2,Z A1AB= / A1AD=60 .(1) 求证:A1o丄平面ABcD;(2) 求二面角C1-BD-C的余弦值.解:⑴证明:连接A1B,A1D,由题意知厶ABA1A ADA1均是边长为2的等边三角形,所以A1B=A1D=2所以△ ABM A A1BD.因为底面ABcD是正方形,所以Ac与BD相互垂直且平分,所以A1o丄BD,且A1o=Ao=,因为A1o2+Ao2=4=A1A2所以A1o丄Ao,又Ao n BD=o,Ao,BD 平面ABcD,所以A1o丄平面ABcD.(2) 连接A1c1,oc1,由⑴可知BD丄平面AcclAI,所以BD 丄oc,BD 丄oc1,所以/ cloc为二面角C1-BD-C的平面角,易知/ cloc为锐角.以o为原点,oA,oB,oA1所在直线分别为x,y,z轴建立空间直角坐标系,如图所示,则o(0,0,0),c(-,0,0),A1(0,0,),A(,0,0), 所以=(-,0,0),=+=+=(-2,0,),所以cos / c1oc=cos===.故二面角C1-BD-C的余弦值为.例2 [配例3使用]如图所示,四棱柱ABcD-A1B1c1D1 的底面为菱形,/ BAD=120 ,AB=2,E,F分别为cD,AA1的中占八、、・⑴求证:DF //平面B1AE;(2) 若AA1丄底面ABcD,且直线AD1与平面B1AE所成角的正弦值为,求AA1的长.解:(1)证明:设G为AB1的中点,连接EG,GF,因为FGA1B1QEA1B1 所以FGDE,所以四边形DEGF是平行四边形,所以DF/ EG,又DF?平面B1AE,EG平面B1AE,所以DF//平面B1AE.(2) 连接Ac,因为四边形ABcD是菱形,且/ ABc=60° ,所以△ ABc是等边三角形,取Bc的中点Q,则AQL AD,因为AA1丄平面ABcD,所以AA1丄AQ,AA1丄AD.以A为原点,AQ,AD,AA1所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,设AA1=t(t>0),则A(0,0,0),E,B1(,-1,t),D1(0,2,t),=,=(,-1,t),=(0,2,t).设平面B1AE的法向量为n=(x,y,z),贝U即令y=t,则x=-t,z=4,所以n=(-t,t,4).设直线AD1与平面B1AE所成的角为B ,贝U sin 0 ===,解得t=2,故线段AA1的长为2.例3 [配例4使用]如图所示,四边形ABcD是梯形,AD II Bc, / BAD=90° ,四边形CC1D1D为矩形,已知AB丄Bc1,AD=4,AB=2,Bc=1.(1) 求证:Bc1 I 平面ADD1.(2) 若DD仁2,求平面Ac1D1与平面ADD1所成的锐二面角的余弦值.(3) 设P为线段c1D上的一个动点(端点除外),判断直线Bc1与直线cP能否垂直?并说明理由.解:⑴证明:由四边形CC1D1D为矩形,得cc1 II DD1,又因为DD1平面ADD1,cc1平面ADD1所以cc1 I平面ADD1.同理,Bc I平面ADD1,因为Bc n cc仁c,所以平面Bcc1 I 平面ADD1,又因为Bc1平面Bcc1,所以Bc1 I平面ADD1.(2) 由AD// Bc, / BAD=90 ,得AB丄Bc,又因为AB丄Bc1,Bc n Bc1=B,所以AB丄平面Bcc1,所以AB丄cc1.因为四边形CC1D1D为矩形,且底面ABcD中AB与cD相交于一点,所以cc1丄平面ABcD,又因为cc1 I DD1,所以DD1丄平面ABcD.过点D在底面ABcD中作D丄AD,则DA,D,DD1两两垂直,以DA,D,DD1所在直线分别为x,y,z轴,建立空间直角坐标系如图,则D(0,0,0),A(4,0,0),B(4,2,0),c(3,2,0),c1(322),D1(0,0,2),所以=(-1,2,2),=(-4,0,2).设平面Ac1D1的法向量为=(x,y,z),贝U即令x=2,则y=-3,z=4,所以=(2,-3,4),易得平面ADD1的一个法向量为n=(0,1,0),所以cos==-,故平面Ac1D1与平面ADD1所成的锐二面角的余弦值为.(3) 直线Bc1与直线cP不可能垂直.设DD1=(>0),=入(入€ (0,1)),由B(4,2,0),c(3,2,0),c1(3,2,),D(0,0,0),得=(-1,0,),=(3,2,),= 入=(3 入,2入,入),=(-3,-2,0),=+=(3 入-3,2 入-2,入).若Bc1± cP,则?=-(3 入-3)+ 入2=0,即(2-3)入=-3,因为入工0,所以2=-+3>0,解得入>1,这与0 所以直线Bc1与直线cP不可能垂直.★精品文档★-独家原创27 / 27。
数学高三立体几何与空间向量专题复习检测(含答案)

数学2019届高三立体几何与空间向量专题复习检测(含答案)立体几何是3维欧氏空间的几何的传统名称,下面是立体几何与空间向量专题复习检测,请考生练习。
一、选择题1.(2019武汉调研)一个几何体的三视图如图所示,则该几何体的直观图可以是()解析A、B、C与俯视图不符.答案D2.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧(左)视图为()解析抓住其一条对角线被遮住应为虚线,可知正确答案在C,D中,又结合直观图知,D正确.答案D3.(2019安徽卷)一个多面体的三视图如图所示,则该多面体的表面积为()A.21+3B.18+3C.21D.18解析由三视图知,该多面体是由正方体割去两个角所成的图形,如图所示,则S=S正方体-2S三棱锥侧+2S三棱锥底=24-231211+234(2)2=21+3.4.已知S,A,B,C是球O表面上的点,SA平面ABCD,ABBC,SA=AB=1,BC=2,则球O的表面积等于()A.4B.3C.2解析如图所示,由ABBC知,AC为过A,B,C,D四点小圆直径,所以ADDC.又SA平面ABCD,设SB1C1D1-ABCD为SA,AB,BC为棱长构造的长方体,得体对角线长为12+12+22=2R,所以R=1,球O的表面积S=4.故选A.答案A5.(2019湖南卷)一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4解析由三视图可得原石材为如图所示的直三棱柱A1B1C1-ABC,且AB=8,BC=6,BB1=12.若要得到半径最大的球,则此球与平面A1B1BA,BCC1B1,ACC1A1相切,故此时球的半径与△ABC内切圆的半径相等,故半径r=6+8-102=2.故选B.6.点A,B,C,D均在同一球面上,其中△ABC是正三角形,AD平面ABC,AD=2AB=6,则该球的体积为()A.323B.48C.643D.163解析如图所示,O1为三角形ABC的外心,过O做OEAD,OO1面ABC,AO1=33AB=3.∵OD=O A,E为DA的中点.∵AD面ABC,AD∥OO1,EO=AO1=3.DO=DE2+OE2=23.R=DO= 23.V=43(23)3=323.答案A二、填空题7.某四棱锥的三视图如图所示,该四棱锥的体积是________.解析由三视图可知,四棱锥的高为2,底面为直角梯形ABCD.其中DC=2,AB=3,BC=3,所以四棱锥的体积为132+3322=533.答案5338.如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1V2=________.解析设三棱柱A1B1C1-ABC的高为h,底面三角形ABC的面积为S,则V1=1314S12h=124Sh=124V2,即V1V2=124.答案1249.在四面体ABCD中,AB=CD=6,AC=BD=4,AD=BC=5,则四面体ABCD的外接球的表面积为________.解析构造一个长方体,使得它的三条面对角线分别为4、5、6,设长方体的三条边分别为x,y,z,则x2+y2+z2=772,而长方体的外接球就是四面体的外接球,所以S=4R2=772.答案772三、解答题10.下列三个图中,左边是一个正方体截去一个角后所得多面体的直观图.右边两个是其正(主)视图和侧(左)视图.(1)请在正(主)视图的下方,按照画三视图的要求画出该多面体的俯视图(不要求叙述作图过程).(2)求该多面体的体积(尺寸如图).解(1)作出俯视图如图所示.(2)依题意,该多面体是由一个正方体(ABCD-A1B1C1D1)截去一个三棱锥(E-A1B1D1)得到的,所以截去的三棱锥体积VE-A1B1D1=13S△A1B1D1A1E=1312221=23,正方体体积V正方体AC1=23=8,所以所求多面体的体积V=8-23=223.11.(2019安徽卷)如图,四棱柱ABCD-A1B1C1D1中,A1A底面ABCD.四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为,BB1与的交点为Q.(1)证明:Q为BB1的中点;(2)求此四棱柱被平面所分成上下两部分的体积之比.解(1)证明:因为BQ∥AA1,BC∥AD,BCBQ=B,ADAA1=A,所以平面QBC∥平面A1AD.从而平面A1CD与这两个平面的交线相互平行,即QC∥A1D.故△QBC与△A1AD的对应边相互平行,于是△QBC∽△A1AD.所以BQBB1=BQAA1=BCAD=12,即Q为BB1的中点.(2)如图,连接QA,QD.设AA1=h,梯形ABCD的高为d,四棱柱被平面所分成上下两部分的体积分别为V上和V下,BC=a,则AD=2a.VQ-A1AD=13122ahd=13ahd,VQ-ABCD=13a+2a2d12h=14ahd,所以V下=VQ-A1AD+VQ-ABCD=712ahd,又V四棱柱A1B1C1D1-ABCD=32ahd,所以V上=V四棱柱A1B1C1D1-ABCD-V下=32ahd-712ahd=1112ahd.故V上V下=117.B级能力提高组1.(2019北京卷)在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,2).若S1,S2,S3分别是三棱锥D-ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则()A.S1=S2=S3B.S2=S1且S2S3C.S3=S1且S3 S2D.S3=S2且S3S1解析作出三棱锥在三个坐标平面上的正投影,计算三角形的面积.如图所示,△ABC为三棱锥在坐标平面xOy上的正投影,所以S1=1222=2.三棱锥在坐标平面yOz上的正投影与△DE F(E,F 分别为OA,BC的中点)全等,所以S2=1222=2.三棱锥在坐标平面xOz上的正投影与△DGH(G,H分别为AB,OC的中点)全等,所以S3=1222=2.所以S2=S3且S1S3.故选D.答案D2.(2019山东卷)三棱锥P-ABC中,D,E分别为PB,PC的中点,记三棱锥D-ABE的体积为V1,P-ABC的体积为V2,则V1V2=________. 解析由于VP-ABE=VC-ABE,所以VP-ABE=12VP-ABC,又因VD-ABE=12VP-ABE,所以VD-ABE=14VP-ABC,V1V2=14.答案143.(理)(2019课标全国卷Ⅱ)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角D-AE-C为60,AP=1,AD=3,求三棱锥E-ACD的体积.解(1)连接BD交AC于点O,连接EO.因为ABCD为矩形,所以O为BD的中点.又E为PD的中点,所以EO∥PB.EO平面AEC,PB平面AEC,所以PB∥平面AEC.(2)因为PA平面ABCD,ABCD为矩形,所以AB,AD,AP两两垂直.如图,以A为坐标原点,AB的方向为x轴的正方向,|PA|为单位长,建立空间直角坐标系A-xyz.则D(0,3,0),E0,32,12,AE=0,32,12.设B(m,0,0)(m0),则C(m,3,0),AC=(m,3,0),设n1=(x,y,z)为平面ACE的法向量,则n1AC=0,n1AE=0,即mx+3y=0,32y+12z=0,可取n1=3m,-1,3.又n2=(1,0,0)为平面DAE的法向量,由题设|cos〈n1,n2〉|=12,即33+4m2=12,解得m=32.因为E为PD的中点,所以三棱锥E-ACD的高为12.三棱锥E-ACD的体积V=131233212=38.3.(文)如图,在Rt△ABC中,AB=BC=4,点E在线段AB上.过点E 作EF∥BC交AC于点F,将△AEF沿EF折起到△PEF的位置(点A 与P重合),使得PEB=30.(1)求证:EF(2)试问:当点E在何处时,四棱锥P-EFCB的侧面PEB的面积最大?并求此时四棱锥P-EFCB的体积.解(1)证明:∵AB=BC,BCAB,又∵EF∥BC,EFAB,即EFBE,EFPE.又BEPE=E,EF平面PBE,EFPB.(2)设BE=x,PE=y,则x+y=4.S△PEB=12BEPEsinPEB=14xy14x+y22=1.当且仅当x=y=2时,S△PEB的面积最大.此时,BE=PE=2.由(1)知EF平面PBE,平面PBE平面EFCB,在平面PBE中,作POBE于O,则PO平面EFCB.即PO为四棱锥P-EFCB的高.又PO=PEsin30=212=1.S梯形EFCB =12(2+4)2=6.VP-BCFE=1361=2.我国古代的读书人,从上学之日起,就日诵不辍,一般在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第讲空间几何体、空间中的位置关系.()[·全国卷Ⅲ]中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()图图()[·全国卷Ⅱ]一个四面体的顶点在空间直角坐标系中的坐标分别是(),(),(),(),画该四面体三视图中的正视图时,以平面为投影面,则得到的正视图可以为()图[试做]命题角度由直观图求三视图的问题关键一:注意正视图、侧视图和俯视图的观察方向;关键二:注意看到的轮廓线和棱是实线,看不到的轮廓线和棱是虚线..[·全国卷Ⅰ]某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为()图[试做]命题角度与三视图有关的几何体的表面积和体积问题()关键一:由三视图想象几何体的结构特征,并画出该几何体的空间图形;关键二:搞清楚几何体的尺寸与三视图尺寸的关系;关键三:利用外部补形法,将几何体补成长方体或正方体等常见几何体.()看三视图时,需注意图中的虚实线.()求不规则几何体的表面积和体积时,通常将所给几何体分割为基本的柱、锥、台体..()[·全国卷Ⅱ]已知圆锥的顶点为,母线所成角的余弦值为与圆锥底面所成角为°.若△的面积为,则该圆锥的侧面积为.()[·全国卷Ⅰ]在长方体中与平面所成的角为°,则该长方体的体积为()[试做]命题角度空间几何体的面积与体积()求规则几何体的体积,只需确定底面与相应的高,而求一些不规则几何体的体积往往需采用分割或补形思想,转化求解.()求组合体的表面积时,需注意组合体衔接部分的面积,分清侧面积和表面积..()[·全国卷Ⅰ]如图,在下列四个正方体中为正方体的两个顶点为所在棱的中点,则在这四个正方体中,直线与平面不平行的是()图()[·全国卷Ⅱ]α,β是两个平面是两条直线,有下列四个命题:①如果⊥⊥α∥β,那么α⊥β.②如果⊥α∥α,那么⊥.③如果α∥β⊂α,那么∥β.④如果∥,α∥β,那么与α所成的角和与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号)[试做]命题角度空间中线面位置关系的判定关键一:逐个寻找反例作出否定的判断,逐个进行逻辑证明作出肯定的判断;关键二:结合长方体模型或实际空间位置作出判断,但要注意准确应用定理,考虑问题全面细致..()[·全国卷Ⅲ]设是同一个半径为的球的球面上四点,△为等边三角形且其面积为,则三棱锥体积的最大值为()()[·全国卷Ⅲ]在封闭的直三棱柱内有一个体积为的球.若⊥,则的最大值是()ππ.[试做]命题角度多面体与球()解决与球有关的组合体问题:关键一:分清球是内切还是外接;关键二:确定球心在多面体中的位置,确定球的半径或直径与多面体相关元素之间的关系;关键三:球的每个截面都是圆.()设正四面体的棱长为,则其外接球的半径,内切球的半径..[·全国卷Ⅰ]已知正方体的棱长为,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为().[试做]命题角度解决平面截正方体所形成的图形问题关键一:根据已知条件确定所求平面或与所求平面平行的平面;关键二:根据平面特点利用数形结合思想确定截面形状..()[·全国卷Ⅱ]在长方体中,则异面直线与所成角的余弦值为().()[·全国卷Ⅱ]已知直三棱柱中,∠°,则异面直线与所成角的余弦值为().[试做]命题角度解决异面直线所成角问题()关键一:先通过作图(三角形中位线、平行四边形补形)来构造平行线,再通过解三角形求解; 关键二:补形法(补成长方体、正方体)求解.()当异面直线所成角为时,两异面直线互相垂直.()用空间向量法解决.小题空间几何体的三视图与直观图()如图,在正方体中分别为棱的中点,用过点的平面截正方体,则位于截面以下部分的几何体的侧视图为()图图()已知某几何体的三视图如图所示,则该几何体最长棱的长为()图. . .[听课笔记]【考场点拨】识别三视图应注意以下几方面:()看线型,是线段、虚线还是曲线,确定此几何体是简单多面体还是旋转体;()分部分,想整体,看是简单几何体还是组合体;()对比一些熟悉的三视图模型分析,如正方体、圆锥、三棱锥的三视图模型. 【自我检测】.某几何体的正视图与俯视图如图,则其侧视图可能是()图图.某几何体的三视图如图所示,则此几何体的各个面中最大面的面积为 ()图.[·北京卷]某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()图.如图所示,在正方体中为的中点,则△在该正方体各个面上的射影可能是()图①②③④图.①④.②③.②④.①②小题空间几何体的表面积与体积()已知矩形中,把这个矩形分别以所在直线为轴旋转一周,所成几何体的侧面积分别记为,则与的比值为()()在三棱锥中⊥底面,△为正三角形,若∥,则三棱锥与三棱锥的公共部分构成的几何体的体积为()..[听课笔记]【考场点拨】高考中求几何体的表面积和体积易失分点:()计算表面积时,有些面没有计算到,有遗漏;()求组合体的表面积时没注意重合部分的面积.【自我检测】.某几何体的三视图如图所示,则该几何体的表面积为()图.在三棱柱中分别为棱的中点,过的截面把三棱柱分成两部分,则这两部分的体积之比为() ∶∶∶∶.《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如“堑堵”指的是底面为直角三角形,且侧棱垂直于底面的三棱柱;“阳马”指的是底面为矩形,一侧棱垂直于底面的四棱锥.如图所示,在堑堵中⊥,当堑堵的侧面积取得最大值时,阳马的体积为()图...小题多面体与球角度外接球问题在矩形中,将△沿折起,当平面⊥平面时,四面体的外接球的体积是().π.π.π.π[听课笔记]【考场点拨】解决多面体的外接球问题,关键是确定球心位置,方法是先选择多面体中的一面,确定此面多边形外接圆的圆心,再过此圆心作垂直于此面的垂线,则球心一定在此垂线上,最后根据其他顶点情况确定球心的准确位置.对于特殊的多面体还可以通过补成正方体或长方体的方法找到球心位置.【自我检测】.在三棱锥中⊥⊥,且三棱锥的体积为,则该三棱锥的外接球半径是().设直三棱柱的所有顶点都在一个球面上,且球的表面积是π,若,∠π,则此直三棱柱的高是.角度内切球问题设正三棱锥的高为,且此三棱锥内切球的半径为,若二面角的正切值为,则()[听课笔记]【考场点拨】解决多面体的内切球问题,一般是将多面体分割为以球心为顶点,多面体的各面为底面的棱锥,利用多面体的体积等于各分割棱锥的体积之和求内切球的半径.【自我检测】.在三棱锥中,侧棱,当三棱锥的三个侧面的面积之和最大时,三棱锥内切球的表面积是().()π.()π.()π.()π.已知圆锥的高为,侧面积为π,若此圆锥内有一个体积为的球,则的最大值为.小题空间线面位置关系的判断角度线面位置关系()已知直线,平面α,β,且⊥α⊂β,给出下列说法:①若α∥β,则⊥;②若α⊥β,则∥;③若∥,则α⊥β;④若⊥,则α∥β.其中正确说法的序号是().①②.①③.②④.③④()如图,在正方形中分别是的中点是的中点,沿将正方形折起,使重合于点,构成四面体,则在四面体中,给出下列结论:①⊥平面;②⊥;③⊥平面;④⊥;⑤平面⊥平面.其中正确结论的序号是()图.①②③⑤.②③④⑤.①②④⑤.②④⑤[听课笔记]【考场点拨】判断空间点、线、面的位置关系,主要依赖于四个公理,平行关系和垂直关系的有关定义及定理.具体处理时可以构建长方体或三棱锥等模型,把要考查的点、线、面融入模型中,使判断简洁明了.如要否定一结论,只需找到一个反例即可.【自我检测】.已知α,β是两个不同的平面是一条直线,给出下列说法:①若⊥α,α⊥β,则∥β;②若∥α,α∥β,则∥β;③若⊥α,α∥β,则⊥β;④若∥α,α⊥β,则⊥β.其中正确说法的个数为().若为两条不同的直线,α为一个平面,且⊥α,则“∥α”是“⊥”的().充分不必要条件.必要不充分条件.充要条件.既不充分也不必要条件角度异面直线所成的角、线面角()已知△与△均为正三角形,且.若平面与平面垂直,且异面直线与所成的角为θ,则θ()..()已知三棱柱的侧棱与底面垂直,体积为,底面是边长为的正三角形.若为底面的中心,则与平面所成角的大小为()..[听课笔记]【考场点拨】()求异面直线所成的角,一般是通过平移构建三角形求解,要注意异面直线所成的角是锐角或直角,若计算出钝角,其补角才是异面直线所成的角.()求直线与平面所成角的关键是过直线上一点作出这个平面的垂线,进而直线与直线在平面内的射影所成的角即为直线与平面所成的角.()当空间关系较为复杂时也可以建立空间直角坐标系,利用向量求解.【自我检测】.如图所示为一个半圆柱,△是等腰直角三角形是线段的中点,该半圆柱的体积为π,则异面直线与所成角的正弦值为()图.....在四边形中,且⊥,现将△沿翻折到△'的位置,则在△折起至与平面重合的过程中,直线'与平面所成角最大时的正弦值为()..角度截面问题()在棱长为的正方体中为棱的中点,过点且与平面平行的截面面积为()()已知棱长为的正方体中,球与该正方体的各面都相切,则平面截此球所得的截面面积为()..[听课笔记]【考场点拨】几何体截面面积问题,关键是确定截面图形的位置、形状,所经过的点,截面面积根据有关数量进行计算.【自我检测】.已知一个棱长为的正方体被一个平面截后所得几何体的三视图如图所示,则该截面的面积为() ..图.过半径为的球表面上一点作球的截面,若与该截面所成的角为°,则该截面的面积是.模块四立体几何与空间向量第讲空间几何体、空间中的位置关系典型真题研析.()()[解析] ()卯眼的空间立体图如图,同时需要注意,在三视图中看不见的线用虚线表示,故选.()在空间直角坐标系中画出三棱锥,由已知可知三棱锥为题中所描叙的四面体,而其在平面上的投影为正方形,故选.[解析] 该几何体为一个三棱柱和一个三棱锥的组合体,其直观图如图所示,各个面中有两个全等的梯形,其面积之和为××..()π()[解析] ()设圆锥的底面圆的半径为,因为与圆锥底面所成角为°,所以.由∠得∠,所以··∠×××,所以,所以圆锥的侧面积为ππ.()如图,连接,易知∠即为与平面所成的角,由题易知∠°,易得.设,则有, 解得,所以该长方体的体积××..()()②③④[解析] 因为分别为对应棱的中点,所以在选项中均有∥,在选项中,有∥,所以在选项中均有与平面平行,所以选.()对于①⊥⊥α∥β,则α,β的位置关系无法确定,故错误;对于②,因为∥α,所以可过直线作平面γ与平面α相交于直线,则∥,因为⊥α,所以⊥,所以⊥,故正确;对于③,由两个平面平行的性质可知其正确;对于④,由线面所成角的定义和等角定理可知其正确.故正确的有②③④..()()[解析] ()由题易知当点到平面的距离最大时,三棱锥的体积最大.∵△,∴.设△的中心为,由等边三角形的性质得,.设球心为,则,∴,∴点到平面的距离的最大值为.故三棱锥体积的最大值为××.()当球与三侧面相切时,设球的半径为,∵⊥,∴,解得,不合题意.当球与直三棱柱的上、下底面相切时,设球的半径为,则,即,∴球的体积的最大值为π×π.[解析] 平面α与正方体的每条棱所在直线所成的角都相等,只需与过同一顶点的三条棱所成的角相等即可,如图,则平面与正方体过点的三条棱所成的角相等.若点分别为相应棱的中点,易证得平面平行于平面,且六边形为正六边形.正方体棱长为,所以正六边形的边长为,可得此正六边形的面积为,而在四个选项中,选项中的值都小于,所以选..()()[解析] ()方法一:以为坐标原点所在直线分别为轴建立空间直角坐标系,如图所示,则()(,)(,),所以(,)(,),所以<,>,所以异面直线与所成角的余弦值为.方法二:如图,在长方体的面的一侧再补填一个完全一样的长方体,连接.易知∥,所以异面直线与所成的角即为与所成的角.因为,所以.在△中∠,所以异面直线与所成角的余弦值为.()方法一:建立如图所示的空间直角坐标系,则()()(),所以(),故异面直线与所成角θ的余弦值θ.方法二:如图,将该直三棱柱补充成直四棱柱,其中∥且,则可得∥且,图中∠即为异面直线与所成的角或所成角的补角.在△中,所以∠.故异面直线与所成角的余弦值为.考点考法探究小题例()()[解析] ()取的中点,连接,则为过点的平面与平面的交线.延长,交的延长线于点,连接,交于点,连接,则为过点的平面与平面的交线.同理,连接并延长,交的延长线于点,连接,交于点,连接,则为过点的平面与平面的交线.所以过点的平面截正方体所得的截面为图中的正六边形.故可得位于截面以下部分的几何体的侧视图为选项中的图.故选.()根据三视图作出几何体的直观图如图所示,可计算得,故该几何体最长棱的长为.【自我检测】[解析] 由俯视图与正视图可知,该几何体是一个三棱柱挖去一个圆柱后剩余的部分,因此其侧视图是矩形且内部有一条虚线,虚线靠近矩形的左边部分,只有选项符合题意,故选.[解析] 由三视图可得,该几何体为如图所示的三棱锥.结合三视图中的数据可得△×××××,故此几何体的各个面中最大面的面积为.故选.[解析] 由三视图可得该几何体的直观图如图所示,且⊥平面,∴△和△均为直角三角形.又∵⊥⊥∩,∴⊥平面,∴⊥,∴△为直角三角形.故选.[解析] 从上下方向看,△的射影为图①所示的情况;从左右方向看,△的射影为图④所示的情况;从前后方向看,△的射影为图④所示的情况.故选.小题例()()[解析] ()设,则π··π··,∴.故选.()根据题意画出如图所示的几何体,三棱锥与三棱锥的公共部分构成的几何体为三棱锥.∵△为正三角形,∴△×××.∵⊥底面∥,∴四边形为矩形,则为与的中点,∴三棱锥的高为,∴三棱锥的体积××.故选.【自我检测】[解析] 根据三视图可得,该几何体为如图所示的四棱锥,则该几何体的表面积×××××××××.[解析] 根据题中的条件可知,截面与的交点为靠近的四等分点,所以该截面将三棱柱分成了一个三棱台和一个几何体.设三棱柱的体积,而三棱台的体积,所以几何体的体积,所以所得的两部分的体积之比为∶,故选.[解析] 根据题意,设,则有,堑堵的侧面积侧()×()≤,当且仅当时取等号,此时阳马的体积××××××,故选.小题例[解析] 设矩形的对角线的交点为,由矩形的性质结合题意可知×.在翻折过程中的长度不变,据此可知点为四面体外接球的球心,外接球的半径,∴外接球的体积ππ×π.【自我检测】[解析] 取的中点,连接,则,即为三棱锥的外接球球心.设外接球的半径为,则××,∴.故选.[解析] 设,球的半径为.由题意知△外接圆的半径为·.∵ππ,∴,又,∴,故直三棱柱的高是.例[解析] 取线段的中点,设在底面内的射影为,连接.设,则×,易知∠为二面角的平面角,∴∠,∴.设三棱锥的表面积为,体积为,则,即×××,化简得.【自我检测】[解析] 其中一个侧面的面积△×××∠∠,要使此面积最大,则∠°.同理可知,当两两垂直时,三棱锥的三个侧面的面积之和最大.设三棱锥的内切球的球心为,则到三棱锥的四个面的距离与球的半径相等.因为,所以,可得△,△,△,△的面积分别为,,所以三棱锥×()·××,解得,所以内切球的表面积()π..[解析] 设圆锥的母线长为,底面圆的半径为,则ππ,即,又,所以.当球的体积最大时,该球为圆锥的内切球,设内切球的半径为,则×()×××,故,所以π×π.小题例()()[解析] ()由⊥α,α∥β⇒⊥β,而⊂β,所以⊥,①正确;⊥α⊂β,α⊥β时的位置关系不确定,②不正确;由⊥α∥⇒⊥α,而⊂β,所以α⊥β,③正确;⊥α⊂β⊥时,α,β的位置关系不确定,④不正确.故选.()构成的四面体如图所示.因为⊥⊥,所以折叠后⊥⊥,又∩,所以⊥平面,所以①正确;由⊥平面⊂平面,可知⊥,所以②正确;因为⊥平面,且过一点有且只有一条直线垂直于一个平面,所以⊥平面是不正确的,所以③不正确;连接,由题意知⊥,且,所以⊥,又⊥∩,所以⊥平面,又因为⊂平面,所以⊥,所以④正确;因为⊥平面,且⊂平面,所以平面⊥平面,所以⑤正确.综上可知,正确结论的序号为①②④⑤,故选.【自我检测】[解析] ①若⊥α,α⊥β,则∥β或⊂β,①不正确;②若∥α,α∥β,则∥β或⊂β,②不正确;③若⊥α,α∥β,则⊥β,③正确;④若∥α,α⊥β,则∥β或⊂β或与β相交,④不正确.故选.[解析] 由⊥α且∥α,能推出⊥,充分性成立;若⊥α且⊥,则∥α或⊂α,必要性不成立.因此“∥α”是“⊥”的充分不必要条件,故选.例()()[解析] ()方法一:取的中点,连接.∵正三角形与正三角形所在平面互相垂直,∴⊥.分别取的中点,连接,则∥∥,则∠为异面直线与所成的角,易得,在△中,由余弦定理得∠,即θ.方法二:如图所示,取的中点,连接.∵正三角形与正三角形所在平面互相垂直,∴⊥⊥⊥.以为原点所在直线分别为轴,建立如图所示的空间直角坐标系,则()()()(),∴()(),故<,>,∴θ.()取的中点,连接,则由题易知点在上.∵⊥底面,∴∠为与平面所成的角,又平面∥平面,∴∠的大小等于与平面所成角的大小.∵×(),∴··,解得.又为正三角形的中心,∴,∴在△中∠,∴∠.故选.【自我检测】[解析] 设底面半圆的半径为,由×π,得.易得⊥,所以,又∥,所以异面直线与所成的角为∠,易知∠.[解析] 设与交于点,因为,所以⊥,因此在翻折过程中'在平面内的射影在直线上,所以∠'是直线'与平面所成的角.由已知可得',在△'中,设',则由余弦定理得∠',因为>,所以≥(当且仅当时取等号),此时∠'最大,且∠'.例()()[解析] ()取的中点的中点,则四边形即为所求的截面.根据正方体的性质,可得,易知四边形为菱形,所以其面积××,故选.()由题知△是边长为的等边三角形,所以所求截面为△的内切圆,可得截面圆的半径为,所以截面圆的面积为π.【自我检测】[解析] 如图所示,在正方体中分别为的中点.由三视图可知,该几何体是正方体截取棱台后剩余的部分.易知截面为等腰梯形,且,截面的高为,则截面的面积为.π[解析] 过半径为的球表面上一点作球的截面,若与该截面所成的角为°,则截面圆的半径是× °,故该截面的面积为π×()π.[备选理由] 例为一道高考题,考查对三视图的认识,并且通过计算对直观图中的各棱长作出准确判断;例以正方体为载体,较容易入手,考查空间想象能力和计算能力;例是三视图、多面体、球的综合问题,解决该问题的关键是根据三视图将几何体还原,从而得到该几何体是直三棱柱,最后利用长方体的外接球的特征求得结果;例考查异面直线所成的角,其基本思路是通过平移直线,把异面问题化归为共面问题来解决.例[配例使用] [·北京卷]某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为()[解析] 将四棱锥放在棱长为的正方体中,该四棱锥为''',如图所示.该四棱锥最长的棱为正方体的体对角线'',故选.例[配例使用] [·江苏卷]如图所示,正方体的棱长为,以其所有面的中心为顶点的多面体的体积为.[答案][解析] 该几何体是一个正八面体,而正八面体是由两个相同的正四棱锥组成的,由图可知一个正四棱锥的高为,底面边长为,所以正八面体的体积××()×.例[配例使用]中国古代数学名著《九章算术》中记载了一种名为“堑堵”的几何体,其三视图如图所示,则其外接球的表面积为().ππππ[解析] 由三视图可得该几何体是一个直三棱柱,将其扩展为长方体,易得长方体的长、宽、高分别是,该几何体的外接球为对应的长方体的外接球,而长方体的体对角线长为,所以该几何体外接球的半径为,故外接球的表面积为π×π,故选.例[配例使用]在四棱锥中⊥平面,底面是边长为的正方形为的中点,则异面直线与所成角的余弦值为()..[解析] 延长到,使,过作∥,且,连接.因为∥,所以四边形为平行四边形,所以∥.又∥∥,所以四边形为平行四边形,所以与共线,则∠为异面直线与所成的角或其补角.在△中,所以由余弦定理得∠.。
