人教版-数学-七年级上册-第四章图形认识初步单元测试14

合集下载

人教版数学七年级上册第四章《几何图形初步》单元测试题含答案

人教版初中数学七年级上册第四章《几何图形初步》测试一、选择題（每小題3分.共36分）1. 在的内部任取一点C作射线OC,则一定成立的是（）A. AAOB > ZAOC B・ZAOC > ZBOCC・ZLAOC = Z1BOC D. ZAOC < ZBOC2. 下列描述正确的是（）A. 若乙1+乙2+/3=180。

，则厶1、Z2、乙3互补.B. 两个锐角的和一定是钝角.C. 互补的两个角一定是一个锐角，一个钝角.D. 钝角的一半是锐角.3. 如图1是一块手表，早上8点时针、分针的位置如图所示，那么时针与分针所成的角度是（）A. 60°B. 80°C. 120°D. 150°4. 已知：ZJ=25. 12°, Z^ = 25°12%那么ZA、ZB的大小关系为（）A・ZA>ZB B. ZA<ZB C. ZB = AA D. ZB>Z^5. 用一对三角尺画出小于180。

的角，一共能画出（）个A. 10 B・ 11 C. 12 D. 136. 如图2,若Z1 = Z2,则下列结论正确的是（）A. OB 平分Z AOCB. OB、OC是ZAOD的三等分线C. ZAOC=ZBODD. ZAOD=3ZBOC1.如果Za + Z^ = 90°＞而Z0与互余.那么Za 与Zy 的关系是（） A ・一定互余 B ・一定互补 C. 一定相等 D.不能确定8.如图3,是O 直线AB 上一点.OD 是ZAOC 的平分线，OE 是ZCOB 的平分线，则 ZDOE 的度数是（）A. 70°B. 80°C. 90°D. 100°9. 如图4所示.下列说法中错误的是（）A. 04的方向是北偏东40。

•B. 的方向是北偏两 C. OC 的方向是南僞西30。

・D. OD 的方向是正东南方向•10. 如图 5. ZAOD=ZCOB=90°t ZAOC=a.则ZBOD的D. 180°-2aA. 90°+aB. 90°+2aC. 180°-a11. 一个角的余角比它的补角的丄少20°.则这个角为（）2A. 30°B・ 40° C. 60° D. 75°12、如图3・OB、OC是乙4OD内部的两条射线，OM平分乙4OB・ ON平分厶COD、若M0D=a・ 3ON=p・则MOC可表示为（）A. a—flB. 2a—ftC. a—2fl D・—a二、境空題（毎小題3分，共12分）13. 如图7・厶OC = 90。

完整版人教版七年级上册数学第四章几何图形初步含答案

人教版七年级上册数学第四章几何图形初步含答案一、单选题(共15题，共计45分)1、如图所示为几何体的平面展开图，则从左到右，其对应的几何体名称分别为（）A.圆锥，正方体，三棱锥，圆柱B.圆锥，正方体，四棱锥，圆柱C.圆锥，正方体，四棱柱，圆柱D.正方体，圆锥，圆柱，三棱柱2、把如图所示的纸片沿着虚线折叠，可以得到的几何体是（）A.三棱柱B.四棱柱C.三棱锥D.四棱锥3、笔尖在纸上快速滑动写出一个又一个字，用数学知识解释为（）A.点动成线B.线动成面C.面动成体D.以上答案都不对4、如图，是一个正方体纸盒的外表面展开图，则这个正方体纸盒是（）A. B. C. D.5、如图，直线l1∥l2，且分别与直线l交于C，D两点，把一块含30°角的三角尺按如图所示的位置摆放，若∠1＝50°，则∠2的度数为（）A.90°B.110°C.108°D.100°6、下列叙述：①最小的正整数是0；② 的系数是6π；③用一个平面去截正方体，截面不可能是六边形；④若AC=BC，则点C是线段AB的中点；⑤三角形是多边形；⑥绝对值等于本身的数是正数，其中正确的个数有（）A.2B.3C.4D.57、如图所示，从A地到达B地，最短的路线是（）A.A→C→E→BB.A→F→E→BC.A→D→E→BD.A→C→G→E→B8、如图，马聪同学用剪刀沿虚线将一片平整的银杏叶剪掉一部分，发现剩下的叶片的周长比原叶片的周长要小，能正确解释这一现象的数学知识是（）A.两点确定一条直线B.经过一点有无数条直线C.两点之间线段最短D.两直线相交只有一个交点9、下列说法正确的有（）①一个数的相反数不是正数就是负数；②海拔表示比海平面低；③负分数不是有理数；④由两条射线组成的图形叫做角；⑤把一个角放到一个放大5倍的放大镜下观看，角的度数也扩大5倍.A.0个B.1个C.2个D.3个10、如图，点C是线段AB的中点，点D是线段BC的中点，下列等式不正确的是（）A.CD=AC﹣DBB.CD=AD﹣BCC.CD=AB﹣ADD.CD=AB﹣BD11、下列图形中，经过折叠不能围成一个正方体的是（）A. B. C. D.12、“笔尖在纸上快速滑动写出数字6”，运用数学知识解释这一现象（）A.点动成线B.线动成面C.面动成体D.面面相交得线13、若一个角的补角等于它的余角的3倍，则这个角为（）A.75°B.60°C.45°D.30°14、如果一个角的补角为144°，那么这个角的余角为( )A.36°B.44°C.54°D.64°15、如图，下列说法中错误的是( )A.OD方向是东南方向B.OB方向是北偏西l5。

(新版人教版)七年级上第四章《图形认识初步》单元测试卷及解析答案

第四章《图形认识初步》综合测试题（满分120分时间 90分钟）一、选择题（每题3分，共30分）1． ①平角是一条直线；②射线是直线的一半；③射线AB 与射线BA 表示同一条射线；④用一个扩大2倍的放大镜去看一个角，这个角会扩大2倍；⑤两点之间，线段最短；⑥120.5°= 120°50׳.以上说法正确的有( )A .0个 B.1个 C.2个 D.3个2．下列四个图中，能用∠1、∠AOB 、∠O 三种方法表示同一个角的是（）3．下列叙述正确的是（）A ．180°是补角B 120°和60°互为补角C 120°和60°是补角D 60°是30°的补角4. 如图1表示一个用于防震的L 形的包装用泡沫塑料，当从上面看这一物体时看到的图形形状是（）5．下列图形中，哪一个是正方体的展开图（）6．甲看乙的方向为南偏西25°，那么乙看甲的方向是（）A ．北偏东75°B ．南偏东75°C ．北偏东25°D ．北偏西25°7．若∠A 的余角是70°，则∠A 的补角是（）A ．70°B ．110°C ．20°D ．160°8．如图，AOC ∠和BOD ∠都是直角，如果 ︒=∠150AOB ，那么=∠COD （） A 、︒30 B 、︒40 C 、︒50 D 、︒609.经过任意三点中的两点共可画出（）A ．1条直线B ．2条直线C ．1条或3条直线D ．3条直线AC B O DA ．B ．C ．D ．(图1)10.如图所示，从O 点出发的五条射线，可以组成角的个数是（）．A ．10个B ．9个C ．8个D ．4个二、填空题（每题3分，共30分）11．橙子类似______体，菠萝类似_______体，角柜类似_______体，金字塔类似_______体，粉笔盒类似_______体。

【数学】人教版七年级数学上册第四章几何图形的初步单元测试(含答案)

人教版七年级数学上册第四章几何图形的初步单元测试（含答案）一、单选题1．如图，图、图、图均由四个全等的等边三角形组成，其中能够折叠围成一个立体图形的有（）A．只有图①B．只有图①、图②C．图①、图②、图③D．只有图②、图③2．下列平面图形中不能围成正方体的是（）A．B．C．D．3．某校年级（1）班在“迎中考日誓师”活动中打算制作一个带有正方体挂坠的倒计时牌挂在班级，正方体的每个面上分别书写“成功舍我其谁”六个字如图是该班同学设计的正方体挂坠的平面展开图，那么“谁”对面的字是（）A．成B．功C．其D．我4．将一个底面直径是10厘米，高为36厘米的圆柱体锻压成底面直径为20厘米的圆柱体，在这个规程中不改变的是圆柱的（）A.高B.侧面积C.底面积D.体积5．用一个平面去截下列立体图形，截面可以得到三角形的立体图形有（）A．1个B．2个C．3个D．4个6．下列现象，能说明“线动成面”的是（）A．天空划过一道流星B．汽车雨刷在挡风玻璃上刷出的痕迹C．抛出一块小石子，石子在空中飞行的路线D．旋转一扇门，门在空中运动的痕迹7．点A，B，C在一条直线上，AB＝6，BC＝2，点M是AC的中点，则AM的长度为（）A．4 B．6 C．2或6 D．2或48．如图，小李同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是（）A.垂线段最短B.经过一点有无数条直线C.两点之间线段最短D.经过两点有且仅有一条直线9．将直角三角尺和长方形纸片如图放置，图中与∠1互余的角有A.2个B.3个C.4个D.5个10．如图，点位于点的（）.A.南偏东方向上B.北偏西方向上C.南偏东方向上D.南偏西方向上11．如图，直线AB，CD相交于点O，OE⊥AB于O,∠COE=55°,则∠BOD的度数是（）A.35°B.45°C.30°D.40°12．过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图几何体，其正确展开图正确的为（）A．B．C．D．二、填空题13．如图，C岛在A岛的北偏东60°方向，在B岛的北偏西45°方向，则从C岛看A、B两岛的视角∠ACB＝_______.14．如图，平面展开图折叠成正方体后，相对面上的两个代数式值相等，则x+y=________．15．如图，将一副三角板叠放在一起，使直角顶点重合于O，则∠AOC+∠DOB＝_____．16．线段,C是线段AB上一点，AC=4,M是AB的中点，点N是AC的中点，则线段NM的长是________.三、解答题17．从正面、左面、上面观察如图所示的几何体，分别画出你所看到的几何体的形状图。

人教版七年级上册数学第四章几何图形初步单元测试(含解析)

第四章几何图形初步单元测试一．选择题1．对如图所示几何体的认识正确的是（）A．棱柱的底面是四边形B．棱柱的侧面是三角形C．几何体是四棱柱D．棱柱的底面是三角形2．电视剧《西游记》中，孙悟空的“金箍棒”飞速旋转，形成一个圆面，是属于（）A．点动成线B．线动成面C．面动成体D．以上都不对3．下列说法正确的是（）A．延长直线AB到点CB．延长射线AB到点CC．延长线段AB到点CD．射线AB与射线BA是同一条射线4．如图，C为线段AD上一点，点B为CD的中点，且AD＝9，BD＝2．若点E在直线AD 上，且EA＝1，则BE的长为（）A．4B．6或8C．6D．85．下列说法正确的是（）A．两点之间的线段，叫做这两点之间的距离B．87'等于1.45°C．射线OA与射线AO表示的是同一条射线D．延长线段AB到点C，使AC＝BC6．线段AB＝9，点C在线段AB上，且有AC＝AB，M是AB的中点，则MC等于（）A．3B．C．D．7．某公司员工分别在A、B、C三个住宅区，A区有30人，B区有15人，C区有10人，三个区在一条直线上，位置如图所示，该公司的接送车打算在此间只设一个停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠点的位置应设在（）A．A区B．B区C．C区D．A、B两区之间8．如图，将一副三角板叠在一起使直角顶点重合于点O，（两块三角板可以在同一平面内自由转动），下列结论一定成立的是（）A．∠BOA＞∠DOC B．∠BOA﹣∠DOC＝90°C．∠BOA+∠DOC＝180°D．∠BOC≠∠DOA9．下列说法正确的是（）A．射线比直线短B．从同一点引出的两条射线所组成的图形叫做角C．若AP＝BP，则P是线段AB的中点D．两点之间的线段叫做这两点之间的距离10．如图，O在直线AB上，OC平分∠DOA（大于90°），OE平分∠DOB，OF⊥AB，则图中互余的角有（）对．A．6B．7C．8D．10二．填空题11．若一个六棱柱，则它有条棱，有个面．12．秒针旋转一周时，形成一个圆面，用数学知识可以理解为．13．已知点A、B、C在同一直线上，若AB＝10cm，AC＝16cm，点M、N分别是线段AB、AC中点，则线段MN的长是．14．如图，线段AB＝3，延长AB到点C，使BC＝2AB，则AC＝．15．如图，已知CD＝AD＝BC，E、F分别是AC、BC的中点，且BF＝40cm，则EF 的长度为cm．16．人们会把弯曲的河道改直，这样能够缩短航程．这样做的道理是．17．如图，有一种电子游戏，电子屏幕上有一条直线，在直线上有A，B，C，D四点，且AB＝BC＝CD，点P沿直线l从右向左移动，当出现点P与A，B，C，D四点中的至少两个点距离相等时，就会发出警报，则直线l上会发出警报的点P有个．18．如图，已知A、B是线段EF上两点，EA：AB：BF＝1：2：3，M、N分别为EA、BF 的中点，且MN＝8cm，则EF长为．19．如图，C、D是线段AB上的两点，E是AC的中点，F是BD的中点，若AB＝m，CD ＝n，则线段EF的长为．20．如图，射线OC，OD在∠AOB内，∠AOB和∠BOC互为补角，．若∠COD比∠BOD大m°（m＜30），则∠AOC＝°．（用含m的式子表示）三．解答题21．如图所示是一张铁皮．（1）计算该铁皮的面积；（2）它能否做成一个长方体盒子？若能，画出来，计算它的体积；若不能，说明理由．22．如图，线段AB＝20，BC＝15，点M是AC的中点．（1）求线段AM的长度；（2）在CB上取一点N，使得CN：NB＝2：3．求MN的长．23．如图，是小明家和学校所在地的简单地图，已知OA＝2km，OB＝3.5km，OP＝4km，点C为OP的中点，回答下列问题：（1）图中到小明家距离相同的是哪些地方？（2）由图可知，公园在小明家东偏南30°方向2km处．请用方向与距离描述学校、商场、停车场相对于小明家的位置．24．如图，在直线AD上任取一点O，过点O做射线OB，OE平分∠DOB，OC平分∠AOB，∠BOC＝26°时，求∠BOE的度数．25．如图，C是线段AB上一点，AC＝5cm，点p从点A出发沿AB以3cm/s的速度匀速向点B运动，点Q从点C出发沿CB以1cm/s的速度匀速向点B运动，两点同时出发，结果点P比点Q先到3s．（1）求AB的长；（2）设点P、Q出发时间为ts，①求点P与点Q重合时（未到达点B），t的值；②直接写出点P与点Q相距2cm时，t的值．26．线段与角的计算．（1）如图1，已知点C为AB上一点，AC＝15cm，CB＝AC，若D、E分别为AC、AB 的中点，求DE的长．（2）已知：如图2，∠AOB被分成∠AOC：∠COD：∠DOB＝2：3：4，OM平分∠AOC，ON平分∠DOB，且∠MON＝90°，求∠AOB的度数．参考答案1．解：如图所示的几何体是三棱柱，它有两个全等的三角形的底面，三个矩形的侧面，因此选项ABC均不符合题意，选项D符合题意；故选：D．2．解：孙悟空的“金箍棒”飞速旋转，形成一个圆面，是属于线动成面，故选：B．3．解：A、直线可以沿两个方向无限延伸，故不能说延长直线AB，故本选项不符合题意；B、射线可沿延伸方向无限延伸，故不能说延长射线AB，故本选项不符合题意；C、线段不能延伸，可以说延长线段AB到点C，故本选项符合题意；D、射线AB与射线BA不是同一条射线，故本选项不符合题意；故选：C．4．解：若E在线段DA的延长线，如图1，∵EA＝1，AD＝9，∴ED＝EA+AD＝1+9＝10，∵BD＝2，∴BE＝ED﹣BD＝10﹣2＝8，若E线段AD上，如图2，EA＝1，AD＝9，∴ED＝AD﹣EA＝9﹣1＝8，∵BD＝2，∴BE＝ED﹣BD＝8﹣2＝6，综上所述，BE的长为8或6．故选：B．5．解：A、应为：连结两点的线段的长度叫做这两点间的距离，故本选项错误；B、87'＝60'+27'＝1°+（）°＝1.45°，故本选项正确；C、射线OA的端点是点O，射线AO的端点是点A，所以，它们不是同一条射线，故本选项错误；D、延长线段AB到点C，则AC一定大于BC，不能使AC＝BC，故本选项错误．故选：B．6．解：∵AB＝9，∴AC＝AB＝3，∵M是AB的中点，∴AM＝AB＝∴MC＝AM﹣AC＝﹣3＝故选：B．7．解：∵当停靠点在A区时，所有员工步行到停靠点路程和是：15×100+10×300＝4500m，当停靠点在B区时，所有员工步行到停靠点路程和是：30×100+10×200＝5000m，当停靠点在C区时，所有员工步行到停靠点路程和是：30×300+15×200＝12000m，当停靠点在A、B区之间时，设在A区、B区之间时，设距离A区x米，则所有员工步行路程之和＝30x+15（100﹣x）+10（100+200﹣x），＝30x+1500﹣15x+3000﹣10x，＝5x+4500，∴当x＝0时，即在A区时，路程之和最小，为4500米；综上，当停靠点在A区时，所有员工步行到停靠点路程和最小，那么停靠点的位置应该在A区．故选：A．8．解：因为是直角三角板，所以∠AOC＝∠BOD＝90°，所以∠BOA+∠DOC＝∠AOC+∠BOC+∠DOC＝∠AOC＝∠BOD＝180°，故选：C．9．解：A．射线和直线不可以比较长短，原说法错误，故本选项不符合题意；B．从同一点引出的两条射线所组成的图形叫做角，原说法正确，故本选项符合题意；C．若点P在线段AB上，AP＝BP，则P是线段AB的中点，原说法错误，故本选项不符合题意；D．两点之间的线段的长度叫做这两点之间的距离，原说法错误，故本选项不符合题意；故选：B．10．解：∵OC平分∠DOA，∴∠AOC＝∠COD，∵OE平分∠DOB，∴∠DOE＝∠BOE，∴∠COE＝90°，∴∠AOC+∠BOE＝90°，∠AOC+∠DOE＝90°，∠COD+∠BOE＝90°，∠COD+∠DOE ＝90°，∠COF+∠EOF＝90°，∵OF⊥AB，∴∠AOC+∠COF＝90°，∠COD+∠COF＝90°，∠BOE+∠EOF＝90°，∠BOD+∠DOF ＝90°，∠DOE+∠EOF＝90°，∴互余的角有10对．故选：D．11．解：因为六棱柱上下两个底面是6边形，侧面是6个长方形，所以共有18条棱，8个面；故答案为18，8．12．解：根据点、线、面、体之间的关系可得，线动成面．13．解：（1）如图1，，∵AB＝10cm，点M是线段AB的中点，∴AM＝10÷2＝5（cm）；∵AC＝16cm，点N是线段AC的中点，∴AN＝16÷2＝8（cm），∴MN＝AM+AN＝5+8＝13（cm）（2）如图2，，∵AB＝10cm，点M是线段AB的中点，∴AM＝10÷2＝5（cm）；∵AC＝16cm，点N是线段AC的中点，∴AN＝16÷2＝8（cm），∴MN＝AN﹣AM＝8﹣5＝3（cm），综上，线段MN的长是13cm或3cm．故答案为：13cm或3cm．14．解：∵AB＝3，∴BC＝2AB＝6，∴AC＝AB+BC＝3+6＝9．故答案为：9．15．解：∵点F是BC的中点，且BF＝40cm，∴BC＝2BF＝80cm，∵CD＝AD＝BC，∴CD＝×80＝16cm，AD＝64cm，∴AC＝AD﹣CD＝48cm，∵E、F分别是AC、BC的中点，∴CE＝AC＝24cm，CF＝BF＝40cm，∴EF的长度为CE+CF＝64cm，故答案为：64．16．解：由线段的性质可知，把弯曲的河道改直，能够缩短航程，这样做根据的道理是两点之间线段最短，故答案为：两点之间线段最短．17．解：根据题意可知：当点P经过任意一条线段中点时会发出报警，∵图中共有线段DC、DB、DA、CB、CA、BA，∵BC和AD中点是同一个∴发出警报的可能最多有5个．故答案为5．18．解：∵EA：AB：BF＝1：2：3，可以设EA＝x，AB＝2x，BF＝3x，而M、N分别为EA、BF的中点，∴MA＝EA，NB＝BF，∴MN＝MA+AB+BN＝x+2x+x＝4x ∵MN＝8cm，∴4x＝8，∴x＝2，∴EF＝EA+AB+BF＝6x＝12，∴EF的长为12cm，故答案为：12cm．19．解：∵AB＝m，CD＝n．∴AB﹣CD＝m﹣n，∵E、F分别是AC、DB的中点，∴CE＝AC，DF＝DB，∴CE+DF＝（m﹣n），∴EF＝CE+DF+DC＝（m﹣n）+n＝m+n，故答案为：m+n．20．解：∵∠AOB和∠BOC互为补角，∴∠AOB+∠BOC＝180°，∵∠BOD＝，∴3∠BOD+∠BOC＝180°，即∠BOC＝180°﹣3∠BOD，∵∠COD+∠BOD＝∠BOC，∴180°﹣3∠BOD＝∠COD+∠BOD，∴∠COD+4∠BOD＝180°，∵∠COD比∠BOD大m°（m＜30），∴∠COD﹣∠BOD＝m°，∴∠BOD＝（）°，∠COD＝（）°∴∠BOC＝（）°，∴∠AOB＝180°﹣∠BOC＝（108﹣）°，∴∠AOC＝∠AOB﹣∠BOC＝（108﹣）°﹣（）°＝（36﹣m）°．故答案为（36﹣m）．21．解：（1）（1×3+2×3+1×2）×2＝22（m2），（2）根据棱柱的展开与折叠，可得可以折叠成长方体的盒子，其长、宽、高分别为3cm，2cm，1cm，因此体积为：1×2×3＝6（m3），22．解：（1）线段AB＝20，BC＝15，∴AC＝AB﹣BC＝20﹣15＝5．又∵点M是AC的中点．∴AM＝AC＝×5＝，即线段AM的长度是．（2）∵BC＝15，CN：NB＝2：3，∴CN＝BC＝×15＝6．又∵点M是AC的中点，AC＝5，∴MC＝AC＝，∴MN＝MC+NC＝，即MN的长度是．23．解：（1）因为点C为OP的中点，所以OC＝2km，因为OA＝2km，所以可得出距小明家距离相同的是学校和公园；（2）由图可知，学校在小明家东偏北45°方向2km处，商场在小明家西偏北60°方向3.5km处，停车场在东偏南30°方向4km处．24．解：∵OC平分∠AOB，∠BOC＝26°，∴∠AOB＝2∠BOC＝52°．∴∠BOD＝180°﹣52°＝128°．∵OE平分∠DOB，∴∠BOE＝∠DOB＝×128°＝64°．25．解：（1）设AB＝xcm，根据题意可得：（x﹣5）﹣＝3，解得：x＝12，答：AB的长为12cm；（2）①由题意可得：3t＝t+5，解得：t＝，故点P与点Q重合时（未到达点B），t的值为；②当点P追上点Q前相距2cm，由题意可得：3t+2＝t+5，解得：t＝，当追上后相距2cm，由题意可得：3t﹣2＝t+5，解得：t＝，总上所述：t＝或t＝．26．解：（1）∵AC＝15cm，CB＝AC，∴CB＝×15＝10（cm），∴AB＝15+10＝25（cm）．∵D，E分别为AC，AB的中点，∴AE＝BE＝AB＝12.5cm，DC＝AD＝AC＝7.5cm，∴DE＝AE﹣AD＝12.5﹣7.5＝5（cm）；（2）设∠AOC＝2x，∠COD＝3x，∠DOB＝4x，则∠AOB＝9x，∵OM平分∠AOC，ON平分∠DOB，∴∠MOC＝x，∠NOD＝2x，∴∠MON＝x+3x+2x＝6x，又∵∠MON＝90°，∴6x＝90°，∴x＝15°，∴∠AOB＝135°．。

人教版初中数学七年级上册第四章图形认识初步单元测试

初中数学-七年级上册-第四章图形认识初步-单元测试一、单选题（选择一个正确的选项）1 、如图是一个正方体，用一个平面去截这个正方体，截面形状不可能为下图中的（）A、B、C、D、2 、两个完全相同的正方体，将一面完全重合，构成的几何体面数有（）A、12个B、11个C、10个D、6个3 、下列哪个图形阴影部分的面积与已知图形阴影部分的面积不相等（）A、图形阴影部分的面积=1×1=1面积单位，与已知图形阴影部分的面积相等；B、图形阴影部分的面积=1×2÷2=1面积单位，与已知图形阴影部分的面积相等；C、图形阴影部分的面积=1×2÷2=1面积单位，与已知图形阴影部分的面积相等；D、图形阴影部分的面积=1×1÷2=面积单位，与已知图形阴影部分的面积不相等．4 、圆锥可以看作是由一个( )旋转得到的A、矩形（长方形）B、等腰梯形C、半圆D、直角三角形5 、两个角的大小之比是7:3,它们的差是,则这两个角的关系是( )A、相等B、互补C、互余D、无法确定6 、如图所示的图形绕虚线旋转一周，所形成的几何体是（）A、B、C、D、7 、将如图所示的直角梯形绕直线l旋转一周，得到的立体图形是（）A、B、C、D、8 、用一个平面去截一个几何体，不能截得三角形截面的几何体是（）A、圆柱B、圆锥C、三棱柱D、正方形9 、如图，点A位于点O的方向上（）A、南偏东35°B、北偏西65°C、南偏东65°D、南偏西65°10 、下面的几何体是棱柱的是（）A、B、C、D、二、填空题（在空白处填写正确的答案）11 、下列图形各能叠成什么图形？答：图A____________，图B____________12 、如图，数一数，图中共有____________个三角形．13 、时钟表面3点30分时，时针与分针所夹角的度数是____14 、把正六面体的各面分别涂上不同的颜色，不同的颜色对应的数字如表．现将三个大小、颜色完全相同的正六面体摆成如图所示的长方体，则这个长方体底面上的数字和为________15 、如图，MN是圆柱底面的直径，NO是圆柱的高，在圆柱的侧面上，过点M，P．有一条绕了四周的路径最短的金属丝，现将圆柱侧面沿NO剪开，所得的侧面展开图可以是：_________（填序号）．三、解答题（在题目下方写出解答过程）16 、如图12，小张从家（图中A处）出发，向南偏东40°的方向走到学校（图中B处），再从学校出发，向北偏西75°的方向走到小明家（图中C处），试问∠ABC为多少度？说明你的理由。

(新版人教版)七年级上第四章《图形认识初步》测试题及答案

D CB AB A第1题图会社谐和设建DC BAβββααα第3题图七级数学第四章几何图形初步测试题（新课标）（时限：100分钟总分：100分）一、选择题：将下列各题正确答案的代号填在下表中。

每小题2分，共24分。

1.如图是一个小正方体的展开图，把展开图折叠成小正方体后，有“建”字一面的相对面上的字是（）A.和B.谐C.社D.会2.下面左边是用八块完全相同的小正方体搭成的几何体，从上面看该几何体得到的图是（）A B C D3.如图，四个图形是由立体图形展开得到的，相应的立体图形顺次是（） A. 正方体、圆柱、三棱柱、圆锥 B. 正方体、圆锥、三棱柱、圆柱 C. 正方体、圆柱、三棱锥、圆锥 D. 正方体、圆柱、四棱柱、圆锥4.如图，对于直线AB ，线段CD ，射线EF ，其中能相交的是（）5.下列说法中正确的是（）A.画一条3厘米长的射线B.画一条3厘米长的直线C.画一条5厘米长的线段D.在线段、射线、直线中直线最长 6.如图，将一副三角尺按不同位置摆放，摆放方式中∠α 与∠β 互余的是（）1乙甲N MP D C B A B ()D C A D C B A 第9题图BA 7.点E 在线段CD 上，下面四个等式①CE ＝DE ；②DE ＝21CD ；③CD ＝2CE ； ④CD ＝21DE.其中能表示E 是线段CD 中点的有（） A. 1个 B. 2个 C. 3个 D. 4个 8. C 是线段AB 上一点，D 是BC 的中点，若AB ＝12cm ，AC ＝2cm ，则BD 的长为（） A. 3cm B. 4cm C. 5cm D. 6cm9.如图是一正方体的平面展开图，若AB ＝4，则该正方体A 、B 两点间的距离为（）A. 1B. 2C. 3D. 410.用度、分、秒表示91.34°为（） A. 91°20/24// B. 91°34/ C. 91°20/4// D. 91°3/4// 11.下列说法中正确的是（）A.若∠AOB ＝2∠AOC ，则OC 平分∠AOBB.延长∠AOB 的平分线OCC.若射线OC 、OD 三等份∠AOB ，则∠AOC ＝∠DOCD.若OC 平分∠AOB ，则∠AOC ＝∠BOC12.甲、乙两人各用一张正方形的纸片ABCD 折出一个45°的角（如图），两人做法如下：甲：将纸片沿对角线AC 折叠，使B 点落在D 点上，则∠1＝45°；乙：将纸片沿AM 、AN 折叠，分别使B 、D 落在对角线AC 上的一点P ，则∠MAN ＝45°对于两人的做法，下列判断正确的是（）A.甲乙都对B.甲对乙错C.甲错乙对D.甲乙都错二、填空题：本大题共8小题，每小题3分，共24分。

人教版数学七年级上册第第四章几何图形初步基础检测题含答案

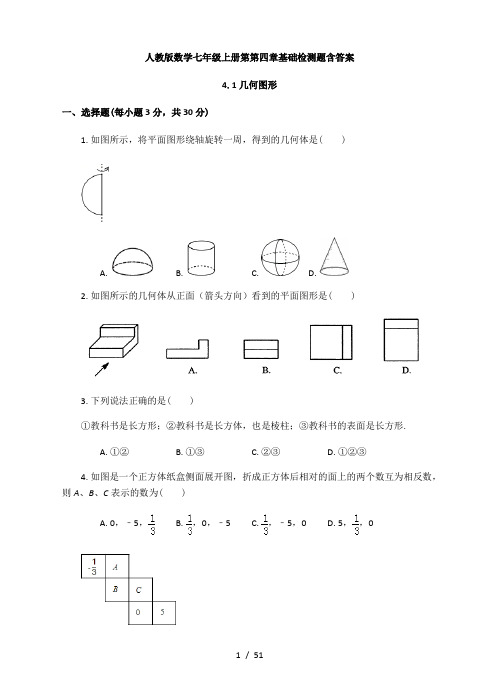
人教版数学七年级上册第第四章基础检测题含答案4.1几何图形一、选择题(每小题3分，共30分)1.如图所示，将平面图形绕轴旋转一周，得到的几何体是()A.B.C.D.2.如图所示的几何体从正面（箭头方向）看到的平面图形是()3.下列说法正确的是()①教科书是长方形；②教科书是长方体，也是棱柱；③教科书的表面是长方形.A.①②B.①③C.②③D.①②③4.如图是一个正方体纸盒侧面展开图，折成正方体后相对的面上的两个数互为相反数，则A、B、C表示的数为()A.0，﹣5，B.，0，﹣5C.，﹣5，0D.5，，05.如下图，下列图形全部属于柱体的是()6.骰子是一种特别的数字立方体(见右图)，它符合规则：相对两面的点数之和总是7，下面四幅图中可以折成符合规则的骰子的是()A.B.C.D.7.如图所示的几何体，从上面看得到的平面图形是()8.下列图形中为三棱柱的表面展开图的是()A.B.C.D.9.图(1)是一个正方体的表面展开图，小正方体从图(2)所示的位置依次翻到第1格、第2格、第3格、第4格，这时小正方体朝上一面的字是( )A.家B.乡C.是D.伊4 的网格图剪去5个小正方形后，图中还剩下7个小正方形，为了使余10.如图，将3下的部分(小正方形之间至少要有一条边相连)恰好能．．．折成一个正方体，需要再剪去1个小正方形，则应剪去的小正方形的编号是()A.7B.6C.5D.4二、填空题(每小题3分，共30分)11.写出一个主视图、左视图、俯视图都相同的几何体：.12.一个矩形绕着它的一边旋转一周，所得到的立体图形是.13.一个棱锥的棱数是12，则这个棱锥的面数是.14.一个几何体的从三个方向看到的平面图形，如图所示，则这个几何体的名称是____________.第14题图第15题图第16题图15.如图，该平面展开图按虚线折叠成正方体后，相对面上两个数之和为8，则x+y ＝.16.立方体木块的六个面分别标有数字1、2、3、4、5、6，如图，是从不同方向观察这个立方体木块看到的数字情况，数字1和5对面的数字的和是.17.如图，一长方体木板上有两个洞，一个是正方形形状的，一个是圆形形状的，对于以下4种几何体，你觉得哪一种作为塞子既可以堵住圆形空洞又可以堵住方形空洞？(填序号).18.一个立体图形的三视图如图所示，请你根据图中给出的数据求出这个立体图形的表面积为.第18题图第19题图第20题图19.如图，从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如所示的零件，则这个零件的表面积为20.如图，用小木块搭一个几何体，它的从正面看和从上面看如图所示.问：最少需要__________个小正方体木块.三、解答题(共40分)21.(9分)如图所示由五个小立方体构成的立体图形,请你分别画出从它的正面、左面、上面三个方向看所得到的平面图形.从正面看从左面看从上面看22.(6分)下面是一个正方体纸盒的展开图，请把－10，7，10，－2，－7，2分别填入六个正方形，使得按虚线折成正方体后，相对面上的两数互为相反数.23.(12分)如图，一个多面体的展开图中，每个面内的大写字母表示该面，被剪开的棱边所注的小写字母可表示该棱.(1)说出这个多面体的名称；(2)写出所有相对的面 _ ；(3)若把这个展开图折叠起来成立体时，被剪开的棱b 与重合，f 与重合.24.(13分)将一个正方体表面全部涂上颜色把正方体的棱三等分，然后沿等分线把正方体切开，得到27个小正方体，我们把仅有i 个面涂色的小正方体的个数记为i x ，例如：通过观察我们可以发现仅有3个面涂色的小正方体个数83=x ，仅有2个面涂色的小正方体个数122=x ，仅有1个面涂色的小正方体个数61=x ，6个面均不涂色的小正方体个数10=x ；(1)如果把正方体的棱四等分，同样沿等分线把正方体切开，得到64个小正方体，那么=3x ________，=2x _______，=1x _______，=0x _________；(2)如果把正方体的棱n 等分(n 大于3)，然后沿等分线把正方体切开，得到3n 个小正方体，且满足184232=-x x ，请求出n 的值.参考答案1.C2.B3.C∴不能说它是一个长方形，∵有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱∴它是棱柱.教科书的表面是一个长方形.故选C.4.A【解析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点求出A、B、C的值，然后代入进行计算即可求解.解：正方体的表面展开图，相对的面之间一定相隔一个正方形，∴A与0是相对面，B与5是相对面，C与﹣是相对面，∵折成正方体后相对的面上的两个数互为相反数，∴A＝0，B＝﹣5，C＝.故选：A.5.C【解析】A选项中含有三棱锥，就是锥体；B选项中含有圆锥，就是锥体；D选项中含有圆台，就是台体.6.A【解析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点对各选项分析判断后利用排除法求解.解：根据正方体的表面展开图，相对的面之间一定相隔一个正方形，A.4点与3点是向对面，5点与2点是向对面，1点与6点是向对面，所以可以折成符合规则的骰子，故本选项正确；B.1点与3点是向对面，4点与6点是向对面，2点与5点是向对面，所以不可以折成符合规则的骰子，故本选项错误；C.3点与4点是向对面，1点与5点是向对面，2点与6点是向对面，所以不可以折成符合规则的骰子，故本选项错误；D.1点与5点是向对面，3点与4点是向对面，2点与6点是向对面，所以不可以折成符合规则的骰子，故本选项错误.故选A.7.B.【解析】根据所看位置，找出此几何体的三视图即可.解：从上面看得到的平面图形是两个同心圆，故选：B.8.B【解析】利用棱柱及其表面展开图的特点解题.解：A、C、D围成三棱柱时，两个三角形重合为同一底面，而另一底面没有.故不能围成三棱柱；B、中间三个长方形能围成三棱柱的侧面，左、右两个三角形围成三棱柱的上、下两底面，故能围成三棱柱，是三棱柱的表面展开图.故选B.9.C.【解析】由图1可得，“伊”和“乡”相对；“春”和“我”相对；“是”和“家”相对；由图2可得，小正方体从图2的位置依次翻到第4格时，“家”在下面，则这时小正方体朝上面的字是“是”.10.C.【解析】根据只要有“田”字格的展开图都不是正方体的表面展开图，应剪去的小正方形的编号是5.故选C.11.球或正方体.【解析】试题分析：主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形.解：球的三视图都为圆；正方体的三视图为正方形；所以应填球或正方体.12.圆柱体【解析】本题是一个矩形绕着它的一边旋转一周，根据面动成体的原理即可解.解：以矩形的一边所在直线为旋转轴，形成的旋转体叫做圆柱体.故答案为圆柱体.13.7.【解析】因为一个棱锥的棱数是12，可得多面体为六棱锥，所以多面体的面数为714.三棱柱.【解析】根据图中三视图的形状，符合条件的只有三棱柱，因此这个几何体的名称是三棱柱.15.10.【解析】∵“4”与“y”是对面，“x”与“2”是对面，∴x＝6，y＝4.∴x+y＝10.【解析】从3个图形看，和1相邻的有2，4，5，6，那么和1相对的就是3.则和2相邻的有1，3，4，5，那么和2相对的就是6.则和5相对的就是4.再将数字1和5对面的数字相加即可.解：根据三个图形的数字，可推断出来，1对面是3；2对面是6；5对面是4.∴3+4＝7.则数字1和5对面的数字的和是7.故答案为：7.17.②.【解析】本题中圆柱的俯视图是圆，可以堵住圆形空洞，它的正视图和左视图是长方形，可以堵住方形空洞，据此选择即可.解：圆柱的俯视图是圆，可以堵住圆形空洞，它的正视图和左视图是长方形，可以堵住方形空洞，故圆柱是最佳选项，故答案为②.18.8π.【解析】从三视图可以看正视图以及俯视图为矩形，而左视图为圆形，可以得出该立体图形为圆柱，再由三视图可以圆柱的半径，长和高求出体积.解：∵正视图和俯视图是矩形，左视图为圆形，∴可得这个立体图形是圆柱，∴这个立体图形的侧面积是2π×3＝6π，底面积是：21ππ⋅=，∴这个立体图形的表面积为6π+2π＝8π；故答案为：8π.【解析】挖去一个棱长为1的小正方体，得到的图形与原图形表面积相等，则表面积是2×2×6＝24.20.10【解析】根据俯视图可以判定就至少需要7个，再根据主视图上面还需要3个，则最少需要10个.21.见解析【解析】分别画出三视图即可解：如图：22.(1)正方体；(2)P与X，Q与Y，R与Z；(3)i；g【解析】根据正方体的展开图我们就可以得到答案，自己也可以动手叠一下试试看.解：(1)这个多面体是正方体.(2)相对的面有三对：P与X，Q与Y，R与Z.(3)将会重合的棱有b与i，f与g23.见解析【解析】如图，A－A’、B－B’、C－C’是相对面，填入互为相反数的两个数即可.解：如图所示：(答案不唯一，符合即可)4.2直线、射线、线段一．选择题1．下列说法正确的是（）A．射线P A和射线AP是同一条射线B．射线OA的长度是3cmC．直线ab，cd相交于点PD．两点确定一条直线2．如图，C为AB的中点，D是BC的中点，则下列说法错误的是（）A．CD＝AC﹣BD B．CD＝AB﹣BD C．CD＝BC D．AD＝BC+CD 3．平面上有A、B、C三点，经过任意两点画一条直线，可以画出直线的数量为（）A．1条B．3条C．1条或3条D．无数条4．如图，线段CD在线段AB上，且CD＝3，若线段AB的长度是一个正整数，则图中以A，B，C，D这四点中任意两点为端点的所有线段长度之和可能是（）A．28B．29C．30D．315．已知点A、B、C、D在同一条直线上，线段AB＝8，C是AB的中点，DB＝1.5．则线段CD的长为（）A．2.5B．3.5C．2.5或5.5D．3.5或5.56．点M在线段AB上，给出下列四个条件，其中不能判定点M是线段AB的中点的是（）A．AM＝BM B．AB＝2AM C．AM+BM＝AB D．BM＝AB7．如图，线段AB＝18cm，点M为线段AB的中点，点C将线段MB分成MC：CB＝1：2，则线段AC的长度为（）A．6cm B．12cm C．9cm D．15cm8．如图，已知线段AB＝8，点C是线段AB是一动点，点D是线段AC的中点，点E是线段BD的中点，在点C从点A向点B运动的过程中，当点C刚好为线段DE的中点时，线段AC的长为（）A．3.2B．4C．4.2D．9．如图，D、E顺次为线段AB上的两点，AB＝19，BE﹣DE＝7，C为AD的中点，则AE ﹣AC的值为（）A．5B．6C．7D．810．如图，C，D，E是线段AB上的三个点，下面关于线段CE的表示：①CE＝CD+DE；②CE＝CB﹣EB；③CE＝CD+DB﹣AC；④CE＝AE+CB﹣AB．其中，正确的是（）A．①②B．①②③C．①②④D．①②③④二．填空题11．数学来源于生活而又高于生活，比如当我们在植树的时候，要想整齐地栽一行树，只需要确定两端树坑的位置即可．用数学知识可以解释为．12．如图，已知C为线段AB的中点，D在线段CB上．若DA＝6，DB＝3，则CD＝．13．如图，点C在线段AB上，且AC＝AB，点D在线段BC上，AD＝5，BD＝3，则线段CD的长度为．14．如图，点C、D在线段AB上，AC＝6cm，CD＝4cm，AB＝12cm，则图中所有线段的和是cm．15．如图，已知A、B是线段EF上两点，EA：AB：BF＝1：2：3，M、N分别为EA、BF 的中点，且MN＝8cm，则EF长为．三．解答题16．如图，已知点A、B、C．D，根据下列语句画图．（不写作图过程）作射线AB、直线AC，连接AD并延长线段AD．17．如图，A，B，C三棵树在同一直线上，若小明正好站在线段的AC中点Q处，BC＝2BQ．（1）填空：AQ＝＝AC，AQ﹣BC＝．（2）若BQ＝3米，求AC的长．18．如图，线段AB上顺次有三个点C，D，E，把线段AB分为了2：3：4：5四部分，且AB＝28．（1）求线段AE的长；（2）若M，N分别是DE，EB的中点，求线段MN的长度．参考答案一．选择题1．解：A、射线P A和射线AP不是同一条射线，故本选项错误；B、射线是无限长的，故本选项错误；C、直线ab，cd，直线的写法不对，故本选项错误；D、两点确定一条直线是正确的．故选：D．2．解：∵C是AB的中点，D是BC的中点，∴AC＝BC＝AB，CD＝BD＝BC，∵CD＝BC﹣BD∴CD＝AC﹣BD，故A正确；∵CD＝BC﹣DB，∴CD＝AB﹣DB，故B正确；∴AD＝AC+CD＝BC+CD，故D正确；∵CD＝BD＝BC；故C错误；故选：C．3．解：①如果三点共线，过其中两点画直线，共可以画1条；②如果任意三点不共线，过其中两点画直线，共可以画3条．故选：C．4．解：所有线段之和＝AC+AD+AB+CD+CB+BD，∵CD＝3，∴所有线段之和＝AC+AC+3+AC+3+BD+3+3+BD+BD＝12+3（AC+BD）＝12+3（AB﹣CD）＝12+3（AB﹣3）＝3AB+3＝3（AB+1），∵AB是正整数，∴所有线段之和是3的倍数，故选：C．5．解：∵AB＝8，C是AB的中点，∴AC＝BC＝4，∵DB＝1.5．当点D在点B左侧时，CD＝BC﹣BD＝4﹣1.5＝2.5，当点D在点B右侧时，CD＝BC+BD＝4+1.5＝5.5，则线段CD的长为2.5或5.5．故选：C．6．解：A、由AM＝BM可以判定点M是线段AB中点，所以此结论正确，故这个选项不符合题意；B、由AB＝2AM可以判定点M是线段AB中点，所以此结论正确，故这个选项不符合题意；C、由AM+BM＝AB不可以判定点M是线段AB中点，所以此结论不正确，故这个选项符合题意；D、由BM＝AB可以判定点M是线段AB中点，所以此结论不正确，故这个选项不符合题意；故选：C．7．解：∵线段AB＝18cm，点M为线段AB的中点，∴AM＝BM＝AB＝9，∵点C将线段MB分成MC：CB＝1：2，设MC＝x，CB＝2x，∴BM＝MC+CB＝3x，∴3x＝9，解得x＝3，∴AC＝AM+MC＝9+3＝12．则线段AC的长度为12．故选：B．8．解：∵点D是线段AC的中点，∴AD＝CD，∵点E是线段BD的中点，∴BE＝DE，∵点C为线段DE的中点，∴CD＝CE，∴AD＝CD＝CE，∵AB＝AD+DC+CE+BE＝3AD+BE＝3AD+DE＝3AD+2CD＝5AD，∴AD＝1.6，∴AC＝2AD＝3.2，故选：A．9．解：∵AB＝19，设AE＝m，∴BE＝AB﹣AE＝19﹣m，∵BE﹣DE＝7，∴19﹣m﹣DE＝7，∴DE＝12﹣m，∴AD＝AB﹣BE﹣DE＝19﹣（19﹣m）﹣（12﹣m）＝19﹣19+m﹣12+m＝2m﹣12，∵C为AD中点，∴AC＝AD＝×（2m﹣12）＝m﹣6．∴AE﹣AC＝6，故选：B．10．解：由图可知：①CE＝CD+DE，正确；②CE＝CB﹣EB，正确；③CE＝CD+DB﹣EB，错误；④CE＝AE+CB﹣AB，正确；故选：C．二．填空题11．解：两端两个树坑的位置，可看做两个点，根据两点确定一条直线，即可确定一行树所在的位置．故答案为：两点确定一条直线．12．解：∵DA＝6，DB＝3，∴AB＝DB+DA＝3+6＝9，∵C为线段AB的中点，∴BC＝AB＝×9＝4.5，∴CD＝BC﹣DB＝4.5﹣3＝1.5．故答案为：1.5．13．解：∵AD＝5，BD＝3，∴AB＝AD+BD＝8，∵AC＝AB＝，∴CD＝AD﹣AC＝5﹣＝，故答案为：．14．解：由线段的和差，得AC+DB＝AB﹣CD＝12﹣4＝8（cm）．图中所有线段的和AC+AD+AB+CD+CB+DB＝AC+（AC+CD）+AB+CD+（CD+DB）+DB ＝2（AC+DB）+3CD+AB＝2×8+3×4+12＝40（cm）．答：图中所有线段的和是40cm，故答案为：40．15．解：∵EA：AB：BF＝1：2：3，可以设EA＝x，AB＝2x，BF＝3x，而M、N分别为EA、BF的中点，∴MA＝EA，NB＝BF，∴MN＝MA+AB+BN＝x+2x+x＝4x∵MN＝8cm，∴4x＝8，∴x＝2，∴EF＝EA+AB+BF＝6x＝12，∴EF的长为12cm，故答案为：12cm．三．解答题16．解：作射线AB、直线AC，连接AD并延长线段AD，如图所示：17．解：（1）∵O是线段AC的中点，∴AQ＝CQ＝AC，AQ﹣BC＝CQ﹣BC＝QB，故答案为；（2）∵BQ＝3米，BC＝2BQ，∴BC＝2BQ＝6米，∴CQ＝BC+BQ＝6+3＝9（米），∵Q是AC中点，∴AQ＝QC＝9（米），∴AC＝AQ+QC＝9+9＝18（米），∴AC的长是18米．18．解：（1）设AC＝2x，则CD、DE、EB分别为3x、4x、5x，由题意得，2x+3x+4x+5x＝28，解得，x＝2，则AC、CD、DE、EB分别为4、6、8、10，则AE＝AC+CD+DE＝4+6+8＝18；（2）如图：∵M是DE的中点，∴ME＝DE＝4，∵N是EB的中点∴EN＝EB＝5，∴MN＝ME+EN＝4+5＝9．4.3角一．选择题1．25°的补角是（）A．155°B．145°C．55°D．65°2．已知∠A＝30°45'，∠B＝30.45°，则∠A（）∠B．A．两点之间直线最短B．一个有理数，不是正数就是负数C．平角是一条直线D．整数和分数统称为有理数4．下列语句中：正确的个数有（）①画直线AB＝3cm；②连接点A与点B的线段，叫做A、B两点之间的距离；③两条射线组成的图形叫角；④任何一个有理数都可以用数轴上的一个点来表示．A．0B．1C．2D．35．如图，∠AOC＝90°，OC平分∠DOB，且∠DOC＝22°36′，∠BOA度数是（）A．67°64′B．57°64′C．67°24′D．68°24′6．如图，射线OA表示的方向是（）A．北偏东65°B．北偏西35°C．南偏东65°D．南偏西35°7．已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（）A．120°B．60°C．30°D．150°8．如图所示的是正方形网格，则∠AOB___∠COD（）A．＞B．＜C．＝D．≥9．如图，OA是北偏东30°方向的一条射线，若射线OB与OA垂直，则射线OB表示的方向是（）A．东偏北30°B．东偏北60°C．北偏西30°D．北偏西60°10．如图，甲、乙两人同时从A地出发，甲沿北偏东50°方向步行前进，乙沿图示方向步行前进．当甲到达B地，乙到达C地时，甲与乙前进方向的夹角∠BAC为100°，则此时乙位于A地的（）A．南偏东30°B．南偏东50°C．北偏西30°D．北偏西50°二．填空题11．计算：18°13′×5＝．12．若此时时钟表上的时间是8：20分，则时针与分针的夹角为度．13．若两个角互补，且度数之比为3：2，求较大角度数为．14．若∠AOB＝45°，∠BOC＝75°，OD平分∠AOB，OE平分∠BOC，则∠DOE的度数为．15．将一副三角板按如图方式摆放在一起，且∠1比∠2大20°，则∠1的度数等于．三．解答题16．已知：如图，∠AOB＝30°，∠COB＝20°，OC平分∠AOD，求∠BOD的度数．17．如图，已知∠MON＝150°，∠AOB＝90°，OC平分∠MOB，（1）若∠AOC＝35°，则∠BOC＝°，∠NOB＝°；（2）若∠NOB＝10°，则∠BOC＝°，∠AOC＝°；（3）若∠AOC＝α，∠NOB＝β，请直接写出α与β之间的数量关系．18．已知O为直线AB上一点，射线OD，OC，OE位于直线AB上方，OD在OE的左侧，∠AOC＝120°，∠DOE＝50°，设∠BOE＝n．（1）若射线OE在∠BOC的内部（如图1），①若n＝43°，求∠COD的度数；②当∠AOD＝3∠COE时，求∠COD的度数．（2）若射线OE恰为图中某一个角（小于180°）的角平分线，试求n的值．19．如图，已知∠AOB内部有三条射线，OE平分∠AOD，OC平分∠BOD．（1）若∠AOB＝90°，求∠EOC的度数；（2）若∠AOB＝α，求∠EOC的度数；（3）如果将题中“平分”的条件改为∠EOA＝∠AOD，∠DOC＝∠DOB且∠DOE：∠DOC＝4：3，∠AOB＝90°，求∠EOC的度数．参考答案与试题解析一．选择题1．【解答】解：25°的补角是：180°﹣25°＝155°．故选：A．2．【解答】解：30.45°＝30°+0.45×60′＝30°27′，∵30°45′＞30°27′，∴30°45'＞30.45°，∴∠A＞∠B，故选：A．3．【解答】解：A、两点之间线段最短，原说法错误，故本选项不符合题意；B、一个有理数，不是正数就是负数或零，原说法错误，故本选项不符合题意；C、平角的两边在一条直线上，原说法错误，故本选项不符合题意；D、整数和分数统称为有理数，原说法正确，故本选项符合题意；故选：D．4．【解答】解：①因为直线不可以度量，所以画直线AB＝3cm是错误的；②连接点A与点B的线段的长度，叫做A、B两点之间的距离，原说法错误；③有公共端点是两条射线组成的图形叫做角，原说法错误；④任何一个有理数都可以用数轴上的一个点来表示，原说法正确；正确的有1个，故选：B．5．【解答】解：∵OC平分∠DOB，∴∠DOC＝∠BOC＝22°36′．∵∠AOC＝∠AOB+∠BOC＝90°，∴∠AOB＝∠AOC﹣∠BOC＝90°﹣22°36′＝67°24′．故选：C．6．【解答】解：射线OA表示的方向是南偏东65°，故选：C．7．【解答】解：∵∠1和∠2互为余角，∠1＝60°，∴∠2＝90°﹣∠1＝90°﹣60°＝30°，∵∠2与∠3互补，∴∠3＝180°﹣∠2＝180°﹣30°＝150°．故选：D．8．【解答】解：∵∠AOC＝∠BOD＝90°，∴∠AOB+∠BOC＝90°，∠COD+∠BOC＝90°，∴∠AOB＝∠COD．故选：C．9．【解答】解：由题意得，∠AOC＝30°，∵射线OB与射线OA垂直，∴∠BOC＝60°，∴OB的方向角是北偏西60°．故选：D．10．【解答】解：如图所示：由题意可得：∠1＝50°，∠BAC＝100°，则∠2＝180°﹣100°﹣50°＝30°，故乙位于A地的南偏东30°．故选：A．二．填空题（共5小题）11．【解答】解：原式＝90°+65′＝91°5′．故答案是：91°5′．12．【解答】解：∵时针在钟面上每分钟转0.5°，分针每分钟转6°，∴钟表上8点20分，时针与分针的夹角可以看成30°×4+0.5°×20＝130°．故答案为：130．13．【解答】解：因为两个角的度数之比为3：2，所以设这两个角的度数分别为（3x）°和（2x）°．根据题意，列方程，得3x+2x＝180，解这个方程，得x＝36，所以3x＝108．即较大角度数为108°．故答案为108°．14．【解答】解：如图1，∵∠AOB＝45°，∴∠BOD＝22.5°，∵∠BOC＝75°，∴∠BOE＝37.5°，∴∠DOE＝22.5°+37.5°＝60°；如图2，∵∠AOB＝45°，∴∠BOD＝22.5°，∵∠BOC＝75°，∴∠BOE＝37.5°，∴∠DOE＝37.5°﹣22.5°＝15°，故答案为：60°或15°．15．【解答】解：设∠2为x，则∠1＝x+20°；根据题意得：x+x+20°＝90°，解得：x＝35°，则∠1＝35°+20°＝55°；故答案为：55°．三．解答题（共4小题）16．【解答】解：∵∠AOB＝30°，∠COB＝20°，∴∠AOC＝∠AOB+∠BOC＝30°+20°＝50°，∵OC平分∠AOD，∴∠AOC＝∠COD＝50°，∴∠BOD＝∠BOC+COD＝20°+50°＝70°．17．【解答】解：（1）∠BOC＝∠AOB﹣∠AOC＝90°﹣35°＝55°；∵OC平分∠MOB，∴∠MOB＝2∠BOC＝110°，∴∠NOB＝∠MON﹣∠MOB＝150°﹣110°＝40°．故答案为：55，40；（2）∠MOB＝∠MON﹣∠NOB＝150°﹣10°＝140°，∵OC平分∠MOB，∴∠BOC＝；∴∠AOC＝90°﹣∠BOC＝20°．故答案为70，20；（3）∵∠AOC＝α，∠NOB＝β，∴∠BOC＝90°﹣α，∵OC平分∠MOB，∴∠MOB＝2∠BOC＝180°﹣2α，∵∠MOB+∠NOB＝150°，∴180°﹣2α+β＝150°，即β＝2α﹣30°．18．【解答】解：（1）①∠BOC＝180°﹣∠AOC＝60°，由n＝43°，可得∠COE＝∠BOC﹣∠BOE＝17°，∴∠COD＝∠DOE﹣∠COE＝50°﹣17°＝33°；②∵∠AOD＝3∠COE，∠AOD+∠COD＝120°，∠DOE＝50°，∴3∠COE+50°﹣∠COE＝120°，解得∠COE＝35°，∴∠COD＝∠DOE﹣∠COE＝50°﹣35°＝15°；（2）当OE平分∠BOC时，如图所示：∵∠AOC＝120°，∴∠BOC＝180°﹣∠AOC＝60°，∴∠BOE＝＝30°．即n＝30°；当OE平分∠AOC时，如图所示：∠BOE＝2∠BOC＝120°，即n＝120°；当OE平分∠BOD时，如图所示：∠BOE＝∠DOE＝50°，即n＝50°；当OE平分∠COD时，∠BOE＝∠EOC+∠BOC＝50°+60°＝110°，即n＝110°；OE平分∠AOD是不成立．所以n＝30°、50°、110°或120°．19．【解答】解：（1）∵OE平分∠AOD，OC平分∠BOD，∴∠EOD＝∠AOD，∠DOC＝∠DOB，∴∠EOC＝（∠AOD+∠DOB）＝45°；（2）由（1）可知：∠EOC＝（∠AOD+∠DOB）＝α；（3）∵∠DOE：∠DOC＝4：3，∴设∠DOE＝4x，∠DOC＝3x，∵∠EOA＝∠AOD，∴∠DOE＝∠AOD，∴∠AOD＝5x，∵∠DOC＝∠DOB，∴∠DOB＝4x4.4课题学习制作长方形形状一．选择题1．给出一个正方形，请你动手画一画，将它剖分为n个小正方形．那么，通过实验与思考，你认为下列自然数n不可以取到的是（）A．5B．6C．7D．82．有一块两条直角边长分别为3m和4m的直角三角形绿地，现在要扩充成等腰三角形，且扩充部分是直角边长为4m的直角三角形，则扩充后的等腰三角形绿地的周长不可能是（）A．16m B．m C．（10+）m D．（10+）m 3．某地有三家工厂，分别位于矩形ABCD的顶点A、B及边CD的中点P处，已知AB＝16km，BC＝12km，为了处理三家工厂的污水，现要在矩形ABCD的区域上（含边界），且与A，B等距离的一点O处建造一个污水处理厂，并铺设排污管道AO，BO，OP．记管道总长为S km．下列说法正确的是（）A．S的最小值是8B．S的最小值应该大于28C．S的最小值是26D．S的最小值应该小于264．某乡镇的4个村庄A、B、C、D恰好位于正方形的4个顶点上，为了解决农民出行难问题，镇政府决定修建连接各村庄的道路系统，使得每两个村庄都有直达的公路，设计人员给出了如下四个设计方案（实线表示连接的道路）在上述四个方案中最短的道路系统是方案（）A．一B．二C．三D．四5．有甲、乙、丙三个村庄分别位于等边△ABC的顶点，在城中村改造时，为保护环境，改善居民的生活条件，政府决定铺设能够连结这三个村庄的天然气管道．设计人员给出了如图四个设计方案（点D为BC边的中点，点O为△ABC的中心，实线表示天然气管道），其中天然气管道总长最短的是（）A．方案1B．方案2C．方案3D．方案46．如图，直线m表示一条河，点M、N表示两个村庄，计划在m上的某处修建一个水泵向两个村庄供水．在下面四种铺设管道的方案中，所需管道最短的方案是（图中实线表示铺设的管道）（）A．B．C．D．7．将一块长为a米，宽为b米的矩形空地建成一个矩形花园，要求在花园中修两条入口宽均为x米的小道，其中一条小道两边分别经过矩形一组对角顶点，剩余的地方种植花草，现有从左至右三种设计方案如图所示，种植花草的面积分别为S1，S2和S3，则它们的大小关系为（）A．S3＜S1＜S2B．S1＜S2＜S3C．S2＜S1＜S3D．S1＝S2＝S38．四座城市A，B，C，D分别位于一个边长为100km的大正方形的四个顶点，由于各城市之间的商业往来日益频繁，于是政府决定修建公路网连接它们，根据实际，公路总长设计得越短越好，公开招标的信息发布后，一个又一个方案被提交上来，经过初审后，拟从下面四个方案中选定一个再进一步论证，其中符合要求的方案是（）A．B．C．D．9．如图：有一块三角形状的土地平均分给四户人家，现有四种不同的分法，（如图中，D、E、F分别是BC、AC、AB的中点，G、H分别是BF、AF的中点），其中正确的分法有（）A．1种B．2种C．3种D．4种10．王老师用28米长的木条给花圃做围栏，他想把花圃设计成以下四种造型，不能用28米的长木条围成的设计有（）种．A．1B．2C．3D．4二．填空题11．如图，笔直的公路旁有A、B两车站，相距15km，C、D为同旁的两个村庄，DA⊥AB 于A，CB⊥AB于B，AD＝10cm，CB＝5cm，要在这段公路AB旁建一个公路管理站E，使C、D两村到公路管理站的距离相等，那么公路管理站E应建在距A站km处．12．面积为1个平方单位的正三角形，称为单位正三角形．下面图中的每一个小三角形都是单位正三角形，三角形的顶点称为格点．在图1，2，3中分别画出一个平行四边形、梯形和对边都不平行的凸四边形，要求这三个图形的顶点在格点、面积都为12个平方单位．．13．如图，有两个正方形的花坛，准备把每个花坛都分成形状相同的四块，种不同的花草．下面左边的两个图案是设计示例，请你在右边的两个正方形中再设计两个不同的图案．．14．有一块方角形钢板如图所示，请你用一条直线将其分为面积相等的两部分（不写作法，保留作图痕迹，在图中直接画出）．15．如图，平原上有A、B、C、D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池，不考虑其他因素，请你画图确定蓄水池H点的位置，使它与四个村庄的距离之和最小．三．解答题16．如图为正方形网格，每个小正方形的边长均为1，各个小正方形的顶点叫做格点，请在下面的网格中按要求分别画图，使得每个图形的顶点均在格点上．（1）在图中画一个以AB为一边的菱形ABCD，且菱形ABCD的面积等于20．（2）在图中画一个以EF为对角线的正方形EGFH，并直接写出正方形EGFH的面积．17．通过文明城市的评选，人们增强了卫生意识，大街随地乱扔生活垃圾的人少了，人们自觉地将生活垃圾倒入垃圾桶中，如图所示，A，B，C为市内的三个住宅小区，环保公司要建一垃圾回收站，为方便起见，要使得回收站建在三个小区都相等的某处，请问如果你是工程师，你将如何选址．18．图①、图②、图③均是4×4的正方形网格，每个小正方形的顶点称为格点，线段AB 的端点均在格点上，在图②、图③中仿照图①，只用无刻度的直尺，各画出一条线段CD，将线段AB分为2：3两部分．要求：所画线段CD的位置不同，点C、D均在格点上19．小名准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如图所示的拼接图形（实线部分），经折叠后发现还少一个面，你能在图中的拼接图形上再接一个正方形画出阴影，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子吗？请在下面的图①和图②中画出两种不同的补充方法．参考答案与试题解析一．选择题1．【解答】解：对任一正方形，容易分为大于等于4的偶数个小正方形（大小不等），比如2N，（N≥2）．具体分法为：设原正方形边长为1，按在水平和垂直方向划两条线，这可分出边长为和两个正方形及长宽分别为和的两个小长方形，而每个小长方形又可分为（N ﹣1）个边长为的小正方形，因此总的正方形数为2+2×（N﹣1）＝2N．而对于奇数（N≥7），显然原正方形先可一分为四，而其中之一的小正方形又可分为大于等于4的偶数个小正方形（前一结论），计为2N，因此可分为3+2N＝2（N+1）+1个奇数个小正方形，其中（N≥2），故N＝4或N≥6的所有自然数．故选：A．2．【解答】解：如图所示：（1）图1：当BC＝CD＝3m时；由于AC⊥BD，则AB＝AD＝5m；此时等腰三角形绿地的周长＝5+5+3+3＝16（m）；（2）图2：当AC＝CD＝4m时；∵AC⊥CB，∴AB＝BD＝5m，此时等腰三角形绿地的周长＝5+5+4+4＝18（m）；。

【数学】人教版七年级上册第四章《几何图形初步》单元测试(解析版)

人教版七年级上册第四章《几何图形初步》单元测试（解析版）一、选择题1、如图所示，该几何体的主视图是（）A． B． C． D．2、图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①②③④某一位置，所组成的图形不能围成正方体的位置是（）A．① B．② C．③ D．④3、已知一个几何体的三种视图如图所示，则这个几何体是（）A．圆柱 B．圆锥 C．球体 D．正方体4、下列四个生活、生产现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；③从A地到B地架设电线，总是尽可能沿着线段AB架设；④把弯曲的公路改直，就能缩短路程，其中可用公理“两点之间，线段最短”来解释的现象有( )A．①② B．①③ C．②④ D．③④5、已知∠AOB＝30°，自∠AOB顶点O引射线OC，若∠AOC︰∠AOB＝4︰3，那么∠BOC的度数是（）A．10° B．40° C．70° D．10°或70°6、．下列说法正确的是（）A．两点之间的连线中，直线最短 B．若P是线段AB的中点，则AP=BPC．若AP=BP，则P是线段AB的中点 D．若A，B，C在同一直线上，且AB=2，BC=3，则AC=57、如图，C，D是线段AB上两点．若CB=4cm，DB=7cm，且D是AC的中点，则AC的长等于（）A．3cm B．6cm C．11cm D．14cm8、如图，下列说法中错误的是（）A．OA的方向是东北方向 B．OB的方向是北偏西60°C．OC的方向是南偏西60° D．OD的方向是南偏东60°9、钟表盘上指示的时间是10时40分，此刻时针与分针之间的夹角为（）。

（A）60°（B）70°（C）80°（D）85°10、如图，已知∠AOC=∠BOD=900, ∠AOD=1500,则∠BOC的度数为（）A、450B、300C、500D、60011、∠α=40.4°，∠β=40°4′，则∠α与∠β的关系是（）A. ∠α=∠β；B. ∠α＞∠β；C. ∠α＜∠β；D. 以上都不对；12、如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC=100°，则∠BOD的度数是（）A. 20°；B. 40°；C. 50°；D. 80°；二、填空题13、一个角的余角比这个角的补角的一半小40°，则这个角为度．14、17°14′24″＝___度．15、．计算：153°﹣26°40′=_______．16、如图所示，将图沿虚线折起来，得到一个正方体，那么“我”的对面是（填汉字）.17、图1，是一个由边长为1的小正方形木块摆放在地上而成的图形，图2，图3也是由边长为1的小正方体木块叠放在地上而成，要给露在外面的小正方体表面涂上油漆（底面不涂），按照这样的规律继续叠放下去，到第7个叠放的图形中，涂到油漆部分的面积是．18、五棱柱有__________个顶点，有__________个面，有__________条棱．19、如图，AC=CD=DE=EB,则点C是线段的中点，点D是线段的中点，如果AB=8 cm，则AD= cm,AE= cm。

人教版七年级上数学第四章《图形认识初步》单元卷含答案

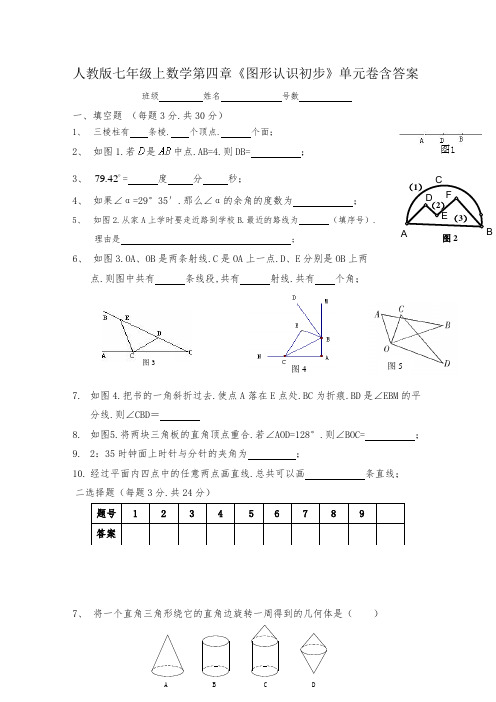
人教版七年级上数学第四章《图形认识初步》单元卷含答案班级姓名号数一、填空题（每题3分.共30分）1、三棱柱有条棱. 个顶点. 个面；2、如图1.若是中点.AB=4.则DB= ；3、 42.79= 度分秒；4、如果∠α=29°35′.那么∠α的余角的度数为；5、如图2.从家A 上学时要走近路到学校B.最近的路线为（填序号）.理由是；6、如图3.OA 、OB 是两条射线.C 是OA 上一点.D 、E 分别是OB 上两点.则图中共有条线段,共有射线.共有个角；7. 如图4.把书的一角斜折过去.使点A 落在E 点处.BC 为折痕.BD 是∠EBM 的平分线.则∠CBD ＝8. 如图5.将两块三角板的直角顶点重合.若∠AOD=128°.则∠BOC= ； 9. 2：35时钟面上时针与分针的夹角为；10. 经过平面内四点中的任意两点画直线.总共可以画条直线；二选择题（每题3分.共24分）7、将一个直角三角形绕它的直角边旋转一周得到的几何体是（）题号 123456789答案C BADE F（1）（2）（3）图2图3图5图412、如果与互补.与互余.则与的关系是（）A.=B.C.D.以上都不对13、对于直线.线段.射线.在下列各图中能相交的是（）AB；③AM=BM；④AM+BM=AB。

15、已知M是线段AB的中点.那么.①AB=2AM；②BM=2上面四个式子中.正确的有（）A．1个 B．2个 C．3个 D．4个16、在海上.灯塔位于一艘船的北偏东40度方向.那么这艘船位于这个灯塔的（）方向A.南偏西50度B.南偏西40度C.北偏东50度D.北偏东40度17、如右图.AB、CD交于点O.∠AOE=90°.若∠AOC：∠COE=5：4.则∠AOD等于（）A．120° B．130° C．140° D．150°18、图中(1)-(4)各图都是正方体的表面展开图.若将他们折成正方体.各面图案均在正方体外面.则其中两个正方体各面图案完全一样.他们是（）A. (1)(2)B.（2）（3）C.（3）（4）D.（2）（4）三、作图题（各7分.共21分）19、已知、求作线段AB使AB=2a－b（不写作法.保留作图痕迹）20、按照要求.在图中画出表示下列方向的射线：(1)南偏东300 (2)北偏西600 (3)西南方向四、解答题（8+8+9分.共25分）21、若一个角的补角等于它的余角的4倍.求这个角的度数。

初中数学人教版(2012)七年级上册第四章几何图形初步单元测试(有答案)

初中数学人教版(2012)七年级上册第四章几何图形初步单元测试一、单选题1.如图，将一副三角尺按不同的位置摆放，下列方式中α∠与β∠互余的是（）.A.①B.②C.③D.④2.由5个棱长为1的小正方体组成的几何体如图放置，一面着地，两面靠墙．如果要将露出来的部分涂色，则涂色部分的面积为（）A．9 B．11 C．14 D．183.用一个平面去截正方体(如图),下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是( )A.①②B.①④C.①②④D.①②③④4.如图,码头A在码头B的正西方向，甲、乙两船分别从,A B同时出发.并以等速驶向某海域，甲的航向是北偏东35°，为避免行进中甲、乙相撞，则乙的航向不能是( )A.北偏东55°B.北偏西55°C.北偏东35°D.北偏西35°5.线段12cm AB =，点C 在线段AB 上，且1,3AC BC M =为BC 的中点，则AM 的长为( ) A.4.5cm B.6.5cm C.7.5cm D.8cm6.下面关于余角、补角的说法，正确的是( )A.若123180∠+∠+∠=°，则1,2,3∠∠∠互补B.若1290∠+∠=°，则1∠与2∠互余C.若12180∠+∠=°，则1∠与2∠互余D.一个角的余角和它的补角相等7.下列关于角的平分线的说法中，正确的是( )A.角的平分线是一条线段B.角的平分线是平分这个角的一条直线C.以一个角的顶点为端点且把这个角分成相等的两个角的一条线段D.以一个角的顶点为端点且把这个角分成相等的两个角的一条射线8.下列说法中，正确的是( )A.两条射线所组成的图形叫做角B.有公共端点的两条线段组成的图形叫做角C.角是一条射线绕着它的端点旋转而形成的图形D.角是一条线段绕着它的一个端点旋转而形成的图形9.下列四个图形中，能用1,,AOB O ∠∠∠三种方法表示同一个角的是( )A. B.C. D.10.如图，AB CD =，则AC 与BD 的大小关系是( )A.AC BD >B.AC BD <C.AC BD =D.无法确定11.下列判断中，正确的是( )①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的补角，那么它们相等;④锐角和钝角互补.A.①②B.①③C.①④D.②③12.下列图形中，能通过折叠围成一个三棱柱的是( )A. B.C. D.13.如图，将三角形绕直线l 旋转一周，可以得到图5所示的立体图形的是( )A.图1B.图2C.图3D.图414.在灯塔O 处观测到轮船A 位于北偏西54°的方向，同时轮船B 在南偏东15°的方向，那么AOB ∠的大小为( )A.69°B.111°C.141°D.159°15.下列说法中，正确的有( )①射线OP 和射线PO 是同一条射线；②连接两点的线段叫两点间的距离；③两点确定一条直线；④若AC BC =，则C 是线段AB 的中点.A.1个B.2个C.3个D.4个16.因为1290,2390∠+∠=︒∠+∠=︒,所以13∠=∠理由是( )A.同角的余角相等B.同角的补角相等C.等角的余角相等D.等角的补角相等17.点C 在AOB ∠内部，现有四个等式1,2COA BOC BOC AOB ∠=∠∠=∠，12,2AOB COA ∠=∠2AOB AOC ∠=∠，其中能表示OC 是角平分线的等式的个数是( ) A.1 B.2 C.3 D.418.下列关于平角、周角的说法正确的是( )A.平角是一条直线B.周角是一条射线C.反向延长射线OA ，就形成一个平角D.两个锐角的和不一定小于平角19.如图.下列表示角的方法中.不正确的是( )A.A ∠B.E ∠C.α∠D.1∠20.如果点B 在线段AC 上，那么下列表达式中：①12AB AC =；②AB BC =；③2AC AB =；④AB BC AC +=.能表示点B 是线段AC 的中点的有( )A.1个B.2个C.3个D.4个二、填空题21.如果一个角的补角是150°，那么这个角的余角的度数是______________度.22.若要使图中的展开图按虚线折叠成正方体后，相对面上两个数之和为10，则x y +=_____.23.把弯曲的河道改直，能够缩短航程.这样做根据的道理是___________________.24.已知一条直线上有,,A B C 三点，线段AB 的中点为,16P AB =cm ，线段BC 的中点为Q ，且6BC =cm,则线段PQ 的长为 .25.下图是一个无盖的长方体盒子的展开图(重叠部分及厚度不计)，根据图中数据，则该无盖长方体盒子的容积为 .26.如果一个角的补角比这个角的余角的3倍大10°，则这个角的度数是________27.如图，是由一些小立方块所搭几何体的三种视图，若在所搭几何体的基础上(不改变原几何体中小立方块的位置)，继续添加相同的小立方块，以搭成一个大正方体，至少还需要________个小立方块.28.如图，从图书馆A到教室B，不少人没有走人行道，而是直接沿图中虚线由A穿过草坪到达B，他们这样做的数学依据是，你对此的看法是 .29.已知线段AB,延长AB到C,使得12BC AB=,延长BA到D,使得2AD AB=,M,N分别为,BC AD的中点，若18MN=,则AB=_______.30.一个几何体的展开图如图所示.请根据图中所标的尺寸，这个几何体的侧面积为 .三、解答题31.如图，AB与CD相交于,O OE平分AOC∠，OF AB⊥于,O OG OE⊥于O，若40BOD∠=︒，求AOE∠和FOG∠的度数.32.已知线段10cm AB =,直线AB 从上有一点C ,6cm BC =,M 为线段的中点,N 为线段BC 的中点,求线段MN 的长.33.如图，90AOB ∠=︒，2BOC BOD ∠=∠，OD 平分AOC ∠，求BOD ∠的度数.34.已知点C 在线段AB 上,线段7cm AC =,5cm BC =,点,M N 分别是,AC BC 的中点,求 MN 的长度.参考答案1.答案：A解析：图①中，1809090αβ∠+∠=+=°°°，互余；图②中，根据同角的余角相等，得αβ∠=∠图③中，根据等角的补角相等，得αβ∠=∠;图④中，180αβ∠+∠=°，互补.2.答案：B解析：由图可知涂色部分是从上、前、右三个方向所涂面积相加的和，即涂色部分面积为44311++=，3.答案：B解析：用平面去截正方体，得到的截面可能为三角形、四边形、五边形、六边形，而三角形只能是锐角三角形，不能是直角三角形和钝角三角形.4.答案：D解析：因为甲的航向是北偏东35°且甲、乙等速，为避免行进中甲、乙相撞，所以乙的航向不能是北偏西35°.故选D.5.答案：C解析：如图，因为13AC BC =，所以11123(cm)44AC AB ==⨯= 所以1239(cm)BC AB AC =-=-=因为点M 为BC 的中点，所以119 4.5(cm)22CM BC ==⨯= 所以3 4.57.5(cm)AM AC CM =+=+=.6.答案：B解析：1,2∠∠与3∠是3个角，不符合互补的定义，故选项A 错误;若1290∠+∠=°，则1∠与2∠互余，故选项B 正确;若12180∠+∠=°，则1∠与2∠互补，故选项C 错误;若设这个角为x °，则它的余角为90x -°°，补角为180x -°°.因为(180)(90)90x x ---=°°°°°，所以一个角的余角比它的补角小90°，故选项D 错误.故选B.7.答案：D解析：根据角平分线的定义可知选项A,B,C 都不对.只有D 选项符合题意.8.答案：C解析：A 中有两条射线，但未强调有公共端点，所以不正确，B,D 中说的是两条线段，所以也不正确.故选C.9.答案：C解析：能用1,,AOB O ∠∠∠三种方法表示同一个角的图形是选项C 中的图形，选项A,B,D 中的图形都不能同时用1,,AOB O ∠∠∠三种方法表示同一个角，故选C.10.答案：C解析：因为AB CD =，所以AB BC CD BC +=+，即AC BD =.故选C.11.答案：B解析：由互补的定义和性质可知，①③正确；因为90︒角的补角还是90︒，150︒角的补角是30︒，所以②错误；因为60︒和100︒的和不是180︒，所以④错误.故选B.12.答案：C解析：根据三棱柱及其表面展开图的特点对各选项分析判断即可得解．试题解析：A 、折叠后少一面，故本选项错误；B 、折叠后两侧面重叠，不能围成三棱柱，故本选项错误；C 、折叠后能围成三棱柱，故本选项正确；D 、折叠后两侧面重叠，不能围成三棱柱，故本选项错误．故选C ．考点：展开图折叠成几何体．13.答案：B解析：绕直角三角形一条直角边旋转一周可得到圆锥，绕斜边旋转一周可得到两个有公共底面的圆锥.故选B.14.答案：C解析：由题意得154,215,3905436∠=︒∠=︒∠=︒-︒=︒369015141AOB ∠=︒+︒+︒=︒.故选C.15.答案：A解析：射线OP 的端点是O ，从O 向P 无限延伸，射线PO 的端点是P ，从P 向O 无限延伸，所以不是同一条射线，故①错误，连接两点间的线段的长度，叫两点间的距离，故②错误。

新人教版七年级上第四章《图形认识初步》单元测试卷

七年级上期《图形认识初步》测验试卷（满分100分）班级姓名座号成绩一、填空题（每题3分，共30分）1．圆柱的侧面展开图是；2．若要使右图中平面展开图折叠成正方体后，相对面上两个数之和为6，则x=_ ___， y=______.3．已知α∠与β∠互余，且40α=∠51'，则β∠为.4．如图，若是中点，是中点，若，，_________。

5．俯视图为圆的立体图形可能是____________ 。

(填两个即可)6．要在墙上固定一根木条，至少要个钉子，根据的原理是。

7．⑴°；⑵0.5°=______′=______″8．不在同一直线上的四点最多能确定条直线。

9．小明每天下午5:30回家，这时分针与时针所成的角的度数为____度。

10. 一个角的补角等于它的余角的3倍,则这个角的度数为 .二、选择题（每题3分，共30分）1．如果与互补，与互余，则与的关系是…………（）（A）=（B）（C）（D）以上都不对2．对于直线，线段，射线，在下列各图中能相交的是（）12 3x yA650O3.下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个的是（）4．如图，∠1＝︒15,∠AOC=︒90点B、O、D在同一直线上，则的度数为（）（A）（B）（C）（D）5．如图的几何体，左视图是（）6．如图，点A位于点O的方向上．（）.（A）南偏东35°（B）北偏西65°（C）南偏东65°（D）南偏西65°7．将下列图形绕直线l旋转一周, 可以得到右图所示的立体图形的是( )8．下图中, 是正方体的展开图是( )DCBA9、平面上A 、B 两点间的距离是指（）A 、经过A 、B 两点的直线 B 、射线ABC 、 A 、B 两点间的线段D 、 A 、B 两点间线段的长度 10、一个立体图形的三视图如图所示，那么它是（） A ．圆锥 B ．圆柱 C ．三棱锥 D ．四棱锥三、作图题：（6分）根据下列要求画图：（1）连接线段AB ；（2）画射线OA ，射线OB ；（3）在线段AB 上取一点C ，在射线OA 上取一点D （点C 、D 不与点A 重合），画直线CD ，使直线CD 与射线OB 交于点E 。

(新版人教版)七年级上第四章《图形认识初步》单元测试卷及解析答案

第四章《图形认识初步》综合测试题（满分120 分时间90 分钟）一、选择题（每题 3 分，共 30 分）1． ①平角是一条直线；②射线是直线的一半；③射线一个扩大 2 倍的放大镜去看一个角，这个角会扩大= 120 °50. ?AB 与射线 BA 表示同一条射线；④用2 倍；⑤两点之间，线段最短； ⑥ 120.5 °以上说法正确的有 (A.0 个B.12．以下四个图中，能用∠)个 C.2 个 D.3 个1、∠ AOB 、∠ O 三种方法表示同一个角的是（）3．以下表达正确的选项是（） A ． 180°是补角B 120°和 60°互为补角 C 120 °和 60°是补角 D 60°是 30°的补角4. 如图 1 表示一个用于防震的 L 形的包装用泡沫塑料，当从上边看这一物体时看到的图形形状是（）A ．B ．C ．D ．(图 1)5．以下图形中，哪一个是正方体的睁开图（）6．甲看乙的方向为南偏西25°，那么乙看甲的方向是（）A ．北偏东 75° B．南偏东 75° C．北偏东 25° D ．北偏西 25°7．若∠ A 的余角是 70°，则∠ A 的补角是（）A ． 70°B ．110°C ． 20°D ． 160°8．如图，AOC和BOD都是直角，假如D CAOB150 ，那么 COD（）AA 、30B 、40C 、50D 、60BO9.经过随意三点中的两点共可画出（）A ．1 条直线B ． 2 条直线C ．1 条或 3 条直线D ． 3 条直线10. 如下图，从O点出发的五条射线，能够构成角的个数是（）．A．10个B．9个C．8个D．4个二、填空题（每题 3 分，共 30 分）11．橙子近似 ______ 体，菠萝近似 _______ 体，角柜近似 _______ 体，金字塔近似 _______体，粉笔盒近似 _______体。

人教版数学七年级上册《几何图形初步》单元检测卷附答案

【详解】正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,所以在此正方体上与“动”字相对的面上的汉字是“乐”．
故选D．
【点睛】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题．
4.与红砖、足球类似的图形是（）
A.长方形、圆B.长方体、圆
C.长方体、球D.长方形、球
16.天上一颗颗闪烁的星星给我们以“_____”的形象；中国武术中有“枪扎一条线,棍扫一大片”的说法,这句话给我们以“_____”的形象；宾馆里旋转的大门给我们以“_____”的形象．
17.定义：两个直角三角形,若一个三角形的两条直角边分别与另一个三角形的两条直角边相等,我们就说这两个直角三角形是“同胞直角三角形”．如图,在边长为10的正方形中有两个直角三角形,当直角三角形①和直角三角形②是同胞直角三角形时,a的值是_____．
9.A,B,C三点在同一直线上,线段AB＝5cm,BC＝4cm,那么A,C两点的距离是（）
A.1cmB.9cmC.1cm或9cmD. 以上答案都不对
二、填空题
10.如图,有一个长方形纸片,减去相邻的两个角,使∠ABC=90°,如果∠1=152°,那么∠2=_____________°.
11.一个长方体形状的粉笔盒展开如图所示,相对的两个面上的数字之和等于6,则a+b+c=_____．
(1)数一下每一个多面体具有的顶点数、棱数和面数 .并且把结果记入表中.
多面体
顶点数
面数
棱数
正四面体
4
4
6
正方体
正八面体
正十二面体
正ห้องสมุดไป่ตู้十面体
12
20
30
(2)观察表中数据,猜想多面体的顶点数、棱数和面数之间的关系.

【数学】人教版七年级上册数学第四章几何图形初步单元测试题(含答案)

人教版七年级上册数学第四章几何图形初步单元测试题（含答案）一、选择题1.角是指（）A. 由两条线段组成的图形B. 由两条射线组成的图形C. 由两条直线组成的图形D. 有公共端点的两条射线组成的图形2.如果一个角的补角是150°，那么这个角的余角的度数是（）A. 30°B. 60°C. 90°D. 120°3.下列说法正确的是（）A. 经过两点有且只有一条线段B. 经过两点有且只有一条直线C. 经过两点有且只有一条射线D. 经过两点有无数条直线4.如图，四条线段中，最短和最长的一条分别是（）A. acB. bdC. adD. bc5.如图，B在线段AC上，且BC=2AB，D，E分别是AB，BC的中点．则下列结论：①AB= AC；②B是AE的中点；③EC=2BD；④DE=AB．其中正确的有（）A. 1个B. 2个C. 3个D. 4个6.已知∠α=70°，则∠α的补角为（）A. 120°B. 110°C. 70°D. 20°7.下列语句中，正确的是（）．A. 比直角大的角钝角;B. 比平角小的角是钝角C. 钝角的平分线把钝角分为两个锐角;D. 钝角与锐角的差是锐角8.如图，已知AD平分∠BAE，若∠BAD=62°，则∠CAE的度数是（）A. 55°B. 56°C. 58°D. 62°9.如图，下列关系式中与图不符合的式子是（）A. AD-CD=AB+BCB. AC-BC=AD-BDC. AC-BC=AC+BDD. AD-AC=BD-BC10.如图是一个正方体的平面展开图，当把它拆成一个正方体，与空白面相对的字应该是（）A. 北B. 京C. 欢D. 迎二、填空题11.已知线段AB=8 cm，在直线AB上画线段BC，使它等于3 cm，则线段AC=________.12.若∠α=32°22′，则∠α的余角的度数为________．13.已知一个角的补角等于155°，则这个角的余角等于________14.八棱柱有________个顶点，________条棱，________个面．15.和互补，且-=50°，求和的度数． ________、 ________16.34.42°=________（用度、分、秒表示）.17.一个角的补角加上10°后，等于这个角的余角的3倍，则这个角=________ °．18.用一个平面去截长方体，截面________是平行四边形（填“可能”或“不可能”）．19.一条直线上有A、B、C三个点，AB=7cm，BC=4cm，则AC=________ ．20.已知线段AB=1996，P、Q是线段AB上的两个点，线段AQ=1200，线段BP=1050，则线段PQ=________．三、解答题21.已知∠BOC＝120°，∠AOB＝70°，求∠AOC的大小。

人教版-数学-七年级上册-第四章 图形认识初步 单元测试14

人教版数学七年级上册第四章《几何图形初步》单元测试题含答案

完整版人教版七年级上册数学第四章 几何图形初步含答案

(新版人教版)七年级上第四章《图形认识初步》单元测试卷及解析答案

【数学】人教版七年级数学上册第四章几何图形的初步单元测试(含答案)

人教版七年级上册数学 第四章 几何图形初步 单元测试(含解析)

人教版初中数学七年级上册第四章图形认识初步单元测试

(新版人教版)七年级上第四章《图形认识初步》测试题及答案

人教版数学七年级上册第第四章 几何图形初步 基础检测题含答案

【数学】人教版七年级上册第四章《几何图形初步》单元测试(解析版)

人教版七年级上数学第四章《图形认识初步》单元卷含答案

初中数学人教版(2012)七年级上册 第四章几何图形初步 单元测试(有答案)

新人教版七年级上第四章《图形认识初步》单元测试卷

(新版人教版)七年级上第四章《图形认识初步》单元测试卷及解析答案

人教版数学七年级上册《几何图形初步》单元检测卷附答案

【数学】人教版七年级上册数学第四章几何图形初步单元测试题(含答案)

人教版-数学-七年级上册-第四章图形认识初步单元测试14

完整版人教版七年级上册数学第四章几何图形初步含答案

人教版七年级上册数学第四章几何图形初步单元测试(含解析)

人教版数学七年级上册第第四章几何图形初步基础检测题含答案

初中数学人教版(2012)七年级上册第四章几何图形初步单元测试(有答案)