大小偏心受压构件的承载力计算公式ppt课件
偏心受压构件的承载力
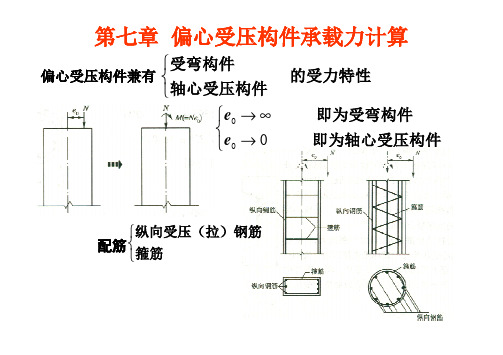
三、M — N相关曲线
对偏压短柱其承载力: Nu与 e0/h0 有关 <=> Nu与Mu有关
对小偏压:增加轴向力会使构件 构件 N Na 的抗弯能力减小 Nb 对大偏压 对大 偏压:增加 :增加轴向力会使构件 构件 的抗弯能力增大 界限破坏:构件 构件的 的抗弯能力最大.Nc O
a
短柱
b
长柱
截面承载力
D = βε cu Es As (h0 − as' )
h / h0 > ξ > ξb
由7-4 γ 0 N d − f cd bx + σ s As As′ = ' f sd
选钢筋 并合理布置
x < ξ b h0
若ξ ≥ h / h0 , 令x = h
由7-5 γ 0 N d es − f cd bh(h0 − h / 2) ' As = ' f sd (h0 − as' )
N
ζ 2 = 1.15 − 0.01l0 / h ≤ 1
试验研究表明:对于两端铰接柱的侧向挠度曲线近似符合正弦曲线
d2y π2 πx π2 挠度曲线曲率 φ = − = u 2 sin =y 2 2 d x l0 l0 l0 2 l 10 π 2 ≈10 →φ = y 2 或 y =φ 0 10 l0 εc + εs
β = 0.8
' γ 0 N d es ≤ f sd As ( h0 − a′ s ) (7-12)
(3)对小小偏心,As不得小于按下式计算的数量
'2 ' γ 0 N d e ' ≤ 0.5 f cd bh0 + f sd As ( h0 '− a s ) (7-13)
06受压构件承载力计算 (新的课件)134页PPT

6.1 概述
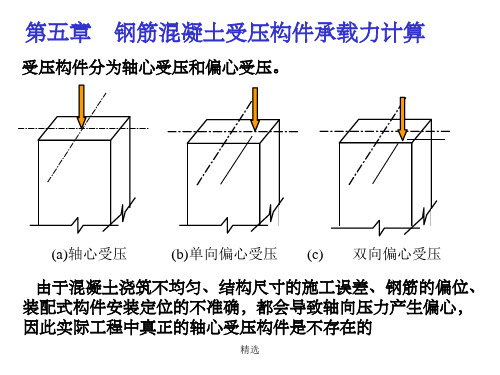
受压构件分为轴心受压构件和偏心受压构件。
轴心受压构件:轴向力作用在构件截面的形心上。矩和轴力共同作用的构件)。
N
N
N
M
(a)轴心受压
(b) 单向偏心受压
第六章 受压构件承载力计算
要说明的是,实际工程中真正的轴心受压构件是没 有的。由于施工的偏差及混凝土的不均匀性和钢筋 的不对称性,都将使构件产生初始偏心距,所以即时设 计时理论计算是轴心受压构件, 也不一定为轴心受压 构件,但对于一些偏心距较小的构件,可按轴心受压构 件计算。
第六章 受压构件承载力计算
Highway interchange structure. Spans are all multi-cell reinforced concrete box girders. Being stiff in torsion, these sections can be supported on a single line of columns, as well as on double columns or bents. (Oakland, California)
第六章 受压构件承载力计算
第六章 受压构件承载力计算
第六章 受压构件承载力计算
第六章 受压构件承载力计算
偏心受 压构件
工业和民用建 筑中的单层厂 房和多层框架 柱
偏心受压构件 第六章 受压构件承载力计算
偏心受压构件拱和 屋架上弦杆,以及 水塔、烟囱的筒壁 等属于偏心受压构 件
第六章 受压构件承载力计算
受压构件在实际工程中应用比较广泛。
第六章 受压构件承载力计算
第六章 受压构件承载力计算
New Antioch Bridge. This high-level bridge completed in 1979 replaced an older truss-type lift bridge crossing the main shipping channel. The bridge consists of continuous spans of variable depth in Cor-Ten steel. Maximum span is 460 ft, and maximum height of roadway above water level is 135 ft. (California)
第八章 偏心受压构件承载力计算公式

第8章 偏心受压构件正截面承载力知 识 点 回 顾•破坏形式及特点 •大小偏心划分 •大偏心算法第8章 偏心受压构件正截面承载力8.1.4 矩形截面偏心受压构件正截面承载力 1. 大偏心受压x £ xb 正截面破坏åN =0g 0 N £ N u = a1 f c bx + f y¢ As¢ - f y Asxö æ ¢ g 0 Ne £ N u e = a1 f c bx ç h0 - ÷ + f y¢ As¢ ( h0 - as ) 2ø èå M As = 0适用条件: x £ xb ¢ x ³ 2 as As 配筋率: r= ³ r min = max ( 0.45 ft fy, 0.2% ) bh第8章 偏心受压构件正截面承载力¢ 当 x < 2as 时,受压钢筋(此时不屈服)计算, 有两种处理方式: (1)规范算法设混凝土合力中心与 As¢ 形心重合。
åM¢ As=0¢ Ne¢ £ N u e¢ = f y As ( h0 - as )(2)平截面假定算法¢ s s¢ = Ese cu (1 - b1 as x )第8章 偏心受压构件正截面承载力2. 小偏心受压构件 (1)基本计算公式 x > xb矩形截面小偏心受压构件承载力计算简图第8章 偏心受压构件正截面承载力小偏心受压构件计算公式:åN =0åMAsg 0 N £ N u = a1 f c bx + f y¢ As¢ - s s Asxö æ ¢ g 0 Ne £ N u e = a1 f c bx ç h0 - ÷ + f y¢ As¢ ( h0 - as ) 2ø è=0依据平截面假定( b1 = 0.8 ):æ b1hoi ö s si = Ese cu ç - 1÷ è x ø公路桥规:æ b1 - x ö s si = ç ÷ fy è b1 - xb øxb < x £ 2 b1 - xb第8章 偏心受压构件正截面承载力依据平截面假定:公路桥规:第8章 偏心受压构件正截面承载力(2) “反向破坏”的计算公式 偏心距很小,且远离轴向压力一侧的钢筋配置得 不够多,偏心压力有可能位于换算截面形心轴和 截面几何中心之间。
钢筋混凝土结构设计原理第六章偏心受压构件承载力

第六章偏心受压构件承载力计算题1. (矩形截面大偏压)已知荷载设计值作用下的纵向压力N 600KN ,弯矩M 180KN • m,柱截面尺寸b h 300mm 600mm,a$ a$ 40mm,混凝土强度等级为 C30, f c=14.3N/mm2,钢筋用HRB335级,f y=f y=300N/mm2,b 0-550,柱的计算长度I。
3.0m,已知受压钢筋A 402mm2(£尘1&|),求:受拉钢筋截面面积A s。
2. (矩形不对称配筋大偏压)已知一偏心受压柱的轴向力设计值N = 400KN,弯矩M = 180KN- m,截面尺寸b h 300mm 500m , a s a s40mm ,计算长度 l° = 6.5m,混凝土等级为C30 ,f c=14.3N/mm 2,钢筋为 HRB335 , , f y f y300N/mm2,采用不对称配筋,求钢筋截面面积。
3. (矩形不对称配筋大偏压)已知偏心受压柱的截面尺寸为b h 300mm 400mm ,混凝土为C25级, f c=11.9N/mm 2,纵筋为HRB335级钢,f y f y300N / mm2,轴向力N,在截面长边方向的偏心距e。
200mm。
距轴向力较近的一侧配置4「16纵向钢筋A'S804mm2,另一侧配置2十20纵向钢筋A S628mm2,a s a s' 35mm,柱的计算长度1。
= 5m。
求柱的承载力N。
4. (矩形不对称小偏心受压的情况)某一矩形截面偏心受压柱的截面尺寸b h 300mm 500mm,计算长度I0 6m, a s a s 40mm,混凝土强度等级为 C30, f c=14.3N/mm2, 1 1.0 ,用 HRB335 级钢筋,f y=f y =300N/mm 2,轴心压力设计值 N = 1512KN,弯矩设计值 M = 121.4KN • m,试求所需钢筋截面面积。
混凝土结构设计原理PPT课件第7章 偏心受压构件正截面承载力计算

钢筋的应力
si cu E s ( hoi
x 1)
ci
为了保证构件破坏时,大偏心 受压构件截面上的受压钢筋能达 到抗压强度设计值,必须满足
0 Nd
es
e 0
x 2a s
若x 2a x 2a s,近似取 s,则:
e s
0 N d e s M u f sd As (h0 as )
7.3.4矩形截面偏心受压构件对称配筋的计算方法 对称配筋: 截面设计 大、小偏心受压构件的判别: 假设为大偏心受压,则:
N f cd bx x N f cd b
As = A's,
fsd = f'sd , as = a's
若ξ ≤ ξ b,为大偏心受压构件,则:
若2a s x b h0 若x 2a s
A´s已知,As未知。 根据基本公式:
x As (h0 a Ne s f cd bx (h0 ) f sd s) 2
求得受压区高度:
As (h0 a 2Nes f sd s ) x h0 h0 f cd b
2
若满足:
2a s x b h0 取 s f sd
f cd bf x( e s h0 x As e ) f sd As e s f sd s 2
As f sd As
es
e 0
N
e s
ys
f cd bf x
hf
As f sd As
适用条件: x b h0
b
bf
a s
2a s x hf
短柱
柱:在压力作用下产 生纵向弯曲 ––– 材料破坏 ––– 失稳破坏
第七章偏心受压构件的正承载力计算-PPT

基本计算公式
受压区混凝土都能达到极限压应变; As’达到抗压强度设计值fsd’ ;
As受拉,也可能受压,大小ss。
es e0 h 2 as
es' e0 h 2 as'
es 、 es' —分别为偏心应力 0 Nd 至钢筋 As 合力点和钢筋 As' 合力作用点的距离;
1 2
ei
N
f
s
t
c
h0
偏心距增大系数
1 f
ei
f
1 1717
l0 2 h0
1 2
1
1 1717ei
l0 2 h0
1
2
h 1.1h0
1 1
1400 ei
l0 h
2
1
2
h0
ei
N
f
s
t
c
h0
根据偏心压杆得极限曲率理论分析,《公路桥规》规定
1 1 1400
e0
(
l0 h
)2
1
2
h0
1
0.2 2.7
as 、 as' —分别为钢筋 As 合力点和钢筋 As' 合力作用点至截面边缘的距离。
基本计算公式
纵轴方向得合力为零
0 Nd
Nu
fcdbx
f
' sd
As'
s s As
对钢筋As合力点得力矩之与等于零
0 Nd es
Mu
fcd
bx(h0
x 2
)
f
' sd
As'
(h0
as'
)
1
2
偏心受压构件承载力计算

轴心受压构件承载力计算一、偏心受压构件破坏特征偏心受压构件在承受轴向力N和弯矩M 的共同作用时,等效于承受一个偏心距为e0=M/N的偏心力N的作用,当弯矩M相对较小时,e0就很小,构件接近于轴心受压,相反当N相对较小时,e0就很大,构件接近于受弯,因此,随着e0 的改变,偏心受压构件的受力性能和破坏形态介于轴心受压和受弯之间。
按照轴向力的偏心距和配筋情况的不同,偏心受压构件的破坏可分为受拉破坏和受压破坏两种情况。
1.受拉破坏当轴向压力偏心距e0 较大,且受拉钢筋配置不太多时,构件发生受拉破坏。
在这种情况下,构件受轴向压力N后,离N较远一侧的截面受拉,另一侧截面受压。
当N增加到一定程度,首先在受拉区出现横向裂缝,随着荷载的增加,裂缝不断发展和加宽,裂缝截面处的拉力全部由钢筋承担。
荷载继续加大,受拉钢筋首先达到屈服,并形成一条明显的主裂缝,随后主裂缝明显加宽并向受压一侧延伸,受压区高度迅速减小。
最后,受压区边缘出现纵向裂缝,受压区混凝土被压碎而导致构件破坏(图4.3.1)。
此时,受压钢筋一般也能屈服。
由于受拉破坏通常在轴向压力偏心距e0 较大发生,故习惯上也称为大偏心受压破坏。
受拉破坏有明显预兆,属于延性破坏。
2.受压破坏当构件的轴向压力的偏心距e0 较小,或偏心距e0 虽然较大但配置的受拉钢筋过多时,就发生这种类型的破坏。
加荷后整个截面全部受压或大部份受压,靠近轴向压力一侧的混凝土压应力较高,远离轴向压力一侧压应力较小甚至受拉。
随着荷载逐渐增加,靠近轴一侧混凝土出现纵向裂缝,进而混凝土达到极限应变εcu 被压碎,受压钢筋的应力也达到f y′,远离一侧的钢筋可能受压,也可能受拉,但因本身截面应力太小,或因配筋过多,都达不到屈服强度(图4.3.2)。
由于受压破坏通常在轴向压力偏心距e0 较小时发生,故习惯上也称为小偏心受压破坏。
受压破坏无明显预兆,属脆性破坏。
3.受拉破坏与受压破坏的界限综上可知,受拉破坏和受压破坏都属于材料破坏”。
受压构件计算PPT课件

两端铰
1.0l
一端固定,一端铰支 0.7l 实际结构按
两端固定
规范规定取值 0.5l
一端固定,一端自由 2.0l
4、公式应用
• 截面设计: 已知:fc, f y, l0, N, 求As、A
设ρ’(0.6%~2%), φ=1
N A
0.9(fc ' fy' )
初估截面尺 寸
As
(
N
0.9
-f
c
Ac
)
f y
第五章
受压构件承载力计算
1
5.1 概 述
受压构件的类型
N N
N
N
(a)轴心受压
(b)单偏压
(c)双偏压
偏心受压构件
2
5.2 轴心受压构件的承载力计算
◆ 在实际结构中,理想的轴心受压构件几乎是不存在的。
◆ 通常由于施工制造的误差、荷载作用位置的不确定性、混凝 土质量的不均匀性等原因,往往存在一定的初始偏心距。
18
混凝土圆柱体三向受压状态的纵向抗压强度
1fc42
2 、 正截面受压承载力计算
(a)
(b)
2
s
(c)
s
1fc42
dcor fyAss1
2
fyAss1
达到极限状态时(保护层已剥落,不考虑)
Nu1Aco r fyAs
10
短柱极限承载力: Nu'sAscAc
条件: c s
混凝土: 当 cm , a x00.0时 02c, fck
钢 筋:
N
普通钢筋(HPB235,HRB335、HRB400)
y c,ma, x 则钢筋先屈服,
s fyk As
钢筋混凝土受拉构件承载力计算—偏心受拉构件正截面承载力计算

这时本题转化为已知As´求As的问题。
(3)求As
= −
+ ′ ′ ( − ′ )
得
× × = . × . × − .
+ × × ( − )
偏心受拉构件正截面受拉承载力计算
− =
×
属于大偏心受拉构件。
(2) 计算As´
= − + = −
+ =
由式(5-6)可得
′
− ² ( − . )
=
′ ( − ′ )
As=1963mm2
,
(1-1)、(1-2)式可得
′
=
=
− ( −. ) ²
′ ( −′ )
+′ ′ +
(5-6)
(5-7)
当采用对称配筋时,求得x为负值,取 = 2′ ,并对As´合力点取矩,计算As 。
偏心受拉构件正截面受拉承载力计算
315×103 ×125−1.0×14.3×1000×1752 ×0.55×(1−0.5×0.55)
=
<0
300×(175−25)
偏心受拉构件正截面受拉承载力计算
取
′ = ′ = . × × = ²
取2
16,
选2
16,A's=402mm2
偏心受拉构件的正截面受力原理及承载能力计算
判别条件:
M h
e
as
N 2
M h
e
as
N 2
水工钢筋混凝土结构学第5章PPT课件
三、 纵筋
纵筋:采用Ⅱ、Ⅲ级钢筋,不宜采用高强度钢筋。 轴心受压构件纵筋沿截面的四周均匀放置,钢筋根数不得少于4 根,直径不小于12mm,常用12~32mm。。 偏心受压构件纵筋放置在偏心截面的两边,截面高度≥600mm时, 侧面应设置直径10~16mm的纵向构造钢筋,并设附加箍筋或拉 筋。
承重墙内竖向钢筋的直径不应小于10mm,间距不应大于300mm。
荷载较小,砼和钢筋应力比符合弹模比。
荷载加大,应力比不再符合弹模比。
荷载长期持续作用,砼徐变发生,砼与钢筋之间引起
应力重分配。
破坏时,砼的应力达到 f c ,钢筋应力达到
f
y
。
精选
5.2 轴心受压构件正截面承载力计算
不同箍筋短柱的荷载—应变图
普通钢箍柱
A——不配筋的素砼短柱; B——配置普通箍筋的钢筋砼短柱; C——配置螺旋箍筋的钢筋砼短柱。
令 x h0
KN
Nu
1 d
( fcb h0
f y As
f y As )
KNe
fc
s
b
h
2 0
f y As ( h0 a ' )
得到
s
KNe
f y As ( h0
Байду номын сангаас
f
c
b
h
2 0
a')
1- 1-2 s
若 b ,可 以 保 证 构 件 破 坏 时 受 拉 钢 筋 的 应 力 先 达 到 fy ,因 而
y y f ?sin px
le f
考虑二阶效应的计算方法目前主要有非 线性有限元法和偏心距增大系数法精选
ei N
le
建筑结构第5章钢筋混凝土受压构件承载力计算参考课件

(4)圆柱中纵向钢筋不宜少于8根,不应少于6根,且 宜沿周边均匀布置。
(5)在偏心受压柱中,垂直于弯矩作用平面的侧面上 的纵向受力钢筋以及轴心受压柱中各边的纵向受力筋,其 中距不宜大于300mm。
(6)全部纵向受力钢筋的配筋率,对强度等级为 300MPa、335 MPa的钢筋不应小于0.6%,对强度等级为 400MPa的钢筋不应小于0.55%,对强度等级为500MPa的 钢筋不应小于0.5%,同时一侧钢筋的配筋率不应小于0.2%。 全部纵向钢筋和一侧纵向钢筋的配筋率均按构件的全截面 面积计算。
5.2.2 截面形式和尺寸
常用的截面:方形和矩形;用于桥墩、桩和公共建筑 中的柱,可采用圆形或多边形截面;单层工业厂房的预制 柱也常采用I字形截面。
截面的最小边长不宜小于250 mm。柱截面尺寸宜取 整数,边长在800mm以下者,取50mm为模数,边长在 800mm以上者,取100mm为模数。
5.2.3 纵向钢筋
N N u 0 .9fc A fy A s
当纵向普通钢筋配筋率ρ′ 大于3%时,公式中的A应改用 (A-As′)代替。
(2)配筋率
4.设计计算方法
(1)截面设计 已知:轴向力设计值N,柱的计算长度l0和材料的强 度等级fc、fy′。计算柱的截面尺寸b×h及配筋As′。
此时,As′、A、φ均为未知数,有许多组解答。求 解时先假设φ=1,ρ′=0.6%~5%(一般取ρ′=1%),估算
【学习重点】 配筋构造要求;轴心受压构件的正截面承载力计算; 对称配筋矩形截面偏心受压构件正截面承载力计算。
5.1 概 述
受压构件分为轴心受压构件和偏心受压构件。
当轴向力作用线与构件截面形心轴重合时,称为轴心受 压构件;当弯矩和轴力共同作用于构件上或轴向力作用线与 构件截面形心轴不重合时,称为偏心受压构件。
偏心受压构件承载力计算ppt课件

破坏特征:截面受拉侧混凝土较早出现裂
N
缝,As的应力随荷载增加发展较快,首先 达到屈服。最后受压侧钢筋A‘s 受压屈服, 压区混凝土压碎而达到破坏。有明显预兆,
变形能力较大,与适筋梁相似。
fyAs
f'yA's
精选ppt课件
2
第六章 受压构件承载力计算
精选ppt课件
3
第六章 受压构件承载力计算
二、受压破坏compressive failur(小偏心受压破坏)
24
第六章 受压构件承载力计算
对于大偏心受压: ss fy
N1fcb xfyAsfyAs Ne1fcb(xh0x2)fyAs(h0as' )
公式适用条件: 1xbh0,保证受拉钢筋屈服 2x2as' ,保证受压钢筋屈服
对于小偏心受压:
N1fcb xfyAsssAs Ne1fcb(xh0x2)fyAs(h0as' )
第六章 受压构件承载力计算
6.3 矩形截面偏心受压构件计算
N
6.3.1 偏心受压构件的破坏形态
M=N e0
As
As = As
e0 N As
N
As
As
As
M=N e0
As
As
N M=N e0
As
精选ppt课件
1
第六章 受压构件承载力计算
试验表明,钢筋混凝土偏心受压构件的破坏,有两种 情况:
1.受拉破坏情况 tensile failure(大偏心受压破坏) 2. 受压破坏情况 compressive failure(小偏心受压破坏) 一.受拉破坏情况 tensile failure(大偏心受压破坏) ◆ 形成这种破坏的条件是:偏心距e0较大,且受拉侧纵 向钢筋配筋率合适,是延性破坏。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
示。为简化计算,将其简化为图4.3.4b所示的等效矩形图。
17
18
由静力平衡条件可得出大偏心受压的基本公式:
N=αx1fcbx + fy′As′-fyAs Ne=α1fcbx2(h0- )+As′fy′(h0-as′)
附加弯矩。引入偏心距增大系数η ,相当于用代替 ei +f
。
11
12
2.偏心矩增大系数 钢筋混凝土偏心受压构件按其长细比 l0 / h 不同分
为短柱、长柱和细长柱,其偏心距增大系数 分别按下
述方法确定:
(1)对短柱(矩形截面 l0 / h≤5),可不考虑纵向弯曲
对偏心距的影响,取 = 1.0。 (2)对长柱(矩形截面5< l0 / h ≤30),偏心距增大
按照轴向力的偏心距和配筋情况的不同,偏心受压构件 的破坏可分为受拉破坏和受压破坏两种情况。
3
1.大偏心钢筋混凝土受压构件破坏过程(受拉破坏) (点击播放视频)
4
受拉破坏
5
破坏特征:受拉钢筋首先达到屈服强度,最后受压 区混凝土达到界限压应变而被压碎,构件破坏。此时, 受压区钢筋也达到屈服强度。
破坏性质:延性破坏
9
3.受拉破坏与受压破坏的界限 界限破坏:在受拉钢筋达到受拉屈服强度时,受压区 混凝土也达到极限压应变而被压碎,构件破坏,这就是大 小偏心受压破坏的界限。 判断条件:当§≤§b,属于大偏心受压构件;
当§>§ ,属于小偏心受压构件; b
10
6.3.2 偏心距增大系数η
1.压弯效应:在偏心力作用下,钢筋混凝土受压构件
系数按下式计算:
13
1
1 1400ei
/
h0
( l0 h
) 2 1 2
1
0.5 fc N
A
ζ2=1.15-0.01
l0 h
(6.3.1) (6.3.2) (6.3.3)
14
式中l0—构件的计算长度; h—矩形截面的高度; h 0—截面的有效高度; ζ1——偏心受压构件的截面曲率修正系数,当ζ1>1.0时,
将产生纵向弯曲变形,即会产生侧向挠度,从而导致截面的
初始偏心距增大(图4.3.3)。如1/2柱高处的初始偏心距将
由增大为ei +f ,截面最大弯矩也将由Nei增大为N( ei +f ),致使柱的承载力降低。这种偏心受压构件截面内的
弯矩受轴向力和侧向挠度变化影响的现象称为“压弯效应”
。
截面弯矩中的Nei称为一阶弯矩,将N·f称为二阶弯矩或
e'
eih 2Fra bibliotekas'
(6.3.13) (6.3.14)
22
(3) 小偏心受压(ξ>ξb): 矩形截面小偏心受压的基本公式可按大偏心受压的方
法建立。但应注意,小偏心受压构件在破坏时,远离纵
向力一侧的钢筋 As 未达到屈服,其应力 s 用来表示,
s
f
或
y
f
' y
。根据如图4.3.5所示等效矩形图,由静力平
第六章 受压构件
教学目标:
第三讲
1.了解大小偏心受压构件破坏特征 ;
2. 掌握大小偏心受压构件的承载力计算公式 及其适用条件。
1
重点
1、大小偏心受压构件破坏特征。 2、大小偏心受压构件的承载力计算公式及其适用
条件。
难点
大小偏心受压构件的承载力计算公式的建立。
2
§6.3 偏心受压构件承载力计算 6.3.1 偏心受压构件破坏特征
混凝土轴心抗压强度设计值fc乘以系数α1,矩形应力图形
的受压区高度 x 1xn ,xn 为由平面假定确定的中和轴高度
,1 、1 仍按表3.2.1取用;
16
4)考虑到实际工程中由于施工的误差、混凝土质量的不 均匀性,以及荷载实际作用位置的偏差等原因,都会造成轴 向压力在偏心方向产生附加偏心距ea,因此在偏心受压构件 的正截面承载力计算中应考虑ea的影响,ea应取20mm和偏心 方 向 截 面 尺 寸 h 的 1/30 中 的 较 大 值 , 即 ea=max(h/30 , 20 mm ) 。
6
2.小偏心钢筋混凝土受压构件破坏过程(受压破坏) (点击播放视频)
7
受压破坏
8
破坏特征:临近破坏时,构件截面压应力较大一 侧混凝土达到极限压应变而被压碎。构件截面压应力 较大一侧的纵向钢筋应力也达到了屈服强度;而另一 侧混凝土及纵向钢筋可能受拉,也可能受压,但应力 较小,均未达到屈服强度。
破坏性质:脆性破坏
M N
。
As'
As
Ne
1
f
y
fcbx
h0
h0 as
x 2
Ne 1 fcbh02 1 0.5
f
y
h0 as
(6.3.9)
20
2)基本公式适用条件 l为了保证构件在破坏时,受拉钢筋应力能达到抗拉强度设
计值fy,必须满足:
x
ξ= h0 ≤ξb
(6.3.10)
l为了保证构件在破坏时,受压钢筋应力能达到抗压强度设
将对称配筋条件As=As′,fy= fy′代入式(4.3.1)得
N=α1fcbx
(6.3.4) (6.3.5)
(6.3.6)
式中N—轴向压力设计值; x—混凝土受压区高度; e—轴向压力作用点至纵向受拉钢筋合力点之间的距
离;
19
—偏心剧增大系数;
ei —初始偏心距;
E0 —轴向压力N对截面重心的偏心距,e0=
取ζ1=1.0;
ζ2—构件长细比对截面曲率的影响系数,当l0/h<15时,
取ζ2=1.0;
A—构件的截面面积。
15
6.3.3 对称配筋矩形截面偏心受压构件 正截面承载力计算
1.基本公式及适用条件 (1)基本假定
1)截面应变保持为平面; 2)不考虑混凝土的受拉作用; 3)受压区混凝土采用等效矩形应力图,其强度取等于
衡条件可得出小偏心受压构件承载力计算基本公式为:
N =α1fcbx+fy′As′-σsAs
(6.3.15)
Ne =α1fcbx(h0-)+fy′As′(h0-as′) (6.3.16)
23
式中σs—距轴向力较远一侧的钢筋应力:
s
b
fy
1
(
1)
1 —系数,按表3.2.1取用。
(6.3.17)
解式(6.3.15)~式(6.3.17)得对称配筋时纵向
计值fy′,必须满足:
x≥2as′
(6.3.11)
当x<2as′时,表示受压钢筋的应力可能达不到fy′,此时,
近似取x=2as′,构件正截面承载力按下式计算:
Ne′=fyAs(h0-as′)
(6.3.12)
21
相应的,对称配筋时纵向钢筋截面面积计算公式为
As' As
fy
N e h0 as
