一次函数图像和性质ppt
合集下载
《一次函数》课件

REPORTING
经济问题中的一次函数
总结词:经济模型
详细描述:一次函数在经济领域中常被用作简化经济模型,例如,消费和收入之 间的关系、生产成本和产量之间的关系等。通过一次函数,可以更直观地理解经 济现象和预测未来的经济趋势。
物理问题中的一次函数
总结词:物理定律
详细描述:在物理学中,许多定律和公式都可以用一次函数来表示,例如,重力与距离的关系、电流与电压的关系等。通过 一次函数,可以更准确地描述物理现象和预测实验结果。
2023
《一次函数最新》 ppt课件
REPORTING
2023
目录
• 一次函数简介 • 一次函数的表达式 • 一次函数的应用 • 一次函数的解析方法 • 一次函数的实际案例
2023
PART 01
一次函数简介
REPORTING
一次函数的定义
一次函数是形如y=kx+b的函 数,其中k和b是常数,k≠0。
一次函数在数学问题中的应用
线性规划
利用一次函数解决资源分 配问题,实现资源利用的 最大化。
代数方程求解
通过一次函数表示代数方 程,简化方程求解过程。
几何图形面积计算
利用一次函数计算几何图 形的面积,如三角形、矩 形等。
一次函数与其他数学知识的结合
与二次函数的结合
利用一次函数和二次函数的性质 ,解决更复杂的数学问题。
一次函数是线性函数的一种, 它的图像是一条直线。
一次函数在平面坐标系中表示 为一条直线,该直线经过点 (0,b)和斜率为k。
一次函数的图像
一次函数的图像是一 条直线,其斜率为k ,截距为b。
通过代入不同的x值 ,可以求出对应的y 值,从而得到函数的 图像。
一次函数图像和性质ppt课件
一次函数的图像和性质
y
0
x
深圳市龙翔学校
刘国平
提问复习,引入新课
1、什么叫正比例函数、一次函数?它们之间有 什么关系?
一般地,形如 y=kx(k是常的数函,k数≠0,) 叫做正比 例函数; 一般地,形如 y=kx+b(k,的b是函常数数,,k≠叫0)做一次函 数。
当b=0时,y=kx+b就变成了 y=k,x所以说正比 例函数是一种特殊的一次函数。 2、正比例函数的图象是什么形状?
(3)直线 y=kx+b可以看作由直线y=kx_平__移___b_个__单__位
而得到
当b>0,向上平移b个单位;
当b<0,向下平可移编辑b课个件单PPT位。
11
• 用简单方法作函数y=2x+3,y=-x+3,y=5x-2的 图象
可编辑课件PPT
12
一次函数图象上点的确定
• 1、判断(2,3),(2,1),(0,3), (3,0)是否在一次函数y=2x-3的图象上
可编辑课件PPT
13
• 2、图象与x轴、y轴交点坐标及与x轴、y轴 围成的三角形面积的求解.
• 例题 已知一次函数y=-2x-2 • (1)画出函数的图象 (2)求图象与x轴、y轴的交点A、B的坐标 (3)求其图象与坐标轴围成的图形的面积 (4)利用图象求当x为何值时,y≥0
可编辑课件PPT
14
• 基础训练
b=0
b>0
b<0
一,三 一,二,三 一,三,四 二,四 一,二,四 二,三,四 当k>0时,y的值随x的增大而增大可编辑课件P当PTk<0时,y的值随x的增大而减小9
观察:比较上面第二组作的三个函数的相同点与 不同点,根据你的观察结果回答下列问题:
y
0
x
深圳市龙翔学校
刘国平
提问复习,引入新课
1、什么叫正比例函数、一次函数?它们之间有 什么关系?
一般地,形如 y=kx(k是常的数函,k数≠0,) 叫做正比 例函数; 一般地,形如 y=kx+b(k,的b是函常数数,,k≠叫0)做一次函 数。
当b=0时,y=kx+b就变成了 y=k,x所以说正比 例函数是一种特殊的一次函数。 2、正比例函数的图象是什么形状?
(3)直线 y=kx+b可以看作由直线y=kx_平__移___b_个__单__位
而得到
当b>0,向上平移b个单位;
当b<0,向下平可移编辑b课个件单PPT位。
11
• 用简单方法作函数y=2x+3,y=-x+3,y=5x-2的 图象
可编辑课件PPT
12
一次函数图象上点的确定
• 1、判断(2,3),(2,1),(0,3), (3,0)是否在一次函数y=2x-3的图象上
可编辑课件PPT
13
• 2、图象与x轴、y轴交点坐标及与x轴、y轴 围成的三角形面积的求解.
• 例题 已知一次函数y=-2x-2 • (1)画出函数的图象 (2)求图象与x轴、y轴的交点A、B的坐标 (3)求其图象与坐标轴围成的图形的面积 (4)利用图象求当x为何值时,y≥0
可编辑课件PPT
14
• 基础训练
b=0
b>0
b<0
一,三 一,二,三 一,三,四 二,四 一,二,四 二,三,四 当k>0时,y的值随x的增大而增大可编辑课件P当PTk<0时,y的值随x的增大而减小9
观察:比较上面第二组作的三个函数的相同点与 不同点,根据你的观察结果回答下列问题:
一次函数图像与性质精选教学PPT课件

生死教会她锐利果敢。所以她说,那一刻,没有一个母亲,会如苏珊般高贵沉着。 九天九夜的追捕,孩子们找到了。不在暗夜不在森林,而沉在冰冷的湖底。苏珊,终于向警方自首,的确是她,因为一点情欲的贪念,亲手杀了自己的孩子。
1994年的事了。偶尔在一本书里,读到前因后果,和那陌生女子的信。我低一低头,其实并没有泪。我想我懂。 我尚不及为人母,也不曾遭逢死亡,我却曾站在高处林下,看着爱人轻快远去,仿佛有鹳雀在他鞋底翻飞,他是急着赶另一个女子的约会吧?真相凄厉地直逼眼前。不是不知道,在泪落之前应该说再见,我却做不到。因为我爱他。
女子说,她也是母亲,也曾在山崩石裂瞬间,下车问路,一转头,车被人开走,而车上,有她还是稚婴的女儿。 她说她疯了一般扑向大团尾气和泥尘,手袋脱手而飞,惨号大叫,不知道自己说了什么,旁人也听不懂——她是归华美籍,此刻却忘尽英语,只用母语声声狂呼“救命”或者“放下我的孩子”。再也不可能是别的语言了。 高跟鞋妨碍她,一把拽脱劈手扔过去,她死命追赶。忘了人的速度不可能与车抗衡,看不见脚下的石砾、玻璃屑、柏油,唯一的念头就是:女儿。她只是一个纤细的亚裔女子,那一刻却如豹如鹰,势如疯虎,连歹徒也被吓倒了,弃车而逃。而她裙摆全撕,脚踝扭伤,脚底流下殷红的血。
教学重点
1、从实际问题中抽象概括出运动变化的规律,建 立函数关系式. 2、通过函数的性质及定义域范围求函数的最值.
教学难点 从实际问题中抽象概括出运动变化的规律,建立函 数关系式.
典型例题
例1 A校和B校各有旧电脑12台和6台,现决定送 给C校10台、D校8台,已知从A校调一台电脑到 C校、D校的费用分别是40元和80元,从B校调运 一台电脑到C校、D校的运费分别是30元和50元, 试求出总运费最低的调运方案,最低运费是多少?
我开始虚伪,听着谎言却装做一无所知;我学会窥探,四处打听如蛇之祟行,而十分看轻自己; 我的故事越编越好,好莱坞金牌编剧也没这般丰富多采,只为让他多留一分钟。
1994年的事了。偶尔在一本书里,读到前因后果,和那陌生女子的信。我低一低头,其实并没有泪。我想我懂。 我尚不及为人母,也不曾遭逢死亡,我却曾站在高处林下,看着爱人轻快远去,仿佛有鹳雀在他鞋底翻飞,他是急着赶另一个女子的约会吧?真相凄厉地直逼眼前。不是不知道,在泪落之前应该说再见,我却做不到。因为我爱他。
女子说,她也是母亲,也曾在山崩石裂瞬间,下车问路,一转头,车被人开走,而车上,有她还是稚婴的女儿。 她说她疯了一般扑向大团尾气和泥尘,手袋脱手而飞,惨号大叫,不知道自己说了什么,旁人也听不懂——她是归华美籍,此刻却忘尽英语,只用母语声声狂呼“救命”或者“放下我的孩子”。再也不可能是别的语言了。 高跟鞋妨碍她,一把拽脱劈手扔过去,她死命追赶。忘了人的速度不可能与车抗衡,看不见脚下的石砾、玻璃屑、柏油,唯一的念头就是:女儿。她只是一个纤细的亚裔女子,那一刻却如豹如鹰,势如疯虎,连歹徒也被吓倒了,弃车而逃。而她裙摆全撕,脚踝扭伤,脚底流下殷红的血。
教学重点
1、从实际问题中抽象概括出运动变化的规律,建 立函数关系式. 2、通过函数的性质及定义域范围求函数的最值.
教学难点 从实际问题中抽象概括出运动变化的规律,建立函 数关系式.
典型例题
例1 A校和B校各有旧电脑12台和6台,现决定送 给C校10台、D校8台,已知从A校调一台电脑到 C校、D校的费用分别是40元和80元,从B校调运 一台电脑到C校、D校的运费分别是30元和50元, 试求出总运费最低的调运方案,最低运费是多少?
我开始虚伪,听着谎言却装做一无所知;我学会窥探,四处打听如蛇之祟行,而十分看轻自己; 我的故事越编越好,好莱坞金牌编剧也没这般丰富多采,只为让他多留一分钟。
一次函数的图像及性质PPT
5
4
3
2
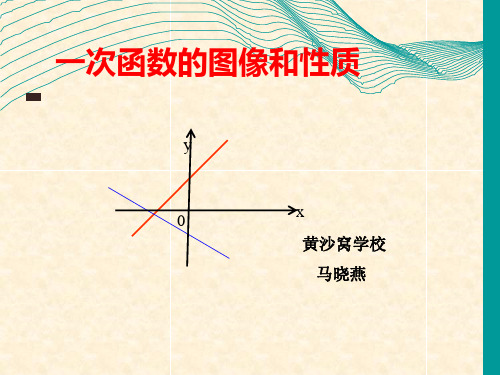
y=-2x+3
1
-6 -5 -4 -3 -2 -1 o 1 2 3 4
-1
y=-2x-3
-2
-3
-4
-5
y=-2x
-6
5 6x
观察:比较上面三个函数的相同点与不同点,根 据你的观察结果回答下列问题:
(1)这三个函数的图象形状都是_直_线_,并且倾斜程 度_相_同_;
(2)函数y=-2x图象经过原点,一次函数y=-2x+3
的图象与y轴交于点(_0_,_3)_,即它可以看作由直线
y=-2x向_上_平移_3个_单位长度而得到;
一次函数y=-2x-3的图象与y轴交于点(_0_,_-_3), 即它可以看作由直线y=-2x向_下_平移_3个_单位长
度而得到;
推广: (1) 所有一次函数y=kx+b的图象都是_一__条__直__线_ ;
正比例函数的图象是( 经过原点的一条直线 )
提问复习,引入新课
3、正比例函数 y=kx(k是常数,k≠0)中, k的正负对函数图象有什么影响?
y=kx
图象
性质
K>0
y
经过一、三象限 x y随x增大而增大
K<0
y
x 经过二、四象限 y随x增大而减小
特权福利
特权说明
VIP用户有效期内可使用VIP专享文档下载特权下载或阅读完成VIP专享文档(部分VIP专享文档由于上传者设置不可下载只能 阅读全文),每下载/读完一篇VIP专享文档消耗一个VIP专享文档下载特权。
年VIP
月VIP
连续包月VIP
VIP专享文档下载特权
享受60次VIP专享文档下载特权,一 次发放,全年内有效。
4
3
2
y=-2x+3
1
-6 -5 -4 -3 -2 -1 o 1 2 3 4
-1
y=-2x-3
-2
-3
-4
-5
y=-2x
-6
5 6x
观察:比较上面三个函数的相同点与不同点,根 据你的观察结果回答下列问题:
(1)这三个函数的图象形状都是_直_线_,并且倾斜程 度_相_同_;
(2)函数y=-2x图象经过原点,一次函数y=-2x+3
的图象与y轴交于点(_0_,_3)_,即它可以看作由直线
y=-2x向_上_平移_3个_单位长度而得到;
一次函数y=-2x-3的图象与y轴交于点(_0_,_-_3), 即它可以看作由直线y=-2x向_下_平移_3个_单位长
度而得到;
推广: (1) 所有一次函数y=kx+b的图象都是_一__条__直__线_ ;
正比例函数的图象是( 经过原点的一条直线 )
提问复习,引入新课
3、正比例函数 y=kx(k是常数,k≠0)中, k的正负对函数图象有什么影响?
y=kx
图象
性质
K>0
y
经过一、三象限 x y随x增大而增大
K<0
y
x 经过二、四象限 y随x增大而减小
特权福利
特权说明
VIP用户有效期内可使用VIP专享文档下载特权下载或阅读完成VIP专享文档(部分VIP专享文档由于上传者设置不可下载只能 阅读全文),每下载/读完一篇VIP专享文档消耗一个VIP专享文档下载特权。
年VIP
月VIP
连续包月VIP
VIP专享文档下载特权
享受60次VIP专享文档下载特权,一 次发放,全年内有效。
第2课时一次函数的图象和性质PPT课件(北师大版)

当堂练习
1. 一次函数y=x-2的大致图象为( C )
y
y
y
y
x
x
x
x
A
B
C
D
2.下列函数中,y的值随x值的增大而增大的函数是( C ).
A.y=-2xLeabharlann B.y=-2x+1
C.y=x-2
D.y=-x-2
3.直线y=3x-2可由直线y=3x向 下 平移 2 单位得到.
4.直线y=x+2可由直线y=x-1向 上 平移 3 单位得到.
y
y=2x-1
2… -3 …
2·
x
o ·1
再画出y=2x-1 的图象
y=-2x+l
总结归纳
一次函数
一次函数y=kx+b的图象是一条直线,
因此画一次函数图象时,只要确定两个点,
再过这两点画直线就可以了.一般过
(0,b)和(1,k+b)或( b ,0) k
(
y
, 0) (0, b)
O
x
一次函数y=kx+b的图象也称为直线y=kx+b.
总结归纳
一次函数y=kx+b中,k的正负对函数图象有什么影响? 当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大 而增大.
① b>0时,直线经过一、二、三象限; ② b<0时,直线经过一、三、四象限. 当k<0时,直线y=kx+b由左到右逐渐降落,y随x的增大 而减小.
① b>0时,直线经过 一、二、四象限; ② b<0时,直线经过二、三、四象限.
y=5-6x, 这个函数也可以写成
y=-6x+5.
讲授新课
一 一次函数的图象的画法
一次函数的图像和性质说课ppt

斜率与函数增减性的关系
斜率决定了函数的增减性。斜率为正表示函数为增函数,斜率为负表示函数为 减函数。
一次函数的增减性
单调性
一次函数的单调性由其斜率决定。在区间(-∞, +∞)上,当k>0时,函数为增函数; 当k<0时,函数为减函数。
增减性的判断方法
通过求导数或利用区间内任取两点连线的斜率来判断。在定义域内任取两点x1, x2 (x1<x2),如果y1<y2,则函数在此区间内为增函数;如果y1>y2,则函数在此 区间内为减函数。
03 一次函数的性质
一次函数的定义域和值域
定义域
对于一次函数y=kx+b(k≠0), 其定义域为全体实数R,即x可以取 任意实数值。
值域
由于一次函数的图像是一条直线, 其值域也为全体实数R,即y可以取 任意实数值。
一次函数的斜率
斜率
一次函数的斜率是函数图像在平面坐标系中的倾斜度,由参数k决定。当k>0 时,函数图像为增函数;当k<0时,函数图像为减函数。
课程目标
理解一次函数的概念 和图像。
能够应用一次函数解 决实际问题。
掌握一次函数的性质, 如斜率和截距。
02 一次函数图像的绘制
函数图像的基本概念
01
02
03
函数图像
表示函数关系的一种图形 表示,通过坐标系中的点 来表示函数中自变量和因 变量的对应关系。
坐标系
用于表示平面内点的位置, 通常由x轴和y轴组成,每 个轴上的单位长度表示一 定的数值。
教师自我反思
教师需要自我反思,思考课程中存在的问题和不足,以及如何改进。
调整教学方法和内容
根据学生的表现和反馈,调整教学方法和内容,以提高教学效果。
斜率决定了函数的增减性。斜率为正表示函数为增函数,斜率为负表示函数为 减函数。
一次函数的增减性
单调性
一次函数的单调性由其斜率决定。在区间(-∞, +∞)上,当k>0时,函数为增函数; 当k<0时,函数为减函数。
增减性的判断方法
通过求导数或利用区间内任取两点连线的斜率来判断。在定义域内任取两点x1, x2 (x1<x2),如果y1<y2,则函数在此区间内为增函数;如果y1>y2,则函数在此 区间内为减函数。
03 一次函数的性质
一次函数的定义域和值域
定义域
对于一次函数y=kx+b(k≠0), 其定义域为全体实数R,即x可以取 任意实数值。
值域
由于一次函数的图像是一条直线, 其值域也为全体实数R,即y可以取 任意实数值。
一次函数的斜率
斜率
一次函数的斜率是函数图像在平面坐标系中的倾斜度,由参数k决定。当k>0 时,函数图像为增函数;当k<0时,函数图像为减函数。
课程目标
理解一次函数的概念 和图像。
能够应用一次函数解 决实际问题。
掌握一次函数的性质, 如斜率和截距。
02 一次函数图像的绘制
函数图像的基本概念
01
02
03
函数图像
表示函数关系的一种图形 表示,通过坐标系中的点 来表示函数中自变量和因 变量的对应关系。
坐标系
用于表示平面内点的位置, 通常由x轴和y轴组成,每 个轴上的单位长度表示一 定的数值。
教师自我反思
教师需要自我反思,思考课程中存在的问题和不足,以及如何改进。
调整教学方法和内容
根据学生的表现和反馈,调整教学方法和内容,以提高教学效果。
一次函数的图象和性质 ppt

(2)因为点P (x,-2x+8), 所以SΔAPO=OA×(-2x+8)
= 1 ×4×(-2x+8)
2
=-4x+16(0<x<4).
中考链接
5.(2019•辽阳)若ab<0且a>b,则函数y=ax+b的图象可能 是( A )
A
B
C
D
中考链接
6.(2019•临沂)下列关于一次函数y=kx+b(k<0,b>0)的说 法,错误的是( D )
课堂练习
1. 在同一直角坐标系中,描绘出了下列函数: ①y=-x+1;②y=x+1;③y=-x-1;④y=-2(x+1)的图象, 则下列说法正确的是( C ) A.过点(-1,0)的是①③ B.交点在y轴上的是②④ C.互相平行的是①③ D.关于x轴对称的是①②
课堂练习
2.已知点(-4,y1),(2,y2)都在直线y=-x+2上,则y1,y2的大小关 系是( A ) A.y1>y2 B.y1=y2 C.y1<y2 D.不能比较
新知讲解
【知识拓展】 1.直线y=kx+b(k≠0,b≠0)与直线y=kx(k≠0)的位置关系: ①直线y=kx+b平行于直线y=kx; ②当b>0时,把直线y=kx向上平移b个单位长度,可得直线y=kx+b; ③当b<0时,把直线y=kx向下平移|b|个单位长度,可得直线y=kx+b.
2.一次函数y1=k1x+b1与y2=k2x+b2中: 若k1=-k2,b1=b2,则两直线关于y轴对称; 若k1=-k2,b1=-b2,则两直线关于x轴对称;若k1=k2,b1≠b2,则两直线平行.
= 1 ×4×(-2x+8)
2
=-4x+16(0<x<4).
中考链接
5.(2019•辽阳)若ab<0且a>b,则函数y=ax+b的图象可能 是( A )
A
B
C
D
中考链接
6.(2019•临沂)下列关于一次函数y=kx+b(k<0,b>0)的说 法,错误的是( D )
课堂练习
1. 在同一直角坐标系中,描绘出了下列函数: ①y=-x+1;②y=x+1;③y=-x-1;④y=-2(x+1)的图象, 则下列说法正确的是( C ) A.过点(-1,0)的是①③ B.交点在y轴上的是②④ C.互相平行的是①③ D.关于x轴对称的是①②
课堂练习
2.已知点(-4,y1),(2,y2)都在直线y=-x+2上,则y1,y2的大小关 系是( A ) A.y1>y2 B.y1=y2 C.y1<y2 D.不能比较
新知讲解
【知识拓展】 1.直线y=kx+b(k≠0,b≠0)与直线y=kx(k≠0)的位置关系: ①直线y=kx+b平行于直线y=kx; ②当b>0时,把直线y=kx向上平移b个单位长度,可得直线y=kx+b; ③当b<0时,把直线y=kx向下平移|b|个单位长度,可得直线y=kx+b.
2.一次函数y1=k1x+b1与y2=k2x+b2中: 若k1=-k2,b1=b2,则两直线关于y轴对称; 若k1=-k2,b1=-b2,则两直线关于x轴对称;若k1=k2,b1≠b2,则两直线平行.
《一次函数的图像和性质》一次函数PPT优秀课件

2020/8/19
例2:在同一坐标系作出下列函数的图象
(1)y = 2x+1 (2)y = -2x+1
根据图象回答,当自变量x逐渐增大时,函数
y的值怎样变化?
y
解: x 0 -1/2
4
y =2x+1 1 0
3
y =2x+1
x
0 1/2
2
y=-2x+1 1 0
1 (0,1)
(-1/2,0)
(1/2,0)
(1)函数值y 随x的增大而增大;
m 1 2
(2)函数图象与y
轴的负半轴相交;
m
1且m
1 2
(3)函数的图象过第二、三、四象限; 1 m 1
2
(4)函数的图象过原点。 m 1
2020/8/19
会画一次函数的图象 一次函数的图象与性质,常 数k,b的意义和作用. 数形结合的思想与方法,从 特殊到一般的思想与方法. 进一步体验研究函数的一般 思路与方法.
x
-4 -3 -2 -1 o 1 2 3 4 -1
2020/8/19
-2 y= -2x+1
一次函数通常选取(0,b), (-b/k,0)两点连线
• 一次函数 y = kx + b ( k ≠ 0 ) 有以 下性质:
• (1)当 k > 0 时,y 随 x 的增大 而 增大 。
• (2)当 k < 0 时,y 随 x 的增大 而 减小 。
2020/8/19
o
y=kx+b
y=kx
y
特性:
▲k1=k2=k3 b1≠b2≠b3三 线平行
2020/8/19
x
o y = k1x+b1 y = k2x+b2
例2:在同一坐标系作出下列函数的图象
(1)y = 2x+1 (2)y = -2x+1
根据图象回答,当自变量x逐渐增大时,函数
y的值怎样变化?
y
解: x 0 -1/2
4
y =2x+1 1 0
3
y =2x+1
x
0 1/2
2
y=-2x+1 1 0
1 (0,1)
(-1/2,0)
(1/2,0)
(1)函数值y 随x的增大而增大;
m 1 2
(2)函数图象与y
轴的负半轴相交;
m
1且m
1 2
(3)函数的图象过第二、三、四象限; 1 m 1
2
(4)函数的图象过原点。 m 1
2020/8/19
会画一次函数的图象 一次函数的图象与性质,常 数k,b的意义和作用. 数形结合的思想与方法,从 特殊到一般的思想与方法. 进一步体验研究函数的一般 思路与方法.
x
-4 -3 -2 -1 o 1 2 3 4 -1
2020/8/19
-2 y= -2x+1
一次函数通常选取(0,b), (-b/k,0)两点连线
• 一次函数 y = kx + b ( k ≠ 0 ) 有以 下性质:
• (1)当 k > 0 时,y 随 x 的增大 而 增大 。
• (2)当 k < 0 时,y 随 x 的增大 而 减小 。
2020/8/19
o
y=kx+b
y=kx
y
特性:
▲k1=k2=k3 b1≠b2≠b3三 线平行
2020/8/19
x
o y = k1x+b1 y = k2x+b2
一次函数的图象和性质(第1课时)PPT课件
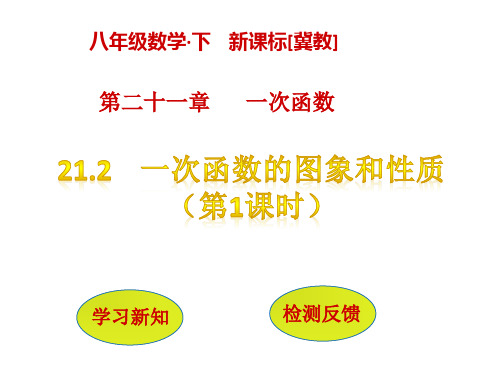
7.若一次函数y=kx+4的图像经过点(1,2).
(1)求k的值;
(2)在所给直角坐标系中画出此函数的图像;
(3)根据图像回答:当x
时,y>0.
解析:(1)把点(1,2)代入函数解析式,利用方程来求得k的值;(2)由 两点确定一条直线进行作图;(3)根据图像解答即可.
解:(1)依题意,得2=k+4,解得k=-2,即k的值是-2.
A.x<-2
B.x>-2
C.x<2
D.x>2
解析:由图像可得一次函数的图像与x轴的 交点为(-2,0),当y<0时,x<-2.故选A.
6.连降6天大雨,某水库的蓄水量随时间的增加而直线上升.若
该水库的蓄水量v(万米3)与降雨的时间t(天)的关系如图所示,
则下列说法正确的是
( B)
A.降雨后,蓄水量每天减少5万米3
达成共识. 1.图像为一条直线. 2.由画图过程,知一次函数y=2x-1的图像是由所有满足关系式y=2x-1 的点(x,y)连线而得到的.因此,凡满足关系式y=2x-1的x,y的值所对应 的点都在一次函数y=2x-1的图像上.
因为一次函数的图像是一条直线,所以也把一次函数y=kx+b 的图像称为直线y=kx+b.
为(0,2),与x轴的交点为
2 3
,0
.故选C.
4.函数
yk x
的图像经过点(1,-1),则函数y=kx-2的图像是
图中的
(A)
解析:∵
y
k x
的图像经过点(1,-1),∴k=xy=-1,∴函数解析式
为y=-x-2,所以函数图像经过(-2,0)和(0,-2).故选A.
《一次函数的图像和性质》一次函数PPT 图文

回忆的老墙,偶尔依靠,黄花总开不败 ,所有 囤积下 来的风 声雨声 ,天晴 天阴, 都是慈 悲。时 光不管 走多远 ,不管 有多老 旧,含 着眼泪 ,伴着 迷茫, 读了一 页又一 页,一 直都在 ,轻轻 一碰, 就让内 心温软 。旧的 时光被 揉进了 岁月的 折皱里 ,藏在 心灵的 沟壑, 直至韶 华已远 ,才知 道走过 的路不 能回头 ,错过 的已不 可挽留 ,与岁 月反复 交手, 沧桑中 变得更 加坚强 。
4.对于一次函数y = mx-(m-2),若y
随x 的增大而增小,则其图象不
过三
象限。
5.若直线 y = kx -3 过(2, 5),
则k = 4
;
若此直线平行于直线y = - 3x - 5,
则k= -3 .
抢答题
1在平面直角坐标系中,函数y=-2x+3的图象经过( A.一、二、三象限 B.二、三、四象限
x
0-
1-
2-
3-
4-
5
练
1、有下列函数:①y=2x+1,
一
③ y=0.5x,
②y=-3x+4, ④y=x-6;
练
其中过原点的直线是___③_____; 函数y随x的增大而增大的是___①__3__④___;
函数y随x的增大而减小的是____②_______;
图象在第一、二、三象限的是___①_____ 。
唯用一枝瘦笔,剪一段旧时光,剪掉喧 嚣尘世 的纷纷 扰扰, 剪掉终 日的忙 忙碌碌 。情也 好,事 也罢, 细品红 尘,文 字相随 ,把寻 常的日 子,过 得如春 光般明 媚。光 阴珍贵 ,指尖 徘徊的 时光唯 有珍惜 ,朝圣 的路上 做一个 谦卑的 信徒, 听雨落 ,嗅花 香,心 上植花 田,蝴 蝶自会 来,心 深处自 有广阔 的天地 。旧时 光难忘 ,好的 坏的一 一纳藏 ,不辜 负每一 寸光阴 ,自会 花香满 径,盈 暗香满 袖。尘 。但就 是无数 个小小 的你我 点燃了 万家灯 火,照 亮了整 个世界 。这人 间的生 与死, 荣与辱 ,兴与 衰,从 来都让 人无法 左右, 但我们 终不负 韶光, 不负自 己,守 着草木 ,守着 云水, 演绎着 一代又 一代的 传奇。
一次函数图像(共14张PPT)
-2
向上平移b个单位而来。
-3
-4
会用两点作一次函数图象; 会求一次函数与坐标轴的交点坐标; 会判断点是否在函数图象上及图象所经过的象限; 会求两函数的交点坐标,理解其实际意义。
思考
在同一坐标系中画出下列直线
y =—2x-1 ; y = —2x+3.
y 1 x2 2
y 1x2 2
观察图像,你发现了什么?
智力冲 浪
一个长方形的周长是12厘米,一边长是X厘米,
另一边长为y厘米,下列表示y关于x的函数关
系的图像中,正确的是( )B
4
A C
B D
(1)一次函数y=kx+b的图像是一条直线; 正比例函数y=kx的图像是一条过原点的直线。
y
7
6
y=2x+1
5
4
y=2x
3
2
1
-7 -6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 7 x
-1
-2
-3
-4
-5
-6
-7
练一练
1.下列各点中,在直线y=2x-3上的是( C )
(A)(0,3)
(B)(1,1)
(C)(2,1) (D)( -1,5)
2.若点(a,3)在直线y=2x-5上,则a=__4____
3 2 1 -7 -6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 7 x -1
-2
描点法
-3
-4
-5
-6
-7
画函数y=2x+1的图象。
1.列表 x y=2x+1 点( x, y)
2.描点
3.连线
…
-2
人教版数学八年级下册课件 19.2一次函数的图像和性质 (共28张PPT)

(3)若直线y=(3-k)x-k经过 第二、三、四象限,求k的取值 范围:__________(4分)
课堂小结
说一说你在这节课上都收 获到了什么知识?
时间是一个常数,但对勤 奋者来说,是一个“变数”.
你在学业上的收获与你 平时的付出是成正比的
求出y=kx+b(k,b为常数,k≠0) 的图像与x轴、y轴的交点,你发现 了什么规律?
结论:
函数y=kx+b(k,b为
常数,k≠0)的图像
与x轴交于(-
b k
,0)
与y轴交于(0,b)
用你认为最简单的方法画出函 数y=2x-1与y=-2x+l的图象.
思考:一次函数解析式y=kx+b (k, b是常数,k≠0)中,k的正负对 函数图象有什么影响?(3分钟)
即它可以看作由直线
y=x向_上___平移 2 个
1 2 3 x 单位长度而得到.
函数y=x-2的图象与y轴 交于点(0,-2),即它可以看
作由直线y=x向下 平移_2_
个单位长度而得到.
一次函数y=3x-4的图象是 什么形状?它与直线y=3x有什 么关系?
函数y=-2x+3的图像是由 哪个正比例函数的图像平移 得到的? 需要平移几个单位 长度?
y=-2x+1
y
o·· x
y=-2x-1
k的取值范围 b的取值范围
的象限
一、三、二
k>0
b<0
一、三、四
k<0
b>0
二、四、一
k<0
b<0
二、四、三
比一比看谁记得快,你发现 什么规律了么?
直线y=2x-3与x轴交点坐标为_(_23__,0_)_, 与y轴交点坐标为_(__0_,_-_3_)__ 图象经过第__一_、__三_、__四__象限, y随x增大而__增__大_______.
课堂小结
说一说你在这节课上都收 获到了什么知识?
时间是一个常数,但对勤 奋者来说,是一个“变数”.
你在学业上的收获与你 平时的付出是成正比的
求出y=kx+b(k,b为常数,k≠0) 的图像与x轴、y轴的交点,你发现 了什么规律?
结论:
函数y=kx+b(k,b为
常数,k≠0)的图像
与x轴交于(-
b k
,0)
与y轴交于(0,b)
用你认为最简单的方法画出函 数y=2x-1与y=-2x+l的图象.
思考:一次函数解析式y=kx+b (k, b是常数,k≠0)中,k的正负对 函数图象有什么影响?(3分钟)
即它可以看作由直线
y=x向_上___平移 2 个
1 2 3 x 单位长度而得到.
函数y=x-2的图象与y轴 交于点(0,-2),即它可以看
作由直线y=x向下 平移_2_
个单位长度而得到.
一次函数y=3x-4的图象是 什么形状?它与直线y=3x有什 么关系?
函数y=-2x+3的图像是由 哪个正比例函数的图像平移 得到的? 需要平移几个单位 长度?
y=-2x+1
y
o·· x
y=-2x-1
k的取值范围 b的取值范围
的象限
一、三、二
k>0
b<0
一、三、四
k<0
b>0
二、四、一
k<0
b<0
二、四、三
比一比看谁记得快,你发现 什么规律了么?
直线y=2x-3与x轴交点坐标为_(_23__,0_)_, 与y轴交点坐标为_(__0_,_-_3_)__ 图象经过第__一_、__三_、__四__象限, y随x增大而__增__大_______.
一次函数的图像和性质 课件

k的正负性
k>0
k<0
b取正、负、0 b>0 b=0 b<0 b>0 b=0 b<0
正比例函数
正比例函数
示意图
图像经过的 一、二、三 一、三 一、三、四一、二、四 二、四 二、三、四
象限
象限 象限 象限 象限 象限 象限
性质
y随x的增大而增大
y随x的增大而减小
画图常用 (0,b) (0,0) (0,b) (0,b) (0,0) (0,b) 的两个点 (1,k+b) (1,k) (1,k+b) (1,k+b) (1,k) (1,k+b)
探索新知识
一次函数
对比
正比例函数
下面我们将通过画一次函数的图象来 探索一次函数的性质
比较与发现
画函数y=-2x与y=-2x+3的图象
y6
y =- 2x
5
4
3
2
1
O -6 -5 -4 -3 -2 -1 -1
x 1 2 3 4 5 6
-2
-3
-4
几何 -5
-6
猜想 y=-y2x=+3-的2x图象
会是什么样的呢?
代数
例1.画出函数y=-2x与y=-2x+3的图象:
1.列表: x
-2 -1 0 1 2
y=-2x 2.描点: y=-2x+3
3.连线:
函数y=kx+b图象
函数y=-2x+3图像和函 数y=-2x图像平行.
和函数y=kx图象 平行.
y=-2x+3 y=-2x
例1.画出函数y=-2x与y=-2x+3的图象:
1.列表: x
-2 -1 0 1 2
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x 01
联系: 3.函数y=-6x+5可以看作由直线y=-6x向 上 平移 5 个 单位长度而得到.
比较两个函数解析式,你能说出这两个函数图 象有平移关系的道理吗?
相同点: 1.这两个函数解析式都是自 变量x的 -6 (常数)倍, 与一个常数的和。
y= -6x+5 y= -6x
不同点: 2.这两个函数解析式仅在 有区别。
(3)将直线y=-2x-1向上平移3个单 位,得到的直线是y_=_-_2_x_+_2.
2、用两点法画一次函数图像
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
y
6
x
0 0.5
5
y=2x-1 -1 0 y=-0.5x+1 4
y=2x-1
3
经过(0,-1)和(0.5,0)两点
5
两个函数 图象有什 么关系?
0
X
-7
合作探究(一)
问比题较3:上请面大两家个观函察数这的两图个象函的数相图同象点的与形不状同,点倾. 斜程度
你有什么发现?
y
相同点:
1.这两个函数的图象形状都 是 直线, 并且倾斜程度 相同 .
5 y=-6x+5 y=-6x
不同点: 2.函数y=6x的图象经过原点, 函数y=-6x+5的图象与y轴交 于点 (0,5.)
联系:
3.对于自变量x的任一值,这两个函数相应
的y值总相差 5
。
请比较下列函数y=x, y=x+2,y=x-2的图 象有什么异同点?
这几个函数的图象形状都 是 直线,并且倾斜程度__相_同
函数y=x的图象经过原点,
函数y=x+2的图象与y轴交于
点(__0_,_ 2),即它可以看作由 直线y=x向_上_平移 2 个单位 长度而得到.函数y=x-2的 图象与y轴交于点(_0,-2_)_,
D.第四象限
3、已知一次函数y=x-2的大致图像为 ( C )
y
y
y
y
x
x
x
x
A
B
C
D
4.下列哪个图像是一次函数y=-3x+5 和y=2x-4的大致图像( B )
(A)
(B)
(C)
(D)
5. 直线y=2x-3与x轴交点坐标为(__1_.5_,_0)_;与y 轴的交点坐标为(__0_,_-_3_);图象经过_一_、_三__、_四__象 限,y随x的增大而___.增大
二、新课精讲
例2.画出函数y =-6x与 y =-6x +5的图 象。
x
-2 -1 0 1 2
y=-6x 12 6
0
-6 -12
y=-6x+5 17 11 5 -1 -7
解:函数y =-6x与 y =-6x +5中,自变量x 可以是任意的实数,列表表示几组对应值:
y
y=-6x+5 17
11
y=-6x
一次函数的图像和性质
y
0
x
提问复习,引入新课
1、什么叫正比例函数、一次函数?它们之间有 什么关系?
一般地,形如 y=kx(k是常的数函,k数≠0,) 叫做正比 例函数; 一般地,形如 y=kx+b(k,的b是函常数数,,k≠叫0)做一次函 数。
当b=0时,y=kx+b就变成了 y=k,x所以说正比 例函数是一种特殊的一次函数。 2、正比例函数的图象是什么形状?
正比例函数的图象是( 经过原点的一条直线 )
提问复习,引入新课
3、正比例函数 y=kx(k是常数,k≠0)中, k的正负对函数图象有什么影响?
y=kx
图象
性质
K>0
y
经过一、三象限 x y随x增大而增大
K<0
y
x 经过二、四象限 y随x增大而减小
提问复习,引入新课
既然正比例函数是特殊的一次 函数,正比例函数的图象是直线, 那么一次函数的图象也会是一条直 线吗? 它们图象之间有什么关系? 一次函数又有什么性质呢?
告诉大家本节课你的收获!
2
1
x
02
y= -0.5x+1 1 0
-6 -5 -4 -3 -2 -1 o 1 2 3 4 5 6 x -1
-2
-3
经过(0,1)和(2:
• 画一次函数的图像时,只要描出合
适关系式的两点,再连接两点即可,
我们通常选 取(0,b)和(-
,b 0 )
k
这两个点,也就是选取图像与x轴和 y轴的交点坐标。
即它可以看作由直线y=x向 下 平移___2_ 个单位长度而得 到.
.
.
.
y
...0...
.
.
.
y... =yyx==+xx2-2
2
x
一次函数y=kx+b的图象是经过(0,b)点且平行于
直线y=kx的一条直线, y y=x+2
(0,b)
3 y=x-2
02
x
y=x
我们称它为直线y=kx+b,它可以看作由直线y=kx平 移|b|个单位长度得到. (当b>0时,向上平移;当 b<0时,向下平移)
一次函数y=kx+b(k、b是常数,k≠0)的图象
k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0
y
(0,b)
0
b k
,0
x
y
b k
,0
0
x
(0,b)
y
(0,b)
0
b k
,0
x
y
b k
,0
0
(0,b) x
图象经过 一,二,三象限
6、直线y=kx+b与直线y=5x+2平行, 与y轴的交点为(0,-7),则解 析式为_y_=_5_x-_7__.
7、 一次函数y=kx+b的图象不经过 第二象限,则 k、b的符号是:
解析:∵图象不过第二象限
∴图象必过一、三象限
∴k > 0 由于图象不过第二象限,说明图象 可能过 第四象限或原点
∴b≤0 ∴k > 0 b ≤0
活动与探究
在同一直角坐标系中画出下列每组 函数图象,并归纳y=kx+b(k、b是常 数,k≠0)中b对函数图象的影响. 1.y=x-1 y=x y=x+1 2.y=-2x+1 y=-2x y=-2x-1
b决定直线y=kx+b与y轴交点的坐标(0,b).
当b>0时,交点在y轴正半轴(x轴上方). 当b=0时,交点即原点. 当b<0时,交点在y轴负半轴(x轴下方).
练习(1)直线y=2x-3可以由直线y=2x经过 __向__下__平__移__3_个_单位 而得到;
直线y=-3x+2可以由直线y=-3x经过 向__上__平__移__2_个__单__位__而得到;
直线y=x+2可以由直线y=x-3经过 _向__下__平__移__5_个__单__位___而得到.
(2)直线y=2x+5与直线y=-3x+5都 经过轴上的同一点(_0__,_5__).
y随x的增大 而增大
图象经过 一,三,四象限
y随x的增大 而增大
图象经过 一,二,四象限
y随x的增大 而减小
图象经过 二,三,四象限
y随x的增大 而减小
练习1、一次函数y=3x-2的图象不经过( B )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2、一次函数y=2x+1的图象不经过( D )
A.第一象限 B.第二象限C.第三象限
