高三第一轮复习第1讲集合及其运算

合集下载

2022高考数学一轮总复习第一章集合与常用逻辑用语第1讲集合及其运算学案文(含答案)

高考数学一轮总复习学案：第1讲集合及其运算1．集合与元素(1)集合元素的三个特征：确定性、互异性、无序性．(2)元素与集合的关系是属于或不属于关系，用符号∈或∉表示．(3)集合的表示法：列举法、描述法、图示法．(4)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号N N*(或N＋)Z Q R [注意] N为自然数集(即非负整数集)，包含0，而N*和N＋的含义是一样的，表示正整数集，不包含0.2．集合间的基本关系表示关系自然语言符号语言Venn图子集集合A中所有元素都在集合B中(即若x∈A，则x∈B)A⊆B(或B⊇A)真子集集合A是集合B的子集，且集合B中至少有一个元素不在集合A中A B(或B A)集合相等集合A，B中元素相同A＝B集合的并集集合的交集集合的补集图形语言符号语言A ∪B ＝{x |x ∈A 或x ∈B }A ∩B ＝{x |x ∈A 且x ∈B }∁U A ＝{x |x ∈U 且x ∉A }4.集合的运算性质(1)A ∩A ＝A ，A ∩∅＝∅，A ∩B ＝B ∩A . (2)A ∪A ＝A ，A ∪∅＝A ，A ∪B ＝B ∪A . (3)A ∩(∁U A )＝∅，A ∪(∁U A )＝U ，∁U (∁U A )＝A . 常用结论(1)对于有限集合A ，其元素个数为n ，则集合A 的子集个数为2n ，真子集个数为2n－1，非空真子集个数为2n－2.(2)A ⊆B ⇔A ∩B ＝A ⇔A ∪B ＝B ⇔∁U A ⊇∁U B .(3)∁U (A ∩B )＝(∁U A )∪(∁U B )，∁U (A ∪B )＝(∁U A )∩(∁U B )．一、思考辨析判断正误(正确的打“√”，错误的打“×”)(1){x |y ＝x 2＋1}＝{y |y ＝x 2＋1}＝{(x ，y )|y ＝x 2＋1}．( ) (2)若{x 2，1}＝{0，1}，则x ＝0，1.( ) (3){x |x ≤1}＝{t |t ≤1}．( )(4)对于任意两个集合A ，B ，(A ∩B )⊆(A ∪B )恒成立．( ) (5)若A ∩B ＝A ∩C ，则B ＝C .( ) 答案：(1)× (2)× (3)√ (4)√ (5)× 二、易错纠偏常见误区| (1)忽视集合中元素的互异性致误； (2)忽视空集的情况致误； (3)忽视区间端点值致误．1．已知集合A ＝{1，3，m }，B ＝{1，m }，若B ⊆A ，则m ＝________．解析：因为B ⊆A ，所以m ＝3或m ＝m ，即m ＝3或m ＝0或m ＝1，根据集合元素的互异性可知，m ≠1，所以m ＝0或3.答案：0或32．已知集合M ＝{x |x －2＝0}，N ＝{x |ax －1＝0}，若M ∩N ＝N ，则实数a 的值是________．解析：易得M ＝{2}．因为M ∩N ＝N ，所以N ⊆M ，所以N ＝∅或N ＝M ，所以a ＝0或a ＝12.答案：0或123．已知集合A ＝{x |x 2－4x ＋3＜0}，B ＝{x |2＜x ＜4}，则A ∩B ＝________，A ∪B ＝________，(∁R A )∪B ＝________．解析：由已知得A ＝{x |1＜x ＜3}，B ＝{x |2＜x ＜4}，所以A ∩B ＝{x |2＜x ＜3}，A ∪B ＝{x |1＜x ＜4}，(∁R A )∪B ＝{x |x ≤1或x ＞2}．答案：(2，3) (1，4) (－∞，1]∪(2，＋∞)集合的概念(自主练透)1．设集合A ＝{0，1，2，3}，B ＝{x |－x ∈A ，1－x ∉A }，则集合B 中元素的个数为( ) A ．1 B ．2 C ．3D ．4解析：选A ．若x ∈B ，则－x ∈A ，故x 只可能是0，－1，－2，－3，当0∈B 时，1－0＝1∈A ；当－1∈B 时，1－(－1)＝2∈A ；当－2∈B 时，1－(－2)＝3∈A ；当－3∈B 时，1－(－3)＝4∉A ，所以B ＝{－3}，故集合B 中元素的个数为1.2．已知集合A ＝{x |x ∈Z ，且32－x ∈Z }，则集合A 中的元素个数为( )A ．2B ．3C ．4D ．5解析：选C ．因为32－x ∈Z ，所以2－x 的取值有－3，－1，1，3，又因为x ∈Z ，所以x的值分别为5，3，1，－1，故集合A 中的元素个数为4.3．已知集合A ＝{m ＋2，2m 2＋m }，若3∈A ，则m 的值为________．解析：由题意得m ＋2＝3或2m 2＋m ＝3，则m ＝1或m ＝－32.当m ＝1时，m ＋2＝3且2m 2＋m ＝3，根据集合中元素的互异性可知不满足题意；当m ＝－32时，m ＋2＝12，而2m 2＋m ＝3，符合题意，故m ＝－32.答案：－324．设a ，b ∈R ，集合{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，ba，b ，则b －a ＝________．解析：因为{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，a ≠0，所以a ＋b ＝0，则b a ＝－1，所以a ＝－1，b ＝1.所以b －a ＝2.答案：2解决集合概念问题的3个关键点(1)确定构成集合的元素； (2)确定元素的限制条件；(3)根据元素特征(满足的条件)构造关系式解决相应问题．[提醒] 含字母的集合问题，在求出字母的值后，需要验证集合的元素是否满足互异性．集合的基本关系(典例迁移)(1)已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R }，B ＝{x |0<x <5，x ∈N }，则( ) A ．B ⊆A B ．A ＝B C ．AB D ．BA(2)已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R }，B ＝{x |0<x <5，x ∈N }，则满足条件A ⊆C ⊆B 的集合C 的个数为( )A ．1B ．2C ．3D ．4(3)已知集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}，若B ⊆A ，则实数m 的取值范围为________．【解析】 (1)由x 2－3x ＋2＝0得x ＝1或x ＝2，所以A ＝{1，2}．由题意知B ＝{1，2，3，4}，比较A ，B 中的元素可知AB ，故选C ．(2)因为A ＝{1，2}，B ＝{1，2，3，4}，A ⊆C ⊆B ，则集合C 可以为{1，2}，{1，2，3}，{1，2，4}，{1，2，3，4}，共4个．(3)因为B ⊆A ，所以①若B ＝∅，则2m －1<m ＋1，此时m <2. ②若B ≠∅，则⎩⎪⎨⎪⎧2m －1≥m ＋1，m ＋1≥－2，2m －1≤5.解得2≤m ≤3.由①②可得，符合题意的实数m 的取值范围为m ≤3. 【答案】 (1)C (2)D (3)(－∞，3]【迁移探究1】 (变条件)本例(3)中，若B A ，求m 的取值范围？解：因为BA ，①若B ＝∅，成立，此时m ＜2.②若B ≠∅，则⎩⎪⎨⎪⎧2m －1≥m ＋1，m ＋1≥－2，2m －1≤5，且边界点不能同时取得，解得2≤m ≤3.综合①②，m 的取值范围为(－∞，3]．【迁移探究2】 (变条件)本例(3)中，若A ⊆B ，求m 的取值范围．解：若A ⊆B ，则⎩⎪⎨⎪⎧m ＋1≤－2，2m －1≥5，即⎩⎪⎨⎪⎧m ≤－3，m ≥3.所以m 的取值范围为∅.【迁移探究3】 (变条件)若将本例(3)中的集合A 改为A ＝{x |x <－2或x >5}，试求m 的取值范围．解：因为B ⊆A ，所以①当B ＝∅时，2m －1<m ＋1，即m <2，符合题意．②当B ≠∅时，⎩⎪⎨⎪⎧m ＋1≤2m －1，m ＋1>5或⎩⎪⎨⎪⎧m ＋1≤2m －1，2m －1<－2，解得⎩⎪⎨⎪⎧m ≥2，m >4或⎩⎪⎨⎪⎧m ≥2，m <－12.即m >4.综上可知，实数m 的取值范围为(－∞，2)∪(4，＋∞)．[提醒] 题目中若有条件B ⊆A ，则应分B ＝∅和B ≠∅两种情况进行分类讨论．1．设集合M ＝{x |x 2－x >0}，N ＝⎩⎨⎧x ⎪⎪⎪⎭⎬⎫1x<1，则( )A ．MN B ．N MC ．M ＝ND ．M ∪N ＝R解析：选C ．集合M ＝{x |x 2－x >0}＝{x |x >1或x <0}，N ＝⎩⎨⎧x ⎪⎪⎪⎭⎬⎫1x<1＝{x |x >1或x <0}，所以M ＝N .故答案为C ．2．设M 为非空的数集，M ⊆{1，2，3}，且M 中至少含有一个奇数元素，则这样的集合M 共有( )A ．6个B ．5个C ．4个D ．3个解析：选A ．由题意知，M ＝{1}，{3}，{1，2}，{1，3}，{2，3}，{1，2，3}，共6个．3．若集合A ＝{1，2}，B ＝{x |x 2＋mx ＋1＝0，x ∈R }，且B ⊆A ，则实数m 的取值范围为________．解析：①若B ＝∅，则Δ＝m 2－4＜0，解得－2＜m ＜2，符合题意； ②若1∈B ，则12＋m ＋1＝0，解得m ＝－2，此时B ＝{1}，符合题意； ③若2∈B ，则22＋2m ＋1＝0，解得m ＝－52，此时B ＝⎩⎨⎧⎭⎬⎫2，12，不合题意．综上所述，实数m 的取值范围为[－2，2)．答案：[－2，2)集合的基本运算(多维探究) 角度一集合的运算(1)(2020·高考全国卷Ⅰ)已知集合A ＝{x |x 2－3x －4<0}，B ＝{－4，1，3，5}，则A ∩B ＝( )A ．{－4，1}B ．{1，5}C ．{3，5}D ．{1，3}(2)(2021·东北三校第一次联考)已知全集U ＝R ，集合A ＝{x |x 2－2x －3＜0}，B ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1x ＞1，则∁U (A ∪B )＝ ( ) A ．(－∞，－1)∪(3，＋∞) B ．(－∞，－1]∪[3，＋∞) C ．[3，＋∞)D ．(－∞，－1]∪[1，＋∞)(3)(2020·高考全国卷Ⅲ)已知集合A ＝{(x ，y )|x ，y ∈N *，y ≥x }，B ＝{(x ，y )|x ＋y ＝8}，则A ∩B 中元素的个数为( )A ．2B ．3C ．4D ．6【解析】 (1)方法一：由x 2－3x －4<0，得－1<x <4，即集合A ＝{x |－1<x <4}，又集合B ＝{－4，1，3，5}，所以A ∩B ＝{1，3}，故选D ．方法二：因为(－4)2－3×(－4)－4>0，所以－4∉A ，故排除A ；又12－3×1－4<0，所以1∈A ，则1∈(A ∩B )，故排除C ；又32－3×3－4<0，所以3∈A ，则3∈(A ∩B )，故排除B ．故选D ．方法三：观察集合A 与集合B ，发现3∈A ，故3∈(A ∩B )，所以排除选项A 和B ，又52－3×5－4>0，所以5∉A ，5∉(A ∩B )，排除C ．故选D ．(2)由已知，得A ＝{x |－1＜x ＜3}，B ＝{x |0＜x ＜1}，所以A ∪B ＝{x |－1＜x ＜3}，所以∁U (A ∪B )＝{x |x ≤－1或x ≥3}，故选B ．(3)由题意得，A ∩B ＝{(1，7)，(2，6)，(3，5)，(4，4)}，所以A ∩B 中元素的个数为4，选C ．【答案】 (1)D (2)B (3)C集合运算的常用方法(1)若集合中的元素是离散的，常用Venn 图求解．(2)若集合中的元素是连续的实数，则用数轴表示，此时要注意端点的情况．角度二利用集合的运算求参数(1)(2020·高考全国卷Ⅰ)设集合A ＝{x |x 2－4≤0}，B ＝{x |2x ＋a ≤0}，且A ∩B＝{x |－2≤x ≤1}，则a ＝( )A ．－4B ．－2C ．2D ．4(2)(2021·福州市适应性考试)已知集合A ＝{(x ，y )|2x ＋y ＝0}，B ＝{(x ，y )|x ＋my ＋1＝0}．若A ∩B ＝∅，则实数m ＝( )A ．－2B ．－12C ．12D ．2【解析】 (1)方法一：易知A ＝{x |－2≤x ≤2}，B ＝{x |x ≤－a2}，因为A ∩B ＝{x |－2≤x ≤1}，所以－a2＝1，解得a ＝－2.故选B ．方法二：由题意得A ＝{x |－2≤x ≤2}．若a ＝－4，则B ＝{x |x ≤2}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤2}，不满足题意，排除A ；若a ＝－2，则B ＝{x |x ≤1}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤1}，满足题意；若a ＝2，则B ＝{x |x ≤－1}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤－1}，不满足题意，排除C ；若a ＝4，则B ＝{x |x ≤－2}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |x ＝－2}，不满足题意．故选B ．(2)因为A ∩B ＝∅，所以直线2x ＋y ＝0与直线x ＋my ＋1＝0平行，所以m ＝12，故选C ．【答案】 (1)B (2)C利用集合的运算求参数的值或取值范围的方法(1)对于与不等式有关的集合，一般利用数轴解决，要注意端点值能否取到； (2)若集合能一一列举，则一般先用观察法得到不同集合中元素之间的关系，再列方程(组)求解．[提醒] 在求出参数后，注意对结果的验证(满足互异性)．1．(2021·河北九校第二次联考)已知集合A ＝{x |x 2－x －2＜0，x ∈Z }，B ＝{y |y ＝2x，x ∈A }，则A ∪B ＝( )A ．{1}B ．{0，1，2}C ．⎩⎨⎧⎭⎬⎫12，1，2，4 D ．{0，1，2，4}解析：选B ．A ＝{x |－1＜x ＜2，x ∈Z }＝{0，1}，B ＝{y |y ＝2x，x ∈A }＝{1，2}，所以A ∪B ＝{0，1，2}，故选B ．2．(2021·四省八校第二次质量检测)若全集U ＝R ，集合A ＝(－∞，－1)∪(4，＋∞)，B ＝{x ||x |≤2}，则如图阴影部分所表示的集合为( )A ．{x |－2≤x ＜4}B ．{x |x ≤2或x ≥4}C ．{x |－2≤x ≤－1}D ．{x |－1≤x ≤2}解析：选D ．∁U A ＝{x |－1≤x ≤4}，B ＝{x |－2≤x ≤2}，则所求阴影部分所表示的集合为C ，则C ＝(∁U A )∩B ＝{x |－1≤x ≤2}．3．(2021·广东省七校联考)设集合A ＝{1，2，4}，B ＝{x |x 2－4x ＋m ＝0}，若A ∩B ＝{1}，则B ＝( )A ．{1，－3}B ．{1，0}C ．{1，3}D ．{1，5}解析：选C ．由题意可得1－4＋m ＝0，解得m ＝3，所以B ＝{x |x 2－4x ＋3＝0}＝{1，3}，故选C ．核心素养系列1 数学抽象——集合的新定义问题以集合为背景的新定义问题常以“问题”为核心，以“探究”为途径，以“发现”为目的，这类试题只是以集合为依托，考查考生对新概念的理解，充分体现了核心素养中的数学抽象．若集合A 具有以下性质： (1)0∈A ，1∈A ；(2)若x ∈A ，y ∈A ，则x －y ∈A ，且x ≠0时，1x∈A .则称集合A 是“好集”．给出下列说法：①集合B ＝{－1，0，1}是“好集”；②有理数集Q 是“好集”③设集合A 是“好集”，若x ∈A ，y ∈A ，则x ＋y ∈A .其中，正确说法的个数是( )A ．0B ．1C ．2D ．3【解析】 ①集合B 不是“好集”，假设集合B 是“好集”，因为－1∈B ，1∈B ，所以－1－1＝－2∈B ，这与－2∉B 矛盾．②有理数集Q 是“好集”，因为0∈Q ，1∈Q ，对任意的x ∈Q ，y ∈Q ，有x －y ∈Q ，且x ≠0时，1x∈Q ，所以有理数集Q 是“好集”．③因为集合A 是“好集”，则0∈A ，由性质(2)知，若y ∈A ，则0－y ∈A ，知－y ∈A ，因此x －(－y )＝x ＋y ∈A ，所以③正确．故正确的说法是②③.故选C ．【答案】 C解决集合的新定义问题的两个切入点(1)正确理解新定义．这类问题不是简单的考查集合的概念或性质问题，而是以集合为载体的有关新定义问题．常见的命题形式有新概念、新法则、新运算等；(2)合理利用集合性质．运用集合的性质(如元素的性质、集合的运算性质等)是破解新定义型集合问题的关键．在解题时要善于从题设条件给出的数式中发现可以使用集合性质的一些因素，但关键之处还是合理利用集合的运算与性质．1．如果集合A 满足若x ∈A ，则－x ∈A ，那么就称集合A 为“对称集合”．已知集合A ＝{2x ，0，x 2＋x }，且A 是对称集合，集合B 是自然数集，则A ∩B ＝________．解析：由题意可知－2x ＝x 2＋x ，所以x ＝0或x ＝－3.而当x＝0时不符合元素的互异性，所以舍去．当x＝－3时，A＝{－6，0，6}，所以A∩B＝{0，6}．答案：{0，6}2．设A，B是非空集合，定义A⊗B＝{x|x∈A∪B且x∉A∩B}．已知集合A＝{x|0<x<2}，B＝{y|y≥0}，则A⊗B＝________．解析：由已知A＝{x|0<x<2}，B＝{y|y≥0}，又因为新定义A⊗B＝{x|x∈A∪B且x∉A∩B}，结合数轴得A⊗B＝{0}∪[2，＋∞)．答案：{0}∪[2，＋∞)。

高三数学第一轮复习1.1 集合的概念与运算

B.{1,2,4}
C.{1,2,4,6} D.{x∈R|-1≤x≤5}
∵A={1,2,6},B={2,4},∴A∪B={1,2,4,6}. ∵C={x∈R|-1≤x≤5}, ∴(A∪B)∩C={1,2,4}.故选B.
B解析-21-关闭关闭答案第一章
1.1 集合的概念与运算
知识体系
知识梳理
核心考点
≥ <
2��, -1
或
�� + 3 2�� >
≥ 4,
2��,解得
a<-4
或
2<a≤3.
综上可得,实数 a 的取值范围为(-∞,-4)∪(2,+∞).
(-∞,-4)∪(2,+∞)
图(1) 图(2)
关闭
解析答案
第一章
1.1 集合的概念与运算
知识体系
知识梳理
核心考点
-19-
考点1
考点2
考点3
解题心得1.判定集合间的基本关系有两种方法.方法一:化简集合, 从表达式中寻找集合的关系;方法二:用列举法(或图示法等)表示各个集合,从元素(或图形)中寻找关系.
2.解决集合间的基本关系的常用技巧:(1)若给定的集合是不等式的解集,则用数轴求解;(2)若给定的集合是点集,则用数形结合法求解;(3)若给定的集合是抽象集合,则常用Venn图求解.
()
A.A=B
B.A∩B=⌀
C.A⊆B
D.B⊆A
思考判定集合间的基本关系有哪些方法?解决集合间的基本关系
的常用技巧有哪些? 关闭
∵A={x|y=ln(x+3)},∴A={x|x>-3}.
又B={x|x≥2},∴B⊆A.

《新课标》第01讲集合

《新课标》高三数学（人教版）第一轮复习单元讲座第一讲集合一．课标要求：1．集合的含义与表示（1）通过实例，了解集合的含义，体会元素与集合的“属于”关系；（2）能选择自然语言、图形语言、集合语言（列举法或描述法）描述不同的具体问题，感受集合语言的意义和作用；2．集合间的基本关系（1）理解集合之间包含与相等的含义，能识别给定集合的子集；（2）在具体情境中，了解全集与空集的含义；3．集合的基本运算（1）理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集；（2）理解在给定集合中一个子集的补集的含义，会求给定子集的补集；（3）能使用V enn图表达集合的关系及运算，体会直观图示对理解抽象概念的作用。

二．命题走向有关集合的高考试题，考查重点是集合与集合之间的关系，近年试题加强了对集合的计算化简的考查，并向无限集发展，考查抽象思维能力，在解决这些问题时，要注意利用几何的直观性，注意运用Venn图解题方法的训练，注意利用特殊值法解题，加强集合表示方法的转换和化简的训练。

考试形式多以一道选择题为主，分值5分。

预测2007年高考将继续体现本章知识的工具作用，多以小题形式出现，也会渗透在解答题的表达之中，相对独立。

具体题型估计为：（1）题型是1个选择题或1个填空题；（2）热点是集合的基本概念、运算和工具作用。

三．要点精讲1．集合：某些指定的对象集在一起成为集合。

a∈；若b不是集合A的元（1）集合中的对象称元素，若a是集合A的元素，记作Ab∉；素，记作A（2）集合中的元素必须满足：确定性、互异性与无序性；确定性：设A是一个给定的集合，x是某一个具体对象，则或者是A的元素，或者不是A的元素，两种情况必有一种且只有一种成立；互异性：一个给定集合中的元素，指属于这个集合的互不相同的个体（对象），因此，同一集合中不应重复出现同一元素；无序性：集合中不同的元素之间没有地位差异，集合不同于元素的排列顺序无关；（3）表示一个集合可用列举法、描述法或图示法；列举法：把集合中的元素一一列举出来，写在大括号内；描述法：把集合中的元素的公共属性描述出来，写在大括号{}内。

【名师导学】高考数学第一轮总复习 1

A．{0}
B．{1}
C．{1,2}
D．{0,2}
【解析】∵N＝{x|x＝2a＋1，a∈M}＝{1,3,5}． ∴M∩N＝{1}，选B.
3．已知全集U＝R，则正确表示集合M＝{－1,0,1}和 N＝{x|x2＋x＝0}关系的韦恩图是( B)
【解析】∵N＝{x|x2＋x＝0}＝{－1,0} M＝{－1,0,1}． ∴选B.
4．(2011辽宁)已知M，N为集合I的非空真子集，且 M，N不相等，若N∩∁IM＝∅，则M∪N＝( A)
A．M
B．N
C．I
D．∅
【解析】利用韦恩图：N M，∴M∪N＝M，∴选A.
5．已知全集U＝{1,2,3,4,5}，集合A＝{x|x2－3x＋2＝0}， B＝{x|x＝2a，a∈A}，则集合∁U(A∪B)中元素的个数共有__2__个．
【解析】由已知得M∩N＝{2,3}，∴∁U(M∩N)＝ {1,4}，选D.
4．(2011广东)已知集合A＝{(x，y)|x，y为实数，且
x2＋y2＝1}，B＝{(x，y)|x，y为实数，且y＝x}，则
A∩B的元素的个数为( C)
A．0
B．1
C．2
D．3
【解析】集合A表示的是圆心在原点的单位圆，集合 B表示的是直线y＝x，画图可知选C.
1．确定一个集合的依据是：一是判断集合的元素是什么？二是理解元素的属性有哪些？
2．判断集合之间的包含关系，关键是理解符号 “⊆”的含义．注意∅对问题的影响．
3．对求解含有参数的集合运算问题，能化简的集合应先化简，以便使问题进一步明朗化．
4．集合问题多与函数、方程、不等式、解析几何等有关．在解题时，要注意相关知识间的联系．
③理解必要条件、充分条件与充要条件的意义．

高考数学一轮复习讲练测专题1.1集合的概念及其基本运算(讲)理(含解析)

1}，专题1.1集合的概念及其基本运算（讲）【辭析】由已知得^ = {1,4}.当口 = ＜时.A = [3],则討二〔12*卜・4厂直=0,当也=1时,J = ；L3j ; 则JU5 = {1.3r 4} p = 当a = 4时.^ = {4.3}, = （1,3.4}, -40-8={4}.当疽产1,戊戸吳。

否4时…儿丘二卩”丸好，JO^ =0,综上所述，当a = 3时—儿P = {1S4齐AClB^Qi 当应"时，血JH"4}, /仃丘二{1»当*4时,则加UE 二口34、“5={4}f 当口工1, 口产3, a 芦4时I dl-再三卜 B =0.2.【2015高考天津，理1】已知全集U 1,2,3,4,5,6,7,8 ，集合A 2,3,5,6，集合B 1,3,4,6,7则集合AI ejB （） (A )2,5( B )3,6 (C ) 2,5,6 ( D ) 2,3,5,6,8【答案】A【赭斤】^5 = （2,5,8}_所以二冷5},故选九3. 【云南省玉溪一中 2015届高三上学期第一次月考试卷】设集合B {(x, y) y 3x }，则A B 的子集的个数是( )A. 4 B. 3C. 2D. 1【答案】A1.【课本典型习题，P12第3题】设集合Ax(x a)(x 3) 0,a R , Bx(x 4)(x 1) 0 ,AUB , AI B .【答案】当a 3时，AU B 1,3,4 , AI B ;当a 1 时，AU B1,3,4,AI B 1 ;当 a时，贝U AU B 1,3,4 , AIB 4 ;当 a 1 ,a 3, a 4时， AU B1,3,4, a , AI B【课前小测摸底细】求4{(“)話【解析】篥會話为橢區|兰+匸=1上的昌集合卫为扌無心煎i' = 丁上的点，由于指纹函数恒过点(Q1)・16 -4* 斗由于点121在椭圆兰十二“曲内部，因此扌旨数函数与椭圆有2个交点.，的子篥的个数次F =4个，16 4故答累为扎4. 【基础经典试题】集合M ={y | y= x2—1, x R}，集合N={x|y= 9 x2, x R}，则MIN等于( )A. {t|0 t 3} B . {t|—1 t 3} C . {(- . 2,1),( .2,1) D •【答案】B【鱷析】■・」=/—in —h 二対=[—h +工)・又丫)=嗣-》匸9 - ? > 0 +/■[- 3,3]. ■- M A -V = [-l(3].5. 【改编自2012年江西卷理科】若集合A={— 1,1}, B= 0,2，则集合{z|z= x+ y, x A, y B}中的元素的非空子集个数为()A. 7 B . 6 C . 5 D . 4【答案】A【鋒析】由已知得，集台V尸K+F送用ye ^={-1.1.3}-所以其非空子集个数冷2为二7,故选【考点深度剖析】高考对集合知识的考查要求较低，均是以小题的形式进行考查，一般难度不大，要求考生熟练掌握与集合有关的基础知识•纵观近几年的高考试题，主要考查以下两个方面：一是考查具体集合的关系判断和集合的运算•解决这类问题的关键在于正确理解集合中元素所具有属性的含义，弄清集合中元素所具有的形式以及集合中含有哪些元素•二是考查抽象集合的关系判断以及运算•【经典例题精析】考点1集合的概念K【1-1 】若a, b R，集合{1 , a b, a 0,-,b，求b a的值_____________________ .a【答案】2iy【解析】由d d+方卫｝=0—血可知“山则只能卄庄0,则有以下对应关爲CJ - b = 0.b—=c ab = 1.Jl_2【1-2】已知集合A=｛x|x+ m好4 = 0｝为空集，则实数m的取值范围是()A. ( —4, 4) B . [ —4, 4] C . ( —2, 2) D . [ —2, 2]【答案】A【解析】依题意知一元二次方程F十ww十4二0无解，^flzA A= w;_16 < 0(解得一4€楞羔4.故选A.【1-3】已知A=｛a+ 2, (a+ 1)2, a2+ 3a+ 3｝，若1€ A,则实数a构成的集合B的元素个数是()A. 0 B . 1 C . 2 D . 3【答案】B丽析】若口则1,代入集合」」得川=｛1"1｝,与集合元责的互异性若S+1F=1,帶住=0或一2,代入集合4帰/=匸切｝或去｛0二1｝,后■看与集合的互异性矛盾，故尸0 符合要求J若/+3卄3=1,则尸—诫-拿代人黑皆出得沪｛山1｝或看•戶｛轴助都与集合的互异性相矛盾, 無上可如只有口二。

备战高考数学一轮复习讲义第一章

答案与解析二配套精练第一章集合与常用逻辑用语、不等式第1讲集合及其运算1. D 解析： M ＝{x |0≤x <16}，N ＝{x ⎪⎪⎪⎭⎬⎫x ≥13，则M ∩N ＝{x ⎪⎪⎪⎭⎬⎫13≤x <16. 2. A 解析：因为U ＝{x ∈N |x ≤4}＝{0,1,2,3,4}，∁U (A ∩B )＝{0,2,3}，所以A ∩B ＝{1,4}，即1∈A 且4∈A .又A ＝{1，m }，所以m ＝4.3. C 解析：由题意，非空且互不相等的集合A ，B ，C 满足A ∪B ＝A ，可得B ⊆A .又因为B ∩C ＝C ，可得C ⊆B ，所以C ⊆A ，所以A ∩C ＝C .4. C 解析：由题可知A ＝{－1,0,1}，所以A ∩B ＝{0,1}，所以其子集分别是∅，{1}，{0}，{0,1}，共有4个子集．5. C 解析：因为集合M ＝{x |x ＝2k ＋1，k ∈Z }，集合N ＝{y |y ＝4k ＋3，k ∈Z }＝{y |y ＝2(2k ＋1)＋1，k ∈Z }，且x ∈N 时，x ∈M 成立，所以M ∪N ＝{x |x ＝2k ＋1，k ∈Z }．6. ABC 解析：当B ＝∅时，m ＋1>2m －1，即m <2，此时∁U B ＝R ，符合题意；当B ≠∅时，m ＋1≤2m －1，即m ≥2，由B ＝{x |m ＋1≤x ≤2m －1}，得∁U B ＝{x |x <m ＋1或x >2m －1}．因为A ⊆∁U B ，所以m ＋1>7或2m －1<－2，可得m >6或m <－12.因为m ≥2，所以m >6.综上，实数m 的取值范围为{m |m <2或m >6}．7. BD 解析：因为N ∩(∁R M )＝∅，所以N ⊆M .若N 是M 的真子集，则M ∩(∁R N )≠∅，故A 错误；由N ⊆M ，得M ∪(∁R N )＝R ，故B 正确；由N ⊆M ，得∁R N ⊇∁R M ，故C 错误，D 正确．8. BD 解析：对于A ，由B －A ＝{x |x ∈B 且x ∉A }，知B －A ＝{3,8}，A 错误；对于B ，由A －B ＝{x |x ∈A 且x ∉B }，A －B ＝∅，知A ⊆B ，B 正确；对于C ，由韦恩图知B －A 如图中阴影部分所示，则B －A ＝B ∩(∁U A )，C 错误；对于D ，∁U B ＝{x |x <－2或x ≥4}，则A －B ＝A ∩(∁U B )＝{x |x <－2或x ≥4}，D 正确．(第8题)9. (－∞，1] 解析：由x －a ≥0，得x ≥a ，所以B ＝[a ，＋∞)．因为A＝[1,6]，且A ⊆B ，所以a ≤1，所以实数a 的取值范围是(－∞，1]．10. (－∞，－1]∪[1，＋∞)∪{0} 解析：由题意，原问题转化为方程ax 2－2x ＋a ＝0至多只有一个根．当a ＝0时，方程为－2x ＝0，解得x ＝0，此时方程只有一个实数根，符合题意；当a ≠0时，方程ax 2－2x ＋a ＝0为一元二次方程，所以Δ＝4－4a 2≤0，解得a ≤－1或a ≥1.综上，实数a 的取值范围为(－∞，－1]∪[1，＋∞)∪{0}．11. 15 解析：因为1∈A ，11＝1∈A ；－1∈A ，1－1＝－1∈A ；2∈A ，12∈A ；3∈A ，13∈A ，所以所求集合即为由1，－1，“3和13”，“2和12”这“四大”元素所组成的集合的非空子集，所以满足条件的集合的个数为24－1＝15.12. 【解答】 (1) 当a ＝0时，A ＝{x |－1<x <1}，所以∁R A ＝{x |x ≤－1或x ≥1}，所以(∁R A )∩B ＝{x |1≤x <4}．(2) 因为A ⊆B ，所以集合A 可以分为A ＝∅和A ≠∅两种情况讨论．当A ＝∅时，2a －1≥3a ＋1，即a ≤－2；当A ≠∅时，得⎩⎨⎧ 2a －1≥－1，3a ＋1≤4，2a －1<3a ＋1，即0≤a ≤1.综上，a ∈(－∞，－2]∪[0,1]．13. 【解答】集合A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x |0<x －13≤1＝{x |1＜x ≤4}，B ＝⎩⎨⎧⎭⎬⎫x |y ＝1－x 2＋10x －16＝{x |2＜x ＜8}． (1) 因为集合C ＝{x |x ≤a }满足A ∩C ＝A ，所以A ⊆C ，所以a ≥4，所以实数a 的取值范围是[4，＋∞)．(2) 因为A ∩B ＝{x |2＜x ≤4}，A ∪B ＝{x |1＜x ＜8}，所以集合D ＝{x |1＜x ≤2或4＜x ＜8}．14. 【解答】 (1) 因为集合A ＝{x |x 2－ax ＋a 2－19＝0}，B ＝{x |x 2－5x ＋6＝0}＝{2,3}，且A ∩B ＝{2}，所以2∈A ，所以4－2a ＋a 2－19＝0，即a 2－2a －15＝0，解得a ＝－3或a ＝5.当a ＝－3时，A ＝{x |x 2＋3x －10＝0}＝{－5,2}，A ∩B ＝{2}，符合题意；当a ＝5时，A ＝{x |x 2－5x ＋6＝0}＝{2,3}，A ∩B ＝{2,3}，不符合题意．综上，实数a 的值为－3.(2) 因为A ＝{x |x 2－ax ＋a 2－19＝0}，B ＝{2,3}，C ＝{x |x 2＋2x －8＝0}＝{－4,2}，且A ∩B ≠∅，A ∩C ＝∅，所以3∈A ，所以9－3a ＋a 2－19＝0，即a 2－3a －10＝0，解得a ＝－2或a ＝5.当a ＝－2时，A ＝{x |x 2＋2x －15＝0}＝{－5,3}，满足题意；当a ＝5时，A ＝{x |x 2－5x ＋6＝0}＝{2,3}，不满足题意．综上，实数a 的值为－2.第2讲充分条件、必要条件、充要条件1. B 解析：若x <0，y ＝0满足x <y ，则(x －y )·y 2＝0，即(x －y )·y 2<0不成立；若(x －y )·y 2<0，则有y ≠0，必有y 2>0，从而得x －y <0，即x <y 成立．所以“x <y ”是“(x －y )·y 2<0”成立的必要不充分条件．2. D 解析：非有志者不能至，是必要条件；但“有志”也不一定“能至”，不是充分条件．3. B4. A 解析：因为x <z ，y <z ，所以x ＋y <2z ，故充分性成立；当x ＝3，y ＝1，z ＝2.5时，满足x ＋y <2z ，但不满足x <y <z ，故必要性不成立．5. C 解析： x －1x >0⇒x 2－1x >0⇒x (x ＋1)(x －1)>0⇒x >1或－1<x <0.因为{x |－1<x <0}{x |x >1或－1<x <0}，所以不等式x －1x >0成立的一个充分条件是－1<x <0.6. BC 解析： x 2>x 的解集为(－∞，0)∪(1，＋∞)．对于A ，因为(1，＋∞)为(－∞，0)∪(1，＋∞)的真子集，故A 不符合；对于B ，因为2x 2>2x 等价于x 2>x ，解集也是(－∞，0)∪(1，＋∞)，故B 符合；对于C ，1x <1即为x (x －1)>0，解集为(－∞，0)∪(1，＋∞)，故C 符合；对于D ，|x (x －1)|＝x (x －1)即为x (x －1)≥0，解集为(－∞，0]∪[1，＋∞)，(－∞，0)∪(1，＋∞)为(－∞，0]∪[1，＋∞)的真子集，故D 不符合．7. AC 解析：对于p ：|2x －1|<3，解得x ∈A ＝{x |－1<x <2}．对于q ：2x 2－ax －a 2≤0，得(2x ＋a )(x －a )≤0，当a ≥0时，解得x ∈B ＝{x ⎪⎪⎪⎭⎬⎫－a 2≤x ≤a ；当a <0时，解得x ∈B ＝{x ⎪⎪⎪⎭⎬⎫a ≤x ≤－a 2.因为p 是q 的一个必要不充分条件，所以B A .当a ≥0时，⎩⎪⎨⎪⎧ －a 2>－1，a <2，解得0≤a <2.当a <0时，⎩⎪⎨⎪⎧ a >－1，－a 2<2，解得－1<a <0.综上，可得－1<a <2.故只要实数a 的取值集合是集合{a |－1<a <2}的真子集即可．8. BCD 解析：对于A ，方程为x 2＋3＝0，方程没有实数根，所以A 错误；对于B ，如果方程没有实数根，则Δ＝(m －3)2－4m ＝m 2－10m ＋9<0，所以1<m <9，m >1是1<m <9的必要条件，所以B 正确；对于C ，因为方程有两个正根，所以⎩⎨⎧ Δ＝m 2－10m ＋9≥0，－(m －3)>0，m >0，所以0<m ≤1，所以方程有两个正根的充要条件是0<m ≤1，所以C 正确；对于D ，如果方程有一个正根和一个负根，则⎩⎨⎧Δ＝m 2－10m ＋9>0，m <0，所以m <0，所以方程有一个正根和一个负根的充要条件是m <0，所以D 正确．9. [1，＋∞) 解析：由不等式|x ＋1|>2，可得x >1或x <－3，所以綈p ：－3≤x ≤1.又由綈q ：x ≤a ，且綈p 是綈q 的充分不必要条件，可知a ≥1，所以实数a 的取值范围为[1，＋∞)．10. m ＝1(答案不唯一) 解析：当x ∈(2,3)时，易知x 2－x ＝⎝ ⎛⎭⎪⎫x －122－14∈(2,6)．又∃x ∈(2,3)，mx 2－mx －3>0⇔∃x ∈(2,3)，m >3x 2－x ⇔m >⎝ ⎛⎭⎪⎫3x 2－x min ，x ∈(2,3)⇔m ≥12.显然m ＝1⇒m ≥12，m ≥12D ⇒/m ＝1，故“m ＝1”是命题“∃x ∈(2,3)，mx 2－mx －3>0”成立的充分不必要条件．11. [1,2] 解析：由(x －a )2<1得a －1<x <a ＋1.因为1<x <2是不等式(x －a )2<1成立的充分不必要条件，所以满足⎩⎨⎧a －1≤1，a ＋1≥2且等号不能同时取得，即⎩⎨⎧a ≤2，a ≥1，解得1≤a ≤2. 12. 【解答】 (1) 当m ＝2时，A ＝{x |1<x <5}，B ＝{x |－2<x <2}，所以A ∪B ＝{x |－2<x <5}，A ∩B ＝{x |1<x <2}．(2) 由“x ∈A ”是“x ∈B ”成立的充分不必要条件，得A B .当A ＝∅，即m－1≥m 2＋1时，m 无解，所以A ≠∅，所以⎩⎨⎧m －1≥－2，m 2＋1≤2且等号不能同时取得，解得－1≤m ≤1.当m ＝－1时，A ＝B ＝(－2,2)，不成立．故实数m 的取值范围为{m |－1<m ≤1}．13. 【解答】 (1) 不存在，理由如下：由|4x －3|≤1，得－1≤4x －3≤1，故12≤x ≤1，即p ：12≤x ≤1.假设存在a ，使得p 是q 的充要条件，则不等式x 2－4ax ＋3a －1≤0的解集为{x ⎪⎪⎪⎭⎬⎫12≤x ≤1，所以x 1＝12，x 2＝1是方程x 2－4ax ＋3a －1＝0的两个根，故⎩⎪⎨⎪⎧ 12＋1＝4a ，12×1＝3a －1，此方程组无解，故假设不成立，所以不存在实数a ，使得p 是q 的充要条件．(2) 若p 是q 的充分不必要条件，则集合{x ⎪⎪⎪⎭⎬⎫12≤x ≤1为不等式x 2－4ax ＋3a －1≤0的解集的真子集．令f (x )＝x 2－4ax ＋3a －1，则由二次函数的图象性质可得⎩⎪⎨⎪⎧ f ⎝ ⎛⎭⎪⎫12≤0，f (1)≤0，即⎩⎪⎨⎪⎧ ⎝ ⎛⎭⎪⎫122－4a ×12＋3a －1≤0，1－4a ＋3a －1≤0，解得⎩⎪⎨⎪⎧ a ≤34，a ≥0，故0≤a ≤34.当a ＝0时，x 2－4ax ＋3a －1≤0⇒x 2－1≤0，解得－1≤x ≤1，满足题意；当a ＝34时，x 2－4ax ＋3a －1≤0⇒x 2－3x ＋54≤0，解得12≤x ≤52，满足题意．所以实数a 的取值范围为⎣⎢⎡⎦⎥⎤0，34. 14. 【解答】必要性：若方程ax 2＋2x ＋1＝0有且只有一个负数根，当a ＝0时，方程为2x ＋1＝0，解得x ＝－12，符合题意；当a <0时，Δ＝4－4a >0，设方程ax 2＋2x ＋1＝0的两根分别为x 1，x 2，则x 1x 2＝1a <0，此时方程ax 2＋2x ＋1＝0有且只有一个负数根；当a >0时，由Δ＝4－4a ≥0，可得0<a ≤1，设方程ax 2＋2x ＋1＝0的两根分别为x 1，x 2，则⎩⎪⎨⎪⎧ x 1x 2＝1a >0，x 1＋x 2＝－2a <0，则x 1，x 2均为负数．由题意可知Δ＝0，可得a ＝1，符合题意．所以“方程ax 2＋2x ＋1＝0有且只有一个负数根”⇒“a ≤0或a ＝1”．充分性：当a ＝0时，原方程变为2x ＋1＝0，解得x ＝－12，原方程只有一个负数根；当a ＝1时，方程为x 2＋2x ＋1＝0，解得x ＝－1，原方程只有一个负数根；当a <0时，对于原方程，Δ＝4－4a >0，此时方程ax 2＋2x ＋1＝0有两根，设为x 1，x 2，则x 1x 2＝1a <0，此时方程ax 2＋2x ＋1＝0有且只有一个负数根．所以“方程ax 2＋2x ＋1＝0有且只有一个负数根”⇐“a ≤0或a ＝1”．综上所述，方程ax 2＋2x ＋1＝0有且只有一个负数根的充要条件为a ≤0或a ＝1.第3讲全称量词和存在量词1. C 解析：因为集合M ，N 满足M ∩N ≠∅，所以根据交集的定义可得∃x ∈M ，x ∈N .2. A 解析：命题“∀x ∈R,2x >0”为全称量词命题，该命题的否定为“∃x ∈R,2x ≤0”．3. A 解析：由题意，①若甲说的是真话，则甲不会证明，乙会证明，丙不会证明，丁不会证明，此时丁说的也是真话，与题意矛盾；②若乙说的是真话，则丙会证明，甲和丁均会证明，与题意矛盾；③若丙说的是真话，则丁会证明，甲和丁均会证明，与题意矛盾；④若丁说的是真话，则丁不会证明，甲会证明，丙不会证明，满足题意．4. A 解析：若p 为真，则Δ1＝4－4a ≤0，解得a ≥1.若q 为真，则Δ2＝4a 2－4(2－a )<0，解得－2<a <1.若p 真q 假，则a ≥1；若p 假q 真，则－2<a <1.综上所述，若p ，q 一真一假，则实数a 的取值范围为(－2，＋∞)．5. A 解析：若不等式(m ＋1)x 2＋(m ＋1)x ＋1>0对任意x ∈R 恒成立，则有①当m ＋1＝0，即m ＝－1时，不等式显然成立；②当m ＋1>0时，Δ＝(m ＋1)2－4(m ＋1)<0，解得－1<m <3；③当m ＋1<0时，不等式(m ＋1)x 2＋(m ＋1)x ＋1>0对任意x ∈R 显然不恒成立，舍去．综上①②③可知，不等式(m ＋1)x 2＋(m＋1)x ＋1>0对任意x ∈R 恒成立，则－1≤m <3，所以当“∀x ∈R ，(m ＋1)x 2＋(m ＋1)x ＋1>0”是假命题时，m ∈(－∞，－1)∪[3，＋∞)．6. AB 解析：由条件可知∀x ∈⎣⎢⎡⎦⎥⎤12，2，2x 2－λx ＋1≥0是真命题，即λ≤2x 2＋1x ＝2x ＋1x ，即λ≤⎝ ⎛⎭⎪⎫2x ＋1x min ，x ∈⎣⎢⎡⎦⎥⎤12，2.设f (x )＝2x ＋1x ≥22x ·1x ＝22，x ∈⎣⎢⎡⎦⎥⎤12，2，等号成立的条件是2x ＝1x ⇒x ＝22∈⎣⎢⎡⎦⎥⎤12，2，所以f (x )的最小值是22，即λ≤22，满足条件的是AB.7. BC 解析：当x ＝0时，1x 2＋1＝1，A 错误．当x ＝－1时，1x <x ＋1，B 正确．命题“∃n ∈N ，n 2>2n ”的否定是命题“∀n ∈N ，n 2≤2n ”，C 正确．命题“∀n >4,2n >n 2”的否定是命题“∃n >4,2n ≤n 2”，D 错误．8. AD 解析：函数f (x )＝x ＋4x 在[1,2]上单调递减，在[2,6]上单调递增，f (x )min＝f (2)＝4，f (x )max ＝f (6)＝203.对任意a ，b ，c ∈[1,6]，不妨令f (a )≥f (b )≥f (c )，则f (b )＋f (c )≥2f (c )≥2f (x )min >f (x )max ≥f (a )，即f (a )，f (b )，f (c )均能作为一个三角形的三条边长，A 正确，B 错误；取a ＝b ＝2，c ＝22＋2，满足a ，b ，c ∈[1,6]，则f (a )＝f (b )＝4，f (c )＝42，显然有[f (a )]2＋[f (b )]2＝[f (c )]2，即以f (a )，f (b )，f (c )为边的三角形是直角三角形，C 错误，D 正确．9. ⎣⎢⎡⎭⎪⎫52，＋∞ 解析：因为∀x ∈[1,2]，x 2－ax ＋1≤0为真命题，所以a ≥⎝ ⎛⎭⎪⎫x ＋1x max ，x ∈[1,2]．因为y ＝x ＋1x 在区间[1,2]上单调递增，所以⎝ ⎛⎭⎪⎫x ＋1x max ＝2＋12＝52，即a ≥52，所以实数a 的取值范围为⎣⎢⎡⎭⎪⎫52，＋∞. 10. (－∞，2] 解析：设x 1，x 2是方程的两个负实数根，则⎩⎨⎧ Δ＞0，x 1＋x 2＝－m ＜0，x 1x 2＝1＞0，即⎩⎨⎧m 2－4＞0，m ＞0，解得m ＞2，所以当綈p 是真命题时，m 的取值范围是(－∞，2]．11. ∀x ∈[1,2]，x 2＋2ax ＋2－a ≤0 (－3，＋∞)解析：綈p ：∀x ∈[1,2]，x 2＋2ax ＋2－a ≤0.若綈p 是真命题，令f (x )＝x 2＋2ax ＋2－a ，则 ⎩⎨⎧ f (1)≤0，f (2)≤0，即⎩⎨⎧1＋2a ＋2－a ≤0，4＋4a ＋2－a ≤0，解得a ≤－3，故满足题意的实数a 的取值范围为(－3，＋∞)．12. 【解答】 (1) 因为命题p ：∀x ∈R ，x 2＋ax ＋2≥0为真命题，所以Δ＝a 2－4×1×2≤0，解得－22≤a ≤22，所以实数a 的取值范围为[－22，22]．(2) 因为命题q ：∃x ∈⎣⎢⎡⎦⎥⎤－3，－12，x 2－ax ＋1＝0为真命题，所以a ＝x 2＋1x ＝x ＋1x ，又y ＝x ＋1x 在[－3，－1]上单调递增，在⎣⎢⎡⎦⎥⎤－1，－12上单调递减，所以当x ＝－1时，a 取最大值－2.当x ＝－3时，a ＝－103；当x ＝－12时，a ＝－52.所以实数a 的取值范围为⎣⎢⎡⎦⎥⎤－103，－2. 13. 【解答】若命题p 为真命题，则Δ＝(m －2)2－4≥0，解得m ≤0或m ≥4.若命题q 为真命题，由a ，b ∈(0，＋∞)，知b ＝2a a －1>0，所以a －1>0，则a (b －1)＝a ⎝ ⎛⎭⎪⎫2a a －1－1＝a ·a ＋1a －1＝(a －1＋1)⎝⎛⎭⎪⎫1＋2a －1＝a －1＋2a －1＋3≥3＋22，m ＋22≤22＋3⇒m ≤3.当命题p 为真，命题q 为假时，⎩⎨⎧ m ≤0或m ≥4，m >3，解得m ≥4；当命题p 为假，命题q 为真时，⎩⎨⎧0<m <4，m ≤3，解得0<m ≤3.综上所述，实数m 的取值范围为{m |0<m ≤3或m ≥4}．14. 【解答】 (1) 由题设知f ′(x )＝x 2＋2x ＋a ≥0在[1，＋∞)上恒成立，即a ≥－(x ＋1)2＋1在[1，＋∞)上恒成立，而函数y ＝－(x ＋1)2＋1在[1，＋∞)上单调递减，则y max ＝－3，所以a ≥－3，所以a 的最小值为－3.(2) 由题可知，当x ∈⎣⎢⎡⎦⎥⎤12，2时，f ′(x )max ≤g (x )max .因为f ′(x )＝x 2＋2x ＋a ＝(x ＋1)2＋a －1在⎣⎢⎡⎦⎥⎤12，2上单调递增，所以f ′(x )max ＝f ′(2)＝8＋a .而g ′(x )＝1－xe x ，由g ′(x )＞0，得x ＜1，由g ′(x )＜0，得x ＞1，所以g (x )在(－∞，1)上单调递增，在(1，＋∞)上单调递减，所以当x ∈⎣⎢⎡⎦⎥⎤12，2时，g (x )max ＝g (1)＝1e .由8＋a ≤1e ，得a ≤1e －8，所以实数a 的取值范围为⎝ ⎛⎦⎥⎤－∞，1e －8. 第4讲不等式的性质、基本不等式1. D 解析：对于A ，取a ＝－1，b ＝1，则1a <1b ，A 错误；对于B ，取a＝－1，b ＝1，则a 2＝b 2，B 错误；对于C ，取a ＝－1，b ＝1，则1a 2＝1b 2，C 错误；对于D ，由a <b ，可得b 3－a 3＝(b －a )·(b 2＋ab ＋a 2)＝(b －a )⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫b ＋12a 2＋34a 2>0，所以a 3<b 3，D 正确．2. D 解析：对于A ，当c ＝0时，显然不成立，故A 为假命题；对于B ，当a ＝－3，b ＝－2时，满足a <b <0，但a 2<ab <b 2不满足，故B 为假命题；对于C ，当c ＝3，a ＝2，b ＝1时，a c －a ＝23－2>b c －b＝12，不满足，故C 为假命题；对于D ，因为a >b >c >0，所以a b －a ＋c b ＋c ＝a (b ＋c )－b (a ＋c )b (b ＋c )＝ac －bc b (b ＋c )＝(a －b )c b (b ＋c )>0，即a b >a ＋c b ＋c，故D 为真命题． 3. B 解析：由题知4b ＋1a ＝12⎝ ⎛⎭⎪⎫4b ＋1a (a ＋b )＝12⎝ ⎛⎭⎪⎫4a b ＋b a ＋5≥12(4＋5)＝92，当且仅当4a b ＝b a 时等号成立．4. C 解析： 7＝(a ＋2b )2－ab ＝(a ＋2b )2－12a ·2b ≥(a ＋2b )2－12⎝ ⎛⎭⎪⎫a ＋2b 22＝7(a ＋2b )28，则(a ＋2b )2≤8，当且仅当a ＝2b ＝2时等号成立，又a ，b ∈(0，＋∞)，所以0<a ＋2b ≤22，当且仅当a ＝2b ＝2时等号成立，所以a ＋2b 的最大值为2 2.5. BCD 解析：对于A ，当c ＝0时，ac ＝bc ，故A 错误；对于B ，若ac 2>bc 2，则a >b ，故B 正确；对于C ，若a <b <0，则|a |>|b |，故C 正确；对于D ，若c >a >b >0，则0<c －a <c －b ，从而1c －a >1c －b，故D 正确． 6. AB 解析：对于A ，ab ≤⎝ ⎛⎭⎪⎫a ＋b 22＝⎝ ⎛⎭⎪⎫122＝14，当且仅当a ＝b ＝12时取等号，故A 正确．对于B ，(a ＋b )2＝a ＋b ＋2ab ≤a ＋b ＋a ＋b ＝2，故a ＋b ≤2，当且仅当a ＝b ＝12时取等号，故B 正确．对于C ，1a ＋1b ＝⎝ ⎛⎭⎪⎫1a ＋1b (a ＋b )＝2＋b a ＋a b ≥2＋2b a ·a b ＝4，当且仅当a ＝b ＝12时取等号，所以1a ＋1b 有最小值4，故C 错误．对于D ，(a ＋b )2＝1⇒a 2＋2ab ＋b 2＝1≤a 2＋(a 2＋b 2)＋b 2，即a 2＋b 2≥12，故a 2＋b 2有最小值12，故D 错误．7. －1，－2，－3(答案不唯一) 解析：－1>－2>－3，(－1)＋(－2)＝－3>－3，矛盾，所以－1，－2，－3可验证该命题是假命题．8. 9 解析：因为0<x <1，所以0<1－x <1，则1x ＋41－x ＝⎝ ⎛⎭⎪⎫1x ＋41－x [(1－x )＋x ]＝1＋4＋1－x x ＋4x 1－x ≥5＋21－x x ·4x 1－x ＝9，当且仅当1－x x ＝4x 1－x，即x ＝13时，等号成立，故1x ＋41－x的最小值为9. 9. 6 解析：设矩形空地的长为x m ，则宽为32x m ．由题意，试验区的总面积S ＝(x －0.5×4)⎝ ⎛⎭⎪⎫32x －0.5×2＝34－x －64x ≤34－2x ·64x ＝18，当且仅当x＝64x ，即x ＝8时，等号成立，所以每块试验区的面积的最大值为183＝6(m 2)．10. 【解答】 (1) 由不等式4a 2＋b 2≥4ab ，解得ab ≤12，当且仅当2a ＝b ＝1时取等号，所以ab 的最大值为12，此时a ＝12，b ＝1.(2) 由4a 2＋b 2＝2，得4a 2＋(1＋b 2)＝3.由4a 2＋(1＋b 2)≥24a 2·(1＋b 2)＝4a 1＋b 2，解得a 1＋b 2≤34，当且仅当4a 2＝1＋b 2，即a ＝64，b ＝22时取等号，所以a 1＋b 2的最大值为34，此时a ＝64，b ＝22.11. 【解答】 (1) 因为a >1，b >2，所以a －1>0，b －2>0，所以1a －1＋1b －2＝14⎝ ⎛⎭⎪⎫1a －1＋1b －2(a －1)(b －2)＝14[(b －2)＋(a －1)]≥14×2(b －2)(a －1)＝1，当且仅当⎩⎨⎧b －2＝a －1，(a －1)(b －2)＝4时，等号成立，解得a ＝3，b ＝4，所以1a －1＋1b －2的最小值为1，此时a ＝3，b ＝4.(2) 由2a ＋b ＝6，得2(a －1)＋(b －2)＝2，所以(a －1)＋b －22＝1，所以1a －1＋1b －2＝⎝ ⎛⎭⎪⎫1a －1＋1b －2×1＝⎝ ⎛⎭⎪⎫1a －1＋1b －2×⎣⎢⎡⎦⎥⎤(a －1)＋b －22＝32＋a －1b －2＋b －22(a －1)≥3＋222，当且仅当⎩⎨⎧b －2＝2(a －1)，2(a －1)＋(b －2)＝2时，等号成立，解得a ＝3－2，b ＝22，所以1a －1＋1b －2的最小值为3＋222，此时a ＝3－2，b ＝2 2.(3) 因为b >2，由1a ＋1b ＝1，可得a ＝b b －1，所以a －1＝1b －1，所以1a －1＋1b －2＝b －2＋1b －2＋1≥3，当且仅当a ＝32，b ＝3时，等号成立，所以1a －1＋1b －2的最小值为3，此时a ＝32，b ＝3.12. D 解析：因为A ＝{1,2,3}，B ＝{0,1,2}，所以A ∩B ＝{1,2}，A ∪B ＝{0,1,2,3}，所以当x ∈A ∩B ，y ∈A ∪B 时，z ＝0,1,2,3,4,6，所以A *B ＝{0,1,2,3,4,6}，所以∁(A *B )A ＝{0,4,6}．13. BC 解析： A 错误，当a <0时，显然有P <0.B 正确，当a >1时，P ＝a ＋2a ≥2a ·2a ＝22，故充分性成立，而P ≥22只需a >0即可．C 正确，P ＝a＋2a >3可得0<a <1或a >2，当a >2时，P >3成立．D 错误，当a >3时，a ＋2a >3＋23>3.14. 【解答】 (1) 当m ＝1时，B ＝{x |2<x <3}．因为A ＝{x |－1≤x ≤2}，所以∁R A ＝{x |x <－1或x >2}，所以A ∪B ＝{x |－1≤x <3}，(∁R A )∩B ＝{x |2<x <3}．(2) 因为∅是A ∩B 的真子集，所以A ∩B ≠∅.因为A ＝{x |－1≤x ≤2}，B ＝{x |2m <x <3}，所以⎩⎨⎧2m <3，2m <2，解得m <1，即实数m 的取值范围为(－∞，1)．(3) 因为B ∩(∁R A )中只有一个整数，∁R A ＝{x |x <－1或x >2}，B ＝{x |2m <x <3}，所以B ≠∅，且－3≤2m <－2，解得－32≤m <－1，所以实数m 的取值范围是{m ⎪⎪⎪⎭⎬⎫－32≤m <－1. 第5讲一元二次不等式1. A 解析：因为不等式x 2＋kx ＋1<0的解集为空集，所以Δ＝k 2－4≤0，解得－2≤k ≤2.2. D 解析：当a ＝1时，不等式为－4<0恒成立，故满足题意；当a ≠1时，要满足⎩⎨⎧a －1<0，Δ<0，解得－3<a <1.综上，实数a 的取值范围是(－3,1]．3. C 解析：由x ＋a x －b ＝(1－b )x ＋ax ≥0，可知⎩⎨⎧x [(b －1)x －a ]≤0，x ≠0的解集为[－1,0)，所以⎩⎪⎨⎪⎧b －1>0，ab －1＝－1，则b >1且a ＋b ＝1.4. C 解析：因为关于x 的一元二次不等式ax 2＋bx ＋c >0的解集为{x |1<x <3}，所以1,3为方程ax 2＋bx ＋c ＝0的两个根，由韦达定理得⎩⎪⎨⎪⎧1＋3＝－ba ，1×3＝c a ，所以⎩⎨⎧c ＝3a ，b ＝－4a ，且a <0，则ax ＋b cx ＋a >0等价于x －43x ＋1>0，即(3x ＋1)(x －4)>0，故原不等式的解集为⎝ ⎛⎭⎪⎫－∞，－13∪(4，＋∞)．5. ACD 解析：对于A ，ax 2>0(a >0)的解集为{x |x ≠0}，A 错误；对于B ，因为Δ＝1－4＝－3<0，所以x 2＋x ＋1<0的解集为∅，B 正确；对于C ，若a <0，Δ＝0，则ax 2＋bx ＋c ≥0的解集为{x ⎪⎪⎪⎭⎬⎫x ＝－b 2a ，C 错误；对于D ，x 2＋3x －4>0的解集为(－∞，－4)∪(1，＋∞)，不等式组⎩⎨⎧x －1>0，x ＋4>0的解集为(1，＋∞)，D错误．6. BD 解析：设x 小时后蓄水池中的水量为y t ，则y ＝400＋60x －1206x .设6x ＝u ，则u 2＝6x (u ∈[0,12])，所以y ＝400＋10u 2－120u ＝10(u －6)2＋40.因为u ∈[0,12]，故当u ＝6，即x ＝6时，y min ＝40，即从供水开始到第6个小时时，蓄水池中的存水量最少，为40t ，所以A 错误，B 正确．令400＋10u 2－120u >80，即u 2－12u ＋32>0，解得u <4或u >8，所以0≤x <83或323<x ≤24，所以C 错误．由400＋10u 2－120u <80，得83<x <323，又323－83＝8，所以每天约有8小时蓄水池中水量少于80t ，所以D 正确．7. [1，＋∞) 解析： x －1x >0⇒x (x －1)>0⇒x >1或x <0，则当x >a 时，x －1x >0成立，所以a ≥1.8. (－1,2) 解析：由表中二次函数y ＝ax 2＋bx ＋c (x ∈R )的部分对应值，得⎩⎨⎧c ＝2，a ＋b ＋c ＝2，a －b ＋c ＝0，解得⎩⎨⎧a ＝－1，b ＝1，c ＝2，所以y ＝－x 2＋x ＋2.不等式ax 2＋bx ＋c ＞0化为－x 2＋x ＋2＞0，即x 2－x －2＜0，解得－1＜x ＜2，所以该不等式的解集为(－1,2)．9. ⎝ ⎛⎭⎪⎫－12，32 解析：由题意可知，不等式(x －a )(x ＋a )<1对任意实数x 都成立，又由(x －a )(x ＋a )＝(x －a )(1－x －a )，即x 2－x －a 2＋a ＋1>0对任意实数x 都成立，所以Δ＝1－4(－a 2＋a ＋1)<0，即4a 2－4a －3<0，解得－12<a <32.10. 【解答】 (1) 因为不等式ax 2＋bx －1>0的解集是{x |1<x <2}，所以a <0，且1和2是方程ax 2＋bx －1＝0的两个根，所以⎩⎨⎧a ＋b －1＝0，4a ＋2b －1＝0，解得⎩⎪⎨⎪⎧a ＝－12，b ＝32.(2) 由(1)知不等式ax ＋1bx －1≥0即为－12x ＋132x －1≥0⇔x －23x －2≤0⇔⎩⎨⎧3x －2≠0，(x －2)(3x －2)≤0，解得23<x ≤2，所以不等式的解集是{x ⎪⎪⎪⎭⎬⎫23<x ≤2.11. 【解答】 (1) 由已知易得y ≥4＋2a 即为x 2－(a －2)x －2a ≥0.令x 2－(a －2)x －2a ＝0，可得x ＝－2或x ＝a ，所以，当a <－2时，原不等式的解集为{x |x ≤a 或x ≥－2}；当a ＝－2时，原不等式的解集为R ；当a >－2时，原不等式的解集为{x |x ≤－2或x ≥a }．(2) 由y －2a ＋14≥0，可得a (x ＋2)≤x 2＋2x ＋18.由1≤x ≤6，得x ＋2>0，所以a ≤x 2＋2x ＋18x ＋2.因为x 2＋2x ＋18x ＋2＝x ＋18x ＋2＝(x ＋2)＋18x ＋2－2≥218－2＝62－2，当且仅当x ＋2＝18x ＋2，即x ＝32－2时等号成立，所以a ≤62－2，所以a 的取值范围是{a |a ≤62－2}．12. C 解析：因为B ＝{x ∈N *|x 2－x －2≤0}＝{x ∈N *|(x －2)(x ＋1)≤0}＝{1,2}，A ＝{－2，－1}，所以A ∪B ＝{－2，－1,1,2}．13. C 解析：命题“∀x ∈R ，cos x ≤1”的否定是“∃x 0∈R ，cos x 0>1”，A 正确．在△ABC 中，因为sin A ≥sin B ，所以由正弦定理可得a 2R ≥b2R (R 为△ABC 外接圆的半径)，所以a ≥b ，则由大边对大角可得A ≥B ；反之，由A ≥B 可得a ≥b ，所以由正弦定理可得sin A ≥sin B .即为充要条件，B 正确．当a ＝b ＝0，c ≥0时，满足ax 2＋bx ＋c ≥0，但是得不到“a >0，且b 2－4ac ≤0”，即不是充要条件，C 错误．“若sin α≠12，则α≠π6”是真命题，D 正确．14. 【解答】 (1) 当a ＝1时，B ＝{x ⎪⎪⎪⎭⎪⎬⎪⎫x －51－x >0，因为x －51－x >0⇔(x －1)(x －5)<0⇒1<x <5，所以B ＝{x |1<x <5}．(2) 因为|x －1|<3⇒－3<x －1<3⇒－2<x <4，所以A ＝{x |－2<x <4}．因为A ∩B ＝B ，所以B ⊆A .①当B ＝∅时，3a ＋2＝1，解得a ＝－13，满足题意；②当B ≠∅时，若3a ＋2>1，即a >－13，则B ＝{x ⎪⎪⎪⎭⎪⎬⎪⎫x －3a －21－x >0＝{x |1<x <3a ＋2}，故3a ＋2≤4，所以－13<a ≤23.若3a ＋2<1，即a <－13，则B ＝{x ⎪⎪⎪⎭⎪⎬⎪⎫x －3a －21－x >0＝{x |3a ＋2<x <1}，43≤a<－13.综上所述，a的取值范围为⎣⎢⎡⎦⎥⎤－43，23.故3a＋2≥－2，所以－。

第1章第1讲集合的概念与运算-2021版高三数学(新高考)一轮复习课件共45张PPT

第一章集合与常用逻辑用语
高考一轮总复习 • 数学 • 新高考
返回导航
[解析] (1)B＝{x|x∈A}＝{1,2,3}＝A，故选 C．
(2)∵集合 A＝{x|x＝sin n3π，n∈Z}＝{0， 23，－ 23}，且 B⊆A，∴集合 B 的个数为 23＝8，故选 C．
(3)解法一：(列举法)，由题意知
高考一轮总复习 • 数学 • 新高考
返回导航
(2)(多选题)(2020·湖南长郡中学模拟改编)已知集合 M＝{y|y＝x－|x|，x∈R}，N
＝{y|y＝(12)x，x∈R}，则下列不正确的是(ABD )
A．M＝N
B．N⊆M
C．M＝∁RN
D．(∁RN)∩M＝∅
(3)已知集合 A＝{x|x2－3x－10≤0}，B＝{x|mx＋10>0}，若 A⊆B，则 m 的取值范
返回导航
(3)若 a＋2＝1，则 a＝－1，A＝{1,0,1}，不合题意；若(a＋1)2＝1，则 a＝0 或－
2，当 a＝0 时，A＝{2,1,3}，当 a＝－2 时，A＝{0,1,1}，不合题意；若 a2＋3a＋3＝1，
则 a＝－1 或－2，显然都不合题意；因此 a＝0，所以 2 0200＝1.
∵1∉A，∴a＋2≠1，∴a≠－1；(a＋1)2≠1，解得 a≠0，－2；a2＋3a＋3≠1 解
A．(－1,1)
B．(1,2)
C．(－1，＋∞)
D．(1，＋∞)
[解析] 由题意得A∪B＝{x|x>－1}，即A∪B＝(－1，＋∞)，故选C．
第一章集合与常用逻辑用语
高考一轮总复习 • 数学 • 新高考
返回导航
6． (2019·全国卷Ⅱ，5分)设集合A＝{x|x2－5x＋6>0}，B＝{x|x－1<0}，则A∩B

旧教材适用2023高考数学一轮总复习第一章集合与常用逻辑用语第1讲集合及其运算课件

(2)已知 a，b∈R，若a，ba，1＝{a2，a＋b，0}，则 a＋b 为(
)
A．1 B．0 C．－1 D．±1
答案 C 解析由已知得 a≠0，则ba＝0，所以 b＝0，于是 a2＝1，即 a＝1 或 a ＝－1，又根据集合中元素的互异性可知 a＝1 应舍去，因此 a＝－1，故 a ＋b＝－1.故选 C.
1．若有限集 A 中有 n 个元素，则集合 A 的子集个数为 2n，真子集的个数为 2n－1，非空真子集的个数为 2n－2.
2．A∪∅＝A，A∪A＝A，A⊆ (A∪B)，B⊆ (A∪B). 3．A∩∅＝∅，A∩A＝A，A∩B⊆ A，A∩B⊆ B. 4．A∩B＝A∪B⇔A＝B.
5．A⊆ B⇔A∩B＝A⇔A∪B＝B⇔(∁UA)⊇ (∁UB)⇔A∩(∁UB)＝∅. 6．A∩(∁UA)＝∅，A∪(∁UA)＝U，∁U(∁UA)＝A. 7．(∁UA)∩(∁UB)＝∁U(A∪B)，(∁UA)∪(∁UB)＝∁U(A∩B).
2
PART TWO
核心考向突破
考向一集合的基本概念例 1 (1)已知集合 A＝{0，1，2}，则集合 B＝{x－y|x∈A，y∈A}中元素的个数是( ) A．1 B．3 C．5 D．9
答案 C
解析当 x＝0 时，若 y＝0，则 x－y＝0；若 y＝1，则 x－y＝－1；若 y ＝2，则 x－y＝－2.同理可得，当 x＝1 时，x－y＝1，0，－1；当 x＝2 时，x －y＝2，1，0.综上，根据集合中元素的互异性，可知 B 中元素有－2，－1， 0，1，2，共 5 个．
6．(2021·福建泉州质量检测(三))已知集合 A＝{(x，y)|x＋y＝8，x，y∈ N*}，B＝{(x，y)|y＞x＋1}，则 A∩B 中元素的个数为( )

高考数学一轮复习课件浙江专版-第1讲集合

一集合的运算及应用
【例 1】若集合A＝{x|x2－2x－8<0}，B＝{x|x－m<0}． (1)若m＝3，全集U＝A∪B，试求∁UB； (2)若A∩B＝∅，求实数m的取值范围； (3)若A∩B＝A，求实数m的取值范围．
【解析】 (1)由 x2－2x－8<0，得－2<x<4，所以 A＝{x|－2<x<4}；当 m＝3 时，由 x－m<0，得 x<3，所以 B＝{x|x<3}．所以 U＝A∪B＝{x|x<4}，所以∁UB＝{x|3≤x<4}． (2)因为 A＝{x|－2<x<4}，B＝{x|x<m}，又 A∩B＝∅，所以 m≤－2. (3)因为 A＝{x|－2<x<4}，B＝{x|x<m}．又 A∩B＝A，即 A⊆B，所以 m≥4，
则
下
面
论
断
正
确
的
是
A． IS1
S
＝
2
B． S1 IS2
C ． I S1 I S2
D ． S2 IS1
【解析】
1因为P＝[0，＋)，Q＝[－ 2，2]，
所以P Q＝[0，2]，故选D.
2因为S1 S2＝I，所以 I (S1 S2 )＝ I I＝
即 I S1 I S2＝，故选C.
【解析】 (1)由 M∩{a1，a2，a3}＝{a1，a2}，可知 a1∈M，a2∈M，且 a3∉M. 又 M⊆{a1，a2，a3，a4}，从而 M＝{a1，a2} 或 M＝{a1，a2，a4}，共 2 个．
(2)由 x2＋x－6＝0 得 x＝2 或 x＝－3，所以 M＝{2，－3}． N∩M＝N⇔N⊆M. (ⅰ)当 a＝0 时，N＝∅，此时 N⊆M； (ⅱ)当 a≠0 时，N＝{1a}．由 N⊆M 得1a＝2 或1a＝－3，即 a＝12或 a＝－13. 故所求实数 a 的值为 0 或12或－13.

2025版高考数学一轮总复习考点突破第1章集合常用逻辑用语不等式第1讲集合考点3集合的基本运算

集合的基本运算角度1 集合的运算1.(2024·江苏盐城模拟)已知集合U＝{x|1<x<6，x∈N}，A＝{2,3}，B＝{2,4,5}，则(∁U A)∩B等于( A )A．{4,5} B．{2,3,4,5}C．{2} D．{2,4,5}[解析]由题意得，U＝{2,3,4,5}，又A＝{2,3}，则∁U A＝{4,5}，因为B＝{2,4,5}，所以(∁U A)∩B＝{4,5}．故选A.[解析]集合M中的元素是被3除余1的数，集合N中的元素是被3除余2的数，所以集合∁U(M∪N)中的元素是被3整除的数，即∁U(M∪N)＝{x|x＝3k，k∈Z}，故选A.3．(多选题)(2022·潍坊质检)已知集合A＝{x|－1<x≤3}，集合B＝{x||x|≤2}，则下列关系式正确的是( BD )A．A∩B＝∅B．A∪B＝{x|－2≤x≤3}C．A∪∁R B＝{x|x≤－1或x>2}D．A∩∁R B＝{x|2<x≤3}[解析]∵A＝{x|－1<x≤3}，B＝{x||x|≤2}＝{x|－2≤x≤2}，∴A∩B＝{x|－1<x≤3}∩{x|－2≤x≤2}＝{x|－1<x≤2}，A不正确；A∪B＝{x|－1<x≤3}∪{x|－2≤x≤2}＝{x|－2≤x≤3}，B正确；∵∁R B＝{x|x<－2或x>2}，∴A∪∁R B＝{x|－1<x≤3}∪{x|x<－2或x>2}＝{x|x<－2或x>－1}，C不正确；A∩∁R B＝{x|－1<x≤3}∩{x|x<－2或x>2}＝{x|2<x≤3}，D正确．角度2 利用集合的运算求参数1.已知集合A＝{x|x2－3x<0}，B＝{1，a}，且A∩B有4个子集，则实数a的取值范围是( B )A．(0,3) B．(0,1)∪(1,3)C ．(0,1)D ．(－∞，1)∪(3，＋∞)[解析] 因为A ∩B 有4个子集，所以A ∩B 中有2个不同的元素，所以a ∈A ，所以a2－3a <0，解得0<a <3.又a ≠1，所以实数a 的取值范围是(0,1)∪(1,3)，故选B.2．已知集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}≠∅，若A ∩B ＝B ，则实数m 的取值范围为_[2,3]__. [解析] 由A ∩B ＝B 知，B ⊆A .又B ≠∅，则⎩⎪⎨⎪⎧ 2m －1≥m ＋1，m ＋1≥－2，2m －1≤5，解得2≤m ≤3，则实数m 的取值范围为[2,3]．[引申1]本例2中若B ＝{x |m ＋1≤x ≤2m －1}情况又如何？[解析] 应对B ＝∅和B ≠∅进行分类．①若B ＝∅，则2m －1<m ＋1，此时m <2.②若B ≠∅，由例得2≤m ≤3.由①②可得，符合题意的实数m 的取值范围为(－∞，3]．[引申2]本例2中是否存在实数m ，使A ∪B ＝B ？若存在，求实数m 的取值范围；若不存在，请说明理由．[解析] 由A ∪B ＝B ，即A ⊆B 得⎩⎪⎨⎪⎧ m ＋1≤－2，2m －1≥5，即⎩⎪⎨⎪⎧ m ≤－3，m ≥3，不等式组无解，故不存在实数m ，使A ∪B ＝B .[引申3]本例2中，若B ＝{x |m ＋1≤x ≤1－2m }，AB ，则m 的取值范围为 (－∞，－3] .[解析] 由题意可知⎩⎪⎨⎪⎧ m ＋1≤－2，1－2m ≥5，解得m ≤－3.名师点拨：集合的基本运算的关注点1．集合是由元素组成的，从研究集合中元素的构成入手是解决集合运算问题的前提．2．有些集合是可以化简的，先化简再研究其关系并进行运算，可使问题简单明了，易于解决．3．注意数形结合思想的应用，常用的数形结合形式有数轴、坐标系和Venn 图．4．根据集合运算结果求参数，先把符号语言译成文字语言，然后应用数形结合求解．【变式训练】1．(角度1)(2023·全国乙文，2,5分)设全集U ＝{0,1,2,4,6,8}，集合M ＝{0,4,6}，N ＝{0,1,6}，则M ∪∁U N ＝( A )A ．{0,2,4,6,8}B ．{0,1,4,6,8}C ．{1,2,4,6,8}D ．U[解析] 易得∁U N ＝{2,4,8}，又M ＝{0,4,6}，∴M ∪∁U N ＝{0,2,4,6,8}．故选A.2．(角度1)(2024·上海控江中学月考)设集合A ＝{x ∈Z |x 2<4}，B ＝{x |y ＝x －1}，则A ∩(∁R B )＝( C )A ．{x |－2<x <1}B ．{x |－2<x ≤1}C ．{－1,0}D ．{－1} [解析] A ＝{x ∈Z |x 2<4}＝{－1,0,1}，B ＝{x |y ＝x －1}＝[1，＋∞)，则∁R B ＝(－∞，1)，所以A ∩(∁R B )＝{－1,0}，故选C.3．(多选题)(角度2)若集合A ＝{x |x <a }，B ＝{x |lg x ≥0}，且满足A ∪B ＝R ，则实数a 的值可以为( AC )A ．2B ．－1C ．1D ．－2[解析] 集合A ＝{x |x <a }，B ＝{x |lg x ≥0}，由题意得B ＝{x |x ≥1}，因为A ∪B ＝R ，所以a ≥1.所以实数a 的取值范围是[1，＋∞)．故选AC.4．(角度2)已知集合A ＝{x |－3≤x ≤4}，B ＝{x |2m －1≤x ≤m ＋1}，且B ⊆A ，则实数m 的取值范围是 [－1，＋∞) .[解析] ∵B ⊆A ，①当B ＝∅时，2m －1>m ＋1，解得m >2，②当B ≠∅时，⎩⎪⎨⎪⎧ 2m －1≤m ＋1，2m －1≥－3，m ＋1≤4，解得－1≤m ≤2.综上，实数m 的取值范围是[－1，＋∞)．。

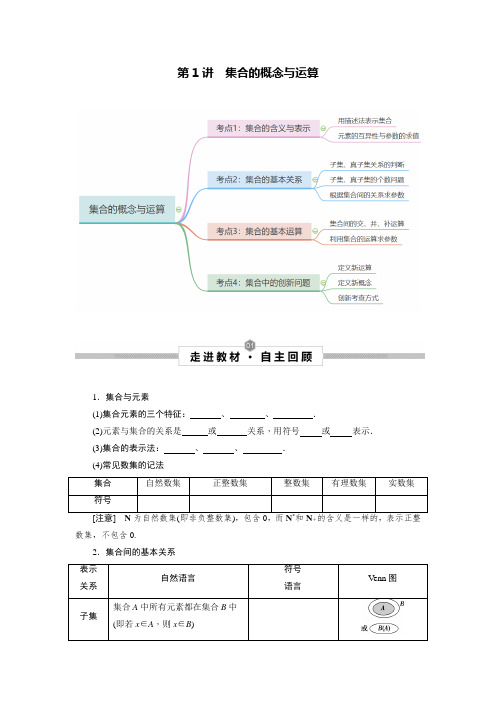
2023届高考数学一轮复习讲义：第1讲集合的概念与运算

第1讲集合的概念与运算1．集合与元素(1)集合元素的三个特征：、、．(2)元素与集合的关系是或关系，用符号或表示．(3)集合的表示法：、、．(4)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号[注意]N为自然数集(即非负整数集)，包含0，而N*和N＋的含义是一样的，表示正整数集，不包含0.2．集合间的基本关系表示关系自然语言符号语言Venn图子集集合A中所有元素都在集合B中(即若x∈A，则x∈B)真子集集合A 是集合B 的子集，且集合B 中至少有一个元素不在集合A 中集合相等集合A ，B 中元素相同A ＝B3.集合的基本运算集合的并集集合的交集集合的补集图形语言符号语言A ∪B ＝A ∩B ＝∁U A ＝➢考点1 集合的含义与表示[名师点睛]与集合元素有关问题的解题策略(1)研究集合问题时，首先要明确构成集合的元素是什么，即弄清该集合是数集、点集，还是其他集合；然后再看集合的构成元素满足的限制条件是什么，从而准确把握集合的含义． (2)利用集合元素的限制条件求参数的值或确定集合中元素的个数时，要注意检验集合是否满足元素的互异性．2＋y 2≤3，x ∈Z ，y ∈Z }，则A 中元素的个数为( )A ．9B ．8C ．5D ．4(2)设A ＝⎩⎨⎧⎭⎬⎫2，3，a 2－3a ，a ＋2a ＋7，B ＝{|a －2|,3}，已知4∈A 且4∉B ，则a 的取值集合为________．[举一反三]1．（2022·江西·新余四中模拟预测（理））已知集合()(){}20A x a x x a =--<，若2A ∉，则实数a 的取值范围为（）A ．()(),12,-∞+∞ B ．[)1,2 C ．()1,2D ．[]1,22．（2022·菏泽模拟）设a ，b ∈R ，集合{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，则b －a ＝( ) A ．1 B ．－1 C ．2D ．－23．(多选)（2022· 广州一调）已知集合{x |mx 2－2x ＋1＝0}＝{n }，则m ＋n 的值可能为( )A ．0B ．12C ．1D ．24．（2022·福建·模拟预测）设集合{2,1,1,2,3}A =--，{}2|log ||,B y y x x A ==∈ ，则集合B 元素的个数为（）A ．2B ．3C ．4D ．55．（2022·武汉校级月考）已知集合A ＝{m ＋2，2m 2＋m }，若3∈A ，则m 的值为________．➢考点2 集合的基本关系R N )＝( )A ．∅B ．MC ．ND ．R(2)[2022·广东阳江月考]已知集合A ＝{x |y ＝4－x 2}，B ＝{x |a ≤x ≤a ＋1}，若B ⊆A ，则实数a 的取值范围为( )A ．(－∞，－3]∪[2，＋∞)B ．[－1，2]C ．[－2，1]D ．[2，＋∞)[举一反三]1.（2022·广东广州·一模）已知集合{}11A x x =∈-≤≤Z ，{}02B x x =≤≤，则A B 的子集个数为（）A ．2B ．3C ．4D ．62．[2022·湖北武汉摸底]已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R }，B ＝{x |0<x <5，x ∈N }，则满足条件A ⊆C ⊆B 的集合C 的个数为( ) A ．1 B ．2 C ．3D ．43．（2022·山东·潍坊一中模拟预测）已知集合M ，N 是全集U 的两个非空子集，且()U M N ⊆，则（）A ．M N ⋂=∅B ．M N ⊆C ．N M ⊆D ．()U N M U ⋃=4.[2021·湖南长沙长郡中学适应性考试]已知集合A ＝{x ∈Z |x ≥a }，集合B ＝{x ∈Z |2x ≤4}．若A ∩B 只有4个子集，则实数a 的取值范围是( )A ．(－2，－1]B ．[－2，－1]C ．[0,1]D ．(0,1]5．[2022·吉林辽源五校期末联考]已知集合M ＝{x |x －a ＝0}，N ＝{x |ax －1＝0}，若M ∩N ＝N ，则实数a 的值是________．➢考点3 集合的基本运算[典例]1.(1)（2021·全国·高考真题）设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===，则()UAB =（）A ．{3}B ．{1,6}C ．{5,6}D ．{1,3}(2)(多选)[2022·湖南长沙模拟]已知全集U ＝R ，集合M ＝{x |－3≤x <4}，N ＝{x |x 2－2x －8≤0}，则( )A ．M ∪N ＝{x |－3≤x <4}B ．M ∩N ＝{x |－2≤x <4}C ．(∁U M )∪N ＝(－∞，－3)∪[－2，＋∞)D ．M ∩(∁U N )＝(－3，－2)2.(1)(2020·高考全国卷Ⅰ)设集合A ＝{x |x 2－4≤0}，B ＝{x |2x ＋a ≤0}，且A ∩B ＝{x |－2≤x ≤1}，则a ＝( )A ．－4B ．－2C ．2D ．4(2)[2022·湖南六校联考]集合A ＝{0，2，a }，B ＝{1，a 2}，若A ∪B ＝{0，1，2，4，16}，则a 的值为( )A ．0B ．1C ．2D ．4[举一反三]1．（2022·河北石家庄·二模）已知集合{3,2,1,0,1}A =---，301x B x Zx +⎧⎫=∈<⎨⎬-⎩⎭，则A B =（）A ．[3,1)-B ．[3,1]-C ．{3,2,1,0,1}---D ．{2,1,0}--2．[2022·华南师范大学附属中学月考]已知集合A ＝{x |x <3}，B ＝{x |x >a }，若A ∩B ≠∅，则实数a 的取值范围为( )A ．[3，＋∞)B ．(3，＋∞)C ．(－∞，3)D ．(－∞，3]3．(2020·高考全国卷Ⅲ)已知集合A ＝{(x ，y )|x ，y ∈N *，y ≥x }，B ＝{(x ，y )|x ＋y ＝8}，则A ∩B 中元素的个数为( )A ．2B ．3C ．4D ．64．（2022·重庆·二模）已知集合{}{}21,3,5,6,7,8,9,14480A B xx x ==-+∣，则下图中阴影部分表示的集合为（）A ．{}1,3,5,7,9B ．{}1,3,5,9C ．{}1,3,5D ．{}1,3,95．（2021·全国·高考真题（理））已知集合{}21,S s s n n ==+∈Z ，{}41,T t t n n ==+∈Z ，则S T （）A ．∅B ．SC ．TD ．Z6.[2021·豫北名校联考]设集合A ＝{x |x 2＋2x －3>0}，集合B ＝{x |x 2－2ax －1≤0，a >0}，若A ∩B 中恰含有一个整数，则实数a 的取值范围是( )A ．⎝⎛⎭⎫0，34 B ．⎣⎡⎭⎫34，43 C ．⎣⎡⎭⎫34，＋∞ D ．(1，＋∞)7.（2020·浙江·高考真题）设集合S ，T ，S ⊆N *，T ⊆N *，S ，T 中至少有两个元素，且S ，T 满足：①对于任意x ，y ∈S ，若x ≠y ，都有xy ∈T ②对于任意x ，y ∈T ，若x <y ，则yx∈S ；下列命题正确的是（）A ．若S 有4个元素，则S ∪T 有7个元素B ．若S 有4个元素，则S ∪T 有6个元素C ．若S 有3个元素，则S ∪T 有5个元素D ．若S 有3个元素，则S ∪T 有4个元素➢考点4 集合中的创新问题[典例] 1.（2022·北京房山·一模）已知U 是非实数集，若非空集合A 1，A 2满足以下三个条件，则称（A 1，A 2）为集合U 的一种真分拆，并规定（A 1，A 2）与（A 2，A 1）为集合U 的同一种真分拆 ①A 1∩A 2=0 ②A 1A 2=U③(1,2)i A i =的元素个数不是i A 中的元素.则集合U ={1，2，3，4，5，6}的真分拆的种数是（） A ．5B ．6C ．10D ．152.[2022·广东六校联考]已知集合A 0＝{x |0<x <1}．给定一个函数y ＝f (x )，定义集合A n＝{y |y ＝f (x )，x ∈A n －1}，若A n ∩A n －1＝∅对任意的x ∈N *成立，则称该函数具有性质 “∅”． (1)具有性质“∅”的一个一次函数的解析式可以是________．(2)给出下列函数：①y ＝1x ；②y ＝x 2＋1；③y ＝cos π2x ＋2.其中具有性质“∅”的函数的序号是________．3.[2022·河北保定质检]现有100名携带药品出国的旅游者，其中75人带有感冒药，80人带有胃药，那么对既带感冒药又带胃药的人数统计中，下列说法正确的是( ) A ．最多人数是55 B ．最少人数是55 C ．最少人数是75 D ．最多人数是80[举一反三]1．（2022·湖南·雅礼中学一模）已知集合{}22(,)|1,,A x y x y x y Z =+≤∈，{}(,)|2,2,,B x y x y x y Z =≤≤∈，定义集合{}12121122(,)|(,),(,)A B x x y y x y A x y B ⊕=++∈∈，则A B ⊕中元素的个数为A ．77B ．49C ．45D ．302．[2021·四川成都联考]已知集合A ＝{1,2,3,4,5,6}的所有三个元素的子集记为B 1，B 2，B 3，…，B k ，k ∈N *.记b i 为集合B i (i ＝1,2,3，…，k )中的最大元素，则b 1＋b 2＋b 3＋…＋b k ＝( )A ．45B ．105C ．150D ．2103．[多选][2022·湘赣皖十五校第一次联考]已知集合M ，N 都是非空集合U 的子集，令集合S ＝{x |x 恰好属于M ，N 中的一个}，下列说法正确的是( )A ．若S ＝N ，则M ＝∅B ．若S ＝∅，则M ＝NC ．若S ⊆M ，则M ⊆ND ．∃M ，N ，使得S ＝(∁U M )∪(∁U N )4．[2022·湖北华大新联盟考试]中国古代重要的数学著作《孙子算经》下卷有题：今有物，不知其数．三三数之，剩二；五五数之，剩三；七七数之，剩二．问：物几何？现有如下表示：已知A ＝{x |x ＝3n ＋2，n ∈N *}，B ＝{x |x ＝5n ＋3，n ∈N *}，C ＝{x |x ＝7n ＋2，n ∈N *}，若x ∈(A ∩B ∩C )，则整数x 的最小值为( ) A ．128 B ．127 C ．37D ．235．[2022·山东省实验中学第二次诊断]若集合{a ，b ，c ，d }＝{1,2,3,4}，且下列四个关系：①a ＝1；②b ≠1；③c ＝2；④d ≠4有且只有一个是正确的．请写出满足上述条件的一个有序数组(a ，b ，c ，d )＝________，符合条件的全部有序数组(a ，b ，c ，d )的个数是________．6．[2022·山东潍坊重点高中联考]已知U ＝{a 1，a 2，a 3，a 4}，集合A 是集合U 中的两个元素所组成的集合，且同时满足下列三个条件：①若a 1∈A ，则a 2∈A ；②若a 3∉A ，则a 2∉A ；③若a 3∈A ，则a 4∉A .求集合A .第1讲集合的概念与运算1．集合与元素(1)集合元素的三个特征：确定性、互异性、无序性．(2)元素与集合的关系是属于或不属于关系，用符号∈或∉表示．(3)集合的表示法：列举法、描述法、图示法．(4)常见数集的记法集合自然数集正整数集整数集有理数集实数集符号N N*(或N＋)Z Q R [注意]N为自然数集(即非负整数集)，包含0，而N*和N＋的含义是一样的，表示正整数集，不包含0.2．集合间的基本关系表示关系自然语言符号语言Venn图子集集合A中所有元素都在集合B中(即若x∈A，则x∈B)A⊆B(或B⊇A)真子集集合A是集合B的子集，且集合B中至少有一个元素不在集合A中A⫋B(或B⫌A)集合相等集合A ，B 中元素相同 A ＝B3.集合的基本运算集合的并集集合的交集集合的补集图形语言符号语言A ∪B ＝ {x |x ∈A 或x∈B }A ∩B ＝ {x |x ∈A 且x ∈B }∁U A ＝ {x |x ∈U 且 x ∉A }➢考点1 集合的含义与表示[名师点睛]与集合元素有关问题的解题策略(1)研究集合问题时，首先要明确构成集合的元素是什么，即弄清该集合是数集、点集，还是其他集合；然后再看集合的构成元素满足的限制条件是什么，从而准确把握集合的含义． (2)利用集合元素的限制条件求参数的值或确定集合中元素的个数时，要注意检验集合是否满足元素的互异性．2＋y 2≤3，x ∈Z ，y ∈Z }，则A 中元素的个数为( )A ．9B ．8C ．5D ．4(2)设A ＝⎩⎨⎧⎭⎬⎫2，3，a 2－3a ，a ＋2a ＋7，B ＝{|a －2|,3}，已知4∈A 且4∉B ，则a 的取值集合为________．[解析] (1)将满足x 2＋y 2≤3的整数x ，y 全部列举出来，即(－1，－1)，(－1,0)，(－1,1)，(0，－1)，(0,0)，(0,1)，(1，－1)，(1,0)，(1,1)，共有9个．故选A.(2)因为4∈A ，即4∈⎩⎨⎧⎭⎬⎫2，3，a 2－3a ，a ＋2a ＋7，所以a 2－3a ＝4或a ＋2a ＋7＝4.若a 2－3a ＝4，则a ＝－1或a ＝4；若a ＋2a ＋7＝4，即a 2＋3a ＋2＝0，则a ＝－1或a ＝－2.由a 2－3a 与a ＋2a ＋7互异，得a ≠－1.故a ＝－2或a ＝4.又4∉B ，即4∉{|a －2|,3}，所以|a －2|≠4，解得a ≠－2且a ≠6. 综上所述，a 的取值集合为{4}． [答案] (1)A (2){4} [举一反三]1．（2022·江西·新余四中模拟预测（理））已知集合()(){}20A x a x x a =--<，若2A ∉，则实数a 的取值范围为（）A ．()(),12,-∞+∞B ．[)1,2C ．()1,2D ．[]1,2【答案】D【解析】因为2A ∉，所以()()2220a a --≥，解得12a ≤≤．故选：D ．2．（2022·菏泽模拟）设a ，b ∈R ，集合{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，则b －a ＝( )A ．1B ．－1C ．2D ．－2解析：选C.因为{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，b a ，b ，a ≠0，所以a ＋b ＝0，则ba ＝－1，所以a＝－1，b ＝1.所以b －a ＝2.3．(多选)（2022· 广州一调）已知集合{x |mx 2－2x ＋1＝0}＝{n }，则m ＋n 的值可能为( )A ．0B ．12C ．1D ．2解析：选BD.因为集合{x |mx 2－2x ＋1＝0}＝{n }，所以⎩⎪⎨⎪⎧m ＝0，－2n ＋1＝0或⎩⎪⎨⎪⎧m ≠0，Δ＝4－4m ＝0，n ＝－－22m ，解得⎩⎪⎨⎪⎧m ＝0，n ＝12或⎩⎨⎧m ＝1，n ＝1，所以m ＋n ＝12或m ＋n ＝2.故选BD.4．（2022·福建·模拟预测）设集合{2,1,1,2,3}A =--，{}2|log ||,B y y x x A ==∈ ，则集合B 元素的个数为（）A ．2B ．3C ．4D ．5【答案】B 【解析】当2x =±时，y ＝1；当1x =±时，y ＝0；当x ＝3时，2log 3y =．故集合B 共有3个元素．故选：B.5．（2022·武汉校级月考）已知集合A ＝{m ＋2，2m 2＋m }，若3∈A ，则m 的值为________．解析：由题意得m ＋2＝3或2m 2＋m ＝3，则m ＝1或m ＝－32.当m ＝1时，m ＋2＝3且2m 2＋m ＝3，根据集合中元素的互异性可知不满足题意；当m ＝－32时，m ＋2＝12，而2m 2＋m ＝3，符合题意，故m ＝－32.答案：－32➢考点2 集合的基本关系R N )＝( )A ．∅B ．MC ．ND ．R(2)[2022·广东阳江月考]已知集合A ＝{x |y ＝4－x 2}，B ＝{x |a ≤x ≤a ＋1}，若B ⊆A ，则实数a 的取值范围为( )A ．(－∞，－3]∪[2，＋∞)B ．[－1，2]C ．[－2，1]D ．[2，＋∞)【解析】 (1)因为M ，N 均为R 的子集，且∁R M ⊆N ，所以N ＝∁R M ，所以M ∪(∁R N )＝M .故选B.(2)集合A ＝{x |y ＝4－x 2}＝{x |－2≤x ≤2}，因为B ⊆A ，所以有⎩⎨⎧a ≥－2，a ＋1≤2，所以－2≤a ≤1. 【答案】 (1)B (2)C [举一反三]1.（2022·广东广州·一模）已知集合{}11A x x =∈-≤≤Z ，{}02B x x =≤≤，则A B 的子集个数为（）A ．2B ．3C ．4D ．6【答案】C【解析】由题可知{}1,0,1A =-，所有{}0,1A B =，所有其子集分别是{}{}{},1,0,0,1∅，所有共有4个子集，故选：C2．[2022·湖北武汉摸底]已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R }，B ＝{x |0<x <5，x ∈N }，则满足条件A ⊆C ⊆B 的集合C 的个数为( ) A ．1 B ．2 C ．3D ．4解析：选D 求解一元二次方程，得A ＝{x |x 2－3x ＋2＝0，x ∈R }＝{x |(x －1)(x －2)＝0，x ∈R }＝{1,2}，易知B ＝{x |0<x <5，x ∈N }＝{1,2,3,4}．因为A ⊆C ⊆B ，所以根据子集的定义，集合C 必须含有元素1,2，且可能含有元素3,4，原题即求集合{3,4}的子集个数，即有22＝4个，故选D.3．（2022·山东·潍坊一中模拟预测）已知集合M ，N 是全集U 的两个非空子集，且()U M N ⊆，则（）A ．M N ⋂=∅B ．M N ⊆C ．N M ⊆D ．()U N M U ⋃=【答案】A 【解析】UN 表示集合N 的补集，因为()U M N ⊆，所以M N ⋂=∅．故选：A4.[2021·湖南长沙长郡中学适应性考试]已知集合A ＝{x ∈Z |x ≥a }，集合B ＝{x ∈Z |2x ≤4}．若A ∩B 只有4个子集，则实数a 的取值范围是( )A ．(－2，－1]B ．[－2，－1]C ．[0,1]D ．(0,1][答案] D [解析] 本题考查根据集合的子集个数求参数的取值．集合A ＝{x ∈Z |x ≥a }，集合B ＝{x ∈Z |2x ≤4}＝{x ∈Z |x ≤2}，故A ∩B ＝{x ∈Z |a ≤x ≤2}．因为A ∩B 只有4个子集，所以A ∩B 中元素只能有2个，即A ∩B ＝{1,2}，所以0<a ≤1，故选D.5．[2022·吉林辽源五校期末联考]已知集合M ＝{x |x －a ＝0}，N ＝{x |ax －1＝0}，若M ∩N ＝N ，则实数a 的值是________．解析：由题易得M ＝{a }．因为M ∩N ＝N ，所以N ⊆M ，所以N ＝∅或N ＝M ，所以a ＝0或a ＝±1. 答案：0或1或－1➢考点3 集合的基本运算[典例]1.(1)（2021·全国·高考真题）设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===，则()UAB =（）A ．{3}B ．{1,6}C ．{5,6}D ．{1,3}【答案】B【解析】由题设可得{}U1,5,6B =，故(){}U 1,6A B ⋂=，故选：B.(2)(多选)[2022·湖南长沙模拟]已知全集U ＝R ，集合M ＝{x |－3≤x <4}，N ＝{x |x 2－2x －8≤0}，则( )A ．M ∪N ＝{x |－3≤x <4}B ．M ∩N ＝{x |－2≤x <4}C ．(∁U M )∪N ＝(－∞，－3)∪[－2，＋∞)D ．M ∩(∁U N )＝(－3，－2)【解析】 (1)方法一：由题意，得A ∪B ＝{－1，0，1，2}，所以∁U (A ∪B )＝{－2，3}，故选A.方法二：因为2∈B ，所以2∈A ∪B ，所以2∉∁U (A ∪B )，故排除B ，D ；又0∈A ，所以0∈A ∪B ，所以0∉∁U (A ∪B )，故排除C ，故选A.(2)由x 2－2x －8≤0，得－2≤x ≤4，所以N ＝{x |－2≤x ≤4}，则M ∪N ＝{x |－3≤x ≤4}，A 错误；M ∩N ＝{x |－2≤x <4}，B 正确；由于∁U M ＝(－∞，－3)∪[4，＋∞)，故(∁U M )∪N ＝(－∞，－3)∪[－2，＋∞)，C 正确；由于∁U N ＝(－∞，－2)∪(4，＋∞)，故M ∩(∁U N )＝[－3，－2)，D 错误．故选BC.【答案】 (1)A (2)BC2.(1)(2020·高考全国卷Ⅰ)设集合A ＝{x |x 2－4≤0}，B ＝{x |2x ＋a ≤0}，且A ∩B ＝{x |－2≤x ≤1}，则a ＝( )A ．－4B ．－2C ．2D ．4(2)[2022·湖南六校联考]集合A ＝{0，2，a }，B ＝{1，a 2}，若A ∪B ＝{0，1，2，4，16}，则a 的值为( )A ．0B ．1C ．2D ．4【解析】 (1)方法一：易知A ＝{x |－2≤x ≤2}，B ＝{x |x ≤－a2}，因为A ∩B ＝{x |－2≤x ≤1}，所以－a2＝1，解得a ＝－2.故选B.方法二：由题意得A ＝{x |－2≤x ≤2}．若a ＝－4，则B ＝{x |x ≤2}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤2}，不满足题意，排除A ；若a ＝－2，则B ＝{x |x ≤1}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤1}，满足题意；若a ＝2，则B ＝{x |x ≤－1}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤－1}，不满足题意，排除C ；若a ＝4，则B ＝{x |x ≤－2}，又A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |x ＝－2}，不满足题意．故选B.(2)根据集合并集的概念，可知{a ，a 2}＝{4，16}，故a ＝4. 【答案】 (1)B (2)D [举一反三]1．（2022·河北石家庄·二模）已知集合{3,2,1,0,1}A =---，301x B x Zx +⎧⎫=∈<⎨⎬-⎩⎭，则A B =（）A ．[3,1)-B ．[3,1]-C ．{3,2,1,0,1}---D ．{2,1,0}--【答案】D 【解析】因为30311x x x +<⇒-<<-，所以{}2,1,0B =--，而{3,2,1,0,1}A =---，所以A B ={2,1,0}--，故选：D2．[2022·华南师范大学附属中学月考]已知集合A ＝{x |x <3}，B ＝{x |x >a }，若A ∩B ≠∅，则实数a 的取值范围为( )A ．[3，＋∞)B ．(3，＋∞)C ．(－∞，3)D ．(－∞，3]解析：选C 因为A ∩B ≠∅，所以结合数轴可知实数a 的取值范围是a <3，故选C. 3．(2020·高考全国卷Ⅲ)已知集合A ＝{(x ，y )|x ，y ∈N *，y ≥x }，B ＝{(x ，y )|x ＋y ＝8}，则A ∩B 中元素的个数为( )A ．2B ．3C ．4D ．6解析：选C.由题意得，A ∩B ＝{(1，7)，(2，6)，(3，5)，(4，4)}，所以A ∩B 中元素的个数为4，选C.4．（2022·重庆·二模）已知集合{}{}21,3,5,6,7,8,9,14480A B xx x ==-+∣，则下图中阴影部分表示的集合为（）A ．{}1,3,5,7,9B ．{}1,3,5,9C ．{}1,3,5D ．{}1,3,9【答案】B【解析】由图可知，图中阴影部分表示()R A B ⋂，由214480x x -+≤，得68x ≤≤，所以{}68B x x =≤≤，所以{R 6B x x =<或}8x >，因为{}1,3,5,6,7,8,9A =，所以(){}R1,3,5,9AB =，故选：B5．（2021·全国·高考真题（理））已知集合{}21,S s s n n ==+∈Z ，{}41,T t t n n ==+∈Z ，则S T （）A ．∅B ．SC ．TD ．Z【答案】C【解析】任取t T ∈，则()41221t n n =+=⋅+，其中n Z ∈，所以，t S ∈，故T S ⊆，因此，S T T =.故选：C.6.[2021·豫北名校联考]设集合A ＝{x |x 2＋2x －3>0}，集合B ＝{x |x 2－2ax －1≤0，a >0}，若A ∩B 中恰含有一个整数，则实数a 的取值范围是( )A ．⎝⎛⎭⎫0，34 B ．⎣⎡⎭⎫34，43 C ．⎣⎡⎭⎫34，＋∞D ．(1，＋∞)[答案] B [解析] A ＝{x |x 2＋2x －3>0}＝{x |x >1或x <－3}，设函数f (x )＝x 2－2ax －1，因为函数f (x )＝x 2－2ax －1图象的对称轴为直线x ＝a (a >0)，f (0)＝－1<0，根据对称性可知，若A ∩B 中恰有一个整数，则这个整数为2，所以有⎩⎪⎨⎪⎧ f (2)≤0，f (3)>0，即⎩⎪⎨⎪⎧4－4a －1≤0，9－6a －1>0，所以⎩⎨⎧a ≥34，a <43，即34≤a <43.故选B. 7.（2020·浙江·高考真题）设集合S ，T ，S ⊆N *，T ⊆N *，S ，T 中至少有两个元素，且S ，T 满足：①对于任意x ，y ∈S ，若x ≠y ，都有xy ∈T ②对于任意x ，y ∈T ，若x <y ，则yx∈S ；下列命题正确的是（）A ．若S 有4个元素，则S ∪T 有7个元素B ．若S 有4个元素，则S ∪T 有6个元素C ．若S 有3个元素，则S ∪T 有5个元素D ．若S 有3个元素，则S ∪T 有4个元素【答案】A 【解析】首先利用排除法：若取{}1,2,4S =，则{}2,4,8T =，此时{}1,2,4,8S T =，包含4个元素，排除选项 C ；若取{}2,4,8S =，则{}8,16,32T =，此时{}2,4,8,16,32S T =，包含5个元素，排除选项D ；若取{}2,4,8,16S =，则{}8,16,32,64,128T =，此时{}2,4,8,16,32,64,128S T =，包含7个元素，排除选项B ；下面来说明选项A 的正确性：设集合{}1234,,,S p p p p =，且1234p p p p <<<，*1234,,,p p p p N ∈，则1224p p p p <，且1224,p p p p T ∈，则41p S p ∈，同理42p S p ∈，43p S p ∈，32p S p ∈，31p S p ∈，21p S p ∈，若11p =，则22p ≥，则332p p p <，故322p p p =即232p p =，又444231p p p p p >>>，故442232p p p p p ==，所以342p p =，故{}232221,,,S p p p =，此时522,p T p T ∈∈，故42p S ∈，矛盾，舍.若12p ≥，则32311p p p p p <<，故322111,p pp p p p ==即323121,p p p p ==，又44441231p p p p p p p >>>>，故441331p p p p p ==，所以441p p =，故{}2341111,,,S p p p p =，此时{}3456711111,,,,p p p p p T ⊆.若q T ∈，则31q S p ∈，故131,1,2,3,4i qp i p ==，故31,1,2,3,4i q p i +==，即{}3456711111,,,,q p p p p p ∈，故{}3456711111,,,,p p p p p T =，此时{}234456711111111,,,,,,,S T p p p p p p p p ⋃=即S T 中有7个元素.故A 正确. 故选：A .➢考点4 集合中的创新问题[典例] 1.（2022·北京房山·一模）已知U 是非实数集，若非空集合A 1，A 2满足以下三个条件，则称（A 1，A 2）为集合U 的一种真分拆，并规定（A 1，A 2）与（A 2，A 1）为集合U 的同一种真分拆 ①A 1∩A 2=0 ②A 1A 2=U③(1,2)i A i =的元素个数不是i A 中的元素.则集合U ={1，2，3，4，5，6}的真分拆的种数是（） A ．5 B ．6C ．10D ．15【答案】A 【解析】解：由题意，集合U ={1，2，3，4，5，6}的真分拆有{}{}125,1,2,3,4,6A A ==；{}{}121,4,2,3,5,6A A ==；{}{}123,4,1,2,5,6A A ==；{}{}124,5,1,2,3,6A A ==；{}{}124,6,1,2,3,5A A ==，共5种，故选：A.2.[2022·广东六校联考]已知集合A 0＝{x |0<x <1}．给定一个函数y ＝f (x )，定义集合A n＝{y |y ＝f (x )，x ∈A n －1}，若A n ∩A n －1＝∅对任意的x ∈N *成立，则称该函数具有性质 “∅”． (1)具有性质“∅”的一个一次函数的解析式可以是________．(2)给出下列函数：①y ＝1x ；②y ＝x 2＋1；③y ＝cos π2x ＋2.其中具有性质“∅”的函数的序号是________．[解析] (1)答案不唯一，合理即可．示例：对于解析式y ＝x ＋1，因为A 0＝{x |0<x <1}，所以A 1＝{x |1<x <2}， A 2＝{x |2<x <3}，…，显然符合A n ∩A n －1＝∅.故具有性质“∅”的一个一次函数的解析式可以是y ＝x ＋1. (2)对于①，A 0＝{x |0<x <1}，A 1＝{x |x >1}，A 2＝{x |0<x <1}，…，依次循环下去，符合A n ∩A n －1＝∅.对于②，A 0＝{x |0<x <1}，A 1＝{x |1<x <2}，A 2＝{x |2<x <5}，A 3＝{x |5<x <26}，…，根据函数y ＝x 2＋1的单调性得相邻两个集合不会有交集，符合A n ∩A n －1＝∅.对于③，A 0＝{x |0<x <1}，A 1＝{x |2<x <3}，A 2＝{x |1<x <2}，A 3＝{x |1<x <2}，不符合A n ∩A n －1＝∅.所以具有性质“∅”的函数的序号是①②. [答案] (1)y ＝x ＋1 (2)①②3.[2022·河北保定质检]现有100名携带药品出国的旅游者，其中75人带有感冒药，80人带有胃药，那么对既带感冒药又带胃药的人数统计中，下列说法正确的是( ) A ．最多人数是55 B ．最少人数是55 C ．最少人数是75D ．最多人数是80解析：选B 设100名携带药品出国的旅游者组成全集I ，其中带感冒药的人组成集合A ，带胃药的人组成集合B .设所携带药品既非感冒药又非胃药的人数为x ，则0≤x ≤20.设以上两种药都带的人数为y .由图可知，x ＋card(A )＋card(B )－y ＝100.∴x ＋75＋80－y ＝100，∴y ＝55＋x .∵0≤x ≤20，∴55≤y ≤75，故最少人数是55. [举一反三]1．（2022·湖南·雅礼中学一模）已知集合{}22(,)|1,,A x y x y x y Z =+≤∈，{}(,)|2,2,,B x y x y x y Z =≤≤∈，定义集合{}12121122(,)|(,),(,)A B x x y y x y A x y B ⊕=++∈∈，中元素的个数为则A BA．77 B．49 C．45 D．30【答案】C【解析】因为集合，所以集合中有5个元素（即5个点），即图中圆中的整点，集合中有25个元素（即25个点）：即图中正方形中的整点，集合的元素可看作正方形中的整点（除去四个顶点），即个．2．[2021·四川成都联考]已知集合A＝{1,2,3,4,5,6}的所有三个元素的子集记为B1，B2，B3，…，B k，k∈N*.记b i为集合B i(i＝1,2,3，…，k)中的最大元素，则b1＋b2＋b3＋…＋b k＝()A．45 B．105C．150 D．210[答案]B[解析]本题考查集合的新定义问题．集合A的含有3个元素的子集共有C36＝20个，所以k＝20.在集合B i(i＝1,2,3，…，k)中，最大元素为3的集合有C22＝1个；最大元素为4的集合有C23＝3个；最大元素为5的集合有C24＝6个；最大元素为6的集合有C25＝10个，所以b1＋b2＋b3＋…＋b k＝3×1＋4×3＋5×6＋6×10＝105.故选B.3．[多选][2022·湘赣皖十五校第一次联考]已知集合M，N都是非空集合U的子集，令集合S＝{x|x恰好属于M，N中的一个}，下列说法正确的是()A．若S＝N，则M＝∅B．若S＝∅，则M＝NC．若S⊆M，则M⊆ND．∃M，N，使得S＝(∁U M)∪(∁U N)[答案] ABD [解析]本题考查Venn 图．用Venn 图表示，集合S 为如图1中的阴影部分，对于A 选项，若S ＝N ，利用S 的Venn 图观察，则有M ∩N ＝∅，M ＝∅，故A 选项正确；对于B 选项，若S ＝∅，则M ＝N ，故B 选项正确；对于C 选项，反例：如图集合S 为如图2中的阴影部分，N ⊆M ，故C 选项错误；对于D 选项，例如U ＝{1,2,3,4}，M ＝{1,2,3}，N ＝{4}，S ＝{x |x 恰好属于M ，N 中的一个}＝{1,2,3,4}＝U ，而(∁U M )∪(∁U N )＝{4}∪{1,2，3}＝{1,2,3,4}＝S ，故D 选项正确，故选ABD.图1 图24．[2022·湖北华大新联盟考试]中国古代重要的数学著作《孙子算经》下卷有题：今有物，不知其数．三三数之，剩二；五五数之，剩三；七七数之，剩二．问：物几何？现有如下表示：已知A ＝{x |x ＝3n ＋2，n ∈N *}，B ＝{x |x ＝5n ＋3，n ∈N *}，C ＝{x |x ＝7n ＋2，n ∈N *}，若x ∈(A ∩B ∩C )，则整数x 的最小值为( ) A ．128 B ．127 C ．37D ．23解析：选D ∵求整数的最小值，∴先将23代入检验，满足A ，B ，C 三个集合，故选D.5．[2022·山东省实验中学第二次诊断]若集合{a ，b ，c ，d }＝{1,2,3,4}，且下列四个关系：①a ＝1；②b ≠1；③c ＝2；④d ≠4有且只有一个是正确的．请写出满足上述条件的一个有序数组(a ，b ，c ，d )＝________，符合条件的全部有序数组(a ，b ，c ，d )的个数是________．解析：显然①不可能正确，否则①②都正确；若②正确，则⎩⎪⎨⎪⎧ a ＝2，b ＝3，c ＝1，d ＝4或⎩⎪⎨⎪⎧ a ＝3，b ＝2，c ＝1，d ＝4.若③正确，则⎩⎪⎨⎪⎧ a ＝3，b ＝1，c ＝2，d ＝4.若④正确，则⎩⎪⎨⎪⎧ a ＝2，b ＝1，c ＝4，d ＝3或⎩⎪⎨⎪⎧ a ＝3，b ＝1，c ＝4，d ＝2或⎩⎪⎨⎪⎧a ＝4，b ＝1，c ＝3，d ＝2.所以符合条件的数组共6个．答案：(3,2,1,4)(填一个正确的即可) 66．[2022·山东潍坊重点高中联考]已知U ＝{a 1，a 2，a 3，a 4}，集合A 是集合U 中的两个元素所组成的集合，且同时满足下列三个条件：①若a1∈A，则a2∈A；②若a3∉A，则a2∉A；③若a3∈A，则a4∉A.求集合A.解：假设a1∈A，则a2∈A.又若a3∉A，则a2∉A，∴a3∈A，与集合A中有且仅有两个元素不符，∴假设不成立，∴a1∉A.假设a4∈A，则a3∉A，则a2∉A，且a1∉A，与集合A中有且仅有两个元素不符，∴假设不成立，∴a4∉A.故集合A＝{a2，a3}，经检验知符合题意．。

高三数学一轮复习(1)集合概念、子集

集合的概念及运算（1）总第1个教案【复习目标】：准确理解和使用集合概念；理解元素与集合、集合与集合之间的关系,能识别给定集合的子集.学会对简单的含参变量的讨论. 【复习重点】：注重集合中元素的形式，集合元素的互异性、子集与真子集、空集的特殊性【复习难点】：根据集合的含义求参数；分类讨论思想的培养 1、已知集合A ＝{}N a a a ∈<≤,40 ，用列举法能够表示为 2、已知集合A ＝{}m m m ++22,2，若A ∈3，则=m 3、下列集合表示同一集合的有（1）(){}2,3= M ,(){}3,2= N （2）(){}{}1,1,=+==+=y x y N y x y x M （3）{}5,4 =M ，{}4,5 =N （4）{}21，＝M ，{}），（＝21N 4、设集合A ＝{}R a a a x x ∈+-=,452，{}R b b b y y B ∈++==,2442 ，则A 、B 的关系是5、已知集合A ＝[)4,1，B ＝()a ,∞-，B A ⊆，则∈a 二、交流质疑精讲点拔例1、若R b a ∈，,集合{}⎭⎬⎫⎩⎨⎧=+b a ba b a ，，，，01,求a b -的值. 变式训练：已知集合A ＝{}b a b a a 2,,++，B ＝{}2,,acac a ．若A ＝B ，求c 的值例2、已知集合A ＝{}R a x ax x ∈=+-,0232．(1) 若A 是空集，求a 的取值范围；(2) 若A 中只有一个元素，求a 的值，并将这个元素写出来；(3) 若A 中至多有一个元素，求a 的取值范围．变式练习：已知1≤a 时，集合[]a a -2,中有且只有3个整数，则a 的取值范围是_______．例3、（1）若集合{}{}01,062=+==-+ax x S x x x P ＝，且P S ⊆，求由a 的可取值组成的集合。

（2）集合{}52≤≤-x x A ＝，集合{}121-≤≤+m x m x B ＝．若A B ⊆，求实数m 的取值范围。

第1讲集合的概念及运算

因为既参加数学竞赛又参加物理竞赛的有12人，
所以card(D)=12-2=10. 同理，得card(E)=6-2=4，
card(F)=5-2=3. 又因为参加数学、物理、化学竞赛的人
数分别为21,17,10. 所以card(A)=21-2-10-4=5，
card(B)=17-2-10-3=2，
card(C)=10-3-2-4=1. 故需预定火车票的张数为 5+2+1+10+4+3+2=27.
解析
（ 1 ）因为 z=xy ， x∈{1,2} ， y∈{0,2} ，故 xy=0,2,4 ，从而 A*B={0,2,4} ，故集合A*B的所有元素之和为6.故选D.
（2）该班学生参加竞赛如图所示，集合A、B、C、D、E、F、F中的任何两个无公共元素，其中G表示三科都参加的学生集合，card(G)=2.
分析
求m的取值范围，关键在于做好等价转换.
解析 A∩B≠
x2+mx-y+2=0 x-y+1=0(0≤x≤2)有解
方程x2+(m-1)x+1＝0在［0,2］上有解.
令f(x)=x2+(m-1)x+1,则f(0)=1>0.
(ⅰ)若有一解，则f(2)=3+2m≤0，所以m≤
;
3 2
(ⅱ)若有两解，则 f(2)≥0
点评本题是属于创新型的概念理解题.
准确理解A*B是解决本题的关键所在，并且又考查了集合元素的互异性，因此要准确理解集合的含义，明确题目所要解决的问题，从而使问题得以解决.
备选题
已知集合A={(x,y)|x2+mx-y+2=0}, B={(x,y)|x-y+1=0,0≤x≤2}. 如果A∩B≠ ，求实数m的取值范围.

高考数学(文)一轮课件【第1讲】集合及其运算

返回目录
第1讲
双向固基础
集合及其运算
2．集合的基本关系
表示关系子集基真本子关集系相等空集文字语言
元素集合 A 的________ 都是集合 B 的元素集合 A 是集合 B 的子集，但集合 B 中至少有一个元 ________ 素不属于 A 集合 A， B 的元素完全________ 相同 ________ 子集任何元素的集合．空集是任何集合 A 的_______ 不含
[答案] (1)B A B
(2)(∁UB) (∁UB)
返回目录
第1讲
双向固基础
集合及其运算
[解析] (1)根据韦恩图分析可知，当 A⊆B 时，显然 A∩B＝A；当 A∩B＝A 时，对任意 x∈A，有 x∈(A∩B)，得 x∈B，即 x∈A⇒x∈B，故 A⊆B；当 B⊆A 时，显然 A∪B ＝A；当 A∪B＝A 时，对任意 x∈B，有 x∈(A∪B)，得 x∈A，即 x∈B⇒x∈A，即 B⊆A. (2)设 x∈∁U(A∪B)，则 x∉(A∪B)，得 x∉A 且 x∉B，即 x∈ ∁ UA 且 x∈∁UB ，即 x∈(∁UA)∩(∁UB) ，即 ∁U(A∪B) ⊂ (∁UA)∩(∁UB)；反之，当时 x∈(∁UA)∩(∁UB)时，得 x∈∁UA 且 x∈∁UB，得 x∉A 且 x∉B，即 x∉(A∪B)，得 x∈∁U(A∪B)，即∁U(A∪B)⊇(∁UA)∩(∁UB)．根据集合相等的定义得∁U(A∪B) ＝(∁UA)∩(∁UB)．同理可证第二个结论成立．
返回目录
第1讲
双向固基础
集合及其运算
2．集合问题中的两个难点 (1)[2013· 山东卷改编] 已知集合 A＝{0，1，2}，则集合 B＝{x－y|x∈A，y∈A}中元素的个数是 9.( )

2024年高考数学一轮复习第1章第1讲：集合(附答案解析)

第1页共23页2024年高考数学一轮复习第1章第1讲：集合学生版考试要求 1.了解集合的含义，了解全集、空集的含义.2.理解元素与集合的属于关系，理解集合间的包含和相等关系.3.会求两个集合的并集、交集与补集.4.能用自然语言、图形语言、集合语言描述不同的具体问题，能使用Venn
图表示集合间的基本关系和基本运算．知识梳理
1．集合与元素
(1)集合中元素的三个特性：确定性、互异性、无序性．
(2)元素与集合的关系是属于或不属于，用符号∈或∉表示．
(3)集合的表示法：列举法、描述法、图示法．
(4)常见数集的记法集合
非负整数集(或自然数集)正整数集整数集有理数集实数集符号N N *(或N ＋)Z Q R
2.集合的基本关系
(1)子集：一般地，对于两个集合A ，B ，如果集合A 中任意一个元素都是集合B 中的元素，就称集合A 为集合B 的子集，记作A ⊆B (或B ⊇A )．
(2)真子集：如果集合A ⊆B ，但存在元素x ∈B ，且x ∉A ，就称集合A 是集合B 的真子集，记作A B (或B A )．
(3)相等：若A ⊆B ，且B ⊆A ，则A ＝B .
(4)
空集：不含任何元素的集合叫做空集，记为∅.空集是任何集合的子集，是任何非空集合的真子集．
3．集合的基本运算表示
运算
集合语言图形语言记法并集{x |x ∈A ，或x ∈B }A ∪B。