高斯烟羽模型
高斯烟羽模型

模型假设:1、 坐标系高斯模型的坐标系如图2.1所示,原点为排放点(若为高架源,原点为排放点在地面的投影),x 轴正向为风速方向,y 轴在水平面上垂直于x 轴,正向在x 轴的左侧,z 轴垂直于水平面xoy ,向上为正向。
在此坐标系下烟流中心线或烟流中心线在xoy 面的投影与x 轴重合。
2、模型假设(1)污染物的浓度在y 、z 轴上的分布是高斯分布(正态分布)的;(2)污染源的源强是连续且均匀的,初始时刻云团内部的浓度、温度呈均匀分布;(3)扩散过程中不考虑云团内部温度的变化,忽略热传递、热对流及热辐射;(4)泄漏气体是理想气体,遵守理想气体状态方程;(5)在水平方向,大气扩散系数呈各向同性;(6)取x 轴为平均风速方向,整个扩散过程中风速的大小、方向保持不变,不随地点、时间变化而变化;(7)地面对泄漏气体起全反射作用,不发生吸收或吸附作用;(8)整个过程中,泄漏气体不发生沉降、分解,不发生任何化学反应等。
3、模型公式推导由正态分布假设可以导出下风向任意一点X (x,y,z )处泄漏气体浓度的函数为:22)(),,(bz ay e e x A z y x X --=(1)由概率统计理论可以写出方差的表达式为:⎪⎪⎪⎩⎪⎪⎪⎨⎧==⎰⎰⎰⎰∞∞∞∞00220022Xdz Xdz z Xdy Xdy y z yσσ (2) 由假设可以写出源强的积分公式:⎰⎰∞∞-∞∞-=uXdydz Q (3)式中:y σ、z σ为泄漏气体在y 、z 方向分布的标准差,单位为 m ;X (x,y,z )为任一点处泄漏气体的浓度,单位为 kg/m 3;u 为平均风速,单位为 m/s ;Q 为源强(即泄漏速度),单位为 kg/s ;将(1)式代入(2)式,积分可得:⎪⎪⎩⎪⎪⎨⎧==222121z y b a σσ (4)将(1)式和(4)式代入(3)式,积分可得:zy u Q x A σσπ2=)( (5) 再将(4)式和(5)式代入(1)式,可得:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=222222exp 2,,z y z y z y u Q z y x X σσσσπ)( (6) 上式为无界空间连续点源扩散的高斯模型公式,然而在实际中,由于地面的存在,烟羽的扩散是有界的。
高斯烟羽模型课件

温度和湿度影响大气稳定度和湍流强 度,进而影响污染物的扩散。这些数 据可以通过气象观测站获取。
排放参数的估算方法
源强
源强表示污染物的排放速率。根据工厂或设施的工艺流程、设备运行状况等因素进行估算。
排放高度
排放高度决定了烟羽在垂直方向上的扩散范围。根据工厂或设施的建筑高度、排放设备的位置等因素进行估算。
案例一:城市空气质量预测
总结词:动态模拟
详细描述:高斯烟羽模型能够模拟城市空气质量的动态变化过程,揭示不同气象条件和地形地貌对空气质量的影响。
案例一:城市空气质量预测
总结词
可视化展示
详细描述
通过可视化技术,高斯烟羽模型能够将预测结果以直观的方式呈现出来,便于分析和理 解。
案例二:工业区污染物扩散模拟
特点
高斯烟羽模型适用于污染物在大气中扩散的情况,特别是对 于低空污染物的扩散,如工厂排放、汽车尾气等。该模型能 够考虑气象条件、地形等因素对污染物扩散的影响,提供较 为准确的预测结果。
模型的应用领域
环境评估
高斯烟羽模型广泛应用于环境评 估领域,用于评估工厂、交通工 具等污染源对周围环境的影响, 为环境管理和污染控制提供依据。
z
垂直距离,表示烟 羽扩散的垂直方向 上的距离。
公式的应用场景
高斯烟羽模型适用于描述烟羽 在大气中的扩散情况,特别是
在稳定气象条件下。
该模型广泛应用于环境科学、 大气污染控制等领域,用于 预测烟羽的扩散范围、浓度 分布等。
通过高斯烟羽模型,可以评估 烟羽对周围环境和居民的影响,
为制定相应的污染控制措施提 供科学依据。
03
高斯烟羽模型的参数估算
扩散参数的估算方法
扩散系数
高斯烟羽模型
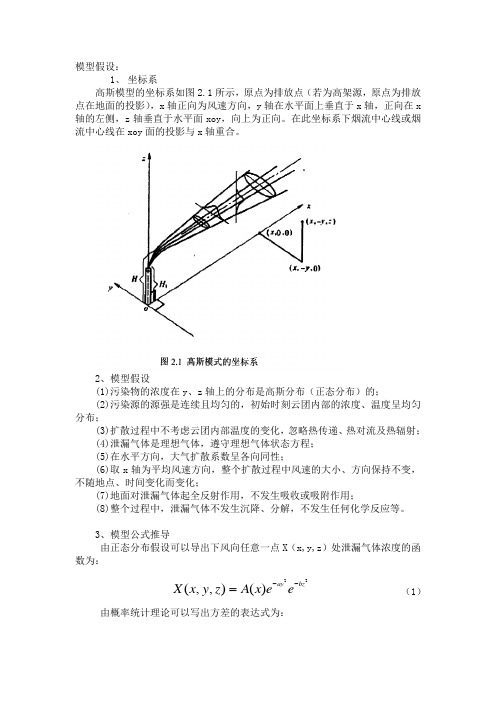
模型假设:1、 坐标系高斯模型的坐标系如图2.1所示,原点为排放点(若为高架源,原点为排放点在地面的投影),x 轴正向为风速方向,y 轴在水平面上垂直于x 轴,正向在x 轴的左侧,z 轴垂直于水平面xoy ,向上为正向。
在此坐标系下烟流中心线或烟流中心线在xoy 面的投影与x 轴重合。
2、模型假设(1)污染物的浓度在y 、z 轴上的分布是高斯分布(正态分布)的;(2)污染源的源强是连续且均匀的,初始时刻云团内部的浓度、温度呈均匀分布;(3)扩散过程中不考虑云团内部温度的变化,忽略热传递、热对流及热辐射; (4)泄漏气体是理想气体,遵守理想气体状态方程; (5)在水平方向,大气扩散系数呈各向同性;(6)取x 轴为平均风速方向,整个扩散过程中风速的大小、方向保持不变,不随地点、时间变化而变化;(7)地面对泄漏气体起全反射作用,不发生吸收或吸附作用;(8)整个过程中,泄漏气体不发生沉降、分解,不发生任何化学反应等。
3、模型公式推导由正态分布假设可以导出下风向任意一点X (x,y,z )处泄漏气体浓度的函数为:22(,,)()aybzX x y z A x ee--= (1)由概率统计理论可以写出方差的表达式为:22022y z y XdyXdyz Xdz Xdzσσ∞∞∞∞==⎧⎪⎪⎪⎨⎪⎪⎪⎩⎰⎰⎰⎰(2) 由假设可以写出源强的积分公式:⎰⎰∞∞-∞∞-=uXdydz Q (3)式中:y σ、z σ为泄漏气体在y 、z 方向分布的标准差,单位为 m ;X (x,y,z )为任一点处泄漏气体的浓度,单位为 kg/m 3;u 为平均风速,单位为 m/s ;Q 为源强(即泄漏速度),单位为 kg/s ;将(1)式代入(2)式,积分可得:221212y za b σσ==⎧⎪⎪⎨⎪⎪⎩ (4)将(1)式和(4)式代入(3)式,积分可得:zy u Qx A σσπ2=)( (5)再将(4)式和(5)式代入(1)式,可得:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=222222exp 2,,z y z y zy u Qz y x X σσσσπ)( (6) 上式为无界空间连续点源扩散的高斯模型公式,然而在实际中,由于地面的存在,烟羽的扩散是有界的。
基于高斯烟羽模型的铁路气体类危险货物泄漏扩散研究

Logistics Sci-Tech No.8, 2018物流科技2018年第8期•交通运输!文章编号:1002-3100 (2018) 08-0109-05Research on Leakage and Diffusion of Gas Dangerous Goods Based on Gaussian Plume Model李丹,杨睿,宋辉(兰州交通大学交通运输学院,甘肃兰州730070)L I D an,Y A N G R u i,SONG H u i(School o f Traffic and Transportation,Lanzhou Jiaotong U n ive rsity,Lanzhou730070, C hina)摘要:铁路运输的危险货物中,气体类危险货物占有较大的比重。
故文章针对易燃气体在铁路运输过程中的泄漏事故,以丙烷气体为例,运用高斯烟羽模型,通过m a tla b模 拟出在不同大气状况下,单个泄漏源和多个泄漏源的气体平面扩散范围和扩散高度,分析了大气稳定度对于气体在扩散半径、扩散高度以及浓度方面的影响。
最后得出结论,随着 大气状况从极不稳定到稳定,易燃气体的扩散半径逐渐扩大,扩散高度逐渐降低,因此,大气状况越稳定越有利于易燃气体在平面内的扩散,并且大气状况越稳定,沿水平方向的气体浓度下降越快。
关键词:高斯烟羽模型;易燃气体运输;m a tla b仿真中图分类号:F530 文献标识码:AAbstract:A m on g the dangerous goods transported by ra il,gas dangerous goods occu py a large p ro p o rtio n.T h ere fore,in view o f the leakage a ccid e n t o f flam m able gas d u rin g the ra ilw a y tra n sp o rta tio n,ta k in g propane gas as an exa m ple,G aussian plum e m odel is used to sim ula te the gas d iffu s io n range of single and m u ltip le leakage sources u n d e r d iffe re n t atm ospheric c o n d itio n s b y m a tla b.W ith the h e ig h t o f d iffu s io n,the e ffe c t of atm ospheric s ta b ility on the d iffu s io n ra d iu s,d iffu s io n h e ig h t,and con ce n tra tio n o f the gas was analyzed.F in a lly,it is con clu d e d th a t as the atm ospheric co n d itio n s change fro m extrem e ly unstable to stable,the d iffu s io n ra dius of flam m able gases g ra d u a lly expands and the d iffu s io n h e ig h t g ra d u a lly d ecreases.T h ere fore,the more stable the atm ospheric c o n d itio n s, the more con ducive to the d iffu s io n of flam m able gases in the p la n e,and the atm osphere The m ore stable the s itu a tio n,the faster the con centration of gas in the h o rizonta l d ire c tio n drops.Key words:G aussian plum e m o d e l;fla m m a b le gas tra n sp o rt; m atlab s im u la tio n随着化工行业的持续发展,化工气体的用量也在持续增长,而铁路承载了相当一部分的气体运输量。
高斯烟羽模式公式

高斯烟羽模式
高斯烟羽模式是计算释入大气中的气载污染物下风向浓度的应用最广的方法。
此模式假定烟羽中污染物浓度在水平方向和垂直方向都遵循高斯分布。
对于在恒定气象条件(指风向、风速、大气稳定度不随时间而改变)高架点源的连续排放,在考虑了烟羽在地面的全反射后,下风向任一点的污染物浓度C (x ,y ,z )由下式给出:
][2),,(2z 22z 2y 22)(2)(2σσσzyσπσσHe z He z y e e e u z y x C +----+=
式中 C (x ,y ,z )—— 下风某点(x ,y ,z )处的空气中污染物浓度,g/m 3。
x —— 下风向距离,m ;
y —— 横截风向距离,m ;
Q —— 气载污染物源强,即释放率,g/s ;
U —— 排放高度处的平均风速,m/s ;
He —— 有效排放高度;m 。
σy ,σz —— 水平方向和垂直方向扩散参数,m ,它们是下风距离x 急大气稳
定度的函数:
下风地面处(z = 0)的污染物浓度则为:
y 2z 222z y σσσσπy H e e u Q C --=。
云团扩散模型

1 云团扩散模型根据物质泄漏后所形成的气云的物理性质的不同,可以将描述气云扩散的模型分为非重气云模型和重气云模型两种[5-13]。
非重气云模型高斯模型是一种常用的非重气扩散模型,高斯烟羽(Plume model)模型又称高架点连续点源扩散模型,适用于连续源的扩散,即连续源或泄放时间大于或等于扩散时间的扩散。
高斯烟团(Puff model)模型适用于短时间泄漏的扩散,即泄放时间相对于扩散时间比较短的情形,如突发性泄放等。
若假设气体云内空间上的分布为高斯分布,则地面地处风向的烟团浓度分布算式为式中,c(x,y,H)——点(x,y,H)处浓度值,mg/m3;Q——源强,即单位时问的排放量,mg/s;u——环境平均风速,m/s;σx,σy,σz——扩散参数;H——源高(烟团高度),m;x——下方向到泄漏原点的距离,m;y,z——侧风方向、垂直向上方向离泄漏原点的距离,m。
高斯模式的实际应用效果很大程度上依赖于如何给定模式中的一些参数,尤其要注意源强、扩散参数等的确定。
源强与污染物的物理化学属性、扩散方式、释放点的地理环境等有关。
扩散参数表征大气边界层内湍流扩散的强弱,是高斯模式的一项重要数据。
高斯扩散模式所描述的扩散过程(实质上也包含了在实际应用中对高斯模式的一些限制)主要有:1)下垫面平坦、开阔、性质均匀,平均流场稳定,不考虑风场的切变。
2)扩散过程中,污染物本身是被动、保守的,即污染物和空气无相对运动,且扩散过程中污染物无损失、无转化,污染物在地面被反射。
3)扩散在同一温度层结中发生,平均风速大于 m/s。
4)适用范围一般小于10~20 km。
重气云模型由于重气本身的特殊性,在重气扩散领域也有大量基于不同理论的模型。
鉴于重气扩散与中性或浮性气体扩散有着明显的区别,目前国内外已开发大量的不同复杂程度的重气扩散模型,如箱模型、相似模型、LTA-HGDM模型、CFD模型等。
箱(BOX)模型箱模型是指假定浓度、温度和其他场,在任何下风横截面处为矩形分布等简单形状,这里的矩形分布是指在某些空间范围内场是均匀的,而在其他地方为零。
基于高斯烟羽模型的放射性气体的扩散

关于核电站泄漏放射性气体扩散的预估模型摘要由于核泄漏导致放射性气体扩散对经济和人身造成巨大损失的报道在国内外屡见不鲜,本文中日本福岛核泄漏事件更加使我们认识到对放射性气体扩散进行合理性的预估从而为以后类似于此的突发性事件作积极有效的补救措施的重要性。
对于问题一我们运用了点源烟羽扩散模型,用抛物型二阶偏微分方程解出理想状态下的不同时刻、不同地点的浓度表达式:222432 (,,,)(4)x y zktQC x y z t ektπ++-=。
此模型是建立在以泄漏点为圆心的一个无界球形区域内的。
为了使模型更符合实际情况,能够被应用于现实生活中,我们在泄漏源有效高度的确定和考虑地面反射与吸收作用下对此模型进行了修正,最终得到问题一浓度的确定公式(14)(,,,)C x y z t的表达式。
对于问题二,我们采用高位连续点源烟羽扩散模式,其扩散服从正态分布,并根据概率论的相关知识通过数学公式推导,得到理想状态下的高斯模型,由泄漏源有效高度,地面反射等因素的影响对其进行修正,又由于重力干沉积,雨洗湿沉积以及核衰变等因素对源强的影响,对高斯烟羽模型再次进行修正,最终得到泄漏源周边浓度变化情况即公式(32),在风速为k m/s的条件下浓度为(,,,)C x y z H。
对于问题三,我们在第二问建立的模型的基础上,引入时间变量rt和t,和扩散速度变量s,在风速和扩散速度的共同影响下,可分别求出上风向和下风向浓度预估模型即公式(40)和(41)。
对于问题四,本文参阅整理大量气象、地理、新闻资料,选择我国东海岸典型地域---山东半岛和美国西海岸典型地域---加利福尼亚州作为研究对象,综合考虑对应海域平均风速及风向、地理距离、海水对放射性物质扩散的部分反射系数等因素,并通过计算机模拟,预测出放射性核物质将经过6天到达我国东海岸,且131I浓度预测值为:0.1053mBq m-⋅,,经过6.8天到达美国西海岸,且氙-133浓度的预测值几乎为零,与实际情况比较吻合。
高斯烟羽模型

模型假设:1、坐标系高斯模型的坐标系如图2.1所示,原点为排放点(若为高架源,原点为排放点在地面的投影),x轴正向为风速方向,y轴在水平面上垂直于x轴,正向在x轴的左侧,z轴垂直于x轴重时间变化而变化;(7)地面对泄漏气体起全反射作用,不发生吸收或吸附作用;(8)整个过程中,泄漏气体不发生沉降、分解,不发生任何化学反应等。
3、模型公式推导由正态分布假设可以导出下风向任意一点X (x,y,z )处泄漏气体浓度的函数为:22)(),,(bz ay e e x A z y x X --= (1)由概率统计理论可以写出方差的表达式为:⎧∞2⎪⎪⎩⎪⎪⎨⎧==222121z y b a σσ (4)将(1)式和(4)式代入(3)式,积分可得:zy u Q x A σσπ2=)( (5) 再将(4)式和(5)式代入(1)式,可得:⎤⎡⎫⎛22一部分P 其中,像源的贡献为:))(21exp()21exp(2,,22222zy z y H z y u Q z y x X σσσσπ+--=)( (8) 则该处的实际浓度为:)()()(z y x X z y x X z y x X ,,,,,,21+= (9) 由以上条件公式可得到高架连续点源扩散的高斯烟羽模型公式为:)])(1exp())(1[exp()21exp(2,,,,222222yz y H z H z y u Q H t z y x X σσσπ+-+--⨯-=)( (10)为y σ为水s ;H m 。
其中,X (x,y,0)为下风向x 米、横向y 米处的地面扩散气体浓度,单位为kg/m 3;若令y=0,则可以得到下风向中心线上的浓度分布。
4、泄漏源有效高度(烟云抬升高度的计算):以上式中的泄漏源有效高度是指泄漏气体形成的气云基本上变成水平状的时候气云中心的离地高度。
实际上,泄漏源有效高度就等于泄漏源几何高度加泄漏烟云抬升高度。
影响烟云抬升高度的因素有很多,主要包括:泄漏气体的初始速度和方向、初始温度、泄漏口直径、环境风速及风速岁高度的变化率、环境温度及大气稳定度。
高斯烟羽模型

高斯烟羽模型 Prepared on 22 November 2020模型假设:1、坐标系高斯模型的坐标系如图所示,原点为排放点(若为高架源,原点为排放点在地面的投影),x轴正向为风速方向,y轴在水平面上垂直于x轴,正向在x轴的左侧,z 轴垂直于水平面xoy,向上为正向。
在此坐标系下烟流中心线或烟流中心线在xoy面的投影与x轴重合。
2、模型假设(1)污染物的浓度在y、z轴上的分布是高斯分布(正态分布)的;(2)污染源的源强是连续且均匀的,初始时刻云团内部的浓度、温度呈均匀分布;(3)扩散过程中不考虑云团内部温度的变化,忽略热传递、热对流及热辐射;(4)泄漏气体是理想气体,遵守理想气体状态方程;(5)在水平方向,大气扩散系数呈各向同性;(6)取x轴为平均风速方向,整个扩散过程中风速的大小、方向保持不变,不随地点、时间变化而变化;(7)地面对泄漏气体起全反射作用,不发生吸收或吸附作用;(8)整个过程中,泄漏气体不发生沉降、分解,不发生任何化学反应等。
3、模型公式推导由正态分布假设可以导出下风向任意一点X(x,y,z)处泄漏气体浓度的函数为:22)(),,(bz ay eex A z y x X --=(1)由概率统计理论可以写出方差的表达式为:⎪⎪⎪⎩⎪⎪⎪⎨⎧==⎰⎰⎰⎰∞∞∞∞22022XdzXdz z XdyXdyy z y σσ (2)由假设可以写出源强的积分公式:⎰⎰∞∞-∞∞-=uXdydz Q (3)式中:y σ、z σ为泄漏气体在y 、z 方向分布的标准差,单位为 m ;X (x,y,z )为任一点处泄漏气体的浓度,单位为 kg/m 3;u 为平均风速,单位为 m/s ;Q 为源强(即泄漏速度),单位为 kg/s ;将(1)式代入(2)式,积分可得:⎪⎪⎩⎪⎪⎨⎧==222121z y b a σσ (4)将(1)式和(4)式代入(3)式,积分可得:zy u Qx A σσπ2=)( (5)再将(4)式和(5)式代入(1)式,可得:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=222222exp 2,,z yz y zy u Qz y x X σσσσπ)( (6) 上式为无界空间连续点源扩散的高斯模型公式,然而在实际中,由于地面的存在,烟羽的扩散是有界的。
大气污染扩散的高斯烟羽模型及其GIS集成研究

[7]
2 ∏ [ dj ( x, y ) ] 2
n
k =1j= k
∑ ∏ [ dj ( x, y ) ]
3 系统实现 3. 1 系统平台
克里金插值法是常用的一种空间插值方法 。 它利用区域化变量的原始数据和变异函数的结构 特点 ,对未采样点的区域化变量的值进行线性无偏 最优估计 。它在分析已测样点的形状 、 大小 、 空间 位置 ,已测样点与待估样点的相互空间位置关系 , 以及变异函数提供的结构信息基础上 ,对待估样点
[ 10 - 11 ]
。
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
第 20 卷 第 5期
张斌才等 . 大气污染扩散的高斯烟羽模型及其 GIS集成研究
Q
(2 π) 3 / 2σxσyσz +e
e
σ2 - ( x - u t) 2 / 2 x
×
[e
σ2 - ( z - h - w t) 2 / 2 z
σ2 - ( z + 2H + h - w t) 2 / 2 z
]
( 1)
式中 : t— — — 时间 , s; Q — — — 污染释放率 , m g / s; u, v, σ σ σz — w— — — 风速矢量值 ; x 、 y 、 — — 水平和垂直方向 扩散 系 数 ; h — — — 事 故 点 高 度 , m; H — — — 混合层 高 , m。 烟羽模型以事故点为坐标原点 , 风向为 x 轴 , 得出空间一点 ( x, y, z)的污染物质量浓度值 C。当 v = w = 0, 且 z = 0 时 , 方程为 :
高斯烟雨扩散模型在空气中PM2.5实际问题的应用

高斯烟雨扩散模型在空气中PM2.5实际问题的应用董赫;翟哲;李夺;李伟凯【摘要】通过建立高斯烟雨扩散模型并采用多元线性回归等数学方法,进一步探索产生雾霾的主要因素PM2.5的形成、扩散过程以及与风速之间的关系。
以武汉市和西安市2013年AQI监测数据为基础,得到空气中PM2.5与其他污染物之间的相关性。
预测了西安市某一区域PM2.5浓度骤增并持续数小时的情况下,污染严重和相对安全的区域。
为研究空气中PM2.5成因、监测和治理提供了一定的理论依据。
%Through establishing gauss misty rain diffusion model and adopting mathematical methods of multiple linear regression,the relations of the formation and diffusion process of PM2.5 with wind speed were explored further. Basing on AQI monitoring data of Wuhan City and Xi’an City in 2013,the correlation between PM2.5 and other pollutants was obtained,and the seriously polluted and relatively secure area were predicted under the circumstances of the sharp increase in PM2.5 content for several hours in certain region of Xi’an. The articl e could provide certain theoretical basis to research the cause,monitoring and governance of PM2.5 in air.【期刊名称】《黑龙江八一农垦大学学报》【年(卷),期】2014(000)003【总页数】6页(P69-73,118)【关键词】PM2.5;多元线性回归;高斯烟雨扩散模型【作者】董赫;翟哲;李夺;李伟凯【作者单位】黑龙江八一农垦大学信息技术学院,大庆 163319;黑龙江八一农垦大学信息技术学院,大庆 163319;黑龙江八一农垦大学工程学院;黑龙江八一农垦大学信息技术学院,大庆 163319【正文语种】中文【中图分类】X502随着国民经济飞速发展和城市化进程的日益加快,我国已有1/4的国土面积相继出现因大气细粒子污染增多而导致的雾霾天气,影响近6亿人的工作和生活。
最新-高斯烟羽扩散模型再研究 精品

高斯烟羽扩散模型再研究篇一:高斯烟羽模型模型假设:1、坐标系高斯模型的坐标系如图21所示,原点为排放点(若为高架源,原点为排放点在地面的投影),轴正向为风速方向,轴在水平面上垂直于轴,正向在轴的左侧,轴垂直于水平面,向上为正向。
在此坐标系下烟流中心线或烟流中心线在面的投影与轴重合。
2、模型假设(1)污染物的浓度在、轴上的分布是高斯分布(正态分布)的;(2)污染源的源强是连续且均匀的,初始时刻云团内部的浓度、温度呈均匀分布;(3)扩散过程中不考虑云团内部温度的变化,忽略热传递、热对流及热辐射;(4)泄漏气体是理想气体,遵守理想气体状态方程;(5)在水平方向,大气扩散系数呈各向同性;(6)取轴为平均风速方向,整个扩散过程中风速的大小、方向保持不变,不随地点、时间变化而变化;(7)地面对泄漏气体起全反射作用,不发生吸收或吸附作用;(8)整个过程中,泄漏气体不发生沉降、分解,不发生任何化学反应等。
3、模型公式推导由正态分布假设可以导出下风向任意一点(,,)处泄漏气体浓度的函数为:(,,)?()?2?2(1)由概率统计理论可以写出方差的表达式为:???2?????2???????????02???002(2)????0由假设可以写出源强的积分公式:????(3)式中:?、?为泄漏气体在、方向分布的标准差,单位为;(,,)为任一点处泄漏气体的浓度,单位为3;为平均风速,单位为;为源强(即泄漏速度),单位为;将(1)式代入(2)式,积分可得:1???2?2????12?2??()?(4)将(1)式和(4)式代入(3)式,积分可得:(5)2???????(6)????再将(4)式和(5)式代入(1)式,可得:2??2(,,)????2?2?2?2???2????上式为无界空间连续点源扩散的高斯模型公式,然而在实际中,由于地面的存在,烟羽的扩散是有界的。
根据假设可以把地面看做一镜面,对泄漏气体起全反射作用,并采用像源法处理,原理如图22所示。
基于遗传-模拟退火算法修正高斯烟羽模型参数

现代电子技术Modern Electronics TechniqueMar. 2024Vol. 47 No. 62024年3月15日第47卷第6期0 引 言在当今的社会环境下,工业化进程的迅猛发展导致大量的废气排放[1],且城市化快速扩张[2],加剧了大气污染问题。
我国部分城市的PM 2.5污染已经到达甚至超过了世界卫生组织的标准。
因此,为了有效地改善大气环境质量,减少污染物的排放和扩散对人类及生态环境带来的危害,建立一个高效、准确的数学模型来描述和预DOI :10.16652/j.issn.1004‐373x.2024.06.002引用格式:王彦骄,张绍阳,梁玉泉,等.基于遗传‐模拟退火算法修正高斯烟羽模型参数[J].现代电子技术,2024,47(6):9‐14.基于遗传⁃模拟退火算法修正高斯烟羽模型参数王彦骄, 张绍阳, 梁玉泉, 马丹晨(长安大学 信息工程学院, 陕西 西安 710018)摘 要: 高斯烟羽模型由于受到地形地貌与气象条件等因素的影响,难以准确反映大气的实际扩散过程。
为解决上述问题,首先在经验参数作为先验值的基础上,通过遗传算法对实际观测数据进行参数反演修正,根据观测结果调整模型参数,提高模型的准确性;然后,为进一步优化参数修正结果,引入模拟退火算法,通过随机搜索和逐步降温的策略来跳出遗传算法可能陷入的局部最优解,进一步改善模型的性能。
为了评估修正效果,建立一个基于权重的模型值与观测值之间差异的适应度函数,通过比较修正前后的误差率来判断参数修正对高斯烟羽模型的影响程度。
仿真实验的结果表明,所提出的遗传‐模拟退火算法模型能够有效地修正高斯烟羽模型中的扩散参数,修正后的模型在预测污染物浓度方面的误差率下降了89.40%。
所提模型可为环境保护和污染防治提供重要的理论支撑和决策依据,具有较大的应用潜力。
关键词: 高斯烟羽模型; 遗传算法; 模拟退火算法; 参数修正; 适应度函数; 误差率中图分类号: TN957.52+4‐34; TP391.9 文献标识码: A 文章编号: 1004‐373X (2024)06‐0009‐06Gaussian plume model parameters modification based on genetic⁃simulatedannealing algorithmWANG Yanjiao, ZHANG Shaoyang, LIANG Yuquan, MA Danchen(School of Information Engineering, Chang ’an University, Xi ’an 710018, China)Abstract : Gaussian plume model is difficult to accurately reflect the actual diffusion process of the atmosphere due to the influence of topography and meteorological conditions and other factors. In order to solve the above situation, on the basis of the empirical parameters as a priori values, the actual observation data are used to carry out parameter inversion correction by means of the genetic algorithm, and the model parameters are adjusted according to the observation results to improve the accuracy of the model. A simulated annealing algorithm is introduced to further optimize the parameter correction results, which can jump out of the local optimal solutions that the genetic algorithm may fall into and further improve the performance of the model bymeans of the strategy of random search and gradual cooling. In order to evaluate the correction effect, a weight ‐based fitness function for the difference between the model value and the observed value is calculated. By comparing the error rate before and after the correction, the degree of influence of the parameter correction on the Gaussian plume model can be judged. The results of simulation experiments show that the diffusion parameters in the Gaussian plume model can be effectively corrected by means of the genetic ‐simulated annealing algorithm model proposed in this paper. The error rate of the corrected model in predicting pollutant concentrations is reduced by 89.40%. This experiment can provide important theoretical support and decision basis for the environmental protection and the pollution prevention, and has important application potential.Keywords : Gaussian plume model; genetic algorithm; simulated annealing algorithm; parameter correction; fitness function;error rate收稿日期:2023‐10‐07 修回日期:2023‐11‐20基金项目:陕西省交通运输科技项目(21‐12R );重点产业创新链(群)(2021ZDLGY07‐06)9现代电子技术2024年第47卷测空气污染物的扩散和浓度分布情况变得越来越重要。
高斯烟羽扩散模型再评估

汇报人: 日期:
目录
• 引言 • 高斯烟羽扩散模型理论基础 • 高斯烟羽扩散模型的应用 • 高斯烟羽扩散模型的局限性和
改进方法 • 案例分析 • 结论与展望 • 参考文献
01
引言
研究背景和意义
环境保护的重要性
环境保护是当今社会面临的重要问题之一,而空气污染是环境保护领域的关键 问题之一。高斯烟羽扩散模型是预测空气污染的重要工具,因此对其进行再评 估具有重要的实际意义。
详细描述
高斯烟羽扩散模型在风险评估中应用前景 广阔,能够较为准确地评估大气污染物排 放对周边环境和人类健康造成的风险和危 害。该模型在制定风险防范措施和应急预 案方面具有重要的应用价值,为保障公共 安全和生态环境提供了有力支持。
04
高斯烟羽扩散模型的局限性和 改进方法
高斯烟羽扩散模型的局限性
无法准确预测复杂地 形下的烟羽扩散情况
总结词
客观评价、科学性强、符合实际
详细描述
高斯烟羽扩散模型在环境影响评价中具有较高的应用价值。 通过对建设项目实施前后大气污染物排放量的预测和分析, 能够较为客观地评价建设项目对周边环境的影响程度和范围 ,为环境管理决策提供科学依据。
高斯烟羽扩散模型在风险评估中的应用
总结词
评估准确、应用前景广阔
VS
总结词
广泛使用、可靠性高、应用范围广
详细描述
高斯烟羽扩散模型在空气质量预测中应用广泛,通过对大气扩散参数和气象条件的测量和计算,能够 较为准确地预测空气污染物的浓度分布和变化趋势。该模型在国内外得到广泛应用,为环境保护部门 制定相应的污染控制措施提供了科学依据。
高斯烟羽扩散模型在环境影响评价中的应用
高斯烟羽扩散模型适用于风力较 大、气象条件稳定的情况,但在 静风或逆温等条件下,模型的预
高斯烟羽扩散模型再研究

高斯烟羽扩散模型再研究孙志宽【摘要】高斯烟羽扩散模型自二十世纪50年代提出后,一直在空气污染扩散研究及大气环境质量预测领域广泛使用,我国及美国、欧盟将其列为环境影响评价中大气环境预测的基本模型.不少国内外学者发现,该模型与实际监测有一定的误差.作者通过认真研究,对模型的两个重要参数U和△H的选取和计算方法提出质疑,并通过严密的数学推导,得到严谨数学表达式,进而提出新的高斯烟羽扩散模型.通过边界层污染气象观测、烟羽对比观测和对比计算证明,修正后的高斯烟羽扩散模型更接近实际.【期刊名称】《环境与可持续发展》【年(卷),期】2013(038)005【总页数】3页(P107-109)【关键词】高斯模型;平均风速;抬升高度【作者】孙志宽【作者单位】神华国能集团(神东电力)集团公司,北京10033【正文语种】中文【中图分类】X211 引言在大气环境质量预测及空气污染等问题中,用数学模型模拟并预测大气污染物输送与扩散是一种常用且有效的手段。
对连续的气态污染源在有风时对周围空气质量的影响预测,无论是我国目前现行的《境影响评价技术导则-大气环境》(HJ 2.2-2008)[1],还是美国EPA推荐的AERMOD模型[2],其基本形式都是高斯烟流扩散模型,其数学表达式为:式中,C(x,y,z)为污染源下方向任一点(x,y,z)处的污染物浓度,mg/m3;Q为源强,mg/m;U为水平输送速度,m;σy和σz分别为横向扩散参数和垂直扩散参数,m;h为混合层高度,m;k为反射次数;He为烟囱有效高度,m,其值为烟囱几何高度(Hs)与烟气抬升高度(△H)之和,即:通常所需预测的是地面浓度,在无界情况下,其表达式为:有不少国内外学者发现,上式计算结果与实测值有较大的偏差[2,5],Herman 和 Mccaffrey 的实验研究[4]和我国原水电部及南京大学在徐州所做的烟流抬升和扩散试验的结果[6]都表明:一是高斯模型预报的峰值浓度几乎全部低于实测值,预报与实测的误差以D类稳定度最大,A类最小。
基于高斯烟羽模型和ISSA算法的油气站场泄漏检测研究

基于高斯烟羽模型和ISSA算法的油气站场泄漏检测研究刘若兮;陶野;赵元东;李彦华;王婷婷;梁昌晶
【期刊名称】《石油工程建设》
【年(卷),期】2024(50)2
【摘要】为提高油气站场泄漏检测的预测精度,降低事后处理带来的经济损失和环境污染,将高斯烟羽模型作为前向气体扩散模型,通过Circle混沌映射初始化麻雀种群,将蝴蝶算法加入麻雀发现者搜索策略中,随后利用算法实现质量浓度误差最小化的迭代计算,并从迭代次数、种群规模、网格尺寸和噪声强度等方面衡量其对反演结果的影响。
结果表明,算法在时间算法复杂度上与SSA算法一致,优化后算法的全局搜索能力和局部开发能力增强;通过将地理坐标系转化为标准风向坐标系,简化了计算过程;在最大迭代次数100、种群规模100、网格尺寸0.5 m×0.5 m×0.5 m 的设置下,当站场内存在2个监测点受噪声影响时,3个方向上泄漏位置的最大误差分别为1.37%、1.02%、9.70%,泄漏速率的最大相对误差为0.22%,符合现场定位检测的需求。
研究结果可为油气站场完整性管理水平的提升提供实际参考。
【总页数】7页(P71-76)
【作者】刘若兮;陶野;赵元东;李彦华;王婷婷;梁昌晶
【作者单位】中国石油华北油田分公司第五采油厂;中国石油华北油田分公司新能源事业部;中国石油华北油田公司二连分公司
【正文语种】中文
【中图分类】TP3
【相关文献】
1.基于高斯烟羽扩散模型的空气污染研究
2.基于高斯烟羽扩散模型的蚌埠市空气质量的研究
3.基于高斯烟羽扩散模型的成都市空气质量的研究
4.基于高斯烟羽模型的山区含硫天然气泄漏扩散研究
因版权原因,仅展示原文概要,查看原文内容请购买。
高斯烟羽模型

X ( x, y, z ) = A( x)e
− ay
2
e
− bz
2
• (1) • 由概率统计理论可以写出方差的表达式为: y Xdy σ = ∫ • (2) Xdy
∞ 2 2 y 0
σ ∫∞源自02 z=
∫
∞
0
z 2 Xdz
∞
∫
0
Xdz
• 由假设可以写出源强的积分公式: ∞ ∞ • (3) Q = ∫ ∫ uXdydz −∞ −∞
• 将(1)式和(4)式代入(3)式,积分可 得: Q • (5) A(x) =
2πuσ yσ z
• 再将(4)式和(5)式代入(1)式,可得:
y2 z2 X(x, y, z) = exp− 2 + 2σ 2πuσ y σ z 2σ z2 y Q
• 为泄漏后是时间,单位为s;H为泄漏源有 效高度,单位为m;y为横向距离,单位为 m;z为垂直方向距离,单位为m。 • 如:式中,令z=0,即可得到地面气体浓度 计算公式: • 1 y H2 (11) Q
X( , y,0, H) x =
2 exp − ( ) exp 2 πuσ yσz 2 σ y 2σz
• (6)取x轴为平均风速方向,整个扩散过程中 风速的大小、方向保持不变,不随地点、 时间变化而变化; • (7)地面对泄漏气体起全反射作用,不发生 吸收或吸附作用; • (8)整个过程中,泄漏气体不发生沉降、分 解,不发生任何化学反应等。 • 3、模型公式推导 • 由正态分布假设可以导出下风向任意一点X (x,y,z)处泄漏气体浓度的函数为:
• 式中:、为泄漏气体在y、z方向分布的标 准差,单位为 m;X(x,y,z)为任一点处泄 漏气体的浓度,单位为 kg/m;u为平均风 速,单位为 m/s;Q为源强(即泄漏速度), 单位为 kg/s; • 将(1)式代入(2)式,积分可得:
高斯烟羽模型

模型假设:1、坐标系高斯模型的坐标系如图2.1所示;原点为排放点若为高架源;原点为排放点在地面的投影;x轴正向为风速方向;y轴在水平面上垂直于x轴;正向在x轴的左侧;z轴垂直于水平面xoy;向上为正向..在此坐标系下烟流中心线或烟流中心线在xoy面的投影与x轴重合..2、模型假设1污染物的浓度在y、z轴上的分布是高斯分布正态分布的;2污染源的源强是连续且均匀的;初始时刻云团内部的浓度、温度呈均匀分布;3扩散过程中不考虑云团内部温度的变化;忽略热传递、热对流及热辐射;4泄漏气体是理想气体;遵守理想气体状态方程;5在水平方向;大气扩散系数呈各向同性;6取x轴为平均风速方向;整个扩散过程中风速的大小、方向保持不变;不随地点、时间变化而变化;7地面对泄漏气体起全反射作用;不发生吸收或吸附作用;8整个过程中;泄漏气体不发生沉降、分解;不发生任何化学反应等..3、模型公式推导由正态分布假设可以导出下风向任意一点Xx;y;z处泄漏气体浓度的函数为:22)(),,(bz ay eex A z y x X --=1由概率统计理论可以写出方差的表达式为:⎪⎪⎪⎩⎪⎪⎪⎨⎧==⎰⎰⎰⎰∞∞∞∞22022XdzXdz z XdyXdyy z y σσ 2由假设可以写出源强的积分公式:⎰⎰∞∞-∞∞-=uXdydz Q 3式中:y σ、z σ为泄漏气体在y 、z 方向分布的标准差;单位为 m ;Xx;y;z为任一点处泄漏气体的浓度;单位为 kg/m 3;u 为平均风速;单位为 m/s ;Q 为源强即泄漏速度;单位为 kg/s ;将1式代入2式;积分可得:⎪⎪⎩⎪⎪⎨⎧==222121z y b a σσ 4将1式和4式代入3式;积分可得:zy u Qx A σσπ2=)( 5再将4式和5式代入1式;可得:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-=222222exp 2,,z yz y zy u Qz y x X σσσσπ)( 6 上式为无界空间连续点源扩散的高斯模型公式;然而在实际中;由于地面的存在;烟羽的扩散是有界的..根据假设可以把地面看做一镜面;对泄漏气体起全反射作用;并采用像源法处理;原理如图2.2所示..可以把任一点p 处的浓度看做两部分的贡献之和:一部分是不存在地面时所造成的泄漏物浓度;一部分是由于地面反射作用增加的泄漏物浓度..该处的泄漏物浓度即相当于不存在地面时由位于0;0;H 的实源和位于0;0;-H 的像源在P 点处所造成的泄漏物浓度之和..其中;实源的贡献为:))(21exp()21exp(2),,(22221zy z y H z y u Q z y x X σσσσπ---= 7 其中;像源的贡献为:))(21exp()21exp(2,,22222zy z y H z y u Q z y x X σσσσπ+--=)( 8 则该处的实际浓度为:)()()(z y x X z y x X z y x X ,,,,,,21+= 9 由以上条件公式可得到高架连续点源扩散的高斯烟羽模型公式为:)])(21exp())(21[exp()21exp(2,,,,222222zz y z y H z H z y u Q H t z y x X σσσσσπ+-+--⨯-=)( 10其中:Xx;y;z 为下风向x 米、横向y 米、地面上方z 米处的扩散的气体浓度;单位为kg/m 3;Q 为源强即源释放速率;单位为kg/s ;u 为平均风速;单位为m/s ;y σ为水平扩散参数;单位为m ;z σ为垂直扩散参数;单位为 m ;t 为泄漏后是时间;单位为s ;H 为泄漏源有效高度;单位为m ;y 为横向距离;单位为m ;z 为垂直方向距离;单位为m..如:式中;令z=0;即可得到地面气体浓度计算公式:⎪⎪⎭⎫⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡-=2222exp 21exp ,0,,z y z y H y u QH y x X σσσσπ)()( 11 令y=z=0;即可得到地面轴线气体浓度计算公式:)2exp(),0,0,(22zz y H u QH x X σσσπ-= 12其中;Xx;y;0为下风向x 米、横向y 米处的地面扩散气体浓度;单位为kg/m 3;若令y=0;则可以得到下风向中心线上的浓度分布..4、泄漏源有效高度烟云抬升高度的计算:以上式中的泄漏源有效高度是指泄漏气体形成的气云基本上变成水平状的时候气云中心的离地高度..实际上;泄漏源有效高度就等于泄漏源几何高度加泄漏烟云抬升高度..影响烟云抬升高度的因素有很多;主要包括:泄漏气体的初始速度和方向、初始温度、泄漏口直径、环境风速及风速岁高度的变化率、环境温度及大气稳定度..有效源高: HH HS ∆+=其中;s H 为泄漏源几何架高;H ∆为烟云抬升高度.. 实验表明;泄漏源抬升高度可以用下面公式近似计算: V d V HS /.42=∆ 13其中;S V 是气云释放速度;单位为m/s ;d 是泄漏出口直径;单位为 m ;V 为环境风速;单位为m/s ;13式是20世纪70年代末、80年代初;Wilson 根据管道破裂泄漏实验所得的实验公式..实验时气体的喷射方向与风速垂直并且气体喷射路径上无障碍物..实验表明;当气体喷射方向垂直向上时;预测值与实际值之比在洗漱2以内..计算出泄漏烟云抬升高度以后;将泄漏源抬升高度与泄漏源实际几何高度相加就得到了泄漏源有效高度..5、扩散系数的选取:扩散系数x σ、y σ、z σ的大小与大气湍流结构、离地高度、地面粗糙度、泄漏持续时间、抽样时间间隔、风速以及离开泄漏源的距离等因素有关..大气的湍流结构和风速在大气稳定度中考虑..大气稳定度由10米高度以上的风速、白天的太阳辐射或夜间的云量等参数决定..按照Pasquill 的分类方法;随着气象条件稳定性的增加;大气稳定度可以分为A 、B 、C 、D 、E 、F 六类..其中A 、B 、C 三类表示气象条件不稳定;E 、F 两类表示气象条件稳定;D 类表示中性气象条件;也就是说气象条件的稳定性在稳定和不稳定之间..A 、B 、C 三种类型的稳定度中;A 类表示气象条件极其不稳定;B 类表示气象条件中等程度不稳定;C 类表示气象条件弱不稳定..E 和F 两种类型的稳定度中;E 类表示气象条件弱稳定;F 类表示气象条件中等程度稳定..大气稳定度具体分类方法见下表1、表2..表1 Pasquill 大气稳定度的确定日照强度的确定表2表1和表2中的云量是指当地天空层覆盖率..例如;云量为3/8是指当地3/8的天空有云层覆盖..日照角是指当地太阳光线与地平线之间的夹度..例如;阳光垂直照射地卖弄时的日照角为90°..一般来说;随着大气稳定度的增加;扩散系数减小..根据Hanna和Drivas的建议;化学危险品事故泄漏扩散系数与大气稳定度类型和下风向的关系如下表3..表3 扩散系数的计算方法。
烟羽模型的建立
• FLUENT 解算器有如下模拟能力: • ������ 用非结构自适应网格模拟 2D 或者3D 流场,它所使用的非结构 网格主要有三角形/五边形、四边形/五边形,或者混合网格,其中混 合网格有棱柱形和金字塔形。(一致网格和悬挂节点网格都可以) • 不可压或可压流动 • 定常状态或者过渡分析 • 无粘,层流和湍流 • 牛顿流或者非牛顿流 • 对流热传导,包括自然对流和强迫对流 • 耦合热传导和对流 • 辐射热传导模型 • 惯性(静止)坐标系非惯性(旋转)坐标系模型 • 学组分混合和反应,包括燃烧子模型和表面沉积反应模型 • 热,质量,动量,湍流和化学组分的控制体源 • 粒子,液滴和气泡的离散相的拉格朗日轨迹的计算,包括了和连续相 的耦合 多孔流动 • 一维风扇/热交换模型 • 两相流,包括气穴现象 • 复杂外形的自由表面流动
烟羽模型的建立
•
烟羽模型的构建是为移动机器人主动嗅觉研究而服务 的。移动机器人主动嗅觉定位技术的研究起源于上个世纪 90 年代欧美和日本一些发达的国家,距今只有十几年的历 史,但受到了广大专家和学者的关注。它集成了智能技术﹑ 传感器及信息处理技术﹑仿生学﹑控制科学、计算机科学﹑ 流体力学等多种学科的知识。主动嗅觉可以主动对目标化学 物质感知并确定其位置,在环境监测﹑灾难营救、危险物品 泄漏检测和大型工厂仓库保安等方面具有重要的研究意义和 潜在的应用前景。但是机器人主动嗅觉的研究受硬件和外界 环境的影响较大,这很不利于其发展,再考虑到其成本问题, 能够建立一个合理的研究模型就显得很有必要了,而烟羽模 型的构建正是此模型研究的前提,这也就说明了构建一个合 理烟羽模型的意义所在。
• ������
• 当我们决定使 FLUENT 解决某一问题时,首先要考虑如下几点问题: 定义模型目标:从CFD 模型中需要得到什么样的结果?从模型中需要 得到什么样的精度;选择计算模型;如何隔绝所需要模拟的物理系统, 计算区域的起点和终点是什么?在模型的边界处使用什么样的边界条 件?二维问题还是三维问题?什么样的网格拓扑结构适合解决问题? 物理模型的选取:无粘,层流还湍流?定常还是非定常?可压流还是 不可压流?是否需要应用其它的物理模型?确定解的程序:问题可否 简化?是否使用缺省的解的格式与参数值?采用哪种解格式可以加速 收敛?使用多重网格计算机的内存是否够用?得到收敛解需要多久的 时间? • 确定所解决问题的特征之后,解决问题的一般步骤是: • 创建网格; • 运行合适的解算器; • 输入网格; • 检查网格; • 选择解的格式; • 选择需要的基本方程;层流还是湍流(无粘),化学组分还是化学反 应、热传导模型; • 指定材料物理性质; • 指定边界条件; • 调节器的控制参数;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Most probable wind direction
6
Simple Model #2:
Conc at 2 =
( wind speed)(area of disk 2 )
Mass emission rate
[Gaussian distribution function ]
µg µg/sec [ ] = − 3 2 m (m/sec )( m )
*Pollutant is well mixed and confined within the cone *Pollutant is continuously swept thru the cone by the wind
2 1
3
mass/time passing point 1
=
mass/time passing thru disk area 2 C1 > C 2 > C 3
1
Instantaneous Plume Shape
Time-averaged Plume Shape
Describing Plume Concentrations
wind
Fig 4 -3, p.44 in Martin et al
2
Tim’s Simple Plume Model
h
x
Simplified Steady-State Plume Model
“Eddy” Diffusion
Consider two enclosed air volumes separated by a wall
(arrows represent eddy motions; balls represent pollutant molecules)
Size of eddies > size of pollutant molecules
8
The rate of pollutant molecules crossing plane AA depends upon the concentration difference between the two sides. Specifically, this rate =K δc/δx ,where K is termed an “eddy diffusivity” with units of m2 /sec. The magnitude of K depends upon the magnitude of the eddy motions.
“Advection-Diffusion” Equation
∂C ∂C ∂ ∂C ∂ ∂C + other losses = −u + K + K due to ∂t ∂x ∂y y ∂y ∂z z ∂z deposition and
chemical reactions = 0 for steadystate models “Advection”, i.e., transport by the mean wind, u Effect of turbulent “diffusion”, i.e., exchange of polluted air parcel with surrounding air parcels. If the surrounding air is cleaner, δC/δz & δC/δy are negative. K is the “eddy diffusivity” and represents the intensity of turbulent motions and varies with stability
Source: Slade et al “Meteorology and Atomic Energy, 1968”
5
unstable
neutral
stable
More Detailed Plume Model
Mass is not uniformly distributed within the cone’s volume
* Constant wind speed with height (u does not depend on z) * Constant eddy diffusivity (K does not depend on y or z)
Define:
ó2 z =
2 Kz x u
ó2 y =
2 Ky x u
A similar result is obtained in the y direction. Given that the net rate of change in the volume [ = V(δc/δt)] is the change in all three directions , we obtain an overall expression in terms of x, y and z.
7
z
y x dy dz dx
*Transport of mass in x direction depends on the average horizontal wind *Transport of mass in the y and z directions depends on turbulent motions
Pollutant molecules are moving around in random directions due to random eddy motions
Random eddy motions in pollution-free air
Now remove the wall between the enclosures
Mass emission rate “Effective” stack height, including rise of the hot plume near the source
Q C(x, y, z) = 2π u σyσz
Wind speed evaluated at “effective” release height
µg = µg/sec m 3 (m/sec)( m2 )
2 1
Disk shape depends upon stability category
More unstable and thus more pronounced vertical spreading
4
Perspective View of “Fanning” Plume in Very Stable Air Less vertical motion
Changes in z Direction via “ Turbulent Diffusion”:
Mass Flow Rate In = - A xy ∂ { K z C} ∂z [m 2 ][m-1 ][ µg m -3 ][m 2 sec-1 ]
Net Rate of Change =
∂ ∂ (K z C ) V ∂ z ∂z
Gaussian Plumes from “Point” Sources
• • • • • • • • • • Time averaged vs instantaneous plumes Simplified steady-state plume model “Eddy” diffusion, advection/diffusion equation Gaussian point source plume model Plume sigma values vs stability and distance Plume reflection Non-gaussian plumes Plume Rise; plume trajectories Buoyancy-induced dispersion Stack downwash
* Mass is conserved
∞
−∞
∫∫
∞
−∞
Cdydz = Q
[for x > 0]
{µg/sec }
Pollutant concentration as a function of downwind position (x,y,z)
Gausቤተ መጻሕፍቲ ባይዱian “Point” Source Plume Model:
=
mass/time passing thru disk area 3
Concentration vs. distance downwind depends upon cone shape
3
Simple Model #1:
Concentration of air at 2 = Mass emission rate (wind speed )(area of disk 2)
2 1 y
z x
X is the time-averaged wind direction, Y is the cross-wind direction, Z is the vertical dimension
Gaussian Plume Model
2 1
In order to derive an equation describing the distribution of mass within the plume, we must first consider the transport of mass within a small control volume
dx dy dz
V =Volume = dxdydz Axy = dxdy Ayz = dydz Axz = dxdz
Changes in x Direction:
