优选动态规划习题课

合集下载

动态规划例题讲解精品PPT课件

动态规划例题讲解
山东师大附中
Preview
本节课主要通过几道例题，总揽NOIp中较常见的动态规划模型，不会过多涉及优化内容。
Preview
最长上升子序列内存碎片背包问题最长公共子序列石子合并
括号序列决斗三取方格数选课贪吃的九头龙
最长上升子序列
给出一个数列{a1,a2,...,an}，要求你选出尽量多的元素，使这些元素按其相对位置单调
完全背包问题
共有N种物品，每种物品有一定的重量w[i] 和一定的价值v[i]，每种物品有无限个。现在我们有一个最大载重量limit的包，问放入哪些物品能使得总价值最高？
w[i]和v[i]均为整数，N<=100，limit<=10000
完全背包问题
fillchar(f,sizeof(f),0); for i:=1 to n do for j:= w[i] to limit do f[j] = max(f[j], f[j-w[i]]+v[i]); writeln(f[limit]);
1400
共有3件物品重量分别为30/80/10 价值分别为300/1200/200 背包最大载重量为100
0/1背包问题
令f[i,j]表示考虑完前i项物品，并且当前背包承重不大于j的情况下能获得的最大价值
f[i,j]=max( f[i-1,j], //不选第i项物品 f[i-1,j–w[i]]+v[i]) //选择第i项物品
2
插入a6后 -inf
1
插入a7后 -inf
1
插入a8后 -inf
1
插入a9后 -inf
1
inf
inf
inf
8

动态规划练习例题

c(m,n)为最终最小代价，反向追踪获得编辑序列
动态规划方法总结
动态规划算法的设计步骤
– – – – – – – 将问题表示成多步判断确定是否满足优化原则——必要条件确定子问题的重叠性——估计算法效率列出关于优化函数的递推方程(或不等式)和边界条件自底向上计算子问题的优化函数值----非递归的算法备忘录方法记录中间结果标记函数追踪问题的解
• S(i)表示结束于位置i的最大子区间和 • max{S(i)}即为所求最大子区间和 • 考虑如何递推求解并反算问题解
最大子矩阵
• 已知矩阵的大小定义为矩阵中所有元素的和。给定一个矩阵，找到最大的非空(大小至少是1 * 1)子矩阵。 • 例如这个矩阵的最大子矩阵大小为15。
0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2
动态规划练习例题在棋盘上移动在一个nn的棋盘上棋子可以向上方右上方或左上方移动每次从x方格移动到y方格将获得pxy元钱pxy不一定是正数现求一个获得钱最多的从底边到顶边的一种移动棋子的方案
动态规划练习例题
在棋盘上移动
• 在一个n×n的棋盘上，棋子可以向上方、右上方或左上方移动，每次从x方格移动到y 方格将获得p(x,y)元钱， p(x,y)不一定是正数，现求一个获得钱最多的从底边到顶边的一种移动棋子的方案。
解题思路
Qx, y 1 Q x, y max Qx 1, y 1 Q x 1, y 1 y 1 px, y 1, x, y y 1 px 1, y 1, x, y y 1且x 1 px 1, y 1, x, y y 1且x 字符串X=x1,x2,…xm和Y=y1,y2,…yn 使用一系列编辑操作将字符串X转变成Y。允许使用插入，删除，修改三种操作，每种操作都有一定的代价，求一个总代价最小的操作序列。 – 设从字符X中删除符号xi的代价为D(xi) – 将符号yj插入X的代价为I(yj) – 将X中的符号xi修改成yj的代价为C(xi,yj)

动态规划练习题及解答1

动态规划练习题[题1] 多米诺骨牌（DOMINO）问题描述：有一种多米诺骨牌是平面的，其正面被分成上下两部分，每一部分的表面或者为空，或者被标上1至6个点。

现有一行排列在桌面上：顶行骨牌的点数之和为6+1+1+1=9；底行骨牌点数之和为1+5+3+2=11。

顶行和底行的差值是2。

这个差值是两行点数之和的差的绝对值。

每个多米诺骨牌都可以上下倒置转换，即上部变为下部，下部变为上部。

现在的任务是，以最少的翻转次数，使得顶行和底行之间的差值最小。

对于上面这个例子，我们只需翻转最后一个骨牌，就可以使得顶行和底行的差值为0，所以例子的答案为1。

输入格式：文件的第一行是一个整数n（1〈=n〈=1000〉，表示有n个多米诺骨牌在桌面上排成一行。

接下来共有n行，每行包含两个整数a、b（0〈=a、b〈=6，中间用空格分开〉。

第I+1行的a、b分别表示第I个多米诺骨牌的上部与下部的点数（0表示空）。

输出格式：只有一个整数在文件的第一行。

这个整数表示翻动骨牌的最少次数，从而使得顶行和底行的差值最小。

[题2] Perform巡回演出题目描述:Flute市的Phlharmoniker乐团2000年准备到Harp市做一次大型演出,本着普及古典音乐的目的,乐团指挥L.Y.M准备在到达Harp市之前先在周围一些小城市作一段时间的巡回演出,此后的几天里,音乐家们将每天搭乘一个航班从一个城市飞到另一个城市,最后才到达目的地Harp市(乐团可多次在同一城市演出).由于航线的费用和班次每天都在变,城市和城市之间都有一份循环的航班表,每一时间,每一方向,航班表循环的周期都可能不同.现要求寻找一张花费费用最小的演出表.输入: 输入文件包括若干个场景.每个场景的描述由一对整数n(2<=n<=10)和k(1<=k<=1000)开始,音乐家们要在这n个城市作巡回演出,城市用1..n标号,其中1是起点Flute市,n是终点Harp市,接下来有n*(n-1)份航班表,一份航班表一行,描述每对城市之间的航线和价格,第一组n-1份航班表对应从城市1到其他城市(2,3,...n)的航班,接下的n-1行是从城市2到其他城市(1,3,4...n)的航班,如此下去.每份航班又一个整数d(1<=d<=30)开始,表示航班表循环的周期,接下来的d个非负整数表示1,2...d天对应的两个城市的航班的价格,价格为零表示那天两个城市之间没有航班.例如"3 75 0 80"表示第一天机票价格是75KOI,第二天没有航班,第三天的机票是80KOI,然后循环:第四天又是75KOI,第五天没有航班,如此循环.输入文件由n=k=0的场景结束.输出:对每个场景如果乐团可能从城市1出发,每天都要飞往另一个城市,最后(经过k天)抵达城市n,则输出这k个航班价格之和的最小值.如果不可能存在这样的巡回演出路线,输出0.样例输入: 样例输出：3 6 4602 130 150 03 75 0 807 120 110 0 100 110 120 04 60 70 60 503 0 135 1402 70 802 32 0 701 800 0[题3] 复制书稿（BOOKS）问题描述：假设有M本书（编号为1，2，…M），想将每本复制一份，M本书的页数可能不同（分别是P1，P2，…PM）。

动态规划练习题(含答案)

动态规划练习题USACO 2.2 Subset Sums题目如下：对于从1到N的连续整集合合，能划分成两个子集合，且保证每个集合的数字和是相等的。

举个例子，如果N=3，对于{1，2，3}能划分成两个子集合，他们每个的所有数字和是相等的：and {1,2}这是唯一一种分发（交换集合位置被认为是同一种划分方案，因此不会增加划分方案总数）如果N=7，有四种方法能划分集合{1，2，3，4，5，6，7}，每一种分发的子集合各数字和是相等的:{1,6,7} and {2,3,4,5} {注1+6+7=2+3+4+5}{2,5,7} and {1,3,4,6}{3,4,7} and {1,2,5,6}{1,2,4,7} and {3,5,6}给出N，你的程序应该输出划分方案总数，如果不存在这样的划分方案，则输出0。

程序不能预存结果直接输出。

PROGRAM NAME: subsetINPUT FORMAT输入文件只有一行，且只有一个整数NSAMPLE INPUT (file subset.in)7OUTPUT FORMAT输出划分方案总数，如果不存在则输出0。

SAMPLE OUTPUT (file subset.out)4参考程序如下：#include <fstream>using namespace std;const unsigned int MAX_SUM = 1024;int n;unsigned long long int dyn[MAX_SUM];ifstream fin ("subset.in");ofstream fout ("subset.out");int main() {fin >> n;fin.close();int s = n*(n+1);if (s % 4) {fout << 0 << endl;fout.close ();return ;}s /= 4;int i, j;dyn [0] = 1;for (i = 1; i <= n; i++)for (j = s; j >= i; j--)dyn[j] += dyn[j-i];fout << (dyn[s]/2) << endl;fout.close();return 0;}USACO 2.3 Longest Prefix题目如下：在生物学中，一些生物的结构是用包含其要素的大写字母序列来表示的。

第六章动态规划习题课

* u5 s5
max {3u4 5s4 8[0.7u4 0.9( s4 u4 )]} max {1.4u4 12.2s4 } 13.6s4
0 u4 s4 0 u4 s4
* u4 s4
f 3 ( s3 ) max {8u3 5( s3 u3 ) 13.6s4 }
0 u1 s1
f 3 ( s3 ) max {8u3 5( s3 u3 ) 13.6s4 } 900 s3 810 s4 567 s5 397 s6 278 s1 1000 0s2u3s3 max {3u3 5s3 13.6[0.7u3 0.9( s3 u3 )]} * * * * 0* 3 s3 u u1 0 u2 0 u3 810 u4 567 u5 397 * max {0.28u3 17.24s3 } 17.52s3 u3 s3 0 .6912 f1 ( s1 ) 23u3 s3 1000 236912 .
1 4 2 6 3 11 4 12 5 12
0 1 2 2 1,2 2
f(s3)
f1 ( s1 ) max { p1 ( x1 ) f 2 ( s2 )} max { p1 ( x1 ) f 2 ( s1 x1 )}
0 x1 s1 0 x1 s1
其计算如下表：
x1
s1
（ } k f（sk ) max { gk ( xk ) f k 1 sk xk） 0 x k s k k n, n 1,,2,1 f n1 ( sn1 ) 0
例1 某部门拟建某种高效设备五台分配给所属的甲、乙、丙三个工厂，各工厂获得这种设备后，可以提供的盈利如下表，问应如何分配，才能使总盈利最大？

动态规划习题完整版

动态规划习题Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】动态规划专题分类视图数轴动规题：题1.2001年普及组第4题--装箱问题【问题描述】有一个箱子容量为V(正整数,0≤V≤20000),同时有n个物品(0<n≤30),每个物品有一个体积（正整数）。

要求从n个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。

【输入格式】输入文件box.in有若干行。

第一行：一个整数，表示箱子容量V；第二行：一个整数，表示物品个数n；接下来n行，分别表示这n个物品的各自体积。

【输出格式】输出文件box.out只有一行数据，该行只有一个数，表示最小的箱子剩余空间。

【输入样例】2468312797【输出样例】题2.1996年提高组第4题--砝码秤重__数据加强版【问题描述】设有n种砝码,第k种砝码有Ck 个,每个重量均为Wk,求：用这些砝码能秤出的不同重量的个数，但不包括一个砝码也不用的情况。

【输入格式】输入文件weight.in的第一行只有一个数n,表示不同的砝码的种类数.第2行至第n+1行,每行有两个整数.第k+1行的两个数分别表示第k种砝码的个数和重量.【输出格式】输出文件weight.out中只有一行数据:Total=N。

表示用这些砝码能秤出的不同重量数。

【输入样例】22223【输出样例】Total=8【样例说明】重量2,3,4,5,6,7,8,10都能秤得【数据限制】对于100%的数据,砝码的种类n满足:1≤n≤100;对于30%的数据,砝码的总数量C满足:1≤C≤20;对于100%的数据,砝码的总数量C满足:1≤C≤100;对于所有的数据,砝码的总重量W满足:1≤W≤400000;题3.石子归并-szgb.pas【问题描述】有一堆石头质量分别为W1,W2,…,Wn.(Wi≤10000),将石头合并为两堆,使两堆质量的差最小。

【输入】输入文件szgb.in的第一行只有一个整数n(1≤n≤50),表示有n堆石子。

动态规划练习题

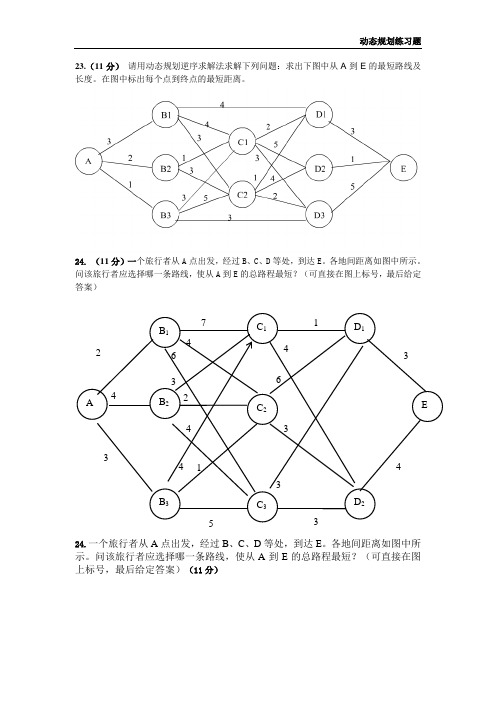
23.（11分）请用动态规划逆序求解法求解下列问题：求出下图中从A到E的最短路线及长度。

在图中标出每个点到终点的最短距离。

24. （11分）一个旅行者从A点出发，经过B、C、D等处，到达E。

各地间距离如图中所示。

问该旅行者应选择哪一条路线，使从A到E的总路程最短？（可直接在图上标号，最后给定答案）
24.一个旅行者从A点出发，经过B、C、D等处，到达E。

各地间距离如图中所示。

问该旅行者应选择哪一条路线，使从A到E的总路程最短？（可直接在图上标号，最后给定答案）（11分）
解：此为动态规划之“最短路问题”，可用逆向追踪“图上标号法”解决如下：
最佳策略为：A →B 2→C 1→D 1→E 或A →B 3→C 1→D 1→E 此时从A 到E 的总路程的最短距离都是11
23. 请用动态规划逆序求解法求解下列问题：
各点标号依次为：A:8, B1：7，B2:6, B3:8, C1：5， C2：4，D1：3，D2：1，D3：5.
25. 某厂生产C B A ,,三种产品，其所需劳动力、材料等有关数据见下表。

要求：建立模型，并用单纯形法计算，确定获利最大的产品生产计划。

解：（1）设C B A ,,
各生产321,,x x x 件。

有
32143min x x x z ++=
st.⎪⎩⎪
⎨⎧=≥≤++≤++)3,2,1(,03054345
536321321j x x x x x x x j
（4分）
获利最大的生产计划是C B A ,,各生产5件、0件、3件，最大利润为273453=⨯+⨯=z 元。

（15分）。

动态规划习题答案

2.某公司有资金4百万元向A,B和C3个项目追加投资，各个项目可以有不同的投资额（百万元计），相应的效益如表所示。

问怎样分配资金，使总效益值最大？##表8－47W k (X k)投资额（项目k#012341#（A）－414860662#（B ）40425060－3#（C）－64687884解：设S1－A,B,C项目的总投资额，S2－B、C项目的总投资额S3－C项目的投资额；X k－k项目的投资额；（X1－A项目的投资额，X2－B项目的投资额，X3－C项目的投资额）W k（S k,X k）－对K项目投资X k后的收益：W k（S k,X k）＝W k (X k)T k (S k,X k)－S k+1=S k-X kf k (S k)－当K至第3项目允许的投资额为S k时所能获得的最大收益。

为获得最大利润，必须将4百万全部投资，假设有4阶段存在，有S4＝0，建立递归方程f4 (S k)=0f k (S k)=max{ W k (X k)+f k +1(S k+1)} k=3,2,1X k∈D k(S k)第一步，K=3f4(S4)=0f3 (S3)=max{W3 (X3)+f4 (S4)}X3∈D3(S3)S4=S3-X3S3f3 (S3)X3* 1641268237834844第二步：K=2 f2 (S2)=max{W2 (X2)+f3 (S3)}X2∈D2(S2)S3=S2-X2W2 (X2)+f3 (S2-X2)S2X2 =0X2 =1X2 =2X2 =3f2 (S2)X2 * 140+64－－－1040 240+6842+64－－1080 340+7842+6850+64－1180 440+8442+7850+6860+641240，3第三步：K=1 f1 (S1) =max {W1 (X1)+ f2 (S2)}X1∈D1(S1)S2= S1- X1W1 (X1)+ f2 (S1- X1)S1X1=0X1=1X1=2X1=3f1 (S1)X1 * 4－41+118 48+10860+1041643S1=4 →S2=1 →S3=1↓↓↓X1*=3 X2*=0 X3*=1A投资3百万，B不投资C投资1百万。

动态规划练习解答

Var a:array[1..1000000] of longint; c,p:array[1..100] of longint; k,n,tmp,s,min,i:longint; begin assign(input,'panda.in'); assign(output,'panda.out'); reset(input); rewrite(output); readln(k, n); inc(n); for i:=1 to k do read(c[i]); i-1; end; for i:=1 to n do if k[i]>0 then writeln(i,' ',k[i]); close(input); close(output); end.
2、最小乘车费用（work.pas）、最小乘车费用（）假设某条街上每一公里就有一个公共汽车站，假设某条街上每一公里就有一个公共汽车站，并且乘车费用如下表：且乘车费用如下表：
For i:=1 to 10 do read(a[i]); readln(n); fillchar(b,sizeof(b),0); for i:=1 to n do begin max:=maxlongint; for j:=1 to 10 do if (i-j>=0) and (a[j]+b[i-j]<max) then max:=a[j]+b[i-j]; b[i]:=max; end; writeln(b[n]); close(input); close(output); end.
输入：输入：panda.in 行有2个数代表质因数的个数，代表那个宇宙系数第1行有个数行有个数n,k,n代表质因数的个数，k代表那个宇宙系数代表质因数的个数（1<=n<=100,1<=k<=1e5））行有n个数个质因数。（每个均小于1000，且第2行有个数，代表这个质因数。（每个均小于行有个数，代表这n个质因数。（每个均小于，不相同）不相同）输出：输出：panda.out 个质因数的数中第k小的数仅1行，即至多只包含这个质因数的数中第小的数。行即至多只包含这n个质因数的数中第小的数。这个数不会超过2e9）（这个数不会超过）输入样例 27 35 输出样例 45（前6个分别是个分别是3,5,9,15,25,27）（个分别是）

动态规划习题集全

动态规划专题训练护卫队【问题描述】护卫车队在一条单行的街道前排成一队，前面河上是一座单行的桥。

因为街道是一条单行道，所以任何车辆都不能超车。

桥能承受一个给定的最大承载量。

为了控制桥上的交通，桥两边各站一个指挥员。

护卫车队被分成几个组，每组中的车辆都能同时通过该桥。

当一组车队到达了桥的另一端，该端的指挥员就用电话通知另一端的指挥员，这样下一组车队才能开始通过该桥。

每辆车的重量是已知的。

任何一组车队的重量之和不能超过桥的最大承重量。

被分在同一组的每一辆车都以其最快的速度通过该桥。

一组车队通过该桥的时间是用该车队中速度最慢的车通过该桥所需的时间来表示的。

问题要求计算出全部护卫车队通过该桥所需的最短时间值。

【输入格式】输入文件中的第一行包含三个正整数（用空格隔开），第一个整数表示该桥所能承受的最大载重量（用吨表示），第二个整数表示该桥的长度（用千米表示），第三个整数表示该护卫队中车辆的总数（n<1000）。

接下来的几行中，每行包含两个正整数W和S（用空格隔开），W表示该车的重量（用吨表示），S表示该车过桥能达到的最快速度（用千米/小时表示）。

车子的重量和速度是按车子排队等候时的顺序给出的。

【输出格式】输出文件中应该是一个实数，四舍五入精确到小数点后1位，表示整个护卫车队通过该桥所需的最短时间（用分钟表示）。

【输入输出样例】输入：100 5 1040 2550 2050 2070 1012 509 7049 3038 2527 5019 70输入：75.0DOLLARS【问题描述】在以后的若干天里戴维将学习美元与德国马克的汇率。

编写程序帮助戴维何时应买或卖马克或美元，使他从100美元开始，最后能获得最高可能的价值。

【输入格式】输入文件中的第一行是一个自然数N（1<=N<=100），表示戴维学习汇率的天数。

接下来的N行中每行是一个自然数A（1<=A<=1000）。

第i+1行的A表示预先知道的第i+1天的平均汇率，在这一天中，戴维既能用100美元买A马克也能用A马克购买100美元。

动态规划讲解大全(含例题及答案)

动态规划算法的应用
一、动态规划的概念
近年来，涉及动态规划的各种竞赛题越来越多，每一年的 NOI 几乎都至少有一道题目需要用动态规划的方法来解决；而竞赛对选手运用动态规划知识的要求也越来越高，已经不再停留于简单的递推和建模上了。
要了解动态规划的概念，首先要知道什么是多阶段决策问题。 1. 多阶段决策问题如果一类活动过程可以分为若干个互相联系的阶段，在每一个阶段都需作出决策(采取措施)，一个阶段的决策确定以后，常常影响到下一个阶段的决策，从而就完全确定了一个过程的活动路线，则称它为多阶段决策问题。各个阶段的决策构成一个决策序列，称为一个策略。每一个阶段都有若干个决策可供选择，因而就有许多策略供我们选取，对应于一个策略可以确定活动的效果，这个效果可以用数量来确定。策略不同，效果也不同，多阶段决策问题，就是要在可以选择的那些策略中间，选取一个最优策略，使在预定的标准下达到最好的效果. 2．动态规划问题中的术语阶段：把所给求解问题的过程恰当地分成若干个相互联系的阶段，以便于求解，过程不同，阶段数就可能不同．描述阶段的变量称为阶段变量。在多数情况下，阶段变量是离散的，用 k 表示。此外，也有阶段变量是连续的情形。如果过程可以在任何时刻作出决策，且在任意两个不同的时刻之间允许有无穷多个决策时，阶段变量就是连续的。
解决方法：
我们尝试从正面的思路去分析问题，如上例，不难得出一个非常简单的递归过程 : f1:=f(i-1,j+1); f2:=f(i-1,j); if f1>f2 then f:=f1+a[i,j] else f:=f2+a[i,j]; 显而易见，这个算法就是最简单的搜索算法。时间复杂度为 2n，明显是会超时的。分析一下搜索的过程，实际上，很多调用都是不必要的，也就是把产生过的最优状态，又产生了一次。为了避免浪费，很显然，我们存放一个 opt 数组：Opt[i, j] - 每产生一个 f(i, j)，将 f(i, j)的值放入 opt 中，以后再次调用到 f(i, j)的时候，直接从 opt[i, j]来取就可以了。于是动态规划的状态转移方程被直观地表示出来了，这样节省了思维的难度，减少了编程的技巧，而运行时间只是相差常数的复杂度，避免了动态规划状态转移先后的问题，而且在相当多的情况下，递归算法能更好地避免浪费，在比赛中是非常实用的.

第3章-动态规划-习题

租用游艇问题
长江游艇俱乐部在长江上设置了n 个游艇出租站1，，，长江游艇俱乐部在长江上设置了个游艇出租站，2，…， n。游客可在这些游艇出租站租用游艇，并在下游的任何。游客可在这些游艇出租站租用游艇，一个游艇出租站归还游艇。游艇出租站i 到游艇出租站j 一个游艇出租站归还游艇。游艇出租站到游艇出租站之间的租金为r(i,j),1≤i<j≤n。试设计一个算法，计算出从游间的租金为。试设计一个算法，艇出租站1 到游艇出租站n 所需的最少租金。艇出租站到游艇出租站所需的最少租金。编程任务：编程任务：对于给定的游艇出租站i 到游艇出租站j 对于给定的游艇出租站到游艇出租站之间的租金为 r(i,j),1≤i<j≤n，编程计算从游艇出租站到游艇出租站所，编程计算从游艇出租站1 到游艇出租站n所需的最少租金。需的最少租金。
10
编辑距离问题
a f x p i u
长度：长度：n
m
长度：长度：m
b
x
w
r
s
d
1
2
3
4
5
删除一个字符：删除一个字符：插入一个字符：插入一个字符：将一个字符改为另一个字符：将一个字符改为另一个字符：
y z
del (δ)
11
编辑距离问题
char a[100],b[100]; scanf("%s%s", a, b); x w r int m = strlen(a); i d[1] d[2] d[3] int n = strlen(b); f 1 1 2 3 int d[101]; int i, j; x 2 1 2 3 for (i=1; i<=n; i++) d[i] = i; p 3 2 2 3 for (i=1; i<=m; i++) { i 4 3 3 3 int y = i-1; for (j=1; j<=n; j++) { u 5 4 4 4 int x = y; m 6 5 5 5 y = d[j]; int z = j>1?d[j-1]:i; int del = a[i-1]==b[j-1]?0:1; d[j] = min(x+del, y+1, z+1); } 删除一个字符： y 删除一个字符： } 插入一个字符： z 插入一个字符： printf("%d\n",d[n]); 将一个字符改为另一个字符：将一个字符改为另一个字符： del (δ) 12 s d[4] 4 4 4 4 4 5

动态规划习题课

练习1：某厂生产三种产品，多种产品重量与利润旳关系如表所示。现将此三种产品运往市场出售，运送能力总重量不超出 6 吨，问怎样安排运送，使总利润最大？
种类
123
重量（吨/公斤）
234
单件利润（元） 80 130 180
最优方案：X1 =（0.2.0）X2 =（1.0.1） Z=260
例4 投资问题
w2(5,3)+f3(2) w2(5,2)+f3(3) =max
12+8 10+11
=21
w2(5,1)+f3(4)
5+15
当k=1时，有s1=5 D1(s1)={0,1,2,3,4}
w1(5,4)+f2(1)
12+4
w1(5,3)+f2(2)
10+9
f1(5)=max w1(5,2)+f2(3) =max 6+14 =21
可提高成绩 aij , (i, j 1,2,3,4) 。用动态规划方法求使其成绩提高最多的复习天数安排计划。要求写出问题的阶段变量，状态变量，决策变量，阶段指标函数，基本方程（递推公式）。
max
0x3x整3 数 a53
12 x3 f2 (5 5 x3 )
＝max
0
x3
5 5
12 x3 f2 (5 5 x3 )
x3整数
＝max x3＝0，1
12 x3
f2(5 5x3 )
＝max0 f2 (5),
12 f2 (0)
( x3 0)
( x3 1)
f2(5)
w1(5,1)+f2(4)
3+18
w1(5,0)+f2(5)

动态规划专项练习（1）

动态规划专项练习（1）动态规划专项练习(1)1、警卫安排（security.pas/c/cpp）一个重要的基地被分为n个连通的区域。

出于某种神秘的原因，这些区域以一个区域为核心，呈一颗树形分布。

在每个区域安排警卫所需要的费用是不同的，而每个区域的警卫都可以望见其相邻的区域，只要一个区域被一个警卫望见或者是安排有警卫，这个区域就是安全的。

你的任务是：在确保所有区域都是安全的情况下，找到安排警卫的最小费用。

输入数据第一行n，表示树中结点的数目。

接下来的n行描述了n个区域的信息，每一行包含的整数依次为：区域的标号i(0<i<=n)，在区域i安排警卫的费用k，区域i的子结点数目m，接下来m个数为区域i p="" 的子结点编号。

<=""> 输出数据一行一个整数，为最小的安排费用。

样例输入:security.in61 30 323 42 16 2 5 63 5 04 4 05 11 06 5 0输出security.out25数据范围对于所有的数据，0<n<=720。

< p="">2、最长上升子序列（LIS.pas/c/cpp）LIS问题是最经典的动态规划基础问题之一。

如果要求一个满足一定条件的最长上升子序列，你还能解决吗？给出一个长度为N整数序列，请求出它的包含第K个元素的最长上升子序列。

例如：对于长度为6的序列<2,7,3,4,8,5>，它的最长上升子序列为<2,3,4,5>，但如果限制一定要包含第2个元素，那么满足此要求的最长上升子序列就只能是<2,7,8>了。

输入数据第一行为两个整数N,K，如上所述。

接下来是N个整数，描述一个序列。

输出数据请输出一个整数，即包含第K个元素的最长上升子序列长度。

样例输入8 665 158 170 299 300 155 207 389输出4数据范围对于所有的数据，满足0<n<=200000，0<k<=n< p="">3、最短回文串（palindrome.pas/c/cpp）如果一个字符串正过来读和倒过来读是一样的，那么这个字符串就被称作回文串。

动态规划习题课共32页

谢谢！
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯力做你应该做的事吧。——美华纳
动态规划习题课
11、获得的成功越大，就越令人高兴。野心是使人勤奋的原因，节制使人枯萎。 12、不问收获，只问耕耘。如同种树，先有根茎，再有枝叶，尔后花实，好好劳动，不要想太多，那样只会使人胆孝懒惰，因为不实践，甚至不接触社会，难道你是野人。(名言网) 13、不怕，不悔(虽然只有四个字，但常看常新。 14、我在心里默默地为每一个人祝福。我爱自己，我用清洁与节制来珍惜我的身体，我用智慧和知识充实我的头脑。 15、这世上的一切都借希望而完成。农夫不会播下一粒玉米，如果他不曾希望它长成种籽；单身汉不会娶妻，如果他不曾希望有小孩；商人或手艺人不会工作，如果他不曾希望因此而有收益。-- 马钉路德。
40、学而不思则罔，思而不学则殆。——孔子

动态规划习题

第七章动态规划规划问题的最终目的就是确定各决策变量的取值，以使目标函数达到极大或极小。

在线性规划和非线性规划中，决策变量都是以集合的形式被一次性处理的；然而，有时我们也会面对决策变量需分期、分批处理的多阶段决策问题。

所谓多阶段决策问题是指这样一类活动过程：它可以分解为若干个互相联系的阶段，在每一阶段分别对应着一组可供选取的决策集合；即构成过程的每个阶段都需要进行一次决策的决策问题。

将各个阶段的决策综合起来构成一个决策序列，称为一个策略。

显然，由于各个阶段选取的决策不同，对应整个过程可以有一系列不同的策略。

当过程采取某个具体策略时，相应可以得到一个确定的效果，采取不同的策略，就会得到不同的效果。

多阶段的决策问题，就是要在所有可能采取的策略中选取一个最优的策略，以便得到最佳的效果。

动态规划（dynamic programming）同前面介绍过的各种优化方法不同，它不是一种算法，而是考察问题的一种途径。

动态规划是一种求解多阶段决策问题的系统技术，可以说它横跨整个规划领域（线性规划和非线性规划）。

当然，由于动态规划不是一种特定的算法，因而它不象线性规划那样有一个标准的数学表达式和明确定义的一组规则，动态规划必须对具体问题进行具体的分析处理。

在多阶段决策问题中，有些问题对阶段的划分具有明显的时序性，动态规划的“动态”二字也由此而得名。

动态规划的主要创始人是美国数学家贝尔曼（Bellman）。

20世纪40年代末50年代初，当时在兰德公司（Rand Corporation）从事研究工作的贝尔曼首先提出了动态规划的概念。

1957年贝尔曼发表了数篇研究论文，并出版了他的第一部著作《动态规划》。

该著作成为了当时唯一的进一步研究和应用动态规划的理论源泉。

1961年贝尔曼出版了他的第二部著作，并于1962年同杜瑞佛思（Dreyfus）合作出版了第三部著作。

在贝尔曼及其助手们致力于发展和推广这一技术的同时，其他一些学者也对动态规划的发展做出了重大的贡献，其中最值得一提的是爱尔思（Aris）和梅特顿（Mitten）。

动态规划入门练习题

动态规划入门练习题一些动态规划的入门练习题，难度不大，适合初学者练习，以便掌握动态规划这个高效算法。

欢迎您将以下各题的解答投稿至本站：drs@，标题中请包含“drs”字样。

石子合并在一个圆形操场的四周摆放着N堆石子(N<= 100),现要将石子有次序地合并成一堆.规定每次只能选取相邻的两堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分.编一程序,由文件读入堆栈数N及每堆栈的石子数(<=20).(!)选择一种合并石子的方案,使用权得做N－1次合并,得分的总和最小;(2)选择一种合并石子的方案,使用权得做N－1次合并,得分的总和最小;输入数据:第一行为石子堆数N;第二行为每堆的石子数,每两个数之间用一个空格分隔.输出数据:从第一至第N行为得分最小的合并方案.第N+1行是空行.从第N+2行到第2N+1行是得分最大合并方案.每种合并方案用N行表示,其中第i行(1<=i<=N)表示第i次合并前各堆的石子数(依顺时针次序输出,哪一堆先输出均可).要求将待合并的两堆石子数以相应的负数表示. 输入输出范例:输入:44 5 9 4输出:－４５９－４－８－５９－１３－９２２４－５－９４４－１４－４－４－１８２２最小代价子母树设有一排数，共ｎ个，例如：22 14 7 13 26 15 11.任意2个相邻的数可以进行归并,归并的代价为该两个数的和,经过不断的归并,最后归为一堆,而全部归并代价的和称为总代价,给出一种归并算法,使总代价为最小.输入、输出数据格式与“石子合并”相同。

输入样例：412 5 16 4输出样例：－１２－５１６４１７－１６－４－１７－２０３７背包问题设有ｎ种物品，每种物品有一个重量及一个价值。

但每种物品的数量是无限的，同时有一个背包，最大载重量为ＸＫ，今从ｎ种物品中选取若干件（同一种物品可以多次选取），使其重量的和小于等于ＸＫ，而价值的和为最大。

输入数据：第一行两个数：物品总数Ｎ，背包载重量ＸＫ；两个数用空格分隔；第二行N个数,为Ｎ种物品重量；两个数用空格分隔；第三行N个数,为N种物品价值; 两个数用空格分隔；输出数据：第一行总价值；以下N行，每行两个数，分别为选取物品的编号及数量；输入样例：4 102 3 4 71 3 5 9输出样例：122 14 1商店购物某商店中每种商品都有一个价格。

动态规划练习题

最小乘车费用 (bus)【问题描述】而任意一辆汽车从不行驶超过1 0公里。

某人想乘车到达n公里远的地方，假设他可以任意次换车，请你帮他找到一种乘车方案，使得总费用最小。

注意：1 0公里的费用比1公里小的情况是允许的。

【输入文件】共两行：第一行为1 0个不超过200的整数，依次表示行驶1～1 0公里的费用，相邻两数间用一个空格隔开：第二行为某人想要乘车的公里数(不超过20000的整数)。

【输出文件】仅一行，包含一个整数，表示到达n公里所需要的最小费用。

【样例输入】12 21 31 40 49 58 69 79 90 10115【样例输出】147船 (ships)【问题描述】PALMIA国家被一条河流分成南北两岸，南北两岸上各有N个村庄。

北岸的每一个村庄有一个唯一的朋友在南岸，且他们的朋友村庄彼此不同。

每一对朋友村庄想要一条船来连接他们，他们向政府提出申请以获得批准。

由于河面上常常有雾，政府决定禁止船只航线相交（如果相交，则很可能导致碰船）。

你的任务是编写一个程序，帮助政府官员决定批准哪些船只航线，使得不相交的航线数目最大。

【输入文件】ships.in输入文件由几组数据组成。

每组数据的第一行有2个整数X，Y，中间有一个空格隔开，X代表PALMIA河的长度（10<=X<=6000），Y代表河的宽度（10<=Y<=100）。

第二行包含整数N，表示分别坐落在南北两岸上的村庄的数目（1<=N<=5000）。

在接下来的N行中，每一行有两个非负整数C，D，由一个空格隔开，分别表示这一对朋友村庄沿河岸与PALMIA 河最西边界的距离（C代表北岸的村庄，D代表南岸的村庄），不存在同岸又同位置的村庄。

最后一组数据的下面仅有一行，是两个0，也被一空格隔开。

【输出文件】ships.out对输入文件的每一组数据，输出文件应在连续的行中表示出最大可能满足上述条件的航线的数目。

【输入样例】30 4722 42 610 315 129 817 174 20 0【输出样例】4DOLLARS (dollars)【问题描述】在以后的若干天里戴维将学习美元与德国马克的汇率。

优选动态规划习题课

动态规划例题讲解精品PPT课件

动态规划练习例题

动态规划练习题及解答1

动态规划练习题(含答案)

第六章 动态规划习题课

动态规划习题完整版

动态规划 练习题

动态规划习题答案

动态规划练习解答

动态规划习题集全

动态规划讲解大全(含例题及答案)

第3章-动态规划-习题

动态规划习题课

动态规划专项练习（1）

动态规划习题课共32页

动态规划习题

动态规划入门练习题

动态规划练习题

第六章动态规划习题课

动态规划练习题