余弦函数的图像与性质PPT
合集下载
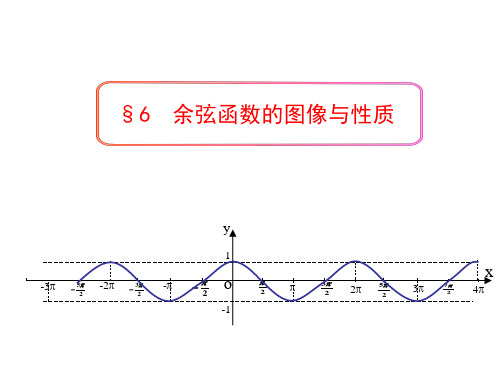
余弦函数的图像与性质
[ 2 2k, 2 2k ](k z),单调递增 [(2k 1),2k ](k z),单调递增 [ 2 2k,3 2 2k ](k z),单调递减 [2k , (2k 1) ](k z),单调递减
函数y=cosx有对称性吗?
y
1
-3 5 -2 3
2
2
-
o 2
2
-1
3
2
2
5 2
§6 余弦函数的图像与性质
y
1
-3 5 -2 3
2
2
-
o 2
-1
2
3
2
2
5 2
x
3
7 2
4
1.会用“五点法”作余弦函数的图像. 2.掌握余弦函数y=cosx的图像和性质. 3.会应用余弦函数y=cosx的图像与性质解决一些简单问题.
利用变换法作余弦函数的图
像
y
余弦曲线
1
6
4
2
o
-1
3
2
2
5 2
x
3
7 2
4
例2:比较 cos 5 和 cos( 7 ) 大小
y
4
5
1-
-
-1
o
6
2
3
2 3
5
7
6
6
4 3
3 2
5 3
11 6
2
x
-1 -
cos 5 cos( 7 )
4
5
对于实数范围内的x,分别写出满足sinx=cosx, sinx>cosx, sinx<cosx的x的集合.
x
3
7 2
4
对称轴方程x=k(k∈Z) 对称中心为(k+/2,0)(k∈Z)
余弦函数和正切函数的图像及性质课件

π 2π 3π 4π 5π 6π
-4π
-3π
-2π
-π
o-1Biblioteka 余弦函数的单调性y
1
-3π
5π 2
-2π
3π 2
-π
π
2
o
-1
π
2
π
3π 2
2π
5π 2
3π
7π 2
4π
x
y=cosx (x∈R) ∈ π π ∈ 增区间为 [ π +2kπ, 2kπ],k∈Z π π ∈ 减区间为 [2kπ, 2kπ + π], k∈Z , 其值从-1增至 其值从 增至1 增至 减至-1 其值从 1减至 减至
π
x= 2kπ时 ymax=1 x= 2kπ+ π时 ymin=-1 周期为T=2π 偶
π
在x∈[2kπ, 2kπ+ π ] 上都是增函数 , 在x∈[2kπ- π , 2kπ ] 上都是减函数 。 (kπ+ π ,0) 2
对称中心 对称轴
π
2
x = kπ
正切函数的图像和性质
回忆: 回忆:怎样利用单位圆中的正弦线作出 图像的? y = sin x 图像的?
一、y=sinx 与 y=cosx 的性质
函 数 y= sinx 性质
(k∈z) ∈
y= cosx x∈ R [-1,1]
(k∈z) ∈
定义域 值域 最值及相应的 x 的集合 周期性 奇偶性 单调性
x∈ R [-1,1] x= 2kπ+ 2 时 ymax=1 x=2kπ- π 时 ymin=-1 2 周期为T=2π 奇 在x∈[2kπ- π, 2kπ+ ]2上 2 都是增函数 , 在 π 3 x∈[2kπ+ ,2kπ+ ]上π 2 2 都是减函数. (kπ,0) x = kπ+
-4π
-3π
-2π
-π
o-1Biblioteka 余弦函数的单调性y
1
-3π
5π 2
-2π
3π 2
-π
π
2
o
-1
π
2
π
3π 2
2π
5π 2
3π
7π 2
4π
x
y=cosx (x∈R) ∈ π π ∈ 增区间为 [ π +2kπ, 2kπ],k∈Z π π ∈ 减区间为 [2kπ, 2kπ + π], k∈Z , 其值从-1增至 其值从 增至1 增至 减至-1 其值从 1减至 减至
π
x= 2kπ时 ymax=1 x= 2kπ+ π时 ymin=-1 周期为T=2π 偶
π
在x∈[2kπ, 2kπ+ π ] 上都是增函数 , 在x∈[2kπ- π , 2kπ ] 上都是减函数 。 (kπ+ π ,0) 2
对称中心 对称轴
π
2
x = kπ
正切函数的图像和性质
回忆: 回忆:怎样利用单位圆中的正弦线作出 图像的? y = sin x 图像的?
一、y=sinx 与 y=cosx 的性质
函 数 y= sinx 性质
(k∈z) ∈
y= cosx x∈ R [-1,1]
(k∈z) ∈
定义域 值域 最值及相应的 x 的集合 周期性 奇偶性 单调性
x∈ R [-1,1] x= 2kπ+ 2 时 ymax=1 x=2kπ- π 时 ymin=-1 2 周期为T=2π 奇 在x∈[2kπ- π, 2kπ+ ]2上 2 都是增函数 , 在 π 3 x∈[2kπ+ ,2kπ+ ]上π 2 2 都是减函数. (kπ,0) x = kπ+
【高职数学课件】余弦函数的图像与性质

\ cos 5 < cos 7
4
5
(2) c os( 23 ) c os 23 c os 3 ,
5
5
5
c os( 17 ) c os17 c os ,
4
4
4
又 0 < < 3 < , 且函数y c os x在[0, ]上是减函数,
45
\ c os 3 < c os .
5
4
即c os( 23 ) < c os( 17 )
3.知识理解方面: (1)、用五点法做余弦函数图像时五个关键点的确
定; (2)、函数定义域一定要写成集合或区间的形式; (3)、单调性的确定要注意说法步骤。
[-1,1]
问题五:单调性
观察余弦曲线,余弦函数在哪些区间上是增函数?在哪些
区间上是减函数?如何将这些单调区间进行整合?
y y=cosx
2
2
1 22
2
2
x
2
O
2
2
-1
2
2
2
在 [ 2k 上2都k是单 调递增;
在 [2k 2k上都是单调 递减.
问题六:最值
y y=cosx
[2k,(2k 1)]上是减函数
当x
2k
2
时,ymax
1
当x
2k
3
2
时,ymin
1
例题讲解
例1 求下列函数的最大值、最小值和周期T
(1)y=5cosx (2)y 8cos(2x )
4
解 (1) ymax 5, ymin 5,T 2
(2) ymax 8, ymin 8,T
2
2
当堂检测
正弦函数和余弦函数的图像与性质.ppt

, 0), (2 ,1)
2
2
并注意-4 曲线的“凹凸”变化.
课堂练习
1.作函数 y sin x 与 y sin x 1在 [0, 2 ]
上的大致图像. 2.指出1.中各图像与正弦函数图像的位置关系.
3.作函数 y cos x, x [ , ]的大致图像.
4.利用3.解不等式:cos x sin x, x [ , ]
-2
五个关键点:(0, 0), ( ,1), ( , 0), (3 , 1), (2 , 0)
2
2
利用五个关-4键点作简图的方法称为“五点法”
10
三、余弦函数的图像
根据诱导公式
cos
8
x
sin(
x) 可知余弦函数
y
cos
6
x的图像可由
y
2 sin
x
的图像向左平移
2
4
个单位得到.
1
2
2
-10
3-5
0
2
1
-2
余弦函数的值域是[1,1] -4
当且仅当 x 2k , k Z 时, -6
余弦函数取得最大值1;-8
5
2
35
x10
2
yP
OM x
当且仅当 x 2k , k-10 Z 时,
余弦函数取得最小值-1-1.2例1.求下列函数的源自大值与最小值,及取到最值6
课堂练习答案
12
1. y sin x, x [0, 2 ] y4
10
x
0
2
3 2
2
2 8
5
-10
中职数学基础模块上册《余弦函数的图像和性质》ppt课件2

增 2 k 区 ,2 kk 间 Z
减 2 k 区 ,2 kk 间 Z
对称轴: xk,kZ 对称中心:(k,0) kZ
2
典例1:求下列函数的最大值和最小值 以及取得最大,最小值时x的值
(分析)利(用1)余y弦函 值数3域c求ox s1
(换元法)
令 t cx o , ts 1 ,1
y 3 t 1 ,t 1 ,1
对称性
y=sinx xR
y
1
y=cosx xR
y
1
2
0
2
-1
3
2 5 x
2
2
0
2
3
2 5 x
2
2
-1
R
x x 22 y22 kk [((k1k,1 ]Z Z))yym m inax1 1
R
y [1,1]
x2k(k Z)ym ax1
x 2 k(k Z )y m in 1
2
2
奇函数
偶函数
减 增 区 区 对间 间 称 轴 2:2 2 xk2 k,3 22 ,2 k22 k k, k (k (k Z ZZ )) 对称中心: (k,0) kZ
对称中心: (k,0) kZ
化简:sin(x2) c o s x
如何作余弦函数 y=cosx (x∈R) 的图象?
◎平移法:
只需将 ysinx的图象向左平移 个单位即可得到。
2
y ycosx
1
ysinx
正弦曲线
3
2
0
2
3 2
2
3 x 形状一样
1
位置不同
余弦曲线
正弦、余弦函数的图象
y=cosx,x[0, 2]
《余弦函数、正切函数的图像与性质》课件1

,0 2
正切函数y=tanx的主要性质: x | x , 1. 定义域: 2 2.值域:实数集R. 3.周期性:周期是π. 4.奇偶性:由tan(-x)=-tan(x),知正切函 数是奇函数,它的图象关于原点成中心 对称. 5.单调性:正切函数在每一个开区间 , 内都是增函数.
• 小结 1.通过本节学习,应掌握余弦函数 图象的画法.
2.会用“五点法”画出余弦曲线简图. 3.能结合余弦函数图象理解余弦函数的 性质(定义域、值域、周期性、奇偶性、 单调性)
正切函数的图象与性质
• 学习目标 1.理解利用正切线画出正切函数图象 的方法 2.掌握正切函数的图象与性质 3.会画正切函数简图
• 课堂练习二 1.判断下列函数的奇偶性 (1)f(x)=|x|+cosx; (2)f(x)=sinx+cosx; (3)f(x)=cosx|sinx|+sinx|cosx|. 2.已知f(x)是定义在R上的奇函数, 且x>0时, f(x)=sinx+cosx,则在定义域R 上,f(x)=___________. 3.已知函数y=a-bcos3x的最大值为6,最小值为-2, 求a,b的值. 4.求y=cos2x的单调区间. 5.教材56页-4,5.
• 学法指导: 1. 余弦曲线是中心对称图形,其所有的 ,0 对称中心坐标是_____________ ; 2 2.余弦曲线是轴对称图形,其所有的对 x , 称轴方程是_______________. 余弦曲线的对称轴一定是过余弦曲线的 最高点或最低点,此时余弦值为最大值 或最小值.
• 余弦型函数 y Acosx A0, 0的 2 定义域R;值域[-A,A];周期 T . 当 时 y Acos(x ) 为偶函数, 当 2 时y Acos(x )为奇函数; 对称轴由x 求得 x 对称中心横坐标由 x 求得. 2 其单调区间求法与正弦型函数相同。
正切函数y=tanx的主要性质: x | x , 1. 定义域: 2 2.值域:实数集R. 3.周期性:周期是π. 4.奇偶性:由tan(-x)=-tan(x),知正切函 数是奇函数,它的图象关于原点成中心 对称. 5.单调性:正切函数在每一个开区间 , 内都是增函数.
• 小结 1.通过本节学习,应掌握余弦函数 图象的画法.
2.会用“五点法”画出余弦曲线简图. 3.能结合余弦函数图象理解余弦函数的 性质(定义域、值域、周期性、奇偶性、 单调性)
正切函数的图象与性质
• 学习目标 1.理解利用正切线画出正切函数图象 的方法 2.掌握正切函数的图象与性质 3.会画正切函数简图
• 课堂练习二 1.判断下列函数的奇偶性 (1)f(x)=|x|+cosx; (2)f(x)=sinx+cosx; (3)f(x)=cosx|sinx|+sinx|cosx|. 2.已知f(x)是定义在R上的奇函数, 且x>0时, f(x)=sinx+cosx,则在定义域R 上,f(x)=___________. 3.已知函数y=a-bcos3x的最大值为6,最小值为-2, 求a,b的值. 4.求y=cos2x的单调区间. 5.教材56页-4,5.
• 学法指导: 1. 余弦曲线是中心对称图形,其所有的 ,0 对称中心坐标是_____________ ; 2 2.余弦曲线是轴对称图形,其所有的对 x , 称轴方程是_______________. 余弦曲线的对称轴一定是过余弦曲线的 最高点或最低点,此时余弦值为最大值 或最小值.
• 余弦型函数 y Acosx A0, 0的 2 定义域R;值域[-A,A];周期 T . 当 时 y Acos(x ) 为偶函数, 当 2 时y Acos(x )为奇函数; 对称轴由x 求得 x 对称中心横坐标由 x 求得. 2 其单调区间求法与正弦型函数相同。
高中数学第一章三角函数1.6余弦函数的图像与性质课件北师大版必修4

•§6 余弦函数的图像与性质
•学习目标 1.了解余弦函数与正弦函数之间的关系.2. 理解“五点法”作出余弦函数的图像(重点).3.掌握余弦 函数的图像性质及其运用(难点).
知识点 1 余弦函数的图像 余弦函数 y=cos x(x∈R)的图像叫余弦曲线. 根据诱导公式 sinx+π2=cos x,x∈R.只需把正弦函数 y=sin x, x∈R 的图像向左平移π2个单位长度即可得到余弦函数图像(如 图).
• 答案 B
• 3.函数y=cos x,x∈[0,2π]的图像和直线y=1围成 一个封闭的平面图形,这个封闭图形的面积是 ________.
• 解析 如图,可把x轴下方图形补到x轴上方阴影 部分,此时所围面积可变成一个矩形.
• 答案 2π
4.使 cos x=11-+mm有意义的实数 m 的取值范围是________. 解析 -1≤11-+mm≤1;即11+-mm≤1;|1+m|≤|1-m|且 m≠1, 得 m≤0.
答案 D
(2)作出函数 y=1-13cos x 在[-2π,2π]上的图像. 解 ①列表:
x y=cos x
0
π 2
π
3π 2
2π
1 0 -1 0 1
y=1-13cos x
2 3
1
4 3
1
2 3
②作出 y=1-13cos x 在 x∈[0,2π]上的图像.由于该函数为偶函数, 作关于 y 轴对称的图像.从而得出 y=1-13cos x 在 x∈[-2π,2π] 上的图像.
•规律方法 对于余弦函数的性质,要善于结合余弦函 数图像并类比正弦函数的相关性质进行记忆,其解题 规律方法与正弦函数的对应性质解题方法一致.
【训练 2】 (1)求函数 y=1-12cos x 的单调区间; (2)比较 cos-π7与 cos187π的大小. 解 (1)∵-12<0, ∴y=1-12cos x 的单调性与 y=cos x 的单调性相反. ∵y=cos x 的单调增区间是[2kπ-π,2kπ](k∈Z),减区间是[2kπ, 2kπ+π](k∈Z). ∴y=1-12cos x 的单调减区间是[2kπ-π,2kπ](k∈Z),增区间 是[2kπ,2kπ+π](k∈Z).
•学习目标 1.了解余弦函数与正弦函数之间的关系.2. 理解“五点法”作出余弦函数的图像(重点).3.掌握余弦 函数的图像性质及其运用(难点).
知识点 1 余弦函数的图像 余弦函数 y=cos x(x∈R)的图像叫余弦曲线. 根据诱导公式 sinx+π2=cos x,x∈R.只需把正弦函数 y=sin x, x∈R 的图像向左平移π2个单位长度即可得到余弦函数图像(如 图).
• 答案 B
• 3.函数y=cos x,x∈[0,2π]的图像和直线y=1围成 一个封闭的平面图形,这个封闭图形的面积是 ________.
• 解析 如图,可把x轴下方图形补到x轴上方阴影 部分,此时所围面积可变成一个矩形.
• 答案 2π
4.使 cos x=11-+mm有意义的实数 m 的取值范围是________. 解析 -1≤11-+mm≤1;即11+-mm≤1;|1+m|≤|1-m|且 m≠1, 得 m≤0.
答案 D
(2)作出函数 y=1-13cos x 在[-2π,2π]上的图像. 解 ①列表:
x y=cos x
0
π 2
π
3π 2
2π
1 0 -1 0 1
y=1-13cos x
2 3
1
4 3
1
2 3
②作出 y=1-13cos x 在 x∈[0,2π]上的图像.由于该函数为偶函数, 作关于 y 轴对称的图像.从而得出 y=1-13cos x 在 x∈[-2π,2π] 上的图像.
•规律方法 对于余弦函数的性质,要善于结合余弦函 数图像并类比正弦函数的相关性质进行记忆,其解题 规律方法与正弦函数的对应性质解题方法一致.
【训练 2】 (1)求函数 y=1-12cos x 的单调区间; (2)比较 cos-π7与 cos187π的大小. 解 (1)∵-12<0, ∴y=1-12cos x 的单调性与 y=cos x 的单调性相反. ∵y=cos x 的单调增区间是[2kπ-π,2kπ](k∈Z),减区间是[2kπ, 2kπ+π](k∈Z). ∴y=1-12cos x 的单调减区间是[2kπ-π,2kπ](k∈Z),增区间 是[2kπ,2kπ+π](k∈Z).
高一数学正弦函数、余弦函数的图像和性质课件

....
描点法: 查三角函数表得三角函数值,描点 ( x, sin x),连线.
y sin 如: x 3 0.8660 3 查表 ) 描点 ( 3 ,0.8660
y
P
3
y 1 1
O
M
x 0
2
- 3 2
2
-
x
1 -
几何法: 作三角函数线得三角函数值,描点 ( x, sin x) ,连线
-
-
-
-
-
-1
用诱导公式来作余弦函数y=cosx,x∈R的的图像 y= cosx = cos(-x) = sin[
y
2
-(-x)] = sin(x+ 2 )
从图像中我们看到cosx由sinx 向左平移 2 个单位后得到
1
-
4
2
o
-
2
4
x
-
-
因为终边相同的角的三角函数值相同,所以y=cosx的图象在……, 4 ,2 , 2 ,0, 0,2 , 2 ,4 , ……与y=cosx,x∈[0,2π]的图象 形状相同
正弦、余弦函数y=sinx,y=cosx的图象
o x
1-
-
-
-
-
-
6
-
4
2
2
-1 -
4
6
-
4 , 2 因为终边相同的角的三角函数值相同,所以 y=cosx的图象在……, , 2 , 0 , ……与y=cosx,x∈[0,2π ]的图象相同
-
-
-
-
-
-1
想一想
正弦余弦函数的图像性质(周期、对称、奇偶)经典课件25页PPT

新知探究 :
1、正弦函数的单调性 y
1
y
1
2
o
2
o
-1
-1
3
2
2
x x
y=sinx x[0,2]
y
y=sinx xR
-4 -3
-2
1
- o
-1
正弦曲 线
2
3
4
5 6 x
新知探究:
1、正弦函数的单调性
y
-4 -3
-2
- 2
1
o
-1
2
2
3
4
5 6 x
x
2
…
0
…
正 正弦弦函数余.余弦弦函函数的数图象对和称性质性
-
-
-
6
4
2
对称轴:无数条
xk,kZ
2
-
-
-
6
4
2
对称轴:无数条 x=kπ,k∈Z
-
y
正弦 函数 y=sinx的 图象
1-
-
-
-
o - 1-
2
4
6
x
对称中心:无数个
(kπ,0),k∈Z
y
余 弦函 数 y =co sx的 图象
1-
-
-
-
o
复习回顾
一、正弦函数、余弦函数的图像及画法
正弦曲线
y
1-
-
-
6
4
2
o
-1-
2
4
6
x
6
4
余弦曲线
y-
1
2
o-
-1
2
4
6
探索发现
高三数学正弦余弦函数的性质,图像课件

例1: 求函数
3 cos x y 2 cos x
的值域
解法二: ∵ ∴
2y 3 cos x ( y 1) y 1 1 cos x 1
1 2y 3 1且y 1 y 1
∴
4 函数值域为 2 3,
反函数法
练习:
①若 2 ,则 y 2 cos 2
例3: 求方程lg x sin x的实根的个数
在同一坐标系中作出 y lg x和y sin x的图象如下:
y=sinx
数形结合思想
两图象有三个交点,即方程有三个实数根。
练习:
⒈已知 f ( x) 4m sin x cos 2 x( x R) ,
③ 函数
y 1 2 cos x lg(2 sin x 1) 的定义域为
5 2 k , 2 k , k Z 6 3
例 2: 若函数 f ( x) cos 2 x 2a cos x a 2 2a(0 x )的 最 小 值
2
, 知0 cos x 1, 可 得
1 当0 a 2时, f ( x) 最 小 值 为 a 2 2a 1 2解 得 2 a 2 2 , 此 时f ( x)的 最 大 值 为 1 当a 2时 ,f ( x)的 最 小 值 为 a 2 4a 1 2, 解 得a 3 此 时f ( x)的 最 大 值 为 2 a 0时, f ( x)的 最 小 值 a 2 2a 1 2, 解 得a 1, 显 然 不 成 立
y=sinx xR
ห้องสมุดไป่ตู้
y
1
正弦曲 线
3
-4
-3
正余弦函数图像和性质PPT课件

(2)余弦函数“五点作图法”:
y 1 y=cosx
3 2
2
o
2
-1
3 2
Y=sinx 2 5 3 x
2
五个关 键点:
( 0 ,1),
( ,0 ), 2
( , 1), ( 3 , 0 ) , ( 2 ,1)
2
(3)正、余弦函数图象的关系
cosx=sin(x+
2
y=cosx
y
) sinx=cos( -x)=cos(x- )
定义域 值域 周期性 对称性 单调性
性质的应. 用
3
一.基础知识复习
(一)正、余弦函数图象
“五点作图法”
(1)正弦函数“五点作图法”:
y
1
4
3
2
-
3 2
-
-
2
o
2
3 2
2
3
4 x
-1
五个关键点:
( 0 , 0 ) ,(
2
, 1 ) , ( , 0 ) ,( 3
2
, 1)(, 2 , 0 )
正 余弦函数的图象与性质(1)
y
1
ysinx,x[0,2
3p
π
2
2π
O
p
x
2
-1
思考4:观察函数y=sin在[0,2π]内的 图象,其形状、位置、凸向等有何变化 规律?
《正弦函数、余弦函数的图象和性质》的知识框架
正弦线 正弦函数的图象 平移变换 余弦函数的图象
正弦函数的性质 “五点法”作 图
余弦函数的性质
⑤奇偶性:
奇偶性的y1定义y=:sif f n( ( x x x ) ) ( x ff R( ( x x )) ) ff( ( x x ) ) 为 为 偶 奇 函 函 数 数
7.2 余弦函数的图像与性质(课件)-高一数学(沪教版2020必修第二册)

9. 已知函数 = 2cos − ;
3 2
(1)求f(x)的最小正周期T;
(2)求f(x)的单调递增区间.
−
解: 由已知 =
= − , 则 = = .
当 − ≤ − ≤ ∈ ,
即 − ≤ ≤ +
3
点的坐标是 0,1 、 , 0 、 , −1 、
,0 、 2, 1
2
2
2.余弦函数的性质
利用余弦函数 = cos与正弦函数 = 的关系cos = sin +
2
,由正弦函
数的性质就容易推出余弦函数的性质:
(1)余弦函数 = cos是周期函数,2 ∈ , ≠ 0 均是它的周期,而2π是
A.
,1
2
C.(0,1)
B.(π,1)
D.(2π,1)
【答案】B;
【解析】用五点作图法作出函数y=-cos x(x>0)的一个周期的图像如图所示,
由图易知与y轴最近的最高点的坐标为(π,1);
2.函数 y=cos x 与函数 y=-cos x 的图象(
)
A.关于直线 x=1 对称
B.关于原点对称
3.求函数 = 2cos
2
−
6
的最小正周期及单调区间.
解:函数 = 2cos − 的最小正周期为4,
2 6
5
单调增区间为 4 −
,4 +
∈ ,
3
3
7
单调减区间为 4 + ,4 +
课件3:1.3.2 余弦函数、正切函数的图像与性质

(5)单调性:
在开区间 k , k k z 内,函数单调递增。
2
2
例1、比较
tan 13
4
与
tan 17 5
的大小。
解:
tan
13
4
tan
4
tan
17
5
tan
2
5
又 0 2 ,
45
y
tan
x在
0,
2
内单调递增,
tan tan 2 , tan tan 2 ,
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
y
--
-
4 3 2
定义域
值域
周期
奇偶性
单调性
对称轴 对称中心
1
-
o
-1
2
R
34
5 6x
[-1,1]
2
奇函数
单调递增区间:[ 2k , 2k ] (k Z )
2
2
单调递减区间:[ 2k , 3 2k ] (k Z )
34
3 42
2sin(1 x )
34
小结:
所以这个函数的周期为2
1
6
3
一般地,函数 y Acos(x )( x R)(其中A,,
为常数,且 A 0, 0)的周期为 T 2 .
1、知识要点
定义域 值域 周期 奇偶性
R [-1,1]
2
偶函数
单调性 单调递增区间: [2k , 2k ] (k Z ) 单调递减区间: [2k ,2k 2 ] (k Z)
(A) y=tan 1 x
余弦函数图像与性质

的函数图象y ?
-
-
1-
P1
p1/6o1M-源自 1Ao63
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2 2
x
-1 -
作法:
(1) 等分 (2) 作正弦线 (3) 平移 (4) 连线
以上有不当之处,请大家给与批评指正, 谢谢大家!
32
2
正弦曲 线
形状完全一样 只是位置不同
余弦函数的图象
y
余弦曲
-4 -3
-2
(0,11)
3
( 2 ,1)
-
(o2 ,0)
( 2 ,0)
2
3
-1
( ,-1)
线
4
5 6 x
正弦函数的性质
• 我们已经学习了正弦函数的性质,能不能 类比学习余弦函数的性质呢?
1. 定义域 2. 值域 3. 周期性 4. 单调性 5. 奇偶性 6. 对称性
都是这两个函数的周期。
即2k k Z,k 0 是它的周期,
最小正周期为 2
-4 -3
正弦、余弦函数的相同性质
y
1
-2
- o
-1
2
3
4
y=sinx (xR) 定义域 xR
值 域 y[ - 1, 1 ]
y=cosx (xR) 周期性 T = 2
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x 5 6 x
一定义域内的偶函数。
关于y轴对称
cos(-x)= cosx (xR)
y=cosx (xR) 是偶函数
-4 -3
-
-
1-
P1
p1/6o1M-源自 1Ao63
2
2 3
5 6
7 6
4 3
3 2
5 3
11 6
2 2
x
-1 -
作法:
(1) 等分 (2) 作正弦线 (3) 平移 (4) 连线
以上有不当之处,请大家给与批评指正, 谢谢大家!
32
2
正弦曲 线
形状完全一样 只是位置不同
余弦函数的图象
y
余弦曲
-4 -3
-2
(0,11)
3
( 2 ,1)
-
(o2 ,0)
( 2 ,0)
2
3
-1
( ,-1)
线
4
5 6 x
正弦函数的性质
• 我们已经学习了正弦函数的性质,能不能 类比学习余弦函数的性质呢?
1. 定义域 2. 值域 3. 周期性 4. 单调性 5. 奇偶性 6. 对称性
都是这两个函数的周期。
即2k k Z,k 0 是它的周期,
最小正周期为 2
-4 -3
正弦、余弦函数的相同性质
y
1
-2
- o
-1
2
3
4
y=sinx (xR) 定义域 xR
值 域 y[ - 1, 1 ]
y=cosx (xR) 周期性 T = 2
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x 5 6 x
一定义域内的偶函数。
关于y轴对称
cos(-x)= cosx (xR)
y=cosx (xR) 是偶函数
-4 -3
余弦函数的图像和性质PPT

余弦函数的图像及性质
一、余弦函数图像
y=cos x x [0, 2 ]
x
y cos x
y
0
1
2
0
2
1
3 2
2
0 1
3 2
1
0
-1ຫໍສະໝຸດ x 2例1 画出函数[0,2π]上的图像
y=1-cos x
y sin x
x
cosx
y 1 cos x
2 0 2 1 0 -1 0 1 0 1 2 1 0
在x 2k ,2k 上是增函数;
在x 2k , 2k 上是减函数;
例2 求出使下列函数取得最值的x的集合,
并写出最值,定义域和值域
• y=2-3cos x
解: 当x k 2 , k Z时 cosx取得最大值1
此时y 2 3cosx的最小值2-3 = 1
x
3 2
2 1
y
0
2
3 2
2
练习:画出函数[0,2π]上的图像
y=2cos x -3
二、余弦函数y cosx的性质
1、定义域 2、值域 3、周期性 4、最值
5、单调性
y cos x , x R
y 1
2
2
-1
0
3 2
2
4x
y cos x , x R
y 1
2
2
-1
0
3 2
2
4
x
二、正弦函数y cosx的性质
1、定义域 2、值域 3、周期性 4、最值
xR y 1,1
一、余弦函数图像
y=cos x x [0, 2 ]
x
y cos x
y
0
1
2
0
2
1
3 2
2
0 1
3 2
1
0
-1ຫໍສະໝຸດ x 2例1 画出函数[0,2π]上的图像
y=1-cos x
y sin x
x
cosx
y 1 cos x
2 0 2 1 0 -1 0 1 0 1 2 1 0
在x 2k ,2k 上是增函数;
在x 2k , 2k 上是减函数;
例2 求出使下列函数取得最值的x的集合,
并写出最值,定义域和值域
• y=2-3cos x
解: 当x k 2 , k Z时 cosx取得最大值1
此时y 2 3cosx的最小值2-3 = 1
x
3 2
2 1
y
0
2
3 2
2
练习:画出函数[0,2π]上的图像
y=2cos x -3
二、余弦函数y cosx的性质
1、定义域 2、值域 3、周期性 4、最值
5、单调性
y cos x , x R
y 1
2
2
-1
0
3 2
2
4x
y cos x , x R
y 1
2
2
-1
0
3 2
2
4
x
二、正弦函数y cosx的性质
1、定义域 2、值域 3、周期性 4、最值
xR y 1,1
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所以 cos 3<sin 1 < cos 7 .
2
10
4
答案: cos 3<sin 1 < cos 7
2
10
4
类型一 余弦函数的图像及应用 【典例】用“五点法”作函数y=1-cosx(0≤x≤2π)的 简图.
世纪金榜导学号70034021
【审题路线图】用“五点法”作函数y=1-cosx(0≤x≤2π) 的简图⇒根据余弦函数图像的五个关键点列表⇒在坐标 系中描出五个关键点⇒用平滑的曲线连接五个点.
2.比较下列各组数的大小.
(1)-sin46°与cos221°.
2cos( 23 )与cos( 17 ).
5
4
【审题路线图】1.配方法⇒求出最值⇒写出值域. 2.用诱导公式化角在同一单调区间内⇒利用正(余)弦函 数单调性⇒写出答案.
【解析】1.y (cos x 1 )2 1 .
24
因为-1≤cosx≤1,
所以当cosx=1
2
时,ymax=
1 4
.
当cosx=-1时,ymin=-2.
所以函数y=-cos2x+cosx的值域是[2,1 ].
4
答案: [2,1]
4
2.(1)-sin46°=-cos44°=cos136°, cos221°=-cos41°=cos139°. 因为180°>139°>136°>0°, 所以cos139°<cos136°,即-sin46°>cos221°.
【解析】列表:
x cosx
0
π 3
2π
2
2
1
0
-1
0
1
1-cosx
01
2
1
0
描点并用光滑的曲线连接起来,如图所示.
【方法技巧】“五点法”画函数图像的三个步骤
【变式训练】(2017·新余高一检测)用“五点法”作 函数y=2cosx+1,x∈[0,2π]的简图.
【解析】因为x∈[0,2π],
所以令x=0, ,π, ,23π,列表得:
提醒: (1)正、余弦函数取得最值时自变量的取值易混. (2)正、余弦函数的单调区间易混.
【自我检测】 1.对于余弦函数y=cosx的图像,有以下描述: ①向左、向右无限伸展;②与y=sinx的形状完全一样, 只是位置不同;③与x轴有无数个交点;④关于y轴对称. 其中描述正确的是________.
偶函数 当x=2kπ(k∈Z)时取 最大值; 当x=2kπ+π(k∈Z)时 取最小值
y=sinx
性质
在 [2k ,2k ]
2
2
(k∈Z)上是增加的;
在[2k ,2k 3]
2
2(k∈Z)上是减少的y=cosx在[2kπ-π,2kπ] (k∈Z)上是增加的; 在[2kπ,2kπ+π] (k∈Z)上是减少的
2.求本例1中x∈[ ,] 时的函数值域.
23
【解析】y (cos x 1 )2 1 .
24
因为x∈[ ,所 ],以0≤cosx≤1,
23
所以当cosx=1
2
时,ymax=
1 4
.
当cosx=0或1时,ymin=0.
所以函数y=-cos2x+cosx的值域是[0,1 ].
4
【方法技巧】 1.关于余弦函数性质的应用 应用余弦函数的性质时一般要结合余弦函数的图像,特 别注意余弦函数单调区间、最值、对称性等性质在图 像中的体现,解题中要善于利用图像发现函数的性质用 于解题.
2cos( 23 ) cos 23 cos(4 3 ) cos 3 ,
5
5
5
5
cos( 17 ) cos 17 cos(4 ) cos .
4
4
4
4
因为0< 3<π,且y=cosx在[0,π]上是减少的,
45
所以 cos 3 cos ,即cos( 23 ) cos( 17 ).
【解析】由题意,x满足不等式组
cos x 0,
25
x2
0,
即 co5sxx作0,出5,y=cosx的图像,如图所示.
结合图像可得:
x [5, 3 ) ( , ) ( 3 ,5].
2
22 2
【核心素养培优区】 【易错案例】判断三角函数的奇偶性 【典例】判断函数f(x)= lg cos x 的奇偶性. 【失误案例】
6
【解析】由 T 2 2 .
2
答案:π
4.三个数 cos 3,sin 1 , cos 7 的大小关系是________.
2 10
4
【解析】 sin 1 cos( 1 ); cos 7 cos( 7 ),
10
2 10
4
4
又 >3> 1 > 7>0,
2 2 10 4
又y=cosx在[0,π]上是减函数,
2.余弦函数的性质 函数
性质
图像
定义域 值域
余弦函数y=cosx
R [-1,1]
函数 性质
余弦函数y=cosx
最值
周期性 奇偶性 单调性
当x=2kπ(k∈Z)时,ymax=1 当x=(2k+1)π(k∈Z)时,ymin=-1 是周期函数,最小正周期为_2_π__
是偶函数,图像关于y轴对称 在[(2k-1)π,2kπ](k∈Z)上是_增__加__的 在[2kπ,(2k+1)π](k∈Z)上是_减__少__的
因为f(-x)= lg cosx lg cos x f x,
所以f(x)为偶函数.
【错解分析】分析解题过程,请找出错误之处. 提示:上述做法忽视了函数的定义域,从而导致判断失误, 判断函数的奇偶性时,应先求函数定义域,再在其定义域 内将原函数式化简,然后判断f(-x)与f(x)的关系.
【自我纠正】由lg cosx≥0,得cosx≥1.又cosx≤1,所 以cosx=1,此函数的定义域为{x|x=2kπ(k∈Z)},关于 原点对称,此时f(x)=0,所以f(x)既是奇函数,又是偶函数.
5
4
5
4
【延伸探究】 1.求本例1中x∈[0, ]时的函数值域.
3
【解析】y (cos x 1 )2 1 .
24
因为x∈[0, ],
3
所以 1≤cosx≤1,
2
所以当cosx=1
2
时,ymax=14
.
当cosx=1时,ymin=0.
所以函数y=-cos2x+cosx的值域是[0,1 ].
4
【解析】如图,y=2cosx的图像在[0,2π]上与直线y=2 围成封闭图形的面积为S=4π,所以在[0,1000π]上封 闭图形的面积为4π×500=2000π. 答案:2000π
类型二 余弦函数的性质及应用
【典例】1.函数y=-cos2x+cosx的值域为________.
世纪金榜导学号70034022
§6 余弦函数的图像与性质
1.余弦函数图像的画法
(1)变换法:y=sinx图像向左平移_2_个单位即得y=cosx
的图像. (2)五点法:利用五个关键点_(_0_,_1_)_,_(_2_,_0_) ,_(_π__,_-_1_)_, _(_32__,0_),_(_2_π__,_1_)_画出[0,2π]上的图像,再左右扩展即可.
【点拨】正、余弦函数比较
y=sinx
y=cosx
①都介于直线y=1与y=-1之间; 图像 ②都向两边无限延伸;
关于原点对称
关于y轴对称
y=sinx
①定义域相同 ②值域(最值)相同 ③周期相同
性质
奇函数
当x=2kπ+ (k∈Z)
2
时取最大值; 当x=2kπ- (k∈Z) 时取最小值2
y=cosx
2
2
x
0
π
3
2π
2
2
cosx 1 0 -1 0
1
y
3 1 -1 1
3
描点,连线得:
【补偿训练】1.用“五点法”画出函数y=2+3cosx在 x∈[0,2π]内的图像.
【解析】
x y=cosx
0
2
π 3 2π
2
1 0 -1 0 1
y=2+3cosx 5 2 -1 2 5
2.已知函数y=2cosx(0≤x≤1000π)的图像和直线y=2 围成一个封闭的平面图形,则这个封闭图形的面积是 ________.
2.与正、余弦函数有关的函数值域求法 (1)利用sinx,cosx的有界性. (2)利用sinx,cosx的单调性. (3)化为sinx=f(y)或cosx=f(y),利用|f(y)|≤1来确定. (4)通过换元转化为二次函数.
【补偿训练】(2017·池州高一检测)求函数f(x) lgcos x 25 x2 的定义域.
【解析】由函数y=cosx的图像可知①②③④都正确. 答案:①②③④
2.函数y=-2cosx+10取最小值时,自变量x的取值集合是 ________. 【解析】由于-1≤cosx≤1,所以当cosx=1,即 x=2kπ(k∈Z)时,y取得最小值8. 答案:{x|x=2kπ,k∈Z}
3.函数y=cos (2x ) 的周期为________.
