第十讲 多剂量给药
第十章-多剂量给药

f ss
AUC0 AUC AUC
AUC0t AUC
例:已知某药注射剂量为0.5克,Vd为 128升,半衰期为3.5小时,有效浓度
为1.6ug/ml,试确定给药间隔τ。
例:某抗生素在体内为单室模型, 在多次用药过程中,要求该病人 的 血 药 浓 度 高 于 25μg/ml , 而 不 超过50μg/ml,问(1)每隔6h静 注250mg是否合理?(2)若每次 仍静注250mg,则给药间隔如何选 择?
二.间歇静脉滴注 (单室模型)
重要意义: ①静脉滴注与停止静脉滴注过程的血药浓度
P243 (10-39) (10-40) (10-41) (10-42)
②稳态时滴注过程与停止静脉滴注过程的血药浓度 滴注过程中CSS ; 停止静脉滴注后CSS`
(10-48) 求给药时间间隔
三.血管外给药 (单室模型)
如果第二次给药间隔长于上次药物消除所需 要的时间(>7 T1/2),药物将不会累积。
稳态时,每个给药时间间隔任意时间的血药 浓度是相等的。
2
药 物 浓 度
1
Css.max
Css.min 稳态浓度
波波动度动度
0
0
1
2
3
4
5
6
7
图2-10 多次给药的时-量曲线 (Css.max,峰浓度,Css.min,谷浓度
– 基本假设:
药物按一级动力学消除 单次(首次)给药后的药物动力学
不因以后的多次给药而改变。
一.静脉注射(单室模型)
血药浓度和时间的关系:
1)理论分析(多剂量函数通式)
多剂量函数 = r =(1-e-nkτ )/( 1-e-kτ )
τ为给药间隔
第十讲多剂量给药
第十章多剂量给药临床用药过程中,象镇痛药、催眠药、止喘药等药物一次用药就可以获得满意的疗效,我们可以采用单剂量给药的方案。
但多数疾病是需要多次给药才能达到治疗目的,也就是要采用多剂量给药方案。
多剂量给药又称重复给药,是指按一定剂量、一定给药间隔、多次重复给药,才能达到并保持在一定有效治疗血药浓度范围内的给药方法。
多剂量给药血药浓度预测,可用单剂量给药函数导出的多剂量给药函数式求算,也可用叠加法求算。
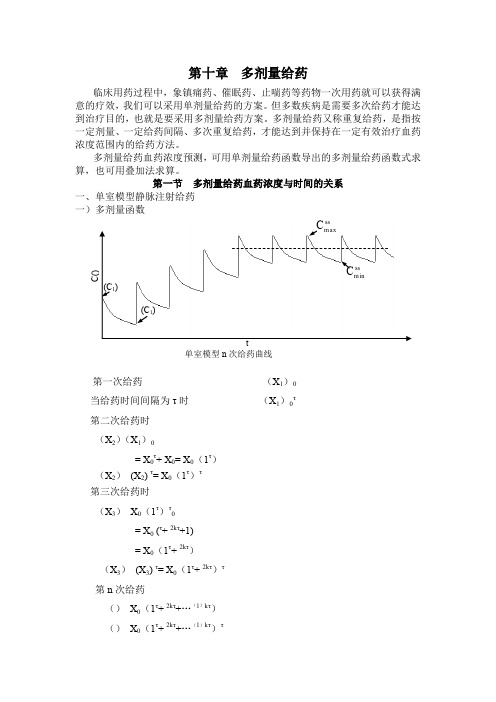
第一节多剂量给药血药浓度与时间的关系一、单室模型静脉注射给药一)多剂量函数ss单室模型n次给药曲线第一次给药(X1)0当给药时间间隔为τ时(X1)0τ第二次给药时(X2)(X1)0= X0τ+ X0= X0(1τ)(X2)(X2) τ= X0(1τ)τ第三次给药时(X3)X0(1τ)τ0= X0 (τ+ 2kτ+1)= X0(1τ+ 2kτ)(X3)(X3) τ= X0(1τ+ 2kτ)τ第n次给药()X0(1τ+ 2kτ+…(1)kτ)()X0(1τ+ 2kτ+…(1)kτ)τ我们看1、τ、 2kτ、…、(1)kτ是一组公比为τ的等比数列,其首项为1,第n项为(1)kτ,根据等比数列前n 和的公式则有:∴式中 就是多剂量函数,用r 表示,n 为给药次数,τ为给药周期。
二)多剂量给药血药浓度与时间的关系前面讲到的多剂量函数,可以说就是一个转换因子,在等时间间隔,维持剂量相同的前提下,多剂量给药的体内动态规律可以用相应的单剂量公式经一定转换成多剂量公式。
对多剂量静脉注射给药,第n 次给药的血药浓度与时间t 的关系就等于单剂量给药的函数式与多剂量函数的乘积,即:三)稳态血药浓度多剂量给药时,随着n 的增大,血药浓度不断增加,当增加到一定程度时,血药浓度不再升高,随每次给药做周期性的变化,此时药物进入体内的速度等于体内消除的速度,这时的血药浓度叫稳态血药浓度或坪浓度,记为。
四)稳态最大血药浓度如图,在一个给药周期(τ)内,稳态血药浓度也有波动,会在一个恒定的水平范围内波动。
多剂量给药

k=0.693/3=0.231 h-1
Css 10 k min e ss Cmax 351 35 l来自 5.4h 0.231 10
将C0=25μg/ml代入得
C0 25 C 35.1g / ml k 0.2315.4 1e 1e C0 ss k ss k 0.2315.4 Cmin e C e 35 . 1 e max k 1e 10.1g / ml
( C1 )max
滴注停止期间血药浓度与时间的关系式为:
C 1 k0 (1 e kT ) e kt kV
第二次滴注开始时,即第一次滴注停止经过了 (τ-T )时间,此时的血药浓度最小,即:
( C1 ) min k0 (1 e kT ) e k ( T ) kV
1e r k 1e
nk
多剂量函数
1 e r 1 e k
nk
n为给药次数,τ为给药周期
由单剂量一室模型静脉注射的药时曲线方 程 ,引入多剂量函数可得多剂量给药的药 时曲线方程:
1 e nk kt C n C0 e k 1e
最高血药浓度
稳态血药浓度
多剂量给药时,随着给药次数n的增加,血 药浓度不断增加,但增加的速度逐渐减慢, 当n充分大时,血药浓度不再升高,达到稳 态(steady state)水平。
若继续给药则血药浓度在稳态水平上下波动, 随每次给药作周期性变化,药物在体内的消 除速率等于给药速率,此时的血药浓度称为 稳态血药浓度(stedy state plasma concentrtion),亦称坪浓度(plateau level),记为Css。
( C2 )max
k0 (1 e kT )( e k 1) kV
第十章 多剂量给药

∫
τ
0
Cssdt = ∫ Cdt
0
∞
公式推导: 公式推导:
X0 C= ss VKτ
如何用单剂量的研究来预测相同剂量多剂量给 药后的平均稳定浓度。 药后的平均稳定浓度。 1)从单剂量给药后求出 、K值,代入公 从单剂量给药后求出V、 值 从单剂量给药后求出
nKτ nKaτ
Ka FX 0 1 e 1 e Kaτ Kτ ( = e e ) Kaτ Kτ Ka K V 1 e 1 e
稳态时, 稳态时,
t →∞a FX0 1 Kt 1 Kat Css = ( Kτ e Kaτ e ) Ka K V 1e 1e
1 1 αt βt Css = A e +B e ατ βτ 1 e 1 e 1 1 (Css )max = A +B ατ βτ 1 e 1 e
1 1 ατ βτ (Css )min = A e +B e ατ βτ 1 e 1 e
血管外给药
1 e 1 e 1 e Kat αt βt Cn = L e +M e +N e Kaτ ατ βτ 1 e 1 e 1 e (Cn )max = (Cn )min =
2
Css.max 药 物 浓 度
波动度 波动度
Css.min
1
稳态浓度
0 0 1 2 3 4 5 6 7
多次给药的时Css.max,峰浓度,Css.min ,Css.min, 图2-10 多次给药的时-量曲线 (Css.max,峰浓度,Css.min,谷浓度
– 基本假设: 基本假设:
药物按一级动力学消除 单次(首次)给药后的药物动力学 不因以后的多次给药而改变。
Css
∫ =
药科大生物药剂学课件第十章 多剂量给药

(1) iv bolus injection, iv A. one-compt. drugs s.d. m.d.
B. two-compt. drugs
X 0 kel t C e Vd X 0 1 e nkel t kel t Cn e k el t Vd 1 e
C Ae t Be t
ss
ss C max k el t e ss C min
在一个 t内
ss t 0, C max
X0 1 Vd 1 e kel t X0 1 kel t e Vd 1 e kel t
t t, C
ss min
Bo Wang Associate Professor of Pharmaceutics Department of Pharmaceutics China Pharmaceutical University
1
LOGO
Chapter 11 多剂量给药药物动力学
• • • • •
3rd dose
( X e
0
kel t
X 0 )e kel t X 0 e k kel t X 0 )e kel t X 0 体内药量最 小值 ( X 0e kel t X 0 )e kel t X 0 e kel t
C
ka FX 0 (e kel t e ka t ) Vd ( ka kel )
m i 1
C Ne ka t Le t Me t
C Ai e l i t
li: 相关过程的表观一级速度常数
13
LOGO
single dosing
多剂量给药

二、重复给药血药浓度的波动程度
1、波动百分数(PF)
指稳态最大血药浓度与稳态最小血药浓度之
差与稳态最大血药浓度或稳态最小血药浓度比值
的百分数。
PF=Cmssax
C ss min
C ss max
100%
PF=Cmssax
C ss min
C ss min
100%
2、波动度(DF)
指稳态最大血药浓度与稳态最小血药浓度之 差与平均稳态血药浓度的百分数。
• 指稳态血药浓度波动的幅度。
C ss max
C ss min
X0 V (1 ek
)
V
X0 (1 ek
)
ek
X0 V
X ss max
X ss min
X0
可见,达稳态时体内药量波动范围等于给药剂量。
(五)达坪分数fss (Fraction of steady state concentration) 达到稳态平均血药浓度某一分数为达坪分数fss。
2、血管外给药负荷剂量的求算
给首剂量X0*,经过一给药周期τ后,血药浓度C1*为:
*
C
FX
* 0
ka
(ek eka )
1 V (ka k)
因为稳态最低血药浓度为:
Css min
FX V (ka
0 ka k)
( 1
ek ek
eka 1 eka )
假设
即
*
C 1
=Cmssin
FX
* 0
ka
DF=
C ss max
C ss min
100%
Css
波动度是评价缓控释制剂质量的重要指标 之一,新药申报需提供该参数。
第十讲多剂量给药

第十章多剂量给药临床用药过程中,象镇痛药、催眠药、止喘药等药物一次用药就可以获得满意的疗效,我们可以采用单剂量给药的方案。
但多数疾病是需要多次给药才能达到治疗目的,也就是要采用多剂量给药方案。
多剂量给药又称重复给药,是指按一定剂量、一定给药间隔、多次重复给药,才能达到并保持在一定有效治疗血药浓度范围内的给药方法。
多剂量给药血药浓度预测,可用单剂量给药函数导出的多剂量给药函数式求算,也可用叠加法求算。
第一节多剂量给药血药浓度与时间的关系一、单室模型静脉注射给药一)多剂量函数C SSC max(C l)maxt单室模型n次给药C-t曲线第一次给药(X I) max=X 0当给药时间间隔为T时(X i) min=X o e"T第二次给药时(X2 ) max= (X i ) min+X o=X o e-k+ X o= X o (1+e-k T)(X2) min= (X2)max 吐X o ( 1+尹) 尹第三次给药时(X3 ) max= X0 ( 1+尹)寸袄0-k T-2 k T=X o (e + e +1)-k T-2k T=X o (1+e + e )-k T-k T -2k T、 -k T(X3 ) min= (X3)max e = X o (1+e + e ) e第n次给药-k T -2k T- (n-1) k T(X n) max= X o (1+e + e + …+e、-k-k T -2k T- (n-1) k T(X n) min= X o (1+e + e + …+e ) e我们看1、尹、严为1,第n 项为,n-1)k、、根据等比数列前e -(n-1)k、是一组公比为e -kT 的等比数列,其首项 n 和的公式则有:1 e k e-2-ke -(n-1)k -(n -1)k. -k -nk. 1 - e e 1 - e -k-k.1 - e1- e(X n )max(X n )max1-e -nkXo 厂厂1 - e V e -nk 1 - e1 - e -nk - 式中W 就是多剂量函数,用 )多剂量给药血药浓度与时间的关系 r 表示,n 为给药次数,T 为给药周期。
生物药剂学与药物动力学_第十章多剂量给药

达坪分数 f ss(n)= Cn / Css
f ss(n)=1- e-nkτ = 1 – e -0.693nτ/ t 1/2
nτ = -
2.303lg(1-
k
f
ss(n))
=
-3.32
t
1/2
lg(1-
f
ss(n))
蓄积系数(积累系数,蓄积因子) R= Css / C1 =1 /(1- e -kτ )
治疗浓度范围。
第一节 多剂量给药的血药浓度与时间关系
一、单室模型静脉注射 1. n次给药后血药浓度与时间的关系
(Xss)max
(X3)max (X2)max
(X4)max
(Xn)max
(X1)max
(X1)min
(X4)mix (X3)mix (X2)mix
(Xn)mix (Xss)mix
第一次给药: (X1)max=Xo (X1)mix =Xo e- Kτ
Css=
Xo
VKτ
口服给药时: Css=
FXo
VKτ
=
Xo V
×1.44
t 1/2
(τ
)
双室模型:
Xo
静脉给药时: Css= Vββτ
口服给药时: Css= FXo Vββτ
第三节 重复给药时体内药物量的蓄积
1. 稳态最低血药浓度
静脉给药:
Css min = C1
min
1 =R (蓄积因子)
1- e-Kτ
r• e- Kτ = e- Kτ+ e- 2Kτ+ …… + e- (n-1)2Kτ + e- nKτ
1- e-nKτ r=
1- e-Kτ
多剂量给药

= 2.74 μg/ml
稳态血药浓度
多剂量给药时,随着给药次数n的增加,血 药浓度不断增加,但增加的速度逐渐减慢, 当n充分大时,血药浓度不再升高,达到稳 态(steady state)水平。
若继续给药则血药浓度在稳态水平上下波动, 随每次给药作周期性变化,药物在体内的消 除速率等于给药速率,此时的血药浓度称为 稳态血药浓度(stedy state plasma concentrtion),亦称坪浓度(plateau level),记为Css。
(C 2)ma x k k0V (1ek)Te(k1)
C 2k k0V (1ek)Te(k 1)ek t
( C 2 ) m ( iC n 2 ) m e a k ( x T ) k k 0( e k V T 1 )e ( 2 k e k )
第三次滴注过程中的血药浓度C3、最大血药浓 度(C3)max、滴注停止期间的血药浓度、最小血 药浓度(C3)min为:
当n充分大时,此时达到稳态血药浓度
ln im C nln i (m C 01 1 e e n kkek)t
1 CssC01ek
ekt
稳态血药浓度是时间的函数,随时间的 变化而变化
稳态最大血药浓度
– 对于静注来说,当t = 0 时血药浓度最大,此 时即稳态最大血药浓度
Csmsax
X0 V(1ek)
例题
某抗生素静脉滴注给药,剂量为40mg, 经过2h后停止滴注,第一次滴注开始 10h后再次滴注2h,剂量仍为40mg,假 定该抗生素k=0.2h-1,V=10L。第一次滴 注2h后的血药浓度是多少?第二次滴注 开始后经过5h的血药浓度是多少?
多剂量给药

- kτ
• 体内最小药物量为
给予第二个剂量后的体内最大药物量,等于静脉注射第一 个剂量在体内的剩余量与第二个剂量之和。静脉注射经过 一个给药间隔的 指数衰减,即为体内最小药物量
第三次给药
• 体内最大药物量为
• 体内最小药物量为
第n次给药
• 体内最大药物量为
• 体内最小药物量为
令:
上式乘以e -kτ,得:
3. 稳态达峰时间与稳态最大血药浓度
∵ ka>>k , 则(tmax)稳态< (tmax)单剂量
4. 稳态最小血药浓度
5. 达坪分数
因为ka >>k,在t =τ 时吸收基本结束,故e-nkaτ →0,则:
二、双室模型
(一)血药浓度与时间的关系 静脉注射
1− e 1− e −αt − βt ) + ( ) Cn = A( e B e 1 − e −ατ 1 − e − βτ
(二)间歇静脉滴注给药
1. 间歇静脉滴注给药的特点
静脉滴注速度为k0,固定滴注时间T,然后停止滴注τ-T时间, 给药间隔时间为τ,如此反复进行。 在每次滴注时血药浓度逐渐升高,停止滴注后血药浓逐渐下降, 由于第二次再滴注时,体内药物量未完全消除,所以体内药物 量不断蓄积,血药浓度曲线不断升高,直到达到稳定状态,才 维持在一个相应时间上相等的血药浓度水平。
Cn
C dt ∫ =
0 n
τ
τ
第三节 体内药量的蓄积与血药浓度的波动 一、多剂量给药体内药量的蓄积
蓄积系数: 又称为蓄积因子或积累系数,系指稳态血药浓 度与第一次给药后的血药浓度的比值,以R表示。
1. 以稳态最小血药浓度与第一次给药后的最小血 药浓度的比值表示
生物药剂学与药物动力学:第十章 多剂量给药

二、单室模型血管外给药 (一)多剂量血管外给药血药浓度与时间关系
单次给药: C ka FX 0 ekt ekat V (ka k)
多剂量给药:
Cn
ka FX V (ka
0
k
)
1 enk 1 ek
ekt
1 enka 1 eka
ekat
二、单室模型血管外给药 (二)稳态最大血药浓度与达峰时
第十章 多剂量给药
第一节 多剂量给药血药浓度与时 间的关系
一、单室模型静脉注射给药 二、单室模型血管外给药 三、双室模型多剂量给药 四、利用叠加原理预测多剂量给药
一、单室模型静脉注射给药 (一)多剂量函数
1 enk r 1 ek
其中:n 为给药次数,τ 为给药间隔
c
MTC
(X4)max (X5)max (X6)max (X3)max
第三次给药: 第四次给药: 第 n次给药:
( X 3 )max X 0 (1 ek e2k ) ( X 3 )min X 0 (ek e2k e3k )
( X 4 )max X 0 (1 ek e2k e3k ) ( X 4 )min X 0 (ek e2k e3k e4k ) ( X n )max X 0 (1 ek e2k e(n1)k ) ( X n )min X 0 (ek e2k enk )
解:
C ss max
X0 V (1 ek
)
1000
0.6936
66.7(mg/L)
20(1 e 3 )
C ss m in
C ss max
e k
0.6936
66.7 e 3
16.7(mg/L)
C
1000
0.6936
第十章 多剂量给药

1 Cn = C0
1
e nk e k e
kt
多剂量给药稳态血药浓度
按一定剂量、一定给药间隔,多次重复给药,随着 给药次数n的增大,血药浓度不断增加,当n充分大时, 血药浓度不再升高,随每次给药作周期性变化,此时, 药物进入体内的速率等于从体内消除的速率,这时的 血药浓度称为稳态血药浓度,或称坪浓度(plateau level),记为Css。
所以 n = 3.32t1/ 2 lg(1 0.99) = 6.645t1/ 2
答:给药时间为4个半衰期,可达坪浓度的93.75%;达 到坪浓度的99%,需要6.645个半衰期。
(二)单室模型间歇静脉滴注给药
(二)单室模型间歇静脉滴注给药
(一)间歇静脉滴注给药的特点
• 每次固定滴注时间T,然后停止滴注τ-T 时间,给 药间隔时间为τ,如此反复进行。
当时间t=0时,体内最大药量为:
( X 3 ) max = X 0 (ek+ e 2 k ) + X 0 = X 0 (1 + e k+ e 2 k)
当时间t=τ时(即经过第三个给药周
期),体内最小药量为:
( X 3 ) min = X 0 (1 + e k + e 2 k ) e k = X 0 ( e k + e 2 k + e 3 k )
令 r =1+e k+e 2k+......+ e (n 1)k a
上式两边同时乘以e-kτ得:
r.e k=e
k +e2k
+.....+e(n +1)k e
nk
b
将上述两式相减后,再整理得单室模型多 剂量静脉注射给药,多剂量函数公式为:
重复给药

第一节 多剂量给药血药浓度与时间的关系
一、单室模型静脉注射
第一次给药 (X1)max=X0 经过一个给药周期τ (X1)min=X0e-kτ 第二次给药
(X2)max=(X1)min+X0=X0(1+e-kτ) (X2)min=(X2)maxe-kτ=X0(1+e-kτ) e-kτ 第三次给药 (X3)max=(X2)min+X0
Cn
C0
1 enk 1 ek
ekt
=
10 ´
1 e8´0.173´6 1 e 0.173´6
´ e 0.173´10
= 2.74 μg/ml
稳态血药浓度
❖ 多剂量给药时,随着给药次数n的增加,血 药浓度不断增加,但增加的速度逐渐减慢, 当n充分大时,血药浓度不再升高,达到稳 态(steady state)水平。
❖ 若继续给药则血药浓度在稳态水平上下波动, 随每次给药作周期性变化,药物在体内的消 除速率等于给药速率,此时的血药浓度称为 稳态血药浓度(stedy state plasma concentrtion),亦称坪浓度(plateau level),记为Css。
❖ 当n充分大时,此时达到稳态血药浓度
由题意可知滴注时间T=2h,给药间隔时间τ=10h (1)第一次滴注2h后的血药浓度
(2C)1 第kkV0二(1次 e停kt 止) 滴104注0 02时.2 的1 血e0药.22浓度3.30mg L
第(C2二)ma次x 滴10注40开02.2始(1后 e经0.2过2 )(511h的ee2血0.02.2药1010 )浓度3.7,5m即g为L第
(Cn )max
ek(T)
k0 (ekT kV
1)(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章 多剂量给药临床用药过程中,象镇痛药、催眠药、止喘药等药物一次用药就可以获得满意的疗效,我们可以采用单剂量给药的方案。
但多数疾病是需要多次给药才能达到治疗目的,也就是要采用多剂量给药方案。
多剂量给药又称重复给药,是指按一定剂量、一定给药间隔、多次重复给药,才能达到并保持在一定有效治疗血药浓度范围内的给药方法。
多剂量给药血药浓度预测,可用单剂量给药函数导出的多剂量给药函数式求算,也可用叠加法求算。
第一节 多剂量给药血药浓度与时间的关系一、单室模型静脉注射给药 一)多剂量函数第一次给药 (X 1)max =X 0当给药时间间隔为τ时 (X 1)min =X 0e -kτ 第二次给药时(X 2)max =(X 1)min +X 0= X 0e -kτ+ X 0= X 0(1+e -kτ) (X 2)min = (X 2)max e -kτ= X 0(1+e -kτ)e -kτ第三次给药时(X 3)max = X 0(1+e -kτ)e -kτ+X 0 = X 0 (e -kτ+ e -2kτ+1) = X 0(1+e -kτ+ e -2kτ)(X 3)min = (X 3)max e -kτ= X 0(1+e -kτ+ e -2kτ)e -kτ 第n 次给药(X n )max = X 0(1+e -kτ+ e -2kτ+…+e -(n-1)kτ)(X n )min = X 0(1+e -kτ+ e -2kτ+…+e -(n-1)kτ)e -kτtC (u g /m l )单室模型n 次给药C-t 曲线(C 1)max(C 1)maxss C m axssC min我们看1、e -kτ、 e -2kτ、…、e -(n-1)kτ是一组公比为e -kτ的等比数列,其首项为1,第n 项为e -(n-1)kτ,根据等比数列前n 和的公式则有:∴式中 就是多剂量函数,用r 表示,n 为给药次数,τ为给药周期。
二)多剂量给药血药浓度与时间的关系前面讲到的多剂量函数,可以说就是一个转换因子,在等时间间隔,维持剂量相同的前提下,多剂量给药的体内动态规律可以用相应的单剂量公式经一定转换成多剂量公式。
对多剂量静脉注射给药,第n 次给药的血药浓度C n 与时间t 的关系就等于单剂量给药的函数式与多剂量函数的乘积,即:三)稳态血药浓度多剂量给药时,随着n 的增大,血药浓度不断增加,当增加到一定程度时,血药浓度不再升高,随每次给药做周期性的变化,此时药物进入体内的速度等于体内消除的速度,这时的血药浓度叫稳态血药浓度或坪浓度,记为C ss 。
四)稳态最大血药浓度如图,在一个给药周期(τ)内,稳态血药浓度也有波动,会在一个恒定的水平范围内波动。
当t =0时,就是稳态最大血药浓度,以 表示。
ττττττττk --nk k --k 1)k --(n 1)k -(n -k -k -e 1e 1e 1e e 1e 2-e e 1--=--=+⋅⋅⋅+++ττk --nk 0max n e 1e 1)(X --=X τττk -k --nk 0max n e e1e 1)(X --=X ττk --nk e 1e 1--tC k -k --nk 0n e e1e 1C ⋅--=ττttn n C C k -k -0ss k -k --nk 0n ss ee 11C )e e1e 1(lim C lim C ⋅-=⋅--==∞→∞→τττssm ax C五)稳态最小血药浓度当t =τ时,即达到稳态血药浓度以后,经过一个给药周期时的血药浓度,为稳态最小血药浓度,以 表示。
六)坪幅坪浓度的波动幅度称为坪幅。
七)达坪分数是指n 次给药后的血药浓度与坪浓度相比,相当于坪浓度的分数,以f ss (n )表示。
它的引入,主要是为了回答用药多长时间或多少个给药周期才能接近坪浓度,达到坪浓度的什么程度这个问题。
∵ t 1/2=0.693/k ∴移项,取对数,整理,得或 八)蓄积系数又叫累积系数,或称蓄积因子,指坪浓度与第一次给药后的浓度的比值,以R 表示。
ττk -0k -k -0ss max e 11e e 11C -=⋅-=C C tssm in C τττk -k -0k -k -0ss mine e 11e e 11C-=⋅-=C C t 0ss min ss max k -k -0k -0ssmin ss max C -C e e 11e 11C -C C C C =---=τττττττnk -k -k -0k -k --nk 0ss n ss(n)e 1e e 11e e 1e 1 C Cf -=⋅-⋅--==ttC C 2/1/-0.693n ss(n)e 1f t τ-=)1lg(303.2n )(n ss f k--=τ)1lg(32.3n )(2/1n ss f t --=τ二、单室模型血管外给药一)多剂量血管外给药血药浓度与时间的关系我们已经介绍过,多剂量函数是一个转换因子,n 次给药后的血药浓度C n 与时间t 的函数关系式,就是在单剂量给药后的血药浓度与时间的函数关系式中,将每一个指数项乘以多剂量函数,该函数的速度常数与指数项的速度常数相同。
二)稳态血药浓度多剂量血管外途径给药与静脉注射给药一样,随着给药次数的不断增加,体内药物不断积蓄,当n 充分大时,血药浓度逐渐趋向并达到稳定状态。
三)稳态最大血药浓度与达峰时多剂量血管外给药,由于由于有一个吸收过程,每一个给药周期内,峰浓度不象静脉注射给药那样,紧跟在给药之后,而是在两次给药间隔内的某一点。
求ττk -k -0k -k -01sse 11e ee 11 C C R -=⋅-==t tC C )e e1e 1e e 1e 1()(C a a a k -k --nk k -k --nk 0n tt a a k k V FX k ττττ---⋅---=Ctss m axC ss m inC )e e11e e 11()(C )e e 1e 1e e 1e 1()(lim C lim C a a a a a k -k -k -k -0ss k -k --nk k -k --nk 0n ss t ta a tt a a n n k k V FX k k k V FX k ττττττ--⋅--=---⋅---==∞→∞→其最大血药浓度与达峰时,就是求函数的极大值,也就是求它的一阶导数,并另其等于零,得:∵ k a >> k∴ e -k τ > e -ka τ1-e -k τ <1- e -ka τ< 因此稳态时的达峰时小于单次给药的达峰时。
将t max 代入,求得:∵ k a >> k ,该式可简化为:四)稳态最小血药浓度当t =τ时,为稳态最小血药浓度。
∵ ∴五)达坪分数多剂量血管外给药,达坪分数可用给药周期内平均稳态血药浓度计算。
六)蓄积系数多剂量血管外给药,体内药物蓄积程度与该给药周期内的时间有关,不同时刻蓄积程度不同,通常以最低坪浓度为标准计算。
)1()1(ln1max ττa k k a a e k e k k k t -----=)1()1(ττa k k a e k e k ----k k a)e1e e 1e ()(Ca maxa max k --k k --k 0ss maxττ----=t t a a k k V FX k )e1e (C k --k 0ss max max τ-=t V FX )e e11e e 11()(Ca a k -k -k -k -0ss m inττττ--⋅--=k k V FX k a a ττττττττττττττa a a a a a a k -k -k -k --k -k k -k --k -k k --k k --k e 11e 11)e 1)(e 1()e 1()e (1)e 1)(e 1(e e e 1e e 1e ---=-----=---=---)e11e 11()(Ca k -k -0ssm inττ----=k k V FX k a a ⎰⎰=ττττ0ss(n))(1)(1f dtt C dt t C ss n三、双室模型多剂量给药双室模型多剂量给药,n 次给药后的血药浓度与时间的关系,等于在单剂量给药血药浓度与时间的函数关系式中,每一个指数项乘以多剂量函数,该函数的速度常数与指数项的速度常数相同。
iv :血管外:四、利用叠加原理预测多剂量给药血药浓度给药具有线性药物动力学特征的药物,多剂量给药后的血药浓度,可以从单剂量给药后相应浓度预测。
认为每一剂量不受其它任何剂量的影响而独立发挥其作用,且每个间隔内药物吸收的速度与程度及平均全身清除率相同,这样只需要简单叠加即可预测血药浓度。
第二节 平均稳态血药浓度从多剂量给药的C-t 曲线可以看出,在达到稳态后,其血药浓度亦有波动,C ss 仍然是时间t (0≤t ≤τ)的函数。
我们把血药浓度达到稳定后,一个剂量间隔时间内,血药浓度-时间曲线下面积除以时间间隔τ称为平均稳态血药浓度,用 表示。
一、单室模型平均稳态血药浓度 一)静脉注射给药平均稳态血药浓度多剂量静脉注射给药,达稳态后血药浓度-时间曲线下面积为:)e 1)(e 1(1)e e ()()e 11e 11()(C C R a a a k -k -k -k -0k -k -0m inss m in ττττττ--=------==k k V FX k k k V FX k a a a a tn t n n e ee B e e e A C ββτβταατατ--------+--=)11()11(tk k nk t n t n n a a a e ee N e e e M e e e L C -----------+--+--=)11()11()11(ττββτβταατατss C ττ⎰=)(dtt C C ss ssVkX e k k e V X dt e e V X dt t C k k k kt ss 00000)11(11)1()(=⋅--⋅=-=----⎰⎰τττττ单剂量静脉注射给药,血药浓度-时间曲线下面积为:多剂量药给药达稳态血药浓度后,在一个给药周期(t =0→τ)内,血药浓度-时间曲线下面积,等于单剂量给药,时间从0至∞范围内血药浓度-时间曲线下面积。
根据平均稳态血药浓度的定义,则平均稳态血药浓度可用多剂量或单剂量给药所得血药浓度时间数据估算。
将t 1/2=0.693/k 代入上式,得被称为给药频数要达到所希望的平均稳态血药浓度,可根据上式选择τ调节X 0或固定X 0调τ,进行给药方案设计。
