第1章 真空中的静电场2015(王晓平)
真空中的静电场(一) - 重庆邮电大学精品课程管理平台
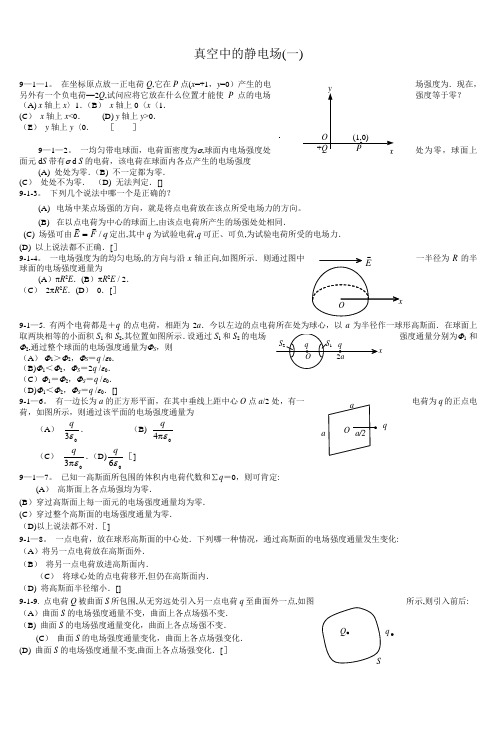
真空中的静电场(一)9—1—1。
在坐标原点放一正电荷Q ,它在P 点(x =+1,y =0)产生的电场强度为.现在,另外有一个负电荷—2Q ,试问应将它放在什么位置才能使P 点的电场强度等于零?(A) x 轴上x 〉1.(B ) x 轴上0〈x 〈1. (C ) x 轴上x <0. (D) y 轴上y >0. (E ) y 轴上y 〈0. [ ]9—1—2。
一均匀带电球面,电荷面密度为σ,球面内电场强度处处为零,球面上面元d S 带有σ d S 的电荷,该电荷在球面内各点产生的电场强度(A) 处处为零.(B) 不一定都为零. (C ) 处处不为零. (D) 无法判定.[] 9-1-3。
下列几个说法中哪一个是正确的?(A) 电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向。
(B) 在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同.(C) 场强可由q F E /=定出,其中q 为试验电荷,q 可正、可负,为试验电荷所受的电场力. (D) 以上说法都不正确.[]9-1-4。
一电场强度为的均匀电场,的方向与沿x 轴正向,如图所示.则通过图中一半径为R 的半球面的电场强度通量为(A )πR 2E .(B )πR 2E / 2. (C ) 2πR 2E .(D ) 0.[]9-1—5. 有两个电荷都是+q 的点电荷,相距为2a .今以左边的点电荷所在处为球心,以a 为半径作一球形高斯面.在球面上取两块相等的小面积S 1和S 2,其位置如图所示.设通过S 1和S 2的电场强度通量分别为Φ1和Φ2,通过整个球面的电场强度通量为ΦS ,则 (A ) Φ1>Φ2,ΦS =q /ε0.(B)Φ1<Φ2,ΦS =2q /ε0.(C )Φ1=Φ2,ΦS =q /ε0. (D)Φ1<Φ2,ΦS =q /ε0.[]9-1—6。
有一边长为a 的正方形平面,在其中垂线上距中心O 点a /2处,有一电荷为q 的正点电荷,如图所示,则通过该平面的电场强度通量为(A )03εq . (B) 04επq (C ) 03επq .(D)06εq[]9—1—7。
第一章 真空中的静电场

教
“物理学不应该教成一堆技术, 而应教成思想概念的诗剧。应该强 调思想概念的演变,强调我们企图 了解物理世界的历史,以使学生具 备洞察未来的能力。”
——爱因斯坦
学
“学问”:“求学问,需学问; 只学答,非学问” — 李政道 “学习”:预习、复习、练习 “学而不思则罔” “如切如磋、如琢如磨”—
交流、求精
电磁学与电动力学
(上册:电磁学部分)
程福臻 中国科技大学理学院 fzhen@ 3606844 下载 “电磁学pdf”网址: 下载“
/~fzhen/dcx
绪论
1、什么是电磁学 :是研究电磁现象、电磁相互 什么是电磁学:是研究电磁现象、电磁相互 作用规律及其应用的学科。 2、研究的对象 :电磁场,与力学、热学区别。 研究的对象:电磁场,与力学、热学区别。 :尺度 (1%的原子尺度) 3、适用范围 适用范围: 尺度( −10 10 cm ∞ 速度 低速 高速 :四大相互作用之一;物质结构的基 4、重要性 重要性:四大相互作用之一;物质结构的基 础;高新技术的基础;其它学科的基础。
§1-2 库仑定律
1. 库仑定律建立的基础
16世纪—18世纪中叶,摩擦起电机;正电、 负电两种,同性电荷相斥,异性电荷相吸;天 电和地电统一 ;掌握了电荷转移及储存方法 ; 认识到电荷守恒定律。 电荷之间作用力的大小和方向 ? 1750年前后,德国的埃皮诺斯发现:电荷 之间的相互作用力随其距离的减小而增大,但 是没有给出定量的规律;
3. 电荷守恒定律
一个孤立系统(与外界不发生电荷交换的 系统)的电荷总量(代数和)是保持不变的, 它既不能创生,也不会消灭。电荷只能从系统 内的一个物体转移到另一个物体,系统的总电 量既不随时间而变,也与参考系的选取无关。 对核反应也是成立的: 1 1 − β衰变 : 0 n1 →1 p 0 + e + ve . 中子(n) (n)β 226 222 4 Ra → Rn + 镭的α衰变 : 88 138 86 136 2 He 2
第一章真空中的静电场一

点电荷:带电体自身的几何线度比它到其他带电 体的距离小很多时的抽象模型。集中了带电体的所 有电量,没有形状和大小。
二、库仑定律
1785年,库仑通过扭称实验得到。
库仑定律的表述: 在真空中, 两个静止点电荷之间的相互
关于较详细的发展史,可பைடு நூலகம்从课本上看到。
三、参考书目:
电磁学 . 赵凯华 .高等教育出版社
其他参考书很多,图书馆有,因为“经典” 物理,所以各种参考书都大同小异。
有兴趣的同学可以借阅一本外文原版书阅读, 可以掌握一些词汇,提高阅读外文资料的能力。
另外希望能找一本习题书。 ➢与课本比较,组织形式不同,内容相近,以讲授
作用力,大小与它们的电量的乘积成正比, 与它们之间距离的平方成反比;作用力的方 向沿着它们的联线,同号电荷相斥,异号电 荷相吸。
f k q1q2 r2
q1
q2
r
f12
k
q1q2 r2
rˆ12
rˆ12 :从电荷1指向电
荷2的单位矢量。
f12 :电荷1对电荷2的作用力。
同理:
f 21
k
q1q2 r2
3、认真完成作业,不得抄写。(计入平时成绩)
4、课后多习题,从习题中发现问题。
5、参加期中、期末考试。
6、多提意见:关于讲授的方法、内容。
第一章 真空中的静电场
静电场:
相对于观测者是静止的,数量不随时间变化 的电荷在自身周围空间中产生的电场。
真空: 除了静止的电荷及静电场以外,无其他物质
的空间,并非一无所有。
一、电场概念
1、什么是电场
大学物理课件-真空中的静电场

8.1
静电场中的导体
导体(Conductor) 导体中存在大量的可自由移动的电荷
例如:各种金属、电解质溶液。
绝缘体也称电介质 (Dielectric) 理论上认为电介质中一个自由移动的电荷也没有。 例如:云母、胶木等。
半导体 (Semiconductor) 带电性质介于上述两者之间。
在静电场中总是存在导体或电介质。 静电场与静电场中导体或电介质之间有相互作用。 它们的相互作用体现在: 任何物质(实物)都是由带正电的原子核和 带负电的电子组成,它们在电场中受到电场力的 作用而重新分布。电荷的重新分布的结果反过来 又将影响电场的分布。这两种过程相互制约,直 到达到某种新的平衡。 这一部分只限于讨论各向同性均匀金属导体 与电场的相互作用。
q1
+ q1
3、导体表面的电荷面密度与邻近表面处场强的关系
S , E dS
S
为表面电荷面密度
E表 n
0
S E S 0
作钱币形高斯面 S
0
, E ; E
结论:导体外邻近表面处 的电场强度大小与该表面 处电荷面密度成正比。 + +
一、导体的静电平衡及条件 1、静电感应 导体的静电平衡 ( Electrostatic Equilibrium ) 静电感应: 在静电场力作用下,导 体中电荷重新分布的现象。
+
++ + ++ +
+
+
感应电荷
E0
' E
E 0
E0 ' E
+ + + + + + + +
大学物理课件-真空中的静电场-55页精选文档

例:两球半径分别为R1、R2 ,带电量为q1、q2,设 两球相距很远,求:当用导线将彼此连接时,电
荷将如何分布?
这一部分只限于讨论各向同性均匀金属导体 与电场的相互作用。
一、导体的静电平衡及条件
1、静电感应 导体的静电平衡 ( Electrostatic Equilibrium )
静电感应: 在静电场力作用下,导
体中电荷重新分布的现象。
+
+ ++++ + + +
感应电荷
E0 E'
+
E0 E'
+ + + + +
均匀带电无 限大平面
d
U Ed
20
典型电场的场强
3.高斯定理
均匀带电 球面
EE 40qr0r3
球面内 球面外
均匀带电无 限长直线
E 2 0r
方向垂直于直线
均匀带电无 限大平面
E
2 0
方向垂直于平面
本章讨论:电场与物质的相互作用(影响)
主要内容有: 静电场中导体 电容器 *电介质 *有介质时的高斯定理 电场的能量
U dQ (连续)
Q 4 0r
2、根据电势的定义 EU
0势
Ur Edr
1、点电荷场的场强及叠加原理
E
i
E
Qir
40ri3
(分立)
rdQ (连续)
Q4 0r3
2、可 由 U U EE
U x
Ex
典型电场电势
均匀带 电球面
U q
4 0 R
U q
4 0r
均匀带电无 限长直线
大学物理12真空中的静电场

03
电势与电势差
电势的概念
总结词
电势是描述电场中某点电荷所具有的势能,其值与零电势点的选 择有关。
详细描述
电势是描述电场中某点电荷所具有的势能,通常用符号"φ"表示。它 是一个标量,其值与零电势点的选择有关。在静电场中,零电势点 是任意选择的,通常选择大地或无穷远处作为零电势点。
电势的计算方法
计算电场能量
利用高斯定理可以计算电场的能量密度和总能量。
静电场的散度与源电荷的关系
02
01
03
静电场的散度等于该点源电荷的密度。
数学表达式:divE = ρ/ε0
其中,divE是电场强度的散度,ρ是电荷的密度,ε0是 真空中的电容率。
05
静电场的环路定理与电场线的引入
静电场的环路定理
总结词
静电场的环路定理描述了电场与磁场之 间的关系,是电磁学中的基本定理之一 。
大学物理12真空中的静电场
目
CONTENCT
录
• 引言 • 电场与电场强度 • 电势与电势差 • 高斯定理与静电场的散度 • 静电场的环路定理与电场线的引入 • 静电场的边界条件与导体表面的电
场线分布 • 静电场的能量与力
01
引言
主题简介
静电场是静止电荷产生的电场,是电 磁学的重要概念之一。
在真空环境中,静电场不受其他电磁 场的影响,因此具有独特的性质和规 律。
指导电路设计
在电路设计中,通过合理 布置导线和元件的位置, 利用电场线的分布来优化 电路性能。
07
静电场的能量与力
静电场的能量分布
静电场的能量分布由电场强度和电势的乘积积分得 到,表示电场中各点的能量密度。
在真空中的静电场,能量分布与电荷分布有关,电 荷密度越大,能量密度越高。
电磁学_01_真空中的静电场

第一讲 真空中的静电场本讲主要介绍真空中相对于观察者静止的电荷产生的电场和电场的性质 从电荷受力的角度,引出描写电场特性的物理量 —— 电场强度 从电场力做功的角度,引出描述电场特性的势能函数 —— 电势01 电荷 库仑定律1 电荷的量子性自然界存在两种基本电荷:电子和质子,分别带电:19191.62101.6210e p q Cq C--⎧=-⨯⎪⎨=+⨯⎪⎩ 基本电量:191.6210e C -=⨯物体带电:,2,3,4,,q e e e e ne =±±±±± 这一特性称为电荷的量子性。
夸克模型:强子(中子和质子)由若干种夸克或反夸克组成 夸克的电量:13e ±或23e ±电子的电量分布:负电荷集中分布在18~10m -范围,可以将电子看作是无内部结构的电荷点 质子的电量分布:正电荷集中分布在15~10m -范围,一般问题中可看作无内部结构的电荷点,如图XCH003_001所示。
中子的电量分布:正负电荷集中分布在15~10m -范围,正负电量相等,对外呈现中性,如图XCH003_001所示。
宏观物体的电量:q>>e ,带电为准连续的2 电荷守恒定律 —— 一个封闭的带电系统,系统正负电荷的代数和保持不变重核的裂变:238234492902U Th He →+ —— 重核裂变前后,电荷代数和不变,电荷守恒γ光子与重核的碰撞:e e γ+-→+ —— 光子转化为一个正电子和一个负电子高速运动的正负电子对作用:e e γ+-+⇒ —— 正负电子对湮灭产生γ光子 3 电荷的相对性不变性实验研究表明:电荷的电量与带电体的运动状态无关;电荷的测量与参照系无关。
氦原子中两个质子能量为氢分子中两个质子的能量100万倍,实验研究表明氦原子和氢分子精确地为电中性。
说明氦原子和氢分子质子的电量和运动状态无关,即电荷相对论不变性。
《真空中静电场》课件

静电复印的工作原理
静电复印利用静电场原理将图像或文字复制到纸张上。
在静电复印过程中,先通过曝光将原稿的图像转换为静电荷,然后在电场力的作用下将带电 墨粉吸附到纸张上,最后通过热压或冷压将墨粉固定在纸张上,形成复制的图像或文字。
静电复印技术具有高效、方便、灵活等优点,已成为现代办公和印刷领域的重要技术手段。
电势差的概念与计算
要点一
总结词
电场力做功,高电势到低电势,单位
要点二
详细描述
电势差是描述电场中两点之间电势差异的物理量。在电场 中,若电荷从某点移动到另一点,若电场力做正功,则这 两点的电势差为正,反之为负。电势差的计算公式为$U = frac{W}{q}$,其中$U$是电势差,$W$是电场力做的功, $q$是电荷的电量。在国际单位制中,电势差的单位是伏 特(V)。
电场强度的计算
点电荷的电场强度公式
E=k*Q/r^2,其中E为电场强度,k为静 电力常量,Q为点电荷的电量,r为点电 荷到某点的距离。
VS
匀强电场的电场强度公式
E=U/d,其中E为电场强度,U为两点间 的电势差,d为这两点沿电场线方向的距 离。
03
电势与电势差
电势的概念
总结词
标量,相对性,单位
电容器在电路中的作用
电容器在电路中可以起到滤波、耦合、旁路等作用,是电子设备中不可或缺的元件之一 。
静电场的能量分布与计算
静电场的能量分布
在静电场中,电场能量密度与电场强 度的大小和方向有关,能量分布不均 匀,主要集中在导体表面。
电场能量的计算
电场能量的计算公式为 $W = frac{1}{2} CU^2$,其中 $C$ 是电容 器的电容,$U$ 是电容器两端的电压 。
大学物理教案真空中的静电场

真空中的静电场一、教学目标1. 了解静电场的基本概念,掌握电场强度、电势和电势差等基本物理量。
2. 学习静电场的叠加原理,理解高斯定律及其应用。
3. 掌握静电场的能量和能量密度,了解静电场的几种常见分布。
4. 能够运用所学知识分析解决实际问题,提高学生的科学素养。
二、教学内容1. 静电场的基本概念电场强度电势电势差2. 静电场的叠加原理场强的叠加电势的叠加3. 高斯定律高斯定律的表述应用高斯定律求解电荷分布4. 静电场的能量和能量密度静电场的能量能量密度5. 静电场的几种常见分布均匀电场非均匀电场点电荷电场线性电场三、教学方法1. 采用讲授法,系统地介绍静电场的基本概念、叠加原理、高斯定律、能量和能量密度以及常见分布。
2. 利用多媒体动画和图片,直观地展示静电场的现象,增强学生的理解。
3. 结合实际例子,让学生学会分析解决实际问题。
4. 布置适量练习题,巩固所学知识。
四、教学环境1. 教室环境舒适,通风良好。
2. 教学设备:计算机、投影仪、黑板、粉笔。
3. 教材、教案、练习题等相关教学资源。
五、教学评价1. 课堂表现:观察学生在课堂上的参与程度、提问回答等情况,了解学生的学习状态。
2. 练习题:检查学生对静电场基本概念、叠加原理、高斯定律、能量和能量密度的掌握程度。
3. 课后反馈:收集学生对教学内容的意见和建议,不断改进教学方法。
4. 期中考试:评估学生在静电场部分的知识水平和应用能力。
六、教学内容6. 静电场中的电势能和势能曲线静电势能的概念势能曲线的绘制与分析静电力做功与势能变化的关系7. 静电场的能量与能量守恒静电场的能量表达式能量守恒在静电场中的应用静电场的能量与电场强度、电势的关系8. 电场线与等势面电场线的定义与性质等势面的概念与绘制电场线与等势面的关系及其在静电场中的应用9. 静电场的边界条件狄拉克原理边界条件的数学表达应用边界条件解静电场问题10. 静电场的数值计算方法有限差分法有限元法蒙特卡洛法数值计算方法在静电场中的应用实例七、教学方法1. 采用案例分析法,深入讲解静电场中的电势能和势能曲线,让学生理解静电力做功与势能变化的关系。
20150430---01、库仑定律、电场、电场强度

E E1 + E2 + + En Ei
i 1
n
2)如果带电体电荷连续分布,如图 把带电体看作是由许多个电荷元组成, 然后利用场强叠加原理求解。 q r
dE
P
E
q
dE
dq e 2 r q 4π 0 r
dq
er
dq 体电荷密度 dV dq 面电荷密度 ds
解:(方法一)设盘心 o 点处为原点,x 轴沿轴线 方向,如图所示,在任意半径 r 处取一宽为 dr 的 圆环,其电量 dq 2rdr
dq dE cos 2 4 0 l
dr
R
r
l
p dE
X
rd dE sin d 2 0l 2 0
E sin d 2 0 0 2 1 cos 2 0 2 0
一、静电的基本现象及基本规律 1、几个名词 2、基本电现象 3、电荷的单位和量子化 研究宏观电磁现象时不必考虑电子量子化问题
二、两个基本规律 1、电荷守恒定律及电荷不变性
电荷守恒定律 对某系统,如没有净电荷出入其边界,则 系统的电荷的代数和保持不变.
电荷的不变性:电荷量不因坐标的变换而改变
2、库仑定律 1、点电荷
点电荷在外场中受的电场力: 一般带电体在外场中受的电场力:
F qE
F dF
(q)
(q)
Edq
由库仑定律有 F
二、电场强度的计算 1.点电荷Q的场强公式 q× 首先,将试验点电荷q放置场点P处 r F 由场强定义 E q Q
er
·
Qq er 2 4 0 r
第1章 真空中静电场

L2
q0
0
LE dl 0
a
L1
在静电场中,场强沿任意闭合路径的 线积分(称为场强的环流)恒为零。
41
讨论
E dl 0
L
1)静电场的基本方程之一
静电场是保守场或无旋场 2) 微分形式 E 0
3)表征静电场的性质有两个方程
E dl 0
L
qi
E dS i
S
0
---有源无旋场
解:选择高斯面——
E
+ + ++ ++ ++ + +
与平面正交 对称的 柱面
dS E
底面 E 平行dS 侧面 E dS
dS
e
Ed S
S
S 0
E
2 0
2SE
思考:密度为ρ无限长带电平板(厚为b)的E? 38
请点击你认为是对的答案
若通过一闭合曲面的 通量为零, 则此闭合曲面上的 一定是
(1)处处为零。
高斯
Φe
E
SE
dS
V
1
0
dV
是所有电荷产生的;
(连续分布的源电荷)
e 只与内部电荷有关。
真空中的任何静电场中,穿过任一闭合曲面的电通量,
等于该曲面所包围的电荷电量的代数和除以 0
意义
反映静电场的性质 —— 有源场 ,电荷就是它的源。
31
说明
e
SE
dS
1
0
q内
(1) 适用于一切静电场;闭合曲面称为高斯面
(2)电场的环路定理 电势能
一、静电场力的功
❖单个点电荷产生的电场
b
第1章 静电场基本规律 课后习题PPT课件

(1)计算与球心相距 r 1.00cm, 3.00cm, 5.00cm 的场强。
(2)画出场强随距离变化的曲线。
解:由对称性可以判定,场强具有球对称 性。小球表面上和球壳内外表面上的电荷
解:以P点到带电细棒的垂足O为坐标原点建立坐标系如图。
dE
y
电荷元在P点产生的电场强度大小为
dq
dx
dE 4π 0r 2 4π 0r 2
dE x
dE cos
cos dx 4 0r 2
P
ra
dx
O
x
l
x
dx 4 0r 2
l
r
x
4 0
(l
l x dx
x)2 a2 3/2
dq=dx
解:在半球面上取圆环形面元.其带 电量为
Y R
利用P34例3结论, 知其在O点的电场强度
θ
大小为
O
X
方向沿X轴负向.如图所示.
O点的总电场强度为
Y
R θ
O
X
“-”表示电场方向沿X轴负向.
法二:在球面上取面元ds ,如图:
dq ds Rd R sin d
R O
dEz
dE cos
dq
4 0 R2
Ex 40
l l x dx
1 l d l x2
0
(l
x)2
a2 3/2
4 0
(
) 2
0
(l
x)2
a2 3/2
8 0
l d[ l x 2 a2 ]
0 (l x)2 a2 3/2
l
[ l x 2 a2 ]1/2
[ l x 2 a2 ]1/2 l
第1章真空中的静电场

电磁学 认识物质微观构造和性质的基础和 途径;其它许多学科的基础;
在中学物理基础上,主要从场的观点讨 论电磁运动规律; 要求掌握
电磁学的基本内容和基本方法
真空中的静电场
真空中稳恒电流的磁场
介质中的电场和磁场 ➢电磁感应与电磁场
Electrostatic field
求: 均匀带电圆环轴线上的场强。
解:在圆环上任取电荷元
dQ Qdl 2R
R
rx
dE
dE
dE
dE// x
r dE
dE dQ
4 0r 2
dE dE// dE
E E// E
由对称性分析知 垂直x 轴的场强为0
E L dE 0
E//
L dE //
Lcorxs4ddEQ0r 2
一、电场线(电力线): 描述场强分布的一族空间曲线
1.规定
场强方向:电场线上每一点的切线方向为 该点电场的方向;
电场线的疏密表征场强的大小
场强大小
(通过每一点垂直于电场方向单位 面积上的电场线条数为该点电场 强度的大小)
dS
E
E de dS
﹡电场线图形可通过实验显现出来。如:将针状晶体碎屑撒在绝缘油中使之
电荷面密度为 . 求通过盘心且垂直盘面的轴线上
任意一点处的电场强度.
解 由例3
y dq 2π RdR
E
4π
qx
0(x2
R2 )3
2
dEx
4π
dq x
0(x2 R2)3
2
R
(x2 R2 )1/ 2
zR0
o x P dEx
dR q π R02
xRdR
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.2 Coulomb定律
(1) 历史背景
18世纪中叶,定性观察电磁现象 1785年,Coulomb发明扭秤:力与电量、距离的关系?
(2) Coulomb定律 点电荷: 理想模型。突出电量及位置,忽略形状、大小、
电荷分布等次要因素。(类似力学中质点) 实际应用要求:当两带电体距离 > > 带电体尺寸
F0 q0 E(r )
(2)电场——矢量场
大小:单位电荷所受力的大小 方向:正电荷所受力的方向
静电场:电场分布不随时间变化; 匀强电场:大小与方向均不随位置发生变化的电场
(3)点电荷q的电场 E (r ) 1 q r 4 0 r 3
球对称
1.2.3 连续分布电荷产生的电场
定律表述
真空中两点电荷间的作用力大小正比于两点电荷电
量的乘积,反比于两点电荷间距离的平方;方向沿两点
电荷的连线,同种电荷相互排斥,异种电荷相互吸引。
数学表述
q1q2 q1q2 F12 2 e12 k 2 e12 r12 r1 r2
k 1 4 0
F21
q1
r12 r2 r1
~1745:穆欣布洛克(荷) :存储电方法——莱顿瓶 存储电 ~1760:伯努利(荷):猜测平方反比? ~1747:富兰克林(美):电荷守恒律、电的一元流体理论 尖端放电现象 ~1766:普里斯特利:金属容器内部没有电力,内表面无电荷
~1773:卡文迪许(英):推测电力与距离平方成反比(1879麦 克斯韦整理) (检验导体球内表面电荷) ~1785:库仑(法):库仑定律(定量描述电荷间作用) ~1811:泊松(法):静电学解析理论 ~1780:伽伐尼(意):观察到“生物电” ~1799:伏打 Volta (意):制造出化学电池 Cu-Zn ~1822:塞贝克:温差电效应 ~1820:奥斯特(丹):电流磁效应 ~1820:安培(法):物质磁性的分子电流假说、 毕奥-萨伐尔(法):长直通电导线对磁极作用 电流元间的相互作用——安培定律
p cos p
点电荷 电偶极子
1 E 2 r
1 E 3 r
p sin
作用力的距离关系
电四极子?
1 E 4 r
(2)均匀带电细棒中垂面上任一点的电场强度?
L, q,
由对称性
Ex 0
P
x r
r dx dEr 4 0 (r 2 x 2 )3 / 2 1
dx l / 2 (r 2 x 2 )3/ 2 lr qr 2 2 2 1/ 2 4 0 r (r l ) 4 0 r 2 (r 2 l 2 )1/ 2
~1905:爱因斯坦(德):狭义相对论(洛伦兹变换) ——电力与磁力的统一
电磁学的主要内容
电磁理论 电磁感应 静电学
静磁学
场
交流电路 直流电路
路
教材与参考书
教科书 《电磁学》叶邦角编 参考书 《电磁学》 张玉民等编 《电磁学》赵凯华等编 《电磁学》贾起民等编 科学出版社 高教出版社 高教出版社
+q
B 延长线上 (B点)
E// 2p 4 0 r 3
一般情况
当r>>l时(远场)
2 p cos E// 4 0 r 3 3e ( p er ) p E r 4 0 r 3
p sin E 4 0 r 3
对照电势解法
绪 论
为什么学? 电磁学是什么? 如何演化? 主要内容? 考核方式?
1
电磁学的重要性
基础方面: 物质的电结构是物质的基本组成形式
电磁作用是物质的基本作用之一
电磁场是物质世界的重要组成部分 应用方面: 能源(第二次技术革命——电力革命) 通讯、导航定位 电子器件与科技、控制技术 ………… 生活与活动的任何场合
流速V的通量为 V ds
s s
v n S
s 电通量为 E ds E n ds
n 为指向曲面凸出一侧的外法线方向
电通量物理意义:通过s的电力线根数,是标量。
若 > 0 有净电力线穿出 对于闭合曲面: E ds 若 < 0 有净电力线穿入 s
l/2
r Er 4 0
l 0
Er
qr 4 0 r
3
l
Er
r er 2 2 0 r 2 0 r
(3)均匀带电圆环通过圆心中 垂线上任一点的电场强度? R, q,
(4)均匀带电圆盘通过中垂 线上任一点的电场强度?
R, q,
r12 q2 F12
r1
o
r2
0 8.851012 C 2 N 1 m2
满足牛顿第三定律
(3) 几点说明
静止参考系中成立。静止电荷对运动电荷的力仍可由库仑 定律描述,反之不成立。 库仑定律两特点。 (1)有心力——环路定理——静电场无 旋;(2)平方反比——Gauss定理——静电场为有源场 精度: F r 2
利用 q(r ) (r )dV 则任一带电体对q0 的作用力为
F
1 4 0
V
( r ) q0
3 (r0 r )dV r0 r
对面电荷和线电荷只要用相应的电荷密度与电荷元带入
利用 q(r ) (r )dV 或 q' (r ' ) (r ' )dV ' 原则上可求解 任意两带电体间的作用力
5
~1826:欧姆(德) : 欧姆定律——电流与电压成正比 ~1848:基尔霍夫(德) :复杂电路理论 ~1831:法拉第(英):电磁感应现象、力线、场观点 ~1834: 电解定律 ~1845: 磁光效应,统一解释顺次、抗磁性 ~1856-1864:麦克斯韦(英):涡旋电场、位移电流—— 电磁理论——电磁波——光是电磁波 ~1888:赫兹(德):验证电磁波
性质
+q-q 或 +q -q:不能在无电荷处中断。静电场 为有源场 两电力线不能在无电荷的地方相交,电力线不能从电力x 线管中穿过.
静电场的电力线不能闭合——静电场的无旋性
几种常见电荷分布对应的电力线与等位面示意
+
点电荷
电偶极子
(2)电通量
定义:
由流体的不可压缩来引入通量概念 E s
电磁学的发展历史
公元前~600:摩擦吸引物体 磁石吸引物体,吸引、排斥 ~1600:吉尔伯特(英):摩擦——验电器 ~1660:盖力克(德):摩擦起电机 制造电 ~1729:格雷(英):导体、绝缘体分类 运输电 ~1733:杜费(法):电荷二元论:两种电荷(树脂电、玻璃电;
同电排斥、异电吸引)
微观上:电荷是分立的;宏观上:连续
(1) 场强的叠加原理:
根据静电力的叠加原理
N E (r ) i 1 Ei (r )
(2)点电荷组电场
1 E (r ) 4πε0
i
3 (r ri ) r ri
(r ' ) 3 (r r ' )dV r r '
1773年,卡文迪许 < 0.02 ;1879年,麦克斯韦 < 5x10-5
1936年,采用灵敏静电计, < 2x10-9 ;1971年, <(2.73.1)x10-16 理论上, =0和光子静止质量为零有关, m0<10-49g。
适用范围:库伦力为长程力 1910年Rutherford 10-14m, 现代高能粒子散射实验:< 10-15m 精确成立 大尺度上:人造卫星地磁场 107m 成立 同引力的比较 : (电荷 vs 质量) (e~p):电力/引力~1039,平方反比、引力、斥力
F
1 4 0
( r ) ( r ' )
r r'
3
(r r ' )dldl'
17
L L'
1.2 电场与电场强度
1.2.1 电场的引入 库仑力作用的机制,作用是如何体现的?
超距(直接、瞬时)? 近距作用:以太,场(需要传播时间)?
带电体1
场
带电体2
在静电学研究范围内,超距作用观点与场观点所得到的结果是等效的
ห้องสมุดไป่ตู้
《电磁学》胡友秋等编
《物理学》 哈理德瑞斯尼克 《伯克利教程》
高教出版社
考评方法
平时:30 %;期中:30 %;期末:40 %。
第1章 真空中的静电场
本章讨论的内容主要限制在 真空(无极化电荷) 静止电荷(无运动) 静电场的特性:有源性——Gauss定律 无旋性——环路定理 描述电场的方法: 电场强度与电势 两者间关系
F
1 4 0
V V'
(r ) (r ' )
r r'
3
(r r ' )dVdV '
对面电荷和线电荷只要用相应的电荷密度与电荷元带入
F
1 4 0
S S'
(r ) (r ' )
r r'
3
(r r ' )dSdS'
(4)叠加原理
实验证明:两个静止点电荷间的相互作用力不因第三 个静止点电荷的存在而改变。 数学表述:N个电荷构成的电荷组对q0的作用
1 F0 4 0
i 1
N
q0 qi 3 (r0 ri ) r0 ri
只能由实验证实,且和电荷叠加原理相一致(即ri = rj) 叠加原理并不是一个理所当然的结果,它反映了一个新的 实验事实,即电的作用没有三体力存在,因而它是库仑定 律的一个基本性质,是计算任意复杂系统的总库仑力的理 论基础。
