三角形全等的判定同步练习1

合集下载

人教版八年级数学上册全等三角形的判定同步训练习题

人教版八年级数学上册12.2《全等三角形的判定》同步训练习题一．选择题（共10小题）1．（2015•莆田）如图，AE∥DF，AE=DF，要使△EAC≌△FDB，需要添加下列选项中的（）A．AB=CD B．EC=BF C．∠A=∠D D．AB=BC2．（2015春•南京校级期末）下列说法中：①如果两个三角形可以依据“AAS”来判定全等，那么一定也可以依据“ASA”来判定它们全等；②如果两个三角形都和第三个三角形不全等，那么这两个三角形也一定不全等；③要判断两个三角形全等，给出的条件中至少要有一对边对应相等．正确的是（）A．①和②B．②和③C．①和③D．①②③3．（2015•宁波）如图，▱ABCD中，E，F是对角线BD上的两点，如果添加一个条件，使△ABE≌△CDF，则添加的条件不能为（）A．BE=DF B．BF=DE C．AE=CF D．∠1=∠24．（2015•泰州）如图，△ABC中，AB=AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等三角形的对数是（）A．1对B．2对C．3对D．4对5．（2015•滨湖区一模）在△ABC中，∠ABC=30°，AB边长为4，AC边的长度可以在1、2、3、4、5中取值，满足这些条件的互不全等的三角形的个数是（）A．3个B．4个C．5个D．6个6．（2015•沂源县校级模拟）如图，用尺规作出∠AOB的角平分线OE，在作角平分线过程中，用到的三角形全等的判定方法是（）A．ASA B．SSS C．SAS D．AAS7．（2015•启东市模拟）如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②AB=DE，∠B=∠E．BC=EF；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，AC=DF，∠B=∠E．其中，能使△ABC≌△DEF的条件共有（）A．1组 B．2组 C．3组 D．4组8．（2015•漳州一模）小明不小心把一块三角形形状的玻璃打碎成了三块，如图①②③，他想要到玻璃店去配一块大小形状完全一样的玻璃，你认为应带（）A．① B．② C．③ D．①和②9．（2015春•陕西校级期末）如图，CE⊥AB，DF⊥AB，垂足分别为E、F，AC∥DB，且AC=BD，那么Rt △AEC≌Rt△BFC的理由是（）A．SSS B．AAS C．SAS D．HL10．（2014•厦门）如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F．若AC=BD，AB=ED，BC=BE，则∠ACB等于（）A．∠EDB B．∠BED C．∠AFB D．2∠ABF二．填空题（共10小题）11．（2015•南昌）如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有对全等三角形．12．（2015•齐齐哈尔）如图，点B、A、D、E在同一直线上，BD=AE，BC∥EF，要使△ABC≌△DEF，则只需添加一个适当的条件是．（只填一个即可）13．（2015•永州）如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE= ．14．（2015•怀化）如图，在正方形ABCD中，如果AF=BE，那么∠AOD的度数是．15．（2015•盐亭县模拟）如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是度．16．（2015•姜堰市一模）如图，E为正方形ABCD边CD上一点，DE=3，CE=1，F为直线BC上一点，直线DF与直线AE交于G，且DF=AE，则DG= ．17．（2015春•锡山区）如图，∠B=∠D=90°，BC=DC，∠1=40°，则∠2= °．18．（2015春•揭西县期末）如图所示，已知点D为等腰直角三角形ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA，则∠DCE的度数是．19．（2015春•瑶海区期末）如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，G在AD 上，且DF=BE．①CE=CF；②EC⊥CF；③△ECG≌△FCG，④若∠GCE=45°，则EG=BE+GD，以上说法正确的是．20．（2015春•苏州期末）如图，△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点P从A点出发沿A﹣C 路径向终点C运动；点Q从B点出发沿B﹣C﹣A路径向终点A运动．点P和Q分别以每秒1cm和3cm 的运动速度同时开始运动，其中一点到达终点时另一点也停止运动，在某时刻，分别过P和Q作PE⊥l 于E，QF⊥l于F．则点P运动时间为时，△PEC与△QFC全等．三．解答题（共10小题）21．（2015•云南）如图，∠B=∠D，请添加一个条件（不得添加辅助线），使得△ABC≌△ADC，并说明理由．22．（2015•通辽）如图，四边形ABCD中，E点在AD上，其中∠BAE=∠BCE=∠ACD=90°，且BC=CE，求证：△ABC与△DEC全等．23．（2015•泸州）如图，AC=AE，∠1=∠2，AB=AD．求证：BC=DE．24．（2015•南充）如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：（1）△AEF≌△CEB；（2）AF=2CD．25．（2015•温州）如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．（1）求证：AB=CD．（2）若AB=CF，∠B=30°，求∠D的度数．26．（2015•金溪县模拟）请从以下三个等式中，选出一个等式填在横线上，并加以证明．等式：AB=CD，∠A=∠C，∠AEB=∠CFD，已知：AB∥CD，BE=DF，．求证：△ABE≌△CDF．证明：27．（2015•大兴区一模）已知，在△ABC中，DE∥AB，FG∥AC，BE=GC．求证：DE=FB．28．（2015•西安模拟）如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于Q．（1）求证：△ADC≌△BEA；（2）若PQ=4，PE=1，求AD的长．29．（2015•铁岭一模）已知：△ABC中，BD、CE分别是AC、AB边上的高，BQ=AC，点F在CE的延长线上，CF=AB，求证：AF⊥AQ．30．（2015春•鄄城县期末）如图1，△ABC中，∠BAC=90°，AB=AC，AE是过点A的一条直线，且点B，C在AE的异侧，BD⊥AE于点D，CE⊥AE于点E．（1）BD=DE+CE成立吗？为什么？（2）若直线AE绕点A旋转到如图2位置时，其他条件不变，BD与DE，CE关系如何？请说明理由．人教版八年级数学上册12.2《全等三角形的判定》同步训练习题参考答案一．选择题（共10小题）1．（2015•莆田）如图，AE∥DF，AE=DF，要使△EAC≌△FDB，需要添加下列选项中的（）A．AB=CD B．EC=BF C．∠A=∠D D．AB=BC选A【点评】此题主要考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．2．（2015春•南京校级期末）下列说法中：①如果两个三角形可以依据“AAS”来判定全等，那么一定也可以依据“ASA”来判定它们全等；②如果两个三角形都和第三个三角形不全等，那么这两个三角形也一定不全等；③要判断两个三角形全等，给出的条件中至少要有一对边对应相等．正确的是（）A．①和②B．②和③C．①和③D．①②③【考点】全等三角形的判定．【分析】熟练综合运用判定定理判断，做题时要结合已知与全等的判定方法逐个验证．【解答】解：因为两个三角形的两个角对应相等，根据内角和定理，可知另一对对应角也相等，那么总能利用ASA来判定两个三角形全等，故选项①正确；两个全等的直角三角形都和一个等边三角形不全等，但是这两个全等的直角三角形可以全等，故选项②错误；判定两个三角形全等时，必须有边的参与，否则不会全等，故选项③正确．故选C．【点评】AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．3．（2015•宁波）如图，▱ABCD中，E，F是对角线BD上的两点，如果添加一个条件，使△ABE≌△CDF，则添加的条件不能为（）A．BE=DF B．BF=DE C．AE=CF D．∠1=∠2【考点】全等三角形的判定；平行四边形的性质．【分析】利用平行四边形的性质以及全等三角形的判定分别得出三角形全等，再进行选择即可．【解答】解：A、当BE=FD，∵平行四边形ABCD中，∴AB=CD，∠ABE=∠CDF，在△ABE和△CDF中，∴△ABE≌△CDF（SAS），故此选项错误；C、当AE=CF无法得出△ABE≌△CDF，故此选项符合题意；B、当BF=ED，∴BE=DF，∵平行四边形ABCD中，∴AB=CD，∠ABE=∠CDF，在△ABE和△CDF中，∴△ABE≌△CDF（SAS），故此选项错误；D、当∠1=∠2，∵平行四边形ABCD中，∴AB=CD，∠ABE=∠CDF，在△ABE和△CDF中，∴△ABE≌△CDF（ASA），故此选项错误；故选C．【点评】本题考查了平行四边形的性质以及全等三角形的判定等知识，熟练掌握全等三角形的判定方法是解题关键．4．（2015•泰州）如图，△ABC中，AB=AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等三角形的对数是（）A．1对B．2对C．3对D．4对【考点】全等三角形的判定；线段垂直平分线的性质；等腰三角形的性质．【专题】压轴题．【分析】根据已知条件“AB=AC，D为BC中点”，得出△ABD≌△ACD，然后再由AC的垂直平分线分别交AC、AD、AB于点E、O、F，推出△AOE≌△EOC，从而根据“SSS”或“SAS”找到更多的全等三角形，要由易到难，不重不漏．【解答】解：∵AB=AC，D为BC中点，∴CD=BD，∠BDO=∠CDO=90°，在△ABD和△ACD中，，∴△ABD≌△ACD；∵EF垂直平分AC，∴OA=OC，AE=CE，在△AOE和△COE中，，∴△AOE≌△COE；在△BOD和△COD中，，∴△BOD≌△COD；在△AOC和△AOB中，，∴△AOC≌△AOB；故选：D．【点评】本题考查的是全等三角形的判定方法；这是一道考试常见题，易错点是漏掉△ABO≌△ACO，此类题可以先根据直观判断得出可能全等的所有三角形，然后从已知条件入手，分析推理，对结论一个个进行论证．5．（2015•滨湖区一模）在△ABC中，∠ABC=30°，AB边长为4，AC边的长度可以在1、2、3、4、5中取值，满足这些条件的互不全等的三角形的个数是（）A．3个B．4个C．5个D．6个【考点】全等三角形的判定．【分析】根据30°角所对的直角边等于斜边的一半以及垂线段最短的性质求出AC边的最短值，然后选择即可得解．【解答】解：如图，AC⊥BC时，∵∠ABC=30°，AB=4，∴AC=AB=×4=2，∵垂线段最短，∴AC≥2，∴在1、2、3、4、5中可取的值有2、3、4、5，当AC=2时可以作1个三角形，当AC=3时可以作2个三角形，当AC=4时可以作1个三角形，当AC=5时可以作1个三角形，共1+2+1+1=5，所以，三角形的个数是5个．故选C．【点评】本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质，垂线段最短，求出AC边的最小值是解题的关键．6．（2015•沂源县校级模拟）如图，用尺规作出∠AOB的角平分线OE，在作角平分线过程中，用到的三角形全等的判定方法是（）A．ASA B．SSS C．SAS D．AAS【考点】全等三角形的判定；作图—基本作图．【分析】由作图可得CO=DO，CE=DE，OE=OE，可利用SSS定理判定三角形全等．【解答】解：在△OCE和△ODE中，，∴△OCE≌△ODE（SSS）．故选：B．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．7．（2015•启东市模拟）如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②AB=DE，∠B=∠E．BC=EF；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，AC=DF，∠B=∠E．其中，能使△ABC≌△DEF的条件共有（）A．1组B．2组C．3组D．4组【考点】全等三角形的判定．【分析】要使△ABC≌△DEF的条件必须满足SSS、SAS、ASA、AAS，可据此进行判断．【解答】解：第①组满足SSS，能证明△ABC≌△DEF．第②组满足SAS，能证明△ABC≌△DEF．第③组满足ASA，能证明△ABC≌△DEF．第④组只是SSA，不能证明△ABC≌△DEF．所以有3组能证明△ABC≌△DEF．故符合条件的有3组．故选：C．【点评】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关键．8．（2015•漳州一模）小明不小心把一块三角形形状的玻璃打碎成了三块，如图①②③，他想要到玻璃店去配一块大小形状完全一样的玻璃，你认为应带（）A．①B．②C．③D．①和②【考点】全等三角形的应用．【分析】根据全等三角形的判定方法解答即可．【解答】解：带③去可以利用“角边角”得到全等的三角形．故选C．【点评】本题考查了全等三角形的应用，熟练掌握三角形全等的判定方法是解题的关键．9．（2015春•陕西校级期末）如图，CE⊥AB，DF⊥AB，垂足分别为E、F，AC∥DB，且AC=BD，那么Rt △AEC≌Rt△BFC的理由是（）A．SSS B．AAS C．SAS D．HL【考点】全等三角形的判定．【分析】根据垂直定义求出∠AEC=∠BFD=90°，根据平行线的性质得出∠A=∠B，根据全等三角形的判定定理AAS推出即可．【解答】解：∵CE⊥AB，DF⊥AB，∴∠AEC=∠BFD=90°．∵AC∥DB，∴∠A=∠B．在△AEC和△BFD中，∴Rt△AEC≌Rt△BFC（AAS），故选B．【点评】本题考查了全等三角形的判定，平行线的性质，垂直定义的应用，能熟练地运用定理进行推理是解此题的关键，注意：全等三角形的判定定理有SAS，AAS，ASA，SSS，直角三角形全等的判定定理除了具有以上定理外，还有HL定理．10．（2014•厦门）如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F．若AC=BD，AB=ED，BC=BE，则∠ACB等于（）A．∠EDB B．∠BED C．∠AFB D．2∠ABF【考点】全等三角形的判定与性质．【分析】根据全等三角形的判定与性质，可得∠ACB与∠DBE的关系，根据三角形外角的性质，可得答案．【解答】解：在△ABC和△DEB中，，∴△ABC≌△DEB （SSS），∴∠ACB=∠DBE．∵∠AFB是△BFC的外角，∴∠ACB+∠DBE=∠AFB，∠ACB=∠AFB，故选：C．【点评】本题考查了全等三角形的判定与性质，利用了全等三角形的判定与性质，三角形外角的性质．二．填空题（共10小题）11．（2015•南昌）如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有 3 对全等三角形．【考点】全等三角形的判定；角平分线的性质．【分析】由OP平分∠MON，PE⊥OM于E，PF⊥ON于F，得到PE=PF，∠1=∠2，证得△AOP≌△BOP，再根据△AOP≌△BOP，得出AP=BP，于是证得△AOP≌△BOP，和R t△AOP≌R t△BOP．【解答】解：OP平分∠MON，PE⊥OM于E，PF⊥ON于F，∴PE=PF，∠1=∠2，在△AOP与△BOP中，，∴△AOP≌△BOP，∴AP=BP，在△EOP与△FOP中，，∴△EOP≌△FOP，在R t△AEP与R t△BFP中，，∴R t△AEP≌R t△BFP，∴图中有3对全等三角形，故答案为：3．【点评】本题考查了角平分线的性质，全等三角形的判定和性质，熟练掌握全等三角形的判定定理是解题的关键．12．（2015•齐齐哈尔）如图，点B、A、D、E在同一直线上，BD=AE，BC∥EF，要使△ABC≌△DEF，则只需添加一个适当的条件是BC=EF或∠BAC=∠EDF ．（只填一个即可）【考点】全等三角形的判定．【专题】开放型．【分析】BC=EF或∠BAC=∠EDF，若BC=EF，根据条件利用SAS即可得证；若∠BAC=∠EDF，根据条件利用ASA即可得证．【解答】解：若添加BC=EF，∵BC∥EF，∴∠B=∠E，∵BD=AE，∴BD﹣AD=AE﹣AD，即BA=ED，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）；若添加∠BAC=∠EDF，∵BC∥EF，∴∠B=∠E，∵BD=AE，∴BD﹣AD=AE﹣AD，即BA=ED，在△ABC和△DEF中，，∴△ABC≌△DEF（ASA），故答案为：BC=EF或∠BAC=∠EDF【点评】此题考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解本题的关键．13．（2015•永州）如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE= 3 ．【考点】全等三角形的判定与性质．【分析】由已知条件易证△ABE≌△ACD，再根据全等三角形的性质得出结论．【解答】解：△ABE和△ACD中，，∴△ABE≌△ACD（AAS），∴AD=AE=2，AC=AB=5，∴CE=BD=AB﹣AD=3，故答案为3．【点评】本题主要考查了全等三角形的性质和判定，熟记定理是解题的关键．14．（2015•怀化）如图，在正方形ABCD中，如果AF=BE，那么∠AOD的度数是90°．【考点】全等三角形的判定与性质；正方形的性质．【专题】压轴题．【分析】根据全等三角形的判定与性质，可得∠ODA与∠BAE的关系，根据余角的性质，可得∠ODA与∠OAD的关系，根据直角三角形的判定，可得答案．15．（2015•盐亭县模拟）如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE的度数是60 度．【考点】全等三角形的判定与性质；等边三角形的性质．【专题】几何图形问题．【分析】根据题目已知条件可证△ABD≌△BCE，再利用全等三角形的性质及三角形外角和定理求解．【解答】解：∵等边△ABC，∴∠ABD=∠C，AB=BC，在△ABD与△BCE中，，∴△ABD≌△BCE（SAS），∴∠BAD=∠CBE，∵∠ABE+∠EBC=60°，∴∠ABE+∠BAD=60°，∴∠APE=∠ABE+∠BAD=60°，∴∠APE=60°．故答案为：60．【点评】本题利用等边三角形的性质来为三角形全等的判定创造条件，是中考的热点．16．（2015•姜堰市一模）如图，E为正方形ABCD边CD上一点，DE=3，CE=1，F为直线BC上一点，直线DF与直线AE交于G，且DF=AE，则DG= 或．【考点】全等三角形的判定与性质；勾股定理；正方形的性质．【专题】分类讨论．【分析】分两种情况：①由正方形的性质得出∠ADE=∠DCF=90°，AD=DC=4，由勾股定理求出AE，由HL证明Rt△ADE≌Rt△DCF，得出∠AED=∠DFC，证出∠DGE=90°，由△ADE的面积=AE×DG=AD×DE，即可求出DG的长；②如图2所示：同①得：Rt△ADE≌Rt△DCF，得出CF=DE，DF=AE，作GM⊥BC于M，作GN⊥DC于N；证出△GMF∽△DCF，△GNE∽△ADE，得出比例式，，设GM=4x，则FM=3x，GF=5x，GN=MC=3+3x，EN=4x+1，解方程求出x，得出GF，即可得出DG的长．【解答】解：分两种情况：①如图1所示：∵四边形ABCD是正方形，∴∠ADE=∠DCF=90°，AD=DC=3+1=4，AD∥BC，∴AE===5，在Rt△ADE和Rt△DCF中，，∴Rt△ADE≌Rt△DCF（HL），∴∠AED=∠DFC，∵∠DFC+∠CDF=90°，∴∠AED+∠CDF=90°，∴∠DGE=90°，∵△ADE的面积=AE×DG=AD×DE，∴DG==；②如图2所示：同①得：Rt△ADE≌Rt△DCF，∴CF=DE=3，DF=AE=5，作GM⊥BC于M，作GN⊥DC于N；则GM∥DC，GN∥AD，∴△GMF∽△DCF，△GNE∽△ADE，∴=，=，设GM=4x，则FM=3x，∴GF=5x，GN=MC=3+3x，EN=4x+1，∴，解得：x=，∴GF=，∴DG=DF+GF=5+=；综上所述：DG的长为或；故答案为：或．【点评】本题考查了正方形的性质、勾股定理、全等三角形的判定与性质、相似三角形的判定与性质；本题有一定难度，需要进行分类讨论，特别是②中，需要证明三角形相似才能得出结果．17．（2015春•锡山区期末）如图，∠B=∠D=90°，BC=DC，∠1=40°，则∠2= 50 °．【考点】全等三角形的判定与性质．【分析】易证△ABC和△ADC均为直角三角形，即可证明RT△ABC≌RT△ADC，可得∠1=∠CAD，即可解题．【解答】解：∵∠B=∠D=90°，∴△ABC和△ADC均为直角三角形，在RT△ABC和RT△ADC中，，∴RT△ABC≌RT△ADC（HL），∴∠1=∠CAD，∴∠2=90°﹣∠CAD=50°．故答案为 50°．【点评】本题考查了全等三角形的判定，考查了全等三角形对应角相等的性质，本题中求证RT△ABC ≌RT△ADC是解题的关键．18．（2015春•揭西县期末）如图所示，已知点D为等腰直角三角形ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA，则∠DCE的度数是105°．【考点】全等三角形的判定与性质；等腰三角形的性质；等腰直角三角形．【分析】根据等腰直角△ABC，求出CD是边AB的垂直平分线，求出CD平分∠ACB，根据CE=CA，∠CAD=15°，求出∠ACE=150°即可利用角的和差求解．【解答】解：∵△ABC是等腰直角三角形，∴∠BAC=∠ABC=45°，∵∠CAD=∠CBD=15°，∴∠BAD=∠ABD=45°﹣15°=30°，∠ABD=∠ABC﹣15°=30°，∴BD=AD，∴D在AB的垂直平分线上，∵AC=BC，∴C也在AB的垂直平分线上，即直线CD是AB的垂直平分线，∴∠ACD=∠BCD=45°，∵∠CAD=15°，CE=CA，∴∠CED=∠CAD=15°，∴∠ECA=150°，∴∠DCE=∠ECA﹣∠ACD=150°﹣45°=105°．故答案为：105°．【点评】此题主要考查等腰直角三角形，线段垂直平分线的性质与判定、等腰三角形的性质等知识点，难易程度适中，是一道很典型的题目．。

1.2.2 直角三角形全等的判定同步练习(答案版)

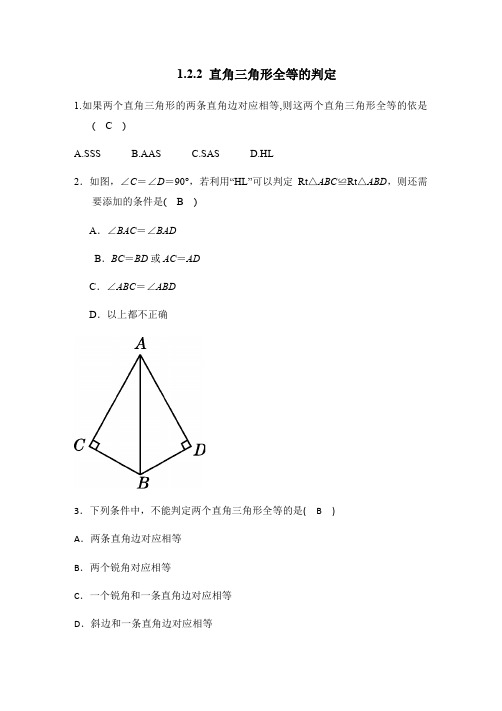
1.2.2 直角三角形全等的判定1.如果两个直角三角形的两条直角边对应相等,则这两个直角三角形全等的依是(C)A.SSSB.AASC.SASD.HL2．如图，∠C＝∠D＝90°，若利用“HL”可以判定Rt△ABC≌Rt△ABD，则还需要添加的条件是(B)A．∠BAC＝∠BADB．BC＝BD或AC＝ADC．∠ABC＝∠ABDD．以上都不正确3．下列条件中，不能判定两个直角三角形全等的是(B)A．两条直角边对应相等B．两个锐角对应相等C．一个锐角和一条直角边对应相等D．斜边和一条直角边对应相等4.如图，在△ABC中，∠C＝90°，E为AC上一点，ED⊥AB于点D，BD＝BC，连接BE，若AC＝6 cm，则AE＋DE等于(C)A．4 cm B．5 cm C．6 cm D．7 cm【点拨】由已知可证Rt△BDE≌Rt△BCE，∴DE＝CE.∴AE＋DE＝AE＋CE＝AC＝6 cm.5.如图，BD＝CF，FD⊥BC于点D，DE⊥AB于点E，BE＝CD，若∠AFD＝134°，则∠EDF的度数为(A)A．44° B．36° C．46° D．34°【点拨】∵BD＝CF，BE＝CD，FD⊥BC，DE⊥AB，∴Rt△BDE≌Rt△CFD(HL)．∴∠BDE＝∠CFD.又∵∠CFD＝180°－∠AFD＝46°，∠EDF＋∠EDB＝90°，∴∠EDF＝90°－46°＝44°.【答案】A6．如图，在△ABC中，△C＝90°，AD＝AC，DE△AB交BC于点E.若△B＝28°，则△AEC＝(B)A．28°B．59°C．60°D．62°7．如图，在△ABC中，AB＝AC，BD⊥AC于点D，CE⊥AB于点E，BD，CE 相交于点O，AO的延长线交BC于点F，则图中全等的直角三角形有(D) A．3对B．4对C．5对D．6对8．如图，H是△ABC的高AD，BE的交点，且DH＝DC.下列结论：①BD＝AD；②BC＝AC；③BH＝AC；④CE＝CD.其中正确的有(B)A．1个B．2个C．3个D．4个9．(中考·凉山州)如图，∠E＝∠F＝90°，∠B＝∠C，AE＝AF.下列结论：①EM＝FN；②CD＝DN；③∠F AN＝∠EAM；④△ACN≌△ABM.其中正确的有(C)A．1个B．2个C．3个D．4个10.(中考·南京)如图，AB⊥CD，且AB＝CD，E，F是AD上两点，CE⊥AD，BF⊥AD.若CE＝a，BF＝b，EF＝c，则AD的长为(D)A．a＋c B．b＋cC．a－b＋c D．a＋b－c【点拨】∵AB⊥CD，CE⊥AD，BF⊥AD，∴∠AFB＝∠CED＝90°，∠A＋∠D＝90°，∠C＋∠D＝90°.∴∠A＝∠C.又∵AB＝CD，∴△ABF≌△CDE(AAS)．∴AF＝CE＝a，DE＝BF＝b.∵EF＝c，∴AD＝AF＋DF＝a＋(b－c)＝a＋b－c.【答案】D二．填空题11.如图所示,在△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件__AB=AC__ ,若加条件∠B=∠C,则可用_______AAS__________判定.第11题图第12题图第13题图12.如图所示,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是____HL或斜边直角边定理_____13.如图所示,已知AB⊥CD,垂足为点B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是__AC=DE____14．如图，MN∥PQ，AB⊥PQ，点A，D在直线MN上，点B，C在直线PQ上，点E在AB上，AD＋BC＝7，AD＝EB，DE＝EC，则AB＝___7_____．【点拨】∵MN∥PQ，AB⊥PQ，∴∠DAE＝∠EBC＝90°.∵AD＝BE，DE＝EC，∴Rt△ADE≌Rt△BEC.∴AE＝BC.∵AD＋BC＝7，∴AB＝AE＋BE＝BC＋AD＝7.三．计算证明题15.如图，在△ABC中，AB＝42，D为BC上一点，AD＝BD＝4，在AD上找一点E，使BE＝AC.(1)判断△ABD的形状，并说明理由；(2)求证：△BDE≌△ADC.解：(1)△ABD是等腰直角三角形．理由：在△ABD中，∵AD＝BD＝4，∴AD2＋BD2＝32.又∵AB＝42，∴AB2＝32，∴AD2＋BD2＝AB2，∴△ABD为等腰直角三角形．(2)证明：∵∠ADB＝90°且∠ADB＋∠ADC＝180°，∴∠ADC＝∠ADB＝90°，∴△ADC 和△BDE 为直角三角形．在Rt △ADC 和Rt △BDE 中，⎩⎨⎧AC ＝BE ，AD ＝BD ，∴Rt △ADC ≌Rt △BDE (HL)．16．如图，AC △BC ，AD △BD ，AD ＝BC ，CE △AB ，DF △AB ，垂足分别是E ，F .求证：CE ＝DF .证明：∵AC ⊥BC ，AD ⊥BD ，CE ⊥AB ，DF ⊥AB ，∴∠ACB ＝∠ADB ＝∠AEC ＝∠BFD ＝90°.在Rt △ABC 和Rt △BAD 中，⎩⎨⎧AB ＝BA ，BC ＝AD ，∴Rt △ABC ≌Rt △BAD (HL)，∴AC ＝BD ，∠CAE ＝∠DBF .∵在△ACE 和△BDF 中，⎩⎨⎧∠CAE ＝∠DBF ，∠AEC ＝∠BFD ，AC ＝BD ，∴△ACE ≌△BDF (AAS)，∴CE ＝DF .17．如图，在△ABC 中，AB ＝CB ，∠ABC ＝90°，F 为AB 延长线上一点，点E 在BC 上，且AE ＝CF.(1)求证：Rt △ABE ≌Rt △CBF ；(2)若∠CAE＝30°，求∠ACF的度数．（1）证明：∵∠ABC＝90°，∴∠CBF＝∠ABE＝90°.在Rt△ABE和Rt△CBF中，∵AE＝CF，AB＝CB，∴Rt△ABE≌Rt△CBF(HL)．(2）解：∵AB＝BC，∠ABC＝90°，∴∠CAB＝∠ACB＝45°.∴∠BAE＝∠CAB－∠CAE＝45°－30°＝15°.由(1)知Rt△ABE≌Rt△CBF，∴∠BCF＝∠BAE＝15°，∴∠ACF＝∠BCF＋∠ACB＝15°＋45°＝60°.18.【中考·哈尔滨】已知：△ACB和△DCE都是等腰直角三角形，∠ACB＝∠DCE ＝90°，连接AE，BD交于点O，AE与DC交于点M，BD与AC交于点N.(1) 如图①，求证：AE ＝BD ； (2) 如图②，若AC ＝DC ，在不添加任何辅助线的情况下，请直接写出图②中四对全等的直角三角形．（1）证明：∵△ACB 和△DCE 都是等腰直角三角形，∠ACB ＝∠DCE ＝90°，∴AC ＝BC ，DC ＝EC ，∠ACB ＋∠ACD ＝∠DCE ＋∠ACD ，∴∠BCD ＝∠ACE ，在△ACE 与△BCD 中，⎩⎨⎧AC ＝BC ，∠ACE ＝∠BCD ，CE ＝CD ，∴△ACE ≌△BCD (SAS)，∴AE ＝BD .（2）解：△ACB ≌△DCE ，△EMC ≌△BNC ，△AON ≌△DOM ，△AOB ≌△DOE.19．如图，∠C ＝∠D ，AC ＝AD .求证：BC ＝BD .【思路点拨】当图中的一对三角形根据已知条件无法证明全等时，可通过作辅助线将图形进行分割或添补，构造全等三角形．本题可过点A 分别作BC ，BD 的垂线，构造出几组全等的直角三角形．证明：过点A 作AM ⊥BC ，AN ⊥BD ，分别交BC ，BD 的延长线于点M ，N ，∴∠M ＝∠N ＝90°.∵∠ACB ＝∠ADB ，∴∠ACM ＝∠ADN .在△ACM 和△ADN 中，⎩⎨⎧∠M ＝∠N ，∠ACM ＝∠ADN ，AC ＝AD ，∴△ACM ≌△ADN (AAS)．∴AM ＝AN ，CM ＝DN .在Rt △ABM 和Rt △ABN 中，⎩⎨⎧AB ＝AB ，AM ＝AN ，∴Rt △ABM ≌Rt △ABN (HL)．∴BM ＝BN .∴BM －CM ＝BN －DN ，即BC ＝BD .20.如图,在△ABC 中,AB=AC,点P 从点B 出发沿线段BA 移动,同时,点Q 从点C 出发沿线段AC 的延长线移动,点P,Q 移动的速度相同,PQ 与直线BC 相交于点D.(1)如图①,求证PD=QD.(2)如图②,过点P 作直线BC 的垂线,垂足为E,当P,Q 在移动过程中,线段BE,ED,CD 中是否存在长度保持不变的线段?请说明理由.图3 图4(1)证明:如图3,过点P作PF//AC交BC于点F.∵点P和点Q同时出发,且速度相同,∴BP=CQ.∴PF//AQ,∴∠PFB=∠ACB,∠DPF=∠CQD.∵AB=AC,∴∠B=∠ACB.∴∠B=∠PFB.∴BP=FP.∴FP=CQ.在△PFD和△QCD中,∠DPF=∠DQC,∠PDF=∠QDC,FP=CQ,∴△PFD≌△QCD(AAS),∴PD=QD.(2)解:ED的长度保持不变.理由如下:如图4,过点P作PF//AC交BC于点F.由(1)知PB=PF.△PE△BF,△BE=EF.由(1)知△PFD△△QCD,△FD=CD.△ED=EF+FD=BE+CD=1BC.2△ED的长度为定值.。

练习-三角形全等的条件同步训练 1

三角形全等的条件同步训练一、选择题1．如图1，OA=OC ，OB=OD ，则图中有多少对全等三角形（）A ．2B ．3C ．4D ．5ODCBA21DCBDCB A(1) (2) (3) 2．如图2，AB=AC ，AD=AE ，欲证△ABD ≌△ACE ，可补充条件（） A ．∠1=∠2 B ．∠B=∠C C ．∠D=∠E D ．∠BAE=∠CAD 3．如图3，AD=BC ，要得到△ABD 和△CDB 全等，可以添加的条件是（） A ．AB ∥CD B ．AD ∥BC C ．∠A=∠C D ．∠ABC=∠CDA 二、填空题4．如图4，AB 与CD 交于点O ，OA=OC ，OD=OB ，∠AOD=________，•根据__________可得到△AOD ≌△COB ，从而可以得到AD=_________．O DCBADC BA21EDB A(4) (5) (6)5．如图5，已知△ABC 中，AB=AC ，AD 平分∠BAC ，请补充完整过程说明△ABD ≌△ACD 的理由．∵AD 平分∠BAC∴∠________=∠_________（角平分线的定义）在△ABD 和△ACD 中∵___________________________________________ ∴△ABD ≌△ACD （）三、解题题6．如图6，已知AB=AD ，AC=AE ，∠1=∠2，求证∠ADE=∠B.7．如图，已知AB=AD ，若AC 平分∠BAD ，问AC 是否平分∠BCD ？为什么？CBA8．如图（1），AB ⊥BD ，DE ⊥BD ，点C 是BD 上一点，且BC=DE ，CD=AB ．（1）试判断AC 与CE 的位置关系，并说明理由．（2）如图（2），若把△CDE 沿直线BD 向左平移，使△CDE 的顶点C 与B 重合，此时第（1）问中AC 与BE 的位置关系还成立吗？（注意字母的变化）(1)EDC B A(2)EDC A答案:1．C 2．A 3．B 4．∠COB ；SAS ；CB 5．略 6．证△ABC ≌△ADE 7．平分；证△ABC ≌△ADC 8．①AC ⊥CE ，证△ABC ≌△CDE ；②结论仍成立。

人教版数学八上《三角形全等的判定HL(第4课时)》同步练习1

本资源的初衷，是希望通过网络分享，能够为广大读者提供更好的服务，为您水平的提高提供坚强的动力和保证。

内容由一线名师原创，立意新，图片精，是非常强的一手资料。

三角形全等的判定要点感知1 斜边和一条_______分别相等的两个直角三角形全等(可以简写成_____或“_____”).预习练习1-1 如图,∠B=∠E=90°,AB=DE,AC=DF,则△ABC≌△DEF的理由是( )A.SASB.ASAC.AASD.HL要点感知2 直角三角形全等除“HL”外,还有SSS,SAS,ASA,AAS都适合.预习练习2-1 下列命题：①两直角边分别相等的两个直角三角形全等；②两锐角分别相等的两个直角三角形全等；③斜边和一直角边分别相等的两个直角三角形全等；④一锐角和一直角边分别相等的两个直角三角形全等；⑤一锐角和斜边分别相等的两个直角三角形全等.其中,正确的命题有_____.(填写正确的序号)知识点1 用“HL”判定直角三角形全等1.已知如图，AC⊥BC，AD⊥BD，垂足分别为C、D，AC=BD，Rt△ABC与Rt△BAD全等吗？为什么？2.已知，在△ABC中，AB=AC，AD⊥BC，垂足为D，求证：AD平分∠BAC.3.如图，∠ACB=∠CFE＝90°，AB=DE，BC=EF，求证：AD=CF.知识点2 直角三角形全等的判定方法的选用4.在Rt△ABC和Rt△A′B′C′中，∠C=∠C′=90°，如图，那么下列各条件中，不能使Rt△ABC≌Rt△A′B′C′的是( )A.AB=A′B′=5，BC=B′C′=3B.AB=B′C′=5，∠A=∠B′=40°C.AC=A′C′=5，BC=B′C′=3D.AC=A′C′=5，∠A=∠A′=40°5.如图，在△ABC中，点D是BC的中点，DE⊥AB于点E，DF⊥AC于点F，BE＝CF.(1)图中有几对全等的三角形？请一一列出；(2)选择一对你认为全等的三角形说明理由.6.如图,在Rt△ABC中,∠BAC=90°,DE⊥BC,AC=6,EC=6,∠ACB=60°,则∠ACD的度数为( )A.45°B.30°C.20°D.15°7.如图,在直角三角形ABC中,∠C=90°,一条线段PQ=AB,点P，Q两点分别在AC和AC的垂线AX上移动,当AP=_____时,才能使△ABC≌△QPA.8.如图，已知方格纸中是4个相同的正方形，则∠1+∠3=_____.9.如图,已知AE=DE,AB⊥BC,DC⊥BC,且AB=EC.求证：BC=AB+DC.10.如图,在△ABC中,AD是中线,分别过点B，C作AD及其延长线的垂线BE，CF,垂足分别为点E，F.求证：BE=CF.11.如图所示,已知AB＝CD,DE⊥AC于E,BF⊥AC于F，且BF=DE，求证：AB∥CD.12.如图,已知AD，AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.求证：BC=BE.挑战自我13.已知：点O到△ABC的两边AB，AC所在直线的距离相等,且OB=OC.(1)如图1,若点O在边BC上,求证：∠ABO=∠ACO；(2)如图2,若点O在△ABC的内部,求证：∠ABO=∠ACO.参考答案课前预习要点感知1 直角边斜边、直角边 HL预习练习1-1 D预习练习2-1 ①③④⑤当堂训练1.Rt△ABC≌Rt△BAD.理由如下：∵AC⊥BC，AD⊥BD，∴∠C＝∠D＝90°.在Rt△ABC和Rt△BAD中，AB＝BA，AC ＝BD，∴Rt△ABC≌Rt△BAD(HL).2.证明：∵AD⊥BC，∴∠ADB=∠ADC=90°.在Rt△ABD和Rt△ACD中，AB=AC，AD=AD，∴Rt△ABD≌Rt△ACD(HL).∴∠BAD=∠CAD，即AD平分∠BAC.3.证明：∵∠ACB=∠CFE＝90°，∴∠ACB=∠DFE=90°.在Rt△ACB和Rt△DFE中，AB=DE，BC=EF，∴Rt△ACB≌Rt △DFE(HL).∴AC=DF.∴AC-AF=DF-AF，即AD=CF.4.B5.(1)△BDE≌△CDF，△AED≌△AFD，△ABD≌△ACD.(2)∵DE⊥AB，DF⊥AC，∴△BDE和△CDF是直角三角形.∵D 是BC的中点，∴BD＝CD.又∵BE＝CF，∴Rt△BDE≌Rt△CDF(HL).课后作业6.B7.CB8.90°9.证明：∵AB⊥BC,DC⊥BC,∴∠B=∠C=90°.在Rt△ABE和Rt△ECD中,AE=DE,AB=EC,∴Rt△ABE≌Rt△ECD.∴BE=CD.∵BC=BE+EC,∴BC=AB+DC.10.证明：∵在△ABC中,AD是中线,∴BD=CD.∵CF⊥AD,BE⊥AD,∴∠CFD＝∠BED＝90°.在△BED与△CFD中,∵∠BED ＝∠CFD,∠BDE＝∠CDF,BD＝CD,∴△BED≌△CFD(AAS).∴BE=CF.11.证明：∵DE⊥AC,BF⊥AC,∴∠AFB=∠CED=90°.在Rt△ABF和Rt△CDE中,AB=CD，BF=DE，∴Rt△ABF≌Rt△CDE(HL).∴∠BAF=∠DCE.∴AB∥CD.12.证明：∵AD，AF分别是两个钝角△ABC和△ABE的高,∴∠ADB=∠AFB=90°.∵AB=AB，AD=AF，∴Rt△ABD≌Rt△ABF.∴DB=FB.∵AC=AE,AD=AF，∴Rt△ADC≌Rt△AFE.∴DC=FE.∴DB-DC=FB-FE,即BC=BE.13.(1)证明：过点O作OE⊥AB于E,作OF⊥AC于F,则∠BEO=∠CFO=90°,OE=OF.又∵OB=OC,∴Rt△BOE≌Rt△COF(HL).∴∠ABO=∠ACO.(2)证明：过点O分别作OE⊥AB,OF⊥AC,E，F分别是垂足,则∠BEO=∠CFO=90°,OE=OF.又OB=OC,∴Rt△OEB≌Rt△OFC.∴∠EBO=∠FCO.即∠ABO=∠ACO.本资源的初衷，是希望通过网络分享，能够为广大读者提供更好的服务，为您水平的提高提供坚强的动力和保证。

《直角三角形全等的判定》同步练习题

直角三角形第2课时直角三角形全等的判定一、选择题:1. 两个直角三角形全等的条件是( )A.一锐角对应相等;B.两锐角对应相等;C.一条边对应相等;D.两条边对应相等（2. 如图,∠B=∠D=90°，BC=CD ，∠1=30°，则∠2的度数为( )A. 30°B. 60°C. 30°和60°之间D. 以上都不对3. 如果两个直角三角形的两条直角边对应相等,那么两个直角三角形全等的依据是( )A. AAS4. 已知在△ABC 和△DEF 中,∠A=∠D=90°,则下列条件中不能判定△ABC 和 … △DEF 全等的是( )=DE,AC=DF =EF,BC=DF=DE,BC=EF D.∠C=∠F,BC=EF5. 如图,AB ∥EF ∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( ) 对; 对; 对; 对6. 要判定两个直角三角形全等,下列说法正确的有( ) |①有两条直角边对应相等; ②有两个锐角对应相等; ③有斜边和一条直角边对应相等; ④有一条直角边和一个锐角相等; ⑤有斜边和一个锐角对应相等; ⑥有两条边相等.个个个个12A BCD第2题图第5题图第7题图第8题图7. 如图，已知AB AD =，那么添加下列一个条件后，仍无法判定ABC ADC △≌△的是（）A ．CB CD = B ．BAC DAC =∠∠ C ．BCA DCA =∠∠D ．90B D ==︒∠∠BAEFD8. 如图，已知AD是△ABC的BC边上的高，下列能使△ABD≌△ACD的条件是（）]A．A B=AC B．∠BAC=90°C．B D=AC D．{∠B=45°二、填空题:9.有________和一条________对应相等的两个直角三角形全等,简写成“斜边直角边”或用字母表示为“___________”.10.判定两个直角三角形全等的方法有______________________________.·11.如图，已知AC⊥BD于点P，AP=CP，请增加一个条件，使△ABP≌△CDP（不能添加辅助线），你增加的条件是_________________________________12.如图，在Rt△ABC和Rt△DCB中，AB=DC，∠A=∠D=90°，AC与BD交于点O，则有△________≌△________，其判定依据是________，还有△________≌△________，其判定依据是________．第11题图第12题图第13题图13.如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF=AC，则∠ABC=_______…第14题图第15题图第16题图14.如图，已知∠1=∠2=90°，AD=AE，那么图中有对全等三角形.15.如图，Rt△ABC中，∠C=90°，AC=8，BC=4，PQ=AB，点P与点Q分别在AC和AC的垂线AD上移动，则当AP=_______时，△ABC≌△APQ．16.如图，在Rt△ABC中，∠BAC=90°，AB=AC，分别过点B，C作过点A的直线的垂线BD，CE，若BD=4cm，CE=3cm，则DE=________cm .《17.如图，有两个长度相同的滑梯（即BC=EF），左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则∠ABC+∠DFE=__________度18.如图，南京路与八一街垂直，西安路也与八一街垂直，曙光路与环城路垂直．如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程为__________m.第17题图第18题图）三、解答题:19. 如图，,于点，，平分交于点，请=⊥=∠AB AC AD BC D AD AE AB DAE DE F你写出图中三对．．全等三角形，并选取其中一对加以证明．【20.在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.-(1)求证: Rt△AB E≌Rt△CBF;(2)若∠CAE=30º,求∠ACF度数.21. 如图 AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．（1）求证AD=AE；&（2）连接OA，BC，试判断直线OA，BC的关系并说明理由．：22. 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.B AC D23. 如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.(1)用圆规比较EM与FM的大小.(2)你能说明由(1)中所得结论的道理吗B AE MF D—~"@参考答案一、选择题…二、填空题9. 斜边,直角边,HL 10. SSS 、ASA 、AAS 、SAS 、HL 11. BP=DP 或AB=CD 或∠A=∠C 或∠B=∠D ． ,DCB,HL,AOB,DOC,AAS. `13. 45° 14. 3 15. 4或8 16. 7 17. 90° 18. 500三、解答题】19.解：（1）ADB ADC △≌△、ABD ABE △≌△、AFD AFE △≌△、BFD BFE △≌△、 ABE ACD △≌△（写出其中的三对即可）. （2）以△ADB ≌ADC 为例证明．证明：,90AD BC ADB ADC ⊥∴∠=∠=°.在Rt ADB △和Rt ADC △中，,,AB AC AD AD == ∴ Rt ADB △≌Rt ADC △.[20.解：（1）∵∠ABC=90°,∴∠CBF=∠ABE=90°.在Rt △ABE 和Rt △CBF 中,∵AE=CF, AB=BC, ∴Rt △ABE ≌Rt △CBF(HL)(2) ∵AB=BC, ∠ABC=90°, ∴ ∠CAB=∠AC B=45°.∵∠BAE=∠CAB-∠CAE=45°-30°=15°.由（1）知 Rt △ABE ≌Rt △CBF ， ∴∠BCF=∠BAE=15°, ∴∠ACF=∠BCF+∠ACB=45°+15°=60°.?21.（1）证明：在△ACD 与△ABE 中，∵∠A=∠A ，∠ADC=∠AEB=90°，AB=AC ， ∴△ACD ≌△ABE ， ∴AD=AE ．（2）互相垂直，在Rt △ADO 与△AEO 中，—∵OA=OA ，AD=AE ， ∴△ADO ≌△AEO ， ∴∠DAO=∠EAO ，即OA 是∠BAC 的平分线，又∵AB=AC ， ∴OA ⊥BC ．22.证明：∵BD ⊥AE 于D,CE ⊥AE 于E ∴∠ADB=∠AEC=90° ∵∠BAC=90°∴∠ABD+∠BAD=∠CAE+∠BAD ∴∠ABD=∠CAE在△ABD 和△CAE 中ABD CAE ADB CEA AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△CAE(AAS) ∴BD=AE,AD=CE ∵AE=AD+DE ∴BD=CE+DE23. 解：(1)EM=FM(2)作EH ⊥AM,垂足为H,FK ⊥AM,垂足为K 先说明Rt △EHA ≌Rt △ADB 得EH=AD Rt △FKA ≌Rt △ADC 得FK=AD 得EH=F K在Rt△EHK与Rt△FKM中,Rt△EHM≌Rt△FKM 得EM=FM.。

2023-2024学年人教版八年级数学上册《第十二章三角形全等的判定》同步练习题附带答案

2023-2024学年人教版八年级数学上册《第十二章三角形全等的判定》同步练习题附带答案学校:___________班级：___________姓名：___________考号：___________一、选择题1．如图，在△ACD与△ABD中∠C=∠B，再添加下列哪个条件，能判定△ADC≌△ADB（）A．AC=AB B．AC⊥CD C．DA平分∠BDC D．CD=BD2．如图，一块玻璃碎成三片，小智只带了第③块去玻璃店，就能配一块一模一样的玻璃，你能用三角形的知识解释，这是为什么？（）A．ASA B．AAS C．SAS D．SSSBC若ΔABC的面积3．如图，AE垂直于∠ABC的平分线于点D，交BC于点E，CE=13为12，则ΔCDE的面积是（）A．2B．3C．4D．64．工人常用角尺平分一个任意角，做法如下：如图，∠AOB是一个任意角，在边OA、OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分別与点M、N重合，过角尺顶点C作射线OC，由此作法便可得△NOC≅△MOC，共依据是（）A．SSS B．SAS C．ASA D．AAS5．如图，在△ABC中∠C=90°，D是AC上一点，DE⊥AB于点E，BE=BC连接BD，若AC=8cm，则AD+DE等于（）A．6cm B．7cm C．8cm D．10cm6．如图，为了测出池塘两端A，B间的距离，小铱在地面上取一个可以直接到达A点和B点的点O，连接AO并延长到C，使OC=OA；连接BO并延长到D，使OD=OB，连接CD并和测量出它的长度，小铱认为CD的长度就是A，B间的距离，她是根据△OAB≌△OCD来判断的AB=CD，那么判定这两个三角形全等的依据是（）．A．SSS B．SAS C．ASA D．AAS7．“又是一年三月三”．在校内劳动课上，小明所在小组的同学们设计了如图所示的风筝框架．已知∠B=∠E，AB=DE，BF=EC，△ABC的周长为24cm，FC=3cm制作该风筝框架需用材料的总长度至少为（）A．44cm B．45cm C．46cm D．48cm8．如图，AB⊥BC，EC⊥BC，AD⊥DE，AD=DE，AB=3，BC=8，则CE长为（）A．4 B．5 C．8 D．10二、填空题9．如下图，已知AC=AB，要使△ABE≌△ACD．则需添加一个条件．10．数学实践活动课中，老师布置了“测量小口圆柱形瓶底部内径”的探究任务，某学习小组设计了如下方案：如图，用螺丝钉将两根小棒AC，BD的中点O固定，现测得C，D之间的距离为75mm，那么小口圆柱形瓶底部的内径AB=mm．11．如图，在Rt△ABC中∠BAC=90°，AB=AC分别过点B、C作经过点A的直线的垂线段BD、CE，若BD=5厘米，CE=8厘米，则DE的长为.12．如图，△ABC中，AD是中线AC=3，AB=5则AD的取值范围是．13．如图，在四边形ABEF中，AB=4，EF=6，点C是BE上一点，连接AC、CF，若AC=CF，∠B=∠E=∠ACF，则BE的长为.三、解答题14．图1是郝老师制作的风筝，图2是风筝骨架的示意图，其中AB=AC，BD=CD，∠C=23°．求∠B的度数．15．如图，已知在△ABC中，D、E是BC上两点，且∠ADE=∠AED，∠BAD=∠EAC，求证：AB=AC．16．如图，C是AB上一点，点D，E分别在AB两侧AD∥BE，且AD=BC，BE=AC求证：CD=EC．17．如图所示，点O在一块直角三角板ABC上（其中∠ABC=30°），OM⊥AB于点M，ON⊥BC于点N，若OM=ON，求∠ABO度数．18．课间，小明拿着老师的直角三角尺玩，不小心掉到两堆砖块之间，如图所示，已知∠ACB= 90°，AC=BC，AD⊥DE，BE⊥DE.（1）试说明：△ADC≌△CEB；（2）已知DE=35cm，请你帮小明求出砖块的厚度a(每块砖的厚度相同)参考答案1．C2．A3．A4．A5．C6．B7．B8．B9．∠C=∠B （答案不唯一）10．7511．13厘米12．1＜AD ＜413．1014．解：在△ABD 和△ACD 中{AB =AC AD =AD BD =CD ∴△ABD ≌△ACD(SSS) ∴∠B =∠C ∵∠C =23° ∴∠B =23°．15．证明：∵∠ADE =∠AED∴AD =AE ，∠ADB =∠AEC在△ABD 与△ACE 中{∠BAD =∠EAC AD =AE ∠ADB =∠AEC∴△ABD ≌△ACE(ASA)∴AB =AC16．证明：∵AD ∥BE∴∠A =∠B在△ADC 和△BCE 中{AD =BC∠A =∠B AC =BE∴△DAC ≌△CBE∴CD =CE ；17．解：∵OM ⊥AB ，ON ⊥BC ∴∠OMB =∠ONB =90°在Rt △OMB 和Rt △ONB 中{OM =ON OB =OB∴Rt △OMB ≌Rt △ONB(HL)∴∠OBM =∠OBN∵∠ABC =30°∴∠ABO =15°．18．（1）解：∵∠ACB =90°∴∠ACD +∠BCE =90°∵AD ⊥DE∴∠ACD +∠DAC =90°∴∠BCE =∠DAC在△ADC 与△CEB 中{∠ADC =∠BEC =90°∠BCE =∠DACAC =BC∴△ADC ≌△CEB(AAS)；（2）解：∵△ADC ≌△CEB∴DC =BE ，AD =CE∴DE =DC +CE =BE +AD =35cm ∵一共有7块砖∴每块砖块的厚度a 为：35÷7=5cm ．。

8年级数学人教版上册同步练习全等三角形三角形全等的判定(含答案解析)

8年级数学人教版上册同步练习全等三角形三角形全等的判定（含答案解析）12.1全等三角形12.2三角形全等的判定专题一三角形全等的判定1．如图，BD是平行四边形ABCD的对角线，∠ABD的平分线BE交AD于点E，∠CDB 的平分线DF交BC于点F．求证：△ABE≌△CDF．2．如图，在△ABC中，D是BC边上的点（不与B，C重合），F，E分别是AD及其延长线上的点，CF∥BE. 请你添加一个条件，使△BDE≌△CDF (不再添加其他线段，不再标注或使用其他字母)，并给出证明．（1）你添加的条件是：__________；（2）证明：3．如图，△ABC中，点D在BC上，点E在AB上，BD=BE，要使△ADB≌△CEB，还需添加一个条件．（1）给出下列四个条件：①AD=CE；②AE=CD；③∠BAC=∠BCA；④∠ADB=∠CEB；请你从中选出一个能使△ADB≌△CEB的条件，并给出证明；（2）在（1）中所给出的条件中，能使△ADB≌△CEB的还有哪些？直接在题后横线上写出满足题意的条件序号．__________________．专题二全等三角形的判定与性质4．如图，已知△ABC中，∠ABC=45°，AC=4，H是高AD和BE的交点，则线段BH的长度为（）A6B．4 C．23D．55．【2013·襄阳】如图，在△ABC中，AB＝AC，AD⊥BC于点D，将△ADC绕点A顺时针旋转，使AC与AB重合，点D落在点E处，AE的延长线交CB的延长线于点M，EB的延长线交AD的延长线于点N.求证：AM＝AN.NMEDB CA6．【2012·泸州】如图，△ABC是等边三角形，D是AB边上一点，以CD为边作等边三角形CDE，使点E﹨A在直线DC的同侧，连接AE．求证：AE∥BC．专题三全等三角形在实际生活中的应用7．如图，有两个长度相同的滑梯靠在一面墙上．已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是（）A．60°B．90°C．120°D．150°8．有一座小山，现要在小山A﹨B的两端开一条隧道，施工队要知道A﹨B两端的距离，于是先在平地上取一个可以直接到达A和B的点C，连接AC并延长到D，使CD=CA，连接BC并延长到E，使CE=CB，连接DE，那么量出DE的长，就是A﹨B两端的距离，你能说说其中的道理吗？9．已知如图，要测量水池的宽AB，可过点A作直线AC⊥AB，再由点C观测，在BA延长线上找一点B′，使∠ACB′=∠ACB，这时只要量出AB′的长，就知道AB的长，对吗？为什么？状元笔记【知识要点】1．全等三角形能够完全重合的两个三角形叫做全等三角形．2．全等三角形的性质全等三角形的对应边相等，全等三角形的对应角相等．3．三角形全等的判定方法(1)三边分别相等的两个三角形全等(简写成“边边边”或“SSS”)．(2)两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”)．(3)两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)．(4)两个角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”)．4．直角三角形全等的判定方法斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边﹨直角边”或“HL”)．【温馨提示】1．两个三角形全等的条件中必须有一条边分别相等，只有角分别相等不能证明两个三角形全等．2．有两边和其中一边的对角分别相等的两个三角形不一定全等．3．“HL”定理指的是斜边和一条直角边分别相等，而不是斜边和直角分别相等．【方法技巧】1．应用全等三角形性质解决问题的前提是准确地确定全等三角形的对应边和对应角，其规律主要有以下几点：（1）以对应顶点为顶点的角是对应角；（2）对应顶点所对应的边是对应边；（3）公共边（角）是对应边（角）；（4）对顶角是对应角；（5）最大边（角）是对应边（角），最小边（角）是对应边（角）．全等三角形的对应边和对应角可以依据字母的对应位置来确定，如若△ABC≌△DEF，说明A与D，B与E，C与F是对应点，则∠ABC与∠DEF是对应角，边AC与边DF 是对应边．2．判定两个三角形全等的解题思路：SAS SSS AAS SAS ASA AAS ASA AAS ⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪⎪⎧⎪⎪⎨⎨⎪⎨⎪⎪⎪⎪⎪⎩⎩⎪⎪⎧⎪⎨⎪⎩⎩找夹角——已知两边找另一边——边为角的对边——找任一角——找夹角的另一边——已知一边一角边为角的邻边找夹边的另一角——找边的对角——找夹边——已知两角找任一边——参考答案:1．证明：平行四边形ABCD 中，AB=CD ，∠A=∠C ，AB ∥CD ， ∴∠ABD=∠CDB ．∵∠ABE=21∠ABD ，∠CDF=21∠CDB ，∴∠ABE=∠CDF ．在△ABE 与△CDF 中，⎪⎩⎪⎨⎧∠=∠=∠=∠CDF ABE CDAB C A ∴△ABE ≌△CDF ． 2．解：（1）DC BD =(或点D 是线段BC 的中点)，ED FD =，BE CF =中任选一个即可﹒ （2）以DC BD =为例进行证明： ∵CF ∥BE ，∴∠FCD ﹦∠EBD ．又∵DC BD =，∠FDC =∠EDB ， ∴△BDE ≌△CDF ． 3．解：（1）添加条件②，③，④中任一个即可，以添加②为例说明．证明：∵AE=CD ，BE=BD ， ∴AB=CB ．又∠ABD=∠CBE ，BE=BD ， ∴△ADB ≌△CEB ．（2）③④．4．B 解析：∵∠ABC =45°，AD ⊥BC ，∴AD =BD ，∠ADC =∠BDH ， ∠AHE =∠BHD =∠C ．∴△ADC ≌△BDH ．∴BH =AC =4．故选B ． 5．证明：如图所示，M∵△AEB由△ADC旋转而得，∴△AEB≌△ADC.∴∠3＝∠1，∠6＝∠C．∵AB＝AC，AD⊥BC，∴∠2＝∠1，∠7＝∠C.∴∠3＝∠2，∠6＝∠7．∵∠4＝∠5，∴∠ABM＝∠ABN．又∵AB＝AB，∴△AMB≌△ANB．∴AM＝AN．6．证明：∵△ABC和△EDC是等边三角形，∴∠BCA＝∠DCE＝60°．∴∠BCA－∠ACD＝∠DCE－∠ACD，即∠BCD＝∠ACE．在△DBC和△EAC中，BC＝AC，∠BCD＝∠ACE，DC＝EC，∴△DBC≌△EAC（SAS）．∴∠DBC＝∠EAC．又∵∠DBC＝∠ACB＝60°，∴∠ACB＝∠EAC．∴AE∥BC．7．B 解析：∵滑梯﹨墙﹨地面正好构成直角三角形，又∵BC=EF，AC=DF，∴Rt△ABC≌Rt△DEF．∴∠ABC=∠DEF，∵∠DEF+∠DFE=90°，∴∠ABC+∠DFE=90°．故选B．8．解：在△ABC和△CED中，AC=CD，∠ACB=∠ECD，EC=BC，∴△ABC≌△CED．∴AB=ED．即量出DE的长，就是A﹨B两端的距离．9．解：对．理由：∵AC ⊥AB,∴∠CAB=∠CAB′=90°. 在△ABC 和△AB′C 中，ACB ACB AC AC CAB CAB =⎧⎪=⎨⎪=⎩∠∠′，，∠∠′， ∴△ABC ≌△AB′C （ASA ）． ∴AB′=AB ．。

B112-11.2全等三角形的判定(1)配套练习

11．2全等三角形的判定（1）配套练习一、填空题．1、下列判断两个三角形全等的条件中，正确的是（）A、一条边对应相等B、两条边对应相等C、三个角对应相等D、三条边对应相等2、如图，在①AB＝AE；②AD＝AE；③∠B＝∠C；④BD＝CE四个条件中，能证明△ABD 与△ACE全等的条件序号是（）A、①②③B、②③④C、①②④D、①③④3、如图，在△ABC中，AB＝AC，D、E两点在BC上，且有AD＝AE，BD＝CE，若∠BAD ＝30°，∠DAE＝50°，则∠BAC的度数为（）A、130°B、120°C、110°D、100°4、下列画图语句表述正确的是（）A、延长线段AB至点C，使AB＝BCB、以点O为圆心作弧C、以点O为圆心，以AC的长为半径画弧D、在射线OA上截取CB＝a，BC＝b，则有OC＝a+b二、选择题．5、如图，AB＝AC，BE＝CD，要使△ABE≌△ACD的依据是“SSS”，则还需添加的条件____6、如图，AB＝ED，AC＝EC，C是BD的中点，若∠A＝36°，则∠E＝7、如图，已知AB＝AC，EB＝EC，AE的延长线交BC于D，则图中全等的三角形共有对。

8、在平面直角坐标系中有两点A（4,0）、B（0,2），如果点C在坐标平面内，当点C的坐标为时，由点B、O、C组成的三角形与△AOB全等。

三、解答题．9、已知：如图，AD=BC，AB=DC，求证：∠A=∠C．10、已知：如图，AB=EF，BC=FD，AD=EC，求证：∠B=∠F ．11、如图，已知AB=AC，AD=AE，BD=CE，你能运用上面条件证明出几对三角形全等？•写出你的证明过程．12、操作并回答：取一长方形纸片，用A、B、C、D表示其四个顶点．将其折叠，使点D与点B重合（如图）．回答问题：（1）图中有没有全等形？如果有，请指出；（2）图中的△BEF与△BFD′虽然有公共边，但却不全等，试说明理由；（3）在图中画一条线段，使图形中出现全等三角形，并写出所出现的全等三角形（只画一条线段，并且是连接图中已用字母标出的某两个点）．BC DEB D EB CD EAB C D EAB CDEAAAC。

八年级数学直角三角形全等的判定同步练习1

1.1 探索勾股定理1. 下列说法正确的是（）A.若 a 、b 、c 是△ABC 的三边，则a 2＋b 2＝c 2；B.若 a 、b 、c 是Rt △ABC 的三边，则a 2＋b 2＝c 2；C.若 a 、b 、c 是Rt △ABC 的三边， 90=∠A ，则a 2＋b 2＝c 2；D.若 a 、b 、c 是Rt △ABC 的三边， 90=∠C ，则a 2＋b 2＝c 2． 2. △ABC 的三条边长分别是a 、b 、c ，则下列各式成立的是（）A ．c b a =+ B. c b a >+ C. c b a <+ D. 222c b a =+ 3．直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（）A ．121B ．120C ．90D ．不能确定4．△ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为（） A ．42 B ．32 C ．42 或 32 D ．37 或 33 5．斜边的边长为cm 17，一条直角边长为cm 8的直角三角形的面积是． 6．假如有一个三角形是直角三角形，那么三边a 、b 、c 之间应满足，其中边是直角所对的边；如果一个三角形的三边a 、b 、c 满足222b c a =+，那么这个三角形是三角形，其中b 边是边，b 边所对的角是． 7．一个三角形三边之比是6:8:10，则按角分类它是三角形．8．若三角形的三个内角的比是3:2:1，最短边长为cm 1，最长边长为cm 2，则这个三角形三个角度数分别是，另外一边的平方是． 9．如图，已知ABC ∆中，︒=∠90C ，15=BA ，12=AC ，以直角边BC 为直径作半圆，则这个半圆的面积是．10．一长方形的一边长为cm 3，面积为212cm ，那么它的一条对角线长是．11．如图，一个高4m 、宽3m 的大门，需要在对角线的顶点间加固一个木条，求木条的长．ACB12.一个三角形三条边的长分别为cm 15，cm 20，cm 25，这个三角形最长边上的高是多少？13．如图，小李准备建一个蔬菜大棚，棚宽4m ，高3m ，长20m ，棚的斜面用塑料薄膜遮盖，不计墙的厚度，请计算阳光透过的最大面积.14．如图，有一只小鸟在一棵高13m 12m ，高8m 的一棵小树树梢上发出友好的叫声，它立刻以2m/s 的速度飞向小树树梢，那么这只小鸟至少几秒才可能到达小树和伙伴在一起？15．“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70km/h.如图，，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪正前方30m 处，过了2s 后，测得小汽车与车速检测仪间距离为50m ，这辆小汽车超速了吗？16.如下图所示，△ABC 中，AB =15 cm ，AC =24 cm ，∠A =60°，求BC 的长.观测点A17.如图，在四边形ABCD 中，∠BAD=90°，∠DBC=90°，AB=3，AD=4，BC=12，求CD 的长。

八年级数学下册1.3直角三角形全等的判定同步练习1(新版)湘教版

1.3直角三角形全等的判定同步练习一、选择题（本大题共8小题）1.如图，/ A=Z D=90°, AC=DB 则厶 AB3A DCB 的依据是（）2. 在下列条件中，不能判定两个直角三角形全等的是（）A. 两条直角边对应相等B. 两个锐角对应相等C. 一个锐角和它所对的直角边对应相等D. 一条斜边和一条直角边对应相等3. 如图所示，AB=CD,AE 丄BD 于点E,CF 丄BD 于点F,AE=CF,则图中全等的三角形有（）A.HLB.ASAC.AASA.1 对B.2 D.44.在 Rt △ ABC 和 Rt △ A B' C'中，/ C=Z C =90°,/ A=Z B ', AB=B A ,则下列结论中正确的是（） A. AC=A ' CB.BC=B' CC.AC=B' CD. /A=/ A 5.如图所示，△ ABC 中, AE =AC ADL BC 交 D 点，E 、 F 分别是DB D.SAS 对A.1B.2C.3D.4三角形的对数是（）6.已知在△ ABC 和厶DEF 中，/ A=Z D=90° ,则下列条件中不能判定厶 ABC 和厶DEF 全等的是8. 如图，南京路与八一街垂直，西安路也与八一街垂直，曙光路与环城路垂直•如果小明站在南京路与八一街的交叉口，准备去书店，按图中的街道行走，最近的路程为（）m.二、填空题（本大题共6小题）9. 已知一条斜边和一条直角边，求作直角三角形，作图的依据是___________ .10. 已知：如图，AE ± BC DF 丄BC 垂足分别为 E 、F, AE=DF AB=DC 则厶ABE^A ____________A. AB=DE,AC=DFB. AC=EF,BC=DFC.AB=DE,BC=EFD. / C=Z F,BC=EF 7.如图，在Rt △ ABC 的斜边 BC 上截取CD=CA 过点D 作DEI BC 交AB 于点E,则有（） A.DE=DB B.DE=AE C.AE=BED.AE=BDA.400B.60011. 如图,已知BD 丄AE 于点B,C 是BD 上一点,且BC=BE 要使Rt △ AB3 Rt △ DBE,应补充的条件是/ A=Z D 或 __________ 或 ___________ 或 ___________14.用三角尺可按下面方法画角平分线：如图，在已知/ AOB两边上分别取 0M=0,再分别过点M N 作OA 0B 的垂线，两垂线交于点 P,画射线0P 则0P 平分/ AOB 作图过程用到了厶 OPM PA 0PN 那么△ 0PM PA 0PN 的依据是 __________ .12.如图，△ ABC 中，AD ± BC 于点D,要使△ ABD^A ACD 若根据“ HL ”判定，还需要加一个条件 __________iy c/ D=60°,则/ A=13.16. 已知：Rt △ ABC 中，/ ACB 是直角，D 是AB 上一点，BD=BC 过D 作AB 的垂线交求证：CD L BE17.用尺规作一个直角三角形，使其中一条边长为 a ,这条边所对的角为 30°a已知：线段a ,求作：Rt △ ABC 使 BC=a / ACB=90，/ A=30°18. 已知△ ABC 中，CD L AB 于D,过D 作DEI AC F 为BC 中点，过F 作FG L DC 求证: 参考答案: 一、选择题(本大题共8小题) 1. A分析：已知/ A=Z D=90 , 题中隐含BC=BC,根据HL 即可推出△ AB 笑 △ DCB■Vi f三、计算题（本大题共4小题）15. 已知：如图△ ABC 中，BD 丄 AC, CE L AB, BD CE 交于O 点，且BD=CE 求证：OB=OC.AC 于 E ,DG=EG解：解：HL,理由是：•/ / A=Z D=90 ,•••在Rt△ ABC和Rt△ DCB 中AC 二BDBC =BC•Rt△ ABC^ Rt△ DCB( HL)，故选A.2. D分析：针对每一个条件进行判定验证，从而判断结论。

12.2 三角形的全等判定(1)练习(含答案)

12.2三角形全等的判定第1课时三角形全等的判定—SSS预习要点：1．按下列步骤在下面方框中画一个△A′B′C′，使A′B′=AB，A′C′=AC，B′C′=BC，保留作图痕迹：（1）画B′C′=BC；（2）分别以点B′，C′为圆心，线段AB，AC长为半径画弧，两弧相交于点A′；（3）连接线段A′B′，A′C′，得△A′B′C′。

2．三边分别的两个三角形全等（可以简写成“”或“”）3．按下列步骤在下面方框中画∠A′O′B′，使得∠A′O′B′=∠AOB，保留作图痕迹。

（1）以点O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；（2）画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′；（3）以点C′为圆心，CD长为半径画弧，与第2步中所画的弧相交于点D′；（4）过点D′画射线O′B′，则∠A′O′B′=∠AOB。

判断∠A′O′B′=∠AOB的依据是。

4．如图，AD=AC，BD=BC，则△ABC≌△ABD的根据是（）A．SSS B．ASA C．AAS D．SAS5．如图，下列三角形中，与△ABC全等的是（）A．①B．②C．③D．④6．如图，D、C为AF上两点，AD=CF，AB=DE，要用SSS判定△ABC≌△DEF，需补充边的条件为．7．如图，E在BC边上，AD=AB，AE=AC，DE=BC，若∠1=25°，则∠3= 度．8．如图，AC=AD，BC=BD，∠1=35°，∠2=65°，则∠C= ．9．用尺规法画一个角等于已知角．同步小题12道一．选择题1．如图，在△ABC和△DEF中，已知AB=DE，BC=EF，根据（SAS）判定△ABC≌△DEF，还需的条件是（）A．∠A=∠D B．∠B=∠EC．∠C=∠F D．以上三个均可以2．如图，已知AB=AD，BC=DC，则图中能用“SSS”判定三角形全等的是（）A．△ACD≌△ACB B．△ABE≌△ADEC．△CDE≌△CBE D．△ABE≌△CBE3．如图，点C在∠AOB的边OB上，用尺规作出了∠BCN=∠AOC，作图痕迹中，弧FG是（）A．以点C为圆心，OD为半径的弧B．以点C为圆心，DM为半径的弧C．以点E为圆心，OD为半径的弧D．以点E为圆心，DM为半径的弧4．如图，BA=BC，DA=DC，则判定△ABD和△CBD全等的依据是（）A．SSS B．ASA C．HL D．SAS5．如图，点E，F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加的一个条件是（）A．∠A=∠C B．AE=CF C．AD∥BC D．DF∥BE6．如图，AB=AD，CB=CD，∠B=30゜，∠BAD=46゜，则∠ACD的度数是（）A．120゜B．125゜C．127゜D．104゜二．填空题7．如图，AB=CD，还需要加上一个条件或就可得到△ABD≌△CD B．8．将图中的全等三角形用全等符号表示出来：．9．如图所示，AB=AC，AD=AE，BD=CE，∠1=35°，∠2=30°，则∠3= ．10．如图，AB=CD，DE=AF，CF=BE，∠AFB=80°，∠CDE=60°，那么∠ABC等于．三．解答题11．如图，AB=AD，CB=CD，求证：△ABC≌△AD C．12．如图，A、D、B、E在同一直线上，AC=EF，AD=BE，BC=DF，求证：∠C=∠F．参考答案12.2三角形全等的判定第1课时三角形全等的判定—SSS预习要点： 1．图略2．相等边边边 SSS 3．图略 SSS4．解析：在△ABC 和ABD 中，⎩⎪⎨⎪⎧ AD ＝ACBD ＝BC AB ＝AB，∴△ABC ≌△ABD （SSS ），故选A5．解析：因为三角形要全等对应边必须相等，所以只有③与△ABC 的各边都相等，只有③正确，故选C6．解析：补充条件：BC =EF ，理由如下：∵AD =CF ，∴AD +DC =CF +DC ，即AC =FD ，∵在△ABC 和△DEF中，⎩⎪⎨⎪⎧ AB ＝DEAC ＝DF CB ＝FE，∴△ABC ≌△DEF （SSS ）．答案：BC =EF ．7．解析：在△ABC 与△ADE 中⎩⎪⎨⎪⎧AD ＝ABAE ＝AC DE ＝BC∴△ABC ≌△ADE ，∴∠BAC =∠DAE ，AC =AE ，∠C =∠AED ，∴∠1=∠2，∵∠1=25°，∴∠2=25°，∴∠C =∠AEC =77.5°，∴∠3=180°-2×77.5°=25°．答案：25°．8．解析：∵在△ACB 和△ADB 中，⎩⎪⎨⎪⎧AC ＝ADBC ＝BD AB ＝AB，∴△ACB ≌△ADB （SSS ），∴∠C =∠D ，∵∠1=35°，∠2=65°，∴∠D =180°-35°-65°=80°，∴∠C =80°，答案：80°．9．用尺规法画一个角等于已知角．解：如图：同步小题12道1．解析：要使两三角形全等，且SAS 已知AB =DE ，BC =EF ，还差夹角，即∠B =∠E ；A 、C 都不满足要求，D 也就不能选取．故选B2．解析：∵AD =AB ，BD =DC ，AC =AC ，∴△ACD ≌△ACB （SSS ）．故选A3．解析：根据作一个角等于已知角可得弧FG 是以点E 为圆心，DM 为半径的弧．故选：D ．4．解析：△ABD 和△CBD 中，BD =BD ，BA =BC ，DA =DC ∴△ABD ≌△CBD （SSS ）故选A5．解析：当∠D =∠B 时，在△ADF 和△CBE 中∵⎩⎪⎨⎪⎧ AD ＝BCAE=CF DF ＝BE，∴△ADF ≌△CBE （SSS ），故选：B6．解析：∵在△ABC 和△ADC 中⎩⎪⎨⎪⎧AB ＝AD AC ＝AC BC ＝CD ，∴△ABC ≌△ADC ，∴∠B =∠D =30°，∠BAC =∠DAC =12∠BAD =12×46°=23°，∠ACD =180°-∠D -∠DAC =180°-30°-23°=127°，故选C7．解析：添加条件是AD =CB 或∠ABD =∠CDB ，理由是：∵在△ABD 和△CDB 中⎩⎪⎨⎪⎧BD ＝BD AD ＝BC AB ＝CD∴△ABD ≌△CDB （SSS ），∵在△ABD 和△CDB 中⎩⎪⎨⎪⎧AB ＝CD∠ABD ＝∠CDB BD ＝BD∴△ABD ≌△CDB （SAS ），答案：AD =CB ，∠ABD =∠CD B ．8．解析：在△ABC 和△DFE 中⎩⎪⎨⎪⎧ AB ＝DE BC ＝EF AC ＝DE ，∴△ABC ≌△DFE （SSS ），在△RPQ 和△MNG 中⎩⎪⎨⎪⎧ PQ ＝GNPR ＝MN QR ＝GM，∴△RPQ ≌△MNG （SSS ），答案：△ABC ≌△DFE ，△RPQ ≌△MNG ．9．解析：∵∠BAC =∠DAE ，∴∠BAC -∠DAC =∠DAE -∠DAC ，∴∠1=∠CAE ．在△ABD 和△ACE 中⎩⎪⎨⎪⎧ AB ＝AC∠1＝∠CAE AD ＝AE ，∴△ABD ≌△ACE （SAS ），∴∠ABD =∠2=30°．∵∠3=∠1+∠ABD ，∴∠3=35°+30°=65°．答案：65°．10．解析：∵CF =BE ，∴CF +EF =BE +EF ，∴CE =BF ，在△AFB 和△DEC 中，⎩⎪⎨⎪⎧ AF ＝DE AB ＝CD BF ＝CE，∴△AFB ≌△DEC（SSS ），∴∠A =∠CDE =60°，∵∠AFB =80°，∴在△AFB 中，∠ABC =180°-∠A -∠AFB =180°-60°-80°=40°，答案：40°．11．证明：∵在△ABC 和△ADC 中⎩⎪⎨⎪⎧ AB ＝ADBC ＝CD AC ＝AC，∴△ABC ≌△ADC （SSS ）． 12．证明：∵AD =BE ∴AD +DB =BE +DB ，即：AB =DE ，在△ABC 和△DEF 中，⎩⎪⎨⎪⎧ AC ＝EFAB ＝DE BC ＝DF ， ∴△ABC ≌△DEF （SSS ）， ∴∠C =∠F ．。

2022-2023学年人教版八年级数学上册《三角形全等的判定》同步练习

人教版数学八年级上册《12.2三角形全等的判定》同步练习一、单选题（本大题共15小题，共45分）1.（3分）不能确定两个三角形全等的条件是()A. 三条边对应相等B. 两边及其夹角对应相等C. 两角及其中一角的对边对应相等D. 两条边和一条边所对的角对应相等2.（3分）如图，线段AD与BC交于点O，且AC=BD，AD=BC，则下面的结论中不正确的是()A. ΔABC≌ΔBADB. OB=OCC. ∠CAB=∠DBAD. ∠C=∠D3.（3分）在△ABC中，∠C=90°，∠CBA的外角平分线，交AC的延长线于F，交斜边上的高CD的延长线于E，EG∥AC交AB的延长线于G，则下列结论：①CF=CE；②GE=CF；③EF是CG的垂直平分线；④BC=BG．其中正确的是（）A. ①②③④B. ①③④C. ②③④D. ①②4.（3分）如图，AD是ΔABC的高，AD也是ΔABC的中线，则下列结论不一定成立的是()A. AB=ACB. AD=BCC. ∠B=∠CD. ∠BAD=∠CAD5.（3分）B为AC上一点，在AC同侧作等边△EAB及等边△DBC,那么下列式子错误的是( )A. △ABD≌△EBCB. ∠BDA=∠BCEC. △ABE≌△BCDD. 若BE交AD于M，CE交BD于N，那么△NBC≌△MBD6.（3分）如图所示，AB=AC，要说明△ADC≌△AEB，需添加的条件不能是()A. ∠B=∠CB. AD=AEC. ∠ADC=∠AEBD. DC=BE7.（3分）把点M(-2，1)向右平移3个单位长度，再向下平移2个单位长度后得到点N，则N的坐标为( )A. (-4，4)B. (-5，3)C. (1，-1)D. (-5，-1)8.（3分）如图，AB交CD于点O，点O分别是AB与CD的中点，则下列结论中错误的是（）A. ∠A=∠BB. AC=BDC. ∠A+∠B=90°D. AC∥BD9.（3分）如图，∠1=∠2，∠C=∠D，AC、BD交于E点，下列结论中不正确的是（）A. ∠DAE=∠CBEB. △DEA不全等于△CEBC. CE=DED. △EAB是等腰三角形10.（3分）如图，在正方形ABCD中，点E，F分别在BC和CD上，过点A作GA⊥AE，CD的延长线交AG于点G，BE+DF=EF，若∠DAF=30°，则∠BAE的度数为()A. 15°B. 20°C. 25°D. 30°11.（3分）下列说法正确的是( )A. 有两边和一个角相等的两个三角形全等B. 两条直角边对应相等的两个直角三角形全等C. 三角形的一条中线把三角形分成的两个小三角形全等D. 有两边和其中一边的对角对应相等的两个三角形全等12.（3分）在下列命题中，是假命题的个数有（）①相等的角是对顶角；②两条直线被第三条直线所截，同位角相等；③面积相等的两个三角形全等；④三角形的一个外角等于两个内角的和．A. 4个B. 3个C. 2个D. 1个13.（3分）如图，已知O是线段AC和BD的中点，要说明ΔABO≌ΔCDO，以下回答最合理的是()A. 添加条件∠A=∠CB. 添加条件AB=CDC. 不需要添加条件D. ΔABO和ΔCDO不可能全等14.（3分）如图，∠1=∠2，∠3=∠4，则下面结论中错误的是（）A. △ADC≌△BCDB. △ABD≌△BACC. △AOB≌△CODD. △AOD≌△BOC15.（3分）如图是5×5的正方形网络，以点D，E为两个顶点作位置不同的格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出（）A. 2个B. 4个C. 6个D. 8个二、填空题（本大题共5小题，共15分）16.（3分）如图，∠BAC=∠ABD，BD、AC交于点O，要使OC=OD，还需添加一个条件，这个条件可以是____．17.（3分）同学们知道：只有两边和其中一边的对角对应相等的两个三角形不一定全等．你如何处理这三个条件，使这两个三角形全等？如方案（1）：若这两个三角形是直角三角形，则这两个三角形全等．请你仿照方案（1）写出另外一个方案：____．18.（3分）如图，∠1=∠2=30°，∠A=∠B，AE=BE，点D在边AC上，AE与BD相交于点O，则∠C的度数为______.19.（3分）如图，AB=AC，AD=AE，∠BAC=∠DAE，∠1=21°，∠2=30°，∠3= ______ ．20.（3分）如图，已知AD=BC，根据“SAS”，还需要一个条件____，可证明△ABC≌△BAD．三、解答题（本大题共5小题，共40分）21.（8分）如图所示，在四边形ABCD中，AC与BD交于O，AB=AD，CB=CD，∠BCD=45°，BE⊥CD于E，BE与AC交于F.(1)求证：CF=2BO；(2)若DE=1，求CF⋅FO的值．22.（8分）已知：∠A=90°，∠ADE=120°，BD平分∠ADE，AD=DE.(1)ΔBAD与ΔBED全等吗？请说明理由；(2)若DE=2，试求AC与EC的长．23.（8分）已知：如图，点E，D，B，F在同一条直线上，AD//CB，∠BAD=∠BCD，DE=BF.求证：(1)AD=BC；(2)AE//CF．24.（8分）如图，在RtΔABC中，∠ABC=90°，延长AB至E，使AE=AC，过E作EF⊥AC于F，EF交BC于G.(1)求证：BE=CF；(2)若∠E=40°，求∠AGB的度数．25.（8分）如图，AD=BC，请添加一个条件，使图中存在全等三角形并给予证明．你所添加的条件为：____；得到的一对全等三角形是△____≌△____．答案和解析1.【答案】D;【解析】解：A、三条边对应相等，符合SSS，能判定三角形全等；B、两边及其夹角对应相等，符合SAS，能判定三角形全等；C、两角及其中一角的对边对应相等，能判定三角形全等，符合AAS．D、两条边和一条边所对的角对应相等，满足SSA，不能判定三角形全等．故选D．判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS，HL，做题时要结合各选项的已知逐个进行验证．该题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS，HL.注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．2.【答案】B;【解析】解：A、根据SSS可以证明ΔABC≌ΔBAD，故本选项正确；B、OB和OC显然不是对应边，故本选项错误；C、根据全等三角形的对应角相等，得∠CAB=∠DBA，故本选项正确；D、根据全等三角形的对应角相等，得∠C=∠D，故本选项正确．故选：B．根据SSS可以证明ΔABC≌ΔBAD，从而得到其对应角相等、对应边相等．该题考查全等三角形的判定和性质，解答该题的关键是熟练掌握基本知识，属于中考常考题型．3.【答案】A;【解析】解：∵BF平分∠GBC，∴∠GBF=∠CBF，而∠GBF=∠EBD，∴∠CBF=∠EBD，∵∠BCA=90°，CD为高，∴∠F=∠BED，∴CF=CE，所以①正确；又∵GE∥AF，∴∠F=∠GEB，∴∠GEB=∠CEB，而∠GBF=∠CBF，∴∠GBE=∠CBE，∴△BEG≌△BEC，∴GE=CE，∴GE=CF，所以②正确；在△EGC中，EC=EG，BE平分∠CEG，∴EB垂直平分GC，所以③正确；∴BG=BC，所以④正确．故选A．4.【答案】B;【解析】解：∵AD是ΔABC的高，AD也是ΔABC的中线，∴BC⊥AD，BD=CD，在ΔABD和ΔACD中，{AD=AD∠ADB=∠ADC=90°BD=CD，∴ΔABD≌ΔACD(SAS)，∴AB=AC，∠B=∠C，∠BAD=∠BAD．故选：B．证明ΔABD≌ΔACD，可得AB=AC，∠B=∠C，∠BAD=∠BAD.则答案得出．考查了等腰三角形的性质及全等三角形的判定与性质，熟练掌握全等三角形的判定方法是解答该题的关键．5.【答案】C;【解析】△ABE与△BCD未必全等，故选C。

人教版初中数学八年级上册 12.2全等三角形的判定同步练习(含答案)

人教版初中数学八年级上册12.2全等三角形的判定同步练习（含答案）一、选择题（本大题共8道小题）1. 如图，AD＝AE，若利用“SAS”证明△ABE△△ACD，则需要添加的条件是()A．AB＝ACB．△B＝△CC．△AEB＝△ADCD．△A＝△B2. 下列三角形中全等的是()A．△△ B．△△ C．△△ D．△△3. 如图，小强画了一个与已知△ABC全等的△DEF，他画图的步骤是：(1)画DE ＝AB；(2)在DE的同旁画△HDE＝△A，△GED＝△B，DH，EG相交于点F，小强画图的依据是()A．ASA B．SASC．SSS D．AAS4. 如图所示，△C＝△D＝90°，若要用“HL”判定Rt△ABC与Rt△ABD全等，则可添加的条件是()A．AC＝AD B．AB＝ABC．△ABC＝△ABD D．△BAC＝△BAD5. 如图，点B，F，C，E在一条直线上，AB△ED，AC△FD，那么添加下列一个条件后，仍无法判定△ABC△△DEF的是()A．AB＝DE B．AC＝DFC．△A＝△D D．BF＝EC6. 如图所示，P是△BAC内一点，且点P到AB，AC的距离PE，PF相等，则△PEA△△PF A的依据是()A．HL B．ASA C．SSS D．SAS7. 在Rt△ABC和Rt△DEF中，△C＝△F＝90°，下列条件不能判定Rt△ABC△Rt△DEF的是()A．AC＝DF，△B＝△E B．△A＝△D，△B＝△EC．AB＝DE，AC＝DF D．AB＝DE，△A＝△D8. 如图，有两个长度相同的滑梯靠在一面墙上，已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，且左边的滑梯与地面的夹角△ABC＝35°，则右边的滑梯与地面的夹角△DFE等于()A．60° B．55° C．65° D．35°二、填空题（本大题共4道小题）9. 如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于点H，请你添加一个适当条件：________，使△AEH△△CEB.10. 如图，在△ABC中，AD△BC于点D，要使△ABD△△ACD，若根据“HL”判定，还需要添加条件：____________．11. 如图，已知AD＝BC，AB＝CD，若△C＝40°，则△A＝________°.12. 如图K－10－10，CA＝CD，AB＝DE，BC＝EC，AC与DE相交于点F，ED 与AB相交于点G.若△ACD＝40°，则△AGD＝________°.三、解答题（本大题共2道小题）13. 如图，点A，B，C，D在同一条直线上，CE∥DF，EC＝BD，AC＝FD.求证：AE＝FB.14. 如图，C是线段BD的中点，AB＝EC，△B＝△ECD.求证：△ABC△△ECD.人教版初中数学八年级上册12.2全等三角形的判定同步练习-答案一、选择题（本大题共8道小题）1. 【答案】A2. 【答案】A[解析] △△符合证明三角形全等的判定方法“SAS”．△△中相等的角所对的边不相等，所以不可能全等．故选A.3. 【答案】A4. 【答案】A5. 【答案】C[解析] 选项A中添加AB＝DE可用“AAS”进行判定，故本选项不符合题意；选项B中添加AC＝DF可用“AAS”进行判定，故本选项不符合题意；选项C中添加△A＝△D不能判定△ABC△△DEF，故本选项符合题意；选项D中添加BF＝EC可得出BC＝EF，然后可用“ASA”进行判定，故本选项不符合题意．故选C.6. 【答案】A7. 【答案】B[解析] 选项A，D均可由“AAS”判定Rt△ABC△Rt△DEF，选项C 可由“HL”判定Rt△ABC△Rt△DEF，只有选项B不能判定Rt△ABC△Rt△DEF.8. 【答案】B [解析] 在Rt△ABC 和Rt△DEF 中，⎩⎨⎧BC ＝EF ，AC ＝DF ，△Rt△ABC△Rt△DEF(HL)． △△DEF ＝△ABC ＝35°.△△DFE ＝90°－35°＝55°.二、填空题（本大题共4道小题）9. 【答案】AH ＝CB (符合要求即可)【解析】∵AD ⊥BC ，CE ⊥AB ，垂足分别为点D 、E ，∴∠BEC ＝∠AEC ＝90°，在Rt △AEH 中，∠EAH ＝90°－∠AHE ，在Rt △HDC 中，∠ECB ＝90°－∠DHC ，∵∠AHE ＝∠DHC ，∴∠EAH ＝∠ECB ，∴根据AAS 添加AH ＝CB 或EH ＝EB ；根据ASA 添加AE ＝CE.可证△AEH ≌△CEB.故答案为：AH ＝CB 或EH ＝EB 或AE ＝CE 均可．10. 【答案】AB ＝AC 11. 【答案】40[解析] 如图，连接DB.在△ADB 和△CBD 中，⎩⎨⎧AD ＝CB ，AB ＝CD ，DB ＝BD ，△△ADB△△CBD(SSS)． △△A ＝△C ＝40°.12. 【答案】40[解析] 在△ABC 和△DEC 中，⎩⎨⎧CA ＝CD ，AB ＝DE ，BC ＝EC ，△△ABC△△DEC(SSS)． △△A ＝△D.又△△AFG ＝△DFC ，△△AGD ＝△ACD ＝40°.三、解答题（本大题共2道小题）13. 【答案】证明：∵CE ∥DF ，∴∠ACE ＝∠FDB ，(2分)在△ACE 和△FDB 中，⎩⎨⎧EC ＝BD∠ACE ＝∠FDB AC ＝FD，∴△ACE ≌△FDB(SAS )，(5分) ∴AE ＝FB.(7分)14. 【答案】证明：△C 是线段BD 的中点，△BC ＝CD.在△ABC 与△ECD 中，⎩⎨⎧BC ＝CD ，△B ＝△ECD ，AB ＝EC ，△△ABC△△ECD.。

人教版八年级上册数学三角形全等的判定同步练习(含答案)

人教版八年级上册数学12.2.1 三角形全等的判定同步练习一、单选题1．下列条件中，能判定△ABC △△DEF 的是（）A ．AB =DE ，BC =EF ，△A =△DB ．△A =△D ，△C =△F ，AC =EF C ．△B =△E ，△A =△D ，AC =EF D ．△B =△E ，△A =△D ，AB =DE 2．如图，已知AB AC =，D 、E 分别为AB 、AC 上两点，B C ∠=∠，则下列结论不一定成立的是（）A ．AD AE =B ．DB EC = C ．DO EO =D ．AD DB = 3．如图，已知△ABD ＝△CBD ，添加以下条件，不一定能判定△ABD △△CBD 的是( )A ．△A ＝△CB ．AB ＝CBC ．△BDA ＝△BDCD ．AD ＝CD 4．如图，AB △BC ，EC △BC ，AD △DE ，AD =DE ，AB =3，BC =8，则CE 长为（）A ．4B ．5C ．8D ．10 5．如图，A 、B 、C 、D 在同一直线上，AE DF ∥，AE =DF ,添加一个条件，不能判定△AEC △△DFB 的是（）A．EC BF∥B．EC=BF C．AB=CD D．△E=△F 6．如图，在△ACD和△BCE中，DA△AB，EB△AB，点C是AB的中点，添加下列条件后，不能判定△ACD△△BCE的是（）A．CD＝CE B．AD＝BE C．AD∥BE D．△D＝△E 7．如图，点B，F，C，E在同一直线上，AC＝DF，△1＝△2，如果根据“ASA”判断△ABC△△DEF，那么需要补充的条件是（）A．AB＝DE B．△A＝△D C．BF＝CE D．△B＝△D 8．如图，在△ABC中，△ACB=90°，AC=BC，BE△CE于点E，AD△CE于点D，若AD=12，CD=5，则ED的长度是（）A．8B．7C．6D．5二、填空题9．如图，在ABC 和DEF 中，点A 、E 、B 、D 在同一直线上，BC EF ∥，AB DE =，只添加一个条件，能判定ABC DEF △≌△的是_________（写出一个即可）．10．如图，△ABC 中AC △BC ，AC ＝8cm ，BC ＝4cm ，AP △AC 于A ，现有两点D 、E 分别在AC 和AP 上运动，运动过程中总有DE ＝AB ，当AD ＝_____cm 时，能使△ADE 和△ABC 全等．11．如图，在ABC 中，CD AB ⊥，AE BC ⊥，垂足分别为点D ，E ，CD 与AE 交于点F ，若3BD DF ==，6ADF S =△，则CF 的长是________．12．如图，90B D ∠=∠=︒，AB AD =，130BAD ∠=︒，则DCA ∠=______°．13．如图，点P 在直线AB 外，点C ，D 在直线AB 上，AC BD =，请你补充一个条件______（写出一个即可），使APC BPD △△≌．14．如图，点B ，F ，C ，E 在一条直线上，已知BF CE =，AC DF ∥，请你添加一个适当的条件______使得ABC DEF △≌△．（要求不添加任何线段）．15．如图，点P 在AOB ∠内部，PM OA ⊥于点M ，PN OB ⊥于点N ，且PM PN =．若70OPM ∠=︒，则AOB ∠=__________°．16．如图，点D 是△ABC 的边AB 上一点，FC △AB ，连接DF 交AC 于点E ，若CE =AE ，AB =7，CF =4，则BD 的长为________．三、解答题17．已知，如图，点B 、F 、C 、E 在同一条直线上，A D ∠=∠，AB DE ∥，BF EC =．求证：(1)ABC DEF△≌△(2)AC DF∥．AC DF18．如图，△ABC中，△BAC=90°，AB=AC，AF是过点A的一条直线，且B，C在AE 的两侧，BD△AE于D，CE△AE于点E．(1)试说明△BAD△△ACE；(2) BD与DE、CE有什么数量关系？并说明理由．19．如图，CA=CD，△BCE=△ACD，BC=EC，求证：△ABC△△DEC．20．如图，在△ABC和△BDE中，90∠为锐角，AB BC=，ABC DBE∠=∠=︒，CBE=，连接AE、CD，AE与CD交于点M，AE与BC交于点N．BE BD(1)△ABE与△CBD全等吗？为什么？(2)AE与CD有何特殊的位置关系，并说明理由．答案第1页，共1页参考答案：1．D2．D3．D4．B5．B6．C7．B8．B9．BC EF =（或C F ∠=∠或A D ∠=∠或AC DF ∥） 10．8或411．112．2513．PC =PD （答案不唯一） 14．B E ∠=∠（答案不唯一） 15．4016．318． (2)BD =DE +CE ， 20．(1)全等，(2)AE 与CD 互相垂直，。

人教版八年级上册数学 12.2 全等三角形的判定同步训练(含答案)

人教版八年级数学12.2 全等三角形的判定同步训练一、选择题（本大题共10道小题）1. 如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能．．判定△ABE≌△ACD()A. ∠B＝∠CB. AD＝AEC. BD＝CED. BE＝CD2. 如图，小强画了一个与已知△ABC全等的△DEF，他画图的步骤是：(1)画DE ＝AB；(2)在DE的同旁画∠HDE＝∠A，∠GED＝∠B，DH，EG相交于点F，小强画图的依据是()A．ASA B．SASC．SSS D．AAS3. 如图所示，已知AB∥DE，点B，E，C，F在同一直线上，AB＝DE，BE＝CF，∠B＝32°，∠A＝78°，则∠F等于()A．55°B．65°C．60°D．70°4. 如图，李颖同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最合理的办法是带哪块玻璃去()A．只带①B．只带②C．只带③D．带①和②5. 已知△ABC的六个元素，下列甲、乙、丙三个三角形中标出了某些元素，则与△ABC全等的三角形是()A．只有乙B．只有丙C．甲和乙D．乙和丙6. 如图，已知∠ABC＝∠DCB，添加以下条件，不能判定△ABC≌△DCB的是()A．∠A＝∠DB．∠ACB＝∠DBCC．AC＝DBD．AB＝DC7. 在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，下列条件不能判定Rt△ABC≌Rt△DEF的是()A．AC＝DF，∠B＝∠E B．∠A＝∠D，∠B＝∠EC．AB＝DE，AC＝DF D．AB＝DE，∠A＝∠D8. 如图，AB⊥BC，BE⊥AC，垂足分别为B，E，∠1=∠2，AD=AB，则下列结论正确的是()A.∠1=∠EFDB.BE=ECC.BF=CDD.FD∥BC9. 如图，在等腰直角△ABC中，∠C＝90°，点O是AB的中点，且AB＝6，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为D、E，则CD＋CE等于()A. 2B. 3C. 2D. 610. 现已知线段a，b(a<b)，∠MON=90°，求作Rt△ABO，使得∠O=90°，OA=a，AB=b.小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.小雷:①以点O为圆心、线段a的长为半径画弧，交射线ON于点A;②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求.则下列说法中正确的是()A.小惠的作法正确，小雷的作法错误B.小雷的作法正确，小惠的作法错误C.两人的作法都正确D.两人的作法都错误二、填空题（本大题共7道小题）11. 如图，AB＝DE，∠1＝∠2，添加一个适当的条件，使△ABC≌△DEC，则需添加的条件是__________(不添加任何辅助线，填一个即可)．12. 如图，已知在△ABC和△DEF中，∠B＝∠E，BF＝CE，点B，F，C，E在同一条直线上，若使△ABC≌△DEF，则还需添加的一个条件是________(只填一个即可)．13. 如图K－10－10，CA＝CD，AB＝DE，BC＝EC，AC与DE相交于点F，ED与AB相交于点G.若∠ACD＝40°，则∠AGD＝________°.14. 如图，在△ABC中，D，E分别是边AB，AC上的点，过点C作平行于AB 的直线交DE的延长线于点F.若DE＝FE，AB＝5，CF＝3，则BD的长是________．15. 如图，若AB＝AC，BD＝CD，∠A＝80°，∠BDC＝120°，则∠B＝________°.16. 如图，在Rt△ABC中，∠ACB＝90°，BC＝2 cm，CD⊥AB，在AC上取一点E，使EC＝BC，过点E作EF⊥AC交CD的延长线于点F.若EF＝5 cm，则AE ＝________cm.17. 如图，已知△ABC(AC＞AB)，DE＝BC，以D，E为顶点作三角形，使所作的三角形与△ABC全等，则这样的三角形最多可以作出________个．三、解答题（本大题共4道小题）18. 如图，点B，C分别在∠MAN的边AM，AN上，点E，F在∠MAN内部的射线AD上，∠1，∠2分别是△ABE，△CAF的外角．已知AB＝AC，∠1＝∠2＝∠BAC.求证：△ABE ≌△CAF.19. 在四边形ABCD 中，AB ＝AD .(1)如图①，若∠B ＝∠D ＝90°，E ，F 分别是边BC ，CD 上的点，且∠EAF ＝12∠BAD .请直接写出线段EF ，BE ，FD 之间的数量关系：____________．(2)如图②，若∠B ＋∠D ＝180°，E ，F 分别是边BC ，CD 上的点，且∠EAF ＝12∠BAD ，(1)中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由． (3)如图③，若∠B ＋∠ADC ＝180°，E ，F 分别是边BC ，CD 延长线上的点，且∠EAF ＝12∠BAD ，请直接写出EF ，BE ，FD 三者的数量关系．20. 如图①，点A ，B ，C ，D 在同一直线上，AB=CD ，作EC ⊥AD 于点C ，FB⊥AD 于点B ，且AE=DF . (1)求证:EF 平分线段BC ;(2)若将△BFD 沿AD 方向平移得到图②，其他条件不变，(1)中的结论是否仍成立?请说明理由.21. (1)如图①，在△ABC 中，∠BAC ＝90°，AB ＝CA ，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为D ，E.求证：DE ＝BD ＋CE.(2)如图②，将(1)中的条件改为：在△ABC 中，AB ＝CA ，D ，A ，E 三点都在直线m 上，并且有∠BDA ＝∠AEC ＝∠BAC ＝α，其中α为任意锐角或钝角，则结论DE ＝BD ＋CE 是否成立？若成立，请你给出证明；若不成立，请说明理由．人教版八年级数学 12.2 全等三角形的判定同步训练-答案一、选择题（本大题共10道小题）1. 【答案】D【解析】A.当∠B ＝∠C 时，在△ABE 与△ACD 中，⎩⎨⎧∠A ＝∠AAB ＝AC ∠B ＝∠C，∴△ABE ≌△ACD (ASA)；B.当AD ＝AE 时，在△ABE 与△ACD 中，⎩⎨⎧AB ＝AC∠A ＝∠A AE ＝AD，∴△ABE ≌△ACD (SAS)；C.当BD ＝CE 时，∵AB ＝AC ，∴AD ＝AE ，在△ABE与△ACD 中，⎩⎨⎧AB ＝AC∠A ＝∠A AE ＝AD，∴△ABE ≌△ACD (SAS)；D.当BE ＝CD 时，在△ABE与△ACD 中，有AB ＝AC ，BE ＝BD ，∠A ＝∠A ，只满足两边及一对角对应相等的两个三角形不一定全等．故选D.2. 【答案】A3. 【答案】D[解析] 因为AB∥DE，所以∠B＝∠DEF.由条件BE＝CF知BC＝EF.结合条件AB＝DE，可由“SAS”判定△ABC≌△DEF，所以∠F＝∠ACB＝180°－(∠A＋∠B)＝180°－(78°＋32°)＝70°.4. 【答案】C[解析] 由“ASA”的判定方法可知只带③去就可以配出一块和以前一样(全等)的三角形玻璃．5. 【答案】D6. 【答案】C[解析] A．∠A＝∠D，∠ABC＝∠DCB，BC＝BC，符合“AAS”，即能推出△ABC≌△DCB，故本选项不符合题意；B．∠ABC＝∠DCB，BC＝CB，∠ACB＝∠DBC，符合“ASA”，即能推出△ABC ≌△DCB，故本选项不符合题意；C．∠ABC＝∠DCB，AC＝DB，BC＝BC，不符合全等三角形的判定条件，即不能推出△ABC≌△DCB，故本选项符合题意；D．AB＝DC，∠ABC＝∠DCB，BC＝CB，符合“SAS”，即能推出△ABC≌△DCB，故本选项不符合题意．故选C.7. 【答案】B[解析] 选项A，D均可由“AAS”判定Rt△ABC≌Rt△DEF，选项C 可由“HL”判定Rt△ABC≌Rt△DEF，只有选项B不能判定Rt△ABC≌Rt△DEF.8. 【答案】D[解析] 在△AFD和△AFB中，∴△AFD≌△AFB.∴∠ADF=∠ABF.∵AB⊥BC，BE⊥AC，∴∠BEC=∠ABC=90°.∴∠ABF+∠EBC=90°，∠C+∠EBC=90°. ∴∠ADF=∠ABF=∠C. ∴FD ∥BC.9. 【答案】B【解析】如解图，连接OC ，由已知条件易得∠A ＝∠OCE ，CO ＝AO ，∠DOE ＝∠COA ，∴∠DOE －∠COD ＝∠COA －∠COD ，即∠AOD ＝∠COE ，∴△AOD ≌△COE (ASA)，∴AD ＝CE ，进而得CD ＋CE ＝CD ＋AD ＝AC＝22AB ＝3，故选B.10. 【答案】A[解析] AB=b ，AB 是斜边，小惠作的斜边长是b 符合条件，而小雷作的是一条直角边长是b.故小惠的作法正确，小雷的作法错误.二、填空题（本大题共7道小题）11. 【答案】答案不唯一，如∠B ＝∠E12. 【答案】答案不唯一，如AB ＝DE[解析] ∵BF ＝CE ，∴BC ＝EF.在△ABC 和△DEF 中，⎩⎨⎧AB ＝DE ，∠B ＝∠E ，BC ＝EF ，∴△ABC ≌△DEF(SAS)．13. 【答案】40[解析] 在△ABC 和△DEC 中，⎩⎨⎧CA ＝CD ，AB ＝DE ，BC ＝EC ，∴△ABC ≌△DEC(SSS)． ∴∠A ＝∠D.又∵∠AFG ＝∠DFC ， ∴∠AGD ＝∠ACD ＝40°.14. 【答案】2[解析] ∵CF ∥AB ，∴∠A ＝∠FCE.在△ADE 和△CFE 中，⎩⎨⎧∠A ＝∠FCE ，∠AED ＝∠CEF ，DE ＝FE ，∴△ADE ≌△CFE(AAS)． ∴AD ＝CF ＝3.∴BD ＝AB －AD ＝5－3＝2.15. 【答案】20[解析] 如图，过点D 作射线AF.在△BAD 和△CAD 中，⎩⎨⎧AB ＝AC ，AD ＝AD ，BD ＝CD ，∴△BAD ≌△CAD(SSS)． ∴∠BAD ＝∠CAD ，∠B ＝∠C.∵∠BDF ＝∠B ＋∠BAD ，∠CDF ＝∠C ＋∠CAD ， ∴∠BDF ＋∠CDF ＝∠B ＋∠BAD ＋∠C ＋∠CAD ，即∠BDC ＝∠B ＋∠C ＋∠BAC. ∵∠BAC ＝80°，∠BDC ＝120°， ∴∠B ＝∠C ＝20°.16. 【答案】3[解析] ∵∠ACB ＝90°，∴∠ECF ＋∠BCD ＝90°.∵CD ⊥AB ，∴∠BCD ＋∠B ＝90°. ∴∠ECF ＝∠B.在△ABC 和△FCE 中，⎩⎨⎧∠B ＝∠ECF ，BC ＝CE ，∠ACB ＝∠FEC ，∴△ABC ≌△FCE(ASA)．∴AC ＝FE. ∵AE ＝AC －CE ，BC ＝2 cm ，EF ＝5 cm ， ∴AE ＝5－2＝3(cm)．17. 【答案】4[解析] 能画4个，分别是：以点D 为圆心，AB 长为半径画圆；以点E 为圆心，AC 长为半径画圆，两圆相交于两点(DE 上下各一个)，分别与点D ，E 连接后，可得到两个三角形．以点D 为圆心，AC 长为半径画圆；以点E 为圆心，AB 长为半径画圆，两圆相交于两点(DE 上下各一个)，分别与点D ，E 连接后，可得到两个三角形．因此最多能画出4个三角形与△ABC 全等．如图．三、解答题（本大题共4道小题）18. 【答案】证明：∵∠1＝∠2＝∠BAC ，且∠1＝∠BAE ＋∠ABE ，∠2＝∠CAF ＋∠ACF ，∠BAC ＝∠BAE ＋∠CAF ，∴∠BAE ＝∠ACF ，∠ABE ＝∠CAF.在△ABE 和△CAF 中，⎩⎨⎧∠BAE ＝∠ACF ，AB ＝CA ，∠ABE ＝∠CAF ，∴△ABE ≌△CAF(ASA)．19. 【答案】解：(1)EF ＝BE ＋FD(2)(1)中的结论EF ＝BE ＋FD 仍然成立．证明：如图，延长EB 到点G ，使BG ＝DF ，连接AG .∵∠ABC ＋∠D ＝180°，∠ABG ＋∠ABC ＝180°，∴∠ABG ＝∠D.在△ABG 与△ADF 中，⎩⎨⎧AB ＝AD ，∠ABG ＝∠D ，BG ＝DF ， ∴△ABG ≌△ADF(SAS)．∴AG ＝AF ，∠1＝∠2.∴∠1＋∠3＝∠2＋∠3＝∠BAD －∠EAF.又∵∠EAF ＝12∠BAD ，∴∠1＋∠3＝12∠BAD ＝∠EAF ，即∠EAG ＝∠EAF.在△AEG 和△AEF 中，⎩⎨⎧AG ＝AF ，∠EAG ＝∠EAF ，AE ＝AE ， ∴△AEG ≌△AEF.∴EG ＝EF.∵EG ＝BE ＋BG ，∴EF ＝BE ＋FD.(3)EF ＝BE －FD.20. 【答案】解:(1)证明:∵EC ⊥AD ，FB ⊥AD ， ∴∠ACE=∠DBF=90°.∵AB=CD ，∴AB+BC=BC+CD ，即AC=DB.在Rt △ACE 和Rt △DBF 中， ∴Rt △ACE ≌Rt △DBF (HL).∴EC=FB. 在△CEG 和△BFG 中，∴△CEG ≌△BFG (AAS).∴CG=BG ，即EF 平分线段BC.(2)EF 平分线段BC 仍成立.理由:∵EC ⊥AD ，FB ⊥AD ，∴∠ACE=∠DBF=90°.∵AB=CD ，∴AB-BC=CD-BC ，即AC=DB.在Rt △ACE 和Rt △DBF 中， ∴Rt △ACE ≌Rt △DBF (HL).∴EC=FB.在△CEG 和△BFG 中，∴△CEG ≌△BFG (AAS).∴CG=BG ，即EF 平分线段BC.21. 【答案】解：(1)证明：∵BD ⊥直线m ，CE ⊥直线m ， ∴∠BDA ＝∠AEC ＝90°.∴∠BAD ＋∠ABD ＝90°.∵∠BAC ＝90°，∴∠BAD ＋∠CAE ＝90°. ∴∠CAE ＝∠ABD.在△ADB 和△CEA 中，⎩⎨⎧∠ABD ＝∠CAE ，∠BDA ＝∠AEC ，AB ＝CA ， ∴△ADB ≌△CEA(AAS)．∴BD ＝AE ，AD ＝CE.∴DE ＝AE ＋AD ＝BD ＋CE.(2)成立．证明：∵∠BDA ＝∠BAC ＝α，∴∠DBA ＋∠BAD ＝∠BAD ＋∠EAC ＝180°－α. ∴∠DBA ＝∠EAC.在△ADB 和△CEA 中，⎩⎨⎧∠DBA ＝∠EAC ，∠BDA ＝∠AEC ，AB ＝CA ，∴△ADB≌△CEA(AAS)．∴BD＝AE，AD＝CE.∴DE＝AE＋AD＝BD＋CE.。

人教版八年级数学上册三角形全等的判定同步练习及答案

三角形全等的判定同步练习题一. 选择题1. 下列条件不能判定两个三角形全等的是（）A. 有两边和夹角对应相等B. 有三边分别对应相等C. 有两边和一角对应相等D. 有两角和一边对应相等2. 下列条件能判定两个三角形全等的是（）A. 有三个角相等B. 有一条边和一个角相等C. 有一条边和一个角相等D. 有一条边和两个角相等3. 如图所示，已知AB∥CD，AD∥BC，那么图中共有全等三角形（）AB C DO第3题A. 1对B. 2对C. 4对D. 8对4. 如图所示，已知∠A＝∠D，∠1＝∠2，那么要得到△ABC≌△DEF，还应给出的条件是（）AB CDE12第4题FA. ∠E ＝∠BB. ED ＝BCC. AB ＝EFD. AF ＝CD5. 如图所示，点E 在△ABC 外部，点D 在BC 边上，DE 交AC 于F ，若∠1＝∠2，∠E ＝∠C ，AE ＝AC ，则（）A B CD E123第5题FA. △ABC ≌△AFEB. △AFE≌△ADC C. △AFE ≌△DFC D. △ABC ≌△ADE6. 我们学过的判定两个直角三角形全等的条件，有（）A. 5种B. 4种C. 3种D. 2种7. 如图所示，AB ∥EF ∥CD ，∠ABC ＝90°，AB ＝DC ，那么图中的全等三角形有（）A B C DEF 第7题A. 1对B. 2对C. 3对D. 4对8. 如图，在△ABC 中，AB ＝AC ，AD ⊥BC ，垂足为D ，且BC ＝6cm ，则BD ＝__________.（）AB C D 第8题A. 1cmB. 2cmC. 3cmD. 4cm9. 如图所示，DE ⊥AB ，DF ⊥AC ，AE ＝AF ，则下列结论成立的是（）AB C DEF 第9题 A. BD ＝CD B. DE ＝DF C. ∠B ＝∠C D. AB ＝AC二. 填空题10. 如图所示，AC ∥BD ，AC ＝BD ，那么__________，理由是__________.B CD O第10题11. 已知△ABC ≌△A'B'C'，AB ＝6cm ，BC ＝7cm ，AC ＝9cm ，∠A'＝70°，∠B'＝80°，则A'B'＝__________，B'C'＝__________，A'C'＝__________，∠C'＝__________，∠C ＝__________.12. 如图所示，已知AB ＝AC ，在△ABD 与△ACD 中，要使△ABD ≌△ACD ，还需要再添加一个条件是____________________.AB CD13. 如图所示，已知△ABC≌△DEF，AB＝4cm，BC＝6cm，AC＝5cm，CF＝2cm，∠A＝70°，∠B＝65°，则第12题∠D＝__________，∠F＝__________，DE＝__________，BE＝__________.14. （2007年福州）如图，点D、E分别在线段AB、AC上，BE、CD相交于点O，AE＝AD，要使△ABE≌△ACD，需添加一个条件是__________（只要求写一个条件）.15. （2007年沈阳）如图，AC、BD相交于点O，∠A＝∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是__________.三. 解答题16. （2007年浙江温州）已知：如图，∠1＝∠2，∠C ＝∠D ，求证：AC ＝AD.A BCD1217. （2007年浙江金华）如图，A 、E 、B 、D 在同一直线上，在△ABC 和△DEF 中，AB ＝DE ，AC ＝DF ，AC ∥DF. （1）求证：△ABC ≌△DEF ；（2）你还可以得到的结论是__________（写出一个即可，不再添加其他线段，不再标注或使用其它字母）A B CDEF18. （2007年武汉）你一定玩过跷跷板吧！如图是小明和小刚玩跷跷板的示意图，横板绕它的中点O 上下转动，立柱OC 与地面垂直. 当一方着地时，另一方上升到最高点. 问：在上下转动横板的过程中，两人上升的最大高度AA'、BB'有何数量关系？为什么？C O A'AB'B19. MN 、PQ 是校园里的两条互相垂直的小路，小强和小明分别站在距交叉口C 等距离的B 、E 两处，这时他们分别从B 、E 两点按同一速度沿直线行走，如图所示，经过一段时间后，同时到达A 、D 两点，他们的行走路线AB 、DE 平行吗？请说明你的理由.MNP20. 有一块不规则的鱼池，下面是两位同学分别设计的能够粗略地测量出鱼池两端A 、B 的距离的方案，请你分析一下两种方案的理由.方案一：小明想出了这样一个方法，如图①所示，先在AB 的垂线BF 上取两点C 、D ，使CD ＝BC ，再定出BF 的垂线DE ，使A 、C 、E 在同一条直线上，测得DE 的长就是AB 的长. 你能说明一下这是为什么吗？方案二：小军想出了这样一个方法，如图②所示，先在平地上取一个可以直接到达鱼池两端A 、B 的点C ，连结AC 并延长到点D ，使CD ＝CA ，连结BC 并延长到E ，使CE ＝CB ，连结DE ，量出DE 的长，这个长就是A、B之间的距离. 你能说明一下这是为什么吗？A BCD EF①A B②CE D21. 我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等. 那么在什么情况下，它们会全等?（1）阅读与证明：对于这两个三角形均为直角三角形，显然它们全等.对于这两个三角形均为钝角三角形，可证它们全等（证明略）.对于这两个三角形均为锐角三角形，它们也全等，可证明如下：已知：△ABC、△A1B1C1均为锐角三角形，AB＝A1B1，BC＝B1C1，∠C＝∠C1.求证：△ABC≌△A1B1C1. （请你将下列证明过程补充完整）证明：分别过点B，B1作BD⊥CA于D，B1D1⊥C1A1于D1.则∠BDC＝∠B1D1C1＝90°，∵BC＝B1C1，∠C＝∠C1，∴△BCD≌△B1C1D1，∴BD＝B1D1.______________________________。

最新人教版八年级数学上册课时同步练：全等三角形的判定(含答案)

课时同步练：全等三角形的判定基础题训练（一）：限时35分钟1．如图，在△ABC和△DBE中，点D在边AC上，BC与DE交于点P，AB＝DB，∠A＝∠BDE，∠ABD＝∠CBE．（1）求证：BC＝BE；（2）若AD＝DC＝2.5，BC＝4，求△CDP与△BEP的周长之和．2．如图，AB∥CD，∠B＝∠D，O是CD的中点，连接AO并延长，交BC的延长线于点E．（1）试判断AD与BE有怎样的位置关系，并说明理由；（2）试说明△AOD≌△EOC．3．如图，已知AD＝AE，BD和CE相交于点O，BD＝CE，∠B＝∠C．求证：AB＝AC．小明同学的证明过程如下框．小明同学的证法是否正确？若正确，请在方框内打“√”；若错误，请写出你的证明过程．4．已知两组邻边分别相等的四边形叫做“筝形”．如图，四边形ABCD 是一个筝形，其中AD＝CD，AB＝CB，小明在探究筝形的性质时，得到如下结论：①BD平分∠ADC；②AO＝CO＝AC；③AC⊥BD；④S四边形ABCD＝AC•BD．（1）在以上结论中，正确的有（只填序号）；（2）请选择一个你认为正确的结论进行证明．5．如图，△ACD中，∠ACD＝60°，以AC为边作等腰三角形ABC，AB＝AC，E、F分别为边CD、BC上的点，连结AE、AF、EF，∠BAC＝∠EAF＝60°（1）求证：△ABF≌△ACE；（2）若∠AED＝70°，求∠EFC的度数；（3）请直接指出：当F点在BC何处时，AC⊥EF？6．填空：把下面的推理过程补充完整，并在括号内注明理由，如图，已知△ABC中，E、F分别是AB、AC上的两点，且EF∥BC，D为EF上一点，且BD＝CD，ED＝FD，请说明BE＝CF．解：∵BD＝CD（已知）∴∠DBC＝∠DCB（）∵EF∥BC（已知）∴∠EDB＝∠DBC∠FDC＝（）∴∠EDB＝∠FDC（等量代换）在△EBD和△FCD中，∴△EBD≌△FCD（）∴BE＝CF（）7．如图，点P是△ABC内一点，E、F分别是边AC、BC上的两点，连接PE、PF，且PE＝PF，点D为AC延长线上一点，连接PD，且DE＝BF，∠AEP+∠BFP＝180°．（1）求证：△DEP≌△BFP；（2）已知AB＝AE+BF，若∠ACB＝80°，求∠APB的度数．基础题训练（二）：限时35分钟8．如图，在∠ABC＝90°，∠DBE＝90°，BA＝BC，BD＝BE，连接AE、CD，AE所在直线交CD于点F，连接BF．（1）连接AD，EC，求证：AD＝EC；（2）若BF⊥AF，求证：点F为CD的中点．9．在△ABC和△ADE中，点E在BC边上，∠EAC＝∠DAB，∠B＝∠D，AB＝AD．（1）求证：△ABC≌△ADE；（2）如果∠AEC＝70°，求∠BAD的度数．10．（1）如图1，已知，AB∥CD，AD∥BC．求证：△ABC≌△CDA；（2）如图2，已知AB＝DC，AE＝DF，BF＝CE．求证：AF＝DE．11．如图，边长为a的正方形ABCD被两条与正方形的边平行的线段EF，GH分割成四个小矩形，EF与GH交于点P，连接AF，AH．（1）若BF＝DH，求证：AF＝AH．（2）连接FH，若∠FAH＝45°，求△FCH的周长（用含a的代数式表示）．12．如图，在△ABC中，AB＝AC，DE是过点A的直线，BD⊥DE 于点D，CE⊥DE于点E，AD＝CE．（1）若BC在DE的同侧（如图①）．求证：AB⊥AC．（2）若BC在DE的两侧（如图②），其他条件不变，（1）中的结论还成立吗？（不需证明）13．如图，已知BC是△ABD的角平分线，BC＝DC，∠A＝∠E＝30°，∠D＝50°．（1）写出AB＝DE的理由；（2）求∠BCE的度数．14．如图，点M是线段AB中点，AD、BC交于点N，连接AC、BD、MC、MD，∠1＝∠2，∠3＝∠4．（1）求证：△AMD≌△BMC；（2）图中在不添加新的字母的情况下，请写出除了“△AMD≌△BMC”以外的所有全等三角形，并选出其中一对进行证明．15．已知，如图，△ABC中，AB＝AC，∠ABC＝30°，过点B作BD ⊥AB交CA延长线于点D，过点C作CE⊥AC交BA延长线于点E，点F为AE中点，连接CF．（1）求证：AD＝BF；（2）请直接写出长度等于CF的线段（线段CF本身除外）．参考答案1．（1）证明：∵∠ABD＝∠CBE，∴∠ABC＝∠DBE，∵∠A＝∠BDE，AB＝BD，∴△ABC≌△DBE（SAS），∴BC＝BE；（2）∵△ABC≌△DBE，∴DE＝AC＝AD+DC＝2.5+2.5＝5，BE＝BC＝4，∴△CDP和△BEP的周长和＝DC+DP+CP+BP+PE+BE＝DC+DE+BC+BE＝15.5．2．解：（1）AD∥BE，理由：∵AB∥CD，∴∠B＝∠DCE，∵∠B＝∠D，∴∠DCE＝∠D，∴AD∥BE；（2）∵O是CD的中点，∴DO＝CO，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠D＝∠OCE，在△ADO和△ECO中，∴△AOD≌△EOC（ASA）．3．解：小明同学的证法不正确．证明：∵∠B＝∠C，∠BOE＝∠COE，∴∠BDC＝∠BEC，∴∠ADB＝∠AEC，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS），∴AB＝AC．4．解：在△ABD与△CBD中，，∴△ABD≌△CBD（SSS），∴∠BDA＝∠BDC，故①正确，∵DA＝DC，∴DO⊥AC，∴∠AOD＝∠COD＝90°，AO＝OC，∴AC⊥DB，故②③正确；四边形ABCD的面积＝S△ADB+S△BCD＝DB×OA+DB×OC＝AC•BD，故④正确；故答案为①②③④5．（1）证明：∵∠BAC＝∠EAF＝60°，∴∠BAC﹣∠CAF＝∠EAF﹣∠CAF，∴∠EAC＝∠BAF，∵AB＝AC，∴∠B＝∠ACB＝（180°﹣6°）÷2＝60°，∵∠ACD＝60°，∴∠ACD＝∠D，在△CAE和△BAF中，，∴△CAE≌△BAF．（2）解：∵△CAE≌△BAF，∴AE＝AF，∠AEC＝∠AFB，∴∠AEF＝∠AFE＝（180°﹣60°）÷2＝60°，∵∠AEC+∠AED＝∠AFC+∠AFB＝180°，∴∠AED＝∠AFC＝70°，∴∠EFC＝∠AFC﹣∠AFE＝70°﹣60°＝10°．（3）解：当F点是BC的中点时，AC⊥EF．理由：∵△CAE≌△BAF．∴AE＝AF，CE＝BF，∵BF＝CF，∴CE＝CF，∴AC⊥EF．6．解：∵BD＝CD（已知）∴∠DBC＝∠DCB（等边对等角）∵EF∥BC（已知）∴∠EDB＝∠DBC∠FDC＝∠DCB（两直线平行，内错角相等）∴∠EDB＝∠FDC（等量代换）在△EBD和△FCD中，，∴△EBD≌△FCD（SAS）∴BE＝CF（全等三角形的对应边相等），故答案为：等边对等角；∠DCB；两直线平行，内错角相等；SAS；全等三角形的对应边相等．7．（1）证明：∵∠AEP+∠BFP＝180°，∠AEP+∠DEP＝180°，∴∠DEP＝∠BFP，∴DE＝BF，PE＝FP，∴△DEP≌△BFP．（2）解：∵△DEP≌△BFP，∴BF＝DE，PB＝PD，∠D＝∠FBP，∵AB＝AE+BF＝AE+DE＝AD，AP＝AP，∴△APD≌△APB，∴∠D＝∠ABP＝∠FBP，∠PAD＝∠PAB，∵∠ACB＝80°，∴∠CAB+∠CBA＝100°，∴∠PAB+∠PBA＝50°，∴∠APB＝130°．8．证明：（1）∵∠ABC＝90°，∠DBE＝90°，∴∠ABD＝∠EBC，又∵AB＝BC，BD＝BE，∴△ABD≌△BEC，∴AD＝EC．（2）如图2中：作CP⊥BF交BF的延长线于P，作DN⊥BF于N．∵∠ABC＝90°，BF⊥AE∴∠ABF+∠A＝90°，∠ABF+∠PBC＝90°∴∠A＝∠PBC，且AB＝BC，∠P＝∠AFB＝90°∴△ABF≌△BPC∴BF＝CP∵∠DBN+∠EBF＝90°，∠DBN+∠BDN＝90°，∴∠BDN＝∠EBF，∵∠DNB＝∠BFE＝90°，BD＝BE，∴△DNB≌△BFE，∴DN＝BF＝CP，∵∠DNF＝∠FPC，∠DEN＝∠PFC，∴△PFC≌△NFD，∴DF＝FC即点F是CD中点．9．证明：（1）∵∠EAC＝∠DAB，∴∠BAC＝∠DAE，在△ABC和△ADE中∵，∴△ABC≌△ADE；（2）∵△ABC≌△ADE，∴AC＝AE，∴∠C＝∠AEC＝70°，∴∠CAE＝180°﹣∠C﹣∠AEC＝40°，∴∠BAD＝40°．10．（1）证明：∵AB∥CD，∴∠BAC＝∠DCA，∵AD∥BC∴∠BCA＝∠DAC，在△ABC和△CDA中∴△ABC≌△CDA（ASA）（2）∵BF＝CE，∴BF+EF＝CE+EF．∴BE＝CF．在△ABE和△DCF中∴△ABE≌△DCF（SSS）．∴∠B＝∠C，在△ABF和△DCE中∴△ABF≌△DCE（SAS）∴AF＝DE．11．证明：（1）∵四边形ABCD是正方形，∴AD＝AB，∠D＝∠B＝90°，在△ABF和△ADH中，，∴△ABF≌△ADH（SAS），∴AF＝AH；（2）将△ADH绕点A顺时针旋转90°到△ABM的位置，如图所示，则AM＝AH，∠DAH＝∠BAM，∵∠FAH＝45°，∠DAB＝90°，∴∠DAH+∠BAF＝45°，∴∠BAM+∠BAF＝45°，即∠FAM＝45°，∴∠FAM＝∠FAH，在△FAM和△FAH中，，∴△FAM≌△FAH（SAS），∴MF＝HF，∵MF＝BF+BM＝BF+DH，∴△FCH的周长为：CF+CH+FH＝CF+CH+BF+DH＝BC+CD＝2a，即△FCH的周长为2a．12．（1）证明：∵BD⊥DE于点D，CE⊥DE于点E，∴△ABD和△CAE均为直角三角形．在Rt△ABD和Rt△CAE中，，∴Rt△ABD≌Rt△CAE（HL），∴∠ABD＝∠CAE．又∵∠ABD+∠BAD＝90°，∴∠CAE+∠BAD＝90°，∴∠BAC＝180°﹣（∠CAE+∠BAD）＝90°，∴AB⊥AC．（2）解：AB⊥AC，理由如下：同（1）可证出：Rt△ABD≌Rt△CAE（HL），∴∠ABD＝∠CAE．又∵∠ABD+∠BAD＝90°，∴∠BAC＝∠CAE+∠BAD＝90°，∴AB⊥AC．13．解：（1）∵BC是△ABD的角平分线，∴∠CBD＝∠CBA，∵BC＝DC，∴∠CBD＝∠D＝50°，∴∠CBD＝∠CBA，在△CDE和△CBA中，，∴△CDE≌△CBA，∴DE＝AB；（2）由（1）知，∠CBD＝∠D＝50°，∴∠BCD＝80°，∴∠ACB＝100°由（1）知，△CDE≌△CBA，∴∠DCE＝∠BCA，∴∠BCD＝∠ACE＝80°，∴∠BCE＝∠ACB﹣∠ACE＝20°．14．（1）解：∵点M是AB中点，∴AM＝BM，∵∠1＝∠2，∴∠AMD＝∠BMC，在△AMD和△BMC中，，∴△AMD≌△MBC（ASA）；（2）△AMC≌△BMD，△ABC≌△BAD，△ACN≌△BDN．理由：∵△AMD≌△MBC，∴AD＝BC，∵∠3＝∠4，AB＝BA，∴△BAD≌△ABC（SAS），∴AC＝BD，∠BDN＝∠ACN，∵∠ANC＝∠BND，∴△ANC≌△BND（AAS），∵AC＝BD，∠CAM＝∠DBM，AM＝BM，∴△AMC≌△BMD（SAS）．15．（1）证明：∵BD⊥AB，EC⊥CA，∴∠DBA＝∠ECA＝90°，在△DBA和△ECA中，，∴△DBA≌△ECA（ASA），∴AD＝AE，∵AB＝AC，∴∠ABC＝∠ACB＝30°，∴∠FAC＝∠ABC+∠ACB＝60°，∵AF＝FE，∠ACE＝90°，∴CF＝AF＝EF，∴△AFC是等边三角形，∴AF＝AC＝FC＝AB＝EF，∴BF＝AE，∴BF＝AE，∴AD＝BF．（2）∵AF＝FE，∠ECA＝90°，∴CF＝AF＝EF，∵AB＝AC，∴∠ABC＝∠ACB＝30°，∴∠FAC＝∠ABC+∠ACB＝60°，∴△CAF是等边三角形，∴AC＝CF，∴与CF相等的线段有AB，AC，AF，EF．。