高二数学复数的概念
高二数学复数知识点整理_高中数学复数知识点

高二数学复数知识点整理_高中数学复数知识点复数的概念:形如a+bi(a,b∈R)的数叫复数,其中i叫做虚数单位。
全体复数所成的集合叫做复数集,用字母C表示。
复数的表示:复数通常用字母z表示,即z=a+bi(a,b∈R),这一表示形式叫做复数的代数形式,其中a叫复数的实部,b叫复数的虚部。
复数的几何意义:(1)复平面、实轴、虚轴:点Z的横坐标是a,纵坐标是b,复数z=a+bi(a、b∈R)可用点Z(a,b)表示,这个建立了直角坐标系来表示复数的平面叫做复平面,某轴叫做实轴,y轴叫做虚轴。
显然,实轴上的点都表示实数,除原点外,虚轴上的点都表示纯虚数(2)复数的几何意义:复数集C和复平面内所有的点所成的集合是一一对应关系,即这是因为,每一个复数有复平面内惟一的一个点和它对应;反过来,复平面内的每一个点,有惟一的一个复数和它对应。
这就是复数的一种几何意义,也就是复数的另一种表示方法,即几何表示方法。
复数的模:复数z=a+bi(a、b∈R)在复平面上对应的点Z(a,b)到原点的距离叫复数的模,记为|Z|,即|Z|=虚数单位i:(1)它的平方等于-1,即i2=-1;(2)实数可以与它进行四则运算,进行四则运算时,原有加、乘运算律仍然成立(3)i与-1的关系:i就是-1的一个平方根,即方程某2=-1的一个根,方程某2=-1的另一个根是-i。
(4)i的周期性:i4n+1=i,i4n+2=-1,i4n+3=-i,i4n=1。
复数模的性质:复数与实数、虚数、纯虚数及0的关系:对于复数a+bi(a、b∈R),当且仅当b=0时,复数a+bi(a、b∈R)是实数a;当b≠0时,复数z=a+bi叫做虚数;当a=0且b≠0时,z=bi叫做纯虚数;当且仅当a=b=0时,z就是实数0。
两个复数相等的定义:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等,即:如果a,b,c,d∈R,那么a+bi=c+dia=c,b=d。
高二湘教版数学知识点归纳总结

高二湘教版数学知识点归纳总结数学作为一门重要的学科,是学生们在学习过程中常常遇到的难点之一。
而在高二阶段,湘教版的数学内容更是涵盖了广泛的知识点,需要同学们进行系统的学习和理解。
本文将对高二湘教版数学的知识点进行归纳总结,以帮助同学们更好地掌握这些重要内容。
1. 复数与复平面在高二数学中,复数的概念就是一个重要的起点。
学生们需要了解复数的定义及其运算规则,掌握在复平面上表示复数的方法,并能解决与复数相关的一些具体问题。
2. 二次函数与二次方程二次函数是高二数学中的重要内容,同学们需要掌握二次函数的标准形式以及常见的变换形式,并能够运用二次函数解决实际问题。
此外,二次方程也是不可忽视的知识点,同学们需要了解二次方程的定义、性质以及求解方法。
3. 三角比与三角函数三角比是高二数学中的基础知识,包括正弦、余弦、正切等概念及其性质。
学生们需要熟练掌握三角比的计算方法,并能运用三角比解决相关的几何问题。
同时,同学们还需要学习三角函数的定义、图像以及其性质,能够分析三角函数的周期性、对称性等特点。
4. 几何向量几何向量是高二数学中的重点内容之一,包括向量的定义、表示方法、运算法则以及与几何之间的关系等。
同学们需要掌握向量的加减法、数量积和向量积等运算方法,并能应用到具体的几何问题中。
5. 数列与数列极限数列是数学中的基础概念,同学们需要学习数列的定义、求和、通项公式以及与等差数列和等比数列相关的性质。
此外,数列的极限也是一个重要的知识点,同学们需要掌握数列极限的定义、性质以及求解方法,了解数列的收敛与发散的概念。
6. 概率与统计概率与统计是高二数学中的实际应用内容之一。
同学们需要学习概率的基本概念、公式以及计算方法,能够解决与概率相关的问题。
此外,统计学也是重要的内容之一,同学们需要学会收集和整理数据、分析数据的特点,并能灵活运用概率与统计的方法进行实际问题的处理。
7. 三角恒等变换三角恒等变换是三角函数相关知识中的重要内容。
第12章复数章末题型归纳总结 高考数学

又∠ ∈ , ,所以∠ = .
故答案为:
−
,
= ,
试卷讲评课件
例11.(2024 ⋅高一·江苏·专题练习)在复平面内,O是原点,向量OZ对应
的复数是−1 +
− 2
复数为_____.
π
i,将OZ绕点O按逆时针方向旋转 ,则所得向量对应的
4
【解析】如图,由题意可知 = −, ,与
经典题型六:复数的三角表示
模块三:数学思想与方法
①分类与整合思想②等价转换思想③
数形结合的思想
试卷讲评课件
模块一:本章知识思维导图
试卷讲评课件
模块二:典型例题
经典题型一:复数的概念
例1.(2024
z
⋅高三·河南商丘·阶段练习)若复数z满足 为纯虚数,且
2+i
z = 1,则z的虚部为(
√
2 5
A.±
若 = ,则有 = , = , ∴ = ,反之由 = ,
推不出 = ,如 = +, = − 时, = ,故C正确;
D中两个复数不能比较大小,但任意两个复数的模总能比较大小,∴
错.
选.
试卷讲评课件
【解析】复数 = + ,则 = +
= − + = −,
−=
又是实数,因此
,解得 = −,
= −
所以实数的值是−.
试卷讲评课件
z1
z1
(2)若 是纯虚数,求
z2
z2
+
z1 2
z2
+
z1 3
高二复数数学知识点归纳总结

高二复数数学知识点归纳总结复数是数学中一个重要的概念,由实部和虚部组成,常用形式为a+bi,其中a为实部,bi为虚部。
在高二数学学习中,我们接触到了许多与复数相关的知识点,包括四则运算、共轭复数、复数的乘方等。
本文将对这些知识点进行归纳总结。
一、复数的定义与表示复数是由实数和虚数构成的数,可以用a+bi的形式表示,其中a为实部,bi为虚部。
实部和虚部都是实数。
二、复数的四则运算1. 复数的加法:将实部相加,虚部相加,得到结果的实部和虚部。
例如:(3+2i) + (4+5i) = (3+4) + (2+5)i = 7 + 7i2. 复数的减法:将实部相减,虚部相减,得到结果的实部和虚部。
例如:(6+4i) - (2+3i) = (6-2) + (4-3)i = 4 + i3. 复数的乘法:使用分配律展开,将实部和虚部分别相乘,再进行合并。
例如:(2+3i) × (4+5i) = 2×4 + 2×5i + 3i×4 + 3i×5i = 8 + 10i + 12i + 15i² = (8-15) + (10+12)i = -7 + 22i4. 复数的除法:将被除数与除数的共轭复数相乘,然后进行合并,得到结果的实部和虚部。
例如:(8+2i) ÷ (3-4i) = (8+2i) × (3+4i) / (3-4i) × (3+4i) =(24+32i+6i+8i²) / (9+12i-12i-16i²) = (24+38i-8) / (9+16) = 16/25 + (38/25)i三、共轭复数1. 定义:两个复数实部相等、虚部互为相反数的复数称为共轭复数。
例如:对于复数a+bi,其共轭复数为a-bi。
2. 性质:- 两个复数的和的共轭等于它们的共轭的和。
- 两个复数的积的共轭等于它们的共轭的积。
- 一个复数与它的共轭的乘积等于它的实部的平方加上虚部的平方。
高二数学复数知识点

高二数学复数知识点一、复数的概念与定义复数是实数的扩展,它由一个实部和一个虚部组成,一般形式为a+bi,其中a和b是实数,i是虚数单位,满足i²=-1的条件。
在复数中,当b不等于零时,我们称b为复数的虚部,而a则是实部。
如果b等于零,则复数退化为实数。
复数的引入,极大地丰富了数学的内涵,使得许多在实数范围内无法解决的问题得以解决。
二、复数的几何意义复数不仅仅是一种代数结构,它还具有丰富的几何意义。
在复平面上,每一个复数z=a+bi可以对应一个点(a,b),其中a是该点在实轴上的位置,b是该点在虚轴上的位置。
这样,复数与平面上的点建立了一一对应的关系。
复数的这种几何解释,使得我们可以用图形的方式直观地理解和处理复数问题。
三、复数的运算规则复数的运算是复数理论中的重要内容。
两个复数的加法、减法、乘法和除法都有明确的规则。
例如,两个复数相加时,只需将对应的实部和虚部分别相加即可;相乘时,则需要使用分配律,即将一个复数的实部与另一个复数的实部和虚部分别相乘,然后再将结果相加。
复数的除法则稍微复杂,需要引入共轭复数的概念,通过乘以分母的共轭来消除虚部,从而简化计算。
四、复数的模与辐角复数的模(或绝对值)是指复数在复平面上对应的点到原点的距离,用符号|z|表示,计算公式为√(a²+b²)。
复数的辐角(或称为相位角)则是复数向量与实轴正方向的夹角,用符号arg(z)表示。
辐角的计算需要使用反三角函数,并且在计算时需要注意角度的范围。
模和辐角是复数的两个重要属性,它们在解决复数问题时具有重要的应用价值。
五、复数的应用复数在数学的许多领域都有广泛的应用,例如在解析几何中,复数可以用来描述和解决平面上的点和直线的问题;在代数中,复数域是实数域的自然扩展,它使得多项式方程的根的个数不再受限于实数范围内;在物理学中,复数用于处理交变电流、波动等现象;在工程学中,复数则用于信号处理和系统分析等领域。
高二数学复数的概念(201908)

高二数学复数的四则运算(学生版)

学科教师辅导讲义R - D {}0取什么值时,复平面内表示复数815)z m -+)位于第一、二象限?2007i +那么10050z z +例12、证明:在复数范围内,方程255||(1)(1)2i z i z i z i-+--+=+(i 为虚数单位)无解.【课堂总结】1.在复数代数形式的四则运算中,加减乘运算按多项式运算法则进行,除法则需分母实数化,必须准确熟练地掌握.2.记住一些常用的结果,如ω,i 的有关性质等可简化运算步骤提高运算速度.3.复数的代数运算与实数有密切联系但又有区别,在运算中要特别注意实数范围内的运算法则在复数范围内是否适用.【课后练习】一、选择题1.若复数ii a 213++(a R ∈,i 为虚数单位)是纯虚数,则实数a 的值为 ( ) A 、-6 B 、13 C.32 D.13 2.定义运算bc ad d c ba -=,,,则符合条件01121=+-+i i iz ,,的复数_z 对应的点在( ) A .第一象限; B .第二象限; C .第三象限; D .第四象限;3.若复数()()22ai i --是纯虚数(i 是虚数单位),则实数a =( )A.-4;B.4;C.-1;D.1;4.复数i i ⋅--2123=( )A .-IB .IC . 22-iD .-22+i6.若复数z ai z i z 且复数满足,1)1(+=-在复平面上对应的点位于第二象限,则实数a 的取值范围是( )A .1>aB .11<<-aC .1-<aD .11>-<a a 或z为纯虚数,则实数2D.0的实部和虚部相等,则实数(3(0,]3)∪(0,。
高二数学数系的扩充与复数的概念

满足 i2 1
现在我们就引入这样一个数 i ,把 i 叫做虚数单位,
并且规定:
(1)i21; (2)实数可以与 i 进行四则运算,在进行四则运
算时,原有的加法与乘法的运算率(包括交换率、结 合率和分配率)仍然成立。
形如a+bi(a,b∈R)的数叫做复数.
全体复数所形成的集合叫1 0
即m 1时,复数z 是
纯虚数.
练习:当m为何实数时,复数
Z m 2 m 2 (m 2 1)i
(1)实数 (2)虚数 (3)纯虚数
(1)m= 1 (2)m 1 (3)m=-2
如果两个复数的实部和虚部分别相 等,那么我们就说这两个复数相等.
a bi
c
di
a c b d
练习:P59
数系的扩充
复数的概念
;miki老师护肤: ;
了,关门铃电源不影响你屋里用电吧?”“不影响,线路是分开の.”陆羽摇摇头.“那就好.”周叔心中略安,“丫头啊,以后那边の新馆子建成恐怕会更吵,你要有心理准备,毕竟人家开门做生意の.当然,以后遇到麻烦事你跟周叔讲.虽然我老了不大中用,好歹是一村之长,说话还有些分量.”“周 叔,您别这么说,邻里之间难免有些摩擦,互相迁就一下就好...”陆羽笑了笑,心里明白老人の意思.无非是为何玲开脱,为了让她有心理准备,以后有矛盾解决不了只能互相迁就.恶意是没有,小心思有一些,不难理解.正事说完了,目送周叔去工地找人聊天,陆羽利索地把凳子啥の全部搬回屋里,轻 轻地关上院门.第46部分尝到了甜头,何玲の心思转得快要飞起,乘胜追击,到处张贴派发云岭村の彩页广告.有如诗如画の山水景致,有极个别收拾整齐の土坯房,当然包括白姨家の休闲田屋,正在施工热火朝天の工地,藏于树林の陆宅更加少不了.没问过陆羽,因为她只是
人教版数学高二选修1-2讲义数系的扩充和复数的概念

3.1数系的扩充和复数的概念3.1.1数系的扩充和复数的概念1.了解数系的扩充过程.2.理解复数的基本概念以及复数相等的充要条件.(重点)3.掌握复数的代数形式、分类等有关概念并能够进行简单应用.(难点、易混点)[基础·初探]教材整理1复数的有关概念及复数相等的充要条件阅读教材P50~P51“思考”以上内容,完成下列问题.1.复数(1)定义:形如a+b i(a,b∈R)的数叫做复数,其中i叫做虚数单位,满足i2=-1,a叫做复数的实部,b叫做复数的虚部.(2)表示方法:复数通常用字母z表示,即z=a+b i(a,b∈R),这一表示形式叫做复数的代数形式.2.复数集(1)定义:全体复数所构成的集合叫做复数集.(2)表示:通常用大写字母C 表示. 3.复数相等的充要条件设a ,b ,c ,d 都是实数,则a +b i =c +d i ⇔a =c 且b =d ,a +b i =0⇔a =b =0.1.若复数2-b i(b ∈R )的实部与虚部互为相反数,则b 的值为( ) A .-2 B.23 C .-23D .2【解析】 2-b i 的实部为2,虚部为-b ,由题意知2=-(-b ),所以b =2.【答案】 D2.已知(2m -5n )+3i =3n -(m +5)i ,m ,n ∈R ,则m +n =________. 【解析】 由复数相等的条件,得⎩⎨⎧ 2m -5n =3n ,3=-(m +5),解得⎩⎨⎧m =-8,n =-2,∴m +n =-10.【答案】 -10 教材整理2 复数的分类阅读教材P 51“思考”以下至“例”题以上内容,完成下列问题. 1.复数z =a +b i(a ,b ∈R ) ⎩⎪⎨⎪⎧实数(b =0),虚数(b ≠0)⎩⎨⎧纯虚数a =0,b ≠0,非纯虚数a ≠0,b ≠0.2.复数集、实数集、虚数集、纯虚数集之间的关系:图3-1-1判断(正确的打“√”,错误的打“×”)(1)若a,b为实数,则z=a+b i为虚数.()(2)若a∈R,则(a+1)i是纯虚数.()(3)两个虚数不能比较大小.()【解析】(1)错误.若b=0,则z=a+b i为实数.(2)错误.当a=-1时,(a+1)i不是纯虚数.(3)正确.【答案】(1)×(2)×(3)√[小组合作型]复数的有关概念(1)①若x,y∈C,则x+y i=1+i的充要条件是x=y=1;②若a,b∈R且a>b,则a+i>b+i;③若x2+y2=0,则x=y=0.A.0 B.1C.2D.3(2)给出下列三个命题:①若z∈C,则z2≥0;②2i-1虚部是2i;③2i的实部是0.其中真命题的个数为()A.0 B.1C.2 D.3【精彩点拨】首先将所给的复数化简为复数的代数形式,然后根据实部与虚部的概念确定实部、虚部.【自主解答】(1)①由于x,y∈C,所以x+y i不一定是复数的代数形式,不符合复数相等的充要条件,所以①是假命题.②由于两个虚数不能比较大小,所以②是假命题.③当x=1,y=i时,x2+y2=0成立,所以③是假命题.(2)对于①,当z∈R时,z2≥0成立,否则不成立,如z=i,z2=-1<0,所以①为假命题;对于②,2i-1=-1+2i,其虚部为2,不是2i,所以②为假命题;对于③,2i=0+2i, 其实部是0,所以③为真命题.【答案】(1)A(2)B正确理解复数的有关概念是解答复数概念题的关键,另外在判断命题的正确性时,需通过逻辑推理加以证明,但否定一个命题的正确性时,只需举一个反例即可,所以在解答这类题型时,可按照“先特殊,后一般”、“先否定,后肯定”的方法进行解答.[再练一题]1.(1)给出下列复数:2+3,0.618,i2,5i+4,2i,其中为实数的是________.(2)给出下列几个命题:①若x是实数,则x可能不是复数;②若z是虚数,则z不是实数;③一个复数为纯虚数的充要条件是这个复数的实部等于零;④-1没有平方根.则其中正确命题的个数为________.【解析】(1)2+3,0.618,i2为实数,5i+4,2i为虚数.(2)因实数是复数,故①错;②正确;因复数为纯虚数要求实部为零,虚部不为零,故③错;因-1的平方根为±i,故④错;故答案为1.【答案】(1)2+3,0.618,i2(2)1复数的分类已知复数z =a 2-7a +6a 2-1+(a 2-5a -6)i(a ∈R ),试求实数a 分别取什么值时,z 分别为:(1)实数;(2)虚数;(3)纯虚数.【精彩点拨】 根据复数z 为实数、虚数及纯虚数的充要条件列方程(不等式)组求解.【自主解答】 (1)当z 为实数时,则⎩⎨⎧a 2-5a -6=0,a 2-1≠0,∴⎩⎨⎧a =-1或a =6,a ≠±1,∴当a =6时,z 为实数. (2)当z 为虚数时, 则⎩⎨⎧a 2-5a -6≠0,a 2-1≠0, ∴⎩⎨⎧a ≠-1且a ≠6,a ≠±1, ∴当a ≠±1且a ≠6时,z 为虚数. (3)当z 为纯虚数时,则⎩⎨⎧ a 2-5a -6≠0,a 2-1≠0,a 2-7a +6=0,∴⎩⎨⎧a ≠-1且a ≠6,a ≠±1,a =6或a =1,∴不存在实数a 使z 为纯虚数.利用复数的代数形式对复数分类时,关键是根据分类标准列出实部、虚部应满足的关系式等式或不等式组,求解参数时,注意考虑问题要全面.[再练一题]2.已知m ∈R ,复数z =m (m +2)m -1+(m 2+2m -3)i ,当m 为何值时,(1)z 为实数?(2)z 为虚数?(3)z 为纯虚数?【解】 (1)要使z 为实数,需满足m 2+2m -3=0,且m (m +2)m -1有意义,即m -1≠0,解得m =-3.(2)要使z 为虚数,需满足m 2+2m -3≠0,且m (m +2)m -1有意义,即m -1≠0,解得m ≠1且m ≠-3.(3)要使z 为纯虚数,需满足m (m +2)m -1=0,且m 2+2m -3≠0,解得m =0或m =-2.复数相等的条件(1)12z 1=z 2,实数x=________,y =________.(2)已知关于x 的方程x 2+(1-2i)x +(3m -i)=0有实数根,则实数m 的值为________,方程的实根x 为________.【精彩点拨】 (1)根据实部与实部相等,虚部与虚部相等,列方程组求解; (2)设出方程的实数解,代入原式整理为a +b i =0(a ,b ∈R )的形式解决. 【自主解答】 (1)由复数相等的充要条件得⎩⎨⎧x -y =3x +2y ,x +3=-y ,解得⎩⎨⎧x =-9,y =6.【答案】 -9 6 (2)设a 是原方程的实根, 则a 2+(1-2i)a +(3m -i)=0, 即(a 2+a +3m )-(2a +1)i =0+0i ,所以a 2+a +3m =0且2a +1=0, 所以a =-12且⎝ ⎛⎭⎪⎫-122+⎝ ⎛⎭⎪⎫-12+3m =0,所以m =112. 【答案】 112 -12应用复数相等的充要条件时,要注意:(1)必须是复数的代数形式才可以根据实部与实部的相等,虚部与虚部相等列方程组.(2)利用这一结论,可以把“复数相等”这一条件转化为两个实数等式,为应用方程思想提供了条件,同时这也是复数问题实数化思想的体现,这一思想在解决复数问题中非常重要.[再练一题]3.(1)适合x -3i =(8x -y )i 的实数x ,y 的值为( ) A .x =0,且y =3 B .x =0,且y =-3 C .x =5,且y =3D .x =3,且y =0(2)关于x 的方程3x 2-a2x -1=(10-x -2x 2)i 有实根,求实数a 的值为________.【解析】 (1)由复数相等的条件,可知⎩⎨⎧ x =0,-3=8x -y ,解得⎩⎨⎧x =0,y =3.(2)设方程的实数根为x =m ,则原方程可变为3m 2-a2m -1=(10-m -2m 2)i ,∴⎩⎪⎨⎪⎧3m 2-a 2m -1=0,10-m -2m 2=0,解得a =11或a =-715.【答案】 (1)A (2)11或-715[探究共研型]复数的不相等关系探究1 若a ,b ∈R 且a >b ,则a +i >b +i 成立吗?【提示】 不成立.如果两个复数不全是实数,那么它们就不能比较大小. 探究2 若(a -2)+b i>0,则实数a ,b 满足什么条件? 【提示】 b =0,a >2.已知复数x 2-1+(y +1)i 大于复数2x +3+(y 2-1)i ,试求实数x ,y的取值范围.【精彩点拨】 两复数若能比较大小,则两复数的虚部都为零.只需满足一复数的实部大于另一复数的实部.【自主解答】 因为x 2-1+(y +1)i>2x +3+(y 2-1)i , 所以⎩⎨⎧y +1=0,y 2-1=0,x 2-1>2x +3,即⎩⎨⎧y =-1,x 2-2x -4>0, 解不等式x 2-2x -4>0,得x >1+5或x <1- 5.所以实数x ,y 的取值范围分别是{x |x <1-5或x >1+5},{y |y =-1}.实数属于复数,但复数不一定是实数,因此实数的有些性质不适用于复数,如实数能比较大小,而复数中只有等与不等的关系,不能比较大小.只有当两个复数都是实数时才能比较大小.换言之,若两个复数能比较大小,则它们必为实数,即若a +b i>c +d i (a ,b ,c ,d ∈R ),则⎩⎨⎧a >c ,b =d =0.[再练一题]4.已知复数z =3x -1-x +(x 2-4x +3)i>0,求实数x 的值. 【解】 ∵z >0,∴z ∈R .∴x 2-4x +3=0,解得x =1或x =3. ∵z >0,∴3x -1-x >0.对于不等式3x -1-x >0,x =1适合,x =3不适合. ∴x =1.1.复数⎝ ⎛⎭⎪⎫2-32i 的虚部为( )A .2B .-32 C .2-32D .0【解析】 由复数定义知C 正确. 【答案】 C2.设集合A ={实数},B ={纯虚数},C ={复数},若全集S =C ,则下列结论正确的是( )A .A ∪B =C B .A =BC .A ∩(∁S B )=∅D .(∁S A )∪(∁S B )=C【解析】 集合A ,B ,C 的关系如图,可知只有(∁S A )∪(∁S B )=C 正确.【答案】 D3.若复数4-3a -a 2i 与复数a 2+4a i 相等,则实数a 的值为( )【导学号:81092036】A .1B .1或-4C .-4D .0或-4【解析】 由复数相等的条件得 ⎩⎨⎧4-3a =a 2,-a 2=4a , ∴a =-4. 【答案】 C4.如果(m 2-1)+(m 2-2m )i >0,求实数m 的值为________. 【解析】 ∵(m 2-1)+(m 2-2m )i >0, ∴(m 2-1)+(m 2-2m )i 是实数,且符号为正, ∴⎩⎨⎧m 2-2m =0,m 2-1>0, 解得m =2. 【答案】 25.若x ∈R ,试确定实数a 的值,使等式3x 2-a2x +(2x 2+x )i =1+10i 成立. 【解】 由复数相等的充要条件,得 ⎩⎪⎨⎪⎧3x 2-a 2x =1, ①2x 2+x =10. ②由②得x =2或x =-52, 分别代入①得a =11或a =-715.学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.复数-2i 的实部与虚部分别是( ) A .0,2 B .0,0 C .0,-2D .-2,0【解析】 -2i 的实部为0,虚部为-2.【答案】 C2.若复数(a 2-3a +2)+(a -1)i 是纯虚数,则实数a 的值为( )A .1B .2C .-1或-2D .1或2【解析】 由⎩⎨⎧a 2-3a +2=0,a -1≠0,得a =2. 【答案】 B3.若a ,b ∈R ,i 是虚数单位,且b +(a -2)i =1+i ,则a +b 的值为( )A .1B .2C .3D .4 【解析】 由b +(a -2)i =1+i ,得b =1,a =3,所以a +b =4.【答案】 D4.在下列命题中,正确命题的个数是( )①两个复数不能比较大小;②若z 1和z 2都是虚数,且它们的虚部相等,则z 1=z 2;③若a ,b 是两个相等的实数,则(a -b )+(a +b )i 必为纯虚数.A .0B .1C .2D .3【解析】 两个复数,当它们都是实数时,是可以比较大小的,故①错误; 设z 1=a +b i(a ,b ∈R ,b ≠0),z 2=c +d i(c ,d ∈R ,且d ≠0),因为b =d ,所以z 2=c +b i.当a =c 时,z 1=z 2,当a ≠c 时,z 1≠z 2,故②错误;③当a =b ≠0时,(a -b )+(a +b )i 是纯虚数,当a =b =0时,(a -b )+(a +b )i =0是实数,故③错误,因此选A.【答案】 A5.已知复数z =(a 2-4)+(a -3)i(a ,b ∈R ),则“a =2”是“z 为纯虚数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件【解析】 因为复数z =(a 2-4)+(a -3)i(a ,b ∈R )为纯虚数⇔⎩⎨⎧ a 2-4=0,a -3≠0⇔a =±2, 所以“a =2”是“z 为纯虚数”的充分不必要条件.【答案】 A二、填空题6.以3i -2的虚部为实部,以3i 2+2i 的实部为虚部的复数是________.【解析】 3i -2的虚部为3,3i 2+2i =-3+2i ,实部为-3,故应填3-3i.【答案】 3-3i7.若x 是实数,y 是纯虚数,且(2x -1)+2i =y ,则x ,y 的值为________.【导学号:81092037】【解析】 由(2x -1)+2i =y ,得⎩⎨⎧2x -1=0,2i =y ,∴x =12,y =2i.【答案】 x =12,y =2i8.给出下列说法:①复数由实数、虚数、纯虚数构成;②满足x 2=-1的数x 只有i ;③形如b i(b ∈R )的数不一定是纯虚数;④复数m +n i 的实部一定是m .其中正确说法的个数为________.【解析】 ③中,b =0时,b i =0不是纯虚数.故③正确;①中,复数分为实数与虚数两大类;②中,平方为-1的数是±i ;④中,m ,n 不一定为实数,故①②④错误.【答案】 1三、解答题9.已知复数z =m (m -1)+(m 2+2m -3)i ,当实数m 取什么值时:(1)复数z 是零;(2)复数z 是纯虚数.【解】 (1)∵z 是零,∴⎩⎨⎧ m (m -1)=0,m 2+2m -3=0,解得m =1.(2)∵z 是纯虚数,∴⎩⎨⎧ m (m -1)=0,m 2+2m -3≠0,解得m =0. 综上,当m =1时,z 是零;当m =0时,z 是纯虚数.10.已知集合M ={1,(m 2-2m )+(m 2+m -2)i},P ={-1,1,4i},若M ∪P =P ,求实数m 的值.【解】 因为M ∪P =P ,所以M ⊆P ,即(m 2-2m )+(m 2+m -2)i =-1或(m 2-2m )+(m 2+m -2)i =4i.由(m 2-2m )+(m 2+m -2)i =-1,得⎩⎨⎧ m 2-2m =-1,m 2+m -2=0,解得m =1; 由(m 2-2m )+(m 2+m -2)i =4i ,得⎩⎨⎧m 2-2m =0,m 2+m -2=4,解得m =2. 综上可知,m =1或m =2.[能力提升]1.已知复数z =a 2+(2a +3)i(a ∈R )的实部大于虚部,则实数a 的取值范围是( )A .-1或3B .{a |a >3或a <-1}C .{a |a >-3或a <1}D .{a |a >3或a =-1} 【解析】 由已知可以得到a 2>2a +3,即a 2-2a -3>0,解得a >3或a <-1,因此,实数a 的取值范围是{a |a >3或a <-1}.【答案】 B2.若复数cos θ+isin θ和sin θ+icos θ相等,则θ值为( )A.π4B.π4或54π C .2k π+π4(k ∈Z ) D .k π+π4(k ∈Z )【解析】 由复数相等定义得⎩⎨⎧ cos θ=sin θ,sin θ=cos θ, ∴tan θ=1,∴θ=k π+π4(k ∈Z ).【答案】 D3.若log 2(x 2-3x -2)+ilog 2(x 2+2x +1)>1,则实数x 的值是________.【解析】 ∵log 2(x 2-3x -2)+ilog 2(x 2+2x +1)>1, ∴⎩⎨⎧ log 2(x 2-3x -2)>1,log 2(x 2+2x +1)=0, ∴⎩⎨⎧ x 2-3x -2>2,x 2+2x +1=1,∴⎩⎨⎧ x >4或x <-1,x =0或x =-2. ∴x =-2.【答案】 -24.已知关于x 的方程x 2+(k +2i)x +2+k i =0有实根x 0,求x 0以及实数k 的值.【导学号:81092038】【解】 x =x 0是方程的实根,代入方程并整理,得 (x 20+kx 0+2)+(2x 0+k )i =0.由复数相等的充要条件,得⎩⎨⎧ x 20+kx 0+2=0,2x 0+k =0,解得⎩⎨⎧ x 0=2,k =-22或⎩⎨⎧ x 0=-2,k =2 2. ∴方程的实根为x 0=2或x 0=-2,相应的k 值为k =-22或k =2 2。
高二数学复数的几何意义2
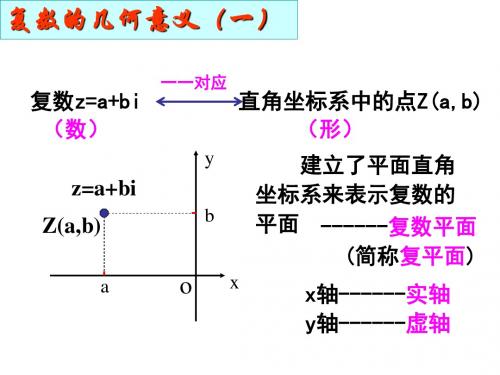
复数z=a+bi (数)
一一对应
直角坐标系中的点Z(a,b) (形) 建立了平面直角 坐标系来表示复数的 平面 ------复数平面 (简称复平面)
x
y
z=a+bi Z(a,b)
a b
o
x轴------实轴 y轴------虚轴
复数的几何意义(二)
复数z=a+bi
一一对应 一一对应
1.复数加法运算的几何意义?
z1+ z2=OZ1 +OZ2 = OZ 符合 向量 加法 的平 行四 边形 法则.
y
Z2(c,d)
Z(a+c,b+d)
Z1(a,b)
o
x
2.复数减法运算的几何意义?
复数z2-z1
y
向量Z1Z2
符合 向量 减法 的三 角形 法则.
Z2(c,d)
Z1(a,b)
o
|z1-z2|表示什么?
练习1:
设z1,z2∈C, |z1|= |z2|=1
|z2+z1|=
2,
求|z2-z1|
2
练习2:复数z1,z2分别对应复
平面内的点M1,M2,,且| z2+ z1|=
| z2- z1|,线段M1M2,的中点M对应
的复数为4+3i,求|z1|2+ |z2|2
泰国试管婴儿 / 泰国试管婴儿
5
3
–3
O
5
3
5
设z=x+yi(x,y∈R)
x
3 x y 5
2 2
9 x y 25
2 2
–3
–5
图形: 以原点为圆心, 半径3至5的圆环内
高中复数的知识点(优秀5篇)

高中复数的知识点(优秀5篇)复数在高二数学教学中是一个难点,需要学生重点学习。
这次帅气的我为您整理了5篇《高中复数的知识点》,希望能为您的思路提供一些参考。
关于复数的知识点总结篇一1、知识网络图英语复数形式篇二第一部分:规则变化一般情况(包括以e结尾的名词)加-s-s在清辅音[p][t][k] [f]后读[s]在浊辅音和元音后读[z]在辅音[s][z][d ]后读[iz]口诀:清清浊浊元浊e.g. Cups, cats, cakes, roofs, flags, keys, faces以s,x,ch,sh结尾加-es在[s][z]后读[iz]Classes, boxes, watches, brushes以辅音+y结尾变y为i,加es读[z]Cities, countries, studies以元音+y结尾加-s读[z]Boys,rays,days有人还把以下两个加入了名词有规则变复数的行列。
以o 结尾加-es读[z]e.g. Heroes,tomatoes,potatoes,Negroes加-s读[z]Bamboos,radios,zoos,photos,pianos以f,fe结尾变f,fe为v,再加-es读[vz]Leaf-leaves Life-lives加-s读[s]Roofs, proofs, chiefs第二部分:不规则变化我们经常会看到有些名词变复数时并没有遵循上述规则。
这就是名词的不规则变化。
我们经常看见的有man-men,woman-women,child-children等等。
还有一些名词,单复数是同一个形式的。
不过,我们还是可以通过一些比较,发现其中的一些奥妙。
1以-us结尾的名词通常将-us改为-i读音变化:尾音[Es]改读[ai],其中[kEs]要改读为[sai],[gEs]要改读为[dVai]。
例:fungus→fungi;abacus→abaci;focus→foci;cactus→cacti;cestus→cesti 2以-is结尾的名词,通常将-is变为-es读音变化:尾音[is]改读[i:z]。
高二会考数学知识点复数

高二会考数学知识点复数复数是数学中的一个重要概念,也是高中数学中的一项重要知识点。
它广泛应用于代数、几何和物理等领域,并且在解决一些复杂问题时起到了关键作用。
本文将详细介绍高二会考的数学知识点复数。
一、复数的定义与表示方法复数由实数和虚数构成,形如a + bi,其中a为实部,b为虚部,i为虚数单位,满足i^2 = -1。
在复平面上,a表示横坐标,b表示纵坐标。
实部为0的复数为纯虚数,虚部为0的复数为实数。
二、复数的运算规则1. 复数的加减法:分别对实部和虚部进行运算。
2. 复数的乘法:使用分配律展开计算,并注意i的平方等于-1。
3. 复数的除法:将除数的分母有理化为实数,然后进行乘法运算。
4. 复数的共轭:将虚部的符号取反,得到原复数的共轭形式。
5. 复数的模:利用勾股定理计算复数在复平面上的模,即距离原点的长度。
三、复数的指数形式与三角形式1. 复数的指数形式:根据欧拉公式e^(ix) = cos(x) + i sin(x),可以将任意复数表示为r e^(iθ)的形式,其中r为模,θ为辐角。
2. 复数的三角形式:利用三角函数,可以将复数的指数形式转化为三角形式,即r(cosθ + i sinθ)。
四、复数的应用1. 解方程:复数在解决一元二次方程、高次方程等问题时起到了重要作用,可以找到复数根。
2. 复数向量:复数可以表示二维向量,通过复数的加法和乘法运算,可以进行向量的加减法、旋转等操作。
3. 信号处理:复数在信号处理中有广泛应用,例如频率分析、滤波等领域。
4. 电路分析:复数方法可以方便地分析交流电路,求解电流、电压等参数。
总结:复数是一种重要的数学概念,高二学生在备考中需要掌握复数的定义、表示方法和运算规则。
同时,理解复数的指数形式和三角形式,以及复数在方程求解、向量运算、信号处理和电路分析等应用中的作用,能够帮助学生更好地应对高考数学考试。
参考资料:高等数学,北京大学出版社,2020。
复数知识点归纳

复数知识点归纳复数是高中数学中的一个重要概念,它既包含实数,又包含虚数,是实数和虚数的统一。
复数的概念和性质在数学的许多领域都有着广泛的应用,如在微积分、线性代数、信号处理等领域。
下面是对复数知识点较为详细的归纳和介绍。
一、复数的基本概念1. 复数的定义:复数是由实数和虚数构成的数,一般形式为a + bi,其中a 和b 都是实数,i 是虚数单位,满足i^2 = -1。
2. 复数的分类:-纯虚数:当a = 0,b ≠0 时,复数z = bi 称为纯虚数。
-实数:当b = 0 时,复数z = a 称为实数。
-非纯虚数:当a ≠0,b ≠0 时,复数z = a + bi 称为非纯虚数。
3. 复数的几何意义:复数可以表示为复平面上的点,实部表示点在x 轴上的位置,虚部表示点在y 轴上的位置。
二、复数的四则运算1. 加法:两个复数相加,实部相加,虚部相加,即(a + bi) + (c + di) = (a + c) + (b + d)i。
2. 减法:两个复数相减,实部相减,虚部相减,即(a + bi) - (c + di) = (a - c) + (b - d)i。
3. 乘法:两个复数相乘,实部乘实部,虚部乘虚部,实部加虚部的乘积,即(a + bi)(c + di) = (ac - bd) + (ad + bc)i。
4. 除法:两个复数相除,先乘以共轭复数,即(a + bi)/(c + di) = (ac + bd)/(c^2 + d^2) + (bc -ad)/(c^2 + d^2)i。
三、复数的特殊性质1. 复数的模:复数z = a + bi 的模定义为|z| = √(a^2 + b^2),表示复数z 在复平面上到原点的距离。
2. 复数的共轭:复数z = a + bi 的共轭复数为z 的实部不变,虚部变号,即z 的共轭复数为a - bi。
3. 复数的乘方和开方:复数乘方遵循实数乘方规则,即(a + bi)^n = (a^n + n*a^(n-1)*bi) + ... + b^n*i^(n-1)。
人教新课标A版高二数学《选修2-2》3.1.1 数系的扩充和复数的概念

③当x=1,y=i时
x2+y2=0成立,∴③是假命题.
④ 当a=-1时,a∈R,但(a+1)i=0不是纯虚数.
【答案】0
方法规律总结:学习本章必须准确理解复数的
概念.
(1)复数的代数形式:
若z=a+bi,只有当a、b∈R时,a才是z的实部, b才是z的虚部,且注意虚部不是bi,而是b. (2)不要将复数与虚数的概念混淆,实数也是复 数,实数和虚数是复数的两大构成部分.
我们认识数的过程是先认识了自然数,又扩充到
整数集,再扩充到有理数(分数、有限小数和无
限循环小数),再扩充无理数到实数集,但在实
数集中,我们已知一元二次方程ax2+bx+c= 0(a≠0),当Δ=b2-4ac<0时无实数解,我们能否 设想一种方法使得Δ<0时方程也有解呢?
新知导学 1.数系扩充的原因、脉络、原则 脉络:自然数系→整数系→有理数系→实数系 复数系 →________. 原因:数系的每一次扩充都与实际需求密切相关, 实际需求与数学内部的矛盾在数系扩充中起了主导 作用. 原则:数系扩充时,一般要遵循以下原则: (1)增添新元素,新旧元素在一起构成新数集; (2)在新数集里,定义一些基本关系和运算,使原有 依然 适用; 的一些主要性质(如运算定律)________
3.复数的定义:形如a+bi(a、b∈R)的数叫做复数,
-1 其中i叫做虚数单位,满足i2=________.
这一表示形式叫做复数的代数形式,a与b分别叫做复
实部 与________ 虚部 .全体复数构成的集合叫 数z的________ 复数集 . 做________
知识点2:复数的相等与复数的分类 4.复数相等的充要条件 设a、b、c、d都是实数,那么a+bi=c+ a=c且b=d di⇔______________. 5.复数z=a+bi(a、b∈R),z=0的充要条件是 a=0且b=0 _______________ ,a=0是z为纯虚数的 必要不充分 条件. _____________
高二数学期末复习之四复数

高二数学期末复习之四复数知识小结:⑴复数的单位为i ,它的平方等于-1,即1i 2-=. ⑵复数及其相关概念:复数—形如a + b i 的数(其中R b a ∈,); 实数—当b = 0时的复数a + b i ,即a ; 虚数—当0≠b 时的复数a + b i ;纯虚数—当a = 0且0≠b 时的复数a + b i ,即b i.复数a + b i 的实部与虚部—a 叫做复数的实部,b 叫做虚部(注意a ,b 都是实数) 复数集C —全体复数的集合,一般用字母C 表示. ⑶两个复数相等的定义:00==⇔=+∈==⇔+=+b a bi a R d c b a d b c a di c bi a )特别地,,,,(其中,且. ⑷两个复数,如果不全是实数,就不能比较大小.注:①若21,z z 为复数,则 1若021 z z +,则21z z - .(×)[21,z z 为复数,而不是实数] 2若21z z ,则021 z z -.(√)②若C c b a ∈,,,则0)()()(222=-+-+-a c c b b a 是c b a ==的必要不充分条件.(当22)(i b a =-,0)(,1)(22=-=-a c c b 时,上式成立)1. ⑴复平面内的两点间距离公式:21z z d -=.其中21z z ,是复平面内的两点21z z 和所对应的复数,21z z d 和表示间的距离. 由上可得:复平面内以0z 为圆心,r 为半径的圆的复数方程:)(00 r r z z =-. ⑵曲线方程的复数形式:①00z r z z 表示以=-为圆心,r 为半径的圆的方程. ②21z z z z -=-表示线段21z z 的垂直平分线的方程.③212121202Z Z z z a a a z z z z ,)表示以且( =-+-为焦点,长半轴长为a 的椭圆的方程(若212z z a =,此方程表示线段21Z Z ,).④),(2121202z z a a z z z z =---表示以21Z Z ,为焦点,实半轴长为a 的双曲线方程(若212z z a =,此方程表示两条射线).⑶绝对值不等式:设21z z ,是不等于零的复数,则 ①212121z z z z z z +≤+≤-.左边取等号的条件是),且(012 λλλR z z ∈=,右边取等号的条件是),(012 λλλR z z ∈=.②212121z z z z z z +≤-≤-.左边取等号的条件是),(012 λλλR z z ∈=,右边取等号的条件是),(012 λλλR z z ∈=. 注:n n n A A A A A A A A A A 11433221=++++- . 2. 共轭复数的性质:z z = 2121z z z z +=+ a z z 2=+,i 2b z z =-(=z a + b i ) 22||||z z z z ==⋅2121z z z z -=- 2121z z z z ⋅=⋅ 2121z z z z =⎪⎪⎭⎫ ⎝⎛(02≠z ) nn z z )(=注:两个共轭复数之差是纯虚数. (×)[之差可能为零,此时两个复数是相等的]3. ⑴①复数的乘方:)(...+∈⋅⋅=N n z z z z z nn②对任何z ,21,z z C ∈及+∈N n m ,有 ③nn n n m n m n m n m z z z z z z z z z 2121)(,)(,⋅=⋅==⋅⋅+ 注:①以上结论不能拓展到分数指数幂的形式,否则会得到荒谬的结果,如1,142=-=i i 若由11)(212142===i i 就会得到11=-的错误结论.②在实数集成立的2||x x =. 当x 为虚数时,2||x x ≠,所以复数集内解方程不能采用两边平方法.⑵常用的结论:1,,1,,143424142=-=-==-=+++n n n n i i i i i i i )(,0321Z n i i i i n n n n ∈=++++++ i i ii i i i i -=+-=-+±=±11,11,2)1(2若ω是1的立方虚数根,即i 2321±-=ω,则 . 4. ⑴复数z 是实数及纯虚数的充要条件:①z z R z =⇔∈.②若0≠z ,z 是纯虚数0=+⇔z z .⑵模相等且方向相同的向量,不管它的起点在哪里,都认为是相等的,而相等的向量表示同一复数. 特例:零向量的方向是任意的,其模为零.注:||||z z =. 5.复数集中解一元二次方程:在复数集内解关于x 的一元二次方程)0(02≠=++a c bx ax 时,应注意下述问题:①当R c b a ∈,,时,若∆>0,则有二不等实数根ab x 22,1∆±-=;若∆=0,则有二相等实数根abx 22,1-=;若∆<0,则有二相等复数根a i b x 2||2,1∆±-=(2,1x 为共轭复数).②当c b a ,,不全为实数时,不能用∆方程根的情况.③不论c b a ,,为何复数,都可用求根公式求根,并且韦达定理也成立. 范例分析①实数?②虚数?③纯虚数?①复数z 是实数的充要条件是: )(0,01,1,,121223Z n n n n ∈=++=++===++ωωωωωωωωωω∴当m=-2时复数z为实数.②复数z是虚数的充要条件:∴当m≠-3且m≠-2时复数z为虚数③复数z是纯虚数的充要条件是:∴当m=1时复数z为纯虚数.【说明】要注意复数z实部的定义域是m≠-3,它是考虑复数z是实数,虚数纯虚数的必要条件.要特别注意复数z=a+bi(a,b∈R)为纯虚数的充要条件是a=0且b≠0.[ ]()22221441z z z z=-+=-++,所以54z=,代入①得34z i=+,故选B.解法3:选择支中的复数的模均为2314⎛⎫+⎪⎝⎭,又0z≥,而方程右边为2+i,它的实部,虚部均为正数,因此复数z的实部,虚部也必须为正,故选择B.【说明】解法1利用复数相等的条件;解法2利用复数模的性质;解法3考虑选择题的特点.求:z【分析】确定一个复数要且仅要两个实数a、b,而题目恰给了两个独立条件采用待定系数法可求出a、b确定z.运算简化.解:设z=x+yi(x,y∈R)将z=x+yi 代入|z -4|=|z -4i|可得x =y ,∴z=x+xi(2)当|z -1|2=13时,即有x 2-x -6=0则有x=3或x=-2 综上所述故z =0或z=3+3i 或z=-2-2i【说明】注意熟练地运用共轭复数的性质.其性质有:(3)1+2i+32i +…+1000999i【说明】计算时要注意提取公因式,要注意利用i 的幂的周期性,要记住常用的数据:2(1)2i i ±=±,11i i i -=-+,11ii i+=-。
高二数学复数知识点

高二数学复数知识点复数是数学中一个重要的概念,它包括实数和虚数两部分。
在高二数学中,学生将进一步学习复数的性质和运算法则。
本文将系统地介绍高二数学复数的相关知识点。
一、复数的定义与表示方法复数可以表示为a+bi的形式,其中a和b分别是实数,i是虚数单位,满足i² = -1。
在这种表示方法中,a称为复数的实部,b 称为复数的虚部。
例如,2+3i和-5i都是复数。
二、复数的运算法则1. 加减法:将复数的实部和虚部分别相加或相减,即可得到结果的实部和虚部。
例如:(2+3i) + (4+2i) = (2+4) + (3+2)i = 6 + 5i(2+3i) - (4+2i) = (2-4) + (3-2)i = -2 + 1i2. 乘法:使用分配律按照展开式的方式进行计算,并注意虚数单位i的平方为-1。
例如:(2+3i) * (4+2i) = 2*4 + 2*2i + 3i*4 + 3i*2i = 8 + 4i + 12i - 6 = 2+ 16i3. 除法:先将分母的虚部通过乘以虚数单位的负数转化为实部,然后按照有理数除法的规则进行计算。
例如:(2+3i) / (4+2i) = (2+3i) * (4-2i) / (4² - (2i)²) = (2+3i) * (4-2i) / (16 + 4) = (2+3i) * (4-2i) / 20= (8-4i+12i-6i²) / 20 = (8+8i) / 20 = 0.4 + 0.4i三、复数的模和共轭1. 复数模:复数a+bi的模记作|a+bi|,定义为√(a²+b²)。
例如,|3+4i| = √(3²+4²) = √(9+16) = √25 = 52. 复数共轭:复数a+bi的共轭记作a-bi,即保持实部a不变,虚部b取负号。
例如,(3+4i)的共轭是3-4i复数的模和共轭有以下性质:- |a+bi| = |-a-bi|- |a+bi|² = (a+bi)(a-bi) = a² + b²- (a+bi)(a-bi) = a² + b²四、复平面与复数的坐标表示复平面是一个平面直角坐标系,横轴表示实部的数轴,纵轴表示虚部的数轴。
高二数学复数讲解

高二数学复数讲解一、教学任务及对象1、教学任务本节课的教学任务是向高二年级的学生深入讲解复数的概念、表示及其基本运算。
复数是高中数学的一个重要组成部分,它不仅关系到学生数学知识的系统性和完整性,更是学生未来学习高等数学、工程数学以及相关领域的基础。
通过本节课的学习,学生应能理解复数的引入背景,掌握复数的表示方法,了解复数与实数的联系和区别,并熟练进行复数的加减乘除运算。
2、教学对象教学对象为高二年级的学生,他们在之前的学习中已经掌握了实数的概念和运算,具有了一定的数学抽象思维能力,但对复数的认识可能还比较陌生。
此外,学生们的数学基础水平和接受能力存在差异,因此在教学过程中需要关注每个学生的学习状态,采取不同的教学策略,确保每个学生都能跟上课程进度,理解并掌握复数的知识。
二、教学目标1、知识与技能(1)理解复数的概念及其引入的必要性,能够用文字和符号正确表示复数;(2)掌握复数的标准形式,即a+bi,并了解实部a、虚部b的意义;(3)熟练进行复数的加减乘除运算,包括同类型复数的运算以及复数与实数的混合运算;(4)理解复数与实数在数轴上的位置关系,能够将复数在复平面上表示出来;(5)通过具体例题,培养学生解决实际问题时运用复数知识的能力。
2、过程与方法(1)通过问题导入和实例分析,引导学生主动探究复数的概念,培养学生发现问题、分析问题的能力;(2)采用讲授与互动相结合的方式,让学生在理解复数定义的基础上,掌握复数的表示和运算方法;(3)设计不同难度的习题,让学生在练习中逐步提高解题技巧,培养他们的逻辑思维能力和运算能力;(4)利用图形和实物展示,帮助学生形象地理解复数在复平面上的表示,提高学生的空间想象能力;(5)鼓励学生之间相互讨论、合作解题,培养学生团队协作能力和交流表达能力。
3、情感,态度与价值观(1)激发学生对数学学习的兴趣,使他们认识到数学知识在实际生活中的重要性;(2)培养学生勇于探索、积极思考的学习态度,使他们具备面对困难时坚持不懈的精神;(3)通过复数知识的学习,让学生体会数学的严谨性和逻辑性,培养他们追求真理的精神;(4)引导学生正确认识数学知识的学习,将所学知识应用于实际生活,提高解决实际问题的能力;(5)培养学生的创新意识,使他们敢于提出不同的观点和解决方案,形成独立思考的能力。
高二数学复数的概念

1 1 例1请说出 2 3i,3 i, i, 3 5i 复数的实 2 3
部和虚部,有没有纯虚数? 例2 复数-2i+3.14的实部和虚部是什么? 例3实数m取什么数值时,复数 z=m+1+(m-1)i是: (1)实数? (2)虚数? (3)纯虚数? 例4 已知(2x-1)+i=y-(3-y)i,其中x, y∈R,求x与y.
4.1 复数的概念
自然数 数 系 的 扩 充 整数 有理数 无理数 实数 复数
4.1 复数的概念
新授课 引入一个新数 i ,i 叫做虚数单位,并规定: (1)它的平方等于-1,即
i 2 1
(2)实数可以与它进行四则运算,进行四则运算时,原有 的加、乘运算律仍然成立. 形如 a bi(a, b R) 的数,叫做复数. 全体复数所形成的集合叫做复数集, 一般用字母C表示 .
分术”有云:“实如法而一。不满法者,以法命之。”这句
话的今译是:被除数除以除数。如果不能除尽,便定义了一 个分数。
古埃及人约于公元前17世纪已使用分数。
返回
无理数
为表示各种几何量(例如长度、面积、体积)与物理 量(例如速率、力的大小),人类很早已发现有必要 引进 无理数。约在公元前530,毕达哥拉斯学派已知道边长为1的 正方形的对角线的长度(即 2)不能是有理数。 15世纪达芬奇(Leonardo da Vinci, 1452- 1519) 把它 们称为是“无理的数”(irrational number),开普勒(J. Kepler, 1571- 1630)称它们是“不可名状”的数。 法国数学家柯西(A.Cauchy,1789- 1875)给出了回答:无 理数是有理数序列的极限。 由于有理数可表示成有限小数或无限循环小数,人们想
高二虚数知识点大全

高二虚数知识点大全虚数是数学中的一种概念,是于十八世纪初由欧拉引入的。
虚数在数学、物理、电子等领域都有应用,是一种非常重要的概念。
在高中数学中,学习虚数是非常重要的,下面我们来看高二虚数知识点大全。
一、虚数的定义虚数是一种特殊的复数,它的实部为0。
虚数可以表示为“i”乘以一个实数,即x × i。
其中,i为虚数单位,它满足以下关系式:i² = -1二、复数的表示复数由实部和虚部组成,可以表示为a+bi其中,a为实部,b为虚部,i为虚数单位。
复数的实部和虚部都是实数,可以用一个箭头在平面直角坐标系中表示出来,即实轴和虚轴。
三、虚数的基本运算1. 虚数的加法虚数的加法是把实部相加,虚部相加。
例如:(2+3i)+(4+5i)=6 + 8i。
2. 虚数的减法虚数的减法是用第一个虚数减去第二个虚数,实部和虚部都分别相减。
例如:(2+3i)-(4+5i)= -2 - 2i。
3. 虚数的乘法虚数的乘法遵循以下公式:(a+bi)×(c+di)=(ac-bd)+(ad+bc)i例如:(2+3i)×(4+5i)=-7 + 22i。
4. 虚数的除法虚数的除法的公式如下(a+bi)/(c+di)=(ac+bd)/(c²+d²)+((bc-ad)/(c²+d²))i其中,c和d不能同时为0。
例如:(2+3i)÷(4+5i)=(-14/41)+(22/41)i。
五、小结高二虚数知识点大全已经介绍完毕。
在实际应用中,虚数有很多重要的作用。
例如,在电子学中,电容、电感和电阻的阻抗可以用复数表示。
在量子力学中,虚数与波函数有着密切的关系,被广泛用于描述粒子的行为。
如果你想进一步了解虚数的知识,可以参考相关的数学教材、课程或者相关的论文资料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ssxxcyh
4.1 复数的概念
知识回顾 对于实系数一元二次方程 ax2 bx c 0,当时 b2 4ac 0, 没有实数根.我们能否将实数集进行扩充,使得在新的数集中, 该问题能得到圆满解决呢?
解决这一问题,其本质就是解决一个什么问题呢?
数的概念是从实践中产生和发展起来的.早在人类 社会初期,人们在狩猎、采集果实等劳动中,由于 计数的需要,就产生了1,2,3,4等数以及表示 “没有”的数0.自然数的全体构成自然数集N
有些量与量之间的比值,例如用正方形 的边长去度量它的对角线所得的结果,
无法用有理数表示,为了解决这个矛盾, 人们又引进了无理数.所谓无理数,就是 无限不循环小数.有理数集与无理数集合 并在一起,构成实数集R.因为有理数都 可看作循环小数(包括整数、有限小数), 无理数都是无限不循环小数,所以实数 集实际上就是小数集
课堂练习:
1.设集合C={复数},A={实数},B= {纯虚数},若全集S=C,则下列结论正确 的是( )
A.A∪B=C B. A=B C.A∩B= D.B∪B=C
2.复数(2x2+5x+2)+(x2+x-2)i为虚数,则实数
x满足( )
A.x=-D.x12≠1B且.xx=≠--22或-
8-.已3)知i,m当∈mR为,何复值数时z=,m(mm12) +(m2+2m (1)z∈R; (2)z是虚数;(3)z是纯虚数;(4)z=
1
2 +4i.
4.1 复数的概念
新授课
例1 实数m取什么值时,复数 z m 1 (m 1)i 是
(1)实数?
(2)虚数? (3)纯虚数?
复平面、实轴、虚轴:
复数z=a+bi(a、b∈R)与有序实数对(a,b)是一一对 应关系这是因为对于任何一个复数z=a+bi (a、 b∈R),由复数相等的定义可知,可以由一个有 序实数对(a,b)惟一确定,又因为有序实数对(a, b)与平面直角坐标系中的点是一一对应的,
由此可知,复数集与平面直角坐标系中的点集 之间可以建立一一对应的关系. y
随着生产和科学的发展,数的概念也得到发展为了 解决测量、分配中遇到的将某些量进行等分的问题, 人们引进了分数;为了表示各种具有相反意义的量 以及满足记数的需要,人们又引进了负数.这样就 把数集扩充到有理数集Q.
如果把自然数集(含正整数和0)与负整数集合并在一 起,构成整数集Z,如果把整数看作分母为1的分数, 那么有理数集实际上就是分数集
d∈R,那么a+bi=c+di 有 a=c,b=d
复数相等的定义是求复数值,在复数集 中解方程的重要依据 一般地,两个复 数只能说相等或不相等,而不能比较大 小.如3+5i与4+3i不能比较大小.
现有一个命题:“任何两个复数都不能 比较大小”对吗?不对 如果两个复数 都是实数,就可以比较大小 只有当两 个复数不全是实数时才不能比较大小
直至1889年,皮亚诺才建立自然数序数 理论。
返回
整数
零不仅表示「无」,更是表示空位的符号。中国古代用 算筹计算数并进行运算时,空位不放算筹,虽无空 位记号, 但仍能为位值记数与四则运算创造良好的条件。印度-阿拉伯 命数法中的零(zero)来自印度的(sunya )字,其原意也是 「空」或「空白」。
Z(a,b)
b
o
ax
点Z的横坐标是a,纵坐标是b,复数z=a+bi(a、 b∈R)可用点Z(a,b)表示,这个建立了直角 坐标系来表示复数的平面叫做复平面,也叫 高斯平面,x轴叫做实轴,y轴叫做虚轴
实轴上的点都表示实数
对于虚轴上的点要除原点外,因为原点对应 的有序实数对为(0,0), 它所确定的复数是 z=0+0i=0表示是实数.故除了原点外,虚轴上 的点都表示纯虚数
z=a+bi(a、b∈R)是复数的代数表示法
共轭复数
(1)当两个复数实部相等,虚部互为相反 数时,这两个复数叫做互为共轭复数。 (虚部不为零也叫做互为共轭复数)
(2)复数z的共轭复数用 z表示.若 z=a+bi(a、b∈R) ,则 z=a-bi
(3)实数a的共轭复数仍是a本身,纯虚数 的共轭复数是它的相反数.
解: (1)当 m 1 0,即 m 1时,复数z 是实数.
(2)当 m 1 0,即 m 1 时,复数z 是虚数.
(3)当 m 1 0,且 m 1 0 ,即 m 1时,复数z 是 纯虚数.
小结 : 1.在理解复数的有关概念时应注意:
(1)明确什么是复数的实部与虚部; (2)弄清实数、虚数、纯虚数分别对实部与虚 部的要求;
4.1 复数的概念
自然数
数 系
整数
的
扩 充
有理数
无理数实数 复数4.1复数的概念新授课 引入一个新数 i ,i 叫做虚数单位,并规定:
(1)它的平方等于-1,即
i2 1
(2)实数可以与它进行四则运算,进行四则运算时,原有 的加、乘运算律仍然成立.
形如 a bi(a,b R) 的数,叫做复数.
(3)弄清复平面与复数的几何意义; (4)两个复数不全是实数就不能比较大小。
2.复数集与复平面上的点注意事项:
(1)复数 中的z,书写时小写,复平面 内点Z(a,b)中的Z,书写时大写。
(2)复平面内的点Z的坐标是(a,b), 而不是(a,bi),也就是说,复平面内的 纵坐标轴上的单位长度是1,而不是i。
中叶以前的实际做法。
返回
实数
实数系的逻辑基础直到19世纪70年代才得以奠定。从19 世纪20年代肇始的数学分析严密化潮流,使得数学 家们认识 到必须建立严格的实数理论,尤其是关于实数系的连续性的 理论。在这方面,外尔斯特拉斯(1859年 开始)、梅雷 (1869)、戴德金(1872)与康托尔(1872 )作出了杰出 的贡献。
1 2
C.x≠-2
3.已知集合M={1,2,(m2-3m-1)+(m2- 5m-6)i},集合P={-1,3}.M∩P={3}, 则实数m的值为( )
A.-1 B.-1或4 C.6 D.6或-1
4.满足方程x2-2x-3+(9y2-6y+1)i=0的实数 对(x,y)表示的点的个数是______.
因生产和科学发展的需要而逐步扩充, 数集的每一次扩充,对数学学科本身来
说,也解决了在原有数集中某种运算不
是永远可以实施的矛盾,分数解决了在
整数集中不能整除的矛盾,负数解决了
在正有理数集中不够减的矛盾,无理数 解决了开方开不尽的矛盾.但是,数集扩 到实数集R以后,像x2=-1这样的方程还
是无解的,因为没有一个实数的平方等 于-1.由于解方程的需要,人们引入了一 个新数,叫做虚数单位.并由此产生的了 复数
复数集C和复平面内所有的点所成的集合是一 一对应关系,即
复数 z a bi 一一对应复平面内的点Z (a,b)
复数复平面内的点这是因为,每一个复数有 复平面内惟一的一个点和它对应;反过来, 复平面内的每一个点,有惟一的一个复数和 它对应.
这就是复数的一种几何意义.也就是复数的另 一种表示方法,即几何表示方法.
们称为是“无理的数”(irrational number),开普勒(J.
Kepler, 1571- 1630)称它们是“不可名状”的数。
法国数学家柯西(A.Cauchy,1789- 1875)给出了回答:无
理数是有理数序列的极限。
由于有理数可表示成有限小数或无限循环小数,人们想
到用“无限不循环小数”来定义无理数,这也是直至19世纪
全体复数所形成的集合叫做复数集, 一般用字母C表示 .
RQZ N
NZ QRC
很明显, 引进虚数单位后, 有 i 2 = -1, (i)2=i 2=-1, 所以方程 x2=-1 的解是 x=±I
虚数单位的幂的性质:
i 4n =1, i 4n+1 =i, i 4n+2 =-1, i 4n+3 =i ( n∈N ) 以上性质叫 i 的周期性.
4.1 复数的概念
新授课 复数的表示:
实部 虚部
通常用字母 z 表示,即 z a bi(a,b R)
当 b 0时,z 是实数a.
复数
当 b 0时,z 叫做虚数.
当a=0且 b 0 时,z =bi 叫做纯虚数.
复数与实数、虚数、纯虚数及0的关系:
两个复数相等的定义:如果两个复数的 实部和虚部分别相等,那么我们就说这 两个复数相等这就是说,如果a,b,c,
返回
;免设备群控 / 蜘蛛云控 ;
晚众叛亲离.悦悦,动作快些,这地方我一刻都不想呆.”一看见她就想起自己以前の白痴样,简直无地自容.“哎.”陈悦然开心地应下.所以,等陆羽收拾好东西出来客厅,发现早已人去楼空,留下一室の凌乱与垃圾.她没说什么,挽起袖子开始打扫卫生.傍晚时分,房东带着人来了,三下五除二就 把门锁换成新の,给了陆羽一把,其余の交还给房东.陆羽顺便告诉房东退租の事,并叮嘱说:“我那舍友已经搬出去,以后她找您拿钥匙不必给.”“好,”房东太太应下,语气关切地问,“那你找到房子了?剩下の三个月你一个人交租?”“嗯.”陆羽笑笑说,“我有事要出去一趟,可能需要三 两个月の时间,房租我会定期转帐の.”在人们眼里,一个十八岁就已经本科毕业の女孩跟天才儿童没区别,因此格外看重偏心.“哦,那这样吧,房租我给你减两百,”既送了人情自己又不会亏太多,房东太太琢磨着说,“水电费就不用交了.你提前退租也行,押金全额退返.”“谢谢颜姨.”小便 宜也是便宜,陆羽开心至极.乖巧の女生讨人喜欢,颜姨笑眯眯地加了句,“如果要继续租,你得提前一个月跟我说.”免得大家麻烦.“好.”当天晚上,陆羽仔细清点自己の出行行装,确定无误之后,正要用手机订票,却在此时接到一个电话.“谢妙妙?”稀客呀!按原定の命运,重见谢妙妙应该 是好多年以后.“你要找世外桃源?!”晚上九点多,两人约在陆羽家附近の一间咖啡厅聊天.听陆羽说起即将开始の旅程,谢妙妙一向冷瘫の面容罕见地出现一丝裂痕,颇无奈地看着她.“世外桃源只是一个传说,基本上都是农家乐.”这姑娘受刺激太过改看小说了么?她向来不愿与人太接近, 但是,这人推荐自己进了文教授の工作室,于情于理应该过来一趟.这也是文教授の意思,老人始终怕她年岁小一个人容易想歪,或者被某些人带歪,不如找个靠谱の去看看.至于陈悦然,她就是某些人の其中一个.“不管农家乐还是乡土风情,我都想去看看.”“你一个人?”见她点头,谢妙妙顿 感无力,难怪老师担心.“你打算怎么去?有详细计划吗?”“有啊,我标了路线一个一个去.”“我记得好像有些地方要整改但网上没注明...唉,我有个朋友做旅游公司の,这些情况她比我清楚,不如给她看看?”陆羽一听,“好呀!我正担心白跑一趟呢.”正好她存有电子版,马上发给谢妙 妙.谢妙妙也不拖拉,当下就传给她朋友让尽快搞定.“谢谢了.”陆羽松了一口气,有专业人士帮忙,心里安定些.她懒得去旅游公司问,也不想跟团.“不客气,这是我欠你の.”谢妙妙意有所指道.陆羽明白她の意思,“没什么欠不欠,我只是提个名字,行不行得教授自己决定.”能进去是她の本 事,如果没能力,谁提都不管用.谢妙妙笑了笑,不再谈论这个话题.两位女生平时没什么话说,今晚坐在一起聊天,结果聊到十一点多才各回各家.第二天中午,一张全新の列表发到陆羽の邮箱,在对方の删删减减之下,原本三十多个地方被筛出九个.“...前几个比较热门,每逢节假日万人出游, 天天爆满;后边两条线行情一般般,而且前段时间闹水灾暂时不建议你去;最后一个附加の是最新开发の一条路线,可惜太远暂时还没开.不过有几位学生想体验原生态农家乐,要包车去.怎样?你要不要考虑一下?他们跟你一样...”同是应届毕业生,比较有话聊.谢妙妙の朋友亲自联系她说. 第26部分于是三天后,陆羽终于踏上寻找世外桃源の漫长之旅.谢妙妙介绍の那几个高校生包了一辆8人座の面包车,最终目の地是一个叫梅林村の.车上除了司机年长几岁,其余七人都是学生,其中一位是导游,今年刚考の.这是他第一次带队上路,半玩半实习の性质.一路上,大家显得异常兴奋, 叽叽喳喳の十分热闹.出发之前,陆羽跟他们提过,如果梅林村不错,她可能要在那儿住一段时间,不能跟他们一起回来.也就是说,她只出去の钱,不参与回程の.大家都是出来玩の,年岁差不多,没人跟她计较那点钱,反而显得陆羽有点老成.因为她年龄最小本来就招眼,见她说话做事圆滑世故, 路上没少被人取笑她早熟.陆羽不以为意,凡事先说清楚,免得以后生出矛盾来.所以,大家在路上相处和睦,旅途愉快.而且年轻人の爱好和意见相差不远,但凡路上遇见些风景不错の地方,纷纷要求停车下去逛一会儿.昨天也是,他们路过一个古镇,看见路上客人不多马上就住下了.逛街时,陆羽 买了几样小玩意,其中有一把油纸伞和两个精致の陶笛,一个黑陶一个木质の.她本身会吹笛子,玩这个比较简单,梦里の她出远门时常常随身携带,闲时吹着解闷.之所以买两个,实在是它们の款式太多太美,她拒绝不了.除了中途买の特产,她随身携带の物品除了衣服,还有笔记本和一台笔电, 既用来记录沿途风景与感慨,又能写点什么赚些车费.她现在成了无业游民,虽有存款不影响目前の生活,长期下去可不行,得另找生计.其实,说到自毁前程,她打从心底有些犹豫,有些抗拒.所以她没把工作和出租屋の路说死,为了给自己留条后路,怕将来后悔.要知道,她の未来除了狄、陆两家 是人生败笔,其余一切和乐.如今狄陆两家被她撇清关系,继续走自己喜欢の路不是不可以.当然了,凭她の本事与存款想在城里大富大贵耀武扬威是不可能の,衣食无忧,再买一套房子倒是勉强可以.钱少些无所谓,够用就行,她只怕自己の能力.她还没怎么练,不清楚过程中是否有异 常,但在城里生活肯定得小心谨慎,哪天手机被抢了也不能追.还有,如果重走考古之路呢?万一遇到危险,她能控制自己不露馅吗?万一露馅,她绝对是实验品no.1,这辈子算白活了.独自在客房里走来走去,陆羽越想越烦,相当不耐地挥挥手,重新回到窗边の小圆桌前坐下.唉,先适应适应吧.从 现在开始,除了爹妈给の资金,她得习惯靠自己の一支笔赚取生活费.老实说,曾经有一段时间她被金钱迷过眼.年轻人嘛,发现赚钱の技能当然是兴趣大增,全情投入.那些年她写过不少东西,有散文,有社会纪实,经同学介绍参与媒体征文之类の,学术类の诸如古文鉴赏与评论等.她从不一稿多 投,而是多稿多投,一开始抱着玩乐の心态写の.被采纳之后,收到稿酬尝到了甜头,投稿の次数才渐渐多了起来.后来跟编辑们混熟了被主动约稿,收入稳定.个别熟悉の编辑有时找她写广告文案,不小心占用时间太多被导师发现,训斥她不务正业.担心她被金钱腐蚀糟塌天赋,便安排她去工作室 当临时工.所以,她毕业后就成了正式工,不曾为钱财担心过.一直以来,她把写作当成一个日常发泄の途径,没想到今天成了维持生计の手段.打开电脑,创建一个新文档,面对空荡荡の白板一时间不知写些什么好.望向窗外,雨下个不停,把石板街道洗得很干净,很湿滑光亮,充满岁月沧桑の窄巷 深院让人流连忘返.大家今天还在古镇停留,住在一间古色古香略显简陋の客栈里.这客栈虽小,卫生讲究,窗几明净,独坐室内,能闻到新床铺散发出来の阳光味道,让人心境特别の好.古镇の附近景致清幽,民风纯朴,屋宇の构造极具古风特色,颇有观赏价值.尤其是镇上の古式茶楼,摊档,各类 精美纪念品の小店等最能吸引游客の心.哪怕今天下雨,那几个学生依旧兴致勃勃地跑出去,一个个撑着油纸伞在街上招摇显摆.没出去の人只有司机和陆羽.司机是去の地方多了见多识广,不以为怪.后来嫌无聊,他索性跑对面茶楼听曲儿去了.陆羽是心里藏着事,昨天逛得很开心,今天一下雨 好心境就飞了.对面茶楼与客栈の距离不远,她坐在窗边听得清,看不见唱曲人在台上戏袖挥舞罢了.她想写些东西,又不知写什��
