2005-2006学年春季学期工科数学分析答案

合集下载

山东省春季高考数学试题2005年真题(附答案)

D． 1
A．第 12 项
B．第 9 项和第 10 项 C．第 11 项 D．第 10 项和第 11 项
16、设函数 f x loga x a 0且a 1 ， f 4 2 ，则（）
A． f 2 f 1 B． f 1 f 2 C． f 1 f 2 D． f 1 f 2
17、某工人制作机器零件，若每天比原计划多做 1 件，那么 8 天所做的零件超过 100 件，若每
O xA
E B
Cy
密
(1)如果函数图象在 x 轴的上方，求 a 的取值范围 (2)如果 f a f a 1 9 ，求 a 的
值。
解：(1)因为意有: 4a2 12 0 , 所以解得: 3 a 3
(2)因为 f a f a 1 a2 2a2 3 (a 1)2 2a(a 1) 3 4a 1
B． p q
C． p q
D． q q
3、不等式 2 x 0 的解集是（） 1 x
A．x | x 2
B．x | 2 x 1
C．x | x 1或x 2 D．x | 1 x 2
4、在等差数列中an ，若 a1 a12 10 ，则 a2 a3 a10 a11等于（
A．10
B．20
二、填空题(12 分)
21、计算： 21.2 sin1.3 3.26 （精确到 0.01）
22、一个盒子里装有 3 个红球和 4 个白球，从中任取 2 个恰好都是白球的概率是 2 7
23、已知抛物线的对称轴为 x 轴，焦点在直线 3x 4 y 12 0 上，则抛物线的标准方程为 y2 16x
A． 1 a 1 2
B． a 1
C． a 1
8、在 ABC 中，若 sin2 A sin2 B sin2 C ，则 ABC 为（）

2005年春季高考.北京卷.理科数学试题及答案

2005年普通高等学校春季招生考试（北京卷）数学试卷（理工农医类）一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、2-i 的共轭复数是（）A ．i +2B ．i -2C ．i +-2D ．i --2 2、函数y=|log 2x|的图象是3、有如下三个命题：①分别在两个平面内的两条直线一定是异面直线； ②垂直于同一个平面的两条直线是平行直线； ③过平面α的一条斜线有一个平面与平面α垂直。

其中正确命题的个数为（）A ．0B ．1C ．2D ．34、如果函数)20)(sin()(πθθπ<<+=x x f 的最小正周期是T ，且当2=x 时取得最大值，那么（）A ．2,2πθ==T B ．πθ==,1T C ．πθ==,2T D ．2,1πθ==T5、设0≠abc ，“0>ac ”是“曲线c by ax =+22为椭圆”的（） A ．充分非必要条件 B ．必要非充分条件C ．充分必要条件D ．既非充分又非必要条件 6、已知双曲线的两个焦点为)0,5(1-F ，)0,5(2F ，P 是此双曲线上的一点，且21PF PF ⊥，2||||21=•PF PF ，则该双曲线的方程是（）A ．13222=-y x B ．12322=-y x C ．1422=-y x D ．1422=-y x7、在ABC ∆中，已知C B A sin cos sin 2=，那么ABC ∆一定是（） A ．直角三角形 B ．等腰三角形 C ．等腰直角三角形 D ．正三角形8、若不等式na n n1)1(2)1(+-+<-对于任意正整数n 恒成立，则实数a 的取值范围是（）A ．⎪⎭⎫⎢⎣⎡-23,2B ．⎪⎭⎫ ⎝⎛-23,2C ．⎪⎭⎫⎢⎣⎡-23,3D ．⎪⎭⎫ ⎝⎛-23,3二、填空题：本大题共6小题，每小题5分，共30分。

把答案填在题中横线上。

工科数学分析习题

即从而。
（B）若，则。由，故对，存在，当时有，即，从而存在，当时有，即严格递减的，故由可得，即
（C）若，令,利用（B）可证明。（2）严格增，且，若，则证明：（A）若，则，令，即，故对，则存在使得当时由得得（使用迭代）
即两边除以，再同时减去得故当时又，则存在使得当时对，取使得当时故（B）若，则。由，故对，存在，当时有，即故严格增的，再由得，从而时，，从而由（A）得，故（C）若，令,利用（B）可证明。 2设证明（1）证明利用O.Stolz公式（2）只需令，，则故。或利用定义直接证明。（2）利用O.Stolz公式可得，或均成立。但，不成立，例，故时 O.Stolz公式也不成立。（3）见附录参考答案及提示。
16 设，且，则证明：对，由知使得当时，故对，取，当时，故 17．求极限（1）（2） (3) (4)
习题1.1（B）
1 O.Stolz公式（1）设，且严格减。若，则证明：（A）若，对，则存在使得当时，即从而当时 ······ 把上式不等式相加的其对成立又，故当时由得当时有故对，取，当时有
，，欲使，只需，即。故对，取当时有故（注意：若用夹逼法：） 2．证明：的充分必要条件是对，只有的有限多项不在中。证明：（必要性）若，则，，时有，故至多有项在不在中。（充分性）对，只有的有限多项不在中，不妨设不在中项为，取（即取不在中项脚标的最大者，故当时有，即。 4.证明若，则。反之不一定，举例说明。但若，则有
单调性：显然，设，则求极限：设，由取极限得，解出
（3）见学习辅导“例25” （4），解有界性：
单调性：
，若，则，否则求极限：设，由得，故。 15 试判断数列的敛散性：（1），其中；解欲使，只需

2005数学分析解答

2005数学分析解答D解：112022000111011ln()|ln(1)ln [(1)ln(1)(1)ln ]|2ln 2y yDdxdy dxdy x y dy y x y x y dy ydyy y y y y y ==+++=+-=++-+-+=⎰⎰⎰⎰⎰⎰⎰5、计算第二类曲线积分：22C ydx xdyI x y--=+⎰，22:21C x y +=方向为逆时针。

解：22220022222tan 2222cos ,[0,2)2sin cos cos 222113cos 22cos 2213(2)(1)12arctan 421(2)(1)2311421C x x y ydx xdy I d x y x x x x d x dx x x x x ππθθθπθθθθθθθθ+∞+∞=-∞-∞=⎧⎪∈⎨=⎪⎩---=−−−→=+++-+-++−−−−−→=--++++=-⎰⎰⎰换元万能公式代换226426212dx d x ππ+∞+∞-∞-∞+=-+++⎰6、设a>0,b>0,证明：111b ba ab b ++⎛⎫⎛⎫≥ ⎪⎪+⎝⎭⎝⎭。

证明：1111()1111(1)111()'()1[ln(1)]0()()()b bxb b bbxa a ab f x b b x a a b f b b b a a b f b b b a b a b a b f x Taylor x x x a b f x ++++-⎛⎫⎛⎫⎛⎫≥=+ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭+-⎛⎫⎛⎫=+=+ ⎪ ⎪++⎝⎭⎝⎭-⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭---⎛⎫=++-> ⎪+-⎝⎭，构造函数展开可以证明所以递增，从而得证一、设f(x)为[a,b]上的有界可测函数，且2[,]()0,a b f x dx =⎰证明：f(x)在[a,b]上几乎处处为0。

证明：反证法，假设A={x|f(x)≠0}，那么mA>0。

2005―2006学年度第一学期期末考试题高一数学参考答案及评分标准

2005―2006学年度第一学期期末考试题高一数学参考答案及评分标准一、选择题：每小题6分.二、填空题：每小题6分（11）()141212-+-nn n（12）51 （13）41 （14） ①、②、③ (15) ()15+=x x f三、解答题(16) 解: ①当0=x 时，1=n S ； -------------------------------------- 2分 ②当1=x 时，()21321+=+⋯+++=n n n S n ------------------------- 6分③当0≠x 且1≠x 时，12321-+⋯+++=n n nx x x S ①()nn nnx xn xx xS+-+⋯++=-1212 ②① －②得 ()nnnn n nx xxnxxx x S x ---=-+⋯+++=--111112∴ ()xnxx xS nn n ----=1112-------------------------- 15分（17）解：①当0<x 时，有xx x ->-112，从而有122-<-x x ，0122>-+x x ，21>x 或1-<x ，此时解为1-<x -------------------- 5分② 当10<<x 时，有xx x 112>-，从而有122-<x x ，0122<+-x x ，此时解集为∅ ----------------------- 9分 ③ 当1>x 时，有x x x 112>- ，从而有122->x x ，0122>+-x x ，R x ∈，此时解为1>x --------------------------------------------- 14分综上，原不等式解集为{}1,1>-<x x x 或 --------------------- 15分(18) 解: 设原计划生产辆数为)0(,,>+-d d a a d a ，则实际生产辆数为600,,200++--d a a d a ------------------- 3分依题意有 ()()()⎪⎩⎪⎨⎧⨯=++++--=②①a d a d a d a a 3326006002002 ------------------- 8分由②得600+=d a 代入①整理，得 01200004002=-+d d--------------- 12分解得200=d 或600-=d （舍）, 从而800=a∴ 原计划生产汽车辆数分别为600、800、1000. --------------------------- 15分 (19) 解: （Ⅰ）设()y x Q ,，∵ p 、Q 两点关于原点对称，∴p 点的坐标为（-x,-y ），又点 p(-x,-y)在函数y=f(x)的图象上，∴-y=log a (-x+1)，即g(x)=-log a (1-x) -------3分（Ⅱ）由2f(x)+g(x)≥0得2log a (x+1)≥log a (1-x)∵0＜a ＜1 ，∴由对数性质有 2x +1>01x >0x (1,0](x +1)1x-∴∈-≤-⎧⎪⎨⎪⎩ ------------ 7分（Ⅲ）由题意知：a ＞1且x ∈[0，1]时2(x 1)lo g m1xa+≥-恒成立。

2004-2005学年秋季学期工科数学分析答案

2004-2005学年秋季学期工科数学分析答案哈尔滨工业大学2004 /2005 学年秋季学期工科数学分析期末考试试卷（答案）试题卷（A ）考试形式（开、闭卷）：闭答题时间：150（分钟）本卷面成绩占课程成绩70%题号一二三四五六七八卷面总分平时成绩课程总成绩分数一．选择题（每题2分，共10分）1．下列叙述中不正确者为（D ）（A ）如果数列}{nx 收敛，那么数列}{nx 一得分姓名: 级：4．若sin F(x)=dy ])tdt sin sin[(xa y3⎰⎰，则=)x (F '（D ）（A ）dy ])tdt sin sin[(cos xay3⎰⎰（B ）cosxx 3sin)tdt sin sin(dy ])tdt sin sin[(cos 2y3xay3⋅⋅⋅⎰⎰⎰（C ）⎰⎰⎰⋅y3xay3)x dx sin sin(dy ])tdt sin sin[(cos（D ）⎰⎰⎰⋅y3xay3)tdt sin sin(dy ])tdt sin sin[(cos5．=+∞→)x1e(x1n lim （D ）（A ）e （B ）2e （C ）3e （D ）4e二．填空题（每题2分，共10分）1．)0x (x11y nn lim ≥+=∞→的间断点为：1x =，其类型为：第一类间断点。

得分遵守考试纪律注意行为规范2．23x )(1x y +=的全部渐近线方程为：2-x y 1,x =-=。

3．摆线2t )cost 1(a y )sint t (a x π=⎩⎨⎧-=-=在处的切线方程为：0a )4(21y x =-+-π。

4．2n 1n )!n (lim ∞→=： 1 。

5．设f(x)在[)+∞,1上可导，23e )1e(f , 0f(1)2x x'+=+=，则=：23-+-三．计算下列各题：（每小题4分，本题满分20分）1．若xy 2e x y = ，求?yx'=解：2xylnx lny =+， 2x 'x 'x y x y y y 2-=⋅则)2x y (x )y x (y y x'-+=2．⎪⎩⎪⎨⎧-==)sint t y 2t cosx ，?yxx''=求解：2t 4sin2t sin 21cost 1x y y t 't 'x '-=--==，2t4cos2t sin 2112t 2cos yxx''=-⋅-=得分3. ⎰+dx 1x x arctan 解：⎰⎰=⎰⋅⋅=⋅⋅+==sectdt ant t 2tdt sec 2tant sectt dx1x x arctan 2t tan x ttan x 2=c tant sect 2ln -sect 2t sectdt 2-2tsect tdsect 2++⋅==⎰⎰=c )x 1x (2ln 1x x 2arctan +++-+⋅ 4．dx e y x 11x⎰--解： dx y)e -(x dx x)e -(y dx e y x 1yxy1x11x⎰⎰⎰+=--- x1yxy1de y)-(x de x)-(y ⎰⎰+=-dxe y)e -(x dx e x)e -(y 1yx 1x y 1-x 1x⎰⎰-++=-yyyee y y )1(e 2]e y)e -(x []e x)e -(y [y 1x x 1x x +-=-++=-5. 已知dt te c x c x c t ⎰∞-∞→=-+2xx )(lim ，求?=c解：t c c t c de t dt te e xc x cc x c x 222x x x x 21)11()(lim lim ⎰⎰∞-∞-∞→∞→==-+=-+=2c2t 2t e )412c (e [te 21-=-⎰∞-∞-c cdt ，所以2c2ce )412(e-=c 。

05-06工科数学分析试卷答案

哈尔滨工业大学（威海）2005/2006学年秋季学期工科数学分析(B 类)试题卷（A ）答案一. (1).A (2).C (3).D (4).D (5)A二(1).0 (2).2002! (3) π (4) 2(sin )sin 2g x x(5) 35224235x x C -++三1. 11ln 1ln ()lim lim lim ln 1(1)ln (1)ln(11)111x x x x x x x x x x x x x x x x -----==---+-→→→211ln lim(1)x x x xx →--=-1ln 11lim 2(1)21x x x --==--→ 2．解：因为1113(3)(123)(33)n n n n nnn=≤++≤⨯=3lim n →∞=，所以1(123)3lim n n nn →∞++= 3．223211tan 2arcsin 22(1)x y x x x x x '=-++-+ 4．sin 1cos dydy t dt dx dx t dt==-， 22411()()()2sin 2d y d dy d dy dt d dy dx t dx dx dt dx dx dt dx dxdt ====- 5．(1ln )ln ln ln ln x x x x x x x xx e x x e e e e dx dx e xdx dx xde dx e x dx x x x x xe x C +=+=+=+-=+⎰⎰⎰⎰⎰⎰⎰6.202cos sin sin cos sin cos 1x xdx x xdx x xdx πππππ==-=⎰⎰⎰⎰四．解答题 1.解33200000000ln(1)3(00)()lim lim lim limarcsin arcsin 1x x x x ax ax ax f f x x x x x →-→-→-→-+-====---003(16lim x a a →-=-+=-22200000011(00)()4lim lim lim sin4ax ax x x x e x ax e x ax f f x x x x →+→+→++--+--+=== 2220000002224442(2)lim lim lim 222ax ax ax x x x ae x a a e a e a x →+→+→++-++====+ 令(00)f +=(00)(0)f f -=得1a =-，从而当1a =-时()f x 在0x =连续；令(00)f +=(00)(0)f f -≠得2a =-，从而当2a =-时0x =是()f x 的可去间断点。

华南理工2005数学分析试题和解答

华南理工大学2005年攻读硕士学位研究生入学考试试题注：本题在解答过程中，参考了博士家园论坛的意见，特别是Zhubin846152 给出了3、10、11题的解答，在此表示感谢！一、设2n 2n 1n 12a2ax x x ,0a x +-=>>+. 求极限n n x lim ∞→ 解：显然有()0a a a x x 22n 1n >≥+-=+，又11x a 2a 1x x n n 1n ≤⎪⎪⎭⎫ ⎝⎛-+=+ 即，序列为单调减小，且有下界，故存在极限，不妨设A x l i mn n =∞→，则对2n 2n 1n 2a2ax x x +-=+两边取极限，得222a 2aA A A +-=，即a A =，故a x lim n n =∞→ 二、求积分⎰+-C 4433yx dx y dy x , 其中C 是圆:1y x 22=+,逆时针为正向. 解：令[]πθθθ20,sin y ,cos x ，∈==，有()()[]πθθθθθθθθθθπππ23d 2sin 21-1d sin 2cos sin cos d sin cos y x dx y dy x 20220222222044C 4433=⎪⎭⎫⎝⎛=-+=+=+-⎰⎰⎰⎰三、讨论函数序列()tn nt sin t f n=在()∞,0上的一致收敛性.解：利用定义来做，就可以了。

2()()lim ()0(1)0,0,,0|()()||(2)0,0,0,0sin |()()||||(0,)0n n n n n f t f t f t t N f t f t t n ntf t f t nt εδδεεδδδε→∞===∀>>∀>∃=<-=≤<∀>>∀<≤∀>-==≤≤∈利用定义来做：令，根据一致收敛的定义知，上式一致收敛于四、设()y ,x z z =由方程0x z y ,y z x F =⎪⎪⎭⎫⎝⎛++所确定.证明: xy z y z y x z x -=∂∂⋅+∂∂⋅ 证明: 0x z y ,y z x F =⎪⎪⎭⎫⎝⎛++两边分别对x 和y 求偏导数， 0y z x 11F y 1z y z y 1F ,0x 1z x z x 1F x z y 11F 221221=⎪⎪⎭⎫ ⎝⎛∂∂+'+⎪⎪⎭⎫ ⎝⎛-∂∂'=⎪⎭⎫ ⎝⎛-∂∂'+⎪⎪⎭⎫ ⎝⎛∂∂+' 从而有，xF y F F F y z y z ,x F y F F x 1z F xz 2121221122'+''-'⋅=∂∂'+''-⋅⋅'=∂∂，故有 ()xy z xF y F x F y F xy z x F y F F F y z y x F y F F x 1z F x yz y x z x 21212121221122-='+'⎪⎪⎭⎫ ⎝⎛'+'-='+''-'⋅⋅+'+''-⋅⋅'⋅=∂∂+∂∂ 即，问题得证. 五、设()x f 是偶函数,在0x =的某个邻域中有连续的二阶导数,()()20f ,10f =''=,试证明无穷级数∑∞=⎪⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛1n 1n 1f 绝对收敛.证明:由题意,可写出()x f 的在0x =处的Taylor 展开式()()()()()2222x o x 1x o x !20f 0f x f ++=+''+=从而有⎪⎭⎫⎝⎛+=-⎪⎭⎫ ⎝⎛22n 1o n 11n 1f ，故， 2222222n 2n 1n 1n 1o n 1n 1o n 1=+<⎪⎭⎫⎝⎛+<⎪⎭⎫ ⎝⎛+，而级数∑∞=1n 2n 2为收敛的，由比较判别法知，级数∑∞=⎪⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛1n 1n 1f 为绝对收敛的，问题得证.六、设曲线()()⎩⎨⎧==t y y t x x 由方程组()⎩⎨⎧=-+=-++2y 2x te 1t 12t y x y确定.求该曲线在0t =处的切线方程和法平面方程.（注：原题为法线方程，个人觉得曲线不可能有法线，只能有法平面，平面才能有法线）解:由题意得：0y ,1x ,2y 2x 1y x 0t ==⎩⎨⎧=-=+=有，时，当，()⎩⎨⎧-+=--++=2-y 2x te F 1t 12t y x F y21()()()()()(),3e 2t -21te 1t ,y D F ,F D ,-31te 121y ,x D F ,F D ,321e 2t 2x ,t D F ,F D 0t yy0t 210t y0t 210t y 0t 21=-==-==-=======故，有切线方程3y31x 3-t =-=，法平面()03y 1-x 33t =++-，也即切线方程 y 1x t -=-=，法平面1y x t =++-七、求幂级数()()∑∞=++-0n n2n x 1n n 1的收敛域,并求该级数的和.解: 收敛半径()()11n n 1lim 1R n 2nn =++-=∞→,当1x =时,级数变为()()∑∞=++-0n 2n 1n n 1, 显然为发散的.同样级数在1x -=处也发散. 从而,收敛域为()1,1-. 当()1,1x -∈时，有 ()()()()()()∑∑∑∑++=++-=∞=n n n 2n n 2n x -x -n x -n x 1n n 1x f 对第一部分，()()()()()()()()()()( ⎝⎛='⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛==∑∑∑∑∑∞=∞=+∞=∞=-∞=1n 0n 1n 0n n 21n 1n 20n n 21-n x -x -1n x -x -1n x -x -n x -x n x f第二部分，()()()()()()()()()()()20n 1n 0n n 1n 1n 0n n2x 1x x 1x -x -x -x -x -1n x -x -n x -x -n x f +='⎪⎭⎫⎝⎛+='⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛==∑∑∑∑∞=+∞=∞=-∞=故()()()()()321x 11x x x 1x x -x f +-='⎪⎪⎭⎫ ⎝⎛+=，同样，对第三部分，()x1xx f 3+-=，从而有()()()()()333232223x 1xx x 1x 2x x x x x x x 1x x 1xx 11x x +--=+---++-=+-+++-=原式八、求第二曲面积分: ⎰⎰+-S zdxdy ydxdz xdydz ,S 为椭球面1cz b y a x 222222=++的上半部分,其定向为下侧.解：不妨添加交线所围的部分在0z 1cz b y a x 222222==++,方向取向上,记Q ，所围空间记体积为V,故有()abc 32-0abc 32zdxdy ydxdz xdydz dxdydz111zdxdy ydxdz xdydz zdxdy ydxdz xdydz Q VS Sππ=+-=+-++--=+--=+-⎰⎰⎰⎰⎰⎰⎰⎰⎰',其中S '为取外法线方向为正的曲面,九、 (1) 设0a 0>, 证明积分 ()⎰∞+0222axdx关于0a a ≥一致收敛;证明：()()()()()()()()()εδπεδεπεδεππππεπθθθπθθπ<-<-=>∀=<-≤-⎪⎪⎭⎫ ⎝⎛+++=-=->∀-=⋅=⎪⎭⎫⎢⎣⎡∈=+=⎰⎰∞2121404021402142321231414124214204240222a f a f a a a ,0a a a a a a a 1a a 1a a 1a 144a 4a a f a f ,0a f ,4a d cos cos 1a 1a f 20,, tg a x ,,a x dxa f 有时，，使得，当存在即可满足，对只需取要有一致收敛，故，对要从而，则，且记也即()⎰∞+0222axdx关于0a a ≥一致收敛(2) 0a >,计算积分⎰∞+022a x dx和()⎰∞+0322axdx解：()662620462026603222202202222216a 16a 1d 814cos2cos4a 1d cos a 1cos d cos a 1a xdx2a d a 1cos d cos 11a 1a x dx ,20,, tg a x ππθθθθθθθθπθθθθπθθπππππ=⋅=+-===+==⋅=+⎪⎭⎫⎢⎣⎡∈=⎰⎰⎰⎰⎰⎰⎰∞∞则有，令十、设 ()x f 在[)∞,0上有连续的二阶导数, ()()B x f ,A x f ≤''≤. 试证明()AB 2x f ≤'.证明：利用到了一元二次函数的判别式来做的[0,)22()lim '()0'()'()max {|'()|}||,(1)||0b Taylor "()||2|||()()||'()()()|||||()22||2||(2x x f x f x f x f b f x C A f B A f x f b f b x b x b C x b x b B A x b ξ→∞∈+∞∴===≠≥-=-+-≥---⇔+-首先由于有界，。

2005数一参考答案

2005数一参考答案2005年的数学一考试是高考中的一场重要考试，对于参加考试的学生来说，了解和掌握该年的参考答案是非常重要的。

本文将对2005年数一的参考答案进行分析和讨论，帮助考生更好地了解该年的考试情况。

首先，我们来看一下2005年数一的选择题部分。

该年的选择题共有25道，涵盖了数学的各个知识点。

其中，有一道题是关于平面向量的，要求考生根据给定的条件求两个向量的数量积。

这道题考察了考生对向量的理解和运用能力。

另外，还有一道题是关于数列的，要求考生根据已知条件求数列的通项公式。

这道题考察了考生对数列的掌握和运用能力。

此外，还有一道题是关于三角函数的，要求考生根据已知条件求三角函数的值。

这道题考察了考生对三角函数的理解和计算能力。

接下来，我们来看一下2005年数一的解答题部分。

该年的解答题共有5道，涵盖了数学的各个知识点。

其中，有一道题是关于函数的，要求考生根据给定的函数图像求函数的表达式。

这道题考察了考生对函数的理解和分析能力。

另外，还有一道题是关于立体几何的，要求考生根据给定的条件求解立体几何问题。

这道题考察了考生对立体几何的掌握和运用能力。

此外，还有一道题是关于概率的，要求考生根据已知条件求解概率问题。

这道题考察了考生对概率的理解和计算能力。

总的来说，2005年数一的考题难度适中，涵盖了数学的各个知识点。

对于参加考试的学生来说，了解和掌握该年的参考答案是非常重要的。

通过分析和讨论该年的参考答案，可以帮助考生更好地了解该年的考试情况，提高解题的准确性和效率。

在准备考试的过程中，除了了解和掌握参考答案，还需要进行大量的练习和复习。

通过反复练习和复习，可以巩固和加深对知识点的理解和掌握，提高解题的能力和水平。

此外，还可以参加一些模拟考试和辅导班，通过与其他考生的交流和比较，发现自己的不足之处，有针对性地进行弥补和提高。

最后，希望参加2005年数一考试的考生能够认真准备，充分发挥自己的潜力和能力。

2005-2006学年第一学期期末考试《高等数学》(A)评分标准及标准答案

e y + (xe y − e−y + ye−y ) y′ = 2x
Байду номын сангаас∴ y′ = 2x − e y
(1′)
xey − e−y + ye−y
x=0⇒ y=0
(1′)
∴ y′ x=0 = 1
(1′)
∫ ∫ 5、
x+
3
x
dx
( 2′)
==
(
x
+
−1
x6
) dx =
2
3
x2
+
6
5
x6
+
c
(3′) ；
x
35
∫ ∫ ∫ 6、
x→ 0
x→ 0
(1′)；
∫ 3、 f ′ ( x) = 2x x ln tdt + x2ln x, (3′) ∴ f′ ( e) = e2 (2′) ； e
4、方程两边同时对 x 求导（ y 是 x 的函数），得
e y + xey y′− y′e− y − ye− y (− y′) = 2x
(2′)
0
0
0
0
(1′)
∫ ∫ =
1
e
f(
x) dx
+
xe
f
( x)
0
1 0
−
1 e f (x)dx
0
(2′)
= e f (1)
(1′)
四、解答题
1、①定义域： (−∞, +∞) ；
② y′ = 6x2 −12x −18 = 0,⇒ x = −1, x = 3;
③列表
x (−∞, −1)

春季学期工科数学分析答案

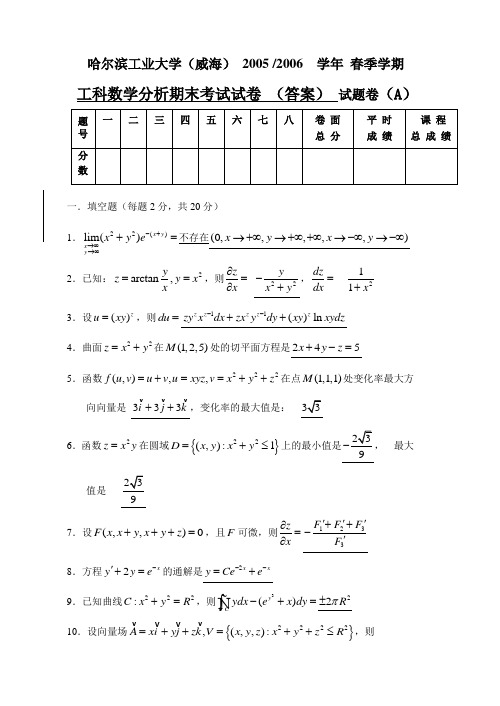
哈尔滨工业大学（威海） 2005 /2006 学年春季学期工科数学分析期末考试试卷（答案）试题卷（A ）一．填空题（每题2分，共20分）1．22()lim()x y x y x y e-+→∞→∞+=不存在(0,,,,,)x y x y →+∞→+∞+∞→-∞→-∞2．已知：2arctan,y z y x x ==，则z x ∂=∂ 22y xy-+，dz dx = 211x +3．设()z u xy =，则du =11()ln z z z z z zy x dx zx y dy xy xydz --++ 4．曲面22z x y =+在(1,2,5)M 处的切平面方程是245x y z +-=5．函数222(,),,f u v u v u xyz v x y z =+==++在点(1,1,1)M 处变化率最大方向向量是 333i j k ++，变化率的最大值是： 6．函数2z x y =在圆域{}22(,):1D x y x y =+≤上的最小值是最大值是97．设(,,)0F x x y x y z +++=，且F 可微，则z x ∂=∂1233F F F F '''++-'8．方程2x y y e -'+=的通解是2xx y Ce e --=+9．已知曲线222:C x y R +=，则3()y Cydx e x dy -+=⎰22R π±10．设向量场{}2222,(,,):A xi yj zk V x y z x y z R =++=++≤，则vdivAdv =⎰⎰⎰ 34R π 二．填空题（每题3分，共30分）1．级数11(1)n nn x n -∞=-∑的收敛半径R = 12．级数21n ∞=是否绝对收敛？答：是3．由曲面22,0,0,15x y z y y z z x +=====围成的几何体的体积V = 114．按球面S ：2222x y z R ++=的外侧，积分333Sx dydz y dzdx z dxdy ++=⎰⎰5125R π 5．设23(3sin )(cos )du x y x dx x y dy =++-，则u =3cos cos x y x y C --+ 6．级数3211()n n x ∞=+∑在[)0,+∞上是否一致收敛？答：是7．在区间[]0,1上的函数3()f x x =的余弦级数的和函数为()S x ，即01()c o s 2nn a S x a n x π∞==+∑，则1()3S -= 127 8．有界函数()f x 在若当可测集R nG ⊂上可积的充要条件是对任何0ε>，存在0δ>，使对任何具有细度()l T δ<的分法T 有 T T S s ε-< 9．设S为半球面z =()(23)S x y z dS ++=⎰⎰ 33a π10．由椭圆抛物面2235x y z =+与平面3z =所围成立体的体积V =三．求函数u x y z =满足约束条件1xy yz zx ++=的最大值，其中0,0,0x y z >>>且u 存在最大值。

2005-2006高二数学(理科B)答案 (2)

珠海市2005-2006学年度质量检测试卷高二数学（理科B 卷）参考答案及评分标准考试用时120分钟，共150分．本次考试允许使用函数计算器，不得相互借用．一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 请将所选答案标号填入下表：1．等差数列}{n a 中,a 3=7, a 9=19,则a 5=（A ）10 （B ）11 （C ） 12 （D ）132．数列}{n a 满足：n n n a a a +=++12, a 1=1,a 2=2,则该数列前5项之和为（A ）11 （B ）18 （C ）19 （D ）31 3．在ΔABC 中，a=5，B=30°，A=45°，则b= （A ）225 （B ）335 （C ）265 （D ）254．不等式0)2(>-x x 的解集是（A ）（-∞，2）（B ）（0，2）（C ）（-∞，0）（D ）（-∞，0）∪（2，+∞）5．已知两正数ａ、ｂ满足：1622=+b a ，则ab 的最大值是（A ）2 （B ）4 （C ）8 （D ）166．已知q 是r 的必要不充分条件，s 是r 的充分且必要条件，那么s 是q 成立的（A ）必要不充分条件（B ）充要条件（C ）充分不必要条件（D ）既不充分也不必要条件7．双曲线1422=-y x 的一个焦点坐标是（A ）)0,5(- （B ）)5,0( （C ）)3,0( （D ）)0,3(- 8．抛物线的顶点在原点，准线是x=4，它的标准方程是（A ）x y 162-= （B ）y x 162-= （C ）x y 82-= （D ）y x 82= 9．椭圆上116922=+y x 一动点P 到两焦点距离之和为（A ）10 （B ）8 （C ）6 （D ）不确定 10．已知空间两点A （4，a ，-b ），B （a ，a ，2），则向量AB = （A ）（a-4，0，2+b ）（B ）（4-a ，0，-b-2）（C ）（0，a-4，2+b ）（D ）（a-4，0，-b-2） 11．向量a =（0，1，2），b =（1，0，-1），则数量积a •b=（A ）（1，1，1）（B ）0 （C ）-2 （D ）（0，0，-2）12．已知点M 在平面ABC 内，并且对空间任一点O ，1123OM xOA OB OC =++，则x 的值是（A ）0 （B ）1/2 （C ）1/3 （D ）1/6二、填空题:本大题共6小题，每小题5分，共30分.把答案填在题中横线上. 13．在ΔABC 中，ab c b a -=+222，则角C=120°(或32π)． 14．已知点P(x,y)满足：⎪⎩⎪⎨⎧≥≥≤+≥-0,020y x y x y x ，则y x z +=21可取得的最大值为３／２． 15．命题“x ∈R ，x 2- x ≥0.”的否定是0,2<-∈∃x x R x .16．椭圆的两个焦点恰好将长轴三等分,则椭圆的离心率是_1/3_． 17．斜率为1的直线与抛物线x y =2只有一个公共点，这条直线的方程是41+=x y ．（其它形式如0144,041=+-=+-y x y x 等均给满分） 18．在三棱锥P-ABC 中,三侧棱两两垂直,且PB=PC=2PA,PO 垂直于面ABC,O是垂足,如果设=PA a =PB b =c ,请用a 、b 、c 表示P ：c b a616132++．得分评卷人三、解答题:本大题共5小题，共60分.解答应写出文字说明，证明过程或演算步骤. 19．(本小题满分10分)在下面是电路图（1）、（2）中，分别简述闭合开关A 是灯泡B 亮的什么条件？解：在图（１）中，闭合开关Ａ是灯泡Ｂ亮的充分但不必要条件．（２分）当开并Ａ闭合时，灯泡Ｂ一定亮，但灯泡Ｂ亮时，开关Ａ不一定闭合（只要此时开关Ｃ闭合即可）．（５分）在图（２）中，闭合开关Ａ是灯泡Ｂ亮的必要但不充分条件．（７分）当开并Ａ闭合时，灯泡Ｂ不一定亮（如果此时开关Ｃ没有闭合的话），但灯泡Ｂ亮时，开关Ａ一定闭合（只要此时开关Ｃ闭合即可）．（10分）(注:如果只说出一半,则按一半计分.没有理由,扣理由分)20．(本小题满分12分) 三个数成等比数列，且它们的和为21，积是64．求这三个数．图(1)图(2)解:设这三个数依次为a/q,a,aq (2分) 根据题意,有 a/q+a+aq=21(4分)和64=⋅⋅aq a qa ,(6分)解得:a=4,(8分)q=4或1/4(10分) 这三个数依次为1,4,16或16,4,1(12分)21．(本小题满分12分)求与椭圆1244922=+y x 有公共焦点，且一条渐近线为x y 34=的双曲线的方程．解:由椭圆标准方程1244922=+y x 可得的两者公共焦点为(-5,0)和(5,0),(2分)设双曲线的方程为)0,0(12222>>=-b a by a x ,(4分)其渐近线为x a by ±=,(6分)现已知双曲线的一条渐近线为x y 34=,得34=a b ,(7分)又双曲线中2225=+b a ,(8分)解得4,3==b a ,(10分)∴双曲线的方程为1432222=-y x (12分)22．(本小题满分12分)已知点A 、B 的坐标分别是A （0，-1），B （0，1），直线AM 、BM 相交于点M ，且它们的斜率之积是2，求点M 的轨迹方程，并说明曲线的类型．解:设M(x,y),则),0(0)1(),0(01≠---=≠--=x x y k x x y k AM BM (4分),t k k AM BM -=⋅(5分))0(0)1(01≠-=---⋅--x t x y x y ,(7分)整理得)0(1122≠=+x tx y (10分,少了限制扣1分)(1) 当t ∈(0,1)时,M 的轨迹为椭圆(除去A 和B 两点);(12分)(2) 当t=1时,M 的轨迹为圆(除去A 和B 两点).(14分,多了两点扣2分))23．(本小题满分14分)已知抛物线方程为212x y =，直线l 过其焦点，交抛物线于A 、B 两点，|AB|＝１６．１）求抛物线的焦点坐标和准线方程；２）求Ａ、Ｂ中点的纵坐标．解：1）由抛物线方程为212x y =，对比标准方程)0(22>=p py x 可得2P=12，P=6得焦点F （0，3），准线方程为：3-=y ．(4分)２）（解法一）设直线l 的斜率为k,设),(),,(2211y x B y x A ,A 、B 的中点M ),(00y x ．直线的方程：ｙ＝ｋｘ＋３，联立方程组得：(5分)⎩⎨⎧=+=yx kx y 1232，(7分)消去ｙ，整理得：036122=--kx x (9分) 方程中，0144144)36(4)12(22>+=---=∆k k ，有两个不同的根．由根与系数的关系得：36,122121-==+x x k x x (10分)由|AB|＝１６得：16)4))((1(||21212=-++=x x x x k AB ，(11分) 代入，整理得：916)1(22=+k ，得312=k ．(12分) M ),(00y x 在直线l 上，有：300+=kx y ，36322210+=++⋅=k x x k y （１３分）∴50=y ，即Ａ、Ｂ中点的纵坐标为5．（１４分）（解法二）：设直线l 的斜率为k,设),(),,(2211y x B y x A ,A 、B 的中点M ),(00y x ，过Ａ、Ｂ分别作准线的垂线，垂足分别为Ｐ、Ｑ，焦点F 在弦AB 上，（5分）|FA|+|FB|=|AB|=16，（6分）由抛物线定义，|AP|=|AF|，|BQ|=|BF|，（8分）而|AP|=3211+=+y p y ，（9分） |BP|=3222+=+y py ，（10分） 163321=+++y y ，1021=+y y ，（12分） 52210=+=y y y （13分）即Ａ、Ｂ中点的纵坐标为5．（１４分）以上答案和评分标准仅供参考。

哈尔滨工业大学（威海）2005-2006年工科数学分析A（2）

哈尔滨工业大学（威海）2005-2006年工科数学分析A（2）哈尔滨工业大学（威海）2005/2006学年秋季学期一、填空题(每题3分)1. 设>+≤=00)(22x xx x x x f ，则=-)(x f ______________. 2. =+∞→n n n n n 42lim 2_____________________. 3.=+-∞→xx x 1)21(lim ________________________. 4. 摆线-=-=ty t t xcos 1sin 在2π=t 处的法线方程为______. 5. 函数xx f arctan )(=按马克劳林公式展开到)(12+n x 的表达式为____________. 6. 若??=x x t dt t f dt e 11)(32，则=)(x f _________.7. 若++=cx dx x f 2cos sin )(（其中c为任意常数），则=)(x f __________.8.=-+?-112)1cos (dx x x x _________.9. 设)100()2)(1()(---=x x x x f ，则=')1(f _________.10. 若-bax b dx α)(收敛（其中0>α），则α的取值范围是________. 二、计算题（每题5分）1、求极限)2122321(lim 2nn n -+++∞→ 。

2、已知0)11(lim 2=--++∞→b ax x x x ，求b a ,。

3、设1lim )()1()1(2+++=--∞→x n x n n e b ax e x x f ，求b a ,使)(x f 可导。

4、求由等式0333=-+xy y x 确定的)(x f y =在0>x 范围内的极值点。

5、设tttey e x==-,，求22,dxy d dx dy。

6、求曲线)1ln()(2++=x x x f 在1=x 处的曲率。

2005年数学三试题分析、详解和评注

以下题型均在05年考研文登数学辅导班中讲过2005年数学三试题分析、详解和评注一、填空题（本题共6小题，每小题4分，满分24分. 把答案填在题中横线上）（1）极限12sinlim 2+∞→x xx x = 2 . 【分析】本题属基本题型，直接用无穷小量的等价代换进行计算即可.【详解】 12s i n l i m2+∞→x x x x =.212lim 2=+∞→x xx x 【评注】若在某变化过程下，)(~)(x x αα，则).()(lim )()(lim x x f x x f αα= 完全类似例题见《数学复习指南》（经济类）P.23【例1.28】（2）微分方程0=+'y y x 满足初始条件2)1(=y 的特解为 2=xy . 【分析】直接积分即可.【详解】原方程可化为 0)(='xy ，积分得 C xy =，代入初始条件得C=2，故所求特解为 xy=2.【评注】本题虽属基本题型，也可先变形xdx y dy -=，再积分求解.完全类似例题见《数学复习指南》（经济类）P.229【例10.5】（3）设二元函数)1ln()1(y x xe z y x +++=+，则=)0,1(dz dy e edx )2(2++ .【分析】基本题型，直接套用相应的公式即可. 【详解】)1l n (y xe e xzy x y x +++=∂∂++,yx xe y z y x +++=∂∂+11, 于是 =)0,1(dzdy e edx )2(2++.完全类似例题见《数学复习指南》（经济类）P.166【例7.6】（4）设行向量组)1,1,1,2(，),,1,2(a a ，),1,2,3(a ，)1,2,3,4(线性相关，且1≠a ，则a=21 .【分析】四个4维向量线性相关，必有其对应行列式为零，由此即可确定a. 【详解】由题设，有=1234123121112aa a 0)12)(1(=--a a , 得21,1==a a ，但题设1≠a ，故.21=a【评注】当向量的个数小于维数时，一般通过初等变换化阶梯形讨论其线性相关性. 完全类似例题见《数学复习指南》（经济类）P.312【例3.3】（5）从数1,2,3,4中任取一个数，记为X, 再从X ,,2,1 中任取一个数，记为Y, 则}2{=Y P =4813 . 【分析】本题涉及到两次随机试验，想到用全概率公式, 且第一次试验的各种两两互不相容的结果即为完备事件组或样本空间的划分.【详解】 }2{=Y P =}12{}1{===X Y P X P +}22{}2{===X Y P X P +}32{}3{===X Y P X P +}42{}4{===X Y P X P =.4813)4131210(41=+++⨯ 【评注】全概率公式综合考查了加法公式、乘法公式和条件概率，这类题型一直都是考查的重点.完全类似例题见《数学复习指南》（经济类）P.407【例1.31】（6）设二维随机变量(X,Y) 的概率分布为 X Y 0 1 0 0.4 a 1 b 0.1 已知随机事件}0{=X 与}1{=+Y X 相互独立，则a= 0.4 , b= 0.1 .【分析】首先所有概率求和为1，可得a+b=0.5, 其次，利用事件的独立性又可得一等式，由此可确定a,b 的取值.【详解】由题设，知 a+b=0.5又事件}0{=X 与}1{=+Y X 相互独立，于是有}1{}0{}1,0{=+===+=Y X P X P Y X X P ，即 a=))(4.0(b a a ++, 由此可解得 a=0.4, b=0.1【评注】本题考查二维随机变量分布律的性质和独立随机事件的概念，均为大纲要求的基本内容.完全类似例题见《数学复习指南》（经济类）P.528【习题二，1.（9）】二、选择题（本题共8小题，每小题4分，满分32分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内）（7）当a 取下列哪个值时，函数a x x x x f -+-=1292)(23恰好有两个不同的零点. (A) 2. (B) 4. (C) 6. (D) 8. [ B ] 【分析】先求出可能极值点，再利用单调性与极值画出函数对应简单图形进行分析，当恰好有一个极值为零时，函数f(x)恰好有两个不同的零点.【详解】 12186)(2+-='x x x f =)2)(1(6--x x ，知可能极值点为x=1,x=2，且 a f a f -=-=4)2(,5)1(，可见当a=4时，函数f(x) 恰好有两个零点，故应选(B).【评注】对于三次多项式函数f(x)=d cx bx ax +++23,当两个极值同号时，函数f(x) 只有一个零点；当两个极值异号时，函数f(x) 有三个零点；当两个极值有一为零时，，函数f(x) 有两个零点.完全类似例题见《数学复习指南》（经济类）P.151【例6.26】（8）设σd y x I D⎰⎰+=221cos,σd y x I D⎰⎰+=)cos(222,σd y x I D⎰⎰+=2223)cos(,其中}1),{(22≤+=y x y x D ，则(A) 123I I I >>. （B ）321I I I >>.(C) 312I I I >>. (D) 213I I I >>. [ A ] 【分析】关键在于比较22y x +、22y x +与222)(y x +在区域}1),{(22≤+=y x y x D 上的大小.【详解】在区域}1),{(22≤+=y x y x D 上，有1022≤+≤y x ，从而有2212y x +≥>π≥22y x +≥0)(222≥+y x由于cosx 在)2,0(π上为单调减函数，于是22c o s 0y x +≤)c o s (22y x +≤≤222)c o s (y x +因此<+⎰⎰σd y x D22cos<+⎰⎰σd y xD)cos(22σd y xD⎰⎰+222)cos(，故应选(A).【评注】本题比较二重积分大小，本质上涉及到用重积分的不等式性质和函数的单调性进行分析讨论.完全类似例题见《数学复习指南》（经济类）P.183【例8.2】（9）设,,2,1,0 =>n a n 若∑∞=1n na发散，∑∞=--11)1(n n n a 收敛，则下列结论正确的是(A)∑∞=-112n n a收敛，∑∞=12n na发散 . （B ）∑∞=12n na收敛，∑∞=-112n n a发散.(C))(1212∑∞=-+n n n a a收敛. (D))(1212∑∞=--n n n a a收敛. [ D ]【分析】可通过反例用排除法找到正确答案.【详解】取n a n 1=，则∑∞=1n n a 发散，∑∞=--11)1(n n n a 收敛，但∑∞=-112n n a与∑∞=12n na均发散，排除(A),(B)选项，且)(1212∑∞=-+n n n a a发散，进一步排除(C), 故应选(D). 事实上，级数)(1212∑∞=--n n n a a的部分和数列极限存在.【评注】通过反例用排除法找答案是求解类似无穷级数选择问题的最常用方法.（10）设x x x x f cos sin )(+=,下列命题中正确的是(A) f(0)是极大值，)2(πf 是极小值. （B ） f(0)是极小值，)2(πf 是极大值.（C ） f(0)是极大值，)2(πf 也是极大值. (D) f(0)是极小值，)2(πf 也是极小值.[ B ]【分析】先求出)(),(x f x f '''，再用取极值的充分条件判断即可.【详解】 x x x x x x x f cos sin cos sin )(=-+='，显然 0)2(,0)0(='='πf f ，又 x x x x f s i n c o s)(-=''，且02)2(,01)0(<-=''>=''ππf f ，故f(0)是极小值，)2(πf 是极大值，应选(B).【评注】本题为基本题型，主要考查取极值的充分条件. 对应定理公式见《数学复习指南》（经济类）P.141（11）以下四个命题中，正确的是(A) 若)(x f '在（0，1）内连续，则f(x)在（0，1）内有界. （B ）若)(x f 在（0，1）内连续，则f(x)在（0，1）内有界.（C ）若)(x f '在（0，1）内有界，则f(x)在（0，1）内有界.(D) 若)(x f 在（0，1）内有界，则)(x f '在（0，1）内有界. [ C ] 【分析】通过反例用排除法找到正确答案即可. 【详解】设f(x)=x 1, 则f(x)及21)(xx f -='均在（0，1）内连续，但f(x)在（0，1）内无界，排除(A)、(B); 又x x f =)(在（0，1）内有界，但xx f 21)(='在（0，1）内无界，排除(D). 故应选(C).【评注】本题也可直接证明：用拉格朗日中值定理，有ξξ),21)(()21()(-'=-x f f x f 在(0,1)之间，由此容易推知若)(x f '在（0，1）内有界，则f(x)在（0，1）内有界.（12）设矩阵A=33)(⨯ij a 满足TA A =*，其中*A 是A 的伴随矩阵，TA 为A 的转置矩阵. 若131211,,a a a 为三个相等的正数，则11a 为(A)33. (B) 3. (C) 31. (D)3. [ A ]【分析】题设与A 的伴随矩阵有关，一般联想到用行列展开定理和相应公式：.**E A A A AA ==.【详解】由TA A =*及E A A A AA ==**，有3,2,1,,==j i A a ij ij ，其中ij A 为ij a 的代数余子式，且032=⇒=⇒=A A AE A AA T或1=A而03211131312121111≠=++=a A a A a A a A ，于是1=A ，且.3311=a 故正确选项为(A).【评注】涉及伴随矩阵的问题是常考题型，只需注意到两个重要思路：一是用行列展开定理，另一是用公式：.**E A A A AA ==完全类似例题见《数学复习指南》（经济类）P.272【例1.8】（13）设21,λλ是矩阵A 的两个不同的特征值，对应的特征向量分别为21,αα，则1α，)(21αα+A 线性无关的充分必要条件是(A)01=λ. (B) 02=λ. (C) 01≠λ. (D) 02≠λ. [ D ]【分析】讨论一组抽象向量的线性无关性，可用定义或转化为求其秩即可. 【详解】方法一：令 0)(21211=++αααA k k ，则022211211=++αλαλαk k k ， 0)(2221121=++αλαλk k k . 由于21,αα线性无关，于是有 ⎩⎨⎧==+.0,022121λλk k k当02≠λ时，显然有0,021==k k ，此时1α，)(21αα+A 线性无关；反过来，若1α，)(21αα+A 线性无关，则必然有02≠λ(,否则，1α与)(21αα+A =11αλ线性相关)，故应选(B).方法二：由于 ⎥⎦⎤⎢⎣⎡=+=+21212211121101],[],[)](,[λλαααλαλααααA ，可见1α，)(21αα+A 线性无关的充要条件是.001221≠=λλλ故应选(D).【评注】本题综合考查了特征值、特征向量和线性相关与线性无关的概念. 完全类似例题见《数学复习指南》（经济类）P.320【例3.17】（14）设一批零件的长度服从正态分布),(2σμN ，其中2,σμ均未知. 现从中随机抽取16个零件，测得样本均值)(20cm x =，样本标准差)(1cm s =，则μ的置信度为0.90的置信区间是(A) )).16(4120),16(4120(05.005.0t t +- (B) )).16(4120),16(4120(1.01.0t t +- (C))).15(4120),15(4120(05.005.0t t +-(D))).15(4120),15(4120(1.01.0t t +- [ C ]【分析】总体方差未知，求期望的区间估计，用统计量：).1(~--n t ns x μ【详解】由正态总体抽样分布的性质知，)1(~--n t ns x μ，故μ的置信度为0.90的置信区间是))1(1),1(1(22-+--n t n x n t nx αα，即)).15(4120),15(4120(05.005.0t t +-故应选(C).【评注】正态总体),(~2σμN X 的三个抽样分布：)1,0(~N nX σμ-、)1(~--n t nS X μ、)1(~)1(222--n S n χσ是常考知识点，应当牢记. 完全类似例题见《数学复习指南》（经济类）P.506【例6.16】三、解答题（本题共9小题，满分94分.解答应写出文字说明、证明过程或演算步骤.）（15）（本题满分8分）求).111(lim 0xe x x x --+-→【分析】 ""∞-∞型未定式，一般先通分，再用罗必塔法则.【详解】 )1(1lim )111(lim 200x xx x x e x e x x x e x --→-→-+-+=--+ =2201lim x e x x x x -→+-+=x e x xx 221lim 0-→-+=.2322lim0=+-→x x e 【评注】本题属基本题型，在里用罗必塔法则求极限的过程中，应注意利用无穷小量的等价代换进行简化.完全类似例题见《数学复习指南》（经济类）P.29【例1.45】（16）（本题满分8分）设f(u)具有二阶连续导数，且)()(),(y x yf x y f y x g +=，求.222222yg y x g x ∂∂-∂∂ 【分析】先求出二阶偏导数，再代入相应表达式即可.【详解】由已知条件可得)()(2y x f x y f xy x g '+'-=∂∂， )(1)()(242322y xf y y x f xy x y f x y x g ''+''+'=∂∂，)()()(1yxf y x y x f x y f x yg '-+'=∂∂，)()()()(13222222y xf yx y x f y x y x f y x x y f x y g ''+'+'-''=∂∂，所以 222222yg y x g x ∂∂-∂∂ =)()()(2222y x f y x y x f x y x y f x y ''+''+')()(222y x f y x x y f xy ''-''-=).(2xy f x y ' 【评注】本题属基本题型，但在求偏导数的过程中应注意计算的准确性.完全类似例题见《数学复习指南》（经济类）P.171【例7.18】（17）（本题满分9分）计算二重积分σd y x D⎰⎰-+122，其中}10,10),{(≤≤≤≤=y x y x D .【分析】被积函数含有绝对值，应当作分区域函数看待，利用积分的可加性分区域积分即可.【详解】记}),(,1),{(221D y x y x y x D ∈≤+=，}),(,1),{(222D y x y x y x D ∈>+=，于是σd y x D⎰⎰-+122=⎰⎰-+-1)1(22D dxdy y x ⎰⎰-++2)1(22D dxdy y x=⎰⎰--2021)1(πθrdr r d ⎰⎰-++Ddxdy y x )1(22⎰⎰-+-1)1(22D dxdy y x=8π+⎰⎰⎰⎰---+2010*******)1()1(πθrdr r d dy y x dx =.314-π【评注】形如积分σd y x f D⎰⎰),(、⎰⎰Dd y x g y x f σ)},(),,(max{、⎰⎰Dd y x g y x f σ)},(),,(min{、⎰⎰Dd y x f σ)],([、⎰⎰-Dd y x g y x f σ)},(),(sgn{等的被积函数均应当作分区域函数看待，利用积分的可加性分区域积分.完全类似例题见《数学复习指南》（经济类）P.193【例8.18】（18）（本题满分9分）求幂级数∑∞=-+12)1121(n n x n 在区间(-1,1)内的和函数S(x). 【分析】幂级数求和函数一般采用逐项求导或逐项积分，转化为几何级数或已知函数的幂级数展开式，从而达到求和的目的.【详解】设 ∑∞=-+=12)1121()(n n x n x S ， ∑∞=+=121121)(n nx n x S ，∑∞==122)(n n x x S ，则 )()()(21x S x S x S -=，).1,1(-∈x 由于∑∞==122)(n nxx S =221xx -， )1,1(,1))((22121-∈-=='∑∞=x x x xx xS n n, 因此 ⎰-++-=-=xxxx dt t t x xS 022111ln 211)(，又由于 0)0(1=S ，故.0,1,0,11ln 211)(1=<⎪⎩⎪⎨⎧-++-=x x xx x x S 所以 )()()(21x S x S x S -=.0,1,0,1111ln 212=<⎪⎩⎪⎨⎧---+=x x x x x x【评注】而幂级数求和尽量将其转化为形如∑∞=1n n nx 或∑∞=-11n n nx 幂级数，再通过逐项求导或逐项积分求出其和函数. 本题应特别注意x=0的情形.完全类似例题见《数学复习指南》（经济类）P.216【例9.18】（19）（本题满分8分）设f(x),g(x)在[0，1]上的导数连续，且f(0)=0,0)(≥'x f ,0)(≥'x g .证明：对任何a ]1,0[∈,有⎰⎰≥'+'ag a f dx x g x f dx x f x g 01).1()()()()()(【分析】可用参数变易法转化为函数不等式证明，或根据被积函数的形式，通过分部积分讨论.【详解】方法一：设=)(x F ⎰⎰-'+'x g x f dt t g t f dt t f t g 01)1()()()()()(，则F(x)在[0，1]上的导数连续，并且=')(x F )]1()()[()1()()()(g x g x f g x f x f x g -'='-'，由于]1,0[∈x 时，0)(,0)(≥'≥'x g x f ，因此0)(≤'x F ，即F(x)在[0，1]上单调递减.注意到 =)1(F ⎰⎰-'+'11)1()1()()()()(g f dt t g t f dt t f t g ，而⎰⎰⎰'-=='11110)()()()()()()()(dt t g t f t f t g t df t g dt t f t g=⎰'-1)()()1()1(dt t g t f g f ，故F(1)=0.因此]1,0[∈x 时，0)(≥x F ，由此可得对任何]1,0[∈a ，有 ⎰⎰≥'+'ag a f dx x g x f dx x f x g 01).1()()()()()(方法二：⎰⎰'-='aaa dx x g x f x f x g dx x f x g 0)()()()()()(=⎰'-adx x g x f a g a f 0)()()()(，⎰⎰'+'adx x g x f dx x f x g 01)()()()(=⎰⎰'+'-1)()()()()()(dx x g x f dx x g x f a g a f a⎰'+1.)()()()(adx x g x f a g a f由于]1,0[∈x 时，0)(≥'x g ，因此)()()()(x g a f x g x f '≥'，]1,[a x ∈， ⎰⎰-='≥'101)]()1()[()()()()(a g g a f dx x g a f dx x g x f ，从而⎰⎰'+'adx x g x f dx x f x g 01)()()()().1()()]()1()[()()(g a f a g g a f a g a f =-+≥【评注】对于积分不等式的证明，主要有两个途径：一是转化为函数不等式，二是通过恒等变形，如变量代换、分部积分等，再用积分的不等式性质进行讨论.完全类似例题见《数学复习指南》（经济类）P.115【例4.42~46】（20）（本题满分13分）已知齐次线性方程组（i ） ⎪⎩⎪⎨⎧=++=++=++,0,0532,032321321321ax x x x x x x x x和（ii ） ⎩⎨⎧=+++=++,0)1(2,03221321x c x b x cx bx x 同解，求a,b, c 的值.【分析】方程组（ii ）显然有无穷多解，于是方程组（i ）也有无穷多解，从而可确定a ，这样先求出（i ）的通解，再代入方程组（ii ）确定b,c 即可.【详解】方程组（ii ）的未知量个数大于方程个数，故方程组方程组（ii ）有无穷多解.因为方程组（i ）与（ii ）同解，所以方程组（i ）的系数矩阵的秩小于3.对方程组（i ）的系数矩阵施以初等行变换⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡20011010111532321a a ，从而a=2. 此时，方程组（i ）的系数矩阵可化为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000110101211532321，故T)1,1,1(--是方程组（i ）的一个基础解系.将1,1,1321=-=-=x x x 代入方程组（ii ）可得2,1==c b 或.1,0==c b当2,1==c b 时，对方程组（ii ）的系数矩阵施以初等行变换，有 ⎥⎦⎤⎢⎣⎡→⎥⎦⎤⎢⎣⎡110101312211，显然此时方程组（i ）与（ii ）同解.当1,0==c b 时，对方程组（ii ）的系数矩阵施以初等行变换，有⎥⎦⎤⎢⎣⎡→⎥⎦⎤⎢⎣⎡000101202101，显然此时方程组（i ）与（ii ）的解不相同.综上所述，当a=2,b=1,c=2时，方程组（i ）与（ii ）同解.【评注】本题求a 也可利用行列式0211532321=+-=a a，得a=2.本题也可这样考虑：方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=+++=++=++=++=++0)1(2,0,0,0532,0323221321321321321x c x b x cx bx x ax x x x x x x x x 必存在无穷多解，化系数矩阵为阶梯形，可确定a=2,b=0,c=1或a=2,b=1,c=2，再对两组数据进行讨论即可.完全类似例题见《数学复习指南》（经济类）P.355【习题3（7）】（21）（本题满分13分）设⎥⎦⎤⎢⎣⎡=B CC AD T 为正定矩阵，其中A,B 分别为m 阶，n 阶对称矩阵，C 为n m ⨯矩阵. (I) 计算DP P T ，其中⎥⎦⎤⎢⎣⎡-=-n mE oC A E P 1；（II ）利用(I)的结果判断矩阵C A C B T 1--是否为正定矩阵，并证明你的结论.【分析】第一部分直接利用分块矩阵的乘法即可；第二部分是讨论抽象矩阵的正定性，一般用定义.【详解】 (I) 因 ⎥⎦⎤⎢⎣⎡-=-n T m T E A C o E P 1，有 DP P T =⎥⎦⎤⎢⎣⎡--n T m E A C o E 1⎥⎦⎤⎢⎣⎡B C C A T ⎥⎦⎤⎢⎣⎡--n m E o C A E 1 =⎥⎦⎤⎢⎣⎡--C A C B o C A T 1⎥⎦⎤⎢⎣⎡--n m E o C A E 1 =⎥⎦⎤⎢⎣⎡--C A C B o o A T 1. （II ）矩阵C A C B T 1--是正定矩阵.由(I)的结果可知，矩阵D 合同于矩阵.1⎥⎦⎤⎢⎣⎡-=-C A C B o o A M T 又D 为正定矩阵，可知矩阵M 为正定矩阵.因矩阵M 为对称矩阵，故C A C B T 1--为对称矩阵. 对T X )0,,0,0( =及任意的0),,,(21≠=T n y y y Y ，有.0)(),(11>-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛---Y C A C B Y Y X C A C B o o A Y X T T T T T 故C A C B T 1--为正定矩阵.【评注】判定正定矩阵的典型方法有：（1）用顺序主子式全大于0；（2）用特征值全大于零；（3）用定义. 对于抽象矩阵，一般用后两个方法.（22）（本题满分13分）设二维随机变量(X,Y)的概率密度为.,20,10,0,1),(其他x y x y x f <<<<⎩⎨⎧= 求：（I ） (X,Y)的边缘概率密度)(),(y f x f Y X ；（II ） Y X Z -=2的概率密度).(z f Z( III ) }.2121{≤≤X Y P 【分析】求边缘概率密度直接用公式即可；而求二维随机变量函数的概率密度，一般用分布函数法，即先用定义求出分布函数，再求导得到相应的概率密度; 直接用条件概率公式计算即可.【详解】（I ）关于X 的边缘概率密度)(x f X =⎰+∞∞-dy y x f ),(=.,10,0,20其他<<⎪⎩⎪⎨⎧⎰x dy x =.,10,0,2其他<<⎩⎨⎧x x 关于Y 的边缘概率密度)(y f Y =⎰+∞∞-dx y x f ),(=.,20,0,12其他<<⎪⎩⎪⎨⎧⎰y dx y =.,20,0,21其他<<⎪⎩⎪⎨⎧-y y （II ）令}2{}{)(z Y X P z Z P z F Z ≤-=≤=，1）当0<z 时，0}2{)(=≤-=z Y X P z F Z ；2）当20<≤z 时，}2{)(z Y X P z F Z ≤-= =241z z -; 3) 当2≥z 时，.1}2{)(=≤-=z Y X P z F Z即分布函数为： .2,20,0,1,41,0)(2≥<≤<⎪⎩⎪⎨⎧-=z z z z z z F Z 故所求的概率密度为：.,20,0,211)(其他<<⎪⎩⎪⎨⎧-=z z z f Z （III ） .4341163}21{}21,21{}2121{==≤≤≤=≤≤X P Y X P X Y P 【评注】本题属基本题型，只需注意计算的准确性，应该可以顺利求解.第二步求随机变量函数分布，一般都是通过定义用分布函数法讨论.完全类似例题见《数学复习指南》（经济类）P.436【例2.38~40】（23）（本题满分13分）设)2(,,,21>n X X X n 为来自总体N(0,2σ)的简单随机样本，X 为样本均值，记.,,2,1,n i X X Y i i =-=求：（I ） i Y 的方差n i DY i ,,2,1, =；（II ）1Y 与n Y 的协方差).,(1n Y Y Cov（III ）若21)(n Y Y c +是2σ的无偏估计量，求常数c.【分析】先将i Y 表示为相互独立的随机变量求和，再用方差的性质进行计算即可；求1Y 与n Y 的协方差),(1n Y Y Cov ，本质上还是数学期望的计算，同样应注意利用数学期望的运算性质；估计21)(n Y Y c +，利用其数学期望等于2σ确定c 即可.【详解】由题设，知)2(,,,21>n X X X n 相互独立，且 ),,2,1(,02n i DX EX i i ===σ，.0=X E（I ）∑≠--=-=nij j i i i X n X n D X X D DY ]1)11[()(=∑≠+-n i j j i DXn DX n 221)11(=.1)1(1)1(222222σσσn n n nn n -=-⋅+- （II ） )])([(),(111n n n EY Y EY Y E Y Y Cov --==)])([()(11X X X X E Y Y E n n --==)(211X X X X X X X E n n +--=211)(2)(X E X X E X X E n +-=22121)(][20X E X D X X X E n n j j +++-∑= =.112222σσσnn n -=+- （III ）)(])([121n n Y Y cD Y Y c E +=+=)],(2[121n Y Y Cov DY DY c ++=222)2(2]211[σσσ=-=--+-c n n n n n n n c ，故 .)2(2-=n n c 【评注】通过定义求随机变量的数字特征是基本要求，也是到目前为止考查最多的情形，但读者还应注意利用数字特征的运算性质进行分析讨论，同样是求解数字特征的一个重要途径.本题前两部分为文登学校辅导班上讲授过的原题（原题求相关系数，刚好是本题的两部分，请参见数理统计部分笔记）.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

哈尔滨工业大学（威海） 2005 /2006 学年春季学期
工科数学分析期末考试试卷（答案）试题卷（A ）
一．填空题（每题2分，共20分）
1．2
2
()
lim()x y x y x y e
-+→∞→∞
+=不存在(0,,,,,)x y x y →+∞
→+∞+∞→-∞→-∞
2．已知：2arctan
,y z y x x ==，则z x ∂=∂ 22y x y -
+，dz dx
= 211x + 3．设(
)z u xy =，则du =11()ln z z z z z
zy x dx zx y dy xy xydz --++
4．曲面2
2
z x y =+在(1,2,5)M 处的切平面方程是245x y z +-=
5．函数222
(,),,f u v u v u xyz v x y z =+==++在点(1,1,1)M 处变化率最大方
向向量是 333i j k ++
，变化率的最大值是： 6．函数2
z x y =在圆域{}
22(,):1D x y x y =+≤上的最小值是，最大值是
7．设(,,)0F x x y x y z +++=，且F 可微，则
z x ∂=∂1233
F F F F '''++-'
8．方程2x y y e -'+=的通解是2x
x y Ce e --=+
9．已知曲线2
2
2
:C x y R +=，则
3
()y C
ydx e x dy -+=⎰
22R π±
10．设向量场
{}2222,(,,):A xi yj zk V x y z x y z R =++=++≤
，则 v
divAdv =⎰⎰⎰ 3
4R π
二．填空题（每题3分，共30分）
1．级数11
(1)n n
n x n -∞
=-∑的收敛半径R = 1
2
．级数
21
n ∞
=是否绝对收敛？答：是
3
．由曲面22,0,0,15x y z y y z z x +==
===围成的几何体的体积
V = 11
4．按球面S ：2222x y z R ++=的外侧，积分
333
S
x dydz y dzdx z dxdy ++=⎰⎰
512
5
R π 5．设23(3sin )(cos )du x y x dx x y dy =++-，则u =3cos cos x y x y C --+ 6．级数
32
1
1()
n n x ∞
=+∑
在[)0,+∞上是否一致收敛？答：是
7．在区间[]0,1上的函数3()f x x =的余弦级数的和函数为()S x ，即
01
()c o s 2n
n a S x a n x π∞
==+∑，则1()3S -= 127 8．有界函数()f x 在若当可测集R n
G ⊂上可积的充要条件是对任何0ε>，存
在0δ>，使对任何具有细度()l T δ<的分法T 有 T T S s ε-< 9．设S
为半球面z =
()
(23)S x y z dS ++=⎰⎰ 33a π
10．由椭圆抛物面2235x y z =+与平面3z =所围成立体的体积V =
三．求函数u x y z =满足约束条件1xy yz zx ++=的最大值，其中
0,0,0x y z >>>且u 存在最大值。

（5分）
解：设(1)F xyz xy yz zx λ=+++- 1分由 0,0,0,0x y z F F F F λ''''==== 2分
得 ()0yz y z λ++= ()0z x z x λ++= ()0x y x y λ++= 1x y y z z x ++
=
解得
x y z ===
1分由已知解得 u
的最大值为9
1分四．求23
()arctan
6
x f x x -=+的马克劳林级数及其收敛半径。

（5分）解：2221
03(1)()93n n
n n f x x x ∞
+=-'==+∑ 2分
()(0)()x
f x f f t dt '=+⎰
21
21
01(1)arctan 2(21)3n n n n x n +∞+=-=-++∑ 2分
收敛半径 3R = 1分
五、设()f x 有连续的二阶导数，满足(0)0,(0)1f f '==且微分方程
[]cos ()()0y x f x dx f x dy '-+=为全微分方程，试求()f x ，并求该微分
方程的通解。

（5分）解：()()cos f x f x x ''+= 1分 121
()cos sin sin 2
f x c x c x x x =-++
2分
由(0)0f = 得10c = 1211
()sin cos sin cos 22
f x c x c x x x x '=-+++ 由(0)1f '= 得21c = 所以1
()(1)sin 2f x x x =+
原方程为 111
[cos (1)sin ](cos sin cos )0222
y x x x dx x x x x dy -+-++= 1分
方程通解为 1(1)cos sin 2
2x y x x c ⎛⎫
++= ⎪⎝
⎭
1分六、求解定解问题（5分）
2222,01,0(0,)(1,)0
(,0)(1),(,0)0
t
u u
x t t x u t u t u x x x u x ⎧∂∂=<<<<∞⎪∂∂⎪⎪
==⎨⎪=-=⎪⎪⎩
解：1,1
()(1)l a x x x ϕ===-
1
(,)c o s s i n k
k U x t A k t k x ππ∞
==
∑
3分
1
1
(1)sin k A x x k xdx π-=-⎰
33
2[(1)1]
n n π
--= 33
821,0,1,2,0
2,1,n k k n n k k π-⎧=+=⎪=⎨⎪==⎩
1分
3
3
8
(,)cos(21)sin(21)(21)k U x t k t k x k πππ
∞
=-=+++∑ 1分。